Как бороться с реактивной мощностю
Реактивная мощность представляет собой часть полной мощности, которая не производит работы, но необходима для создания электромагнитных полей в сердечниках магнитопроводов.
Физика процесса и практика применения установок компенсации реактивной мощности
Чтобы разобраться с понятием реактивной мощности, вспомним сначала, что такое электрическая мощность. Электрическая мощность – это физическая величина, характеризующая скорость генерации, передачи или потребления электрической энергии в единицу времени.
Чем больше мощность, тем большую работу может совершить электроустановка в единицу времени. Измеряется мощность в ваттах (произведение Вольт х Ампер). Мгновенная мощность – это произведение мгновенных значений напряжения и силы тока на каком-то участке электрической цепи.
Физика процесса
В цепях постоянного тока значение мгновенной и средней мощности за какой-то промежуток времени совпадают, а понятие реактивной мощности отсутствует.
Если нагрузка индуктивная (трансформаторы, электродвигатели), то ток отстает по фазе от напряжения, если нагрузка емкостная (различные электронные устройства), то ток по фазе опережает напряжение. Поскольку ток и напряжение не совпадают по фазе (реактивная нагрузка), то в нагрузку (потребителю) передается только часть мощности (полной мощности), которая могла бы быть передана в нагрузку, если бы сдвиг фаз был равен нулю (активная нагрузка).
Активная и реактивная мощности
Часть полной мощности, которую удалось передать в нагрузку за период переменного тока, называется активной мощностью. Она равна произведению действующих значений тока и напряжения на косинус угла сдвига фаз между ними (cos φ ).
Мощность, которая не была передана в нагрузку, а привела к потерям на нагрев и излучение, называется реактивной мощностью. Она равна произведению действующих значений тока и напряжения на синус угла сдвига фаз между ними (sin φ).
Таким образом, реактивная мощность является величиной характеризующей нагрузку. Она измеряется в вольт амперах реактивных (вар, var). На практике чаще встречается понятие косинус фи, как величины характеризующей качество электроустановке с точки зрения экономии электроэнергии.
Действительно, чем выше cos φ, тем больше энергии, подаваемой от источника, попадает в нагрузку. Значит можно использовать менее мощный источник и меньше энергии пропадает зря.
Реактивная мощность бытовых потребителей
Итак, потребители переменного тока имеют такой параметр, как коэффициент мощности cosφ.
На графике ток сдвинут на 90° (для наглядности), то есть на четверть периода. Например, электрооборудование имеет cosφ = 0,8, что соответствует углу arccos 0,8 ≈ 36.8°. Этот сдвиг происходит из-за наличия в потребителе электроэнергии нелинейных компонентов – ёмкостей и индуктивностей (например, обмотки электродвигателей, трансформаторов и электромагнитов).
Например, электрооборудование имеет cosφ = 0,8, что соответствует углу arccos 0,8 ≈ 36.8°. Этот сдвиг происходит из-за наличия в потребителе электроэнергии нелинейных компонентов – ёмкостей и индуктивностей (например, обмотки электродвигателей, трансформаторов и электромагнитов).
Для дальнейшего понимания происходящего требуется учет того факта, что, чем выше коэффициент мощности (максимум 1), тем более эффективно потребитель использует получаемую из сети электроэнергию (то есть большее количество энергии преобразуется в полезную работу) – такую нагрузку называют резистивной.
При резистивной нагрузке ток в цепи совпадает с напряжением. А при низком коэффициенте мощности нагрузку называют реактивной, то есть часть потребляемой мощности не совершает полезной работы.
Таблица ниже демонстрирует классификацию потребителей по коэффициенту мощности.
Классификация потребителей переменного тока
Следующая таблица демонстрирует коэффициент мощности распространённых в быту потребителей электроэнергии.
Коэффициент мощности бытовых электроприборов
Юмор электрика
Что такое реактивная мощность? Все очень просто!
Способы компенсации реактивной мощности
Из сказанного выше вытекает, если нагрузка индуктивная, то следует компенсировать ее с помощью емкостей (конденсаторов) и наоборот емкостную нагрузку компенсируют с помощью индуктивностей (дросселей и реакторов). Это помогает увеличить косинус фи (cos φ) до приемлемых значений 0.7-0.9. Этот процесс называется компенсацией реактивной мощности.
Экономический эффект от компенсации реактивной мощности
Экономический эффект от внедрения установок компенсации реактивной мощности может быть очень большим. По статистике он составляет от 12 до 50% от оплаты электроэнергии в различных регионах России. Установка компенсации реактивной мощности окупается не более чем за год.
Для проектируемых объектов внедрение конденсаторной установки на этапе разработки позволяет экономить на стоимости кабельных линий за счет снижения их сечения.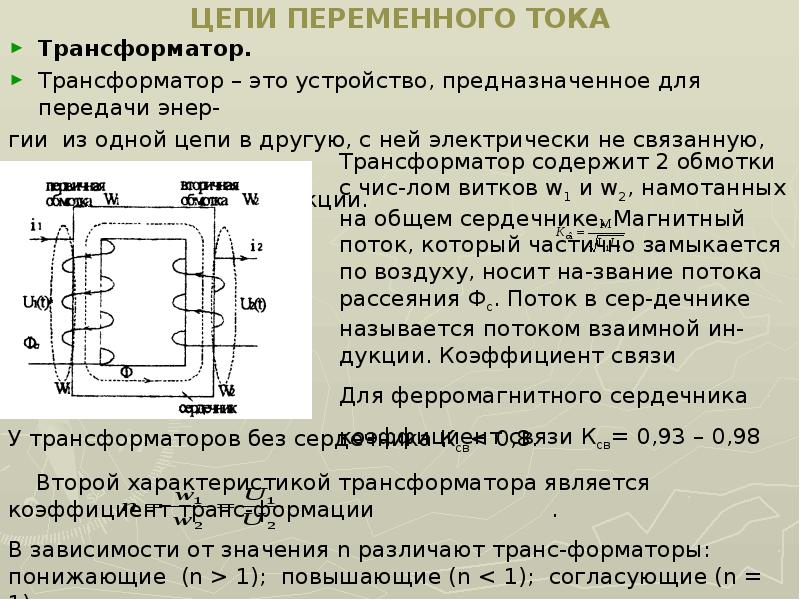 Автоматическая конденсаторная установка, например, может поднять cos φ с 0.6 до 0.97.
Автоматическая конденсаторная установка, например, может поднять cos φ с 0.6 до 0.97.
Выводы
Итак, установки по компенсации реактивной мощности приносят ощутимые финансовые выгоды. Они также позволяют дольше сохранять оборудование в рабочем состоянии.
Вот несколько причин, по которым это происходит.
1. Уменьшение нагрузки на силовые трансформаторы, увеличение в связи с этим срока их службы.
2. Уменьшение нагрузки на провода и кабели, возможность использования кабелей меньшего сечения.
3. Улучшение качества электроэнергии у электроприемников.
4. Ликвидация возможности штрафов за снижение cos φ.
5. Уменьшение уровня высших гармоник в сети.
6. Снижение уровня потребления электроэнергии.
Ранее ЭлектроВести писали, что в Ямпольском районе Винницкой области восстановят работу двух гидроэлектростанций. «Вторую жизнь» получат Мироновская и Клембовская ГЭС в рамках национальной программы стимулирования развития возобновляемой энергетики.
По материалам: electrik.info.
Пример решения контрольной по электротехнике
Ниже приведены условия и решения задач. Закачка решений в формате doc начнется автоматически через 10 секунд.
На рисунке, изображён магнитопровод с воздушным зазором. Материал сердечника — электротехническая сталь. Размеры сердечника по средней магнитной линии в мм : ℓ1=280 мм ; ℓ2=330 мм ; ℓ3=370 мм ; ℓ0=2 мм. Толщина сердечника 50 мм. В сердечнике требуется создать магнитный поток Ф=0,0048 Вб. Определить ток, который должен проходить по обмотке катушки, если она имеет w=800 витков. Вычислить, также ток катушки, для создания заданного магнитного потока, если в сердечнике будет отсутствовать воздушный зазор.
Дано : ℓ1=280 мм ; ℓ2=330 мм ; ℓ3=370 мм ; ℓ0=2 мм ; d=50 мм ; w=800 ; Ф=0,0048 Вб.
Найти : I
Решение.
1. Начертим схему замещения магнитной цепи.
Цепь содержит три участка : первый состоит из одного участка – электротехнической стали ; второй из одного участка – электротехнической стали ; третий из двух участков — электротехнической стали и воздушного зазора.
Найдём длины и площади сечения участков.
Первый участок : S1=0.05×0.1=5×10-3 м2 ; ℓ1=280 мм=0,28 м
Второй участок : S2=0.05×0.08=4×10-3 м2 ; ℓ2=330 мм=0,33 м ;
Третий участок : S3=0.05×0.08=4×10-3 м2 ; ℓ3=370 мм=0,37 м.
2. Составим для магнитной цепи уравнения по законам Кирхгофа.
По второму закону Кирхгофа составляем одно уравнение.
Ф(Rм1+Rм2+Rм3+R0)=F (1)
Найдём магнитные индукции на каждом участке : B1=Ф/S1=0.0048/0.005=0.96 Тл ;
B2=B3=B0=Ф/S2=Ф/S3=0.0048/0.004=1.2 Тл
Найдём напряжённости магнитного поля на каждом участке : на участках из электротехнической стали напряжённость поля находим по кривой намагничивания
h2=600 А/м ; h3=h4=1400 А/м.
Напряжённость магнитного поля находим по формуле : H0=B0/μ0=1. 2/(4π×10-7)=9.6×105 А/м
2/(4π×10-7)=9.6×105 А/м
(где μ0=4π×10-7 Гн/м – магнитная постоянная).
Запишем уравнение (1) :
F=Iw=h2ℓ1+h3ℓ2+h4ℓ3+H0ℓ0=600×0.28+1400×0.33+1400×0.37+9.6×105×0.002=3068 А
Откуда находим ток, который должен проходить по обмотке : I=3068/800=3.8 А
Найдём ток в обмотке катушки, необходимый для создания магнитного потока Ф=0,0048 Вб, если воздушный зазор отсутсвует.
F=Iw=h2ℓ1+h3ℓ2+h4(ℓ3+ℓ0)=600×0.28+1400×(0.33+0.37+0.002)=1150.8
Откуда ток катушки : I=1150.8/800=1.4 А
Ответ : 1) I=3.8 A ; 2) I=1.4 A.
Задача 7.
К переменному напряжению U=150 В частотой f=50 Гц подключены последовательно соединённые резистор и конденсатор. По цепи проходит ток I=3 А, при этом на резисторе возникает падение напряжения Ua=90 В. Начертить схему цепи. Определить полное сопротивление цепи z, сопротивление резистора R, сопротивление XC и ёмкость С конденсатора, коэффициент мощности cosφ, напряжение UC на ёмкостном сопротивлении. Построить в масштабе mu=20 В/см векторную диаграмму напряжений, отложив горизонтально вектор тока.
Построить в масштабе mu=20 В/см векторную диаграмму напряжений, отложив горизонтально вектор тока.
Дано : U=150 В ; f=50 Гц ; I=3 А ; Ua=90 В.
Найти : z , R , XC , C , cosφ , UC.
Решение.
Находим полное сопротивление цепи : z=U/I=150/3=50 Ом.
Сопротивление резистора : R=Ua/I=90/3=30 Ом.
Находим сопротивление XC : XC==40 Ом.
Находим ёмкость конденсатора : C=1/(2πfXC)=1/(2×50×3.14×40)=79.6×10-6 Ф=79,6 мкФ.
Находим коэффициент мощности цепи : cosφ=R/z=30/50=0.6
Находим напряжение на ёмкости : UC=IXC=3×40=120 В.
Для построения векторной диаграммы, найдём длины векторов : ℓUa=Ua/mu=90/20=4.5 см ;
ℓUc=UC/mu=120/20=6 см.
Построение векторной диаграммы начинаем с построения вектора тока I, который откладываем горизонтально. Вектор напряжения Ua откладываем параллельно вектору тока I. От конца вектора Ua откладываем вектор напряжения UC перпендикулярно вектору тока I, в сторону его опережения. Геометрическая сумма векторов Ua и UC даёт вектор U.
Геометрическая сумма векторов Ua и UC даёт вектор U.
Схема цепи и векторная диаграмма построены на рисунке.
Ответ : z=50 Ом ; R=30 Ом ; XC=40 Ом ; C=79,6 мкФ ; cosφ=0.6 ; UC=120 В.
Задача 13.
Последовательно с катушкой, активное сопротивление которой R=5 Ом и индуктивное XL=
=26 Ом, включен конденсатор, ёмкостное сопротивление которого XC=14 Ом. Ток в цепи I=12 А, частота f=50 Гц. Начертить схему цепи. Определить полное сопротивление цепи z ; коэффициент мощности cosφ и напряжение на зажимах цепи U. Вычислить индуктивность катушки L0, при которой в цепи наступает резонанс напряжений. Для режима резонанса напряжений определить полное сопротивление цепи z0 ; ток I0 ; падение напряжения на активном Ua0 и ёмкостном UC0 сопротивлениях ; коэффициент мощности цепи cosφ0 ; полную S, активную P и реактивную Q мощности цепи. Построить в масштабе mu=50 В/см векторную диаграмму напряжений для режима резонанса, отложив горизонтально вектор тока.
Дано : R=5 Ом ; XL=260 Ом ; XC=14 Ом ; I=12 A ; f=50 Гц.
Найти : z ; cosφ ; U ; L0 ; z0 ; I0 ; Ua0 ; UC0 ; cosφ0 ; S ; P ; Q.
Решение.
Схема цепи приведена на рисунке.
Полное сопротивление цепи : z==13 Ом
Коэффициент мощности цепи : cosφ=R/z=5/13=0,38
Напряжение, приложенное к цепи : U=Iz=12×13=156 В
Найдём индуктивность катушки, которую нужно включить в сеть с конденсатором, чтобы в цепи возник резонанс напряжений. Условие резонанса :
XL0=XC=14 Ом
Индуктивность катушки : L0=XL0/(2πf)=14/(2×3.14×50)=0.045 Гн=45 мГн.
Полное сопротивление цепи в режиме резонанса напряжений равно активному сопротивлению : z0=R=5 Ом.
Ток в цепи в режиме резонанса напряжений : I0=U/z0=156/5=31,2 А.
Падение напряжения на активном сопротивлении в режиме резонанса напряжений : Ua0=I0R=31.2×5=156 В.
Падение напряжения на ёмкостном сопротивлении в режиме резонанса напряжений :
UC0=I0XC=31. 2×14=436.8 В.
2×14=436.8 В.
Коэффициент мощности цепи в режиме резонанса напряжений : cosφ0=R/z0=5/5=1
Активная P, реактивная Q и полная S мощности цепи в резонансе напряжений :
P=I02R=31.22×5=4867.2 Вт ; Q=0 ; S=P=4867.2 В∙А.
Для построения векторной диаграммы найдём длины векторов : ℓUa=156/50=3.1 см ;
ℓUc0=436.8/50=8.7 см.
Построение векторной диаграммы начинаем с построения вектора тока I, который откладываем горизонтально. Вектор напряжения Ua0 откладываем параллельно вектору тока I. От конца вектора Ua0 откладываем вектор напряжение UC0 перпендикулярно вектору тока I в сторону отставания от него. От конца вектора UC0 откладываем вектор напряжения UL0 перпендикулярно вектору тока I в сторону его опережения (по модулю вектора UC0 и UL0 равны).
Геометрическая сумма векторов Ua0 , UC0 и UL0 даёт вектор напряжения U, приложенного к цепи (U=Ua0).
Ответ : z=13 Ом ; cosφ=0.38 ; U=156 В ; L0=45 мГн ; z0=5 Ом ; I0=31.2 A ; Ua0=156 В ; UC0=
=436. 8 В ; cosφ0=1 ; P=4867.2 Вт ; Q=0 ; S=4867.2 В∙А.
8 В ; cosφ0=1 ; P=4867.2 Вт ; Q=0 ; S=4867.2 В∙А.
№ 19
Цепь переменного тока состоит из двух параллельных ветвей. В первую ветвь включены последовательно активное и индуктивное сопротивления : R1=12 Ом ; XL=9 Ом. Вторая ветвь состоит из последовательно соединённых активного и ёмкостного сопротивлений : R2=12 Ом ; XC=16 Ом. Напряжение на зажимах цепи U=220 В. Начертить схему цепи. Определить токи I1 , I2 в параллельных ветвях и ток I в неразветвленной части цепи ; коэффициент мощности всей цепи ; активную P , реактивную Q и полную S мощности цепи. Задачу решить методом разложения токов на активные и реактивные составляющие. Построить векторную диаграмму токов в масштабе mi=2 А/см. Вычислить активную g и реактивную bc проводимости второй ветви.
Дано : R1=12 Ом ; XL=9 Ом ; R2=12 Ом ; XC=16 Ом ; U=220 В.
Найти : I1 , I2 , I , cosφ , P , Q , S , g2 , bc.
Решение.
Схема цепи изображена на рисунке.
Находим полные сопротивления параллельных ветвей.
Z1==15 Ом ; Z2= =20 Ом.
Находим токи в параллельных ветвях : I1=U/Z1=220/15=14.7 A ; I2=U/Z2=220/20=11 A
Найдём углы сдвига фаз между токами I1 и I2 и напряжением U.
φ1=arctg[XL/R1]=arctg[9/12]=37°
φ2=arctg[-XC/R2]=arctg[-16/12]=-53°
Находим активные составляющие токов I1, I2 и I.
Ia1=I1cosφ1=14.7×cos(37°)=11.7 A ; Ia2=I2cosφ2=11×cos(-53°)=6.6 A ;
Ia=Ia1+Ia2=11.7+6.6=18.3 A
Находим реактивные составляющие токов I1 , I2 и I.
Ip1=I1sinφ1=14.7×sin(37°)=8.84 A ; Ip2=I2sinφ2=11×sin(-53°)=-8.78 A
Ip=Ip1+Ip2=8.84-8.78=0,06 А
Полный ток в неразветвленной части цепи : I==18.3 A.
Найдём коэффициент мощности цепи : cosφ=Ia/I=18.3/18.3=1
В цепи имеет место резонанс токов.
Найдём активную P, реактивную Q и полную S мощности цепи.
P=I12R1+I22R2=14. 72×12+112×12=4045.08 Вт
72×12+112×12=4045.08 Вт
Q=I12XL-I22XC=14.72×9-112×16=8.8 вар
S=UI=220×18.3=4026 В∙А , или S==4045 В∙А.
Вычислим активную g2 и реактивную bc составляющие второй ветви.
g2=R2/Z22=12/202=0.05 сим ; bc=-XC/Z22=-16/202=-0.04 сим.
Для построения векторной диаграммы найдём длины векторов :
ℓIa1=Ia1/mI=11.7/2=5.9 см ; ℓIp1=Ip1/mI=8.84/2=4.4 см ; ℓI1=I1/mI=14.7/2=7.4 см ;
ℓIa2=Ia2/mI=6.6/2=3.3 см ; ℓIp2=Ip2/mI=8.78/2=4.4 см ; ℓI2=I2/mI=11/2=5.5 см.
ℓIa=Ia/mI=18.3/2=9.2 см ; ℓIp=Ip/mI=0.06/2=0.03 см ; ℓI=I/mI=18.3/2=9.2 см.
Построение векторной диаграммы начинаем с построения вектора напряжения U , который откладываем горизонтально. Вектор тока Ia1 откладываем параллельно вектору напряжения U. От конца вектора Ia1 откладываем вектор тока Ip1 перпендикулярно вектору U в сторону отставания от него. Геометрическая сумма векторов Ia1 и Ip1 дают вектор I1. Вектор тока Ia2 откладываем параллельно вектору напряжения U. От конца вектора Ia2 откладываем вектор тока Ip2 перпендикулярно вектору напряжения U в сторону его опережения.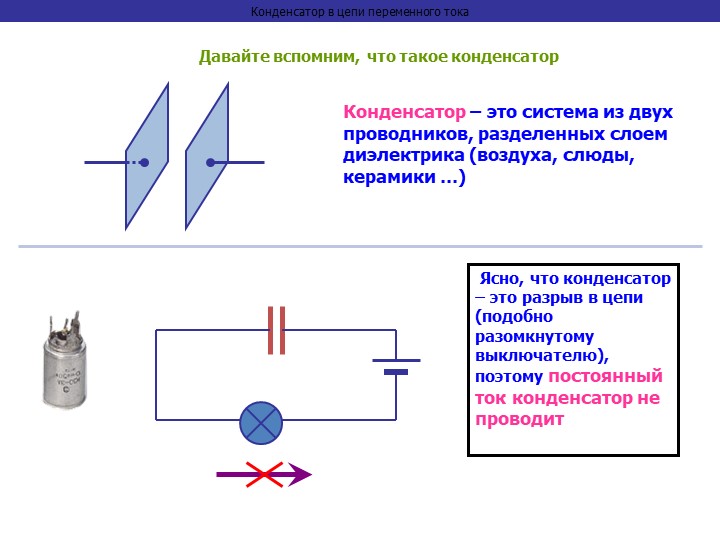 Геометрическая сумма векторов Ia2 и Ip2 дают вектор I2. Вектор I строим как геометрическая сумма векторов I1 и I2 , или как геометрическую сумму векторов Ia и Ip.
Геометрическая сумма векторов Ia2 и Ip2 дают вектор I2. Вектор I строим как геометрическая сумма векторов I1 и I2 , или как геометрическую сумму векторов Ia и Ip.
Ответ : I1=14.7 A ; I2=11 A ; I=18.3 A ; cosφ=1 ; P=4045 Вт ; Q=8.8 вар ; S=4045 В∙А ; g2=0.05 сим ; bc=-0.04 сим.
№ 21
Три одинаковых приёмника с сопротивлениями ZA=ZB=ZC=12+j16 Ом, соединены звездой и питаются от трёхфазной сети с линейным напряжением Uл=220 В. Начертить схему цепи. Определить фазное напряжение Uф ; фазные Iф и линейные Iл токи ; полную S , активную P и реактивную Q мощности ; коэффициент мощности cosφ трёхфазного потребителя. Построить в масштабе mu=40 В/см , mI=2 А/см векторную диаграмму напряжений и токов.
Дано : ZA=ZB=ZC=12+j16 Ом ; Uл=220 В
Найти : Uф , Iф , Iл , S , P , Q , cosφ.
Решение.
Так как приёмник симметричный, то полное сопротивление фаз :
Z=ZA=ZB=ZC===20 Ом.
Фазное напряжение : Uф=Uл/=220/=127 В
Так как приёмник соединён звездой, то фазные и линейные токи равны :
Iф=Iл=Uф/Z=127/20=6.35 А.
Коэффициент мощности цепи : cosφ=R/Z=12/20=0.6 ; угол сдвига фаз между током Iф и напряжением Uф : φ=arccos(0.6)=53°
Активная мощность цепи : P=3Iф2R=3×6.352×12=1452 Вт.
Реактивная мощность цепи : Q=3Iф2X=3×6.352×16=1935 вар
Полная мощность цепи : S==2419 В∙А.
Для построения векторной диаграммы найдём длины векторов :
ℓUф=Uф/mu=127/40=3.2 см ; ℓIф=Iф/mI=6.35/2=3.2 см.
Построение диаграммы начинаем с построения векторов фазных напряжений UA, UB и UC , которые откладываем под углом 120° относительно друг – друга, предварительно отложив вектор UA вдоль вещественной оси.
Вектора фазных токов откладываем под углом φ=53° от соответствующих фазных напряжений. Соединив концы векторов фазных напряжений, получим треугольник линейных напряжений.
Ответ : Uф=127 В ; Iф=6,35 А ; S=2419 В∙А ; P=1452 Вт ; Q=1935 вар ; cosφ=0.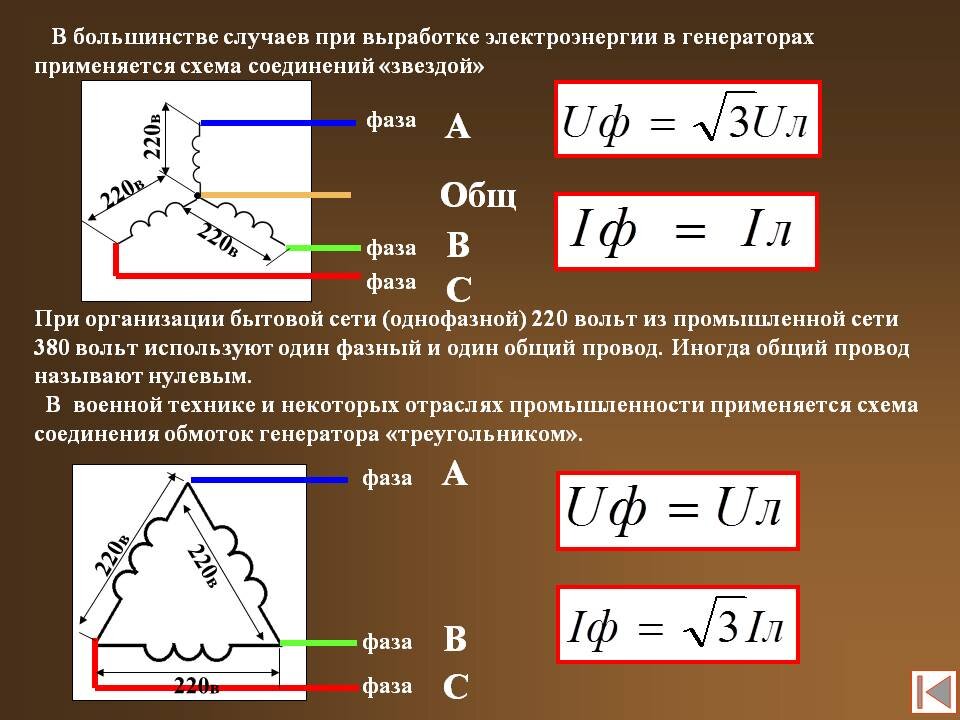 6.
6.
№ 30
Конденсатор С=30 мкФ, соединённый последовательно с резистором R=0.5 МОм, заряжается от сети с постоянным напряжением U=220 В. Определить постоянную времени цепи τ и значение разрядного тока и напряжения в конденсаторе для моментов времени t=0, τ, 2τ, 3τ, 4τ, 5τ. Начертить схему цепи. Построить в масштабе кривые iзар=f(t) ; uc=f(t).
Дано : С=30 мкФ ; R=0.5 МОм ; U=220 В.
Найти : τ ; iзар=f(t) ; uc=f(t).
Решение.
Постоянная времени цепи : τ=RC=0.5×106×30×10-6=15 c
Напряжение на конденсаторе при заряде : uc=U(1-e-t/τ)=220(1-e-t/τ) В
Вычислим значение напряжения на конденсаторе в моменты времени : t=0, τ, 2τ, 3τ, 4τ, 5τ. Вычисления сведём в таблицу.
|
t, c |
0 |
τ |
2τ |
3τ |
4τ |
5τ |
|
e-t/τ |
1 |
0. |
0.14 |
0.05 |
0.02 |
0.01 |
|
uc , В |
0 |
138.6 |
189.2 |
209 |
215.6 |
217.8 |
По результатам расчёта строим кривую : uc=f(t).
Ток переходного режима, или зарядный ток : i=Ie-t/τ===440e-t/τ мкА
Вычислим значение зарядного тока в моменты времени : t=0, τ,2τ, 3τ, 4τ, 5τ.
Вычисления сведём в таблицу.
|
t, c |
0 |
τ |
2τ |
3τ |
4τ |
5τ |
|
e-t/τ |
1 |
0,37 |
0,14 |
0,05 |
0,02 |
0,01 |
|
I, мкA |
440 |
162,8 |
61,6 |
22 |
8,8 |
4,4 |
По результатам расчёта строим кривую : i=440e-t/τ мкА.
Ответ : τ=15 с ; uc=220(1-e-t/τ) В ; i=440e-t/τ мкА.
Компенсация реактивной мощности как фактор энергосбережения
Как платить за электричество меньше, повысить КПД оборудования и более эффективно использовать электрическую энергию, — сегодня эти вопросы волнуют многих руководителей производственных предприятий и владельцев коммерческих объектов.
Из данной статьи вы подробнее узнаете, что такое компенсация реактивной мощности, как правильно рассчитать мощность для потребителей и подобрать оборудование, чтобы сократить потери электроэнергии до 65%.
Немного теории
Для оценки и расчетов цепей переменного тока используются действующие значения тока и напряжения.
Действующее значение переменного тока определяется как величина такого эквивалентного постоянного тока, который проходя через то же активное сопротивление, что и переменный ток, выделяет на нем за период то же количество тепла. Математически действующее значение определяется как среднеквадратичное за период.
Полная мощность вычисляется как произведение действующих значений тока и напряжения цепи.
S = U * I
В случае активной нагрузки фазы тока и напряжения совпадают и вся полная мощность выделяется на нагрузке. Расчеты для переменного тока соответствуют анализу цепей постоянного тока, только используются действующие значения тока и напряжения.
Полная мощность фактически показывает требования к электрической сети. Измеряется она в вольт-амперах (ВА).
Если в цепи переменного тока появляются реактивные элементы (индуктивные нагрузки и емкостные нагрузки) расчёты приходится корректировать. Реактивные элементы обладают способностью накапливать энергию и отдавать ее обратно в цепь. Появляется сдвиг фаз между током и напряжением и как следствие появляется реактивная мощность.
Реактивные элементы обладают способностью накапливать энергию и отдавать ее обратно в цепь. Появляется сдвиг фаз между током и напряжением и как следствие появляется реактивная мощность.
Реактивная мощность может быть, как положительной (для индуктивных цепей), так и отрицательной (для емкостной составляющей).
Реактивная мощность не выделяется на нагрузке, не создает полезной работы. Она накапливается на реактивных элементах нагрузки (конденсаторах, катушках индуктивности), а затем возвращается обратно в питающую сеть. Возвращаясь, она увеличивает текущий по проводам ток. Этот реактивный ток, присутствуя в линиях, дополнительно нагревает их. Поэтому в любой энергосистеме стремятся уменьшить реактивную мощность до минимума.
На нагрузке остается активная мощность. Она и совершает полезную работу: приводит в движение двигатель, переходит в световую волну в лампах и др. Активная мощность — это среднее значение мгновенной мощности за период.
Активная мощность — это среднее значение мгновенной мощности за период.
Полная мощность в цепях переменного тока равна квадратному корню из суммы квадратов активной и реактивной мощностей.
S = ? ( P2 + Q2)
Активная мощность вычисляется как:
P = I * U * cos ?
I и U это действующие значения тока и напряжения.
Или:
P = S * cos ?
Т.е. активная и полная мощности связаны через коэффициент — cos ?.
Коэффициент мощности – это соотношение полезной активной мощности к полной мощности, то есть cos?=P/S этот коэффициент характеризует, насколько эффективно используется электроэнергия. cos ? – это косинус угла сдвига между напряжением питающей сети и током, потребляемым нагрузкой.
При cos ? = 1 (когда фаза тока совпадает с фазой напряжения) активная мощность на нагрузке равна
полной. Вся энергия питающей сети используется для полезной работы. Происходит это только на чисто
активной нагрузке, без реактивной составляющей.
Вся энергия питающей сети используется для полезной работы. Происходит это только на чисто
активной нагрузке, без реактивной составляющей.
Попробуем рассчитать мощность, когда угол между напряжением и током составляет 90 градусов.
На графике ? равно 90 косинус фи (cos?)=0(нулю). Для простоты вычислений возьмем максимальное значение напряжения равное 1 (100%). В этот момент ток равен 0 (нулю). Соответственно их произведение, то есть мощность равны 0(нулю). И наоборот, когда ток максимальный, напряжение равно нулю. Получается, что полезная, активная мощность равна 0 (нулю).
Конечно, устройств с cos ? = 0 на практике не бывает, но промежуточных вариантов может быть
множество. Например, бестрансформаторный блок питания, приведенный в качестве примера выше, имеет
коэффициент мощности 0,6 — 0,7.
Значимость коэффициента мощности
Приведем простые расчеты, демонстрирующие значимость данного показателя.
Два потребителя электроэнергии с одинаковой активной (полезной) мощностью. У первого cos ? = 1,
а у второго – 0,5. Это означает, что второй потребитель потребляет от сети ток в два раза больше,
чем первый. Т.к. зависимость потерь в проводах от тока имеет квадратичный характер (P = I2 * R), то
потери на активном сопротивлении проводов во втором случае будут в 4 раза больше. Соответственно
потребуются провода большего сечения.
Высокий коэффициент мощности особенно важен для мощных нагрузок и длинных линий электропередач.
Реактивная мощность в электрических сетях продуцирует следующие негативные факторы:- Увеличение потерь в проводниках
- Нагрев проводников вызывает ускорение старения изоляции, снижение срока службы, способствует возникновению коротких замыканий
- Снижение пропускной способности энергосистемы при генерации дополнительной мощности для компенсации потерь
- Нагрев обмоток трансформаторов и снижение нагрузочной способности без видимых причин
- Перегрузка генераторов и трансформаторов.

Повышение тока из-за низкого коэффициента мощности вызывает перегрузку генераторов и трансформаторов, и, как следствие, уменьшение их срока службы вследствие превышения расчётных характеристик - Увеличение падения напряжения
Протекающий по электрическому проводнику ток вызывает падение на нем напряжения, величина которого определяется по закону Ома. Возрастание величины тока из-за низкого значения коэффициента мощности вызывает увеличение падения напряжения, что приводит к снижению напряжения на нагрузке относительно требуемого значения, и приводит к снижению мощности, поступающей на нагрузку - Повышение эффективности использования электрической энергии за счет снижения тепловых потерь на передачу электроэнергии.
- Повышение качества электроснабжения за счёт уменьшения падения напряжения в линии электропередач.

- Экономия до 30% на оплате электроэнергии.
 При компенсированном коэффициенте мощности нет
необходимости платить за реактивную мощность. Значительное сокращение энергопотребления.
При компенсированном коэффициенте мощности нет
необходимости платить за реактивную мощность. Значительное сокращение энергопотребления.
- Увеличение срока службы электрических машин. Недостаток реактивной мощности приводит к увеличению тока, что вызывает снижение срока службы электрооборудования.
- Стоимость прокладки кабеля сокращается до 30%. Оптимизация конструкции оборудования за счёт уменьшения сечения проводников позволяет снизить стоимость используемых материалов.
- Снижения тепловых потерь на передачу электроэнергии. Повышение эффективности использования
электроэнергии и качества электроснабжения за счёт уменьшения падения напряжения в линии
электропередач.

- Дополнительный прирост мощности системы электроснабжения. При скомпенсированном коэффициенте мощности часть избыточной энергии, высвобождающейся за счёт уменьшения потерь, может быть использована потребителем.
- Компенсация четко соответствует нагрузке
- Конденсаторная батарея может быть размещена непосредственно у нагрузки
- Конденсаторы используются только во время работы нагрузки
- Низкая стоимость установки
- Реактивная мощность полностью исключена из распределительной сети
- Простота установки
- Низкая стоимость решения
- Конденсаторная батарея может быть размещена в щите управления
- Конденсаторы используются только во время работы нагрузки
- Низкая стоимость установки
- Реактивная мощность полностью исключена из распределительной сети
- Распределительная сеть до щита питания нагружена реактивной мощностью
- Компенсация четко соответствует изменяющейся во времени нагрузке
- Конденсаторная батарея размещена рядом со щитом питания
- Более эффективное использование конденсаторов: контроллер равномерно распределяет нагрузку на конденсаторы, что увеличивает срок службы конденсаторов
- Лучшее регулирование напряжения в энергосистеме
- Конденсаторы КПС-0,40-ХХ-3, рассчитанные на работу в трехфазных сетях переменного тока 400В с номинальными емкостями до 50 кВАр
- Регуляторы на 3,5,7,14 подключаемых ступеней компенсации
- Контакторы для конденсаторов номиналами от 12,5 кВАр до 50 кВАр с катушками управления 230В и 400В
- Щиты ШМП и ВРУ с удобной внутренней конфигурацией, которые можно подобрать для любого варианта компенсации реактивной мощности.
Использование КРМ для снижения нагрузки в электросетях. Виды компенсаторов
Для уменьшения нагрузки в электрических сетях от реактивной мощности применяются компенсаторы реактивной мощности. Это может быть использование синхронного компенсатора. Данное оборудование представлено синхронным двигателем, работающим на холостом ходу. Одновременно с ним применяются системы регулировок, влияющих на эффективность оборудования.
Кроме синхронного устройства, компенсация производится с помощью батарей конденсаторов. Этот вариант считается более простым и дешевым в эксплуатации.
Данное оборудование представлено синхронным двигателем, работающим на холостом ходу. Одновременно с ним применяются системы регулировок, влияющих на эффективность оборудования.
Кроме синхронного устройства, компенсация производится с помощью батарей конденсаторов. Этот вариант считается более простым и дешевым в эксплуатации.
Преимущества компенсации реактивной мощности
Снижение тепловых потерь можно рассчитать, если значение тока в законе Джоуля-Ленца выразить через соотношение для активной мощности. Получается следующая зависимость:
Потери комп./Потери нач. =( COS ? нач./ COS ? комп)?
В результате расчётов получаем следующие зависимости:
В таблице показано возможное уменьшение тепловых потерь
| COS ? начальнй | COS ? компенсированный | |||
|---|---|---|---|---|
| 0,85 | 0,90 | 0,95 | 1,00 | |
| 0,50 | 65,40% | 69,14% | 72,30% | 75,00% |
| 0,55 | 58,13% | 62,65% | 66,48% | 69,75% |
| 0,60 | 50,17% | 55,56% | 60,11% | 64,00% |
| 0,65 | 41,52% | 47,84% | 53,19% | 57,75% |
| 0,7 | 32,18% | 39,51% | 45,71% | 51,00% |
| 0,75 | 22,15% | 30,59% | 37,67% | 43,75% |
| 0,80 | 11,42% | 20,99% | 29,09% | 36,00% |
| 0,85 | — | 10,80% | 19,94% | 27,75% |
| 0,90 | — | — | 10,25% | 19,00% |
| 0,95 | — | — | — | 9,75% |
В процессе передачи электроэнергии на расстоянии ток вынужден преодолевать сопротивление (R) проводов, что вызывает падение напряжения в линии. Падения напряжения можно определить по закону Ома. Оно равно произведению величины тока на сопротивление. Если выразить величину тока через активную мощность, то в конце преобразований получим следующее выражение:
?U=?Uкомп./?Uнач.* COS ? нач./ COS ? комп
В таблице показано возможное уменьшение падения напряжения
| COS ? начальнй | COS ? компенсированный | |||
|---|---|---|---|---|
| 0,85 | 0,90 | 0,95 | 1,00 | |
| 0,50 | 41,18% | 44,44% | 47,37% | 50,00% |
| 0,55 | 35,29% | 38,89% | 42,11% | 45,00% |
| 0,60 | 29,41% | 33,33% | 36,84% | 40,00% |
| 0,65 | 23,53% | 27,78% | 31,58% | 35,00% |
| 0,7 | 17,65% | 22,22% | 26,32% | 30,00% |
| 0,75 | 11,76% | 16,67% | 21,05% | 25,00% |
| 0,80 | 5,88% | 11,11% | 15,76% | 20,00% |
| 0,85 | — | 5,56% | 10,53% | 15,00% |
| 0,90 | — | — | 5,26% | 10,00% |
| 0,95 | — | — | — | 5,00% |
Как выбрать оборудование для компенсации реактивной мощности
Оптимальный выбор оборудования для коррекции коэффициента мощности будет зависеть от типа имеющихся нагрузок и режимов их работы.
Если загрузка оборудования мало подвержена колебаниям, т.е. она почти постоянна, то выгоднее всего использовать индивидуальную компенсацию реактивной мощности. В этом случае конденсатор включается и выключается вместе с относящейся к нему нагрузкой, поэтому компенсация соответствует cos ? нагрузки и синхронизирована с ее суточными колебаниями. Индивидуальная компенсация реактивной мощности наиболее эффективна, если большая часть реактивной мощности потребляется несколькими мощными нагрузками, которые работают непрерывно или длительное время.
рис.1
Индивидуальная компенсация (см. рис.1) реактивной мощности имеет следующие преимущества:
Однако во многих системах не все нагрузки задействованы одновременно, и некоторые из них работают всего несколько часов в день. В этом случае индивидуальная компенсация реактивной мощности становится более дорогой из-за необходимости установки большого количества конденсаторов. При этом основная масса конденсаторов не будет использоваться большую часть времени.
При этом основная масса конденсаторов не будет использоваться большую часть времени.
рис.2
Если в такой системе часть потребителей всегда работает, а часть стоит, периодически меняясь местами, но суммарная нагрузка получается примерно одинаковая по времени, то используют нерегулируемую групповую компенсацию реактивной мощности (см. рис. 2).
Такая конфигурация имеет следующие преимущества:
Групповая компенсация имеет и недостаток:
Если потребность в реактивной мощности сильно колеблется, целесообразно использовать батареи с автоматическим регулированием (см.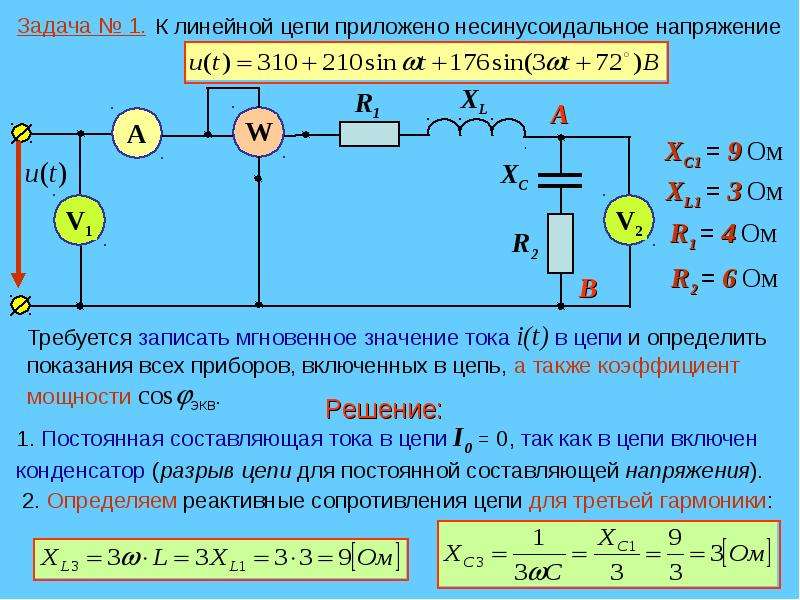 рис. 3), а не конденсаторы, емкость которых постоянна. В этой системе конденсаторы устанавливаются рядом со щитом питания. Суммарная емкость батареи конденсаторов разделяется на ступени. Контроллер регистрирует текущий коэффициент мощности в сети и подключает или отключает необходимую реактивную мощность. При этом контроллер выбирает ту ступень, которая меньше всего проработала до этого момента.
рис. 3), а не конденсаторы, емкость которых постоянна. В этой системе конденсаторы устанавливаются рядом со щитом питания. Суммарная емкость батареи конденсаторов разделяется на ступени. Контроллер регистрирует текущий коэффициент мощности в сети и подключает или отключает необходимую реактивную мощность. При этом контроллер выбирает ту ступень, которая меньше всего проработала до этого момента.
рис.3
Преимущества централизованной компенсации реактивной мощности с автоматическим регулированием:
Важно обратить внимание, что распределительная сеть до щита питания нагружена реактивной мощностью. Необходим контроллер и аппарат управления ступенями, что усложняет решение, но при этом делает его более оптимальным по функционалу и стоимости.
Необходим контроллер и аппарат управления ступенями, что усложняет решение, но при этом делает его более оптимальным по функционалу и стоимости.
В ассортименте компании EKF представлены все элементы компенсации реактивной мощности:
Кроме того, в компании EKF проводится сертификация сборщиков данного оборудования. Подробнее о том, как осуществить квалифицированный подбор и сборку компенсаторных установок в вашем регионе, можно уточнить по электронной почте info@ekf. su.
su.
Лабораторная работа 12. по дисциплине Электротехника. название Исследование электрической цепи переменного тока в режиме компенсации реактивной мощности.
ЛАБОРАТОРНАЯ РАБОТА № 16
Наименование работы: Исследование электрической цепи переменного тока в режиме компенсации реактивной мощности.
Цель работы: Исследовать работу электрической цепи переменного тока в режиме компенсации реактивной мощности. Исследовать искусственный и естественный способы компенсации.
Пояснения к работе.
cos = P / S = Р / √Р2 + Q2 — отношение активной мощности приемника энергии к полной называется коэффициентом мощности
Коэффициент мощности – показывает, какую часть от полной мощности составляет активная мощность и характеризует энергию, которая безвозвратно преобразуется в другие виды энергии. Обычно активная мощность меньше полной, cos<и, только при чисто активной нагрузке, когда P = S cos Чемменьше cosпотребителя, тем больше ток потребителя, тем больший ток проходит по проводам линий электропередачи, тем больше потери энергии в этой линии и меньше КПД её и всей системы. Кроме того, увеличение тока требует для его передачи проводов большего сечения, т.е. большего расхода цветных металлов. В России установлен минимально допустимый коэффициент мощности не менее 0,93. У большинства приемников cosменяется во время их работы. Например, cosасинхронного двигателя изменяется от 0,2 до 0,8, при увеличении его механической мощности от 0 до номинальной. Поэтому работу установки характеризуют средневзвешенным коэффициентом мощности. Его находят за определенный промежуток времени по показаниям счетчиков активной и реактивной энергии.
Обычно активная мощность меньше полной, cos<и, только при чисто активной нагрузке, когда P = S cos Чемменьше cosпотребителя, тем больше ток потребителя, тем больший ток проходит по проводам линий электропередачи, тем больше потери энергии в этой линии и меньше КПД её и всей системы. Кроме того, увеличение тока требует для его передачи проводов большего сечения, т.е. большего расхода цветных металлов. В России установлен минимально допустимый коэффициент мощности не менее 0,93. У большинства приемников cosменяется во время их работы. Например, cosасинхронного двигателя изменяется от 0,2 до 0,8, при увеличении его механической мощности от 0 до номинальной. Поэтому работу установки характеризуют средневзвешенным коэффициентом мощности. Его находят за определенный промежуток времени по показаниям счетчиков активной и реактивной энергии. cos φ = Wa / √Wa2 + Wp2 . Один и тот же генератор при номинальной полной мощности может отдавать приемникам энергии различную активную мощность. Это зависит от cos φ нагрузки. Наилучшее использование номинальной мощности генератора возможно при его работе с номинальным напряжением и током и cos φ=1. Различают естественные и искусственные способы улучшения коэффициента мощности. Электродвигатели переменного тока, трансформаторы работают с наибольшим cos φ при полной их загрузке, поэтому электродвигатели и трансформаторы нужно выбирать по требуемой мощности не допуская их недогрузки и работы в холостую. Способы повышения коэффициента мощности, связанные с выбором оборудования и его эксплуатации, называются естественными. Часто естественные способы дополняют искусственными.
cos φ = Wa / √Wa2 + Wp2 . Один и тот же генератор при номинальной полной мощности может отдавать приемникам энергии различную активную мощность. Это зависит от cos φ нагрузки. Наилучшее использование номинальной мощности генератора возможно при его работе с номинальным напряжением и током и cos φ=1. Различают естественные и искусственные способы улучшения коэффициента мощности. Электродвигатели переменного тока, трансформаторы работают с наибольшим cos φ при полной их загрузке, поэтому электродвигатели и трансформаторы нужно выбирать по требуемой мощности не допуская их недогрузки и работы в холостую. Способы повышения коэффициента мощности, связанные с выбором оборудования и его эксплуатации, называются естественными. Часто естественные способы дополняют искусственными. Так как большинство потребителей представляет собой нагрузку индуктивного характера, то для улучшения cos φ потребителя параллельно приемнику подключают статические конденсаторы, так называемой компенсационной установки.
Так как большинство потребителей представляет собой нагрузку индуктивного характера, то для улучшения cos φ потребителя параллельно приемнику подключают статические конденсаторы, так называемой компенсационной установки.
а
I Ic Iп
R
u
С L
б
Векторная диаграмма токов такой установки имеет вид:
Iпа – активная составляющая тока приемника
Iпp – реактивная составляющая тока приемника
Iс
Iпа
φк U
φ
Iк
Iс
Iпp
Iп
Ток приемника Iп отстает от напряжения на угол φ, а ток конденсаторов Iс опережает
это же напряжение на угол 900. Общий ток в цепи равен геометрической сумме токов Iп и Iс. Реактивная составляющая тока приемника Iпp частично или полностью компенсируется током конденсатора Iс. В связи с этим, уменьшая общий ток цепи с Iп до Iк и угол сдвига фаз с φ до φк, активная составляющая тока приемника Iпа не меняется.
Общий ток в цепи равен геометрической сумме токов Iп и Iс. Реактивная составляющая тока приемника Iпp частично или полностью компенсируется током конденсатора Iс. В связи с этим, уменьшая общий ток цепи с Iп до Iк и угол сдвига фаз с φ до φк, активная составляющая тока приемника Iпа не меняется.
Треугольники мощности установки до и после включения конденсаторов имеют вид:
Р Pк
φк Qк
φ
Q
S
Реактивная мощность установки выраженная через неизменную активную мощность Р до подключения конденсаторов: Q = Р tgφ, после подключения конденсаторов Qк=Ркtgφк. Реактивная мощность статических конденсаторов равна: Qс = Q — Qк= Р ( tgφ— tgφк ). Эту же мощность можно выразить через напряжение сети U и проводимость конденсаторов Вс : Qс = U2 Вс = U2ωС = U22πƒС
Реактивная мощность статических конденсаторов равна: Qс = Q — Qк= Р ( tgφ— tgφк ). Эту же мощность можно выразить через напряжение сети U и проводимость конденсаторов Вс : Qс = U2 Вс = U2ωС = U22πƒС
U22πƒС = Р ( tgφ— tgφк ) С = Р ( tgφ— tgφк ) / U22πƒ
При полной компенсации, когда φк = 0, С = Р tgφ / U22πƒ
Приборы и оборудование: 1. Лабораторный стенд
2. Вольтметр В 3-38
3. Генератор Г 3-109
Генератор Г 3-109
Задание:
1. В лабораторной работе необходимо исследовать работу электрической цепи переменного тока в режиме компенсации реактивной мощности.
2. Для исследования естественной компенсации собрать на лабораторном стенде данную принципиальную схему.
а i Rи1 R8
Uг = 8 В
Rи1 = 10 Ом
Г3-109 L2 ƒг = 2кГц
Rк = 0
б
3. Установить напряжение на генераторе Uг = 8 В, ƒг = 2кГц.
4. Изменяя значения сопротивления R8 с помощью вольтметра В 3-38 измерить действующие значения падений напряжения на элементах цепи Rи1, R8, L2 и на выходе генератора Uаб.
5. Результаты измерений занести в таблицу.
6. Произвести расчеты, применяя следующие формулы:
I = Uи1 / Rи1; Р = I2 RЭ; S = I Uаб; cos = P /S; φ = arccos P /S; Q= S sin φ.
7. Результаты расчета занести в таблицу.
8. По результатам естественной компенсации построить векторные диаграммы напряжений относительно тока для различных значений R8.
Uаб
φ/ UL
Uи1 U8 I
9. По диаграммам определить угол сдвига φ/ между током и напряжением Uаб. Значения φ/ записать в таблицу.
Значения φ/ записать в таблицу.
10.Для исследования искусственной компенсации использовать ранее рассмотренную схему, подключая параллельно к катушке индуктивности конденсаторы.
а
i Rи1
Г 3-109 R8
С5 С4 С3 L2
б
11.Установить напряжение на генераторе Uг = 8 В, ƒг = 20 кГц, сопротивление переменного резистора R8 = 100 Ом.
12.С помощью вольтметра В 3-38 измерить действующие значения падений напряжения на элементах цепи Rи1, R8, L2 и на выходе генератора Uаб.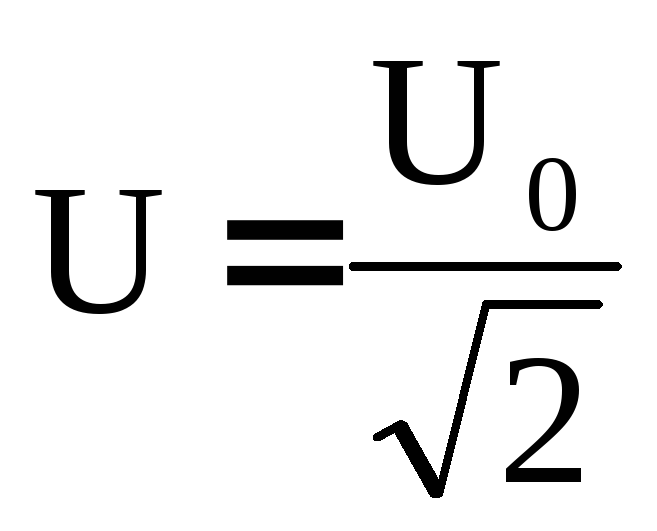
13. Результаты измерений занести в таблицу.
14. Подключить параллельно к катушке индуктивности L2 конденсатор С3. С помощью вольтметра В3-38 измерить действующие значения падений напряжения на элементах цепи Rи1, R8, L2 и на выходе генератора Uаб.
15. Результаты измерений занести в таблицу.
16.Подключить параллельно к конденсатору С3 конденсатор С4. С помощью вольтметра В3-38 измерить действующие значения падений напряжения на элементах цепи Rи1, R8, L2 и на выходе генератора Uаб.
17. Результаты измерений занести в таблицу.
18. Подключить параллельно к конденсаторам С3 и С4 конденсатор С5. С помощью вольтметра В3-38 измерить действующие значения падений напряжения на элементах цепи Rи1, R8, L2 и на выходе генератора Uаб.
19. Произвести расчеты, применяя следующие формулы:
I = Uи1 / Rи1; Р = I2 RЭ; S = I Uаб; cos = P /S; φ = arccos P /S; Q= S sin φ.
20. Результаты расчета занести в таблицу.
21. По результатам искусственной компенсации построить в масштабе векторную диаграмму общего напряжения и тока в неразветвленной части цепи для различных емкостей компенсации. При построении использовать значение угла сдвига φ между общим напряжением и током в неразветвленной части цепи из таблицы.
При построении использовать значение угла сдвига φ между общим напряжением и током в неразветвленной части цепи из таблицы.
Uаб
φ
I
22. Оформить отчет по проделанной работе.
23. Сделать соответствующие выводы по работе.
Работа в лаборатории.
1.В соответствии с принципиальной схемой, используя предлагаемые комплектующие, собрать на лабораторном стенде электрическую цепь.
2.В качестве источника питания использовать низкочастотный генератор Г 3-109
3.Установить на генераторе напряжение 8 В, частоту 2 кГц.
4.С помощью вольтметра В 3-38 измерить действующие значения падений напряжения на каждом участке цепи: Uаб, UL , Uи1, U8.
5.Повторить измерения, устанавливая поочередно значения R8 = 30 Ом, 50 Ом, 100 Ом.
6.Установить на генераторе напряжение 8 В, частоту 20 кГц.
7.С помощью вольтметра В 3-38 измерить действующие значения падений напряжения на каждом участке цепи: Uаб, UL , Uи1, U8.
8. Подключить параллельно к катушке индуктивности L2 конденсатор С3.
9.С помощью вольтметра В 3-38 измерить действующие значения падений напряжения на каждом участке цепи: Uаб, UL , Uи1, U8.
10.Подключить параллельно к конденсатору С3 конденсатор С4.
11.С помощью вольтметра В 3-38 измерить действующие значения падений напряжения на каждом участке цепи: Uаб, UL , Uи1, U8.
12.Подключить параллельно к конденсаторам С3 и С4 конденсатор С5.
13.С помощью вольтметра В 3-38 измерить действующие значения падений напряжения на каждом участке цепи: Uаб, UL , Uи1, U8.
14.По окончании измерений – отключить источник питания, отключить измерительные приборы, разобрать электрическую цепь.
Содержание отчета.
1.Цель работы.
2.Приборы и оборудование.
3.Принципиальные электрические схемы.
4.Таблицы с результатами измерений.
5.Формулы, необходимые для расчета.
6.Векторные диаграммы напряжений, построенные для естественной компенсации.
7.Векторная диаграмма общего напряжения и тока в неразветвленной части цепи для различных емкостей компенсации.
8.Вывод по работе.
Контрольные вопросы.
1.Определение коэффициента мощности.
2.В чем состоит экономическое значение коэффициента мощности?
3.Каким образом величина коэффициента мощности влияет на капитальные затраты и расходы по эксплуатации электрооборудования?
4.В чем состоят меры естественного повышения коэффициента мощности?
5.В чем состоят меры искусственного повышения коэффициента мощности с помощью конденсаторов?
Литература.
1. Ф.Е.Евдокимов. Теоретические основы электротехники.- М.: Высшая школа, 2004.
Ф.Е.Евдокимов. Теоретические основы электротехники.- М.: Высшая школа, 2004.
Стр. 310 — 314.
2.Конспект лекций. Тема: «Коэффициент мощности и его технико-экономическое значение».
Помогите умоляю. 1) Общее сопротивление цепи переменного тока Z=40 Ом, коэффициент мощности
Решите срочно 30 баллов даю
чему равно количество вещества в двух кубических дециметрах воды
сколько молекул в 4 молях углекислого газа
2 вариант
ВЫБЕРИТЕ ОДИН ПРАВИЛЬНЫЙ ОТВЕТ
1. Изобарный процесс в идеальном газе представлен графиком
2. Выражение p1 V1 =p2 V2 (при T=const, m=const) я
… вляется
А) законом Бойля-Мариотта, Б) законом Гей-Люссака, В) законом Шарля,
Г) уравнением Менделеева-Клапейрона.
3. При изобарном процессе в газе не изменяется (при т = сonst) его:
А) давление. Б) объем. В) температура.
4. При осуществлении какого изопроцесса увеличение абсолютной температуры идеального газа в 2 раза приводит к увеличению давления газа тоже в 2 раза? Выберите правильный ответ. А. Изобарного.
Б. Изохорного.
В. Изотермического.
5. Изохорный процесс при m = сonst описывается уравнением
А) p1 V1=p2 V2; Б) p1 T2=p2 T1; В) pV=mRT/M; Г) V1 T2=V2 T1.
6. При нагревании газ переведен из состояния 1 в состояние 2. При этом его давление
7. Нагревание на спиртовке воздуха в закрытом сосуде следует отнести к процессу
А) изотермическому. Б) изобарному. В) изохорному.
8. Если среднюю кинетическую энергию молекул увеличить в 3 раза (при n = сonst), то давление идеального газа увеличится в
А) 9 раз. Б) 3 раза. В) 6 раз.
9. При нагревании идеального газа средняя кинетическая энергия теплового движения молекул увеличилась в 2 раза. При этом абсолютная температура газа увеличилась в
А) 2 раза, Б) 3 раза. В) 4 раза;
10. Давление идеального газа при Т = сonst с увеличением объема
А) увеличивается. Б) уменьшается. В) не изменяется.
УСТАНОВИТЕ СООТВЕТСТВИЕ
11. Физическая величина Единица измерения (СИ)
1) p (давление) А) 1/м3 (1/метр3)
2) n (концентрация молекул) Б) м3 (метр3)
3) М (молярная масса) В) Па (паскаль)
Г) Дж (джоуль)
Д) кг/моль(килограмм/моль)
12.
А. Изобарного.
Б. Изохорного.
В. Изотермического.
5. Изохорный процесс при m = сonst описывается уравнением
А) p1 V1=p2 V2; Б) p1 T2=p2 T1; В) pV=mRT/M; Г) V1 T2=V2 T1.
6. При нагревании газ переведен из состояния 1 в состояние 2. При этом его давление
7. Нагревание на спиртовке воздуха в закрытом сосуде следует отнести к процессу
А) изотермическому. Б) изобарному. В) изохорному.
8. Если среднюю кинетическую энергию молекул увеличить в 3 раза (при n = сonst), то давление идеального газа увеличится в
А) 9 раз. Б) 3 раза. В) 6 раз.
9. При нагревании идеального газа средняя кинетическая энергия теплового движения молекул увеличилась в 2 раза. При этом абсолютная температура газа увеличилась в
А) 2 раза, Б) 3 раза. В) 4 раза;
10. Давление идеального газа при Т = сonst с увеличением объема
А) увеличивается. Б) уменьшается. В) не изменяется.
УСТАНОВИТЕ СООТВЕТСТВИЕ
11. Физическая величина Единица измерения (СИ)
1) p (давление) А) 1/м3 (1/метр3)
2) n (концентрация молекул) Б) м3 (метр3)
3) М (молярная масса) В) Па (паскаль)
Г) Дж (джоуль)
Д) кг/моль(килограмм/моль)
12. Температура по шкале Температура по шкале
Цельсия (° С) Кельвина (Т, К)
(Абсолютная температура)
1) 20 А) О
2)-273 Б) 303
3)0 В) 273
Г) 293
13. Физическая величина Определяется по формуле
1) Средняя А) mRT/MV
кинетическая Б) 3nT/2
энергия молекул В) m 0V — 2/2
2) давление Г) nm0v- 2/2
Решите задачи:
14. Каково количество вещества в газе, если при температуре -13 °С и давлении 500 кПа объем газа равен 30 л?
15. На сколько градусов надо изобарно нагреть газ, чтобы он занял объем, вдвое больший по сравнению с объемом при 0 °С?
Температура по шкале Температура по шкале
Цельсия (° С) Кельвина (Т, К)
(Абсолютная температура)
1) 20 А) О
2)-273 Б) 303
3)0 В) 273
Г) 293
13. Физическая величина Определяется по формуле
1) Средняя А) mRT/MV
кинетическая Б) 3nT/2
энергия молекул В) m 0V — 2/2
2) давление Г) nm0v- 2/2
Решите задачи:
14. Каково количество вещества в газе, если при температуре -13 °С и давлении 500 кПа объем газа равен 30 л?
15. На сколько градусов надо изобарно нагреть газ, чтобы он занял объем, вдвое больший по сравнению с объемом при 0 °С?
2 вариант
ВЫБЕРИТЕ ОДИН ПРАВИЛЬНЫЙ ОТВЕТ
1. Изобарный процесс в идеальном газе представлен графиком
2. Выражение p1 V1 =p2 V2 (при T=const, m=const) я
… вляется
А) законом Бойля-Мариотта, Б) законом Гей-Люссака, В) законом Шарля,
Г) уравнением Менделеева-Клапейрона.
3. При изобарном процессе в газе не изменяется (при т = сonst) его:
А) давление. Б) объем. В) температура.
4. При осуществлении какого изопроцесса увеличение абсолютной температуры идеального газа в 2 раза приводит к увеличению давления газа тоже в 2 раза? Выберите правильный ответ. А. Изобарного.
Б. Изохорного.
В. Изотермического.
5. Изохорный процесс при т = сonst описывается уравнением
А) p1 V1=p2 V2; Б) p1 T2=p2 T1; В) pV=mRT/M; Г) V1 T2=V2 T1.
6. При нагревании газ переведен из состояния 1 в состояние 2. При этом его давление
7. Нагревание на спиртовке воздуха в закрытом сосуде следует отнести к процессу
А) изотермическому. Б) изобарному. В) изохорному.
8. Если среднюю кинетическую энергию молекул увеличить в 3 раза (при n = сonst), то давление идеального газа увеличится в
А) 9 раз. Б) 3 раза. В) 6 раз.
9. При нагревании идеального газа средняя кинетическая энергия теплового движения молекул увеличилась в 2 раза. При этом абсолютная температура газа увеличилась в
А) 2 раза, Б) 3 раза. В) 4 раза;
10. Давление идеального газа при Т = сonst с увеличением объема
А) увеличивается. Б) уменьшается. В) не изменяется.
УСТАНОВИТЕ СООТВЕТСТВИЕ
11. Физическая величина Единица измерения (СИ)
1) p (давление) А) 1/м3 (1/метр3)
2) n (концентрация молекул) Б) м3 (метр3)
3) М (молярная масса) В) Па (паскаль)
Г) Дж (джоуль)
Д) кг/моль(килограмм/моль)
12.
А. Изобарного.
Б. Изохорного.
В. Изотермического.
5. Изохорный процесс при т = сonst описывается уравнением
А) p1 V1=p2 V2; Б) p1 T2=p2 T1; В) pV=mRT/M; Г) V1 T2=V2 T1.
6. При нагревании газ переведен из состояния 1 в состояние 2. При этом его давление
7. Нагревание на спиртовке воздуха в закрытом сосуде следует отнести к процессу
А) изотермическому. Б) изобарному. В) изохорному.
8. Если среднюю кинетическую энергию молекул увеличить в 3 раза (при n = сonst), то давление идеального газа увеличится в
А) 9 раз. Б) 3 раза. В) 6 раз.
9. При нагревании идеального газа средняя кинетическая энергия теплового движения молекул увеличилась в 2 раза. При этом абсолютная температура газа увеличилась в
А) 2 раза, Б) 3 раза. В) 4 раза;
10. Давление идеального газа при Т = сonst с увеличением объема
А) увеличивается. Б) уменьшается. В) не изменяется.
УСТАНОВИТЕ СООТВЕТСТВИЕ
11. Физическая величина Единица измерения (СИ)
1) p (давление) А) 1/м3 (1/метр3)
2) n (концентрация молекул) Б) м3 (метр3)
3) М (молярная масса) В) Па (паскаль)
Г) Дж (джоуль)
Д) кг/моль(килограмм/моль)
12. Температура по шкале Температура по шкале
Цельсия (° С) Кельвина (Т, К)
(Абсолютная температура)
1) 20 А) О
2)-273 Б) 303
3)0 В) 273
Г) 293
13. Физическая величина Определяется по формуле
1) Средняя А) mRT/MV
кинетическая Б) 3nT/2
энергия молекул В) m 0V — 2/2
2) давление Г) nm0v- 2/2
Решите задачи:
14. Каково количество вещества в газе, если при температуре -13 °С и давлении 500 кПа объем газа равен 30 л?
15. На сколько градусов надо изобарно нагреть газ, чтобы он занял объем, вдвое больший по сравнению с объемом при 0 °С?
Температура по шкале Температура по шкале
Цельсия (° С) Кельвина (Т, К)
(Абсолютная температура)
1) 20 А) О
2)-273 Б) 303
3)0 В) 273
Г) 293
13. Физическая величина Определяется по формуле
1) Средняя А) mRT/MV
кинетическая Б) 3nT/2
энергия молекул В) m 0V — 2/2
2) давление Г) nm0v- 2/2
Решите задачи:
14. Каково количество вещества в газе, если при температуре -13 °С и давлении 500 кПа объем газа равен 30 л?
15. На сколько градусов надо изобарно нагреть газ, чтобы он занял объем, вдвое больший по сравнению с объемом при 0 °С?
Велосипедное колесо вращается с частотой n=2 c−1. Под действием сил трения оно остановилось через интервал времени Δt=5 мин. Определить число N оборот … ов, которое сделает колесо за это время. N= ?
Диск радиусом r=19 см, находившийся в состоянии покоя, начал вращаться с постоянным угловым ускорением ε=0,8 рад/с2. Найти полное a ускорения точек на … окружности диска в конце 3-ой секунды после начала вращения. a=? см/c2
Миномет установлен под углом α=34o к горизонту на крыше здания, высота которого h=33 м. Начальная скорость мины v0=44 м/с. горизонтальную дальность по
… лета. S=? м.
Ускорение свободного падения g=9.8м/с2. Сопротивлением воздуха пренебречь.
Начальная скорость мины v0=44 м/с. горизонтальную дальность по
… лета. S=? м.
Ускорение свободного падения g=9.8м/с2. Сопротивлением воздуха пренебречь.
Миномет установлен под углом α=42∘ к горизонту на крыше здания, высота которого h=40 м. Начальная скорость мины v0=59 м/с. Определить время τ полета м … ины. τ=? c. Ускорение свободного падения g=9.8м/с2. Сопротивлением воздуха пренебречь.
Точка движется по кривой с постоянным тангенциальным ускорением aτ=1,8 м/с2. Определить полное ускорение a точки на участке кривой с радиусом кривизны … R=2,2 м, если точка движется на этом участке со скоростью v=3,5 м/с a=? м/c2
Понимание коэффициента мощности — Laurens Electric Cooperative
Корректировка коэффициента мощности с помощью конденсаторов
Описание:
Коэффициент мощности — это соотношение (фазы) тока и напряжения в электрических распределительных системах переменного тока. В идеальных условиях ток и напряжение «синфазны», а коэффициент мощности равен «100%». При наличии индуктивных нагрузок (двигателей) коэффициент мощности менее 100% (обычно может составлять от 80 до 90%).
При наличии индуктивных нагрузок (двигателей) коэффициент мощности менее 100% (обычно может составлять от 80 до 90%).
Низкий коэффициент мощности, с точки зрения электричества, вызывает протекание более сильного тока в линиях распределения электроэнергии, чтобы обеспечить заданное количество киловатт сверх электрической нагрузки.
Эффекты?
Система распределения электроэнергии в здании или между зданиями может быть перегружена избыточным (бесполезным) током.
Мощность генерирующих и распределительных систем, принадлежащих Laurens Electric, измеряется в кВА (килоамперах).
кВА = НАПРЯЖЕНИЕ X АМПЕР X 1,73 (трехфазная система) / 1000
При единичном коэффициенте мощности (100%) потребуется 2000 кВА мощности генерирующей и распределительной сети для обеспечения 2000 кВт. Однако если коэффициент мощности упадет до 85%, потребуется 2 353 кВА мощности.Таким образом, мы видим, что более низкий коэффициент мощности оказывает обратное влияние на генерирующую и распределительную мощность.
Перегрузка с низким коэффициентом мощности для генерации, распределения и сетей с избыточным значением кВА.
Если вы владеете большим зданием, вам следует подумать о корректировке низкого коэффициента мощности по любой из этих причин или по обеим этим причинам:
- Чтобы снизить вероятность дополнительных расходов на коэффициент мощности в случае, если Laurens Electric начнет выставлять счет за корректировку коэффициента мощности и
- To восстановить мощность (кВА) перегруженных фидеров в здании или строительном комплексе.
Существует несколько методов коррекции более низкого коэффициента мощности. Обычно используются: емкость.
Конденсаторные батареи
Самым практичным и экономичным устройством коррекции коэффициента мощности является конденсатор. Это улучшает коэффициент мощности, поскольку влияние емкости прямо противоположно влиянию индуктивности.
Вариант номинальной мощности конденсатора в кВАр показывает, сколько реактивной мощности будет выдавать конденсатор. Поскольку этот вид реактивной мощности нейтрализует реактивную мощность, вызванную индуктивностью, каждый киловар емкости снижает чистую потребляемую реактивную мощность на ту же величину.Конденсатор на 15 кВАр, например, нейтрализует 15 кВА индуктивной реактивной мощности.
Поскольку этот вид реактивной мощности нейтрализует реактивную мощность, вызванную индуктивностью, каждый киловар емкости снижает чистую потребляемую реактивную мощность на ту же величину.Конденсатор на 15 кВАр, например, нейтрализует 15 кВА индуктивной реактивной мощности.
Конденсаторы могут быть установлены в любой точке электрической системы и улучшат коэффициент мощности между точкой приложения и источником питания. Однако коэффициент мощности между нагрузкой и конденсатором останется неизменным. Конденсаторы обычно добавляются в каждую часть неисправного оборудования, перед группами двигателей (перед центрами управления двигателями или распределительными щитами) или в основных службах.
Почему фактор мощности важен при измерении эффективности?
Инженеры, использующие внешние источники питания (EPS), не привыкать к измерениям эффективности. Однако, поскольку их приложения обычно работают на постоянном токе, при измерении мощности на стороне переменного тока источника питания могут быть сделаны типичные ошибки. Эти распространенные ошибки включают неправильное измерение или полное отсутствие коэффициента мощности при расчете потребляемой мощности источника питания, что приводит к неправильным измерениям КПД.В этом сообщении блога мы рассмотрим основы коэффициента мощности и эффективности, а затем дадим рекомендации о том, как учитывать коэффициент мощности при измерении эффективности источника питания постоянного и переменного тока.
Эти распространенные ошибки включают неправильное измерение или полное отсутствие коэффициента мощности при расчете потребляемой мощности источника питания, что приводит к неправильным измерениям КПД.В этом сообщении блога мы рассмотрим основы коэффициента мощности и эффективности, а затем дадим рекомендации о том, как учитывать коэффициент мощности при измерении эффективности источника питания постоянного и переменного тока.
Коэффициент мощности и КПД, обзор
КПД (η) — это отношение выходной мощности к входной:
Уравнение 1: КПДРасчет выходной мощности EPS, которая является постоянным током, представляет собой просто выходное напряжение, умноженное на выходной ток:
Уравнение 2: Выходная мощность Распространенной ошибкой является применение этого же расчета для получения входной мощности.Это представляет проблему, потому что произведение вольт-ампер в цепях переменного тока не всегда равно реальной мощности, и фактически, в случае внешних адаптеров, произведение вольт-ампер никогда не будет равняться реальной мощности. В цепях переменного тока произведение вольт-ампер равно полной мощности (S), которая связана с реальной мощностью через термин, называемый коэффициентом мощности (PF):
В цепях переменного тока произведение вольт-ампер равно полной мощности (S), которая связана с реальной мощностью через термин, называемый коэффициентом мощности (PF):
По определению, коэффициент мощности — это отношение реальной мощности к полной мощности, где полная мощность является произведением действующего напряжения и действующего тока.Только когда коэффициент мощности равен 1, произведение вольт-ампер равно реальной мощности:
Уравнение 4: Коэффициент мощностиЕсли коэффициент мощности учитывается при расчете КПД, он должен быть рассчитан правильно. Многим инженерам приходится возвращаться к своим ранним инженерным занятиям, чтобы вспомнить, что такое коэффициент мощности и как его измерять. Однако в школе часто сосредотачиваются на линейном случае, когда и напряжение, и ток представляют собой чистые синусоиды одинаковой частоты. В этом случае коэффициент мощности представляет собой просто косинус разности фаз между напряжением и током и более точно известен как коэффициент мощности смещения:
Уравнение 5: Коэффициент вытесненияМногим инженерам знаком треугольник мощности, показанный на рисунке 1, который визуально представляет взаимосвязь уравнения 5.По определению косинус θ равен отношению смежной стороны к гипотенузе. В треугольнике мощности это равно отношению реальной мощности к полной мощности, что соответствует нашему определению в уравнении 4. С другой стороны, когда дело доходит до нелинейных систем, одним из примеров которых являются источники питания постоянного и переменного тока, это имеет место. не представляю всей картины.
Рисунок 1: Треугольник мощности для линейных системНе хватает коэффициента мощности искажения, который добавляет третье измерение к треугольнику мощности, как показано на рисунке 2.Этот момент является критическим, потому что в источниках питания коэффициент искажения является основным фактором снижения коэффициента мощности, поскольку коэффициент смещения стремится быть близким к единице.
Рисунок 2: Треугольник мощности для нелинейных системАнализ Фурье показывает, что этот нелинейный сигнал тока может быть разбит на серию гармонических составляющих различной величины. Эти гармоники уменьшают коэффициент мощности, но не учитываются в уравнении 5. Для расчета коэффициента мощности искажения вводится полное гармоническое искажение (THD).THD учитывает ток, связанный с каждой гармоникой, как показано в следующем уравнении:
Уравнение 6: Суммарные гармонические искаженияКогда THD равен 0, коэффициент мощности искажения равен 1, что было бы в случае линейной системы:
Уравнение 7: Коэффициент мощности искаженияИзображение коэффициента мощности дополняется умножением коэффициента мощности смещения и коэффициента мощности искажения, что дает истинный коэффициент мощности:
Уравнение 8: Истинный коэффициент мощностиНа рисунке 3 показаны формы входного тока и напряжения типичного источника питания.При сравнении с синусоидальным напряжением можно ясно увидеть нелинейный характер тока.
Рисунок 3: Осциллограф, показывающий формы сигналов тока и напряжения типичного источника питанияЭто вызвано комбинацией мостового выпрямителя и конденсатора большой емкости, которые создают высоковольтную шину постоянного тока внутри источника. Выпрямитель имеет прямое смещение и проводит ток только тогда, когда входное напряжение превышает напряжение на конденсаторе большой емкости.
Измерение коэффициента мощности
Лучший способ измерить коэффициент мощности — использовать измеритель мощности, подобный показанному на Рисунке 4 ниже.Эти устройства будут напрямую выводить реальную мощность, поэтому коэффициент мощности не нужно учитывать при расчете КПД. Помимо реальной мощности, эти измерители могут измерять коэффициент мощности, THD, ток для каждой гармоники и многое другое. В то время как внешние адаптеры малой мощности не имеют определенного коэффициента мощности или пределов гармоник, блоки питания с более высокой мощностью имеют определенные нормативные ограничения на содержание гармоник и коэффициент мощности. Стандарты, такие как EN 61000-3-2, определяют пределы гармонического тока до 39 -й гармоники включительно для определенных уровней мощности.При измерении гармонического тока источника питания необходим измеритель мощности.
Рисунок 4: Измеритель мощности WT210, показывающий измерения, соответствующие сигналам на Рисунке 3Коэффициент мощности в источниках питания
Вы можете подумать, что игнорирование коэффициента мощности приведет только к небольшой ошибке и / или что коэффициент мощности внешнего адаптера не может быть настолько плохим. Фактически, без коррекции коэффициента мощности коэффициент мощности внешнего адаптера может легко достигнуть нуля.5 при номинальной нагрузке. Адаптер с коэффициентом мощности 0,5 будет иметь кажущуюся мощность в два раза больше реальной мощности, что приведет к неверным результатам. Даже если бы источник питания имел реальный КПД 100%, это измерение показало бы только 50%.
Помимо общего включения коэффициента мощности в расчеты КПД, важно отметить, что коэффициент мощности зависит от линии и нагрузки. Требования к эффективности, такие как DoE Level VI, требуют измерения эффективности в нескольких точках (25%, 50%, 75% и 100% нагрузки) как при высоком, так и при низком линейном напряжении.Если при расчете реальной мощности используется коэффициент мощности, его необходимо повторно измерить для каждого из этих условий.
Пример из реального мира
В качестве реального примера возьмем рисунки 3 и 4, которые были получены от внешнего источника питания мощностью 20 Вт, работающего на 10,8 Вт. С измерениями, полученными с помощью осциллографа на рисунке 3, мы получаем произведение вольт-ампер, равное 22,5. VA. Если бы мы забыли включить коэффициент мощности, то, используя это число, мы получили бы показатель КПД 48%:
Используя измеритель мощности, подобный показанному на рисунке 4, мы видим, что реальная входная мощность на самом деле составляет всего 12.8 Вт, и, используя это значение, мы получаем КПД 84%, что почти вдвое больше, чем мы получили без учета коэффициента мощности:
Теперь, если коэффициент мощности учитывался, но для его расчета использовались осциллограф и уравнение 5 (коэффициент искажения опущен), возникает несколько проблем. Во-первых, как показано на рисунке 3, у осциллографов могут возникнуть проблемы с автоматическим вычислением разности фаз. Осциллограф, использованный на рисунке 3, рассчитал фазовый угол 72 градуса, что невооруженным глазом кажется неверным.При использовании курсоров осциллографа для ручного измерения фазового угла мы замечаем, что пытаемся измерить смещение двух сигналов разной формы и что текущий импульс формы сигнала является асимметричным.
Возникает вопрос: куда поставить курсор, на пик или в центр импульса? В любом случае значение не превышает нескольких градусов. Если бы мы использовали уравнение 5 для расчета коэффициента мощности смещения с углом 5 °, мы получили бы значение 0,996. Если мы умножим наш результат на 22.5 ВА, собранные выше по нашему рассчитанному коэффициенту мощности, мы находим, что результат почти не изменился при 22,4 ВА. Это должно подтвердить наше предыдущее утверждение о том, что коэффициент смещения близок к единице, а коэффициент мощности искажения является доминирующим членом в уравнении 8. Таким образом, мы можем видеть, что метод осциллографа бесполезен для нас, и единственным методом, который дал правильные результаты, был использование измерителя мощности.
Заключение
Десятилетия ужесточающегося регулирования сделали тестирование эффективности одним из наиболее важных факторов при выборе и оценке характеристик источников питания.Отсутствие опыта работы с цепями переменного тока может привести к тому, что инженеры-испытатели будут не учитывать или неправильно рассчитывать коэффициент мощности, что приводит к неверным показателям эффективности. При тестировании внешних адаптеров или любого источника питания постоянного и переменного тока лучший метод расчета реальной потребляемой мощности — использование измерителя мощности. Эти устройства не только напрямую измеряют реальную мощность, но и могут измерять ток, связанный с отдельными гармониками, и обеспечивать полную картину входа источника питания.
Категории: Основы , Тестирование и анализ отказов
Вам также может понравиться
У вас есть комментарии к этому сообщению или темам, которые вы хотели бы, чтобы мы освещали в будущем?
Отправьте нам письмо по адресу powerblog @ cui.ком
— Прикладное промышленное электричество
Рассмотрим схему для однофазной системы питания переменного тока, в которой источник переменного напряжения 120 В и 60 Гц подает питание на резистивную нагрузку: (рисунок ниже)
Источник переменного тока управляет чисто резистивной нагрузкой.[латекс] Z = 60 + j0 \ Omega \ textbf {или} 60 \ Omega \ angle \ text {0 °} [/ latex]
[латекс] \ begin {align} I & = \ frac {E} {Z} \\ & = \ frac {120V} {60Ω} \\ & = \ mathbf {2A} \ end {align} [/ latex]
В этом примере ток нагрузки будет 2 ампера, среднеквадратичное значение.Мощность, рассеиваемая на нагрузке, составит 240 Вт. Поскольку эта нагрузка является чисто резистивной (без реактивного сопротивления), ток находится в фазе с напряжением, и расчеты выглядят аналогично расчетам в эквивалентной цепи постоянного тока. Если бы мы построили кривые напряжения, тока и мощности для этой схемы, это выглядело бы так, как показано на рисунке ниже.
Рисунок 7.1 Ток синфазен с напряжением в резистивной цепи.Обратите внимание, что форма сигнала мощности всегда положительная, а не отрицательная для этой резистивной цепи.Это означает, что мощность всегда рассеивается резистивной нагрузкой и никогда не возвращается к источнику, как это происходит с реактивной нагрузкой. Если бы источником был механический генератор, для вращения вала потребовалось бы 240 Вт механической энергии (около 1/3 лошадиных сил).
Также обратите внимание, что форма сигнала мощности не соответствует частоте напряжения или тока! Скорее, его частота составляет удвоить частоты сигнала напряжения или тока. Эта другая частота запрещает выражение мощности в цепи переменного тока с использованием тех же сложных (прямоугольных или полярных) обозначений, которые используются для напряжения, тока и импеданса, потому что эта форма математического символизма подразумевает неизменные фазовые отношения.Когда частоты не совпадают, фазовые отношения постоянно меняются.
Как ни странно это может показаться, лучший способ продолжить вычисления мощности переменного тока — это использовать скалярную нотацию и обрабатывать любые соответствующие фазовые отношения с помощью тригонометрии.
Цепь переменного тока с чисто реактивной нагрузкой
Для сравнения рассмотрим простую цепь переменного тока с чисто реактивной нагрузкой на рисунке ниже.
Цепь переменного тока с чисто реактивной (индуктивной) нагрузкой.[латекс] X_L = 60.319 \ Omega [/ латекс]
[латекс] Z = 0 + j60,319 \ Omega \ text {или} 60,319 Ом \ угол \ текст {90 °} [/ латекс]
[латекс] \ begin {align} I & = \ frac {E} {Z} \\ & = \ frac {120V} {60.319 \ Omega} \\ & \ mathbf {= 1.989A} \ end {align} [ / латекс]
Рисунок 7.2 Мощность не рассеивается в чисто реактивной нагрузке. Хотя он попеременно поглощается источником и возвращается обратно.Обратите внимание, что мощность одинаково чередуется между положительными и отрицательными циклами.(Рисунок выше) Это означает, что мощность поочередно поглощается и возвращается к источнику. Если бы источником был механический генератор, для вращения вала не потребовалось бы (практически) никакой полезной механической энергии, потому что нагрузка не использовала бы никакой энергии. Вал генератора можно было бы легко вращать, а катушка индуктивности не нагревалась бы, как резистор.
Цепь переменного тока с резистивной и чисто реактивной нагрузкой
Теперь давайте рассмотрим цепь переменного тока с нагрузкой, состоящей из индуктивности и сопротивления, как показано на рисунке ниже.
цепь с реактивным сопротивлением и сопротивлением.[латекс] X_L = 60,319 \ Omega [/ латекс]
[латекс] Z_L = 0 + j60.319 \ Omega [/ latex] или [латекс] 60.319 \ Omega \ угол 90 ° [/ латекс]
[латекс] Z_R = 60 + j0 \ Omega [/ латекс] или [латекс] 60 \ Omega \ угол 0 ° [/ латекс]
[латекс] Z _ {\ text {total}} = 60+ j60.319 \ Omega [/ latex] или [латекс] 85.078 \ Omega \ angle 45.152 ° [/ latex]
[латекс] \ text {I} = \ frac {E} {Z _ {\ text {total}}} = \ frac {120V} {85.078 \ Omega} = \ mathbf {1.410A} [/ латекс]
При частоте 60 Гц индуктивность 160 миллигенри дает нам индуктивное сопротивление 60,319 Ом. Это реактивное сопротивление в сочетании с сопротивлением 60 Ом образует полное сопротивление нагрузки 60 + j60,319 Ом, или 85,078 Ом 45,152 или . Если нас не интересуют фазовые углы (чего мы еще не достигли), мы можем рассчитать ток в цепи, взяв полярную величину источника напряжения (120 вольт) и разделив ее на полярную величину импеданса. (85.078 Ом). При напряжении источника питания 120 вольт RMS ток нагрузки составляет 1,410 ампер. Это цифра, которую покажет амперметр RMS, если он подключен последовательно с резистором и катушкой индуктивности.
Мы уже знаем, что реактивные компоненты рассеивают нулевую мощность, поскольку они в равной степени поглощают мощность и возвращают мощность к остальной части схемы. Следовательно, любое индуктивное реактивное сопротивление в этой нагрузке также будет рассеивать нулевую мощность. Единственное, что здесь остается для рассеивания мощности, — это резистивная часть импеданса нагрузки.Если мы посмотрим на график формы волны напряжения, тока и полной мощности для этой схемы, мы увидим, как эта комбинация работает на рисунке ниже.
Рисунок 7.3 Комбинированная резистивная / реактивная цепь рассеивает больше мощности, чем возвращается к источнику. Реактивное сопротивление не рассеивает мощность; хотя резистор делает.Как и в любой реактивной цепи, мощность с течением времени чередуется между положительными и отрицательными мгновенными значениями. В чисто реактивной схеме чередование положительной и отрицательной мощности делится поровну, в результате чего рассеиваемая полезная мощность равна нулю.Однако в схемах со смешанным сопротивлением и реактивным сопротивлением, подобных этой, форма волны мощности по-прежнему будет чередоваться между положительной и отрицательной, но количество положительной мощности будет превышать количество отрицательной мощности. Другими словами, комбинированная индуктивная / резистивная нагрузка потребляет больше энергии, чем возвращается к источнику.
Глядя на график формы волны для мощности, должно быть очевидно, что волна проводит больше времени на положительной стороне центральной линии, чем на отрицательной, что указывает на то, что нагрузка потребляет больше энергии, чем возвращается в цепь.То небольшое возвращение мощности происходит из-за реактивного сопротивления; Несбалансированность положительной и отрицательной мощности происходит из-за сопротивления, поскольку она рассеивает энергию за пределами цепи (обычно в виде тепла). Если бы источником был механический генератор, количество механической энергии, необходимое для вращения вала, было бы суммой мощности, усредненной между положительным и отрицательным циклами мощности.
Математическое представление мощности в цепи переменного тока является сложной задачей, потому что волна мощности не имеет той же частоты, что и напряжение или ток.Кроме того, фазовый угол для мощности означает нечто совершенно иное, чем фазовый угол для напряжения или тока. В то время как угол для напряжения или тока представляет собой относительный сдвиг по времени между двумя волнами, фазовый угол для мощности представляет собой отношение между рассеиваемой мощностью и возвращаемой мощностью. Из-за того, что мощность переменного тока отличается от напряжения или тока переменного тока, на самом деле легче получить цифры для мощности, вычислив с помощью скаляра величин напряжения, тока, сопротивления и реактивного сопротивления, чем пытаться получить их из вектор или комплексные величины напряжения, тока и импеданса, с которыми мы работали до сих пор.
- В чисто резистивной цепи вся мощность схемы рассеивается резисторами. Напряжение и ток синфазны.
- В чисто реактивной цепи мощность цепи не рассеивается нагрузкой (ами). Напротив, мощность поочередно поглощается и возвращается к источнику переменного тока. Напряжение и ток сдвинуты по фазе на 90 °.
- В цепи, состоящей из смешанного сопротивления и реактивного сопротивления, мощность, рассеиваемая нагрузкой (ами), будет больше, чем возвращаемая, но некоторая мощность определенно будет рассеиваться, а некоторая будет просто поглощаться и возвращаться.Напряжение и ток в такой цепи будут сдвинуты по фазе на величину где-то между 0 ° и 90 °.
Реактивная мощность
Мы знаем, что реактивные нагрузки, такие как катушки индуктивности и конденсаторы, рассеивают нулевую мощность, но тот факт, что они понижают напряжение и потребляют ток, создает обманчивое впечатление, что они на самом деле рассеивают мощность. Эта «фантомная мощность» называется реактивной мощностью , и она измеряется в единицах, называемых вольт-ампер-реактивная мощность (ВАР), а не в ваттах.Математическим обозначением реактивной мощности является (к сожалению) заглавная буква Q.
.Истинная сила
Фактическая мощность, используемая или рассеиваемая в цепи, называется истинной мощностью и измеряется в ваттах (как всегда, обозначается заглавной буквой P).
Полная мощность
Комбинация реактивной мощности и истинной мощности называется кажущейся мощностью , и она является произведением напряжения и тока цепи без учета фазового угла.Полная мощность измеряется в единицах Вольт-Ампер (ВА) и обозначается заглавной буквой S.
Расчет реактивной, истинной или полной мощности
Как правило, истинная мощность зависит от рассеивающих элементов схемы, обычно от сопротивления (R). Реактивная мощность зависит от реактивного сопротивления цепи (X). Полная мощность — это функция полного сопротивления цепи (Z). Поскольку для расчета мощности мы имеем дело со скалярными величинами, любые комплексные начальные величины, такие как напряжение, ток и импеданс, должны быть представлены их полярными величинами , а не действительными или мнимыми прямоугольными составляющими.Например, если я вычисляю истинную мощность по току и сопротивлению, я должен использовать полярную величину для тока, а не просто «реальную» или «мнимую» часть тока. Если я рассчитываю полную мощность по напряжению и импедансу, обе эти ранее комплексные величины должны быть уменьшены до их полярных величин для скалярной арифметики.
Уравнения, использующие скалярные величины
Существует несколько уравнений мощности, связывающих три типа мощности с сопротивлением, реактивным сопротивлением и импедансом (все с использованием скалярных величин):
Истинная мощность[латекс] \ begin {align} \ tag {7.2} {Z} \ end {align} [/ latex]
Измеряется в единицах Вольт-Ампер (ВА)
Обратите внимание, что существует два уравнения для расчета истинной и реактивной мощности. Для расчета полной мощности доступны три уравнения, P = IE используется только для для этой цели. Изучите следующие схемы и посмотрите, как эти три типа мощности взаимосвязаны: чисто резистивная нагрузка, чисто реактивная нагрузка и резистивная / реактивная нагрузка.2Z = 169,256ВА [/ латекс]
Истинная мощность, реактивная мощность и полная мощность для резистивной / реактивной нагрузки.
Треугольник власти
Эти три типа мощности — истинная, реактивная и полная — связаны друг с другом в тригонометрической форме. Мы называем это треугольником мощности : (рисунок ниже).
Рисунок 7.4 Треугольник мощности, связывающий кажущуюся мощность с реальной и реактивной мощностью.Используя законы тригонометрии, мы можем найти длину любой стороны (количество любого типа мощности), учитывая длины двух других сторон или длину одной стороны и угол.
- Мощность, рассеиваемая нагрузкой, обозначается как истинная мощность . Истинная мощность обозначается буквой P и измеряется в ваттах (Вт).
- Мощность, просто поглощаемая и возвращаемая нагрузкой из-за ее реактивных свойств, называется реактивной мощностью . Реактивная мощность обозначается буквой Q и измеряется в вольт-амперных реактивных единицах (ВАР).
- Полная мощность в цепи переменного тока, как рассеиваемая, так и поглощенная / возвращаемая, обозначается как полная мощность .Полная мощность обозначается буквой S и измеряется в вольт-амперах (ВА).
- Эти три типа мощности тригонометрически связаны друг с другом. В прямоугольном треугольнике P = смежная длина, Q = противоположная длина и S = длина гипотенузы. Противоположный угол равен фазовому углу импеданса цепи (Z).
Как упоминалось ранее, угол этого «треугольника мощности» графически показывает соотношение между количеством рассеиваемой (или потребляемой ) мощности и количеством потребляемой / возвращаемой мощности.Кроме того, это тот же угол, что и импеданс цепи в полярной форме. Выраженное в виде дроби, это соотношение между истинной мощностью и полной мощностью называется коэффициентом мощности для этой схемы. Поскольку истинная мощность и полная мощность образуют смежные стороны и стороны гипотенузы прямоугольного треугольника, соответственно, коэффициент мощности также равен косинусу этого фазового угла. Используя значения из схемы последнего примера:
Коэффициент мощности[латекс] \ tag {7.4} PF = \ frac {P} {S} = \ frac {IECosθ} {IE} = Cosθ [/ латекс]
[латекс] Коэффициент мощности = \ frac {119,365 Вт} {169,256 ВА} [/ латекс]
[латекс] Коэффициент мощности = 0,705 [/ латекс]
[латекс] \ mathbf {Cos 45,152 ° = 0,705} [/ латекс]
Следует отметить, что коэффициент мощности, как и все измерения коэффициента мощности, является безразмерной величиной , равной .
Значения коэффициента мощности
Для чисто резистивной схемы коэффициент мощности равен 1 (идеальный), потому что реактивная мощность равна нулю.Здесь треугольник мощности будет выглядеть как горизонтальная линия, потому что противоположная сторона (реактивная мощность) будет иметь нулевую длину.
Для чисто индуктивной цепи коэффициент мощности равен нулю, потому что истинная мощность равна нулю. Здесь треугольник мощности будет выглядеть как вертикальная линия, потому что прилегающая сторона (истинная мощность) будет иметь нулевую длину.
То же самое можно сказать и о чисто емкостной цепи. Если в цепи нет диссипативных (резистивных) компонентов, то истинная мощность должна быть равна нулю, что делает любую мощность в цепи чисто реактивной.Треугольник мощности для чисто емкостной цепи снова будет вертикальной линией (направленной вниз, а не вверх, как это было для чисто индуктивной цепи).
Важность коэффициента мощности
Коэффициент мощностиможет быть важным аспектом, который следует учитывать в цепи переменного тока, поскольку любой коэффициент мощности меньше 1 означает, что проводка схемы должна пропускать больший ток, чем это было бы необходимо при нулевом реактивном сопротивлении в цепи для обеспечения того же количества ( true) мощность резистивной нагрузки.Если бы наша последняя примерная схема была чисто резистивной, мы могли бы подавать на нагрузку полную мощность 169,256 Вт при том же токе 1,410 А, а не просто 119,365 Вт, которые она в настоящее время рассеивает с тем же количеством тока. Низкий коэффициент мощности приводит к неэффективной системе подачи энергии.
Низкий коэффициент мощности
Низкий коэффициент мощности можно исправить, как это ни парадоксально, добавив в схему еще одну нагрузку, потребляющую равную и противоположную величину реактивной мощности, чтобы нейтрализовать влияние индуктивного реактивного сопротивления нагрузки.Индуктивное реактивное сопротивление можно нейтрализовать только емкостным реактивным сопротивлением, поэтому мы должны добавить конденсатор параллельно нашей примерной схеме в качестве дополнительной нагрузки. Влияние этих двух противоположных реактивных сопротивлений, включенных параллельно, состоит в том, чтобы довести полное сопротивление цепи до ее полного сопротивления (чтобы фазовый угол импеданса был равен нулю или, по крайней мере, ближе к нему).
Поскольку мы знаем, что (нескорректированная) реактивная мощность составляет 119,998 ВАР (индуктивная), нам необходимо рассчитать правильный размер конденсатора, чтобы получить такое же количество (емкостной) реактивной мощности.2} {119.998VAR} [/ латекс]
[латекс] X = 120,002 Ом [/ латекс]
[латекс] X_C = \ frac {1} {2πfC} [/ латекс]
Решение для C:
[латекс] C = \ frac {1} {2πfX_C} [/ латекс]
[латекс] C = \ frac {1} {2π (60 Гц) (120,002 Ом} [/ латекс]
[латекс] C = 22,105 мкФ [/ латекс]
Давайте возьмем округленное значение емкости конденсатора 22 мкФ и посмотрим, что произойдет с нашей схемой: (рисунок ниже)
[латекс] Z _ {\ text {total}} = Z_C // (Z_L — Z_R) [/ латекс]
[латекс] Z _ {\ text {total}} = (120.2Z = 119,366ВА [/ латекс]
Коэффициент мощности схемы в целом был существенно улучшен. Основной ток был уменьшен с 1,41 ампера до 994,7 миллиампера, в то время как мощность, рассеиваемая на нагрузочном резисторе, осталась неизменной и составила 119,365 Вт. Коэффициент мощности намного ближе к 1:
.[латекс] PF = \ frac {P} {S} [/ латекс]
[латекс] PF = \ frac {119.365W} {119.366VA} [/ латекс]
[латекс] PF = 0,9999887 [/ латекс]
[латекс] \ text {Импендансный (полярный) угол} = 0.272 ° [/ латекс]
Поскольку угол импеданса по-прежнему является положительным числом, мы знаем, что схема в целом по-прежнему является более индуктивной, чем емкостной. Если бы наши усилия по коррекции коэффициента мощности были точно намечены, мы бы достигли угла импеданса, равного точно нулю, или чисто резистивного. Если бы мы добавили слишком большой конденсатор параллельно, мы бы получили отрицательный угол импеданса, что указывало на то, что цепь была более емкостной, чем индуктивной.
Следует отметить, что слишком большая емкость в цепи переменного тока приведет к низкому коэффициенту мощности, а также к слишком большой индуктивности.Вы должны быть осторожны, чтобы не чрезмерно скорректировать при добавлении емкости в цепь переменного тока. Вы также должны быть очень осторожны, , , чтобы использовать подходящие конденсаторы для работы (рассчитанные на соответствующие напряжения в энергосистеме и случайные скачки напряжения от ударов молнии, для непрерывной работы переменного тока и способные выдерживать ожидаемые уровни тока).
Если схема является преимущественно индуктивной, мы говорим, что ее коэффициент мощности составляет , отстающий от (потому что волна тока для схемы отстает от волны приложенного напряжения).И наоборот, если схема преимущественно емкостная, мы говорим, что ее коэффициент мощности составляет перед . Таким образом, наша примерная схема была запущена с коэффициентом мощности 0,705 с запаздыванием и была скорректирована до коэффициента мощности с запаздыванием 0,999.
Низкий коэффициент мощности в цепи переменного тока может быть «скорректирован» или восстановлен до значения, близкого к 1, путем добавления параллельного реактивного сопротивления, противоположного влиянию реактивного сопротивления нагрузки. Если реактивное сопротивление нагрузки является индуктивным по своей природе (что почти всегда будет), параллельная емкость — это то, что необходимо для корректировки низкого коэффициента мощности.
Когда возникает необходимость исправить низкий коэффициент мощности в системе питания переменного тока, у вас, вероятно, не будет роскоши знать точную индуктивность нагрузки в генри, чтобы использовать ее для своих расчетов. Возможно, вам повезло иметь прибор, называемый измерителем коэффициента мощности, который сообщит вам, каков коэффициент мощности (число от 0 до 1) и полную мощность (которую можно вычислить, сняв показания вольтметра в вольтах и умножив их на показание амперметра в амперах). В менее благоприятных обстоятельствах вам, возможно, придется использовать осциллограф для сравнения форм сигналов напряжения и тока, измерения фазового сдвига в градусах и вычисления коэффициента мощности по косинусу этого фазового сдвига.Скорее всего, у вас будет доступ к ваттметру для измерения истинной мощности, показания которого вы можете сравнить с расчетом полной мощности (умножением общего напряжения на измерения общего тока). По значениям истинной и полной мощности вы можете определить реактивную мощность и коэффициент мощности.
Давайте рассмотрим пример задачи, чтобы увидеть, как это работает: (Рисунок ниже)
Как рассчитать полную мощность в кВА
Во-первых, нам нужно рассчитать полную мощность в кВА.Мы можем сделать это, умножив напряжение нагрузки на ток нагрузки:
[латекс] S = IE [/ латекс]
[латекс] S = (9,615A) (240 В) [/ латекс]
[латекс] S = 2,308 кВА [/ латекс]
Как мы видим, 2,308 кВА — это намного больше, чем 1,5 кВт, что говорит нам о том, что коэффициент мощности в этой цепи довольно низкий (существенно меньше 1). Теперь рассчитаем коэффициент мощности этой нагрузки, разделив истинную мощность на полную:
[латекс] PF = \ frac {P} {S} [/ латекс]
[латекс] PF = \ frac {1.5кВт} {2,308кВА} [/ латекс]
[латекс] PF = 0,65 [/ латекс]
Используя это значение для коэффициента мощности, мы можем нарисовать треугольник мощности и по нему определить реактивную мощность этой нагрузки: (Рисунок ниже) Реактивная мощность может быть рассчитана из истинной мощности и полной мощности.
Как использовать теорему Пифагора для определения неизвестного количества треугольников
Чтобы определить неизвестную величину треугольника (реактивная мощность), мы используем теорему Пифагора «в обратном направлении», учитывая длину гипотенузы (полная мощность) и длина смежной стороны (истинная мощность):
[латекс] Q = √ (S ^ 2 -P ^ 2) [/ латекс]
[латекс] Q = 1. 2} {1.754kVAR} [/ латекс]
[латекс] X = 32,845 Ом [/ латекс]
[латекс] X_C = \ frac {1} {2πfC} [/ латекс]
Решение для C:
[латекс] C = \ frac {1} {2πfX_C} [/ латекс]
[латекс] C = \ frac {1} {2π (60 Гц) (32,845 Ом} [/ латекс]
[латекс] C = 80,761 мкФ [/ латекс]
Округляя этот ответ до 80 мкФ, мы можем поместить конденсатор этого размера в схему и вычислить результаты: (рисунок ниже)
Конденсатор 80 мкФ будет иметь емкостное реактивное сопротивление 33.157 Ом, что дает ток 7,238 ампер и соответствующую реактивную мощность 1,737 кВАр (для конденсатора только ). Поскольку ток конденсатора на 180 o не совпадает по фазе с индуктивным вкладом нагрузки в потребляемый ток, реактивная мощность конденсатора будет напрямую вычитаться из реактивной мощности нагрузки, в результате чего получится:
[латекс] X_L — X_C = X [/ латекс]
[латекс] 1,754 кВАр — 1,737 кВАр = 16,519 вар [/ латекс]
Эта коррекция, конечно, не изменит количество истинной мощности, потребляемой нагрузкой, но приведет к существенному снижению полной мощности и общего тока, потребляемого от источника 240 В: (рисунок ниже)
Новая полная мощность может быть найдена из истинных и новых значений реактивной мощности, используя стандартную форму теоремы Пифагора:
[латекс] S = √Q ^ 2 + P ^ 2 [/ латекс]
[латекс] S = 1.50009кВА [/ латекс]
Назад к основам: что означает коэффициент мощности и почему мы должны его корректировать?
Сегодняшние коммерческие, промышленные, розничные и даже домашние помещения все чаще заполняются электронными устройствами, такими как ПК, мониторы, серверы и копировальные аппараты, которые обычно питаются от импульсных источников питания (SMPS). Если они не спроектированы должным образом, они могут представлять нелинейные нагрузки, которые создают гармонические токи и, возможно, напряжения в сети электропитания.Гармоники могут повредить кабели и оборудование в этой сети, а также другое подключенное к ней оборудование. Проблемы включают перегрев и риск возгорания, высокое напряжение и циркулирующие токи, сбои в работе оборудования и отказы компонентов, а также другие возможные последствия. Нелинейная нагрузка может генерировать эти гармоники, если у нее низкий коэффициент мощности. Другие нагрузки могут иметь низкие коэффициенты мощности, не создавая гармоник. В этом посте рассматриваются эти проблемы, обстоятельства, которые могут привести к разрушительной генерации гармоник, и практические подходы к их уменьшению.
Две причины низкого коэффициента мощности
На самом простом уровне мы могли бы сказать, что коэффициент мощности электрического или электронного устройства — это соотношение мощности, которую оно потребляет от сети, и мощности, которую оно фактически потребляет. «Идеальное» устройство имеет коэффициент мощности 1,0 и потребляет всю потребляемую мощность. Он будет представлять нагрузку, которая является линейной и полностью резистивной, то есть такой, которая остается постоянной независимо от входного напряжения и не имеет значительной индуктивности или емкости.На рисунке 1 показаны формы входных сигналов, которые может показывать такое устройство. Во-первых, форма волны тока совпадает по фазе с напряжением, а во-вторых, обе формы волны синусоидальны.
Рис. 1. Осциллограммы входного напряжения и тока для устройства с коэффициентом мощности = 1,0
Рис. 1. Осциллограммы входного напряжения и тока для устройства с коэффициентом мощности = 1,0
На практике некоторые устройства имеют единичный коэффициент мощности, а многие другие нет.Устройство имеет низкий коэффициент мощности по одной из двух причин; либо он потребляет ток, не совпадающий по фазе с напряжением питания, либо потребляет ток несинусоидальной формы. Случай несинусоидальности, известный как коэффициент мощности смещения, обычно связан с электродвигателями внутри промышленного оборудования, в то время как несинусоидальный случай, известный как коэффициент мощности искажения, обычно наблюдается с электронными устройствами, такими как ПК, копировальные аппараты. и зарядные устройства аккумуляторов, приводимые в действие импульсными источниками питания (SMPS).Мы кратко рассмотрим коэффициент мощности смещения, прежде чем перейти к случаю искажения, который имеет более непосредственное отношение к проектировщикам электронных систем питания. Однако важно помнить об обоих случаях. Например, на некоторых инженерных курсах вопрос о коэффициенте мощности обсуждается только с точки зрения двигателей, что вызывает путаницу, когда их студенты позже сталкиваются с низким коэффициентом мощности, который демонстрирует SMPS.
Проблемы с электродвигателями и смещением коэффициента мощности
Электродвигатели создают мощные магнитные поля, которые создают напряжение или противодвижущую силу, противоположную приложенному напряжению.Это заставляет ток питания отставать от приложенного напряжения. Возникающая в результате противофазная составляющая тока не может обеспечить полезную мощность, но увеличивает требуемую мощность поставки и затраты на электроэнергию. Установка конденсаторов на двигатели снижает фазовую задержку и улучшает их коэффициент мощности.
SMPS и проблемы с коэффициентом мощности искажения
В то время как нагрузки с коэффициентом мощности смещения не вызывают гармоник и связанных с ними проблем, нагрузки с коэффициентом мощности с искажениями, такие как SMPS, будут делать это, если их коэффициент мощности не будет улучшен.
Входной каскад переменного тока SMPS обычно включает в себя мостовой выпрямитель, за которым следует большой конденсатор фильтра. Эта схема потребляет ток из сети только тогда, когда линейное напряжение превышает напряжение на конденсаторе. Это приводит к прерывистому течению тока, что приводит к несинусоидальной форме волны тока, показанной на рисунке 2.
Рис. 2: Несинусоидальная форма волны тока, полученная SMPS с низким коэффициентом мощности
Рис. 2: Несинусоидальная форма волны тока, полученная SMPS с низким коэффициентом мощности
Можно использовать преобразование Фурье, математический процесс, чтобы проанализировать этот сигнал и разбить его на набор синусоидальных компонентов.Они включают в себя основную частоту — 50 Гц в Европе, 60 Гц в Америке — и набор преимущественно нечетных кратных основной частоты, известных как гармоники. Третья гармоника — 150 Гц (или 180 Гц), пятая — 250 Гц (300 Гц) и так далее. На рисунке 3 показан типичный спектр гармоник для электронной нагрузки SMPS. Основная составляющая потребляется SMPS, в то время как гармоники являются реактивными и создают проблемы, описанные выше. Отношение основной амплитуды к сумме амплитуд всех гармоник дает коэффициент мощности устройства.
Рис. 3: Типичный спектр гармоник для электронной нагрузки SMPS
Рис. 3: Типичный спектр гармоник для электронной нагрузки SMPS
Международный стандарт
Существует международный стандарт для описания и установки допустимых пределов генерации гармоник в сети. В ЕС используется стандарт IEC 61000-3-2, охватывающий уровни мощности оборудования от 75 до 600 Вт.Стандарт разделяет оборудование на четыре класса — A, B, C и D. Класс D охватывает персональные компьютеры, мониторы персональных компьютеров и телевизионные приемники.
Проверенные и инновационные решения PFC
Несмотря на то, что существуют пассивные решения для определения коэффициента мощности, в целом отрасль считает, что активные конструкции обеспечивают наилучшее улучшение коэффициента мощности. Обычно они основаны на технологии повышающего преобразователя, как в примере, показанном на Рисунке 4.
Фиг.4: Схема активной коррекции коэффициента мощности с использованием повышения напряжения
Рис.4: Схема активной коррекции коэффициента мощности с использованием повышения напряжения
Рис. 5: Формы напряжения и тока для активной цепи повышения
Рис. 5: Формы напряжения и тока для активной цепи повышения
Для этого схема управления использует форму волны входного напряжения в качестве шаблона.Схема управления измеряет входной ток, сравнивает его с формой волны входного напряжения и регулирует повышающее напряжение для получения формы волны входного тока той же формы (5 – I). В то же время схема управления отслеживает напряжение на шине и регулирует повышающее напряжение для поддержания грубо регулируемого выходного постоянного тока (5 – B). Поскольку основной функцией схемы управления является подача синусоидального входного тока, напряжение шины постоянного тока может незначительно изменяться.
Использование схемы активной коррекции коэффициента мощности приводит к небольшому количеству разрывов входного тока и, как следствие, к низким искажениям и гармоническим составляющим, накладываемым на входной ток, потребляемый из линии.Однако недавно Vicor представила модульный интерфейс переменного тока, основанный на их новой архитектуре динамического преобразователя, названной Adaptive Cell.
Внешний интерфейс AC предлагает ряд улучшений для разработчиков систем. В частности, он обеспечивает универсальный вход AC от 85 В до 264 В, высокую эффективность и высокую удельную мощность, особенно с учетом того, что это полное решение, включающее изолированный и регулируемый выход постоянного тока, а также выпрямление и коррекцию коэффициента мощности. Устройство снижает распространение гармоник в сети переменного тока, улучшая общее качество электроэнергии на уровне системы и объекта.Суммарные гармонические искажения превышают требования EN61000-2-3, а высокая частота переключения и резонансные переходы упрощают внешнюю фильтрацию и соответствие стандартам EMI.
Понимание коэффициента мощности | electricaleasy.com
Энергия нужна и используется повсюду в мире. С точки зрения удобства, эффективности и экономии, лучше всего, чтобы мы генерировали, передавали и распространяли его в электрической форме, прежде чем он будет преобразован в требуемый с помощью подходящего оборудования.По тем же причинам экономии и эффективности мы используем переменный ток, а не постоянный ток. На практике мы производим, передаем и распределяем энергию почти исключительно в форме переменного тока. Постоянный ток используется либо в приложениях постоянного тока (машины постоянного тока и электронные схемы), либо в линиях передачи постоянного тока высокого напряжения. Везде, где используется питание переменного тока, возникает вопрос о коэффициенте мощности.
Коэффициент мощности
- Определяется как « косинус угла между напряжением и током ».
- В цепи переменного тока напряжение и ток идеально совпадают по фазе.
- Но практически между ними существует разность фаз.
- Косинус этой разности фаз называется коэффициентом мощности.
- Его можно определить и математически представить следующим образом:
Из рис. (a) выше, можно ясно отметить, что существует разность фаз угла ɸ между вектором напряжения и вектором тока.
Коэффициент мощности = cosɸ
Рис. (b) называется треугольником мощности
Здесь VI sinɸ = реактивная мощность (в ВАр)
VI cosɸ = активная мощность (в ваттах)
VI = полная мощность (в ВА)
PF = cosɸ = активная мощность ( Вт) / Полная мощность (ВА)
Рис.(c) называется треугольником импеданса
Здесь R = сопротивление, X = реактивное сопротивление, Z = импеданс
Z 2 = R 2 + X 2
PF = cosɸ = R / Z
Коэффициент мощности может быть запаздывающим, опережающим или единичным.
Отстающий коэффициент мощности
- Когда ток отстает от напряжения, коэффициент мощности цепи называется «запаздывающим».
- Когда цепь индуктивная, коэффициент мощности отстает.
- Нагрузки, такие как асинхронные двигатели, катушки, лампы и т. Д., Являются индуктивными и имеют запаздывание pf.
Ведущий коэффициент мощности
- Когда ток опережает напряжение (или напряжение отстает от тока), коэффициент мощности цепи называется опережающим.
- Когда цепь емкостная, опережает pf.
- Емкостные нагрузки, такие как синхронные конденсаторы, конденсаторные батареи и т. Д., Потребляют опережающий ток. Такие схемы имеют опережающий коэффициент мощности.
Коэффициент мощности Unity
- Коэффициент мощности равен единице (т.е.е. 1) для идеальных схем.
- Когда ток и напряжение в фазе, PF = 1
- Коэффициент мощности не может быть больше единицы.
- Практически он должен быть максимально приближен к единице.
Влияние низкого коэффициента мощности
- Ток нагрузки
Мощность в цепи переменного тока может быть задана как: P = VI cosɸ
Следовательно, cosɸ = P / VI
I ∝ 1 / cosɸ
Аналогичное соотношение может быть получено и для трехфазной цепи.Мы видим, что ток обратно пропорционален pf.Например, предположим, что мы хотим передать мощность 10 кВА при 100 В
Если PF = 1,
I = P / (V cosɸ) = 10000 / (100 x 1) = 100 A
Если PF = 0,8 ,
I = P / (V cosɸ) = 10000 / (100 x 0,8) = 125 A
Следовательно, потребляемый ток выше при низком коэффициенте мощности. - Потери: Как указано выше, для низкого pf потребляемый ток будет большим. Следовательно, потери в меди (потери I 2 R) также будут высокими.Это снижает эффективность оборудования.
- Перегрев оборудования: I 2 R при потерях выделяется тепло (закон Джоуля). Следовательно, повышение температуры будет относительно большим при низком коэффициенте мощности, что приведет к дальнейшему увеличению нагрузки на изоляцию.
- Размер проводника: Низкий коэффициент мощности приводит к более высокому току нагрузки. Если ток нагрузки увеличивается, размер необходимого проводника также увеличивается. Это еще больше увеличит стоимость кондуктора.
- кВА Номинальная мощность машины: Машины не рассчитываются в кВт при производстве, потому что коэффициент мощности источника питания неизвестен. Вместо этого они оцениваются в кВА.
Согласно определению, Cosɸ = Активная мощность (кВт) / Полная мощность (кВА)
Следовательно, номинальная мощность кВА = 1 / cosɸ
Следовательно, для низкого коэффициента мощности необходимо оборудование с большей номинальной мощностью кВА. Но чем выше рейтинг кВА, тем больше размер оборудования. Если размер увеличивается, увеличивается и стоимость. - Регулировка напряжения: Определяется как разница между конечным напряжением отправителя и получателя на единицу конечного напряжения отправления.Когда мощность передается с одного конца на другой, напряжение падает по нескольким причинам. Это падение напряжения должно быть в допустимых пределах.
P = VI cosɸ, поэтому I 1 / V
При низком коэффициенте мощности ток будет больше и, следовательно, будет увеличиваться падение напряжения. Следовательно, регулирование напряжения при низком коэффициенте мощности плохое. - Активная и реактивная мощность (передаваемая мощность): Активная и реактивная мощность передаются по линии вместе. Для питания нагрузки требуется активная мощность.Реактивная мощность необходима для поддержания напряжения в линии. Но если реактивная мощность больше, то передаваемая активная мощность уменьшается. Для низкого коэффициента мощности активная мощность мала, поскольку cosɸ = активная мощность (Вт) / полная мощность (ВА). Это приводит к неэкономичной работе.
[Также прочтите: Сравнение различных электростанций]
Автор: Манодж Арора — студент-электрик и писатель из Гуджарата, Индия.Он пишет стихи и рассказы, когда не погружается в книгу.
Кредиты для Графика: Киран Давэр.
Узнать | OpenEnergyMonitor
Общие сведения о питании переменного тока
Общие сведения о питании переменного тока
Энергомонитор всего дома измеряет энергию, потребляемую приборами, подключенными к домашней электросети. Чтобы понять, как это происходит, полезно знать кое-что о том, как приборы взаимодействуют с электрической системой.
Не все приборы одинаково взаимодействуют с электросетью.В этой статье сначала будут обсуждаться резистивные нагрузки и расчет потребляемой мощности. Затем мы переходим к обсуждению реактивных нагрузок и немного о нелинейных нагрузках. Наконец, он покажет, как мы измеряем направление потока энергии, что важно, если энергия генерируется, а также потребляется.
Резистивные нагрузки
Лампы накаливания, чайники, утюги, электрические водонагреватели, электрические плиты — все довольно просто. Они используют всю отданную им энергию. Это резистивные нагрузки, что означает, что их потребляемый ток равен напряжению, деленному на их сопротивление (закон Ома).Чисто резистивная нагрузка дает выходной сигнал напряжения и тока, подобный следующему:
Диаграмма 1 — Соотношение фаз напряжения и тока в резистивной нагрузке
Желтая линия — мощность в данный момент времени (в любой данный момент она называется мгновенной мощностью , ), которая равна произведению напряжения и тока в данный момент времени. Обратите внимание, сила всегда положительная. В этом случае положительное направление — это энергия, текущая к нагрузке.
Частично реактивные нагрузки
Однако такие вещи, как холодильники, стиральные машины, сверлильные станки и аппараты для дуговой сварки, не так просты, поскольку эти устройства потребляют определенное количество энергии, а затем возвращают часть энергии обратно в сеть. Они имеют индуктивные (например, двигатели) или емкостные (например, аппараты для дуговой сварки) компоненты в дополнение к резистивному компоненту. Частично индуктивная нагрузка дает выходные сигналы напряжения и тока, подобные приведенным ниже:
Диаграмма 2 — Соотношение фаз напряжения и тока в частично реактивной нагрузке
Обратите внимание, что желтая линия теперь на некоторое время становится отрицательной, положительный бит — это энергия, текущая к нагрузке, а отрицательный бит — энергия, текущая обратно от нагрузки.
Еще одна вещь, которую следует учитывать, — это то, что формы сигналов напряжения и тока смещены друг от друга. Представьте себе зарядку довольно большого конденсатора с помощью резистора последовательно (так, чтобы он не мог заряжаться мгновенно): для начала конденсатор разряжается. Напряжение питания возрастает и превышает напряжение на конденсаторе, поэтому ток течет в конденсатор (положительное направление на графике), что вызывает повышение напряжения на конденсаторе. Напряжение питания падает. Теперь напряжение на заряженном конденсаторе выше, чем напряжение питания.Ток начинает течь обратно в направлении источника питания (отрицательное направление на графике). Это приводит к тому, что текущая форма волны выглядит так, как если бы она была сдвинута, как показано на графике. (Это называется фазовым сдвигом).
Реальная мощность, реактивная мощность и полная мощность
Если посмотреть на приведенные выше графики напряжения, тока и мощности при частоте сети, потребляемая мощность колеблется 50/60 раз в секунду. Мы не можем угнаться за изменениями на этой скорости, поэтому у нас есть более полезное значение мощности: среднее значение мгновенной мощности, которое мы называем реальной мощностью или активной мощностью .
Реальная мощность часто определяется как мощность, используемая устройством для выполнения полезной работы. Ссылаясь на график выше, положительные биты — это мощность, поступающая на нагрузку от источника питания, а отрицательные биты — это мощность, возвращающаяся к источнику питания от нагрузки. Мощность, которая фактически использовалась нагрузкой, то есть мощность, которая была включена, за вычетом мощности, возвращаемой обратно, является реальной мощностью.
Реактивная мощность или мнимая мощность — это мера мощности, передаваемой между нагрузкой и источником питания, которая не выполняет полезной работы.
Еще одним полезным показателем мощности является полная мощность , которая является произведением среднеквадратичного (RMS) напряжения и RMS-тока. Для чисто резистивных нагрузок активная мощность равна полной мощности. Но для всех остальных нагрузок реальная мощность меньше полной мощности. Полная мощность является мерой реальной и реактивной мощности, но не является суммой двух, так как сумма двух не учитывает разности фаз.
Соотношение между реальной, реактивной и полной мощностью для ИДЕАЛЬНЫХ синусоидальных нагрузок:
Действительная мощность = Полная мощность x cosΦ
Реактивная мощность = Полная мощность x sin Φ
cosΦ также известен как коэффициент мощности.
Однако примечание о нелинейных нагрузках:
Это соотношение коэффициента мощности действительно только для линейных синусоидальных нагрузок. Большинство источников питания для устройств постоянного тока, таких как портативные компьютеры, создают нелинейную нагрузку на сеть. Их текущий розыгрыш часто выглядит так:
Мы все еще можем рассчитать коэффициент мощности по следующему уравнению:
Коэффициент мощности = фактическая мощность / полная мощность
но отношение
(полная мощность) 2 = (активная мощность) 2 + (реактивная мощность) 2
, которое верно для чистых синусоидальных волн, больше не является правильным.Кроме того, коэффициент мощности не равен cosΦ , поскольку необходимо учитывать влияние гармоник более высокого порядка на формы сигналов как напряжения, так и тока.
Значение коэффициента мощности измеряет, насколько эффективность сети зависит от ОБОИХ фазовых задержек φ И содержания гармоник входного тока.
Ссылка: понимание коэффициента мощности от L Wuidart
Определение направления потока мощности
До сих пор в этой статье предполагалось, что нагрузка потребляет мощность.Однако если мы генерируем электроэнергию, то направление тока меняется на противоположное. Но поскольку ток переменный, направление все равно меняется на противоположное, 50 (или 60) раз в секунду. Нам нужна ссылка для сравнения текущего направления. К счастью, у нас есть это в виде напряжения. На диаграмме 1 волны напряжения и тока как нарастали, так и падали вместе. Когда напряжение было положительным (выше оси X), ток был положительным, а когда напряжение было отрицательным (ниже оси x), ток был отрицательным.Мощность равна произведению напряжения и тока, поэтому мощность всегда была положительной — вся кривая мощности находится выше оси X.
Если дом вырабатывает электроэнергию, направление тока меняется на противоположное по сравнению с нашим предыдущим примером. Теперь, когда напряжение положительное (выше оси X), ток отрицательный (ниже оси X), а когда напряжение отрицательное, ток положительный. Мощность всегда отрицательная — вся кривая мощности находится ниже оси X.
Диаграмма 4 — Соотношение фаз напряжения и тока при выработке энергии.
Знак мощности, следовательно, указывает, потребляется или генерируется мощность.
Подвести итог
Есть много параметров, которые мы можем измерить в отношении использования энергии в системах переменного тока. У каждого есть свои достоинства. Для измерения энергии в домах реальная мощность, вероятно, будет наиболее полезной величиной, поскольку она показывает, сколько энергии фактически потребляют все ваши приборы, и это то, за что вам выставляет счет коммунальное предприятие.
Далее: Теория мощности переменного тока — Математика Arduino — Как рассчитываются действительная и полная мощность, среднеквадратичное напряжение и ток, а также коэффициент мощности.
Дополнительная литература
https://en.wikipedia.org/wiki/AC_power
Мощность в резистивных и реактивных нагрузках: https://www.allaboutcircuits.com/vol_2/chpt_11/1.html
Однофазные системы питания: https://www.allaboutcircuits.com/vol_2/chpt_10/1.html
Блок питания
Формула коэффициента мощностии полная мощность для цепей переменного тока — Wira Electrical
Коэффициент мощности — это отношение рабочей мощности.
Этот термин часто используется в электротехнической промышленности, но знаете ли вы, что он означает?
Обязательно сначала прочтите, что такое цепь переменного тока.
Существует несколько типов мощности в цепи переменного тока:
- Максимальная средняя передаваемая мощность
- Среднеквадратичное значение напряжения и тока
- Коэффициент мощности и полная мощность
- Треугольник мощности и силовой комплекс
- Сохранение мощности переменного тока
Полная мощность и коэффициент мощности
Мы видели, что если напряжение и ток на выводах схемы равны
| (1) |
или, в векторной форме, В = В м ∠θ v и I = I m ∠θ i , средняя мощность
| (2) | (2) | 972 909
| (3) |
Мы добавили новый член в уравнение:
| (4) |
Средняя мощность — это произведение двух членов.Продукт V rms I rms известен как полная мощность S .
Коэффициент cos (θ v — θ i ) называется коэффициентом мощности (pf).
Полная мощность (в ВА) является произведением среднеквадратичных значений напряжения и тока.
Полная мощность называется так, потому что кажется очевидным, что мощность должна быть произведением напряжения на ток по аналогии с резистивными цепями постоянного тока.
Он измеряется в вольт-амперах или ВА, чтобы отличить его от средней или реальной мощности, которая измеряется в ваттах.
Коэффициент мощности безразмерен, поскольку он представляет собой отношение средней мощности к полной,
| (5) |
Угол θ v — θ i равен называется углом коэффициента мощности , поскольку это угол, косинус которого является коэффициентом мощности.
Угол коэффициента мощности равен сопротивлению нагрузки, если V — напряжение на нагрузке, а I — ток через нее.Это очевидно из того факта, что
| (6) |
В качестве альтернативы, поскольку
| (7a) |
| (7b) |
импеданс равен
| (8) |
Напряжение соответствует косинусоидальному коэффициенту мощности .Это также косинус угла импеданса нагрузки.
Из уравнения (5) коэффициент мощности можно рассматривать как тот коэффициент, на который необходимо умножить полную мощность, чтобы получить реальную или среднюю мощность.
Значение pf находится в диапазоне от нуля до единицы.
Для чисто резистивной нагрузки напряжение и ток синфазны, так что θ v — θ i = 0 и pf = 1.
Это означает, что полная мощность равна средней мощности.
Для чисто реактивной нагрузки θ v — θ i = ± 90 o и pf = 0. В этом случае средняя мощность равна нулю. В промежутке между этими двумя крайними случаями pf считается равным , опережающему , или , отстающему .
Опережающий коэффициент мощности означает, что ток ведет к напряжению, что подразумевает емкостную нагрузку.
Отстающий коэффициент мощности означает, что ток отстает от напряжения, что подразумевает индуктивную нагрузку.
Коэффициент мощности влияет на счета за электроэнергию, которые потребители оплачивают коммунальным предприятиям.Мы узнаем, как исправить коэффициент мощности с помощью коррекции коэффициента мощности.
Примеры полной мощности и коэффициента мощности
Для лучшего понимания рассмотрим примеры ниже:
1. Последовательно подключенная нагрузка потребляет ток i (t) = 4 cos (100π t + 10 o ) A когда приложенное напряжение составляет v (t) = 120 cos (100π t — 20 o ) V.
Найдите полную мощность и коэффициент мощности нагрузки. Определите значения элементов, которые образуют последовательно подключенную нагрузку.
Решение:
Полная мощность
Коэффициент мощности
ПФ является опережающим, потому что ток опережает напряжение. Коэффициент мощности также можно получить из импеданса нагрузки.
Импеданс нагрузки Z можно смоделировать с помощью резистора 25,98 Ом, включенного последовательно с конденсатором с
или
2. Определите коэффициент мощности всей схемы рисунка (1), видимой источником. Рассчитайте среднюю мощность, отдаваемую источником.
| Рисунок 1 |
Решение:
Общий импеданс составляет
Коэффициент мощности
, так как сопротивление является емкостным.




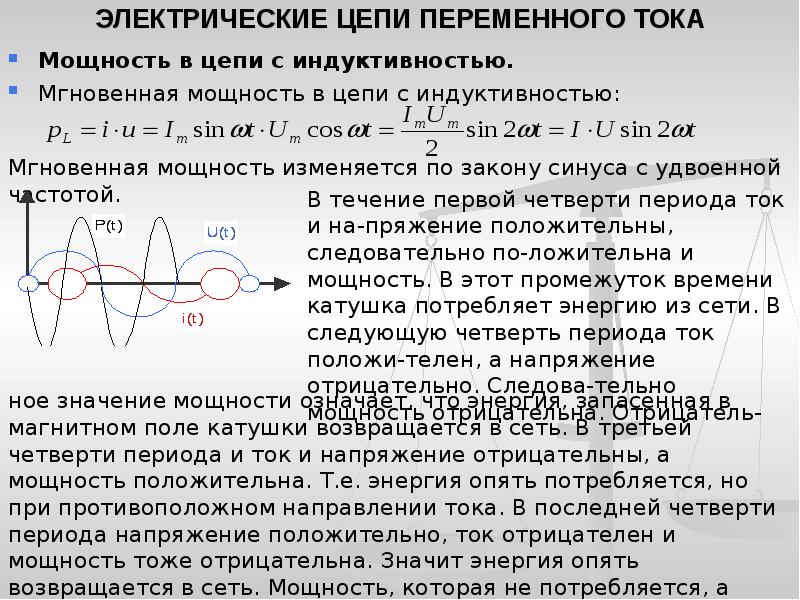 37
37
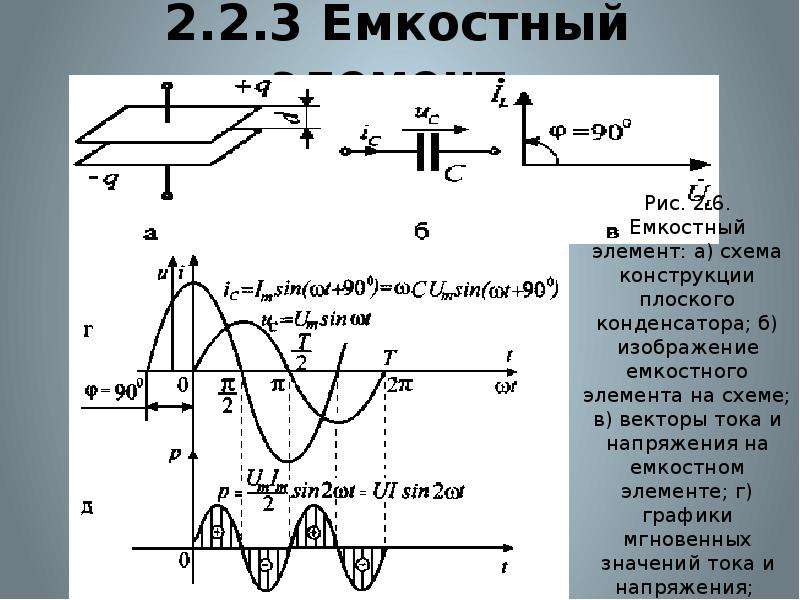
 При компенсированном коэффициенте мощности нет
необходимости платить за реактивную мощность. Значительное сокращение энергопотребления.
При компенсированном коэффициенте мощности нет
необходимости платить за реактивную мощность. Значительное сокращение энергопотребления.
