Скважность — Википедия

Материал из Википедии — свободной энциклопедии

Сигнал с различным коэффициентом заполнения D

Сква́жность (в физике, электронике) — безразмерная величина, один из классификационных признаков импульсных систем, определяющий отношение периода следования (повторения) импульсов к длительности импульса. Часто используется величина, обратная скважности, которая называется коэффициент заполнения (англ. duty cycle).

Таким образом, для импульсного сигнала справедливы следующие соотношения:

S=Tτ=1D,{\displaystyle S={\frac {T}{\tau }}={\frac {1}{D}},}

D=τT=1S,{\displaystyle D={\frac {\tau }{T}}={\frac {1}{S}},}

где S{\displaystyle S} — скважность, D{\displaystyle D} — коэффициент заполнения, T{\displaystyle T} — период импульсов, τ{\displaystyle \tau } — длительность импульса.

T{\displaystyle T} — период импульсов, τ{\displaystyle \tau } — длительность импульса

Скважность и коэффициент заполнения — безразмерные величины, однако коэффициент заполнения часто указывают в процентах. Коэффициент заполнения в ряде применений более удобен, поскольку его относительное изменение происходит в интервале от 0 до 1, тогда как соответствующая скважность изменяется от бесконечности до 1.

Понятие скважности используется, например, в радиолокации, где эта величина определяет отношение пиковой мощности импульсной установки (например, передатчика радиолокационной станции) к её средней мощности и является важным показателем работы импульсных систем.

Известный в радиотехнике сигнал меандр имеет скважность 2 (коэффициент заполнения 0,5). Скважность импульсов в радиолокационных станциях может достигать тысяч.

коэффициент заполнения — это… Что такое коэффициент заполнения?

3.15 коэффициент заполнения (fill ratio), φ: Отношение объема источника шума под кожухом к внутреннему объему кожуха.

Примечание — Если форма источника шума затрудняет расчет его объема, то можно в качестве объема источника принять объем огибающего параллелепипеда по ГОСТ 31275.

Коэффициент заполнения — максимально возможный объем СПГ по отношению к общему объему резервуара (определяет разработчик резервуара).

3.13 коэффициент заполнения (fill ratio) φ: Отношение объема источника шума под кожухом к внутреннему объему кожуха.

Примечание — Если форма источника шума затрудняет расчет его объема, то можно в качестве объема источника принять объем огибающего параллелепипеда по ГОСТ 31275.

2.15 коэффициент заполнения: Отношение площади пикселя, отведенной для отображения информации, к полной площади пикселя.

3.11 коэффициент заполнения: Отношение теоретического объема, заполненного металлом, определяемого исходя из массы и плотности, к действительному объему, полученному после сдавливания при определенной нагрузке набора (пакета) листов.

3.10 коэффициент заполнения: Отношение теоретического объема, заполненного металлом, определяемого исходя из массы и плотности, к действительному объему, полученному после сдавливания при определенной нагрузке набора (пакета) листов.

3.10 коэффициент заполнения (duty factor): Отношение длительности импульса к периоду следования импульсов в периодической импульсной последовательности.

11. Коэффициент заполнения

Отношение длительности импульса к длительности периода

Смотри также родственные термины:

47. Коэффициент заполнения вихретокового проходного преобразователя

Fill factor of encircling eddy current probe

Отношение площади поперечного сечения объекта контроля к меньшей из площадей поперечного сечения, эквивалентного витка измерительной или возбуждающей обмотки проходного вихретокового преобразователя

где  — площадь поперечного сечения эквивалентного витка измерительной обмотки;

 — площадь поперечного сечения эквивалентного витка обмотки возбуждения

57. Коэффициент заполнения графика нагрузки энергоустановки потребителя

Коэффициент заполнения

D. Belastungsfaktor

Отношение среднеарифметического значения нагрузки энергоустановки потребителя к максимальному за установленный интервал времени

3.1.63 коэффициент заполнения графика нагрузки энергоустановки потребителя (коэффициент заполнения): Отношение среднеарифметического значения нагрузки энергоустановки потребителя к максимальному за установленный интервал времени.

[ГОСТ 19431-84, пункт 57]

207. Коэффициент заполнения жилы

Коэффициент заполнения

Отношение площади поперечного сечения многопроволочной токопроводящей жилы к площади, ограниченной описанным около нее контуром

13.5.2. Коэффициент заполнения кабельных каналов

Необходимо, чтобы коэффициент заполнения основывался на показателях длины и прямолинейности канала и гибкости проводов. Рекомендуется, чтобы расположение каналов и их размеры позволяли легко укладывать на место провода и кабели.

7.1.9. Коэффициент заполнения круга

Отношение площади поперечного сечения стержня к площади круга с диаметром, равным диаметру стержня трансформатора

Примечание. При наличии в сечении стержня каналов площадь поперечного сечения каналов не включается в площадь поперечного сечения стержня

34. Коэффициент заполнения лесосплавного хода

Е. Coefficient of floating route filling

Отношение площади, занятой плывущими бревнами или сплоточными единицами в пределах рассматриваемого участка лесосплавного хода, к общей площади этого участка

19. Коэффициент заполнения несущего винта

Коэффициент заполнения

σ

Величина, определяемая соотношением

7.1.15. Коэффициент заполнения окна магнитной системы

Отношение суммарной площади поперечного сечения металла всех витков всех обмоток в окне магнитной системы к площади окна

68. Коэффициент заполнения питателя роторного снегоочистителя

Коэффициент заполнения питателя

Отношение фактической объемной производительности снегоочистителя к пропускной способности питателя

67. Коэффициент заполнения ротора снегоочистителя

Коэффициент заполнения ротора

Отношение фактической объемной производительности снегоочистителя к пропускной способности ротора

7.1.10. Коэффициент заполнения сечения стержня (ярма)

Отношение активного сечения стержня (ярма) к площади его поперечного сечения

7.1.11. Коэффициент заполнения сталью

Отношение активного сечения стержня к площади круга с диаметром, равным диаметру стержня трансформатора.

Примечание. Коэффициент заполнения сталью равен произведению коэффициента заполнения круга и коэффициента заполнения сечения стержня

Словарь-справочник терминов нормативно-технической документации. academic.ru. 2015.

Понятие скважности импульса и коэффициента заполнения

Общеизвестно, что регулировать количество оборотов электродвигателя можно периодическим включением и отключением его от энергосети, кроме того при изменении времени включения и отключения можно задавать дополнительные параметры скорости. Это явление характерно не только для электродвигателя – его действие можно заметить во всех потребителях тока, способных запасать энергию, иначе говоря, инерционных системах.

Скважность

Принцип широтно-импульсной модуляции основан именно на этом эффекте, он нашёл себе достаточно широкое применение при управлении электротехническими устройствами и источниками освещения, где требуется циклическая подача энергии. В английском языке этот принцип получил название – Pulse-Width Modulation.

Что такое ШИМ

Что такое электрический импульс? Это резкий конечный всплеск напряжения в системе. Поскольку он конечен, то он имеет начало, обычно называемое фронтом, ширину и спад, его окончание, период.

Такие всплески можно охарактеризовать следующими параметрами:

• периодичность – это временной период до фронта следующего импульса, обозначается литерой T;
• скважность – отношение периода к ширине, это величина безразмерная и выражается чаще всего в процентах, на схеме можно обозначить участок между спадом первого импульса и фронтом нового, обозначается литерой S;
• частота сигнала – количество всплесков за определённый промежуток времени, величина, обратная периоду колебаний;
• ширина импульса – период времени, в течение которого его амплитуда стабильна;
• коэффициент заполнения – значение, обратное скважности, обычно обозначается в формулах литерой t.

Таким образом, скважность импульса – это соотношение:

S = T/t.

Благодаря этому, широтно-импульсная модуляция позволяет управляемо изменять напряжение в системе от нулевого значения до максимальной амплитуды сигнала, это используется для установки оптимальных режимов работы инерциальных систем.

Схема

Применение

Для формирования прямоугольных колебаний применяется микросхема аналогового типа или чип-контроллер. Сами колебания управляют только нагрузкой, идущей от источника тока. Подключение производится через ключевую схему на полупроводнике. Ключ имеет всего два состояния: либо он включён в сеть, либо размыкает её.

Грубо говоря, все зависит от характеристик колебаний. Так, если светильник подключен через подобную схему, то при низкой частоте работы устройства лампа будет мигать с определенной периодичностью, но при превышении её сверх 50Гц в человеческих глазах отдельные всплески света сольются в одно ровное свечение. Это особенность человеческого глаза, который не улавливает колебания свыше этого значения. Но и яркость свечения можно регулировать. Чем ниже коэффициент заполнения, а, следовательно, и значение, обратное ему, тем меньше яркость свечения источника.

Аналогичный пример можно использовать и с двигателем постоянного тока, под управлением широтно-импульсного регулятора. При этом низкая частота приведёт к снижению оборотов двигателя, в то время как высокая – к его эффективной работе. Для её достижения используются ключи-полупроводники, обладающие значительным быстродействием и низким коэффициентом проводимости, так как в противном случае возможно запаздывание сигнала.

При необходимости сигналы схемы импульсного регулятора можно усреднять, для этого используются фильтры низких частот, но при подключении двигателя с большой механической инерцией и хорошим значением индуктивности. В этом случае снижение амплитуды и частоты происходит самопроизвольно.

Скважность, а также её обратное значение зависят от уровня моделирующего сигнала, частота таких устройств определяется частотой дублирующего генератора, подающего дополнительный сигнал.

Генератор для получения скважности

Видео

Оцените статью:

Коэффициент заполнения Википедия

Сигнал с различным коэффициентом заполнения D

Сква́жность (в физике, электронике) — безразмерная величина, один из классификационных признаков импульсных систем, определяющий отношение периода следования (повторения) импульсов к длительности импульса. Часто используется величина, обратная скважности, которая называется коэффициент заполнения (англ. duty cycle).

Таким образом, для импульсного сигнала справедливы следующие соотношения:

S=Tτ=1D,{\displaystyle S={\frac {T}{\tau }}={\frac {1}{D}},}

D=τT=1S,{\displaystyle D={\frac {\tau }{T}}={\frac {1}{S}},}

где S{\displaystyle S} — скважность, D{\displaystyle D} — коэффициент заполнения, T{\displaystyle T} — период импульсов, τ{\displaystyle \tau } — длительность импульса.

T{\displaystyle T} — период импульсов, τ{\displaystyle \tau } — длительность импульса

Скважность и коэффициент заполнения — безразмерные величины, однако коэффициент заполнения часто указывают в процентах. Коэффициент заполнения в ряде применений более удобен, поскольку его относительное изменение происходит в интервале от 0 до 1, тогда как соответствующая скважность изменяется от бесконечности до 1.

Понятие скважности используется, например, в радиолокации, где эта величина определяет отношение пиковой мощности импульсной установки (например, передатчика радиолокационной станции) к её средней мощности и является важным показателем работы импульсных систем.

Известный в радиотехнике сигнал меандр имеет скважность 2 (коэффициент заполнения 0,5). Скважность импульсов в радиолокационных станциях может достигать тысяч.

См. также

Ссылки

отношение периода следования к длительности импульса

Электрические сигналы, которые имеют только 2 допустимых состояния «0» или «1», что соответствует уровню напряжения 0.2 вольта (В) или 4.9В, называются импульсными. В основном, оперируют с последовательностью импульсов. Одна из простейших последовательностей импульсов показа на рис. ниже.

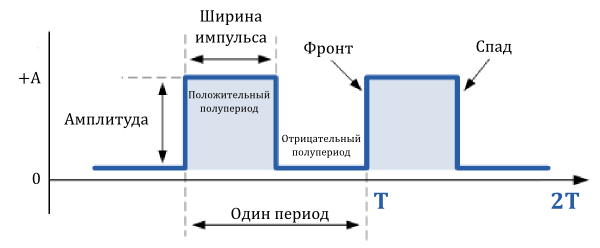
Последовательность импульсов

Общая информация

К основным параметрам последовательности импульсов относятся:

• l амплитуда импульса – Um,
• l длительность импульса – tu,
• l длительность паузы – tn,
• l период следования T или частота f = 1/T следования.

Если длительность tu всех импульсов, входящих в состав последовательности, и всех пауз tn постоянна в течение времени, то она называется периодической.

Важным параметром периодического импульсного процесса является скважность импульсов S. Скважность импульсов – это отношение периода следования к длительности импульса,  рассчитывается по формуле:

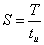
Эффективность S при управлении устройства достигается при стабильной частоте сигнала. Иногда используют обратную величину D – коэффициент заполнения, рассчитывается по формуле:

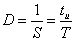
При равенстве tu и tn скважность равна 2, и сигнал называется меандром. S и D – безразмерные величины, так как время делится на время. В цифровых устройствах применяются импульсы различной формы. Формой импульса называется графическое изображение закона изменения импульсного напряжения во времени. На рис. ниже показаны формы сигналов:

• а – прямоугольная,
• б – трапецеидальная,
• в – экспоненциальная,
• г – колокольная,
• д – ступенчатая,
• е – пилообразная.

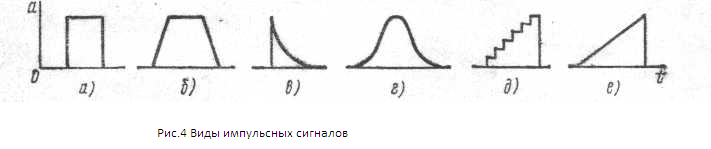
Виды импульсных сигналов

Техническая характеристика формы импульсов связана с количественной оценкой основных параметров импульса, свойств отдельных его участков, которые играют разную роль при воздействии импульса на устройство. На рис. выше изображены идеализированные формы импульса. Из-за переходных процессов в устройствах (формирования и усиления импульсов) существует реальная форма, например, прямоугольного импульса (рис. ниже).

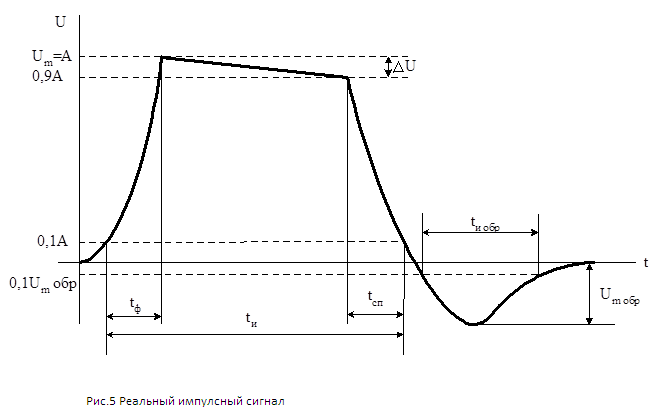
Реальная форма импульса

Основные параметры импульса – это:

• l Размах импульса – Um,
• l Длительность импульса – tи,
• l Длительность переднего фронта – tф,
• l Длительность заднего фронта – tсп,
• l Спад вершины – ΔU,
• l Размах выброса заднего фронта – Um обр,
• l Длительность выброса заднего фронта – tи обр.

Указанные величины считываются между уровнями 0.1 и 0.9 от амплитуды в микросекундах, в зависимости от частоты сигнала. Амплитудные – в вольтах.

Определить параметры импульсного сигнала можно с помощью осциллографа, частотомера или мультиметра.

Управление скважностью

С помощью цифровых сигналов происходит управление разнообразными устройствами. Первое применение такого управления использовалось при передаче информации кодом Морзе. Сигнал передаётся короткими и длинными импульсами. Каждой букве соответствует определённый набор точек и тире. Сегодня этот метод управления используется для ШИМ-управления.

При изменении D (коэффициент заполнения) от 0 до 1 добиваются нужного напряжения на выходе электронного устройства. Таким образом, можно управлять оборотами двигателя, освещением, яркостью дисплея и т.д. При формировании прямоугольных импульсов используются специально разработанные микросхемы, например, NE555, NL494, КР1006ВИ1, IR2153, и микроконтроллеры: Arduino, AVR, SG2525A.

Для обеспечения надёжной работы управляемых устройств к  параметрам импульсного сигнала предъявляются жестокие требования по их стабильности. Это достигается применением кварцевого генератора и хорошей переходной характеристикой схемы формирования управляющих импульсов.

Видео

КОЭФФИЦИЕНТ ЗАПОЛНЕНИЯ — это… Что такое КОЭФФИЦИЕНТ ЗАПОЛНЕНИЯ?



КОЭФФИЦИЕНТ ЗАПОЛНЕНИЯ

— численность особей на пробе или на единице площади, обладающих каким-то заданным свойством.

Словарь ботанических терминов. — Киев: Наукова Думка. Под общей редакцией д.б.н. И.А. Дудки. 1984.

• КОЭФФИЦИЕНТ ЗАВЯДАНИЯ
• КОЭФФИЦИЕНТ ОБЩНОСТИ

Смотреть что такое «КОЭФФИЦИЕНТ ЗАПОЛНЕНИЯ» в других словарях:

• коэффициент заполнения — отношение длительности разноименных импульсов — [http://www.iks media.ru/glossary/index.html?glossid=2400324] Тематики электросвязь, основные понятия Синонимы отношение длительности разноименных импульсов EN mark space ratio …   Справочник технического переводчика

• коэффициент заполнения — 3.15 коэффициент заполнения (fill ratio), φ: Отношение объема источника шума под кожухом к внутреннему объему кожуха. Примечание Если форма источника шума затрудняет расчет его объема, то можно в качестве объема источника принять объем огибающего …   Словарь-справочник терминов нормативно-технической документации

• коэффициент заполнения — ГОСТ Р 54480 2011 коэффициент заполнения Отношение теоретического объема, заполненного металлом, определяемого исходя из массы и плотности, к действительному объему, полученному после сдавливания при определенной нагрузке набора (пакета) листов.… …   Металлургия. Терминология ГОСТ

• коэффициент заполнения — užpildos faktorius statusas T sritis fizika atitikmenys: angl. fill factor; filling factor vok. Füllfaktor, m; Füllungsgrad, m rus. коэффициент заполнения, m pranc. facteur de remplissage, m …   Fizikos terminų žodynas

• коэффициент заполнения — [coefficient of charge, lamination factor] 1. Показатель степени заполнения пресс формы порошком и его усадки при прессовании, выраженный отношением высоты засыпки шихты к высоте полученной прессовки. 2. Показатель степени заполнения калибра при… …   Энциклопедический словарь по металлургии

• коэффициент заполнения импульсного режима работы ЖРДМТ — коэффициент заполнения Отношение включения ЖРДМТ к циклу включения. Примечание Коэффициент заполнения равен также произведению частоты включения на включение. Обозначение: Kз [ГОСТ 17655 89] Тематики двигатели ракетные жидкостные Синонимы… …   Справочник технического переводчика

• коэффициент заполнения жилы — коэффициент заполнения Отношение площади поперечного сечения многопроволочной токопроводящей жилы к площади, ограниченной описанным около нее контуром. [ГОСТ 15845 80] Тематики кабели, провода … Синонимы коэффициент заполнения …   Справочник технического переводчика

• коэффициент заполнения изделия из волоконных световодов — коэффициент заполнения Отношение суммы площадей торцов сердцевин к площади торца изделия из волоконных световодов. [ГОСТ 25462 82] Тематики оптические линии связи Синонимы коэффициент заполнения …   Справочник технического переводчика

• коэффициент заполнения питателя роторного снегоочистителя — коэффициент заполнения питателя Отношение фактической объемной производительности снегоочистителя к пропускной способности питателя. [ГОСТ 15840 70] Тематики снегоочистители Обобщающие термины параметры снегоочистителей Синонимы коэффициент… …   Справочник технического переводчика

• коэффициент заполнения ротора снегоочистителя — коэффициент заполнения ротора Отношение фактической объемной производительности снегоочистителя к пропускной способности ротора. [ГОСТ 15840 70] Тематики снегоочистители Обобщающие термины параметры снегоочистителей Синонимы коэффициент… …   Справочник технического переводчика

Скважность Википедия

Сигнал с различным коэффициентом заполнения D

Сква́жность (в физике, электронике) — безразмерная величина, один из классификационных признаков импульсных систем, определяющий отношение периода следования (повторения) импульсов к длительности импульса. Часто используется величина, обратная скважности, которая называется коэффициент заполнения (англ. duty cycle).

Таким образом, для импульсного сигнала справедливы следующие соотношения:

S=Tτ=1D,{\displaystyle S={\frac {T}{\tau }}={\frac {1}{D}},}

D=τT=1S,{\displaystyle D={\frac {\tau }{T}}={\frac {1}{S}},}

где S{\displaystyle S} — скважность, D{\displaystyle D} — коэффициент заполнения, T{\displaystyle T} — период импульсов, τ{\displaystyle \tau } — длительность импульса.

T{\displaystyle T} — период импульсов, τ{\displaystyle \tau } — длительность импульса

Скважность и коэффициент заполнения — безразмерные величины, однако коэффициент заполнения часто указывают в процентах. Коэффициент заполнения в ряде применений более удобен, поскольку его относительное изменение происходит в интервале от 0 до 1, тогда как соответствующая скважность изменяется от бесконечности до 1.

Понятие скважности используется, например, в радиолокации, где эта величина определяет отношение пиковой мощности импульсной установки (например, передатчика радиолокационной станции) к её средней мощности и является важным показателем работы импульсных систем.

Известный в радиотехнике сигнал меандр имеет скважность 2 (коэффициент заполнения 0,5). Скважность импульсов в радиолокационных станциях может достигать тысяч.

См. также[ | ]

Ссылки[ | ]