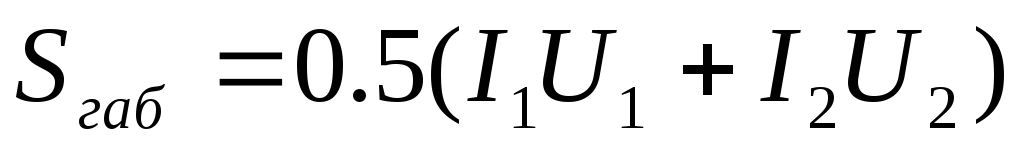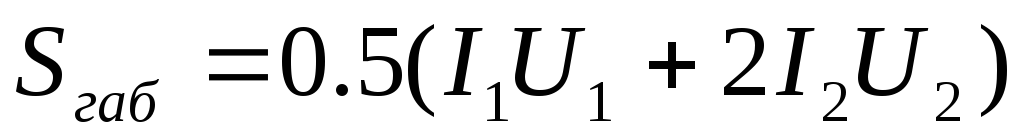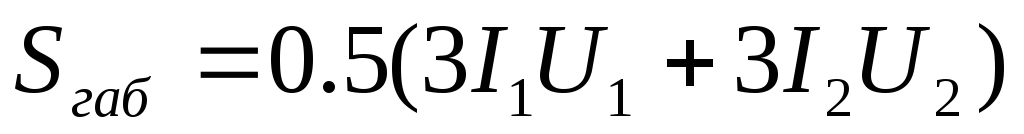Коэффициент пульсации выпрямителя
Выпрямители обладают на выходе абсолютно различными коэффициентами пульсаций. Чем выше чувствительность подключаемого к выпрямителю устройства, тем пульсации должны быть ниже, а коэффициент пульсаций меньше.
Существует несколько схем выпрямителей:
• однополупериодные;
• двухполупериодные, выполненные по схеме со средней точкой;
• двухполупериодные мостовые;
• трехфазные.
Кроме применяемой схемы, на пульсации выходного напряжения большое влияние оказывает рабочая частота выпрямителя. Чем она выше, тем меньше в конечном результате будут пульсации.
Свойства различных схем выпрямителей
Самые большие пульсации наблюдаются на выходе однополупериодного выпрямителя, работающего на частоте промышленной сети – 50 Гц. Эта схема начисто срезает каждую вторую полуволну из периода, поскольку для ее осуществления используется только один диод.
Однако однополупериодное выпрямление сигнала получило большое распространение в импульсных выпрямителях напряжения, так как для получения необходимого уровня напряжения там используется сигнал высокой (до 200-300 кГц) частоты. Поскольку на выходе выпрямителя традиционно установлен конденсатор очень большой емкости, а время между периодами минимально, пульсации также не выходят за допустимый техническими условиями предел.
Двухфазные – мостовая и со средней точкой – схемы с точки зрения пульсаций имеют совершенно одинаковые значения. В таких выпрямителях используются обе полуволны периода. Как только напряжение одной полуволны доходит до нуля, в следующий момент начинается его подъем благодаря нарастанию второй полуволны.
Трехфазная сеть состоит из трех сдвинутых относительно друг друга на 120º фаз. Благодаря этому, даже в случае выпрямления только одним полупериодом, на выходе такого выпрямителя просто нет момента, при котором напряжение равно нулю. Что же касается двухполупериодного выпрямления такого тока, то даже без применения каких-либо дополнительных мер пульсации имеют довольно невысокий уровень.
Специальная оценка условий труда
Дополнительные элементы, позволяющие снизить пульсации
Самым простым способом, позволяющим значительно уменьшить коэффициент пульсаций выпрямителя, является установка конденсатора параллельно его выходу. При нарастании напряжения часть тока идет в нагрузку, а другая заряжает конденсатор. За счет частичного разряда конденсатора, отдающего энергию в нагрузку, во время спада полуволны напряжение на выходе выпрямителя не успевает дойти до нуля (или нижнего значения в случае использования трехфазного выпрямителя), за счет чего пульсации значительно уменьшаются.
Существует еще несколько способов уменьшения коэффициента пульсаций выпрямителя. Они применяются каждый для своих конкретных случаев и позволяют достичь очень неплохих результатов.
Основные характеристики выпрямителей:
29
Основными характеристиками выпрямителей являются:
Номинальное напряжение постоянного тока
Номинальный выпрямленный ток I0– среднее значение выпрямленного тока, т.е. его постоянная составляющая, заданная техническими требованиями. Определяется результирующим током всех цепей питаемых выпрямителем.
Напряжение сети Uсети– напряжение сети переменного тока, питающей выпрямитель. Стандартное значение этого напряжения для бытовой сети –220 вольт с допускаемыми отклонениями не более 10 %.
Пульсация
Частота пульсаций– частота наиболее резко выраженной гармонической составляющей напряжения или тока на выходе выпрямителя. Для самой простой однополупериодной схемы выпрямителя частота пульсаций равна частоте питающей сети. Двухполупериодные, мостовые схемы дают пульсации, частота которых равна удвоенной частоте питающей сети. Многофазные схемы выпрямления имеют частоту пульсаций, зависящую от схемы выпрямителя и числа фаз.
Коэффициент пульсаций– отношение амплитуды наиболее резко выраженной гармонической составляющей напряжения или тока на выходе выпрямителя к среднему значению напряжения или тока. Различают
Коэффициент фильтрации (коэффициент сглаживания)– отношение коэффициента пульсаций на входе фильтра к коэффициенту пульсаций на выходе фильтра k с = p0 / p. Для многозвенных фильтров коэффициент фильтрации равен произведению коэффициентов фильтрации отдельных звеньев.
Колебания (нестабильность) напряженияна выходе выпрямителя –изменение напряжения постоянного тока относительно номинального. При отсутствии стабилизаторов напряжения определяются отклонениями напряжения сети.
Схемы выпрямителей.
Чаще всего используются трехфазные схемы выпрямителей. Основные показатели, характеризующие схемы выпрямителей могут быть разбиты на 3 группы:
Относящиеся ко всему выпрямителю в целом: U0 -напряжение постоянного тока до фильтра, I0 – среднее значение выпрямленного тока, p0 – коэффициент пульсаций на входе фильтра.
Определяющие выбор выпрямительного элемента (вентиля): Uобр – обратное напряжение (напряжение на выпрямительном элементе (вентиле) в непроводящую часть периода), Iмакс – максимальный ток проходящий через выпрямительный элемент (вентиль) в проводящую часть периода.
Определяющие выбор трансформатора: U2 – действующее значение напряжения на вторичной обмотке трансформатора, I2 – действующее значение тока во вторичной обмотке трансформатора, Pтр – расчетная мощность трансформатора.
Глава 2. Методики анализа и расчета выпрямителей
2.1. Анализ работы выпрямителя гармонического напряжения при нагрузке, начинающейся с емкостного элемента
Проведем анализ работы выпрямителя гармонического напряжения с нагрузкой, начинающейся с емкостного элемента, и рассмотрим процессы в многофазных схемах выпрямителей (рис. 2.1, а). Возьмем в качестве вентиля идеализированный диод с потерями, а в трансформаторе учтем только сопротивления обмоток. Примем за
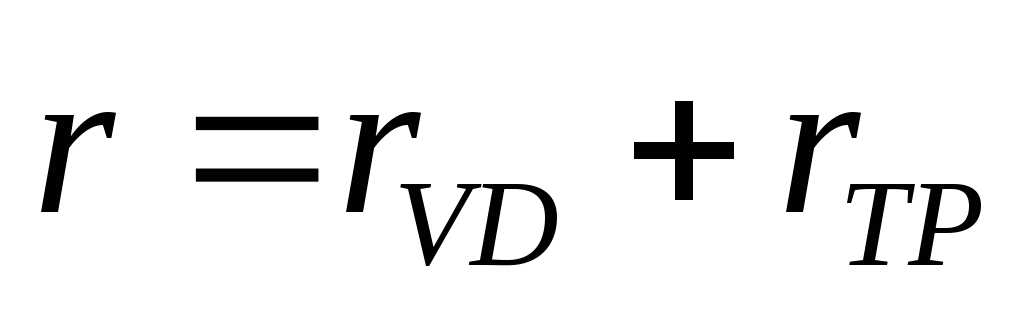 (2.1)
(2.1)
Рассмотрение
начнем с момента 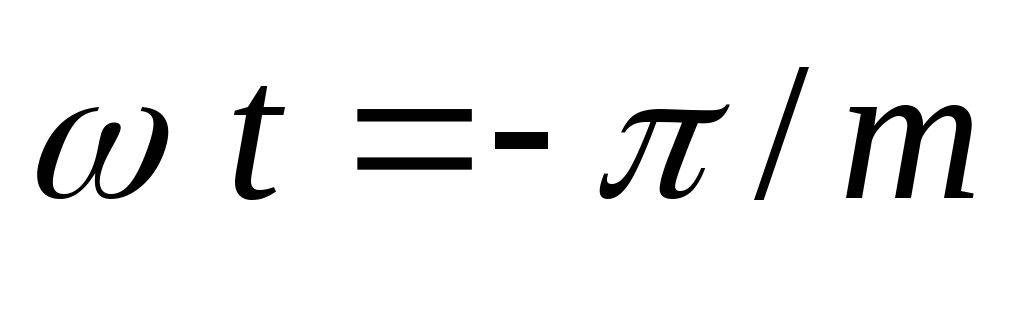 .
В этот момент (рис. 2.1, в) напряжение на
конденсаторе больше ЭДС любой из фаз и
все вентили закрыты. Разряжаясь,
конденсатор создает на нагрузке
экспоненциально спадающее напряжение.
При
.
В этот момент (рис. 2.1, в) напряжение на
конденсаторе больше ЭДС любой из фаз и
все вентили закрыты. Разряжаясь,
конденсатор создает на нагрузке
экспоненциально спадающее напряжение.
При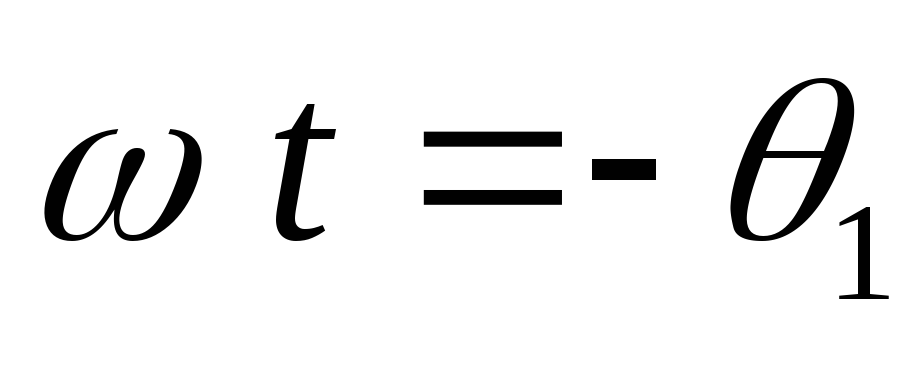
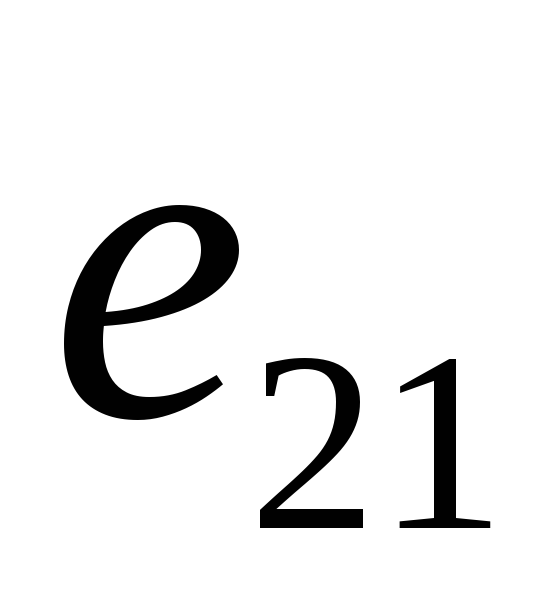 ,
вентиль этой фазы откроется и начнет
пропускать ток. Ток вентиля частично
идет на подзарядку конденсатора, а
частично в нагрузку.
,
вентиль этой фазы откроется и начнет
пропускать ток. Ток вентиля частично
идет на подзарядку конденсатора, а
частично в нагрузку. При зарядке
конденсатора напряжение на нем растет
и при угле 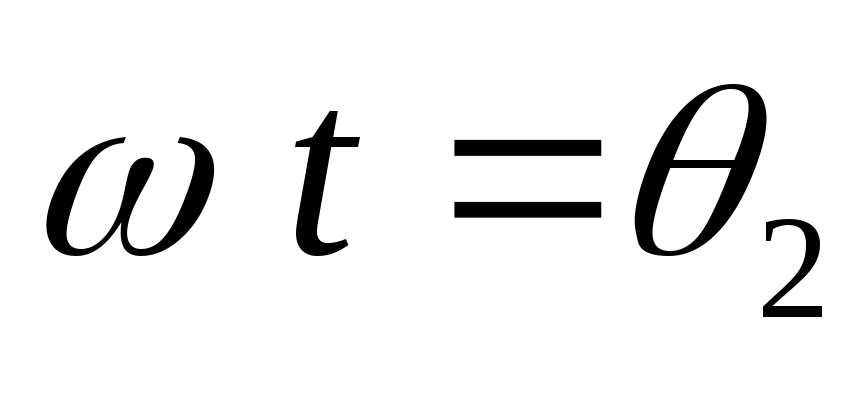 сравнивается с уменьшающейся ЭДС первой
фазы. Вентиль закрывается и начинается
разрядка конденсатора на нагрузку,
которая продолжается до угла
сравнивается с уменьшающейся ЭДС первой
фазы. Вентиль закрывается и начинается
разрядка конденсатора на нагрузку,
которая продолжается до угла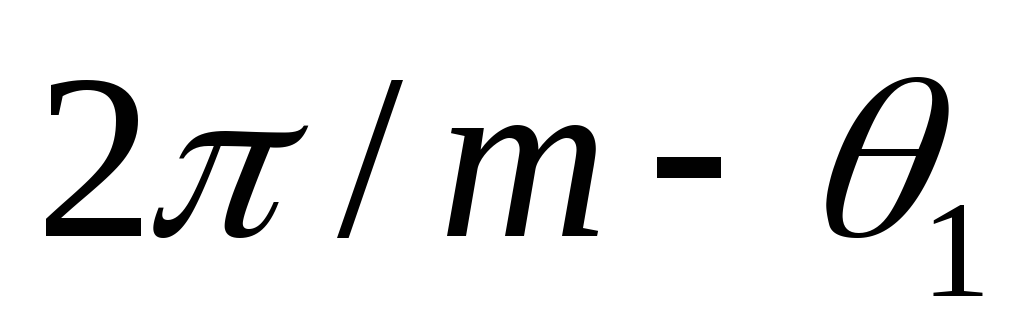
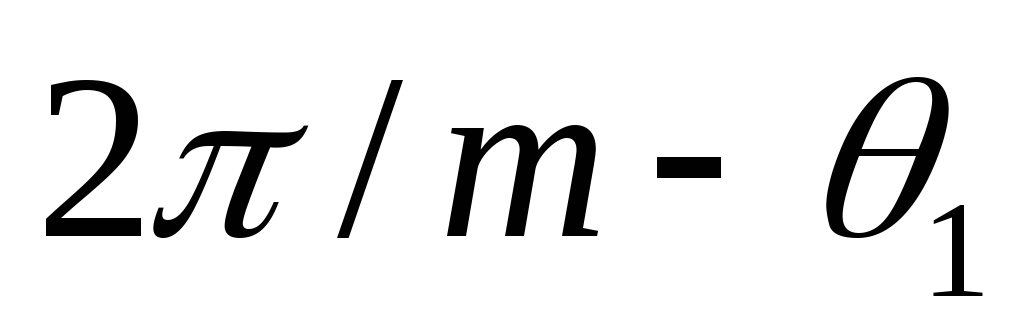 открывается вентиль второй фазы,
конденсатор вновь подзаряжается и т.д.
За один период выпрямляемого напряжения
поочередно срабатывают вентили всех
фаз.
открывается вентиль второй фазы,
конденсатор вновь подзаряжается и т.д.
За один период выпрямляемого напряжения
поочередно срабатывают вентили всех
фаз.Определим ток вентиля, исходя из эквивалентной схемы открытой фазы (рис. 2.1, б). В данной схеме разность ЭДС фазы и выпрямленного напряжения получается из-за падения напряжения на сопротивлении r и, следовательно,
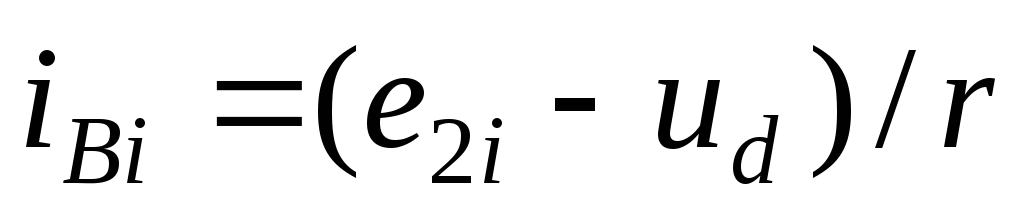
Таким образом, по
форме ток вентиля совпадает с напряжением 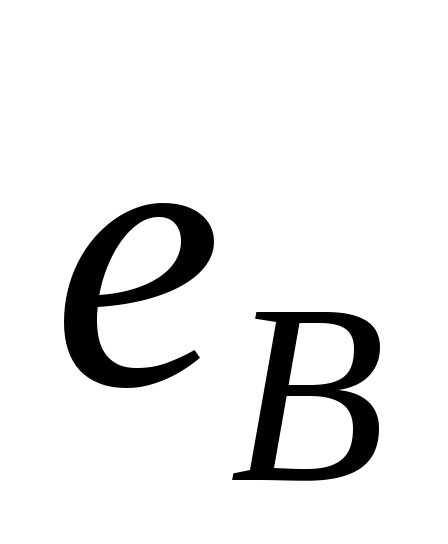 ,
равным разности ЭДС фазы и выпрямленного
напряжения (рис. 2.1, в, г).
,
равным разности ЭДС фазы и выпрямленного
напряжения (рис. 2.1, в, г).
Импульс тока
вентиля второй фазы совпадает по значению
и форме с импульсом тока первой фазы,
но запаздывает на угол 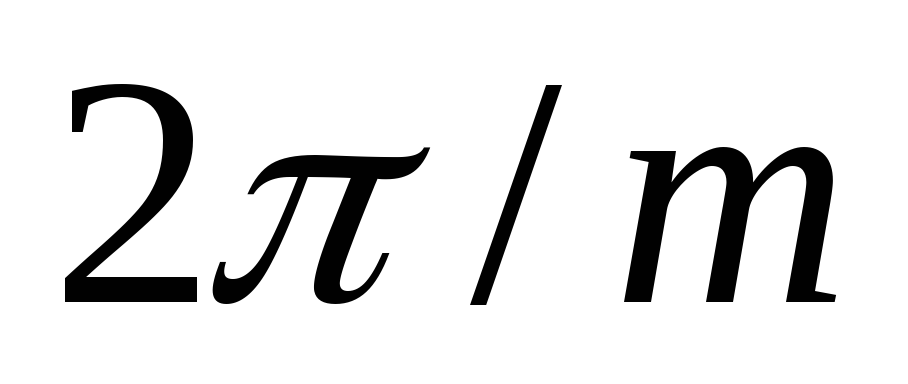 (рис. 2.1, д). Общий выпрямленный ток
(рис. 2.1, д). Общий выпрямленный ток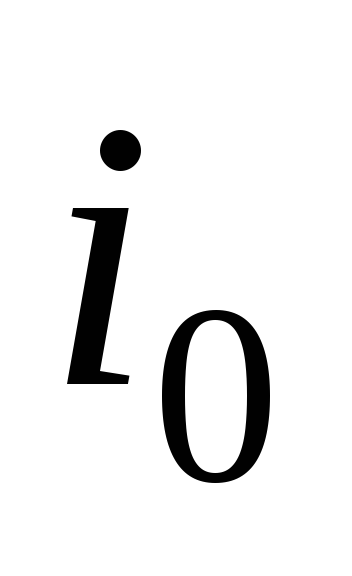 представляет собой сумму токов всех
вентилей, подходя к точке
представляет собой сумму токов всех
вентилей, подходя к точке
 течет через нагрузку, а часть
течет через нагрузку, а часть – через конденсатор. Ток
– через конденсатор. Ток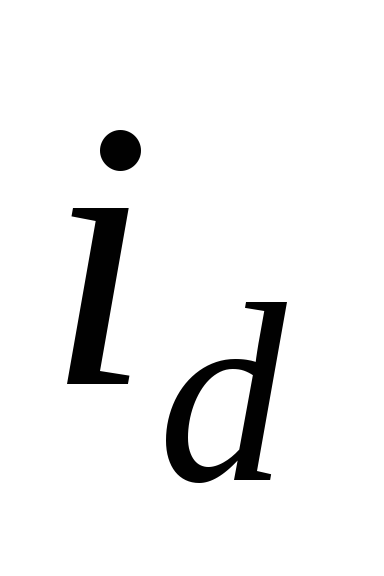 ,
проходящий в нагрузке, повторяет по
форме выпрямленное напряжение (рис.
2.1, ж). Ток, проходящий через конденсатор,
можно найти, вычтя ток нагрузки из общего
выпрямленного тока (рис. 2.1, з).
,
проходящий в нагрузке, повторяет по
форме выпрямленное напряжение (рис.
2.1, ж). Ток, проходящий через конденсатор,
можно найти, вычтя ток нагрузки из общего
выпрямленного тока (рис. 2.1, з).
Рис. 2.1. Схемы (а, б) и диаграммы электромагнитных процессов выпрямителя гармонического напряжения с емкостным фильтром (в — и).
Напряжение на
вентиле первой фазы  меняется по сложному закону, близкому
к косинусоидальному (рис. 2.1, и), оно
положительно лишь в небольшой части
периода
меняется по сложному закону, близкому
к косинусоидальному (рис. 2.1, и), оно
положительно лишь в небольшой части
периода .
Отрицательное обратное напряжение
достигает максимума при
.
Отрицательное обратное напряжение
достигает максимума при :
:
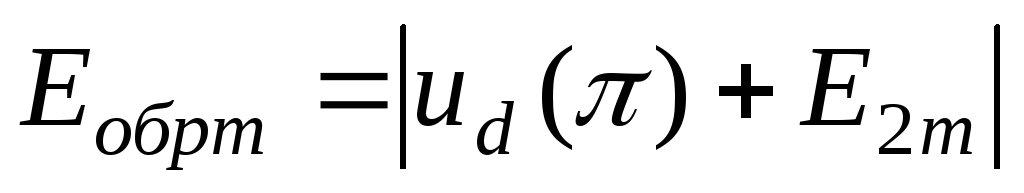 ,
(2.3)
,
(2.3)
что значительно больше выпрямленного напряжения.
Увеличение
сопротивления нагрузки 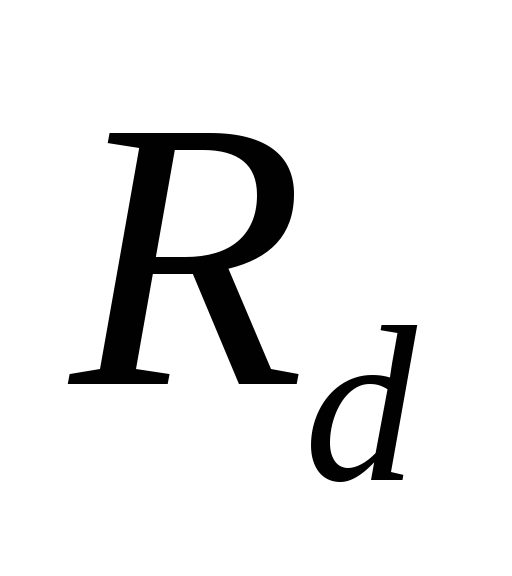 приводит к уменьшению тока нагрузки
приводит к уменьшению тока нагрузки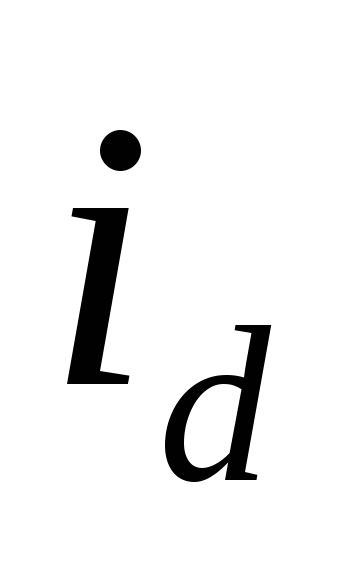 и замедлению разрядки конденсатора.
Поэтому ЭДС первой фазы становится
равным выпрямленному напряжению
несколько позже, т.е. угол
и замедлению разрядки конденсатора.
Поэтому ЭДС первой фазы становится
равным выпрямленному напряжению
несколько позже, т.е. угол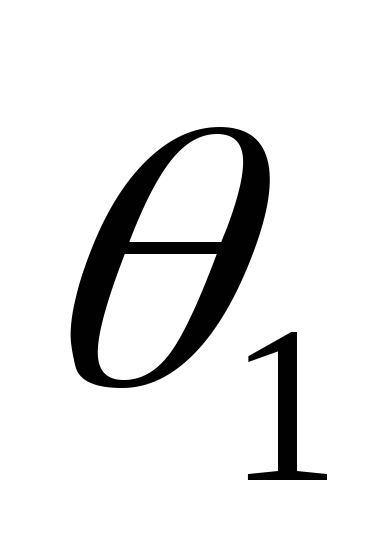 по абсолютному значению уменьшается
(рис. 2.2, а). При зарядке конденсатора
через большое сопротивление нагрузки
ответвляется меньшая часть тока вентиля.
Следовательно, конденсатор зарядится
быстрее, что вызовет уменьшение угла
по абсолютному значению уменьшается
(рис. 2.2, а). При зарядке конденсатора
через большое сопротивление нагрузки
ответвляется меньшая часть тока вентиля.
Следовательно, конденсатор зарядится
быстрее, что вызовет уменьшение угла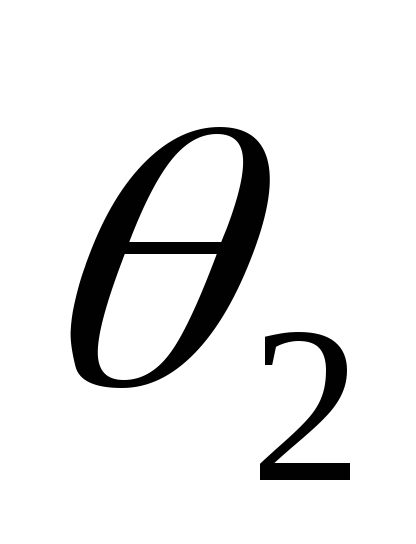 .
Таким образом, уменьшение тока нагрузки
приводит к уменьшению углов отсечки
тока (рис. 2.2, б), увеличению значения
выпрямленного напряжения от
.
Таким образом, уменьшение тока нагрузки
приводит к уменьшению углов отсечки
тока (рис. 2.2, б), увеличению значения
выпрямленного напряжения от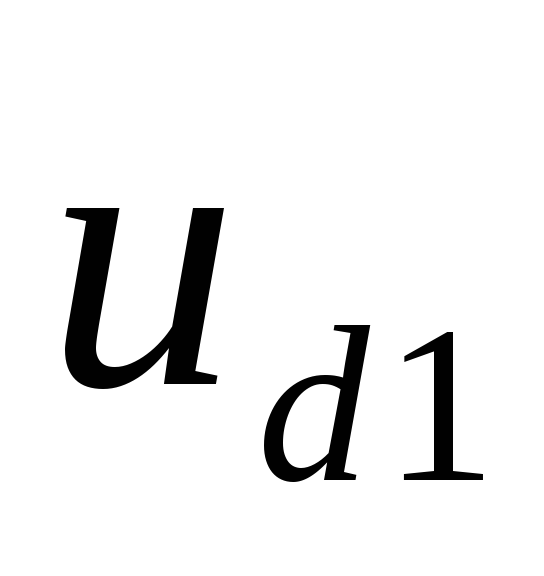 до
до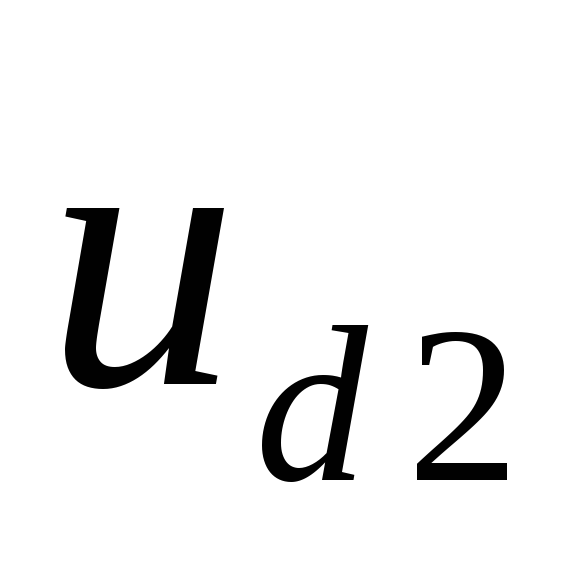 и сокращению его пульсаций. При токе
нагрузке, равном нулю, конденсатор не
разряжается и на нем создается постоянное
напряжение
и сокращению его пульсаций. При токе
нагрузке, равном нулю, конденсатор не
разряжается и на нем создается постоянное
напряжение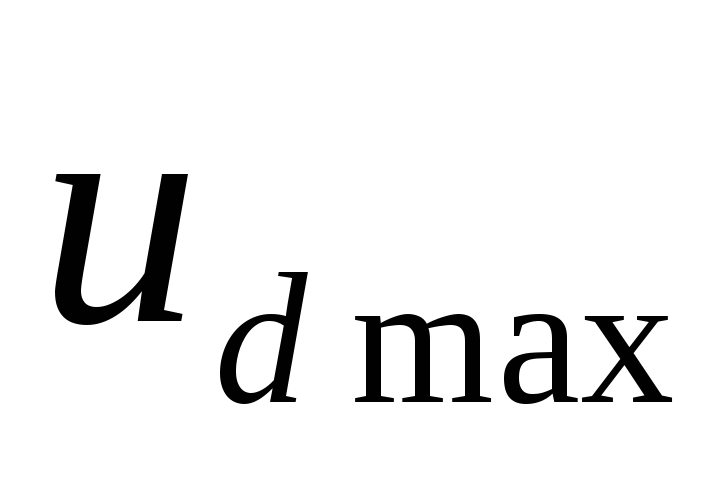 ,
равное амплитуде ЭДС
,
равное амплитуде ЭДС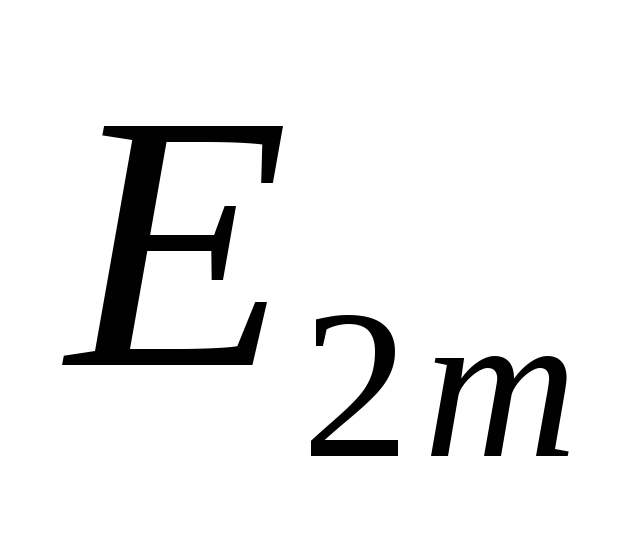 .
Амплитуда обратного напряжения на
вентиль получается при этом максимальной:
.
Амплитуда обратного напряжения на
вентиль получается при этом максимальной:
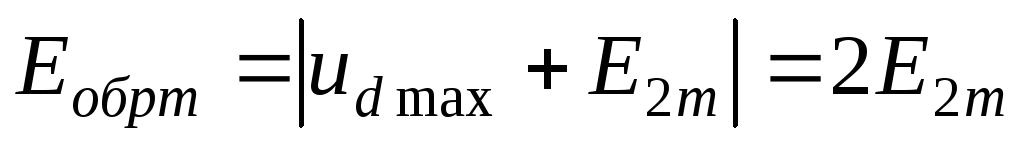 (2.4)
(2.4)
Из рассмотренного можно сделать вывод, что внешняя характеристика выпрямителя, работающего на нагрузку, начинающуюся с емкостного элемента, есть ниспадающая кривая (рис. 2.2, в), а угол отсечки зависит от тока нагрузки.
Емкость конденсатора
сказывается не только на пульсациях
выпрямленного напряжения, но и на форме
импульса тока вентиля. При очень большой
емкости конденсатора выходное напряжение
почти постоянно и импульс тока симметричен,
т.к. углы отсечки  и
и равны. При уменьшении емкости импульс
немного искажается по форме и сдвигается
в сторону опережения. Угол отсечки
равны. При уменьшении емкости импульс
немного искажается по форме и сдвигается
в сторону опережения. Угол отсечки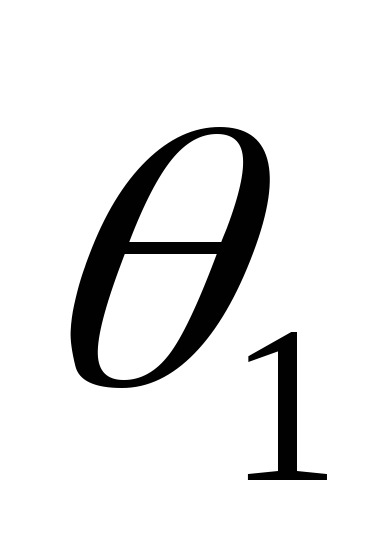 становится больше угла
становится больше угла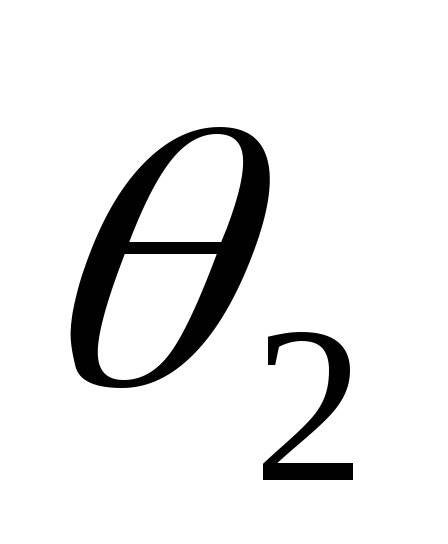 .
.
В итоге необходимо отметить следующее [6]:
1) при нагрузке, начинающейся с конденсатора, выпрямитель работает с отсечкой тока. Импульсы тока вентилей имеют длительность, меньшую T/m;
2) выпрямленное напряжение и ток нагрузки имеют пилообразную форму;
3) чем больше ток нагрузки, тем больше угол отсечки тока и тем меньше выпрямленное напряжение;
4) емкость конденсатора определяет как напряжение пульсаций, так и отклонение от косинусоидальной формы импульса тока.
С уменьшением сопротивления фазы r зарядный ток возрастает и напряжение на выходном конденсаторе нарастает круче, чем это показано на рис. 2.1, в.
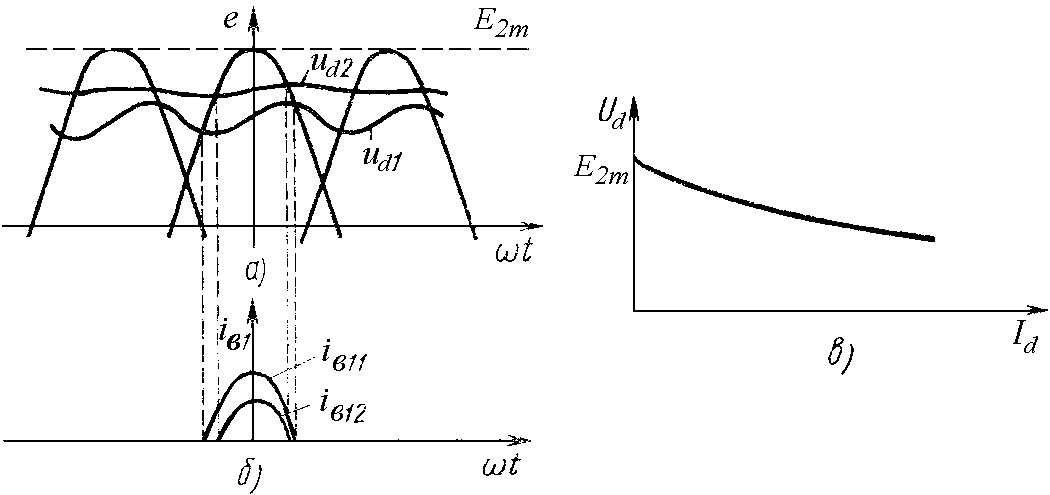
Рис.
2.2. Диаграммы электромагнитных процессов
(а, б) для нагрузок 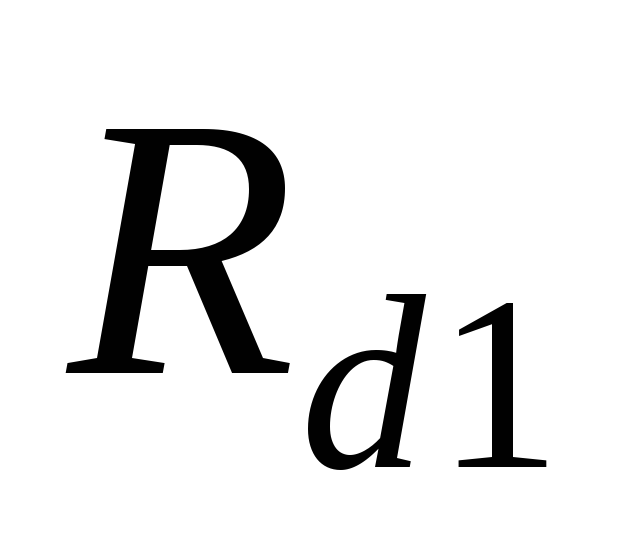 и
и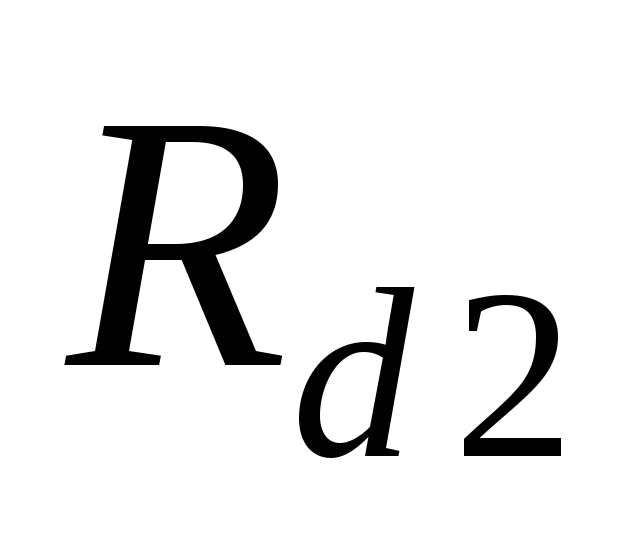 (
( )
и внешняя характеристика выпрямителя
(в).
)
и внешняя характеристика выпрямителя
(в).
В бестрансформаторных выпрямителях сопротивление вентилей и проводов, подводящих энергию к выпрямителю, настолько мало, что напряжение на конденсаторе при его зарядке следует за ЭДС работающей фазы (рис. 2.3, а). При этом ток вентиля:
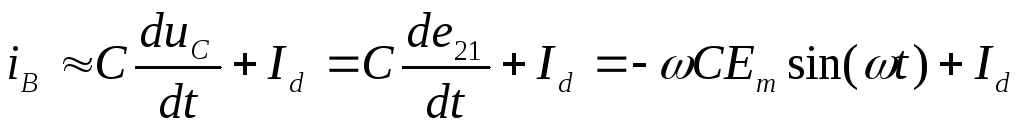 ,
(2.5)
,
(2.5)
где 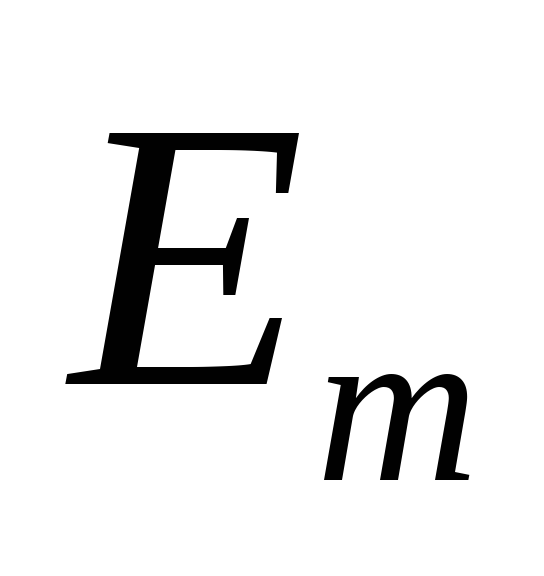 — амплитуда фазного напряжения сети,
— амплитуда фазного напряжения сети,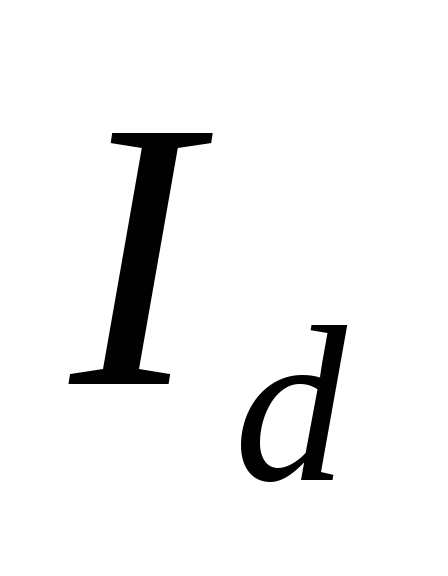 — ток нагрузки, принятый постоянным.
— ток нагрузки, принятый постоянным.
По сравнению со
случаем, когда зарядный ток ограничивался
сопротивлением зарядной цепи, импульс
тока (рис. 2.3, б) становится асимметричным.
Выходной конденсатор выпрямителя
заряжается до напряжения 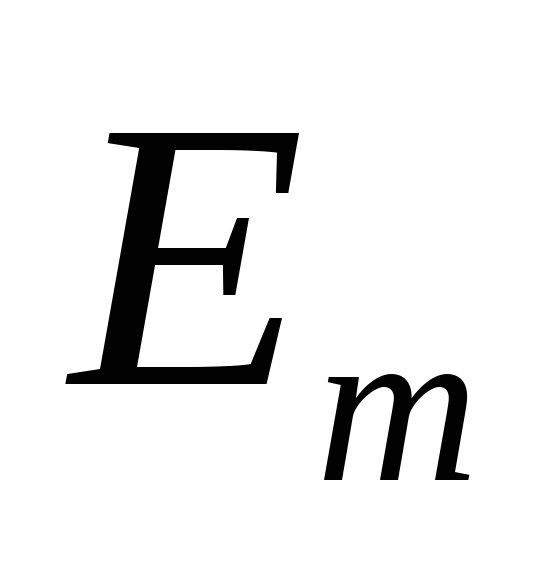 от каждой из фаз сети. Зарядка конденсатора
током вентиля продолжается до угла
от каждой из фаз сети. Зарядка конденсатора
током вентиля продолжается до угла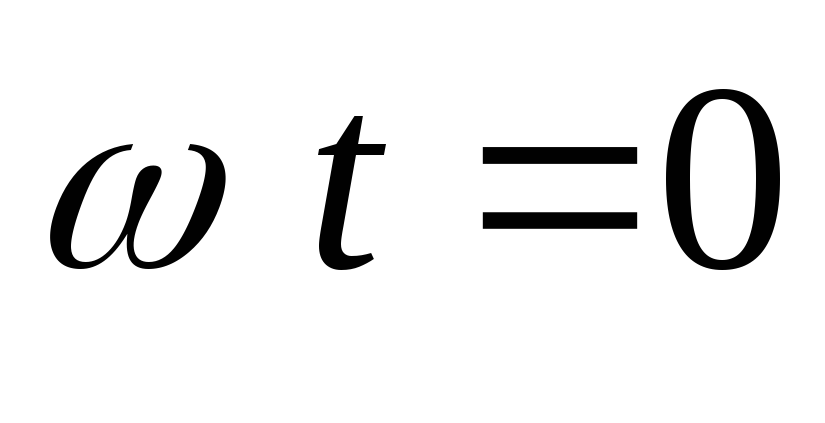 (первая фаза). При
(первая фаза). При >
0 ток вентиля становится меньше тока
нагрузки и при
>
0 ток вентиля становится меньше тока
нагрузки и при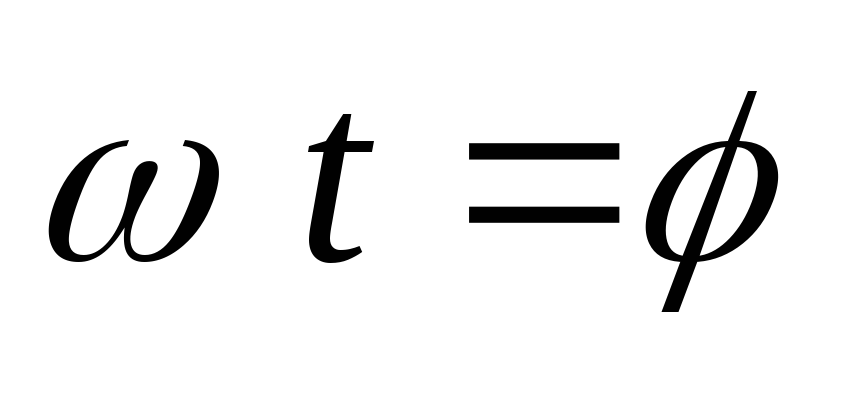 достигает нуля, вентиль закрывается.
Положив в (2.5)
достигает нуля, вентиль закрывается.
Положив в (2.5)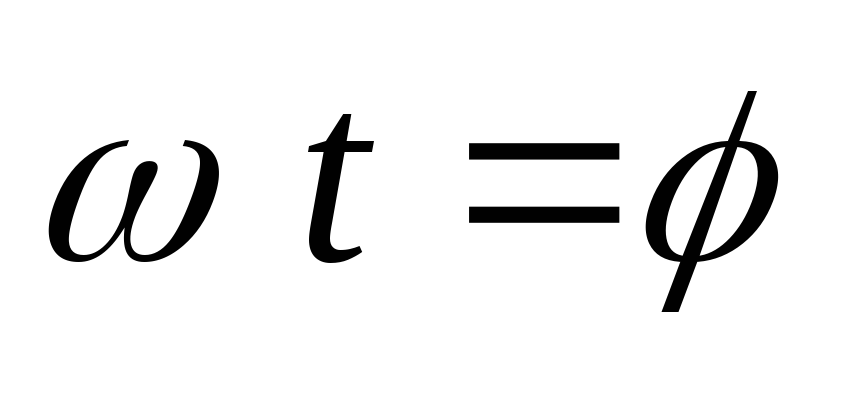 ,
получим выражение для определения угла
выключения вентилей
,
получим выражение для определения угла
выключения вентилей :
:
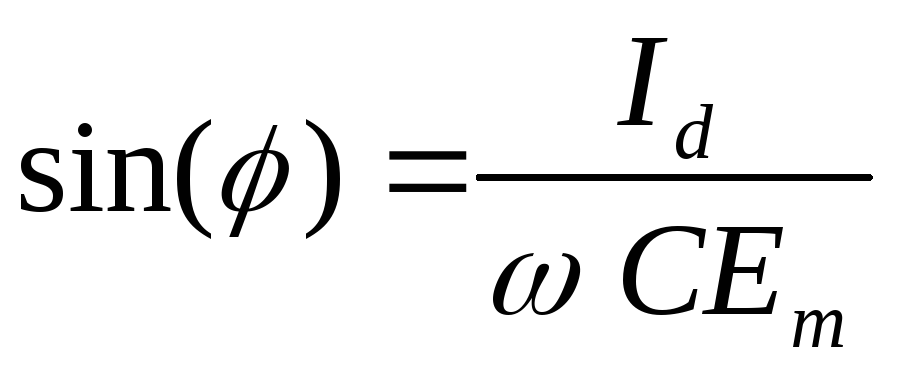 (2.6)
(2.6)
При 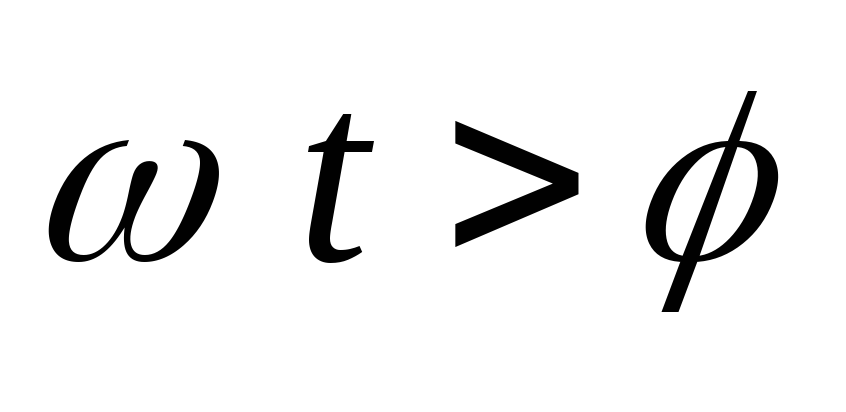 напряжение на конденсаторе спадает
линейно, т.к. ток нагрузки считается
постоянным. Когдаωt достигает значения
напряжение на конденсаторе спадает
линейно, т.к. ток нагрузки считается
постоянным. Когдаωt достигает значения 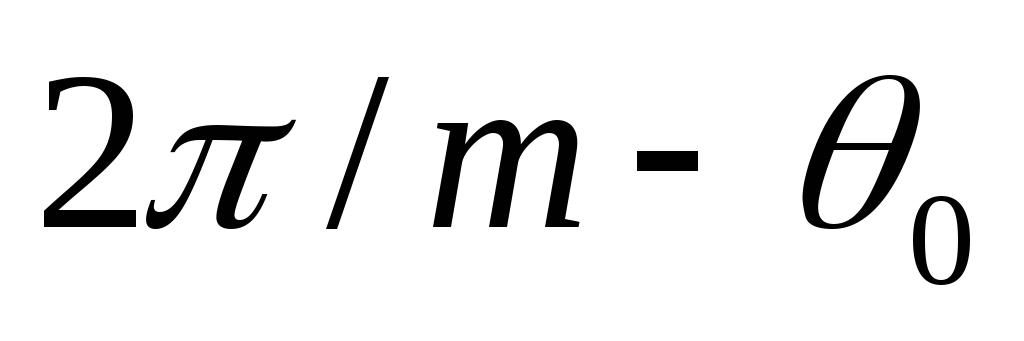 ,
спадающее напряжение на конденсаторе
сравнивается с возрастающей ЭДС второй
фазы
,
спадающее напряжение на конденсаторе
сравнивается с возрастающей ЭДС второй
фазы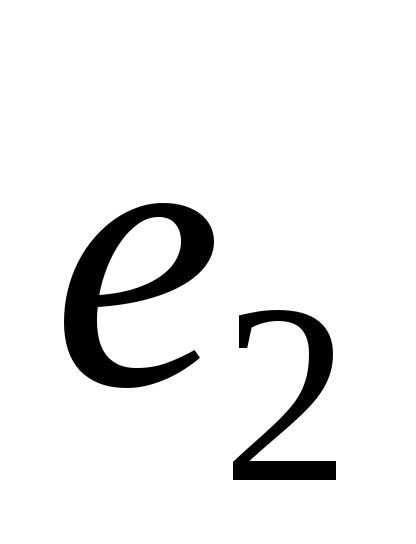 ,
после чего начинается подзарядка
конденсатора током второй фазы. Таким
образом, минимальное напряжение на
выходном конденсаторе оказывается
равным
,
после чего начинается подзарядка
конденсатора током второй фазы. Таким
образом, минимальное напряжение на
выходном конденсаторе оказывается
равным
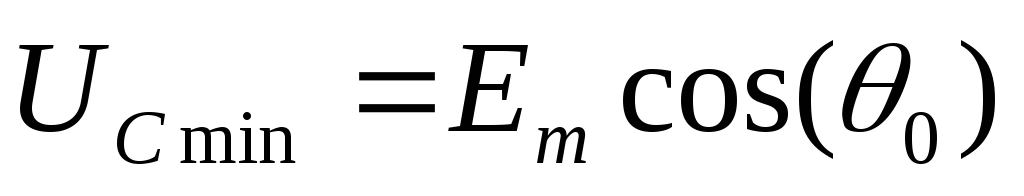 (2.7)
(2.7)
Углы  и
и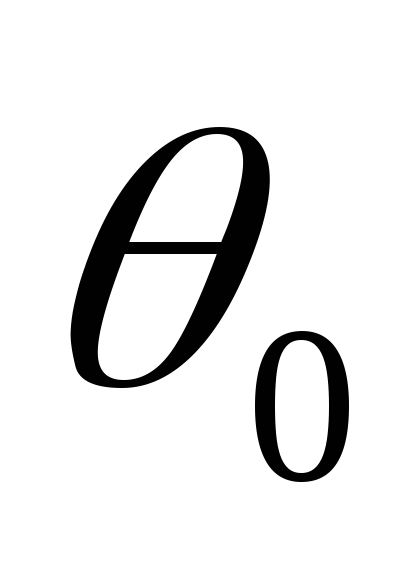 связаны нелинейной зависимостью (рис.
2.3, в).
связаны нелинейной зависимостью (рис.
2.3, в).
Рис.
2.3. Диаграммы электромагнитных процессов
в бестрансформаторном выпрямителе (а,
б) и зависимость углов  и
и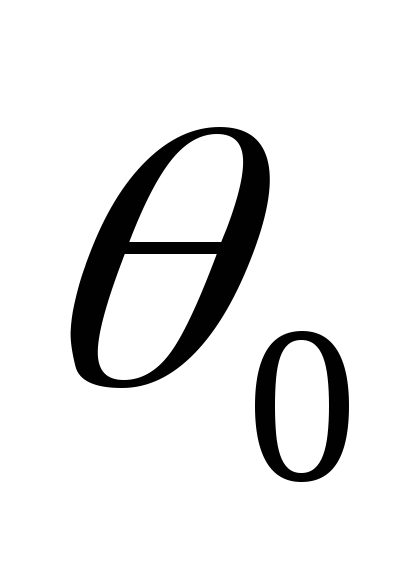 (в).
(в).
Среднее значение выпрямленного напряжения мало отличается от:
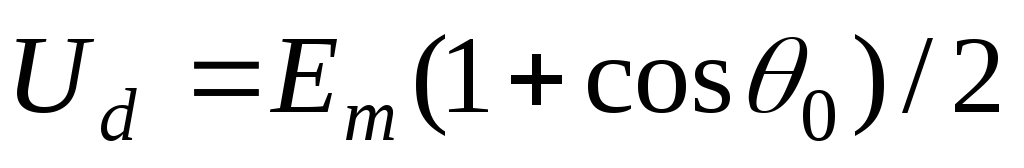 ,
(2.8)
,
(2.8)
которое
получилось бы при линейном нарастании 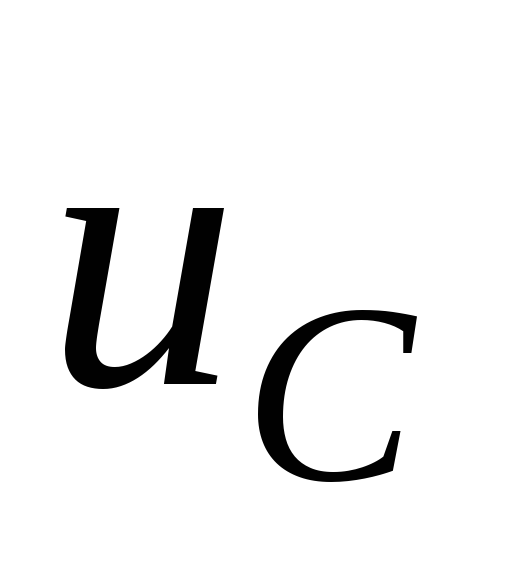 при зарядке конденсатора.
при зарядке конденсатора.
Важно отметить
заметную зависимость выходного напряжения
выпрямителя от емкости выходного
конденсатора. При увеличении емкости С спадание напряжения из-за разрядки
конденсатора замедляется и угол
открывания вентиля 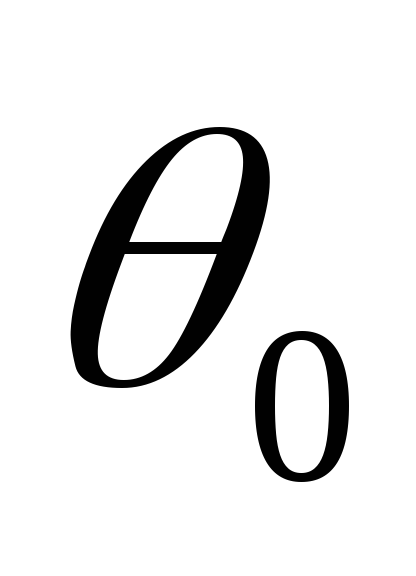 становится меньше.
становится меньше.
Таким образом, при расчете выпрямителя пользуются двумя расчетными моделями [6]. Первую расчетную модель применяют при расчетах трансформаторных выпрямителей, когда ток зарядки выходного конденсатора ограничивается активным и индуктивным сопротивлением фазы трансформатора, а также сопротивлением вентиля.
Вторая модель хорошо отражает процессы в бестрансформаторном выпрямителе. В нее закладываются малые активное и индуктивное сопротивление фазы сети и малое падение напряжения на вентилях.
Поскольку характер
выпрямителей определяется не только
сопротивлением зарядной цепи, а и
емкостью выходного конденсатора, т.е.
постоянной времени заряда, применимость
первой или второй моделей зависит от
соотношения сопротивлений фаз r и 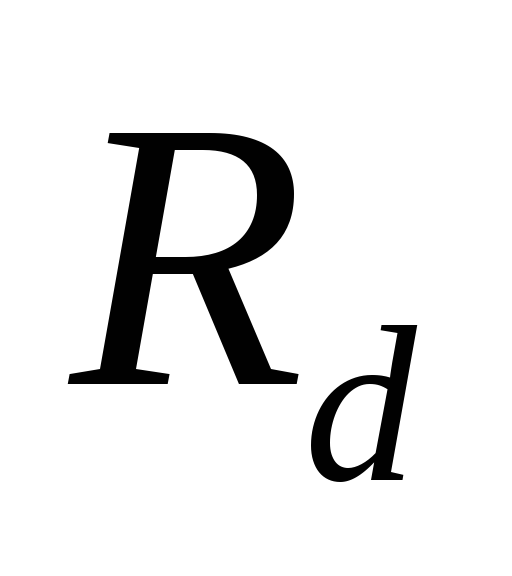 и емкости выходного конденсатораС [6].
и емкости выходного конденсатораС [6].
Пояснить методику
получения расчетных формул для первой
модели проще всего при анализе схемы
выпрямителя, приведенной на рис. 2.1, б,
где ток зарядки конденсатора ограничивается
сопротивлением r.
Так как выпрямитель всегда характеризуется
относительно небольшим напряжением
пульсаций (его значение ограничивают
допустимой реактивной мощностью
выходного конденсатора фильтра на
уровне 5-10% от 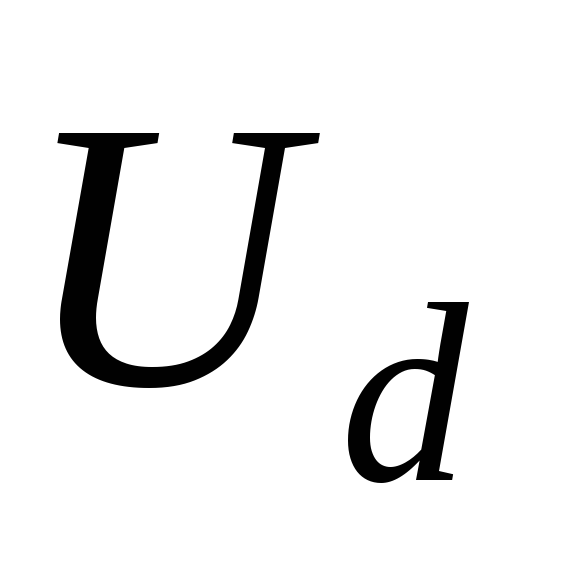 ),
то можно принять без больших погрешностей
[6] выходное выпрямленное напряжение
постоянным, каким оно становится при
бесконечно большой емкости конденсатораС.
При этом углы отсечки
),
то можно принять без больших погрешностей
[6] выходное выпрямленное напряжение
постоянным, каким оно становится при
бесконечно большой емкости конденсатораС.
При этом углы отсечки 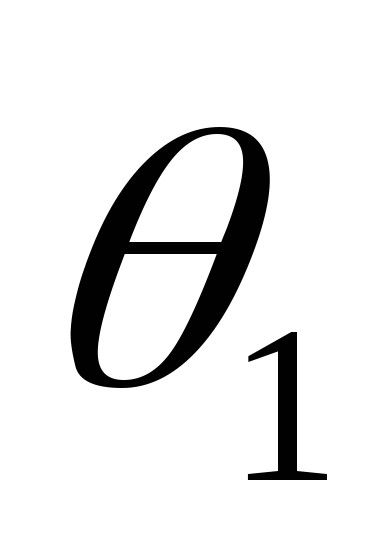 и
и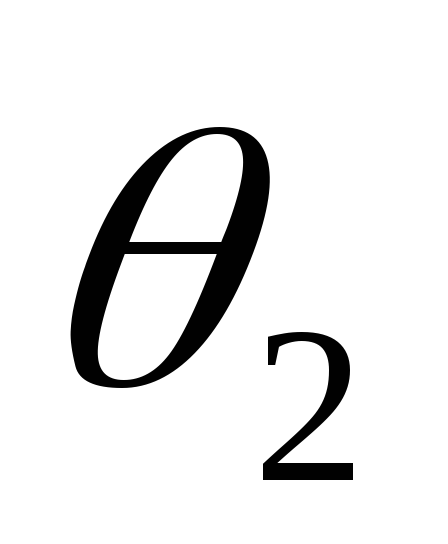 становятся равными и импульс тока
вентиля приобретает косинусоидальную
форму:
становятся равными и импульс тока
вентиля приобретает косинусоидальную
форму:
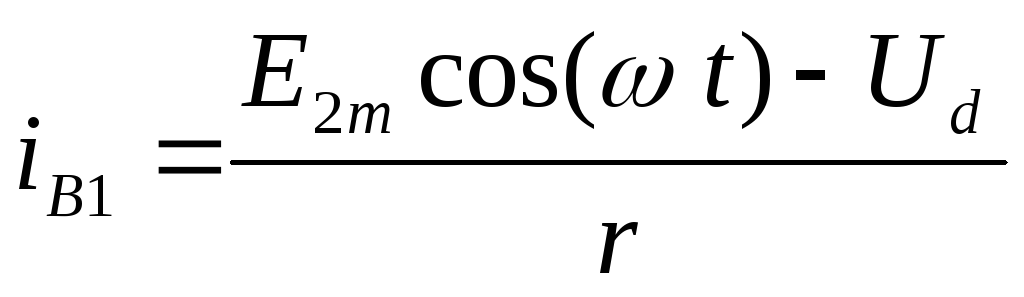 (2.9)
(2.9)
при 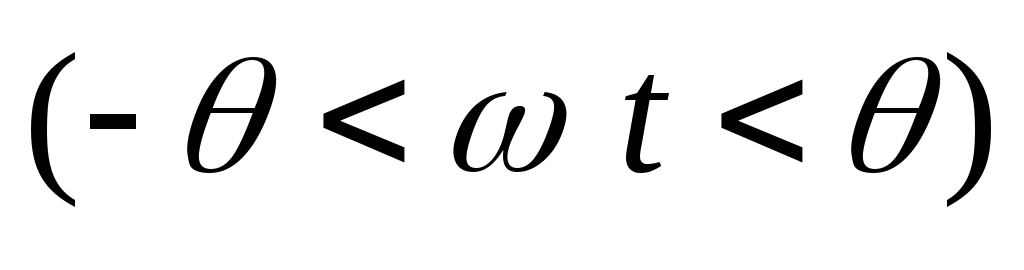 и
и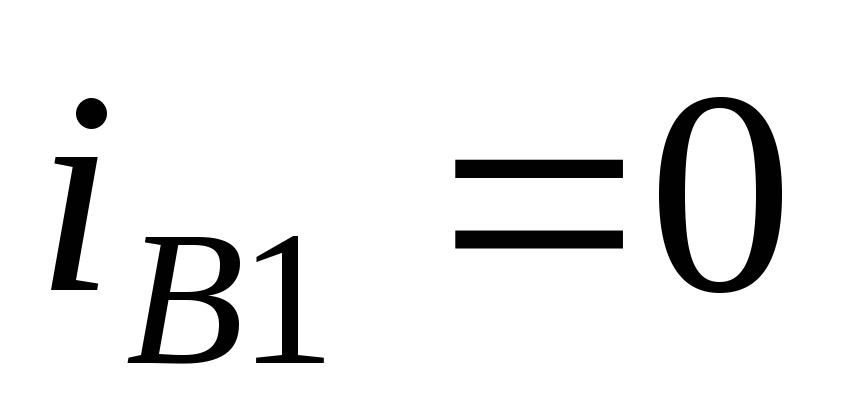 на остальной части периода.
на остальной части периода.
Постоянный ток в нагрузке выпрямителя равен сумме постоянных составляющих токов всех вентилей:
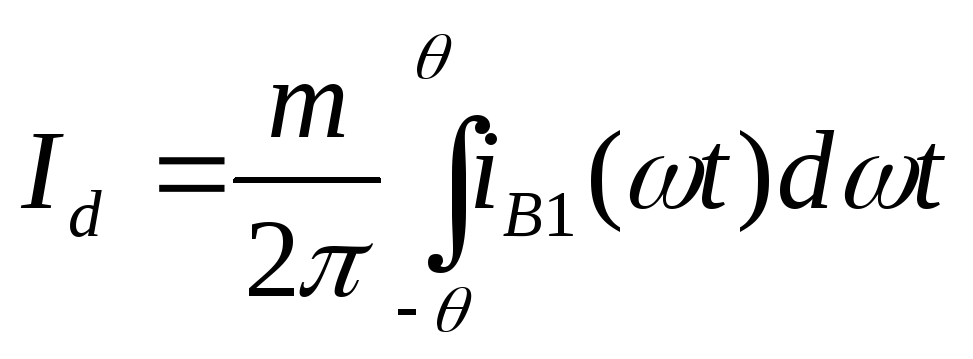 (2.10)
(2.10)
При углах 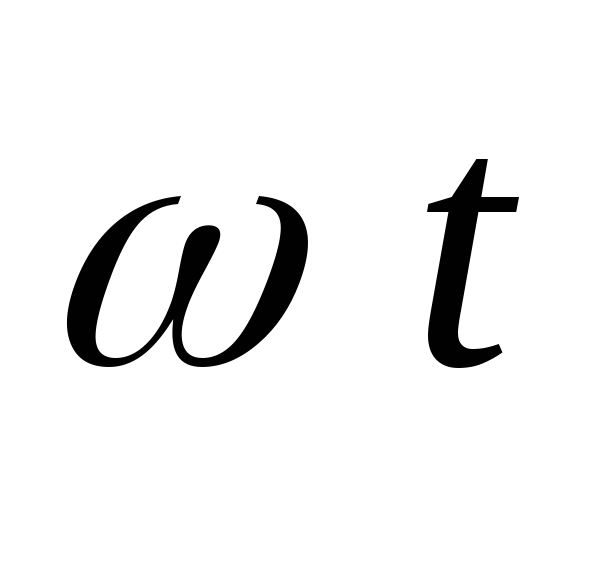 ,
равных
,
равных и,
выпрямляемое переменное напряжение
и,
выпрямляемое переменное напряжение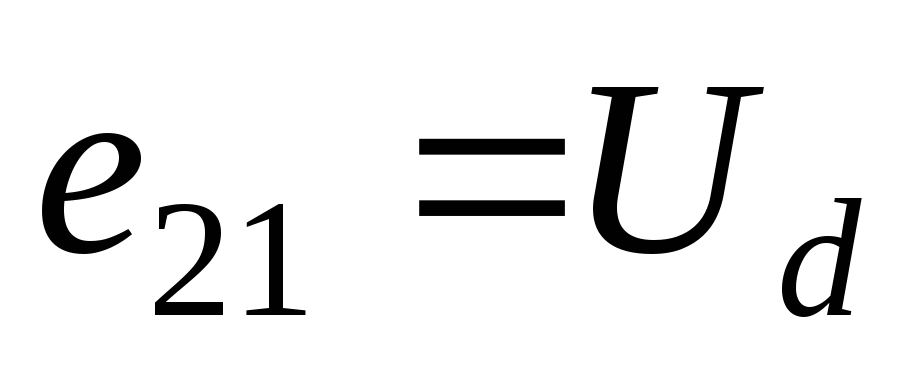 ,
что позволяет записать:
,
что позволяет записать:
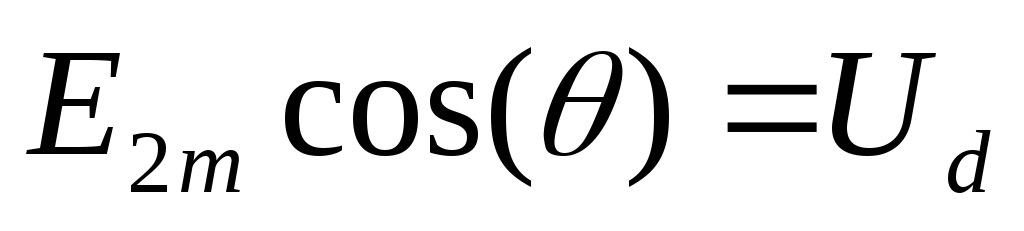 (2.11)
(2.11)
Следует отметить,
что в схеме Ларионова используется не
фазное напряжение, а линейное, поэтому
амплитудное напряжение фазы на вторичной
обмотке трансформатора будет в 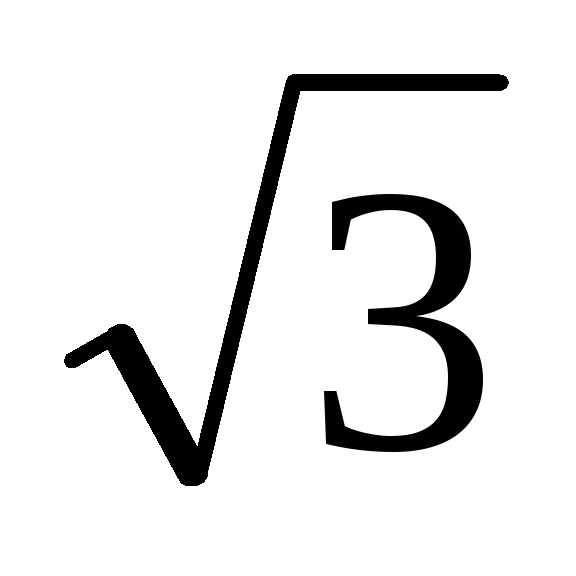 раз меньше
раз меньше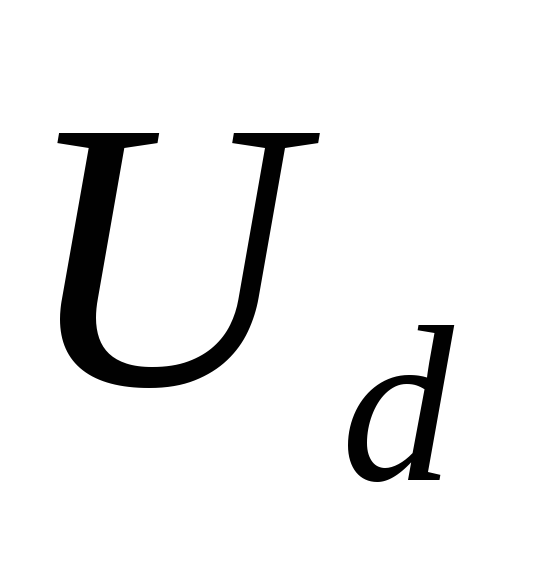 .
Максимум напряжения будет здесь не при
.
Максимум напряжения будет здесь не при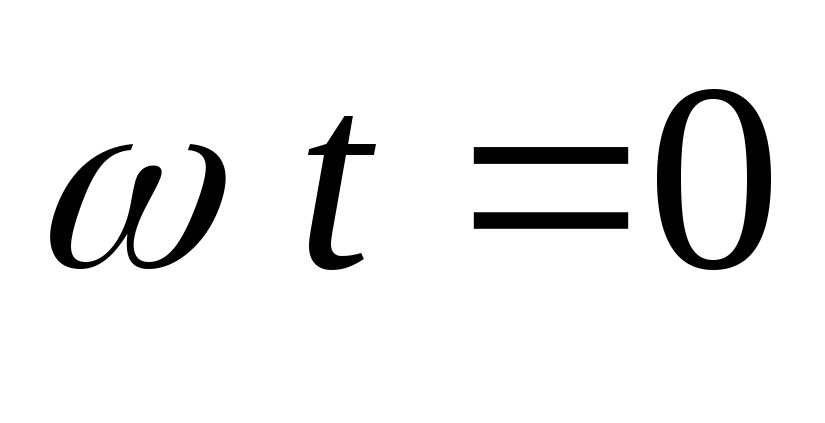 ,
а при
,
а при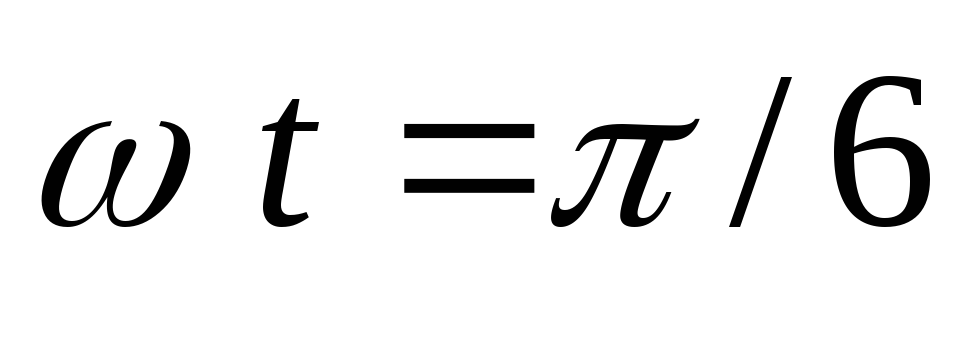 .
Форма тока в фазе вторичной обмотки
здесь также будет отличаться от однофазных
схем (см. таблицу 2.1).
.
Форма тока в фазе вторичной обмотки
здесь также будет отличаться от однофазных
схем (см. таблицу 2.1).
Произведя интегрирование (2.10), придем к выражению:
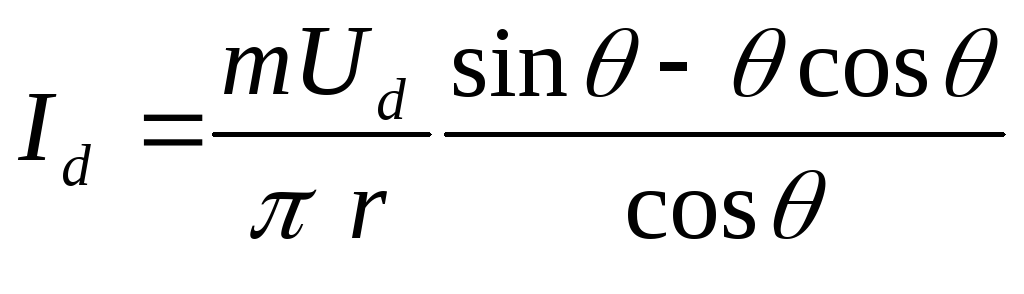 ,
(2.12)
,
(2.12)
связывающему
параметр режима работы выпрямителя  с выходным выпрямленным напряжением
с выходным выпрямленным напряжением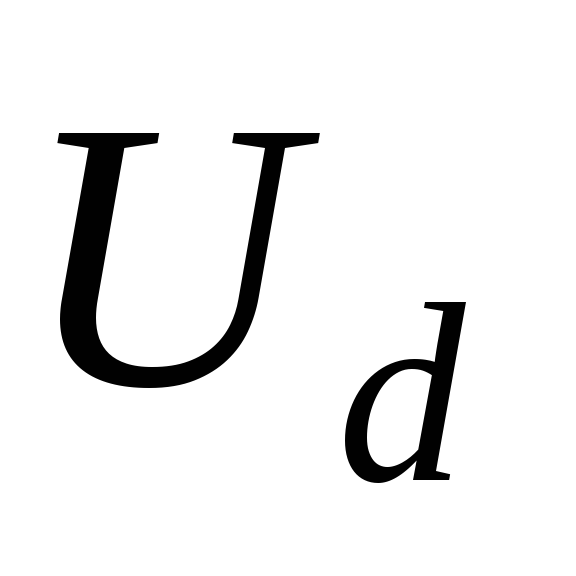 и током нагрузки
и током нагрузки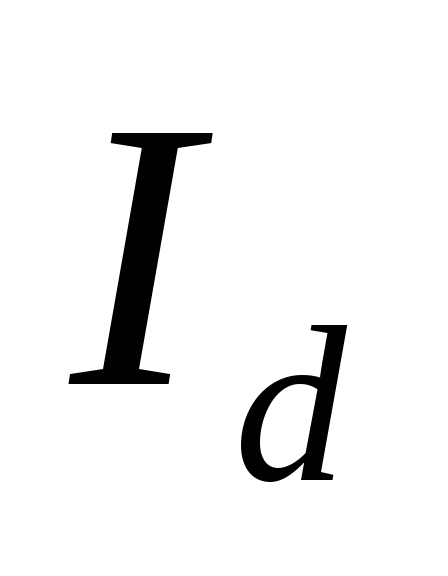 .
Обычно его записывают в несколько ином
виде [6 — 8]:
.
Обычно его записывают в несколько ином
виде [6 — 8]:
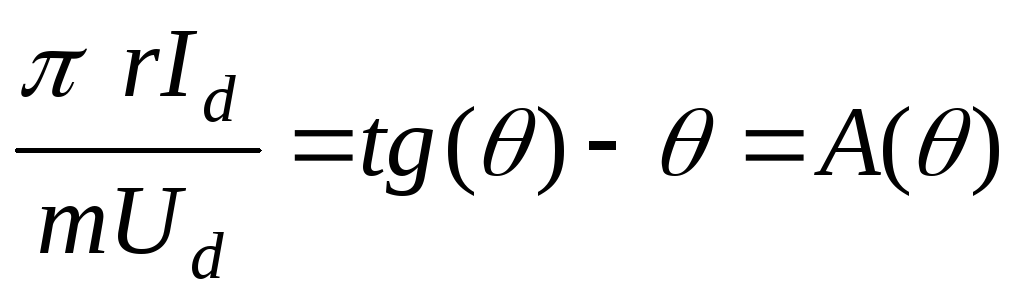 или
или 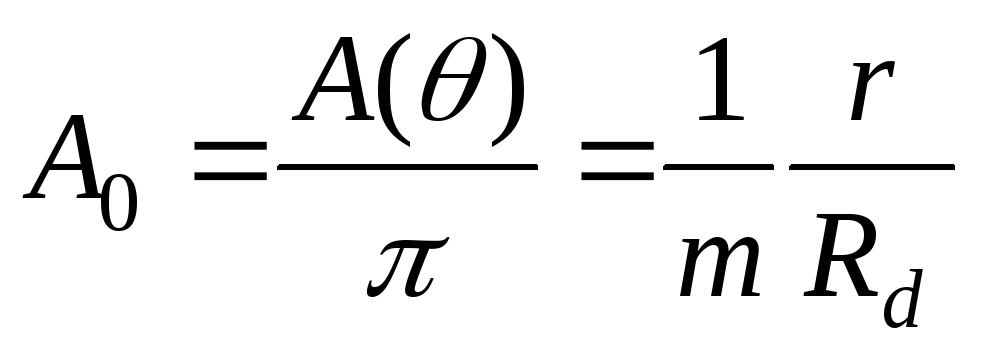 . (2.13)
. (2.13)
В этом выражении
правая часть является однозначной
функцией угла
отсечки  .
.
Соотношение (2.13)
позволяет по выходным данным выпрямителя
(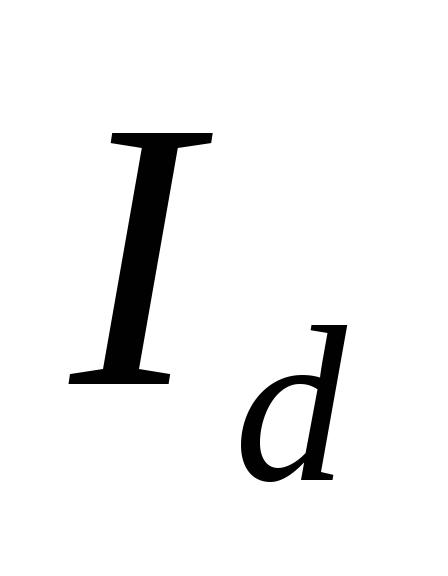 ,
,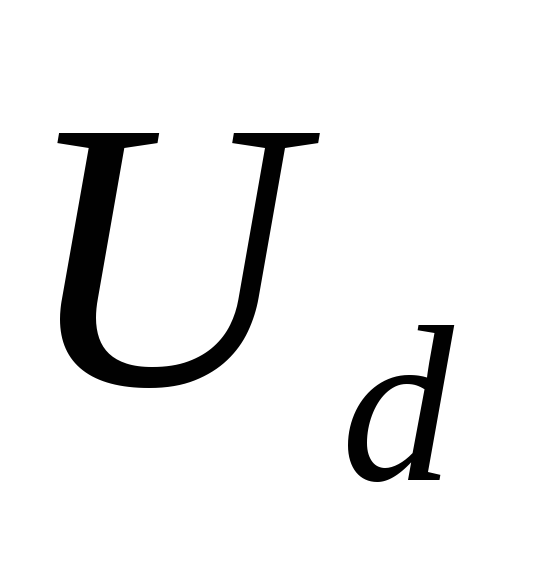 )
и оценке сопротивления фазыr определить режим работы выпрямителя,
т.е. угол отсечки
)
и оценке сопротивления фазыr определить режим работы выпрямителя,
т.е. угол отсечки  .
Когда режим работы известен, все
интересующие расчетчика зависимости
находятся легко, т.к. полностью известна
форма импульса тока одной из фаз
выпрямителя (это усеченный косинусоидальный
импульс).
.
Когда режим работы известен, все
интересующие расчетчика зависимости
находятся легко, т.к. полностью известна
форма импульса тока одной из фаз
выпрямителя (это усеченный косинусоидальный
импульс).
Действующее значение ЭДС вторичной обмотки, согласно (2.11) ,
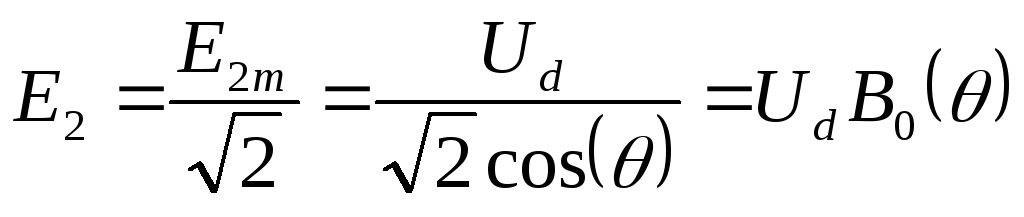 (2.14)
(2.14)
Действующее значение тока найдем по (2.9):
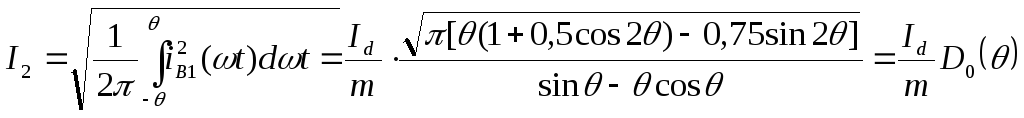 (2.15)
(2.15)
где
функция угла отсечки 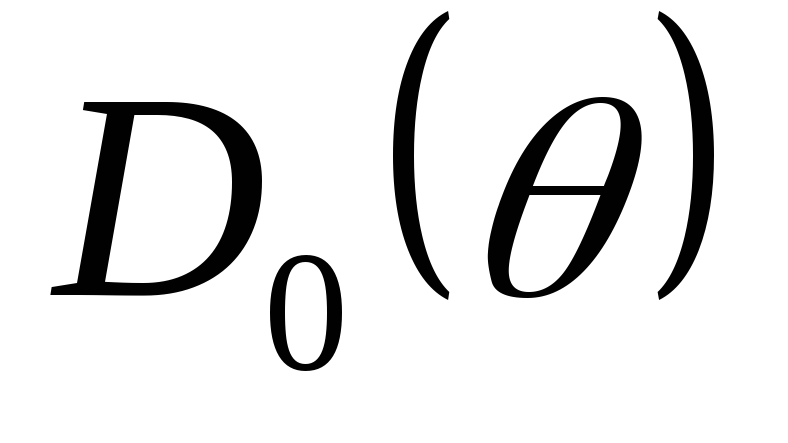 характеризует отношение действующего
значения импульса тока к его постоянной
составляющей. Для схемы Ларионова
разница в формуле (2.15) связана с тем, что
вентили в ней проводят ток 2 раза за 1
период, а во всех остальных схемах
вентили проводят ток по одному разу.
характеризует отношение действующего
значения импульса тока к его постоянной
составляющей. Для схемы Ларионова
разница в формуле (2.15) связана с тем, что
вентили в ней проводят ток 2 раза за 1
период, а во всех остальных схемах
вентили проводят ток по одному разу.
Следует отметить,
что имеется разница в схемах между
действующим значением тока во вторичной
обмотке трансформатора 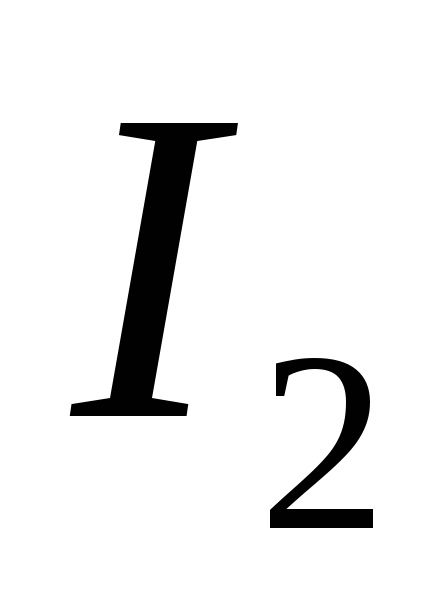 и током вентиля
и током вентиля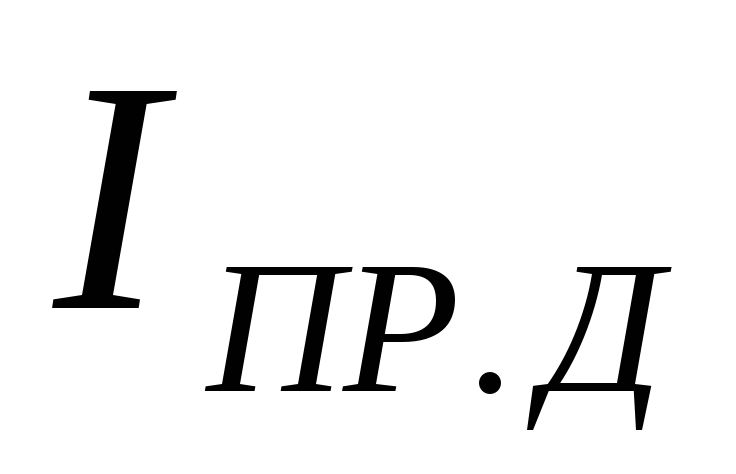 .
Это связано с тем, что вторичные обмотки
мостовых схем проводят ток в обе стороны,
а остальные схемы проводят ток только
в одну сторону.
.
Это связано с тем, что вторичные обмотки
мостовых схем проводят ток в обе стороны,
а остальные схемы проводят ток только
в одну сторону.
Максимального
значения ток вентиля достигает при 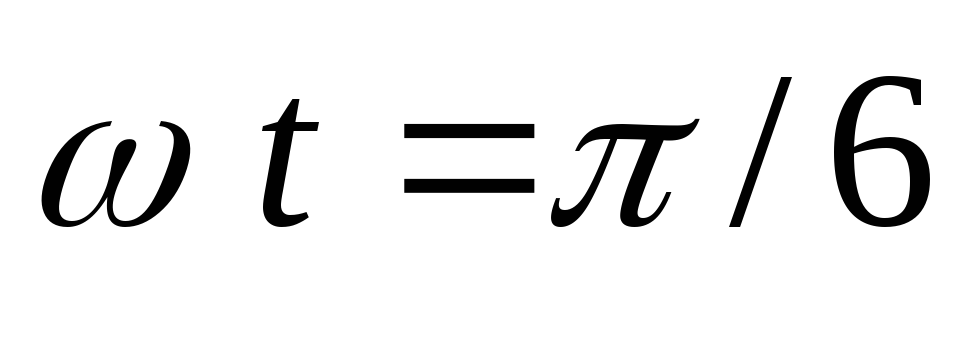 в схеме Ларионова и при
в схеме Ларионова и при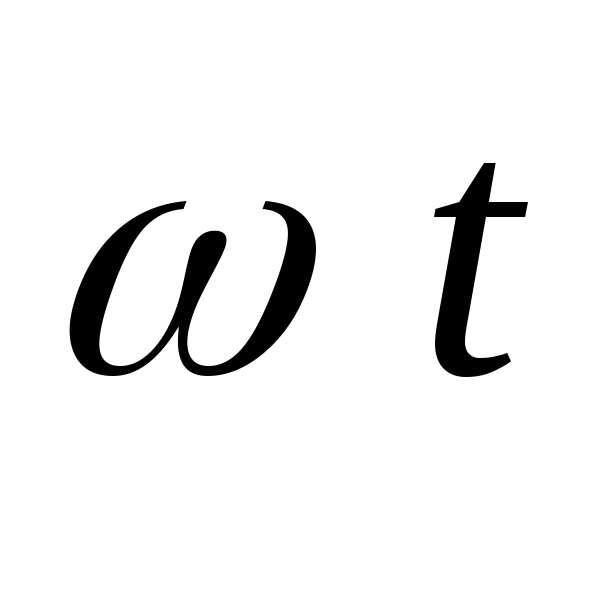 = 0 во всех остальных схемах:
= 0 во всех остальных схемах:
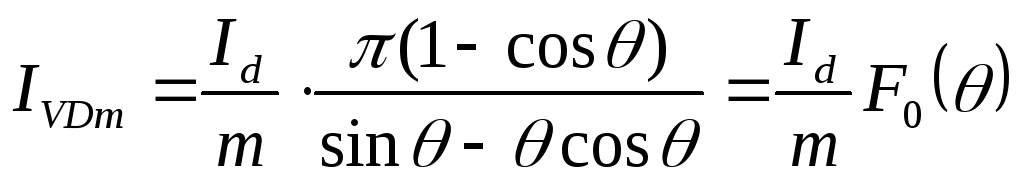 (2.16)
(2.16)
где 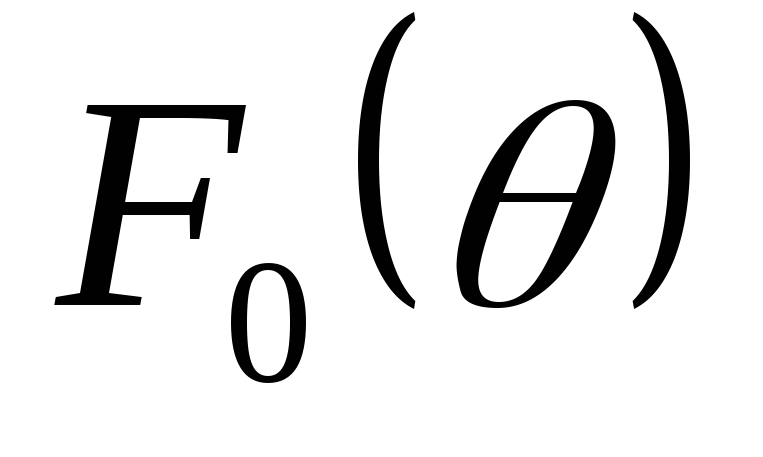 —
функция, связывающая значение амплитуды
импульса тока и его постоянной
составляющей.
—
функция, связывающая значение амплитуды
импульса тока и его постоянной
составляющей.
Трудность возникает
при расчете коэффициента пульсаций
выпрямителей, поскольку, положив 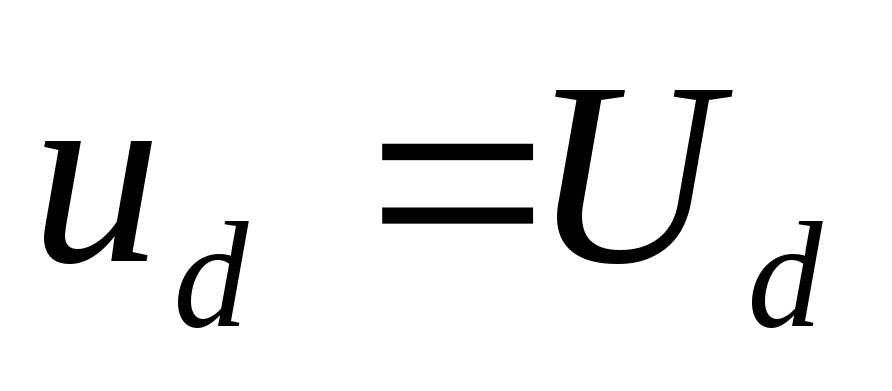 ,
приняли пульсации выпрямителя равными
нулю. Однако если пульсации выходного
напряжения небольшие, то и отклонения
формы тока вентиля от косинусоидальной
также окажутся небольшими. В результате
для расчета переменной составляющей
тока всех вентилей, проходящей через
выходной конденсатор выпрямителя и
определяющий его пульсации, можно
воспользоваться формулой (2.9), но уже не
как точной, а как приближенной. Так как
выходное напряжение выпрямителя
фильтруется сглаживающим фильтром,
который сильно ослабляет высшие гармоники
выходного напряжения, то достаточным
для практики явится расчет коэффициента
пульсаций по первой гармонике.
,
приняли пульсации выпрямителя равными
нулю. Однако если пульсации выходного
напряжения небольшие, то и отклонения
формы тока вентиля от косинусоидальной
также окажутся небольшими. В результате
для расчета переменной составляющей
тока всех вентилей, проходящей через
выходной конденсатор выпрямителя и
определяющий его пульсации, можно
воспользоваться формулой (2.9), но уже не
как точной, а как приближенной. Так как
выходное напряжение выпрямителя
фильтруется сглаживающим фильтром,
который сильно ослабляет высшие гармоники
выходного напряжения, то достаточным
для практики явится расчет коэффициента
пульсаций по первой гармонике.
Таким образом,
общий ток всех вентилей представляет
собой совокупность импульсов тока,
определяемых (2.9) и следующих друг за
другом с интервалом 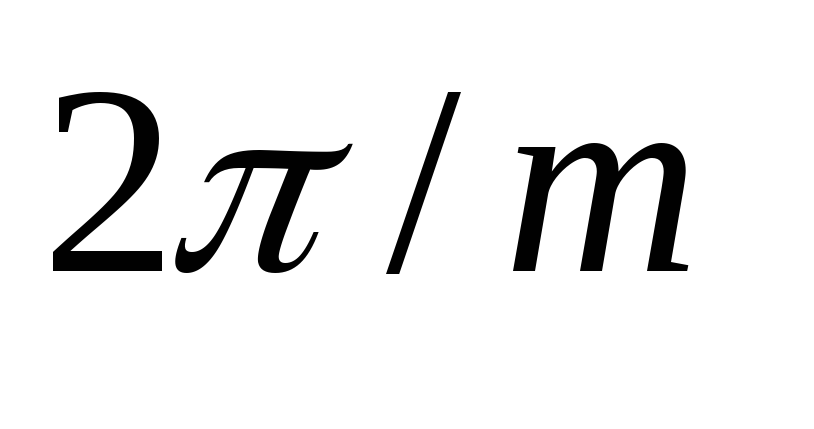 .
Амплитуда первой гармоники тока:
.
Амплитуда первой гармоники тока:
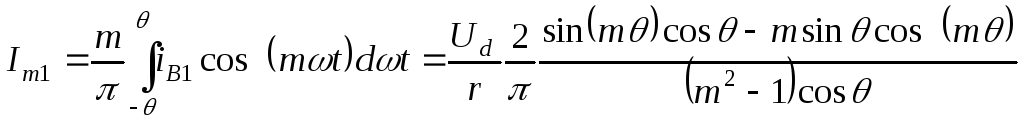 (2.17)
(2.17)
Амплитуда первой гармоники напряжения:
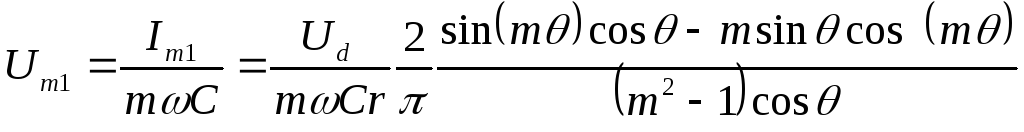 (2.18)
(2.18)
Коэффициент пульсаций по первой гармонике:
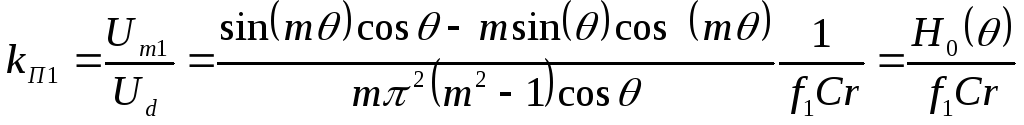 (2.19)
(2.19)
где 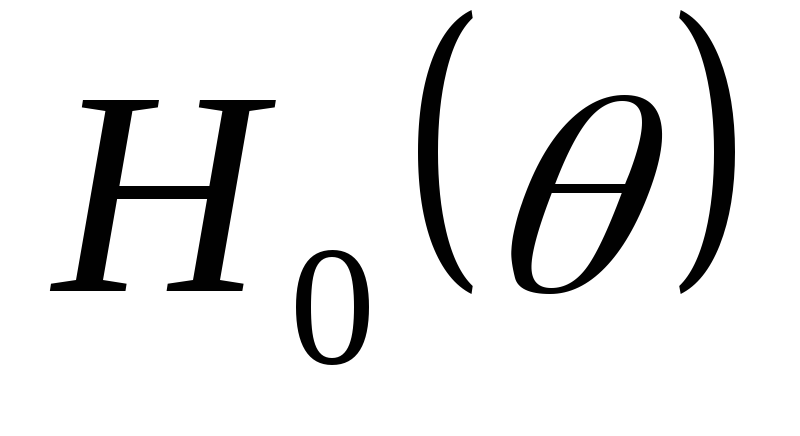 —
функция угла отсечки и числа фаз
выпрямителя.
—
функция угла отсечки и числа фаз
выпрямителя.
Данный
метод расчета из-за приближения 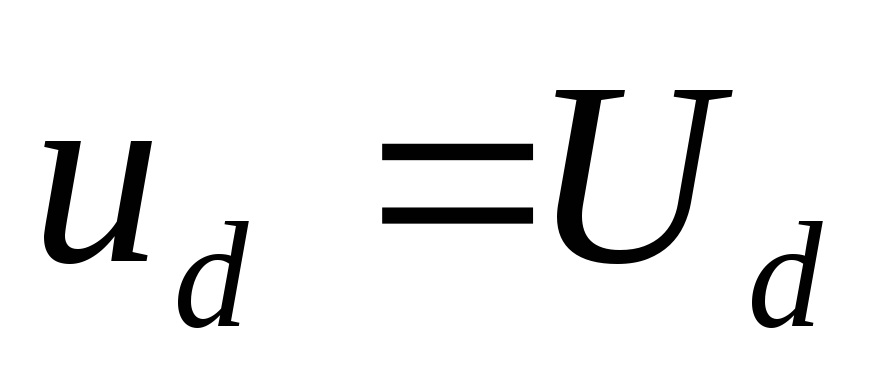 достаточно точен лишь при малых значениях
коэффициента пульсаций (
достаточно точен лишь при малых значениях
коэффициента пульсаций (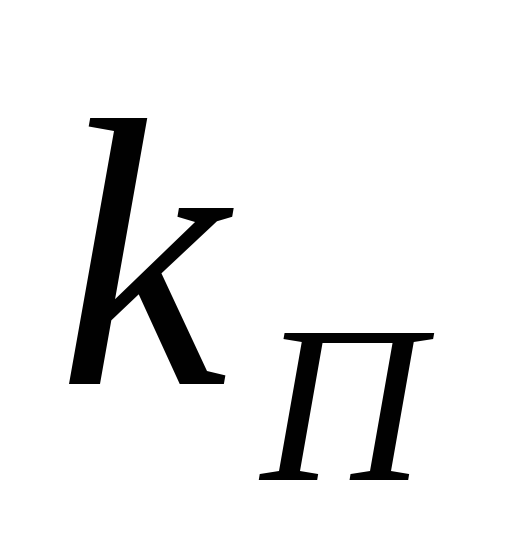 <0,1÷0,12).
Поэтому формула (2.19) определяет и
применимость изложенного метода. Если
при расчете окажется, что
<0,1÷0,12).
Поэтому формула (2.19) определяет и
применимость изложенного метода. Если
при расчете окажется, что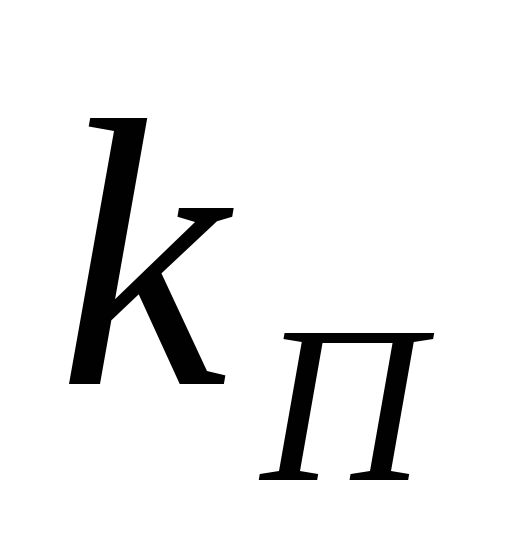 >0,12,
то точность будет ниже требуемой (
>0,12,
то точность будет ниже требуемой (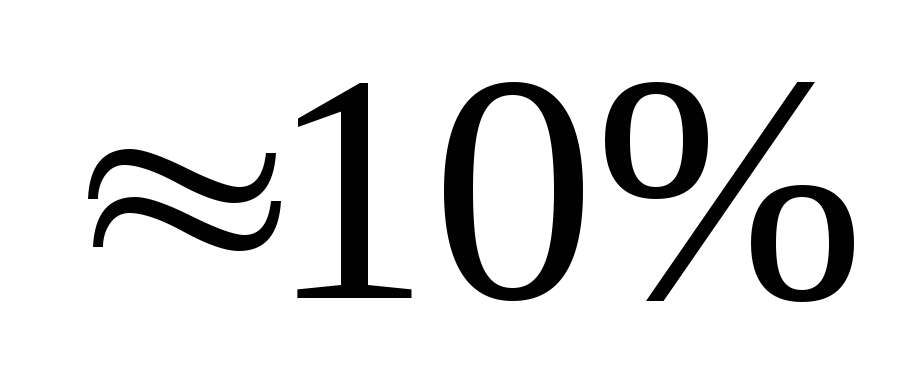 )
и возникнет необходимость изменения
расчетной модели.
)
и возникнет необходимость изменения
расчетной модели.
Самым простым
способом достижения требуемой точности
расчета является увеличение емкости
выходного конденсатора выпрямителя до
значения, которое обеспечивает выполнение
условия 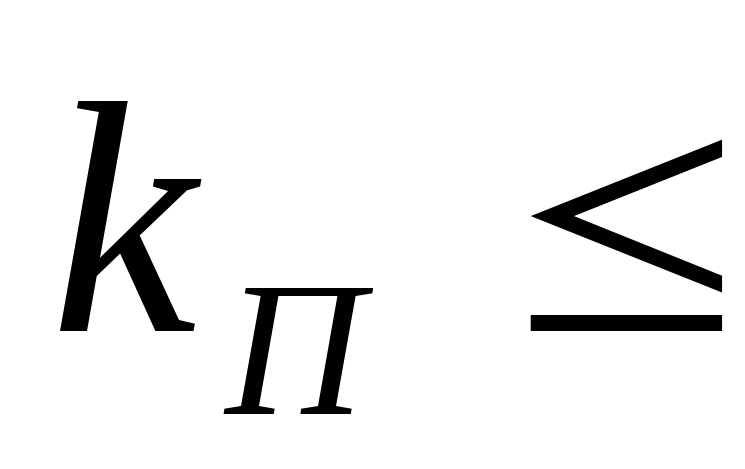 0,1÷0,12.
При этом вводят понятиеминимальной
емкости выходного конденсатора выпрямителя. При
0,1÷0,12.
При этом вводят понятиеминимальной
емкости выходного конденсатора выпрямителя. При 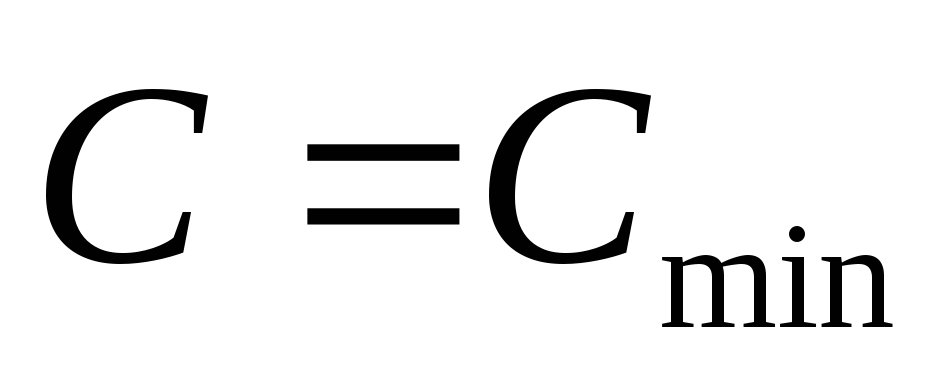 коэффициент пульсаций
коэффициент пульсаций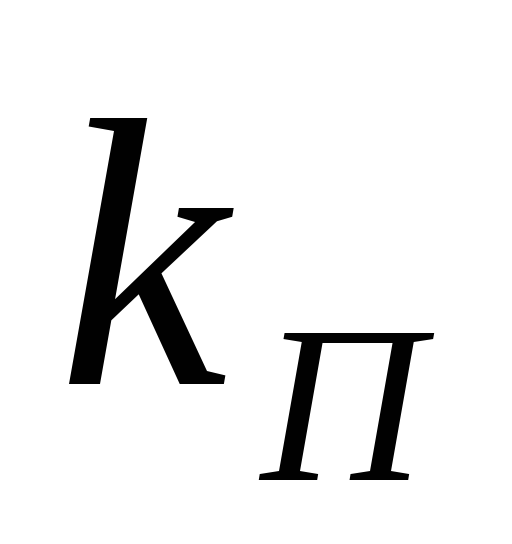 = 0,1.
= 0,1.
Недостатком
использования формулы (2.19) является то,
что о выполнении или нарушении условия
малости пульсаций узнают только в конце
расчета, когда определен угол отсечки  и найдена функция
и найдена функция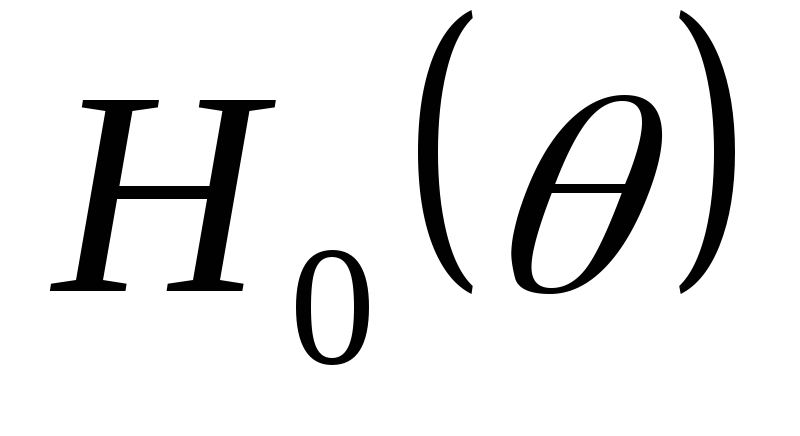 .
Удобнее было бы иметь такое соотношение,
которое позволило бы определить емкость
.
Удобнее было бы иметь такое соотношение,
которое позволило бы определить емкость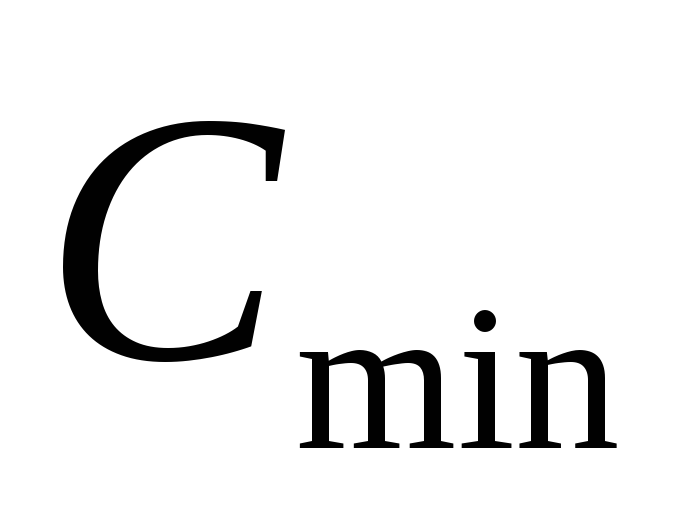 до начала расчета, после чего вынести
решение о возможности применения
выходного конденсатора заданной емкости
в выбранной схеме выпрямителя.
до начала расчета, после чего вынести
решение о возможности применения
выходного конденсатора заданной емкости
в выбранной схеме выпрямителя.
Прийти к такому
соотношения можно представив зависимость 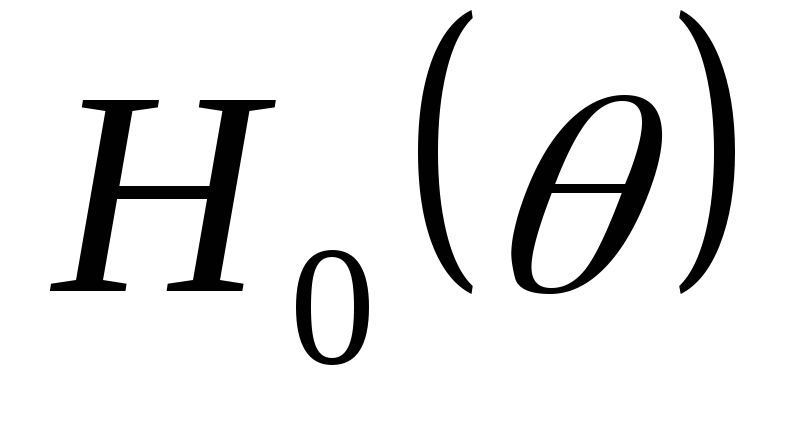 в приближенном виде. Так, для двухфазного
выпрямителя
в приближенном виде. Так, для двухфазного
выпрямителя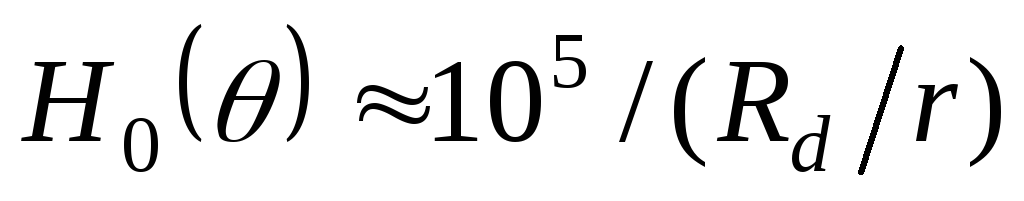 .
Подставив это приближение в (2.19), при
.
Подставив это приближение в (2.19), при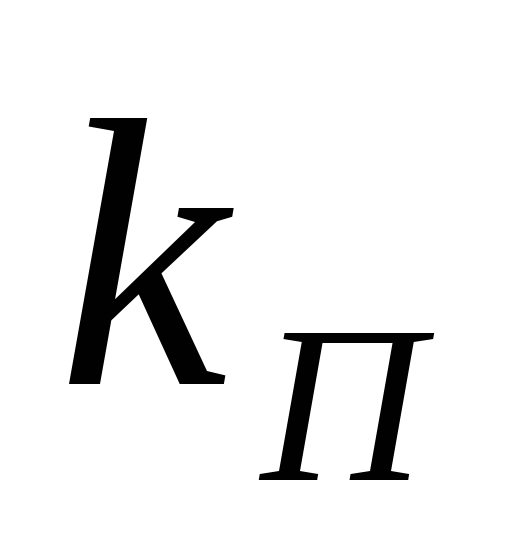 = 0,1 получим:
= 0,1 получим:
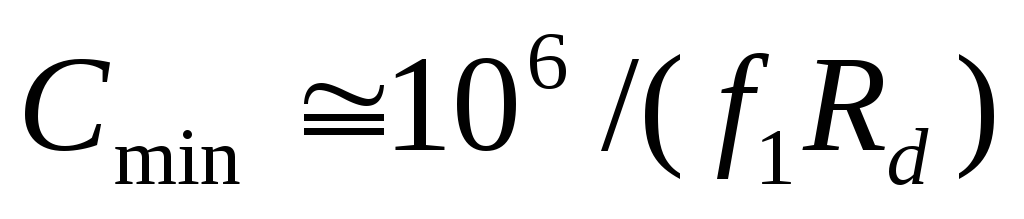 ,
(2.20)
,
(2.20)
где 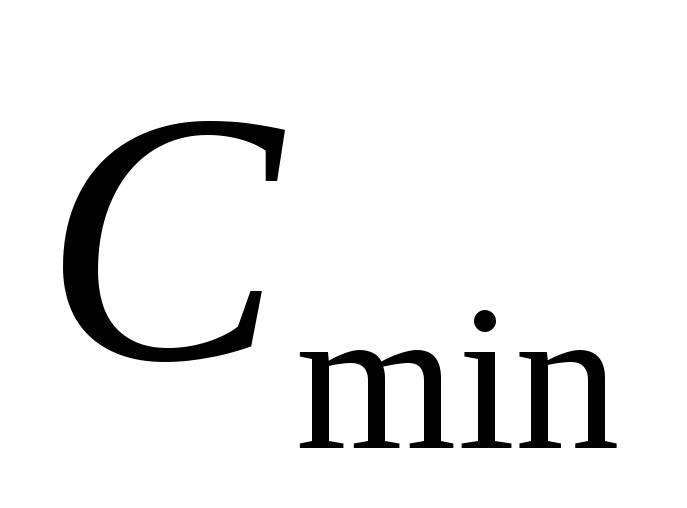 —
в мкФ.
—
в мкФ.
Таким образом, данный метод расчета выпрямителя заключается в проверке условия (2.20) с последующим определением режима работы по выражению (2.13) и нахождения расчетных показателей по формулам (2.14), (2.15), (2.16), (2.19).
Как было показано
ранее, выбранная модель (рис. 2.1, б)
достаточно проста, однако расчеты по
полученным на ее основе формулам дают
во многих случаях неплохую точность.
Вместе с тем в выпрямителях на относительно
высокие напряжения заметное влияние
на выходные показатели оказывает
индуктивность рассеяния трансформатора.
При ее учете придем к расчетной модели,
приведенной на рис. 2.4, а. Импульс тока
вентиля в такой модели заметно отличается
от косинусоидального (рис. 2.4, б) и имеет
длительность, большую 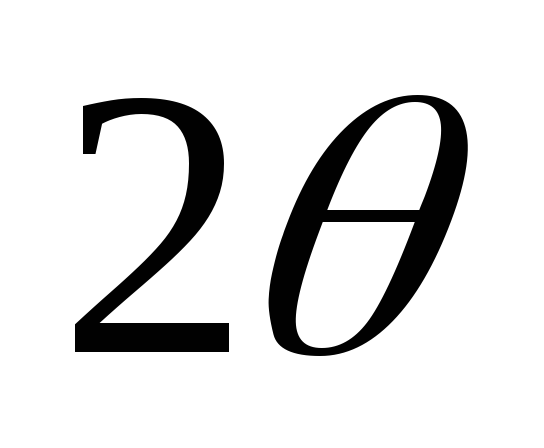 .
.
Проведя анализ
подобный ранее изложенному, получим
зависимости коэффициентов  не только от угла
не только от угла ,
но и от относительного реактивного
сопротивления фазыx.
,
но и от относительного реактивного
сопротивления фазыx.
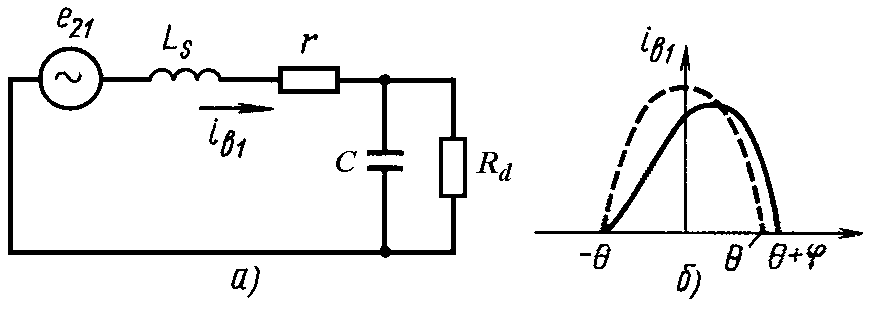
Рис. 2.4. Расчетная модель выпрямителя с учтенной индуктивностью
рассеяния (а) и кривые импульса тока вентиля в исходной и данной моделях (б).
Также может быть
определен тангенс угла  ,
характеризующего соотношение между
индуктивным и активным сопротивлениями
фазы выпрямителя:
,
характеризующего соотношение между
индуктивным и активным сопротивлениями
фазы выпрямителя:
 (2.21)
(2.21)
Найденные ранее
выражения для коэффициентов  соответствуют значению параметра
соответствуют значению параметра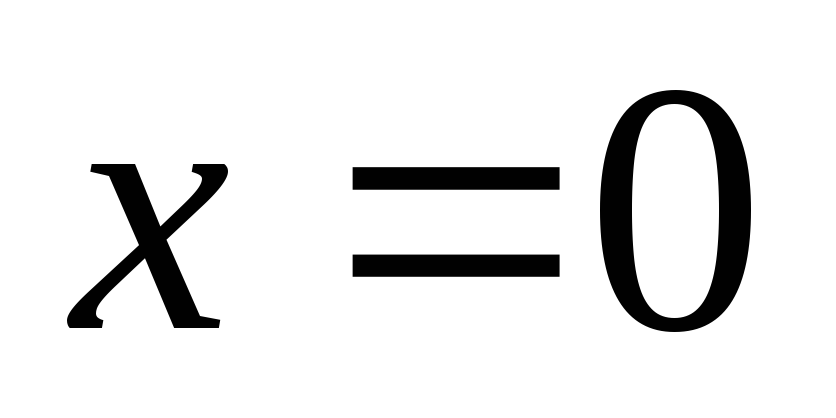 или
или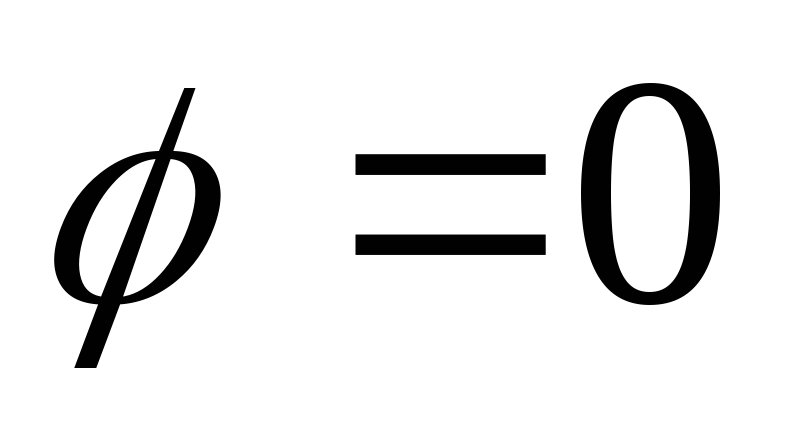 .
Зависимости коэффициентов
.
Зависимости коэффициентов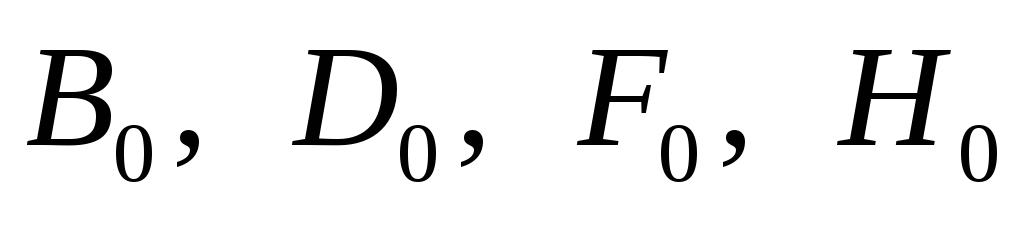 от функции параметра режима
от функции параметра режима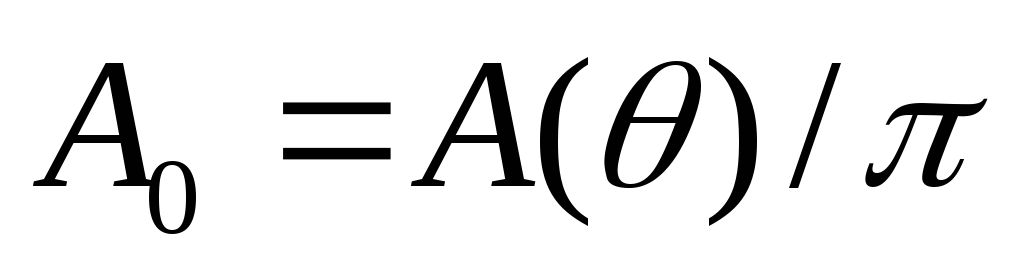 и угла
и угла приведены на рис. 2.5 — 2.9 [7, 8].
приведены на рис. 2.5 — 2.9 [7, 8].
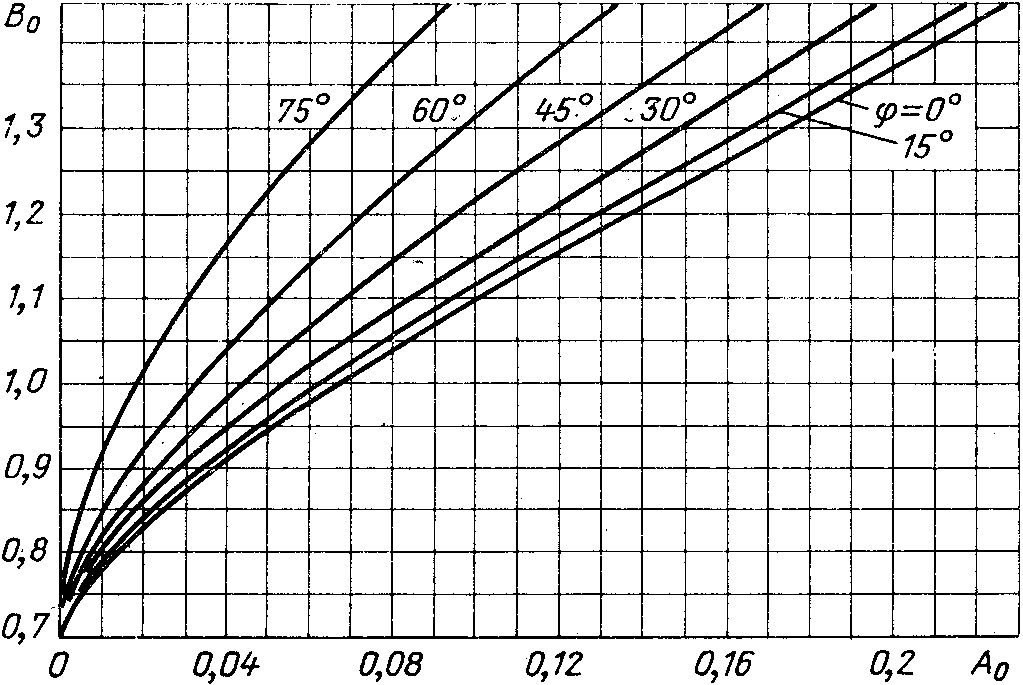
Рис.
2.5. Зависимость коэффициента  от
от при различных значениях
при различных значениях .
.
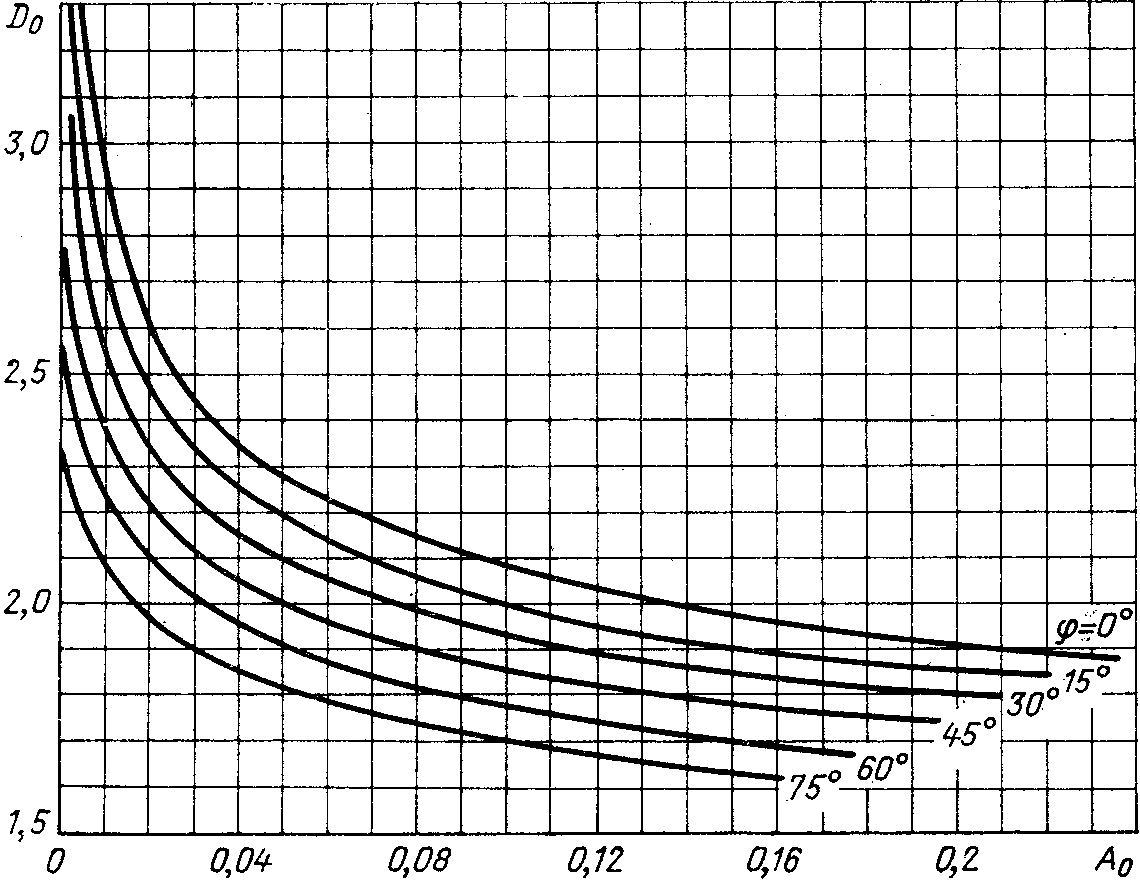
Рис.
2.6. Зависимость коэффициента 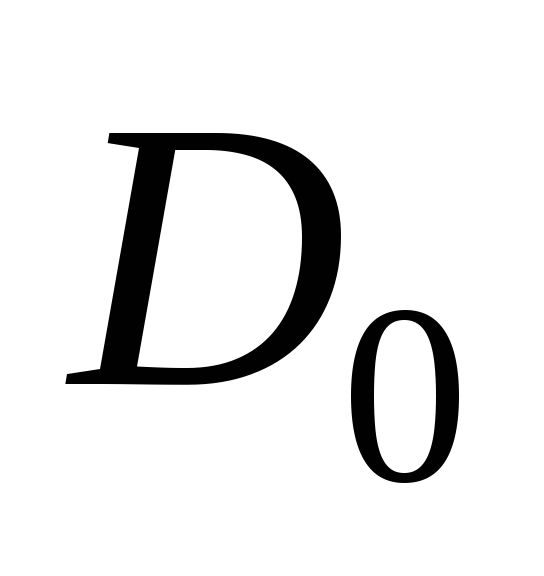 от
от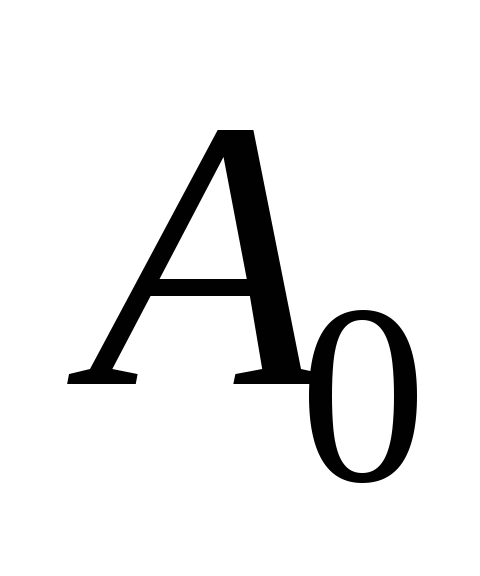 при различных значениях
при различных значениях .
.
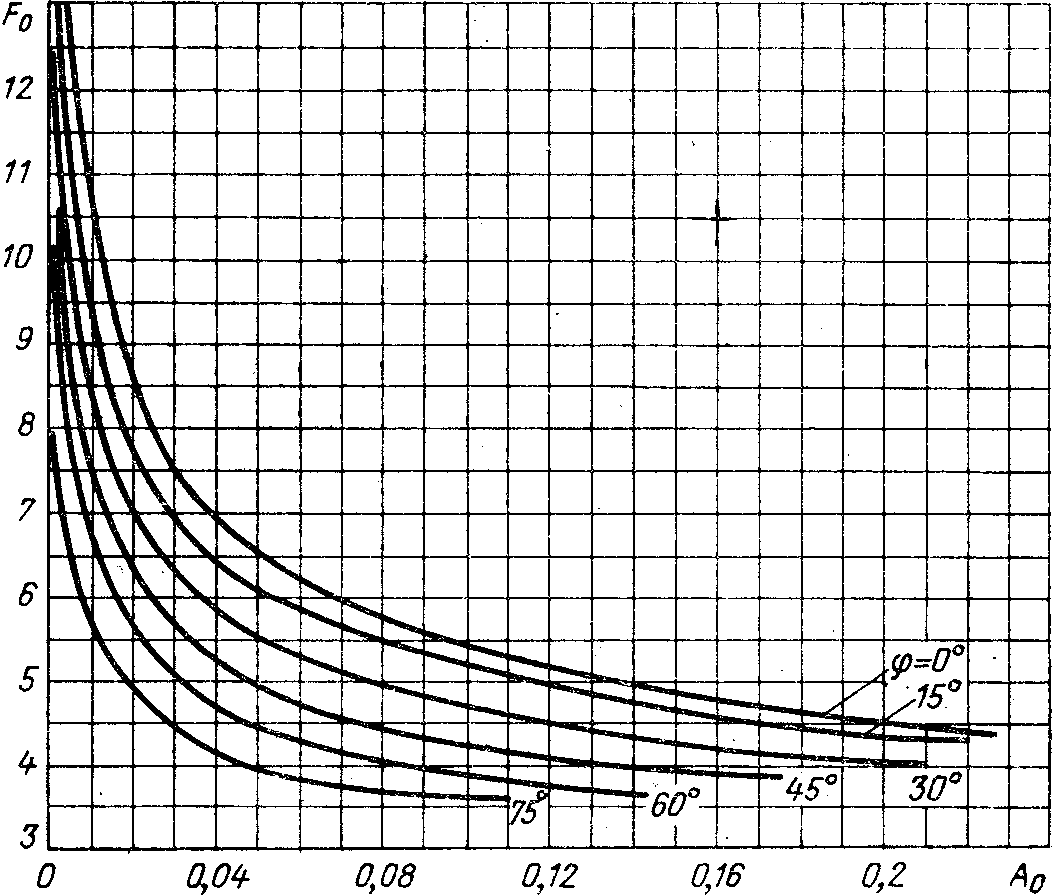
Рис.
2.7. Зависимость коэффициента 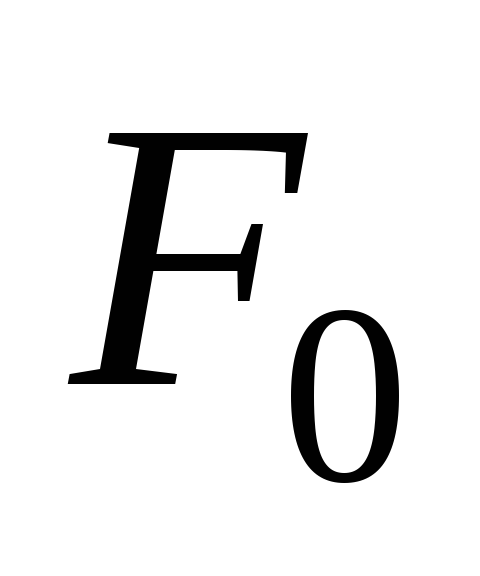 от
от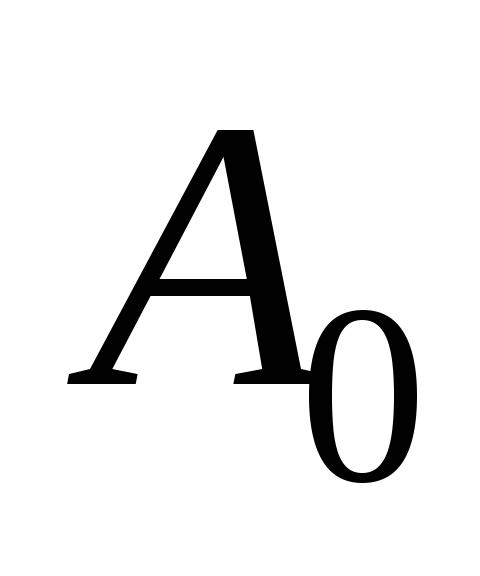 при различных значениях
при различных значениях .
.
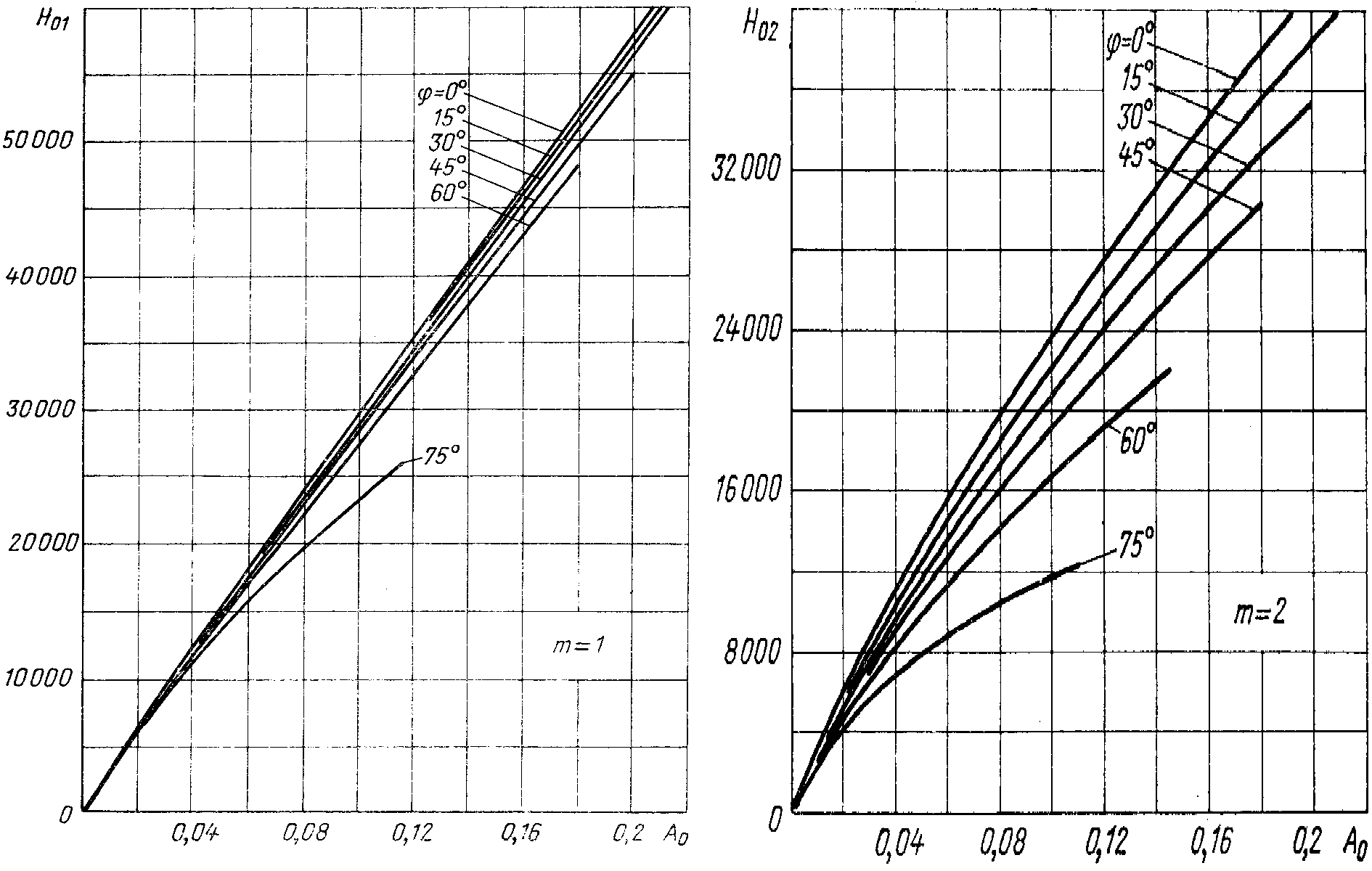
Рис.
2.8. Зависимости коэффициентов 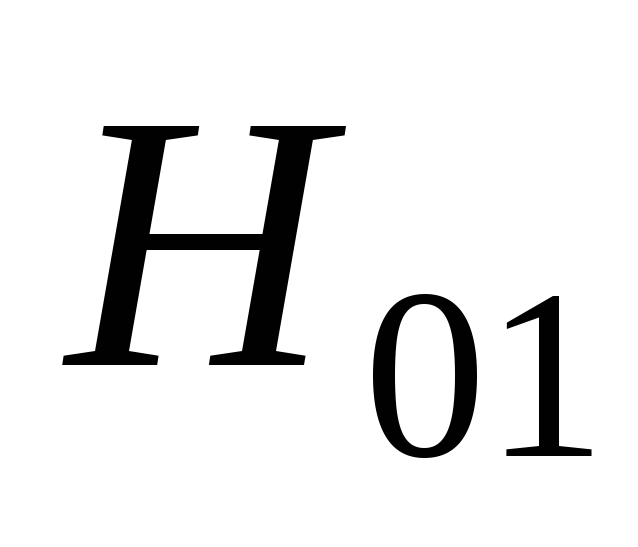 и
и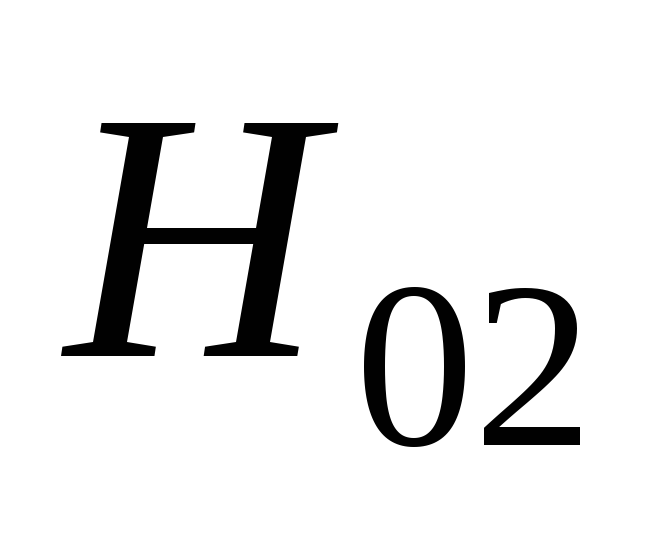 от
от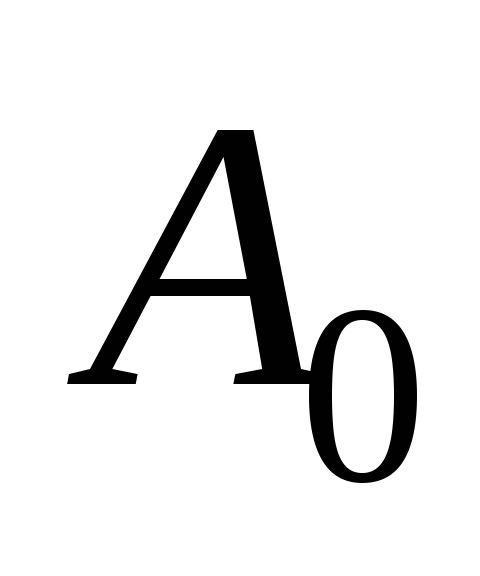 и
и .
.
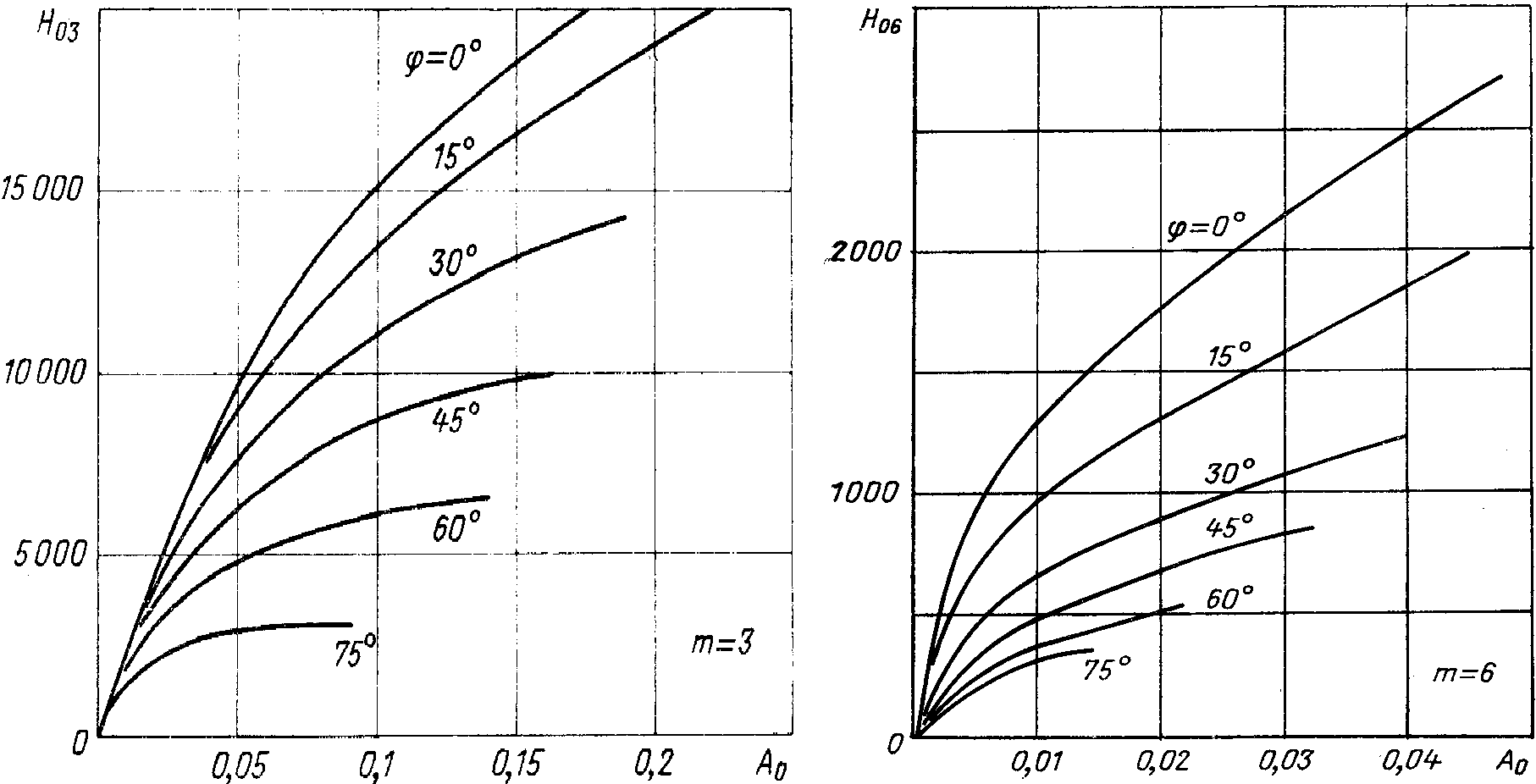
Рис.
2.9. Зависимости коэффициентов 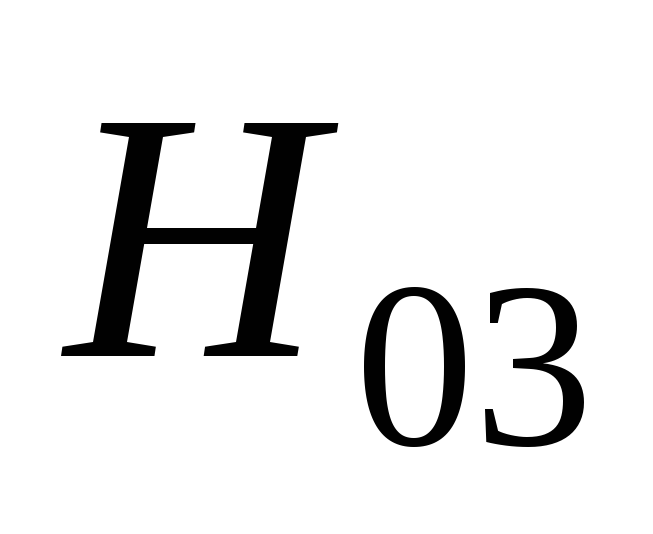 и
и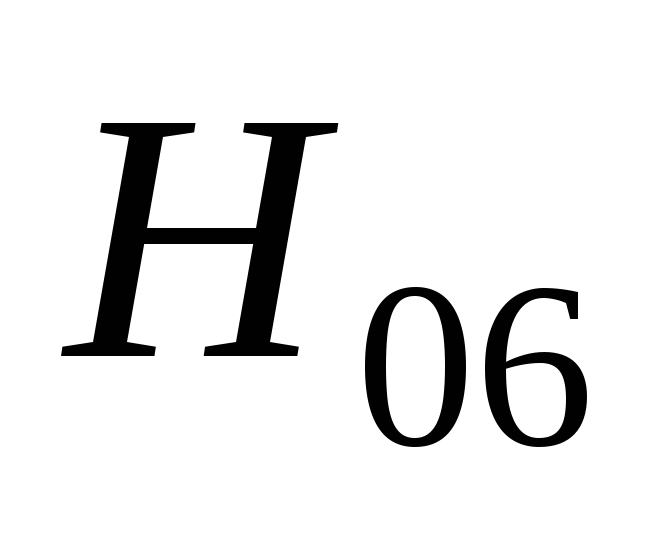 от
от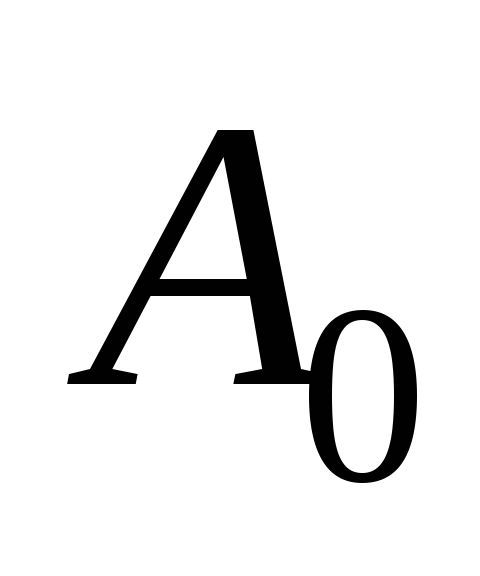 и
и .
.
Действующий ток 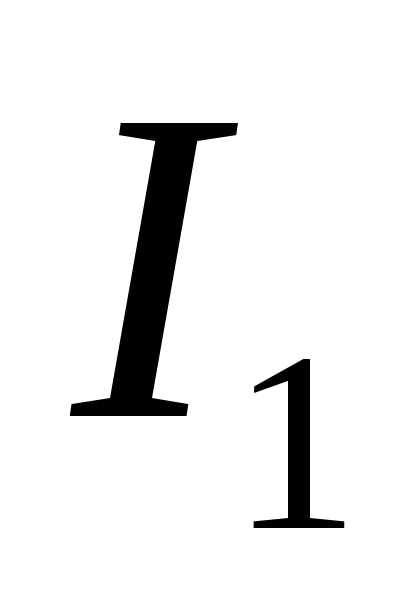 первичных обмоток (см. таблицу 2.1) можно
найти, зная коэффициент трансформации
[8]:
первичных обмоток (см. таблицу 2.1) можно
найти, зная коэффициент трансформации
[8]:
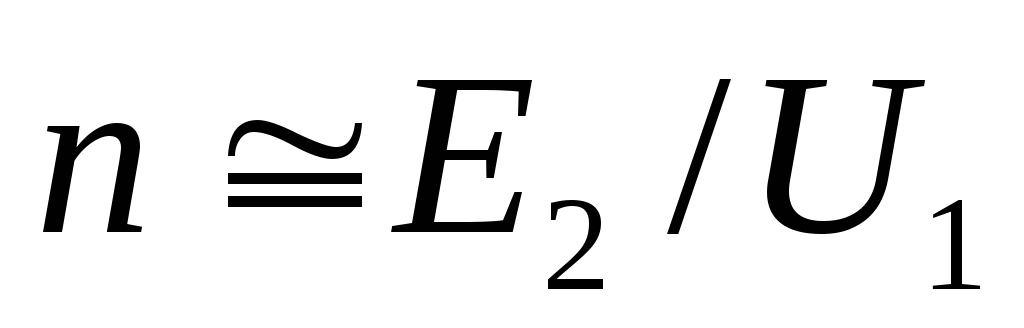 (2.22)
(2.22)
и
действующий ток во вторичных обмотках
трансформатора 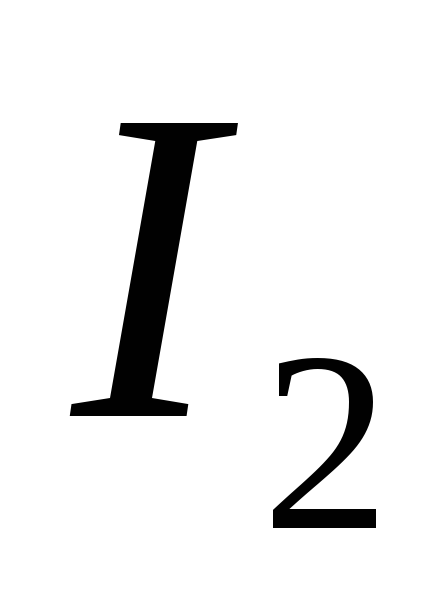 .
.
Габаритная мощность
трансформатора 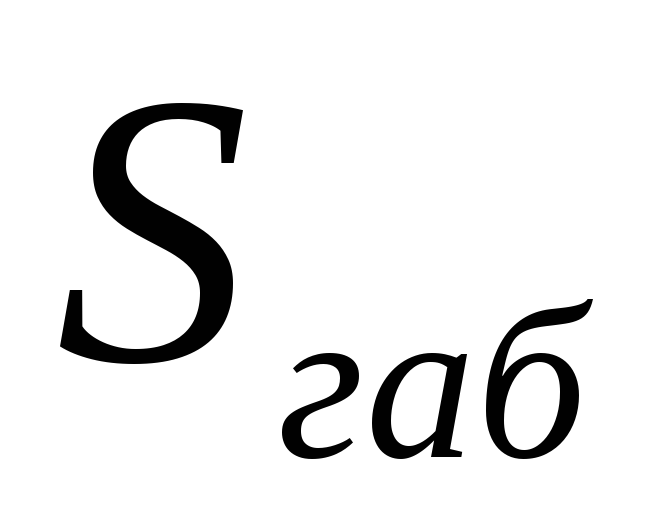 определяется согласно данным таблицы
2.2. Через габаритную мощность трансформатора
находится один из важнейших показателей
выпрямителя —коэффициент
использования трансформатора по мощности (1.1).
определяется согласно данным таблицы
2.2. Через габаритную мощность трансформатора
находится один из важнейших показателей
выпрямителя —коэффициент
использования трансформатора по мощности (1.1).
Таблица 2.2.
Схема | Габаритная мощность трансформатора |
Однополупериодная |
|
Мостовая | |
2-х полупериодная со средней точкой |
|
3-х фазная нулевая |
|
Ларионова |
Внешнюю (нагрузочную) характеристику выпрямителя, т.е. зависимость выпрямленного напряжения от тока нагрузки, рассчитывают по формуле [8]:
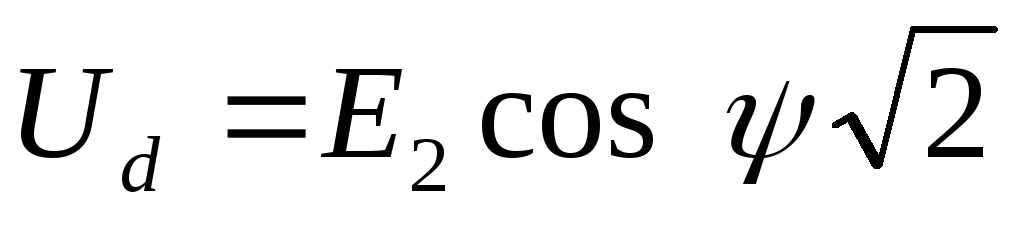 (2.23)
(2.23)
Задаваясь
различными значениями 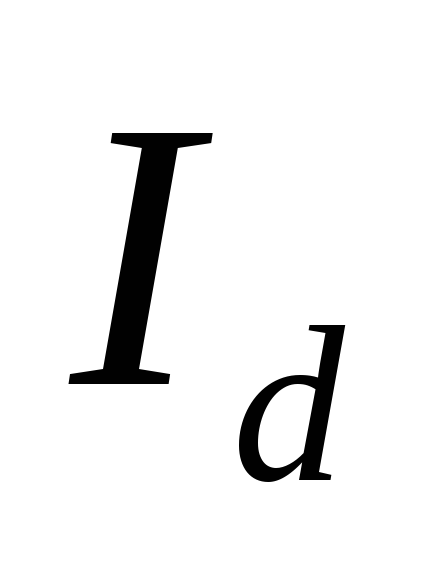 ,
определяют коэффициент
,
определяют коэффициент
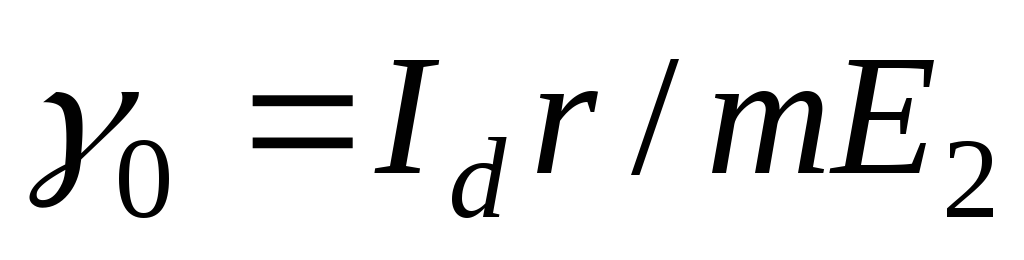 (2.24)
(2.24)
Значения  находят в зависимости от коэффициента
находят в зависимости от коэффициента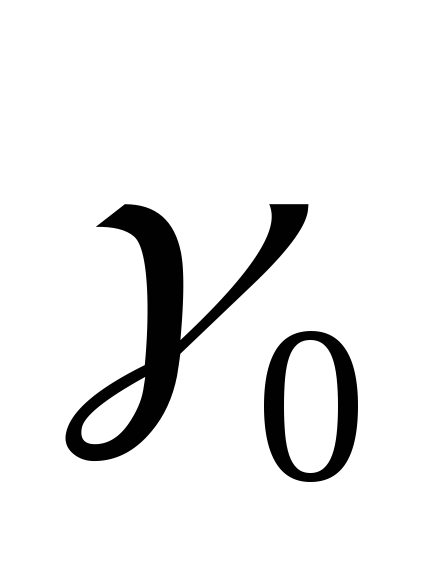 и угла φ по графику на риc.
2.10 [8]. Подставляя величину
и угла φ по графику на риc.
2.10 [8]. Подставляя величину 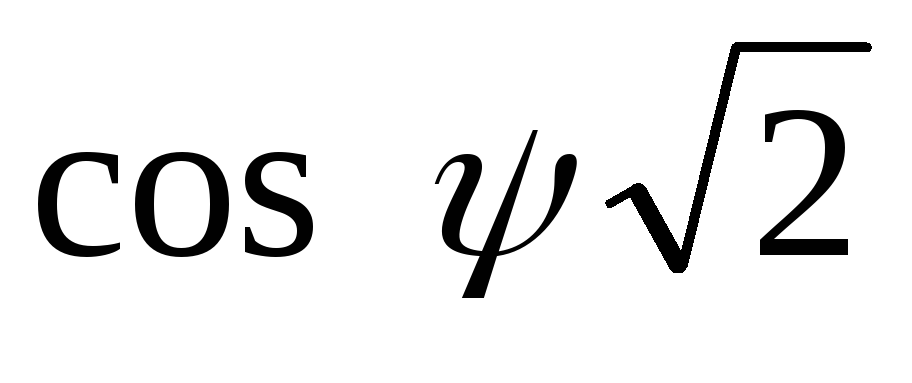 в формулу (2.23), находят
в формулу (2.23), находят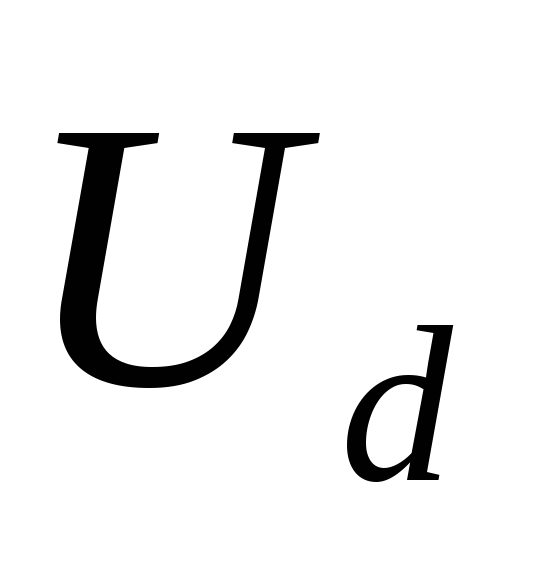 для различных значений
для различных значений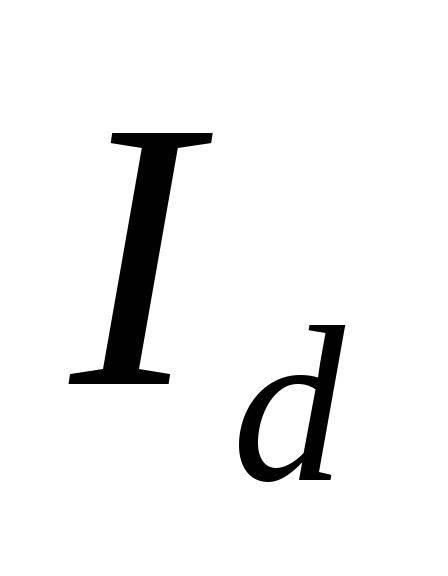 .
.
Напряжение на
конденсаторе будет равно напряжению
на нагрузке, но на случай отсоединения
нагрузки необходимо выбирать конденсатор
рассчитанный на напряжение
холостого хода выпрямителя – Uхх.
Очевидно, что при холостом ходе (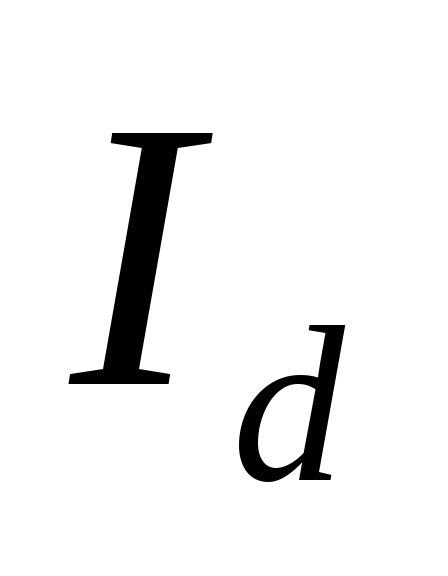 = 0)
= 0)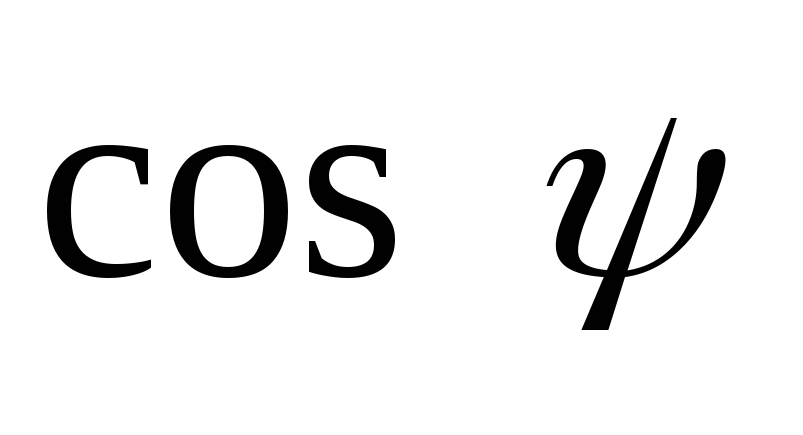 = 1 и значение напряжения холостого хода
выпрямителя для всех схем, кроме схемы
Ларионова:
= 1 и значение напряжения холостого хода
выпрямителя для всех схем, кроме схемы
Ларионова:
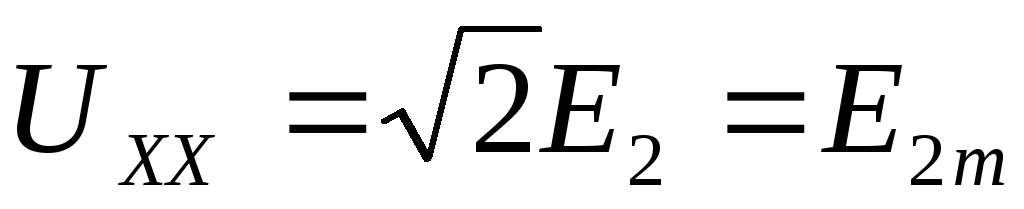 (2.25)
(2.25)
В схеме Ларионова при соединении вторичной обмотки в звезду:
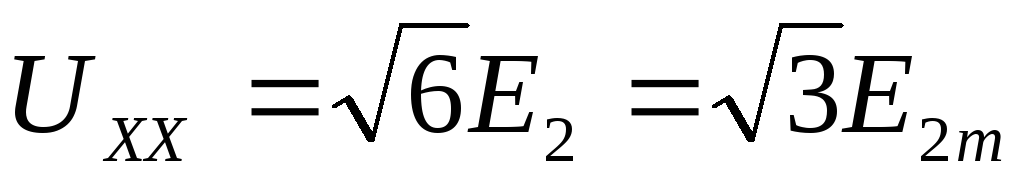 (2.26)
(2.26)
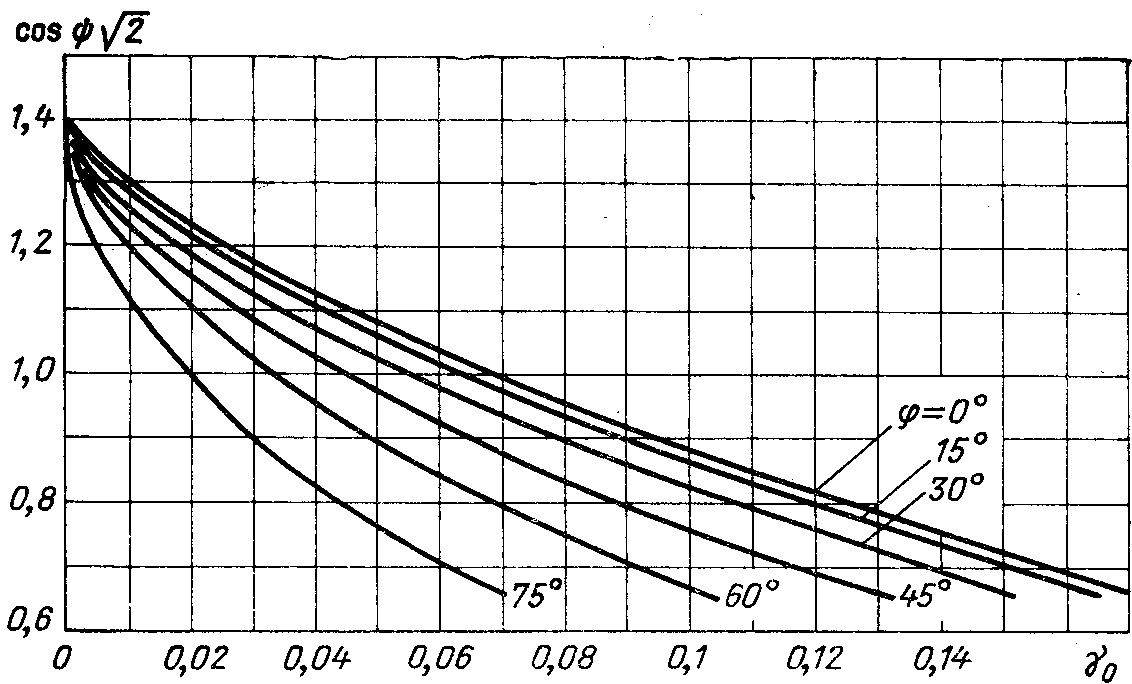
Рис.
2.10. Зависимость 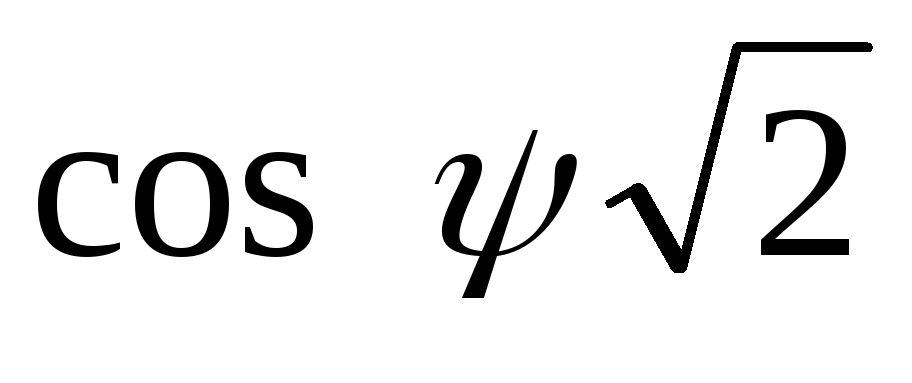 от коэффициента
от коэффициента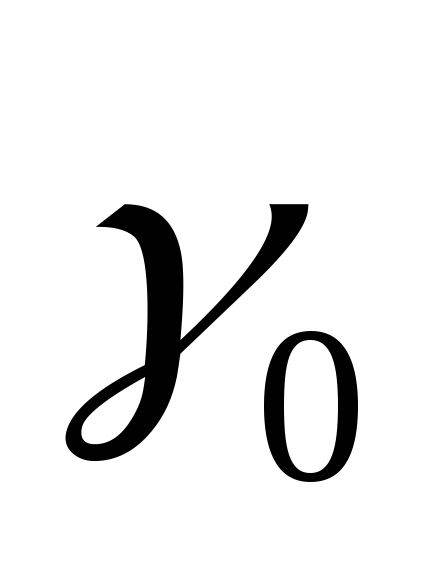
при различных значениях φ.
Учитывая то, что на фильтре знакопостоянное напряжение, конденсатор следует выбирать полярный, c номинальным напряжением не менее чем на 10% больше чем напряжение холостого хода выпрямителя (на случай скачков напряжения в электросети). Также следует учесть изменение емкости конденсатора в течение минимальной наработки, допустимое отклонение емкости, при этом допустимые напряжения переменной составляющей пульсирующего тока не должны превышать предельных значений для выбранного типа конденсатора. Переменная составляющая пульсирующего напряжения рассчитывается согласно (2.18). Поскольку допустимая переменная составляющая приводится в справочниках для частоты 50 Гц, ее следует пересчитать на частоту пульсаций напряжения на конденсаторе:
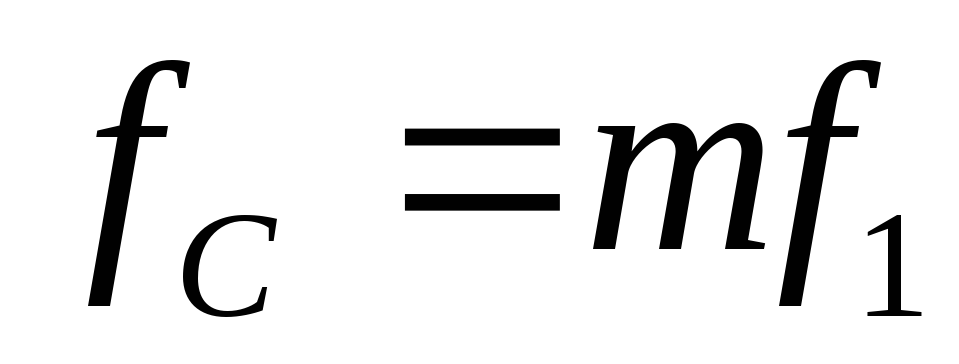 (2.27)
(2.27)
Приведенные соотношения получены для модели вентиля без порога выпрямления. Они обеспечивают хорошую точность расчета при выпрямленном напряжении более 15-20 В. При меньших значениях выпрямленного напряжения следует учитывать порог выпрямления [6].
ЭДС 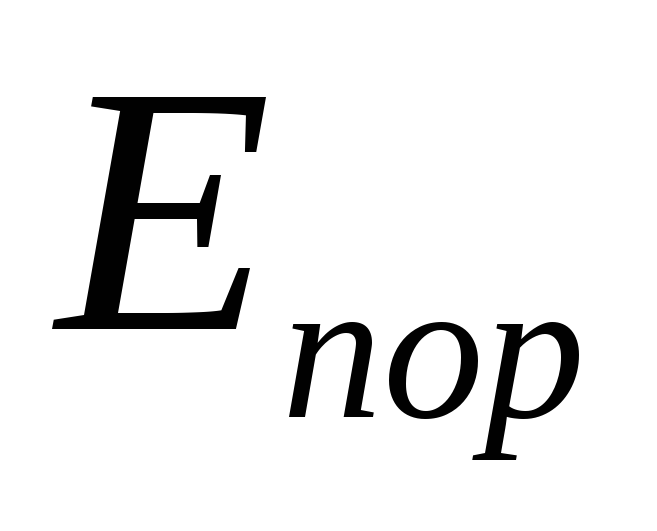 оказывается включенной согласно с
выпрямленным напряжением (по полярности).
Поэтому рассчитанное по (2.11) выходное
напряжение больше реального напряжения
на конденсатореС на величину порога выпрямления вентилей
схемы.
оказывается включенной согласно с
выпрямленным напряжением (по полярности).
Поэтому рассчитанное по (2.11) выходное
напряжение больше реального напряжения
на конденсатореС на величину порога выпрямления вентилей
схемы.
Если считать напряжение:
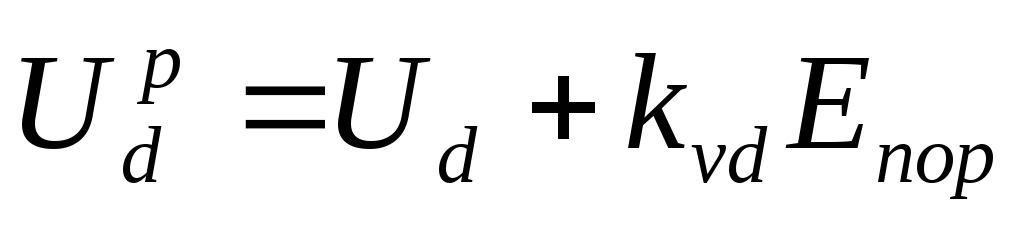 ,
(2.28)
,
(2.28)
которое
получается на выходном конденсаторе,
расчетным 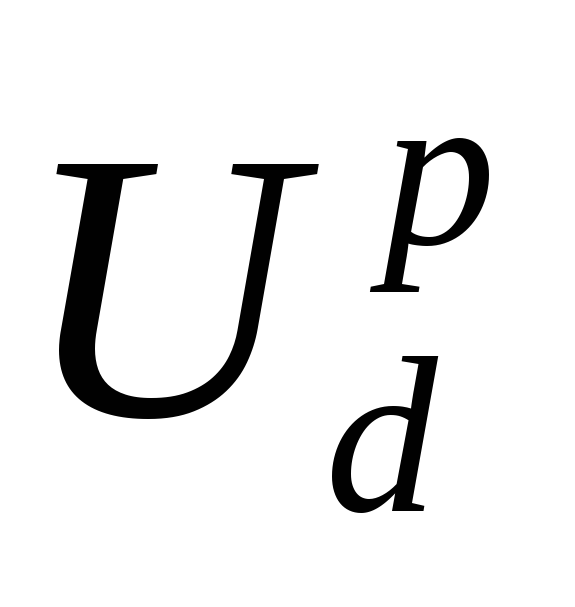 и равным сумме порогового напряжения
вентилей и заданного постоянного
выходного напряжения
и равным сумме порогового напряжения
вентилей и заданного постоянного
выходного напряжения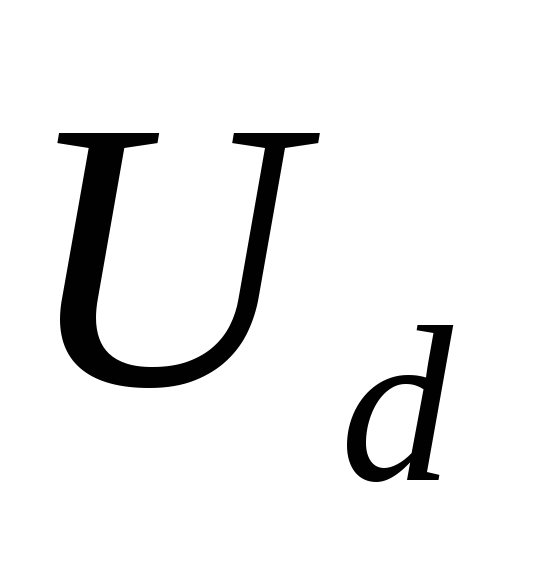 ,
то все расчетные формулы будут справедливы
и для выпрямителя с выходным напряжением
менее 5-7 В [6]. Коэффициент
,
то все расчетные формулы будут справедливы
и для выпрямителя с выходным напряжением
менее 5-7 В [6]. Коэффициент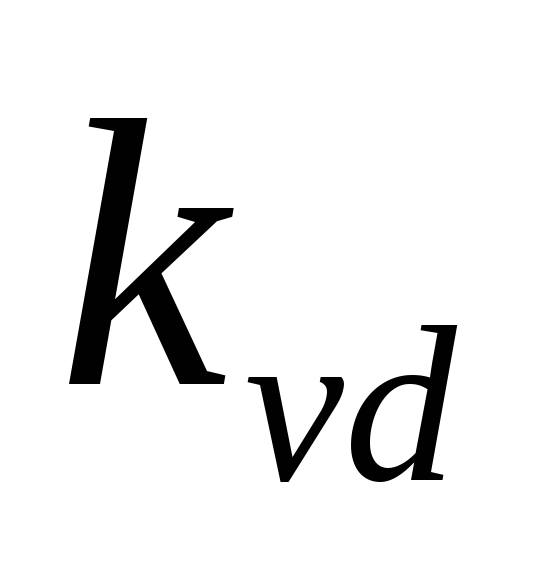 в формуле (2.28) определяется числом
проводящих вентилей, т.е. схемой
выпрямления: для мостовых схем —
в формуле (2.28) определяется числом
проводящих вентилей, т.е. схемой
выпрямления: для мостовых схем —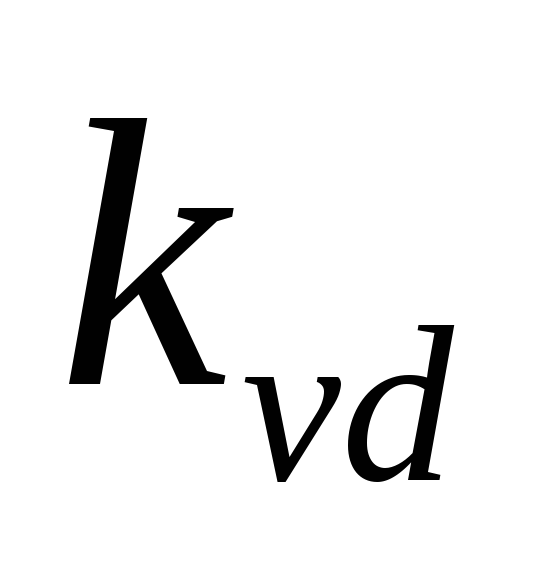 = 2, для остальных схем —
= 2, для остальных схем —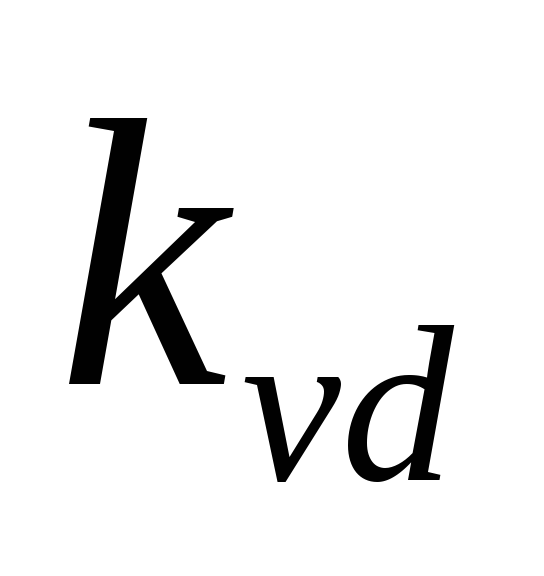 = 1.
= 1.
VII. Переменная составляющая напряжения Коэффициент пульсаций
Периодическая последовательность импульсов тока выпрямителя может быть, на основе разложения в ряд Фурье, представлена выражением
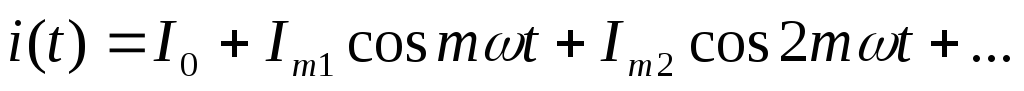 , (11)
, (11)
где m – число фаз выпрямителя, I0 – постоянная составляющая тока выпрямителя, Imi – амплитуда i-той гармонической составляющей тока, члены разложения с синусами пропадут в силу симметричности кривой импульса тока. Постоянная составляющая выпрямленного тока пройдет через сопротивление нагрузки выпрямителя RH и создаст на нем падение напряжения
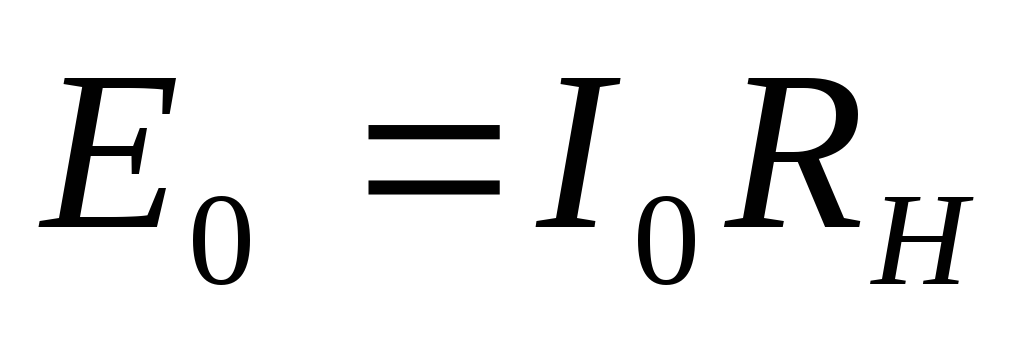 .
.
По
условию фильтрации емкостное сопротивление
конденсатора фильтра 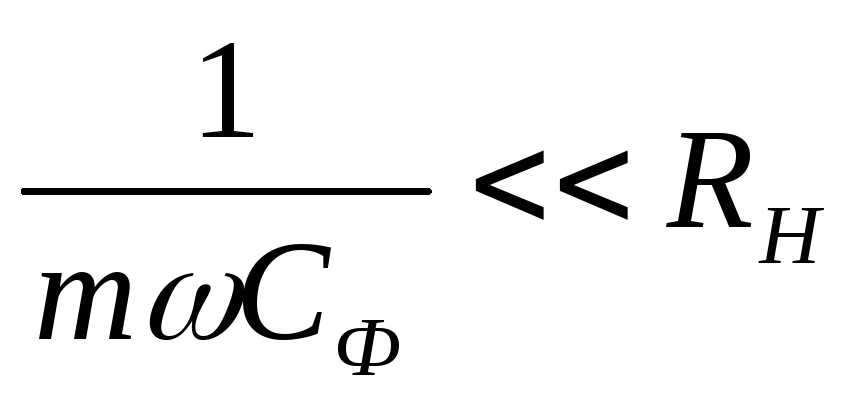 .
Поэтому полное сопротивление нагрузки
для переменной составляющей, состоящее
изRH и СФ,
включенных параллельно (рис.12), определяется
главным образом сопротивлением емкости.
Таким образом, для первой гармоники
выпрямленного тока сопротивление
нагрузки равно
.
Поэтому полное сопротивление нагрузки
для переменной составляющей, состоящее
изRH и СФ,
включенных параллельно (рис.12), определяется
главным образом сопротивлением емкости.
Таким образом, для первой гармоники
выпрямленного тока сопротивление
нагрузки равно 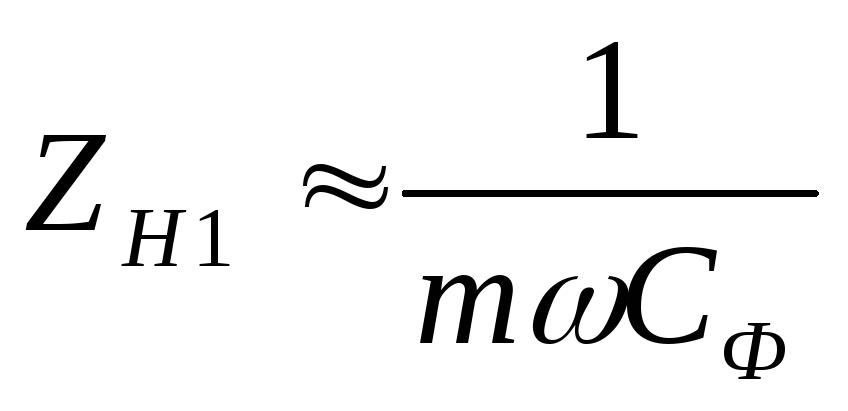 ,
для второй гармоники —
,
для второй гармоники —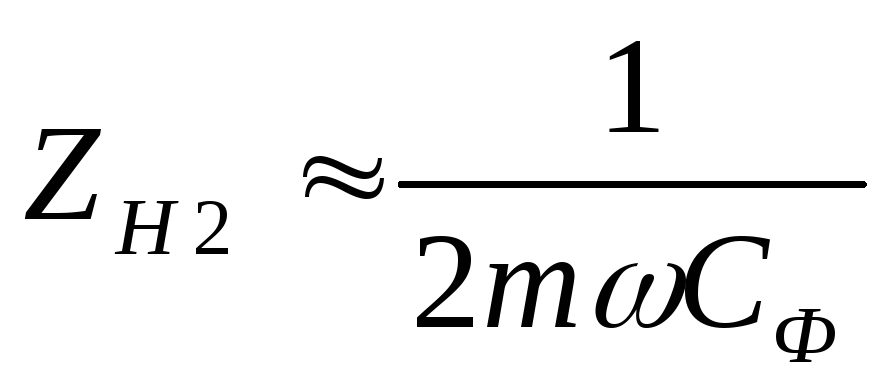 и т.д.
и т.д.
Ввиду того, что сопротивление конденсатора имеет наибольшую величину для первой гармоники, и первая гармоника имеет наибольшую (по сравнению с другими) амплитуду, очевидно, что переменная составляющая напряжения на нагрузке содержит почти исключительно первую гармонику напряжения. Все остальные гармоники очень малы. Поэтому с достаточной для практики точностью можно принять, что переменная составляющая напряжения на нагрузке выпрямителя
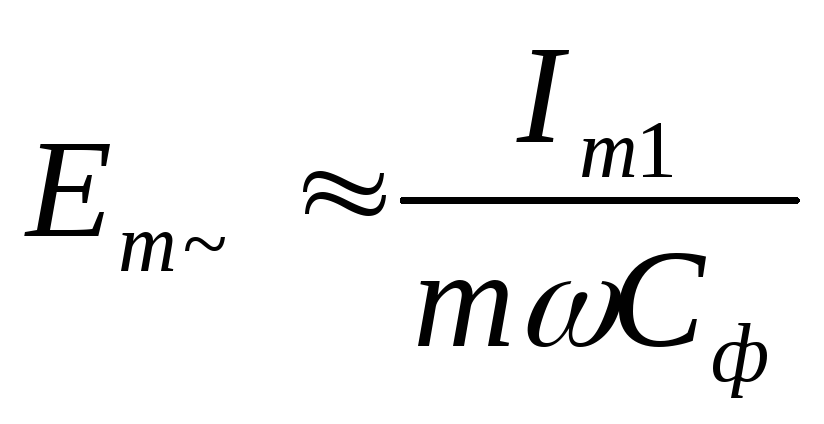 ,
(11)
,
(11)
где для амплитуды первой гармоники, согласно разложению отрезка косинусоиды в ряд Фурье, имеем
. (12)
Подставляя из (12) выражение для Im1 в (11), получим
, (13)
где, если Сф выразить в мкФ, и частоту питающей сети принять равной 50 Гц, имеем для H выражение
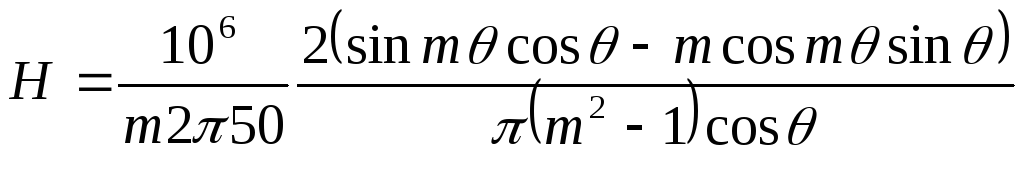 . (14)
. (14)
Кривая зависимости H от параметра A дана на рис.15.
Обычно
пользуются не абсолютным значением
переменной составляющей напряжения Em~,
а ее относительное значение 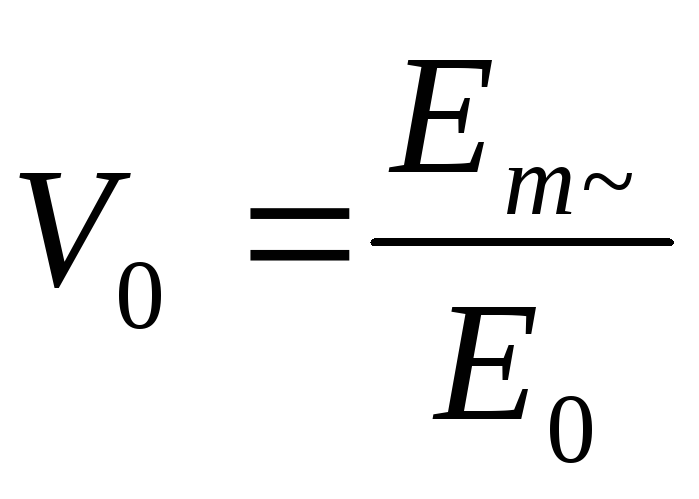 ,
называемымкоэффициентом
пульсаций.
В этом случае из (13)
,
называемымкоэффициентом
пульсаций.
В этом случае из (13)
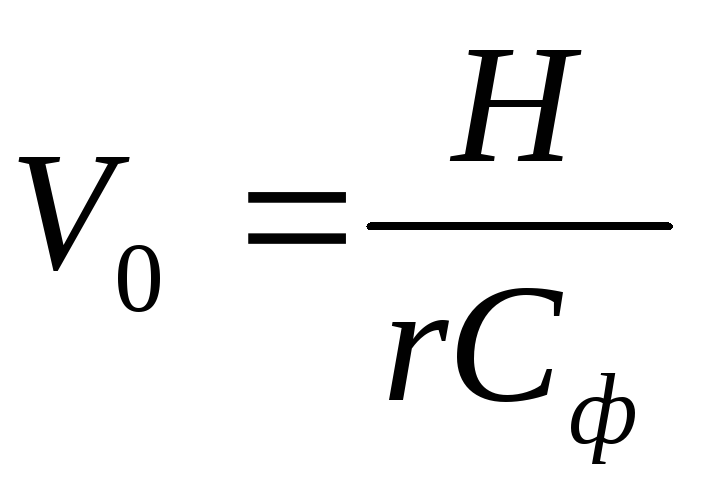 (15)
(15)
или, если для расчета задан коэффициент пульсаций, то
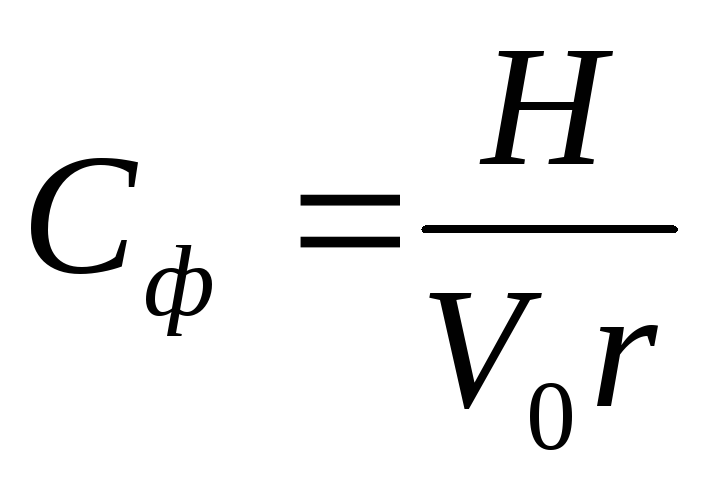 . (16)
. (16)
VIII. Внешняя характеристика выпрямителя
Под
внешней характеристикой выпрямителя
понимают зависимость 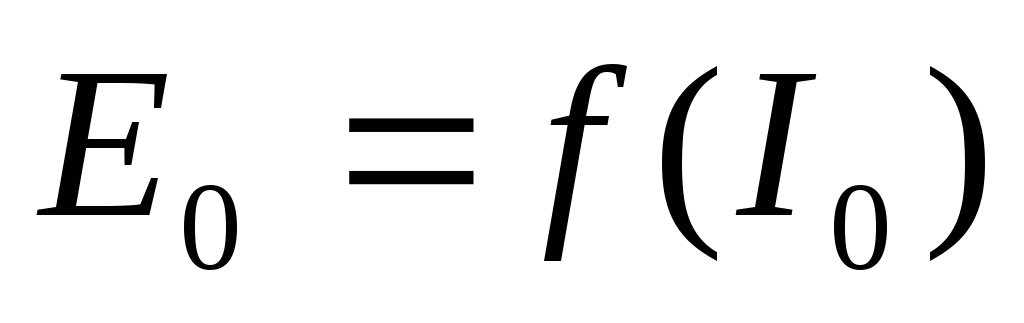 .
Внешняя характеристика выпрямителя
при переменном напряжении на его входе
(напряжении сети) зависит от параметров
выпрямителя. При данныхm, r,
и Em величины E0 и I0 являются
функциями угла отсечки. Действительно,
согласно уравнению (5)
.
Внешняя характеристика выпрямителя
при переменном напряжении на его входе
(напряжении сети) зависит от параметров
выпрямителя. При данныхm, r,
и Em величины E0 и I0 являются
функциями угла отсечки. Действительно,
согласно уравнению (5)
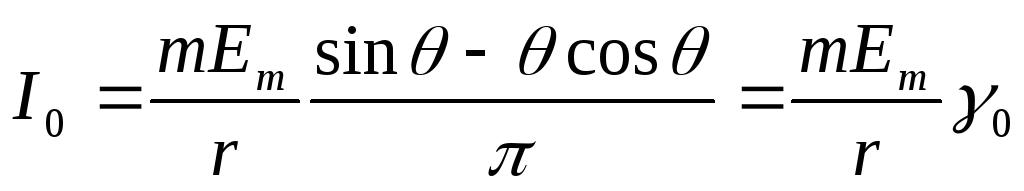 , (17)
, (17)
где 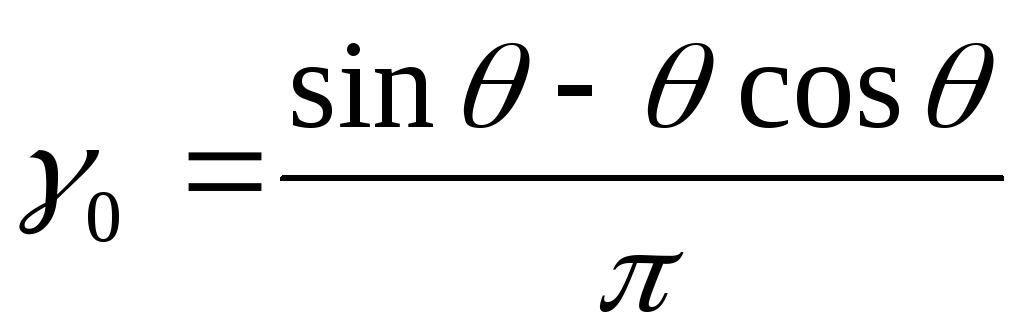 .
.
С
другой стороны, согласно (2), 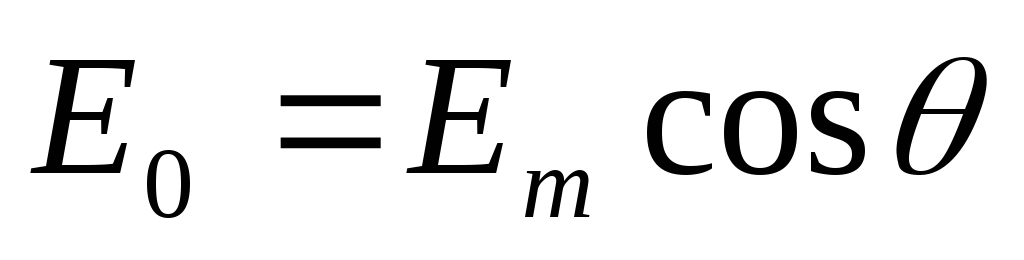 .
Отсюда, т.к. величинаγ0 пропорциональна I0,
а cosθ пропорционален Е0,
то кривая
.
Отсюда, т.к. величинаγ0 пропорциональна I0,
а cosθ пропорционален Е0,
то кривая 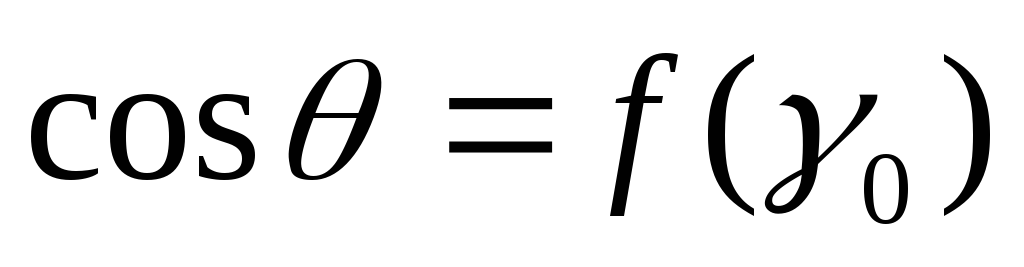 (рис.16)
дает в известном масштабе зависимостьЕ0 от I0.
Необходимо отметить, что при холостом
ходе выпрямителя (I0=0)
выпрямленное напряжение равно амплитуде
напряжения вторичной обмотки Е0= Еm.
Так как обычно Еm значительно выше Е0,
то при сбросе нагрузки напряжение на
зажимах конденсатора резко возрастает
и, если он выбран правильно (допустимое
рабочее напряжение конденсатора < Еm),
может произойти пробой емкости фильтра.
(рис.16)
дает в известном масштабе зависимостьЕ0 от I0.
Необходимо отметить, что при холостом
ходе выпрямителя (I0=0)
выпрямленное напряжение равно амплитуде
напряжения вторичной обмотки Е0= Еm.
Так как обычно Еm значительно выше Е0,
то при сбросе нагрузки напряжение на
зажимах конденсатора резко возрастает
и, если он выбран правильно (допустимое
рабочее напряжение конденсатора < Еm),
может произойти пробой емкости фильтра.
IX. Коэффициент сглаживания фильтра
П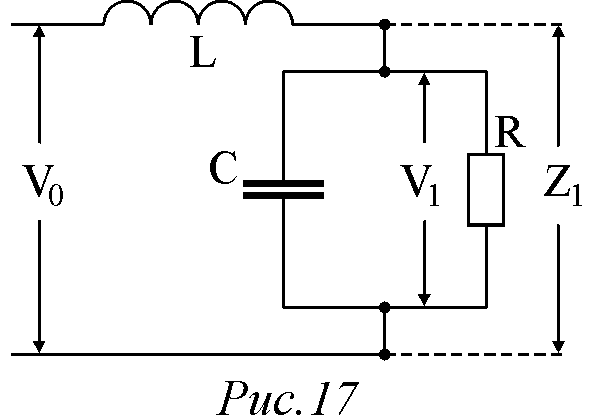 усть
на входе фильтра (рис.17) действует
некоторая переменная составляющая
выпрямленного напряжения
усть
на входе фильтра (рис.17) действует
некоторая переменная составляющая
выпрямленного напряжения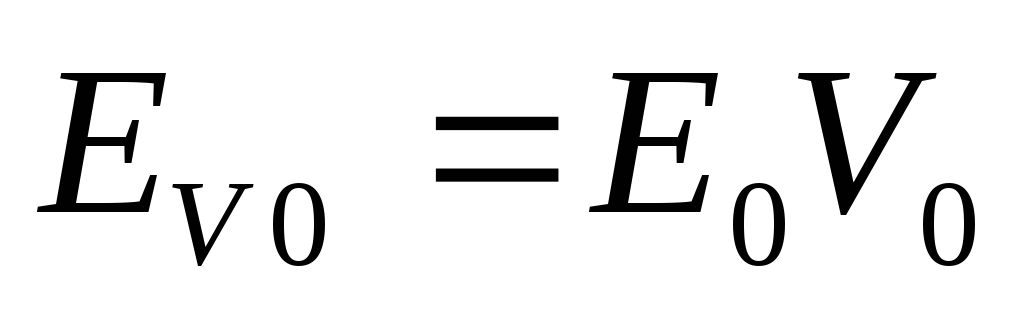 .
При этом на выходе фильтра получится
напряжениеEV1,
равное
.
При этом на выходе фильтра получится
напряжениеEV1,
равное
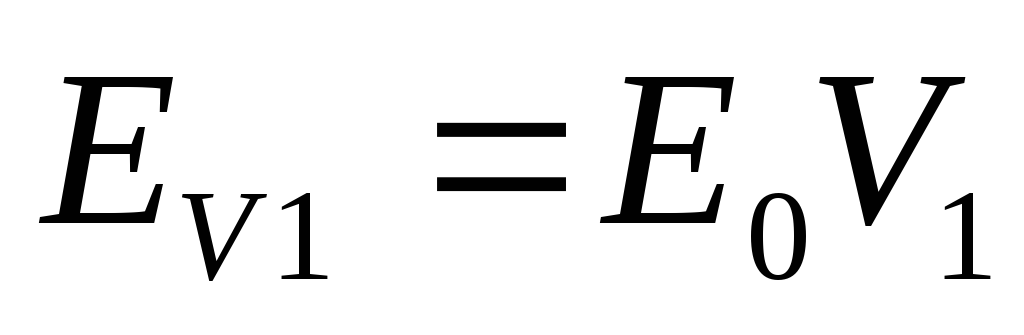 , (18)
, (18)
откуда коэффициент пульсаций на выходе фильтра
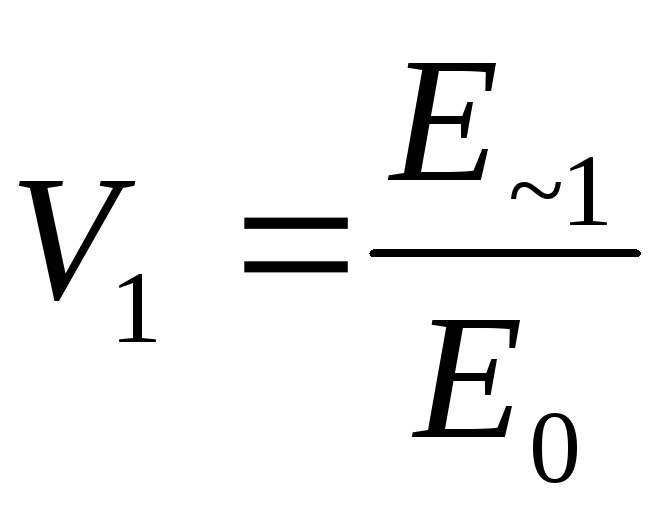 . (18а)
. (18а)
Уменьшение пульсаций выпрямленного напряжения определяется коэффициентом сглаживания фильтра, показывающем во сколько раз фильтр ослабляет первую гармонику переменной составляющей выпрямленного напряжения, то есть
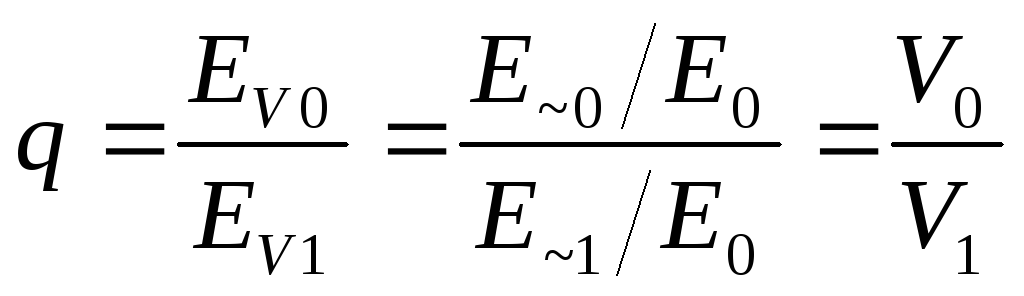 .
(19)
.
(19)
Р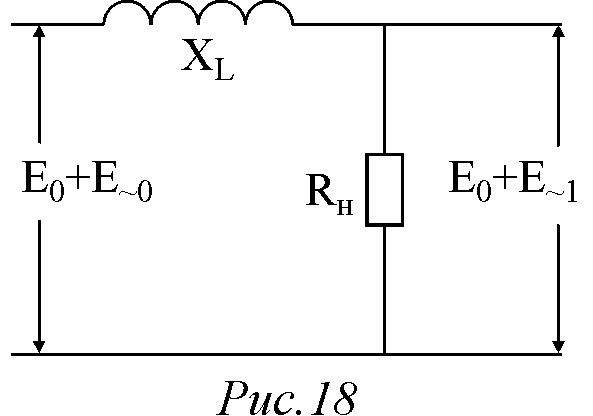 анее
было рассмотрено влияние емкостного
фильтра на коэффициент пульсацийV0.
Рассмотрим теперь влияние Г-образных
фильтров типа LC и RC (рис.11б и 11г) на уменьшение величины
пульсаций выпрямленного напряжения.
Для этого, предварительно для схемы
рис.18 (только индуктивный фильтр),
исследуем влияние индуктивности фильтра
на уменьшение величины пульсаций.
Простоты ради считаем активное
сопротивление индуктивности равно
нулю. Напряжение входа схемы
перераспределяется между индуктивным
сопротивлением и сопротивлением
нагрузки. Пусть XL1 – величина сопротивления индуктивности
для 1-ой гармоники периодической
составляющей E~0на
входе фильтра. Тогда величина переменной
составляющей 1-ой гармоники на выходе
фильтра
анее
было рассмотрено влияние емкостного
фильтра на коэффициент пульсацийV0.
Рассмотрим теперь влияние Г-образных
фильтров типа LC и RC (рис.11б и 11г) на уменьшение величины
пульсаций выпрямленного напряжения.
Для этого, предварительно для схемы
рис.18 (только индуктивный фильтр),
исследуем влияние индуктивности фильтра
на уменьшение величины пульсаций.
Простоты ради считаем активное
сопротивление индуктивности равно
нулю. Напряжение входа схемы
перераспределяется между индуктивным
сопротивлением и сопротивлением
нагрузки. Пусть XL1 – величина сопротивления индуктивности
для 1-ой гармоники периодической
составляющей E~0на
входе фильтра. Тогда величина переменной
составляющей 1-ой гармоники на выходе
фильтра
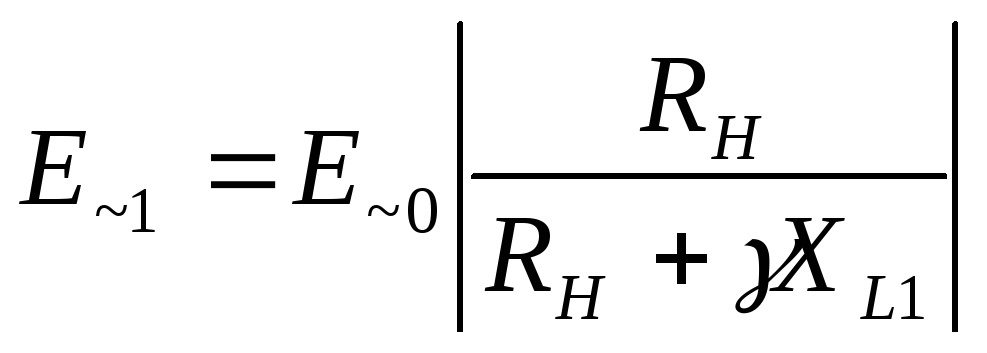 . (20)
. (20)
Для более эффективной фильтрации принимают
 . (21)
. (21)
Тогда
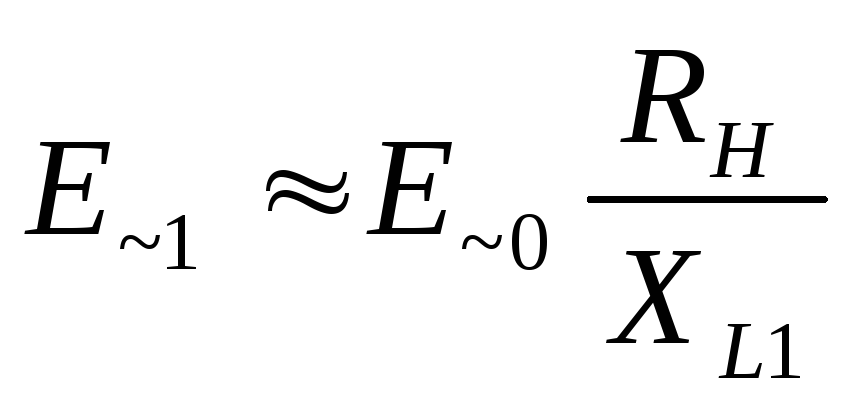 . (22)
. (22)
Так как активным сопротивлением индуктивности пренебрегли, считаем (ради упрощения рассуждений), что постоянная составляющая выпрямленного тока не вызывает падения напряжения на выходе фильтра, т.е. величина Е0 на входе и выходе фильтра одна и та же. Отсюда, для того, чтобы определить связь между коэффициентами пульсаций на входе и выходе фильтра, разделим правую и левую части на Е0. Получим
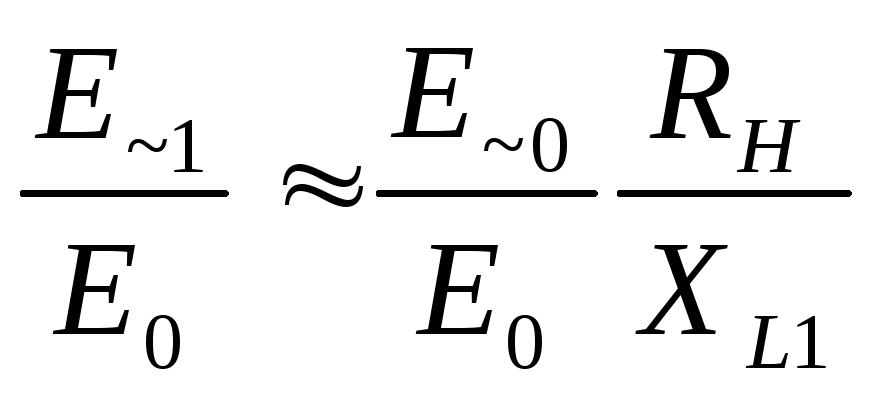
или
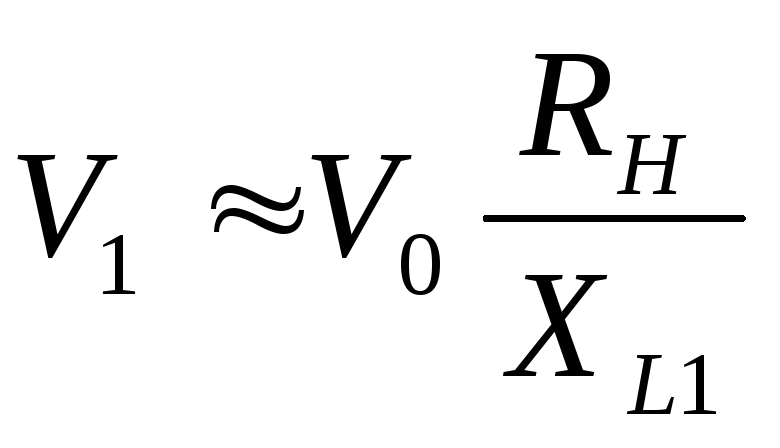 . (22а)
. (22а)
Учитывая формулу (19), коэффициент фильтрации определится из (22а) как
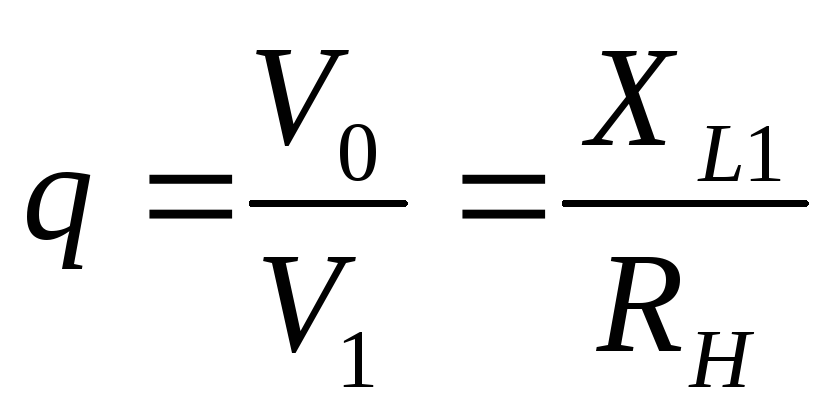 . (23)
. (23)
Так как сопротивление индуктивности, равное ωL будет для высших составляющих гармоник пульсирующего напряжения более высоким (пропорциональном номеру гармоники), то, как видно из (22а) и (23), фильтрующее воздействие индуктивности по отношению к ним оказывается более высоким. Кроме того, при разложении пульсирующего на входе фильтра напряжения в ряд Фурье удельный вес 2-ой и т.д. составляющих падает с ростом номера гармоники. Поэтому при расчете коэффициентов сглаживания и коэффициентов пульсаций влиянием высших гармонических составляющих можно пре с ростом номера гармоники. Поэтому при расчете коэффициентов сглаживания и коэффициентов пульсаций влиянием высших гармонических составляющих можно пренебречь и, таким образом, расчет вести только по отношению к 1-ой гармонике выпрямленного напряжения.
Л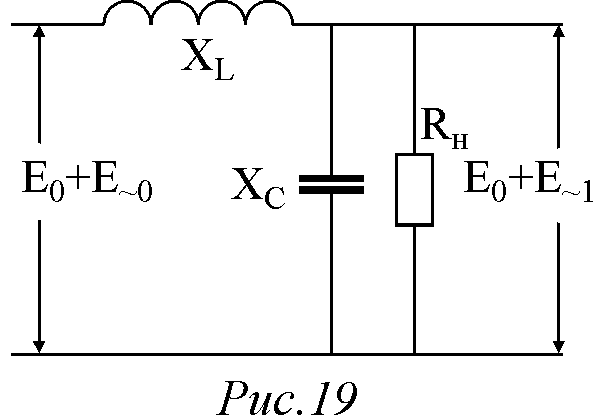 учшими
фильтрующими качествами по сравнению
с одной индуктивностью является
Г-образныйLC фильтр (рис.11б), который представим в
обозначениях рис.19.
учшими
фильтрующими качествами по сравнению
с одной индуктивностью является
Г-образныйLC фильтр (рис.11б), который представим в
обозначениях рис.19.
Сопротивление параллельно включенной емкости Cф и сопротивление RH определяется как
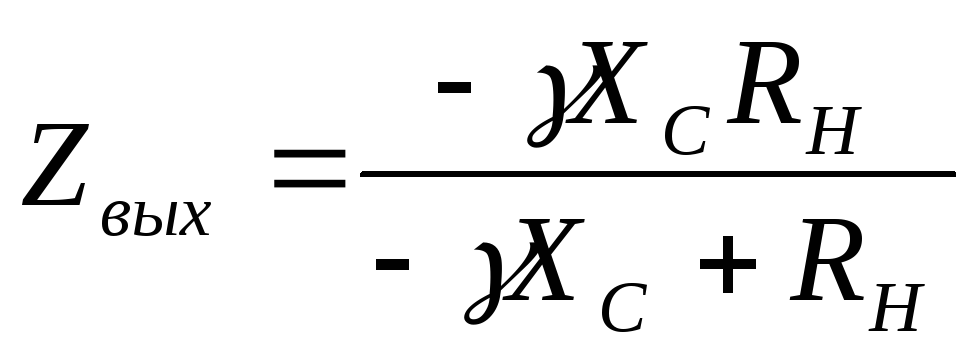 ,
(24)
,
(24)
где
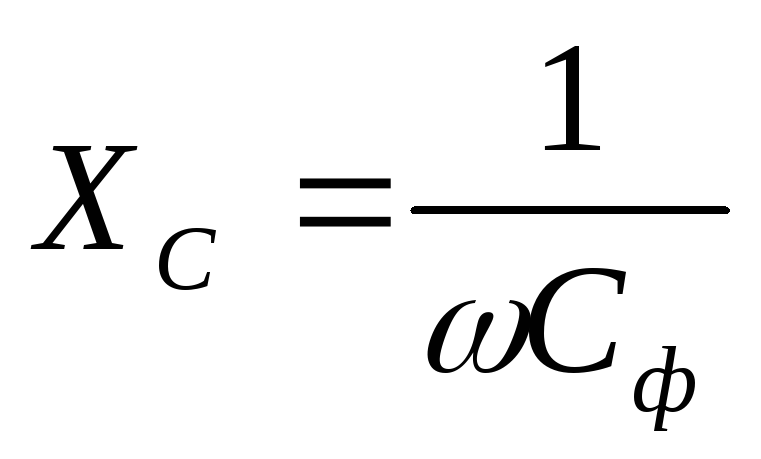 .
.
Для фильтров обычно выполняется условие
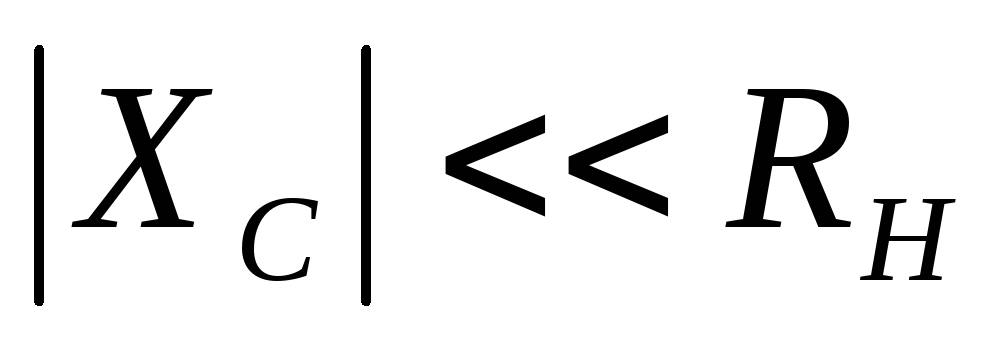 .
(25)
.
(25)
Тогда (24) перепишем в виде

или по модулю
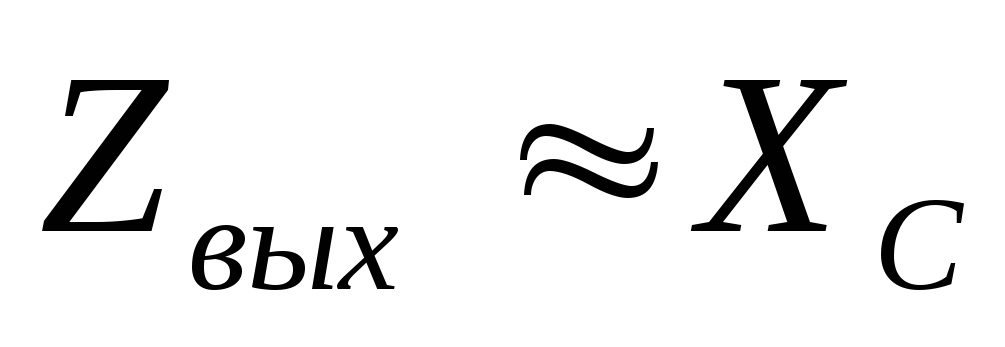 .
.
Очевидно, если (25) выполняется для 1-ой гармоники пульсирующего напряжения, то тем более оно будет выполняться для более высокочастотных его составляющих. Поэтому при расчете пульсаций, принимая во внимание неравенство (25), активное сопротивление нагрузки не учитываем, а сопротивление емкости XC рассматриваем для 1-ой гармоники — XC1.
Таким образом, схему рис.19 можно представить как делитель, где переменная составляющая перераспределяется между индуктивным и емкостным сопротивлениями. Тогда, аналогично (20), имеем выражение
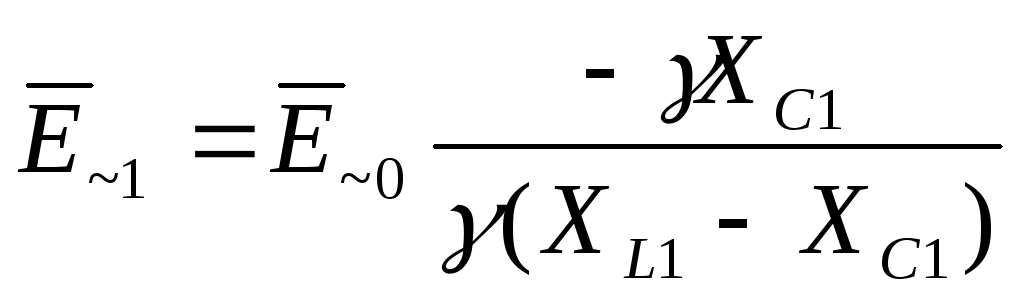 ,
,
или
для соотношения модулей E~1 и E~0 (без учета аргументов комплексных
амплитуд 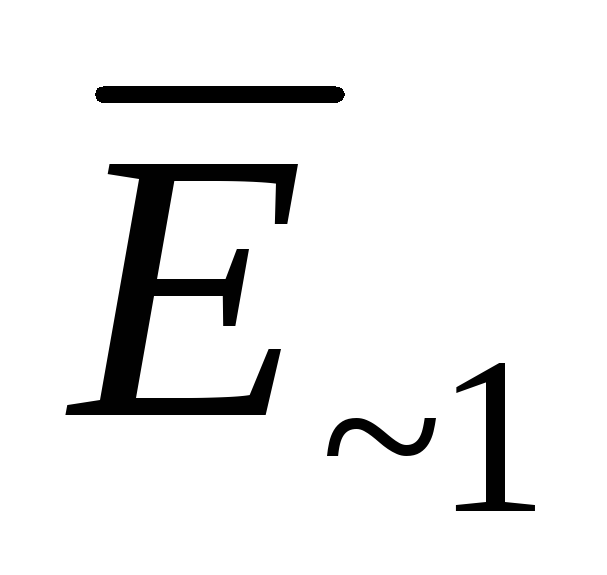 и
и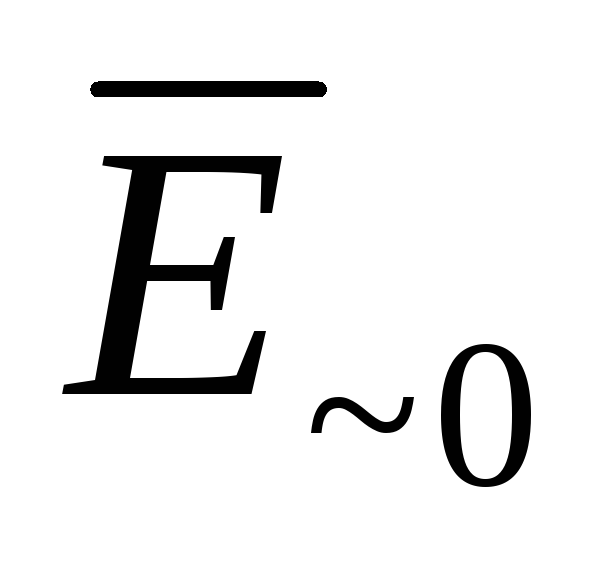 )
имеем
)
имеем
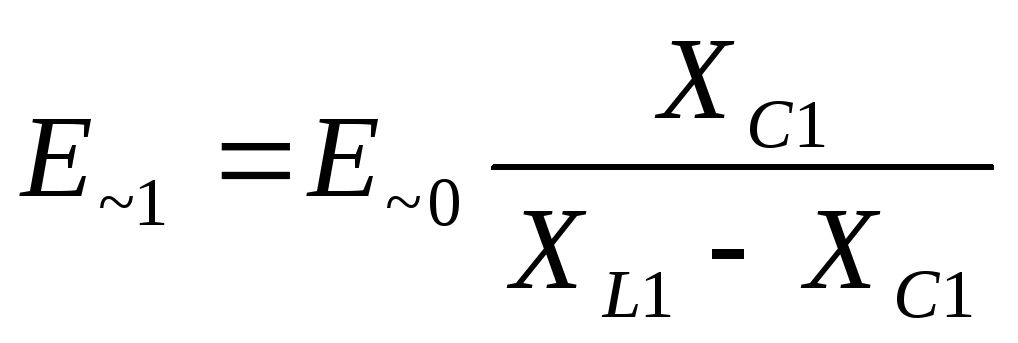 . (26)
. (26)
Отсюда, коэффициент сглаживания фильтра
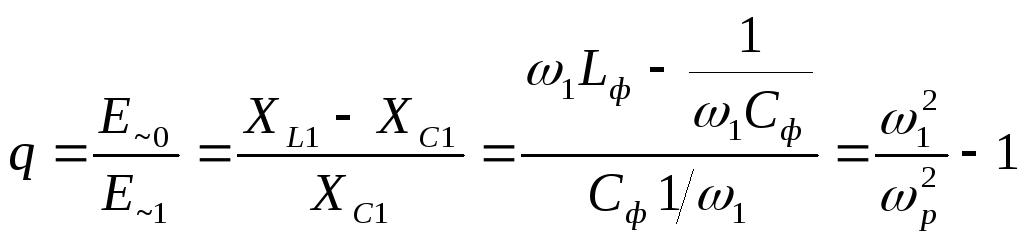 , (27)
, (27)
где 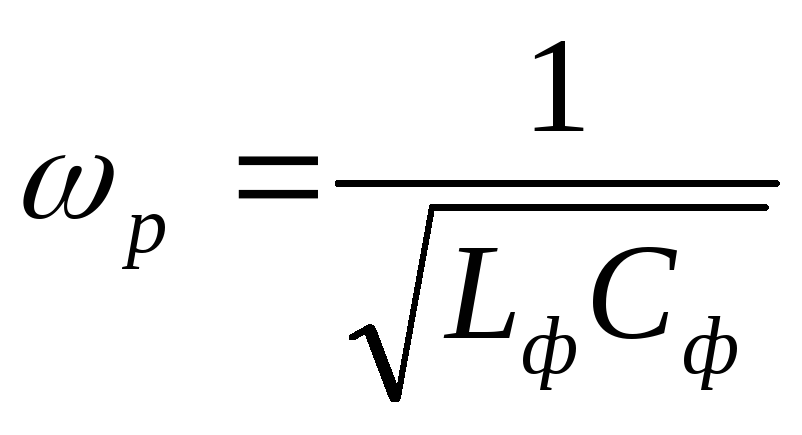 — резонансная угловая частота фильтра,ω1 – угловая частота 1-ой гармоники.
— резонансная угловая частота фильтра,ω1 – угловая частота 1-ой гармоники.
Из объяснения неравенств (21) и (25) имеем для фильтра LC
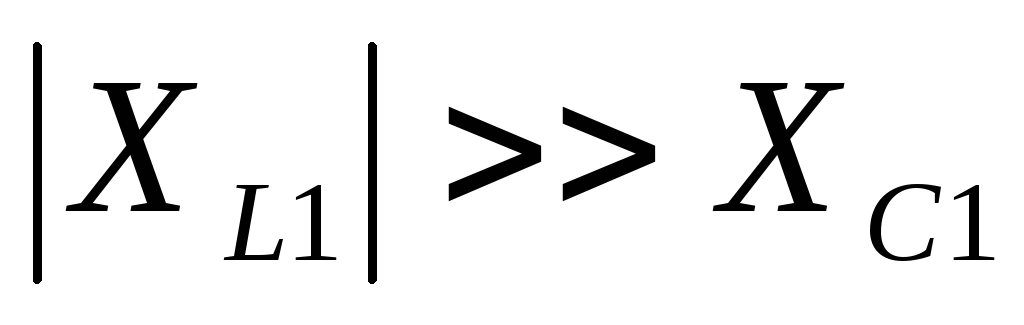 ,
то есть
,
то есть 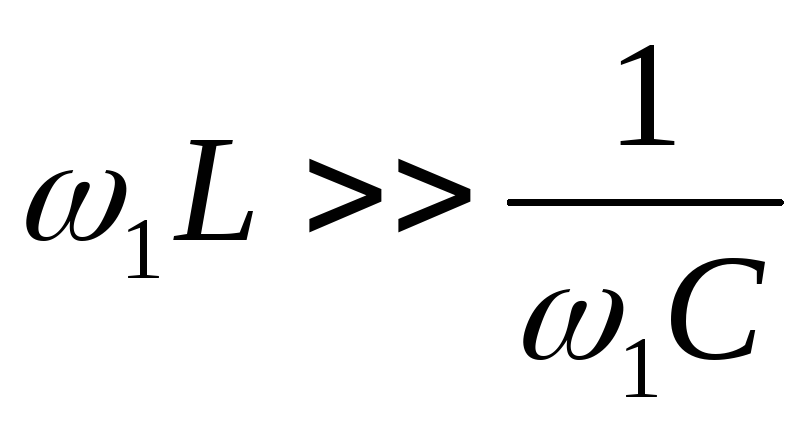 ,
,
откуда
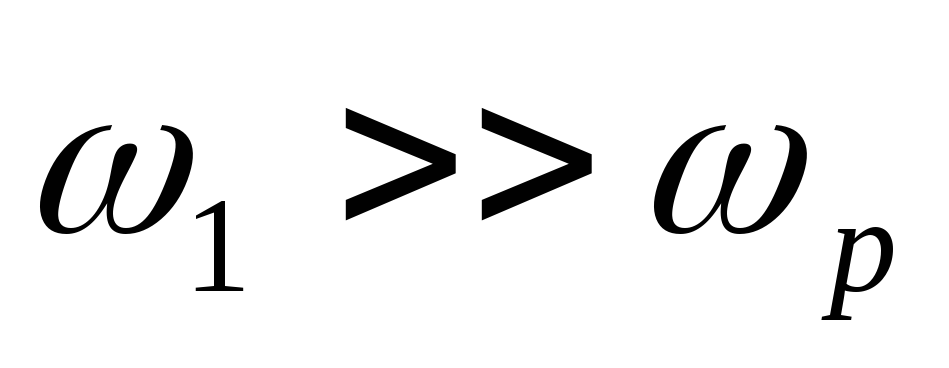 . (28)
. (28)
Значит, соотношение (27) приближенно можем переписать в более простом виде
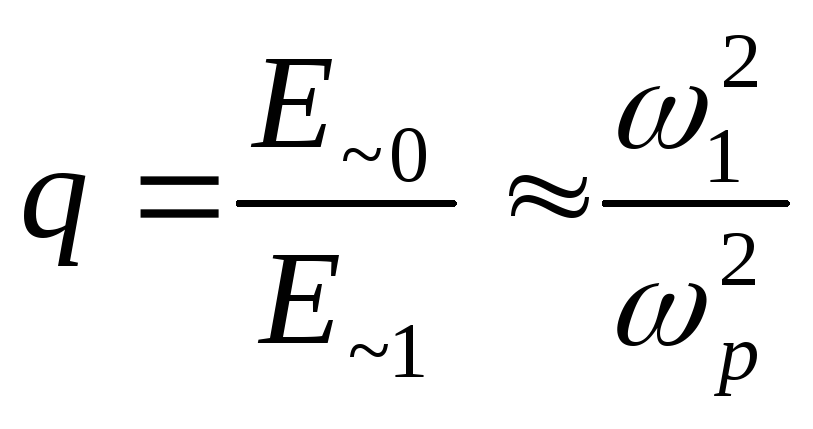
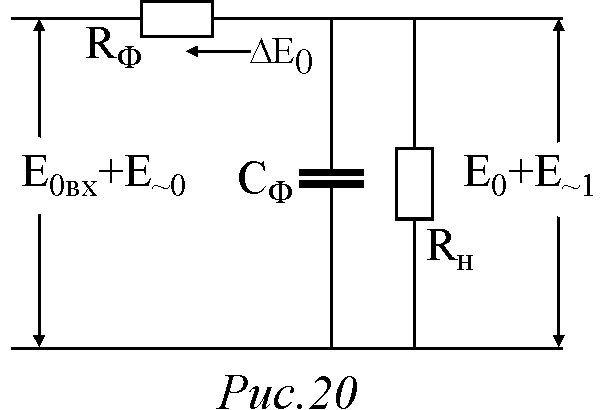 .
(27а)
.
(27а)
Г-образный фильтр RC (рис.11г) используется, как правило, в источниках напряжения, в которых потребление тока невелико и поэтому относительное падение постоянной составляющей напряжения на сопротивлении Rф небольшое.
Для обозначений, принятых на рис.20, имеем: Е0вх – постоянная составляющая напряжения на входе фильтра, равная Е0вх = ΔЕ0 + Е0, ΔЕ0 –падение постоянной составляющей напряжения на сопротивлении фильтра.
Из рис.20 имеем очевидное соотношение
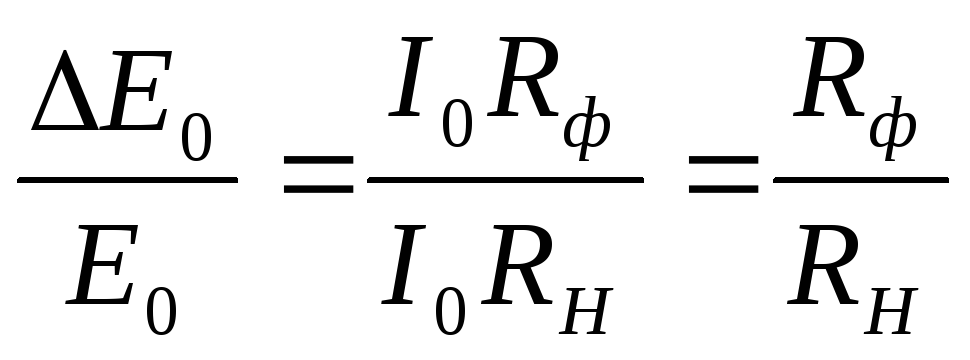 .
.
Как
уже отмечалось, обычно выполняется
соотношение 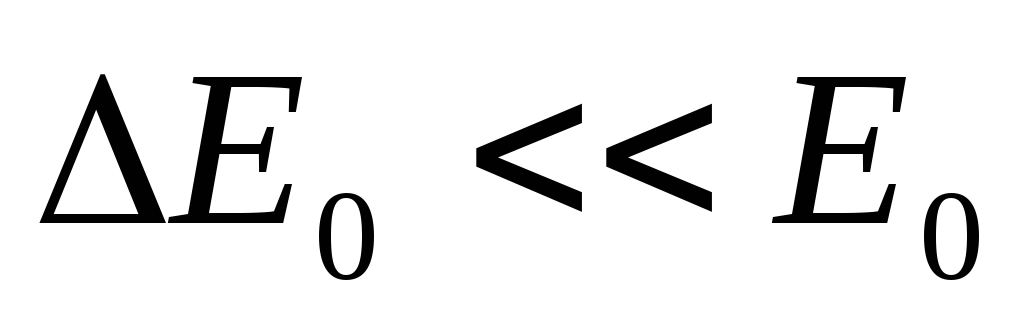 ,
откуда
,
откуда
 . (29)
. (29)
При
этом емкость фильтра выбирают из условия 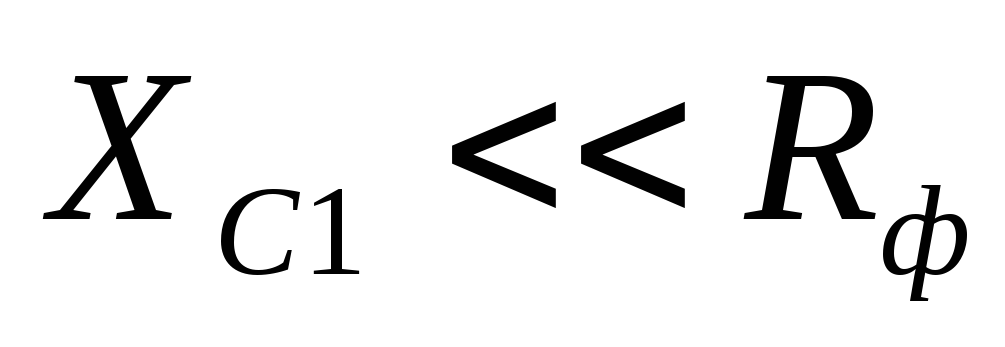 ,
что дает неравенства
,
что дает неравенства
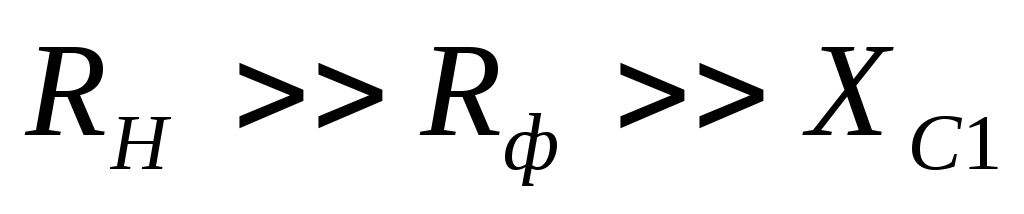 . (30)
. (30)
Неравенства (30) обеспечивают выполнение условия (25). Это позволяет рассчитывать ослабление переменной составляющей RC фильтром, представляя его для переменной составляющей как RC делитель напряжения. Тогда для коэффициента сглаживания RC фильтра имеем
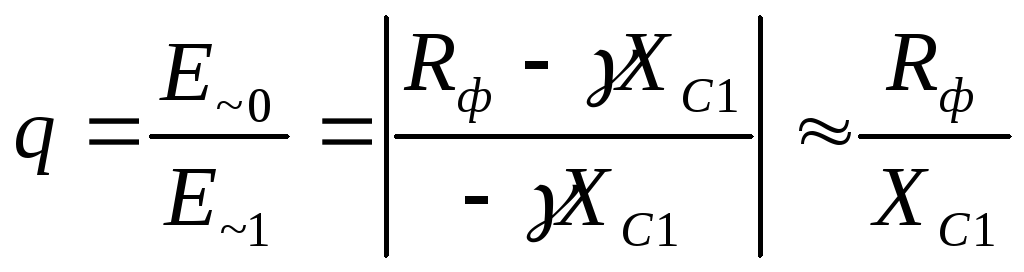 ; (31)
; (31)
или
т.к. через коэффициенты пульсаций
коэффициент сглаживания запишется в
виде 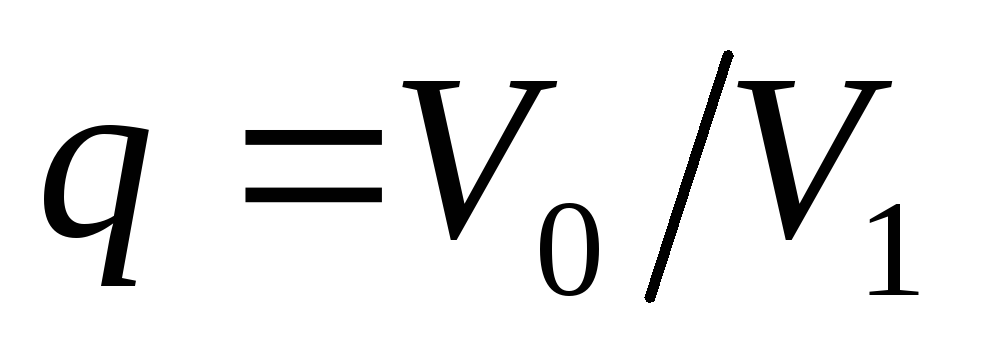 ,
получим связь между коэффициентами
пульсаций на входе и выходе фильтра в
виде
,
получим связь между коэффициентами
пульсаций на входе и выходе фильтра в
виде
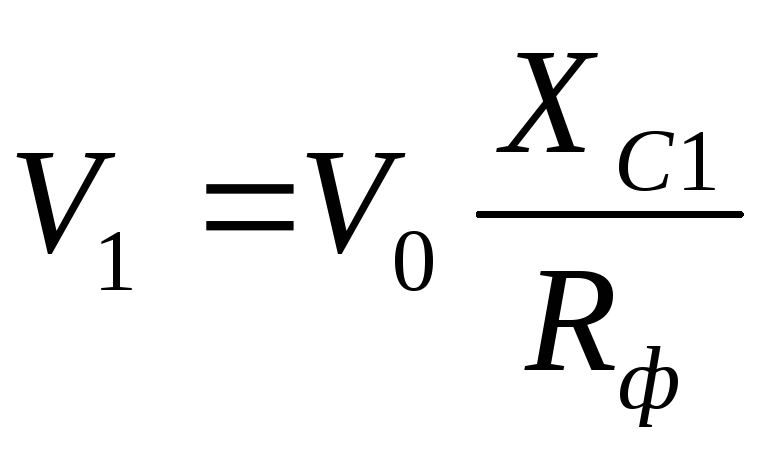 . (32)
. (32)
В заключение рассмотрим определение коэффициента сглаживания в случае двухзвенного фильтра (рис.21).
Н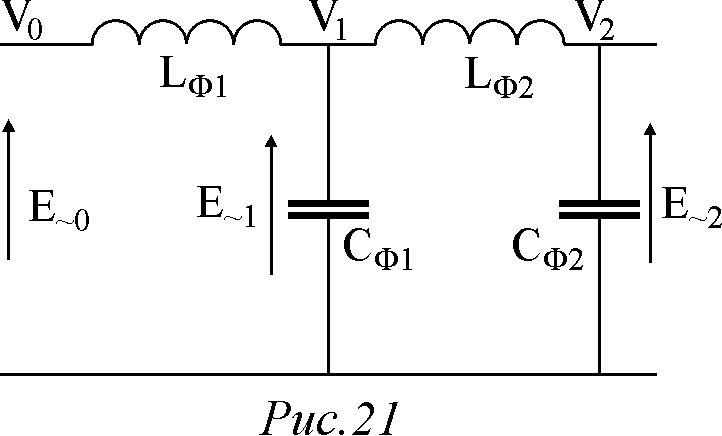 а
рисункеЕ~0, Е~1, Е~2 – уровень
первой гармоники на входе фильтра, после
первого звена и на выходе фильтрации,
соответственно. Для этого случая запишем
коэффициенты сглаживания 1-ым и 2-ым
звеньями:
а
рисункеЕ~0, Е~1, Е~2 – уровень
первой гармоники на входе фильтра, после
первого звена и на выходе фильтрации,
соответственно. Для этого случая запишем
коэффициенты сглаживания 1-ым и 2-ым
звеньями:
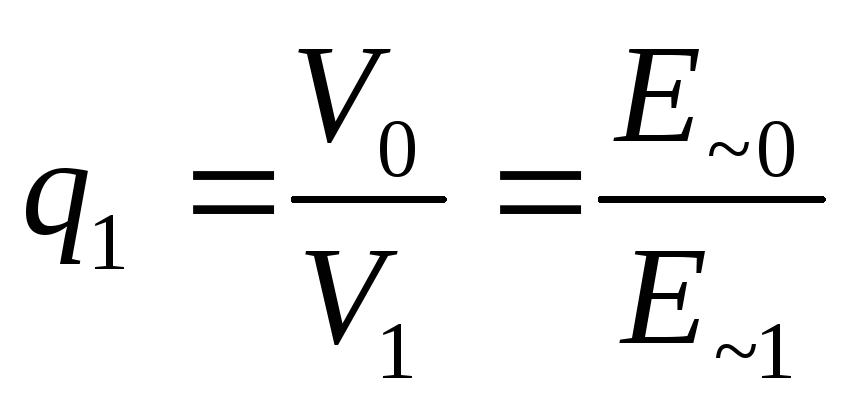 ;
; 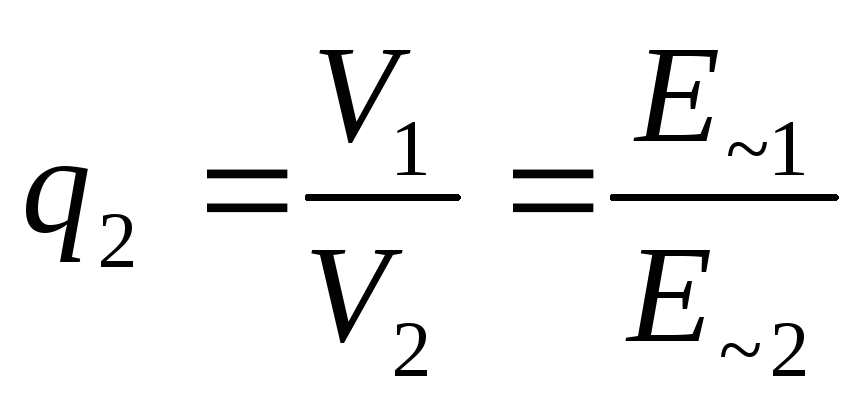 .
.
Итоговый коэффициент сглаживания
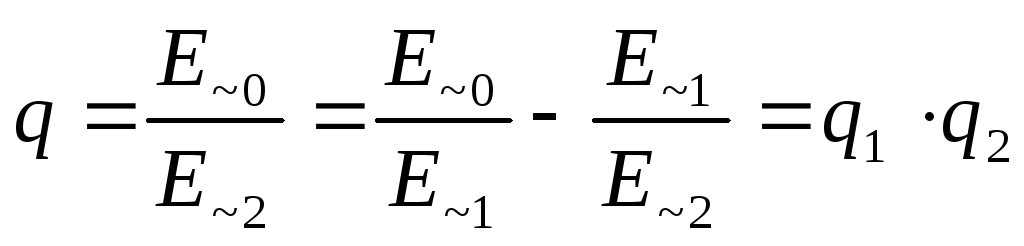 .
.
Таким образом, общий коэффициент сглаживания равен произведению коэффициентов сглаживания отдельных звеньев. Аналогично рассчитываются многозвенные фильтры.
Изложенное позволяет по данным опыта определять величины коэффициентов пульсаций и сглаживания, а также (в случае необходимости) по заданному допустимому уроню пульсаций рассчитать фильтр.
При
выводах мы положили справедливым
неравенство 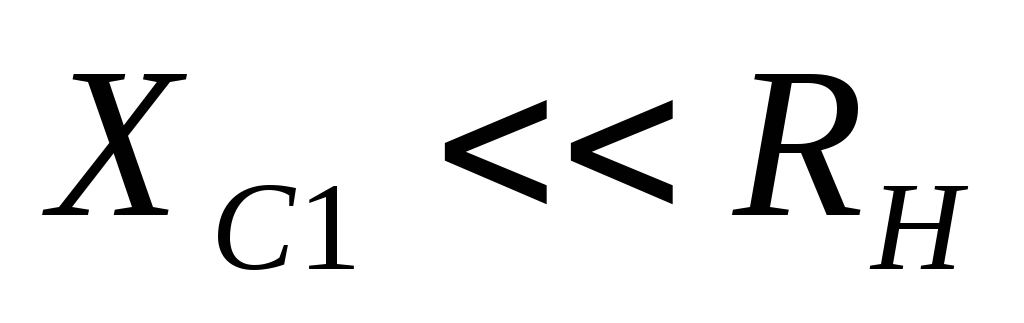 .
Таким образом, пренебрегли шунтирующим
сопротивлением нагрузки. В общем случае,
чем хуже выполняется это неравенство,
тем больше влияние RH на
уменьшение фильтрации. В этом можно
убедиться, если исследовать уровень
пульсаций при изменении величины
сопротивления нагрузки RH.
.
Таким образом, пренебрегли шунтирующим
сопротивлением нагрузки. В общем случае,
чем хуже выполняется это неравенство,
тем больше влияние RH на
уменьшение фильтрации. В этом можно
убедиться, если исследовать уровень
пульсаций при изменении величины
сопротивления нагрузки RH.
Основы преобразовательной техники — Стр 4
31
Лекция №6. Трехфазные мостовые выпрямители.
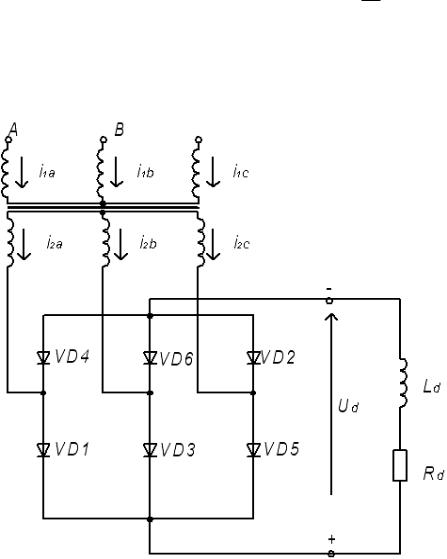
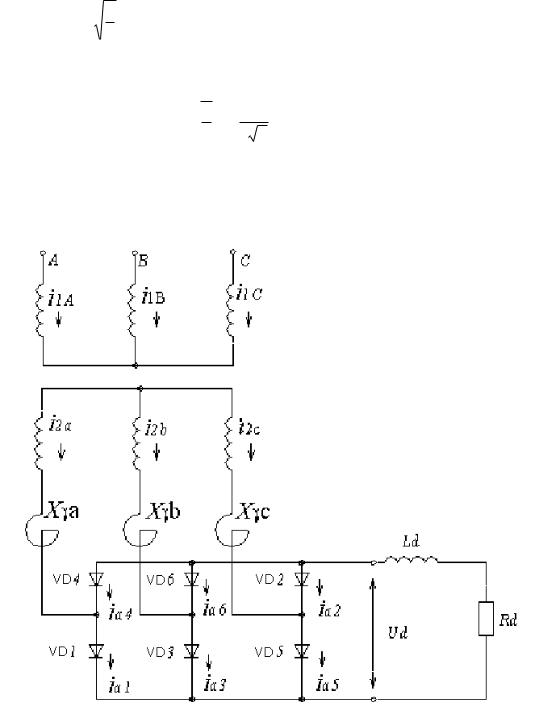
Принципиальная схема мостового выпрямителя изображена на рис.6.1.
Режим Lγ = 0, Lc = 0, ra = 0, Ld → ∞ .
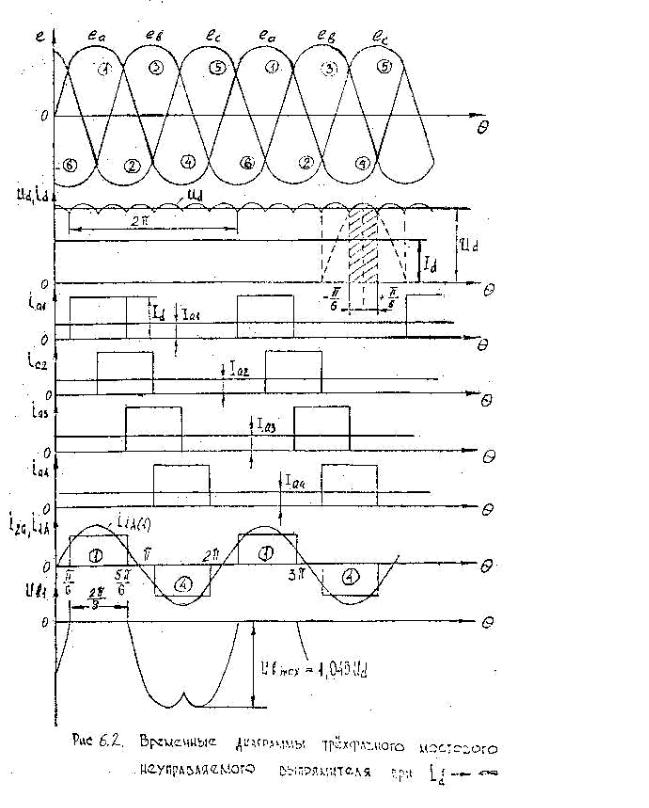
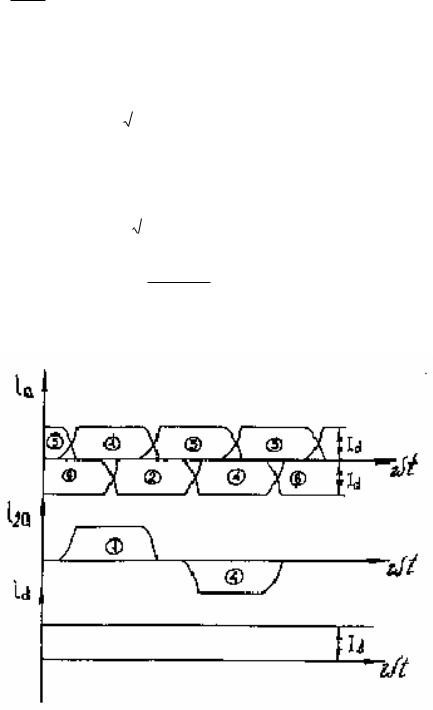
Схема выпрямителя содержит выпрямительный мост, состоящий из шести диодов VD1…VD6. Временные диаграммы приведены на рис.6.2.
Из катодной группы в открытом состоянии будет находится тот из диодов, напряжение анода которого имеет положительную полярность относительно нулевого вывода и наибольшую величину по сравнению с другими диодами. Из анодной группы открытое состояние принимает тот из вентилей, напряжение катода которого в данный момент является наибольшим и имеет отрицательную полярность. Иными словами в проводящем состоянии будут находится те два накрест лежащих диода выпрямительного моста, между которыми действует в проводящем направлении наибольшее линейное напряжение.
На диаграмме фазных напряжений (рис.6.2.) указаны интервалы проводимости диодов. Интервал проводимости каждого вентиля составляет 23π , а интервал совместной
работы двух диодов равен π3 . За период напряжения питания происходит 6 переключений
диодов. Схема работает в шесть тактов в связи с чем, ее часто называют шестипульсной. Кривая ud (рис.6.2.) состоит из участков линейных напряжений вторичных обмоток трансформатора.
32
Рис.6.1. Принципиальная схема трехфазного мостового выпрямителя.
33
Среднее значение выпрямленного напряжения находят по среднему значению ud за период повторяемости p/3 (заштрихованный участок на рис.6.2):
|
| 3 | π / 6 |
|
| 3 |
| U2Л = 2,34 ×U2Ф . | |
U d | = |
| ×U2Л × cosθdθ = | 2 | |||||
2 | |||||||||
π | ò | ||||||||
|
|
|
| π | |||||
|
|
| −π / 6 |
|
|
|
|
| |
Напряжение на нагрузке по сравнению с трёхфазной схемой с нулевым выводом получается вдвое больше. Это объясняется тем, что трёхфазная мостовая схема представляет собой как бы две трёхфазные схемы с нулевым выводом, выходы которых включаются последовательно. При заданном напряжении Ud здесь требуется вдвое меньшее напряжение
U2:
U2Ф = 3π6 U d = 0,425×U d .
Коэффициент пульсаций по первой гармонике:
КП (1) | = | U dm(1) | = | 2 | . | ||
| U d | m2 | -1 | ||||
|
|
|
|
| |||
Поскольку период повторяемости кривой Ud равен 2p/6, трёхфазная мостовая схема эквивалентна шестифазной в отношении коэффициента пульсаций и частоты её первой гармоники, то есть m=6,
КП | = |
|
| 2 | = 0,057 | = 5,7 %. |
| 2 | -1 | ||||
| 6 |
|
| |||
Таким образом, амплитуда первой гармоники пульсации составляет 5,7% от напряжения Ud против 25% для трёхфазной схемы с нулевым выводом. Частота первой гармоники 300Гц, второй – 600Гц и так далее. Ток нагрузки из-за наличия в ней индуктивности сглажен:
Id = U d . Rd
Поскольку каждый вентиль проводит ток в течение трети периода, среднее значение анодного тока Iа=1/3*Id .Кривые токов вентилей показаны на рис.6.2.
При открытом состоянии двух вентилей выпрямительного моста другие четыре вентиля закрыты, приложенным к ним обратным напряжением, максимальное значение которого
Uв.max = 
 3 ×
3 × 
 2 ×U2Ф =
2 ×U2Ф = 
 6 ×U2Ф =
6 ×U2Ф = 
 6 3π6 U d = 1,045×U d .
6 3π6 U d = 1,045×U d .
Таким образом, вентили в трехфазной мостовой схеме следует выбирать на напряжение близкое к Ud.
Кривая тока вторичной обмотки трансформатора определяется токами двух вентилей, подключенных к данной фазе. Один из вентилей входит в анодную группу, а другой в катодную. Так, например, ток i2а состоит из токов вентилей VD1и VD4. Вторичный ток является переменным, имеет форму прямоугольных импульсов с амплитудой Id и паузой между импульсами длительностью p/3, когда оба вентиля фазы закрыты. Постоянная составляющая во вторичном токе отсутствует, в связи с чем магнитный поток вынужденного намагничивания магнитопровода трансформатора в мостовой схеме не создаётся.
Для расчёта сечения вторичных обмоток трансформатора определим действующее значение тока вторичной обмотки:
| 1 |
| 5π / 62 |
| 1 |
| 5π / 6 | 2 |
| 2 |
|
| ||
I2 = |
|
| × | òi2 dθ = |
|
|
| × | òId dθ = | 3 | ×Id . | |||
π | π | |||||||||||||
|
|
|
| π / 6 |
|
|
|
| π / 6 |
|
|
|
|
|
34
Ток первичной обмотки трансформатора:
i1=кi2,
где к=w2/w1.
Действующее значение:
2
I1=к 3 Id.
Первая гармоника потребляемого тока, как и во всех неуправляемых выпрямителях (приγ=0) совпадает по фазе с напряжением питания.
Расчётные мощности:
ST = S1 = S2 = 3× 
 23 Id × 3π6 ×U d = π3 × Pd = 1.045× Pd .
23 Id × 3π6 ×U d = π3 × Pd = 1.045× Pd .
Учёт коммутации вентилей в схеме трёхфазного мостового неуправляемого выпрямителя.
Lγ ¹ 0 , LC ¹ 0, ra=0, Ld ® ¥ .
Эквивалентная схема приведена на рис.6.3.
Рис.6.3. Схема трёхфазного мостового неуправляемого выпрямителя с учётом индуктивностей рассеяния трансформатора.
Ввиду наличия индуктивности рассеяния трансформатора и индуктивности сети каждый переход тока с одного вентиля на другой в пределах анодной и катодной групп происходит в течении интервала коммутации γ. На эквивалентной схеме указанные индук-
35
тивности учитываются приведенными ко вторичной обмотке трансформатора “анодными” реактивными сопротивлениями хγ:
xγ | æ w2 | ö | 2 |
= xc ç | ÷ | + xтр , | |
| è w1 | ø |
|
U 2
где xc= лин — эквивалентное индуктивное сопротивление сети;
Sк.з.
Uлин – линейное напряжение сети;
Sк.з. – мощность трёхфазного короткого замыкания сети.
xтр=xS2+xS1(w2/w1)2,
где xS2 и xS1 — индуктивности рассеяния вторичной и первичной обмоток трансформатора. Среднее значение коммутационного снижения напряжения:
|
|
|
|
|
|
|
| |
DU | dγ | = | 3 6 | (1- cosγ )×U |
| , | ||
2π | 2 | |||||||
|
|
|
| |||||
|
|
|
|
|
| |||
U d | = U do − U dγ . |
|
| |||||
Угол g может быть найден из уравнения:
1- cosγ = | 2 | xγ | × Id | . |
|
|
| ||
|
| 2 ×U2 | ||
Уравнение внешней характеристики:
Ud = Udo — 3× Id × xγ .
π
Уменьшение напряжения на нагрузке с увеличением её тока связано с повышением коммутационных падений напряжения ввиду роста угла коммутации γ. Временные диаграммы токов, учитывающие явления коммутации приведены на рис.6.4.
Рис.6.4. Временные диаграммы токов, учитывающие явление коммутации.
Мы рассмотрели режим, когда попеременно проводят ток два или три диода (режим 2-3). При увеличении тока Id или сопротивления хγ может наступить режим, когда ток будут проводить сразу три вентиля (режим 3), при этом угол γ=const=60°. При дальнейшем
36
увеличении тока Id или (и) сопротивления хγ наступает режим, когда ток проводят сразу четыре вентиля.
Контрольные вопросы
1.Нарисуйте принципиальную схему трёхфазного мостового неуправляемого выпрямителя.
2.Нарисуйте временные диаграммы ЭДС вторичной обмотки трансформатора и укажите последовательность переключения диодов выпрямительного моста. Объясните эту последовательность.
3.Какую форму имеют импульс анодных токов при Ld→∞ и Lγ=0?
4.Существует ли явление вынужденного намагничивания сердечника трансформатора в трёхфазной мостовой схеме выпрямителя?
5.Напишите соотношения между максимальным обратным напряжением на диоде и постоянной составляющей выпрямленного напряжения.
6.Напишите соотношения между мощностью Pd, постоянных составляющих тока Id и напряжения Ud и типовой мощностью Sт трансформатора.
7.Нарисуйте временную диаграмму выпрямленного напряжения и выведите формулу для вычисления среднего значения выпрямленного напряжения Ud.
8.Почему трёхфазный мостовой выпрямитель называют шестипульсным?
9.Чему равен коэффициент пульсаций трёхфазного мостового выпрямителя по первой гармонике?
Раздел 3. Управляемые выпрямители.
Лекция №7. Управляемый однофазный выпрямитель с нулевым выво- дом при статической нагрузке.
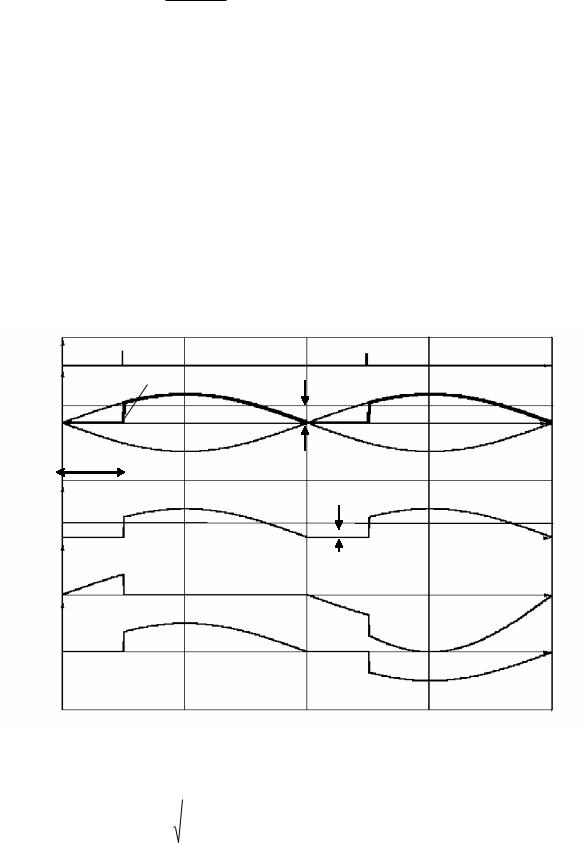
Принципиальная схема приведена на рис.7.1., эквивалентная – на рис.7.2. На рис. 7.3. представлены временные диаграммы напряжений и токов идеальной (ra=0, rпр=0, Lγ=0) однофазной схемы с нулевым выводом при активной нагрузке для произвольного значения угла регулирования α, определяемого положением отпирающих импульсов управляемых вентилей Uу1 и Uу2 по отношению к ЭДС полуобмоток трансформатора e21 и e22.
Среднее значение выпрямленного напряжения:
U d = | 1 π | E2m sin(Θ)dΘ = | E | 2m | (1 | + cos(α)) . | |
|
|
|
| ||||
π αò |
|
| |||||
|
| π |
| ||||
Для нерегулируемого режима:
U do = E2m /π .
37
При α≠0:
Ud = Udo1+ cos(α) . 2
Полученное выражение представляет собой регулировочную характеристику выпрямителя Ud=f(α). Для данного режима среднее значение выпрямленного напряжения будет равно нулю при α=π.
В отличие от нерегулируемого режима, в рассматриваемой схеме напряжение на вентиле на интервале α перед отпиранием имеет положительное значение. Прямое напряжение на вентиле будет максимальным и равным Е2м при α=π/2. Обратное напряжение на вентиле после перехода тока через нуль на интервале α определяется отрицательным значением анодной ЭДС того же вентиля. С моментом вступления в работу очередного вентиля, обратное напряжение определяется результирующей ЭДС е1-е2 вторичной обмотки трансформатора. Обратное напряжение на вентиле будет максимальным и равным Е2м при α≥π/2. Среднее значение выпрямленного тока:
Id | = | Udo | × | (1+ cos(α)) | . |
|
| ||||
|
| rd | 2 |
| |
Среднее значение тока вентиля: Ia=Id/2.
Uy |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
e |
| Ud | e21 |
| Ud | e22 | ||
|
| |||||||
|
|
| ||||||
0 |
|
|
|
|
|
|
| θ |
α |
|
| π |
|
|
| 2π | |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
id |
|
| ia1 |
|
|
| ia2 | |
0 |
|
|
|
|
|
| Id | |
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
| |
Uvs1 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
e21 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
0 |
|
|
|
|
|
|
|
|
i1 |
|
|
|
| e21 | e21-e22 | ||
0 |
|
|
|
|
|
| ||
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
|
|
|
Рис.7.3. Временные диаграммы однофазного управляемого выпрямителя с нулевым выводом при активной нагрузке (ключ К1 замкнут, К2-разомкнут).
Действующее значение тока вентиля (или вторичной обмотки трансформатора):
|
|
| 1 | π | 2 |
| |
Ia эфф = I2 | = |
|
| ò0 | ia dQ = Д*Ia, | ||
2π | |||||||
|
|
|
|
| |||

38
где Д= |
| I | аэфф |
|
|
|
|
|
|
| — коэффициент формы кривой тока вентиля: | |||||||
|
| I a |
|
|
|
|
|
|
| |||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| |
|
|
|
|
|
|
| 1 | (π | — α | + | 1 | sin(2α)) |
| |||||
|
|
|
|
| 2 | π |
|
| π |
|
| |||||||
|
|
| Д = |
| × | 2 | 2 | 4 |
| . | ||||||||
|
|
|
|
|
|
|
|
|
| 1+ cos(α) | ||||||||
|
|
| 2 |
| ||||||||||||||
|
|
|
|
|
|
|
|
|
| |||||||||
| С увеличением угла регулирования коэффициент формы кривой тока растёт. | |||||||||||||||||
| Действующее значение тока первичной обмотки трансформатора определяется по | |||||||||||||||||
формуле: |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
| ||
|
|
| I1= | 2 | k·I2. |
|
|
|
|
|
| |||||||
Расчетную мощность обмоток и типовую мощность трансформатора определяют исходя из неуправляемого режима.
Активно – индуктивная нагрузка (ключ К1 разомкнут, ключ К2 — разомкнут).
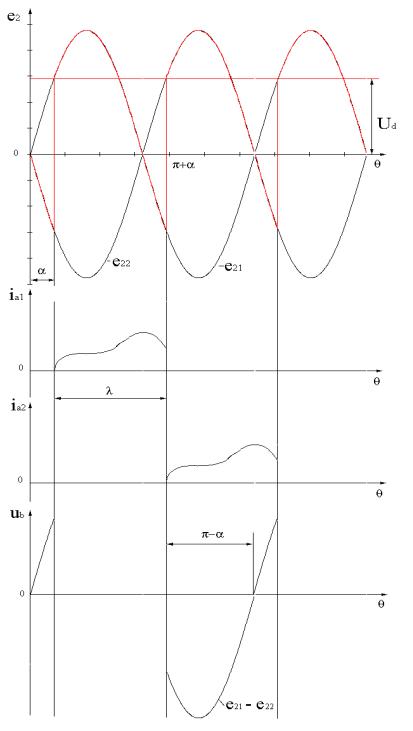
При активно – индуктивной нагрузке схема может работать в двух режимах: в режиме непрерывного тока нагрузки (λ=π) и в режиме прерывистого тока нагрузки (λ<π). На рис.7.4 показаны временные диаграммы токов и напряжений идеальной схемы для первого режима. В отличие от режима при активной нагрузке, здесь выпрямленное напряжение на интервале α имеет отрицательное значение. Это обуславливается тем, что энергия магнитного поля индуктивности нагрузки поддерживает ток вентиля и после перехода анодного ЭДС через нуль (на интервале α). Поэтому среднее значение выпрямленного напряжения будет
| 1 | π +α | 2E2m | cosα =Ud 0 cosα . | |
Ud = | òE2m sinθdθ = | ||||
π |
| ||||
| α | π | |||
|
|
|
| ||
Обратное напряжение на вентиле в отличие от режима при активной нагрузке определяется линейным значением ЭДС вторичной обмотки (e21-e22) как на интервале a, так и на интервале p-a. Форма токов в элементах схемы зависит от величины xd/rd . При xd стремящейся к бесконечности, соотношения между токами определяются также как в случае неуправляемого режима. Коэффициент мощности выпрямителя в данном режиме тем ниже, чем больше угол регулирования a. Это объясняется тем, что сдвиг по фазе основной гармоники тока первичной обмотки трансформатора j(1), по отношению к напряжению сети, с увеличением угла a так же увеличивается.
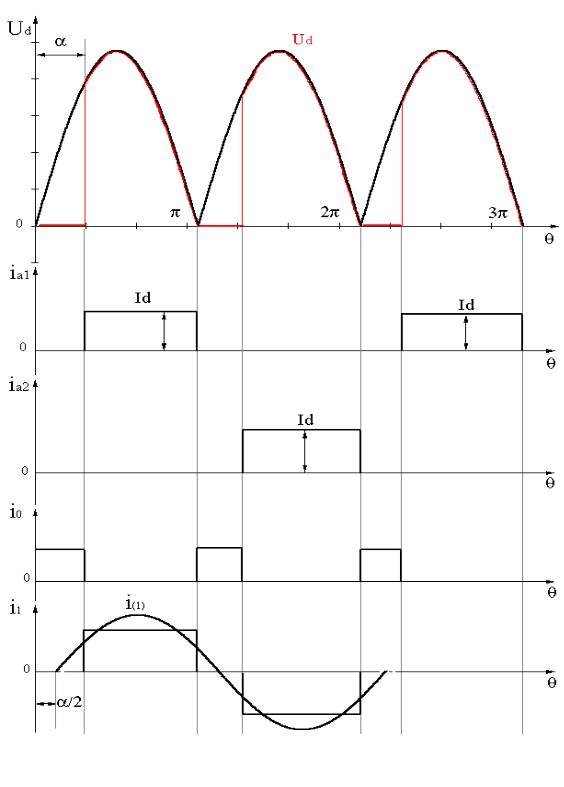
На принципиальной схеме рис.7.1. ключ К1 — разомкнут, К2 — замкнут. Нулевой вентиль VD0 шунтирующий нагрузку, применяется при больших индуктивностях Ld, для уменьшения потребляемой из сети реактивной мощности, а следовательно для увеличения коэффициента мощности выпрямителя. На рис.7.5. представлены временные диаграммы, поясняющие принцип работы схемы без учета параметров: ra, rпр, Lγ.
39
Рис.7.4. Временные диаграммы управляемого однофазного выпрямителя с выводом нулевой точки при активно-индуктивной нагрузке.
40
Активно-индуктивная нагрузка выпрямителя с нулевым вентилем.
Рис.7.5. Временные диаграммы однофазного управляемого выпрямителя с нулевым выводом при активно-индуктивной нагрузке, шунтируемой нулевым вентилем.