§57. Мощность переменного тока и коэффициент мощности
Мгновенное значение мощности. В цепи, содержащей активное, индуктивное и емкостное сопротивления, в которой ток I и напряжение u в общем случае сдвинуты по фазе на некоторый угол ?, мгновенное значение мощности р равно произведению мгновенных значений силы тока i и напряжения u. Кривую мгновенной мощности р можно получить перемножением мгновенных значений тока i и напряжения u при различных углах ?t (рис. 199, а. Из этого рисунка видно, что в некоторые моменты времени, когда ток и напряжение направлены навстречу друг другу, мощность имеет отрицательное значение. Возникновение в электрической цепи отрицательных значений мощности является вредным. Это означает, что в такие периоды времени приемник возвращает часть полученной электроэнергии обратно источнику; в результате уменьшается мощность, передаваемая от источника к приемнику. Очевидно, что чем больше угол сдвига фаз ?, тем больше время, в течение которого часть электроэнергии возвращается обратно к источнику, и тем больше возвращаемая обратно энергия и мощность.
Активная и реактивная мощности. Мгновенная мощность может быть представлена в виде суммы двух составляющих 1 и 2 (рис. 199,б). Составляющая 1 соответствует изменению мощности в цепи с активным сопротивлением (см. рис. 175,б).

Среднее ее значение, которое называют активной мощностью,
P = UI cos ? (75)
Она представляет собой среднюю мощность, которая поступает от источника к электрическим установкам при переменном токе.
Составляющая 2 изменяется подобно изменению мощности в цепи с реактивным сопротивлением (индуктивным или емкостным, см. рис. 179, а и б). Среднее ее значение равно нулю, поэтому для оценки этой составляющей пользуются ее амплитудным значением, которое называют
Q = UI sin ? (76)
Рассматривая кривые мощности (см. рис. 199,б), можно установить, что только активная мощность может обеспечить преобразование в приемнике электрической энергии в другие виды энергии. Эта мощность в течение всего периода имеет положительный знак, т. е. соответствующая ей электрическая энергия 2, называемая активной, непрерывно переходит от источника 1 к приемнику 4 (рис. 200, а). Реактивная мощность никакой полезной работы создать не может, так как среднее значение ее в течение одного периода равно нулю
Рис. 199. Зависимость мгновенной мощности р (а) и ее составляющих (б) от угла ?t
Рис. 200. Диаграмма, иллюстрирующая передачу электрической энергии между источником и приемником, содержащим активное и реактивное сопротивления, при отсутствии компенсатора (а) и при наличии его (б): 1 — источник; 2,3 — условные изображения активной и реактивной энергии; 4 — приемник; 5 — компенсатор
непрерывно циркулирует по электрической цепи от источника электрической энергии 1 к приемнику 4 и обратно (см. рис. 200, а).
Возникновение реактивной мощности в цепи переменного тока возможно только при включении в эту цепь накопителей энергии, таких как катушка индуктивности или конденсатор. В первом случае электрическая энергия, поступающая от источника, накапливается в электромагнитном поле катушки индуктивности, а затем отдается обратно; во втором случае она накапливается в электрическом поле конденсатора, а затем возвращается обратно к источнику. Постоянная циркуляция реактивной мощности от источника к приемникам загружает генераторы переменного тока и электрические сети реактивными токами, не создающими полезной работы, и тем самым не дает возможности использовать их по прямому назначению для выработки и передачи потребителям активной мощности. Поэтому в производственных условиях стараются по возможности уменьшить реактивную мощность, потребляемую электрическими установками.
Полная мощность. Источники электрической энергии переменного тока (генераторы и трансформаторы) рассчитаны на определенный номинальный ток Iном и определенное номинальное напряжение Uном, которые зависят от конструкции машины, размеров ее основных частей и пр. Увеличить значительно номинальный ток или номинальное напряжение нельзя, так как это может привести к недопустимому нагреву обмоток машины или пробою их изоляции. Поэтому каждый генератор или трансформатор может длительно отдавать без опасности аварии только вполне определенную мощность, равную произведению его номинального тока на номинальное напряжение.
S = UI
Следовательно, полная мощность представляет собой наибольшее значение активной мощности при заданных значениях тока и напряжения. Она характеризует ту наибольшую мощность, которую можно получить от источника переменного тока при условии, что между проходящим по нему током и напряжением отсутствует сдвиг фаз. Полную мощность измеряют в вольт-амперах (В*А) или киловольт-амперах (кВ*А).
Связь между мощностями Р, Q и S можно определить из векторной диаграммы напряжений (рис. 201, а). Если умножить на ток I все стороны треугольника ABC, то получим треугольник мощностей А’В’С’ (рис. 201,б), стороны которого равны Р, Q и S. Из треугольника мощностей имеем:
S = ?(P2 + Q2)
Из этого выражения следует, что при заданной полной мощности S (т. е. напряжении U и токе I) чем больше реактивная мощность Q, которая проходит через генератор переменного тока или трансформатор, тем меньше активная мощность Р, которую он может отдать приемнику. Иными словами, реактивная мощность не позволяет полностью использовать всю расчетную мощность источников переменного тока для выработки полезно используемой электрической энергии. То же самое относится и к электрическим сетям. Ток I = ?(I
Рис. 201. Векторная диаграмма напряжений (а) и треугольник мощностей (б) для цепи переменного тока
Если задана активная мощность Р, то при увеличении реактивной мощности Q возрастут реактивный ток I
Таким образом, бесполезная циркуляция электрической энергии между источником переменного тока и приемником, обусловленная наличием в нем реактивных сопротивлений, требует также затраты определенного количества энергии, которая теряется в проводах всей электрической цепи.
Коэффициент мощности. Из формулы (75) следует, что активная мощность Р зависит не только от тока I и напряжения U, но и от величины cos?, называемой
cos ? = P/(UI) = P/S = P/?(P2 + Q2)
По значению cos ? можно судить, как использует мощность источника данный приемник или электрическая цепь. Чем больше cos ?, тем меньше sin ?, следовательно, согласно формулам (75) и (76) при заданных U и I, т. е. S, тем больше активная и меньше реактивная мощности, отдаваемые источником. При повышении cos ? и постоянной активной мощности Р, поступающей в приемник, уменьшается ток в цепи I = P/(U cos ?). При этом уменьшаются потери мощности ?P = I2Rпp в проводах и обеспечивается возможность дополнительной загрузки источника и электрической сети, т. е. лучшего их использования. Если приемник питается от источника при неизменном токе нагрузки, то повышение cos ? ведет к возрастанию активной мощности Р, используемой приемником. При cos?=1 реактивная мощность равна нулю, и вся мощность, отдаваемая источником, является активной. Поэтому на всех предприятиях и во всех отраслях народного хозяйства стремятся всемерно повышать коэффициент мощности и доводить его по возможности до единицы.
Значения коэффициента мощности электрических установок переменного тока различны. Электрические лампы обладают, главным образом, активным сопротивлением, поэтому при их включении сдвиг фаз между током и напряжением практически отсутствует. Следовательно, для осветительной нагрузки коэффициент мощности можно считать равным единице. Коэффициент мощности для двигателей переменного тока зависит от нагрузки. При номинальной расчетной нагрузке двигателя cos? = 0,8-0,9, а у крупных двигателей даже выше. При недогрузке двигателей коэффициент мощности их резко снижается (при холостом ходе cos ? = 0,25-0,3).
Повышение коэффициента мощности. Cos ? повышают различными способами. Основной из них — включение параллельно приемникам электрической энергии специальных устройств, называемых компенсаторами. В качестве последних чаще всего используют батареи конденсаторов (статические компенсаторы), но могут быть применены также и синхронные электрические машины (вращающиеся компенсаторы).
Способ повышения cos ? с помощью статического компенсатора (рис. 202, а) называют компенсацией сдвига фаз, или компенсацией реактивной мощности. При отсутствии компенсатора от источника к приемнику, содержащему активное и индуктивное сопротивления, поступает ток i1 который отстает от напряжения и на некоторый угол сдвига фаз ?1. При включении компенсатора Хс по нему проходит ток ic, опережающий напряжение и на 90°. Как видно из векторной диаграммы (рис. 202,б), при этом в цепи источника будет проходить ток i<i1 и угол сдвига фаз его ? относительно напряжения также будет меньше ?1.
Для полной компенсации угла сдвига фаз ?, т. е. для получения cos ? =1 и минимального значения тока Imin, необходимо, чтобы ток компенсатора Iс был равен реактивной составляющей I1p = I1 sin ?1 тока I1.
При включении компенсатора 5 (см. рис. 200,б) источник 1 и электрическая сеть разгружаются от реактивной энергии 3, так как она циркулирует уже по цепи «приемник — компенсатор». Благодаря этому достигаются существенное повышение использования генераторов переменного тока и электрических сетей и уменьшение потерь энергии, возникающих при бесполезной циркуляции реактивной энергии между источником 1 и приемником 4. Компен-
Рис. 202. Схема, иллюстрирующая способ повышения cos ? с помощью компенсатора (а), и векторная диаграмма (б)
сатор в этом случае выполняет роль генератора реактивной энергии, так как токи Iсв конденсаторе и I1р в катушке индуктивности (см, рис. 202,б) направлены навстречу один другому (первый опережает по фазе напряжение на 90°, второй отстает от него на 90°), вследствие чего включение компенсатора уменьшает общий реактивный ток Iр и сдвиг фаз между током I и напряжением U. При надлежащем подборе реактивной мощности компенсатора можно добиться, что вся реактивная энергия 3 (см. рис. 200,б), поступающая в приемник 4, будет циркулировать внутри контура «приемник — компенсатор», а генератор и сеть не будут участвовать в ее передаче. При этих условиях от источника 1 к приемнику 4 будет передаваться только активная мощность 2, т. е. cos ? будет равен единице.
В большинстве случаев по экономическим соображениям в электрических установках осуществляют неполную компенсацию угла сдвига фаз и ограничиваются значением cos ? = 0,95.

Коэффициент мощности, формула и примеры
Определение и формула коэффициента мощности
Средняя мощность переменного электрического тока , выражаемая через действующие значения силы тока (I) и напряжение (U) равна:
где — действующее (эффективное) значение силы тока, — амплитуда силы тока, — действующее (эффективное) значение напряжения, — амплитуда напряжения.
Коэффициент мощности используют для характеристики потребителя переменного тока как реактивную составляющую нагрузки. Величина этого коэффициента отражает сдвиг фазы () переменного тока, который течет через нагрузку, по отношению к приложенному к нагрузке напряжению. Из выражения (1) видно, что по величине коэффициент мощности равен косинусу от этого сдвига. Если сила тока отстает от напряжения, то сдвиг фаз считают большим нуля, если обгоняет, то
Практическое значение коэффициента мощности
На практике коэффициент мощности стараются сделать максимально большим. Так как при малом для выделения в цепи необходимой мощности надо пропускать ток большой силы, а это приводит к большим потерям в подводящих проводах (см. закон Джоуля — Ленца).
Коэффициент мощности учитывают при проектировании электрических сетей. Если коэффициент мощности является низким, это приводит к росту части потерь электрической энергии в общей сумме потерь. Для увеличения данного коэффициента применяют компенсирующие устройства.
Ошибки при расчетах коэффициента мощности ведут к повышенному потреблению электрической энергии и уменьшению коэффициента полезного действия оборудования.
Коэффициент мощности измеряют фазометром.
Способы расчета коэффициента мощности
Коэффициент мощности рассчитывают как отношение активной мощности (P) к полной мощности (S)
где — реактивная мощность.
Коэффициент мощности для трехфазного асинхронного двигателя вычисляют при помощи формулы:
Коэффициент мощности можно определить, используя, например треугольник сопротивлений (рис.1а) или треугольник мощностей (рис.1b).
Треугольники на рис. 1(a и b) подобны, так как из стороны пропорциональны.
Единицы измерения
Коэффициент мощности — безразмерная физическая величина.
Примеры решения задач
Коэффициент мощности
Дата публикации: .
Категория: Электротехника.
Коэффициентом мощности, или «косинусом фи» (cos φ), цепи называется отношение активной мощности к полной мощности.

В общем случае активная мощность меньше полной мощности, то есть у этой дроби числитель меньше знаменателя, и поэтому коэффициент мощности меньше единицы.
Только в случае чисто активной нагрузки, когда вся мощность является активной мощностью, числитель и знаменатель этой дроби равны между собой, и поэтому коэффициент мощности равен единице.
Реактивная энергия потребляется нагрузкой и, если не принимать специальных мер, она будет загружать линию, идущую от генератора к нагрузке. Нельзя лишить реактивной энергии цепь, содержащую индуктивную нагрузку, но разгрузить генератор от реактивной мощности необходимо.
Чем большую часть полной мощности составляет активная мощность, тем меньше числитель отличается от знаменателя дроби и тем ближе коэффициент мощности к единице. Задача состоит в том, чтобы заставить протекать по линии к потребителю только минимально необходимую величину реактивной энергии.
Из треугольника мощностей (смотрите рисунок 1, в статье «Треугольник мощностей») получаем:

Cos φ, или коэффициент мощности, измеряется особым прибором фазометром.
Пример 1. Амперметр показывает ток 10 А, вольтметр – 120 В, ваттметр – 1 кВт. Определить cos φ потребителя.
S = I × U = 10 × 120 = 1200 ВА,

Пример 2. Определить активную мощность, отдаваемую генератором однофазного переменного тока в сеть, если вольтметр на щите генератора показывает 220 В, амперметр – 20 А и фазометр 0,8.
P = I × U × cos φ = 20 × 220 × 0,8 = 3520 Вт = 3,52 кВт.
Полная мощность.
S = I × U = 20 × 220 = 4400 ВА = 4,4 кВА.
Пример 3. Вольтметр, установленный на щитке электродвигателя показывает 120 В, амперметр – 450 А, ваттметр – 50 кВт. Определить z, r, xL, S, cos φ, Q.

Так как P = I2 × r, то


S = I × U = 450 × 120 = 54000 ВА = 54 кВА ,


 |
| Рисунок 1. Определение коэффициента мощности из треугольников сопротивлений, напряжений и мощностей |
Из построения треугольников сопротивлений, напряжений и мощностей для определенной цепи видно, что эти треугольники подобны один другому, так как их стороны пропорциональны. Из каждого треугольника можно найти «косинус фи» цепи, как показано на рисунке 1. Этим можно воспользоваться для решения самых разнообразных задач.
Пример 4. Определить z, xL, U, Uа, UL, S, P, Q, если I = 6 А, r = 3 Ом, cos φ = 0,8 и ток отстает от по фазе от напряжения.
Из треугольника сопротивлений известно, что

отсюда

U = I × z = 6 × 3,75 = 22,5 В .


Uа = I × r = 6 × 3 =18 В .
UL = I × xL = 6 × 2,24 = 13,45 В .
S = I × U = 6 × 22,5 = 135 ВА .
P = I2 × r = 36 × 3 = 108 Вт
или
P = I × U × cos φ = 6 × 22,5 × 0,8 = 108 Вт .
Q = I × UL = 6 × 13,45 = 81 вар
или

или
Q = I2 × xL = 62 × 2,24 = 81 вар .
Источник: Кузнецов М. И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560 с.
Закон Ома для полной цепи переменного тока. | |
Если в цепи переменного тока имеются нагрузки разных типов, то закон Ома выполняется только для максимальных (амплитудных) и действующих значений тока и напряжения. В этом случае:
|
|
| |
Учитывая, что отношение напряжения к силе тока – это сопротивление, и подставляя конкретные выражения для соответствующих сопротивлений, получим: |
|
Сдвиг фаз в цепи переменного тока определяется характером нагрузки:
|
|
Мощность в цепи переменного тока. | |
Активной мощностью переменного тока называется средняя за период мощность необратимых преобразований в цепи переменного тока (преобразование энергии электрического тока во внутреннюю энергию): |
|
или, переходя к действующим значениям, |
|
Величина |
коэффициент мощности |
Резонанс в электрической цепи. | |
Резонанс в электрической цепи — явление резкого возрастания амплитуды вынужденных колебаний тока при приближении частоты внешнего напряжения (эдс) и собственной частоты колебательного контура. |
|
Из выражения для полного сопротивления переменному току видим, что сопротивление будет минимальным (сила тока при заданном напряжении – максимальной) при условии
|
|
Следовательно, |
|
Амплитуды колебаний напряжения на индуктивности и емкости будут равны и — т.е. они равны по величине и противоположны по фазе (напряжение на индуктивности опережает по фазе напряжение на емкости на p). |
|
Следовательно, |
|
Полное падение напряжения в контуре равно падению напряжения на активном сопротивлении. Амплитуда установившихся колебаний тока будет определяться уравнением |
|
При этом если величина то напряжения на емкостной и индуктивной нагрузках могут оказаться много больше внешнего напряжения (эдс генератора)! |
|
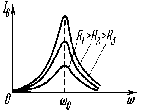
На рисунке представлена зависимость тока в колебательном контуре от частоты при значениях R, где R1<R2<R3. | |
В параллельном контуре при малых активных сопротивлениях R1 и R2 токи в параллельных ветвях противоположны по фазе. Тогда, согласно правилу Кирхгофа |
|
В случае резонанса |
|
Применение: одно из основных применений резонанса в электрической цепи – настройка радио и телевизионных приемников на частоту передающей станции. Необходимо учитывать резонансные явления, когда в цепи, не рассчитанной на работу в условиях резонанса, возникают чрезмерно большие токи или напряжения (расплавление проводов, пробой изоляции и т.д.). |
|
2.9. Повышение коэффициента мощности в электрической цепи
Активная мощность потребителя определена формулой
P = U I cos φ.
Величину cos φ здесь называют коэффициентом мощности. Ток в линии питающей потребителя с заданной мощностью Р равен
(2.51)
I = P / (U cos φ).
и будет тем больше, чем меньше cos φ. При этом возрастают потери в питающей линии. Для их снижения желательно увеличивать cos φ. Большинство потребителей имеет активно-индуктивную нагрузку. Увеличение cos φ возможно путем компенсации индуктивной составляющей тока путем подключения параллельно нагрузке конденсатора (рис. 2.24).

Расчет емкости дополнительного конденсатора для обеспечения заданного cos φ проводится следующим образом. Пусть известны параметры нагрузки Pн, U и Iн . Можно определить cosφн
cos φн = P / (U Iн).
Из п. 2.8.3 следует, что подключение емкости не изменяет активную составляющую нагрузки
(2.52)
Iна = Iн cos φн = Pн / U
Реактивная составляющая нагрузки Iнр может быть выражена через tg φн
Iнр = Iна tg φн.
При подключении емкости величина Iнр уменьшается на величину IC.
Если задано, что коэффициент мощности в питающей линии должен быть равен cos φ, то можно определить величину реактивной составляющей тока в линии
Iр = Iа tg φ.
Уменьшение реактивной составляющей нагрузки с Iнр до Iр определяет величину тока компенсирующей емкости
(2.53)
IC = Iнр — Iр = Iа (tg φн — tg φ).
Подставляя в уравнение (2.53), значение Iна из (2.52) и учитывая, что IC = U / XC = U ωC, получим U ωC = Pн / U · (tg φн — tg φ), откуда для емкости конденсатора имеем
C = Pн / ωU2 · (tg φн — tg φ).
Для больших значений Pн величина емкости C может оказаться слишком большой, что технически трудно реализовать. В этом случае используют синхронные компенсирующие машины.
2.10. Комплексный (символический) метод расчета цепей синусоидального тока
Все параметры цепи представляются в комплексной форме.


 –комплексное
мгновенное значение;
–комплексное
мгновенное значение; 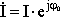 –
комплексное действующее значение силы
тока;
–
комплексное действующее значение силы
тока;  –
комплексное действующее значение
напряжения.
–
комплексное действующее значение
напряжения.
Пример.

Законы Ома и Кирхгофа в комплексной форме
Достоинство комплексного метода: при его применении в анализе цепей переменного тока можно применять все известные методы анализа постоянного тока.
Закон Ома
Под законом Ома в комплексной форме понимают:
Í = Ú / Z

Комплексное сопротивление участка цепи представляет собой комплексное число, вещественная часть которого соответствует величине активного сопротивления, а коэффициент при мнимой части – реактивному сопротивлению.
По виду записи комплексного сопротивления можно судить о характере участка цепи:
R + j X — активно-индуктивное сопротивление; R – j X — активно-емкостное.
Примеры.

Первый закон Кирхгофа в комплексной форме
Алгебраическая сумма комплексных действующих значений токов в узле равна нулю.

Второй закон Кирхгофа в комплексной форме
В замкнутом контуре электрической цепи алгебраическая сумма комплексных действующих значений ЭДС равна алгебраической сумме комплексных падений напряжений в нём.
 .
.
При использовании символического метода можно пользоваться понятиями мощностей. Но в комплексной форме можно записать только полную мощность:

где Ï — комплексно-сопряженный ток
S cos φ ± j S sin φ = P ± j Q.
Полная мощность в комплексной форме представляет собой комплексное число, вещественная часть которого соответствует активной мощности рассматриваемого участка, а коэффициент при мнимой части – реактивной мощности участка. Значение знака перед мнимой частью: “+” означает, что напряжение опережает ток, нагрузка – активно-индуктивная; “–” означает, что нагрузка — активно-емкостная.

Лицензия | Model.Exponenta.Ru | Jigrein |
|
|
© Н.В. Клиначёв, 1999-2008. Все права защищены. 800×600.





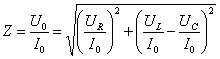 — полное сопротивление переменному току.
— полное сопротивление переменному току.
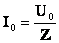
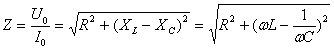 .
.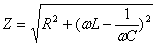
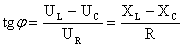 или
или 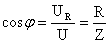 .
.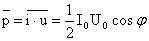
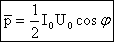
 .
.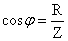 наз. коэффициентом мощности. При малом коэффициенте мощности потребляется лишь малая часть мощности, вырабатываемой генератором. Остальная часть мощности периодически перекачивается от генератора к потребителю и обратно и рассеивается в линиях электропередач.
наз. коэффициентом мощности. При малом коэффициенте мощности потребляется лишь малая часть мощности, вырабатываемой генератором. Остальная часть мощности периодически перекачивается от генератора к потребителю и обратно и рассеивается в линиях электропередач.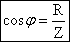
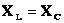 или
или  .
.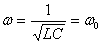 — т.е. частота изменения внешнего напряжения равна собственной частоте колебаний в контуре.
— т.е. частота изменения внешнего напряжения равна собственной частоте колебаний в контуре.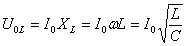
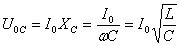
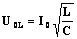
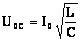
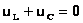 .
.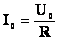 . В этом и состоит смысл явления резонанса.
. В этом и состоит смысл явления резонанса.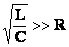 ,
,
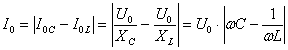 .
.
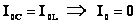 . Резкое уменьшение амплитуды силы тока во внешней цепи, питающей параллельно соединенные емкостное и индуктивное сопротивления при приближении частоты внешнего напряжения к собственной частоте колебательного контура наз. резонансом токов.
. Резкое уменьшение амплитуды силы тока во внешней цепи, питающей параллельно соединенные емкостное и индуктивное сопротивления при приближении частоты внешнего напряжения к собственной частоте колебательного контура наз. резонансом токов.
