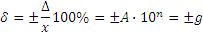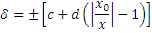Класс точности — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 мая 2018; проверки требуют 8 правок. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 24 мая 2018; проверки требуют 8 правок.

Класс точности — обобщённая характеристика средств измерений, определяемая пределами допускаемых основных и дополнительных погрешностей, а также рядом других свойств, влияющих на точность осуществляемых с их помощью измерений.

Погрешность может нормироваться, в частности, по отношению к:

• результату измерения (по относительной погрешности)

в этом случае, по ГОСТ 8.401-80 (взамен ГОСТ 13600-68), цифровое обозначение класса точности (в процентах) заключается в кружок.

• длине (верхнему пределу) шкалы измерительного прибора (по приведенной погрешности).

Для стрелочных приборов принято указывать класс точности, записываемый в виде числа, например, 0,05 или 4,0. Это число дает максимально возможную погрешность прибора, выраженную в процентах от наибольшего значения величины, измеряемой в данном диапазоне работы прибора. Так, для вольтметра, работающего в диапазоне измерений 0—30 В, класс точности 1,0 определяет, что указанная погрешность при положении стрелки в любом месте шкалы не превышает 0,3 В.

Относительная погрешность результата, полученного с помощью указанного вольтметра, зависит от значения измеряемого напряжения, становясь недопустимо высокой для малых напряжений. При измерении напряжения 0,5 В погрешность составит 60 %. Как следствие, такой прибор не годится для исследования процессов, в которых напряжение меняется на 0,1—0,5 В.

Обычно цена наименьшего деления шкалы стрелочного прибора согласована с погрешностью самого прибора. Если класс точности используемого прибора неизвестен, за погрешность s прибора всегда принимают половину цены его наименьшего деления. Понятно, что при считывании показаний со шкалы нецелесообразно стараться определить доли деления, так как результат измерения от этого не станет точнее.

Следует иметь в виду, что понятие класса точности встречается в различных областях техники. Так, в станкостроении имеется понятие класса точности металлорежущего станка, класса точности электроэрозионных станков (по ГОСТ 20551).

Обозначения класса точности могут иметь вид заглавных букв латинского алфавита, римских цифр и арабских цифр с добавлением условных знаков. Если класс точности обозначается латинскими буквами, то класс точности определяется пределами абсолютной погрешности. Если класс точности обозначается арабскими цифрами без условных знаков, то класс точности определяется пределами приведённой погрешности и в качестве нормирующего значения используется наибольший по модулю из пределов измерений. Если класс точности обозначается арабскими цифрами с галочкой, то класс точности определяется пределами приведённой погрешности, но в качестве нормирующего значения используется длина шкалы. Если класс точности обозначается римскими цифрами, то класс точности определяется пределами относительной погрешности.

Аппараты с классом точности 0,5 (0,2) проходят метрологические испытания с 5 % загрузки, а 0,5s (0,2s) уже с 1 % загрузки.^[1]

Точность обработки деталей. Классы точности

Взаимозаменяемость деталей.

Выпуск велосипедов, мотоциклов, тракторов, автомобилей, электродвигателей, швейных и других машин осуществляется на заводах такими темпами, когда счет времени обработки и сборки ведется не только минутами, но и секундами. Детали этих машин должны быть изготовлены точно по чертежам и техническим условиям так, чтобы при сборке они подходили одна к другой без слесарной подгонки, что сокращает время на сборку и удешевляет стоимость изделия. Важно также, чтобы при ремонте машины новая деталь, заменяющая изношенную, могла быть установлена на ее место без подгонки. Детали, удовлетворяющие таким требованиям, называются

взаимозаменяемыми. Взаимозаменяемость – это свойство деталей занимать свои места в узлах и изделиях без предварительного подбора или подгонки по месту.

Сопряжение деталей.

Две детали, подвижно или неподвижно соединяемые друг с другом, называют сопрягаемыми. Размеры, по которым происходит соединение этих деталей, называют сопрягаемыми размерами. Размеры, по которым не происходит соединение деталей, называют свободными размерами. Примером сопрягаемых размеров может служить наружный диаметр фрезерной оправки и соответствующий ему диаметр отверстия в насадной фрезе, диаметр шейки оправки и соответствующий ему диаметр отверстия в подшипнике подвески. Примером свободных размеров может служить наружный диаметр установочных колец фрезерной оправки, длина фрезерной оправки, ширина цилиндрической фрезы.

Сопрягаемые детали должны быть выполнены взаимозаменяемыми.

Понятие о точности обработки.

Изготовить партию взаимозаменяемых деталей абсолютно одинакового размера невозможно, так как на точность обработки влияют неточность и износ станка, износ фрезы, неточности при установке и закреплении заготовки и другие причины. Как правило, все детали данной партии при обработке имеют отклонения от заданных размеров и формы. Но величины этих отклонений должны быть назначены таким образом, чтобы сопрягаемые размеры могли обеспечить сборку деталей без подгонки, т.е. чтобы детали были взаимозаменяемыми.

Конструкторы изделий при назначении величины допускаемых отклонений на сопрягаемые детали руководствуются установленными государством стандартами – ГОСТ. Ниже вкратце излагаются основные понятия о допусках и предельных отклонениях, вытекающие их ГОСТ 7713-55.

Понятие о допуске и предельных отклонениях. Величина допустимых отклонений указывается в чертежах детали со знаками плюс и минус.

Знак минус показывает, что деталь может быть изготовлена с отклонением в меньшую сторону; знак

плюс показывает, что деталь может быть изготовлена с отклонением в большую сторону. Например, поставленный в чертеже бруска размер 10_-0,1 мм показывает, что брусок может быть отфрезерован так, чтобы после его обработки его размер лежал в пределах между 10 мм и 9,9 мм. Точно также поставленный в чертеже диаметр паза 10^+0,2 мм показывает, что паз может быть отфрезерован так, чтобы после обработки его размер лежал в пределах между 10 мм и 10,2 мм.

Поставленный в чертеже размер 10^+0,2_-0,1 мм показывает, что обработанная деталь будет годной, если ее размер составляет не менее

9,9 мм и не более 10,2 мм, т.е. лежит в этих пределах.

Номинальным размером называется основной расчетный размер, от которого исходят при назначении отклонений. Если в чертеже указан размер 10^+0,2_-0,1 мм, то размер 10 мм называется номинальным.

Действительным размером называется размер, полученный при измерении обработанной детали. Размеры, между которыми может находиться действительный размер годной детали, называются предельными размерами. Действительный размер детали с размерами

10^+0,2_-0,1 мм может лежать в пределах 10+0,2 = 10,02 мм и 10-0,1 =9,9 мм. Больший размер называется наибольшим предельным размером, а меньший – наименьшим предельным размером.

Разность между наибольшим и наименьшим предельными размерами называется допуском размера.

• Верхним предельным отклонением называется разность между наибольшим предельным размером и номинальным размером.
• Нижним предельным отклонением называется разность между наименьшим предельным размером и номинальным размером.

Допуск можно также определить, как разность между верхним и нижним предельными отклонениями.

Действительным отклонением называется разность между действительным и номинальным размерами.

При графическом изображении допусков отклонения размеров откладываются от линии, соответствующей номинальному размеру и называемой нулевой линией; положительные отклонения откладываются вверх от нулевой линии, а отрицательные – вниз.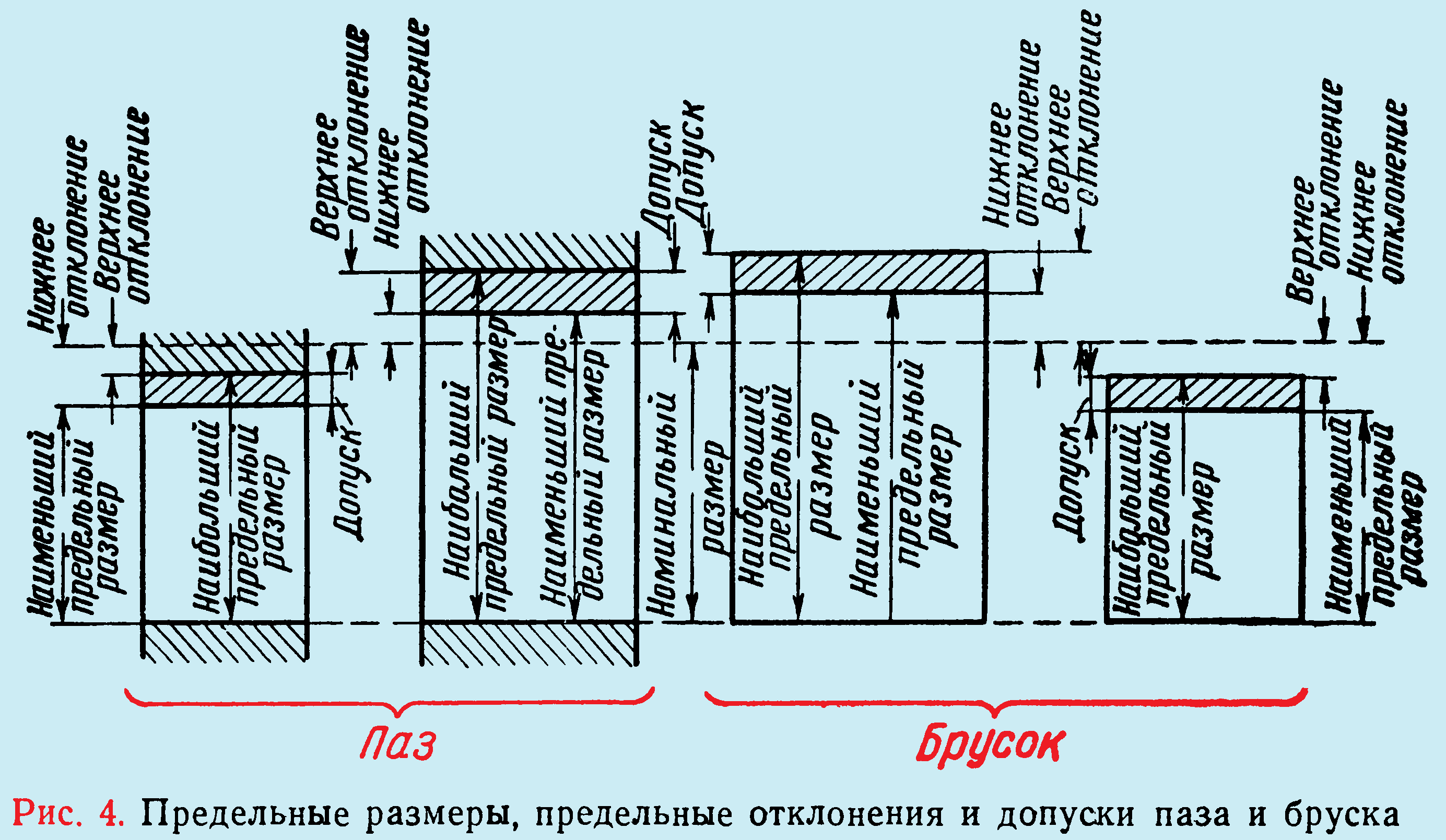

Зазоры и натяги.

Если брусок с размерами грани 10_-0,1 мм посадить в паз с размерами грани

10^+0,2_+0,1 мм, то в соединении бруска с пазом получится зазор, и брусок можно будет передвигать вдоль паза. Такая посадка (сопряжение двух деталей) называется свободной. Наибольший зазор в этом случае составит 0,3 мм, а наименьший будет равен 0,1 мм.

Если же размер бруска будет 10^+0,2_+0,1 мм, а паза 10_-0,1 мм, то брусок не войдет свободно в паз и его придется вставлять с силой или запрессовывать. В соединении получится натяг или отрицательный зазор, наименьшая величина которого равна 0,1 мм. А наибольшая

0,3 мм. Такая посадка называется неподвижной, так как брусок нельзя будет передвигать вдоль паза.

Таким образом, можно сделать следующие заключения.

• Зазором называется положительная разность между размером паза и размером бруска, обеспечивающая свободу их движения относительно друг друга.
• Натягом называется отрицательная разность между размером паза и размером бруска (размер бруска больше размера паза), которая после посадки бруска в паз создает неподвижное их соединение.

Посадки.

Посадкой называется характер соединения сопрягаемых деталей, определяемый разностью между размерами паза и бруска, создающий большую или меньшую свободу (зазор или натяг) их относительного перемещения или степень сопро­тивления взаимному перемещению. В зависимости от наличия в сопряжении бруска и паза зазора или натяга различают посадки с зазором, с натягом и переходные.

Посадками с зазором, или свободными, называют такие посадки, при которых обеспечивается возможность относительного перемещения сопряженных деталей во время работы. В зависимости от величины зазора степень относительного перемещения деталей, сопряженных свободной посадкой, может быть различной. Для вращения шпинделя фрезерного станка в подшипниках зазор должен быть меньшим и, следовательно, посадка более тугой, чем для посадки колец на фрезерную оправку.

Посадками с натягом, или неподвижными, называют посадки, при которых во время работы не должно происходить перемещения сопряженных деталей относительно друг друга. В зависимости от величины натяга степень свободы сопряженных деталей неподвижной посадки может быть различной. Так, посадку шейки вала в кольцо шарикоподшипника производят с меньшим натягом, чем посадку колеса железнодорожного вагона на шейку оси.

При переходных посадках возможно получение, как натягов, так и зазоров. При наибольшем предельном размере бруска и наименьшем предельном размере паза получается натяг, а при наименьшем предельном размере бруска и наибольшем предельном размере паза получается зазор (в таблицах допусков в графе «натяг» обозначен знаком минус).

Ниже приводятся посадки, относящиеся к рассмотренным трем группам; в скобках даются их сокращенные обозначения.

Наибольший натяг получается при горячей посадке, меньший — при прессовых посадках; наименьший зазор получается при скользящей посадке, немного больший — при посадке движения, почти втрое больший при ходовой, затем еще больший при легкоходовой и, наконец, наибольший при широкоходовой посадке.

При глухой, тугой, напряженной и плотной посадках, как указывалось выше, возможны натяги и зазоры в зависимости от получающихся отклонений размера.

Классы точности.

Точность изготовления характеризуется величиной допускаемых отклонений от заданных размеров и формы. Для разных машин требуются детали с различной точностью обработки. Очевидно, что детали плуга, дорожного катка и других сельскохозяйственных и дорожных машин могут быть изготовлены менее точно, чем детали фрезерного станка, а детали фрезерного станка требуют меньшей точности, чем детали измерительного прибора. В связи с этим в машиностроении детали разных машин изготовляют по разным классам точности. В СССР (были) приняты десять классов точности.

• пять из них: 1-й, 2-й, 2а, 3-й, За — требуют наибольшей точности обработки;
• два других: 4-й и 5-й — меньшей;
• три остальных: 7-й, 8-й, 9-й — еще меньшей.

Применение классов точности в различных областях

• 1-й класс точности применяют при изготовлении особо точных изделий. Вследствие очень малых допусков работа по 1-му классу точности требует высокой квалификации рабочего и точного оборудования, приспособлений и инструмента.
• 2-й и 2а классы точности применяют наиболее часто. По ним изготовляют ответственные детали станков, автомобильных, тракторных, авиационных и электрических двигателей, текстильных и других машин.Наряду с этим в отраслях машиностроения, выпускающих указанные машины, детали менее ответственных соединений из­готовляют по 3-му, 4-му, 5-му и другим более грубым классам точности.
• 3-й и За классы точности применяют главным образом в тяжелом машиностроении при производстве турбин, паровых машин, двигателей внутреннего сгорания, трансмиссионных деталей и т. д.
• По 4-му классу точности изготовляют детали сельскохозяйственных машин, паровозов, железнодорожных вагонов и т. д.
• 5-й класс точности применяют в машиностроении для неответственных деталей менее точных механизмов.
• 7-й, 8-й и 9-й классы точности применяют при изготовлении более грубых деталей и особенно при заготовительных операциях: литье, штамповке, медницко-слесарных работах и т. д.
• Свободные размеры деталей выполняют обычно по 5-му или 7-му классам точности.

Чтобы показать, с какой посадкой и по какому классу точности нужно изготовить деталь, в чертежах на номинальных сопрягаемых размерах ставится буква, обозначающая посадку, и цифра, соответствующая классу точности. Например, С₄ означает: скользящая посадка 4-го класса точности; Х₃ — ходовая посадка 3-го класса точности и т. п. Для посадок 2-го класса точности (особенно широко распространенных) цифра 2 не ставится. Поэтому, если в чертеже на сопрягаемом размере рядом с буквой посадки нет цифры, то это значит, что деталь надо изготовить по 2-му классу точности. Например, Л означает легкоходовая посадка 2-го класса точности.

---

 

Автор: С. В. Аврутин
Источник: Основы фрезерного дела, С. В. Аврутин, 1962г
Дата в источнике: 1962г

Классы точности приборов измерения — MOREREMONTA

Конспект КСР1 (п. 8)

КЛАССЫ ТОЧНОСТИ ИЗМЕРИТЕЛЬНЫХ ПРИБОРОВ

Класс точности измерительного прибора — это характеристика, определяемая нормированными предельными значениями погрешности средства измерений.

Способы нормирования допускаемых погрешностей и обозначения классов точности средств измерений установлены ГОСТ 8.401-80.

Способы нормирования допускаемых погрешностей:

— по абсолютной погрешности,

— по относительной погрешности,

— по приведенной погрешности – по длине или верхнему пределу шкалы прибора.

Обозначения классов точности измерительных приборов:

— арабскими цифрами без условных знаков — класс точности определяется пределами приведённой погрешности, в качестве нормирующего значения используется наибольший по модулю из пределов измерений.

— арабскими цифрами с галочкой, то класс точности определяется пределами приведённой погрешности, но в качестве нормирующего значения используется длина шкалы.

По приведенной погрешности приборы делятся на классы: 0,05; 0,1; 0,2; 0,5; 1,0; 1,5; 2,5; 4,0.

Приборы класса точности 0,05; 0,1; 0,2; 0,5 применяются для точных лабораторных измерений и называются прецизионными.

В технике применяются приборы классов 1,0; 1,5: 2,5 и 4,0 (технические).

Если на шкале такого обозначения нет, то данный прибор внеклассный, то есть его приведенная погрешность превышает 4%.

— арабскими цифрами в кружке — класс точности определяется пределами относительной погрешности.

— латинскими буквами, то класс точности определяется пределами абсолютной погрешности.

Когда на приборе класс точности не указан, абсолютная погрешность принимается равной половине цены наименьшего деления. При считывании показаний со шкалы нецелесообразно стараться определить доли деления, так как результат измерения от этого не станет точнее.

Пример: вольтметр, диапазон измерений 0 — 30 В, класс точности 1,0 определяет, указанная погрешность при положении стрелки в любом месте шкалы не превышает 0,3 В. Соответственно, среднее квадратичное отклонение s прибора составляет 0,1 В.

Относительная погрешность результата зависит от значения напряжения, становясь недопустимо высокой для малых напряжений. При измерении напряжения 0,5 В погрешность составит 60 %. Такой прибор не годится для исследования процессов, в которых напряжение меняется на 0,1 — 0,5 В.

Во время лабораторных измерений требуется знать точность измерительных средств, которые в свою очередь обладают определенными характеристиками и различаются по устройству. Каждое из средств измерения (СИ) имеют определенные неточности, которые делится на основные и дополнительные. Зачастую возникают ситуации, когда нет возможности или просто не требуется производить подробный расчет. Каждому средству измерения присвоен определенный класс точности, зная который, можно выяснить его диапазон отклонений.

Вовремя выяснить ошибки измерительного средства помогут нормированные величины погрешностей. Под этим определением стоит понимать предельные, для измерительного средства показатели. Они могут быть разными по величине и зависеть от разных условий, но пренебрегать ими не стоит ни в коем случае, ведь это может привести к серьезной ошибке в дальнейшем. Нормированные значения должны быть меньше чем покажет прибор. Границы допустимых величин ошибок и необходимые коэффициенты вносятся в паспорт каждого замеряющего размеры устройства. Узнать подробные значения нормирования для любого прибора можно воспользовавшись соответствующим ГОСТом.

Класс точности измерительного прибора

Обобщающая характеристика, которая определяется пределами погрешностей (как основных, так и дополнительных), а также другими влияющими на точные замеры свойствами и показатели которых стандартизированы, называется класс точности измерительного аппарата. Класс точности средств измерений дает информацию о возможной ошибке, но одновременно с этим не является показателем точности данного СИ.

Средство измерения – это такое устройство, которое имеет нормированные метрологические характеристики и позволяет делать замеры определенных величин. По своему назначению они бывают примерные и рабочие. Первые используются для контроля вторых или примерных, имеющих меньший ранг квалификации. Рабочие используются в различных отраслях. К ним относятся измерительные:

• приборы;
• преобразователи;
• установки;
• системы;
• принадлежности;
• меры.

На каждом средстве для измерений имеется шкала, на которой указываются классы точности этих средств измерений. Они указываются в виде чисел и обозначают процент погрешности. Для тех, кто не знает, как определить класс точности, следует знать, что они давно стандартизованы и есть определенный ряд значений. Например, на устройстве может быть одна из следующих цифр: 6; 4; 2,5; 1,5; 1,0; 0,5; 0,2; 0,1; 0,05; 0,02; 0,01; 0,005; 0,002; 0,001. Если это число находится в круге, то это погрешность чувствительности. Обычно ее указывают для масштабных преобразователей, таких как:

• делители напряжения;
• трансформаторы тока и напряжения;
• шунты.

Обозначение класса точности

Обязательно указывается граница диапазона работы этого прибора, в пределах которой значение класса точности будет верно.

Те измерительные устройства, которые имеют рядом со шкалой цифры: 0,05; 0,1; 0,2; 0,5, именуются как прецизионные. Сфера их применения – это точные и особо точные замеры в лабораторных условиях. Приборы с маркировкой 1,0; 1,5; 2,5 или 4,0 называются технические и исходя из названия применяются в технических устройствах, станках, установках.

Возможен вариант, что на шкале такого аппарата не будет маркировки. В такой ситуации погрешность приведенную принято считать более 4%.

Если значение класса точности устройства не подчеркнуто снизу прямой линией, то это говорит о том, что такой прибор нормируется приведенной погрешностью нуля.

Грузопоршневой манометр, класс точности 0,05

Если шкала отображает положительные и отрицательные величины и отметка нуля находится посередине такой шкалы, то не стоит думать, что погрешность во всем диапазоне будет неизменной. Она будет меняться в зависимости от величины, которую измеряет устройство.

Если замеряющий агрегат имеет шкалу, на которой деления отображены неравномерно, то класс точности для такого устройства указывают в долях от длины шкалы.

Возможны варианты измерительных аппаратов со значениями шкалы в виде дробей. Числитель такой дроби укажет величину в конце шкалы, а число в знаменателе при нуле.

Нормирование

Классы точности средств измерений сообщают нам информацию о точности таких средств, но одновременно с этим он не показывает точность измерения, выполненного с помощью этого измерительного устройства. Для того, чтобы выявить заблаговременно ошибку показаний прибора, которую он укажет при измерении люди нормируют погрешности. Для этого пользуются уже известными нормированными значениями.й

Нормирование осуществляется по:

Формулы расчета абсолютной погрешности по ГОСТ 8.401

Каждый прибор из конкретной группы приспособлений для замера размеров имеет определенное значение неточностей. Оно может незначительно отличаться от установленного нормированного показателя, но не превышать общие показатели. Каждый такой агрегат имеет паспорт, в который записываются минимальные и максимальные величины ошибок, а также коэффициенты, оказывающие влияние в определенных ситуациях.

Все способы нормирования СИ и обозначения их классов точности устанавливаются в соответствующих ГОСТах.

Виды маркирования

Классы точности абсолютно всех измерительных приборов подлежат маркировке на шкале этих самых приборов в виде числа. Используются арабские цифры, которые обозначают процент нормированной погрешности. Обозначение класса точности в круге, например число 1,0, говорит о том, что ошибочность показаний стрелки аппарата будет равна 1%.

Если в обозначении используется кроме цифры еще и галочка, то это значит, что длина шкалы применяется в роли нормирующего значения.

Латинские буквы для обозначения применяются если он определяется пределами абсолютной погрешности.

Существуют аппараты, на шкалах которых нет информации о классе точности. В таких случаях абсолютную следует приравнивать к одной второй наименьшего деления.

Пределы

Как уже говорилось раньше, измерительный прибор, благодаря нормированию уже содержит случайную и систематические ошибки. Но стоит помнить, что они зависят от метода измерения, условий и других факторов. Чтобы значение величины, подлежащей замеру, было на 99% точным, средство измерения должно иметь минимальную неточность. Относительная должна быть примерно на треть или четверть меньше погрешности измерений.

Базовый способ определения погрешности

При установке класса точности в первую очередь нормированию подлежат пределы допустимой основной погрешности, а пределы допускаемой дополнительной погрешности имеют кратное значение от основной. Их пределы выражают в форме абсолютной, относительной и приведенной.

Приведенная погрешность средства измерения – это относительная, выраженная отношением предельно-допустимой абсолютной погрешности к нормирующему показателю. Абсолютная может быть выражена в виде числа или двучлена.

Если класс точности СИ будет определяться через абсолютную, то его обозначают римскими цифрами или буквами латиницы. Чем ближе буква будет к началу алфавита, тем меньше допускаемая абсолютная погрешность такого аппарата.

Класс точности 2,5

Благодаря относительной погрешности можно назначить класс точности двумя способами. В первом случае на шкале будет изображена арабская цифра в кружке, во втором случае дробью, числитель и знаменатель которой сообщают диапазон неточностей.

Основная погрешность может быть только в идеальных лабораторных условиях. В жизни приходится умножать данные на ряд специальных коэффициентов.

Дополнительная случается в результате изменений величин, которые каким-либо образом влияют на измерения (например температура или влажность). Выход за установленные пределы можно выявить, если сложить все дополнительные погрешности.

Случайные ошибки имеют непредсказуемые значения в результате того, что факторы, оказывающие на них влияние постоянно меняются во времени. Для их учета пользуются теорией вероятности из высшей математики и ведут записи происходивших раньше случаев.

Пример расчета погрешности

Статистическая измерительного средства учитывается при измерении какой-либо константы или же редко подверженной изменениям величины.

Динамическая учитывается при замерах величин, которые часто меняют свои значения за небольшой отрезок времени.

Классы точности болтов

Болты и другие крепежные изделия изготавливают нескольких классов:

Каждый из них имеет свои допуски измеряемой величины, отличные от остальных и применяется в различных сферах.

Крепеж С используют в отверстиях с диаметром немногим больше диаметра болта (до 3мм). Болты без труда устанавливаются, не отнимая много времени на работу. Из минусов стоит отметить то, что при физическом воздействии на такой крепеж, болтовое соединение может сместиться на несколько миллиметров.

Крепеж В подразумевает использование болтов, диаметр которых меньше отверстия в пределах 1-1,5 мм. Это позволяет конструкции меньше подвергаться смещениям и деформациям, но повышаются требования к изготовлению отверстий в креплениях.

Гайки шестигранные класса точности В

Крепеж А создается по проекту. Диаметр болта такого типа, меньше диаметра отверстия максимум на 0,3 мм и имеет допуск только со знаком минус. Это делает крепеж неподвижным, не позволяет происходить смещению узлов. Изготовление болтов А-класса стоит дороже и не всегда используется в производстве.

Класс точности присутствует в описании всех измерительных приборов и является одной из самых важных характеристик. Чем выше его значение, тем более дорогостоящий будет прибор, но в то же время он сможет предоставить более точную информацию. Выбор стоить делать исходя из сложившейся ситуации и целей в которых будет использоваться такое средство. Важно понимать, что в некоторых ситуациях экономически выгодно будет приобрести дорогостоящее сверхточное оборудование, чтобы в дальнейшем сберечь деньги.

Если вы нашли ошибку, пожалуйста, выделите фрагмент текста и нажмите Ctrl+Enter.

Класс точности измерительного прибора — это обобщенная характеристика, определяемая пределами допускаемых основных и дополнительных погрешностей, а также другими свойствами, влияющими на точность, значения которых установлены в стандартах на отдельные виды средств измерений. Класс точности средств измерений характеризует их свойства в отношении точности, но не является непосредственным показателем точности измерений, выполняемых при помощи этих средств.

Для того чтобы заранее оценить погрешность, которую внесет данное средство измерений в результат, пользуются нормированными значениями погрешности . Под ними понимают предельные для данного типа средства измерений погрешности.

Погрешности отдельных измерительных приборов данного типа могут быть различными, иметь отличающиеся друг от друга систематические и случайные составляющие, но в целом погрешность данного измерительного прибора не должна превосходить нормированного значения. Границы основной погрешности и коэффициентов влияния заносят в паспорт каждого измерительного прибора.

Основные способы нормирования допускаемых погрешностей и обозначения классов точности средств измерений установлены ГОСТ.

На шкале измерительного прибора маркируют значение класса точности измерительного прибора в виде числа, указывающего нормированное значение погрешности. Выраженное в процентах, оно может иметь значения 6; 4; 2,5; 1,5; 1,0; 0,5; 0,2; 0,1; 0,05; 0,02; 0,01; 0,005; 0,002; 0,001 и т. д.

Если обозначаемое на шкале значение класса точности обведено кружком, например 1,5, это означает, что погрешность чувствительности δ s =1,5%. Так нормируют погрешности масштабных преобразователей (делителей напряжения, измерительных шунтов, измерительных трансформаторов тока и напряжения и т. п.).

Это означает, что для данного измерительного прибора погрешность чувствительности δ s= d x/x — постоянная величина при любом значении х. Граница относительной погрешности δ (х) постоянна и при любом значении х просто равна значению δ s, а абсолютная погрешность результата измерений определяется как d x= δ sx

Для таких измерительных приборов всегда указывают границы рабочего диапазона, в которых такая оценка справедлива.

Если на шкале измерительного прибора цифра класса точности не подчеркнута, например 0,5, это означает, что прибор нормируется приведенной погрешностью нуля δ о=0,5 %. У таких приборов для любых значений х граница абсолютной погрешности нуля d x= d о=const, а δ о= d о/хн.

При равномерной или степенной шкале измерительного прибора и нулевой отметке на краю шкалы или вне ее за хн принимают верхний предел диапазона измерений. Если нулевая отметка находится посредине шкалы, то хн равно протяженности диапазона измерений, например для миллиамперметра со шкалой от -3 до +3 мА, хн= 3 — (-3)=6 А.

Однако будет грубейшей ошибкой полагать, что амперметр класса точности 0,5 обеспечивает во всем диапазоне измерений погрешность результатов измерений ±0,5 %. Значение погрешности δ о увеличивается обратно пропорционально х, то есть относительная погрешность δ (х) равна классу точности измерительного прибора лишь на последней отметке шкалы (при х = хк). При х = 0,1хк она в 10 раз больше класса точности. При приближении х к нулю δ (х) стремится к бесконечности, то есть такими приборами делать измерения в начальной части шкалы недопустимо.

На измерительных приборах с резко неравномерной шкалой (например на омметрах) класс точности указывают в долях от длины шкалы и обозначают как 1,5 с обозначением ниже цифр знака «угол».

Если обозначение класса точности на шкале измерительного прибора дано в виде дроби (например 0,02/0,01), это указывает на то, что приведенная погрешность в конце диапазона измерений δ прк = ±0,02 %, а в нуле диапазона δ прк = -0,01 %. К таким измерительным приборам относятся высокоточные цифровые вольтметры, потенциометры постоянного тока и другие высокоточные приборы. В этом случае

δ (х) = δ к + δ н (хк/х — 1),

где хк — верхний предел измерений (конечное значение шкалы прибора), х — измеряемое значение.

2. Классы точности средств измерений

Класс точности — это обобщенная характеристика средства измере­ний, выражаемая пределами его допускаемых основной и дополнитель­ных погрешностей, а также другими характеристиками, влияющими на точность. Класс точности средств измерений обозначают числом. В общем случае класс точности дает возможность судить о том, в каких пределах находится погрешность средств измерений этого класса, но не является непосредственным показателем точности измерений, выпол­няемых с помощью этих средств. Это обстоятельство является важным при выборе средств измерений в зависимости от заданной точности из­мерений.

С целью ограничения номенклатуры средств измерения по точно­сти для средств измерения конкретного вида устанавливают ограничен­ное число классов точности, определяемое технико-экономическими обоснованиями.

Итак, классом точности средств измерений называется обобщенная характеристика средств измерений, определяемая пределами допускае­мых основных и дополнительных погрешностей, значения которых ус­танавливаются в стандартах на отдельные виды средств измерений. При этом учитываются другие свойства средств измерений, влияющие на точность.

В числовом виде класс точности определяется максимальной абсо­лютной погрешностью прибора, отнесенной к пределу измерения, вы­раженной в процентах

К_n=,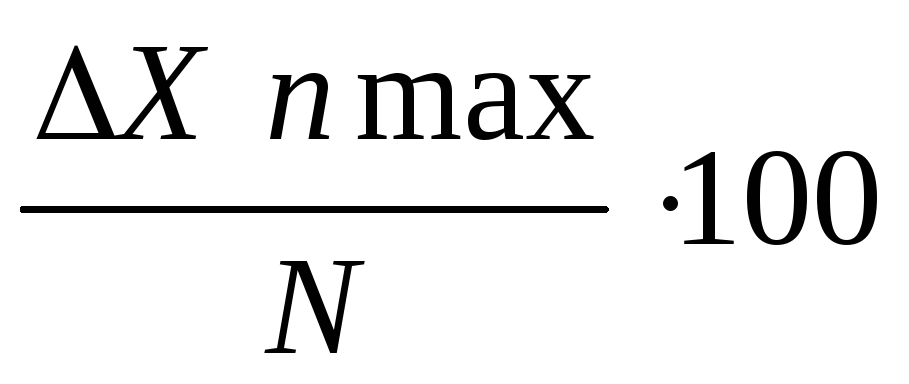

где nmax — максимальная абсолютная погрешность прибора;

N — предел измерения прибора.

Классы точности присваиваются типам средств измерений с уче­том результатов государственных приемочных испытаний.

Средствам измерений с несколькими диапазонами измерений одной и той же физической величины или предназначенным для измерения разных физических величин могут быть присвоены различные классы точности для каждого диапазона или каждой измеряемой величины. Так, амперметр с диапазонами 0 — 25; 0 — 50; 0 — 100  может иметь разные классы точности для каждого из диапазонов; электрическому измери­тельному прибору, предназначенному для измерения напряжения и со­противления, могут быть присвоены два класса точности: один — как вольтметру, другой — как омметру.

Обозначения классов точности наносятся на циферблаты, щитки, корпуса приборов, приводятся в нормативно-технических документах. Указывается также ссылка на стандарт или технические условия, в ко­торых установлены классы точности для этих конкретных средств из­мерений.

Чтобы ограничить произвол в установлении погрешности средств измерений, определить единый критерий для оценки погрешности из­мерения, а также для облегчения выбора средств измерений с необхо­димой точностью измерений, устанавливают ряд классов, обозначаемых арабскими цифрами: (1; 1.5; 1.6; 2.0; 2.5; 3.0; 4.0; 5.0; 6 ) • 10ⁿ , где п = 0; 1; -1; -2; -3 и т. д.

Выбранное из такого ряда значение класса точности означает, что значение измеряемой величины не отличается оттого, что показывает указатель отсчетного устройства более чем на соответствующее число процентов от верхнего предела измерения.

Пример 1. Указатель отсчетного устройства вторичного прибора класса точности 0.5, служащего для измерения величины давления в трубопроводе, показывает 124 кПа. Шкала вторичного прибора приве­дена на рис. 2. Чему равно измеренное давление?

кПа

025 5075 100 125 150 175 200

0.5 ГОСТ 8711-90

Рис. 2. Шкала вторичного прибора класса точности 0.5, служащего для измерения давления

Решение. Для указанного прибора измеряемое давление не может отличаться оттого, что показывает указатель, более чем на 1 кПа, т. е. если 200 кПа — 100 %, то 0.5 % соответствует

Х=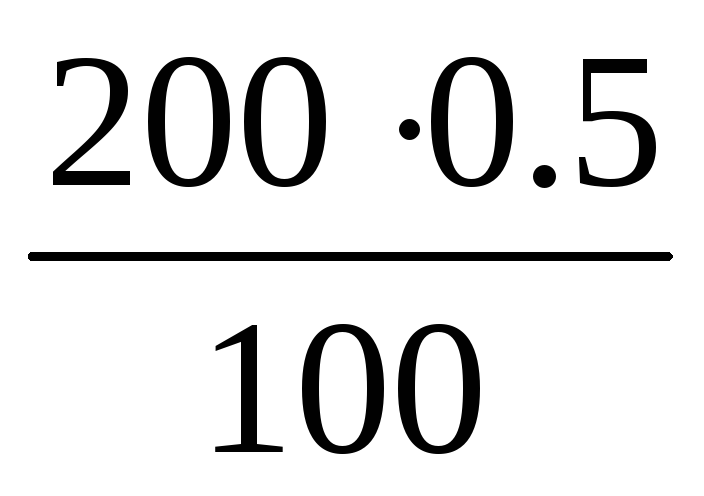= 1 кПа,

следовательно, измеренное значение давления Р будет

123 кПа ≤ Р ≤ 125 кПа.

Если при тех же условиях (шкала равномерная, линейная) нулевое значение находится внутри диапазона измерения, то значение измеряе­мой величины не отличается от того, что показывает указатель, больше чем на соответствующее классу точности число процентов от большего из модулей пределов измерений.

Пример 2. Указатель отсчетного устройства мановакууметра класса точности -1.5, шкала которого дана на рис.3, показывает 4 кПа. Чему равна измеряемая величина давления (разряжения)?

кПа

-5 -2.5 0 2.5 5 7.5 10 12.5 15

1.5 ГОСТ 8711-90

Рис. 3. Шкала мановакууметра класса точности 1.5

Решение. Для указанного прибора измеренное давление (разряжение) не может отличаться оттого, что показывает указатель, более чем на 0.225 кПа, т. к. 15 кПа соответствует 100 %, а 1,5 % — соот­ветственно

Х = = 0,225 кПа,

Поэтому измеряемое давление (разряжение) будет

3,775 кПа ≤ Р ≤ 4,225 кПа.

У средств измерений с установленным номинальным значением от­личие измеряемой величины от той, что показывает указатель, не может превышать соответствующего числа процентов от номинального значе­ния.

Пример 3. Цифровой измерительный прибор класса точности 2.0, предназначенный для измерения температуры с номинальным значени­ем 100 °С, показывает 97 °С. Чему равна измеряемая температура?

Решение. У такого прибора измеряемая температура не отличается от цифры на табло больше чем на 2 °С, т. к. 100 °С соответствует 100 %, а 2,0 % соответствует

Х =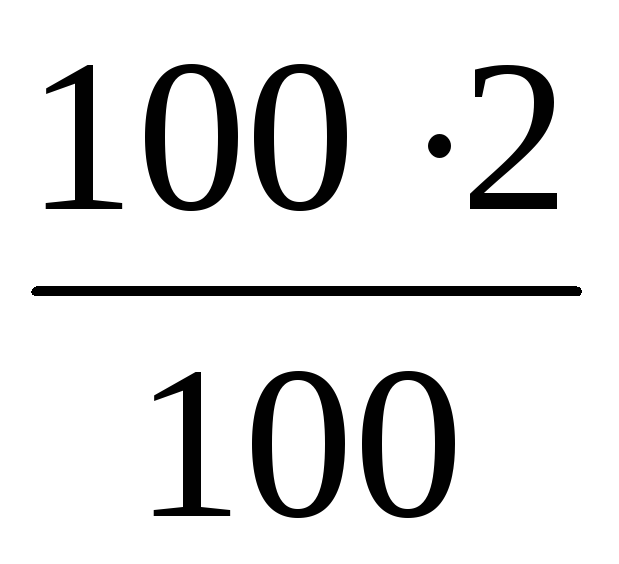= 2 С,

следовательно, измеряемая температура

95 °С ≤ t ≤ 99 °С.

Заключение в окружность, например , и т. д., означа­ет, что проценты, соответствующие классу точности, исчисляются не­посредственно от того значения, которое показывает указатель.

Пример 4. Указатель отсчетного устройства рН-метра класса точ­ности 0,5 с неравномерной шкалой, представленной на рис. 4, пока­зывает 8,5 рН. Чему равно измеренное значение величины рН?

02 4 6 7 8 9 10 11 12

ГОСТ 8778-90

Рис. 4. Шкала измерительного прибора, предназначенного для измерения величины рН

Решение. При таком обозначении класса точности измеряемая ве­личина не может отличаться от того, что показывает указатель, больше чем на 0,04 ед. рН, так как 8,5 ед. рН соответ­ствует 100 %, а 0,5 % соответству­ет

,

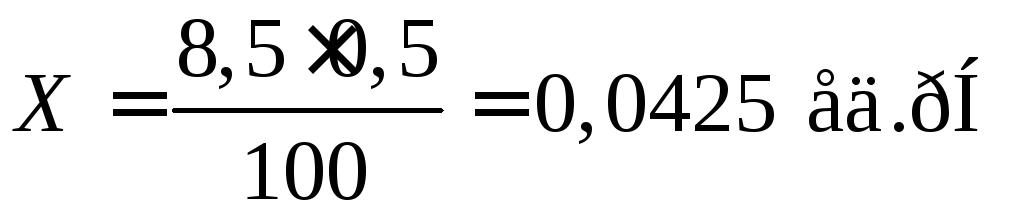следовательно, измеренное значение величины рН:

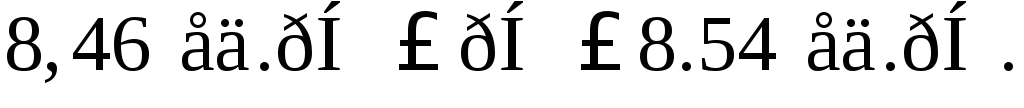
Иногда обозначение классов точности пишется в виде дроби, на­пример 0,02/0,01, 0,03/0,01 и т. д. Такое обозначение класса точности означает, что измеряемая величина не может от­личаться от значения X, показанного указателем, больше чем на

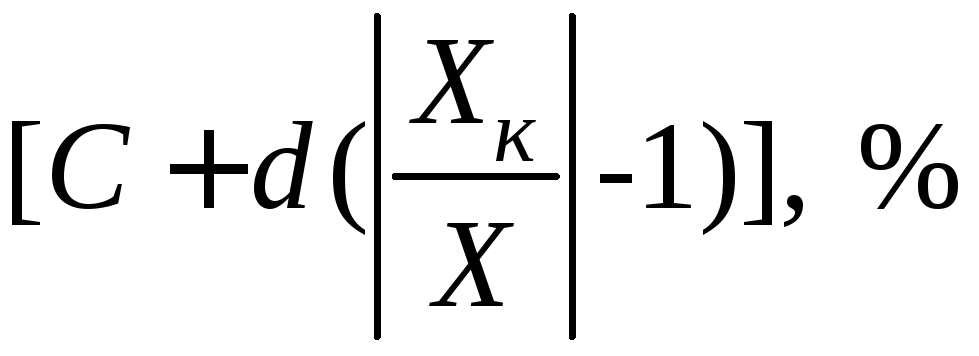
где С и d — соответственно числитель и знаменатель в обозна­чениикласса точности;

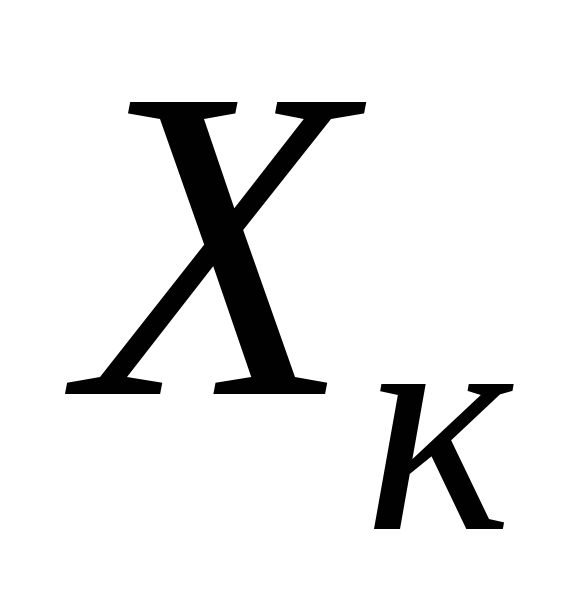— больший (по модулю) из пределов измерений;

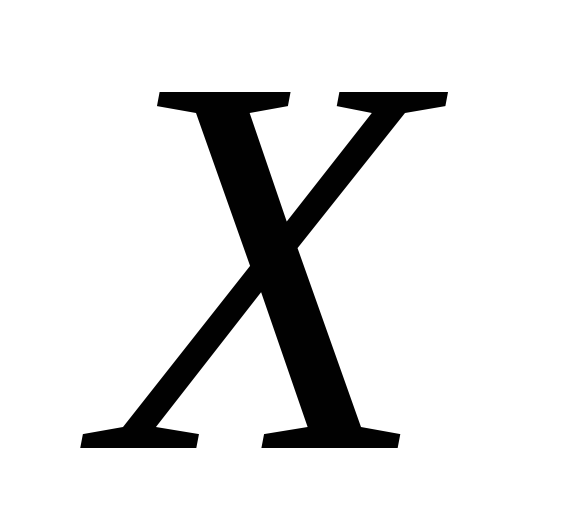— значение измеряемой величины, показываемое указателем.

Пример 5. Указатель отсчетного устройства ампервольт­метра клас­са точности 0.02/0.01 со шкалой (рис. 6) показывает -25 А. Чему рав­на измеряемая сила электрического тока?

-50 -25 0 25 50 А

-100 -50 0 50 100 В

0.02/0.01 ГОСТ 8711-927

Рис. 5. Шкала ампервольтметра с классом точности 0.02/0.01

Решение. Измеряемая сила электрического тока отличается от той, что показывает прибор, не больше чем на

,

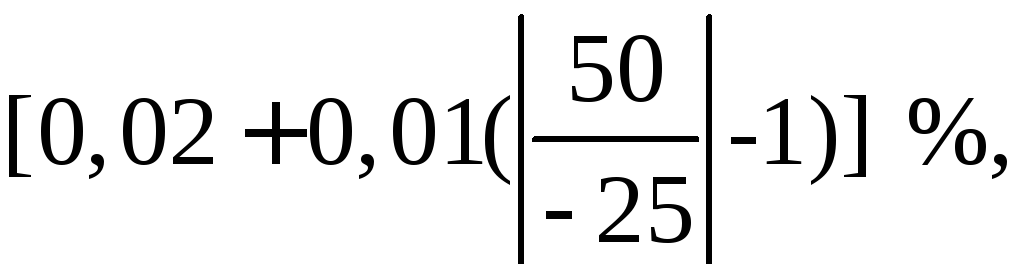что составляет 0,03 %.

Так как 25 А — 100 %, а 0,03 % составляет

.

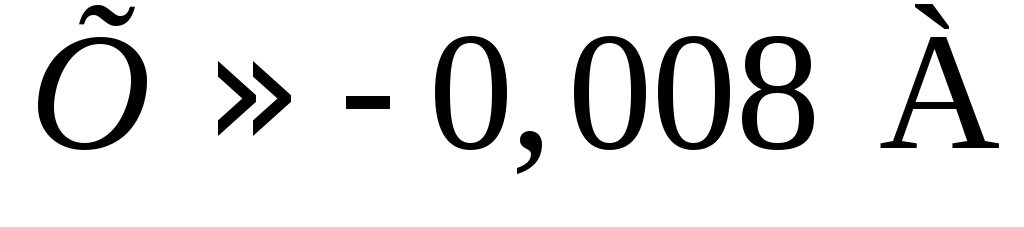Таким образом, измеренное значение тока будет

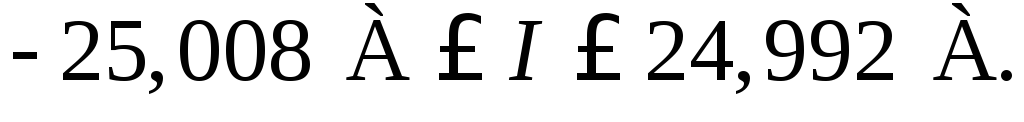
В заключение подчеркнем еще раз, что класс точности, явля­ясь обобщенной характеристикой средств измерения, позволяет определить пределы, в которых находится значение измеряемой величины.

2.5.1 Классы точности средств измерений

При высокоточных лабораторных измерениях предполагается строгое нормирование метрологических характеристик средства измерений (диапазон измерений, предел измерения, цена деления шкалы, чувствительность и др.). Основная метрологическая характеристика СИ – погрешность СИ – есть разность между показаниями СИ и истинными (действительными) значениями ФВ. Все погрешности СИ в зависимости от внешних условий делятся на основные и дополнительные .

При технических измерениях, когда не предусмотрено выделение случайных и систематических составляющих, когда не существенна динамическая погрешность СИ, когда не учитываются влияющие (дестабилизирующие) факторы и т.д., можно пользоваться более грубым нормированием – присвоением СИ определенного класса точности по ГОСТ 8.401-80.

Класс точности — это обобщенная метрологическая характеристика СИ, определяемая предельными значениями допустимых основной и дополнительной погрешностей в рабочих диапазонах влияющих величин. Например, для основного параметра окружающей среды — температуры — в паспорте на прибор может быть записано: «……диапазон рабочих температур:0….+40⁰С, диапазон температур хранения: -10…+60⁰С». Класс точности СИ уже включает систематическую и случайную погрешности. Однако он не является непосредственной характеристикой точности измерений, выполняемых с помощью этих СИ, поскольку точность измерения зависит как от метода измерения, так и условий измерения. В частности, чтобы измерить величину с точностью до 1%, выбранное СИ должно обладать гораздо меньшей погрешностью. Для гарантированной заданной или расчетной погрешности измерений δ_из относительная погрешность СИ δ_СИ должна быть на 25%-30% ниже чем δ_и (т.е. δ_си=0,7 δ_из). Определяя класс точности, нормируют, прежде всего пределы допустимой основной погрешности δ_осн. Пределы допускаемой дополнительной погрешности устанавливают в виде дольного (кратного) значения ( δ_осн). Пределы допускаемых основной и дополнительной погрешностей выражают в форме абсолютной (), относительной (δ) или приведенной () погрешностей.

Приведенной погрешностью СИ (прибора) называют относительную погрешность, определяемую по формуле:

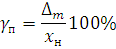
где — предельно допустимая (максимальная) абсолютная погрешность СИ, а Х_н — нормирующее значение (чаще всего в качестве Х_н выбирается верхний или конечный предел диапазона измерения прибора Х_к).

ГОСТ 8.401-80 «Классы точности средств измерений. Общие требования» в качестве основных устанавливает три вида классов точности СИ:

1) для пределов допускаемой абсолютной основной погрешности в единицах измеряемой величины или делениях шкалы;

2) для пределов допускаемой относительной погрешности в виде ряда чисел

где А=1; 1,5; 2; 2,5; 4; 5; n= 1; 0; -1; -2; -3……

3) для пределов допускаемой приведенной погрешности с тем же рядом чисел γ=±А10ⁿ. Например для класса точности 0,05 , А=5, n= -2. При этом проценты в обозначении класса точности не указываются;

Абсолютная погрешность может выражаться одним числом =а при аддитивном характере погрешности (ширина коридора значений 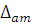не изменяется во всем измеряемом диапазоне значении Х, см. рисунок 2а), или двучленом Δ=(а+bх) при совместном проявлении аддитивной и мультипликативной составляющих, либо в виде таблицы (графика функции) при нелинейном изменении границ абсолютной погрешности (например, табл.1).

Таблица 1

Пределы допускаемой абсолютной погрешности вольтметра М-366

Показания СИ, В	0	10	20	30	40	50	60	70	75
Погрешность Δ, В	-0,2	-0,1	0	0,1	0,2	0,35	0,45	0,55	0,7

Классы точности СИ, выраженные через абсолютные погрешности, обозначают прописными буквами латинского алфавита или римскими цифрами. При этом чем дальше буква от начала алфавита тем больше значения допускаемой абсолютной погрешности. Буквенное обозначение принято для мер с аддитивной погрешностью, цифра ΙΙΙ для мер с обоими составляющими погрешности (см. табл.2).

Класс точности через относительную погрешность СИ назначается двумя способами:

— Если погрешность СИ имеет в основном мультипликативный характер 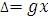(при этом относительная погрешность остается постоянной величиной g во всем измеряемом диапазоне), то пределы допускаемой основной относительной погрешности устанавливают по формуле [4 с.140.]

(2)

Так определяют классы точности мостов переменного тока, счетчиков электроэнергии, делителей напряжения, измерительных трансформаторов и др. При этом класс точности на СИ обозначается цифрой в кружке. Например .

— Если СИ имеют обе составляющих погрешности, то класс точности обозначается двумя цифрами c/d , соответствующими значениям с и d формулы

(3)

Здесь c и d выражаются также через ряд (1). Причем c>d, Х_{к —} конечное значение шкалы, X – значение отсчета. Например, класс точности 0,02/0,01 означает, что с=0,02; а d=0,01.

Для некоторых СИ характерна сложная зависимость относительной погрешности от измеряемой величины или влияющих факторов, которая приводит к логарифмической характеристике точности. В основном это широкополосные СИ, например мосты постоянного тока, мосты сопротивлений, цифровые частомеры и т.д. Для них ГОСТ 8.401-80 допускает нормирование класса точности трехчленной формулой [4 c. 143]

δ(x)=(xmin/x+ δ3+x/xk)

(4)

где Х_min и Х_к — порог и предел чувствительности, δ_з — относительная погрешность, ограничивающая снизу рабочий диапазон. При δ_з =0,5%, Х_min=0,02 Ом и Х_к =20*10⁶ Ом для любого Х относительная погрешность составит:

δx=(0,02/x+0,5/100+x/20∙10^6)100%.

(5)

Для приборов с существенно неравномерной шкалой нормирующее значение 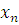устанавливается равным длине шкалы или ее части, соответствующей диапазону измерений. В этом случае предел абсолютной погрешности выражают, как и длину шкалы, в единицах длины, а на шкалу прибора наносится обозначение класса точности в виде цифры под которой находится знак 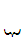.Например, обозначение класса точности означает, что для данного прибора установлен предел допускаемой погрешности, составляющей 2,5% от длины шкалы, действительное значение измеряемой величины должно находиться в пределах ±2,5% от длины шкалы, отсчитанных от установившегося положения стрелки.

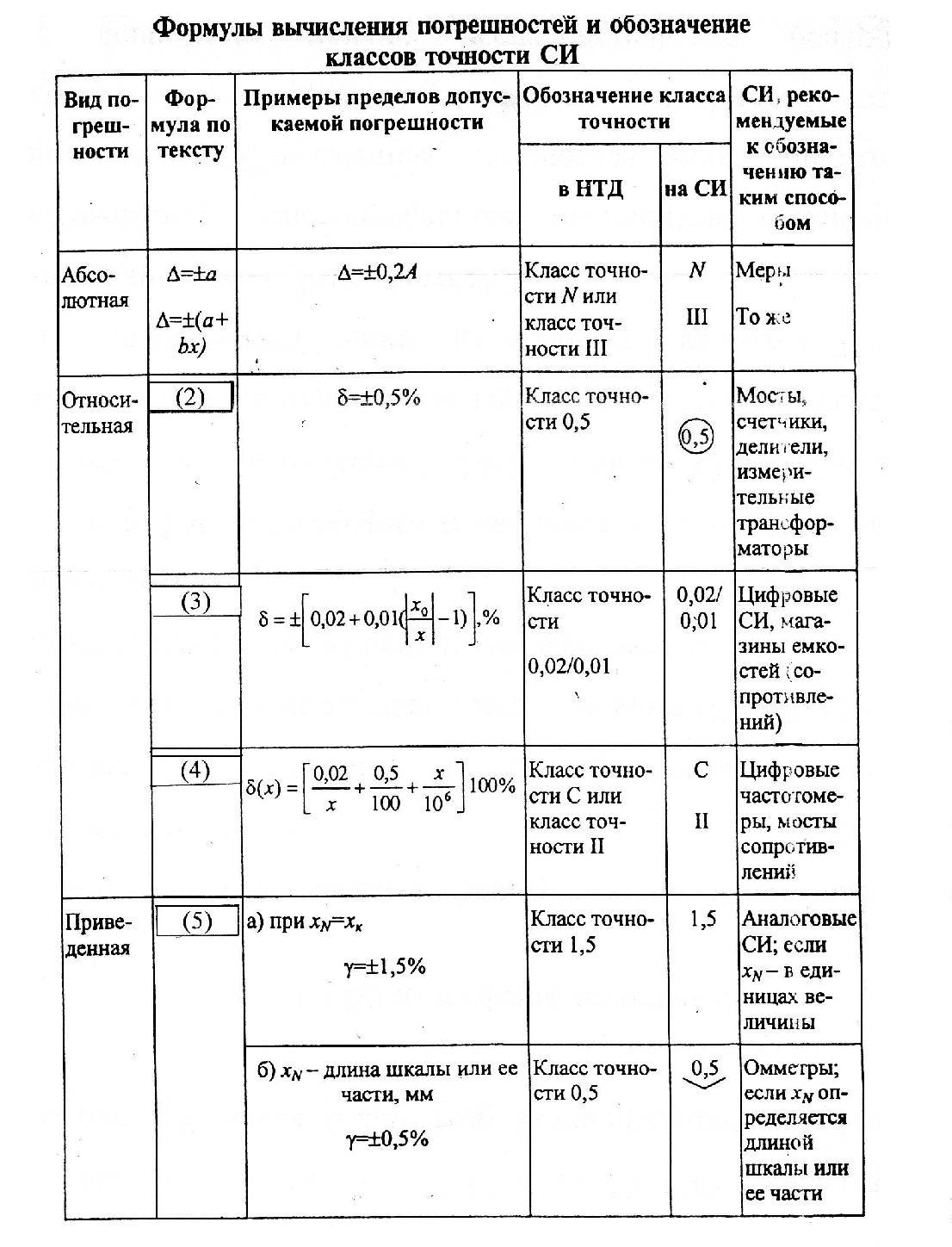
Обозначения классов точности в документах и на приборах приведены в табл. 2.

Таблица 2

Необходимо подчеркнуть, что класс точности является обобщенной характеристикой СИ данного типа. Значение его позволяет не определить погрешность конкретного измерения, а лишь указать пределы, в которых находится погрешность при измерении физической величины данным средством.

Пример. Отсчет по шкале прибора с приделами измерений 0-50А и равномерной шкалой составил 25А.Пренебрегаю другими видами погрешностей измерений, оценить пределы абсолютной погрешности этого отсчета при использовании амперметров с классами точности 0,02/0,01 , , 0,5. Выбрать амперметр, который бы давал погрешность отсчета, не превышающую 0,01А.

1.Для СИ класс точности 0,02/0,01 из табл.2 находим

,

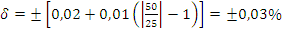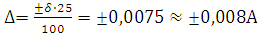
2.Для СИ класс точности

% ,

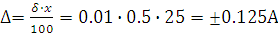
3.Для СИ класс точности 0,5

,

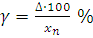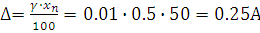
Вывод. Погрешность отсчета не превышающую 0,01А обеспечит амперметр класса точности 0,02/0,01, а при использовании амперметра класса точности 0,5 погрешность отсчета будет превышать требуемую в 25 раз.

Что такое класс точности манометра — Детейлинг-мастерская Adrenaline Garage

Манометры выпускаются следующих классов точности: 0,6; 1; 1,5; 2,5; 4 (цифры расположены в порядке уменьшения значения класса точности приборов).

Класс точности – это максимально допустимая относительная погрешность прибора, приведенная к диапазону его шкалы, выраженная в процентах. Чем ниже значение класса точности тем меньше погрешность манометра.

Согласно ГОСТ 2405-88 класс точности приборов должен выбираться из ряда: 0,4; 0,6; 1,0; 1,5; 2,5; 4,0. В случае с дифференцированным значением основной погрешности устанавливают следующие условные обозначения классов точности: 0,6-0,4-0,6; 1-0,6-1; 1,5-1-1,5; 2,5-1,5-2,5; 4-2,5-4.

Обозначение класса точности	Предел допускаемой основной погрешности, % диапазона показаний, в диапазоне шкалы
	от 0 до 25%	от 25 до 75%	св. 75 до 100%
0,4	±0,4	±0,4*	±0,4
0,6-0,4-0,6	±0,6	±0,4	±0,6
0,6	±0,6	±0,6	±0,6
1-0,6-1	±1,0	±0,6	±1,0
1	±1,0	±1,0	±1,0
1,5-1-1,5	±1,5	±1,0	±1,5
1,5	±1,5	±1,5	±1,5
2,5-1,5-2,5	±2,5	±1,5	±2,5
2,5	±2,5	±2,5	±2,5
4-2,5-4	±4,0	±2,5	±4,0
4	±4,0	±4,0	±4,0

Классом точности называют выраженную в процентах максимально допустимую погрешность манометра, приведенную к его диапазону измерений.

Чем ниже значение класса точности, тем меньше погрешность измерительного прибора.

Какие существуют классы точности

Согласно ГОСТ 2405-88 класс точности манометра должен выбираться из ряда чисел:

• 0,4;
• 0,6;
• 1,0;
• 1,5;
• 2,5;
• 4,0.

Как связаны диаметр и класс точности

Диаметр и класс точности манометра параметры взаимосвязанные, чем выше точность прибора для измерения давления, тем больше диаметр его шкалы.

Какая погрешность у манометра с классом точности 1,5

Погрешность измерения манометра, зависит не только от его класса точности, но и от диапазона измерений.

Рассмотрим пример, диапазон измерения манометра составляет 10 МПа, класс точности прибора 1,5. Это означает, что максимальная погрешность манометра не должна превышать 10*1,5/100=0,15 МПа.

Манометр класса точности 2,5

Обозначение 2,5 означает, что максимально допустимая погрешность измерений манометра составляет 2,5% от его диапазона измерений.

Как узнать класс точности манометра

Класс точности указывается на шкале прибора, перед числовым значением могут располагаться буквы KL или CL.

Вычисление класса точности прибора

Предположим, что на шкале указан класс точности 1,0, а диапазон измерения прибора 250 Bar. При сравнении результатов измерения давления с показаниями образцового манометра выяснилось, что погрешность составляет 2 Bar. Соответствует ли манометр указанному классу точности?

Для того, чтобы ответить на этот вопрос произведем вычисление класса точности, для этого соотнесем погрешность измерений с диапазоном измерения прибора и выразим результат в процентах.

2*100/250=0,8

 

Полученный результат не превышает 1, это означает, что манометр соответствует указанному классу точности 1,0.