При проведении эксперимента надо ограничить ток в цепи, посредством включенной последовательно с катушкой нагрузки, иначе возникнет короткое замыкание.

Катушка индуктивности в цепи переменного тока

В цепи переменного тока в катушке индуктивности происходит следующий процесс:

1. ток возбуждает в катушке электромагнитное поле. Поскольку он переменный, то и параметры электромагнитного поля во времени меняются, то есть оно тоже переменное;
2. переменное магнитное поле в соответствии с законом электромагнитной индукции возбуждает в самой катушке ЭДС. Ее так и называют — ЭДС самоиндукции. Она всегда идет против направления изменения силы тока. Следовательно, в первой половине полупериода, когда сила тока возрастает, катушка это нарастание сдерживает. При этом часть энергии электричества накапливается в формируемом катушкой магнитном поле;
3. во второй половине полупериода, катушка, наоборот, противостоит снижению силы тока, возвращая в цепь накопленную в виде магнитного поля энергию.

Таким образом, катушка индукции оказывает сопротивление источнику переменного тока. Это сопротивление имеет иную природу, нежели активное, преобразующее электрическую энергию в тепло.

Сопротивление катушки энергию не потребляет, а лишь аккумулирует ее и затем снова возвращает в цепь, меняя характер протекания в ней тока. Его называют индуктивным. В противоположность активному, оно, как и емкостное сопротивление конденсатора, является реактивным.

Эффект проявляется тем сильнее, чем выше частота переменного тока, то подтверждается формулой расчета индуктивного сопротивления: XL = w*L = 2 π * f * L, где:

• XL — индуктивное сопротивление, Ом;
• W — круговая частота переменного тока, рад/с;
• F — частота переменного тока, Гц;
• L — индуктивность катушки, Гн.

Индуктивное сопротивление, несмотря на иной принцип действия, измеряется в тех же единицах, что и активное — Омах. Таким образом, в цепях переменного тока катушка индуктивности выступает ограничителем силы тока и нагрузку, в отличие от цепи постоянного, вводить не требуется.

Зависимость индуктивного сопротивления катушки от частоты тока позволяет использовать данный элемент помимо прочего, для фильтрации высокочастотных помех или сигналов. Например, при установке его в схеме динамика, последний воспроизводит только низкие частоты, то есть играет роль сабвуфера.

На преодоление индуктивного сопротивления источник расходует часть мощности — это реактивная мощность (Wр). Остальное называют активной или полезной мощностью (Wа) — она производит полезную работу. Вместе реактивная и активная мощности образуют полную: Wр + Wа = Wпол.

График происходящих процессов в катушке индуктивности

Доля активной мощности характеризуется параметром cosϕ: cosϕ = Wа / W пол. Полную мощность принято измерять в вольт-амперах (ВА). Именно эти единицы указываются в характеристике источников бесперебойного питания (ИБП) и дизельных электрогенераторов. Активная мощность измеряется в привычных ваттах (Вт).

Все сказанное имеет отношение к потребителям с электродвигателями и трансформаторами, поскольку обмотки этих элементов по сути, являются катушками индуктивности. То есть если на шильдике импульсного блока питания компьютера указано, что его мощность составляет 400 Вт и cosϕ = 0,7, то от «бесперебойника» данное устройство потянет мощность Wпол = Wа / cosϕ = 400 0,7 = 571,4 ВА.

При большом количестве подобных потребителей, затраты на реактивную мощность существенно перегружают генераторы электростанций, ввиду чего в энергосетях применяют установки компенсации реактивной мощности (УКРМ).

При включении катушки индуктивности в цепь постоянного тока процесс, описанный в пунктах 1-3, также имеет место, только не все время, а в момент включения/отключения.

Если собрать простейшую цепь из последовательно установленных выключателя, катушки и лампы, можно видеть, что лампочка загорается при замыкании цепи с запаздыванием и также с запаздыванием гаснет после размыкания.

Объясняется это тем, что ток в момент включения меняется от нулевого значения до максимума, также в момент отключения его значение меняется, хоть и очень быстро, от максимума до нуля. В первом случае катушка накапливает в себе часть энергии в виде магнитного поля, во втором — отдает ее лампе, отчего та и горит после размыкания цепи.

График зависимости тока и ЭДС самоиндукции от времени

Графически характер изменения тока в цепи и ЭДС самоиндукции с течением времени выглядит так:

Зависимость тока и ЭДС самоиндукции в катушке в цепи переменного тока

Из графика видно, что ЭДС самоиндукции тем больше, чем выше скорость изменения силы тока. В начале периода (участок вблизи т.1 на графике) сила тока возрастает быстро, потому и ЭДС самоиндукции здесь максимальна. К концу первой четверти периода (т. 2) скорость изменения снижается почти до нуля (синусоида принимает горизонтальное положение), после чего сила тока все стремительнее уменьшается (участок между т. 2 и т. 3).

Соответственно, ЭДС самоиндукции снижается в т. 2 до нуля, а затем снова возрастает, но при этом меняет знак на противоположный: теперь она противодействует падению силы тока, то есть ток и ЭДС по знаку совпадают. В следующем полупериоде картина повторяется.

График зависимости тока и напряжения в цепи от времени

Графически зависимость тока в цепи и напряжения с течением времени выглядит так:

График зависимости тока и напряжения в цепи от времени

Как видно, синусоиды тока и напряжения не совпадают: первая смещена относительно второй на угол в 90⁰ или ¼ периода вправо, то есть, отстает от нее. Данное явление называют сдвигом фаз.

Сдвиг фаз между напряжением и током

Данное явление обусловлено противодействием катушки индуктивности изменению силы тока.

Изучить явление поможет простой опыт, для которого понадобятся следующие устройства и элементы:

Все элементы последовательно подключаются к источнику постоянного тока. На осциллографе видно две синусоиды, отображающие напряжение на генераторе частоты (красная) и на резисторе (желтая).

Вторую синусоиду можно считать отображением колебаний тока на резисторе, так как он по амплитуде, фазе и частоте всегда соответствует напряжению на данном участке.

Ход опыта:

1. генератор настраивается на частоту в 1 кГц. По осциллографу видно, что фазы обеих синусоид совпадают. Амплитуда на второй синусоиде составляет почти 2 В;
2. увеличивают частоту тока до 100 кГц. Осциллограф отражает два изменения: амплитуда колебаний напряжения на резисторе уменьшилась, а синусоида резистора сдвинулась относительно синусоиды генератора: это и есть сдвиг фаз;
3. при дальнейшем увеличении частоты, наблюдается следующее: амплитуда напряжения на резисторе падает до 480 мВ, а сдвиг фаз увеличивается;
4. при установке максимально возможной частоты, амплитуда напряжения на резисторе падает до 120 мВ. Сдвиг фаз приближается к 90⁰ (четверть периода).

Опыт подтвердил, что индуктивное сопротивление катушки при увеличении частоты возрастает. Попутно наблюдается сдвиг фаз между напряжением источника и током нагрузки, стремящийся к 90⁰.

Видео по теме

Кратко о катушке индуктивности в цепи переменного тока в видео:

Катушка индуктивности при всей своей простоте, применяется довольно широко. Это и индукционные нагреватели, и обмотки трансформаторов, двигателей и генераторов, и дроссели (сглаживание пульсаций и подавление помех), и реактор (ограничение силы тока при замыкании на ЛЭП), и многое другое. Правильно применяя данный элемент, радиолюбитель повысит качество работы электросхемы.

Катушка индуктивности в цепи переменного тока

Катушка индуктивности в цепи переменного тока

«Физика — 11 класс»

Индуктивность в цепи влияет на силу переменного тока.
Есть цепь из катушки с большой индуктивностью и электрической лампы накаливания.

При подключении с помощью переключателя цепи к источнику постоянного напряжения или к источнику переменного напряжения постоянное напряжение и действующее значение переменного напряжения будут равны.
Однако лампа светится ярче при постоянном напряжении.
Значит действующее значение силы переменного тока в цепи меньше силы постоянного тока.

Это объясняется явлением самоиндукции.
При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно.
Возникающее при этом вихревое электрическое поле тормозит движение электронов.
По прошествии некоторого времени сила тока достигает наибольшего (установившегося) значения, соответствующего данному постоянному напряжению.
Если напряжение быстро меняется, то сила тока не будет успевать достигнуть тех значений, которые она приобрела бы с течением времени при постоянном напряжении.

Максимальное значение силы переменного тока (его амплитуда) ограничивается индуктивностью цепи и будет тем меньше, чем больше индуктивность и чем больше частота приложенного напряжения.

Если сопротивление катушки равно нулю, то и напряженность электрического поля внутри проводника в любой момент времени должна быть равна нулю.
Иначе сила тока, согласно закону Ома, была бы бесконечно большой.
Равенство нулю напряженности поля оказывается возможным потому, что напряженность вихревого электрического поля _i, порождаемого переменным магнитным полем, в каждой точке равна по модулю и противоположна по направлению напряженности кулоновского поля _к, создаваемого в проводнике зарядами, расположенными на зажимах источника и в проводах цепи.

Из равенства _i = —_к следует, что удельная работа вихревого поля (т. е. ЭДС самоиндукции) равна по модулю и противоположна по знаку удельной работе кулоновского поля.

Так как удельная работа кулоновского поля равна напряжению на концах катушки, можно записать:

e_i = —u

При изменении силы тока по гармоническому закону

i = Im sin ωt

ЭДС самоиндукции равна:

е_i = —Li’ = —LωI_m cos ωt

Так как u = —e_i напряжение на концах катушки оказывается равным

где
U_m = LωI_m — амплитуда напряжения.

Колебания напряжения на катушке опережают по фазе колебания силы тока на , или, что то же самое, колебания силы тока отстают по фазе от колебаний напряжения на .

Амплитуда силы тока в катушке равна:

Если ввести обозначение

ωL = Х_L

и действующие значения силы тока и напряжения, то получим:

Величину X_L, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.

Действующее значение силы тока связано с действующим значением напряжения и индуктивным сопротивлением соотношением, подобным закону Ома для цепи постоянного тока.

Индуктивное сопротивление зависит от частоты ω.
Постоянный ток вообще «не замечает» индуктивности катушки.
При ω = 0 индуктивное сопротивление равно нулю (X_L = 0).
Чем быстрее меняется напряжение, тем больше ЭДС самоиндукции и тем меньше амплитуда силы тока.

Итак,
Катушка индуктивности оказывает сопротивление переменному току.
Это сопротивление, называемое индуктивным, равно произведению циклической частоты на индуктивность.
Колебания силы тока в цепи с индуктивностью отстают по фазе от колебаний напряжения на .

Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин

Электромагнитные колебания. Физика, учебник для 11 класса — Класс!ная физика

Свободные и вынужденные электромагнитные колебания. Колебательный контур. Превращение энергии при электромагнитных колебаниях — Аналогия между механическими и электромагнитными колебаниями — Уравнение, описывающее процессы в колебательном контуре. Период свободных электрических колебаний — Переменный электрический ток — Активное сопротивление. Действующие значения силы тока и напряжения — Конденсатор в цепи переменного тока — Катушка индуктивности в цепи переменного тока — Резонанс в электрической цепи — Генератор на транзисторе. Автоколебания — Краткие итоги главы

Катушка Индуктивности в Цепи Переменного Тока: Принцип Действия

Катушки индуктивности различных модификаций

Сегодня нами будет рассмотрена катушка индуктивности в цепи переменного тока, узнаем, в чем бы была разница, если бы цепь питалась от постоянного тока, а также много интересных особенностей этого простого, но очень важного радиоэлемента.

Теоретика

Для начала давайте определим назначение этой детали, а также основные понятия и термины, связанные с ней.

Что такое катушка индуктивности

Разнообразие размеров катушек

Катушка индуктивности – это радиоэлемент, применяющийся в разных схемах для следующего:

• Сглаживание биений;
• Подавление помех;
• Ограничение переменного тока;
• Накопление энергии и прочее.

Представляет собой данный элемент спиральную, винтовую или винтоспиральную катушку, сделанную из изолированного проводника. Деталь обладает относительно малой емкостью и малым активным сопротивлением, при этом у него имеет высокая индуктивность, то есть способность возникновения ЭДС (электродвижущей силы) в проводнике, при протекании в цепи электрического тока.

Дроссели на печатной плате

• Катушка индуктивности, в зависимости от места и цели применения может иметь и другие названия. Например, если элемент используется для изоляции по высокой частоте в разных частях схемы, накоплении энергии магнитного поля сердечника, сглаживания пульсаций и подавления помех, катушку называют дросселем либо реактором (второе название употребляется редко).
• Если говорить про силовую электротехнику, то там устоялось название ректор – его применяют при необходимости ограничения тока, например, если произошло замыкание на ЛЭП.

Соленоид

• Бывают также и цилиндрические катушки индуктивности, называемые соленоидами. Длина такого цилиндра в несколько раз превышает его диаметр.

Интересно знать! Магнитное поле внутри соленоида однородно. Данное магнитное поле может выполнять механическую работу, втягивая ферритовый сердечник.

Обмотка с втягивающего реле на стартере

• Применяются катушки индуктивности и в электромагнитных реле, где их называют обмоткой реле.
• Устанавливаются подобные элементы и в индукционные нагреватели – тут их называют нагревательными индукторами.

Схема сверхпроводящего индуктивного накопителя

• Также можно услышать термины вроде индукционного накопителя или накопительного дросселя, если речь идет об устройствах импульсной стабилизации напряжения.

Конструкционные особенности

Строение катушки индуктивности

Конструкционно катушка индуктивности представляет собой намотанную по спирали или винтом изолированную одножильный или многожильный проводник (чаще, лакированная медная проволока), вокруг диэлектрического сердечника (каркаса). Форма сердечника может быть круглой, тороидальной, прямоугольной, квадратной. Материалы, применяемые для сердечника, имеют магнитную проницаемость выше, чем у воздуха, что дополнительно удерживает магнитное поле возле катушки, а значит, увеличивается и индуктивность.

Существуют и катушки, вовсе не имеющие сердечника, или же он является регулируемым, что позволяет менять индуктивность детали.

Тороидальная катушка

Намотка проводника может быть как однослойной, ее еще называют рядовой с шагом, или многослойной (применяются названия универсал, внавал, рядовая). Расстояние между витками называется шагом.

Интересно знать! Шаг намотки может быть прогрессивным, то есть его величина изменяется по длине катушки. Применяется такая намотка для снижения «паразитной» емкости.

Применение

Используются катушки в схемах обработки сигналов и аналоговых схемах. В сочетании с конденсаторами и прочими радиокомпонентами могут формировать участки схем, которые усиливают или отфильтровывают определенные сигналы.

Широко применяются дроссели в источниках питания, где они вместе с конденсаторами фильтра призваны устранить остаточные помехи и прочие колебания, возникающие на выходе.

Строение трансформатора

Если две катушки соединить одним магнитным полем, то получится трансформатор – устройство, способное передавать электричество от одной части цепи к другой, за счет электромагнитной индукции, попутно меняя величину напряжения.

Для справки! Трансформаторы способны функционировать только с переменным током.

Основные характеристики катушек индуктивности

Прежде чем разбираться с тем, как ведет себя ток, проходя в цепи через катушку индуктивности, давайте сначала узнаем главные характеристики этого элемента.

Определение индуктивности: формула

• Прежде всего, нас интересует индуктивность – значение, численно выражающаяся соотношением потока магнитного поля, которое создается протекающим током, к силе этого самого тока. Измеряется этот параметр в Генри (Гн).
• Если говорить более простым языком, то это явление можно описать так. При протекании тока через катушку индуктивности создается электромагнитное поле, которое напрямую связано с ЭДС, которая оказывает противодействие изменению переменного напряжения, то есть в цепи возникает ток, который течет в обратном направлении основному.
• Измерение силы тока на катушке индуктивности и переменного напряжения, противостоят данной силе, точнее наоборот. Это свойство элемента называется индуктивным сопротивлением, которое находится в противофазе реактивному емкостному сопротивлению конденсатора, включенному в цепь переменного тока.

Совет! Изменение величины индуктивности катушки происходит пропорционально изменению числа витков.

Расчет энергии магнитного поля катушки

• Давно известно, что любое магнитное поле обладает некоторой энергией. Отсюда следует, что магнитное поле катушки тоже имеет определенный запас магнитной энергии. Величина этого запаса равна затраченной энергии на обеспечение протекания тока (I) в противодействие ЭДС. Расчеты производятся по приведенной выше формуле.

Гидротурбина

• Чтобы было еще понятнее давайте сравним катушку с гидротурбиной. Итак, водяной поток, который направлен через турбину, будет ощущать ее сопротивление, пока турбина до конца не раскрутится. Она имеет некоторую инерцию, а значит, будет вращаться синхронно с потоком воды, не оказывая ему практически никакого сопротивления.
• Если вы попробуете остановить поток воды или сменить его направление, то увидите, что турбина продолжит вращаться по инерции, заставляя двигаться воду в прежнем направлении. Чем выше инерция у турбины, тем сильнее она будет сопротивляться изменению направления потока воды.
• Ровно то же самое происходит в катушке индуктивности, когда переменный ток начинает течь в обратном направлении.

При последовательном соединении катушек их индуктивность складывается

• Влияние тока на индуктивность катушки выражается не только в виде основного эффекта взаимодействия. Часто наблюдаются паразитные эффекты, из-за которых сопротивление переменному току катушки индуктивности чисто реактивным назвать нельзя. Из-за этих эффектов в катушке возникают некоторые потери, оценивающиеся как сопротивление потерь. Данное значение составляет сумму потерь в сердечнике, проводе, экране и диэлектрике.
• Каждая из потерь вызвана разными причинами. В проводах их целых три: они обладают хоть и малым, но все же активным омическим сопротивлением; данное сопротивление растет с увеличением частоты, что обусловлено уменьшением амплитуды электромагнитных волн, по мере того как они проникают в глубину проводящей среды (это явление называется скин-эффектом) – другими словами, ток вытесняется на верхние слои провода, из-за чего изменяется площадь проводника, а значит, и его сопротивление; если провода свиты в спираль, возникает эффект близости, из-за которого тоже меняется активное сечение проводника, и общее сопротивление.

Дроссель сварочного аппарата

• Потери в диэлектрике могут возникать из-за межвиткового конденсатора, или по причине его электромагнитных свойств. Однако справедливости ради стоит отметить, что потери в этой части детали настолько малы, что ими часто пренебрегают при расчетах.
• Потери на сердечнике складываются из двух величин: потери на перемагничивание ферромагнетика (потери на гистерезис) и потери на вихревые токи. Переменное магнитное поле, возникающее от протекающего в проводнике тока, индуцирует вихревые ЭДС в соседних проводниках – сердечнике, проводах ближайших витков, и даже экране. Возникшие токи, имеющие название помимо вихревых, токи Фуко, также являются причиной потерь, из-за активного сопротивления провода.
• С потерями на сопротивление связана и другая характеристика, называемая добротностью. Ее величина – это соотношение реактивного и активного сопротивления катушки индуктивности.

Паразитная емкость катушки индуктивности

• Следующий параметр – это паразитная емкость. Явление состоит в том, что между витками катушки возникает некоторая нежелательная емкостная связь.
• ТКИ (температурный коэффициент индуктивности) – все мы знаем, что при нагревании вещества увеличиваются в размерах. Когда это происходит с катушкой, мы получаем нестабильность индуктивности, из-за изменения длины и диаметра проводника, длины и диаметра каркаса, а значит, изменения диаметра и шага витков. Помимо этого перемена температуры влияет на диэлектрическую проницаемость материала каркаса, что влечет изменение емкости катушки и влияет на проницаемость магнитным полем ферромагнетика сердечника.
• ТКД (температурный коэффициент дробности) – тут все понятно! Это изменение параметров добротности в зависимости от температуры.

Включение катушки индуктивности в цепи с постоянным и переменным током

В целом, мы определили, что такое катушка индуктивности, для чего она нужна, и какие характеристики для расчета ее параметров важны, однако до сих пор неискушенному читателю наверняка не понятно, как будут изменяться параметры протекающего через эту деталь тока.

Цепь, питаемая постоянным током

Катушка индуктивности в цепи постоянного тока

Чтобы упростить изложение, будем проводить очень простой опыт:

• Для начала нам потребуется блок питания, способный выдавать стабильные 12 Вольт напряжения на выходе, 12-ти вольтовая лампочка накаливания для создания сопротивления, а также сама катушка индуктивности.

Стержень из феррита

• Катушку мы соберем своими руками из куска лакированной медной проволоки и ферритового стержня.

Изготовление катушки индуктивности

• Инструкция предельно проста — берем проволоку и наматываем ее на стержень, после чего зачищаем ножом концы, чтобы можно было подсоединить клеммы от блока питания и подпаять провода.
• Цена такой схемы минимальна, так что можете без проблем повторить опыт при желании дома.

Измерение индуктивности собранной катушки

• При помощи LC-метра измеряем индуктивность полученной детали. Как видно из фото выше, в рассматриваемом примере она составила 132 мкГн.

Схема с включенной катушкой индуктивности

• Теперь берем все наши детали и соединяем их по приведенной выше схеме.

Схема включена в сеть

• Вот что получилось на практике. Как видим, постоянный ток протекает через катушку практически беспрепятственно, если не учитывать естественное сопротивление проводника, ведь ток не меняет своего направления на противоположное.

На данной схеме лампочку заменяет резистор, но это не важно

• Значит ли это, что катушка индуктивности неприменима в цепях с постоянным током? Вовсе нет! Вот другая схема, в которую, как мы видим, уже включен некий выключатель, способный размыкать цепь. Именно в момент замыкания и происходит самое интересное.
• Поскольку до этого ток был равен нулю, он начнет изменяться и расти, из-за чего изменится магнитное поле катушки, что в свою очередь приведет к возникновению ЭДС. В катушке появится индукционный ток, который потечет в обратном направлении основного потока от источника питания.
• Именно в момент включения величина ЭДС будет максимальной, так как скорость изменения тока в этот момент наиболее высока, а значит, ток катушки индуктивности равен нулю.
• Что произойдет дальше? А дальше мы увидим, что ток в катушке индуктивности начнет расти, тогда как ЭДС, наоборот, снижаться. Вот как это выглядит на графике.

Uвх – входное напряжение питания; Il- изменение величины тока; Ul – напряжение на катушке

• На верхнем графике изображено изменение напряжения входной сети, сразу после включения. Как видим, моментально появляется постоянное значение.
• Дальше показано, как меняется величина тока, протекающего через катушку. Он тоже достигает постоянно значения, но не сразу, а спустя какое-то время.
• Напряжение на катушке (нижний график) также вырастает моментально, но тут же начинает падать. При этом обратите внимание, что графики силы тока и напряжения зеркально противоположны.
• Если все это перенести на наш опыт с лампой, то мы увидим, что после соединения цепи через выключатель, она загорится не сразу, а с некоторой задержкой.

Похожая ситуация будет и при размыкании цепи.

Физические процессы в катушке при размыкании цепи

По графикам видна противоположная ситуация, означающая, что лампочка продолжить гореть еще какое-то время после размыкания цепи.

Дело в том, что при прекращении подачи питания, в катушке снова возникнет ЭДС, однако ток индукции потечет теперь в том же направлении, что и от источника питания, то есть запасенная энергия в катушке, поддержит питание цепи.

Включение в цепь с переменным током

Теперь давайте проведем другой опыт, в котором подключим сделанную ранее катушку к источнику питания переменного тока.

Схема включения катушки индуктивности в цепь переменного тока

• Для создания приведенной схемы и снятия показаний нам потребуются: генератор частоты, осциллограф, резистор на 100 Ом и сама катушка.

Схема в сборе

• На фото выше виден осциллограф, отображающий 2 синусоиды. Это каналы, соответствующие частотам генератора (красная) и резистора (желтая), который включен в цепь уже после катушки индуктивности.
• Опыт с постоянным током показал, что катушка индуктивности при неизменном токе, никак не изменяет параметры тока, то есть не оказывает ему никакого сопротивления, а изменения случаются лишь во время включения и выключения питания.
• Теперь же, при помощи генератора, мы сможем посмотреть, как изменится сопротивление катушки, вследствие увеличения частот.

Ток имеет частоту 1 кГц

• Для начала подадим ток частотой в 1 кГц. Как видно из показаний, сигнал на выходе ничем не отличается от входного – сохранились и частота, и амплитуда.

Частота в 100 кГц

• Наращиваем частоту, останавливаясь на 100 кГц-ах. По графикам видно, что произошло какое-то изменение. А именно, уменьшилась амплитуда (ток стал выравниваться) и желтый график сместился вправо (появилась задержка) – это явление называет сдвигом фаз, то есть разницей между начальными и итоговыми замерами величин.

Интересно знать! Чтобы иметь возможность измерить сдвиг фаз, необходимо чтобы сигналы имели одинаковую частоту. Амплитуда значения не имеет.

Сдвиг фаз

Давайте посмотрим, что произойдет, если частоту увеличить еще.

Частота в 500 кГц

• По графикам видно, что тенденция сохранилась. Фаза сдвинулась еще сильнее, а амплитуда упала до 480 милливольт, хотя изначально равнялась практически 2 Вольтам.

Частота в 2 Мегагерца

• Выставляем максимальную частоту, что способен выдать наш генератор, и видим падение амплитуды до 120 мВ, и смещение фазы практически на 90 градусов.
• Отсюда можно сделать вывод, что с увеличением частоты питающего тока сопротивление катушки индуктивности будет расти. При этом происходит сдвиг фаз, максимальное значение которого составляет 90 градусов.

Сопротивление катушки напрямую зависит от ее индуктивности и рассчитывается по следующей формуле.

Расчет сопротивления катушки индуктивности

Работает при этом катушка все по тому же принципу.

Изменение тока и ЭДС самоиндукции

На графике показана зависимость тока и ЭДС от времени. Почему она выглядит именно так?

• Мы уже выяснили на примере постоянного тока, что ЭДС прямопропорциональна скорости, с которой изменяется сила тока. Собственно на графике и показывается эта зависимость.
• Рассмотрим часть графика. Между точками 1 и 2 ток изменяется, причем вначале изменение весьма резкое, но чем ближе к точке 2, тем оно сильнее замедляется, а в некотором промежутке времени и вовсе остается почти одинаковым.
• Отсюда следует, что скорость изменения тока выше около точки 1, а значит, в тот момент времени ЭДС и будет самым высоким.
• Также мы помним, что направление ЭДС противоположно основному току, то есть принимает отрицательное значение. Вот собственно и показанная зависимость – ток от точки 1 до точки 2 растет, а ЭДС падает, при прямой зависимости от скорости изменения тока.
• Идем дальше – промежуток 2-3. Ток у нас падает – сначала с медленной, а затем быстрой скоростью. ЭДС же, наоборот, растет, принимая положительное значение. И так далее, по аналогии.

Теперь, что касается знаков. На участке 1-2, у тока и ЭДС они противоположные, а значит, ЭДС тормозит ток, препятствуя его возрастанию, из-за того что они направлены навстречу друг другу. Далее идет участок 2-3, на котором ток и ЭДС выравниваются по знакам, а значит ЭДС побежит в ту же сторону, поддерживая убывающий ток.

Вот мы и пришли к тому факту, что току, протекающему в цепи, катушка индуктивности оказывает индуктивное или реактивное сопротивление. Возвращаясь к формуле расчета этого сопротивления, видим, что, так как частота в постоянном токе равно 0, сопротивление не оказывается, и наоборот, высокая частота переменного тока, увеличивает сопротивление катушки.

Так, мы что-то забыли! Да, конечно же! Что будет в это время с напряжением?

Зависимость напряжения и тока от времени

Из графика видно, что ток относительно напряжения сдвинут по фазе на ¼ такта, или на 90 градусов (отстает), что является одним из важнейших свойств цепей переменного тока, с включенной катушкой индуктивности.

Как все это можно задействовать на практике. Самый банальный пример – это фильтр низких частот (ФНЧ). Мы увидели, что сигнал с высокой частотой проходит намного хуже, тогда как низкочастотный, не испытывает никакого сопротивления. Если включить катушку индуктивности  в цепь, запитывающую динамик, то мы получим обрезку высоких частот, превращая конструкцию в сабвуфер, играющий только басы.

На этом все. Мы разобрали, как меняется ток катушки индуктивности, ЭДС и напряжение. Кто бы мог подумать, что это простое устройство совершает такую работу? Этим то и прекрасен мир электротехники. Изучайте его, и вам откроется много интересного! В дополнение просмотрите лекцию из видео в этой статье. Удачи!

Катушка индуктивности в цепи переменного тока

Мы предполагаем, что катушка индуктивности обладает пренебрежимо малым активным сопротивлением R. Такой элемент включать в цепь постоянного тока нельзя, потому что произойдет короткое замыкание.

В цепи переменного тока мгновенному нарастанию силы тока препятствует ЭДС самоиндукции. При этом для сверхпроводника e_i+u=0.

Используя закон Фарадея для самоиндукции e_i= -Li^/ ,

можно показать, что, если сила тока в цепи изменяется по гармоническому закону

i= I₀cos(ωt),

то колебания напряжения на катушке описываются

уравнением

U = — I₀ Lωsin ωt = I₀ Lω cos(ωt+π/2),

то есть колебания напряжения опережают по фазе колебания силы тока на π/2. Произведение U₀ = I₀Lω является амплитудой напряжения:

U = U₀ cos(ωt+π/2)

Индуктивное сопротивление

Величину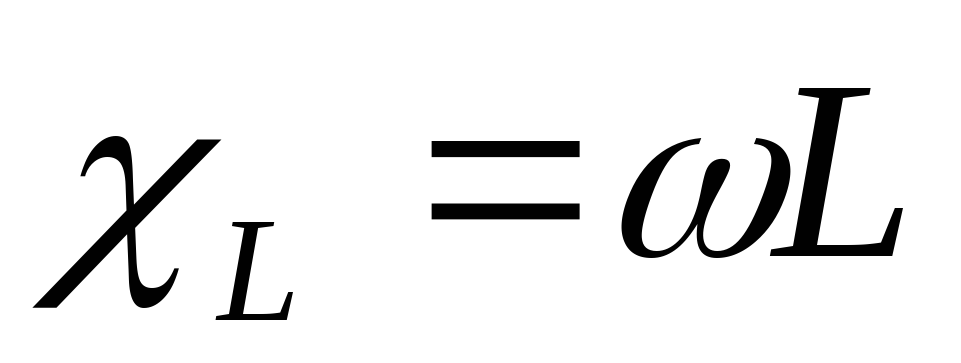

называют индуктивным сопротивлением.

Связь между амплитудными значениями силы тока и напряжения формально совпадает с законом Ома для участка цепи

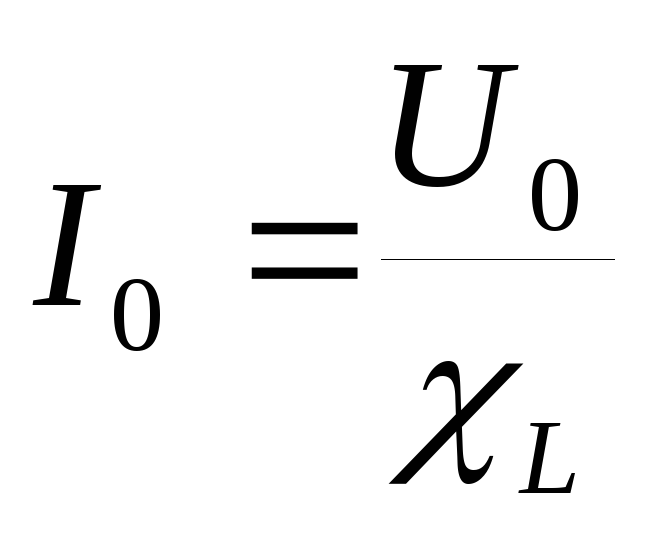
Такое же соотношение выполняется для действующих значений силы тока и напряжения.

Индуктивное сопротивление зависит от частоты переменного напряжения. С увеличением частоты колебаний напряжения индуктивное сопротивление увеличивается, поэтому амплитуда силы тока уменьшается обратно пропорционально частоте I₀ = U₀ /ωL.

При уменьшении частоты амплитуда силы тока возрастает и при ω=0 стремится к бесконечности. Отметим, что нулевая частота колебаний означает, что в цепи протекает постоянный ток.

Мощность в цепи переменного тока

Рассчитаем тепловую мощность, выделяющуюся на конденсаторе в цепи переменного тока. По закону Джоуля-Ленца, мгновенное значение мощности определяется как произведение мгновенных значений силы тока и напряжения:

P = UI =U₀cos ω t* I₀sin ω t =1/2 I₀U₀sin 2ωt

Среднее значение мощности за период

<P> = <1/2I₀U₀sin 2 ω t> = 1/2I₀U₀<sin 2 ω t>

<sin 2 ω t>= 0

<P> = 0

Аналогичный результат получается и для мощности на катушке индуктивности.

Вывод В цепи переменного тока тепловая мощность выделяется только на участке цепи с резистором, где нет сдвига фаз между током и напряжением.

По этой причине резистор в цепи переменного тока называют активным сопротивлением, а конденсатор и катушку индуктивности – реактивным.

Вопрос: Директор кинотеатра собирается установить систему, которая обеспечивала бы медленное затухание осветительных ламп перед сеансом и медленное их включение – после. Ему предлагают на выбор два способа: 1) – воспользоваться реостатом, чтобы постепенно изменять активное сопротивление цепи и 2) использовать соленоид с большой индуктивностью, чтобы мгновенному изменению силы тока в цепи препятствовала ЭДС индукции. Какой из двух способов выгоднее?

Ответ: Использование реактивного сопротивления не связано с дополнительным выделением Джоулевого тепла, и поэтому всегда экономичнее.

Лекция 7 Полная цепь переменного тока

Любая реальная цепь переменного тока содержит одновременно активное сопротивление (нагревательные приборы, лампы накаливания, соединительные провода и т.п.), емкостное сопротивление (емкости проводников, конденсаторов и т.п.) и индуктивное сопротивление (обмотки электродвигателей, катушки электромагнитных приборов и т.п.).

П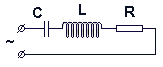усть все эти элементы соединены последовательно, как показано на рисунке.

В такой цепи колебания тока и напряжения не совпадают по фазе. Фазовый сдвиг между этими величинами зависит от индуктивности катушки и емкости конденсатора.

Во всех последовательно включенных элементах цепи сила тока изменяется практически одновременно, потому что распространение электромагнитных взаимодействий происходит со скоростью света. Поэтому можно считать, что колебания тока во всех элементах последовательной цепи совпадают по фазе и выражаются формулой:

I = I₀·cos ω ·t

Тогда

Напряжение на резисторе U = U₀ cos(ωt)

Напряжение на конденсаторе U = U₀ cos(ωt—π/2) =+ U₀ sin(ωt)

Напряжение на катушке U = U₀ cos(ωt+π/2) =­ — U₀ sin(ωt)

Uc. выходит из нуля, возрастает, первую четветь>0

Разность фаз колебаний напряжения на конденсаторе и катушке индуктивности в любой момент времени равна π. О таких колебаниях говорят, что они присходят в противофазе.

Uc. выходит из нуля, возрастает, первую четветь>0

U_L выходит из нуля, убывает, первую четветь<0

,

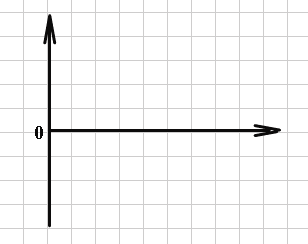
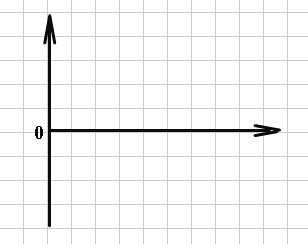
Uc(t) UL(t)

Катушка индуктивности в цепи переменного тока

Если катушка индуктивности включена в цепь переменного тока, то в такой цепи, фаза тока всегда отстает от фазы напряжения. Разберем причины этого отставания на простейшем примере, когда в цепи имеется только индуктивное сопротивление, а омического сопротивления нет вовсе, или вернее омическим сопротивлением провода катушки самоиндукции можно пренебречь, так как оно мало.

Для удобства рассмотрения явлений будем считать, что мы присоединяем катушку индуктивности к источнику переменного тока в тот момент, когда напряжение U на его зажимах имеет максимальное амплитудное значение (рис. 1а.). Этот момент будем считать началом периода.

 Рисунок 1. Самоиндукция-инерция. а) соотношения фаз тока, напряжения и ЭДС самоиндукции при включение катушки индуктивности в цепь переменного тока; б) соотношение фаз скорости движения, внешней силы и силы инерции

В момент включения катушки в ней немедленно возникнет электрический ток. Но ток не может сразу достичь своего амплитудного значения потому, что при его возникновении вокруг катушки начнет появляться магнитное поле, которое будет наводить в катушке ЭДС самоиндукции, направленную против внешнего напряжения, т. е. напряжения источника переменного тока. Электродвижущая сила самоиндукции будет препятствовать быстрому нарастанию силы тока в катушке. Поэтому нарастание тока будет длиться целую четверть периода.

По мере приближения к концу первой четверти периода скорость нарастания тока в катушке постепенно уменьшается.

Но вместе с тем ослабевает и ЭДС самоиндукции, так как величина ее зависит от скорости изменения силы тока.

Итак, в конце первой четверти периода внешнее напряжение, приложенное к катушке, будет равно нулю, ЭДС самоиндукции также будет, равна нулю, а ток в катушке и магнитный поток вокруг нее будут иметь максимальные амплитудные значения. В магнитном поле катушки будет запасено некоторое количество энергии, полученной от источника тока.

С началом второй четверти периода внешнее напряжение, переменив свое направление, будет возрастать, вследствие чего ток в катушке, текущий все еще в прежнем направлении, начнет уменьшаться. Но теперь в катушке снова возникнет ЭДС самоиндукции, обусловленная уменьшением магнитного потока, которая будет поддерживать ток в прежнем направлении.

В течение всей второй четверти периода внешнее напряже¬ние будет увеличиваться, а сила тока — уменьшаться. Ско¬рость уменьшения силы тока, оставаясь небольшой в начале второй четверти, станет постепенно нарастать и в конце этой четверти достигнет наибольшей величины.

Итак, к концу второй четверти периода внешнее напряжение приближается к амплитудному значению, а сила тока и магнитный ноток приближаются к нулю, убывая все с большей скоростью, вследствие чего ЭДС самоиндукции достигает своего амплитудного значения. Направление ЭДС самоиндукции, как всегда, остается противоположным направлению внешнего напряжения. Энергия, запасенная в магнитном поле за первую четверть периода, теперь возвращается обратно в цепь.

В течение второй половины (третья и четвертая четверти) периода все явления будут происходить в том же порядке, с той лишь разницей, что направления тока, внешнего напряжения и ЭДС самоиндукции изменяются на противоположные (рис. 1а.).

Таким образом, фаза тока все время отстает от фазы напряжения, причем нетрудно заметить, что сдвиг фаз тока и напряжения равен 90°.

Представим себе, что мы толкаем вдоль по рельсам груженую вагонетку. В первый момент, когда вагонетка только начинает трогаться с места, мы прилагаем к ней максимум усилий, которые по мере увеличения скорости вагонетки будем постепенно уменьшать. При этом мы почувствуем, что вагонетка, обладая инерцией, как бы сопротивляется нашим усилиям. Это противодействие (реакция) вагонетки будет особенно сильным вначале, по мере же ослабления наших усилий будет ослабевать и противодействие вагонетки, она постепенно будет переставать «упрямиться» и покорно покатится по рельсам.

Затем мы вовсе перестанем толкать вагонетку и даже, наоборот, начнем понемногу тянуть ее в обратном направлении. При этом мы почувствуем, что вагонетка снова сопротивляется нашим усилиям. Если мы будем все сильнее и сильнее тянуть вагонетку назад, то и ее противодействие будет соответственно все более и более возрастать. Наконец, нам удастся остановить вагонетку и даже изменить направление ее движения. Когда вагонетка покатится обратно, мы будем постепенно ослаблять наши усилия, т. е. будем тянуть ее все слабее и слабее, однако, несмотря на это, скорость вагонетки будет все-таки увеличиваться (при слабом трении в подшипниках).

Когда вагонетка пройдет половину пути в обратном направлении, мы совсем перестанем тянуть ее и снова переменим направление наших усилий, т. е. начнем ее снова задерживать, постепенно увеличивая силу торможения до тех пор, пока вагонетка не остановится, заняв первоначальное (исходное) положение. После этого мы можем продолжать все наши действия сначала.

В этом примере наши усилия, прилагаемые к вагонетке, соответствуют внешней ЭДС, противодействие вагонетки, обусловленное ее инерцией, — ЭДС самоиндукции, а скорость вагонетки — электрическому току. Если изобразить графически изменение наших усилий, а также изменение противодействия вагонетки и ее скорости с течением времени, то мы получим графики (рис. 1б), в точности соответствующие графикам рис.1а.

Из этого примера становится более понятной сущность реактивного (безваттного) сопротивления. В самом деле, в течение первой четверти периода мы толкали вагонетку, а она противодействовала нашим усилиям; в течение второй четверти периода она катилась сама, а мы «упирались»; в течение третьей четверти периода мы опять тянули ее, а вагонетка снова оказывала противодействие нашим усилиям и, наконец, в течение четвертой четверти периода она снова катилась сама, а мы ее тормозили.

Короче говоря, в течение первой и третьей четверти периода мы работали «на вагонетку», а в течение второй и четвертой четвертей она работала «на нас», возвращая обратно полученную то нас энергию. В результате наша работа оказалась «безваттной».

Таким образом катушка индуктивности в цепи переменного тока может работать как безваттный резистор.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

Урок 9. конденсатор и катушка индуктивности в цепи переменного электрического тока — Физика — 11 класс

Физика, 11 класс

Урок 9. Конденсатор и катушка индуктивности в цепи переменного электрического тока

Перечень вопросов, рассматриваемых на уроке:

Процессы, происходящие в цепи переменного электрического тока при наличии конденсатора и катушки индуктивности;

Устройство и принцип действия генератора переменного тока и трансформатора;

Автоколебания;

Проблемы передачи электроэнергии и способы повышения эффективности её использования.

Глоссарий по теме

Автоколебания – незатухающие колебания в системе, поддерживаемые за счет постоянного источника энергии.

Электрические машины преобразующие механическую энергию в электрическую называются генераторами.

Трансформатор – устройство, применяемое для повышения или понижения переменного напряжения.

Коэффициент трансформации – величина равная отношению напряжений в первичной и вторичной обмотках трансформатора.

Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б.Б., Чаругин В.М. Физика.11 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2014. – С. 86 – 95.

Рымкевич А.П. Сборник задач по физике. 10-11 класс. — М.: Дрофа, 2014. – С. 128 – 132.

Степанова. Г.Н. Сборник задач по физике. 10-11 класс. М., Просвещение 1999 г.

Е.А. Марон, А.Е. Марон. Контрольные работы по физике. М., Просвещение, 2004

Основное содержание урока

Переменный ток, которым мы пользуемся, вырабатывается с помощью генераторов переменного тока на электростанциях. Для передачи произведенной электроэнергии строятся линии электропередачи. В каждом населенном пункте имеются трансформаторы. Какую роль играют трансформаторы при передаче электроэнергии? Об этом мы поговорим на данном уроке.

В июле 1832 года Фарадей получил анонимное письмо, в котором автор описывал устройство созданного им генератора постоянного тока. Ознакомившись с содержанием письма Фарадей тут же отослал его в редакцию научного журнала. Автор этого письма не назвал себя, его фамилия осталась неизвестной.

Электрические машины преобразующие механическую энергию в электрическую называются генераторами. Впоследствии генераторы постоянного тока непрерывно совершенствовались. Потом, когда начали использовать переменный ток они уступили место генераторам переменного тока. Переменный ток в основном вырабатывается генераторами переменного тока. Простой моделью генератора может служить прямоугольная рамка, вращающаяся в магнитном поле. При вращении рамки, магнитный поток пронизывающий площадь поверхности, ограниченную рамкой, меняется по гармоническому закону:

N- число витков.

Возникает ЭДС индукции который меняется по гармоническому закону.

ЭДС индукции в рамке равна:

Если с помощью контактных колец и скользящих по ним щёток соединить концы рамки с электрической цепью, то в цепи возникнет переменный ток.

В современной энергетике для производства электроэнергии используются электромеханические индукционные генераторы. Принцип действия таких генераторов основан на явлении электромагнитной индукции. Основными частями генератора являются статор и ротор. Неподвижная часть генератора называется статором, а вращающаяся – ротором.

Постоянный ток не может идти по цепи содержащей конденсатор, т. к. цепь оказывается разомкнутой. При включении конденсатора в цепь переменного тока конденсатор будет периодически заряжаться и разряжаться с частотой равной частоте приложенного напряжения. В результате периодически меняющихся процессов зарядки и разрядки конденсатора в цепи течет переменный ток. Лампа накаливания, включенная в цепь переменного тока последовательно с конденсатором кажется горящей непрерывно, т.к. при высокой частоте колебаний силы тока человеческий глаз не способен заметить периодического ослабления нити накала. Конденсатор оказывает сопротивление прохождению тока. Это сопротивление называют ёмкостным.

Величину Х_C, обратную произведению циклической частоты на электрическую ёмкость конденсатора называют ёмкостным сопротивлением.

Ёмкостное сопротивление не является постоянной величиной. Мы видим, что конденсатор оказывает бесконечно большое сопротивление постоянному току. Чем больше ёмкость конденсатора и частота колебаний, тем больше ток перезарядки. При наличии в цепи переменного тока конденсатора колебания силы тока опережают по фазе колебания напряжения конденсаторе на 90º. Сдвиг фазы колебаний силы тока на 90º относительно фазы колебания напряжения на конденсаторе приводит к тому, что мощность переменного тока в течение одной четверти периода имеет положительный знак, а в течение второй четверти – отрицательный. Поэтому среднее значение мощности за период равно нулю.

Индуктивность в цепи, так же, как и ёмкость, влияет на силу переменного тока. Объясняется это явлением самоиндукции. В любом проводнике, по которому протекает переменный ток, возникает ЭДС самоиндукции. При подключении катушки к источнику постоянного напряжения сила тока в цепи нарастает постепенно. Возникающее при этом вихревое электрическое поле тормозит движение электронов. Лишь спустя некоторое время сила тока достигает максимального значения, соответствующего данному постоянному напряжению. Если напряжение быстро меняется, то сила тока не будет успевать достигать тех значений, которые она приобрела бы при постоянном напряжении. Следовательно, максимальное значение силы переменного тока ограничивается индуктивностью цепи и его частотой колебаний.

Величину Х_L, равную произведению циклической частоты на индуктивность, называют индуктивным сопротивлением.

Если частота равна нулю, то индуктивное сопротивление тоже равно нулю. Поэтому постоянный ток как бы не «замечает» катушку индуктивности в цепи.

Колебания напряжения на катушке опережают по фазе колебания силы тока на 90º.

Сдвиг фазы колебаний приводит к тому, что средняя мощность за период колебаний равна нулю.

Генератор на транзисторе используется для создания высокочастотных электромагнитных колебаний.

Для потребления электрической энергии нужно доставить его от источника к потребителю. Для этого строят линии электропередачи. При передаче электроэнергии на расстояние возникают потери энергии вследствие нагревания проводов. Тепловые потери можно определить используя закон Джоуля – Ленца:

Из этой формулы следует, что для уменьшения потерь энергиинужно уменьшить сопротивление или повысить напряжение. Уменьшения сопротивления проводов ЛЭП требует увеличения их площади поперечного сечения, что приведет к увеличению массы проводов. Увеличение массы проводов связано с большими расходами на укрепление столбов линии электропередачи, для их удержания и на производство металла для них. Наиболее эффективным является увеличение напряжения.

Для изменения напряжения в сети используют трансформаторы. Трансформатор был изобретен в 1876 году Яблочковым и в 1882 году усовершенствован Усагиным. Простейший трансформатор состоит из двух катушек, надетых на общий замкнутый стальной сердечник. Эти катушки называются обмотками трансформатора. Обмотка трансформатора, подключаемая к источнику переменного напряжения, называют первичной, а другая к которой присоединяют нагрузку – вторичной. Действие трансформатора основано на явлении электромагнитной индукции. При прохождении переменного тока по первичной обмотке в трансформаторе возникает переменное магнитное поле. Это поле пронизывает обе обмотки и в них возникает вихревое электрическое поле, которое действуя на заряженные частицы во вторичной обмотке способствует возникновению в ней переменного напряжения.

Величина равная отношению напряжений в первичной и вторичной обмотках трансформатора называют коэффициентом трансформации. Его обозначают буквой «k».

k– коэффициент трансформации.

U₁ и_{U2 – напряжения на первичной и на вторичной обмотке.}

N₁ и _{N2— число витков на первичной и на вторичной обмотке.}

Если k < 1 — трансформатор повышающий,

k > 1 — трансформатор понижающий.

КПД трансформатора равен отношению мощности в нагрузке к мощности, подаваемой из сети на первичную обмотку:

Для передачи электроэнергии на расстояние напряжение повышают с помощью трансформатора, а для потребления — понижают. В массивных проводниках при изменении магнитного поля возникают индукционные токи (токи Фуко), которые нагревают проводник. Чтобы эти индукционные токи не нагревали сердечник трансформатора его делают не сплошным, а из отдельных пластин, скрепленных вместе.

Закон Ома гласит: значение тока в цепи переменного тока прямо пропорционально напряжению в цепи и обратно пропорционально полному сопротивлению цепи.

Из формулы закона Ома для переменного тока мы видим, что при постоянной амплитуде напряжения, амплитуда силы тока зависит от частоты. Амплитуда силы тока будет максимальной, если полное сопротивление минимально. Полное сопротивление цепи минимально при равенстве индуктивного и ёмкостного сопротивления. В этом заключается условие возникновения резонанса в электрической цепи.

Резонанс в электрической цепи – это явление резкого возрастания амплитуды колебаний силы тока в контуре при совпадении частоты вынужденных колебаний с частотой собственных колебаний контура.

 Явление резонанса широко используется в радиотехнике, в схемах настройки радиоприемников. Меняя электроемкость конденсатора в колебательном контуре можно настроить его на нужную волну, т.е. выделить частоту на которой работает передающая станция

Разбор тренировочных заданий

1. Каково амплитудное значение ЭДС, возникающей в рамке из 50 витков, если она вращается с циклической частотой 180 рад/с в магнитном поле индукцией 0,4 Тл? Площадь рамки 0,02 м².

Дано:

N=50

ω=180 рад/с

B=0,4 Тл

S=0,02 м²

_________

Ԑ_m=?

Решение:

Ответ: 72 В.

2. Катушка с индуктивностью 0,08 Гн присоединена к источнику переменного тока частотой 1000 Гц. При этом вольтметр показывает 100 В. Определить амплитуду тока в цепи. Ответ округлить до десятых.

Дано:

L=0,08 Гн

ν= 1000 Гц

U=100 В

__________

I_m=?

Решение:

Напишем закон Ома для переменного тока

Т.к. Х_C и R равны нулю, то

Учитывая, что , получаем:

Найдем амплитудное значение напряжения:

Подставим числовые данные в формулу для расчета амплитуды силы тока:

Ответ: I_m = 0,3 А.

Катушка индуктивности в цепи переменного тока

Разглядим цепь, содержащую внутри себя катушку индуктивности, и представим, что активное сопротивление цепи, включая провод катушки, так не достаточно, что им можно пренебречь. В данном случае подключение катушки к источнику неизменного тока вызвало бы его куцее замыкание, при котором, как понятно, сила тока в цепи оказалась бы очень большой.

По другому обстоит дело, когда катушка присоединена к источнику переменного тока. Недлинного замыкания в данном случае не происходит. Это гласит о том. что катушка индуктивности оказывает сопротивление проходящему по ней переменному току.

Каковой нрав этого сопротивления и чем оно обусловливается?

Чтоб ответить ил этот вопрос, вспомним явление самоиндукции. Всякое изменение тока в катушке вызывает возникновение в ней ЭДС самоиндукции, препятствующей изменению тока. Величина ЭДС самоиндукции прямо пропорциональна величине индуктивности катушки и скорости конфигурации тока в ней. Но потому что переменный ток безпрерывно меняется, то безпрерывно возникающая в катушке ЭДС самоиндукции делает сопротивление переменному току.

Для уяснения процессов, происходящих в цепи переменного тока с катушкой индуктивности, обратимся к графику. На рисунке 1 построены кривые полосы, характеризующие соответственно тик в цепи, напряжение на катушке и возникающую в ней ЭДС самоиндукции. Убедимся в корректности сделанных па рисунке построений.

Цепь переменного тока с катушкой индуктивности

С момента t = 0, т. е. с исходного момента наблюдения за током, он начал стремительно возрастать, но по мере приближения к собственному наибольшему значению скорость нарастания тока уменьшалась. В момент, когда ток достигнул наибольшей величины, скорость его конфигурации на мгновение стала равной нулю, т. е. закончилось изменение тока. Потом ток начал поначалу медлительно, а позже стремительно убывать и по истечении 2-ой четверти периода уменьшился до нуля. Скорость же конфигурации тока за эту четверть периода, возрастая от пуля, достигнула большей величины тогда, когда ток станет равным нулю.

Набросок 2. Нрав конфигураций тока во времени зависимо от величины тока

Из построений на рисунке 2 видно, что при переходе кривой тока через ось времени повышение тока за маленький отрезок времени t больше, чем за тот же отрезок времени, когда кривая тока добивается собственной верхушки.

Как следует, скорость конфигурации тока миниатюризируется по мере роста тока и возрастает по мере его уменьшения, независимо от направления тока в цепи.

Разумеется, и ЭДС самоиндукции в катушке должна быть большей тогда, когда скорость конфигурации тока большая, и уменьшаться до нуля, когда прекращается его изменение. Вправду, на графике кривая ЭДС самоиндукции e_L за первую четверть периода, начиная от наибольшего значения, свалилась до нуля (см. рис. 1).

В протяжении последующей четверти периода ток от наибольшего значения уменьшался до нуля, но скорость его конфигурации равномерно росла и была большей в момент, когда ток стал равным нулю. Соответственно и ЭДС самоиндукции за время этой четверти периода, появившись вновь в катушке, равномерно росла и оказалась наибольшей к моменту, когда ток стал равным нулю.

Но направление свое ЭДС самоиндукции изменила на оборотное, потому что возрастание тока в первой четверти периода сменилось во 2-ой четверти его убыванием.

Продолжив далее построение кривой ЭДС самоиндукции, мы убеждаемся в том, что за период конфигурации тока в катушке и ЭДС самоиндукции совершит в ней полный период собственного конфигурации. Направление ее определяется законом Ленца: при возрастании тока ЭДС самоиндукции будет ориентирована против тока (1-ая и 3-я четверти периода), а при убывании тока, напротив, совпадать с ним по направлению (2-ая и 4-ая четверти периода).

Таким макаром, ЭДС самоиндукции, вызываемая самим переменным током, препятствует его возрастанию и, напротив, поддерживает его при убывании.

Обратимся сейчас к графику напряжения на катушке (см. рис. 1). На этом графике синусоида напряжения на зажимах катушки изображена равной и обратной синусоиде ЭДС самоиндукции. Как следует, напряжение на зажимах катушки в хоть какой момент времени равно и обратно ЭДС самоиндукции, возникающей в ней. Напряжение это создается генератором переменного тока и идет на то, чтоб погасить действие в цепи ЭДС самоиндукции.

Таким макаром, в катушке индуктивности, включенной в цепь переменного тока, создается сопротивление прохождению тока. Но потому что такое сопротивление вызывается в конечном счете индуктивностью катушки, то и именуется оно индуктивным сопротивлением.

Индуктивное сопротивление обозначается через X_L и измеряется, как и активное сопротивление, в омах.

Индуктивное сопротивление цепи тем больше, чем больше частота источника тока, питающего цепь, и чем больше индуктивность цепи. Как следует, индуктивное сопротивление цепи прямо пропорционально частоте тока и индуктивности цепи; определяется оно по формуле XL = ωL, где ω — радиальная частота, определяемая произведением 2πf. — индуктивность цепи в гн.

Закон Ома для цепи переменного тока, содержащей индуктивное сопротивление, звучит так: величина тока прямо пропорциональна напряжению и назад пропорциональна индуктивному сопротивлению цепи, т. е. I = U / X_L, где I и U — действующие значения тока и напряжения, а X_L— индуктивное сопротивление цепи.

Рассматривая графики конфигурации тока в катушке. ЭДС самоиндукции и напряжения на ее зажимах, мы направили внимание на то, что изменение этих величин не совпадает по времени. По другому говоря, синусоиды тока, напряжения и ЭДС самоиндукции оказались для рассматриваемой нами цепи сдвинутыми по времени одна относительно другой. В технике переменных токов такое явление принято именовать сдвигом фаз.

Если же две переменные величины меняются по одному и тому же закону (в нашем случае по синусоидальному) с схожими периодами, сразу добиваются собственного наибольшего значения как в прямом, так и в оборотном направлении, также сразу уменьшаются до нуля, то такие переменные величины имеют однообразные фазы либо, как молвят, совпадают по фазе.

В качестве примера на рисунке 3 приведены совпадающие по фазе кривые конфигурации тока и напряжения. Такое совпадение фаз мы всегда смотрим в цепи переменного тока, состоящей только из активного сопротивления.

В этом случае, когда цепь содержит индуктивное сопротивление, фазы тока и напряжения, как это видно из рис. 1 не совпадают, т. е. имеется сдвиг фаз меж этими переменными величинами. Кривая тока в данном случае вроде бы отстает от кривой напряжения на четверть периода.

Как следует, при включении катушки индуктивности в цепь переменного тока в цепи возникает сдвиг фаз меж током и напряжением, при этом ток отстает по фазе от напряжения на четверть периода. Это означает, что максимум тока наступает через четверть периода после того, как наступил максимум напряжения.

ЭДС же самоиндукции находится в противофазе с напряжением на катушке, отставая, в свою очередь, от тока на четверть периода. При всем этом период конфигурации тока, напряжения, также и ЭДС самоиндукции не изменяется и остается равным периоду конфигурации напряжения генератора, питающего цепь. Сохраняется также и синусоидальный нрав конфигурации этих величин.

Набросок 3. Совпадение по фазе тока и напряжения в цепи с активным сопротивлением

Выясним сейчас, каково отличие нагрузки генератора переменного тока активным сопротивлением от нагрузки его индуктивным сопротивлением.

Когда цепь переменного тока содержит внутри себя только одно активное сопротивление, то энергия источника тока поглощается в активном сопротивлении, нагревая проводник.

Когда же цепь не содержит активного сопротивления (мы условно считаем его равным нулю), а состоит только из индуктивного сопротивления катушки, энергия источника тока расходуется не на нагрев проводов, а лишь на создание ЭДС самоиндукции, т. е. она преобразуется в энергию магнитного поля. Но переменный ток безпрерывно меняется как по величине, так и по направлению, а как следует, и магнитное поле катушки безпрерывно меняется в такт с конфигурацией тока. В первую четверть периода, когда ток растет, цепь получает энергию от источника тока и припасает ее в магнитном поле катушки. Но как ток, достигнув собственного максимума, начинает убывать, он поддерживается за счет энергии, запасенной в магнитном поле катушки средством ЭДС самоиндукции.

Таким макаром, источник тока, отдав в течение первой четверти периода часть собственной энергии в цепь, в течение 2-ой четверти получает ее назад от катушки, выполняющей приэтом роль типичного источника тока. По другому говоря, цепь переменного тока, содержащая только индуктивное сопротивление, не потребляет энергии: в этом случае происходит колебание энергии меж источником и цепью. Активное же сопротивление, напротив, поглощает внутри себя всю энергию, сообщенную ему источником тока.

Молвят, что катушка индуктивности, в противоположность омическому сопротивлению, не активна по отношению к источнику переменного тока, т. е. реактивна. Потому индуктивное сопротивление катушки именуют также реактивным сопротивлением.