Видимый горизонт и дальность видимости
Калькулятор ниже предназначен для расчета видимого горизонта и дальности видимости в зависимости от высоты наблюдателя и наблюдаемого объекта. Под ним, как водится, немного теории.

Видимый горизонт и дальность видимости
Высота наблюдателя (метры)
Высота наблюдаемого объекта (метры)
Точность вычисленияЗнаков после запятой: 3
Видимый горизонт
Дальность видимости
save Сохранить share Поделиться extension Виджет
Видимый горизонт
Так как земля изогнута, наблюдателю, находящемуся, например, в море, представляется, что он находится в центре круга, по краям которого небо как бы смыкается с морской поверхностью. Эта окружность и называется видимым горизонтом наблюдателя. На картинке слева видимый горизонт обозначен пунктирной линией. То есть для наблюдателя, находящегося в точке А на высоте h от земли, видимый горизонт будет образован всеми точками касания лучей зрения земной поверхности (угол BCO равен 90 градусов).
Говоря о видимом горизонте чаще всего имеют в виду длину d отрезка BC. Длину d легко вывести из теоремы Пифагора.
где R — радиус Земли, который обычно принимают за 6378 километров.
В реальной жизни на стороне человека выступает атмосфера. Она, благодаря явлению рефракции, то есть отражения лучей в верхних слоях атмосферы, расширяет его горизонты примерно на 6% 🙂
Формула, таким образом, принимает вид
В принципе, везде (по крайней мере, насколько я находил в Интернете) для расчетов используют упрощенную формулу, из которой исключен радиус Земли. Она, кстати, вполне выводится из верхней.
, для результата в километрах
Дальность видимости
Дальность видимости предметов определяется наибольшим расстоянием, на котором наблюдатель увидит вершину наблюдаемого объекта на линии горизонта. Как видно из рисунка, она зависит как от высоты наблюдателя, так и от высоты наблюдаемого объекта. Собственно, это сумма дальности видимого горизонта наблюдателя и дальности видимого горизонта наблюдаемого объекта. Это довольно важный параметр для навигации.
В калькуляторе я ее вычисляю, а на практике, насколько я понимаю, дальности видимости береговых ориентиров указываются во всяческих лоциях, мореходных таблицах и тому подобном для высоты наблюдателя, равной пяти метрам. Для поправки на фактическую высоту наблюдателя используется «номограмма для расчета дальности видимости предметов в море в дневное время при среднем состоянии атмосферы».
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Длина, расстояние, линейный размер / / Расстояние до горизонта. Правильная таблица расстояния до горизонта (удаления горизонта) в зависимости от высоты глаз наблюдателя. Поделиться:
| |||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||||
Горизонт — Википедия
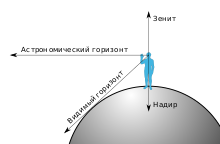
Горизо́нт (др.-греч. ὁρίζων — буквально: ограничивающий) — граница неба с земной или водной поверхностью[1]. По другому определению в понятие включают также видимую часть этой поверхности[2]. Различают горизонт видимый и горизонт истинный. Угол между плоскостью истинного горизонта и направлением на видимый горизонт называют
Видимым горизонтом называют и линию, по которой небо кажется граничащим с поверхностью Земли, и пространство неба над этой границей, и видимую наблюдателем поверхность Земли, и всё видимое вокруг наблюдателя пространство, до конечных пределов его
Синонимы: небосклон, кругозор, небозём, небоскат, закат неба, глазоём, зреймо, завесь, закрой, озор, овидь, окоём, оглядь[6].
Расстояние до видимого горизонта[править | править код]

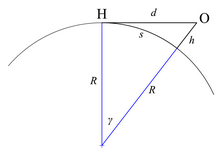
- В случае, если видимый горизонт определять как границу между небом и Землёй, то рассчитать геометрическую дальность видимого горизонта можно, воспользовавшись теоремой Пифагора:
- d=(R+h)2−R2{\displaystyle d={\sqrt {(R+h)^{2}-R^{2}}}}
- Здесь d — геометрическая дальность видимого горизонта, R — радиус Земли, h — высота точки наблюдения относительно поверхности Земли[7].
- В приближении, что Земля — идеально круглая и без учёта рефракции эта формула даёт хорошие результаты вплоть до высот расположения точки наблюдения порядка 100 км над поверхностью Земли.
- Принимая радиус Земли равным 6371 км и отбрасывая из-под корня величину h2, которая не слишком значима ввиду малого отношения h/R, получим ещё более простую приближённую формулу[8]:
- d≈113h,{\displaystyle d\approx 113{\sqrt {h}}\,,}
где d и h в километрах или
d≈3,57h,{\displaystyle d\approx 3,57{\sqrt {h}}\,,}
где d в километрах, а h в метрах. - Ниже приведено расстояние до горизонта при наблюдении с различных высот[9]:
| Высота над поверхностью Земли h | Расстояние до горизонта d | Пример места наблюдения |
|---|---|---|
| 1,75 м | 4,7 км | стоя на земле |
| 25 м | 17,9 км | 8-этажный дом |
| 50 м | 25,3 км | колесо обозрения |
| 150 м | 43,8 км | воздушный шар |
| 2 км | 159,8 км | гора |
| 10 км | 357,3 км | самолёт |
| 350 км | 2114,0 км | космический корабль |
 Расстояние до горизонта в зависимости от высоты точки наблюдения. Щёлкните по изображению, чтобы увеличить его.
Расстояние до горизонта в зависимости от высоты точки наблюдения. Щёлкните по изображению, чтобы увеличить его.- Для облегчения расчётов дальности горизонта в зависимости от высоты точки наблюдения и с учётом рефракции составлены таблицы и номограммы. Действительные значения дальности видимого горизонта могут значительно отличаться от табличных, особенно в высоких широтах, в зависимости от состояния атмосферы и подстилающей поверхности[10][11].
- Поднятие (снижение) горизонта относится к явлениям, связанным с рефракцией (рисунок 2). При положительной рефракции видимый горизонт поднимается (расширяется), географическая дальность видимого горизонта увеличивается по сравнению с геометрической дальностью, видны предметы, обычно скрытые кривизной Земли. При нормальных температурных условиях поднятие горизонта составляет 6—7 %. При усилении температурной инверсии видимый горизонт может подняться до истинного (математического) горизонта, земная поверхность как бы распрямится, станет плоской, дальность видимости станет бесконечно большой, радиус кривизны луча станет равным радиусу земного шара. При ещё более сильной температурной инверсии видимый горизонт поднимется выше истинного. Наблюдателю будет казаться, что он находится на дне огромной котловины. Из-за горизонта поднимутся и станут видимыми (как бы парить в воздухе) предметы, находящиеся далеко за геодезическим горизонтом. При наличии сильных температурных инверсий создаются условия для возникновения верхних миражей.
- Большие градиенты температуры создаются при сильном нагреве земной поверхности солнечными лучами, часто в пустынях, в степях. Большие градиенты могут возникнуть и в средних, и даже в высоких широтах в летние дни при солнечной погоде: над песчаными пляжами, над асфальтом, над обнажённой почвой. Такие условия являются благоприятными для возникновения нижних миражей[12].
- При отрицательной рефракции видимый горизонт снижается (сужается), не видны даже те предметы, которые видны в обычных условиях.
- В случае, если видимый горизонт определять как всё видимое вокруг наблюдателя пространство, до конечных пределов его, то расстояние до видимого горизонта, например, в лесу — это максимальное расстояние на которое уходит взгляд, пока не упрётся в деревья (несколько десятков метров), а для наблюдаемой Вселенной расстояние до видимого горизонта (то есть до самых далёких звёзд, которые мы можем наблюдать) составит около 13—14 млрд световых лет[13].
- Кстати: Космический горизонт (горизонт частиц) — это и мысленно воображаемая сфера с радиусом, равным расстоянию, которое свет прошёл за время существования Вселенной, и все множество точек Вселенной, находящихся на этом расстоянии[14].
Дальность видимости[править | править код]
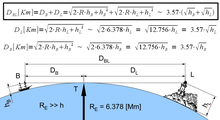 Формула и рисунок для вычисления геометрической дальности видимости.
Формула и рисунок для вычисления геометрической дальности видимости.Щёлкните по изображению, чтобы увеличить его.
На рисунке справа дальность видимости объекта определяют по формуле
DBL=3.57(hB+hL){\displaystyle D_{\mathrm {BL} }=3.57\,({\sqrt {h_{\mathrm {B} }}}+{\sqrt {h_{\mathrm {L} }}})},
где DBL{\displaystyle D_{\mathrm {BL} }} — дальность видимости в километрах,
hB{\displaystyle h_{\mathrm {B} }} и hL{\displaystyle h_{\mathrm {L} }} — высоты точки наблюдения и объекта в метрах.
Если учесть земную рефракцию, то формула примет вид:
DBL<3.86(hB+hL).{\displaystyle D_{\mathrm {BL} }<3.86\,({\sqrt {h_{\mathrm {B} }}}+{\sqrt {h_{\mathrm {L} }}})\,.}
То же самое, но DBL{\displaystyle D_{\mathrm {BL} }} — в морских милях:
DBL<2.08(hB+hL).{\displaystyle D_{\mathrm {BL} }<2.08\,({\sqrt {h_{\mathrm {B} }}}+{\sqrt {h_{\mathrm {L} }}})\,.}
 Диаграмма Струйского: Наблюдатель на высоте 10 м (шкала C) увидит утес высотой 50 м (шкала A) с расстояния примерно 21 морской мили (шкала B).
Диаграмма Струйского: Наблюдатель на высоте 10 м (шкала C) увидит утес высотой 50 м (шкала A) с расстояния примерно 21 морской мили (шкала B).Для приближённого расчёта дальности видимости объектов применяют номограмму Струйского (см. илл.): на двух крайних шкалах номограммы отмечают точки, соответствующие высоте точки наблюдения и высоте объекта, затем проводят через них прямую и на пересечении этой прямой со средней шкалой получают дальность видимости объекта[15].
На морских картах, в лоциях и других навигационных пособиях дальность видимости маяков и огней указывается для высоты точки наблюдения равной 5 м[10]. Если высота точки наблюдения иная, то вводится поправка[16].
Горизонт на Луне[править | править код]
 Земля над горизонтом Луны
Земля над горизонтом ЛуныНужно сказать, что расстояния на Луне очень обманчивы. Благодаря отсутствию воздуха удалённые предметы видятся на Луне более чётко и поэтому всегда кажутся ближе.
Лунный горизонт практически вдвое ближе земного. При этом расстояние до лунного горизонта зрительно определить крайне сложно по причине отсутствия атмосферы[17], а также объектов известного размера, по которым можно бы судить о масштабе.
Истинный горизонт — мысленно воображаемый большой круг небесной сферы, плоскость которого перпендикулярна отвесной линии в точке наблюдения. Аналогично общему понятию, истинным горизонтом может называться не круг, а окружность, то есть линия пересечения небесной сферы и плоскости, перпендикулярной отвесной линии.
Синонимы: математический горизонт, астрономический горизонт[18].
Искусственный горизонт — прибор, которым пользуются для определения истинного горизонта.
Например, истинный горизонт легко определить, если поднести к глазам стакан с водой так, чтобы уровень воды был виден как прямая линия[19].
Понятие горизонта в философию вводит Эдмунд Гуссерль, а Гадамер определяет его следующим образом: «Горизонт — поле зрения, охватывающее и обнимающее все то, что может быть увидено из какого-либо пункта»[20]
- ↑ Значения слова «горизонт» на сайте gramota.ru (неопр.).
- ↑ Статья «Горизонт» в Большой советской энциклопедии
- ↑ Ермолаев Г. Г., Андронов Л. П., Зотеев Е. С., Кирин Ю. П., Черниев Л. Ф. Морское судовождение / под общей редакцией капитана дальнего плавания Г. Г. Ермолаева. — издание 3-е, переработанное. — М.: Транспорт, 1970. — 568 с.
- ↑ Словари и энциклопедии на Академике (неопр.). Толкования выражения «видимый горизонт». Архивировано 3 февраля 2012 года.
- ↑ Изучение Солнечной системы (неопр.) (недоступная ссылка). Горизонт. Космос и астрономия. Архивировано 3 февраля 2012 года.
- ↑ Даль В. И. Толковый словарь живого великорусского языка. — М.: ОЛМА Медиа Групп, 2011. — 576 с. — ISBN 978-5-373-03764-8.
- ↑ Верюжский Н. А. Мореходная астрономия: Теоретический курс. — М.: РКонсульт, 2006. — 164 с. — ISBN 5-94976-802-7.
- ↑ Перельман Я. И. Горизонт // Занимательная геометрия. — М.: Римис, 2010. — 320 с. — ISBN 978-5-9650-0059-3.
- ↑ Вычислено по формуле «расстояние = 113 корней из высоты», таким образом, влияние атмосферы на распространение света не учитывается и предполагается, что Земля имеет форму шара.
- ↑ 1 2 Мореходные таблицы (МТ-2000). Адм. № 9011 / главный редактор К. А. Емец. — СПб: ГУН и О, 2002. — 576 с.
- ↑ Мир путешествий и приключений (неопр.). Расчёт расстояния до горизонта и прямой видимости онлайн.
- ↑ Всё о космосе (неопр.) (недоступная ссылка). Какой горизонт дальше?. Архивировано 3 февраля 2012 года.
- ↑ Лукаш В. Н., Михеева Е. В. Физическая космология. — М.: Физико-математическая литература, 2010. — 404 с. — ISBN 5922111614.
- ↑ Климушкин Д. Ю.; Граблевский С. В. Космология (неопр.). Космический горизонт (2001).
- ↑ starpomlom Учебник судоводителя любителя (неопр.). Глава VII . Навигация.
- ↑ Яхтенная энциклопедия (неопр.) (недоступная ссылка). Видимый горизонт и дальность видимости. Архивировано 3 февраля 2012 года.
- ↑ Skeptic.net (неопр.) (недоступная ссылка). Были ли американцы на Луне?. Архивировано 14 марта 2016 года.
- ↑ Словари и энциклопедии на Академике (неопр.). Толкования выражения «истинный горизонт». Архивировано 3 февраля 2012 года.
- ↑ Запаренко Виктор. Большая энциклопедия рисования Виктора Запаренко. — М.: АСТ, 2007. — 240 с. — ISBN 978-5-17-041243-3.
- ↑ Истина и метод. С.358
Азимут и высота солнца над горизонтом
Продолжаем тему, начатую статьей Восход и закат солнца.
На повестке дня вычисление азимута солнца и его высоты над горизонтом в любой момент времени в точке с заданными координатами. Азимут мы откладываем от севера по часовой стрелке.
Алгоритм расчета взят отсюда. Описал его какой-то хороший швед. Он старался как мог, но все равно для стороннего человека ничего не понятно. Например, я могу еще понять, как мы переходим от одной системы координат к другой, но понять, почему долгота перигелия солнца вычисляется как
, где d — количество дней от эпохи J2000 — это уже выше моих сил.
Видимо где-то далеко, в башне из слоновой кости, сидят астрономы, и все эти цифры рассчитывают, а потом все остальные смертные их используют. Может быть какой-нибудь астроном когда-нибудь расскажет о том, как это все происходит; пока же пришлось взять на веру все эти магические цифры и воплотить расчет в жизнь. Очевидно, так делает большинство.
Есть несколько книг, которые обычно рекомендуют людям на форумах, когда не хотят отвечать развернуто, типа, «смотри вон там», и я тоже приведу их здесь:
Jean Meeus. Astronomical algorithms
Peter Duffett-Smith. Practical Astronomy with your calculator.
Как и в случае калькуляторов для расчета времени восхода и захода солнца, ниже представлены два калькулятора — первый берет информацию о координатах и часовом поясе из справочника городов, т. е. остается только выбрать город и ввести время наблюдения; а второй позволяет задать координаты и часовой пояс «вручную». Информацию о городах могут добавлять в справочник зарегистрированные пользователи.
Отрицательная высота над горизонтом соответствует темному времени суток — солнце «под» горизонтом. Пересечение с горизонтом утром происходит примерно на азимуте 90 градусов, из чего можно сделать смелый вывод, что солнце восходит все-таки на востоке.
Paul Schlyter (это швед) утверждает, что ошибка в расчетах не превышает одной угловой минуты для дат в диапазоне 1900 – 2100.

Положение солнца по городам
ГородОбновление…Точность вычисленияЗнаков после запятой: 2
Азимут (градусы)
Высота над горизонтом (градусы)
save Сохранить share Поделиться extension Виджет

Положение Солнца
Точность вычисленияЗнаков после запятой: 2
Азимут (градусы)
Высота над горизонтом (градусы)
save Сохранить share Поделиться extension Виджет
Расстояние до горизонта — Математическая составляющая
Расстояние до горизонта
Какова дальность до линии горизонта для наблюдателя, стоящего на земле? Ответ — приближённое расстояние до горизонта — можно найти с помощью теоремы Пифагора.
Для проведения приближённых расчётов сделаем допущение, что Земля имеет форму шара. Тогда стоящий вертикально человек будет продолжением земного радиуса, а линия взгляда, направленного на горизонт, — касательной к сфере (поверхности Земли). Так как касательная перпендикулярна радиусу, проведённому в точку касания, то треугольник (центр Земли) —(точка касания) —(глаз наблюдателя) является прямоугольным.
Две стороны в нём известны. Длина одного из катетов (стороны, прилегающей к прямому углу) равна радиусу Земли $R$, а длина гипотенузы (стороны, лежащей против прямого угла) равна $R+h$, где $h$ — расстояние от земли до глаз наблюдателя.
По теореме Пифагора, сумма квадратов катетов равна квадрату гипотенузы. Значит, расстояние до горизонта равно
$$
d=\sqrt{(R+h)^2-R^2} = \sqrt{(R^2+2Rh+h^2)-R^2} =\sqrt{2Rh+h^2}.
$$
Величина $h^2$ очень мала по сравнению со слагаемым $2Rh$, поэтому верно приближённое равенство
$$
d≈ \sqrt{2Rh}.
$$
Известно, что $R≈ 6400$ км, или $R≈ 64\cdot10^5$ м. Будем считать, что $h≈ 1{,}6$ м. Тогда
$$
d≈\sqrt{2\cdot64\cdot10^5\cdot 1{,}6}=8\cdot 10^3 \cdot \sqrt{0{,}32}.
$$
Используя приближённое значение $\sqrt{0{,}32}≈ 0{,}566$, находим
$$
d≈ 8\cdot10^3 \cdot 0{,}566=4528.
$$
Полученный ответ — в метрах. Если перевести найденное приближённое расстояние от наблюдателя до горизонта в километры, то получим $d≈ 4,5$ км.
Онлайн калькулятор: Баллистическое движение
Калькулятор ниже предназначен для решении задач школьного курса физики на баллистическое движение. Баллистическое движение — движение тела в пространстве под действием внешних сил, в данном случае речь идет только о силе тяжести.
Параметры баллистического движения изображены на картинке, это:
дальность полета ,
максимальная высота полета ,
длительность полета ,
угол броска ,
начальная скорость .
Основные формулы, определяющие баллистическое движение:
, ,
Формулы выводятся из формул для скорости и расстояния при равноускоренном движении, в предположении, что по оси х на тело не действует никакое ускорение, а по оси y на тело действует ускорение свободного падения g.
Калькулятор позволяет рассчитать неизвестные параметры баллистического движения по известным.
То есть, если задать угол броска и начальную скорость, то калькулятор найдет дальность полета, время полета и максимальную высоту, на которую поднимется тело. Если задать время полета и дальность полета, то калькулятор найдет начальную скорость, угол броска и максимальную высоту, и так далее.
Единственная неопределенная комбинация — это время полета и высота полета. Зная только эти параметры, рассчитать остальные невозможно.

Баллистическое движение
Значениеначальной скорости (м/с)угла броска (градусы)времени полета (сек)дальности полета (м)максимальной высоты полета (м)Значениеначальной скорости (м/с)угла броска (градусы)времени полета (сек)дальности полета (м)максимальной высоты полета (м)Ускорение свободного падения (м/с2)
Точность вычисленияЗнаков после запятой: 2
Начальная скорость (м/с)
Угол броска (градусы)
Время полета (сек)
Дальность полета (м)
Максимальная высота полета (м)
save Сохранить share Поделиться extension Виджет
Онлайн калькулятор: Восход и закат солнца
Наблюдая за улучшением погоды в своей местности, внезапно задался мыслью о том, что неплохо было бы знать время восхода и заката Солнца. Сказано — сделано. Алгоритм расчета нашелся здесь. Источник алгоритма — Almanac for Computers, 1990, published by Nautical Almanac Office, United States Naval Observatory, Washington, DC 20392
В комментариях к алгоритму также было указано, что он верен для периода с 1980 по 2050 год, и обладает точностью до одной минуты. Точность, впрочем, уменьшается для мест, лежащих на широтах выше 60 градусов северной или южной широты. Выше 80 градусов погрешности в расчете солнечной эклиптики (так, кажется) приводят к еще большим ошибкам (каким — не сказано).
Также для высоких широт зимой и летом солнце может либо никогда не заходить (полярный день) либо никогда не восходить (полярная ночь). В этом случае в результатах указывается продолжительность дня 24 часа либо 00 часов соответственно.
Надо еще рассказать про зенитный угол (zenith angle), который задается параметром «Граница дня/ночи» и оказывает существенное влияние на расчет. Зенит — это линия, направленная из точки на поверхности земли вертикально вверх, а зенитный угол (я не уверен в термине, это калька с английского) — это угол между вертикалью и направлением на центр небесного объекта. В данном случае речь идет о том, какой величины должен быть этот угол, чтобы считать, что солнце уже «совсем» взошло или уже село и день сменился ночью или наоборот.
Если бы Солнце было точкой, а Земля не имела атмосферы, то зенитный угол, определяющий полный закат солнца, был бы равен 90 градусам. Но поскольку Солнце не точка и имеет угловой диаметр, а его свет отражается твердыми частицами в атмосфере, то для того, чтобы верхний край солнечного диска скрылся за горизонтом, его центр должен лежать уже чуть ниже горизонта. При нормальных атмосферных условиях это соответствует углу в 90 градусов 50 минут. Этот угол считается углом «официального» заката солнца.
Но хотя солнце и скрылось за горизонтом, за счет отражения его света от атмосферы все еще довольно светло. Начинается период времени, называемый сумерками. Сумерки делятся на три этапа, и конец каждого из этапов тоже можно взять за точку заката солнца.
Первый этап называется гражданскими сумерками. Это время, когда еще достаточно светло, чтобы работать вне помещения без искусственного освещения. Концу гражданских сумерек соответствует зенитный угол в 96 градусов, после чего начинаются навигационные сумерки.
Навигационные сумерки — это время, когда на воде все еще заметна линия горизонта. Концу навигационных сумерек соответствует зенитный угол в 102 градуса, после чего начинаются астрономические сумерки.
Астрономические сумерки — это время, когда Солнце все еще является источником света и мешает видимости самых слабых звезд. Для обычного наблюдателя это время неотличимо от ночи. Концу астрономических сумерек соответствует момент, когда Солнце полностью прекращает быть источником света, и это зенитный угол в 108 градусов.
Впрочем, как оказалось, реализация алгоритма это еще не все. Дело в том, что алгоритм выдает результат в гринвичском времени. Очевидно, что для большего удобства пользователя надо перевести это время в местное. В идеальном мире часовой пояс можно было бы получить, используя значение долготы места. В самом деле, земной сфероид делится на 24 сферических двуугольника, по меридианам, отстоящим друг от друга на 15 градусов, и часовой пояс вычисляется тривиально.
Но в реальном мире все не так — политические, административные и географические границы придали весьма забавную форму часовым поясам, так что от определения пояса по долготе пришлось отказаться. Вместо этого я добавил в калькулятор дополнительное поле для задания смещения от гринвичского времени.
Тут пришла в голову мысль — почему бы не объединить этот алгоритм со справочником Информация о городах, который используется для калькулятора Расстояние между двумя городами и не сделать еще один калькулятор — расчет времени восхода и заката солнца в городах, с использованием данных из справочника. Координаты городов в нем есть, часовые пояса теперь тоже есть — выбираешь дату и город и получаешь местное время восхода и заката без лишних хлопот.
Правда, надо еще было понять, какое сейчас местное время — зимнее или летнее. Дело в том, что в тех странах, которые используют зимнее и летнее время, смена времени осуществляется по разному. Например, в Новой Зеландии летнее время действует с 30 апреля до последнего воскресенья сентября, а в Ираке — с первой пятницы апреля до последней пятницы октября. В общем, на такие подробности меня уже не хватило, и я немного упростил, использовав правило перехода на зимнее/летнее время, принятое в Европе и в России — с последнего воскресенья марта по последнее воскресенье октября.
Так что для некоторых городов (ну например, для городов Новой Зеландии) местное время в калькуляторе может вычисляться неправильно для марта-апреля и сентября-октября. Но, к слову, далеко не все страны используют зимнее/летнее время. Например, в районе экватора оно совсем и не нужно, так как сезонных изменений в солнечном свете практически не наблюдается. Да и вообще, многим странам такое деление навязывалось искусственно, в их бытность колониями, или, как в случае с Японией, под американской оккупацией (1948-1951). Некоторые страны, как говорится, пробовали, но им не понравилось. На территории бывшего СССР от разного времени уже отказались страны Центральной Азии и Грузия. Мол, люди напрягаются, а экономического эффекта не видно.
Вообще придумали зимнее/летнее время, как я и подозревал, англичане. В 1907 году предложил его некий Вильям Виллет (William Willett).
Англичане вообще славятся придумыванием всяких забавных штук вроде имперской системы мер (см. Перевод мер площади из метрической в английскую систему и обратно) или нестандартных размеров обуви (см. Соответствие размеров обуви), так что ничего удивительного. Но многие страны Европы им последовали в годы Первой Мировой Войны, чтобы экономить что? Неправильно, совсем не электричество — а уголь. Первыми были практичные немцы и их союзники (30 апреля 1916 года), ну а потом подтянулась Великобритания с союзниками и затем нейтральные страны.
Собственно, ниже калькулятор времени восхода и заката в городах (если вашего города в нем нет, зарегистрируйтесь и добавьте его в справочник), а еще ниже — по заданным географическим координатам (для вывода правильного местного времени надо самому ввести смещение от гринвичского).
P.S. По просьбе пользователя (смотри обсуждение статьи ниже) в калькуляторы добавлен расчет времени истинного полудня, т. е. времени, когда солнце солнце имеет наибольшее восхождение. Это время, в общем, не совпадает с 12:00.

Восход и закат солнца по городам
ГородОбновление…Граница дня/ночивидимый заход солнца за линию горизонтаконец гражданских сумерекконец навигационных сумерекконец астрономических сумерекВремя восхода по Гринвичу
Время заката по Гринвичу
Продолжительность дня
Время восхода местное
Время заката местное
Истинный полдень
save Сохранить share Поделиться extension Виджет

Восход и закат солнца
Граница дня/ночивидимый заход солнца за линию горизонтаконец гражданских сумерекконец навигационных сумерекконец астрономических сумерекВремя восхода по Гринвичу
Время заката по Гринвичу
Продолжительность дня
Время восхода местное
Время заката местное
Истинный полдень




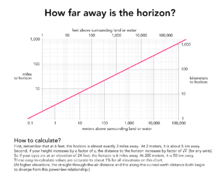 Расстояние до горизонта в зависимости от высоты точки наблюдения. Щёлкните по изображению, чтобы увеличить его.
Расстояние до горизонта в зависимости от высоты точки наблюдения. Щёлкните по изображению, чтобы увеличить его.