Вынужденные колебания. Резонанс (практика)
Данная тема посвящена решению задач на вынужденные колебания и резонанс.
Задача 1. На рисунке изображена зависимость амплитуды установившихся колебаний маятника от частоты вынуждающей силы (резонансная кривая). Определите резонансную частоту и амплитуду колебаний этого маятника при резонансе.
Задача 2. Капли воды падают через одинаковые промежутки времени с некоторой высоты на пластину, закреплённую на пружине. Частота собственных колебаний пластины равна ω0. Известно, что амплитуда колебаний пластины при этом оказывается максимальной. Найдите расстояние между отрывающейся каплей и ближайшей к ней падающей каплей.
Задача 3. К динамометру подвесили груз, вывели его из состояния равновесия и отпустили. Определите частоту колебаний, возникших в системе, если после их прекращения указатель динамометра остановился на расстоянии 6 см от нулевого положения.
Задача 4. Вагон массой 80 т имеет четыре рессоры, жёсткостью 200 кН/м каждая. Через какой промежуток времени должны повторяться толчки от стыков рельсов, чтобы вагон начало сильно раскачивать?
Задача 5. При какой скорости поезда рессоры вагонов будут особенно сильно колебаться под действием толчков колёс на стыках рельсов? Длина рельса l, нагрузка на рессору F, рессора прогибается на h при нагрузке F1.
Задача 6. На чашку, подвешенную на пружине жёсткостью 300 Н/м, с высоты 1,5 м падает груз массой 200 г и остаётся лежать на чашке. Определите амплитуду установившихся колебаний, если массой чашки и пружины можно пренебречь.
«Не подражайте другим.
Найдите себя и будьте собой».
Д. Карнеги
Гармонические, затухающие, вынужденные колебания. Резонанс (Колебошин С.В.)
На данном уроке, тема которого «Гармонические, затухающие, вынужденные колебания. Резонанс», мы продолжим изучать различные виды колебательного движения, познакомимся с таким явлением, как резонанс.
На прошлом уроке мы начали изучать новый вид механического движения – механические колебания. Напомним также, что на прошлом уроке мы договорились, что будем изучать так называемые свободные колебания – колебания, которые система производит под действием первоначально запасенной энергии. Но в реальности такие колебания встречаются нечасто. Итак, начнем с первого раздела – гармонических колебаний.
Гармонические колебания мы наблюдали на прошлом уроке, когда следили за поведением пружинного и математического маятников. Что же это за вид колебаний? Мы помним, что для возникновения колебательного движения необходимо, чтобы в системе было положение устойчивого равновесия, при выводе из которого возникает сила, стремящаяся вернуть тело в это положение. Если эта сила (возвращающая сила) пропорциональна величине отклонения тела от положения равновесия, то говорят, что система совершает гармонические колебания. Более строгое определение вы получите в одиннадцатом классе, нам же для нашей работы достаточно и этого.
Характерной чертой гармонических колебаний является независимость периода таких колебаний от амплитуды. Именно гармонические колебания являются самыми простыми с точки зрения математического описания такого движения. Отличными моделями для гармонических колебаний являются пружинный и математический маятники. Давайте более подробно рассмотрим гармонические колебания на примере пружинного маятника.
Пружинный маятник
Пусть возвращающая сила (в данном случае сила упругости) (см. рис. 1) определяется формулой: 
, где x – отклонение от положения равновесия; k – коэффициент упругости.
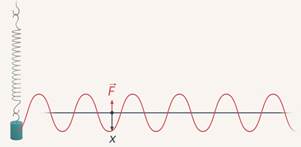
Рис. 1. Колебания пружинного маятника
Запишем второй закон Ньютона для данной системы: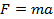 
.
Мы договорились, что в данном случае действует только сила упругости. Итак, мы получаем: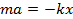 
. Разделим это выражение на массу m и получим выражение для ускорения колеблющегося тела: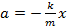 
Записав это выражение для ускорения, мы вплотную приблизились к главной задаче механики для гармонических колебаний (ведь сюда входит x, а мы знаем, что ускорение зависит от времени, то есть время сюда входит неявно). Решить такое уравнение строго математически мы пока не умеем, такие уравнения называются дифференциальными. Строгое решение такого уравнения мы запишем в 11 классе, а я отмечу тот факт, что решение будет выражаться периодическим законом – законом синуса или косинуса. А сейчас только обсудим, к какому результату приводит такое вот решение главной задачи для гармонических колебаний.
Обратите внимание, что у нас ускорение зависит от координаты x и в этой зависимости есть некоторая величина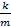 
. Так вот это отношение равно квадрату угловой частоты колебания системы: 
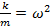. Это доказательство мы получим в 11 классе. Таким образом, если нам при решении задачи удается представить второй закон Ньютона в виде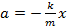
.
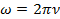Только что мы получили выражение для угловой частоты пружинного маятника, аналогичным образом можно получить выражение для угловой частоты математического маятника, естественно, там роль этого коэффициента будут выполнять другие величины. Об этом вы узнаете, если посмотрите ответвление к уроку.
Зависимость E(t) при свободных колебаниях
Вы уже знаете, что энергия во время колебаний непрерывно меняется: кинетическая переходит в потенциальную и наоборот. Логично, что так же, как и координата, скорость, и ускорение, энергия будет меняться по гармоническому закону. Убедимся в этом. Давайте рассмотрим превращение колебаний на примере математического маятника, но расчеты будем вести для пружинного маятника – в данном случае это проще. Итак, как же происходит превращение энергии при колебаниях маятника? В верхней точке максимальна потенциальная энергия, а кинетическая равна 0 (см. рис. 2).
Рис. 2. Верхняя точка математического маятника
Когда отпустим маятник, он начнет колебаться. Рассмотрим маятник, когда он проходит положение равновесия: здесь кинетическая максимальная, а потенциальная 0. Потенциальная энергия равна 0, потому что мы выберем именно этот уровень (см. рис. 3), а не уровень земли.
Рис. 3. Уровень нулевой потенциальной энергии
Дальше происходит обратное превращение энергии: кинетическая начинает падать, а потенциальная увеличиваться (и так происходит постоянно). Теперь попытаемся вывести закон, по которому меняются потенциальная и кинетическая энергии (см. рис. 4).
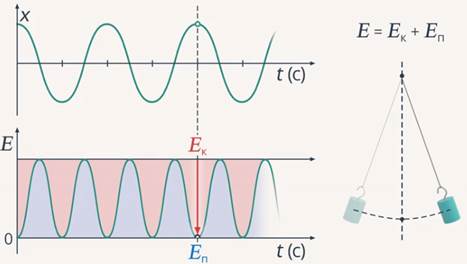
Рис. 4. Изменение энергий
Потенциальная энергия пружинного маятника имеет вид: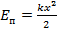 
, где k – коэффициент жесткости пружины, x – координата. Кинетическая энергия: 
.
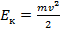Координата меняется по такому закону: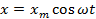 
.
Скорость тоже изменяется по гармоническому закону: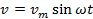 
.
Подставим выражение для координаты и для скорости в формулы для энергий и получим закон, по которому изменяется со временем энергия потенциальная и кинетическая для пружинного маятника: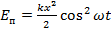 
.
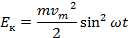
Для математического маятника формула для кинетической энергии будет идентичной, а для потенциальной, с математической точки зрения, тоже похожей, но перед значением косинуса будет стоять другой коэффициент. Так как квадрат величины всегда неотрицательная величина, то график (см. рис. 4) расположен выше оси времени. В каждый момент времени сумма кинетической и потенциальной энергии одинакова – выполняется закон сохранения энергии.
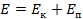
В реальности энергия, конечно же, не сохраняется. Любая колебательная система тратит часть своей энергии на преодоление силы сопротивления, силы трения. Энергия уменьшается, колебания на самом деле являются затухающими. В тех случаях, которые мы рассматриваем в 9 классе, этим затуханием можно пренебречь, но в реальной жизни это нужно учитывать
А каким же образом мы может заставить колебаться маятник гармонически? Это можно сделать двумя способами. Вывести груз из положения равновесия и отпустить его. В этом случае график движения (график x(t)) будет иметь такой вид (см. рис. 5).
Рис. 5. График движения x(t)
Второй вариант: заставить тело совершать гармонические колебания с помощью импульса (например, толкнуть его). Вспомните, например, как вы раскачиваете качели: либо толкнуть их, либо вывести их из положения равновесия и отпустить. Естественно, можно вывести их из положения равновесия и сообщить некий импульс.
Свободные колебания могут совершаться за счет первоначального запаса энергии. Вернемся к предыдущим рассуждениям: в первом примере, который мы приводили, это была первоначальная энергия грузика, мы выводили его из положения равновесия, а потом отпускали. А во втором случае этот первоначальный запас энергии – это кинетическая энергия (в случае, когда мы толкали грузик). Согласно закону сохранения энергии в обоих случаях сумма кинетической и потенциальной энергий маятника должна оставаться неизменной с течением времени. То есть, какое бы промежуточное значение маятника мы бы ни рассмотрели, в любой из них эта сумма равна начальной энергии маятника (см. рис. 6), при этом маятник мог совершать колебания довольно долго.
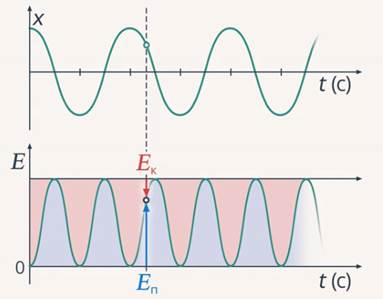
Рис. 6. Иллюстрация закона сохранения энергии
Однако на самом деле мы понимаем, что маятников, которые могли бы совершать колебания довольно долго, не существует – это какая-то абстракция.
Учтём, что система маятников незамкнутая, то есть в системе присутствует сила трения. В реальных условиях мы можем взять тяжелый груз, подвесить его на очень длинную и легкую нить или проволоку, закрепить один конец на опоре и получить систему, близкую по своим свойствам к математическому маятнику. Однако нельзя сказать, что механическая энергия такого маятника будет сохраняться – мы прекрасно знаем, что рано или поздно он остановится. В чем же наша недоработка? Ответ прост: в данной системе присутствуют различные виды трения, действие которых приводит к потере на каждом периоде колебаний маятника какой-то части его энергии (см. рис. 7).
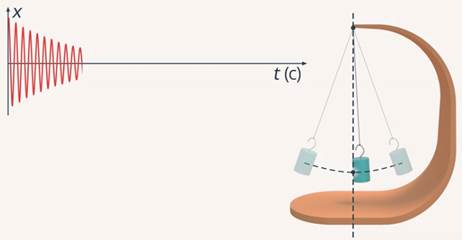
Рис. 7. В системе присутствуют различные виды трения
Силы трения могут быть внутренними (например, в подвесе маятника), а могут быть и внешними (например, со стороны окружающего воздуха или другой среды, в которой может находиться маятник). Естественно, что силы трения зависят от свойств среды: в воде колебания будут затухать быстрее, чем в воздухе (см. рис. 8).
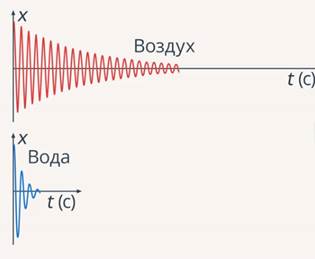
Рис. 8. Затухание в воздухе и воде
В итоге амплитуда колебаний будет постепенно уменьшаться, и в конце маятник остановится. На рисунке представлены смещения груза маятника от времени: видно, что амплитуда постепенно уменьшается, стремясь к нулю, такие колебания называются затухающими (см. рис. 8).
Затухающие колебания – это колебания, которые происходят в незамкнутой системе, то есть колебания, которые происходят в том числе под действием силы трения. Амплитуда таких колебаний постепенно затухает. Большинство колебаний в мире – затухающие, так как в окружающем нас мире, постоянно существуют силы трения.
Итак, мы выяснили: в реальности колебания маятников механических систем затухающие, то есть их амплитуда постепенно уменьшается, стремясь к нулю. Что же нам сделать, чтоб колебания не были такими, чтоб амплитуда постоянно поддерживала свое значение? Для этого нам необходимо разомкнуть систему и подкачивать энергию извне. Таким образом, мы добьемся незатухающих колебаний. Как же разомкнуть систему?
Вспомним простой пример из жизни: катание на качелях. Для того чтобы качели колебались без остановки, человек периодически толкает их, а если перевести это на язык физики, то человек действует на качели с силой, величина которой зависит от времени периодическим образом. Если построить график зависимости модуля силы от времени, то получим следующий результат: сила зависит от времени периодически (см. рис. 9).
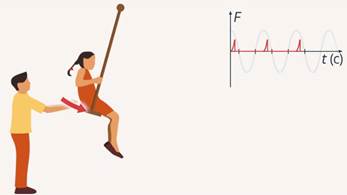
Рис. 9. Зависимость силы от времени
Мы прекрасно понимаем, что если мы будем воздействовать на качели постоянно, то они не будут колебаться.
Колебания системы, совершающие ею под действием внешней периодической силы, называются вынужденными. Силу, являющейся мерой этого внешнего воздействия, называют вынуждающей. При этом, как вы понимаете, мы уже не можем считать систему замкнутой, то есть в системе уже не совершаются свободные колебания – в системе совершаются вынужденные колебания. Примерами систем, в которых совершаются вынужденные колебания, могут быть также в полнее привычные вам часы – это могут быть настенные маятниковые часы, а могут быть и обычные пружинные механические часы. В каждом таком случае колебания совершаются за счет подвода энергии извне.
Вынужденные колебания
Самым простым видом колебаний являются свободные незатухающие колебания. О них подробнее мы говорили на предыдущих занятиях. Давайте поговорим о некоторых характерных особенностях затухающих колебаний и вынужденных колебаний. Начнем с затухающих колебаний. Как вы уже знаете, любая реальная колебательная система – затухающая, ведь нам всегда приходится преодолевать силу трения или силу сопротивления. Если мы говорим об электромагнитных колебаниях, то там тоже есть факторы, вызывающие их затухания, – это сопротивление проводников.
Итак, как же выглядят затухающие колебания? Если вывести маятник из положения равновесия, то со временем его колебания затухают, здесь два основных фактора: сопротивление воздуха, а также трение в подвесе. Здесь речь идет об амплитуде колебаний, то есть максимальном отклонении от положения равновесия. Со временем амплитуда становится все меньше, меньше и меньше – именно этот факт отображен на рисунке (см. рис. 10).
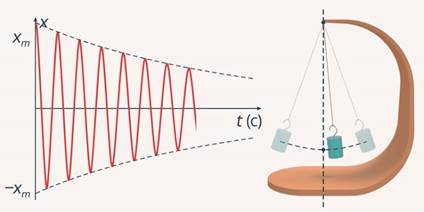
Рис. 10. Уменьшение амплитуды колебаний
Обратите внимание: колебания все равно остаются периодическими, но амплитуда непрерывно уменьшается – колебания затухают. Хорошо это или плохо – смотря для чего. Если речь идет о часах, то плохо, поскольку хотелось бы, чтоб затухание было как можно меньше, а колебания – больше, чтобы нам не доводилось подводить дополнительную энергию. Но есть и обратная сторона: если распахнуть двери и бросить их, то нам будет хотеться, чтобы они колебались как можно меньше. Для этого на двери ставят демпферы – гасители колебаний.
Теперь переходим к вынужденным колебаниям. Представим себе, что мы раскачиваем брата или сестру на качелях: если мы толкнем качели один раз, то они рано или поздно остановятся. Поэтому мы продолжаем раскачивать качели, и тем самым колебания из свободных становятся вынужденными, потому что появляется некая внешняя сила. Какой же характеристикой должна обладать эта внешняя сила? Эта сила обязательно должна меняться во времени, должна быть периодической. И тут нужно поговорить о двух частотах: собственная частота колебаний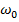 
– та частота, с которой бы колебалась система, если бы она была выведена из равновесия и больше её никто не сообщал её энергию (то есть никто бы больше не раскачивал её), и частота внешней силы 
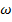– это та частота, с которой будут раскачивать качели. Запомните, чтобы колебания были вынужденными, внешняя сила должна периодически меняться.
Во время затухающих колебаний энергия системы непрерывно уменьшается, а во время вынужденных колебаний энергия подводится к системе извне
Приведем исторический факт: в Петербурге сильно раскачался и в результате обвалился Египетский мост (см. рис. 11).
Рис. 11. Обвал Египетского моста
В это время по мосту маршевым шагом, то есть в ногу, проходил кавалерийский эскадрон. Почему же в данном случае вынужденные колебания (а именно: воздействие эскадрона и вызвало вынужденные колебания) привели к разрушению моста? Ответим на этот вопрос. На рисунке изображены два маятника, висящие на общем шнуре (см. рис. 12).
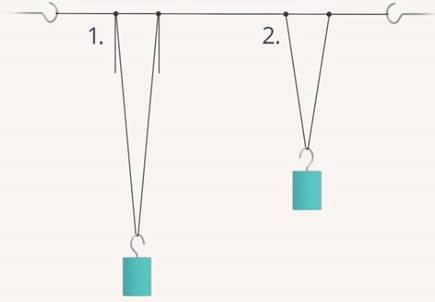
Рис. 12. Два маятника на шнуре
Длина второго маятника неизменная. Этой длине соответствует определенная частота свободных колебаний, назовем её собственная частота маятника. Длину первого маятника можно менять, подтягивая свободные концы его нити. При изменении длины нити 1, меняется его собственная частота. Если отклонить первый маятник от положения равновесия и предоставить его самому себе, то он будет совершать свободные колебания. Это вызовет колебания шнура, в результате чего на маятник 2 через его точки подвеса будет действовать вынуждающая сила, которая периодически меняется по модулю и направлению с такой же частотой, с которой колеблется первый маятник. Под действием этой силы второй маятник будет совершать вынужденные колебания (см. рис. 13).
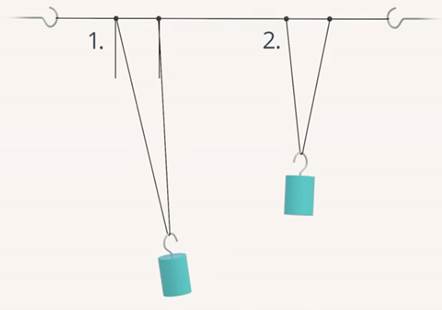
Рис. 13. Второй маятник начинает совершать вынужденные колебания
Начнем уменьшать длину первого маятника – частота его колебаний, а значит, и частота изменения вынуждающей силы, действующей на второй маятник, будет увеличиваться, приближаясь к собственной частоте второго маятника (см. рис. 14).
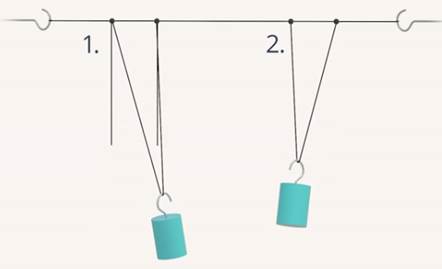
Рис. 14. Уменьшаем длину первого маятника
При этом можно увидеть, что амплитуда установившихся вынужденных колебаний второго маятника будет возрастать (см. рис. 15).
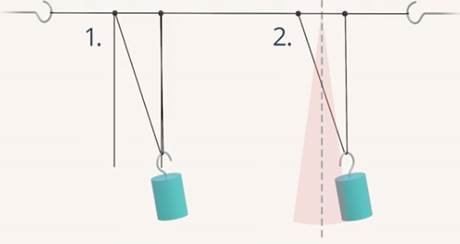
Рис. 15. Возрастание амплитуды второго маятника
В момент, когда длины маятников сравняются, то есть когда частота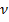 
вынуждающей силы совпадет с собственной частотой 
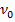второго маятника, амплитуда колебаний достигнет максимального значения. Если и в дальнейшем уменьшать длину первого маятника, то это приведет к тому, что частота вынуждающей силы станет больше собственной частоты второго маятника – амплитуда колебаний начнет уменьшаться (см. рис. 16).
Рис. 16. Уменьшение амплитуды колебаний
Можно обратиться к графику зависимости амплитуды колебаний от частоты внешней вынуждающей силы (см. рис. 17), в данном случае частоты колебания маятника 1.
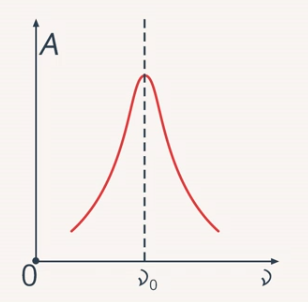
Рис. 17. Зависимость амплитуды от частоты
Вынужденные колебания и резонанс
Если
на тело с массой m
действуют упругая сила Fу = -kX,
сила трения 
и
внешняя периодическая сила 
,
то оно совершает вынужденные колебания.
В этом случае дифференциальное уравнение
движения имеет вид
,
или
,
(33)
где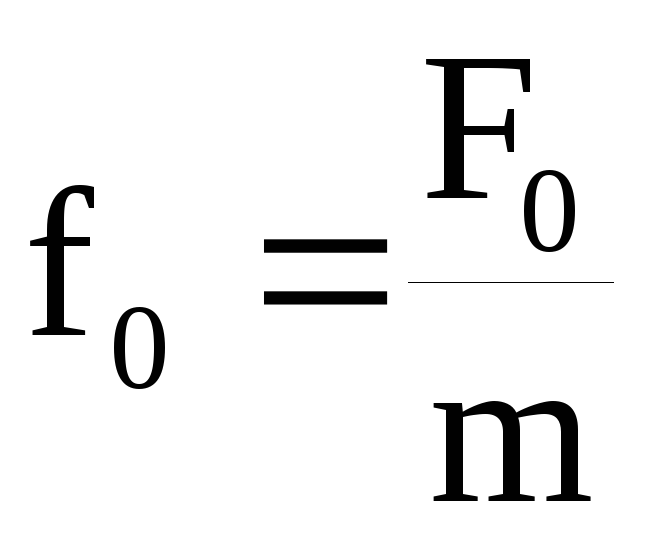
,
—
коэффициент затухания,
— собственная частота свободных
незатухающих колебаний тела,F0 – амплитуда, ω – частота периодической
силы.
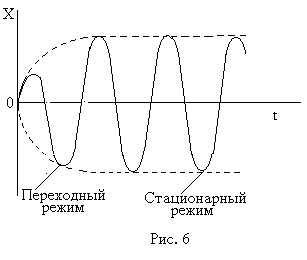В
начальный момент времени работа внешней
силы превосходит энергию, которая
расходуется на трение (рис. 6). Энергия
и амплитуда колебаний тела будет
возрастать до тех
пор, пока вся сообщаемая внешней силой энергия не будет целиком расходоваться на преодоление трения, которое пропорционально скорости. Поэтому устанавливается равновесие, при котором сумма кинетической и потенциальной энергии оказывается постоянной. Это условие характеризует стационарное состояние системы.
В таком состоянии движение тела будет гармоническим с частотой, равной частоте внешнего возбуждения, но вследствие инерции тела его колебания будут сдвинуты по фазе по отношению к мгновенному значению внешней периодической силы:
X
= AСos(ωt
+ φ). (34)
В отличие от свободных колебаний амплитуда А и фаза вынужденных колебаний
зависят не от начальных условий движения, а будут определяться только свойствами колеблющейся системы, амплитудой и частотой вынуждающей силы:
, (35)
. (36)
Видно, что амплитуда и сдвиг по фазе зависят от частоты вынуждающей силы (рис.7 и 8).
Характерной
особенностью вынужденных колебаний
является наличие резонанса. Явление
резкого возрастания амплитуды вынужденных
колебаний при приближении частоты
вынуждающей силы к собственной частоте
свободных незатухающих колебаний тела
ω0носит название механического
резонанса. Амплитуда колебаний тела
при резонансной частоте
достигает
максимального значения:
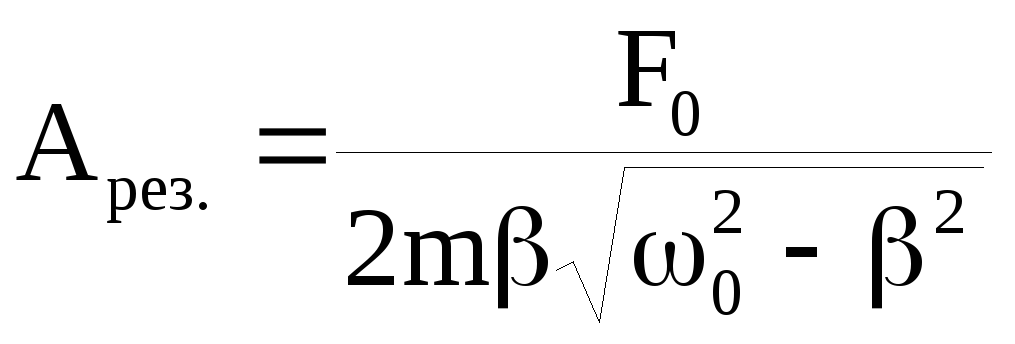(37)
По
поводу резонансных кривых (см. рис. 7)
сделаем следующие замечания. Если ω→
0, то все кривые (см. также (35)) приходят
к одному и тому же, отличному от нуля,
предельному значению 
,
так называемому статистическому
отклонению. Если ω→ ∞, то все кривые
асимптотически стремятся к нулю.
При условии малого затухания (β2 ‹‹ω02) резонансная амплитуда (см.(37))
(37а)
При этом условии возьмем отношение резонансного смещения к статическому отклонению.
,
из
которого видно, что относительное
увеличение амплитуды колебаний при
резонансе определяется добротностью
колебательной системы. Здесь добротность
является по сути коэффициентом усиления
отклика 
системы
и при малом затухании может достигать
больших значений.
Это обстоятельство обусловливает огромное значение явления резонанса в физике и технике. Его используют, если хотят усилить колебания, например, в акустике – для усиления звучания музыкальных инструментов, в радиотехнике – для выделения нужного сигнала из множества других, отличающихся по частоте. Если резонанс можетпривести к нежелательному росту колебаний, пользуются системой с малой добротностью.
СВЯЗАННЫЕКОЛЕБАНИЯ
Источником внешней периодической силы может служить вторая колебательная система, упруго связанная с первой. Обе колебательные системы могут действовать одна на другую. Так, например, случай двух связанных маятников (рис. 9).
Система
может совершать как синфазные (рис. 9б),
так и противофазные (рис. 9с) колебания.
Такие колебания называются нормальным
типом или нормальной модой колебаний
и характеризуются своей собственной
нормальной частотой. При синфазных
колебаниях смещения маятников во все
моменты времени Х1 = Х2,
а частота ω1 точно такая же, как частота отдельно
взятого маятника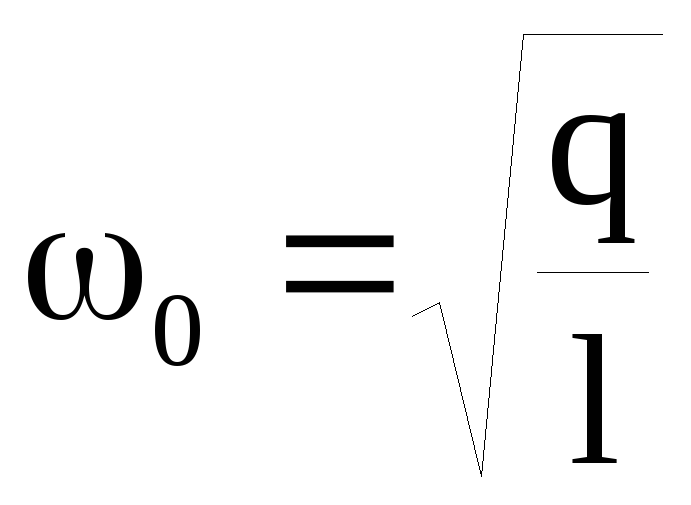 
.
Это объясняется тем, что легкая пружина
находится в свободном состоянии и не
оказывает никакого влияния на движение.
При противофазных колебаниях во все
моменты времени – Х1 = Х2.
Частота таких колебаний больше и равна 
,
так как пружина, обладающая жесткостьюk
и осуществляющая связь, все время
находится то в растянутом, то в сжатом
состоянии.
Любое состояние нашей связанной системы,
в том числе и начальное смещение Х (рис.
9а), можно представить в виде суперпозиции
двух нормальных мод:
и
.
Если
привести систему в движение из начального
состояния Х1 = 0, 
,
Х2 = 2А,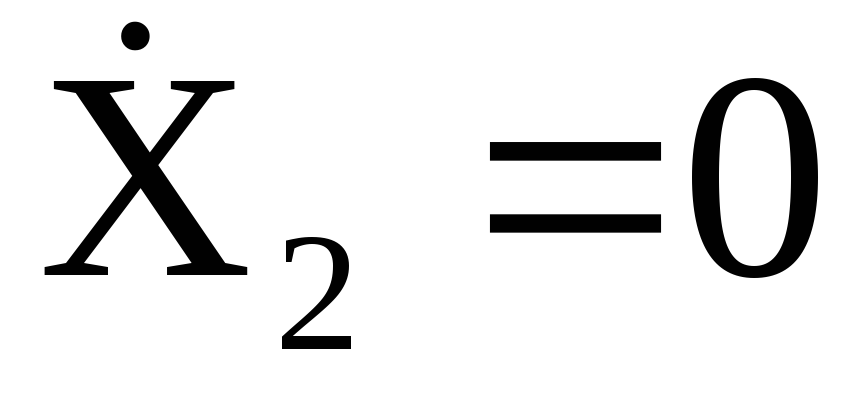 
,
то смещения маятников будут описываться выражениями:
,
(38)
На
рис. 10 представлено изменение смещения
отдельных маятников во времени.
Частота колебаний маятников равна средней частоте двух нормальных мод
(39)
а их амплитуда изменяется по закону синуса или конуса с меньшей частотой, равной половине разности частоты нормальных мод
. (40)
Медленное
изменение амплитуды с частотой, равной
половине разности частот нормальных
мод, называется “биениями” двух колебаний с почти одинаковыми
частотами. Частота “биений” равна
разности ω1 –ω2 частот, (а не половине этой разности),
поскольку максимум амплитуды 2А
достигается дважды за период,
соответствующий частоте
Отсюда период биений оказывается равным
(41)
При биениях между маятниками происходит обмен энергией. Однако полный обмен энергией возможен только тогда, когда обе массы одинаковы и отношение (ω1+ω2 / ω1-ω2) равно целому числу. Необходимо отметить один важный момент: хотя отдельные маятники могут обмениваться энергией, обмен энергией между нормальными модами отсутствует.
Наличие таких колеблющихся систем, которые взаимодействуют между собой и способны передавать друг другу свою энергию, составляют основу волнового движения.
ВОЛНЫ
Колеблющееся материальное тело, помещенное в упругую среду, увлекает за собой и приводит в колебательное движение прилегающие к нему частицы среды. Благодаря наличию упругих связей между частицами колебания распространяются с характерной для данной среды скоростью по всей среде.
Процесс распространения колебаний в упругой среде называется волной. Различают два основных типа волн: продольные и поперечные. В продольных волнах частицы среды колеблются вдоль направления распространения волны, а в поперечных – перпендикулярно к направлению распространения волны. Не во всякой упругой среде возможно распространение поперечной волны. Поперечная упругая волна возможна лишь в таких средах, в которых имеет место упругая деформация сдвига. Например, в газах и жидкостях распространяются только продольные упругие волны (звук).
Геометрическое место точек среды, до которых к данному моменту времени дошло колебание, называется фронтом волны. Фронт волны отделяет часть пространства, уже вовлеченную в волновой процесс, от области, в которой колебания еще не возникали. В зависимости от формы фронта различают волны плоские, сферические, цилиндрические и т.д.
Уравнение плоской волны, распространяющейся без потерь в однородной среде, имеет вид
, (42)
где
ξ(Х,t)
– смещение частиц среды с координатой
Х от положения равновесия в момент
времени t,
А – амплитуда, 
— фаза волны,
— круговая частота колебания частиц
среды,v
– скорость распространения волны.
Длиной волны λ называется расстояние между точками, колеблющимися с разностью фаз 2π, другими словами, длиной волны называется путь, проходимый любой фазой волны за один период колебаний:
λ = vT, (43)
фазовая скорость, т.е. скорость распространения данной фазы:
λ
/ Т (44)
Волновое число – число длин волн, укладывающихся на длине 2π единиц:
k = ω / v = 2π / λ. (45)
Подставляя эти обозначения в (42), уравнение плоской бегущей монохроматической волны можно представить в виде
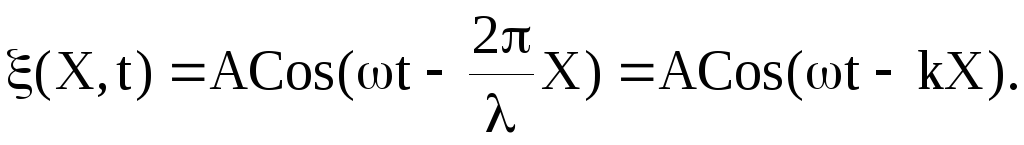
(46)
Отметим, что уравнение волны (46) обнаруживает двойную периодичность по координате и времени. Действительно, фазы колебаний совпадают при изменении координаты на λ и при
изменении времени на Т (период). Поэтому изобразить графически волну на плоскости нельзя. Часто фиксируют время t и на графике представляют зависимость смещения ξ от координаты Х, т.е. мгновенное распределение смещений частиц среды вдоль направления распространения волны (рис.11). Разность фаз Δφ колебаний точек среды зависит от расстояния ΔХ =Х2 – Х1 между этими точками
(47)
Если волна распространяется противоположно направлению Х, то уравнение обратной волны запишется в виде:
ξ (Х,t) = АСos(ωt + kX). (48)
СТОЯЧИЕ ВОЛНЫ – это результат особого вида интерференции волн. Они образуются при наложении двух бегущих волн, распространяющихся навстречу друг другу с одинаковыми частотами и амплитудами.
Уравнения двух плоских волн, распространяющихся вдоль оси Х в противоположных направлениях, имеют вид:
ξ1 =АСos(ωt – kX)
ξ2 = AСos(ωt + kX). (49)
Складывая эти уравнения по формуле суммы косинусов и учитывая, что k = 2π / λ, получим уравнение стоячей волны
. (50)
Множитель
Сos
ωt
показывает, что в точках среды возникает
колебание той же частоты ω
с амплитудой 
,
зависящей от координаты Х рассматриваемой
точки. В точках среды, где
, (51)
амплитуда колебаний достигает максимального значения, равного 2А. Эти точки называются пучностями. Из выражения (51) можно найти координаты пучностей:
(52)
В
точках, где 
, (53)
амплитуда колебаний обращается в нуль. Эти точки называются узлами. Координаты узлов
. (54)
Р
асстояния
между соседними пучностями и соседними
узлами одинаковы и равны λ/2. Расстояние
между узлом и соседней пучностью равно
λ / 4. При переходе через узел множитель
меняет знак, поэтому фазы колебаний по
разные стороны от узла отличаются на
π, т.е. точки, лежащие по разные стороны
от узла, колеблются в противофазе. Точки,
заключенные между двумя соседними
узлами, колеблются с разными амплитудами,
но с одинаковыми фазами.
Распределение
узлов и пучностей в стоячей волне зависит
от условий, имеющих место на границе
раздела двух сред, от которой происходит
отражение. Если отражение волны происходит
от среды более плотной, то фаза колебаний
в месте отражения волны меняется на
противоположную или, как говорят,
теряется половина волны. Поэтому, в
результате сложения колебаний
противоположных направлений смещение
на границе равно нулю, т.е. имеет место
узел (рис. 12).
При отражении волны от границы менее
плотной среды фаза колебаний в месте
отражения остается без изменения и у
границы складываются колебания с
одинаковыми фазами – получается
пучность.
В стоячей волне нет перемещения фаз, нет распространения волны, нет переноса энергии, с чем и связано название такого типа волн.
Вынужденные колебания. Резонанс
Вынужденные колебания
В отличие от свободных колебаний, когда система получает энергию лишь один раз (при выведении системы из состояния равновесия), в случае вынужденных колебаний система поглощает эту энергию от источника внешней периодической силы непрерывно. Эта энергия восполняет потери, расходуемые на преодоление трения, и потому полная энергия колебательной системы no-прежнему остается неизменной.
Вынужденные колебания в отличие от свободных могут происходить с любой частотой. Частота вынужденных колебаний совпадает с частотой внешней силы, действующей на колебательную систему. Таким образом, частота вынужденных колебаний определяется не свойствами самой системы, а частотой внешнего воздействия.
Примерами вынужденных колебаний являются колебания детских качелей, колебания иглы в швейной машине, поршня в цилиндре автомобильного двигателя, рессор автомобиля, движущегося по неровной дороге и т.д.
Резонанс
Резонанс возникает из-за того, что при внешняя сила, действуя в такт со свободными колебаниями, все время имеет одинаковое направление со скоростью колеблющегося тела и совершает положительную работу: энергия колеблющегося тела увеличивается, и амплитуда его колебаний становится большой. Если же внешняя сила действует «не в такт», то эта силы попеременно совершает то отрицательную, то положительную работу и вследствие этого энергия системы меняется незначительно.
На рис.1 показана зависимость амплитуды вынужденных колебаний от частоты вынуждающей силы. Видно, что эта амплитуда достигает максимума при определенном значении частоты, т.е. при , где собственная частота колебательной системы. Кривые 1 и 2 отличаются величиной силы трения. При малом трении (кривая 1) резонансная кривая имеет резкий максимум, при большей силе трения (кривая 2) такого резкого максимума нет.
Рис.1. Резонансные кривые для различных значений силы трения.
С явлением резонанса мы часто встречаемся в повседневной жизни. Если в комнате задрожали стекла при прохождении по улице тяжелого грузовика, это значит, что собственная частота колебаний стекол равна частоте колебаний машины. Если морские волны попадают в резонанс с периодом корабля, то качка становится особенно сильной.
Явление резонанса необходимо учитывать при проектировании мостов, зданий и других сооружений, испытывающих вибрацию под нагрузкой, в противном случае при определенных условиях эти сооружения могут быть разрушены. Однако резонанс также может быть полезен. Явление резонанса используется при настройке радиоприемника на определенную частоту радиовещания, а также во многих других случаях.
Примеры решения задач
Самостоятельная работа по физике Затухающие колебания. Вынужденные колебания. Резонанс 9 класс
Самостоятельная работа по физике Затухающие колебания. Вынужденные колебания. Резонанс 9 класс с ответами. Самостоятельная работа по физике включает 2 варианта, в каждом по 4 задания.
Вариант 1
1. Приведите примеры вынужденных колебаний. Являются ли они затухающими?
2. При каком условии наблюдается резонанс?
3. Приведите примеры полезного проявления резонанса.
4. На рисунке представлен график зависимости амплитуды А вынужденных колебаний от частоты ν вынуждающей силы.
При какой частоте происходит резонанс?
Вариант 2
1. Чем вынужденные колебания отличаются от свободных?
2. Какие изменения амплитуды происходят при резонансе?
3. Приведите примеры вредного проявления резонанса.
4. На рисунке представлен график зависимости амплитуды А вынужденных колебаний от частоты ν вынуждающей силы.
Определите амплитуду колебаний при резонансе.
Ответы на самостоятельную работа по физике Затухающие колебания. Вынужденные колебания. Резонанс 9 класс
Вариант 1
1. Колебания мембраны телефона, игла в швейной машинке, движение поршня в двигателе. Не являются.
2. Резонанс наблюдается в том случае, если собственная частота системы совпадает с частотой вынуждающей силы
3. Звучание музыкальных инструментов, генераторы переменного тока
4. 10 Гц
Вариант 2
1. Вынужденные колебания происходят в том случае, если на систему влияет внешнее периодическое воздействие, они не затухают. Свободные колеблются под действием внутренних сил, являются затухающими.
2. Амплитуда резко увеличивается, так как амплитуда собственных колебаний складывается с амплитудой колебаний внешней силы.
3. При переходе через мост, если человеческий шаг совпадет с частотой колебаний моста, то мост начнет сильно раскачиваться. Вагон сильно раскачивается, если частота ударов колес совпадает с частотой свободных колебаний вагона.
4. 10 см
§ 30. Резонанс. —
Вопросы.1. С какой целью и как проводился опыт с двумя маятниками, изображенными на рисунке 64, а?
Цель опыта: Демонстрация явления резонанса. Ход опыта: 1) колебания маятника 1, через нить передаются маятнику 2, длина нити которого неизменна, вызывая его колебания; 2) при уменьшении длины нити маятника 1 частота его колебаний начнет приближаться к собственной частоте маятника 2; 3) при этом амплитуда вынужденных колебаний маятника 2 будет возрастать; 4) в момент, когда частота вынуждающей силы маятника 1 совпадет с частотой собственных колебаний маятника 2 (одинаковая длина нитей маятников) маятники будут колебаться в одинаковых фазах; 5) при дальнейшем уменьшении длины нити маятника 1 частота колебаний маятника 2 будет уменьшаться.
2. В чем заключается явление, называемое резонансом?
Явление резонанса заключается в том, что при совпадении частоты вынуждающей силы с собственной частотой системы амплитуда вынужденных колебаний достигает своего максимального значения.
3. Какой из маятников, изображенных на рисунке 64, б) колеблется в резонанс с маятником 3? По каким признакам вы это определили?
В резонанс колеблется маятник 1, т.к. его длина нити равна длине нити маятника 3.
4. К каким колебаниям — свободным или вынужденным — применимо понятие резонанса?
Понятие резонанса применимо к вынужденным колебаниям.
5. Приведите примеры, показывающие, что в одних случаях резонанс может быть полезным явлением, а в других — вредным.
Вредное проявление резонанса можно увидеть на примере разрушения мостов, высотных сооружений, затопления пароходов на волнах. Положительное явление резонанса проявляется например при настройке музыкальных инструментов с помощью камертона, в радиоэлектронике.
Упражнения.
1. Маятник 3 (см.рис. 64, б) совершает свободные колебания.
а) Какие колебания — свободные или вынужденные — будут совершать при этом маятники 1, 2 и 4?
б) Благодаря чему возникает вынуждающая сила, действующая на маятники 1, 2 и 4?
в) Каковы собственные частоты маятников 1, 2 и 4 по сравнению с частотой колебаний маятника 3?
г) Почему маятник 1 колеблется в резонанс с маятником 3, а маятники 2 и 4 — нет?
а) маятники 1, 2 и 4 будут совершать вынужденные колебания, т.к. они колеблются под действием шнура; б) вынуждающая сила возникает благодаря колебанию маятника; в) частота маятника 1 равна частоте маятника 3, частота маятника 2 больше частоты маятника 3, частота маятника 4 меньше частоты маятника 3; г) т.к их длины одинаковы, то их собственные частоты совпадают и они колеблются в резонансе.
2. Вода, которую мальчик несет в ведре, начинает сильно расплескиваться. Мальчик меняет темп ходьбы (или просто «сбивает ногу»), и расплескивание прекращается. Почему так происходит?
Вода начинает расплескиваться когда частота шагов мальчика совпадает с собственной частотой колебаний ведра с водой в руках мальчика. Если частоты не совпадают, то ведро перестает сильно раскачиваться.
3. Собственная частота качелей равна 0,5 Гц. Через какие промежутки времени нужно подталкивать их, чтобы раскачать как можно сильнее, действуя относительно небольшой силой?
Амплитуда колебаний маятника зависит
27974. Амплитуда колебаний маятника зависит от частоты вынуждающей силы, определяемой по формуле
ω — частота вынуждающей силы (в с–1)
А0 — постоянный параметр
ωр = 360с–1 — резонансная частота.
Найдите максимальную частоту ω, меньшую резонансной, для которой амплитуда колебаний превосходит величину А0 не более чем на 12,5%. Ответ выразите в с–1.
Сказано, что амплитуда колебаний Аω превосходит величину А0 не более, чем на 12,5%. Это означает, что Аω числа равного 112,5% от А0.
Как выразить 112,5% от числа А0?
Составим пропорцию:
А0 – 100%
х – 112,5%
Значит можем записать:
Подставим данные и найдём ω:
Величина А0 постоянная и положительная, поэтому знак неравенства не изменится:
Знак модуля можно снять, так как в условии сказано, что ω < ωр (это означает, что их разность положительна):
Решением неравенства будет интервал [–120;120]. Учитывая то, что ω величина положительная, означает что она принадлежит интервалу [0;120]. Таким образом, максимальная частота ω для которой амплитуда колебаний превосходит величину А0 не более чем на 12,5% равна 120 с–1.
Ответ: 120
Другие статьи из категории:Физические задачи
- Ёмкость высоковольтного конденсатора
- Груз массой 0,08 кг колеблется
- Катер должен пересечь реку шириной
- При адиабатическом процессе для идеального
- При сближении источника и приёмника
- Находящийся в воде водолазный
- Для обогрева помещения, температура
- На сколько метров нужно подняться
- Для определения эффективной температуры звёзд
- Деталью некоторого прибора является