Методическая разработка для самостоятельной работы студентов по теме Электродинамика

ГОСУДАРСТВЕННОЕ АВТОНОМНОЕ ПРОФЕССИОНАЛЬНОЕ ОБРАЗОВАТЕЛЬНОЕ УЧРЕЖДЕНИЕ НОВОСИБИРСКОЙ ОБЛАСТИ «КУПИНСКИЙ МЕДИЦИНСКИЙ ТЕХНИКУМ»

МЕТОДИЧЕСКАЯ РАЗРАБОТКА

Для самостоятельной работы студентов

По дисциплине: ФИЗИКА

Тема: «ЭЛЕКТРОДИНАМИКА»

Специальность: 34.02.01 Сестринское дело Курс: 1

(базовой подготовки)

Купино

2019

Рассмотрено на заседании предметной цикловой

Методической комиссии по общеобразовательным дисциплинам,

общему гуманитарному и социально-экономическому, математическому и

естественно-научному циклу

Протокол № _____ от «_____» _________20____г.

Председатель ПЦМК: _____________

Автор – составитель: преподаватель математики высшей категории Тюменцева О.Н.

Купино

2019 г

Пояснительная записка

Методическое пособие предназначено для самостоятельного изучения теоретических и практических знаний по теме.

Цель пособия – изучить понятия: сил, действующих на проводник с током в магнитном поле, сил, действующих на электрический заряд, движущийся в магнитном поле, индукции и самоиндукции. Данное пособие рекомендовано для студентов первого курса специальности 34.02.01 Сестринское дело. Пособие содержит определения основных понятий по теме электромагнитная индукция, вопросы для самопроверки, образцы решения задач и задачи для самостоятельного решения.

Пособие направлено на формирование навыков самостоятельной работы с учебным материалом, формирование навыков решения задач, формирование и развитие творческого потенциала, повышение интереса к дисциплине.

Электромагнитная индукция

1.Магнитный поток

Вектор магнитной индукции  B ⃗   характеризует силовые свойства магнитного поля в данной точке пространства. Введем еще одну величину, зависящую от значения вектора магнитной индукции не в одной точке, а во всех точках произвольно выбранной поверхности. Эту величина называется

магнитным потоком и обозначается греческой буквой Φ (фи).

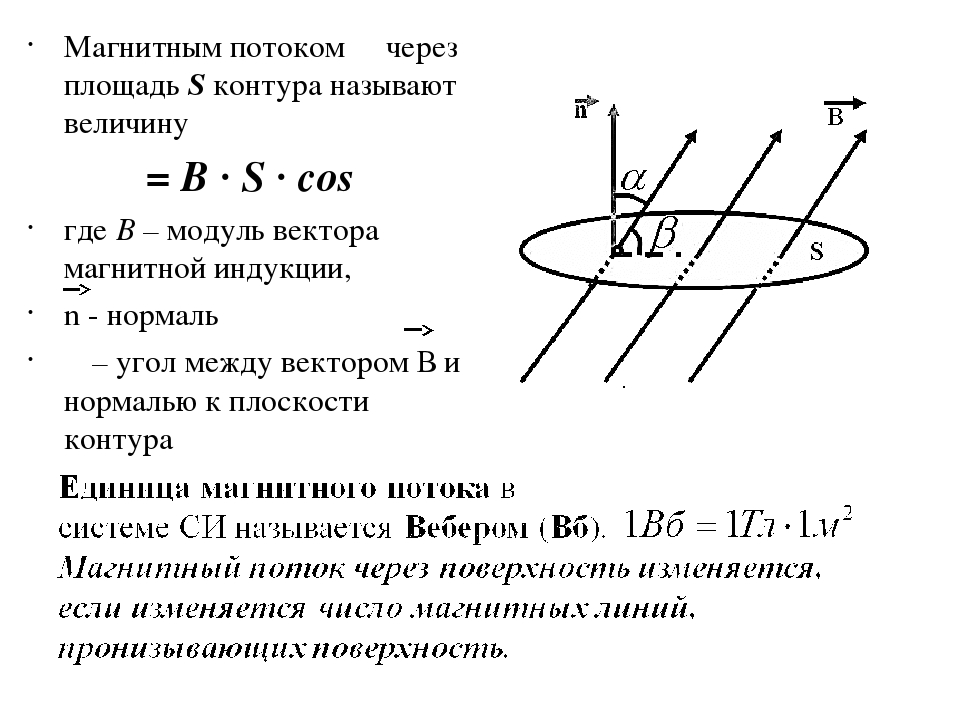
Магнитный поток Φ однородного поля через плоскую поверхность — это скалярная физическая величина, численно равная произведению модуля индукции B магнитного поля, площади поверхности S и косинуса угла α между нормалью  n ⃗   к поверхности и вектором индукции  B ⃗:

Φ=B⋅S⋅cosα.  (1) В СИ единицей магнитного потока является вебер (Вб): 1 Вб = 1 Тл ⋅ 1 м².

Магнитный поток в 1 Вб — это магнитный поток однородного магнитного поля с индукцией 1 Тл через перпендикулярную ему плоскую поверхность площадью 1 м

2.

Поток может быть как положительным, так и отрицательным в зависимости от значения угла α.

Поток магнитной индукции наглядно может быть истолкован как величина, пропорциональная числу линий вектора индукции  B ⃗  , пронизывающих данную площадку поверхности.

Из формулы (1) следует, что магнитные поток может изменяться:

• или только за счет изменения модуля вектора индукции B магнитного поля, тогда ΔΦ=(B 2 −B 1 )⋅S⋅cosα  ;

• или только за счет изменения площади контура S, тогда

 ΔΦ=B⋅(S 2 −S 1 )⋅cosα  ;

 ΔΦ=B⋅S⋅(cosα 2 −cosα 1 )  ;

 ΔΦ=B 2 ⋅S 2 ⋅cosα 2 −B 1 ⋅S 1 ⋅cosα 1  .

2. Электромагнитная индукция (ЭМИ)

Открытие ЭМИ

Вам уже известно, что вокруг проводника с током всегда существует магнитное поле. А нельзя наоборот, с помощью магнитного поля создать ток в проводнике? Именно такой вопрос заинтересовал английского физика Майкла Фарадея, который в 1822 г. записал в своем дневнике: «Превратить магнетизм в электричество». И только через 9 лет эта задача была им решена.

Открытие электромагнитной индукции

, как назвал Фарадей это явление, было сделано 29 августа 1831 г. Первоначально была открыта индукция в неподвижных друг относительно друга проводниках при замыкании и размыкании цепи. Затем, ясно понимая, что сближение или удаление проводников с током должно приводить к тому же результату, что и замыкание и размыкание цепи, Фарадей с помощью опытов доказал, что ток возникает при перемещении катушек относительно друг друга.

17 октября, как зарегистрировано в его лабораторном журнале, был обнаружен индукционный ток в катушке во время вдвигания (или выдвигания) магнита.

В течение одного месяца Фарадей опытным путем открыл, что в замкнутом контуре возникает электрический ток при любом изменении магнитного потока через него. Полученный таким способом ток называется

индукционным током I_i.

Известно, что в цепи возникает электрический ток в том случае, когда на свободные заряды действуют сторонние силы. Работу этих сил при перемещении единичного положительного заряда вдоль замкнутого контура называют электродвижущей силой. Следовательно, при изменении магнитного потока через поверхность, ограниченную контуром, в нем появляются сторонние силы, действие которых характеризуется ЭДС, которую называют ЭДС индукции и обозначают E_i.

Индукционный ток I_i в контуре и ЭДС индукции E_i связаны следующим соотношением (законом Ома):

 I i =−E i/R  , 

где R — сопротивление контура.

Явление возникновения ЭДС индукции при изменении магнитного потока через площадь, ограниченную контуром, называется явлением электромагнитной индукции.

Если контур замкнут, то вместе с ЭДС индукции возникает и индукционный ток.

Джеймс Клерк Максвелл предложил такую гипотезу: изменяющееся магнитное поле создает в окружающем пространстве электрическое поле, которое и приводит свободные заряды в направленное движение, т.

е. создает индукционный ток. Силовые линии такого поля замкнуты, т.е. электрическое поле вихревое.

Индукционные токи, возникающие в массивных проводниках под действием переменного магнитного поля, называются токами Фуко или вихревыми токами.

История

Вот краткое описание первого опыта, данное самим Фарадеем.

«На широкую деревянную катушку была намотана медная проволока длиной в 203 фута (фут равен 304,8 мм), и между витками ее намотана проволока такой же длины, но изолированная от первой хлопчатобумажной нитью. Одна из этих спиралей была соединена с гальванометром, а другая — с сильной батареей, состоящей из 100 пар пластин… При замыкании цепи удалось заметить внезапное, но чрезвычайно слабое действие на гальванометр, и то же самое замечалось при прекращении тока. При непрерывном же прохождении тока через одну из спиралей не удавалось отметить ни действия на гальванометр, ни вообще какого-либо индукционного действия на другую спираль, не смотря на то что нагревание всей спирали, соединенной с батареей, и яркость искры, проскакивающей между углями, свидетельствовали о мощности батареи».

3. Правило Ленца

Русский физик Эмилий Ленц в 1833 г. сформулировал правило (

правило Ленца), которое позволяет установить направление индукционного тока в контуре:

• возникающий в замкнутом контуре индукционный ток имеет такое направление, при котором созданный им собственный магнитный поток через площадь, ограниченную контуром, стремится препятствовать тому изменению внешнего магнитного потока, вызвавшее данный ток.

Или

Например, при увеличении магнитного потока через витки катушки индукционный ток имеет такое направление, что создаваемое им магнитное поле препятствует нарастанию магнитного потока через витки катушки, т.е. вектор индукции B ⃗  ′   этого поля направлен против вектора индукции B ⃗   внешнего магнитного поля. Если же магнитный поток через катушку ослабевает, то индукционный ток создает магнитное поле с индукцией B ⃗ , увеличивающее магнитный поток через витки катушки.

4. Закон ЭМИ

Опыты Фарадея показали, что ЭДС индукции (и сила индукционного тока) в проводящем контуре пропорциональна скорости изменения магнитного потока. Если за малое время Δt магнитный поток меняется на ΔΦ, то скорость изменения магнитного потока равна ΔΦ Δt   . С учетом правила Ленца Д. Максвелл в 1873 г. дал следующую формулировку закона электромагнитной индукции:

• ЭДС индукции в замкнутом контуре равна скорости изменения магнитного потока, пронизывающего этот контур, взятой с противоположным знаком

 E i =−ΔΦ/ Δt  . 

• Знак «минус» в законе следует из закона Ленца. При увеличении магнитного потока (ΔΦ > 0), ЭДС отрицательная (E_i < 0), т.е. индукционный ток имеет такое направление, что вектор магнитной индукции индукционного

• магнитного поля направлен против вектора магнитной индукции внешнего (изменяющегося) магнитного поля (рис. 4, а). При уменьшении магнитного потока (ΔΦ < 0), ЭДС положительная (E_i > 0) (рис. 4, б).

В Международной системе единиц закон электромагнитной индукции используют для установления единицы магнитного потока. Так как ЭДС индукции E_i выражают в вольтах, а время в секундах, то из закона ЭМИ вебер можно определить следующим образом:

магнитный поток через поверхность, ограниченную замкнутым контуром, равен 1 Вб, если при равномерном убывании этого потока до нуля за 1 с в контуре возникает ЭДС индукции равная 1 В:

1 Вб = 1 В ∙ 1 с.

5. ЭДС индукции в движущемся проводнике

При движении проводника длиной l со скоростью υ ⃗   в постоянном магнитном поле с вектором индукции B ⃗   в нем возникает ЭДС индукции E i =B⋅υ⋅l⋅cosα, 

где α – угол между направлением скорости υ⃗проводника и вектором магнитной индукции B ⃗.

Причиной появления этой ЭДС является сила Лоренца, действующая на свободные заряды в движущемся проводнике. Поэтому направление индукционного тока в проводнике будет совпадать с направлением составляющей силы Лоренца на этот проводник.

С учетом этого можно сформулировать следующее для определения направления индукционного тока в движущемся проводнике (правило левой руки):

нужно расположить левую руку так, чтобы вектор магнитной индукции B ⃗   входил в ладонь, четыре пальца совпадали с направлением скорости υ ⃗   проводника, тогда отставленный на 90° большой палец укажет направление индукционного тока (рис. 5).

Если проводник движется вдоль вектора магнитной индукции, то индукционного тока не будет (сила Лоренца равна нулю).

Вопросы для самопроверки

1. Сформулируйте определение магнитного потока

2. Сформулируйте правило Ленца

3. Сформулируйте определение ЭДС индукции

4. Сформулируйте определение вихревого электрического поля

5. Сформулируйте определение самоиндукции

6. Сформулируйте определение индуктивности

7. Перечислите свойства электромагнитного поля

Примеры решения задач по теме: Электромагнитная индукция

1. 1. 1. 1. Медное кольцо, диаметр которого — 20 см, а диаметр провода кольца 2 мм, расположено в однородном магнитном поле. Плоскость кольца перпендикулярна вектору магнитной индукции. Определите модуль скорости изменения магнитной индукции поля со временем, если при этом в кольце возникает индукционный ток 10 А. Удельное сопротивление меди ρ_Сu = 1,72 • 10^-8 Ом·м.

1. 1. 1. 2. Плоская рамка из провода сопротивлением 5 Ом находится в однородном магнитном поле. Проекция магнитной индукции поля на ось Ох, перпендикулярную плоскости рамки, меняется от В_1х = 3 Тл до В_2х = -1 Тл. За время изменения поля по рамке протекает заряд 1,6 Кл. Определите площадь рамки.  

1. 1. 1. 3. Замкнутый контур из тонкой проволоки помещён в магнитное поле. Плоскость контура перпендикулярна вектору магнитной индукции поля. Площадь контура S = 2•10^–3 м². В контуре возникают колебания тока с амплитудой i_м = 35 мА, если магнитная индукция поля меняется с течением времени в соответствии с формулой B = acos(bt), где а = 6•10^–3 Тл, b = 3500 с^–1. Чему равно электрическое сопротивление контура R? 

Задачи для самостоятельного решения

1. Медное кольцо из провода диаметром 2 мм расположено в однородном магнитном поле, магнитная индукция которого меняется по модулю со скоростью 1,09 Тл/с. Плоскость кольца перпендикулярна вектору магнитной индукции. Каков диаметр кольца, если возникающий в нём индукционный ток равен 10 А? Удельное сопротивление меди ρ_Cu = 1,72·10^-8 Ом·м.

2. Плоская горизонтальная фигура площадью 0,1 м², ограниченная проводящим контуром с сопротивлением 5 Ом, находится в однородном магнитном поле. Пока проекция вектора магнитной индукции на вертикальную ось Oz медленно и равномерно возрастает от В_1Z = – 0,15 Тл до некоторого конечного значения В_2Z, по контуру протекает заряд 0,008 Кл. Найдите В_2Z. 

3. Проводящий стержень длиной l = 20 см движется поступательно в однородном магнитном поле со скоростью v = 1 м/с так, что угол между стержнем и вектором скорости α = 30° (см. рисунок). ЭДС индукции в стержне равна 0,05 В. Какова индукция магнитного поля? 

Магнитная индукция — Основы электроники

Магнитная индукция это способность влиять магнитным полем  на объект.

При помещении в катушку железного стержня (сердеч­ника) ее магнитный поток увеличивается во много раз. Объ­ясняется это следующим. Железо имеет кристаллическое строе­ние. Отдельные кристаллы железа, вследствие того, что внутри их происходит круговое движение электронов, т. е. существуют электрические токи, обладают свойствами маленьких магни­тиков. В обычном состоянии эти молекулярные магнитики рас­положены в беспорядке. Магнитные поля их взаимно нейтра­лизуются, и поэтому кусок железа в целом не проявляет маг­нитных свойств. Схематически это изображено на рисунке 1. Отдельные молекулярные кристаллики изображены в виде ма­леньких магнитиков.

Рисунок 1. Беспорядочное расположение малекулярных кристалликов в обыном состоянии железа.

При помещении железа в магнитное поле молекулярные магнитики подобно магнитной стрелке компаса поворачиваются на некоторый угол и устанавливаются вдоль силовых линий магнитного поля. Чем сильное магнитное поле, тем большее число молекулярных магнитиков поворачивается и тем одно­роднее становится их расположение. Поля одинаково ориен­тированных магнитов не нейтрализуют уже друг друга, а на­оборот, складываются, создавая дополнительные силовые линии.

Магнитный поток, создаваемый элементарными магнити­ками железа, во много раз больше основного магнитного по­тока, создаваемого катушкой; именно поэтому магнитный поток катушки при помещении в нее железного сердечника увеличивается во много раз.

Если постепенно увеличивать ток, протекающий по виткам катушки, то магнитный поток в железном сердечнике будет увеличиваться до тех пор, пока все молекулярные магнитики не повернутся точно по направлению силовых линий магнит­ного поля (рисунок 2).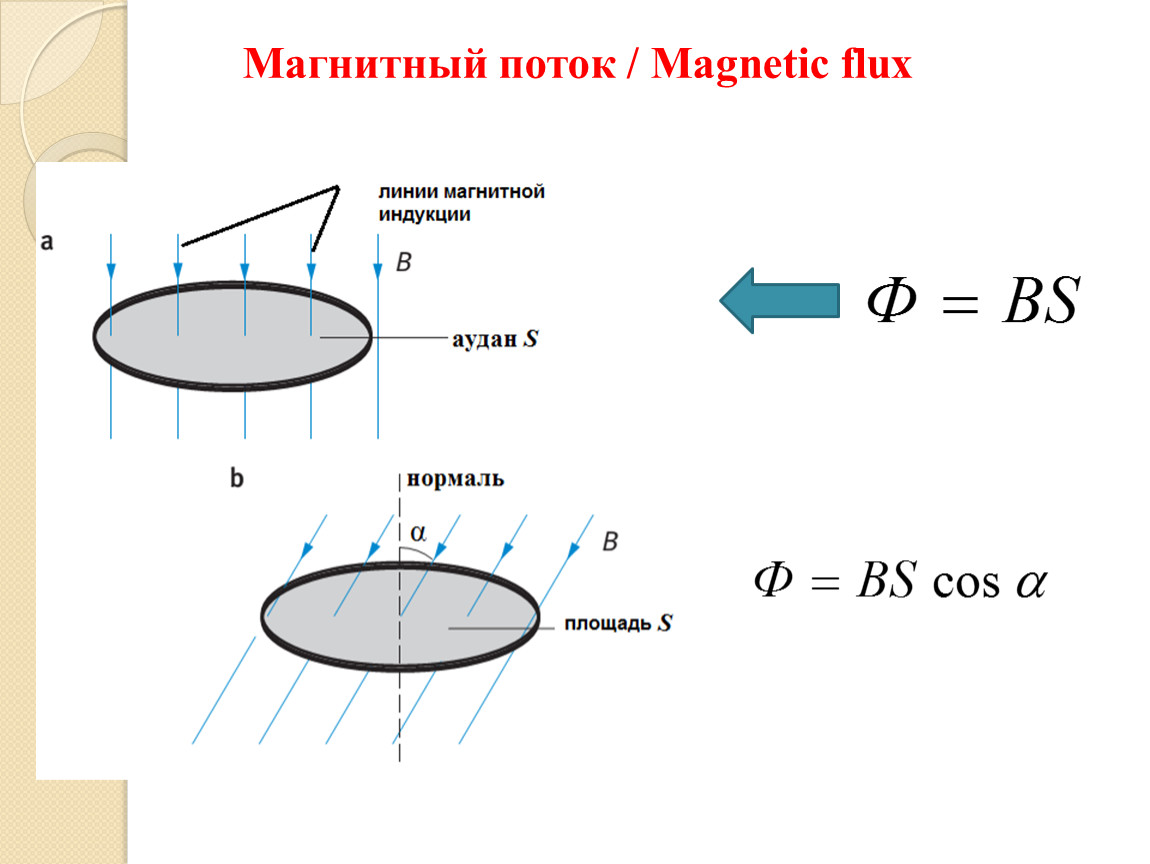 После этого возрастание магнитного по­тока за счет железа прекратится. Это состояние железного сердечника называется магнитным насыщением.

Рисунок 2. В магнитном поле кристаллики направлены вдоль магнитных силовых линий.

Способностью увеличивать магнитный поток катушки об­ладают кроме железа и другие металлы (кобальт и никель), но у них эта способность выражена значительно слабее, чем у железа.

Очень сильными магнитными свойствами обладают также некоторые специальные сплавы. В радиотехнике эти сплавы применяются для изготовления постоянных магнитов для ди­намиков и магнетронов.

Число, показывающее, во сколько раз увеличивается маг­нитный поток соленоида при введении в него сердечника из какого-нибудь материала, называется магнитной проницае­мостью данного материала и обозначается буквой µ

Магнитная проницаемость некоторых сортов железа и спе­циальных сплавов достигает нескольких сотен тысяч. Для боль­шинства же материалов она близка к единице.

Произведение из напряженности магнитного поля Н на проницаемость материала µ называется магнитной индук­цией В.

Таким образом

B = µ *H.

Магнитная индукция определяет количество силовых линий в данном материале, проходящих через 1 см² поперечного се­чения материала.

После прекращения тока в катушке сердечник, если он сделан из мягкого железа, теряет свои магнитные свойства, потому что молекулярные магнитики снова располагаются бес­порядочно. Если же сердечник стальной, то он сохраняет при­обретенные магнитные свойства и после прекращения действия на него магнитного поля катушки. Объясняется это тем, что в стали молекулярные магнитики сохраняют свое упорядочен­ное расположение и после прекращения тока в катушке.

Катушка с железным сердечником называется электромаг­нитом, так как ее магнитные свойства обусловлены электриче­ским током.

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Похожие материалы:

Добавить комментарий

это высокое наслаждение» (Лев Ландау): 9 класс

КИНЕМАТИКА

ЛАБОРАТОРНЫЕ РАБОТЫ

Урок «Индукция магнитного поля», «Магнитный поток»

1. Посмотрите видеофрагмент.

2. Прочитайте параграф «Индукция магнитного поля»

3. Письменно ответьте на вопросы:

а) Какой величиной можно охарактеризовать магнитное поле? Напишите определение.

б) По какой формуле определяется модуль вектора магнитной индукции однородного поля? Напишите определение, формулу, составьте треугольник для этой формулы, выразите остальные физические величины из формулы для магнитной индукции.

в) Напишите единицу измерения магнитной индукции, какая взаимосвязь между единицей магнитной индукции и единицами других величин.

г) Что называется линиями магнитного поля?

д) Дайте определение однородному магнитному полю. 

Изобразите однородное и неоднородное магнитное поле  с векторами магнитной индукции.

е) Решите задачу из видеоролика.

4. Посмотрите видеофрагмент

5. Прочитайте параграф «Магнитный поток»

6. Письменно ответьте на вопросы 

а) От чего и как зависит магнитный поток, пронизывающий площадь плоского контура, помещённого в однородное магнитное поле? Сделайте соответствующие рисунки .

б) Какой буквой обозначается магнитный поток и когда он равен нулю?

Урок «Реактивное движение. Ракеты»

1. Прочтите параграф «Реактивное движение. Ракеты»

2. Посмотрите видеоурок по теме.

3. В тетради оформите конспект параграфа.

Урок № 40. Явление электромагнитной индукции.

1. Посмотрите видеоурок по теме.

2. Письменно в тетради ответьте на вопросы:

а) В каком году и кто открыл явление электромагнитной индукции?

б) Дайте определение явлению электромагнитной индукции.

в) В однородном магнитном поле помещена проволочная рамка (см. рисунок). Будет ли возникать индукционный ток в рамке, если её:

— перемещать поступательно вверх,

— вращать вокруг оси, параллельной магнитному полю,

— вращать вокруг оси, перпендикулярно магнитному полю? (Рисунок перерисовать в тетрадь)

3. Назовите главное условие возникновения индукционного тока.

4.Изобразите схему опыта Фарадея и опишите его.

5. Изобразите схему опыта с двумя катушками, одна из которых подключена к источнику питания, а вторая к гальванометру, и опишите опыт.

  

Домашнее задание по теме

«Явление самоиндукции»

1.Посмотрите видеоуроки по теме.

2.Письменно ответьте на вопросы после параграфа

Урок . Электромагнитное поле. Электромагнитные волны.

Домашнее задание по теме.

1. Посмотрите видеоуроки по теме.

2. Прочтите параграфы  по теме.

3. Письменно ответьте на вопросы после параграфов.

4. Выполните   ТЕСТ

Урок «Преломление света», «Дисперсия света»
Домашнее задание:

1.Посмотрите видеоуроки по темам

2. Сделайте конспект параграфа , ответив на следующие вопросы:

а)Сформулируйте закон преломления.
б)Какое вещество называется «оптически более плотным»? Изобразите ход луча из среды оптически менее плотной в среду оптически более плотную и наоборот.
в)Что такое «абсолютный показатель преломления» и «относительный показатель преломления»? Как определяются показатели преломления через скорость света в средах?
г)Где свет распространяется с наибольшей скоростью? Какова физическая причина уменьшения скорости света при его переходе из среды с меньшей оптической плотностью в среду с большей?
д)Расскажите об учёный, работающих в этой области
ССЫЛКА НА ПАРАГРАФ «ПРЕЛОМЛЕНИЕ»

3. Сделайте конспект параграфа , ответив на следующие вопросы:

а)Расскажите об опыте  по преломлению белого света в призме (Ход опыта, результаты, выводы)
б)Что такое дисперсия света?
в)Каковы были взгляды древних на понятие «цвет»?В чем причина различия цветов окружающих нас тел?
г)Изобразите спектроскоп, опишите его устройство, чем спектрограф отличается от спектроскопа?
д)Расскажите об учёных , работающих в этой области.
ССЫЛКА НА ПАРАГРАФ «ДИСПЕРСИЯ»

4. Пройдите тест.

Урок №50 и №51. Типы оптических спектров. Поглощение и испускание света атомами.

   

1. Посмотрите два видеоурока.

2. Напишите конспекты двух параграфов  по темам, ответив на вопросы после параграфов.

Подготовка к контрольной работе по главе №3″Электромагнитное поле».
Основные вопросы.

1. Повторите основные формулы из главы: длины волны э/м волн, абсолютного показателя преломления, закона преломления, магнитной индукции, энергии магнитного поля, магнитного потока, формула для периода э/м волн. Вы должны уметь решать такие задачи , как №1845,1840,1778 (но для э/м волн).
2. Правила левой и правой руки для различных случаев. Вы должны уметь решать такие задачи , как №1791, 1792, 1793,1780.
3. Понимать  понятия и явления: явление э/м индукции, переменный ток, дисперсия, преломление, спектральный анализ, магнитное поле, линии магнитной индукции и т.д.
4. Понимать как изображается магнитное поле вокруг проводника с током, как получают переменный ток, как его передают, как происходит радиопередача , какие энергии и как изменяются в колебательном контуре, что происходит и как с лучом света  при переходе из одной среды в другую.

5. О каких учёных шла речь в этой главе, что они сделали.

6. От чего зависит и не зависит магнитная индукция. От чего зависит магнитный поток. Где скорость света наибольшая, что с ней происходит, например в воде. Когда угол падения равен углу преломления, а когда какой больше.

Урок № 79 «Экспериментальные методы регистрации заряженных частиц.»

1.  Внимательно прочтите §54 «Экспериментальные методы регистрации частиц», посмотрите видеофильм и письменно заполните таблицу в тетрадях (отчёт вышлите мне на почту). 

Название прибора, метода. Кем и когда был предложен.	Схема строения	Рабочее вещество	Принцип действия	Что позволяет делать. Достоинства

В таблице рассмотрите 

2.   Ссылка на видеофильм.

Урок №80, 81″Открытие протона и нейтрона», «Состав атомного ядра. Ядерные силы»

1. Посмотрите видеофильм.

2. Прочтите § 55,56.

3. Сделайте конспект (вам помогут подсказки внизу задания) , ответив на следующие вопросы.

А)  Как был открыт протон: кем, когда, как. Дайте полную характеристику протону.

Б)  Как был открыт нейтрон: кем, когда, как. Дайте полную характеристику нейтрону.

В)  Что такое число «А», «Z», «N». Что каждое число показывает и как они связаны между собой?

Г)  дайте определение понятию «Изотоп».

Д)  Дайте определение понятию «Ядерные силы». Какими свойствами они обладают?

Отчёт вышлите мне на почту.

Подсказки для конспекта:

Урок №82,83 «Энергия связи. Дефект масс»

1. Посмотрите видеоурок.

2.Прочтите параграф «Энергия связи. Дефект масс».

3. Письменно в тетрадях (фотоотчёт пришлите по почте):

А)  Что называется энергией связи ядра?

Б)  Запишите формулу для определения дефекта массы любого ядра.

В)  Как перевести из !а.е.м. в кг?

Г)  Запишите формулу для расчёта энергии связи ядра.

Д)  Запишите задачу по нахождению энергии связи для гелия (см.фильм).

Е) Самостоятельно решите такую же задачу, но для фтора (см. фильм или таблицу Менделеева ;помните, что для нахождения числа всех нуклонов массу ядра надо округлить).

Урок №84 «Повторительно-обобщающий урок по теме»Состав атома и атомного ядра»

Урок №85, 86 «Деление ядер урана. Цепная реакции», «Ядерный реактор. Атомная энергетика»

1. Посмотрите видеоурок.

2. Ознакомтесь с  §58,59,60
3. Пройдите ТЕСТ

Урок № 87. Биологическое действие радиации. Период полураспада.

1. Посмотрите презентацию по теме. ( ССЫЛКА на презентацию) и видеосюжет 

2. Прочтите параграф  по теме.

3. Напишите конспект параграфа.

4. Найдите в интернете информацию о крупных авариях на АЭС. И сделайте по этой информации отчётную таблицу, где будут отображены следующие сведения:

Урок №89 «Термоядерная реакция»

Прочтите параграф на соответствующую тему

Пройдите

ТЕСТ

Урок №90 «Элементарные частицы. Античастицы»

1. Прочтите текст из рубрики «Это любопытно…» про элементарные частицы и античастицы.

2. Сделайте лабораторную работу №9 «Изучение треков заряженных частиц по готовым фотографиям». Отчёт пришлите на почту.

АСТРОНОМИЯ

Урок №95-99 «Строение и эволюция Вселенной»

1. Прочтите § 63

2. Посмотрите видеоурок.

3. Прочтите § 64.65

4. Посмотрите видеоурок.

5. Прочтите § 66.67

6. Посмотрите видеоурок.

Проверочная работа по теме «СТРОЕНИЕ И ЭВОЛЮЦИЯ ВСЕЛЕННОЙ»

Индукция магнитного поля и магнитный поток

Магнитное поле характеризуется векторной величиной, которая называется магнитной индукцией, обозначается буквой Bи измеряется в Теслах (Тл).

На практике чем больше величина B, тем сильнее притягивает (или отталкивает) магнит. Ближе к магниту B будет больше, дальше – меньше.

Модуль магнитной индукции можно определить через силу Ампера.

B = F/(IL), где – это значение индукции, F – величина силы Ампера, I – сила тока, проходящего через проводник, L – длина проводника. Формула работает, лишь если проводник расположен перпендикулярно B (и F тогда перпендикулярно и проводнику, и B).

Направление B совпадает с направлением линий магнитного поля в данной точке.

Также магнитное поле часто характеризуют магнитным потоком – потоком вектора B через некоторый заданный контур. Поток рассчитывается по формуле:

Ф = B * S * cos(α), где Ф – это поток, B – индукция, S – площадь контура, α – угол между вектором индукции и перпендикуляром к контуру.

Чтобы лучше «ощутить» поток, взглянем на картинки.

На картинке 2 поток больше, чем на картинке 1, так как при равной площади больше индукция. На картинке 3 поток тоже больше, чем на картинке 1 – при равной индукции больше площадь. На картинке 4 поток меньше, чем на картинке 1 – индукция и площадь такие же, на cos(α) околонулевой.

Удобно представлять себе поток как ветер, дующий в парус. Парус побольше – корабль идёт быстрее. Ветер посильнее – опять же, корабль ускорился. Парус поставили параллельно ветру – усилие пропало и корабль потерял скорость.

Поток магнитного поля измеряется в Веберах (Вб).

Когда магнитный поток изменяется, в контуре возникает ток, называемый индукционным током. Это явление называется электромагнитной индукцией.

Индукционный ток направлен в соответствии с правилом Ленца – то есть так, чтобы этотток порождал магнитное поле, противодействующее изменению магнитного потока. То есть если магнитный поток ослабевает, то индукционный ток идёт так, что порождает магнитное поле, усиливающее поток.

Редактировать этот урок и/или добавить задание Добавить свой урок и/или задание

Добавить интересную новость

11 класс — Физика

 

Явление электромагнитной индукции было открыто Майлом Фарадеем в 1831 году. Еще за 10 лет до этого Фарадей думал о способе превратить магнетизм в электричество. Он считал, что магнитное поле и электрическое поле должны быть как-то связаны.

Открытие электромагнитной индукции

Например, с помощью электрического поля можно намагнитить железный предмет. Наверное, должна существовать возможность с помощью магнита получить электрический ток.  

Сначала Фарадей открыл явление электромагнитной индукции в неподвижных относительно друг друга проводниках. При возникновении в одной из них тока в другой катушке тоже индуцировался ток. Причем в дальнейшем он пропадал, и появлялся снова лишь при выключении питания одной катушки. 

Через некоторое время Фарадей на опытах доказал, что при перемещении катушки без тока в цепи относительно другой, на концы которой подается напряжение, в первой катушке тоже будет возникать электрический ток.

Следующим опытом было введение в катушку магнита, и при этом тоже в ней появлялся ток. 

Фарадеем была сформулирована основная причина появления тока в замкнутом контуре.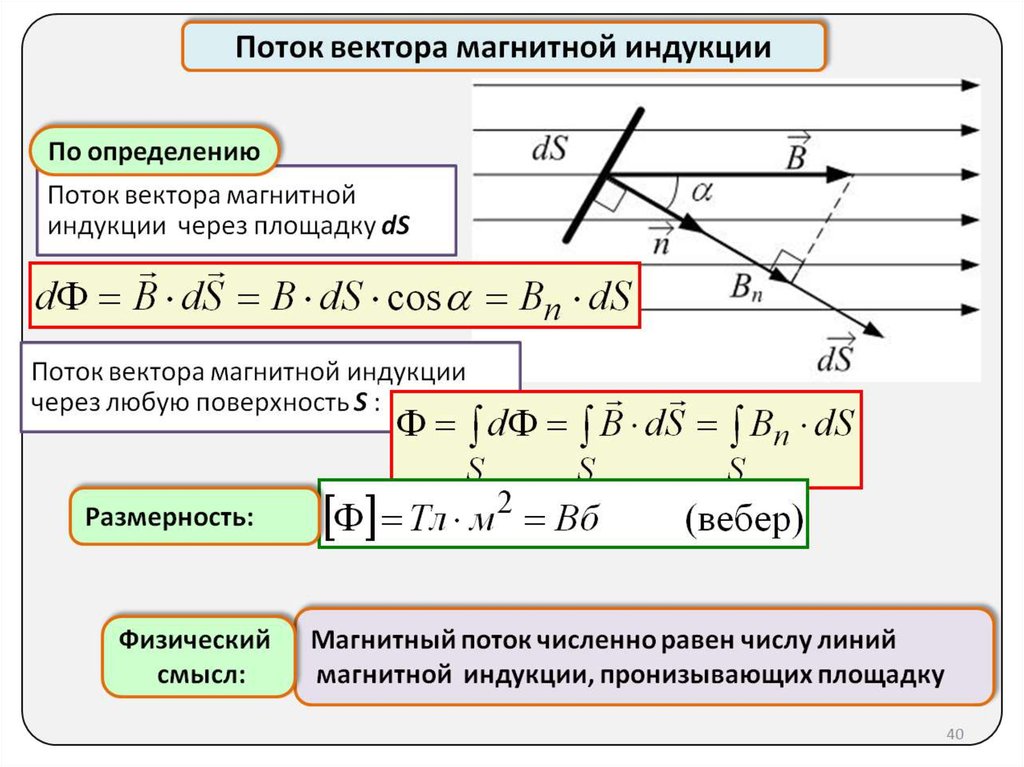 В замкнутом проводящем контуре ток возникает при изменении числа линий магнитной индукции, которые пронизывают этот контур.

Чем больше будет это изменение, тем сильнее получится индукционный ток. Неважно, каким образом мы добьемся изменения числа линий магнитной индукции. Например, это можно сделать движением контура в неоднородном магнитном поле, как это происходило в опыте с магнитом или движением катушки. А можем, например, изменять силу тока в соседней с контуром катушке, при этом будет изменяться магнитное поле, создаваемое этой катушкой.

Формулировка закона

Подведем краткий итог. Явление электромагнитной индукции – это явление возникновения тока в замкнутом контуре, при изменении магнитного поля в котором находится этот контур.

Для более точной формулировки закона электромагнитной индукции необходимо ввести величину, которая бы характеризовала магнитное поле – поток вектора магнитной индукции.

Магнитный поток

Вектор магнитной индукции обозначается буквой B. 2, которая расположена перпендикулярно вектору магнитной индукции.

 

При внесении в катушку магнита в ней возникает индукционный ток. Если к катушке присоединить гальванометр, то можно заметить, что направление тока будет зависеть от того приближаем ли мы магнит или удаляем его.

Магнит будет взаимодействовать с катушкой либо притягиваясь, либо отталкиваясь от нее. Это будет возникать вследствие того, что катушка с проходящим по ней током, будет подобна магниту с двумя полюсами. Направление индуцируемого тока будет определять, где у катушки будет находиться какой из полюсов.

Если приближать к катушке магнит, то в ней будет возникать индукционный ток такого направления, что катушка обязательно будет отталкиваться от магнита. Если мы будет удалять магнит от катушки, то при этом в катушке возникнет такой индукционный ток, что она будет притягиваться к магниту.

Стоит отметить, что не важно каким полюсом мы подносим или убираем магнит, всегда при подносе катушка будет отталкиваться, а при удалении притягиваться. Различие состоит в том, что при приближении магнита к катушке магнитный поток, который будет пронизывать катушку, увеличивается, так как у полюса магнита кучность линий магнитной индукции увеличивается. А при удалении магнита, магнитный поток, пронизывающий катушку, будет уменьшаться.

Узнать направление индукционного тока можно. Для этого существует правило Ленца. Оно основано на законе сохранения. Рассмотрим следующий опыт.

рисунок

Имеется катушка с подключенным к ней гальванометром. К одному и краев катушки начинаем подносить магнит, например, северным полюсом. Количество линий, которые будут пронизывать поверхность каждого витка катушки, будет увеличиваться. Следовательно, будет увеличиваться и значение магнитного потока.

Так как должен выполняться закон сохранения, должно возникнуть магнитное поле, которое будет препятствовать изменению магнитного потока. В нашем случае магнитный поток увеличивался, следовательно, ток должен течь в таком направлении, чтобы линии вектора магнитной индукции, создаваемые катушкой, были направлены в противоположном направлении линиям магнитной индукции, создаваемым магнитом.  

То есть они должны в нашем случае быть направлены вверх. Теперь воспользуемся правилом буравчика. Направляем большой палец правой руки по необходимому нам направлению линий магнитной индукции, то есть — вверх. Тогда остальные пальцы укажут, в какую сторону должен быть направлен индукционный ток. В нашем случае, слева на право.

Аналогичный процесс происходит при удалении магнита. Убираем магнит, магнитный поток уменьшается, следовательно, должно возникнуть поле которое будет увеличивать магнитный поток. То есть поле линии магнитной индукции, которого будут сонаправлены с линиями магнитной индукции, создаваемыми постоянным магнитом. В нашем случае эти лини направлены вниз. Опять пользуемся правилом буравчика и определяем направление индукционного тока.

 

После возникновения понятия о явлении электромагнитной индукции, интересно было бы узнать её количественные характеристики. Согласно опытам сила индукционного тока, которая возникнет в замкнутом контуре, будет пропорциональна изменению магнитного потока, который пронизывает этот контур.

Магнитный поток

Магнитный поток — это не что иное, как количество пронизывающих контур линий магнитной индукции. Чем больше их пронизывает контур, тем больше будет магнитный поток. Поэтому скорость изменения магнитного потока, можно представить как скорость изменения количество линий магнитной индукции, которые пронизывают контур.

За некоторое достаточно малое время ∆t магнитный поток изменится на некоторую величину ∆Ф. Следовательно, сила индукционного тока в замкнутом контуре будет пропорциональна скорости изменения магнитного потока, который пронизывает поверхность, ограниченную этим контуром.

Ii = ∆Ф/∆t.

Электродвижущая сила

Ток в цепи будет возникать при направленном движении заряженных частиц, под действием некоторых сторонних сил. Электродвижущая сила, величина численно равная работе сил по перемещению, единичного положительного заряда вдоль замкнутого контура, называется электродвижущей силой. 

При изменении магнитного потока в контуре возникает электрический ток, а следовательно, возникает электродвижущая сила, которая в этом случае называется ЭДС индукции. Для её обозначение используют прописную букву Е. Мы будем обозначать ЭДС индукции Ei.

Согласно закону Ома для замкнутой цепи, будет выполняться следующее равенство:

Ii = Ei/R.

Теперь сформулируем закон электромагнитной индукции. Он будет говорить об ЭДС индукции, так как сила тока, будет зависеть от свойств проводника, а ЭДС будет определяться только изменением магнитного потока, пронизывающего замкнутый контур.

Закон электромагнитной индукции

ЭДС индукции возникающая в замкнутом контуре равна по модулю скорости изменения магнитного потока через поверхность, которую ограничивает этот контур.

Ei = |∆Ф/∆t |.

Теперь необходимо учесть направление индукционного тока, который возникает в контуре. Для этого в формуле необходимо раскрыть модуль и поставить перед частным знак минус.

Ei = -∆Ф/∆t.

Индукционный ток должен быть направлен в направлении против положительного обхода контура. ЭДС индукции будет отрицательна.

 

Нахождение ЭДС индукции через силу Лоренца

Магнитный поток через контур может изменяться по следующим причинам:

В обоих этих случаях будет выполняться закон электромагнитной индукции. При этом происхождение электродвижущей силы в этих случаях различное. Рассмотрим подробнее второй из этих случаев

В данном случае проводник движется в магнитном поле. Вместе с проводником совершают движение и все заряды, которые находятся внутри проводника. На каждый из таких зарядов со стороны магнитного поля будет действовать сила Лоренца. Она и будет способствовать перемещению зарядов внутри проводника.

• ЭДС индукции в данном случае будет иметь магнитное происхождение.

Рассмотрим следующий опыт: магнитный контур, у которого одна сторона подвижная, помещают в однородное магнитное поле. Подвижная сторона длиной l начинает скользить вдоль сторон MD и NC с постоянной скоростью V. При этом она постоянно остаётся параллельной стороне СD. Вектор магнитной индукции поля будет перпендикулярен проводнику и составлять угол а с направлением его скорости. На следующем рисунке представлена лабораторная установка для этого опыта:

Сила Лоренца, действующая на движущуюся частицу, вычисляется по следующей формуле:

Fл = |q|*V*B*sin(a).

Сила Лоренца будет направлена вдоль отрезка MN. Рассчитаем работу силы Лоренца:

A = Fл*l = |q|*V*B*l*sin(a).

ЭДС индукции — это отношение работы, совершаемой силой при перемещении единичного положительного заряда, к величине этого заряда. Следовательно, имеем:

Ei = A/|q| = V*B*l*sin(a).

Эта формула будет справедлива для любого проводника, движущегося в с постоянной скоростью в магнитном поле. ЭДС индукции будет только в этом проводнике, так как остальные проводники контура остаются неподвижными. Очевидно, что ЭДС индукции во всем контуре будет равняться ЭДС индукции в подвижном проводнике.

ЭДС из закона электромагнитной индукции 

Магнитный поток через тот же контур, что и в примере выше, будет равняться: 

Ф = B*S*cos(90-a) = B*S*sin(a).

Здесь угол (90-а) = угол между вектором магнитной индукции и нормалью к поверхности контура. За некоторое время ∆t площадь контура будет изменяться на ∆S = -l*V*∆t. Знак «минус» показывает, что площадь уменьшается. При этом за это время магнитный поток изменится:

∆Ф = -B*l*V*sin(a).

Тогда ЭДС индукции равна:

Ei = -∆Ф/∆t = B*l*V*sin(a).

Если весь контур будет двигаться внутри однородного магнитного поля с постоянной скоростью, то ЭДС индукции будет равняться нулю, так как будет отсутствовать изменение магнитного потока.

• ЭДС индукции будет возникать и при повороте рамки внутри магнитного поля.

Микрофон – электрическое устройство, которое преобразует звуковые колебания воздуха в колебания электрического тока. Микрофоны получили широко распространение в радиовещании, телевидении и т.д.

Электродинамический микрофон

Рассмотрим, как работает микрофон, на самом простом из микрофонов – электородинамическом. Его работа основана на явлении электромагнитной индукции. Рассмотрим устройство электродинамического микрофона.

картинка

Диафрагма микрофона (2) сделана из полистирола или алюминиевой фольги. Она жестко связана со звуковой катушкой. Звуковая катушка (1) изготавливается из очень тонкой проволоки.

Катушку помешают в кольцевой зазор сильно постоянного магнита (3). Линии магнитной индукции будут перпндикулярны виткам катушки.

Когда человек говорит, возникает звуковая волна. Эта волна вызывает колебание диафрагмы, а следовательно и колебание звуковой катушки. Катушка движется в магнитном поле, в её витка индуцируется ток, и на концах катушки возникает переменная ЭДС индукции.

Это переменное напряжение вызывает колебание тока в цепи микрофона. Данные колебания могут быть поданы на громкоговоритель. Электродинамический микрофон имеет очень простую конструкцию.

Так же микрофоны этого типа имеют небольшие габариты и надежны в эксплуатации. При этом искажение преобразуемых колебаний в звуковом диапазоне невелики.

Самоиндукция

Как уже известно, если по катушке идет переменный ток, то магнитный поток, который пронизывает катушку, будет изменяться. При этом, в этом же самом проводнике возникает ЭДС индукции. Это явление называется самоиндукция.

Во время самоиндукции контур, через который проходит ток, выполняет сразу две функции. Переменный ток в проводнике вызовет появление магнитного потока, через поверхность ограниченную контуром. Магнитный поток будет изменяться с течением времени, следовательно, в контуре будет возникать ЭДС индукции.

Напряженность возникающего вихревого поля будет направлена против тока. То есть, вихревое поле будет препятствовать нарастанию тока. Если бы ток уменьшался, то вихревое поле поддерживало бы ток. Явление самоиндукции можно наблюдать, например, на следующем опыте.

Рассмотрим следующую принципиальную электрическую схему. 

Параллельно источнику питания подключены две одинаковые лампочки. В цепь одной из них последовательно включено сопротивление, а в цепь другой – катушка индуктивности. При замыкании ключа, первая лампочка вспыхнет почти мгновенно.

Вторая лампочка включится только спустя некоторое время. ЭДС самоиндукции катушки будет достаточно большим, и будет препятствовать нарастанию силы тока, поэтому свое максимальное значение сила тока достигнет только спустя некоторое время. Теперь рассмотрим следующую схему.

Здесь при размыкании ключа в катушке возникнет ЭДС самоиндукции, которая будет стараться поддерживать ток. В момент размыкания ключа через гальванометр будет протекать ток, обратно направленный по отношению к первоначальному. Сила тока при размыкании может даже превысить силу тока, который был первоначально. Следовательно, ЭДС самоиндукции будет больше ЭДС батареи.

Индукция магнитного поля. Магнитный поток

Многие из вас наверняка замечали, что внешне похожие магниты создают разные по силе магнитные поля.

С другой стороны, вы также знаете, что, например, рамка с током, помещённая между полюсами подковообразного магнита, принимает ориентированное положение, при котором линии магнитного поля перпендикулярны плоскости рамки.

— Так какой же величиной можно охарактеризовать магнитное поле?

Для описания магнитного поля вводится векторная физическая величина, называемая индукцией магнитного поля (или просто магнитной индукцией). Обозначается она большой латинской буквой B.

Давайте поясним смысл этой величины и укажем способ её измерения. Для этого проведём такой опыт. Возьмём проводник, длиной пол метра, подвешенный на динамометре, и поместим его между полюсами подковообразного магнита перпендикулярно его магнитным линиям.

Первоначально проводник уравновешен, а показание динамометра численно равно модулю силы тяжести, действующей на проводник.

Теперь наша задача пропустить по проводнику ток такого направления, чтобы на него подействовала сила Ампера, направленная вертикально вниз. Для этого мы используем правило левой руки: линии магнитного поля должны входить в ладонь перпендикулярно к ней, а отставленный на девяносто градусов большой палец должен быть направлен вертикально вниз. При этом четыре сомкнутых пальца покажут направление тока в проводнике.

Замкнув цепь снимем показания динамометра. Далее определим значение силы Ампера, действующей на проводник, как разность показаний динамометра в конце и начале опыта.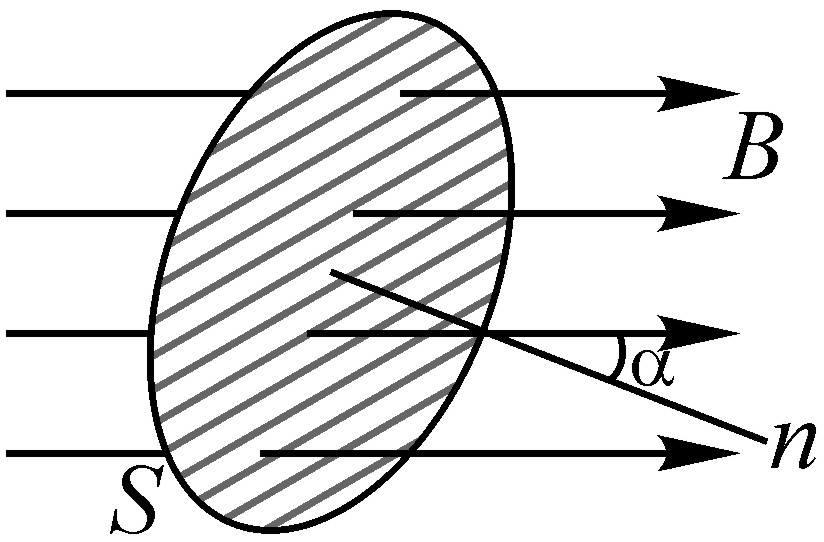 Теперь повторим эксперимент при неизменной силе тока, заменив проводник на более длинный и, как и в прошлый раз, найдём значение действующей на проводник силы Ампера.

Видно, что чем длиннее проводник, тем большая сила Ампера на него действует. Следовательно, сила Ампера пропорциональна длине проводника.

Теперь при неизменной длине проводника будем изменять силу тока в нём и, как и в прошлый раз, будем находить значение силы Ампера.

Можно прийти к заключению, что сила Ампера пропорциональна силе тока в проводнике.

Опыты показывают, что сила Ампера зависит и от ориентации проводника в магнитном поле. Она достигает своего максимального значения в случае, когда проводник расположен перпендикулярно линиям поля.

Однако отношение модуля силы Ампера к длине проводника и силе тока не зависит ни от длины проводника, ни от силы тока в нём:

Следовательно, отношение F/l зависит только от свойств магнитного поля и поэтому может служить его количественной характеристикой. Эту характеристику поля называют модулем магнитной индукции.

Таким образом, модуль вектора магнитной индукции — это физическая величина, равная отношению силы, действующей на расположенный перпендикулярно магнитным линиям проводник с током, к произведению силы тока в нём на длину проводника.

Сразу обращаем ваше внимание на то, что по этой формуле можно определить индукцию однородного магнитного поля.

В международной системе единиц за единицу магнитной индукции принята индукция такого магнитного поля, в котором на каждый метр длины проводника при силе тока 1 А действует максимальная сила, равная 1 Н. Эту единицу называют тесла в честь выдающегося югославского физика Николы Тесла.

Отметим, что тесла — это очень крупная единица. Так, например, большой лабораторный электромагнит может создать поле не более 5 Тл. Магнитное поле нашей планеты приблизительно равно 0,5 ∙ 10−4 Тл. И лишь в солнечных пятнах индукция магнитного поля достигает 10 Тл. Поэтому на практике используются более мелкие единицы индукции:

До сегодняшнего дня для графического изображения магнитных полей мы с вами пользовались магнитными линиями — воображаемыми линиями, направление которых совпадает с направлением, на которое указывает северный полюс магнитной стрелки.

За направление же вектора магнитной индукции принимается направление от южного полюса к северному полюсу свободно устанавливающейся стрелки, помещённой в данную точку поля.

Сравните два определения.

Не трудно заметить, что они очень похожи. И это не случайно, дело в том, что более точное название магнитных линий — линии магнитной индукции.

Или, другими словами, линиями магнитной индукции называют линии, касательные к которым в каждой точке поля в направлены так же, как и вектор магнитной индукции.

Например, картина линий магнитной индукции поля, образованного прямолинейным проводником с током, представляет собой систему концентрических окружностей, лежащих в плоскости, перпендикулярной этому проводнику. Проведённые к любой из этих окружностей касательные в любой точке совпадают с направлением вектора магнитной индукции.

Линии магнитной индукции условились проводить так, чтобы по их густоте можно было судить о модуле магнитной индукции: чем гуще линии магнитной индукции, тем больше её модуль.

Теперь, пользуясь понятием «магнитная индукция», дадим более строгое определение однородного и неоднородного магнитного поля. Для начала рассмотрим однородное магнитное поле между полюсами дугообразного магнита.

Магнитные линии здесь расположены параллельно друг другу. А так как во всех точках поля вектор магнитной индукции не только одинаково направлен, но и имеет одно и то же значение, то и густота линий магнитной индукции в любой области поля между полюсами будет одна и та же.

А теперь сравним это поле с неоднородным полем полосового магнита. Не трудно увидеть, что в таком поле вектор магнитной индукции меняется от точки к точке как по направлению, так и по величине.

Таким образом, магнитное поле называют однородным, если во всех его точках магнитная индукция одинакова как по направлению, так и по значению. В противном случае магнитное поле называют неоднородным.

Для объяснения опытов, которые будут проводиться в дальнейшем, нам необходимо ввести ещё одну физическую величину — магнитный поток, которая также является одной из важных характеристик магнитного поля.

Что мы понимаем под потоком в обычной жизни? Кому-то на ум придут потоки воды в реке, кому-то — потоки воздуха. Например, возьмём лист картона с отверстием. Подставив руку с обратной стороны листа, подуем в отверстие — рука явно ощущает поток воздуха. Сильнее дуем — больший поток воздуха. Будем дуть с такой же силой, но уменьшим отверстие — поток уменьшится. И наконец, если плоскость листа бумаги поставим параллельно направлению потока выдуваемого воздуха, ваша рука практически не почувствует влияние воздушного потока.

Аналогично и с магнитным потоком, который можно рассматривать как величину, пропорциональную числу магнитных линий, проходящих через площадь, ограничивающую некоторую поверхность. Поскольку число магнитных линий зависит от их густоты, то, очевидно, что магнитный поток пропорционален модулю вектора индукции магнитного поля: чем больше индукция, тем больший магнитный поток, пронизывает контур.

Вместе с тем магнитный поток зависит и от площади контура: при том же значении магнитной индукции магнитный поток, пронизывающий контур большей площади, будет больше. Следовательно, магнитный поток пропорционален также площади контура.

Очевидно и то, что в случаях, когда линии магнитной индукции перпендикулярны плоскости контура, магнитный поток принимает наибольшее значение. А при изменении ориентации контура в магнитном поле, например, при его вращении вокруг оси, магнитный поток будет уменьшаться, так как будет уменьшаться число линий магнитной индукции, пронизывающей контур. А когда плоскость контура окажется параллельной линиям магнитной индукции, магнитный поток станет равным нулю.

Магнитный поток будет равен нулю и в том случае, если линии магнитной индукции лежат в плоскости контура, не пересекая ограниченную им площадь.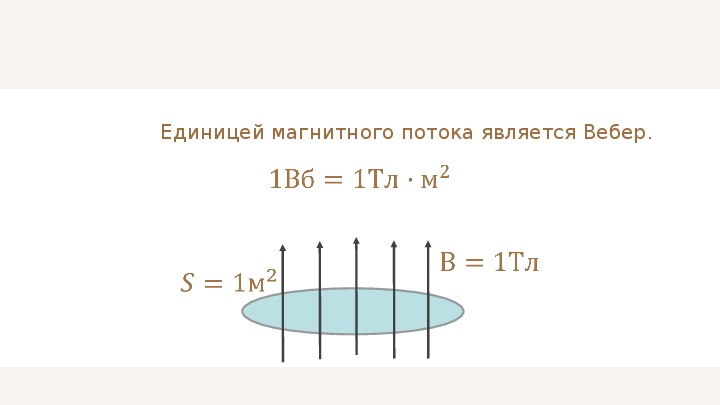

В Международной системе единиц за единицу магнитного потока принят вэбэр, названный в честь немецкого физика Вильгельма Эдуарда Вебера.

1 Вб — это магнитный поток через поверхность площадью 1 м², расположенную в однородном магнитном поле индукцией 1 Тл, перпендикулярной линиям индукции.

Закрепления материала.

Основы электротехники и электроники: Курс лекций, страница 24

Нелинейные магнитные свойства ферромагнетика задают с помощью основной кривой намагничивания – зависимости индукции от напряженности магнитного поля, представленной в табличном или графическом виде (Рис. 27.1).

Рис. 27.1

Рассмотрим некоторую магнитную цепь, состоящую из замкнутого ферромагнитного сердечника, на который намотана катушка, содержащая W витков. По катушке течет неизменный во времени ток I (Рис. 27. 2 а). Магнитные свойства сердечника заданы кривой намагничивания (Рис. 27.2 б). Геометрия системы известна.

а)

б)

Рис. 27.2

Источником магнитного поля в цепи является магнитодвижущая сила (МДС), определяемая как произведение числа витков катушки на протекающий по катушке ток:

                                                                           .                    (27.2)

Магнитодвижущая сила (МДС) является аналогом известной нам электродвижущей силы (ЭДС) и обозначается на схемах замещения аналогично ЭДС (Рис. 27.3). Размерность МДС – амперы.

Рис. 27.3

МДС создает в сердечнике замкнутый магнитный поток  (греческая буква фи). Направление магнитного потока в сердечнике определяется правилом правой руки. Правой рукой надо обхватить катушку так, чтобы четыре пальца были направлены в ту же сторону, что и ток в катушке. Тогда большой палец укажет направление магнитного потока. Магнитный поток является аналогом электрического тока. Единица магнитного потока – Вебер (Вб).

Требуется рассчитать магнитный поток в сердечнике при заданной МДС.

Наконец, в схеме замещения должен быть потребитель. Это нелинейное магнитное сопротивление R_M, моделирующее реакцию ферромагнитного сердечника на магнитное поле в нем. В окончательном виде схема замещения выглядит так, как показано на Рис. 27.4. В этой схеме один контур, так как магнитный поток в сердечнике не разветвляется. МДС источника уравновешивается падением магнитного напряжения U_M на нелинейном магнитном сопротивлении.

Обратить внимание! Размерность магнитного напряжения и МДС – амперы (ни в коем случае не вольты!).

Рис.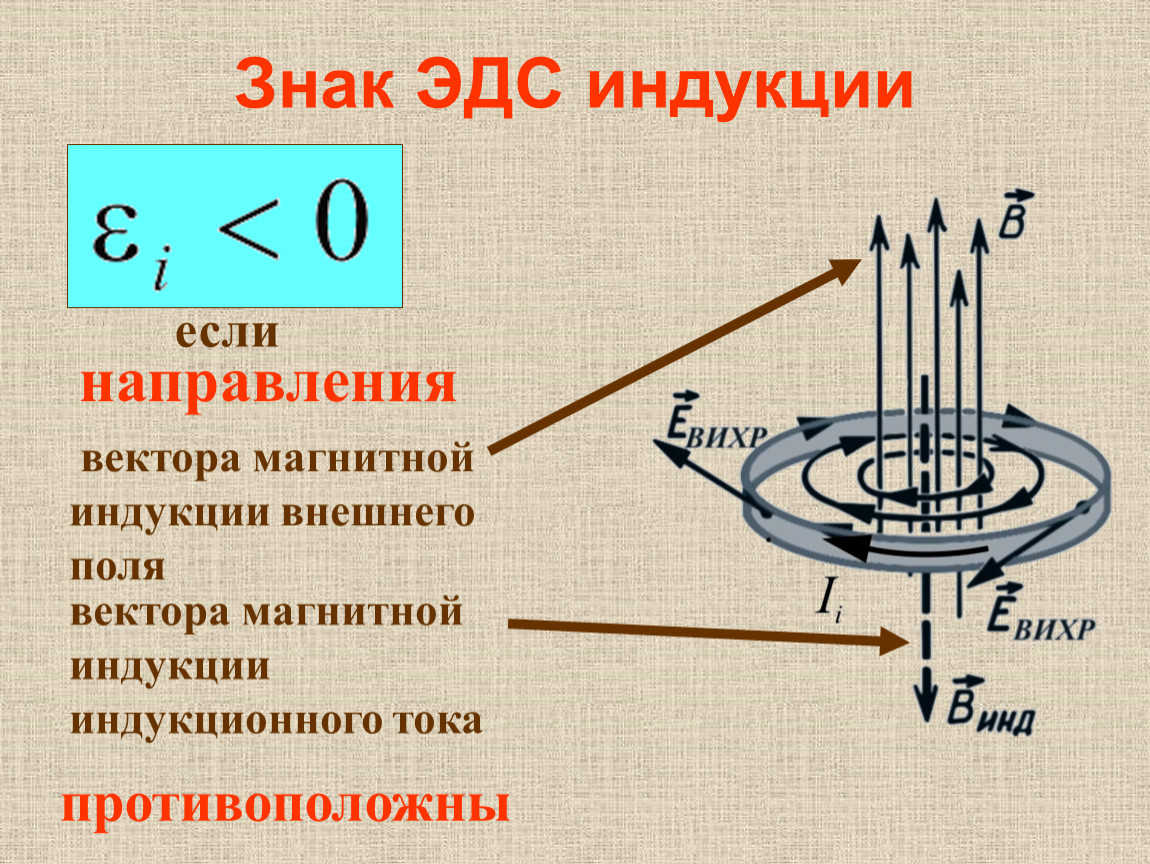  27.4

Так как нелинейное магнитное сопротивление R_M моделирует в схеме замещения ферромагнитный сердечник, магнитное напряжение U_M связано с напряженностью магнитного поля в сердечнике:

                                                                          ,                   (27.3)

где       –      длина средней линии сердечника в направлении потока; иными словами, это путь,

                        который преодолевает магнитный поток в сердечнике.

Магнитный поток связан с индукцией магнитного поля в сердечнике следующей зависимостью:

                                                                           ,                    (27.4)

где       –     площадь поперечного сечения сердечника в направлении перпендикулярном,

                        направлению магнитного потока.

Ни индукция, ни напряженность магнитного поля нам пока неизвестны. Но анализ задачи показывает, что к ней можно применить те же принципы, на которых основываются расчеты нелинейных цепей постоянного тока.

Рассмотрим кривую намагничивания ферромагнитного сердечника (Рис. 27.2 б). По оси абсцисс здесь отложена напряженность магнитного поля. Если абсциссу текущей точки графика умножить на длину средней линии сердечника, получим значение магнитного напряжения в текущей точке (27.3).

По оси ординат отложена индукция магнитного поля. Если ординату текущей точки графика умножить на площадь поперечного сечения сердечника, получим значение магнитного потока в текущей точке (27.4).

Таким образом, можно получить так называемую вебер-амперную характеристику нелинейного магнитного элемента (Рис. 27.5).

Для магнитной цепи справедлив второй закон Кирхгофа: сумма падений магнитных напряжений в замкнутом контуре равна сумме МДС, включенных в контур. В данном случае:

                                                                          .                   (27.5)

На оси абсцисс откладываем значение МДС, вычисленное по выражению (27.2). На вебер-амперной характеристике находим рабочую точку. Ордината этой точки – это искомый магнитный поток в сердечнике. Задача решена.

Рис. 27.5

Усложним только что решенную задачу. Пусть теперь в сердечнике пропилен воздушный зазор шириной δ (Рис. 27.6 а). При этом длина средней линии сердечника стала меньше. Для упрощения дальнейших рассуждений будем считать, что площадь поперечного сечения воздушного зазора равна площади сечения сердечника. Магнитные свойства сердечника по-прежнему заданы кривой намагничивания (Рис. 27.6 б). Требуется рассчитать магнитный поток в воздушном зазоре при заданной МДС катушки.

а)

б)

Рис. 27.6

В схеме замещения магнитной цепи, как и в предыдущей задаче, будет один контур, так как магнитный поток не разветвляется.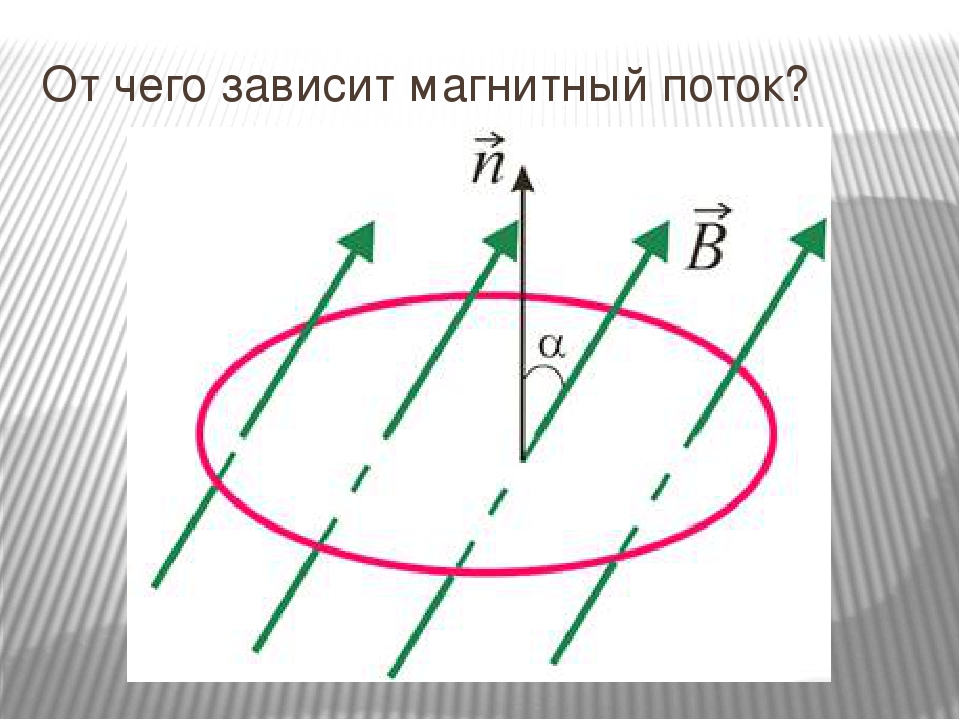 Также, в силу известного принципа непрерывности магнитного потока, поток при выходе из незамкнутого сердечника и входе в зазор не может измениться скачком. Значит и в сердечнике, и в зазоре будет один и тот же магнитный поток. Сердечник будет моделироваться нелинейным магнитным сопротивлением R_M. Но кроме сердечника сопротивление магнитному потоку оказывает и воздушный зазор. Индукция в воздушном зазоре связана с магнитной напряженностью в зазоре следующей зависимостью:

                                                                          .                   (27.6)

Левую часть уравнения (27.6) умножим и разделим на площадь поперечного сечения зазора . Правую часть уравнения (27.6) умножим и разделим на ширину зазора δ:

                                                                  .           (27.7)

Произведение  в правой части уравнения (27.7) – это падение магнитного напряжения в зазоре (ср. с выражением (27.3)). Произведение  в левой части уравнения (27. 7) – это магнитный поток в зазоре, а значит и в сердечнике (ср. с выражением (27.4)). Преобразуя (27.7), получаем зависимость между магнитным потоком и магнитным напряжением в зазоре. Это линейная функция:

                                                                     .              (27.8)

Выражение  в (27.8) называют магнитной проводимостью воздушного зазора и обозначают греческой буквой лямбда:

                                                                         .                 (27.9)

Размерность магнитной проводимости – Генри (Гн).

Так как функция (27.8) линейна, воздушный зазор в схеме замещения будет моделироваться линейным магнитным сопротивлением R_δ. Схема замещения магнитной цепи представлена на Рис. 27.7.

Плотность магнитного потока | Магнит-Лексикон / Глоссарий

Плотность магнитного потока определяется как плотность силовых линий. Как так называемое поле B, это косвенная мера силы магнитного поля. Обозначение B-field желательно: это не настоящее магнитное поле, даже если эти два термина иногда используются как синонимы в литературе.

Расчет плотности магнитного потока

В то время как по определению плотность магнитного потока описывается буквой B , буква для магнитного поля — H. Следующее соотношение применяется с так называемыми константами проницаемости μ0 (для вакуума) и μ (для дополнительных материалов):

Константа проницаемости может варьироваться в зависимости от типа материала:

• Пока материал не является ферромагнитным, константа проницаемости для материала μ около 1.
• В случае ферромагнитных материалов, это значение иногда может доходить до 100000.
• Если это снова сверхпроводник, то μ = 0 .

Произведение двух констант проницаемости и магнитного поля H , таким образом, по определению дает плотность магнитного потока B. Она измеряется в единицах Тесла (Тл).

Справочная информация

Многие не могут реально использовать формулу плотности магнитного потока, упомянутую выше. Описательное объяснение физического фона должно немного помочь: так называемое магнитное поле образуется вокруг проводника, по которому течет электричество.Это будет воздействовать на близлежащие кобальт, никель, железо или другие ферромагнитные материалы. Плотность магнитного потока B , в свою очередь, показывает, насколько сильным является это магнитное поле на самом деле. Иногда его еще называют , магнитная индукция . B описывает плотность магнитного потока через поверхность. Для выполнения этого расчета существует множество формул.

Зависимость плотности магнитного потока от магнитного потока — есть ли здесь разница?

Плотность магнитного потока, проходящего через воображаемую поверхность, и есть магнитный поток.Полезно представить себе изображение с силовыми линиями магнитного поля между двумя полюсами. Плотность силовых линий в поперечном сечении — это, так сказать, плотность магнитного потока.

Согласно так называемым уравнениям Максвелла — хорошо известному физическому закону в электродинамике — силовые линии не могут просто остановиться. Таким образом, магнитная индукция магнита продолжает работать снаружи. Магнитный поток сам по себе имеет символ формулы Φ и в основном обозначает всех силовых линий магнитного поля. Следовательно, магнитный поток возникает из определенной области A к изделию с плотностью магнитного потока B. Область должна быть перпендикулярна потоку.

Движущиеся заряды — т. Е. Токи — вызывают магнитный поток. У этого нет ни начала, ни конца, потому что токи создают только замкнутые силовые линии. Физически корректно, это означает, что нет источников и стоков магнитного потока или плотности магнитного потока. Этот факт является причиной того, что два полюса всегда образуют магнит: южный полюс и северный полюс.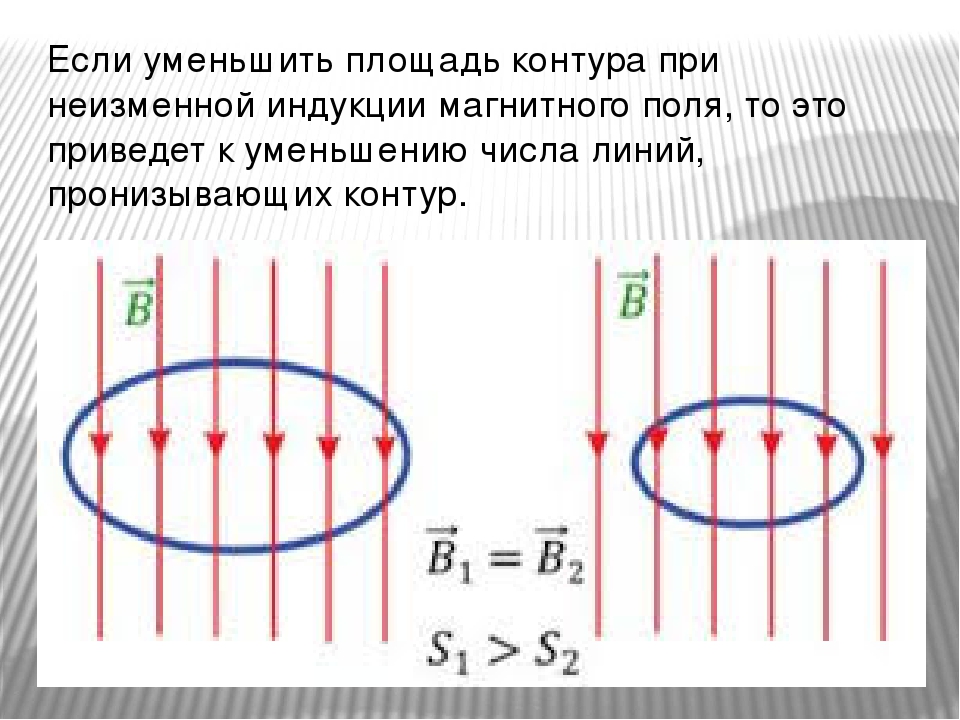

Уравнения Максвелла из электродинамики выражают этот факт математически. Важно понимать, что постоянные магниты также основаны на этом поведении в отношении плотности магнитного потока: там образуются микроскопических круговых токов с током I, , вызванные перемещениями электронов в материале. Они отвечают за магнитный поток или магнитное поле. Круговой ток создает так называемый магнитный момент с южным полюсом ниже проводящей петли и северным полюсом над этой проводящей петлей.Если бы направление тока было изменено на противоположное, полюса поменяли бы местами.

Таким образом, с физической точки зрения магнитный поток определяется индуктивным эффектом, который он оказывает на проводящую петлю. Если петля проводника с известной площадью попадает в магнитное поле, это указывает на наличие там скачка напряжения. Магнитный поток равен интегралу по времени по этому скачку:

Магнитный поток измеряется с помощью этой проводящей петли и индуцируемого в ней напряжения.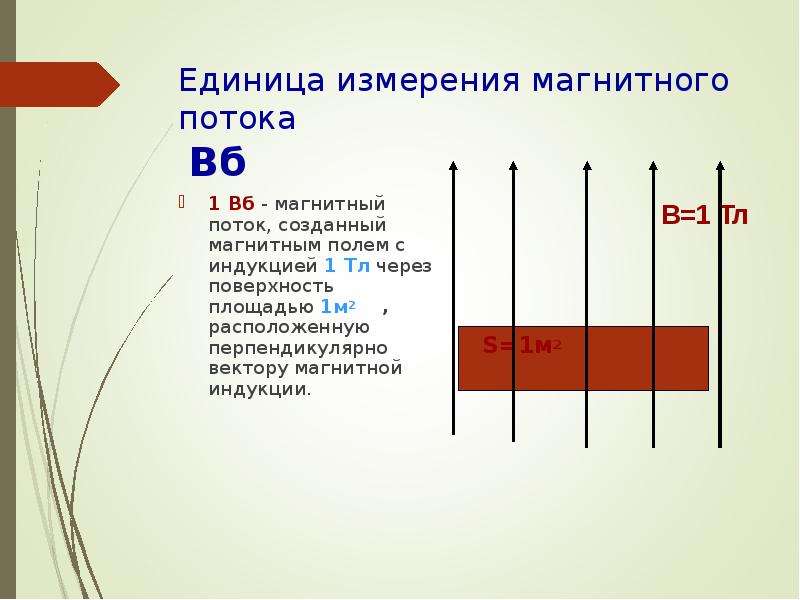 Однако это уже не распространенный метод: так называемый зонд Холла намного точнее. Если плотность магнитного потока проходит через изогнутую поверхность, магнитный поток должен быть определен как интеграл по нормали к поверхности векторной плотности потока:

Линии поля, проходящие через замкнутую поверхность, например поверхность сферы, также должны выходить оттуда. Такова природа замкнутых силовых линий: Математически это проявляется в том, что магнитный поток через замкнутые поверхности всегда равен нулю. Следовательно, нет никаких источников или стоков в плотности магнитного потока.

Эквивалент этого — утверждение одного из четырех уравнений Максвелла о так называемой свободе от дивергенции плотности магнитного потока.

магнитное поле | Определение и факты

Наблюдайте за действием магнитного поля и взаимодействием между магнитными полюсами

Узнайте о магнитных полях и взаимодействиях между магнитными полюсами.

Encyclopædia Britannica, Inc. Посмотреть все видео к этой статье

магнитное поле , векторное поле в окрестности магнита, электрический ток или изменяющееся электрическое поле, в котором наблюдаются магнитные силы.Магнитные поля, такие как у Земли, заставляют стрелки магнитного компаса и другие постоянные магниты выстраиваться в линию в направлении поля. Магнитные поля заставляют электрически заряженные частицы двигаться по круговой или винтовой траектории. Эта сила, действующая на электрические токи в проводах в магнитном поле, лежит в основе работы электродвигателей. (Для получения дополнительной информации о магнитных полях, см. магнетизм.

Вокруг постоянного магнита или провода, по которому проходит постоянный электрический ток в одном направлении, магнитное поле является стационарным и называется магнитостатическим полем.В любой момент его величина и направление остаются неизменными. Магнитное поле вокруг переменного или постоянного тока постоянно меняет свою величину и направление.

Подробнее по этой теме

Магнетизм: основы

Основными для магнетизма являются магнитное поле с и их влияние на материю, как, например, отклонение движущихся зарядов…

Магнитные поля могут быть представлены непрерывными силовыми линиями или магнитным потоком, которые исходят из магнитных полюсов, направленных на север, и входят в магнитные полюсы, направленные на юг. Плотность линий указывает величину магнитного поля. Например, на полюсах магнита, где сильное магнитное поле, силовые линии сжимаются или становятся более плотными. Дальше, где магнитное поле слабое, они разветвляются, становясь менее плотными. Однородное магнитное поле представлено параллельными прямыми, расположенными на одинаковом расстоянии друг от друга.Направление потока — это направление, в котором указывает северный полюс небольшого магнита. Линии потока непрерывны, образуя замкнутые контуры. Для стержневого магнита они выходят из северного полюса, разветвляются и вращаются, входят в магнит на южном полюсе и проходят через магнит к северному полюсу, где они снова появляются. Единицей измерения магнитного потока в системе СИ является вебер. Количество веберов — это мера общего количества линий поля, пересекающих данную область.

Магнитные поля могут быть представлены математически величинами, называемыми векторами, которые имеют направление, а также величину.Два разных вектора используются для представления магнитного поля: один, называемый плотностью магнитного потока или магнитной индукцией, обозначается как B ; другой, называемый напряженностью магнитного поля или напряженностью магнитного поля, обозначается как H . Магнитное поле H можно рассматривать как магнитное поле, создаваемое протеканием тока в проводах, а магнитное поле B — как полное магнитное поле, включая также вклад, вносимый магнитными свойствами материалов в поле.Когда ток течет по проволоке, намотанной на цилиндр из мягкого железа, намагничивающее поле H довольно слабое, но фактическое среднее магнитное поле ( B ) внутри утюга может быть в тысячи раз сильнее, поскольку B значительно усилен выравниванием бесчисленных крошечных естественных атомных магнитов железа в направлении поля. См. Также магнитную проницаемость .

Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчас

2.5: Плотность магнитного потока — Engineering LibreTexts

Плотность магнитного потока — это векторное поле, которое мы идентифицируем с помощью символа \ ({\ bf B} \) и которое имеет единицы СИ в тесла (Т). Прежде чем предложить формальное определение, полезно рассмотреть более широкую концепцию магнитного поля .

Магнитные поля являются неотъемлемым свойством некоторых материалов, особенно постоянных магнитов. Основное явление, вероятно, знакомо и показано на рисунке \ (\ PageIndex {1} \).У стержневого магнита есть «полюса», обозначенные как «N» («север») и «S» («юг»). N-конец одного магнита притягивает S-конец другого магнита, но отталкивает N-конец другого магнита и так далее. Существование векторного поля очевидно, поскольку наблюдаемая сила действует на расстоянии и утверждается в определенном направлении. В случае постоянного магнита магнитное поле возникает из-за механизмов, происходящих в масштабе атомов и электронов, составляющих материал. Эти механизмы требуют некоторого дополнительного объяснения, которое мы пока отложим.

Рисунок \ (\ PageIndex {1} \): свидетельство векторного поля из наблюдений силы, воспринимаемой стержневыми магнитами справа в присутствии стержневых магнитов слева. (CC BY 3.0; Ю. Цинь).

Магнитные поля также появляются при наличии тока. Например, катушка с проводом, по которой проходит ток, влияет на постоянные магниты (и наоборот) так же, как постоянные магниты влияют друг на друга. Это показано на рисунке \ (\ PageIndex {2} \). Из этого мы заключаем, что основной механизм тот же — i.е. векторное поле, создаваемое токонесущей катушкой, представляет собой то же явление, что и векторное поле, связанное с постоянным магнитом. Каким бы ни был источник, теперь мы заинтересованы в количественной оценке его поведения.

Рисунок \ (\ PageIndex {2} \): Доказательство того, что ток также может создавать магнитное поле. (CC BY 4.0; Ю. Цинь).

Для начала рассмотрим действие магнитного поля на электрически заряженную частицу. Во-первых, представьте себе область свободного пространства без электрических или магнитных полей. Затем представьте, что появляется заряженная частица.Эта частица не будет испытывать силы. Далее появляется магнитное поле; возможно, это связано с постоянным магнитом или током поблизости. Эта ситуация показана на рисунке \ (\ PageIndex {2} \) (вверху). Тем не менее, к частице не приложена сила. Фактически, ничего не происходит, пока частица не придет в движение. На рисунке \ (\ PageIndex {3} \) (внизу) показан пример. Внезапно частица воспринимает силу. Мы скоро перейдем к деталям о направлении и величине, но основная идея теперь очевидна.Магнитное поле — это то, что прилагает силу к движущейся заряженной частице, отличную от силы, связанной с электрическим полем (фактически, в дополнение к ней).

Рисунок \ (\ PageIndex {3} \): сила, воспринимаемая заряженной частицей, которая (вверху) неподвижна и (внизу) движется со скоростью \ (\ mathbf {v} = \ hat {\ mathbf {z}} v \ ), которая перпендикулярна плоскости этого документа и по направлению к читателю (CC BY 4.0; Y. Qing).

Стоит отметить, что движущаяся одиночная заряженная частица представляет собой простейшую форму тока.Помните также, что для того, чтобы магнитное поле влияло на частицу, необходимо движение. Следовательно, не только ток является источником магнитного поля, магнитное поле также оказывает влияние на ток. Обобщение:

Магнитное поле описывает силу, действующую на постоянные магниты и токи в присутствии других постоянных магнитов и токов.

Итак, как мы можем количественно определить магнитное поле? Ответ из классической физики включает другое экспериментально выведенное уравнение, которое предсказывает силу как функцию заряда, скорости и векторного поля \ ({\ bf B} \), представляющего магнитное поле.Вот оно: сила, приложенная к частице, несущей заряд \ (q \), равна

.

\ [\ mathbf {F} = q \ mathbf {v} \ times \ mathbf {B} \ label {m0005_eFqvB} \]

где \ ({\ bf v} \) — скорость частицы, а «\ (\ times \)» обозначает перекрестное произведение. Перекрестное произведение двух векторов находится в направлении, перпендикулярном каждому из двух векторов, поэтому сила, создаваемая магнитным полем, перпендикулярна как направлению движения, так и направлению, в котором указывает магнитное поле.

Читатель будет вправе задаться вопросом, почему сила, создаваемая магнитным полем, должна быть на перпендикулярна к \ ({\ bf B} \). В таком случае, почему сила должна зависеть от \ (\ bf v \)? Это вопросы, на которые классическая физика не дает очевидных ответов. Эффективные ответы на эти вопросы требуют концепций из квантовой механики, где мы обнаруживаем, что магнитное поле является проявлением фундаментальной и удачно названной электромагнитной силы .Электромагнитная сила также усиливает электрическое поле, и только ограниченная интуиция, основанная на классической физике, заставляет нас воспринимать электрические и магнитные поля как отдельные явления. Для наших настоящих целей — и для наиболее часто встречающихся инженерных приложений — нам не нужны эти концепции. Достаточно принять эту кажущуюся странность как факт и действовать соответственно.

Анализ размеров \ ref {m0005_eFqvB} показывает, что \ ({\ bf B} \) имеет единицы измерения (N \ (\ cdot \) s) / (C \ (\ cdot \) m).В системе СИ эта комбинация единиц известна как тесла (Т).

Мы называем \ ({\ bf B} \) плотностью магнитного потока , и поэтому тесла — это единица плотности магнитного потока. Здесь уместно задать вопрос: что делает это плотностью потока? Короткий ответ заключается в том, что эта терминология несколько произвольна и на самом деле даже не является общепринятой. В инженерной электромагнетизме предпочтение называть \ ({\ bf B} \) «плотностью потока» объясняется тем, что мы часто обнаруживаем, что интегрируем \ ({\ bf B} \) по математической поверхности.2 \)) представляет собой описание магнитного поля, которое можно определить как решение уравнения \ ref {m0005_eFqvB}.

Рисунок \ (\ PageIndex {4} \): Магнитное поле стержневого магнита, иллюстрирующее силовые линии. (CC BY 4.0; Ю. Цин).

При описании магнитных полей мы иногда ссылаемся на концепцию силовой линии , определяемую следующим образом:

Линия магнитного поля — это кривая в пространстве, очерченная в направлении, в котором указывает вектор магнитного поля.

Эта концепция проиллюстрирована на рисунке \ (\ PageIndex {4} \) для постоянного стержневого магнита и на рисунке \ (\ PageIndex {5} \) для токонесущей катушки.

Рисунок \ (\ PageIndex {5} \): Магнитное поле токонесущей катушки, иллюстрирующее силовые линии. (CC BY 4.0; Ю. Цин).

Силовые линии магнитного поля примечательны по следующей причине:

Линия магнитного поля всегда образует замкнутый контур.

В некотором смысле это верно даже для силовых линий, которые кажутся прямыми (например, линии вдоль оси стержневого магнита и катушки на рисунках \ (\ PageIndex {4} \) и \ (\ PageIndex {5) } \), поскольку силовая линия, уходящая в бесконечность в одном направлении, снова появляется из бесконечности в противоположном направлении.

Авторы и авторство

Уравнение электромагнитного поля Максвелла № 1

Уравнение электромагнитного поля Максвелла № 1

Максвеллс Электромагнитный Полевое уравнение № 1

Автор Джордж Дж. Спикс

1.0 Формулировка уравнения

Следующее электростатическое поле уравнения будут разработаны в этом разделе:

Интегральная форма	Дифференциальные формы

Первое уравнение Максвелла основано на Гауссе закон электростатики, опубликованный в 1832 году, в котором Гаусс установил взаимосвязь между статическими электрическими зарядами и их сопутствующими статические поля.

Приведенное выше интегральное уравнение утверждает, что электрический поток через закрытая поверхность равна общему приложенному заряду.

Дифференциальная форма уравнения утверждает, что дивергенция или исходящий поток электрического потока из точки равен объемному заряду плотность в этой точке.

1.1. Уравнение Максвелла № 1; Площадь Интеграл

Выведем интеграл уравнение, рассматривая сумму плотности электрического потока на площадь поверхности, а затем как сумма объемов, содержащих электрические плата.Показано, что два интеграла равны, если они основаны на такое же обвинение. Два примера с использованием уравнений: показано.

1.1.1 Закон Гаусса

Закон электростатики Гаусса гласит, что линии электрического поток,

f _E , исходит от положительного заряда, q , и прекращаются, если они прекращаются, на отрицательном заряде. Пространство внутри на которое оказывают свое влияние заряды, называется электростатическим полем.

Схема на рис. 1.1 представляет заряды и три размерное поле. Поле визуализируется как состоящее из линий поток. Для изолированного заряда линии потока не оканчиваются и имеют вид считается продолжающимся до бесконечности.

Чтобы получить уравнение, связывающее электрическую заряда q и его потока

f _E , предположим, что заряд центрирован в сфере радиус r метров. Плотность электрического потока D тогда равна электрический поток, исходящий от заряда, q , деленный на площадь сфера.

кулонов на квадратный метр; где площадь перпендикулярно линиям потока. (Один кулон равен величина заряда 6,25

X 10 ¹⁸ электронов.) Тогда заряд, заключенный в сфере, равен электрическому потоку плотность на его поверхности, умноженная на площадь, вмещающую заряд.

q (кулоны включены) =

D x 4 r ² .

Линии потока, вносящие вклад в плотности потока те, которые оставляют сферу перпендикулярно поверхности сферы.Это приводит к интегральной формулировке этой части Закон Гаусса;

Знак интеграла указывает на суммирование бесконечно малые площади, d

a , чтобы получить всю площадь поверхности.

Кружок на знаке интеграла означает, что интеграл или Суммирование площадей ведется по замкнутой сплошной поверхности.

Полужирные буквы обозначают, что буква представляет вектор, т. Е. эта величина имеет величину и направление.Расстояние, скорость, ускорение и сила — общие примеры векторов.

Д

— вектор плотности электрического потока в кулонах на квадратный метр.

(указанная точка) следующий Д показывает, что при умножении двух векторы, D и d а .

Скалярное произведение (обсуждается ниже) указывает, что величины два вектора умножаются вместе, а затем этот продукт умножается косинусом угла между двумя векторами.Точечный продукт здесь позволяет определить эффективные линии потока, протекающего через поверхность.

1.1.2 Векторное произведение точек

Приложение векторного скалярного произведения может быть проиллюстрировано вычислением работать над следующей проблемой физики.

Напомним, что работа = сила, умноженная на расстояние. Работа равна продукту силы, то есть в направлении движения силы, умноженное на расстояние, на которое движется сила.

В следующем примере предположим, что человек толкает швабру по пол с ручкой швабры под углом 60 градусов к полу, как в Рисунок 1.2. На этих диаграммах стрелки используются для обозначения векторов.

Через ручка швабры. Как показано на диаграмме, только эта составляющая силы в направление параллельно полу используется при расчете работ. Мы видим, что сила параллельна полу;

20 фунтов x косинус 60 ⁰ = 10 фунтов.

Какая работа выполняется при проталкивании швабры на 8 футов по полу?

10 фунтов x 8 футов = 80 футов.фунты.

Используя скалярное произведение, уравнение работы выглядит так:

Работа = F orce d istance.

Скалярное произведение означает, что работа равна величине силы. умножить на величину пройденного расстояния, умножить на косинус угла между двумя векторами.

Или, работа = сила на ручке швабры, умноженная на расстояние, на которое сила перемещается, умноженное на косинус угла между силой и полом.

Работа = 20 фунтов умножить на 8 футов умножить на 1/2 = 80 фут-фунтов.

Только та составляющая полной силы в направлении, параллельном пол, полученный с помощью скалярного произведения, используется в расчет работы.

Это показывает, что скалярное произведение определяется как метод вектора умножение, в котором векторные величины умножаются вместе и затем этот продукт умножается на косинус включенных векторов угол.Всегда должен быть вектор на каждую сторону точки в скалярном произведении.

Следовательно, когда скалярное произведение используется в законе Гаусса, только то, что составляющая потока, параллельная вектору, представляющему площадь, будет вносят свой вклад в общую вложенную плату.

1.2 Закон Гаусса; Интегральная площадь Примеры

Способ определения заряда с помощью скалярного произведения аналогично нахождению Работы как скалярного произведения между приложенной Силой и Расстояние.С помощью этого метода только те компоненты векторных линий потока в том же направлении, что и вектор, представляющий площадь, будет суммируется в расчете начисления. Или, иначе говоря: только эти силовые линии, перпендикулярные поверхности, включены в результат скалярного произведения для получения заряда прилагается.

Скалярное значение всегда является результатом скалярного произведения. В этом случае, результат — количество кулонов. Примеры других скалярных величин температура, масса и мощность.Скалярная величина, в отличие от вектор, не имеет направления.

Дифференциальный элемент площади равен

d a . Вектор Представляющая область указывается перпендикулярно этой области. Использование скалярного произведения между вектором, представляющим площадь d a и плотность потока D , приводит к получению эффективного потока через площадь. Суммирование всей площади в квадратные метры.

Предварительное уравнение (закон Гаусса) в нашей процедуре для получения Первое уравнение Максвелла теперь;

Это интегральное уравнение утверждает, что величина плотности электрического потока, нормального к поверхности, вызвана определенное количество заряда, q , заключенное на поверхность.

Рассмотрим следующие примеры определения плотности электрического потока на сферической поверхности и на цилиндрической поверхности.

1.2.1 Определение плотности потока на сфере

Предположим, что заряд в один кулон центрирован в сфере радиуса r. метров как на рисунке 1.3. Рассчитайте плотность электрического потока

Д по поверхность на сфере. Интеграл или сумма площадей сфера 4 p r ² кв.

Вектор, представляющий область, направлен нормально к этой области. Вектор, представляющий небольшую область,

d a , тогда находится прямо на одной линии с линия электрического потока, выходящая из сферы. D представляет плотность линий электрического потока, выходящих из сфера. Угол между плотностью смещения, D , и стрелкой представляющий бесконечно малую область — ноль градусов. Косинус нуля градусов один.

Переформулируя интегральное уравнение площадей закона Гаусса:

q (кулоны включены) =

один кулон = D x 4 p r ² .

кулонов на квадратный метр на поверхности сфера.

1.2.2 Определение плотности потока на цилиндре

Предположим, что длинная линия стационарных зарядов составляет q кулонов на метр, как показано на рисунке 1.4. Имеется цилиндр длиной «L» и радиусом «r» с центром на зарядах. Какая плотность электрического потока на поверхность цилиндра?

Уравнение Гаусса:

Q _T , полный прилагаемый заряд, = q кулонов на метр x L метров.

= Q _T = D x 2pr x L.

D

в кулонах на квадратный метр =

1,3 Уравнение Максвелла № 1; Объемный интеграл

Закон электростатики Гаусса также записано в виде интеграла по объему:

Это уравнение утверждает, что заряд заключенный в объем, равен объемной плотности заряда,

r , (rho) суммированы для весь том.

q — заряд, заключенный в томе.

r

— объемная плотность заряда в кулонах на кубический метр.

— бесконечно малый элемент объема.

Весь объем в кубических метрах.

Суммарный заряд, заключенный в объем, — это объем в кубических метрах. умноженное на плотность заряда в кулонах на кубический метр. Средняя громкость Плотность заряда, просуммированная для всего объема, является вложенным зарядом.А обсуждение r можно найти в разделе 1.5.3.

1,4 Уравнение Максвелла № 1; Полная форма заполнена

Для получения интегральной формы Уравнение Максвелла № 1, предположим, что эксперимент настроен так, что одинаковый заряд q кулонов содержится в каждом из уравнений закона Гаусса. Тогда интегралы от одного заряда должны быть равны.

Затем,

Таким образом, мы получили интегральный вид Уравнение Максвелла No.1. Это уравнение утверждает, что эффективная электрическая поле через поверхность, ограничивающую объем, равно полному заряду в объеме. Уравнение показывает что область, заключенная в левом интеграле, должна охватывать объем правого интеграла. Это похоже на утверждение, что площадь поверхности шара или коробки включает в себя объем мяча или коробки. Площадь и объем, указанный в уравнениях потребность не наблюдаемые физические поверхности, часто они будут математическими пределы.

Чтобы запомнить интегральную форму уравнения Максвелла № 1, рассмотрим что заряд q , заключенный в объем, должен быть равен объему плотность заряда,

r, умноженная на объем. Кроме того, тот же заряд q вызовет поток определенной площади. плотность, D , раз больше определенной площади. Площадь должна охватывать объем. В интегралы (суммы) должны быть равны, поскольку одинаковые количество кулонов должно быть получено с каждой стороны от знака равенства.

1,5 уравнение Максвелла № 1; Дифференциальная форма

Дифференциальная форма Уравнение Максвелла № 1:

это дифференциальный оператор читается как «del» (обсуждается ниже).

читается как «расхождение».

Д

— плотность электрического потока в кулонах на квадратный метр.

р

(rho) — объемная плотность заряда в кулонов на кубический метр.

1.5.1 Обсуждение (del)

— это математическое расширение обычного одномерного измерения. производная исчисления в трех измерениях.

Мы начнем обсуждение с обзора обычных производных.

В качестве примера для обозначения скорости используется производная. Скорость (v) — это увеличение расстояния, с , для увеличения время, т .

Скорость (v) =.

Поскольку изменение во времени очень мало, дифференциальное исчисление символ используется для скорости.

Теперь рассмотрим обычное одномерное измерение. производная для ускорения.

Вспомните уравнение для получения скорости объекта, когда он упал с высоты. Скорость, которой достигает объект, определяется;

Скорость, v, = ускорение свободного падения, g, умноженное на время в течение который объект падает.

Скорость = v = g t. Или

В интегральной форме закона Гаусса мы просуммировали бесконечно малые значения площади и объема, да и дв.Здесь мы используем дифференциала, ds, dv и dt, чтобы найти мгновенные скорости изменения расстояние и скорость относительно времени.

Существует правило дифференциального исчисления, на которое мы укажем здесь. так как мы будем использовать правило ниже.

Обратите внимание, что скорость равна ускорению (g), умноженному на время (t). Итак, мы можно взять производную от скорости следующим образом:

Правило исчисления состоит в том, что производная от умноженная на константу переменная — это константа.

Теперь мы расширим эту концепцию обычных производных до частичных производные, что позволит нам получить скорость изменения объема в трех измерениях, что, в свою очередь, приводит к определению

Ñ (дел). Чтобы проиллюстрировать скорость изменения трех измерений, предположим, что коробка находится в начале прямоугольного систему координат, как показано на рисунке 1.5.

Объем коробки, V, = длина x ширина x высота; знак равно Д x Ш x В.

Какова скорость изменения объема, когда только длина увеличивается на небольшое количество, но ширина и высота остаются неизменными?

Здесь используется символ частной производной. В символ для частных производных немного отличается от символа для обыкновенные (одномерные) производные. Символ указывает, что только один независимых переменных меняется на данный момент на рассмотрении. Зависимая переменная, объем,

v изменений, определяемых изменениями независимых переменных; L, W и H.Когда меняется только длина;

Символ частной производной показывает, что изменение объема только из-за изменения длины. Ширина и высота удерживаются постоянный. Мы также видим, что производная переменной, умноженная на константу — постоянная, W умноженная на H. Из симметрии следует, что скорость изменение объема в зависимости от ширины или высоты выражается как частная производная.

Когда изменение объема происходит из-за одновременного изменения длины, ширины и высоты, изменения будут происходить в направлениях x, y и z и частные производные складываются, чтобы найти результирующую скорость изменения объем.Это достигается в векторной форме путем умножения каждого частичного производная по единичным векторам, указывающим в направлениях x, y и z. Ед. изм векторы указаны здесь и обсуждаются далее в разделе 1.5.2. С использованием единичные векторы и одновременные изменения в трех измерениях, общая изменение объема обозначено:

Для более общего случая тома

V изменение в направления x , y и z ;

Это обсуждение обычных и частичных производных была направлена ​​на получение группы трех частных производных термины в скобках выше.

означает градиент. В этой статье мы не будем использовать градиент.

Нам понадобится Ñ (del dot, обсуждается ниже) и Ñ 5 (дель-крест, обсуждается в Раздел 3).

1.5.2 Обсуждение компонентов вектора по отношению к

Прежде чем продолжить части дифференциальной формы уравнения Максвелла № 1, мы должны Рассмотрим компоненты x, y и z вектора в прямоугольные координаты.

В разделе 1.1.2 скалярное произведение двух векторов, силы и расстояния, использовался для расчета работы. Здесь мы рассчитаем ту же работу, используя компоненты вектора силы и расстояния и используют скалярное произведение.

Обратите внимание, что компоненты вектора силы в прямоугольном координаты размещаются либо на нуле, либо на 90 градусах к расстоянию движение. Косинус нуля градусов равен единице, а косинус 90 градусов. равно нулю.

Из рисунка 1.3;

Компоненты вектора силы = 17,3 фунта. y + 10 фунтов. х .

Компоненты вектора расстояния = 0 футов y + 8 футов x .

Теперь процедура умножения векторов (точек) заключается в умножении величины компонент вектора и косинус угла между ними, посрочно.

Нулевое расстояние y, умноженное на две составляющие силы, равно нулю.

8 футов x расстояние, умноженное на 17.8 фунтов силы в направлении y раз косинус 90 градусов равен нулю. Направленное расстояние 8 футов x, умноженное на Сила 10 фунтов в направлении x, умноженная на косинус нуля градусов, составляет те же 80 фут-фунтов, которые мы нашли в предыдущем примере.

Следуют этой процедуре умножения компонент вектора x, y и z. при выполнении продукта ниже. Умножение компонентов вектора, которые всегда равны нулю или 90 градусов друг от друга, значительно упрощает векторную математику.

Мы определили компоненты в разделе 1.5.1. Выше мы обсуждали умножение скалярного произведения векторов, используя их компоненты. Эти две концепции сейчас используются для рассчитать

1.5.3 Рассчитать

Компоненты вектора D являются его проекциями на x, y и z ось. Векторные направления D компонентов обозначены единичные векторы x, y и z .На рисунке 1.6 вектор D начинается в начале координат, указывает вверх и вправо и является обозначен как выходящий из бумаги. Величины проекций Д по осям D _x , Dy, и D _z . На рисунке 1.7 показаны единичные векторы в направлениях x, y и z, которые дают компоненты D их векторные отношения. Одинаковый единичные векторы обозначены в

Уравнение вектора

D в проекции на три оси координат: D = D _x x + D _y y + D _z z. Теперь займемся указано скалярное произведение.

Скалярное произведение означает, что мы должны умножить скобки, член по члену, умноженному на косинус включенного угла между каждой парой термины. Эта серия умножений может дать девять членов, но обратите внимание, что единичный вектор, разделенный точками на один и тот же единичный вектор:

Остальные шесть комбинаций единичного вектора Умножение скалярного произведения содержит косинус 90 градусов и следовательно, ноль.

Окончательный результат операция — это скаляр из трех членов:

Это уравнение указывает сумму изменения по плотности электрического потока,

D , в каждом из трех ортогональных направлений. В изменение происходит из-за небольшого (приближающегося ноль), расстояние изменяется в тех же ортогональных направлениях.

Изменение расстояния в трех ортогональных направлениях представляет собой объем измените, как показано в разделе 1.5.1. Следовательно, электрическая плотность ( D ) изменение в трех направлениях, что мы получили с использованием скалярного произведения с единичными векторами в del, на самом деле изменение объема блока. Поскольку заряд измеряется в кулонах, сумма заряд в кулонах. Результат сложения трех электрических плотностей изменения — кулоны на кубический метр. Это определяет

r , объемная плотность заряда, , как указано в разделе 1.3.

1,6 Уравнение № 1, дифференциальное Форма заполнена

Выполняя указанные операция, которую мы получили

r , объемная плотность заряда. Это дифференциал формулировка уравнения Максвелла №1.

Уравнение утверждает, что дивергенция плотность электрического потока в точке равна заряду на единицу объем в этот момент. Скалярное произведение, как всегда, дает скаляр результат.В этом случае результат

р, количество кулонов расход за кубометр.

1.7 Теорема о расходимости

Здесь поучительно продолжить использование только что разработанных интегральных и дифференциальных уравнений для уравнения Максвелла № 1, чтобы проиллюстрировать векторную идентичность называется «Теорема о расходимости Гаусса». Этот тождество приравнивает векторный интеграл по поверхности к векторному интегралу по объему, и потребуется позже в Разделе 2.5.

Из раздела 1.4,

из раздела 1.5;

Путем замены на

r в интегральном уравнении получаем;

Это типичная иллюстрация Гаусса. теорема о расходимости на примере вектора

D . В Дело в том, что каждый раз, когда у нас есть векторный поверхностный интеграл этого типа мы можем заменить интеграл объема. Если у нас есть векторный объем интеграл указанного выше типа можно заменить поверхностным интегралом.В интеграл расходимости вектора, просуммированный по объему, равен равный интегралу произведения вектора на его эффективную площадь просуммирована по площади. Это аналогично заявлению о том, что объем шара содержится в пределах его площади поверхности. Круг на знак интеграла означает, что интеграл берется по непрерывной площадь.

Если бы мы просто использовали теорему о расходимости Гаусса из списка учебников векторных тождеств, мы могли бы сразу записать дифференциальная форма уравнения Максвелла No.1 из интегральной формы. Этот более подробный способ получения личности будет полезно в более поздних выводах.

1,8 Связь

D , E и e

Пространство, в котором электрическая заряды, оказывающие свое влияние, называют полем электрического заряда. Электрический заряд q окружает электрическое поле поля Прочность

E . Напряженность электрического поля E вызывает величина плотности потока, D , в зависимости от диэлектрической проницаемости, e окружающая среда.

D

находится в кулонов на квадратный метр.

E

в ньютонах на кулон или в вольтах на метр.

e

в кулонах ² на ньютон-метр ² .

E

— это напряжение в пространстве, которое вызывает проявление D . В связи к этому уравнению и по причинам, обсуждаемым в разделе 3.7, D есть часто обозначается как плотность смещения электрического потока в дополнение к плотность электрического потока.Кроме того, в разделе 4 будет показано, что магнитно-индуцированное электрическое поле также обозначен E , с размером вольт на метр. Это индуцированное электрическое поле то же поле, что и напряженность статического поля, обсуждаемая здесь, но это генерируется изменяющимся магнитным полем.

Диэлектрическая проницаемость

е — это степень, в которой окружающая среда позволяют плотности электрического потока, D , возникать из-за с учетом напряженности электрического поля, E .В воздухе или в свободном пространстве,

е

= 8,85×10 ^-12 кулон ² на ньютон-метр ² .

Эти понятия и определения будут использоваться в разделах 6 и 7.

1.9 Закон Кулона

В разделе 1.2.1 мы обнаружили, что плотность электрического потока D за счет заряда q, находящегося внутри сфера:

Затем, используя E и e, как определено в разделе 1.8;

При следующем заряде q ₂ , размещены на расстоянии r метров от q ₁ , сила испытывает q ₂ . Сила составляет

E раз q ₂ Ньютон. Или,

, где q ₁ и q ₂ обозначают физическое лицо обвинения. Это уравнение является законом Кулона. Напомним, что сила одного Ньютон разгонит массу в один килограмм на один метр в секунду ² .

Закон Кулона гласит, что сила между двумя зарядами пропорционально произведению двух зарядов на расстояние между двумя зарядами в квадрате. Уравнение — это основа для экспериментального определения силы между двумя зарядами и диэлектрическая проницаемость различных сред. Этот важный электрический закон не включен в список Максвелла, поскольку считается производным от Гаусса закон, и не используется в этих уравнениях поля.

На этом обсуждение уравнения Максвелла завершено. Нет.1.

Коалесценция жгутов магнитного потока в области диффузии ионов при магнитном пересоединении

Жгуты магнитного потока (также называемые плазмоидами или токовыми нитями) представляют собой локализованные спиральные магнитные структуры ^9,10,11 и обычно погружаются в поток пересоединения ^12,13 . Недавнее численное моделирование показало, что неустойчивость плазмоида имеет место как в токовом слое Свита – Паркера для большого числа Лундквиста ^14,15,16,17 , так и в вытянутых слоях тока электронного масштаба ^17,18,19,20 .Более того, взаимодействие этих плазмоидов приводит к быстрому пересоединению и заряжает электроны ^18,19 . Однако слияние, посредством которого пара магнитных жгутов сливается в более крупную ^21,22,23 , еще не было подтверждено напрямую наблюдениями на месте , хотя сообщалось о дистанционных наблюдениях ^24,25 . Здесь мы представляем первое обнаружение in situ слияния флюсового жгута во время повторного соединения. Наблюдения показали, что коалесценция преобладает и играет решающую роль в диссипации энергии при пересоединении.

Повторное соединение с направляющим полем ( B _g ≍ −10 нТл) уходило в хвост 17 августа 2003 года при −17 R _E в хвосте магнитосферы. Область диффузии ионов, отмеченная зеленой полосой в верхней части рис.1, уже была идентифицирована на основе совпадающих разворотов высокоскоростных потоков V _L (рис. 1a) и B _N (рис.1b), а также искаженная квадрупольная структура Холла в локальной токовой системе ( LMN ; исх.26). В это время были доступны данные о магнитном поле, полученные с интервалом 1/67 с, а расстояние между космическими аппаратами было меньше 200 км, так что тонкая структура в области диффузии ионов могла быть исследована дополнительно.

Рис. 1. Обзор тросов магнитного пересоединения и магнитного потока.

Данные представлены в координатах LMN , определенных путем применения анализа минимальной дисперсии к данным магнитного поля в интервале 15: 50–16: 20 UT 17 августа 2003 г., когда токовый слой был спокойным, чтобы избежать влияния система токов Холла внутри области диффузии ионов, L = (0.957,0,237, -0,166), M = (-0,271,0,935, -0,228) и N = (0,102,0,263,0,959) относительно координат GSM. Компонент M в основном расположен в направлении рассвета и заката. a , Объемные потоки в направлении L , доступно только на C4. b , N (черная кривая) и L (серая кривая) компоненты магнитного поля в точке C2. Синяя заливка указывает на отдельные веревки, розовая — на пары соединяющихся веревок. c , d , B _N и B _M , выборка 67 с ^-1 (красная кривая) и 0.25 с ⁻¹ (черная кривая) с 16:32 до 16:46 UT. Звездочка над панелью c указывает на растянутые веревки на фиг. 2, тогда как три стрелки соответствуют веревкам, показанным на фиг. 3a – c. e , Каждый кружок соответствует одной веревке в области диффузии ионов. Его положение определяется средними значениями V _L и B _L каната. Скорость V _L оценивается по временной задержке между C2 и C3, которые широко разнесены в направлении L и близко друг к другу в двух других направлениях

Космический корабль в основном пересек область пересоединения в Южном полушарии с несколькими экскурсиями в Северное полушарие (рис.1б). Магнитное поле сильно колебалось внутри области диффузии ионов. Изучая флуктуации, было идентифицировано большое количество локализованных спиральных магнитных структур, которые характеризовались отчетливо биполярной сигнатурой B _N со сменой знака и значительным B _M — B _г вблизи точки разворота B _N (рис. 1в, г). Этот тип магнитной структуры обычно интерпретируется как жгут магнитного потока ^{9,10,11,12,13} .Мы сосредоточились только на веревках, которые были одновременно обнаружены всеми четырьмя спутниками, и всего 19 веревок были идентифицированы (см. Дополнительную таблицу) и обозначены цветом на рис. 1b. Каждая бледно-голубая полоса обозначает одну веревку, тогда как каждая розовая полоса включает пару веревок, которые, как позже было подтверждено, сливаются. Для наглядности веревки во время 16: 32–16: 46 UT, включая все срастания в хвосте X-линии, растянуты на рис. 1c, d. Большинство веревок идентифицируются только с данными с высоким разрешением (красная кривая), например, веревки, отмеченные стрелками над рис.1c, которые увеличены на рис. 3a – c. Используя данные, полученные на интервале 0,25 с ^-1 (черная кривая), в 16:40:47 UT можно было различить только одну веревку, отмеченную звездочкой на рис. 1c, тогда как другая биполярная сигнатура появилась в задней части, когда Использовались данные, полученные при 67 с ^-1 (красная кривая). Две веревки дополнительно исследуются на рис. 2, чтобы подтвердить слияние.

Рисунок 2: Пример слияния.

a , Плотность электронов, полученная из потенциала космического аппарата. b — e , N ( b ), M ( c ), L ( d ) компоненты и величина ( e ) магнитного поля на всех четырех спутниках . f , Дифференциальные потоки энергии электронов (DEF) на C4, белая линия — температура электронов. Вертикальные черные пунктирные линии в точках ∼16: 40: 47 и ∼16: 41: 15 UT соответствуют центрам веревок, а розовая пунктирная линия обозначает точку слияния. Розовая полоса в b представляет область взаимодействия между двумя веревками.Измерения в области взаимодействия в C4 увеличены до g — k . г , B _N и B _L . ч , Электронная плотность. i , электрическое поле E _y в системе отсчета перевернутого спина. j , Три составляющие плотности тока. k , Дифференциальные потоки энергии электронов от датчика HEEA прибора PEACE.

Если соединялась попарная веревка, для выполнения диссипации энергии в области их взаимодействия должны быть индуцированы электрическое поле и ток слияния. В случае хвоста магнитосферы Земли, как индуцированное электрическое поле слияния, так и ток будут указывать на сторону рассвета ^21,22,23 . Два упомянутых выше каната наблюдались с сильным полем ядра до -40 нТл (рис. 2c) вблизи центров в 16:40:47 и 16:41:15 UT (вертикальные черные линии) на рис. 2a – f. . Электронная плотность (рис.2а) и температура (белая линия на рис. 2е) также увеличились. Область взаимодействия заштрихована розовым цветом на рис. 2б и увеличена на рис. 2ж – к. При ∼16: 41: 11.6 UT (вертикальная розовая линия) измеряется узкий токовый слой, направленный на рассветную сторону ( j _M ≍ −40 нА м ⁻² , рис. 2j) . Измеряется кажущееся асимметричное распределение B _N и N _e между двумя сторонами текущего слоя. B _N ( N _e ) изменяется от −20 (1.6 см ⁻³ ) слева до 10 нТл (1,1 см ⁻³ ) справа. Используя метод синхронизации, мы оцениваем скорости v _L веревок в 16:40:47 и 16:41:15 UT как -375 и -629 км с ^-1 , соответственно. А именно, веревка в 16:41:15 UT сталкивается с веревкой впереди нее (рис. 4а), что может быть причиной асимметричного распределения B _N и N _e . Продолжительность текущего слоя около 0.3 с, и поэтому пространственный масштаб слоя оценивается как 0,3 с × 375 км с ^-1 ∼ 6,6 d _e ( d _e : инерционная длина электрона для N _e = 0,1 см ⁻³ ) в направлении L . Ожидается, что этот токовый слой будет диссипативной областью слияния.

Электрическое поле в остальной рамке слоя можно оценить как E _M ′ = E _M + ( V × B ) _M .Скорость ( V ) в основном находится в направлении L , а B _N близка к 0 в точке разворота B _N , поэтому E _M ′ ≍ E _M вокруг этой точки. Электрическое поле измерялось только в плоскости спина Кластера ( x — y ) системы Inverted Spin Reference. Компонент y равен (0, 0,948, -0.319) в координатах GSM и в основном в направлении M , поэтому E _y близок к E _M ( E _M ≍ E 902 y ) вокруг точки. E _y отображает локализованное минимальное значение (−2,8 мВ м ⁻¹ ) около точки разворота B _N (рис. 2i). Полярности j _M и E _M ′ соответствуют ожидаемому току слияния и электрическому полю.Таким образом, мы делаем вывод, что веревки срослись. j _M E _M ′> 0 указывает, что была выделена магнитная энергия. Центральное поле веревок в два раза больше поля слияния (рис. 2g) и, по-видимому, является направляющим полем слияния. Таким образом, эта коалесценция по сути является асимметричным пересоединением компонентов. В окрестностях текущего слоя текущий j _N значительно увеличивается и указывает на юг, его ширина оценивается как 0.8 d _i ( d _i ≍ 720 км). Отрицательный j _N может быть объяснен сливающимся истечением.

Таким же образом можно было идентифицировать еще пять слияний. Сращивания в хвостовом потоке в ∼16: 35: 49 и ∼16: 42: 45 UT и в потоке от земли в 16:55:47 UT показаны на рис. 3b, c и рис. 3d, соответственно. В точках слияния j _M и E _y отрицательны, то есть указывают на сторону рассвета.Иногда космический аппарат неоднократно пересекал одну область диссипации слияния (рис. 3г). На рис. 3e, f показан анализ наложенных эпох для E _y и j _M в 6 слияниях, временная область составляет ± 3 с. Минимальное значение E _y ( j _M ) было принято в качестве нулевой эпохи на рис. 3e (рис. 3f). В среднем скорость диссипации энергии этих слияний составляет около 200 пВт м ^-3 , что намного выше, чем у обычного пересоединения в хвосте магнитосферы ²⁷ (45 пвт м ^-3 ).Используя закон Фарадея (Δ E _y ∼ 10 мВ м ⁻¹ , Δ L ∼ 100 км, Δ B _N ∼ 10 нТл), мы оцениваем динамический временной масштаб слияние 0,1 τ _A (альфвеновское время τ _A ≍ 1 с).

Рисунок 3: Средние свойства коалесценции.

a — d , Данные отображаются в том же формате на графиках a — d : B _L (зеленый), B _M (синий ) и B _N (красный) отображаются на первой панели, а плотность тока j _M , а также электрическое поле E _y показаны в вторая панель.Вертикальные черные пунктирные линии соответствуют центру веревки, а розовые пунктирные линии представляют точки слияния. Электрическое поле E _y вариация сильна внутри канатов, но отрицательна вблизи точки слияния. e , f , анализ наложенных эпох E _y ( e ) и j _M ( f ) в областях взаимодействия 6 слияний (серые линии ), идентифицированные внутри области диффузии ионов.Использовались данные электрического поля на C4.

Различные веревки в области диффузии ионов имеют поле сердцевины, противоположное направляющему полю (рис. 1c, d и дополнительная информация), например, веревки на рис. 3a, c были обнаружены в точке B _L <-25 нТл, а поле ядра было больше 10 нТл. Пики основного поля B _M и тока j _M указывают на то, что космический аппарат пересек центры канатов.Несоответствие знаков между основным полем и направляющим полем означает, что направляющее поле не было единственным источником для основного поля. Диаграмма рассеяния средних значений v _L и B _L в точке C2 этих веревок показана на рис. 1e. Отрицательное поле сердцевины (кружки с крестом) преимущественно появляется в верхнем правом и нижнем левом квадрантах, тогда как положительное поле сердцевины (кружки с точкой) в основном находится в правом нижнем квадранте, что согласуется с искаженной квадрупольной структурой Холла ²⁶ .Следовательно, это указывает на то, что основное поле генерируется сжатием окружающего поля Холла. Другими словами, большинство веревок находится в области холловского поля, а не центрировано в плазменном слое. Этот вывод согласуется с предыдущими наблюдениями ²⁸ . Следовательно, новый сценарий для диффузионной области показан на рис. 4b. Цветные эллипсы вдоль траектории представляют собой веревки, отмеченные тем же цветом на рис. 1b.

Рис. 4: Схема области коалесценции и диффузии ионов.

a , Попарное слияние флюсового жгута, соответствующее сливающимся жгутам, отмеченным звездочкой на рисунках 1c и 2 и b . Эллипсы красного (синего) цвета указывают на то, что плотность тока положительная (отрицательная) в направлении M . Зеленая кривая обозначает траекторию космического корабля. b , Новый сценарий для ионно-диффузионной области бесстолкновительного пересоединения в хвосте магнитосферы. Эллипсы с цветовой кодировкой представляют собой магнитные жгуты, обнаруженные космическим аппаратом в области диффузии ионов.Розовые эллипсы обозначают сливающиеся веревки.

Во время этого события пересоединения тонкие токовые слои вблизи нейтральной плоскости и сепаратрис расширились до десятков инерционной длины иона в направлении L ²⁶ . Таким образом, идентифицированные веревки могли возникнуть только в результате разрыва токовых слоев, как предполагалось при моделировании ^{14,15,16,17,18,19} и подтверждено только в лаборатории ²⁹ . После того, как жгуты сформированы, они сливаются и образуют небольшие области диффузии в электронном масштабе.А именно, небольшие диффузионные области были погружены в большую диффузионную область нормального пересоединения. Наблюдения показывают четкий каскад турбулентной энергии. Недавнее моделирование ¹⁹ показало, что в пересоединении преобладает образование и взаимодействие жгутов магнитного потока, большинство из которых генерируется нестабильностью слоев электронного тока вдоль сепаратрис и превращается в турбулентность. Эта картина согласуется с нашими наблюдениями. Однако необходимо дальнейшее количественное сравнение наблюдений и моделирования.

Определение Tesla от Merriam-Webster

тес · ля | \ ˈTe-slə \

: единица плотности магнитного потока в системе метр-килограмм-секунда, эквивалентная одному Веберу на квадратный метр.

Tes · la | \ ˈTe-slə \

Никола 1856–1943 Американский (хорватский) инженер-электрик и изобретатель.

Закон Гаусса, Закон Фарадея, Закон Ленца

Магнитный поток — очень важная физическая величина в области электромагнетизма.Это измерение общего магнитного поля, проходящего через область. Измерение магнитного потока зависит от конкретной выбранной области. В данной статье мы подробно обсудим магнитный поток и изучим другие величины, такие как силовые линии магнитного поля и магнитное поле. Мы узнаем об одном из четырех уравнений Максвелла, которое аналогично закону Гаусса, который мы изучали в электростатике. Мы также обсудим различные явления, связанные с магнитным потоком, такие как электромагнитная индукция.

Узнайте об электромагнитной индукции здесь

Магнитное поле

Мы все видели, как магниты притягивают железные гвозди, находящиеся рядом с ними, но как они притягивают их, не соприкасаясь? Это явление можно объяснить с помощью поля, поэтому у нас также есть магнитное поле, как у нас было электрическое и гравитационное поле.
Как создаются магнитные поля?
Некоторым материалам присуще магнитное свойство, они создают магнитное поле и известны как магниты.
Статический заряд создает только электрическое поле, но он создает как электрическое поле, так и магнитное поле, когда заряд движется. Можно сказать, что движущийся заряд создает магнитное поле.
Когда электрический ток течет внутри проводника, свободные электроны в проводнике находятся в движении. Из-за движения этих свободных электронов вокруг проводника создается магнитное поле.
Магнитное поле является векторной величиной и обозначается \ (\ overrightarrow B \). Его единица СИ — Тесла.

Что такое магнитный поток?

Магнитный поток можно определить как количество силовых линий магнитного поля, проходящих через область. Он обозначает как направление, так и величину магнитного поля, проходящего через поверхность. Обозначается греческой буквой фи \ ((\ phi) \). Его единица СИ — Вебер \ ((\ rm {Wb}) \).
Магнитный поток определяется как скалярное произведение магнитного поля и вектора площади,

\ (\ phi = \ overrightarrow B \ cdot \ overrightarrow S \)
Где
\ (\ overrightarrow B \) — магнитное поле.
\ (\ overrightarrow S \) — вектор площади.

Линии магнитного поля

Силовые или магнитные силовые линии — это способ наглядно представить магнитное поле. Плотность и направление линий в пространстве обозначают величину и направление магнитного поля.
Свойства магнитного поля следующие:

1. Две линии магнитного поля никогда не пересекаются.
   Это происходит потому, что силовые линии магнитного поля задают направление чистого магнитного поля, и если они пересекаются, будет два направления для чистого магнитного поля, что невозможно.
2. Силовые линии магнитного поля образуют замкнутый контур.
3. Силовые линии магнитного поля исходят от северного полюса и заканчиваются на южном полюсе.

Закон Гаусса для магнетизма

Закон Гаусса для магнитного поля — одно из четырех уравнений Максвелла для электромагнетизма.
Согласно этому закону, магнитный поток через любую замкнутую поверхность будет равен нулю.
\ ({\ phi _ {{\ text {closed}} \, {\ text {surface}}}} = \ oint \ overrightarrow B \ cdot \ overrightarrow {dA} = 0 \)
Где,
\ (\ стрелка вверху B \) — магнитное поле.
\ (\ overrightarrow {dA} \) — вектор небольшой площади.

Электромагнитная индукция

Электромагнитная индукция была открыта известным ученым Майклом Фарадеем в 1931 году. Электромагнитная индукция — это явление, при котором электрический ток генерируется в проводнике из-за изменения магнитного потока.
Это можно рассматривать как обратное магнитному эффекту тока, так как при магнитном действии тока магнитное поле создается из-за тока, а при электромагнитной индукции электрический ток создается из-за магнитного поля.

Закон электромагнитной индукции Фарадея

Согласно закону электромагнитной индукции Фарадея, ЭДС, индуцированная в контуре из-за электромагнитной индукции, прямо пропорциональна скорости изменения потока во времени.
\ (E = — \ frac {{d \ phi}} {{dt}} \)

Закон Ленца

Закон Ленца гласит, что индуцированный электрический ток в петле течет в таком направлении, что ток противодействует вызвавшему его изменению потока.
Закон Ленца дает нам только направление тока. Проще говоря, если поток через контур уменьшается, то индуцированный ток увеличивает поток через контур, а если ток создается из-за увеличения потока, то индуцированный ток уменьшает поток.

Самоиндукция и взаимная индукция

Самоиндукция — это явление, при котором ЭДС индуцируется в катушке или контуре из-за изменения потока через них из-за изменения тока в цепи.Благодаря этому катушка или петля сопротивляются любому изменению тока через нее.
Взаимная индукция — это явление, при котором ток индуцируется в контуре или катушке из-за тока, протекающего в другом контуре, находящемся рядом с ним. Это явление используется в трансформаторах.

Индуцированное электрическое поле

Это индуцированное электрическое поле возникает из-за изменения потока через петлю из-за изменения магнитного поля. Важно отметить, что это индуцированное электрическое поле отличается от электрического поля, вызванного статическим зарядом.Индуцированное электрическое поле — неконсервативное поле. Электрический потенциал и разность потенциалов не определены.
\ (\ oint {\ overrightarrow E} \ cdot \ overrightarrow {dl} = \ frac {{d \ phi}} {{dt}} \)
Единственное сходство индуцированного поля с электрическим полем из-за статического заряда состоит в том, что сила, действующая на заряд из-за поля, представляет собой величину заряда, умноженную на напряженность поля.
\ (\ overrightarrow {{F_E}} = \ overrightarrow {q {E_E}} \)
И,
\ (\ overrightarrow {{F_ {IE}}} = \ overrightarrow {q {E_I}} \).

Примеры задач по магнитному потоку

Q.1. Если проводящий стержень \ (AB \) движется со скоростью «\ (v \)» на данном рисунке, найдите ЭДС, индуцированную в цепи. Длина проводника «\ (l \)», и постоянное магнитное поле \ (\ overrightarrow B \) выходит из плоскости.

Ответ: Дано,
Длина проводника «\ (l \)».
Скорость проводника «\ (v \)».
Величина магнитного поля равна \ (\ overrightarrow B \).
Поток цепи определяется выражением
\ (\ phi = \ oint \ overrightarrow B \ cdot \ overrightarrow {dA} \)
\ (= \ phi = Blx \)
Из закона электромагнитной индукции Фарадея имеем ,
\ (E = — \ frac {{d \ phi}} {{dt}} \)
\ (\ Rightarrow E = Bl \ frac {{dx}} {{dt}} \)
\ (= E = Blv \).

Q.2. Найдите поток через заданную область, когда магнитное поле \ (\ overrightarrow B \) составляет угол \ (60 \) градусов с вектором площади \ (\ overrightarrow S \).\ circ \).
Магнитный поток определяется выражением
\ (\ phi = \ oint {\ overrightarrow B} \ cdot \ overrightarrow {dS} \)
\ (\ Rightarrow \ phi = BS \, \ cos \ left ( {60} \ right) = \ frac {1} {2} BS \).

Сводка

Магнитный поток — это величина магнитного поля, проходящего через область. Поток через замкнутую поверхность всегда равен нулю. Это потому, что магнитного монополя не существует. Силовые линии магнитного поля всегда образуют замкнутый контур. Магнетизм и электрический ток связаны друг с другом.Изменение потока через проводящую петлю вызывает внутри петли ЭДС. Фарадей объяснил это. Индуцированная ЭДС равна скорости изменения потока. Закон Ленца определяет направление индуцированного тока. Самоиндукция сопротивляется любому изменению тока в петле, тогда как взаимная индукция индуцирует ток в другой петле, находящейся рядом с токоведущей петлей.

Часто задаваемые вопросы по M

agnetic Flux

Q.1. Что такое магнитный поток?
Ответ: Магнитный поток — это величина магнитного поля, проходящего через область.Его также можно определить как количество линий магнитного поля, проходящих через область. Его единица СИ — Тесла. Он рассчитывается как скалярное произведение магнитного поля и вектора площади.
\ (\ phi = \ overrightarrow B \ cdot \ overrightarrow A \).
Где
\ (\ overrightarrow B \) — магнитное поле.
\ (\ overrightarrow {A} \) — вектор площади.

Q.2. Каков закон Гаусса для магнитного поля?
Ответ: Закон Гаусса для магнетизма гласит, что магнитный поток через любую замкнутую поверхность всегда будет равен нулю.
\ ({\ phi _ {{\ text {closed}} \, {\ text {surface}}}} = \ oint {\ overrightarrow B} \ cdot \ overrightarrow A = 0 \).
Где
\ ({\ overrightarrow B} \) — магнитное поле.
\ (\ overrightarrow {A} \) — вектор площади.

Q.3. Можно ли изолировать магнитные монополи?
Ответ: Нет, магнитные монополи нельзя изолировать. Магнитные полюса всегда существуют парами, известными как северный и южный полюсы.

Q.4. Что такое электромагнитная индукция?
Ответ: Электромагнитная индукция — это явление, при котором электродвижущая сила индуцируется из-за изменения магнитного потока.Закон электромагнитной индукции Фарадея дает значение наведенной ЭДС. ЭДС, индуцированная в контуре из-за электромагнитной индукции, прямо пропорциональна скорости изменения потока во времени.
\ (E = — \ frac {{d \ phi}} {{dt}} \)
Закон Ленца дает направление наведенной ЭДС. Индуцированный электрический ток в петле течет в таком направлении, что ток противодействует вызвавшему его изменению магнитного потока. Проще говоря, эффект противодействует изменению.

В.5. Что такое индуцированное электрическое поле?
Ответ: Индуцированное электрическое поле — это силовое поле, которое прикладывает силу к заряду в этом поле, как,
\ (\ overrightarrow {{F_ {IE}}} = \ overrightarrow {q {E_I}} \)
Это поле отличается от электрического поля, которое создается статическим зарядом. Линии индуцированного электрического поля могут образовывать замкнутый контур. Электрический потенциал и разность потенциалов не определены для точек в наведенном электрическом поле.
Индуцированное электрическое поле создается путем изменения магнитного потока через область.