Какое соединение сопротивлений называют последовательным — MOREREMONTA
1. Собрать поочередно электрические схемы в соответствии с рис. 2.4; 2.6; 2.7 и произвести измерения величин токов и напряжений. В качестве приемников энергии использовать проволочные реостаты, одни и те же для всех трех схем, не изменяя их сопротивлений, при этом ползунки реостатов установить в положения, соответствующие максимальным значениям их сопротивлений.
2. Согласно измеренным величинам токов и напряжений, вычислить сопротивления каждого реостата и эквивалентное сопротивление каждой цепи относительно зажимов источников энергии. Полученные результаты свести в табл. 2.1.
3. Вычислить, исходя из величин r1, r2, r3 эквивалентное сопротивление rэкв каждой из цепей. Сравнить полученные результаты с опытами.
4. Вычислить аналитическую силу токов в приемниках для всех трех схем, считая известными сопротивления приемников и напряжение источника питания. Полученные токи сравнить с измеренными.
5. Сделать выводы по работе.
| Соедине- ние | Измерения | Вычисления | |||||||||
| U В | U1 В | U2 В | U3 В | I А | I1 А | I2 А | I3 А | rэкв Ом | r1 Ом | r2 Ом | r3 Ом |
| Последова-тельное | |||||||||||
| Параллель-ное | |||||||||||
| Смешан- ное |
Контрольные вопросы:
1. Какое соединение резисторов называется последовательным?
2. Чему равно эквивалентное сопротивление цепи с последовательно включенными резисторами?
3. При каких условиях применяется последовательное включение резисторов (приемников)?
4. Какое соединение резисторов называется параллельным?
5. Как определить для параллельного соединения эквивалентное сопротивление и эквивалентную проводимость?
6. При каких условиях можно включать параллельно приемники электрической энергии?
7. Почему схема параллельного включения приемников является основной?
8. Какое соединение резисторов называется смешанным?
9. Как определить для смешанного соединения эквивалентное сопротивление?
Работа 3. Цепь переменного синусоидального тока с последовательным соединением катушки и конденсатора. Резонанс напряжений.
Пояснения к работе
Рассмотрим процессы в цепи с последовательным соединением катушки и конденсатора (рис. 3.1).
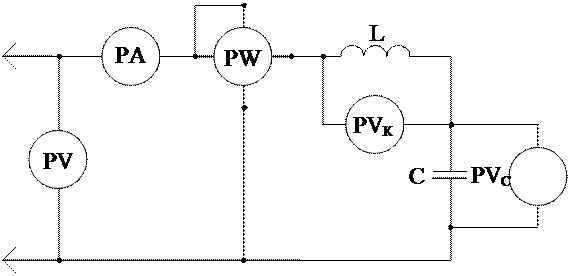
Рис.3.1. Схема цепи с последовательным соединением
катушки и конденсатора
Реальная катушка обладает индуктивным сопротивлением xL=wL и активным сопротивлением r = r 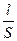
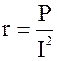 . Его можно определить также, пропуская через катушку постоянный ток. В цепи постоянного тока катушка обладает только активным сопротивлением, так как угловая частота w=2p¦=0 и x
. Его можно определить также, пропуская через катушку постоянный ток. В цепи постоянного тока катушка обладает только активным сопротивлением, так как угловая частота w=2p¦=0 и x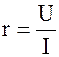 , где U – постоянное напряжение, приложенное к катушке, а I – сила постоянного тока, протекающего через катушку.
, где U – постоянное напряжение, приложенное к катушке, а I – сила постоянного тока, протекающего через катушку.Эквивалентная схема замещения катушки может быть представлена в виде последовательного соединения резистивного и индуктивного идеальных элементов (рис. 3.2).
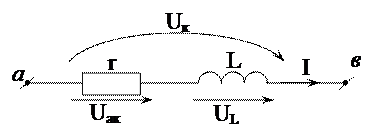 |
Рис.3.2. Эквивалентная схема замещения катушки
Напряжение на катушке Uк можно разложить на две составляющие – активную Uак и индуктивную UL Векторная диаграмма напряжений и тока для катушки приведена на рис. 3.3.
Напряжение Uк можно измерить на выводах катушки с помощью вольтметра, ток I – с помощью амперметра. Угол сдвига фаз между током и напряжением катушки jк можно определить из формулы Pк = Uк I cosjк , если измерить с помощью ваттметра активную мощность катушки Pк. Составляющие напряжения Uк, UL и Uак можно вычислить из треугольника напряжений ОАВ (рис.3.3): Uак=Uкcosjк или определить графически, опустив перпендикуляр из конца вектора U

Рис.3.3. Векторная диаграмма напряжения и тока для катушки
Конденсатор в цепи переменного тока обладает емкостным сопротивлением  , где C – емкость конденсатора. Следует указать, что в конденсаторе также имеются активные потери энергии в диэлектрике. Однако величина этих потерь настолько мала, что ими можно пренебречь. На схеме замещения конденсатор можно представит в виде идеального емкостного элемента с параметром С, равным емкости конденсатора.
, где C – емкость конденсатора. Следует указать, что в конденсаторе также имеются активные потери энергии в диэлектрике. Однако величина этих потерь настолько мала, что ими можно пренебречь. На схеме замещения конденсатор можно представит в виде идеального емкостного элемента с параметром С, равным емкости конденсатора.
Последовательное соединение катушки и конденсатора изображено в виде схемы замещения на рис. 3.4.
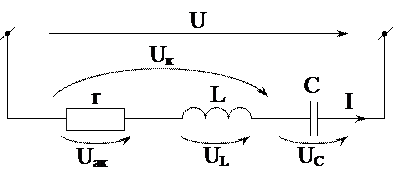 |
Рис.3.4. Схема замещения цепи с последовательным
соединением катушки и коденсатора
При подключении такой цепи под напряжение U в ней возникает ток I.
Вектор активной составляющей напряжений на катушке 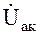 будет совпадать по направлению с вектором тока İ (рис.3.5), так как соответствующие синусоиды мгновенных значений совпадают по фазе:
будет совпадать по направлению с вектором тока İ (рис.3.5), так как соответствующие синусоиды мгновенных значений совпадают по фазе:
i = Imsinwt и U = i r =Im r sinwt. (3.1)
Вектор индуктивного напряжения 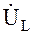 =İхL опережает по фазе вектор тока İ на
=İхL опережает по фазе вектор тока İ на 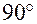 (рис. 3.6), так как синусоида напряжения UL на индуктивности опережает по фазе синусоиду тока i на
(рис. 3.6), так как синусоида напряжения UL на индуктивности опережает по фазе синусоиду тока i на 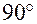 .
.
UL = L 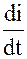
Вектор емкостного напряжения  =İхC отстает по фазе от вектора тока İ на
=İхC отстает по фазе от вектора тока İ на 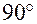 (рис. 3.7), так как синусоида напряжения на емкости при нулевых начальных условиях отстает от синусоиды тока i на
(рис. 3.7), так как синусоида напряжения на емкости при нулевых начальных условиях отстает от синусоиды тока i на 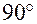 .
.
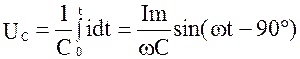 . (3.3)
. (3.3)
 |
Рис.3.5. Векторная диаграмма напряжения и тока
при активной нагрузке цепи.
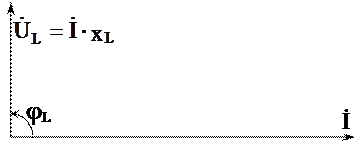 |
Рис. 3.6. Векторная диаграмма напряжения и тока
при индуктивной нагрузке цепи
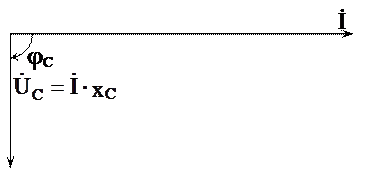
Рис. 3.7. Векторная диаграмма напряжения и тока
при емкостной нагрузке цепи
Для рассматриваемой цепи уравнений по второму закону Кирхгофа имеет следующий вид:
 , (3.4)
, (3.4)где 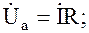
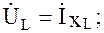
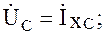
Согласно уравнению (3.4) и рис.3.5 – 3.7, векторная диаграмма напряжений цепи (рис.3.4) будет иметь вид, показанный на рис. 3.8, где вектор 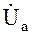 совпадает по фазе с вектором İ, а вектор
совпадает по фазе с вектором İ, а вектор 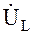
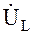 и
и 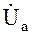 дает вектор напряжения катушки:
дает вектор напряжения катушки:
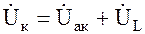 ,
,
Опережающий по фазе ток на угол jк.
Вектор  отстает по фазе на 90˚ от вектора тока İ. Сумма векторов
отстает по фазе на 90˚ от вектора тока İ. Сумма векторов 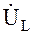 ,
, 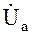 ,
,  дает вектор напряжения сети
дает вектор напряжения сети 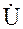 , опережающий ток по фазе на угол j.
, опережающий ток по фазе на угол j.
Разделив и умножив стороны треугольника (рис.3.8) на величину тока İ, получим подобные треугольники сопротивлений и мощностей (рис.3.9, 3.10).
Из треугольника сопротивлений (см. рис.3.9) найдем полное сопротивление Z и cosj цепи
Z= 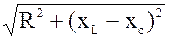 . (3.5)
. (3.5)
cosj = 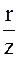 . (3.6)
. (3.6)
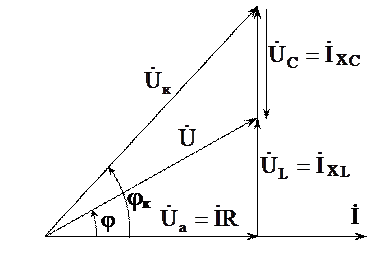
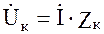
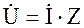
Рис. 3.8. Векторная диаграмма тока и напряжений
для цепи с последовательным соединением
 |
Рис. 3.9. Треугольник сопротивлений для цепи с последовательным
соединением элементов r, L, C.
Из векторной диаграммы напряжений (см.рис.3.8) получим формулу тока I, которая является выражением закон Ома для последовательной цепи переменного тока:
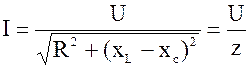 . (3.7)
. (3.7)
Из диаграммы мощностей (рис.3.10) получим соотношение между полной S, активной P и реактивными QL и Qc мощностями
 . (3.8)
. (3.8)
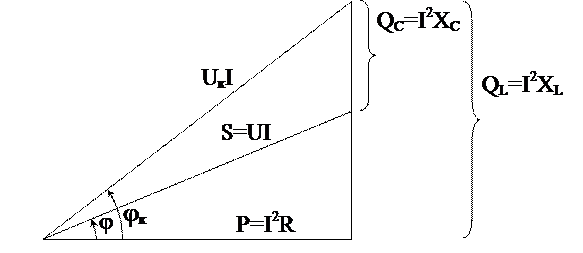 |
Рис. 3.10. Треугольник мощностей для цепи с последовательным
соединением элементов r, L, C.
Изменяя величину емкости в цепи, можно изменять соотношение между емкостными и индуктивными сопротивлениями и напряжениями:
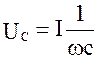 и
и  UL=I ω L
UL=I ω L
и получать различные значения угла сдвига φ между вектором тока İ и вектора напряжения сети  согласно уравнению (3.6). Если величина L>
согласно уравнению (3.6). Если величина L> 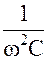 имеем: ωL>
имеем: ωL>  и UL>UC, т.е. в цепи преобладает индуктивное сопротивление xL и напряжение
и UL>UC, т.е. в цепи преобладает индуктивное сопротивление xL и напряжение 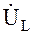 , поэтому вектор тока İ отстает по фазе от вектора напряжение сети
, поэтому вектор тока İ отстает по фазе от вектора напряжение сети 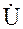 на угол φ (см.рис. 3.8).
на угол φ (см.рис. 3.8).
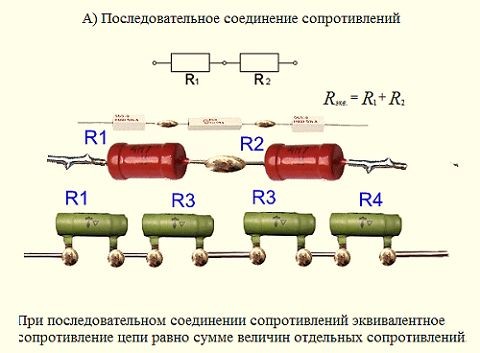
Последовательное соединение резисторов
Последовательное соединение – это соединение двух или более резисторов в форме цепи, в которой каждый отдельный резистор соединяется с другим отдельным резистором только в одной точке.

Общее сопротивление Rобщ
При таком соединении, через все резисторы проходит один и тот же электрический ток. Чем больше элементов на данном участке электрической цепи, тем «труднее» току протекать через него. Следовательно, при последовательном соединении резисторов их общее сопротивление увеличивается, и оно равно сумме всех сопротивлений.
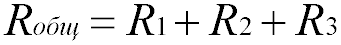
Напряжение при последовательном соединении
Напряжение при последовательном соединении распределяется на каждый резистор согласно закону Ома:
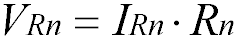

Т.е чем большее сопротивление резистора, тем большее напряжение на него падает.
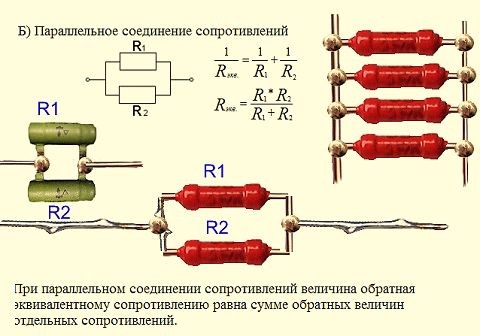
Параллельное соединение резисторов
Параллельное соединение – это соединение, при котором резисторы соединяются между собой обоими контактами. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов.

Общее сопротивление Rобщ
При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора. В результате общая проводимость такого участка электрической цепи увеличивается, а общее сопротивление в свою очередь уменьшается.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора.
Формула общей проводимости при параллельном соединении резисторов:
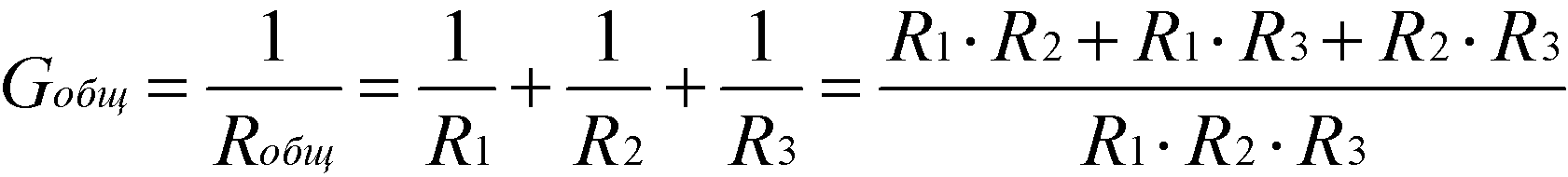
Формула эквивалентного общего сопротивления при параллельном соединении резисторов:
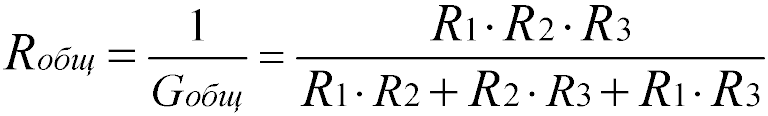
Для двух одинаковых резисторов общее сопротивление будет равно половине одного отдельного резистора:
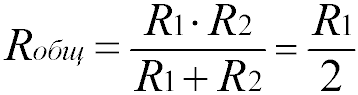
Соответственно, для n одинаковых резисторов общее сопротивление будет равно значению одного резистора, разделенного на n.
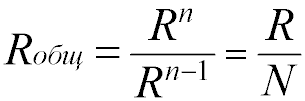
Напряжение при параллельном соединении
Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Поэтому при параллельном соединении на все резисторы упадет одинаковое напряжение.

Электрический ток при параллельном соединении
Через каждый резистор течет ток, сила которого обратно пропорциональна сопротивлению резистора. Для того чтобы узнать какой ток течет через определенный резистор, можно воспользоваться законом Ома:

Смешанное соединение резисторов
Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно. В свою очередь, смешанное соединение бывает последовательного и параллельного типов.

Общее сопротивление Rобщ
Для того чтобы посчитать общее сопротивление смешанного соединения:
- Цепь разбивают на участки с только пареллельным или только последовательным соединением.
- Вычисляют общее сопротивление для каждого отдельного участка.
- Вычисляют общее сопротивление для всей цепи смешанного соединения.
Так это будет выглядеть для схемы 1:

Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Можно, в соответствии схеме, сразу записывать формулу следующим образом:
- Если резисторы соединяются последоватеьно — складывать.
- Если резисторы соединяются параллельно — использовать условное обозначение «||».
- Подставлять формулу для параллельного соединения где стоит символ «||».
Так это будет выглядеть для схемы 1:

После подстановки формулы параллельного соединения вместо «||»:
Ответ

1) При последовательном соединении все элементы связаны друг с другом так, что включающий их участок цепи не имеет ни одного узла.
При последовательном соединении проводников сила тока во всех проводниках одинакова.
При последовательном соединении напряжение в цепи равно сумме напряжений на каждом участке:
2) например, гирлянда на елку
3) при последовательном соединении проводников общее сопротивление на участке цепи находится суммой всех сопротивлений на всех участках цепи.
4) При параллельном соединении все входящие в цепь элементы объединены двумя узлами и не имеют связей с другими узлами.
Сила тока при параллельном соединении проводников равна сумме сил токов во всех параллельно соединенных участках:
5) При параллельном соединении сопротивлений складываются величины, обратные сопротивлению:
= +
Смешанное соединение резисторов
Содержание:
- Особенности последовательного соединения
- Параметры цепи при параллельном соединении
- Схема смешанного соединения резисторов
- Видео: смешанное соединение проводников
Резистор представляет собой устройство, обладающее устойчивым, стабильным значением сопротивления. Это позволяет выполнять регулировку параметров на любых участках электрической цепи. Существуют различные виды соединений, в том числе и смешанное соединение резисторов. От использования того или иного способа в конкретной схеме, напрямую зависит падение напряжений и распределение токов в цепи. Вариант смешанного соединения состоит из последовательного и параллельного подключения активных сопротивлений. Поэтому в первую очередь нужно рассматривать эти два вида соединений, чтобы понять, как работают другие схемы.
Последовательное соединение
Последовательная схема подключения предполагает расположение резисторов в схеме таким образом, что конец первого элемента соединяется с началом второго, а конец второго – с началом третьего и т.д. То есть все резисторы поочередно следуют друг за другом. Сила тока при последовательном соединении будет одинаковой в каждом элементе. В виде формулы это выглядит следующим образом: Iобщ = I1 = I2, где Iобщ является общим током цепи, I1 и I2 – соответствуют токам 1-го и 2-го резистора.
В соответствии с законом Ома, напряжение источника питания будет равно сумме падений напряжения на каждом резисторе: Uобщ = U1 + U2 = I1r1 + I2r2, в которой Uобщ – напряжение источника электроэнергии или самой сети; U1 и U2 – значение падений напряжения на 1-м и 2-м резисторах; r1 и r2 – сопротивления 1-го и 2-го резисторов. Поскольку токи на любом участке цепи имеют одинаковое значение, формула приобретает вид: Uобщ = I(r1 + r2).
Таким образом, можно сделать вывод, что при последовательной схеме включения резисторов, электрический ток, протекающий через каждый из них равен общему значению тока во всей цепи. Напряжение на каждом резисторе будет разное, однако их общая сумма составит значение, равное общему напряжению всей электрической цепи. Общее сопротивление цепи также будет равно сумме сопротивлений каждого резистора, включенного в эту цепь.
Параметры цепи при параллельном соединении
Параллельное соединение представляет собой включение начальных выходов двух и более резисторов в единой точке, и концов этих же элементов в другой общей точке. Таким образом, фактически происходит соединение каждого резистора непосредственно с источником электроэнергии.
В результате, напряжение каждого резистора будет одинаковым с общим напряжением цепи: Uобщ = U1 = U2. В свою очередь, значение токов будет разным на каждом резисторе, их распределение становится прямо пропорциональным сопротивлению этих резисторов. То есть, при увеличении сопротивления, сила тока уменьшается, а общий ток становится равен сумме токов, проходящих через каждый элемент. Формула для данного положения выглядит следующим образом: Iобщ= I1 + I2.
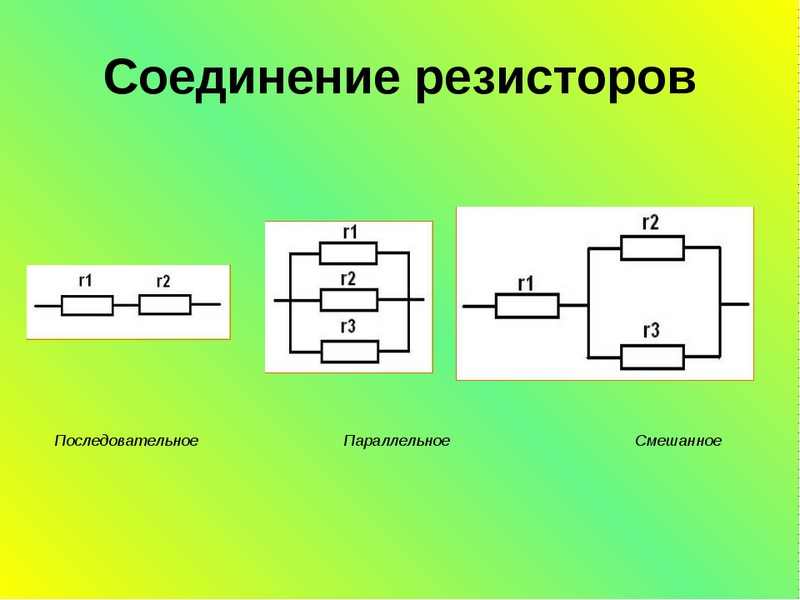
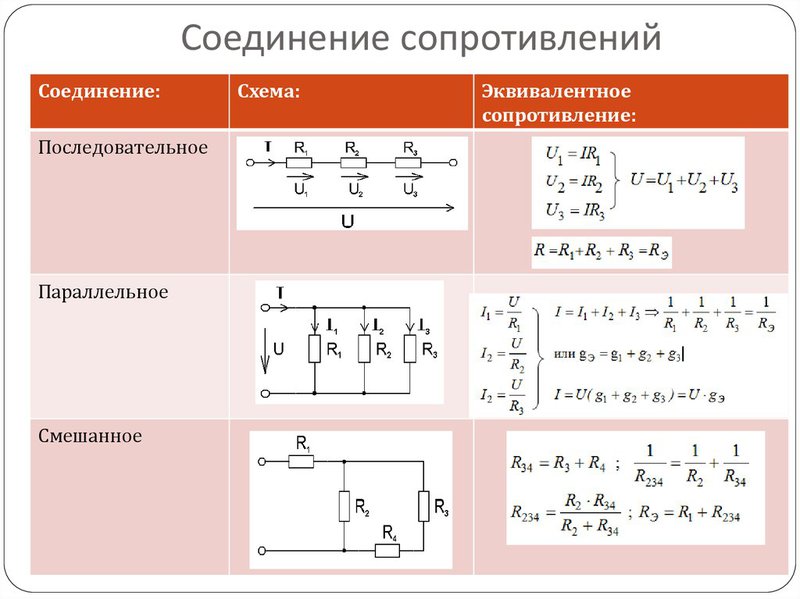
Для расчетов общего сопротивления используется формула: 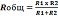 . Она используется при наличии в цепи только двух сопротивлений. В тех случаях, когда сопротивлений в цепи подключено три и более, применяется другая формула:
. Она используется при наличии в цепи только двух сопротивлений. В тех случаях, когда сопротивлений в цепи подключено три и более, применяется другая формула:
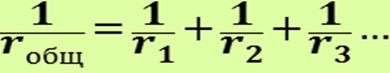
Таким образом, значение общего сопротивления электрической цепи будет меньше, чем самое минимальное сопротивление одного из резисторов, подключенных параллельно в эту цепь. На каждый элемент поступает напряжение, одинаковое с напряжением источника электроэнергии. Распределение тока будет прямо пропорциональным сопротивлению резисторов. Значение общего сопротивления резисторов, соединенных параллельно, не должно превышать минимального сопротивления какого-либо элемента.
Схема смешанного соединения резисторов
Схема смешанного соединения обладает свойствами схем последовательного и параллельного соединения резисторов. В этом случае элементы частично подключаются последовательно, а другая часть соединяется параллельно. На представленной схеме резисторы R1 и R2 включены последовательно, а резистор R3 соединен параллельно с ними. В свою очередь резистор R4 включается последовательно с предыдущей группой резисторов R1, R2 и R3.

Расчет сопротивления для такой цепи сопряжен с определенными трудностями. Для того чтобы правильно выполнить расчеты используется метод преобразования. Он заключается в последовательном преобразовании сложной цепи в простейшую цепь за несколько этапов.
Если для примера вновь использовать представленную схему, то в самом начале определяется сопротивление R12 резисторов R1 и R2, включенных последовательно: R12 = R1 + R2. Далее, нужно определить сопротивление резисторов R123, включенных параллельно, по следующей формуле: R123=R12R3/(R12+R3) = (R1+R2)R3/(R1+R2+R3). На последнем этапе выполняется расчет эквивалентного сопротивления всей цепи, путем суммирования полученных данных R123 и сопротивления R4, включенного последовательно с ним: Rэк = R123 + R4 = (R1 + R2) R3 / (R1 + R2 + R3) + R4.
В заключение следует отметить, что смешанное соединение резисторов обладает положительными и отрицательными качествами последовательного и параллельного соединения. Это свойство успешно используется на практике в электрических схемах.
Смешанное соединение резисторов. Расчет смешанного соединения
26 Ноя 2018г | Раздел: Радио и Электрика начинающим
Здравствуйте, уважаемые читатели сайта sesaga.ru. Смешанное соединение резисторов представляет собой сложную электрическую цепь, в которой часть резисторов соединена последовательно, а часть параллельно.
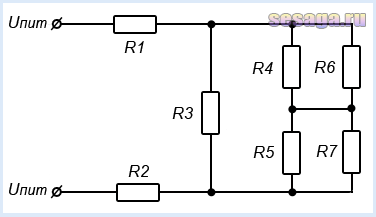
В радиолюбительской практике такое включение резисторов встретить трудно, так как нет смысла подбирать сопротивление таким сложным способом. Достаточно соединить два, ну максимум три резистора последовательно или параллельно, чтобы подобрать нужный номинал.
Смешанное соединение встречается в основном в учебниках физики или электротехники в виде задач. Мне вспоминается такая задачка из школьной программы, но тогда она мне показалась сложной и правильно решить ее не получилось.
И вот, исходя из полученного опыта, хочу рассказать Вам, как вычислить общее сопротивление смешанного соединения резисторов. Вдруг кому-нибудь в жизни да и пригодится.
Расчет смешанного соединения резисторов.
Расчет начинают от дальнего участка цепи по отношению к источнику питания.
Определяют участок с параллельным или последовательным соединением двух резисторов и высчитывают их общее сопротивление Rобщ. Затем полученное сопротивление складывают с рядом стоящим резистором и т.д.
Суть данного метода заключается в уменьшении количества элементов в цепи с целью упрощения схемы и, соответственно, упрощению расчета общего сопротивления.
Разберем схему смешанного соединения из семи резисторов:
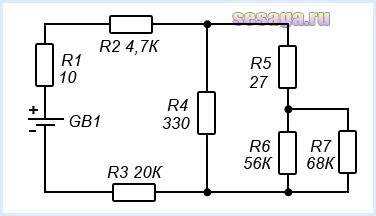
Самым дальним участком схемы оказались резисторы R6 и R7, соединенные параллельно:
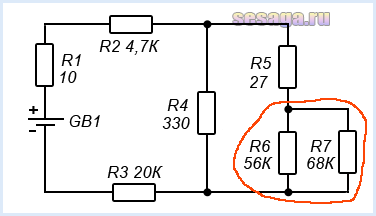
Вычисляем их общее сопротивление используя формулу параллельного соединения:
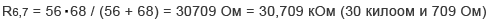
Теперь если сравнить первоначальную схему с получившейся, то здесь мы видим, что она уменьшилась на один элемент и вместо двух резисторов R6 и R7 остался один R6 с суммарным сопротивлением равным 30, 709 кОм.
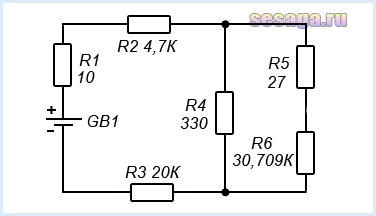
Продолжим расчет и следующим дальним участком схемы оказались резисторы R5 и R6, соединенные последовательно:
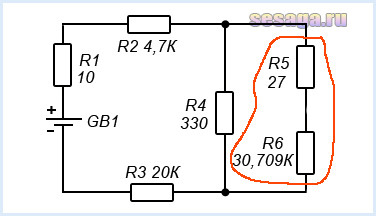
Вычисляем их общее сопротивление используя формулу последовательного соединения. Сопротивление резистора R5 составляет 27 Ом, а R6 = 30,709 кОм, поэтому для удобства расчета килоомы переводим в Омы (1 кОм = 1000 Ом):
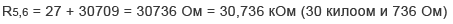
Схема уменьшилась еще на один элемент и приняла вид:
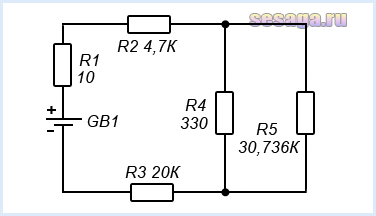
Теперь дальним участком оказались резисторы R4 и R5 соединенные параллельно:
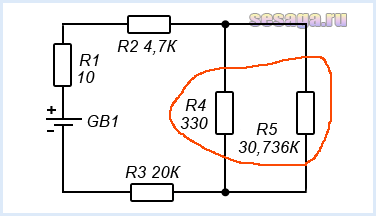
Вычисляем их общее сопротивление:
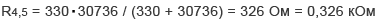
Первоначальная схема опять изменилась и теперь состоит всего из четырех резисторов соединенных последовательно. Таким образом мы максимально упростили схему и привели ее к удобному расчету.
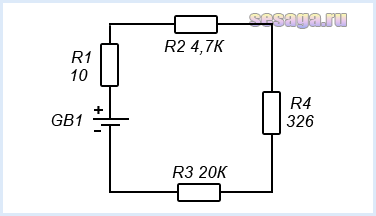
Теперь все просто. Складываем сопротивления оставшихся четырех резисторов, используя формулу последовательного соединения, и получаем общее сопротивление всей цепи:
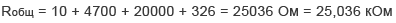
Вот в принципе и все, что хотел сказать о смешанном соединении резисторов и расчете смешанного соединения.
Удачи!
Поделиться с друзьями:
Еще интересно почитать:
Параллельное и смешанное соединение резисторов: разные способы подключения сопротивления
 Ни одна операция в электронике или электротехнике не обходится без вычисления сопротивления. В этом случае рассматривают только тот участок цепи, в котором находится смешанное соединение резисторов. Инженерам и физикам необходимо понимать то, как именно происходят расчёты в таких схемах. Всего разделяют несколько видов подключения, которые используются в цепях различной сложности.
Ни одна операция в электронике или электротехнике не обходится без вычисления сопротивления. В этом случае рассматривают только тот участок цепи, в котором находится смешанное соединение резисторов. Инженерам и физикам необходимо понимать то, как именно происходят расчёты в таких схемах. Всего разделяют несколько видов подключения, которые используются в цепях различной сложности.
Последовательное соединение
Выделяют такие способы соединения резисторов: последовательное, параллельное и комбинированное. При последовательном подключении конец первого резистора подключают к началу второго, его часть к третьему. Так действуют со всеми составляющими. То есть все компоненты цепи следуют друг за другом. Через них в таком подключении будет проходить один общий электрический ток. Для таких схем физики применяют формулу, в которой между точками А и В есть только один путь протекания заряженных электронов.
От количества подключённых резисторов зависит сопротивление протекающему электричеству. Чем больше составляющих, тем оно выше. Его рассчитывают по формуле: R общее = R1+R2+…+Rn, где:
- R общее — это сумма всех сопротивлений;
- R1 — первый резистор;
- R2 — второй компонент;
- Rn — последняя составляющая в цепи.
Параллельное подключение
Параллельное соединение подразумевает подключение начал резисторов к одной точке, а концов к другой. Сами компоненты при этом расположены на одинаковом расстоянии друг от друга, а их количество не ограничено. По каждой составляющей электричество протекает отдельно, выбирая один из нескольких путей.
 Из-за того, что в цепи находится несколько компонентов и путей прохода тока, сопротивление значительно меньше, чем при последовательном соединении. То есть общая сумма противодействия уменьшается пропорционально увеличению количества составляющих. Формула для определения общей суммы противостояния электричеству: 1/R общее = 1/R1+1/R2+…+1/Rn.
Из-за того, что в цепи находится несколько компонентов и путей прохода тока, сопротивление значительно меньше, чем при последовательном соединении. То есть общая сумма противодействия уменьшается пропорционально увеличению количества составляющих. Формула для определения общей суммы противостояния электричеству: 1/R общее = 1/R1+1/R2+…+1/Rn.
В расчётах общее сопротивление всегда должно быть меньше любого из составляющих цепи. Способ вычисления суммы противостояния для схемы из двух резисторов немного отличается: 1/R общее = (R1 х R2)/(R1+R2). Если в системе у компонентов одинаковые показатели сопротивления, то общее число будет равно половине одного из составляющих.
Смешанный вариант
В смешанном соединении сопротивлений комбинируют последовательную и параллельную схему подключений. В этом случае несколько компонентов соединяют одним способом, а другие — вторым, но все они включены в одну цепь. В физике такой метод соединения называют последовательно-параллельным.
Для вычисления суммы противостояния электричеству схему нужно разбить на мелкие участки, в которых резисторы подключены одинаковым способом. Затем расчёты проводят по алгоритму:
- в цепи с параллельно соединёнными компонентами высчитывают эквивалентное сопротивление;
- после этого высчитывают противостояние на последовательно подключённых участках схемы;
- наглядную иллюстрацию нужно перерисовать, обычно получается цепь с последовательным соединением резисторов;
- рассчитывают сопротивление в новой схеме по одной из двух формул.
Лучше понять методы вычислений поможет пример. Если в схеме всего пять компонентов, они могут располагаться по-разному. Начало первого резистора подключено к точке А, конец — к В. От неё идёт отдельная схема с комбинированным соединением. Вторая и третья составляющие находятся на последовательной линии, четвёртый компонент параллелен им. От конечной точки этой цепи — Г — исходит последний резистор.
Сначала высчитывают сумму сопротивления последовательного участка внутренней схемы: R2+R3. После этого цепь перерисовывают так, чтобы второй и третий компоненты были соединены в один. В результате внутренняя цепь имеет параллельное подключение. Теперь высчитывают её противостояние: (R2,3xR4)/(R2,3+R4). Можно второй раз изобразить полученную цепь.
В схеме будет три резистора, соединённые последовательным методов. Причём средний включает параметры второго, третьего и четвёртого компонента.
 Теперь можно узнать общую сумму сопротивлений. Для этого складывают показатели противостояний электричеству первого, пятого и остальных составляющих. Формула будет иметь вид: R1+(R2,3xR4)/(R2,3+R4)+R5. Можно сразу подставить в неё все параметры компонентов.
Теперь можно узнать общую сумму сопротивлений. Для этого складывают показатели противостояний электричеству первого, пятого и остальных составляющих. Формула будет иметь вид: R1+(R2,3xR4)/(R2,3+R4)+R5. Можно сразу подставить в неё все параметры компонентов.
На практике последовательный и параллельный метод соединения используются редко, ведь в приборах схемы обычно сложные. Поэтому в цепях резисторы часто соединены комбинированным способом. Сопротивление в таких случаях высчитывают пошагово.
Если сразу выводить числа в общую формулу, то можно ошибиться и получить неверные результаты. А это может отрицательно сказаться на работе электрического прибора.
как подключить резистор в цепь
Резистор — это прибор, который обладает устойчивым, стабильным показателем сопротивления. Это помогает производить регулировку параметров на любом участке схемы. В этой статье говорится о том, как подключить резистор в цепь и какие методы для этого существуют. Также продемонстрированы несколько простых, но полезных схем, которые могут пригодиться при работе с электрикой.
Что такое соединение резисторов
Подключение приборов различными методами помогает получить нужное число мощности одной единицы цепи. Есть три основных метода подключения прибора — последовательное, параллельное и смешанное. Ниже подробно рассказано о каждом из них.

Как выглядят резисторы
Внимание! Для работы необходимо использовать только качественные приборы, на которые действует гарантия.
Как подключить резистор в цепь
Для сборки составного устройства необходимо соединить несколько элементов одним из основных методов и таким образом получить нужный номинальный показатель. В практике это используется очень часто. Навыки правильного подключения устройств и расчета их общего сопротивления используются мастерами для ремонта проводки или радиолюбителями при сборке устройства. В интернете можно найти много схем с различным видом подключения. Ниже описано какое соединение резисторов называется параллельным.

Параллельное соединение резисторов схема
Параллельно
Параллельное — это одно из двух типов электрических соединений, когда два вывода единственного устройства соединены с соответствующими выводами других элементов. Очень часто их могут соединять последовательно или параллельно, чтобы сделать более усложненные электрические схемы.
При этом виде соединения напряжение на всех устройствах будет равным, а проходящий через них ток — пропорционален их сопротивлению.
Такой вариант подключения один из простых, очень часто именно его рекомендуют использовать тем, кто не имеет опыта работы с электрикой.
Последовательно
Формула расчета достаточно легкая. Общее сопротивление при параллельном соединении формула:
Rобщ. = R1+R2+R3+…+Rn.
Сопротивление двух и более параллельно соединенных резисторов указано как Rобщ.

Последовательный способ подключения
Остальные элементы указываются как R, R2, R3 и так далее.
Обратите внимание! Используя последовательное соединение, необходимо запомнить один важный нюанс. Из общего количества компонентов, соединённых последовательным методом, основную роль занимает тот, у которого самое высокое сопротивление.
Как это понять? Для примера, если необходимо соединить три устройства, номинал которых будет равняться 1, 10 и 100 Ом, то в итоге получится составной на 111 Ом.

Смешанный тип подключения
Если исключить прибор на 100 Ом, то все сопротивление схемы резко снизится до 11 Ом. А если исключить, например, на 1 Ом, то показатель получится уже 110 Ом. В итоге устройства с небольшим сопротивлениями в последовательной цепочке почти не влияют на все показатели.
Какая мощность тока при последовательном и параллельном соединении
При соединении устройств последовательным методом ток будет проходить через каждое сопротивление. Показатель тока в любом месте цепочки будет равным. Это правило определяется при помощи закона Ома. Если суммировать все показатели в цепи, получится такое выражение:

Образец цепи
R = 200+100+51+39 = 390 Ом.
Напряжение на схеме равняется 100 В, по правилу Ома сила тока будет выражаться:
I = U/R = 100/390 = 0,256 A.
Теперь с помощью этих уравнений можно посчитать мощность при последовательном подключении, используя это выражение:
P = I2 x R = 0,2562×390 = 25,55 Вт.
При параллельном соединении все основания нужно подсоединить к одному узлу цепи, а концы — к другому. В таком варианте получается разветвление тока, и он будет проходить по каждому узлу. По правилу Ома, сила тока будет обратно пропорциональна всем имеющимся устройствам, а показатель напряжения везде одинаковый.
При смешанном подключении используются свойства обоих видов соединений.

Закон Ома для участка цепи
Как правильно рассчитать сопротивление
Для выбора и установки элементов в цепь нужно заранее просчитать номинал и мощность составных частей.
Применяют для этого правило Ома для участка цепи, чтобы рассчитать сопротивление, выражение выглядит так:
R = U/I.
U — будет напряжением на выводах компонента.
I — показатель тока на участке цепи.
Это выражение используется для токов постоянного направления.
Если трудно самостоятельно рассчитать этот показатель, то существуют специальные онлайн-калькуляторы. Туда необходимо вставить имеющиеся значения и можно получить результат за секунды. Но поскольку закон Ома изучается еще в школе, то не составит проблем провести вычисления самостоятельно.
Внимание! Если нет опыта в работе с электрикой, желательно не выполнять ремонт проводки самостоятельно, потому что при неправильной работе может случиться короткое замыкание, что чревато возникновением пожара. Также необходимо помнить, что при работе с проводкой нужно полностью обесточить сеть.

Подключение для светодиодов
В заключении необходимо отметить, что подключать резисторы можно тремя способами: параллельно, последовательно и смешанно. Для тех, кто не имеет особых навыков работы с электрикой, рекомендуется выбирать последовательный метод соединения.
1.8.3. Смешанное соединение резисторов
Смешаннымсоединением называют сочетание последовательного и параллельного соединений резисторов. Большое разнообразие этих соединений не позволяет вывести общую формулу для определения эквивалентного сопротивления цепи. Поэтому в каждом конкретном случае, используя методы расчета при последовательном и параллельном соединениях, можно рассчитать эквивалентное сопротивление при смешанном соединении. Поясним это на конкретном примере расчета электрической цепи (рис. 1.20 а).
Электрическую цепь постепенно упрощают и приводят к простейшему виду (рис. 1.20 б, в)
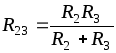 ;
;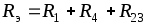 ;
;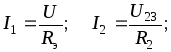
 ;
;
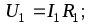
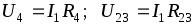 .
.
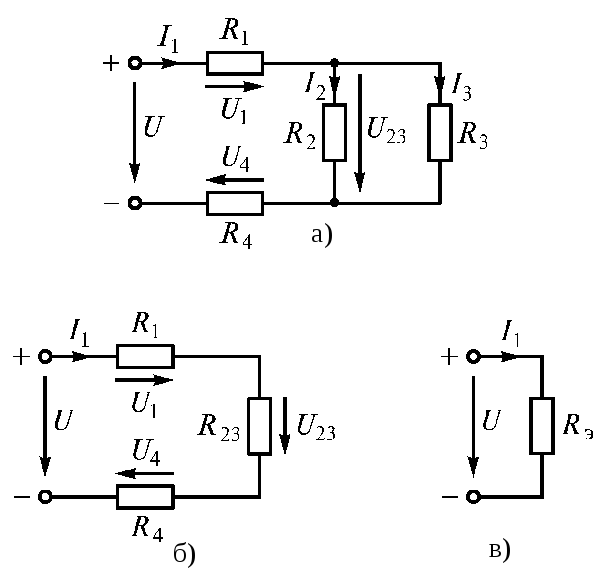
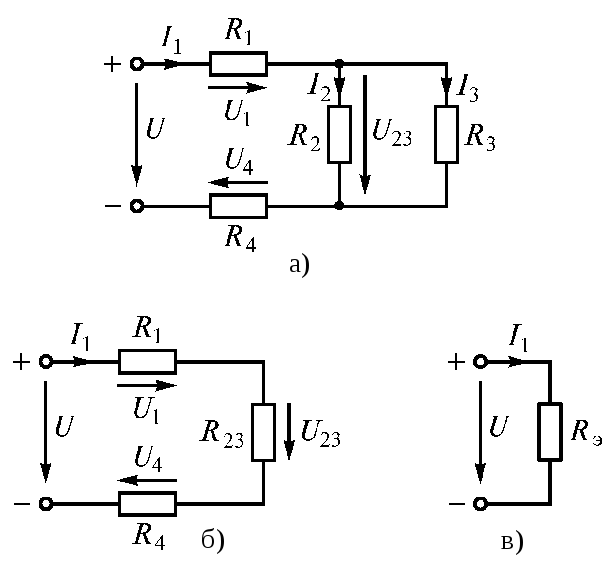
Рис. 1.20
Проверка: 1)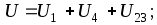 2)
2)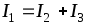 .
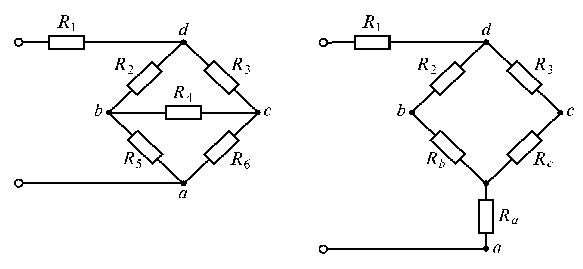
.1.8.4. Метод преобразований треугольника резисторов в эквивалентную звезду и наоборот
Рассмотрим две электрические цепи (рис. 1.21). Одна из них имеет вид треугольника, другая – трехлучевой звезды. В дальнейшем такие соединения будем называть соответственно соединением в треугольник и соединением звездой.

Рис. 1.21
Соединения такого вида очень распространены в трехфазных цепях, в которых часто возникает необходимость перехода от одного вида соединения к другому (эквивалентному). Эквивалентность треугольника и звезды резисторов заключается в том, что их замена не изменяет потенциалов узловых точек (φа, φb иφс), являющихся вершинами треугольника и эквивалентной звезды. Не изменяются также токи, напряжения и мощности в остальной части схемы, не затронутой преобразованием.
Формулы пересчета без вывода сопротивлений
ветвей треугольника 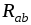 ,
,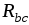 ,
,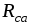 в эквивалентную звезду
в эквивалентную звезду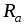 ,
,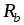 ,
, имеют вид
имеют вид
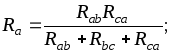
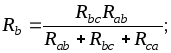
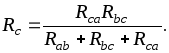 (1.39)
(1.39)
При переходе от звезды к треугольнику можно воспользоваться следующими формулами

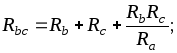
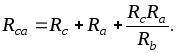 (1.40)
(1.40)
Если сопротивления всех ветвей цепи
по схеме треугольник одинаковы, т.е. 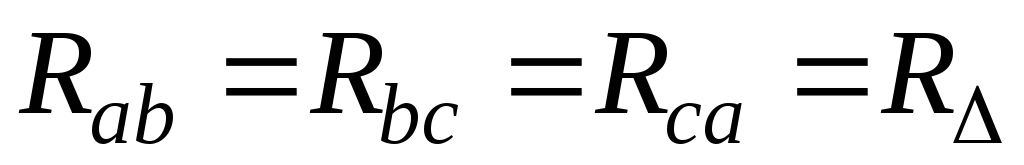 ,
сопротивления эквивалентной звезды
будут также одинаковые:
,
сопротивления эквивалентной звезды
будут также одинаковые: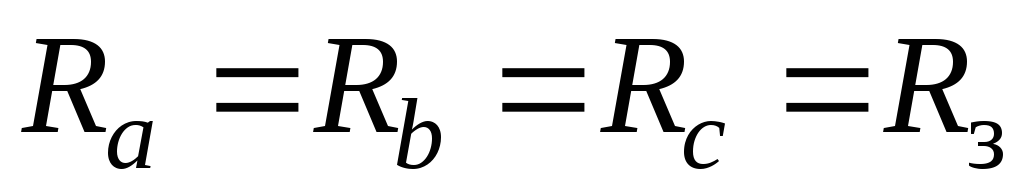 ,
причем
,
причем
 .
.
1.8.5. Последовательное соединение источников энергии
В практике последовательное и согласное включение источников применяют для увеличения напряжения. Рассмотрим схему с двумя согласно и одним встречно включенными источниками (рис. 1.22).
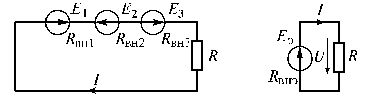
Рис. 1.22
По второму закону Кирхгофа запишем
 .
(1.41)
.
(1.41)
Отсюда
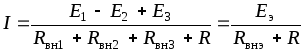 ,
(1.42)
,
(1.42)
где 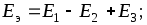
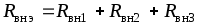 .
.
Напряжения на зажимах источников и приемника
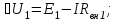
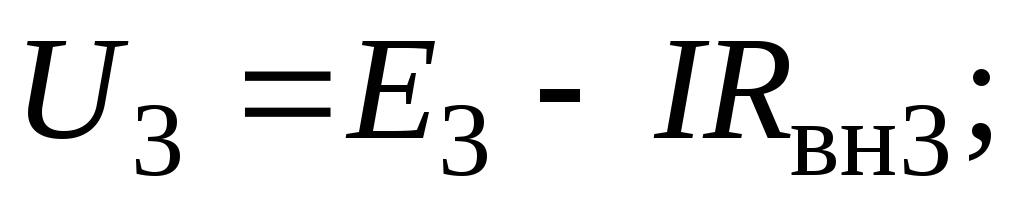
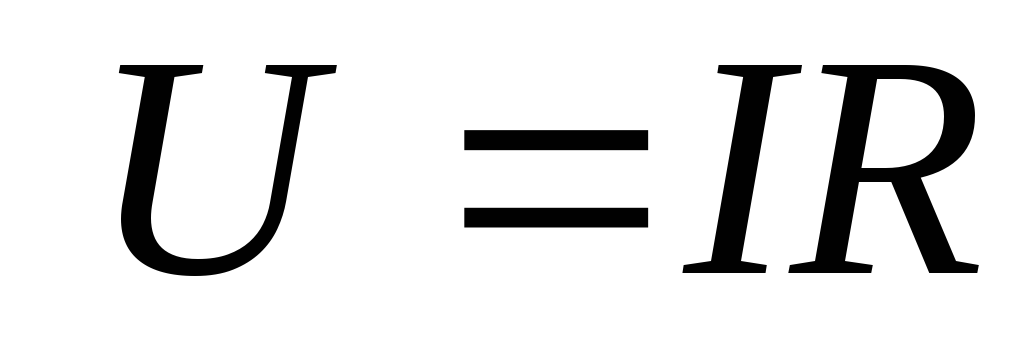 .
.
При последовательном соединении  источников с одинаковыми параметрами
источников с одинаковыми параметрами
 .
(1.43)
.
(1.43)
1.8.6. Параллельное соединение источников энергии
В тех случаях, когда номинальное напряжение приемника равно напряжению одного источника, а его ток больше допустимого тока одного источника, применяют параллельное соединение источников (рис. 1.23 а).
При параллельном
соединении источников с одинаковыми
параметрами их общая ЭДС не изменится,
но уменьшатся токи через каждый источник
и внутреннее сопротивление общего
источника. Тогда эквивалентный источник
(рис. 1.23 б) имеет следующие параметры: 
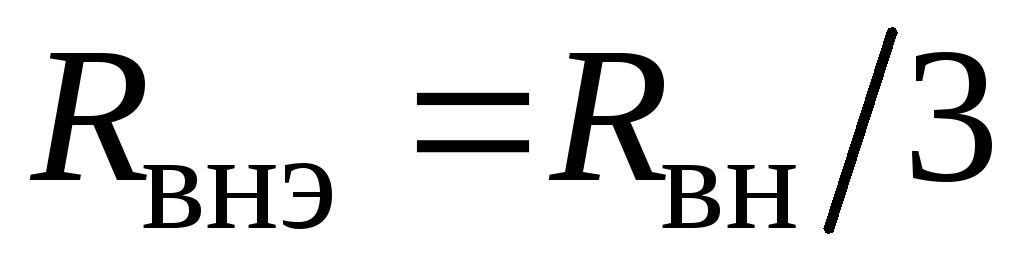 .
.
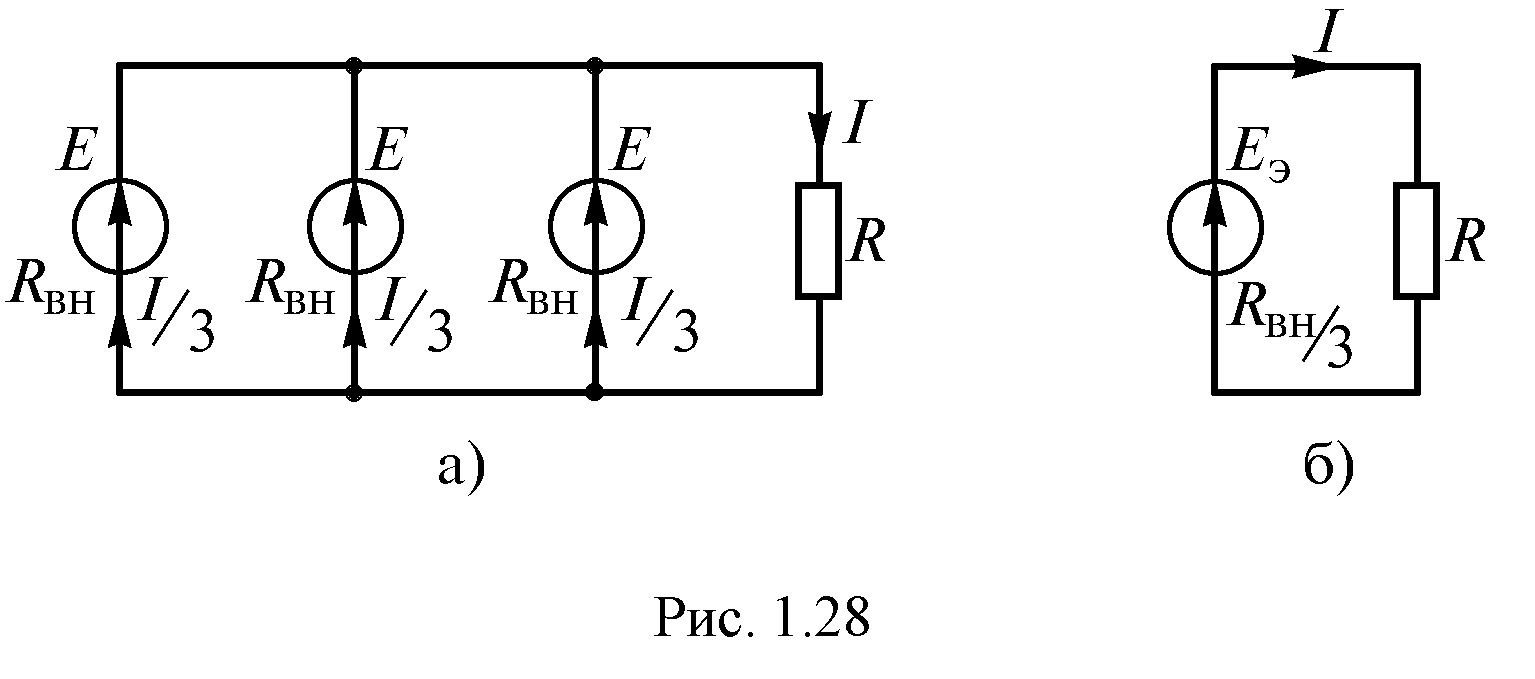
Рис. 1.23
При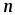 источниках
источниках
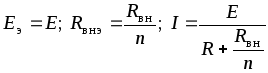 .
(1.44)
.
(1.44)
 Пример
1.1. Определить
эквивалентное сопротивление цепи (рис.
1.24 а),
если
Пример
1.1. Определить
эквивалентное сопротивление цепи (рис.
1.24 а),
если  1Ом;
1Ом; 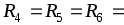 3Ом.
3Ом.
а) б)
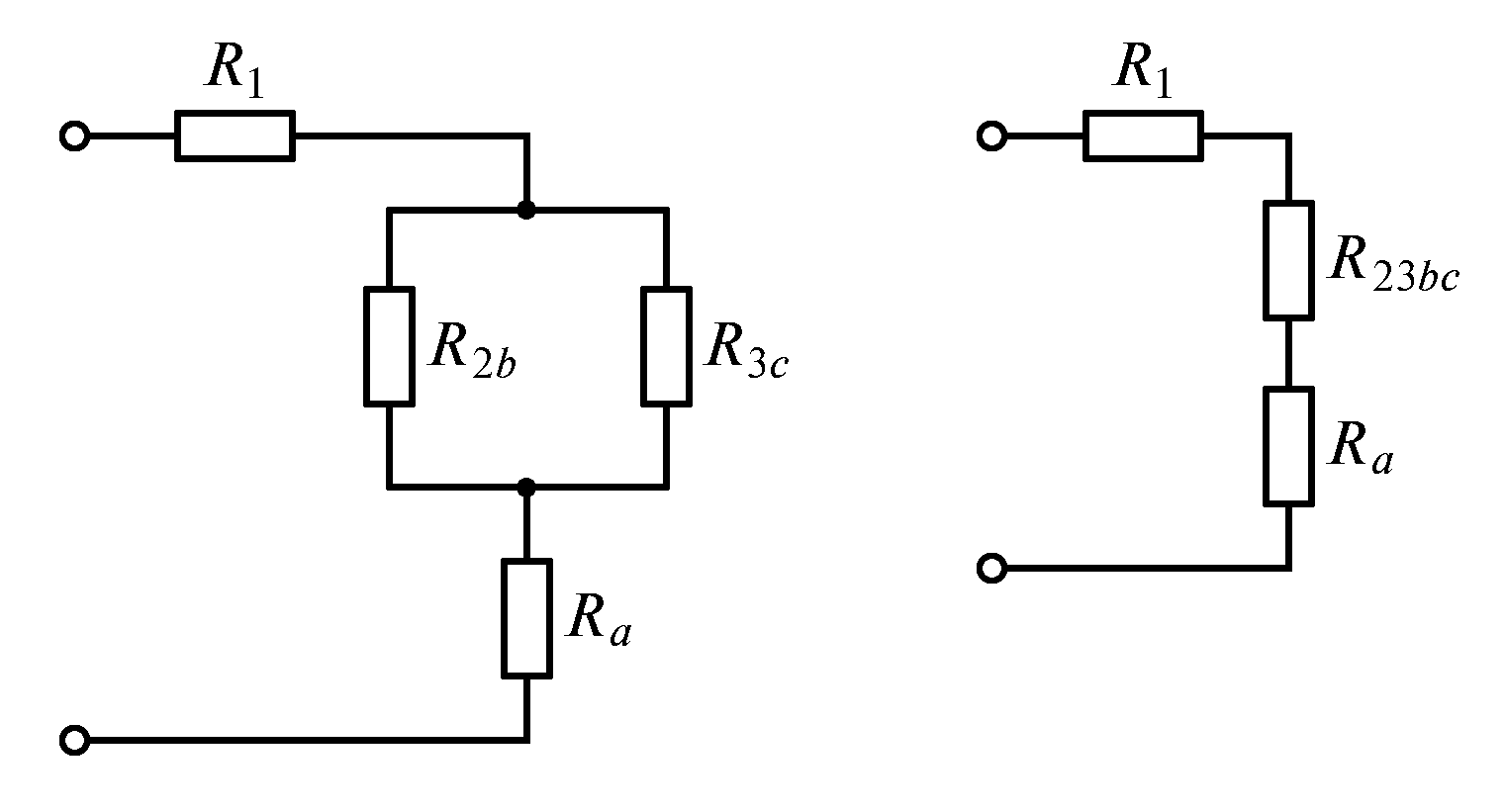
в) г)
Рис. 1.24
Решение. Преобразуем
треугольник сопротивлений  в эквивалентную
звезду сопротивлений
в эквивалентную
звезду сопротивлений 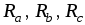 (рис. 1.24 б).
Так как
(рис. 1.24 б).
Так как 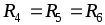 ,
то
,
то
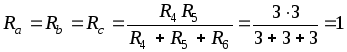 Ом.
Ом.
Дальнейшее решение
выполним преобразованием последовательно или параллельно
соединенных сопротивлений резисторов
их эквивалентными сопротивлениями
«свертыванием» схемы. Резисторы 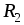 и
и ,
а также
,
а также и
и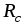 соединены последовательно, поэтому их
общие сопротивления
соединены последовательно, поэтому их
общие сопротивления
 Ом;
Ом; Ом.
Ом.
Полученная схема приведена на рис. 1.24 в.
Резисторы 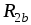 и
и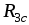 соединены параллельно, поэтому (рис.
1.24 г)
соединены параллельно, поэтому (рис.
1.24 г)
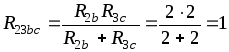 Ом.
Ом.
Эквивалентное сопротивление всей цепи
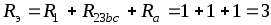 Ом.
Ом.
Пример 1.2.Определить токи в ветвях
цепи (рис. 1.25 а), если задано: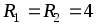 Ом;
Ом;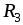 = 6Ом;
= 6Ом;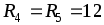 Ом;
Ом;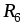 = 2Ом;
= 2Ом;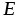 = 100В.
= 100В.
Решение. Резисторы  и
и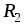 соединены последовательно и образуют
ветвь с током
соединены последовательно и образуют
ветвь с током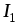 .
Резисторы
.
Резисторы и
и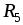 включены параллельно, а относительно
резистора
включены параллельно, а относительно
резистора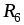 – последовательно. Вычислим эквивалентные
сопротивления:
– последовательно. Вычислим эквивалентные
сопротивления:
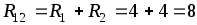 Ом;
Ом;
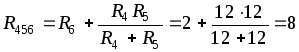 Ом.
Ом.
Рис. 1.25
Резисторы  и
и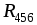 соединены параллельно, а по отношению
к
соединены параллельно, а по отношению
к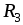 – последовательно, поэтому (рис. 1.25
б, в)
– последовательно, поэтому (рис. 1.25
б, в)
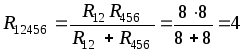 Ом.
Ом.
Эквивалентное сопротивление цепи
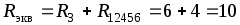 Ом.
Ом.
Ток в ветви с источником
 А.
А.
Так как сопротивления резисторов 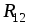 и
и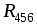 одинаковы, то
одинаковы, то
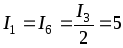 А.
А.
Аналогично, при 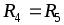
 А.
А.
Смешанное соединение резисторов
Смешанное соединение резисторов. Смешанным соединением резисторов называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
Рис. 27. Схемы смешанного соединения сопротивлений
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле

R123=R12R3/(R12+R3)=(R1+R2)R3/(R1+R2+R3).
При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:
Rэк = R123 + R4 = (R1 + R2) R3 / (R1 + R2 + R3) + R4
Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.




