Силы, действующие на движущиеся заряды в магнитном поле
Закон Ампера: сила
 ,
с которой магнитное поле действует на
элемент
,
с которой магнитное поле действует на
элемент  проводника с током, находящегося в
магнитном поле, прямо пропорциональна
силе тока I в проводнике и векторному произведению
элемента длины проводника на магнитную
индукцию
проводника с током, находящегося в
магнитном поле, прямо пропорциональна
силе тока I в проводнике и векторному произведению
элемента длины проводника на магнитную
индукцию  :
:
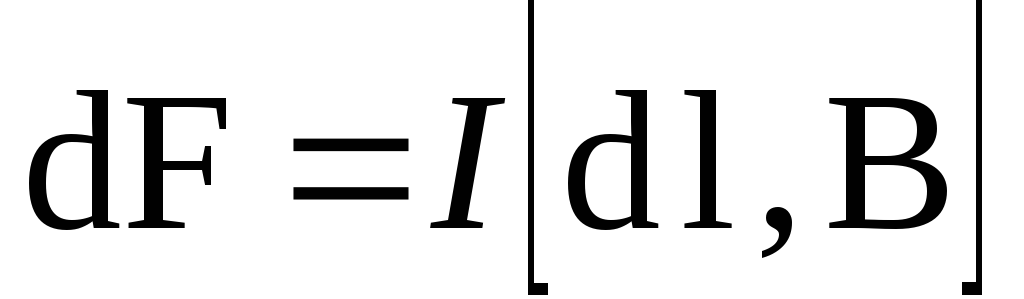 или
или  .
.
 .
. 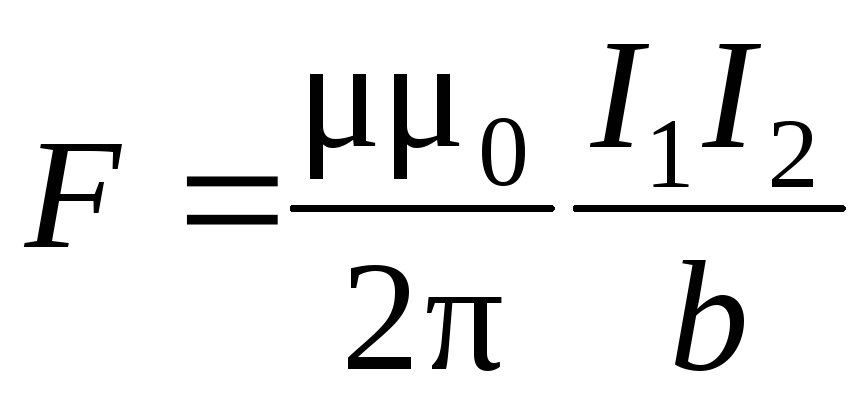 .
.
Сила Лоренца – это сила, действующая со стороны магнитного поля на движущийся со скорость
 положительный заряд (здесь
положительный заряд (здесь  скорость
упорядоченного движения носителей
положительного заряда):
скорость
упорядоченного движения носителей
положительного заряда):
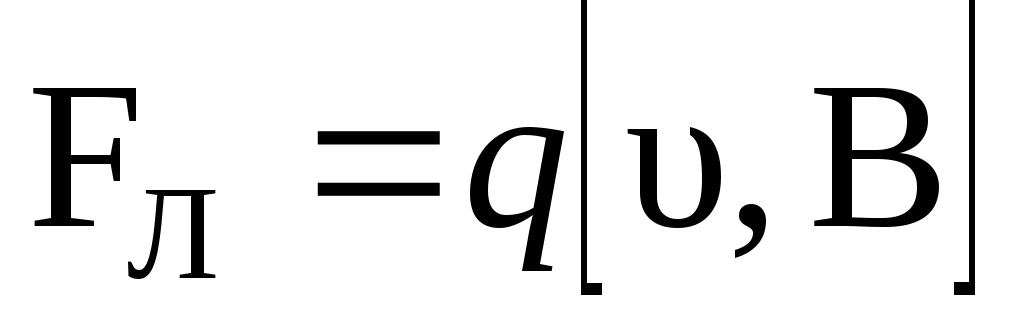
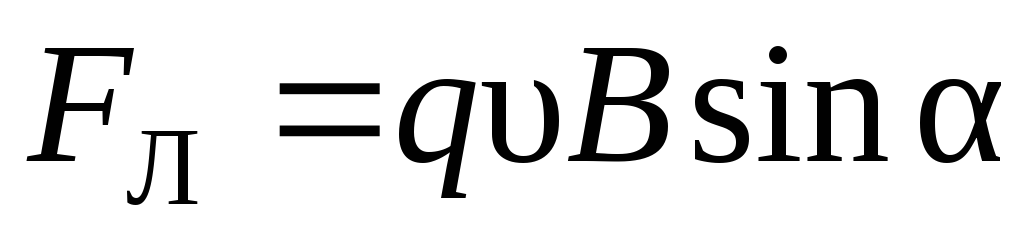 ,
, 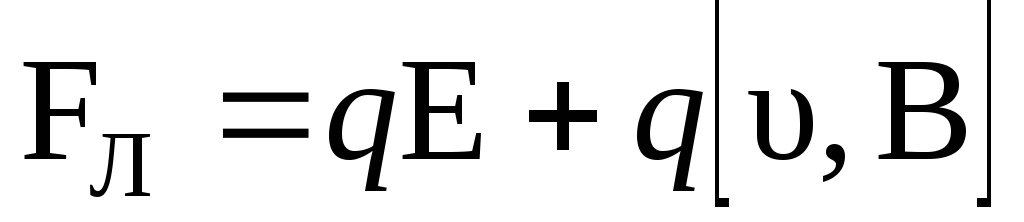 .
.Теорема о циркуляции вектора
 :
циркуляция вектора магнитной индукции
равна току, охваченному контуром,
умноженному на магнитную постоянную:
:
циркуляция вектора магнитной индукции
равна току, охваченному контуром,
умноженному на магнитную постоянную:

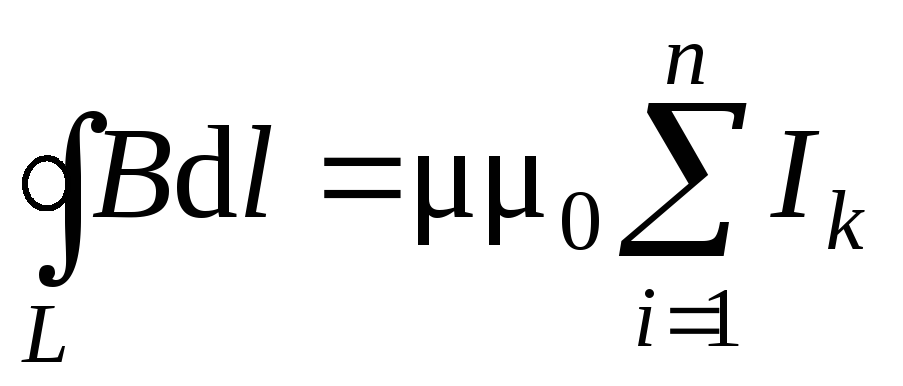
т.е. циркуляция
вектора  равна алгебраической сумме токов,
охваченных контуром произвольной формы.
равна алгебраической сумме токов,
охваченных контуром произвольной формы.
Теорема о циркуляции вектора
 :
циркуляция вектора напряженности
магнитного поля равна току, охваченному
контуром
:
циркуляция вектора напряженности
магнитного поля равна току, охваченному
контуром

Работа по перемещению проводника с током в магнитном поле – это работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересеченный этим проводником:
 .
.
Работа по перемещению замкнутого контура в магнитном поле – это работа, совершаемая при перемещении замкнутого контура, с током в магнитном поле, равна произведению величины тока на изменение магнитного потока, сцепленного с эти контуром:
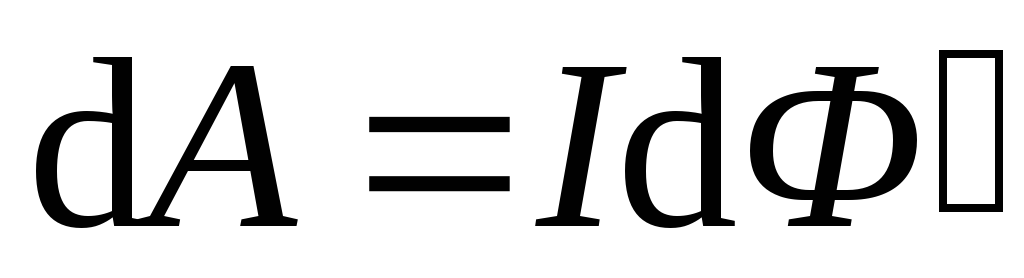 .
.

где 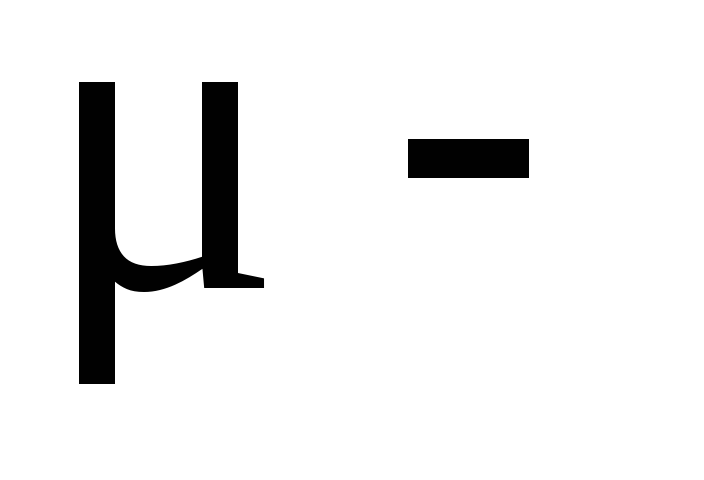 магнитная
проницаемость вещества; п – число витков на единицу длины; I – ток в соленоиде.
магнитная
проницаемость вещества; п – число витков на единицу длины; I – ток в соленоиде.
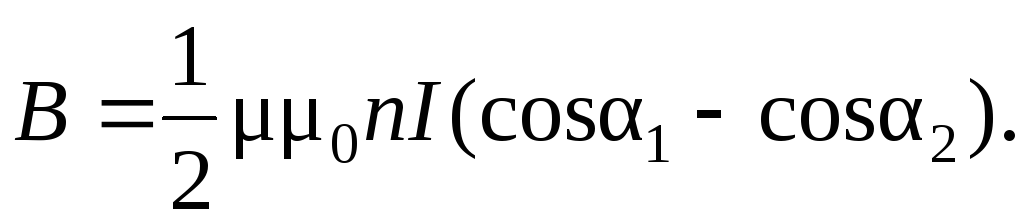
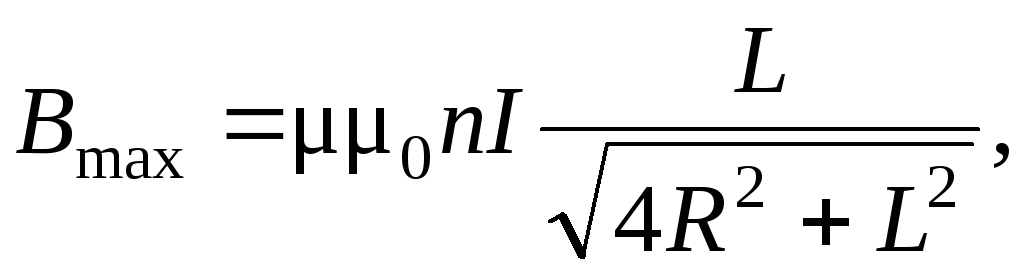
где L – длина соленоида; R – радиус витков.
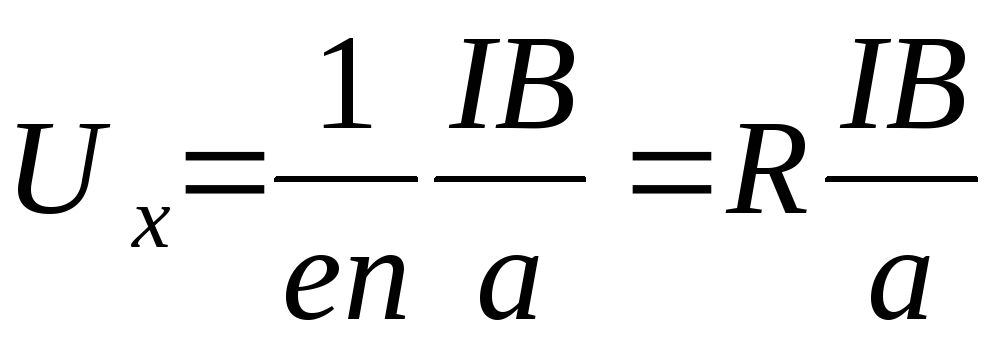
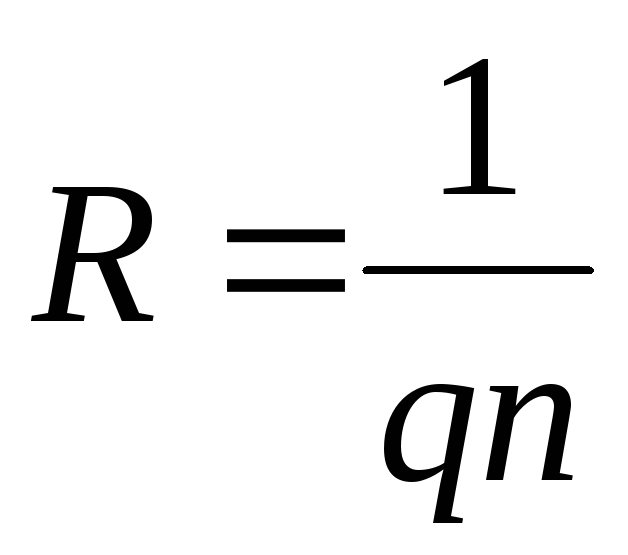 .
.
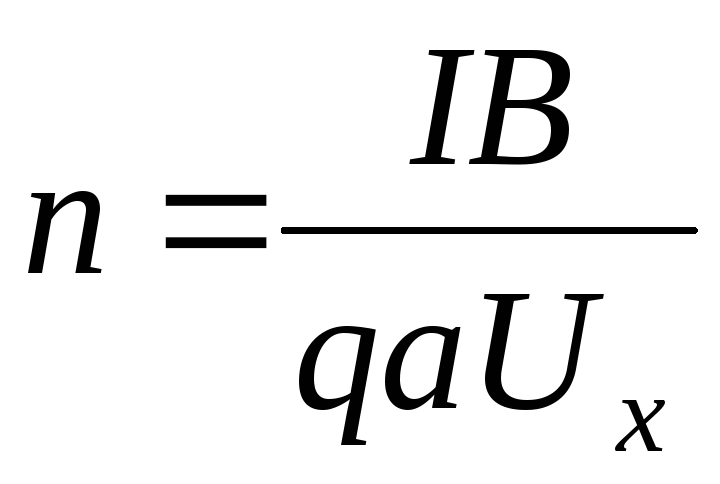 .
.
Явление электромагнитной индукции
Закон фарадея: ЭДС индукции контура равна скорости изменения потока магнитной индукции, пронизывающей этот контур.
 или
или  ,
,
где 
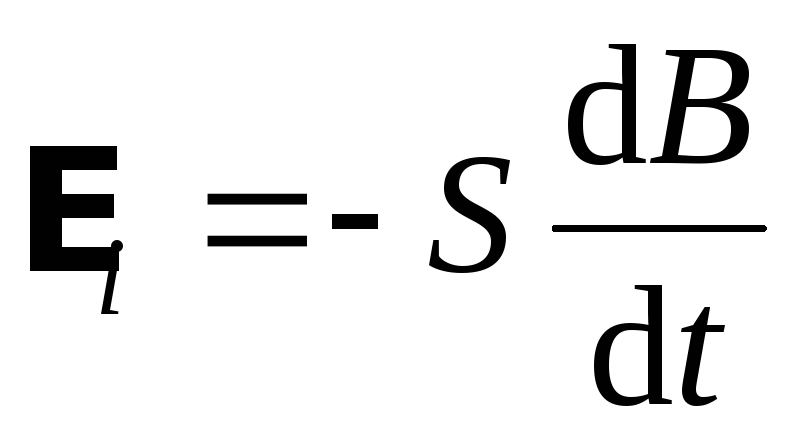 .
.
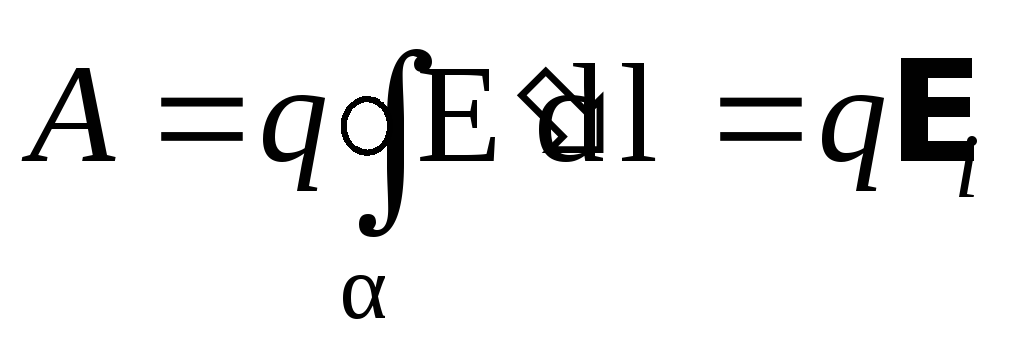 .
.
Ускорители заряженных частиц
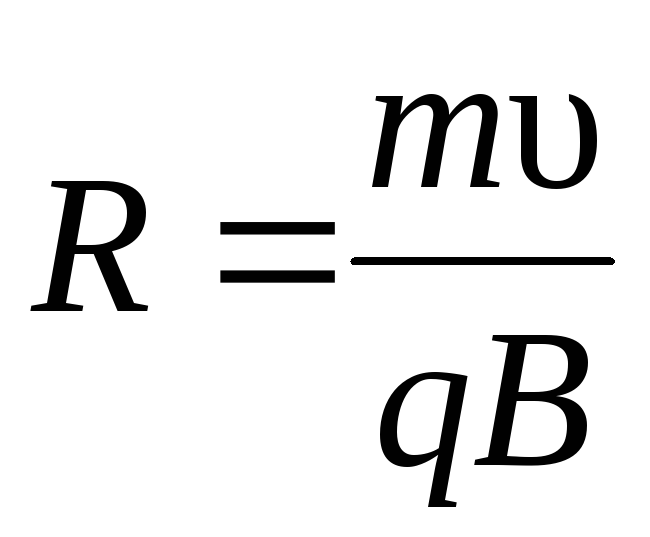 .
.
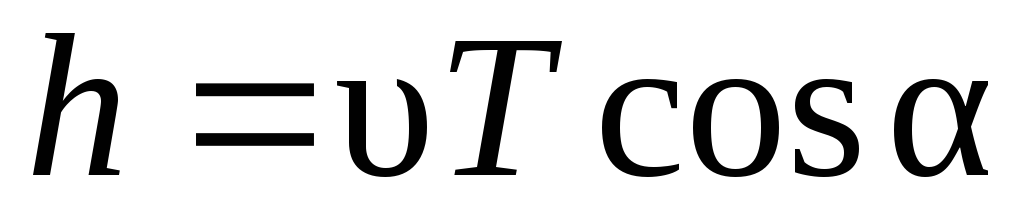 .
.
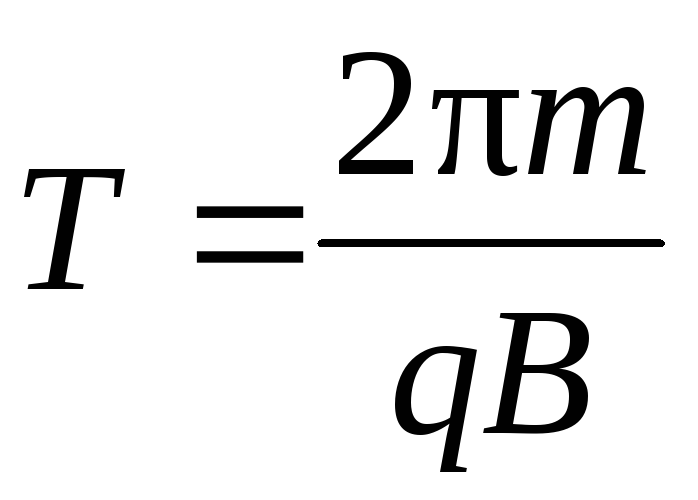
 ,
,
где с – скорость света в вакууме; 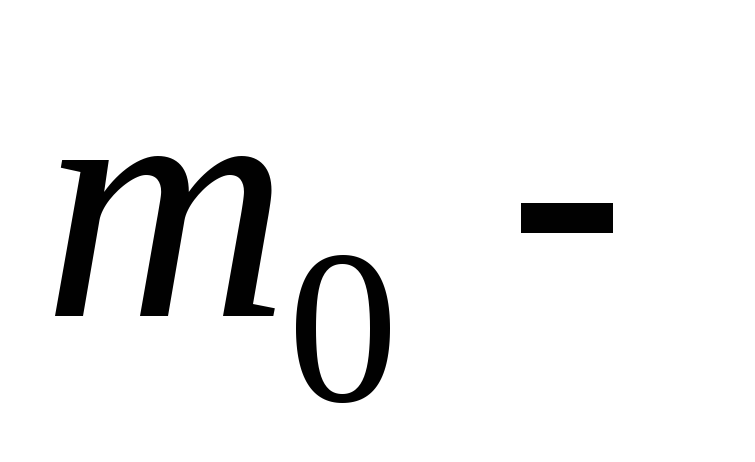 масса
покоя частицы.
масса
покоя частицы.
,
где Е – полная энергия частицы; Е0 – энергия покоя.
 .
.
.
 .
.
формулы. Движение заряженных частиц в однородном магнитном поле :: SYL.ru
Как известно, электрическое поле принято характеризовать величиной силы, с которой оно действует на пробный единичный электрический заряд. Магнитное поле традиционно характеризуют силой, с которой оно действует на проводник с «единичным» током. Однако при его протекании происходит упорядоченное движение заряженных частиц в магнитном поле. Поэтому мы можем определить магнитное поле B в какой-то точке пространства с точки зрения магнитной силы FB, которую поле оказывает на частицу при ее движении в нем со скоростью v.
Общие свойства магнитной силы
Эксперименты, в которых наблюдалось движение заряженных частиц в магнитном поле, дают такие результаты:
- Величина FB магнитной силы, действующей на частицу пропорциональна заряду q и скорости v частицы.
- Если движение заряженной частицы в магнитном поле происходит параллельно вектору этого поля, то сила, действующая на нее, равна нулю.
- Когда вектор скорости частицы составляет любой Угол θ ≠ 0 с магнитным полем, то сила действует в направлении, перпендикулярном к v и B; то есть, FB перпендикулярна плоскости, образованной v и B (см.рис. ниже).
- Величина и направление FB зависит от скорости частицы и от величины и направления магнитного поля B.
- Направление силы, действующей на положительный заряд, противоположно направлению такой же силы, действующей на отрицательный заряд, движущийся в ту же сторону.
- Величина магнитной силы, действующей на движущуюся частицу, пропорциональна sinθ угла θ между векторами v и B.
Сила Лоренца
Мы можем суммировать вышеперечисленные наблюдения путем записи магнитной силы в виде FB= qv х B.
Когда происходит движение заряженной частицы в магнитном поле, сила Лоренца FB при положительном q направлена вдоль векторного произведения v x B. Оно по определению перпендикулярно как v, так и B. Считаем это уравнение рабочим определением магнитного поля в некоторой точке в пространстве. То есть оно определяется в терминах силы, действующей на частицу при ее движении. Таким образом, движение заряженной частицы в магнитном поле кратко можно определить как перемещение под действием этой силы.
Заряд, движущийся со скоростью v в присутствии как электрического поля E, так и магнитного B, испытывает действие как электрической силы qE, так и магнитной qv х В. Полное приложенное к нему воздействие равно FЛ = qE + qv х В. Его принято называть так: полная сила Лоренца.
Движение заряженных частиц в однородном магнитном поле
Рассмотрим теперь частный случай положительно заряженной частицы, движущейся в однородном поле, с начальным вектором скорости, перпендикулярным ему. Предположим, что вектор B поля направлен за страницу. Рисунок ниже показывает, что частица движется по кругу в плоскости, перпендикулярной к B.
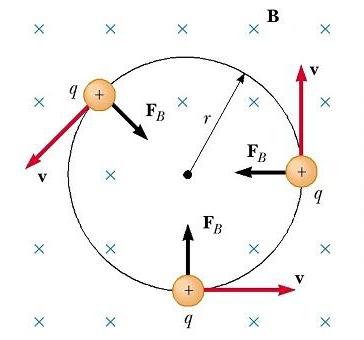
Движение заряженной частицы в магнитном поле по окружности происходит потому, что магнитная сила FB направлена под прямым углом к v и B и имеет постоянную величину qvB. Поскольку сила отклоняет частицы, направления v и FB изменяются непрерывно, как показано на рисунке. Так как FB всегда направлена к центру окружности, она изменяет только направление v, а не ее величину. Как показано на рисунке, движение положительно заряженной частицы в магнитном поле происходит против часовой стрелки. Если q будет отрицательным, то вращение произойдет по часовой стрелке.
Динамика кругового движения частицы
Какие же параметры характеризуют вышеописанное движение заряженной частицы в магнитном поле? Формулы для их определения мы можем получить, если возьмем предыдущее уравнение и приравняем FB центробежной силе, требуемой для сохранения круговой траектории движения:
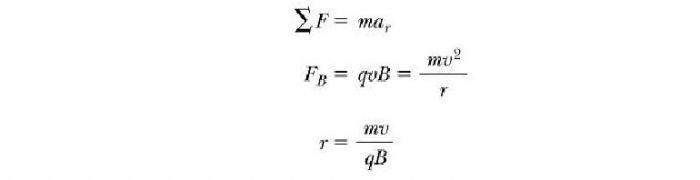
То есть радиус окружности пропорционален импульсу mv частицы и обратно пропорционален величине ее заряда и величине магнитного поля. Угловая скорость частицы
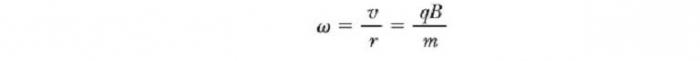
Период, с которым происходит движение заряженной частицы в магнитном поле по кругу, равен длине окружности, разделенной на ее линейную скорость:
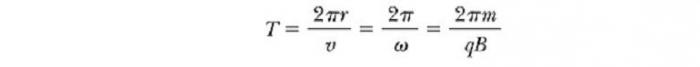
Эти результаты показывают, что угловая скорость частицы и период кругового движения не зависит от линейной скорости или от радиуса орбиты. Угловую скорость ω часто называют циклотронной частотой (круговой), потому что заряженные частицы циркулируют с ней в типе ускорителя под названием циклотрон.
Движение частицы под углом к вектору магнитного поля
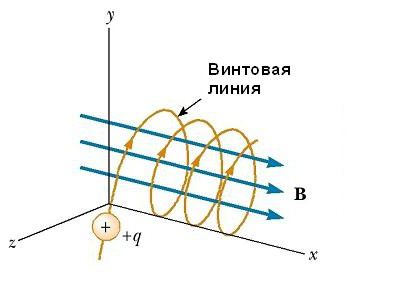
Если вектор v скорости частицы образует некоторый произвольный угол по отношению к вектору B, то ее траектория является винтовой линией. Например, если однородное поле будет направлено вдоль оси х, как показано на рисунке ниже, то не существует никакой компоненты магнитной силы FB в этом направлении. В результате составляющая ускорения ax= 0, и х-составляющая скорости движения частицы является постоянной. Однако магнитная сила FB = qv х В вызывает изменение во времени компонентов скорости vy и vz. В результате имеет место движение заряженной частицы в магнитном поле по винтовой линии, ось которой параллельна магнитному полю. Проекция траектории на плоскости yz (если смотреть вдоль оси х) представляет собой круг. Проекции ее на плоскости ху и xz являются синусоидами! Уравнения движения остаются такими же, как и при круговой траектории, при условии, что v заменяется на ν⊥ = √(νу2 + νz2).
Неоднородное магнитное поле: как в нем движутся частицы
Движение заряженной частицы в магнитном поле, являющемся неоднородным, происходит по сложным траекториям. Так, в поле, величина которого усиливается по краям области его существования и ослабляется в ее середине, как, например, показано на рисунке ниже, частица может колебаться вперед и назад между конечными точками.
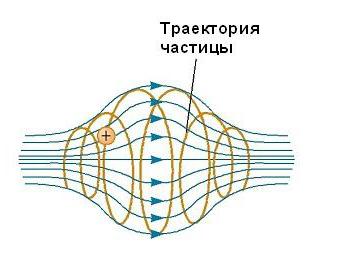 Заряженная частица стартует с одного конца винтовой линии, накрученной вдоль силовых линий, и движется вдоль нее, пока не достигнет другого конца, где она поворачивает свой путь обратно. Эта конфигурация известна как «магнитная бутылка», поскольку заряженные частицы могут быть захвачены в нее. Она была использована, чтобы ограничить плазму, газ, состоящий из ионов и электронов. Такая схема плазменного заключения может выполнять ключевую роль в контроле ядерного синтеза, процессе, который представит нам почти бесконечный источник энергии. К сожалению, «магнитная бутылка» имеет свои проблемы. Если в ловушке большое число частиц, столкновения между ними вызывают утечку их из системы.
Заряженная частица стартует с одного конца винтовой линии, накрученной вдоль силовых линий, и движется вдоль нее, пока не достигнет другого конца, где она поворачивает свой путь обратно. Эта конфигурация известна как «магнитная бутылка», поскольку заряженные частицы могут быть захвачены в нее. Она была использована, чтобы ограничить плазму, газ, состоящий из ионов и электронов. Такая схема плазменного заключения может выполнять ключевую роль в контроле ядерного синтеза, процессе, который представит нам почти бесконечный источник энергии. К сожалению, «магнитная бутылка» имеет свои проблемы. Если в ловушке большое число частиц, столкновения между ними вызывают утечку их из системы.Как Земля влияет на движение космических частиц
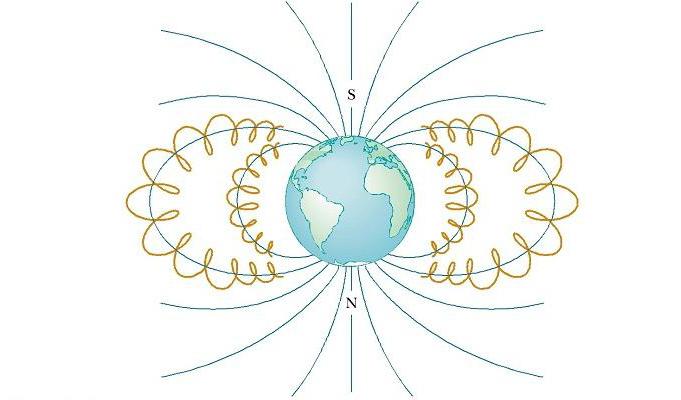
Околоземные пояса Ван Аллена состоят из заряженных частиц (в основном электронов и протонов), окружающих Землю в форме тороидальных областей (см. рис. ниже). Движение заряженной частицы в магнитном поле Земли происходит по по спирали вокруг силовых линий от полюса до полюса, покрывая это расстояние в несколько секунд. Эти частицы идут в основном от Солнца, но некоторые приходят от звезд и других небесных объектов. По этой причине они называются космическими лучами. Большинство их отклоняется магнитным полем Земли и никогда не достигает атмосферы. Тем не менее, некоторые из частиц попадают в ловушку, именно они составляют пояса Ван Аллена. Когда они находятся над полюсами, иногда происходят столкновения их с атомами в атмосфере, в результате чего последние излучают видимый свет. Так возникают красивые Полярные сияния в Северном и Южном полушариях. Они, как правило, происходят в полярных регионах, потому что именно здесь пояса Ван Аллена расположены ближе всего к поверхности Земли.
Иногда, однако, солнечная активность вызывает большее число заряженных частиц, входящих в эти пояса, и значительно искажает нормальные силовые линии магнитного поля, связанные с Землей. В этих ситуациях полярное сияние можно иногда увидеть в более низких широтах.
Селектор скоростей
Во многих экспериментах, в которых происходит движение заряженных частиц в однородном магнитном поле, важно, чтобы все частицы двигались с практически одинаковой скоростью. Это может быть достигнуто путем применения комбинации электрического поля и магнитного поля, ориентированного так, как показано на рисунке ниже. Однородное электрическое поле направлено вертикально вниз (в плоскости страницы), а такое же магнитное поле приложено в направлении, перпендикулярном к электрическому (за страницу).
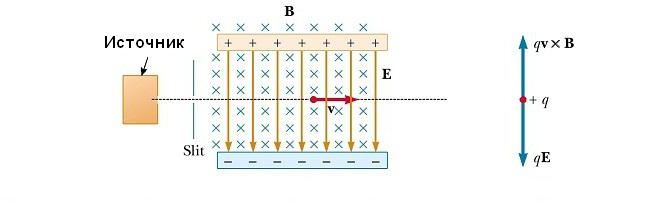 Для положительного q магнитная сила FB=qv х В направлена вверх, а электрическая сила qE – вниз. Когда величины двух полей выбраны так, что qE = qvB, то частица движется по прямой горизонтальной линии через область поля. Из выражения qE = qvB мы находим, что только частицы, имеющие скорость v=E/B, проходят без отклонения через взаимно перпендикулярные электрическое и магнитное поля. Сила FB, действующая на частицы, движущиеся со скоростью большей, чем v=E/B, оказывается больше электрической, и они отклоняются вверх. Те же из них, которые движутся с меньшей скоростью, отклоняются вниз.
Для положительного q магнитная сила FB=qv х В направлена вверх, а электрическая сила qE – вниз. Когда величины двух полей выбраны так, что qE = qvB, то частица движется по прямой горизонтальной линии через область поля. Из выражения qE = qvB мы находим, что только частицы, имеющие скорость v=E/B, проходят без отклонения через взаимно перпендикулярные электрическое и магнитное поля. Сила FB, действующая на частицы, движущиеся со скоростью большей, чем v=E/B, оказывается больше электрической, и они отклоняются вверх. Те же из них, которые движутся с меньшей скоростью, отклоняются вниз.Масс-спектрометр
Этот прибор разделяет ионы в соответствии с соотношением их массы к заряду. По одной из версий этого устройства, известного как масс-спектрометр Бэйнбриджа, пучок ионов проходит сначала через селектор скоростей и затем поступает во второе поле B0, также однородное и имеющее то же направление, что и поле в селекторе (см. рис. ниже). После входа в него движение заряженной частицы в магнитном поле происходит по полукругу радиуса r перед ударом в фотопластинку Р. Если ионы заряжены положительно, луч отклоняется вверх, как показано на рисунке. Если ионы заряжены отрицательно, луч будет отклоняться вниз. Из выражения для радиуса круговой траектории частицы, мы можем найти отношение m/q
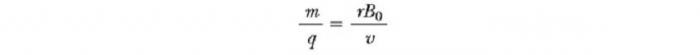
и затем, используя уравнение v=E/B, мы находим, что
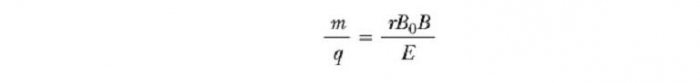
Таким образом, мы можем определить m/q путем измерения радиуса кривизны, зная поля величин B, B0, и E. На практике, так обычно измеряет массы различных изотопов данного иона, поскольку все они несут один заряд q. Таким образом, отношение масс может быть определено, даже если q неизвестно. Разновидность этого метода была использована Дж. Дж. Томсоном (1856-1940) в 1897 году для измерения отношение е/mе для электронов.
Циклотрон
Он может ускорить заряженные частицы до очень высоких скоростей. И электрические, и магнитные силы играют здесь ключевую роль. Полученные высокоэнергетические частицы используются для бомбардировки атомных ядер, и тем самым производят ядерные реакции, представляющие интерес для исследователей. Ряд больниц использует циклотронное оборудование для получения радиоактивных веществ для диагностики и лечения.
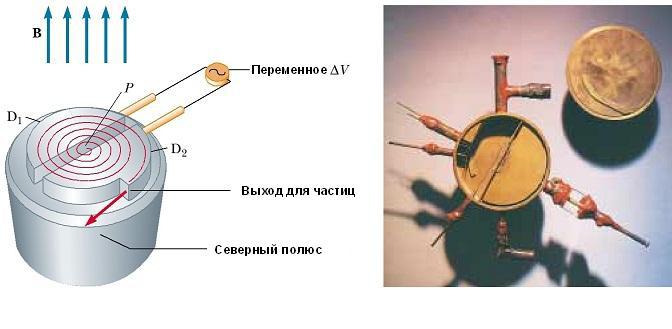
Схематическое изображение циклотрона показан на рис. ниже. Частицы движутся внутри двух полуцилиндрических контейнеров D 1 и D 2, называемых дуантами. Высокочастотная переменная разность потенциалов приложена к дуантам, разделенным зазором, а однородное магнитное поле направлено вдоль оси циклотрона (южный полюс его источника на рис. не показан).
Положительный ион, выпущенный из источника в точке Р вблизи центра устройства в первом дуанте, перемещается по полукруглой траектории (показана пунктирной красной линией на рисунке) и прибывает обратно в щель в момент времени Т / 2, где Т — время одного полного оборота внутри двух дуантов.
Частота приложенной разности потенциалов регулируется таким образом, что полярность дуантов меняется на обратную в тот момент времени, когда ион выходит из одного дуанта. Если приложенная разность потенциалов регулируется таким образом, что в этот момент D2 получает более низкий электрический потенциал, чем D1 на величину qΔV, то ион ускоряется в зазоре перед входом в D2, и его кинетической энергии увеличивается на величину qΔV. Затем он движется вокруг D2 по полукруглой траектории большего радиуса (потому что его скорость увеличилась).
Через некоторое время T / 2 он снова поступает в зазор между дуантами. К этому моменту полярность дуантов снова изменяется, и иону дается еще один «удар» через зазор. Движение заряженной частицы в магнитном поле по спирали продолжается, так что при каждом проходе одного дуанта ион получает дополнительную кинетическую энергию, равную qΔV. Когда радиус его траектории становится близким к радиусу дуантов, ион покидает систему через выходную щель. Важно отметить, что работа циклотрона основана на том, что Т не зависит от скорости иона и радиуса круговой траектории. Мы можем получить выражение для кинетической энергии иона, когда он выходит из циклотрона в зависимости от радиуса R дуантов. Мы знаем, что скорость кругового движения частицы — ν = qBR /m. Следовательно, ее кинетическая энергия
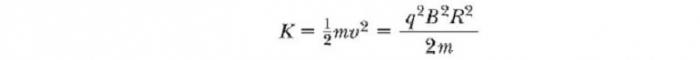
Когда энергии ионов в циклотрон превышает около 20 МэВ, в игру вступают релятивистские эффекты. Мы отмечаем, что T увеличивается, и что движущиеся ионы не остаются в фазе с приложенной разностью потенциалов. Некоторые ускорители решают эту проблему, изменяя период прикладываемой разности потенциалов, так что она остается в фазе с движущимися ионами.
Эффект Холла
Когда проводник с током помещается в магнитное поле, то дополнительная разность потенциалов создается в направлении, перпендикулярном к направлению тока и магнитного поля. Это явление, впервые наблюдаемое Эдвином Холлом (1855-1938) в 1879 году, известно как эффект Холла. Он всегда наблюдается, когда происходит движение заряженной частицы в магнитном поле. Это приводит к отклонению носителей заряда на одной стороне проводника в результате магнитной силы, которую они испытывают. Эффект Холла дает информацию о знаке носителей заряда и их плотности, он также может быть использован для измерения величины магнитных полей.
Устройство для наблюдения эффекта Холла состоит из плоского проводника с током I в направлении х, как показано на рисунке ниже.
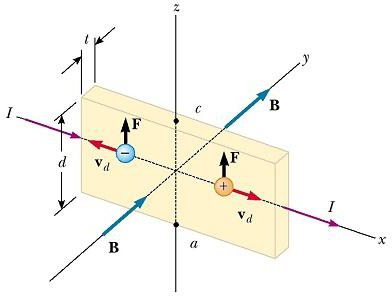 Однородное поле B приложено в направлении у. Если носителями заряда являются электроны, движущиеся вдоль оси х со скоростью дрейфа vd, то они испытывают направленную вверх (с учетом отрицательного q) магнитную силу FB = qvd х B, отклоняются вверх и накапливаются на верхнем краю плоского проводника, в результате чего появляется избыток положительного заряда на нижнем краю. Это накопление заряда на краях увеличивается до тех пор, пока электрическая сила, появившаяся в результате разделения зарядов, не уравновешивает магнитную силу, действующую на носители. Когда это равновесие будет достигнуто, электроны больше не отклоняются вверх. Чувствительный вольтметр или потенциометр, подключенный к верхней и нижней граням проводника, может измерить разность потенциалов, известную как ЭДС Холла.
Однородное поле B приложено в направлении у. Если носителями заряда являются электроны, движущиеся вдоль оси х со скоростью дрейфа vd, то они испытывают направленную вверх (с учетом отрицательного q) магнитную силу FB = qvd х B, отклоняются вверх и накапливаются на верхнем краю плоского проводника, в результате чего появляется избыток положительного заряда на нижнем краю. Это накопление заряда на краях увеличивается до тех пор, пока электрическая сила, появившаяся в результате разделения зарядов, не уравновешивает магнитную силу, действующую на носители. Когда это равновесие будет достигнуто, электроны больше не отклоняются вверх. Чувствительный вольтметр или потенциометр, подключенный к верхней и нижней граням проводника, может измерить разность потенциалов, известную как ЭДС Холла.33 Действие магнитного поля на движущийся электрический заряд. Сила Лоренца. Движение заряженных частиц в магнитном поле.
С ила
Лоренца (сила, действующая со стороны
магнитного поля на движущийся заряд) .
ила
Лоренца (сила, действующая со стороны
магнитного поля на движущийся заряд) .
Правило левой руки.
Если расположить ладонь так чтобы в нее вход силовые линии поля, а 4 пальца – по направлению скор полож заряда (против в-ра скорости для отриц зарядов) Большой палец пакажет направл силы Л.
Зависит от угла. 1)Вдоль а=0 F=0 2)Перпенд. a=п/2 3)п>a>0 Движ по спирали
34 Эффект Холла. Мгд-генератор. Масс-спектрограф. Циклотрон.
Возникновен эл тока в пров-ке /полупр с током помещ в магн поле, в-р индукц перп в-ру пл-ти тока
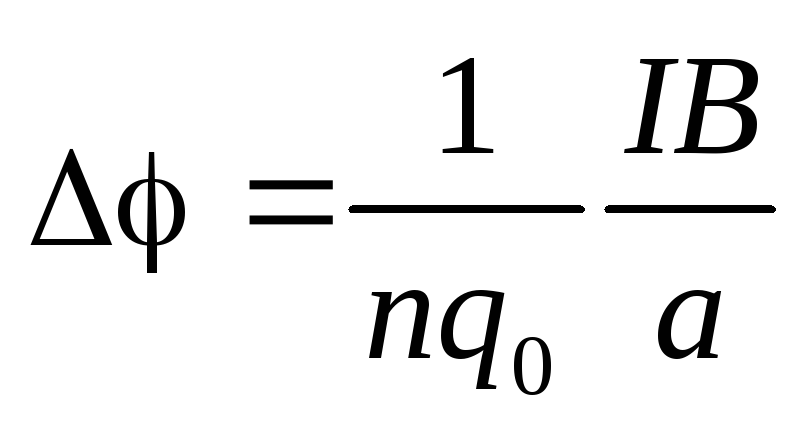 .
МГД-генератор Находит применение в
методе преобр внутр энерг ионизир газа
в электр энергию
.
МГД-генератор Находит применение в
методе преобр внутр энерг ионизир газа
в электр энергию
спектром масс частиц наз совокупность значений их масс. Весьма точно измеряют массы и относительные концентрации различных изотопов химических элементоа.
Для ускорения протонов, дейтронов и других более тяжелых частиц применяются резонансные циклические ускорители, в которых частица многократно проходит через переменное электр поле, каждый раз увеличивая свою скорость.Простейшим резонанс цикличес ускорителем – циклотрон.
35 Магнитный поток. Теорема Остроградского-Гаусса для магнитного поля.
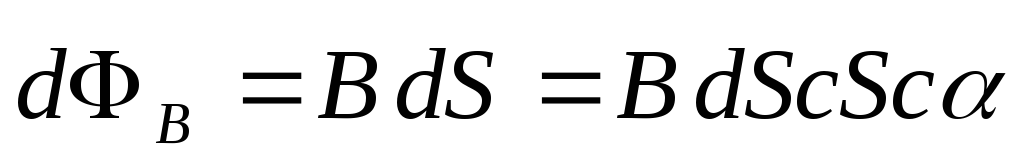
теорема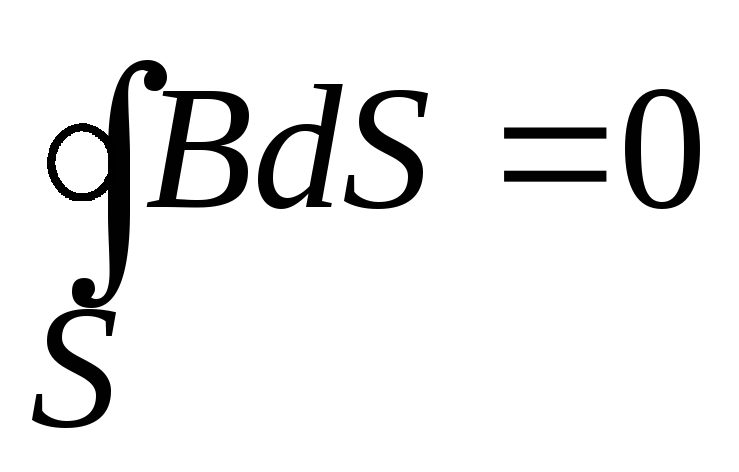 Магн поток через замкнут пов-ть =0
Магн поток через замкнут пов-ть =0
36 Работа по перемещению проводника и контура с током в магнитном поле.
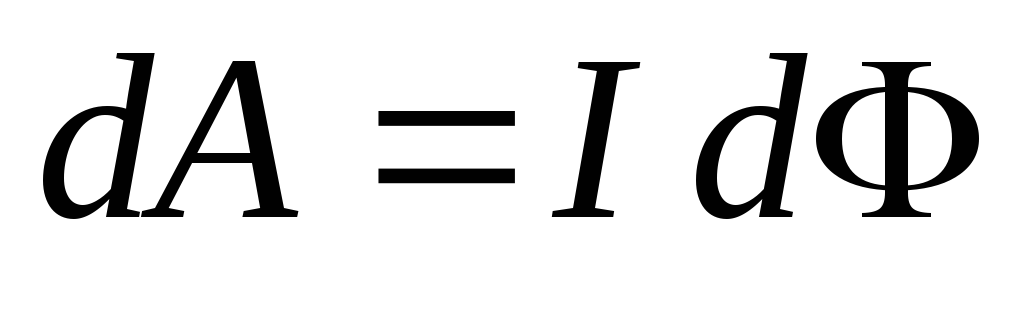 =произведению
силы тока в проводнике на перес им
магнитн поток
=произведению
силы тока в проводнике на перес им
магнитн поток
I=const A1-2=I(Ф2-Ф1)
37 Явление электромагнитной индукции. Закон электромагнитной индукции. Правило Ленца. Вывод закона электромагнитной индукции из закона сохранения энергии.
1) Возникновение электрического тока в замкнутом проводящем контуре при изменении магнитного поля, пронизывающего контур. Этот ток получил название индукционного. Индукция магнитного поля может меняться как по величине, так и по направлению.
2) Возникновение индукционного тока в замкнутом проводящем контуре при его движении в постоянном магнитном поле. Движение контура может быть поступательным, вращательным, а также означать его деформацию.
3) Разделение зарядов в незамкнутом отрезке проводника при его движении в постоянном магнитном поле. При этом в проводнике возникает электрическое поле, создаваемое разделенными зарядами. Обнаружить это явление можно, измеряя разность потенциалов (напряжение) между концами проводника.
Общими чертами всех трех явлений являются возникновение сторонних сил в проводниках.
Различающимися чертами является природа сторонних сил. Во втором и третьем явлениях сторонние силы – силы Лоренца. В первом явлении изменяющееся магнитное поле создает в окружающем пространстве особый вид электрического поля – вихревое электрическое поле. Оно по некоторым свойствам похоже на электростатическое (характеризуется напряженностью электрического поля, действует как на неподвижные, так и на движущиеся заряды), а по некоторым – напоминает магнитное (силовые линии замкнуты). В данном случае сторонние силы – силы, действующие со стороны вихревого электрического поля на заряженные частицы в проводниках (носители тока).
П равило
Ленца.
Возникающий в замкнутом контуре
индукционный ток противодействует тому
изменению магнитного потока, которым
вызван данный ток.
равило
Ленца.
Возникающий в замкнутом контуре
индукционный ток противодействует тому
изменению магнитного потока, которым
вызван данный ток.
Закон электромагнитной индукции .
З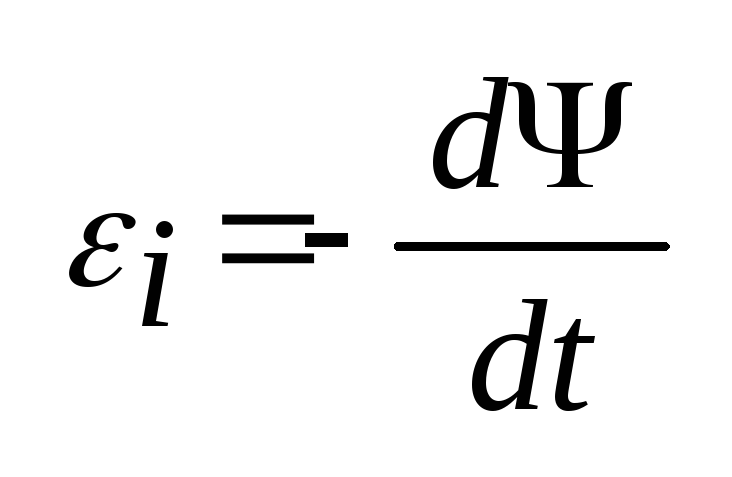 акон
электромагнитной индукции (для многих
витков) .
акон
электромагнитной индукции (для многих
витков) .
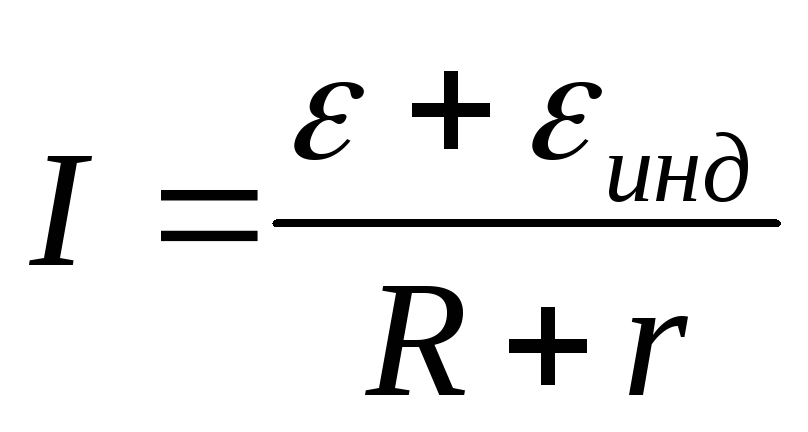
38 Заряд, проходящий через поперечное сечение цепи при электромагнитной индукции. Генератор переменного тока.

39 Поток самоиндукции. Индуктивность контура. Явление самоиндукции.
Контур прониз магн поле сцеплен с контуром магнитного потока наз потоком самоиндукции. Коэф пропорц L между силой тока и полным магн потоком – идуктив-ть.
Ток
протек в замкнут контур созд вокруг
себя магн поле. Велеч этого поля пропор
силе тока в контуре, это поле прониз и
сам контур. З-н Фарадея 
40 Токи при размыкании и замыкании цепи.
при размыкании

размыкании замыкании
41 Взаимная индукция. Коэффициент взаимной индукции. Трансформатор.
Взаимной индукцией наз явление возбуждения ЭДС электомагнитной индукции в одной электрической цепи при изменении электрического тока в другой цепи или изм взаимного расположения этих двух цепей.
Явл возникнов ЭДС в одном из контуров пр изм силы тока в др. L12 и L21 коф вз инд.
Трансформатор – устройство, преобразующее переменный ток одного напряжения в переменный ток другого напряжения.
Трансформатор 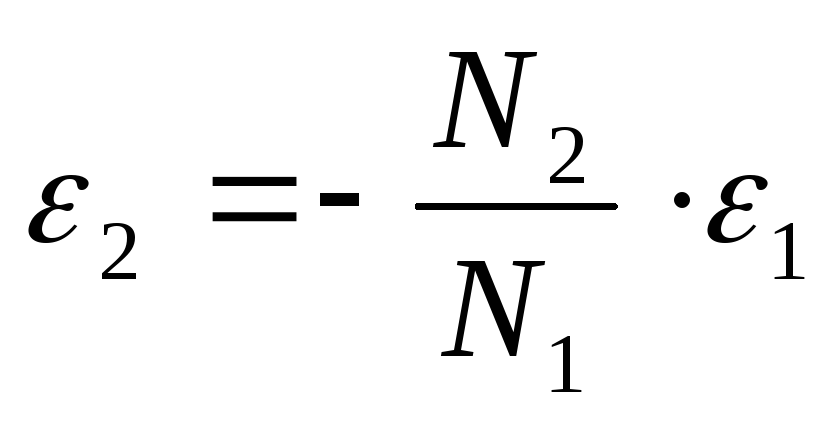
Коэффициент
трансформации (К)
– отношение
числа витков в первичной обмотке к числу
витков во вторичной обмотке 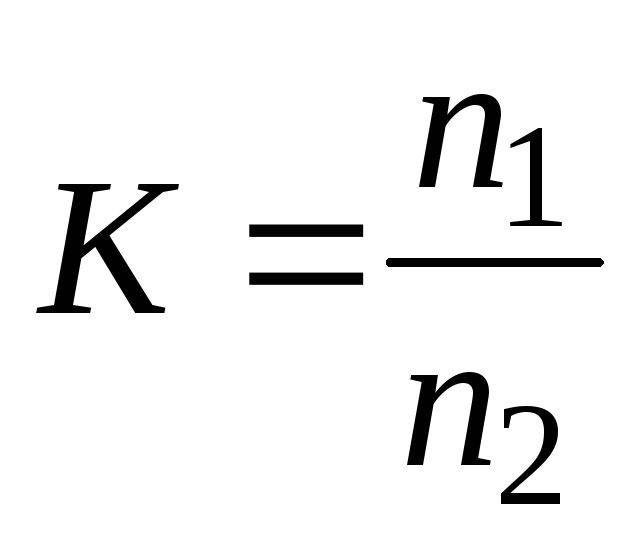 .
.
При К > 1 трансформатор называется понижающим, а при К < 1 — повышающим
44. Действие магнитного поля на движущийся заряд. Сила Лоренца.
Сила, действующая на электрический заряд Q, движущийся в магнитном поле со скоростью v, называется силой Лоренца и выражается формулой F=Q[vB], где В — индукция магнитного поля, в котором заряд движется.
Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q> 0 направления I и v совпадают, для Q<0—противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд. На рис. 169 показана взаимная ориентация векторов v, В (поле направлено к нам, на рисунке показано точками) и F для положительного заряда. На отрицательный заряд сила действует в противоположном направлении.
М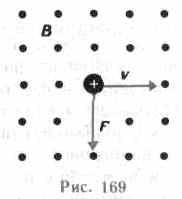 одуль
силы Лоренца равенF=QvBsin,
где
— угол между v и В. Магнитное
поле действует только на движущиеся в
нем заряды. Так
как по действию силы Лоренца можно
определить модуль и направление вектора
В, то выражение для силы Лоренца может
быть использовано для определения
вектора магнитной индукции В.
одуль
силы Лоренца равенF=QvBsin,
где
— угол между v и В. Магнитное
поле действует только на движущиеся в
нем заряды. Так
как по действию силы Лоренца можно
определить модуль и направление вектора
В, то выражение для силы Лоренца может
быть использовано для определения
вектора магнитной индукции В.
Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает. Иными словами, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется.
Если на движущийся электрический заряд помимо магнитного поля с индукцией В действует и электрическое поле с напряженностью Е, то результирующая сила F, приложенная к заряду, равна векторной сумме сил — силы, действующей со стороны электрического поля, и силы Лоренца: F=QE + Q[vB]. Это выражение называется формулой Лоренца. Скорость v в этой формуле есть скорость заряда относительно магнитного поля.
45. Движение заряженных частиц в магнитном поле. Ускорители элементарных частиц.
Н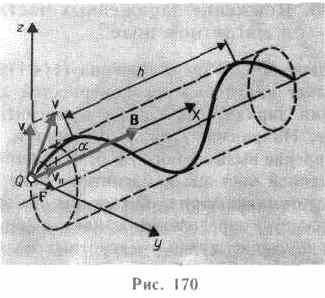 аправление
силы Лоренца и направление вызываемого
ею отклонения заряженной частицы в
магнитном поле зависят от знака
зарядаQ частицы. На этом основано определение
знака заряда частиц, движущихся в
магнитных полях.
аправление
силы Лоренца и направление вызываемого
ею отклонения заряженной частицы в
магнитном поле зависят от знака
зарядаQ частицы. На этом основано определение
знака заряда частиц, движущихся в
магнитных полях.
Для вывода общих закономерностей будем считать, что магнитное поле однородно и на частицы электрические поля не действуют. Если заряженная частица движется в магнитном поле со скоростью v вдоль линий магнитной индукции, то угол а между векторами v и В равен 0 или . Тогда сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно.
Если заряженная
частица движется в магнитном поле со
скоростью v,
перпендикулярной вектору В, то сила
Лоренца F=Q[vB]
постоянна по модулю и нормальна к
траектории частицы. Согласно второму
закону Ньютона, эта сила создает
центростремительное ускорение. Отсюда
следует, что частица будет двигаться
по окружности, радиус r которой
определяется из условия QvB = mv2/r, откуда  Период
вращения частицы, т.
е. время Т, затрачиваемое
ею на один полный оборот,
Период
вращения частицы, т.
е. время Т, затрачиваемое
ею на один полный оборот, 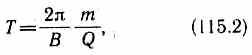 т.
е. период вращения частицы в однородном
магнитном поле определяется только
величиной, обратной удельному заряду(Q/m) частицы, и
магнитной индукцией поля, но не зависит
от ее скорости (при v << с)).
т.
е. период вращения частицы в однородном
магнитном поле определяется только
величиной, обратной удельному заряду(Q/m) частицы, и
магнитной индукцией поля, но не зависит
от ее скорости (при v << с)).
Если скорость v
заряженной частицы направлена под углом
а к вектору В (рис. 170), то ее движение
можно представить в виде суперпозиции:
1) равномерного прямолинейного
движения вдоль поля со скоростью
v||=vcos;
2) равномерного движения со скоростью
v┴= vsin
по окружности в плоскости, перпендикулярной
полю. В результате сложения обоих
движений возникает движение по спирали,
ось которой параллельна магнитному
полю. Шаг винтовой линии h=v||T=vTcos.
Радиус окружности определяется формулой  (в данном случае надо заменитьv на v┴=vsin).
(в данном случае надо заменитьv на v┴=vsin).
Ускорителями заряженных частиц называются устройства, в которых под действием электрических и магнитных полей создаются и управляются пучки высокоэнергетичных заряженных частиц (электронов, протонов, мезонов и т.д.).
Любой ускоритель характеризуется типом ускоряемых частиц, энергией, сообщаемой частицам, разбросом частиц по энергиям и интенсивностью пучка. Ускорители делятся на непрерывные (из них выходит равномерный по времени пучок) и импульсные (из них частицы вылетают порциями — импульсами). Последние характеризуются длительностью импульса. По форме траектории и механизму ускорения частиц ускорители делятся на линейные, циклические и индукционные. В линейных ускорителях траектории движения частиц близки к прямым линиям, в циклических и индукционных — траекториями частиц являются окружности или спирали.
Рассмотрим некоторые типы ускорителей заряженных частиц.
1. Линейный ускоритель. Ускорение частиц осуществляется электростатическим полем, создаваемым, например, высоковольтным генератором Ван-де-Граафа. Заряженная частица проходит поле однократно: заряд Q, проходя разность потенциалов 1-2, приобретает энергию W=Q(1-2). Таким способом частицы ускоряются до 10 МэВ. Их дальнейшее ускорение с помощью источников постоянного напряжения невозможно из-за утечки зарядов, пробоев и т. д.
2. Линейный резонансный ускоритель. Ускорение заряженных частиц осуществляется переменным электрическим полем сверхвысокой частоты, синхронно изменяющимся с движением частиц. Таким способом протоны ускоряются до энергий порядка десятков мегаэлектрон-вольт, электроны — до десятков гигаэлектрон-вольт.
3. Циклотрон —
циклический резонансный ускоритель
тяжелых частиц (протонов, ионов).
Между полюсами 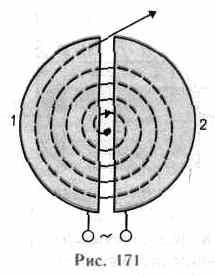 сильного
электромагнита помещается вакуумная
камера, в которой находятся два электрода
(1 и 2) в
виде полых металлических полуцилиндров,
или дуантов. К дуантам приложено
переменное электрическое поле.
Магнитное поле, создаваемое электромагнитом,
однородно и перпендикулярно плоскости
дуантов.
сильного
электромагнита помещается вакуумная
камера, в которой находятся два электрода
(1 и 2) в
виде полых металлических полуцилиндров,
или дуантов. К дуантам приложено
переменное электрическое поле.
Магнитное поле, создаваемое электромагнитом,
однородно и перпендикулярно плоскости
дуантов.
Если заряженную частицу ввести в центр зазора между дуантами, то она, ускоряемая электрическим и отклоняемая магнитным полями, войдя в дуант 1, опишет полуокружность, радиус которой пропорционален скорости частицы. К моменту ее выхода из дуанта 1 полярность напряжения изменяется (при соответствующем подборе изменения напряжения между дуантами), поэтому частица вновь ускоряется и, переходя в дуант 2, описывает там уже полуокружность большего радиуса и т. д.
Для непрерывного ускорения частицы в циклотроне необходимо выполнить условие синхронизма (условие «резонанса») — периоды вращения частицы в магнитном поле и колебаний электрического поля должны быть равны. При выполнении этого условия частица будет двигаться по раскручивающейся спирали, получая при каждом прохождении через зазор дополнительную энергию. На последнем витке, когда энергия частиц и радиус орбиты доведены до максимально допустимых значений, пучок частиц посредством отклоняющего электрического поля выводится из циклотрона.
Циклотроны позволяют ускорять протоны до энергий примерно 20 МэВ. Дальнейшее их ускорение в циклотроне ограничивается релятивистским возрастанием массы со скоростью, что приводит к увеличению периода обращения, и синхронизм нарушается. Поэтому циклотрон совершенно неприменим для ускорения электронов (при E=0,5 МэВ m = 2m0, при E=10 МэВ m=28m0!).
4. Фазотрон (синхроциклотрон) — циклический резонансный ускоритель тяжелых заряженных частиц (например, протонов, ионов, -частиц), в котором управляющее магнитное поле постоянно, а частота ускоряющего электрического поля медленно изменяется с периодом. Движение частиц в фазотроне, как и в циклотроне, происходит по раскручивающейся спирали. Частицы в фазотроне ускоряются до энергий, примерно равных 1 ГэВ (ограничения здесь определяются размерами фазотрона, так как с ростом скорости частиц растет радиус их орбиты).
5. Синхротрон — циклический резонансный ускоритель ультрарелятивистских электронов, в котором управляющее магнитное поле изменяется во времени, а частота ускоряющего электрического поля постоянна. Электроны в синхротроне ускоряются до энергий 5—10 ГэВ.
6. Синхрофазотрон — циклический резонансный ускоритель тяжелых заряженных частиц (протонов, ионов), в котором объединяются свойства фазотрона и синхротрона, т. е. управляющее магнитное поле и частота ускоряющего электрического поля одновременно изменяются во времени так, чтобы радиус равновесной орбиты частиц оставался постоянным. Протоны ускоряются в синхрофазотроне до энергий 500 ГэВ.
7. Бетатрон — циклический индукционный ускоритель электронов, в котором ускорение осуществляется вихревым электрическим полем (см. §137), индуцируемым переменным магнитным полем, удерживающим электроны на круговой орбите. В бетатроне в отличие от рассмотренных выше ускорителей не существует проблемы синхронизации. Электроны в бетатроне ускоряются до энергий 100 МэВ. При W> 100 МэВ режим ускорения в бетатроне нарушается электромагнитным излучением электронов. Особенно распространены бетатроны на энергии 20—50 МэВ.
44. Действие магнитного поля на движущийся заряд. Сила Лоренца.
С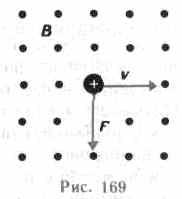 ила,
действующая на электрический зарядQ,
движущийся в магнитном поле со
скоростью v,
называется силой
Лоренца и
выражается формулой F=Q[vB],
где В — индукция магнитного поля, в
котором заряд движется.
ила,
действующая на электрический зарядQ,
движущийся в магнитном поле со
скоростью v,
называется силой
Лоренца и
выражается формулой F=Q[vB],
где В — индукция магнитного поля, в
котором заряд движется.
Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора v (для Q> 0 направления I и v совпадают, для Q<0—противоположны), то отогнутый большой палец покажет направление силы, действующей на положительный заряд. На рис. 169 показана взаимная ориентация векторов v, В (поле направлено к нам, на рисунке показано точками) и F для положительного заряда. На отрицательный заряд сила действует в противоположном направлении.
Модуль силы Лоренца равен F=QvBsin, где — угол между v и В. Магнитное поле действует только на движущиеся в нем заряды. Так как по действию силы Лоренца можно определить модуль и направление вектора В, то выражение для силы Лоренца может быть использовано для определения вектора магнитной индукции В.
Сила Лоренца всегда перпендикулярна скорости движения заряженной частицы, поэтому она изменяет только направление этой скорости, не изменяя ее модуля. Следовательно, сила Лоренца работы не совершает. Иными словами, постоянное магнитное поле не совершает работы над движущейся в нем заряженной частицей и кинетическая энергия этой частицы при движении в магнитном поле не изменяется.
Если на движущийся электрический заряд помимо магнитного поля с индукцией В действует и электрическое поле с напряженностью Е, то результирующая сила F, приложенная к заряду, равна векторной сумме сил — силы, действующей со стороны электрического поля, и силы Лоренца: F=QE + Q[vB]. Это выражение называется формулой Лоренца. Скорость v в этой формуле есть скорость заряда относительно магнитного поля.
45. Движение заряженных частиц в магнитном поле. Ускорители элементарных частиц.
Н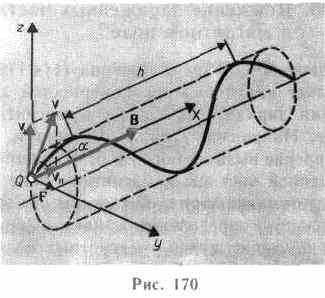 аправление
силы Лоренца и направление вызываемого
ею отклонения заряженной частицы в
магнитном поле зависят от знака
зарядаQ частицы. На этом основано определение
знака заряда частиц, движущихся в
магнитных полях.
аправление
силы Лоренца и направление вызываемого
ею отклонения заряженной частицы в
магнитном поле зависят от знака
зарядаQ частицы. На этом основано определение
знака заряда частиц, движущихся в
магнитных полях.
Для вывода общих закономерностей будем считать, что магнитное поле однородно и на частицы электрические поля не действуют. Если заряженная частица движется в магнитном поле со скоростью v вдоль линий магнитной индукции, то угол а между векторами v и В равен 0 или . Тогда сила Лоренца равна нулю, т. е. магнитное поле на частицу не действует и она движется равномерно и прямолинейно.
Если заряженная
частица движется в магнитном поле со
скоростью v,
перпендикулярной вектору В, то сила
Лоренца F=Q[vB]
постоянна по модулю и нормальна к
траектории частицы. Согласно второму
закону Ньютона, эта сила создает
центростремительное ускорение. Отсюда
следует, что частица будет двигаться
по окружности, радиус r которой
определяется из условия QvB = mv2/r, откуда  Период вращения
частицы, т.
е. время Т, затрачиваемое
ею на один полный оборот,
Период вращения
частицы, т.
е. время Т, затрачиваемое
ею на один полный оборот, 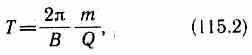 т.
е. период вращения частицы в однородном
магнитном поле определяется только
величиной, обратной удельному заряду(Q/m) частицы, и
магнитной индукцией поля, но не зависит
от ее скорости (при v << с)).
т.
е. период вращения частицы в однородном
магнитном поле определяется только
величиной, обратной удельному заряду(Q/m) частицы, и
магнитной индукцией поля, но не зависит
от ее скорости (при v << с)).
Если скорость v
заряженной частицы направлена под углом
а к вектору В (рис. 170), то ее движение
можно представить в виде суперпозиции:
1) равномерного прямолинейного
движения вдоль поля со скоростью
v||=vcos;
2) равномерного движения со скоростью
v┴= vsin
по окружности в плоскости, перпендикулярной
полю. В результате сложения обоих
движений возникает движение по спирали,
ось которой параллельна магнитному
полю. Шаг винтовой линии h=v||T=vTcos.
Радиус окружности определяется формулой  (в данном случае надо заменитьv на v┴=vsin).
(в данном случае надо заменитьv на v┴=vsin).
Ускорителями заряженных частиц называются устройства, в которых под действием электрических и магнитных полей создаются и управляются пучки высокоэнергетичных заряженных частиц (электронов, протонов, мезонов и т.д.).
Любой ускоритель характеризуется типом ускоряемых частиц, энергией, сообщаемой частицам, разбросом частиц по энергиям и интенсивностью пучка. Ускорители делятся на непрерывные (из них выходит равномерный по времени пучок) и импульсные (из них частицы вылетают порциями — импульсами). Последние характеризуются длительностью импульса. По форме траектории и механизму ускорения частиц ускорители делятся на линейные, циклические и индукционные. В линейных ускорителях траектории движения частиц близки к прямым линиям, в циклических и индукционных — траекториями частиц являются окружности или спирали.
Рассмотрим некоторые типы ускорителей заряженных частиц.
1. Линейный ускоритель. Ускорение частиц осуществляется электростатическим полем, создаваемым, например, высоковольтным генератором Ван-де-Граафа. Заряженная частица проходит поле однократно: заряд Q, проходя разность потенциалов 1-2, приобретает энергию W=Q(1-2). Таким способом частицы ускоряются до 10 МэВ. Их дальнейшее ускорение с помощью источников постоянного напряжения невозможно из-за утечки зарядов, пробоев и т. д.
2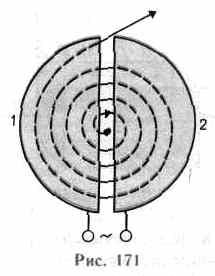 .
Линейный резонансный ускоритель.Ускорение
заряженных частиц осуществляется
переменным электрическим полем
сверхвысокой частоты, синхронно изменяющимся
с движением частиц. Таким способом
протоны ускоряются до энергий порядка
десятков мегаэлектрон-вольт, электроны
— до десятков гигаэлектрон-вольт.
.
Линейный резонансный ускоритель.Ускорение
заряженных частиц осуществляется
переменным электрическим полем
сверхвысокой частоты, синхронно изменяющимся
с движением частиц. Таким способом
протоны ускоряются до энергий порядка
десятков мегаэлектрон-вольт, электроны
— до десятков гигаэлектрон-вольт.
3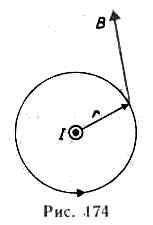 .
Циклотрон—
циклический резонансный ускоритель
тяжелых частиц (протонов, ионов).
Между полюсами сильного электромагнита
помещается вакуумная камера, в которой
находятся два электрода (1 и 2) в
виде полых металлических полуцилиндров,
или дуантов. К дуантам приложено
переменное электрическое поле.
Магнитное поле, создаваемое электромагнитом,
однородно и перпендикулярно плоскости
дуантов.
.
Циклотрон—
циклический резонансный ускоритель
тяжелых частиц (протонов, ионов).
Между полюсами сильного электромагнита
помещается вакуумная камера, в которой
находятся два электрода (1 и 2) в
виде полых металлических полуцилиндров,
или дуантов. К дуантам приложено
переменное электрическое поле.
Магнитное поле, создаваемое электромагнитом,
однородно и перпендикулярно плоскости
дуантов.
Если заряженную частицу ввести в центр зазора между дуантами, то она, ускоряемая электрическим и отклоняемая магнитным полями, войдя в дуант 1, опишет полуокружность, радиус которой пропорционален скорости частицы. К моменту ее выхода из дуанта 1 полярность напряжения изменяется (при соответствующем подборе изменения напряжения между дуантами), поэтому частица вновь ускоряется и, переходя в дуант 2, описывает там уже полуокружность большего радиуса и т. д.
Для непрерывного ускорения частицы в циклотроне необходимо выполнить условие синхронизма (условие «резонанса») — периоды вращения частицы в магнитном поле и колебаний электрического поля должны быть равны. При выполнении этого условия частица будет двигаться по раскручивающейся спирали, получая при каждом прохождении через зазор дополнительную энергию. На последнем витке, когда энергия частиц и радиус орбиты доведены до максимально допустимых значений, пучок частиц посредством отклоняющего электрического поля выводится из циклотрона.
Циклотроны позволяют ускорять протоны до энергий примерно 20 МэВ. Дальнейшее их ускорение в циклотроне ограничивается релятивистским возрастанием массы со скоростью, что приводит к увеличению периода обращения, и синхронизм нарушается. Поэтому циклотрон совершенно неприменим для ускорения электронов (при E=0,5 МэВ m = 2m0, при E=10 МэВ m=28m0!).
4. Фазотрон (синхроциклотрон) — циклический резонансный ускоритель тяжелых заряженных частиц (например, протонов, ионов, -частиц), в котором управляющее магнитное поле постоянно, а частота ускоряющего электрического поля медленно изменяется с периодом. Движение частиц в фазотроне, как и в циклотроне, происходит по раскручивающейся спирали. Частицы в фазотроне ускоряются до энергий, примерно равных 1 ГэВ (ограничения здесь определяются размерами фазотрона, так как с ростом скорости частиц растет радиус их орбиты).
5. Синхротрон — циклический резонансный ускоритель ультрарелятивистских электронов, в котором управляющее магнитное поле изменяется во времени, а частота ускоряющего электрического поля постоянна. Электроны в синхротроне ускоряются до энергий 5—10 ГэВ.
6. Синхрофазотрон — циклический резонансный ускоритель тяжелых заряженных частиц (протонов, ионов), в котором объединяются свойства фазотрона и синхротрона, т. е. управляющее магнитное поле и частота ускоряющего электрического поля одновременно изменяются во времени так, чтобы радиус равновесной орбиты частиц оставался постоянным. Протоны ускоряются в синхрофазотроне до энергий 500 ГэВ.
7. Бетатрон — циклический индукционный ускоритель электронов, в котором ускорение осуществляется вихревым электрическим полем (см. §137), индуцируемым переменным магнитным полем, удерживающим электроны на круговой орбите. В бетатроне в отличие от рассмотренных выше ускорителей не существует проблемы синхронизации. Электроны в бетатроне ускоряются до энергий 100 МэВ. При W> 100 МэВ режим ускорения в бетатроне нарушается электромагнитным излучением электронов. Особенно распространены бетатроны на энергии 20—50 МэВ.
Сила, действующая на заряд, движущийся в магнитном поле
⇐ ПредыдущаяСтр 5 из 7Следующая ⇒Основные формулы и указания к решению задачи
Сила, действующая на провод с током в магнитном поле (закон Ампера),
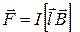 или
или 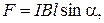
 (5.1)
(5.1)
где l – длина провода;
a – угол между направлением тока в проводе и вектором магнитной индукции 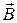 .
.
Это выражение справедливо для однородного магнитного поля и прямого отрезка провода. Если поле неоднородно и провод не является прямым, то закон Ампера можно применять к каждому элементу провода в отдельности:
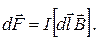 (5.2)
(5.2)
Сила Лоренца – 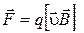 или
или 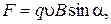 (5.3)
(5.3)
где  – скорость заряженной частицы;
– скорость заряженной частицы;
 – угол между векторами
– угол между векторами  и
и 
Направление силы Лоренца определяется с помощью правила левой руки: если ладонь левой руки расположить так, чтобы в нее входил вектор В, а четыре вытянутых пальца направить вдоль вектора u (если заряд положительный), то отогнутый большой палец покажет направление силы Лоренца.
Отметим, что магнитное поле действует только на движущиеся в нем заряды, на покоящиеся электрические заряды магнитное поле не действует.
Пример решения задачи
Рассмотрев фотографию треков заряженных частиц, двигавшихся в магнитном поле определить отношение заряда к массе неизвестной частицы, а также знак заряда этой частицы, если известно, что левый трек принадлежит ядру атома водорода, правый неизвестной частице. Отношение заряда атома водорода к его массе равно 9,6×107Кл/кг. Модули начальных скоростей частиц одинаковы. Индукция магнитного поля 2,2 Тл. Направление магнитного поля показано на рис. 5.1.
Решение. Для решения этой задачи оба трека осторожно переносят на кальку или делают ксерокопию рисунка. Затем измеряют радиусы кривизны треков. Для этого вначале находят центры кривизны. В средних участках треков проводят по две хорды и в середине к ним восстанавливают перпендикуляры. Точки пересечения перпендикуляров будут центрами кривизны треков. Затем измеряют радиусы кривизны с помощью измерительной линейки, учитывая масштаб снимка.
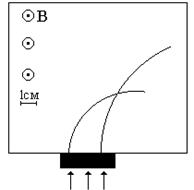
Рис. 5.1. Треки заряженных частиц в магнитном поле
Для нашего случая R1 = 0,032 м, R2 = 0,072 м.
На заряженную частицу, движущуюся в магнитном поле, действует сила Лоренца, вектор которой перпендикулярен вектору скорости частицы. Эта сила является центростремительной силой:
Fл = quB, 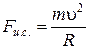 , Fл = Fц.с., (5.4)
, Fл = Fц.с., (5.4)
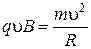 . (5.5)
. (5.5)
Отсюда модуль скорости неизвестной частицы u1 будет равен:
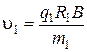 , (5.6)
, (5.6)
где q1 – заряд частицы;
m1 – масса частицы;
R1 – радиус кривизны трека;
B – модуль магнитной индукции.
Модуль скорости ядра атома водорода u2 равен:
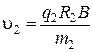 , (5.7)
, (5.7)
где q2 – заряд ядра водорода;
m2 – масса ядра атома водорода;
R2 – радиус кривизны трека.
Так как по условию u1 = u2, то
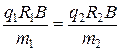 . (5.8)
. (5.8)
Отсюда получаем:
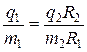 . (5.9)
. (5.9)
Подставляя в последнюю формулу числовые данные, находим:
 Кл/кг.
Кл/кг.
Выполним проверку единиц измерения величин.
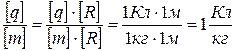 . (5.10)
. (5.10)
Воспользовавшись правилом левой руки определяем, что наша частица заряжена положительно.
5.3 Задание для самостоятельного выполнения по вариантам
Неизвестные частицы 1 и 2 (см. рис. 5.2) прошли ускоряющую разность потенциалов U и влетели перпендикулярно линиям магнитной индукции В в камеру Вильсона. По фотографии трека определите удельный заряд частиц q/m и укажите знаки их заряда. При измерении радиусов треков учитывайте масштаб снимка, указанный на рис. 5.2. Направление линий магнитной индукции указано на рисунке обозначением: – перпендикулярно листу бумаги «к нам», Ä – перпендикулярно листу бумаги «от нас». Данные приведены в табл. 5.1.
Таблица 5.1
Значения величин.
| № варианта | U, B | В, Tл |
| 2,1 | ||
| 2,2 | ||
| 2,3 | ||
| 2,4 | ||
| 2,5 | ||
| 2,6 | ||
| 2,7 | ||
| 2,8 | ||
| 2,9 | ||
| 3,0 | ||
| 3,1 | ||
| 3,2 | ||
| 3,3 | ||
| 3,4 | ||
| 3,5 |
Рис. 5.2. Треки частиц в магнитном поле
Продолжение рис. 5.2. Треки частиц в магнитном поле
 | 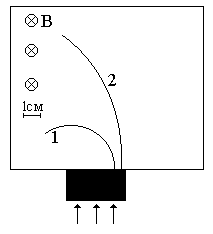 |
| вариант 13 | вариант 14 |
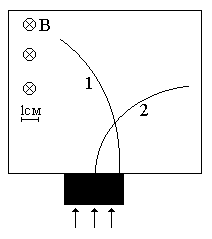 | 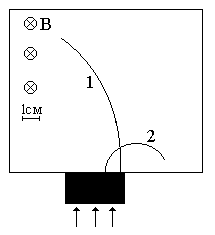 |
| вариант 15 | вариант 16 |
Продолжение рис. 5.2. Треки частиц в магнитном поле
Физика. Магнитное поле. Силы, действующие в магнитном поле на движущиеся заряды и токи. .Магнитное поле равномерно движущегося заряда.
Магнитное поле
Магнитное поле – особый вид материи. Оно проявляется в действии на движущиеся электрические заряды и тела, которые обладают собственным магнитным моментом (постоянные магниты).
Важно: на неподвижные заряды магнитное поле не действует! Создается магнитное поле также движущимися электрическими зарядами, либо изменяющимся во времени электрическим полем, либо магнитными моментами электронов в атомах. То есть любой провод, по которому течет ток, становится также и магнитом!
Магнит
Магнит — тело, обладающее собственным магнитным полем.
У магнита есть полюса, называемые северным и южным. Обозначения «северный» и «южный» даны лишь для удобства (как «плюс» и «минус» в электричестве).
Магнитное поле изображается посредством силовых магнитных линий. Силовые линиинепрерывны и замкнуты, а их направление всегда совпадает с направлением действия сил поля. Если вокруг постоянного магнита рассыпать металлическую стружку, частицы металла покажут наглядную картину силовых линий магнитного поля, выходящих из северного и входящих в южный полюс. Графическая характеристика магнитного поля — силовые линии.
Картина магнитного поля
Характеристики магнитного поля
Основными характеристиками магнитного поля являются магнитная индукция, магнитный потоки магнитная проницаемость. Но давайте обо всем по порядку.
Сразу отметим, что все единицы измерения приводятся в системе СИ.
Магнитная индукция B – векторная физическая величина, являющаяся основной силовой характеристикой магнитного поля. Обозначается буквой B. Единица измерения магнитной индукции – Тесла (Тл).
Магнитная индукция показывает, насколько сильно поле, определяя силу, с которой оно действует на заряд. Данная сила называется силой Лоренца.
Здесь q — заряд, v — его скорость в магнитном поле, B — индукция, F — сила Лоренца, с которой поле действует на заряд.
Магнитный поток Ф – физическая величина, равная произведению магнитной индукции на площадь контура и косинус между вектором индукции и нормалью к плоскости контура, через который проходит поток. Магнитный поток — скалярная характеристика магнитного поля.
Можно сказать, что магнитный поток характеризует количество линий магнитной индукции, пронизывающих единицу площади. Магнитный поток измеряется в Веберах (Вб).
Магнитный поток
Магнитная проницаемость – коэффициент, определяющий магнитные свойства среды. Одним из параметров, от которых зависит магнитная индукция поля, является магнитная проницаемость.
Магнитное поле Земли
Наша планета на протяжении нескольких миллиардов лет является огромным магнитом. Индукция магнитного поля Земли изменяется в зависимости от координат. На экваторе она равна примерно 3,1 на 10 в минус пятой степени Тесла. К тому же существуют магнитные аномалии, где значение и направление поля существенно отличаются от соседних областей. Одни из самых крупных магнитных аномалий на планете — Курская и Бразильская магнитные аномалии.
Происхождение магнитного поля Земли до сих пор остается загадкой для ученых. Предполагается, что источником поля является жидкое металлическое ядро Земли. Ядро движется, значит, движется расплавленный железо-никелевый сплав, а движение заряженных частиц – это и есть электрический ток, порождающий магнитное поле. Проблема в том, что эта теория (геодинамо) не объясняет того, как поле сохраняется устойчивым.
Магнитное поле земли
Земля – огромный магнитный диполь. Магнитные полюса не совпадают с географическими, хотя и находятся в непосредственной близости. Более того, магнитные полюса Земли движутся. Их смещение регистрируется с 1885 года. Например, за последние сто лет магнитный полюс в Южном полушарии сместился почти на 900 километров и сейчас находится в Южном океане. Полюс арктического полушария движется через Северный Ледовитый океан к Восточно-Сибирскоймагнитной аномалии, скорость его передвижения (по данным 2004 года) составила около 60 километров в год. Сейчас наблюдается ускорение движения полюсов — в среднем скорость растет на 3 километра в год.
Каково значение магнитного поля Земли для нас? В первую очередь магнитное поле Земли защищает планету от космических лучей и солнечного ветра. Заряженные частицы из далекого космоса не падают прямо на землю, а отклоняются гигантским магнитом и движутся вдоль его силовых линий. Таким образом, все живое оказывается защищенным от пагубной радиации.
Магнитное поле Земли
За историю Земли происходило несколько инверсий (смен) магнитных полюсов. Инверсия полюсов – это когда они меняются местами. Последний раз это явление произошло около 800 тысяч лет назад, а всего геомагнитных инверсий в истории Земли было более 400. Некоторые ученые полагают, что с учетом наблюдающегося ускорения движения магнитных полюсов следующей инверсии полюсов следует ожидать в ближайшие пару тысяч лет.
К счастью, в нашем веке смены полюсов пока не ожидается. А значит, можно думать о приятном и наслаждаться жизнью в старом добром постоянном поле Земли, рассмотрев основные свойства и характеристики магнитного поля.




 ,
с которой магнитное поле действует на
элемент
,
с которой магнитное поле действует на
элемент 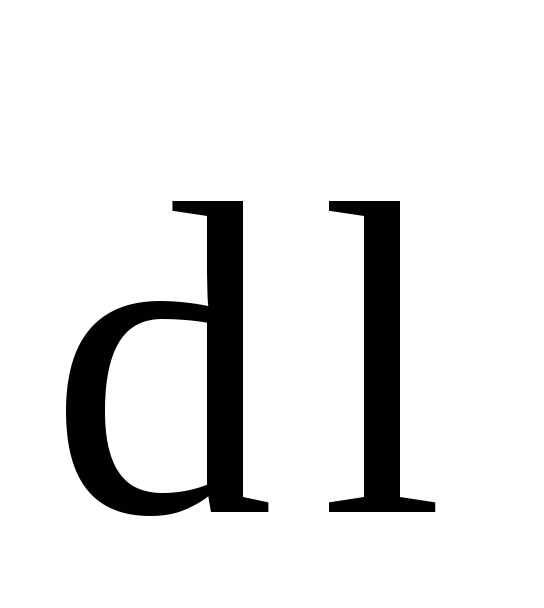 проводника с током, находящегося в
магнитном поле, прямо пропорциональна
силе тока I в проводнике и векторному произведению
элемента длины проводника на магнитную
индукцию
проводника с током, находящегося в
магнитном поле, прямо пропорциональна
силе тока I в проводнике и векторному произведению
элемента длины проводника на магнитную
индукцию  :
: положительный заряд (здесь
положительный заряд (здесь 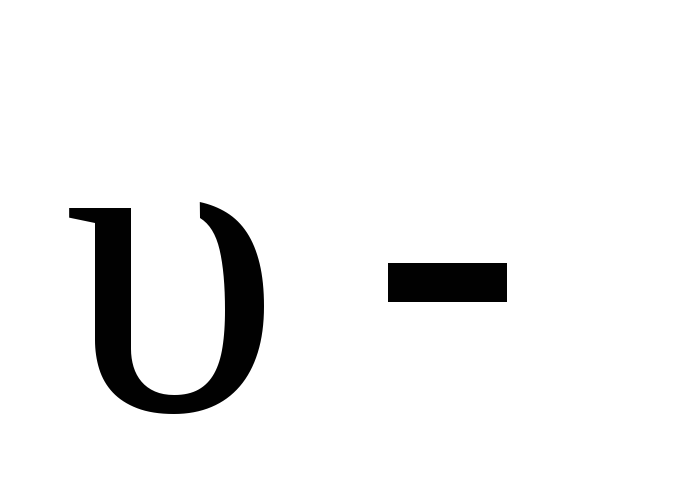 скорость
упорядоченного движения носителей
положительного заряда):
скорость
упорядоченного движения носителей
положительного заряда): :
циркуляция вектора магнитной индукции
равна току, охваченному контуром,
умноженному на магнитную постоянную:
:
циркуляция вектора магнитной индукции
равна току, охваченному контуром,
умноженному на магнитную постоянную: :
циркуляция вектора напряженности
магнитного поля равна току, охваченному
контуром
:
циркуляция вектора напряженности
магнитного поля равна току, охваченному
контуром