22. Как рассчитать фазный ток, если известны линейное напряжение и сопротивление нагрузки в схеме треугольник.
Схема треугольник
В
этой схеме (рис. 10.2,) токи в фазах при
несимметричной нагрузке различны 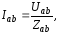
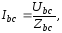 но напряжения
остаются неизменными (номинальные).
Линейные токи определяют по закону
Кирхгофа
но напряжения
остаются неизменными (номинальные).
Линейные токи определяют по закону
Кирхгофа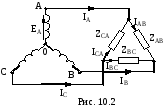
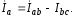
Мощность трехфазной несимметричной цепи.
Для измерения активной мощности трехфазной нагрузки в общем случае, когда нагрузка несимметрична, используют 3 ваттметра (рис. 10.3,
Трехфазную
цепь с тремя проводами,
соединяющими генератор с потребителем,
всегда можно рассматривать как две
двухпроводные линии, имеющие один общий
провод, например как линии АВ и СВ с общим
проводом В (рис. 10.3, б), в котором ток 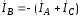 .
При этом по первой линии при напряжении
.
При этом по первой линии при напряжении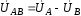 идет ток
идет ток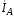
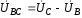 идет ток
идет ток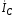 .
. 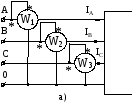
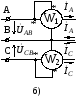
Рис. 10.3
Мощность,
передаваемая по первой линии 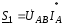 ,
,
а
мощность, передаваемая по второй линии, 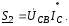
Полная мощность, передаваемая по трехпроводной линии, S = S1 + S2.
Из сказанного вытекает возможность измерять мощность, передаваемую по трехпроводной линии трехфазной системы, двумя ваттметрами, каждый из которых определяет мощность, передаваемую по одной из двух двухпроводных линий. Такая схема включения ваттметров (схема Арона) изображена на рис. 10.3, б.
При выводе не делалось никаких предположений о симметрии системы, следовательно, найденный метод измерения мощности двумя ваттметрами
При чисто активной нагрузке (=0) показания обоих ваттметров одинаковы.
Полное значение передаваемой (активной) мощности равно алгебраической сумме показаний обоих ваттметров. На практике часто два ваттметра ставятся на общую ось. Показания такого сдвоенного ваттметра непосредственно равны всей (активной) мощности, передаваемой по трехпроводной линии.
Если определить разность показаний ваттметров
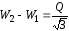 .
На основании последних выражений легко
вывести формулу, позволяющую определить
угол по показаниям ваттметров:
.
На основании последних выражений легко
вывести формулу, позволяющую определить
угол по показаниям ваттметров: 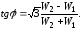
23. Как определяется мощность в трёхфазных цепях?.
Вычисление величины полной мощности. Расчет полной мощности электрической цепи требует знания ее активной и реактивной составляющих, соотношение которых в любой схеме описывается треугольником мощностей.
Для вычисления активной (Р) и реактивной (Q) составляющих 3-х фазной цепи проводится суммирование их величин в каждой фазе по формулам:
Р=РA+РB+РC=UAIAcosφA+UВIВcosφВ+UСIAСcosφС;
Q=QA+QB+QC=UAIAsinφA+UВIВ
IA, IВ, IС, UA, UВ, UС – вектора токов и напряжений в фазах, Φ – угол сдвига фаз векторов тока относительно напряжения.
Для симметричного режима работы схемы во всех фазах выполняется равенство мощностей. Поэтому общую величину мощности можно получить простым умножением фазной составляющей на количество фаз в системе:
Р=3РФ=3UФ∙IФ
Делаем замену фазных составляющих линейными по их соотношениям для схемы звезды: IЛ=IФ, UФ=UЛ/√3.
В результате получаем:
Р=3UФ∙IФ∙cosφ=(3UЛ∙IЛ/√3)∙cosφ=√3∙UЛ∙IЛ∙cosφ.
Заменяем фазные составляющие линейными для схемы треугольника по их соотношениям:
Итог вычисления:
Р=3UФ∙IФ∙cosφ=(3UЛ∙IЛ/√3)∙cosφ=√3∙UЛ∙IЛ∙cosφ.
Таким образом, получилось, что зависимость от вариантов соединения элементов цепи схемой γ либо Δ в 3-х фазной симметричной системе значения мощностей отсутствует. Они вычисляются по одним и тем же формулам:
Р=√3∙U∙I∙cosφ
[Вт];
Q=√3∙U∙I∙sinφ
[вар];
S=√(Р2+Q
Для данных выражений сложилось правило: подставлять линейные значения векторов U и I без указания их линейных индексов.
Способы измерений мощности В энергетике существует постоянная необходимость измерения электрических величин. Активная составляющая полной мощности замеряется ваттметром, а реактивная – варметром. Ваттметр работает по алгоритму, описанному формулой:
W=UW∙IW∙cos(UW^IW)=Re│UW∙IW*│.
UW, IW – те вектора, которые подвели к клеммам прибору для замера активной составляющей.
Практика
электрических измерений предлагает
несколько вариантов подключения к
электросети ваттметров. Они выбираются
в зависимости от схемы выполненный
коммутации нагрузок и ее характеристик.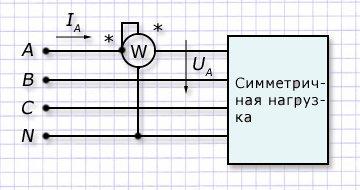
В симметричной 3-х фазной системе достаточно включить один ваттметр в любую фазу для постоянного замера активной мощности с последующим утроением полученного результата по алгоритму Р=3W=3UФ∙IФ∙cosφ.
Однако, этот простой способ только ориентировочно оценивает замеряемые величины, имеет большие погрешности. Поэтому, он малоприемлем для выполнения замеров, требующих высокой точности и в решении коммерческих задач.
Более точные замеры активной составляющей для звезды с нейтральным проводом обеспечивает использование в измерении трех ваттметров.
9.4. Расчет трехфазных цепей с несимметричной нагрузкой
Исходными данными являются:
— схема трехфазной цепи;
— фазные ЭДС генератора;
— сопротивления фаз несимметричной нагрузки.
Искомыми величинами являются токи и напряжения отдельных участков схемы.
Обмотки генератора и сопротивления нагрузки соединены в звезду с нулевым проводом
(рис. 9.29).
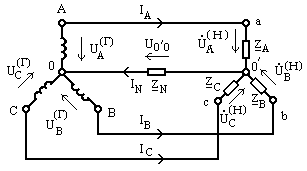
Рис. 9.29
Напряжение между нейтральными точками нагрузки и генератора, называемое напряжением
смещения нейтрали, найдем по методу двух узлов
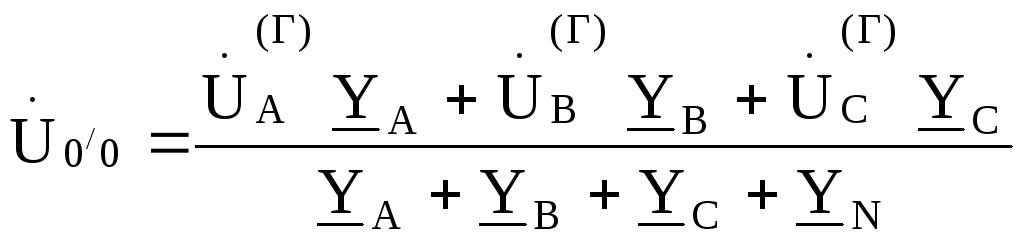 ,
,
где 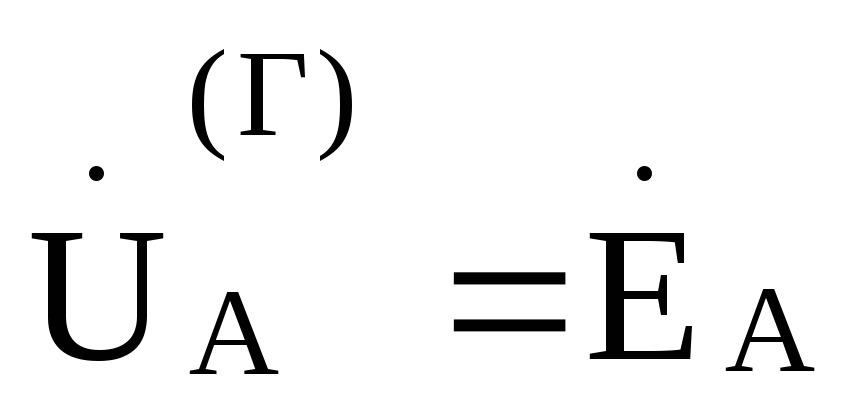 ,
,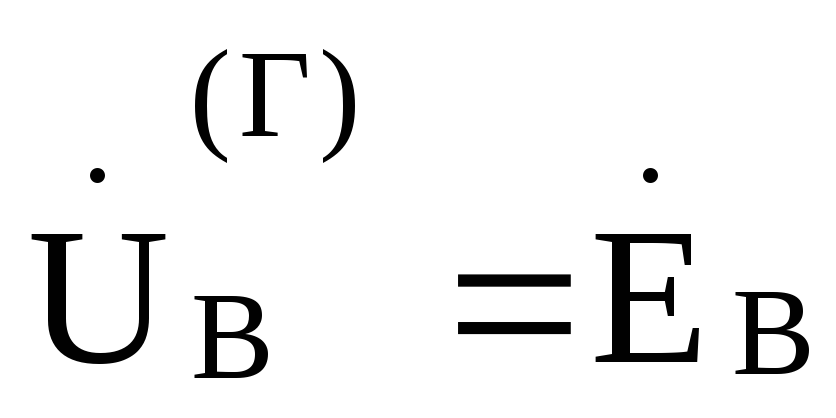 ,
,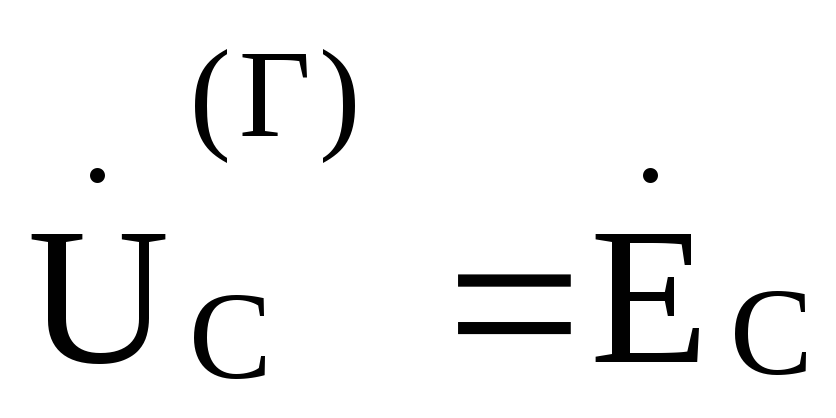 .
.
На основании обобщенного закона Оманайдем токи:
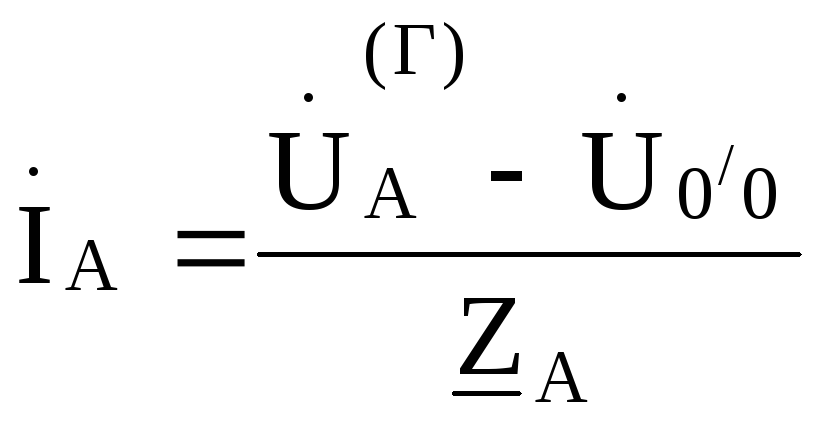 ,
,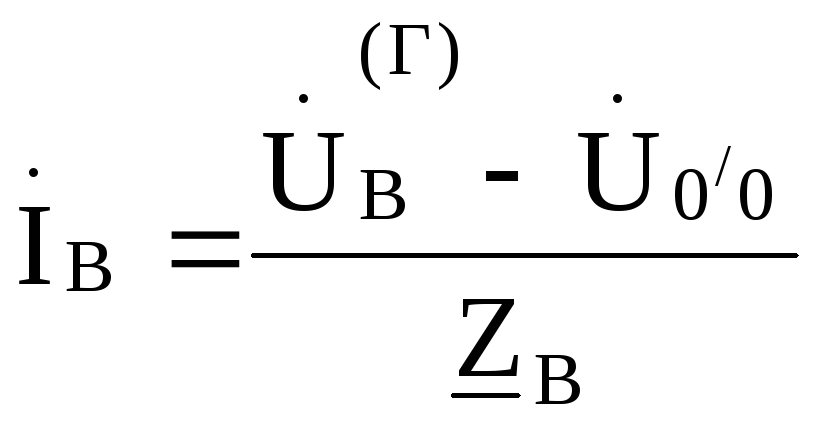 ,
,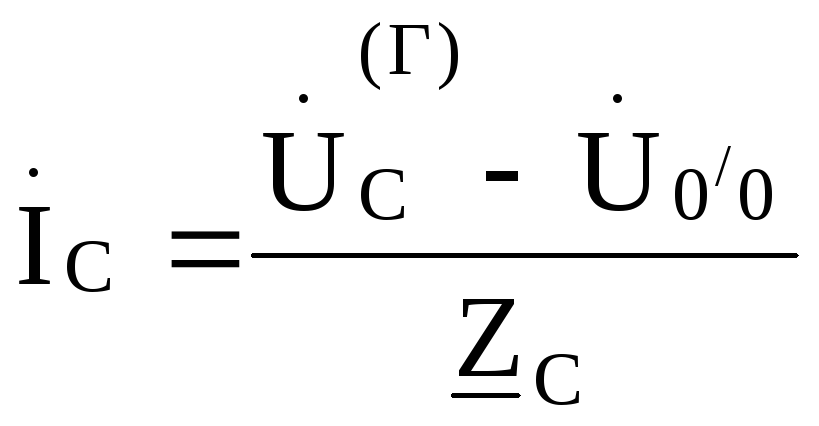
Ток в нулевом проводе
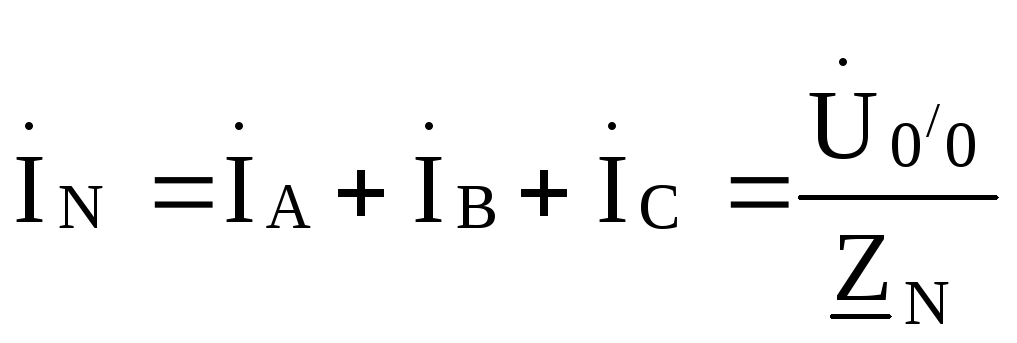
Если сопротивление нулевого провола,
равно нулю (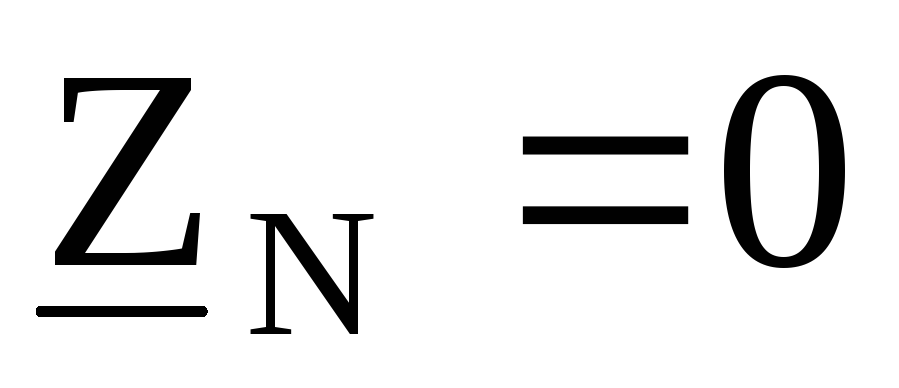 ),
то напряжение смещения нейтрали
),
то напряжение смещения нейтрали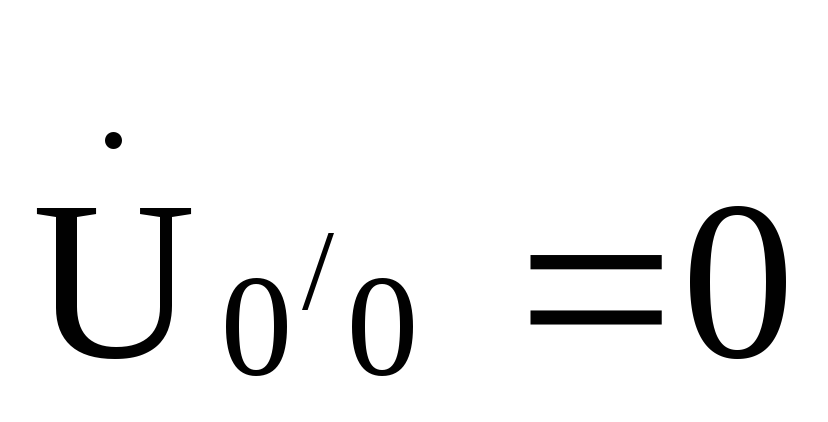 и
и
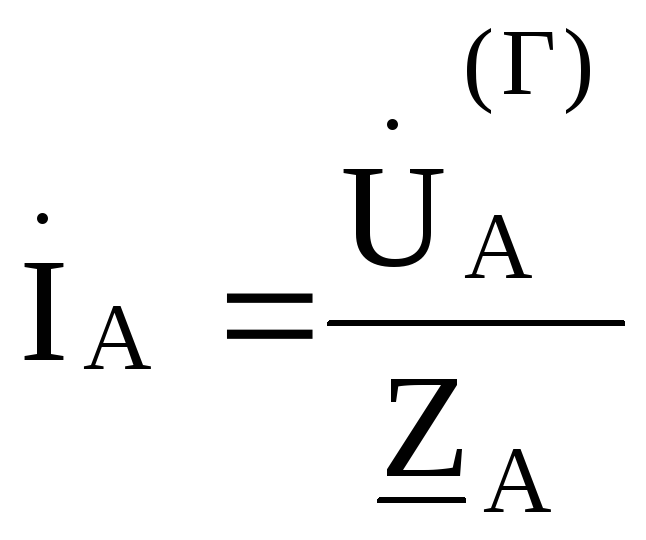 ,
,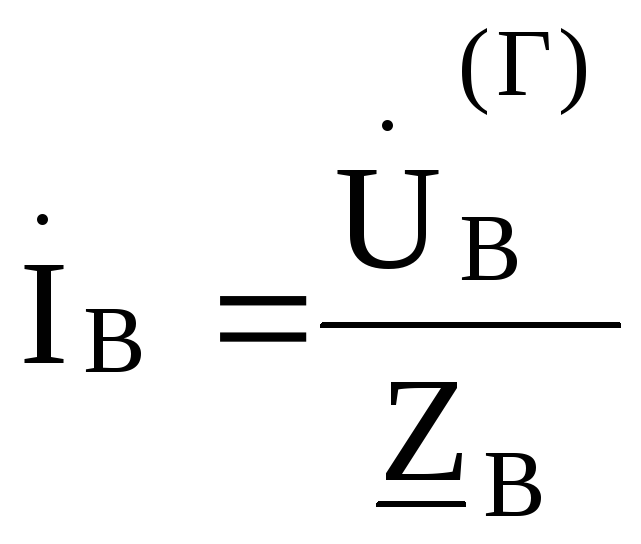 ,
,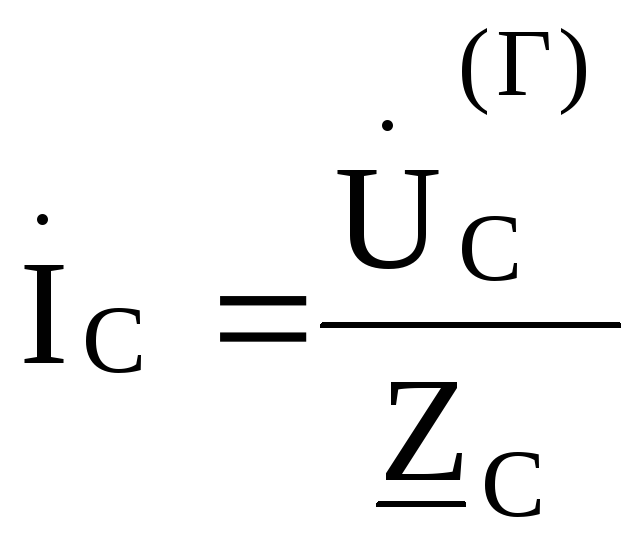
В этом случае фазные напряжения нагрузки иуяут равны соответствующим фазнымнапряжениям генератора и не будут зависеть от величины сопротивления в фазах нагрузки. Такой режим работы чаще всего встречается при питании однофазных приемников.
Если 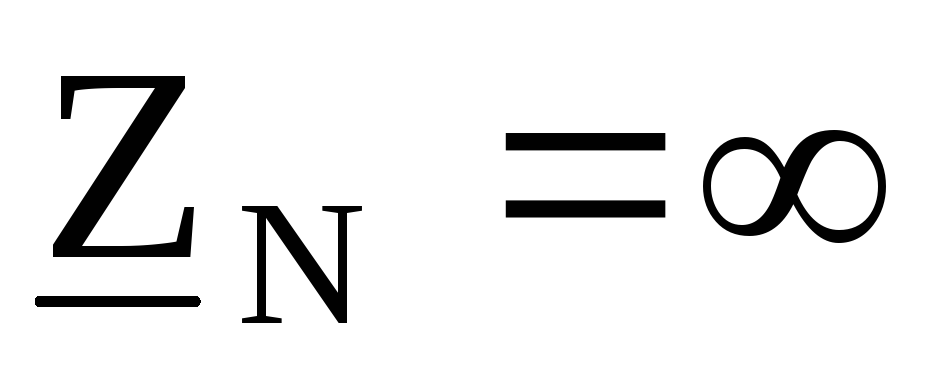 ,
то
,
то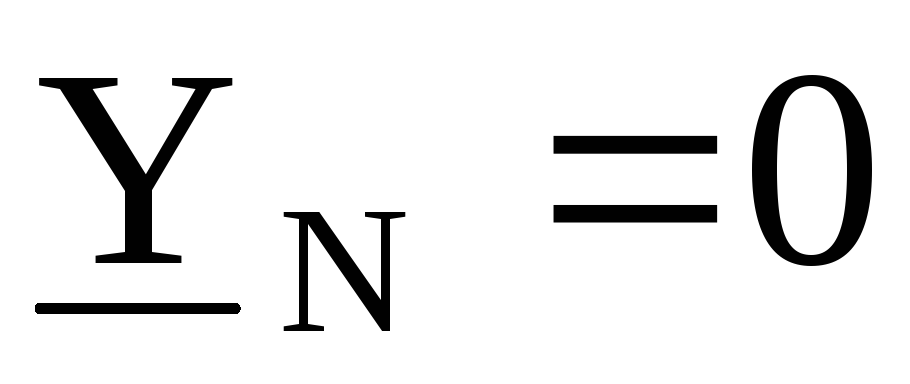 и
и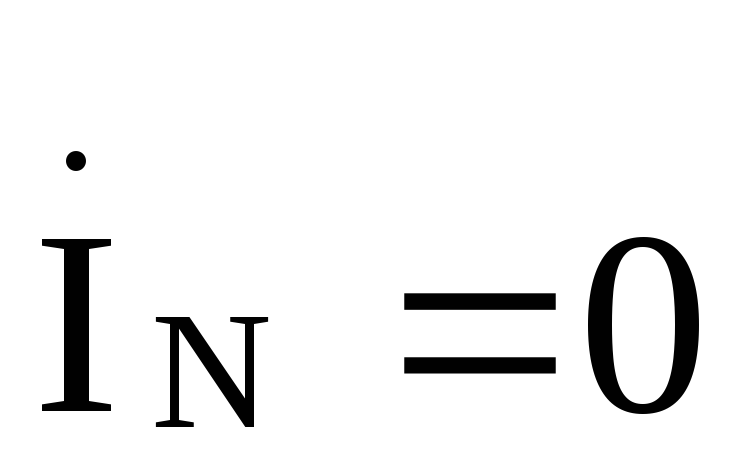 .
В этом случае напряжения на фаззах
нагрузки могут существенно отличаться
от номинальных напряжений, что
нежелательно. Приведем пример для
этого случая.
.
В этом случае напряжения на фаззах
нагрузки могут существенно отличаться
от номинальных напряжений, что
нежелательно. Приведем пример для
этого случая.
Пример 9.6.Для цепи рис. 9.30определить напряжения в фазах нагрузки и токи
при 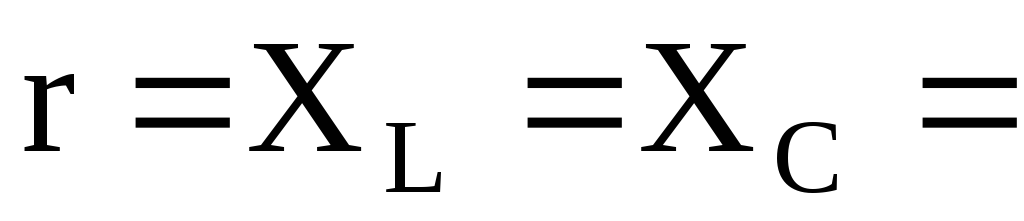 2 Ом.
2 Ом.
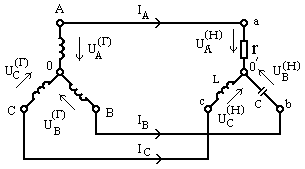
Рис. 9.30.
Фазное напряжение генератора 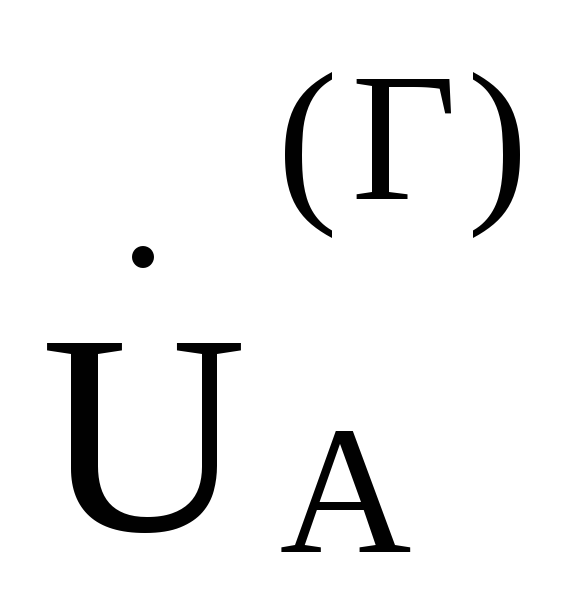 =220В.
=220В.
Решение
Найдем смещение нейтрали
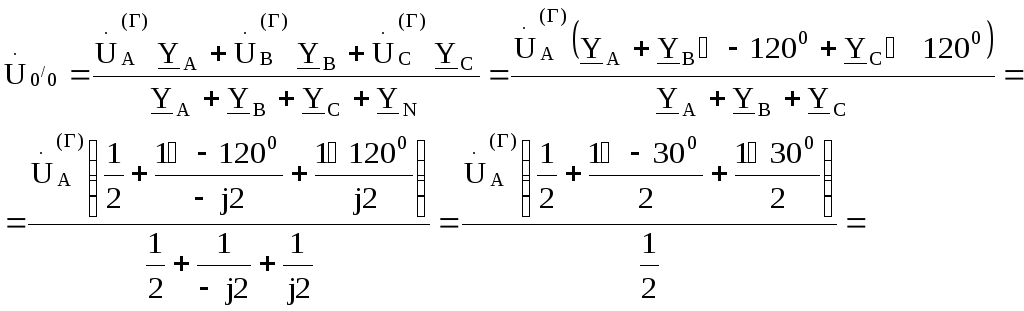
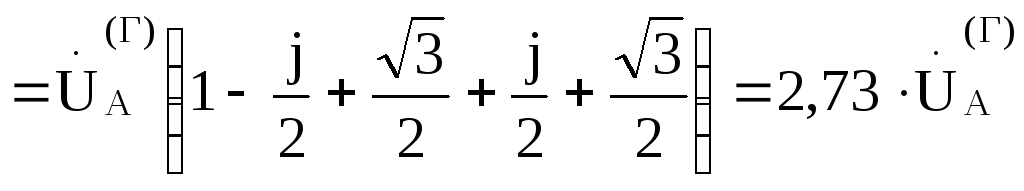
Тогда:
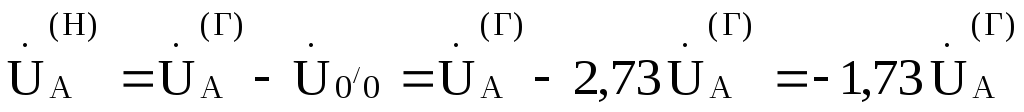 ;
;
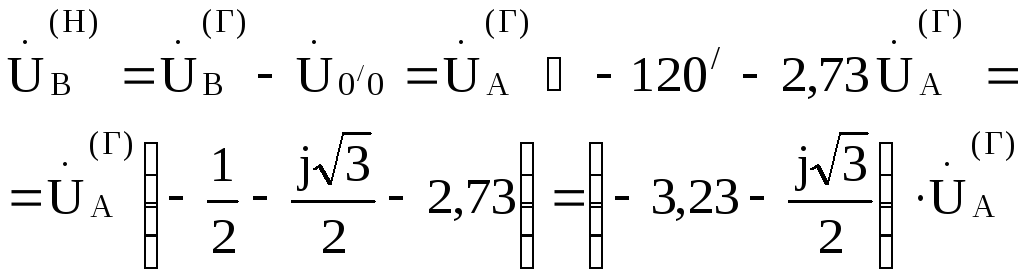 ;
;
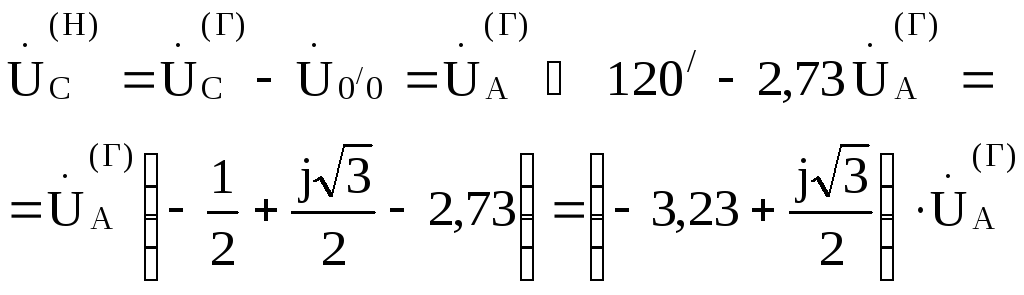 .
.
Считая 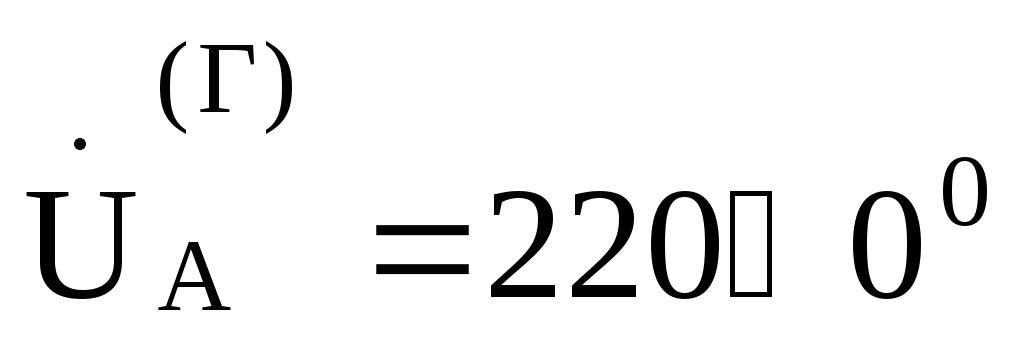 В, найдем токи:
В, найдем токи:
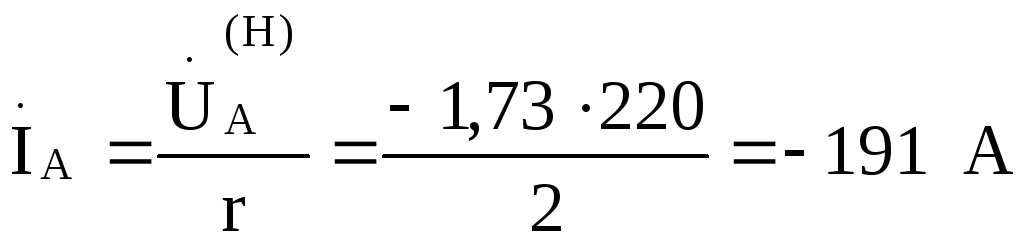
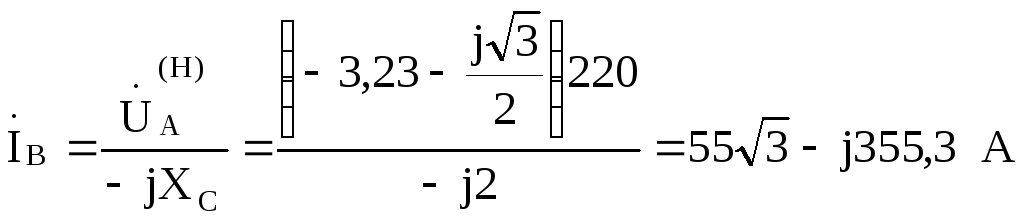
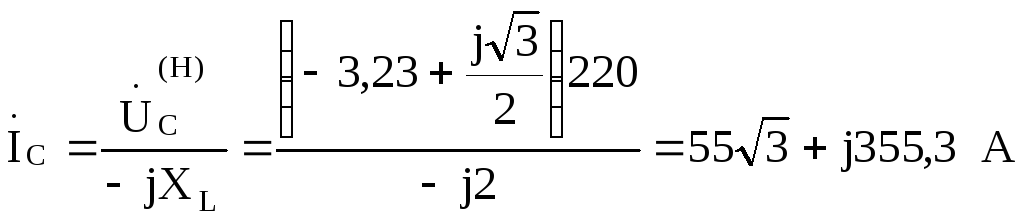
По найденным величинам построим векторно-топографическую диаграмму, показанную
на рис. 9.31.
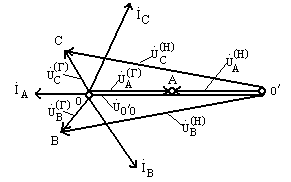
Рис. 9.31
2.Обмотки генератора и сопротивления нагрузки соединены в треугольник (рис. 9.32).
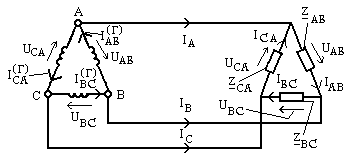
Рис. 9.32 Фазные токи нагрузки определяются по формулам
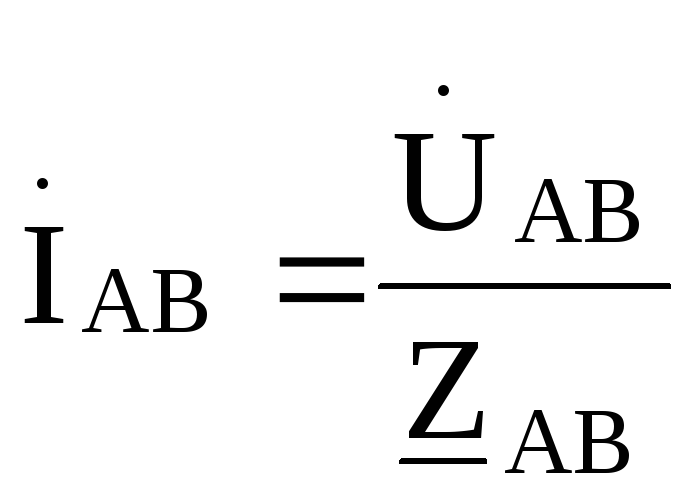
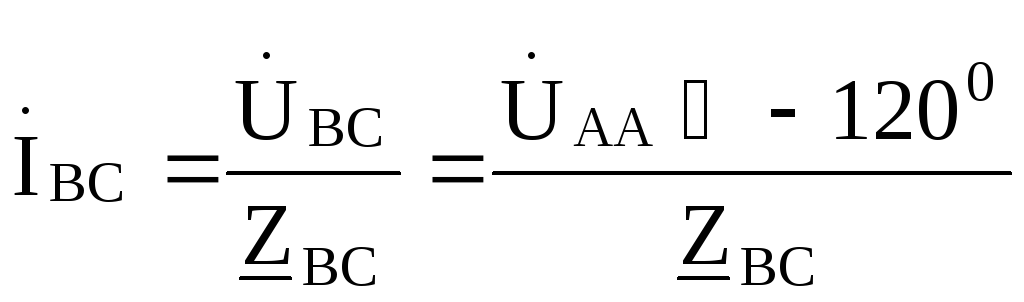
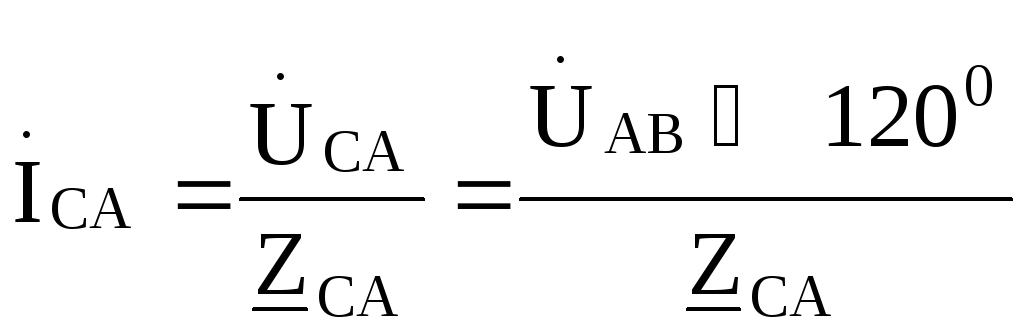
Токи в линиях (линейные токи):
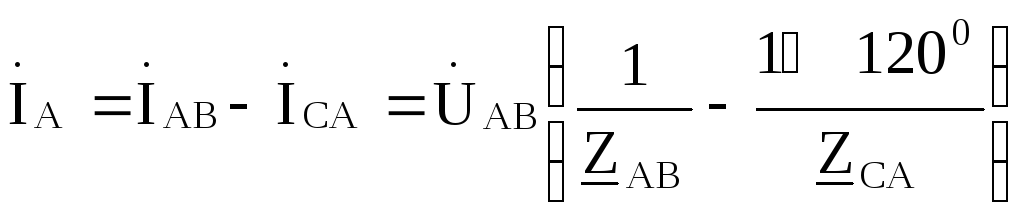
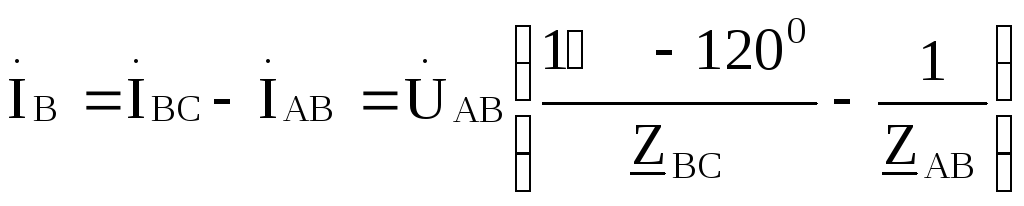
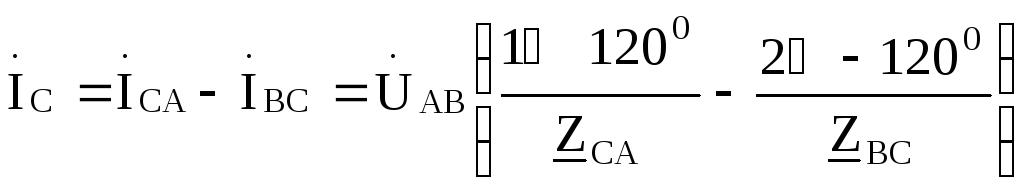
С помощью метода контурных токов можно показать, что фазные токи генератора оказываются равными соответствующим фазным токам нагрузки, т .е.
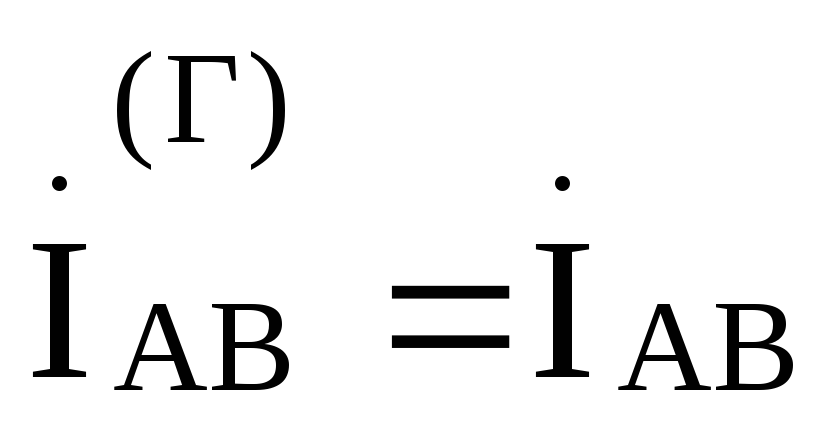 ,
,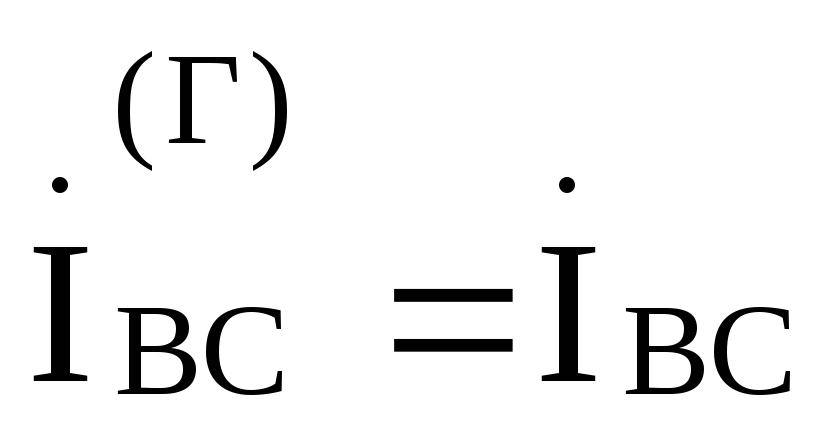 ,
,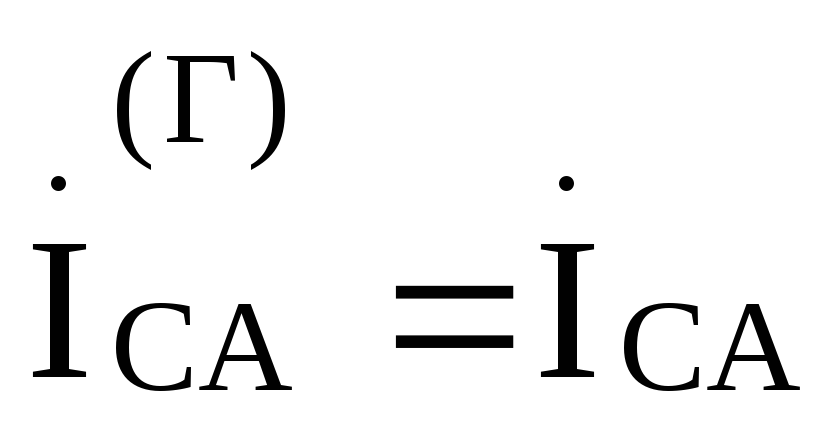
Пример 9.7.В цепи рис. 9.33определить фазные и линейные токи и построить векторно —
топографическую диаграмму.
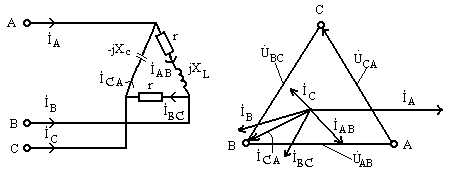
Рис. 9.33Рис. 9.34
если 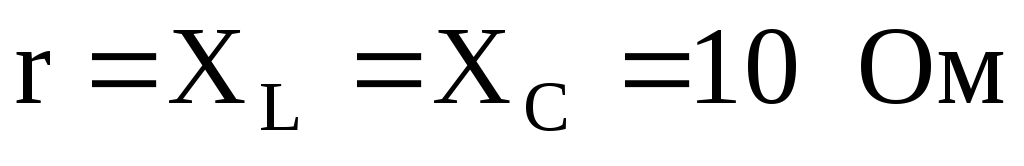 и фазное напряжение генератора обмотки
которого соединены в
и фазное напряжение генератора обмотки
которого соединены в
треугольник, равно 380В.
Решение
Принимаем 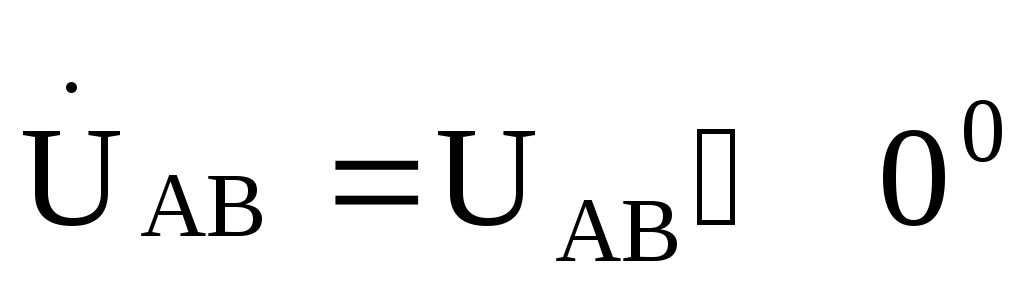 ,
тогда фазные токи нагрузки будут
,
тогда фазные токи нагрузки будут
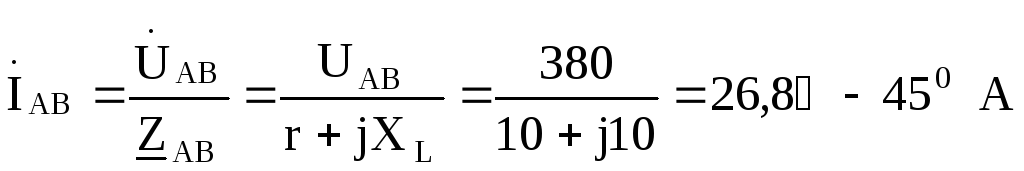
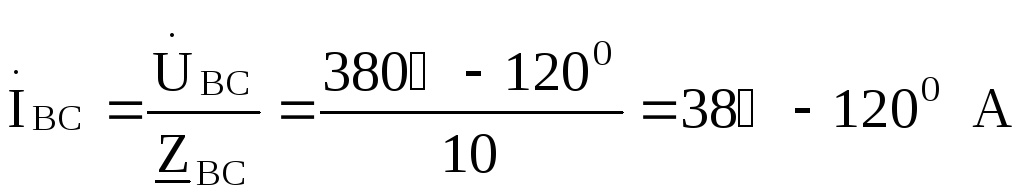
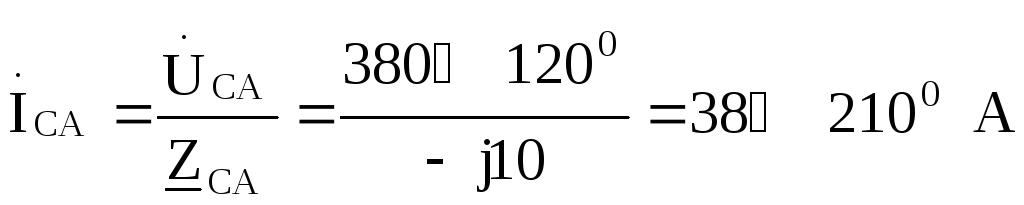
Линейные токи выражаем через фазные:

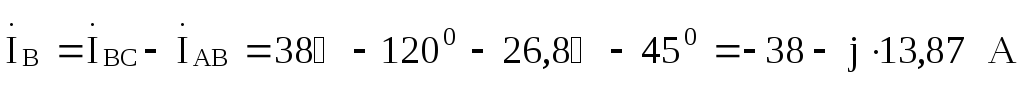

.
Векторно-топографическая диаграмма приведена на рис. 9.34.
3.Смешанное соединение сопротивлений нагрузки (cм.рис. 9.35).
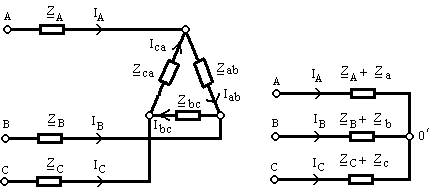
Рис.9.35 Рис. 9.36
Линейные напряжения на зажимах генератора
в зависимости от способа соединения
его обмоток могут отличаться в 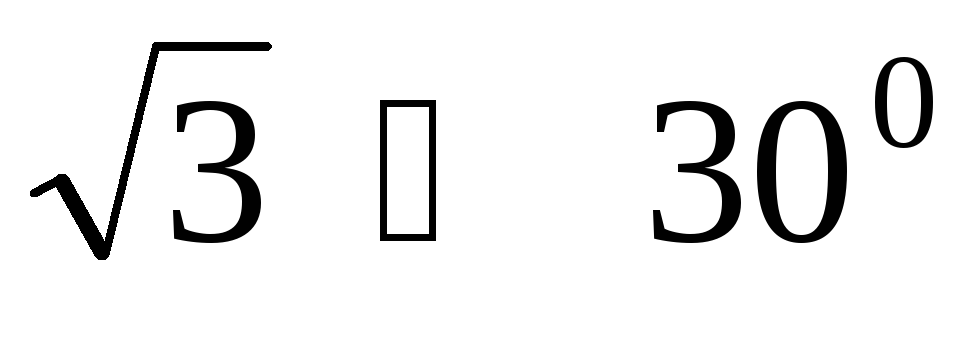 раз от соответствующих фазных напряжений.
Способ
раз от соответствующих фазных напряжений.
Способ
соединения обмотокгенератора иногда на схеме не указывают, тогда обязательно задается его
линейное напряжение, хотя бы по модулю. Для расчета токов в линии неснмметричную нагрузку
со смешанным соединением сопротивленнй преобразуют к единственной звезде или
единственному треугольнику, в которых токи в каждой фазе находятся известными приемами.
Например, в схеме рис. 9.35треугольник сопротивлений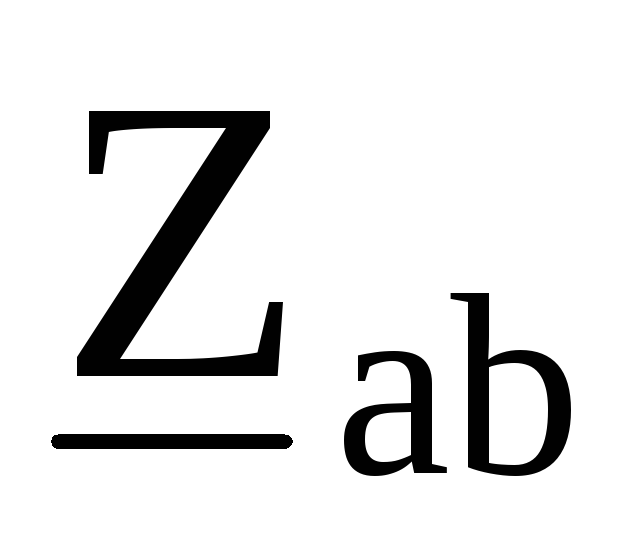 ,
,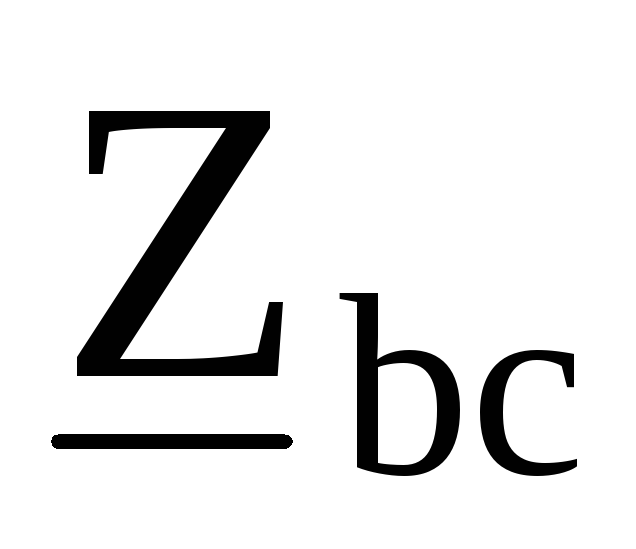 ,
,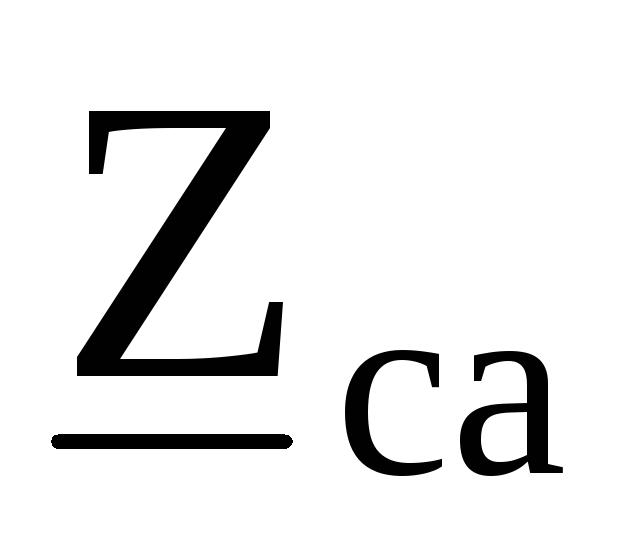 преобразуется
в
преобразуется
в
эквивалентную звезду с сопротивлениями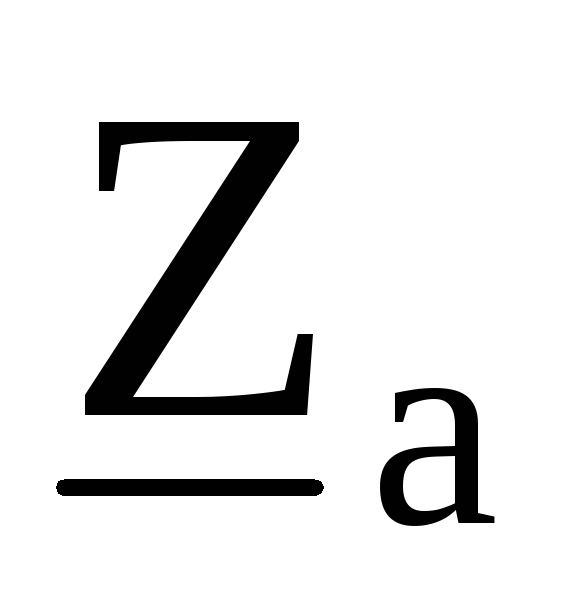 ,
,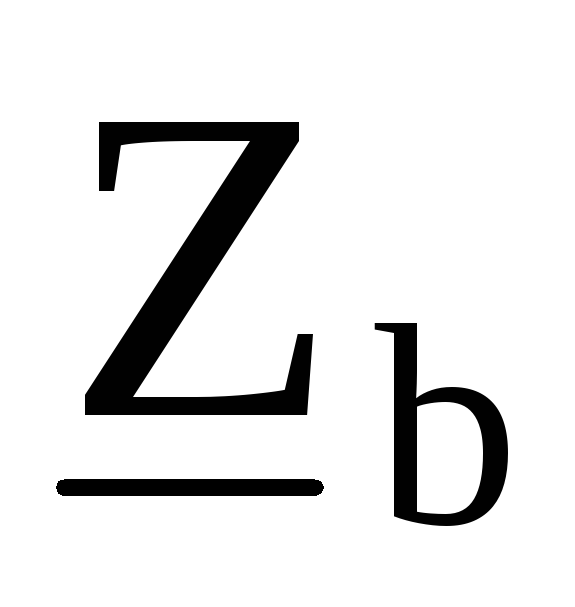 ,
,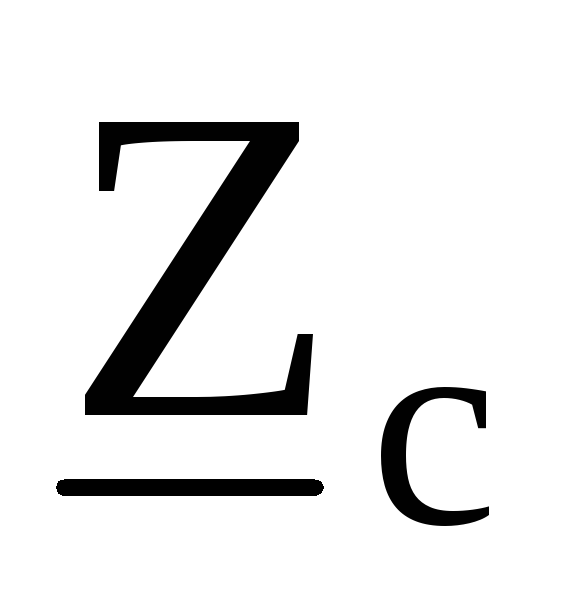 .
.
Полученные сопротивления:
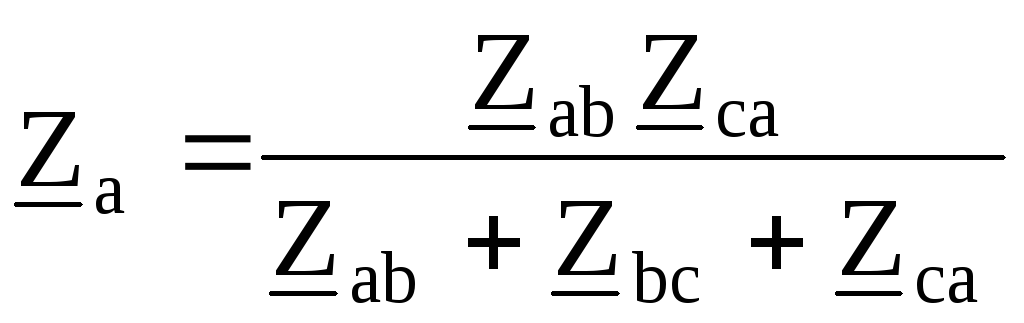 ;
;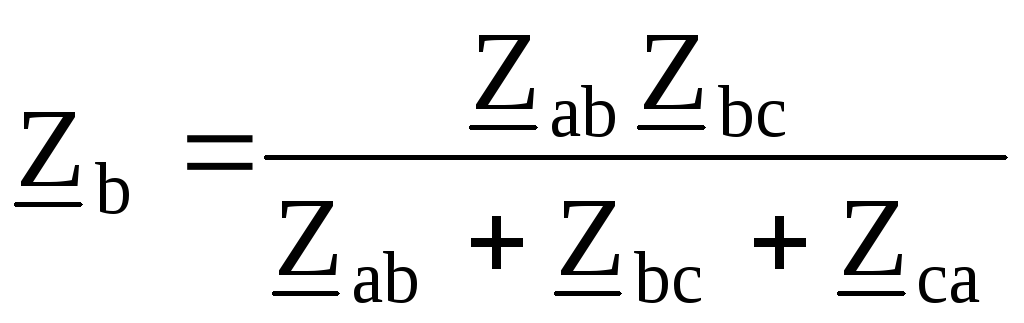 ;
;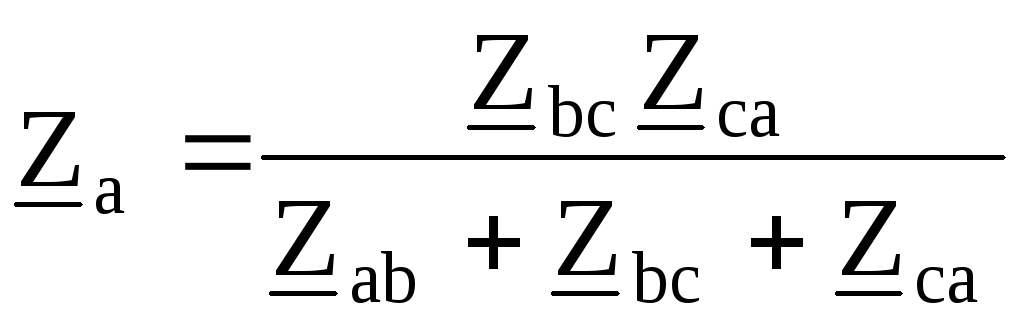 ;
;
объединяются с соответствующими
сопротивлениями 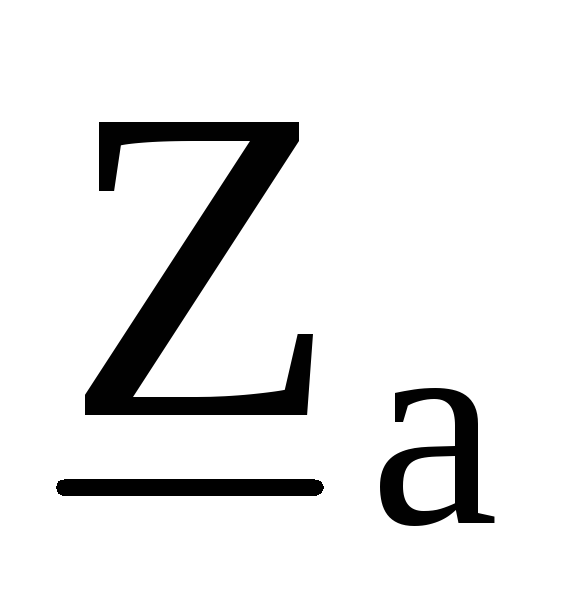
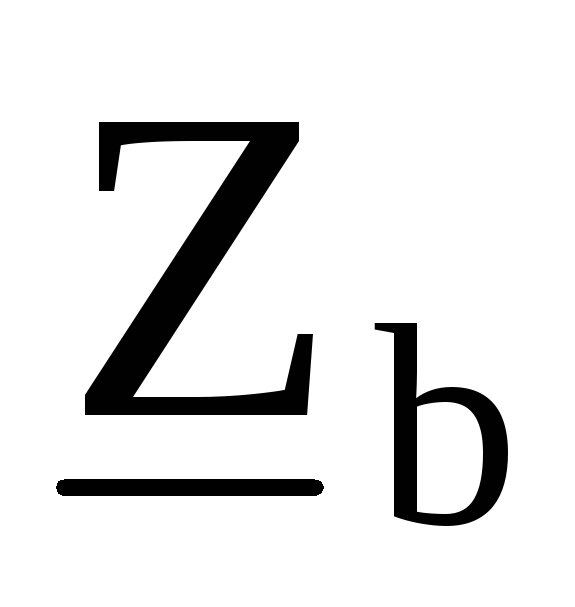 ,
,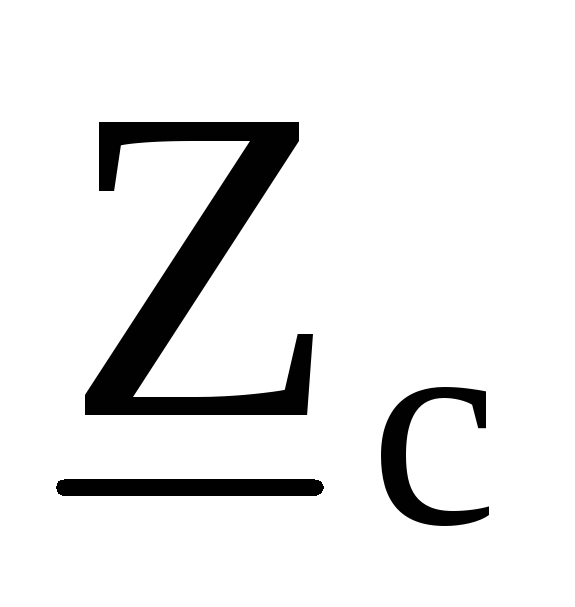 в результате чего получается
в результате чего получаетсянесимметричная звезда, показанная на рис. 9.36.Для этой звезды можно найти смещение
нейтрали нагрузки по отношению к «центру тяжести »треугольника линейных напряжений
генератора по формуле
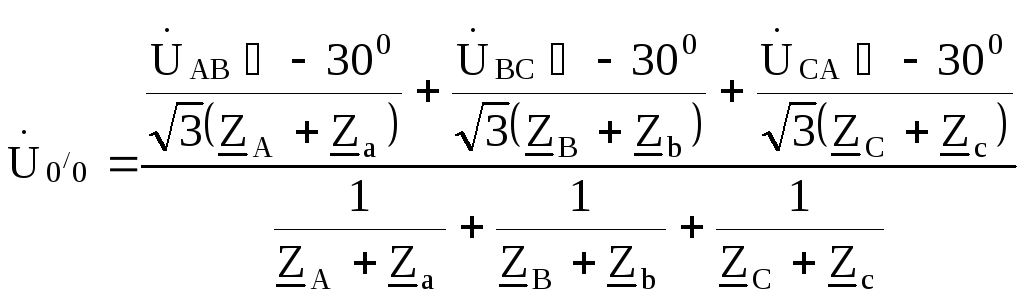
Тогда фазные напряжения на нагрузке будут
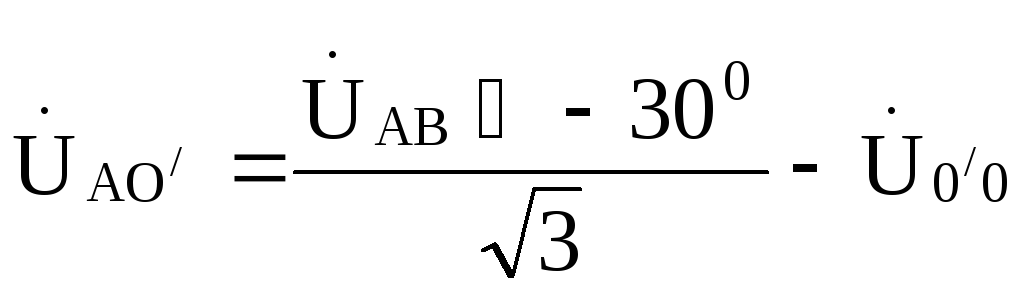 ;
;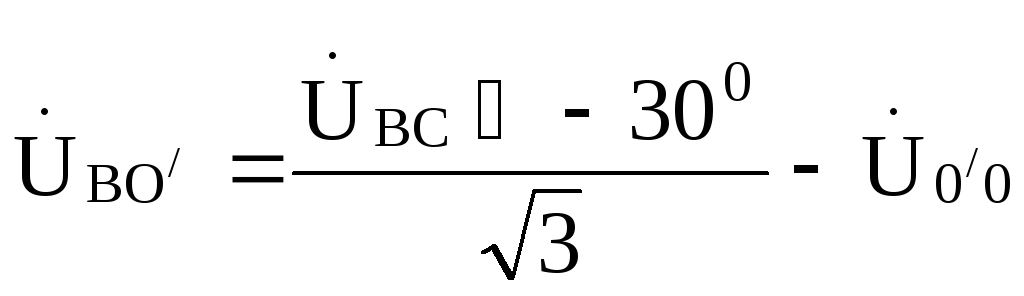
По этим напряжениям находим токи
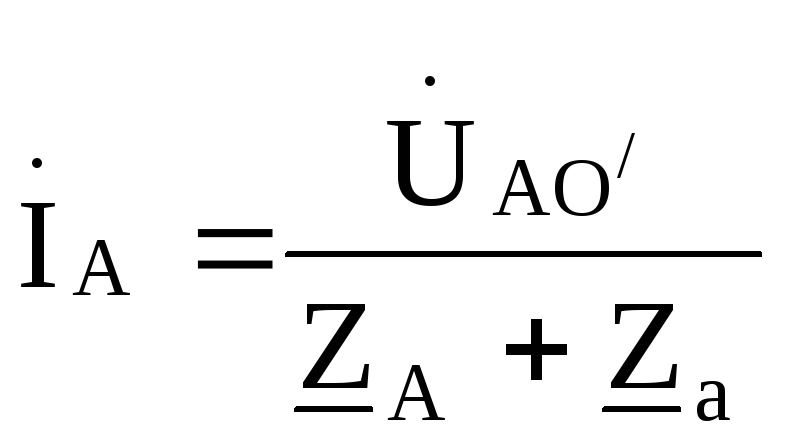 ;
;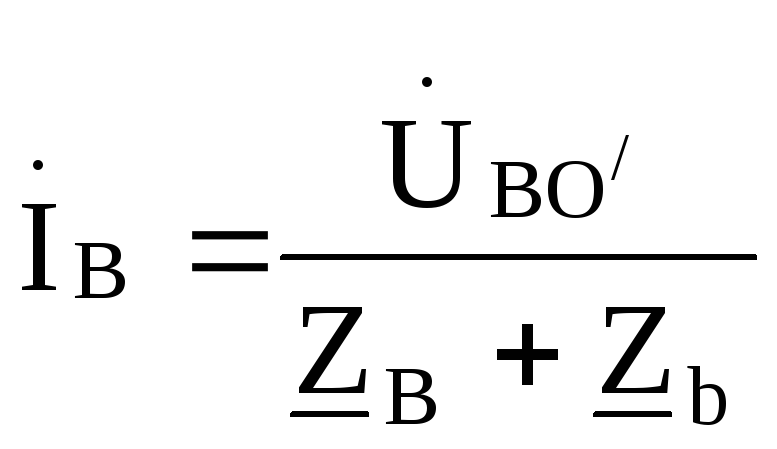 ;
; ;
;
По найденным токам ,
, ,
,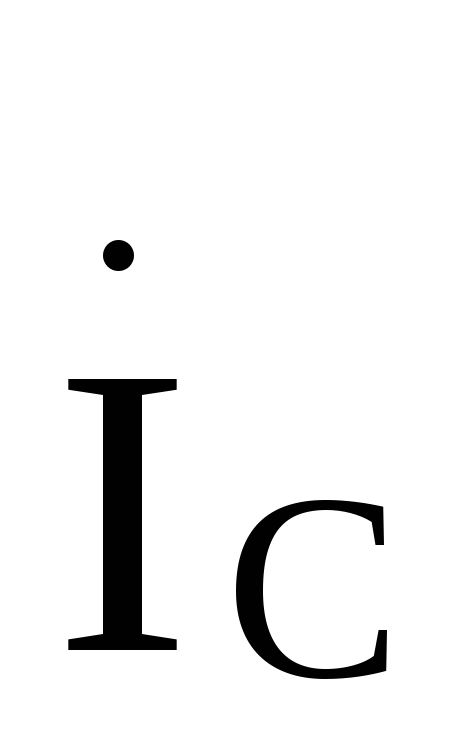 ,
находим напряжения на фазах звезды
с
,
находим напряжения на фазах звезды
с
сопротивлениями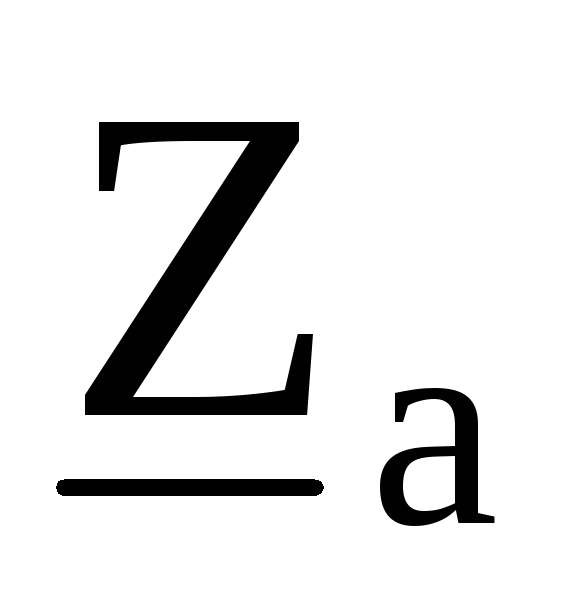
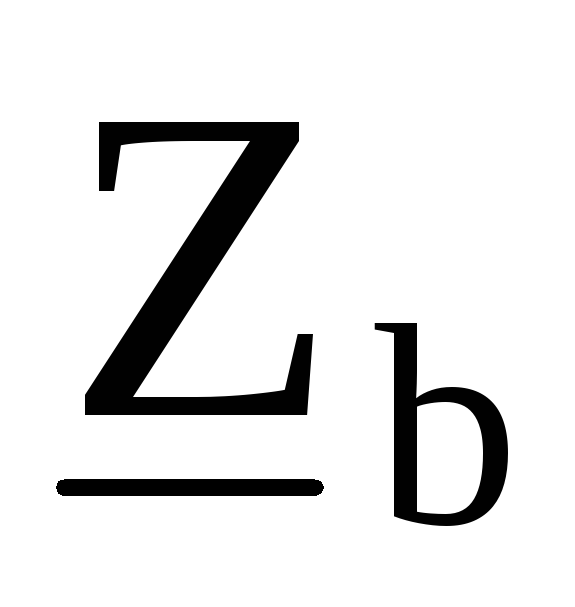 ,
,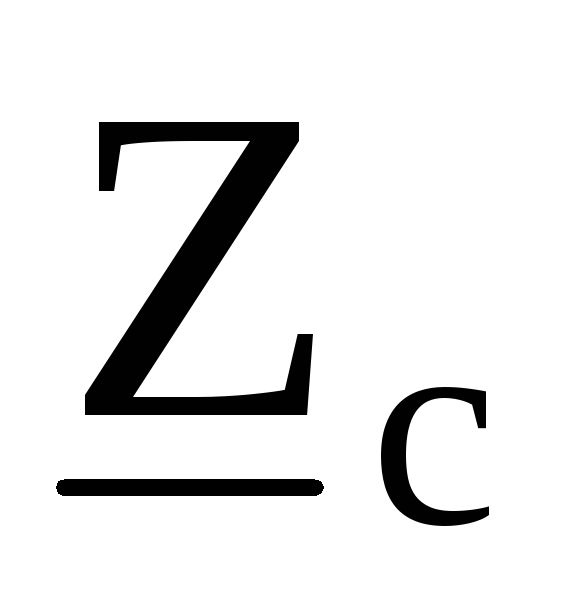 .
. 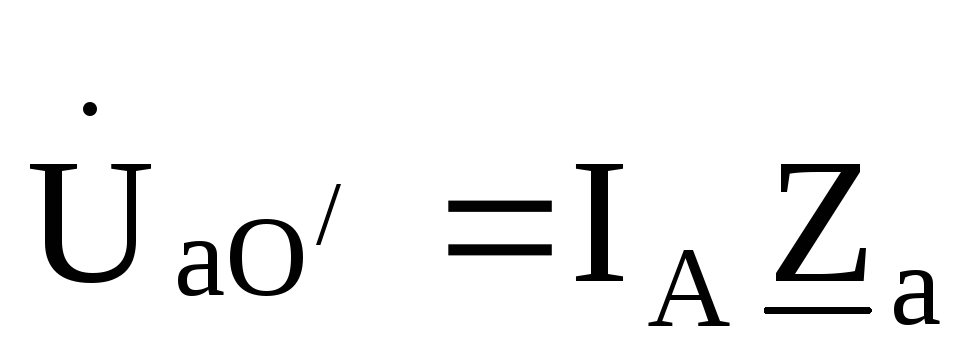 ,
,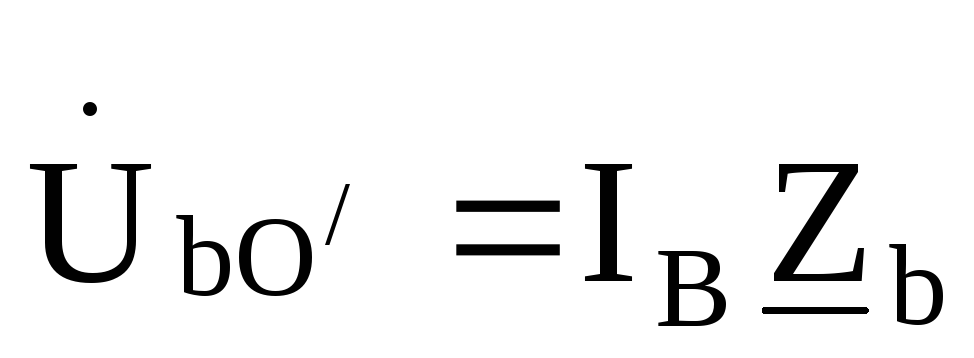 ,
,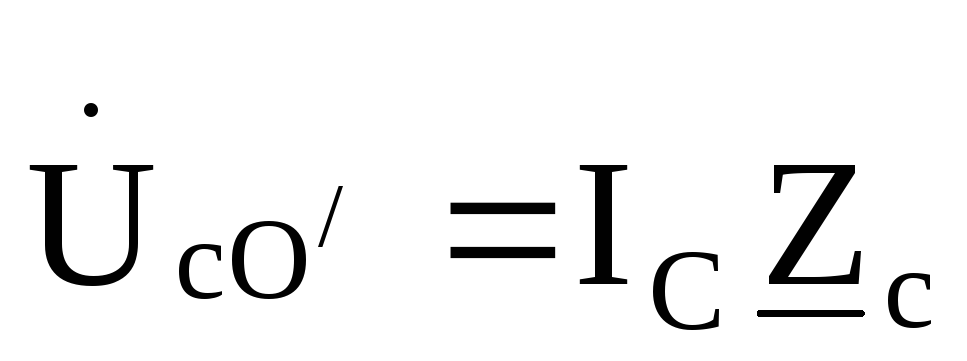 .
.
По этим фазным напряжениям находим напряжения зажимах треугольника
 ,
,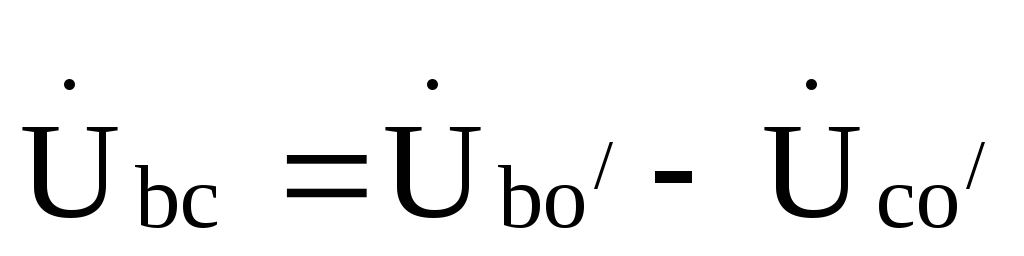 ,
,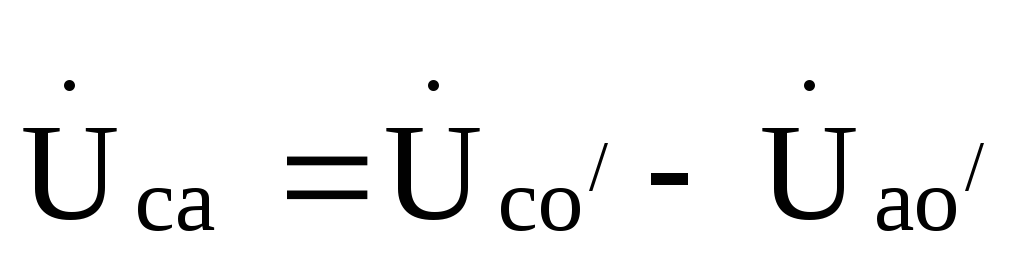 ,
,
Токи в фазах
треугольника находятся из выражений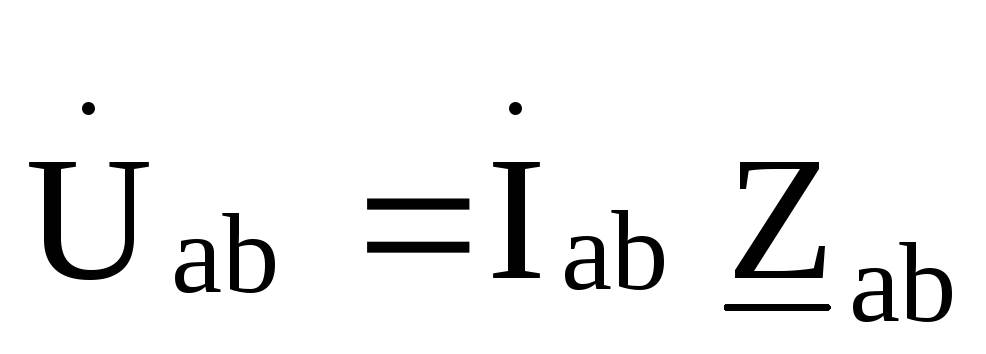 ,
,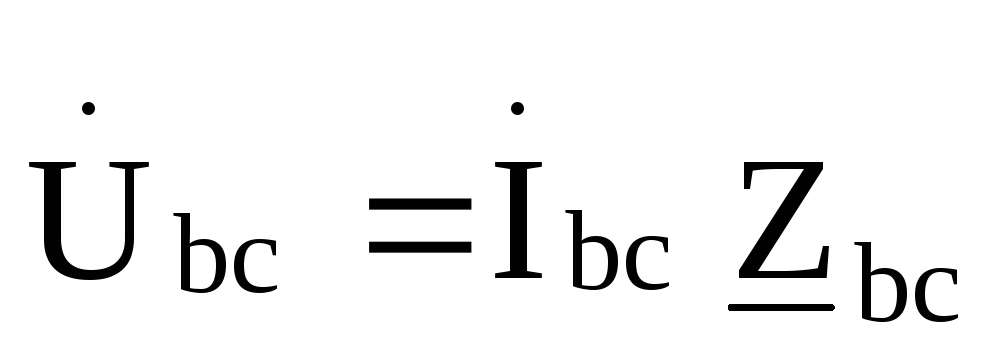 ,
,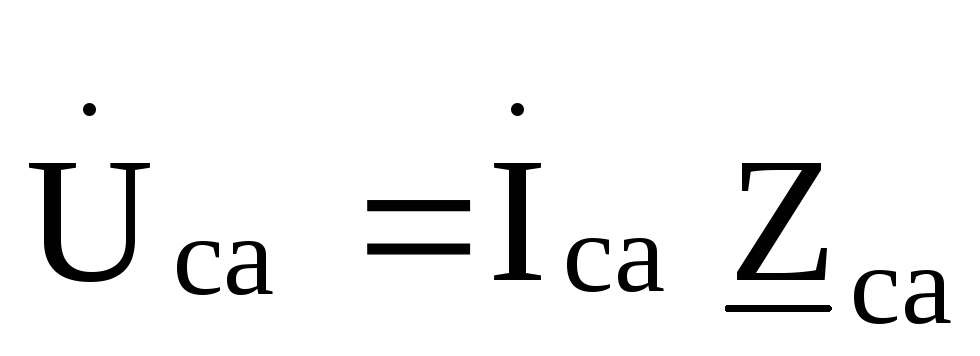 ,
,
Пример 9.8.Для цепи рис. 9.37определить токи и напряження. Построить векторно-
топографическую диаграмму
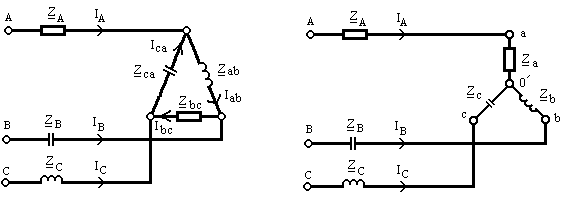
Рис. 9.37 Рис. 9.38
Линейное напряжение 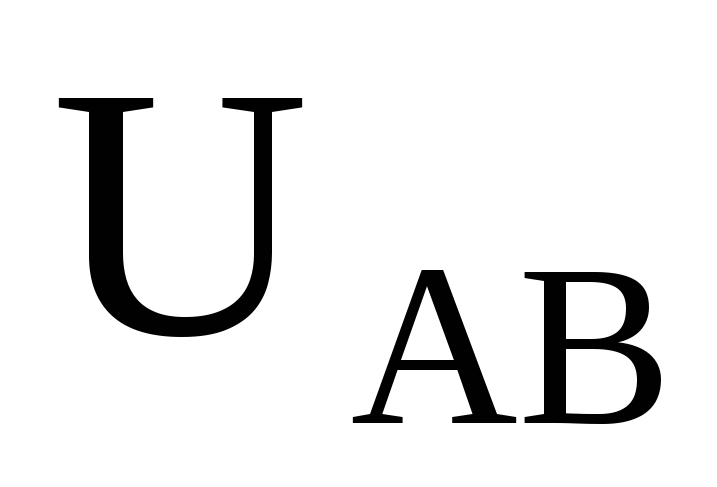 =220
В,
=220
В,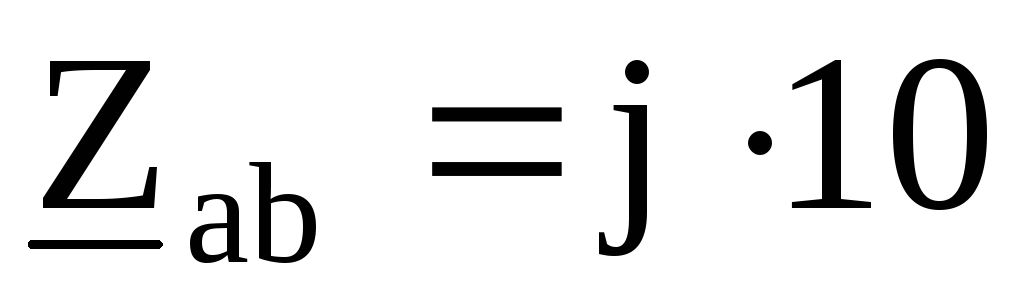 Ом,
Ом,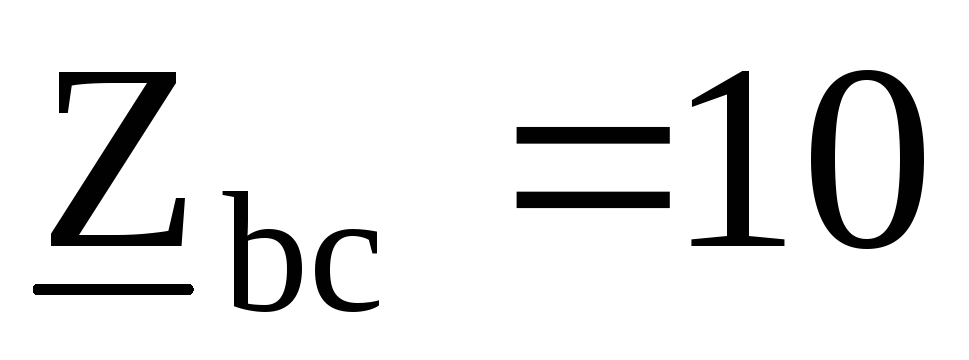 Ом ,
Ом ,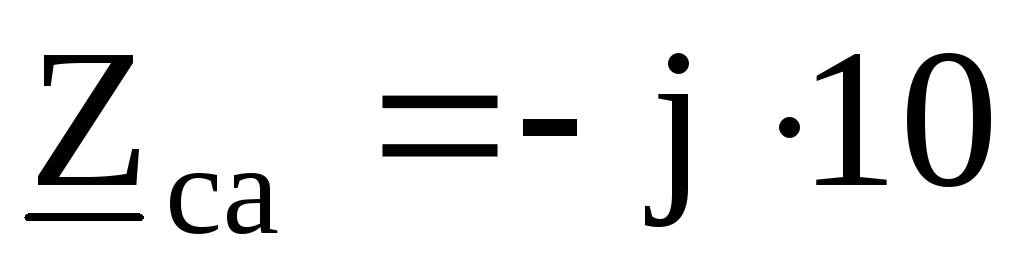 Ом,
Ом,
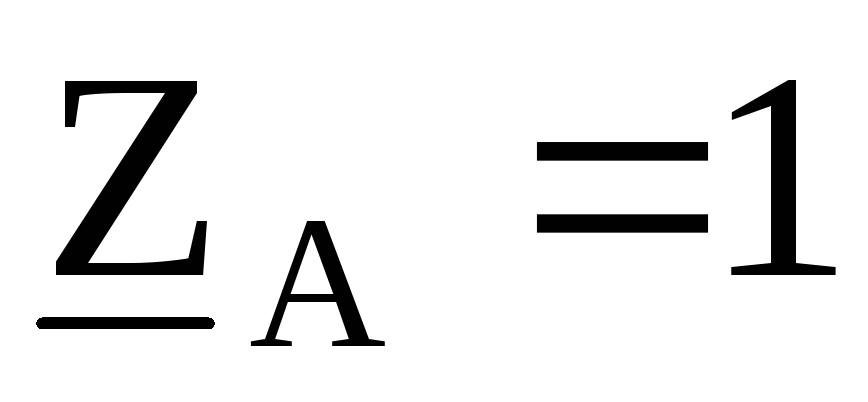 Ом,
Ом,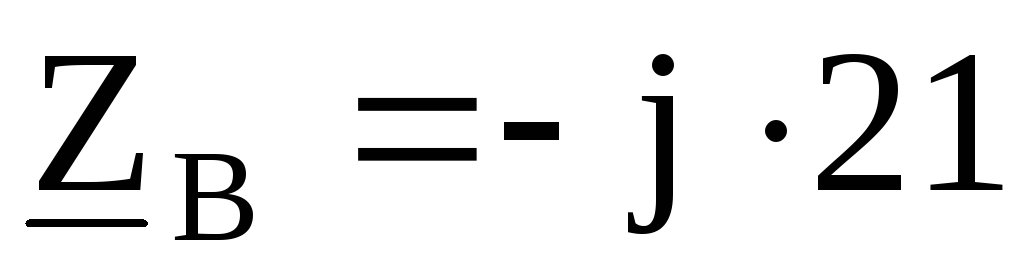 Ом,
Ом,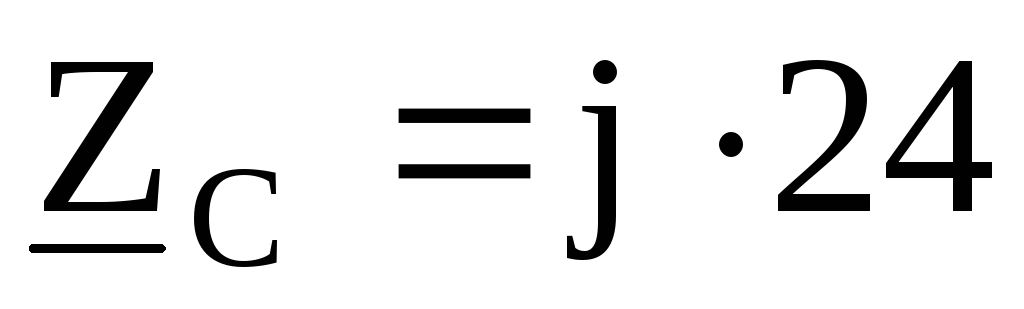 Ом
.
Ом
.
Решение
Преобразуем треугольник сопротивлений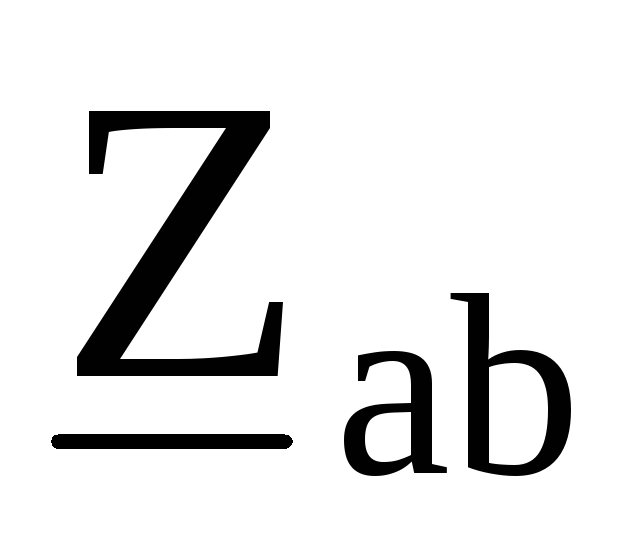 ,
,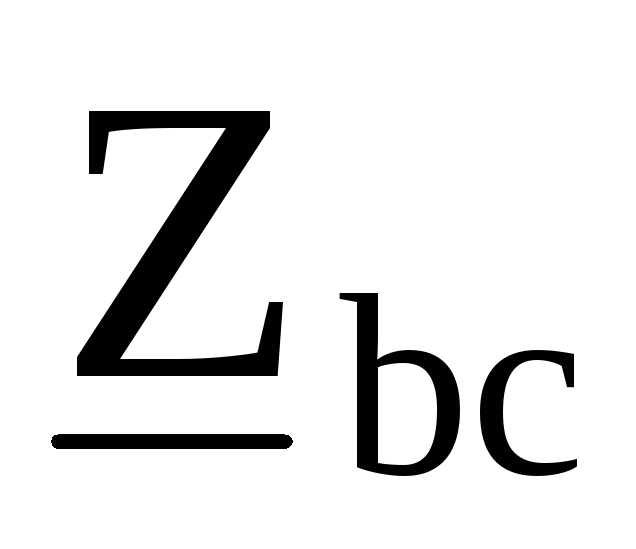 ,
,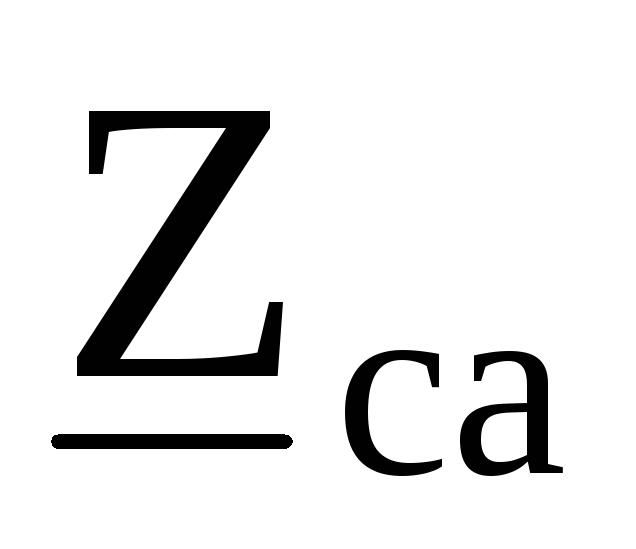 в эквивалентную звезду с
сопротивлениями
в эквивалентную звезду с
сопротивлениями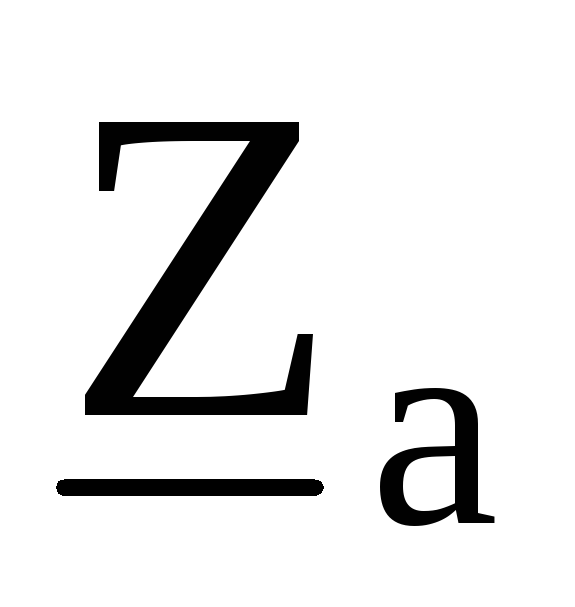 ,
,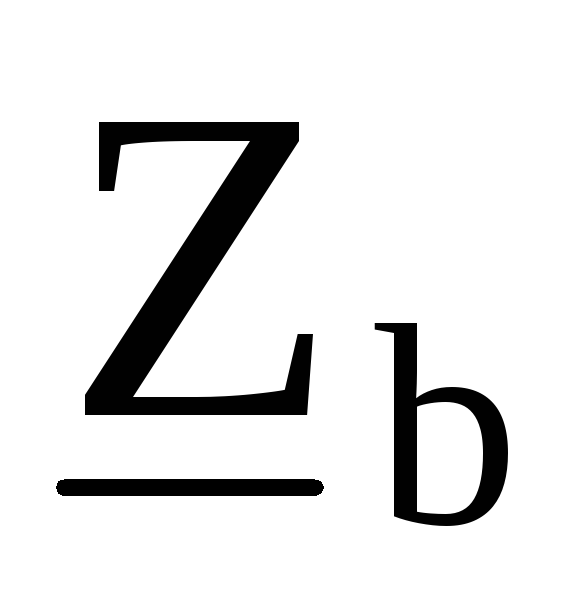 ,
,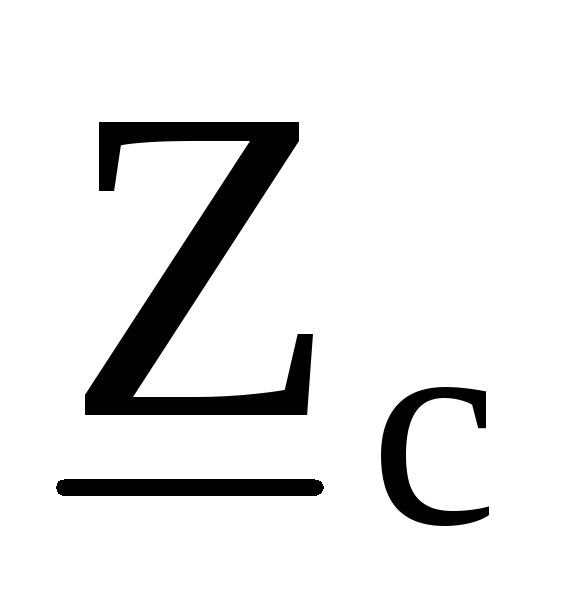 :
:
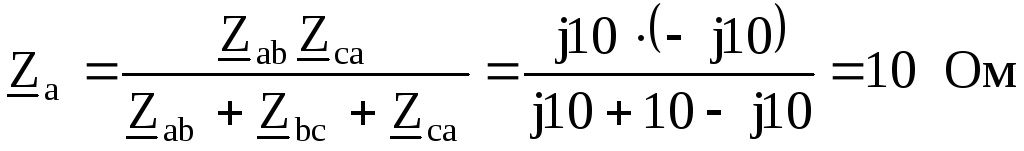
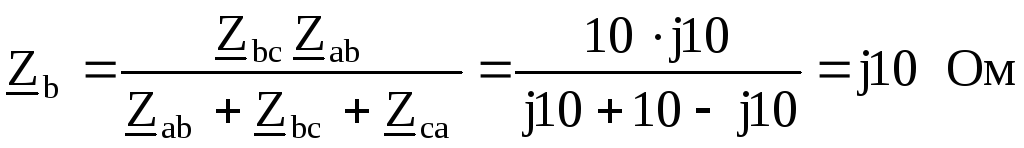
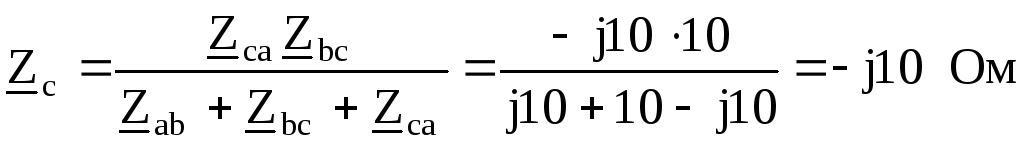
Полученные сопротивления оказываются соединенными последовательно с
соответствующимисопротивлениями в
линии 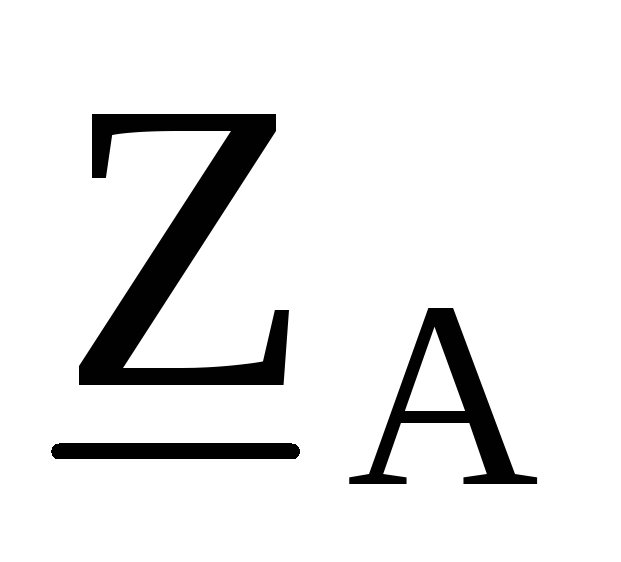 ,
,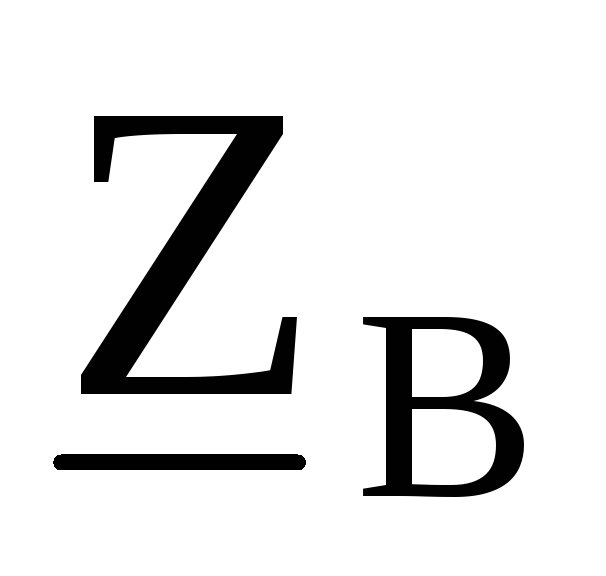 ,
,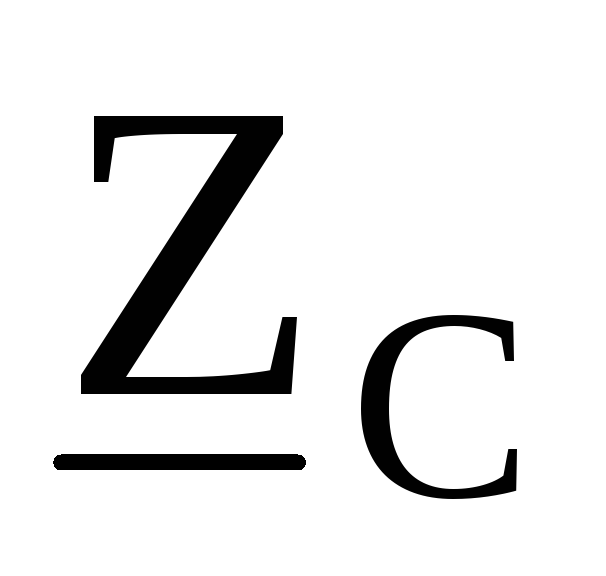 ,
как это показано на рис. 9.38.
,
как это показано на рис. 9.38.
Объединяя сопротивления в фазах, получим эквивалентную несимметричную звезду с
сопротивлениями 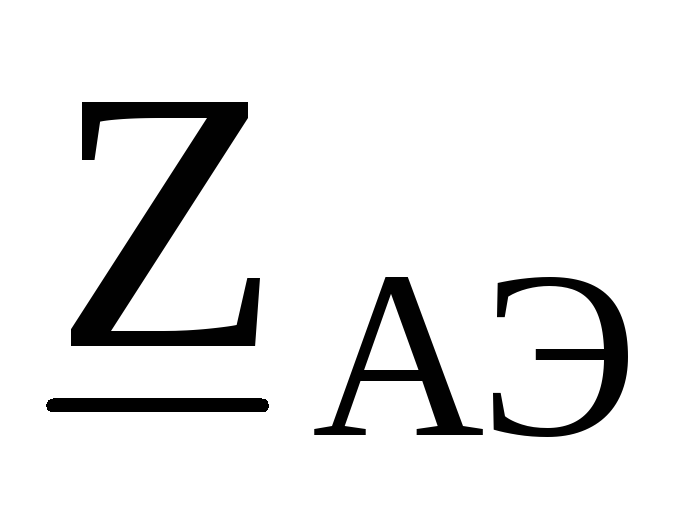 ,
,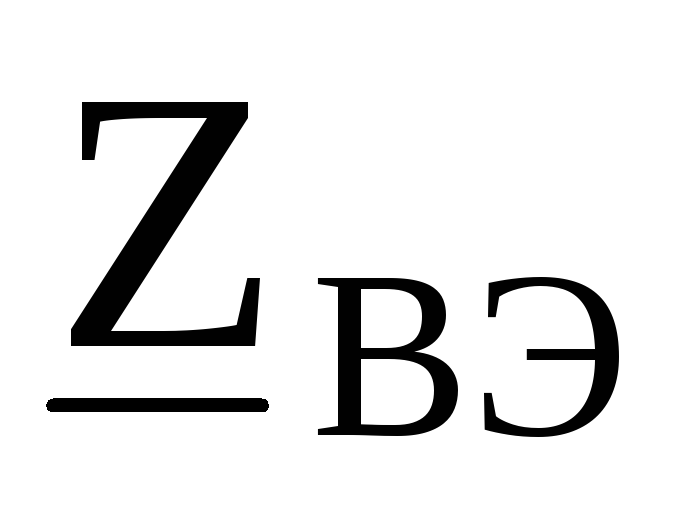 ,
,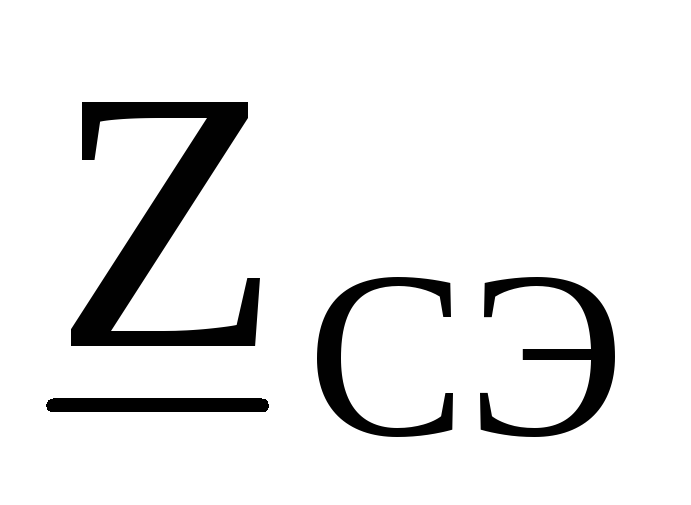 :
:
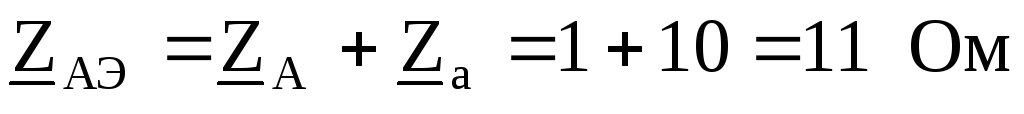
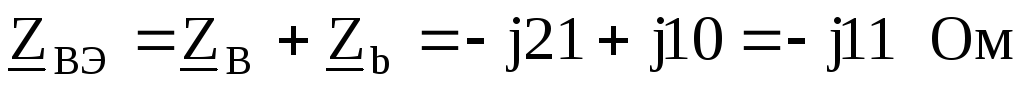
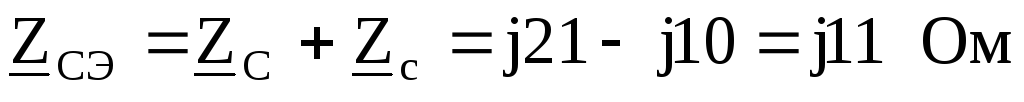
По заданному линейному напряжению найдем фазное напряжение генератора, обмотки которого соединены звездой.
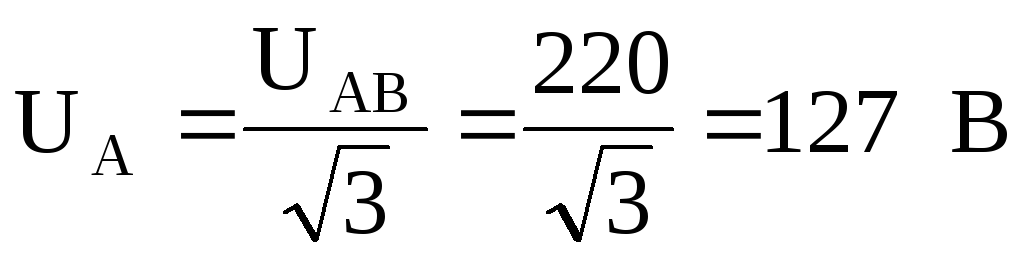
Принимаем 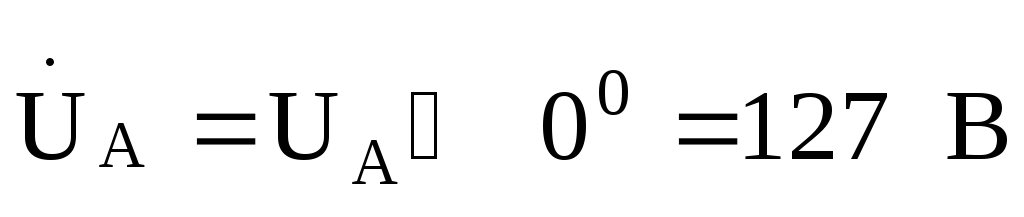 ,
тогда смещение нейтрали
,
тогда смещение нейтрали
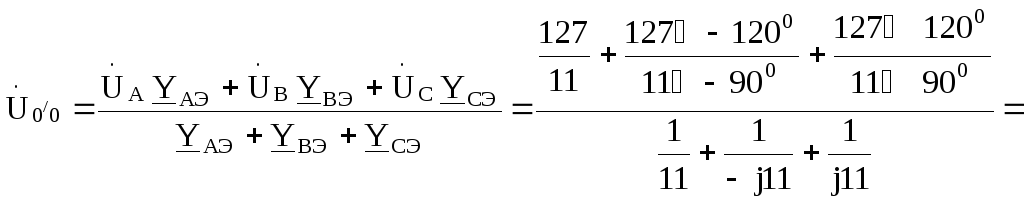
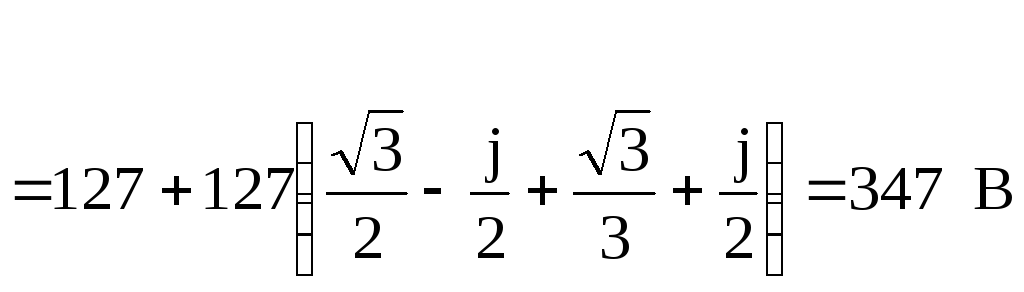
позволяет найти фазные напряжения
эквивалентной звезды с сопротивлениями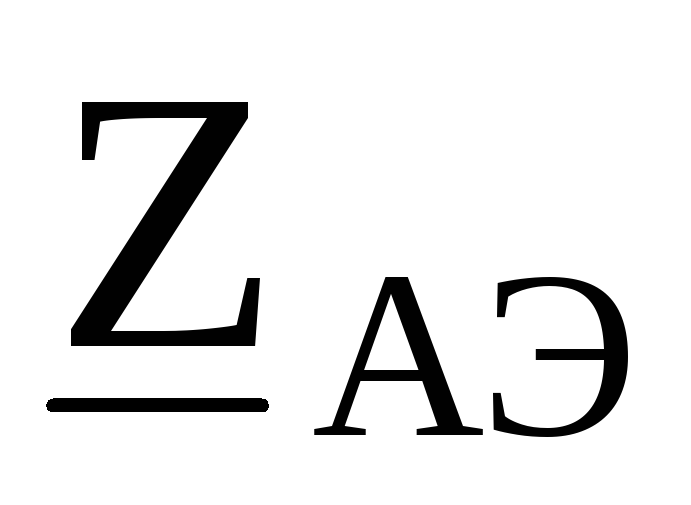 ,
,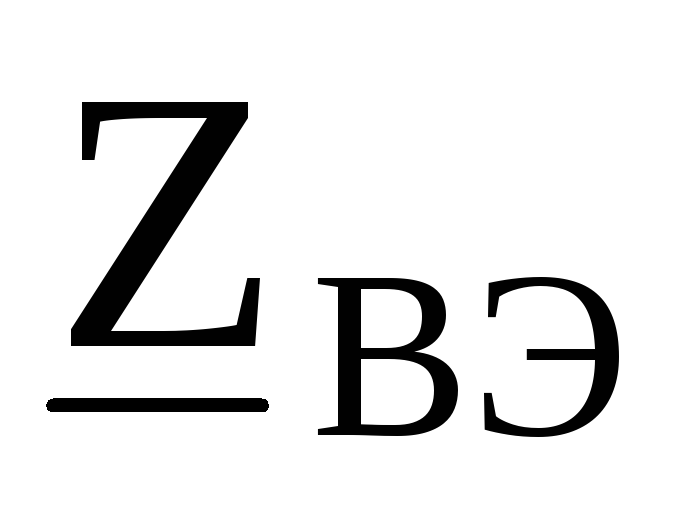 ,
,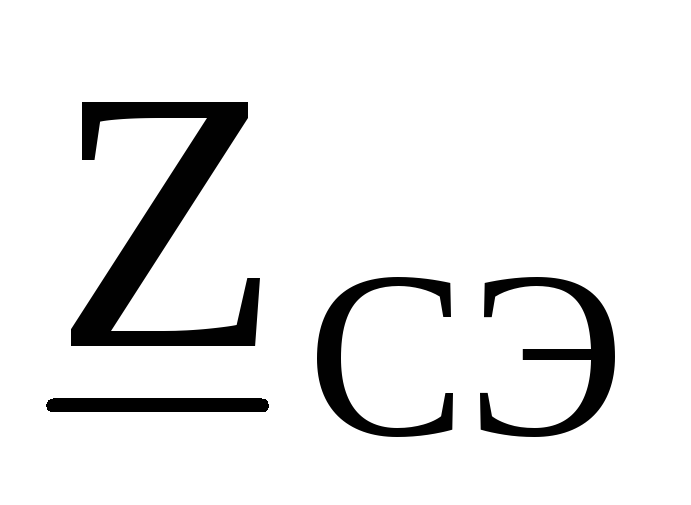 :
:
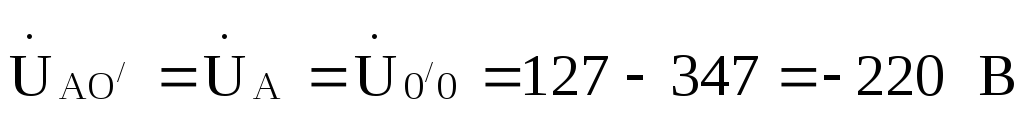
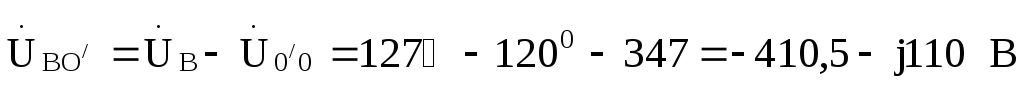
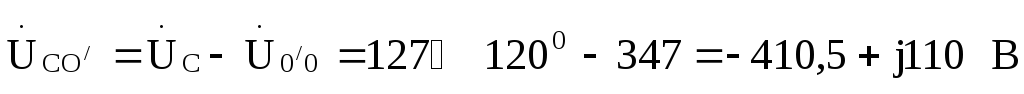
По этим напряжениям находим токи 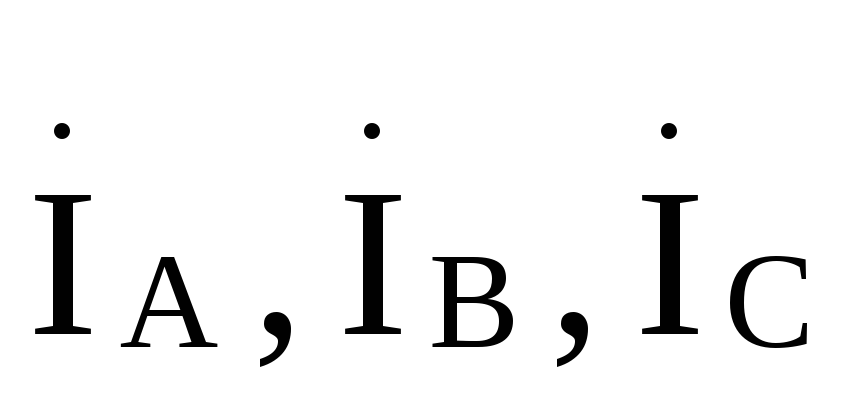 :
:
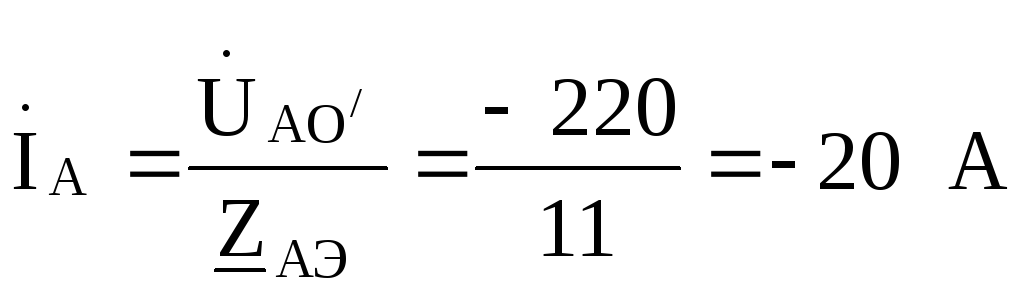
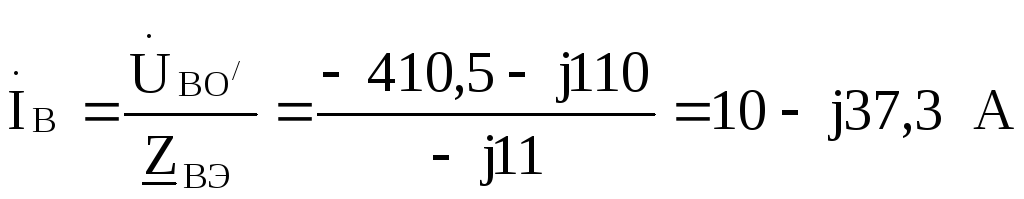
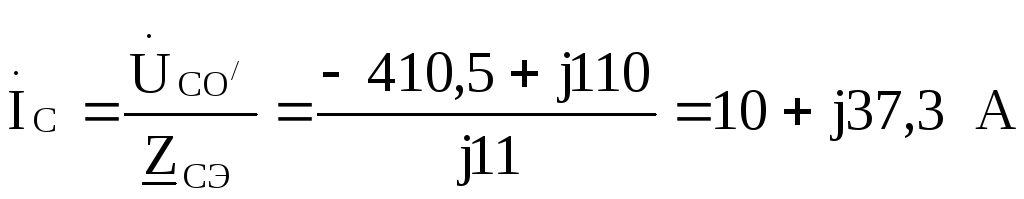
Проверка: 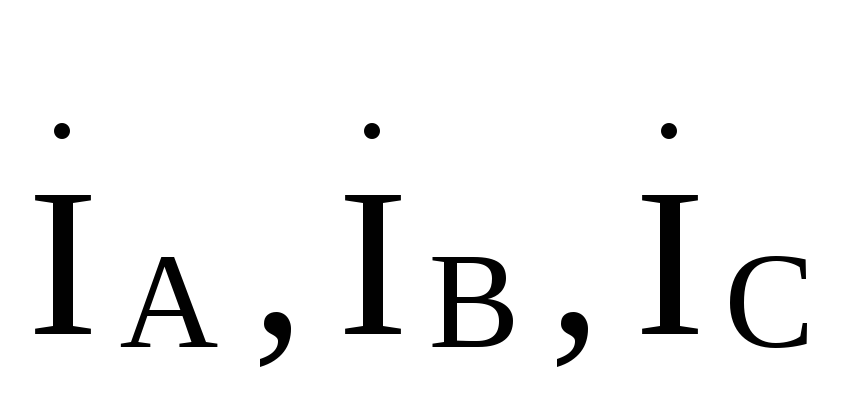 =
=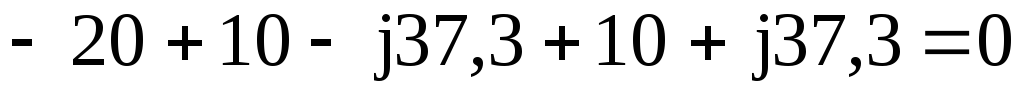 .
Теперь можно найти потенциалы точека, в, сно
отношению к потенциалу точки
.
Теперь можно найти потенциалы точека, в, сно
отношению к потенциалу точки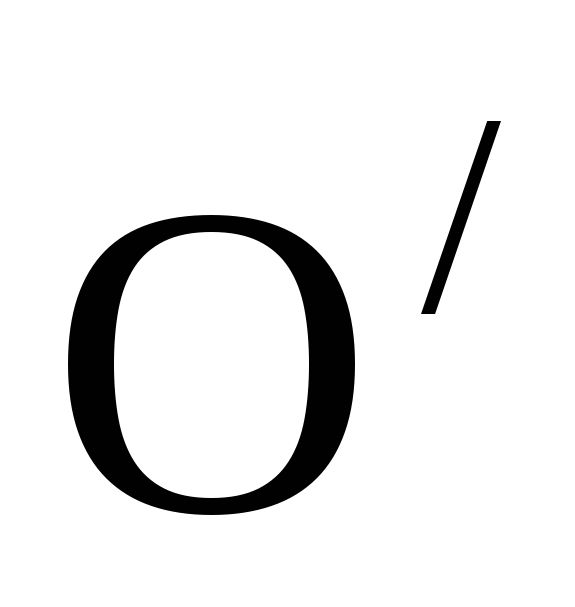 и напряжения на зажимах треугольника
и напряжения на зажимах треугольника
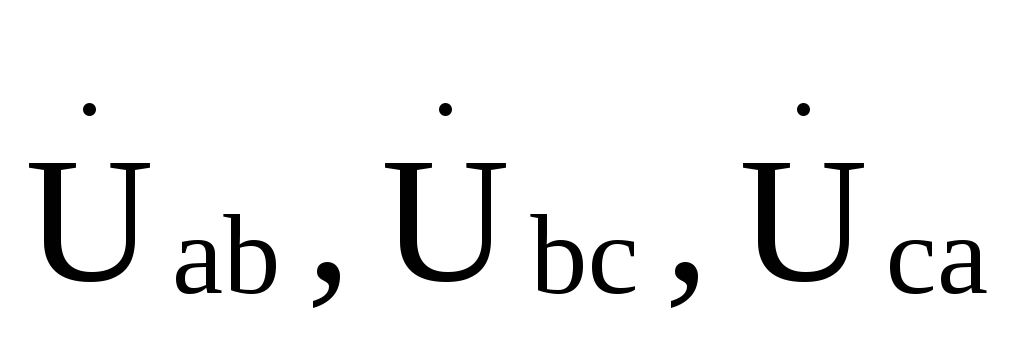 :
:
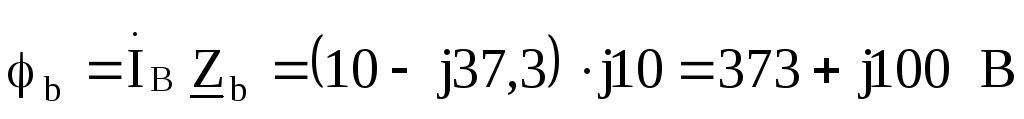
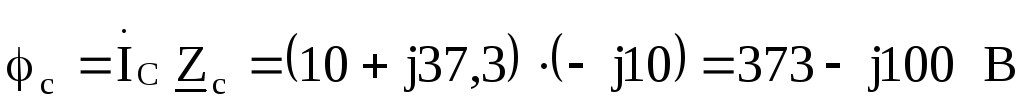

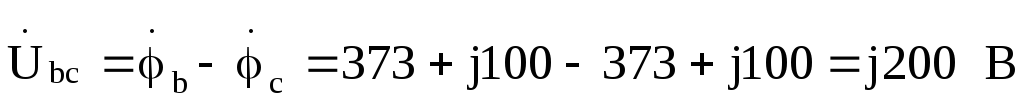
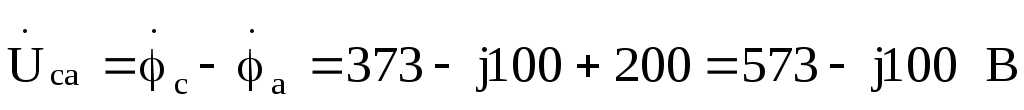
Токи в фазах треугольника:
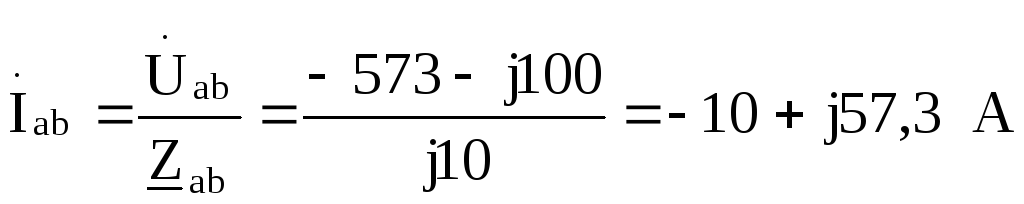 ;
;
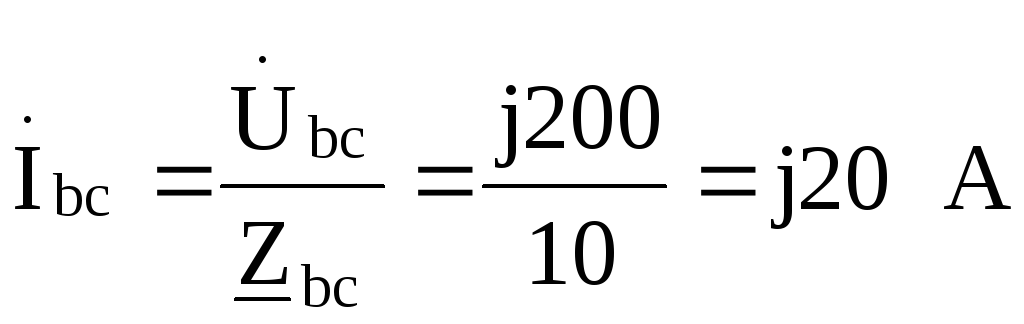 ;
;
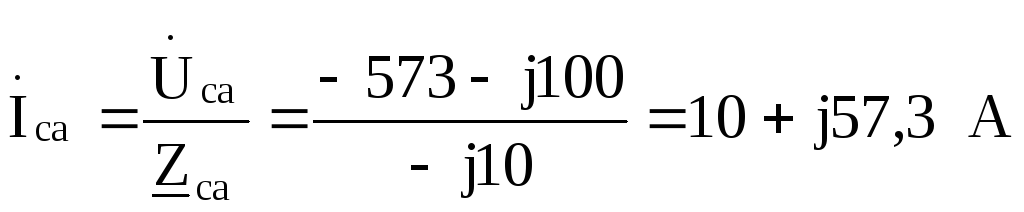 .
.
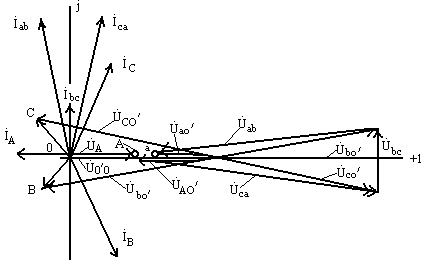
Рис. 9.39
Векторно-топографическая диаграмма приведена на рис. 9.39.
17. Преимущества трехфазных систем. Мощность в трехфазной цепи. Способы измерения активной и реактивной мощности в трехфазных цепях.
В современных системах передачи электрической энергии на дальние расстояния, электроснабжения и распределения электрической энергии применяются трехфазные цепи, которые по сравнению с однофазными имеют значительные преимущества:
Меньший расход проводникового материала, меньшая стоимость и более высокая экономичность линии электропередачи при одинаковой мощности и напряжении ЛЭП.
Возможность получения двух эксплуатационных напряжений (линейного и фазного) в одной трёхфазной четырёхпроводной системе.
Возможность простого получения вращающегося магнитного поля (ВМП), на использовании которого основана работа самых распространённых потребителей электрической энергии — трёхфазных асинхронных и синхронных электродвигателей.
Мощность трехфазной цепи
Мощность трехфазной цепи – это сумма соответствующих мощностей всех трех фаз (потерями мощности в нейтральном проводе обычно пренебрегают):
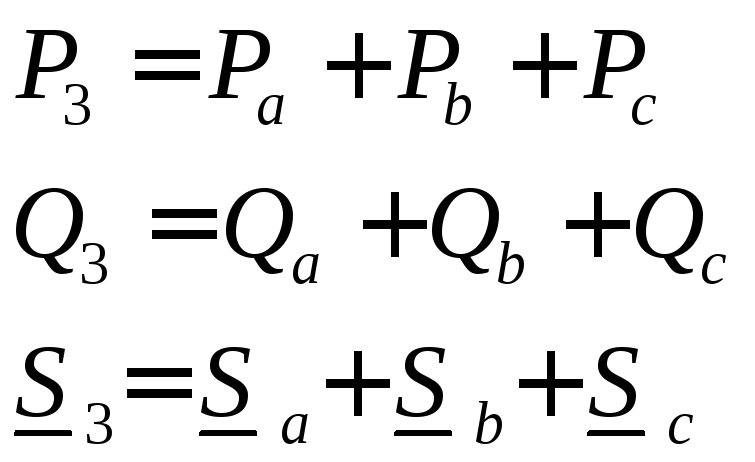
Как
и в однофазной цепи активная, реактивная
и полная мощности трёхфазной цепи
связаны соотношением: 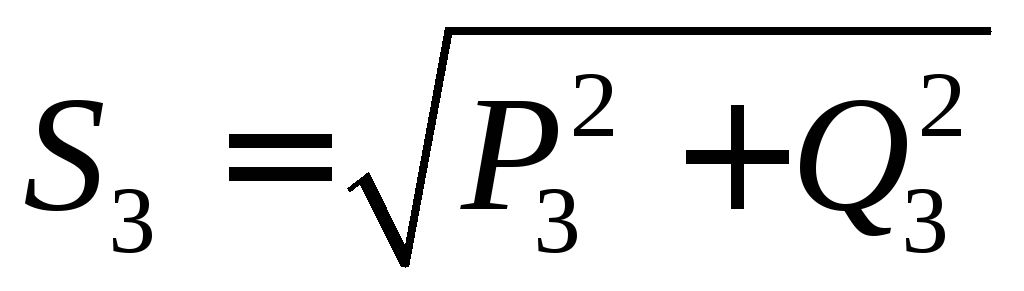 .
.
Мощность любой из фаз выражается обычной формулой:
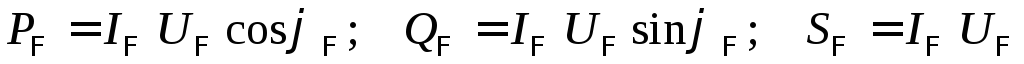 .
.
В случае симметричной нагрузки мощности всех трёх фаз соответственно равны:
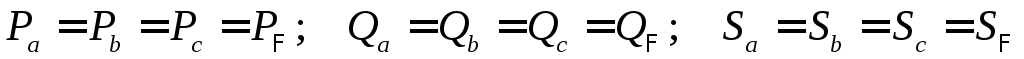
и
для мощности трёхфазной цепи можно
записать: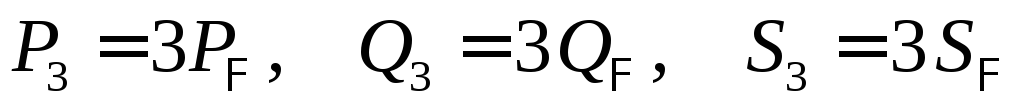 .
.
В
трёхфазной цепи при симметричной
нагрузке: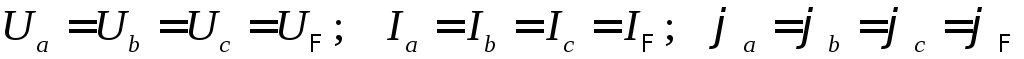 ,
,
поэтому
для мощности трёхфазной цепи можно
записать: 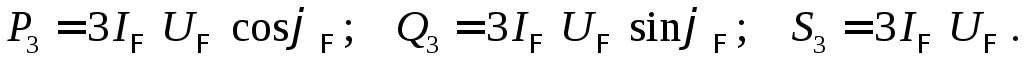
Кроме
того, при симметричной нагрузке известны
соотношения между линейными и фазными
напряжениями и токами: I Л = I Ф , U Л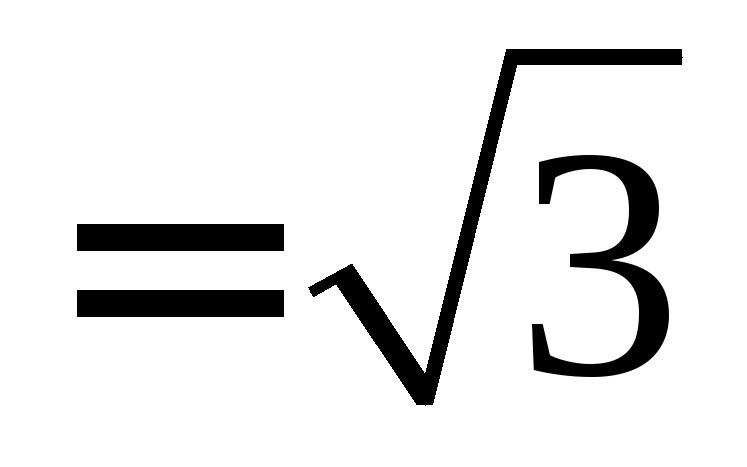 U Ф — при
соединении по схеме «звезда», I Л
U Ф — при
соединении по схеме «звезда», I Л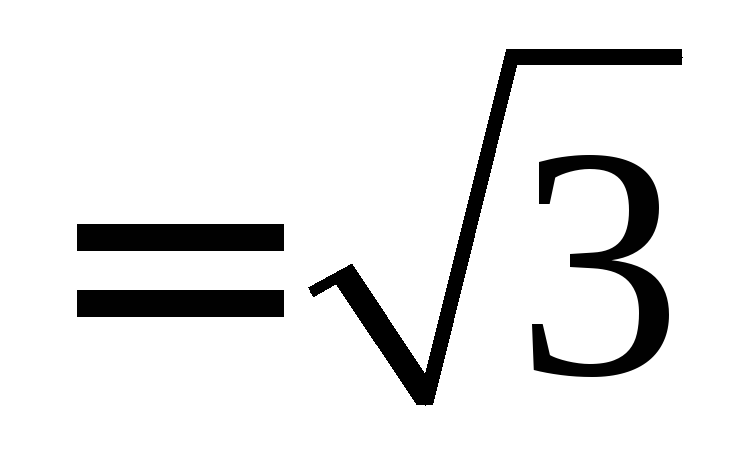 I Ф , U Л = U Ф — при
соединении по схеме «треугольник».
I Ф , U Л = U Ф — при
соединении по схеме «треугольник».
После
подстановки этих выражений в формулу
мощности трёхфазной цепи в общем случае
при симметричной нагрузке получаем: 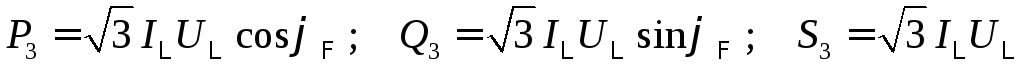 .
.
В
случае несимметричной нагрузки мощность
трёхфазной цепи следует находить как
сумму соответствующих мощностей всех
трёх фаз (т.е. как сумму соответствующих
фазных мощностей): 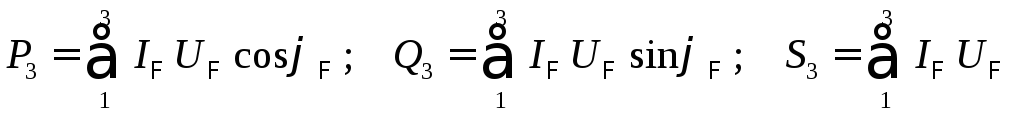
Измерение активной мощности трёхфазной цепи
Активная мощность в цепи переменного тока P = I U cos φ измеряется с помощью электродинамического ваттметра, измерительный механизм которого состоит из двух катушек, одна из которых может вращаться.
Обмотка неподвижной катушки – последовательная или токовая обмотка – обладает малым сопротивлением и включается в измеряемую цепь последовательно, а обмотка подвижной катушки — обмотка напряжения — имеет большое сопротивление и включается параллельно на зажимы нагрузки (потребителя). где k — конструкционный коэффициент, I — ток в последовательной обмотке ваттметра.
При включении ваттметра в цепь следует обращать внимание на правильное подключение обмоток ваттметра, начала которых ( генераторные зажимы) обозначаются звёздочками (* ). Оба генераторных зажима должны быть присоединены к одному и тому же проводу со стороны источника электрической энергии (генератора).
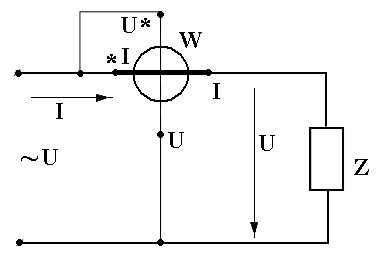 Для
измерения активной мощности трёхфазной
цепи часто используется однофазный
ваттметр активной мощности, включаемый
по различным схемам.
Для
измерения активной мощности трёхфазной
цепи часто используется однофазный
ваттметр активной мощности, включаемый
по различным схемам.
Измерение активной мощности методом одного ваттметра
Метод
одного ваттметра применяется в трёхфазных
цепях только при симметричной нагрузке
фаз. При симметричной нагрузке мощность,
потребляемая каждой из трёх фаз,
одинакова, поэтому достаточно измерить
мощность одной фазы и, умножив результат
измерения на число фаз, получить мощность
трёхфазной цепи: 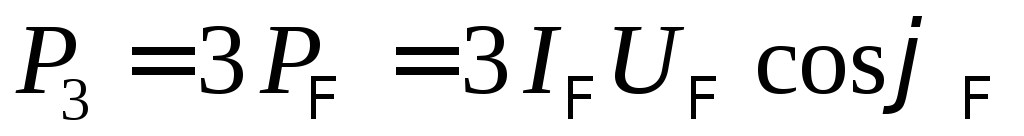 .
.
Следовательно, для измерения мощности при симметричной нагрузке достаточно одного ваттметра, токовая обмотка которого включается последовательно с фазной нагрузкой, а обмотка напряжения – включается на фазное напряжение.
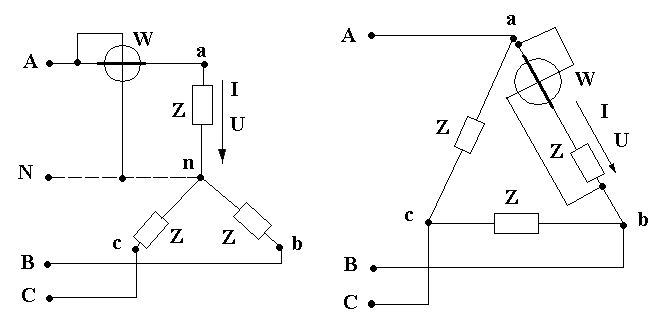
Если
нейтральная точка нагрузки недоступна,
то измерение фазной мощности в соединении
звезда выполняют по схеме с искусственной
нейтральной точкой, созданной соединёнными
в звезду обмоткой напряжения ваттметра Z Vи двух
равных ей по сопротивлению добавочных
резисторов Z 2 и Z 3 : 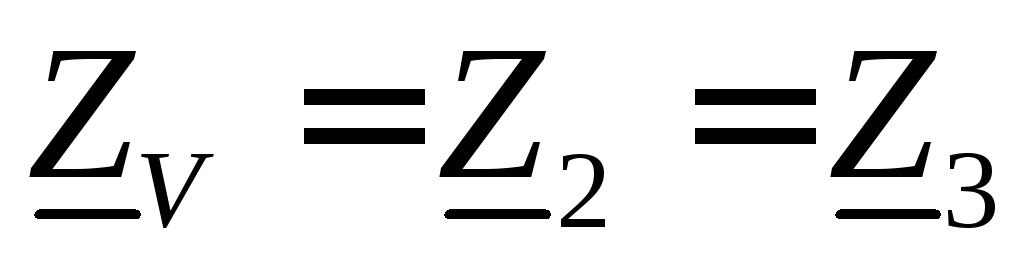 .
.
9.3. Расчет трехфазных цепей с симметричной нагрузкой
Исходными данными являются:
— схема трехфазной цепи,
— фазные ЭДС генератора,
— сопротивления фаз нагрузки.
Искомыми величинами являются токи.
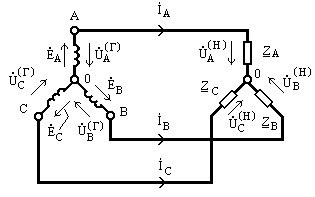
Рис. 9.9
Обмотки генератора и сопротивления нагрузки соединены в звездy, как показано нaрис. 9.9
(без нулевого провода).
По условию: 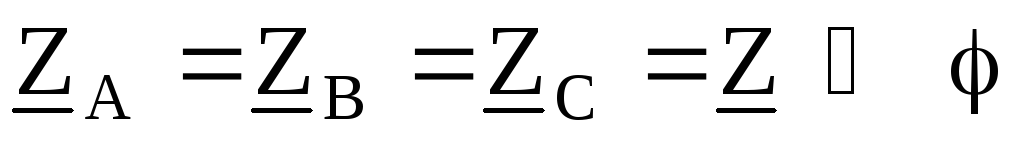
Заданные фазные ЭДС генератора в комплексной форме можно записать так
если 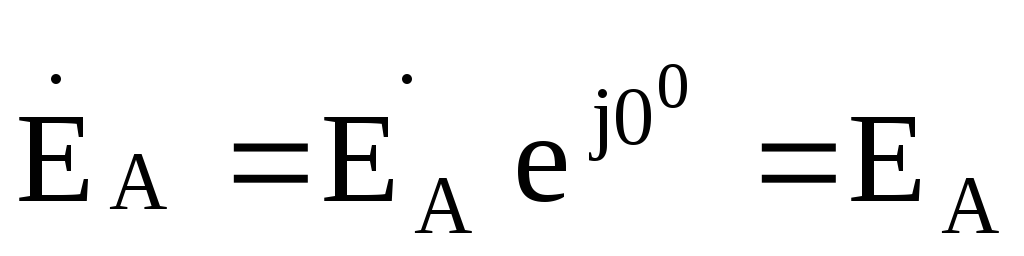 ,
то
,
то
 ,
,
Напряжение между нейтральными точками нагрузки и генератора находим по методу двух узлов
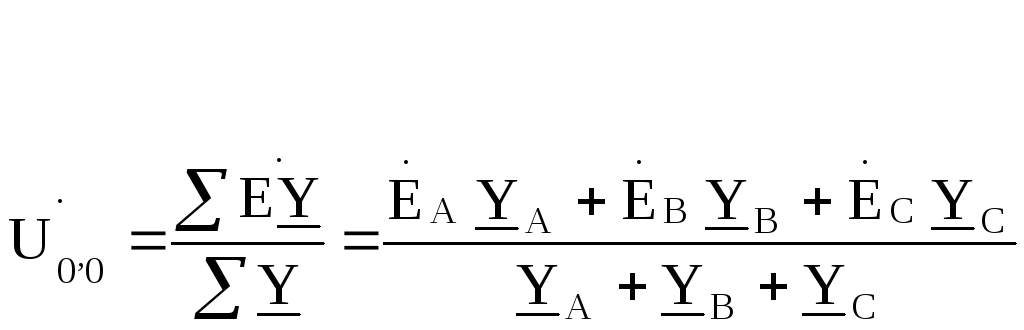
Так как для симметричной нагрузки 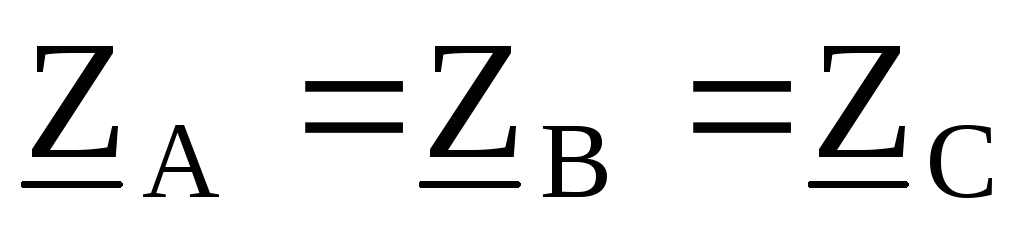 и
и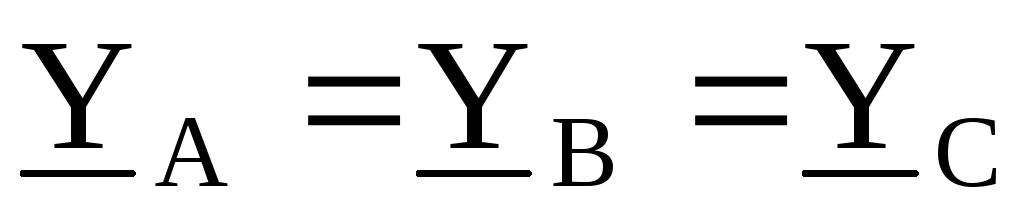 ,
то, учитывая
,
то, учитывая
соотношение (9.2),найдем
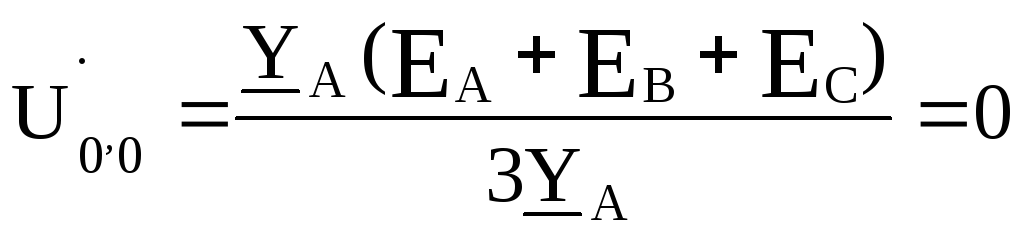
Вывод , который необходимо запомнить: у симметричной нагрузки, соединенной звездой,
потенциал нейтральной точки 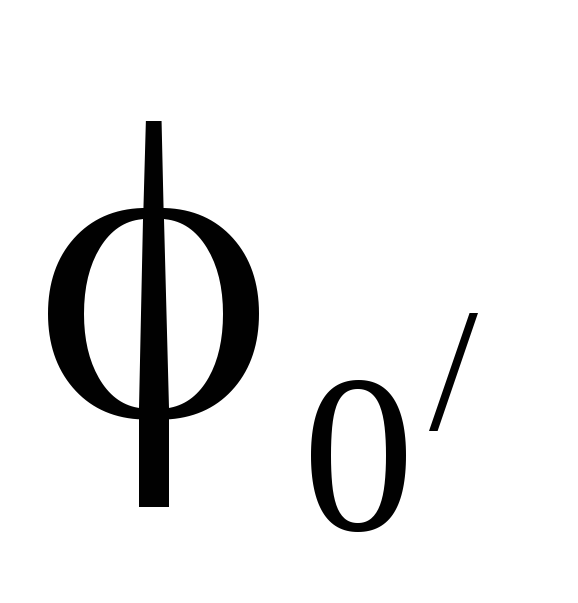 равен потенциалу нейтральной точки
генератора
равен потенциалу нейтральной точки
генератора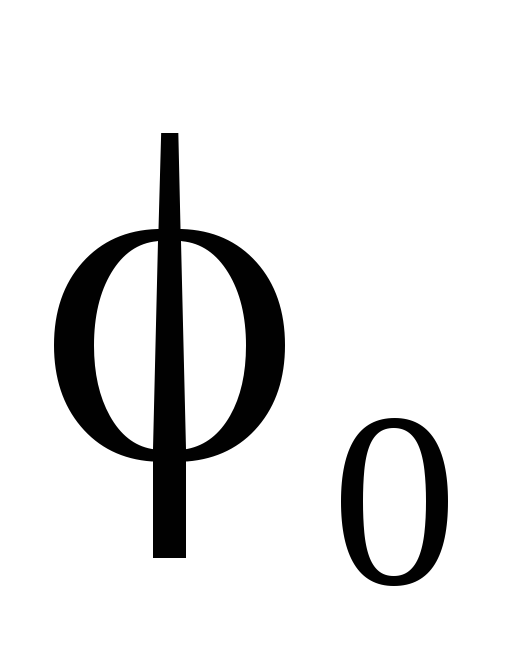 .
Отсюда
.
Отсюда
следует, что эти точки можно соединить между собой проводником и тогда становится ясным,
что 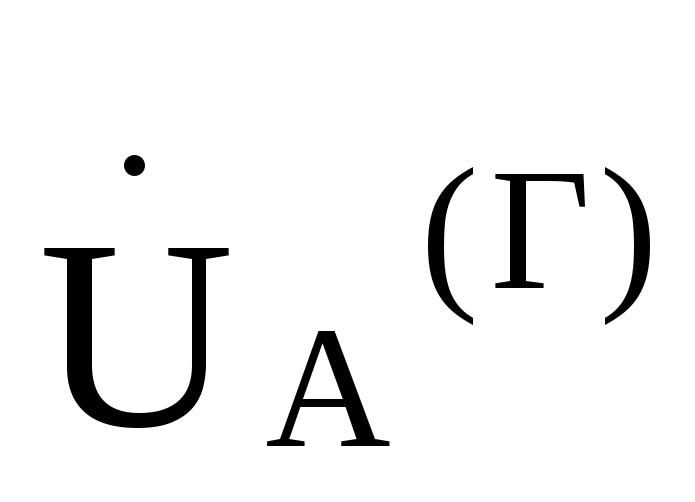 =
=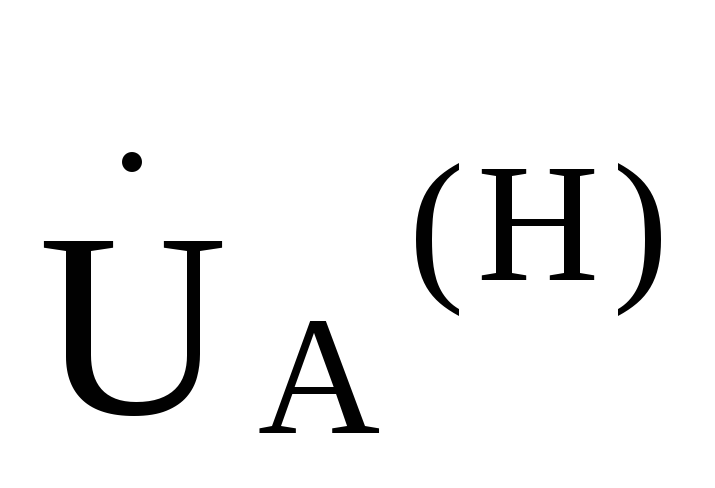 ,
,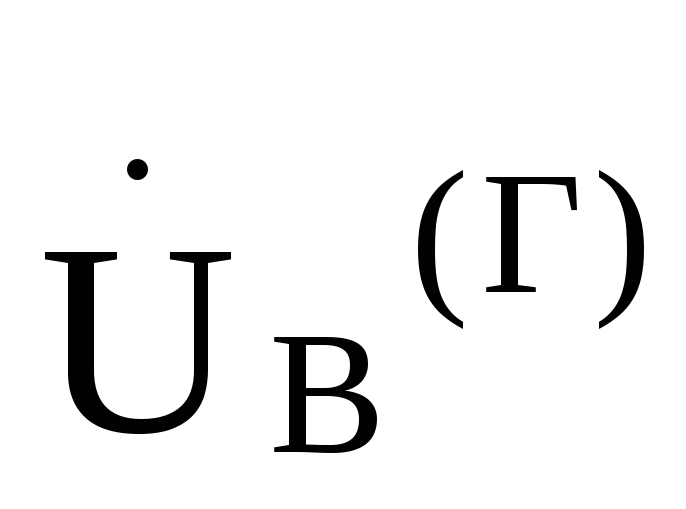 =
=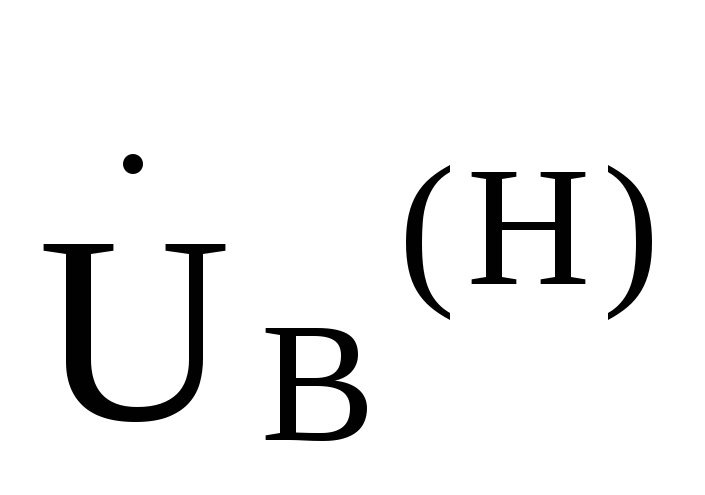 ,
,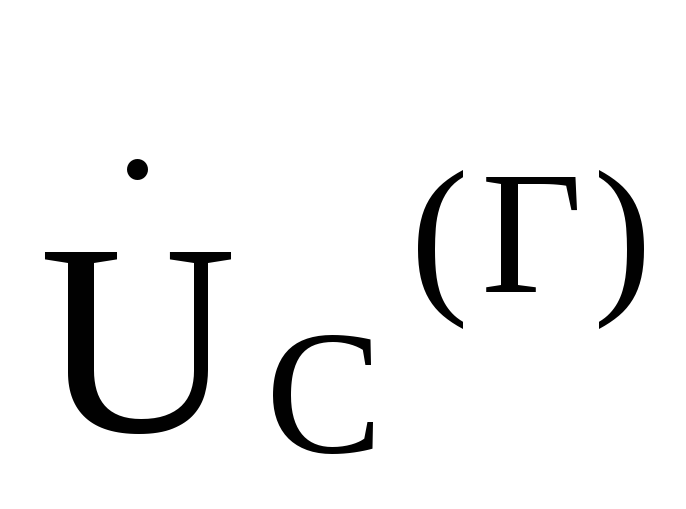 =
=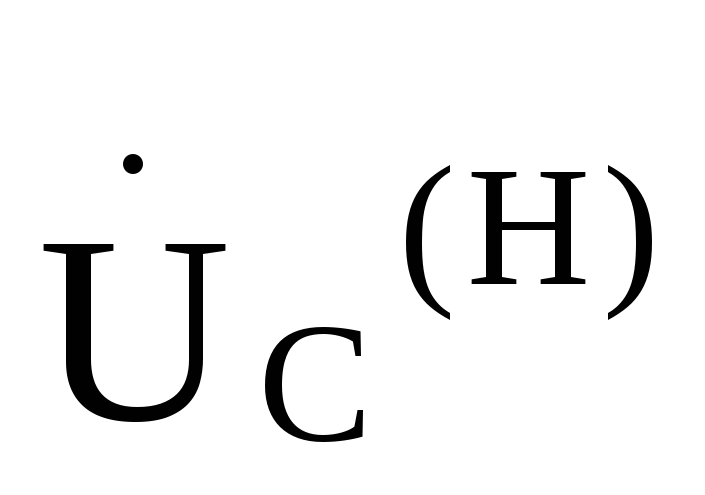 и токи в фазах нагрузки будут
и токи в фазах нагрузки будут
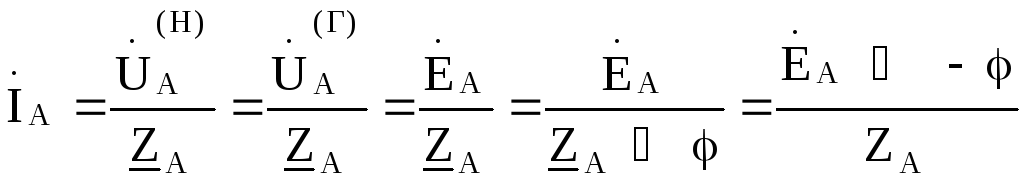

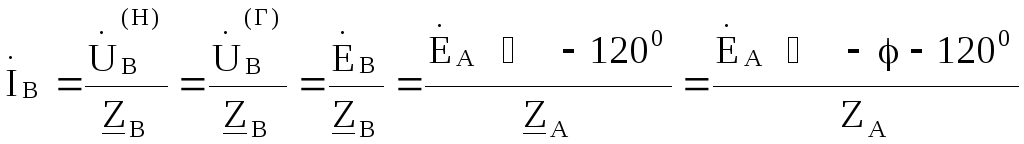
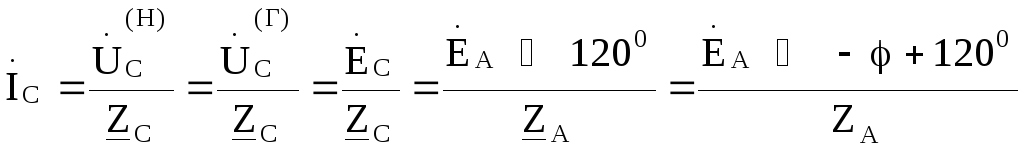
Из схемы очевидно, что фазный ток нагрузки является линейным током и он же есть ток в фазе
генератора.
Покажем, что напряжение между любыми двумя линейными проводами, называемое —
линейным напряжением, в 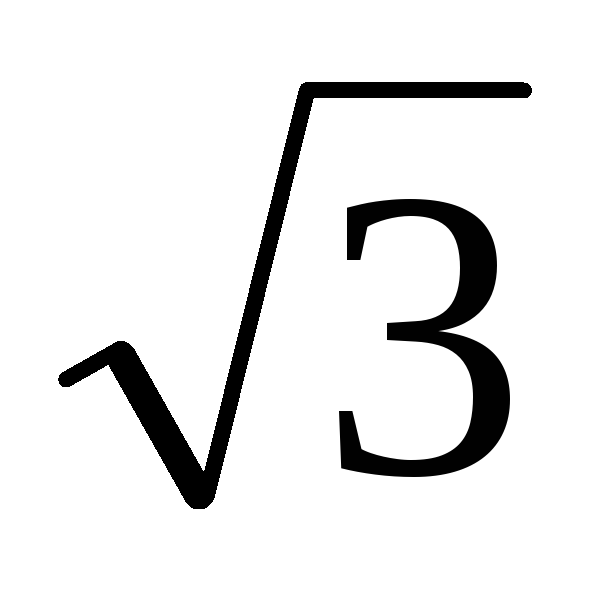 раз
больше фазного напряжения, т. е.
раз
больше фазного напряжения, т. е.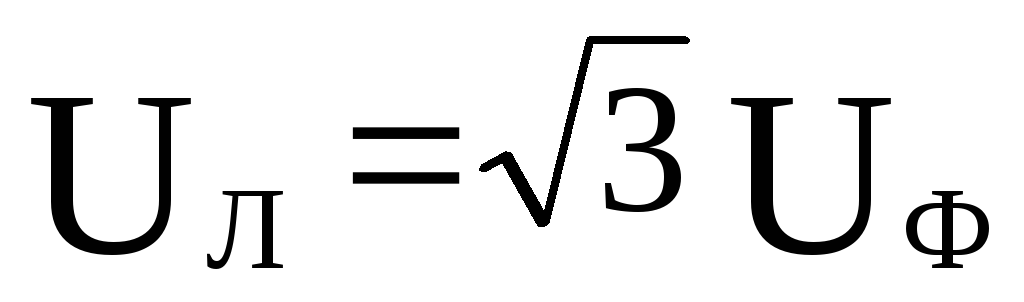 .
.
Для этого найдем, например, разность комплексных потенциалов точек А и В
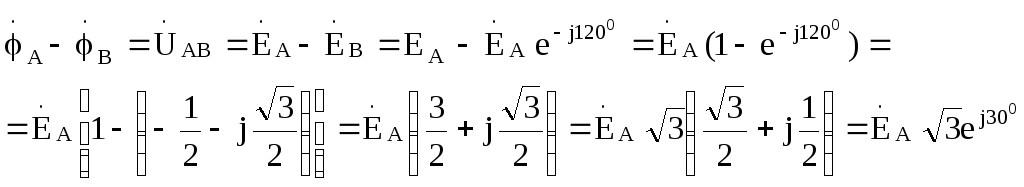
Таким
образом, линейное напряжение 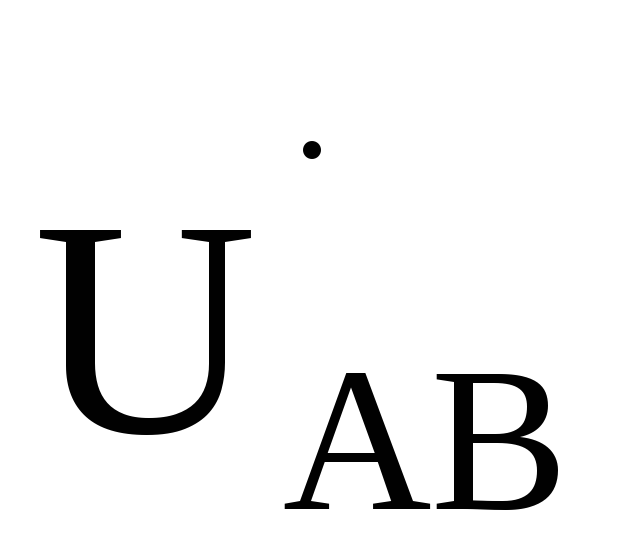 в
в 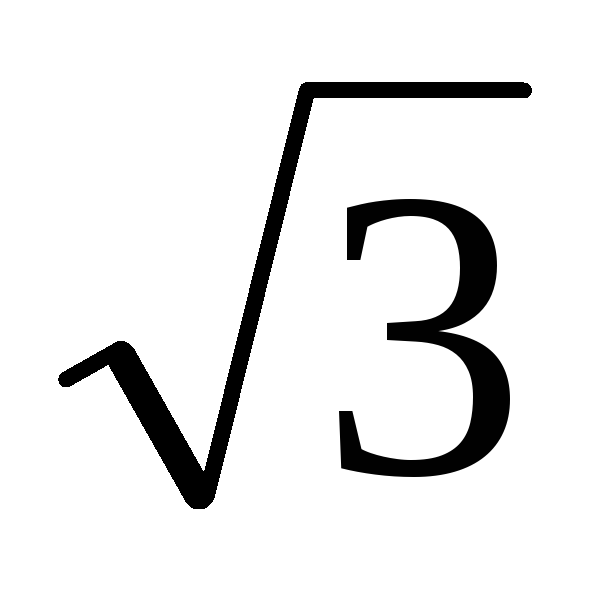 раз
больше фазного
раз
больше фазного 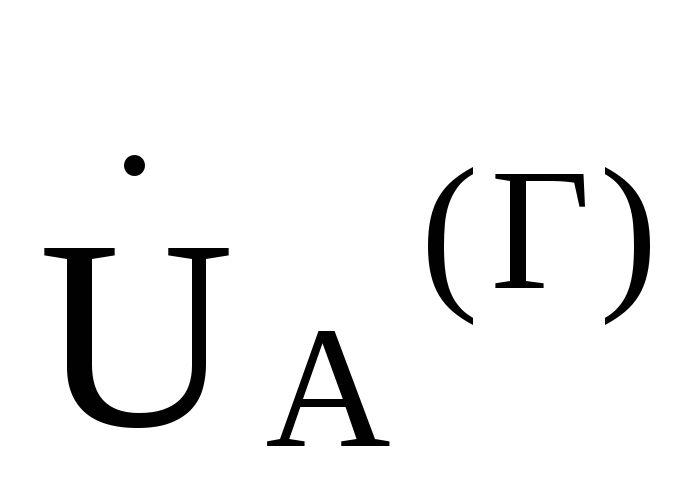 и
на
30°
и
на
30°
опережает его. Аналогично можно
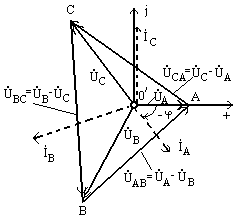
Рис. 9.10
получить, что линейное напряжение 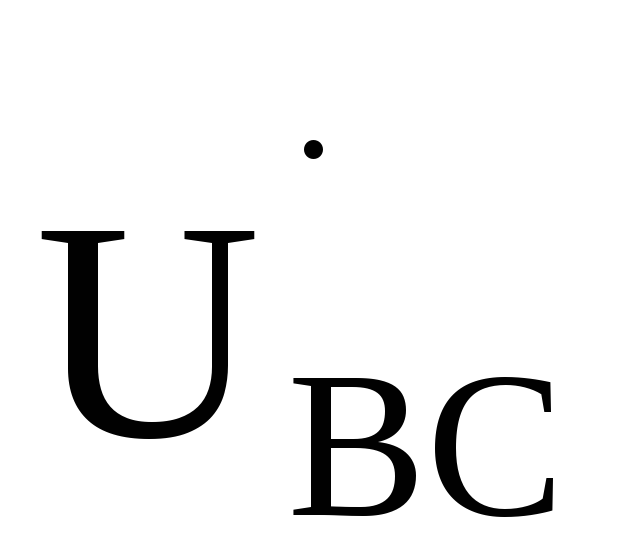 опережает фазное напряжение
опережает фазное напряжение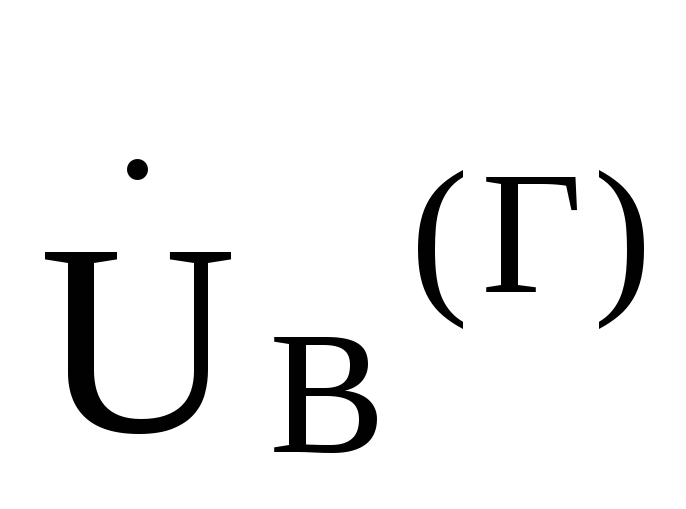 на
30°и в
на
30°и в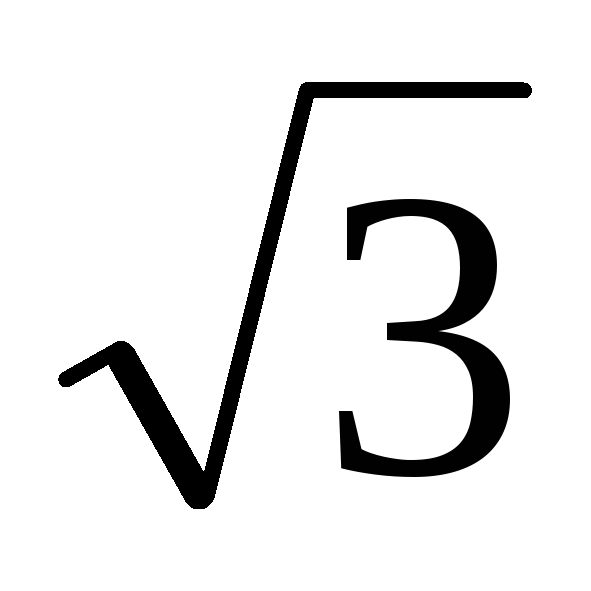 раз
больше его и линейное напряжение
раз
больше его и линейное напряжение опережает фазное напряжение
опережает фазное напряжение 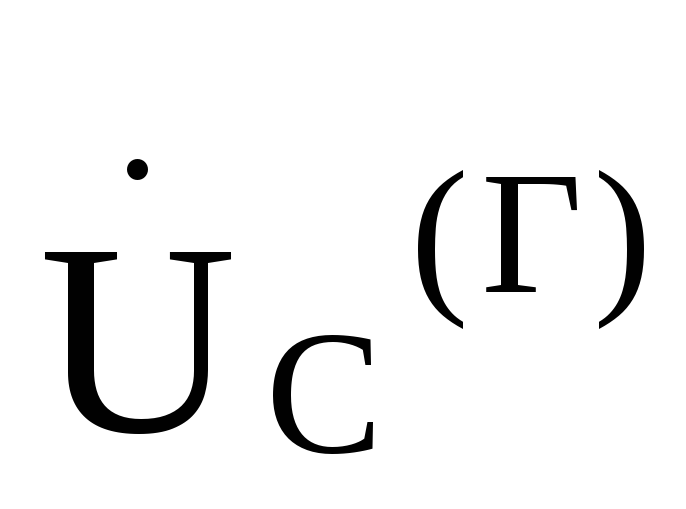 на 30°
на 30°
uв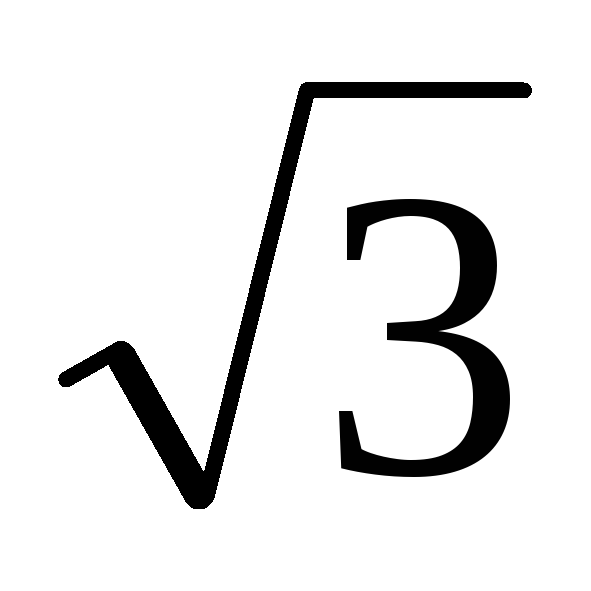 раз
больше, его. Приведенные соотношения
проще всего запомнить с помощью построения
топографической диаграммы для фазных
и линейных напряжений, приведенной
на рис. 9.10.Векторы фазных
напряжений
раз
больше, его. Приведенные соотношения
проще всего запомнить с помощью построения
топографической диаграммы для фазных
и линейных напряжений, приведенной
на рис. 9.10.Векторы фазных
напряжений ,
,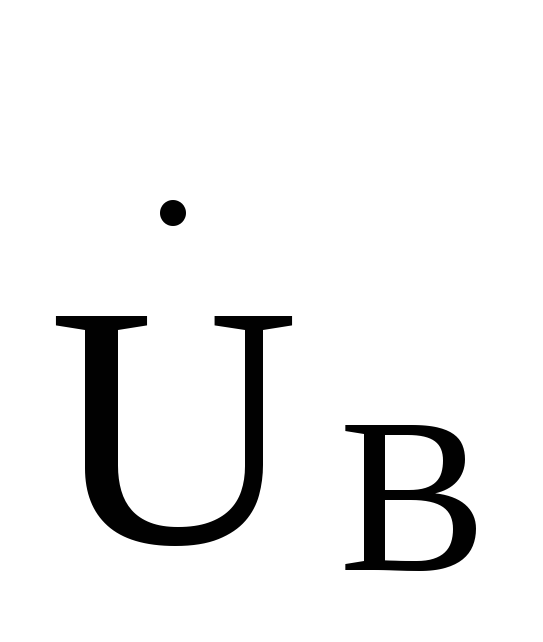 ,
и
,
и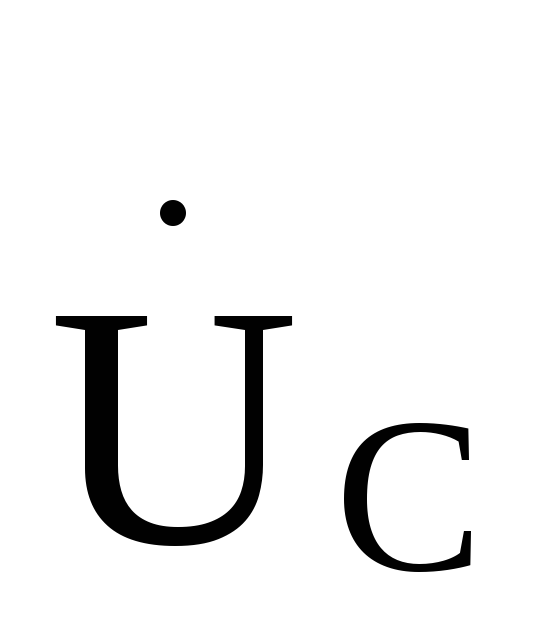 этой диаграммы относятся ках к фазным
напряжениям генератора, так и к фазным
напряжениям нагрузки, т. е. топографические
диаграммы фазных напряжений генератора
и нагрузки совпадают. Векторная диаграмма
токов для схемы рис. 9.9показана на рис. 9.10пунктирными линиями.
этой диаграммы относятся ках к фазным
напряжениям генератора, так и к фазным
напряжениям нагрузки, т. е. топографические
диаграммы фазных напряжений генератора
и нагрузки совпадают. Векторная диаграмма
токов для схемы рис. 9.9показана на рис. 9.10пунктирными линиями.
Следует отметить, что расчет токов и напряжений на отдельных участках трехфазной цепи с симметричной нагрузкой можно и нужно проводить на одну фазу, например, на фазу А, тогда соответствующие величины в фазе Вбудут отличаться только аргументом (углом) величиной
-120°,а в фазеС.– аргументом величиной +120°.
Пример 9.1.В цепи
рис. 9.11. рассчитать токи и построить
векторно-топографическую диаграмму
приr=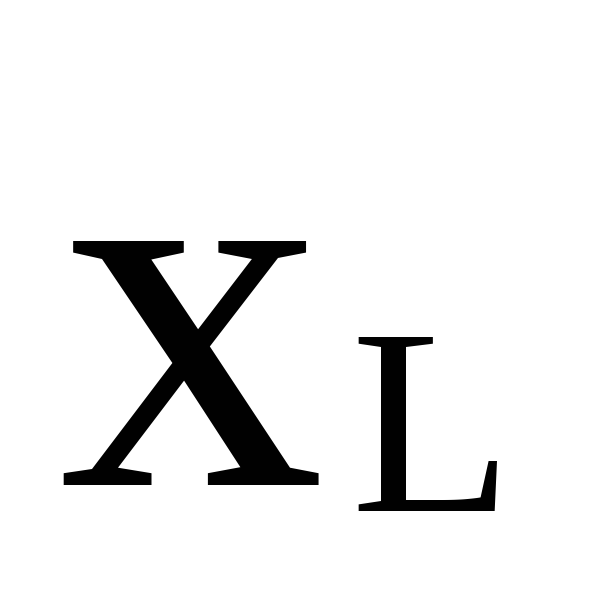 =10
Ом и фазном напряжении генератора
=10
Ом и фазном напряжении генератора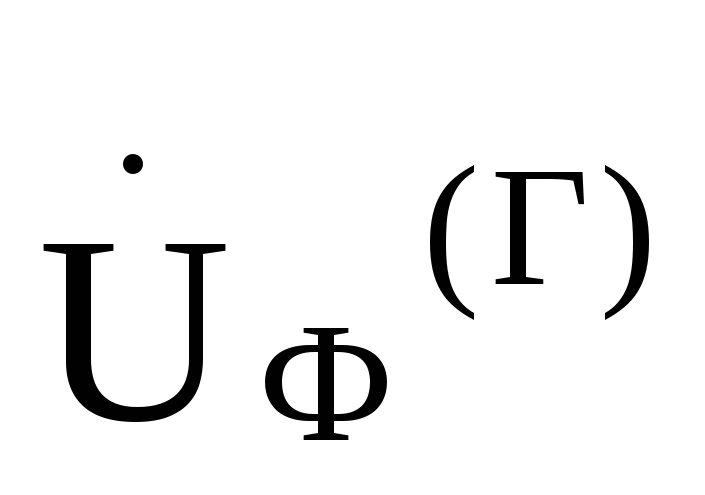 =220В.
=220В.
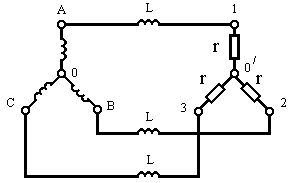
Рис. 9.11
Решение
Так как точки 0и
0’имеют одинаковые потенциалы, то
для фазы А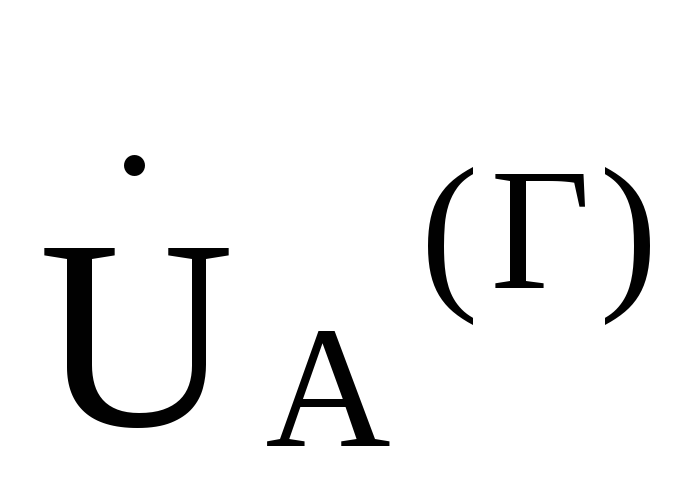 =
=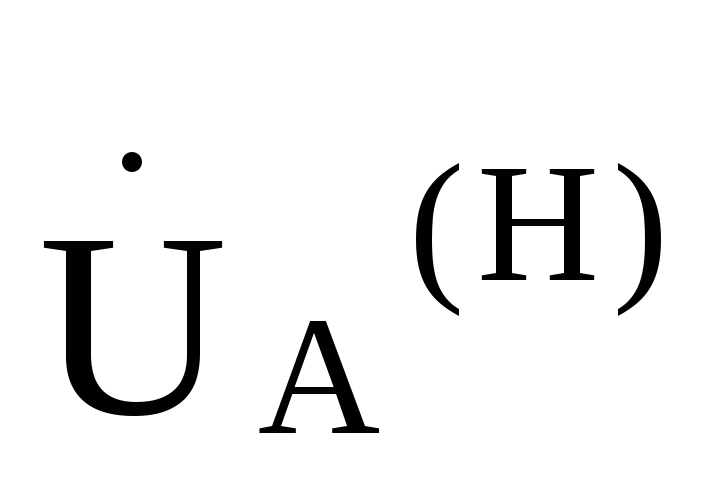 .
.
Принимаем
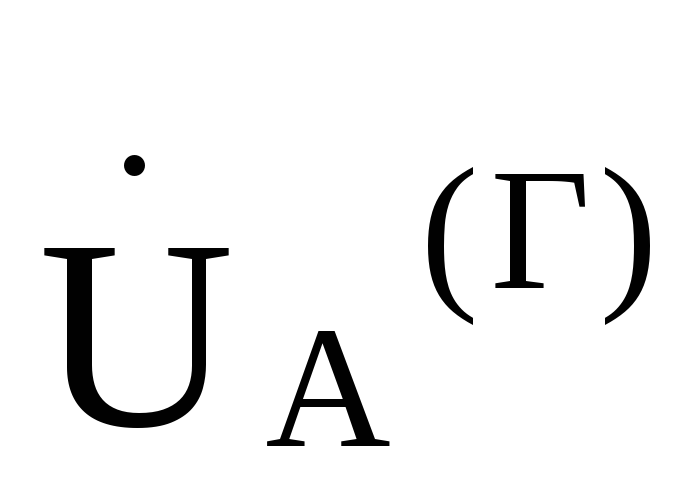 ==220
==220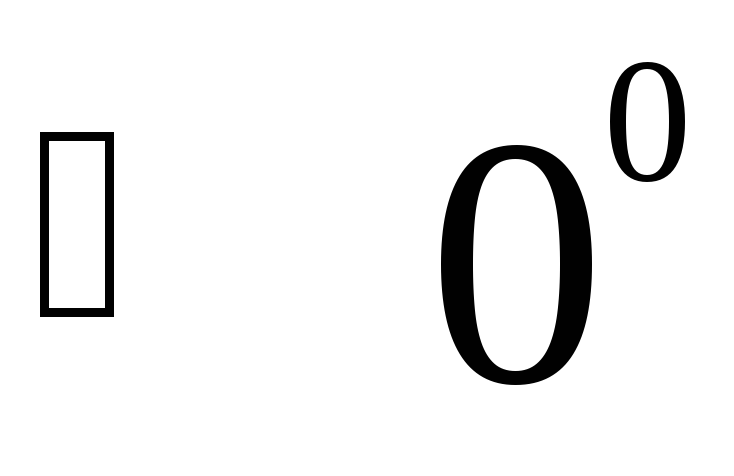 В,
тогда
В,
тогда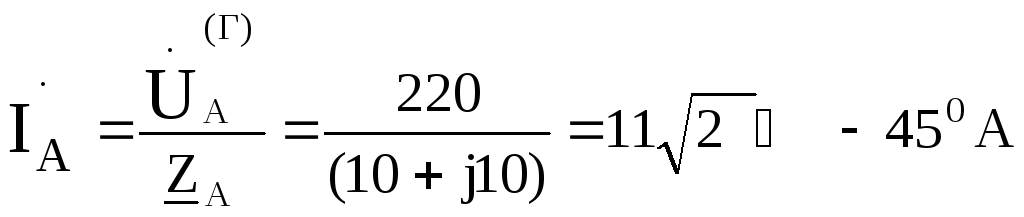 .
.
Токи в фазах ВиСотличаются
от тока только своими аргументами, т.е.
только своими аргументами, т.е.
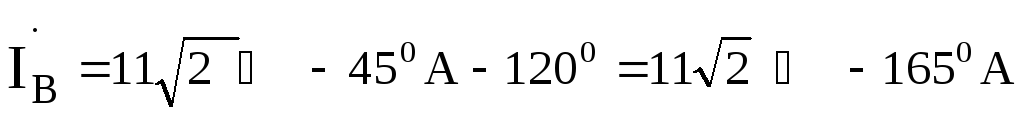

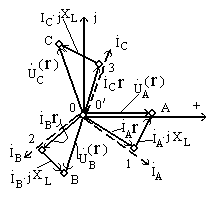
Рис. 9.12
Построение векторно-топографической
диаграммы проведем в следующей
последовательности. Отложим по
действительной оси вектор фазного
напряжения фазы А генератора 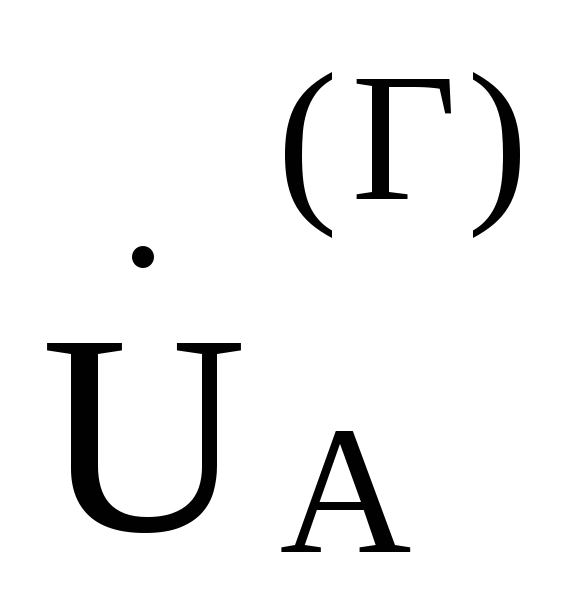 .
.
Затем в выбранном масштабе для напряжения под углами —120°и +120°по отношению к этому вектору из точки 0,потенциал которой принят равным нулю, отложим соответственно векторы
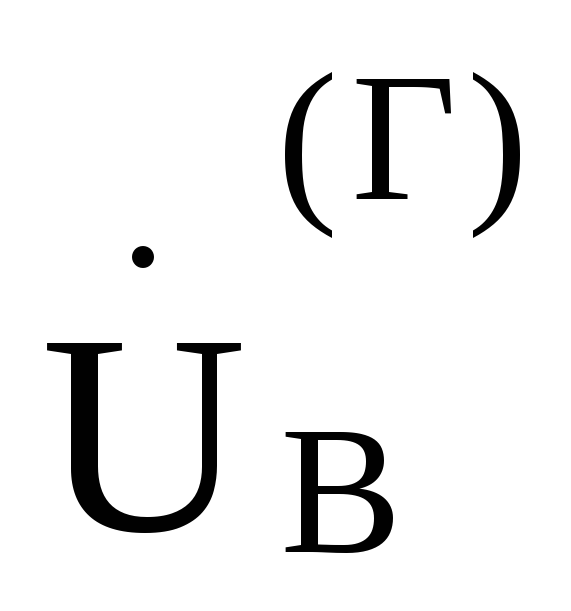 и
и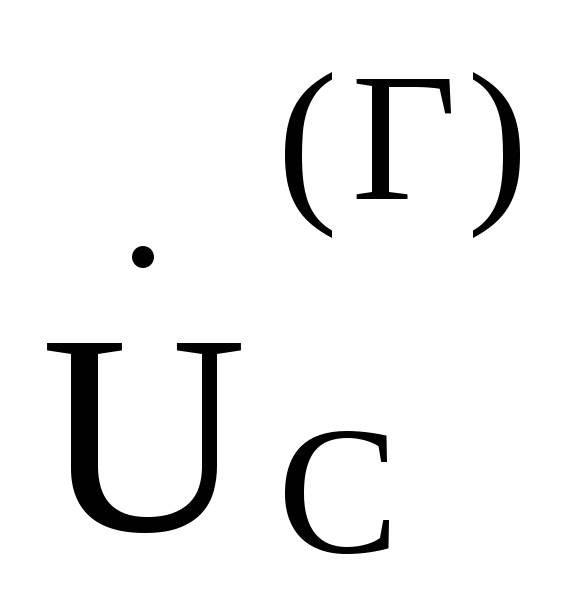 ,
как показано на рис. 9.I
2.Далее под углом —45°по
отношению к вектору
,
как показано на рис. 9.I
2.Далее под углом —45°по
отношению к вектору
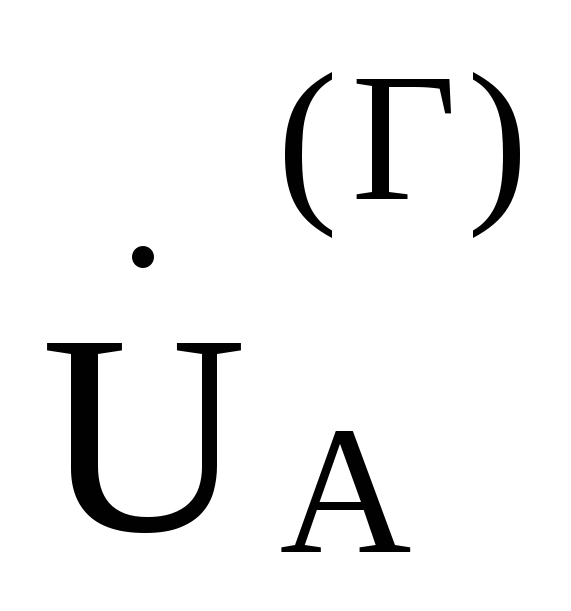 откладываем
в маштабе для тока вектор тока
откладываем
в маштабе для тока вектор тока Векторы токов
Векторы токов и
и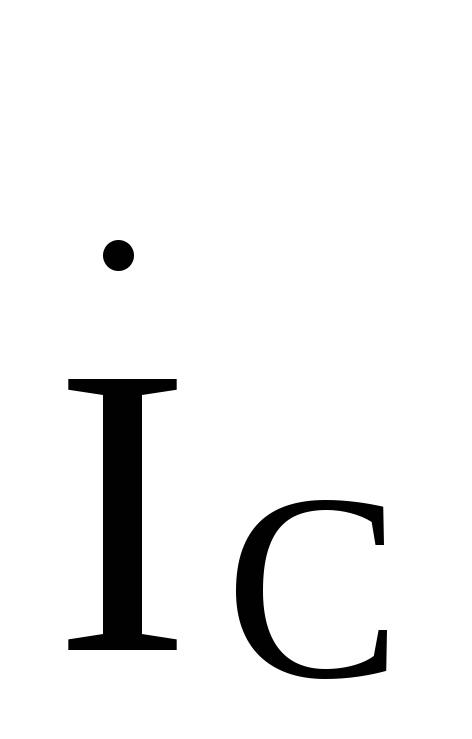 строим
строим
соответственно, под углами
—120°и+120°по отношению
к вектору тока .
Затем для каждой
.
Затем для каждой
из фаз нагрузки определяем комплексные потенциалы точек 1, 2 и 3 по отношеную к потенциалу
точки 0′,равному так-же нулю:


Найденные комплексные потенциалы откладываем от точки О’ по направлениям соответствующих токов в масштабе для напряжения.
Далее определяем потенциалы точек А, В, Спо отношению к потенциалу точки О’:
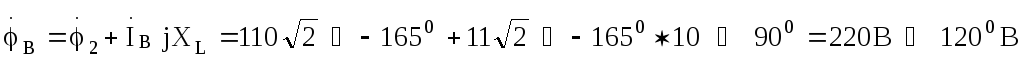
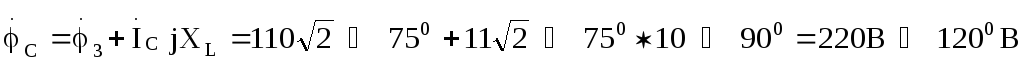
Отметим, что напряжения на индуктивностях нагрузки можно было бы найти графически,
используя соотношения:
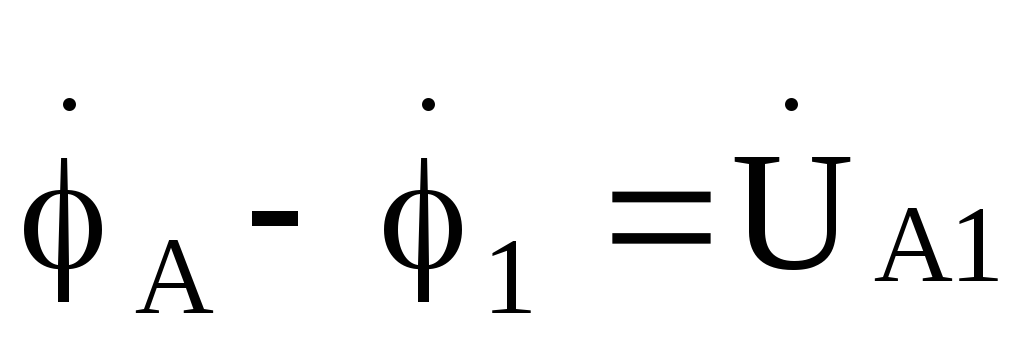 ;
;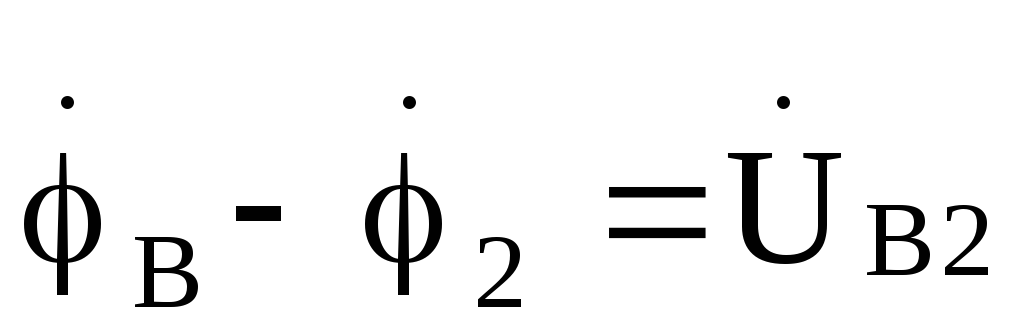 ;
;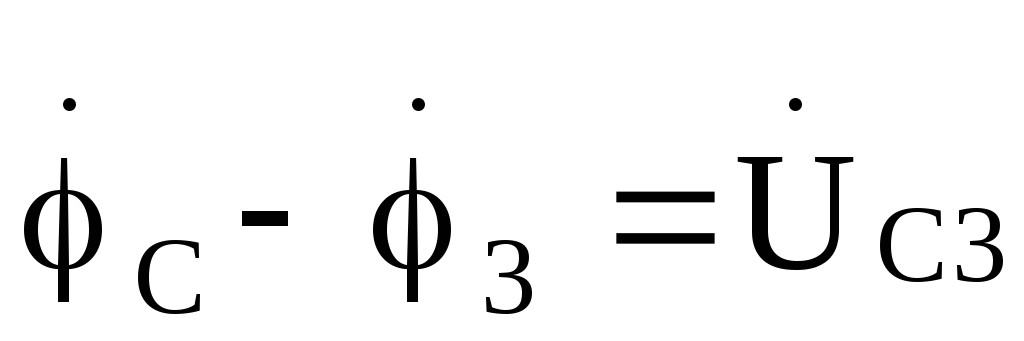
При этом для получения .напряжения  надо на диаграмме соединить точкиАи 1прямой и указать
направление этой прямой к первому
индексу, т.е. к точкеА.Аналогично
. получают напряжения
надо на диаграмме соединить точкиАи 1прямой и указать
направление этой прямой к первому
индексу, т.е. к точкеА.Аналогично
. получают напряжения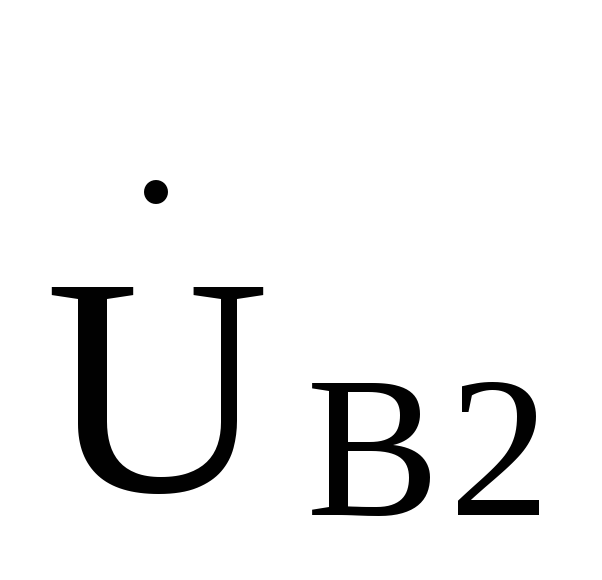 ;
;
2.Обмотки генератора и сопротивления нагрузки соединены в треугольник, как показано на рис. 9.13.
Из схемы рис .9.13непосредственно следует, что фазные
напряжения генератора, именуемые теперь
как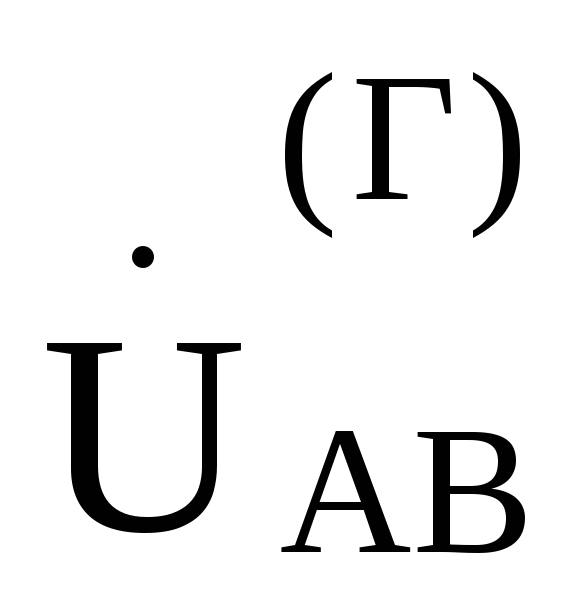 ,
,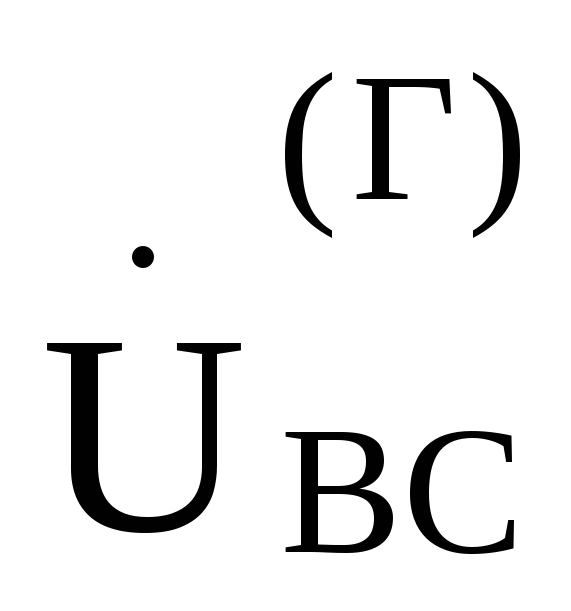 ,
,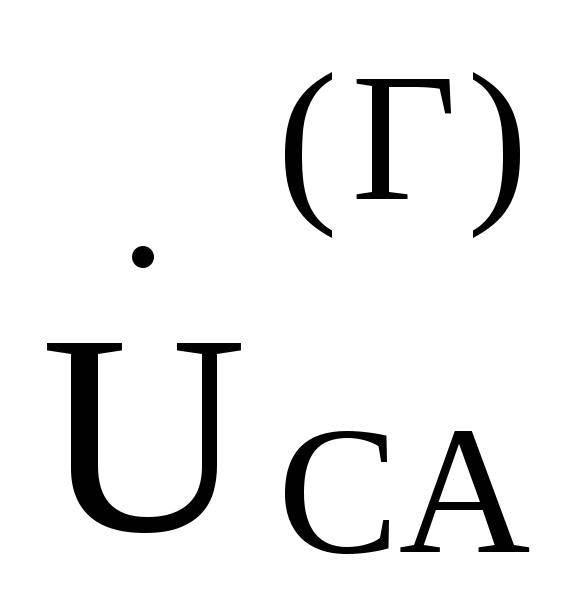 ,
,
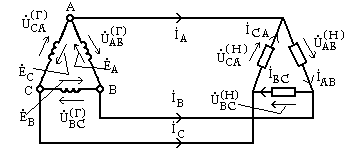
Рис. 9.13
линейные напряжения между соответствующими парами проводов и фазные напряжения
нагрузки 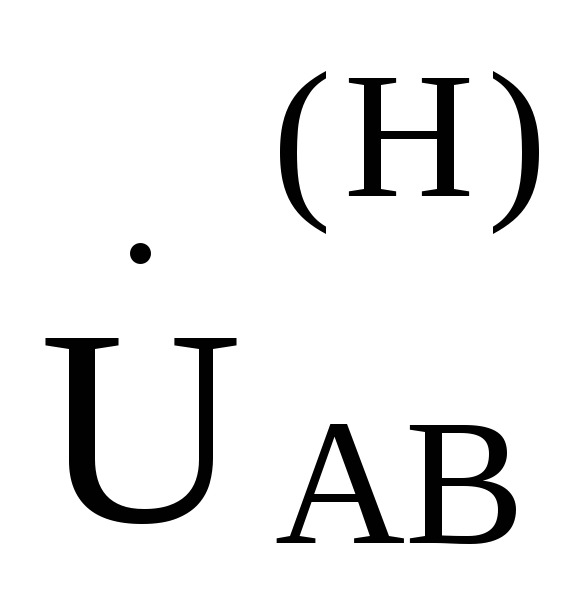 ,
,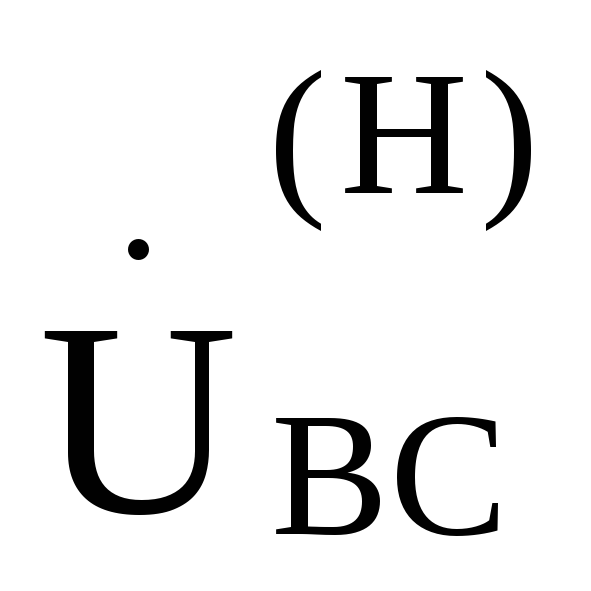 ,
,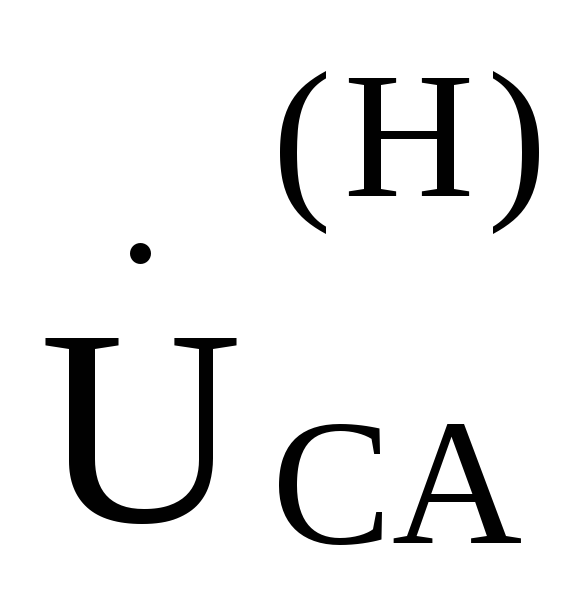 ,—соответственно равны друг другу.
Другими словами, при
,—соответственно равны друг другу.
Другими словами, при
соединений треугольником линейные напряжения равны соответствующим фазным
напряжениям. Поэтому фазные токи нагрузки определяются через заданные фазные ЭДС и
сопротивления нагрузки по соотношениям:
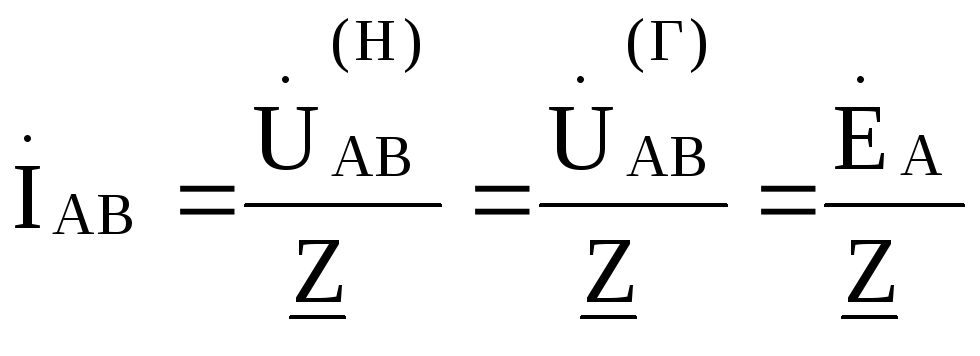

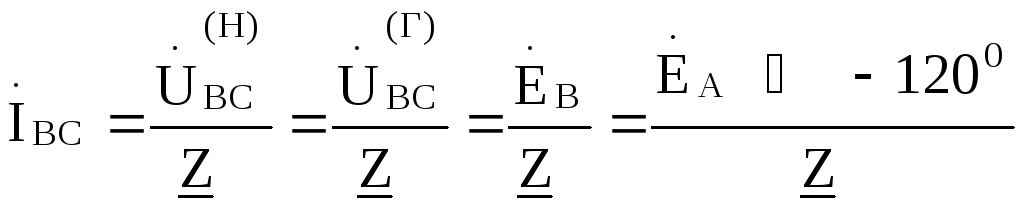
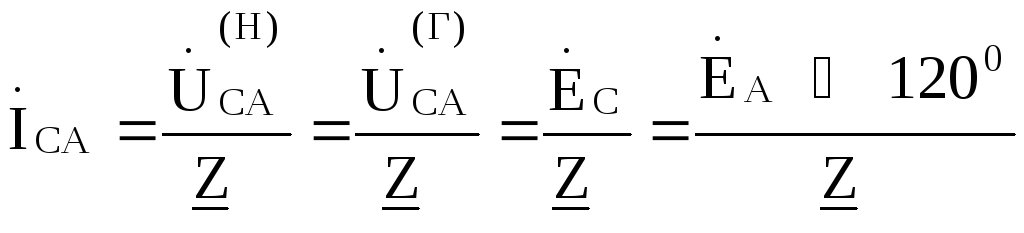
Линейные токи  ,
, ,
,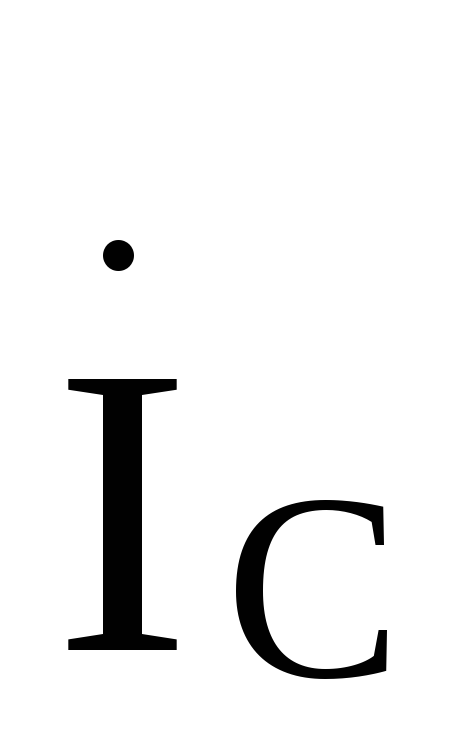 определяются через фазные по первому
закону Кирхгофа:
определяются через фазные по первому
закону Кирхгофа:
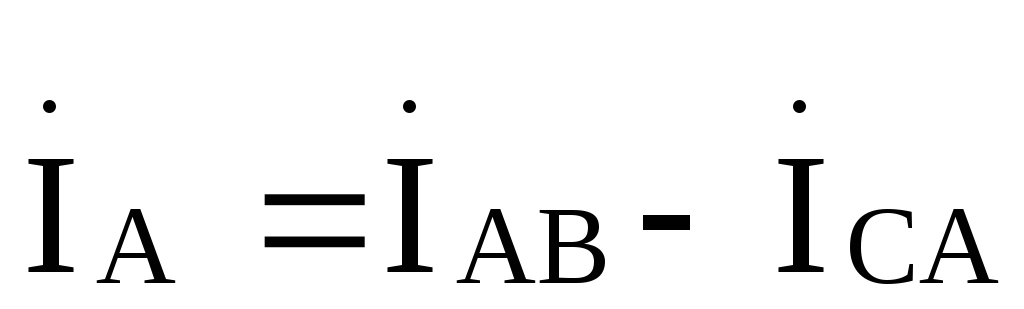 ,
,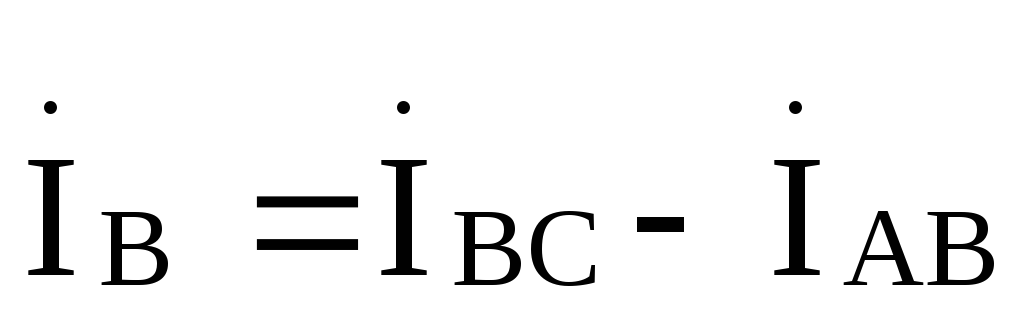 ,
,
Покажем, что при симметричной нагрузке
линейный ток в 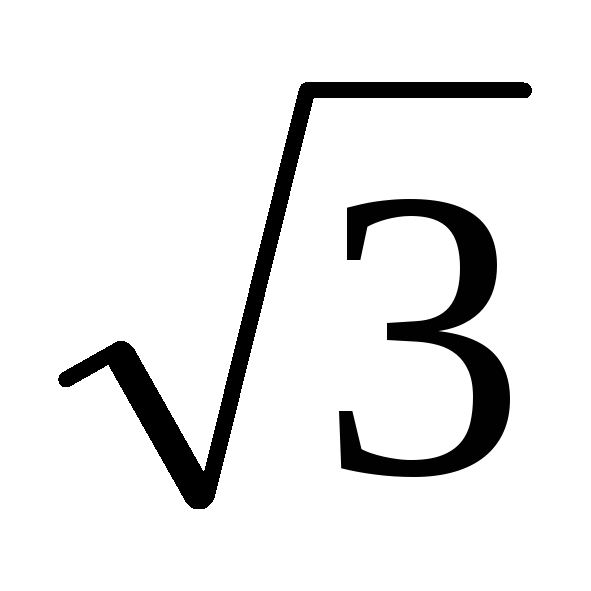 раз больше фазного,
раз больше фазного,
т. е. 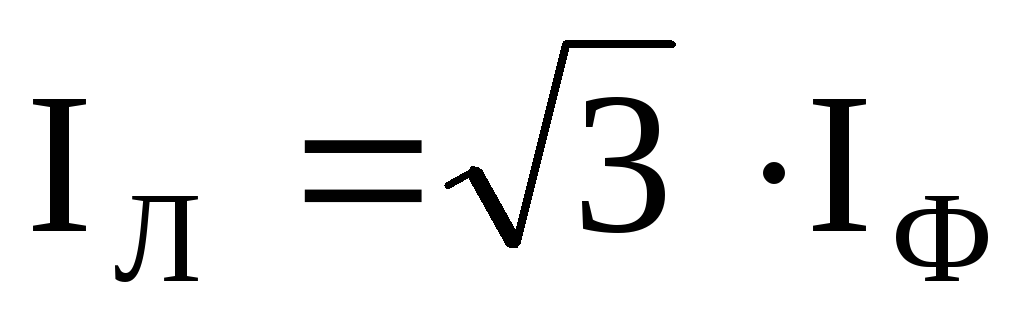
Таким образом, линейный ток  в
в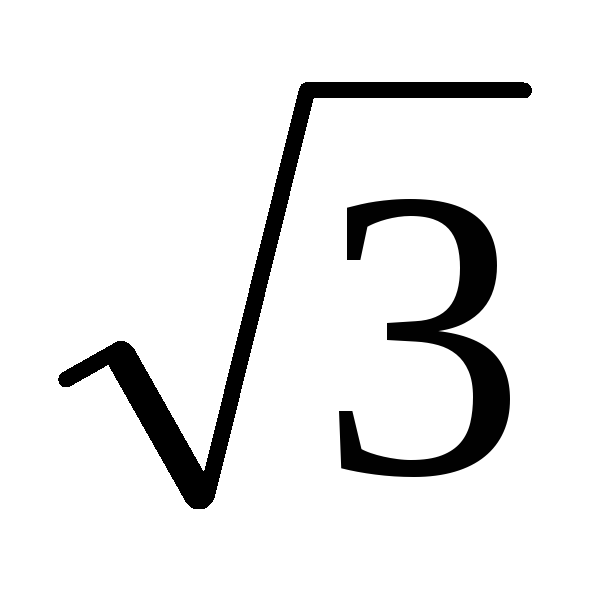 раз больше фазного
раз больше фазного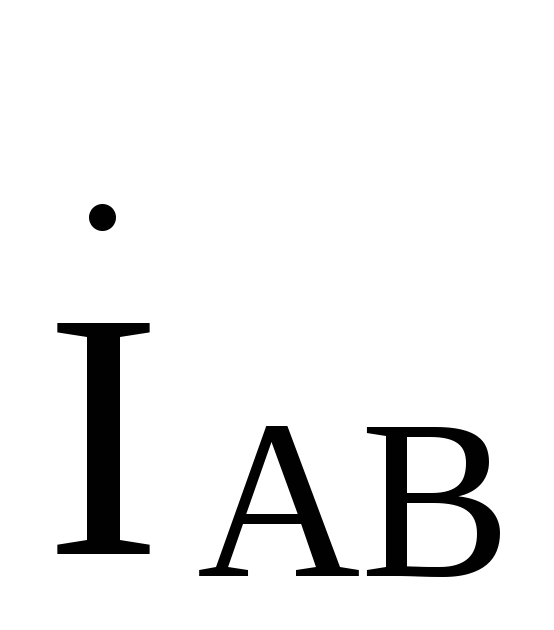 и на 30°отстает от него.
и на 30°отстает от него.
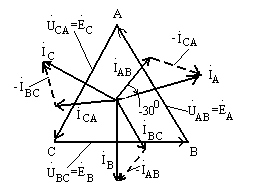
Рис. 9.14
Аналогично можно получить, что линейный
ток  илиотстает соответственно от фазного
илиотстает соответственно от фазного
тока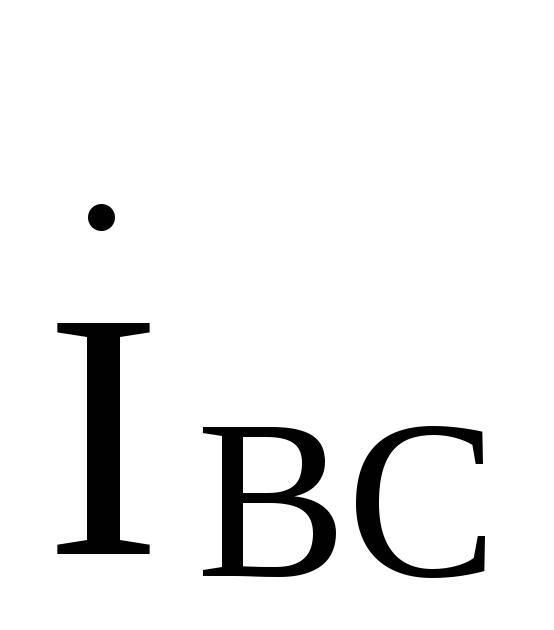 или
или и в
и в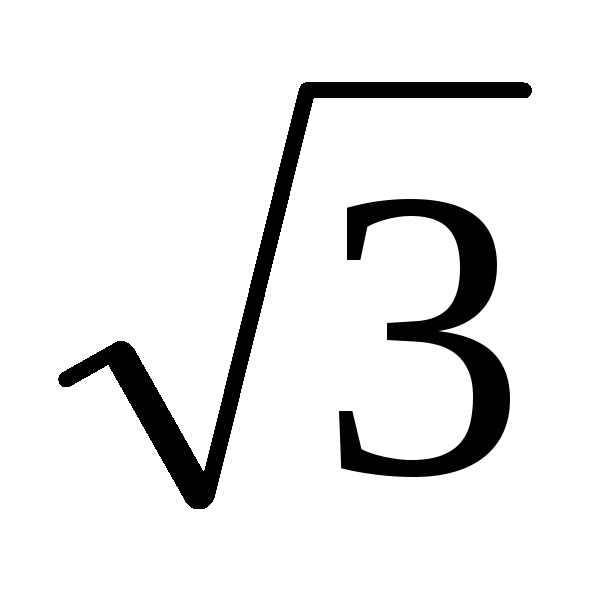 раз больше последнего.
раз больше последнего.
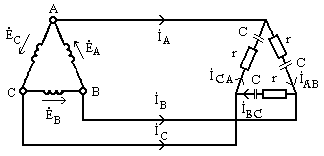
Рис. 9.15
Эти соотношения проще запомнить, если построить векторно-топографическую диаграмму, показанную на рис 9.14.Следует отметить, что фазные токи генератора, если их
положительное направление выбрать совпадающим с положительным направлением ЭДС, будут равны фазным тикам нагрузки одноименных фаз.
Пример 9.2. Вцепи рис. 9.15определить фазные и линейные токи, если r =25Ом, С = 100мкФ
и eA(f)=141sin(400е+30°)В.
Решение
Запишем действующее значение ЭДС фазы Агенератора в комплексной форме
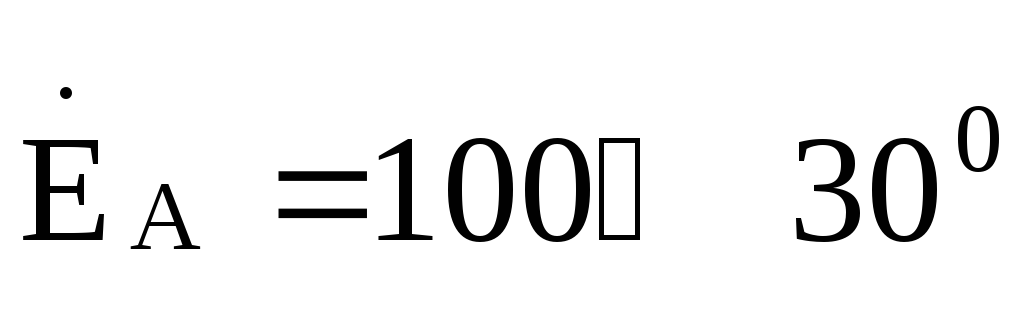 В.
Вычислим емкостное сопротивление
В.
Вычислим емкостное сопротивление
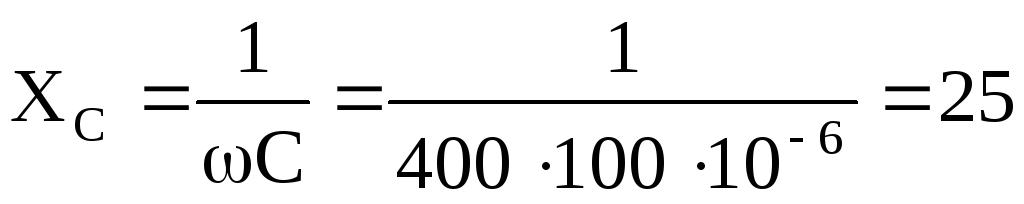 Ом
Ом
Так как 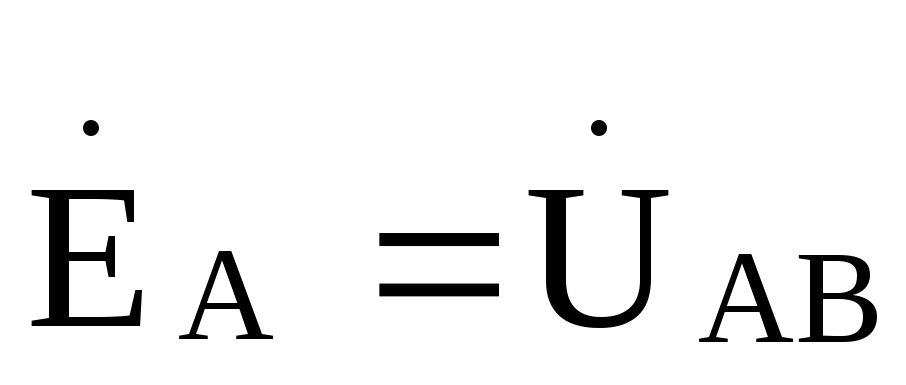 ,
то
,
то
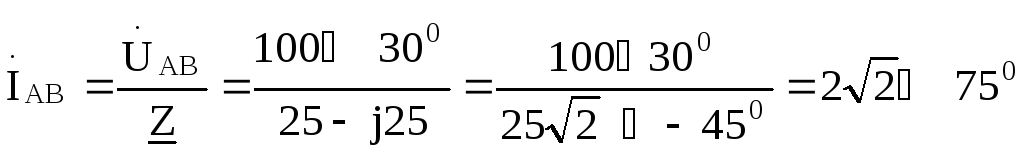 A
A
Ток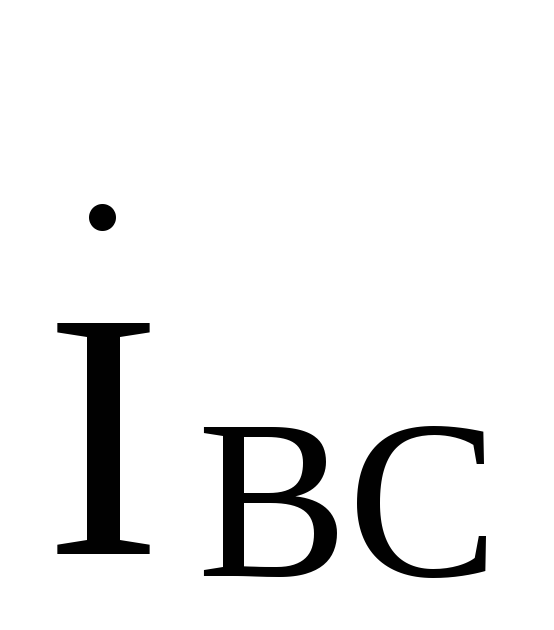 будет отставать от тока
будет отставать от тока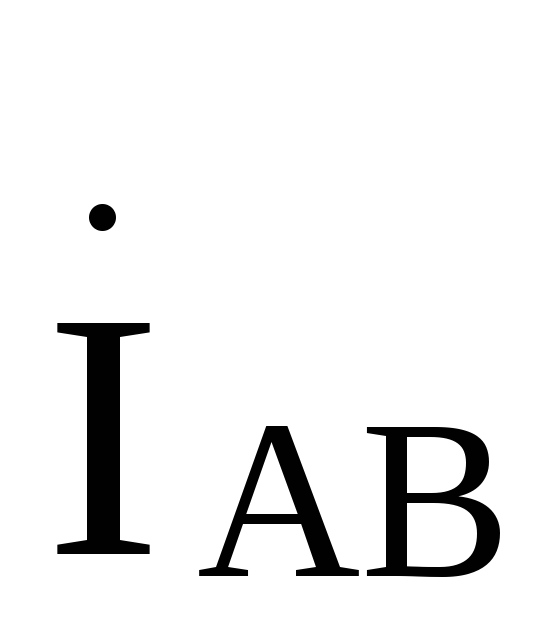 на
120й, а ток
на
120й, а ток будет опережать ток
будет опережать ток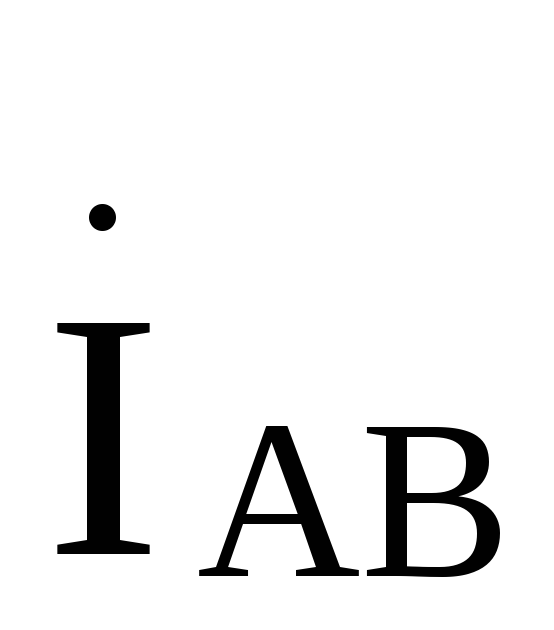 на 120°,поэтому
на 120°,поэтому
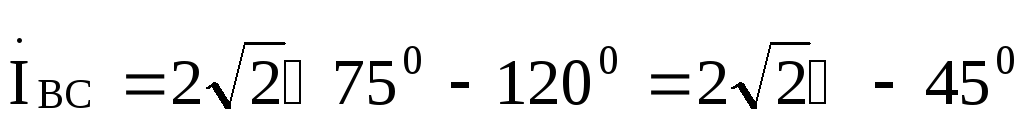 A
A
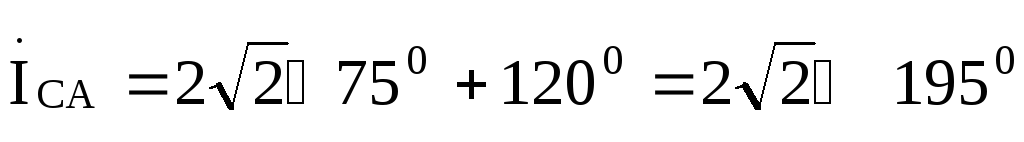 A
A
Линейные токи найдем на основании первого закона Кирхгофа:
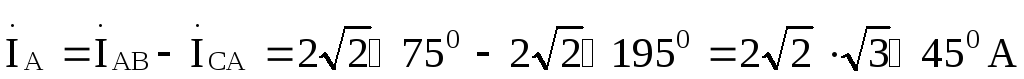
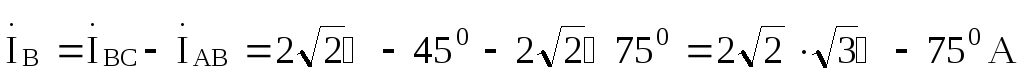
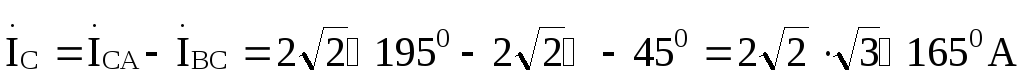
По результатам вычислений построена векторно-топографическая диаграмма,
показанная на рис. 9.16.
3.Обмотки генератора соединены в звезду, а сопротивления нагрузки соединены в треугольник, ‘как показано на рис. 9.17. .
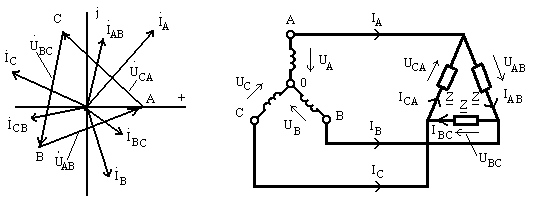
Рис. 9.16 Рис. 9.17
Если принять, что фазная ЭДС фазы Агенератора имеет нулевую начальную
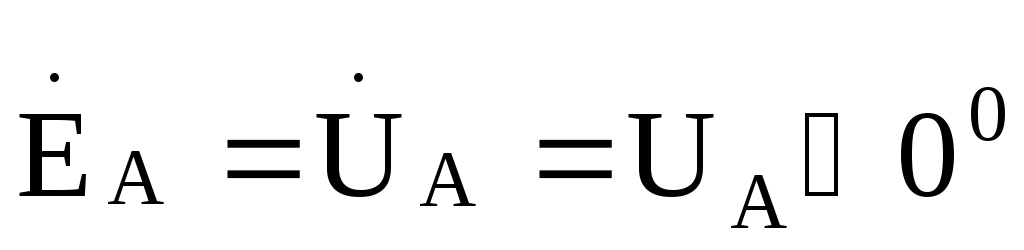 ,то
,то
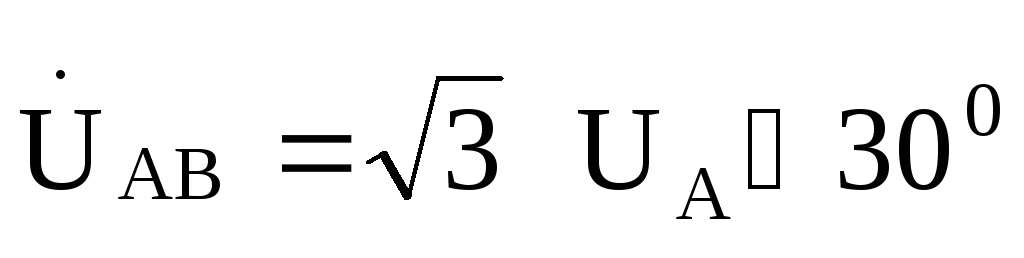
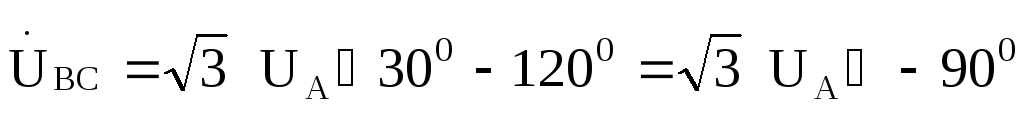
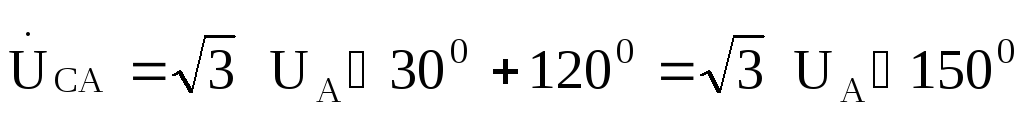
Фазные токи в фазах нагрузки найдем .по закону Ома:
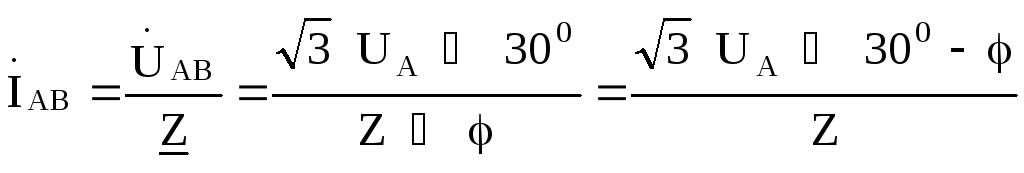
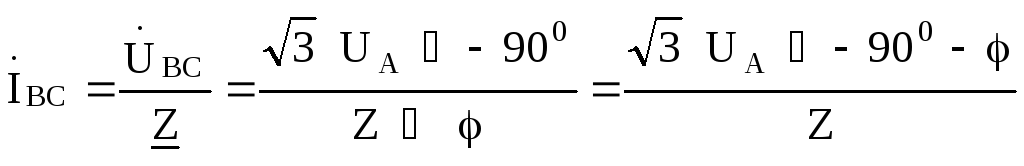
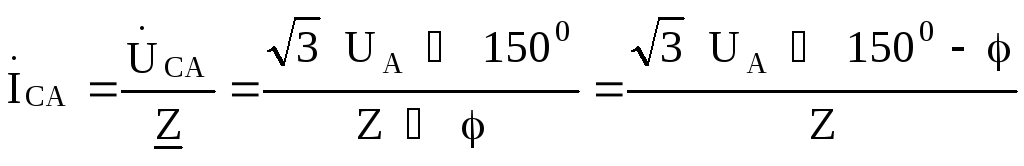
Линейные токи найдем по первому закону Кирхгофа:
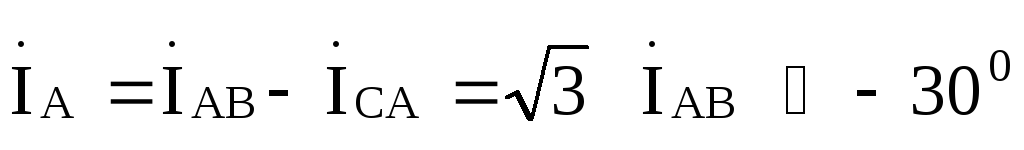
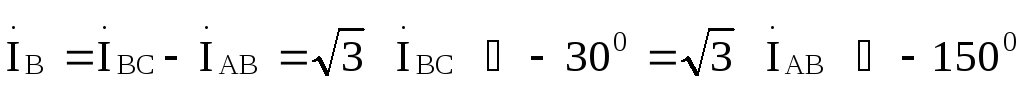
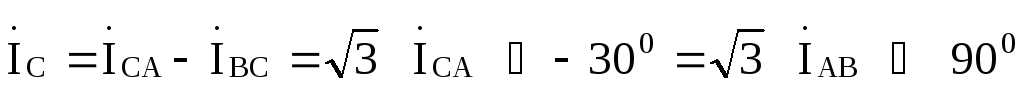
Найденные величины иллюстрируются векторно-топографической диаграммой, приведенной на рис. 9.18,где ось вещественных чисел направлена по вертикали.
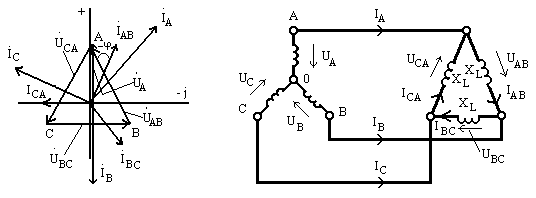
Рис. 9.18Рис. 9.19
Пример 9.3.В цепи
рис. 9.19определить фазные
и линейные токи при ХL=22
Ом и фазном напряжении генератора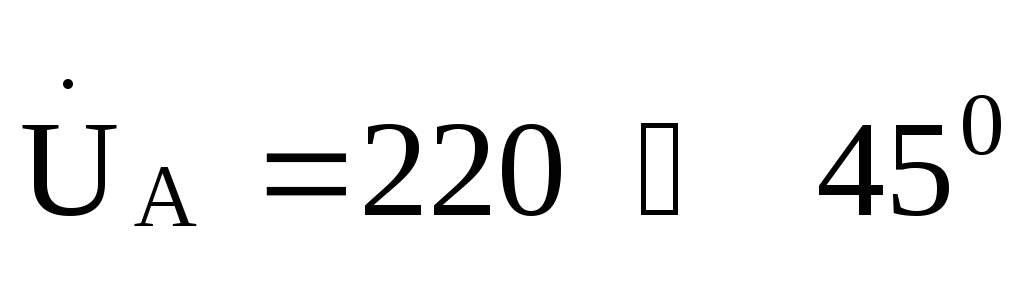 .
.
Расчет мощности трехфазной сети: формулы для расчета
Содержание:
- Специфика и особенности трехфазных сетей
- Расчет мощности потребителей
- Как рассчитать трехфазную сеть
- Использование калькулятора для расчета мощности
Электрическая энергия на все объекты изначально поступает через трехфазную сеть. В частные дома она может заводиться напрямую, а в многоквартирном доме доходит лишь до вводного распределительного устройства. Далее по квартирам расходятся уже однофазные линии. В любом случае потребуется выполнить расчет мощности трехфазной сети, чтобы заранее определить ее способность выдерживать запланированные нагрузки по току.
Для того чтобы сделать правильные вычисления, нужно знать особенности таких сетей, принципы их работы и технические характеристики. Все необходимые расчеты выполняются вручную при помощи формул или с использованием онлайн-калькулятора.
Специфика и особенности трехфазных сетей
Трехфазные электрические сети наиболее эффективно передают ток через промежуточные звенья, вплоть до потребителя. В процессе доставки потери энергии минимальны.
Наличие трехфазной сети в квартире или частном доме очень легко определить. Для этого нужно просто заглянуть в щиток и посчитать количество проводов. Если в наличии 2 или 3 проводника, значит сеть однофазная. В ней два провода являются фазой и нулем. При наличии заземления может быть третий провод. В трехфазных сетях проводов больше на два из-за двух дополнительных фаз. При отсутствии заземления – их всего четыре, а при наличии заземляющего контура – пять.

Эту же задачу можно решить и с помощью вводного автоматического выключателя. К нему также подводится определенное количество проводов, подключаемых в соответствующие клеммы.
В процессе эксплуатации трехфазной сети велика вероятность неравномерного распределения нагрузки по отдельным фазам. Если к одной из них будет подключено только мощное оборудование, а к другим – обычные бытовые приборы, в этом случае может возникнуть ситуация, называемая перекосом фаз. В результате асимметрии тока и напряжения, отдельные потребители могут выйти из строя. Во избежание негативных последствий, нагрузка должна быть равномерно спланирована еще на стадии проектирования и выполнен расчет мощности трехфазной сети.

Трехфазная сеть, по сравнению с однофазной, отличается большим количеством кабельно-проводниковой продукции, автоматов и других устройств. К ней подключается специфическое трёхфазное оборудование Суммарная мощность будет выше ровно в три раза. Значение мощности рассчитывается по току и напряжению с использованием формул.
Расчет мощности потребителей
В первую очередь нужно заранее установить объемы потребляемой электроэнергии. Для этого суммируется мощность всех потребителей, находящихся в доме. Сюда входит мощное оборудование, обычная бытовая техника и осветительные приборы. У некоторых хозяев этот список может быть дополнен теплыми электрическими полами.
Все необходимы сведения можно посмотреть в техническом паспорте, который прилагается к каждому устройству. На некоторые приборы наносится соответствующая маркировка. Вначале идут самые мощные агрегаты и далее – все остальное оборудование, по мере уменьшения мощности.

Для вычислений берется стиральная машина-автомат, мощностью 2600 Вт, электрический водонагреватель – 1900 Вт, утюг – 1500 Вт, пылесос – 1000 Вт, микроволновка – 800 Вт, компьютер и оргтехника – 600 Вт, осветительные приборы (с лампами эконом) – 400 Вт, холодильник – 300 Вт, телевизор – 100 Вт. Итоговый результат получился 9200 Вт и его необходимо перевести в киловатты. Для этого 9200 Вт делится на 1000, получается 9,2 кВт, что и будет расчетным потреблением электроэнергии.
С данной мощностью может справиться и одна фаза, однако в частных домах устанавливается более мощное оборудование, для работы которого лучше пользоваться сетями 380в. В этом случае гарантируется бесперебойное функционирование отопительных и водонагревательных котлов, насосов, электродвигателей и других агрегатов.
Как рассчитать трехфазную сеть
В качестве примера можно взять некие производственные площади с установленным оборудованием и по этим исходным данным делать расчет мощности трехфазного тока.
В каждом станке используется электродвигатель. Их общая мощность Ру1 составляет 50 кВт, с учетом активной мощности. Кроме того, в помещении установлены осветительные приборы общей мощностью (Ру2) – 3 кВт. Символ Ру обозначает величину установленной суммарной мощности для конкретных групп потребителей. Работа оборудования осуществляется от трехфазной сети с 4 проводами и номинальным напряжением 380 В.

Кроме того, при расчетах учитывается коэффициент спроса Кс, действующий в режиме максимальной нагрузки. Он учитывает наивысшее количество включений потребителей данной группы. Для электродвигателей Кс1 берется с учетом величины их загруженности и составляет 0,35. Для приборов освещения Кс2 составляет 0,9. Все потребители выравниваются усредненным коэффициентом мощности cos φ = 0,75.
Расчеты начинаются с определения силовой нагрузки Р1 = 0,35 х 50 = 17,5 кВт. Далее рассчитывается осветительная нагрузка Р2 = 0,9 х 3 = 2,7 кВт. Таким образом, величина полной расчетной нагрузки составит Р = Р1 + Р2 = 17,5 + 2,7 = 20,2 кВт.
Для определения и расчета тока используется формула I = (1000 x P)/(1,73 x Uн x cos φ), в которой Р является расчетной мощностью потребителей, Uн – номинальным напряжением 380 вольт, cos φ – коэффициентом мощности.
Подставив нужные значения, находим значение силы и мощности по току: I = (1000 x 20,2)/(1,73 x 380 x 0,75) = 41 А. Полученный результат дает возможность узнать, сможет ли сеть обеспечить нормальную работу потребителей.
Использование калькулятора для расчета мощности
Онлайн-калькулятор существенно ускоряет проведение расчетов мощности в трехфазной сети. Для этого должны быть заранее известны мощность и характер нагрузки – активной и реактивной, сетевое напряжение, а также тип сети – одно- или трехфазный. Все параметры рассчитываются по формулам и методикам, приведенным выше. Достаточно всего лишь вставить в окна необходимые данные и нажать кнопку «Рассчитать ток». В окне с обозначением тока в А появится искомый результат, показывающий величину тока по мощности.
Расчет мощности 3 фазной сети. Трехфазная сеть: расчет мощности, схема подключения
Равномерное значение трехфазной нагрузки представляет собой протекание по каждому фазному проводнику одинакового тока. При этом, значение силы тока в нулевом проводнике будет равным нулю. Наиболее ярко, равномерная нагрузка фаз проявляется в трехфазных электрических двигателях. Для них расчет мощности фазного тока производится по формуле P = 3*Uф*I* cos(φ) = 1,73Uл*I* cos(φ) .
В случае протекания по фазам токов, различных по величине, то данная нагрузка будет неравномерная или несимметричная. В такой ситуации, по нулевому проводу будет происходить протекание электрического тока. При неравномерной нагрузке, определение мощности будет производиться по формуле Pобщ = Ua*Ia* cos(φ1) + Ub*Ib* cos(φ2) + Uc*Ic* cos(φ3).
Измерение мощности ваттметром
Измерение мощности электрического тока производится при помощи специальных измерительных приборов, в роли которых выступают ваттметры.
При условии симметричной нагрузки, мощность, поступающая от трехфазной системы, легко определяется с использованием одного однофазного ваттметра. В четырехпроводную систему, имеющую нулевой провод, включение токовой обмотки ваттметра производится последовательным способом с одним из проводов фаз. Для подключения обмотки напряжения используется фазный и нулевой провод. Такое включение дает возможность определить с помощью ваттметра мощность одной из фаз (Рф). Поскольку равномерная нагрузка предполагает одинаковую мощность всех трех фаз, то общая мощность трехфазной системы будет равна: Р = 3Рф .
В системе, состоящей из трех проводов, включение обмотки ваттметра осуществляется к сети, а через токовую обмотку проходит линейный ток. Таким образом, показатель мощности трехфазной системы враз превышает данные ваттметра Pω, т. е. Р= Рω .
Расчет мощности фаз при несимметричной нагрузке
В случае несимметричной нагрузки, расчет мощности фазного тока и ее практическое определение производится с помощью нескольких ваттметров.
В такой ситуации, для определения мощности системы из четырех проводов, используются сразу три ваттметра. Обмотка напряжения каждого из них, включается между нулевым проводом и соответствующим проводом фазы. Таким образом, общая мощность системы из трех фаз будет равна суммарной мощности каждой из них.
Для трехпроводной системы применяется два ваттметра. Здесь соединяются обмотки напряжений в каждом ваттметре, входные зажимы обмотки тока и свободный линейный провод. Общая мощность будет состоять из показаний двух ваттметров.
Не всякому обывателю понятно, что такое электрические цепи. В квартирах они на 99 % однофазные, где ток поступает к потребителю по одному проводу, а возвращается по другому (нулевому). Трехфазная сеть представляет собой систему передачи электрического тока, который течет по трем проводам с возвратом по одному. Здесь обратный провод не перегружен благодаря сдвигу тока по фазе. Электроэнергия вырабатывается генератором, приводимым во вращение внешним приводом.
Увеличение нагрузки в цепи приводит к росту силы тока, проходящего по обмоткам генератора. В результате магнитное поле в большей степени сопротивляется вращению вала привода. Количество оборотов начинает снижаться, и регулятор скорости вращения подает команду на увеличение мощности привода, например путем подачи большего количества топлива к двигателю внутреннего сгорания. Число оборотов восстанавливается, и генерируется больше электроэнергии.
Трехфазная система представляет собой 3 цепи с ЭДС одинаковой частоты и сдвигом по фазе 120°.
Особенности подключения питания к частному дому
Многие считают, что трехфазная сеть в доме повышает потребляемую мощность. На самом деле лимит устанавливается электроснабжающей организацией и определяется факторами:
- возможностями поставщика;
- количеством потребителей;
- состоянием линии и оборудования.
Для предупреждения скачков напряжения и перекоса фаз их следует нагружать равномерно. Расчет трехфазной системы получается примерным, поскольку невозможно точно определить, какие приборы в данный момент будут подключены. Наличие импульсных приборов в настоящее время приводит к повышенному энергопотреблению при их пуске.
Распределительный электрощит при трехфазном подключении берется больших размеров, чем при однофазном питании. Возможны варианты с установкой небольшого вводного щитка, а остальных — из пластика на каждую фазу и на надворные постройки.
Подключение к магистрали реализуется по подземному способу и по воздушной линии. Предпочтение отдают последней благодаря небольшому объему работ, низкой стоимости подключения и удобству ремонта.
Сейчас воздушное подключение удобно делать с помощью Минимальное сечение алюминиевой жилы составляет 16 мм 2 , чего с большим запасом хватит для частного дома.
СИП крепится на опорах и стене дома с помощью анкерных кронштейнов с зажимами. Соединение с главной воздушной линией и кабелем ввода в электрощит дома производится ответвительн
3.5. Мощность трехфазной системы
Активные и реактивные мощности каждой фазы трехфазной системы при соединении звездой в случае несимметричной нагрузке рассчитываются по следующим формулам:
РA=UAIA сosφA, РВ=UBIB cosφB, РC=UCIC cosφC
QA=UAIA sinφA, QB=UBIB sinφB, QC=UCIC sinφC
Активная и реактивная мощности трехфазной системы звезда при несимметричной нагрузке равна сумме активных и реактивных мощностей фаз
Р=РА + РВ + РС,
Q = QA + QB + QC
При симметричной нагрузке независимо от схемы включения
P = 3Pф = 3 UфIф сosφ,
Q = 3Qф = 3 UфIф sinφ,
S=3UфIф.
Для линейных
величин тока и напряжения, учитывая,
что при соединении звездой IЛ = IФ и UЛ = 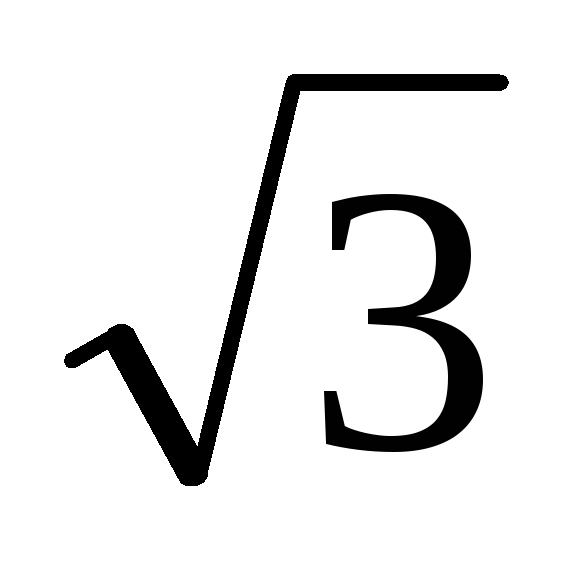 Uф,
а при соединении треугольником
Uф,
а при соединении треугольником
IЛ = 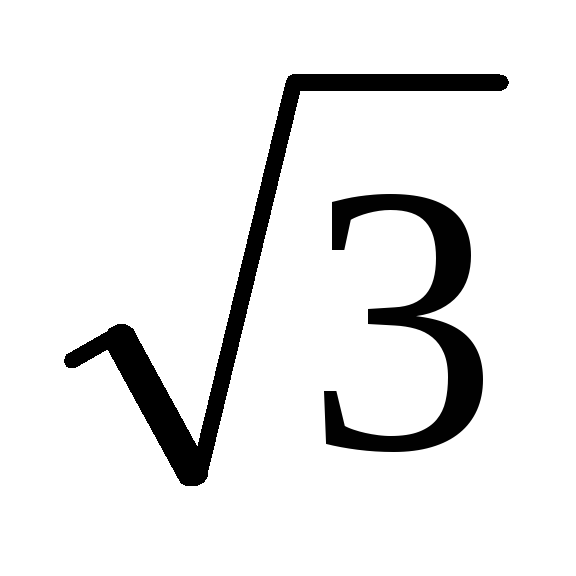 IФ и UЛ = Uф , получим:
IФ и UЛ = Uф , получим:
P
= 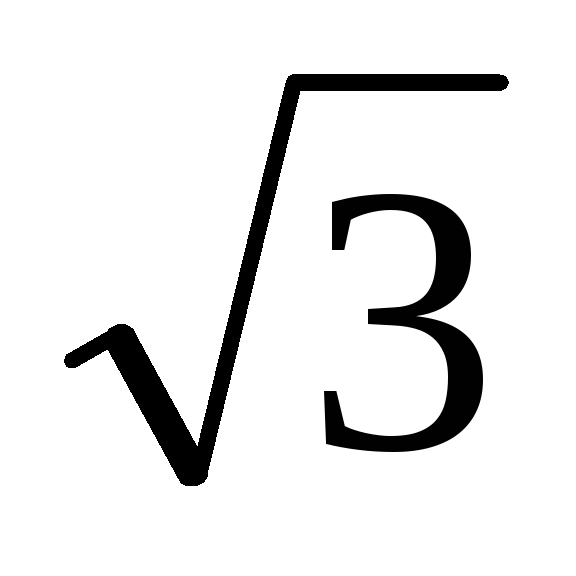 UЛIЛ cosφ,
(3.6)
UЛIЛ cosφ,
(3.6)
Q = UЛIЛ sinφ, (3.7)
S
= 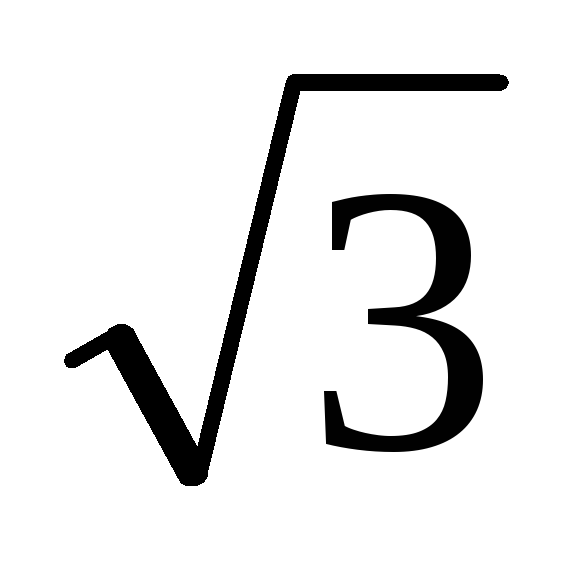 UЛIЛ.
UЛIЛ.
3.6. Измерения мощности потребляемой трехфазными электроприемниками.
Измерение активной мощности в трехфазной системе при симметричной нагрузке может быть осуществлено измерением мощности в одной любой фазе с последующим умножением полученного значения на три (рис. 3.11).
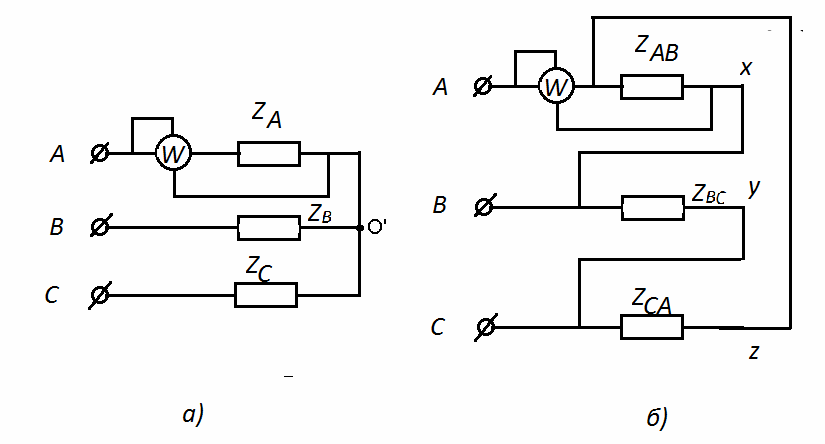
Рис. 3.11 Схемы измерения активной мощности в симметричных трехфазных цепях: а) соединение звездой; б) соединение треугольником.
Активная мощность, потребляемая каждой схемой, определятся по формуле P = 3W, где W – показания ваттметра.
В несимметричной четырехпроводной трехфазной системе, активная мощность определяется методом трех ваттметров (рис. 3.12)
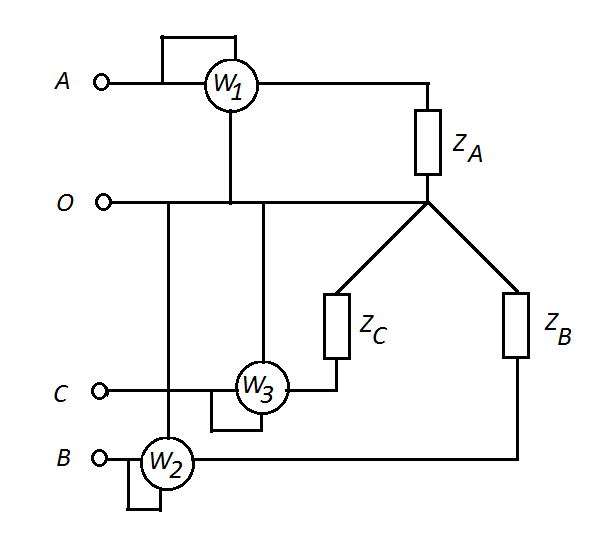
Рис. 3.12 Схема измерения мощности в четырехпроводных цепях трехфазного тока.
Активная мощность, потребляемая цепью, определяется как арифметическая сумма показаний всех ваттметров P = W1 + W2 + W3.
В трехпроводных системах трехфазного тока при любой нагрузке для определения мощности широко применяют схему измерения мощности двумя ваттметрами, показанную на рис. 3.13.
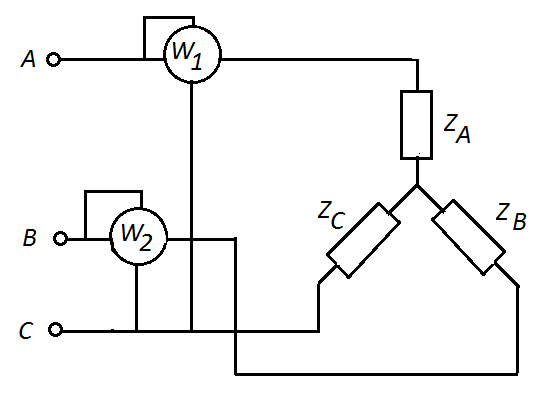
Рис.3.13 Схема измерения мощности в трехпроводных системах двумя ваттметрами
Токовые обмотки ваттметров включены в линейные провода А и В и измеряют линейные токи IA и IB, а обмотки напряжений измеряют линейные напряжения UAC и UBC.
Т
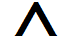 аким
образом, первый ваттметр покажет значение
мощностиW1=IAUACcos
аким
образом, первый ваттметр покажет значение
мощностиW1=IAUACcos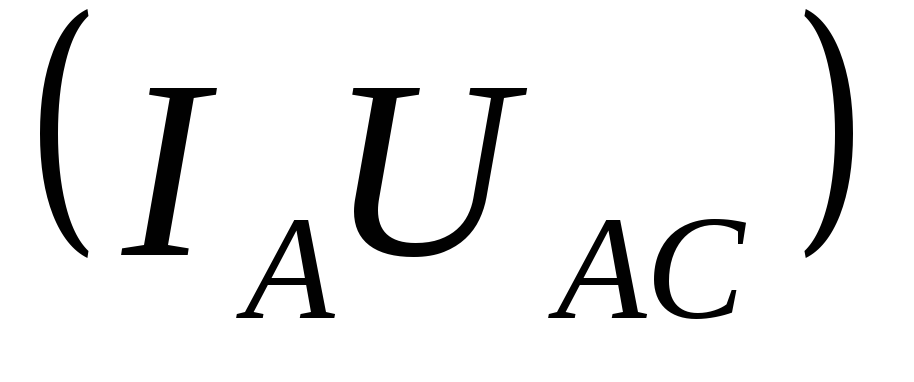 ,
а второй ваттметр W2=IВUВСcos
,
а второй ваттметр W2=IВUВСcos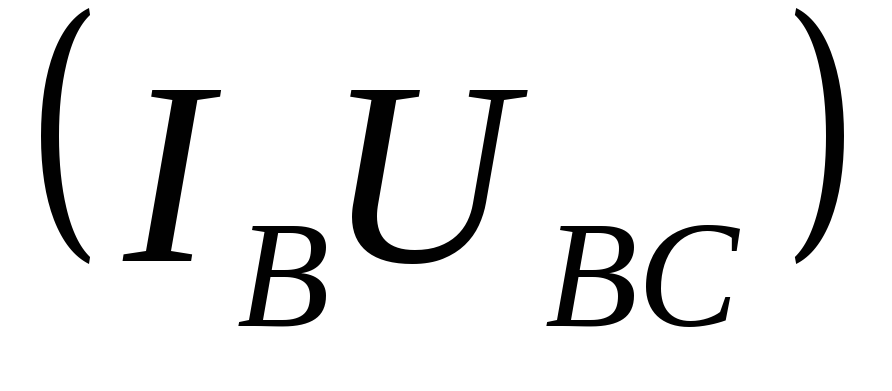 .
.
Покажем, что сумма показаний ваттметров равна полезной мощности всей цепи с помощью векторной диаграммы измеряемых токов и напряжений при симметричной нагрузке (рис. 3.14).
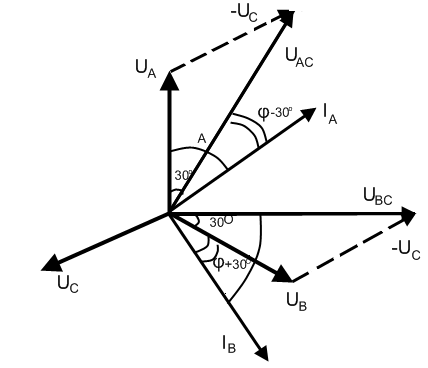
Рис. 3.14. Векторная диаграмма при соединении звездой.
И з
векторной диаграммы следует
з
векторной диаграммы следует
W 1=IAUACcos
1=IAUACcos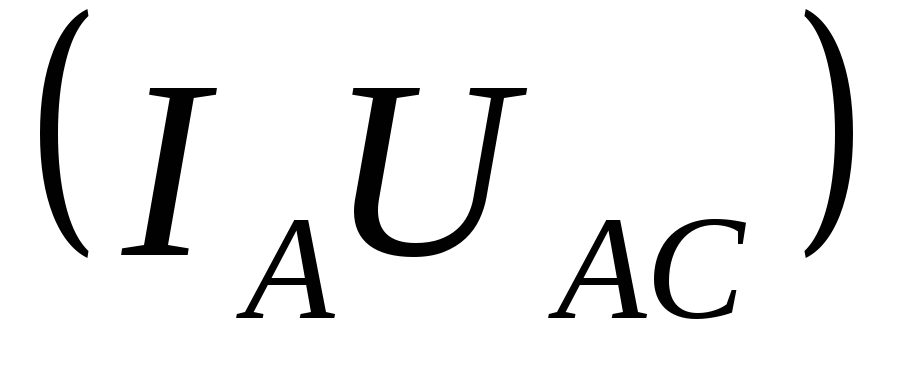 = IЛUЛ cos (φ-30o)
= IЛUЛ cos (φ-30o)
W2=IВUВСcos = IЛUЛ cos (φ+30o).
= IЛUЛ cos (φ+30o).
W1 +
W2 = IЛUЛ cos (φ-30o)
+ IЛUЛ cos (φ+30o)
= IЛUЛ (cosφ cos30о + sinφ sin30o + cosφ cos30о — sinφ
sin30o)
= 2 IЛUЛcosφ
cos30о= 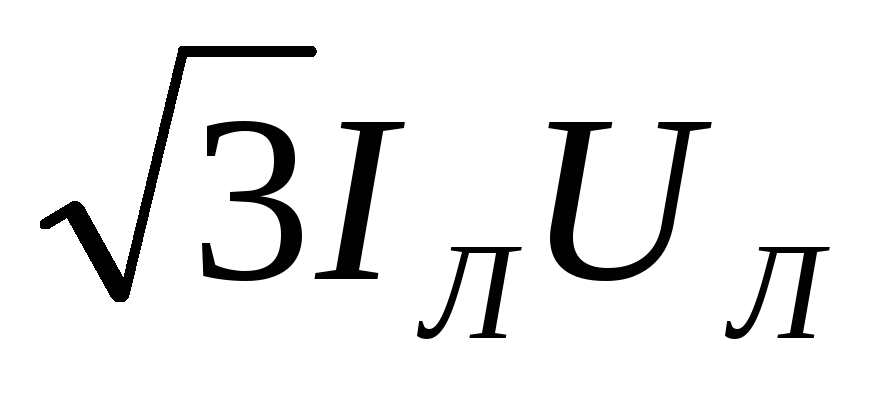 cosφ .
cosφ .
Полученное выражение совпадает с выражением (3.6), т.е. W1 + W2 = P, что и требовалось доказать.
По разности показаний ваттметров можно определить реактивную мощность трехфазной системы. Действительно
W1-W2 = IЛUЛcos(φ-30o) — IЛUЛcos(φ+30o) = IЛUЛ (cosφ cos30о+ sinφsin30o — cosφ cos30о+ sinφ sin30o) = 2 IЛUЛ sinφsin30o) = IЛUЛsinφ, (3.8)
Сравнивая (3.8) и
(3.7) получаем Q
= 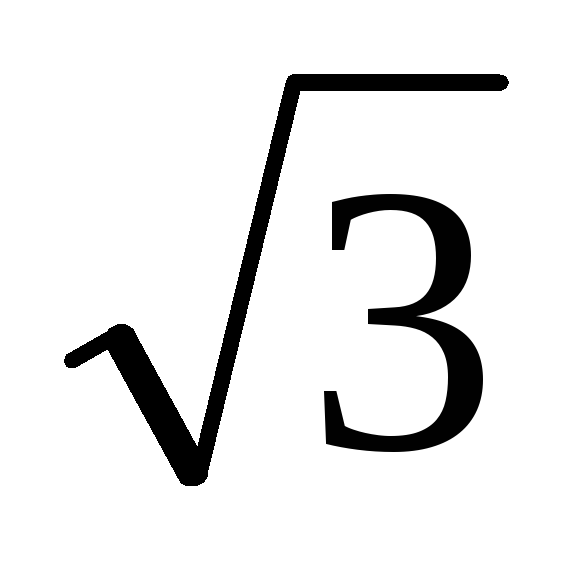 (W1-W2)
(W1-W2)



