Как измерить мощность в цепи трехфазного переменного тока

Мощность в цепи трехфазного тока может быть измерена с помощью одного, двух и трех ваттметров. Метод одного прибора применяют в трехфазной симметричной системе. Активная мощность всей системы равна утроенной мощности потребления по одной из фаз.

При соединении нагрузки звездой с доступной нулевой точкой или если при соединении нагрузки треугольником имеется возможность включить обмотку ваттметра последовательно с нагрузкой, можно использовать схемы включения, показанные на рис. 1.

Рис. 1 Схемы измерения мощности трехфазного переменного тока при соединении нагрузок а — по схеме звезды с доступной нулевой точкой; б — по схеме треугольника с помощью одного ваттметра

Если нагрузка соединена звездой с недоступной нулевой точкой или треугольником, то можно применить схему с искусственной нулевой точкой (рис. 2). В этом случае сопротивления должны быть равны Rвт+ Rа = Rb =Rc.

Рис 2. Схема измерения мощности трехфазного переменного тока одним ваттметром с искусственной нулевой точкой

Для измерения реактивной мощности токовые концы ваттметра включают в рассечку любой фазы, а концы обмотки напряжения — на две другие фазы (рис. 3). Полная реактивная мощность определяется умножением показания ваттметра на корень из трех. (Даже при незначительной асимметрии фаз применение данного метода дает значительную погрешность).

Рис. 3. Схема измерения реактивной мощности трехфазного переменного тока одним ваттметром

Методом двух приборов можно пользоваться при симметричной и несимметричной нагрузке фаз. Три равноценных варианта включения ваттметров для измерения активной мощности показаны на рис. 4. Активная мощность определяется как сумма показаний ваттметров.

При измерении реактивной мощности можно применять схему рис. 5, а с искусственной нулевой точкой. Для создания нулевой точки необходимо выполнить условие равенства сопротивлений обмоток напряжений ваттметров и резистора R. Реактивная мощность вычисляется по формуле

где Р1 и Р2 — показания ваттметров.

По этой же формуле можно вычислить реактивную мощность при равномерной загрузке фаз и соединении ваттметров по схеме рис. 4. Достоинство этого способа в том, что по одной и той же схеме можно определить активную и реактивную мощности. При равномерной загрузке фаз реактивная мощность может быть измерена по схеме рис. 5, б.

Метод трех приборов применяется при любой нагрузке фаз. Активная мощность может быть замерена по схеме рис. 6. Мощность всей цепи определяется суммированием показаний всех ваттметров.

Рис. 4. Схемы измерения активной мощности трехфазного переменного тока двумя ваттметрами а — токовые обмотки включены в фазы А и С; б — в фазы А и В; в — в фазы В и С

Реактивная мощность для трех- и четырехпроводной сети измеряется по схеме рис. 7 и вычисляется по формуле

где РA, РB, РC — показания ваттметров, включенных в фазы А, В, С.

Рис. 5. Схемы измерения реактивной мощности трехфазного переменного тока двумя ваттметрами

Рис. 6. Схемы измерения активной мощности трехфазного переменного тока тремя ваттметрами а — при наличии нулевого провода; б — с искусственной нулевой точкой

На практике обычно применяют одно-, двух- и трехэлементные трехфазные ваттметры соответственно методу измерения.

Чтобы расширить предел измерения, можно применить все указанные схемы при подключении ваттметров через измерительные трансформаторы тока и напряжения. На рис. 8 в качестве примера показана схема измерения мощности по методу двух приборов при включении их через измерительные трансформаторы тока и напряжения.

Рис. 7. Схемы измерения реактивной мощности тремя ваттметрами

Рис.

8. Схемы включения ваттметров через измерительные трансформаторы.

Калькулятор мощности трехфазного переменного тока • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения

Однофазный и трехфазный ток

Однофазную сеть можно сравнить с проселочной дорогой — оно не позволяет получить большую мощность. Трехфазную сеть можно сравнить с автомагистралью — она обычно имеется в промышленных зданиях для питания оборудования большой мощности

Установленный на столбе однофазный трансформатор, предназначенный для подачи электроэнергии в индивидуальные жилые дома (Канада)

Термин «фаза» относится к распределению электрической энергии. Для далеких от физики людей однофазную и трехфазную сеть можно сравнить с иллюстрациями выше. Однофазная сеть — как проселочная дорога, ее возможности по мощности невысоки и используется она в основном в жилых домах и квартирах. Однофазная сеть проста и экономична. Однако однофазную сеть нельзя использовать для питания эффективных трехфазных электродвигателей. С другой стороны, трехфазная сеть — как автомагистраль, она позволяет использовать мощные нагрузки и обычно применяется в промышленных зданиях и намного реже в индивидуальных жилых домах и квартирах. Все мощные потребители энергии, такие как водонагреватели, большие электродвигатели и системы кондиционирования воздуха обычно подключаются к трехфазной сети.

В однофазной сети используются два или три провода. Всегда имеется один фазный провод и один провод, называемый нейтралью или нулевым проводом. Ток течет между этими двумя проводами. Если однофазная сеть содержит заземляющий провод, то используется трехпроводная сеть. Однофазная сеть хороша в тех случаях, когда типичными нагрузками являются чисто активные потребители, например, традиционные лампы накаливания и электрические обогреватели. Однофазная система не годится для питания мощных электродвигателей.

Установленная на столбе группа из трех трансформаторов, обеспечивающая трехфазное питание небольшой промышленной установки

В трехфазной сети используются три провода, называемые фазными или просто фазами. По этим проводам текут синусоидальные токи со сдвигом фаз относительно друг друга на 120°. В трехфазной системе может быть три или четыре провода. Если имеется четвертый провод, то трехфазную сеть можно использовать для подачи однофазного питания (три линии), например, в индивидуальные жилые дома. При этом от каждой фазы в нагрузку (дом) подается примерно одинаковая мощность. Нейтральный провод часто имеет меньшее сечение, потому что фазные токи взаимно гасятся и по нейтральному проводу обычно течет совсем небольшой ток. Трехфазная система обеспечивает постоянную передачу мощности в нагрузку, что позволяет подключить более высокую нагрузку.

Определения и формулы

Генерация трехфазного тока

В простейшем трехфазном генераторе имеется три идентичных обмотки, расположенных под углом 120° по отношению друг к другу. В результате с обмоток снимаются напряжения (фазы) со сдвигом по фазе 120°. Эти три напряжения не зависят друг от друга и их мгновенные значения определяются формулами:

Здесь U_p — пиковое значение (амплитуда) напряжения в вольтах, ω — угловая частота в радианах в секунду и t — время в секундах. Напряжение, наведенное в обмотке 2, отстает от напряжения в обмотке 1 на 120°, а напряжение, наведенное в обмотке 3, отстает от напряжения в обмотке 1 на 240°. Ниже на рисунке приведены векторные диаграммы и формы колебаний напряжений генератора:

Если коэффициент мощности равен единице, то в каждой фазе трехфазной системы напряжение, ток и мощность сдвинуты относительно друг друга на 120°; последовательность фаз на этом рисунке U₁, U₂, U₃, потому что U₁ опережает U₂, U₂ опережает U₃, и U₃ опережает U₁.

Преимущества трехфазных систем

• По сравнению с однофазными двигателями, трехфазные двигатели имеют более простую конструкцию, высокий пусковой момент, высокие коэффициент мощности и эффективность, более компактны.
• Передача и распределение трехфазной электроэнергии дешевле в сравнении с однофазной, так как для этого можно использовать провода меньшего сечения при существенном уменьшении стоимости материалов и трудозатрат.
• В отличие от пульсирующей мощности однофазной системы, мгновенная мощность трехфазной системы постоянна, что обеспечивает плавность вращения и отсутствие вибрации двигателей и другого оборудования.
• Размеры трехфазных трансформаторов меньше однофазных трансформаторов аналогичной мощности.
• Трехфазную сеть можно использовать для питания однофазных нагрузок.
• Выпрямление трехфазного тока происходит с меньшей амплитудой пульсаций, по сравнению с выпрямлением однофазного тока.

Последовательность фаз

Последовательность фаз определяется временем, при котором напряжения трех фаз достигают положительного максимума. Последовательность фаз называют также порядком фаз. На рисунке выше последовательность фаз 1-2-3, так как фаза 1 достигает положительного максимума раньше, чем фаза 2, а фаза 3 достигает положительного максимума позже фазы 2. Отметим, что нам безразлично направление вращения ротора генератора, потому вращающийся по часовой стрелке ротор можно обойти и мы будем наблюдать вращение против часовой стрелки. Нам интересен только порядок чередования фаз напряжений, вырабатываемых генератором.

Для определения порядка фаз на векторной диаграмме нужно знать, что векторы всегда вращаются против часовой стрелки. Например, на этих трех чертежах последовательность чередования фаз снова U₁, U₂, U₃:

Фазное напряжение и фазный ток

Фазным называется напряжение между каждым из трех фазных проводов и нейтралью. Его также называют напряжением между фазой и нейтралью. Ток, которые течет в нагрузке между фазным проводом и нейтралью, называется фазным током.

Линейное напряжение и ток

Линейным называется напряжение между любыми двумя фазами (линиями). Ток, протекающий в каждой из линий, называется линейным.

Симметричные и несимметричные системы и нагрузки

В сбалансированной (симметричной) трехфазной системе токи во всех трех фазах равны, а сумма всех токов равна нулю, поэтому ток по нейтрали не течет. Амплитуды и частоты напряжений и токов одинаковые. Отличаются они только сдвигом фаз: напряжение в каждой фазе отстает от предыдущей на 2π/3, или на 1/3 цикла, или на 120°. Векторная сумма трех напряжений равна нулю:

То же можно сказать и о токах в симметричной системе:

Если три нагрузки, присоединенные к трем линиям, имеют одинаковую величину и коэффициент мощности, она также называются сбалансированными или симметричными.

Линейные и нелинейные нагрузки

В линейных нагрузках в цепях переменного тока напряжения и токи имеют синусоидальную форму и в любое время ток в нагрузке прямо пропорционален напряжению на ней. Примерами линейных нагрузок являются нагреватели, лампы накаливания. конденсаторы и катушки индуктивности. Все линейные нагрузки подчиняются закону Ома. В линейных нагрузка коэффициент мощности равен cos φ. Подробнее о нелинейных нагрузках — в нашем Калькуляторе активной и реактивной мощности.

В нелинейных нагрузках ток не пропорционален напряжению и содержит гармоники основной частоты 50 или 60 Гц. Примерами нелинейных нагрузок являются блоки питания компьютеров, лазерные принтеры, светодиодные и компактные люминесцентные лампы, электронные регуляторы оборотов электродвигателей и многие другие потребители электроэнергии. Искажение формы гармонических колебаний тока приводит к искажению формы напряжения. К нелинейным нагрузкам неприменим закон Ома. В таких нагрузках коэффициент мощности не равен cos φ.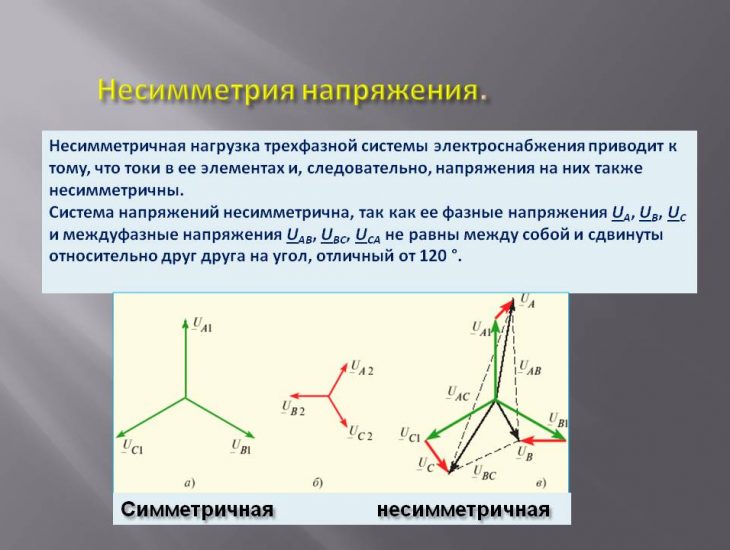

Соединение треугольником и звездой

Три обмотки трехфазного генератора можно присоединить к нагрузке шестью проводами, по два на обмотку. Для уменьшения количества проводов обмотки присоединяются к нагрузке тремя или четырьмя проводами. Эти два способа подключения называются треугольником (Δ) и звездой (Y).

В соединении треугольником начало каждой обмотки соединяется с концом следующей обмотки. Таким образом энергию можно передавать только по трем проводам.

Соединение звездой (слева) и треугольником (справа)

В симметричной соединении треугольником напряжения равны по амплитуде, отличаются по фазе на 120° и их сумма равна нулю:

В симметричной четырехпроводной системе соединения звездой с тремя одинаковыми подключенными к каждой фазе нагрузками мгновенное значение тока, текущего по нейтрали, равно сумме трех фазных токов i₁, i₂, и i₃, которые имеют одинаковые амплитуды I_p и сдвинуты по фазе на 120°:

Напряжение и мощность в симметричной трехфазной нагрузке при соединении звездой

Соединение звездой; I₁, I₂, и I₃ — фазные токи, которые равны линейным токам

Полная мощность в трехфазной системе является суммой мощностей, потребляемых нагрузками в каждой из трех фаз. В связи с тем, что нагрузки симметричные, в каждой фазе потребляется одинаковая мощность и полная активная мощность во всех трех фазах равна

Здесь φ — разность фаз между током и напряжением. Поскольку в трехфазном соединении звездой фазное U_ph и линейное среднеквадратичное напряжение U_L связаны как

а среднеквадратичное значения линейного и фазного токов равны

полная активная мощность определяется следующим уравнением:

Полная реактивная мощность равна

Комплексная мощность:

И, наконец, полная мощность в трех фазах определяется формулой:

Напряжение и мощность в симметричной трехфазной нагрузке при соединении треугольником

Соединение треугольником; I₁₃, I₂₃, и I₃₂ — фазные токи, а I₁, I₂, и I₃ — линейные токи; при этом I_L = √3∙I_ph

При соединении треугольником нейтральный проводник отсутствует и конец одной обмотки генератора соединяется с началом следующей обмотки. Фазное напряжение — это напряжение на каждой обмотке. Линейное напряжение — это напряжение между двумя фазами, то есть также на каждой из обмоток. Таким образом, среднеквадратичные напряжения на обмотках и между фазами одинаковые, то есть для соединения треугольником можно написать

При соединении треугольником фазные токи — это токи, текущие через фазные нагрузки. Мы рассматриваем симметричную систему, поэтому фазные среднеквадратичные значения токов I_p1, I_p2 и I_p3 по амплитуде равны (I_p) и отличаются по фазе на 120°:

Как мы уже упоминали, общая мощность в трехфазной системе — это сумма мощностей, потребляемых в нагрузках трех фаз:

где φ — сдвиг фаз между током и напряжением. Поскольку при соединении треугольником среднеквадратичные значения фазного U_ph и линейного напряжений U_L равны,

а среднеквадратичные значения линейного и фазного токов связаны формулой

активная мощность определяется следующим уравнением:

Полная реактивная мощность равна

Комплексная мощность:

И полная мощность в трех фазах:

Отметим, что приведенные выше уравнения для мощности при соединении звездой и треугольником одинаковые. Мы используем их в этом калькуляторе.

То, что эти формулы мощности для звезды и треугольника одинаковые, иногда приводит к ошибочным выводам о том, что можно соединить обмотки одного и того же электродвигателя звездой или треугольником и потребляемая мощность (и ток!) не изменятся. Конечно, это неправильно. И если мы в калькуляторе соединение звездой изменим на треугольник, не изменяя нагрузку, мы увидим, что мощность и потребляемый ток изменятся.

Рассмотрим пример. Трехфазный электродвигатель подключен по схеме треугольника и работает на полной номинальной мощности при линейном напряжении U_L и линейном токе I_L. Полная мощность в вольт-амперах (ВА) равна

Затем обмотки того же двигателя соединили звездой. Линейное напряжение, приложенное к каждой обмотке, уменьшилось в 1/1,73 раза, при этом сетевое напряжение осталось прежним. Ток в каждой обмотке уменьшился в 1/1,73 раза по сравнению с током, потребляемым при соединении треугольником. Полная мощность также уменьшилась:

Таким образом, полная мощность при соединении звездой равна одной трети мощности при соединении треугольником для нагрузки с тем же импедансом. Очевидно, что полный момент двигателя, обмотки которого соединены звездой, будет в три раза меньше момента того же двигателя при соединении обмоток треугольником.

Иными словами, хотя новая мощность для соединения звездой рассчитывается по той же формуле, что и для треугольника, в расчет нужно вставить другие величины, а именно, напряжение и ток. уменьшенные в 1,73 раза (то есть в квадратный корень из 3).

Расчет симметричной нагрузки по известным напряжению, току и коэффициенту мощности

Для расчета симметричной нагрузки (одинаковой в каждой фазе) по известным напряжению, току и коэффициенту мощности (опережающему или отстающему) используются следующие формулы:

Импеданс нагрузки

Z

В полярной форме:

В комплексной форме:

Расчет тока и мощности по известным напряжению и нагрузке

Фазный ток

По закону Ома, имеем:

Преобразование из прямоугольных координат в полярные и наоборот

Для преобразования из прямоугольных координат R, X в полярные координаты |Z|, φ, используйте следующие формулы:

Треугольник импеданса

В этих формулах R всегда положительно, а X положительно для индуктивной нагрузки (ток отстает от напряжения) и отрицательно для емкостной нагрузки (ток опережает напряжение).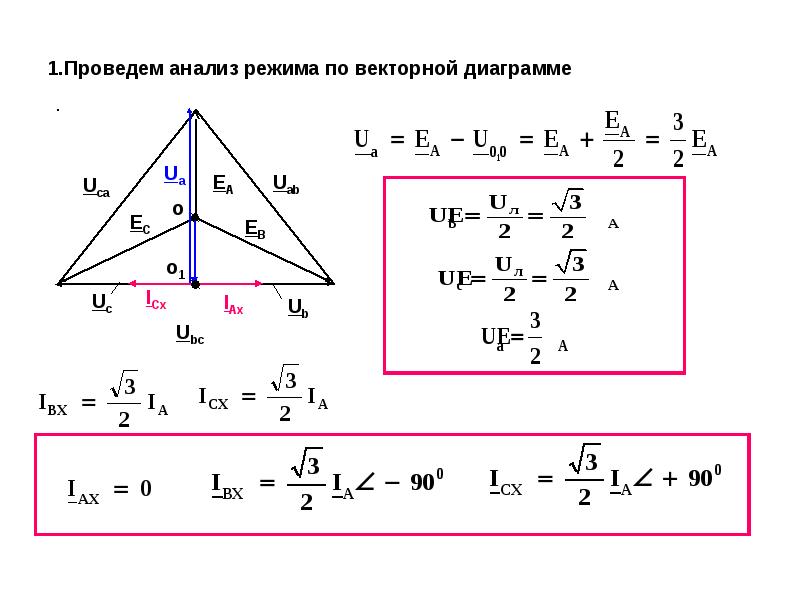

Активное

R_ph и реактивное X_ph сопротивление нагрузки

Импеданс конденсатора и катушки индуктивности

Параллельная нагрузка RLC

Параллельное соединение RLC

Для расчета используйте наш Калькулятор импеданса параллельной RLC-цепи.

Последовательная нагрузка RLC

Последовательное соединение RLC

Для расчета используйте наш Калькулятор импеданса последовательной RLC-цепи

Более подробную информацию о нагрузки в форме RLC-цепи вы найдете в наших калькуляторах для расчета импеданса:

Примеры расчетов

Пример 1. Расчет мощности и тока по заданным напряжению и нагрузке

Индуктивная нагрузка из трех цепей с равными импедансами Z_ph = 5+j3 Ом подключена звездой к трехфазной сети с линейным напряжением 400 В 50 Гц. Рассчитать фазное напряжение U_ph, фазовый угол φ_ph, фазный ток I_ph, линейный ток I_L, активную P, реактивную Q, полную |S|, и комплексную S мощности.

Пример 2. Расчет мощности и тока по заданным напряжению и нагрузке

Индуктивная нагрузка из трех цепей с равными импедансами Z_ph = 15 ∠60° Ом подключена звездой к трехфазной сети с фазным напряжением (между фазой и нейтралью) 110 В 50 Гц. Определить тип нагрузки (емкостная или индуктивная) фазное напряжение U_ph, фазовый угол φ_ph, фазный ток I_ph, линейный ток I_L, активную P, реактивную Q, полную |S|, и комплексную S мощности.

Пример 3. Расчет мощности и тока по заданным напряжению и нагрузке

Индуктивная нагрузка из трех обмоток с равными импедансами и эквивалентной схемой в виде включенных последовательно сопротивления R_ph = 20 Ом и индуктивности L_ph = 440 мГн подключена звездой к трехфазной сети с фазным напряжением (между фазой и нейтралью) 230 В 50 Гц. Рассчитайте фазное напряжение U_ph, фазовый угол φ_ph, фазный ток I_ph, линейный ток I_L, активную P, реактивную Q, полную |S|, и комплексную S мощности. Найти линейный ток и потребляемую мощность для той же нагрузки, но соединенной треугольником. Совет: Для определения импеданса каждой обмотки воспользуйтесь Калькулятором последовательной RL-цепи.

Пример 4. Расчет мощности и нагрузки по заданным напряжению и току

Симметричный трехфазный генератор подает фазное напряжение 230 В на включенную звездой нагрузку с отстающим (активно-индуктивным) коэффициентом мощности 0,75. Ток в каждой фазе равен 28,5 А. Рассчитать импеданс нагрузки, активное и реактивное сопротивление в каждой фазе. Также рассчитать полную, активную и реактивную мощности. Описать что произойдет, если для той же нагрузки изменить соединение со звезды на треугольник. Совет: используйте режим определения мощности и нагрузки по заданным току и напряжению, а затем для ответа на последний вопрос воспользуйтесь этим же калькулятором в режиме определения мощности и тока по заданным напряжению и нагрузке.

Пример 5. Расчет мощности и тока по заданным напряжению и нагрузке

Нагрузка, состоящая из трех одинаковых обмоток, имеющих сопротивление R_ph = 10 Ом и индуктивность L_ph = 310 мГн, подключена треугольником к трехфазной сети с напряжением между фазой и нейтралью 120 В, 60 Гц. Рассчитайте линейное напряжение U_L, фазовый угол φ_ph, фазный ток I_ph, линейный ток I_L, активную P, реактивную Q, полную |S|, и комплексную S мощности. Как изменятся ток и мощность, если эту же нагрузку подключить звездой? Совет: воспользуйтесь нашим Калькулятором импеданса последовательной RL-цепи для определения импеданса каждой катушки, а затем введите данные в этот калькулятор.

Пример 6. Расчет мощности и тока по заданным напряжению и нагрузке

Нагрузка из трех цепей с равными импедансами Z_ph = 7 – j5 Ом подключена треугольником к трехфазной сети с линейным напряжением (между двумя фазами) 208 В 60 Гц. Определить тип нагрузки (резистивно-емкостная или резистивно-индуктивная) фазное напряжение U_ph, фазовый угол φ_ph, фазный ток I_ph, линейный ток I_L, активную P, реактивную Q, полную |S|, и комплексную S мощности.

Пример 7. Расчет мощности и нагрузки по заданным напряжению и току

Симметричная нагрузка подключена звездой к симметричному трехфазному генератору с линейным (между двумя фазами) напряжением 208 В 60 Гц. В каждом фазном проводе протекает ток I_ph = 20 А с запаздыванием относительно напряжения на 15°. Определите фазное напряжение, импеданс нагрузки в каждой фазе в полярной и комплексной форме, активную и реактивную мощности.

Автор статьи: Анатолий Золотков

Расчет цепи с несимметричной нагрузкой

В нормальных условиях несимметричные режимы в высоковольтных трехфазных цепях встречаются относительно редко (преимущественно в цепях с дуговыми электроплавильными печами и однофазными электротяговыми двигателями). Обычно несимметричные режимы получаются в аварийных условиях, когда в какой-либо цепи появляется несимметрия.
Различают два вида несимметрии — поперечную и продольную. Поперечная несимметрия у симметричной трехфазной цепи возникает при несимметричной нагрузке. К ней, в частности, относятся различные виды несимметричных коротких замыканий (замыкания между фазами, замыкание одной или двух фаз на землю). Продольная несимметрия возникает, если в рассечку фаз линии включаются элементы с неодинаковыми сопротивлениями или при обрыве одного или двух проводов (несимметричный участок линии).
Для расчетов несимметричных режимов трехфазных цепей удобно пользоваться принципом компенсации, заменяя несимметричный приемник или несимметричный участок в линии источниками ЭДС (напряжений), значения которых до окончания всего расчета остаются неизвестными. Целесообразность этого приема заключается в том, что после такой замены цепь становится симметричной и для нее разноименные симметричные составляющие токов и напряжений не зависят друг от друга. Связи же между симметричными составляющими токов и напряжений различных последовательностей, обусловленные несимметрией, вводятся позднее.

Рассмотрим метод расчета на примере схемы рис. 11.13, содержащей симметричную динамическую () и несимметричную статическую нагрузки. Пусть заданы ЭДС генераторов и сопротивления элементов схемы. Требуется найти токи и напряжения. На рис. 11.13 схема и сопротивления несимметричной нагрузки не показаны, так как на первом этапе расчета они не нужны.
Заменим несимметричную нагрузку тремя источниками ЭДС с неизвестными напряжениями и получим симметричную схему, которая помимо генератора с симметричной системой ЭДС содержит источники с несимметричными напряжениями .

Разложим напряжения на симметричные составляющие , приняв фазу А за основную. В результате получим симметричную схему (рис. 11.14), причем в ответвлении, где была несимметричная нагрузка, находятся источники трех симметричных систем напряжений прямой, обратной и нулевой последовательностей.
В симметричной цепи симметричная система напряжений какой-либо последовательности вызывает симметричную систему токов той же самой последовательности. Следовательно, можно составить три независимые схемы, показанные на рис. 11.15, а-в. Для упрощения в этих схемах не учтены частичные емкости линии (см. раздел).
Режим фазы А исходной схемы (см. рис. 11.13) определим путем наложения режимов этих трех схем.
Конфигурации схем прямой и обратной последовательностей всегда одинаковы. Схема нулевой последовательности обычно существенно отличается. В данном примере она не имеет разветвления, так как в правой части трехфазной цепи (см. рис. 11.13) токов нулевой последовательности не может быть. Следует обратить особое внимание на то, что сопротивление в нейтральном проводе вводится в схему нулевой последовательности утроенной величиной (см. раздел).
Из рассмотрения составленных схем видно, что наибольшие значения симметричных составляющих напряжений обратной и нулевой последовательностей наблюдаются в месте подключения несимметричного приемника, так как в схемах именно там находятся источники ЭДС обратной и нулевой последовательностей.
Для дальнейшего расчета целесообразно преобразовать схемы отдельных последовательностей к простейшему виду, не затрагивая при этом ветвей с источниками неизвестных напряжений .

В схеме прямой последовательности заменим ветви генератора и симметричного приемника эквивалентным генератором (рис. 11.16, а):

В схеме обратной последовательности объединяем ветви генератора и симметричного приемника (рис. 11.16,б):

Схема нулевой последовательности в данном примере в преобразовании не нуждается, так как она имеет простейший вид.
Для каждой из трех схем напишем уравнения по второму закону Кирхгофа:

В этих трех уравнениях шесть неизвестных: Дополнительные три уравнения, связывающие эти шесть неизвестных величин, могут быть составлены на основании заданной схемы и параметров несимметричного приемника.
Рис. 11.16

Составим дополнительные уравнения для некоторых видов несимметричных приемников. Для приемника, представленного на рис. 11.17, а

Для приемника, показанного на рис. 11.17,6

При отсутствии соединения несимметричного приемника с землей, например, для схемы, приведенной на рис. 11.17, в,симметричные составляющие токов нулевой последовательности равны нулю и составление схемы цепи нулевой последовательности на предыдущих этапах расчета выпадает. Получаются два основных уравнения с четырьмя неизвестными, и нужно составить только два дополнительных уравнения, а именно:

Аналогично составляют дополнительные уравнения и при других видах статической несимметричной нагрузки. При совместном решении уравнений Кирхгофа для схем различных последовательностей с дополнительными уравнениями определяются симметричные составляющие тока фазы А в ответвлении к несимметричному приемнику. Затем находят распределение этих составляющих по отдельным ветвям схем прямой, обратной и нулевой последовательностей. Зная составляющие токов в любой ветви, вычисляют действительный ток в каждой фазе и составляющие падений напряжения различных последовательностей, а затем и фазные напряжения на отдельных участках схемы.
Приведем расчет режима схемы (см. рис. 11.13) для случая несимметричной нагрузки, представленной на рис. 11.17, a при условии, что (однофазное замыкание на землю). Составим дополнительные уравнения

Вычитая (11.24) из (11.23), получаем

Подставляя этот результат в (11.23), имеем

Заменяем в (11.21) затем их суммируем и с учетом (11.22) получим

Симметричные составляющие напряжений (в месте замыкания на землю) определяются из (11.21):

Для схем рис. 11.15, а

рис. 11.15, б

рис. 1115, в

Симметричные составляющие напряжений на выводах генератора могут быть найдены по тем же схемам на рис. 11.15:

Измерение мощности в четырехпроводной системе с использованием ваттметров

4-проводная система для несбалансированных нагрузок

Четырехпроводная система подходит для подачи несбалансированных, трехфазных нагрузок или однофазных нагрузок, распределенных на всех трех фазах установки низкого напряжения.

Измерение мощности на четырехпроводной системе (на фото: измерительная мощность с устройством Метрела MI 3102 Eurotest XE; кредит: itrservis.ru)

При измерении мощности на трехфазной системе действительно необходимо учитывать тот факт, что трехфазная система питания может быть не сбалансирована (указатели фаз-фазных напряжений U _{L1 / L2}, U _{L2 / L3} и U

L3 / L1 в последовательности не образуют равносторонний треугольник).

Проблема возникает из-за мощных несбалансированных трехфазных нагрузок, подключенных к сети.

Остановимся теперь на трехфазных и однофазных методах ваттметра //

1. Трехфазный ваттметр

Рисунок 1 — Принцип измерения мощности на трехфазной четырехпроводной системе с использованием трехфазного ваттметра

Трехфазный ваттметр измеряет все трехфазные напряжения, фазные токи и задержки между напряжениями и токами. На этой основе он может рассчитать три уровня мощности отдельно для каждой фазы, а также уровень общей трехфазной системы.

Рисунок 2 — Измерение мощности на трехфазной четырехпроводной системе с использованием измерительного устройства

Все три уровня мощности можно считывать непосредственно на дисплее измерительного устройства. Этот метод позволяет измерять мощность на всех трех фазах одновременно и особенно подходит для несбалансированной мощности. В случае сбалансированной мощности один ваттметр можно использовать и перемещать на все три этапа в три этапа.

2. Однофазный ваттметр

При наличии несимметричных трехфазных нагрузок или однофазных нагрузок, обычно подключаемых к четырехпроводной системе, необходимо измерить мощность на всех трех фазах (невозможно измерить только одну фазу и вычислить мощность общей трехфазной нагрузки система).

Измерение с использованием измерительного устройства выполняется в три этапа, где каждый шаг равен измерению в однофазной системе.

Первый шаг //

Рисунок 3 — Измерение мощности в трехфазной системе (первый шаг)

Результат 1 P ₁ = U ₁ × I ₁ × cos φ1 (активная мощность)

Результат 2 Q ₁ = U ₁ × I ₁ × sin φ1 (реактивная мощность)

Результат 3 PA ₁ = U ₁ × I ₁ (кажущаяся мощность)

Второй шаг //

Рисунок 4 — Измерение мощности в трехфазной системе (второй шаг)

Результат 1 P ₂ = U ₂

× I ₂ × cos φ2

…

(активная мощность)

Третий шаг //

Рисунок 5 — Измерение мощности на трехфазной системе (третий шаг)

Результат 1 P ₃ = U ₃ × I ₃ × cos φ3 (активная мощность)

Результат 2 Q ₃ = U ₃ × I ₃ × sin φ3 (реактивная мощность)

Результат 3 PA ₃ = U ₃ × I ₃ (кажущаяся мощность)

На каждом шаге прибор измеряет фазное напряжение, фазовый ток и задержку между напряжением и током.

На основе измеренных результатов для каждой фазы мы можем вычислить все три полные мощности трехфазной системы в соответствии со следующими уравнениями //

P _tot

= P ₁ + P ₂ + P ₃ (общая активная мощность трехфазной системы)

Q _tot = Q ₁ + Q ₂ + Q ₃ (полная реактивная мощность трехфазной системы)

PA _tot = √ (P _tot² + Q _tot² ) (полная кажущаяся мощность трехфазной системы)

PF _tot = P _tot / PA _tot (коэффициент мощности)

Ссылка // Измерения на электрических установках в теории и практике — Руководство по эксплуатации Metrel

Связанные электрические направляющие и изделия

4.2. Измерение мощности

Мощность измеряют различными способами.

Мощность в электрических цепях постоянного и однофазного переменного тока, измеряют в основном ваттметрами электродинамической системы. На рис. 4.4 приведены схемы включения ваттметра для измерения мощности, потребляемой сопротивлением нагрузки R

НАГ в цепях постоянного и однофазного переменного тока.

В цепях напряжения включено добавочное сопротивление R_Д. Начало токовой обмотки напряжения, так же как и в последующих схемах, показано, соответственно, левой и верхней точками на обмотках ваттметра W; перемена полярности одной из обмоток приведет к отклонению стрелки ваттметра в обратную сторону. Если включить ваттметр в цепь постоянного тока (рис. 4.4, схема а), то он учтёт потребляемую электроприемниками мощность и потери в токовой обмотке ваттметра. Мощность Р определяют по формуле

P=IU’=I(U+IRт)=IU+I²RT=Pпp+Pт,

где I и U — соответственно, ток  и напряжение на нагрузке; U’ — напряжение питания; Rт — сопротивление токовой обмотки ваттметра; Рпр и Рт — соответственно, потребляемая приемниками мощность и потери мощности в токовой обмотке.

При включении (рис. 4.4, схема б) по схеме ваттметра учитываются дополнительные потери в обмотке напряжения Рн:

P=U(I+Iн)=UI+UIн=Pнр+Pн.

Таким образом, систематической погрешности, возникающей в следствии того, что цепи тока и напряжения измерительного механизма должны включаться также, как и приборы для измерения тока и напряжения избежать не удается. Если ожидаются значительные колебания мощности за счёт колебаний тока, то предпочтительней будет схема а. При включении ваттметра (рис. 4.4, схема в) на добавочном сопротивлении Rд окажется почти полное напряжение источника, на которое не может быть рассчитана изоляция подвижной катушки. Кроме того, появляется дополнительная погрешность за счет электростатического взаимодействия обмоток. Такую схему не следует применять.

Показания ваттметра, включенного в цепь переменного тока, пропорциональны произведению подведенного к нему напряжения U, тока в токовой обмотке I и cosφ:

Р = с·U·I·cosφ, где с — цена деления ваттметра.

При определенном положении переключателей пределов по току и напряжению цена деления составит

с = (U_ПРI_ПР)/_ПР, Вт/дел,

где U_ПР и I_ПР — верхние пределы ваттметра, _ПР — количество делений шкалы ваттметра.

При определении мощности косвенным методом в цепи постоянного тока измеряют ток и напряжение, а в цепи переменного тока (дополнительно, с помощью фазометра), коэффициент мощности cosφ.

Для расширения пределов измерения по току и напряжению применяют шунты, добавочные сопротивления и измерительные трансформаторы (рис. 4.5). Цену деления ватт-метра при пользовании измерительными трансформаторами определяют по уравнению:

С_ИЗМ= СК_IHК_UH, Вт/дел.

На сверхвысоких частотах (СВЧ) способы измерения мощности, рассмотренные выше очень трудно реализуемы, поэтому применяются другие способы измерения мощности. Несмотря на кажущееся разнообразие, все они сводятся к преобразованию энергии электромагнитных колебаний в другой вид энергии, более применяемый для измерения (тепловую, механическую и другие) с последующим вторичным преобразованием в электрический сигнал. Измерение производится в основном цифровыми приборами.

При измерении активной мощности в трёхфазных цепях (три фазовых провода и один нулевой — четырех проводная сеть) используют три однофазных ваттметра, включенных в отдельные фазы; измеряемую мощность определяют как сумму мощностей всех фаз. В, этом случае не следует пользоваться ваттметром, включенным в одну из фаз, так как велика вероятность неравномерности нагрузки, и погрешность измерения может оказаться значительно больше допустимой.

В трехфазных цепях без нулевого провода возникает затруднение с подключением цепи напряжения ваттметра, потому что в цепи имеется линейное напряжение. Однако при симметричной, нагрузке можно измерить мощность одним ваттметром. Для этого в месте измерения создается искусственная нулевая точка. Сопротивления всех фаз, образующие звезду, должны быть равными. Мощность в этом случае равна утроенному показанию ваттметра.

В несимметричных трехфазных трехпроводных цепях мощность можно измерить так же, как и в четырехпроводных цепях, т.е. как сумму трех мощностей. Здесь также необходима искусственная нулевая точка, однако ее можно очень просто создать соединением в звезду трех (одинаковых!) цепей напряжения ваттметров.

Более универсальным и точным методом измерения трехфазной мощности является метод двух ваттметров или так называемая схема Арона (рис. 4.6).

Токовые обмотки ваттметров включены на линии А, В; обмотки по напряжению на АС и ВС (рис. 4.6, а).

Токовые обмотки ваттметров включены на линии А, С; обмотки по напряжению — на АВ и СВ (рис. 4.6, б).

Токовые обмотки ваттметров включены в линии В, С; обмотки по напряжению – на ВА и СА (рис. 4.6, в).

Построим векторную диаграмму (рис. 4.7) для схемы Арона (рис. 4.6, схема б).

Мощность определяют по сумме показаний ваттметров

P=P₁+P₂=U_авI_аcosψ1+U_свI_сcosψ2.

В зависимости от характера нагрузки один из углов (ψ1 или ψ2) может стать больше 90°. В этом случае один из ваттметров будет показывать отклонение в противоположную сторону. Чтобы получить отсчет, надо изменить направление тока в одной из обмоток этого ваттметра. Показания берут со знаком минус, т.е. общая мощность равна алгебраической сумме показаний. В частном случае, когда система симметрична, ψ1=30+φ, ψ2=30-φ и общую мощность находят по формуле

P=P₁+P₂=U_авI_аcos(30+φ)+U_свI_сcos(30-φ)=U_лI_л2cos30cosφ= U_лI_лcosφ.

Даже при полной симметрии показания ваттметров не равны и зависят от величины и знака угла φ. При значении φ, равном 0-60 показания обоих положительны; при φ=60 показания первого ваттметра Р₁=0; при φ>60 оба покажут отрицательные значения.

При измерении реактивной мощности однофазные реактивные ваттметры применяют для лабораторных измерений и поверки индукционных счетчиков. В отличии от обыкновенного ваттметра реактивный имеет усложненную схему параллельной цепи, в которую включают реактивное сопротивление для получения сдвига по фазе на 90° между током и напряжением. Тогда угол отклонения подвижной части будет пропорционален реактивной мощности. При измерении реактивной мощности в трехфазных цепях нет необходимости получать сдвиг по фазе на 90°, так как при переходе от схемы звезды к схеме треугольника всегда имеется напряжение, которое пропорционально измеряемому и сдвинуто по фазе на 90°. В соответствии с этим, например в несимметрично нагруженной трех- и четырехфазной сети, реактивную мощность Q определяют по схеме трех активных ваттметров, включенных по напряжению на «чужие» фазы (рис. 4.8).

Тогда реактивная мощность Q = (P₁+P₂+P₃)/

При равномерной нагрузке можно ограничиться одним из ваттметров. Тогда Q =·Р₁. В трехфазной сети с равномерной нагрузкой (рис. 4.6, любая схема), реактивную мощность Q определяют по формуле

Q =·(P₁-P₂).

Реактивную мощность в трехфазной сети с равномерной и неравномерной загрузкой фаз Q находят по схеме с искусственной нулевой точкой (рис. 4.9):

Q = ·(P₁+ Р₂).

Сопротивление, включенное на свободную фазу (R), подбирают так, чтобы оно вместе с обмотками напряжения ваттметров образовало симметричную звезду, а к ваттметрам были подведены фазовые напряжения:

R=R_w1=R_w2.

Для определении реактивной мощности указанными выше методами необходимо знать порядок чередования фаз сети. Если он окажется обратным, показания ваттметров во многих случаях будут отрицательными.

4.1. Измерение тока и напряжения< Предыдущая		Следующая >4.3. Измерение энергии

Полный анализ несимметричных трехфазных систем — Wira Electrical

Специальным методом работы с несбалансированными трехфазными системами является метод симметричных компонентов, который выходит за рамки этого текста. Мы узнаем об этом в ближайшее время.

Обязательно сначала прочтите «что такое трехфазная цепь».

После того, как мы узнаем о трехфазной цепи, мы узнаем:

1. Сбалансированное трехфазное напряжение
2. Сбалансированное трехфазное питание
3. Несбалансированное трехфазное питание
4. Измерение трехфазной мощности

Несбалансированные трехфазные системы

Обучение и понимание трехфазных систем было бы неполным без изучения и анализа несбалансированных трехфазных систем.

Несбалансированная трехфазная система — не редкость при передаче и распределении электроэнергии.

Когда мы имеем дело с:

1. Сбалансированной трехфазной системой
2. Несбалансированной трехфазной системой

Нам нужно знать, что заставило их стать «сбалансированными» или «несбалансированными».

Есть две причины этой несбалансированной системы:

1. Источники напряжения не равны по величине и / или имеют разницу в фазовом угле между фазами.
2. Полные сопротивления нагрузки не равны друг другу.

В сбалансированной системе всегда есть:

1. Источники равного напряжения по величине и фазовому углу. Например, трехфазная система с источником напряжения 120 В и частотой 50 Гц для каждой фазы.
2. Равное сопротивление нагрузки. Например, трехфазная система только с резистивными нагрузками или индуктивными нагрузками или емкостными нагрузками с одинаковым значением для всех линий.

Таким образом,

Несбалансированная система возникает из-за несимметричных источников напряжения или несимметричной нагрузки.

Также нужно помнить, что несимметричный трехфазный источник напряжения — очень редкое явление.

Анализ несбалансированных трехфазных систем займет много времени. Следовательно, в этом посте мы будем предполагать, что каждая используемая нами схема имеет сбалансированные источники напряжения и несимметричный импеданс нагрузки.

Несбалансированная нагрузка в трехфазной системе

Трехфазная система сбалансирована, если все линейные нагрузки равны друг другу. Если одну из нагрузок увеличить, то это будет неуравновешенная система.

Почему?

Потому что эта линия потребляет больше тока, чем две другие.

Влияние несбалансированной трехфазной системы

• Повышенный нагрев от трехфазных двигателей.
• Уменьшение срока службы машины из-за повышенного нагрева.
• Потери мощности I ² R увеличились.
• Моторные приводы становятся ненадежными.

Свойства несбалансированной трехфазной системы

• Трехфазный сигнал искажен.
• Линейные токи не равны друг другу.
• Необходим нейтральный провод.
• Более высокие потери мощности.

Как решить несбалансированную трехфазную систему

Даже если мы имеем дело с трехфазными системами, мы все равно можем использовать сеточный и узловой анализ. Конечно, KCL и KVL тоже полезны.

Обратите внимание на схему на Рисунке (1) ниже. Здесь у нас есть четырехпроводная несимметричная трехфазная система, соединенная звездой, состоит из:

• Сбалансированный трехфазный источник напряжения (не показан в схеме)
• Несимметричный импеданс нагрузки при соединении звездой (Z ₁ , Z ₂ и Z ₃ ).

Рис. 1. Несбалансированная трехфазная нагрузка, подключенная по схеме Y

Поскольку мы уже установили несимметричные импедансы нагрузки, все Z _A , Z _B и Z _C не равны.

Используя закон Ома, мы получаем линейные токи как:

(1)

В сбалансированной трехфазной системе ток, производимый в нейтральной линии, должен быть равен нулю. Но здесь ток в нейтральной линии не равен нулю.

Применение KCL в узле N дает ток нейтральной линии как

(2)

Если мы имеем дело с трехфазной системой, у которой нет нейтральной линии, мы все равно можем использовать анализ сетки, чтобы найти линейные токи I. _a , I _b и I _c .Сюда входят трехфазные (и трехпроводные) системы треугольник-звезда, звезда-треугольник и треугольник-треугольник.

Если мы говорим о распределении и передаче электроэнергии на большие расстояния, мы имеем дело с несколькими трехпроводными системами с заземлением в качестве нейтрального проводника.

Для расчета мощности в несбалансированной трехфазной системе необходимо найти мощность в каждой фазе.

Общая мощность — это не просто трехкратная мощность в одной фазе, а сумма мощностей в трех фазах.

Несимметричные трехфазные системы Примеры проблем

1. Несимметричная нагрузка звезды на рисунке (1) имеет сбалансированные источники напряжения 100 В и последовательность a c b. Вычислите линейные токи и ток нейтрали, если они известны

Z _A = 15 Ом
Z _B = 10 + j5 Ом
Z _C = 6 — j8 Ом.

Решение:

Используя уравнение (1), линейные токи равны

Используя уравнение (2), ток в нейтральной линии равен

2.Обратите внимание на схему на рисунке (2) ниже. Здесь мы имеем несимметричную схему с трехпроводным соединением звезда-звезда. Найдите:
(a) линейные токи
(b) полную комплексную мощность, потребляемую нагрузкой
(c) полную комплексную мощность, отдаваемую источником.

Решение:

(a) Мы используем анализ сетки, чтобы найти требуемые токи. Для сетки 1:

Или

(2,1)

Для сетки 2,

Или

(2.2)

Уравнения (2.1) и (2.2) образуют матричное уравнение:

Детерминанты

Сеточные токи

Линейные токи равны

(b) Мы можем Теперь рассчитайте комплексную мощность, потребляемую нагрузкой.
Для фазы A,

Для фазы B,

Для фазы C,

Общая комплексная мощность, потребляемая нагрузкой, составляет

(c) Мы проверяем результат выше, найдя мощность предоставлено источником.Для источника напряжения в фазе a,

Для источника в фазе b,

Для источника в фазе c,

Общая комплексная мощность, подаваемая трехфазным источником, составляет

показывающий, что Ss + S _L = 0, и подтверждающий принцип сохранения переменного тока.

Несбалансированные трехфазные нагрузки — Inst Tools

Важным свойством трехфазной сбалансированной системы является то, что сумма векторов трех линейных или фазных напряжений равна нулю, а сумма векторов трех линейных или фазных токов равна нулю.Когда три импеданса нагрузки не равны друг другу, сумма векторов и нейтральный ток (I _n ) не равны нулю, и, следовательно, нагрузка несимметрична. Дисбаланс возникает при появлении обрыва или короткого замыкания в нагрузке.

Если трехфазная система имеет несимметричную нагрузку и несимметричный источник питания, методы ремонта системы сложны. Поэтому мы будем рассматривать только несимметричную нагрузку со сбалансированным источником питания.

Пример:

Сбалансированная система с 3 фазой, показанная на рисунке 16a, содержит нагрузку звездой.Линейное напряжение составляет 240 В, а сопротивление — 40 Ом в каждой ветви.

Рисунок 16: Несбалансированная нагрузка 3φ

Найдите линейный ток и ток нейтрали для следующих условий нагрузки.

1. сбалансированная нагрузка
2. обрыв цепи, фаза A (рисунок 16b)
3. короткое замыкание в фазе А (рисунок 16в)

Решение: сбалансированная нагрузка

I _L = 138,7 / 40

I _L = 3.5 ампер

I _N = 0

Решение: Ответ для обрыва цепи, фаза A

2. Ток в линиях B и C становится результатом нагрузки в B и C, соединенных последовательно.

I _B = 240/40 + 40

I _B = 3 А

так, I _C = 3 ампера

I _N = I _{B +} I _C = 6 ампер

3. Ответ на короткое замыкание в фазе А

I _B = 240/40

I _B = 6 ампер

, поэтому я _C = 6 ампер

Ток в фазе A равен току нейтрали, I _A = I _N

Следовательно, I _N — это векторная сумма I _B = I _C

I _N = √3 I _B

I _N = 1.73 х 6

I _N = 10,4 А

В состоянии неисправности нейтраль в нагрузке, соединенной звездой, будет пропускать больше тока, чем фаза при сбалансированной нагрузке. Несимметричные трехфазные цепи обозначаются аномально высокими токами в одной или нескольких фазах. Это может привести к повреждению оборудования, если дисбаланс будет продолжаться.

(PDF) База быстрой несимметричной трехфазной регулировки при однофазной нагрузке

TELKOMNIKA e-ISSN: 2087-278X 

Быстрая несимметричная трехфазная регулировка при однофазной нагрузке… (Yanwei Zheng)

4333

5.Заключение

Целью данной статьи является быстрое регулирование трехфазной нагрузки для распределительной сети с большим количеством одиночных нагрузок

. В данной статье предложена идея регулировки трех нагрузок и модель контроллера

, которая изменила схему подключения однофазной нагрузки. Некоторые однофазные нагрузки

подключаются ко всем трем фазам магистрали с помощью контроллера. Устройство контроллера может обнаруживать

3-фазную нагрузку в режиме реального времени. Когда коэффициент несимметрии трех фаз превышает пороговое значение,

может переключать соответствующие однофазные нагрузки с одной фазы на другую, таким образом, коэффициент несимметрии трех фаз

будет отрегулирован до допустимого значения.

Результаты показывают, что алгоритм MCLA может отрегулировать соотношение трехфазного несимметрии до

грубо сбалансировать, а алгоритм MBA подходит для использования, когда трехфазный несимметричный сигнал является серьезным.

Эти два алгоритма могут эффективно улучшить качество электроэнергии и снизить потери в сети.

Благодарности

Настоящий документ поддержан Национальным фондом естественных наук Китая (№

61173079 и № 60973093) и ключевым проектом Фонда естественных наук провинции Шаньдун

(ZR2011FZ003).

Ссылки

[1] Ли Чаоин, Ли Баосянь, Ван Жуйци. Анализ трехфазной несимметричной технологии распределения

Трансформатор и меры управления. Ценностная инженерия. 2011; (14): 47-48.

[2] Го Фэн, Яо Лина, Лю Хэн, У Шаньшань. Расчет теоретических потерь в линии с трехфазной степенью асимметрии

для низковольтной распределительной сети. Электроэнергетическая автоматизация. 2007;

27 (11): 51-54.

[3] Линь Чжисюн, Чэнь Янь, Цай Цзиньдин, Ли Тянью.Воздействие и противодействие трехфазной несимметричной работе

для низковольтных распределительных систем. Журнал электроэнергетики и

технологий. 2009; 24 (3): 63-67.

[4] Тонг Сянцянь, Ван Хайян, Инь Цзюнь. Метод расчета коэффициента трехфазного дисбаланса на основе

мощности нагрузки. Труды CSU-EPSA. 2011; 23 (2): 24-30.

[5] Чжоу Линь, Чжан Юй, Лю Цян, Ма Юнцян, У Цзянь. Сравнительное исследование трехфазного алгоритма дисбаланса

.East China Electric Power. 2010; 38 (2): 210-215.

[6] Лю Яньхуа, У Чжэнцю, Линь Шуньцзян. Исследование несбалансированного трехфазного потока мощности

Метод расчета

в изолированной микросети. Журнал Хунаньского университета (естественные науки). 2009;

36 (7): 36-40.

[7] Чжао Цзинцзин, Ли Синь, Сюй Чжун. Расчет трехфазного несимметричного потока мощности в распределительной сети

Сеть, содержащая распределенную генерацию. Технология энергосистем. 2009; 33 (3): 94-98.

[8] Цюань Хуэйминь, Дай Юсин, Тянь Ли. Трехфазная система контроля дисбаланса на основе DSP. Контроль

Машиностроение Китая. 2009; 16 (S0): 180-185.

[9] Чжэн Яньвэй, Пань Юци, Фэн Чжицюань. Исследование раннего предупреждения о перегрузке и несимметричном трехфазном распределительном трансформаторе

. Материалы Международной конференции по вопросам энергетики и окружающей среды

2011 г. Шэньчжэнь. 2011; 2: 439-441.

[10] Сунь Чжэ, Лян Цинъян, Лян Хунъян, Го Сицин.Алгоритм компенсации трехфазного дисбаланса

на основе теории мгновенной реактивной мощности и нечеткого ПИД-регулирования. Метрология и

Измерительная техника. 2010; 30 (5): 1-29.

[11] Ли Цинчуань. Исследование нового алгоритма компенсации реактивной нагрузки для трехфазного дисбаланса

Нагрузка. Цветное металлургическое оборудование. 2009; (4): 9-12.

[12] Вэй Ган, Чен Сенхуань, Цай Ян, Лу Вэй. Компенсация трехфазной несимметричной нагрузки на основе

на основе теории мгновенной реактивной мощности.Электроэнергетическая автоматизация. 2010; 30 (2): 59-63.

[13] Линь Чжисюн, Ли Тянью, Цай Цзиньдин. Исследование полностью конденсаторной скорректированной компенсации для распределительной сети трехфазного дисбаланса низкого напряжения

. Распространение и использование. 2009; 26 (6): 66-69.

[14] Хуан Годун, Ян Ренган, Фэн Сяомин. Исследование метода компенсации реактивной мощности для несбалансированной нагрузки

. Электрические измерения и приборы. 2011; 48 (544): 23-26.

[15] Лю Вэньхуа, Лю Вэньхуэй, Лу Цзюньфэн, Лю Бин.Балансировочная компенсация трехфазной несимметричной нагрузки

с однофазным STATCOM. Силовая электроника. 2003; 37 (4): 10-12.

[16] Чэнь Юй-синь, Фу Сян-юнь, Гу Цян. Метод управления STATCOM с компенсацией трехфазной несимметричной нагрузки

. Журнал Хэйлунцзянского гидравлического инженерного колледжа. 2007; 34 (4): 75-77.

[17] Сяо Сян-нин, Гао Бен-фэн, Чжао Чэн-юн, Ли Гуан-кай. Компенсация гибридной серии

Схема

с использованием однофазного SSSC.Техника высокого напряжения. 2010; 36 (11): 2803-2807.

[18] Чжан Юнгао, Гао Яньли, Лю Хуань, Лун Личжун. Конструкция мягкого контура фазовой синхронизации в трехфазном ШИМ-выпрямителе

при несимметричной электросети. Журнал Восточно-Китайского университета Цзяотун. 2011;

28 (5): 14-17.

Трехфазная балансировка нагрузки | Sunbird DCIM

Трехфазная балансировка нагрузки происходит, когда нагрузки источников питания, таких как трехфазный стоечный блок распределения питания, равномерно распределяются по всем трем фазам (L1 / L2, L2 / L3 и L3 / L1).

Этого можно достичь, подключив одинаковое количество устройств к розеткам PDU для каждой фазы и используя одинаковую мощность нагрузки на каждой фазе. Некоторые производители предоставляют трехфазные PDU с переменно-фазированным питанием для каждой розетки, а не ветви.

Трехфазная балансировка нагрузки желательна, поскольку несбалансированная система может привести к снижению эффективности, срабатыванию выключателей и сокращению срока службы оборудования.

Преимущества сбалансированного трехфазного питания

• Повышенное использование мощностей электрической инфраструктуры верхнего уровня, что приводит к повышению общей эффективности центра обработки данных и может отсрочить капитальные вложения.
• Способность поддерживать значительно более высокую удельную мощность по сравнению с однофазной схемой с аналогичной силой тока.
• Поддерживайте коэффициент мощности входящей мощности и избегайте штрафов, налагаемых электросетью.
• Масштабируемость для будущих требований к нагрузке.
• Требуется меньше хлыстов и кабелей, что снижает препятствия для воздушного потока, создает более чистую рабочую среду и упрощает установку и обслуживание.
• Продлить срок эксплуатации оборудования.

Мониторинг трехфазной мощности с помощью программного обеспечения DCIM

Расчет мощности для трехфазных энергосистем может значительно усложниться, если нагрузка не сбалансирована.Это происходит, когда ток нагрузки между любыми двумя линиями значительно отличается от тока нагрузки между оставшимися линиями. Когда есть несбалансированная нагрузка, эффективность системы и количество подаваемой мощности будут снижены. Поставщики интеллектуальных стоечных БРП с трехфазным питанием предоставляют локальные измерители нагрузки тока для каждой фазы на БРП, что значительно упрощает мониторинг и балансировку мощности, чем выполнение ручных вычислений.

Для мониторинга энергопотребления и емкости рекомендуется использовать программное обеспечение для управления инфраструктурой центра обработки данных (DCIM).Современное программное обеспечение DCIM имеет предупреждения о трехфазном дисбалансе для всего оборудования предприятия, включая стоечные PDU, напольные PDU, ИБП, RPP, счетчики и шинопроводы. Ранее это была чрезвычайно сложная задача, теперь менеджеры центров обработки данных имеют простое решение для мониторинга, которое автоматически вычисляет процент дисбаланса и предупреждает их о любом дисбалансе в тракте питания на основе настраиваемых пороговых значений. Пользователи могут сообщать о текущих показаниях трехфазного тока и процентном дисбалансе.

Хотите увидеть, как ведущее в мире программное обеспечение DCIM от Sunbird значительно упрощает трехфазную балансировку нагрузки? Получите бесплатный тест-драйв прямо сейчас!

Асимметричный / трехфазный поток мощности — pandapower 2.3.0 документация

алгоритм (str, «nr») — алгоритм, который используется для решения степени проблема с потоком.

Доступны следующие алгоритмы:

ускорений)

Используется только для сети прямой последовательности

В сетях нулевой и обратной последовательности используется метод ввода тока

Vnew = Y.inv * Ispecified (из s_abc / v_abc old)

Icalculated = Y * Vnew

calculate_voltage_angles (bool, «авто») — учитывать углы напряжения в расчете расхода

Если True, углы напряжения ext_grids и сдвиги трансформатора равны учитывается при расчете потока нагрузки.Учитывая напряжение углов требуется только в ячеистых сетях, которые обычно найдено в более высоких уровнях напряжения. Calcul_voltage_angles в автоматическом режиме по умолчанию:

Уровень сетевого напряжения определяется как максимальное номинальное напряжение. любой шины в сети, подключенной к линии.

max_iteration (int, «auto») — максимальное количество переносимых итераций в алгоритме потока мощности.

В автоматическом режиме значение по умолчанию зависит от решателя потока мощности:

Для трехфазных вычислений расширено до 3 * max_iteration

толерантность_mva (float, 1e-8) — условие прекращения потока нагрузки относится к несоответствию P / Q мощности узла в MVA

trafo_model — трансформаторный аналог модели

• «т» — трансформатор смоделирован как эквивалент Т-модели.

• «пи» — Не рекомендуется, так как он менее точен, чем Т-модель.

Итак, для трехфазного потока нагрузки это не

реализовано

trafo_loading (str, «текущий») — режим расчета для трансформатор нагрузки

Нагрузка трансформатора может быть рассчитана относительно номинальной ток или номинальная мощность. В обоих случаях общий трансформатор нагрузка определяется как максимальная нагрузка с двух сторон трансформатор.

расход и номинальный ток трансформатора. Это рекомендуемый настройки, так как тепловые, а также магнитные эффекты в трансформатор зависит от тока. — «мощность» — нагрузка трансформатора дана как отношение полной мощность потока к номинальной полной мощности трансформатора.

enforce_q_lims (булево, ложь)

(не тестировался с трехфазным потоком нагрузки) — учитывать реактивную мощность генератора лимиты

Если True, ограничивает реактивную мощность в сети.gen.max_q_mvar / min_q_mvar соблюдаются в потоке загрузки. Это делается путем запуска второго расход нагрузки при нарушении пределов реактивной мощности на любом генераторе, так что время выполнения для потока нагрузки увеличится, если реактивный власть должна быть сокращена.

Примечание: enforce_q_lims работает, только если алгоритм = ”nr”!

check_connectivity (bool, True) — выполнить дополнительное подключение тест после конвертации с pandapower на PYPOWER

Если True, дополнительный тест подключения на основе SciPy Compressed Выполняются подпрограммы разреженных графиков.Если проверка обнаружит неподтвержденные автобусы, они выведены из эксплуатации в ппк

Voltage_depend_loads (булево, True)

(не тестировался с трехфазным потоком нагрузки) — рассмотрение нагрузки, зависящие от напряжения. Если False, net.load.const_z_percent и net.load.const_i_percent не учитываются, т.е. net.load.p_mw и net.load.q_mvar считаются нагрузками с постоянной мощностью.

рассмотреть_линию_температуру (булево, ложь)

(не тестировался с трехфазным потоком нагрузки) — регулировка линии полное сопротивление зависит от температуры в линии.Если True, net.line должен содержат столбец «temperature_degree_celsius». Температура коэффициент зависимости альфа должен быть указан в net.line.alpha

столбец, в противном случае используется значение по умолчанию 0,004

** КВАРГ:

numba (bool, True) — Активация JIT-компилятора numba в решатель ньютона

Если установлено значение True, JIT-компилятор numba используется для генерации матрицы для потока мощности, что приводит к значительному быстродействию улучшения.

switch_rx_ratio (поплавок, 2)

(не тестировался с 3-фазным потоком нагрузки) — rx_ratio переключателей шины. Если импеданс равен нулю, шины, подключенные замкнутым переключателем шина-шина сплавлены, чтобы смоделировать идеальный автобус. В противном случае они моделируются как ветви с сопротивлением, определенным как столбец z_ohm в переключателе таблица и этот параметр

delta_q

(не тестировался с трехфазным потоком нагрузки) — Допуск реактивной мощности для опции «enforce_q_lims» в квар — помогает сходимости в некоторых случаях.

trafo3w_losses

(Не тестировался с 3-фазным потоком нагрузки) — определяет, где потери разомкнутого контура трехобмоточного трансформаторы рассмотрены. Допустимые варианты: «hv», «mv», «lv». для стороны ВН / СН / НН или «звезда» для точки звезды.

v_debug (bool, Ложь)

(не тестировался с 3-фазным потоком нагрузки) — если True, значения напряжения в каждом итерация Ньютона-Рэфсона регистрируется в ppc

init_vm_pu (строка / с плавающей точкой / массив / серия, нет)

(не тестировался с трехфазным потоком нагрузки) — позволяет определить инициализация специально для значений напряжения.Работает только с init == «auto»!

элемента управления напряжением в сети — «flat» для плоского старта от 1.0 — «результаты»: вектор величины напряжения берется из таблицы результатов. — поплавок, которым инициализируются все величины напряжения — итерация со значением величины напряжения для каждой шины (длина и порядок должны соответствовать автобусам в net.bus) — серия панд со значением величины напряжения для каждой шины (индексы должны совпадать с индексами в net.bus)

init_va_degree (строка / число с плавающей запятой / массив / серия, нет)

(не тестировался с трехфазным потоком нагрузки) —

Позволяет определить инициализацию специально для углов напряжения.Работает только с init == «auto»!

, если углы вычисляются, или 0 в противном случае — «dc»: углы напряжения инициализируются из потока мощности постоянного тока. — «flat» для плоского старта от 0 — «результаты»: вектор угла напряжения берется из таблицы результатов. — поплавок, которым инициализируются все углы напряжения — итерация со значением угла напряжения для каждой шины (длина и заказ должен совпадать с автобусами в net.bus) — серия панд со значением угла напряжения для каждой шины (индексы должны соответствовать индексам в net.автобус)

переработка (dict, none)

(не тестировался с трехфазным потоком нагрузки) — повторное использование внутренних переменных потока мощности для расчет временного ряда

Содержит dict со следующими параметрами: _is_elements: если True в сервисных элементах снова не фильтруется и берутся из последнего результата в net [«_ is_elements»] ppc: Если True, ppc берется из сети [«_ ppc»] и обновляется. вместо того, чтобы полностью реконструировать Ybus: Если True, матрица проводимости (Ybus, Yf, Yt) берется из ppc [«внутренний»] и без реконструкции

neglect_open_switch_branches (bool, Ложь)

(не тестировался с 3-фазным потоком нагрузки) — Если верно, то вспомогательный автобусы создаются для филиалов, когда в филиале открываются переключатели.Вместо филиалов выведены из строя

Несимметрия напряжения — искажение напряжения

В трехфазных системах несимметрия напряжения или дисбаланс напряжения возникает, когда фазное или линейное напряжение отличается от номинального сбалансированного состояния. Нормальное сбалансированное состояние — это когда три фазных напряжения идентичны по величине, а фазовые углы смещены на 120 градусов векторно. Неуравновешенность может быть вызвана разницей в величине напряжения или фазового угла или обоих .С точки зрения надежности и качества электроэнергии первостепенное значение имеет хороший баланс напряжений в системе.

Связь с дисбалансом тока

Векторы симметричного и несимметричного напряжения

Ниже приведены некоторые факторы, которые могут способствовать несимметрии напряжения:

• Несимметричное напряжение источника от электросети
• Неравное сопротивление трехфазной распределительной сети
• Несимметричная нагрузка на конденсаторы коррекции коэффициента мощности [Как перегоревший предохранитель на одной фазе]
• Неравномерное распределение однофазных нагрузок
• Несимметричные нагрузки даже при трехфазном подключении
• Отводы трансформатора несовместимы

Ниже приведены некоторые эффекты несимметрии напряжения.

• Повышенный нагрев и сокращение срока службы асинхронных двигателей
• Уменьшение срока службы входных диодов частотно-регулируемого привода и / или конденсаторов шины.
• В зависимости от типа нагрузки пониженное напряжение может привести к увеличению тока в одной или нескольких фазах и, следовательно, к увеличению потерь.

Вышеупомянутые моменты будут подробно обсуждены после того, как будет введено определение несимметрии напряжений.

Определение дисбаланса напряжения или дисбаланса напряжений:

В промышленности есть два наиболее часто используемых определения разбаланса напряжений.Это:

Определение NEMA : NEMA означает Национальную ассоциацию производителей оборудования в США. Определение асимметрии напряжения по NEMA:

Определение NEMA также называется коэффициентом несимметрии линейного напряжения (LVUR), поскольку линейные напряжения (то есть межфазные напряжения) используются только для расчета . Не следует использовать напряжение между фазой и нейтралью, поскольку компоненты нулевой последовательности могут дать неверные результаты. Кроме того, в уравнение не входят фазовые углы.Как можно заметить, расчет дисбаланса напряжений NEMA относительно прост.

Следующий калькулятор можно использовать для расчета несимметрии напряжения на основе метода NEMA.

Истинное определение: Это определение дисбаланса напряжений также известно как « Истинное определение», «Определение IEC» или «Коэффициент несимметрии напряжений» . На основании этого процентный дисбаланс напряжений определяется как отношение напряжения обратной последовательности (V2) к напряжению прямой последовательности (V1).

Если вам интересно, что такое напряжения прямой и обратной последовательности, вот простое объяснение. Трехфазные напряжения (или токи), сбалансированные или несимметричные, могут быть математически выражены как сумма компонентов прямой, обратной и нулевой последовательности. Это математический метод, который широко используется в энергетике, и его подробности можно найти во многих учебниках по энергетике. Например, если у нас есть несимметричное напряжение, которое представлено векторно, как показано ниже, его можно разделить на составляющие его компоненты положительной, отрицательной и нулевой последовательности, как показано.Из них мы будем использовать величины напряжения обратной и прямой последовательности для расчета дисбаланса. Обратите внимание, что напряжение прямой последовательности создает магнитный поток в том направлении, в котором двигатель должен вращаться. Напряжение обратной последовательности вращается в направлении, противоположном (векторно) положительной последовательности, и, следовательно, создает магнитный поток в противоположном направлении. Напряжение прямой последовательности будет намного больше, чем напряжение обратной последовательности, и, следовательно, направление вращения двигателя не изменится. Однако встречный поток обратной последовательности вызывает дополнительный нагрев в двигателе.

Почему не используется асимметрия напряжений нулевой последовательности? Это связано с тем, что токи нулевой последовательности не могут протекать в нагрузках асинхронных двигателей, которые больше всего подвержены дисбалансу напряжений. Обмотки асинхронных двигателей почти всегда соединяются треугольником или незаземленной звездой. Следовательно, вычисление небаланса напряжений нулевой последовательности практически не очень полезно.

Ниже приведен калькулятор, который можно использовать для расчета несимметрии напряжений с использованием истинного определения или определения IEC.Калькулятор вычисляет положительные и отрицательные составляющие напряжения системы и использует их для оценки «истинного» дисбаланса напряжений.

Может быть разница в% дисбаланса, рассчитанном обоими методами, что совершенно нормально. Определение NEMA не учитывает фазовые углы, и, следовательно, этого можно ожидать. Асинхронный двигатель всегда будет реагировать на «истинное» значение дисбаланса напряжений, поскольку это единственное уравнение, в котором используются напряжения как прямой, так и обратной последовательности.Отрицательная последовательность лежит в основе создания встречно вращающегося магнитного потока внутри двигателя и, как следствие, нагрева.

Влияние несимметрии напряжений

Асинхронные двигатели : Возможно, единственным устройством, которое больше всего страдает от несимметрии напряжения, является старый и заслуживающий доверия асинхронный двигатель. Когда на трехмоторный двигатель подается несимметричное напряжение, линейные токи обычно в несколько раз превышают несимметрию напряжения в процентном отношении. Это означает, что двигатель, питаемый, скажем, с небалансом напряжения 5%, может иметь небаланс тока на 20-30%.Дополнительный ток вызовет резистивные (I ² R) потери в двигателе, что приведет к повышению температуры. Температура — убийца номер один для изоляции двигателя. Подсчитано, что срок службы изоляции двигателя сокращается вдвое на каждые 10 градусов Цельсия повышения температуры обмотки.

NEMA разработало кривые снижения номинальных характеристик двигателя, работающего в условиях несимметричного напряжения. Curve предполагает, что двигатель обеспечивает номинальную нагрузку, указанную на паспортной табличке.

Из кривой видно, что любой двигатель должен выдерживать небаланс напряжения до 1% без снижения номинальных характеристик.Для 3% дисбаланса мощность двигателя должна быть снижена до 0,9. Не рекомендуется эксплуатация двигателя при несимметрии напряжений выше 5%.

Преобразователи частоты:

Частотно-регулируемые приводы

становятся все более и более распространенными на промышленных и коммерческих предприятиях в качестве средства эффективного управления скоростью двигателя. Скорее всего, не очень хорошо известно или понятно, что дисбаланс напряжений также может быть плохим для частотно-регулируемых приводов. Фактически, другие устройства, которые используют аналогичную схему внешнего интерфейса с диодным выпрямлением, также имеют аналогичные проблемы с несимметричным напряжением.Это могут быть трехфазные ИБП, большие источники питания постоянного тока с трехфазным входом и т. Д.

Входные схемы с трехфазными диодами, подобные показанной выше, потребляют ток в импульсах. Для 6-пульсного привода, который является наиболее распространенным приводом, мы можем видеть 6 импульсов тока за один цикл переменного тока. Каждый импульс тока возникает, когда напряжение питания переменного тока превышает напряжение конденсатора шины постоянного тока.

Форма волны 6 импульсов — сбалансированное напряжение

Когда напряжение питания сбалансировано, каждый диод проводит одинаковое количество тока в течение одинаковой продолжительности.Площадь под кривой тока по существу представляет мощность, необходимую для работы нагрузки, подключенной к частотно-регулируемому преобразователю.

По мере увеличения дисбаланса напряжений один или несколько диодов перестанут проводить, и потребляемый ток будет выглядеть как одиночный большой импульс, аналогичный тому, что наблюдается в однофазном выпрямителе мощности. Теперь большой импульс тока будет передаваться только меньшему количеству диодов, что приведет к чрезмерной нагрузке на диоды. Поскольку мощность, подаваемая на нагрузку, является постоянной величиной, площадь под кривой тока должна оставаться неизменной.Кроме того, дисбаланс напряжения питания также приведет к увеличению пульсации постоянного тока в конденсаторе шины постоянного тока, что приведет к дополнительным тепловым потерям и сокращению срока службы конденсатора шины. В зависимости от настроек привод может отключиться при перегрузке по току или пониженном напряжении на шине постоянного тока.

Каждый раз, когда пара диодов проводит, они потребляют большой импульс тока, как описано выше. По сути, это подключение конденсатора к источнику питания, при котором возникает большой импульс тока, величина которого будет зависеть от существующего заряда на конденсаторе, а также от импеданса источника.Если одна фаза имеет немного более высокий импеданс по сравнению с другой фазой, то это обычно отражается в импульсе тока. Обратите внимание, что на рисунке ниже, фаза C имеет сопротивление 1 Ом, а две другие фазы — 0,1 Ом. Обратите внимание на разницу в величине потребляемого тока для каждого импульса.

6-пульсный сигнал с несимметричным напряжением

Разница в импульсе тока по высоте частотно-регулируемых приводов переменного тока обычно является признаком:

• Несимметрия напряжения питания
• Импеданс питания одной или нескольких фаз отличается от здоровой фазы.

Полное сопротивление источника питания может отличаться между одной или несколькими фазами из-за:

• Слабое соединение в любом месте источника питания.
• Несоответствие импедансов выходного трансформатора между различными фазами. Обычно это бывает редко для трехфазных трансформаторов. Однако для трехфазных трансформаторов, собранных с использованием трех однофазных трансформаторов, это возможно, если импеданс не будет точно согласован.

Методы уменьшения несимметрии трехфазного напряжения на уровне предприятия :

1. Равномерно распределяйте однофазные нагрузки.
2. Используйте трехфазный регулятор напряжения. Ищите устройства с независимой фазовой регулировкой. При низком напряжении они доступны от 5 кВА до более 2500 кВА.

Решения, которые необходимо рассмотреть для смягчения последствий несимметрии трехфазного напряжения на уровне оборудования :

1. Трехфазный регулятор напряжения. Ищите устройства с независимой регулировкой фазного напряжения.
2. Трехфазный ИБП с двойным преобразованием: ИБП с двойным преобразованием всегда питает нагрузку от батареи.Это означает, что аккумулятор является основным источником выходной мощности, а вход переменного тока используется для зарядки аккумулятора. Нарушение или несимметрия линейного напряжения не повлияют на нагрузку. Однако каждый производитель ИБП устанавливает уровень несимметрии входного напряжения, который может выдержать секция входного выпрямителя. Этот параметр необходимо сравнить с существующим дисбалансом напряжения на объекте, чтобы убедиться, что ИБП будет работать должным образом.
3. ИБП с трехфазным преобразованием в треугольник: они обладают теми же преимуществами, что и ИБП с двойным преобразованием, но обеспечивают повышенную эффективность работы.Преобразование в треугольник также имеет преимущества за счет снижения гармонического тока на стороне питания.
4. Если небаланс напряжения создается из-за больших однофазных двигателей, рассмотрите возможность добавления пассивной или активной компенсации переменного тока (коррекция коэффициента мощности). Это будет работать только в том случае, если потребляемая реактивная мощность однофазного двигателя вызывает несимметрию напряжения. Пассивная компенсация будет заключаться в добавлении конденсаторов коррекции коэффициента мощности в двигатель. Доступны конденсаторы для определения коэффициента мощности однофазного двигателя, которые обычно подключаются к стороне нагрузки выключателя двигателя.

Методы защиты двигателя или оборудования от разрушительного воздействия несимметрии напряжения:

1. Реле баланса фаз: используйте реле баланса фазных напряжений для отключения двигателя / нагрузки в случае чрезмерного дисбаланса напряжений. В продаже имеются как однофазные, так и трехфазные реле баланса фаз. Обычно эти реле предлагают дополнительную защиту, такую ​​как потеря фазного напряжения, защита от чередования фаз и т. Д.

Как рассчитать трехфазный несимметричный ток? — MVOrganizing

Как рассчитать трехфазный несимметричный ток?

Расчет состоит из трех этапов:

1. Определите среднее значение напряжения или тока.
2. Рассчитайте наибольшее отклонение напряжения или тока.
3. Разделите максимальное отклонение на среднее напряжение или ток и умножьте на 100% дисбаланс = (максимальное отклонение от среднего значения V или I / среднего значения V или I) x 100.

Как рассчитать мощность неуравновешенной нагрузки?

Несимметричная трехфазная система: как рассчитать полную мощность?

1. Линия нейтрали (фаза) напряжение VLN = 208 / √3 = 120 В.
2. Полная мощность фазы 1 = 42 x 120 = 5040 ВА = 5.04 кВА.
3. Полная мощность фазы 2 = 84 x 120 = 10080 ВА = 10,08 кВА.
4. полная мощность фазы 3 = 80 x 120 = 9600 ВА = 9,6 кВА.

Как рассчитывается трехфазная мощность?

Потребляемая электрическая мощность в киловаттах для трехфазного двигателя рассчитывается путем умножения среднего напряжения всех трех фаз, измеренного на двигателе, на среднюю силу тока всех трех фаз, измеренную на двигателе, на средний коэффициент мощности всех трех фаз, измеренный при постоянная времени двигателя…

Что такое уравнение для кВт в случае несбалансированной нагрузки?

IL = кВт / √3VL.Для соединения треугольником это IL = √3 × I / ph. Теперь в случае несимметричной нагрузки IR + IY + IB = 3I0.

Какова формула полной мощности?

Полная мощность: S = V x I (кВА) Активная мощность: P = V x Ia (кВт)

Что подразумевается под трехфазной сбалансированной нагрузкой?

Сбалансированное трехфазное напряжение или ток — это напряжение, в котором размер каждой фазы одинаков, а фазовые углы трех фаз отличаются друг от друга на 120 градусов. При такой сбалансированной нагрузке, если применяется сбалансированное трехфазное питание, токи также будут сбалансированы.

Что такое трехфазная линия?

Трехфазное питание — это трехпроводная силовая цепь переменного тока, в которой каждый фазный сигнал переменного тока разнесен на 120 электрических градусов. Жилые дома обычно питаются от однофазного источника питания, в то время как коммерческие и промышленные объекты обычно используют трехфазное питание.

Есть ли нейтраль в 3-фазном режиме?

Трехфазные системы могут иметь или не иметь нейтральный провод. Нейтральный провод позволяет трехфазной системе использовать более высокое напряжение, поддерживая при этом однофазные приборы с более низким напряжением.Три — это самый низкий фазовый порядок, демонстрирующий все эти свойства. Большинство бытовых нагрузок однофазные.

Сколько ампер в трехфазном?

Например, трехфазная цепь, использующая мощность 25 000 Вт и напряжение сети 250, будет иметь ток 25 000 / (250 x 1,73), что равно 57,80 ампер.