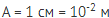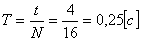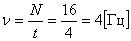Длина волны. Скорость распространения волны (Ерюткин Е.С.)
В ходе урока вы сможете самостоятельно изучить тему «Длина волны. Скорость распространения волны». На этом уроке вы сможете познакомиться с особенными характеристиками волн. В первую очередь вы узнаете, что такое длина волны. Мы рассмотрим ее определение, способ ее обозначения и измерения. Затем мы также подробно рассмотрим скорость распространения волны.
Для начала вспомним, что механическая волна – это колебание, которое распространяется с течением времени в упругой среде. Раз это колебание, волне будут присущи все характеристики, которые соответствуют колебанию: амплитуда, период колебания и частота.
Кроме этого, у волны появляются свои особые характеристики. Одной из таких характеристик является длина волны. Обозначается длина волны греческой буквой  (лямбда, или говорят «ламбда») и измеряется в метрах. Перечислим характеристики волны:
(лямбда, или говорят «ламбда») и измеряется в метрах. Перечислим характеристики волны:
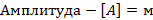
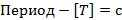
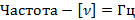
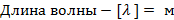
Что такое длина волны?
Длина волны – это наименьшее расстояние между частицами, совершающими колебание с одинаковой фазой.

Рис. 1. Длина волны, амплитуда волны
Говорить о длине волны в продольной волне сложнее, потому что там пронаблюдать частицы, которые совершают одинаковые колебания, гораздо труднее. Но и там есть характеристика – длина волны, которая определяет расстояние между двумя частицами, совершающими одинаковое колебание, колебание с одинаковой фазой.
Также длиной волны можно назвать расстояние, пройденное волной, за один период колебания частицы (рис. 2).
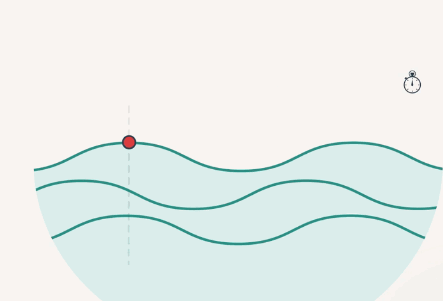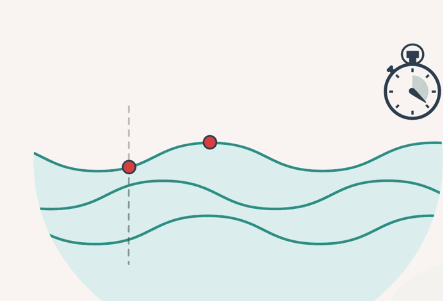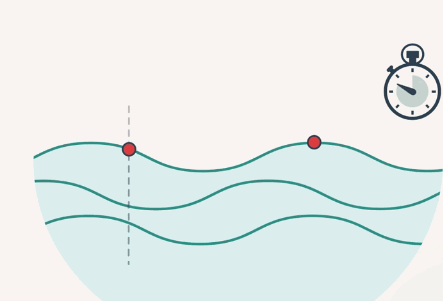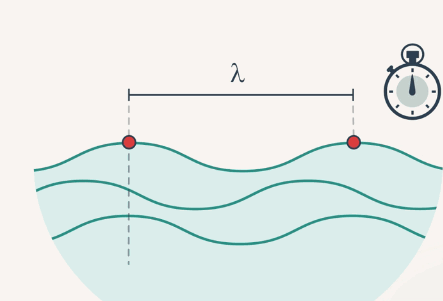
Рис. 2. Длина волны
Следующая характеристика – это скорость распространения волны (или просто скорость волны). Скорость волны обозначается так же, как и любая другая скорость, буквой  и измеряется в
и измеряется в  . Как наглядно объяснить, что такое скорость волны? Проще всего это сделать на примере поперечной волны.
. Как наглядно объяснить, что такое скорость волны? Проще всего это сделать на примере поперечной волны.
Поперечная волна – это волна, в которой возмущения ориентированы перпендикулярно направлению ее распространения (рис. 3).
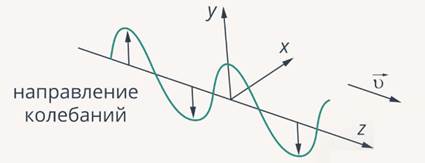
Рис. 3. Поперечная волна
Представьте себе летящую над гребнем волны чайку. Ее скорость полета над гребнем и будет скоростью самой волны (рис.4).
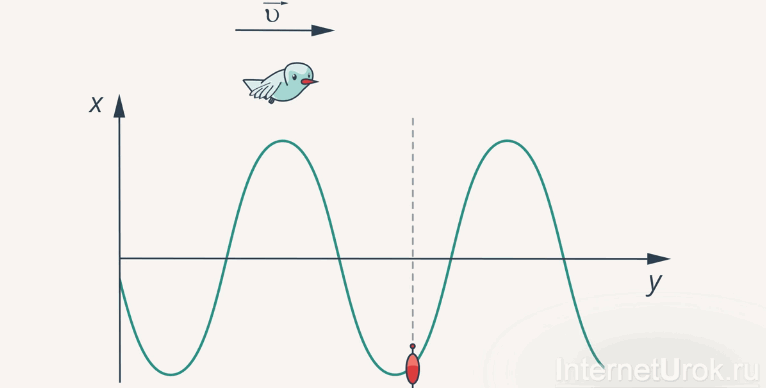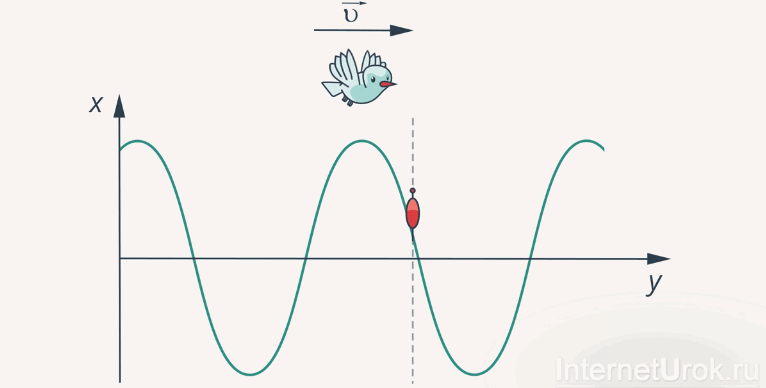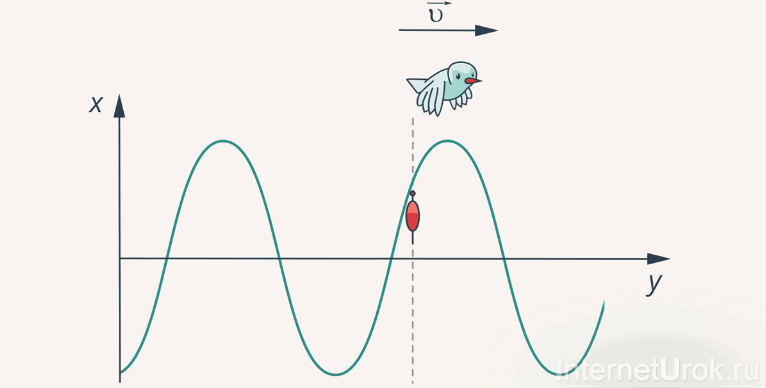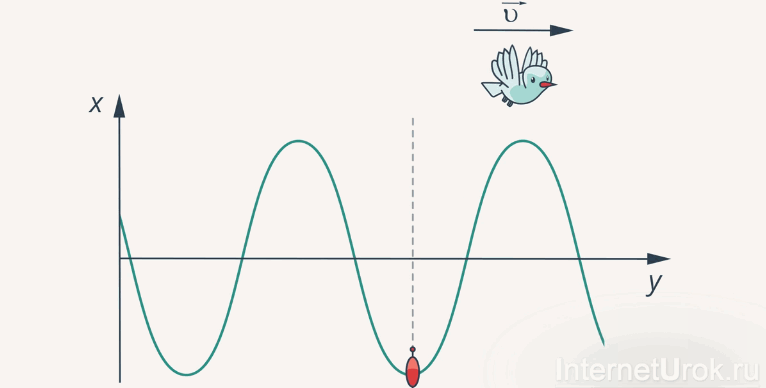
Рис. 4. К определению скорости волны
Скорость волны зависит от того, какова плотность среды, каковы силы взаимодействия между частицами этой среды. Запишем связь между скоростью волны, длиной волны и периодом волны: 
Скорость можно определить, как отношение длины волны, расстояние, пройденное волной за один период, к периоду колебания частиц среды, в которой распространяется волна. Кроме этого, вспомним, что период связан с частотой следующим соотношением:
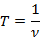
Тогда получим соотношение, которое связывает скорость, длину волны и частоту колебаний: 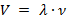
Мы знаем, что волна возникает в результате действия внешних сил. Важно заметить, что при переходе волны из одной среды в другую изменяются ее характеристики: скорость движения волн, длина волны. А вот частота колебания остается прежней.
Список литературы
- Соколович Ю.А., Богданова Г.С. Физика: справочник с примерами решения задач. – 2-е издание передел. – X.: Веста: издательство «Ранок», 2005. – 464 с.
- Перышкин А.В., Гутник Е.М., Физика. 9 кл.: учебник для общеобразоват. учреждений / А.В. Перышкин, Е.М. Гутник. – 14-е изд., стереотип. – М.: Дрофа, 2009. – 300 с.
Дополнительные рекомендованные ссылки на ресурсы сети Интернет
- Интернет-портал «eduspb» (Источник)
- Интернет-портал «eduspb» (Источник)
- Интернет-портал «class-fizika.narod.ru» (Источник)
Домашнее задание
- Поплавок совершает колебания на волнах. За 10 с он совершил 10 колебаний. Какова скорость распространения волны, если расстояние между соседними гребнями волны равно 1 м?
- Тело совершает гармонические колебания по закону
 м. Определите амплитуду, период, частоту, смещение и скорость в момент времени 0,1 с.
м. Определите амплитуду, период, частоту, смещение и скорость в момент времени 0,1 с. - Определите длину звуковой волны ноты, если ее частота колебаний 430 Гц, а скорость звука в воздухе 340 м/с?
ФИЗИКА: Задачи на Механические волны — Ответы и решения
Задачи на Механические волны с решениями
Формулы, используемые на уроках «Задачи на Механические волны».
Название величины | Обозначение | Единица измерения | Формула |
Длина волны | λ | м | λ = vT ;λ = v / v |
Скорость волны | v | м/с | v = λ / T ;v = λv |
Период колебаний | T | с | T = λ / v ;T = t / N |
Частота колебаний | v | Гц | v = v / λ ;v = N / t |
Число колебаний | N | N = t / T ;N = vt |
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Лодка качается на волнах, распространяющихся со скоростью 4 м/с, и за 10 с совершает 20 колебаний. Каково расстояние между соседними гребнями волн?

Задача № 2. Голосовые связки певца, поющего тенором (высоким мужским голосом), колеблются с частотой от 130 до 520 Гц. Определите максимальную и минимальную длину излучаемой звуковой волны в воздухе. Скорость звука в воздухе 330 м/с.

Задача № 3. Скорость звука в эбоните 2400 м/с, а в кирпиче — 3600 м/с. В каком веществе звуковому сигналу требуется большее время для распространения? Во сколько раз?

Задача № 4. Расстояние между ближайшими гребнями волн в море 6 м. Лодка качается на волнах, распространяющихся со скоростью 2 м/с. Какова частота ударов волн о корпус лодки?

Задача № 5. Наблюдатель, находящийся на расстоянии 2 км 150 м от источника звука, слышит звук, пришедший по воздуху, на 4,8 с позднее, чем звук от того же источника, пришедший по воде. Определите скорость звука в воде, если скорость звука в воздухе равна 345 м/с.
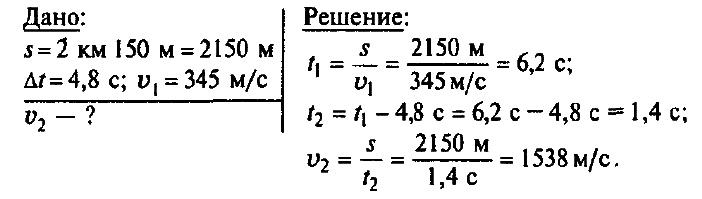
Задача № 6. Охотник выстрелил, находясь на расстоянии 170 м от лесного массива. Через сколько времени после выстрела охотник услышит эхо?
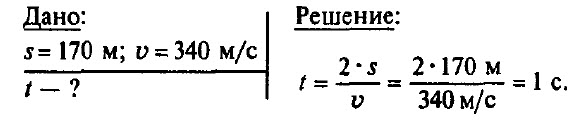
Задача № 7. Мимо неподвижного наблюдателя, стоящего на берегу озера, за 6 с прошло 4 гребня волны. Расстояние между первым и третьим гребнями равно 12 м. Определить период колебания частиц волны, скорость распространения и длину волны.

Задача № 8. Скорость звука в воде 1450 м/с. На каком расстоянии находятся ближайшие точки, совершающие колебания в противоположных фазах, если частота колебаний равна 725 Гц?

Задача № 9. Длина волны в воздухе 17 см (при скорости 340 м/с). Найти скорость распространения звука в теле, в котором при той же частоте колебаний длина волны равна 1,02 м.

Задача № 10. ОГЭ Расстояние между гребнями волн в море λ = 5 м. При встречном движении катера волна за t = 1 с ударяет о корпус катера N1 = 4 раза, а при попутном — N2 = 2 раза. Найти скорость катера и волны.

Задача № 11. ОГЭ Звуковые колебания, имеющие частоту v = 500 Гц и амплитуду А = 0,25 мм, распространяются в воздухе. Длина волны λ = 70 см. Найти скорость распространения колебаний v и максимальную скорость частиц среды.

Краткая теория для решения Задачи на Механические волны.
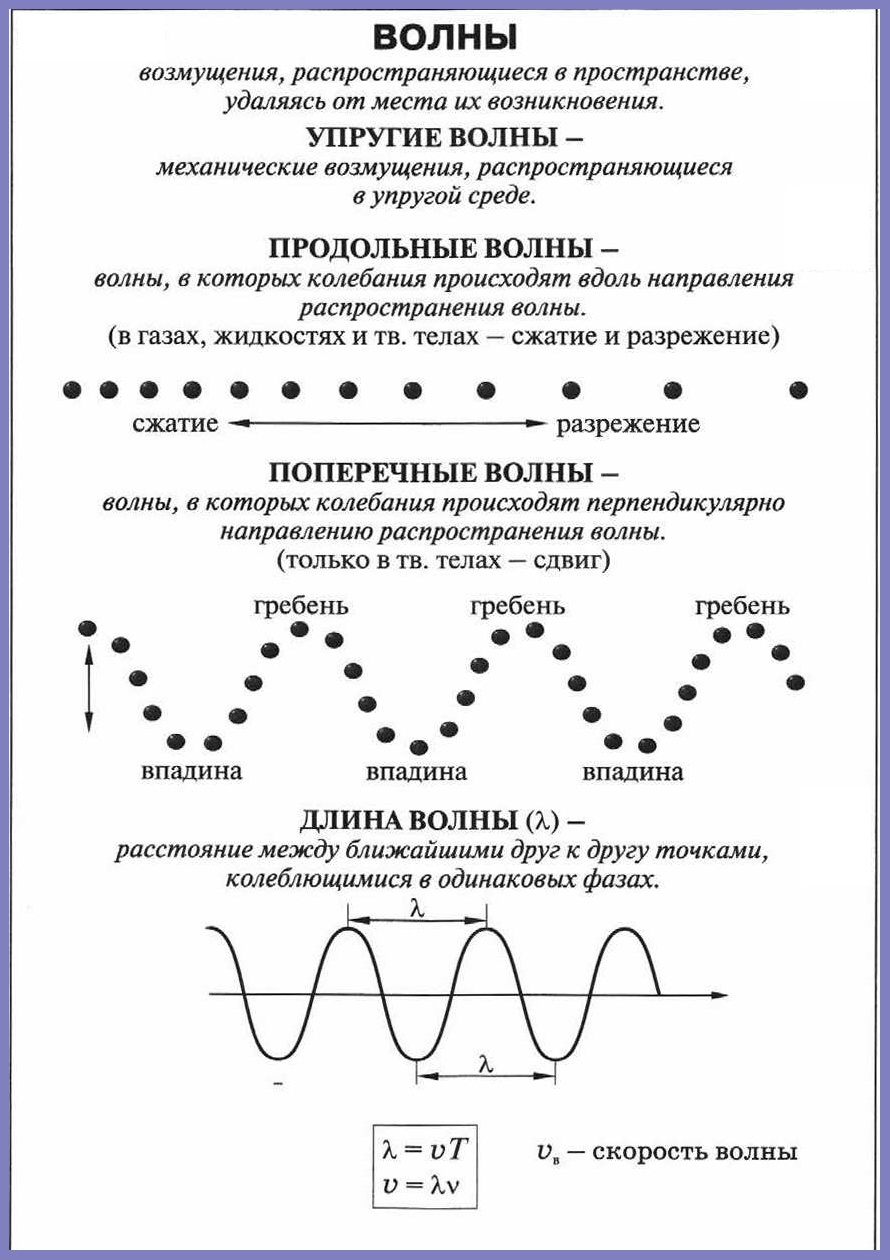

Это конспект по теме «ЗАДАЧИ на Механические волны». Выберите дальнейшие действия:
Частота волны | Все формулы
Сообщение от администратора:
Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока в школе английского языка SkyEng!
Занимаюсь там сам — очень круто. Прогресс налицо.
В приложении можно учить слова, тренировать аудирование и произношение.
Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА
Частота волны — число полных колебаний или циклов волны, совершенных в единицу времени
В Формуле мы использовали :
— Частота волны
— Скорость света
— Длина волны
— Фазовая скорость
— Период колебаний
— Волновое число
— Длина волны
Решение задач по теме «Механические колебания и волны. Звук» (Ерюткин Е.С.)
На этом занятии мы приступим к решению задач по теме «Механические колебания и волны. Звук». На этом завершающем уроке раздела «Механические колебания и волны» мы рассмотрим различные примеры, посвящённые распространению звука в природе и колебаниям. Вместе с преподавателем мы научимся правильно решать задачи по этой теме.
Здравствуйте! Наш завершает тему «Механические колебания и волны», поэтому он будет посвящен контрольной работе. Наша контрольная работа так и называется «Механические колебания и волны. Звук». Мы рассмотрим различные задачи, посвященные этой теме. Первая задача, которую будем рассматривать, посвящена колебаниям обыкновенного нитяного маятника, звучит она следующим образом.
Задача 1
По представленному графику определите амплитуду и период колебаний нитяного маятника.
|
|
Решение:
Ответ: А = 10-2 м, Т = 1 с. |
Мне бы хотелось отметить, что такого рода задачи часто встречаются в контрольных работах. Именно по графику определить характеристики колебаний. Давайте обратимся к записи, посмотрим на график и ответим на поставленный вопрос.
Итак, в данном случае график представлен на рисунке и выглядит он следующим образом. Сначала мы должны отметить точку равновесия. В данной точке тело когда находилось, оно находилось в положении равновесия. Дальше начинается движение маятника. С течением времени у нас смещение произошло сначала в одну сторону, затем в другую. Таким образом, мы представляем себе движение маятника в сочетании с осью времени. Мы знаем, что амплитудой является максимальное смещение от положения равновесия. Посмотрите, в данном случае смещение произошло на 1, на 1 в одну сторону относительно положения равновесия. И относительно положения равновесия в другую сторону тоже на 1. Если вы посмотрите, то смещение, обозначенное буквой х, измеряется в сантиметрах. По всему представленному графику смещение в данном случае максимальное постоянно, равно 1, т.е. 1 см. Это и есть амплитуда колебаний. Обратите внимание: необходимо сразу записать, что А = 1 см, или в системе интернациональной А = 1 см = 10-2 м.
Чтобы определить период колебаний, нам надо рассмотреть все колебания, представленные на этом графике. Что такое одно полное колебание? Это когда тело сходило в противоположную точку и вернулось обратно. Этот промежуток времени будет соответствовать периоду колебаний маятника. Таких движений за указанное время маятник совершил 2, таким образом, мы должны отметить, что число колебаний равно 2, а время этих колебаний составляет 2 с. Воспользуемся уравнением для определения периода колебаний: 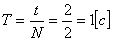 .
.
Обязательно необходимо записать ответ этой задачи. Ответ: А = 10-2 м, Т = 1 с.
Следующая задача, которую мы будем разбирать, – задача, посвященная колебаниям пружинного маятника. Звучит текст этой задачи следующим образом.
Задача 2
Пружинный маятник совершил за 4 с 16 полных колебаний. Необходимо определить период и частоту колебаний этого маятника.
Давайте посмотрим на краткую запись этой задачи и рассмотрим ее решение. Посмотрите, краткое условие следующее.
| Дано: | Решение: |
| N =16 |
Ответ: Т = 0,25 с, ν = 4 Гц. |
Волны. Физика. Курс лекций
1. Упругие волны
1.1. Упругие продольные и поперечные волны
1.2. Характеристики бегущих волн
1.2.1. Длина волны
1.2.2. Фазовая скорость волны
1.2.3. Фазовая скорость различна для разных сред
1.2.4. Фронт волны. Волновая поверхность
1.2.5. Уравнение бегущей волны
1.2.6. Волновое уравнение
1.2.7. Скорость и ускорение колеблющейся точки. Относительное смещение точек среды
1.3. Энергия упругих волн
1.4. Принцип суперпозиции волн. Групповая скорость
1.5. Интерференция волн. Стоячие волны
2. Звуковые волны
3. Электромагнитные волны
Как происходит распространение колебаний? Необходима среда для передачи колебаний или они могут передаваться без нее? Как звук от звучащего камертона доходит до слушателя? Каким образом быстропеременный ток в антенне радиопередатчика вызывает появление тока в антенне приемника? Как свет от далеких звезд достигает нашего глаза? Для рассмотрения подобного рода явлений необходимо ввести новое физическое понятие – волна. Волновые процессы представляют общий класс явлений, несмотря на их разную природу.
Процесс распространения колебаний в пространстве называется волной.
Волны, образованные внешним воздействием, приложенным к упругой среде, называются бегущими волнами: они “бегут” от создающего их источника. Важное свойство бегущих волн заключается в том, что они переносят энергию и импульс. Если внешняя сила совершает гармонические колебания, то вызванные ею волны называются гармоническими бегущими волнами.
Волновой процесс обусловлен наличием связей между отдельными частями системы, в зависимости от которых, мы имеем упругую волну той или иной природы.
1. Упругие волны
1. Упругими или механическими волнами называются механические возмущения (деформации), распространяющиеся в упругой среде.
Деформации в теле или среде называются упругими, если они полностью исчезают после прекращения внешних воздействий.
Тела, которые воздействуют на среду, вызывая колебания, называются источниками волн. Распространение упругих волн не связано с переносом вещества, но волны переносят энергию, которой обеспечивает волновой процесс источник колебаний.
2. Среда называется однородной, если ее физические свойства, рассматриваемые в данной задаче, не изменяются от точки к точке.
Среда называется изотропной, если ее физические свойства, рассматриваемые в задаче, одинаковы по всем направлениям.
Среда называется линейной, если между величинами, характеризующими внешнее воздействие на среду, которое и вызывает ее изменение, существует прямо пропорциональная связь. Например, выполнение закона Гука означает, что среда линейна по своим механическим свойствам.
1.1. Упругие продольные и поперечные волны
Все волны делятся на продольные и поперечные.
Поперечные волны – упругие волны, при распространении которых частицы среды совершают колебания в направлении, перпендикулярном направлению распространения волны.
Продольные волны – упругие волны, при распространении которых частицы среды совершают колебания вдоль направления распространения волны.
Поперечные упругие волны возникают только в твердых телах, в которых возможны упругие деформации сдвига. Продольные волны могут распространяться в жидкостях или газах, где возможны объемные деформации среды, или в твердых телах, где возникают деформации удлинения или сжатия. Исключение составляют поперечные поверхностные волны. Простые продольные колебания – это процесс распространения в пространстве областей сжатий и растяжений среды. Сжатия и растяжения среды образуются при колебаниях ее точек (частиц) около своих положений равновесия.
1.2. Характеристики бегущих волн
1.2.1. Длина волны
Минимальное расстояние, на которое распространяется волна за время, равное периоду колебания точки среды около положения равновесия, называется длиной волны.
Длиной волны 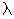 называется наименьшее расстояние между двумя точками среды, совершающими колебания в фазе (т.е. разность их фаз равна
называется наименьшее расстояние между двумя точками среды, совершающими колебания в фазе (т.е. разность их фаз равна 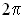 ).
).
Если точки разделены расстоянием  , их колебания происходят в противофазе.
, их колебания происходят в противофазе.
1.2.2. Фазовая скорость волны
Из повседневного опыта известно, что бегущие по воде волны распространяются с постоянной скоростью, пока свойства среды, например, глубина воды, не меняется, что говорит о том, что скорость распространения волнового процесса в пространстве остается постоянной. В случае гармонических бегущих волн (см. определение выше) эта скорость называется фазовой.
Фазовая скорость 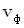 — это скорость распространения данной фазы колебаний, т.е. скорость волны.
— это скорость распространения данной фазы колебаний, т.е. скорость волны.
Связь длины волны 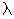 , фазовой скорости
, фазовой скорости 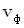 и периода колебаний Т задается соотношением:
и периода колебаний Т задается соотношением:
 .
.
Учитывая, что 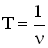 , где
, где 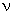 — линейная частота волны,
— линейная частота волны, 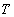 — период, а циклическая частота волны
— период, а циклическая частота волны 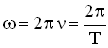 , получим разные формулы для фазовой скорости:
, получим разные формулы для фазовой скорости:
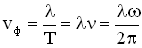 .
.
Для волнового процесса характерна периодичность по времени и по пространству.
Т – период колебаний точек среды. Роль пространственного периода играет длина волны 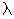 . Соотношение между периодом и циклической частотой задается формулой:
. Соотношение между периодом и циклической частотой задается формулой:  . Аналогичное соотношение можно записать для длины волны и величиной k, называемой волновым числом:
. Аналогичное соотношение можно записать для длины волны и величиной k, называемой волновым числом: 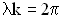 .
.
Таким образом. Можно добавить еще одно уравнение для фазовой скорости:
 .
.
1.2.3. Фазовая скорость различна для разных сред
В случае упругих поперечных волн (в твердом теле) фазовая скорость равна:
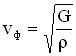 ,
,
где  — модуль сдвига среды,
— модуль сдвига среды,  -ее плотность в невозбужденном состоянии (т.е. когда в этой среде не распространяется упругая волна).
-ее плотность в невозбужденном состоянии (т.е. когда в этой среде не распространяется упругая волна).
Фазовая скорость упругих продольных волн в твердом теле равна
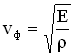 ,
,
где Е — модуль Юнга,  — плотность невозмущенной среды (твердого тела до момента распространения по нему волны).
— плотность невозмущенной среды (твердого тела до момента распространения по нему волны).
Фазовая скорость продольных волн в жидкости и газе определяется соотношением: 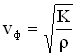 ,
,
где К – модуль объемной упругости среды – величина, характеризующая способность среды сопротивляться изменению ее объема,  — плотность невозмущенной среды.
— плотность невозмущенной среды.
Фазовая скорость продольных волн в идеальном газе задается формулой: 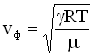 ,
,
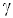 — показатель адиабаты,
— показатель адиабаты,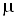 — молярная масса, Т – абсолютная температура, R – универсальная газовая постоянная. Фазовая скорость в газе зависит от сорта газа (
— молярная масса, Т – абсолютная температура, R – универсальная газовая постоянная. Фазовая скорость в газе зависит от сорта газа (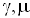 ) и от его термодинамического состояния (Т).
) и от его термодинамического состояния (Т).
1.2.4. Фронт волны. Волновая поверхность
При прохождении волны по среде ее точки вовлекаются в колебательный процесс последовательно друг за другом.
Геометрическое место точек, до которого к некоторому моменту времени дошел колебательный процесс, называется волновым фронтом.
Геометрическое место точек, колеблющихся в фазе, называется волновой поверхностью.
Волновой фронт – частный случай волновой поверхности. Волновой фронт все время перемещается. Волновые поверхности остаются неподвижными. Они проходят через положения равновесия частиц среды, которые колеблются в одинаковой фазе.
При описании распространения волн широко используют понятие луча. Направления, в которых распространяются колебания, называются лучами. В изотропной среде (см. определение выше) лучи перпендикулярны волновым поверхностям (фронту) и имеют вид прямых линий. В анизотропной среде, а также при дифракции волн, лучи могут искривляться.
Форма волнового фронта определяет вид волны: сферические (от точечного источника в изотропной среде), эллиптические (в анизотропной среде), цилиндрические (от протяженных источников), плоские и другие. На достаточно большом расстоянии от источника небольшой участок любого фронта можно считать плоским.
Если известно положение фронта волны в некоторый момент времени и скорость волны 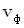 , то его положение в последующий момент времени можно определить на основе принципа Гюйгенса. Согласно этому принципу все точки поверхности волнового фронта являются источниками вторичных волн. Искомое положение волнового фронта совпадает с поверхностью, огибающей фронты вторичных волн.
, то его положение в последующий момент времени можно определить на основе принципа Гюйгенса. Согласно этому принципу все точки поверхности волнового фронта являются источниками вторичных волн. Искомое положение волнового фронта совпадает с поверхностью, огибающей фронты вторичных волн.
1.2.5. Уравнение бегущей волны
Уравнением упругой волны называется зависимость от координат и времени скалярных или векторных величин, характеризующих колебания среды при прохождении по ней волны.
Так, для волн в твердом теле такой величиной является смещение от положения равновесия любой точки тела в произвольный момент времени. Для характеристики продольных волн в жидкости или газе используют понятие избыточного давления. Избыточное давление равно разности между давлением в данный момент времени, когда по среде проходит волна, и равновесным, когда возмущений в среде нет.
Получим уравнение бегущей волны в одномерном пространстве, которое предполагаем изотропным и однородным (см. определения выше). Кроме того, силы сопротивления в среде считаем пренебрежимо малыми (т.е. нет затухания колебаний). Пусть точка О — центр (источник) колебаний, она колеблется по закону:
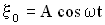 ,
,
где 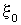 — смещение точки О от положения равновесия,
— смещение точки О от положения равновесия, 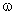 — частота, А – амплитуда колебаний. Часы или секундомер №1 включаются сразу, как только начинаются колебаний точки О, и отсчитывают время t (Рисунок 2.1.1). Ось ОУ совпадает с направлением распространения волны.
— частота, А – амплитуда колебаний. Часы или секундомер №1 включаются сразу, как только начинаются колебаний точки О, и отсчитывают время t (Рисунок 2.1.1). Ось ОУ совпадает с направлением распространения волны.
Через промежуток времени 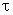 процесс колебаний дойдет до точки В, и она будет колебаться по закону:
процесс колебаний дойдет до точки В, и она будет колебаться по закону: 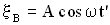 .
.
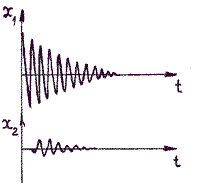
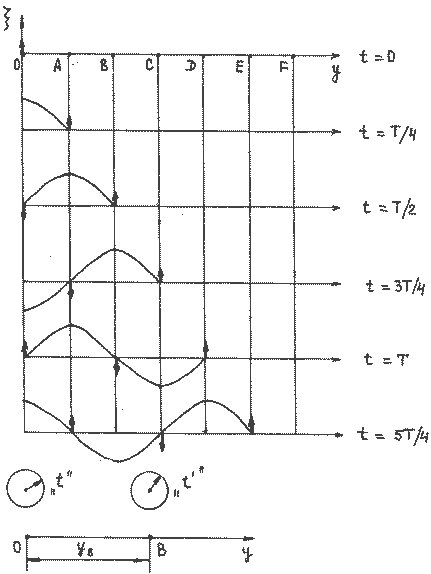
Рисунок 2.1.1.
Амплитуда колебаний в случае отсутствия затухания процесса будет такой же как и амплитуда точки О. Часы или секундомер №2 включаются тогда, когда колебательный процесс дойдет до точки В (т.е. когда начинает колебаться точка В), и отсчитывают время 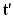 . Моменты времени t и
. Моменты времени t и 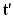 связаны между собой соотношением
связаны между собой соотношением 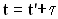 или
или  . Расстояние между точками О и В обозначим
. Расстояние между точками О и В обозначим 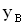 . Фазовая скорость волны равна
. Фазовая скорость волны равна 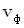 , тогда
, тогда 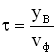 . Учитывая соотношения для
. Учитывая соотношения для 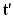 и
и 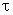 и формулы
и формулы 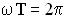 и
и 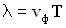 , можно записать уравнение колебаний точки В в разных видах:
, можно записать уравнение колебаний точки В в разных видах:
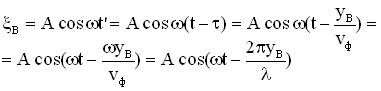 .
.
Аналогично уравнению колебаний точки В запишем уравнение колебаний любой точки среды, расположенной на расстоянии y от источника колебаний:
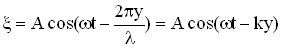 ,
,
где 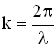 — волновое число (см. определение выше).
— волновое число (см. определение выше).
Это уравнение и есть уравнение для смещения  любой точки пространства в любой момент времени, т.е. уравнение бегущей волны, где А – амплитуда, величина
любой точки пространства в любой момент времени, т.е. уравнение бегущей волны, где А – амплитуда, величина 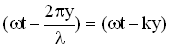 — фаза волны, которая в отличии от фазы колебаний зависит и от времени “t”, и от расстояния “y” колеблющейся точки от источника колебаний.
— фаза волны, которая в отличии от фазы колебаний зависит и от времени “t”, и от расстояния “y” колеблющейся точки от источника колебаний.
Вернемся к разделению волн по форме фронта волны и к понятию луча, как направления распространения колебательного процесса. Учтем, что в изотропной среде лучи перпендикулярны фронту и имеют вид прямых линий. Тогда уравнение бегущей волны, полученное выше, есть уравнение плоской бегущей волны, т.е. когда фронт волны – плоскость.
Уравнение плоской отраженной волны в одномерном пространстве легко получить, если представить ее как бегущую волну в отрицательном направлении оси ОУ, что приведет к замене в уравнении бегущей волны координаты “y” на “-y”:
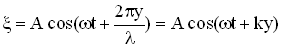 .
.
Упругая волна называется синусоидальной или гармонической, если соответствующие ей колебания частиц среды являются гармоническими. Так, рассмотренные выше бегущая и отраженная волны являются гармоническими волнами.
1.2.6. Волновое уравнение
Когда мы рассматривали колебания, то для любой колебательной системы получали дифференциальное уравнение, для которого соответствующее уравнение колебаний являлось решением. Аналогично уравнение бегущей и отраженной волны являются решениями дифференциального уравнения второго порядка в частных производных, называемого волновым уравнением и имеющего вид:
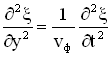 , где
, где 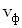 — фазовая скорость волны.
— фазовая скорость волны.
Уравнения бегущей и отраженной волн и волновое уравнение представлены для случая одного измерения, т.е. распространения волны вдоль оси ОУ. В волновое уравнение входят вторые частные производные по времени и координате от смещения потому, что  есть функция двух переменных t и y.
есть функция двух переменных t и y.
1.2.7. Скорость и ускорение колеблющейся точки. Относительное смещение точек среды
Если смещение любой точки среды с координатой y в момент времени t задано уравнением:
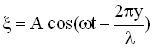 ,
,
то скорость этой точки есть величина 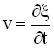 , а ускорение —
, а ускорение —  :
:
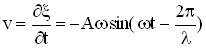 ,
, 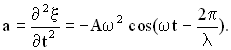
1.3. Энергия упругих волн
В среде распространяется плоская упругая волна и переносит энергию, величина которой в объеме  равна:
равна: 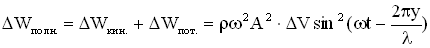 , где
, где 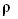 — объемная плотность среды.
— объемная плотность среды.
Если выбранный объем записать как 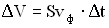 , где S – площадь его поперечного сечения, а
, где S – площадь его поперечного сечения, а  — его длина, то среднее количество энергии, переносимое волной за единицу времени через поперечное сечение S, называется потоком
— его длина, то среднее количество энергии, переносимое волной за единицу времени через поперечное сечение S, называется потоком 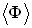 через его поверхность:
через его поверхность:
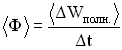 .
.
Количество энергии, переносимое волной за единицу времени через единицу площади поверхности, расположенной перпендикулярно направлению распространения волны, называется плотностью потока энергии волны.
Эта величина определяется соотношением:
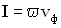 ,
,
где  -объемная плотность энергии волны,
-объемная плотность энергии волны,  — фазовая скорость волны. Так как фазовая скорость волны
— фазовая скорость волны. Так как фазовая скорость волны  — вектор, направление которого совпадает с направлением распространения волны, то можно величине плотности потока энергии I придать смысл векторной величины:
— вектор, направление которого совпадает с направлением распространения волны, то можно величине плотности потока энергии I придать смысл векторной величины:
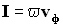 .
.
Величина 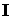 , вектор плотности энергии волны, впервые была введена Н.А. Умовым в 1984 году и получила название вектора Умова. Подобная величина для электромагнитных волн называется вектором Умова — Пойнтинга.
, вектор плотности энергии волны, впервые была введена Н.А. Умовым в 1984 году и получила название вектора Умова. Подобная величина для электромагнитных волн называется вектором Умова — Пойнтинга.
Интенсивностью волны называется модуль среднего значения вектора Умова 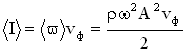 .
.
1.4. Принцип суперпозиции волн. Групповая скорость
Принцип суперпозиции (наложения) волн установлен на опыте. Он состоит в том, что в линейной среде волны от разных источников распространяются независимо, и накладываясь, не изменяют друг друга. Результирующее смещение частицы среды в любой момент времени равно геометрической сумме смещений, которые частица получит, участвуя в каждом из слагаемых волновых процессов.
Согласно принципу суперпозиции накладываться друг на друга без взаимного искажения могут волны любой формы. В результате наложения волн результирующее колебание каждой частицы среды может происходить по любому сложному закону. Такое образование волн называется волновым пакетом. Скорость движения волнового пакета не совпадает со скоростью ни с одной из слагаемых волн. В этом случае говорят о скорости 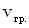 волнового пакета. Скорость перемещения максимума группы волн (волнового пакета) называется групповой скоростью. Она равна скорости переноса энергии волнового пакета.
волнового пакета. Скорость перемещения максимума группы волн (волнового пакета) называется групповой скоростью. Она равна скорости переноса энергии волнового пакета.
На практике мы всегда имеем дело с группой волн, так как синусоидальных волн, бесконечных в пространстве и во времени, не существует. Любая ограниченная во времени и пространстве синусоидальная волна есть волновой пакет (его называют цуг волны). Групповая скорость такого пакета совпадает с фазовой скоростью бесконечных синусоидальных волн, результатом сложения которых он является.
В общем виде связь между групповой и фазовой скоростями имеет вид:
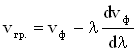 .
.
1.5. Интерференция волн. Стоячие волны
1. Интерференцией волн называется явление наложение двух и более волн, при котором в зависимости от соотношения между фазами этих волн происходит устойчивое во времени их взаимное усиление в одних точках пространства и ослабление в других.
В пространстве всегда найдутся такие точки, в которых разность фаз складываемых колебаний равна величине 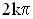 , где k – целое число, т.е. волны (от разных источников) приходят в такие точки в фазе. В них будет наблюдаться устойчивое, неизменно продолжающееся все время усиление колебаний частиц. Найдутся в пространстве, где распространяется несколько волн, и такие точки, где разность фаз будет равна
, где k – целое число, т.е. волны (от разных источников) приходят в такие точки в фазе. В них будет наблюдаться устойчивое, неизменно продолжающееся все время усиление колебаний частиц. Найдутся в пространстве, где распространяется несколько волн, и такие точки, где разность фаз будет равна 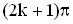 , т.е. волны приходят в эти точки в противофазе. В таких точках пространства будет наблюдаться устойчивое ослабление колебаний частиц.
, т.е. волны приходят в эти точки в противофазе. В таких точках пространства будет наблюдаться устойчивое ослабление колебаний частиц.
Устойчивая интерференционная картина возникает только при наложении таких волн, которые имеют одинаковую частоту, постоянную во времени разность фаз в каждой точке пространства. Волны, удовлетворяющие этим условиям и источники, создающие такие волны, называются когерентными. Плоские синусоидальные волны, частоты которых одинаковы, когерентны всегда.
2. Запишем условия максимумов и минимумов при интерференции. Когерентные точечные источники 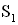 и
и 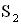 испускают волны по всем направлениям. До точки наблюдения М расстояние от первого источника
испускают волны по всем направлениям. До точки наблюдения М расстояние от первого источника 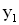 , а от второго —
, а от второго —  .
.
Колебания точки М под действием волн от двух источников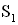 и
и 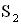 описываются уравнениями:
описываются уравнениями:
 ,
, 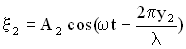 . Амплитуда результирующего колебания в точке М определится следующим образом (см. раздел “Сложение колебаний”):
. Амплитуда результирующего колебания в точке М определится следующим образом (см. раздел “Сложение колебаний”): 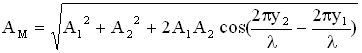 . Амплитуда колебаний точки М максимальна (
. Амплитуда колебаний точки М максимальна (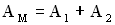 ), если
), если 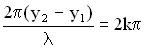 , где
, где 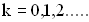 Величина
Величина 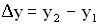 называется разностью хода двух волн. Условие максимума при интерференции имеет вид:
называется разностью хода двух волн. Условие максимума при интерференции имеет вид: 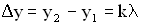 . Если целое число волн укладывается на разности хода двух волн, то при их сложении наблюдается интерференционный максимум. Амплитуда колебаний точки М минимальна (
. Если целое число волн укладывается на разности хода двух волн, то при их сложении наблюдается интерференционный максимум. Амплитуда колебаний точки М минимальна (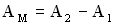 ), если
), если 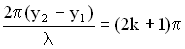 , (
, (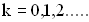 ). Условие минимума при интерференции имеет вид:
). Условие минимума при интерференции имеет вид:  . Если нечетное число полуволн укладывается на разности хода двух волн, то при их сложении наблюдается интерференционный минимум. 3. Простейший случай интерференции наблюдается при наложении бегущей и отраженной волн, что приводит к образованию стоячей волны. Уравнения бегущей и отраженной волны имеют вид:
. Если нечетное число полуволн укладывается на разности хода двух волн, то при их сложении наблюдается интерференционный минимум. 3. Простейший случай интерференции наблюдается при наложении бегущей и отраженной волн, что приводит к образованию стоячей волны. Уравнения бегущей и отраженной волны имеют вид: 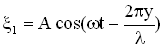 ,
, 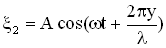 Суммарное смещение
Суммарное смещение  частицы среды, находящейся на расстоянии y от источника колебаний, равно сумме смещений
частицы среды, находящейся на расстоянии y от источника колебаний, равно сумме смещений 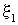 и
и 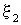 :
: 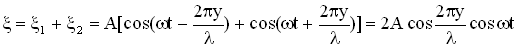 .
.
Это и есть уравнение стоячей волны. Величина  — амплитуда, а (
— амплитуда, а (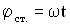 ) — фаза стоячей волны. Можно сказать, что частицы в стоячей волне имеют одну фазу колебаний. Амплитуда колебаний частиц в стоячей волне зависит от их координат (расстояний до источника колебаний), но не зависит от времени. Знак модуля поставлен в формуле для амплитуды стоячей волны, потому что амплитуда – величина положительная.
) — фаза стоячей волны. Можно сказать, что частицы в стоячей волне имеют одну фазу колебаний. Амплитуда колебаний частиц в стоячей волне зависит от их координат (расстояний до источника колебаний), но не зависит от времени. Знак модуля поставлен в формуле для амплитуды стоячей волны, потому что амплитуда – величина положительная.
В стоячей волне есть точки, которые все время остаются неподвижными. Такие точки называются узлами смещения, их положение определяется из условия:
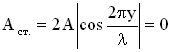 , отсюда следует
, отсюда следует 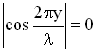 . Выполнение этого соотношения будет при условии
. Выполнение этого соотношения будет при условии 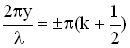 для
для 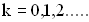 Итак, координаты узлов задаются формулой:
Итак, координаты узлов задаются формулой:
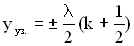 .
.
Расстояние между двумя соседними узлами равно  .
.
Точки среды, колеблющиеся с наибольшей амплитудой, называются пучностями стоячей волны, их положение (координаты) определяются соотношением:
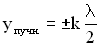 .
.
Это уравнение можно получить из условия максимума амплитуды
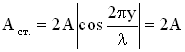 , т.е.
, т.е. 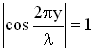 . Последнее соотношение выполняется при значениях аргумента
. Последнее соотношение выполняется при значениях аргумента 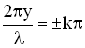 (
(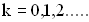 ).
).
Расстояние между двумя соседними пучностями равно  .
.
4. Изменение фазы волны при ее отражении.
Как отмечалось ранее, стоячая волна образуется при сложении бегущей и отраженной волн. Отраженную волну можно рассматривать как бегущую волну, распространяющуюся в обратном направлении и ее можно получить при отражении бегущей волны от границы двух сред. Для синусоидальных волн это означает, что при отражении от более плотной среды фаза волны скачком изменяется на  радиан, а при отражении от менее плотной среды фаза волны не изменяется. Изменение фазы на
радиан, а при отражении от менее плотной среды фаза волны не изменяется. Изменение фазы на  радиан соответствует появлению дополнительного хода луча, равного
радиан соответствует появлению дополнительного хода луча, равного 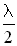 .
.
2. Звуковые волны
1. Важным видом продольных волн являются звуковые волны. Так называются волны с частотами 17 – 20000 Гц. Учение о звуке называется акустикой. В акустике изучаются волны, которые распространяются не только в воздухе, но и в любой другой среде. Упругие волны с частотой ниже 17 Гц называются инфразвуком, а с частотой выше 20000 Гц – ультразвуком.
Звуковые волны – упругие колебания, распространяющиеся в виде волнового процесса в газах, жидкостях, твердых телах.
2. Избыточное звуковое давление. Уравнение звуковой волны.
Уравнение упругой волны позволяет вычислить смещение любой точки пространства, по которому проходит волна, в любой момент времени. Но как говорить о смещении частиц воздуха или жидкости от положения равновесия? Звук, распространяясь в жидкости или газе, создает области сжатия и разряжение среды, в которых давление соответственно повышается или понижается по сравнению с давлением невозмущенной среды.
Если 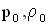 — давление и плотность невозмущенной среды (среды, по которой не проходит волна), а
— давление и плотность невозмущенной среды (среды, по которой не проходит волна), а 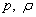 — давление и плотность среды при распространении в ней волнового процесса, то величина
— давление и плотность среды при распространении в ней волнового процесса, то величина 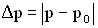 называется избыточным давлением. Величина
называется избыточным давлением. Величина 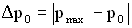 есть максимальное значение избыточное давление (амплитуда избыточного давления).
есть максимальное значение избыточное давление (амплитуда избыточного давления).
Изменение избыточного давления для плоской звуковой волны (т.е. уравнение плоской звуковой волны) имеет вид:
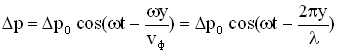 ,
,
где y – расстояние от источника колебаний точки, избыточное давление в которой мы определяем в момент времени t.
Если ввести величину избыточной плотности 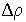 и ее амплитуды
и ее амплитуды 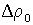 так же, как мы вводили величину избыточного звукового давления, то уравнение плоской звуковой волны можно было бы записать так:
так же, как мы вводили величину избыточного звукового давления, то уравнение плоской звуковой волны можно было бы записать так: 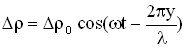 . 3. Объективные и субъективные характеристики звука.
. 3. Объективные и субъективные характеристики звука.
Само слово “звук” отражает два различных, но взаимосвязанных понятия: 1)звук как физическое явление; 2)звук – то восприятие, которое испытывает слуховой аппарат (человеческое ухо) и ощущения, возникающие у него при этом. Соответственно характеристики звука делятся на объективные, которые могут быть измерены физической аппаратурой, и субъективные, определяемые восприятием данного звука человеком.
К объективным (физическим) характеристикам звука относятся характеристики, которые описывают любой волновой процесс: частота, интенсивность и спектральный состав. В таблицу 3 включены сравнительные данные объективных и субъективных характеристик.
Таблица 3.
| Субъективные Характеристики | Объективные характеристики |
| Высота звука | Высота звука определяется частотой волны |
| Тембр (окраска звука) | Тембр звука определяется его спектром |
| Громкость (сила звука) | Сила звука определяется нтенсивностью волны (или квадратом ее амплитуды) |
Остановимся на некоторых определениях.
Частота звука измеряется числом колебаний частиц среды, участвующих в волновом процессе, в 1 секунду.
Интенсивность волны измеряется энергией, переносимой волной в единицу времени через единичную площадь (расположенную перпендикулярно направлению распространению волны).
Спектральный состав (спектр) звука указывает из каких колебаний состоит данный звук и как распределены амплитуды между отдельными его составляющими.
Различают сплошные и линейчатые спектры. Для субъективной оценки громкости используются величины, называемые уровнем силы звука и уровнем громкости. Все акустические величины и их размерности в СИ приведены в приложении.
3. Электромагнитные волны
1. Электромагнитными волнами называются возмущения электромагнитного поля (т.е. переменное электромагнитное поле), распространяющиеся в пространстве.
Утверждение о существовании электромагнитных волн является непосредственным следствием решения системы уравнений Максвелла. Согласно этой теории следует, что переменное электромагнитное поле распространяется в пространстве в виде волн, фазовая скорость которых равна:
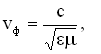
где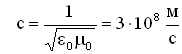 — скорость света в вакууме,
— скорость света в вакууме, 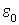 ,
,  — электрическая и магнитная постоянные,
— электрическая и магнитная постоянные,  ,
, 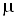 — соответственно диэлектрическая и магнитная проницаемость среды.
— соответственно диэлектрическая и магнитная проницаемость среды.
2. Электромагнитные волны — поперечные волны. Векторы Е и Н поля электромагнитной волны взаимно перпендикулярны друг другу. Вектор скорости волны 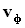 и векторы Е и Н образуют правую тройку векторов (Рисунок 2.1.4).
и векторы Е и Н образуют правую тройку векторов (Рисунок 2.1.4).
Для сравнения ориентации тройки векторов 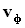 , Е и Н на рисунке приведено расположение осей декартовой системы координат. Такое сопоставление уместно и в дальнейшем будет использовано для определения проекций векторов Е и Н на координатные оси.
, Е и Н на рисунке приведено расположение осей декартовой системы координат. Такое сопоставление уместно и в дальнейшем будет использовано для определения проекций векторов Е и Н на координатные оси.
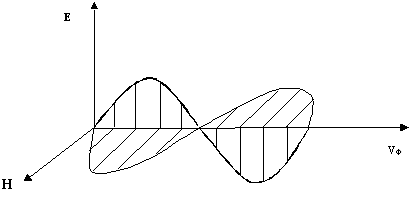
Рисунок 2.1.4
Взаимно перпендикулярные векторы Е и Н колеблются в одной фазе (их колебания синфазные). Модули этих векторов связаны соотношением:
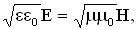
которое справедливо для любой бегущей электромагнитной волны независимо от формы ее волновых поверхностей.
3. По форме волновых поверхностей волны могут быть плоские, эллиптические, сферические и т.д..
Монохроматической волной называется электромагнитная волна одной определенной частоты. Монохроматическая волна не ограничена в пространстве и во времени. В каждой точке электромагнитного поля монохроматической волны проекции векторов Е и Н на оси координат совершают гармонические колебания одинаковой частоты 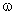 . Например, для плоской монохроматической волны, распространяющейся вдоль положительного направления оси ОУ, как показано на рисунке 2.1.3.,ее уравнение имеет вид:
. Например, для плоской монохроматической волны, распространяющейся вдоль положительного направления оси ОУ, как показано на рисунке 2.1.3.,ее уравнение имеет вид:
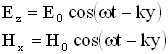
Такие волны называются плоско (или линейно) поляризованными волнами.
Плоскость, в которой происходит колебание вектора Е называют плоскостью поляризации линейно поляризованной волны, а плоскость колебаний вектора Н – плоскостью колебаний. Ранее эти названия были обратными (см. [1]).
4. Все сказанное о стоячих волнах в упругих средах относится и к электромагнитным волнам. В этом случае, однако, волна характеризуется не одним вектором, а двумя взаимно перпендикулярными векторами Е и Н.
Стоячая электромагнитная волна состоит из двух стоячих волн — магнитной и электрической, колебания которых сдвинуты по фазе на 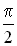 .
.
5. Энергия электромагнитных волн. Объемная плотность энергии электромагнитного поля в линейной изотропной среде задается соотношением: 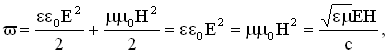 с — скорость света в вакууме.
с — скорость света в вакууме.
В случае плоской линейно поляризованной монохроматической волны, распространяющейся вдоль положительного направления ОY, напряженность электрического поля задается уравнением:
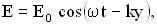
соответственно объемная плотность энергии этой волны 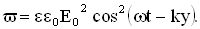
Значение объемной плотности энергии волны меняется за период от 0 до 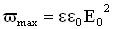 .Среднее за период значение энергии равно:
.Среднее за период значение энергии равно:
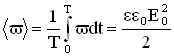 .
.
6. Вектор плотности потока энергии электромагнитной волны называется вектором Умова — Пойнтинга:
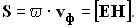
Для линейно поляризованной монохроматической волны вектор Пойнтинга направлен в сторону распространения волны и численно равен: 
Интенсивность электромагнитной волны равна модулю среднего значения вектора Пойнтинга за период его полного колебания:

Интенсивностью электромагнитной волны называется физическая величина, численно равная энергии, переносимая волной за единицу времени через единицу площади поверхности, расположенной перпендикулярно к направлению распространения волны.
Интенсивность бегущей монохроматической волны: 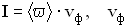 — фазовая скорость волны,
— фазовая скорость волны,  среднее значение объемной плотности энергии поля волны.
среднее значение объемной плотности энергии поля волны.
Интенсивность света (электромагнитных волн, рассматриваемых в оптике) прямо пропорциональна квадрату амплитуды колебаний вектора напряженности Е поля световой волны.
Длина волны. Скорость распространения волны (Серов А.Ю.). Видеоурок. Физика 9 Класс
К изучению предлагается тема «Длина волны. Скорость распространения волны». Вначале дадим определения упругой среды и механической волны. Затем на этом уроке мы обсудим такие количественные характеристики волн, как длина волны и скорость её распространения. Также мы познакомимся с такими новыми характеристиками, как волновой фронт и луч.
Волны на поверхности жидкости; волна, пробегающая по веревке, если дернуть ее за один из концов; даже звук – всё это примеры механических волн. Сегодня мы познакомимся с параметрами, которые количественно характеризуют волны.
Вспомним определение: волна – это изменение некоторой совокупности физических величин, которое распространяется в пространстве от места возникновения с течением времени.
Представим себе бильярдные шары, расставленные в ряд с интервалом в несколько сантиметров (см. рис. 1).

Рис. 1. Расставленные бильярдные шары
После удара по крайнему шару (см. рис. 2) мы увидим, как он перемещается и сталкивается со вторым шаром.

Рис. 2. Шар ударяет крайний шар
Затем второй шар ударяет третий и так далее. Таким образом, мы наблюдаем распространение волны. Изменение величин (в данном случае это перемещение, скорость, кинетическая энергия шаров) распространяется в пространстве с течением времени (см. рис. 3).

Рис. 3. Принцип распространения волны
Такая волна является одиночной – изменение физических величин распространяется разово.
Цунами, волна, пробегающая по веревке, если дернуть ее за один из концов, даже продвижение на одного человека привычной нам очереди за мороженым – тоже примеры одиночных волн.
Очередь за мороженым
Представим очередь за мороженым (см. рис. 4).

Рис. 4. Продвижение очереди
Люди, стоящие в очереди, находятся на равном расстоянии друг от друга. Затем, расплатившись и получив свое мороженое, довольный покупатель покидает очередь. Человек, стоящий за ним, смещается на шаг к прилавку, тоже освобождая свое место. Дальше смещение на шаг вперед совершит третий покупатель, затем четвертый и т. д. То есть смещение будет распространяться в пространстве от места возникновения (от начала очереди к концу) с течением времени. Такая волна является одиночной – смещение каждого покупателя происходит однократно. Повторно волна «прокатится» по очереди лишь после того, как следующий покупатель отойдет от прилавка и стоящий за ним сместится на его место – то есть возникнет уже новое смещение, новое изменение физической величины.
А что будет происходить, если соединить шары пружинками? Тогда при перемещении первого шара прикрепленная к нему пружина будет сжиматься и в ней будет возникать сила упругости, которая с одной стороны будет толкать второй шар и передавать ему энергию, а с другой стороны – возвращать первый шар в исходное положение (см. рис. 5).

Рис. 5. Сила упругости в пружине
Описанная ситуация моделирует упругую среду (газ, жидкость, твердое тело).
Между частицами упругих сред присутствуют силы упругого взаимодействия
Физика колебаний и волн — Википедия
Физика колебаний и волн — раздел общей физики, изучающий физические явления, характеризующиеся циклическим изменением физических величин во времени и в пространстве. Это — одна большая часть школьного курса физики, изучается после электромагнетизма ( рассматривая механические и электромагнитные процессы вместе ) или сразу с механикой ( в связи с тем, что теория колебаний и волн развивается на основе кинематики и динамики, что охватывает механика ). [1][2]
В колебательных и волновых процессах численные значения физических величин циклически изменяются. Для упрощения анализа физических явлений в пространственных и временных координатах можно рассматривать проекции. Если зафиксировать какой-либо момент времени, волновой характер проявляется в определённом распределении характеризующей величины в пространстве, в котором налюдаемо чередование максимумов и минимумов физической величины. Если, напротив, зафиксировать пространственные координаты, локально наблюдаемая физическая величина совершает колебания.
Волновой циклический процесс состоит из циклов, которые повторяются в пространстве и времени. Колебания — это циклический процесс, в котором циклы повторяются во времени. Например, проекция точки, которая движится по единичной окружности, совершает колебания на отрезке [-1,1]. Соответствие между этими двумя циклическими процессами ( движением по окружности и движением проекции ) используют для графического отображения колебаний. Отображение колебаний с помощью вращающегося вектора амплитуды называется методом векторных диаграмм.[3]
Колебаниями называются процессы, которые повторяются ( во времени ), так, что то в одну сторону, то в противоположную сторону меняется физическая величина, характеризующая явление.[1][3] В зависимости от физической природы процесса, различают:
- Механические колебания:
- Колебания пружины, колебания струны ( и мембраны ), колебания маятника.
- Колебания поршня в цилиндре двигателя внутреннего сгорания, колебания Земной коры во время землетрясений.
- Колебания давления воздуха во время распространения звука, волнение моря и качка корабля.
- Электромагнитные колебания: колебания в цепи переменного тока, колебания поля.
- Электромеханические колебания: колебания мембраны телефона, колебания диффузора электродинамического громкоговорителя. [3]
Колебания механической природы и электромагнитной природы подчиняются одинаковым количественным законам. Раздел физики, в котором колебания различной природы рассматривают с одной точки зрения, называется физикой колебаний. [1]
Система, совершающая колебания, называется колебательной системой.[3] Основные свойства колебательных систем:
- У любой колебательной системы есть устойчивое состояние равновесия.
- Как только колебательная система оказывается выведеной из устойчивого состояния равновесия, появляется сила, возвращающая систему в устойчивое состояние.
- Вернувшись в устойчивое состояние, колеблющееся тело по инерции продолжает движение.[2]
Если колебательная система в начальный момент времени находится в устойчивом состоянии равновесия, колебания не происходят пока на систему не подействует внешняя сила. Если колебательная система выведена из этого состояния, перечисленные свойства приводят к тому, что в системе происходят колебания, которые какое-то время продолжаются.
Колебания, которые происходят без переменных внешних воздействий на колебательную систему, называются свободными колебаниями. В противном случае — колебания называются вынужденными колебаниями. [3]
Колебания называются периодическими, если численные значения всех физических величин, характеризующих колебательную систему и меняющихся в процессе колебаний, повторяются через равные промежутки времени. Периодические колебания величины s(t){\displaystyle s(t)} называются гармоническими колебаниями, если s(t)=Asin(ωt+φ0){\displaystyle s(t)=Asin(\omega t+\varphi _{0})} или s(t)=Acos(ωt+φ1){\displaystyle s(t)=Acos(\omega t+\varphi _{1})}. Начальные фазы в аргументах этих тригонометрических функций связаны соотношением φ1=φ0−π/2{\displaystyle \varphi _{1}=\varphi _{0}-\pi /2}. [3]
Можно доказать, что величина ( s{\displaystyle s} ) совершает гармонические колебания ( с циклической частотой ω{\displaystyle \omega } ) тогда и только тогда, если она удовлетворяет уравнению d2sdt2+ω2s=0{\displaystyle {\frac {d^{2}s}{dt^{2}}}+\omega ^{2}s=0}. Поэтоту это уравнение называется дифференциальным уравнением гармонических колебаний. [3]
Когда система одновременно участвует в разных колебательных процессах, получение закона результирующих колебаний системы называется сложением колебаний. Гармонические колебания двух колебательных процессов называются когерентными, если разность их фаз не зависит от времени. В сложении некогерентных колебаний получаются негармонические результирующие колебания. Для сложения двух одинаково направленных гармонических колебаний можно использовать метод векторных диаграмм. [3]
При сложении одинаково направленных гармонических колебаний с циклическими частотами ω,2ω,3ω{\displaystyle \omega ,2\omega ,3\omega } и т. д. получаются периодические негармонические колебания с периодом 2π/ω{\displaystyle 2\pi /\omega }. Любое гармоническое колебание можно представить в виде суммы гармонических колебаний с такими частотами: s=f(t)=a02+∑n=1∞(ancos(nωt)+bnsin(nωt))=a02+∑n=1∞Ansin(nωt+φn){\displaystyle s=f(t)={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }(a_{n}cos(n\omega t)+b_{n}sin(n\omega t))={\frac {a_{0}}{2}}+\sum _{n=1}^{\infty }A_{n}sin(n\omega t+\varphi _{n})}, где
an=2T∫−T/2T/2f(t)cos(nωt)dt,(n=0,1,2,…){\displaystyle a_{n}={\frac {2}{T}}\int \limits _{-T/2}^{T/2}f(t)cos(n\omega t)\,dt,\,\,(n=0,1,2,…)},
bn=2T∫−T/2T/2f(t)sin(nωt)dt,(n=1,2,…){\displaystyle b_{n}={\frac {2}{T}}\int \limits _{-T/2}^{T/2}f(t)sin(n\omega t)\,dt,\,\,(n=1,2,…)}[4]
Такое представление периодической функции f(t){\displaystyle f(t)} называется её разложением в ряд Фурье. Члены ряда Фурье, соответствующие колебаниям с циклическими частотами ω,2ω,3ω{\displaystyle \omega ,2\omega ,3\omega } и т. д. называются первой, второй, третьей и т. д. гармониками сложного периодического колебания. Совокупность этих гармоник образует спектр колебания. Периодические колебания имеют дискретный спектр частот. [3]
Непериодические колебания в общем случае имеют сплошной спектр частот. В гармоническом анализе эти сложные колебания представляются в виде интеграла Фурье. [3]
Некоторые непериодические колебания ( они называются почти периодическими, квазипериодическими ) имеют дискретный спектр частот. Но эти циклические частоты выражаются иррациональными числами. [3]
Различают 2 вида волн: упругие волны и электромагнитные волны.
Упругими волнами называются механические возмущения ( деформации ), которые распространяются в упругой среде. Тело называется упругим, если его деформации, которые появляются под влиянием внешних воздействий, полностью исчезают после прекращения этих воздействий.
Упругие волны в неограниченной среде распространяются, в результате вовлечения в вынужденные колебания всё более и более удалённых от источника волн частей среды. За колеблющиеся частицы сплошной среды, в которой распространяются упругие волны, принимают небольшие элементы объёма.
Упругая волна называется продольной, если частицы среды колеблются в направление распространения волны. Пример — звуковые волны в воздухе ( это — упругие волны малой интенсивности ).
Упругая волна называется поперечной, если частицы среды колеблются перпендикулярно направлению распространения волны. Пример — волны, которые распространяются вдоль струн музыкальных инструментов.
Особое место занимают поверхностные волны. Имеются в виду волны на поверхности жидкости ( возмущения поверхности жидкости ). В поверхностных волнах частицы жидкости одновременно совершают и продольные, и поперечные колебания. [3]
Бегущая волна[править | править код]
Бегущей волной называется волна, которая, в отличие от стоячей волны, переносит энергию в пространстве. Уравнением бегущей волны называется зависимость величин, характеризующих колебания среды в распространении волны, от координат и времени.
Упругая волна называется синусоидальной, или гармонической, если соответствующие ей колебания частиц среды являются гармоническими. Частота этих колебаний называется частотой волны.
Волновой поверхностью, или волновым фронтом, называется геометрическое место точек с одинаковой фазой колебаний. Волна называется плоской, если её поверхности представляют собой совокупность параллельных плоскостей. Волна называется сферической, если её поверхности представляют собой концентрические сферы; центр этих сфер называется центром волны.
Уравнение плоской синусоидальной волны: s=Asin(ωt−{\displaystyle s=Asin(\omega t-}kr+α){\displaystyle +\alpha )}, где есть
k – волновой вектор,
r – радиус-вектор,
α{\displaystyle \alpha } – начальная фаза колебаний в
Уравнение сферической синусоидальной волны: s=a0rsin(ωt−kr+α){\displaystyle s={\frac {a_{0}}{r}}sin(\omega t-kr+\alpha )}, где a0{\displaystyle a_{0}} – это физическая величина, численно равная амплитуде волны на единичном расстоянии от центра волны.
Распространение волны в однородной изотропной среде описывается следующим дифференциальным уравнением в частных производных: Δs=1v2∂2s∂t2{\displaystyle \Delta s={\frac {1}{v^{2}}}{\frac {\partial ^{2}s}{\partial t^{2}}}}, где Δ{\displaystyle \Delta } – это оператор Лапласа и v{\displaystyle v} – скорость распространения волны. Плоская и сфирическая волна удовлетворяют этому уравнению. Функция s{\displaystyle s}, которая характеризует синусоидальную волну с волновым числом k{\displaystyle k}, распространяющуюся в однородной изотропной среде, одновременно удовлетворяет двум уравнениям: Δs=−k2s{\displaystyle \Delta s=-k^{2}s} и ∂2s∂t2=−ω2s{\displaystyle {\frac {\partial ^{2}s}{\partial t^{2}}}=-\omega ^{2}s}. [3]
Ссылки: использованная литература, список – в разделе «Примечания».
См. также на других языках: https://lv.wikipedia.org/wiki/Svārstību_un_viļņu_fizika
- ↑ 1 2 3 G. Mjakiševs, B. Buhovcevs. Fizika 11. klasei. 303 с.
- ↑ 1 2 Н. М. Шахмаев, С. Н. Шахмаев, Д. Ш. Шодиев. Физика 9. Москва, «Просвещение», 1994. 239 с.
- ↑ 1 2 3 4 5 6 7 8 9 10 11 12 13 Б. М. Яворский, А. А. Детлаф. Справочник по физике. 512 с.
- ↑ А. А. Детлаф, Б. М. Яворский. Курс физики. Москва, «Высшая школа», 1989. 607 с.




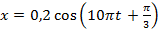 м. Определите амплитуду, период, частоту, смещение и скорость в момент времени 0,1 с.
м. Определите амплитуду, период, частоту, смещение и скорость в момент времени 0,1 с.