Сборник задач по электротехнике с решениями. Учебное пособие

	I	+ I	2	−	I	3	= 0;
	1
0,8I1				+	0,8I3		=1,8;
		0,7I2 +			0,8I3		=1,2.

определяют ток I1 в первой ветви

I1 = 1,2 −1,5I2 . 0,8

Ток I2 во второй ветви находят по значению тока I1 из уравнений для эдс E1 и E2:

1,8 = 1,6 1,2 −1,5I2 + 0,8I2

0,8

или

1,8 = 2,4 – 3I2 + 0,8I2,

откуда

I2 = 0,272 A.

Величину тока I1 в первой ветви определяют по величине тока I2 из уравнения для эдс E1

1,8 = 1,6I1 + 0,8·0,27,

откуда

I1 = 0,99 А.

Ток I3 в третьей ветви находят из уравнения для токов

I3 = I1 + I2 = 0,99 + 0,27 = 1,26 A.

2.1.2)В электрической цепи постоянного тока (рис. 2.1.2) амперметр А показывает I5 = 5 А. Методом уравнений Кирхгофа рассчитать токи I1, I2, I3, I4 в ветвях цепи. Сопротивления резисторов:

R1 = 1 Ом; R2 = 10 Ом; R3 = 10 Ом;

R4 = 4 Ом;	R5 = 3 Ом;	R6 = 1 Ом;
R7 = 1 Ом;	R8 = 6 Ом;	R9 = 7 Ом.

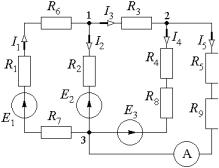
Величины эдс:

E1 = 162 В; E2 = 50 В; E3 = 30 В.

Внутренними сопротивлениями источников питания пренебречь. Решить задачу для случая, когда показание амперметра неизвестно.

1 2

3

Рис. 2.1.2

Решение. При заданном включении источников питания за положительные направления токов принимаем направления, указанные на схеме рис. 2.1.2. В схеме – три узла и пять ветвей, следовательно, необходимо определить пять неизвестных токов. В соответствии с этим составляют два уравнения по первому закону Кирхгофа и три – по второму закону Кирхгофа. Для узлов 1 и 2 цепи составляют уравнения для токов по первому закону Кирхгофа:

			I1 = I2 + I3;		I3 = I4 + I5.
По	второму	закону	Кирхгофа	уравнение		для	левого	контура	с	эдс

E1 и E2

E1 – E2 = (R1 + R6 + R7)I1 + R2I2.

Для контура с эдс E2 и E3

E2 – E3 = –R2I2 + R3I3 + (R4 + R8)I4.

Для правого контура с амперметром А в ветви

E3 = –(R4 + R8)I4 + (R5 + R9)I5.

Ток в цепи резистора R4 определяют из последнего уравнения:

30 = –(4 + 6) I4 + (3 + 7) 5 = –10I4 + 50,

откуда I4 = 2 A.

Ток I3 в ветви резистора R3 находят из уравнения, составленного для узла 2 цепи

I3 = I4 + I5 = 7 А.

Ток в ветви резистора R2 находят из уравнения, записанного для среднего замкнутого контура

E2 – E3 = –10I2 + 10·7 + (4 + 6)·2,

откуда I2 = 7 A.

Ток в ветви с резисторами R1, R6, R7 находят из уравнения

I1 = I2 + I3 = 14 A.

Ток I1 можно также определить из уравнения

E2 – E3 = –R2I2 + R3I3 + (R4 + R8)I4,

откуда I1 = 14 A.

Если ток в ветви резисторов R5 и R9 не задан, то искомые токи и их направления в других ветвях определяют, решая систему пяти уравнений, составленных по законам Кирхгофа.

Положительные значения токов свидетельствуют о том, что действительные направления токов в соответствующих ветвях совпадают с условными направлениями.

Задача

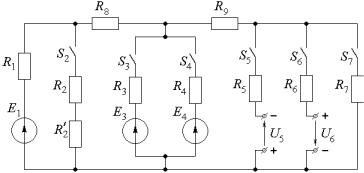
2.1.3)Методом уравнений Кирхгофа рассчитать токи I1, … , I9 в ветвях электрической цепи, показанной на рис. 2.1.3. Электродвижущая сила и напряжения источников, сопротивления резисторов и положения выключателей для соответствующих вариантов задания указаны в табл. 2.1.1. Внутренними сопротивлениями источников пренебречь.

Рис. 2.1.3

8При замене звезды сопротивлений эквивалентным треугольником сопротивлений сопротивления его сторон рассчитывают по формулам:

R31 = R3 + R1 + R3R1 ;

R2

R12 = R1 + R2 + R1R2 ;

R3

R23 = R2 + R3 + R2R3 .

R1

Примеры решения задач

2.3.1)Найти эквивалентное сопротивление, токи в неразветвленной части и в отдельных ветвях цепи, показанной на рис. 2.3.5. К цепи приложено напряжение U.

Рис. 2.3.5

Решение. Сопротивления R1, R2, R3 соединены параллельно. Их эквивалентная проводимость Gэ1 и сопротивление Rэ1 равны:

	Gэ1 = G1 + G2 + G3			=		1	+	1	+	1	;
						R		R		R
						1		2		3
	Rэ1	=		1	.
			Gэ1

В результате исходная схема (рис. 2.3.5) приводится к эквивалентной схеме (рис. 2.3.6, а), в которой сопротивления R4 и Rэ1 соединены последовательно. Их эквивалентное сопротивление Rэ2 = R4 + Rэ1. На участке cd (рис. 2.3.6, б) сопротивления R5 и Rэ2 соединены параллельно; их эквивалентное сопротивле-

ние	R	=	R5Rэ2	. В результате «свертки» исходная схема приводится к схеме (рис. 2.3.6, в), в которой
	э3		R5 + Rэ2

сопротивления R6, Rэ3 и R7 соединены последовательно. Эквивалентное сопротивление исходной цепи

Rэ = R6 + Rэ3 + R7.

а)

б)		в)

Рис. 2.3.6

Ток в неразветвленной части цепи I = U . Для расчета токов в ветвях по закону Ома для пассивного

Rэ

участка цепи определим напряжение на разветвленном участке цепи Ucd = IRэ1. Токи в ветвях:

I4 =	Ucd		;	I5 =	Ucd	.
	R	э2			R
					5

Напряжение

Uab = I4Rэ1.

Токи в ветвях:

I1 =	Uab	;	I2 =	Uab		;	I3 =	Uab	.
	R			R	2			R
	1							3

2.3.2)Задана мостовая схема (рис. 2.3.7, а). Сопротивления и эдс схемы известны. Рассчитать ток в сопротивлении R.

		2						2
						1				4
	1	3		4				3

Рис. 2.3.7

Решение. Заменим треугольник сопротивлений R12, R23, R31 эквивалентной звездой сопротивлений R1, R2, R3, в результате получим схему со смешанным соединением сопротивлений (рис. 2.3.7, б). Эквивалентное сопротивление этой схемы

Rэ = R + R1 + (R2 + R4 )(R3 + R5 ) .

R2 + R4 + R3 +R5

Ток в неразветвленной части цепи
I =	E	.
	R
	э
Задачи
2.3.3)Для схемы (рис. 2.3.8) заданы:	R1 = 2 Ом; R2 = 30 Ом; R3 =

= 12 Ом; R4 = 8 Ом; R5 = 1,5 Ом; E = 160 В; Rвт = 0,5 Ом. Определить токи во всех элементах схемы и кпд источника.

Рис. 2.3.8

2.3.4)В схеме (рис. 2.3.8) ток I3 = 3 A. Определить эдс и мощность источника, приняв величины сопротивлений по условию задачи 2.3.3.

2.3.5)Задана цепь (рис. 2.3.9), в которой известны сопротивления R1 = 4 Ом; R2 = 4 Ом; R3 = 6 Ом; R4 = R5 = 120 Ом; R6 = 4 Ом и ток I6 = 2 A. Определить токи остальных ветвей и эдс Е.

Рис. 2.3.9

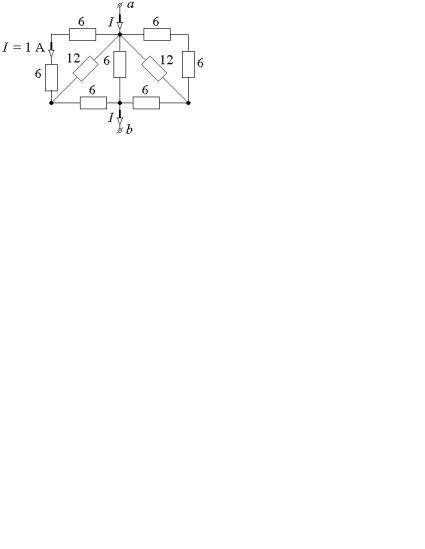
2.3.6)Определить эквивалентное сопротивление относительно выводов а – b схем (рис. 2.3.10, а – е). Величины сопротивлений на схемах указаны в омах.

2.3.7)Определить напряжение Uab в схеме рис. 2.3.10, е.

	а)				б)

в)		г)

Рис. 2.3.10

2.3.8) Как нужно соединить три сопротивления и выбрать их отношение, чтобы при питании от одного источника отношение напряжений на этих сопротивлениях было 1 : 2 : 3?

2.3.9) Как нужно соединить два сопротивления и выбрать их отношение, чтобы при питании от одного источника отношение токов в сопротивлениях было 1 : 3?

2.3.10) Преобразовать схему, показанную на рис. 2.3.11, в одноконтурную.

1

3

2

Рис. 2.3.11

2.3.11) Преобразовать эквивалентный источник эдс (рис. 2.3.12, а) в источник тока (рис. 2.3.12, б), определить параметры этого источника и потери в обоих источниках, если Rн = 10 Ом; E = 60 В; Rвт = 2 Ом.

а)

б)

Рис. 2.3.12

2.3.12) Определить

параметры

эквивалентного

источника

эдс

(рис.

2.3.12,

а),

если

известны

параметры

источника

тока

(рис.

2.3.12,

б):

I = 5 A; Gвт = 0,1 См. Определить, при каком сопротивлении нагрузки мощность потерь обоих источни-

ков одинакова?

а),

2.3.13) Рассчитать

параметры

источника

(рис.

2.3.12,

если

Rн = 4 Ом; Uab = 12 B, а мощность потерь 9 Вт.

2.3.14) Для измерения малых сопротивлений применяют двойной мост Томсона (рис. 2.3.13). Выведите условия равновесия моста, если сопротивления R1, R2, R3 и R4 подобраны так, что R2R3 = R4R1.

x

Рис. 2.3.13

2.3.15) За неимением одинаковых гальванических элементов пришлось включить параллельно два гальванических элемента с эдс E1 и E2 с внутренними сопротивлениями Rвт1 и Rвт2 соответственно. Во внешней цепи, сопротивление которой R, протекает ток I. Найти эдс E и внутреннее сопротивление Rвт гальванического элемента, который дает во внешнюю цепь такой же ток при любом сопротивлении R, и показать, что E всегда меньше наибольшей из эдс E1 и E2.

2.3.16) В цепи, схема которой приведена на рис. 2.3.14, известны все сопротивления и ток I4 через резистор R4. Найти эдс E источника. Внутренним сопротивлением источника пренебречь.

Рис. 2.3.14

2.3.17) В цепи постоянного тока (рис. 2.3.15) E = 10 В; R1 = 5 Ом; R2 = R3 = 1 Ом; R4 = R5 = 3 Ом. Найти токи в каждой ветви. Внутренним сопротивлением источника пренебречь.

		Рис. 2.3.15
2.3.18) В	электрической	цепи,	схема	которой	приведена	на

рис. 2.3.16, известны сопротивления R1, R2 и R3, ток I в источнике эдс E и разность потенциалов U21 между точками 2 и 1. Найти сопротивление резистора R4.

1

2

Рис. 2.3.16

2.3.19) Сопротивления ветвей цепи (рис. 2.3.17) R1 = R2 = R3 = 60 Ом; R4 = R5 = R6 = 30 Ом, внутрен-

нее сопротивление источника не учитывается. Определить эдс источника, если ток I = 3 A.
2.3.20) Определить	мощность	цепи	(рис.	2.3.18),	если	напряжение
U = 20 В; сопротивления ветвей		R1 = R4	= 5 Ом;	R2 = R3	= 2 Ом;	R5 = R6 =
= R7 = 6 Ом.

Электрические цепи постоянного тока и методы их расчета

Практические занятия проводятся с целью успешного освоения студентами теоретического материала и применения его для решения задач и анализа полученных результатов. На практических занятиях №1 и №2 подробно рассмотрены примеры расчета электрических цепей с помощью различных методов, показано, как надо проверять правильность решения задачи и проанализированы возможные режимы работы всей цепи и отдельных ее элементов.

6.1. Практическое занятие №1 Расчет электрических цепей с использованием законов Ома и Кирхгофа

Рабочие файлы: [Инструмент решения СЛАУ]

6.1.1. Вопросы для подготовки к занятиям

1. Сформулировать закон Ома для участка и для замкнутого контура.

2. Нарисовать схемы с последовательным и параллельным соединением пассивных элементов, указать основные свойства этих соединений, схему со смешанным соединением пассивных элементов; дать порядок расчета этих схем.

3. Нарисовать схемы соединения пассивных элементов звездой и треугольником и объяснить порядок их расчета.

4. Сформулировать первый и второй законы Кирхгофа, объяснить правила знаков.

5. Сформулировать уравнение баланса мощностей.

6. Как составляется система уравнений для расчета сложных схем при помощи уравнений Кирхгофа?

6.1.2. Расчет цепи с одним источником питания

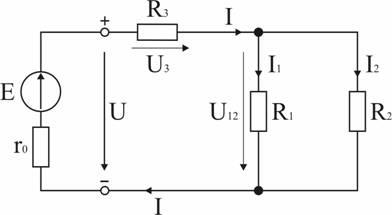
Задача 1. В цепи, схема которой приведена на рис. 1.29, ЭДС аккумуляторной батареи Е = 78 В, ее внутреннее сопротивление r₀ = 0,5 Ом. Сопротивления резисторов R₁ = 10 Ом, R₂ = 5 Ом, R₃ = 4 Ом. Вычислить токи во всех ветвях цепи и напряжения на зажимах батареи и на каждом их резисторов.

Анализ и решение задачи 1

1. Обозначение токов и напряжений на участках цепи.

Резистор R₃ включен последовательно с источником, поэтому ток I для них будет общим, токи в резисторах R₁ и R₂ обозначим соответственно I₁ и I₂. Аналогично обозначим напряжения на участках цепи.

2. Определение эквивалентного сопротивления цепи:

R_э = r₀ + R₃ + R₁ R₂ / (R₁ + R₂) = 0,5 + 4 + 5 * 10 / (5 +10) = 7,8 Ом

3. Ток в цепи источника рассчитываем по закону Ома:

I = E / R_э = 78 / 7,8 = 10 А.

4. Определение напряжений на участках цепи:

U₁₂ = R₁₂ I = 3,3 * 10 = 33 В; U₃ = R₃ I = 4 * 10 = 40 В;

U = E — r₀ I = 78 — 0,5 * 10 = 73 В.

5. Определение токов и мощностей всех участков:

I₁ = U₁₂ / R₁ = 33 / 10 = 3,3 А; I₂ = U₁₂ / R₂ = 33 / 5 = 6,6 А;

P₁ = R₁ I₁² = U₁₂ I₁ = 108,9 Вт; P₂ = R₂ I₂² = U₁₂ I₂ = 217,8 Вт;

P₃ = R₃ I² = U₃ I = 400 Вт.

Мощность потерь на внутреннем сопротивлении источника

P = r₀ I² = 50 Вт.

Мощность источника P = E I = 780 Вт.

Дополнительные вопросы к задаче 1

1. Как проверить правильность решения задачи?

Правильность вычисления токов можно проверить, составив уравнение на основании первого закона Кирхгофа: I = I₁ + I₂.

Правильность расчета мощностей проверяют по уравнению баланса мощностей: P = P₁ + P₂ + P₃ + P.

2. Каким будет напряжение на зажимах источника, при обрыве в цепи резистора R₃?

Это будет режим холостого хода источника ЭДС, при котором U = E, т.к. ток I равен 0 и I r₀ = 0.

3. Каким будет ток в цепи источника при коротком замыкании на его зажимах?

В режиме короткого замыкания U = 0 и ток источника ограничивается только его внутренним сопротивлением

I_кз = E / r₀ = 78 / 0,5 = 156 А.

4. Как изменятся токи в схеме при увеличении R₁?

При увеличении R₁ увеличивается сопротивление параллельного участка схемы R₁₂, поэтому увеличивается сопротивление R_экв, что приводит к уменьшению тока I. При уменьшении I уменьшаются падения напряжения I R₃ и I r₀ и, в соответствии со вторым законом Кирхгофа, напряжение на разветвлении U₁₂ = E — I (R₃ + r₀) возрастает, что приводит к увеличению тока в резисторе R₂. Т.к. ток I уменьшается, а ток I₂ возрастает, ток I₁ = I — I₂ уменьшается.

Задачи на трехфазные цепи

Трехфазные электрические цепи получили широкое распространение в промышленности, благодаря своим немалым преимуществам перед другими системами электрических цепей. К ним относятся – экономичность передачи энергии, относительная простота создания вращающегося магнитного поля, а также возможность получения двух значений напряжения. Основными потребителями трехфазных систем являются асинхронные двигатели, а основными источниками – трехфазные генераторы. 

В разделе электротехники трехфазным цепям переменного тока посвящено немало задач, рассмотрим решение некоторых из них.

Задача 1

Обмотки трехфазного генератора соединены по схеме “звезда”, э.д.с. в них 220 В. Построить векторные диаграммы  и определить линейные напряжения для схемы соединения, в которой в одной точке сходятся: a) X Y Z б) X B Z в) X B C . Начала обмоток – A,B,C, концы обмоток – X,Y,Z. Принять нагрузку на генераторе равной нулю.

а) Для данной схемы соединения векторная диаграмма будет выглядеть следующим образом

 

Линейные напряжения в данном случае будут равны и определяться как 

б) Так как обмотка BY подключена началом в нейтральную точку, то вектор напряжения оказывается повернутым на 180 относительно нормального положения.

 

Линейные напряжения в данном примере будут разными по значению 

в) В данном случае относительно нормального положения повернуты вектора двух обмоток – BY и CZ. 

Как и в предыдущем примере, линейные напряжения не будут равны 

Задача 2

К зажимам приемника подсоединён трехфазный генератор, как показано на схеме. Определить показания амперметров A₁,A₂ и фазные токи зная, что U_л=380В, R=50 Ом, x_L=35 Ом.

 

Определим комплексные значения сопротивления (для удобства вычислений будем переводить в показательную форму)

Напряжения в фазах будет равно

Токи в фазах

Ток в нейтральном проводе равен (для удобства сложения сначала переведем из показательной формы в алгебраическую, а затем наоборот)

Соответственно, показания амперметров будут следующими:

Задача 3

К зажимам приемника, подсоединён трехфазный генератор, обмотки которого соединены по схеме “треугольник”. Определить фазные и линейные токи, показания вольтметра, зная, что линейное напряжение равно 220 В,  R=25 Ом, x_L=x_C=10 Ом.

 

Как и в предыдущей задаче, в первую очередь определим комплексы сопротивлений 

Фазное напряжение при данном соединении будет равно линейному, следовательно 

Фазные токи при несимметричной нагрузке не равны 

Для определения линейных токов представим фазные токи в алгебраической форме комплексного числа

Сумма линейных токов 

Равенство нулю суммы линейных токов является свойством любой трёхфазной системы.

Чтобы определить показания вольтметра, найдём сумму падений напряжения на x_L и R в соответствующих обмотках. 

Так решаются задачи на трехфазные цепи. Спасибо за внимание! Читайте также — задачи на цепи переменный ток

Просмотров: 19039

Сборник задач по электротехнике с решениями. Учебное пособие

Рис. 2.3.17

		Рис. 2.3.18
2.3.21) Найти	распределение	токов	в	цепи	(рис.	2.3.19),	если

R1 = R2 = 0,5 Ом; R3 = 6 Ом; R4 = 6 Ом; R5 = R6 = 1 Ом; R7 = 2 Ом, а напряжение на входе U = 120 В. 2.3.22) В схеме цепи (рис. 2.3.20) определить напряжение Uab. Значения эдс и сопротивлений указа-

ны соответственно в В и Ом.

Рис. 2.3.19

a

			Рис. 2.3.20
2.3.23) В	схеме	цепи	(рис.	2.3.21)	определить	ток	Icd	(по
значению и	направлению),	если	E = 48	В; R1 =	R3 = 8 Ом;	R2 = R4	=	4 Ом;
R5 = R6 = 2 Ом.

cd

Рис. 2.3.21

2.3.24) Определить входное сопротивление схемы Rab (рис. 2.3.22) относительно точек a и b, если J5 и J6 – источники тока.

Рис. 2.3.22

2.3.25) В цепи (рис. 2.3.23) сопротивления резисторов даны в омах. Определить входное сопротивление схемы относительно точек a и b.

Рис. 2.3.23

2.4 МЕТОД УЗЛОВОГО НАПРЯЖЕНИЯ

Метод узлового напряжения целесообразно использовать для расчета электрических цепей, содержащих несколько параллельных ветвей, присоединенных к паре узлов. Преимущество этого метода перед другими возрастает с увеличением числа параллельных ветвей электрических цепей, при этом определяется узловое напряжение, что позволяет достаточно просто определять токи в параллельных ветвях и другие величины, характеризующие подобные электрические цепи.

Узловое напряжение между двумя точками разветвлений (узлами) определяют в соответствии с выражением

			N	N	N
			∑Ek Gk + ∑Uk Gk + ∑Jk
		U =	k =1	k =1	k =1	,
				N
				∑Gk
				k =1
		N
	где	∑Ek Gk – алгебраическая сумма произведений эдс на проводимости соответствующих ветвей;
	k =1
	N
	∑Uk Gk – алгебраическая сумма произведений напряжений на проводимости соответствующих ветвей;
	k =1
	N						1
	∑Jk	– алгебраическая сумма токов источников тока в ветвях; Gk =						– проводимость k-й ветви цепи;
	k =1						Rk
	N
	∑Gk	– сумма проводимостей всех ветвей.

k =1

При расчете электрических цепей по методу узлового напряжения задают условное положительное направление указанного напряжения, рассчитывая его по соответствующей формуле. При этом определяют проводимости всех ветвей, выбирая условно положительные направления токов в ветвях.

При определении токов в параллельных ветвях для соответствующих замкнутых контуров выбирают направления обхода контура и составляют уравнение по второму закону Кирхгофа. При этом эдс, напряжения и токи источников тока принимаются положительными, если они направлены по направлению обхода контура, и отрицательными, если они направлены против направления обхода контура.

При отсутствии в цепи источников тока (рис. 2.4.1, а) выражение для определения узлового напряжения принимает вид

	N			N
	∑Ek Gk + ∑Uk Gk
U =	k =1		k =1		.
		N
		∑Gk
		k =1
1			1

2	2
а)	б)
	Рис. 2.4.1

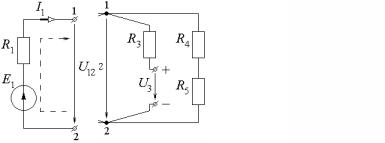
При заданном условном положительном направлении напряжения U12, действующего между узлами 1 и 2 (рис. 2.4.1, б), эдс в замкнутом контуре, образованном соответствующей ветвью и замыкающим его напряжением U12, считается положительной, если совпадает с направлением обхода контура, и отрицательной, если не совпадает. Знаки в расчетной формуле не зависят от направления токов в ветвях электрической цепи, поэтому выражение для напряжений между узлами 1 и 2 цепи записывается в виде

U12 =	E1G1 − E2G2 +U3G3	.
	G1 +G2 +G3

Для расчетов тока в ветвях электрической цепи составляют замкнутый контур, состоящий из рассматриваемой ветви цепи, замыкаемой напряжением U12 между узлами с учетом действительного его направления. Расчетная схема ветви с резистором R1 и эдс E1 приведена на рис. 2.4.1, б. Задавшись условным положительным направлением обхода полученного контура, например, по часовой стрелке (пунктирная линия на рис. 2.4.1, б), по второму закону Кирхгофа с учетом знаков составляется уравнение

E1 = I1R1 + U12,

из которого определяется величина тока I1 в данной ветви цепи. Аналогичным образом определяются токи в других ветвях электрической цепи.

Примеры решения задач

2.4.1)Для электрической цепи постоянного тока (рис. 2.4.2) определить при какой величине эдс E3 ток I3 в ветви с резистором R3 уменьшится в три раза по сравнению с его первоначальным значением. Электродвижущая сила источников питания: E1 = 100 B; E2 = 120 B; E3 = 150 B.

1

2

Рис. 2.4.2

Сопротивления резисторов: R1 = 20 Ом; R3 = 100 Ом; R4 = 60 Ом. Внутренними сопротивлениями источников питания пренебречь.

Решение. По второму закону Кирхгофа напряжение, действующее между двумя узлами 1 и 2 электрической цепи U12 = E2 = 120 В. Ток I3 в ветви резистора R3 для первоначальных условий определяется из выражения, записанного для ветви по второму закону Кирхгофа:

E3 = U12 + I3R3,

откуда

I3 = E3 −U12 = 150 −120 = 0,3 A.

R3 100

Электродвижущая сила E3′ , при которой ток I3′ в цепи резистора R3 уменьшается в три раза, определяется из выражения для эдс E3

E3′ = U12 + I3′ R3 = 120 – 100 I3′ .

Из условия

I3′ = I33 = 0,1 A

находим

E3′ = 120 + 100 0,1 = 130 B.

2.4.2)Два источника постоянного тока с эдс E1 = E2 = 115 B и внутренними сопротивлениями R01 = 0,2 Ом и R02 = 0,4 Ом включены параллельно в нагрузку Rн = 5 Ом (рис. 2.4.3). Определить токи I, I1, I2 в ветвях цепи и составить баланс мощностей.

1

2

Рис. 2.4.3

Решение. Проводимости ветвей электрической цепи:

G	=	1	=	1	= 5 См;
1		R01	0,2

Gн = 1 = 1 = 0,2 См;

Rн 5

	G2 =	1	=	1	= 2,5 См.
		R02		0,4

Узловое напряжение, действующее между узлами 1 и 2 цепи:

	U12 =	E1G1 + E2G2	=	115 5 +115 2,5		=112 B.
		Gн +G1 +G2			0,2 +5 +2,5

Принимаем положительные направления токов в ветвях в соответствии с рис. 2.4.3. По второму закону Кирхгофа для ветви генератора с эдс E1 можно записать уравнение электрического равновесия:

U12 + I1R01 = E1,

откуда

I1 = E1 −U12 = (E1 – U12) G1 = (115 – 112)·5 = 5 A.

R01

Задачи

2.4.3)На рис. 2.4.4 приведена мостовая электрическая схема соединения сопротивлений R1…R5. Определить величину и направление тока I5 в диагонали моста с резистором R5, если напряжение источни-

ка

питания

U

=

150

B;

сопротивления

резисторов в

плечах

моста:

R1

=

20

Ом;

R2 = 40 Ом; R3 = 10 Ом; R4 = 30 Ом; R5 = 50 Ом.

2.4.4)Методом двух узлов определить токи I1…I3 в ветвях электрической цепи (рис. 2.4.5). Электро-

движущая

сила

источников:

E1

=

60

B,

E2

=

65

B,

E3 =

50 B.

Сопротивления

резисторов:

R1 =

R2

=

0,5

Ом;

R3

= 1 Ом. Внутренними сопротивлениями источников пренебречь.

2.4.5)Решить задачу 2.1.3 методом узлового напряжения.

1

2

Рис. 2.4.4

1

2

РИС. 2.4.5

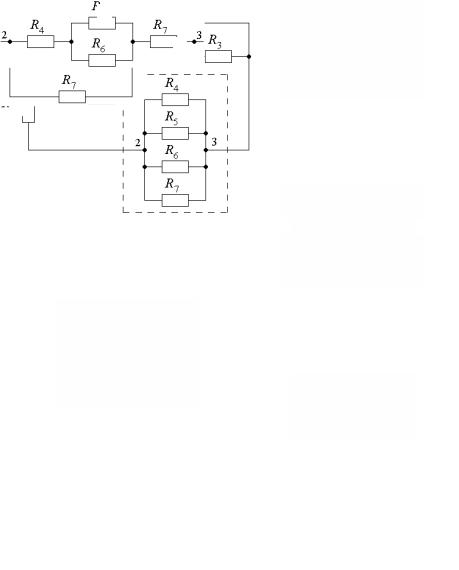
2.4.6)Определить токи в ветвях электрической цепи постоянного тока (рис. 2.4.6, а). Электродвижущая сила источников питания E1 и E2; внутренние сопротивления R01 и R02; сопротивления резисторов R1…R7, а также схема включения резисторов на участке 2 – 3 (ограниченная пунктиром на рис. 2.4.6, б – е) для соответствующих вариантов задания приведены в табл. 2.4.1. Задачу решить методом узлового напряжения.

2.5 МЕТОД НАЛОЖЕНИЯ ТОКОВ

Метод наложения токов (метод суперпозиции) применяется для расчета сложных электрических цепей постоянного тока с несколькими источниками энергии. Наиболее целесообразно применять его при небольшом числе источников. По сравнению с другими методами он имеет преимущества в тех случаях, когда не требуется полный расчет цепи, а можно ограничиться, например, определением токов только в некоторых ветвях электрической цепи.

1

02

01

б)

а)

в)

г)

д)

2		3

е)

Рис. 2.4.6

В методе наложения электрическая цепь с несколькими источниками эдс и напряжений заменяется расчетными электрическими цепями с одним источником. Число расчетных цепей равно числу источников, действующих в электрической цепи. Источники питания, кроме рассматриваемого, из цепи удаляют, оставляя в цепи только их внутренние сопротивления. В результате расчета каждой преобразованной цепи определяются частичные токи от действия данного источника.

Значение действительных токов ветвей определяется алгебраическим суммированием частичных токов в этих ветвях. Применительно к исходной электрической цепи (рис. 2.5.1, а), на которой предва-

рительно нанесены положительные направления токов в ветвях, приведены расчетные электрические цепи (рис. 2.5.2, б – в) для частичных токов от действия эдс

01	02		01		02

01 02

в)

Рис. 2.5.1

E1 и E2. При расчете этих цепей определяются частичные токи во всех ветвях. С учетом направления частичных токов и токов в ветвях исходной электрической цепи определяют действительные токи в ветвях рассматриваемой цепи путем наложения (алгебраического суммирования) частичных токов в ветвях:

		I1 = I1′ − I1′′ ;		I2 = I2′′ − I2′ ; I3 = I3′ + I3′′.
			Примеры решения задач
2.5.1)Определить	ток	I	в	электрической	цепи	постоянного	тока

(рис. 2.5.2, а), а также диапазон изменения сопротивления резистора R для зарядки аккумуляторной батареи до эдс E2 = 16 B в конце зарядки при неизменном токе нагрузки цепей. Сопротивление резистора R = 4 Ом; эдс генератора E1 = 36 B; внутреннее сопротивление R01 = 0,3 Ом. Электродвижущая сила ак-

кумуляторной	батареи	в	начале	зарядки	E2	=	12	B;
ее внутреннее сопротивление R02 = 0,01 Ом. Задачу решить методом наложения.

					02
01	02		01
а)					б)

01

02

в)

Рис. 2.5.2

Решение.

По

закону

Ома

для

полной

цепи

ток

в

цепи

при

эдс

E2 = 0 (рис. 2.5.2, б)

I ′ =

E1

=

36

= 8,35 A.

R

+ R

+ R

0,3 +4 +0,01

01

02

Ток в цепи при эдс E1 = 0 (рис. 2.5.2, в)

I ′′ =

E2

=

12

= 2,78 A.

R

+ R

+ R

0,3 +4 +0,01

01

02

Ток в электрической цепи при наличии обоих источников питания

I = I ′− I ′′ = 8,35 – 2,78 = 5,57 A.

Сопротивление электрической цепи в начале зарядки аккумуляторной батареи при токе I = 5,57 A

Rн′ = E1 −I E2 = 365,−5712 = 4,31 Ом.

Сопротивление нагрузочного резистора в начале зарядки батареи

R′ = Rн′ −(R01 + R02 ) = 4,31 – (0,3 + 0,01) = 4 Ом.

Сопротивление электрической цепи в конце зарядки аккумуляторной батареи при токе I = 5,57 A

Rн′′ = E1 −I E2 = 365,−5716 = 3,59 Ом.

Сопротивление нагрузочного резистора в конце зарядки аккумуляторной батареи при токе I = 5,57

A

R′′ = Rн′′ −(R01 + R02 ) = 3,59 – (0,3 + 0,01) = 3,28 Ом.

Диапазон изменения сопротивления нагрузочного резистора при заданных условиях

KR = RR′′′ = 34,,2831 =1,31.

Задачи

📝 решение задач любой сложности. Заказывайте без посредников

Курс ТОЭ (теоретические основы электротехники) и решение задач по нему имеют серьезное значение для студентов технико-энергетических специальностей. Основой для изучения многих дисциплин  являются знания, которые дают непосредственно теоретическая электротехника и электроника, решение задач и практические занятия по этому предмету.

Решение задач по ТОЭ необходимо в первую очередь самим студентам, ведь для большинства из них хорошая успеваемость напрямую связана с умением свободно ориентироваться в таком базовом предмете, как электротехника и электроника. Решение задач по ТОЭ не только способно поднять ваш уровень специальной подготовки, но и заставит творчески и неординарно мыслить, создавать сложные многоступенчатые комбинации.

Чтобы вникнуть в основы электротехники, решение задач является одним из наиболее быстрых и эффективных способов. Изучать теоретику электромагнетизма, электричества и множество научных выкладок лучше всего, держа перед глазами правильные решения задач по ТОЭ: пошаговые объяснения и наглядность заданий позволяют отлично преуспеть в такой сложной, но необходимой дисциплине, как электротехника и электроника. Решение задач (в том числе и задачи по химии на заказ) с поэтапным описанием и объяснением всех используемых формул, терминов, символов для вас быстро и недорого выполнят профессионалы портала «ВсёСдал!».

Решение задач по ТОЭ всех уровней сложности

Трудности с решением задач по электротехники и электронике могут возникнуть практически у каждого студента. Курс настолько тесно связан с другими дисциплинами, что если недоучить физику или высшую математику на начальных курсах, в дальнейшем решение задач по теоретическим основам электротехники будет вызывать серьезные затруднения. А предмет, между тем, очень важен, да и портить диплом плохой оценкой не хочется.

Онлайн решение задач по ТОЭ предлагает портал ВсёСдал!», на котором зарегистрированы опытные исполнители самых разных профилей. Вы сами сможете выбрать автора, исходя из его рейтинга, отзывов о предыдущих проектах, опыта и цены.

 Заказать ТОЭ —  самый оптимальный выход из ситуации, когда нет времени или возможности самостоятельно выполнить решение задач по переходным процессам, четырехполосникам, узловым напряжениям.

Что собой представляет сайт? Это база исполнителей-профессионалов, в числе которых и студенты старших курсов, и научные работники, и преподаватели ВУЗов. Вы заполняете простую форму онлайн заявки на решение задач по ТОЭ, в которой по возможности даете информацию о характере требуемой услуги:

·         решение задач (трехфазные цепи, трехфазныегенераторы)

·         решение задач (электротехника, переменный ток)

·         решение задач (четырехполюсники, передаточные и вольт-амперные характеристики)

·         онлайн решение задач по ТОЭ(помощь на экзамене онлайн)

·         решение задач (магнитные цепи) и т.д.

Нелишним будет указать и то, какой именно объем заданий предстоит решить, и как должна выглядеть запись готовой работы (оформление, сноски, последовательность и т.д.).

Помните, что у вас впереди сессия. Возможно, решение задач по электротехнике и электронике — не единственная услуга, которая поможет вам высвободить время для занятий по другим дисциплинам. Можно заказать решение задач по физике, реферат по зарубежной литературе или курсовую по биологии — «ВсёСдал!» поможет найти специалиста любого профиля.

Заказать ТОЭ без переплаты

Исполнители сами связываются с вами, предлагают свои цены и уточняют все необходимые для работы моменты (срок, требования к оформлению, подробное описание и т.п.). Окончательное решение принимаете вы.

На сайте нет менеджеров, чьи услуги должен был бы оплачивать заказчик и которые «ненавязчиво» включаются в общий счет за работу исполнителя на сторонних ресурсах.

Заказываете ли вы решение задач на трехфазные цепи, хотите ли полностью законченный и оформленный диплом по ТОЭ на заказ или же заинтересовались услугой химическая термодинамика решение задач — в любом случае вы не заплатите ни одной лишней копейки, договариваясь обо всех нюансах работы и расчетах за ее выполнение напрямую с исполнителем.

Заказать решение нескольких типовых задач по электротехнике и электронике стоит еще и для того, чтобы грамотно подготовиться к экзамену, зачету или другой форме контроля знаний. Ведь кроме учебника и конспектов, которые дают лишь теоретические знания, у вас на руках окажется подробное пошаговое решение задач по электротехнике (переменный ток, узловые потенциалы, первый и второй Кирхгофа, цепи синусоидального тока, интеграл Дюамеля и т.д.).

Специалисты «ВсёСдал!» оперативно и грамотно решат, а при необходимости — снабдят подробными пояснениями задания:

·         на законы Кирхгофа

·         на МЭГ, МКТ, МУП

·         по двигателям (асинхронным, синхронным),тормозным нагрузкам и т.д.

С таким подспорьем вы легко сможете усвоить материал и будете уверенно чувствовать себя на экзамене.

Практические занятия по электротехнике для профессии наладчик

Практическое занятие №1.

«Изучение обозначений элементов электрических цепей постоянного тока. Составление простых электрических цепей из заданных элементов».

Задание для практической работы разработано на основе программы «Основы электротехники» для профессии «Наладчик станков и оборудования в механообработке».

Целями работы являются:

1. Изучить обозначения элементов электрических цепей постоянного тока.

2. Научиться составлять простые электрические цепи из заданных элементов.

3. Научиться использовать основные законы электротехники при решении задач.

4. Закрепить полученные на уроке знания .

5. Приобрести навыки самостоятельной работы.

При выполнении практической работы обучающиеся, должны :

• изучить таблицу «Элементы цепи и величины их характеризующие»;

• выполнить самостоятельную работу по составлению цепи;

• решить задачи на основные законы постоянного тока.

Основные электрические величины и формулы для их определения.

_стор/q

А_стор- работа сторонних сил(Дж)

q- переносимый заряд(Кл)

2

Сила тока

I

А(ампер)

I =q/t

3

Электрическое сопротивление

R

Ом

R =ρ·l/S

ρ — удельное эл. сопротивление (Ом^.м)

l- длина проводника (м)

S- площадь поперечного сечения проводника (м²)

4

Напряжение (разность потенциалов)

U(∆φ)

В

U=∆φ=А/ q

5

Работа эл. тока

А

Дж(джоуль)

Вт^.ч(ватт-час)

А=I·U·∆t

6

Эл. мощность

Р

Вт(ватт)

Р= I·U

Основные законы электротехники.

1. Закон Ома для замкнутой (полной) цепи: ток в замкнутой неразветвленной электрической цепи прямопропорционален ЭДС и обратно пропорционален полному сопротивлению: I=ε /(R+r)

R- сопротивление внешнего участка цепи (Ом)

r- сопротивление внутреннего участка (источника тока) (Ом).

2. Закон Ома для участка цепи: ток на участке цепи прямопропорционален падению напряжения на концах этого участка и обратно пропорционален сопротивлению участка: I =U/R .

3. Первый закон (правило) Кирхгофа: алгебраическая сумма токов в узле эл. цепи равна нулю: Σ I = 0 т.е. I₁+ I₂+ I₃+…+ I_n=0.

4. Закон Джоуля – Ленца: количество теплоты, выделяемое проводником при прохождении по нему тока прямопропорционально квадрату силы тока, сопротивлению проводника и времени прохождения тока:

Q = I²·R·∆t Q- количество теплоты (Дж).

Карточка №1.

1. Определить время прохождения заряда в 0,6 Кл по проводнику при значении тока 0,5А.

2. Для радиоприёмника необходимо намотать сопротивление в 30 Ом из никелиновой проволоки сечением 0,21 мм². Определить необходимую длину проволоки(ρ_{никелина}=42·10^-8Ом·м).

3. Через эл. паяльник, включённый в сеть напряжением 220В, проходит ток 0,3А. Определить сопротивление эл. паяльника.

4. Аккумулятор с внутренним сопротивлением 0,4 Ом работает на лампочку с сопротивлением 12,5Ом, при этом ток в цепи равен 0,26 А. Определить ЭДС аккумулятора.

5. На цоколе эл. лампы написано 220В и 200Вт.Определить силу тока и сопротивление нити накаливания.

Карточка №2.

1. Определить время прохождения заряда в 0,9 Кл по проводнику при значении тока 0,03А.

2. определить сечение нихромовой проволоки длиной 20 м, если её сопротивление 25 Ом(ρ_{нихрома}=110·10^-8Ом·м).

3. По эл. лампе сопротивлением 210 Ом протекает ток 0,2 А. Определить напряжение в эл.сети.

4. Аккумулятор с внутренним сопротивлением 0,4 Ом и ЭДС 3,5 В питает лампочку , при этом ток в цепи равен 0,26 А. Определить сопротивление лампочки.

5. На масляном обогревателе написано 1000Вт и 220В. Определить силу тока и сопротивление обогревателя.

Карточка №3.

1. Определить время прохождения заряда в 1,6 Кл по проводнику при значении тока 1А.

2. Проволока сечением 0,5 мм² и длиной 40 м имеет сопротивление 16 Ом, Определить материал проводника( удельное сопротивление поводника).

3. Через обогреватель включённый в сеть 220в проходит ток0,5 А Определить сопротивление обогревателя.

4. Кислотный аккумулятор с ЭДС 3В замкнут на потребитель сопротивлкнием 2,6 Ом при этом сила тока в цепи 1А. Определить внутреннее сопротивление аккумулятора.

5. На вентиляторе написано 45Вт и 220В. Определить силу тока и работу , совершаемую его электродвигателем за 5 часов.

Практическое занятие №2.

«Расчёт сопротивления разветвлённой электрической цепи».

Задание для практической работы разработано на основе программы «Основы электротехники» для профессии «Наладчик станков и оборудования в механообработке».

Целями работы являются:

1. Научится применять законы последовательного и параллельного соединения резисторов при расчёте общего сопротивления участка цепи со смешанным соединением потребителей.

2. Научиться строить схемы замещения и определять эквивалентные сопротивления.

3. Закрепить знания , полученные на уроках.

4. Приобретать навыки самостоятельной работы.

При выполнении практической работы, обучающиеся, должны:

• Изучить законы последовательного и параллельного соединения резисторов;

• Выполнить самостоятельно расчет цепи со смешанным соединением резисторов.

Вариант №1.

Определить общее сопротивление участка цепи, если величина всех сопротивлений резисторов, включённых в цепь равна 1кОм.

Вариант №2.

Определить общее сопротивление участка цепи, если величина всех сопротивлений резисторов, включённых в цепь равна 2кОм.

Вариант №3.

Определить общее сопротивление участка цепи, если величина всех сопротивлений резисторов, включённых в цепь равна 3кОм.

Вариант №4.

Определить общее сопротивление участка цепи, если величина всех сопротивлений резисторов, включённых в цепь равна 0,5кОм.

Вариант №1.

Начертить неразветвлённую электрическую цепь, содержащую два резистора, амперметр, вольтметр подключённый к первому резистору, источник тока, ключ, соединительные проводники.

Вариант №2.

Начертить неразветвлённую электрическую цепь, содержащую два резистора, лампочку, амперметр, вольтметр подключённый ко второму резистору, источник тока, ключ, соединительные проводники.

Вариант №3.

Начертить неразветвлённую электрическую цепь, содержащую резистор, лампочку, амперметр, вольтметр подключённый к резистору, источник тока, ключ, соединительные проводники.

Вариант №4.

Начертить неразветвлённую электрическую цепь, содержащую два резистора, амперметр, вольтметр подключённый к двум резисторам, источник тока, ключ, соединительные проводники.

Практическое занятие №3.

Активные и реактивные элементы цепи переменного тока.

Цель работы: закрепить теоретические знания на практике путём решения задач.

Краткая теория.

_а[Ом]

R_а=ρ·l/s

ρ- удельное сопротивление [Ом·м]

l-длина проводника [м]

s-площадь поперечного сечения проводника [м²]

I=U/R

Ток i и напряжение u совпадают по фазе т.е. φ =0.

Реактивные сопротивления:

Индуктивное сопротивление (создаётся при включении катушки индуктивности).

Χ_L [Ом]

Χ_L=ω·L

Χ_L=2πfL

L-индуктивность катушки[ Гн]

I=U/Χ_L=

U/ ω·L

Напряжение u опережает ток i на φ=90⁰.

Емкостное сопротивление (создаётся при включении конденсатора).

Χ_С [Ом]

Χ_С=1/ω·C

Χ_С=1/2πfС

С-ёмкость конденсатора[ Ф]

I=U/Χ_С=

U· ω·C

Ток i опережает напряжение u на φ =90⁰.

Материальное оснащение урока: 1.таблица;

2.В.М. Прошин, Г.В. Ярочкина Сборник

задач по электротехнике.

Решить задачи.

1. Дроссель пускорегулирующей аппаратуры для люминесцентных ламп

имеет индуктивность 1,3 Гн. Вычислить индуктивное сопротивление на промышленной частоте.

2. При частоте 50 Гц емкостное сопротивление конденсатора равно

Ом. Вычислить ёмкость конденсатора.

3. Как изменится ёмкостное сопротивление конденсатора, если частота увеличится вдвое?

Практическое занятие №4.

«Резонанс токов и напряжений».

Цель работы: закрепить теоретические знания, полученные на уроке, путём решения задач.

Краткая теория.

Если собственные колебания в контуре, содержащем последовательно соединённые катушку индуктивности L и конденсатор ёмкостью C, совпадают с вынужденными колебаниями, поступающими от источника питания, а это возможно только, если Χ_L= Χ_С и φ=0, т.е. сдвиг фаз между I и U отсутствует. Величина тока I=U/R максимальна, так как минимальна величина сопротивления. В связи с этим напряжение на катушке индуктивности и конденсаторе возрастают и могут значительно превышать напряжение питания, если Χ_L= Χ_С>>R.

Резонанс напряжений — это явление увеличения напряжения на отдельных элементах цепи по отношению к напряжению источника питания.

Условием резонанса напряжений является равенство реактивных сопротивлений конденсатора и катушки индуктивности: Χ_L= Χ_С.

Получение резонанса напряжений возможно либо за счёт изменения частоты источника питания. Либо за счёт изменений собственной частоты контура. Т.е. индуктивности L и ёмкости C , т.к. собственная частота колебаний в контуре ω=1/√ LС. На практике чаще используют переменную ёмкость, изменение которой позволяет настроить контур в резонанс.

Резонанс напряжений — явление опасное и вредное, поскольку возможен пробой изоляции проводов и конденсаторов. В то же время в радиотехнике это явление нашло применение в приёмопередающих устройствах.

Резонанс токов – это явление резкого возрастания тока, возникающее в контуре, содержащем параллельно соединённые катушку индуктивности L и конденсатор ёмкостью C.

Явление резонанса токов широко используется в технике, например в технике связи и автоматике. В энергетических устройствах резонанс токов в отличие от резонанса напряжений—явление безопасное , так как совпадение частоты источника питания с собственной частотой контура не приводит к нежелательным последствиям.

Материальное оснащение урока: 1.справочник;

2.В.М. Прошин, Г.В. Ярочкина Сборник

задач по электротехнике.

Решить задачи.

1. Определить резонансную частоту последовательного колебательного контура с параметрами: L=10 мГн; C=100 мкФ.

2. Параллельный колебательный контур имеет следующие параметры: сопротивление и индуктивность катушки — соответственно R_к=11Ом и L_к=53,2 мГн; подводимое напряжение U=220В частотой f=50 Гц. Определить ёмкость конденсатора С при настройке контура в резонанс.

3. На какое рабочее напряжение необходимо выбрать конденсатор при резонансе, если напряжение питания 21В, активное сопротивление катушки индуктивности 30 Ом, индуктивность 0.64 Гн?

Практическое занятие №6.

«Расширение пределов измерения вольтметра и амперметра».

Цель работы: закрепить теоретические знания, полученные на уроке, путём решения задач.

Краткая теория.

Расширение пределов измерения вольтметра или амперметра даёт возможность измерить данным прибором напряжение или силу тока значительно превышающих номинальные (то есть максимальное напряжение или силу тока обозначенное на шкале прибора). Для этой цели используют добавочное сопротивление или шунт.

Добавочное сопротивление – это резистор, включённый последовательно с вольтметром, который берёт на себя часть измеряемого напряжения.

Для определения величины добавочного сопротивления используют формулу: R_д =(n—1)R_v

• R_д— добавочное сопротивление [Ом ];

• R_v– внутреннее сопротивление вольтметра [Ом];

• n – число, показывающее во сколько раз необходимо увеличить предел измерения: n =U _{измеренное}/ U _{номинальное}

Шунт— это резистор, включённый параллельно амперметру, через который будет проходить большая часть тока цепи.

Для определения сопротивления шунта используют формулу: R_ш=R_А/(n-1)

• R_ш— сопротивление шунта [Ом];

• R_А – внутреннее сопротивление амперметра [Ом];

• n – число, показывающее во сколько раз необходимо увеличить предел измерения: n = I _{измеренное} / I _{номинальное}

Решить задачи.

1. Амперметр с пределом измерения 0,3 А имеет внутреннее сопротивление R_А=0,008 Ом. Определить сопротивление шунта, обеспечивающего расширение предела измерения до 1,5 А.

2. Вольтметр, рассчитанный на 30 В с внутренним сопротивлением

3 кОм используется для измерения напряжения величиной 210 В. Какое минимальное добавочное сопротивление необходимо подключить к вольтметру для расширения предела измерения до нужной величины?

3. Верхний предел измерения вольтметра 100 В, его внутреннее сопротивление 10000 Ом, шкала имеет 100 делений. Определить цену деления вольтметра, если он включён с добавочным сопротивлением 30000 Ом.

Практическое занятие №7.

«Расчёт обмотки трансформатора».

Цель работы: закрепить теоретические знания, полученные на уроке, путём решения задач.

Краткая теория.

Трансформатор—это статический (без подвижных частей) электромагнитный аппарат, который служит для преобразования переменного напряжения одной величины в переменное напряжение другой величины (понижения или повышения напряжения).

Принцип действия трансформатора основан на явлении электромагнитной индукции или на взаимоиндукции т.е. на возможности передавать энергию с помощью электромагнитного поля от одной обмотки к другой.

Устройство однофазного трансформатора:

1. магнитопровод — выполнен из листов трансформаторного железа, назначение, которого состоит в передаче электромагнитного поля от одной обмотки к другой;

2. первичная обмотка – подключается к источнику переменного тока;

3. вторичная обмотка — к ней подключается нагрузка. Если число витков во вторичной обмотке больше числа витков в первичной, то трансформатор – повышающий. Если меньше, то понижающий.

Коэффициент трансформации k —это отношение напряжения на вторичной обмотке U₂ к напряжению на первичной обмотке U₁:

k =U₂/ U₁= W₂/ W₁= ε₂/ ε₁= I₁/ I₂

• U₂; U₁ – напряжение во вторичной и первичной обмотках [В];

• W₂; W₁ – число витков во вторичной и первичной обмотках;

Решить задачи.

Вариант №1.

1. Как называется обмотка трансформатора, подключаемая к сети?

2. На какое количество витков необходимо уменьшить вторичную обмотку трансформатора, напряжение в которой 24В, чтобы получить напряжение 12 В. Первоначальное количество витков в ней составляло 33, а в первичной — 300 витков. Трансформатор подключён к сети 220 В.

Вариант №2.

1. Как называется трансформатор, у которого количество витков в первичной обмотке больше , чем во вторичной?

2. Определить длину вторичной обмотки трансформатора, если известно, что напряжение в ней составляет 36 В, сила тока – 0,2А. выполнена она из медного проводника сечением 0,1 мм² (ρ_меди= 1,7·10^-8 Ом·м).

Вариант №3.

1. Как называется трансформатор, у которого количество витков во — вторичной обмотке больше, чем в первичной?

2. На какое количество витков необходимо уменьшить вторичную обмотку трансформатора, напряжение в которой 36В, чтобы получить напряжение 9 В. Первоначальное количество витков в ней составляло 150, а в первичной — 500 витков. Трансформатор подключён к сети

220 В.

Вариант №4.

1. Как называется обмотка трансформатора, к которой подключен потребитель?

2. Рассчитать длину первичной обмотки однофазного трансформатора, подключенного к сети 220В и определить её сопротивление, если известно, что обмотка выполнена из медного проводника сечением 0,05 мм² (ρ_меди= 1,7·10^-8 Ом·м).

Практическое занятие №8.

«Изучение однофазного двигателя постоянного тока».

Цель работы: закрепить теоретические знания, полученные на уроке, путём решения задач.

Краткая теория.

Электрические машины служат для преобразования электрической энергии в механическую (двигатели) и преобразования механической энергии в электрическую (генераторы).

Принцип действия электрических машин основан на явлении электромагнитной индукции.

В режиме двигателя машина постоянного тока преобразует подводимую электрическую энергию в механическую энергию вращения вала. Конструктивная схема электрического двигателя аналогична схеме генератора и включает в себя те же основные узлы: статор, ротор и коллектор. Схемы включения обмоток возбуждения двигателя те же, что и для генератора. Они служат для создания постоянного магнитного потока, в котором вращается якорь, если в его обмотках течёт электрический ток.

Если к обмотке якоря приложить напряжение U, то в ней потечёт ток. Взаимодействие тока и магнитного потока создаст электромагнитный момент, который заставит якорь вращаться. Как только он начнёт вращаться (пересекать магнитное поле), в его обмотках наведётся ЭДС, создающая ток, направленный навстречу току от приложенного напряжения.

Суммарный ток в якоре определяется по формуле:

I_я = (U – E_я )/ Σ R_я

В момент пуска при n=0 пусковой ток I _я.п равен : I _я.п = U/ R_я

Для ограничения пускового тока на время пуска в якорную цепь вводят реостат. В этом случае: I_я.п = U/ ( R _я + R _п.р.)

В двигателе с последовательным возбуждением ток якоря I_я и ток возбуждения I_в один и тот же ток , следовательно, поток возбуждения пропорционален току якоря : Ф= к I_я. В этом случае вращающий момент пропорционален току якоря в квадрате:

М_вр =с_мФ_в I_я =к₁ I_я² ,

Т.е. плавное увеличение тока якоря ведёт к довольно резкому увеличению вращающего момента. В то же время: n = Е_я /с_еФ_в = k₂/ I_я.

Решить задачи.

1. Пусковой ток в двигателе постоянного тока с номинальным напряжением 120 В и пусковым реостатом с сопротивлением 2,1 Ом составил 50 А. Определить пусковой ток рои отсутствии пускового реостата.

2. Определить сопротивление пускового реостата, обеспечивающего пусковой ток в цепи якоря, равный 40 а, если напряжение питания 120 В. А сопротивление обмотки якоря 0,5 Ом.

Практическое занятие №9.

«Изучение вольт — амперной характеристики полупроводникового диода».

Цель работы: закрепить теоретические знания, полученные на уроке, путём решения задач.

Краткая теория.

Полупроводниковый диод- это элемент цепи, обладающий односторонней проводимостью (пропускает ток только одного направления).

Р-n — переход является основой полупроводниковых диодов, которые применяются для выпрямления переменного тока.

Наибольшее применение в полупроводниковой технике находят германий (Gе) и кремний (Si). Это четырехвалентные элементы, у которых на внешней оболочке имеется четыре электрона. Связь валентных электронов с ядром непрочная, и электроны под действием внешней энергии (температуры, электрического поля, освещенности) могут покидать свой атом, становясь свободными. Освободившееся место, называемое дыркой, может заполниться электроном с соседнего атома, а образовавшаяся там дырка в свою очередь заполняется соседним электроном и т.д.

Таким образом, полупроводниковые материалы способны к электронной и дырочной проводимости под действием внешнего поля.

Главным признаком полупроводниковых материалов является сильная зависимость их удельного сопротивления от примесей.

Если в кристаллическую решетки чистого германия или кремния ввести примесь пятивалентной сурьмы(Sb), то в кристалле германия или кремния появляются свободные электроны. Такой полупроводник будет обладать электронной проводимостью, и будет называться «полупроводник

n-типа»( negative).

Если в кристаллическую решетки чистого германия или кремния ввести примесь трехвалентного индия (In) или вольфрама (W), то одна ковалентная связь останется свободной и может заполняться электроном с соседнего атома, Дырку, образовавшуюся после ухода электрона, занимает другой электрон и т.д. Такой полупроводник будет обладать дырочной проводимостью, и будет называться «полупроводник р-типа»(positive).

При соединении двух полупроводников n – р – типов между ними образуется n – р- переход, ширина зоны которого зависит от величины и направления внешнего электрического поля.

Основным свойством n – р- перехода является односторонняя проводимость т.е. хорошо проводит ток прямого направления и практически не проводит ток обратного направления.

ВАХ – вольт — амперная характеристика – это график зависимости силы тока от напряжения f=I(U), состоит из двух ветвей прямой I_пр (возрастающей) и обратной I_обр (практически совпадающей с осью абсцисс).

Прямой ток велик, так как создан основными носителями заряда, а их очень много при подключении напряжения прямой полярности (направление внешнего поля противоположно направлению контактного поля, что уменьшает запирающий слой у границы раздела р — и n- областей) ширина двойного слоя уменьшается, и в цепи возникает большой прямой ток I_пр.

Обратный ток очень мал, так как создан неосновными носителями заряда при подключении напряжения обратной полярности (направление внешнего поля совпадает по направлению с контактным полем и вызывает рост запирающего слоя и не даёт возможности проходить основным носителям заряда через n – р- переход ).

Основные параметры полупроводникового диода:

Прямое и обратное статическое сопротивление диода:

R_пр = U_пр / I_пр R _обр = U_обр / I_обр.

Прямое и обратное дифференциальное сопротивление диода:

R_пр =ΔU_пр / I_пр R _обр = ΔU_обр / I_обр.

Решить задачи.

1. Назовите основное свойство n – р – перехода.

2. Изобразите вольт — амперную характеристику идеального диода.

3. В соответствии со справочными данными выпрямительный диод КД203А имеет при токе 5А прямое падение напряжения 0,4 В, а при обратном напряжении 400 В обратный ток составляет 100 мкА. Вычислить прямое и обратное сопротивление диода.

ЭЛЕКТРОТЕХНИКА решение задач Рассчитать простую электрическую цепь

ЭЛЕКТРОТЕХНИКА (решение задач)

Рассчитать простую электрическую цепь постоянного тока • Используя формулы последовательного и параллельного соединения резисторов схема сворачивается (находится общее сопротивление цепи) • Разворачивая в обратном порядке цепь находятся токи во всех ветвях, используя законы Ома

Рассчитать сложную электрическую цепь постоянного тока методом наложения или методом законов Кирхгофа • Метод наложения: схема разбивается на простые (по количеству источников ЭДС). Решается каждая из простых схем. Токи в ветвях находятся как геометрическая сумма токов простых схем • Метод законов Кирхгофа. По первому закону составляется (n 1, n – количество узлов в схеме) уравнение, по второму закону – недостающие. Решается система уравнений • Проверка решения – составление баланса мощностей

Рассчитать неразветвленную цепь переменного тока • 1. 2. 3. 4. 5. 6. Активное сопротивление катушки Rк = 6 Ом, индуктивное ХL = 10 Ом. Последовательно с катушкой включено активное сопротивление R = 2 Ом и конденсатор сопротивлением Хс = 4 Ом. К цепи приложено напряжение U = 50 В (действующее значение). Определить: 1) полное сопротивление цепи: 2) ток; 3) коэффициент мощности; 4) активную, реактивную и полную мощности; 5) напряжения на каждом сопротивлении. Начертите в масштабе векторную диаграмму цепи. Определяем полное сопротивление цепи Определяем ток Определяем коэффициент мощности цепи и угол: = 36 50´. Угол сдвига фаз находим по синусу во избежание потери знака угла Определяем активную мощность цепи (любая из формул) Определяем реактивную мощность цепи (любая из формул) Определяем полную мощность цепи (любая из формул)

Рассчитать неразветвленную цепь переменного тока 7. Определяем падения напряжения на сопротивлениях цепи 8. Построение векторной диаграммы начинаем с выбора масштаба для тока и напряжения. Задаемся масштабом по току: в 1 см — 1, 0 А и масштабом по напряжению: в 1 см — 10 В. Построение векторной диаграммы начинаем с вектора тока, который откладываем по горизонтали в масштабе. Вдоль вектора тока откладываем векторы падений напряжения на активных сопротивлениях Из конца вектора UR откладываем в сторону опережения вектора тока на 90º вектор падения напряжения UL на индуктивном сопротивлении Из конца вектора UL откладываем в сторону отставания от вектора тока на 90° вектор падения напряжения на конденсаторе UС Геометрическая сумма векторов равна полному напряжению U, приложенному к цепи

Рассчитать разветвленную цепь переменного тока • 1. 2. 3. 4. 5. Катушка с активным сопротивлением R = 6 Ом и индуктивным ХL 1 = 8 Ом соединена параллельно с конденсатором, емкостное сопротивление которого ХС = 10 Ом. Определить: 1) токи в ветвях и в неразветвленной части цепи; 2) активные к реактив ные мощности ветвей и всей цепи; 3) полную мощность цепи; 4) углы сдвига фаз между током и напряжением в каждой ветви и во всей цепи. Начертить в масштабе векторную диаграмму цепи. К цепи приложено напряжение U = 100 В Определяем токи в ветвях Углы сдвига фаз в ветвях находим по синусам углов во избежание потери знака угла Определяем косинусы угла Определяем активные и реактивные составляющие токов в ветвях Определяем ток в неразветвленной части цепи

Рассчитать разветвленную цепь переменного тока 6. Определяем коэффициент мощности всей цепи 7. Определяем активные и реактивные мощности ветвей и всей цепи 8. Определяем полную мощность цепи 9. Для построения векторной диаграммы задаемся масштабом со току: в 1 см — 2, 5 А и масштабом по напряжению: в 1 см — 25 В. Построение начинаем с вектора напряжения U. Под углом 1 к нему (в сторону отставания) откладываем в масштабе вектор тока I 1, под углом 2 (в сторону опережения) — вектор тока I 2. Геометрическая сумма этих токов равна току в неразветвленной части цепи. На диаграмме показаны также проекции векторов токов на вектор напряжения (активная составляющая Iа 1) и вектор, перпендикулярный ему (реактивные составляющие Iр1 и Iр2).

Рассчитать трехфазную цепь, соединенную звездой • 1. 2. 3. В трехфазную четырехпроводную сеть включили звездой несимметричную нагрузку: в фазу А — конденсатор с емкостным со противлением. ХА = 10 Ом; в фазу В — активное сопротивление RВ = 0 Ом и индуктивное ХВ = 6 Ом, в фазу С — активное сопротивление RС = 5 Ом. Линейное напряжение сети UН = 380 В. Определить фазные токи, начертить в масштабе векторную диаграмму цепи и найти графически ток в нулевом проводе Определяем фазные напряжения установки Находим фазные токи Для построения векторной диаграммы выбираем масштабы по току: 1 см — 10 А и по напряжению: 1 см — 100 В. Построение диаграммы начинаем с векторов фазных напряжений UА, UВ, UС, располагая их под углом 120º друг относительно друга. Ток IА опережает напряжение UА на угол 90 º; ток IВ отстает от напряжения UВ на угол В, который определяется из выражения: . Ток IС совпадает с напряжением UС. Ток в нулевом проводе равен геометрической сумме трех фазных токов. Измеряя длину вектора тока I 0, которая сказалась равной 6, 8 см. находим ток I 0 = 68 А

Рассчитать трехфазную цепь, соединенную треугольником • 1. 2. 3. В трехфазную сеть включили треугольником несимметричную нагрузку : в фазу AВ — конденсатор с емкостным сопротивлением ХАВ = 10 Ом; в фазу ВС— катушку с активным сопро тивлением R = 4 Ом и индуктивным Х ВС = 3 ВС Ом; в фазу СА — активное сопротивление R СА = 10 Ом. Линейное напряжение сети U Н = 220 В. Определить фазные токи, углы сдвига фаз и начертить в масштабе векторную диаграмму цепи. По векторной диаграмме определить числовые значения линейных токов. Определяем фазные токи и углы сдвига фаз Для построения векторной диаграммы выбираем масштабы по току: 1 см — 10 А и по напряжению: 1 см — 80 В. Затем в принятом масштабе откладываем векторы фазных (они же линейные) напряжений U АВ, UВС, UСА под углом 120º друг относительно друга. Под углом АВ = — 90° к вектору напряжения U АВ откладываем вектор тока IАВ; в фазе ВС вектор тока IВС должен отставать от вектора напряже ния U на угол ВС ВС = 36° 50´, а в фазе СА вектор тока I СА совладает с вектором напряжения UСА. Затем строим векторы линейных токов на основании известных уравнений Измеряя длины векторов линейных токов и пользуясь принятым масштабом, находим значения линейных токов: IА = 11 А, IВ = 57 А, IС = 47 А

Рассчитать добавочные сопротивления к многопредельному вольтметру • Предел измерения вольтметра электромагнитной системы составляет 7, 5 В при внутреннем сопротивлении Rв = 200 Ом. Определить добавочное сопротивление, которое необходимо включить для расширения предела измерения до 600 В. • Решение:

Рассчитать емкость или индуктивность с помощью авометра и источников постоянного и переменного токов • • Для расчета емкости необходим источник питания переменного тока с известной частотой (измеряются напряжение, ток) Для расчета индуктивности необходимы оба источника (измеряются напряжение, ток). Если источник постоянного тока – определяем активное сопротивление катушки, если источник переменного тока – полное сопротивление катушки

Рассчитать шунт и проверить амперметр • Предел измерения микроамперметра на 150 мк. А должен быть расширен до 15 А. Определить сопротивление шунта, если внутреннее его сопротивление RА = 400 А. • Решение: