Построение векторных диаграмм | FaultAn.ru

Задание исходных данных

Для построения векторной диаграммы необходимо задать напряжения и токи в полярной форме. Для этого предусмотрены соответствующие поля (рис. 1). Угол напряжений и токов задаётся в градусах.

Рис. 1. Задание исходных данных

Для построения векторной диаграммы только для токов либо только для напряжений, необходимо выбрать соответствующие параметры чекбоксов (рис. 2).

Рис. 2. Выбор данных для отображения

После задания всех параметров необходимо нажать кнопку «Построить», в результате чего будет отображена векторная диаграмма для заданных величин (рис. 3). Все величины отображаются в относительных единицах. За базисную величину для напряжений и для токов берутся максимальное из трёх заданных напряжений и токов соответственно.

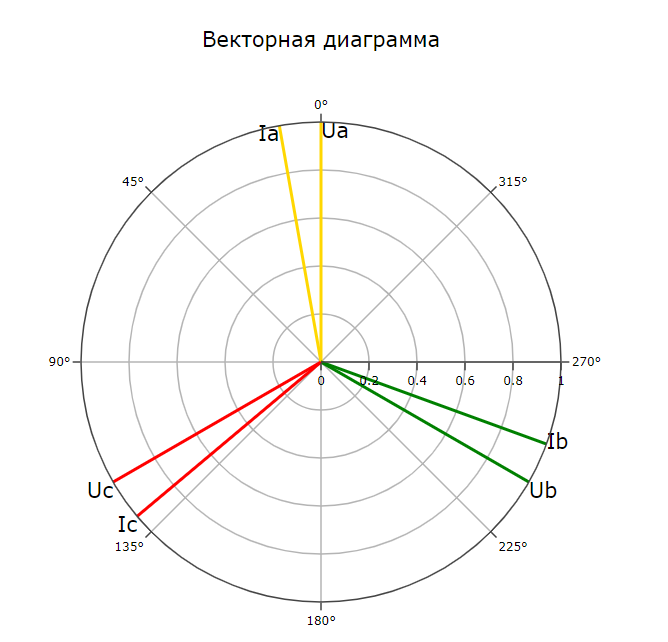
Рис. 3. Векторная диаграмма

Выбор базового вектора

При построении векторной диаграммы доступен выбор базового вектора (рис. 4). При выборе вектора базовым его угол принимается равным 0°, а углы остальных векторов отсчитываются относительно него.

Рис. 4. Выбор базового вектора

В выпадающем списке появляются только те данные, которые выбраны для отображения чекбоксами (рис. 2). Более подробно про выбор базового вектора можете прочитать здесь.

Инструменты

Для векторной диаграммы доступны инструменты для анализа: увеличение/уменьшение графика, отображение значений. Полученные результаты можно экспортировать в рисунок в формате png.

правила построения диаграмм, онлайн построение

В целом, для лучшего понимания процедур, происходящих в радиотехнических цепях, их взаимосвязи между собой, бывает недостаточно оперировать характеристиками и параметрами данной цепи, имеющими цифровое отображение. В связи с тем, что основная масса цепей характеризуется переменными значениями приложенного напряжения и протекающего тока, являющимися синусоидальными функциями времени, то исчерпывающий ответ по состоянию цепи может дать ее графическая презентация посредством векторной гистограммы.

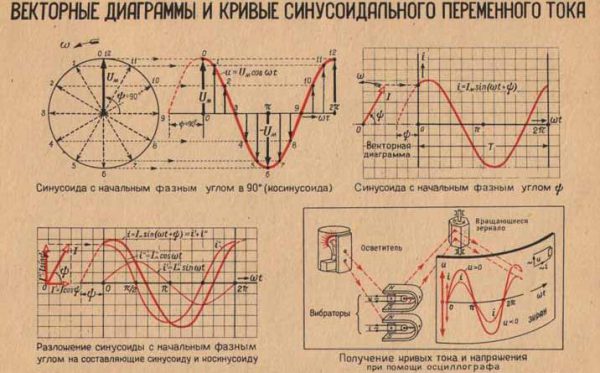
Векторная диаграмма напряжений и токов

Разновидности векторных диаграмм

Любую характеристику электротехнической цепи, изменяющуюся по синусоидальному или косинусоидальному принципу, можно отобразить посредством точки на поверхности, в соответствующей системе величин. В качестве размерности по оси Х выступает действительный компонент параметра, по оси Y размещается воображаемая составляющая. Именно такие составляющие входят в алгебраическую модель записи комплексной величины. Последующее соединение точки на поверхности и нулевой точки системы координат позволит рассматривать эту прямую и ее угол с действительной осью как изображение комплексного числа. На практике положительно направленный отрезок принято называть вектором.

Векторной диаграммой принято называть множество положительно направленных отрезков на комплексной поверхности, которая соответствует комплексным значениям и параметрам гальванической цепи и их взаимосвязям. По своему характеру векторные диаграммы подразделяются на:

• Точные гистограммы;
• Качественные гистограммы.

Особенностями достоверных гистограмм является соблюдение пропорций всех характеристик и параметров, полученных путем вычислений. Данные диаграммы находят свое применение в проверке ранее проведенных расчетов. В основе использования качественных гистограмм лежит учет взаимного влияния характеристик друг на друга, и в основном они предшествуют расчетам либо заменяют их.

Векторные диаграммы токов и напряжений визуально отображают процесс достижения цели по расчету электротехнической цепи. При соблюдении всех правил по построению векторных отрезков можно просто из гистограммы установить фазы и амплитуды вещественных характеристик. Построение качественных гистограмм поможет контролировать правильный процесс решения задачи и с легкостью определить сектор с определяемыми векторами. В зависимости от особенностей построения, графические диаграммы делятся на такие типы:

1. Круговая диаграмма, представляющая собой графическую гистограмму, образованную вектором, описывающим своим концом круг или полукруг, при любых изменениях характеристик цепи;
2. Линейная диаграмма, представляющая собой графический рисунок в виде прямой линии, образованной вектором, посредством изменения характеристик цепи.

Построение векторной диаграммы напряжений и токов

Для лучшего понимания того, как построить векторную диаграмму токов и напряжений, следует рассматривать RLC цепь, состоящую из пассивного элемента в виде резистора и реактивных элементов в виде катушки индуктивности и конденсатора.

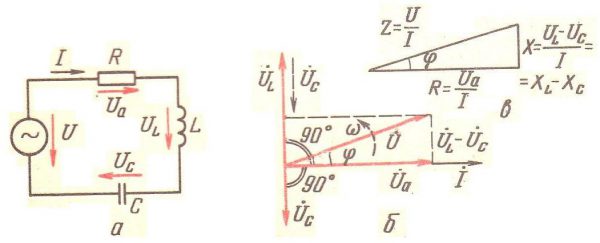
Схема цепи с последовательным соединением элементов

Перед тем, как построить векторную диаграмму токов и напряжений, необходимо охарактеризовать все известные параметры цепи. Согласно схемы цепи, изображенной на картинке а:

• U – величина переменного напряжения в текущий момент времени;
• I – мощность тока в заданный момент времени;
• UА – напряжение, падающее на активном сопротивлении;
• UC – напряжение, падающее на емкостной нагрузке;
• UL – напряжение, падающее на индуктивной нагрузке.

Поскольку входное напряжение U изменяется по колебательному закону, то сила тока характеризуется уравнением:

I=Im*cosωt, где:

• Im – максимальная амплитуда тока;
• ω – частота тока;
• t – время.

Суммарное входное напряжение, в соответствии со вторым законом Кирхгофа, равно общей величине напряжений на всех элементах цепи:

U=UC+UL+UA.

В соответствии с законом Ома, падение напряжения на резистивном компоненте равняется:

UA= Im*R*cosωt.

Противодействие току активного элемента зависит сугубо от свойства проводника и не обуславливается ни характеристиками тока, ни аспектом времени и, соответственно, имеет идентичный с напряжением фазовый сдвиг.

Поскольку конденсатору в цепи с электротоком, изменяющимся по синусоиде, свойственно наличие реактивного емкостного сопротивления, и ввиду того, что напряжение на нем постоянно имеет фазовое отставание от протекающего тока на π/2, то уместно выражение:

1. RC=XC=1/ωC;
2. UC=Im*RС*cos(ωt-π/2), где:

• RC – сопротивление конденсатора;
• XC – реактивный импеданс конденсатора;
• C – емкость конденсатора.

Реактивное индуктивное сопротивление катушки индуктивности обуславливается наличием изменяющегося по синусоидальному закону электротока, и поскольку напряжение на любом отрезке времени имеет фазовое опережение по отношению к электротоку на π/2, то формула, описывающая колебательный процесс на элементе, выглядит как:

1. RL=XL=ωL;
2. UL=Im*RL*cos(ωt+π/2), где:

• RL – сопротивление катушки индуктивности;
• XL – реактивный импеданс катушки индуктивности;
• L – индуктивность катушки.

Следовательно, общее напряжение, подведенное к цепи, выглядит:

U=Um*cos(ωt±φ), где:

• Um – максимальная величина напряжения;
• φ – фазовый сдвиг.

Ввиду того, что напряжение и электроток изменяются по синусоидальному закону, и их фиксированные показатели отличаются лишь фазовым сдвигом, то данные величины строятся как вектора.

В соответствии с законом сохранения электрического заряда, в любой момент времени сила протекающего тока одинакова, то целесообразно сформировать векторную гистограмму токов.

Векторная диаграмма токов и напряжений RLC цепочке

Пусть по оси Х отображается амплитудное значение электротока в цепочке. Поскольку напряжение и электроток на резисторе имеют одинаковый фазовый сдвиг, то вектора данных характеристик будут ориентированы в одну сторону, согласно картинке а.

Напряжение на емкостной нагрузке отстает от электрического тока на π/2, и его вектор будет направлен под прямым углом вниз, перпендикулярно напряжению активного сопротивления, согласно картинке в.

Напряжение на индуктивной нагрузке опережает электрический ток на π/2, и ее вектор будет ориентирован под прямым углом вверх, перпендикулярно напряжению на активном сопротивлении, согласно картинке б.

Для наглядности векторных преобразований пусть UL>UС. Сложив вектора напряжений на реактивных компонентах, получаем, что вектор UL-UС будет направлен перпендикулярно вверх. Суммировав вектора разности напряжений на реактивных компонентах и напряжения на сопротивлении получаем вектор, характеризующий дисперсное значение общего напряжения, согласно картинке 2(б).

Аналогично электрическому току, изменяющемуся по синусоидальному закону, напряжение меняется по такому же закону, однако с некоторым фазовым сдвигом. Наблюдается постоянный фазовый сдвиг между напряжением и током.

После простых преобразований по постулату Ома, уравнение полного импеданса заданной электрической цепи выглядит как:

Z=√R2+(1/ωC- ωL)2.

Векторная гистограмма общего и реактивных сопротивлений изображена на картинке 2в.

Построение векторных диаграмм токов и напряжений может значительно упростить процесс расчета характеристик контура. Вместе с тем сама процедура позволит наглядно видеть поведение исследуемых характеристик, в зависимости от входных величин. При большом объеме вычислительных операций целесообразно воспользоваться одной из онлайн программ по построению векторных графиков.

Видео

Оцените статью:

Построение векторных диаграмм токов и напряжений — Студопедия

Порядок построения векторных диаграмм рассмотрен для случая с исправным нулевым проводом. Векторные диаграммы напряжений и токов даны на рисунках 15 и 16; на рисунке 17 дана совмещенная диаграмма токов и напряжений

1. Строятся оси комплексной плоскости: действительных величин (+1) – горизонтально, мнимых величин (j) – вертикально.

2. Исходя из значений модулей токов и напряжений и размеров полей листов, отведеных для построения диаграмм, выбираются масштабы тока mI и напряжения mU. При использовании формата А4 (размеры 210х297 мм) при наибольших модулях (см. табл. 8) тока 54 А и напряжения 433 В приняты масштабы: mI = 5 А/см, mU = 50 В/см.

3. С учетом принятых масштабов mI и mU определяется длина каждого вектора, если диаграмма строится с использованием показательной формы его записи; при использовании алгебраической формы находятся длины проекций векторов на оси действительных и мнимых величин, т.е. длины действительной и мнимой частей комплекса.

Например, для фазы А:

— длина вектора тока / 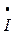ф.А / = 34,8 А/ 5 А/см = 6,96 см; длина его действительной части

I 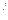ф.А = 30 А/ 5 А/см = 6 см,

длина его мнимой части

I 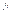ф.А = -17,8 А/5 А/см = — 3,56 см;

— длина вектора напряжения / 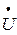А нагр./ = 348 В/ 50 В/см = 6,96 см; длина его действительной части

U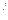

А нагр. = 340,5 В/ 50 В/см = 6,8 см;

длина его мнимой части

U 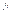Анагр. = 37,75 В/ 50 В/см = 0,76 см.

Результаты определения длин векторов, их действительных и мнимых частей отражены в таблице 9.

Таблица 9 — Длины векторов тока и напряжения, их действительных и мнимых частей для случая неповрежденного нулевого провода.

Величина	Масштаб, 1/см	Длина вектора, см	Длина действительной части, см	Длина мнимой части, см
Напряжения фаз сети	U А	50 В/см	7,6	7,6
UВ	7,6	— 3,8	— 6,56
UС	7,6	— 3,8	6,56
Напряжения фаз нагрузки	U Анагр.	50 В/см	6,96	6,8	0,76
UВ нагр.	7,4	— 4,59	— 5,8
UС нагр.	8,66	-4,59	7,32
U0	1,08	0,79	— 0,76

Продолжение таблицы 9

Токи фаз нагрузки	I ф.А	5 А/см	6,96	6.0	— 3,56
I ф.В	7,4	1,87	— 7,14
I ф.С	3,13	0,1	3,12
I 0	10,8	7,9	— 7,6

4. Построение векторной диаграммы напряжений.

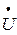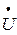4.1 На комплексной плоскости строятся векторы фазных напряжений питающей сети А, В, 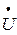С; соединив их концы, получают векторы линейных напряжений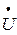

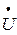АВ, ВС, 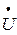СА. Затем строятся векторы фазных напряжений нагрузки 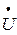А нагр., 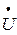В нагр., 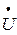С нагр. Для их построения можно использовать обе формы записи комплексов токов и напряжений.

Например, вектор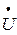

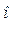А нагр. строится по показательной форме следующим образом: от оси +1 под углом 6 10 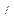, т.е. против часовой стрелки, откладывается отрезок длиной 6,96 см; по алгебраической форме его можно построить, отложив по оси +1 отрезок длиной 6,81 см, а по оси + j отрезок длиной 0,76 см, концы этих отрезков являются координатами конца вектора 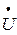А нагр.

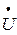4.2 Т.к. линейные напряжения нагрузки заданы питающей сетью, для определения положения нейтрали нагрузки необходимо выполнить параллельный перенос векторов фазных напряжений нагрузки А нагр., 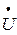В нагр., 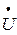С нагр. так, чтобы их концы совпали с концами фазных напряжений питающей сети.

Точка 0, в которой окажутся их начала, есть нейтраль нагрузки. В этой точке находится конец вектора напряжения смещения нейтрали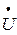

0, его начало расположено в точке 0. Этот вектор можно также построить, используя данные таблицы 9.

5. Построение векторной диаграммы токов.

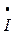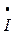5.1 Построение векторов фазных токов нагрузки ф.А, ф.В, 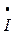ф.С подобно построению векторов фазных напряжений.

5.2 Сложением векторов фазных токов находится вектор тока в нулевом проводе 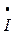0; его длина и длины его проекций на оси должны совпасть с указанными в таблице 8.

Векторные диаграммы токов и напряжений для случая обрыва нулевого провода строятся аналогично.

Следует выполнить анализ результатов расчета и построения векторных диаграмм и сделать выводы о влиянии несимметрии нагрузки на величину ее фазных напряжений и на напряжение нейтрали; особое внимание необходимо обратить на последствия обрыва нулевого провода сети при несимметричной нагрузке.

Примечание. Допускается совмещение диаграмм токов и напряжений при условии их выполнения разными цветами.

Рисунок 15. Векторная диаграмма напряжений

Рисунок 16. Векторная диаграмма токов.

Рисунок 17. Совмещенная векторная диаграмма напряжений и токов.

Как построить векторную диаграмму трансформатора тока

В этой статье будем строить схему замещения трансформатора тока и векторную диаграмму. Начнем со схемы замещения. Как и на векторной диаграмме, все величины мы приводим к вторичному току. Величины токов приводятся через коэффициент трансформации в первой степени, значения сопротивлений – через коэффициент трансформации в квадрате.

Первичный ток разделяется на ветвь тока намагничивания и ветвь вторичного тока.

Теперь, на основе этой схемы замещения можно построить векторную диаграмму.

Для начала строим из начала координат вектор вторичного тока I₂ и его активную составляющую I₂*R_н. Затем из конца вектора I₂*R_н откладываем на 90 градусов вектор I₂*Х_н. Сумма двух векторов будет равна U₂, т.е.:

U₂= I₂(R_н+jX_н)

Или другими словами – вторичное напряжение равно падению напряжения в сопротивлении нагрузки. Далее аналогично откладываем вектора I₂*R₂ и I₂*X₂. В итоге получим вектор ЭДС E₂

E₂=I₂(Z_н+Z₂)

Вектор между вторичным током I₂ его ЭДС E₂ обозначим «альфа». Его величина зависит от отношения активных и индуктивных сопротивлений вторичной цепи:

tg«альфа»= (R₂+ R_н)/(X₂+X_н)

Из вводной статьи про трансформаторы тока мы узнали, что первичный ток I’₁ состоит из тока намагничивания I_нам и вторичного тока I₂.

Угол между током намагничивания и ЭДС зависит от активных потерь в стали сердечника. Чем больше угол, тем меньше потери. Более подробно про углы на векторной диаграмме можно почитать в статье про погрешности в трансформаторах тока.

Угол гамма называется углом потерь и показывает отношение активной составляющей тока намагничивания к реактивной. Угол потерь определяют по экспериментальной кривой, которую снимают для конкретного трансформатора тока.

Сохраните в закладки или поделитесь с друзьями

---

---

Последние статьи

---

Самое популярное

Полезные сервисы

---

Векторные диаграммы — Студопедия

В цепях переменного тока все токи и напряжения являются синусоидальными функциями времени. Поэтому аналитические зависимости в виде уравнений не дают представления о реальных соотношениях величин. При переходе от оригиналов функций и параметров к их изображениям в виде комплексных чисел задача анализа несущественно упрощается, т.к., в отличие от цепей постоянного тока, где все величины однозначно характеризуются одним числом, в области изображений каждая величина определяется двумя числами, каждое из которых в общем случае недостаточно для полной оценки состояния цепи. Помочь в анализе соотношений между величинами и параметрами электрический цепи может их геометрическое представление в виде векторной диаграммы.

Из курса математики известно, что любое комплексное число может быть изображено в виде точки на плоскости с ортогональной системой координат, в которой на оси абсцисс откладывается вещественная составляющая, а на оси ординат мнимая. Такое изображение соответствует алгебраической форме записи комплексного числа. Если начало координат соединить отрезком прямой с точкой изображающей комплексное число, то длина этого отрезка и его угол с вещественной осью также могут служить изображением комплексного числа. Причем, для однозначного определения угла нужно задать положительное направление отрезка, т.е. определить его как радиус-векторили просто вектор.

Векторной диаграммой называется совокупность векторов на комплексной плоскости, соответствующая комплексным величинам и/или параметрам электрической цепи и их связям.

Векторные диаграммы могут быть точными и качественными. Точные диаграммы строятся с соблюдением масштабов всех величин по результатам численного анализа. Они предназначены в основном для проверки расчетов. Качественные векторные диаграммы строятся с учетом взаимных связей между величинами и обычно предшествуют расчету или заменяют его. В качественных диаграммах масштаб изображения и конкретные значения величин несущественны, важно только, чтобы в них были правильно отражены все связи между величинами, соответствующие связям и параметрам элементов электрической цепи. Качественные диаграммы являются важнейшим инструментом анализа цепей переменного тока.

В цепях переменного тока одной из самых распространенных задач является анализ поведения цепи при изменении в широких пределах какой-либо величины или параметра.

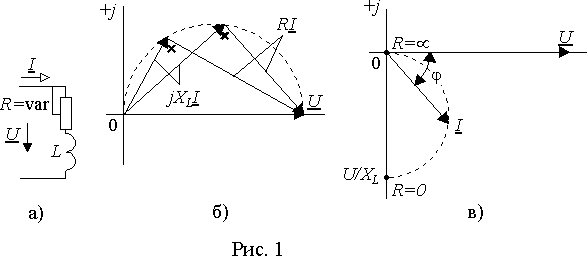
Пусть, например, требуется исследовать изменение тока в цепи, представленной на рис. 1 а), при постоянном напряжении на входе и изменении резистивного сопротивления в пределах 0 > R > µ .

Падение напряжения на входе уравновешивается суммой падений напряжения на R и L, т.е. u = u_R+u_L = Ri + Ldi/dt или для изображений

U = UR + UL = RI + jw LI = RI + jXLI.

(1)

Из выражения (1) следует, что

• векторы U_R и U_L всегда перпендикулярны друг другу, т.к. каждый из них представляет собой вектор тока I, умноженный на соответствующую константу (R или X_L), а в падении напряжения U_L присутствует в качестве множителя оператор поворота на 90° — j;
• сумма векторов U_R и U_L постоянная и равна вектору U .

Для упрощения построений, не ограничивая в то же время общности рассуждений, совместим вектор U с вещественной осью (рис. 1 б)). Тогда в соответствии с условиями (1) при любых значениях R векторы U_R и U_L будут составлять с вектором U прямоугольные треугольники. Как известно, любой треугольник может быть вписан в окружность, причем дуги, на которые опираются углы вписанного треугольника равны двойному значению угла. Так как во всех векторных треугольниках угол между U_R и U_L равен 90° , то все они опираются на дугу в 180° , т.е. на диаметр, которым является постоянный вектор входного напряжения U. Следовательно, все треугольники векторов U_R , U_L и U вписываются в одну и ту же полуокружность, которая является геометрическим местом точек перемещения конца вектора U_R при всех изменениях значения R.

Векторная диаграмма, в которой при вариации параметров геометрическим местом точек перемещения конца какого-либо вектора является окружность или полуокружность, называется круговой диаграммой.

Так как векторы U_R и U_L связаны с вектором тока I постоянными коэффициентами, то из круговой диаграммы вектора U_R можно получить векторную диаграмму тока и она также будет круговой. Для получения вектора I, в соответствии с выражением (1), достаточно разделить все элементы треугольников U_R , U_L и U на R или jX_L. При этом мы получим подобный треугольник, одним из катетов которого будет I. Однако деление на R нецелесообразно, т.к. эта величина переменная и для сохранения масштаба треугольников следует произвести деление на jX_L. В результате диаметр полуокружности станет равным U/X_L и она вследствие деления на оператор поворота j повернется относительно начала координат на угол — 90° (рис. 1 в)). Полученная полуокружность и будет круговой диаграммой вектора входного тока I. Из нее можно заключить, что при R = 0 вектор тока отстает от напряжения на 90° и по модулю равен U/X_L. При R ® µ модуль и аргумент вектора тока стремятся к нулю.

Другой важной разновидностью векторных диаграмм являются линейные диаграммы.

Линейной диаграммой называется векторная диаграмма, в которой геометрическим местом точек конца какого-либо вектора при вариации параметра является прямая линия.

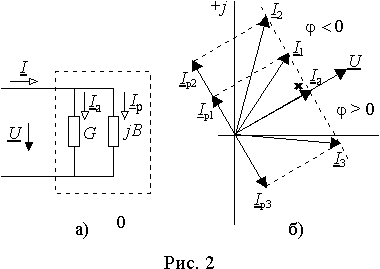Примером такой диаграммы может служить диаграмма входного тока I пассивного двухполюсника при постоянном напряжении на входе U=const и изменении его реактивной проводимости в пределах — µ > B > +µ , если активная составляющая проводимости G остается постоянной. Примером электрической цепи с такой вариацией реактивной проводимости является параллельный резонансный контур при вариации частоты 0 < w <µ .

Действительно, активная составляющая тока любого двухполюсника равна I_а=GU, а реактивная I_р=jBU, т.е. эти составляющие всегда перпендикулярны друг другу или, иначе говоря, находятся в квадратуре, т.к. являются производными от одного и того же вектора U, но I_р содержит оператор поворота на 90° — j. Входной ток представляет собой сумму активной и реактивной составляющих I = I_а+ I_р, причем, активная составляющая отличается от вектора U постоянным вещественным множителем G, поэтому всегда совпадает с ним по фазе (рис. 2 б)) и имеет постоянный модуль. Вектор реактивной составляющей имеет переменный модуль — µ < | I_р| < + µ и I_а ^ I_р , следовательно, он будет располагаться на прямой проходящей через начало координат перпендикулярно вектору U . Поэтому суммарный вектор входного тока I при изменении реактивной проводимости будет скользить своим концом по линии перпендикулярной векторам I_а и U и проходящей через конец вектора I_а.

Для качественного анализа электромагнитных процессов в электрической цепи переменного тока можно строить векторные диаграммы, пользуясь только принципиальной схемой.

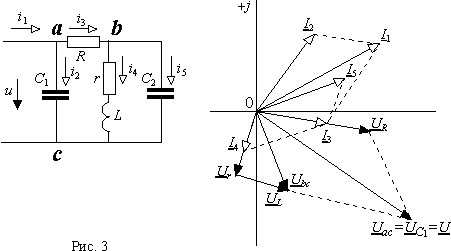Построим качественную векторную диаграмму для цепи рис. 3.

Построение всегда можно начинать с произвольно выбранной величины, но т.к. операции суммирования векторов производятся проще, чем операции разложения на составляющие, то лучше в качестве начального вектора выбирать напряжение или ток элемента цепи, расположенного как можно дальше от входа. Тогда входные величины будут получены постепенным сложением векторов.

Пусть вектор тока I₅ расположен так, как это показано на рис. 3. Ток I₅ протекает в емкости C₂, подключенной к узлам b и c цепи. Поэтому U_bc=U_C2. Но падение напряжения на емкости отстает от тока в ней на 90° , следовательно, U_bc нужно расположить на луче перпендикулярном вектору I₅ и смещенном в сторону отставания, т.е. по часовой стрелке.

Между узлами b и c помимо емкости C₂ включена ветвь, содержащая резистор r и индуктивность L. Ток в активно-резистивном двухполюснике отстает от напряжения на некоторый угол j , конкретное значение которого определяется отношением индуктивного сопротивления w L к резистивному r. Поэтому конец вектора тока I₄ в r—L ветви рис. 3 может находиться в любой точке сектора комплексной плоскости в 90° , ограниченного лучом совпадающим по направлению с U_bc и перпендикулярным ему лучом, смещенным в сторону отставания. Зададим произвольно точку конца вектора I₄ в этом секторе. Тогда падение напряжения на резисторе r должно совпадать по направлению с I₄, а падение напряжение на индуктивности L — опережать I₄ на 90°, причем в сумме U_r и U_L должны быть равны U_bc. Построение векторов U_r и U_L, удовлетворяющих этим условиям, проще всего произвести проектированием конца вектора U_bc на направление вектора I₄. Тогда вектор, совпадающий с I₄ по направлению, будет U_r, а перпендикулярный ему — U_L.

Уравнение Кирхгофа для узла b цепи можно записать в виде I₃ = I₄ + I₅, поэтому сложение векторов I₄ и I₅ по правилу параллелограмма даст нам вектор тока I₃, протекающего в резисторе R рис. 3. Падение напряжения на нем U_R = U_ab, как у любого резистора, будет совпадать по фазе с током, следовательно, его можно построить на луче совпадающем по направлению с I₃.

По второму закону Кирхгофа разность потенциалов U_ac можно представить суммой U_ac = U_ab+ U_bc = U. Соответственно, вектор входного напряжения U получается сложением по правилу параллелограмма векторов U_ab и U_bc рис. 3. Но U_ac= U_С1. Следовательно, ток в емкости C₁ должен опережать напряжение U_ac на 90° , поэтому его нужно построить на луче перпендикулярном U_ac и смещенном в сторону опережения.

Для узла a цепи справедливо I₁ = I₂ + I₃. В соответствии с этим равенством входной ток I₁ получен геометрическим суммированием векторов I₂ и I₃.

Порядок построения векторной диаграммы

Пост­роение векторной диаграммы начинают с выбора масштаба для напря­жения и токов

(в контрольной работе эти масштабы вам заданы).Пусть m _U = 55 В / см и m _I = 10 А / см

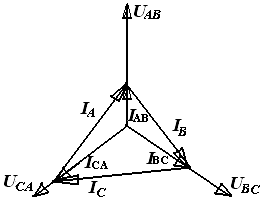
Из точки 0 проводим три вектора фазных напряжений U_АВ, U_ВС, U_СА, между которыми 120° (эти углы строят с макси­мальной точностью, используя циркуль или транспортир). В выбранном масштабе их длина будет L_UФ =U_Ф / m _U = 220 В / 55 (В / см)=4 см

Следует иметь ввиду, что эти векторы напряжений одновре­менно являются и векторами линейных напряжений.

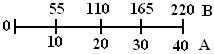
Нагрузка Фаз активная (электрические лампы накаливания обла­дают активным сопротивлением), поэтому токи I_АВ , I_ВС, I_СА будут совпадать по фазе с соответствующими фазными напряжениями, В выбранном масштабе их длина будет:

L_IAВ =I_АВ / m _I = 10 А / 10 (A / см) = 4 см

L_IСВ =I_ВС / m _I = 20 А / 10 (A / см) = 2 см

L_IСА =I_СА / m _I = 30 А / 10 (A / см) = 3 см

Соединив концы векторов фазных токов, получим треугольник линейных токов I_А , I_В, I_С, направление этих векторов совпа­дает с обходом по часовой стрелке. Возможны и другие способы изображения линейных токов (см. их в учебной литературе). Измерив длину линейных токов и учитывая масштаб, определяем их значение

I_А = m _I ·L_IA = 10 (A / см) ·3,5 см = 36 А

I_В = m _I ·L_IВ = 10 (A / см) · 2,6 см = 26 А

I_С = m _I ·L_IС = 10 (A / см) · 4,4 см = 44 А

4.5. Задания контрольной работе Задачи вариантов 1 -10

В четырехпроводную сеть трехфазного тока /рис.1/ включены по схеме «звезда» три группы электрических ламп накаливания оди­наковой мощности. В каждой, фазе /группе/ лампы соединены парал­лельно.

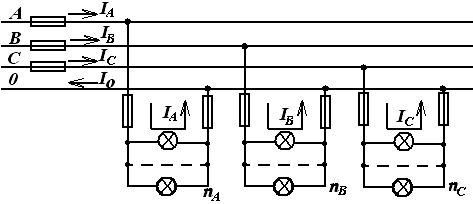Рис. 1

Известны:

U_Л (U_АВ, U_ВС, U_СА) — -линейные напряжения;

Рламр. — мощность одной лампы;

п_А, п_в п_с — число ламп в каждой фазе /группе/.

Определить:

U_Ф (U_А, U_В, U_С) — Фазные напряжения /на эти напряжения рассчитаны все включенные в сеть лампы накалива­ния/;

I_А, I_В, I_С — Фазные (они же линейные) токи.

Рф (Ра , Р_В, Рс) — мощности, потребляемые каждой фазой /группой ламп/.

Р — мощность, потребляемую цепью /всеми лампами/.

Построить в заданных масштабах m _U , m _I векторную диаграм­му напряжений и токов и из нее графически определить величину то­ка в нулевом проводе I₀.

Данные для своего варианта взять из таблицы.

Известная величина	I	2	3	4	5	6	7	8	9	10
UЛ ,В	380	220	380	220	380	220	380	220	380	270
Р гламп , Вт	40	100	500	60	200	25	100	40	75	150
пА, шт	44	42	11	17	66	36	22	54	50	44
пв шт	44	42	22	51	22	142	66	100	12	11
пс шт	88	14	33	51	44	36	88	54	12	11
m I А/см	4	11	25	8	20	7	10	8,5	4	13
m U В/см	44	25,4	55	25,4	55	25,4	44	25,4	44	25,4

Указание. При определении фазных токов полученные расчеты округлите до целой величины.

Как я могу построить векторные диаграммы? + Пример

физика

Наука

• Анатомия и физиология
• астрономия
• астрофизика
• Биология
• Химия
• наука о планете Земля
• Наука об окружающей среде
• Органическая химия
• физика

математический

• Алгебра
• Исчисление
• Геометрия

.

python — Создание векторной диаграммы ветра

Переполнение стека

1. Около
2. Товары
3. Для команд

1. Переполнение стека Общественные вопросы и ответы
2. Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
3. работы Программирование и связанные с ним технические возможности карьерного роста
4. Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
5. реклама Обратитесь к разработчикам и технологам со всего мира

.

Как нарисовать векторные диаграммы скорости?

физика

Наука

• Анатомия и физиология
• астрономия
• астрофизика
• Биология
• Химия
• наука о планете Земля
• Наука об окружающей среде
• Органическая химия
• физика

математический

.

chisel — Как создать вектор вектора, когда я определяю IO

Переполнение стека

1. Около
2. Товары
3. Для команд

1. Переполнение стека Общественные вопросы и ответы
2. Переполнение стека для команд Где разработчики и технологи делятся частными знаниями с коллегами
3. работы Программирование и связанные с ним технические возможности карьерного роста
4. Талант Нанимайте технических специалистов и создавайте свой бренд работодателя
5. реклама Обратитесь к разработчикам и технологам со всего мира
6. О компании

,