Векторные диаграммы. Построение векторных диаграмм


При расчете электрических цепей переменного тока пользуются весьма простым и наглядным способом графического изображения синусоидальных величин при помощи вращающихся векторов.
Обоснование векторной диаграммы
Предположим, что ток задан уравнением
i = Imsin(ωt +Ψ)
Проведем две взаимно перпендикулярные оси и из точки пересечения осей проведем вектор Im, длина которого в определённом масштабе Mi выражает амплитуду тока Im:
Im = Im/Mi
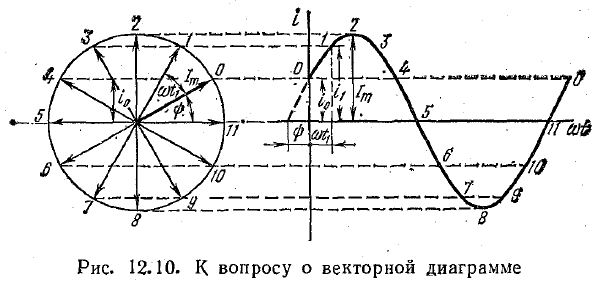

Направление вектора выберем так, чтобы с положительным направлением горизонтальной оси вектор составлял угол, равный начальной фазе Ψ (рис. 12.10).
Проекция этого вектора на вертикальную ось определяет мгновенный ток в начальный момент времени: i0 = ImsinΨ.
Представим себе, что вектор Im вращается против движения часовой стрелки с угловой скоростью, равной угловой частоте ω. Его положение в любой момент времени определяется углом ωt +Ψ ,
Тогда мгновенный ток для произвольного момента времени t можно определить проекцией вектора Im на вертикальную ось в этот момент времени.
Следующая статья сложение и вычитания векторов векторной диаграммы.
Например, для t = t1
i1 = Imsin(ωt1 +Ψ)
в общем случае
i = Imsin(ωt +Ψ)
Получили такое же уравнение, каким был задан переменный ток, что свидетельствует о возможности изображения тока вращающимся вектором при нанесении его на чертеж в начальном положении.
Построение векторной диаграммы
Вращая вектор Im‘ против движения часовой стрелки, в прямоугольной системе координат построим график изменения проекции его на вертикальную ось в пределах одного оборота (одного периода). Получим известный уже график синусоидальной функции, соответствующий заданному уравнению.
При построении векторов положительные углы отсчитывают от положительного направления горизонтальной оси против вращения часовой стрелки, а отрицательные — по ее движению.
В процессе расчета электрической цепи определяется ряд синусоидальных величин. Все их можно изобразить на одном чертеже при помощи вращающихся векторов, привязав к одной паре взаимно перпендикулярных осей.
Совокупность векторов, изображающих на одном чертеже несколько синусоидальных величин одинаковой частоты в начальный момент времени, называется векторной диаграммой.
Например, напряжение и ток в электрической цепи выражаются уравнениями:
u = 125 sin(ωt + 30°)
i = 12 sin(ωt — 20°).
Векторная диаграмма такой цепи изображена на рис. 12.11. Если выбрать масштабы напряжения и тока
Mu = 50 В/см; Mi = 4 А/см;
то
Um = Um/Mu = 125/50 = 2,5 см; Im = Im = im/Mi = 12/4 = 3 см.
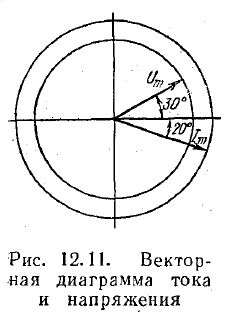

Векторная диаграмма содержит векторы синусоидальных величин одинаковой частоты, поэтому они вращаются с одинаковой частотой и их взаимное расположение не меняется.
Начало отсчета времени выбирают произвольно, поэтому один из векторов диаграммы можно направить произвольно; остальные же нужно располагать с учетом сдвига фаз по отношению к первому или предыдущему вектору.
Сложение и вычитание векторов
Главным достоинством векторных — это возможность простого сложения и вычитания двух величин. Например: требуется сложить, два тока, заданных уравнениями
Сложим два заданных тока i1 и i2 по известному правилу сложения векторов (рис. 12.12, а). Для этого изобразим токи в виде векторов из общего начала 0. Результирующий вектор найдем как диагональ параллелограмма, построенного на слагаемых векторах:
Im = Im1 + Im2
Сложение векторов, особенно трех и более, удобнее вести в таком порядке: один вектор остается на месте, другие переносятся параллель
но самим себе так, чтобы начало последующего вектора совпало с концом предыдущего.
Вектор Im, проведенный из начала первого вектора в конец последнего, представляет собой сумму всех векторов (рис. 12.12, б).
Вычитание одного вектора из другого выполняют сложением прямого вектора (уменьшаемого) и обратного (вычитаемого) (рис. 12.13):
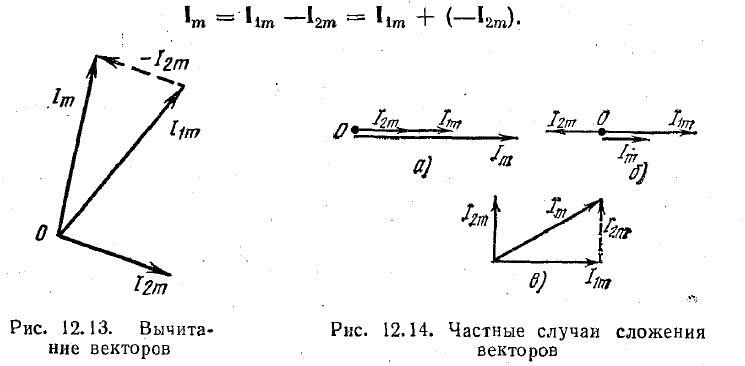

При сложении синусоидальных величин в отдельных случаях можно применить аналитическое решение: применительно к рис. 12.12, а — по теореме косинусов; к рис. 12.14, а — сложение модулей векторов; б — вычитание модулей векторов, в — по теореме Пифагора.
Построение векторной диаграммы напряжений. Катушка. Конденсатор. Сопротивление. Сдвиг фаз.
Достаточно сложным и чаще всего не изучаемым аспектом темы переменный ток является метод построения векторных диаграмм. Анализируя вынужденные электромагнитные колебания, мы уже обсудили сдвиг тока и напряжения на реактивных сопротивлениях (катушка индуктивности и конденсатор) по сравнению с активным сопротивлением (резистор). Тогда одним из задаваемых вопросов задачи является вопрос о направлении суммарного тока или напряжения в данный конкретный момент времени. Для ответа на этот вопрос и используется метод построения векторных диаграмм.
Векторная диаграмма — это изображение гармонически изменяющихся величин (текущего тока и напряжения) в виде векторов на плоскости.
Рис. 1. Векторная диаграмма
Построение векторных диаграмм происходит в прямоугольной декартовой системе координат. Построение начинается с проведения вектора, численно равного амплитудному значению тока в цепи. Данный вектор сонаправим в осью ОХ (рис. 1.1).
Т.к. напряжение на активном сопротивлении находится в одной фазе с током, то вектор амплитуды напряжения сонаправлен с вектором тока (рис. 1.2. красный).
На катушке напряжение опережает ток, поэтому отложим вектор амплитуды напряжения на катушке (
) вверх под углом относительно вектора тока (рис. 1.2. синий).На конденсаторе напряжение отстаёт от тока, поэтому отложим вектор амплитуды напряжения на конденсаторе (
) вниз под углом относительно вектора тока (рис. 1.2. зелёный).Угол
, используемый в логике построений, используется в случае идеальности контура и катушки.Для построения общего вектора напряжения достаточно векторно сложить напряжения:
(1)Проще всего сначала найти вектор-сумму
(т.к. они расположены вдоль одной прямой). В нашем случае, эти вектора разнонаправлены, найдём (рис. 1.3. жёлтый).И последнее, осталось сложить получившийся вектор с вектором
для получения значения полного напряжения в цепи (рис. 1.4. оранжевый). Для получения модуля вектора воспользуемся теоремой Пифагора, т.к. вектора находятся под прямым углом. Тогда: (2)Угол
— угол между вектором силы тока и полного напряжения называется сдвигом фаз между колебаниями силы тока и напряжения. Данный параметр можно найти и исходя из параметров системы: (3)Вывод: задачи на данную тематику касаются поиска сдвига фаз между колебаниями силы тока и напряжения через график (рис. 1.4) или через соотношение (3), а также поиска полного напряжения в цепи также через график (рис. 1.4) или через соотношение (2).
Поделиться ссылкой:
Понравилось это:
Нравится Загрузка…
Построение в заданном масштабе векторной диаграммы напряжений, отложив горизонтально вектор тока
Контрольная работа №3.
Задача 1.
К источнику переменного тока с синусоидально
изменяющимся напряжением 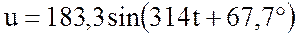 В подключена
катушка, индуктивное сопротивление которой
В подключена
катушка, индуктивное сопротивление которой 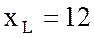 Ом
и активное
Ом
и активное 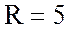 Ом.
Ом.
Начертить схему цепи. Определить полное сопротивление 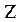 и индуктивность
и индуктивность 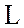 катушки; действующее значение
напряжения
катушки; действующее значение
напряжения 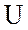 и тока
и тока 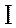 в
цепи; коэффициент мощности
в
цепи; коэффициент мощности 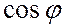
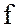 и период
и период 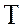 переменного
тока; полную
переменного
тока; полную 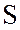 , активную
, активную 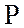 и
реактивную
и
реактивную 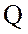 мощности катушки.
мощности катушки.Построить в масштабе 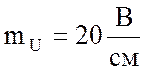
 Дано:
Дано:
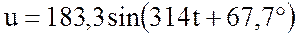 В;
В;
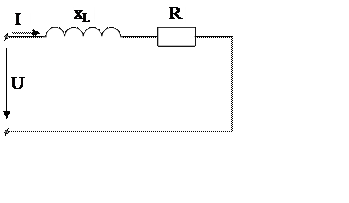
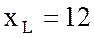 Ом;
Ом;
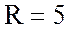 Ом.;
Ом.;
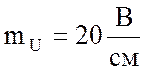

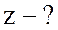 ;
; 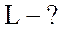 ;
; 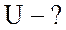 ;
; 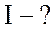 ;
;
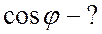 ;
; 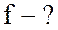 ;
; 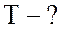
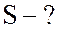 ;
;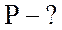 ;
; 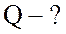 .
.
Решение.
1. Найду полное сопротивление цепи:
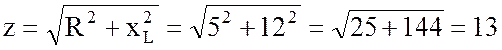 Ом.
Ом.
2. Найду индуктивность катушки:
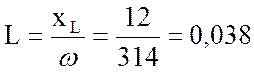 Гн.
Гн.
3. Найду действующие значения напряжения и тока:
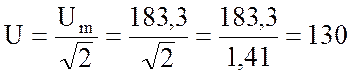
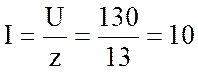 А.
А.
4.
Из уравнения переменного тока и
напряжения следует, что ток опережает напряжение на угол 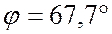 , следовательно
, следовательно
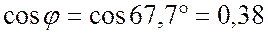 ;
;
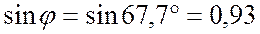 .
.
5. Найду частоту переменного тока:
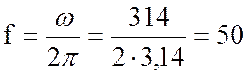 Гц.
Гц.
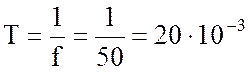 с.
с.
7. Определю полную мощность цепи:
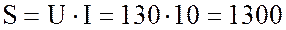 ВА.
ВА.
8. Определю активную мощность цепи:
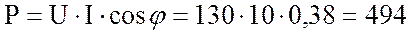 Вт.
Вт.
9. Определю реактивную мощность цепи:
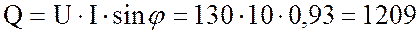 вар.
вар.
10. Построю векторную диаграмму. Для построения векторной диаграммы вычислю составляющие напряжения:
активную 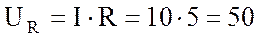
реактивную 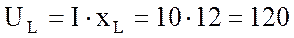 В
В
Построение векторной диаграммы начну с вектора тока 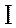 , откладывая его горизонтально в
произвольном масштабе. Принимаю масштаб для векторов напряжения
, откладывая его горизонтально в
произвольном масштабе. Принимаю масштаб для векторов напряжения 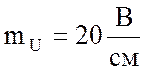 и определяю соответственно длины
векторов напряжений:
и определяю соответственно длины
векторов напряжений:
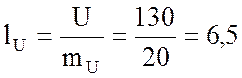 см;
см;
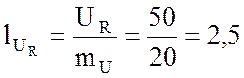
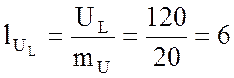 см.
см.
Откладываю «по току» (совпадающим по фазе с вектором
тока), вектор активной составляющей напряжения 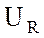 ;
на конце вектора
;
на конце вектора 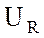 перпендикулярно вектору
тока строю опережающий ток на
перпендикулярно вектору
тока строю опережающий ток на 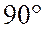 вектор реактивной
составляющей напряжения
вектор реактивной
составляющей напряжения 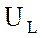
Замыкающий вектор, равный сумме векторов 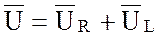 является вектором приложенного
напряжения. Вектор
является вектором приложенного
напряжения. Вектор 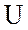 опережает вектор
опережает вектор 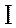 на угол
на угол 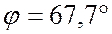 .
.
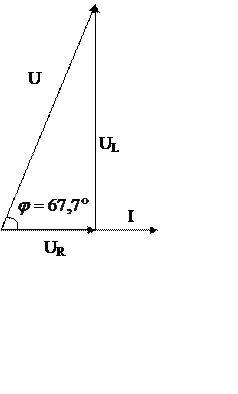
Ответ: полное
сопротивление 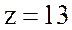
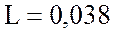 Гн; действующее значение напряжения в
цепи
Гн; действующее значение напряжения в
цепи 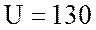 В и тока в цепи
В и тока в цепи 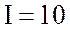 А; коэффициент мощности
А; коэффициент мощности 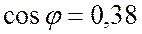 ; частота переменного тока
; частота переменного тока 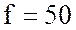 Гц и период переменного тока
Гц и период переменного тока 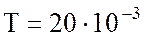
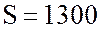 ВА, активная мощности катушки
ВА, активная мощности катушки 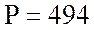 Вт и реактивная мощности катушки
Вт и реактивная мощности катушки 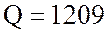 вар.
вар.Контрольная работа №3.
Задача 2.
По катушке проходит синусоидально изменяющийся ток 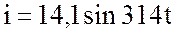 А. Катушка имеет полное
сопротивление
А. Катушка имеет полное
сопротивление 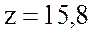
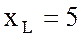 Ом.
Ом.Начертить схему цепи. Определить действующее значение
тока 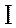 и напряжения
и напряжения 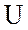 в
цепи; активное сопротивление
в
цепи; активное сопротивление 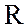 и индуктивность
и индуктивность 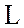 ; коэффициент мощности
; коэффициент мощности 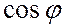
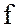 и
период
и
период 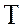 переменного тока; полную
переменного тока; полную 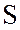 , активную
, активную 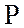 и
реактивную
и
реактивную  мощности катушки.
мощности катушки.Построить в масштабе 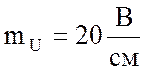 векторную
диаграмму напряжений, отложив горизонтально вектор тока.
векторную
диаграмму напряжений, отложив горизонтально вектор тока.
 Дано:
Дано:
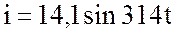 А;
А;

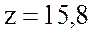 Ом;
Ом;
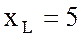 Ом;
Ом;
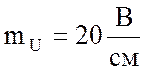
 Найти:
Найти:
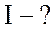 ;
; 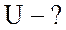 ;
; 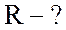 ;
; 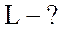 ;
;
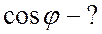 ;
; 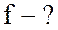 ;
; 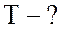 ;
; 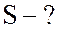 ;
;
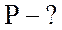 ;
; 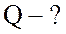 .
.
Решение.
1. Найду действующие значения напряжения и тока:
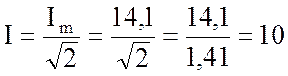 А.
А.
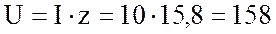 В;
В;
2. Найду активное сопротивление цепи:
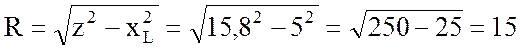 Ом.
Ом.
3. Найду индуктивность катушки:
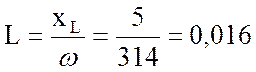 Гн.
Гн.
4. Определю коэффициент мощности:
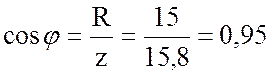 ;
;
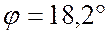
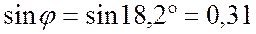 .
.
5. Найду частоту переменного тока:
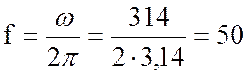 Гц.
Гц.
6. Найду период переменного тока:
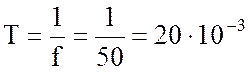 с.
с.
7. Определю полную мощность цепи:
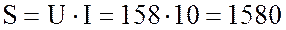 ВА.
ВА.
8. Определю активную мощность цепи:
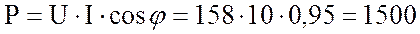 Вт.
Вт.
9. Определю реактивную мощность цепи:
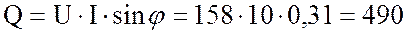 вар.
вар.
10. Построю векторную диаграмму. Для построения векторной диаграммы вычислю составляющие напряжения:
активную 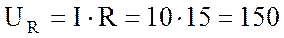 В
В
реактивную 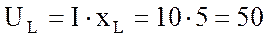 В
В
Построение векторной диаграммы начну с вектора тока 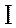 , откладывая его горизонтально в
произвольном масштабе. Принимаю масштаб для векторов напряжения
, откладывая его горизонтально в
произвольном масштабе. Принимаю масштаб для векторов напряжения 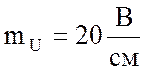 и определяю соответственно длины
векторов напряжений:
и определяю соответственно длины
векторов напряжений:
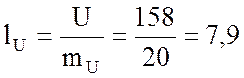 см;
см;
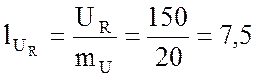 см;
см;
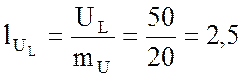 см.
см.
Откладываю «по току» (совпадающим по фазе с вектором
тока), вектор активной составляющей напряжения 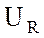 ;
на конце вектора
;
на конце вектора 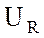 перпендикулярно вектору
тока строю опережающий ток на
перпендикулярно вектору
тока строю опережающий ток на  вектор реактивной
составляющей напряжения
вектор реактивной
составляющей напряжения 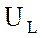 .
.
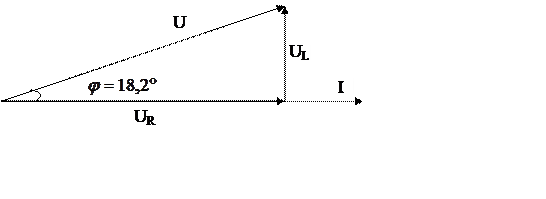
Замыкающий вектор, равный сумме векторов 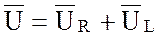 является вектором приложенного
напряжения. Вектор
является вектором приложенного
напряжения. Вектор 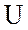 опережает вектор
опережает вектор 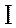 на угол
на угол 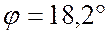 .
.
Ответ: действующее
значение тока в цепи 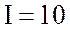 А и напряжения в цепи
А и напряжения в цепи 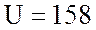 В; активное сопротивление
В; активное сопротивление 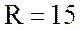 Ом и индуктивность
Ом и индуктивность 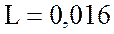 Гн; коэффициент мощности
Гн; коэффициент мощности 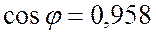 ; частота переменного тока
; частота переменного тока 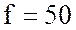 Гц и период переменного тока
Гц и период переменного тока 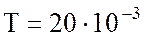 с; полная мощности катушки
с; полная мощности катушки 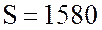 ВА, активная мощности катушки
ВА, активная мощности катушки 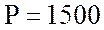 Вт и реактивная мощности катушки
Вт и реактивная мощности катушки 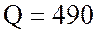 вар.
вар.
Контрольная работа №3.
Задача 3.
К источнику переменного тока с синусоидально
изменяющимся напряжением 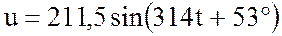 В подключена
катушка, индуктивность которой
В подключена
катушка, индуктивность которой 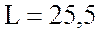 мГн и активное
сопротивление
мГн и активное
сопротивление 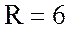 Ом.
Ом.
Начертить схему цепи. Определить индуктивное
сопротивление 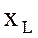 и полное сопротивление
и полное сопротивление 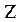 катушки; действующее значение
напряжения
катушки; действующее значение
напряжения 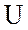 и тока
и тока 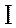 в
цепи; коэффициент мощности
в
цепи; коэффициент мощности 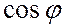 ; частоту
; частоту 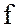 и период
и период 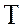 переменного
тока; полную
переменного
тока; полную 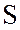 , активную
, активную 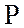 и
реактивную
и
реактивную 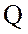 мощности катушки.
мощности катушки.
Построить в масштабе 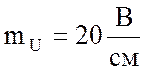 векторную
диаграмму напряжений, отложив горизонтально вектор тока.
векторную
диаграмму напряжений, отложив горизонтально вектор тока.
 Дано:
Дано:
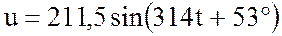 В;
В;
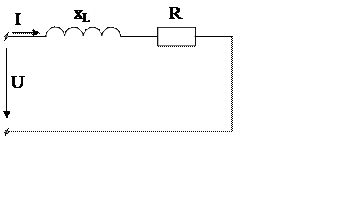
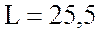 мГн;
мГн;
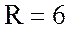 Ом;
Ом;
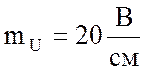
 Найти:
Найти:
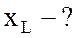 ;
;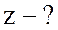 ;
; 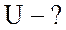 ;
; 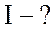 ;
;
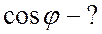 ;
; 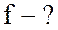 ;
; 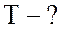 ;
; 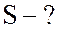 ;
;
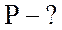 ;
; 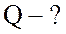 .
.
Решение.
1. Найду индуктивное сопротивление катушки:
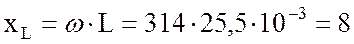 Ом.
Ом.
2. Найду полное сопротивление цепи:
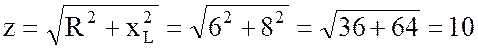 Ом.
Ом.
3. Найду действующие значения напряжения и тока:
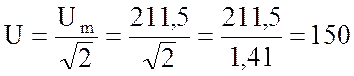 В;
В;
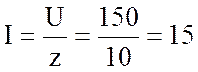 А.
А.
4.
Из уравнения переменного тока и
напряжения следует, что ток опережает напряжение на угол 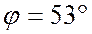 , следовательно
, следовательно
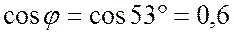 ;
;
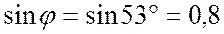 .
.
5. Найду частоту переменного тока:
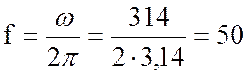 Гц.
Гц.
6. Найду период переменного тока:
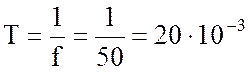 с.
с.
7. Определю полную мощность цепи:
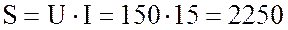 ВА.
ВА.
8. Определю активную мощность цепи:
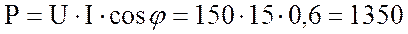 Вт.
Вт.
9. Определю реактивную мощность цепи:
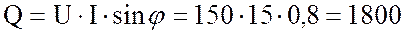 вар.
вар.
10. Построю векторную диаграмму. Для построения векторной диаграммы вычислю составляющие напряжения:
активную 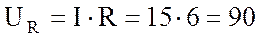 В
В
реактивную 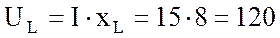 В
В
Построение векторной диаграммы начну с вектора тока 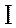 , откладывая его горизонтально в
произвольном масштабе. Принимаю масштаб для векторов напряжения
, откладывая его горизонтально в
произвольном масштабе. Принимаю масштаб для векторов напряжения 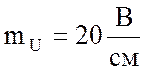 и определяю соответственно длины
векторов напряжений:
и определяю соответственно длины
векторов напряжений:
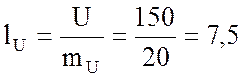 см;
см;
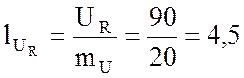 см;
см;
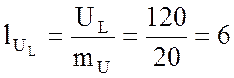 см.
см.
Откладываю «по току» (совпадающим по фазе с вектором
тока), вектор активной составляющей напряжения 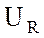 ;
на конце вектора
;
на конце вектора 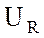 перпендикулярно вектору
тока строю опережающий ток на
перпендикулярно вектору
тока строю опережающий ток на 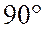 вектор реактивной
составляющей напряжения
вектор реактивной
составляющей напряжения 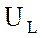 .
.
Замыкающий вектор, равный сумме векторов 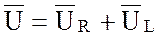 является вектором приложенного
напряжения. Вектор
является вектором приложенного
напряжения. Вектор 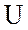 опережает вектор
опережает вектор 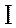 на угол
на угол 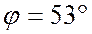 .
.
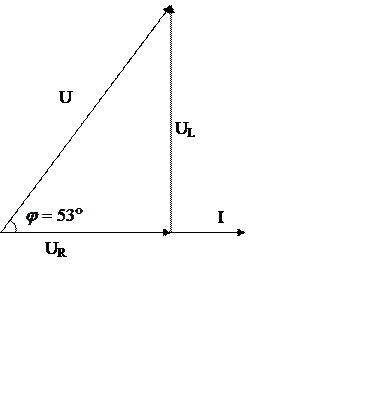
Ответ: индуктивное
сопротивление катушки 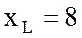 Ом и полное сопротивление
катушки
Ом и полное сопротивление
катушки 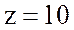 Ом; действующее значение напряжения
в цепи
Ом; действующее значение напряжения
в цепи 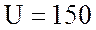 В и тока в цепи
В и тока в цепи 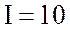 А; коэффициент мощности
А; коэффициент мощности 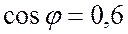 ; частота переменного тока
; частота переменного тока 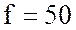 Гц и период переменного тока
Гц и период переменного тока 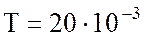 с; полная мощности катушки
с; полная мощности катушки 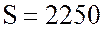 ВА, активная мощности катушки
ВА, активная мощности катушки 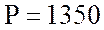 Вт и реактивная мощности катушки
Вт и реактивная мощности катушки 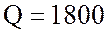 вар.
вар.
Контрольная работа №3.
Задача 4.
По катушке, подключенной к источнику переменного тока
с напряжением 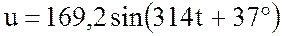 В проходит ток
В проходит ток 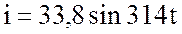 А.
А.
Начертить схему цепи. Определить действующее значение
тока 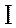 и напряжения
и напряжения 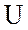 в
цепи; полное
в
цепи; полное 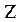 ; активное
; активное 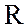 ,
индуктивное
,
индуктивное 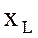 сопротивления и индуктивность
сопротивления и индуктивность 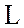 ; коэффициент мощности
; коэффициент мощности 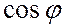 ; частоту
; частоту 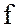 и
период
и
период 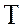 переменного тока; полную
переменного тока; полную 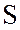 , активную
, активную 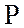 и
реактивную
и
реактивную 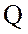 мощности катушки.
мощности катушки.
Построить в масштабе 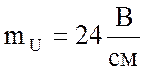 векторную
диаграмму напряжений и тока, отложив горизонтально вектор тока.
векторную
диаграмму напряжений и тока, отложив горизонтально вектор тока.
 |
 Дано:
Дано:
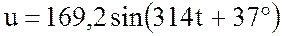 В;
В;
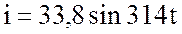 А;
А;
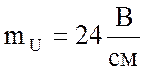
 Найти:
Найти:
 ;
; 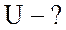 ;
; 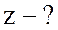 ;
; 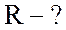 ;
;
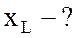 ;
; 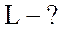 ;
; 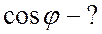 ;
; 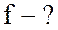 ;
;
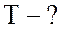 ;
; 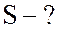 ;
; 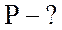 ;
; 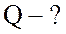 .
.
Решение.
1. Найду действующие значения напряжения и тока:
12. Построение волновой и векторной диаграмм
12.1. Волновая диаграмма
По найденному комплексному значению тока мы можем записать уравнение его мгновенного значения:
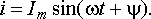 (12.1)
(12.1)
Амплитуду
тока 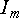 мы
получаем, умножив на
мы
получаем, умножив на 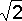 модуль
комплекса действующего значения тока,
а начальная фаза
модуль
комплекса действующего значения тока,
а начальная фаза 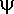 равна
аргументу последнего. Так, мгновенное
значение тока первой ветви, определяемое
по найденному выше его комплексному
значению, имеет вид:
равна
аргументу последнего. Так, мгновенное
значение тока первой ветви, определяемое
по найденному выше его комплексному
значению, имеет вид:
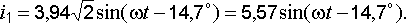 (12.2)
(12.2)
Аналогично:
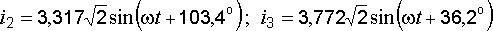 .
.
Графическое изображение уравнения (12.1) называется волновой диаграммой.
При
построении графика 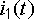 прежде
всего определяем те значения угла
прежде
всего определяем те значения угла 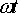 ,
при которых ток имеет максимальное
значение и равен нулю:
,
при которых ток имеет максимальное
значение и равен нулю:
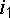 =
0 при
=
0 при 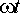 –
14,7° =
0, т. е. при
–
14,7° =
0, т. е. при 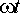 =
14,7° и
=
14,7° и
при 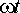 –
14,7° =
180°, т. е. при
–
14,7° =
180°, т. е. при 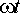 =
194,7°;
=
194,7°;
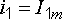 при
при 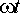 –
14,7° =
90°, т. е. при
–
14,7° =
90°, т. е. при 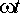 =
104,7°.
=
104,7°.
Кроме того, необходимо взять еще несколько промежуточных точек. Причем достаточно взять их только для первой полуволны синусоиды, так как остальная часть кривой может быть построена из условий симметрии.
В
табл. 12.1 приведены различные значения
угла 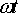 и
соответствующие им значения тока,
вычисленные по формуле (12.2).
и
соответствующие им значения тока,
вычисленные по формуле (12.2).
Таблица 12.1
Данные для построения волновой диаграммы тока первой ветви
| 0 | 14,7 | 30 | 45 | 60 | 75 | 90 | 104,7 |
| -1,41 | 0 | 1,47 | 2,81 | 3,96 | 4,84 | 5,39 | 5,57 |
Построенная по этим данным кривая представлена на рис. 12.1.
Обращаем внимание на то, что при отрицательной начальной фазе синусоида смещается вправо относительно начала координат.
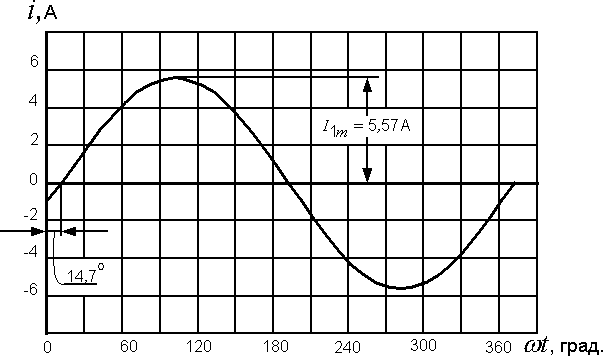
Рис. 12.1. Волновая диаграмма тока первой ветви
12.2. Векторная топографическая диаграмма
Обычно
векторы напряжений и токов на диаграмме
не отделяются друг от друга, а показываются
вместе, образуя общую картину. Если
расчет ведется в символической форме,
то диаграмма строится на комплексной
плоскости в осях  и
и 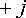 .
Построение каждого вектора в этом случае
затруднений не вызывает.
.
Построение каждого вектора в этом случае
затруднений не вызывает.
Прежде всего выбираются масштабы. Требования к ним те же, что и при оформлении графиков. Удобны, например, такие масштабы:
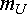 =
20 В/см;
=
20 В/см; 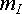 =
1 А/см
=
1 А/см
или
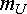 =
50 В/см;
=
50 В/см; 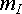 =
0,5 А/см и т. д.
=
0,5 А/см и т. д.
Предположим,
что построение диаграммы мы начинаем
с вектора 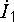 .
.
С помощью транспортира мы можем отложить его аргумент. Так как он отрицательный, то откладывается по часовой стрелке (рис. 12.2). Длина вектора определяется делением величины тока на масштаб:
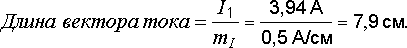
Так как транспортир недостаточно точный инструмент, то для построения вектора лучше пользоваться алгебраической формой комплексного числа. Разделив его вещественную и мнимую составляющие на масштаб, найдем проекции вектора тока на оси:
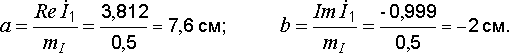
Так
как вещественная часть комплекса тока
( 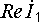 )
положительна, то величину
)
положительна, то величину 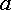 откладываем
вправо от начала координат, т.е. в
положительном направлении вещественной
оси. Мнимая часть (
откладываем
вправо от начала координат, т.е. в
положительном направлении вещественной
оси. Мнимая часть ( 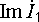 )
отрицательна, поэтому
)
отрицательна, поэтому 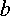 направляется
вниз.
направляется
вниз.
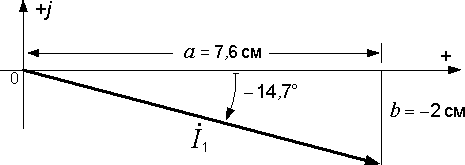
Рис. 12.2. Построение вектора на комплексной плоскости
Правильно
построенная векторная диаграмма токов
должна отражать первый закон Кирхгофа.
На рис. 12.5 видно, что для рассматриваемой
цепи этот закон выполняется: сумма
векторов  и
и  дает
вектор
дает
вектор 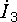 .
.
Обычно мы имеем дело со свободными векторами, когда каждый из них может переноситься параллельно самому себе. Поэтому возможны различные варианты одной и той же диаграммы (рис. 12.3). Все эти варианты характеризуются тем, что, во-первых, каждый вектор имеет одни и те же длину и направление, и во-вторых, на диаграмме выполняется первый закон Кирхгофа: сумма первого и второго токов равна третьему.
Аналогично (из свободных векторов) может строиться и векторная диаграмма напряжений. Однако, очень часто последнюю строят так, что каждой точке электрической цепи соответствует точка на комплексной плоскости. Векторы напряжений в этом случае оказываются привязанными к этим точкам и уже не являются свободными. Векторная диаграмма такого типа называется топографической. Для ее построения необходимо, приняв потенциал одной из точек равным нулю, рассчитать потенциалы остальных точек.
Примем,
как и в расчете, 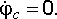
Так
как в емкости  ток
протекает от точки
ток
протекает от точки 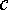 к
точке
к
точке 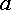 ,
то потенциал точки
,
то потенциал точки 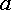 меньше
потенциала точки
меньше
потенциала точки  на
величину падения напряжения на
конденсаторе
на
величину падения напряжения на
конденсаторе  (сопротивление
токовой обмотки ваттметра мы принимаем
равным нулю и падение напряжения на ней
не учитываем):
(сопротивление
токовой обмотки ваттметра мы принимаем
равным нулю и падение напряжения на ней
не учитываем):
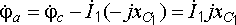 .
.
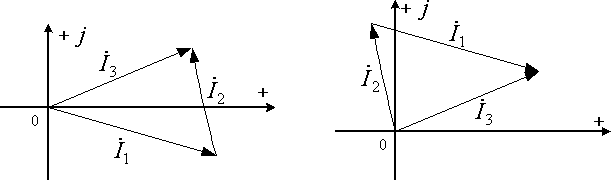
Рис. 12.3. Варианты диаграммы токов
Аналогично:
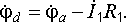
Потенциалы
всех точек первой ветви мы определили.
Однако с целью проверки желательно
рассчитать и потенциал точки 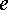 :
:
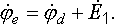
Здесь
величина 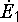 прибавляется
к
прибавляется
к 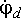 ,
так как по ходу стрелки ЭДС внутри
источника потенциал повышается (мы идем
от минуса источника к плюсу).
,
так как по ходу стрелки ЭДС внутри
источника потенциал повышается (мы идем
от минуса источника к плюсу).
Найденное
по последней формуле значение 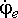 должно
совпадать с тем, которое мы нашли при
расчете цепи методом узловых потенциалов.
должно
совпадать с тем, которое мы нашли при
расчете цепи методом узловых потенциалов.
Аналогичный
проверочный расчет потенциала
точки 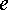 следует
выполнять и при обходе остальных ветвей.
следует
выполнять и при обходе остальных ветвей.
В рассматриваемом примере комплексные потенциалы всех точек цепи имеют следующие значения:
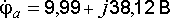 ;
;
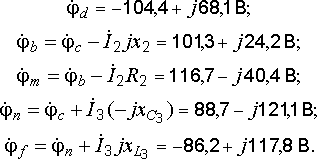
Порядок построения топографической диаграммы.
1. Выбираем
масштаб напряжения 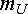 .
.
2. Разделив
комплексные потенциалы на этот масштаб,
находим отрезки в сантиметрах, определяющие
положение каждой точки на диаграмме.
Отмечаем эти точки на комплексной
плоскости. Например, при 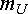 =
20 В/см точка
=
20 В/см точка 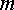 находится
на 116,7 : 20 = 5,8 см правее
находится
на 116,7 : 20 = 5,8 см правее
вертикальной оси и на 40,4 : 20 = 2 см ниже горизонтальной (рис. 12.5).
3. Соединяем
отрезками прямых точки, обозначающие
на схеме зажимы каждого отдельного
элемента ( 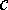 и
и 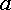 ,
, 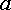 и
и 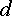 ,
, 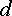 и
и 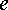 ,
, 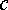 и
и 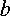 и
т. д.).
и
т. д.).
4. Даем
наименование каждому вектору ( 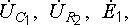 и
т. д.) и указываем его направление.
и
т. д.) и указываем его направление.
На последнем пункте следует остановиться подробнее.
Рассмотрим
фрагмент диаграммы, содержащей
точки 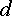 и
и 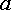 (рис.
12.4).
(рис.
12.4).
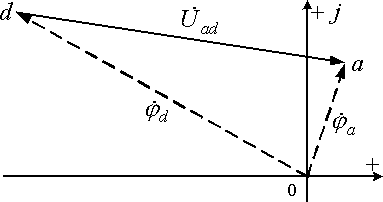
Рис. 12.4. Определение направления вектора напряжения
На
схеме электрической цепи (см. рис. 11.1)
эти точки определяют зажимы сопротивления 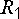 ,
,
поэтому
на векторной 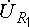 диаграмме
(рис. 12.5) соединяющий их вектор мы
обозначаем символом .
Но куда этот вектор должен быть направлен?
диаграмме
(рис. 12.5) соединяющий их вектор мы
обозначаем символом .
Но куда этот вектор должен быть направлен?
Так
как по сопротивлению 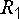 ток
протекает в направлении от точки
ток
протекает в направлении от точки 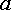 к
точке
к
точке 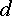 ,
то
,
то 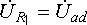 (порядок
следования индексов
(порядок
следования индексов 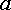 и
и 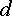 у
буквы U определяется
направлением стрелки
у
буквы U определяется
направлением стрелки 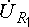 ,
а последняя всегда направляется по
направлению
,
а последняя всегда направляется по
направлению
тока).
Но 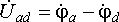 .
.
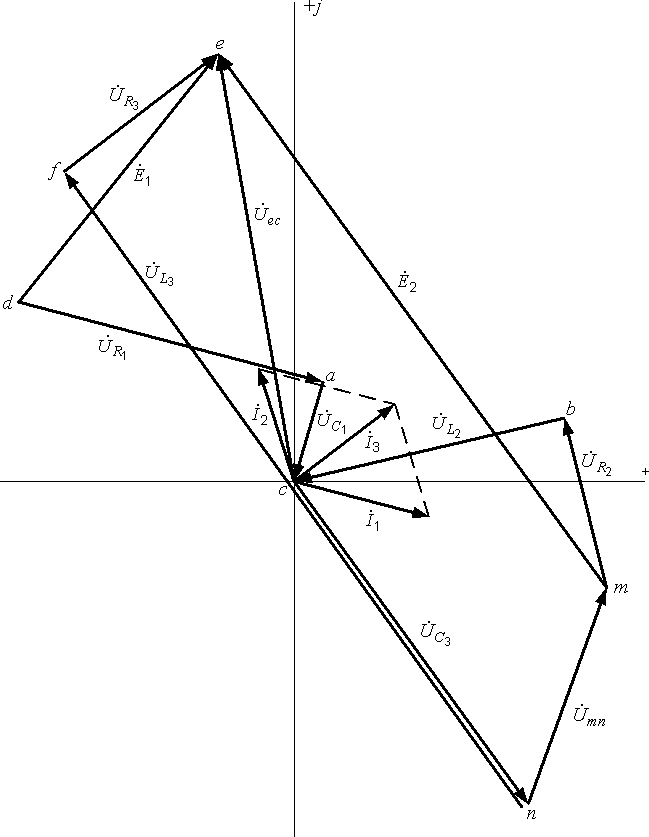
Рис. 12.5. Векторная топографическая диаграмма
Комплексным
числам 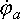 и
и 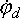 на
комплексной плоскости соответствуют
векторы, начинающиеся в начале координат
и оканчивающиеся соответственно в
точках
на
комплексной плоскости соответствуют
векторы, начинающиеся в начале координат
и оканчивающиеся соответственно в
точках 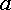 и
и 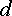 .
На рис. 12.4 эти векторы изображены
пунктирными линиями, а на топографической
диаграмме (см. рис. 12.5) они не показаны.
По правилу вычитания векторов
вектор-разность
.
На рис. 12.4 эти векторы изображены
пунктирными линиями, а на топографической
диаграмме (см. рис. 12.5) они не показаны.
По правилу вычитания векторов
вектор-разность 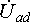 направляется
из конца вектора-вычитаемого
направляется
из конца вектора-вычитаемого 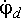 в
конец вектора-уменьшаемого
в
конец вектора-уменьшаемого 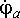 ,
т. е. из точки
,
т. е. из точки 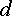 в
точку
в
точку 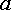 (от
второго индекса в обозначении напряжения
к первому). Аналогично, вектор
(от
второго индекса в обозначении напряжения
к первому). Аналогично, вектор 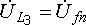 (см.
рис. 11.1 и 12.5) должен быть направлен на
диаграмме от точки
(см.
рис. 11.1 и 12.5) должен быть направлен на
диаграмме от точки 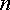 к
точке
к
точке 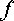 и
т.д.
и
т.д.
ЭДС 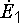 на
схеме направлена от
на
схеме направлена от 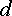 к
к 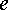 (от
минуса к плюсу), поэтому потенциал
точки
(от
минуса к плюсу), поэтому потенциал
точки 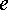 выше
потенциала точки
выше
потенциала точки 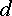 на
величину ЭДС. Следовательно,
на
величину ЭДС. Следовательно, 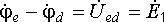 ,
и на векторной диаграмме вектор
,
и на векторной диаграмме вектор 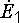 направляется
точно так же, как и
направляется
точно так же, как и 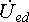 ,
т. е. от
,
т. е. от 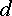 к
к 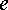 .
.
По
аналогичной причине вектор 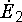 направлен
от
направлен
от 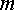 к
к 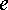 .
.
Проверка диаграммы.
1. Сопоставляем
направления вектора напряжения на
каждом элементе и вектора тока,
протекающего по этому элементу. Для
активного сопротивления эти векторы
параллельны и направлены в одну сторону
как совпадающие по фазе
( 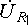 и
и 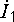 ,
, 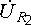 и
и 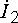 ,
, 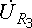 и
и 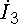 ).
).
На
участке с индуктивностью ток отстает
от напряжения по фазе на угол 90° (при
вращении векторной диаграммы против
часовой стрелки), а в емкости ток опережает
напряжение на этот же угол. Проверим,
например, правильность проведения
вектора 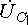 .
Перенесем мысленно вектор
.
Перенесем мысленно вектор
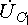 параллельно
самому себе так, чтобы его начало
оказалось в точке
параллельно
самому себе так, чтобы его начало
оказалось в точке 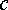 (в
начале вектора тока
(в
начале вектора тока
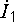 ).
При вращении этой пары векторов против
часовой стрелки вектор
).
При вращении этой пары векторов против
часовой стрелки вектор 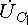 будет
отставать от
будет
отставать от
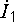 как
раз на 90°. Сравните подобным же образом
взаимные направления векторов
как
раз на 90°. Сравните подобным же образом
взаимные направления векторов 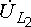 и
и 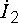 ,
,
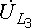 и
и 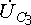 с
с 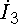 .
.
2. На векторной диаграмме должен выполняться второй закон Кирхгофа.
Посмотрим
на рис. 11.1. Напряжение между
точками 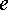 и
и 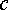 равно
сумме напряжений на элементах третьей
ветви
равно
сумме напряжений на элементах третьей
ветви 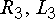 и
и 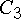 :
:
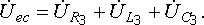
На
топографической диаграмме мы видим,
что вектор 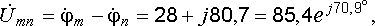 ,
направленный от
,
направленный от 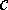 к
к 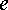 ,
равен сумме
,
равен сумме
векторов 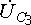 ,
, 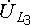 и
и 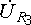 (чтобы
попасть из точки
(чтобы
попасть из точки 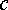 в
точку
в
точку 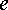 ,
мы сначала идем вправо вниз от
,
мы сначала идем вправо вниз от
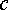 к
к 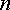 –
по стрелке напряжения
–
по стрелке напряжения 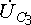 ,
затем по
,
затем по 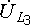 к
точке
к
точке 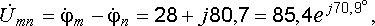 ,
и наконец, замыкаем многоугольни
,
и наконец, замыкаем многоугольни
к
вектором 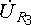 ).
).
Для
контура, образованного первой ветвью
и стрелкой 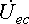
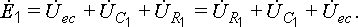
А
для контура, включающего напряжение 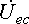 и
вторую ветвь,
и
вторую ветвь,
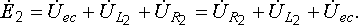
Рассмотрите внимательно топографическую диаграмму и убедитесь, что она удовлетворяет последним двум уравнениям.
Топографическая
диаграмма позволяет очень легко находить
напряжение между двумя любыми точками
электрической цепи. Например,
напряжение 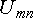 (напряжение
между точками m и n)
(напряжение
между точками m и n)
определяется длиной вектора, направленного из точки n в точку m :
Umn = mnּmU = 4,3 см ּ 20 В/см = 86 В.
Расчет
дает для 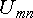 следующее
значение:
следующее
значение:
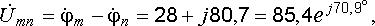
т.
е. 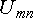 =
85,4 В.
=
85,4 В.
Топографическая диаграмма | Электрикам


Напряжение на выводах цепи переменного тока или на любом из её участков можно выразить комплексным числом – комплексным напряжением и изобразить на комплексной плоскости вектором. Напряжение между двумя точками электрической цепи представляет собой разность потенциалов между этими точками. Следовательно, потенциалы отдельных точек цепи также можно представить комплексами – комплексными потенциалами и изображать соответствующими векторами. Вектор, изображающие комплексный потенциал, начинается в начале координат; его конец обозначают той же буквой (или цифрой), что в точке цепи, потенциал которой изображает вектор. Например, на рисунке 1 построены векторы комплексных потенциалов ϕа = 10 + j20 В и ϕб = 30 – j15 В и разность векторов или вектор напряжения Uаб = ϕа — ϕб = 10 + j20 – 30 + j15 = -20 + j35 В.
Напряжение Uаб построено по правилу вычитания векторов, так что ϕа = ϕб + Uаб рисунок 1. Поэтому напряжение Uаб изображается вектором, направленным от точки б (второй индекс у напряжения Uаб) к точке а (первый индекс).
Напряжение Uба = ϕб — ϕа = 30 – j15 -10 — j20 В = 20 – j35 В. Очевидно, Uба = — Uаб и изображается вектором, направленным от точки а к точке б (штриховая линия на рисунке 1).
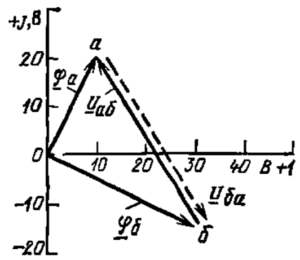
 Рисунок 1 — Комплексные потенциалы
Рисунок 1 — Комплексные потенциалыТакая векторная диаграмма называется топографической; она удовлетворяет двум условиям:
- Каждой точке электрической цепи соответствует определенная точка на векторной диаграмме и
- вектор, проведённый из начала координат в какую-либо точку диаграммы изображает комплексный потенциал соответствующей точки цепи.
Построение топографической диаграммы
При построении топографической диаграммы потенциал одной из точек цепи принимают равным нулю и на диаграмме точку нулевого потенциала совмещают с началом координат. На такой диаграмме отрезок, соединяющий любые две точки, также определяет комплексное напряжение между соответствующими точками цепи.
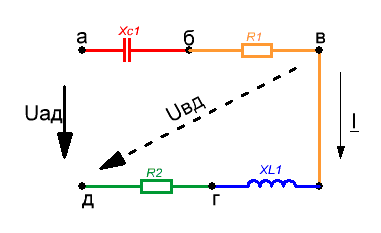
 Рисунок 2 а — Неразветвлённая цепь
Рисунок 2 а — Неразветвлённая цепьНа рисунке 2, а представлена неразветвлённая цепь.
1) Для построения топографической диаграммы примем, например, потенциал точки д равным нулю, т.е. ϕд = 0.

2) Обходим контур в направлении, встречно току, определим потенциалы всех точек цепи. Начальную фазу общего тока примем равной нулю, т. е. I = I, поэтому вектор тока I направлен вдоль положительной полуось действительных величин.
 3) Потенциал точки г или ϕг выше потенциала ϕд на падение напряжения в сопротивлении R2, т.е. на R2*I или ϕг = ϕд R2*I = 0 + R2*I = R2*I. Построив вектор R2*I, получим на диаграмме точку г.
3) Потенциал точки г или ϕг выше потенциала ϕд на падение напряжения в сопротивлении R2, т.е. на R2*I или ϕг = ϕд R2*I = 0 + R2*I = R2*I. Построив вектор R2*I, получим на диаграмме точку г.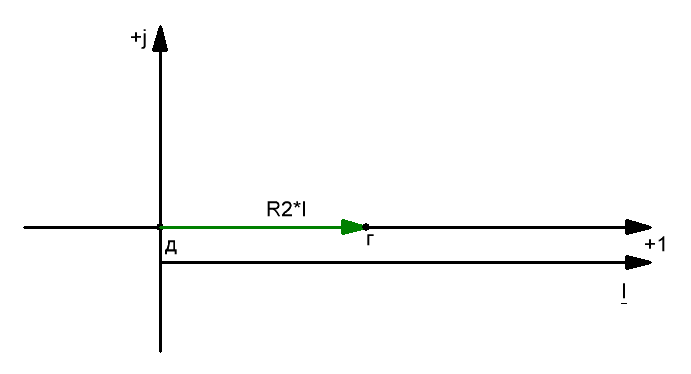
 4) Потенциал точки в или ϕв больше потенциала ϕг, на падение напряжения на индуктивном сопротивлении XL2 или в комплексной форме на jXL2*I. Построив вектор напряжения Uвг = ϕв — ϕг = jXL2*I, начинающийся в точке г и опережающий ток по фазе на 90 градусов (индуктивное сопротивление — вектор направлен вверх), получим точку в.
4) Потенциал точки в или ϕв больше потенциала ϕг, на падение напряжения на индуктивном сопротивлении XL2 или в комплексной форме на jXL2*I. Построив вектор напряжения Uвг = ϕв — ϕг = jXL2*I, начинающийся в точке г и опережающий ток по фазе на 90 градусов (индуктивное сопротивление — вектор направлен вверх), получим точку в.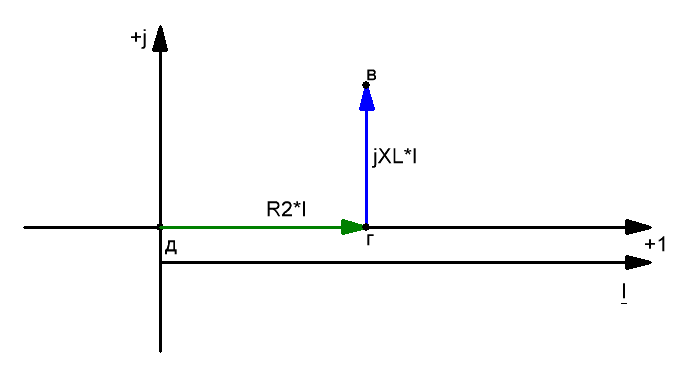
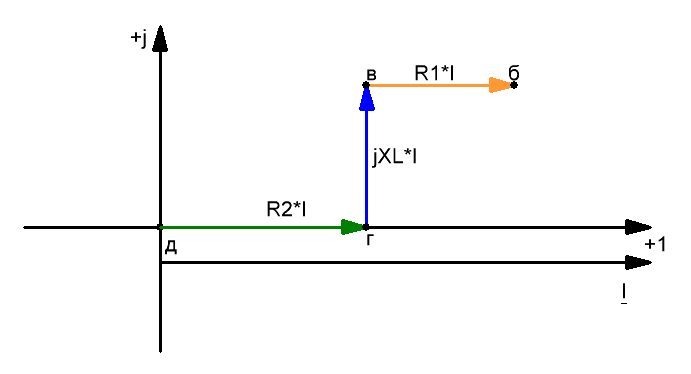
 5) Потенциал точки б или ϕб больше ϕв на падение напряжения R1*I. Построив из точки в вектор напряжения Uбв = ϕб — ϕв = R1*I, параллельный току, находим точку б.
5) Потенциал точки б или ϕб больше ϕв на падение напряжения R1*I. Построив из точки в вектор напряжения Uбв = ϕб — ϕв = R1*I, параллельный току, находим точку б.
 6) Потенциал точки а или ϕа больше ϕб на падение напряжения на емкости -jXc1*I. Построив из точки б вектор напряжения Uаб = ϕа — ϕб = -jXc1*I, отстающий по фазе от тока на угол 90 градусов (емкостное сопротивление — вектор напряжения направлен вниз), получим точку а.
6) Потенциал точки а или ϕа больше ϕб на падение напряжения на емкости -jXc1*I. Построив из точки б вектор напряжения Uаб = ϕа — ϕб = -jXc1*I, отстающий по фазе от тока на угол 90 градусов (емкостное сопротивление — вектор напряжения направлен вниз), получим точку а.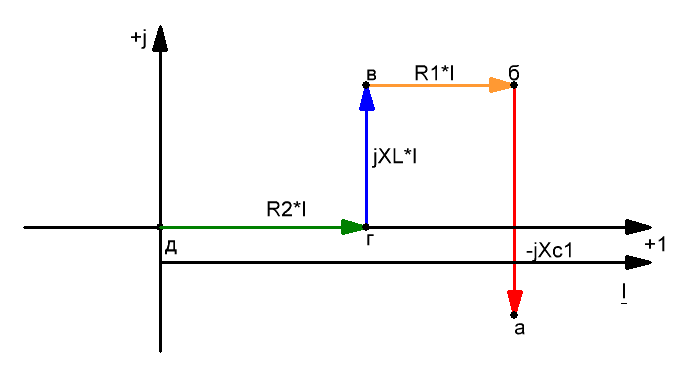

Вектор, соединяющий точки д и а направленный от точки д к точке а, изображает напряжение Uад на выходах цепи.
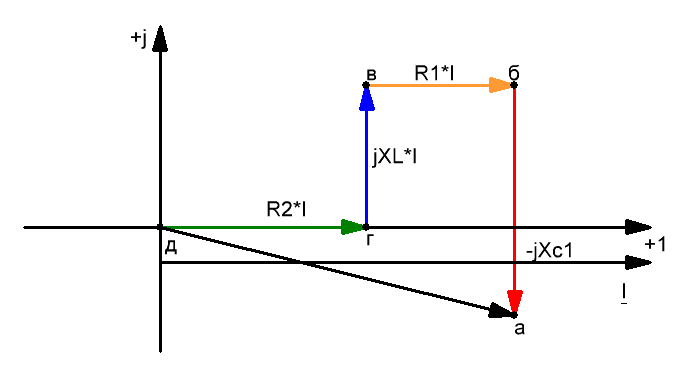

Необходимо учесть, что векторы напряжений на топографической диаграмме имеют по отношению к точкам цепи направления, обратные положительным направлениям напряжений относительно тех же точек цепи.
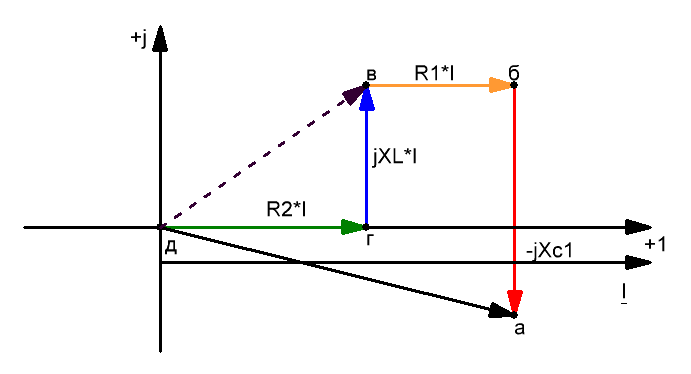

Например, напряжение Uвд = ϕв — ϕд , направленное на схеме от точки в к точке д (по направлению тока), на топографической диаграмме имеет противоположное направление относительно этих точек, что согласуется с правилом вычитания векторов, согласно которому вектор разности всегда направлен в одну сторону с уменьшаемым вектором.
Решение задач по электротехнике (ТОЭ)
В электрической цепи однофазного синусоидального тока, схема и параметры элементов которой заданы для каждого варианта в таблице, определить:
1) полное сопротивление электрической цепи и его характер;
2) действующие значения токов в ветвях;
3) показания вольтметра и ваттметра;
4) построить векторную диаграмму токов и топографическую диаграмму напряжений для всей цепи.
Дано
E = 130 В;
f = 50 Гц;
R1 = 9 Ом;
L1 = 15,9 мГн;
C2 = 318 мкФ;
L2 = 9,4 мГн;
R3 = 8 Ом;
C3 = 500 мкФ;
Схема 1.5.
Решение
Рисунок 1. Исходная схема цепи Выбираем произвольные направления токов в ветвях. Заменяем измерительные приборы их внутренними сопротивлениями: Рисунок 2. Расчётная схема цепиЦиклическая частота цепи:
ω=2πf=2•3,14•50=314рад⁄с;
Сопротивления реактивных элементов:
XL1=ωL1=314•15,9•10^(-3)=4,99 Ом;
XC2=1/(ωC2)=1/(314•318•10^(-6))=10,01 Ом;
XL2=ωL2=314•9,4•10^(-3)=2,95 Ом;
XC3=1/(ωC1 )=1/(314•500•10^(-6))=6,37 Ом;
Общее сопротивление цепи:
Характер входного сопротивления активно-индуктивный, на это указывает наличие действительной части и положительная мнимая часть сопротивления.
Комплекс действующего значения входного напряжения:
E=E•(cosφ+jsinφ)=130•(cos0o+jsin0o)=130+0j В;
Действующие комплексные токи в цепи:
I1=E/Zвх =130/(10,632+0,669j)=12,179-0,767j=12,203•e(-4oj) А;
I2=I1•((R3-jXC3))/(R3+j(XL2-XC2-XC3))=(12,179-0,767j)•(8-6,37j)/(8+j•(2,95-10,01-6,37))=
=7,631+2,346j=7,983•e(17oj) А;
I3=I1-I2=12,179-0,767j-7,631-2,346j=4,548-3,113j=5,511•e(-35oj) А;
Падения напряжения на элементах:
UL1=I1•jXL1=(12,179-0,767j)•4,99j=3,83+60,77j В;
UR1=I1•R1=(12,179-0,767j)•9=109,61-6,90j В;
UL2=I2•jXL2=(7,631+2,346j)•2,95j=-6,92+22,51j В;
UC2=I2•(-jXC2)=(7,631+2,346j)•(-10,01j)=23,48-76,39j В;
UR3=I3•R3=(4,548-3,113j)•8=36,38-24,90j В;
UC3=I4•(-jXC3)=(4,548-3,113j)•(-6,37j)=-19,83-28,97j=35,11•e(-124oj) В;
Показания вольтметра (измеряющего действующее значение напряжения):
UV=UC3=35,11 В;
Показания ваттметра (измеряющего активную мощность):
Pw=Re(E•I1*)=Re(130•(12,179+0,767j))=1583,3 Вт;I* — сопряженный ток.Например,если I=a+jb,то I*=a-jb;
Рисунок 3. Топографическая диаграмма напряжений Рисунок 4. Векторная диаграмма токовМетодические рекоменд по переменному току
I ОБЩИЕ МЕТОДИЧЕСКИЕ УКАЗАНИЯ
1.1 Принятые буквенные обозначения основных электрических величин
u, e, i, p — мгновенные значения напряжения, ЭДС, тока и мощности;
U, E, I — постоянные или действующие значения напряжения,
ЭДС и тока;
Um, Em, Im — амплитудные значения напряжения, ЭДС и тока;
P,Q,S — активная, реактивная и полная мощности;
R, X, Z — активное, реактивное и полное сопротивления;
G, B, Y — активная, реактивная и полная проводимости;
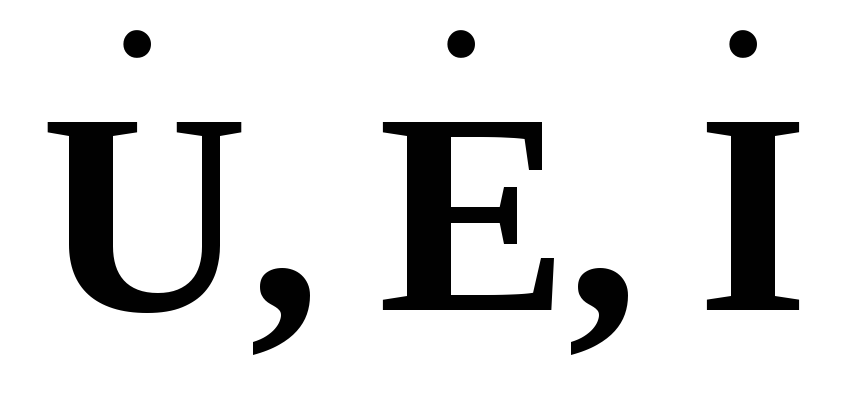
 —
комплексы действующих значений
напряжения, э.д.с. и тока;
—
комплексы действующих значений
напряжения, э.д.с. и тока;
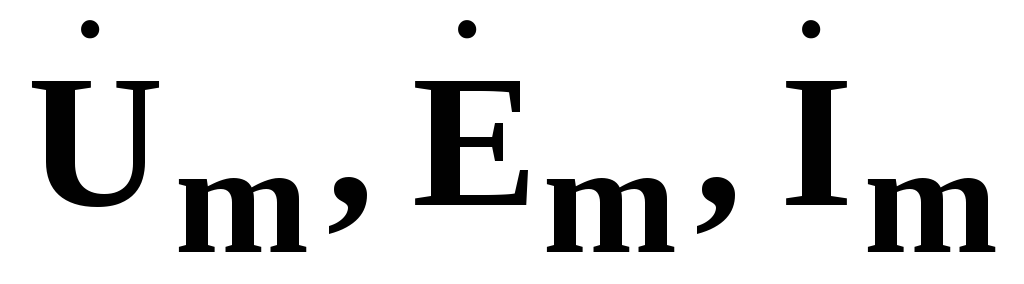 —
комплексы амплитудных значений
напряжения, э.д.с. и тока;
—
комплексы амплитудных значений
напряжения, э.д.с. и тока;
 —
комплексы реактивной и полной мощности;
—
комплексы реактивной и полной мощности;
 —
комплексы полного сопротивления и
проводимости;
—
комплексы полного сопротивления и
проводимости;
u, i, — начальные фазы напряжения и тока, разность фаз;
f, , T — частота, угловая частота, период.
III. РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ
ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА.
3.1. Краткие теоретические сведения, методы и примеры расчета.
3.1.1. Аналитическое и графическое представление синусоидальных функций напряжения и тока
Мгновенные значения напряжения и тока записываются в виде функций:
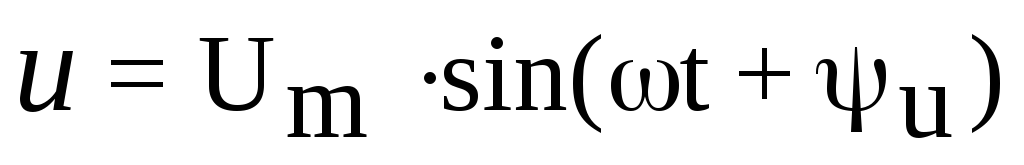
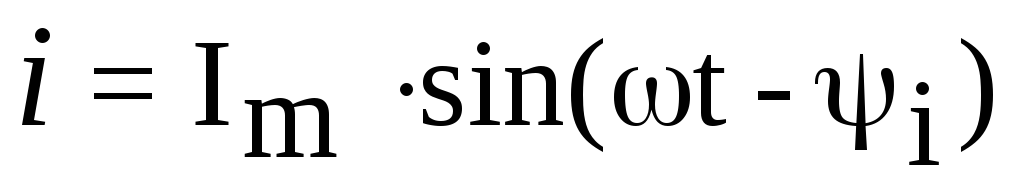 ,
,
где: u, i, — мгновенные значения напряжения и тока;
Um, Im — амплитудные значения напряжения и тока;
u, i, — начальные фазы напряжения и тока;
— угловая частота.
Комплексные выражения для действующих значений синусоидального напряжения и тока записываются в трех формах:
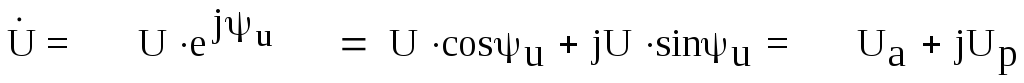 ,
,
 ,
,
где: Uа, Iа – активные составляющие комплексов;
Uр, Iр – реактивные составляющие комплексов.
Формулы переходов из алгебраической формы комплексного числа в показательную и обратно дают возможность легко проводить расчеты в комплексных выражениях, например:
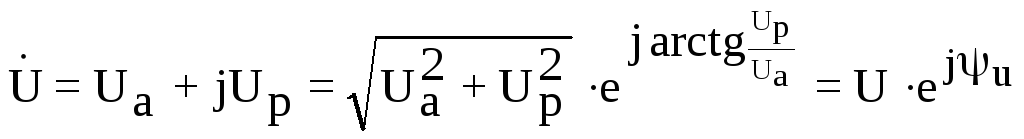
Мощность в цепях однофазного тока
Формула полной мощности определяет соотношение всех мощностей:
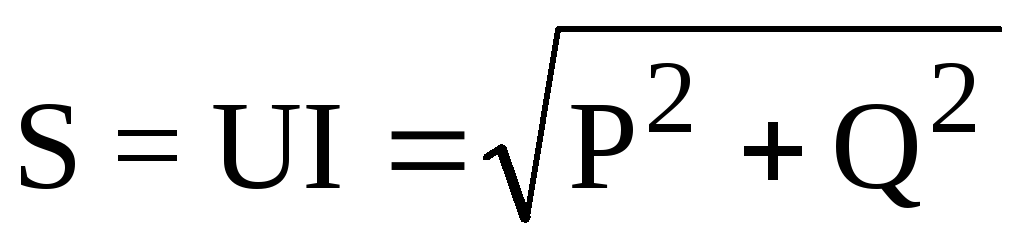 ,
,
где: S — полная мощность цепи;
P — активная мощность цепи;
Q — реактивная мощность цепи.
В комплексной форме формула приобретает вид:
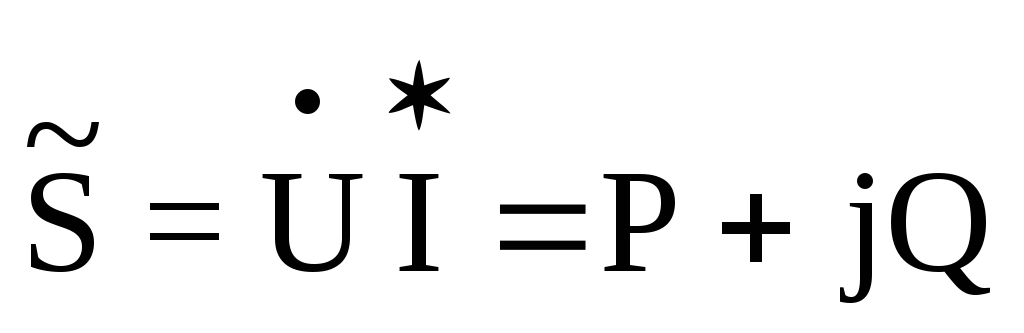 , где:
, где: — сопряженный комплекс тока.
— сопряженный комплекс тока.
Например,
если ток в комплексной форме представлен
формулой 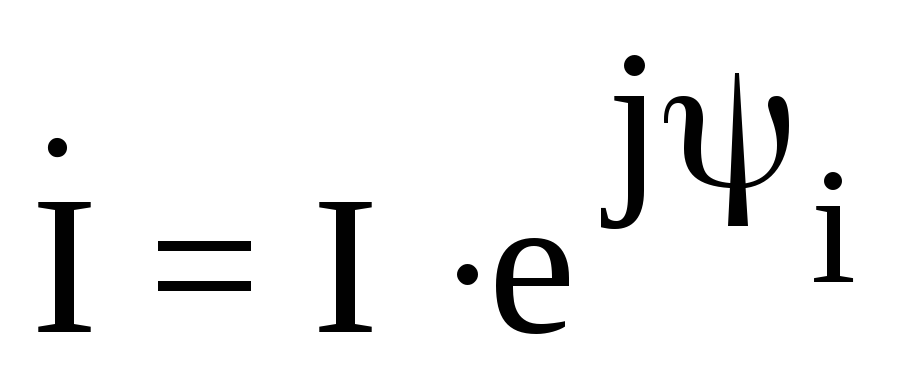 ,
то сопряженный комплекс будет
,
то сопряженный комплекс будет 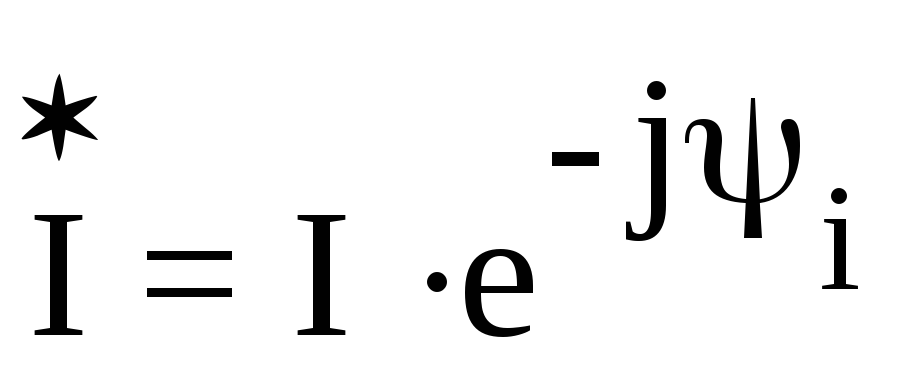 .
.
Построение векторных диаграмм
В основном векторные диаграммы строятся на комплексной плоскости и
бывают двух типов: — векторные диаграммы токов и напряжений;
— векторные топографические диаграммы напряжений.
Все векторные диаграммы строятся в масштабе, как для токов, так и для напряжений. На комплексной плоскости обозначаются оси координат +1 и +j. Методика построения диаграмм зависит от схемы соединения электрической цепи. Если элементы цепи R, L, C соединены последовательно, то «опорным» в диаграмме является вектор тока, как общий для всех элементов. Далее строятся векторы напряжений с учетом сдвига фаз между током и напряжениями на элементах (см. диаграмму А). Геометрическая сумма векторов напряжений должна быть равна вектору напряжения, приложенному к электрической цепи.
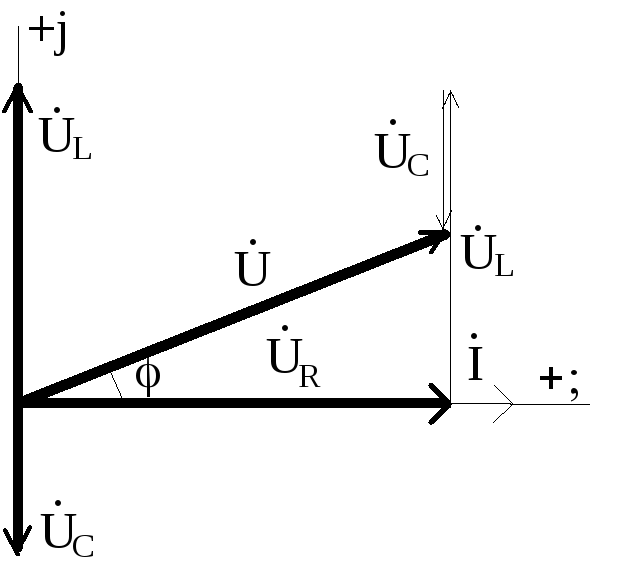
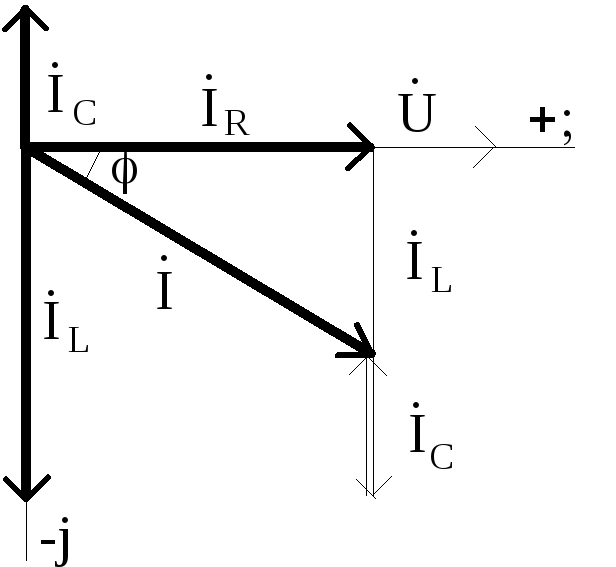
Диаграмма А Диаграмма Б
Если элементы цепи R, L, C соединены параллельно, то «опорным» в диаграмме является вектор напряжения, как общий для всех элементов. Далее строятся векторы токов с учетом сдвига фаз между напряжением и токами в ветвях цепи (см. диаграмму Б). Геометрическая сумма векторов токов в ветвях должна быть равна общему току в электрической цепи.
Топографическая диаграмма напряжений представляет собой диаграмму комплексных потенциалов точек электрической цепи, отложенных в определенном порядке. Потенциал одной из точек принимается равным нулю и далее возможны два варианта построения: первый-относительно этого потенциала рассчитываются потенциалы остальных точек; второй-от этой точки откладываются модули напряжений на элементах с соответствующими углами сдвига фаз. Порядок построения топографической диаграммы виден на простом примере (см. схему В и диаграмму В).
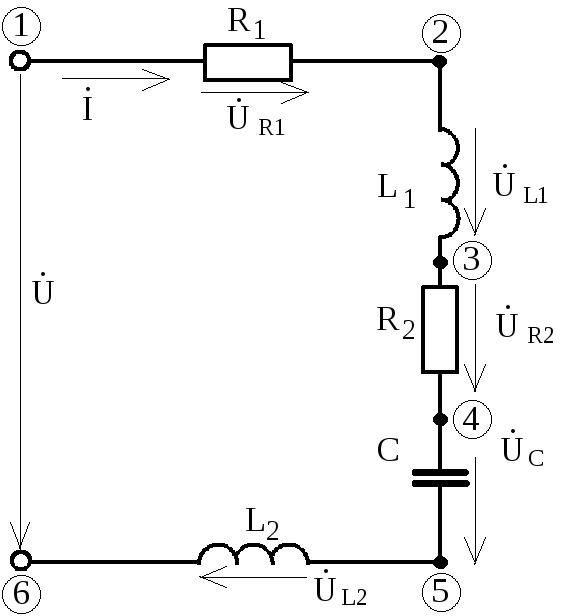
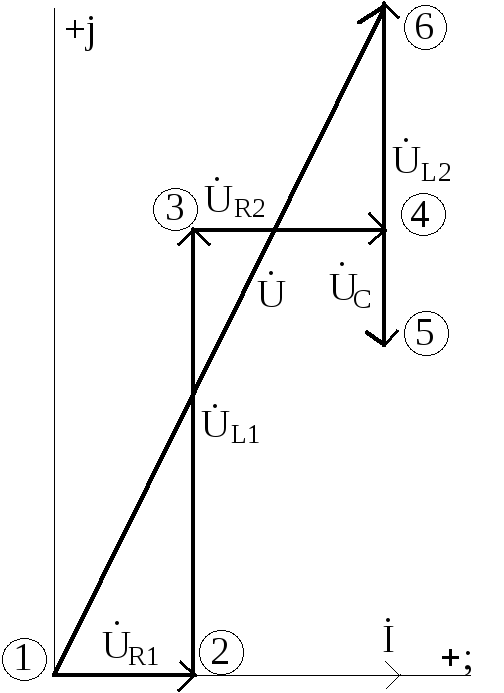
Схема В Диаграмма В
В электрических цепях со смешанным соединением элементов топографическая диаграмма напряжений обычно строится в несколько этапов. При этом сначала строятся диаграммы для отдельных ветвей цепи, что предполагает наличие векторной диаграммы токов для всей цепи, а потом объединяются в общую топографическую диаграмму.
Расчет сопротивлений
Обычно сопротивления задаются, как в явной форме R = 5Ом, так и в виде индуктивностей и емкостей L = 19,1мГн или С = 99,5мкФ. В случае индуктивных и емкостных сопротивлений расчет ведется следующим образом:
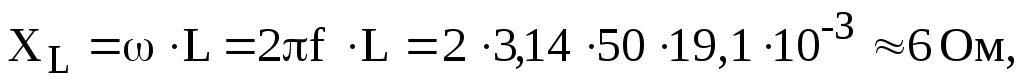
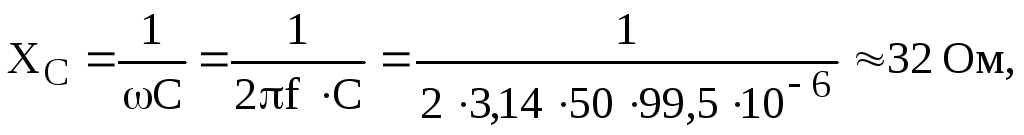 где
f =
50Гц.
где
f =
50Гц.
Методика решения задач
3.2.1. ЗАДАЧА №1.
Последовательное соединение элементов R, L, C.
Дана электрическая цепь переменного тока (см. схему). Используя данные:
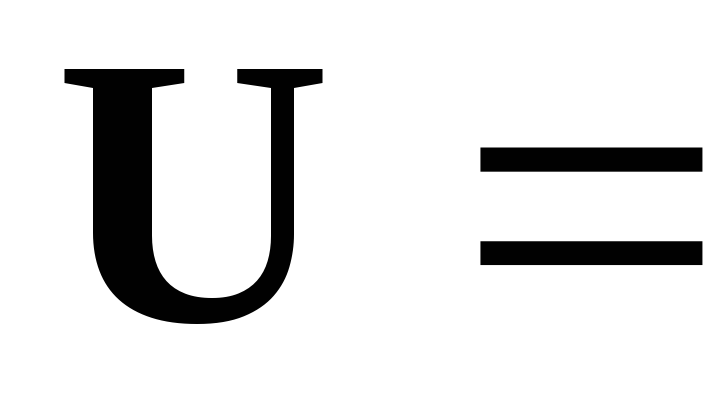 100
[В], f =
50 [Гц],
100
[В], f =
50 [Гц],
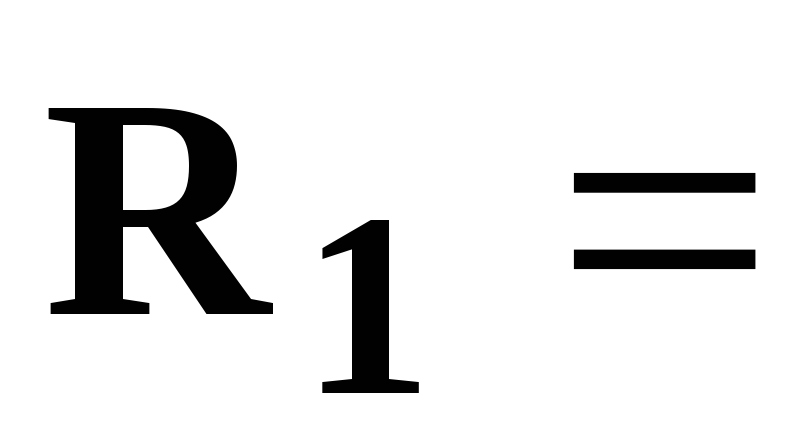 3
[Ом],
3
[Ом], 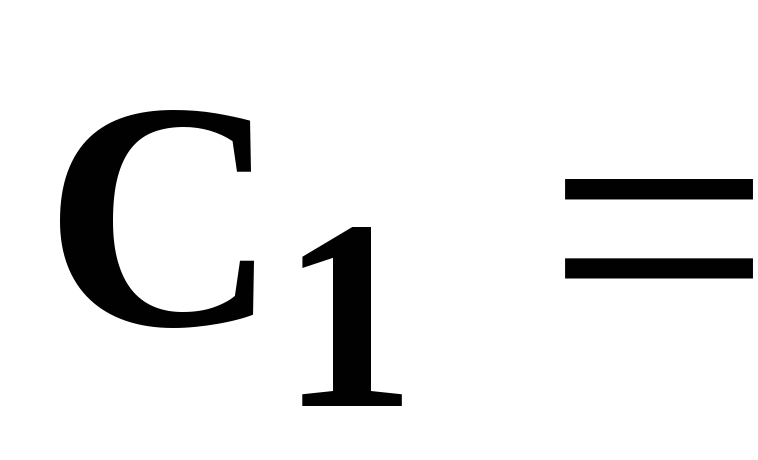 177
[мкФ],
177
[мкФ], 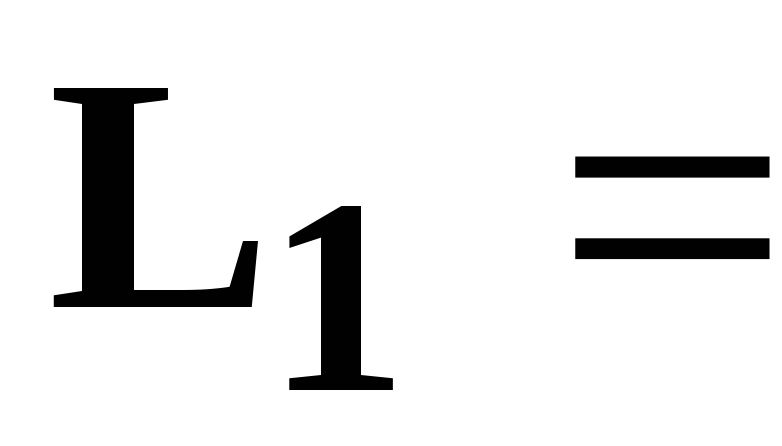 37,2
[мГн], необходимо определить:
37,2
[мГн], необходимо определить:
1) ток в цепи;
2) показания ваттметра W;
Построить векторную диаграмму напряжений.
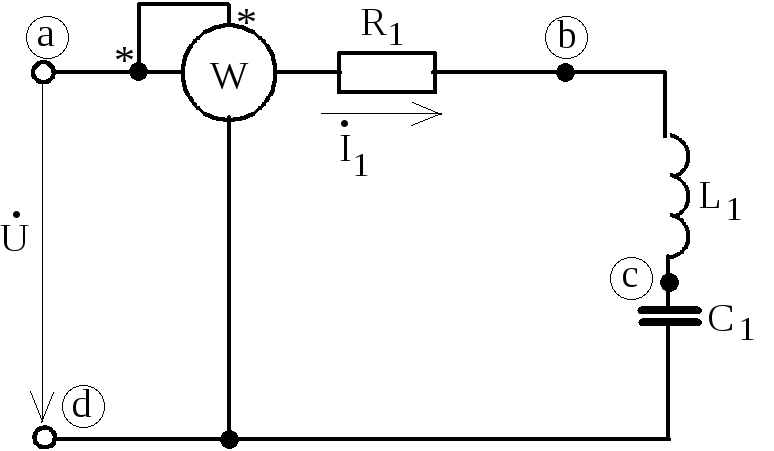
Схема электрической цепи.
1) Расчет тока.
В начале рассчитываем реактивные сопротивления цепи:
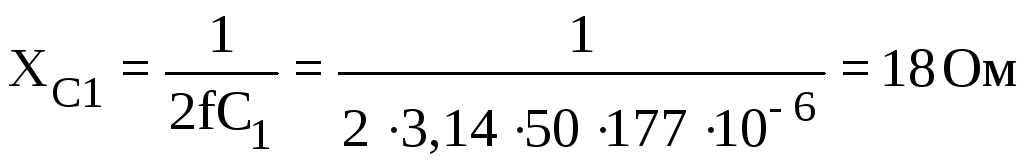 ;
;
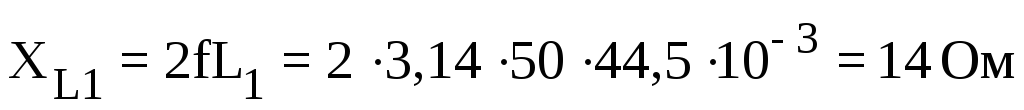 ,
,
а затем полное комплексное сопротивление цепи:
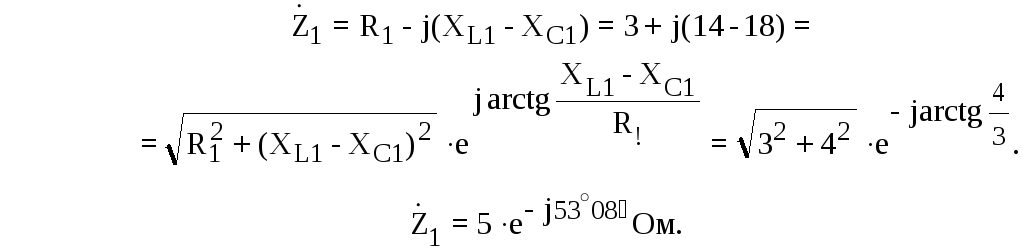
Далее рассчитываем ток и падения напряжения на элементах цепи:
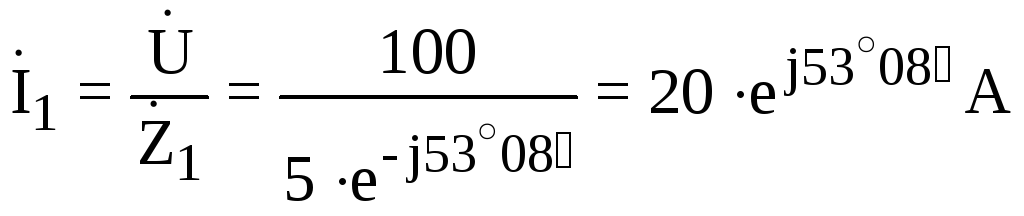 .
.
 ;
;
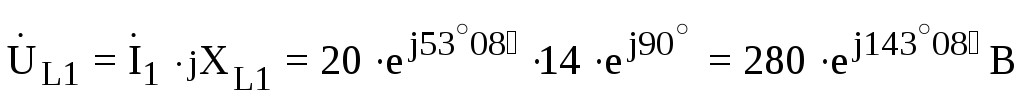 ;
;
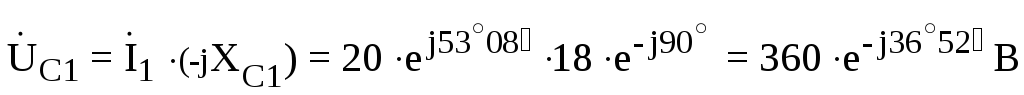 .
.
2) Определение показаний ваттметра.
Ваттметр измеряет активную мощность, которую можно определить как:
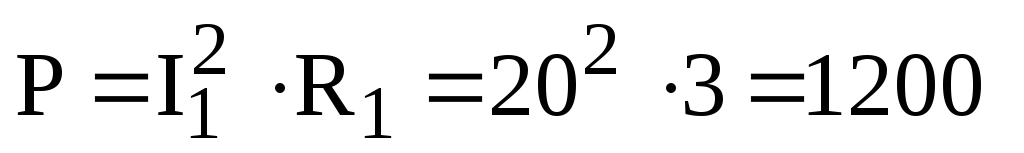 Вт.
Вт.
Построение топографической диаграммы напряжений.
Определим основное уравнение цепи, данные, расчеты и правила построения диаграммы:
— уравнение 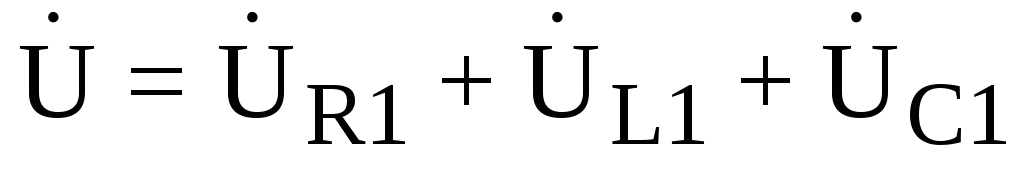 ;
;
— данные 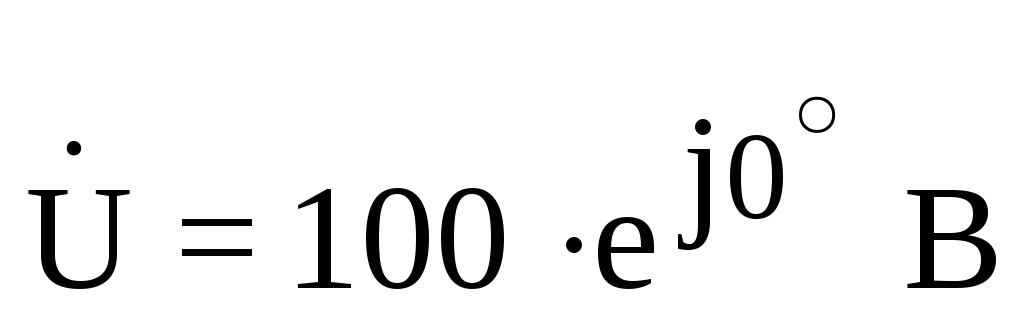
— расчеты 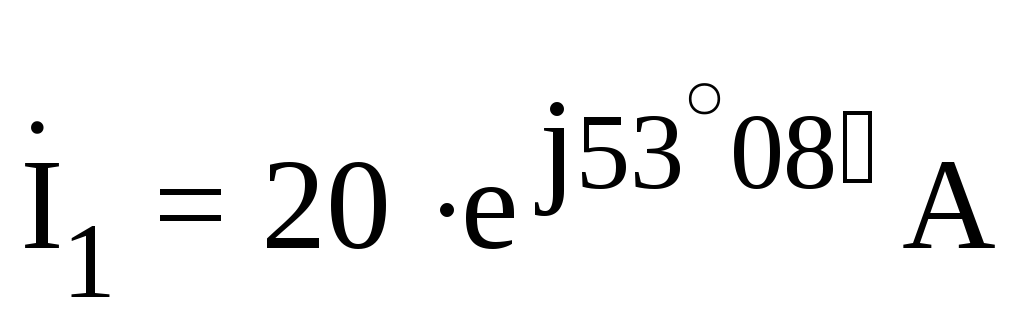 ;
; 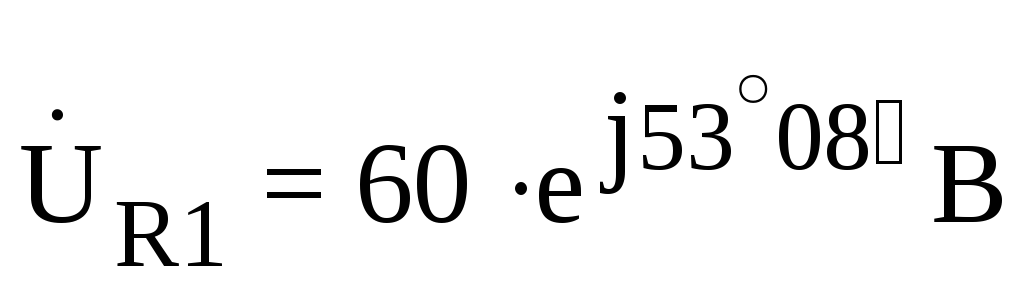 ;
;
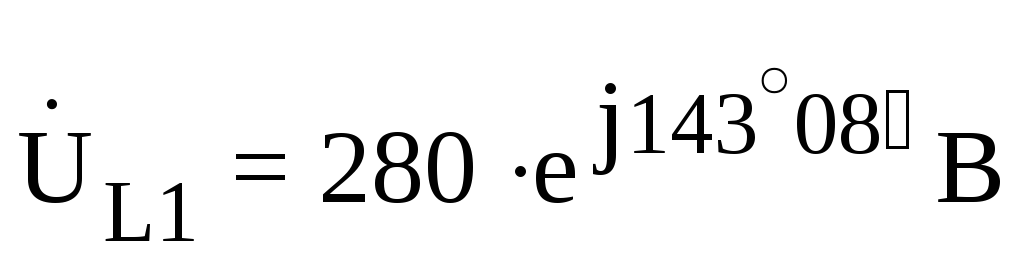 ;
; 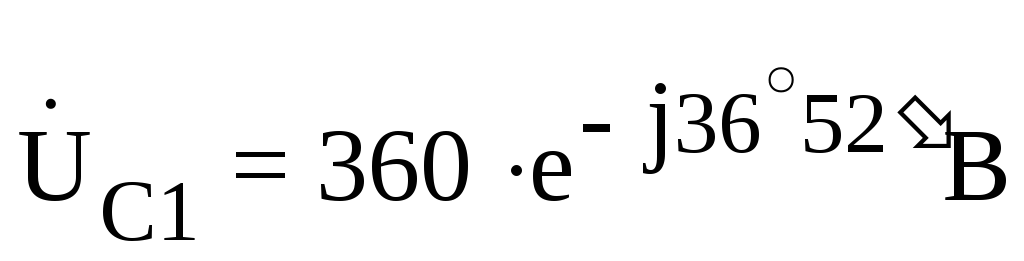 .
.
— правила первое: выбираем масштаб 2A/дел и 25В/дел;
второе: чертим вектор тока в качестве опорного;
третье: чертим векторы всех напряжений;
четвертое: геометрическая сумма напряжений должна быть равна приложенному напряжению питания или э.д.с.
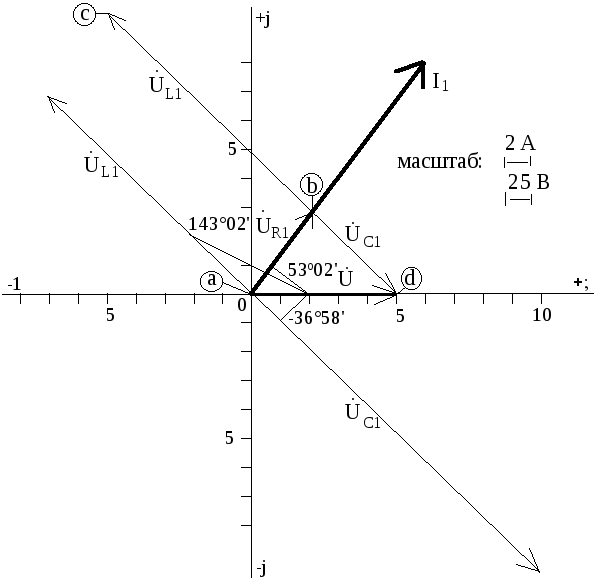
Топографическая диаграмма напряжений
ЗАДАЧА №2.
Параллельное соединение элементов RC, RL, R.
Дана электрическая цепь переменного тока (см. схему). Используя данные:
 200
[В], f =
50 [Гц],
200
[В], f =
50 [Гц],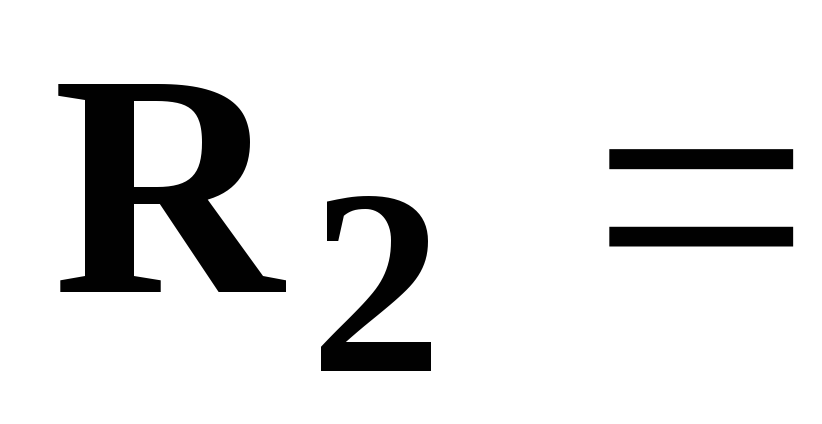 10
[Ом],
10
[Ом], 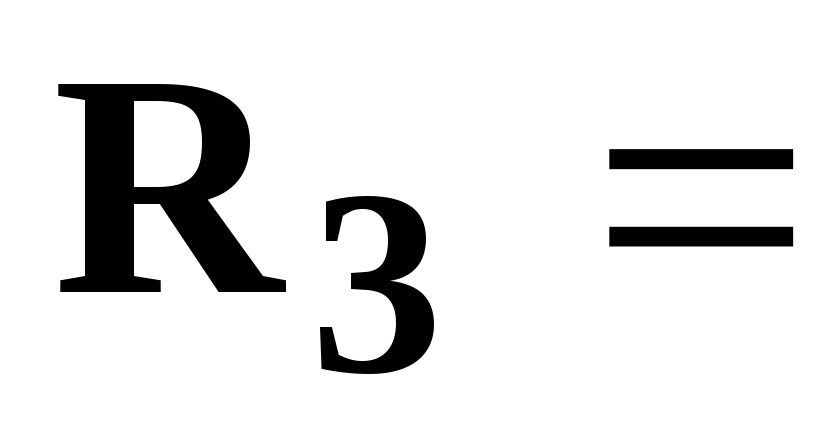 8
[Ом],
8
[Ом], 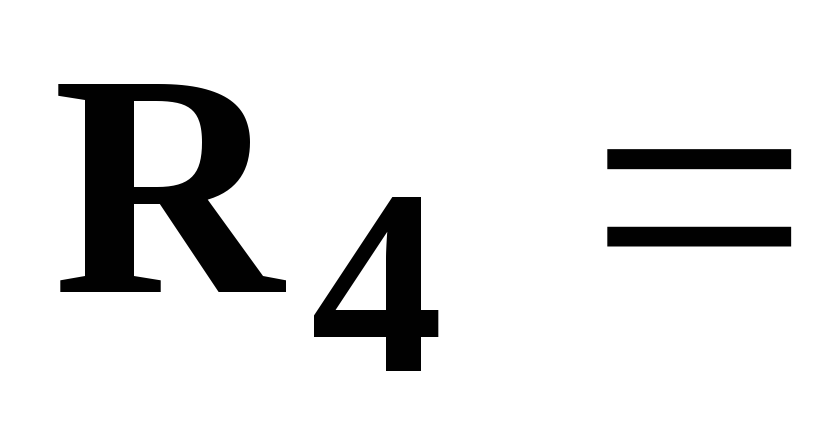 4
[Ом],
4
[Ом],
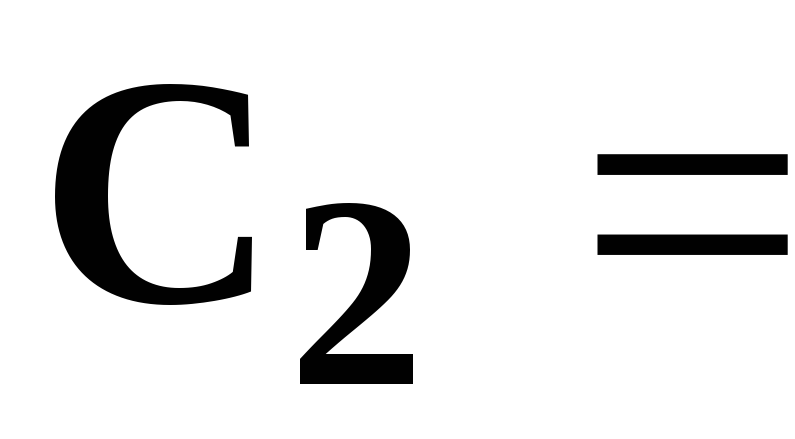 354
[мкФ],
354
[мкФ], 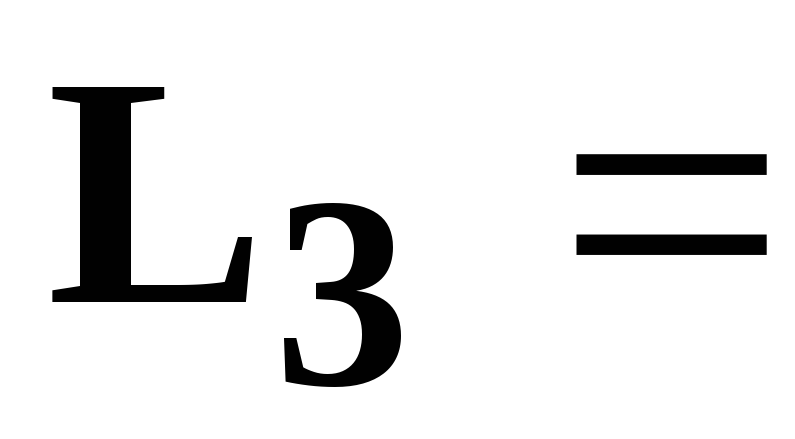 19,1
[мГн], необходимо определить:
19,1
[мГн], необходимо определить:
1) токи в цепи;
2) активную, реактивную и полную мощность цепи;
Построить векторную диаграмму токов и напряжений.
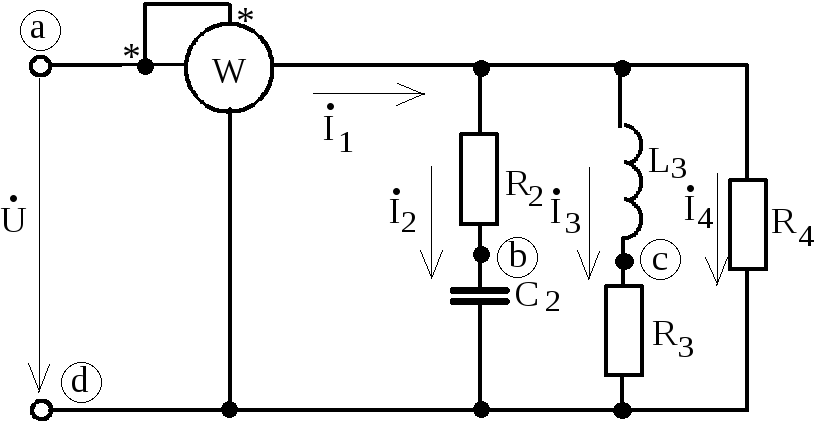
Схема электрической цепи
1) Расчет токов.
Сначала рассчитываем реактивные сопротивления цепи:
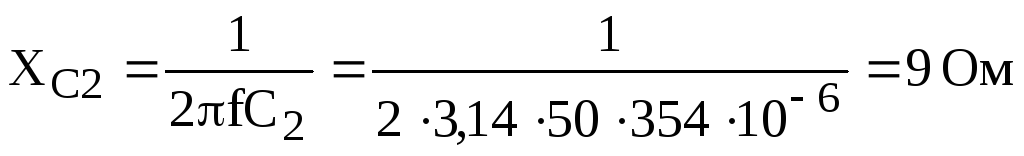 ;
;
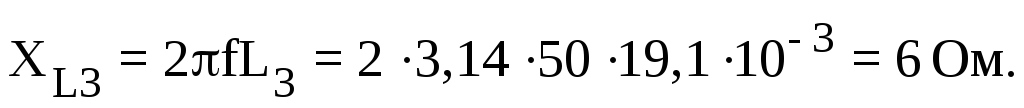
После этого, находим комплексы проводимостей всех параллельных ветвей:
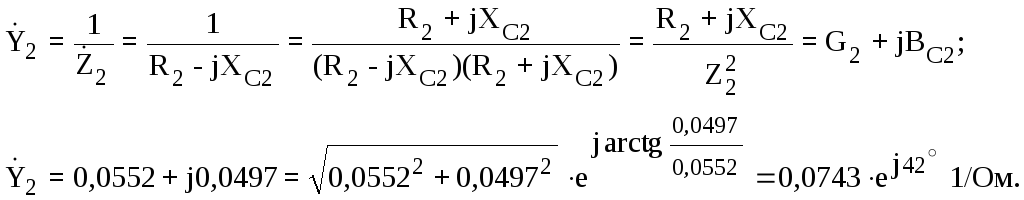
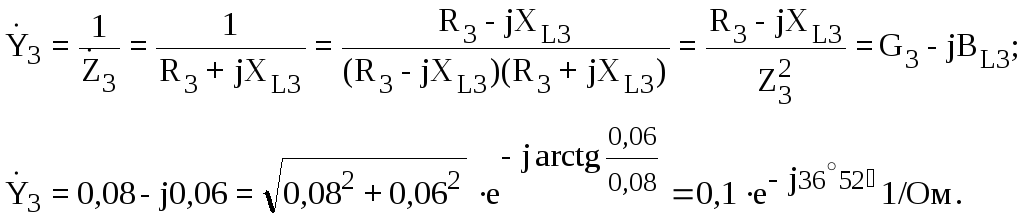
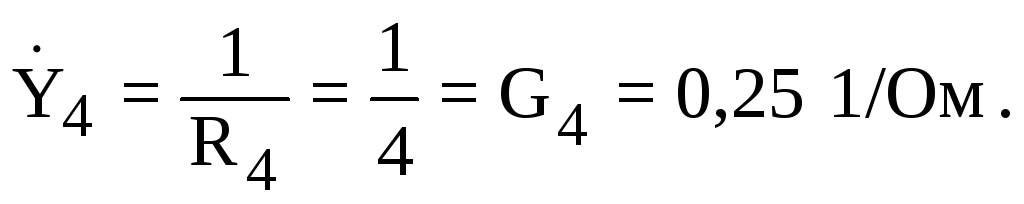
Используя рассчитанные проводимости, найдем комплекс эквивалентной проводимости всей цепи:
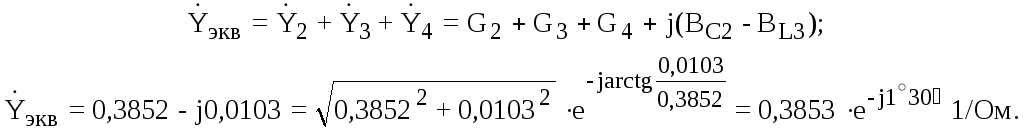
И, наконец, рассчитаем токи:
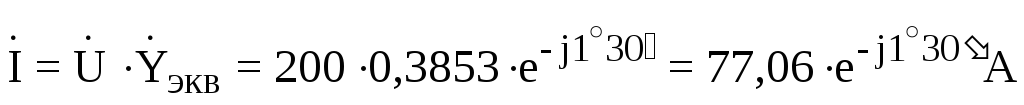 ;
;
 ;
;
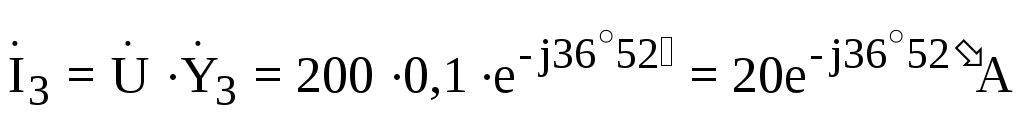 .
.
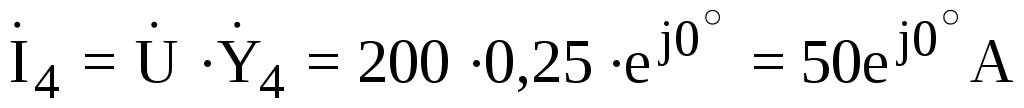 .
.
2) Определение мощностей P,Q и S
С помощью формулы комплексной, полной мощности можно определить активную и реактивную составляющие:

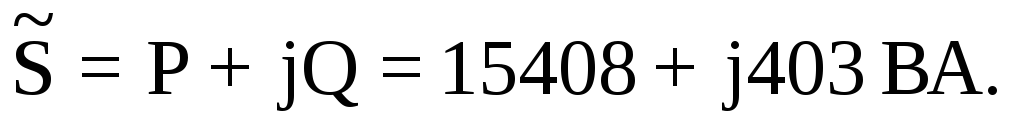
где:
активная мощность  ;
;
реактивная
мощность 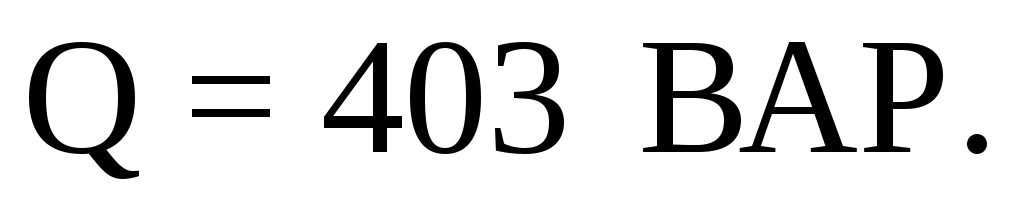
Построение векторной диаграммы токов и топографической диаграммы напряжений.
Определим основные уравнения цепи, данные, расчеты и правила построения диаграммы:
— уравнения 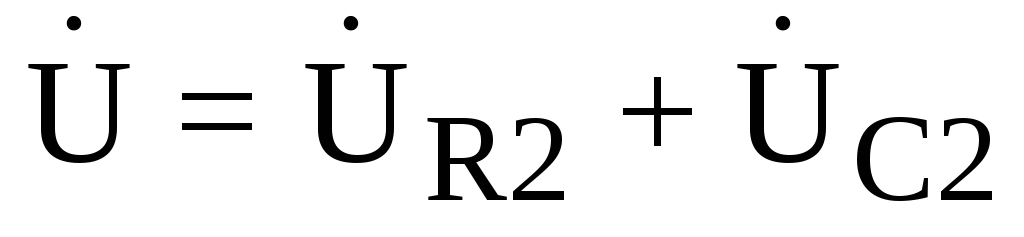 ;
; 
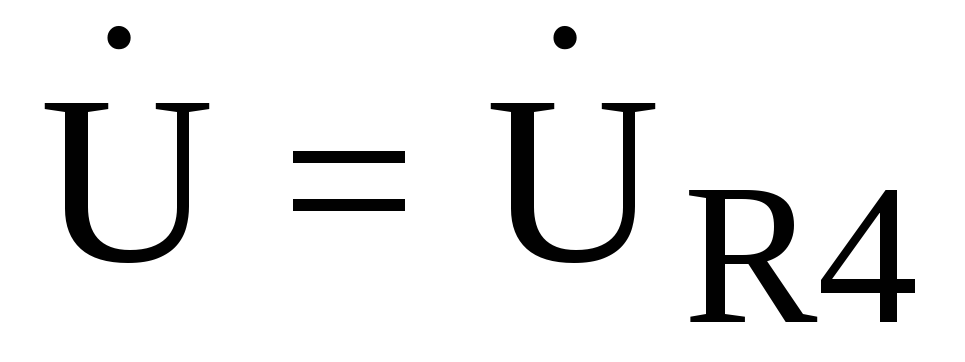
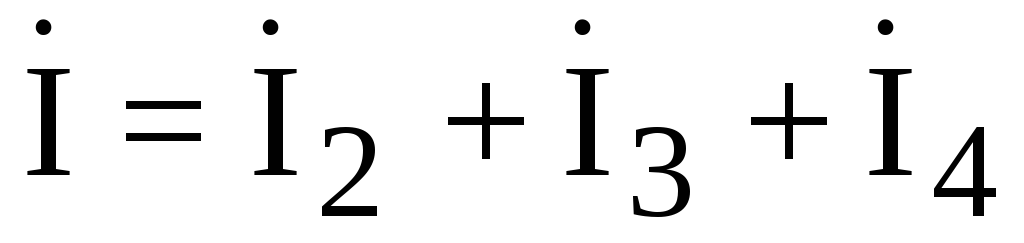 .
.
— данные 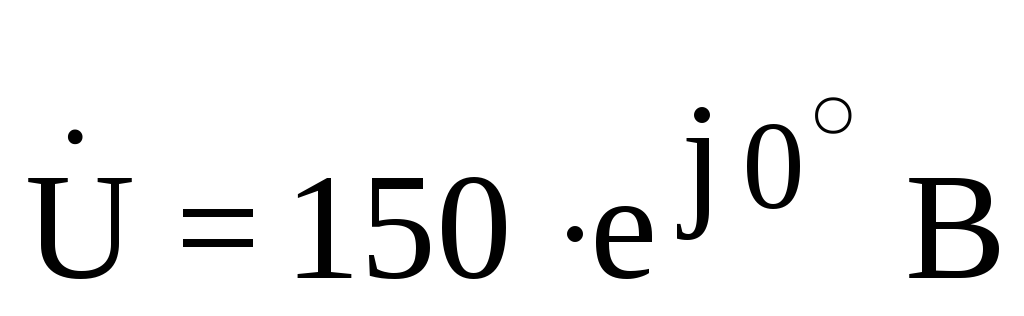
— расчеты 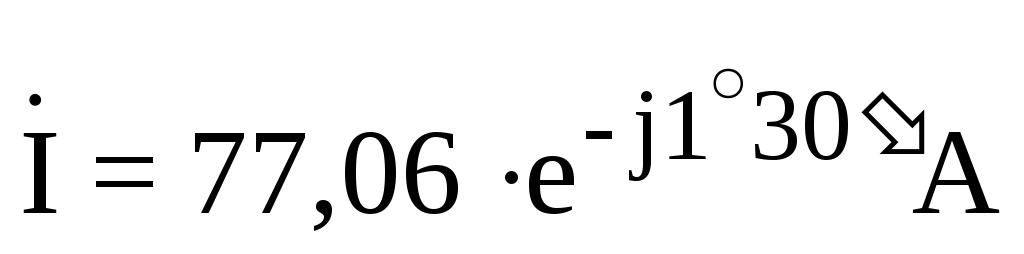 ;
; 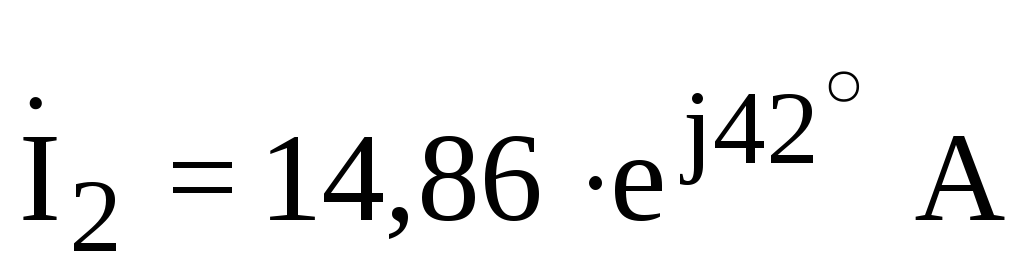 ;
;
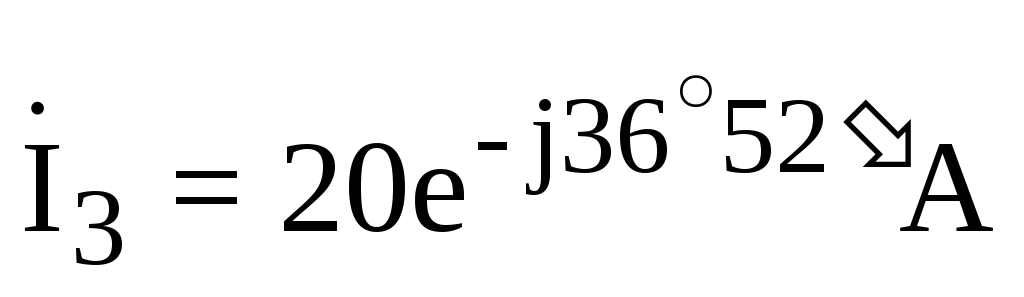 ;
; 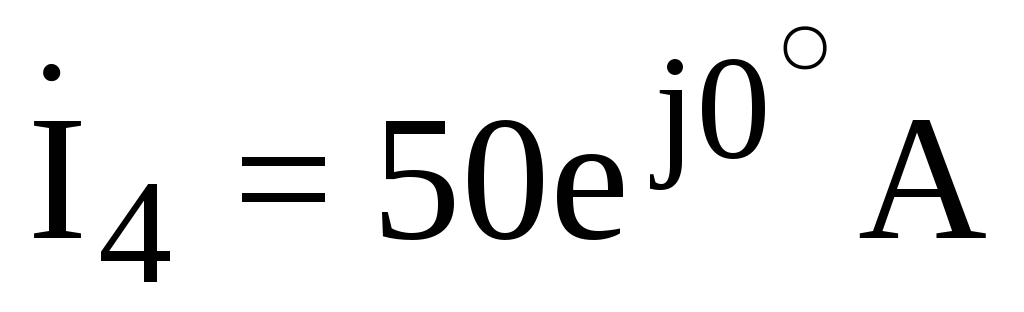 .
.  ;
; 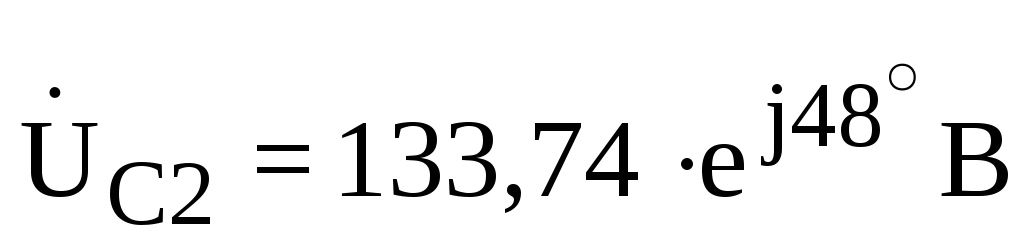 ;
; 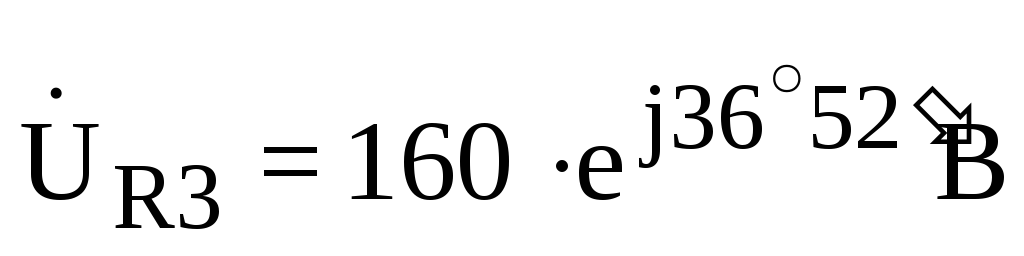 ;
; 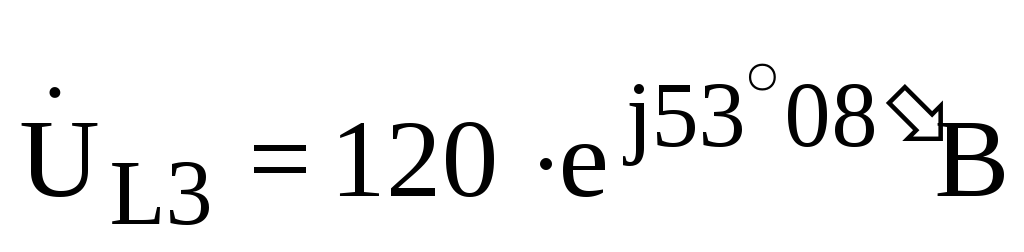 ;
; 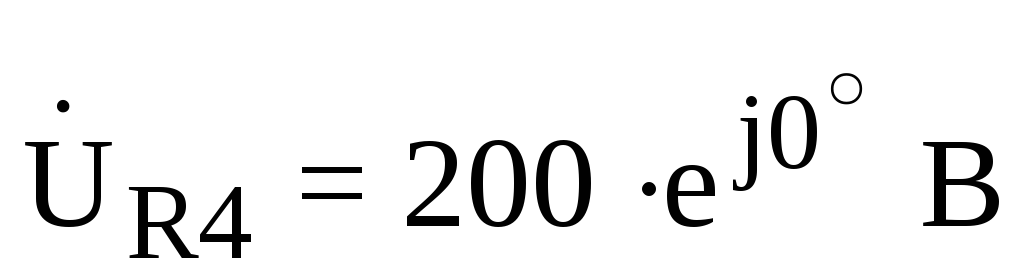 .
.
— правила первое: выбираем масштаб по току и напряжению 4A/дел и 20В/дел;
второе: начертим векторы токов в ветвях цепи и составим геометрическую сумму этих токов, которая должна быть равна вектору общего тока.
третье: начертим векторы всех напряжений по точкам на схеме и составим геометрическую сумму этих напряжений в каждой ветви, которая должна быть равна вектору напряжения источника питания.
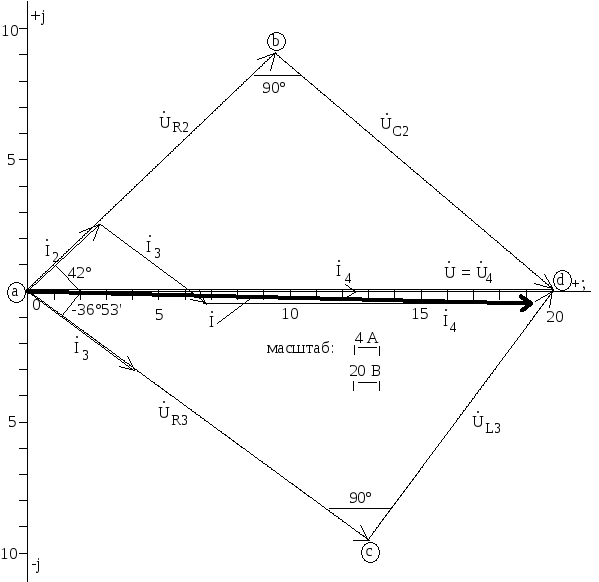
Векторная диаграмма токов и топографическая диаграмма напряжений
3.2.3. ЗАДАЧА N° 3.
Смешанное соединение элементов R, L, C.
Дана электрическая цепь переменного тока (см. схему). Используя данные:
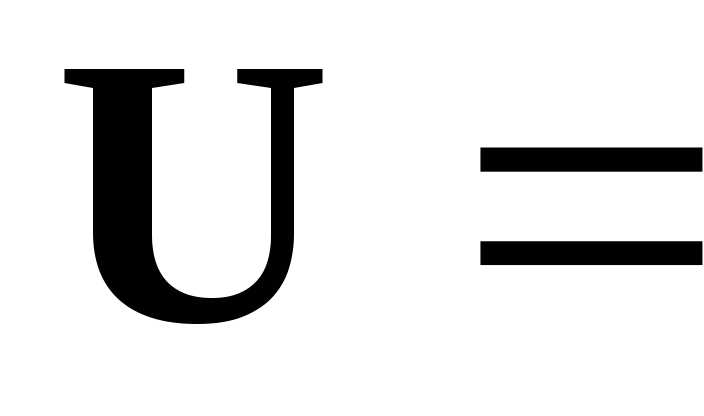 150
[В], f =
50 [Гц],
150
[В], f =
50 [Гц], 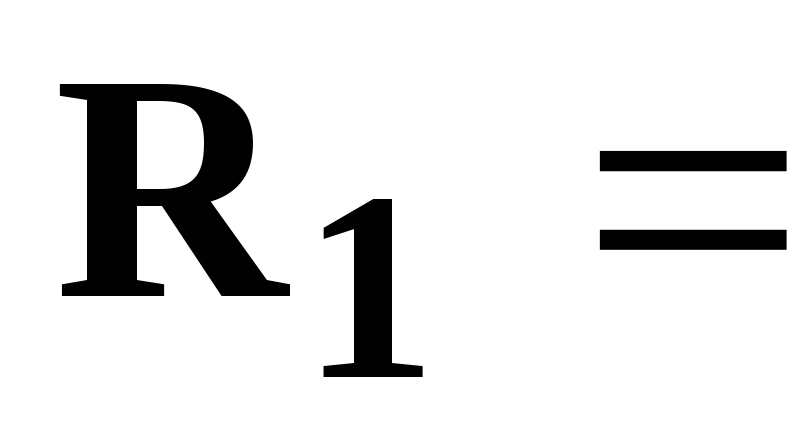 2
[Ом],
2
[Ом], 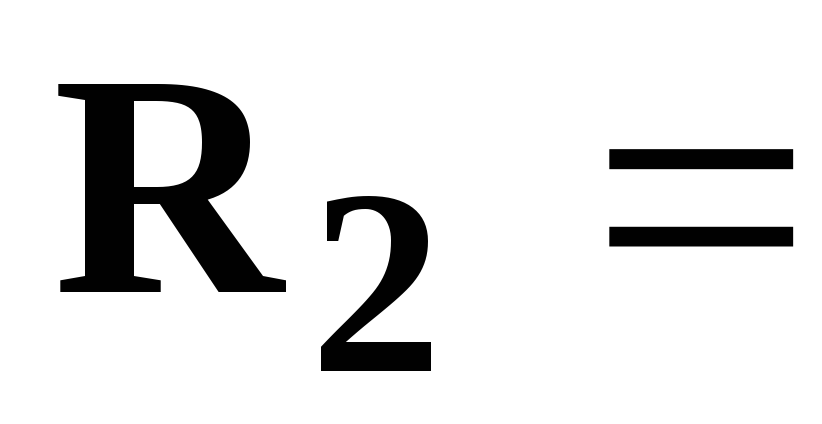 3
[Ом],
3
[Ом],
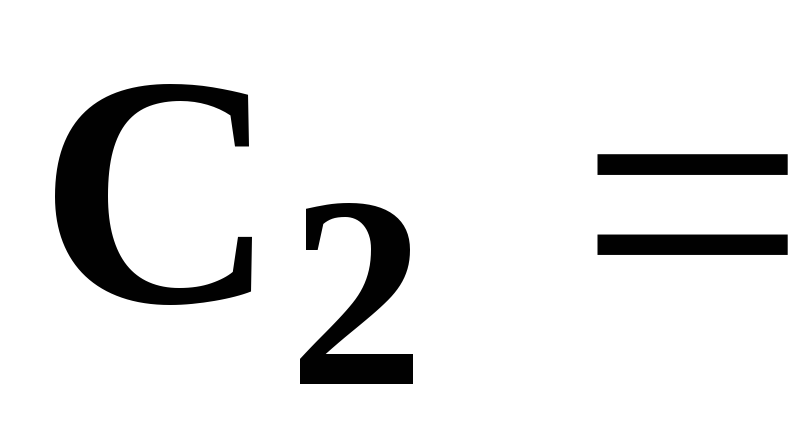 354
[мкФ],
354
[мкФ], 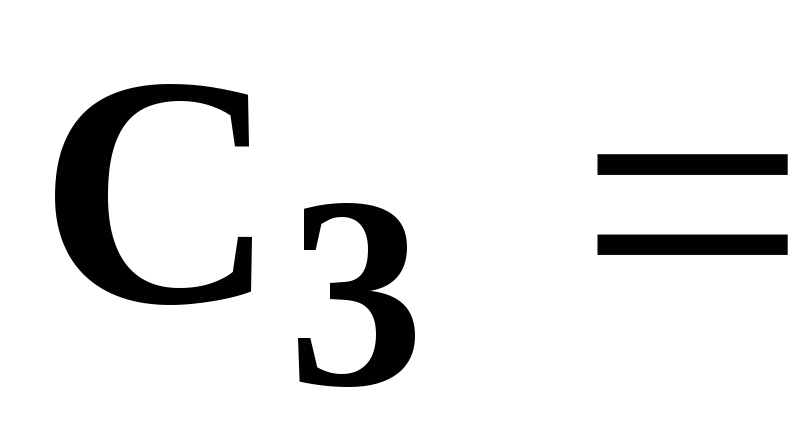 798
[мкФ],
798
[мкФ], 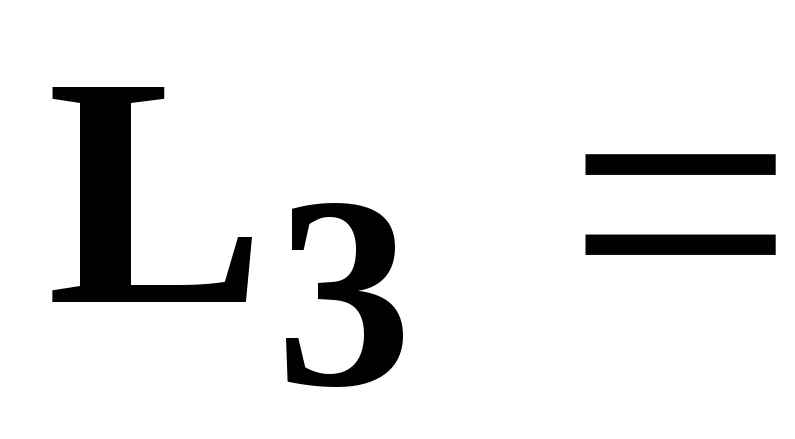 19,1
[мГн], необходимо определить:
19,1
[мГн], необходимо определить:
1) ток в цепи;
2) показания ваттметра W;
Построить векторную диаграмму токов и топографическую диаграмму напряжений по внутреннему контуру электрической цепи.
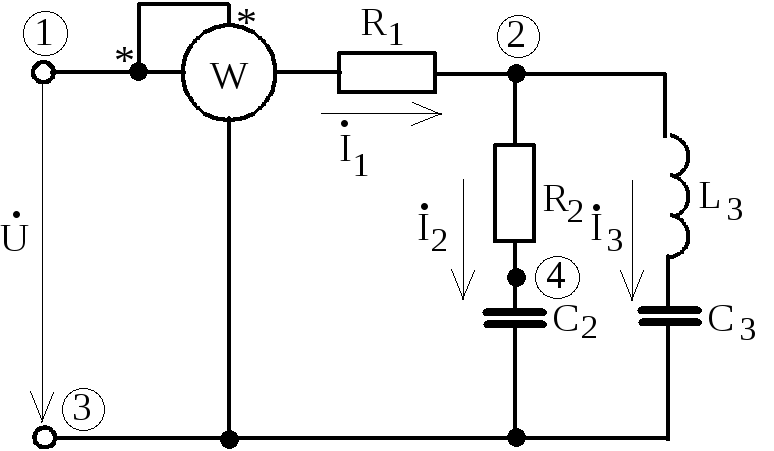
Схема электрической цепи
1) Расчет токов
Сначала рассчитаем реактивные сопротивления цепи:
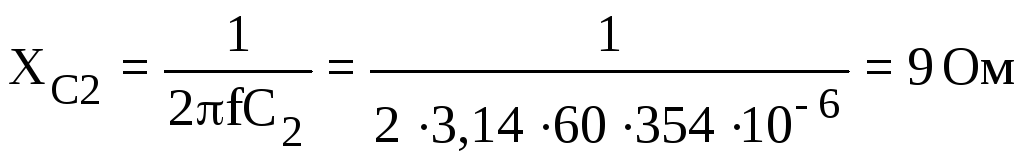 ;
;  ;
;
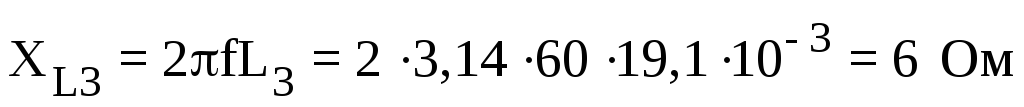 ,
,
а потом комплексы полных сопротивлений всех ветвей:
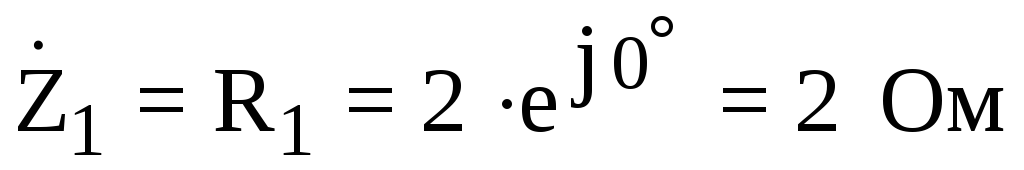 ;
;
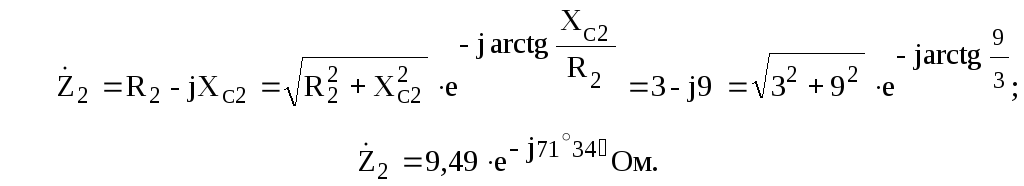
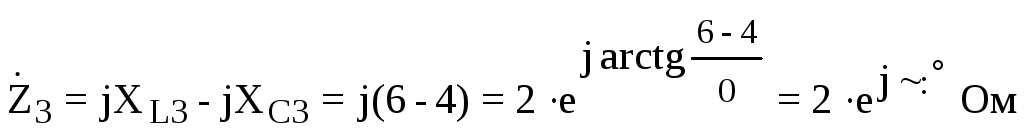 .
.
Используя рассчитанные величины, найдем комплекс сопротивления между точками 2-3 и комплекс полного эквивалентного сопротивления цепи:
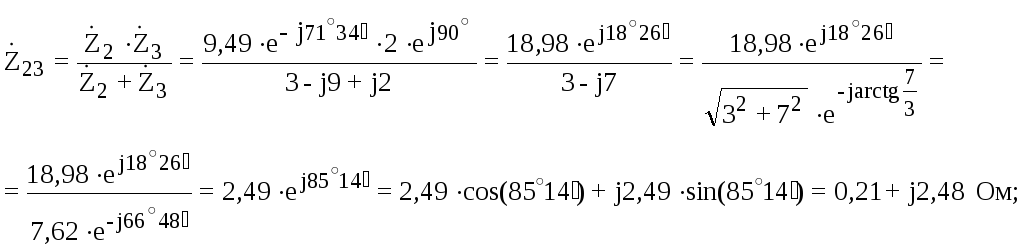
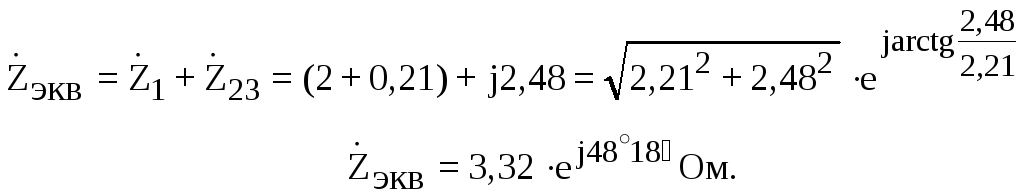 .
.
И, наконец, рассчитываем токи:
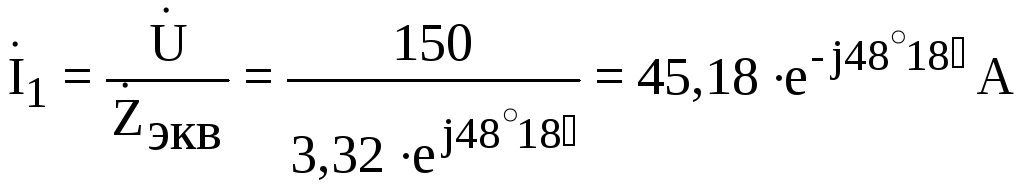 ;
;
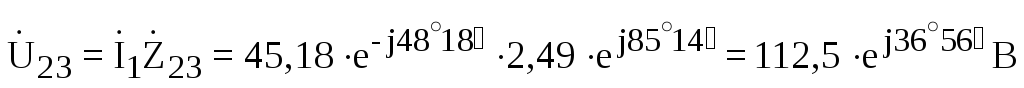
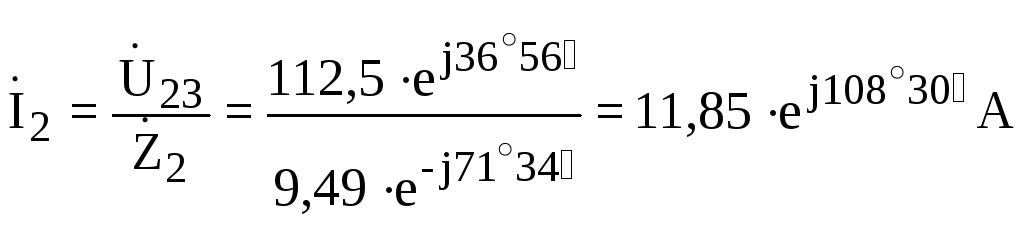 ;
;
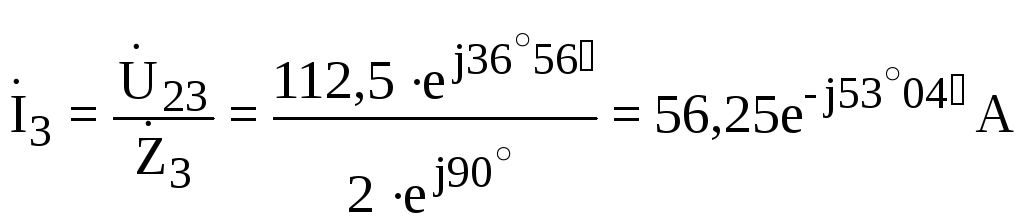 .
.
2) Определение показаний ваттметра
Зная комплекс полного эквивалентного сопротивления цепи, можно рассчитать полную, активную и реактивную мощности цепи:
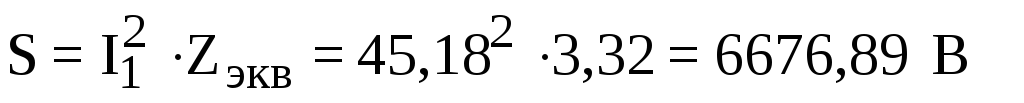
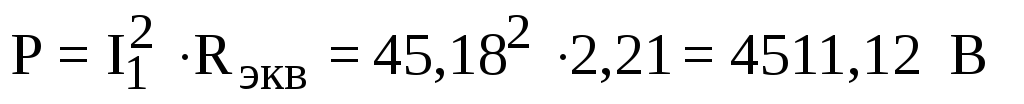 ;
;
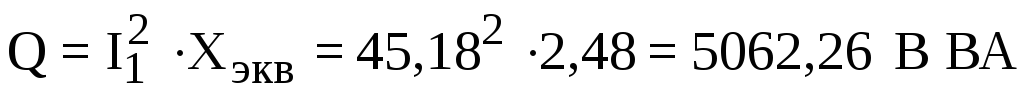
Таким образом, показания ваттметра будут 4511,12 Вт.
Построение векторной диаграммы токов и топографической диаграммы напряжений.
Определим основные уравнения цепи, данные, расчеты и правила построения диаграммы:
— уравнения 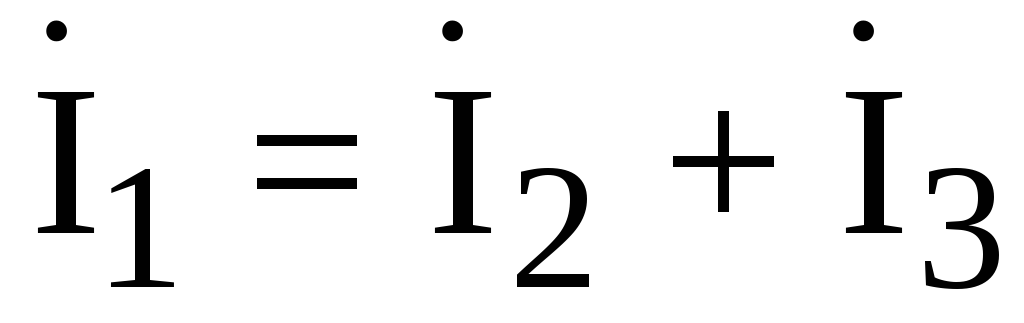 ;
;  ;
; 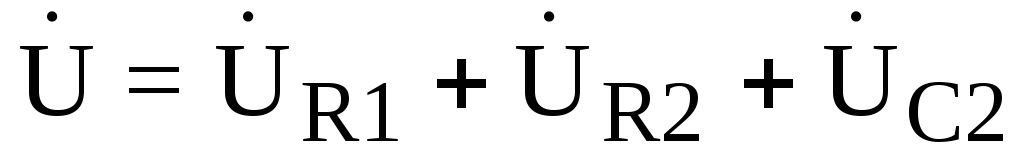 ;
;
— данные 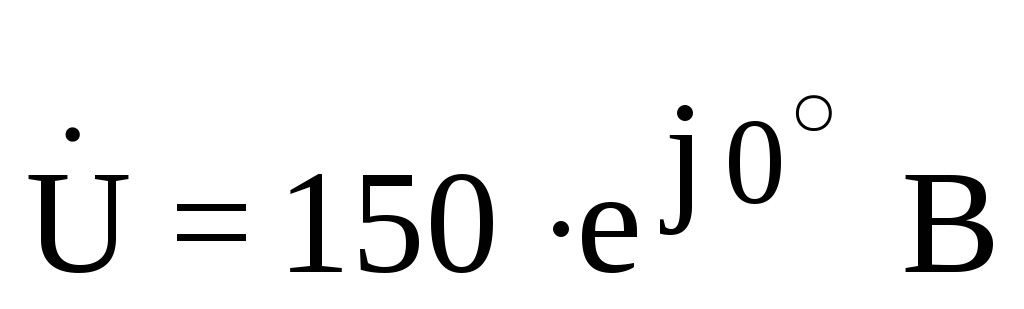 ;
;
— расчеты 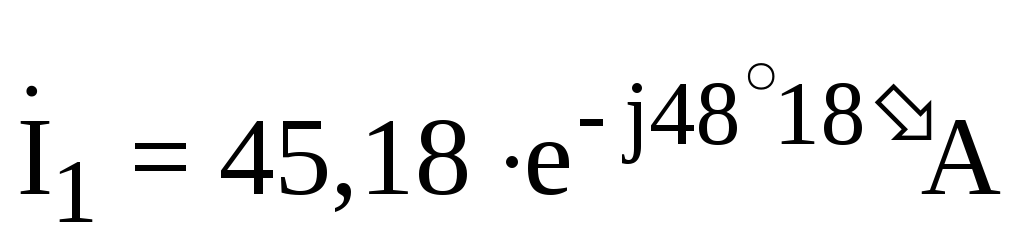 ;
; 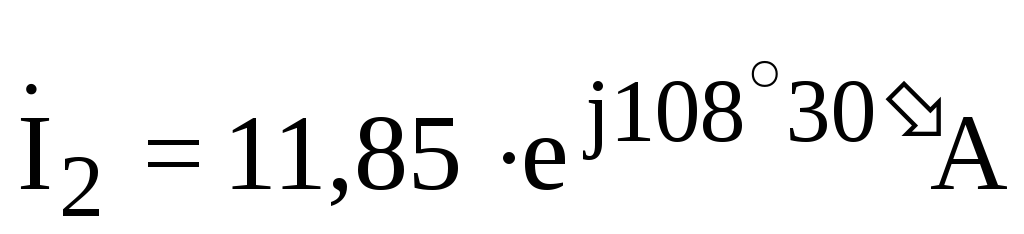 ;
; 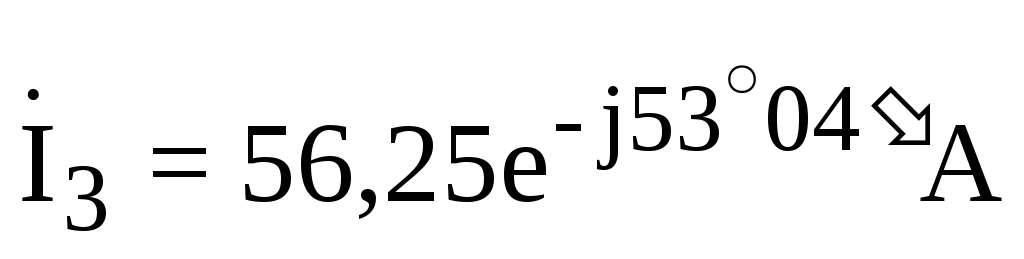 ;
;
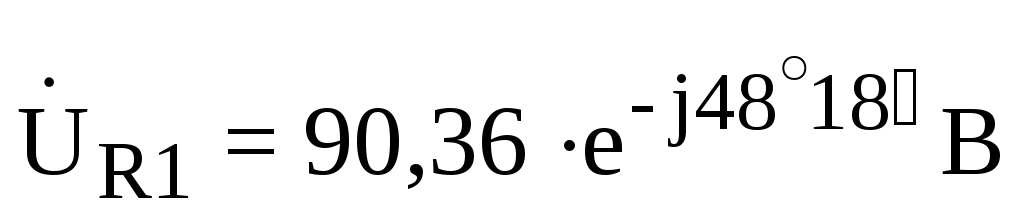 ;
;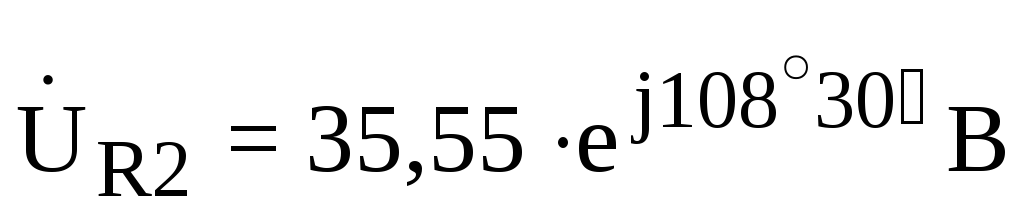 ;
;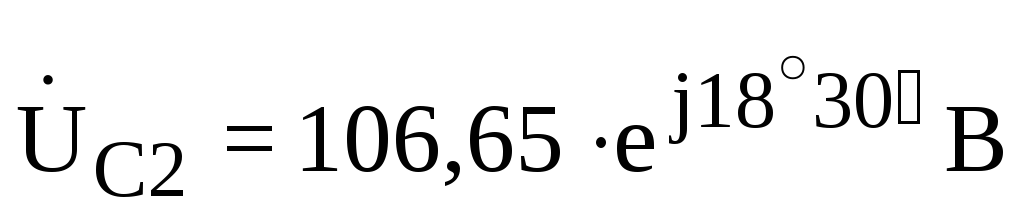
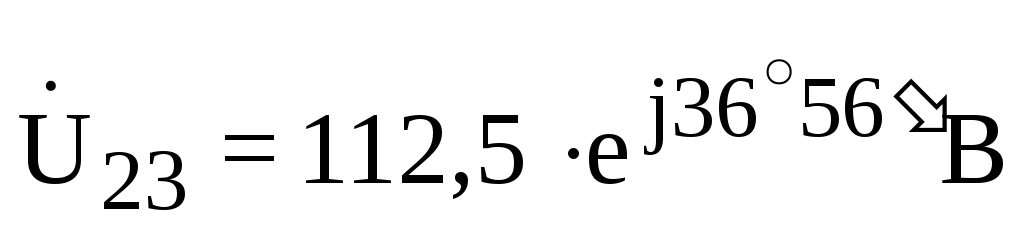 .
.
— правила первое: выбираем масштаб по току и напряжению 3A/дел и 10В/дел;
второе: начертим векторы токов в ветвях цепи и составим геометрическую сумму этих токов, которая должна быть равна вектору общего тока.
третье: начертим векторы всех напряжений по точкам на схеме и составим геометрическую сумму этих напряжений, которая должна быть равна вектору напряжения источника питания.
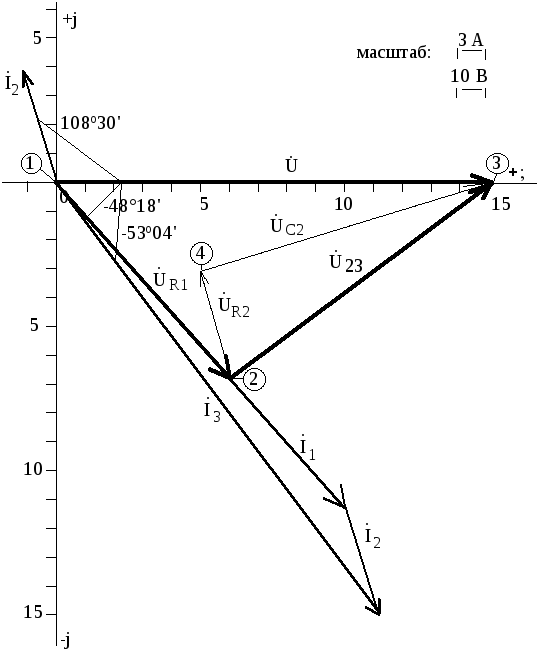
Векторная диаграмма токов и топографическая диаграмма напряжений
11




 ,
град.
,
град. ,
А
,
А