27.Магнитное поле. Силовые линии магнитного поля. Принцип суперпозиции магнитных полей.

Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения;магнитная составляющая электромагнитного поля.

Силовые линии магнитного поля – это воображаемые линии, касательные к которым в каждой точке поля совпадают по направлению с вектором магнитной индукции. 

Для магнитного поля справедлив принцип суперпозиции: в каждой точке пространства вектор магнитной индукции B∑→B∑→ созданных в этой точке всеми источниками магнитных полей равен векторной сумме векторов магнитных индукций Bk→Bk→

, созданных в этой точке всеми источниками магнитных полей:

28.Закон Био-Савара-Лапласа. Закон полного тока.

 Формулировка закона Био Савара Лапласа имеет вид: При прохождении постоянного тока по замкнутому контуру, находящемуся в вакууме, для точки, отстоящей на расстоянии r0, от контура магнитная индукция будет иметь вид.

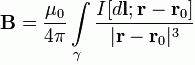
где I     ток в контуре

     гамма контур, по которому идет интегрирование

     r0    произвольная точка

Закон полного тока это закон, связывающий циркуляцию вектора напряженности магнитного поля и ток.

Циркуляция вектора напряженности магнитного поля по контуру равна алгебраической сумме токов, охватываемых этим контуром.

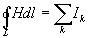
29.Магнитное поле проводника с током. Магнитный момент кругового тока.

30. Действие магнитного поля на проводник с током. Закон Ампера. Взаимодействие токов.

F = B I l sinα,

где α — угол между векторами магнитной индукции и тока,

B — индукция магнитного поля, I — сила тока в проводнике, l — длина проводника.

Взаимодействие токов. Если в цепь постоянного тока включить два провода, то: Последовательно включенные параллельные близко расположенные проводники отталкиваются.  Параллельно включенные проводники притягиваются. 

31. Действие электрических и магнитных полей на движущийся заряд. Сила Лоренца.

Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамике

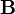 действует на точечную заряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью заряд лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1], иначе говоря, со стороны электрического и  магнитного полей.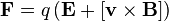

32. Действие магнитного поля на вещество. Диа-, пара- и ферромагнетики. Магнитный гистерезис.

B=B₀+B₁

где  B⃗  B→ — магнитная индукция поля в веществе;  B⃗ 0 B→0 — магнитная индукция поля в вакууме,  B⃗ 1 B→1 — магнитная индукция поля, возникшего благодаря намагничиванию вещества. 

Вещества, для которых магнитная проницаемость незначительно меньше единицы (μ < 1), называются

 диамагнетиками, незначительно больше единицы (μ > 1) — парамагнетиками.

ферромагнетик — вещество или материал, в котором наблюдается явление ферромагнетизма, т. е. появление спонтанной намагниченности при температуре ниже температуры Кюри.

Магнитный гистерезис — явление зависимости вектора намагничивания и вектора напряженностимагнитного 

поля в веществе не только от приложенного внешнего поля, но и от предыстории данного образца

Магнитное поле прямого тока — урок. Физика, 8 класс.

Существование магнитного поля вокруг проводника с электрическим током можно обнаружить различными способами. Один из таких способов заключается в использовании мелких железных опилок.

 

В магнитном поле опилки — маленькие кусочки железа — намагничиваются и становятся магнитными стрелочками. Ось каждой стрелочки в магнитном поле устанавливается вдоль направления действия сил магнитного поля.

Линии, вдоль которых в магнитном поле располагаются оси маленьких магнитных стрелок, называют магнитными линиями магнитного поля.

С помощью магнитных линий удобно изображать магнитные поля графически. Так как магнитное поле существует во всех точках пространства, окружающего проводник с током, то через любую точку можно провести магнитную линию. Магнитные линии магнитного поля тока представляют собой замкнутые кривые, охватывающие проводник.

 

Обрати внимание!

Направление, которое указывает северный полюс магнитной стрелки в каждой точке поля, принято за направление магнитной линии магнитного поля.

Цепочки, которые образуют в магнитном поле железные опилки, показывают форму магнитных линий магнитного поля (рис. 1).

 

Рис. 1

 

Если прямой проводник пропустить сквозь лист картона, на который насыпан тонкий слой железных опилок, включить ток и опилки слегка встряхнуть, то под действием магнитного поля тока железные опилки расположатся вокруг проводника не беспорядочно, а по концентрическим окружностям (рис. 2).

 

Рис. 2

 

На рисунке показано расположение магнитных стрелок вокруг проводника с током, расположенного перпендикулярно плоскости чертежа, ток в нём направлен от нас, что условно обозначено кружком с крестиком. Оси этих стрелок устанавливаются вдоль магнитных линий магнитного поля прямого тока (рис. 3, а).

При изменении направления тока в проводнике на противоположное (к нам), что условно обозначено кружком с точкой, все магнитные стрелки поворачиваются на \(180\)° (рис. 3, б).

 

Рис. 3

 

Направление магнитных линий магнитного поля тока связано с направлением тока в проводнике.

Направление линий магнитного поля можно определить с помощью правила правой руки:

если обхватить проводник с током ладонью правой руки так, чтобы отставленный большой палец был сонаправлен с током (рис. 4), то согнутые четыре пальца укажут направление линий магнитного поля.

 

Рис. 4

Силовые линии векторного поля — Википедия

Материал из Википедии — свободной энциклопедии

Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 января 2019; проверки требует 1 правка. Текущая версия страницы пока не проверялась опытными участниками и может значительно отличаться от версии, проверенной 3 января 2019; проверки требует 1 правка. Силовые линии, изображающие электрическое поле, созданное положительным зарядом (слева), отрицательным зарядом (по центру) и незаряженным объектом (справа).

Силовая линия, или интегральная кривая, — это кривая, касательная к которой в любой точке совпадает по направлению с вектором, являющимся элементом векторного поля в этой же точке. Применяется для визуализации векторных полей, которые сложно наглядно изобразить каким-либо другим образом. Иногда (не всегда) на этих кривых ставятся стрелочки, показывающие направление вектора вдоль кривой. Для обозначения векторов физического поля, образующих силовые линии, обычно используется термин «напряжённость».

Различные виды реальных физических полей имеют свои особенности, которые проявляются в изображении интегральных кривых. В частности, электрический заряд является центром, в котором сходятся силовые линии.

Электрическое поле, согласно уравнениям Максвелла ∇→×E→=−dB→dt{\displaystyle {\vec {\nabla }}\times {\vec {E}}=-{\frac {d{\vec {B}}}{dt}}} и ∇⋅D→=ρ{\displaystyle \nabla \cdot {\vec {D}}=\rho }, может быть как потенциальным (обусловлено наличием электрических зарядов), так и вихревым (возникающим за счёт явления электромагнитной индукции), или комбинацией этих двух случаев. Потенциальное электрическое поле имеет интегральные кривые, которые начинаются на положительном заряде и заканчиваются на отрицательном; сила Кулона, действующая на пробный заряд, будет направлена по касательной к интегральной кривой

[1]^[2]. Силовые линии вихревого поля замкнуты, их плотность в точке пространства определена значением производной по времени магнитной индукции в этой точке, а направление определяется правилом буравчика.

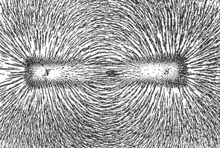Силовые линии магнитного поля магнита, визуализированные железными опилками.

Согласно уравнениям Максвелла ∇⋅B=0{\displaystyle \nabla \cdot B=0} и ∇→×H→=dD→dt+j→{\displaystyle {\vec {\nabla }}\times {\vec {H}}={\frac {d{\vec {D}}}{dt}}+{\vec {j}}}, и пока неизвестны магнитные монополи, магнитное поле может возникать лишь в результате изменения электрической индукции (первое слагаемое в правой части 2-го уравнения) и протекания электрического тока (второе слагаемое в правой части 2-го уравнения). Отсюда следует, что магнитное поле является вихревым, а его силовые линии (линии магнитной индукции) всегда замкнуты, то есть дивергенция магнитного поля везде равна 0.

Линии магнитной индукции могут быть наглядно визуализированы при помощи ферромагнитных порошков, либо суспензий их в жидкости, помещённых в магнитное поле.

Гравитационное поле в ньютоновском приближении является потенциальным.

Силовые линии векторного поля, применённые для описания мгновенного поля скоростей жидкости или газа, называют линиями тока. Они изображают картину течения в данный момент времени. Для стационарного течения они совпадают с траекториями частиц. Линии тока, выходящие из замкнутой кривой (не лежащей ни одной своей частью вдоль любой линии тока), образуют трубку тока.

• Силовые линии — Большая советская энциклопедия. — М.: Советская энциклопедия. 1969—1978.

43. Индукция поля прямого тока. Магнитное поле прямого тока — создается током, текущего по тонкому прямому бесконечному проводу

44. Сила Ампера.

Действие магнитного поля на проводник с током Сила, действующая на проводник с током в магнитном поле, называется силой Ампера.
Сила действия однородного маг­нитного поля на проводник с током прямо пропорциональна силе тока, длине проводника, модулю вектора индукции магнитного поля, синусу угла между вектором индукции магнитного поля и проводником: F=B.I.ℓ. sin α — закон Ампера.
Направление силы Ампера (правило левой руки) Если левую руку расположить так, чтобы перпендикулярная составляющая вектора В входила в ладонь, а четыре вытянутых пальца были направлены по направлению тока, то отогнутый на 90° большой палец покажет направление силы, действующей на проводник с током.

45. Рассмотрим взаимодействие двух параллельных проводников с токами, расположенными на расстоянии а один от другого. Пусть длина проводников равна l.

Магнитная индукция, созданная током I₁ на линии расположения второго проводника, равна

На второй проводник будет действовать электромагнитная сила

Магнитная индукция, созданная током I₂ на линии расположения первого проводника, будет равна

и на первый проводник действует электромагнитная сила

46. Сила Лоренца — Сила, с которой, электромагнитное поле действует на точечную заряженную частицу

  

  

Направление силы Лоренца определяется по правилу левой руки — Если поставить левую руку так, чтобы перпендикулярная скорости составляющая вектора индукции входила в ладонь, а четыре пальца были бы расположены по направлению скорости движения положительного заряда (или против направления скорости отрицательного заряда), то отогнутый большой палец укажет направление силы Лоренца

47. Магнитный поток

Магнитный поток — , поток вектора магнитной индукции В через какую-либо поверхность. Магнитный поток через малую площадку dS, в пределах которой вектор В неизменен, равен dФ = ВndS, где Bn — проекция вектора на нормаль к площадке dS. Магнитный поток Ф через конечную поверхность равен интегралу от dФ по этой поверхности. Для замкнутой поверхности магнитный поток равен нулю, что отражает отсутствие в природе магнитных зарядов — источников магнитного поля. ;

( Или поток магнитной индукции)

Магнитным потоком через поверхность площадью S называют величину, равную произведению модуля вектора магнитной индукции В на площадь S и косинус угла между векторами В и n.

Електро магнитная индукция.

Явление электромагнитной индукции — возникновение электрического тока в замкнутом проводящем контуре, который либо покоится в переменном во времени магнитном поле, либо движется в постоянном магнитном поле так, что число линий магнитной индукции, пронизывающих контур, меняется. Чем быстрее меняется число линий магнитной индукции, тем больше индукционный ток.

48.Индуктивность.ЭДС. ИНДУКЦИЯ

Индукти́вность (или коэффициент самоиндукции) — коэффициент пропорциональности между электрическим током, текущим в каком-либо замкнутом контуре, и магнитным потоком, создаваемым этим током через поверхность^[1], краем которой является этот контур^[2][3][4].

В формуле

 — магнитный поток,  — ток в контуре,  — индуктивность.

ЭДС индукции.

Электродвижущая сила (ЭДС) — скалярная физическая величина, характеризующая работу сторонних сил, то есть любых сил неэлектрическогопроисхождения, действующих в квазистационарных цепях постоянного или переменного тока. В замкнутом проводящем контуре ЭДС равна работеэтих сил по перемещению единичного положительного заряда вдоль всего контура

49. Самоиндукция — это явление возникновения ЭДС индукции в проводящем контуре ^[1]при изменении протекающего через контур тока.

При изменении тока в контуре пропорционально меняется^[2] и магнитный поток через поверхность, ограниченную этим контуром^[3]. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.

Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока :

.

50. Правило Ленца определяет направление индукционного тока и гласит:

Индукционный ток всегда имеет такое направление, что он ослабляет действие причины, возбуждающей этот ток.

50_)Правило ленца

Правило Ленца: индукционный ток в контуре имеет такое направление,

что создаваемое им магнитное поле препятствует изменению магнитного

потока, вызвавшего этот ток.

51_)

52_)электромагнитные волны.виды электромагнитных волн

53_)свет.природа света. корускулярно-волновой дуализм света.

свет — сложный электромагнитный процесс, обладающий как волновыми, так и корпускулярными свойствами.

54_)световой поток, сила света. Освещенность, яркость, интенсивность света

55)поляризация света кристаллами. Закон малюса

ромагнитных волн).

56_)фотон. Энергия, масса и импульс фотона. Фотоэффект. Виды фотоэффект. Законы фотоэффекта уравнение энштена

57_) строение атома. Постулаты бора

58_)строение ядра. Закон радиоактивного распада и период полраспада

59_) ядерные реакции. Дефект массы, энергия связи,энергия реакции

60_) взаимодействие альфа, бета, гамма излучений с веществом

Взаимодействие ионизирующих излучений с веществом Альфа-частицы, бета-частицы, выброшенные из ядра, обладают значительной кинетической энергией и, воздействуя на вещество, с одной стороны производят его ионизацию, а с другой проникают на определенную глубину. Взаимодействуя с веществом, они теряют эту энергию, в основном, в результате упругих взаимодействий с ядрами атомов или электронами, отдавая им всю или часть своей энергии, вызывая ионизацию или возбуждение атомов (т.е. перевод электрона с более близкой на более удаленную от ядра орбиту). Ионизация и проникновение на определенную глубину имеют принципиальное значение для оценки воздействия ионизирующего излучения на биологическую ткань различных видов излучений. Зная свойства различных видов излучений проникать через разные материалы, последние можно использовать как для защиты человека, так и некоторых объектов, приборов и т.д. Результаты взаимодействия ионизирующего излучения с веществом зависят: от массы, заряда потока частиц и их энергий; от вида фотонов и их энергий; от типа и плотности вещества; от значения энергий внутримолекулярных сил облучаемого вещества. Взаимодействие ионизирующего излучения с веществом зависит от соотношения масс и энергий частиц и может носить упругий или неупругий характер. С учетом выше сказанного можно сделать некоторые выводы: · заряженные частицы, проходящие через вещество, взаимодействуют как с орбитальными электронами атома, так и с его ядром; · при взаимодействии с орбитальными электронами, энергия частиц растрачивается на ионизацию атомов, если она не менее 35 эВ и на возбуждение атомов (перевод электрона с ближней орбиты на более удаленную), если она менее 35 эВ; · в процессе ионизации атома образуются заряженные частицы (свободные электроны), а атомы, потерявшие один или несколько электронов, превращаются в положительно заряженные ионы; · при взаимодействии с ядром заряженная частица может или тормозиться электрическим полем ядра и менять свое направление движения или поглощаться ядром. В первом случае происходит испускание тормозного излучения, во втором случае заряженная частица (при достаточно большой энергии) поглощается ядром, при этом выбрасываются элементарные частицы и фотоны. Поглощение частицы ядром обычно происходит, если энергия частицы превышает 1,02 МэВ. Процесс взаимодействия, при котором исчезают первоначальные и появляются новые частицы, называют ядерной реакцией. Рассмотрим взаимодействие различных видов излучений с веществом. Гамма-излучение Взаимодействие гамма-квантов с веществом может сопровождаться фотоэффектом, комптоновским рассеянием и образованием электрон-позитронных пар. Вид эффекта зависит от энергии гамма-кванта: Ек = hн — Еи, (1) где: h — постоянная Планка; н — частота излучения; Еи — энергия ионизации соответствующей атомной оболочки (энергия связи выбитого электрона из атома). Фотоэффект возникает при Е = 10 эВ-1 МэВ, то есть при относительно малых значениях энергий. В этом случае вся энергия гамма-кванта передается орбитальному электрону, и он выбивается из орбиты (рис.3). Выбитый электрон называется фотоэлектроном. В результате его отрыва в атоме появляется свободный уровень, который заполняется одним из наружных электронов. При этом, либо испускается вторичное мягкое характеристическое излучение (процесс флюоресценции), либо энергия передается одному из электронов, который покидает атом (электрон Оже). Флюоресцентное излучение наблюдают в материалах с большим атомным номером. В материалах с низким атомным номером преобладает образование электронов Оже. Вероятность фотоэффекта увеличивается с ростом атомного номера материала и уменьшается с ростом энергии фотона. С ростом энергии гамма-квантов явление фотоэффекта становится все меньше, а при энергии 100-200 кэВ начинает преобладать Комптон эффект.

3.3.2 Опыт Эрстеда. Магнитное поле проводника с током. Картина линий поля длинного прямого проводника и замкнутого кольцевого проводника, катушки с током

Видеоурок: Магнитное поле, его свойства

 

Лекция: Опыт Эрстеда. Магнитное поле проводника с током. Картина линий поля длинного прямого проводника и замкнутого кольцевого проводника, катушки с током 

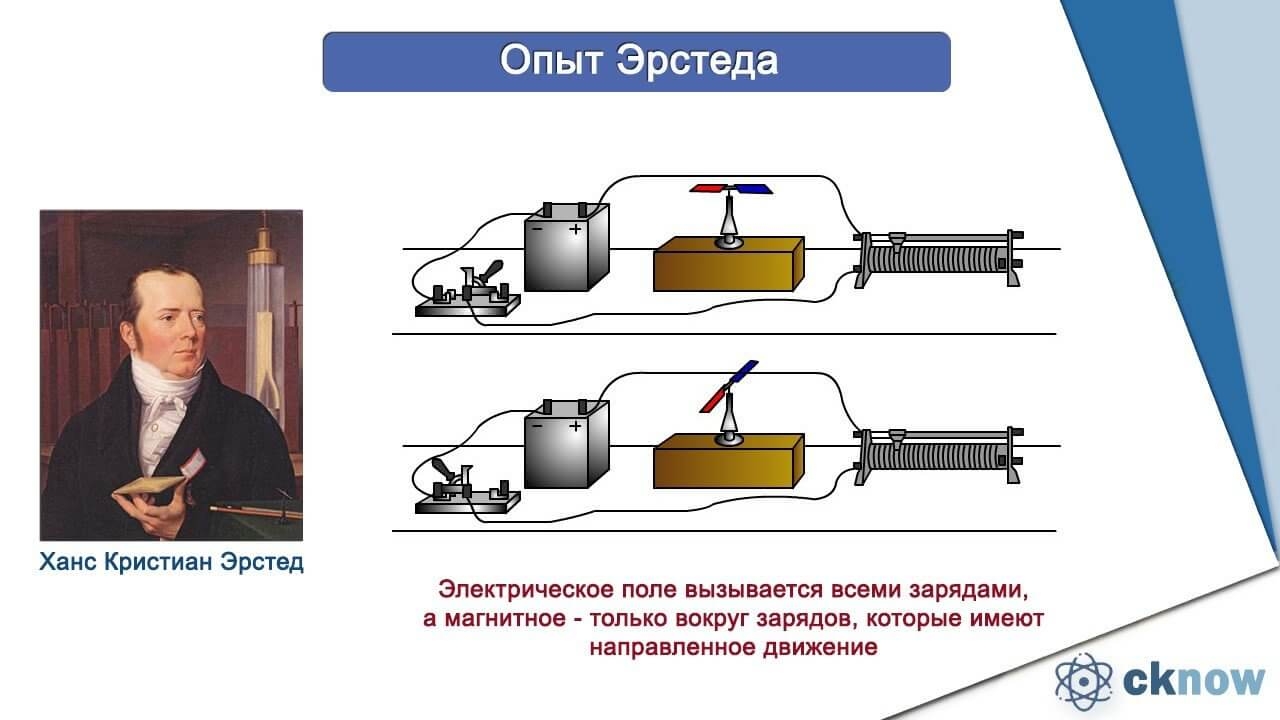
Опыт Эрстеда

Магнитные свойства некоторых веществ известны людям достаточно давно. Однако не столь давним открытием стало то, что магнитные и электрические природы веществ связанны между собой. Эту связь показал Эрстед, проводивший опыты с электрическим током. Совершенно случайно рядом с проводником, по которому бежал ток, находится магнит. Он достаточно резко менял свое направление в то время, когда ток бежал по проводам, и становился в исходное положение, когда ключ схемы был разомкнут.

С данного опыта был сделан вывод, что вокруг проводника, по которому бежит ток, образуется магнитное поле. То есть можно сделать вывод: электрическое поле вызывается всеми зарядами, а магнитное — только вокруг зарядов, которые имеют направленное движение.

Магнитное поле проводника

Если рассматривать поперечное сечение проводника с током, то его магнитные линии будут иметь окружности различного диаметра вокруг проводника.

Чтобы определить направление тока или линий магнитного поля вокруг проводника, следует воспользоваться правилом правого винта:

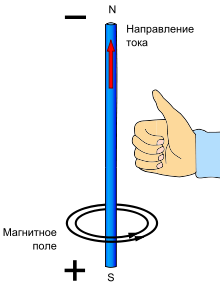
Если правой рукой обхватить проводник и направить большой палец вдоль него по направлению тока, то согнутые пальцы покажут направление линий магнитного поля.

Силовой характеристикой магнитного поля является магнитная индукция. Иногда линии магнитного поля называют линиями индукции.

Индукция обозначается и измеряется следующим образом: [В] = 1 Тл.

Как Вы можете вспомнить, для силовой характеристики электрического поля был справедлив принцип суперпозиций, то же самое можно сказать и для магнитного поля. То есть результирующая индукция поля равна сумме векторов индукции в каждой точке.

Виток с током

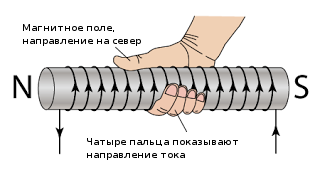
Как известно, проводники могут иметь различную форму, в том числе состоять из нескольких витков. Вокруг такого проводника также образуется магнитное поле. Для его определения следует воспользоваться правилом Буравчика:

Если рукой обхватить витки так, чтобы 4 согнутых пальца их обхватывали, то большой палец покажет направление магнитного поля.

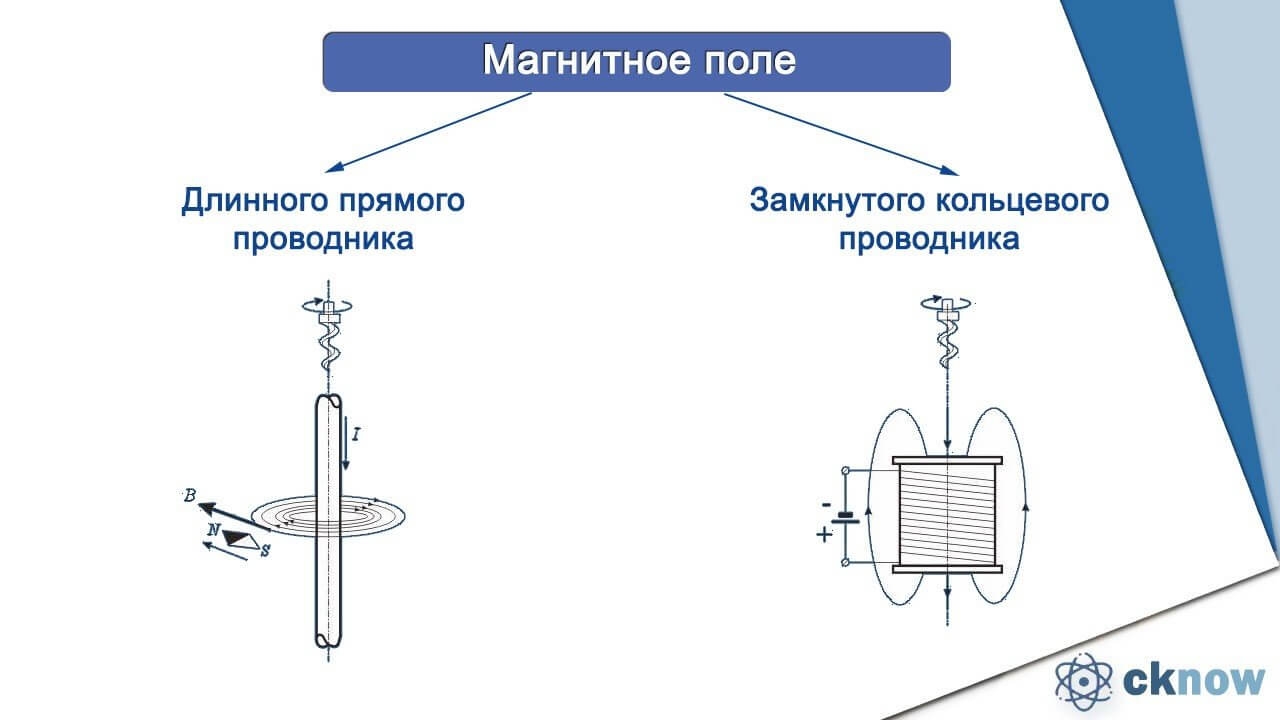
Магнитное поле постоянного электрического тока

Сегодня на уроке мы с вами поговорим о магнитном поле постоянного электрического тока

 «Так как я уже давно рассматривал силы,

проявляющиеся в электрических явлениях,

всеобщими природными силами, то я

должен был отсюда вывести и магнитные действия»

Ханс Кристиан Эрстед

В прошлой теме говорилось о том, что вокруг движущихся электрических зарядов, существует магнитное поле, т.е. особый вид материи, посредством которой осуществляется взаимодействие между движущимися электрическими заряженными частицами. Магнитное поле порождается электрическим током и обнаруживается по действию на него.

Из курса физики 10 класса известно, что электрическое поле характеризуется векторной физической величиной, называемой напряженностью электрического поля. Возникает вопрос: существует ли величина, которая количественно будет характеризовать магнитное поле?

Для количественного описания магнитного поля можно воспользоваться контуром с током. Так как контур с током испытывает ориентирующее действие поля, то на него в магнитном поле действует пара сил, которая создает момент сил относительно некоторой неподвижной оси.

Вращающий момент сил зависит как от свойств поля в данной точке, так и от свойств контура. Для плоского контура с током I величина, равная произведению силы тока I на площадь S, ограниченную контуром, называется магнитным моментом контура и обозначается .

Таким образом, магнитный момент — это векторная величина, направление которой совпадает с направлением положительной нормали к контуру.

Опыт показывает, что вращающий момент зависит от расположения контура в магнитном поле. Он равен нулю, если магнитное поле перпендикулярно плоскости контура, и максимален, если нормаль к контуру перпендикулярна магнитному полю.

Как показывает опыт, максимальный вращающий момент пропорционален силе тока и площади контура рамки с током.

Если в данную точку магнитного поля помещать контуры с разными магнитными моментами, то на них будут действовать различные вращающие моменты, однако отношение максимального вращающего момента к магнитному моменту для всех контуров одно и то же и поэтому может служить характеристикой магнитного поля. Эту величину, в физике, назвали магнитной индукцией.

Таким образом, магнитная индукция — это векторная физическая величина, являющаяся силовой характеристикой магнитного поля, численно равная максимальному вращающему моменту, действующему на контур с единичным магнитным моментом, и направленная вдоль положительной нормали к контуру.

Единицей магнитной индукции в системе СИ является тесла (Тл), названная в честь великого сербского ученого и экспериментатора Николы Тесла.

[B] = [Тл]

1 Тл — это магнитная индукция такого однородного поля, в котором на контур с магнитным моментом 1 А×м² действует вращающий момент 1 Н×м.

Магнитная индукция полностью характеризует магнитное поле, так как в каждой точке поля может быть найден ее модуль и направление.

Как же направлен вектор магнитной индукции?

Известно, что в магнитном поле рамка с током на гибком подвесе, со стороны которого не действуют силы упругости, поворачивается до тех пор, пока она не установится определенным образом. Также известно, что подобным образом ведет себя и магнитная стрелка (маленький продолговатый магнит) помещенная в любую точку поля. Поэтому, ориентирующее действие магнитного поля на рамку с током или магнитную стрелку, можно использовать для определения направления вектора магнитной индукции. За направление вектора магнитной индукции принимается направление, которое показывает северный полюс магнитной стрелки, свободно устанавливающейся в магнитном поле. Это направление совпадает с направлением положительной нормали к замкнутому контуру с током.

Для наглядного представления магнитного поля, его можно изображать графически с помощью линий магнитной индукции, подобно тому, как электрическое поле изображают с помощью линий напряженности.

Линией магнитной индукции называется линия, касательная к которой в каждой точке поля совпадает с вектором магнитной индукции.

Так как в каждой точке магнитного поля характеризуется определенным значением вектора магнитной индукции, то через каждую точку поля можно провести линию магнитной индукции причем только одну. При этом линии магнитной индукции не пересекаются.

Наглядное представление о линиях магнитной индукции можно получить, если на лист стекла, сквозь который проходит проводник с током, насыпать железные опилки и встряхнуть их. Опилки намагничиваются, становятся маленькими магнитными стрелками и располагаются вдоль вектора магнитной индукции.

Исследования различных магнитных полей показало, что линии магнитной индукции, в отличии от линий напряженности электростатического поля являются замкнутыми линиями.

Поля с замкнутыми векторными линиями называют вихревыми. Поэтому магнитное поле — это вихревое поле.

Замкнутость линий индукции представляет собой фундаментальное свойство магнитного поля: оно свидетельствует о том, что магнитных зарядов, подобных электрическим, в природе нет. Источником магнитного поля являются движущиеся заряды и переменные электрические поля.

Рассмотрим более подробно на спектре магнитных линий различных токов. Сначала рассмотрим магнитное поле прямолинейного проводника с током потому, что именно с такими проводниками будем чаще всего сталкиваться.

Для получения спектра магнитного поля прямого проводника с током воспользуемся старым приемом. Пропустим проводник сквозь лист картона. На картон, тонким слоем насыплем железные опилки и пропустим электрический ток по проводнику.

Как видно, под действием магнитного поля железные опилки располагаются по концентрическим окружностям. По касательной к ним расположатся и магнитные стрелки вокруг такого проводника стоком.

Таким образом, линии магнитной индукции магнитного поля прямолинейного тока представляют собой концентрические окружности, расположенные в плоскости, перпендикулярной проводнику, с центром на оси проводника.

Направление же вектора магнитной индукции определяют с помощью правила буравчика (или правила правого винта): если поворачивать головку винта так, чтобы поступательное движение острия винта происходило вдоль тока в проводнике, то направление вращения головки указывает направление линий магнитной индукции поля прямого проводника с током.

Для изображения магнитного поля пользуются следующим приемом. Если линии однородного магнитного поля расположены перпендикулярно к плоскости чертежа и направлены от нас за чертеж, то их изображают крестиками, а если из-за чертежа к нам — то точками. Как и в случае с током, каждый крестик — это как бы видимое хвостовое оперение летящей стрелы, а точка — острие стрелы, летящей к нам.

Как показывают расчеты, модуль магнитной индукции поля прямолинейного тока может быть рассчитан по формуле:

где m – магнитная проницаемость среды;

m⁰ = 4p×10^–7 Н/А² – магнитная постоянная;

I – сила тока в проводнике;

r – расстояние от проводника до точки, в которой вычисляется магнитная индукция.

В формуле появилась новая физическая величина — магнитная проницаемость среды. Что это за величина?

Магнитная проницаемость среды — это физическая величина, показывающая, во сколько раз модуль магнитной индукции поля в однородной среде отличается от модуля магнитной индукции в той же точке поля в вакууме.

Рассмотрим магнитное поле кругового тока. Исследования показали, что линии магнитной индукции поля кругового тока не являются правильными окружностями, но они замыкаются, обходя проводник, по которому идет ток.

Направление линий магнитной индукции можно определить с помощью правила правого винта: если головку винта вращать в направлении тока в проводнике, то поступательное движение острия винта покажет направление магнитной индукции в центре кругового тока.

Модуль магнитной индукции в центре кругового тока прямо пропорционален магнитной проницаемости среды, магнитной постоянной и силе тока в проводнике, и обратно пропорционален удвоенному радиусу кругового витка.

 

Рассмотрим магнитное поле соленоида.

Соленоид — это катушка цилиндрической формы из проволоки, витки которой намотаны вплотную друг к другу в одном направлении, а длина катушки значительно больше радиуса витка.

Магнитное поле соленоида можно представить как результат сложения полей, создаваемых несколькими круговыми токами, имеющими общую ось. На рисунке видно, что внутри соленоида линии магнитного поля каждого отдельного витка имеют одинаковое направление, тогда как между соседними витками они имеют противоположное направление. Поэтому, при достаточно плотной намотке соленоида, противоположно направленные участки линий магнитного поля соседних витков взаимно уничтожаться, а одинаково направленные участки сольются в общую линию.

Изучение этого поля с помощью железных опилок показало, что внутри соленоида магнитные линии поля представляют собой прямые, параллельные оси соленоида, которые расходятся на его концах и замыкаются вне соленоида.

Зная направление тока в витке, полюсы соленоида можно определить с помощью правила правой руки: если обхватить соленоид ладонью правой руки, направив четыре пальца по направлению тока в витках, то отставленный большой палец покажет направление линий магнитного поля внутри соленоида.

Модуль магнитной индукции внутри однослойного соленоида можно определить по формуле:

где N – количество витков в соленоиде;

l – длина соленоида;

n – количество витков в соленоиде, приходящееся на единицу длины.

На рисунке показано магнитное поле Земли. Линии магнитной индукции поля Земли подобны линиям магнитной индукции поля соленоида. Магнитный северный полюс близок к Южному географическому полюсу, а магнитный южный полюс — к северному географическому полюсу. Ось такого большого магнита составляет с осью вращения Земли угол 11,5⁰ градуса. Периодически магнитные полюсы меняют свою полярность. Последняя такая замена произошла около 30 000 лет назад.

Основные выводы:

– Для количественного описания магнитного поля вводится физическая величина, называемая магнитной индукцией.

– Магнитная индукция — это векторная физическая величина, являющаяся силовой характеристикой магнитного поля, численно равная максимальному вращающему моменту, действующему на контур с единичным магнитным моментом, и направленная вдоль положительной нормали к контуру.

– Единицей магнитной индукции в системе СИ является Тл (тесла).

– Магнитное поле — это вихревое поле, т.е. линии индукции магнитного поля замкнуты. Замкнутость линий говорит нам о том, что магнитных зарядов в природе не существует, источником магнитного поля являются движущиеся заряды и переменные электрические поля.

В каждой точке поля вектор магнитной индукции имеет определенное направление, которое можно определить по правилу буравчика.

Магнитное поле прямого тока

Любой электрический ток можно представить в виде совокупности элементарных токов. Следовательно, можно рассчитать характеристики магнитного поля, порождаемого любыми токами, если использовать:

1. Закон Био – Савара – Лапласа:

   $d\vec{B}=\frac{\mu_{0}}{4\pi }\frac{I}{r^{3}}\left[ d\vec{l}\vec{r}\right]\left( 1 \right)$

   где $d\vec{l}$ – элементарный участок проводника, по которому течет ток $I$; $\vec{r}$ – радиус-вектор, который проводится от элемента $dl$ с током к точке, в которой исследуется поле; $\mu_{0}$– магнитная постоянная.

2. Принцип суперпозиции магнитных полей. Магнитная индукция поля, которое создают несколько элементов с токами, — это векторная сумма индукций полей, каждого элементарного тока отдельно. Для непрерывных токов:

   $\vec{B}=\int\limits_l {d\vec{B}} \left( 2 \right)$.

   Замечание 1

   В выражении (2) следует учитывать, что суммирование является векторным.

Закон Био-Савара-Лапласа дает возможность рассчитывать магнитные поля, которые создают токи, распределенные в пространстве. Плотность этих токов может изменяться в зависимости от координаты (или радиус-вектора, определяющего положение точки) ($\vec{j}(\vec{r})$).

Около избранной точки пространства, в котором находится магнитное поле, выберем бесконечно малую трубку тока, с длиной $dl$, сечением $dS$. В точке $C$, которая находится на расстоянии $r$ от трубки тока, создаваемое ей поле равно:

$d\vec{B}=\frac{\mu_{0}}{4\pi }\frac{\left[ \vec{j\, }\left( \vec{r}\right)\vec{r} \right]}{r^{3}}dldS\left( 3 \right)$.

где $dV=dldS.$

Результирующее поле находят интегрированием выражения (3) по объему в котором текут токи.

Применение закона Био-Савара – Лапласа для нахождения магнитного поля прямого тока

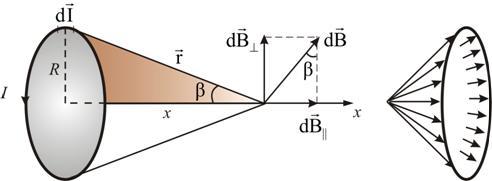
Пусть по очень длинному, тонкому проводу, течет постоянный то $I$ (рис.1). Рассчитаем поле, которое создает этот проводник в некоторой токе $C$, находящейся на расстоянии $R$ от него.

Рисунок 1. Магнитное поле прямого тока. Автор24 — интернет-биржа студенческих работ

По закону Био-Савара – Лапласа в точке $C$ элемент $dl$ с током $I$ создает магнитное поле:

$dB=\frac{\mu_{0}}{4\pi }\frac{Idl\sin \beta }{r^{2}}\left( 4 \right)$.

где $\beta$ – угол между направлением течения тока и $\vec{r}$.

Все элементы нашего проводника с током в точке $C$ создают магнитные поля, направленные вдоль одной прямой, и направлены они перпендикулярно плоскости рисунка к нам. Учтем следующие простые соотношения (см. рис.1):

$r=\frac{R}{\cos \alpha };l=R\, tg\, \alpha ;dl=\frac{R\, d\alpha}{{cos}^{2}\alpha };\sin {\beta =\cos {\alpha (5).}}$

Принимая во внимание формулы (5) закон (4) приведем к виду:

$dB=\frac{\mu_{0}}{4\pi }\frac{I\sin \alpha d\alpha }{R}\left( 6 \right)$

Применим принцип суперпозиции, для этого выражение (6) проинтегрируем, учтем, что $-\frac{\pi }{2}\le \alpha \le \frac{\pi }{2},$ получим:

$B=\frac{\mu_{0}}{4\pi }\frac{I}{R}\int\limits_{-\frac{\pi }{2}}^\frac{\pi}{2} \sin \alpha d\alpha =\frac{\mu_{0}}{2\pi }\frac{I}{R}\left( 7 \right)$

Закон полного тока и его применение для нахождения магнитного поля прямого тока

Допустим, что токи, создающие магнитное поле и контур, по которому мы будем рассматривать интегрирование, находятся в однородном магнитоизотропном веществе, тогда закон полного тока (или закон циркуляции вектора магнитной индукции) запишем в виде:

$\oint\limits_L {\vec{B}d\vec{r}=\mu \mu_{0}I\, \left( 8 \right),}$

где $\mu $ – магнитная проницаемость вещества; $I$ – алгебраическая сумма токов, охватываемых контуром $L$.

Теорема о циркуляции (или закон полного тока), в теории магнетизма, играет роль аналогичную теореме Гаусса для вектора напряженности в электростатике. Если в распределении токов имеется симметрия, то этот закон упрощает процедуру поиска вектора магнитной индукции.

Рассмотрим магнитное поле, которое создается прямым длинным тонким проводом (рис.1). Условия, как и представленные выше. Найдем поле в точке $C$. Применяя закон полного тока.

Магнитное поле прямого тока имеет осевую симметрию (силовые линии поля – окружности с центрами на оси провода). Величина вектора индукции одинакова для всех точек одной такой силовой линии. В качестве контура $L$ возьмем окружность радиуса $R$, тогда циркуляция вектора индукции равна:

$\oint\limits_L {\vec{B}d} \vec{r}=BL=2\pi R B\, \left( 9 \right)$.

Поскольку контур $L$ охватывает только ток $I$, то результат правой части (9) приравняем к величине этого тока, умноженному на магнитную постоянную и магнитную проницаемость вещества:

$2\pi RB=\mu \mu_{0}I\, \, \left( 10 \right)$,

считая, что проводник находится в вакууме ($\mu=1$), получаем:

$B=\mu_{0}\frac{I}{2\pi R}\, \left( 11 \right)$.

Сравнивая формулы (7) и (11), мы видим, что результаты одинаковые.

Магнитное поле прямого тока в проводе, имеющем конечную длину

Допустим, что у нас имеется прямой тонкий провод, конечной длины по которому течет неизменяющийся ток $I$ (рис.2). Определим, какова магнитная индукция поля в точке $C$, создаваемая этим проводом.

Рисунок 2. Магнитное поле прямого тока в проводе, имеющем конечную длину. Автор24 — интернет-биржа студенческих работ

Полярные углы, соответствующие концам проводника будем считать равными $\varphi_{1}=a$ и $\varphi_{2}=b$.

Вектор магнитной индукции перпендикулярен плоскости рисунка. Силовые линии – это окружности, как и у бесконечного проводника.

Модуль элементарного магнитного поля ($dB$), которое создает малый участок $dl$ (рис.2) по закону Био-Савара-Лапласа запишем так:

$dB=\frac{\mu_{0}}{4\pi }\frac{Idl\sin \alpha }{r^{2}}=\frac{\mu_{0}I}{4\pi R}\cos {\varphi d\varphi }\left( 12 \right)$

где из рис.2 видно, что:

• $\sin {\alpha =\cos {\varphi ;}\, }$
• $dl\cos {\varphi =rd\varphi ;\, }$
• $r=\frac{R}{\cos \varphi }.$

Воспользуемся принципом суперпозиции и получим магнитное поле в точке $C$, создаваемое всеми участками проводника с током:

$B=\int\limits_a^b {\frac{\mu_{0}I}{4\pi R}\cos {\varphi d\varphi }=}\frac{\mu_{0}I}{4\pi R}\left( \sin \left( b \right)-\sin \left( a \right)\right)\left( 13 \right)$

Если рассматривать бесконечно длинный проводник, как частный случай прямого проводника с током, то следует учесть, что для него:

$a=-\frac{\pi }{2};\, b=\frac{\pi }{2}$,

тогда из (13) следует:

$B=\frac{\mu_{0}I}{2\pi R}\left( 14 \right)$

Результат (14) снова совпал с (7) и (11).

Магнитное поле внутри прямого тока

Рассмотрим длинный прямой проводник радиуса $R$. Пусть материалом этого проводника будет парамагнетик, магнитная проницаемость которого $\mu$. Материал провода будем считать однородным. Плотность тока, текущего в проводнике при этом может быть представлена:

$j=\frac{I}{\pi R^{2}}\, \left( 15 \right)$.

где $j$ – постоянная величина.

Задачу будем решать, используя закон о циркуляции вектора магнитной индукции (8). Кривую, по которой будем рассматривать циркуляцию совместим с силовой линией магнитного поля. Внутри проводника, магнитное поле так же имеет осевую симметрию. Силовые линии представлены окружностями, с центрами на оси провода. Радиус рассматриваемой силовой линии будем считать равным $r$, тогда

$\oint\limits_L {\vec{B}d} \vec{r}=B 2\pi r\, \left( 16 \right)$.

Из закона полного тока следует, что:

$2\pi rB=I_{1}=\mu \mu_{0}j\pi r^{2}\to $$B=\frac{1}{2}\mu \mu_{0}rj$ при $r\le R(17).$

Для бесконечно длинного провода мы видим:

• что внутри проводника индукция магнитного поля прямо пропорциональна расстоянию от оси провода, до точки рассмотрения.
• вне провода индукция обратно пропорциональна расстоянию.
• у поверхности проводника вектор магнитной индукции претерпевает разрыв, поскольку для внутреннего материала проводника $\mu >1$, для вакуума $\mu =1$.