Презентация по физике на тему » решение задач на правило буравчика, правой и левой руки!(8 класс)

Сила Ампера: варианты расчета

Прежде чем сформулировать данную величину, необходимо разобраться, что такое понятие «сила» в физике. Ей называется величина в физике, которая является мерой воздействия всех окружающих тел на рассматриваемый объект. Обычно любую силу обозначают английской буквой F, от латинского fortis, что означает сильный.

Рассчитывается элементарная сила Ампера по формуле:

где, dl – часть длины проводника, B –индукция магнитного контура, I – сила тока.

Рассчитывается также сила Ампера по формуле:

где, J – направление плотности тока, dv– элемент объема проводника.

Формулировка расчета модуля силы Ампера, согласно литературе, звучит так: данный показатель напрямую зависит от силы тока, протяженности проводника, синуса, образуемого между этим вектором и самим проводником угла, и величины значения вектора магнитного контура в модуле.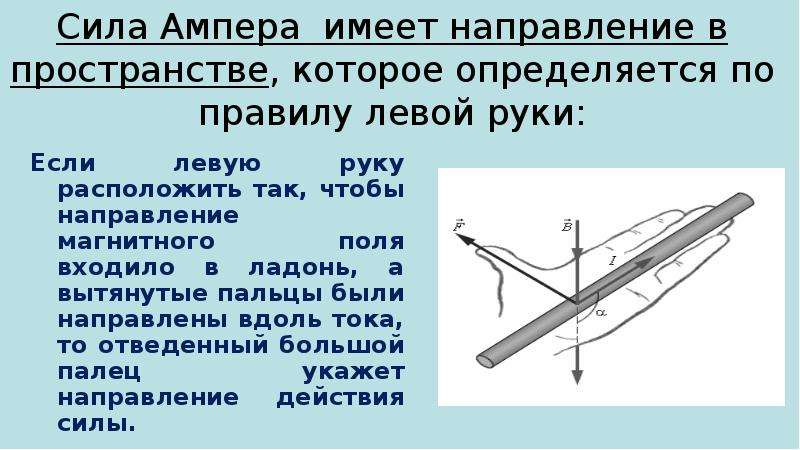 Она и носит название модуля силы Ампера. Формула данного закона математически строится так:

где, B – модуль индукции магнитного контура, I – сила тока, l – длина проводника, α – образуемый угол. Максимальное значение будет при перпендикулярном их пересечении.

Показатель измеряется в ньютонах (условное обозначение – Н) или

. Он является векторной величиной и зависит от вектора индукции и тока.

Существуют и другие формулы для расчета силы Ампера. Но на практике они достаточно редко востребованы и тяжелы для понимания.

Какое правило применить

Слова синонимы: рука, винт, буравчик

Вначале разберем слова-синонимы, многие начали спрашивать себя: если тут повествование должно затрагивать буравчик, почему текст постоянно касается рук. Введем понятие правой тройки, правой системы координат. Итого, 5 слов-синонимов.

Потребовалось выяснить векторное произведение векторов, оказалось: в школе это не проходят. Проясним ситуацию любознательным школьникам.

Декартова система координат

Школьные графики на доске рисуют в декартовой системе координат Х-Y. Горизонтальная ось (положительная часть) направлена вправо – надеемся, вертикальная – указывает вверх. Делаем один шаг, получая правую тройку. Представьте: из начала отсчета в класс смотрит ось Z. Теперь школьники знают определение правой тройки векторов.

В Википедии написано: допустимо брать левые тройки, правые, вычисляя векторное произведение, несогласны. Усманов в этом плане категоричен. С разрешения Александра Евгеньевича приведем точное определение: векторным произведением векторов называют вектор, удовлетворяющий трем условиям:

1. Модуль произведения равен произведению модулей исходных векторов на синус угла меж ними.
2. Вектор результата перпендикулярен исходным (вдвоем образуют плоскость).
3. Тройка векторов (по порядку упоминания контекстом) правая.

Правую тройку знаем. Итак, если ось Х – первый вектор, Y – второй, Z будет результатом.

Почему назвали правой тройкой? По-видимому, связано с винтами, буравчиками. Если закручивать воображаемый буравчик по кратчайшей траектории первый вектор-второй вектор, поступательное движение оси режущего инструмента станет происходить в направлении результирующего вектора:

1. Правило буравчика применяется к произведению двух векторов.
2. Правило буравчика качественно указывает направление результирующего вектора этого действия. Количественно длина находится выражением, упомянутым (произведение модулей векторов на синус угла меж ними).

Простые приемы запоминания правил буравчика

Люди забывают, что силу Лоренца проще определять правилом буравчика с левосторонней резьбой. Желающий понять принцип действия электрического двигателя должен как дважды два щелкать подобные орешки. В зависимости от конструкции число катушек ротора бывает значительным, либо схема вырождается, становясь беличьей клеткой. Ищущим знания помогает правило Лоренца, описывающее магнитное поле, где движутся медные проводники.

Для запоминания представим физику процесса. Допустим, движется электрон в поле. Применяется правило правой руки для нахождения направления действия силы. Доказано: частица несет отрицательный заряд. Направление действия силы на проводник находится правилом левой руки, вспоминаем: физики совершенно с левых ресурсов взяли, что электрический ток течет в направлении противоположном тому, куда направились электроны. И это неправильно. Поэтому приходится применять правило левой руки.

Не всегда следует идти такими дебрями. Казалось бы, правила больше запутывают, не совсем так. Правило правой руки часто применяется для вычисления угловой скорости, которая является геометрическим произведением ускорения на радиус: V = ω х r. Многим поможет визуальная память:

1. Вектор радиуса круговой траектории направлен из центра к окружности.
2. Если вектор ускорения направлен вверх, тело движется против часовой стрелки.

Посмотрите, здесь опять действует правило правой руки: если расположить ладонь так, чтобы вектор ускорения входил перпендикулярно в ладонь, персты вытянуть по направлению радиуса, отогнутый на 90 градусов большой палец укажет направление движения объекта. Достаточно однажды нарисовать на бумаге, запомнив минимум на половину жизни. Картинка действительно простая. Больше на уроке физики не придется ломать голову над простым вопросом – направление вектора углового ускорения.

Аналогичным образом определяется момент силы. Исходит перпендикулярно из оси плеча, совпадает направлением с угловым ускорением на рисунке, описанном выше. Многие спросят: зачем нужно? Почему момент силы не скалярная величина? Зачем направление? В сложных системах непросто проследить взаимодействия. Если много осей, сил, помогает векторное сложение моментов.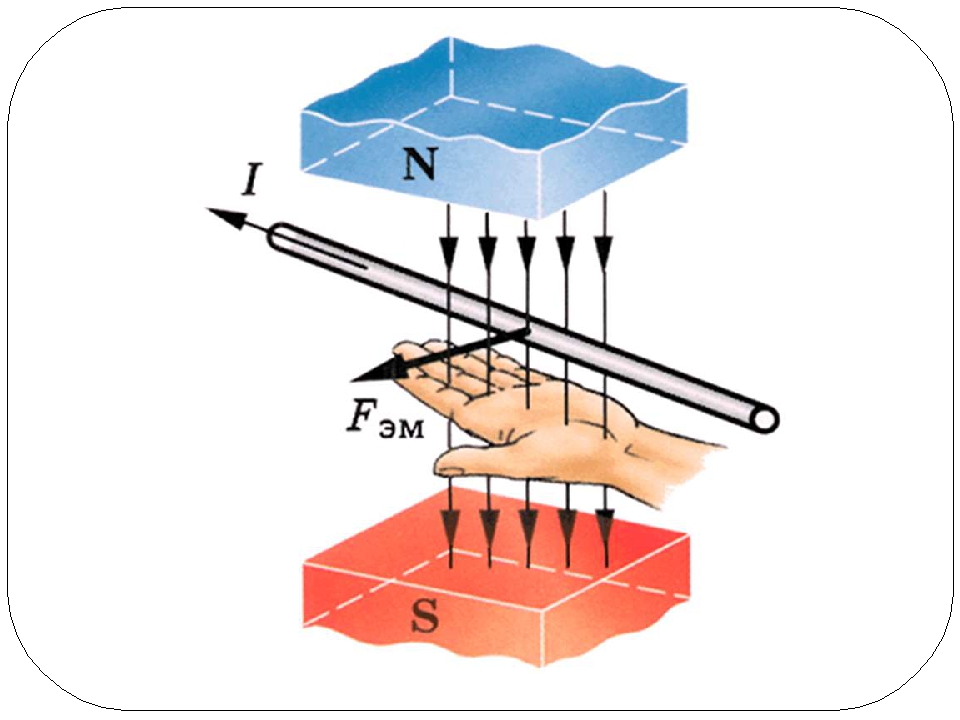 Можно значительно упростить вычисления.

Аналитическая геометрия в пространстве

Каждому известна задачка: стоя на одном берегу реки, определить ширину русла. Кажется уму непостижимым, решается в два счета методами простейшей геометрии, которую изучают школьники. Проделаем ряд несложных действий:

1. Засечь на противоположном берегу видный ориентир, воображаемую точку: ствол дерева, устье ручейка, впадающего в поток.
2. Под прямым углом линии противоположного берега сделать засечку на этой стороне русла.
3. Найти место, с которого ориентир виден под углом 45 градусов к берегу.
4. Ширина реки равна удалению конечной точки от засечки.

Определение ширины реки методом подобия треугольников

Используем тангенс угла. Не обязательно равен 45 градусов. Нужна большая точность – угол лучше брать острым. Просто тангенс 45 градусов равен единице, решение задачки упрощается.

Аналогичным образом удается найти ответы на животрепещущие вопросы. Даже в микромире, управляемом электронами. Можно однозначно сказать одно: непосвященному правило буравчика, векторное произведение векторов представляются скучными, занудными. Удобный инструмент, помогающий в понимании многих процессов. Большинству будет интересным принцип работы электрического двигателя (безотносительно к конструкции). Легко может быть объяснен использованием правила левой руки.

Во многих отраслях науке бок-о-бок идут два правила: левой, правой руки. Векторное произведение иногда может описываться так или эдак. Звучит расплывчато, предлагаем немедленно рассмотреть пример:

Допустим, движется электрон. Отрицательно заряженная частица бороздит постоянное магнитное поле. Очевидно, траектория окажется изогнута благодаря силе Лоренца. скептики возразят, по утверждениям некоторых ученых электрон не частица, а скорее, суперпозиция полей. Но принцип неопределенности Гейзенберга рассмотрим в другой раз. Итак, электрон движется:

Расположив правую руку, чтобы вектор магнитного поля перпендикулярно входил в ладонь, вытянутые персты указывали направление полета частицы, отогнутый на 90 градусов в сторону большой палец вытянется в направлении действия силы.

Правило правой руки, являющееся иным выражением правила буравчика. Слова-синонимы. Звучит по-разному, по сути – одно.

Правило левой руки

Приведем фразу Википедии, отдающую странностью. При отражении в зеркале правая тройка векторов становится левой, тогда нужно применять правило левой руки вместо правой. Летел электрон в одну сторону, по методикам, принятым в физике, ток движется в противоположном направлении. Словно отразился в зеркале, поэтому сила Лоренца определяется уже правилом левой руки:

Если расположить левую руку, чтобы вектор магнитного поля перпендикулярно входил в ладонь, вытянутые персты указывали направление течения электрического тока, отогнутый на 90 градусов в сторону большой палец вытянется, указывая вектор действия силы.

Видите, ситуации похожие, правила просты. Как запомнить, которое применять? Главный принцип неопределенности физики. Векторное произведение вычисляется во многих случаях, причем правило применяется одно.

Как связано магнитное поле с буравчиком и руками

В задачах по физике, при изучении электрических величин, часто сталкиваются с необходимостью нахождения направления тока, по вектору магнитной индукции и наоборот. Также эти навыки потребуются и при решении сложных задач и расчетов, связанных магнитным полем систем.

Прежде чем приступить к рассмотрению правил, хочу напомнить, что ток протекает от точки с большим потенциалом к точке с меньшим. Можно сказать проще — ток протекает от плюса к минусу.

Правило буравчика имеет следующий смысл: при вкручивании острия буравчика вдоль направления тока – рукоятка будет вращаться по направлению вектора B (вектор линий магнитной индукции).

Правило правой руки работает так:

Поставьте большой палец так, словно вы показываете «класс!», затем поверните руку так, чтобы направление тока и пальца совпадали. Тогда оставшиеся четыре пальца совпадут с вектором магнитного поля.

Наглядный разбор правила правой руки:

Чтобы увидеть это более наглядно проведите эксперимент – рассыпьте металлическую стружку на бумаге, сделайте в листе отверстие и проденьте провод, после подачи на него тока вы увидите, что стружка сгруппируется в концентрические окружности.

Опыт Эрстеда

Продолжительное время электрические и магнитные поля изучались раздельно. Но в 1820 году датский учёный Ханс Кристиан Эрстед во время лекции по физике обнаружил, что магнитная стрелка поворачивается возле проводника с током (см. Рис. 1). Это доказало магнитное действие тока. После проведения нескольких экспериментов Эрстед обнаружил, что поворот магнитной стрелки зависел от направления тока в проводнике.

Рис. 1. Опыт Эрстеда

Для того чтобы представить, по какому принципу происходит поворот магнитной стрелки вблизи проводника с током, рассмотрим вид с торца проводника (см. Рис. 2, ток  направлен в рисунок,  – из рисунка), возле которого установлены магнитные стрелки. После пропускания тока стрелки выстроятся определённым образом, противоположными полюсами друг к другу. Так как магнитные стрелки выстраиваются по касательным к магнитным линиям, то магнитные линии прямого проводника с током представляют собой окружности, а их направление зависит от направления тока в проводнике.

Рис. 2. Расположение магнитных стрелок возле прямого проводника с током

Для более наглядной демонстрации магнитных линий проводника с током можно провести следующий опыт. Если вокруг проводника с током высыпать железные опилки, то через некоторое время опилки, попав в магнитное поле проводника, намагнитятся и расположатся по окружностям, которые охватывают проводник (см. Рис. 3).

Рис. 3. Расположение железных опилок вокруг проводника с током (Источник)

Правило буравчика для магнитных полей

Речь шла о постоянных магнитах. У них все всегда понятно: где какой полюс и куда направлены линии магнитного поля — от северного полюса к южному. Но магнитное поле возникает и вокруг проводников, по которым течет ток. Просто оно слабое, так что даже если поднести два участка, по которым течет ток, особого притяжения или отталкивания мы не ощутим. Чтобы создать сильное электромагнитное поле, проводник накручивают вокруг какого-то сердечника. Это изделие называют соленоидом. Когда по нему течет ток, создается ощутимое магнитное поле. Но как направлены линии магнитного поля в электромагнитах? Где у них северный, где южный полюс? Вот это и выясняют с помощью правила буравчика.

Буравчик можно себе представить как обычный штопор с ручкой-перекладиной и витками, накрученными вправо. Чтобы закручивать такой штопор, ручку надо вращать вправо — по часовой стрелке. При этом острие штопора/буравчика продвигается вниз. Чтобы выкручивать его, надо рукоятку вращать влево — против часовой стрелки. Острие при этом движется вверх.

Правило буравчика для магнитного поля

С движением острия буравчика и направлением вращения рукоятки и связано определение направление магнитного поля. Вот как звучит правило буравчика (еще называют правило винта):

С ровными проводниками все просто. Представляете, вкручивать или выкручивать надо буравчик, получаете направление силовых линий. Если по условиям задачи есть только направление линий магнитного поля, при помощи правила буравчика можно установить направление тока. Для этого мысленно представляем, что ручка штопора крутится в указанном направлении. В зависимости от этого, определяем куда движется острие, а, значит, и куда течет ток.

Применение правила буравчика

 правило гласит

Чтобы определить траекторию вращения магнитного контура на представленном графическом изображении нужно знать несколько особенностей.

Часто в задачах по физике нужно, наоборот, определить траекторию движения тока. Чтобы это сделать, дается направление вращения кругов магнитного поля. Ручка буравчика начинается вращаться в сторону, указанную в условиях. Если буравчик движется в поступательном направлении, значит, ток направлен в сторону движения, если же он направлен в обратную, то и ток движется соответственно.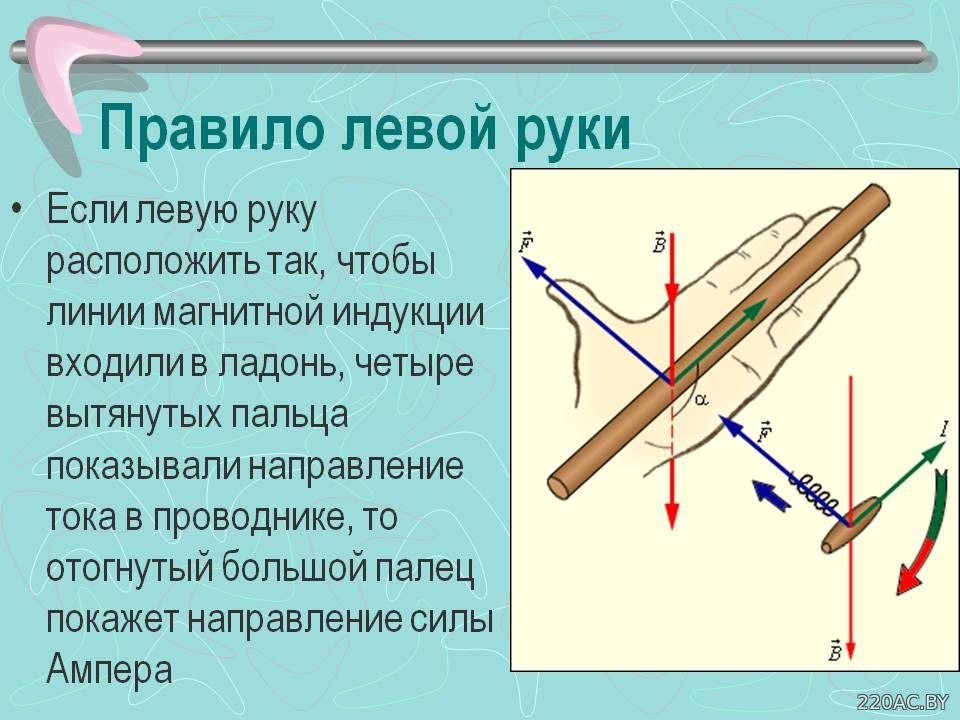

Для определения траектории движения тока в случае, представленном на втором рисунке, тоже можно воспользоваться правилом штопора. Для этого необходимо вращать ручку буравчика в сторону, указанную на изображении контура магнитного поля. Если он будет двигаться поступательно, то ток будет двигаться в сторону от наблюдателя, если же, наоборот, только к наблюдателю.

Важно! Если указана траектория движения потока, то определить траекторию вращения линии магнитного контура можно по вращению ручки буравчика.

Оно обозначается при помощи точки или крестика. Точка означает движение в сторону наблюдателя, крестик означает обратное. Легко запомнить этот случай, используя так называемое правило «стрелы», если острие «смотрит», а в лицо, то траектория движения тока в сторону наблюдателя, если же в лицо «смотрит хвост стрелы», то она двигается от наблюдателя.

Как правило буравчика, так и правило правой руки, достаточно легко применить на практике. Для этого нужно расположить кисть соответствующей руки таким образом, чтобы в лицевую сторону направлялся силовой контур магнитного поля, после чего большой палец, отведенный перпендикулярно, необходимо направить сторону движения тока, соответственно, остальные выпрямленные пальцы укажут на траекторию магнитного контура.

Различают исключительные случаи использования правила правой руки для вычисления:

• уравнения Максвелла;
• момента силы;
• угловой скорости;
• момента импульса;
• магнитной индукции;
• тока в проводе, движущегося через магнитное поле.

Что такое магнитное поле

Все, наверное, знают что такое постоянные магниты — они «липнут» к железу и некоторым другим материалам. Если приблизить два магнита, то они будут притягиваться или отталкиваться — в зависимости от того, как мы их повернем друг относительно друга. Почему и за счет чего так происходит? За счет того, что вокруг магнитов создается магнитное поле. Оно возникает при движении заряженных частиц. Например, вокруг провода, по которому протекает электрический ток, есть магнитное поле. Оно слабое, но оно есть.

Магнитное поле нельзя увидеть, но можно ощутить

Постоянные магниты

Как же тогда с магнитами? Откуда в них магнитное поле, ведь в них нет направленного движения частиц? Все просто. В них магнитное поле создается зарядами частиц. Как известно, любой материал состоит из положительно и отрицательно заряженных частиц. В некоторых материалах частицы можно расположить так, чтобы положительные были сконцентрированы с одной стороны, отрицательные — с другой. Эти «две стороны» называют полюсами магнита. Отрицательный — северный, обозначается латинской буквой N и закрашивается обычно синим цветом, положительный называют «южный» и обозначается S, закрашивается в красный цвет.

Постоянные магниты и их виды

Причем, стоит помнить, что однополюсных магнитов не бывает. Всегда есть два полюса. Если есть у вас большой магнит, его можно распилить пополам. И вы получите два магнита меньшего размера с двумя полюсами. Если распилите их — получите еще более мелкие двухполюсные магнитики.

Постоянные магниты можно сделать далеко не из всех материалов. Для этих целей подходят всего три вещества: железо (Fe), никель (Ni) и кобальт (Co). Если их выдержать в магнитном поле, частицы «рассортируются» по полюсам, материал станет магнитом. Но не все будут долго сохранять эти свойства. По способности удерживать магнитные свойства, материалы разделают на магнитомягкие и магнитотвердые материалы. Первые быстро намагничиваются, но и быстро теряют свои свойства. К таким относится железо (не обработанное). Магнитотвердый материал — например, сталь — в магнитном поле надо выдерживать долго. Зато после «выдержки» он становится магнитом на значительный промежуток времени. Можете поэкспериментировать со стальными скрепками.

Что такое магнитное поле

Приближая магниты друг к другу, на некотором расстоянии вы начнете ощущать, как они притягиваются или отталкиваются. Чем ближе подносите, тем сильнее они взаимодействуют. Все потому, что вокруг них существует магнитное поле. И чем ближе к магниту, тем поле сильнее.  Причем выглядит это поле как округлые линии, которые выходят из северного полюса и «заходят» в южный.

Магнитное поле можно представить в виде линий

Почему так решили? А потому что можно эти линии увидеть «вживую». Для этого надо провести эксперимент. На лист фанеры положить магнит, насыпать вокруг мелких металлических опилок и лист фанеры немного потрусить. Металлические опилки расположатся именно так, как показано на рисунке ниже справа

Обратите внимание — чем ближе к магниту, тем опилок больше, чем дальше — тем меньше. Это потому что магнитное поле ослабевает по мере удаления

Экспериментальное подтверждение: смотрим на магнитное поле и на взаимодействие полюсов

Опилки помогут понять и правила притяжения или отталкивания полюсов. На левом рисунке мы видим что происходит, если приблизить два противоположных полюса. Они притягиваются. Причем когда процесс завершится, картинка будет один в один как та, что справа. Как видите, они даже немного похожи.

Если поднести поближе два одноименных полюса — юг-юг или север-север — они будут отталкиваться. Это демонстрирует средний рисунок. И чем ближе их подносите, тем сильнее будет ощущаться противодействие.

Что связано с левой рукой

Не путайте буравчика и правило левой руки, оно нужно для определения действующей на проводник силы. Выпрямленная ладонь левой руки располагается вдоль проводника. Пальцы показывают в сторону протекания тока I. Через раскрытую ладонь проходят линии поля. Большой палец совпадает с вектором силы – в этом и заключается смысл правила левой руки. Эта сила называется силой Ампера.

Можно это правило применить к отдельной заряженной частице и определить направление 2-х сил:

1. Лоренца.
2. Ампера.

Представьте, что положительно заряженная частица двигается в магнитном поле. Линии вектора магнитной индукции перпендикулярны направлению её движения. Нужно поставить раскрытую левую ладонь пальцами в сторону движения заряда, вектор B должен пронизывать ладонь, тогда большой палец укажет направление вектора Fа. Если частица отрицательная – пальцы смотрят против хода заряда.

Если какой-то момент вам был непонятен, на видео наглядно рассматривается, как пользоваться правилом левой руки:

https://youtube.com/watch?v=vyYK9otQsTw

Важно знать! Если у вас есть тело и на него действует сила, которая стремится его повернуть, вращайте винт в эту сторону, и вы определите, куда направлен момент силы. Если вести речь об угловой скорости, то здесь дело обстоит так: при вращении штопора в одном направлении с вращением тела, завинчиваться он будет в направлении угловой скорости

Примечания

Математические детали общего понятия ориентации базиса, о котором здесь идёт речь — см. в статье Ориентация.

Под определением направления здесь везде имеется в виду выбор одного из двух противоположных направлений (выбор между всего двумя противоположными векторами), то есть сводится к выбору положительного направления.

Это означает, что другие правила могут быть также удобны в любом количестве, но их использование не является необходимым.

Это означает, что при желании можно пользоваться и противоположным правилом, и иногда это может быть даже удобно.

Понятие правого и левого базиса распространяются не только на ортонормированные, но на любые трехмерные базисы (то есть и на косоугольные декартовы координаты тоже), однако мы для простоты ограничимся здесь случаем ортонормированных базисов (прямоугольных декартовых координат с равным масштабом по осям).

Можно проверить, что в целом это действительно так, исходя из элементарного определения векторного произведения: Векторное произведение есть вектор, перпендикулярный обоим векторам-сомножителям, а по величине (длине) равный площади параллелограмма. То же, какой из двух возможных векторов, перпендикулярных двум заданным, выбрать — и есть предмет основного текста, правило, позволяющее это сделать и дополняющее приведённое здесь определение, указано там.

Левая резьба применяется в современной технике только тогда, когда применение правой резьбы привело бы к опасности самопроизвольного развинчивания под влиянием постоянного вращения данной детали в одном направлении — например, левая резьба применяется на левом конце оси велосипедного колеса

Помимо этого, левая резьба применяется в редукторах и баллонах для горючих газов, чтобы исключить подсоединение к кислородному баллону редуктора для горючего газа.

В том числе они могут быть в своих случаях и более удобными, чем общее правило, и даже иногда сформулированы достаточно органично, чтобы особенно легко запоминаться; что, правда, по-видимому, всё же не делает запоминание их всех более лёгким, чем запоминание всего одного общего правила.

Даже если мы имеем дело с достаточно асимметричным (и асимметрично расположенным относительно оси вращения) телом, так что коэффициентом пропорциональности между угловой скоростью и моментом импульса служит тензор инерции, несводимый к численному коэффициенту, и вектор момента импульса тогда вообще говоря не параллелен вектору угловой скорости, тем не менее правило работает в том смысле, что направление указывается приблизительно, но этого достаточно, чтобы сделать выбор между двумя противоположными направлениями.

Строго говоря, при этом сопоставлении есть ещё постоянный коэффициент 2, но в данной теме это не важно, так как речь идет сейчас только о направлении вектора, а не о его величине.

Не обязательное требование.

Выводы

Освоить эти способы определения направления сил и полей очень просто. Такие мнемонические правила в электричестве значительно облегчают задачи школьникам и студентам. С буравчиком разберется даже полный чайник, если он хотя бы раз открывал вино штопором. Главное не забыть, куда течет ток. Повторюсь, что использование буравчика и правой руки чаще всего с успехом применяются в электротехнике.

Напоследок рекомендуем просмотреть видео, благодаря которому вы на примере сможете понять, что такое правило буравчика и как его применять на практике:

Наверняка вы не знаете:

• Зависимость сопротивления проводника от температуры
• Как стать электриком
• Что такое фаза, ноль и земля
• Тесты по электротехнике

Правило правой руки — презентация онлайн

Правило правой руки
Если прямой проводник обхватить
ладонью
так,
чтобы
отогнутый
большой палец указывал направление
тока в проводнике, то оставшиеся
пальцы укажут направление магнитного
поля.
.
N
S
Правило правой руки.
Определение полюсов катушки с током.
N
S
Если обхватить катушку правой рукой так, чтобы
четыре пальца показывали направление тока, то
большой палец укажет направление на северный
полюс катушки.
Определите направление магнитных линий
магнитного поля прямолинейного
проводника с током.
На рисунке изображены магнитные линии
магнитного поля прямолинейного проводника
с током. Определите направление тока в
проводнике.
Определите направление магнитных
линий магнитного поля прямолинейного
проводника с током.
.
Определите направление магнитных линий
магнитного поля рамки с током.
Внутри рамки с током магнитные линии
магнитного поля направлены «от нас».
Магнитное поле катушки с током.
Магнитные линии магнитного
поля катушки с током
замкнутые кривые
и направлены снаружи
катушки от северного
полюса к южному
полюсу.
Определите полюсы магнитного поля
катушки.
N
S
_
+
Определите полюсы источника тока.
+
S
_
N
Определите полюсы источника тока.
N
S
+
_
Определите, как расположены магнитные полюсы
соленоида, подключённого к источнику тока.
Определите, как расположены магнитные полюсы
соленоида, подключенного к источнику тока.
N
–
+
S
Определите, как расположены магнитные полюсы
соленоида, подключенного к источнику тока.
+
Определите, как расположены магнитные полюсы
соленоида, подключенного к источнику тока.
–
+
S
N
Взаимодействие двух проводников с током
Силы, с которыми
проводники с током
действуют друг на
друга, называют
магнитными силами.

18. Сила Ампера

Силу, с которой магнитное поле
действует на проводник с током,
называют силой Ампера.

19. Сила Ампера имеет направление в пространстве, которое определяется по правилу левой руки:

Если
левую
руку
расположить так, чтобы
направление магнитного
поля входило в ладонь, а
вытянутые пальцы были
направлены вдоль тока,
то отведенный большой
палец
укажет
направление
действия
силы.

20. 1.Определить направление силы Ампера:

N
FA
S

21. 2.Определить направление силы Ампера:

N
FA
S

22. 3.Определить направление силы Ампера:

N
S
FA

23. 4.Определить направление силы Ампера:

FA
S
N

24. 9.Применяя правило левой руки, определи направление силы, с которой магнитное поле будет действовать на проводник с током.

Предполагаемые
направления силы Ампера указаны
1
стрелочками.
2
3
4
а) 1,
б)2,
в)3,
г)4

25. 10.Применяя правило левой руки, определи направление силы, с которой магнитное поле будет действовать на проводник с током.

Предполагаемые направления силы
Ампера указаны стрелочками. 1
2
3
4
а) 1,
б)2,
в)3,
г)4

26. 11.Применяя правило левой руки, определи направление силы, с которой магнитное поле будет действовать на проводник с током.

Предполагаемые направления силы
Ампера указаны стрелочками. 1
2
3
4
а) вверх,
б)вниз,
в) к нам,
г) от нас.

27. 12.Применяя правило левой руки, определи направление силы, с которой магнитное поле будет действовать на проводник с током.

Предполагаемые
направления
силы
Ампера
указаны
1
стрелочками.
2
3
4
а) 1,
б) 2,
в) 3,
г) 4

28. 13.Определить положение полюсов магнита, создающего магнитное поле.

а) слева – северный полюс,
б) слева – южный полюс.

29. 14.Определить положение полюсов магнита, создающего магнитное поле.

а) слева – северный полюс,
б) слева – южный полюс.

План Правило левой руки

 

3. Совместно с учащимися определить цели урока/ЦО.

Актуализация знаний.

Просмотр видеофрагмента «Сила Ампера»

После просмотра с учениками обсудить вопросы:

Вопросы к классу

1) Как называется сила, которая действует на проводник с током со стороны магнитного поля?

2) От каких физических величин зависит  сила Ампера?

3) При каких значениях угла сила Ампера принимает максимальное значение?

4) При каких значениях угла сила Ампера принимает минимальное значение?

5) При каких значениях угла сила Ампера принимает среднее значение?

4. Объяснение новой темы.

а) Правило левой руки.

Определяет направление действия силы Ампера.

Расположить ладонь левой руки так, чтобы четыре пальца указывали направление тока в проводнике, а в ладонь входил вектор магнитной индукции, то тогда большой палец отогнутый под прямым углом показывает направление силы Ампера.

 

б) Обсудить различные алгоритмы решения задач.

1)   Определение направления F_A (силы Ампера) по взаимно перпендикулярным векторам В и I.

2)   Определение направления силы тока по взаимно перпендикулярным векторам В и F_A.

3)   Определение направления вектора магнитной индукции по взаимно перпендикулярным векторам F_A и I.

4)   Определение направления вектора магнитной индукции и полюсов постоянного магнита по взаимно перпендикулярным векторам F_A и I.

в) Решение задач (разной уровней сложности.)

Каждая группа получает отдельные карточки с заданиями.

1-3 группа

СР № 30

 

ДУ № (№ 1, 3, 5, 7, 9)

ВУ № (№ 1, 3)

 

2-4 группа

СР № 30

 

ДУ № (№ 2, 4, 6, 8, 10)

ВУ № (№ 2, 4)

 

1 этап: Решение задач —  разминка:

Ученики решают задачи в группах на скорость с  общей сверкой результатов в классе. (2 задачи)

2 этап: Решение задач -закрепление:

Ученики решают задачи в парах на взаимопроверку.(3 задачи)

3 этап: Решение задач —  углубление (2 задачи).

Самостоятельное решение задачи. Первые решившие задачу верно объясняют решение задачи тем, кто испытывает затруднения.

 

Оценивание по критериям

1) Правильно записанное условие задачи;

2) Правильное использование правила левой руки.

3) Запись ответа.

 

Подсчёт стикеров за индивидуальную и групповую работу.

22.9 Магнитные поля, создаваемые токами: закон Ампера — Физика колледжа для курсов AP®

Цели обучения

К концу этого раздела вы сможете:

• Вычислить ток, создающий магнитное поле.
• Используйте правило правой руки 2, чтобы определить направление тока или направление контуров магнитного поля.

Информация, представленная в этом разделе, поддерживает следующие цели обучения AP® и научные практики:

• 2.D.2.1 Учащийся может создать словесное или визуальное представление магнитного поля вокруг длинного прямого провода или пары параллельных проводов. (С.П. 1.1)
• 3.C.3.1 Учащийся может использовать правила правой руки для анализа ситуации, в которой участвует проводник с током и движущийся электрически заряженный объект, чтобы определить направление магнитной силы, действующей на заряженный объект из-за магнитное поле, создаваемое проводником с током. (С.П. 1.4)
• 3.C.3.2 Учащийся может спланировать стратегию сбора данных, соответствующую исследованию направления силы на движущийся электрически заряженный объект, вызванной током в проводе, в контексте определенного набора оборудования. и инструменты и проанализировать полученные данные, чтобы прийти к заключению. (С.П. 4.2, 5.1)

Сколько тока необходимо для создания значительного магнитного поля, возможно, такого же сильного, как поле Земли? Геодезисты скажут вам, что воздушные линии электропередач создают магнитные поля, которые мешают показаниям их компаса.Действительно, когда Эрстед в 1820 году обнаружил, что ток в проводе воздействует на стрелку компаса, он не имел дела с очень большими токами. Как форма проводов, по которым проходит ток, влияет на форму создаваемого магнитного поля? Ранее мы отмечали, что токовая петля создает магнитное поле, подобное магнитному полю, но как насчет прямого провода или тороида (бублика)? Как направление создаваемого током поля связано с направлением тока? Ответы на эти вопросы исследуются в этом разделе вместе с кратким обсуждением закона, регулирующего поля, создаваемые токами.

Магнитное поле, создаваемое длинным прямым токопроводящим проводом: правило правой руки 2

Магнитные поля имеют направление и величину. Как отмечалось ранее, один из способов исследовать направление магнитного поля — это использовать компасы, как показано для длинного прямого токоведущего провода на рис. 22.39. Зонды Холла могут определять величину поля. Поле вокруг длинной прямой проволоки находится в виде кольцевых петель. Правило 2 правой руки (RHR-2) вытекает из этого исследования и справедливо для любого текущего сегмента — указывает большим пальцем в направлении тока, и пальцы сгибаются в направлении петель магнитного поля , созданных им.

Рис. 22.39 (a) Компасы, помещенные рядом с длинным прямым токоведущим проводом, показывают, что силовые линии образуют круговые петли с центром на проводе. (b) Правило 2 правой руки гласит, что, если большой палец правой руки указывает в направлении тока, пальцы сгибаются в направлении поля. Это правило согласуется с полем, отображаемым для длинного прямого провода, и действительно для любого текущего сегмента.

Создание соединений: обозначение

Для провода, ориентированного перпендикулярно странице, если ток в проводе направлен за пределы страницы, правило правой руки говорит нам, что силовые линии магнитного поля будут ориентированы против часовой стрелки вокруг провод.Если ток в проводе направлен на страницу, силовые линии магнитного поля будут ориентированы по часовой стрелке вокруг провода. Мы используем ⊙⊙ чтобы указать, что направление тока в проводе находится вне страницы, и ⊗⊗ для направления на страницу.

Рисунок 22.40 Два параллельных провода имеют токи, направленные внутрь или наружу страницы, как показано. Показано направление магнитного поля вблизи двух проводов.

Экспериментально установлено, что напряженность (величина) магнитного поля, создаваемая длинным прямым проводом с током, равна

. B = μ0I2πr (длинный прямой провод), B = μ0I2πr (длинный прямой провод), размер 12 {B = {{μ rSub {размер 8 {0}} I} над {2πr}} `\ (« длинный прямой провод » \),} {}

22.24

где II размер 12 {I} {} — ток, rr размер 12 {r} {} — кратчайшее расстояние до провода, а константа μ0 = 4π × 10−7T⋅m / Aμ0 = 4π × 10 −7T⋅m / A — проницаемость свободного пространства. (μ0 (μ0 размер 12 {\ (μ rSub {size 8 {0}}} {}) — одна из основных констант в природе. Позже мы увидим, что μ0μ0 размер 12 {μ ​​rSub {размер 8 {0}}} { } связано со скоростью света.) Поскольку провод очень длинный, величина поля зависит только от расстояния до провода размером 12 {r} {}, а не от положения вдоль провода.

Пример 22.6

Расчет тока, создающего магнитное поле

Найдите ток в длинном прямом проводе, который создаст магнитное поле, вдвое превышающее земное, на расстоянии 5,0 см от провода.

Стратегия

Поле Земли составляет около 5,0 × 10–5T5,0 × 10–5T, поэтому здесь размер BB 12 {B} {} из-за проволоки принимается равным 1,0 × 10–4T1,0 × 10–4T. Уравнение B = μ0I2πrB = μ0I2πr можно использовать для нахождения II, так как все остальные величины известны.

Решение

Решение для размера II 12 {I} {} и ввод известных значений дает

I = 2πrBμ0 = 2π5.0 × 10−2m1.0 × 10−4T4π × 10−7T⋅m / A = 25 AI = 2πrBμ0 = 2π5. 0 × 10−2m1.0 × 10−4T4π × 10−7T⋅m / A = 25 A.

22.25

Обсуждение

Таким образом, умеренно большой ток создает значительное магнитное поле на расстоянии 5,0 см от длинного прямого провода. Обратите внимание, что ответ состоит только из двух цифр, поскольку поле Земли в этом примере указано только из двух цифр.

Закон Ампера и другие

Магнитное поле длинного прямого провода имеет большее значение, чем вы можете сначала подумать. Каждый сегмент тока создает магнитное поле, подобное тому, которое имеет длинный прямой провод, а полное поле тока любой формы представляет собой векторную сумму полей, создаваемых каждым сегментом. Формальное определение направления и величины поля, создаваемого каждым сегментом, называется законом Био-Савара. Интегральное исчисление необходимо для суммирования поля для тока произвольной формы.Это приводит к более полному закону, называемому законом Ампера, который связывает магнитное поле и ток в общем виде. Закон Ампера, в свою очередь, является частью уравнений Максвелла, которые дают полную теорию всех электромагнитных явлений. Рассмотрение того, как уравнения Максвелла кажутся разным наблюдателям, привело к современной теории относительности и к осознанию того, что электрические и магнитные поля являются разными проявлениями одного и того же. Большая часть этого выходит за рамки данного текста как на математическом уровне, требующем вычислений, так и на объеме места, которое может быть отведено под него.Но для заинтересованного студента, и особенно для тех, кто продолжает заниматься физикой, инженерией или подобными занятиями, дальнейшее углубление в эти вопросы откроет описания природы, как элегантные, так и глубокие. В этом тексте мы будем иметь в виду общие особенности, такие как RHR-2 и правила для линий магнитного поля, перечисленные в разделе «Магнитные поля» и «Линии магнитного поля», концентрируясь при этом на полях, создаваемых в определенных важных ситуациях.

Установление связей: относительность

Слушая все, что мы делаем об Эйнштейне, у нас иногда создается впечатление, что он из ничего изобрел теорию относительности.Напротив, одной из мотиваций Эйнштейна было решить трудности, связанные с пониманием того, как разные наблюдатели видят магнитные и электрические поля.

Магнитное поле, создаваемое токонесущей круговой петлей

Магнитное поле около токоведущей петли из провода показано на рисунке 22.41. Как направление, так и величина магнитного поля, создаваемого токоведущей петлей, сложны. RHR-2 можно использовать для определения направления поля около петли, но для получения более подробной информации необходимы картографирование с помощью компасов и правила о силовых линиях, приведенные в разделах «Магнитные поля» и «Магнитные линии поля».Существует простая формула для напряженности магнитного поля в центре круговой петли. Это

B = μ0I2R (в центре петли), B = μ0I2R (в центре петли), размер 12 {B = {{μ rSub {size 8 {0}} I} над {2R}} `\ (» в центре петли «\),} {}

22,26

где размер RR 12 {R} {} — радиус петли. Это уравнение очень похоже на уравнение для прямого провода, но действительно только в центре круговой петли провода. Сходство уравнений указывает на то, что аналогичная напряженность поля может быть получена в центре петли.Один из способов увеличить поле — иметь NN размером 12 {N} {} циклов; тогда поле B = Nμ0I / (2R) B = Nμ0I / (2R). Обратите внимание, что чем больше петля, тем меньше поле в ее центре, потому что ток дальше.

Рисунок 22.41 (a) RHR-2 показывает направление магнитного поля внутри и снаружи токоведущей петли. (б) Более подробное картирование с помощью компасов или зонда Холла завершает картину. Поле похоже на поле стержневого магнита.

Магнитное поле, создаваемое токопроводящим соленоидом

Соленоид — это длинная катушка с проводом (с большим количеством витков или петель, в отличие от плоской петли).Из-за своей формы поле внутри соленоида может быть как очень однородным, так и очень сильным. Поле сразу за катушками почти равно нулю. На рис. 22.42 показано, как поле выглядит и как его направление задается RHR-2.

Рис. 22.42 (a) Из-за своей формы поле внутри соленоида длиной 11 размера 12 {l} {} удивительно однородно по величине и направлению, на что указывают прямые и равномерно разнесенные силовые линии. Поле вне катушек почти равно нулю. (b) Этот разрез показывает магнитное поле, создаваемое током в соленоиде.

Магнитное поле внутри соленоида с током очень однородно по направлению и величине. Только ближе к концам он начинает ослабевать и менять направление. Поле снаружи имеет те же сложности, что и плоские петли и стержневые магниты, но напряженность магнитного поля внутри соленоида просто равна

. B = μ0nI (внутри соленоида), B = μ0nI (внутри соленоида), размер 12 {B = μ rSub {size 8 {0}} ital «nI» `\ (» внутри соленоида «\),} {}

22,27

где nn размер 12 {n} {} — количество петель на единицу длины соленоида (n = N / l (n = N / l размер 12 {\ (n = N / l} {}, где размер NN 12 {N} {} — количество петель, а размер 11 — длина 12 {l} {}).Обратите внимание, что BB размер 12 {B} {} — это напряженность поля в любом месте однородной области интерьера, а не только в центре. Как следует из примера 22.7, с соленоидами возможны большие однородные поля, распределенные по большому объему.

Пример 22.7

Расчет напряженности поля внутри соленоида

Что такое поле внутри соленоида длиной 2,00 м, имеющего 2000 петель и пропускающего ток 1600 А?

Стратегия

Чтобы найти напряженность поля внутри соленоида, мы используем B = μ0nIB = μ0nI size 12 {B = μ rSub {size 8 {0}} ital «nI»} {}.Во-первых, отметим, что количество петель на единицу длины составляет

. n = Nl = 20002,00 м = 1000 м − 1 = 10 см − 1. n = Nl = 20002,00 м = 1000 м − 1 = 10 см − 1. размер 12 {n rSup {размер 8 {- 1}} = {{N} больше {l}} = {{«2000»} больше {2 «.» «00» m}} = «1000» «m» rSup {size 8 {- 1}} = «10» «cm» rSup {size 8 {- 1}} «.» } {}

22.28

Раствор

Подстановка известных значений дает

B = μ0nI = 4π × 10−7T⋅m / A1000m − 11600 A = 2,01 T.B = μ0nI = 4π × 10−7T⋅m / A1000m − 11600 A = 2,01 T.

22.29

Обсуждение

Это большая напряженность поля, которая может быть установлена ​​над соленоидом большого диаметра, например, при использовании в медицине магнитно-резонансной томографии (МРТ).Однако очень большой ток указывает на то, что поля такой силы нелегко получить. Такой большой ток через 1000 петель, сжатых до метра, приведет к значительному нагреву. Более высокие токи могут быть достигнуты с помощью сверхпроводящих проводов, хотя это дорого. Существует верхний предел тока, поскольку сверхпроводящее состояние нарушается очень сильными магнитными полями.

Применение научных практик: заряженная частица в магнитном поле

Зайдите сюда и запустите апплет моделирования «Частица в магнитном поле (2D)», чтобы изучить магнитную силу, которая действует на заряженную частицу в магнитном поле.Поэкспериментируйте с симуляцией, чтобы увидеть, как она работает и какие параметры вы можете изменить; затем составьте план методического исследования того, как магнитные поля влияют на заряженные частицы. Некоторые вопросы, на которые вы, возможно, захотите ответить в ходе эксперимента:

• Всегда ли пути заряженных частиц в магнитных полях одинаковы в двух измерениях? Почему или почему нет?
• Как можно сравнить путь нейтральной частицы в магнитном поле с путем заряженной частицы?
• Чем путь положительной частицы отличался бы от пути отрицательной частицы в магнитном поле?
• Какие величины определяют свойства пути частицы?
• Если бы вы пытались измерить массу заряженной частицы, движущейся в магнитном поле, что бы вам нужно было измерить относительно ее пути? Вам нужно было бы увидеть, как он движется с разными скоростями или через разную напряженность поля, или было бы достаточно одной попытки, если бы ваши измерения были правильными?
• Может ли удвоение заряда изменить путь через поле? Предскажите ответ на этот вопрос, а затем проверьте свою гипотезу.
• Изменит ли удвоение скорости путь через поле? Предскажите ответ на этот вопрос, а затем проверьте свою гипотезу.
• Может ли удвоение напряженности магнитного поля изменить его путь? Предскажите ответ на этот вопрос, а затем проверьте свою гипотезу.
• Может ли увеличение массы изменить путь? Предскажите ответ на этот вопрос, а затем проверьте свою гипотезу.

Есть интересные варианты плоской катушки и соленоида.Например, тороидальная катушка, используемая для удержания реактивных частиц в токамаках, очень похожа на соленоид, изогнутый в круг. Поле внутри тороида очень сильное, но круглое. Заряженные частицы движутся по кругу, следуя силовым линиям, и сталкиваются друг с другом, возможно, вызывая синтез. Но заряженные частицы не пересекают силовые линии и не покидают тороид. Целый ряд форм катушек используется для создания всевозможных форм магнитного поля. Добавление ферромагнитных материалов создает большую напряженность поля и может существенно повлиять на форму поля.Ферромагнитные материалы имеют тенденцию улавливать магнитные поля (силовые линии изгибаются в ферромагнитный материал, оставляя более слабые поля за его пределами) и используются в качестве экранов для устройств, на которые неблагоприятно влияют магнитные поля, в том числе магнитное поле Земли.

Генератор

Генерируйте электричество с помощью стержневого магнита! Откройте для себя физику этих явлений, исследуя магниты и узнавая, как с их помощью загорается лампочка.

Правило правой руки для токоведущего провода

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

Что означает Эрстед? — MVOrganizing

Что означает Эрстед?

Напряженность магнитного поля

Выражается в Эрстеде?

Ответ.Эрстед или (Oe) — единица cgs для измерения напряженности магнитного поля, которая обозначается (H). А / м или Ампер / метр — это единица измерения напряженности магнитного поля в системе СИ.

Каковы отношения между Эрстедом Гауссом и Теслой?

Согласно системе гауссовых единиц (cgs), гаусс — это единица плотности магнитного потока B и эквивалент Mx / cm2, а эрстед — единица намагничивающего поля H. Один тесла (T) равен 104 гаусс, а один ампер (А) на метр равен 4π x 10−3 эрстед.

Что доказал эксперимент Эрстеда?

В 1820 году датский физик Ганс Кристиан Эрстед обнаружил связь между электричеством и магнетизмом. Установив компас через провод, по которому проходит электрический ток, Эрстед показал, что движущиеся электроны могут создавать магнитное поле.

Что такое правило снега?

Что такое правило СНЕГА? Правила СНЕГА гласят, что если ток течет в электрической цепи с юга на север и магнитный компас помещается над проводящим проводом, стрелка компаса отклоняется в западном направлении.

Какое правило плавания у Ампера?

Правило плавания

Ампера гласит, что: если человек плывет по токонесущему проводу так, что его лицо всегда обращено к магнитной игле, и ток входит в его ноги и выходит из его головы, то северный полюс магнитной стрелки равен всегда отклоняется в сторону левой руки.

Что такое правило Максвелла Штопора?

Согласно штопору Максвелла по направлению тока, направление, в котором мы поворачиваем его ручку, является направлением магнитного поля.Это правило используется для определения направления магнитного поля вокруг прямолинейного проводника. Ответ проверен Toppr.

Что такое правило винта Максвелла?

Винтовое правило Максвелла 1. Оно гласит, что если правый винт повернуть так, чтобы он двигался вперед в том же направлении, что и обычный ток, его направление вращения будет определять направление магнитного поля.

Для чего используется линейка для правой руки?

Правило для правого захвата используется для определения соотношения между током и магнитным полем в зависимости от направления вращения.

Что такое правило правой руки Максвелла?

Правило для большого пальца правой руки Максвелла гласит: «Когда проводник держится в правой руке, направление большого пальца указывает направление тока, а изогнутый палец указывает направление магнитного пальца. Итак, угол между направлением тока и магнитным полем равен 900.

Какое правило правой руки для магнитной силы?

Правило правой руки гласит, что: чтобы определить направление магнитной силы на положительный движущийся заряд, направьте большой палец правой руки в направлении скорости (v), указательный палец в направлении магнитного поля (B), и ваш средний палец укажет в направлении результирующей магнитной силы…

Каковы два правила правой руки?

Второе правило правой руки имеет дело с магнитным полем, создаваемым током, проходящим через провод.Возьмите правую руку и обхватите пальцами провод, указав большим пальцем в направлении, в котором течет ток. Теперь ваши пальцы представляют направление магнитных силовых линий!

Кто дал правило для большого пальца правой руки?

В математике и физике правило правой руки — это общая мнемоника для понимания условных обозначений для векторов в 3 измерениях. Он был изобретен для использования в электромагнетизме британским физиком Джоном Амброузом Флемингом в конце 19 века.

Какое правило винта правой руки?

Правило для винта с правой рукой можно использовать, когда направление должно быть определено на основе направления вращения, или наоборот. Следовательно, если направление вращения известно, пальцы могут быть согнуты в этой ориентации, а большой палец будет указывать в положительном направлении, и наоборот. …

Как еще называется правило для большого пальца правой руки?

Застежка Правило

Где используется правило правой руки Флеминга?

Правило правой руки Флеминга (для генераторов) показывает направление индуцированного тока, когда проводник, присоединенный к цепи, движется в магнитном поле.Его можно использовать для определения направления тока в обмотках генератора.

Что говорится в правиле большого пальца правой руки?

Если мы держим токопроводящий проводник в правой руке так, чтобы большой палец указывал в направлении силовых линий магнитного поля, тогда пальцы охватывали бы провод в направлении электрического тока. …

Что такое правило левой руки в физике?

: правило в электричестве: если большой и два первых пальца левой руки расположены под прямым углом друг к другу на проводнике, а рука ориентирована так, чтобы первый палец указывал в направлении магнитного поля, а средний палец по направлению электрического тока большой палец укажет на…

Что такое Правило 10 Флеминга для левой руки?

Правило левой руки Флеминга гласит, что: Когда проводник с током помещается во внешнее магнитное поле, на проводник действует сила, перпендикулярная как полю, так и направлению тока.Его изобрел Джон Амброуз Флеминг.

Как правило правой руки работает для векторов?

Длина вектора дает скорость вращения, а направление оси дает направление вращения в соответствии с правилом правой руки: пальцы правой руки согнуты в направлении вращения, а большой палец правой руки указывает в положительном направлении оси. .

Кто сформулировал правило 10 для большого пальца правой руки?

Максвелла

Nerdfighteria Wiki — Закон Ампера: ускоренный курс физики № 33

Итак, сначала эти два параллельных провода: почему они притягиваются и отталкиваются друг от друга? Легче понять, почему два провода действуют именно так, если сначала посмотреть на один провод.

Как мы говорили в нашем последнем эпизоде, ток, проходящий через провод, создает магнитное поле. Допустим, у вас есть длинный прямой провод, по которому проходит ток. Ток создаст вокруг провода магнитное поле.

Это магнитное поле уменьшается по мере удаления от провода. Если вы нарисуете круг, скажем, в сантиметре от провода, магнитное поле вдоль круга будет иметь заданную силу.

Ампер понял, что чем сильнее ток, проходящий через провод, тем сильнее будет магнитное поле вдоль этой окружности.Это основная логика закона Ампера.

Но это физика, и в физике мы склонны выражать отношения в терминах уравнений. Уравнение закона Ампера применимо к любому типу петли, а не только к кругу, окружающему ток, независимо от количества проводов, их расположения или формы. Закон действует до тех пор, пока сила тока постоянна.

Само уравнение говорит, что интеграл магнитного поля «B» вдоль петли, умноженный на косинус тета по отношению к расстоянию, равен константе, называемой мю-ноль, умноженной на ток, протекающий через петлю.Это уравнение просто означает, что полное магнитное поле вдоль петли равно току, протекающему через петлю, умноженному на постоянное число.

Постоянная мю-ноль иногда называется «магнитной постоянной». И это равно четырем умноженным на пи умноженным на десять отрицательным семи Ньютонам на квадрат Ампера.

Теперь вы могли заметить, что в левой части уравнения для закона Ампера есть интеграл. И вы, возможно, помните, что мы используем интегралы, когда нам нужно сложить множество бесконечно маленьких значений.Что ж, в соответствии с законом Ампера мы складываем все маленькие кусочки магнитного поля вдоль петли.

Мы говорим, что все эти биты магнитного поля, сложенные вместе, равны приложенному току, умноженному на магнитную постоянную. «B» — это сила магнитного поля в каждой точке петли, «тета» — это угол между магнитным полем в каждой точке петли, а «ds» относится к каждому бесконечно маленькому участку петли.

Математика закона Ампера может очень быстро усложниться.Но чтобы получить общее представление о том, как это работает, давайте вернемся к нашему сценарию: круг вокруг одного длинного прямого провода.

Мы пытаемся найти магнитное поле в каждой точке круга (то есть B) в терминах приложенного тока и радиуса круга. Итак, сначала давайте решим интеграл в законе Ампера, чтобы получить полное магнитное поле вдоль окружности.

Согласно закону, мы решаем интеграл магнитного поля, умноженный на косинус теты по отношению к точкам на окружности.Но мы можем довольно легко упростить этот интеграл.

Сначала вы заметите, что магнитное поле, исходящее от нашего провода, параллельно окружности в каждой точке. Итак, угол тета равен нулю, а косинус нуля равен единице. Все, что умножено на единицу, равно самому себе. Таким образом, мы можем просто исключить член тета-косинуса из интеграла.

Теперь у нас остался интеграл магнитного поля B относительно точек на окружности. Но каждая часть круга находится на одинаковом расстоянии от провода, поэтому магнитное поле будет одинаковым в каждой точке.Другими словами, B постоянно, поэтому мы можем поставить его перед знаком интеграла.

Теперь все, что нам нужно сделать, это вычислить интеграл всех точек на окружности, который равен длине окружности (то есть удвоить число пи, умноженное на радиус).

Собирая все вместе, мы обнаруживаем, что когда мы применяем закон Ампера к длинному прямому проводу, полное магнитное поле вдоль окружности, окружающей провод, равно B, умноженному на два, умноженных на пи, умноженное на радиус. И это полное магнитное поле равно магнитной постоянной, умноженной на приложенный ток.

Итак, для длинного прямого провода B равно магнитной постоянной, умноженной на приложенный ток, деленной на два-пи-r.

Уравнение магнитного поля вдоль круга, окружающего один провод, оказалось очень важным для Ампера, когда он пытался выяснить, что происходит с двумя проводами. Когда по обоим проводам протекал ток в одном направлении, они притягивались друг к другу. А когда течение шло в противоположных направлениях, они отталкивали друг друга.

Легко понять, почему, если применить первое правило правой руки. Это говорит о том, что если вы укажете большим пальцем правой руки в направлении тока и согнете пальцы, магнитное поле будет указывать в том же направлении, что и ваши пальцы.

Итак, сначала давайте посмотрим на провода, в которых токи протекают в одном направлении. В этом примере мы скажем, что это вертикальные провода с восходящим током. Если вы укажете большим пальцем правой руки в направлении тока в каждом проводе, ваши пальцы будут сгибаться в направлении магнитного поля.

Магнитное поле от провода слева будет направлено вправо, а магнитное поле от провода справа будет направлено влево, поэтому провода будут притягиваться друг к другу.

В случае, когда ток течет в противоположных направлениях, верно обратное, поэтому они будут отталкивать друг друга.

Ампер также хотел найти силу магнитного поля на проводах. Как мы говорили в прошлый раз, сила зависит от угла между током и магнитным полем, силы тока, длины провода и силы магнитного поля.

Вычислить магнитное поле B было непростой задачей. Уравнение, которое он придумал, то, которое мы теперь называем законом Ампера, позволило ему и будущим физикам выяснить, что представляет собой B во многих ситуациях, в том числе в случае двух параллельных проводов.

Итак, два параллельных провода притягивались и отталкивались друг от друга из-за магнитного поля, создаваемого токами. А что насчет катушки с проволокой, которая превратилась в магнит? Что ж, вы, вероятно, можете догадаться, что его поведение также связано с магнитным полем, создаваемым токами.

Обратите внимание на катушку с проволокой особой формы, называемую «соленоидом». И когда через соленоид проходит ток, он создает магнитное поле, которое в основном проходит через внутреннюю часть катушек.

Если вы обхватите соленоид правой рукой так, чтобы пальцы указывали в направлении тока, проходящего через петли, большой палец будет указывать в направлении магнитного поля.

Закон Ампера также применим для соленоидов. В нем говорится, что магнитное поле внутри катушек (B) равно магнитной постоянной, умноженной на ток, протекающий через катушки, умноженный на количество катушек.

Вот что происходит, когда петли из проволоки создают магнитное поле. Когда вы вставляете проволочную петлю в магнитное поле, происходит нечто странное: петля из проволоки поворачивается. Это потому, что магнитное поле создает крутящий момент на проводе.

Взгляните на эту проволочную петлю. Горизонтальные части петли параллельны магнитному полю, поэтому он не будет оказывать на них силу. Но вертикальные части петли перпендикулярны магнитному полю, поэтому на них будет действовать сила: сила, которая поворачивает петлю.

Из последнего эпизода мы знаем, что сила магнитного поля на проводе будет равна току, умноженному на длину этой части катушки, умноженному на магнитное поле. И мы можем использовать второе правило правой руки, чтобы определить направление этой силы.

Если вы укажете рукой в ​​направлении тока, а затем согнете пальцы в направлении магнитного поля, ваш большой палец будет указывать в направлении силы. Которая оказывается от вас для левой стороны катушки и к вам для правой стороны.Катушка вращается по часовой стрелке.

Так работают электродвигатели. У них есть электрический ток, который постоянно меняет направление, заставляя проволочные петли вращаться. Эти движущиеся петли из проволоки можно использовать для выполнения механических работ, таких как вращение барабана в стиральной машине, электродрели или вентилятора, который, вероятно, охлаждает ваш компьютер.

Электродвигатели есть везде. Так что в следующий раз, когда вы будете стирать одежду, собирать мебель, использовать компьютер, не перегревая его, или делать что-нибудь еще, связанное с использованием электродвигателя, вы должны поблагодарить Ампера.

Закон Ампера — объяснение, формула и примеры

Закон Ампера является неотъемлемой частью концепции электромагнетизма и также известен как закон Ампера .

Закон Ампера является альтернативным выражением закона Био Савара.

История

Закон Ампера был впервые открыт французским физиком Андре-Мари Ампер в 1826 . Окончательное уравнение этого закона было получено шотландским ученым Джеймсом Клерком Максвеллом in 1861 .

В 1865 году Максвелл обобщил уравнение для применения к изменяющимся во времени токам, добавив член тока смещения.

Эта современная форма закона иногда также упоминается как Закон Ампера-Максвелла .

Разъяснение закона Ампера

Этот закон определяет взаимосвязь между током через замкнутый контур и магнитным полем , созданным вокруг него.

Заявление

Закон Ампера

«Для любого замкнутого пути линейный интеграл касательной составляющей магнитного поля в направлении элемента пути равен магнитной проницаемости, умноженной на электрический ток, заключенный в петле.”

Направление магнитного поля с использованием правила правой руки (Источник).

Направление магнитного поля можно визуализировать с помощью правила для правой руки : Направьте большой палец в направлении тока, и пальцы сгибаются в направлении петель магнитного поля , созданных им .

Уравнение \ (\ large {\ oint \ overrightarrow {B}. \ overrightarrow {ds} = \ mu_0 I} \)

Где,
\ (B \) — Магнитное поле в позиции \ (ds \),
\ (ds \) — Составляющая длины пути, с
\ (\ mu_0 \) — Проницаемость вакуума,
\ (I \) — Ток через замкнутый контур

Изображает, что при непрерывном прохождении тока через замкнутый контур вокруг проводника создается магнитное поле.

Из уравнений видно, что:

• Общее магнитное поле изменяется при изменении тока, протекающего по замкнутому пути.
• Если магнитное поле известно, ток, протекающий через замкнутый контур, можно рассчитать путем интегрирования магнитного поля в каждой точке / положении контура.
• \ (\ oint \ overrightarrow {B}. \ Overrightarrow {ds} = 0 \) не обязательно означает, что магнитное поле равно нулю, но ток равен нулю.

Существуют определенные условия применения закона Ампера:

• Ток, протекающий через замкнутый контур, должен быть постоянным.
• Учитываются только токи, пересекающие область внутри контура петли, и они вносят некоторый вклад в магнитное поле.
• Токи следует снимать с их алгебраическими знаками ( выходящие «за пределы» поверхности — положительные, входящие «входящие» — отрицательные ) — используйте правило правой руки для определения направлений и знаков.

Для круговых петель \ (\ oint \ overrightarrow {ds} \) становится \ (2 \ pi r \), где r — радиус круговой петли.

Следовательно, уравнение принимает вид

\ (B.2 \ pi r = \ mu_0 I \)
\ (∴ B = \ frac {\ mu_0 I} {2 \ pi r} \)

Применение закона Ампера

• Основное приложение — вычисление магнитного поля , создаваемого электрическим током, которое используется в электромагнитах , двигателях , генераторах , преобразовывает и т. Д.
• Он также применяется вместо Biot Закон Савара , поскольку закон Ампера упрощает расчет за счет использования симметрии.{-6} Т \)
  Часто задаваемые вопросы Что такое Закон Ампера?

  Закон оборота Ампера может быть записан как линейный интеграл магнитного поля, окружающего замкнутый контур, равный магнитной проницаемости, умноженной на алгебраическую сумму токов, проходящих через контур.

  Как Максвелл изменил закон Ампера?

  Максвелл модифицировал закон Ампера, включив в него изменяющиеся во времени электрические поля. Он предположил, что между пластинами конденсатора присутствует некоторый ток, известный как ток смещения.
  Он изменил закон Ампера, включив ток смещения.

  Какое состояние магнитного поля внутри и снаружи проводника?

  Магнитное поле максимально внутри проводника и минимально вне проводника.

  Соленоид

  Соленоид

  Соленоид ^{[nb 1]} представляет собой катушку, намотанную в плотно упакованную спираль. В физике термин соленоид относится к длинной тонкой петле из проволоки, часто намотанной вокруг металлического сердечника, который создает магнитное поле, когда через него проходит электрический ток.Соленоиды важны, потому что они могут создавать контролируемые магнитные поля и могут использоваться в качестве электромагнитов. Термин соленоид относится конкретно к магниту, предназначенному для создания однородного магнитного поля в объеме пространства (где можно провести некоторый эксперимент).

  В технике термин соленоид может также относиться к множеству преобразователей, которые преобразуют энергию в поступательное движение. Этот термин также часто используется для обозначения электромагнитного клапана, который представляет собой интегрированное устройство, содержащее электромеханический соленоид, который приводит в действие пневматический или гидравлический клапан, или электромагнитный переключатель, который представляет собой особый тип реле, внутри которого используется электромеханический соленоид для управлять электрическим выключателем; например, соленоид автомобильного стартера или линейный соленоид, который является электромеханическим соленоидом.

  Магнитное поле соленоида

  Внутри

  Это производное магнитного поля вокруг соленоида, достаточно длинное, чтобы можно было игнорировать краевые эффекты. На диаграмме справа мы сразу знаем, что поле указывает в положительном направлении z внутри соленоида и в отрицательном направлении z вне соленоида.

  Мы видим это, применяя правило захвата правой рукой для поля вокруг проволоки.Если мы обхватим правой рукой провод, указав большим пальцем в направлении тока, изгиб пальцев покажет, как ведет себя поле. Поскольку мы имеем дело с длинным соленоидом, все компоненты магнитного поля, не направленные вверх, компенсируются симметрией. Снаружи происходит аналогичная отмена, а поле только направлено вниз.

  Теперь рассмотрим воображаемую петлю c , которая находится внутри соленоида. По закону Ампера мы знаем, что линейный интеграл B (вектор магнитного поля) вокруг этой петли равен нулю, поскольку он не включает в себя электрические токи (можно также предположить, что циркулирующее электрическое поле, проходящее через петлю, является постоянным при такие условия: постоянный или постоянно меняющийся ток через соленоид).Выше мы показали, что поле направлено вверх внутри соленоида, поэтому горизонтальные участки контура c ничего не вносят в интеграл. Таким образом, интеграл от верхней стороны 1 равен интегралу нижней стороны 2. Поскольку мы можем произвольно изменять размеры контура и получить тот же результат, единственное физическое объяснение состоит в том, что подынтегральные выражения фактически равны, то есть магнитное поле внутри соленоида радиально однородно. Однако обратите внимание, что ничто не запрещает ему изменяться в продольном направлении, что на самом деле так и есть.

  Снаружи

  Аналогичный аргумент можно применить к контуру и , чтобы сделать вывод о том, что поле вне соленоида является радиально однородным или постоянным. Этот последний результат, который строго верен только около центра соленоида, где силовые линии параллельны его длине, важен, поскольку он показывает, что внешнее поле практически равно нулю, поскольку радиусы поля вне соленоида будут стремиться к бесконечность.

  Можно также использовать интуитивный аргумент, чтобы показать, что поле вне соленоида фактически равно нулю.Линии магнитного поля существуют только как петли, они не могут расходиться или сходиться к точке, как силовые линии электрического поля (см. Закон Гаусса для магнетизма). Линии магнитного поля следуют продольной траектории соленоида внутри, поэтому они должны идти в противоположном направлении за пределами соленоида, чтобы линии могли образовывать петлю. Однако объем снаружи соленоида намного больше, чем объем внутри, поэтому плотность силовых линий снаружи значительно снижается. Напомним, что внешнее поле постоянно.Чтобы общее количество силовых линий было сохранено, внешнее поле должно стремиться к нулю по мере того, как соленоид становится длиннее.

  Количественное описание

  Теперь мы можем рассмотреть воображаемую петлю b . Возьмите линейный интеграл B вокруг петли с длиной петли l . Горизонтальные компоненты исчезают, а внешнее поле практически равно нулю, поэтому закон Ампера дает нам:

  , где μ ₀ — магнитная постоянная, N — количество витков, i электрический ток. Этимология : Французский solénoïde , греческий solen «труба, канал» + комбинация греческого eidos «форма, форма» ^[1]

Ссылки

Внешние ссылки

Роль магнитных сил в биологии и биологии. Медицина

Exp Biol Med (Maywood).Авторская рукопись; доступно в PMC 2012 1 февраля.

Опубликован в окончательной отредактированной форме как:

PMCID: PMC3079438

NIHMSID: NIHMS262122

Брэдли Дж. Рот

Департамент физики, Оклендский университет, Рочестер

, Мичиган, 48000 Дж. Рот, факультет физики Оклендского университета, Рочестер, штат Мичиган, 48309, США;

Брэд Рот, физический факультет, Оклендский университет, Рочестер, Мичиган, 48309, (248) 370-4871, факс (248) 370-3408, ude.dnalkao@htor См. Другие статьи в PMC, в которых цитируется опубликованная статья.

Abstract

Сила Лоренца (сила, действующая на токи в магнитном поле) играет все более важную роль в методах визуализации тока и проводимости. В этом обзоре будут обобщены несколько приложений, связанных с силой Лоренца, в том числе 1) магнитоакустическая визуализация тока, 2) визуализация «эффекта Холла», 3) визуализация проводимости с помощью силы Лоренца, индуцированной ультразвуком, 4) магнитоакустическая томография с магнитной индукцией, и 5) визуализация токов действия с помощью силы Лоренца с использованием магнитно-резонансной томографии.

Ключевые слова: сила Лоренца, магнитное поле, ультразвук, магнитно-резонансная томография, проводимость, магнитоакустическая визуализация

Введение

За последние двадцать лет несколько исследовательских групп разработали методы визуализации, которые используют силу, действующую на биотоки при наличии магнитного поля. Механизм, лежащий в основе, знаком любому, кто прошел вводный курс физики ¹ : провод, пропускающий ток I , имеющий длину L и лежащий перпендикулярно магнитному полю B , испытывает магнитную силу F. = ILB , часто называемая «силой Лоренца».Направление силы перпендикулярно как проводу, так и магнитному полю, и его можно определить по «правилу правой руки». Это та же сила, которая заставляет работать электродвигатели.

Поскольку сила Лоренца возникает из-за магнитного поля и вызывает механическое движение, явления, возникающие из-за этого, часто называют «магнитоакустикой». В биологической ткани, где нет проводов, удобнее говорить о силе Лоренца на единицу объема, F , возникающей из плотности тока Дж и магнитного поля B: F = J × B , где «×» обозначает перекрестное произведение ().В общем, магнитоакустические эффекты небольшие, но небольшие эффекты лежат в основе многих важных методов построения изображений.

Сила Лоренца. Плотность тока J течет вправо, а магнитное поле B направлено из бумаги (обозначено символом), в результате чего сила F направлена ​​вниз.

В этом мини-обзоре я расскажу о биологических и медицинских приложениях магнитоакустики. Эти методы могут быть полезны для картирования электрической активности в головном мозге и сердце, а также для обнаружения аномальных тканей, таких как опухоли, по изменению электрических свойств.Я сосредотачиваюсь на магнитных силах, которые действуют на электрический ток, с акцентом на то, как эти силы могут быть использованы для отображения тока или проводимости. Я не буду рассматривать следующие темы: проблемы безопасности, связанные с сильными магнитными полями ^{2 — 4} , эффекты, возникающие из-за присутствия железа, которые приводят к особенно большим магнитным силам (например, частицы магнетита в магнитотатических бактериях ⁵ ), а также явления, связанные со спином электрона или ядра (например, ядерный магнитный резонанс).

Магнитоакустическая визуализация тока

В 1988 году Брюс Тоу и его коллеги ^{6 , 7} разработали «новый метод неинвазивного измерения низкоуровневых ионно-проводимых электрических токов, протекающих в электролитах и ​​тканях. ” Они пропускают переменный ток (3 кГц) силой в несколько микроампер через хомяка, помещенного в магнитное поле 0,2 Тл (). Акустический сигнал, возникающий от силы Лоренца, обнаруживается с помощью микрофона и синхронизирующего усилителя.Они приходят к выводу, что ⁶ «эти эксперименты показывают, что можно неинвазивным образом обнаружить существование ионных токов, текущих внутрь проводящей среды, путем приложения магнитных полей и мониторинга результирующих акустических откликов. Этот принцип представляет интерес как возможная основа для нового метода неинвазивного измерения биоэлектрических токов в живых организмах ». Позже Towe ⁸ разработал инструмент, который «представляет собой очень чувствительный баланс сил, который может измерять силы Лоренца, испытываемые ионными токами, протекающими в небольших объектах при воздействии сильных осциллирующих магнитных полей.«Хотя этот метод еще не получил широкого распространения для получения изображения тока, он демонстрирует возможность измерения магнитоакустических эффектов и иллюстрирует действующие физические принципы.

Эксперимент по магнитно-акустическому обнаружению тока в хомяке. От Towe and Islam ⁶ . (© 1988 IEEE)

Метод Тауэ может обнаруживать приложенные токи переменного тока известной частоты, но можно ли его использовать для обнаружения эндогенных токов действия в нерве и мышцах? Чтобы ответить на этот вопрос, Рот, Бассер и Виксво ⁹ теоретически проанализировали магнитоакустические явления.Они вычисляют давление p и смещение u , создаваемое плотностью тока Дж в эластичной проводящей ткани с модулем сдвига G и подверженной воздействию магнитного поля B , начиная с Уравнение Навье,

G ∇ ² u — ∇ p + J × B = 0.

(1)

Это уравнение мотивировано модель сердечной ткани жидкость-волокно-коллаген ¹⁰ , в которой давление создается жидкостью (считается несжимаемой, ∇ · u = 0), а модуль сдвига возникает из упругих свойств коллагеновые волокна.Уравнение 1 связывает силы, возникающие при упругом сдвиге, градиентах давления и силе Лоренца. Расхождение уравнения. 1 видно, что источником давления является ротор плотности тока

∇ ² p = (∇ × Дж ) · B .

(2)

Этот результат показывает аналогию между магнитоакустической токовой визуализацией и биомагнитной токовой визуализацией ⁹ . Ротор закона Ампера, ∇ × b = μ _o Дж, , управляющий биомагнитным полем b , создаваемым токами действия Дж , дает

∇ ² b = −μ _o ∇ × J ,

(3)

где μ _o — проницаемость свободного пространства.Магнитоакустические записи давления (уравнение 2) и биомагнитные измерения (уравнение 3) отображают токи действия эквивалентным образом: оба они имеют ∇ × Дж в качестве источника.

Roth et al. ⁹ получить аналитические решения для смещения, создаваемого диполем тока силой q в центре проводящей сферы радиусом a . Величина смещения на поверхности сферы составляет порядка qB / ( 4π Ga) .Для диполя с напряженностью q = 1 мкА · м, модуль сдвига G = 10 ⁴ Н / м ² , магнитное поле B = 1 Тл и радиус a = 1 см, смещение поверхности очень мало, порядка 1 нм. Их анализ показывает, что «магнитоакустической визуализации эндогенных биоэлектрических токов может быть значительно труднее достичь, чем можно было бы заключить из экспериментов, о которых сообщалось на сегодняшний день».

Ammari et al. ¹¹ математически исследовали методы локализации для магнитоакустической токовой визуализации. Их подход заключается в усреднении измерений давления, взвешенных по конкретным решениям волнового уравнения, что позволяет им определять местонахождение дипольных источников. Этот метод можно распространить на случай, когда давление измеряется только на части границы ткани.

Визуализация «эффекта Холла»

Хан Вэнь ^{12 — 14} и его сотрудники разработали метод визуализации электрических свойств образца с использованием того, что они называют «классическим эффектом Холла» ().Их сигнал создается ¹² “явлением разделения зарядов в проводящем объекте, движущемся в магнитном поле. Это разделение зарядов является результатом противоположных сил Лоренца на положительный и отрицательный заряды и приводит к внешнему обнаружению напряжения…. [Амплитуда] напряжения определяется силой силы Лоренца, а также плотностью заряда и подвижностью ». Они проверяют свой метод, подавая ультразвуковой сигнал (1 МГц) в камеру солевого раствора, содержащую образец (поликарбонатный блок), помещенный в статическое магнитное поле 4 Тл.Движение образца вызывается ультразвуковой волной. Они измеряют индуцированное напряжение с помощью электродов и могут получать четкие сигналы, соответствующие верхней и нижней поверхности образца. Рот и Виксво ¹⁵ сомневаются, является ли «эффект Холла» правильным названием физического механизма, лежащего в основе этого явления, но в любом случае этот метод представляет собой новое и важное применение сил Лоренца в биомедицинской визуализации.

Напряжение, индуцированное движением.Ткань движется вправо со скоростью v в присутствии магнитного поля B , направленного из бумаги. Отрицательные ионы испытывают восходящую силу Лоренца, а положительные ионы испытывают нисходящую силу Лоренца. Получающееся в результате разделение зарядов создает отрицательное напряжение в верхней части ткани и положительное напряжение в нижней части.

Возможен обратный метод визуализации «эффекта Холла» с током, управляемым источником напряжения, и движением, создаваемым силой Лоренца (как в магнитоакустической визуализации).Wen et al. ¹² пишут, что «в реверсивном режиме или режиме обнаружения ультразвука генератор импульсов, который использовался для управления ультразвуковым преобразователем, теперь подключен к паре электродов, которые использовались для обнаружения… напряжения в прямом режиме, и сигнал -чувствительная электроника подключена к преобразователю. Когда импульсный генератор генерирует импульс напряжения на электродах, он создает плотность тока, пропорциональную локальной кажущейся проводимости. На границах раздела изменяющейся проводимости плотность тока становится прерывистой, как и силы Лоренца, действующие на токи… [приводящие] к ультразвуковым импульсам, исходящим от этих границ раздела.«Они используют этот метод для получения изображений жировых и мышечных слоев бекона (). Рот и Виксво ¹⁵ анализируют этот обратный метод и выводят волновое уравнение для ультразвукового сигнала давления, подобное уравнению. 2 выше

Фотография поперечного сечения бекона, изображение бекона, полученное с помощью метода визуализации с эффектом Холла в обратном режиме, и эхо-ультразвуковое изображение того же поперечного сечения. Из Wen et al. ¹² . (© 1998 IEEE)

∇2p − 1c2∂2p∂t2 = (∇ + J) · B,

(4)

, где c — скорость звука в ткани.Они приходят к выводу, что ¹⁵ «многое из того, что мы узнали из квазистатического анализа магнитоакустических изображений, может быть применено ко второму [обратному] методу построения изображений, предложенному Веном и др.»

Ультразвуковая сила Лоренца для измерения проводимости изображения

Вдохновленная методом Вена и др., Амальрик Монталибет и его коллеги ^{16 , 17} далее разработали методы «ультразвуковой силы Лоренца» для измерения электрическая проводимость ().Суть их методики такая же, как описано Веном и др.: «Ионы растворов, подвергшихся воздействию ультразвука в присутствии магнитного поля, испытывают силу Лоренца. Их движение вызывает локальную плотность электрического тока, которая пропорциональна электропроводности среды… Величина измеренного тока составляет 50 нА в солевом растворе с проводимостью 0,5 См / м. Методика позволила определить проводимость образца крови свиньи по гематокриту » ¹⁷ .

Принципиальная схема экспериментальной установки для обнаружения токов, вызванных силой Лоренца, индуцированной ультразвуком. Ось Oz является осью распространения ультразвука, Ox имеет ту же ориентацию, что и магнитное поле, а ток взаимодействия положительный вдоль Oy . Начало координат, O , расположено в центральной точке преобразователя. Из Montalibet et al. ¹⁶ .

Принимая во внимание, что Montalibet et al. ^{16 , 17} применяют импульсный ультразвук в своих экспериментах, Рот и Шальте ¹⁸ разработали томографический метод для определения проводимости ткани с использованием непрерывного ультразвука.Сила и синхронизация электрического диполя, вызванная ультразвуковой силой Лоренца, определяет амплитуду и фазу преобразования Фурье изображения проводимости. Таким образом, электрические измерения на различных длинах волн и направлениях эквивалентны отображению преобразования Фурье распределения проводимости в пространственно-частотном пространстве. Затем с помощью обратного преобразования Фурье находят изображение самой проводимости. В альтернативном подходе Haider et al. ¹⁹ исследовали эту проблему с точки зрения свинцовых полей. Интересно, что Olaffson et al. ²⁰ показали, что ультразвуковая волна сама может изменять проводимость, и этот эффект, возможно, необходимо учитывать при визуализации проводимости.

Ценг и Рот ²¹ описали новую особенность вызванной ультразвуком силы Лоренца в анизотропной ткани: колеблющийся электрический потенциал распространяется вместе с ультразвуковой волной. Этот потенциал аналогичен потенциалам ультразвуковых колебаний, возникающим из-за разницы в инерции между положительными и отрицательными носителями заряда в коллоидных суспензиях или ионных растворах ²² , но он вызван другим механизмом.показывает три полуволны ультразвуковой волны, которая распространяется вправо в магнитном поле, выходящем из бумаги. Плотность тока из-за силы Лоренца отклоняется от направления z из-за анизотропии (диагональные линии указывают направление волокна). Это вызывает накопление положительного заряда там, где сходятся векторы тока, и отрицательного заряда, где они расходятся. Заряд производит собственный электрический ток и потенциал, который колеблется вместе с ультразвуковой волной.

Три половины длины волны ультразвуковой волны, распространяющейся вправо. Магнитное поле B выходит из бумаги, а смещение u происходит по оси x . Плотность тока, вызванная силой Лоренца, Дж _Лоренц , вращается за счет анизотропии ткани (ось волокна обозначена диагональными линиями), создавая плотность тока и электрический потенциал, вызванные зарядом, Дж _заряд .От Ценга и Рота 31.

Магнитоакустическая томография с магнитной индукцией

Недавно Бин Хе и его коллеги разработали магнитоакустические методы измерения импеданса ^{23 — 31} . Новой особенностью их метода является то, что они индуцируют в образце вихревые токи с помощью магнитной индукции (закон Фарадея: изменяющееся магнитное поле индуцирует электрическое поле). «Образец находится в статическом магнитном поле и изменяющемся во времени магнитном поле.Изменяющееся во времени магнитное поле индуцирует в образце вихревой ток. Следовательно, образец будет излучать ультразвуковые волны силой Лоренца. Ультразвуковые сигналы собираются вокруг объекта для восстановления изображений, связанных с распределением электрического импеданса в образце » ²³ . Ли и др. ²⁵ получили изображения границ проводимости с высоким пространственным разрешением от физиологического раствора и гелевых фантомов (), что указывает на осуществимость их метода, который они называют магнитно-акустической томографией с магнитной индукцией (MAT-MI).Бринкер и Рот ³² проанализировали MAT-MI и обнаружили, что при визуализации нерва или мышцы электрическая анизотропия может иметь значительное влияние на акустический сигнал и должна быть учтена для получения точных изображений. Ammari et al. ¹¹ исследовали методы реконструкции MAT-MI математически.

(a) Двумерное изображение MAT-MI гелевого фантома с двумя колонками геля с 0% -ным содержанием соли, залитыми в гель с содержанием соли 10%. (b) Фотография фантома, вид сверху. Из Li et al. ²⁵ . (© 2007 IEEE)

Силовая визуализация токов действия Лоренца с помощью МРТ

Аллен Сонг и его сотрудники ^{33 — 35} предложили метод МРТ-обнаружения биотоков, названный «визуализацией эффекта Лоренца». При воздействии магнитного поля на ток в теле действует сила Лоренца (). Эта сила деформирует ткань, заставляя перемещаться токопроводящие нервные волокна. Когда присутствует градиент магнитного поля, это движение перемещает нерв в область с другой силой магнитного поля.Если изменение магнитного поля достаточно велико, это вызывает артефакт в сигнале магнитного резонанса, который можно использовать для определения местоположения активных нейронов. Сонг и Такахаши ³³ демонстрируют этот метод, визуализируя движение медной проволоки в гелевом фантоме с помощью МРТ. Совсем недавно Труонг и Сонг ³⁵ применили «серию осциллирующих градиентов (с положительными и отрицательными долями одинаковой амплитуды и продолжительности) синхронно с нервной стимуляцией, так что нейроэлектрическая активность проявляется только в отрицательных долях.Они пришли к выводу, что «успешное обнаружение нейроэлектрической активности in vivo с помощью нашей техники демонстрирует, что активация нейронов может быть визуализирована неинвазивно с помощью МРТ с высоким пространственным и временным разрешением». Basford et al. ³⁶ также исследовали движение, вызванное силой Лоренца, во время магнитно-резонансной томографии.

Рот и Бассер ³⁷ анализируют МРТ с силой Лоренца и предсказывают, что пиковое смещение u нерва радиусом a в плече с радиусом b равно

, где B — магнитное поле, Дж — плотность тока, а G — модуль сдвига.Используя реалистичные параметры медиального нерва человека в поле 4 Тл, они вычисляют максимальное смещение 13 нм или меньше и находят распределение смещения, которое не локализуется вокруг нерва (). Они предполагают, что это смещение слишком мало и размыто, чтобы его можно было обнаружить методами МРТ. Фактически, биомагнитные поля, создаваемые токами действия, должны приводить к большему артефакту в МРТ, чем артефакт, вызванный эффектом Лоренца ³⁸ , и можно ли использовать такие биомагнитные поля с МРТ для изображения токов действия, остается открытым вопросом ³⁹ .Анализ эффекта Лоренца на ионы в растворе также противоречив ^{40 , 41} , и магнитогидродинамические эффекты могут быть важны в этом случае ⁴² .

Вверху: нерв радиуса a , лежащий в руке радиуса b . Магнитное поле имеет направление x . Ток внутри нерва течет в положительном направлении z (за пределы страницы), а ток в окружающей ткани течет в отрицательном направлении z .Внизу: смещение, вызванное силой Лоренца. (а) всю руку и (б) детальный вид смещения вокруг нерва. Для удобства просмотра длина стрелок смещения увеличена. От Рота и Бассера ³⁷ .

Заключение

Сила Лоренца — это новый инструмент для получения изображений тока и проводимости в ткани. В общем, эти силы и результирующие смещения невелики. На сегодняшний день наиболее многообещающие результаты получены при работе на высоких частотах, когда осциллирующая сила порождает ультразвуковые волны, которые можно обнаружить, даже если лежащее в основе смещение очень небольшое.Визуализация проводимости может выполняться двумя способами: с использованием осциллирующей силы Лоренца для создания ультразвуковых изображений () или с применением ультразвука и детектирования результирующего электрического сигнала (). Пока неясно, какой из этих методов будет наиболее полезен в биомедицинской визуализации. Силовые методы Лоренца для измерения тока имеют интересные аналогии с биомагнитными методами и имеют многие из тех же сильных и слабых сторон. Эти методы обычно требуют сильных магнитных полей, создание которых может быть трудным и дорогостоящим.Однако они используют преимущества и сочетают в себе многие сильные стороны как биоэлектрических, так и биомагнитных методов с хорошо зарекомендовавшими себя методами ультразвуковой визуализации. Магнитоакустические методы измерения тока будут конкурировать с такими общепринятыми методами, как электрокардиограмма, магнитокардиограмма, электроэнцефалограмма и магнитоэнцефалограмма. Методы измерения проводимости дадут такую ​​же информацию, как и изображения электрического импеданса.

Таким образом, все большее количество методов визуализации основано на силе Лоренца, и эти методы открывают большие перспективы для получения изображений тока и проводимости.

Благодарности

Я благодарю Штеффана Пувала и Кэтрин Рот за их комментарии к этой рукописи. Я также благодарю Брюса Тоу, Хан Вена, Амальрика Монталибета и Сюй Ли за разрешение воспроизвести их рисунки в этом обзоре. Работа поддержана грантом R01EB008421 Национального института здравоохранения.

Список литературы

1. Хобби Р.К., Рот Б.Дж. Физика среднего уровня для медицины и биологии. 4. Нью-Йорк: Спрингер; 2007. [Google Scholar] 2. Schenck JF. Безопасность сильных статических магнитных полей.J Mag Reson Imag. 2000; 12: 2–19. [PubMed] [Google Scholar] 3. Wikswo JP, Jr, Barach JP. Оценка постоянной напряженности магнитного поля, необходимой для воздействия на нервную проводимость. IEEE Trans Biomed Eng. 1980; 27: 722–723. [PubMed] [Google Scholar] 4. Секино М., Тацуока Х., Ямагути С., Эгути Ю., Уэно С. Влияние сильных статических магнитных полей на нервное возбуждение. IEEE Trans Mag. 2006. 42: 3584–3586. [Google Scholar] 5. Франкель РБ, Блейкмор РП, Вулф РС. Магнетит в пресноводных магнитотактических бактериях. Наука.1979; 203: 1355–1356. [PubMed] [Google Scholar] 6. Тоу BC, Ислам MR. Магнитоакустический метод неинвазивного измерения биоэлектрических токов. IEEE Trans Biomed Eng. 1988; 35: 892–894. [PubMed] [Google Scholar] 7. Ислам MR, Тауэ BC. Реконструкция изображения биоэлектрического тока по магнитно-акустическим измерениям. IEEE Trans Med Imag. 1988; 7: 386–391. [PubMed] [Google Scholar] 8. Towe BC. Исследование биомагнетометра силы Лоренца. IEEE Trans Biomed Eng. 1997; 44: 455–461. [PubMed] [Google Scholar] 9.Рот Б.Дж., Бассер П.Дж., Виксво Дж.П., мл. Теоретическая модель магнитоакустической визуализации биоэлектрических токов. IEEE Trans Biomed Eng. 1994; 41: 723–728. [PubMed] [Google Scholar] 11. Аммари Х., Капдебоск Й., Кан Х., Кожемяк А. Математические модели и методы реконструкции в магнитоакустической визуализации. Euro J Appl Math. 2009. 20: 303–317. [Google Scholar] 14. Вен Х. Возможности биомедицинских приложений визуализации эффекта Холла. Ультразвуковая визуализация. 2000. 22: 123–136. [PubMed] [Google Scholar] 15. Рот BJ, Wikswo JP., Jr Комментарии к «Визуализации эффекта Холла» IEEE Trans Biomed Eng. 1998. 45: 1294–1295. [PubMed] [Google Scholar] 16. Монталибет А., Жосине Дж., Матиас А. Сканирование градиентов электропроводности с помощью силы Лоренца, индуцированной ультразвуком. Ультразвуковая визуализация. 2001; 23: 117–132. [PubMed] [Google Scholar] 17. Montalibet A, Jossinet J, Matias A, Cathignol D. Электрический ток, генерируемый ультразвуковой силой Лоренца в биологических средах. Med Biol Eng Comput. 2001; 39: 15–20. [PubMed] [Google Scholar] 19. Хайдер С., Хрбек А., Сюй Ю.Магнитоакусто-электрическая томография: потенциальный метод для визуализации плотности тока и электрического сопротивления. Physiol Meas. 2008; 29: S41 – S50. [PubMed] [Google Scholar] 20. Олафссон Р., Витте Р.С., Хуанг С.В., О’Доннелл М. Ультразвуковая визуализация плотности источника тока. IEEE Trans Biomed Eng. 2008; 55: 1840–1848. [Бесплатная статья PMC] [PubMed] [Google Scholar] 21. Ценг Н, Рот Б.Дж. Потенциал, индуцированный в анизотропной ткани силой Лоренца, индуцированной ультразвуком. Med Biol Eng Comput. 2008. 46: 195–197. [PubMed] [Google Scholar] 22.Беверидж А.С., Ван С., Диболд Г.Дж. Визуализация на основе потенциала ультразвуковой вибрации. Appl Phys Lett. 2004. 85: 5466–5468. [Google Scholar] 24. Ли X, Xu Y, He B. Магнитоакустическая томография с магнитной индукцией для визуализации электрического импеданса биологической ткани. J Appl Phys. 2006; 99: 066112. [Бесплатная статья PMC] [PubMed] [Google Scholar] 25. Li X, Xu Y, He B. Визуализация электрического импеданса на основе акустических измерений с помощью магнитоакустической томографии с магнитной индукцией (MAT-MI) IEEE Trans Biomed Eng.2007. 54: 323–330. [PubMed] [Google Scholar] 26. Xia R, Li X, He B. Магнитоакустическая томографическая визуализация электрического импеданса с магнитной индукцией. Appl Phys Lett. 2007; 91: 083903. [Бесплатная статья PMC] [PubMed] [Google Scholar] 27. Ma Q, He B. Исследование генерации магнитоакустического сигнала с помощью магнитной индукции и его применение для восстановления электропроводности. Phys Med Biol. 2007. 52: 5085–5099. [PubMed] [Google Scholar] 29. Ли Х, Ли Х, Чжу С.Н., Хэ Б. Решение прямой задачи магнитоакустической томографии с магнитной индукцией с помощью метода конечных элементов.Phys Med Biol. 2009. 54: 2667–2682. [Бесплатная статья PMC] [PubMed] [Google Scholar] 30. Xia RM, Li X, He B. Реконструкция векторных акустических источников во временной томографии. IEEE Trans Med Imag. 2009. 28: 669–675. [Бесплатная статья PMC] [PubMed] [Google Scholar] 31. Ся Р.М., Ли Х, Хе Б. Сравнительное исследование трех различных алгоритмов восстановления изображений для MAT-MI. IEEE Trans Biomed Eng. 2010; 57: 708–713. [Бесплатная статья PMC] [PubMed] [Google Scholar] 32. Бринкер К., Рот Б.Дж. Влияние электрической анизотропии при магнитоакустической томографии с магнитной индукцией.IEEE Trans Biomed Eng. 2008; 55: 1637–1639. [PubMed] [Google Scholar] 33. Песня А. В., Такахаши А. М.. Визуализация эффекта Лоренца. Magn Res Imag. 2001; 19: 763–767. [PubMed] [Google Scholar] 34. Чыонг Т-К, Уилбур Дж. Л., Сонг А. В.. Синхронизированное обнаружение малых электрических токов с МРТ с использованием визуализации на основе эффекта Лоренца. J Magn Res. 2006. 179: 85–91. [Бесплатная статья PMC] [PubMed] [Google Scholar] 35. Чыонг Т-К, Сонг А.В. Обнаружение нейроэлектрической активности при колебаниях магнитного поля (NAMO) с помощью магнитно-резонансной томографии in vivo.PNAS. 2006; 103: 12598–12601. [Бесплатная статья PMC] [PubMed] [Google Scholar] 36. Basford AT, Basford JR, Kugel J, Ehman RL. Движение под действием силы Лоренца в проводящей среде. Магнитно-резонансная томография. 2005; 23: 647–651. [PubMed] [Google Scholar] 38. Мэй И, Рот Би Джей. Смещения, вызванные вихревыми токами, индуцированными во время магнитно-резонансной томографии. Журнал «Встреча умов» по исследованиям в бакалавриате.