Определение шага винтовой линии — Физика дома

Автор: admin. Рубрики: Задачи 30 (С5). Опубликовано: Апрель 20th, 2015

Задача на определение шага винтовой линии при движении частицы в магнитном поле может быть полезна всем, кто сдаёт физику.

Частица, несущая заряд электрона и имеющая импульс 10^-23 кг*м/с, влетает в однородное магнитное поле с индукцией 0,01 Тл под углом 60⁰ к линиям индукции. Определите шаг винтовой линии, вдоль которой будет двигаться частица.

Для начала, как обычно, нужно сделать рисунок и изобразить траекторию движения заряженной частицы.

На частицу в магнитном поле действует сила Лоренца, которая сообщает ей центростремительное ускорение. Но поскольку вектор скорости образует некоторый угол с направлением вектора магнитной индукции, частица будет перемещаться вдоль этой линии по спирали. Шаг этой спирали (винтовой линии) мы должны будем определить.

За радиус винтовой линии отвечает игрековая составляющая вектора скорости, а за перемещение вдоль вектора магнитной индукции — иксовая составляющая вектора скорости.  (В отсутствии электрического поля частица будет двигаться равномерно с постоянным шагом).

Шаг винтовой линии — это то расстояние, которое пролетает заряженная частица за время, равное периоду обращения. И одна из задач будет доказать, что период обращения частицы не зависит от скорости, а следовательно, и от угла ( формула периода обращения частицы в магнитном поле не является обязательной для запоминания).

Умножая проекцию скорости на  ось, совпадающую с направлением вектора магнитной индукции, на период  (время движения частицы по одному звену спирали), получаем итоговую формулу для шага винтовой линии. Остаётся подставить численные значения известных физических величин и определить числовое значение шага винтовой линии (спирали).

Вы можете оставить комментарий, или поставить трэкбек со своего сайта.

Написать комментарий

Винтовая линия — Википедия

Материал из Википедии — свободной энциклопедии

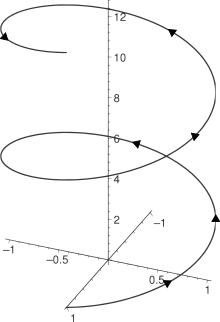Правая винтовая линия (cos t, sin t, t) с t = 0 до 4π Кристаллическая правовинтовая молекулярная структура , по работе сотрудников Lehn, из Helv. Chim. Acta., 2003, 86, 1598—1624 Естественное закручивание усиков винограда (левая спиральновинтовая)

Винтовая ли́ния — кривая в трёхмерном пространстве, расположенная на круглом цилиндре или круглом конусе, пересекающая образующие под одинаковым углом^[1].

Цилиндрическая винтовая линия задаётся в прямоугольных координатах параметрическими уравнениями вида:

t↦(a⋅cos⁡t,a⋅sin⁡t,b⋅t){\displaystyle t\mapsto (a\cdot \cos t,a\cdot \sin t,b\cdot t)},

или в иной записи:

x(t)=a⋅cos⁡t,{\displaystyle x(t)=a\cdot \cos t,}

y(t)=a⋅sin⁡t,{\displaystyle y(t)=a\cdot \sin t,}

z(t)=b⋅t{\displaystyle z(t)=b\cdot t},

где a,b{\displaystyle a,b} — вещественные константы, не равные нулю.

Проекция цилиндрической винтовой линии на плоскость x,y{\displaystyle x,y} представляет собой окружность.

Коническая винтовая линия (также спиральновинтовая линия^[2]), определяется параметрическими уравнениями вида:

t↦(a⋅t⋅cos⁡t,a⋅t⋅sin⁡t,b⋅t){\displaystyle t\mapsto (a\cdot t\cdot \cos t,a\cdot t\cdot \sin t,b\cdot t)},

или:

x(t)=a⋅t⋅cos⁡t{\displaystyle x(t)=a\cdot t\cdot \cos t}

y(t)=a⋅t⋅sin⁡t{\displaystyle y(t)=a\cdot t\cdot \sin t}

z(t)=b⋅t{\displaystyle z(t)=b\cdot t}.

Проекция спиральновинтовой линии на плоскость x,y{\displaystyle x,y} — спираль Архимеда.

Тело, имеющее форму винтовой линии в разговорной речи часто называют спиралью, что не совсем корректно, так как в математике спиралями называют некоторый класс плоских кривых.

Существуют зеркально-симметричные винтовые линии. «Правыми» винтовыми линиями принято называть линии, порождаемые по «правилу буравчика» или по «правилу правой руки». Это свойство винтовых линий называют хиральностью — «правая хиральность» и «левая хиральность». Пару зеркально-симметричных винтовых линий называют энантиоморфами. Если коэффициент b{\displaystyle b} в параметрическом задании цилиндрической винтовой линии в правой тройке координат положителен, то такую линию называют «правой», если отрицателен — то «левой».

Подавляющее число резьб, применяемых в машиностроении, у крепёжных метизов имеют «правую» резьбу или «правую» хиральность, то есть завинчивание производится по часовой стрелке. «Левые» резьбы применяются очень редко в специальных применениях, например, для предотвращения самоотвинчивания шкивов с валов механизмов.

Величину 2⋅π⋅b{\displaystyle 2\cdot \pi \cdot b} называют

шагом винтовой линии, геометрически это расстояние между соседними витками линии, отсчитанное вдоль образующей цилиндра.

Все винтовые линии являются линиями откоса, то есть, касательные к ним образуют постоянный угол с некоторым постоянным направлением. Как и у всякой линии откоса, у цилиндрической винтовой линии кривизна C{\displaystyle C} и кручение S{\displaystyle S} постоянны в любой точке и равны:

C=|a|a2+b2{\displaystyle C={\frac {|a|}{a^{2}+b^{2}}}},

S=ba2+b2{\displaystyle S={\frac {b}{a^{2}+b^{2}}}}.

Элемент длины dL{\displaystyle dL}:

dL=dt⋅a2+b2{\displaystyle dL=dt\cdot {\sqrt {a^{2}+b^{2}}}}.

Угол Φ{\displaystyle \Phi } между касательной к цилиндрической винтовой линии и касательной к окружности цилиндра в этой же точке называют геликальным углом, он равен:

Φ=arctan⁡(ba){\displaystyle \Phi =\arctan({\tfrac {b}{a}})}.

Форму винтовой линии или геликоида имеют, например, следующие молекулы:

Формы винтовых линий имеют также многие детали машин и механизмов — пружины, часть винтовых свёрл, соединительные винты, болты, шпильки, винты (шнеки) мясорубок, экструдеров, винт Архимеда, шнеки снегоуборщиков и другие (реализуют винтовую поверхность — геликоид).

Винтовая линия | Начертательная геометрия

Винтовая линия относится к пространственным кривым. Различают цилиндрические, конические, сферические и другие винтовые линии. Цилиндрическая винтовая линия описывается точкой, которая совершает равномерное движение вдоль образующей кругового цилиндра, а образующая вращается с постоянной угловой скоростью вокруг оси цилиндра. 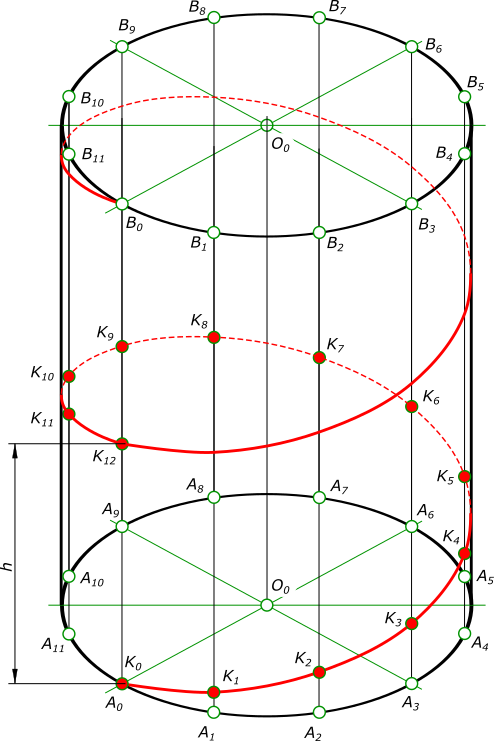Винтовая линия Образующая занимает 12 последовательных положений: A0B0. Дуги A0A1, A1A2 A2A3 и т. д. равны между собой и каждая равна pd/n, где d — диаметр цилиндра, p = 3,14 и n — число положений образующей цилиндра, принятое для построения. Пусть образующая занимает 12 последовательных положений: A0B0, A1B1, A2B2 и т. д. Начальному положению образующей AB соответствует A0B0, а точки K — K0. При перемещении образующей AB в положение A1B1 точка K займет положение K1, и поднимется по образующей на величину отрезка A1K1 = h/12. При последующем перемещении образующая займет положение A2B2, а точка K положение K2 и поднимется на высоту равную A2B2 = 2A1B1 = 2(h/12), и т. д. Когда образующая совершит полный оборот и снова займет начальное положение, точка K будет находится на ней на высоте A12B12 = 12(h/12) = h, величине шага винтовой линии. При этом точка описывает кривую K0K6K12, длина которой равна длине одного витка. На практике эти движения достигаются на токарном станке, где острие резца соответствует данной точке. 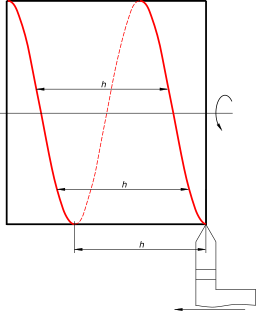Винтовая линия Резец оставит на цилиндрической поверхности след — винтовую линию. Винтовая линия может быть правой или левой. Правой винтовой линией называют линию, совершающую подъем вокруг своей оси против часовой стрелки, а левой — винтовую линию, совершающую подъем по часовой стрелке. Правая цилиндрическая винтовая линия 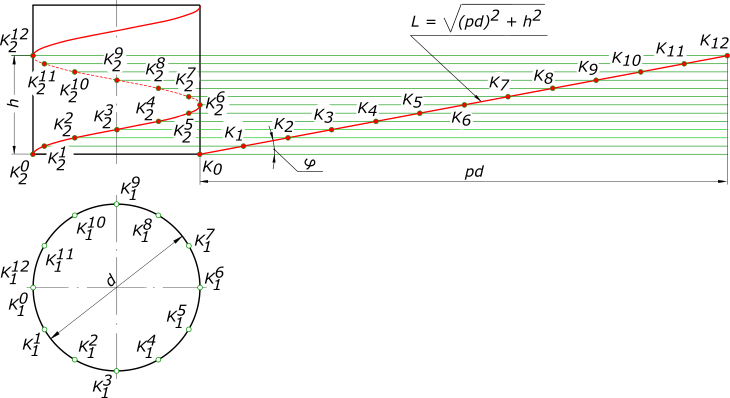Винтовая линия может быть построена, когда заданы ее элементы. Винтовая линия характеризуется следующими элементами: шаг, виток и угол подъема. Шагом винтовой линии называется расстояние между смежными витками, измеренное вдоль образующей кругового цилиндра. Витком называют винтовую линию, описанную точкой за один оборот образующей вокруг оси кругового цилиндра. Длина витка равна L. Углом подъема винтовой линии называют отношение tg(φ)= h/(pd), тогда φ = arctg(φ), где d — диаметр цилиндра, p=3,14. Винтовая линия может быть получена на конической поверхности 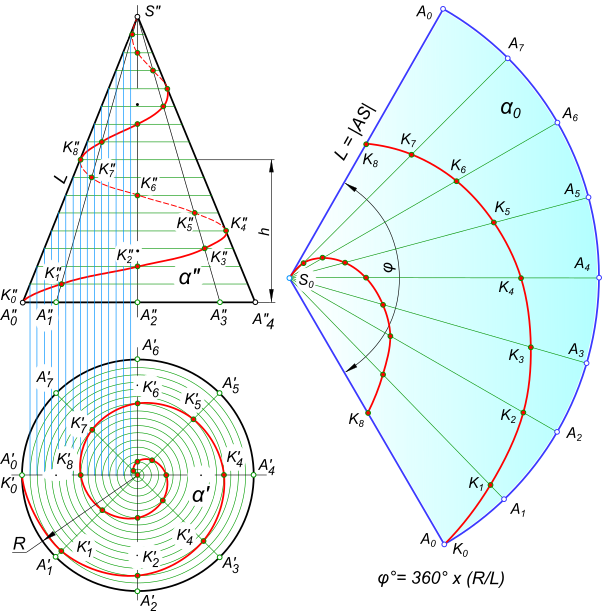Винтовая линия В этом случае, точка совершает равномерно-поступательное движение вдоль образующей прямого кругового конуса, а сама образующая SA вращается вокруг его оси с постоянной угловой скорости. Расстояние между точками смежных витков, измеренное параллельно оси конуса (например между точками A0K8), является шагом h конической винтовой линии. Проекция винтовой линии на фронтальной плоскости проекций представляет собой синусоиду с затухающим колебанием (затухающей волной), а на горизонтальной — спираль Архимеда. При построении развертки боковой поверхности конуса винтовая линия развернется в спираль, а конус — в сектор, угол при вершине которого равен φ= 360°×(h/L), а длина дуги радиуса R, соответствующая углу φ, равна 2πR. +

15.2. Винтовые линии

Пространственные кривые	423

Поэтому пространственные кривые линии иногда называют как линии «двоя-

кой кривизны».

Радиус R соприкасающейся окружности (см. рис. 15.5, а) определяет радиус кривизны пространственной кривой линии, а обратная ей величина — кривизну этой линии. Соприкасающаяся окружность всегда лежит в соприкасающейся плоскости, а ее центр — на главной нормали, проведенной из точки касания.

На рис. 15.6 приведена пространственная кривая b, к которой через точки K1 и K2 проведены две соприкасающиеся плоскости — соответственно плоскости 1 и 2. Средним кручением дуги K1K2 является отношение величины линейного угла между соприкасающимися плоскостями, проведенными

вточках K1 и K2, к длине этой дуги. Линейный угол между соприкасающимися плоскостями может быть измерен углом между бинормалями к кривой b

вточках K1 и K2.

Предельное положение среднего кручения при стремлении точки K2 к точке K1 называется кручением кривой b в точке K1. Чем меньше величина кручения, тем она ближе располагается к соприкасающейся плоскости. Для плоской кривой линии кручение во всех ее точках равно нулю, т. к. кривая целиком лежит в одной плоскости — общей соприкасающейся плоскости всех ее точек.

Рис. 15.6. Пространственная кривая b и две соприкасающиеся плоскости 1 и 2

15.2.1. Свойства винтовых линий

Винтовой линией называется пространственная кривая линия, являющаяся траекторией точки, которая равномерно вращается вокруг неподвижной прямой (оси винтовой линии) и одновременно перемещается поступательно вдоль этой оси.

Винтовая линия может быть правой (с правым ходом) или левой (с левым ходом). Винтовая линия называется правой, если при подъеме она закручивается в направлении против движения часовой стрелки. В обратном случае винтовая линия является левой.

Величина перемещения вдоль оси винтовой линии, соответствующая одному полному обороту вокруг оси, называется шагом, а длина дуги, соответствующая полному обороту точки вокруг оси, — витком. Если величина перемещения точки вдоль оси прямо пропорциональна угловым перемещениям, то винтовая линия имеет постоянный шаг. Если перемещение образующей точки вдоль оси происходит по своему закону, то получается винтовая линия с переменным шагом.

Угол наклона касательной, проведенной в некоторой точке винтовой линии к плоскости, перпендикулярной оси, называется углом подъема винтовой линии.

В зависимости от вида поверхности, по которой происходит перемещение образующей точки, винтовые линии подразделяются на цилиндрические, конические и глобоидные винтовые линии.

15.2.2. Цилиндрическая винтовая линия

Цилиндрическая винтовая линия или гелиса образуется при движении точки по поверхности кругового цилиндра (рис. 15.7). Диаметр цилиндра D и размер шага h являются параметрами цилиндрической винтовой линии.

При равномерном перемещении точки по поверхности цилиндра она совершает сложный вид движения, состоящего из вращательного движения по окружности и поступательного перемещения, перпендикулярного этой окружности. При повороте на некоторый угол точка А переместится в точку А1, а величина ее поступательного перемещения вдоль оси будет равна

h

h 360,

где h — шаг цилиндрической винтовой линии.

При этом ее горизонтальная проекция будет перемещаться по окружности, а фронтальная — по синусоиде.

Построение фронтальной проекции цилиндрической винтовой линии проводится аналогично построению синусоиды (рис. 15.8). Окружность основания цилиндра на горизонтальной плоскости проекций делится на n равных частей (например, на двенадцать). Отрезок оси цилиндра, равный шагу h винтовой линии, делится на то же количество n равных частей. Фронтальные проекции точек, лежащих на винтовой линии, находятся в пересечении горизонтальных и вертикальных прямых, проведенных через соответствующие точки деления.

Пространственные кривые	425

Рис. 15.7. Цилиндрическая винтовая линия	Рис. 15.8. Построение цилиндрической
	винтовой линии

На горизонтальной проекции точка при ее подъеме вращается против часовой стрелки, следовательно, построенная цилиндрическая винтовая линия является правой.

Основные свойства цилиндрической винтовой линии:

на плоскость проекций, перпендикулярную оси, цилиндрическая винтовая линия проецируется в окружность; на плоскость проекций, параллельную оси, — в синусоиду;

 угол подъема цилиндрической винтовой линии с постоянным шагом h не изменяется и может быть определен по формуле

h arctg D ;

винтовая линия пересекает все образующие цилиндра под постоянным углом, равным 90 – ;

кривизна и кручение цилиндрической винтовой линии во всех ее точках постоянны;

цилиндрическая винтовая линия обладает симметрией переноса в направлении по ее оси на расстояние, равное шагу; при этом две симметричные дуги полностью совпадают при наложении друг на друга.

15.2.3. Коническая винтовая линия

Коническая винтовая линия образуется при движении точки по поверхности кругового конуса. При этом точка совершает равномерное поступательное движение по образующей конуса, которая в свою очередь равномерно вращается вокруг оси конуса (рис. 15.9). Размеры конуса (например, диаметр его основания D и высота H), а также размер шага h являются параметрами конической винтовой линии. Иногда шагом конической винтовой линии называют расстояние h2 между точками смежных витков, измеренное по образующей.

Рис. 15.9. Коническая винтовая линия

Для построения проекций конической винтовой линии окружность основания конуса делится на n равных частей (например, на двенадцать), и через точки деления проводятся образующие конуса (рис. 15.10). На оси винтовой линии откладывается отрезок, равный ее шагу h, который делится на то же количе-

Пространственные кривые	427

ство n равных частей. В пересечении горизонтальных прямых, проведенных из точек деления шага, с соответствующими образующими конуса находятся фронтальные проекции точек, принадлежащих искомой винтовой линии. По фронтальным проекциям этих точек строятся их горизонтальные проекции.

Рис. 15.10. Построение конической винтовой линии

На горизонтальной проекции точка при ее подъеме вращается по часовой стрелке, следовательно, построенная коническая винтовая линия является левой.

Основные свойства конической винтовой линии:

на плоскость проекций, перпендикулярную оси, коническая винтовая линия проецируется в архимедову спираль; на плоскость проекций, параллельную оси, — в синусоиду с затухающей амплитудой;

угол подъема конической винтовой линии, имеющей постоянный шаг, не изменяется;

коническая винтовая линия пересекает все образующие под одинаковым углом.

Слободянюк А.И. Физика 10/14.3 — PhysBook

Содержание книги

Предыдующая страница

§14. Движение заряженных частиц в электрическом и магнитном полях

14.3 Движение по винтовой линии в однородном магнитном поле.

Рассмотрим теперь произвольный случай движения заряженной частицы в однородном магнитном поле.

Введем систему декартовых координат, так, чтобы вектор индукции однородного магнитного поля \(~\vec B\) был направлен вдоль оси Oz (рис. 97). Пусть вектор скорости \(~\vec \upsilon_0\) частицы массы m, имеющей электрический заряд q, направлен под произвольным углом α к вектору индукции поля. Разложим этот вектор на две составляющих\[~\vec \upsilon_1\] — параллельную вектору индукции и \(~\vec \upsilon_2\) — перпендикулярную ему. Действующая на частицу сила Лоренца \(~\vec F_L\) перпендикулярна векторам скорости и индукции, то есть лежит в плоскости xOy. Модуль этой силы равен

\(~F_L = q \upsilon_0 B \sin \alpha = q \upsilon_2 B\) . (1)

Если спроецировать уравнение второго закона Ньютона для частицы

\(~m \vec a = q \vec \upsilon \times \vec B\) , (2)

на плоскость xOy, то получим уравнение, в которое только компонента скорости, перпендикулярная полю. Это уравнение описывает движение частицы, движущейся перпендикулярно вектору индукции, которое было подробно рассмотрено ранее. Оно представляет собой равномерное движение по окружности радиуса

\(~R = \frac{m \upsilon_2}{q B} = \frac{m \upsilon_0 \sin \alpha}{q B}\) , (3)

с периодом

\(~T = \frac{2 \pi R}{\upsilon_2} = 2 \pi\frac{m}{q B}\) , (4)

и угловой скоростью

\(~\omega = \frac{2 \pi}{T} = \frac{q}{m} B\) , (5)

не зависящими, ни от модуля скорости частицы, ни от ее направления.

Проекция магнитной силы на ось Oz равна нулю, поэтому проекция скорости на эту остается постоянной. Следовательно, эта координата изменяется по линейному закону

\(~z = z_0 + \upsilon_1 t = z_0 + \upsilon_0 t \cos \alpha\) . (6)

Таким образом, движение частицы можно представить в виде суперпозиции равномерного движения вдоль оси Oz и равномерного движения по окружности в перпендикулярной плоскости. Траекторией этого движения является винтовая линия, радиус которой определяется формулой (3), а шаг рассчитывается по формуле

\(~h = \upsilon_1 t = 2 \pi \frac{m \upsilon_0}{q B} \cos \alpha\) . (7)

Таким образом, заряженные частицы движутся по спиралям (точнее винтовым линиям), навивающимся на силовые линии магнитного поля. Такой же характер движения сохраняется и в неоднородном магнитном поле – частицы движутся по спиралям, навивающимся на силовые линии поля, при этом радиус и шаг спирали плавно изменяются с изменением индукции поля. Направление смещения (дрейфа) частиц в магнитном поле определяется направлением начальной скорости частиц и не зависит ни от знака заряда частицы, ни от направления вектора индукции поля, последние определяют только направление вращения вокруг силовой линии. Такое движение заряженных частиц позволяет конструировать различные «магнитные ловушки» для накопления заряженных частиц, управлять движением сильно ионизованного газа (плазмы). Аналогичный характер имеет движение заряженных частиц и в магнитном поле Земли.

Следующая страница

Цилиндрические и канонические винтовые линии

Реферат

На тему: Цилиндрические и канонические винтовые линии

Образование винтовой линии. Рассмотрим рисунок 113а на нем точка М двигается равномерно по некоторой окружности, которая представляет собой сечение круглого цилиндра плоскостью Р. Здесь эта плоскость перпендикулярна его оси.

Допустим, что и сама окружность движется равномерно вверх или вниз по поверхности цилиндра. При этом плоскость Р, которая содержит окружность, будет оставаться всё время параллельной самой себе. Пять различных положений плоскости, которая содержит движущуюся точку, показаны на рисунке 113 б.

Вследствие этих двух равномерных движений данная точка М пройдет некоторую пространственную кривую М 1М 2М 3М 4М 5. На рисунке 113в показана эта линия, которая располагается на поверхности цилиндра и носит название цилиндрической винтовой линии. Она не может быть совмещена с плоскостью. На рисунке 113 г показано наглядное представление о винтовой линии, которое дает пружина.

Особое внимание следует уделить рассмотрению способности линии перемещаться по самой себе. Прямая линия и окружность обладают способностью перемещаться по самим себе, вследствие чего цилиндрическая винтовая линия также может перемещаться по самой себе. Например, завинчивая металлический винт в специально приготовленное для него отверстие, мы наблюдаем скольжение одной винтовой поверхности по другой.

Шаг винтовой линии. Точка, сделав полный оборот вокруг цилиндра, будет подниматься вверх или опускаться вниз на некоторое расстояние, которое будет одним и тем же для каждого полного оборота точки (рис. 114). Шагом винтовой линии называется подъем точки за один оборот. Витком называется часть винтовой линии, которая описывается точкой за один оборот.

Правая и левая винтовые линии. На рисунке 114 будем рассматривать цилиндр со стороны основания в то время, когда точка, перемещаясь по винтовой линии, будет удаляться от наблюдателя. Вероятны два случая: движение по часовой стрелке или против неё. Если движение проходит по часовой стрелке, то будет иметь место правая винтовая линия (рис. 114а), а если против часовой стрелки – левая (рис. 114б). На рисунке 114(а‑б) в первом случае видимая часть линии будет подниматься слева направо, а во втором – справа налево.

Проекции винтовой линии. Одна проекция прямого кругового цилиндра, на котором расположена винтовая линия, является окружностью, а другая – прямоугольником (рис. 114). Нужно построить фронтальную проекцию правой винтовой линии.

Допустим, движение точки начинается на основании цилиндра в точке 1 (рис. 114). Будем делить шаг винтовой линии и окружность основания на одинаковое число равных частей. На рисунке 114 этих частей 12. За полный оборот точка будет подниматься на величину шага. Следовательно, за 1/12 часть оборота она поднимется на 1/12 часть шага (точка 2).

Затем следует провести через точки деления шага 1, 2,…, 12 горизонтальные прямые, а через точки деления окружности 1, 2,…, 12 – вертикальные. Точки фронтальной проекции винтовой линии 1, 2,…, 12 будут иметь место в пересечении горизонтальных и вертикальных прямых, которые проходят через деления шага и окружности и имеют одинаковые номера. Эти точки 1, 2,…, 12 следует соединить плавной линией, которая будет представлять собой фронтальную проекцию винтовой линии. Этой линией будет синусоида.

При сравнении фронтальных проекций правой и левой винтовых линий убеждаемся в том, что форма кривой одна и та же, лишь видимая часть правой винтовой линии стала невидимой у левой, и наоборот. Кроме того, изменился порядок нумерации точек деления окружности на горизонтальной проекции. Для правой винтовой линии номера точек будут возрастать по часовой стрелке, а для левой будут убывать против часовой стрелки.

Развертка поверхности цилиндра с нанесённой на ней винтовой линией. Если развернуть на плоскость боковую поверхность цилиндра с нанесенной на ней винтовой линией, то винтовая линия предстанет в виде прямой линии (рис. 115), поскольку величина подъема точки пропорциональна ее перемещению вдоль окружности.

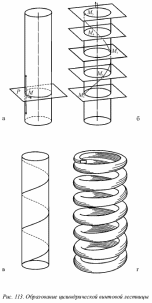
В соответствии с этим несложно изготовить модель винтовой линии, нужно только взять прямоугольник с проведенной в нем диагональю и свернуть его в виде цилиндра. При этом диагональ прямоугольника будет образовывать один виток винтовой линии.

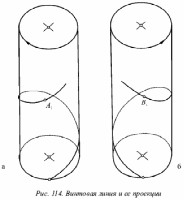
Цилиндрическая винтовая линия

К боковой поверхности прямого кругового цилиндра (стержня) подведен конец резца, принимаем его за точку А (фиг.363,а).

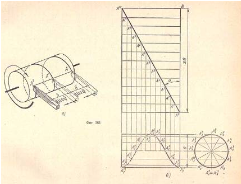
Придадим одновременно резцу равномерно поступательное движение, параллельное оси цилиндра, а цилиндру – равномерно вращательное, вокруг его оси, в результате конец резца, т. е. точки А, оставит на поверхности цилиндра пространственную кривую линию (риску), называемую цилиндрической винтовой линией.

После одного оборота цилиндра точка А – конец резца – переместится в точку А 1 и образует часть винтовой линии, называемую витком. Расстояние АА 1 = А 1А 2, измеряемое по образующей цилиндра, равняется шагу винтовой линии. Цилиндрическая винтовая линия, являясь пространственной кривой, может быть изображена на плоскости только своими проекциями (фиг.363,б).

Так как фронтальной проекцией цилиндрической винтовой линии является синусоида, то построение фронтальной проекции винтовой линии можно выполнить, как построение синусоиды, предварительно разделив окружность – профильную проекцию основания цилиндра – и отрезок A122A02, равный шагу, отложенный на фронтальной проекции оси цилиндра, на одинаковое число равных частей, например на 12 (построение синусоиды см. на фиг.169). винтовой плоскость синусоида

Профильной проекцией цилиндрической винтовой линии является окружность, сливающаяся с профильной проекцией кругового цилиндра, так как все образующие цилиндра перпендикулярны плоскости П 3.

Для построения проекций винтовой линии достаточно иметь размер диаметра цилиндра и величину шага.

Развертка винтовой линии осуществляется вместе с разверткой боковой поверхности цилиндра, на которой она нанесена и выявится прямой линией.

Развернем боковую поверхность цилиндра в плоскость, получим прямоугольник. Сторону, равную ПD, делим на 12 равных частей и через точки деления проводим образующие, а затем с фронтальной проекции переносим точки A02, A12,A22…,A122 на соответствующие образующие. Проведенная через полученные точки прямая А 0 А 12 будет разверткой одного витка винтовой линии.

Заметим, что прямая А 0А 12, являющаяся гипотенузой прямоугольного треугольника, наклонена под одним углом ко всем образующим цилиндра. Угол α называется углом подъема винтовой линии.

Построенная винтовая линия на (фиг.364), а является правой, так как на фронтальной проекции точка А, образующая винтовую линию, перемещается снизу слева вверх направо. В противном случае винтовая линия будет левой (фиг.364,б).

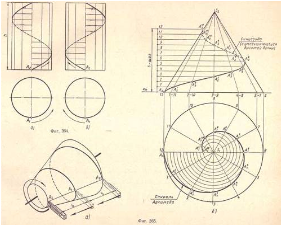
Коническая винтовая линия

К боковой поверхности прямого кругового конуса подведен конец резца, примем его за точку А 0 (фиг.365,a). Придадим одновременно резцу равномерно – поступательное движение, а конусу равномерно – вращательное вокруг его оси; в результате конец резца, т.е. точка А 0, оставит на поверхности конуса пространственную кривую линию – риску называемую конической винтовой линией. Аналогично цилиндрической коническая винтовая линия может быть как правого, так и левого направления.

На (фиг.365,б) показано построение проекций конической винтовой линии: окружность – горизонтальную проекцию основания конуса – и шаг h делим на одинаковое число равных частей, например на 12. Наносим на проекции конуса 12 образующих и, пользуясь делениями шага, находим на фронтальных проекциях соответствующих образующих точки A2, А 12, А 22, A122; соединив найденные точки плавной кривой, получим фронтальную проекцию конической винтовой линии – «затухающую» кривую с уменьшающейся высотой волны.

Горизонтальной проекцией является спираль Архимеда, ее построение видно из чертежа.

Винтовая линия — Математические этюды

Лёг­кость, с ко­то­рой гай­ка на­кру­чи­ва­ет­ся на болт, под­ска­зы­ва­ет, что резь­ба оди­на­ко­ва по всей длине бол­та, а ма­те­ма­ти­че­ская суть резь­бо­вых со­еди­не­ний — ис­поль­зо­ва­ние кри­вой, ко­то­рая мо­жет сколь­зить са­ма по се­бе. Эта за­ме­ча­тель­ная кри­вая на­зы­ва­ет­ся вин­то­вой ли­ни­ей.

Вин­то­вую ли­нию мож­но по­лу­чить, на­мо­тав на ци­линдр пря­мо­уголь­ный про­зрач­ный лист с от­ме­чен­ной диа­го­на­лью. В за­ви­си­мо­сти от дли­ны ли­ста и, со­от­вет­ствен­но, уг­ла на­кло­на на­ри­со­ван­ной ли­нии, бу­дет раз­ли­чать­ся шаг вин­то­вой ли­нии и ко­ли­че­ство вит­ков.

Фор­маль­но вин­то­вой ли­ни­ей (ци­лин­дри­че­ской) на­зы­ва­ет­ся ли­ния, опи­сы­ва­е­мая точ­кой, ко­то­рая вра­ща­ет­ся с по­сто­ян­ной уг­ло­вой ско­ро­стью во­круг непо­движ­ной оси и од­новре­мен­но пе­ре­ме­ща­ет­ся вдоль этой оси с по­сто­ян­ной ско­ро­стью.

На­гляд­ное пред­став­ле­ние и опре­де­ле­ние со­еди­ня­ют­ся в па­ра­мет­ри­че­ском за­да­нии вин­то­вой ли­нии в пря­мо­уголь­ной де­кар­то­вой си­сте­ме ко­ор­ди­нат: $$ x=a \cos t,\quad y=a \sin t,\quad z=ht. $$ Пер­вые два урав­не­ния по­ка­зы­ва­ют, что про­ек­ция точ­ки бе­жит по ос­но­ва­нию пря­мо­го кру­го­во­го ци­лин­дра ра­ди­у­са $a$. Тре­тье урав­не­ние за­да­ёт дви­же­ние вдоль оси ци­лин­дра с по­сто­ян­ной ско­ро­стью.

У «хо­ро­ших» кри­вых в трёх­мер­ном про­стран­стве есть две ба­зо­вые ха­рак­те­ри­сти­ки — кри­виз­на и кру­че­ние.

Кри­виз­на — ха­рак­те­ри­зу­ет ско­рость ис­крив­ле­ния ли­нии в плос­ко­сти и опре­де­ля­ет­ся ра­ди­у­сом окруж­но­сти, ду­га ко­то­рой наи­луч­шим об­ра­зом при­бли­жа­ет неболь­шой от­ре­зок кри­вой, со­дер­жа­щий дан­ную точ­ку). Кру­че­ние — ско­рость, с ко­то­рой кри­вая стре­мит­ся не быть плос­кой, на­сколь­ко кри­вая хо­чет по­ки­нуть плос­кость.

За­ме­ча­тель­но, что для до­ста­точ­но глад­ких кри­вых кри­виз­на и кру­че­ние пол­но­стью опре­де­ля­ют фор­му ли­нии.

У вин­то­вой ли­нии кри­виз­на и кру­че­ние по­сто­ян­ны, а из при­ве­дён­но­го утвер­жде­ния сле­ду­ет, что по­доб­ным свой­ством об­ла­да­ют толь­ко та­кие ли­нии!

По­сто­ян­ство кри­виз­ны и кру­че­ния во всех точ­ках озна­ча­ет, что устрой­ство вин­то­вой ли­нии всю­ду од­но и то же. Как след­ствие, по­лу­ча­ем, что от­ре­зок вин­то­вой ли­нии мо­жет сколь­зить вдоль неё точ­но так же, как от­ре­зок — по пря­мой, ду­га окруж­но­сти — по сво­ей окруж­но­сти. (Пря­мую и окруж­ность мож­но рас­смат­ри­вать как вы­рож­ден­ные, пре­дель­ные слу­чаи вин­то­вой ли­нии.)

Резь­бо­вые со­еди­не­ния, в част­но­сти резь­ба бол­та или вин­та ос­но­ва­ны на вин­то­вой ли­нии. При за­кру­чи­ва­нии резь­ба сколь­зит как буд­то по лыжне.

Вин­то­вая ли­ния — един­ствен­ная кри­вая, ко­то­рая мо­жет сколь­зить са­ма по се­бе. И при ре­ше­нии ин­же­нер­ных за­дач, в ко­то­рых на­ли­чие та­ко­го свой­ства же­ла­тель­но или да­же необ­хо­ди­мо, без вин­то­вых ли­ний не обой­тись.

Вин­то­вой ли­ни­ей яв­ля­ет­ся и гра­ни­ца вин­то­вых лест­ниц. Под­ни­ма­ясь по ним, вы по са­мо­му опре­де­ле­нию под­ни­ма­е­тесь вверх с по­сто­ян­ной ско­ро­стью. Фор­му вин­то­вой ли­нии име­ют и што­пор, и ры­бац­кий бур, сколь­зя­щие в ма­те­ри­а­ле по уже прой­ден­но­му пу­ти.