Напишите формулу закона Кулона.
Стр 1 из 4Следующая ⇒
F1= 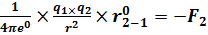
Какое явление определяется с помощью закона Кулона?
Ответ: силу взаимодействия между неподвижными электрическими зарядами.
Каковы формы проявления электромагнитного поля?
Ответ: действие на магнитную стрелку (её отклонение)
При каких условиях электрическое поле называют электростатическим?
Ответ: при условии, что поле создается неподвижными зарядами.
Что произойдет с силой взаимодействия между двумя зарядами если их из воздуха перенести в воду?
Ответ: уменьшиться в E раз.
1.1.6. Величина одного заряда 2.10-5 Кл, другого -4.10-4 Кл. Определить силу взаимодействия между ними, если они помещены в керосин (ε = 2) и находится на расстоянии 10 см друг от друга.
| Дано: | Решение: |
| q1=2×10-5Кл q2=-4×10-4Кл r=10см=0.1м ɛ=2 ф/м | F1=  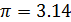 F1= F1=  × × 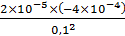 |
| Найти: | |
| F — ? | |
| Ответ: | -3,2×10-7H |
1.1.7. Определите силу взаимодействия между электрическими зарядами q1= 5.10-4 Кл и q2 = 2.10-5 Кл, находящимися в дистиллированной воде (ε =81) на расстоянии 5 см друг от друга.
Выберите правильный ответ:
1.1.8. Два заряда, находящихся на расстоянии 10 см друг от друга, помещены в керосин (ε = 2). Как изменится сила взаимодействия этих зарядов в вакууме? Если взаимное расположение этих зарядов сохраняется.
a) увеличится в два раза;
b) не изменится;
c) уменьшится в два раза.
1.1.9. Расстояние между электрическими зарядами возросло в три раза. Как должны изменится величины зарядов q1и q2, чтобы сила взаимодействия между ними возросла в девять раз?
a) увеличиться в три раза;
b) уменьшиться в три раза;
c) увеличиться в девять раз.
Электрическое поле каких зарядов изображено на рисунке?
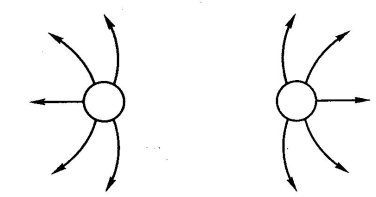
Ответ: одноименные заряды .
Потенциал и напряженность электрического поля
1.2.1. Сформулируйте определения:
Потенциал электрического поля –это отношение потенциальной энергии зарядов поля к этому заряду.
Напряжение— это физическая величина, характеризующая работу электрическое поле по перемещению электрического заряда (разность потенциалов).
Напряженность электрического поля -это физическая величина определяемая силой с которой поле действует на единичный точечный заряд помещенный в эту точку.
В каких единицах измеряется электрический потенциал?
Ответ: Вольт (В)
1.2.3. Как определить работу по переносу заряда из одной точки электрического поля в другую?Ответ: A=q(φ1-φ2)
1.2.4. Определите потенциал точки электрического поля, в которую из бесконечности внесен заряд q= 3.10-6 Кл, если при этом силами поля совершена работа А = 6.10-6 Дж.
| Дано: | Решение: |
| q= 3.10-6 Кл
1.2.5. |  φ=
φ=  =2B =2B
|
| Найти: | |
| φ-? | |
| Ответ: | 2 B |
1.2.5. Потенциал электрического поля в точке А составляет 60 В, а в точке Б – 7 В. Заряд q = 6 Кл перенесен из точки А в точку Б. Какая при этом совершена работа.
| Дано: | Решение: |
| q = 6 Кл
φ | А=q(φa-φб) A =6×(60-7)=318(Дж) |
| Найти: | |
| A — ? | |
| Ответ: | 318(Дж) |
1.2.6. Вычислите напряженность двух различных электрических полей, действующих на заряд q = 0,004 Кл с силами F1 = 0,018 Н и F2 = 0,012 Н.
| Дано: | Решение: |
| q = 0,004 Кл F1 = 0,018 Н 1.2.7. F2 = 0,012 Н | E=   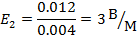 |
| Найти: E1-? E2-? | |
| Ответ: | 4,5B/м; 3 B/м |
Определите напряженность электрического поля плоского конденсатора, если расстояние между пластинами 2 мм, а напряжение 220 В.
| Дано: | Решение: |
| d=2мм=2×10-3м U=220 В | E=   =1,1×105 B/м =1,1×105 B/м
|
| Найти: | |
| E — ? | |
| Ответ: | 1,1×105 B/м |
Электрическая емкость
От чего зависит емкость конденсатора?
Ответ: от геометрических размеров и диэлектрика
Как влияет диэлектрик на емкость конденсаторов?
Ответ: С увеличением диэлектрической проницаемости диэлектрика емкость увеличивается.
В каком случае необходимо применять последовательное соединение конденсаторов?
Ответ: если нужно уменьшить емкость конденсатор
1.3.4. Заполните таблицу.
| 0,0015 Ф | 33 мкФ | 0,047 мкФ | 100 пФ | 6,8 нФ | 820 пФ |
| 1500 мкФ | 3,3×10-5Ф | 47000 пФ | 10-4 мкФ | 6800 пФ | 0,82 нФ |
Определите эквивалентную емкость соединения конденсаторов, схема которых приведена на рисунке, если все конденсаторы имеют емкость по 5 мкФ.

| Дано: | Решение: |
| С1=С2=С3=С4= =5 мкФ | С1,2= 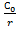 C1,2=
C1,2=  = 2,5 мкФ
С3,4 = = 2,5 мкФ
С3,4 =  = 2,5 мкФ
Сэкв = С1,2+С3,4;
С = 2,5 мкФ
Сэкв = С1,2+С3,4;
С |
| Найти: | |
| Сэк — ? | |
| Ответ: | 5 мкФ |
1.3.6. Конденсатор имеет две пластины. Площадь каждой пластины составляет 15 см2. Между пластинами помещен диэлектрик – слюда толщиной 0,02 см. Определите емкость этого конденсатора.
| Дано: | Решение: |
| E=7 S=15см2 d=0,02см | С =  С =
С =   =9 пФ =9 пФ
|
| Найти: | |
| С — ? | |
| Ответ: | 9 пФ |
Определите эквивалентную емкость конденсаторов, схема включения которых представлена на рисунке, если все конденсаторы имеют емкость по 10 мкФ.

Рекомендуемые страницы:
11. В каких единицах измеряется электрический потенциал?
Ответ:
12. Что называется электрической силовой линией?
Ответ:
13. Как определить работу по переносу заряда из одной точки электрического поля в дрyгyю?
Ответ:
14. Определите потенциал точки электрического поля, в которую из бесконечности внесен заряд q = 3· 10-6 К, если при этом силами поля совершена работа А = 6 . 10-6 Дж.
Дано:
Найти:
Решение:
Ответ:
15. Потенциал электрического поля в точке а составляет 60 в, а в точке б — 76 в. Заряд в 6 к перенесен из точки а в точку б. Какая при этом совершена работа?
Дано:
Найти:
Решение:
Ответ:
16. Вычислите напряженность двух различных электрически полей, действующих на заряд q = 0,004 К с силой F 1 = 0,08 Н и F2 = 0,012 Н.
Д ано:
ано:
Н айти:
айти:
Р ешение:
ешение:
О твет:
твет:
17. Заряд величиной в 0,3 К помещен в однородное электрическое поле, которое действует на него с силой в 4,5 Н. Каков напряженность однородного электрического поля?
Д ано:
ано:
Н айти:
айти:
Р ешение:
ешение:
О твет:
твет:
18. Электрический заряд величиной 2· 10-6 находится в вакууме. Какова напряженность электрического поля на расстоянии 20 см от заряда?
Д ано:
ано:
Н айти:
айти:
Р ешение:
ешение:
О твет:
твет:
19. На шелковых нитках висят два медных шара. Потенциал первого шара 1 = — 18 В, потенциал второго шара 2 = + 32 В Определите напряжение U21 между вторым и первым шарами.
Д ано:
ано:
Н айти:
айти:
Р ешение:
ешение:
О твет:
твет:
1.3. ЭЛЕКТРИЧЕСКАЯ ЕМКОСТЬ. КОНДЕНСАТОРЫ
Ответьте па вопросы:
20. От чего зависит емкость конденсатора?
Ответ:
21. Как влияет диэлектрик на емкость конденсаторов?
Ответ:
22. В каком случае необходимо применять последовательное соединение конденсаторов?
Ответ:
23. Заполните таблицу:
0,0015 Ф | 33 мкФ | 0,047 мкФ | 100 пФ | 6,8нФ | 820 пФ |
?мкФ | ?Ф | ?пФ | ?мкФ | ?пФ | ?нФ |
24. Определите общую емкость соединения конденсаторов, схема которых приведена на рис. 3, если все конденсаторы имеют емкость по 5 мкФ.
Дано:
Найти:
Решение:
Ответ:



 С1
С2
С1
С2















 С3
С4
С3
С4
Рис. 3
Разность потенциалов- работа по переносу заряда из одной точки, в конечную точку.
Циркуляция вектора напряженности электростатического поля по произвольному замкнутому контуру равна нулю
Потенциальная энергия уединенного точечного заряда Q1 равна нулю, поскольку в отсутствие других зарядов на него не действует никакая сила.
Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения, называется эквипотенциальной поверхностью
Разность потенциалов- работа по переносу заряда из одной точки, в конечную точку.
Аддитивность: величина, относящаяся к системе в целом, равна сумме величин, относящихся к её составным частям
6. (6)Электрический диполь. Электрическое поле диполя в дальней зоне (в полярных и декартовых координатах)
Совокупность двух равных по величине разноименных точечных зарядов q, расположенных на некотором расстоянии друг от друга, называется электрическим диполем.
7. (7)Проводники в электростатическом поле. Поведение вектора электрического поля на границе раздела «вакуум – проводник». Связь напряженности электрического поля на поверхности проводника с плотностью индуцированных электрических зарядов. Электростатическая защита.
В отсутствие внешнего поля в любом элементе объема проводника отрицательный свободный заряд компенсируется положительным зарядом ионной решетки. В проводнике, внесенном в электрическое поле, происходит перераспределение свободных зарядов, в результате чего на поверхности проводника возникают нескомпенсированные положительные и отрицательные заряды Этот процесс называют электростатической индукцией, а появившиеся на поверхности проводника заряды – индукционными зарядами
Индукционные заряды создают свое собственное поле которое компенсирует внешнее поле во всем объеме проводника:
Если удалить некоторый объем, выделенный внутри проводника, и образовать пустую полость, то электрическое поле внутри полости будет равно нулю. На этом основана электростатическая защита . Замкнутая металлическая оболочка является «экраном» от электростатический полей.
Поверхностная плотность:
8. (8)Основная задача электростатики. Уравнения Пуассона и Лапласа.
Общей задачей расчета электростатического поля является определение напряженности поля во всех его точках по заданным зарядам
Сис-ма описывает все задачи электростатики.
, тогда
| -ур-ие Пуассона. |
Уравнение Лапласса— частный случай ур-ия Пуассона:
В области простр-ва, где нет заряда: =0
9. (9)Электрическая емкость. Электрическая емкость уединенного проводника. Электрические конденсаторы. Емкость плоского конденсатора.
Электроемкость – способность проводника накапливать заряд.
Уединенным будем называть проводник, размеры которого много меньше расстояний до окружающих тел. Если потенциал на бесконечности принять за 0, то потенциал заряженного уединенного шара
, тогда эл.емкость: проницаемость среды.
Существуют такие проводники, при которых электрическое поле оказывается сосредоточенным в некоторой области пространства. Такие системы называются конденсаторами
-эл.ем. плоского конденсатора.
10. (10)Энергия заряженного конденсатора. Объемная плотность энергии электрического поля.
Заряд конденсатора – перенос заряда с одной обкладки на другую. Тогда система должна совершить работу:
— объемная плотность эл.энергии.
11. Электрическое поле в диэлектриках. Вектор поляризации. Поле электрического смещения в диэлектрике. Емкость плоского конденсатора с линейным изотропным диэлектриком.
Диэлектрик, помещенный во внешнее электрическое поле, поляризуется под действием этого поля. Поляризацией диэлектрика называется процесс приобретения им отличного от нуля макроскопического дипольного момента.
Степень поляризации диэлектрика характеризуется векторной величиной, которая называется поляризованостью или вектором поляризации (P). Поляризованность определяется как электрический момент единицы объема диэлектрика
,
где N — число молекул в объеме . Поляризованность P часто называют поляризацией, понимая под этим количественную меру этого процесса.
В диэлектриках различают следующие типы поляризации: электронную, ориентационную и решеточную (для ионных кристаллов).
Электронный тип поляризации характерен для диэлектриков с неполярными молекулами. Во внешнем электрическом поле (рис. 2.1) положительные заряды внутри молекулы смещаются по направлению поля, а отрицательные в противоположном направлении, в результате чего молекулы приобретают дипольный момент, направленный вдоль внешнего поля
Индуцированный дипольный момент молекулы пропорционален напряженности внешнего электрического поля , где — поляризуемость молекулы. Значение поляризованности в этом случае равно , где n — концентрация молекул ; — индуцированный дипольный момент молекулы, который одинаков для всех молекул и направление которого совпадает с направлением внешнего поля.
Ориентационнный тип поляризации характерен для полярных диэлектриков. В отсутствие внешнего электрического поля молекулярные диполи ориентированы случайным образом, так что макроскопический электрический момент диэлектрика равен нулю.
Если поместить такой диэлектрик во внешнее электрическое поле, то на молекулу-диполь будет действовать момент сил (рис. 2.2), стремящийся ориентировать ее дипольный момент в направлении напряженности поля. Однако полной ориентации не происходит, поскольку тепловое движение стремится разрушить действие внешнего электрического поля.
Такая поляризация называется ориентационной. Поляризованность в этом случае равна , где <p> — среднее значение составляющей дипольного момента молекулы в направлении внешнего поля.
Решеточный тип поляризации характерен для ионных кристаллов. В ионных кристаллах (NaCl и т.д.) в отсутствие внешнего поля дипольный момент каждой элементарной ячейки равен нулю (рис. 2.3.а), под влиянием внешнего электрического поля положительные и отрицательные ионы смещаются в противоположные стороны (рис. 2.3.б). Каждая ячейка кристалла становится диполем, кристалл поляризуется. Такая поляризация называется решеточной. Поляризованность и в этом случае можно определить как , где — значение дипольного момента элементарной ячейки, n — число ячеек в единице объема.
Вектор электрического смещения
| (14.8) |
Вектор направлен в ту же сторону, что и . В отличие от напряженности поля вектор имеет постоянное значение во всех диэлектриках. Поэтому электрическое поле в неоднородной диэлектрической среде удобнее характеризовать не напряженностью , а смещением . С этой целью вводится понятие линий вектора и потока смещения, аналогично понятию силовых линий и потока напряженности
или
| (14.9) |
Используя теорему Гаусса
домножим обе части на
С учетом (14.8) получаем
| (14.10) |
Это уравнение выражает теорему Гаусса для вектора электрического смещения: полный поток вектора электрического смещения через произвольную замкнутую поверхность равен сумме свободных зарядов, заключенных в этой поверхности.
Ёмкость плоского конденсатора находиться по формуле:
Где ε0=8,854187817·10−12 Ф/м — электрическая постоянная, ε — диэлектрическая проницаемость диэлектрика расположенного между обкладками конденсатора, S — площадь обкладки конденсатора, d — расстояние между обкладками.
12. Граничные условия для векторов E и D. Преломление силовых линий электрического поля на границе раздела двух диэлектриков.
На границе двух диэлектриков с различными диэлектрическими проницаемостями , и при наличии внешнего поля возникают поляризационные заряды разного знака с различными поверхностными плотностями зарядов и (рис.14.7).
Дополнительное поле, создаваемое этими зарядами, перпендикулярно поверхности, поэтому нормальные составляющие полей , и в обеих средах у границы раздела различны, а касательный составляющие одинаковы, т.е.
| (14.11) |
Векторы электростатического смещения в обеих средах соответственно равны
| и | (14.12) |
Аналогично рассмотренному выше случаю границы диэлектрик — вакуум нормальная составляющая вектора на границе двух диэлектриков а отсюда следует, что
Из этого выражения следует, что в случае и линии вектора при переходе через границу раздела преломляются, отклоняясь от перпендикуляра к границе раздела. Из (14.11) и (14.12) следует, что
При и
При переходе через границу раздела из диэлектрика с меньшим значением в диэлектрик с большим значением , нормальная составляющая вектора остается неизменной, а касательная увеличивается, так что линии вектора преломляются под таким же углом как и линии напряженности поля (рис. 14.8).
Таким образом, при переходе через границу раздела двух диэлектриков изменяется не только вектор напряженности электрического поля , но и вектор . Однако поток вектора через произвольную площадку на границе раздела, равный по определению , с обеих сторон поверхности на основании остается неизменным. Следовательно, число линий вектора электрического смещения, переходящих через границу, не меняется. Поэтому теорема Гаусса остается справедливой для вектора в самом общем случае при наличии в поле диэлектриков любой формы и размеров.
13. (13)Постоянный электрический ток. Плотность тока. Закон сохранения электрического заряда.
Эл. Ток –направленное движение электрических зарядов. Для существования тока в проводнике необходимо создать в нем электрическое поле.
Ток- это скалярная величина, равна :
Постоянным он называется, если во времени его сила и направление не изм.
Плотность тока j — это векторная физическая величина, модуль которой определяется отношением силы тока I в проводнике к площади S поперечного сечения проводника
З-н сохранения заряда: В телах, которые находятся в покое и электрически нейтральны, заряды противоположных знаков равны по величине и взаимно компенсируют друг друга
14. (14) Закон Ома и Джоуля-Ленца в диф. форме
15. (15) Закон Ома и Джоуля-Ленца в интегральной форме
16. (16)Сторонние силы. Источник ЭДС.
Сторо́нние си́лы— силы неэлектростатического происхождения, действующие на заряды со стороны источников тока и вызывающие перемещение зарядов внутри источника постоянного тока. Сторонние силы совершают работу по поддержанию разности потенциалов на концах цепи.
ЭДС: (дж/(кл)=В)
17. (17+18)Расчет эл.цепей постоянного тока. З-ны Кирхгофа.
1ЗК: сумма сил токов в узле равна нулю
2ЗК: сумма падения напряжения на всех контурах = сумме ЭДС в этом контуре.
1)Определить число ветвей.
2)сост (У-1) ур-ий по 1ЗК
3)сост ур-я по 2ЗК для контуров.
4)с-ма ур-й :В=(У-1)+К
5)решить с-му.
6)проверка баланса мощностей:
18. (19) Магнитное поле. Сила Лоренца.
Магнитное поле – силовое поле, действующее на заряд. Оно возникает из-за движения электронов. Основной силовой характеристикой магнитного поля является вектор магнитной индукции
— сила ампера(сила действия поля на проводник с током, где -угол между индукцией и проводником.)
19. (20)Магнитное поле в вакууме. Закон Био-Савара-Лапласа.
Поле, создаваемое движ. со скорость v зарядом q опр. ф-лой:
| Магнитное поле любого тока может быть вычислено как векторная сумма полей, создаваемых отдельными элементарными участками тока |
Магнитная индукция поля, создаваемая элементом проводника , по которому течёт ток , в некоторой точке А, положение которой относительно элемента определяется радиус-вектором ,
20. (21)Действие магнитного поля на ток. Сила Ампера. Взаимодействие параллельных проводников с токами. Определение Ампера.
Если поместить проводник м/у полюсами магнита, то проводник будет испытывать силу, давящую на него вниз, вследствие того, что ток образует собственное магнитное поле.
Правило левой руки состоит в следующем: если поместить левую руку между полюсами магнита так, чтобы магнитные силовые линии входили в ладонь, а четыре пальца руки совпадали с направлением тока в проводнике, то большой палец покажет направление движения проводника.
Сила Ампера – эта та сила, с которой действует магнитное поле на помещенный в него проводник.
; -угол между индукцией и проводником
Ампер — это сила тока, который проходя по двум прямолинейным параллельным проводникам, расположенным на расстоянии 1 (метр) друг от друга, вызывает на каждом участке длиной силу взаимодействия 2·10−7 Н
21. (22) Действие магнитного поля на контур с током
На обе стороны рамки действует сила Ампера. Получается «пара сил»
22. (23)Теорема о циркуляции магнитного поля постоянных токов. Ее применение для расчета симметричных магнитных полей.
23. (24)Основные уравнение магнитостатики.
24. (25)Магнитное поле в веществе. Вектор намагниченности. Теорема о циркуляции вектора намагниченности. Напряженность магнитного поля. Диа/парамагнетики во внешнем магнитом поле.
Индукция магнитного поля, создаваемого электрическими токами в веществе, отличается от индукции магнитного поля, создаваемого теми же токами в вакууме
| В-во, которые показ. во сколько раз индукциямагнитного поля в однородной среде отличается по модулю от индукции магнитного поля в вакууме, называется магнитной проницаемостью . |
магнитные свойства веществ в основном определяются электронами, входящими в состав атомов, т.к магн.св-ва нейтронов/протонов в 1000 раз слабее.
Слабо-магнитные вещества делятся на две большие группы – парамагнетики и диамагнетики. Они отличаются тем, что при внесении во внешнее магнитное поле парамагнитные намагничиваются так, что их собственное магнитное поле оказывается направленным по внешнему полю, а диамагнитные образцы намагничиваются против внешнего поля
-вектор намагниченности.
Для хар-ки магнитного поля используют понятие напряженности МП. и хар-ют одно поле. Связаны м/у собой: = *
| Циркуляция вектора намагниченности по произвольному замкнутому контуру равна алгебраической сумме токов намагничивания, охватываемых контуром |
25. (27)Ферромагнетизм. Основная кривая намагниченности. Магнитный гистерезис
Ферромагнетизм — магнитоупорядоченное состояние вещества, в котором большинство атомных магнитных моментов параллельны друг другу, так что вещество обладает самопроизвольной намагниченностью Вещества, в которых возникает ферромагнитное упорядочение магнитных моментов, называются ферромагнетиками
| Геометрическое место точек вершин симметричных циклов гистерезиса называется основной кривой намагничивания. При H=0 ферромагнетик оказывается намагниченным, он оставляет остаточную индукцию Br. Hc –напряженность при которой магнитная индукция становится = 0.(коэрцитивная сила). При увеличении магнитного поля противоположного направления, достигается опять насыщение. | |
| Р/м пр-с перемагничивания ферромагнетика. Первоначально он был размагничен. Сначала индукция быстро возрастает за счет того, что магнитные диполи ориентируются по силовым линиям поля, добавляя свой магнитный поток к внешнему. Затем ее рост замедляется по мере того, как количество неориентированных диполей уменьшается и, наконец, когда практически все они ориентируются по внешнему полю рост индукции прекращается и наступает режим насыщения. Если в пр-се намагничивания довести напряженность поля до некоторого значения, а затем начать уменьшать, то уменьшение индукции будет происходить медленнее, чем при намагничивании и новая кривая будет отличаться от первоначальной. Кривая изменения индукции при увеличении напряженности поля для предварительно полностью размагниченного вещества называется начальной кривой намагничивания. |
26. (28)Электромагнитная индукция. Закон электромагнитной индукции Фарадея. Правило Ленца
Электромагнитная индукция заключается в возникновении тока в замкнутом контуре при изменении во времени магнитного потока.
| При изменении магнитного потока в проводящем контуре возникает ЭДС индукции , равная скорости изменения магнитного потока через поверхность | ||
| Правило Ленца — индукционный ток, возбуждаемый в замкнутом контуре при изменении магнитного потока, всегда направлен так, что создаваемое им магнитное поле препятствует изменению магнитного потока, вызывающего индукционный ток | ||
27. (29)Природа электромагнитной индукции. Локальная формулировка закона эм. индукции.
Возьмем произвольный замкнутный контур.
ЭДС:
Видим, что это значит, что E –вихревое поле.
Если в кач-ве контура выбрать проводник
i- индукционный ток, R – сопр. цепи.
При увеличении скорости потока, ток уменьш. и наоборот.
-локальная формулировка з-на эм. индукции.
Изменение во времени магнитного поля, порождает вихревое эл.поле.
28. (30)Самоиндукция. Индуктивность контура с током. Энергия контура с током.
При изменении силы тока в цепи произойдет изменение магнитного поля, в результате чего в этой же цепи возникнет дополнительный индукционный ток. Такое явление называется самоиндукцией, а ток, возникающий при этом, называется током самоиндукции.
| Ф=L*I | Коэффициент пропорциональности L в этой формуле называется коэффициентом самоиндукции | |
| Магнитный поток через виток: МП через катушку | Ф=B*S Ф=NBS, где N- число витков. | |
Индукция поля в катушке: , где -кол-во витков на ед.длины.
29. (31) Взаимная индуктивность. Соединения катушек индуктивностей.
Взаимная индукция- наличие магнитной связи м/у контурами приводит к тому, что изменение тока в одном контуре возникает эдс в другом.
| В первом контуре течет ток I1 . Он создает магнитный поток, который пронизывает и витки второго контура | Аналогично, ток I2 второго контура создает магнитный поток, пронизывающий первый контур | |
| Ф1=L12*I2+L1I1 | Ф2=L21*I1+L2I2 | |
| При изменении тока I1 во втором контуре наводится ЭДС индукции: |
| Последовательное подключение | L=L1+L2+L3 |
| Параллельное соединение | |
| Если катушки, включенные в цепь последовательно, расположены близко друг к другу, т. е. так, что часть магнитного потока одной катушки пронизывает витки другой, т. е. между катушками существует индуктивная связь | Lобщ=L1+L2-2М М-взаимная индукция |
30. (32)Токи смещения. Теорема о циркуляции переменного магнитного поля.
| Для установления количественных соотношений между изменяющимся ЭП и порождаемым им МП Максвелл ввел в рассмотрение ток смещения. | вектор электрического смещения | Теорема циркуляции: |
31. (33)Система ур-й Максвелла
32. Волновое уравнение. Плоские электромагнитные волны.
Волновое уравнение − линейное дифференциальное уравнение в частных производных, описывающее малые колебания струны, колебательные процессы в сплошных средах и в электродинамике.
В общем случае волна, распространяющаяся в пространстве, описывается уравнением
| (1) |
где u = u(x,y,z,t) − возмущение в точке x,y,z в момент времени t, v − скорость распространения волны. Уравнение (1) инвариантно относительно замены v → -v.
Монохроматическая волна − распространение колебаний с определённой
Плоская волна – это волна, имеющая плоский фронт волны. Плоской волне можно дать следующее определение. Волна называется плоской однородной, если векторное поле и в любой точке плоскости перпендикулярны направлению распространения и не изменяются по фазе и амплитуде.
Уравнение плоской волны
. (3.9)
33. Теорема Пойнтинга. Поток энергии электромагнитного поля.
ПОЙНТИНГА ТЕОРЕМА — теорема, описывающая закон сохранения энергии эл—магн. поля. Теорема была доказана в 1884 Дж. Пойнтингом (J. Н. Poynting). Если продифференцировать по времени плотность энергии электромагнитного поля в стационарной среде без дисперсии, с учётом Максвелла уравнений получим:
где — Пойнтинга вектор, j — плотность тока, Е, Ни D, В — напряжённости и индукции электрич. и магн. полей. В интегральной форме П. т. принимает вид
где W — полная энергия эл—магн. поля, заключённого в объёме V; F — поверхность, ограничивающая объём V; dF и dV — элементы поверхности и объёма.
Вектор Умова – Пойнтинга (так же Вектор Пойнтинга) – вектор плотности потока электромагнитной энергии, определяющий количество электромагнитной энергии, переносимой через единицу площади в единицу времени. Вектор Пойнтинга S можно определить через векторное произведение двух векторов:
⃗S=c4π[⃗E×⃗H]{\displaystyle \vec{S} = \frac{c}{4\pi}[\vec{E} \times \vec{H} ]} (в системе СГС),
⃗S=[⃗E×⃗H]{\displaystyle \vec{S} =[\vec{E} \times \vec{H} ]} (в Международной системе единиц (СИ)),
где ⃗E{\displaystyle \vec{E}} и ⃗H{\displaystyle \vec{H}} — векторы напряжённости электрического и магнитного полей соответственно
34. (36) Электрические цепи переменного тока. Элементы R, L, C цепей переменного тока. Правила Кирхгофа для цепей переменного тока.
Читайте также:
Рекомендуемые страницы:
Поиск по сайту
Работа, совершённая силами электростатического поля при переносе заряда
Задача. Работа, совершённая силами электростатического поля при переносе заряда
нКл из бесконечности в некоторую точку поля, нДж. Определите потенциал этой точки поля.Дано:
нКлнДж
Найти:
Решение
Думаем: поле неоднородно значит мы можем воспользоваться соотношением (1).
(1)где
, — потенциалы точек куда и откуда переносят заряд.Решаем: «перенос из бесконечности в некоторую точку» говорит о том, что потенциал в начальной точке (на бесконечности) равен нулю (
). Тогда для (1): (2)Из (2):
(3)Считаем:
ВОтвет:
В.Ещё задачи на тему «Работа электрического поля»
Поделиться ссылкой:
- Telegram
Понравилось это:
Нравится Загрузка…



