Направление вектора магнитной индукции
Магнитное поле характеризуют при помощи вектора магнитной индукции ().
Если свободно вращающуюся магнитную стрелку, которая является небольшим магнитом, обладающим полюсами (северным (N) и южным(S)), поместить в магнитное поле, то она будет поворачиваться до тех пор, пока не установится определённым образом. Аналогично ведет себя рамка с током, повешенная на гибком подвесе, имеющая возможность поворачиваться. Способность магнитного поля ориентировать магнитную стрелку используют для того, чтобы определить направление вектора магнитной индукции.
Направление вектора магнитной индукции
Так, направлением вектора магнитной индукции считают направление, которое указывает северный полюс магнитной стрелки, которая может свободно поворачиваться в магнитном поле.
Такое же направление имеет положительная нормаль к замкнутому контуру с током. Направление положительной нормали определяют при помощи правила правого винта (буравчика): положительная нормаль направлена туда, куда поступательно перемещался бы буравчик, если бы его головку вращали по направлению течения тока в контуре.
Применяя контур с током или магнитную стрелку, можно выяснить, как направлен вектор магнитной индукции магнитного поля в любой точке.
Для определения направления вектора иногда удобно использовать так называемое правило правой руки. Его применяют следующим образом. Пытаются в воображении охватить правой рукой проводник таки образом, чтобы при этом большой палец указывал направление силы тока, тогда кончики остальных пальцев направлены так же как вектор магнитной индукции.
Частные случаи направления вектора магнитной индукции прямого тока
Если магнитное поле в пространстве создается прямолинейным проводником с током, то магнитная стрелка будет в любой точке поля устанавливаться по касательной к окружностям, центры которых лежат на оси проводника, а плоскости перпендикулярны проводу. При этом направление вектора магнитной индукции определим, используя правило правого винта. Если винт вращать так, что он будет поступательно двигаться по направлению силы тока в проводе, то вращение головки винта совпадает с направлением вектора . На рис. 1 направлен от нас, перпендикулярно плоскости рисунка.
Ориентируясь на местности при помощи компаса, мы каждый раз проводим опыт по определению направления вектора Земного поля.
Пусть в магнитном поле движется заряженная частица, тогда на нее действует сила Лоренца (), которая определена как:
где q – заряд частицы; – вектор скорости частицы. Сила Лоренца и вектор магнитной индукции всегда взаимно перпендикулярны. Для заряда большего нуля (), тройка векторов и связана правилом правого винта (рис.2).
Линии магнитного поля и направление вектора B
Визуализировать картину магнитного поля можно при помощи линий магнитной индукции. Линиями магнитной индукции поля называют линий, для которых касательными в любой точке являются векторы магнитной индукции рассматриваемого поля. Для прямого проводника с током линиями магнитной индукции являются концентрические окружности, плоскости их перпендикулярны проводнику, центры на оси провода. Специфика линий магнитного поля заключена в том, что они бесконечны и являются всегда замкнутыми (или уходящими в бесконечность). Это означает, что магнитное поле является вихревым.
Принцип суперпозиции вектора B
Если магнитное поле создано не одним, а совокупностью токов или движущихся зарядов, то оно находится как векторная сумма отдельных полей, создаваемых каждым током или движущимся зарядом отдельно. В виде формулы принцип суперпозиции записывают как:
Или:
Примеры решения задач
Магнитная индукция — Википедия
Материал из Википедии — свободной энциклопедии
Магни́тная инду́кция B→{\displaystyle {\vec {B}}} — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой F→{\displaystyle {\vec {F}}} магнитное поле действует на заряд q{\displaystyle q}, движущийся со скоростью v→{\displaystyle {\vec {v}}}.
Более конкретно, B→{\displaystyle {\vec {B}}} — это такой вектор, что сила Лоренца F→{\displaystyle {\vec {F}}}, действующая со стороны магнитного поля[1] на заряд q{\displaystyle q}, движущийся со скоростью v→{\displaystyle {\vec {v}}}, равна
- F→=q[v→×B→]{\displaystyle {\vec {F}}=q\left[{\vec {v}}\times {\vec {B}}\right]}
- F=qvBsinα{\displaystyle F=qvB\sin \alpha }
где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора F→{\displaystyle {\vec {F}}} перпендикулярно им обоим и направлено по правилу буравчика).
Также магнитная индукция может быть определена[2] как отношение максимального механического момента сил, действующих на рамку с током, помещённую в однородное поле, к произведению силы тока в рамке на её площадь.
Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.
В системе СГС единицей магнитной индукции является гаусс (Гс), в СИ — тесла (Тл)
- 1 Тл = 104 Гс
Магнитометры, применяемые для измерения магнитной индукции, называют тесламетрами.
Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с ним напряжённость магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.
- (Здесь формулы приведем в СИ, в виде для вакуума[3], где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).
В магнитостатике[править | править код]
В магнитостатическом пределе[4] наиболее важными являются:
- Закон Био — Савара — Лапласа: играет в магнитостатике ту же роль, что закон Кулона в электростатике:
- B→(r→)=μ04π∫L1I(r→1)dL1→×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int \limits _{L_{1}}{\frac {I\left({\vec {r}}_{1}\right){\vec {dL_{1}}}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}
- B→(r→)=μ04π∫j→(r→1)dV1×(r→−r→1)|r→−r→1|3,{\displaystyle {\vec {B}}\left({\vec {r}}\right)={\mu _{0} \over 4\pi }\int {\frac {{\vec {j}}\left({\vec {r}}_{1}\right)dV_{1}\times \left({\vec {r}}-{\vec {r}}_{1}\right)}{\left|{\vec {r}}-{\vec {r}}_{1}\right|^{3}}},}
- Теорема Ампера о циркуляции магнитного поля[5]:
- ∮∂SB→⋅dl→=μ0IS≡μ0∫Sj→⋅dS→,{\displaystyle \oint \limits _{\partial S}{\vec {B}}\cdot {\vec {dl}}=\mu _{0}I_{S}\equiv \mu _{0}\int \limits _{S}{\vec {j}}\cdot {\vec {dS}},}
- rotB→≡∇→×B→=μ0j→.{\displaystyle \mathrm {rot} \,{\vec {B}}\equiv {\vec {\nabla }}\times {\vec {B}}=\mu _{0}{\vec {j}}.}
В общем случае[править | править код]
Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции B→{\displaystyle {\vec {B}}}:
- divE→=ρε0, rotE→=−∂B→∂t{\displaystyle \mathrm {div} \,{\vec {E}}={\frac {\rho }{\varepsilon _{0}}},\ \ \ \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}}}
- divB→=0, rotB→=μ0j→+1c2∂E→∂t{\displaystyle \mathrm {div} \,{\vec {B}}=0,\ \ \ \ \,\mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}}
- а именно:
- divB→=0,{\displaystyle \mathrm {div} \,{\vec {B}}=0,}
- rotE→=−∂B→∂t,{\displaystyle \mathrm {rot} \,{\vec {E}}=-{\frac {\partial {\vec {B}}}{\partial t}},}
- rotB→=μ0j→+1c2∂E→∂t.{\displaystyle \mathrm {rot} \,{\vec {B}}=\mu _{0}{\vec {j}}+{\frac {1}{c^{2}}}{\frac {\partial {\vec {E}}}{\partial t}}.}
- F→=qE→+q[v→×B→],{\displaystyle {\vec {F}}=q{\vec {E}}+q\left[{\vec {v}}\times {\vec {B}}\right],}
- Следствия из неё, такие как
- Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)
- dF→=[Idl→×B→],{\displaystyle d{\vec {F}}=\left[I{\vec {dl}}\times {\vec {B}}\right],}
- dF→=[j→dV×B→],{\displaystyle d{\vec {F}}=\left[{\vec {j}}dV\times {\vec {B}}\right],}
- M→=m→×B→,{\displaystyle {\vec {M}}={\vec {m}}\times {\vec {B}},}
- выражение для потенциальной энергии магнитного диполя в магнитном поле:
- U=−m→⋅B→,{\displaystyle U=-{\vec {m}}\cdot {\vec {B}},}
- а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т. д..
- Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:
- F→=Kqmr→r3.{\displaystyle {\vec {F}}=K{\frac {q_{m}{\vec {r}}}{r^{3}}}.}
- (это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).
- Выражение для плотности энергии магнитного поля
- w=B22μ0{\displaystyle w={\frac {B^{2}}{2\mu _{0}}}}
- Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).
- ↑ Если учитывать и действие электрического поля E, то формула (полной) силы Лоренца принимает вид:
- F→=qE→+q[v→×B→].{\displaystyle {\vec {F}}=q{\vec {E}}+q[{\vec {v}}\times {\vec {B}}].}
- ↑ Это определение с современной точки зрения менее фундаментально, чем приведённое выше (и является просто его следствием), однако с точки зрения близости к одному из практических способов измерения магнитной индукции может быть полезным; также и с исторической точки зрения.
- ↑ То есть в наиболее фундаментальном и простом для ознакомления виде.
- ↑ То есть в частном случае постоянных токов и постоянных электрического и магнитного полей или — приближённо — если изменения настолько медленны, что ими можно пренебречь.
- ↑ Являющаяся частным магнитостатическим случаем закона Ампера — Максвелла (см. в статье далее).
Магнитное поле, силовые линии, вектор магнитной индукции, принцип суперпозиции. Курсы по физике
Тестирование онлайн
Магнитное поле. Основные понятия
Магнитное поле. Вектор магнитной индукции
Магнитное поле
Уже в VI в. до н.э. в Китае было известно, что некоторые руды обладают способностью притягиваться друг к другу и притягивать железные предметы. Куски таких руд были найдены возле города Магнесии в Малой Азии, поэтому они получили название магнитов.
Посредством чего взаимодействуют магнит и железные предметы? Вспомним, почему притягиваются наэлектризованные тела? Потому что около электрического заряда образуется своеобразная форма материи — электрическое поле. Вокруг магнита существует подобная форма материи, но имеет другую природу происхождения (ведь руда электрически нейтральна), ее называют магнитным полем.
Для изучения магнитного поля используют прямой или подковообразный магниты. Определенные места магнита обладают наибольшим притягивающим действием, их называют полюсами (северный и южный). Разноименные магнитные полюса притягиваются, а одноименные — отталкиваются.
Для силовой характеристики магнитного поля используют вектор индукции магнитного поля B. Магнитное поле графически изображают при помощи силовых линий (линии магнитной индукции). Линии являются замкнутыми, не имеют ни начала, ни конца. Место, из которого выходят магнитные линии — северный полюс (North), входят магнитные линии в южный полюс (South).
Магнитное поле можно сделать «видимым» с помощью железных опилок.
Магнитное поле проводника с током
А теперь о том, что обнаружили Ханс Кристиан Эрстед и Андре Мари Ампер в 1820 г. Оказывается, магнитное поле существует не только вокруг магнита, но и любого проводника с током. Любой провод, например, шнур от лампы, по которому протекает электрический ток, является магнитом! Провод с током взаимодействует с магнитом (попробуйте поднести к нему компас), два провода с током взаимодействуют друг с другом.
Силовые линии магнитного поля прямого тока — это окружности вокруг проводника.
Направление вектора магнитной индукции
Направление магнитного поля в данной точке можно определить как направление, которое указывает северный полюс стрелки компаса, помещенного в эту точку.
Направление линий магнитной индукции зависит от направления тока в проводнике.
Определяется направление вектора индукции по правилу буравчика или правилу правой руки.
Вектор магнитной индукции
Это векторная величина, характеризующая силовое действие поля.
Индукция магнитного поля бесконечного прямолинейного проводника с током на расстоянии r от него:
Индукция магнитного поля в центре тонкого кругового витка радиуса r:
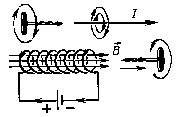
Индукция магнитного поля соленоида (катушка, витки которой последовательно обходятся током в одном направлении):
Принцип суперпозиции
Если магнитное поле в данной точке пространства создается несколькими источниками поля, то магнитная индукция — векторная сумма индукций каждого из полей в отдельности
Земля является не только большим отрицательным зарядом и источником электрического поля, но в то же время магнитное поле нашей планеты подобно полю прямого магнита гигантских размеров.
Географический юг находится недалеко от магнитного севера, а географический север приближен к магнитному югу. Если компас разместить в магнитном поле Земли, то его северная стрелка ориентируется вдоль линий магнитной индукции в направлении южного магнитного полюса, то есть укажет нам, где располагается географический север.
Характерные элементы земного магнетизма весьма медленно изменяются с течением времени — вековые изменения. Однако время от времени происходят магнитные бури, когда в течение нескольких часов магнитное поле Земли сильно искажается, а затем постепенно возвращается к прежним значениям. Такое резкое изменение влияет на самочувствие людей.
Магнитное поле Земли является «щитом», прикрывающего нашу планету от частиц, проникающих из космоса («солнечного ветра»). Вблизи магнитных полюсов потоки частиц подходят гораздо ближе к поверхности Земли. При мощных солнечных вспышках магнитосфера деформируется, и эти частицы могут переходить в верхние слои атмосферы, где сталкиваются с молекулами газа, образуются полярные сияния.
Частицы диоксида железа на магнитной пленке хорошо намагничиваются в процессе записи.
Поезда на магнитной подушке скользят над поверхностью совершенно без трения. Поезд способен развивать скорость до 650 км/ч.
Работа головного мозга, пульсация сердца сопровождается электрическими импульсами. При этом в органах возникает слабое магнитное поле.
| | Адрес этой страницы (вложенность) в справочнике dpva.ru: главная страница / / Техническая информация / / Физический справочник / / Физика для самых маленьких. Шпаргалки. Школа. / / Магнитное поле. Вектор магнитной индукции. Правило буравчика. Закон Ампера и сила Ампера. Сила Лоренца. Правило левой руки. Электромагнитная индукция, магнитный поток, правило Ленца, закон электромагнитной индукции, самоиндукция, энергия магнитного поля Поделиться:
| ||||||||||||||
Магнитная индукция. Линии магнитной индукции
Магнитная индукция. Линии магнитной индукции
«Физика — 11 класс»
Электрическое поле характеризуется напряженностью электрического поля.
Напряженность электрического поля — это величина векторная.
Магнитное поле характеризуется магнитной индукцией.
Магнитная индукция — это векторная величина, она обозначается буквой .
Направление вектора магнитной индукции
За направление вектора магнитной индукци принимается направление, которое показывает северный полюс N магнитной стрелки, свободно устанавливающейся в магнитном поле.
Это направление совпадает с направлением положительной нормали к замкнутому контуру с током.
Используя рамку с током или магнитную стрелку, можно определить направление вектора магнитной индукции в любой точке поля.
В магнитном поле прямолинейного проводника с током магнитная стрелка в каждой точке устанавливается по касательной к окружности, плоскость которой перпендикулярна проводу, а центр ее лежит на оси провода.
Правило буравчика
Направление вектора магнитной индукции устанавливают с помощью правила буравчика.
Если направление поступательного движения буравчика совпадает с направлением тока в проводнике, то направление вращения ручки буравчика указывает направление вектора магнитной индукции.
Линии магнитной индукции
Магнитное поле можно показать с помощью линий магнитной индукции.
Линиями магнитной индукции называют линии, касательные к которым в любой их точке совпадают с вектором в данной точке поля. Линии вектора магнитной индукции аналогичны линиям вектора напряженности электростатического поля.
Линии магнитной индукции можно сделать видимыми, воспользовавшись железными опилками.
Магнитное поле прямолинейного проводника с током
Для пряого проводника с током линии магнитной индукции являются концентрическими окружностями, лежащими в плоскости, перпендикулярной этому проводнику с током. Центр окружностей находится на оси проводника. Стрелки на линиях указывают, в какую сторону направлен вектор магнитной индукции, касательный к данной линии.
Магнитное поле катушки с током (соленоида)
Если длина соленоида много больше его диаметра, то магнитное поле внутри соленоида можно считать однородным.
Линии магнитной индукции такого поля параллельны и находятся на равных расстояниях друг от друга.
Магнитное поле Земли
Линии магнитной индукции поля Земли подобны линиям магнитной индукции поля соленоида.
Периодически магнитные полюсы меняют свою полярность.
Вихревое поле
Силовые линии электростатического поля всегда имеют источники: они начинаются на положительных зарядах и оканчиваются на отрицательных.
А линии магнитной индукции не имеют ни начала, ни конца, они всегда замкнуты.
Поля с замкнутыми векторными линиями называют вихревыми.
Магнитное поле — вихревое поле.
Магнитное поле не имеет источников.
Магнитных зарядов, подобных электрическим, в природе не существует.
Итак, магнитное поле — это вихревое поле, в каждой его точке вектор магнитной индукции указывает магнитная стрелка, направление вектора магнитной индукции можно определить по правилу буравчика.
Источник: «Физика — 11 класс», учебник Мякишев, Буховцев, Чаругин
Магнитное поле. Физика, учебник для 11 класса — Класс!ная физика
Магнитное поле и взаимодействие токов — Магнитная индукция. Линии магнитной индукции — Модуль вектора магнитной индукции. Сила Ампера — Электроизмерительные приборы. Громкоговоритель — Действие магнитного поля на движущийся заряд. Сила Лоренца — Магнитные свойства вещества — Примеры решения задач — Краткие итоги главы
Магнитное действие электрического тока | |
1820 г. X. Эрстед — датский физик, открыл магнитное действие тока. (Опыт: действие электрического тока на магнитную стрелку). 1820 г. А. Ампер — французский ученый, открыл механическое взаимодействие токов и установил закон этого взаимодействия. | |
Магнитное взаимодействие, как и электрическое, удобно рассматриватьвводя понятие магнитного поля:
| |
Для двух параллельных бесконечно длинных проводников было установлено: противоположно направленные токи отталкиваются, однонаправленные токи притягиваются, причем | |
Отсюда устанавливается единица силы тока ампер в СИ: сила тока равна 1 А, если между отрезками двух бесконечных проводников по 1 м каждый, находящимися в вакууме на расстоянии 1 м друг от друга, действует сила магнитного взаимодействия 2.10 7Н. | |
В СИ удобно ввести магнитную проницаемость вакуума | |
Вектор магнитной индукции.Вектор магнитной индукции (В) – аналог напряженности электрического поля. Основной силовой характеристикой магнитного поля является вектор магнитной индукции. | |
Направление этого вектора для поля прямого проводника с током и соленоида можно определить по правилу буравчика: если направление поступательного движения буравчика (винта с правой нарезкой) совпадает с направлением тока, то направление вращения ручки буравчика покажет направление линий магнитной индукции. Вектор магнитной индукции направлен по касательной к линиям. | |
На практике удобно пользоваться следующим правилом: если большой палец правой руки направить по току, то направление обхвата тока остальными пальцами совпадет с направлением линий магнитной индукции. |
|
Модуль вектора магнитной индукции Магнитная индукция В зависит от I и r, где r — расстояние от проводника с током до исследуемой точки. Если расстояние от проводника много меньше его длины (т. е. рассматривать модель бесконечно длинного проводника), то где k — коэффициент пропорциональности. Подставляя эту формулу в уравнение для силы взаимодействия двух проводников с током, получим F=B .I.ℓ. Отсюда Таким образом, модуль вектора магнитной индукции | |
Единица измерения в СИ — тесла (Тл). Единица названа в честь сербского электротехника Н. Тесла. | |
Магнитный поток | |
Магнитный поток (поток линий магнитной индукции) через контур численно равен произведению модуля вектора магнитной индукции на площадь, ограниченную контуром, и на косинус угла между направлением вектора магнитной индукции и нормалью к поверхности, ограниченной этим контуром. | |
| |
Единица магнитного потока в СИ — вебер (Вб). В честь немецкого физика В. Вебера. | |
Опыт показывает, что линии магнитной индукции всегда замкнуты, и полный магнитный поток через замкнутую поверхность равен нулю. Этот факт является следствием отсутствия магнитных зарядов в природе. |
|
А 1 | На каком рисунке правильно изображена картина линий индукции магнитного поля длинного проводника с постоянным током, направленным перпендикулярно плоскости чертежа на нас? | ||||||||
1) 1 | 2) 2 | 3) 3 | 4) 4 | ||||||
А 2 | На каком рисунке правильно изображена картина линий индукции магнитного поля длинного проводника с постоянным током, направленным перпендикулярно плоскости чертежа от нас? | ||||||||
1) 1 | 2) 2 | 3) 3 | 4) 4 | ||||||
А 3 | На рисунке изображен проводник, по которому течет электрический ток. Направление тока указано стрелкой. Как направлен вектор магнитной индукции в точке С? | | |||||||
1)
В плоскости чертежа
4 | |||||||||
А 4 | Н С а рисунке изображен проводник, по которому течет электрический ток. Направление тока указано стрелкой. Как направлен вектор магнитной индукции в точке С? 1)
В плоскости чертежа 2 3)От
нас перпендикулярно плоскости чертежа 4 | | |||||||
А 5 | На рисунке изображен проводник, по которому течет электрический ток. Направление тока указано стрелкой. Как направлен вектор магнитной индукции в точке С? 1)
В плоскости чертежа 2)
В плоскости чертежа 3 4 | С | |||||||
А 6 | Н С а рисунке изображен проводник, по которому течет электрический ток. Направление тока указано стрелкой. Как направлен вектор магнитной индукции в точке С? 1)
В плоскости чертежа 2)
В плоскости чертежа 3 4 | | |||||||
А 7 | На рисунке изображен проводник, по которому течет электрический ток. Направление тока указано стрелкой. Как направлен вектор магнитной индукции в точке С? 1)
В плоскости чертежа 2)
В плоскости чертежа 3 4 | С | |||||||
А 8 | На рисунке изображен проводник, по которому течет электрический ток. Направление тока указано стрелкой. Как направлен вектор магнитной индукции в точке С? 1)
В плоскости чертежа 2 3)
От нас перпендикулярно плоскости
чертежа 4 | С
| |||||||
А 9 | По проводнику течет ток от нас. Вектор индукции магнитного поля в точке, находящейся справа от проводника, направлен | | |||||||
1) вниз 2) вверх | 3) влево 4) вправо | ||||||||
А 10 | На рисунке (вид сверху) показана картина линий индукции магнитного поля прямого проводника с током. В какой из четырех точек индукция магнитного поля наименьшая? |
| |||||||
| |||||||||
А С 11 | По двум тонким
прямым проводникам, параллельным друг
другу, текут одинаковые токи | 1 2
 | |||||||
1) К нам 2) От нас | 3) Вверх 4) Вниз | ||||||||






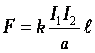 , где k — коэффициент пропорциональности.
, где k — коэффициент пропорциональности.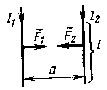
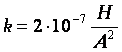
 .
.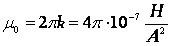
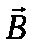
 ,
,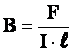 .
.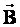 есть отношение максимальной силы, действующей со стороны магнитного поля на участок проводника с током, к произведению силы тока на длину этого участка.
есть отношение максимальной силы, действующей со стороны магнитного поля на участок проводника с током, к произведению силы тока на длину этого участка.
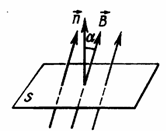
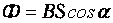 , где Вcosα представляет собой проекцию вектора В на нормаль к плоскости контура. Магнитный поток показывает, какое количество линий магнитной индукции пронизывает данный контур.
, где Вcosα представляет собой проекцию вектора В на нормаль к плоскости контура. Магнитный поток показывает, какое количество линий магнитной индукции пронизывает данный контур.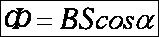
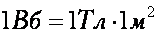




 плоскости чертежа
плоскости чертежа 

 )
К нам перпендикулярно плоскости
чертежа
)
К нам перпендикулярно плоскости
чертежа 
 )
В плоскости чертежа
)
В плоскости чертежа 

 )
К нам перпендикулярно плоскости
чертежа
)
К нам перпендикулярно плоскости
чертежа 



 )
От нас перпендикулярно плоскости
чертежа
)
От нас перпендикулярно плоскости
чертежа 
 )
К нам перпендикулярно плоскости
чертежа
)
К нам перпендикулярно плоскости
чертежа



 )
От нас перпендикулярно плоскости
чертежа
)
От нас перпендикулярно плоскости
чертежа 
 )
К нам перпендикулярно плоскости
чертежа
)
К нам перпендикулярно плоскости
чертежа



 )
От нас перпендикулярно плоскости
чертежа
)
От нас перпендикулярно плоскости
чертежа 
 )
К нам перпендикулярно плоскости
чертежа
)
К нам перпендикулярно плоскости
чертежа 



 )
Вектор магнитной индукции в точке С
равен нулю
)
Вектор магнитной индукции в точке С
равен нулю
 )
К нам перпендикулярно плоскости
чертежа
)
К нам перпендикулярно плоскости
чертежа




 (см. рисунок). Как направлено создаваемое
ими магнитное поле в точке С?
(см. рисунок). Как направлено создаваемое
ими магнитное поле в точке С?




