Как выбрать направление обхода контура

При свертке параллельных ветвей эквивалентное сопротивление всегда меньше наименьшего из сворачиваемых.

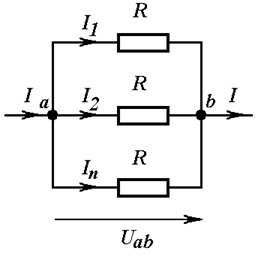
Если параллельно соединены n одинаковых сопротивлений (Рис. 3.3), эквивалентное сопротивление в n раз меньше сопротивления любой из ветвей.

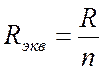
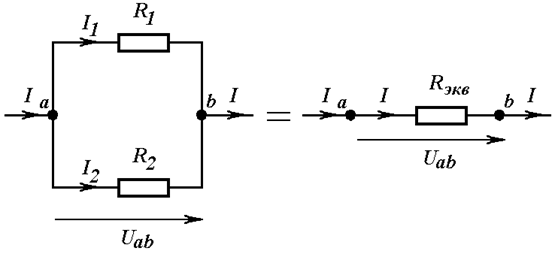
Если на участке цепи параллельно соединены лишь два элемента (Рис. 3.4), выражение (3.2) упрощается. В этом случае эквивалентное сопротивление можно определить как отношение произведения двух сопротивлений к их сумме:

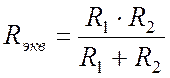
4. ОСНОВНЫЕ ЗАКОНЫ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ

К основным законам электрических цепей относятся закон Ома и законы Кирхгофа.

Если в ветви не содержится ЭДС, к ней применим уже известный закон Ома для пассивного участка цепи (1.1). Его можно сформулировать и следующим образом. Ток в ветви, не содержащей ЭДС, равен падению напряжения в ветви, деленному на сопротивление ветви (Рис. 4.1):

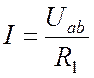
Закон Ома для ветви, содержащей ЭДС, позволяет найти ток этой ветви по известной разности потенциалов на концах ветви. Ток в ветви, содержащей ЭДС, равен дроби, знаменатель которой – это сопротивление ветви. В числителе дроби – напряжение на концах ветви плюс алгебраическая сумма ЭДС, заключенных между концами ветви. С плюсом берутся напряжения и ЭДС, направление которых совпадает с направлением тока, с минусом – противоположные.

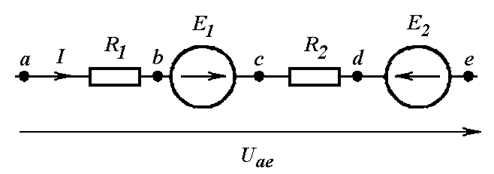
В частности, ток в ветви, изображенной на Рис. 4.2, равен:

.

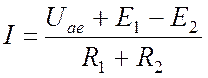Первый закон Кирхгофа

В любом узле цепи алгебраическая сумма токов равна нулю. При этом, токи, направленные к узлу, принято считать положительными, токи, направленные от узла, принято считать отрицательными (

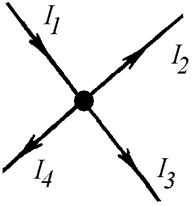
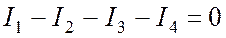
По первому закону Кирхгофа можно написать столько уравнений, сколько узлов содержит схема. Но не все они будут независимыми. Если схема содержит 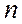узлов, независимыми будут 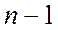уравнений. Оставшееся уравнение будет являться следствием всех предыдущих.

Второй закон Кирхгофа

В любом замкнутом контуре цепи алгебраическая сумма напряжений равна алгебраической сумме ЭДС, включенных в контур.

При этом, положительными считаются те напряжения и ЭДС, которые совпадают с направлением обхода контура, отрицательными считаются напряжения и ЭДС, которые противоположны направлению обхода контура. Направление обхода контура можно выбирать произвольно.

Алгоритм составления уравнения по второму закону Кирхгофа для замкнутого контура цепи

Для заданного контура (Рис. 4.4 а) уравнение по второму закону Кирхгофа составляется в следующем порядке:

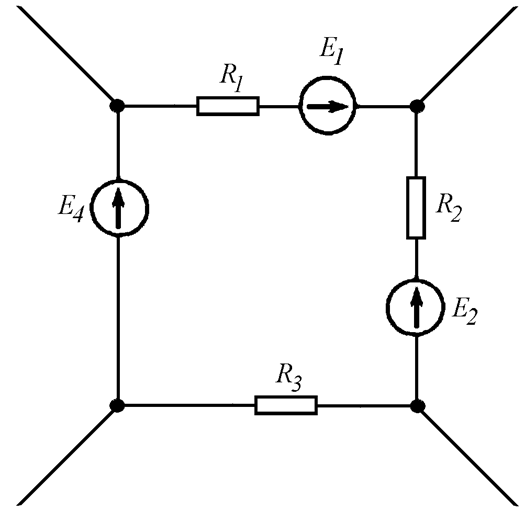
1. Задается направление токов в ветвях (Рис. 4.4 б).

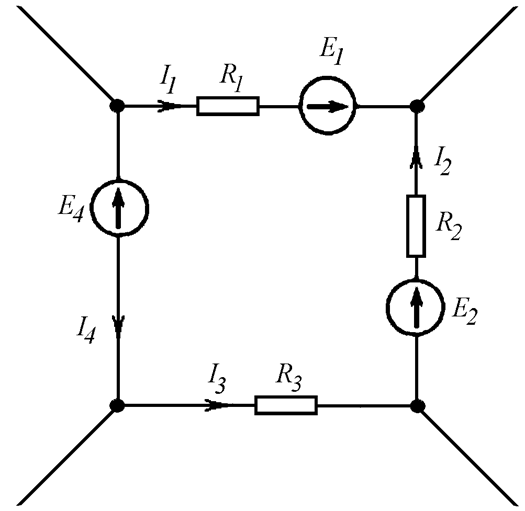
1. Выбирается направление обхода контура (Рис. 4.4 в).

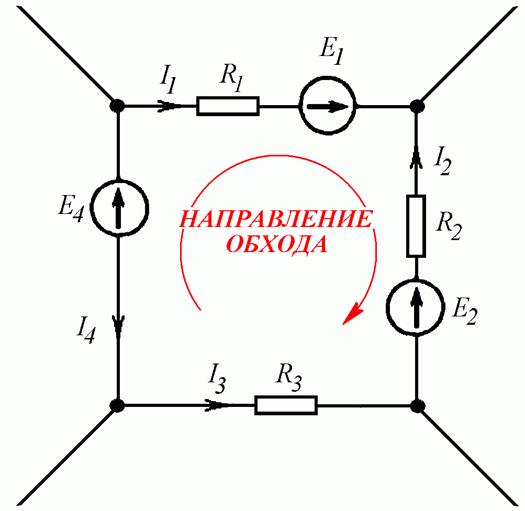
1. Записывается уравнение, в левой части которого – сумма падений напряжений на сопротивлениях ветвей. В правой части – сумма ЭДС контура.

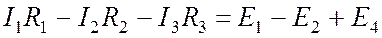
Примечание: Падение напряжения на сопротивлении ветви записывается в соответствии с известным уже законом Ома (1.1):

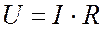
Применение второго закона Кирхгофа для незамкнутого участка цепи

Второй закон Кирхгофа справедлив только для замкнутого контура. При этом, любой незамкнутый участок цепи можно дополнить до замкнутого контура с помощью напряжения в разрыве незамкнутого участка.

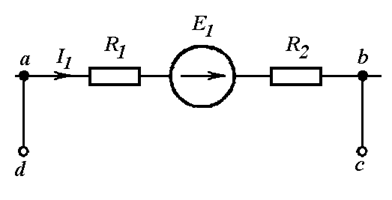
Незамкнутый участок цепи abcd изображен на Рис. 4.5 а.

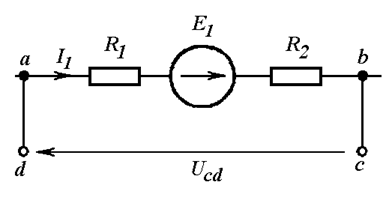
Дополняем участок до замкнутого контура, добавляя напряжение между незамкнутыми точками

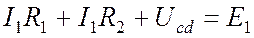
Применение законов Кирхгофа при наличии в цепи источника тока

Источник тока имеет бесконечно большое сопротивление, поэтому не образует замкнутого контура и не может входить в уравнения второго закона Кирхгофа. Однако, в уравнениях первого закона Кирхгофа источник тока должен содержаться обязательно.

При необходимости записать уравнение по второму закону Кирхгофа для контура, содержащего источник тока, его заменяют напряжением на выводах источника тока.

Написать уравнение по первому закону Кирхгофа для узла

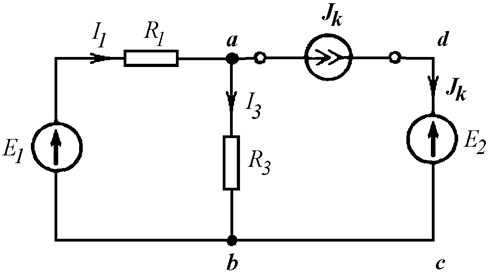
Уравнение по первому закону Кирхгофа для узла a содержит источник тока и имеет вид:

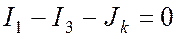
Для того чтобы написать уравнение по второму закону Кирхгофа для контура abcd, заменяем источник тока напряжением на его выводах (

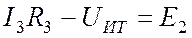
Для упрощения расчетов источник тока с параллельным сопротивлением можно заменить на эквивалентный источник ЭДС (Рис. 4.7). После расчета необходимо обязательно вернуться к исходной схеме.

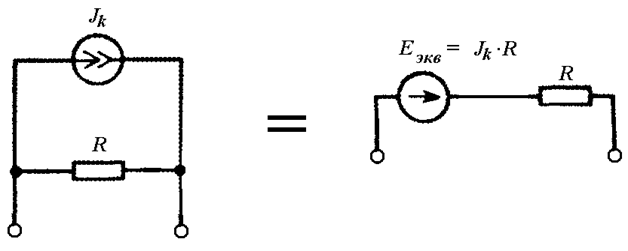
Независимый контур цепи

В принципе, по второму закону Кирхгофа можно составить столько уравнений, сколько контуров содержит цепь. Но не все эти уравнения будут независимыми. Для определения независимости уравнений по второму закону Кирхгофа вводится такое понятие как независимый контур цепи.

Независимый контур цепи – это такой контур, который содержит хотя бы одну новую ветвь, не вошедшую в другие контуры цепи.

Независимые контуры в общем случае выбираются произвольно, но проще всего выбирать их так, чтобы они совпадали с ячейками цепи (Рис. 4.8 б).

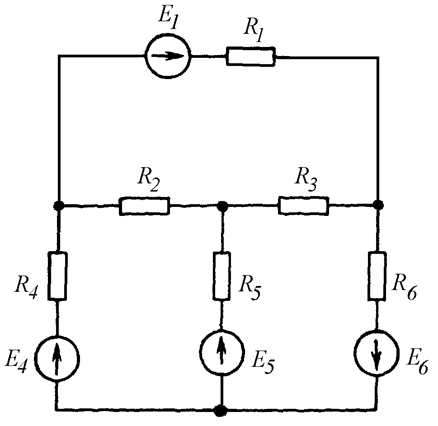
Если схема содержит 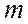ветвей и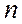

.

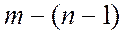Схема на Рис. 4.8 б содержит три независимых контура.

5. СИСТЕМА УРАВНЕНИЙ ПО ЗАКОНАМ КИРХГОФА ДЛЯ РАСЧЕТА ТОКОВ ЦЕПИ

Законы Кирхгофа можно использовать для расчета токов в ветвях цепи. Главное требование при этом – получение системы независимых уравнений, в которой число неизвестных равно количеству токов, подлежащих определению.

Алгоритм составления системы уравнений по законам Кирхгофа

• АлтГТУ 419
• АлтГУ 113
• АмПГУ 296
• АГТУ 266
• БИТТУ 794
• БГТУ «Военмех» 1191
• БГМУ 172
• БГТУ 602
• БГУ 153
• БГУИР 391
• БелГУТ 4908
• БГЭУ 962
• БНТУ 1070
• БТЭУ ПК 689
• БрГУ 179
• ВНТУ 119
• ВГУЭС 426
• ВлГУ 645
• ВМедА 611
• ВолгГТУ 235
• ВНУ им. Даля 166
• ВЗФЭИ 245
• ВятГСХА 101
• ВятГГУ 139
• ВятГУ 559
• ГГДСК 171
• ГомГМК 501
• ГГМУ 1967
• ГГТУ им. Сухого 4467
• ГГУ им. Скорины 1590
• ГМА им. Макарова 300
• ДГПУ 159
• ДальГАУ 279
• ДВГГУ 134
• ДВГМУ 409
• ДВГТУ 936
• ДВГУПС 305
• ДВФУ 949
• ДонГТУ 497
• ДИТМ МНТУ 109
• ИвГМА 488
• ИГХТУ 130
• ИжГТУ 143
• КемГППК 171
• КемГУ 507
• КГМТУ 269
• КировАТ 147
• КГКСЭП 407
• КГТА им. Дегтярева 174
• КнАГТУ 2909
• КрасГАУ 370
• КрасГМУ 630
• КГПУ им. Астафьева 133
• КГТУ (СФУ) 567
• КГТЭИ (СФУ) 112
• КПК №2 177
• КубГТУ 139
• КубГУ 107
• КузГПА 182
• КузГТУ 789
• МГТУ им. Носова 367
• МГЭУ им. Сахарова 232
• МГЭК 249
• МГПУ 165
• МАИ 144
• МАДИ 151
• МГИУ 1179
• МГОУ 121
• МГСУ 330
• МГУ 273
• МГУКИ 101
• МГУПИ 225
• МГУПС (МИИТ) 636
• МГУТУ 122
• МТУСИ 179
• ХАИ 656
• ТПУ 454
• НИУ МЭИ 641
• НМСУ «Горный» 1701
• ХПИ 1534
• НТУУ «КПИ» 212
• НУК им. Макарова 542
• НВ 777
• НГАВТ 362
• НГАУ 411
• НГАСУ 817
• НГМУ 665
• НГПУ 214
• НГТУ 4610
• НГУ 1992
• НГУЭУ 499
• НИИ 201
• ОмГТУ 301
• ОмГУПС 230
• СПбПК №4 115
• ПГУПС 2489
• ПГПУ им. Короленко 296
• ПНТУ им. Кондратюка 119
• РАНХиГС 186
• РОАТ МИИТ 608
• РТА 243
• РГГМУ 118
• РГПУ им. Герцена 124
• РГППУ 142
• РГСУ 162
• «МАТИ» — РГТУ 121
• РГУНиГ 260
• РЭУ им. Плеханова 122
• РГАТУ им. Соловьёва 219
• РязГМУ 125
• РГРТУ 666
• СамГТУ 130
• СПбГАСУ 318
• ИНЖЭКОН 328
• СПбГИПСР 136
• СПбГЛТУ им. Кирова 227
• СПбГМТУ 143
• СПбГПМУ 147
• СПбГПУ 1598
• СПбГТИ (ТУ) 292
• СПбГТУРП 235
• СПбГУ 582
• ГУАП 524
• СПбГУНиПТ 291
• СПбГУПТД 438
• СПбГУСЭ 226
• СПбГУТ 193
• СПГУТД 151
• СПбГУЭФ 145
• СПбГЭТУ «ЛЭТИ» 380
• ПИМаш 247
• НИУ ИТМО 531
• СГТУ им. Гагарина 114
• СахГУ 278
• СЗТУ 484
• СибАГС 249
• СибГАУ 462
• СибГИУ 1655
• СибГТУ 946
• СГУПС 1513
• СибГУТИ 2083
• СибУПК 377
• СФУ 2423
• СНАУ 567
• СумГУ 768
• ТРТУ 149
• ТОГУ 551
• ТГЭУ 325
• ТГУ (Томск) 276
• ТГПУ 181
• ТулГУ 553
• УкрГАЖТ 234
• УлГТУ 536
• УИПКПРО 123
• УрГПУ 195
• УГТУ-УПИ 758
• УГНТУ 570
• УГТУ 134
• ХГАЭП 138
• ХГАФК 110
• ХНАГХ 407
• ХНУВД 512
• ХНУ им. Каразина 305
• ХНУРЭ 324
• ХНЭУ 495
• ЦПУ 157
• ЧитГУ 220
• ЮУрГУ 306

Полный список ВУЗов

Чтобы распечатать файл, скачайте его (в формате Word).

Законы Кирхгофа устанавливают соотношения между токами и напряжениями в разветвленных электрических цепях произвольного типа. Законы Кирхгофа имеют особое значение в электротехнике из-за своей универсальности, так как пригодны для решения любых электротехнических задач. Законы Кирхгофа справедливы для линейных и нелинейных цепей при постоянных и переменных напряжениях и токах.

Первый закон Кирхгофа вытекает из закона сохранения заряда. Он состоит в том, что алгебраическая сумма токов, сходящихся в любом узле, равна нулю.

где – число токов, сходящихся в данном узле. Например, для узла электрической цепи (рис. 1) уравнение по первому закону Кирхгофа можно записать в виде I1 – I2 + I3 – I4 + I5 = 0

В этом уравнении токи, направленные к узлу, приняты положительными.

Физически первый закон Кирхгофа – это закон непрерывности электрического тока.

Второй закон Кирхгофа: алгебраическая сумма падений напряжений на отдельных участках замкнутого контура, произвольно выделенного в сложной разветвленной цепи, равна алгебраической сумме ЭДС в этом контуре

где k – число источников ЭДС; m – число ветвей в замкнутом контуре; Ii , Ri – ток и сопротивление i -й ветви.

Так, для замкнутого контура схемы (рис. 2 ) Е1 – Е2 + Е3 = I1R1 – I2R2 + I3R3 – I4R4

Замечание о знаках полученного уравнения:

1) ЭДС положительна, если ее направление совпадает с направлением произвольно выбранного обхода контура;

2) падение напряжения на резисторе положительно, если направление тока в нем совпадает с направлением обхода.

Физически второй закон Кирхгофа характеризует равновесие напряжений в любом контуре цепи.

Расчет разветвленной электрической цепи с помощью законов Кирхгофа

Метод законов Кирхгофа заключается в решении системы уравнений, составленных по первому и второму законам Кирхгофа.

Метод заключается в составлении уравнений по первому и второму законам Кирхгофа для узлов и контуров электрической цепи и решении этих уравнений с целью определения неизвестных токов в ветвях и по ним – напряжений. Поэтому число неизвестных равно числу ветвей b , следовательно, столько же независимых уравнений необходимо составить по первому и второму законам Кирхгофа.

Число уравнений, которые можно составить на основании первого закона, равно числу узлов цепи, причем только ( y – 1) уравнений являются независимыми друг от друга.

Независимость уравнений обеспечивается выбором узлов. Узлы обычно выбирают так, чтобы каждый последующий узел отличался от смежных узлов хотя бы одной ветвью. Остальные уравнения составляются по второму закону Кирхгофа для независимых контуров, т.е. число уравнений b – (y – 1) = b – y +1 .

Контур называется независимым, если он содержит хотя бы одну ветвь, не входящую в другие контуры.

Составим систему уравнений Кирхгофа для электрической цепи (рис. 3 ). Схема содержит четыре узла и шесть ветвей.

Поэтому по первому закону Кирхгофа составим y – 1 = 4 – 1 = 3 уравнения, а по второму b – y + 1 = 6 – 4 + 1 = 3 , также три уравнения.

Произвольно выберем положительные направления токов во всех ветвях (рис. 4 ). Направление обхода контуров выбираем по часовой стрелке.

Составляем необходимое число уравнений по первому и второму законам Кирхгофа

Полученная система уравнений решается относительно токов. Если при расчете ток в ветви получился с минусом, то его направление противоположно принятому направлению.
Потенциальная диаграмма – это графическое изображение второго закона Кирхгофа, которая применяется для проверки правильности расчетов в линейных резистивных цепях. Потенциальная диаграмма строится для контура без источников тока, причем потенциалы точек начала и конца диаграммы должны получиться одинаковыми.

Рассмотрим контур abcda схемы, изображенной на рис. 4. В ветке ab между резистором R1 и ЭДС E1 обозначим дополнительную точку k.

Рис. 4. Контур для построения потенциальной диаграммы

Потенциал любого узла принимаем равным нулю (например, ?а= 0), выбираем обход контура и определяем потенциалы точек контура: ?а = 0, ?к = ?а – I1R1 , ? b = ? к + Е1, ?с = ? b – I2R2 , ? d = ?c – Е2, ? a = ?d + I3R3 = 0

При построении потенциальной диаграммы необходимо учитывать, что сопротивление ЭДС равно нулю (рис. 5 ).

Рис. 5. Потенциальная диаграмма

Законы Кирхгофа в комплексной форме

Для цепей синусоидального тока законы Кирхгофа формулируются так же, как и для цепей постоянного тока, но только для комплексных значений токов и напряжений.

Первый закон Кирхгофа : «алгебраическая сумма комплексов тока в узле электрической цепи равна нулю»

Второй закон Кирхгофа : «в любом замкнутом контуре электрической цепи алгебраическая сумма комплексных ЭДС равна алгебраической сумме комплексных напряжений на всех пассивных элементах этого контура».

В сложных электрических цепях, то есть где имеется несколько разнообразных ответвлений и несколько источников ЭДС имеет место и сложное распределение токов. Однако при известных величинах всех ЭДС и сопротивлений резистивных элементов в цепи мы можем вычистить значения этих токов и их направление в любом контуре цепи с помощью первого и второго закона Кирхгофа. Суть законов Кирхгофа я довольно кратко изложил в своем учебнике по электронике, на страницах сайта http://www.sxemotehnika.ru.

Пример сложной электрической цепи вы можете посмотреть на рисунке 1.

Рисунок 1. Сложная электрическая цепь.

Иногда законы Кирхгофа называют правилами Кирхгофа, особенно в старой литературе.

Итак, для начала напомню все-таки суть первого и второго закона Кирхгофа, а далее рассмотрим примеры расчета токов, напряжений в электрических цепях, с практическими примерами и ответами на вопросы, которые задавались мне в комментариях на сайте.

Первый закон Кирхгофа

Формулировка №1: Сумма всех токов, втекающих в узел, равна сумме всех токов, вытекающих из узла.

Формулировка №2: Алгебраическая сумма всех токов в узле равна нулю.

Поясню первый закон Кирхгофа на примере рисунка 2.

Рисунок 2. Узел электрической цепи.

Здесь ток I₁ – ток, втекающий в узел , а токи I₂ и I₃ — токи, вытекающие из узла. Тогда применяя формулировку №1, можно записать:

Что бы подтвердить справедливость формулировки №2, перенесем токи I₂ и I ₃ в левую часть выражения (1), тем самым получим:

Знаки «минус» в выражении (2) и означают, что токи вытекают из узла.

Знаки для втекающих и вытекающих токов можно брать произвольно, однако в основном всегда втекающие токи берут со знаком «+», а вытекающие со знаком «-» (например как получилось в выражении (2)).

Можно посмотреть отдельный видеоурок по первому закону Кирхофа в разделе ВИДЕОУРОКИ.

Второй закон Кирхгофа.

Формулировка: Алгебраическая сумма ЭДС, действующих в замкнутом контуре, равна алгебраической сумме падений напряжения на всех резистивных элементах в этом контуре.

Здесь термин «алгебраическая сумма» означает, что как величина ЭДС так и величина падения напряжения на элементах может быть как со знаком «+» так и со знаком «-». При этом определить знак можно по следующему алгоритму:

1. Выбираем направление обхода контура (два варианта либо по часовой, либо против).

2. Произвольно выбираем направление токов через элементы цепи.

3. Расставляем знаки для ЭДС и напряжений, падающих на элементах по правилам:

– ЭДС, создающие ток в контуре, направление которого совпадает с направление обхода контура записываются со знаком «+», в противном случае ЭДС записываются со знаком «-».

– напряжения, падающие на элементах цепи записываются со знаком «+», если ток, протекающий через эти элементы совпадает по направлению с обходом контура, в противном случае напряжения записываются со знаком «-».

Например, рассмотрим цепь, представленную на рисунке 3, и запишем выражение согласно второму закону Кирхгофа, обходя контур по часовой стрелке, и выбрав направление токов через резисторы, как показано на рисунке.

Рисунок 3. Электрическая цепь, для пояснения второго закона Кирхгофа.

Предлагаю посмотреть отдельный видеоурок по второму закону Кирхогфа (теория).

Расчеты электрических цепей с помощью законов Кирхгофа.

Теперь давайте рассмотрим вариант сложной цепи, и я вам расскажу, как на практике применять законы Кирхгофа.

Итак, на рисунке 4 имеется сложная цепь с двумя источниками ЭДС величиной E₁=12 в и E₂=5 в , с внутренним сопротивлением источников r₁=r₂=0,1 Ом, работающих на общую нагрузку R = 2 Ома. Как же будут распределены токи в этой цепи, и какие они имеют значения, нам предстоит выяснить.

Рисунок 4. Пример расчета сложной электрической цепи.

Теперь согласно первому закону Кирхгофа для узла А составляем такое выражение:

так как I₁ и I ₂ втекают в узел А , а ток I вытекает из него.

Используя второй закон Кирхгофа, запишем еще два выражения для внешнего контура и внутреннего левого контура, выбрав направление обхода по часовой стрелке.

Для внешнего контура:

Для внутреннего левого контура:

Итак, у нас получилась система их трех уравнений с тремя неизвестными:

Теперь подставим в эту систему известные нам величины напряжений и сопротивлений:

12 = 0,1I₁ +2I.

Далее из первого и второго уравнения выразим ток I₂

12 = 0,1I₁ + 2I.

Следующим шагом приравняем первое и второе уравнение и получим систему из двух уравнений:

12 = 0,1I₁ + 2I.

Выражаем из первого уравнения значение I

I = 2I₁– 70;

И подставляем его значение во второе уравнение

Решаем полученное уравнение

12 = 0,1I₁ + 4I₁ – 140.

12 + 140= 4,1I₁

Теперь в выражение I = 2I₁– 70 подставим значение

I₁=37,073 (А) и получим:

I = 2*37,073 – 70 = 4,146 А

Ну, а согласно первому закона Кирхгофа ток I₂=I – I₁

I₂=4,146 – 37,073 = -32,927

Знак «минус» для тока I₂ означает, то что мы не правильно выбрали направление тока, то есть в нашем случае ток I ₂ вытекает из узла А .

Теперь полученные данные можно проверить на практике или смоделировать данную схему например в программе Multisim.

Скриншот моделирования схемы для проверки законов Кирхгофа вы можете посмотреть на рисунке 5.

Рисунок 5. Сравнение результатов расчета и моделирования работы цепи.

Для закрепления результатата предлагаю посмотреть подготовленное мной видео:

ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!

Метод контурных токов. — Студопедия

Один из методов анализа электрической цепи является метод контурных токов. Основой для него служит второй закон Кирхгофа. Главное его преимущество это уменьшение количества уравнений до m – n +1, напоминаем что m — количество ветвей, а n — количество узлов в цепи. На практике такое уменьшение существенно упрощает расчет.

Контурный ток — это величина, которая одинакова во всех ветвях данного контура. Обычно в расчетах они обозначаются двойными индексами, например I₁₁, I₂₂ и тд.

Действительный ток в определенной ветви определяется алгебраической суммой контурных токов, в которую эта ветвь входит. Нахождение действительных токов и есть первоочередная задача метода контурных токов.

Контурная ЭДС — это сумма всех ЭДС входящих в этот контур.

Собственным сопротивлением контура называется сумма сопротивлений всех ветвей, которые в него входят.

Общим сопротивлением контура называется сопротивление ветви, смежное двум контурам.

Общий план составления уравнений

1 – Выбор направления действительных токов.

2 – Выбор независимых контуров и направления контурных токов в них.

3 – Определение собственных и общих сопротивлений контуров

4 – Составление уравнений и нахождение контурных токов

5 – Нахождение действительных токов

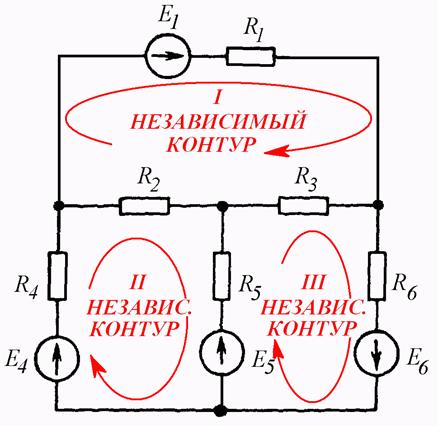
Итак, после ознакомления с теорией предлагаем приступить к практике! Рассмотрим пример.

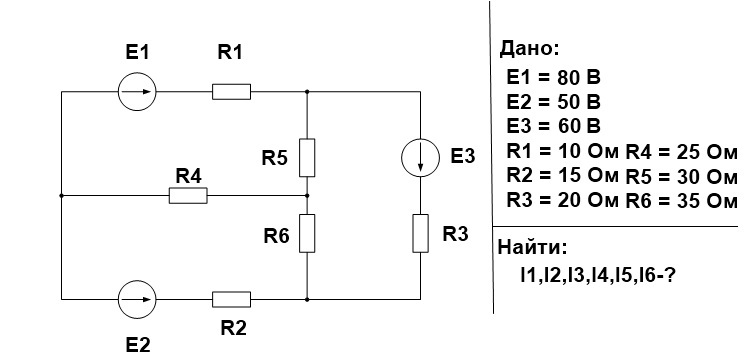
Выполняем все поэтапно.

1. Произвольно выбираем направления действительных токов I₁-I₆.

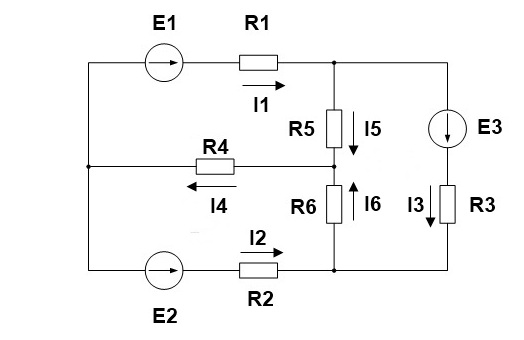
2.Выделяем три контура, а затем указываем направление контурных токов I₁₁,I₂₂,I₃₃. Мы выберем направление по часовой стрелке.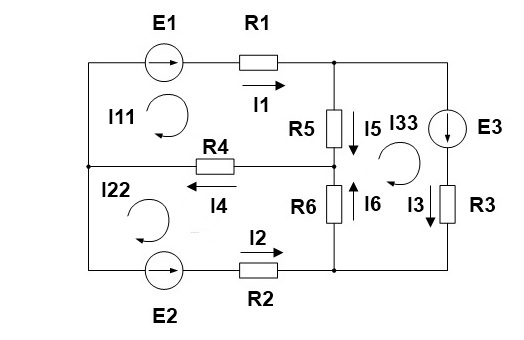

3. Определяем собственные сопротивления контуров. Для этого складываем сопротивления в каждом контуре.

R₁₁=R₁+R₄+R₅=10+25+30= 65 Ом

R₂₂=R₂+R₄+R₆=15+25+35 = 75 Ом

R₃₃=R₃+R₅+R₆=20+30+35= 85 Ом

Затем определяем общие сопротивления, общие сопротивления легко обнаружить, они принадлежат сразу нескольким контурам, например сопротивление R₄ принадлежит контуру 1 и контуру 2. Поэтому для удобства обозначим такие сопротивления номерами контуров к которым они принадлежат.

R₁₂=R₂₁=R₄=25 Ом

R₂₃=R₃₂=R₆=35 Ом

R₃₁=R₁₃=R₅=30 Ом

4. Приступаем к основному этапу – составлению системы уравнений контурных токов. В левой части уравнений входят падения напряжений в контуре, а в правой ЭДС источников данного контура.

Так как контура у нас три, следовательно, система будет состоять из трех уравнений. Для первого контура уравнение будет выглядеть следующим образом:

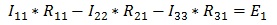
Ток первого контура I₁₁, умножаем на собственное сопротивление R₁₁ этого же контура, а затем вычитаем ток I₂₂, помноженный на общее сопротивление первого и второго контуров R₂₁ и ток I₃₃, помноженный на общее сопротивление первого и третьего контура R₃₁. Данное выражение будет равняться ЭДС E₁ этого контура. Значение ЭДС берем со знаком плюс, так как направление обхода (по часовой стрелке) совпадает с направление ЭДС, в противном случае нужно было бы брать со знаком минус.

Те же действия проделываем с двумя другими контурами и в итоге получаем систему:

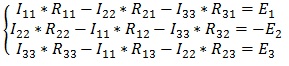
В полученную систему подставляем уже известные значения сопротивлений и решаем её любым известным способом.

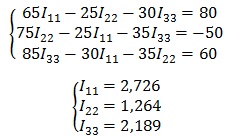
5. Последним этапом находим действительные токи, для этого нужно записать для них выражения.

Контурный ток равен действительному току, который принадлежит только этому контуру. То есть другими словами, если ток протекает только в одном контуре, то он равен контурному.

Но, нужно учитывать направление обхода, например, в нашем случае ток I2 не совпадает с направлением, поэтому берем его со знаком минус.

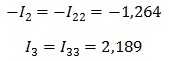
Токи, протекающие через общие сопротивления определяем как алгебраическую сумму контурных, учитывая направление обхода.

Например, через резистор R₄ протекает ток I₄, его направление совпадает с направлением обхода первого контура и противоположно направлению второго контура. Значит, для него выражение будет выглядеть

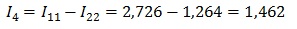
А для остальных

Как расставить направление токов в цепи

Один из методов анализа электрической цепи является метод контурных токов. Основой для него служит второй закон Кирхгофа. Главное его преимущество это уменьшение количества уравнений до m – n +1, напоминаем что m – количество ветвей, а n – количество узлов в цепи. На практике такое уменьшение существенно упрощает расчет.

Основные понятия

Контурный ток – это величина, которая одинакова во всех ветвях данного контура. Обычно в расчетах они обозначаются двойными индексами, например I₁₁, I₂₂ и тд.

Действительный ток в определенной ветви определяется алгебраической суммой контурных токов, в которую эта ветвь входит. Нахождение действительных токов и есть первоочередная задача метода контурных токов.

Контурная ЭДС – это сумма всех ЭДС входящих в этот контур.

Собственным сопротивлением контура называется сумма сопротивлений всех ветвей, которые в него входят.

Общим сопротивлением контура называется сопротивление ветви, смежное двум контурам.

Общий план составления уравнений

1 – Выбор направления действительных токов.

2 – Выбор независимых контуров и направления контурных токов в них.

3 – Определение собственных и общих сопротивлений контуров

4 – Составление уравнений и нахождение контурных токов

5 – Нахождение действительных токов

Итак, после ознакомления с теорией предлагаем приступить к практике! Рассмотрим пример.

Выполняем все поэтапно.

1. Произвольно выбираем направления действительных токов I₁-I₆.

2. Выделяем три контура, а затем указываем направление контурных токов I₁₁,I₂₂,I₃₃. Мы выберем направление по часовой стрелке.

3. Определяем собственные сопротивления контуров. Для этого складываем сопротивления в каждом контуре.

Затем определяем общие сопротивления, общие сопротивления легко обнаружить, они принадлежат сразу нескольким контурам, например сопротивление R₄ принадлежит контуру 1 и контуру 2. Поэтому для удобства обозначим такие сопротивления номерами контуров к которым они принадлежат.

4. Приступаем к основному этапу – составлению системы уравнений контурных токов. В левой части уравнений входят падения напряжений в контуре, а в правой ЭДС источников данного контура.

Так как контура у нас три, следовательно, система будет состоять из трех уравнений. Для первого контура уравнение будет выглядеть следующим образом:

Ток первого контура I₁₁, умножаем на собственное сопротивление R₁₁ этого же контура, а затем вычитаем ток I₂₂, помноженный на общее сопротивление первого и второго контуров R₂₁ и ток I₃₃, помноженный на общее сопротивление первого и третьего контура R₃₁. Данное выражение будет равняться ЭДС E₁ этого контура. Значение ЭДС берем со знаком плюс, так как направление обхода (по часовой стрелке) совпадает с направление ЭДС, в противном случае нужно было бы брать со знаком минус.

Те же действия проделываем с двумя другими контурами и в итоге получаем систему:

В полученную систему подставляем уже известные значения сопротивлений и решаем её любым известным способом.

5. Последним этапом находим действительные токи, для этого нужно записать для них выражения.

Контурный ток равен действительному току, который принадлежит только этому контуру. То есть другими словами, если ток протекает только в одном контуре, то он равен контурному.

Но, нужно учитывать направление обхода, например, в нашем случае ток I2 не совпадает с направлением, поэтому берем его со знаком минус.

Токи, протекающие через общие сопротивления определяем как алгебраическую сумму контурных, учитывая направление обхода.

Например, через резистор R₄ протекает ток I₄, его направление совпадает с направлением обхода первого контура и противоположно направлению второго контура. Значит, для него выражение будет выглядеть

А для остальных

Так решаются задачи методом контурных токов. Надеемся что вам пригодится данный материал, удачи!

Один из методов анализа электрической цепи является метод контурных токов. Основой для него служит второй закон Кирхгофа. Главное его преимущество это уменьшение количества уравнений до m – n +1, напоминаем что m – количество ветвей, а n – количество узлов в цепи. На практике такое уменьшение существенно упрощает расчет.

Основные понятия

Контурный ток – это величина, которая одинакова во всех ветвях данного контура. Обычно в расчетах они обозначаются двойными индексами, например I₁₁, I₂₂ и тд.

Действительный ток в определенной ветви определяется алгебраической суммой контурных токов, в которую эта ветвь входит. Нахождение действительных токов и есть первоочередная задача метода контурных токов.

Контурная ЭДС – это сумма всех ЭДС входящих в этот контур.

Собственным сопротивлением контура называется сумма сопротивлений всех ветвей, которые в него входят.

Общим сопротивлением контура называется сопротивление ветви, смежное двум контурам.

Общий план составления уравнений

1 – Выбор направления действительных токов.

2 – Выбор независимых контуров и направления контурных токов в них.

3 – Определение собственных и общих сопротивлений контуров

4 – Составление уравнений и нахождение контурных токов

5 – Нахождение действительных токов

Итак, после ознакомления с теорией предлагаем приступить к практике! Рассмотрим пример.

Выполняем все поэтапно.

1. Произвольно выбираем направления действительных токов I₁-I₆.

2. Выделяем три контура, а затем указываем направление контурных токов I₁₁,I₂₂,I₃₃. Мы выберем направление по часовой стрелке.

3. Определяем собственные сопротивления контуров. Для этого складываем сопротивления в каждом контуре.

Затем определяем общие сопротивления, общие сопротивления легко обнаружить, они принадлежат сразу нескольким контурам, например сопротивление R₄ принадлежит контуру 1 и контуру 2. Поэтому для удобства обозначим такие сопротивления номерами контуров к которым они принадлежат.

4. Приступаем к основному этапу – составлению системы уравнений контурных токов. В левой части уравнений входят падения напряжений в контуре, а в правой ЭДС источников данного контура.

Так как контура у нас три, следовательно, система будет состоять из трех уравнений. Для первого контура уравнение будет выглядеть следующим образом:

Ток первого контура I₁₁, умножаем на собственное сопротивление R₁₁ этого же контура, а затем вычитаем ток I₂₂, помноженный на общее сопротивление первого и второго контуров R₂₁ и ток I₃₃, помноженный на общее сопротивление первого и третьего контура R₃₁. Данное выражение будет равняться ЭДС E₁ этого контура. Значение ЭДС берем со знаком плюс, так как направление обхода (по часовой стрелке) совпадает с направление ЭДС, в противном случае нужно было бы брать со знаком минус.

Те же действия проделываем с двумя другими контурами и в итоге получаем систему:

В полученную систему подставляем уже известные значения сопротивлений и решаем её любым известным способом.

5. Последним этапом находим действительные токи, для этого нужно записать для них выражения.

Контурный ток равен действительному току, который принадлежит только этому контуру. То есть другими словами, если ток протекает только в одном контуре, то он равен контурному.

Но, нужно учитывать направление обхода, например, в нашем случае ток I2 не совпадает с направлением, поэтому берем его со знаком минус.

Токи, протекающие через общие сопротивления определяем как алгебраическую сумму контурных, учитывая направление обхода.

Например, через резистор R₄ протекает ток I₄, его направление совпадает с направлением обхода первого контура и противоположно направлению второго контура. Значит, для него выражение будет выглядеть

А для остальных

Так решаются задачи методом контурных токов. Надеемся что вам пригодится данный материал, удачи!

Для электрической цепи рис. 1, выполнить следующее:

1. Составить уравнения для определения токов путем непосредственного применения законов Кирхгофа. Решать эту систему уравнений не следует.
2. Определить токи в ветвях методом контурных токов.
3. Построить потенциальную диаграмму для любого замкнутого контура, содержащего обе ЭДС.
4. Определить режимы работы активных элементов и составить баланс мощностей.

Значения ЭДС источников и сопротивлений приемников:
E1 = 130 В, Е2 = 110 В, R1 = 4 Ом, R2 = 8 Ом, R3 = 21 Ом, R4 = 16 Ом, R5 = 19 Ом, R6 = 16 Ом.

Смотрите также
Пример решения схемы методом контурных токов № 1
Пример решения схемы методом контурных токов № 2
Пример решения схемы методом контурных токов № 3
Пример решения схемы методом контурных токов № 4
Пример решения схемы методом контурных токов № 5
Посмотреть видео «Метод контурных токов 2» (пример решения конкретной задачи)

1. Произвольно расставим направления токов в ветвях цепи, примем направления обхода контуров (против часовой стрелки), обозначим узлы.

Рис. 2

2. Для получения системы уравнений по законам Кирхгофа для расчета токов в ветвях цепи составим по 1-му закону Кирхгофа 3 уравнения (на 1 меньше числа узлов в цепи) для узлов 1,2,3:

По второму закону Кирхгофа составим m – (р – 1) уравнений (где m – кол-во ветвей, р – кол-во узлов ), т.е. 6 – (4 – 1) = 3 для контуров I11, I22, I33:



Токи и напряжения совпадающие с принятым направлением обхода с «+», несовпадающие с «-».
Т.е. полная система уравнений для нашей цепи, составленная по законам Кирхгофа:

3. Определим токи в ветвях методом контурных токов. Зададимся направлениями течения контурных токов в каждом контуре схемы и обозначим их I11, I22, I33 (см. рис. 2)

4. Определим собственные сопротивления трех контуров нашей цепи, а так же взаимное сопротивление контуров:

(Ом)
(Ом)
(Ом)
(Ом)
(Ом)
(Ом)

5. Составим систему уравнений для двух контуров нашей цепи:

Подставим числовые значения и решим.

(А)
(А)
(А)

Определим фактические токи в ветвях цепи:
(А) направление совпадает с выбранным
(А) направление совпадает с выбранным
(А) направление совпадает с выбранным
(А) направление тока потивоположно выбранному
(А) направление совпадает с выбранным
(А) направление совпадает с выбранным

6. Проверим баланс мощностей:

(ВА)
Небольшая разница в полученных результатах является результатом погрешности при округлении числовых значений токов и сопротивлений.

7. Построим потенциальную диаграмму контура изображенного на рис. 3. В качестве начальной точки примем узел 1.

Рис.3

Для построения потенциальной диаграммы определим падения напряжения на каждом сопротивлении, входящем в выбранный контур.
(В)
(В)
(В)
(В)
Потенциал увеличивается если обход осуществляется против направления тока, и понижается если направление обхода совпадает с направлением тока. На участке с ЭДС потенциал изменяется на величину ЭДС. Потенциал повышается в том случае, когда переход от одной точки к другой осуществляется по направлению ЭДС и понижается когда переход осуществляется против направления ЭДС.

Рис. 4. Потенциальная диаграмма. ЗАКАЗАТЬ РАБОТУ!

Направление обхода контура — Энциклопедия по машиностроению XXL Матричные уравнения (3.28) и (3,29) соответствуют двум противоположным направлениям обхода контура от звена k к звену О, Приравнивая правые части выражений (3.28) и (3.29), получаем матричное уравнение замкнутости контура  [c.107]

Процедура формирования М-матрицы заключается в следующем каждая хорда графа поочередно включается в дерево, при этом образуется замкнутый контур выполняется обход этого контура в направлении, заданном направлением хорды в строке матрицы, соответствующей данной хорде, ставится -Ы, если направление ветви дерева совпадает с направлением обхода контура,  [c.112]

Направление равнодействующей силы R по контуру силового треугольника противоположно направлению обхода контура треугольника, определяемому слагаемыми силами.  [c.15]

Э. д. с. и токи принимаю положительными, если их направление совпадает с принятым направление обхода контура.  [c.110]

Таким образом, направление положительного изгибающего момента всегда совпадает с направлением обхода контура рамы.  [c.50]

Записываем уравнения изгибающих моментов по участка]и во всех трех системах (направление обхода контура рамы показано на рисунках стрелкой)  [c.115]

Изменение направления обхода контура на обратное влечет изменение знака циркуляции.  [c.50]

Остается сделать некоторые уточнения, относящиеся к выбору знаков. Будем считать, что система координат правая. Положительное направление нормали к поверхности S и положительное направление обхода контура Г таковы, что со стороны положительной нормали обход представляется происходящим против часовой стрелки. При переходе через поверхность 2 со стороны положительной нормали телесный угол получает отрицательное перемещение, равное —4я, и соответственно перемещение изменяется на величину вектора Бюргерса Ь. Следовательно, вектор Бюргерса представляет собою перемещение отрицательной стороны поверхности разреза по отношению к ее положительной стороне.  [c.461]

Что касается изображенных на рис. 16.15, а усилий, то нужно отметить, что ранее было выбрано положительное направление обхода контура, что и предопределило направление составляющих усилия Л/t и N . Равенства моментов, приведенные на рис. 16.15, б, следуют из сопоставления рис. 16.15, б с рис. 16.9, б, где изображены положительные направления моментов М , Му и Мху.  [c.383]

Поскольку в целом по контурам и С, /-интеграл должен быть равен нулю,, то необходимо, чтобы значения /-интеграла вдоль l и Са были взаимно равны (с учетом изменения знака интеграла при изменении направления обхода контура). Таким образом, доказана инвариантность /-интеграла  [c.63]

Стрелки всех векторов должны соответствовать одному п тому же направлению обхода контура.  [c.128]

Нетрудно понять, что интеграл (11.166) является циркуляцией касательного напряжения (см. формулу (11.108), учитывая при этом расположение вдоль касательной к контурной линии), вследствие чего (11.166) совпадает с (11.109), но на сей раз в (11.109) под g понимается Q/2 —площадь, ограниченная контурной линией замкнутого поперечного сечения тонкостенного профиля. Различие знаков в (11.109) и в (11.166) вызвано неодинаковым направлением обхода контура в сопоставляемых случаях.  [c.79]

Векторная сумма таких векторов представляет уравнение замкнутости векторного контура, эквивалентного контуру механизма. При этом векторы считаются положительными или отрицательными в зависимости от совпадения или противоположности их направлений направлению обхода контура. При наличии в цепи механизма нескольких сопряженных контуров соответственно увеличивается количество уравнений замкнутости векторных цепей, причем число этих уравнений должно быть минимальным при условии вхождения в них всех векторов, отображающих соответствующие звенья. Так, например, для сложной векторной цепи (рис. 15) можно составить три уравнения замкнутости цепи  [c.82]

При движении точки вдоль контура области Gi её образ перемещается вдоль контура L области G. Преобразование называется прямым или обратным в зависимости от того, будет ли при этом движении точек направление обхода контуров L i L- одинаковым или взаимно противоположным. Если определитель  [c.180]

Следует задаться положительным направлением обхода контура и совпадающим с ним направлением Положительное направление t2 соответствует вращению вектора tj на 90 против часовой стрелки а — угол между осью х и положительным направлением средней линии данной стенки f, — длина перпендикуляра из начала координат на стенку (касательную в случае криволинейной стенки) Гг — длина перпендикуляра на нормаль к стенке в исследуемой точке Г] и /-2 считаются положительными, если +Т[ и соответственно +Z2 создают вращение вокруг начала против часовой стрелки или, что то же, положительный момент М , вращающий против часовой стрелки, создает -Ьт и — -tj.  [c.183]

Следует задаться положительным направлением обхода контура и совпадающим с ним направлением 4-Ti. Положительное направление xj соответствует  [c.146]

В изолированные точки вырождаются эквидистанты окружности при R = H, а незамкнутые кривые получаются в том случае, если элементы эквидистанты накладываются друг на друга. Усеченная эквидистанта совпадает с полной эквидистантой только при отсутствии самопересечений. Знак параметра Н и направление обхода контура определяют построение внутренне или внешней эквидистанты. Так, при левом  [c.247]

Определим циркуляцию скорости по контрольному контуру При этом направление обхода контура примем совпадаю-ш,им с направлением циркуляции (фиг. 2).  [c.11]

Знаки токов определяются правилом буравчика если при движении рукоятки буравчика по направлению обхода контура тело движется в направлении тока, то последний считается положительным, в противоположном случае — отрицательным.  [c.217]

При вычислении циркуляции скорости знак циркуляции определяется выбранным направлением обхода контура.  [c.14]

Рис. 3.50. Фрагмент чертежа со стрелкой, указывающей направление обхода контура

Произвольный контур О в фазовом пространстве проектируется на двумерную координатную плоскость, соответствующую координате 9 и импульсу р,. При интегрировании на- правление обхода проекции Д это-Рг го контура определено направлением обхода контура О. Площадь 5, счита.-ется положительной, если проекция Д обходится по часовой стрелке.  [c.662]

Построим на свободных векторах а и Ь, приложенных г, точке Л, плоскостной элемент, имеющий форму параллелограмма AB D (рис. 7). Пусть положительное направление обхода контура этого элемента определяется направлением вектора а. Тогда дс-торным произведением векторов а и Ь назовем момент с плоскостного элемента А B D. Векторное произведение с векторов а и Ь обозначим так  [c.32]

Закон дистрибутивности является следствием теоремы о сложении моментов плоскостных элементов, доказанной в предыдущем параграфе. Действительно, векторное произведение с не изменится, если мы произвольным способом преобразуем векторы а и Ь, не изменяя их взаимного расположения, от которого зависит положительное направление обхода контура параллелограмма, а также сохраняя величину площади параллсмюграмма А B D. Следовательно, параллелограмм А B D всегда мо К ю заыенш ь эквивалентным прямоугольником.  [c.33]

Поскольку в целом по контурам L и С. /-интеграл доляам/ быть равегг пулю, то необходимо, мтг)бы значения У-ннтег])ала вдоль С, н С г были взаимтго равны (с учетом измепеини знака интеграла нри изменении направления обхода контура). Таким образом, доказана инвариантность /-интеграла  [c.57]

Пример 2(рис,1.У) демонстрирует возможности пакета ФАП-КФ, позволяющие создавать структурированную модель ГИ (подпрограмма P0LYQ2 рис.1.9,б), выполнять различные преобразования с получением новых моделей, штриховать необходимые области, отображать модели ГИ на графических устройствах (под-нрограммма ЕХАМР2 рис.1.9,а). Программные средства ФАП-КФ позволяют интерпретировать модель ГИ шестиугольника, как часть плоскости, лежаш,ую внутри его границы (отношение внутри/вне определяется направлением обхода контура), и применять теоретико-множественные операции объединения и пересечения над этими областями.  [c.23]

Обратим внимание на то, что АЬсе на плане скоростей подобен АВСЕ на плане механизма по взаимной перпендикулярности сторон. Кроме того, вершины этих треугольников расположены сходственно, т. е. буквы обоих контуров читаются в одной и той же последовательности при одинаковом направлении обхода контура при обходе контуров по ходу часовой стрелки получаем Ь, с, е и В, С, Е. Если Ьсе показать в положении, симметричном относительно отрезка Ьс, то сходственности расположения АЬсе и АВСЕ уже не будет.  [c.38]

Знаки величин S, S , Sy, 1°, /°, 1% зависят от направления обхода контура. Так, величины S, 1х, /у положительны ири обходе контура против часовой стрелки и отрицательны при обходе контура по часовой стрелке. Величины / ах- — тш также выдаются со знаком 1/, аз > 1/minl при обходе контура против часовой стрелки / ах [c.219]

Знак минус при суммировании членов появляется в связи с тем, что направление обхода контура (против часовой стрелки) противоположно направлению скорости на соот-ветствуюшгей стороне контура. Следовательно,  [c.93]

Для выбранного контура играет роль только одна компонента вектора вихря а , а именно компонента uji по оси xi, равная ТУ23- Здесь dS — единичный вектор, направленный вдоль выбранного контура, U — вектор вторичных токов (t/25 t/3), n — единичный вектор нормали к элементу рассматриваемой поверхности dF. Направления обхода контура С и нормаль п связаны так, чтобы обход был по часовой стрелке. Если в начальных сечениях струи вторичные токи отсутствуют, то oji = 0. Чтобы эта компонента вихря появилась, а следовательно, появились и вихревые вторичные токи, необходимо, чтобы было отлично от нуля выражение в правой части (3.1). Запишем уравнения движения для поперечной U2 и трансверсальной U3 компонент скорости, учитывая особенности струйных течений Р = р/р — давление, р = onst — плотность)  [c.583]

---

3. Направление обхода замкнутого контура.

Поскольку значение интеграла по замкнутому контуру зависит от направления интегрирования, условимся в качестве положительного направления обхода контурапринимать направление, при котором внутренняя область, ограниченная данным замкнутым контуром, остаетсяслеваот направления движения. Интегрирование в положительном направлении будем обозначать символом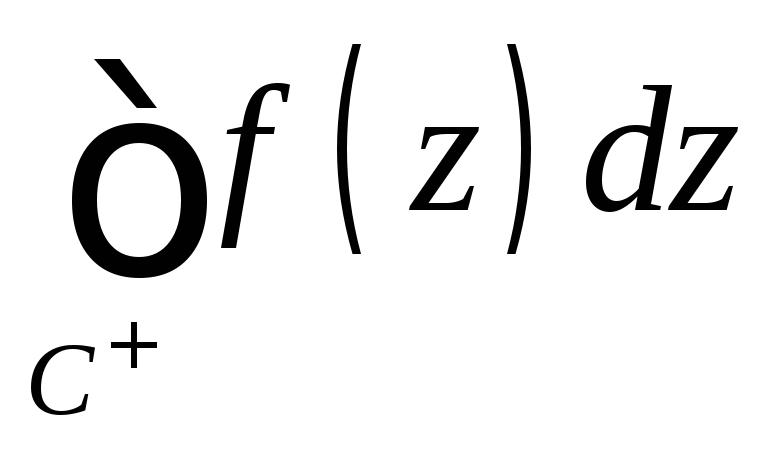или просто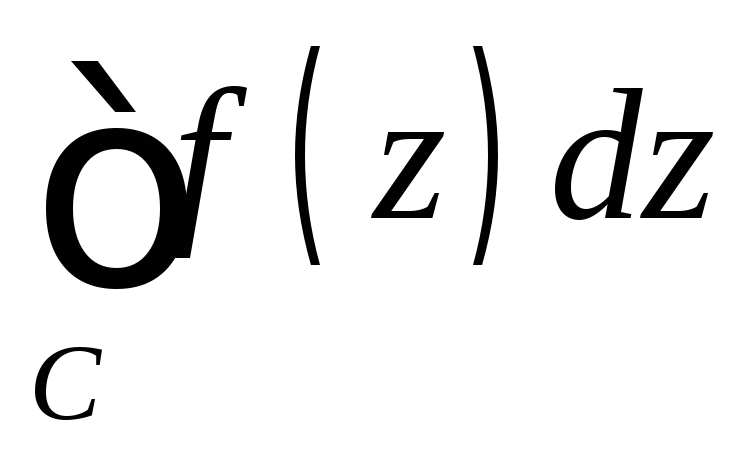, интегрирование в отрицательном направлении — символом.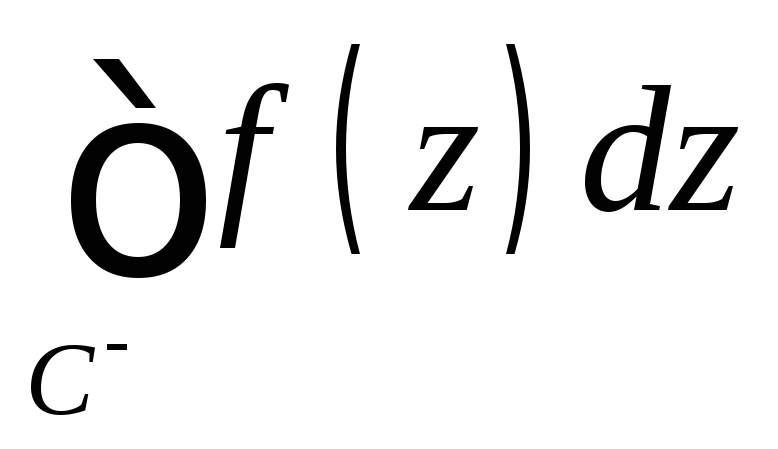

§ 6. Теорема Коши.

1. Вспомогательные положения.

Формула Грина. Пусть P(x,y), Q(x,y) C(),g – кусочно-гладкий контур и P_x, P_y, Q_x, Q_y C(g), тогда

.

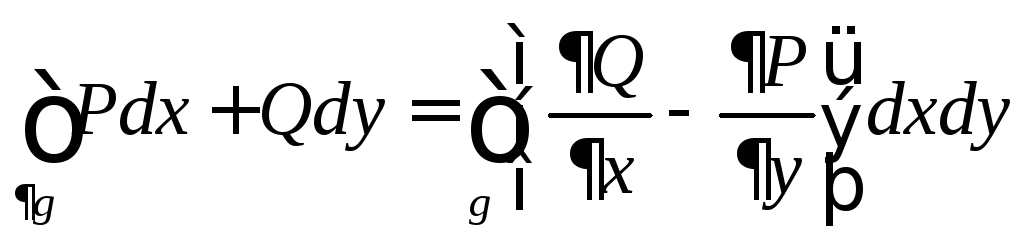2. Теорема Коши. Случай многосвязной области.

Определение. Область называется односвязной, если  две точки ее границы можно соединить непрерывной кривой, полностью принадлежащей границе области. В противном случае область называется многосвязной.

Теорема Коши. Если f(z)C^(g), в односвязной области g, то для замкнутого контура C g

.

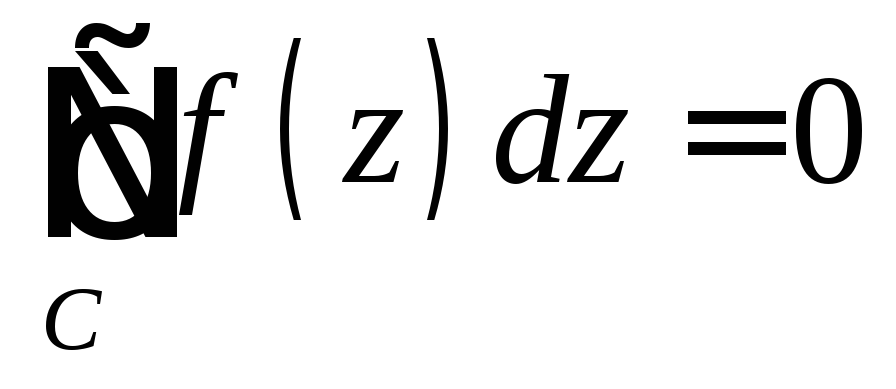Доказательство.

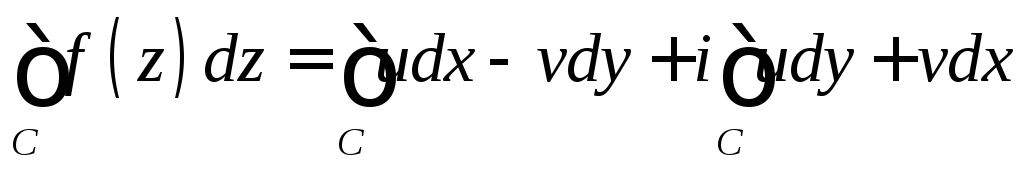=(формула Грина)=

= (-v_x-u_y)dxdy+i(u_x-v_y)dxdy=(условия Коши-Римана)=

= (u_y-u_y)dxdy+i(v_y-v_y)dxdy=0. 

Замечание.1) Требование односвязности области является существенным!

g = {z: 1<|z|<3} f(z)=1/zC^(g).

.

Определение Функция называется аналитической в замкнутой области f(z)C^(), еслиf(z)C^(g). и f(z)C().

Теорема Коши (вторая формулировка). Если f(z)C^(), g-односвязная, то.

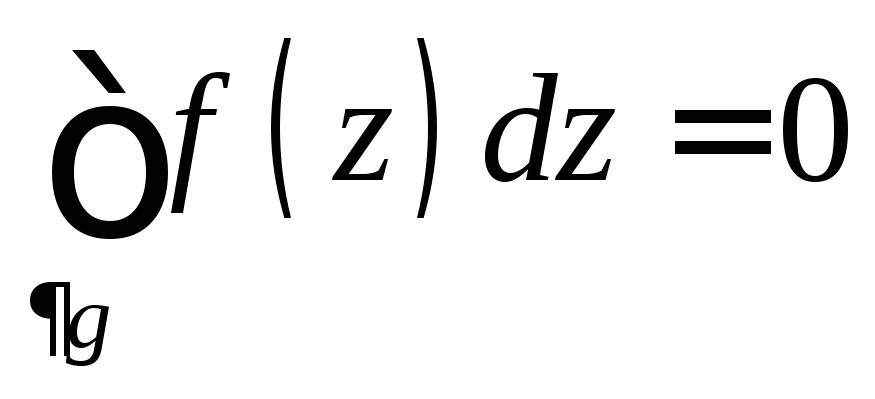Теорема Коши для многосвязной области. Пусть f(z)C^(), g-многосвязная, ограниченная извне контуромC₀, а изнутри контурами C₁, C₂,…,C_n . Тогда .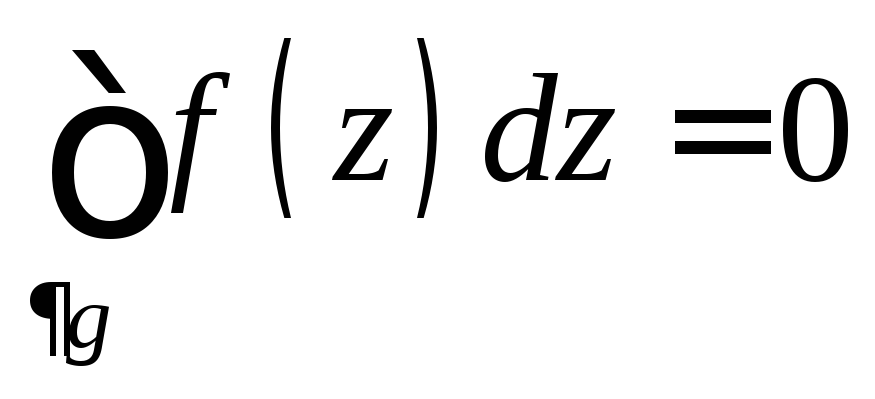

g= C₀C₁C₂…C_n

Доказательство. Проведем гладкие кривые 1,2,…,n, соединяющие контур C0 с контурами C1, C2,…,Cn и не пересекающиеся между собой. Тогда область, ограниченная кривыми C0,C1,C2,…,Cn и кривыми 1,2,…,n, проходимыми дважды в противоположных направлениях

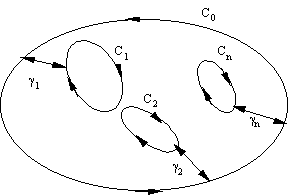
окажется односвязной => интеграл по границе этой области равен 0. Но интегралы по вспомогательным кривым ₁,₂,…,_n проходятся дважды в противоположных направлениях и при суммировании интегралов выпадают.

• .

3. Неопределенный интеграл функции комплексной переменной.

Если g- односвязная и f(z)C^(g), то для z₁, z₂g не зависит от пути интегрирования Т.о. при фиксированномz₀ интеграл 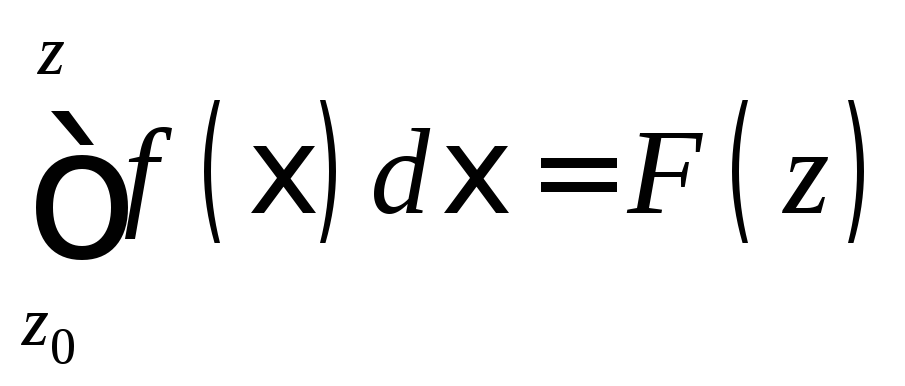— функция толькоz!

Определение. Пусть g-односвязная область, f(z)C(g) (не обязательно аналитическая!) и для  замкнутого контура g 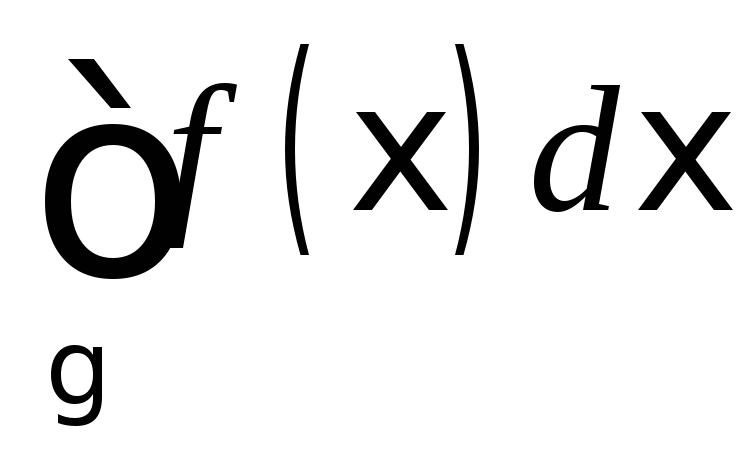=0. Функция— называетсянеопределенным интегралом от f(z).

Теорема 6.1.

Пусть g-односвязная, f(z)C(g) и для  замкнутого контура g 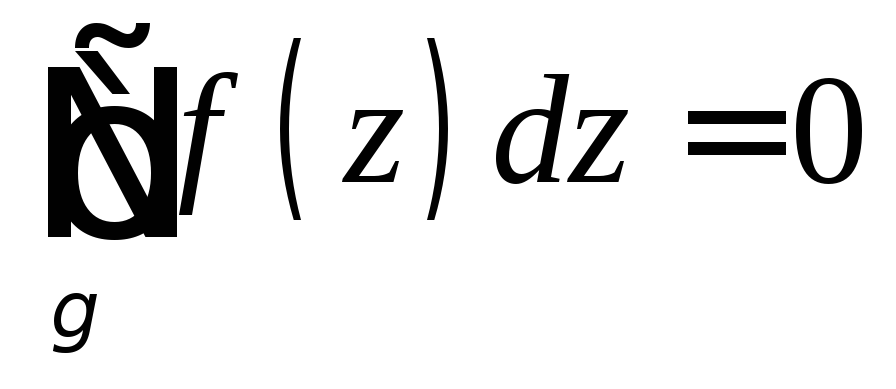, тогда,F(z)C^(g) и .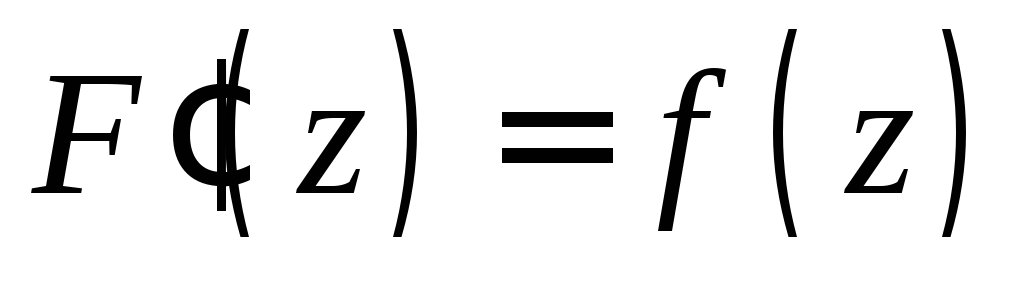

Доказательство.

В силу 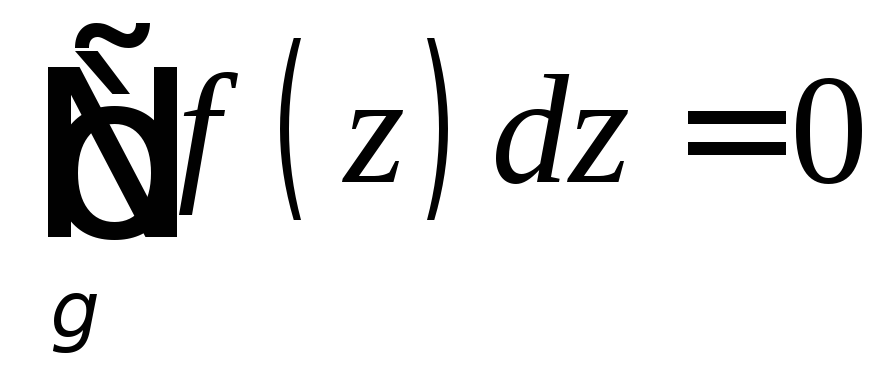длязамкнутого контура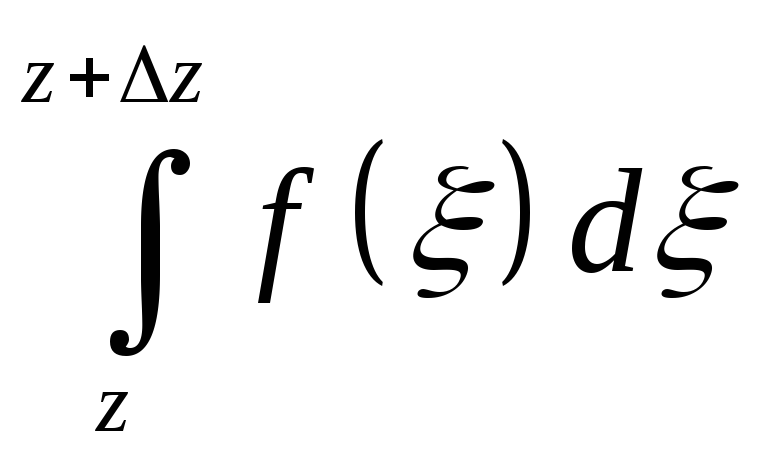не зависит от пути интегрирования => можем взять отрезок прямой, соединяющий точкиz иz

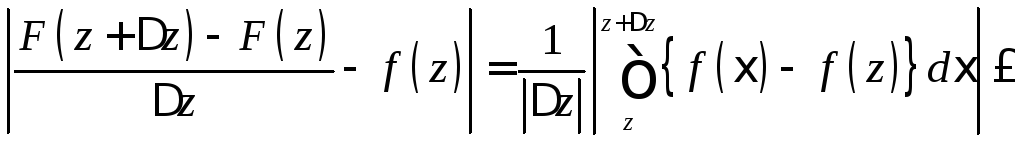
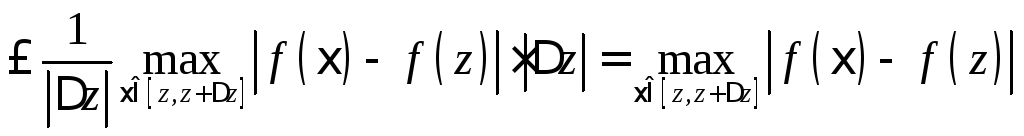
В силу непрерывности f(z) правая часть неравенства может быть сделана меньше<0 для=>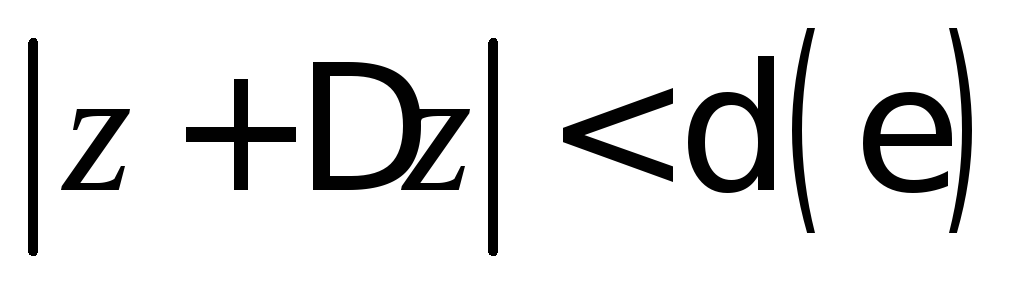

.

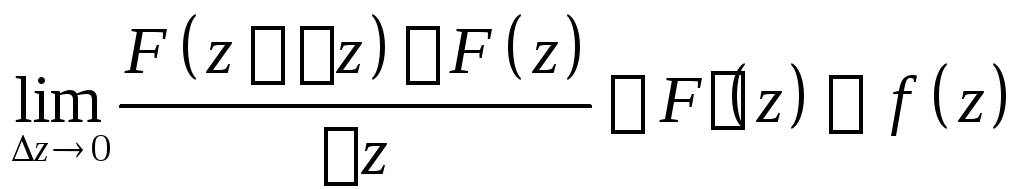Т.о. F(z) – неопределенный интеграл от функции комплексного переменногоf(z).

И F(z)– аналитическая, т.к. ее производная по условию теоремы непрерывна.

§ 7. Интегральная формула Коши. Интеграл Коши.

1. Интегральная формула Коши.

Пусть f(z) C^(). Выразимf(z₀) (z₀g) через значения f(z) на g.

(z)=f(z)/(z—z₀)  C^(/z₀).

Возьмем в области g произвольный такой замкнутый контур  : z₀  . (z)C^(g^*) (g^* — многосвязная область между g и ).

По теореме Коши для многосвязной области

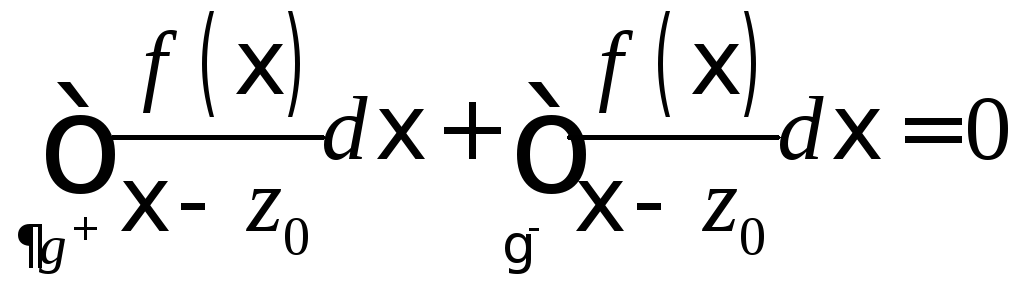
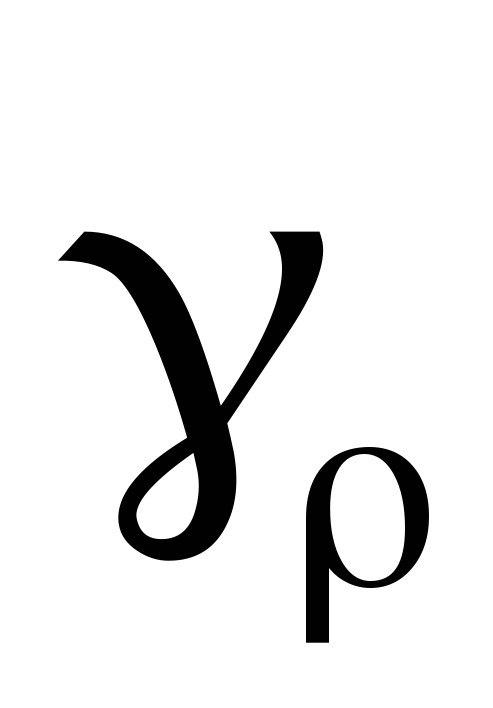: = z₀+e ^i, d = i e ^i d

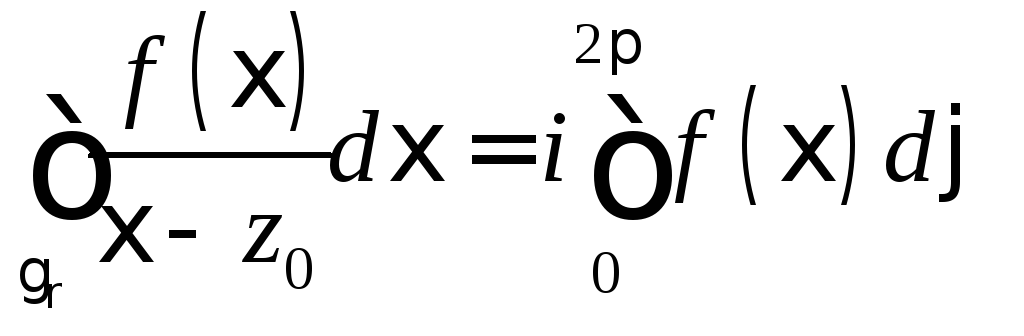
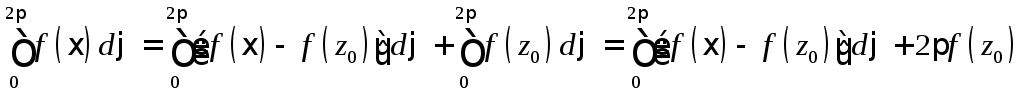
В силу произвольности можем0.

f(z) C^()=> >0  : |f()-f(z₀)|<  как только |-z₀|< (!) =>



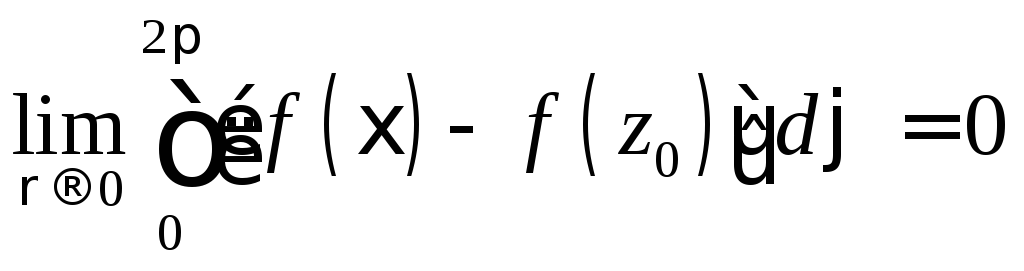
Т.о. или

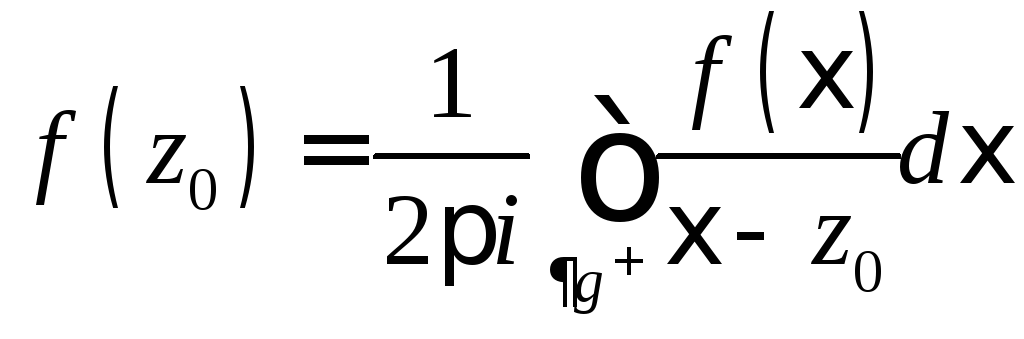—интеграл Коши

Замечания.

1. Формула верна как для g односвязной, так и g- многосвязной, только в последнем случае ⁺— полная граница области, проходимая в положительном направлении.

2. Интеграл Коши имеет смысл для  взаимного расположения точки z₀ и замкнутого контура  (не проходящего через z₀) в области аналитичности f(z)

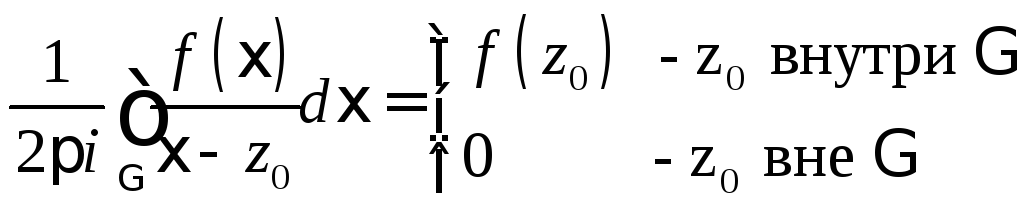
направление обхода контура — это… Что такое направление обхода контура? 

направление обхода контура

1. direction of traversal

 

направление обхода контура
—
[Я.Н.Лугинский, М.С.Фези-Жилинская, Ю.С.Кабиров. Англо-русский словарь по электротехнике и электроэнергетике, Москва, 1999]

Тематики

• электротехника, основные понятия

EN

Русско-английский словарь нормативно-технической терминологии. academic.ru. 2015.

• направление обмена по обходным путям
• направление оптимизации работы

Смотреть что такое «направление обхода контура» в других словарях:

• направление обхода контура — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN direction of traversal …   Справочник технического переводчика

• направление обхода контура — kontūro apėjimo kryptis statusas T sritis automatika atitikmenys: angl. contour bypass direction; traversal direction of contour vok. Maschenumlaufrichtung, f; Maschenumlaufsinn, m rus. направление обхода контура, n pranc. sens du parcours d un… …   Automatikos terminų žodynas

• Правила Кирхгофа —     Классическая электродинамика …   Википедия

• КАРЛЕМАНА ГРАНИЧНАЯ ЗАДАЧА — граничная задача аналитич. функций со сдвигом, изменяющим направление обхода контура на обратное; впервые рассмотрена Т. Карлеманом [1]. Пусть L простая замкнутая кривая Ляпунова на плоскости комплексного переменного z, D конечная область,… …   Математическая энциклопедия

• Ротор (математика) — У этого термина существуют и другие значения, см. Ротор. Ротор, или вихрь  векторный дифференциальный оператор над векторным полем. Обозначается (в русскоязычной[1] литературе) или (в англоязычной литературе), а также как векторное умножение …   Википедия

• Стокса формула —         формула преобразования криволинейного интеграла по замкнутому контуру L в поверхностный интеграл по поверхности Σ, ограниченной контуром L. С. ф. имеет вид:                  ,          причём направление обхода контура L должно быть… …   Большая советская энциклопедия

• Метод Годунова — Метод Годунова  реализация схем сквозного счета, с помощью которых можно рассчитывать газодинамические течения с разрывами параметров внутри расчётной области. Метод Годунова  это вариант метода контрольного объёма. Потоки через боковые …   Википедия

• Maschenumlaufrichtung — kontūro apėjimo kryptis statusas T sritis automatika atitikmenys: angl. contour bypass direction; traversal direction of contour vok. Maschenumlaufrichtung, f; Maschenumlaufsinn, m rus. направление обхода контура, n pranc. sens du parcours d un… …   Automatikos terminų žodynas

• Maschenumlaufsinn — kontūro apėjimo kryptis statusas T sritis automatika atitikmenys: angl. contour bypass direction; traversal direction of contour vok. Maschenumlaufrichtung, f; Maschenumlaufsinn, m rus. направление обхода контура, n pranc. sens du parcours d un… …   Automatikos terminų žodynas

• contour bypass direction — kontūro apėjimo kryptis statusas T sritis automatika atitikmenys: angl. contour bypass direction; traversal direction of contour vok. Maschenumlaufrichtung, f; Maschenumlaufsinn, m rus. направление обхода контура, n pranc. sens du parcours d un… …   Automatikos terminų žodynas

• kontūro apėjimo kryptis — statusas T sritis automatika atitikmenys: angl. contour bypass direction; traversal direction of contour vok. Maschenumlaufrichtung, f; Maschenumlaufsinn, m rus. направление обхода контура, n pranc. sens du parcours d un contour, m …   Automatikos terminų žodynas

направление обхода контура — это… Что такое направление обхода контура? 

направление обхода контура

direction of traversal

Русско-английский политехнический словарь. Академик.ру. 2011.

• направление обхода
• направление падения

Смотреть что такое «направление обхода контура» в других словарях:

• направление обхода контура — — [Я.Н.Лугинский, М.С.Фези Жилинская, Ю.С.Кабиров. Англо русский словарь по электротехнике и электроэнергетике, Москва, 1999] Тематики электротехника, основные понятия EN direction of traversal …   Справочник технического переводчика

• направление обхода контура — kontūro apėjimo kryptis statusas T sritis automatika atitikmenys: angl. contour bypass direction; traversal direction of contour vok. Maschenumlaufrichtung, f; Maschenumlaufsinn, m rus. направление обхода контура, n pranc. sens du parcours d un… …   Automatikos terminų žodynas

• Правила Кирхгофа —     Классическая электродинамика …   Википедия

• КАРЛЕМАНА ГРАНИЧНАЯ ЗАДАЧА — граничная задача аналитич. функций со сдвигом, изменяющим направление обхода контура на обратное; впервые рассмотрена Т. Карлеманом [1]. Пусть L простая замкнутая кривая Ляпунова на плоскости комплексного переменного z, D конечная область,… …   Математическая энциклопедия

• Ротор (математика) — У этого термина существуют и другие значения, см. Ротор. Ротор, или вихрь  векторный дифференциальный оператор над векторным полем. Обозначается (в русскоязычной[1] литературе) или (в англоязычной литературе), а также как векторное умножение …   Википедия

• Стокса формула —         формула преобразования криволинейного интеграла по замкнутому контуру L в поверхностный интеграл по поверхности Σ, ограниченной контуром L. С. ф. имеет вид:                  ,          причём направление обхода контура L должно быть… …   Большая советская энциклопедия

• Метод Годунова — Метод Годунова  реализация схем сквозного счета, с помощью которых можно рассчитывать газодинамические течения с разрывами параметров внутри расчётной области. Метод Годунова  это вариант метода контрольного объёма. Потоки через боковые …   Википедия

• Maschenumlaufrichtung — kontūro apėjimo kryptis statusas T sritis automatika atitikmenys: angl. contour bypass direction; traversal direction of contour vok. Maschenumlaufrichtung, f; Maschenumlaufsinn, m rus. направление обхода контура, n pranc. sens du parcours d un… …   Automatikos terminų žodynas

• Maschenumlaufsinn — kontūro apėjimo kryptis statusas T sritis automatika atitikmenys: angl. contour bypass direction; traversal direction of contour vok. Maschenumlaufrichtung, f; Maschenumlaufsinn, m rus. направление обхода контура, n pranc. sens du parcours d un… …   Automatikos terminų žodynas

• contour bypass direction — kontūro apėjimo kryptis statusas T sritis automatika atitikmenys: angl. contour bypass direction; traversal direction of contour vok. Maschenumlaufrichtung, f; Maschenumlaufsinn, m rus. направление обхода контура, n pranc. sens du parcours d un… …   Automatikos terminų žodynas

• kontūro apėjimo kryptis — statusas T sritis automatika atitikmenys: angl. contour bypass direction; traversal direction of contour vok. Maschenumlaufrichtung, f; Maschenumlaufsinn, m rus. направление обхода контура, n pranc. sens du parcours d un contour, m …   Automatikos terminų žodynas

Path Traversal — шпаргалка, примеры атак и защита

Path Traversal, также известный как «Восхождение по каталогам» и «Обратный путь в каталогах», включает использование конфиденциальной информации, небезопасно хранящейся на веб-серверах. Эта уязвимость постоянно обнаруживается во всемирно признанных ссылках на уязвимости, таких как SANS 25 Top 25 наиболее опасных программных ошибок и OWASP Top-10.

Что такое путь обхода?

На веб-серверах сегодня доступны два основных механизма безопасности:

Списки контроля доступа (ACL) — Это в основном белые списки, которые администратор веб-сервера использует для контроля прав доступа.Эти списки используются в процессе авторизации. Только пользователи с разрешениями могут иметь доступ, изменять или делиться конфиденциальными файлами и информацией.

Корневой каталог — Этот каталог находится в файловой системе сервера, и пользователи просто не могут получить доступ к конфиденциальным файлам выше этого корня. Одним из таких примеров является чувствительный файл cmd.exe на платформах Windows, который находится в корневом каталоге, к которому не каждый может получить доступ.

Обход путей возможен, когда доступ к веб-контенту не контролируется должным образом и веб-сервер скомпрометирован.В основном это эксплойт HTTP, который дает злоумышленникам несанкционированный доступ к закрытым каталогам. В конечном итоге они могут манипулировать веб-сервером и выполнять вредоносные команды вне его корневого каталога / папки.

Эти атаки обычно выполняются с помощью инъекций, таких как инъекции ресурсов, обычно выполняемых с помощью сканеров. Атака обычно включает в себя следующие шаги:

• 1. Пользователь / жертва вводит данные в приложение
• 2.Пользовательский ввод используется для доступа к конкретному файлу (для чтения, записи или отправки)
• 3. Злоумышленник использует идентификаторы ресурсов для манипулирования уязвимым приложением
• 4. Такие параметры, как имена файлов и номера портов, изменяются, чтобы инициировать атаку
• 5. Уязвимое приложение в основном обманывается, предоставляя доступ к конфиденциальному файлу (файлам), даже если у злоумышленника нет необходимых разрешений
• 6. Затем злоумышленник может перезаписать / изменить файлы и даже отправить их на сторонние серверы
.

Примеры обхода пути

Следующие URL показывают, как приложение взаимодействует с используемыми ресурсами:

http: // some_site.com.br/get-files.jsp?file=report.pdf
http://some_site.com.br/get-page.php?home=aaa.html
http://some_site.com. br / some-page.asp? page = index.html

В этих примерах может быть возможно вставить вредоносную строку в качестве параметра переменной для доступа к файлам, расположенным вне каталога веб-публикации.

http://some_site.com.br/get-files?file=../../../../some dir / some file
http: // some_site.com.br/../../../../some dir / файл

Следующие URL-адреса показывают примеры использования файла паролей UNIX / Linux.

http://some_site.com.br/../../../../etc/shadow
http://some_site.com.br/get-files?file=/etc/passwd

Важно: В системе Windows злоумышленник может перемещаться только в разделе, в котором находится веб-root, а в Linux он может перемещаться по всему диску / осуществлять доступ к нему.

Как предотвратить атаки Path Traversal?

Пути снижения риска обхода пути включают в себя:

• 1. Подтвердите ввод пользователя. Принимайте только допустимые значения (белый список).
• 2. Удалите «.. \» и «../» из любого ввода, используемого в контексте файла.
• 3. Используйте индексы вместо фактических частей имен файлов при использовании языковых файлов. (т. е. значение 5 из представления пользователя = индийский, а не ожидание от пользователя возврата «индийский»).
• 4. Внедрите строгие политики доступа к коду, чтобы ограничить место, куда можно сохранять файлы.
• 5. Убедитесь, что пользователь не может указать какую-либо часть пути к файлу, который был прочитан или записан.
• 6. Системным администраторам UNIX рекомендуется использовать chrooted тюрьмы и политики доступа к коду, чтобы ограничить, где файлы могут быть получены или сохранены.
• 7. Настройте установку по умолчанию серверного программного обеспечения в соответствии с требованиями. Серверы также должны быть обновлены и обновлены.

Как предотвратить атаки Path Traversal с помощью CxSAST?

CxSAST обнаруживает потоки данных, которые уязвимы для обхода пути, следуя всем пользовательским данным, которые используются в контексте создания файла или чтения файла. Если входные данные не проверены или не санированы (это «.. \» или «../») перед использованием, CxSAST определяет этот путь как уязвимый для обхода пути. Разработчики могут затем реализовать вышеупомянутые методы исправления.

Назад к Базе знаний об уязвимостях

,Безопасность

— Как предотвратить обход пути в Java

Переполнение стека

1. Товары
2. Клиенты
3. Случаи использования

1. Переполнение стека Публичные вопросы и ответы
2. Команды Частные вопросы и ответы для вашей команды
3. предприятие Частные вопросы и ответы для вашего предприятия
4. работы Программирование и связанные с ним технические возможности карьерного роста
5. Талант Нанимать технический талант
6. реклама Связаться с разработчиками по всему миру

,

Использование объектов обхода | Обходы | Графики | Руководство 3,8 3,7 3,6 3,5 3,4 3,3

• Руководство
• AQL
• HTTP
• Драйверы
• Оазис

• Введение
• Особенности
• ПОЛУЧЕНИЕ СЕМЬИ
• Начиная
  • Монтаж
  • Аутентификация
  • Веб интерфейс
  • Базы данных, коллекции и документы
  • Запрос к базе данных
  • Исходя из SQL
  • Следующие шаги
• Учебники
  • Уменьшить объем памяти
  • ArangoDB Стартер
  • От центра данных к репликации центра обработки данных
  • Kubernetes
    • Амазон ЭКС
    • Google GKE
    • Лазурный АКС
  • DC2DC на Кубернетес
• Программы и инструменты
  • ArangoDB Server
    • Параметры
      • Глобальный
      • Агентство
      • ArangoSearch
      • аудит
      • кэш
      • Резервное копирование
      • кластер
      • уплотнение
      • База данных
      • Foxx
      • Внешний интерфейс
      • HTTP
      • JavaScript
      • LDAP
      • Журнал
      • сеть
      • данное время
      • запрос
      • случайный
      • копирование
      • Rclone
      • RocksDB
      • сервер
      • SSL
      • TCP
      • температура
      • Сделка
      • TTL
      • VST
      • WAL
    • Переменные среды
  • Веб интерфейс
    • Панель приборов
    • кластер
    • Коллекции
    • Документ
    • Запросы
    • диаграммы
    • Сервисы
    • пользователей
    • бревна
  • ArangoDB Shell
    • Примеры
    • подробности
    • Параметры
  • ArangoDB Стартер
    • Параметры
    • Безопасность
    • Архитектура
  • Arangodump
    • Примеры
    • Параметры
    • Maskings
    • Ограничения
  • Arangorestore
    • Примеры
    • Быстрое восстановление кластера
    • Параметры
  • Arangobackup
    • Примеры
    • Параметры
  • Arangoimport
    • Примеры JSON
    • Примеры CSV
    • подробности
    • Параметры
  • Arangoexport
    • Примеры
    • Параметры
  • Arangobench
    • Примеры
    • Параметры
  • Arangoinspect
    • Примеры
    • Параметры
  • Datafile Debugger
    • Примеры
  • Foxx CLI
    • подробности

новейших вопросов прохождения пути — переполнение стека Переполнение стека

1. Товары
2. Клиенты
3. Случаи использования

1. Переполнение стека Публичные вопросы и ответы
2. Команды Частные вопросы и ответы для вашей команды
3. предприятие Частные вопросы и ответы для вашего предприятия
4. работы Программирование и связанные с ним технические возможности карьерного роста
5. Талант Нанимать технический талант
6. Adver

.