ТОЭ Лекции — №10 Линия электропередачи постоянного тока

Если линия электропередачи имеет небольшую длину, при которой можно пренебречь утечкой тока через изоляцию, то ее электрическую схему можно представить в виде последовательного соединения сопротивления линии RЛ, равного суммарному сопротивлению прямого и обратного проводов, и сопротивления нагрузки RН (рис. 10.1).

При анализе работы линии нас интересуют, главным образом, три вопроса: напряжение на нагрузке, величина передаваемой мощности и коэффициент полезного действия передачи. Режимы работы линии удобно рассматривать в виде зависимостей различных величин от тока в линии, равного :

I=U1/(R0+RH)

Падение напряжения в линии ΔU и напряжение на нагрузке U2 определяются следующими выражениями:

Если U1 и RЛ постоянны, то оба выражения представляют собой линейные функции тока (рис. 10.2). В режиме холостого хода (при I = 0) ΔU = 0, а U2 = U1. С ростом тока падение напряжения в линии возрастает, а напряжение на нагрузке уменьшается, и в режиме короткого замыкания (при RН = 0)

Все входное напряжение гасится на сопротивлении линии.

Мощность на входе линии линейно зависит от тока: P1 = U1*I. При холостом ходе она равна нулю, а при коротком замыкании вычисляется по формуле

Потери мощности в линии ΔP=I2Rл представляют собой квадратичную функцию тока. Ее график – парабола, проходящая через начало координат.

При I = 0: ΔP = 0;

при I = Iк:

т.е. в режиме короткого замыкания мощность, поступающая в цепь, полностью теряется в линии.

Мощность, поступающая в нагрузку, равна разности мощности в начале линии и мощности, теряемой в проводах:

Последнее выражение представляет собой уравнение параболы со смещенной вершиной и с обращенными вниз ветвями, проходящими через точки I = 0 и I = IK.

Мощность нагрузки представляет собой довольно сложную зависимость от сопротивления RН:

При RН =0: Р2 = 0; при возрастании RН мощность Р2 сначала возрастает, достигает максимального значения и начинает убывать, стремясь к нулю при RН→∞ (рис. 1.25).

Выясним, при каком сопротивлении нагрузки передаваемая ей мощность максимальна. Для этого продифференцируем функцию (1.15) по RН и приравняем ее к нулю:

Приравняв к нулю числитель производной, получим:

Или Rн = Rл.

То есть мощность, получаемая нагрузкой, максимальна, когда сопротивление нагрузки равно сопротивлению линии.

Ток, протекающий при этом по линии составляет половину тока короткого замыкания, а мощность в конце линии равна:

Коэффициент полезного действия равен отношению мощностей в начале и конце линии:

Из данной формулы следует, что коэффициент полезного действия передачи определяется отношением сопротивлений линии и нагрузки.

При их равенстве, когда нагрузке передается максимальная мощность, η = 0,5 = 50 %. Этот режим, при котором теряется половина передаваемой энергии, на практике, естественно, не пригоден. В реальных линиях при передаче больших мощностей КПД составляет примерно 0,94–0,97. При этом сопротивление нагрузки значительно больше сопротивления линии.

Для анализа режимов электропередачи полезной оказывается еще одна формула. Так как

то

То есть при одной и той же мощности нагрузки Р2, потери ΔР пропорциональны сопротивлению линии и обратно пропорциональны квадрату напряжения. Для увеличения коэффициента полезного действия передачи необходимо повышение напряжения и снижение электрического сопротивления проводов линии путем увеличения их сечения и применения материалов с меньшим удельным сопротивлением.

Пример 1.6. Линия электропередачи с проводами марки А-120 длиной l = 1000 км питает нагрузку мощностью Р2 = 50 МВт. Каким должно быть напряжение в начале линии, чтобы КПД передачи был не ниже 90 %?

Р е ш е н и е. Сопротивление одного километра провода марки А-120 R0 = 0,27 Ом/км. Суммарное сопротивление прямого и обратного проводов линии составляет RЛ = 2lR0 = 540 Ом.

Принимая η = 0,9, из формулы (1.17) получаем:

Так как

Для выполнения условий задачи напряжение в начале линии должно быть не ниже 548 кВ.

Лабораторная работа по дисциплине Электротехника. название Определение потери напряжения и мощности в проводах линии электропередач.

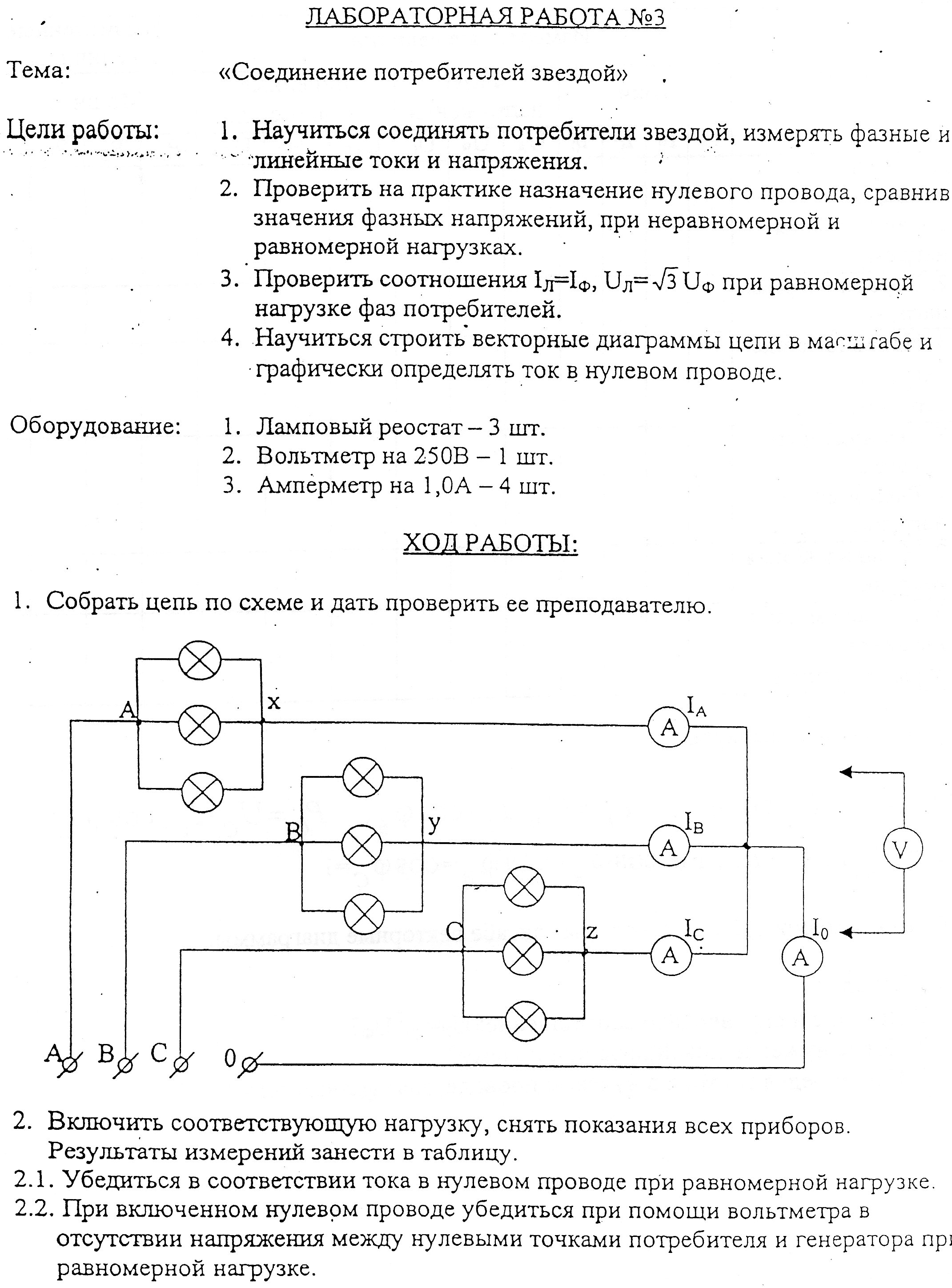
ЛАБОРАТОРНАЯ РАБОТА № 3

Наименование работы: Определение потери напряжения и мощности в проводах линии электропередач.

Цель работы: Рассмотреть, как зависит КПД линии электропередачи от потери напряжения в проводах.

Приборы и оборудование:

1. Лабораторный стенд.

2. Вольтметр универсальный В7-26.

Пояснения к работе.

В линиях электропередачи электрической энергии соединительные провода включаются последовательно с потребителем. Так как провода обладают сопротивлением R= 2ρƖ /S (двухпроводная линия), то при прохождении по ним тока происходит потеря напряжения на них. За счет этой потери напряжение в конце линии электропередачи U₂ меньше, чем напряжение U₁ в начале. Величина потери напряжения в проводах: ΔU = U₁— U₂ =IR_пр. То есть, потеря напряжения в проводах зависит от тока потребителя (нагрузки) и сопротивления проводов R

пр.

Для того, чтобы увеличение тока в линии не приводило к значительной потере напряжения и к ощутимому уменьшению напряжения на потребителе U₂ , расчет сечений проводов ЛЭП производят с учетом допустимой потери напряжения е% = (ΔU/ U₂)*100%. Допустимая потеря напряжения в многокилометровых ЛЭП не должна превышать 10%. Расчет сечения проводов (двухпроводной линии) по допустимой потере напряжения производят по следующему выражению

S = 2ρƖ / R

_пр = 2ρƖI / ΔU = 2ρƖI*100 / е% U₂ = 200ρƖР₂/ е% U₂²,

S – сечение проводов ЛЭП, мм²; ρ – удельное сопротивление материала провода, Ом*мм²/м; Ɩ – длина ЛЭП, м; Р₂ – мощность потребителя, Вт; U₂ – напряжение на потребителе, В.

Выбранное по допустимым потерям напряжения сечение проводов ЛЭП должно быть проверено по допустимому току. Из полученного выражения видно, что сечение проводов зависит от напряжения на потребителе U

2. Поскольку эта зависимость квадратичная, то для уменьшения сечения проводов рационально увеличивать напряжение ЛЭП.

В настоящее время напряжение ЛЭП

переменного тока достигает 1150 кВ, а

+ U₁ U₂ I постоянного тока 1500 кВ. Также

_ полученное выражение справедливо

для ЛЭП с нагрузкой в конце линии.

Ɩ

Если же нагрузка распределена вдоль линии, то сечение проводов определяется выражением S = (200ρ/ е% U

2²)( Р₁Ɩ₁ + Р₂Ɩ₂ + Р₃Ɩ₃)

Линия КПД линии электропередачи в процентах

определяется выражением ɳ = (Р₂/ Р₁)*100% =

Ɩ₁ Р₁ = (U₁ – ΔU)/ U₁ *100% ,

Ɩ₂ Р₂ где Р₂ – мощность потребителя; Р₁— мощность

Ɩ₃ Р₃ источника.

Чем больше потеря напряжения ΔU в проводах, тем меньше КПД линии электропередачи. КПД длинных линий электропередачи лежит в пределах(90-98)%

Задание:

1.В лабораторной работе необходимо определить, как зависит КПД линии электропередачи от потери напряжения в проводах.

2. Измерить ЭДС источника электрической энергии.

3. Собрать на лабораторном стенде данную принципиальную схему.

а R₈

Е R_и1 R₁ = 100 Ом

R₀ R_и1 = 10 Ом

R₁

б

Приемником электрической энергии будем считать резисторы (R_и1 + R₁), а сопротивление линии будем изменять с помощью резистора с переменным сопротивлением R₈.

4. Измерить падения напряжения на всех элементах цепи при различных значениях переменного сопротивления R₈.

5. Результаты измерений занести в таблицу.

R₈

Ом

E

В

U_аб

В

U_и1

В

U₁

В

U₈

В

I

А

ΔU

В

Р₁

Вт

Р₂

Вт

ɳ

%

0

10

30

50

80

100

130

160

200

225

250

6. Произвести расчеты, применяя следующие формулы: I = U_и1/ R_и1; ΔU = U₁— U₂, где U₁ = U_аб – напряжение, отдаваемое источником во внешнюю цепь; U₂ = (U_и1+ U₁) – напряжение на приемнике электрической энергии. Поэтому ΔU определяем по формуле ΔU = U_аб — (U_и1+ U₁); Р₁ = ЕI; Р₂ = I²(R_и1 + R₁); ɳ = Р₂/Р₁ *100%.

7. Результаты расчета занести в таблицу.

8. Построить графики: ΔU( I ); Р₁( I ); Р₂( I ); ɳ( I ).

9. Оформить отчет по проделанной работе.

10. Сделать соответствующие выводы по работе.

Работа в лаборатории.

1. С помощью вольтметра В7-26 измерить ЭДС источника.

2. В соответствии с принципиальной схемой собрать на лабораторном стенде электрическую цепь.

3. Установить сопротивление переменного резистора R₈=0.

4. С помощью вольтметра В7-26 измерить падения напряжения на всех элементах цепи.

5. Меняя поочередно значение переменного сопротивления R₈ , с помощью вольтметра В7-26 измерить падения напряжения на всех элементах цепи.

Содержание отчета.

1. Цель работы.

2. Приборы и оборудование.

3. Принципиальная электрическая схема.

4. Таблица с результатами измерений.

5. Формулы, необходимые для расчета.

6. Графики.

7. Вывод по работе.

Контрольные вопросы.

1. Чем вызваны потери напряжения в линиях электропередачи?

2. От чего зависит величина потери напряжения в проводах?

3. Что такое допустимая потеря напряжения и чему она равна?

4. Как не допустить превышение допустимой потери напряжения?

5. Как зависит КПД линии электропередачи от потери напряжения?

Литература.

1. Е.А.Лоторейчук. Теоретические основы электротехники.- М.: ИД «ФОРУМ»: ИНФРА-М, 2009. Стр. 44-46.

2. Конспект лекций. Тема: «Закон Джоуля-Ленца».

Определение потери напряжения в проводах и КПД линии электропередачи. — МегаЛекции

Лабораторная работа № 2

Цель:выяснить какое влияние оказывает нагрузка линии и сопротивление её проводов на напряжение приемника, а также определить мощность потерь в проводах и КПД линии электропередачи.

Оборудование и приборы: вольтметр и амперметр электромагнитной системы, ламповый реостат, двухполюсный автоматический выключатель, соединительного провода.

Техника безопасности:внимательно слушать указания преподавателя, выполнять сборку и измерение строго в соответствии с инструкцией, перед включением электрической цепи преподаватель должен проверить правильность соединений ее элементов.

Теоретическое обоснование

Каждый приёмник электрической энергии рассчитан на определённое номинальное напряжение. Так как приёмники могут находиться на значительных расстояниях от питающих их электростанций, то потери напряжения в проводах имеют важное значение. Допустимые потери напряжения в проводах для различных установок не одинаковы, но не превышают 4-6% номинального напряжения.

На рис. приведена схема электрической цепи, состоящая из источника электрической энергии, приёмника и длинных соединительных проводов. При прохождении по цепи электрического тока I показания вольтметра U1, включённого в начале линий, больше показаний вольтметра U2, включённого в конце линий.

Уменьшение напряжения в линии по мере удаления от источника вызвано потерями напряжения в проводах линии Ui=U1-U2 и численно равно падению напряжения. Согласно закону Ома, падение напряжения в проводах линии равно произведению тока в ней на сопротивление проводов: Uii=I*R тогда Ui=U1-U2= Uii= — сопротивление проводов линии.

Мощность потерь в линии можно определить двумя способами:

Pi= Ui*I=(U1-U2)*I или Pii=I*R

Уменьшить потери напряжения и потери мощности в линии электропередачи можно уменьшая силу тока в проводах либо увеличивая сечение проводов с целью уменьшения их сопротивления. Силу тока в проводах можно уменьшить увеличивая напряжение в начале линии.

КПД линии электропередачи определяется отношением мощности, отдаваемой электроприёмнику, к мощности, поступающей в линию, или отношением напряжения в конце линии к напряжению в её начале:

 

 

 

Схема передачи электрической энергии:

 

 

Порядок выполнения работы

Ознакомиться с приборами и оборудованием, предназначенными для выполнения лабораторной работы, записать их технические характеристики.

Подать в цепь напряжение. Изменяя нагрузку с помощью лампового реостата, при трёх её значениях записать показания приборов в таблице.

Вычислить потери двумя способами:

1. Как разность напряжений в конце и начале линий.

2. Как произведение силы тока на сопротивление проводов.

Определить мощность потерь в линии и КПД. Результаты вычислений занести в таблицу.

Таблица изменения числа потребителей:

Изменяем напряжение в начале и конце линии.

 

Данные наблюдений	Результаты вычислений
Лампы, Вт	U1	U2	I	U	Pвх	Рвых	Р	%
			0,13
			0,2
			0,3

 

 

Вывод:

На основе проведённого опыта выяснили, что факторами, влияющими на потери в линиях являются: протяжённость линий; сечение проводника; состав материала и количество потребителей. Чем больше потребителей, тем меньше КПД. . Уменьшить потери напряжения и потери мощности в линии электропередачи можно уменьшая силу тока в проводах либо увеличивая сечение проводов с целью уменьшения их сопротивления.

 

 

---

Рекомендуемые страницы:

Читайте также:

Воспользуйтесь поиском по сайту:

Кпд линии

КПД – отношение активной мощности Р_Н , выделяемой в нагрузке к активной мощности, подводимой ко входу: =Р_Н/Р.

Если в линии режим бегущей волны (R_Н=Z_В), то .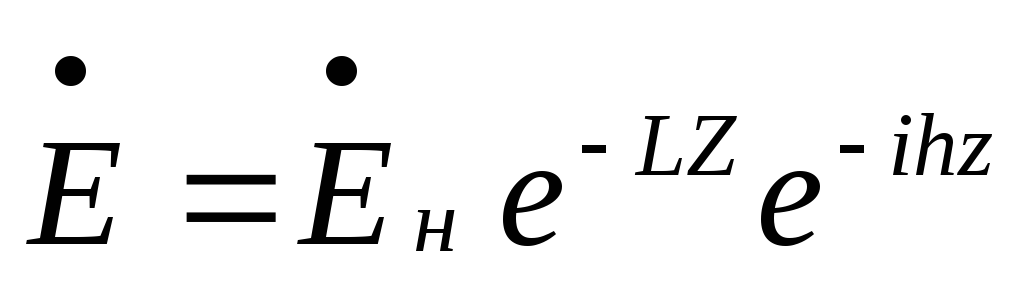

Е и Н связаны через сопротивление линии и =е^-2LZ1-2LZ.

Если нагрузка не согласована, надо учитывать отражение: .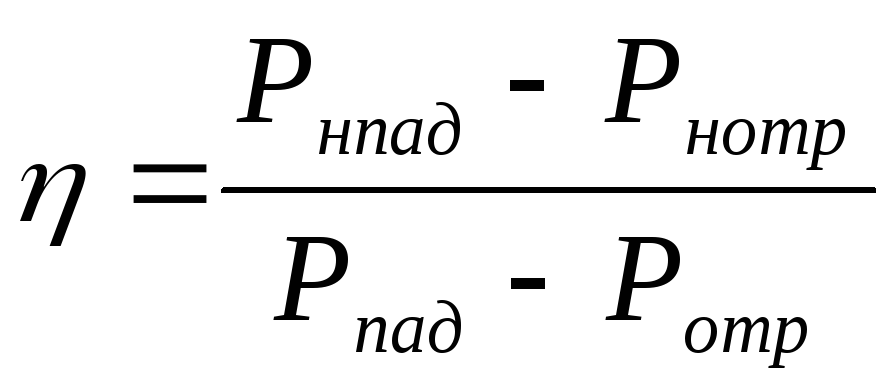

После подставки: =е^-2LZ(1-R²).

Из графика, там, где потери малы,  для различных КБВ почти совпадают (LZ<0,1).

В диапазоне КВ особой степени согласования не надо и допустимы значения КБВ≥0,3 0,5.

В диапазоне СВЧ КБВ0,80,9.



Возбуждение эм колебаний

Для возбуждения ЭМК в линиях передачи необходимо вводить специальные устройства – носители сторонних источников (токов, зарядов и полей).

Эти устройства называют – возбуждающие устройства (ВУ).

В большинстве случаев, это различные модификации электрического и магнитного вибраторов.

Из теоремы единственности следует, что задав функцию распределения сторонних источников и граничные условия, можно однозначно определить структуру поля. Это накладывает ограничения на конструкцию возбуждающего устройства и его положение в линии передачи.

Точное распределение сторонних источников задать практически не возможно, единственный критерий правильности – совпадение расчетных и экспериментальных данных.

Основные требования к ВУ.

1. ВУ должно обеспечивать эффективное возбуждение желаемого типа волны и, по возможности, должно затруднять возбуждение всех других типов волн.

2. Коэффициент отражения от возбуждающего устройства должен быть минимальным в нужной полосе частот.

3. ВУ должно иметь электрическую прочность, достаточную для пропускания необходимой мощности.

Вибратор — это короткозамкнутый отрезок однопроводной линии с косинусоидальным распределением тока, которая теряет энергию на излучение.

В общем случае входное сопротивление вибратора комплексное.

Активная часть характеризует мощность, отдаваемую волне Н, реактивная часть – реактивная мощность полей в близи вибратора.

Желательно, чтобы мнимая часть была равна 0, а активная — равна волновому сопротивлению коаксиальной линии.

Полная мощность, отдаваемая штырю коаксиальной линией: .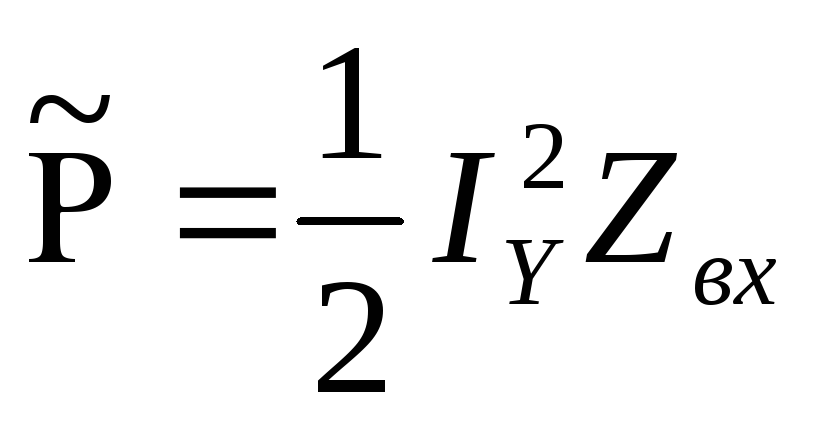

Входное сопротивление:

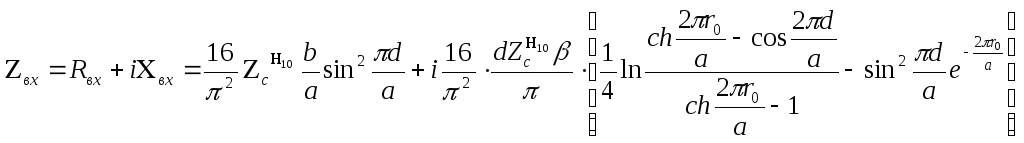
r₀ — радиус вибратора.

По этой формуле, как показывают расчёты, сопротивления коаксиальной линии значительно больше. Снизить сопротивление можно, либо сместив штырь к боковой стенке, либо существенно увеличив его толщину, это, кроме того, позволяет уменьшить индуктивное по характеру реактивное сопротивление линии.

Часто в широкополосных устройствах используют ВУ пестиковой формы.

Т.к. вибратор по обе стороны от себя возбуждает синфазные электрические поля почти равной амплитуды, то пока он расположен по центру, он может возбуждать только колебания типа Н₁₀,Н₃₀,Н₅₀…., а чётные не возбуждает.

Общее для волноводов правило:

Для эффективного возбуждения в волноводе с любой формой поперечного сечения одного из типов волн электрический вибратор необходимо помещать: 1) параллельно силовым линиям электрического поля волны желаемого типа; 2) в сечениях близких к пучности электрического поля этой волны.

Если пучностей несколько – можно помещать вибраторы в каждую с учётом фазового сдвига.

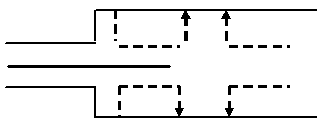
Чтобы обеспечить распространение энергии в одном направлении, надо обеспечить отражённую волну в фазе с прямой.

Расстояние l выбирают с учётом того, что на металле R = -1.

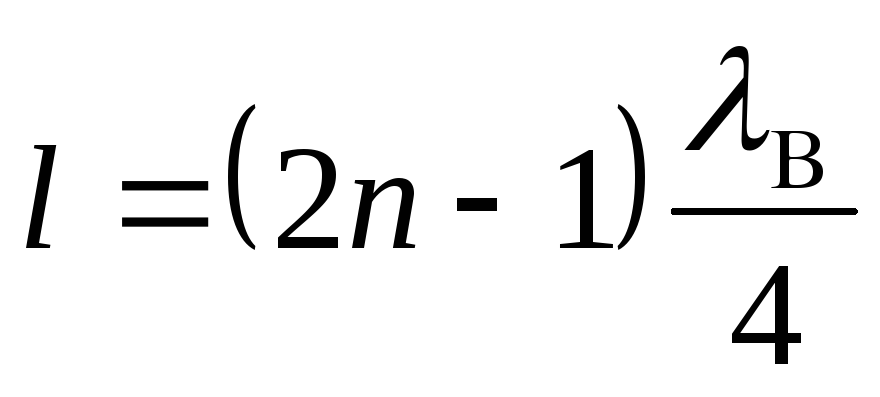
Рамка с током

Обычно периметр рамки выбирают много меньше.

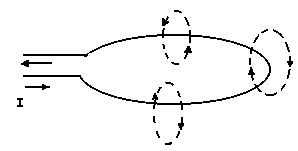
Отверстия связи

Через отверстие в боковой оболочке часть силовых линий ЭМП ответвляется и возбуждает ЭМП в соседнем пространстве.

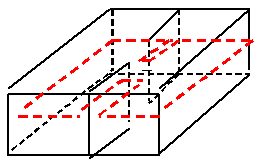
Отверстия эквивалентны одновременно штырю и рамке.

Размеры отверстий, как правило, берут значительно меньше , чтобы не нарушать структуру в основном волноводе.

Причём два волновода не обязательно одинакового сечения.

3.2.4. Натуральная мощность и пропускная способность лэп

Рассмотрим ЛЭП без потерь, для которой активное сопротивление r₀= 0 и активная проводимостьg₀= 0. Выделим на ней отрезок единичной длины∆lс индуктивным сопротивлениемx₀∆lи емкостной проводимостьюb₀∆l. На этом участке имеют место потребление реактивной мощности на индуктивном сопротивлении и генерация реактивной мощности за счет емкостной проводимости:

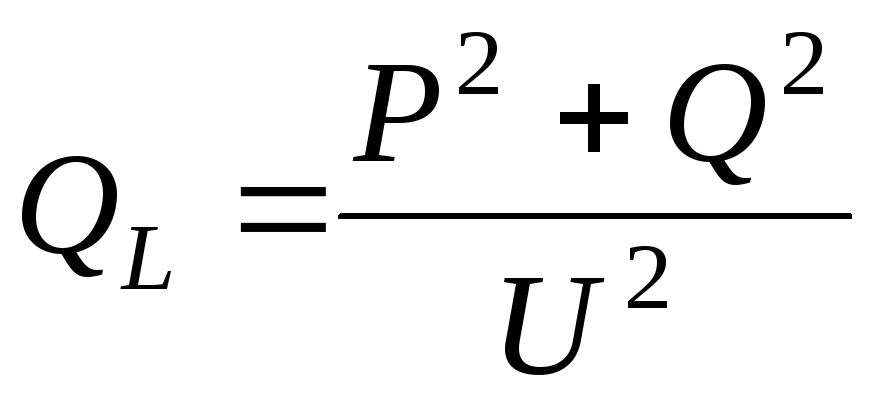x₀∆l,Q_C =U ² b₀∆l.

Мощность Q_Lзависит от величины передаваемой мощности, а мощностьQ_Cот величины передаваемой мощности не зависит. Следовательно, при некоторой активной мощностиPбудет иметь место равенствоQ_L = Q_Cи реактивная мощность ЛЭП будет равна нулю, то есть линия станет идеальной. Мощность, передаваемую в этом режиме, называютнатуральной мощностью P_нат, а сам режим работы ЛЭП — режимом передачи натуральной мощности. При номинальном напряжении

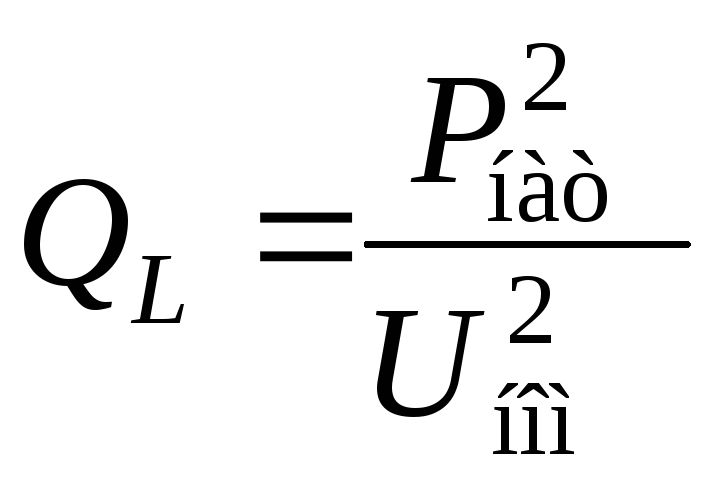x₀∆l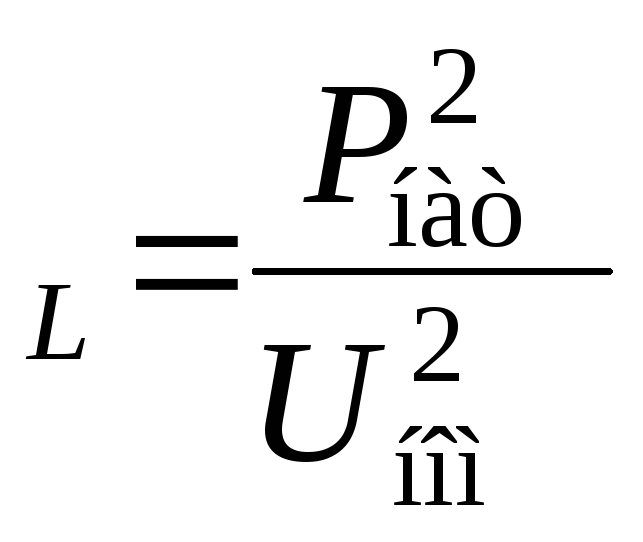ωL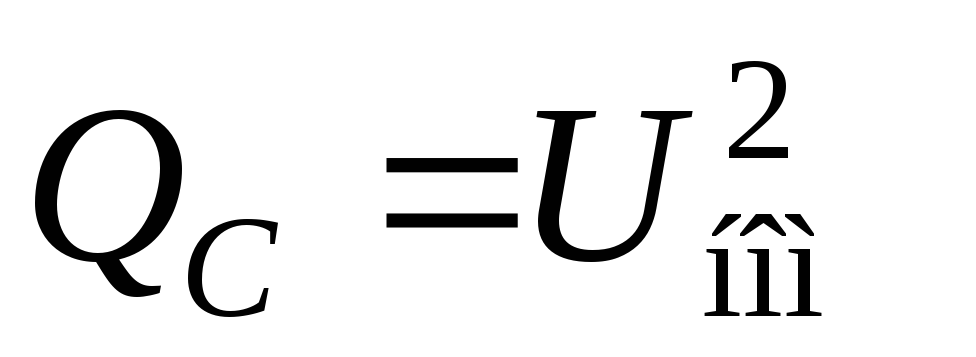₀∆l,

b₀∆l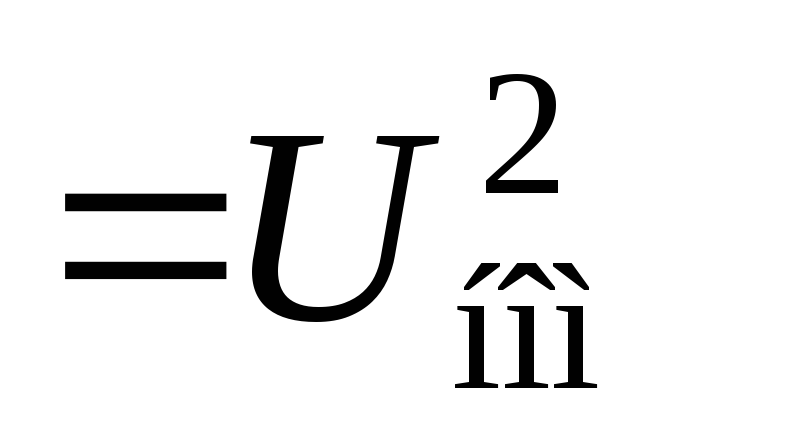ωС₀∆l,

,

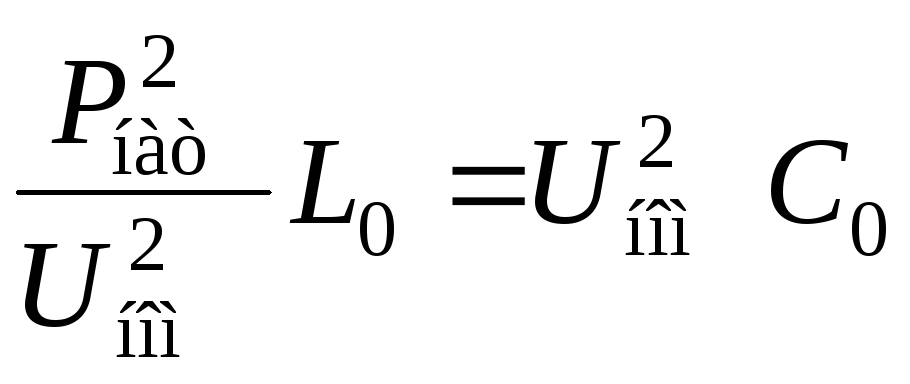откуда находим:

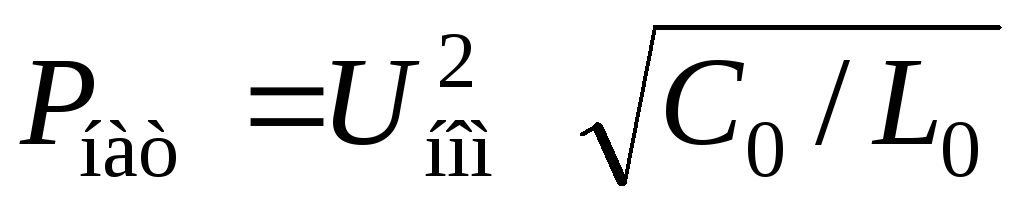
или

,

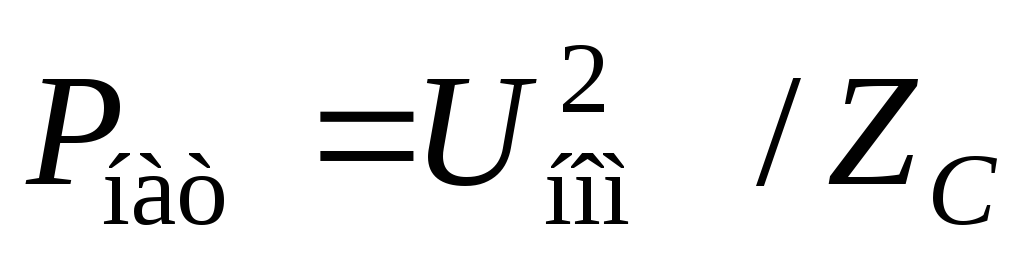где 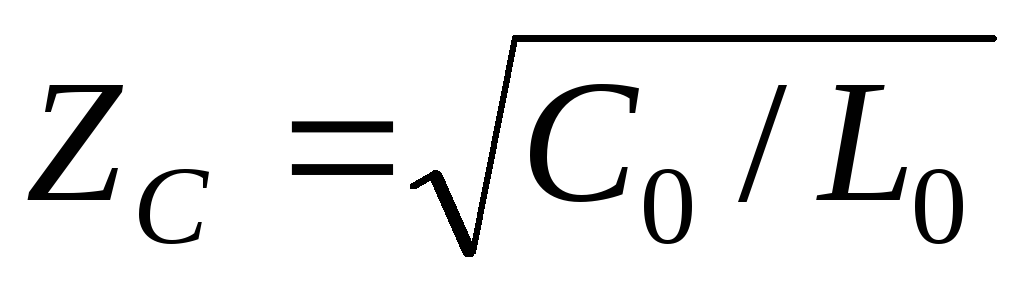— волновое сопротивление линии.

В реальной линии, в которой r₀ ≠ 0 и g₀ ≠ 0, при Q = 0 будут наименьшими:

∆P ,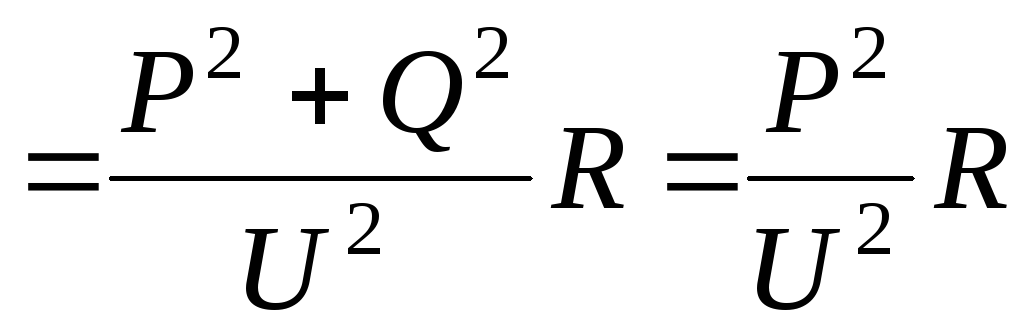

а при P=P_натлиния будет работать с наибольшим КПД вследствие того, что она находится на самобалансе реактивной мощности.

На практике невозможно обеспечить работу всех линий в режиме, близком к натуральному, но этого добиваются для отдельных линий, когда существует возможность регулировать передаваемую мощность за счет ее перераспределения в электрической сети и генерирования реактивной мощности в местах ее потребления.

Пропускная способность ЛЭП определяется величиной активной мощности, которую линия может передать при выполнении всех условий, определяющих ее нормальную работу. Натуральная мощность, пропускная способность и предельная длина воздушных ЛЭП на напряжения 35 кВ и выше приведена в таблице 3.3. Натуральная мощность кабельных линий на порядок больше, чем воздушных.

Таблица 3.3. Пропускная способность и дальность передачи линий 35…1150 кВ

Напряжение линии, кВ	Сечение провода, мм2	Передаваемая мощность, МВт		Длина ЛЭП, км
		натуральная	при плотности тока 1,1 А/мм2	предельная при КПД 0,9	средняя меж- ду двумя со-седними ПС
35	70…150	3	4…10	25	8
110	70…240	30	13…45	80	25
150	150…300	60	38…77	250	20
220	24…400	135	90…150	400	100
330	2∙240…2∙400	360	270…450	700	130
500	3∙300…3∙500	900	770…1300	1200	280
750	5∙300…5∙500	2100	1500…2000	2200	300
1150	8∙300…8∙500	5200	4000…6000	3000	—

Примечание: Передаваемая мощность зависит от длины линии.

3.2.5 Линии электропередач постоянного тока

В настоящее время для выработки электрической энергии, ее передачи на расстояние, распределения и потребления используется переменный ток. Это объясняется, прежде всего, способностью переменного тока к трансформации, т.е. изменению напряжения с помощью достаточно простых аппаратов—трансформаторов, а также и тем, чтоэлектродвигателипеременного тока по своей конструкции значительно проще и, следовательно, надежнее электродвигателей постоянного тока. Тем не менее, в последние десятилетия электроэнергетики разных стран все чаще применяют постоянный ток для решения ряда задач, в том числе связанных с передачей электрической энергии на расстояние.

Для ответа на вопрос, почему это делается, сопоставим характеристики линий переменного и постоянного тока.

При работе воздушной линии на переменном напряжении ее индуктивность оказывает сопротивление протеканию переменного тока и, в конечном итоге, определяет ту максимальную мощность, которую можно передать по этой линии. Индуктивное сопротивление линии возрастает при увеличении ее длины, и, следовательно, при этом снижается максимальная мощность, которую можно передать по линии.

Емкость воздушной линии переменного тока практически не влияет на передаваемую мощность, однако через нее протекает так называемый зарядный ток, который создает зарядную мощность линии и приводит к дополнительному нагреву проводов, т.е. увеличивает потери энергии в линии и снижает ее КПД.

При работе воздушной линии на постоянном напряжении, когда по ней протекает постоянный ток, в установившемся режиме ни ее индуктивность, ни емкость не оказывают никакого влияния на процесс передачи электрической энергии по линии и, следовательно, на максимальную мощность, которую можно передать по линии при увеличении длины последней. Зарядная мощность линии постоянного тока отсутствует.

Из сказанного можно сделать следующие выводы:

1. Для воздушной линии переменного тока существует зависимость максимальной передаваемой мощности от ее длины — чем длиннее линия, тем меньше предельная мощность, которую можно по ней передать; это одна из причин, ограничивающих допустимую длину такой линии;

2. Воздушная линия постоянного тока не имеет такого ограничения, поэтому линия постоянного тока может иметь любую длину и передаваемую мощность, которые диктуются практической целесообразностью.

Кабельные линии переменного токаимеют весьма ограниченную длину — не более 15–20 км. Это объясняется большой зарядной мощностью, возникающей вследствие значительной емкости кабеля. Зарядная мощность приводит к дополнительному нагреву жил кабеля, вынуждая снижать полезную передаваемую мощность и ограничивать длину кабеля. В особенности это относится к высоковольтным кабельным линиям (110–500 кВ). Поэтому кабельные линии переменного тока не могут быть использованы для передачи электроэнергии на достаточно большие расстояния.

В кабельной линии постоянного токазарядная мощность отсутствует и не создает дополнительного нагрева кабеля. Поэтому кабельные линии постоянного тока могут сооружаться достаточно длинными (100–200 км и более) и использоваться для решения задач, которые невозможно решить иными путями, например для пересечения больших водных пространств (морских проливов), ввода больших мощностей в центры крупных городов и др.

Кроме того, с помощью линий постоянного тока можно объединять энергосистемы, работающие несинхронного, а также энергосистемы, работающие на разных частотах. Объединение с помощью линий переменного тока крупных энергосистем, даже работающих синхронно, может приводить к потере устойчивости, что грозит крупными авариями. Если же энергосистемы объединять с помощью звена постоянного тока, то они будут работать независимо друг от друга, но обмениваться между собой мощностью. При этом аварийные возмущения в одной из систем не будут передаваться в другие, как это было бы при связи на переменном токе.

Из сказанного выше могут быть определенывозможные области применения постоянного токав современной электроэнергетике. К ним следует отнести:

— дальние электропередачи, например, от удаленных ГЭС или АЭС. Расстояния здесь могут исчисляться многими сотнями и тысячами километров;

— передача электроэнергии через большие водные пространства;

— глубокие вводы большой мощности в центры крупных городов;

— связь систем переменного тока с различной номинальной частотой;

— несинхронные связи систем одной номинальной частоты, что позволит повысить живучесть объединенной системы.

В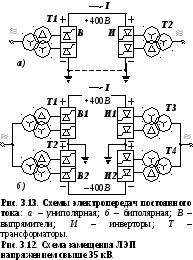настоящее время все электропередачи постоянного тока делятся на две группы. К первой из них относятся собственноэлектропередачи постоянного тока(ППТ), где электрическая энергия передается на какое-то расстояние. Неотъемлемой частью этих электропередач является воздушная или кабельная линия постоянного тока. Ко второй группе относятся так называемыевставки постоянного тока(ВПТ), где линия постоянного тока отсутствует. Все звено постоянного тока расположено на одной подстанции, на которую заходят линии переменного тока от связываемых систем.

Структурные схемы ППТ и ВПТ приведены на рис. 3.13. Электрическая энергия переменного тока, вырабатываемая генераторами передающей системы, выпрямителями Впреобразуется в энергию постоянного тока и передается по линии, а затем с помощью инверторовИснова преобразуется в энергию переменного тока и передается в приемную систему.

Преобразователи построены на основе трехфазных вентильных мостов. С целью повышения напряжения цепи постоянного тока преобразователи выполняются по 12-фазным схемам, образуемым последовательным включением двух трехфазных мостов. Преобразователи являются реверсивными: при необходимости изменения направления передачи мощности выпрямитель становится инвертором, а инвертор — выпрямителем. При этом направление тока в линии остается неизменным, так как вентили в преобразователях пропускают ток только в одном направлении, но меняется полярность самих преобразователей.

Основным элементом преобразовательного мостаявляются вентили. В настоящее время в качестве вентилей чаще всего используютсявысоковольтные тиристорные вентили(ВТВ), собранные из множестватиристоров, включенных последовательно. Кроме того, все более широко применяются полностью управляемые высоковольтные вентили на базеIGBTтранзисторов.

Другим важным элементом преобразовательного блока является трансформатор, который связывает преобразовательный мост с сетью передающей или приемной системы. Этот трансформатор выполняет две функции:

— согласует напряжение сети переменного тока с напряжением линии постоянного тока, что обеспечивается выбором соответствующего коэффициента трансформации;

— электрически отделяет цепь выпрямленного тока от сети переменного тока.

Электропередачи постоянного тока могут выполняться по униполярнойилибиполярнойсхеме. В униполярной схеме (рис. 3.13а) один из полюсов передачи заземляется с обеих сторон. Заземление выполняется обязательно, так как в противном случае потенциалы полюсов относительно земли в этой цепи будут определяться случайными факторами, главным образом токами утечки по изоляции. Это недопустимо, поскольку невозможно будет осуществить координацию изоляции.

В униполярной схеме провод заземленного полюса обычно отсутствует, его роль выполняет земля. Сопротивление земли для постоянного тока равно нулю. Поэтому сопротивление заземленного провода будет определяться только сопротивлением заземлителей, имеющим очень малую величину (0,05–0,15 Ом). Обычно электропередачи такого типа сооружаются при пересечении больших водных пространств, например морских проливов.

Использование земли для возврата тока имеет и свои отрицательные стороны. Наиболее существенным недостатком здесь является возможность коррозионного разрушения металлических инженерных сооружений, проложенных в земле вблизи заземления, — трубопроводов, кабелей. Если линия прокладывается в местности, где много подземных инженерных сооружений, например при глубоком вводе в город, для того чтобы избежать растекания тока по земле, заземленный полюс выполняется в виде кабеля, жила которого заземлена.

Мощные ППТ выполняются по биполярной схеме (рис. 3.13б), где линия выполнена с двумя полюсами, каждый из которых изолирован от земли. Заземляются средние точки преобразовательных подстанций. При этом напряжение между полюсами вдвое выше, чем напряжение полюс земля. Это позволяет повысить КПД передачи. Кроме того, при выходе одной полуцепи из работы другая продолжает работать, но с возвратом тока через землю. При этом мощность передачи уменьшается вдвое, но, тем не менее, передача продолжает работать.

У вставок постоянного тока линия отсутствует, поэтому они выполняются по униполярной схеме на меньшие напряжения цепи постоянного тока.

Стоимость линии постоянного тока меньше стоимости линии переменного тока, главным образом, за счет более легких опор. В то же время стоимость подстанций ППТ будет выше, чем стоимость подстанций переменного тока, за счет более сложного и дорогого оборудования. Следовательно, с превышением некоторой критической длины линии ППТ становится дешевле ЛЭП переменного тока такой же мощности. В зависимости от конкретной ситуации критическая длина линии может составлять от 500 до 1000 км.

По состоянию на 2012 год во всем мире действовало (или готовилось к вводу в эксплуатацию) 83 ППТ общей мощностью около 99 ГВт и 39 ВПТ общей мощностью 18,6 ГВт. Лидером в области строительства ППП является Китай, где имеется 14 ППТ общей мощностью 43,8 ГВт (44,3% от мощности всех ППТ в мире). Наиболее мощной и протяженной воздушной ППТ также станет китайская ППТ Цзиньпин–Восточный Китай (КНР), 2100 км, 7,2 ГВт, ±800 кВ. Напряжение ±800 кВ в настоящее время является самым высоким напряжением ППТ. Ввод этой линии на полную мощность намечен на 2014 г.

Наиболее протяженными кабельными ППТ являются ППТ Герус–Замбези (Намибия), 970 км, 300 МВт и Ява–Суматра (Индонезия) 700 км, 3 ГВт.

Абсолютное большинство действующих ППТ и ВПТ выполнено на тиристорных преобразователях. Однако с 1997 г. началось создание передач и инверторами напряжения на IGBTтранзисторах. Первая такая ППТ, построенная в Швеции, имела мощность всего 3 МВт. Однако к настоящему времени действуют уже 12 ППТ наIGBTтранзисторах, мощность отдельных электропередач достигает 800 МВт (Германия).

В России помимо ВПТ «Выборг» мощностью 1,065 ГВт, связывающей энергосистемы России и Финляндии, действует единственная ППТ Волгоград–Донбасс (400 кВ, 750 МВт, 475 км), построенная еще в 1964 г. Строительство ППТ Экибастуз–Тамбов (Экибастуз–Центр) протяженностью 2400 км, мощностью 6 ГВт и напряжением ±750 кВ, начатое в 80-е годы XXв., прекращено в 90-е годы в связи с распадом СССР.

В период до 2018 года в мире планируется ввести в строй 28 ППТ и ВПТ общей мощностью около 90 ГВт. Лидером по-прежнему является Китай, где планируется ввести 13 ППТ общей мощностью 76,4 ГВт, в том числе ППТ Иркутск–Пекин мощностью 6,4 ГВт. Заслуживает также внимания проект кабельной ППТ между Францией и Испанией на IGBTтранзисторах мощностью 2 ГВт (напряжение ±320 кВ, длина 60 км), которая планируется к пуску в 2014 г.

В Генеральном плане развития электрической сети ЕЭС России на период до 2020 г. рекомендуется строительство ППТ Сибирь – Урал – Центр (±750 кВ, 3 ГВт, 3700 км), Урал – Средняя Волга – Центр (±750 кВ, 3 ГВт, 1850 км), две ППТ Эвенкийская ГЭС – Тюмень ((±500 кВ, 2,5 ГВт, 600 и 800 км), Сибирь – Тюмень (±550 кВ, 2 ГВт, 900 км). С целью объединения энергосистем Сибири и Дальнего Востока рекомендуется установить на подстанциях Могочи и Хани ВПТ мощностью 500 МВт каждая.

Коэффициент полезного действия машины постоянного тока

Дата публикации: 23 января 2013.
Категория: Машины постоянного тока.

Общие положения

Коэффициент полезного действия определяется как отношение полезной, или отдаваемой, мощности P₂ к потребляемой мощности P₁:

(1)

или в процентах

(2)

Современные электрические машины имеют высокий коэффициент полезного действия (к. п. д.). Так, у машин постоянного тока мощностью 10 кВт к. п. д. составляет 83 – 87%, мощностью 100 кВт – 88 – 93% и мощностью 1000 кВт – 92 – 96%. Лишь малые машины имеют относительно низкие к. п. д.; например, у двигателя постоянного тока мощностью 10 Вт к. п. д. 30 – 40%.

Рисунок 1. Зависимость коэффициента полезного действия электрической машины от нагрузки

Кривая к. п. д. электрической машины η = f(P₂) сначала быстро растет с увеличением нагрузки, затем к. п. д. достигает максимального значения (обычно при нагрузке, близкой к номинальной) и при больших нагрузках уменьшается (рисунок 1). Последнее объясняется тем, что отдельные виды потерь (электрические I_а²r_а и добавочные) растут быстрее, чем полезная мощность.

Прямой и косвенный методы определения коэффициента полезного действия

Прямой метод определения к. п. д. по экспериментальным значениям P₁ и P₂ согласно формуле (1)  может дать существенную неточность, поскольку, во-первых, P₁ и P₂ являются близкими по значению и, во-вторых, их экспериментальное определение связано с погрешностями. Наибольшие трудности и погрешности вызывает измерение механической мощности.

Если, например, истинные значения мощности P₁ = 1000 кВт и P₂ = 950 кВт могут быть определены с точностью 2%, то вместо истинного значения к. п. д.

η = 950/1000 = 0,95

можно получить

или

Поэтому ГОСТ 25941-83, «Машины электрические вращающиеся. Методы определения потерь и коэффициента полезного действия», предписывает для машин с η% ≥ 85% косвенный метод определения к. п. д., при котором по экспериментальным данным определяется сумма потерь p_Σ.

Подставив в формулу (1) P₂ = P₁ — p_Σ, получим

(3)

Применив здесь подстановку P₁ = P₂ + p_Σ, получим другой вид формулы:

(4)

Так как более удобно и точно можно измерять электрические мощности (для двигателей P₁ и для генераторов P₂), то для двигателей более подходящей является формула (3) и для генераторов формула (4). Методы экспериментального определения отдельных потерь и суммы потерь p_Σ описываются в стандартах на электрические машины и в руководствах по испытанию и исследованию электрических машин. Если даже p_Σ определяется со значительно меньшей точностью, чем P₁ или P₂, при использовании вместо выражения (1) формул (3) и (4) получаются все же значительно более точные результаты.

Условия максимума коэффициента полезного действия

Различные виды потерь различным образом зависят от нагрузки. Обычно можно считать, что одни виды потерь остаются постоянными при изменении нагрузки, а другие являются переменными. Например, если генератор постоянного тока работает с постоянной скоростью вращения и постоянным потоком возбуждения, то механические и магнитные потери являются также постоянными. Наоборот, электрические потери в обмотках якоря, добавочных полюсов и компенсационной изменяются пропорционально I_а², а в щеточных контактах – пропорционально I_а. Напряжение генератора при этом также приблизительно постоянно, и поэтому с определенной степенью точности P₂ ∼ I_а.

Таким образом, в общем, несколько идеализированном случае можно положить, что

или

где коэффициент нагрузки

Kнг = I / Iн = P2 / P2н

(6)

Определяет относительную величину нагрузки машины.

Суммарные потери также можно выразить через k_нг:

pΣ = p0 + kнг × p1 + kнг² × p2,

(7)

где p₀ – постоянные потери, не зависящие от нагрузки; p₁ – значение потерь, зависящих от первой степени k_нг при номинальной нагрузке; p₂ – значение потерь, зависящих от квадрата k_нг, при номинальной нагрузке.

Подставим P₂ из (5) и p_Σ из (7) в формулу к. п. д.

Тогда

(8)

Установим, при каком значении k_нг к. п. д. достигает максимального значения, для чего определим производную dη/dk_нг по формуле (8) и приравняем ее к нулю:

Это уравнение удовлетворяется, когда его знаменатель равен бесконечности, т. е. при k_нг = ∞. Этот случай не представляет интереса. Поэтому необходимо положить равным нулю числитель. При этом получим

Таким образом, к. п. д. будет максимальным при такой нагрузке, при которой переменные потери k_нг² × p₂, зависящие от квадрата нагрузки, становятся равными постоянным потерям p₀.

Значение коэффициента нагрузки при максимуме к. п. д., согласно формуле (9),

(10)

Если машина проектируется для заданного значения η_макс, то, поскольку потери k_нг × p₁ обычно относительно малы, можно считать, что

p₀ + p₂ ≈ p_Σ = const.

Изменяя при этом соотношение потерь p₀ и p₂, можно достичь максимального значения к. п. д. при различных нагрузках. Если машина работает большей частью при нагрузках, близких к номинальной, то выгодно, чтобы значение k_нг [смотрите формулу (10)] было близко к единице. Если машина работает в основном при малых нагрузках, то выгодно, чтобы значение k_нг [смотрите формулу (10)] было соответственно меньше.

Источник: Вольдек А. И., «Электрические машины. Учебник для технических учебных заведений» – 3-е издание, переработанное – Ленинград: Энергия, 1978 – 832с.

Видео 1. Общее определение коэффициента полезного действия

«Потери напряжения в линии электропередачи»

ЛАБОРАТОРНАЯ РАБОТА №2

ТЕМА: «Потери напряжения в линии электропередачи»

Цели работы:

· Определение потери напряжения в линии электропередачи

· Определение мощности потерь

· Определение КПД линии электропередачи

Приборы, используемые в лабораторной работе:

Двухпроводная линия

Амперметр на 1(А)

Вольтметр с диапазоном не менее 250 (В)

Потребители (ламповый реостат на 1-6 ламп)

Источник питания стенда

Ход работы

Для выполнения работы собрать электрическую цепь в соответствии с данной схемой и дать проверить её преподавателю.

Поочередно включая одну, две и три лампы в ламповом реостате, записать в таблицу показания амперметра и вольтметра.

3. По разнице показаний вольтметра U₁ и U₂ определить величину потери напряжения в каждом замере и занести в таблицу. _∆U₁=U₁-U₂

4. Рассчитать потерю напряжения (U₁-U₂) по закону Ома _∆U₂=I ^. R_л (В) R_л = р ^. 2ℓ/S (Ом) S= ∏d²/4 (мм²) Ρ=0,0175 (Ом ^. мм²/м)

5. Подсчитать потерю мощности для каждого замера по формуле _∆P=_∆U₂ I (Вт) и занести в таблицу.

Определить КПД линии для каждого замера по формуле

ή=(1 — _∆U₂/U₁) ^.100% и занести в таблицу.

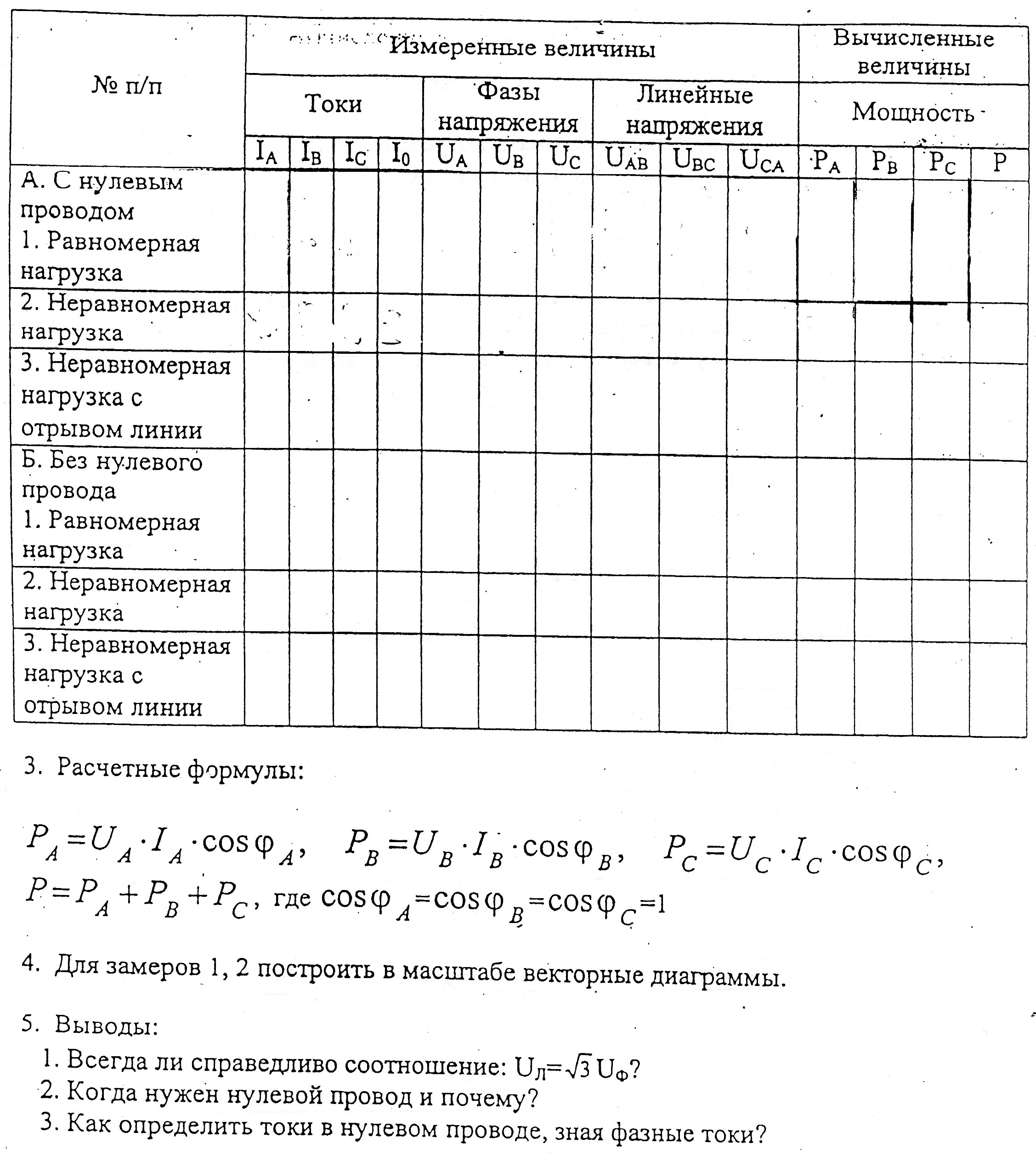
% замера	Измеренные величины	Вычисленные величины
I (A)	U1 (B)	U2 (В)	D (мм)	ℓ (м)	S (мм2)	Rл	∆U1	∆U2	∆P	ή
				0,41
				0,41
				0,41

7. Сделать следующие выводы по работе:

· Как изменяется величина U₂ при увеличении нагрузки?

· Как изменяется мощность потерь _∆P при увеличении нагрузки?

· Как изменяется КПД линии при увеличении нагрузки?

· Учитывая, что для ламп падение напряжения не должно превышать 2%, сделать вывод – соответствует линия данным нагрузкам или нет.

Лабораторная работа №4

Тема: « Измерение сопротивлений методом амперметра-вольтметра и с помощью мультиметра (омметра)

Цели работы:

· Ознакомиться с методикой расчета сопротивлений с помощью амперметра и вольтметра (по закону Ома)

· Научиться пользоваться мультиметром в режиме омметра.

Оборудование и приборы , используемые в лабораторной работе6

Амперметр на 1(А)

Вольтметр с диапазоном измерений до 250 (В)

Ламповый реостат

Цифровой мультиметр

Источник питания стенда

Ход работы.

Для определения сопротивления нагрузки методом амперметра-вольтметра собрать электрическую цепь согласно приведенной схеме и дать проверить преподавателю.

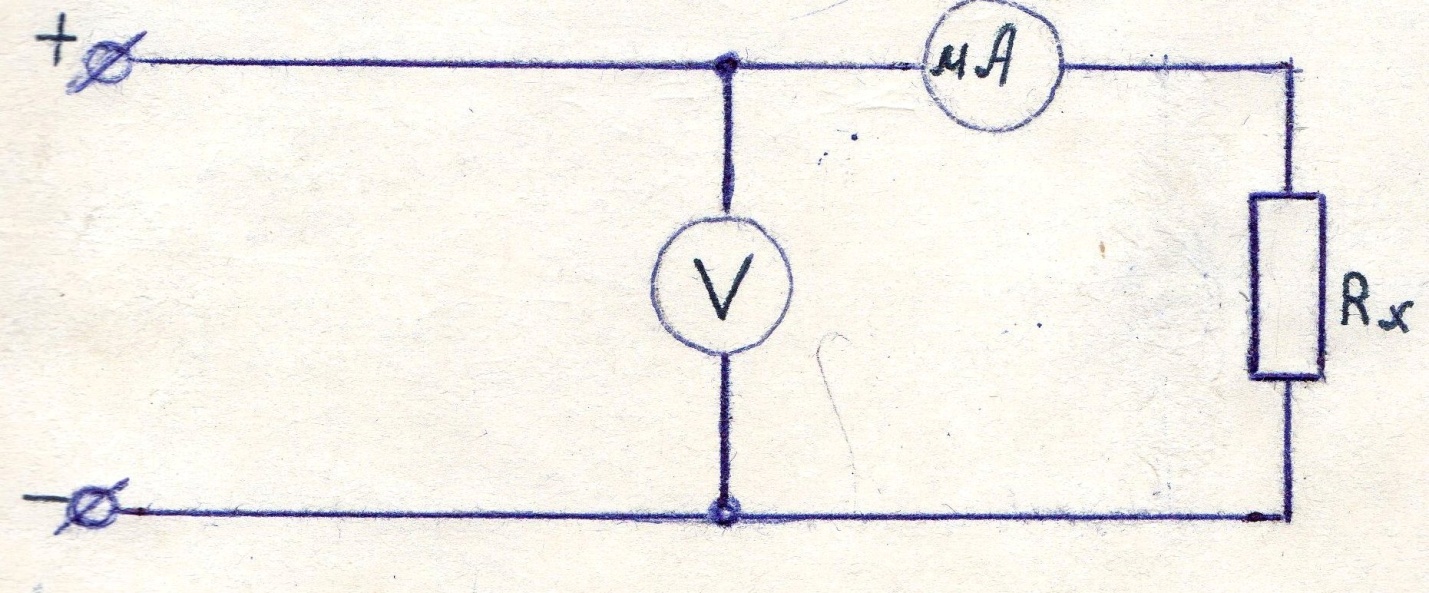
В качестве нагрузки R_x использовать ламповый реостат, размещенный на панели стенда

2. Включить стенд и с помощью регулятора напряжения стенда установить напряжение U=220(В).

Изменяя количество ламп в реостате от одной до пяти, снять показания амперметра и вольтметра в каждом замере и занести в таблицу.

№ замера	U (в)	I (a)	Rx (Ом)	Rм(Ом)	∆R (Ом)

4. Рассчитать для каждого замера величину сопротивления нагрузки R_x c помощью закона Ома для участка цепи R_x=U/I и занести в таблицу.

Снизить напряжение до 0 и выключить питание стенда.

6. С помощью цифрового мультиметра измерить сопротивление реостата R_м . последовательно включая 1,2,3,4 и 5 ламп и показания омметра занести в таблицу.

7. Определить для каждого замера разность значений сопротивления нагрузки, определенных двумя различными способами и занести эту величину _∆R=/R_x – R_м/

После окончания работ сделать следующие выводы6

· Какой способ является наиболее простым

· Какой способ является наиболее точным

· Чем можно объяснить разницу полученных результатов

Лабораторная работа №5

Тема6 «Проверка неразветвленной цепи переменного тока с R L C».

Цель работы:

· Изучить особенности цепи переменного тока с активной, ёмкостной и индуктивной нагрузкой в трех режимах.

· Научиться выполнять построение векторных диаграмм токов и напряжений в каждом из проверяемых режимов.

Приборы и оборудование, используемые в лабораторной работе

Ваттметр

Фазометр (если он есть в наличии)

Источник питания стенда

4. Вольтметр (250-300 в)

5. Амперметр на 1 (а)

Ламповый реостат

Катушка индуктивности

Батарея конденсаторов

Комплект проводов

Ход работы.

Для каждого из трех режимов необходимо произвести следующие вычисления

Z=U/I X_L=U_L/I (U_Lи I взять из 3-го замера и считать X_L=CONST. для всех трех замеров)

X_C=U_C/I U_L=I^.X_L U_a²=U²-(U_L-U_C)² U_a=U^.cosф

R=U_a/I S=U^.I Q=i^.(U_L – U_C) P=i^.U^.cosф

№ замера

Измеренные величины

Вычисленные величины

I

U

UC

P

ф

cosф

Z

XL

XC

UL

Ua

R

S

Q

(а)

(в)

(в)

(вт)

(ом)

(ом)

(ом)

(в)

(в)

(ом)

ва

вар

UL >UC

UL <UC

UL =UC

Лабораторная работа №6

Цель работы: Научиться определять входные и выходные выводы обмоток двигателя, запускать двигатель в работу, соединяя обмотки «звездой» и «треугольником», определять величину пускового и рабочего тока.

Оборудование и приборы: асинхронный двигатель, ламповый реостат, вольтметр 250-300 (В), амперметр 5(А), комплект проводов.

Ход работы.

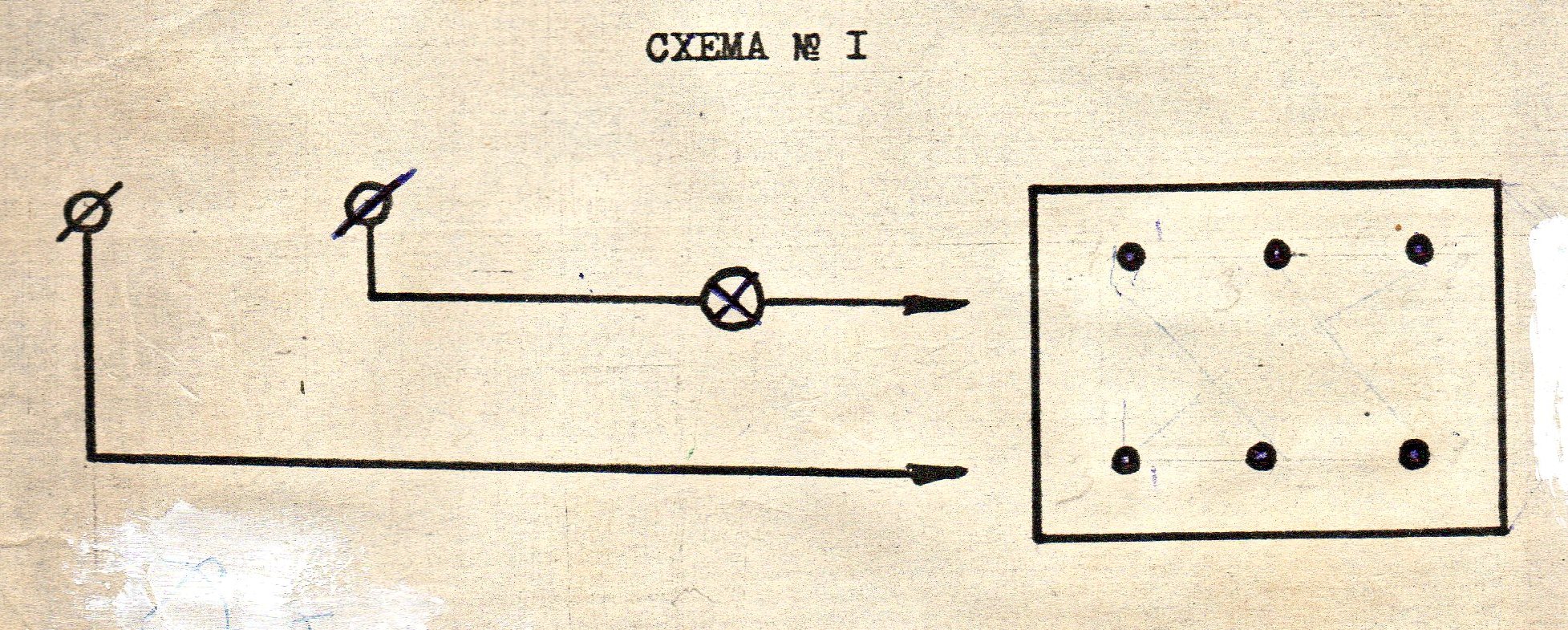
!. Собрать схему №1 и определить выводы каждой из трех обмоток двигателя с помощью контрольной лампы и щупов, последовательно прикасаясь одновременно к двум клеммам (из шести, расположенных на колодке двигателя). Лампа загорится, если две клеммы принадлежат одной из трех обмоток двигателя. Номера выводов проставить на шестиклеммовой колодке, изображенной на рис. 1. (соответственно фактическому расположению – 1-1, 2-2, 3-3).

Лабораторная работа №7

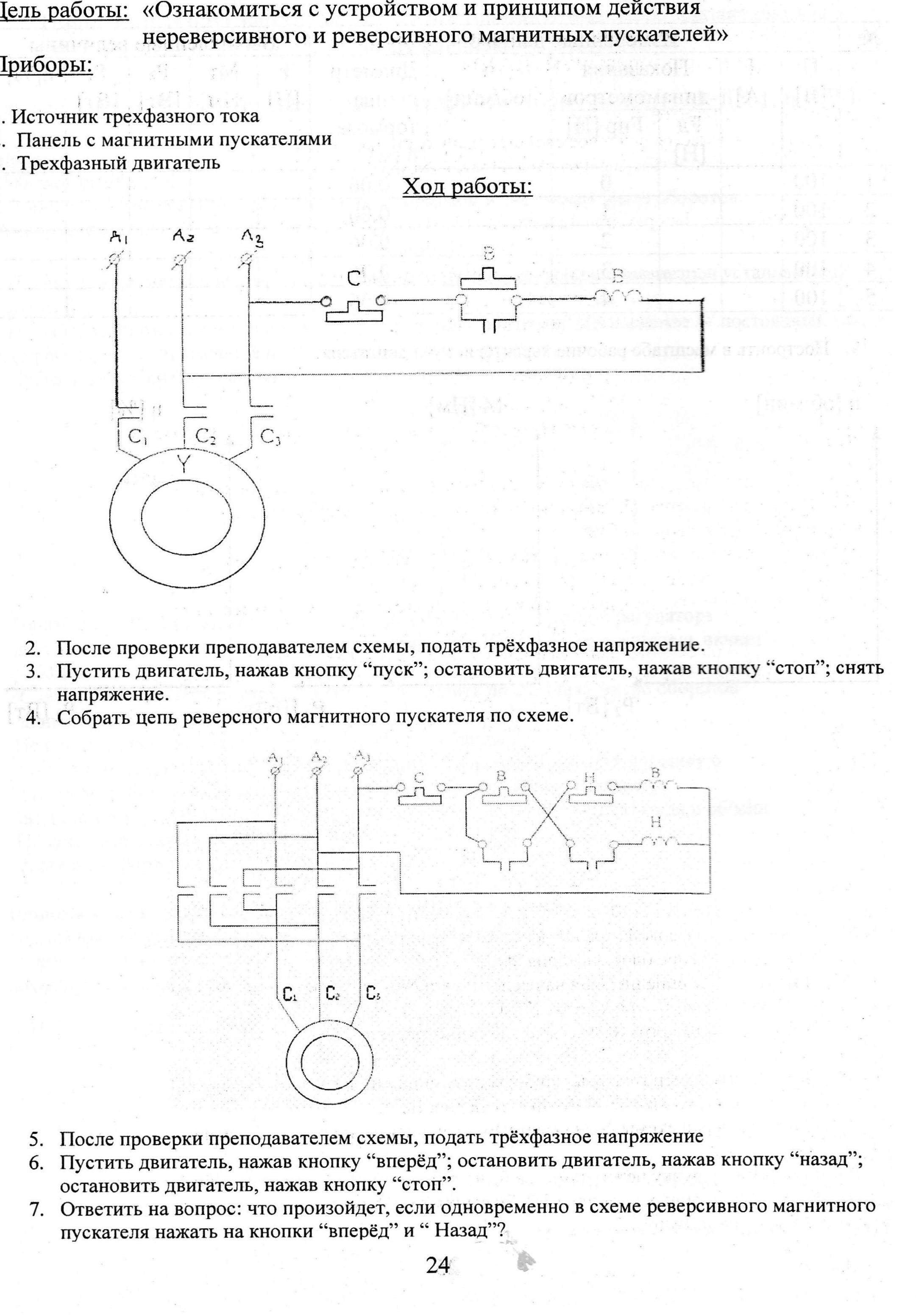
Лабораторная работа №8

 

 

 

Лабораторная работа №9

Лабораторная работа №10

ЛАБОРАТОРНАЯ РАБОТА №2

ТЕМА: «Потери напряжения в линии электропередачи»

Цели работы:

· Определение потери напряжения в линии электропередачи

· Определение мощности потерь

· Определение КПД линии электропередачи

Приборы, используемые в лабораторной работе:

Двухпроводная линия

Амперметр на 1(А)

Вольтметр с диапазоном не менее 250 (В)