Извините такой страницы Wp-content Uploads 2014 02 Dz-1 Zakony-kirhgofa Pdf не существует!
Выбор статьи по меткам03 (1)9 класс (3)10 класс (1)11 класс (2)12 (1)13 (С1) (3)14 ноября (2)14 февраля (1)15 задание ЕГЭ (2)16 задача профиль (1)16 профильного ЕГЭ (1)16 января Статград (1)18 (С5) (2)18 задача ЕГЭ (2)23 марта (1)31 января (1)2016 (2)140319 (1)14032019 (1)C5 (1)RC-цепь (1)А9 (1)Александрова (2)Ампера (2)Архимед (1)Бернулли (1)Бойля-Мариотта (1)В8 (1)В12 (1)В13 (1)В15 (1)ВК (1)ВШЭ (2)ГИА физика задания 5 (1)Герона (1)Герцшпрунга-Рассела (1)Гринвич (1)ДВИ (1)ДПТ (1)Десятичные приставки (1)Дж (1)Диэлектрические проницаемости веществ (1)ЕГЭ 11 (2)ЕГЭ 14 (1)ЕГЭ 15 (2)ЕГЭ 18 (1)ЕГЭ С1 (1)ЕГЭ по математике (25)ЕГЭ по физике (49)ЕГЭ профиль (6)Европа (1)Задача 17 ЕГЭ (6)Задачи на движение (1)Закон Архимеда (2)Законы Ньютона (1)Земля (1)Ио (1)КПД (9)Каллисто (1)Кельвин (1)Кирхгоф (1)Кирхгофа (1)Койпера (1)Колебания (1)Коши (1)Коэффициенты поверхностного натяжения жидкостей (1)Кулона-Амонтона (1)Ломоносов (2)Лоренца (1)Луна (1)МГУ (1)МКТ (7)Максвелл (2)Максвелла (1)Максимальное удаление тела от точки бросания (1)Менделеева-Клапейрона (3)Менелая (3)Метод наложения (2)Метод узловых потенциалов (1)Метод эквивалентных преобразований (1)НОД (1)Нансен (1)НеИСО (1)ОГЭ (11)ОГЭ (ГИА) по математике (27)ОГЭ 3 (ГИА В1) (1)ОГЭ 21 (3)ОГЭ 21 (ГИА С1) (4)ОГЭ 22 (2)ОГЭ 25 (3)ОГЭ 26 (1)ОГЭ 26 (ГИА С6) (1)ОГЭ по физике 5 (1)ОДЗ (12)Обыкновенная дробь (1)Оорта (1)Основные физические константы (1)Отношение объемов (1)Плюк (1)Показатели преломления (1)Показательные неравенства (1)Противо-эдс (1)Работа выхода электронов (1)Радиус кривизны траектории (1)Релятивистское замедление времени (1)Релятивистское изменение массы (1)С1 (1)С1 ЕГЭ (1)С2 (2)С3 (1)С4 (3)С6 (5)СУНЦ МГУ (2)Сиена (1)Синхронная машина (1)Снеллиуса (2)Солнечной системы (1)Солнце (2)СпБ ГУ вступительный (1)Средняя кинетическая энергия молекул (1)Статград физика (3)Таблица Менделеева (1)Текстовые задачи (8)Тьерри Даксу (1)ФИПИ (1)Фазовые переходы (1)Фаренгейт (1)Фобос (1)Френеля (1)Цельсий (1)ЭДС (6)ЭДС индукции (2)Эйлера (1)Электрохимические эквиваленты (1)Эрастофен (1)абсолютная (1)абсолютная влажность (2)абсолютная звездная величина (3)абсолютная температура (1)абсолютный ноль (1)адиабаты (1)аксиомы (1)алгоритм Евклида (2)алгоритм Робертса (1)аморфное (1)амплитуда (3)аналитическое решение (1)анекдоты (1)апериодический переходной процесс (2)аргумент (1)арифметическая прогрессия (5)арифметической прогрессии (1)арки (1)арккосинус (1)арккотангенс (1)арксинус (1)арктангенс (1)архимеда (3)асинхронный (1)атмосферное (2)атмосферном (1)атомная масса (2)афелий (2)база (1)балка (1)банк (1)без калькулятора (1)белого карлика (1)бензин (1)бесконечная периодическая дробь (1)бесконечный предел (1)биквадратные уравнения (1)бипризма (1)биссектриса (4)биссектрисы (2)благоприятный исход (1)блеск (4)блок (2)боковой поверхности (1)большая полуось (1)большем давлении (1)бревно (2)бригада (2)бросили вертикально (1)бросили под углом (3)бросили со скоростью (2)броуновское движение (1)брошенного горизонтально (2)бруски (1)брусок (3)брусок распилили (1)бусинка (1)быстрый способ извлечения (1)вариант (3)вариант ЕГЭ (12)вариант ЕГЭ по физике (18)вариант по физике (1)варианты ЕГЭ (6)вариент по физике (1)введение дополнительного угла (1)вектор (5)векторное произведение (2)велосипедисты (1)вероятность (1)вертикальная составляющая (1)вертикально вверх (1)вертикальные углы (1)вес (3)весов (1)вес тела (1)ветви (1)ветвь (2)ветер (1)взаимодействие зарядов (1)видеоразбор (2)видеоразбор варианта (1)видимая звездная величина (2)виртуальная работа (1)виртуальный банк (1)виртуальных перемещений (1)витка (1)витков (1)виток (1)вклад (1)влажность (3)влажность воздуха (1)влетает (2)вневписанная окружность (2)внутреннее сопротивление (1)внутреннее сопротивление источника (1)внутреннюю энергию (1)внутренняя энергия (8)вода течет (1)воды (1)возведение в квадрат (1)возвратное уравнение (1)возвратность (1)возвратные уравнения (2)воздушный шар (1)возрастающая (1)возрастет (1)волны (1)вписанная (1)вписанная окружность (3)вписанной окружности (1)вписанный угол (4)в правильной пирамиде (1)вращение (1)времени (2)время (24)время в минутах (1)время выполнения (1)время движения (2)время минимально (1)время падения (1)всесибирская олимпиада (1)в стоячей воде (1)встретились (1)встретятся (1)вступительный (1)вступительный экзамен (1)вторая половина пути (1)вторичная (1)вторичная обмотка (1)вторичные изображения (1)второй закон Ньютона (4)выбор двигателя (1)выборка корней (4)выколотая точка (1)выплаты (2)выразить вектор (1)высота (5)высота Солнца (1)высота столба (1)высота столба жидкости (1)высота столбика (1)высоте (3)высоту (1)высоты (3)выталкивающая сила (2)вычисления (2)газ (3)газа (1)газов (1)газовая атмосфера (1)галочка (1)гамма-лучей (1)гармоника (2)гвоздя (1)геометрическая вероятность (1)геометрическая прогрессия (4)геометрические высказывания (1)геометрический смысл (2)геометрическую прогрессию (1)геометрия (7)гигрометр (1)гидродинамика (1)гидростатика (3)гимназия при ВШЭ (1)гипербола (2)гипотенуза (3)гистерезисный двигатель (1)главный период (1)глубина (1)глухозаземленная нейтраль (1)гомотетия (2)гонщик (1)горизонтальная сила (1)горизонтальной спицы (1)горизонтальную силу (1)горка (1)гравитационная постоянная (1)градус (1)грани (2)график (2)графики функций (5)графически (1)графический способ (1)графическое решение (2)груз (2)грузик (2)группа (1)давление (28)давление жидкости (3)давление пара (1)дальность полета (1)двигатель с активным ротором (1)движение под углом (1)движение под углом к горизонту (4)движение по кругу (1)движение по течению (1)движение с постоянной скоростью (2)двойное неравенство (1)двойной фокус (1)двугранный угол при вершине (1)девальвация (1)действительная часть (1)действующее значение (2)деление (1)деление многочленов (2)деление уголком (1)делимость (15)делимость чисел (1)делители (1)делитель (2)делится (3)демонстрационный варант (1)деталей в час (1)диаграмма (1)диаметр (2)диаметру (1)динамика (4)диод (1)диск (1)дискриминант (4)дифракционная решетка (2)дифференцированный платеж (1)диффузия (1)диэлектрик (1)диэлектрическая проницаемость (1)длина (4)длина вектора (1)длина волны (7)длина отрезка (2)длина пружины (1)длина тени (1)длиной волны (2)длину нити (1)длительность разгона (1)длительный режим (1)добротность (1)догнал (1)догоняет (1)докажите (1)долг (1)доля (1)дополнительный угол (1)досок (1)досрочный (2)досрочный вариант (1)дптр (1)дуга (1)единицы продукции (1)единичный источник (1)единичных кубов (1)единственный корень (1)ежесекундно (1)емкость (7)емкость заряженного шара (1)естественная область определения (1)желоб (2)жесткость (6)жеткость (1)живая математика (2)жидкости (1)жидкость (1)завод (1)загадка (2)задание 13 (2)задание 15 (3)задание 23 (1)задания 1-14 ЕГЭ (1)задача 9 (1)задача 13 профиль (1)задача 14 профиль (3)задача 16 (1)задача 16 ЕГЭ (1)задача 16 профиль (3)задача 17 (1)задача 18 (1)задача 26 ОГЭ (2)задача с параметром (6)задачи (1)задачи на доказательство (4)задачи на разрезание (4)задачи на совместную работу (3)задачи про часы (1)задачи с фантазией (1)задерживающее напряжение (1)заземление (1)заказ (1)закон Бернулли (1)закон Гука (1)закон Ома (3)закон Снеллиуса (1)закона сохранения (1)закон движения (1)закон кулона (7)закон палочки (3)закон сложения классических скоростей (1)закон сохранения импульса (6)закон сохранения энергии (4)законы Кирхгофа (6)законы коммутации (1)законы сохранения (1)закрытым концом (1)замена переменной (2)замкнутая система (2)зануление (1)запаянная (2)заряд (9)заряда (1)заряд конденсатора (1)защитная характеристика (1)звездочка (1)звезды (1)зенит (1)зенитное расстояние (1)зеркало (2)знак неравенства (1)знаменатель (1)знаменатель прогрессии (4)значение выражения (1)идеальный блок (1)идеальный газ (5)извлечение в столбик (1)излом (1)излучение (2)изменение длины (2)изобара (1)изобаричесикй (1)изобарический (2)изобарный (1)изобарный процесс (1)изображение (3)изолированная нейтраль (1)изопроцессы (1)изотерма (2)изотермически (1)изотермический (2)изотермический процесс (1)изотоп (1)изохора (1)изохорический (1)изохорный процесс (1)импульс (9)импульса (1)импульс силы (1)импульс системы (1)импульс системы тел (4)импульс тела (4)импульс частицы (1)инвариантность (1)индуктивно-связанные цепи (1)индуктивное сопротивление (1)индуктивность (1)индукцией (1)индукция (8)интеграл Дюамеля (1)интервал (1)интересное (3)интерференционных полос (1)иррациональность (2)испарение (2)исследование функции (4)источник (1)источник света (1)исход (1)камень (1)камешек (1)капилляр (1)карлик (2)касательная (4)касательного (1)касательные (1)касаются (1)катер (2)катет (3)катушка (4)качаний (2)квадлратичная зависимость (1)квадрант (1)квадрат (3)квадратичная функция (3)квадратное (1)квадратное уравнение (4)квадратную рамку (1)квазар (1)квант (1)квантов (1)кинематика (2)кинематическая связь (1)кинематические связи (4)кинетическая (12)кинетическая энергия (4)кинетической (1)кинетической энергии (1)кинетическую энегрию (1)классический метод (3)классический метод расчета (1)клин (2)ключ (1)кодификатор (1)колебаний (1)колене (1)количество вещества (1)количество теплоты (9)коллектор (1)кольцо (2)комбинаторика (1)комбинированное (1)коммутация (1)комплексное сопротивление (1)комплексное число (1)комплексные числа (1)компонент (1)конвекция (3)конденсатор (10)конденсаторы (1)конденсации (1)конечная скорость (1)конечная температура (1)конечная температура смеси (1)конечный предел (1)консоль (1)контрольная (1)контрольные (1)контур (5)конус (4)концентрация (7)концентрическим (1)координата (5)координаты (3)координаты вектора (2)координаты середины отрезка (1)координаты точки (1)корабля (1)корень (2)корень квадратный (1)корень кубический (1)корни (2)корни иррациональные (1)корни квадратного уравнения (3)корни уравнения (1)корпоративных (1)косинус (2)косинусы (1)котангенс (1)коэффициент (1)коэффициент жесткости (1)коэффициент наклона (3)коэффициент поверхностного натяжения (3)коэффициент подобия (5)коэффициент трансформации (1)коэффициент трения (5)коэффициенты (1)красное смещение (1)красной границы (1)красный (1)кратковременный режим (1)кратные звезды (1)кредит (11)кредитная ставка (4)кредиты (1)криволинейная трапеция (2)кристаллизация (1)критерии оценки (1)круговая частота (1)круговой контур (1)кружок (1)кубическая парабола (1)кулонова сила (1)кульминация (1)кусочная функция (1)левом колене (1)лед (2)лет (1)линейная скорость (2)линейное напряжение (1)линейное уравнение (2)линейный размер (1)линза (2)линзы (2)линии излома (1)линиями поля (1)линия отвеса (1)литров (1)лифт (1)лифта (1)лифте (1)логарифм (10)логарифмические неравенства (3)логарифмические уравнения (1)логарифмическое неравенство (3)логарифмы (1)лунка (1)лучевая (1)льда (1)магнитное поле (2)магнитном поле (2)магнитные цепи (1)максимальная высота (1)максимальная скорость (1)максимум (1)малых колебаний (1)масса (23)масса воздуха (1)массе (1)массивная звезда (1)массовое содержание (1)массой (1)массу (1)математика (4)математический маятник (1)математического маятника (1)маятник (4)мгновенный центр вращения (1)медиана (2)меридиан (1)мертвая вода (1)мертвая петля (1)метод виртуальных (1)метод внутреннего проецирования (1)метод замены переменной (4)метод интервалов (3)метод комплексных амплитуд (3)метод контурных токов (1)метод координат (1)метод линий (1)методом внутреннего проецирования (1)метод переброски (1)метод переменных состояния (1)метод подстановки (4)метод рационализации (4)метод решетки (1)метод следов (5)метод сложения (4)метод телескопирования (1)метод узловых напряжений (1)методы расчета цепей (2)методы расчета цепей постоянного тока (1)метод эквивалентного генератора (2)механика (1)механическая характеристика (1)механическое напряжение (1)миля (1)минимальная скорость (1)минимальное (1)минимальной высоты (1)минимальной скоростью (1)минимум (2)мишени (1)мнимая единица (1)мнимая часть (1)многоугольник (1)многочлены (1)мода (2)модули (1)модуль (13)модуль Юнга (1)модуль средней скорости (1)молекулярно-кинетическая теория (2)моль (2)молярная масса (5)момент (7)момент инерции (1)момент инерции двигателя (1)момент нагрузки (1)момент сил (1)монета (1)монотонная (1)монотонность функции (1)монохроматического (1)мощности силы тяжести (1)мощность (9)мощностью (1)мяч (1)наблюдатель (1)нагревание (1)нагреватель (1)нагревателя (1)нагрели (1)наибольшее (1)наивысшая точка (1)наименьшее (1)наименьшее общее кратное (1)наклон (1)наклонная плоскость (2)налог (1)на направление (2)на подумать (2)направление (1)направление обхода (3)направлении (1)направляющий вектор (1)напряжение (9)напряжение на зажимах (1)напряжение смещения нейтрали (2)напряженность (4)напряженность поля (6)насос (2)насоса (1)насыщенный пар (4)натуральное (7)натуральные (7)натуральных (1)натяжение нити (5)натяжения (1)находился в полете (2)начальная температура (1)начальной скоростью (1)недовозбуждение (1)незамкнутая система (2)нелинейное сопротивление (1)неопределенность типа бесконечность на бесконечность (1)неопределенность типа ноль на ноль (1)непериодическая дробь (1)неравенства (8)неравенство (22)неразрывности струи (1)нерастяжимой (1)нерастяжимой нити (1)нерастянутой резинки (1)несимметричная нагрузка (1)несинусоидальный ток (3)нестандартные задачи (1)нестрогое (1)неупругим (1)нецентральный (1)нечетная функция (2)нечетное (1)нечетность (1)неявнополюсный (1)нити (2)нити паутины (1)нить (2)нить нерастяжима (1)новости (1)нормаль (1)нормальное ускорение (11)нулевой ток (2)обкладками (1)обкладках (1)обкладки (1)область допустимых значений (9)область значений (1)область определения (8)область определения функции (4)оборот (1)обратные тригонометрические функции (1)обратные функции (1)общая хорда (1)общее сопротивление (1)общее сопротивление цепи (1)объем (36)объемный расход (1)объемом (1)объем пара (1)объем параллелепипеда (1)объем пирамиды (1)одинаковые части (1)одновременно (1)одновременно из одной точки (1)окружность (13)окружность описанная (1)олимпиада (2)олимпиады по физике (2)они встретятся (1)операторный метод (4)описанная (1)оптика (1)оптимальный выбор (1)оптимизация (1)оптическая разность хода (1)оптический центр (1)орбитам (1)орбитой (1)оригинал (1)осевое сечение (1)оси (1)основание (2)основание логарифма (2)основания трапеции (1)основное тригонометрическое тождество (1)основное уравнение МКТ (2)основной газовый закон (1)основной период (1)основной уровень (1)основные углы (1)остаток (1)ось (1)отбор корней (5)ответ (1)отданное (1)относительная (1)относительная влажность (3)относительная скорость (1)относительно (2)относительность движениия (1)относительность движения (2)относительность скоростей (1)отношение (5)отношение времен (1)отношение длин (1)отношение площадей (3)отношение скоростей (2)отрезок (1)отсечение невидимых граней (1)очки (1)падает (1)падает луч (1)падает под углом (1)падение (3)падение напряжения (2)падения (1)пар (3)парабола (5)параболы (1)параллакс (5)параллелепепед (2)параллелепипед (3)параллелограмм (4)параллелограмм Виньера (1)параллельно (2)параллельно двум векторам (1)параллельное соединение (3)параллельные прямые (1)параллельными граням (1)параметр (30)параметры (1)парообразование (1)парсек (1)парциальное (1)парциальное давление (1)паскаль (1)первая треть (1)первичная (1)переброски (1)перевозбуждение (1)перегородка (1)перегрузок (1)перелетит (1)переливания (1)переменное магнитное поле (1)переменное основание (2)перемещение (6)перемычка (5)перемычке (1)перемычку (1)переносная скорость (1)пересекает (1)пересечение (1)пересечения (1)переходная проводимость (1)переходное сопротивление (1)переходной процесс (1)переходные процессы (9)перигелий (2)периметр (3)период (15)периодическая дробь (1)период колебаний (2)период малых колебаний (1)период обращения (2)период функции (1)периоды (1)перпендикулярно (1)песок (1)пион (1)пипетка (1)пирамида (7)пирамида шестиугольная (1)пирамиды (2)пирсона (1)плавание (1)плавкие предохранители (1)плавление (1)план (1)планете (1)планеты (3)планиметрия (13)планиметрия профиль (1)пластинами (1)пластинка (1)платеж (8)плечо (2)плоского зеркала (1)плоскопараллельная (1)плоскость (4)плоскость сечения (1)плотности веществ (1)плотность (22)плотность пара (3)плотность сосуда (1)плотность энергии (1)площади (2)площади фигур на клетчатой бумаге (1)площадь (30)площадь круга (1)площадь пластин (1)площадь поверхности (1)площадь под кривой (2)площадь проекции (1)площадь проекции сечения (1)площадь сектора (1)площадь сечения (5)площадь треугольника (1)поверхностная плотность заряда (1)поворот (1)повторно-кратковременный режим (1)погрешность (1)погружено (1)подвесили (1)подготовка к контрольным (3)под каким углом (1)подмодульное (1)подмодульных выражений (1)подобен (1)подобие (7)подобия треугольников (1)подобны (1)подпереть (1)под углом (2)под углом к горизонту (3)показателем преломления (1)показательное (1)показатель преломления (4)поле (1)полезной работы (1)полезную мощность (1)полигон частот (1)по линиям сетки (1)полное ускорение (1)половина времени (1)половинный угол (1)положительный знаменатель (1)полония (1)полость (1)полуокружность (1)полупроводник (1)полученное (1)понижение горизонта (1)по окружности (1)по переменному основанию (1)поправка часов (1)по прямой (1)поршень (4)поршня (1)порядок решетки (2)последовательно (1)последовательное соединение (3)последовательность (3)по сторонам клеток (1)посторонние корни (4)постоянная Авогадро (1)постоянная Хаббла (1)постоянная времени (1)постоянная скорость (1)постоянная составляющая (2)постоянный ток (5)построение (2)построение графика функции (1)потенциал (5)потенциал шара (1)потенциальная (13)потенциальная энергия (3)потенциальной (1)потери в стали (2)потеря корней (4)поток (5)по физике (1)правило левой (1)правило моментов (3)правильную пирамиду (1)правильный многоугольник (1)правом колене (1)предел функции (1)преломляющий угол (1)преобразование графиков функций (1)преобразования (3)преподаватели (2)пресс (2)призма (6)призмы (3)признаки подобия (4)признаки равенства треугольников (3)пробн (1)пробник (172)пробник по физике (8)пробниук (1)пробный (1)пробный ЕГЭ (2)пробный ЕГЭ по физике (3)пробный вариант (25)пробный вариант ЕГЭ (17)пробный вариант ЕГЭ по физике (112)пробный вариант по физике (1)провода (1)проводник (1)проводник с током (1)проводящего шара (1)проволока (1)проволоки (1)прогрессия (5)проекции скоростей (1)проекции ускорения (2)проекция (7)проекция перемещения (1)проекция скорости (6)проекция ускорения (2)производительность (2)производная (3)промежутка времени (1)промежуток (1)промежуток знакопостоянства (1)пропорциональны (1)проскальзывает (1)проскальзывания (1)противоположное событие (1)противостояние (1)протона (1)прототипы (1)профиль (2)профильный ЕГЭ (1)процент (5)процентная ставка (6)процентное отношение (1)процентное содержание (2)проценты (3)пружин (1)пружина (6)пружинный маятник (1)пружины (1)прямая (6)прямое восхождение (2)прямой (1)прямой АВ (1)прямоугольник (1)пузырек (1)пульсар (1)пуля (1)пути (1)путь (27)пять корней (1)работа (15)работа газа (5)работа тока (1)работу выхода (2)рабочее тело (1)рабочие (1)равнобедренный (1)равновеликий (1)равновесие (4)равновесия (1)равновесное (1)равнодействующая (1)равномерно (1)равноускоренно (2)равноускоренное (3)равные (1)равные фигуры (1)радиальную ось (1)радикал (1)радиус (11)радиус колеса (1)радиус кривизны (2)радиус описанной сферы (1)радиус темного кольца в отраженном свете (1)разбор (1)разбор Статграда по физике (1)разложение на множители (2)размах (1)разности температур (1)разность (2)разность потенциалов (2)разность прогрессии (3)разность хода (1)разрежьте (2)разрезание (5)разрешающая сила (1)разрыв функции (1)рамка (8)рамка с током (1)раскрытие модуля (1)расписание (1)расположение корней квадратного трехчлена (1)распределение частот (1)рассеивающая (1)расстояние (21)расстояние между зарядами (1)расстояние на карте (1)расстояние от точки (1)расстояния (2)раствор (2)растяжение (2)расходуется (1)расцепители (1)расчеты по формулам (1)рационализация (4)рациональные неравенства (1)реактивные элементы (1)реактивный двигатель (1)реакция опоры (4)реакция якоря (1)ребра (1)ребус (2)резервуар (1)резистор (1)рейки (1)рельса (1)рентгеновскую трубку (1)репетитор (1)решебник (1)решение тригонометрических уравнений (1)решение уравнений (2)решение уравнений больших степеней (1)решить в натуральных (1)решить в целых (1)розетка (1)ромб (1)ряд Фурье (1)сарай с покатой крышей (1)сближаются (1)сближения (1)сбрасывают с высоты (1)сверхгигант (2)сверхновая (1)светимость (3)свободно (1)свободного падения (1)свободно падает (2)свойства (2)свойства отрезков (1)свойства степени (1)свойства функции (1)свойства функций (2)свойства чисел (1)свойство биссектрисы (2)свойству биссектрисы (1)сдвинуть (1)сегмент (1)сектор (1)секущая (2)серия решений (1)сертификация (6)сессия (1)сечение (14)сечение наклонной плоскостью (1)сидерический (1)сила (7)сила Архимеда (5)сила Лоренца (4)сила ампера (9)сила взаимодействия (4)сила давления (1)сила на дно (1)сила натяжения (7)сила натяжения нити (4)сила поверхностного натяжения (3)сила реакции опоры (1)сила трения (3)сила тяготения (1)сила тяжести (5)сила упругости (2)силой (2)силу (1)силу натяжения (1)силы трения (2)символический метод (3)симметричная нагрузка (1)симметрия (3)синодический (1)синус (4)синусоида (1)синусоидальный закон (1)синусоидальный ток (5)синусы (1)синхронный компенсатор (1)система (3)система неравенств (7)система отсчета (3)система счисления (1)система уравнений (3)системы уравнений (3)скалярное произведение (3)склонение (1)скольжение (2)скользит (1)скользит равномерно (1)скоросмть (1)скоростей (1)скорости (3)скорости течения (1)скорость (43)скорость реки (1)скорость сближения (3)скорость света (1)скорость теплохода (1)скорость удаления (1)скорость частицы (1)скоростью (1)с лестницы (1)сложение векторов (1)сложная функция (1)смежные углы (1)смекалка (2)смеси (1)смешанное число (1)смещение (2)снаряд (1)собирающая (2)событие (1)соединение звездой (1)соединение треугольником (1)сокращение (1)сокращение дробей (1)соленоид (1)солнечная постоянная (3)солнечная система (1)сообразительность (1)сообщающиеся сосуды (2)соприкосновения (1)сопротивление (13)сопротивления (1)сопряженное (3)составить квадрат (1)составляет с направлением (1)составляющая скорости (2)составляющие (1)составляющие скорости (3)сосуд (1)сосудах (1)сосуде (1)сохранение энергии (1)спектра (2)спектральный класс (2)спецификация (1)спирт (1)сплава (1)сплавы (1)справочные данные (3)справочные материалы (12)спрос (1)сравнение чисел (2)среднее (1)среднее значение (1)среднеквадратичная скорость (1)среднюю линию (1)средняя квадратичная скорость (1)средняя скорость (6)срок (1)срок кредитования (1)стадии (1)стакан (2)статград (17)статика (2)стенка (1)степенная функция (1)степенные уравнения (1)степень (2)стереометрия (4)стержень (3)стержня (1)столб жидкости (3)столбик (3)столбик жидкости (2)столбик ртути (1)столбчатая диаграмма (1)стрелки поравняются (1)строгое (1)струю (1)студенты (2)ступеньку (1)сумма косинусов (1)сумма прогрессии (1)суммарный импульс (1)сумма ряда (1)сумма синусов (1)сумма углов (2)суммирование (2)сумму (1)суперпозиция (1)сутки (1)сфера (5)сферы (2)таблица (1)таблица частот (1)тангенс (3)тангенс разности (1)тангенс суммы (1)тангенциальная (1)тангенциальное ускорение (1)твердое тело (1)тела вращения (1)тележка (2)телескоп (1)телескопирование (1)тело (1)температура (21)температурный коэффициент сопротивления (1)температуры (2)тени (1)тень (1)теорема Пифагора (3)теорема Штейнера (1)теорема виета (5)теорема косинусов (4)теорема синусов (2)теореме косинусов (1)теоремы (1)теоретическое разрешение (1)теория вероятности (1)теплового двигателя (1)тепловое действие (1)тепловое равновесие (2)тепловой баланс (1)тепловой двигатель (1)тепл
Методы расчета электрических цепей
Постановка задачи: в известной схеме цепи с заданными параметрами необходимо рассчитать токи, напряжения, мощности на отдельных участках. Для этого можно использовать следующие методы:
преобразования цепи;
непосредственного применения законов Кирхгофа;
контурных токов;
узловых потенциалов;
наложения;
эквивалентного генератора.
Будем рассматривать первых два метода.
Метод преобразования цепи. Суть метода: если несколько последовательно или (и) параллельно включенных сопротивлений заменить одним, то распределение токов в электрической цепи не изменится.
а) Последовательное соединение резисторов. Сопротивления включены таким образом, что начало следующего сопротивления подключается к концу предыдущего (рис. 6).
Ток во всех последовательно соединенных элементах одинаков.
З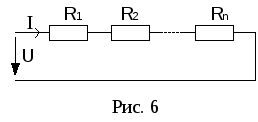
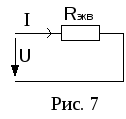 аменим
все последовательно соединенные
резисторы одним эквивалентным
аменим
все последовательно соединенные
резисторы одним эквивалентным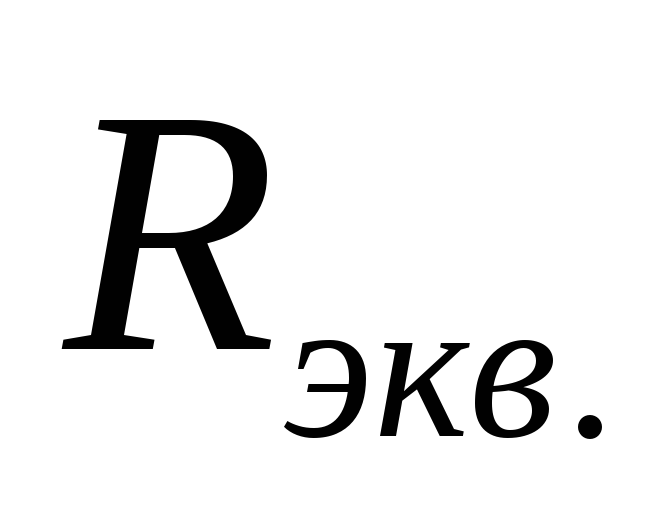 (рис. 7.).
(рис. 7.).
По IIзакону Кирхгофа:
 ;
;
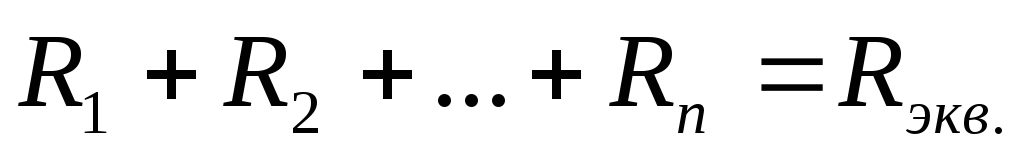 ;
;
т.е. при последовательном соединении резисторов эквивалентное сопротивление участка цепи равно сумме всех последовательно включенных сопротивлений.
б) Параллельное соединение резисторов. При этом соединении соединяются вместе одноименные зажимы резисторов (рис. 8).
В се
элементы присоединяются к одной паре
узлов. Поэтому ко всем элементам приложено
одно и тоже напряжениеU.
се
элементы присоединяются к одной паре
узлов. Поэтому ко всем элементам приложено
одно и тоже напряжениеU.
По Iзакону Кирхгофа: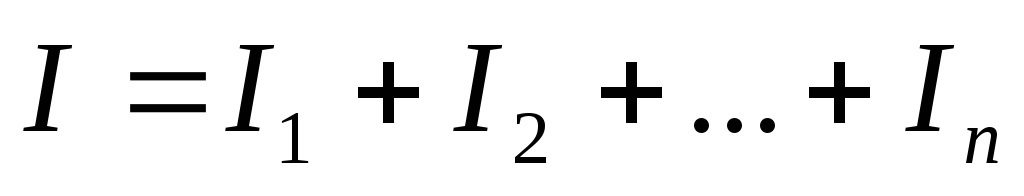 .
.
По
закону Ома 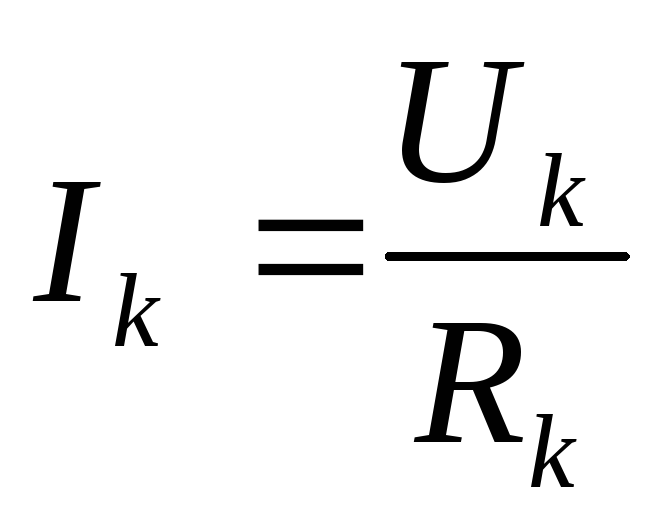 .
Тогда
.
Тогда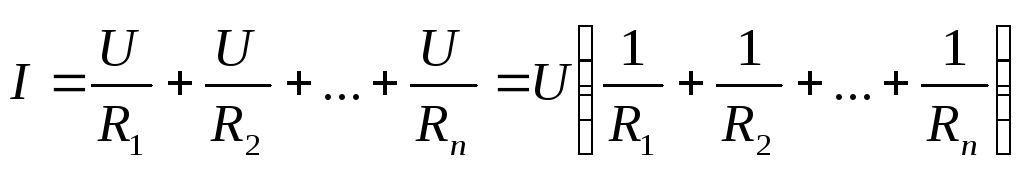 .
.
Для
эквивалентной схемы (см рис. 7): 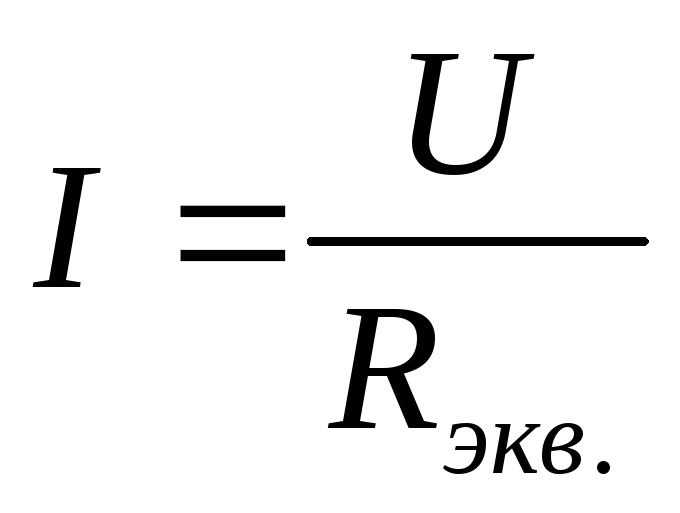 ;
; 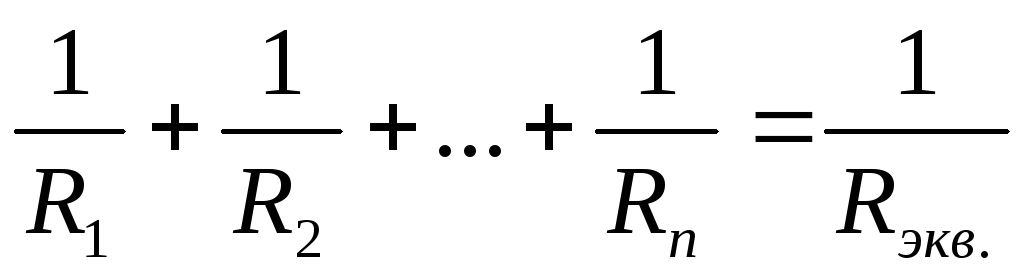 .
.
Величина 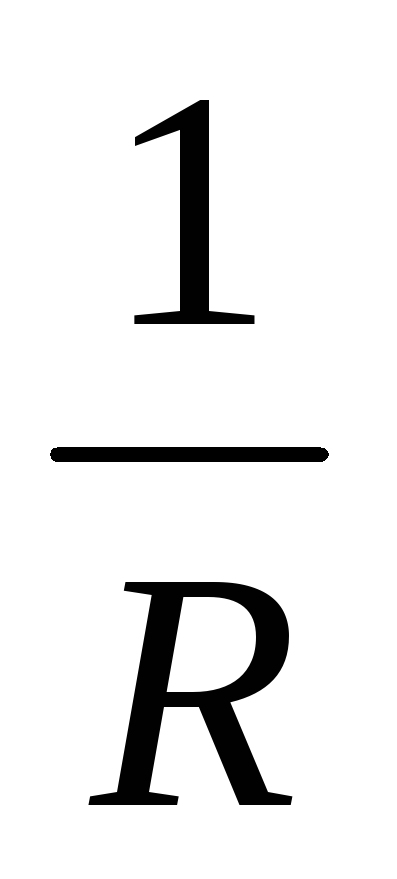 ,
обратная сопротивлению, называется
проводимостьюG.
,
обратная сопротивлению, называется
проводимостьюG.
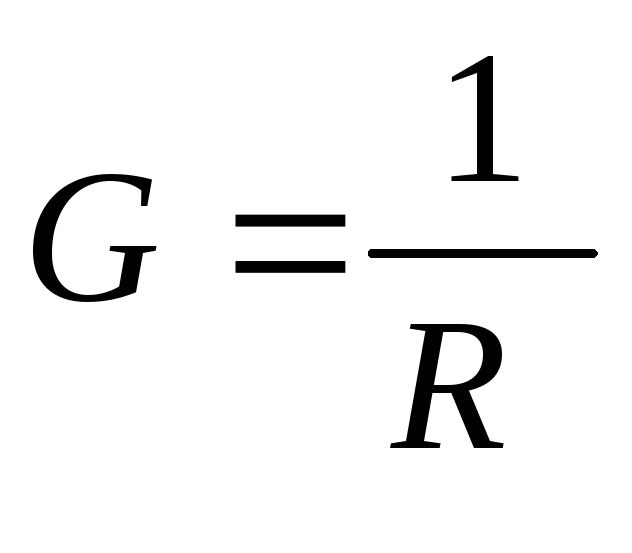 ;
;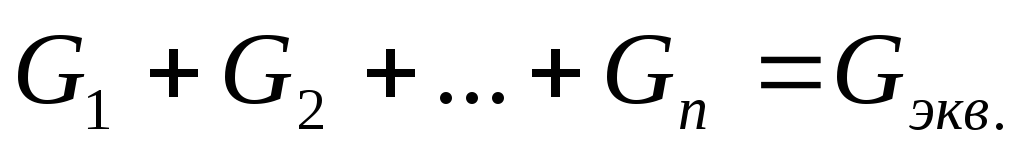
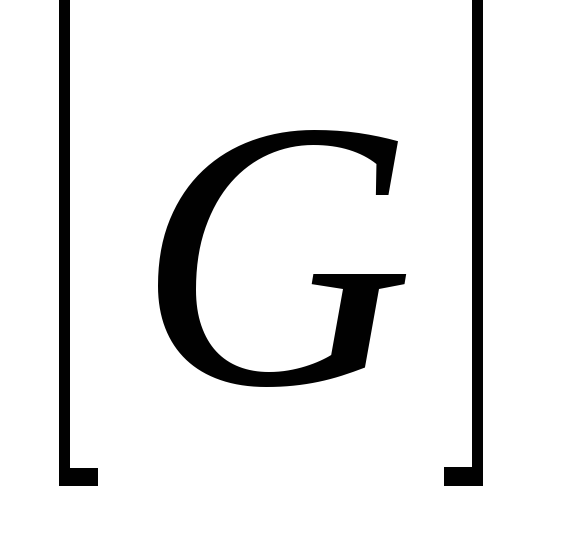 =
Сименс (См).
=
Сименс (См).
Ч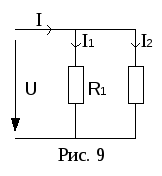 астный
случай: параллельно соединены два
резистора (рис. 9).
астный
случай: параллельно соединены два
резистора (рис. 9).
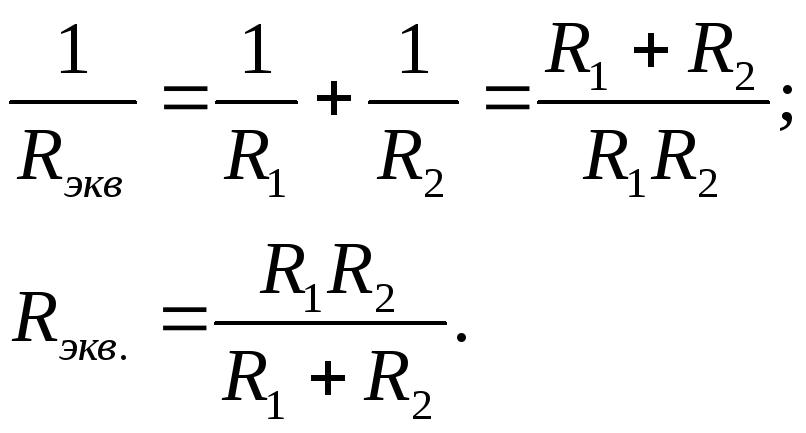


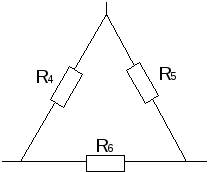
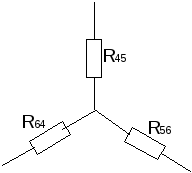
в) Взаимное преобразование звезды (рис.10а) и треугольник сопротивлений (рис. 10б).
— преобразование звезды сопротивлений в треугольник:

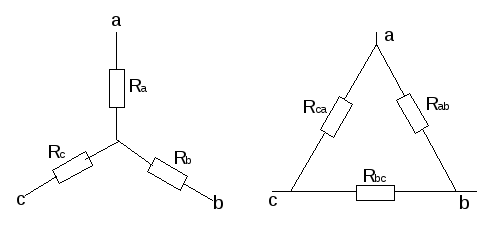
— преобразование «треугольника» сопротивлений в «звезду»:
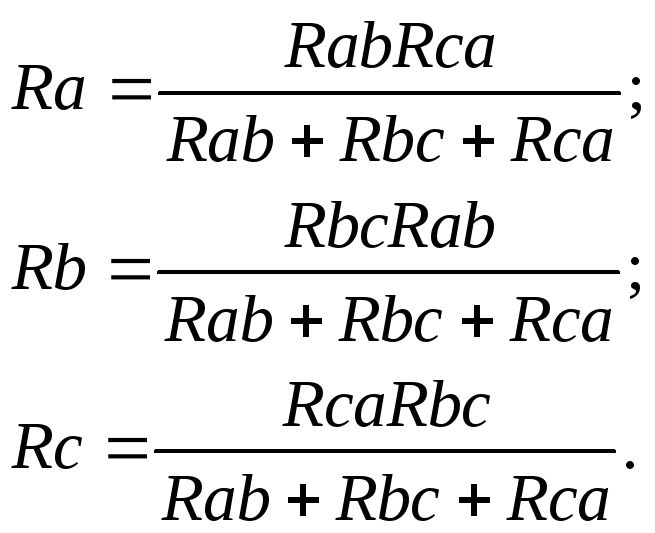
Метод непосредственного применения законов Кирхгофа. Порядок расчета:
Определить число ветвей (т.е. токов) и узлов в схеме.
Произвольно выбрать условно-положительные направления токов. Общее число уравнений должно быть равно числу неизвестных токов.
Определить, сколько уравнений должно быть составлено по Iзакону Кирхгофа, а сколько — поIIзакону Кирхгофа.
Составить уравнения для
 узлов
поIзакону Кирхгофа и
для
узлов
поIзакону Кирхгофа и
для независимых
контуров (отличающихся друг от друга
хотя бы на одну ветвь) — поIIзакону Кирхгофа.
независимых
контуров (отличающихся друг от друга
хотя бы на одну ветвь) — поIIзакону Кирхгофа.Решить система уравнений относительно токов. Если в результате ток получился отрицательным, то его действительное направление противоположно выбранному.
Проверить правильность решения задачи, составив уравнение баланса мощности и смоделировав электрическую цепь средствами моделирующего пакета ElectronicsWorkbench.
Примечание: если есть возможность, то перед составлением системы уравнений по законам Кирхгофа, следует преобразовать «треугольник» сопротивлений в соответствующую «звезду».
Пример расчет электрических цепей постоянного тока
Расчет будем выполнять с применением законов Кирхгофа, предварительно преобразовав треугольник сопротивлений в звезду.
П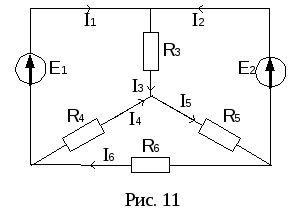 ример.
Определить токи в цепи рис. 11, еслиE1=160
В,E2=100 В,R3=100 Ом,R4=100 Ом,R5=150 Ом,R6=40
Ом.
ример.
Определить токи в цепи рис. 11, еслиE1=160
В,E2=100 В,R3=100 Ом,R4=100 Ом,R5=150 Ом,R6=40
Ом.
Преобразуем треугольник сопротивлений R4 R5 R6в звезду сопротивленийR45 R56 R64, предварительно указав условные положительные направления токов в цепи (рис. 12).
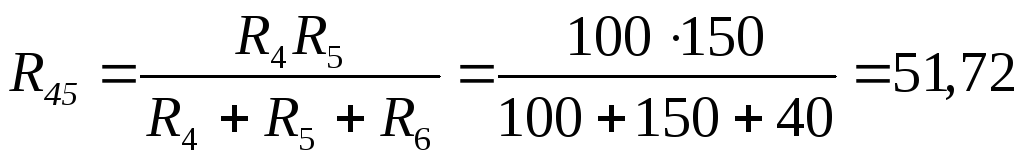 Ом;
Ом;
 Ом;
Ом;
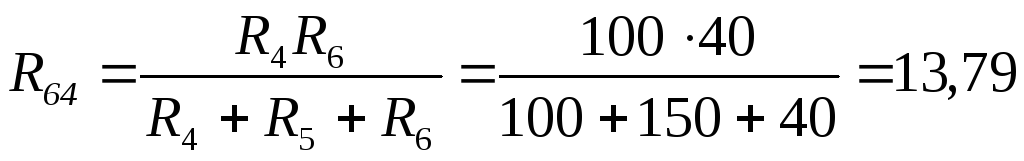 Ом.
Ом.
| |
а) | б) |
Рис. 12 | |
После преобразования электрическая цепь примет вид рис. 13 (в непреобразованной части электрической цепи направления токов не изменятся).
В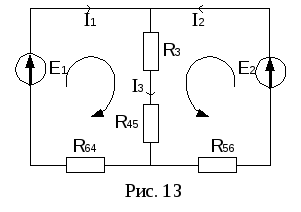 полученной электрической цепи 2 узла,
3 ветви, 2 независимых контура, следовательно,
в цепи протекает три тока (по количеству
ветвей) и необходимо составить систему
трех уравнений, из которых поIзакону Кирхгофа – одно уравнение (на 1
меньше, чем узлов в схеме электрической
цепи) и два уравнения – поIIзакону Кирхгофа:
полученной электрической цепи 2 узла,
3 ветви, 2 независимых контура, следовательно,
в цепи протекает три тока (по количеству
ветвей) и необходимо составить систему
трех уравнений, из которых поIзакону Кирхгофа – одно уравнение (на 1
меньше, чем узлов в схеме электрической
цепи) и два уравнения – поIIзакону Кирхгофа:
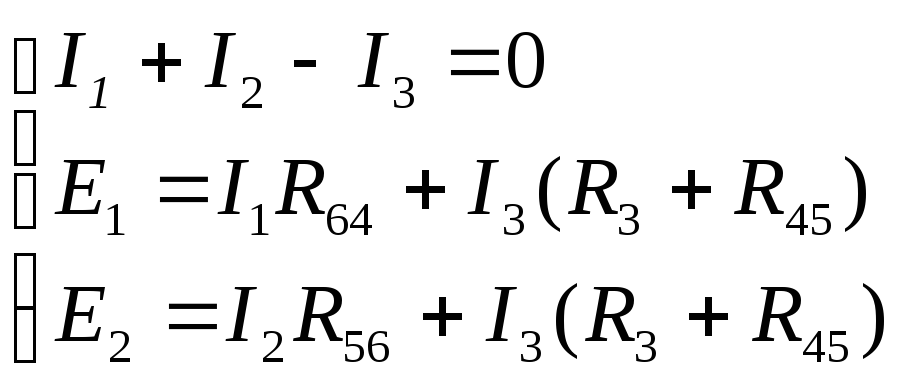
Подставим в полученную систему уравнений известные значения ЭДС и сопротивлений:
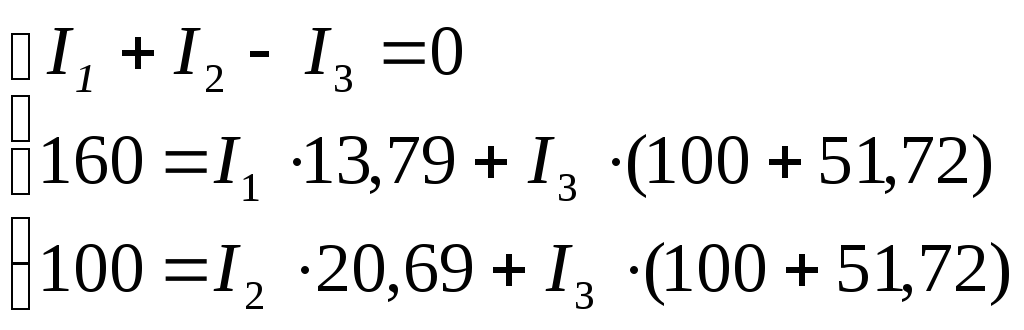
Решая систему уравнений любым способом, определяем токи схемы электрической цепи рис. 13:
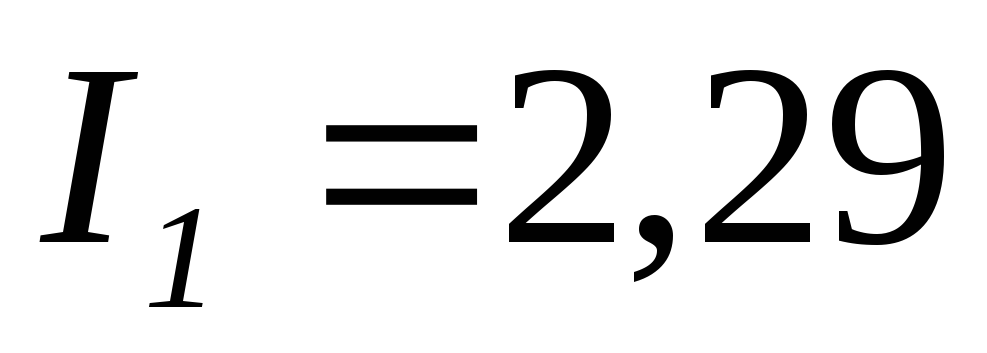 А;
А;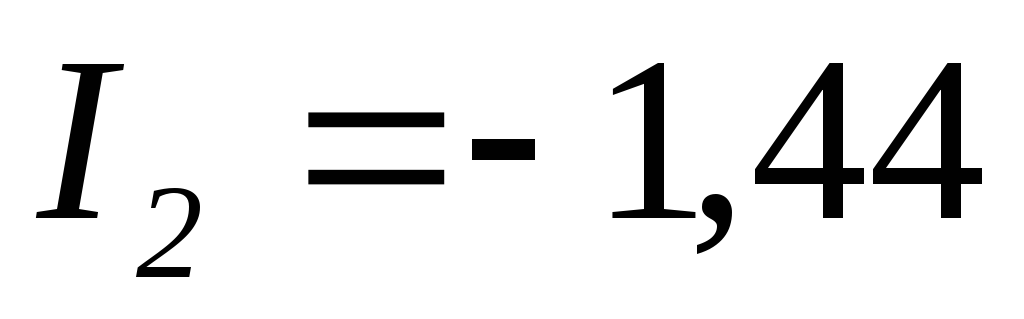 А;
А;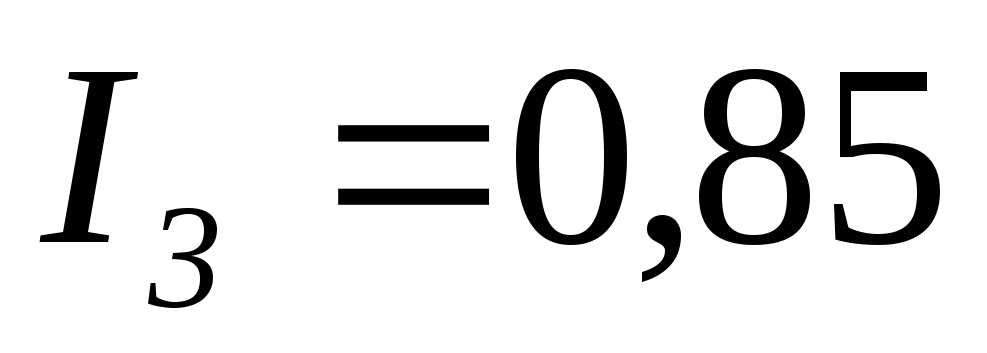 А.
А.
Переходим к исходной схеме (см. рис. 11). По IIзакону Кирхгофа:
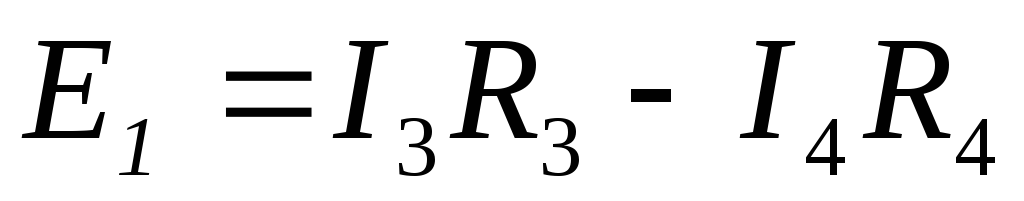 ;
;
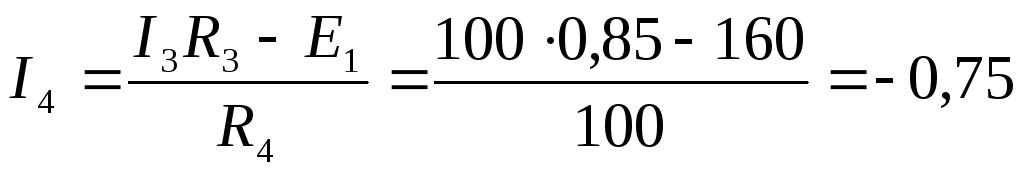 А.
А.
По Iзакону Кирхгофа:
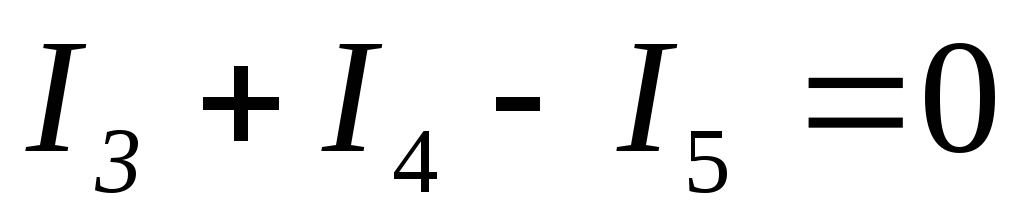 ;
;
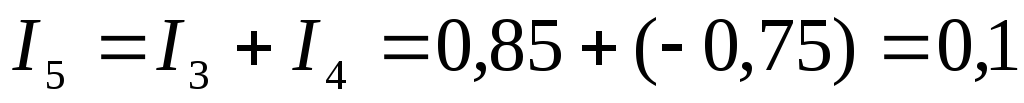 А;
А;
;
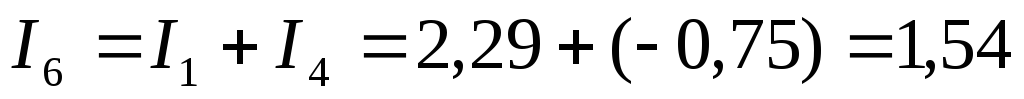 А.
А.
Т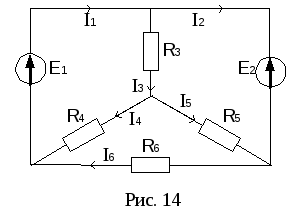 оки
оки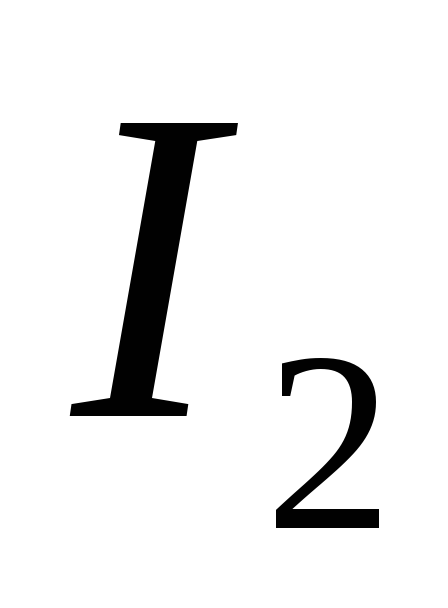 и
и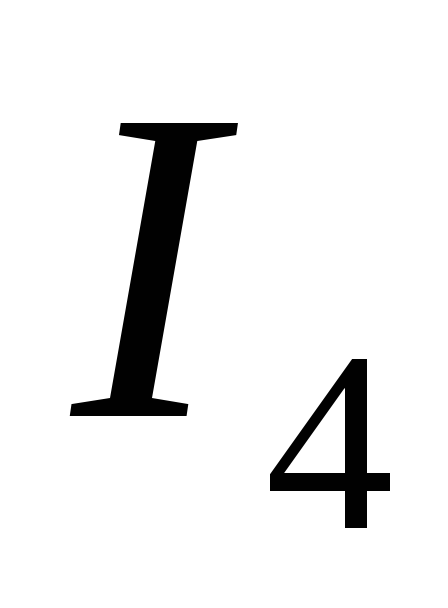 получились отрицательными, следовательно,
их действительное направление
противоположно выбранному нами (рис.
14).
получились отрицательными, следовательно,
их действительное направление
противоположно выбранному нами (рис.
14).
Правильность решения проверяем, составив уравнение баланса мощности. Мощность источников (учтем, что ЭДС источника E2направленно встречно токуI2, протекающему через него):
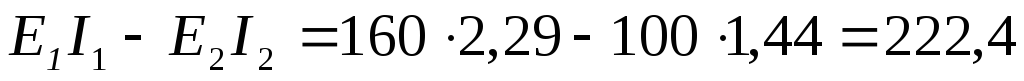 Вт.
Вт.
Мощность потребителей:
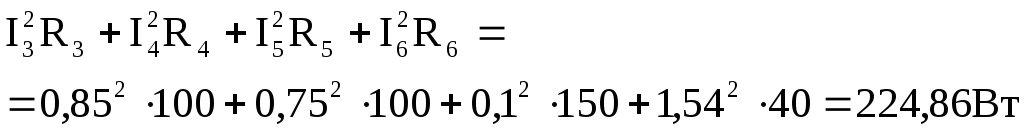
Погрешность вычислений в пределах допустимого (меньше 5%).
Смоделируем электрическую цепь рис. 11 средствами моделирующего пакета ElectronicsWorkbench(рис. 15):
Р ис.
15
ис.
15
При сравнении расчетных результатов и результатов моделирования, можно увидеть, что они отличаются (различия не превышают 5%), т.к. измерительные приборы имеют внутренние сопротивления, которые моделирующая система учитывает
3 Методы расчета электрических цепей с несколькими источниками питания
ЛЕКЦИЯ 3
Методы расчета электрических цепей с несколькими источниками питания
а) Метод с помощью законов Кирхгофа
Самый точный метод, но с его помощью можно определять параметры схемы с небольшим количеством контуров (1-3).
Алгоритм:
1. Определить количество узлов q, ветвей p и независимых контуров;
2. Задаться направлениями токов и обходов контуров произвольно;
3. Установить число независимых уравнений по 1-ому закону Кирхгофа (q — 1) и составить их, где q-количество узлов;
4. Определить число уравнений по 2-ому закону Кирхгофа (p – q + 1) и составить их;
5. Решая совместно уравнения, определяем недостающие параметры цепи;
6. По полученным данным производится проверка расчетов, подставляя значения в уравнения по 1-ому и 2-ому законам Кирхгофа или составив и рассчитав баланс мощностей.
Пример:
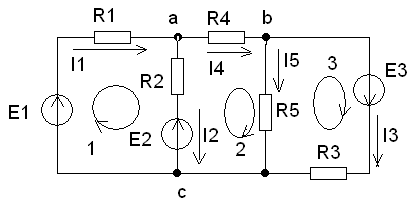
Рис 1. | Согласно предложенному алгоритму, определим количество узлов и ветвей схемы рис. 1 q = 3, p = 5, следовательно, уравнений по 1-ому закону Кирхгофа равно 2, а уравнений по 2-ому закону Кирхгофа равно 3. |
Запишем эти уравнения согласно правилам:
для узла «а» I1 — I2 — I4 = 0
для узла «b» I4 — I5 — I3 = 0
для контура 1 R1·I1+R2·I2 = E1 — E2
для контура 2 R4·I4+R5·I5 — R2·I2 = E2
для контура 3 R3·I3 — R5·I5 =E3
Составим уравнения баланса мощностей:
Pпр= R1·I1² + R2·I2² + R3·I3² + R4·I4² + R5·I5²
Pист= E1·I1 + E3·I3 — E2·I2
б) Метод контурных токов
Используя этот метод, сокращается число уравнений, а именно исключаются уравнения по 1-ому закону Кирхгофа. Вводится понятие контурный ток ( – это виртуальное понятие), составляются уравнения по второму закону Кирхгофа.
Рассмотрим наш пример рис. 2
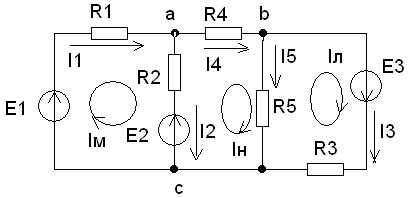
Рис.2
Контурные токи обозначены Iм, Iн, Iл, заданы их направления, как показано на рис. 2
Алгоритм решения:
1. запишем действительные токи через контурные: по внешним ветвям I1 = Iм, I3 = Iл, I4 = Iн и по смежным ветвям I2 = Iм — Iн, I5 = Iн — Iл
2. Составим уравнения по второму закону Кирхгофа, так, как контура три, следовательно будет и три уравнения:
для первого контура Iм·(R1 + R2) — Iн·R2 = E1 — E2, знак «–» перед Iн ставится потому , что этот ток направлен против Iм
для второго контура — Iм·R2 + (R2 + R4 + R5) ·Iн — Iл·R5 = E2
для третьего контура — Iн·R5 + (R3 + R5) ·Iл = E3
3. Решая полученную систему уравнений, находим контурные токи
4. Зная контурные токи, определяем действительные токи схемы (см. пункт 1.)
в) Метод узловых потенциалов
Предлагаемый метод самый эффективный из предложенных методов, при этом конечно теряется точность расчетов, этот метод заложен программу определения параметров схем в инженерных программах EWB MULTISIM, TINA.
Ток в любой ветви схемы можно найти по обобщённому закону Ома. Для этого необходимо определить потенциалы узлов схемы.
Если схема содержит n-узлов, то уравнений будет (n-1):
- Заземлим любой узел схемы φ = 0;
- Необходимо определить (n-1) потенциалов;
- Составляются уравнения согласно первому закону Кирхгофа по типу:
φ1·G11 + φ2·G12 +…+ φ(n-1)·G1,(n-1) = I11
φ1·G21+ φ2·G22 +…+ φ(n-1)·G2,(n-1) = I22
…………………………………………………
…………………………………………………
φ1·G(n-1),1 + φ2·G(n-1),2 +…+ φ(n-1)·G(n-1),(n-1) = I (n-1), (n-1)
где I11… I (n-1), (n-1) узловые токи в ветвях с ЭДС подключенных к данному узлу, Gkk– сумма проводимостей ветвей в узле k, называемая собственной проводимостью, Gkm– сумма проводимостей ветвей соединяющие узлы k и m, взятая со знаком «–», называемая взаимная проводимость между узлами;
- Токи в схеме определяются по обобщенному закону Ома.
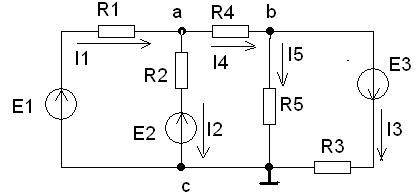
Пример:
| Заземлим узел с, т.е. φс = 0 |
φа ( +
+ 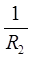 +
+ 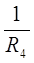 ) — φb
) — φb 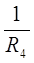 = E1
= E1 + E2
+ E2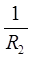
φb(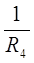 +
+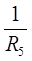 +
+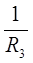 ) — φa
) — φa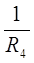 = — E3
= — E3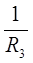
определив потенциалы φа и φb, найдем токи схемы. Составление формул для расчета токов осуществляется в соответствии с правилами знаков ЭДС и напряжений, при расчете по обобщенному закону Ома (см. лекция 1).
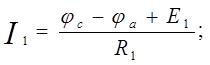
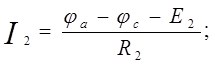
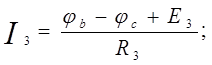
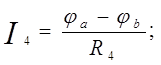
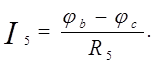
Правильность расчета токов проверяется с помощью законов Кирхгофа и баланса мощностей.
г) Метод двух узлов
Метод двух узлов это частный случай метода узловых потенциалов. Применяется в случае, когда схема содержит только два узла (параллельное соединение).
Алгоритм:
- Задаются положительные направления токов и напряжение между двумя узлами произвольно;
- Уравнение для определения межузлового напряжения
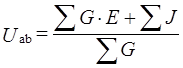 ,
,
где G – проводимость ветви, J – источники тока;
- Правило: G·E и J берутся со знаком «+», если Е и J направлены к узлу с большим потенциалом;
- Токи схемы определяются по обобщенному закону Ома
Пример:
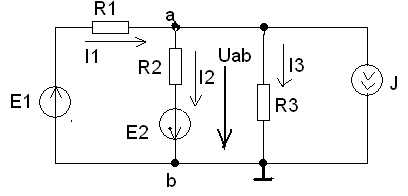

Составление формул для расчета токов осуществляется в соответствии с правилами знаков ЭДС и напряжений, при расчете по обобщенному закону Ома (см. лекция 1).
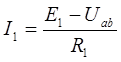
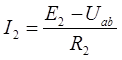

д) Метод активного двухполюсника (генератора)
Данный метод применяется, когда необходимо рассчитать параметры одной ветви в сложной схеме. Метод основан на теореме об активном двухполюснике: «Любой активный двухполюсник может быть заменен эквивалентным двухполюсником с параметрами Еэкв и Rэкв или Jэкв и Gэкв , режим работы схемы при этом не изменится».
Алгоритм:
1. Разомкнуть ветвь, в которой необходимо определить параметры.
2. Определить напряжение на разомкнутых зажимах ветви, т.е. при режиме холостого хода Еэкв = Uхх любимым методом.
3. Заменить активный двухполюсник, т.е. схему без исследуемой ветви, пассивным (исключить все источники питания, оставив их внутренние сопротивления, не забывая, что у идеальной ЭДС Rвн = 0, а у идеального источника тока Rвн = ∞). Определить эквивалентное сопротивление полученной схемы Rэкв.
4. Найти ток в ветви по формуле I = Eэкв/(R+Rэкв) для пассивной ветви и
I = E ± Eэкв/(R+Rэкв) для активной ветви.
Нелинейные цепи постоянного тока
Определение нелинейного элеиента
На практике в промышленной электронике электрические цепи состоят в основном из нелинейных элементов, т.е. из элементов, у которых ВАХ не являются прямой линией (значения параметров резко изменяются с изменением тока)
Нелинейные ВАХ имеют все полупроводниковые приборы:
- Полупроводниковые диоды
- Стабилитроны
- Термисторы
- Транзисторы
- Тиристоры и т.д.
Анализ и расчет нелинейных цепей проводится с помощью метода пересечения характеристик, методом эквивалентного, активного двухполюсника.
Характеристики и параметры нелинейного элемента
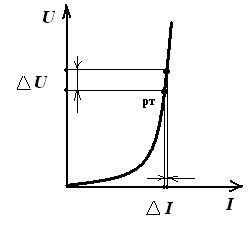
Понятия статического и динамического (дифференциального) сопротивления
Рис 1 | Rcт = Uрт/Iрт – отношение напряжения на элементе к току в заданной точке его характеристики Rдин = dU/dI = ∆U/∆I – отношение изменения напряжения к изменению тока в заданной рабочей области нелинейного элемента Rст > Rдин |
Анализ нелинейных цепей
Осуществляется двумя способами аналитическим или графическим — методом пересечения характеристик — это решение нелинейного уравнения определяющего электрическое состояние графическим способом.
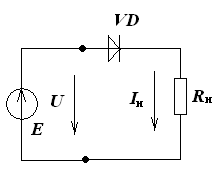
Рассмотри участок цепи с последовательно соединенными линейным и нелинейным элементами (рис 2).
Рис 2 |
Рис 3 |
Составим уравнение электрического состояния для цепи рис.2:
U = E — Rн·I
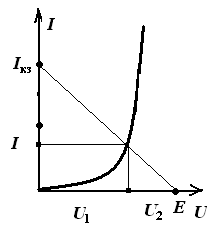
Согласно этому уравнению строится «опрокинутая» ВАХ резистора Rн (или линию нагрузки).
Правило: если нелинейный элемент соединен последовательно с резистором, то строится «опрокинутая» ВАХ, если параллельно, то строится обычная ВАХ резистора.
Как известно, любая прямая строится по двум точкам, которые соответствуют двум режимам двухполюсника с параметрами E и Rн.
Холостой ход: I = 0; U = E
Короткое замыкание: U = 0; Iкз =E/Rн
Пересечение вольтамперных характеристик нелинейного элемента и резистора дают графическое решение задачи, как показано на рис. 3 .
В анализе нелинейных цепей используется метод эквивалентного генератора, в случае сложной цепи: Многоэлементный активный линейный двухполюсник, к выходным зажимам которого подключен нелинейный элемент, может быть заменен эквивалентным двухполюсником. Напряжение и ток на нелинейном элементе находятся методом пересечения характеристик, зная эти параметры можно определить токи и напряжения остальных ветвей цепи.
В случае последовательно соединённых нелинейных элементов сначала графически складывают ВАХ элементов, а затем проводят расчёт как показано ранее.
Сложение ВАХ, при последовательном включении нелинейных элементов
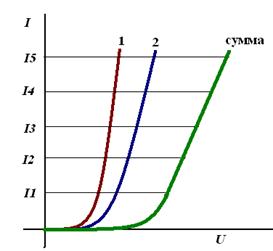
Сложение ВАХ, при параллельном включении нелинейных элементов
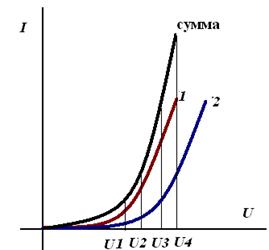
2. Метод токов ветвей | 9. Анализ цепей постоянного тока | Часть1
2. Метод токов ветвей
Метод токов ветвей
Первый и самый простой метод анализа цепей постоянного тока называется методом токов ветвей. В этом методе нам сначала нужно определить направления токов в цепи, а затем написать уравнения, описывающие их отношения друг с другом через законы Кирхгофа и Ома. Как только мы получим уравнения для каждого из неизвестных токов, мы сможем решить систему уравнений, рассчитав тем самым все токи, а затем и все напряжения в цепи.
Для рассмотрения метода мы будем использовать следующую схему:
Первое что нам нужно сделать — это выбрать узел цепи (место соединения проводов), который будет использоваться в качестве точки отсчета для поиска неизвестных токов. Мы выберем узел, соединяющий резистор R1 справа, R2 снизу и R3 слева.
Теперь нам нужно проставить направления токов в примыкающих к этому узлу проводах, обозначив их I1, I2 и I3 соответственно. Имейте ввиду, эти направления будут только предполагаемыми. Если выяснится, что наши предположения оказались ошибочными, то мы это увидим в процессе математического расчета (любые «неправильные» направления токов отобразятся в виде отрицательных чисел).
Согласно Первому Закону Кирхгофа, алгебраическая сумма токов входящих в узел и выходящих из него должна быть равна нулю, поэтому мы можем связать все токи нашей схемы (I1, I2 и I3) друг с другом при помощи одного уравнения. Все входящие в узел токи мы обозначим знаком «плюс», а выходящие из него — знаком «минус»:
На следующем шаге нам нужно промаркировать полярности напряжений всех резисторов в соответствии с предполагаемыми направлениями токов. Конец резистора, в который ток втекает — будет отрицательным, а из которого вытекает — будет положительным (электрон заряжен отрицательно, и течет от минуса к плюсу):
Полярность батареи проставляется в соответствии со стандартом (короткий конец — отрицательный, длинный конец — положительный). В некоторых случаях вы можете обнаружить, что полярность резисторов не соответствует полярности батареи, а ток течет обратно через батарею. Ничего страшного, это только предполагаемое направление тока. Здесь важно помнить, что простановку полярности напряжений на резисторах и последующие расчеты нужно производить по изначально предполагаемым направлениям токов. Как отмечалось ранее, если ваши предположения окажутся неверными, то вы увидите это по окончательным результатам расчетов (они будут отрицательными). Сами же полученные величины все равно будут правильными.
Согласно Второму Закону Кирхгофа, алгебраическая сумма всех напряжений цепи должна равняться нулю. Исходя из этого, мы сможем создать несколько уравнений для нашей системы, подставив в них неизвестные значения токов (I1, I2 и I3). Для получения уравнений Второго Закона Кирхгофа нам нужно знать количество и полярность напряжений в каждой из ветвей цепи. В целях облегчения данной задачи давайте представим, что мы измерили все напряжения реальным вольтметром, обозначив неизвестные значения как положительное или отрицательное напряжение. Сначала мы создадим уравнение для левой ветви схемы, взяв за точку отсчета верхний левый угол, и двигаясь против часовой стрелки (выбор точки отсчета и направление — произвольны). Результат будет выглядеть следующим образом:
Закончив исследование левой ветви схемы, мы можем применить к полученным значениям Второй Закон Кирхгофа (сумма всех напряжений цепи равна нулю):
Нам еще неизвестны значения напряжений на резисторах R1 и R2, поэтому мы не можем вставить их в уравнение в виде числовых величин. Однако, мы знаем, что сумма этих трех напряжений равна нулю, поэтому уравнение верно. Теперь пойдем дальше, и выразим неизвестные напряжения как произведение неизвестных токов и соответствующих им сопротивлений (применив Закон Ома: U = IR), а так же уберем все нулевые значения из левой части уравнения:
Поскольку нам известны сопротивления всех резисторов, давайте подставим в уравнение конкретные числовые значения:
У вас наверняка возник вопрос: зачем мы произвели все эти манипулирования с первоначальным видом уравнения (-28 + ER2 + ER1)? Какая разница в чем будет выражено уравнение, в напряжении или в токе (умноженном на сопротивление), если в обоих случаях последние два члена до сих пор неизвестны? Ответ на данные вопросы прост. Целью всех выше приведенных преобразований является получение уравнения Второго Закона Кирхгофа с использованием тех же неизвестных переменных, что и в уравнении Первого Закона Кирхгофа, так как это является необходимым условием для решения любой системы уравнений. Чтобы найти значения трех неизвестных токов (I1, I2 и I3), у нас должно быть три уравнения, связывающих их вместе.
Применив те же самые действия к правой ветви схемы (начиная с выбранного узла и двигаясь против часовой стрелки), мы получим еще одно уравнение Второго Закона Кирхгофа:
Зная, что напряжение на каждом из резисторов может и должно быть выражено как произведение соответствующих токов и сопротивлений (величина которых известна), мы можем переписать это уравнение следующим образом:
Теперь у нас есть система из трех уравнений (одно уравнение Первого и два уравнения Второго Законов Кирхгофа) с тремя неизвестными:
Далее нам нужно перенести все известные величины в правые части уравнений, а неизвестные оставить в левой, дополнив их отсутствующими нулевыми значениями:
Решив эту систему уравнений мы получим следующий результат:
Таким образом, ток I1 равен 5 амперам, ток I2 равен 4 амперам и ток I3 равен минус 1 амперу. Отрицательное значение тока I3 означает что наше предположение по его направлению оказалось неверным. Давайте вернемся к первоначальной схеме и перерисуем стрелку этого тока на противоположное направление (исправив соответственно полярность напряжения на резисторе R3):
Обратите внимание на тот факт, что в правой ветви схемы ток течет обратно через батарею 2. Это происходит благодаря более высокому напряжению батареи 1 (в которой ток течет «как обычно» — через цепь от минуса к плюсу). Означает ли это, что более «сильная» батарея всегда будет «побеждать» более слабую. Вовсе нет! Данный фактор зависит как от относительных напряжений батарей, так и от сопротивлений резисторов цепи. Единственным способом установления происходящих в цепи процессов является математический анализ.
Итак, величины всех токов данной цепи нам известны. Теперь, при помощи Закона Ома (U = IR), можно рассчитать напряжения на всех ее резисторах:
Давайте теперь проанализируем эту схему при помощи программы PSPICE, проверив тем самым полученные результаты для напряжений. Данная программа, конечно, сможет рассчитать и токи, но тогда нам потребуется включить в схему дополнительные компоненты. Принимая во внимание этот факт, мы с вами пойдем по пути наименьшего сопротивления (если выданные программой значения напряжений совпадут с нашими расчетами, то и токи мы рассчитали правильно). Схема с номерами узлов для программы представлена ниже:
Как видите, результаты работы программы совпадают с нашими рассчетами: 20 вольт на резисторе R1 (узлы 1 и 2), 8 вольт на резисторе R2 (узлы 2 и 0) и 1 вольт на резисторе R3 (узлы 2 и 3). Обратите внимание на знаки всех этих напряжений: они имеют положительные значения! PSPICE основывает свою полярность на порядке, в котором перечислены узлы: первый узел должен быть положительным, а второй — отрицательным. Например, положительное (+) напряжение 20 вольт между узлами 1 и 2 означает, что узел 1 является положительным по отношению к узлу 2. Если бы число получилось отрицательным, то то ошибку следовало бы искать в порядке перечисления узлов.
Тема 3. Законы Кирхгофа и их применение для расчета электрических цепей
1. Ток I3 при I1 = 5A, I2 = 7A равен:
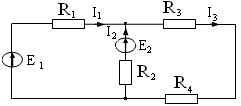
1) 12 А
2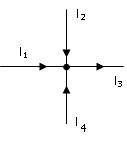 .
Первый закон Кирхгофа имеет вид:
.
Первый закон Кирхгофа имеет вид:
3) I1 + I2 — I3 + I4 = 0
3. Уравнение по второму закону Кирхгофа для цепи постоянного тока имеет вид:
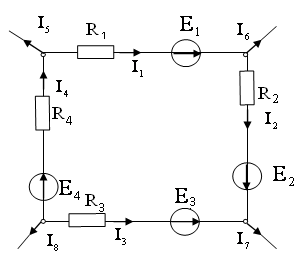
1) I1 R 1+ I2R2 – I3R3+ I4R4= E1+ E2 – E3 + E4
4 .
Для внешнего контура АБВГ электрической
цепи справедливо уравнение:
.
Для внешнего контура АБВГ электрической
цепи справедливо уравнение:
1) E1 – E2 – Е3= I2R2 + I1R1
5. Для внутреннего контура АВГ электрической цепи справедливо уравнение:
2) E1 – Е3= I3R3 + I1R1
6. Для внешнего контура АБВ электрической цепи справедливо уравнение:
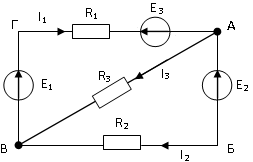
1) E2 = -I2R2 + I3R3
7. Для узла А электрической цепи справедливо уравнение:
1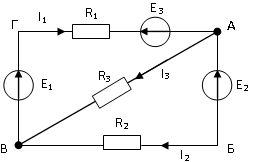 )
)
8. Для узла B электрической цепи справедливо уравнение:
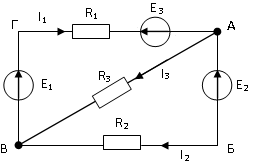
3) 
9. Для электрической цепи указать неправильное уравнение:
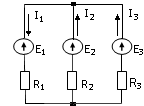
4) 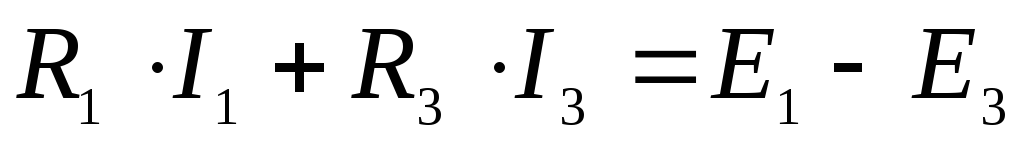 ;
;
10. Уравнение по 2-ому закону Кирхгофа для контура adb имеет вид:
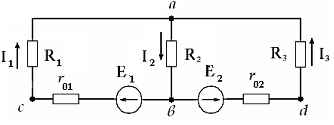
4) 
11. Уравнение по первому закону Кирхгофа для узла а имеет вид:.
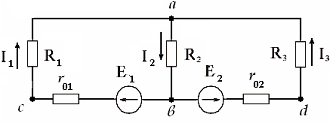
3) 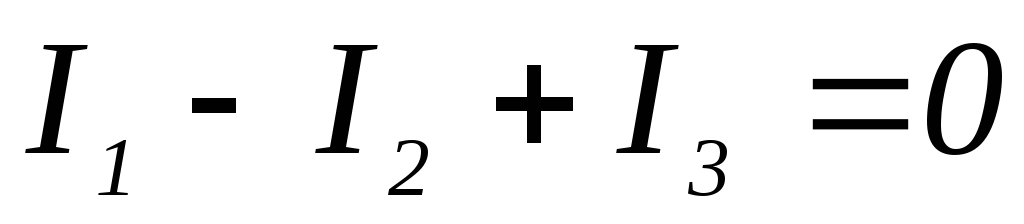
1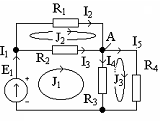 2.
Уравнение по первому закону Кирхгофа
для узла А имеет вид:
2.
Уравнение по первому закону Кирхгофа
для узла А имеет вид:
2) I2+I3-I4-I5=0
1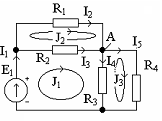 3.
Уравнение по 2-ому закону Кирхгофа для
контураJ1 имеет вид:
3.
Уравнение по 2-ому закону Кирхгофа для
контураJ1 имеет вид:
5) I3R2+I4R3 =E1
1 4.
ТокI2,
если I1=0,5А,
I3=0,3А,
I4=0,6А.
4.
ТокI2,
если I1=0,5А,
I3=0,3А,
I4=0,6А.
4) I2 =0,8А
15. Первый закон Кирхгофа формулируется следующим образом
2) алгебраическая сумма токов ветвей, сходящихся в узле, равна нулю;
16. Второй закон Кирхгофа формулируется следующим образом
1) алгебраическая сумма падений напряжений в контуре равна алгебраической сумме ЭДС в том же контуре;
1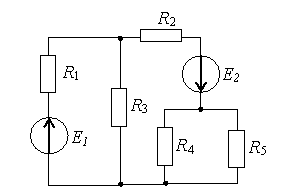 7.
Общее количество независимых уравнений
по законам Кирхгофа, необходимое для
расчета токов в ветвях заданной цепи,
составит…
7.
Общее количество независимых уравнений
по законам Кирхгофа, необходимое для
расчета токов в ветвях заданной цепи,
составит…
4) 5
18. Количество уравнений, которые необходимо составить по первому закону Кирхгофа для заданной цепи, составляет…
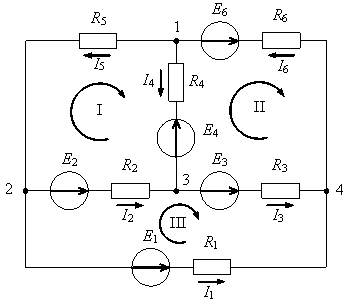
1) 3
Тема 4. Анализ цепей постоянного тока с одним источником энергии
1. Эквивалентное сопротивление цепи относительно источника ЭДС составит…
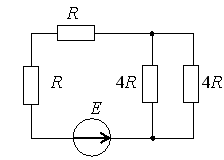
2) 4R
2. Если пять резисторов c сопротивлениями R1= 100 Ом,
R2 = 10 Ом, R3= 20 Ом, R4= 500 Ом, R5= 1000 Ом соединены последовательно, то ток будет …
один и тот же.
3. Внутренние сопротивления rА, rБ, rВ источников энергии находятся в соотношении
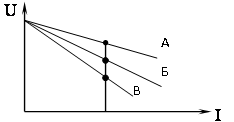
1) rА = rБ = rВ 2) rА < rБ < rВ 3) rА > rБ > rВ
4. К.П.Д. ηА, ηБ, ηВ источников электрической энергии находятся в соотношении …
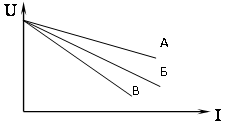
1) А = Б = В 2) А < Б < В 3) А > Б >В
5. Источник ЭДС работает в генераторном режиме, когда
2) ток, протекающий через источник, совпадает по направлению с ЭДС;
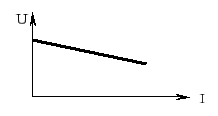
6. Внешняя характеристика источника ЭДС имеет вид:
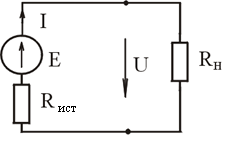
1) 
7. Источник ЭДС работает в режиме потребления энергии, когда
3)ток, протекающий через источник, противоположен по направлению ЭДС.
8 . Показание амперметра при U = 90 В, R = 30 Ом равно …
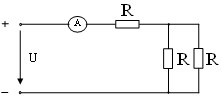 1)
1,5 A 2)
3 A
3) 2 А 4) 9 A 5)
1 A
1)
1,5 A 2)
3 A
3) 2 А 4) 9 A 5)
1 A
9. Показание амперметра при U = 90 B, R = 30 Ом равно…
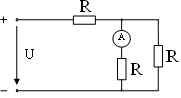
1) I = 1 A
10. Показание вольтметра при U = 90 B, r = 30 Ом равно …
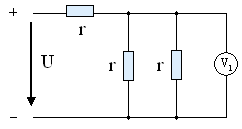
2) U = 30B
11. Ток I в электрической цепи при U = 10 B, E = 20 B, R = 5 Ом равен
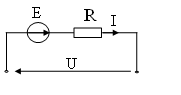
2А
12. Показание амперметра при R1 = R4 = 20 Ом, R2 = R3 = 30 Ом, E = 50В равно
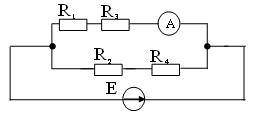
2) 1A
13. Если ток I3 = 0, E1 = 10 В, R1 = 2 Ом, R2 = 4 Ом, E2 равно…

1) 20B 2) 40B 3) 5B 4) 10B 5) 50B
14. Метод эквивалентного генератора применяют, когда необходимо определить
1) контурные токи;
2) потенциалы узлов;
3) ток в выделенной ветви;
4) частичные токи.
15. ЭДС источника энергии Е при сопротивлениях цепи R1 = R4 = 20 Ом, R2 = R3 = 30 Ом и показании амперметра 2 А равна
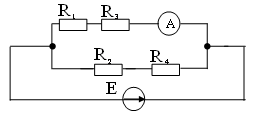
2) 100 В
16. Сопротивление лампы накаливания с номинальными параметрами Uн =220В и Рн = 100 Вт равно …
1) 484 Ом
17. Общее сопротивление двух ламп накаливания мощностью по 100 Вт включенных, параллельно на напряжение U = 200 В, равно …
1) 200 Ом
18. Ток лампы накаливания номинальной мощностью Рн = 200 Вт, включенной на номинальное напряжение Uн = 200B, равен …
3) 1 А
19. Напряжение сети U при падениях напряжения на соответствующих сопротивлениях U1=80B, U2=140B, U3=140B равно …
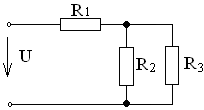
1) 220 В
20. Ток I при потребляемой мощности Р=125 Вт и сопротивлениях цепи R1=10 Ом, R2=2 Ом, R3=8 Ом равен …
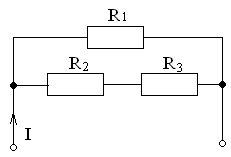
3) I=5 A
21. Показание вольтметра при U = 90 B, R = 30 Ом равно …

2) 60 В
22. Эквивалентное сопротивление цепи, если R1= R2 = R3= R4= R5= R6= R, равно …
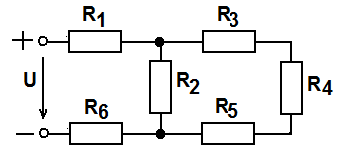
1) 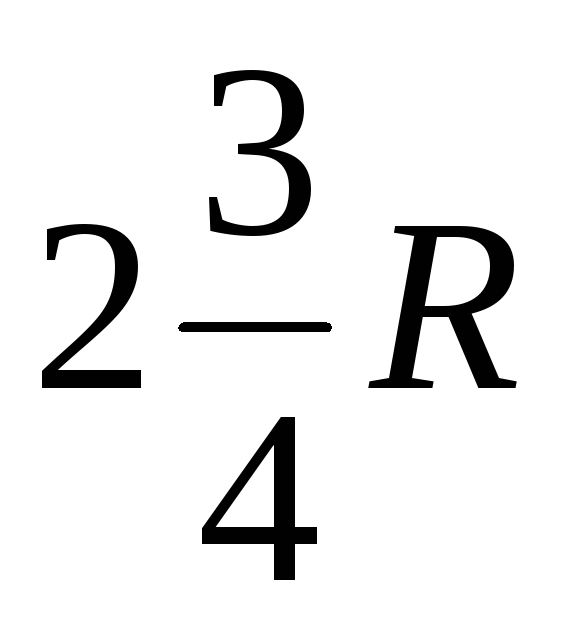
23. Эквивалентное сопротивление R электрической цепи при R = 2Ом равно …

1) 8 Ом
24. Эквивалентное сопротивление RЭ электрической цепи при R = 2 Ом равно …
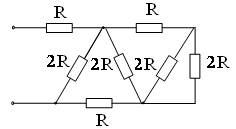
2) 4 Ом
25. Выражение для определения эквивалентного (входного) сопротивления RЭ цепи имеет вид:
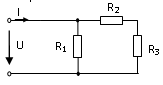
1) 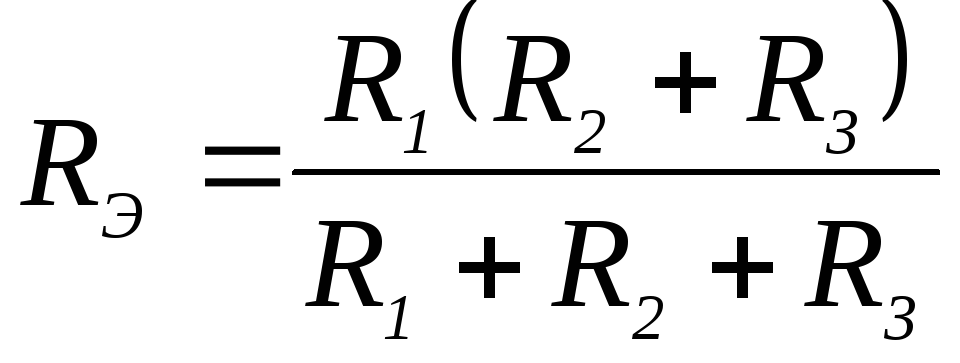
2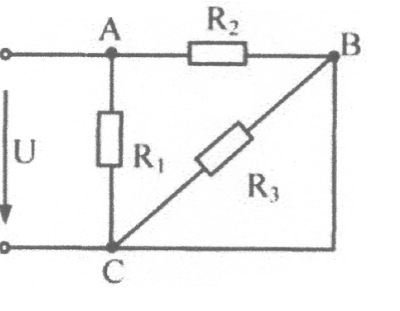 6.
Выражение для определения эквивалентного
(входного)
сопротивления RЭ цепи имеет вид:
6.
Выражение для определения эквивалентного
(входного)
сопротивления RЭ цепи имеет вид:
1) 
27. Выражение для определения эквивалентного (входного) сопротивления RЭ цепи имеет вид:


28. Выражение для определения эквивалентного (входного) сопротивления RЭ цепи имеет вид:

2) 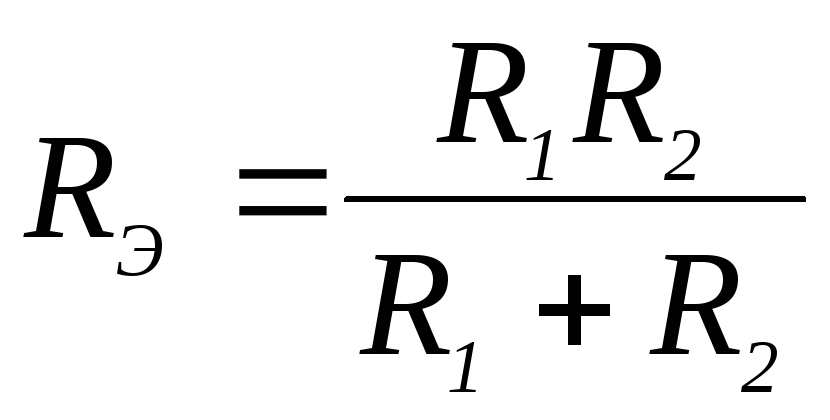
29. Выражение для определения эквивалентного (входного) сопротивления RЭ цепи имеет вид:
2)
3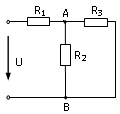 0.
Выражение для определения эквивалентного
(входного)
сопротивления RЭ цепи имеет вид:
0.
Выражение для определения эквивалентного
(входного)
сопротивления RЭ цепи имеет вид:
3) 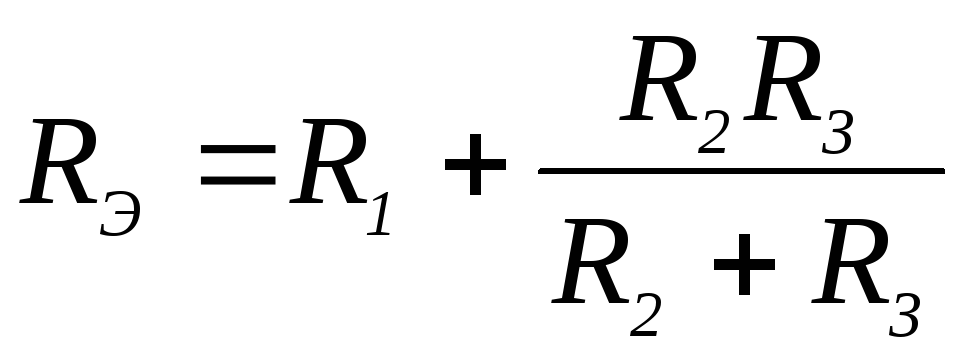
31. Выражение для определения эквивалентного (входного) сопротивления RЭ цепи имеет вид:
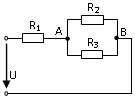
2) 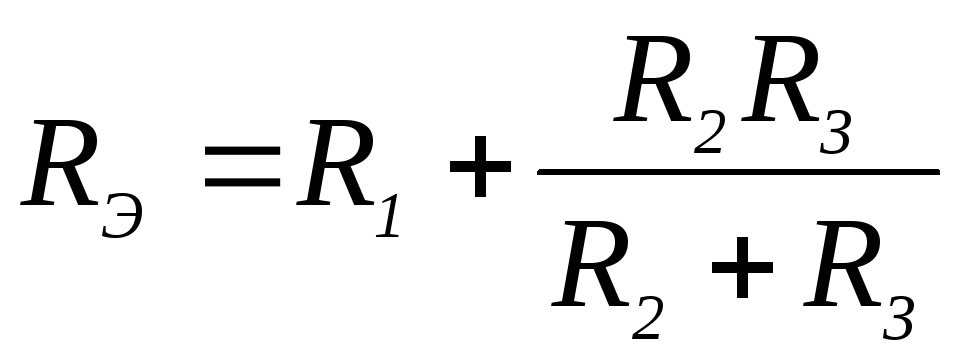
32. Выражение для эквивалентного сопротивления RЭ электрической цепи имеет вид:
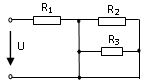 2)
2) 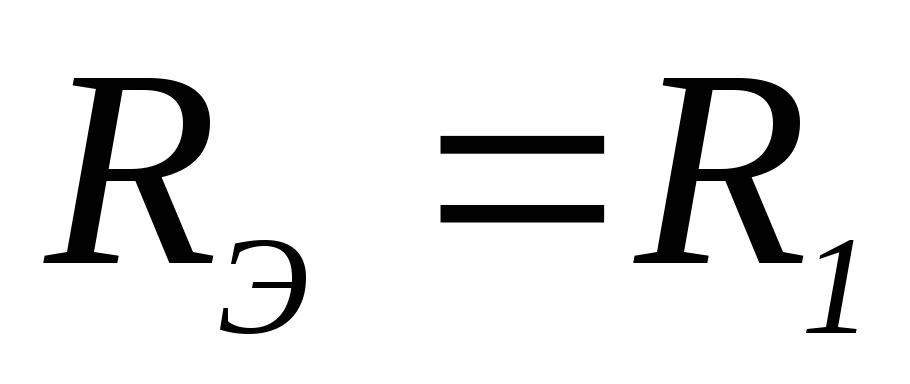
33. Выражение для эквивалентного сопротивления RЭ электрической цепи имеет вид:
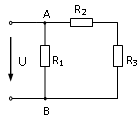
1) 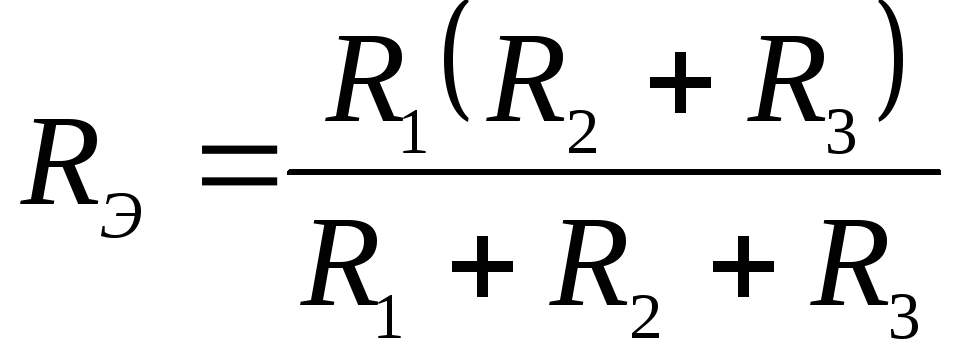
34. Входное сопротивление RЭ электрической цепи при R1 = R2 = R3 = R4 = 50 Ом равно …
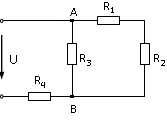
4) 83 Ом
35. Входное сопротивление RЭ цепи R1 = R2 = R3 = R4 = R5 = 50 Ом равно…
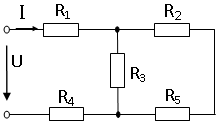
5) 133 Ом
36. Входное сопротивление RЭ электрической цепи при R1 = R2 = R3 = 50 Ом равно …

3) 25 Ом
37. Входное сопротивление RЭ электрической цепи при R1 = R2 = R3 = 50 Ом равно …
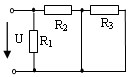
2) 25 Ом
38. Входное сопротивление RЭ электрической цепи при R1 = R2 = R3 = R4 = 50 Ом равно …

1) 50 Ом
39. Входное сопротивление RЭ электрической цепи при R1 = R2=0,5Ом, R3 = R5 = 10 Ом, R4 =R6 = R7 = 5 Ом равно …
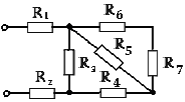
4) 6 Ом
Расчет и анализ линейной электрической цепи по законам Кирхгофа.
Как правило, в задачах заданы все ЭДС, сопротивления и источники тока, при этом нужно определить токи в ветвях электрической цепи. Однако бывают и обратные задачи в которых требуется определить при каких значениях ЭДС и источника тока в ветвях будут протекать заданные токи, при этом сопротивления ветвей известны. Есть задача на определение сопротивлений в ветвях при заданных ЭДС и токах в ветвях. Бывают комбинированные задачи, в которых заданы некоторые источники, некоторые сопротивления и некоторые токи ветвей, при этом требуется найти неизвестные токи, ЭДС и сопротивления.
Количество неизвестных должно совпадать с количеством ветвей электрической цепи за исключением ветвей, содержащих источники тока.
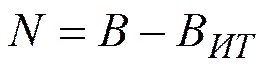
Следовательно, при решении задачи по законам Кирхгофа необходимо составить N уравнений, столько – же, сколько в схеме содержится ветвей без источника тока.
А сколько уравнений нужно взять по 1му и по 2му закону Кирхгофа?
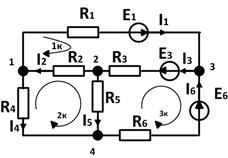 Уравнения по 1му закону Кирхгофа проще, поэтому их нужно брать как можно больше (эти уравнения называют еще узловыми). Для схемы, изображенной на рис.1 можно составить 4е уравнение по первому закону Кирхгофа. Но все ли они нужны? запишем уравнения для 1, 2 и 3 узла:
Уравнения по 1му закону Кирхгофа проще, поэтому их нужно брать как можно больше (эти уравнения называют еще узловыми). Для схемы, изображенной на рис.1 можно составить 4е уравнение по первому закону Кирхгофа. Но все ли они нужны? запишем уравнения для 1, 2 и 3 узла:
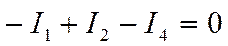
1У
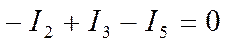
2У
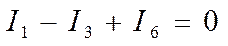
3У
Теперь сложим их левые и правые части:
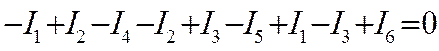
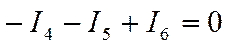 или поменяв знаки
или поменяв знаки 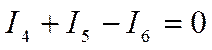 .
.
Мы получили при этом четвертое уравнение. Т.е. три уравнения для этой схемы несут информацию о четвертом, последнем уравнении, которое называется зависимым. 1,2 и 3е уравнения называются независимыми узловыми уравнениями.
Если рассмотреть другую схему с иным количеством узлов, то для нее будет характерна та же картина: последнее уравнение по 1му закону Кирхгофа можно получить, просуммировав уравнения для других узлов.
Из этого следует, что для решения задачи нужно взять узловых уравнений на единицу меньше количества узлов – у.
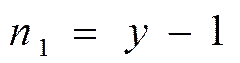
Количество уравнений по 1му закону Кирхгофа — 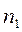 на единицу меньше количества узлов – у, содержащихся в цепи. Последнее уравнение – зависимое.
на единицу меньше количества узлов – у, содержащихся в цепи. Последнее уравнение – зависимое.
Выбор независимых узловых уравнений произволен, т.е. можно было взять в качестве независимых, уравнения для 2, 3, 4 узлов, или 1,3, 4 и т.д.
Теперь легко определить необходимое количество уравнений по 2му закону Кирхгофа – их называют контурными уравнениями. Если общее количество уравнений – N, а узловых уравнений — 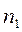 , то количество контурных уравнений —
, то количество контурных уравнений — 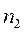 определяется, как
определяется, как 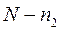 :
:
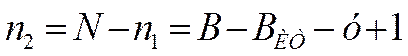
Количество уравнений по 2му закону Кирхгофа равно общему количеству уравнений N минус количество уравнений по 1му закону Кирхгофа 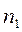 .
.
Контура, уравнения которых используются для решения задачи, называются независимыми контурами, а их уравнения – независимыми контурными уравнениями.
Выбор независимых контуров произволен.
Для цепи в нашем примере неизвестных токов – шесть, ветвей без источников тока – шесть, узлов – четыре, независимых узлов – три, независимых узловых уравнений – три, следовательно независимых контуров — 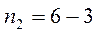 . Только для трех контуров нужно составлять уравнения по второму закону Кирхгофа в нашем примере (а всего контуров – семь). При этом не имеет значения какие три контура взять. Возьмем, для примера, 1, 2 и 3 контура. Посмотрим на ветви схемы: мы видим, что 1я ветвь входит только в 1й контур, 4я ветвь – только во 2й контур, а 6я ветвь — только в 3й контур, а 2я, 3я и 5я ветви входят сразу в два контура.
. Только для трех контуров нужно составлять уравнения по второму закону Кирхгофа в нашем примере (а всего контуров – семь). При этом не имеет значения какие три контура взять. Возьмем, для примера, 1, 2 и 3 контура. Посмотрим на ветви схемы: мы видим, что 1я ветвь входит только в 1й контур, 4я ветвь – только во 2й контур, а 6я ветвь — только в 3й контур, а 2я, 3я и 5я ветви входят сразу в два контура.
Ветви, входящие в несколько независимых контуров называются взаимными ветвями контуров или смежными ветвями.
Ветви, входящие только в один независимый контур называются внешними или собственными ветвями контуров.
Из примера мы видим, что каждый независимый контур имеет собственную ветвь, т.о. мы можем сформулировать еще одно определение независимого контура:
Независимый контур – это контур, имеющий собственную (внешнюю) ветвь, не входящую ни в один другой контур и принадлежащую только ему.
Дата добавления: 2016-05-28; просмотров: 1363;
Похожие статьи:
Символический (комплексный) метод расчета цепей переменного тока


Одним из способов расчета цепей переменного тока является комплексный, или еще как говорят, символический метод расчета. Этот метод применяется при анализе схем с гармоническими ЭДС, напряжениями и токами. В результате решения получают комплексное значение токов и напряжений, используя для решения любые методы (эквивалентных преобразований, контурных токов, узловых потенциалов и т.п.). Но для начала необходимо иметь понятие, в каких именно формах может представляться синусоидальная величина. 1. Одна из форм представления – это вращающийся вектор (см. рис.1):
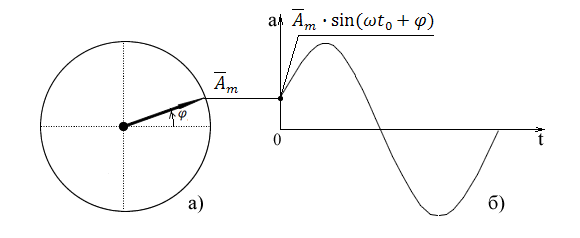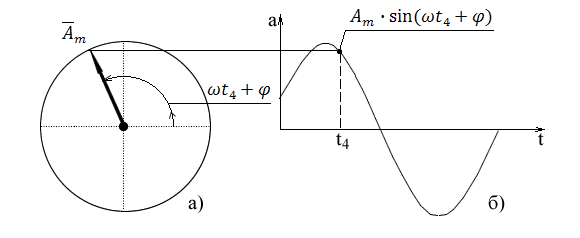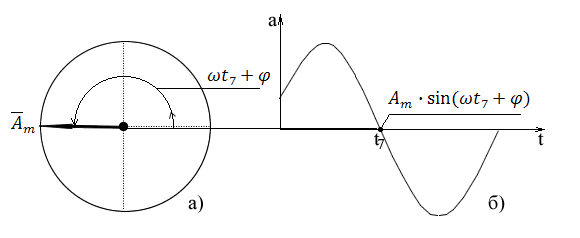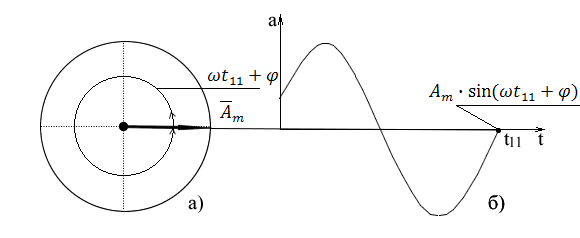
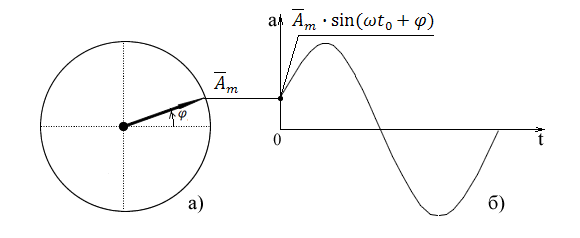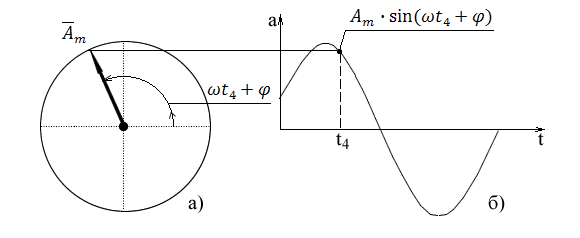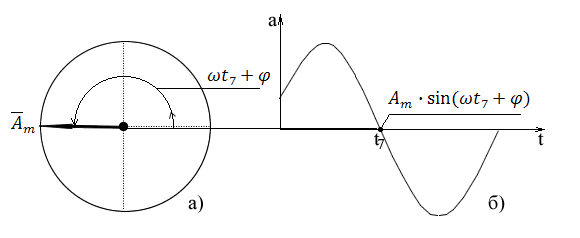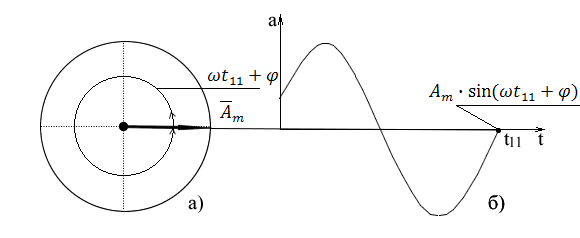
Рис.1. Вращающийся вектор
С помощью рисунка ясно видно, как с течением времени меняется значение синусоидальной величины. В нашем случае – это величина а на графике, которая может быть, например, входным напряжением. Величина имеет некоторое начальное значение при t = 0 при начальной фазе φ
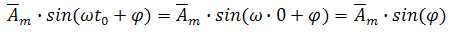
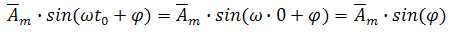
имеет положительное максимальное значение при угле ωt3, когда при времени t3 сумма ωt3 + φ = 90° и соответственно,
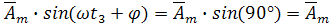
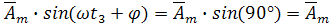
имеет отрицательное максимальное значение при угле ωt7, когда при времени t7 сумма углов ωt7 + φ = 270° и, соответственно,
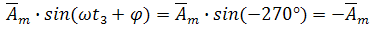
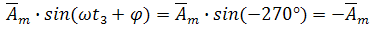
и имеет два нулевых значения при ωtn + φ = 0, когда ωtn = —φ (на рис.1 эта область не показана и находится слева от начала координат)
и тогда
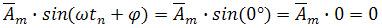
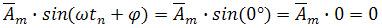
и имеет нулевое значение при угле ωt11, когда при времени t11 сумма ωt11 + φ = 360° и соответственно,
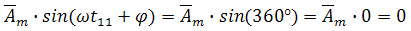
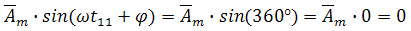
Именно по такому закону и меняется привычное нам переменное напряжение 220 В, изменяясь по синусоидальному закону от значения 0 В до максимальных 311 В и обратно.
2. Другая форма представления – это комплексное число. Чтобы представить ранее рассмотренную форму представления синусоидальной величины, которая имеет некоторую начальную фазу φ, создают комплексную плоскость в виде графика зависимости двух величин (рис.2)
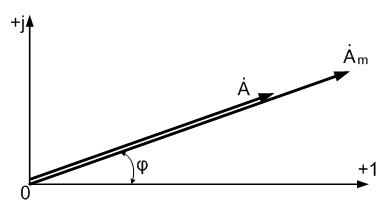

Рис.2. Комплексное число на комплексной плоскости
Длина вектора Am на такой комплексной плоскости равна амплитуде (максимальному значению) рассматриваемой величины. С учетом начальной фазы φ такое число записывают как 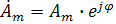
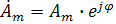 .
.
На практике при использовании для расчетов символического (комплексного) метода расчета используют для некоторых удобств не амплитудное значение величины, а так называемое действующее значение. Его величина в корень из двух раз меньше амплитудного и обозначается без индекса m, т.е. равна
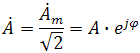
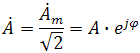
На рисунке выше этот вектор также показан.
Например, при том же нашем напряжении в сети, максимальное значение синусоидально изменяющегося напряжения равно 311 В, а действующее значение, к значению которого мы привыкли
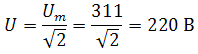
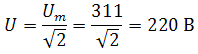
При работе с комплексными числами и расчетов применяют различные формы записи комплексного числа. Например, при сложении комплексных чисел удобнее использовать алгебраическую форму записи таких чисел, а при умножении или делении – показательную форму записи. В некоторых случаях пишут тригонометрическую форму.
Итак, три формы записи комплексного числа:
1) показательная форма в виде
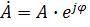
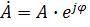
2) тригонометрическая форма в виде
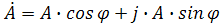
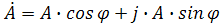
3) алгебраическая форма
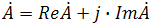
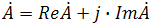
где ReA — это действительная составляющая комплексного числа, ImA — мнимая составляющая.
Например, имеем комплексное число в показательной форме вида
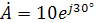
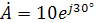
в тригонометрической форме записи это запишется как
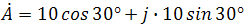
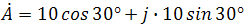
при подсчете получим число, плавно переходящее в алгебраическую форму с учетом того, что
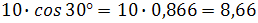
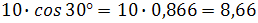
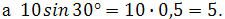
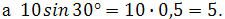
В итоге получим
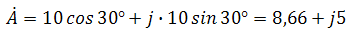
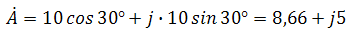
где 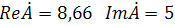
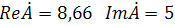
При переходе от алгебраической формы к показательной комплексное число вида
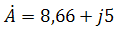
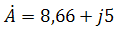
переходит к показательному виду по следующим преобразованиям
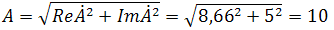
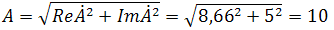
а угол
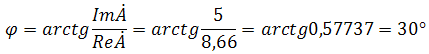
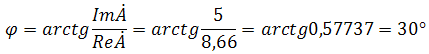
Таким образом, и получим
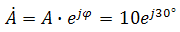
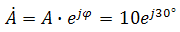
Перейдем к рассмотрению несложных примеров использования символического, или по-другому, комплексного метода расчета электрических цепей. Составим небольшой алгоритм комплексного метода:
- Составить комплексную схему, заменяя мгновенные значения ЭДС, напряжений и токов их комплексным видом
- В полученной схеме произвольно выбирают направления токов в ветвях и обозначают их на схеме.
- При необходимости составляют комплексные уравнения по выбранному методу решения.
- Решают уравнения относительно комплексного значения искомой величины.
- Если требуется, записывают мгновенные значения найденных комплексных величин.
Пример 1. В схеме рис.3 закон изменения ЭДС e = 141sin*ωt. Сопротивления R1 = 3 Ом, R2 = 2 Ом, L = 38,22 мГн, С = 1061,6 мкФ. Частота f = 50 Гц. Решить символическим методом. Найти ток и напряжения на элементах. Проверить 2-ой закон Кирхгофа для цепи.
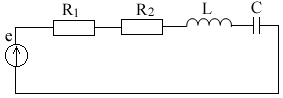

Рис.3. Схема с последовательным соединением элементов
Составляем комплексную схему, обозначив комплексные токи и напряжения (рис.4):
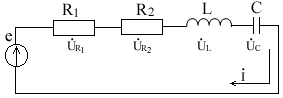

Рис.4. Схема с комплексными обозначениями
По закону Ома ток в цепи равен
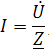
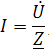
где U — комплексное входное напряжение, Z — полное сопротивление всей цепи. Комплекс входного напряжения находим как
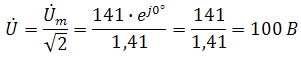
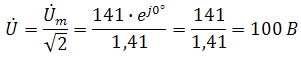
Пояснение: здесь начальная фаза φ = 0°, так как общее выражение для мгновенного значения напряжение вида 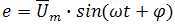
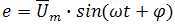 при φ = 0° равно
при φ = 0° равно
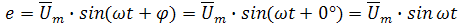
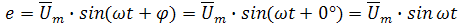
Соответственно, комплекс входного напряжения в показательной форме запишется как
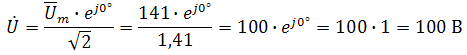
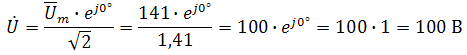
Полное комплексное сопротивление цепи в общем виде
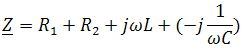
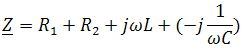
Находим комплексное сопротивление индуктивности
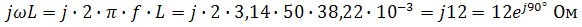
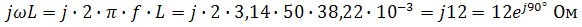
Находим комплексное сопротивление емкости
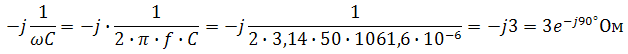
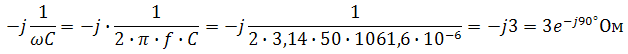
Соответственно, общее комплексное сопротивление цепи
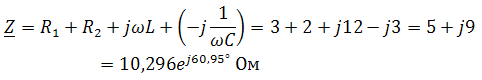
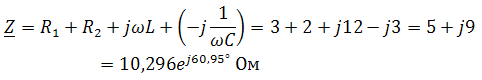
Ток в цепи
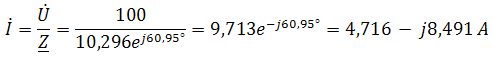
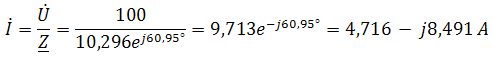
Комплексные напряжения на элементах
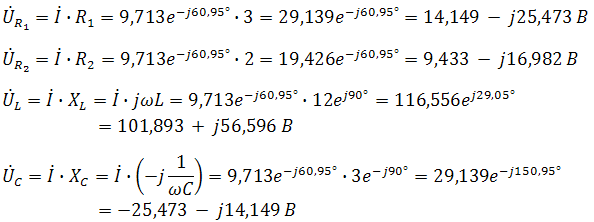
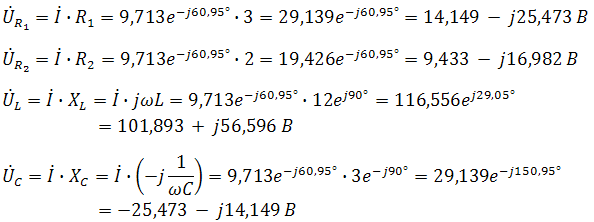
Проверяем второй закон Кирхгофа для замкнутого контура, т.е. должно выполняться равенство 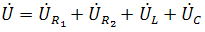
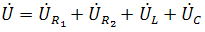
Проверяем
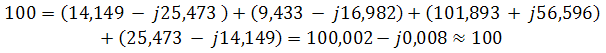
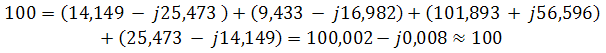
С небольшим расхождением из-за округлений промежуточных вычислений всё верно.
Пример 2. В электрической цепи (рис.5) однофазного синусоидального тока, схема и параметры элементов которой заданы для каждого варианта в таблице, определить:
1) полное сопротивление электрической цепи и его характер;
2) действующие значения токов в ветвях;
3) показания вольтметра и ваттметра;
- Исходные данные: Е = 220 В, f = 50 Гц, L1 = 38,2 мГн, R2 = 6 Ом, С2 = 318 мкФ, L2 = 47,7 мГн, R3 = 10 Ом, С3 = 300 мкФ.
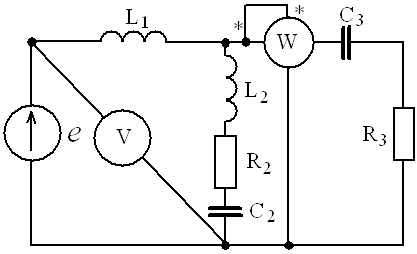

Рис.5.Цепь однофвзного синусоидального тока
Решение:
1. Находим комплексные сопротивления ветвей и всей цепи:
Учитываем, что
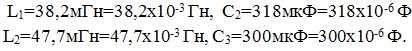
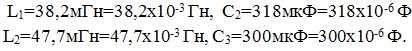
Комплексное сопротивление первой ветви:
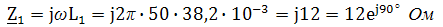
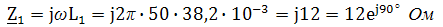
Комплексное сопротивление второй ветви:
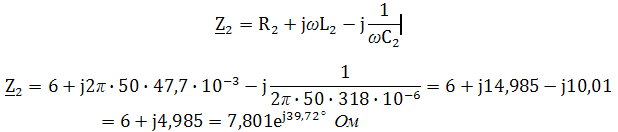
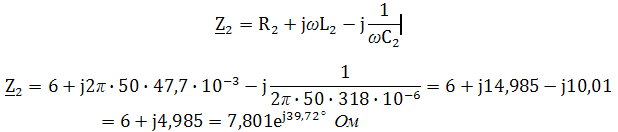
Комплексное сопротивление третьей ветви:
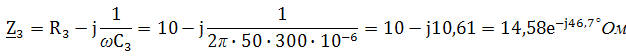
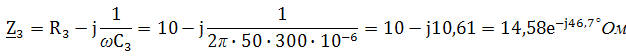
Общее сопротивление цепи
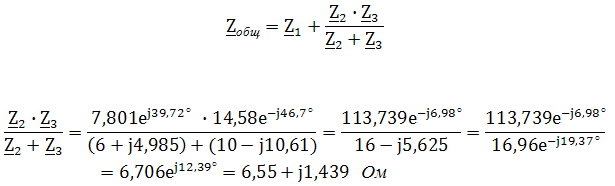
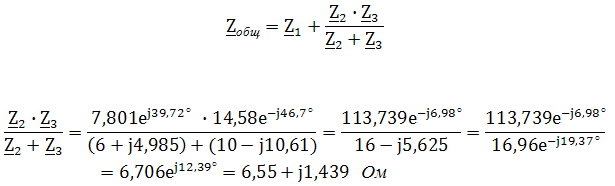
Откуда
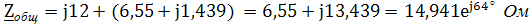
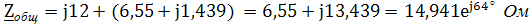
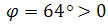
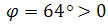 — нагрузка носит активно-индуктивный характер
— нагрузка носит активно-индуктивный характер
2. Находим действующие значения токов в ветвях:
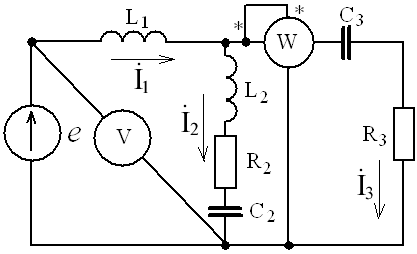

Рис.6. Схема с обозначенными комплексными токами
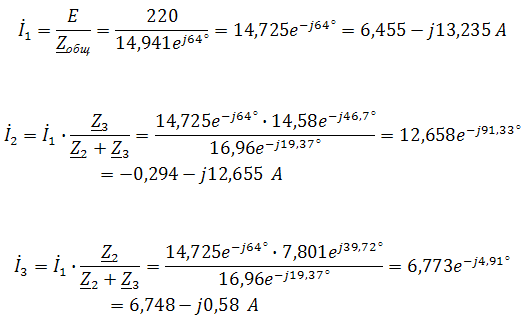
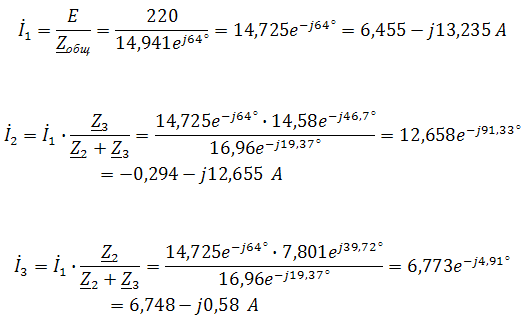
Действующие значения, соответственно,
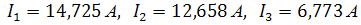
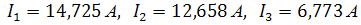
3. Определим показания приборов:
Вольтметр подключен по схеме параллельно источнику питания. Соответственно его показание равно:
U=220 В
Ваттметр включен токовой обмоткой в разрыв третьей ветви, а обмоткой напряжения также к выводам третьей ветви, измеряя, таким образом, активную мощность третьей ветви. Эта мощность равна мощности на сопротивлении R3. Его показания:
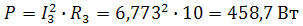
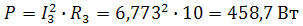




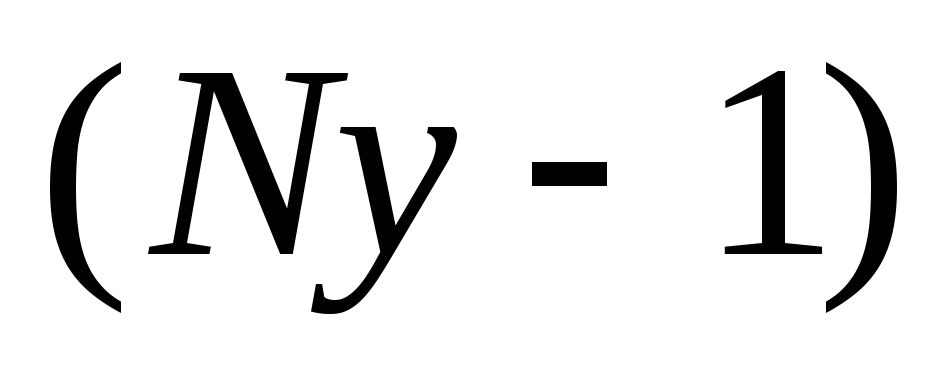 узлов
поIзакону Кирхгофа и
для
узлов
поIзакону Кирхгофа и
для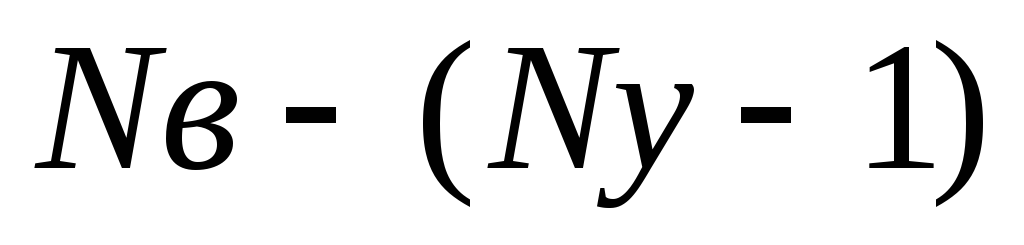 независимых
контуров (отличающихся друг от друга
хотя бы на одну ветвь) — поIIзакону Кирхгофа.
независимых
контуров (отличающихся друг от друга
хотя бы на одну ветвь) — поIIзакону Кирхгофа.