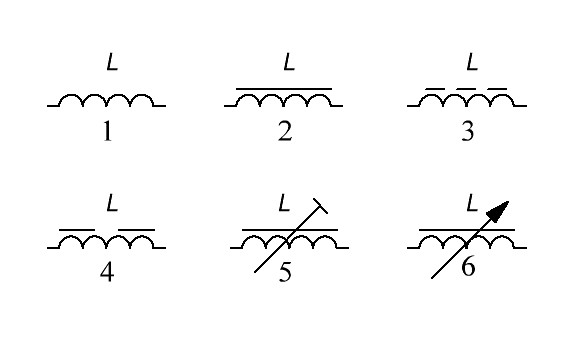Индуктивность
Индуктивность — это физическая (электрическая) величина, которая характеризует магнитные свойства электрической цепи. Как известно электрический ток, протекающий через проводящий контур, создает вокруг него магнитное поле. Это происходит потому, что ток изначально несет в себе энергию. Проходя через проводник, он частично отдает ее, и она превращается в энергию магнитного поля. Индуктивность, по сути, является коэффициентом пропорциональности между протекающим током и возникающим при этом магнитным полем.
Чем выше индуктивность проводника, тем больше будет магнитное поле при одном и том же значении электрического тока. Физически индуктивность в электрической цепи – это катушка, состоящая из пассивного (диэлектрик) или активного (ферромагнитный материал, железо) сердечника и намотанного на него электрического провода.
Если протекающий ток изменяет свою величину во времени, то есть является не постоянным, а переменным, то в индуктивном контуре меняется магнитное поле, вследствие чего возникает ЭДС (электродвижущая сила) самоиндукции. Эта ЭДС также как и электрическое напряжение измеряется в вольтах (В).
Единицей измерения индуктивности является Гн (генри). Она названа в честь Джозефа Генри – американского ученого, открывшего явление самоиндукции. Считается, что контур (катушка индуктивности) имеет величину 1 Гн, если при изменении тока в 1 А (ампер) за одну секунду в нем возникает ЭДС величиною в 1 В (вольт). Обозначается индуктивность буквой L, в честь Эмиля Христиановича Ленца – знаменитого российского физика. Термин «индуктивность» был предложен Оливером Хевисайдом – английским ученым-самоучкой в 1886 году.
| < Предыдущая | Следующая > |
|---|
Явление самоиндукции — урок.
 Физика, 9 класс.
Физика, 9 класс.Согласно правилу Ленца индукционный ток в замкнутом контуре всегда противодействует своим магнитным полем изменению внешнего магнитного потока, которое вызвало его появление.
Рассмотрим случай, когда явление электромагнитной индукции наблюдается при изменении силы тока, проходящего через катушку с большим количеством витков. Если причина возникновения индукционного тока состоит в возрастании тока, то индукционный ток своим магнитным полем будет противодействовать этому возрастанию.
Убедиться в этом можно на следующем опыте.
Соберем цепь по следующему принципу: один участок содержит электрическую лампу и катушку индуктивности, второй участок — электрическую лампу и сопротивление, которое одинаково с сопротивлением катушки. В замкнутом электрическом контуре на первом участке наблюдаем явление запаздывания включения лампы, которое называется самоиндукцией.
Самоиндукция — это явление возникновения индукционного тока в цепи при изменении протекающего по цепи тока.
Возникающий индукционный ток называют током самоиндукции.
На участке цепи, содержащий катушку, возник индукционный ток, который препятствовал нарастанию основного тока, создаваемого источником, поэтому лампа загорелась позже, чем лампа соединенная с резистором. Из этого следует, что индуктивность катушки превышает индуктивность резистора.
Индуктивность — это физическая величина, которую обозначают буквой L.
Индуктивность характеризует способность катушки препятствовать нарастанию силы тока.
Обрати внимание!
За единицу измерения индуктивности принят генри (Гн).
L=1 Гн
Различные катушки могут иметь разную индуктивность. Она зависит от:
- размеров и формы катушки;
- числа витков;
- наличия сердечника;
- материала, из которого изготовлен сердечник.
Чем большей индуктивностью обладает катушка, тем с большим запозданием будет загораться лампа.
Явление самоиндукции можно наблюдать и при размыкании цепи. Изменим цепь.
Изменим цепь.
Параллельно источнику тока включены катушка и лампа.
В такой цепи наблюдается явление кратковременного свечения лампы при размыкании электрической цепи, что также объясняется правилом Ленца о явлении самоиндукции как механизме препятствия изменения тока в контуре.
Применение катушек с большими значениями индуктивности, которые являются одновременно технологическими элементами электрической цепи и источниками больших значений ЭДС самоиндукции, может приводить при разрывах цепи к электризации воздуха.
Катушка индуктивности это в физике — MOREREMONTA
Индукционная катушка — это дроссель или изолированный проводник. Используется электрический каркас, композитные вставки. При рассмотрении понятия необходимо изучить свойства, основные особенности катушки индуктивности.
Определение устройства
Катушка индуктивности — это устройство, которое обладает малой емкостью и значительным сопротивлением. Дроссель является отменным проводником электрического тока, учитывается высокий показатель инерционности.
Важно! Устройство работает в цепях переменного тока при низкой и высокой частоте.
Назначение и принцип действия
Специалисты задаются вопросом, зачем нужна токовая катушка индуктивности в цепи, и для этого необходимо разобраться в показателях. Коэффициент ЭДС (электродвижущая сила) показывает разницу между энергией и магнитным потоком. Устройства самоиндукции способны влиять на изменения в цепи. Чаще всего дроссели применяются в силовых установках. Они способны контролировать уровень напряжения, не допускают разрыва цепи.
Также компоненты устанавливаются на пару с конденсаторами либо резисторами. Благодаря работе катушки фильтры находятся в безопасности. Теперь вызывает интерес, как включается индукционная катушка. Принцип работы построен на изоляции проводников. В конструкции используется электрический каркас с различным сечением.
Интересно! Витки наматываются с определенным шагом, многое зависит от типа катушки.
Виды и типы
Различают низкочастотные, высокочастотные модели. В отдельную категорию выделяют винтовые, спиральные катушки. Также существуют модификации, которые используются в радиотехнике. Они подходят для защиты конденсатора либо резонансных контуров.
Для трансформаторов годятся катушки с усилителем каскадом. В последнюю категорию выделены вариометры, основное отличие — высокая частота колебательных контуров. Дроссели могут быть одинарными либо сдвоенными. От этого зависит показатель индуктивности и питания системы.
Низкочастотные
Для включения в электрическую цепь, применяется низкочастотная катушка индуктивности. Она предназначена для подавления переменного тока. В формуле учитывается циклическая частота и показатели индуктивности. За основу в устройствах берётся сердечник, который изготавливается из стали. Он может быть с фильтрами либо без них.
Он может быть с фильтрами либо без них.
Чтобы влиять на частоту, происходит игра с сопротивлением. В цепи постоянного тока напряжение должно быть неизменным. С целью понижения частоты применяются фильтры. Основная проблема — это малая ёмкость. Чтобы детально ознакомиться с дросселем, стоит подробнее узнать о резонансной частоте, которая выделяется на контуре рабочего сигнала.
Когда в цепях повышается напряжение, на каркас оказывается нагрузка. В цепи постоянного тока задействуются непрозрачные проволочные резисторы. Также для этих целей подходят однослойные катушки типа «универсал». Их особенность — использование ферритовых стержней.
Высокочастотные
Устройства изготавливаются с различными типами обмотки. Речь идет о наборе преимуществ, которые спасают в той или иной ситуации. Сфера применения элементов широка, учитывается значительная частота модуляции. Таким образом удается бороться с повышенным сопротивлением металлов. У катушек имеется сердечник.
Основная задача — это модуляция частоты генератора. Она происходит за счёт усиления сигнала, и за процессом можно проследить при подключении осциллографа. Многие высокочастотные катушки не отличаются стабильной работой, поскольку применяется керамический каркас. У него малый срок годности, плюс они восприимчивы к повышенной влажности.
Интересно! Современные товары изготавливаются из алюминия и являются компактными.
Электрикам известны контурные, безконтурные модификации высокой частоты. В зависимости от намотки учитывается стабильность электрических параметров. У моделей высокой частоты могут применяться магниты и провода. Речь идет о порошковых материалах, сделанных из диэлектриков.
Процесс изготовления связан с методом холодного прессования. Индуктивные датчики отличаются по защищенности. На предприятиях элементы могут погружать в раствор либо продевать в трубку. Это делается с целью избежания коротких замыканий. Мировые производители решают проблему путем использование вторичного витка.
У моделей значительное сопротивление и есть проблема с концентрацией электролита. Таким образом изменяются свойства катушки индуктивности. Проводимость раствора падает и повышается частота электромагнитного поля.
Основные технические параметры
Катушки индуктивности имеют следующие характеристики:
- добротность отклонения;
- эффективность;
- начальная индуктивность;
- температура;
- стабильность;
- предельная емкость;
- номинальная индуктивность.
Стабильность демонстрирует свойства устройства при изменении условий использования. Температура фиксируется вследствие различных причин. Многое зависит от размера каркаса. Когда температура уменьшается, индуктивность также снижается. Современные параметры — это цикличность, которая является отношением температуры к линейному расширению. Учитывается изменение в керамической основе плюс показатель плотности.
Температура отслеживается на горячей намотке.
Номинальная индуктивность — это параметр, который учитывает изменение размеров волны. Измерение происходит в микрогенрах. Если смотреть на формулу, учитывается количество витков, длина намотки, плюс диаметр катушки.
Маркировка
При рассмотрении катушек индуктивности оценивается цветовая и кодовая маркировка. Если смотреть на первые цифры, отображается показатель индуктивности. Далее учитывается параметр отклонения:
- Серебряный 0,01 мкГн, 10%.
- Золотой 0,1 мкГн, 5%.
- Черный 0,1мкГн, 20%.
- Коричневый 1,1 мкГн.
- Красный 2, 2 мкГн.
- Оранжевый 1 мкГн.
- Желтый 4 мкГн.
- Зеленый 5 мкГн.
- Голубой 6 мкГн.
- Фиолетовый 7мкГн.

- Серый 8 мкГн.
- Белый 9 мкГн.
В нестабильной цепи переменного электрического тока не обойтись без катушки индуктивности. Выше описаны основные типы изолированных проводников, продемонстрированы их параметры. Учитывается уровень частоты, а также свойства.
Катушка индуктивности является пассивным компонентом электронных схем, основное предназначение которой является сохранение энергии в виде магнитного поля. Свойство катушки индуктивности чем-то схоже с конденсатором, который хранит энергию в виде электрического поля.
Определение и принцип действия
Катушка индуктивности — это катушка смотанного в спираль или другую форму изолированного проводника. Основные особенности и свойства: высокая индуктивность при низкой ёмкости и активном сопротивлении.
Она накапливает энергию в магнитном поле. На рисунке ниже вы видите её условное графическое обозначение на схеме (УГО) в разных видах и функциональных назначениях.
Она может быть с сердечником и без него. При этом с сердечником индуктивность будет в разы больше, чем если его нет. От материала, из которого изготовлен сердечник, также зависит величина индуктивности. Сердечник может быть сплошным или разомкнутым (с зазором).
Напомним один из законов коммутации:
Ток в индуктивности не может измениться мгновенно.
Это значит, что катушка индуктивности — это своего рода инерционный элемент в электрической цепи (реактивное сопротивление).
Давайте поговорим, как работает это устройство? Чем больше индуктивность, тем больше изменение тока будет отставать от изменения напряжения, а в цепях переменного тока — фаза тока отставать от фазы напряжения.
В этом и заключается принцип работы катушек индуктивности – накопление энергии и задерживание фронта нарастания тока в цепи.
Из этого же вытекает и следующий факт: при разрыве в цепи с высокой индуктивностью напряжение на ключе повышается и образуется дуга, если ключ полупроводниковый — происходит его пробой. Для борьбы с этим используются снабберные цепи, чаще всего из резистора и конденсатора, установленного параллельно ключу.
Для борьбы с этим используются снабберные цепи, чаще всего из резистора и конденсатора, установленного параллельно ключу.
Виды и типы катушек
В зависимости от сферы применения и частоты цепи может отличаться конструкция катушки.
По частоте можно условно разделить на:
- Низкочастотные. Пример — дроссель люминесцентной лампы, трансформатор (каждая обмотка представляет собой катушку индуктивности), реактор, фильтры электромагнитных помех. Сердечники чаще всего выполняются из электротехнической стали, для цепей переменного тока из листов (шихтованный сердечник).
- Высокочастотные. Например, контурные катушки радиоприемников, катушки связи усилителей сигнала, накопительные и сглаживающие дроссели импульсных блоков питания. Их сердечник изготавливают обычно из феррита.
Конструкция отличается в зависимости от характеристик катушки, например, намотка может быть однослойной и многослойной, намотанной виток к витку или с шагом. Шаг между витками может быть постоянным или прогрессивным (изменяющимся по длине катушки). Способ намотки и конструкция влияют на конечные размеры изделия.
Способ намотки и конструкция влияют на конечные размеры изделия.
Отдельно стоит рассказать о том, как устроена катушка с переменной индуктивностью, их еще называют вариометры. На практике можно встретить разные решения:
- Сердечник может двигаться относительно обмотки.
- Две обмотки расположены на одном сердечнике и соединены последовательно, при их перемещении изменяется взаимоиндукция и индуктивная связь.
- Сами витки для настройки контура могут раздвигаться или сужаться приближаясь друг к другу (чем плотнее намотка — тем больше индуктивность).
И так далее. При этом подвижная часть называется ротором, а неподвижная — статором.
По способу намотки бывают также различными, например, фильтры со встречной намоткой подавляют помехи из сети, а намотанные в одну сторону (согласованная намотка) подавляют дифференциальные помехи.
Для чего нужны и какие бывают
В зависимости от того, где применяется катушка индуктивности и её функциональных особенностей, она может называться по-разному: дроссели, соленоиды и прочее. Давайте рассмотрим, какие бывают катушки индуктивности и их сферу применения.
Давайте рассмотрим, какие бывают катушки индуктивности и их сферу применения.
Дроссели. Обычно так называются устройства для ограничения тока, область применения:
- В пускорегулирующей аппаратуре для розжига и питания газоразрядных ламп.
- Для фильтрации помех. В блоках питания — фильтр электромагнитных помех со сдвоенным дросселем на входе компьютерного БП, изображен на фото ниже. Также используется в акустической аппаратуре и прочем.
- Для фильтрации определенных частот или полосы частот, например, в акустических системах (для разделения частот по соответствующим динамикам).
- Основа в импульсных преобразователях — накопитель энергии.
Токоограничивающие реакторы — используются для ограничения токов короткого замыкания на ЛЭП.
Примечание: у дросселей и реакторов должно быть низкое активное сопротивление для уменьшения их нагрева и потерь.
Контурные катушки индуктивности. Используются в паре с конденсатором в колебательном контуре. Резонансная частота подбирается под частоту приема или передачи в радиосвязи. У них должна быть высокая добротность.
Резонансная частота подбирается под частоту приема или передачи в радиосвязи. У них должна быть высокая добротность.
Вариометры. Как было сказано — это настраиваемые или переменные катушки индуктивности. Чаще всего используются в тех же колебательных контурах для точной настройки частоты резонанса.
Соленоид — так называется катушка, длина которой значительно больше диаметра. Таким образом внутри соленоида образуется равномерное магнитное поле. Чаще всего соленоиды используются для совершения механической работы — поступательного движения. Такие изделия называют еще электромагнитами.
Рассмотрим, где используются соленоиды.
Это может быть активатор замка в автомобиле, шток которого втягивается после подачи на соленоид напряжения, и звонок, и различные исполнительные электромеханические устройства типа клапанов, грузоподъёмные магниты на металлургических производствах.
В реле, контакторах и пускателях соленоид также выполняет функцию электромагнита для привода силовых контактов. Но в этом случае его чаще называют просто катушка или обмотка реле (пускателя, контактора соответственно), как выглядит, на примере малогабаритного реле вы видите ниже.
Но в этом случае его чаще называют просто катушка или обмотка реле (пускателя, контактора соответственно), как выглядит, на примере малогабаритного реле вы видите ниже.
Рамочные и кольцевые антенны. Их назначение — передача радиосигнала. Используются в иммобилайзерах автомобилей, металлодетекторах и для беспроводной связи.
Индукционные нагреватели, тогда она называется индуктором, вместо сердечника помещают нагреваемое тело (обычно металл).
Основные параметры
К основным характеристикам катушки индуктивности можно отнести:
- Индуктивность.
- Силу тока (для подбора подходящего элемента при ремонте и проектировании это нужно учитывать).
- Сопротивление потерь (в проводах, в сердечнике, в диэлектрике).
- Добротность — отношение реактивного сопротивления к активному.
- Паразитная емкость (емкость между витками, говоря простым языком).
- Температурный коэффициент индуктивности — изменение индуктивности при нагреве или охлаждении элемента.

- Температурный коэффициент добротности.
Маркировка
Для обозначения номинала катушки индуктивности используют буквенную или цветовую маркировку. Есть два вида буквенной маркировки.
- Обозначение в микрогенри.
- Обозначение набором букв и цифр. Буква r – используется вместо десятичной запятой, буква в конце обозначения обозначает допуск: D = ±0.3 нГн; J = ±5%; К = ±10%; М = ±20%.
Цветовую маркировку можно распознать аналогично таковой на резисторах. Воспользуйтесь таблицей, чтобы расшифровать цветные полосы или кольца на элементе. Первое кольце иногда делают шире остальных.
На это мы и заканчиваем рассматривать, что собой представляет катушка индуктивности, из чего она состоит и зачем нужна. Напоследок рекомендуем посмотреть полезное видео по теме статьи:
Материалы по теме:
Автор: Алексей Бартош
youtube.com/embed/Y8-saxraVlk»/>
ИНДУКТИВНОСТЬ — это… Что такое ИНДУКТИВНОСТЬ?
в электродинамике (коэффициент самоиндукции) (от лат. inductio — наведение, побуждение) — параметр электрич. цепи, определяющий величину эдс самоиндукции, наводимой в цепи при изменении протекающего по ней тока и (или) при её деформации. Термин «И.» употребляется также для обозначения элемента цени (двухполюсника), определяющего её индуктивные свойства (синоним — катушка самоиндукции).И. является количеств. характеристикой эффекта самоиндукции, открытого независимо Дж. Генри (J. Henry) в 1832 и М. Фарадеем (М. Faraday) в 1835. При изменении тока в цепи и (или) при её деформации происходит изменение магн. поля, к-рое, в соответствии с законом индукции, приводит к возникновениювихревого электрич. поля E(r, t )с отличной от нуля циркуляцией
по замкнутым контурам li;пронизываемым магн. ) — циркуляция вектора E вдоль этой линии тока, jn — нормальная к Snp составляющая j. В более сложных ситуациях, когда линии тока замыкаются после неск. обходов по контуру или вообще не являются замкнутыми кривыми, процедура усреднения требует уточнений, однако во всех случаях она должнаудовлетворять энергетич. соотношению: =E сиI ( Р— суммарная мощность взаимодействия поля с током).Усреднённый магн. поток в случае квазистацнонарных процессов пропорц. току:
) — циркуляция вектора E вдоль этой линии тока, jn — нормальная к Snp составляющая j. В более сложных ситуациях, когда линии тока замыкаются после неск. обходов по контуру или вообще не являются замкнутыми кривыми, процедура усреднения требует уточнений, однако во всех случаях она должнаудовлетворять энергетич. соотношению: =E сиI ( Р— суммарная мощность взаимодействия поля с током).Усреднённый магн. поток в случае квазистацнонарных процессов пропорц. току:
Ф=L.I (в СИ), Ф=1/c(LI)(в системе СГС). (1)
Коэф. L и Lназ. И. Величина L измеряется в генри, L — в см.
E си=-d/dt(LI) (в СИ), Ecи=-(1/с 2)(d/dt)(LI)(2) (в системе СГС).
Производная по времени от И. определяет ту часть E си, к-рая связана с деформацией проводящего контура; в случае недеформируемых цепей и квазистационарных процессов И. может быть вынесена из-под знака дифференцирования. энергия, запасённая в создаваемом им магн. поле, записывается в форме, аналогичной выражению для кинетич. энергии.
может быть вынесена из-под знака дифференцирования. энергия, запасённая в создаваемом им магн. поле, записывается в форме, аналогичной выражению для кинетич. энергии.
Wm=1/2LI2 (в СИ), Wm=1/2c2LI2 (в системе СГС). (3)
Соотношение (3) позволяет различать И. внутреннюю Li, определяющую энергию магн. поля, сосредоточенного в проводниках, и внешнюю Le, связанную с внеш. магн. полем (L=Li+Le, L=Li+Le). В важном частном случае токовой цепи, выполненной из проводов, толщина к-рых мала по сравнению с радиусамиих изгибов или расстояниями между соседними проводами, можно считать, что структура токов и ближнего магн. поля такая же, как и для прямого провода того же сечения (подобные проводники наз. квазилинейными). В приближении заданной структуры токов, не зависящей от способа их возбуждения, И. определяется только геометрией проводящей цепи (толщиной и длиной проводов и их формой). Для квазилинейного провода кругового сечения Li=(m0/8p)mil (l — длина провода, mi — магн. проницаемость проводника), а внешняя И. может быть представлена как индуктивность взаимная двух параллельных бесконечно тонких проводящих нитей, одна из к-рых (l1) совпадает с осевой линией проводника, а другая (l2) совмещена с его поверхностью:
определяется только геометрией проводящей цепи (толщиной и длиной проводов и их формой). Для квазилинейного провода кругового сечения Li=(m0/8p)mil (l — длина провода, mi — магн. проницаемость проводника), а внешняя И. может быть представлена как индуктивность взаимная двух параллельных бесконечно тонких проводящих нитей, одна из к-рых (l1) совпадает с осевой линией проводника, а другая (l2) совмещена с его поверхностью:
где r1, r2 — радиус-векторы точек на контурах ll,l2,m е — магн. проницаемость окружающей среды [для аналогия, соотношений в системе СГС L «(m0/4p)L]. Из (4) видно, что Le логарифмически расходится при стремлении радиуса провода к нулю, поэтому идеализацией бесконечно тонкого провода нельзя пользоваться при описании явлений самоиндукции. Приближённые вычисления интеграла в (4) с учётом внутренней И. дают:
дают:
где l и а — длина и радиус провода. Это выражение обладает логарифмич. точностью — его относит. погрешность порядка величины l/ln(l/a). Примеры типичных электрич. цепей и выражения для их И. приведены на рис. 1 и 2.
Рис. 1. Круговой виток. Индуктивность витка (проводящего тора): L=m0R(ln(8R/r)-2+1/4mi), Гн, r<<R.
Особое значение в электротехнике и радиотехнике имеют проволочные катушки с достаточно плотной намоткой — соленоиды (рис. 3), применяемые для увеличения И. Поскольку И. цепей, в к-рые включены соленоиды, ими в основном и определяются, принято говорить об И. соленоида. Под величиной И. идеальногосоленоида понимают И. эфф. проводящей поверхности (совпадающей с его каркасом), по к-рой протекают азимутальные поверхностные токи с плотностью j пов=Ik (I — ток в соленоиде, k — число витков на единице длины).
Понятие И. допускает обобщение на быстропеременные гармонич. ехр(iwt)-процессы, при описании к-рых нельзя пренебрегать запаздыванием эл.-магп. взаимодействий, скин-эффектом в проводниках, дисперсией среды. Комплексные амплитуды тока Iw и эдс самоиндукции Ew связаны соотношением:
ехр(iwt)-процессы, при описании к-рых нельзя пренебрегать запаздыванием эл.-магп. взаимодействий, скин-эффектом в проводниках, дисперсией среды. Комплексные амплитуды тока Iw и эдс самоиндукции Ew связаны соотношением:
И. L(w) зависит от частоты (как правило, уменьшается с её ростом). Эфф. сопротивление RL(w) определяет часть энергетич. потерь, в т. ч. потери на излучение, и связано с L(w) Крамерса — Кронига соотношением:
где интеграл берётся в смысле гл. значения. На низких частотах сопротивлением RL(w) можно пренебречь, тогда Ew и Iw сдвинуты по фазе на p/2. Соотношение (3) для высокочастотных процессов преобразуется к виду:
где Wmw— усреднённая по периоду колебаний энергия ближних (квазистационарных) магн. полей (полная магн. энергия поля не определена из-за линейно растущей во времени энергии поля излучения).Если в цепи действует гармонич. сторонняя эдс , то во втором законе Кирхгофа величина Ew может быть перенесена (со сменой знака) в правую часть равенства:
где С —ёмкость, включённая в цепь. Соотношение (9) позволяет трактовать величину ZL=iwLкак индуктивную часть импеданса цепи (при атом ZC=-i/w С —ёмкостная, a ZR=R— активная части полного импеданса Z=ZL+ZC+ZR). Принято считать, что импеданс двухполюсника имеет индуктивный характер, если его мнимая часть больше нуля [если рассматриваются ехр (-iwt)-процессы, то меньше нуля]. В технике довольно часто И. наз. любой двухполюсник, импеданс к-рого имеет индуктивный характер п в опредсл. диапазоне частот линейно зависит от w. Если индуктивные элементы выполнены в виде катушек самоиндукции, то считать их двухполюсниками можно, вообще говоря, только в том случае, когда взаимодействие через магн. поля между ними и с др. элементами цепи пренебрежимо мало. Тогда их импедансы можно складывать в соответствии с правилами Кирхгофа: при последовательном соединении , а при параллельном При описании сильноточных цепей часто требуется обобщение понятия И.
Соотношение (9) позволяет трактовать величину ZL=iwLкак индуктивную часть импеданса цепи (при атом ZC=-i/w С —ёмкостная, a ZR=R— активная части полного импеданса Z=ZL+ZC+ZR). Принято считать, что импеданс двухполюсника имеет индуктивный характер, если его мнимая часть больше нуля [если рассматриваются ехр (-iwt)-процессы, то меньше нуля]. В технике довольно часто И. наз. любой двухполюсник, импеданс к-рого имеет индуктивный характер п в опредсл. диапазоне частот линейно зависит от w. Если индуктивные элементы выполнены в виде катушек самоиндукции, то считать их двухполюсниками можно, вообще говоря, только в том случае, когда взаимодействие через магн. поля между ними и с др. элементами цепи пренебрежимо мало. Тогда их импедансы можно складывать в соответствии с правилами Кирхгофа: при последовательном соединении , а при параллельном При описании сильноточных цепей часто требуется обобщение понятия И. на случай нелинейных систем. Если неподвижный проводящий контур помещён всреду, в к-рой вектор магн. индукции В и напряжённость магн. поля Н связаны нелинейным локальным соотношением: B(r, t)=B[H(r, t)], то сцепленный с контуром магн. поток можно считать однозначной ф-цией тока Ф=Ф(I). В соответствии с законом индукции Фарадея, эдс самоиндукции в контуре равна:
на случай нелинейных систем. Если неподвижный проводящий контур помещён всреду, в к-рой вектор магн. индукции В и напряжённость магн. поля Н связаны нелинейным локальным соотношением: B(r, t)=B[H(r, t)], то сцепленный с контуром магн. поток можно считать однозначной ф-цией тока Ф=Ф(I). В соответствии с законом индукции Фарадея, эдс самоиндукции в контуре равна:
Величина L Д(I)=d Ф /dIназ. дифференциальной (или иногда динамической) И. Выражение для запасённой энергии пост. тока приобретает вид:
B линейном приближении (при I «0) L Д «L и выражения (10), (11) переходят в (2) и (3) соответственно. Лит.: Тамм И. Е., Основы теории электричества9 изд., М., 1976; Калантаров П. Л., Цейтлин Л. А. Расчет индуктивностей, 3 изд., Л., 1986; Ландау Л. Д. Лифшиц Е. М., Электродинамика сплошных сред, 2 изд. М., 1982. М. А. Миллер, Г. В. Пермитин
Физическая энциклопедия. В 5-ти томах. — М.: Советская энциклопедия.
Главный редактор А. М. Прохоров.
1988.
В 5-ти томах. — М.: Советская энциклопедия.
Главный редактор А. М. Прохоров.
1988.
Индуктивность обозначение в физике — Яхт клуб Ост-Вест
Индуктивность контура — это коэффициент пропорциональности между постоянным током, текущим в заданном замкнутом контуре, и потоком вектора магнитной индукции, создаваемым этим током через поверхность, окружённой этим контуром. Обозначение — , размерность — Гн (генри). Формульно:
- Ф — поток вектора магнитной индукции,
- — индуктивность контура,
- — сила тока в контуре.
В большинстве задач данный параметр задан в условии, однако есть одна система, в которой данный параметр является расчётным. Это соленоид (рис. 1). Соленоидом называется провод, согнутый в виде спирали (он же, в принципе, катушка индуктивности). Формульно:
- — индуктивность соленоида,
- — относительная магнитная проницаемость среды (табличные данные),
- м*кг* * ,
- — число витков,
- — площадь поперечного сечения витка,
- — длинна катушки.

Немного о — относительной магнитной проницаемости среды. Чаще всего в школьных задачах соленоид пустотелый, т.е. внутри него (витков) воздух, тогда . Иногда в него помещают сердечник, т.е. болванку формой повторяющую внутреннюю геометрию соленоида, тогда 1″ title=»displaystyle mu >1″ > и по веществу, из которого состоит сердечник, можно в таблицах найти значение магнитной проницаемости.
Для ряда задач существует всё тот же вопрос о параллельном и последовательном соединении индуктивностей. Будем считать, что взаимной индукции нет (т.е. один контур экранирован от второго). Тогда:
- при параллельном подключении:
- — общая индуктивность системы контуров,
- — сумма обратных индуктивностей, входящих в цепь.
В случае двух элементов, соединённых параллельно:
- при последовательном подключении:
- — общая индуктивность системы контуров,
- — сумма индуктивностей, входящих в цепь.

Индуктивность – это физическая (электрическая) величина, которая характеризует магнитные свойства электрической цепи. Как известно электрический ток, протекающий через проводящий контур, создает вокруг него магнитное поле. Это происходит потому, что ток изначально несет в себе энергию. Проходя через проводник, он частично отдает ее, и она превращается в энергию магнитного поля. Индуктивность, по сути, является коэффициентом пропорциональности между протекающим током и возникающим при этом магнитным полем.
Чем выше индуктивность проводника, тем больше будет магнитное поле при одном и том же значении электрического тока. Физически индуктивность в электрической цепи – это катушка, состоящая из пассивного (диэлектрик) или активного (ферромагнитный материал, железо) сердечника и намотанного на него электрического провода. Это один из самых обсуждаемых электрических компонентов на форумах любителей электроники.
Если протекающий ток изменяет свою величину во времени, то есть является не постоянным, а переменным, то в индуктивном контуре меняется магнитное поле, вследствие чего возникает ЭДС (электродвижущая сила) самоиндукции. Эта ЭДС также как и электрическое напряжение измеряется в вольтах (В).
Эта ЭДС также как и электрическое напряжение измеряется в вольтах (В).
Единицей измерения индуктивности является Гн (генри). Она названа в честь Джозефа Генри – американского ученого, открывшего явление самоиндукции. Считается, что контур (катушка индуктивности) имеет величину 1 Гн, если при изменении тока в 1 А (ампер) за одну секунду в нем возникает ЭДС величиною в 1 В (вольт). Обозначается индуктивность буквой L, в честь Эмиля Христиановича Ленца – знаменитого российского физика. Термин «индуктивность» был предложен Оливером Хевисайдом – английским ученым-самоучкой в 1886 году.
Эл.ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф
B), индукция пропорциональна силе тока в проводнике
(B
I), следовательно магнитный поток пропорционален силе тока (Ф
ЭДС самоиндукции зависит от скорости изменения силы тока в эл.цепи, от свойств проводника
(размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник.
Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.
Индуктивность – физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 Ампер за 1 секунду.
Также индуктивность можно рассчитать по формуле:
где Ф – магнитный поток через контур, I – сила тока в контуре.
Единицы измерения индуктивности в системе СИ:
Индуктивность катушки зависит от: числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды
Индуктивность взаимная – величина, характеризующая магнитную связь двух или более электрических цепей (контуров). Если имеется два проводящих контура , то часть линий магнитной индукции, создаваемых током в первом контуре, будет пронизывать площадь, ограниченную вторым контуром (т. е. будет сцеплена с контуром 2).
е. будет сцеплена с контуром 2).
Магнитный поток Ф12 через контур 2, созданный током I1 в контуре 1, прямо пропорционален току:
Коэффициент пропорциональности M12 зависит от размеров и формы контуров 1 и 2, расстояния между ними, их взаимного расположения, а также от магнитной проницаемости окружающей среды и называется взаимной индуктивностью или коэффициентом взаимной индукции контуров 1 и 2. В системе СИ И. в. измеряется в Генри.
Трансформаторная ЭДС. Принцип действия трансформатора основан на явлении электромагнитной индукции. Линии индукции магнитного поля, создаваемого переменным током в первичной обмотке, благодаря наличию сердечника практически без потерь пронизывают витки вторичной обмотки. Поскольку магнитный поток во вторичной обмотке изменяется со временем (т.к. в первичной обмотке переменный ток), то согласно закону Фарадея в ней возбуждается ЭДС индукции. Трансформатор может работать только на переменном токе, т. к. магнитный поток, созданный постоянным током, не изменяется с течением времени.
к. магнитный поток, созданный постоянным током, не изменяется с течением времени.
Пусть первичная обмотка трансформатора подключена к источнику тока с переменной ЭДС E1 и с действующим значением напряжения U1. На вторичной обмотке ЭДС E2 и напряжение U2.
Из законов Ома следует, что напряжение на обмотке равно
(1)
где r — сопротивление обмотки. При изготовлении трансформатора сопротивление первичной обмотки r1 делают очень малым, поэтому часто им можно пренебречь. Тогда
Если пренебречь потерями магнитного потока в сердечнике, то в каждом витке вторичной обмотки будет индуцироваться точно такая же ЭДС индукции e1, как и ЭДС индукции e2 в каждом витке первичной обмотки, т.е. e1 = e2. Следовательно, отношение ЭДС в первичной E1 и вторичной E2 обмотках равно отношению числа витков в них:
(2)
Трансформаторный ток. Токи обмоток обратно пропорциональны числам витков (I1/I2 приблиз = w1/w2 = 1/n). С увеличением тока активно-индуктивного приемника вторичное напряжение несколько снижается.
Токи обмоток обратно пропорциональны числам витков (I1/I2 приблиз = w1/w2 = 1/n). С увеличением тока активно-индуктивного приемника вторичное напряжение несколько снижается.
Рис.1.11. К определению магнитного потока рассеяния в катушке с ферромагнитным сердечником
часть магнитного потока катушки замыкается не по сердечнику, а по воздуху. Эта часть потока носит название потока рассеивания Фр (рис. 1.11). Таким образом, полный поток, сцепленный с витками катушки равен
| . | (1.14) |
На основании закона Ома для магнитной цепи (1.7) можно написать выражение для потока рассеяния:
| . |
Так как , то .То есть поток рассеяния , в отличие от потока в сердечнике, совпадает по фазе с током и связан с ним линейной зависимостью. Следовательно, на векторной диаграмме вектор потока будет совпадать с вектором тока (рис. 1.12).
1.12).
Рис.1.12. Векторная диаграмма магнитных потоков, ЭДС и токов катушки с ферромагнитным сердечником
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8323 – | 7261 – или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
В чем измеряется индуктивность в физике
Эл.ток создает собственное магнитное поле. Магнитный поток через контур пропорционален индукции магнитного поля (Ф
B), индукция пропорциональна силе тока в проводнике
(B
I), следовательно магнитный поток пропорционален силе тока (Ф
ЭДС самоиндукции зависит от скорости изменения силы тока в эл. цепи, от свойств проводника
цепи, от свойств проводника
(размеров и формы) и от относительной магнитной проницаемости среды, в которой находится проводник.
Физическая величина, показывающая зависимость ЭДС самоиндукции от размеров и формы проводника и от среды, в которой находится проводник, называется коэффициентом самоиндукции или индуктивностью.
Индуктивность — физ. величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 Ампер за 1 секунду.
Также индуктивность можно рассчитать по формуле:
где Ф — магнитный поток через контур, I — сила тока в контуре.
Единицы измерения индуктивности в системе СИ:
Индуктивность катушки зависит от: числа витков, размеров и формы катушки и от относительной магнитной проницаемости среды
Индуктивность взаимная — величина, характеризующая магнитную связь двух или более электрических цепей (контуров). Если имеется два проводящих контура , то часть линий магнитной индукции, создаваемых током в первом контуре, будет пронизывать площадь, ограниченную вторым контуром (т. е. будет сцеплена с контуром 2).
Магнитный поток Ф12 через контур 2, созданный током I1 в контуре 1, прямо пропорционален току:
Коэффициент пропорциональности M12 зависит от размеров и формы контуров 1 и 2, расстояния между ними, их взаимного расположения, а также от магнитной проницаемости окружающей среды и называется взаимной индуктивностью или коэффициентом взаимной индукции контуров 1 и 2. В системе СИ И. в. измеряется в Генри.
Трансформаторная ЭДС. Принцип действия трансформатора основан на явлении электромагнитной индукции. Линии индукции магнитного поля, создаваемого переменным током в первичной обмотке, благодаря наличию сердечника практически без потерь пронизывают витки вторичной обмотки. Поскольку магнитный поток во вторичной обмотке изменяется со временем (т.к. в первичной обмотке переменный ток), то согласно закону Фарадея в ней возбуждается ЭДС индукции. Трансформатор может работать только на переменном токе, т.к. магнитный поток, созданный постоянным током, не изменяется с течением времени.
Пусть первичная обмотка трансформатора подключена к источнику тока с переменной ЭДС E1 и с действующим значением напряжения U1. На вторичной обмотке ЭДС E2 и напряжение U2.
Из законов Ома следует, что напряжение на обмотке равно
(1)
где r — сопротивление обмотки. При изготовлении трансформатора сопротивление первичной обмотки r1 делают очень малым, поэтому часто им можно пренебречь. Тогда
Если пренебречь потерями магнитного потока в сердечнике, то в каждом витке вторичной обмотки будет индуцироваться точно такая же ЭДС индукции e1, как и ЭДС индукции e2 в каждом витке первичной обмотки, т.е. e1 = e2. Следовательно, отношение ЭДС в первичной E1 и вторичной E2 обмотках равно отношению числа витков в них:
(2)
Трансформаторный ток. Токи обмоток обратно пропорциональны числам витков (I1/I2 приблиз = w1/w2 = 1/n). С увеличением тока активно-индуктивного приемника вторичное напряжение несколько снижается.
Рис.1.11. К определению магнитного потока рассеяния в катушке с ферромагнитным сердечником
часть магнитного потока катушки замыкается не по сердечнику, а по воздуху. Эта часть потока носит название потока рассеивания Фр (рис. 1.11). Таким образом, полный поток, сцепленный с витками катушки равен
| . | (1.14) |
На основании закона Ома для магнитной цепи (1.7) можно написать выражение для потока рассеяния:
| . |
Так как , то .То есть поток рассеяния , в отличие от потока в сердечнике, совпадает по фазе с током и связан с ним линейной зависимостью. Следовательно, на векторной диаграмме вектор потока будет совпадать с вектором тока (рис.1.12).
Рис.1.12. Векторная диаграмма магнитных потоков, ЭДС и токов катушки с ферромагнитным сердечником
Не нашли то, что искали? Воспользуйтесь поиском:
Лучшие изречения: Для студентов недели бывают четные, нечетные и зачетные. 9486 — | 7456 — или читать все.
91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.
Отключите adBlock!
и обновите страницу (F5)
очень нужно
Если в проводящем контуре течёт ток, то ток создаёт магнитное поле. Величина магнитного потока, пронизывающего контур, связана с величиной тока следующим образом:
Коэффициент пропорциональности L как раз и называется индуктивностью (или, строго говоря, коэффициентом самоиндукции контура) . Индуктивность зависит от размеров и формы контура, а также от магнитной проницаемости окружающей среды.
В системе единиц СИ индуктивность измеряется в генри, в системе СГС в сантиметрах (1 Гн = 109 см)
Символ L, используемый для обозначения индуктивности, был взят в честь Ленца Эмилия Христиановича (Heinrich Friedrich Emil Lenz). Единица измерения генри названа в честь Джозефа Генри (Joseph Henry). Сам термин индуктивность был предложен Оливером Хевисайдом (Oliver Heaviside) в феврале 1886 года.
Практически участки цепи со значительной индуктивности выполняют в виде катушек индуктивности.
Индуктивность — это коэффициент пропорциональности между электрическом током, проходящим в замкнутом контуре и магнитным потоком, образуемым этим током через поверхность, у которой контур является краем. Индуктивность обозначается символом L, принятым в честь Э.Ленца.
Ф = L I , отсюда
L = Ф / I = 1Вб / 1А = 1 Гн
Ф — величина магнитного потока, которая пронизывает контур с 1 витком;
I — величина тока;
L — индуктивность витка;
L — коэффициент пропорциональности между Ф и I.
Если катушка состоит из N витков, то полным потоком (или потокосцеплением) будет сумма магнитных потоков через все витки, тогда
Индуктивность L зависит от размеров, формы проводника, количества витков и т.п., от магнитной проницаемости среды.
Единица измерения в системе СИ названа генри (Гн) в честь Дж.Генри. В Гауссовой системе и СГС, СГСМ системах индуктивность считают в сантиметрах 1 Гн = 1000000000 см, 1 см = 1 нГн. Для сантиметров используют название абгенри.в качестве единицы. В системе СГСЭ единицу индуктивности называют статгенри, либо оставляют без названия.
1 статгенри приблизительно равен 8,987552 х 10 в 11 степени генри.
1 Гн = 1000 Миллигенри
1 Гн = 1000000 Микрогенри
1 Гн = 0,001 Килогенри
1 Гн = 0,000001 Мегагенри
Рассчитать индуктивность и осуществить быстрый перевод единиц измерения можно с помощью онлайн калькулятора.
Тест по физике 10 класс
Тест по физике 10 класс.
Тест по физике для 10-х классов.Тема: «Электромагнитная индукция».
1. Как обозначается физическая величина, называемая магнитная индукция?
а). В б). L в). H г). Ф
2. Как обозначается физическая величина, называемая индуктивностью?
а). В б). L в). H г). Ф
3. Как обозначается физическая величина, называемая магнитным потоком?
а). В б). L в). H г). Ф
4. Как обозначается физическая величина, называемая индукцией?
а). В б). L в). H г). Ф
5. Какая сила меняет направление скорости частицы?
а). FА б). FЛ в). ЭДС г). сила сопротивления
6. Какое поле создается неподвижными зарядами?
а). магнитное б). электрическое
в). электростатическое г). электродинамическое
7. Какая сила действует на заряженную частицу со стороны магнитного поля?
а). FА б). FЛ в). ЭДС г). сила притяжения
8. Какая физическая величина равна отношению работы сторонних сил к заряду?
а). FА б). FЛ в). ЭДС г). Ф
9. Какая физическая величина равна произведению индуктивности на силу тока?
а). FА б). FЛ в). ЭДС г). Ф
10. В каких единицах измеряется магнитная индукция?
а). Гн б). Вб в). В г). Тл
11. В каких единицах измеряется магнитный поток?
а). Гн б). Вб в). В г). Тл
12. В каких единицах измеряется ЭДС индукции?
а). Гн б). Вб в). В г). Тл
13. В каких единицах измеряется индуктивность?
а). Гн б). Вб в). В г). Тл
14. Какое поле создается движущимися зарядами?
а). магнитное б). электрическое
в). электростатическое г). электродинамическое
15. Какая физическая величина равна произведению вектора магнитной индукции на площадь сечения проводника и на синус угла между ними?
а). FА б). FЛ в). ЭДС г). Ф
Ответы:
1 — а, 2 — б, 3 — г, 4 — в, 5 — б, 6 — б, 7 — б, 8 — в,
9 — г, 10 — г, 11 — б, 12 — в, 13 — а, 14 — а, 15 — г.
Тестирование по физике 10 класс. Механика. Олимпиады по физике 10 класс
14.2 Самоиндуктивность и индукторы — University Physics Volume 2
Цели обучения
К концу этого раздела вы сможете:
- Сопоставьте скорость изменения тока с наведенной ЭДС, создаваемой этим током в той же цепи
- Вывести самоиндукцию цилиндрического соленоида
- Вывести самоиндукцию прямоугольного тороида
Взаимная индуктивность возникает, когда ток в одной цепи создает изменяющееся магнитное поле, которое индуцирует ЭДС в другой цепи.Но может ли магнитное поле повлиять на ток в исходной цепи, создавшей поле? Ответ положительный, и это явление называется самоиндукцией .
Катушки индуктивности
На рис. 14.5 показаны некоторые силовые линии магнитного поля, возникающие из-за тока в кольцевой проволочной петле. Если ток постоянный, магнитный поток через контур также постоянен. Однако, если ток I должен изменяться со временем — скажем, сразу после замыкания переключателя S, — тогда соответственно изменится магнитный поток ΦmΦm.Тогда закон Фарадея говорит нам, что в цепи будет индуцирована ЭДС εε, где
ε = −dΦmdt.ε = −dΦmdt.14,6
Поскольку магнитное поле, создаваемое токоведущим проводом, прямо пропорционально току, поток, создаваемый этим полем, также пропорционален току; то есть
Фигура 14,5 Магнитное поле создается током I в контуре. Если бы I изменялись со временем, магнитный поток через петлю также изменился бы, и в петле была бы индуцирована ЭДС.
Это также можно записать как
, где постоянная пропорциональности L известна как самоиндукция проволочной петли. Если петля имеет N витков, это уравнение становится
По соглашению, положительное значение нормали к петле связано с током по правилу правой руки, поэтому на рис. 14.5 нормаль направлена вниз. При таком соглашении ΦmΦm положительно в уравнении 14.9, поэтому L всегда имеет положительное значение .
Для контура с Н витков ε = −NdΦm / dt, ε = −NdΦm / dt, поэтому наведенная ЭДС может быть записана в терминах самоиндукции как
ε = −LdIdt.ε = −LdIdt.14.10
При использовании этого уравнения для определения L проще всего игнорировать знаки εanddI / dt, εanddI / dt и вычислить L как
L = | ε || dI / dt | .L = | ε || dI / dt |.Поскольку самоиндукция связана с магнитным полем, создаваемым током, любая конфигурация проводников обладает самоиндукцией.Например, помимо проволочной петли, длинный прямой провод имеет самоиндукцию, как и коаксиальный кабель. Коаксиальный кабель чаще всего используется в индустрии кабельного телевидения, и его также можно найти для подключения к кабельному модему. Коаксиальные кабели используются из-за их способности передавать электрические сигналы с минимальными искажениями. Коаксиальные кабели имеют два длинных цилиндрических проводника, которые обладают током и самоиндукцией, что может иметь нежелательные эффекты.
Элемент схемы, используемый для обеспечения самоиндукции, известен как индуктор.Он представлен символом, показанным на рисунке 14.6, который напоминает катушку с проводом, основную форму индуктора. На рисунке 14.7 показано несколько типов индукторов, обычно используемых в схемах.
Фигура 14,6 Символ, используемый для обозначения катушки индуктивности в цепи.
Фигура 14,7 Разнообразные индукторы. Независимо от того, заключены ли они в капсулу, как показанные три верхних, или намотаны в катушку, как самая нижняя, каждая из них представляет собой просто относительно длинную катушку с проволокой.(Источник: Windell Oskay)
В соответствии с законом Ленца отрицательный знак в уравнении 14.10 указывает, что наведенная ЭДС на катушке индуктивности всегда имеет полярность, противоположную изменению тока. Например, если бы ток, протекающий от A, к B на рисунке 14.8 (a), увеличивался, наведенная ЭДС (представленная воображаемой батареей) имела бы указанную полярность, чтобы противодействовать увеличению. Если бы ток от A, до B, уменьшался, то наведенная ЭДС имела бы противоположную полярность, опять же, чтобы противодействовать изменению тока (Рисунок 14.8 (б)). Наконец, если бы ток через катушку индуктивности был постоянным, в катушке не было бы индуцированной ЭДС.
Фигура 14,8 Индуцированная ЭДС на катушке индуктивности всегда препятствует изменению тока. Это можно представить себе как воображаемую батарею, заставляющую течь ток, чтобы противодействовать изменению в (а) и усиливать изменение в (б).
Одно из распространенных применений индуктивности — это возможность светофора определять, когда автомобили ждут на перекрестке.Электрическая цепь с индуктором размещается на дороге под местом остановки ожидающего автомобиля. Кузов автомобиля увеличивает индуктивность, и схема изменяется, посылая сигнал на светофор, чтобы изменить цвет. Точно так же металлоискатели, используемые для безопасности аэропортов, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и как приемник. Импульсный сигнал от катушки передатчика вызывает сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути (рисунок 14.9). Металлоискатели можно настроить на чувствительность, а также они могут определять присутствие металла на человеке.
Фигура 14,9 Знакомые ворота безопасности в аэропорту не только обнаруживают металлы, но также могут указывать их приблизительную высоту над полом. (Источник: «Alexbuirds» / Wikimedia Commons)
При вспышках фотокамер обнаруживаются большие наведенные напряжения. Во вспышках камеры используются аккумулятор, два индуктора, которые работают как трансформатор, и система переключения или генератор для создания больших напряжений.Вспомните из статьи «Колебания при колебаниях», что «колебание» определяется как колебание величины или повторяющиеся регулярные колебания величины между двумя крайними значениями вокруг среднего значения. Также вспомните (из «Электромагнитная индукция об электромагнитной индукции»), что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы вызвать напряжение в другой катушке. Система генератора делает это много раз, когда напряжение батареи повышается до более чем 1000 вольт. (Вы можете услышать пронзительный вой из трансформатора, когда конденсатор заряжается.) Конденсатор сохраняет высокое напряжение для последующего использования при питании вспышки.
Пример 14,2
Самоиндуктивность катушки
Индуцированная ЭДС 20 мВ измеряется на катушке из 50 плотно намотанных витков, в то время как ток через нее равномерно увеличивается от 0,0 до 5,0 А за 0,10 с. а) Какова собственная индуктивность катушки? (б) Каков поток через каждый виток катушки при токе 5,0 А?Стратегия
Обе части этой проблемы предоставляют всю информацию, необходимую для решения самоиндукции в части (а) или потока через каждый виток катушки в части (b).Необходимые уравнения — это уравнение 14.10 для части (a) и уравнение 14.9 для части (b).Решение
- Игнорируя знак минус и используя величины, из уравнения 14.10 имеем L = εdI / dt = 20 мВ5.0A / 0.10s = 4.0 × 10−2H. L = εdI / dt = 20mV5.0A / 0.10s = 4.0 × 10−2H.
- Из уравнения 14.9, поток определяется в терминах тока как Φm = LI / N, Φm = LI / N, поэтому Φm = (4,0 · 10−2H) (5,0A) 50 витков = 4,0 · 10−3Wb. Φm = (4,0 · 10−2H) (5,0A) 50 витков = 4,0 · 10−3Wb.
Значение
Самоиндукция и магнитный поток, вычисленные в частях (а) и (b), являются типичными значениями для катушек, используемых в современных устройствах.Если ток не меняется во времени, поток не изменяется во времени, поэтому ЭДС не индуцируется.Проверьте свое понимание 14,2
Проверьте свое понимание Ток течет через катушку индуктивности на рис. 14.8 от B к A вместо A к B , как показано. Увеличивается или уменьшается ток, чтобы создать ЭДС, показанную на диаграмме (а)? На диаграмме (б)?
Проверьте свое понимание 14.3
Проверьте свое понимание Изменяющийся ток индуцирует ЭДС 10 В на катушке индуктивности 0,25 Гн. С какой скоростью меняется ток?
Хороший подход к расчету самоиндукции катушки индуктивности состоит из следующих шагов:
Стратегия решения проблем
Самоиндуктивность
- Предположим, что через катушку индуктивности протекает ток I .
- Определите магнитное поле B → B →, создаваемое током.Если есть соответствующая симметрия, вы можете сделать это с помощью закона Ампера.
- Получить магнитный поток, Фм.Фм.
- При известном потоке самоиндукция может быть найдена из уравнения 14.9, L = NΦm / IL = NΦm / I.
Чтобы продемонстрировать эту процедуру, мы теперь вычисляем самоиндуктивности двух катушек индуктивности.
Цилиндрический соленоид
Рассмотрим длинный цилиндрический соленоид длиной l , площадью поперечного сечения A, и N, витков провода.Мы предполагаем, что длина соленоида настолько больше, чем его диаметр, что мы можем принять магнитное поле равным B = μ0nIB = μ0nI по всей внутренней части соленоида, то есть мы игнорируем концевые эффекты в соленоиде. При токе –, протекающем через катушки, магнитное поле, создаваемое внутри соленоида, составляет
. B = μ0 (Nl) I, B = μ0 (Nl) I,14.11
, поэтому магнитный поток на один виток равен
Φm = BA = μ0NAlI. Φm = BA = μ0NAlI.14,12
Используя уравнение 14.9, находим для самоиндукции соленоида
L-соленоид = NΦmI = μ0N2Al. L-соленоид = NΦmI = μ0N2Al.14,13
Если n = N / ln = N / l — количество витков на единицу длины соленоида, мы можем записать уравнение 14.13 как
L = μ0 (Nl) 2Al = μ0n2Al = μ0n2 (V), L = μ0 (Nl) 2Al = μ0n2Al = μ0n2 (V),14,14
где V = AlV = Al — объем соленоида. Обратите внимание, что самоиндукция длинного соленоида зависит только от его физических свойств (таких как количество витков провода на единицу длины и объема), а не от магнитного поля или тока.Это верно для индукторов в целом.
Прямоугольный тороид
Тороид прямоугольного сечения показан на рисунке 14.10. Внутренний и внешний радиусы тороида равны R1 и R2, а hR1 и R2, а h — высота тороида. Применяя закон Ампера таким же образом, как в примере 13.8 для тороида с круглым поперечным сечением, мы обнаруживаем, что магнитное поле внутри прямоугольного тороида также равно
B = μ0NI2πr, B = μ0NI2πr,14.15
, где r — расстояние от центральной оси тороида.Поскольку поле внутри тороида изменяется, мы должны вычислить поток путем интегрирования по поперечному сечению тороида. Используя бесконечно малый элемент площади поперечного сечения da = hdrda = hdr, показанный на рисунке 14.10, получаем
Φm = ∫Bda = ∫R1R2 (μ0NI2πr) (hdr) = μ0NhI2πlnR2R1.Φm = ∫Bda = ∫R1R2 (μ0NI2πr) (hdr) = μ0NhI2πlnR2R1.14,16
Фигура 14.10 Расчет самоиндукции прямоугольного тороида.
Теперь из уравнения 14.16 для самоиндукции прямоугольного тороида получаем
L = NΦmI = μ0N2h3πlnR2R1.L = NΦmI = μ0N2h3πlnR2R1.14,17
Как и ожидалось, самоиндукция — постоянная величина, определяемая только физическими свойствами тороида.
Проверьте свое понимание 14,4
Проверьте свое понимание (a) Вычислите самоиндукцию соленоида, который плотно намотан проводом диаметром 0,10 см, имеет площадь поперечного сечения 0,90 см 20,90 см2 и длину 40 см. (b) Если ток через соленоид равномерно уменьшается с 10 до 0 А в 0.10 с, какая ЭДС наводится между концами соленоида?
Проверьте свое понимание 14,5
Проверьте свое понимание (a) Каков магнитный поток через один виток соленоида самоиндукции 8,0 × 10–5H8,0 × 10–5H, когда через него протекает ток 3,0 А? Предположим, что соленоид имеет 1000 витков и намотан из проволоки диаметром 1,0 мм. (б) Какова площадь поперечного сечения соленоида?
Индуктивность — College Physics
Катушки индуктивности
Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока.До сих пор было обсуждено множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы так, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшими потерями энергии в другие формы. Есть ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ — да, и эта физическая величина называется индуктивностью.
Взаимная индуктивность — это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе.См. (Рисунок), где простые катушки индуцируют ЭДС друг в друге.
Эти катушки могут вызывать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает ЭДС в катушке 2. (Обратите внимание, что «индуцированная» представляет собой наведенную ЭДС в катушке 2.)Во многих случаях, когда геометрия устройств фиксирована, магнитный поток изменяется за счет изменения тока. Поэтому мы концентрируемся на скорости изменения тока как на причине индукции.Изменение тока в одном устройстве, катушка 1 на рисунке, вызывает в другом. Мы выражаем это в форме уравнения как
, где определяется как взаимная индуктивность между двумя устройствами. Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность, тем эффективнее связь. Например, катушки на (Рисунок) имеют меньшие размеры по сравнению с катушками трансформатора на (Рисунок). Единицы измерения are, который назван генри (H) в честь Джозефа Генри. То есть, .
Природа здесь симметрична.Если мы изменим ток в катушке 2, мы индуцируем в катушке 1 ток, равный
.где то же, что и для обратного процесса. Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью .
Большая взаимная индуктивность может быть желательной, а может и нежелательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для белья, может вызвать опасную ЭДС на корпусе, если взаимная индуктивность между его катушками и корпусом велика.Один из способов уменьшить взаимную индуктивность состоит в том, чтобы намотать катушки противотоком для подавления создаваемого магнитного поля. (См. (Рисунок).)
Нагревательные катушки электрической сушилки для одежды могут быть намотаны в противоположную сторону, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность по отношению к корпусу сушилки.
Самоиндуктивность, действие закона индукции Фарадея устройства на самого себя, также существует. Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца.И наоборот, если ток уменьшается, индуцируется ЭДС, которая препятствует уменьшению. Большинство устройств имеют фиксированную геометрию, поэтому изменение магнитного потока полностью связано с изменением тока через устройство. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается
, где — самоиндукция устройства. Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначено символом на (Рисунок).
Знак минус является выражением закона Ленца, означающего, что ЭДС препятствует изменению тока.Единицами самоиндукции является генри (Гн), как и для взаимной индуктивности. Чем больше самоиндукция устройства, тем сильнее оно сопротивляется любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большой размер и не позволит току быстро меняться. Чтобы избежать этого эффекта, необходимо добиться небольшого сопротивления, например, за счет встречной намотки катушек, как показано на (Рисунок).
Катушка индуктивностиA 1 Гн — это большая катушка индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство, через которое протекает ток 10 А.Что произойдет, если мы попытаемся быстро отключить ток, возможно, всего за 1,0 мс? ЭДС, заданная параметром, будет противодействовать изменению. Таким образом, будет индуцирована ЭДС, заданная . Положительный знак означает, что это большое напряжение направлено в том же направлении, что и ток, но противодействует его уменьшению. Такие большие ЭДС могут вызвать дуги, повредить коммутационное оборудование, и поэтому может потребоваться более медленное изменение тока.
Есть применение для такого большого наведенного напряжения. Во вспышках камеры используются батарея, два индуктора, которые работают как трансформатор, и система переключения или генератор для создания больших напряжений.(Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы вызвать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи повышается до более чем тысячи вольт. (Вы можете услышать пронзительный вой от трансформатора, когда конденсатор заряжается.) Конденсатор сохраняет высокое напряжение для последующего использования для питания вспышки. (См. (Рисунок).)
Благодаря быстрому переключению катушки индуктивности можно использовать батареи 1,5 В для индукции ЭДС в несколько тысяч вольт.Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, в насадке для вспышки камеры.
Можно произвести расчеты для индуктора, учитывая его геометрию (размер и форму) и зная создаваемое магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Итак, в этом тексте индуктивность — это обычно заданная величина. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму.Поучительно вывести уравнение для его индуктивности. Начнем с того, что наведенная ЭДС определяется законом индукции Фарадея как и, согласно определению самоиндукции, как . Приравнивая эти доходности к
Решение для дает
Это уравнение для самоиндукции устройства всегда верно. Это означает, что самоиндукция зависит от того, насколько эффективен ток для создания магнитного потока; чем эффективнее, тем больше /.
Давайте воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида.Поскольку площадь соленоида фиксирована, изменение магнитного потока составляет. Чтобы найти, отметим, что магнитное поле соленоида равно. (Здесь, где — количество катушек, а — длина соленоида.) Меняется только ток, так что. Подстановка в дает
Это упрощается до
Это самоиндукция соленоида, имеющего площадь поперечного сечения и длину. Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, в соответствии с его определением.
Расчет самоиндукции соленоида среднего размера
Рассчитайте самоиндукцию соленоида длиной 10,0 см и диаметром 4,00 см, который имеет 200 катушек.
Стратегия
Это прямое приложение, поскольку все величины в уравнении, кроме.
Решение
Используйте следующее выражение для самоиндукции соленоида:
Площадь поперечного сечения в этом примере равна 200, а длина равна 0.100 м. Мы знаем проницаемость свободного пространства. Подставляя их в выражение для дает
Обсуждение
Этот соленоид среднего размера. Его индуктивность около миллигенри также считается умеренной.
Одно из распространенных применений индуктивности используется в светофорах, которые могут определить, когда автомобили ждут на перекрестке. Электрическая цепь с индуктором размещается на дороге под местом остановки ожидающей машины. Кузов автомобиля увеличивает индуктивность, и схема изменяется, посылая сигнал на светофор, чтобы изменить цвет.Точно так же металлоискатели, используемые для безопасности аэропортов, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и как приемник. Импульсный сигнал в катушке передатчика вызывает сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать приблизительное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, которая была обнаружена на «бомбардировщике в нижнем белье.») См. (Рисунок).
Знакомые ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (Источник: Alexbuirds, Wikimedia Commons)
где — самоиндукция катушки индуктивности, а — скорость изменения тока через нее. Знак минус указывает на то, что ЭДС противодействует изменению тока, как того требует закон Ленца. Единицей самоиндукции и взаимной индуктивности является генри (H), где. Самоиндукция индуктора пропорциональна тому, насколько поток изменяется с Текущий.Для поворотной катушки индуктивности
, где — количество витков в соленоиде, — площадь его поперечного сечения, — длина и — проницаемость свободного пространства. Энергия, запасенная в катушке индуктивности, составляет
% PDF -1,3 % 3511 0 obj> эндобдж xref 3511 93 0000000016 00000 н. 0000003939 00000 н. 0000002204 00000 н. 0000004198 00000 п. 0000004588 00000 н. 0000004895 00000 н. 0000005042 00000 н. 0000005184 00000 п. 0000005331 00000 п. 0000005473 00000 п. 0000005615 00000 н. 0000005757 00000 н. 0000005904 00000 н. 0000006046 00000 н. 0000006188 00000 п. 0000006330 00000 н. 0000006476 00000 н. 0000006617 00000 н. 0000006759 00000 н. 0000006901 00000 н. 0000007048 00000 н. 0000007194 00000 н. 0000007340 00000 п. 0000007487 00000 н. 0000007629 00000 н. 0000007776 00000 н. 0000007918 00000 п. 0000008065 00000 н. 0000008207 00000 н. 0000008349 00000 п. 0000008496 00000 н. 0000008637 00000 н. 0000008779 00000 н. 0000008921 00000 п. 0000009063 00000 н. 0000009205 00000 н. 0000009345 00000 п. 0000009490 00000 н. 0000009959 00000 н. 0000010530 00000 п. 0000010771 00000 п. 0000010849 00000 п. 0000011096 00000 п. 0000011658 00000 п. 0000012003 00000 п. 0000012041 00000 п. 0000012264 00000 п. 0000012780 00000 п. 0000013996 00000 н. 0000014535 00000 п. 0000014752 00000 п. 0000015344 00000 п. 0000015814 00000 п. 0000016451 00000 п. 0000016948 00000 н. 0000017090 00000 п. 0000017136 00000 п. 0000017614 00000 п. 0000018116 00000 п. 0000051274 00000 п. 0000053945 00000 п. 0000053999 00000 п. 0000054053 00000 п. 0000054107 00000 п. 0000054161 00000 п. 0000054215 00000 п. 0000054269 00000 п. 0000054323 00000 п. 0000054377 00000 п. 0000054431 00000 п. 0000054485 00000 п. 0000054539 00000 п. 0000054593 00000 п. 0000054647 00000 п. 0000054701 00000 п. 0000054755 00000 п. 0000054810 00000 п. 0000054865 00000 п. 0000054920 00000 н. 0000054975 00000 п. 0000055030 00000 п. 0000055085 00000 п. 0000055140 00000 п. 0000055195 00000 п. 0000055250 00000 п. 0000055305 00000 п. 0000055360 00000 п. 0000055415 00000 п. 0000055470 00000 п. 0000055525 00000 п. 0000055580 00000 п. 0000055635 00000 п. 0000003697 00000 н. трейлер ] >> startxref 0 %% EOF 3513 0 obj> поток x ڼ V {LSg? m7iU, \ uFJt @ ˣZn͒p -! «NYh4 šd٢}} j ߾ |; [
23.9 Индуктивность — Физика в колледже, главы 1-17
Индукция — это процесс, при котором ЭДС индуцируется изменением магнитного потока. До сих пор было обсуждено множество примеров, некоторые из которых более эффективны, чем другие. Трансформаторы, например, спроектированы так, чтобы быть особенно эффективными при наведении желаемого напряжения и тока с очень небольшими потерями энергии в другие формы. Есть ли полезная физическая величина, связанная с тем, насколько «эффективно» данное устройство? Ответ — да, и эта физическая величина называется индуктивностью.
Взаимная индуктивность — это влияние закона индукции Фарадея для одного устройства на другое, например, первичная катушка, при передаче энергии вторичной обмотке в трансформаторе. См. [Ссылка], где простые катушки индуцируют ЭДС друг в друге.
Эти катушки могут вызывать ЭДС друг в друге, как неэффективный трансформатор. Их взаимная индуктивность M указывает на эффективность связи между ними. Здесь видно, что изменение тока в катушке 1 вызывает ЭДС в катушке 2. (Обратите внимание, что «E2E2 размер 12 {E rSub {size 8 {2}}} {}индуцированный» представляет наведенную ЭДС в катушке 2.)
Во многих случаях, когда геометрия устройств фиксирована, магнитный поток изменяется за счет изменения тока. Поэтому мы концентрируемся на скорости изменения тока, ΔI / ΔtΔI / Δt размер 12 {ΔI} {}, как на причине индукции. Изменение тока I1I1 размером 12 {I rSub {размер 8 {1}}} {} в одном устройстве, катушка 1 на рисунке, вызывает ЭДС 2-го размера 12 {«ЭДС» rSub {размер 8 {2}}} { } в другом. Мы выражаем это в форме уравнения как
ЭДС2 = −MΔI1Δt, ЭДС2 = −MΔI1Δt, размер 12 {«ЭДС» rSub {размер 8 {2}} = — M {{ΔI rSub {размер 8 {1}}} больше {Δt}}} {}
, где размер MM 12 {M} {} определяется как взаимная индуктивность между двумя устройствами.Знак минус является выражением закона Ленца. Чем больше взаимная индуктивность MM размером 12 {M} {}, тем эффективнее связь. Например, катушки в [link] имеют небольшой размер MM 12 {M} {} по сравнению с катушками трансформатора в [link]. Единицы измерения для MM размера 12 {M} {}: (В⋅с) / A = Ом⋅с (В⋅с) / A = Ом⋅с размер 12 {(В cdot s) «/ A» =% OMEGA cdot s } {}, которого назвали генри (H) в честь Джозефа Генри. То есть 1 H = 1Ω⋅s1 H = 1Ω⋅s размер 12 {1`H = 1`% OMEGA cdot s} {}.
Природа здесь симметрична. Если мы изменим ток I2I2 размером 12 {I rSub {размер 8 {2}}} {} в катушке 2, мы индуцируем ЭДС 1 размера 12 {«ЭДС» rSub {размер 8 {1}}} {} в катушке 1, что дает
ЭДС1 = −MΔI2Δt, ЭДС1 = −MΔI2Δt, размер 12 {«ЭДС» rSub {размер 8 {1}} = — M {{ΔI rSub {размер 8 {2}}} больше {Δt}}} {}
, где размер MM 12 {M} {} такой же, как и для обратного процесса.Трансформаторы работают в обратном направлении с такой же эффективностью или взаимной индуктивностью MM размером 12 {M} {} .
Большая взаимная индуктивность MM размером 12 {M} {} может быть, а может и не быть желательной. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для белья, может вызвать опасную ЭДС на корпусе, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность MM размера 12 {M} {} состоит в том, чтобы намотать катушки против ветра, чтобы нейтрализовать создаваемое магнитное поле.(См. [Ссылку].)
Нагревательные катушки электрической сушилки для одежды могут быть намотаны в противоположную сторону, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность по отношению к корпусу сушилки.Самоиндуктивность, действие закона индукции Фарадея устройства на самого себя, также существует. Когда, например, увеличивается ток через катушку, магнитное поле и магнитный поток также увеличиваются, вызывая противоэдс, как того требует закон Ленца. И наоборот, если ток уменьшается, индуцируется ЭДС, которая препятствует уменьшению.Большинство устройств имеют фиксированную геометрию, и поэтому изменение магнитного потока полностью связано с изменением тока ΔIΔI размером 12 {ΔI} {} через устройство. Индуцированная ЭДС связана с физической геометрией устройства и скоростью изменения тока. Выдается
ЭДС = −LΔIΔt, ЭДС = −LΔIΔt, размер 12 {«ЭДС» = — L {{ΔI} сверх {Δt}}} {}
, где LL размер 12 {L} {} — это собственная индуктивность устройства. Устройство, которое демонстрирует значительную самоиндукцию, называется индуктором и обозначено символом в [ссылка].Знак минус является выражением закона Ленца, означающего, что ЭДС препятствует изменению тока. Единицами самоиндукции является генри (Гн), как и для взаимной индуктивности. Чем больше самоиндукция LL, размер 12 {L} {} устройства, тем сильнее оно сопротивляется любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большой размер LL 12 {L} {} и не позволяет току быстро изменяться. Чтобы избежать этого эффекта, необходимо добиться небольшого размера LL 12 {L} {}, например, за счет встречной намотки катушек, как в [ссылка].
Катушка индуктивностиA 1 Гн — это большая катушка индуктивности. Чтобы проиллюстрировать это, рассмотрим устройство с L = 1,0 HL = 1,0 H размером 12 {L = 1 “.” 0`H} {}, через который протекает ток 10 А. Что произойдет, если мы попытаемся быстро отключить ток, возможно, всего за 1,0 мс? ЭДС, заданная как emf = −L (ΔI / Δt) emf = −L (ΔI / Δt) размер 12 {«emf» = — L (ΔI / Δt)} {}, будет препятствовать изменению. Таким образом, ЭДС будет индуцирована равной ЭДС = −L (ΔI / Δt) = (1.0 H) [(10 A) / (1.0 мс)] = 10,000 Vemf = −L (ΔI / Δt) = (1.0 H) [(10 A) / (1,0 мс)] = 10 000 В.Положительный знак означает, что это большое напряжение направлено в том же направлении, что и ток, но противодействует его уменьшению. Такие большие ЭДС могут вызвать дуги, повредить коммутационное оборудование, и поэтому может потребоваться более медленное изменение тока.
Есть применение для такого большого наведенного напряжения. Во вспышках камеры используются батарея, два индуктора, которые работают как трансформатор, и система переключения или генератор для создания больших напряжений. (Помните, что нам нужно изменяющееся магнитное поле, вызванное изменяющимся током, чтобы вызвать напряжение в другой катушке.) Система генератора будет делать это много раз, когда напряжение батареи повышается до более чем тысячи вольт. (Вы можете услышать пронзительный вой от трансформатора, когда конденсатор заряжается.) Конденсатор сохраняет высокое напряжение для последующего использования для питания вспышки. (См. [Ссылку].)
Благодаря быстрому переключению катушки индуктивности можно использовать батареи 1,5 В для индукции ЭДС в несколько тысяч вольт. Это напряжение можно использовать для хранения заряда в конденсаторе для последующего использования, например, в насадке для вспышки камеры.Можно рассчитать LL размер 12 {L} {} для катушки индуктивности, учитывая ее геометрию (размер и форму) и зная создаваемое ею магнитное поле. В большинстве случаев это сложно из-за сложности создаваемого поля. Таким образом, в этом тексте индуктивность LL размером 12 {L} {} обычно является заданной величиной. Единственным исключением является соленоид, потому что он имеет очень однородное поле внутри, почти нулевое поле снаружи и простую форму. Поучительно вывести уравнение для его индуктивности.Начнем с того, что наведенная ЭДС определяется законом индукции Фарадея как ЭДС = −N (ΔΦ / Δt) ЭДС = −N (ΔΦ / Δt) размер 12 {«ЭДС» = — N (ΔΦ / Δt)} {} и, по определению самоиндуктивности, как ЭДС = −L (ΔI / Δt) ЭДС = −L (ΔI / Δt) размер 12 {«ЭДС» = — L (ΔI / Δt)} {}. Приравнивая эти доходности к
эдс = −NΔΦΔt = −LΔIΔt.emf = −NΔΦΔt = −LΔIΔt. размер 12 {«ЭДС» = — N {{ΔΦ} над {Δt}} = — L {{ΔI} над {Δt}}} {}
Решение для размера LL 12 {L} {} дает
L = NΔΦΔI.L = NΔΦΔI. размер 12 {L = N {{ΔΦ} более {ΔI}}} {}
Это уравнение для самоиндукции LL устройства размером 12 {L} {} всегда верно.Это означает, что величина собственной индуктивности LL 12 {L} {} зависит от того, насколько эффективен ток для создания магнитного потока; чем эффективнее, тем больше ΔΦΔΦ размер 12 {ΔΦ} {} / ΔIΔI размер 12 {ΔI} {}.
Давайте воспользуемся этим последним уравнением, чтобы найти выражение для индуктивности соленоида. Поскольку площадь AA соленоида фиксирована, изменение магнитного потока составляет
ΔΦ = Δ (BA) = AΔBΔΦ = Δ (BA) = AΔB.
Чтобы найти
ΔBΔB, отметим, что магнитное поле соленоида определяется выражением B = μ0nI = μ0NIℓB = μ0nI = μ0NIℓ размер 12 {B = μ rSub {размер 8 {0}} итал «nI» = μ rSub {размер 8 {0}} {{ital «NI»} over {ℓ}}} {}.(Здесь n = N / ℓn = N / ℓ размер 12 {n = N / ℓ} {}, где
NN — количество катушек, а
ℓℓ — длина соленоида.) Меняется только ток, так что ΔΦ = AΔB = μ0NAΔIℓΔΦ = AΔB = μ0NAΔIℓ размер 12 {ΔΦ = AΔB = μ rSub {size 8 {0}} ital «NA» {{ΔI} over {ℓ}}} {}. Подставляя
ΔΦΔΦ в L = NΔΦΔIL = NΔΦΔI, размер 12 {L = N {{ΔΦ} над {ΔI}}} {} дает
L = NΔΦΔI = Nμ0NAΔIℓΔI.L = NΔΦΔI = Nμ0NAΔIℓΔI. размер 12 {L = N {{ΔΦ} больше {ΔI}} = N {{μ rSub {размер 8 {0}} итал «NA» {{ΔI} больше {ℓ}}} больше {ΔI}}} {}
Это упрощается до
L = μ0N2Aℓ (соленоид).L = μ0N2Aℓ (соленоид). размер 12 {L = {{μ rSub {размер 8 {0}} N rSup {размер 8 {2}} A} больше {ℓ}}} {}
Это самоиндукция соленоида с площадью поперечного сечения AA и длиной
. Обратите внимание, что индуктивность зависит только от физических характеристик соленоида, в соответствии с его определением.
Расчет самоиндукции соленоида среднего размера
Рассчитайте самоиндукцию соленоида длиной 10,0 см и диаметром 4,00 см, который имеет 200 катушек.
Стратегия
Это простое применение L = μ0N2AℓL = μ0N2Aℓ размера 12 {L = {{μ rSub {размер 8 {0}} N rSup {размер 8 {2}} A} над {ℓ}}} {}, поскольку все величины в уравнении, за исключением размера LL 12 {L} {}, известны.
Решение
Используйте следующее выражение для самоиндукции соленоида:
L = μ0N2Aℓ.L = μ0N2Aℓ. размер 12 {L = {{μ rSub {размер 8 {0}} N rSup {размер 8 {2}} A} больше {ℓ}}} {}
Площадь поперечного сечения в этом примере A = πr2 = (3.14…) (0,0200 м) 2 = 1,26 × 10−3м2A = πr2 = (3,14…) (0,0200 м) 2 = 1,26 × 10−3м2 размер 12 {A = πr rSup {размер 8 {2}} = (3 “ . »« 14 »«. »«. »«. ») (0«. »« 0200 »` m) rSup {size 8 {2}} = 1 «.» «26» умножить на «10» rSup {размер 8 {- 3}} `m rSup {размер 8 {2}}} {}, NN принимается равным 200, а длина ℓℓ равна 0,100 м. Мы знаем, что проницаемость свободного пространства равна μ0 = 4π × 10−7T⋅m / Aμ0 = 4π × 10−7T⋅m / A. Подставляя их в выражение для
LL, получаем
L = (4π × 10−7 Тм / А) (200) 2 (1,26 × 10−3 м2) 0,100 м = 0,632 мГн. L = (4π × 10−7 Тм / А) (200) 2 (1.26 × 10−3 м2) 0,100 м = 0,632 мГн.
Обсуждение
Этот соленоид среднего размера. Его индуктивность около миллигенри также считается умеренной.
Одно из распространенных применений индуктивности используется в светофорах, которые могут определить, когда автомобили ждут на перекрестке. Электрическая цепь с индуктором размещается на дороге под местом остановки ожидающей машины. Кузов автомобиля увеличивает индуктивность, и схема изменяется, посылая сигнал на светофор, чтобы изменить цвет.Точно так же металлоискатели, используемые для безопасности аэропортов, используют ту же технику. Катушка или индуктор в корпусе металлоискателя действует как передатчик и как приемник. Импульсный сигнал в катушке передатчика вызывает сигнал в приемнике. На самоиндукцию цепи влияет любой металлический предмет на пути. Такие детекторы могут быть настроены на чувствительность, а также могут указывать приблизительное местонахождение обнаруженного на человеке металла. (Но они не смогут обнаружить пластиковую взрывчатку, подобную той, которая была обнаружена на «бомбардировщике в нижнем белье.») См. [Ссылка].
Привычные ворота безопасности в аэропорту могут не только обнаруживать металлы, но и указывать их приблизительную высоту над полом. (Источник: Alexbuirds, Wikimedia Commons)[PDF] RUPHYS (MPCIZEWSKI15079) Мои курсы Настройки курса Университетская физика с современной физикой, 13e Young / Freedman
1 Вы вошли как Джоли Чизевски, инструктор Помогите Выйти RUPHYS (MPCIZEWSKI15079) Мои курсы Настройки курса Университет …
Вы вошли как Джоли Чизевски, инструкторRUPHYS2272014 Мои курсы
Выйти
(MPCIZEWSKI15079)
Настройки курса
Главная страница курса
Помощь
Назначения
Young Physics UniversityРесурсы для инструкторов Библиотека успеваемости
eText
h21 Индуктивность и индуктивности (30.1-3)
[Edit]
Обзор
Просмотр для печати с ответами
Сводный вид
Диагностика
Область исследования
h21 Индуктивность и индуктивности (30.1-3) Срок сдачи: 23:59 в понедельник, ноябрь 17, 2014 Вы не получите баллов за выполненные задания после истечения срока выполнения задания. Политика классификации
Взаимная индуктивность двойного соленоида Описание: Рассмотрение расчета взаимной индуктивности для двойного соленоида. Цель обучения: узнать о взаимной индуктивности на примере длинного соленоида с двумя обмотками.Чтобы проиллюстрировать расчет взаимной индуктивности, полезно рассмотреть конкретный пример двух соленоидов, намотанных на общий цилиндр. Возьмем цилиндр, имеющий радиус ρ и длину L. Предположим, что соленоид намного длиннее своего радиуса, так что его поле можно определить по закону Ампера на всей его длине:
∮ B⃗ (r) ⃗ ⋅ dl ⃗ = µ0 I encl.
Рассмотрим поле, возникающее от соленоида 1, имеющего n 1 витков на единицу длины.Магнитное поле соленоида 1 проходит (в данном случае целиком) через соленоид 2, который имеет n 2 витков на единицу длины. Любое изменение магнитного потока из-за поля, создаваемого соленоидом 1, индуцирует ЭДС в соленоиде 2 в соответствии с законом индукции Фарадея ∮ E⃗ (r) ⃗ ⋅ dl ⃗ = — dtd ΦM (t).
Часть A Рассмотрим сначала создание магнитного поля током I 1 (t) в соленоиде 1. Внутри соленоида (достаточно далеко от его концов), какова величина B 1 (t) магнитного поля, обусловленного этот ток?
B 1 (t)
I 1 (t)
Выразите B 1 (t) через I 1 (t), переменные, указанные во введении, и соответствующие константы.ОТВЕТ:
B 1 (t) = Обратите внимание, что это поле не зависит от радиального положения (расстояния от оси симметрии) для точек внутри соленоида.
Часть B Каков поток Φ 1 (t), создаваемый магнитным полем соленоида 1 за один виток соленоида 2? Выразите Φ 1 (t) через B 1 (t), величины, указанные во введении, и любые необходимые константы.
Подсказка 1. Определение потока
= ∮ B⃗ ⋅ dA⃗. Когда поле постоянное и перпендикулярно поперечному сечению, это просто величина поля, умноженная на площадь.Какова в данном случае площадь А? Определение магнитного потока: Φ M
Выразите A через ρ и другие константы. ОТВЕТ:
A =
ОТВЕТ:
Φ1 (t) =
Часть C Теперь найдите электродвижущую силу E2 (t), индуцированную во всем соленоиде 2 изменением тока в соленоиде 1. Помните, что оба соленоида имеют длину L. Выразите свой ответ в терминах dI 1 (t) / dt, n 1, n 2, других параметров, указанных во введении, и любых соответствующих констант.
Подсказка 1. Найдите поток от I 1 (t) В Части B вы нашли поток через один виток соленоида 2, Φ 1 (t). Теперь выразите Φ 1 (t) через I 1 (t), n 1, другие величины, указанные во введении, и различные константы, такие как µ0.
ОТВЕТ:
Φ1 (t) =
Совет 2. ЭДС для всего соленоида Суммарная ЭДС для многооборотного соленоида может быть довольно большой (это принцип трансформаторов, которые могут вырабатывать киловольты). Выразите полную ЭДС через соленоид 2, E2 (t), через Φ 1 (t), dΦ 1 (t) / dt и другие величины, указанные во введении.ОТВЕТ:
E2 (t) =
Подсказка 3. Собираем все вместе Вы выяснили три вещи: 1. магнитное поле от I 1 (t) 2. поток от этого поля 3. ЭДС для всего второй соленоид Соедините их вместе, и вы получите ответ! ОТВЕТ:
E2 (t) =
Часть D Это общее взаимодействие резюмируется с использованием символа M 21 для обозначения взаимной индуктивности между двумя обмотками. Основываясь на ваших двух предыдущих ответах, какая из следующих формул, по вашему мнению, является правильной? ОТВЕТ:
E2 (t) = −M 21 I 1 (t) d dt
E2 (t) = −M 21 I1 (t)
E2 (t) = −M 21
I1 (t)
I 1 (t) =
E2 (t)
d dt −M 21 dtd
I 1 (t) = −M21 E2 (t)
Взаимная индуктивность показывает, что изменение тока в соленоиде 1 вызывает электродвижущая сила (ЭДС) в соленоиде 2.Когда двойной соленоид рассматривается как элемент схемы, эта электродвижущая сила добавляется в петлевой закон Кирхгофа. Константа пропорциональности — это взаимная индуктивность, обозначенная M 21. Отрицательное значение d I (t) происходит от отрицательного знака в законе Фарадея и отражает знак в уравнении E2 (t) = −M 21 dt 1 Правило Ленца: изменяющееся магнитное поле из-за соленоида 1 будет индуцировать ток в соленоиде 2. ; этот индуцированный ток сам будет генерировать магнитное поле внутри соленоида 2, так что изменения индуцированного магнитного поля противодействуют изменениям магнитного поля соленоида 1.
Часть E Используя формулу для взаимной индуктивности E 2 (t)
= −M 21
d dt
I1 (t), найдите M21.
Выразите взаимную индуктивность M21 через n 1, n 2, величины, указанные во введении, и соответствующие физические константы. ОТВЕТ:
M21 =
Часть F Неудивительно, что если ток проходит через соленоид 2, он индуцирует напряжение в соленоиде 1. Взаимная индуктивность в этом случае обозначается M12, взаимная индуктивность для напряжения, индуцированного в соленоиде 1. от тока в соленоиде 2.Что такое М12? Выразите взаимную индуктивность через n 1, n 2, величины, указанные во введении, и соответствующие физические константы.
Совет 1. Новая симметрия Эта задача имеет новый тип симметрии: обозначение соленоидов как 1 и 2 произвольно. Если мы изменим маркировку соленоидов, единственное изменение будет заключаться в том, чтобы поменять местами n 1 и n 2, количество витков на длину двух соленоидов. Следовательно, решение можно получить, просто сделав эту замену в своем ответе на часть E.ОТВЕТ:
M12 = Этот результат, что M12 равен M21, отражает взаимозаменяемость двух катушек и применяется, даже если катушки соединены лишь частично (например, если одна катушка намотана на гораздо больший цилиндр или если только часть потока большей катушки перехватывается меньшей катушкой). По этой причине индексы обычно опускаются: между двумя катушками существует только одна взаимная индуктивность, обозначенная буквой M: ЭДС генерируется в одной катушке за счет изменения тока в другой катушке.
± Основные свойства индукторов Описание: ± Включает математическое исправление. Практикуйтесь в определении единиц индуктивности (предполагается, что это новая концепция) и некоторых основных концептуальных вопросах об индукторах. Цель обучения: понять единицы индуктивности, потенциальную энергию, запасенную в катушке индуктивности, и некоторые последствия наличия индуктивности в цепи. После батарей, резисторов и конденсаторов наиболее распространенными элементами в схемах являются индукторы. Индукторы обычно выглядят как туго намотанные катушки из тонкой проволоки.В отличие от конденсаторов, которые вызывают физический разрыв цепи между пластинами конденсатора, провод катушки индуктивности обеспечивает непрерывный непрерывный путь, по которому может течь ток. Когда ток в цепи постоянный, индуктор действует по существу как короткое замыкание (то есть путь с нулевым сопротивлением). На самом деле, в обмотках индуктора всегда присутствует по крайней мере небольшое сопротивление — факт, которым обычно пренебрегают во вводных обсуждениях. Напомним, что ток, протекающий по проводу, создает магнитное поле в непосредственной близости от провода.Если провод свернут в бухту, например, в соленоиде или индукторе, магнитное поле будет самым сильным внутри катушки, параллельной ее оси. Магнитное поле, связанное с током, протекающим через катушку индуктивности, требует времени для создания и времени для устранения при отключении тока. При изменении тока в катушке индуктивности генерируется ЭДС, согласно закону Фарадея, которая препятствует изменению тока. Таким образом, индукторы обеспечивают электрическую инерцию цепи за счет уменьшения скорости изменения тока.Индуктивность обычно обозначается буквой L и измеряется в единицах системы СИ — генри (также пишется генри и обозначается сокращенно H), названной в честь Джозефа Генри, современника Майкла Фарадея. ЭДС E, создаваемая в катушке с индуктивностью L, согласно закону Фарадея равна
E = −L ∆I. ∆t
Здесь ∆I / ∆t характеризует скорость, с которой ток I через индуктор изменяется со временем t.
Часть A На основании уравнения, приведенного во введении, каковы единицы индуктивности L в единицах E, t и I (соответственно вольты V, секунды s и амперы A)? ОТВЕТ:
1 H = 1 (V s ⋅ A)
1 H = 1 (V⋅s) A
1 H = 1 (VA s) 1 H = 1 (s⋅A) V
1 1 H = 1 (V⋅s⋅A)
Часть B Какая ЭДС вырабатывается, если вафельница рисует 2.5 ампер и индуктивность 560 миллигенри, внезапно отключается, поэтому ток падает практически до нуля за 0,015 секунды?
Выразите свой ответ в вольтах с двумя значащими цифрами. ОТВЕТ: 93
В
Повышенное напряжение длится недолго, но иногда оно может быть достаточно большим, чтобы вызвать потенциально опасную искру. Мораль: будьте очень осторожны при размыкании переключателей, по которым идет ток, особенно если они являются частью индуктивной цепи!
Электрическая потенциальная энергия U накапливается внутри индуктора в виде магнитного поля, когда через индуктор протекает ток.В терминах тока I и индуктивности L запасенная электрическая потенциальная энергия определяется выражением
U =
1 2
LI 2.
Часть C Какое из следующих изменений увеличило бы потенциальную энергию, запасенную в катушке индуктивности, в 5 раз? Проверить все, что относится. ОТВЕТ: увеличение индуктивности в 5 раз; оставляя ток неизменным, оставляя неизменной индуктивность; увеличение тока в 5 раз без изменения индуктивности; увеличение тока в √5 раз, уменьшение индуктивности в 5 раз; увеличение тока в 5 раз, увеличение индуктивности в 5 раз; уменьшение тока в 5 раз
Как показано уравнением во введении к этой части, ток, протекающий через индуктор, связан с количеством электрической потенциальной энергии, хранящейся в индукторе.Если ток отображается как функция времени, наклон кривой указывает скорость, с которой потенциальная энергия в индукторе увеличивается или уменьшается. Скорость, с которой энергия изменяется с течением времени, называется мощностью. Энергия не может быть доставлена к катушке индуктивности бесконечно быстро и не может быть мгновенно рассеяна в виде тепла или света другими элементами схемы. Таким образом, власть никогда не может быть бесконечной. Это означает, что кривая зависимости тока от времени должна быть непрерывной. График является прерывистым, если он содержит точку, в которой ток перескакивает от одного значения к другому, не принимая все значения между ними.Когда это происходит, наклон кривой в этом месте бесконечен, что в данном случае означает бесконечную мощность.
Часть D Какие из графиков показывают, как ток через индуктивность может изменяться с течением времени? Введите числа, соответствующие правильным ответам, в алфавитном порядке. Не используйте запятые. Например, если вы считаете, что правильными являются только графики C и D, введите CD.
ОТВЕТ: ABC
Все реальные схемы, даже те, в которых специально не используются индукторы, имеют хотя бы небольшую индуктивность, так же как настоящие индукторы имеют небольшое сопротивление в их обмотках.Анализ схем в учебниках часто предполагает идеальные батареи, резисторы, конденсаторы и катушки индуктивности и, следовательно, игнорирует такие тонкие детали реальных схем.
Упражнение 30.5 Описание: Два тороидальных соленоида намотаны вокруг одной и той же формы, так что магнитное поле одного проходит через витки другого. У соленоида 1 N_1 оборотов, а у соленоида 2 — N_2 оборотов. Когда ток в соленоиде 1 равен i_1, средний поток через каждый … Два тороидальных соленоида намотаны вокруг одной и той же формы, так что магнитное поле одного проходит через витки другого.Соленоид 1 имеет 680 витков, а соленоид 2 — 410 витков. Когда ток в соленоиде 1 составляет 6,50 А, средний поток через каждый виток соленоида 2 составляет 3,50 × 10–2 Вт.
Часть A Какова взаимная индуктивность пары соленоидов? ОТВЕТ:
M =
= 2,21
H
Часть B Когда ток в соленоиде 2 составляет 2,60 А, каков средний поток через каждый виток соленоида 1? ОТВЕТ:
Φ =
= 8,44 × 10−3
Wb
Самоиндуктивность соленоида Описание: идет через расчет самоиндукции для одиночного соленоида с некоторым обсуждением в конце.Цель обучения: узнать о самоиндукции на примере длинного соленоида. Чтобы объяснить самоиндукцию, полезно рассмотреть конкретный пример длинного соленоида, как показано на рисунке. Этот соленоид имеет только одну обмотку, поэтому ЭДС, индуцированная его изменяющимся током, появляется на самом соленоиде. Это контрастирует с взаимной индуктивностью, когда это напряжение появляется на второй катушке, намотанной на том же цилиндре, что и первая. Предположим, что соленоид имеет радиус R, длину Z по оси z и намотан с n витками на единицу длины, так что общее количество витков равно nZ.Предположим, что соленоид намного длиннее своего радиуса. При изменении тока через соленоид результирующий магнитный поток через соленоид также изменится, и электродвижущая сила будет генерироваться на соленоиде в соответствии с законом индукции Фарадея: ∮ E⃗ ⋅ dl ⃗ = — dtd ΦM (t). Закон Фарадея подразумевает следующее соотношение между самоиндуцированной ЭДС через соленоид и током, проходящим через него dI (t): E (t) = −L. dt «Направление ЭДС» определяется по отношению к направлению потока положительного тока и представляет собой направление индуцированного электрического поля в катушке индуктивности.Это также направление, в котором будет течь «обратный ток», который пытается создать индуктор.
Часть A Предположим, что ток в соленоиде равен I (t). Какое магнитное поле
B (t) внутри соленоида, но далеко от его концов, возникает из-за этого тока? Выразите свой ответ в терминах I (t), величин, указанных во введении, и соответствующих констант (например,
µ0). ОТВЕТ:
B (t) = Обратите внимание, что это поле не зависит от радиального положения (расстояния от оси симметрии) до тех пор, пока оно измеряется в точке внутри соленоида.
Часть B Каков магнитный поток Φ 1 (t) за один оборот соленоида? Выразите свой ответ в терминах магнитного поля B (t), величин, указанных во введении, и любых необходимых констант. ОТВЕТ:
Φ1 (t) = Также принято:
Часть C Предположим, что ток изменяется со временем, так что dI (t) / dt
≠ 0. Найдите электродвижущую силу E, индуцированную через весь соленоид
из-за к изменению тока через весь соленоид. Выразите свой ответ в терминах dI (t) / dt, n, Z и R.
Подсказка 1. Найдите поток через ток. В Части B вы нашли поток Φ 1 (t) через один оборот соленоида. Теперь найдите поток Φ total (t) через весь соленоид. Выразите свой ответ через I (t), другие величины, указанные во введении, и различные константы, такие как µ0. ОТВЕТ:
Φtotal (t) =
Совет 2. Найдите ЭДС для всего соленоида. Теперь у вас есть выражение для магнитного потока, который проходит через соленоид. Исходя из этого, вы сможете получить выражение для ЭДС в соленоиде.Предположим, что полный магнитный поток через соленоид равен Φ total (t). Какова электродвижущая сила E, создаваемая в соленоиде изменяющимся магнитным потоком
Φtotal (t)? Выразите свой ответ через dΦ total (t) / dt и ее производную, а также другие переменные, указанные во введении. ОТВЕТ:
E =
Подсказка 3. Собираем вместе Вы выяснили три вещи: 1. магнитное поле от I (t); 2. поток от этого поля; 3. ЭДС всего соленоида. Соедините их вместе, и вы получите ответ! ОТВЕТ:
E =
Часть D. Самоиндукция L связана с самоиндуктивной ЭДС E (t) уравнением E (t)
= −LdI (t) / dt.Найдите L для длинного соленоида
. (Подсказка: самоиндуктивность L всегда будет положительной величиной.) Выразите самоиндуктивность через количество витков на длину n, физические размеры R и Z и соответствующие константы. ОТВЕТ:
L = Это определение индуктивности идентично другому определению, которое вы, возможно, встретили: Φ M
= LI, где
ΦM — магнитный поток, обусловленный током I в индукторе. Чтобы увидеть соответствие, вы должны дифференцировать обе части этого уравнения относительно времени и использовать закон Фарадея, т.е.е.,
dΦ M dt
= −E.
Теперь рассмотрим индуктор как элемент схемы. Поскольку теперь мы рассматриваем катушку индуктивности как элемент схемы, мы должны обсудить напряжение на ней, а не ЭДС внутри нее. Важным моментом является то, что предполагается, что индуктор не имеет сопротивления. Это означает, что чистое электрическое поле внутри него должно быть нулевым, когда он включен в цепь. В противном случае ток
⃗
в нем станет бесконечным. Это означает, что индуцированное электрическое поле E n накапливает заряды на индукторе
⃗
→
и вокруг него таким образом, чтобы создать почти равное и противоположное электрическое поле E c, такое что E c
⃗
→ + E n → 0! Петлевой закон Кирхгофа
определяет напряжения только в терминах полей, создаваемых зарядами (например, E c), а не полей, создаваемых изменением магнитных полей
⃗
(например, E n).Поэтому, если мы хотим продолжать использовать закон петель Кирхгофа, мы должны продолжать последовательно использовать это определение B ⃗ ⃗. То есть мы должны определить только напряжение V AB = V A — V B = + ∫ A E c ⋅ dl (обратите внимание, что интеграл идет от A к B, а не от B к A, отсюда положительный знак). Итак, наконец, → → BB dI (t) V AB = ∫ A E⃗ c ⋅ dl ⃗ = ∫ A −E⃗ n ⋅ dl ⃗ = −E = + L dt, где мы использовали E c + E n = 0 и определение E.
Часть E
I (t)
Какое из следующих утверждений верно относительно катушки индуктивности на рисунке во введении к задаче, где I (t) — ток через провод?
Подсказка 1.Основная формула индуктивности Самоиндуктивность L связана с напряжением V
= V A — V B на катушке индуктивности посредством уравнения
V (t) = LdI (t) / dt. Обратите внимание, что в отличие от ЭДС, он не имеет знака минус. ОТВЕТ: Если I (t) положительно, напряжение на конце A обязательно будет больше, чем на конце B. Если dI (t) / dt положительно, напряжение на конце A обязательно будет больше, чем на конце B. Если I (t) положительный, напряжение на конце A обязательно будет меньше, чем на конце B.Если dI (t) / dt положительно, напряжение на конце A обязательно будет меньше, чем на конце B.
Часть F Теперь рассмотрим влияние, которое приложение дополнительного напряжения к катушке индуктивности окажет на ток I (t). уже протекает через него (представьте, что напряжение приложено к концу A, а конец B заземлен). Какое из следующих утверждений верно?
Подсказка 1. Основная формула индуктивности Собственная индуктивность L связана с напряжением V
= V A — V B на катушке индуктивности посредством уравнения
V (t) = LdI (t) / dt.Обратите внимание, что в отличие от ЭДС, он не имеет знака минус. Однако при применении правил Кирхгофа и прохождении через катушку индуктивности в направлении тока будет член −LdI (t) / dt, точно так же, как при обходе резистора возникает член −IR. ОТВЕТ: Если V положительно, то Если V Если V Если V Если V Если V
I (t) обязательно будет положительным, а dI (t) / dt будет отрицательным. положительно, то I (t) обязательно будет отрицательным, а dI (t) / dt будет отрицательным. положительно, то I (t) может быть положительным или отрицательным, тогда как dI (t) / dt обязательно будет отрицательным.положительно, то I (t) обязательно будет положительным, а dI (t) / dt будет положительным. положительно, то I (t) может быть положительным или отрицательным, тогда как dI (t) / dt обязательно будет положительным. положительно, то I (t) обязательно будет отрицательным, а dI (t) / dt будет положительным.
Обратите внимание, что когда вы применяете правила Кирхгофа и перемещаете катушку индуктивности в направлении протекания тока, вас интересует V BA = V B — V A = −LdI (t) / dt, точно так же, как обход резистора дает член −IR. Подводя итог: когда индуктор находится в цепи и ток изменяется, изменяющееся магнитное поле в индукторе создает электрическое поле.Это поле противодействует изменению тока, но в то же время накапливает заряд, создавая еще одно электрическое поле. Чистый эффект этих электрических полей состоит в том, что ток изменяется, но не резко. «Направление ЭДС» относится к направлению первого индуцированного электрического поля.
Задача 30.8 Описание: Тороидальный соленоид имеет площадь поперечного сечения A, средний радиус r и N витков. Пространство внутри обмоток заполнено ферромагнитным материалом с относительной проницаемостью каппа.(а) Рассчитайте индуктивность соленоида. (Вы … Тороидальный соленоид имеет площадь поперечного сечения 0,410 см 2, средний радиус 12,1 см и 1880 витков. Пространство внутри обмоток заполнено ферромагнитным материалом с относительной проницаемостью 550.
Часть A Рассчитайте индуктивность соленоида. (Вы можете игнорировать изменение магнитного поля в поперечном сечении тороида.) 2
Используйте 1,26 × 10−6N / A для проницаемости свободного пространства. ОТВЕТ: = 0.132 H
Часть B Если материал удален изнутри соленоида и заменен воздухом, какова индуктивность соленоида? ОТВЕТ: = 2,40 × 10−4 H
Самоиндуктивность коаксиального кабеля Описание: Найдите самоиндуктивность на единицу длины коаксиального кабеля. Коаксиальный кабель состоит из чередующихся коаксиальных цилиндров из проводящего и изоляционного материала. Коаксиальные кабели являются основным типом кабелей, используемых в индустрии кабельного телевидения, а также широко используются для компьютерных сетей, таких как Ethernet, из-за их превосходной способности передавать большие объемы электрического сигнала с минимальными искажениями.Однако, как и все другие виды кабелей, коаксиальные кабели также обладают некоторой самоиндукцией, которая имеет нежелательные эффекты, такие как искажение и нагрев.
Часть A Рассмотрим длинный коаксиальный кабель, состоящий из двух коаксиальных цилиндрических проводников, по которым проходят равные токи I в противоположных направлениях (см. Рисунок). Внутренний цилиндр представляет собой небольшой твердый проводник радиуса a. Внешний цилиндр представляет собой тонкостенный проводник внешнего радиуса b, электрически изолированный от внутреннего проводника. Рассчитайте самоиндуктивность на единицу длины L этого коаксиального кабеля.(L — это индуктивность l части кабеля, а l — длина этой части.) Из-за так называемого «скин-эффекта» ток I течет по (внешней) поверхности внутреннего проводящего цилиндра и обратно. по внешней поверхности внешнего проводящего цилиндра. Однако вы можете проигнорировать толщину внешнего цилиндра. Выразите свой ответ в терминах некоторых или всех переменных I, a, b и µ0, проницаемости свободного пространства.
Подсказка 1. Как подойти к проблеме. Собственную индуктивность кабеля можно определить, если известны как ток, так и магнитный поток, проходящий через кабель.Используя закон Ампера, вы можете рассчитать магнитное поле, создаваемое кабелем; вы обнаружите, что в области между двумя проводниками существует магнитное поле. Таким образом, рассчитайте магнитный поток на единицу длины через область между двумя цилиндрами. Поскольку ток в кабеле задан, теперь у вас должно быть достаточно информации для расчета самоиндукции кабеля.
Подсказка 2. Найдите магнитное поле внутри внутреннего цилиндра. Рассмотрим внутренний проводящий цилиндр. По внешней поверхности он проводит ток I.Какова величина магнитного поля B 1 на расстоянии r от оси цилиндра в области внутри цилиндра? Выразите свой ответ в терминах некоторых или всех переменных I, r и µ0 — проницаемости свободного пространства.
Подсказка 1. Закон Ампера
⃗
Закон Ампера гласит, что линейный интеграл магнитного поля B, вычисленный вокруг любого замкнутого пути, равен
→ ∮ B⃗ ⋅ dl = µ0 I encl, где µ0 — проницаемость свободное пространство, а I encl — чистый ток через область, ограниченную траекторией.Лучше всего использовать круг с центром на оси цилиндров, потому что магнитное поле будет касаться петли во всех точках, что упрощает вычисление скалярного произведения. ОТВЕТ:
B1 = 0
Подсказка 3. Найдите магнитное поле между цилиндрами. Теперь рассмотрим оба проводящих цилиндра, каждый из которых несет равные токи I в противоположных направлениях. Найти величину магнитного поля B 2 на расстоянии r от оси кабеля в области между двумя цилиндрами. Выразите свой ответ в терминах некоторых или всех переменных I, r и µ0 — проницаемости свободного пространства.
Подсказка 1. Закон Ампера
⃗
Закон Ампера гласит, что линейный интеграл магнитного поля B, вычисленный вокруг любого замкнутого пути, равен
→ ∮ B⃗ ⋅ dl = µ0 I encl, где µ0 — проницаемость свободное пространство, а I encl — чистый ток через область, ограниченную траекторией. Лучше всего использовать круг с центром на оси цилиндров, потому что магнитное поле будет касаться петли во всех точках, что упрощает вычисление скалярного произведения.ОТВЕТ:
B2 =
Между проводящими цилиндрами магнитное поле идентично тому, которое создавалось бы проводом, по которому проходит ток I, расположенным вдоль оси цилиндров.
Подсказка 4. Найдите магнитное поле вне кабеля Наконец, найдите величину магнитного поля B 3 на расстоянии r от оси кабеля в области за пределами кабеля. Снова предположим, что ток I течет по поверхности внутреннего цилиндра и течет обратно по поверхности внешнего цилиндра.Выразите свой ответ в терминах некоторых или всех переменных I, r и µ0 — проницаемости свободного пространства.
Подсказка 1. Закон Ампера
⃗
Закон Ампера гласит, что линейный интеграл магнитного поля B, вычисленный вокруг любого замкнутого пути, равен
→ ∮ B⃗ ⋅ dl = µ0 I encl, где µ0 — проницаемость свободное пространство, а I encl — чистый ток через область, ограниченную
путем. Лучше всего использовать круг с центром на оси цилиндров, потому что магнитное поле будет касаться петли во всех точках, что упрощает вычисление скалярного произведения.ОТВЕТ:
B3 = 0 Поля встречных токов компенсируют друг друга.
Подсказка 5. Найдите магнитный поток в кабеле ΦB в кабеле, обусловленный токами I. Пусть a будет радиусом внутреннего l радиуса внешнего цилиндра.
Найдите магнитный поток на единицу длины цилиндра и b
Выразите свой ответ в терминах некоторых или всех переменных I, a, b и µ0, проницаемости свободного пространства.
Подсказка 1. Как подойти к проблеме Магнитное поле коаксиального кабеля существует только в области между двумя цилиндрами.Следовательно, вам необходимо рассчитать магнитный поток на единицу длины через этот участок кабеля. Для этого подумайте о направлении магнитного поля (используя правило правой руки) и о том, какой элемент площади использовать.
Совет 2. Как рассчитать магнитный поток
⃗
Учитывая конечную площадь A в магнитном поле B, магнитный поток Φ B через площадь определяется следующим интегралом, вычисленным по площади:
ΦB = ∫ B⃗ ⋅ dA⃗, →
, где dA — бесконечно малый элемент площади.Магнитное поле, создаваемое кабелем, существует только в области между цилиндрами и перпендикулярно любой плоскости, содержащей ось кабеля. Поэтому для расчета магнитного потока удобнее всего выбрать элемент площади длиной l, параллельной оси кабеля, и шириной dr, лежащей в плоскости, содержащей ось. На рисунке ниже показан такой элемент площади с поперечным сечением кабеля, параллельным изображенной оси кабеля. Такой элемент площади перпендикулярен магнитному полю, что упрощает скалярное произведение.
ОТВЕТ: ΦB = l
Подсказка 6. Формула для самоиндукции Собственная индуктивность L цепи, по которой проходит ток i, определяется выражением ΦB, i, где Φ B — магнитный поток, проходящий через замкнутый контур цепи.
L =
ОТВЕТ: L = l
Емкость на единицу длины
2πϵ 0 C L такого коаксиального кабеля составляет. Таким образом, произведение l l ln ab
⋅
C l
= µ o ⋅ ϵ0 =
1, c2
, где c — скорость света в вакууме! Как вы могли догадаться, это не совпадение, а результат, который в целом справедлив для таких систем.
Упражнение 30.18 Описание: заполненный воздухом тороидальный соленоид имеет N витков провода, средний радиус r и площадь поперечного сечения A. (a) Если ток равен I, рассчитайте магнитное поле в соленоиде. (b) Рассчитайте самоиндукцию соленоида. (c) Рассчитайте …
c
2
Тороидальный соленоид, заполненный воздухом, имеет 390 витков провода, средний радиус 15,0 см и площадь поперечного сечения 4,20 см 2.
Часть A Если ток 5,60 А, рассчитайте магнитное поле в соленоиде.ОТВЕТ:
B =
= 2,91 × 10−3
T
Часть B Рассчитайте самоиндуктивность соленоида. ОТВЕТ:
L =
= 8,52 × 10-5
H
Часть C Рассчитайте энергию, запасенную в магнитном поле. ОТВЕТ:
U =
= 1,34 × 10-3
Дж
Часть D Рассчитайте плотность энергии в магнитном поле. ОТВЕТ:
u =
= 3,37
Дж / м 3
Часть E Найдите ответ для части D, разделив свой ответ на часть C на объем соленоида.ОТВЕТ:
= 3,37
u =
Дж / м 3
Упражнение 30.20 Описание: Было предложено использовать большие индукторы в качестве накопителей энергии. а) Сколько электрической энергии преобразуется в световую и тепловую энергию лампочки мощностью P за один день? (b) Если количество энергии, рассчитанное в части (a), сохраняется … Было предложено использовать большие индукторы в качестве устройств хранения энергии.
Часть A Сколько электрической энергии преобразуется в световую и тепловую энергию лампочкой мощностью 210 Вт за один день? ОТВЕТ:
U =
= 1.81 × 107
Дж
Часть B Если количество энергии, вычисленное в части (а), хранится в катушке индуктивности с током 85,0 А, какова индуктивность? ОТВЕТ:
L =
= 5020
H
Авторские права © 2014 Pearson. Все права защищены. Официальное уведомление
Политика конфиденциальности
Разрешения
Поддержка
Проблемы индуктивности и решения для AP Physics
В этом руководстве по решенным задачам решаются некоторые из наиболее важных примеров и проблем самоиндукции, которые относятся к уровню C физики AP.{-4}} = 256,5 \] Взяв квадратный корень из обеих частей, получаем количество витков соленоида $ N = 16 $.
(b) Изменяющийся ток вызывает самоиндуцированную ЭДС в соленоиде, величина которой определяется формулой \ [\ mathcal {E} _L = -L \ frac {di} {dt} \], где отрицательное значение означает направление ЭДС. Подставляя известные значения выше и решая для $ di / dt $, мы получаем \ begin {align *} \ mathcal {E} _L & = — L \ frac {di} {dt} \\ \\ -12,5 & = — 0,285 \, \ frac {di} {dt} \\ \\ \ Rightarrow \ frac {di} {dt} & = +43.{2} (20)} {20} = 0.314 \, {\ rm m} \] Таким образом, соленоид имеет длину $ 31.4 \, {\ rm cm} $.
Задача (4): соленоид с $ 100 $ витками имеет длину $ 25 \, {\ rm cm} $ и радиус петли $ 10 \, {\ rm cm} $. Ток в нем постоянно меняется от $ 30 \, {\ rm A} $ до нуля в $ 0.02 \, {\ rm s} $. Какова самоиндуцированная ЭДС соленоида?
Решение : изменяющийся ток связан с изменением магнитного потока с использованием определения самоиндукции как $ \ Delta \ Phi = L \ Delta i $, где $ \ Phi $ — полный магнитный поток, проходящий через катушку с проволокой. имеющий $ N $ витков, который связан с потоком через каждый виток как $ \ Phi = N \ phi $.{2})} {0,25} = 1,5 \, {\ rm mH} \]
Задача (5): В тот момент, когда скорость изменения тока через идеальную катушку индуктивности увеличивается как $ 0,064 \, {\ rm A / s} $, величина самоиндуцированной ЭДС составляет $ 0,016 \, {\ rm V} $.
(а) Какова индуктивность катушки индуктивности?
(b) Пусть этот индуктор представляет собой соленоид с оборотом $ 400. Сколько магнитного потока проходит через каждый его виток при токе $ 0,720 \, {\ rm A} $?
Решение : изменяющийся во времени ток через соленоид создает ЭДС, которая связана друг с другом по следующей формуле \ [\ mathcal {E} _L = -L \ frac {di} {dt} \] Где минус Знак указывает направление самоиндуцированной ЭДС по закону Ленца.{-Rt / L} \ right) \], поэтому в момент $ t = 0 $ ток равен нулю.
С другой стороны, определение индуктивности как $ N \ Delta \ phi = L \ Delta i $ связывает разницу в магнитном потоке через каждый виток $ \ phi $ с разностью токов. Мы можем использовать это определение, чтобы найти поток через каждый виток $ N $ -виткового соленоида. \ begin {align *} N \ Delta \ phi & = L \ Delta i \\ N (\ phi_2- \ phi_1) & = L (i_2-i_1) \\ (400) (\ phi_2-0) & = (0,25) (0.72-0) \\ \ Rightarrow \ phi_2 & = 0.45 \, {\ rm mWb} \ end {align *} В приведенном выше примере $ \ phi_1 $ и $ i_1 $ являются потоком и током в момент времени $ t = 0 $, когда в цепи нет тока, как и магнитного потока.
Проблема (6): В катушке с оборотом $ 500 $ ток меняется от $ 2 \, {\ rm A} $ до $ 2.05 \, {\ rm A} $ в интервале времени $ \ Delta t $. За это время поток меняется от $ 5000 \, {\ rm \ mu Wb} $ до $ 5025 \, {\ rm \ mu Wb} $. Какая у катушки Генри самоиндукция?
Решение . Вспомните, что при изменении магнитного потока в цепи создается электродвижущая сила, ЭДС $ \ mathcal {E} $ как \ [\ mathcal {E} = — \ frac {d \ Phi} {dt} \]
С другой стороны, скорость изменения потока связана со скоростью изменения тока с использованием определения самоиндукции $ \ Phi = LI $.Таким образом, на этот раз индуцированная ЭДС записывается как \ [\ mathcal {E} = — \ frac {d \ Phi} {di} = — L \ frac {di} {dt} \]
Если интервал времени не бесконечно мал, мы имеем \ [\ mathcal {E} = — \ frac {\ Delta \ Phi} {\ Delta i} = — L \, \ frac {\ Delta i} {\ Delta t} \ ] Подставляя известные значения в формулу выше, мы получаем \ begin {align *} — \ frac {\ Delta \ Phi} {\ Delta i} & = — L \ frac {\ Delta i} {\ Delta t} \\ \ \ \ frac {5025-5000} {\ Delta t} & = L \ frac {2.05-2} {\ Delta t} \\ \\ 25 & = L \ times 0,05 \\ \\ \ Rightarrow L & = 500 \ quad { \ rm H} \ end {align *}
Задача (7): В данный момент времени ток и наведенная ЭДС в катушке индуктивности показаны ниже.
(а) Ток увеличивается или уменьшается?
(b) Если наведенная ЭДС составляет $ 25 \, {\ rm V} $ и скорость изменения тока $ 10 \, {\ rm kA / s} $, то найдите индуктивность индуктора.
Решение : Согласно закону Фарадея , самоиндуцированная ЭДС определяется формулой \ [\ mathcal {E} _L = -L \ frac {di} {dt} \], где $ L $ — самоиндукция. {3} \ right) \\ \\ \ Rightarrow L & = 2.5 \ quad {\ rm mH} \ end {align *}
Задача (8): На рисунке ниже изображен график зависимости тока от времени для катушки индуктивности $ 4 \, {\ rm H} $. Какова величина наведенной ЭДС в следующие промежутки времени?
(a) $ 0 \ leq t \ leq 2 $
(b) $ 2 \ leq t \ leq 5 $
(c) $ 5 \ leq t \ leq 6 $
Решение : Когда ток в катушке индуктивности изменяется, магнитный поток также изменяется. Следовательно, согласно закону Фарадея, индуцированная ЭДС получается как $ \ mathcal {E} = — L \ frac {\ Delta i} {\ Delta t} $, где отрицательная величина обусловлена законом Ленца.{-3}} = — 5000 \, {\ rm A / s} \] Следовательно, индуцированная ЭДС равна \ [\ mathcal {E} = (- 4) \ times (-5000) = 20 \, {\ rm kV} \]
Как вы можете видеть, ток и индуцированная ЭДС имеют противоположные направления только во временном интервале $ [0,2] $ и имеют одинаковое направление в другие моменты времени, что и ожидается из закона Ленца.
Задача (9): Ток в длинном соленоиде с индуктивностью $ L = 0,5 \, {\ rm H} $ изменяется как $ I (t) = 0,2 \ sin (500t) $. Найти максимальное значение наведенной ЭДС в соленоиде.
Решение : Переменный ток создает ЭДС в катушке индуктивности (соленоиде или катушке с проводом) с самоиндукцией $ L $, как показано ниже \ [\ mathcal {E} _L = -L \ frac {di} {dt} \ ] Таким образом, самоиндуцированная ЭДС в соленоиде равна \ begin {align *} \ mathcal {E} _L & = — (0.5) \, \ frac {d} {dt} \ left (0.2 \ sin (500t) \ right ) \\ \\ & = — (0.5) (0.2) (500) \ cos (500t) \\ \\ & = — 50 \ cos (500t) \ end {align *} Напомним из тригонометрии, что максимальное значение косинуса функция равна $ 1 $, поэтому максимальное значение индуцированной ЭДС составляет $ \ mathcal {E} _L = -50 \, {\ rm V} $.
Отрицательный показывает направление наведенной ЭДС.
Задача (10): На рисунке ниже показан идеальный индуктор с нулевым сопротивлением $ 0,260 \, {\ rm H} $. Уменьшающийся ток проходит через него с постоянной скоростью $ di / dt = -0,0180 $ в указанном направлении.
(a) Найдите эдс индуктивности индуктивности индуктивности.
(b) Какая из точек a и b имеет более высокий потенциал?
Решение : Согласно закону Фарадея, самоиндуцированная ЭДС индуктора с индуктивностью $ L $ определяется как \ [\ mathcal {E} _L = -L \ frac {di} {dt} \], где минус Знак указывает направление ЭДС.
(a) Подставляя известные значения в приведенную выше формулу, мы получаем \ [\ mathcal {E} _L = — (0,260) (- 0,0180) = + 4,68 \, {\ rm mV} \]
(b) В приведенной выше формуле направление наведенной ЭДС зависит от того, увеличивается или уменьшается ток через катушку индуктивности.
Уменьшающийся ток, $ di / dt <0 $, индуцирует ЭДС в том же направлении, что и ток, чтобы предотвратить дальнейшее уменьшение тока в соответствии с законом Ленца.
В этом случае индуктор действует как батарея со следующей полярностью.
Следовательно, как видно из рисунка выше, точка $ a $ имеет более высокий потенциал.
Автор: Али Немати
Дата публикации: 24.03.2021
Различные типы индукторов с символами и приложениями
Типы индукторовЗдесь представлены различные типы индукторов.
Сюда также входят:
- Определение индуктивности
- Типы
- Приложения
- Индуктивность
- Лот более
Продолжайте читать
Что такое индуктор и для чего он нужен?
Когда кусок провода формируется в катушку, он становится основным индуктором . Термины катушка и индуктор используются как синонимы. Как показано на рисунке, ток через катушку создает электромагнитное поле. Магнитные силовые линии вокруг каждой петли (витка) в обмотке катушки эффективно добавляют к силовым линиям вокруг соседних петель, формируя сильное электромагнитное поле внутри и вокруг катушки. Чистое направление всего электромагнитного поля создает северный и южный полюсы.
Как работает индуктор?
Чтобы понять формирование общего электромагнитного поля в катушке, рассмотрим взаимодействие электромагнитных полей вокруг двух соседних контуров.Каждая из магнитных линий, действующих вокруг соседних петель, отклоняется в единую внешнюю траекторию, когда петли сближаются. Этот эффект возникает из-за того, что магнитные силовые линии находятся в противоположных направлениях между соседними контурами и поэтому нейтрализуются, когда контуры находятся близко друг к другу, как показано. Общее электромагнитное поле для двух контуров показано в части (b). Этот эффект является аддитивным для многих близко расположенных петель в катушке: то есть каждая дополнительная петля увеличивает силу электромагнитного поля.Для простоты показаны только отдельные силовые линии, хотя их много:
Что такое индуктивность?
при прохождении тока по проводнику создается электромагнитное поле. При изменении тока меняется и электромагнитное поле. Увеличение тока расширяет электромагнитное поле, а уменьшение тока уменьшает его. Следовательно, изменяющийся ток создает изменяющееся электромагнитное поле вокруг индуктора. В свою очередь, изменяющееся электромагнитное поле вызывает индуцированное напряжение на катушке в направлении, противодействующем изменению тока.Это свойство называется самоиндуктивностью , но обычно обозначается просто индуктивностью, обозначаемой цифрой L.
«индуктивность — это мера способности катушки создавать наведенное напряжение в результате изменения ее тока, и это индуцированное напряжение направлено против изменения тока».
Единица индуктивности
Генри (H) Это основная единица индуктивности. По определению, индуктивность катушки равна одному Генри, когда ток через катушку, изменяющийся со скоростью один ампер в секунду, индуцирует на катушке один вольт.Во многих практических приложениях наиболее распространенными единицами измерения являются миллигенри (мГн), и микрогенри (мкГн).
Наведенное напряжение зависит от L и di / dt:
Индуктивность (L) катушки и скорость изменения тока (di / dt) во времени определяют индуцированное напряжение (В ind ). Изменение тока вызывает изменение электромагнитного поля, которое, в свою очередь, индуцирует напряжение на катушке, как вы знаете. Индуцированное напряжение прямо пропорционально L и di / dt , как указано в следующей формуле:
В инд = L ( di / dt )
Формула показывает, что чем больше индуктивность, тем больше индуцированное напряжение.также это означает, что чем быстрее изменяется ток катушки (больше di / dt) , тем больше индуцированное напряжение.
Как энергия хранится в индукторе?
Катушка индуктивности накапливает энергию в электромагнитном поле, создаваемом током. Хранение выражается следующим образом:
Как видите, запасенная энергия пропорциональна индуктивности и квадрату тока. Когда ток ( I ) равен Генри, энергия (Вт) выражается в джоулях.
Физические характеристики индукторов
Следующие параметры важны для определения индуктивности катушки: допустимая разрешающая способность материала сердечника, количество витков провода, длина сердечника и площадь поперечного сечения сердечника.
Материал сердечника:
Как обсуждалось ранее, индуктор представляет собой катушку с проволокой, которая окружает магнитный или немагнитный материал, называемый сердечником . Примерами магнитов являются железо, никель, сталь, кобальт или сплав.Эти материалы обладают проницаемостью, в сотни или тысячи раз превышающей проницаемость вакуума, и классифицируются как ферромагнитные. Ферромагнитный сердечник обеспечивает лучший путь для магнитных силовых линий и, таким образом, позволяет создавать более сильное магнитное поле. Примеры немагнитных материалов: воздух, медь, пластик и стекло. Проницаемость этих материалов такая же, как для вакуума.
Магнитная проницаемость (μ) материала сердечника определяет, насколько легко можно установить магнитное поле.Индуктивность прямо пропорциональна проницаемости материала сердечника.
Физические параметры:
Количество витков провода, длина и площадь поперечного сечения сердечника являются факторами при установке значения индуктивности. Индуктивность обратно пропорциональна длине сердечника и прямо пропорциональна площади поперечного сечения. Кроме того, индуктивность напрямую связана с количеством витков в квадрате. Это соотношение выглядит следующим образом:
Где L — индуктивность в генри (Гн), N — количество витков провода, μ — проницаемость в генри на метр (Гн / м), A — площадь поперечного сечения в метрах в квадрате, а I длина жилы в метрах (м).
Сопротивление обмотки:
Когда катушка сделана из определенного материала. Например, изолированный медный провод, этот провод имеет определенное сопротивление на единицу длины. Когда для создания катушки используется много витков провода, общее сопротивление может быть значительным. Это внутреннее сопротивление называется сопротивлением постоянному току или сопротивлением обмотки (R w ).
Хотя это сопротивление распределено по длине провода, оно фактически появляется последовательно с индуктивностью катушки.Во многих случаях сопротивление обмотки может быть достаточно небольшим, чтобы его можно было игнорировать, а катушку рассматривать как идеальный индуктор. В других случаях необходимо учитывать сопротивление.
Емкость обмотки:
, когда два проводника расположены рядом, между ними всегда есть некоторая емкость. Таким образом, когда много витков провода расположены близко друг к другу в катушке, определенная паразитная емкость, называемая емкостью обмотки (C w ), является естественным побочным эффектом.Во многих приложениях эта емкость обмотки очень мала и не оказывает существенного влияния. В других случаях, особенно на высоких частотах, это может стать весьма важным.
Эквивалентная схема для катушки индуктивности с ее сопротивлением обмотки (R w ) и емкостью обмотки (C w ). Емкость эффективно действует параллельно. Суммарная паразитная емкость между каждым витком обмотки обозначена на схеме как емкость, параллельная катушке, и сопротивление ее обмотки.
Типы индукторов
Катушки индуктивностибывают самых разных форм и размеров. В основном они делятся на общие категории:
- Фиксированная катушка индуктивности
- Переменный индуктор
Как фиксированные, так и регулируемые индукторы можно классифицировать по типу материала сердечника. Три распространенных типа — это воздушный сердечник, железный сердечник и ферритовый сердечник.
Регулируемые (переменные) индукторы обычно имеют регулировку винтового типа, которая перемещает скользящий сердечник внутрь и наружу, тем самым изменяя индуктивность.Существует большое разнообразие катушек индуктивности. Небольшие фиксированные индукторы часто заключены в изоляционный материал, который защищает мелкие частицы в катушке. Инкапсулированные катушки индуктивности похожи на резисторы.
Катушки индуктивности серии:
При последовательном соединении катушек индуктивности общая индуктивность, l t , является суммой индивидуальных индуктивностей. Формула для L T выражается в следующем уравнении для общего случая последовательных катушек индуктивности n :
L T = L 1 + L 2 + L 3 + ………… L n
Обратите внимание, что формула для общей индуктивности в серии аналогична формуле для полного сопротивления в серии и общей емкости в параллели.
Параллельные индукторы:
При параллельном подключении катушек индуктивности общая индуктивность меньше наименьшей индуктивности. Формула для полной параллельной индуктивности аналогична формулам для общего параллельного сопротивления и общей последовательной емкости.
Когда только две катушки индуктивности подключены параллельно, можно использовать специальную форму выражения произведения на сумму:
Равнозначные параллельные катушки индуктивности:
Это еще один частный случай, в котором можно использовать сокращенную формулу.