Физика. Период и частота | Частная школа. 9 класс
Конспект по физике для 9 класса «Период и частота». Что такое период обращения. Что такое частота обращения. Как вычислить скорость и ускорение тела, движущегося по окружности, если известны его период и частота обращения.
Конспекты по физике Учебник физики Тесты по физике
Период и частота
Измерить скорость тела, движущегося по окружности, не всегда просто. Однако её можно вычислить, используя такие понятия, как период и частота обращения.
ПЕРИОД
Когда тело движется по окружности с постоянной по модулю скоростью, через определённые промежутки времени движение повторяется снова и снова. Примером этому может служить движение на обычной детской карусели.
Время, в течение которого тело совершает один полный оборот, называют периодом обращения. Период обращения принято обозначать буквой Т. Единица этой физической величины в СИ — секунда.
С понятием периода обращения вы уже знакомились при изучении географии. Например, период обращения Земли вокруг своей оси составляет 23 ч 56 мин 4 с, а период обращения Земли вокруг Солнца — 1,00004 земных года. Самый короткий период обращения вокруг Солнца в нашей Солнечной системе имеет планета Меркурий. Её период обращения составляет 0,24085 земных лет. Интересно, что самая большая планета Солнечной системы — Юпитер — имеет самый короткий период обращения вокруг своей оси — всего 9 ч 50 мин. В 226 000 000 лет оценивается период обращения Солнечной системы вокруг ядра Галактики.
ЧАСТОТА
Число оборотов в единицу времени, которое совершает тело при движении по окружности, называют
Если, катаясь на карусели в парке, мы совершаем один оборот за 20 с, то период обращения в этом случае Т = 20 с. Как определить частоту обращения при этом движении? Сколько оборотов совершает карусель за 1 с?
Очевидно, ν = 1/Т = 1/20 1/с, т. е. за 1 с карусель совершает одну двадцатую часть своего полного оборота.
е. за 1 с карусель совершает одну двадцатую часть своего полного оборота.
Таким образом, частота обращения является величиной, обратной периоду обращения:
Именно поэтому единица этой физической величины обратна секунде, т. е.
СВЯЗЬ МОДУЛЯ СКОРОСТИ С ПЕРИОДОМ И ЧАСТОТОЙ ОБРАЩЕНИЯ
Чтобы определить модуль скорости тела, движущегося по окружности, достаточно знать радиус окружности R и период или частоту обращения. Действительно, один полный оборот тело совершает за время, равное периоду обращения Т. Путь, пройденный телом, в этом случае равен длине окружности: l = 2πR. Тогда можно записать:
или с учётом формулы (1):
С учётом формул (2) и (3) можно найти центростремительное ускорение тела, выразив скорость через период или частоту обращения:
Часто мгновенную скорость движения по окружности называют линейной скоростью

Модуль скорости движения тела по окружности рассчитывается по формуле:
Умение описывать движение тела по окружности чрезвычайно важно, так как движение по криволинейной траектории можно приближённо представить как движение по дугам окружностей различных радиусов.
РЕШЕНИЕ ЗАДАЧ
Задача 1. Найдём модуль скорости вращения ребёнка на карусели, если радиус окружности, по которой происходит движение, равен 2,3 м, а время, за которое карусель совершает один полный оборот, равно 20 с.
Ответ: υ = 0,722 м/с.
Задача 2. Земля делает один оборот вокруг Солнца за 365 дней. Расстояние от Солнца до Земли составляет 149,6 • 106 км. Определим линейную скорость движения Земли вокруг Солнца, считая орбиту окружностью.
Определим линейную скорость движения Земли вокруг Солнца, считая орбиту окружностью.
Ответ: υ ≈ 30 км/с.
Вы смотрели Конспект по физике для 9 класса «Период и частота».
Вернуться к Списку конспектов по физике (Оглавление).
Что такое частота? | Fluke
Частота переменного тока (ac) — это количество синусоидальных колебаний переменного тока в секунду. Частота — это количество изменений направления тока за секунду. Для измерения частоты используется международная единица герц (Гц). 1 герц равен 1 колебанию в секунду.
- Герц (Гц) = 1 герц равен 1 колебанию в секунду.
- Колебание = Одна полная волна переменного тока или напряжения.
- Полупериод = Половина колебания.
- Период = Время, необходимое для выполнения одного полного колебания.
Частота отражает повторяемость процессов. С точки зрения электрического тока частота — это количество повторений синусоиды или, другими словами, полного колебания, которое включает положительную и отрицательную составляющие.
Чем больше колебаний происходит в секунду, тем выше частота.
Пример. Если известно, что частота переменного тока равна 5 Гц (см. схему ниже), это означает, что его форма сигнала повторяется 5 раз за 1 секунду.
Частота обычно используется для описания работы электрооборудования. Ниже приведены некоторые наиболее распространенные диапазоны частот:
- Частота линии питания (обычно 50 Гц или 60 Гц).
- Частотно-регулируемые приводы: обычно используют несущую частоту 1–20 кГц.
- Звуковой диапазон частот: от 15 Гц до 20 кГц (диапазон человеческого слуха).
- Радиочастота: от 30 до 300 кГц.
- Низкая частота: от 300 кГц до 3 МГц.
- Средняя частота: от 3 до 30 МГц.
- Высокая частота: от 30 до 300 кГц.
Обычно цепи и оборудование предназначены для работы с постоянной или переменной частотой. Оборудование, рассчитанное на работу с постоянной частотой, при изменении частоты начинает работать неправильно. Например, двигатель переменного тока, рассчитанный на работу при 60 Гц, работает медленнее при частоте ниже 60 Гц или быстрее при частоте выше 60 Гц. Для двигателей переменного тока любое изменение частоты приводит к пропорциональному изменению частоты вращения двигателя. Другим примером является снижение частоты вращения двигателя на 5 % при снижении частоты сети на 5 %.
Для двигателей переменного тока любое изменение частоты приводит к пропорциональному изменению частоты вращения двигателя. Другим примером является снижение частоты вращения двигателя на 5 % при снижении частоты сети на 5 %.
Порядок измерения частоты
Цифровой мультиметр с режимом частотомера может измерять частоту сигналов переменного тока со следующими функциями:
- регистрация МИН/МАКС значений, позволяющая записывать результаты измерений частоты за заданный интервал времени. Эта функция также применима к измерениям напряжения, тока и сопротивления.
- автоматический выбор диапазона, при котором прибор автоматически подбирает диапазон частот при условии, что частота измеряемого напряжения не выходит за пределы этого диапазона.
Параметры электросетей различаются в зависимости от страны. В США работа сети основана на высокостабильном сигнале с частотой 60 Гц, что соответствует 60 колебаниям в секунду.
Бытовые электросети в США получают питание от однофазного источника питания 120 В перем. тока. Напряжение в настенной розетке дома в США совершает синусоидальные колебания в диапазоне от 170 до −170 В, при этом истинное среднеквадратичное значение этого напряжения будет равно 120 вольт. Частота колебаний составляет 60 циклов в секунду.
тока. Напряжение в настенной розетке дома в США совершает синусоидальные колебания в диапазоне от 170 до −170 В, при этом истинное среднеквадратичное значение этого напряжения будет равно 120 вольт. Частота колебаний составляет 60 циклов в секунду.
Единица измерения получила название «герц» в честь немецкого физика Генриха Герца (1857–1894 гг.), который первым осуществил передачу и принятие радиоволн. Радиоволны распространяются с частотой одно колебание в секунду (1 Гц). (аналогично часы тикают с частотой 1 Гц)
Ссылка: Digital Multimeter Principles by Glen A. Mazur, American Technical Publishers.
Статьи на связанные темы:
План-конспект урока по физике «Период и частота обращения» 9 класс
Тема: Период и частота вращения.
Цель урока: продолжить изучения криволинейного движения, сформировать понятие о частоте и периоде вращения. Познакомить с формулами для нахождения этих величин и единицами измерения.
Задачи урока:
Образовательные: продолжить формирование понятие криволинейном движении, величинах его характеризующих, единицах измерения этих величин и формулах для вычисления.
Воспитательные: Воспитательные задачи: продолжать развивать кругозор учащихся; умение вести записи в тетрадях, наблюдать, замечать закономерности явлений, аргументировать свои выводы.
Тип уроку: изучение и первичное закрепление знаний.
Оборудование: доска, учебник В.В. Белага «Физика, 9», А.Е. Марон «Сборник вопросов и задач, 7-9».
План урока:
Актуализация опорных знаний.
Изучение нового материала.

Закрепление нового материала.
Подведение итогов. Рефлексия.
Содержание урока
І. Орг. момент
ІІ. Актуализация опорных знаний. Проверка Д/з
Фронтальный опрос.
Какое движение называется криволинейным?
Как направлена мгновенная скорость при движении тела по окружности?
Что такое центростремительное ускорение?
Как направлено центростремительное ускорение? По какой формуле оно рассчитывается?
Как направлена центростремительная сила? По какой формуле она рассчитывается?
Тело движется по окружности с постоянной по модулю скоростью. Как изменится его центростремительное ускорение при уменьшении радиуса окружности в 2 раза? Увеличении в 5 раз?
Материальная точка движется по окружности с постоянной по модулю скоростью.
 Как изменится модуль ее центростремительного ускорения, если скорость точки увеличить вдвое?
Как изменится модуль ее центростремительного ускорения, если скорость точки увеличить вдвое?
Решение задач. А.Е. Марон «Сборник вопросов и задач, 7-9» № 1629, 1645, 1648.
III. Изучение нового материала.
Движение тела по окружности характеризуется не только скоростью и ускорением. Когда тело движется по окружности с постоянной по модулю скоростью, то через определённые промежутки времени движение повторяется.
1. Период.
Период – время, в течении которого тело совершает один полный оборот, называют периодом обращения. , где t – время всех оборотов, N – число оборотов.
2. Частота.
Частота – число оборотов за единицу времени (секунду). , (в честь учёного Генриха Герца).
, (в честь учёного Генриха Герца).
Частота и период обращения связаны между собой. , а .
Коленчатые валы двигателей трактора имеют частоту вращения от 60 до 100 оборотов в секунду. Ротор газовой турбины вращается с частотой от 200 до 300 об/с. Пуля, вылетающая из автомата Калашникова, вращается с частотой 3000 об/с.
3. Связь модуля скорости с периодом обращения и частотой.
Чтобы определить модуль скорости тела, движущегося по окружности, достаточно знать радиус окружности и период или частоту обращения. Один полный оборот тело совершает за время, равное периоду обращения. Путь, пройденный телом равен длине окружности: , поэтому .
С учётом этого можно найти центростремительное ускорение:
ІV. Закрепление нового материала.
Что называется периодом и частотой обращения?
В каких единицах они измеряются?
Как эти величины связаны между собой?
Чему равны периоды вращения: часовой, минутной и секундной стрелок часов; Земли вокруг своей оси; Земли вокруг Солнца; Луны вокруг Земли?
Решение задач. А.Е. Марон «Сборник вопросов и задач, 7-9» № 1632, 1631, 1635, 1638, 1641.
А.Е. Марон «Сборник вопросов и задач, 7-9» № 1632, 1631, 1635, 1638, 1641.
V. Д/з. Выучить § 5, решить задачи № 1633, 1634.
VІ. Подведение итогов. Рефлексия.
Кинематика — Физика — Теория, тесты, формулы и задачи
Оглавление:
Основные теоретические сведения
Система СИ
К оглавлению…
Основные единицы измерения величин в системе СИ таковы:
- единица измерения длины — метр (1 м),
- времени — секунда (1 с),
- массы — килограмм (1 кг),
- количества вещества — моль (1 моль),
- температуры — кельвин (1 К),
- силы электрического тока — ампер (1 А),
- Справочно: силы света — кандела (1 кд, фактически не используется при решении школьных задач).
При выполнении расчетов в системе СИ углы измеряются в радианах.
Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.
Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.
Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки. их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.
Таблица дольных и кратных приставок в физике:
Путь и перемещение
К оглавлению…
Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.
Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.
Всякое тело имеет определенные размеры. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой. Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.
Интуитивно понятно, что характеристики движения (скорость, траектория и т.д.) зависят от того, откуда мы на него смотрим. Поэтому для описания движения вводится понятие системы отсчета. Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.
Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют траекторией движения тела.
Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.
Пройденный путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.
При равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:
где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.
Средняя скорость
К оглавлению…
Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.
Средняя скорость пути – это отношение всего пути ко всему времени движения:
где: Lполн – весь путь, который прошло тело, tполн – все время движения.
Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:
Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.
- При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
- И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.
Равноускоренное прямолинейное движение
К оглавлению…
Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:
где: v0 – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t).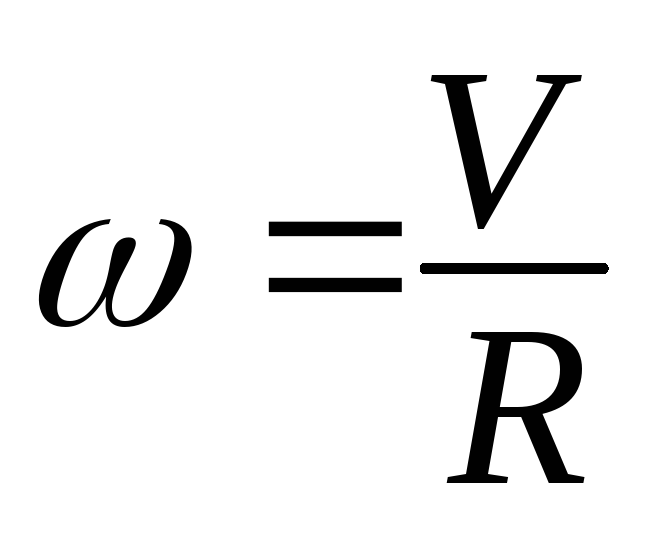
Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным. Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.
Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».
Из предыдущей формулы, следует другая более распространённая формула, описывающая изменение скорости со временем при равноускоренном движении:
Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:
В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):
С расчетом пути все сложнее. Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.
Координата при равноускоренном движении изменяется по закону:
Проекция скорости при равноускоренном движении изменяется по такому закону:
Аналогичные формулы получаются для остальных координатных осей. Формула для тормозного пути тела:
Свободное падение по вертикали
К оглавлению…
На все тела, находящиеся в поле тяготения Земли, действует сила тяжести. В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:
Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:
Это значит, что свободное падение всех тел вблизи поверхности Земли является равноускоренным (но не обязательно прямолинейным) движением. Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали. Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.
Традиционно при свободном падении используют направленную вертикально ось OY. Ничего страшного здесь нет. Просто надо во всех формулах вместо индекса «х» писать «у». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.
Вариантов 2: вверх или вниз.
Приведем несколько формул, которые являются решением некоторых конкретных задач по кинематике на свободное падение по вертикали. Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:
Время падения тела с высоты h без начальной скорости:
Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v0, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):
Горизонтальный бросок
К оглавлению…
При горизонтальном броске с начальной скоростью v0 движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренного движения вдоль оси OY.
Скорость в любой момент времени направлена по касательной к траектории. Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна vx = v0. А вертикальная возрастает по законам ускоренного движения vy = gt. При этом полная скорость тела может быть найдена по формулам:
Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна vx = v0. А вертикальная возрастает по законам ускоренного движения vy = gt. При этом полная скорость тела может быть найдена по формулам:
При этом важно понять, что время падения тела на землю никоим образом не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело. Время падения тела на землю находится по формуле:
Пока тело падает, оно одновременно движется вдоль горизонтальной оси. Следовательно, дальность полета тела или расстояние, которое тело сможет пролететь вдоль оси ОХ, будет равно:
Угол между горизонтом и скоростью тела легко найти из соотношения:
Также иногда в задачах могут спросить о моменте времени, при котором полная скорость тела будет наклонена под определенным углом к вертикали. Тогда этот угол будет находиться из соотношения:
Тогда этот угол будет находиться из соотношения:
Важно понять, какой именно угол фигурирует в задаче (с вертикалью или с горизонталью). Это и поможет вам выбрать правильную формулу. Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:
Преобразуется в следующий закон движения по оси OY для тела брошенного горизонтально:
При ее помощи мы можем найти высоту на которой будет находится тело в любой момент времени. При этом в момент падения тела на землю координата тела по оси OY будет равна нулю. Очевидно, что вдоль оси OХ тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменятся по закону:
Бросок под углом к горизонту (с земли на землю)
К оглавлению…
Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):
Время подъема до максимальной высоты при броске под углом к горизонту:
Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т.е. тело бросали, например, с земли на землю):
Минимальная скорость тела брошенного под углом к горизонту – в наивысшей точке подъёма, и равна:
Максимальная скорость тела брошенного под углом к горизонту – в моменты броска и падения на землю, и равна начальной. Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.
Сложение скоростей
К оглавлению…
Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Таким образом, покой и движение тела относительны. Классический закон сложения скоростей:
Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета. Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.
Равномерное движение по окружности
К оглавлению…
Движение тела по окружности является частным случаем криволинейного движения. Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.
Период – время, за которое тело, двигаясь по окружности, совершает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:
Частота – количество оборотов, которое совершило тело, двигаясь по окружности, в единицу времени. Единица измерения – 1 об/с или 1 Гц. Частота рассчитывается по формуле:
В обеих формулах: N – количество оборотов за время t. Как видно из вышеприведенных формул, период и частота величины взаимообратные:
При равномерном вращении скорость тела будет определяется следующим образом:
где: l – длина окружности или путь, пройденный телом за время равное периоду T. При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах. Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt. Очевидно, что за время равное периоду T тело пройдет угол равный 2π, следовательно при равномерном движении по окружности выполняются формулы:
Угловая скорость измеряется в рад/с. Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:
Связь между модулем линейной скорости v и угловой скоростью ω:
При движении тела по окружности с постоянной по модулю скоростью изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной по модулю скоростью является движением с ускорением (но не равноускоренным), так как меняется направление скорости. В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).
Модуль центростремительного ускорения связан с линейной v и угловой ω скоростями соотношениями:
Обратите внимание, что если тела (точки) находятся на вращающемся диске, шаре, стержне и так далее, одним словом на одном и том же вращающемся объекте, то у всех тел одинаковые период вращения, угловая скорость и частота.
Урок 5. поступательное движение. вращательное движение твердого тела — Физика — 10 класс
Физика, 10 класс
Урок 05. Поступательное движение. Вращательное движение твёрдого тела
Перечень вопросов, рассматриваемых на уроке:
- Поступательное и вращательное движение абсолютно твердого тела.
- Характеристики вращательного движения абсолютно твердого тела.
Глоссарий по теме
1. Абсолютно твердое тело – это тело, расстояние между любыми двумя точками которого остается постоянным при его движении.
2. Поступательным называется такое движение абсолютно твердого тела, при котором любой отрезок, соединяющий любые две точки тела, остается параллельным самому себе. Одинаковыми остаются при поступательном движении перемещение, траектория, путь, скорость, ускорение.
3. Вращением твердого тела вокруг неподвижной оси называется такое движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой перпендикулярной плоскостям этих окружностей. Сама эта прямая есть ось вращения.
4. Угол поворота – угол, на который поворачивается радиус-вектор, соединяющий центр окружности с точкой вращающегося тела.
5. Угловая скорость — отношение угла поворота φ к промежутку времени, в течение которого совершен этот поворот при равномерном движении.
6. Линейная скорость – отношение длины дуги окружности пройденной точкой тела к промежутку времени, в течение которого этот поворот совершен.
7. Период — промежуток времени, за который тело делает один полный оборот.
8. Частота обращения тела – число оборотов за единицу времени
Основная и дополнительная литература по теме урока:
Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н.. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016. – С. 57-61
Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.-С.20-22
Открытые электронные ресурсы:
http://kvant.mccme.ru/1986/11/kinematika_vrashchatelnogo_dvi.htm
Теоретический материал для самостоятельного изучения
1. Вы знаете, что в физике для упрощения исследования реальных ситуаций часто используются модели. Одной из механических моделей, используемых при описании движения и взаимодействия тел, является абсолютно твёрдое тело- тело, расстояние между любыми двумя точками которого остаётся постоянным при его движении.
2. Поступательным называется такое движение абсолютно твёрдого тела, при котором любой отрезок, соединяющий любые две точки тела, остаётся параллельным самому себе. Примером поступательного движения может служить свободное падение тел, движение лифта, поезда на прямолинейном участке дороги. При поступательном движении все точки тела описывают одинаковые траектории, совершают одинаковые перемещения, проходят одинаковые пути, в каждый момент времени имеют равные скорости и ускорения.
Для описания поступательного движения абсолютно твёрдого тела достаточно написать уравнение движения одной из его точек.
3. Вращательным движением абсолютно твёрдого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, называемой осью вращения. При этом плоскости, которым принадлежат эти окружности, перпендикулярны оси вращения.
Вращательное движение позволяет осуществить непрерывный процесс работы с использованием больших скоростей. Вращающиеся механизмы более компактны и более экономичны, так как потери энергии на преодоление сил трения качения меньше, чем на преодоление сил трения скольжения. Поэтому в современной технике вращательное движение рабочих частей машин всё более вытесняет возвратно-поступательное. Например, вместо ножовочной пилы в технике используют вращающуюся дисковую пилу, поршневые насосы в большинстве случаев вытесняются центробежными.
4. Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела ∆φ к промежутку времени ∆t, за которое этот поворот произошёл.
Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению запишем формулу угловой скорости;
При равномерном вращательном движении угловая скорость у всех точек вращающегося тела одинаковая. Поэтому угловая скорость, так же как и угол поворота, является характеристикой движения всего вращающегося тела, а не только отдельных его частей.
Примером вращательного движения, близкого к равномерному, может служить вращение Земли вокруг своей оси.
Угловая скорость в СИ выражается в радианах в секунду (рад/с).
Один радиан – это центральный угол, опирающийся на дугу, длина которой равна радиусу окружности.
Угловая скорость положительна, если угол между радиусом вектором, определяющим положение одной из точек твердого тела, и осью ОХ увеличивается, и отрицательным, когда он уменьшается
5.Число полных оборотов за единицу времени называют частотой обращения.
Частоту обозначают греческой буквой «ню». Единица измерения частоты является секунда в минус первой степени
Время, за которое тело совершает один полный оборот, называют периодом обращения и обозначают буквой Т.
7. Связь между линейной и угловой скоростями:
8. Связь между ускорением и угловой скоростью:
Итак, мы рассмотрели два простейших движения абсолютно твердого тела – поступательное и вращательное. В жизни мы чаще встречаем сложное движение абсолютно твердого тела, однако, в этом случае любое сложное движение можно представить как сумму двух независимых движений: поступательного и вращательного.
Примеры и разбор типового тренировочного задания
- Ротор мощной паровой турбины делает 100 оборотов за 2 с. Определите угловую скорость.
Дано:
N=100 об.
t = 2 c
Найти: ω.
Решение:
2. Два шкива, соединенные друг с другом ремнем, вращаются вокруг неподвижных осей (см.рис). Больший шкив радиусом 20см делает 50 оборотов за 10 секунд, а частота вращения меньшего шкива 2400 оборотов в минуту. Чему равен радиус меньшего шкива? Шкивы вращаются без проскальзывания.
Дано:
Найти —
Решение:
Из условия задачи ученик видит что, шкивы соединены ремнем, следовательно, линейные скорости их равны:
но частота вращения разная.
Сокращает на 2π обе части.
Отсюда имеем:
и так, как в условии известно , то можем записать:
Отсюда находим радиус второго шкива:
Вторая неизвестная величина
Запишем формулу периода обращения для большего шкива:
так как по условию задачи нам известно число оборотов за 10 секунд.
Подставим в формулу (1) и получим конечную формулу:
Вращательное движение вокруг неподвижной оси — еще один частный случай движения твердого тела.Вращательным движением твердого тела вокруг неподвижной оси называется такое его движение, при котором все точки тела описывают окружности, центры которых находятся на одной прямой, называемой осью вращения, при этом плоскости, которым принадлежат эти окружности, перпендикулярны оси вращения (рис.2.4). В технике такой вид движения встречается очень часто: например, вращение валов двигателей и генераторов, турбин и пропеллеров самолетов. Угловая скорость. Каждая точка вращающегося вокруг оси тела, проходящей через точку О, движется по окружности, и различные точки проходят за время разные пути. Так, , поэтому модуль скорости точки А больше, чем у точки В (рис.2.5). Но радиусы окружностей поворачиваются за время на один и тот же угол . Угол — угол между осью ОХ и радиус-вектором , определяющим положение точки А (см. рис.2.5). Пусть тело вращается равномерно, т. е. за любые равные промежутки времени поворачивается на одинаковые углы. Быстрота вращения тела зависит от угла поворота радиус-вектора, определяющего положение одной из точек твердого тела за данный промежуток времени; она характеризуется угловой скоростью. Например, если одно тело за каждую секунду поворачивается на угол , а другое — на угол , то мы говорим, что первое тело вращается быстрее второго в 2 раза. Угловой скоростью тела при равномерном вращении называется величина, равная отношению угла поворота тела к промежутку времени , за который этот поворот произошел. Будем обозначать угловую скорость греческой буквой ω (омега). Тогда по определению Угловая скорость выражается в радианах в секунду (рад/с). Например, угловая скорость вращения Земли вокруг оси равна 0,0000727 рад/с, а точильного диска — около 140 рад/с1. Угловую скорость можно выразить через частоту вращения, т. е. число полных оборотов за 1с. Если тело совершает (греческая буква «ню») оборотов за 1с, то время одного оборота равно секунд. Это время называют периодом вращения и обозначают буквой T. Таким образом, связь между частотой и периодом вращения можно представить в виде: Полному обороту тела соответствует угол . Поэтому согласно формуле (2.1) Если при равномерном вращении угловая скорость известна и в начальный момент времени угол поворота , то угол поворота тела за время t согласно уравнению (2.1) равен: Если , то , или . Угловая скорость принимает положительные значения, если угол между радиус-вектором, определяющим положение одной из точек твердого тела, и осью ОХ увеличивается, и отрицательные, когда он уменьшается. Тем самым мы можем описать положение точек вращающегося тела в любой момент времени. Связь между линейной и угловой скоростями. Скорость точки, движущейся по окружности, часто называют линейной скоростью, чтобы подчеркнуть ее отличие от угловой скорости. Мы уже отмечали, что при вращении твердого тела разные его точки имеют неодинаковые линейные скорости, но угловая скорость для всех точек одинакова. Между линейной скоростью любой точки вращающегося тела и его угловой скоростью существует связь. Установим ее. Точка, лежащая на окружности радиусом R, за один оборот пройдет путь . Поскольку время одного оборота тела есть период T, то модуль линейной скорости точки можно найти так: Так как , то Из этой формулы видно, что, чем дальше расположена точка тела от оси вращения, тем больше ее линейная скорость. Для точек земного экватора , а для точек на широте Санкт-Петербурга . На полюсах Земли . Модуль ускорения точки тела, движущейся равномерно по окружности, можно выразить через угловую скорость тела и радиус окружности: Следовательно, Чем дальше расположена точка твердого тела от оси вращения, тем большее по модулю ускорение она имеет. Итак, мы научились полностью описывать движение абсолютно твердого тела, вращающегося равномерно вокруг неподвижной оси, так как, пользуясь формулами , можем находить положение, модули скорости и ускорения любой точки тела в произвольный момент времени. Знаем мы и направления и , a также форму траекторий точек. |
Скорость вращения черной дыры в центре Млечного Пути оценили по распределению орбит S-звезд
Кстати, несколько этих дней я поразмышлял на тему чёрных дыр, и у меня возникла теория, что, хотя чёрные дыры, как следует из ОТО, теоретически возможны, но в реальности чёрные дыры в строгом смысле не существуют. (Я не уверен, правильна ли эта теория, потому что я плохо знаю ОТО).Вот почему у меня возникла такая теория. В гравитационном поле время замедляется:
en.wikipedia.org/wiki/Gravitational_time_dilation
t = t₀ √(1 — 2GM / rc²) = t₀ √(1 — r₀ / r)
здесь t — время для наблюдателя в гравитационном поле, t₀ — время для наблюдателя вне гравитационного поля, r — расстояние от центра объекта, M — масса объекта, G — гравитационная постоянная, c — скорость света
r₀ = 2GM / c² — это радиус Шварцшильда. То есть при сжатии объекта время на нём замедляется, и когда он сжимается до радиуса Шварцшильда, то время должно замедлиться в бесконечное количество раз, то есть время должно остановиться.
(Кстати, по этой формуле вроде бы получается, что время не замедляется, а наоборот, ускоряется, так как временной интервал становится меньше. Ведь формула специальной теории относительности (СТО) для замедления времени выглядит по-другому:
t = t₀ / √(1 — v² / c²)
то есть тут мы делим на корень, а не умножаем, и тут всё правильно — временной интервал увеличивается, то есть время замедляется. Как это объяснить? Я даже предположил, что в английской Википедии ошибка, я посмотрел в испанской, итальянской и португальской Википедиях, и там то же самое.
Я предположил следующее. В Википедиях вроде как речь идёт об одной и той же паре событий (неважно где происходящих), но с точки зрения разных наблюдателей, один из которых в гравитационном поле, а другой — нет.
В СТО, в принципе тоже — одна и та же пара событий, но в разных системах отсчёта, в одной из которых объект покоится, а в другой — движется. Казалось бы, с точки зрения движущегося тела, так как процессы в нём замедлены, окружающая реальность должна ускориться, но этого не происходит, наоборот, происходит такое же замедление в окружающей реальности, как и в самом теле. Почему так происходит, я пока не очень понимаю (возможно, здесь замешана относительность одновременности). Итак, в СТО получается, что формула t = t₀ / √(1 — v² / c²) описывает одновременно и то, как изменится ход времени внутри объекта, если мы начнём двигаться относительно объекта, и то, как изменится ход времени внутри объекта, если объект сам начнёт двигаться. То есть парадоксальным образом в СТО получается, что одна и та же формула описывает две разные ситуации. Почему так — интересный вопрос, в котором надо разобраться.
Но с гравитационным замедлением времени ситуация другая: если тело попадает в гравитационное поле, то процессы в этом теле замедляются, и, соответственно, с его точки зрения, окружающая реальность должна ускориться. То есть здесь всё более «логично». И здесь уже должны быть две разные формулы, в отличие от СТО.
Так вот, я предположил, что формула t = t₀ √(1 — 2GM / rc²) описывает, как изменится ход времени с точки зрения объекта, когда он попадёт в гравитационное поле. Все процессы в самом объекте замедлятся, поэтому с его точки зрения окружающая реальность ускорится. Именно это ускорение и описывает данная формула (я так думаю). Но если нас интересует, как при этом изменится ход времени внутри самого объекта (а не с его точки зрения), то, я думаю, здесь нужна другая формула
t = t₀ / √(1 — 2GM / rc²)
описывающая замедление процессов в объекте, когда он попадает в гравитационное поле. Здесь t — время в гравитационном поле, t₀ — время вне гравитационного поля).
«Замедление времени» означает замедление всех процессов, в том числе и замедление самого процесса сжатия.
Давайте назовём «радиусом равновесия» такой радиус объекта, при котором размер этого объекта не изменяется (то есть когда гравитационные силы, стремящиеся сжать объект, уравновешиваются силами упругости, которые препятствуют сжатию). То есть если радиус объекта больше его радиуса равновесия, то объект сжимается, а если меньше, то объект взрывается. Например, сейчас радиус Земли равен её радиусу равновесия, так как сейчас Земля не увеличивается и не уменьшается.
Для большинства объектов (например, Земля, Луна, Солнце)
радиус равновесия > радиус Шварцшильда
Но для некоторых (достаточно массивных) объектов
радиус равновесия < радиус Шварцшильда
Такое тело, в принципе, могло бы сжаться до размеров менее радиуса Шварцшильда, но по мере приближения к радиусу Шварцшильда начинает сильно проявляться гравитационное замедление времени, которое может быть сколько угодно большим, ведь в пределе, при достижении радиуса Шварцшильда, время должно остановиться. В результате сам процесс сжатия почти останавливается. Радиус объекта остаётся чуть больше радиуса Шварцшильда, но никогда не достигает его. (Кстати, интересно узнать — насколько больше? На миллиметр? И во сколько раз там замедлено время?) Фактически, горизонт событий так и не появляется, и нет момента времени, который всё делит на «до» и «после» (сначала не было чёрной дыры, и вот она появилась), потому что чёрная дыра, строго говоря, так и не появляется, и объект застывает на стадии сжатия.
И вот, я предположил, что именно таковы все реальные «чёрные дыры» вроде той, что в центре Млечного Пути.
Теоретически, радиус Шварцшильда всё-таки достижим, особенно для наблюдателя на поверхности объекта, с его точки зрения объект будет продолжать сжиматься до размеров менее радиуса Шварцшильда, при этом «снаружи» время пройдёт отметку бесконечности (но ведь есть же трансфинитные числа), то есть ему будет казаться, что он оказался в бесконечно далёком будущем. Или можно просто подождать снаружи бесконечное количество времени.
Но на практике не произойдёт даже этого, так как вследствие излучения Хокинга «чёрная дыра» будет терять массу, пока радиус равновесия объекта не станет равен его радиусу (который чуть больше радиуса Шварцшильда), и дальнейшее сжатие прекратится.
Хотя, если «чёрная дыра» — это не чёрная дыра, то откуда излучение Хокинга? Возникает вопрос: для излучения Хокинга необходимо наличие горизонта событий? Я пока склоняюсь к предположению, что нет, потому что здесь
ru.wikipedia.org/wiki/Излучение_Хокинга
сказано:
прямо из вакуума могут рождаться пары частица-античастица. Такие процессы происходят и вблизи (но всё же снаружи) горизонта событий чёрной дыры
Пары частица-античастица могут родиться только за счёт приливного эффектаИтак, «всё же снаружи», а приливный эффект есть, например, у Луны. Но тогда излучение Хокинга должно быть у любых тел, например, у Земли, или Луны. Тогда у реальных «чёрных дыр», даже если они и не являются, строго говоря, чёрными дырами, всё-таки должно быть излучение Хокинга.
По достижении радиуса равновесия дальнейшее сжатие и дальнейшее замедление времени должны прекратиться, и «чёрная дыра» превращается в нейтронную звезду, но очень замедленную (?). За счёт продолжающегося излучения Хокинга процесс замедления времени должен обратиться вспять, и время должно начать постепенно ускоряться и когда-нибудь «вернуться в норму».
Получается, что реальные «чёрные дыры» — это «обычные» объекты, но очень сильно замедленные. Лёгкая «чёрная дыра» — это коллапсирующая звезда, «замороженная» на стадии сжатия в нейтронную звезду. Наверное, не существует даже чёткой границы между нейтронной звездой и лёгкой «чёрной дырой», разница лишь во времени достижения радиуса равновесия, которое для «чёрной дыры» намного больше, и в массе, теряемой при этом за счёт излучения Хокинга, которая для нейтронной звезды незначительна. Хотя, можно провести условную границу на совпадении радиуса равновесия и радиуса Шварцщильда. Должны быть и «промежуточные» объекты (когда эти радиусы почти равны). Например, когда радиус равновесия чуть-чуть больше радиуса Шварцщильда, то получается коллапс в нейтронную звезду, который может растянуться на миллионы лет. А когда радиус равновесия равен или чуть-чуть меньше радиуса Шварцщильда, то потребуется помощь излучения Хокинга, чтобы часть массы потерялась и радиус равновесия превысил радиус Шварцщильда, и только после этого коллапс сможет завершиться.
Сверхмассивная «чёрная дыра» — это, должно быть, нечто вроде туманности, «замороженной» на стадии сжатия.
Кстати, возникает чисто теоретический вопрос: если бы гравитационное замедление времени не «замораживало» процесс сжатия, то какой объект получился бы в центре Млечного Пути? Наверное, это была бы какая-то сверхмассивная звезда из кварк-глюонной плазмы. Интересно какого размера.
ru.wikipedia.org/wiki/Кварковая_звезда
Но потом у меня появилось подозрение, что любая «чёрная дыра» — это объект, «замороженный» на стадии коллапса в кварковую звезду, а не в нейтронную, так как массы нейтронных звёзд бывают близки к их верхнему теоретическому пределу (предел Оппенгеймера-Волкова). Если это так, то чёткая граница между нейтронными звёздами и «чёрными дырами» всё-таки должна быть. И, возможно, процесс превращения «чёрной дыры» после потери массы в нейтронную звезду должен иметь характер взрыва.
Вообще, я думаю, есть 3 возможных варианта, где теоретически может достигаться равенство радиусов равновесия и Шварцшильда: 1) нейтронные звёзды, 2) между нейтронными и кварковыми звёздами, 3) кварковые звёзды. Я сейчас склоняюсь к 2-ому варианту, потому что при 1-ом…
6.1 Угол вращения и угловая скорость — Физика
Цели обучения разделу
К концу этого раздела вы сможете делать следующее:
- Опишите угол поворота и свяжите его с его линейным аналогом
- Опишите угловую скорость и свяжите ее с ее линейным аналогом
- Решение задач, связанных с углом поворота и угловой скоростью
Поддержка учителей
Поддержка учителей
Цели обучения в этом разделе помогут вашим ученикам овладеть следующими стандартами:
- (4) Научные концепции.Учащийся знает и применяет законы движения в самых разных ситуациях. Ожидается, что студент:
- (C) анализировать и описывать ускоренное движение в двух измерениях с использованием уравнений, включая примеры снарядов и кругов.
Раздел Ключевые термины
| Меры градуса | Меры радиана |
|---|---|
| 30∘30∘ | π6π6 |
| 60∘60∘ | π3π3 |
| 90∘90∘ | π2π2 |
| 120–120– | 2π32π3 |
| 135∘135∘ | 3π43π4 |
| 180∘180∘ | ππ |
Таблица 6.1 Обычно используемые углы в градусах и радианах
Угловая скорость
Поддержка учителя
Поддержка учителя
[BL] Проверьте смещение, скорость, скорость, ускорение.
[AL] Спросите студентов, изменяется ли скорость при равномерном круговом движении. А как насчет скорости? А как насчет разгона?
Насколько быстро вращается объект? Мы можем ответить на этот вопрос, используя понятие угловой скорости. Рассмотрим сначала угловую скорость (ω) (ω) — это скорость, с которой изменяется угол поворота.В форме уравнения угловая скорость равна
ω = ΔθΔt, ω = ΔθΔt,6,2
, что означает, что угловое вращение (Δθ) (Δθ) происходит за время ΔtΔt. Если объект поворачивается на больший угол поворота в данный момент времени, он имеет большую угловую скорость. Единицы измерения угловой скорости — радианы в секунду (рад / с).
Теперь давайте рассмотрим направление угловой скорости, а это значит, что теперь мы должны называть ее угловой скоростью. Направление угловой скорости — вдоль оси вращения.Для объекта, вращающегося по часовой стрелке, угловая скорость указывает от вас вдоль оси вращения. Для объекта, вращающегося против часовой стрелки, угловая скорость указывает на вас вдоль оси вращения.
Угловая скорость (ω) — это угловая версия линейной скорости v . Тангенциальная скорость — это мгновенная линейная скорость объекта во вращательном движении . Чтобы получить точное соотношение между угловой скоростью и тангенциальной скоростью, снова рассмотрим углубление на вращающемся компакт-диске.Эта яма перемещается по длине дуги (Δs) (Δs) за короткое время (Δt) (Δt), поэтому его тангенциальная скорость равна
Из определения угла поворота, Δθ = ΔsrΔθ = Δsr, мы видим, что Δs = rΔθΔs = rΔθ. Подставляя это в выражение для v , получаем
v = rΔθΔt = rω. v = rΔθΔt = rω.Уравнение v = rωv = rω говорит, что тангенциальная скорость v пропорциональна расстоянию r от центра вращения. Следовательно, тангенциальная скорость больше для точки на внешнем крае компакт-диска (с большим r ), чем для точки ближе к центру компакт-диска (с меньшим r ).Это имеет смысл, потому что точка, находящаяся дальше от центра, должна покрывать большую длину дуги за то же время, что и точка ближе к центру. Обратите внимание, что обе точки по-прежнему будут иметь одинаковую угловую скорость, независимо от их расстояния от центра вращения. См. Рисунок 6.4.
Рис. 6.4 Точки 1 и 2 вращаются на один и тот же угол (ΔθΔθ), но точка 2 перемещается на большую длину дуги (Δs2Δs2), поскольку она дальше от центра вращения.Teacher Support
Teacher Support
[AL] Объясните, что период времени ΔtΔt в уравнении, определяющем тангенциальную скорость (v = ΔsΔtv = ΔsΔt), должен быть коротким, чтобы дуга, описываемая движущимся объектом, могла быть аппроксимирована прямой линия.Это позволяет нам определить направление касательной скорости как касательное к окружности. Это приближение становится все более точным по мере того, как ΔtΔt становится все меньше и меньше.
Теперь рассмотрим другой пример: шину движущегося автомобиля (см. Рис. 6.5). Чем быстрее вращается шина, тем быстрее движется автомобиль — большое ωω означает большое v , потому что v = rωv = rω. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью ωω, будет создавать для автомобиля большую линейную (тангенциальную) скорость v, .Это связано с тем, что больший радиус означает, что большая длина дуги должна касаться дороги, поэтому автомобиль должен двигаться дальше за то же время.
Рисунок 6.5 Автомобиль, движущийся со скоростью v, вправо, имеет шину, вращающуюся с угловой скоростью ωω. Скорость протектора шины относительно оси составляет v , такая же, как если бы автомобиль был поднят домкратом и колеса вращались, не касаясь дороги. Непосредственно под осью, где шина касается дороги, протектор шины движется назад по отношению к оси с тангенциальной скоростью v = rωv = rω, где r — радиус шины.Поскольку дорога неподвижна относительно этой точки шины, автомобиль должен двигаться вперед с линейной скоростью v . Большая угловая скорость шины означает большую линейную скорость автомобиля.Однако есть случаи, когда линейная скорость и тангенциальная скорость не эквивалентны, например, когда автомобиль вращает свои колеса по льду. В этом случае линейная скорость будет меньше тангенциальной скорости. Из-за отсутствия трения под шинами автомобиля на льду длина дуги, по которой движутся протекторы шин, больше, чем линейное расстояние, по которому движется автомобиль.Это похоже на бег на беговой дорожке или на велотренажере; вы буквально никуда не денетесь.
Советы для успеха
Угловая скорость ω и тангенциальная скорость v являются векторами, поэтому мы должны включить величину и направление. Направление угловой скорости — вдоль оси вращения и указывает от вас для объекта, вращающегося по часовой стрелке, и к вам для объекта, вращающегося против часовой стрелки. В математике это описывается правилом правой руки.Тангенциальная скорость обычно описывается как вверх, вниз, влево, вправо, север, юг, восток или запад, как показано на рисунке 6.6.
Рис. 6.6. Поскольку муха на краю старинной виниловой пластинки движется по кругу, ее мгновенная скорость всегда находится по касательной к кругу. Направление угловой скорости в данном случае указано на странице.
Watch Physics
Взаимосвязь между угловой скоростью и скоростью
В этом видео рассматриваются определение и единицы угловой скорости и их связь с линейной скоростью.Здесь также показано, как преобразовать число оборотов в радианы.
Проверка захвата
Для объекта, движущегося по круговой траектории с постоянной угловой скоростью, изменится ли линейная скорость объекта при увеличении радиуса пути?
- Да, потому что тангенциальная скорость не зависит от радиуса.
- Да, потому что тангенциальная скорость зависит от радиуса.
- Нет, поскольку тангенциальная скорость не зависит от радиуса.
- Нет, потому что тангенциальная скорость зависит от радиуса.
Решение задач, связанных с углом вращения и угловой скоростью
Snap Lab
Измерение угловой скорости
В этом упражнении вы будете создавать и измерять равномерное круговое движение, а затем сравнивать его с круговыми движениями с разными радиусами.
- Одна струна (длина 1 м)
- Один предмет (резиновая пробка с двумя отверстиями) для привязки к концу
- Один таймер
Процедура
- Привяжите объект к концу строки.
- Раскачивайте объект по горизонтальному кругу над головой (качаясь с запястья). Важно, чтобы круг был горизонтальным!
- Поддерживайте постоянную скорость вращения объекта.
- Измерьте таким образом угловую скорость объекта. Измерьте время в секундах, за которое объект совершит 10 оборотов. Разделите это время на 10, чтобы получить угловую скорость в оборотах в секунду, которую вы можете преобразовать в радианы в секунду.
- Какова приблизительная линейная скорость объекта?
- Переместите руку вверх по тетиве так, чтобы ее длина составляла 90 см.Повторите шаги 2–5.
- Переместите руку вверх по струне так, чтобы ее длина была 80 см. Повторите шаги 2–5.
- Переместите руку вверх по струне так, чтобы ее длина составила 70 см. Повторите шаги 2–5.
- Переместите руку вверх по струне так, чтобы ее длина составляла 60 см. Повторите шаги 2–5 .
- Переместите руку вверх по струне так, чтобы ее длина была 50 см. Повторите шаги 2–5 .
- Постройте графики зависимости угловой скорости от радиуса (т. Е. Длины струны) и линейной скорости от радиуса. Опишите, как выглядит каждый график.
Проверка захвата
Если вы поворачиваете объект медленно, он может вращаться со скоростью менее одного оборота в секунду. Какими были бы обороты в секунду для объекта, который совершает один оборот за пять секунд? Какова была бы его угловая скорость в радианах в секунду?
- Объект будет вращаться в \ frac {1} {5} \, \ text {rev / s}. Угловая скорость объекта будет \ frac {2 \ pi} {5} \, \ text {rad / s}.
- Объект будет вращаться в \ frac {1} {5} \, \ text {rev / s}.Угловая скорость объекта будет \ frac {\ pi} {5} \, \ text {rad / s}.
- Объект будет вращаться со скоростью 5 \, \ text {об / с}. Угловая скорость объекта будет 10 \ pi \, \ text {rad / s}.
- Объект будет вращаться со скоростью 5 \, \ text {об / с}. Угловая скорость объекта будет 5 \ pi \, \ text {rad / s}.
Теперь, когда у нас есть понимание понятий угла поворота и угловой скорости, мы применим их к реальным ситуациям с часовой башней и вращающимся колесом.
Рабочий пример
Угол поворота часовой башни
Часы на часовой башне имеют радиус 1,0 м. (а) На какой угол поворота движется часовая стрелка часов, когда она движется с 12 часов дня. до 15:00? (б) Какова длина дуги по внешнему краю часов между часовой стрелкой в эти два момента времени?
Стратегия
Мы можем вычислить угол поворота, умножив полный оборот (2π2π радиан) на долю 12 часов, покрываемых часовой стрелкой при переходе от 12 к 3.Когда у нас есть угол поворота, мы можем найти длину дуги, переписав уравнение Δθ = ΔsrΔθ = Δsr, поскольку радиус задан.
Решение для (а)
При переходе с 12 на 3 часовая стрелка покрывает 1/4 из 12 часов, необходимых для совершения полного оборота. Следовательно, угол между часовой стрелкой в точках 12 и 3 равен 14 × 2πrad = π214 × 2πrad = π2 (т.е. 90 градусов).
Решение пункта (b)
Преобразование уравнения
получаем
Вставка известных значений дает длину дуги
Δs = (1.0 м) (π2рад) = 1,6 м Δs = (1,0 м) (π2рад) = 1,6 м6,6
Обсуждение
Нам удалось отбросить радианы из окончательного решения в часть (b), потому что радианы фактически безразмерны. Это потому, что радиан определяется как отношение двух расстояний (радиуса и длины дуги). Таким образом, формула дает ответ в метрах, как и ожидалось для длины дуги.
Рабочий пример
Как быстро вращается автомобильная шина?
Рассчитайте угловую скорость 0.Автомобильная шина с радиусом 300 м при движении автомобиля со скоростью 15,0 м / с (около 54 км / ч). См. Рисунок 6.5.
Стратегия
В этом случае скорость протектора шины по отношению к оси шины такая же, как и скорость автомобиля по отношению к дороге, поэтому мы имеем v = 15,0 м / с. Радиус покрышки r = 0,300 м. Поскольку мы знаем v и r , мы можем переписать уравнение v = rωv = rω, чтобы получить ω = vrω = vr и найти угловую скорость.
Решение
Чтобы найти угловую скорость, воспользуемся соотношением: ω = vrω = vr.
Вставка известных величин дает
ω = 15,0 м / с 0,300 м = 50,0 рад / с. ω = 15,0 м / с 0,300 м = 50,0 рад / с.6,7
Обсуждение
Когда мы отменяем единицы измерения в приведенном выше вычислении, мы получаем 50,0 / с (то есть 50,0 в секунду, что обычно записывается как 50,0 с −1 ). Но угловая скорость должна иметь единицы рад / с. Поскольку радианы безразмерны, мы можем вставить их в ответ для угловой скорости, потому что мы знаем, что движение является круговым. Также обратите внимание, что если землеройный трактор с гораздо большими шинами, скажем, 1.Радиус 20 м, двигался с той же скоростью 15,0 м / с, его колеса вращались медленнее. У них будет угловая скорость
ω = 15,0 м / с 1,20 м = 12,5 рад / с ω = 15,0 м / с 1,20 м = 12,5 рад / с6,8
Практические задачи
1.Каков угол в градусах между часовой и минутной стрелками часов, показывающих 9:00 утра?
- 0 °
- 90 °
- 180 °
- 360 °
Каково приблизительное значение длины дуги между часовой и минутной стрелками часов, показывающих 10:00 a.м, если радиус часов 0,2 м?
- 0,1 м
- 0,2 м
- 0,3 м
- 0,6 м
Проверьте свое понимание
3.Что такое круговое движение?
- Круговое движение — это движение объекта по линейному пути.
- Круговое движение — это движение объекта по зигзагообразной траектории.
- Круговое движение — это движение объекта по круговой траектории.
- Круговое движение — это движение объекта по окружности или вращение по круговой траектории.
Что подразумевается под радиусом кривизны при описании вращательного движения?
- Радиус кривизны — это радиус круговой траектории.
- Радиус кривизны — это диаметр круговой траектории.
- Радиус кривизны — это длина окружности круговой траектории.
- Радиус кривизны — это площадь круговой траектории.
Что такое угловая скорость?
- Угловая скорость — это скорость изменения диаметра круговой траектории.
- Угловая скорость — это скорость изменения угла, образованного круговой траекторией.
- Угловая скорость — это скорость изменения площади круговой траектории.
- Угловая скорость — это скорость изменения радиуса круговой траектории.
Какое уравнение определяет угловую скорость \ omega? Предположим, что r — радиус кривизны, \ theta — угол, а t — время.
- \ omega = \ frac {\ Delta \ theta} {\ Delta {t}}
- \ omega = \ frac {\ Delta {t}} {\ Delta \ theta}
- \ omega = \ frac {\ Delta {r}} {\ Delta {t}}
- \ omega = \ frac {\ Delta {t}} {\ Delta {r}}
Назовите три примера объекта, совершающего круговое движение.
- искусственный спутник, вращающийся вокруг Земли, гоночный автомобиль, движущийся по круговой гоночной трассе, и волчок, вращающийся вокруг своей оси
- искусственный спутник, вращающийся вокруг Земли, гоночный автомобиль, движущийся по круговой гоночной трассе, и мяч, привязанный к веревке, вращающийся по кругу вокруг головы человека
- Земля вращается вокруг своей оси, гоночный автомобиль движется по круговой гоночной трассе, и мяч, привязанный к веревке, вращается по кругу вокруг головы человека
- Земля, вращающаяся вокруг своей оси, лопасти рабочего потолочного вентилятора и волчок, вращающийся вокруг своей оси
Какова относительная ориентация векторов радиуса и тангенциальной скорости объекта при равномерном круговом движении?
- Вектор тангенциальной скорости всегда параллелен радиусу круговой траектории, по которой движется объект.
- Вектор тангенциальной скорости всегда перпендикулярен радиусу круговой траектории, по которой движется объект.
- Вектор тангенциальной скорости всегда находится под острым углом к радиусу круговой траектории, по которой движется объект.
- Вектор тангенциальной скорости всегда находится под тупым углом к радиусу круговой траектории, по которой движется объект.
Teacher Support
Teacher Support
Используйте вопросы Check Your Understanding , чтобы оценить, усвоили ли учащиеся учебные цели этого раздела. Если учащиеся борются с определенной целью, формирующая оценка поможет определить, какая цель вызывает проблему, и направит учащихся к соответствующему содержанию.
единиц вращательной кинематики | Безграничная физика
Угловое положение, Theta
Угол поворота — это величина (угол) поворота фигуры относительно фиксированной точки — часто центра круга.
Цели обучения
Оценить взаимосвязь между радианами на обороте CD
Ключевые выводы
Ключевые моменты
- Длина дуги Δs — это расстояние, пройденное по круговой траектории.r — радиус кривизны круговой траектории.
- Угол поворота — это величина поворота, аналогичная линейному расстоянию. Мы определяем угол поворота [latex] \ Delta \ theta [/ latex] как отношение длины дуги к радиусу кривизны: [latex] \ Delta \ theta [/ latex] = Δs / r.
- За один полный оборот угол поворота составляет 2π.
Ключевые термины
- Угловое положение : угол в радианах (градусах, оборотах), на который точка или линия были повернуты в указанном направлении вокруг указанной оси.
Когда объекты вращаются вокруг некоторой оси, например, когда компакт-диск (компакт-диск) вращается вокруг своего центра, каждая точка в объекте движется по дуге окружности. Рассмотрим линию от центра компакт-диска до его края. Каждая яма, используемая для записи звука вдоль этой линии, перемещается под одним и тем же углом за одно и то же время. Угол поворота — это величина поворота, аналогичная линейному расстоянию. Мы определяем угол поворота [latex] \ Delta \ theta [/ latex] как отношение длины дуги к радиусу кривизны:
[латекс] \ Delta \ theta = \ Delta \ text {s} / \ text {r} [/ latex] (показано на).
Угол поворота : Все точки на компакт-диске перемещаются по дугам окружности. Ямки вдоль линии от центра к краю все перемещаются на один и тот же угол Δ за время Δt.
В математике угол поворота (или угловое положение) — это величина (т.е. угол), на которую фигура поворачивается относительно фиксированной точки (часто центра круга, как показано на рисунке).
Угол θ и длина дуги s : Радиус круга поворачивается на угол Δ.Длина дуги Δs указана на окружности.
Длина дуги Δs — это расстояние, пройденное по круговой траектории. r — радиус кривизны круговой траектории. Мы знаем, что за один полный оборот длина дуги равна длине окружности радиуса r. Окружность круга равна 2πr. Таким образом, за один полный оборот угол поворота составляет:
[латекс] \ Delta \ theta = (2 \ pi \ text {r}) / \ text {r} = 2 \ pi [/ latex].
Этот результат является основой для определения единиц измерения углов поворота в радианах (рад), определяемых следующим образом:
2π рад = 1 оборот.
Если [latex] \ Delta \ theta [/ latex] = 2π rad, то компакт-диск сделал один полный оборот, и каждая точка на компакт-диске вернулась в исходное положение. Поскольку в круге 360º или один оборот, отношение между радианами и градусами, таким образом, составляет 2π рад = 360º, так что:
1рад = 360º / 2π = 57,3º.
Угловая скорость, Омега
Угловая скорость ω — это скорость изменения угла, математически определяемая как ω = [latex] \ Delta \ theta [/ latex] [latex] / \ Delta \ text {t} [/ latex].
Цели обучения
Проверить, насколько быстро объект вращается на основе угловой скорости
Ключевые выводы
Ключевые моменты
- Чем больше угол поворота за заданный промежуток времени, тем больше угловая скорость.
- Угловая скорость ω аналогична линейной скорости v.
- Связь между линейной скоростью и угловой скоростью можно записать двумя разными способами: v = rω или ω = v / r.
Ключевые термины
- угловая скорость : векторная величина, описывающая объект в круговом движении; его величина равна скорости частицы, а направление перпендикулярно плоскости ее кругового движения.
Чтобы проверить, насколько быстро объект вращается, мы определяем угловую скорость ω как скорость изменения угла. В символах это
.[латекс] \ omega = \ Delta \ theta / \ Delta \ text {t} [/ latex],
, где угловой поворот Δ происходит за время Δt. Чем больше угол поворота за заданный промежуток времени, тем больше угловая скорость. Единицы измерения угловой скорости — радианы в секунду (рад / с).
Угловая скорость ω аналогична линейной скорости v.Чтобы найти точное соотношение между угловой и линейной скоростью, мы снова рассмотрим ямку на вращающемся CD. Эта яма перемещается на длину дуги Δs за время Δt, поэтому она имеет линейную скорость v = Δs / Δt.
Из [latex] \ Delta \ theta = (\ Delta \ text {s}) / \ text {r} [/ latex] мы видим, что [latex] \ Delta \ text {s} = \ text {r} \ cdot \ Дельта \ тета [/ латекс]. Подстановка этого в выражение для v дает [latex] \ text {v} = (\ text {r} \ cdot \ Delta \ theta) / (\ Delta \ text {t}) = \ text {r} (\ Delta \ theta / \ Delta \ text {t}) = \ text {r} \ omega [/ latex].
Мы можем записать это соотношение двумя разными способами: v = rω или ω = v / r.
Первое соотношение утверждает, что линейная скорость v пропорциональна расстоянию от центра вращения, таким образом, она является наибольшей для точки на ободе (наибольшее значение r), как и следовало ожидать. Мы также можем назвать эту линейную скорость v точки на ободе тангенциальной скоростью. Вторую взаимосвязь можно проиллюстрировать, рассмотрев шину движущегося автомобиля, как показано на рисунке ниже. Обратите внимание, что скорость точки в центре шины такая же, как скорость v автомобиля.Чем быстрее машина движется, тем быстрее вращается шина — большой v означает большой ω, потому что v = rω. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью (ω), будет создавать для автомобиля большую линейную скорость (v).
Угловая скорость : Автомобиль, движущийся со скоростью v вправо, имеет шину, вращающуюся с угловой скоростью ω. Скорость протектора шины относительно оси равна v, как если бы автомобиль был поднят домкратом. Таким образом, автомобиль движется вперед с линейной скоростью v = rω, где r — радиус шины.Чем больше угловая скорость шины, тем больше скорость автомобиля.
Угловое ускорение, Альфа
Угловое ускорение — это скорость изменения угловой скорости, математически выражаемая как [latex] \ alpha = \ Delta \ omega / \ Delta \ text {t} [/ latex].
Цели обучения
Объясните взаимосвязь между угловым ускорением и угловой скоростью
Ключевые выводы
Ключевые моменты
- Чем быстрее происходит изменение угловой скорости, тем больше угловое ускорение.
- При круговом движении линейное ускорение касается окружности в интересующей точке и называется касательным ускорением.
- При круговом движении центростремительное ускорение относится к изменению направления скорости, но не ее величины. Объект, совершающий круговое движение, испытывает центростремительное ускорение.
Ключевые термины
- угловое ускорение : Скорость изменения угловой скорости, часто обозначаемая α.
- тангенциальное ускорение : ускорение в направлении, касательном к окружности, в интересующей точке при круговом движении.
Угловое ускорение — это скорость изменения угловой скорости. В единицах СИ он измеряется в радианах на секунду в квадрате (рад / с 2 ) и обычно обозначается греческой буквой альфа ([латекс] \ альфа [/ латекс]).
Рассмотрим следующие ситуации, в которых угловая скорость непостоянна: когда фигуристка тянет за руки, когда ребенок запускает карусель из состояния покоя или когда жесткий диск компьютера останавливается, когда он выключен.Во всех этих случаях существует угловое ускорение, при котором изменяется [латекс] \ омега [/ латекс]. Чем быстрее происходит изменение, тем больше угловое ускорение. Угловое ускорение определяется как скорость изменения угловой скорости. В форме уравнения угловое ускорение выражается следующим образом:
[латекс] \ alpha = \ Delta \ omega / \ Delta \ text {t} [/ latex]
где [latex] \ Delta \ omega [/ latex] — это изменение угловой скорости, а [latex] \ Delta \ text {t} [/ latex] — это изменение во времени.Единицы углового ускорения: (рад / с) / с или рад / с 2 . Если [latex] \ omega [/ latex] увеличивается, то [latex] \ alpha [/ latex] положительно. Если [latex] \ omega [/ latex] уменьшается, тогда [latex] \ alpha [/ latex] отрицательно.
Полезно знать, как связаны линейное и угловое ускорение. При круговом движении есть ускорение, которое составляет касательных к окружности в интересующей точке (как показано на диаграмме ниже). Это ускорение называется тангенциальным ускорением , a t .
Тангенциальное ускорение : При круговом движении ускорение может происходить из-за изменения величины скорости: a касается движения. Это ускорение называется тангенциальным ускорением.
Касательное ускорение относится к изменениям величины скорости, но не ее направления. При круговом движении центростремительное ускорение, a c , относится к изменениям направления скорости, но не ее величины. Объект, совершающий круговое движение, испытывает центростремительное ускорение (как показано на диаграмме ниже.) Таким образом, t и c перпендикулярны и независимы друг от друга. Касательное ускорение a t напрямую связано с угловым ускорением и связано с увеличением или уменьшением скорости (но не ее направлением).
Центростремительное ускорение : Центростремительное ускорение возникает при изменении направления скорости; он перпендикулярен круговому движению. Таким образом, центростремительное и тангенциальное ускорения перпендикулярны друг другу.
Кинематика вращательного движения | Физика
Цели обучения
К концу этого раздела вы сможете:
- Соблюдайте кинематику вращательного движения.
- Составьте кинематические уравнения вращения.
- Оценить стратегии решения проблем для вращательной кинематики.
Просто используя нашу интуицию, мы можем начать видеть, как вращательные величины, такие как θ , ω и α , связаны друг с другом.Например, если колесо мотоцикла имеет большое угловое ускорение в течение довольно длительного времени, оно быстро вращается и совершает много оборотов. С технической точки зрения, если угловое ускорение α колеса велико в течение длительного периода времени t , то конечная угловая скорость ω и угол поворота θ будут большими. Вращательное движение колеса в точности аналогично тому, что большое поступательное ускорение мотоцикла дает большую конечную скорость, и пройденное расстояние также будет большим.
Кинематика — это описание движения. Кинематика вращательного движения описывает отношения между углом вращения, угловой скоростью, угловым ускорением и временем. Начнем с поиска уравнения, связывающего ω , α и t . Чтобы определить это уравнение, вспомним знакомое кинематическое уравнение поступательного или прямолинейного движения:
[латекс] v = {v} _ {0} + {at} \\ [/ latex] (константа a )
Обратите внимание, что во вращательном движении a = a t , и с этого момента мы будем использовать символ a для тангенциального или линейного ускорения.Как и в линейной кинематике, мы предполагаем, что a является постоянным, что означает, что угловое ускорение α также является постоянным, потому что a = rα . Теперь давайте подставим v = rω и a = rα в приведенное выше линейное уравнение:
rω = rω 0 + крыс.
Радиус r сокращается в уравнении, давая
ω = ω 0 + ат. (константа a )
где ω 0 — начальная угловая скорость. Это последнее уравнение представляет собой кинематическое соотношение между ω , α и t , то есть оно описывает их соотношение без ссылки на силы или массы, которые могут влиять на вращение. Он также точно аналогичен по форме своему трансляционному аналогу.
Выполнение подключений Кинематика вращательного движения полностью аналогична поступательной кинематике, впервые представленной в «Одномерной кинематике».Кинематика занимается описанием движения без учета силы или массы. Мы обнаружим, что поступательные кинематические величины, такие как смещение, скорость и ускорение, имеют прямые аналоги во вращательном движении.Исходя из четырех кинематических уравнений, которые мы разработали в Одномерной кинематике, мы можем вывести следующие четыре кинематических уравнения вращения (представленные вместе с их аналогами для поступательного движения):
| Вращательный | Трансляционный | |
|---|---|---|
| [латекс] \ theta = \ bar {\ omega} t \\ [/ latex] | [латекс] x = \ bar {v} t \\ [/ latex] | |
| ω = ω 0 + αt | v = v o + при | (постоянная α , a ) |
| [латекс] \ theta = {\ omega} _ {0} t + \ frac {1} {2} {\ alpha t} ^ {2} \\ [/ latex] | [латекс] x = {v} _ {0} t + \ frac {1} {2} {\ text {at}} ^ {2} \\ [/ latex] | (постоянная α , a ) |
| ω 2 = ω 0 2 + 2 α θ | v 2 = v o 2 + 2ax | (постоянная α , a ) |
В этих уравнениях индекс 0 обозначает начальные значения ( θ 0 , x 0 и t 0 — начальные значения) и среднюю угловую скорость [латекс] \ bar {\ omega} \\ [/ latex] и средняя скорость [latex] \ bar {v} \\ [/ latex] определяются следующим образом:
[латекс] \ bar {\ omega} = \ frac {{\ omega} _ {0} + \ omega} {2} \ text {и} \ overline {v} = \ frac {{v} _ {0} + v} {2} \\ [/ латекс].
Уравнения, приведенные выше в таблице 1, можно использовать для решения любой задачи вращательной или поступательной кинематики, в которой a и α постоянны.
Стратегия решения проблем вращательной кинематики- Изучите ситуацию, чтобы определить, задействована ли кинематика вращения (вращательное движение) . Должно быть задействовано вращение, но без учета сил или масс, влияющих на движение.
- Определите, что именно необходимо определить в проблеме (определите неизвестные) .Набросок ситуации полезен.
- Составьте список того, что дано или может быть выведено из проблемы, как указано (определить известные) .
- Решите соответствующее уравнение или уравнения для количества, которое необходимо определить (неизвестное) . Может быть полезно думать в терминах трансляционного аналога, потому что теперь вы знакомы с таким движением.
- Подставьте известные значения вместе с их единицами измерения в соответствующее уравнение и получите численные решения вместе с единицами измерения .Обязательно используйте радианы для углов.
- Проверьте свой ответ, чтобы убедиться, что он разумен: Имеет ли смысл ваш ответ ?
Пример 1. Расчет ускорения рыболовной катушки
Глубоководный рыбак ловит большую рыбу, которая отплывает от лодки, выдергивая леску из своей рыболовной катушки. Вся система изначально находится в состоянии покоя, а леска разматывается с катушки на радиусе 4,50 см от оси вращения. Катушке дается угловое ускорение 110 рад / с 2 для 2.00 с, как показано на рисунке 1. (a) Какова конечная угловая скорость барабана? (b) С какой скоростью леска покидает катушку по прошествии 2,00 с? (c) Сколько оборотов делает катушка? (d) Сколько метров лески сошло с катушки за это время?
СтратегияВ каждой части этого примера стратегия такая же, как и для решения задач линейной кинематики. В частности, идентифицируются известные значения и затем ищется взаимосвязь, которая может использоваться для определения неизвестного.
Решение для (а)Здесь даны α и t , и необходимо определить ω . Самым простым уравнением для использования является ω = ω 0 + αt , потому что неизвестное уже находится на одной стороне, а все остальные члены известны. Это уравнение утверждает, что
ω = ω 0 + αt .
Нам также дано, что ω 0 = 0 (начинается с состояния покоя), так что
ω = 0 + (110 рад / с 2 ) (2.00 с) = 220 рад / с
Решение для (b)
Теперь, когда известно ω , скорость v проще всего найти, используя соотношение
v = rω ,
, где радиус r катушки задан равным 4,50 см; таким образом,
v = (0,0450 м) (220 рад / с) = 9,90 м / с.
Еще раз обратите внимание, что радианы всегда должны использоваться в любых вычислениях, касающихся линейных и угловых величин.{2} = \ text {220 рад}. \ End {array} \\ [/ latex]
Преобразование радианов в обороты дает
[латекс] \ theta = (220 \ text {rad}) \ frac {1 \ text {rev}} {2 \ pi \ text {rad}} = 35.0 \ text {rev} \\ [/ latex]
Решение для (d)Количество метров лески x , которое может быть получено через ее соотношение с θ:
x = rθ = (0,0450 м) (220 рад) = 9,90 м.
ОбсуждениеЭтот пример показывает, что отношения между вращательными величинами очень похожи на отношения между линейными величинами.Мы также видим в этом примере, как связаны линейные и вращательные величины. Ответы на вопросы реалистичны. После раскручивания в течение двух секунд катушка вращается со скоростью 220 рад / с, что составляет 2100 об / мин. (Неудивительно, что барабаны иногда издают высокие звуки.) Длина разыгранной лески составляет 9,90 м, что примерно соответствует тому моменту, когда клюет большая рыба.
Рис. 1. Леска, сходящая с вращающейся катушки, движется линейно. В примерах 10.3 и 10.4 рассматриваются отношения между вращательными и линейными величинами, связанными с рыболовной катушкой.
Пример 2. Расчет продолжительности, когда рыболовная катушка замедляется и останавливается
Теперь давайте посмотрим, что произойдет, если рыбак затормозит вращающуюся катушку, получив угловое ускорение -300 рад / с 2 . Как долго катушка останавливается?
СтратегияНам предлагается найти время t , за которое барабан остановится. Начальные и конечные условия отличаются от условий в предыдущей задаче, в которой использовалась та же рыболовная катушка.Теперь мы видим, что начальная угловая скорость равна ω 0 = 220 рад / с, а конечная угловая скорость ω равна нулю. Угловое ускорение составляет α = -300 рад / с 2 . Изучая доступные уравнения, мы видим все величины, но t известны в ω = ω 0 + αt , что упрощает использование этого уравнения.
РешениеУравнение утверждает
ω = ω 0 + αt .{2}} = 0 \ text {.} \ Text {733 s} \\ [/ latex].
ОбсуждениеОбратите внимание, что следует проявлять осторожность со знаками, указывающими направление различных величин. Также обратите внимание, что время остановки барабана довольно мало, потому что ускорение довольно велико. Леска иногда ломается из-за участвующих в ней ускорений, и рыбаки часто позволяют рыбе плавать некоторое время, прежде чем затормозить катушку. Уставшая рыба будет медленнее, требуя меньшего ускорения.
Пример 3. Расчет медленного ускорения поездов и их колес
Большие грузовые поезда очень медленно ускоряются. Предположим, один такой поезд ускоряется из состояния покоя, придавая своим колесам радиусом 0,350 м угловое ускорение 0,250 рад / с 2 . После того, как колеса совершат 200 оборотов (предполагая отсутствие пробуксовки): (а) Как далеко поезд продвинулся по рельсам? б) Какова конечная угловая скорость колес и линейная скорость поезда?
СтратегияВ части (а) нас просят найти x , а в (b) нас просят найти ω и v .Нам даны число оборотов θ , радиус колес r и угловое ускорение α .
Решение для (а)Расстояние x очень легко найти из отношения между расстоянием и углом поворота:
[латекс] \ theta = \ frac {x} {r} \\ [/ latex].
Решение этого уравнения для x дает
x = rθ.
Перед использованием этого уравнения мы должны преобразовать количество оборотов в радианы, потому что мы имеем дело с соотношением между линейными и вращательными величинами:
[латекс] \ theta = \ left (\ text {200} \ text {rev} \ right) \ frac {2 \ pi \ text {rad}} {\ text {1 rev}} = \ text {1257} \ текст {рад} \\ [/ латекс].{1/2} \\ & = & \ text {25,1 рад / с.} \ End {array} \\ [/ latex]
Мы можем найти линейную скорость поезда, v , через ее отношение к ω :
v = rω = (0,350 м) (25,1 рад / с) = 8,77 м / с.
ОбсуждениеПройденное расстояние довольно велико, а конечная скорость довольно мала (чуть менее 32 км / ч).
Существует поступательное движение даже для чего-то, вращающегося на месте, как показано в следующем примере.На рис. 2 изображена муха на краю вращающейся пластины микроволновой печи. В приведенном ниже примере вычисляется общее пройденное расстояние.
Рис. 2. На изображении показана микроволновая пластина. Муха совершает обороты, пока еда разогревается (вместе с мухой).
Пример 4. Расчет расстояния, пройденного мухой на краю плиты микроволновой печи
Человек решает использовать микроволновую печь, чтобы разогреть обед. При этом муха случайно влетает в микроволновку, приземляется на внешний край вращающейся пластины и остается там.Если тарелка имеет радиус 0,15 м и вращается со скоростью 6,0 об / мин, рассчитайте общее расстояние, пройденное мухой за 2,0-минутный период приготовления. (Игнорируйте время запуска и замедления.)
СтратегияСначала найдите общее количество оборотов θ , а затем пройденное линейное расстояние x . [latex] \ theta = \ bar {\ omega} t \\ [/ latex] можно использовать, чтобы найти θ потому что [latex] \ bar {\ omega} \\ [/ latex] задано равным 6,0 об / мин.
РешениеВвод известных значений в [latex] \ theta = \ bar {\ omega} t \\ [/ latex] дает
[латекс] \ theta = \ bar {\ omega} t = \ left (\ text {6.0 об / мин} \ right) \ left (\ text {2.0 min} \ right) = \ text {12 rev} \\ [/ latex].
Как всегда, необходимо преобразовать обороты в радианы перед вычислением линейной величины, такой как x , из угловой величины, такой как θ :
[латекс] \ theta = \ left (\ text {12 rev} \ right) \ left (\ frac {2 \ pi \ text {rad}} {\ text {1 rev}} \ right) = 75,4 \ text { рад} \\ [/ латекс].
Теперь, используя соотношение между x и θ , мы можем определить пройденное расстояние:
x = rθ = (0.15 м) (75,4 рад) = 11 м.
ОбсуждениеНеплохая поездка (если выживет)! Обратите внимание, что это расстояние — это полное расстояние, пройденное мухой. Смещение фактически равно нулю для полных оборотов, потому что они возвращают муху в исходное положение. Различие между общим пройденным расстоянием и перемещением было впервые отмечено в «Одномерной кинематике».
Проверьте свое понимание
Кинематика вращения имеет множество полезных взаимосвязей, часто выражаемых в форме уравнений.Являются ли эти отношения законами физики или они просто описательны? (Подсказка: тот же вопрос относится к линейной кинематике.)
РешениеКинематика вращения (как и линейная кинематика) носит описательный характер и не отражает законы природы. С помощью кинематики мы можем описать многие вещи с большой точностью, но кинематика не учитывает причины. Например, большое угловое ускорение описывает очень быстрое изменение угловой скорости без учета его причины.
Сводка раздела
Задачи и упражнения
1. С помощью струны гироскоп из состояния покоя разгоняется до 32 рад / с за 0,40 с. а) Каково его угловое ускорение в рад / с 2 ? б) Сколько революций происходит в процессе?
2. Допустим, на компакт-диске оказался кусок пыли. Если скорость вращения компакт-диска составляет 500 об / мин, а пылинка находится на расстоянии 4,3 см от центра, какое общее расстояние проходит пыль за 3 минуты? (Игнорируйте ускорения из-за вращения компакт-диска.)
3. Гироскоп замедляется с начальной скорости 32,0 рад / с до 0,700 рад / с 2 . а) Сколько времени нужно, чтобы успокоиться? б) Сколько оборотов он делает до остановки?
4. При очень быстрой остановке автомобиль замедляется со скоростью 700 м / с 2 .
(a) Каково угловое ускорение его шин радиусом 0,280 м, если предположить, что они не скользят по тротуару?
(b) Сколько оборотов делают шины перед остановкой, если их начальная угловая скорость равна 95.0 рад / с?
(c) Сколько времени нужно автомобилю, чтобы полностью остановиться?
(d) Какое расстояние машина проезжает за это время?
(e) Какова была начальная скорость автомобиля?
(f) Кажутся ли полученные значения разумными, учитывая, что эта остановка происходит очень быстро?
Рис. 3. Йо-йо — это забавные игрушки, которые демонстрируют значительную физику и созданы для повышения производительности на основе физических законов. (Источник: Beyond Neon, Flickr)
5. Повседневное применение: Предположим, у йо-йо есть центральный вал с цифрой 0.Радиус 250 см и натягивается его веревка.
(a) Если струна неподвижна и йо-йо ускоряется от нее со скоростью 1,50 м / с 2 , каково угловое ускорение йо-йо?
(б) Какова угловая скорость через 0,750 с, если она начинается из состояния покоя?
(c) Внешний радиус йо-йо составляет 3,50 см. Каково тангенциальное ускорение точки на краю?
Глоссарий
- кинематика вращательного движения:
- описывает отношения между углом поворота, угловой скоростью, угловым ускорением и временем
Избранные решения проблем и упражнения
1.{2} \\ [/ latex] (b) 1.0 rev
3. (а) 45.7 с (б) 116 изм.
5. (а) 600 рад / с 2 (б) 450 рад / с (в) 21,0 м / с
Вращательное движение | Блог Гэри Гарбера
До сих пор в этом семестре нашего изучения классической механики мы изучали поступательное движение. Теперь мы приступим к изучению вращательного движения.
У каждой концепции, которую мы изучили до сих пор, есть вращательный аналог.
В начале года мы обсуждали, как объект может претерпеть смещение x .Мы также могли повернуть объект на угол θ.
Аналогично, скорость объекта или скорость изменения положения
имеет аналог вращения, скорость вращения, скорость изменения угла
ω = Δθ / Δt
Существует также угловое ускорение, которое представляет собой скорость изменения угловой скорости. Мы можем изучить крутящий момент, который представляет собой силу вращения. Момент инерции (или инерции вращения) — это тенденция объекта оставаться в состоянии покоя или оставаться в состоянии вращательного движения.Основываясь на этом, угловой момент — это инерция вращения в состоянии вращательного движения. У нас также может быть кинетическая энергия вращения!
Если мы предположим, что объект непрерывно вращается, то другой способ взглянуть на вращательное движение — это исследовать период вращения, T . Измеряемый в единицах времени ( миллисекунд, секунды, часы, годы, эоны …), период — это время, необходимое для одного полного оборота. Мы также могли бы описать, как часто объект вращается.Частота объекта f обратно пропорциональна периоду вращения.
T = 1 / f
и
ф = 1 / т
Метрическая единица измерения частоты — герцы ( Гц, ), где 1 Гц = 1 циклов в секунду . Вы, вероятно, знакомы с термином Герц по частотам на шкале радиоприемника, например, WBUR 90,9 МГц или WBZ 1030 кГц .
Пример
Представьте себе маленького мальчика, который пытается вызвать головокружение, быстро вращаясь.Если он вращается с частотой 0,8 Гц, сколько времени ему потребуется, чтобы сделать 1 оборот?
f = 0,8 Гц
T = 1 / f = 1 / 0,8 Гц = 1 / 0,8 циклов в секунду = 1,25 секунд
Еще одна традиционная единица измерения частоты — оборотов в минуту или оборотов в минуту . Вы можете увидеть это на старомодном проигрывателе, который мог вращаться со скоростью 33 или 45 об / мин на .
А пока рассмотрим двух маленьких человечков LEGO, стоящих на проигрывателе.Когда проигрыватель поворачивается, мы можем описать движение маленьких человечков LEGO с точки зрения их линейной скорости (метры в секунду) или их скорости вращения. Если мы установим проигрыватель на 45 об / мин, то оба LEGO-человечка будут иметь одинаковую скорость вращения. Однако у них разные линейные или тангенциальные скорости. Мы используем слово «тангенциальный», потому что если человек из LEGO поскользнется и упадет, его собственная инерция заставит его отлететь от проигрывателя по линии, касательной к его круговому движению!
Мы можем рассчитать линейную скорость для каждого человека, используя уравнение
v = 2πr / Т
где r — радиус окружности, а T — период вращения.Помните, что скорость — это расстояние во времени. В этом случае расстояние за один период вращения оказывается длиной окружности.
Если мужчины расположены на нашем проигрывателе на расстоянии 10 см и 4 см от центральной оси:
Пример
f = 45 об / мин
r = 12 см
Сначала вычисляем период. С 45 об / мин = 0,75 об / сек
Таким образом, период вращения равен 1.33 секунд .
Таким образом, скорость будет
v = 2πr / T = 2π (10 см ) / 1,33 с = 47 см / с
Для маленького человечка, стоящего в радиусе 4 см, у него гораздо меньшая линейная скорость, хотя и такая же скорость вращения.
v = 2πr / T = 2π (4 см ) / 1,33 с = 19 см / с
Есть тонкая разница между скоростью вращения и скоростью вращения, которую мы представим позже.
Мы можем определить взаимосвязь между линейной скоростью и угловой скоростью с помощью следующего уравнения
v = ω r
Обратите внимание, что ω, угловая скорость, была определена ранее как изменение угла в единицу времени.
ω = Δθ / Δt
При рассмотрении приведенного выше уравнения возникает интересный вопрос относительно единиц измерения угловой скорости. До сих пор мы использовали такие термины, как обороты в минуту или обороты в секунду. Но революцию можно было бы определить как ПОЛНЫЙ поворот на 360 °.
Вы, наверное, изучали единицы измерения углов в градусах. Но когда мы обсуждаем угловую скорость, мы обычно не говорим об целом числе оборотов. Таким образом, мы могли бы использовать такие единицы измерения, как градусы в секунду. Однако градус не является метрической единицей вращения. Стандартная единица измерения — радиан.
2π радиан = 360 °
Если мы посмотрим на изображение единичного круга, мы сможем увидеть преобразование между радианами и градусами. Это действительно одно и то же, просто разные единицы.
С одной стороны, единственная разница между частотой и угловой скоростью заключается в единицах измерения. Угловая скорость измеряется в радианах в секунду , а частота измеряется в герцах или оборотов в секунду . Таким образом, мы могли бы выразить алгебраическую связь между этими двумя терминами как
2πf = ω
Используя это, мы могли бы фактически найти угловую скорость нашего проигрывателя, который вращается со скоростью 45 об / мин .
ω = 2πf = 2π (0.75 об / с ) = 4,7 радиан / с
Пример
Давайте еще раз посмотрим на человечков LEGO на проигрывателе. Используя соотношение между линейной скоростью и угловой скоростью, находим
v = ω r
v = 4,7 радиан в секунду x 10 см = 47 см / с
и для человека ближе к центру
v = 4,7 радиан в секунду x 4 см = 19 см / с
Важно отметить, что линейная скорость увеличивается как с угловой скоростью, так и с радиусом
Как рассчитать период движения в физике
Обновлено 28 декабря 2020 г.
Крис Дезил
В естественном мире есть множество примеров периодического движения, от орбит планет вокруг Солнца до электромагнитных колебаний фотонов и т. Д. наше собственное сердцебиение.
Все эти колебания связаны с завершением цикла, будь то возвращение движущегося по орбите тела в исходную точку, возврат вибрирующей пружины в точку равновесия или расширение и сжатие сердцебиения. Время, необходимое колебательной системе для завершения цикла, известно как ее период .
Период системы — это мера времени, и в физике он обычно обозначается заглавной буквой T . Период измеряется в единицах времени, подходящих для этой системы, но наиболее распространенными являются секунды.Вторая — это единица времени, первоначально основанная на вращении Земли вокруг своей оси и по ее орбите вокруг Солнца, хотя современное определение основано на колебаниях атома цезия-133, а не на каком-либо астрономическом явлении.
Периоды некоторых систем интуитивно понятны, например, вращение Земли, которое составляет сутки или (по определению) 86 400 секунд. Вы можете рассчитать периоды некоторых других систем, таких как колеблющаяся пружина, используя характеристики системы, такие как масса и жесткость пружины.
Когда дело доходит до колебаний света, все становится немного сложнее, потому что фотоны движутся поперек пространства, пока они колеблются, поэтому длина волны является более полезной величиной, чем период.
Период — величина, обратная частоте
Период — это время, необходимое колебательной системе для завершения цикла, тогда как частота ( f ) — это количество циклов, которое система может завершить за заданный период времени.Например, Земля вращается один раз в день, поэтому период составляет 1 день, а частота также составляет 1 цикл в день. Если вы установите стандарт времени на годы, период составит 1/365 года, а частота — 365 циклов в год. Период и частота являются обратными величинами:
T = \ frac {1} {f}
В расчетах, связанных с атомными и электромагнитными явлениями, частота в физике обычно измеряется в циклах в секунду, также известных как Герцы (Гц), с −1 или 1 / сек. При рассмотрении вращающихся тел в макроскопическом мире число оборотов в минуту (об / мин) также является общепринятой единицей.Период может быть измерен в секундах, минутах или другом подходящем периоде времени.
Период простого гармонического осциллятора
Самый основной тип периодического движения — это движение простого гармонического осциллятора, который определяется как тот, который всегда испытывает ускорение, пропорциональное его расстоянию от положения равновесия и направленное в сторону равновесия. должность. В отсутствие сил трения и маятник, и масса, прикрепленная к пружине, могут быть простыми гармоническими осцилляторами.
Можно сравнить колебания массы на пружине или маятнике с движением тела, вращающегося с равномерным движением по круговой траектории с радиусом r . Если угловая скорость тела, движущегося по окружности, равна ω, его угловое смещение ( θ ) от начальной точки в любой момент времени t составляет θ = ωt , и компоненты x и y его положения равны x = r cos ( ωt ) и y = r sin ( ωt ).
Многие осцилляторы движутся только в одном измерении, а если они движутся горизонтально, они движутся в направлении x . Если амплитуда, наиболее удаленная от положения равновесия, составляет A , то положение в любой момент времени t составляет x = A cos ( ωt ). Здесь ω известна как угловая частота, и она связана с частотой колебаний ( f ) уравнением ω = 2π f .Поскольку f = 1/ T , вы можете записать период колебаний следующим образом:
T = \ frac {2π} {ω}
Пружины и маятники: уравнения периода
Согласно Согласно закону Гука, масса на пружине подвергается действию восстанавливающей силы F = — kx , где k — характеристика пружины, известная как жесткость пружины, а x Это смещение. Знак минус указывает, что сила всегда направлена против направления смещения.Согласно второму закону Ньютона, эта сила также равна массе тела ( m ), умноженной на его ускорение ( a ), поэтому ma = — kx .
Для объекта, колеблющегося с угловой частотой ω , его ускорение равно — Aω 2 cos ωt или, упрощенно, — ω 2 х . Теперь вы можете написать м (- ω 2 x ) = — kx , исключить x и получить ω = √ ( к / м ).Тогда период колебаний массы на пружине равен:
T = 2π \ sqrt {\ frac {m} {k}}
Аналогичные соображения можно применить к простому маятнику, на котором вся масса центрируется на конце строки. Если длина струны составляет L , уравнение периода в физике для малоуглового маятника (т. Е. Такого, в котором максимальное угловое смещение от положения равновесия мало), которое оказывается независимым от массы, имеет вид
T = 2π \ sqrt {\ frac {L} {g}}
, где g — ускорение свободного падения.
Период и длина волны
Как и простой осциллятор, волна имеет точку равновесия и максимальную амплитуду по обе стороны от точки равновесия. Однако, поскольку волна распространяется через среду или пространство, колебания растягиваются вдоль направления движения. Длина волны определяется как поперечное расстояние между любыми двумя идентичными точками в цикле колебаний, обычно точками максимальной амплитуды на одной стороне положения равновесия.
Период волны — это время, за которое одна полная длина волны проходит через контрольную точку, тогда как частота волны — это количество длин волн, которые проходят через контрольную точку за данный период времени. Если период времени равен одной секунде, частота может быть выражена в циклах в секунду (герц), а период выражен в секундах.
Период волны зависит от скорости ее движения и длины волны ( λ ). Волна перемещается на расстояние в одну длину волны за один период времени, поэтому формула скорости волны равна v = λ / T , где v — скорость.Если преобразовать период в другие величины, получим:
T = \ frac {λ} {v}
Например, если волны на озере разделены 10 футами и движутся со скоростью 5 футов в секунду, период каждой волны 10/5 = 2 секунды.
Использование формулы скорости волны
Все электромагнитное излучение, к одному типу которого относится видимый свет, распространяется с постоянной скоростью, обозначенной буквой c , через вакуум. Вы можете написать формулу скорости волны, используя это значение, и поступить так, как обычно делают физики, заменив период волны ее частотой.Формула принимает следующий вид:
c = \ frac {λ} {T} = f × λ
Поскольку c является константой, это уравнение позволяет вычислить длину волны света, если вы знаете его частоту, и наоборот. наоборот. Частота всегда выражается в герцах, и, поскольку свет имеет чрезвычайно малую длину волны, физики измеряют ее в ангстремах (Å), где один ангстрем равен 10 −10 метров.
Детали движения маятника Фуко
Версия этой страницы в формате PDF доступна здесь.
Введение
Этот эксперимент говорит нам, что поверхность Земли не является инерциальной системой отсчета, то есть системой, которая либо находится в состоянии покоя, либо движется с постоянной скоростью в определенном направлении без каких-либо внешних сил. Во вращающихся системах отсчета, например, на поверхности Земли, скорость системы координат постоянно меняет направление. Это то, что в случае маятника заставляет его выглядеть так, как будто угловой момент не сохраняется и законы Ньютона не соблюдаются.Однако, наблюдая из положения покоя в пространстве (инерциальная система отсчета), можно было бы увидеть, что угловой момент на самом деле сохраняется и законы Ньютона соблюдаются.
Можно ожидать, что лучший способ решить эту проблему — это проанализировать механику в инерциальной системе отсчета. На самом деле несколько менее сложно вместо этого использовать неинерциальную вращающуюся раму, прикрепленную к поверхности Земли. Чтобы сделать это, мы должны найти способ перевода из инерциальной системы отсчета в неинерциальную, и следует проявлять осторожность при рассмотрении векторов, в частности их производных по времени, как станет очевидно.
При рассмотрении механики в неинерциальных системах отсчета необходимо учитывать дополнительные силы, которые исчезают в инерциальных системах отсчета. По этой причине эти силы называются фиктивными силами , а те, которые мы рассматриваем здесь, — это центробежные силы и силы Кориолиса . Детали центробежной силы не важны для понимания того, почему плоскость колебаний вращается, однако ее эффекты интересны, и описание естественно вытекает из математики, следующей за этим введением.
Вращающаяся рама
В теле, вращающемся с угловой скоростью, конкретная точка с вектором положения имеет скорость, равную
.| (1) | ||
Фактически для любого вектора (не обязательно вектора положения), закрепленного во вращающемся теле,
| (2) | ||
Таким образом, для единичных векторов и, направленных вдоль осей (восток), (север) и (вверх), закрепленных на поверхности Земли (см. Рисунок 1), мы имеем
| (3) | ||
Рис. 1. Направления осей, и для точки на поверхности Земли с широтой.
Теперь рассмотрим вектор положения частицы в этой системе координат,
| (4) | ||
Обратите внимание, что начало системы координат здесь (где) находится в центре Земли. Скорость изменения этого вектора будет измеряться наблюдателем в инерциальной системе отсчета иначе, чем наблюдателем, стоящим на поверхности Земли. Мы будем использовать для обозначения скорости изменения, измеренной инерционным наблюдателем, и и для обозначения скорости изменения, измеренной неинерциальным наблюдателем на поверхности Земли.Скорость изменения скалярных величин, то есть производных от и, всегда будет одинакова для обоих наблюдателей. Согласно неинерциальному наблюдателю на поверхности Земли, направления единичных векторов постоянны во времени, поэтому
| (5) | ||
Однако для инерциального наблюдателя направления единичных векторов меняются во времени, поэтому мы имеем
| (6) | ||
из уравнений 3 и 4.Применяя ту же формулу, скорость изменения, измеренная инерциальным наблюдателем, составляет
.| (7) | ||
где — скорость изменения, измеренная неинерциальным наблюдателем. Из уравнения 6,
| | ||
Следовательно,
| (8) | ||
Второй закон Ньютона для частицы, движущейся под действием силы тяжести плюс дополнительная сила F, равен
| (9) | ||
, где мы должны учитывать абсолютное ускорение , поскольку уравнение 9 справедливо только в инерциальных системах отсчета.(Если бы вместо этого использовать уравнение 9, то оно не действовало бы). — вектор, направленный к центру Земли, с величиной, равной (). Подставляя уравнение 8 в 9 и переставляя, получаем
| (10) | ||
Уравнение 10 — это уравнение движения частицы в неинерциальной вращающейся системе отсчета. Третий и четвертый члены справа — это силы Кориолиса и центробежные силы соответственно.Пятый член — это сила Эйлера, которой можно пренебречь, поскольку для Земли.
Центробежная сила
Давайте отложим обсуждение силы Кориолиса и сначала сосредоточимся на центробежной силе. Это сила, зависящая от положения, тогда как сила Кориолиса зависит от скорости, что означает, что при любом измерении ускорения свободного падения фактически измеряется эффективное ускорение , обусловленное силой тяжести,
| (11) | ||
Как и следовало ожидать, направление перпендикулярно оси вращения Земли и направлено наружу, таким образом, оно имеет компоненты в направлениях и.Для точки с широтой
| (12) | ||
Таким образом, компоненты и составляют
| (13) | ||
| (14) | ||
и эффект центробежной силы заключается в уменьшении величины ускорения свободного падения и небольшом изменении его направления; в северном полушарии отвес отклонен на юг, а в южном полушарии — на север.
На экваторе () составляющая исчезает и составляющая имеет максимальное значение, тогда как на полюсах () обе составляющие обращаются в нуль. Таким образом, ускорение свободного падения будет меньше на экваторе, чем на полюсах. Это усугубляется тем фактом, что радиус Земли на полюсах меньше, чем на экваторе, что, кстати, связано с центробежной силой. Общий эффект заключается в том, что на экваторе человек весит меньше, чем на полюсах, хотя для читателей, интересующихся похуданием, существуют более простые и экономичные методы.
Сила Кориолиса
Прежде чем углубляться в математику силы Кориолиса, полезно попытаться визуализировать ее действие. Пренебрегая трением, рассмотрим диск, вращающийся против часовой стрелки, при этом частица выстреливается поперек диаметра. Стоя неподвижно (инерциальная рамка) и наблюдая, как диск вращается перед вами, если бы вы катили шар по диаметру диска, вы бы увидели, что шар движется по прямой линии через центр диска. Однако если бы вы вращались вместе с диском (неинерциальная система отсчета) и таким же образом катили шар по направлению к центру, вы бы увидели, что частица отклоняется вправо, как если бы она была подвержена силе, действующей перпендикулярно скорости частицы. .Эта сила и есть сила Кориолиса, и здесь находится хорошее визуальное дополнение к этому описанию. Теперь мы снова обращаем внимание на Землю и представляем, что стоим на Северном полюсе. Если пренебречь сопротивлением воздуха, то птица, летящая на юг, будет, по-видимому, следовать слегка изогнутой траектории на запад, тогда как наблюдатель, наблюдающий из космоса в состоянии покоя, увидит птицу, летящую по прямой линии, в то время как Земля вращается под ней.
В нашем маятнике мы предполагаем, что расстояние, на которое движется боб, достаточно мало, чтобы гравитационные и центробежные силы можно было рассматривать как постоянные, и мы объединяем их вместе в постоянное эффективное ускорение силы тяжести.Из уравнения 10 уравнение движения теперь принимает вид
.| (15) | ||
В нашей системе координат с единичными векторами и, указывая на восток, север и вверх соответственно, угловая скорость точки на поверхности Земли с широтой составляет
| (16) | ||
Отсюда для силы Кориолиса получаем
| (17) | ||
В первую очередь мы занимаемся горизонтальным движением в плоскости.Вертикальной составляющей силы Кориолиса можно пренебречь, поскольку она обеспечивает небольшую поправку к, при этом знак меняется на каждом полупериоде. Предполагая, что длина маятника большая, а амплитуда колебаний сравнительно мала, скоростью в -направлении можно пренебречь () и мы можем использовать приближение малого угла () для угла, который маятник образует с вертикалью. (его положение покоя). Таким образом, из уравнений 15 и 17, предполагая, что нет дополнительных внешних сил (), мы получаем уравнения движения маятника в направлениях и,
| (18) | ||
| (19) | ||
Первые члены в правой части представляют собой знакомые восстанавливающие силы для маятника, демонстрирующего простое гармоническое движение, а вторые члены представляют собой вклады силы Кориолиса.Чтобы получить явное решение этих уравнений, мы можем умножить уравнение 19 на мнимую единицу и добавить его к уравнению 18, получив
| (20) | ||
где и — собственная угловая частота колебаний, то есть частота простых гармонических колебаний в отсутствие силы Кориолиса. Уравнение 20 напоминает уравнение движения для затухающего маятника, за исключением мнимого «демпфирующего» члена.Мы ищем решения этого уравнения формы и подставляя его в уравнение 20, получаем
| | ||
| (21) | ||
где, поскольку частота вращения Земли намного меньше частоты колебаний маятника (). Следовательно, решение
| (22) | ||
Термины в скобках описывают простое гармоническое движение с частотой и являются константами, фиксируемыми начальными условиями.Следовательно, можно ожидать, что предварительный фактор — это член, который расскажет нам о вращении плоскости колебаний. Отбросив условия SHO и взяв действительную часть, получим
| (23) | ||
Определив как период вращения плоскости колебаний, понятно, так
| | ||
| | ||
| (24) | ||
Значение для Земли в удобных единицах равно.Отсюда получаем, что период вращения плоскости колебаний маятника Фуко равен
.| (25) | ||
Из уравнения 23 мы также можем найти угол, на который плоскость колебаний поворачивается за один час, найдя значение аргумента косинуса для часа, таким образом,
| (26) | ||
Широта Уорикского университета составляет 52 ° 22 ’48’ ‘(52 градуса, 22 минуты и 48 секунд).Подставляя это в уравнения 25 и 26, получаем значения 30,3 часа и 11,9 °. Желтые линии на напольном дисплее разделены этим углом.
10.2 Кинематика вращательного движения — College Physics chapters 1-17
Сводка
- Соблюдайте кинематику вращательного движения.
- Составьте кинематические уравнения вращения.
- Оценить стратегии решения проблем для вращательной кинематики.
Просто используя нашу интуицию, мы можем начать видеть, как вращательные величины, такие как [латекс] \ boldsymbol {\ theta}, \: \ boldsymbol {\ omega}, [/ latex] и [латекс] \ boldsymbol {\ alpha} [ / latex] связаны друг с другом. Например, если колесо мотоцикла имеет большое угловое ускорение в течение довольно длительного времени, оно быстро вращается и совершает много оборотов. Говоря более техническим языком, если угловое ускорение колеса [латекс] \ boldsymbol {\ alpha} [/ latex] велико в течение длительного периода времени [латекс] \ boldsymbol {t}, [/ latex], то конечная угловая скорость [ latex] \ boldsymbol {\ omega} [/ latex] и угол поворота [latex] \ boldsymbol {\ theta} [/ latex] большие.Вращательное движение колеса в точности аналогично тому, что большое поступательное ускорение мотоцикла дает большую конечную скорость, и пройденное расстояние также будет большим.
Кинематика — это описание движения. Кинематика вращательного движения описывает отношения между углом вращения, угловой скоростью, угловым ускорением и временем. Начнем с поиска уравнения, связывающего [латекс] \ boldsymbol {\ omega}, \: \ boldsymbol {\ alpha}, [/ latex] и [латекс] \ boldsymbol {t}.[/ latex] Чтобы определить это уравнение, вспомним известное кинематическое уравнение для поступательного или прямолинейного движения:
[латекс] \ boldsymbol {v = v_0 + at \ textbf {(константа a)}} [/ latex]
Обратите внимание, что во вращательном движении [латекс] \ boldsymbol {a = a _ {\ textbf {t}}}, [/ latex] и мы будем использовать символ [латекс] \ boldsymbol {a} [/ latex] для тангенциального или линейного ускорение с этого момента. Как и в линейной кинематике, мы предполагаем, что [латекс] \ boldsymbol {a} [/ latex] является постоянным, что означает, что угловое ускорение [латекс] \ boldsymbol {\ alpha} [/ latex] также является постоянным, потому что [латекс] \ жирный символ {a = r \ alpha}.[/ latex] Теперь давайте заменим [latex] \ boldsymbol {v = r \ omega} [/ latex] и [latex] \ boldsymbol {a = r \ alpha} [/ latex] в приведенное выше линейное уравнение:
[латекс] \ boldsymbol {r \ omega = r \ omega_0 + r \ alpha {t}}. [/ Latex]
Радиус [латекс] \ boldsymbol {r} [/ latex] сокращается в уравнении, давая
[латекс] \ boldsymbol {\ omega = \ omega_0 + at \ textbf {(константа a),}} [/ latex]
где [латекс] \ boldsymbol {\ omega_0} [/ latex] — начальная угловая скорость. Это последнее уравнение представляет собой кинематическое соотношение между [latex] \ boldsymbol {\ omega}, \: \ boldsymbol {\ alpha}, [/ latex] и [latex] \ boldsymbol {t} [/ latex], то есть, он описывает их отношения без ссылки на силы или массы, которые могут повлиять на вращение.Он также точно аналогичен по форме своему трансляционному аналогу.
ПОДКЛЮЧЕНИЕ
Кинематика вращательного движения полностью аналогична поступательной кинематике, впервые представленной в главе 2 «Одномерная кинематика». Кинематика занимается описанием движения без учета силы или массы. Мы обнаружим, что поступательные кинематические величины, такие как смещение, скорость и ускорение, имеют прямые аналоги во вращательном движении.
Исходя из четырех кинематических уравнений, которые мы разработали в главе 2 «Одномерная кинематика», мы можем вывести следующие четыре кинематических уравнения вращения (представленные вместе с их аналогами для поступательного движения):
| Вращающийся | Трансляционный | |
|---|---|---|
| [латекс] \ boldsymbol {\ theta = \ bar {\ omega} t} [/ латекс] | [латекс] \ boldsymbol {x = \ bar {v} t} [/ латекс] | |
| [латекс] \ boldsymbol {\ omega = \ omega_0 + \ alpha {t}} [/ латекс] | [латекс] \ boldsymbol {v = v_0 + at} [/ латекс] | (константа [латекс] \ boldsymbol {\ alpha, \: a} [/ latex]) |
| [латекс] \ boldsymbol {\ omega = \ omega_0 {t} + \ frac {1} {2} \ alpha {t} ^ 2} [/ latex] | [латекс] \ boldsymbol {x = v_0t + \ frac {1} {2} at ^ 2} [/ latex] | (константа [латекс] \ boldsymbol {\ alpha, \: a} [/ latex]) |
| [латекс] \ boldsymbol {\ omega ^ 2 = \ omega_0 ^ 2 + 2 \ alpha \ theta} [/ latex] | [латекс] \ boldsymbol {v ^ 2 = v_0 ^ 2 + 2ax} [/ латекс] | (константа [латекс] \ boldsymbol {\ alpha, \: a} [/ latex]) |
| Таблица 2. Вращательные кинематические уравнения. | ||
В этих уравнениях индекс 0 обозначает начальные значения ([latex] \ boldsymbol {\ theta_0}, \: \ boldsymbol {x_0}, [/ latex] и [latex] \ boldsymbol {t_0} [/ latex] — начальные значения), а средняя угловая скорость [латекс] \ boldsymbol {\ bar {\ omega}} [/ latex] и средняя скорость [латекс] \ boldsymbol {\ bar {v}} [/ latex] определяются следующим образом :
[латекс] \ boldsymbol {\ bar {\ omega} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {\ omega_0 + \ omega} {2}} [/ latex] [латекс] \ textbf {и } \ boldsymbol {\ bar {v} \: =} [/ latex] [латекс] \ boldsymbol {\ frac {v_0 + v} {2}}.[/ латекс]
Уравнения, приведенные выше в таблице 2, могут использоваться для решения любой задачи вращательной или поступательной кинематики, в которой [latex] \ boldsymbol {a} [/ latex] и [latex] \ boldsymbol {\ alpha} [/ latex] являются постоянными.
СТРАТЕГИЯ РЕШЕНИЯ ПРОБЛЕМ ДЛЯ ВРАЩАТЕЛЬНОЙ КИНЕМАТИКИ
- Изучите ситуацию, чтобы определить, задействована ли кинематика вращения (вращательное движение) . Должно быть задействовано вращение, но без учета сил или масс, влияющих на движение.
- Определите, что именно необходимо определить в проблеме (определите неизвестные) . Набросок ситуации полезен.
- Составьте список того, что дано или может быть выведено из проблемы, как указано (определить известные) .
- Решите соответствующее уравнение или уравнения для количества, которое необходимо определить (неизвестное) . Может быть полезно думать в терминах трансляционного аналога, потому что теперь вы знакомы с таким движением.
- Подставьте известные значения вместе с их единицами измерения в соответствующее уравнение и получите численные решения вместе с единицами измерения . Обязательно используйте радианы для углов.
- Проверьте свой ответ, чтобы убедиться, что он разумен: Имеет ли смысл ваш ответ ?
Пример 1: Расчет ускорения рыболовной катушки
Глубоководный рыбак ловит большую рыбу, которая отплывает от лодки, выдергивая леску из своей рыболовной катушки.2} [/ latex] в течение 2,00 с, как показано на рисунке 1.
(а) Какова конечная угловая скорость мотовила?
(b) С какой скоростью леска покидает катушку по истечении 2,00 с?
(c) Сколько оборотов делает катушка?
(d) Сколько метров лески сошло с катушки за это время?
Стратегия
В каждой части этого примера стратегия такая же, как и для решения задач линейной кинематики. В частности, идентифицируются известные значения и затем ищется взаимосвязь, которая может использоваться для определения неизвестного.
Решение для (а)
Здесь даны [латекс] \ boldsymbol {\ alpha} [/ latex] и [latex] \ boldsymbol {t} [/ latex] и необходимо определить [latex] \ boldsymbol {\ omega} [/ latex]. Самым простым в использовании уравнением является [латекс] \ boldsymbol {\ omega = \ omega_0 + \ alpha {t}} [/ latex], потому что неизвестное уже на одной стороне, а все остальные термины известны. Это уравнение утверждает, что
[латекс] \ boldsymbol {\ omega = \ omega_0 + \ alpha {t}. 2) (2.00 \ textbf {s}) = 220 \ textbf {рад / с.}} [/ Latex]
Решение для (b)
Теперь, когда [латекс] \ boldsymbol {\ omega} [/ latex] известен, скорость [латекс] \ boldsymbol {v} [/ latex] легче всего найти с помощью соотношения
[латекс] \ boldsymbol {v = r \ omega,} [/ латекс]
, где радиус [латекс] \ boldsymbol {r} [/ латекс] катушки задан равным 4,50 см; таким образом,
[латекс] \ boldsymbol {v = (0,0450 \ textbf {m}) (220 \ textbf {rad / s}) = 9.90 \ textbf {m / s.}} [/ Latex]
Еще раз обратите внимание, что радианы всегда должны использоваться в любых вычислениях, касающихся линейных и угловых величин.Кроме того, поскольку радианы безразмерны, мы имеем [latex] \ boldsymbol {\ textbf {m} \ times \ textbf {rad} = \ textbf {m}}. [/ Latex]
Решение для (c)
Здесь нас просят найти количество оборотов. Поскольку [latex] \ boldsymbol {1 \ textbf {rev} = 2 \ pi \ textbf {rad}}, [/ latex], мы можем узнать количество оборотов, найдя [latex] \ boldsymbol {\ theta} [/ latex] в радианах. 2}.2 = 220 \ textbf {рад.}} \ End {array} [/ latex]
Преобразование радианов в обороты дает
[латекс] \ boldsymbol {\ theta = (220 \ textbf {rad})} [/ latex] [латекс] \ boldsymbol {\ frac {1 \ textbf {rev}} {2 \ pi \ textbf {rad}}} [/ latex] [latex] \ boldsymbol {= 35.0 \ textbf {rev.}} [/ latex]
Решение для (d)
Длина лески [latex] \ boldsymbol {x}, [/ latex] в метрах может быть получена через ее связь с [latex] \ boldsymbol {\ theta}: [/ latex]
[латекс] \ boldsymbol {x = r \ theta = (0.0450 \ textbf {m}) (220 \ textbf {rad}) = 9.90 \ textbf {m}}. [/ Latex]
Обсуждение
Этот пример показывает, что отношения между вращательными величинами очень похожи на отношения между линейными величинами. Мы также видим в этом примере, как связаны линейные и вращательные величины. Ответы на вопросы реалистичны. После раскручивания в течение двух секунд катушка вращается со скоростью 220 рад / с, что составляет 2100 об / мин. 2}} [/ latex] [латекс] \ boldsymbol {= 0.733 \ textbf {s.}} [/ Latex]
Обсуждение
Обратите внимание, что следует проявлять осторожность со знаками, указывающими направление различных величин. Также обратите внимание, что время остановки барабана довольно мало, потому что ускорение довольно велико. Леска иногда ломается из-за участвующих в ней ускорений, и рыбаки часто позволяют рыбе плавать некоторое время, прежде чем затормозить катушку. Уставшая рыба будет медленнее, требуя меньшего ускорения.
Пример 3: Расчет медленного ускорения поездов и их колес
Большие грузовые поезда очень медленно ускоряются.2}. [/ Latex] После того, как колеса сделали 200 оборотов (предположим, что проскальзывания нет): (a) Как далеко поезд продвинулся по рельсам? б) Какова конечная угловая скорость колес и линейная скорость поезда?
Стратегия
В части (a) нас просят найти [latex] \ boldsymbol {x}, [/ latex], а в (b) нас просят найти [latex] \ boldsymbol {\ omega} [/ latex] и [ латекс] \ boldsymbol {v}. [/ latex] Нам даны количество оборотов [латекс] \ boldsymbol {\ theta}, [/ latex] радиус колес [латекс] \ boldsymbol {r}, [/ латекс ] и угловое ускорение [латекс] \ boldsymbol {\ alpha}.[/ латекс]
Решение для (а)
Расстояние [латекс] \ boldsymbol {x} [/ latex] очень легко найти из зависимости между расстоянием и углом поворота:
[латекс] \ boldsymbol {\ theta \: =} [/ latex] [латекс] \ boldsymbol {\ frac {x} {r}}. [/ Latex]
Решение этого уравнения для [latex] \ boldsymbol {x} [/ latex] дает
[латекс] \ boldsymbol {x = r \ theta}. [/ Latex]
Перед использованием этого уравнения мы должны преобразовать количество оборотов в радианы, потому что мы имеем дело с соотношением между линейными и вращательными величинами:
[латекс] \ boldsymbol {\ theta = (200 \ textbf {rev})} [/ latex] [латекс] \ boldsymbol {\ frac {2 \ pi \ textbf {rad}} {1 \ textbf {rev}}} [/ латекс] [латекс] \ boldsymbol {= 1257 \ textbf {рад. 2 + 2 \ alpha \ theta} [/ латекс]
Извлечение квадратного корня из этого уравнения и ввод известных значений дает
[латекс] \ begin {array} {lcl} \ boldsymbol {\ omega} & \ boldsymbol {=} & \ boldsymbol {[0 + 2 (0.{1/2}} \\ {} & \ boldsymbol {=} & \ boldsymbol {25.1 \ textbf {rad / s.}} \ End {array} [/ latex]
Мы можем найти линейную скорость поезда, [latex] \ boldsymbol {v}, [/ latex] через его связь с [latex] \ boldsymbol {\ omega}: [/ latex]
[латекс] \ boldsymbol {v = r \ omega = (0.350 \ textbf {m}) (25.1 \ textbf {rad / s}) = 8.77 \ textbf {m / s.}} [/ Latex]
Обсуждение
Пройденное расстояние довольно велико, а конечная скорость довольно мала (чуть менее 32 км / ч).
Существует поступательное движение даже для чего-то, вращающегося на месте, как показано в следующем примере. На рис. 2 изображена муха на краю вращающейся пластины микроволновой печи. В приведенном ниже примере вычисляется общее пройденное расстояние.
Рис. 2. На изображении показана микроволновая пластина. Муха совершает обороты, пока еда разогревается (вместе с мухой).Пример 4: Расчет расстояния, пройденного мухой на краю плиты микроволновой печи
Человек решает использовать микроволновую печь, чтобы разогреть обед.При этом муха случайно влетает в микроволновку, приземляется на внешний край вращающейся пластины и остается там. Если тарелка имеет радиус 0,15 м и вращается со скоростью 6,0 об / мин, рассчитайте общее расстояние, пройденное мухой за 2,0-минутный период приготовления. (Игнорируйте время запуска и замедления.)
Стратегия
Сначала найдите общее количество оборотов [latex] \ boldsymbol {\ theta}, [/ latex], а затем линейное расстояние [latex] \ boldsymbol {x} [/ latex], пройденное.[latex] \ boldsymbol {\ theta = \ bar {\ omega} t} [/ latex] можно использовать для поиска [latex] \ boldsymbol {\ theta} [/ latex], потому что [latex] \ boldsymbol {\ bar {\ omega}} [/ latex] задано 6,0 об / мин.
Решение
Ввод известных значений в [latex] \ boldsymbol {\ theta = \ bar {\ omega} t} [/ latex] дает
[латекс] \ boldsymbol {\ theta = \ bar {\ omega} t = (6.0 \ textbf {rpm}) (2.0 \ textbf {min}) = 12 \ textbf {rev}.} [/ Latex]
Как всегда, необходимо преобразовать обороты в радианы перед вычислением линейной величины, такой как [latex] \ boldsymbol {x} [/ latex], из угловой величины, такой как [latex] \ boldsymbol {\ theta}: [/ latex]
[латекс] \ boldsymbol {\ theta = (12 \ textbf {rev})} [/ latex] [латекс] \ boldsymbol {\ frac {2 \ pi \ textbf {rad}} {1 \ textbf {rev}}} [/ латекс] [латекс] \ boldsymbol {= 75.4 \ textbf {rad}.} [/ Latex]
Теперь, используя соотношение между [latex] \ boldsymbol {x} [/ latex] и [latex] \ boldsymbol {\ theta}, [/ latex], мы можем определить пройденное расстояние:
[латекс] \ boldsymbol {x = r \ omega = (0.15 \ textbf {m}) (75.4 \ textbf {rad}) = 11 \ textbf {m}}. [/ Latex]
Обсуждение
Неплохая поездка (если выживет)! Обратите внимание, что это расстояние — это полное расстояние, пройденное мухой. Смещение фактически равно нулю для полных оборотов, потому что они возвращают муху в исходное положение.Различие между общим пройденным расстоянием и перемещением было впервые отмечено в главе 2 «Одномерная кинематика».
Проверьте свое понимание
1: Кинематика вращения имеет множество полезных взаимосвязей, часто выражаемых в форме уравнений. Являются ли эти отношения законами физики или они просто описательны? (Подсказка: тот же вопрос относится к линейной кинематике.)
Задачи и упражнения
1: С помощью струны гироскоп ускоряется из состояния покоя до 32 рад / с за 0.40 с.
(а) Каково его угловое ускорение в рад / с 2 ?
(б) Сколько оборотов он совершает в процессе?
2: Предположим, на компакт-диске оказался кусок пыли. Если скорость вращения компакт-диска составляет 500 об / мин, а пылинка находится на расстоянии 4,3 см от центра, какое общее расстояние проходит пыль за 3 минуты? (Игнорируйте ускорения из-за вращения компакт-диска.)
3: Гироскоп замедляется с начальной скорости 32.2}. [/ Латекс]
(a) Каково угловое ускорение его шин радиусом 0,280 м, если предположить, что они не скользят по тротуару?
(b) Сколько оборотов делают шины перед остановкой, учитывая их начальную угловую скорость [латекс] \ boldsymbol {95.0 \ textbf {rad / s}} [/ latex]?
(c) Сколько времени нужно автомобилю, чтобы полностью остановиться?
(d) Какое расстояние машина проезжает за это время?
(e) Какова была начальная скорость автомобиля?
(f) Кажутся ли полученные значения разумными, учитывая, что эта остановка происходит очень быстро?
Рисунок 3.2}, [/ latex] какое угловое ускорение у йо-йо?(б) Какова угловая скорость через 0,750 с, если она начинается из состояния покоя?
(c) Внешний радиус йо-йо составляет 3,50 см. Каково тангенциальное ускорение точки на краю?
Глоссарий
- кинематика вращательного движения
- описывает отношения между углом поворота, угловой скоростью, угловым ускорением и временем
Решения
Проверьте свое понимание
1: Кинематика вращения (как и линейная кинематика) носит описательный характер и не отражает законы природы.





 Как изменится модуль ее центростремительного ускорения, если скорость точки увеличить вдвое?
Как изменится модуль ее центростремительного ускорения, если скорость точки увеличить вдвое?