Самоиндукция. Индуктивность

 «Науку часто смешивают с знанием.

Это глубокое недоразумение.

Наука есть не только знание, но и сознание,

т.е. умение пользоваться знанием»

В.О. Ключевский

Явление электромагнитной индукции состоит в том, что в замкнутом контуре при изменении магнитного потока в нем возникает электрический ток, который называют индукционным.

Закон электромагнитной индукции гласит: среднее значение ЭДС индукции в проводящем контуре пропорционально скорости изменения магнитного потока через поверхность, ограниченную контуром.

Знак «минус», в математической записи закона, учитывает правило Ленца, согласно которому электромагнитная индукция создает в контуре индукционный ток такого направления, что созданное им магнитное поле препятствует изменению магнитного потока, вызывающего этот ток.

Электромагнитная индукция проявляется во всех случаях изменения магнитного потока через поверхность, ограниченную контуром. Современник Фарадея американский физик Джозеф Генри независимо от своего английского коллеги открыл некоторые из электромагнитных эффектов. В 1829 году Генри обнаружил, что ЭДС индукции возникает в неподвижном контуре и в отсутствии изменения внешнего магнитного поля. Оказалось, что изменяющийся электрический ток, проходящий в контуре, создает изменяющийся магнитный поток. Это явление было названо явлением самоиндукции

.

Примечательно то, что и Генри и Фарадей работали над одной и той же проблемой. И пришли к одним и тем же выводам, касающихся как явления электромагнитной индукции, так и явления самоиндукции. При этом, Генри сделал свои открытия на несколько лет раньше, чем Майкл Фарадей. Но Генри был безответственно нетороплив при опубликовании результатов экспериментов, и Фарадей первым сообщил о своем успехе. Наконец, приоритет открытия электромагнитной индукции был отдан Фарадею, а Генри — открытие явления самоиндукции, которое он описал в той же самой статье, что и явление индукции,— в 1832 г.

Самоиндукция является важным частным случаем явления электромагнитной индукции. Если электрический ток в замкнутом проводящем контуре по каким-либо причинам изменяется, то изменяется и магнитное поле этого тока (т.е. индукция магнитного поля пропорциональна силе тока в контуре). Но при изменении индукции магнитного поля, создаваемого током, проходящим в контуре, изменяется и магнитный поток (т.е. магнитный поток будет пропорционален индукции магнитного поля). Следовательно, магнитный поток через поверхность, ограниченную контуром, пропорционален силе тока в контуре

.

Коэффициент пропорциональности между магнитным потоком и силой тока Томсон (в последствии лорд Кельвин) в 1853 году предложил назвать «коэффициентом самоиндукции».

Коэффициент самоиндукции, который часто называют просто индуктивностью контура, обозначают L.

Индуктивность в СИ измеряют в Гн (генри).

[L] = [Гн]

Эта единица определяется на основании формулы

Индуктивность контура равна 1 Гн, если при силе постоянного тока в контуре 1 А магнитный поток через поверхность, ограниченную этим контуром, равен 1 Вб.

Индуктивность зависит от размеров и формы контура, а также от магнитных свойств среды, в которой этот контур находится.

Например, если взять однослойный соленоид, то его индуктивность будет определяться по формуле

где  — это число витков, приходящихся на единицу длины соленоида,

S — площадь поверхности, ограниченной витком,

l — длина соленоида,

m — магнитная проницаемость среды.

Из формулы для магнитного потока следует, что изменить его можно изменяя силу тока в контуре, или его индуктивность, или и то и другое одновременно.

Согласно закону электромагнитной индукции изменяющийся магнитный поток создает в контуре ЭДС. Возникновение ЭДС индукции в контуре, которое вызвано изменением магнитного поля тока, проходящего в этом же контуре, называют явлением самоиндукции, а появляющуюся ЭДС — электродвижущей силой самоиндукции или ЭДС самоиндукции.

Обозначается ЭДС самоиндукции греческой буквой x_Si. Измеряется ЭДС самоиндукции в В (вольт).

[x_Si] = [В]

По закону электромагнитной индукции среднее значение ЭДС самоиндукции, возникающей в контуре прямо пропорциональна индуктивности контура и скорости изменения силы тока в контуре (при учете, что индуктивность контура остается постоянной).

Из этой формулы следует, что индуктивность — это физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

Используя это выражение, можно дать второе определение единицы индуктивности: элемент электрической цепи обладает индуктивностью в 1 Гн, если при равномерном изменении силы тока в цепи на 1 А за 1 с в нем возникает ЭДС самоиндукции 1 В.

Поскольку контур замкнут, ЭДС самоиндукции создает в нем ток самоиндукции, силу которого определяют по закону Ома

где R — сопротивление контура.

Знак минус в формуле для ЭДС самоиндукции учитывает правило Ленца, согласно которому ток самоиндукции всегда направлен так, что он противодействует изменению тока, создаваемого источником. Если основной ток возрастает, то ток самоиндукции направлен против тока источника, если уменьшается, то направление тока источника и тока самоиндукции совпадают.

Как же пронаблюдать явление самоиндукции?

Для этого соберем электрическую цепь, состоящую из катушки с большой индуктивностью, резистора с электрическим сопротивлением, равным сопротивлению обмотки катушки, двух одинаковых лампочек, ключа и источника постоянного тока.

При замыкании цепи лампочка 2 начинает светиться практически сразу, а лампочка 1 с заметным опозданием. Происходит это из-за того, что при возрастании силы тока I₁, созданного источником, на участке, образованном катушкой и лампочкой 1, ЭДС самоиндукции в катушке имеет такую полярность, что создаваемый ею ток самоиндукции направлен навстречу тока источника. В результате  рост силы тока на этом участке цепи замедляется, и сила тока не сразу достигает своего максимального значения.

Явление самоиндукции можно также пронаблюдать и при размыкании цепи. Для этого соберем цепь, состоящую из катушки с большим количеством витков, намотанных на железном сердечнике, к зажимам которой параллельно подключена лампочка с большим электрическим сопротивлением по сравнению с сопротивлением обмотки катушки. В качестве источника тока возьмем источник с небольшим ЭДС.

При размыкании ключа сохраняется замкнутой часть цепи, состоящая из уже последовательно соединенных катушки и лампочки.

Пока ключ замкнут, лампочка будет тускло светиться, так как отношение сил токов, проходящих через лампочку и катушку, обратно отношению их сопротивлений.

Однако при размыкании ключа можно увидеть, что лампочка ярко вспыхивает.

Почему это происходит?

Все дело в том, что при размыкании цепи сила тока в катушке убывает, что приводит к возникновению ЭДС самоиндукции. Возникающий в цепи ток самоиндукции, согласно правилу Ленца, совпадает по направлению с током катушки, не позволяя ему резко уменьшать силу тока. Это и обеспечивает вспышку лампочки.

Заметим, что явление самоиндукции имеет место в любых случаях изменения силы тока в цепи, содержащей индуктивность, или изменения самой индуктивности.

Вообще, явление самоиндукции подобно явлению инерции в механике.

Известно, что автомобиль не может мгновенно приобрести определенное значение скорости, как не может и мгновенно остановиться, как бы  велика не была тормозящая сила.

Точно так же, за счет самоиндукции при замыкании цепи, сила тока не сразу достигает своего максимального значения, а нарастает постепенно. При выключении источника, ток сразу не прекращается — самоиндукция будет поддерживать его некоторое время, даже не смотря на большое сопротивление цепи.

Упражнения.

Задача: За промежуток времени 9,5 мс сила тока в катушке индуктивности равномерно возросла от 1,6 А до 2,4 А. При этом в катушке возникла ЭДС самоиндукции –14 В. Определите собственный магнитный поток в конце процесса нарастания тока.

Основные выводы:

– Явление возникновения ЭДС индукции в электрической цепи в результате изменения силы тока в этой же цепи, называют явлением самоиндукции.

– ЭДС самоиндукции равна произведению индуктивности контура и скорости изменения силы тока в нем.

– Индуктивность — это физическая величина, численно равная ЭДС самоиндукции, возникающей в контуре при изменении силы тока на 1 А за 1 с.

– Единицей измерения индуктивности в СИ является Гн (генри).

– Индуктивность контура равна 1 Гн, если при силе тока в контуре 1 А магнитный поток через поверхность, ограниченную этим контуром, равен 1 Вб.

Физика

№1

План работы учащегося 11 класса по физике

 

4 четверть «Физический практикум»

Урок № 82/1

Тема урока: «Измерение индуктивности катушки»

1.Цель: учащийся приобретает навыки вычисление индуктивного сопротивления катушки и ее индуктивности по результатам измерений напряжений на катушке и силы тока в цепи.

Оборудование: источник переменного напряжения; катушка школьного разборного трансформатора; вольтметр и миллиамперметр переменного тока; соединительные провода.

 

2.Теория.

   Всякое изменение тока в катушке вызывает появление в ней ЭДС самоиндукции, препятствующей изменению тока. Величина ЭДС самоиндукции прямо пропорциональна величине индуктивности катушки и скорости изменения тока в ней. Но так как переменный ток непрерывно изменяется, то непрерывно возникающая в катушке ЭДС самоиндукции создает сопротивление переменному току. Она препятствует его возрастанию и, наоборот, поддерживает его при убывании. Таким образом, в катушке индуктивности, включенной в цепь переменного тока, создается сопротивление прохождению тока. Но так как такое сопротивление вызывается в конечном счете индуктивностью катушки, то и называется оно индуктивным сопротивлением.

   Индуктивное сопротивление обозначается через Х_L и измеряется, как и активное сопротивление, в омах. Индуктивное сопротивление цепи тем больше, чем больше частота тока, питающего цепь, и чем больше индуктивность цепи. Следовательно, индуктивное сопротивление цепи прямо пропорционально частоте тока и индуктивности цепи; определяется оно по формуле:

 Х_L=ωL , где ω — круговая частота, определяемая произведением 2πν, L — индуктивность цепи в генри (Гн).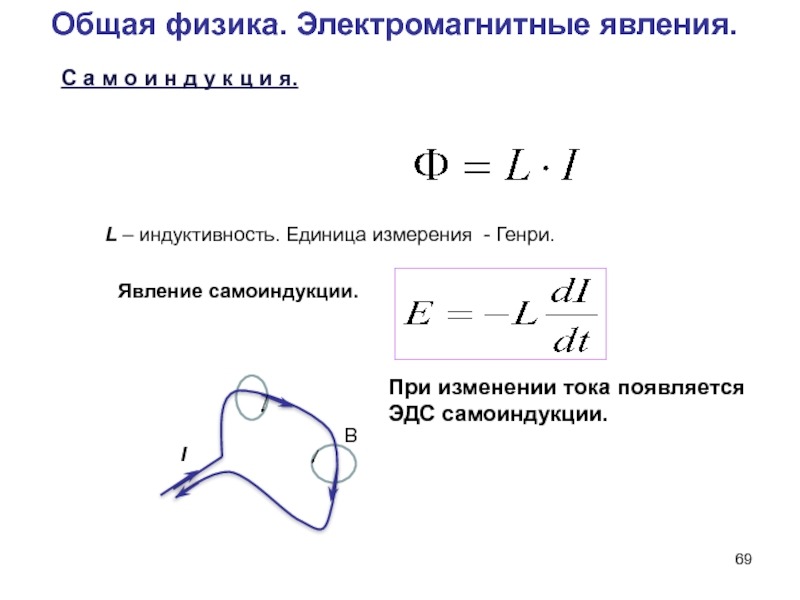

   Т.е.

   Тогда индуктивность катушки можно выразить:

   Закон Ома для цепи переменного тока, содержащей индуктивное сопротивление, звучит так: величина тока прямо пропорциональна напряжению и обратно пропорциональна  индуктивному сопротивлению цепи, т. е

   , где I и U  — действующие значения тока и напряжения, а Х_L — индуктивное сопротивление цепи. 

1. С помощью регулятора напряжения подают на схему напряжение 1,5 В и устанавливают частоту переменного тока 80 Гц. Записывают  показания миллиамперметра.

2. Увеличивая частоту в 2,3,4  раз каждый раз записывают показания миллиамперметра в таблицу.

Напряжение U, В	Сила тока I, мА	Индуктивное сопротивление XL, Ом	Частота ν, Гц	Индуктивность L, мГн
1,5	0,345		80
1,5	0,178		160
1,5	0,121		240
1,5	0,090		320

3. Ссылки на интернет-ресурс: infofiz.ru>index.php>mirfiziri>fizst>lkf

4. задания:

1. В каждом опыте рассчитайте индуктивное сопротивление катушки по формуле:

2. Вычислите в каждом опыте индуктивность катушки L, используя формулу:

3. Сравнивая индуктивности катушек, сделайте вывод, от чего и как зависит индуктивность.

 

Обратная связь: у тебя в тетради должно быть записано и выполнено  задания. Сфотографируй свою работу и отправь мне на проверку. Удачи!

 

 

 

Какой буквой обозначается в физике 1. Скорость движения частицы в магнитном поле 2. Скорость

Помогите пожалуйста ,отдаю последние балы ,на помощь , заранее спасибо)​

U=4 I=1,6 r=1,25 R=2,4 E=? ​

помогите пожалуйста!!!!!​

Як за графіком швидкості руху тіла визначити шлях, подоланий тілом?​

1. Посчитай, какое количество энергии нужно для обращения в пар спирта массой 78 г, взятого(-ой) при температуре 30 °С. (Удельная теплоёмкость спирта … с=2400 Дж/кг·°С, температура кипения спирта равна 78 ° С, удельная теплота парообразования спирта L=857000 Дж/кг).Ответ (округли до целого числа): кДж2. Определи, какое количество теплоты выделится при кристаллизации 3,8 л воды. Удельная теплота кристаллизации воды равна 3,4⋅105 Дж/кг, плотность воды — 1000 кгм3.Ответ (округли до десятых): кДж..

Під час змагань з бігу перший учень пробіг 20 хв зі швидкістю 23 км/год. Другий — 10 км за 55 хв. Третій — 8 км зі швидкістю 26 км/ год. Хто з учнів р … ухався найшвидше? Хто подолав найбільшу відстань? Хто біг довше за всіх. Оберіть ТРИ правильні відповіді: (Баллов: 2) Найшведше — 1 учень. Біг довше за всіх — 2 учень. Біг довше за всіх — 1 учень. Подолав найбільшу відстань — 1 учень. Подолав найбільшу відстань — 2 учень. Найшведше — 2 учень. Біг довше за всіх — 3 учень. Подолав найбільшу відстань — 3 учень. Найшведше — 3 учень.Помогите пожалуйста с заданием, дам много балов!​

У каструлю з окропом кидають шматочок льоду за температури 0°С.Лід якої маси потрібно вкинути в каструлю, щоб температура води стала 40°С.Теплоємність … каструлі 1000дж/кг°с. Допомогите пж

пожалуйста решите через «Дано» ​

Задача 3. На малюнку зображено графік залежності шляху від часу для прямолінійного рівномірного руху до зупинки в одному напрямі, після зупинки — у зв … оротному. Помагите пжпжпж ​

Скільки енергії віддасть вода при утворенні 2 т льоду, та подальшому його охолодженні до -10 С? Накресли схематично графік утворення та охолодження ль … оду.​ МОЖНО ПЖ РЕШЕНИЯ ​

Определение индуктивности катушки (Лабораторная работа № 11)

Лабораторная работа 11

Определение индуктивности катушки

Цель работы: изучение явления электромагнитной индукции.

Задание 1. Определить индуктивность катушки без сердечника.

Задание 2. Определить индуктивность катушки с железным сердечником.

Приборы и принадлежности: исследуемая катушка, сердечник из трансформаторной стали, вольтметр, амперметр, источник переменного тока –  (лабораторный автотрансформатор).

Теория метода

Закон Ома для квазистационарных токов (токи частотой до ) имеет вид

,                                                       (1)

где  – напряжение в цепи переменного тока;  – сопротивление в цепи переменного тока ;  – омическое или активное сопротивление;  – индуктивное сопротивление;  – емкостное сопротивление.

Для цепи с сосредоточенными и

.                                                   (2)

Из выражения (2) можно найти индуктивность катушки

,                                                   (3)

где  – круговая (циклическая) частота – число колебаний тока (или его изменений) в  секунд;  – промышленная частота переменного тока
(50 Гц).

Если катушку включить в цепь переменного тока, то в ней возникает ЭДС самоиндукции

ℰ,                                                      (4)

где  – коэффициент пропорциональности между ℰ и изменением тока во времени  или индуктивность катушки.

Так как по правилу Ленца индукционный ток  направлен против возрастания тока в цепи , то из-за уменьшения тока возникает кажущееся сопротивление индуктивности (реактивное сопротивление) (рис. 1)

.                                                        (5)

Рис. 1. Электрическая схема цепи

Выполнение работы

Задание 1. Определение индуктивности катушки без сердечника

1. Проверьте электрическую цепь по схеме рис. 1. ЛАТР (лабораторный автотрансформатор) должен быть выведен на «0» (вращением ручки ЛАТРа против часовой стрелки).

2. Катушка должна быть без сердечника. Замкните ключ  и, плавно вращая ручку ЛАТРа по часовой стрелке, подайте напряжение на катушку величиной 50 В. Снимите показания амперметра. Подавая затем 60 В и 70 В, снимите     показания амперметра и занесите все в табл. 1.

Таблица 1

Номер опыта	Наименование показателей
	,	,	,	,	,	,	,	, %
Катушка без сердечника
1
2
3
Сердечник в катушку введен
1
2
3

Задание 2. Определение индуктивности катушки с железным сердечником

1. Выведите  на «0». Введите сердечник в катушку и произведите измерения согласно п. 2 задания 1. Все данные занесите в табл. 1.

Данные одной из обмоток катушки индуктивности:  = 1200 витков,      = 14 Ом.

Zи L рассчитайте по (2) и (3). Результаты занесите в табл. 1.

Рассчитайте ошибки методом среднего арифметического для задания 1 и задания 2.

Сделайте выводы по результатам работы.

Контрольные вопросы

1. В чем заключается явление электромагнитной индукции? Как читается правило Ленца? На основании какого закона возникает индуктивный ток?

2. Дайте понятие индуктивности. Единицы измерения.

3. В чем заключается явление самоиндукции?

4. Почему при включении катушки с  (омическое сопротивление)
в цепь переменного тока ее сопротивление возрастает и обозначается
буквой ?

5. Закон Ома для цепи переменного тока.

6. Векторная диаграмма напряжений. Что из нее можно извлечь?

7. Реактивные сопротивления ( и ) называют «кажущимися»
сопротивлениями. Причина такого названия.

8. Линейная частота  и как она связана с периодом колебаний и круговой или циклической частотой ?

9. Что значит омическое, или активное сопротивление?

Библиографический список

1. Савельев И. В. Курс общей физики / И. В. Савельев. – М. : Наука, 1982. – Т. 2. – Гл. XIII. – С. 181–15, 188–191. (Электромагнитная индукция.
§ 60. Явление электромагнитной индукции. § 61. Электродвижущая сила
индукции. § 64. Явление самоиндукции).

2. Грабовский Р. И. Курс физики / Р. И. Грабовский. – М. : Высш. шк., 2002. – Гл. XV. – С. 353-362. (Электрическая индукция и переменный
ток. §103. Электромагнитная индукция. Закон Фарадея. Правило Ленца.
§ 104. Взаимная индукция и самоиндукция).

3. Поцелуйко А. А. Общая физика : курс лекций для студентов торгово-экономических вузов / А. А. Поцелуйко; Краснояр. гос. торг.-экон. ин-т. – Красноярск, 2005. – Раздел 3.– С. 148–152. (Электромагнитная индукция.     Лекция 31).

Решение задач по физике как интеллектуальное приключение — Учителю о решении задач — Методика физики — Каталог статей

Например,  нам надо повесить картину. Мы знаем,  что для этого обычно вбивают в нужное место стены гвоздь (проблема переформулирована для конкретной  ситуации). Очередной шаг — найти подходящий гвоздь (материал) и  молоток (инструмент). Если это  удалось, следующий шаг – умело воспользоваться инструментом,  чтобы забить гвоздь (решить задачу практически). Последний шаг – повесить картину на гвоздь, завершив успешно свои действия.       Ага!  Мы использовали последовательность шагов,  каждый из которых решал частную задачу, однако, постепенно приближающую нас к  цели. Мы кое-что должны были знать и кое-чем уметь пользоваться. Важно заметить,  трудность заключалась в том, что картина, гвоздь и молоток, в явном виде никак не связаны между собой, а  конечный результат мы себе представляли в очень общем виде. Неочевидность шагов  и отсутствие света в конце тоннеля — неизменные атрибуты решения любой  проблемы, ибо, если это не так, то и проблемы нет. Наших детей должно приучать  к тому, чтобы смело ДЕЙСТВОВАТЬ в  условиях неочевидности, а не пасовать, не сидеть и не сопеть, как только  они не видят пути к ответу. И задачи решайте такие, чтобы путь к ответу не был  очевиден. Это научит их решать задачи и далеко не только по физике.         А  теперь конкретно.         Покажем,  как нашим способом можно решить одну из несложных задач части С (С3) из  материалов ЕГЭ. Затем покажем, как эту же задачу обычно решают в школе.  Любопытно сравнить.         В горизонтальном  цилиндрическом сосуде, закрытом подвижным поршнем, находится одноатомный  идеальный газ. Давление окружающего воздуха p = 105 Па. Трение между  поршнем и стенками сосуда пренебрежимо мало. В процессе медленного охлаждения  от газа отведено количество теплоты Q = 75 Дж. При этом поршень передвинулся на  расстояние х = 10 см. Чему равна площадь поперечного сечения поршня?         Не  будем даже записывать кратко условие задачи, так как наш ученик не всегда  знает, как что называется и какой буквой обозначается (но мы обучаем решению  задач и таких учеников тоже).           Первое. Выделим ключевые слова, те, которые, как  кажется ученику, обозначают физические величины или понятия: «идеальный газ»,  «количество теплоты». Поищем,  где встречаются эти слова. Мы, знающие, ищем в голове, а незнающие полезут в  справочник: Q  = cmΔt; Q = λm; Q = rm; Q = qm; Q  = ΔU  + A’; Q = I2Rt. Наступает  время выбора из множества. Вместе  ключевые слова сходятся в формуле первого закона термодинамики: Q  = ΔU  +  A’. Хорошо  бы, были такие справочники, в которых все выстроено не по темам (долгонько  искать незнающему-то), а по алфавиту, и все искомое на одной странице, и сразу  можно понять, что и как обозначено в формуле. Но, допустим, у нас именно такой  справочник. Что-то  нашли, но ответ пока не виден. До неизвестной площади S пока — ой как! —  далеко, но мы ребята упертые! А, главное, верим в силу алгоритма. Второй шаг. Поищем в том же  замечательном справочнике, как можно выразить  ΔU  и A’ через одни и те же величины, ведь Q нам известно: а)  Внимание! Для выбора формулы работы газа A’ всегда надо знать процесс,  происходящий с газом. В данной задаче это проблема. Если внимательно прочитать  условие, можно понять, что поршень никто намеренно не удерживает, трение мало.  Это значит, что давление внутри цилиндра и снаружи одинаково и не меняется (!)  – мы имеем процесс с постоянным давлением, для которого A’ = pΔV  = — pxS (объем уменьшается). Это  соотношение очень полезно, так как позволит нам в дальнейшем связать между  собой величины из условия задачи: x, S и Q (вот и забрезжил свет в конце  тоннеля). б)  Тут же в справочнике:  ΔU = 3/2 νRΔT = 3/2 pΔV =  — 3/2pxS. Третий шаг. Теперь осталось  собрать в одну формулу найденные нами зависимости: Q  = ΔU  + A’ = — 3/2pxS – pxS = — 5/2  pxS. Подставив  сюда значение данных нам величин, легко найдем ответ: S = — 2Q/(5px) = 30·10-4 м2 = 30 см2. Заметим,  что Q = — 75 Дж, так как «от газа  отведено количество тепла». Ответ: S = 30 см2.         Теперь  решение, как его дают обычно в школе.         Воспользуемся  первым законом термодинамики: Q  = ΔU  +  A’.(А почему???)         Подставим  сюда формулы изменения внутренней энергии и работы газа: ΔU = 3/2 νRΔT = 3/2 pΔV =  —  3/2pxS.    A’ = pΔV  = — pxS. (Ловко! А откуда вы все это взяли???)         Тогда  получим: Q  = ΔU  + A’ = — 3/2 pxS – pxS = — 5/2 pxS.         Откуда: S = — 2Q/(5px) = 30·10-4 м2 = 30 см2.         Сравним  для ясности. Сколь много вопросов без ответов возникает у ученика в таком  решении. Насколько необоснованными (для мало знающего ученика, конечно)  выглядят действия учителя! Сколь много подразумевается того, что должно было  быть высказано. Как много возложено на плечи учеников того, что мог бы и должен  был взять на себя учитель! А как использовать это решение? Запомнить как  решение одной из задач? Так мало? Так беспомощно?         Обратите  внимание. Алгоритм, предложенный нами, годится для решения любой школьной  задачи и не только по физике. В нем четко распределены роли: что делается в  слепую по алгоритму, что берем в качестве знания (из головы или справочника),  где все дело за нами (принятие решения, выбор). Вот, только где бы взять такой  удобный для ученика справочник формул?         И  главное. Мы, пытаясь решить задачу, прошли по лабиринту, ранее не хоженому  нами. За каждым поворотом нас ожидало новое интеллектуальное приключение, новый  поворот, новый вопрос и поиск ответа. Как все это далеко от второго решения.  Да, решение в обоих случаях по сути одно и то же. И все же, все же.         Работая  по такому алгоритму, часто наши изначально не слишком умелые дети находят не  одно, а два и более решения. Не мудрено, ведь они обращаются сразу ко всему  массиву возможных формул (зависимостей, законов). А запомнить (заучить) им  нужно только один алгоритм (и небольшое количество приемов), а не решение  полутора тысяч задач из школьного задачника. А их готовность к решению вовсе  неизвестных задач! И не имеет значения, относится ли задача к одной теме  (например, сугубо колебательный контур) или включает в себя еще и механику, и  термодинамику и т.д. (ведь в поиске по алфавиту мы в справочнике получаем  доступ сразу ко всему массиву формул данной величины).         Толково  ли я объяснил здесь разницу? Понятен ли вам выигрыш и его истоки?         Приведем  примеры решения других задач. Например, С5.       В идеальном  колебательном контуре, состоящем из конденсатора и катушки индуктивности,  амплитуда силы тока Im = 50 мА. В таблице приведены значения  разности потенциалов на обкладках конденсатора, измеренные с точностью до 0,1 В  в последовательные моменты времени. Найдите значение электроемкости  конденсатора.                                                                                                                                                                                                                                                                                                       t, мкс 0 1 2 3 4 5 6 7 8 U, В 0,0 2,8 4,0 2,8 0,0 -2,8 -4,0 -2,8 0,0         1.  Ключевые слова условия задачи —  «колебательный контур», «емкость» — дают  по справочнику: C = q/U;  C = ε ε0S/d; W = CU2/2;.         Выберем  формулу Томсона (есть подозрение, что Т мы найдем по таблице):                   или, возведя в квадрат, T2 = 4π2LC.       2.  Осложнение: неизвестные индуктивность L и  период Т. Среди прочих формул L обратим внимание на энергию магнитного  поля: W = LI2/2         Вместе  с формулой энергии конденсатора W = CU2/2 (которая уже раз мелькнула перед нами) можно составить уравнение сохранения  энергии при колебаниях (максимальная энергия магнитного поля катушки равна  максимальной энергии конденсатора):         LIm2/2  = CUm2/2. Это часто встречающийся прием, на который раз за разом надо обращать  внимание. Таких приемов немного в решении задач.         Здесь  Im  нам дано по условию  задачи, а Um можно найти в таблице (наибольшее значение напряжения).         Отсюда: LIm2 = CUm2;        L = CUm2/ Im2.         3.  Подставим значение индуктивности в формулу Томсона:         T2 = 4π2C· CUm2/ Im2.         Извлечем  квадратный корень из обеих частей уравнения и выразим С:         C = Т Im /  2πUm.         4.  Период колебаний найдем в таблице как время полного цикла колебаний (Т = 8 мкс). Поскольку все величины  известны, подставляем численные значения и получаем ответ.         Ответ:  С ≈ 16·10-9 Ф = 16 нФ.         В  этом решении четче видно то, что мы называем   «интеллектуальным путешествием с препятствиями по лабиринту формул»  (число которых для ученика представляется бесконечным). Отыскали формулу  Томсона, да не тут-то было. Нашли формулу, связывающую ток (дано по условию  задачи) и индуктивность (промежуточное неизвестное). Далее потребовалось умение  использовать закон сохранения энергии (ну, наш ученик ходит на уроки, где-то  слышал о сохранении энергии, имеет какие-то представления о колебательных  процессах, чтобы по таблице найти максимум напряжения и период колебаний).         Опора  на ключевые слова, умение выделять главное – одно из важнейших надпредметных  умений, необходимых человеку в информационном мире, которое мы усиленно  развиваем у нашего ученика.       Все  справочник, справочник… А как же знания самого ученика? На первое место мы  ставим успех (сиречь – вера!), а знания появятся как неизбежная объективная  необходимость по мере накопления опыта (становится более понятным, для чего  зубрить).  И еще, становится понятной  особая важность точного знания, не  приблизительного, каким грешат у нас многие.         Задача A19.       В области пространства,  где находится частица с массой 1 мг и зарядом 2 нКл, создано однородное  горизонтальное электрическое поле напряжённостью 50 В/м. За какое время частица  переместится на расстояние 0,45 м по горизонтали, если её начальная скорость  равна нулю? Действием силы тяжести пренебречь.       Ответы:   1) 95 с        2)  4,2 с        3) З с        4) 9,5 с.         1.  Ключевые слова: масса, заряд, напряженность, время и расстояние. Время и расстояние: s = vt; s = (v + v0)t/2;  s = v0t + at2/2; N = A/t; FΔt = Δp. Упоминание  в условии задачи начальной скорости приводит нас к выбору: s = v0t + at2/2 = at2/2.         2.  Осложнение: мы не знаем ускорения a,  без которого ничего не решить. Из  кучи формул ускорения выберем ту, которая не содержит времени (нам его потом  надо будет найти):  F = ma.         3.  Массу m мы знаем по условию  задачи, это вдохновляет, но теперь новая проблема – сила F.         4.  Из всех сил выбираем по смыслу электрическую: F = kq1q2/r2; F = Eq. Последнее  предпочтительнее, так как в условии упоминаются напряженность и заряд.         5.  Собираем найденное вместе: ma = Eq; a = Eq/m.  Далее: t2 = 2s/a = 2sm/(Eq).       Задача  решена: t = 3 с. Правильный ответ №3.         Пять  неочевидных для ученика шагов в задаче! Пять крутых поворотов, за которыми не  виден результат. Как в романе! Целое детективное расследование. А многие ли  ученики рискнут взяться за решение задачи, когда они не видят всего пути  целиком, от начала и до конца. И как мало в этой задаче, в отличие от  предыдущей, надо понимать в физике (что упрощает жизнь тем, кто у нас пока  неуспешен). Полностью выручает работа со справочником (формальное знание).  Алгоритм плюс знание. Плюс математика.         Задача  С5.       В идеальном  колебательном контуре амплитуда колебаний силы тока в катушке индуктивности 5  мА, а амплитуда колебаний заряда конденсатора 2,5 нКл. В момент времени t сила  тока в катушке равна 3 мА. Найдите заряд конденсатора в этот момент.         1.  Ключевые слова: колебательный контур, сила тока, заряд, конденсатор.         По  справочнику имеем в распоряжении формулы: , ω = 2π/T; q =qmcos ωt; i =im sin ωt; Wэл = CU2/2;  Wм =  LI2/2.         ФИПИ рекомендует начинать решение задачи с закона сохранения  энергии, но есть и другое решение.  Для наших детей очевиднее выбрать уравнения заряда и тока (этих величин много в  условии задачи): q =qmcos ωt; i =im sin ωt.         Знание амплитуды тока и текущего значения тока позволят нам  найти sin ωt (пока не понятно зачем, но для наших детей «можно», значит  надо попробовать).         Итак, 3 = 5 sin ωt; значит sin ωt = 3/5.         2. Как бы это использовать? Синус позволит найти косинус,  который мы видим в формуле колебаний заряда. Основное тригонометрическое  тождество: 1 = sin2 ωt + cos2 ωt. Откуда cos ωt = ± 4/5.       3. Зная текущее значение cos ωt, найдем текущее значение заряда, ведь максимальный заряд нам  известен: q = qmcos ωt = ± 2,5·4/5 = ± 2 (нКл). В отличие от ФИПИ мы нашли иное  решение и два правильных ответа вместо одного.         Итак, написать решение — не значит решить задачу. Решить –  это совершить ряд последовательных действий, в каждом из которых необходимо  сделать выбор, что, между прочим, далеко необязательно сразу приводит к ответу,  а, скорее всего,  приведет к новым  вопросам и потребует новых шагов. Решать — значит двигаться в определенном  направлении в условиях неочевидности.         Наши дети довольно часто оказываются в тупике. Ой, как это  полезно. Мы не ставим за это плохую оценку. Попытка, пусть неудачная, тоже  требует своей работы над задачей. Отрицательный результат бывает более полезен,  чем положительный. А многие, пройдя через несколько неудач, понимают, что  где-то надо было пойти другим путем.         Наш подход делает обучаемыми гораздо большее количество  детей, чем это обычно бывает. Наш ученик оптимистичен. Он знает, всегда есть  варианты.    © 2012. Н.В. Смирнов, И.Б. Смирнова

Электричество и магнетизм

Величина	Обозначение	Единица измерения в системе СИ
Сила тока	I	ампер	А
Плотность тока	j	ампер на квадратный метр	А/м2
Электрический заряд	Q, q	кулон	Кл
Электрический дипольный момент	p	кулон-метр	Кл ∙ м
Поляризованность	P	кулон на квадратный метр	Кл/м2
Напряжение, потенциал, ЭДС	U, φ, ε	вольт	В
Напряженность электрического поля	E	вольт на метр	В/м
Электрическая емкость	C	фарад	Ф
Электрическое сопротивление	R, r	ом	Ом
Удельное электрическое сопротивление	ρ	ом-метр	Ом ∙ м
Электрическая проводимость	G	сименс	См
Магнитная индукция	B	тесла	Тл
Магнитный поток	Ф	вебер	Вб
Напряженность магнитного поля	H	ампер на метр	А/м
Магнитный момент	pm	ампер-квадратный метр	А ∙ м2
Намагниченность	J	ампер на метр	А/м
Индуктивность	L	генри	Гн
Электромагнитная энергия	N	джоуль	Дж
Объемная плотность энергии	w	джоуль на кубический метр	Дж/м3
Активная мощность	P	ватт	Вт
Реактивная мощность	Q	вар	вар
Полная мощность	S	ватт-ампер	Вт ∙ А

SI Единица индуктивности, индуктивность и часто задаваемые вопросы

На этой странице мы узнаем о следующем:

Индуктор

Катушка индуктивности представляет собой катушку из проволоки, обернутую вокруг магнитного материала.

Ток, протекающий через индуктор, создает магнитное поле, которое не изменяется, поскольку оно пытается противодействовать изменению потока тока, что означает, что ток остается постоянным внутри индуктора.

Индуктор не будет создавать никаких сил на заряженные частицы, протекающие через него.В таком случае индуктор ведет себя как обычный провод.

Текущему потоку противостоит сопротивление, и приходит время, когда

происходит затухание (спад) тока. Чем больше сопротивление, тем быстрее будет падать ток.

С другой стороны, чем больше индуктивность катушки индуктивности, тем медленнее будет затухать ток.

Что такое индуктивность?

Индуктивность — это способность индуктора или любого проводника с током противодействовать изменению тока, протекающего через него.Индукторы делают это, генерируя внутри себя эдс самоиндуцированной (закон индукции Фарадея) в результате изменения их магнитного поля.

Единица СИ для индуктора

Единица СИ для индуктора — Генри H Единица МКС — Кг м² с² A⁻² Где один Генри равен одному килограмму метр в квадрате на секунду в квадрате на ампер в квадрате.

(изображение скоро будет загружено)

Что такое самоиндуктивность?

Индуктивность также называется самоиндуктивностью.Когда ток устанавливается в замкнутом проводящем контуре, он создает магнитное поле. Это магнитное поле имеет поток, создаваемый в области замкнутого контура. Если ток меняется со временем, поток через контур также изменяется. Следовательно, в петле индуцируется ЭДС. Такой процесс называется самоиндукцией.

Магнитное поле в любой точке из-за тока пропорционально току. Магнитный поток в замкнутой области проводника может быть представлен как коэффициент самоиндукции или просто самоиндукция контура.

(изображение будет загружено в ближайшее время)

Индуктивность в катушке (рис.1) зависит от количества витков, площади поперечного сечения и материала сердечника, на который намотана катушка.

Если i = 1, Φ = L x i или L = Φ

Следовательно, коэффициент самоиндукции численно равен величине магнитного потока, связанного с катушкой, когда через катушку протекает единичный ток.

Согласно закону индукции Фарадея, любое изменение магнитного поля порождает ЭДС, определяемую выражением:

E = — dΦ (t) / dt = — L di / dt

Отрицательный знак указывает на то, что изменяющийся ток индуцирует напряжение в проводнике, и это индуцированное напряжение имеет направление, которое имеет тенденцию противодействовать изменению (увеличению или уменьшению) электрического тока (закон Ленца), называется обратной ЭДС.

Индуктивность для длинного соленоида

Индуктивность соленоида равна,

Плотность магнитного потока может быть получена умножением B на площадь поперечного сечения A, мы получаем,

Φ = B xA = μ₀ N xix A / l…. (1)

Так как общий магнитный поток внутри катушки = поток через каждый виток x общее количество витков.

Φ = B xA = μ₀ N x N i x A / l….(2)

Где μ₀ — магнитная постоянная или абсолютная магнитная проницаемость свободного пространства / воздуха, образующего сердечник соленоида.

N = Общее количество витков соленоида

i = Текущее

l = Длина соленоида

A = Площадь каждого витка длинного соленоида

Мы знаем, что

Из (2) и (3) получаем,

L i = μ₀ N x N x A xi / lx N получаем,

Когда сердечник из любого другого магнитного материала, μ₀ заменяется на

μr (относительная магнитная проницаемость).

Здесь мы делаем следующие выводы:

• Это зависит от магнитной проницаемости материала.

• Площадь поперечного сечения.

• L не зависит от тока.

единица индуктивности S.I.

единица самоиндукции S.I. — вебер / ампер или вольт-секунда / ампер.

Он также обозначается Генри (H), назван в честь американского ученого по имени Джозеф Генри.

Где Генри — величина индуктивности, которая вызывает изменение на один вольт и когда ток изменяется со скоростью один ампер в секунду.

Примечание. Все проводники имеют некоторую индуктивность, которая может иметь как желательные, так и вредные эффекты в электрических цепях, и это зависит от геометрии пути тока и магнитной проницаемости материалов.

Ферромагнитный материал имеет тенденцию иметь высокую индуктивность из-за прохождения через проводник большого количества электрического потока (общего магнитного поля), создаваемого током, протекающим через него, увеличивает индуктивность в этом проводнике.

Сводка

При изменении магнитного потока наведенная ЭДС является обязательной, но наведенный ток появляется только тогда, когда цепь замкнута.

Катушка индуктивности эквивалентна короткому замыканию на постоянный ток, потому что после завершения фазы накопления ток i, который протекает, становится стабильным, ЭДС не индуцируется. Таким образом, индуктор ведет себя как обычный провод, где сопротивление R равно нулю.

Определение самоиндукции в физике.

Примеры самоиндукции в следующих темах:

• Индуктивность

  • Self — индуктивность , также существует влияние закона Фарадея индукции устройства на самого себя.
  • , где L — собственное — индуктивность устройства.
  • Устройство, которое демонстрирует значительную собственную индуктивность — , называется индуктором и обозначено символом в.
  • Единицы собственной индуктивности — — это Генри (Гн), как и для взаимной индуктивности .
  • Собственная — индуктивность соленоида с площадью поперечного сечения A и длиной ℓ составляет

• Индуктивность

  • Ответ — да, и эта физическая величина называется индуктивностью .
  • Чем больше взаимная индуктивность M, тем эффективнее связь.
  • Self — индуктивность , также существует влияние закона Фарадея индукции устройства на самого себя.
  • , где L — собственное — индуктивность устройства.
  • Устройство, которое демонстрирует значительную собственную индуктивность — , называется индуктором.

• RL Схемы

  • Напомним, что индукция — это процесс, в котором ЭДС индуцируется изменением магнитного потока.
  • Взаимная индуктивность — это действие закона Фарадея индукции для одного устройства на другое, в то время как self — индуктивность — это эффект закона Фарадея индукции устройства на самом себе.
  • Катушка индуктивности — это устройство или компонент схемы, который имеет собственную индуктивность — .
  • Характерное время $ \ tau $ зависит только от двух факторов: индуктивности L и сопротивления R.
  • Чем больше индуктивность L, тем она больше, что имеет смысл, поскольку большая индуктивность очень эффективна в противодействии изменениям.

• Обратная ЭДС, вихревые токи и магнитное демпфирование

  • Обратная ЭДС, вихревые токи и магнитное затухание — все это происходит из-за наведенной ЭДС и может быть объяснено законом Фарадея индукции .
  • Когда катушка двигателя поворачивается, магнитный поток изменяется, и возникает электродвижущая сила (ЭДС), соответствующая закону индукции Фарадея.
  Закон
  • Ленца говорит нам, что наведенная ЭДС препятствует любому изменению, так что входной ЭДС, которая питает двигатель, будет противодействовать ЭДС, генерируемая самим двигателя, которая называется обратной ЭДС двигателя.

• Закон индукции Фарадея и закон Ленца

  • Это соотношение известно как закон Фарадея индукции .
  • Знак минус в законе Фарадея индукции очень важен.
  • Когда изменение начинается, закон говорит, что индукция противодействует и, таким образом, замедляет изменение.
  • Это один из аспектов закона Ленца — индукция препятствует любому изменению потока.
  • Выразите закон индукции Фарадея в форме уравнения

• Изменение магнитного потока создает электрическое поле

  • Закон Фарадея индукции гласит, что изменение магнитного поля создает электрическое поле: $ \ varepsilon = — \ frac {\ partial \ Phi_B} {\ partial t} $.
  • Мы изучили закон Фарадея индукции в предыдущих атомах.
  • Вкратце, закон гласит, что изменение магнитного поля $ (\ frac {d \ Phi_B} {dt}) $ создает электрическое поле $ (\ varepsilon) $, закон индукции Фарадея выражается как $ \ varepsilon = — \ frac {\ partial \ Phi_B} {\ partial t} $, где $ \ varepsilon $ — индуцированная ЭДС, а $ \ Phi_B $ — магнитный поток.
  • Следовательно, мы получаем альтернативную форму закона индукции Фарадея : $ \ nabla \ times \ vec E = — \ frac {\ partial \ vec B} {\ partial t} $. Это также называется дифференциальной формой закона Фарадея.
  • Эксперимент Фарадея, демонстрирующий индукцию между витками провода: жидкая батарея (справа) обеспечивает ток, который течет через небольшую катушку (A), создавая магнитное поле.

• Звуковые системы, компьютерная память, сейсмограф, GFCI

  • Микрофон работает за счет индукции , поскольку вибрирующая мембрана индуцирует ЭДС в катушке.
  • Затем динамик приводится в действие модулированными электрическими токами (создаваемыми усилителем), которые проходят и намагничивают (на индуктивность ) катушку динамика из медной проволоки, создавая магнитное поле.
  • Это делается с помощью индуктивности .

• Наведенный заряд

  • Электростатическая индукция — это перераспределение зарядов внутри объекта, которое происходит как реакция на присутствие ближайшего заряда.
  • Электростатическая индукция — это перераспределение заряда внутри объекта, которое происходит как реакция на ближайший заряд.

• Энергия, запасенная в магнитном поле

  • В простом генераторе используется индуктивность для создания тока путем вращения магнита внутри катушки с проволокой.
  • Если ток изменяется, изменение магнитного потока пропорционально скорости изменения тока во времени с коэффициентом, называемым индуктивностью (L).
  • (уравнение 1), где L — индуктивность , в единицах Генри, а I — ток в единицах Ампера.
• Цепь серии

  RLC: на больших и малых частотах; Фазорная диаграмма

  • Отклик цепи RLC зависит от частоты возбуждения — на достаточно больших частотах преобладает индуктивный (емкостной) член.
  • Если частота достаточно высока, так что XL также намного больше, чем R, то в импедансе Z доминирует индуктивный член .

Быстрый ответ: что такое индуктивность в физике?

Индуктивность, свойство проводника (часто в форме катушки), которое измеряется величиной электродвижущей силы или напряжения, индуцированного в нем , по сравнению со скоростью изменения электрического тока, который создает напряжение .

Что такое индуктивность и ее единица?

Индуктивность определяется как отношение индуцированного напряжения к скорости изменения вызывающего его тока.В системе СИ единицей индуктивности является генри (H), то есть величина индуктивности, которая вызывает напряжение в один вольт, когда ток изменяется со скоростью один ампер в секунду.

Что такое индуктивность и емкость?

Емкость, как мы теперь знаем, — это способность сохранять энергию в виде электрического поля. Индуктивность, которая измеряется в генри и обозначается буквой L, — это способность сохранять энергию в виде магнитного поля. Токоведущие провода создают круговое магнитное поле.

Что такое индуктивность на примере?

Единицами самоиндукции является генри (Гн), как и для взаимной индуктивности. Чем больше самоиндукция L устройства, тем сильнее оно сопротивляется любому изменению тока через него. Например, большая катушка с множеством витков и железным сердечником имеет большую L и не позволяет току быстро изменяться.

Какое определение индуктивности в электричестве?

1a: свойство электрической цепи, посредством которого в ней индуцируется электродвижущая сила за счет изменения тока либо в самой цепи, либо в соседней цепи.

Индуктивность — это хорошо или плохо?

Таким образом, индукторы можно определить как пассивные компоненты, поскольку они могут как накапливать, так и передавать энергию в цепь, но не могут генерировать энергию. Идеальный индуктор классифицируется как без потерь, что означает, что он может хранить энергию неограниченно долго, поскольку энергия не теряется.

Что такое формула самоиндукции?

При известном магнитном потоке самоиндукция может быть найдена из уравнения 14.3. 4, L = NΦm / I.

В чем разница между индуктивностью и емкостью?

Ключевое различие между индуктивностью и емкостью состоит в том, что индуктивность — это свойство проводника с током, которое создает магнитное поле вокруг проводника, тогда как емкость — это свойство устройства удерживать и накапливать электрические заряды.

Для чего нужна индуктивность?

Индуктор имеет функции развития электродвижущей силы в направлении, которое уменьшает колебания при протекании флуктуирующего тока, и сохранения электрической энергии в виде магнитной энергии.

Какова функция индуктивности?

Катушки индуктивности обычно используются в качестве накопителей энергии в импульсных силовых устройствах для выработки постоянного тока. Катушка индуктивности, в которой накапливается энергия, подает энергию в схему для поддержания протекания тока во время периодов выключения, что позволяет создавать топографии, в которых выходное напряжение превышает входное.

Какие бывают типы индуктивности?

Базовая электроника — Типы индукторов

• Индуктор с воздушным сердечником. Этот индуктор с воздушным сердечником представляет собой обычный индуктор с простой обмоткой.
• Индуктор с железным сердечником. Эти индукторы имеют ферромагнитные материалы, такие как феррит или железо, в качестве материала сердечника.
• Тороидальные индукторы.
• Катушки индуктивности с ламинированным сердечником.
• Индукторы с порошковым железным сердечником.

Какую самую большую индуктивность можно использовать?

Murata Manufacturing Co., Ltd. недавно разработала пленочный высокочастотный индуктор для кристаллов ( ^{* 1} ), который имеет самое большое в мире значение индуктивности ( ^{* 2} ), равное 39 нГн.

Как измеряется индуктивность?

Индуктивность измеряется в единицах, называемых генри. Определение одного генри простое: один генри — это величина индуктивности, необходимая для индукции одного вольт, когда ток в катушке изменяется со скоростью один ампер в секунду. Как нетрудно догадаться, один генри — это довольно большой индуктор.

Каковы свойства индуктивности?

Индуктивность — свойство проводника (часто в форме катушки), которое измеряется величиной наведенной в нем электродвижущей силы или напряжения, по сравнению со скоростью изменения электрического тока, который создает напряжение.

Индуктивность зависит от тока?

Индуктивность цепи зависит от геометрии пути тока, а также от магнитной проницаемости соседних материалов. Чем больше витков, тем выше индуктивность.Индуктивность также зависит от формы катушки, расстояния между витками и многих других факторов.

Протекает ли ток через катушку индуктивности?

Катушка индуктивности накапливает электрическую энергию в виде магнитной энергии. Катушка индуктивности не позволяет переменному току проходить через нее, но позволяет постоянному току проходить через нее.

Описание собственной индуктивности длинного соленоида

Поскольку самоиндукция связана с магнитным полем, создаваемым током, любая конфигурация проводников обладает самоиндукцией.Катушка обеспечивает индуктивность за счет самоиндуцированной ЭДС, возникающей в самой катушке при изменении тока, протекающего через нее. Это свойство индуктивности или катушки, благодаря которому она противодействует изменению тока через нее, называется индуктивностью, обозначаемой буквой L. Единица индуктивности — Генри (Гн).

Самоиндуктивность длинного соленоида Пояснение —

Рассмотрим соленоид из N витков длиной «l» и площадью поперечного сечения «A». Он несет ток «Я».Если ‘B’ — это магнитное поле в любой точке внутри соленоида, тогда

Магнитный поток на виток = B × площадь каждого витка

Но, B = μ ₀ NI / l

Магнитный поток на виток = мкм ₀ NIA / l

Следовательно, полный магнитный поток (φ), связанный с соленоидом, определяется произведением потока через каждый виток на общее количество витков. Как и конденсатор, индуктор — еще один компонент, обычно используемый в электронных схемах.[Количество силовых линий, проходящих через реальную или вымышленную плоскость в магнитном поле, называется магнитным потоком.]

φ = (μ ₀ NIA / l ) × N

, т.е. φ = ( μ ₀ N ² IA / l )…… (1)

Если L — коэффициент самоиндукции соленоида, то

φ = LI…… (2)

Из уравнений (1) и (2)

LI = (μ ₀ N ² IA / l )

∴ L = (μ ₀ N ² A / l )

Если сердечник заполнен магнитным материалом с проницаемостью μ, то L = (мкН ² A / l )

A Пояснение проблемы: Длинный соленоид с 15 витками на см имеет небольшую петлю площадью 2.0 размещен внутри соленоида перпендикулярно его оси. Если ток, переносимый соленоидом, постоянно изменяется с 2,0 А до 4,0 А за 0,1 с, какова наведенная ЭДС в контуре при изменении тока?

Ответ

Число витков на соленоиде = 15 витков / см = 1500 витков / м

Число витков на единицу длины, n = 1500 витков

Соленоид имеет небольшую петлю площади, A = 2,0 см ² = 2 × 10 ^-4 м ²

Ток, передаваемый соленоидом, изменяется с 2 А до 4 А.

Следовательно, изменение тока в соленоиде, di = 4-2 = 2 A

Изменение во времени, dt = 0,1 с

Индуцированная ЭДС в соленоиде определяется законом Фарадея как:

e = (dΦ / dt )……… (I)

Где, Φ = Индуцированный поток через малую петлю

= BA……… (ii) [Где B = Магнитное поле]

= (μ ₀ ni)……… ( iii)

μ ₀ = Проницаемость свободного пространства

= 4nx10 ^-7 Гн / м

Следовательно, уравнение (i) сводится к:

e = (d / dt) (di / dt)

= Aμ ₀ nx (di / dt)

= 2 × 10 ^-4 x4x3.