Катушка индуктивности

Катушка индуктивности, как показано на рис. 4.11, представляет собой простомоток провода. Условное обозначение катушки индуктивности показано на рис. 4.12. В отличие от конденсатора, который препятствует изменению приложенного к нему напряжения, катушка индуктивности препятствует изменению протекающего через нее тока. Иными словами,

Рис. 4.12. Условное обозначение катушки индуктивности.                         Рис. 4.13           

если ток, подаваемый в схему, которая содержит катушку, резко увеличить, то ток в схеме будет нарастать плавно до достижения своего мак­симального значения.

Способность катушки индуктивности препятствовать изменению силы тока, протекающего через нее, носит название индуктивности этой катушки. Индуктивность обозначается буквой L, единицей ее измерения является генри (Гн).

Постоянная времени RС-цепи

На рис. 4.13 последовательная цепочка из конденсатора и резистора соединяется через ключ с источником питания. Когда ключ находится в положении 1, конденсатор постепенно заряжается через сопротивление, пока напряжение на нем не достигнет уровня Е

т. е. ЭДС или напряжения источника питания.

Процесс заряда конденсатора показан на рис. 4.14(а) экспоненциальной кривой. Время, за которое напряжение на конденсаторе достигает значения 0,63 от максимума, т. е. в данном случае 0,63Е, называется постоянной времени контура или цепи.

 

Вернемся к рис. 4.13. Если ключ установить в положение 2, конденсатор будет сохранять запасенную энергию. При переведении ключа в положение3 конденсатор начинает разряжаться на землю через резистор R, и напряжение на нем постепенно падает до нуля. Процесс разряда конденсаторапоказан на рис. 4.14(б). В этом случае постоянной времени цепи называется время, за которое напряжение на конденсаторе уменьшается 0,63 от своего максимального значения.

 

Рис. 4.14. Кривые заряда (а) и разряда (б) конденсатора, где t — постоянная времени.

Как для случая заряда, так и для случая разряда конденсатора через резистор R постоянная времени цепи выражается формулой

где t — постоянная времени в секундах, С — емкость в фарадах, R — сопротивление, выраженное в омах.

Например, для случая С = 10мкФ и R= 10 кОм постоянная времени цепи равна

На рис. 4.15 изображены графики процессов заряда для цепей с малой и с большой постоянной времени.

 

Рис. 4.15. Процессы заряда для цепей с малой и с большой постоянной времени.

 

Постоянная времени RL-цепи

Рассмотрим схему, изображенную на рис. 4.16. Катушка индуктивности L соединена последовательно с резистором R, имеющим сопротивление 1 кОм. В момент замыкания ключа S ток в цепи равен нулю, хотя под действиемЭДС источника он, казалось бы, должен резко увеличиться.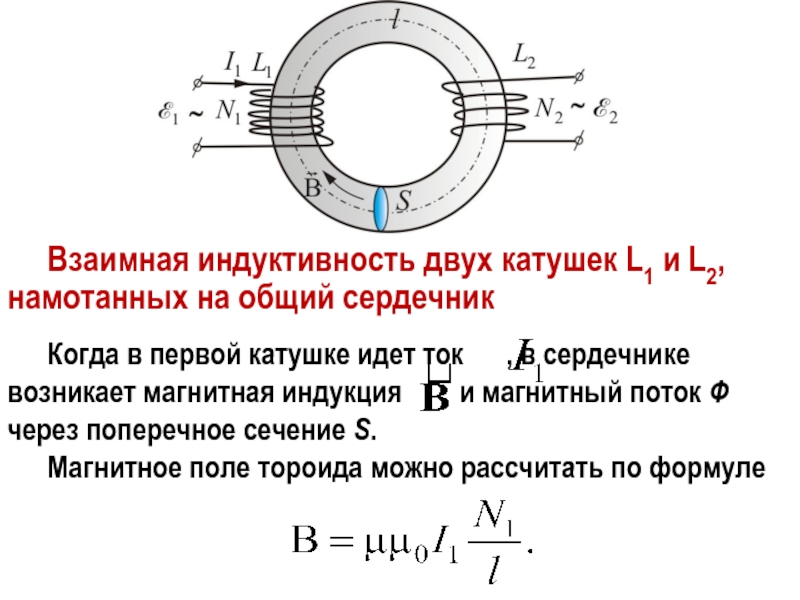 Однако катушка индуктивности, как известно, препятствует всякому изменению силы тока, протекающего через нее, поэтому ток в цепи будет возрастать по экспоненциальному закону, как показано на рис. 4.17. Ток будет возрастать до тех пор, пока не достигнет своего максимального значения. После этого увеличение тока прекратится, а падение напряжения на резисторе

R станет равным приложенному напряжению Е. Установившееся значение тока равно

E/R = 20 В/1 кОм = 20 мА.

Скорость изменения тока в цепи зависит от конкретных значений R и L. Время, необходимое для того, чтобы сила тока достигла значения, равного 0,63 от его максимальной величины, носит название постоянной времени цепи. Постоянная времени вычисляется по формуле

L/R где L выражается в генри, а R — в омах. В этом случае постоянная времени получается в секундах. Используя значения L и R, указанные на рисунке, получаем

Следует заметить, что, чем больше R, тем меньше L/R и тем быстрее изменяется ток в цепи.

Рис. 4.16.

 

Рис. 4.17. Экспоненциальное увеличение тока, протекающего через катушку индуктивности.

 

Сопротивление по постоянному току

Катушка индуктивности, включенная в цепь, не препятствует протеканию постоянного тока, если, конечно, но принимать во внимание очень малое сопротивление провода, из которого она сделана. Следовательно, катушка индуктивности имеет нулевое или очень малое сопротивление и может рассматриваться в цепи постоянного тока как цепь короткого замыкания. Конденсатор же в связи с наличием в нем изолирующего ди­электрика имеет бесконечное или очень большое сопротивление и может рассматриваться в цепи постоянного тока как разрыв.

 

Векторное представление

Сигнал синусоидальной формы может быть представлен в виде век­тора ОА, вращающегося против часовой стрелки с угловой скоростью ω= 2πf, где f – частота сигнала (рис.

4.18). По мере того как поворачивается вектор, ордината его конца характеризует показанный на рисунке синусоидальный сигнал. Один полный оборот вектора (360°, или 2π) со­ответствует одному полному периоду. Половина оборота (180°, или π) со­ответствует половине периода, и так далее. Таким образом, ось времени, как показано на рисунке, может использоваться для нанесения значений угла, на который повернулся вектор. Максимум сигнала достигается при 90° (1/4 периода), а минимум — при 270° (3/4 периода).

Теперь рассмотрим два синусоидальных сигнала, представленных на рис. 4.19(а) векторами ОА и ОВ соответственно. Если оба сигнала имеют одинаковые частоты, то векторы ОА и ОВ будут вращаться с одинаковой угловой скоростью

ω= 2πf. Это означает, что угол между этими векторами

 

Рис. 4.18. Векторное представление синусоидального сигнала.

Рис. 4.19. Разность фаз. Вектор ОА опережает вектор ОВ

 (или вектор ОВ отстает от вектора ОА) на угол θ.

изменяться не будет. Говорят, что вектор ОА опережает вектор ОВ на угол θ, а вектор ОВ отстает от вектора ОА на угол

в. На рис. 4.19(б) эти сигналы развернуты во времени.

Если оба этих синусоидальных сигнала сложить, то в результате получим другой синусоидальный сигнал, имеющий ту же частоту f, но другую амплитуду. Результирующий сигнал может быть представлен вектором ОТ, который, как показано на рис. 4.19(в), является векторной суммой векторов ОА и ОВ. Вектор ОТ опережает вектор ОВ на угол α и отстает от вектора ОА на угол γ. Дальше вы увидите, что векторное представление является весьма удобным приемом при анализе и расчете цепей переменного тока.

В этом видео рассказывается о катушке индуктивности:

 

Добавить комментарий

Урок 46.

Лабораторная работа № 12. Измерение индуктивности катушки.

Тема: Измерение индуктивности катушки

Цель: вычисление индуктивного сопротивления катушки и ее индуктивности по результатом измерений напряжений на катушке и силы тока в цепи.

Оборудование: источник переменного напряжения; катушка школьного разборного трансформатора; вольтметр и миллиамперметр переменного тока; соединительные провода.

Теория.

   Всякое изменение тока в катушке вызывает появление в ней ЭДС самоиндукции, препятствующей изменению тока. Величина ЭДС самоиндукции прямо пропорциональна величине индуктивности катушки и скорости изменения тока в ней. Но так как переменный ток непрерывно изменяется, то непрерывно возникающая в катушке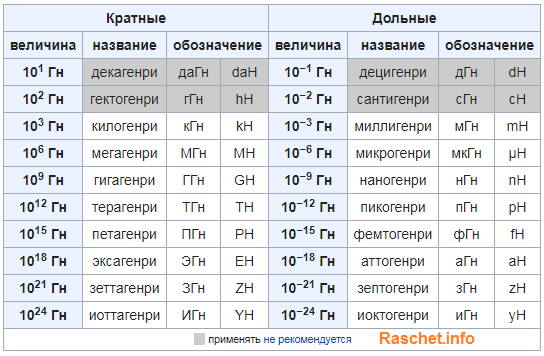

ЭДС самоиндукции создает сопротивление переменному току. Она препятствует его возрастанию и, наоборот, поддерживает его при убывании. Таким образом, в катушке индуктивности, включенной в цепь переменного тока, создается сопротивление прохождению тока. Но так как такое сопротивление вызывается в конечном счете индуктивностью катушки, то и называется оно

индуктивным сопротивлением.

   Индуктивное сопротивление обозначается через Х_L и измеряется, как и активное сопротивление, в омах. Индуктивное сопротивление цепи тем больше, чем больше частота тока, питающего цепь, и чем больше индуктивность цепи. Следовательно, индуктивное сопротивление цепи прямо пропорционально частоте тока и индуктивности цепи; определяется оно по формуле:

 Х_L=ωL , где ω — круговая частота, определяемая произведением 2πν, L — индуктивность цепи в генри (Гн).

   Т.е.

   Тогда индуктивность катушки можно выразить:

   Закон Ома для цепи переменного тока

, содержащей индуктивное сопротивление, звучит так: величина тока прямо пропорциональна напряжению и обратно пропорциональна  индуктивному сопротивлению цепи, т. е

   , где I и U  — действующие значения тока и напряжения, а Х_L — индуктивное сопротивление цепи. 

Выполнение работы:

1. Подготовить таблицу для результатов измерений и вычислений:

Напряжение U, В	Сила тока I, мА	Индуктивное сопротивление XL, Ом	Частота ν, Гц	Индуктивность L, мГн

2. Собрать электрическую схему согласно рисунка 1 и перечертить её в тетрадь:

3. Спомощью регулятора напряжения подать на схему напряжение 1,5 В и установить частоту переменного тока 80 Гц. Записать показания миллиамперметра.

4. Увеличивая частоту в 2,3,4 и 5 раз каждый раз записывать показания миллиамперметра в таблицу.

5. Вынуть сердечник из катушки и, не изменяя напряжения и частоты переменного тока, записать показания миллиамперметра в таблицу.

Напряжение U, В	Сила тока I, мА	Индуктивное сопротивление XL, Ом	Частота ν, Гц	Индуктивность L, мГн
1,5	0,345		80
1,5	0,178		160
1,5	0,121		240
1,5	0,090		320
1,5	0,072		400
1,5	0,284		400

6. В каждом опыте рассчитать индуктивное сопротивление катушки по формуле:

7. Вычислить в каждом опыте индуктивность катушки L, используя формулу:

8. Сравнивая индуктивности катушек, сделайте вывод, от чего и как зависит индуктивность.

9. Ответьте письменно на контрольные вопросы.

Контрольные вопросы.

1. Чем вызвано индуктивное сопротивление у катушки при подключении её в цепь переменного тока?

2. От чего зависит индуктивное сопротивление?

3. Почему уменьшается индуктивное сопротивление при удалении из катушки железного сердечника?

4. Почему на постоянном токе индуктивное сопротивление катушки равно нулю?

5. Чему равно индуктивное сопротивление в цепи переменного тока?

6. Как связаны между собой действующие значения силы тока и напряжения на катушке индуктивности?

    

2. Катушка индуктивности в цепи переменного тока | 3. Реактивное сопр. и импеданс — Индуктивность | Часть2

2.

Катушка индуктивности в цепи переменного тока

Катушка индуктивности в цепи переменного тока

Катушка индуктивности в цепи переменного тока ведет себя не так, как резистор. Если резисторы просто противостоят потоку электронов (напряжение на них прямопропорционально току), то катушки индуктивности противостоят изменению проходящего через них тока (напряжение на них прямопропоционально скорости изменения тока). Согласно Закону Ленца, индуцированное напряжение всегда имеет такую полярность, которая пытается сохранить текущее значение силы тока. То есть, если величина тока возрастает, то индуцированное напряжение будет «тормозить» поток электронов; если величина тока уменьшается, то полярность напряжения развернется и будет «помогать» электронному потоку оставаться на прежнем уровне. Такое противостояние изменению величины тока называется реактивным сопротивлением.

Математическая взаимосвязь между напряжением на катушке индуктивности и скоростью изменения тока через нее выглядит следующим образом:

 

Отношение di/dt представляет собой скорость изменения мгновенного тока (i) с течением времени, и измеряется в амперах в секунду.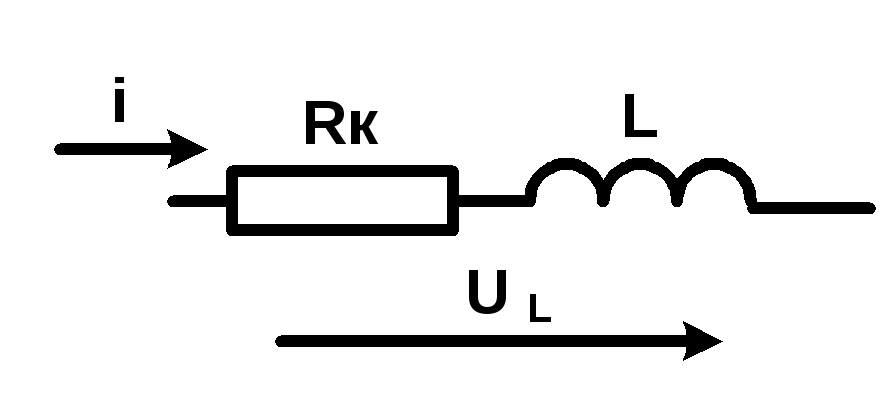 Индуктивность (L) измеряется в Генри, а мгновенное напряжение (u) — в вольтах. Чтобы показать, что происходит с переменным током, давайте проанализируем простую индуктивную схему:

 

Простая индуктивная цепь: ток катушки отстает от напряжения на 90^o.

Если мы построим график тока и напряжения для этой простой цепи, то он будет выглядеть примерно так:

 

Как вы помните, изменение напряжения на катушке индуктивности является реакцией на изменение тока, проходящего через нее. Отсюда можно сделать вывод, что мгновенное напряжение равно нулю всякий раз, когда мгновенное значение тока находится в пике (нулевое изменение, или нулевой наклон синусоидальной волны тока), и мгновенное напряжение равно своему пиковому значению всякий раз, когда мгновенный ток находится в точках максимального изменения (точки самого крутого наклона волны тока, в которых она пересекает нулевую линию). Все это приводит к тому, что волна напряжения на 90^o не совпадает по фазе с волной тока. На графике видно, как волна напряжения дает «фору» волне тока: напряжение «ведет» ток, а ток «запаздывает» за напряжением.

 

Ели мы на этот график нанесем значения мощности нашей схемы, то все станет еще более интересным:

 

Поскольку мгновенная мощность представляет собой произведение мгновенного напряжения  и мгновенного тока (p = iu), она будет равна нулю, если мгновенное напряжение или ток будут равны нулю. Всякий раз, когда мгновенные значения тока и напряжения имеют положительные значения (выше нулевой линии), мощность так же будет положительна. Аналогично примеру с резистивной цепью, мощность примет положительное значение и в том случае, если мгновенный ток и напряжение будут иметь отрицательные значения (ниже нулевой линии). Однако, вследствие того, что волны напряжения и тока не совпадают по фазе на 90^o, бывают случаи, когда ток положителен, а напряжение отрицательно (или наоборот), в результате чего появляются отрицательные значения мгновенной мощности.

Но, что такое отрицательная мощность? Отрицательная мощность означает, что катушка индуктивности отдает энергию обратно в цепь. Положительная же мощность означает, что катушка индуктивности поглощает энергию из цепи. Так как положительные и отрицательные циклы питания равны по величине и продолжительности, в течение полного цикла катушка индуктивности отдает обратно в схему столько же энергии, сколько она потребляет из нее. В практическом смысле это означает, что реактивное сопротивление катушки не рассеивает никакой энергии, чем оно и отличается от сопротивления резистора, рассеивающего энергию в виде тепла. Однако, все вышесказанное справедливо только для идеальных катушек индуктивности, провода которых не имеют никакого сопротивления.

Сопротивление катушки индуктивности, изменяющее силу тока, интерпретируется как сопротивление переменному току в целом, у которого по определению постоянно меняется мгновенная величина и направление. Это сопротивление переменному току похоже на обычное сопротивление, но отличается от него тем, что всегда приводит к фазовому сдвигу между током и напряжением, а так же рассеивает нулевую мощность. Из-за указанных различий, данное сопротивление носит несколько иное название — реактивное сопротивление. Реактивное сопротивление, как и обычное, измеряется в Омах, только обозначается оно символом Х, а не R. Для большей конкретики, реактивное сопротивление катушки индуктивности обычно обозначают заглавной буквой Х с буквой L в качестве индекса: X_L.

Поскольку напряжение на катушке индуктивности пропорционально скорости изменения тока, оно будет больше для быстро меняющихся токов, и меньше — для токов с более медленным изменением. Это означает, что реактивное сопротивление любой катушки индуктивности (в Омах) прямопропорционально частоте переменного тока. Точная формула расчета реактивного сопротивления выглядит следующим образом:

 

Если на катушку индуктивностью 10 мГн воздействовать частотами 60, 120 и 2500 Гц, то ее реактивное сопротивление примет следующие значения:

Частота (Гц)	Реактивное сопротивление (Ом)
60	3. 7699
120	7.5398
2500	157.0796

В уравнении реактивного сопротивления выражение “2πf” имеет важное значение. Оно означает число в радианах в секунду, характеризующее «вращение» переменного тока (один полный цикл переменного тока представляет собой одно полное круговое вращение). Радиан — это единица измерения углов: в одном полном круге есть 2π радиан, точно так же, как в нем есть 360^o. Если генератор переменного тока двухполюсный, то он произведет один полный цикл для каждого полного оборота вала, что будет означать 2π радиан или 360^o. Если постоянную 2π умножить на частоту в герцах (циклах в секунду), то результатом будет число в радианах в секунду, известное как угловая (циклическая) частота переменного тока.

Помимо выражения 2πf, угловая частота переменного тока может обозначаться строчной греческой буквой ω (Омега). В этом случае формула X_L = 2πfL может быть написана как X_L = ωL.

Необходимо понимать, что угловая частота является выражением того, насколько быстро проходит полный цикл волны, равный 2π радиан. Она необязательно представляет фактическую скорость вала генератора, производящего переменный ток. Если генератор имеет более двух полюсов, его угловая частота будет кратной скорости вращения вала. По этой причине ω иногда выражается в единицах электрических радиан в секунду, чтобы отличить ее от механического движения.

При любом способе выражения угловой частоты очевидно, что она прямопропорциональна реактивному сопротивлению катушки индуктивности. При увеличении частоты переменного тока (или скорости вращения вала генератора), катушка индуктивности будет оказывать большее сопротивление прохождению тока и наоборот. Переменный ток в простой индуктивной цепи равен напряжению (в Вольтах) поделенному на реактивное сопротивление катушки индуктивности (в Омах). Как видите, это аналогично тому что переменный или постоянный ток в простой резистивной цепи равен напряжению (в Вольтах) поделенному на сопротивление (в Омах). В качестве примера давайте рассмотрим следующую схему:

 

 

Однако, мы должны иметь в виду, что напряжение и ток имеют разные фазы. Как было сказано ранее, напряжение имеет фазовый сдвиг +90^o по отношению к току (рисунок ниже). Если представить фазовые углы напряжения и тока математически (в виде комплексных чисел), то мы увидим, что сопротивление катушки индуктивности переменному току обладает следующим фазовым углом:

 

 

Ток на катушке индуктивности отстает от напряжения на 90^o.

Математически можно сказать, что фазовый угол сопротивления катушки индуктивности переменному току составляет 90^o. Фазовый угол реактивного сопротивления току очень важен при анализе цепей. Особенно эта важность проявляется при анализе сложных цепей переменного тока, где реактивные и простые сопротивления взаимодействуют друг с другом. Он также окажется полезным для представления сопротивления любого компонента электрическому току с точки зрения комплексных чисел (а не скалярных величин сопротивления и реактивного сопротивления).

Как индуктивность зависит от числа витков. Дроссель, катушка индуктивности. Принцип работы. Математическая модель. Типы, виды, категории, классификация

Катушка индуктивности (inductor. -eng)– устройство, основным компонентом которого является проводник скрученный в кольца или обвивающий сердечник. При прохождении тока, вокруг скрученного проводника (катушки), образуется магнитное поле (она может концентрировать переменное магнитное поле), что и используется в радио- и электро- технике.

К точной и компьютерной технике технике больше близок дроссель (Drossel, регулятор, ограничитель), так как он чаще всего применяется в цепях питания процессоров, видеокарт, материнских плат, блоков питания & etc. В последнее время, применяются индукторы закрытые в корпуса из металлического сплава для уменьшения наводок, излучения, шумов и высокочастотного свиста при работе катушки.

Дроссель служит для уменьшения пульсаций напряжения, сглаживания или фильтрации частотной составляющей тока и устранения переменной составляющей тока. Сопротивление дросселя увеличивается с увеличением частоты, а для постоянного тока сопротивление очень мало. Характеристики дросселя получаются от толщины проводника, количества витков, сопротивления проводника, наличия или отсутствия сердечника и материала, из которого сердечник сделан. Особенно эффективными считаются дроссели с ферритовыми сердечниками (а также из альсифера, карбонильного железа, магнетита) с большой магнитной проницаемостью.

Как работает дроссель.

В цепях переменного тока, для ограничения тока нагрузки, очень часто применяют дроссели — индуктивные сопротивления. Перед обычными резисторами здесь у дросселей имеется серьезные преимущества — значительная экономия электроэнергии и отсутствие сильного нагрева.

Каково устройство дросселя, на чем основан принцип его работы?

Устроен дроссель очень просто — это катушка из электрического провода, намотанная на сердечнике из ферромагнитного материала. Приставка ферро, говорит о присутствии железа в его составе (феррум — латинское название железа), в том или ином количестве.

Принцип работы дросселя основан на свойстве, присущем не только катушкам но и вообще, любым проводникам — индуктивности. Это явление легче всего понять, поставив несложный опыт.

Для этого требуется собрать простейшую электрическую цепь, состоящую из низковольтного источника постоянного тока (батарейки), маленькой лампочки накаливания, на соответствующее напряжение и достаточно мощного дросселя (можно взять дроссель от лампы ДРЛ-400 ватт).

Без дросселя, схема будет работать как обычно — цепь замыкается, лампа загорается. Но если добавить дроссель, подключив его последовательно нагрузке(лампочке), картина несколько изменится.

Присмотревшись, можно заметить, что во первых, лампа загорается не сразу, а с некоторой задержкой, во вторых — при размыкании цепи возникает хорошо заметная искра, прежде не наблюдавшаяся. Так происходит потому что, в момент включения ток в цепи возрастает не сразу — этому препятствует дроссель, некоторое время поглощая электроэнергию и запасая ее в виде электромагнитного поля. Эту способность и называют — индуктивностью.

Чем больше величина индуктивности, тем большее количество энергии может запасти дроссель. Еденица величины индуктивности — 1 Генри В момент разрыва цепи запасеная энергия освобождается, причем напряжение при этом может превысить Э.Д.С. используемого источника в десятки раз, а ток направлен в противоположную сторону. Отсюда заметное искрение в месте разрыва. Это явление называется — Э.Д.С. самоиндукции.

Если установить источник переменного тока вместо постоянного, использовав например, понижающий трансформатор, можно обнаружить что та же лампочка, подключенная через дроссель — не горит вовсе. Дроссель оказывает переменному току гораздо большое сопротивление, нежели постояному. Это происходит из за того, что ток в полупериоде, отстает от напряжения.

Получается, что действующее напряжение на нагрузке падает во много раз(и ток соответственно), но энергия при этом не теряется — возвращается за счет самоиндукции обратно в цепь.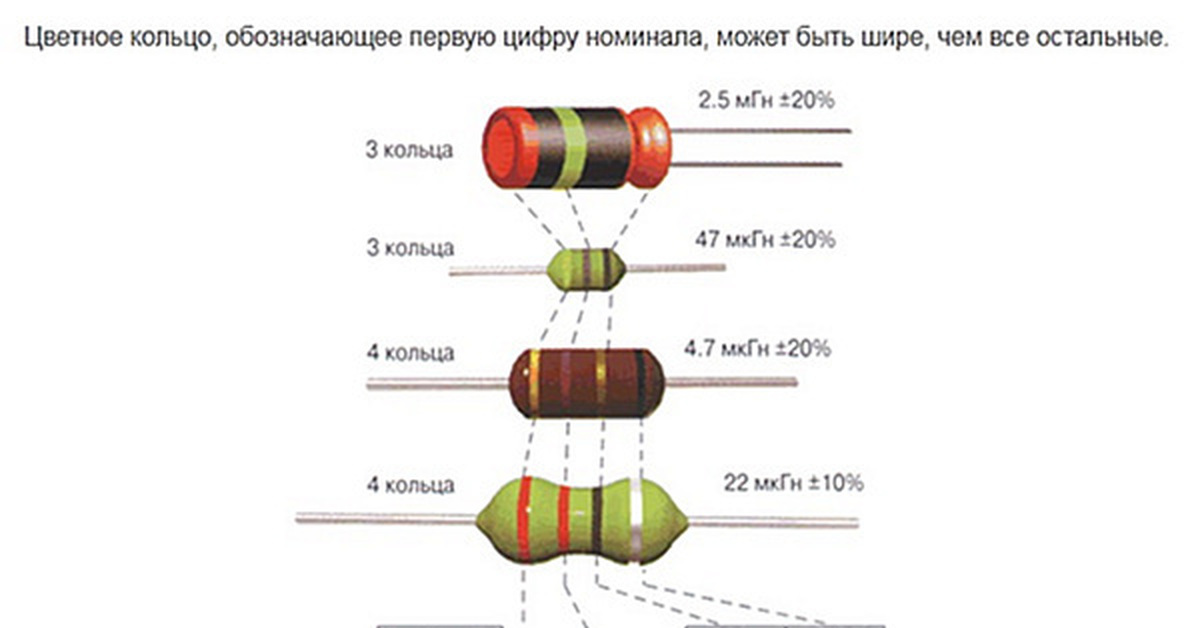 Сопротивление оказываемое индуктивностью переменному току называется — реактивным. Его значение зависит от величины индуктивности и частоты переменного тока. Величина индуктивности в свою очередь, находится в зависимости от количества витков катушки и свойства материала сердечника, называемого — магнитной проницаемостью, а так же его формы.

Магнитная проницаемость — число, показывающее во сколько раз индуктивность катушки больше с сердечником из данного материала, нежели без него(в идеале — в вакууме.)

Т. е — магнитная проницаемость вакуума принята за еденицу.

В радиочастотных катушках малой индуктивности, для точной подстройки применяются сердечники стержеобразной формы. Материалами для них могут являться ферриты с относительно небольшой магнитной проницаемостью, иногда немагнитные материалы с проницаемостью меньше 1.

В электромагнитах реле — сердечники подковоообразной и цилиндрической формы из специальных сталей.

Для намотки дросселей и трансформаторов используют замкнутые сердечники — магнитопроводы Ш — образной и тороидальной формы. Материалом на частотах до 1000 гц служит специальная сталь, выше 1000 гц — различные ферросплавы. Магнитопроводы набираются из отдельных пластин, покрытых лаком.

У катушки, намотанной на сердечник, кроме реактивного(Xl) имеется и активное сопротивление(R). Таким образом, полное сопротивление катушки индуктивности равно сумме активной и реактивной составляющих.

Как работает трансформатор.

Рассмотрим работу дросселя собранного на замкнутом магнитопроводе и подключенного в виде нагрузки, к источнику переменного тока. Число витков и магнитная проницаемость сердечника подобраны таким образом, что его реактивное сопротивление велико, ток протекающий в цепи соответственно — нет.

Ток, переодически изменяя свое направление, будет возбуждать в обмотке катушки (назовем ее катушка номер 1) электромагнитное поле, направление которого будет также переодически меняться — перемагничивая сердечник. Если на этот же сердечник поместить дополнительную катушку(назовем ее — номер 2), то под действием переменного электромагнитного поля сердечника, в ней возникнет наведенная переменная Э. Д.С.

Если количество витков обеих катушек совпадает, то значение наведенной Э.Д.С. очень близко к значению напряжения источника питания, поданного на катушку номер 1. Если уменьшить количество витков катушки номер 2 вдвое, то значение наведенной Э.Д.С. уменьшится вдвое, если количество витков наоборот, увеличить — наведенная Э.Д.С. также, возрастет. Получается, что на каждый виток, приходится какая-то определенная часть напряжения.

Обмотку катушки на которую подается напряжение питания (номер 1) называют первичной. а обмотка, с которой трансформированое напряжение снимается — вторичной.

Отношение числа витков вторичной(Np) и первичной (Ns) обмоток равно отношению соответствующих им напряжений — Up (напряжение первичной обмотки) и Us (напряжение вторичной обмотки).

Таким образом, устройство состоящее из замкнутого магнитопровода и двух обмоток в цепи переменного тока можно использовать для изменения питающего напряжения — трансформации. Соответственно, оно так и называется — трансформатор.

Если подключить к вторичной обмотке какую-либо нагрузку, в ней возникнет ток(Is). Это вызовет пропорциональное увеличение тока(Ip) и в первичной обмотке. Будет верным соотношение:

Трансформаторы могут применяться как для преобразовния питающего напряжения, так и для развязки и согласования усилительных каскадов. При работе с трансформаторами необходимо обратить внимание на ряд важных параметров, таких как:

1. Допустимые токи и напряжения для первичной и вторичной обмоток.

2. Максимальную мощность трансформатора — мощность которая может длительное время передаваться через него, не вызывая перегрева обмоток.

3. Диапазон рабочих частот трансформатора.

Параллельный колебательный контур.

Если соединить катушку индуктивности и конденсатор — получится очень интересный элемент радиотехники — колебательный контур. Если зарядить конденсатор или навести в катушке Э.Д.С. используя электромагнитное поле — в контуре начнут происходить следующие процессы: Конденсатор разряжаясь, возбуждает электромагнитное поле в катушке индуктивности. Когда заряд истощается, катушка индуктивности возвращает запасенную энергию обратно в конденсатор, но уже с противоположным знаком, за счет Э.Д.С. самоиндукции. Это будет повторяться снова и снова — в контуре возникнут электромагнитные колебания синусоидальной формы. Частота этих колебаний называется резонансной частотой контура, и зависит от величин емкости конденсатора(С), и индуктивности катушки (L).

Параллельный колебательный контур обладает очень большим сопротивлением на своей резонансной частоте. Это позволяет использовать его для частотной селекции(выделения) в входных цепях радиоаппаратуры и усилителях промежуточной частоты, а так же — в различных схемах задающих генераторов.

Цветовая и кодовая маркировка индуктивностей.

Обычно для индуктивностей кодируется номинальное значение индуктивности и допуск, т.е. допускаемое отклонение от указанного номинала. Номинальное значение кодируется цифрами, а допуск — буквами. Применяется два вида кодирования.

Кодовая маркировка.

Первые две цифры указывают значение в микрогенри (мкГн), последняя — количество нулей. Следующая за цифрами буква указывает на допуск. Например, код 101J обозначает 100 мкГн ±5%. Если последняя буква не указывается -допуск 20%. Исключения: для индуктивностей меньше 10 мкГн роль десятичной запятой выполняет буква R, а для индуктивностей меньше 1 мкГн — буква N.

D=±0,3 нГн; J=±5%; К=±10%; M=±20%

Примеры обозначений:

Индуктивности маркируются непосредственно в микрогенри (мкГн). В таких случаях маркировка 680К будет означать не 68 мкГн ±10%, как в случае А, а 680 мкГн ±10%.

Как измерить индуктивность катушки, дросселя.

Простите за качество некоторых картинок (чем богаты).

Берегите себя и своих близких!

свернуть

Словосочетание «катушка ниток» знакомо всем, но про катушку индуктивности слышали, думаю, не все. Вот что вы себе представляете под словом «катушка» ? Ну… это, наверное, какая-нибудь фиговинка, на которой намотаны нитки, леска, веревка, да что угодно! Катушка индуктивности представляет из себя точь-в-точь то же самое, но вместо нитки, лески или чего-нибудь еще там намотана обыкновенная медная проволока в изоляции. Изоляция может быть из бесцветного лака, из проводной изоляции, и даже из матерчатой. Тут фишка такая, хоть и провода в катушке индуктивности очень плотно прилегают к друг другу, они все равно изолированы друг от друга. Если будете мотать катушки индуктивности сами, ни в коем случае не вздумайте брать обычный медный голый провод!

Любая катушка индуктивности, как ни странно, обладает индуктивностью:-) Индуктивность катушки измеряется в Генри (Гн), обозначается буковкой L и замеряется LC — метром. Что такое индуктивность? Давайте разбираться. Если через проводок прогнать электрический ток, то он вокруг себя создаст магнитное поле:

где В — магнитное поле, I — сила тока.

А давайте возьмем и намотаем в спиральку этот провод и подадим на его концы электрический ток:

И у нас получилась вот такая картина с магнитными силовыми линиями:

Грубо говоря, чем больше линий магнитного поля пересекут площадь этого соленоида, получается площадь цилиндра, тем больше будет магнитный поток (Ф). Так как по всей этой конструкции течет электрический ток, то значит в этот момент он обладает какой-то Силой тока (I). А коэффициент между магнитным потоком и силой тока называется индуктивностью, и вычисляется так:

С научной же точки зрения, индуктивность — это способность извлекать энергию из источника электрического тока и сохранять ее в виде магнитного поля. Если ток в катушке увеличивается, магнитное поле вокруг катушки расширяется, а если ток уменьшается — магнитное поле сжимается. Катушка индуктивности обладает также очень интересными свойствами. При подаче на катушку электрического тока постоянного напряжения, в катушке возникает напряжение, противоположное напряжению электрического тока и оно потом исчезает через несколько долей секунд. Это противоположное напряжение называется ЭлектроДвижущейСилой самоиндукции, или просто — ЭДС самоиндукции. Это ЭДС зависит от индуктивности катушки. Поэтому в момент подачи напруги на катушку Сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение,в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения, согласно Закон Ома:

где I — сила тока в катушке, U — напряжение в катушке, R — сопротивление катушки.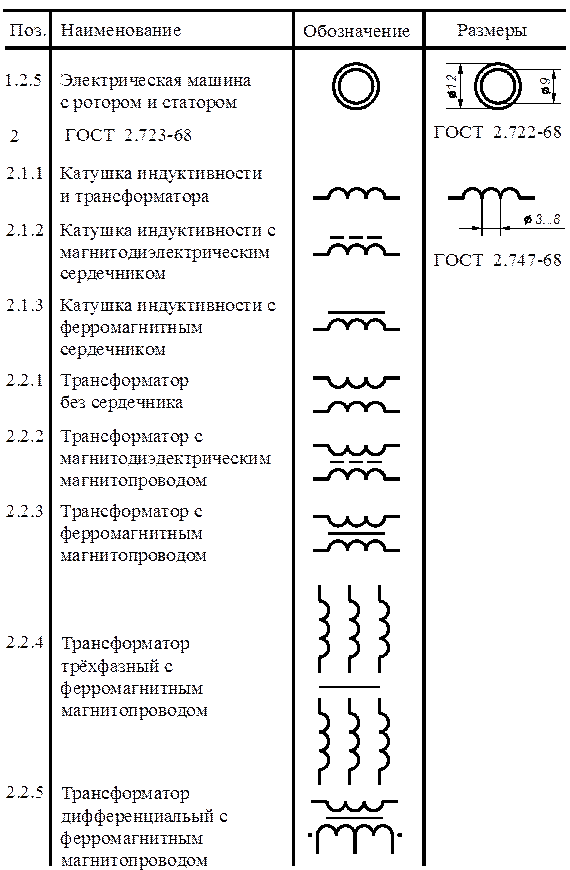

Как мы видим по формуле, напряжение меняется от нуля и до напряжения, подаваемого в катушку, следовательно и ток тоже будет меняться от нуля и до какого то значения. Сопротивление катушки постоянное.

И второй прикол в катушке индуктивности заключается в том, что если мы разомкнем цепь катушка индуктивности — источник тока, то у нас ЭДС самоиндукции будет приплюсовываться к напряжению, которое мы подали на катушку. Следовательно и ток будет в самом начале больше, а потом тихонько спадет до нуля. Время спада силы тока также зависит от индуктивности катушки.

Сделаем первые выводы о работе катушки индуктивности при подаче на нее постоянного тока. При подаче на катушку электрического тока, сила тока будет плавно увеличиваться, а при снятии электрического тока с катушки, сила тока резко возрастет в катушке и плавно убавиться до нуля. Короче говоря,сила тока в катушке мгновенно измениться не может. Это в электронике называют первым законом коммутации. Уфф, ну все, самое тяжелое позади:-).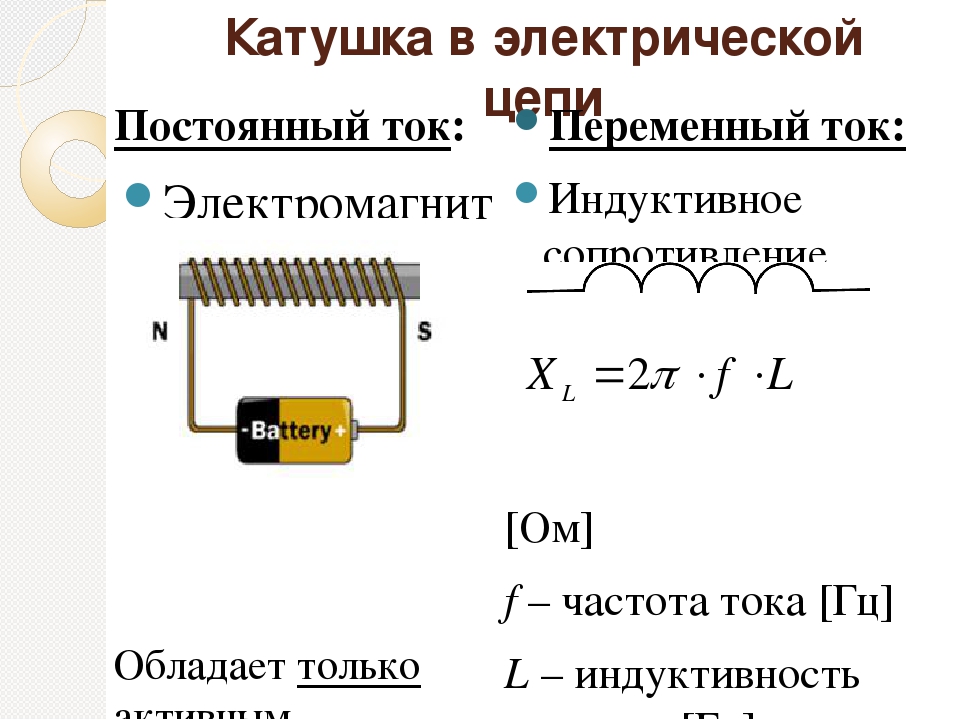

Катушки индуктивности делятся в основном на два класса: с магнитным и немагнитным сердечником. Снизу на фото катушка с немагнитным сердечником.

Но где у нее сердечник? Воздух — это немагнитный сердечник:-). Такие катушки также могут быть намотаны на какой-нибудь цилиндрической бумажной трубочке. Индуктивность катушек с немагнитным сердечником используется, когда индуктивность не превышает 5 миллиГенри.

А вот катушки индуктивности с сердечником:

В основном используют сердечники из феррита и железных пластин. Сердечники повышают индуктивность катушек в разы. Сердечники в виде кольца (тороидальные) позволяют получить большую индуктивность, нежели просто сердечники из цилиндра.

Для катушек средней индуктивности используются ферритовые сердечники:

Катушки с большой индуктивностью делают как трансформатор с железным сердечником, но есть одно различие: у них имеется только одна первичная обмотка:

От каких факторов зависит индуктивность катушки? Давайте проведем несколько опытов. Я намотал катушку с немагнитным сердечником. Ее индуктивность настолько мала, что LC — метр мне показывает ноль.

Имеется ферритовый сердечник

Начинаю вводить катушку в сердечник на самый край

Когда-то в среде «самодельщиков» телевизионных антенн циркулировали мифы о супер эффективности антенны с применением ртути, немного позднее жестяных пивных банок (правда неплохую антенну для Wi-Fi из пивной банки можно сделать, но не телевизионную). Вероятно и по поводу сердечников существуют подобные мифы, тем более сами названия современных магнитных материалов (изоперм, пермендюр) внушают уверенность об их исключительной эффективности. Рассмотрим вопрос применения магнитного сердечника в линейной сигнальной цепи, как он влияет на параметры катушки?

Я не буду углубляться в теорию и рассказывать о диамагнетиках, парамагнетиках, ферромагнетиках, доменах, о петле гистерезиса. Это тема долгого серьезного разговора. Попробую описать доступно, на пальцах.

Итак, магнитный сердечник концентрирует магнитное поле и увеличивает индуктивность при тех же конструктивных параметрах катушки или позволяет уменьшить ее габариты при той же индуктивности. Попробуем подобрать сердечник для фильтра акустической системы — crossover»а для экономии меди. Сердечник должен иметь постоянные магнитные свойства до частот не менее 40 000 Гц при довольно больших токах намагничивания. Какой у нас выбор?

Современные магнитные материалы делятся на три группы:

• Металлические:
  1. Технически чистое железо (электротехническая малоуглеродистая сталь).
  2. Электротехнические кремнистые стали (трансформаторная сталь).
  3. Железоникелевые легированные кристаллические сплавы – пермаллой, суперпермаллой, муметалл, изоперм, пермендюр, перминвар, алфер, алфенол и т.д.
  4. Аморфные и нанокристаллические материалы – витровак, витроперм
• Порошковые материалы, магнитодиэлектрики — тонкие порошки карбонильного железа, пермаллоя или альсифера, смешанные с какой-либо диэлектрической связкой.
• Ферриты — керамические магнитные материалы.

Электротехническая малоуглеродистая сталь может применяться только в цепях постоянного тока, например реле, из-за недопустимо больших вихревых токов на переменном токе и больших потерь на перемагничивание.

Трансформаторная сталь немного лучше. Для уменьшения вихревых токов сердечник набирают из отдельных пластин. Однако выше 1000 Гц такой сердечник имеет недопустимые потери при больших токах намагничивания.

Железоникелевые сплавы имеют очень высокую начальную магнитную проницаемость, могут работать на частотах до 100 Кгц, но при этом у них малая индукция насыщения, т.е. они не могут работать в сильных полях. Зарекомендовали себя как незаменимый материал в магнитных головках магнитофонов, датчиках, магнитных экранах.

Аморфные и нанокристаллические материалы появились позднее чем пермаллои. У них шире частотный диапазон и немного выше индукция насыщения чем у пермаллоя, Применяются как трансформаторы тока в новых электросчетчиках, импульсные трансформаторы в БП, компенсированные дроссели и как более качественная замена пермаллоев.

Магнитодиэлектрики имеют широкий частотный диапазон до десятков мегагерц в зависимости от материала, но малую магнитную проницаемость и индукцию насыщения. Могут работать только в слабых полях. Применяются в технике ВЧ для изготовления магнитопроводов, сердечников катушек индуктивности и т. п

Ферриты

обладают наименьшими потерями на вихревые токи и соответственно могут работать на самых высоких частотах из всех магнитных материалов. Однако имеют малую индукцию насыщения. Отличительной особенностью их является сильная зависимость параметров от температуры, а также старение материала, ухудшение его свойств со временем. Область применения каждой марки феррита определяется критической частотой, выше которой резко возрастают потери и снижается магнитная проницаемость.

Можно проследить общую тенденцию – при улучшении частотных параметров материала падает его индукция насыщения, т.е способность работать в сильных полях, а также магнитная проницаемость.
Самое главное, что любой магнитный материал меняет свои свойства в зависимости от частоты и силы намагничивающего поля . А это значит, что катушка индуктивности с сердечником становится нелинейным элементом и вносит нелинейные искажения в проходящий через нее сигнал, особенно при большой индуктивности и силе тока. Ферриты, кроме того подвержены воздействию температуры.

Для чего мы делаем кроссовер? Чтобы разделить сигнал по частоте, каждый на свою головку. Это позволит уменьшить нелинейные искажения, немного поднять мощность, улучшить качество звучания акустической колонки. Индуктивность в таком фильтре имеет не малую величину и ток тоже. Поэтому, введя в катушку сердечник (любой!), мы не только не добьемся поставленной цели, но и отдалимся от нее, внеся в сигнал дополнительные искажения. Поэтому придется отказаться от экономии на меди и сделать катушку как на рисунке, без сердечника. Правда в случае мощных акустических систем мы получаем монструозную, тяжелую и дорогую катушку. В таком случае приходится идти на компромис и применять сердечник из высококачественных ферромагнетиков. Но его необходимо расчитать так, чтобы он работал далеко от режима насыщения, а это значит, что его размеры тоже будут внушительны.

Сердечники в виде стальных трубок, стержней из «супержелеза» вообще не имеют смысла, ну разве только в установках индукционного нагрева, там вихревые токи в сердечнике играют положительную роль. В цепях, где уровень сигнала слабый и сердечник далек от насыщения, решающий фактор — граничная частота сердечника. При той же индуктивности сердечник даже увеличивает добротность катушки.
В ВЧ дросселях потери в сердечнике играют положительную роль расширяя его частотный диапазон.
Вывод: к подбору сердечника для индуктивности в сигнальной линейной цепи надо подходить взвешенно, учитывая как частотный диапазон, так и максимальный уровень сигнала, а также величину допустимых искажений.
Это не относится к импульсным сигналам и цепям, там все по другому…

Инструкция

Домотайте к катушке дополнительные витки. Это увеличит индуктивность катушки при неизменных параметрах ее остальных конструктивных элементов, а у вариометра (катушки с подвижным сердечником) — сместит оба предела изменения индуктивности (верхний и нижний) в сторону увеличения. При намотке дополнительных витков может оказаться, что они не помещаются на каркасе. Не поддавайтесь соблазну использовать более тонкий провод, чем тот, что использован в катушке первоначально, чтобы не вызвать нагрев обмотки протекающим по ней током.

К катушке, не имеющей сердечника, добавьте таковой. Но помните, что он должен быть выполнен из такого материала, в котором рабочей частоте катушки не возникает потерь на вихревые токи. Для электромагнита , работающего на постоянном токе, подойдет сплошной стальной сердечник, для 50-герцового трансформатора — сердечник, набранный из оксидированных листов стали , в более высокочастотных катушках придется использовать сердечники из ферритов различных марок.

Помните, что даже при одном и том же количестве витков и прочих равных параметрах катушка большего диаметра будет иметь и большую индуктивность. Понятно, однако, что провода для ее изготовления потребуется больше.

Феррит выпускается с различной магнитной проницаемостью. Замените один ферритовый сердечник в катушке на другой, у которого значение этого параметра выше, и ее индуктивность увеличится. Но при этом уменьшится граничная частота, на которой такая катушка сможет работать без возникновения заметных потерь в сердечнике.

Существуют катушки , снабженные специальными механизмами для перемещения сердечника. Для того чтобы увеличить индуктивность в этом случае, вдвиньте сердечник внутрь каркаса.

Замкнутый магнитопровод при прочих равных условиях обеспечивает большую индуктивность, чем разомкнутый. Но старайтесь не применять такое решение в трансформаторах и дросселях, работающих при наличии постоянной составляющей. Она способна подмагничивать и насыщать замкнутый сердечник, тем самым, наоборот, вызывая снижение индуктивности катушки .

Ферритовые сердечники находят широкое применение в бытовой и радиотехнике. Основная цель их использования — устранение помех в контрольных и силовых электрических проводниках.

Ферритами называют химические соединения железного оксида с окислами других металлов. Состав вещества может изменяться в зависимости от необходимых свойств готового изделия.

Производство сердечников

Ферритовые сердечники производят по технологии порошкового литья. Смесь порошков, содержащую необходимые компоненты в тщательно выверенных пропорциях, прессуют в заготовку необходимой формы, которую выпекают при температуре до полутора тысяч градусов. Выпекание может производиться как в воздушной среде, так и в специальной газовой атмосфере. На последнем этапе изготовления изделие из феррита медленно остывает в течение нескольких часов. Такая технология не только позволяет производить сплавы с заданными характеристиками, но также выпускать изделия, не нуждающиеся в последующей обработке

Применение ферритовых сердечников

Наиболее широко ферритовые сердечники применяются в электро- и радиотехнике. Поскольку феррит обладает высокой магнитопропускной способностью и малой удельной электропроводностью, он незаменим при сборке маломощных трансформаторов, в том числе и импульсных. Также сердечники из феррита применяются в качестве средства пассивной защиты от высокочастотных электрических помех. Такое явление наиболее характерно для коммутирующих сетей устройств управления, где даже в экранированном кабеле могут наводиться помехи, снижающие эффективность передачи сигнала.

Типы сердечников из феррита

Для обмоточных трансформаторов выпускают ферриты П-образной и Ш-образной формы. Стержневая форма ферритовых изделий используется при изготовлении магнитопроводов: к примеру, из феррита выполняют сердечники для катушек высокой индуктивности. Обывателю наиболее часто встречаются ферритовые кольца и цилиндры, которые применяются в качестве фильтров помех на кабелях связи: USB, HDMI, LAN и других. Продвинутая технология позволяет изготавливать очень сложные по строению изделия, размер которых иногда составляет меньше десятой доли миллиметра.

Преимущество феррита над аналогичными магнитопроводами

Низкая электропроводность материала позволяет избежать образования вихревых токов при перемагничивании магнитопровода. По этому показателю феррит превосходит даже тонкошихтованную электротехническую сталь. Также ферриту могут быть заданы определенные свойства еще на этапе производства, что позволяет заранее и с высокой точностью адаптировать изделие под нужды определенного устройства, в котором феррит будет задействован. Феррит может активно поглощать, рассеивать или отражать наведенные в кабеле помехи, что особенно актуально в строительстве высокоточных приборов: малый вес и габаритные размеры ферритовых сердечников позволяют применять их без нарушения компоновки оборудования внутри сложных приборов или комплексов.

Катушка индуктивности способна накапливать магнитную энергию при протекании электрического тока. Основной ее характеристикой является ее индуктивность , которая обозначается буквой L и измеряется в Генри (Гн). Индуктивность катушки зависит от ее особенностей.

Вам понадобится

• материал катушки и ее геометрические параметры

Инструкция

По этим данным рассчитайте значение индуктивности катушки . Для этого значение напряжения поделите последовательно на 2, число 3.14, значения частоты тока и силы тока. Результатом будет значение индуктивности для данной катушки в Генри (Гн). Важное замечание : катушку присоединяйте только к источнику переменного тока. Активное сопротивление проводника, используемого в катушке должно быть пренебрежимо мало.

Затем найдите индуктивность соленоида. Для этого, возведите количество его витков во вторую степень, полученный результат умножьте на 3.14, диаметр во второй степени и поделите результат на 4. Полученное число поделите на длину соленоида и умножьте на 0,0000012566 (1,2566*10-6). Это и будет значение индуктивности соленоида.

Если есть такая возможность, для определения индуктивности данного проводника используйте специальный прибор. В его основе лежит схема , именуемая мост переменного тока.

Индуктивность катушки может быть измерена непосредственно либо косвенным способом. В первом случае потребуется прямопоказывающий или мостовой прибор, а во втором придется воспользоваться генератором, вольтметром и миллиамперметром, а затем осуществить ряд вычислений.

Вам понадобится

• — прямопоказывающий или мостовой измеритель индуктивности;
• — генератор синусоидального напряжения;
• — вольтметр и миллиамперметр переменного тока;
• — частотомер;
• — научный калькулятор.

Инструкция

Чтобы измерить индуктивность прямопоказывающим прибором, подключите к нему катушку, а затем, последовательно выбирая пределы измерения переключателем, выберите такой из них, чтобы результат находился примерно в середине диапазона. Прочитайте результат. Если измеритель имеет аналоговую шкалу, при считывании результата принимайте в расчет цену деления, а также коэффициент, указанный рядом с соответствующим положением переключателя.

На мостовом приборе после каждого переключения диапазонов переведите ручку регулятора балансировки моста в любое из крайних положений, а затем вращайте ее до упора в противоположном направлении. Найдите такой диапазон, в котором этой ручкой можно сбалансировать мост. Добившись исчезновения звука в динамике или наушниках либо уменьшения показаний стрелочного индикатора до нуля, прочитайте показания на шкале регулятора (но не стрелочного прибора). При этом, как и в предыдущем случае, учитывайте цену деления и коэффициент, на который следует умножать на данном диапазоне показания.

Для измерения индуктивности косвенным способом соберите измерительную цепь. Вольтметр переменного тока, переключенный на предел, при котором верхней границе диапазона соответствует напряжение в несколько вольт , подключите параллельно выходу генератора. Туда же подключите и частотомер. Также параллельно им присоедините последовательную цепь, состоящую из испытуемой катушки индуктивности, а также милиламперметра переменного тока. Оба прибора должны показывать действующие , а не амплитудные значения измеряемых величин, а также быть рассчитанными на синусоидальную форму колебаний .

На генераторе включите режим выработки напряжения синусоидальной формы. Добейтесь, чтобы вольтметр показывал около двух вольт. Увеличивайте частоту до тех пор, пока показания миллиамперметра не начнут уменьшаться. Добейтесь их уменьшения примерно до половины первоначального значения. Выберите на частотомере предел, соответствующие измеряемой частоте. Прочитайте показания всех трех приборов, а затем отключите генератор и разберите измерительную цепь.-3). Здесь N — это число витков, D — диаметр катушки в сантиметрах. Коэффициент L0 зависит от отношения длины катушки к ее диаметру. Для однослойной катушки он равен: L0 = 1/(0,1*((l/D)+0,45)).

Если в цепи катушки соединены последовательно, то их общая индуктивность равна сумме индуктивностей всех катушек: L = (L1+L2+…+Ln)
Если катушки соединены параллельно, то их общая индуктивность равна: L = 1/((1/L1)+(1/L2)+…+(1/Ln)).
Формулы расчета индуктивности для различных схем соединения катушек индуктивности аналогичны формулам расчета сопротивления при таком же соединении резисторов.

Катушка индуктивности способна накапливать магнитную энергию при протекании электрического тока. Основным параметром катушки является ее индуктивность . Индуктивность измеряется в Генри (Гн) и обозначается буквой L.

Индуктор

— PAL3_Electronics — ~ Confluence ~ Institute ~ for ~ Creative ~ Technologies

Функция катушки индуктивности в контуре цепи заключается в замедлении реакции тока на изменение напряжения.

Катушка индуктивности — это устройство с двумя выводами, которое обозначено схематическими обозначениями ниже:

Хотя для индукторов с воздушным и железным сердечниками используются разные символы, между ними нет электрической разницы. Между двумя клеммами также нет электрической разницы.Таким образом, можно было удалить индуктор из цепи, поменять местами и переустановить; схема будет работать таким же образом с перевернутыми выводами катушки индуктивности.

Часто говорят, что функция индуктивности — накапливать ток. Однако это звучит так, будто катушка индуктивности может накапливать ток сама по себе, как конденсатор или батарея накапливают напряжение сами по себе. Фактически, катушка индуктивности может «накапливать ток» только тогда, когда она установлена ​​в цепи. Электрические токи могут течь только по контуру, поэтому, если индуктор накапливает ток, он должен быть частью контура, по которому может течь ток.Если вы видите катушку индуктивности, которая ни к чему не прикреплена, вы сразу понимаете, что через нее нет тока, поэтому она ничего не сохраняет. Напротив, если вы видите конденсатор или батарею, которые ни к чему не подключены, возможно, они хранят напряжение.

Лучше рассматривать индуктор как устройство, замедляющее реакцию тока на быстрое изменение напряжения. То есть предположим, что имеется петля с источником переменного напряжения и индуктором. Когда источник напряжения включается, индуктор действует как резистор с очень высоким сопротивлением и пропускает лишь небольшой ток.Однако со временем он пропускает все больше и больше тока, пока, наконец, не начнет действовать как короткое замыкание (нулевое сопротивление). Однако короткое замыкание большинства источников напряжения (например, батареи) вызовет кратковременное протекание огромного тока, пока источник напряжения не будет поврежден и перестанет генерировать какое-либо напряжение. Чтобы предотвратить это, предположим, что в цепи есть резистор, который ограничивает ток, протекающий по цепи, до некоторого разумного значения, даже когда катушка индуктивности действует как короткое замыкание.То есть петля выглядит так:

Если бы катушка индуктивности не была в цепи, то, как только подача напряжения была включена, ток немедленно стал бы V / R, что является током, допустимым по закону Ома. пройти через резистор. С индуктором в цепи, ток медленно достигает V / R, поскольку индуктор медленно превращается в разомкнутую цепь.

Теперь предположим, что источник напряжения отключен и действует как короткое замыкание. Если бы катушка индуктивности не была в цепи, то ток вокруг петли немедленно стал бы нулевым по закону Ома: 0 / R = 0.С индуктором в цепи ток медленно падает, пока в конечном итоге не достигнет нуля.

Таким образом, независимо от того, является ли изменение напряжения быстрым увеличением или быстрым уменьшением, катушка индуктивности замедляет реакцию цепи. В конце концов, ток достигает того значения, которое он имел бы, если бы индуктор был коротким замыканием.

Мы обсуждали, какой ток в цепи выше. Теперь давайте обсудим падение напряжения на катушке индуктивности. Когда источник напряжения изначально включается, индуктор действует как резистор, поэтому падение напряжения на нем аналогично резистору.Если ток течет по часовой стрелке, то левый конец индуктора более положительный, чем правый. В конце концов, сопротивление катушки индуктивности равно нулю, а падение напряжения на ней равно нулю. Теперь предположим, что источник напряжения отключился и произошло короткое замыкание. Ток продолжает течь по петле по часовой стрелке, поэтому на резисторе сохраняется такое же падение напряжения, как и раньше. Однако по закону Кирхгофа напряжение на катушке индуктивности должно быть противоположным. Таким образом, его правый конец внезапно становится более положительным, чем его левый конец.Как будто он внезапно становится батареей, которая поддерживает ток, протекающий через резистор. По мере замедления тока падение напряжения как на катушке индуктивности, так и на резисторе уменьшается и в конечном итоге становится равным нулю.

Индуктивность катушки индуктивности определяется как отношение изменения тока к напряжению: индуктивность = изменение тока через катушку индуктивности / напряжение на катушке индуктивности

Как и в случае с конденсаторами, необходимо соблюдать полярность падение напряжения и направление тока.

Основным параметром индуктора является его индуктивность, которая измеряется в генри. То есть падение напряжения на один вольт, приложенное к катушке индуктивности в один генри, вызывает изменение тока на один ампер в течение одной секунды.

Катушка индуктивности состоит из катушки с проволокой. Когда на нее подается падение напряжения, катушка начинает создавать магнитное поле. Однако на это нужно время, поэтому ток увеличивается медленно. В конце концов, поле создано. Его сила определяется током, протекающим через катушку, поэтому внешняя цепь должна накладывать некоторые ограничения на этот ток, чтобы избежать перегорания провода в катушке.Когда напряжение внезапно исчезает и источник напряжения замыкается, магнитное поле не исчезает мгновенно. Вместо этого он заставляет ток продолжать течь. То есть он генерирует напряжение, которое поддерживает ток. Это удаляет энергию из магнитного поля, так что с течением времени генерируемое напряжение падает, а ток замедляется.

элементов схемы | Сопротивление | Емкость

Элементы схемы:

Давайте кратко рассмотрим три основных элемента схемы, а именно сопротивление, емкость и индуктивность.

Сопротивление

Это свойство материала, благодаря которому он препятствует прохождению тока через него. Сопротивление элемента обозначается символом «R». Сопротивление измеряется в омах (Ом).

Связь между напряжением и током определяется законом Ома.

Резистор рассеивает энергию в виде тепла. Таким образом, мощность, потребляемая резистором, равна,

.

Сопротивление преобразует количество энергии в тепло за время t, определяется как,

Сопротивление материала прямо пропорционально его длине и обратно пропорционально площади поперечного сечения.

, где ρ — постоянная пропорциональности, известная как удельное сопротивление или удельное сопротивление , l — длина материала, а A — площадь поперечного сечения материала.

Емкость

Элемент, в котором энергия хранится в форме электростатического поля , известен как емкость. Емкость обозначается буквой «C» и измеряется в фарадах (F).

Для конденсатора напряжение пропорционально заряду.

При нулевом начальном напряжении на конденсаторе, если ток i течет в течение времени t, энергия, подаваемая на конденсатор, будет равна

Индуктивность

Индуктивность — это элемент, в котором хранится энергия в виде электромагнитного поля . Индуктивность обозначается буквой «L» и измеряется в Генри (Гн).

Для индуктивности напряжение пропорционально скорости изменения тока.

Предполагая, что первоначально нулевой ток течет через индуктивность, если ток i протекает через катушку, энергия, запасенная во временном интервале, определяется выражением,

Суммируя поведение трех основных элементов, мы можем написать:

Что такое реактивное сопротивление? — Определение из WhatIs.com

Реактивное сопротивление, обозначенное X , представляет собой форму сопротивления, которое электронные компоненты демонстрируют прохождению переменного тока (переменного тока) из-за емкости или индуктивности.В некоторых отношениях реактивное сопротивление похоже на переменный аналог сопротивления постоянного тока (постоянный ток). Но эти два явления во многом отличаются друг от друга и могут различаться независимо друг от друга. Сопротивление и реактивное сопротивление вместе образуют импеданс , который определяется в терминах двумерных величин, известных как комплексное число.

Когда переменный ток проходит через компонент, обладающий реактивным сопротивлением, энергия попеременно накапливается и высвобождается в магнитном поле или электрическом поле.В случае магнитного поля реактивное сопротивление является индуктивным. В случае электрического поля реактивное сопротивление является емкостным. Индуктивному реактивному сопротивлению присваивается положительное мнимое числовое значение. Емкостному реактивному сопротивлению присваиваются отрицательные значения мнимого числа.

По мере увеличения индуктивности компонента его индуктивное реактивное сопротивление становится больше в мнимом выражении, если частота остается постоянной. По мере увеличения частоты для данного значения индуктивности индуктивное реактивное сопротивление увеличивается в мнимом выражении.Если L — индуктивность в генри (Гн), а f — частота в герцах (Гц), то индуктивное реактивное сопротивление + jX _L в мнимых омах определяется по формуле:

+ jX _L = + j (6,2832 fL )

, где 6,2832 приблизительно равно 2 умноженным на пи, константе, представляющей количество радианов в полном цикле переменного тока, а j представляет собой единичное мнимое число (положительный квадратный корень из -1).Формула также верна для индуктивности в микрогенри (? H) и частоты в МГц (МГц).

В качестве реального примера индуктивного реактивного сопротивления рассмотрим катушку с индуктивностью 10 000 Ом на частоте 2 000 МГц. Используя приведенную выше формулу, + jX _L находится как + j 125,66 Ом. Если частота увеличивается вдвое до 4.000 МГц, то + jX _L удваивается, до + j 251,33 Ом. Если частота уменьшается вдвое до 1.000 МГц, то + jX _L уменьшается вдвое до + j 62.832 Ом.

По мере увеличения емкости компонента его емкостное реактивное сопротивление становится меньше (ближе к нулю) в мнимом выражении, если частота остается постоянной. По мере того, как частота увеличивается для данного значения емкости, емкостное реактивное сопротивление становится меньше отрицательно (ближе к нулю) в мнимом выражении. Если C — это емкость в фарадах (F), а f — частота в Гц, то емкостное реактивное сопротивление -jX _C в мнимых омах определяется по формуле:

-jX _C = — j (6.2832 ФК ) ^-1

Эта формула также верна для емкости в микрофарадах (? F) и частоты в мегагерцах (МГц).

В качестве реального примера емкостного реактивного сопротивления рассмотрим конденсатор номиналом 0,0010000 мкФ на частоте 2,0000 МГц. Используя приведенную выше формулу, -jX _C находится как — j 79,577 Ом. Если частота увеличивается вдвое до 4,0000 МГц, то -jX _C уменьшается вдвое, до — j 39.789 Ом. Если частоту уменьшить вдвое до 1,0000 МГц, то -jX _C увеличится вдвое, до — j 159,15 Ом.

Катушки индуктивности в цепях переменного тока | Электрооборудование A2Z

Когда катушка с проводом (катушка индуктивности) подключена к электричеству постоянного тока ( Рис. 1 ), ток нарастает от нуля, создавая магнитное поле. Сам провод находится в этом поле, и поэтому в нем генерируется напряжение. Это генерируемое напряжение противоположно напряжению, создающему поле; таким образом, он противостоит току.То же самое происходит, когда индуктор отключен от источника постоянного тока.

Только что обсужденное явление называется законом Ленца .

Перед тем, как сформулировать закон Ленца, давайте определим термин индукция . Когда в катушке индуктивности генерируется электромагнитная сила (ЭДС), чаще всего используется утверждение, что «в катушке индуктивности индуцируется ЭДС». Таким образом, индукция используется вместо генерации, что хорошо сочетается с индуктивностью и индуктивностью.

Закон Ленца утверждает , что индуцированная ЭДС всегда противодействует своей причине, что означает, что направление тока, обусловленное индуцированным напряжением, противоположно направлению тока, создавшего индукцию.В результате этого противодействия ток в цепи постоянного тока, содержащей катушку индуктивности, после включения переключателя не является резким изменением, а, вместо этого, представляет собой постепенный рост от нуля до устойчивого значения. Это проиллюстрировано на рис. 2 .

Индукция: Генерация электричества в проводе, когда магнитный поток перерезается проводом (например, когда провод движется относительно магнитного поля или сила и / или направление магнитного поля меняются).

Рисунок 1: При перемещении магнита рядом с витой проволокой в ​​катушке индуцируется электричество.

Рисунок 2 Постепенное изменение тока от нуля до 1,5 А в цепи, содержащей катушку.

Как можно заметить, требуется короткое время, чтобы ток установился на устойчивое значение. Устойчивое значение тока зависит от общего сопротивления в цепи.

Время, необходимое для того, чтобы ток достиг своего конечного значения, зависит от (1) значения индуктивности катушки (измеряется в генри) и (2) общего сопротивления цепи (измеряется в омах).

Индуктор подключен к сети переменного тока

Для лучшего понимания, во-первых, предположим, что прямоугольный сигнал переменного тока подается от источника и подключен к катушке индуктивности, как показано на рис. 3 . Кроме того, мы предполагаем, что сопротивление катушки незначительно и им можно пренебречь.

Когда цепь, содержащая катушку индуктивности, включается, в цепи начинает развиваться ток, начиная с нуля и достигая высокого значения в соответствии с кривой, показанной на Рис. 2 .

Но до того, как ток достигнет максимального значения, напряжение внезапно изменится, и полярность изменится. Следовательно, ток в обратном направлении начинает развиваться таким же образом.

На основе постепенного развития тока и того факта, что напряжение переменного тока переключается с отрицательного на положительное и наоборот, легко понять, что для схемы , рис. 3 , ток выглядит так, как показано на рис. Рисунок 4 .Из рисунка 4 можно понять, что

1. В цепи всегда течет ток.
2. Ток меняется с положительного на отрицательный, т.е. это переменный ток.
3. Ток имеет максимальное (и минимальное) значение в момент, когда напряжение равно нулю (точки A, A ‘, A ″ и т. Д., И точки B, B’, B ″ и т. Д.).

Рисунок 3 Катушка индуктивности, подключенная к источнику переменного тока прямоугольной формы.

Рисунок 4 Ток в катушке индуктивности, подключенной к источнику переменного тока прямоугольной формы.

Рисунок 5 Ток в катушке индуктивности, подключенной к источнику переменного тока с синусоидальной формой волны.

Если вместо прямоугольной волны у нас есть синусоидальная форма волны переменного тока, что является обычным случаем, ток также является синусоидальным и выглядит как Рисунок 5 . Его пики соответствуют моментам, когда значение напряжения равно нулю.

Обратите внимание, что, как показано на Рис. 5 , в цепи переменного тока, содержащей (только катушку индуктивности), ток отстает на 90 ° от приложенного напряжения.Это означает, что ток достигает своего максимума (минимума) после того, как напряжение достигает своего максимума (минимума), а разница между временем, когда напряжение достигает своего пика, и временем, когда ток достигает своего пика, составляет 1/4 цикла или 90 °. Это всегда так для такой схемы.

Переменный ток в индукторе

Мы установили, что при подключении катушки индуктивности к источнику переменного тока в цепи присутствует ток. Это означает, что согласно закону Ома , существует некоторое сопротивление (электрическому потоку) в цепи, связанной с этим током.Это так называемое сопротивление (на самом деле это не сопротивление, потому что в цепи, как предполагается, нулевое значение сопротивления) можно определить.

Но сначала давайте установим еще один факт, что ток в этой цепи изменяется в зависимости от частоты переменного тока. Это легко понять из сравнения токов, показанных для двух случаев в Рис. 6 .

Опять же, для лучшего понимания предполагается прямоугольная форма волны. Форма сигнала на рис. 6b имеет в 2 раза большую частоту, чем на рис. 6а .Ток в , рис. 6b, , меньше, чем ток в , рис. 6а, . Причина разницы в значении тока заключается в том, что в Рис. 6b нет достаточного времени для достижения пикового значения до того, как произойдет переключение полярности. То же верно и для синусоидального сигнала.

Рисунок 6 Сравнение токов в двух прямоугольных сигналах переменного тока при удвоении частоты. (а) Более низкая частота: больший пиковый ток. (b) Более высокая частота: меньший пиковый ток.

Из Рис. 6 видно, что ток через катушку индуктивности имеет обратное влияние на частоту линии переменного тока.

Эффект от включения катушки индуктивности в цепь переменного тока проявляется в виде сопротивления току, но поскольку это не сопротивление (значение в омах, которое можно измерить), его называют реактивным сопротивлением .

Итак, реактивное сопротивление в цепи переменного тока — это то, что демонстрирует сопротивление потоку тока, но это не из-за резистивного элемента, который преобразует электрическую энергию в тепло.Реактивное сопротивление измеряется в омах. Чтобы указать, что реактивное сопротивление связано с катушкой индуктивности, при необходимости, его более конкретно называют индуктивным реактивным сопротивлением .

Реактивное сопротивление катушки индуктивности, обозначенное как X _L , зависит от частоты и индуктивности и может быть определено из

.

Реактивное сопротивление: Кажущееся сопротивление (измеренное в омах), которое конденсатор или катушка индуктивности при подключении к цепи переменного тока демонстрирует потоку электричества.Реактивное сопротивление зависит от частоты переменного тока и, в отличие от резистора, энергия не преобразуется в тепло.

Индуктивное реактивное сопротивление: Кажущееся сопротивление потоку электричества, проявляемое индуктором в цепи переменного тока. Он измеряется в омах и определяет ток в катушке индуктивности в зависимости от приложенного напряжения.

$ \ begin {matrix} {{X} _ {L}} = 2 \ pi fL & {} & \ left (1 \ right) \\\ end {matrix} $

Где π — постоянная (π = 3,14159265), f — частота переменного тока, измеренная в Гц, а L — индуктивность, измеренная в генри.

Пример расчета индуктивного реактивного сопротивления 1

Какое индуктивное сопротивление индуктора при подключении к электричеству 60 Гц? Катушка индуктивности имеет индуктивность 0,05 Гн.

Решение

Из уравнения непосредственно следует, что

$ {{X} _ {L}} = 2 \ pi fL = 2 \ pi * 60 * 0,05 = 18,85 \ Omega $

Пример расчета тока индуктора 2

Найдите ток катушки индуктивности при подключении к источнику переменного тока 9 В, 50 Гц, если ее индуктивность составляет 20 мГн.{9} / {} _ {7.54} = 1.19A \\\ end {align}

долл. США

Из приведенных выше примеров можно заметить, что при повышении частоты реактивное сопротивление катушки индуктивности увеличивается пропорционально ей, а ток в катушке индуктивности уменьшается.

Когда частота электричества, подключенного к катушке индуктивности, увеличивается, реактивное сопротивление катушки индуктивности увеличивается пропорционально частоте, и ток через катушку индуктивности уменьшается.

Катушки индуктивности серии

Точно так же, как резисторы могут быть объединены последовательно и параллельно друг другу, индукторы могут быть включены последовательно или параллельно, когда это необходимо. На рисунке 7 показаны три последовательно включенных индуктора. Соотношение количества катушек индуктивности, включенных последовательно друг с другом, составляет

.

\ [\ begin {matrix} L = {{L} _ {1}} + {{L} _ {2}} + {{L} _ {3}} + \ cdots & {} & \ left (2 \ right) \\\ end {matrix} \]

\ [\ begin {matrix} {{X} _ {L}} = {{X} _ {{{L} _ {1}}}} + {{X} _ {{{L} _ {2} }}} + {{X} _ {{{L} _ {3}}}} + \ cdots & {} & \ left (3 \ right) \\\ end {matrix} \]

L — эквивалентная катушка индуктивности для всех последовательно соединенных катушек индуктивности, а X _L — их эквивалентное индуктивное реактивное сопротивление.

Рисунок 7 Последовательные индукторы.

При последовательном соединении катушек индуктивности все они имеют одинаковый ток. Соответственно, как и в случае резисторов, полное напряжение делится между ними пропорционально их значениям реактивного сопротивления.

Ток в последовательных индукторах Пример 4

Какой ток в трех последовательно соединенных индукторах, когда приложенное напряжение составляет 48 В? Частота источника питания 60 Гц, индуктивности 5, 10 и 15 мГн.{48} / {} _ {11.31} = 4.24A \\\ end {align}

долл. США

Параллельные индукторы

Если необходимо соединить катушки индуктивности параллельно друг другу, как показано на Рис. 8 , то можно использовать правило параллельных катушек индуктивности. Вы заметили, что правило для последовательных катушек индуктивности такое же, как и для последовательных резисторов. То же верно и для катушек индуктивности, включенных параллельно друг другу. Можно использовать любое из следующих уравнений.

\ [\ begin {matrix} \ frac {1} {L} = \ frac {1} {{{L} _ {1}}} + \ frac {1} {{{L} _ {2}}} + \ frac {1} {{{L} _ {3}}} + \ cdots & {} & \ left (4 \ right) \\\ end {matrix} \]

\ [\ begin {matrix} \ frac {1} {{{X} _ {L}}} = \ frac {1} {{{X} _ {{{L} _ {1}}}}} + \ frac {1} {{{X} _ {{{L} _ {2}}}}} + \ frac {1} {{{X} _ {{{L} _ {3}}}}} + \ cdots & {} & \ left (5 \ right) \\\ end {matrix} \]

Ток в параллельных индукторах Пример 5

Три индуктора с индуктивностью 5, 10 и 15 мГн включены параллельно друг другу и подключены к линии 120 В.Если частота линии 60 Гц, какой ток в линии?

Рисунок 8 Катушки индуктивности включены параллельно.

Решение

Для этой задачи проще использовать Уравнение 4 .

\ [\ frac {1} {L} = \ frac {1} {5} + \ frac {1} {10} + \ frac {1} {15} = \ frac {11} {30} \]

Эквивалентная индуктивность для трех катушек индуктивности

.

$ L = 2.727 млн ​​ч $

, а их реактивное сопротивление на частоте 60 Гц —

.

$ {{X} _ {L}} = 2 \ pi * 60 * 0.0002727 = 1,08 \ Омега

долл. США

Таким образом, ток в линии составляет около 120 А (120 В ÷ 1 Ом).

Обратите внимание, что результирующая индуктивность меньше, чем у самой маленькой (5 мГн) индуктивности.

Пример тока индуктора 6

Имейте в виду, что ток в линии при параллельном соединении трех индукторов с индуктивностью 5, 10 и 15 мГн очень велик (120 А). Предположим, что это действительно тот случай, когда вам пришлось заменить поврежденную катушку индуктивности, но у вас нет точного значения, и вы решили изготовить эквивалентную катушку индуктивности, объединив имеющиеся.

Предположим, вы ошиблись и вместо того, чтобы соединять эти индукторы последовательно, вы соединили их параллельно. Во сколько раз ток, вычисленный в примере 5 , сравнивается с ожидаемым током? (Линия 120 В и 60 Гц.)

Решение

Когда эти три катушки индуктивности включены последовательно, их эквивалентная индуктивность составляет

.

$ L = 5 + 10 + 15 = 30 млн. Долл. США

И их реактивное сопротивление

$ {{X} _ {L}} = 2 \ pi * 60 * 0.030 = 11,3 \ Омега

долл. США

и

$ \ begin {align} & I = \ frac {120V} {11.3 \ Omega} = 10.6A \\ & Поскольку, \\ & \ frac {120A} {10.6A} = 11.32 \\\ end {align} $

Таким образом, ток в 11,32 раза больше ожидаемого. В реальной ситуации это может быть очень разрушительным.

Пример расчета индуктивного реактивного сопротивления 7

Три параллельных индуктора в Примере 5 (с индуктивностью 5, 10 и 15 мГн) были фактически взяты из устройства, которое работало с частотой 400 Гц.Найдите, какой ток проходил через каждую отдельную катушку индуктивности и каков был общий ток для приложенного напряжения 48 В.

Решение

Во-первых, нам нужно найти реактивное сопротивление для каждой катушки индуктивности.

$ \ begin {align} & {{X} _ {L1}} = 2 \ times 3,14 \ times 60 \ times 0,005 = 12,566 \ Omega \\ & {{X} _ {L2}} = 2 \ times 3,14 \ раз 60 \ раз 0,010 = 25,133 \ Омега \\ & {{X} _ {L3}} = 2 \ раз 3,14 \ раз 60 \ раз 0,015 = 37,699 \ Омега \\\ end {align} $

Три тока для каждой катушки индуктивности соответственно равны

.

$ \ begin {align} & {{I} _ {1}} = \ frac {48} {12.566} = 3.82A \\ & {{I} _ {2}} = \ frac {48} {25.133} = 1.91A \\ & {{I} _ {3}} = \ frac {48} {37.66} = 1,27A \\\ end {align}

долл. США

А общий ток складывается из трех токов

$ I = 3,82 + 1,91 + 1,27 = 7A $

Концепция самоиндуктивности — электрические концепции

Самоиндуктивность или индуктивность определяется как свойство материала, благодаря которому он препятствует прохождению через него тока. Обычно его обозначают буквой «L», а в системе СИ — Генри. Как материал обладает таким свойством? Чтобы понять, давайте рассмотрим катушку с числом витков N и подключим катушку через источник переменного тока.

Качественный анализ самоиндукции

Пусть через катушку протекает ток i = ImSinωt. Поскольку ток через катушку изменяется, магнитное поле также изменится. Если предполагается, что площадь поперечного сечения катушки равна A, то магнитный поток, связывающий катушку, будет BA, где B — плотность магнитного потока.

Суммарный поток потокосцепления через N витков Ø = NBA

Согласно закону электромагнитной индукции Фарадея изменяющийся магнитный поток вызывает развитие ЭДС.Эта индуцированная ЭДС в катушке будет противодействовать причине в соответствии с законом Ленца. Здесь причина — переменный ток. Следовательно, катушка будет препятствовать прохождению тока. Таким образом, в этот момент мы узнали, как текущее противоположное свойство проявляется в катушке. Но следующая важная вещь — это математическое определение этого свойства, которое называется самоиндуктивностью или индуктивностью.

Количественный анализ самоиндукции

Предположим, что магнитный поток, проходящий через единственную катушку с током I, равен Ø.Тогда собственная индуктивность или индуктивность катушки определяется как «поток, связывающий катушку на единицу тока».

Следовательно,

L = Ø / I

Единица СИ: Тесла / Ампер, известный как Генри.

Расчет собственной индуктивности соленоида

На основании приведенного выше количественного анализа рассчитаем самоиндукцию соленоида. Давайте рассмотрим соленоид из N витков с площадью поперечного сечения «A» и длиной «L», как показано ниже.

Магнитное поле через центр соленоида B = µ ₀ NI / L

«Здесь следует отметить, что магнитное поле внутри длинного соленоида однородно. Но поле вне соленоида почти равно нулю. Здесь длинный соленоид не означает соленоид бесконечной длины, скорее это означает, что длина соленоида намного больше, чем его радиус ».

Следовательно,

Суммарный магнитный поток, соединяющий соленоид Ø = B x количество витков x A

= µ ₀ N ² IA / L

Следовательно,

Собственная индуктивность / индуктивность соленоида = Ø / I

= µ ₀ N ² IA / LI

= µ ₀ N ² A / L

Из приведенного выше выражения самоиндукции ясно, что самоиндукция или индуктивность не зависят от магнитного потока или тока.Это зависит только от геометрии материала. Если взять пример однофазной линии передачи, то индуктивность линии передачи = 4πx10 ^-7 log (D / 0,7788r), где D — расстояние между проводниками, а r — радиус. В этом случае индуктивность также зависит только от геометрии.

Какое значение имеет индуктор в электротехнике

ИНДУКТОР

Индуктор — это пассивное устройство, которое используется для хранения в нем энергии в виде магнитного поля.Индуктор содержит несколько витков проводящего провода вокруг цилиндрической катушки. Это устройство, которое противодействует любому изменению тока, протекающего через него. Они используются в различных приложениях электроники и энергетики, таких как источники питания, радио, телевидение, электродвигатели и т. Д.

Индуктивность измеряется в Генри и обозначается (H). Индуктивность катушки индуктивности зависит от ее физических размеров. то есть: —

Индуктивность, L = N ² мкА / л

Где N = количество витков

L = длина сердечника

U = проницаемость керна

Один Генри

Когда ток в 1 ампер создает напряжение в 1 вольт за одну секунду, считается, что индуктивность катушки равна 1 Генри.

1 Генри = 1 В / 1 кулон

Генри — самые большие единицы, другие более мелкие единицы Генри приведены ниже: —

Милли Генри	мГн	10 -3 H	0,0001
Микро Генри	мкГн	10 -6 H	0,0000001
Нано Генри	нГн	10 -9 H	0,0000000001

Статьи, связанные с индукторами

Типы индукторов

Доступны различные типы индукторов в зависимости от их размеров, номиналов, формы и назначения.Катушки индуктивности доступны от малых до больших, например, трансформаторов.

Индуктор с воздушным сердечником

В индукторе с воздушным сердечником сердечник полностью отсутствует. Этот тип индукторов предлагает путь с высоким сопротивлением для магнитного потока, следовательно, меньшую индуктивность. Катушки индуктивности с воздушным сердечником имеют большие катушки для обеспечения более высокой плотности потока. Эти типы индукторов используются в высокочастотных устройствах, таких как телевизоры, радиоприемники и т. Д.

Индуктор с ферритовым сердечником Катушки индуктивности

с ферритовым сердечником используются там, где требуется высокая частота.Это создает минимальные потери на более высокой частоте. Феррит — это керамический ферромагнитный материал, который действует как изолятор, потому что ток не может проходить через него и, следовательно, вихревой ток не может проходить через него.

Индуктор с железным сердечником

В индукторах этого типа используется шнур из мягкого железа, за счет чего увеличивается индуктивность катушки. Катушки индуктивности с железным сердечником обладают высокой мощностью и высокой индуктивностью, но имеют ограниченную частоту. Они используются для увеличения импеданса и создания высокого напряжения в люминесцентных и натриевых лампах.Кроме того, они используются в схемах фильтров выпрямителя для устранения пульсаций.

Индуктор с тороидальным сердечником

В этих типах индукторов провод наматывается на сердечник круглой формы. Они состоят из ферритов, порошкового железа и намотанной ленты. Утечка потока в индукторах этого типа очень мала на низких частотах. Эти индукторы в основном используются в медицинских устройствах, кондиционерах и холодильниках.

Индуктор на катушке

В этом типе индуктора проволока наматывается на катушку, поэтому его название — катушечный индуктор.В основном они используются в печатных платах, импульсных источниках питания, преобразователях мощности и т. Д.

Многослойные индукторы

Многослойный индуктор включает в себя два рисунка проводящих катушек, которые расположены в два слоя в верхней части многослойного корпуса. Катушки этого индуктора последовательно соединены электрически последовательно с двумя другими проводящими катушками, расположенными под наклоном в нижней части многослойного корпуса.

Тонкослойные индукторы

Тонкопленочные индукторы полностью отличаются от обычных индукторов чипового типа, намотанных медным проводом.В этом типе индукторов мельчайшие индукторы формируются с использованием тонкопленочной обработки, чтобы сделать индуктор микросхемы для высокочастотных (в диапазоне примерно от нано Генри) приложений.

Группировка индукторов

Группирование катушек индуктивности и нахождение их эквивалентных значений аналогично резисторам.

Группирование индукторов последовательно

Когда катушки индуктивности соединены последовательно, общая сумма индуктивностей эквивалентна сумме индуктивностей отдельных индукторов.Формула для последовательного расчета индуктивности: —

L _r = L ₁ + L ₂ + L ₃

Если n индуктивностей соединены последовательно, то эквивалентные индуктивности определяются как: —

Общая индуктивность, L _r = L ₁ + L ₂ + L ₃ + ………… L _n

Группировка индукторов параллельно

При параллельном подключении катушек индуктивности общая сумма индуктивностей эквивалентна сумме индуктивностей отдельных индукторов.Формула для расчета индуктивности при параллельном подключении имеет следующий вид: —

1 / длина _r = 1 / длина ₁ + 1 / длина ₂ + 1 / длина ₃

Если n катушек индуктивности соединены параллельно, то эквивалентные индуктивности равны

.

Общая индуктивность, 1 / L _r = 1 / L ₁ + 1 / L ₂ + 1 / L ₃ ……… + 1 / L _n

Связанные

Самостоятельная и взаимная индуктивность — Материалы для изучения электроники и связи

Собственная индуктивность:

Способность индуктора индуцировать в себе напряжение при изменении тока называется его самоиндуктивностью или просто индуктивностью.Он обозначается буквой L, а его единицы — Генри (H).

Иллюстрация собственной индуктивности

9301 (di / dt)

Где V _L — индуцированное напряжение в вольтах

di / dt — скорость изменения тока в амперах в секунду.

Если di / dt = 1 А / с и V _L = 1 В, то L = 1H

Следовательно, катушка имеет индуктивность в один генри, если в ней индуцируется ЭДС в один вольт, когда ток через нее изменяется на скорость 1 А / с.

Физические факторы, влияющие на значение индуктивности (L):

Было обнаружено, что всякий раз, когда ток через индуктор изменяется (то есть увеличивается или уменьшается), в нем индуцируется противоэдс, которая имеет тенденцию противодействовать этому изменению. Это свойство катушки, благодаря которому она противодействует любому изменению тока через нее, называется индуктивностью (L).

С точки зрения физических факторов

L = μ ₀ μ _r AN ² / l Генри

Где μ ₀ = абсолютная проницаемость для воздуха или вакуума.

μ _r = относительная проницаемость материала сердечника.

A = площадь поперечного сечения сердечника

N = количество витков катушки

l = длина сердечника

Взаимная индуктивность (М):

Возможность изменения тока в одной катушке для индуцирования напряжения в соседняя катушка известна как взаимная индуктивность.Он обозначается буквой M или L _M , а его единицы — Генри (H).

Катушка собственной индуктивности It

Иллюстрация взаимной индуктивности

Его можно выразить как M = V _L2 / (di ₁ / dt)

901 где V L2 взаимно индуцированная ЭДС, производимая во второй катушке (di ₁ / dt), представляет собой скорость изменения тока через первую катушку.

Физические факторы, влияющие на значение взаимной индуктивности (M):

Когда две катушки расположены так близко друг к другу, что расширяющийся и сжимающийся магнитный поток одной катушки соединяется с другой, в другая катушка.В этом случае говорят, что эти две катушки имеют взаимную индуктивность (M).

С точки зрения физических факторов

M = μ ₀ μ _r AN ₁ N ₂ / l

Где ‘ l’ — длина магнитного пути.

Коэффициент сцепления (K):

Степень магнитного сцепления известна как коэффициент сцепления, обозначаемый буквой k. Если L ₁ и L ₂ — индуктивности двух катушек индуктивности, то коэффициент связи выражается как

k = потокосцепления между L ₁ и L ₂ / Общий поток, создаваемый L ₁

(или)

K = M / √ (L ₁ L ₂ )

Если весь поток, создаваемый одной катушкой (L ₁ ), связан с другой, то k = 1.Если магнитный поток одной катушки (L ₁ ) вообще не связан с другой катушкой (L ₂ ), то k = 0. Таким образом, k — постоянная величина, значение которой находится между 0 и 1.

Высокое значение k = 1, так называемая сильная связь, позволяет току в одной катушке индуцировать большее напряжение в другой катушке. Низкое значение k, называемое слабой связью, вызывает меньшее напряжение. Если катушки расположены отдельно или перпендикулярно, коэффициент связи равен нулю и, следовательно, нет взаимной индуктивности.

Типы индукторов:

Катушки индуктивности классифицируются по многим параметрам.Некоторые из них следующие.

1. В зависимости от используемого материала сердечника

(a) индукторы с воздушным сердечником

(b) индукторы с железным сердечником

(c) индукторы с ферритовым сердечником

2. Согласно рабочей частоте

(a) катушки звуковой частоты (AF)

(b) катушки радиочастоты (RF).

3. По способу намотки

(а) однослойные катушки

(б) многослойные катушки

4. По операции

(а) фиксированные катушки

(б) переменные катушки

.