Определить входное сопротивление. Расчет комплексного входного сопротивления цепи

ОБЩИЕ ПОЛОЖЕНИЯ

Для расчета транзисторных усилителей используются два способа: графоаналитический и аналитический . При графоаналитическом методе необходима информация о входных и выходных характеристиках транзистора (по справочнику). Аналитический метод расчета вытекает из теории полупроводниковых приборов и является приближенным. Однако на практике данный метод дает вполне удовлетворительные результаты.

Согласно ЕСКД по выполнению электрических схем в процессе проектирования необходимо составлять перечень элементов принципиально электронных схем (по аналогии со спецификацией механических устройств).

Для составления перечня элементов проектируемого усилителя, элементы его принципиальной схемы необходимо пронумеровать с использованием буквенно-цифровой системы обозначений, принятой в ГОСТ.

С-конденсаторы;

D-микросхемы;

DA-аналоговые микросхемы;

DD-цифровые микросхемы.

L-индуктивности;

R-резисторы;

VD-полупроводниковые диоды;

VT-транзисторы.

Нумерация элементов принципиальной схемы осуществляется в направлении «сверху вниз » и «слева направо ».

Краткие теоретические сведения

Схемы транзисторных усилителей классифицируются по названию заземленного (общего) электрода транзистора-эмиттера, коллектора и базы. Существует три схемы включения биполярных транзисторов: схемы с общим эмиттером , с общим коллектором , с общей базой .

Усилительные свойства транзистора характеризуются следующими статическими параметрами:

Статический коэффициент передачи тока эмиттера транзистора;

статический коэффициент передачи тока базы транзистора.

Параметры a и b связаны соотношениями:

a=b/(1+b) ; b=a/(1-a).

Схема с ОЭ является усилителем мощности входного сигнала. В данной схемевходной и выходной сигналы находятся в противофазе (сдвиг по фазе на угол ). Усилитель с ОЭ обладает сравнительно низким входным сопротивлением и достаточно высоким выходным сопротивлением (импедансом). Вместе с этим схема с ОЭ обеспечивает усиление, как по току , так и по напряжению .

Для обеспечения заданного коэффициента усиления по переменному току в схеме с ОЭ резистор R э в эмиттерной цепи транзистора шунтируется конденсатором С э. Поэтому импеданс эмиттерной цепи соответствует параллельному соединению резистора R э и емкостного сопротивления конденсатора С э.

Комплексный коэффициент усиления в схеме с ОЭ определяется выражением:

,

где R k , R э – активное сопротивление в коллекторной и эмиттерной цепи транзистора соответственно; фазовый сдвиг в эмиттерной цепи транзистора; круговая частота входного сигнала.

Рисунок 1 – Электрическая схема усилителя с общим эмиттером

Методика расчета усилителя с общим эмиттером

Расчет усилителей осуществляется в направлении с выхода к входу устройства (от нагрузки к источнику входного сигнала).

1. Выбор транзистора (по индивидуальному заданию)

Выбор транзистора осуществляется по типу

проводимости и по
параметру b.(bºh 21э -статический коэффициент передачи тока базы для
различных транзисторов b лежит в диапазоне 10…150).

2. Расчет емкости разделительного конденсатора на выходе

Разделительный конденсатор С3 не пропускает постоянный потенциал коллектора в нагрузку. Совместно с сопротивлением нагрузки R н =R5, конденсатор С3 образует RС-цепь, которая подавляет низкие частоты и пропускает высокие частоты.

Величина конденсатора С3 определяются по формуле:

С 3 расч. ³1/(2pf сигн R н).

Рассчитанное значение емкости С3 будет соответствовать ослаблению входного сигнала в раз относительно сигнала на более высоких частотах. Для уменьшения ослабления входного сигнала и расширения за счет этого полосы пропускания усилителя расчетное значение емкости С 3расч увеличиваются на 1-2 порядка (в 10-100 раз).

3. Расчет тока коллектора

При заданном значении тока эмиттера I э ток коллектора I к определяется по формуле

4. Расчет сопротивления в коллекторной цепи транзистора

Для обеспечения усиления сигнала с минимальными искажениями потенциал коллектора относительно земли в статическом режиме U к0 (при отсутствии входного сигнала), выбирается из условия:

U к0 =0,5Е пит.

Сопротивление R к в цепи коллектора определяется по закону Ома

R к =R3= Uк 0 / I к =0,5Е пит /I к.

Определяется мощность Р 3 , рассеиваемая на сопротивлении R3 в коллекторной цепи транзистора

Р 3 = (I k) 2 *R3.

5. Расчет эквивалентного сопротивления нагрузки переменному току

При достаточно большой емкости разделительного конденсатора С3 эквивалентное сопротивление нагрузки на переменном токе R н.экв.оэ определяется параллельным соединением коллекторного резистора R к =R3 и сопротивления нагрузки R н =R5

R н.экв.оэ =.

6. Расчет сопротивления в цепи эмиттера

Сопротивление R э =R4 обеспечивает температурную стабилизацию режима транзистора по постоянному току. Для уменьшения влияния температуры на параметры усилителя в целом потенциал эмиттера U э относительно земли выбирается в диапазоне 1…2 В. Обычно U э =1В.

Сопротивление R э определяется по закону Ома:

R э = U э / I э.

Ток эмиттера I э выбирается в диапазоне (0,5…1,0)мА, либо задается
индивидуально.

Определяется мощность Р 4 , рассеиваемая на сопротивлении R э =R4 в эмиттерной цепи транзистора

Р 4 = (I э) 2 *R4.

7. Расчет входного сопротивления транзистора со стороны базы

Входное сопротивление транзистора со стороны базы h 11 определяется по формуле

h 11 =R э *(b+1).

8. Расчет резистивного делителя в цепи базы транзистора на постоянном токе.

Для температурной стабилизации режима транзистора по постоянному току (при отсутствии входного сигнала) необходимо следить за

разностью потенциалов между эмиттером и базой при изменении температуры . Для обеспечения следящей обратной связи по температуре в цепь эмиттера вводится резистор R э =R4, а в цепь базы — резистивный делитель R1, R2, с помощью которого стабилизируется потенциал базы транзистора относительно земли. Если в режиме максимального сигнала ток делителя I д превышает ток базы I б, то потенциал базы U б будет определяться только напряжением питания Е пит и соотношением резисторов R1, R2. Поэтому обеспечения температурной стабилизации режима обеспечивается условие:

I д = Е п /(R1+R2)= I э.

По второму закону Кирхгофа определяется потенциал базы U б:

U б = j d +U э,

где j d — статический потенциал рn-перехода (для германиевых транзисторов j d =0,3…0,4 В; для кремневых транзисторов j d =0,6…0,8В).

По закону Ома определяются резисторы R1, R2:

R2=U б /I д = (j d +U э) /I э;

R1= (E пит -U б)/I д =(E пит -U б)/I э.

Определяются мощности Р 1 , Р 2 рассеиваемые на сопротивлениях делителя R1, R2:

Р 1 = (I д) 2 *R1;

Р 2 = (I д) 2 *R2.

9. Расчет резистивного делителя в цепи базы транзистора на
переменном токе.

При усилении сигналов переменного тока шина питания Е пит заземлена через конденсатор фильтра С Ф (имеет нулевой потенциал). Поскольку при достаточно большой емкости С Ф емкостное сопротивление фильтра Х С.Ф достаточно мало (X С.Ф =1/wС Ф ®0), резисторы R1, R2

по переменному току соед

Как узнать сопротивление усилителя — MOREREMONTA

Один из немаловажных характеристик усилителя, которые влияют на добротность всей системы, является его выходное сопротивление. От его величины зависит количество интермодуляционных искажений и коэффициент демпфирования.

Выходное сопротивление должно быть в пределах от 0,001 до 0,1% от импеданса нагрузки (сопротивления АС). Выходное сопротивление нынешних усилителей составляет примерно 0,01-0,1 Ом.

Для измерения выходного сопротивления на понадобятся: генератор звуковых частот, проверяемый усилитель, резистор (сопротивлением 4 — 8 Ом соответствующей мощности), вольтметр переменного тока (мультиметр).

На выходе усилителя, параллельно подключить вольтметр, а с генератора звуковых частот подать сигнал с частотой 1000 Гц, регулятором громкости выставить показания вольтметра в пределах 1-5 вольт.

Сперва снимаем показания выходного напряжения без нагрузки, получаем показания Uxxx. (Пример. Uxxx=5 вольт)

Затем повторяем замер, но уже с нагрузкой (Uрез=8Ом) и получаем значение Uнагр= 4,9 Ом.

Имея необходимые показания можем рассчитать сопротивление усилителя по формуле Rвых=((Uxxx-Uнагр)/Uнагр))хRрез=((5-4,9)/4,9))x8=0,163 Ом

Вот таким методом можно измерить выходное сопротивление усилителя.

Топовые усилители имеют ровное сопротивление на всех частотах и оно очень близко к нулевому значению.

Входное и выходное сопротивление является очень важным в электронике.

Предисловие

Ладно, начнем издалека… Как вы знаете, все электронные устройства состоят из блоков. Их еще часто называют каскады, модули, узлы и тд. В нашей статье будем использовать понятие “блок”. Например, источник питания, собранный по этой схеме:

состоит из двух блоков. Я их пометил в красном и зеленом прямоугольниках.

В красном блоке мы получаем постоянное напряжение, а в зеленом блоке мы его стабилизируем. То есть блочная схема будет такой:

Блочная схема – это условное деление. В этом примере мы могли бы даже взять трансформатор, как отдельный блок, который понижает переменное напряжение одного номинала к другому. Как нам удобнее, так и делим на блоки нашу электронную безделушку. Метод “от простого к сложному” полностью работает в нашем мире. На низшем уровне находятся радиоэлементы, на высшем – готовое устройство, например, телевизор.

Ладно, что-то отвлеклись. Как вы поняли, любое устройство состоит из блоков, которые выполняют определенную функцию.

– Ага! Так что же получается? Я могу просто тупо взять готовые блоки и изобрести любое электронное устройство, которое мне придет в голову?

Да! Именно на это нацелена сейчас современная электроника 😉 Микроконтроллеры и конструкторы, типа Arduino, добавляют еще больше гибкости в творческие начинания молодых изобретателей.

На словах все выходит прекрасно, но всегда есть подводные камни, которые следует изучить, чтобы начать проектировать электронные устройства. Некоторые из этих камушков называются входным и выходным сопротивлением.

Думаю, все помнят, что такое сопротивление и что такое резистор. Резистор хоть и обладает сопротивлением, но это активное сопротивление. Катушка индуктивности и конденсатор будут уже обладать, так называемым, реактивным сопротивлением. Но что такое входное и выходное сопротивление? Это уже что-то новенькое. Если прислушаться к этим фразам, то входное сопротивление – это сопротивление какого-то входа, а выходное – сопротивление какого-либо выхода. Ну да, все почти так и есть. И где же нам найти в схеме эти входные и выходные сопротивления? А вот “прячутся” они в самих блоках радиоэлектронных устройств.

Входное сопротивление

Итак, имеем какой-либо блок. Как принято во всем мире, слева – это вход блока, справа – выход.

Как и полагается, этот блок используется в каком-нибудь радиоэлектронном устройстве и выполняет какую-либо функцию. Значит, на его вход будет подаваться какое-то входное напряжение U_вхот другого блока или от источника питания, а на его выходе появится напряжение U_вых(или не появится, если блок является конечным).

Но раз уж мы подаем напряжение на вход (входное напряжение U_вх), следовательно, у нас этот блок будет кушать какую-то силу тока I_вх.

Теперь самое интересное… От чего зависит I_вх? Вообще, от чего зависит сила тока в цепи? Вспоминаем закон Ома для участка цепи :

Значит, сила тока у нас зависит от напряжения и от сопротивления. Предположим, что напряжение у нас не меняется, следовательно, сила тока в цепи будет зависеть от… СОПРОТИВЛЕНИЯ. Но где нам его найти? А прячется оно в самом каскаде и называется входным сопротивлением.

То есть, разобрав такой блок, внутри него мы можем найти этот резистор? Конечно же нет). Он является своего рода сопротивлением радиоэлементов, соединенных по схеме этого блока. Скажем так, совокупное сопротивление.

Как измерить входное сопротивление

Как мы знаем, на каждый блок подается какой-либо сигнал от предыдущего блока или это может быть даже питание от сети или батареи. Что нам остается сделать?

1)Замерить напряжение U_вх, подаваемое на этот блок

2)Замерить силу тока I_вх, которую потребляет наш блок

3) По закону Ома найти входное сопротивление R_вх.

Если у вас входное сопротивление получается очень большое, чтобы замерить его как можно точнее, используют вот такую схему.

Мы с вами знаем, что если входное сопротивление у нас большое, то входная сила тока в цепи у нас будет очень маленькая (из закона Ома).

Падение напряжения на резисторе R обозначим, как U_R

Из всего этого получаем…

Когда мы проводим эти измерения, имейте ввиду, что напряжение на выходе генератора не должно меняться!

Итак, давайте посчитаем, какой же резистор нам необходимо подобрать, чтобы как можно точнее замерять это входное сопротивление. Допустим, что у нас входное сопротивление R_вх=1 МегаОм, а резистор взяли R=1 КилоОм. Пусть генератор выдает постоянное напряжение U=10 Вольт. В результате, у нас получается цепь с двумя сопротивлениями. Правило делителя напряжения гласит: сумма падений напряжений на всех сопротивлениях в цепи равняется ЭДС генератора.

В результате получается цепь:

Высчитываем силу тока в цепи в Амперах

Получается, что падение напряжения на сопротивлении R в Вольтах будет:

Грубо говоря 0,01 Вольт. Вряд ли вы сможете точно замерить такое маленькое напряжение на своем китайском мультиметре.

Какой отсюда вывод? Для более точного измерения высокого входного сопротивления надо брать добавочное сопротивление также очень большого номинала. В этом случае работает правило шунта: на бОльшем сопротивлении падает бОльшее напряжение, и наоборот, на меньшем сопротивлении падает меньшее напряжение.

Измерение входного сопротивления на практике

Ну все, запарка прошла ;-). Давайте теперь на практике попробуем замерить входное сопротивление какого-либо устройства. Мой взгляд сразу упал на Транзистор-метр. Итак, выставляем на блоке питания рабочее напряжение этого транзистор-метра, то есть 9 Вольт, и во включенном состоянии замеряем потребляемую силу тока. Как замерить силу тока в цепи, читаем в этой статье. По схеме все это будет выглядеть вот так:

А на деле вот так:

Итак, у нас получилось 22,5 миллиАмпер.

Теперь, зная значение потребляемого тока, можно найти по этой формуле входное сопротивление:

Выходное сопротивление

Яркий пример выходного сопротивления – это закон Ома для полной цепи, в котором есть так называемое “внутреннее сопротивление”. Кому лень читать про этот закон, вкратце рассмотрим его здесь.

Что мы имели? У нас был автомобильный аккумулятор, с помощью которого мы поджигали галогенную лампочку. Перед тем, как цеплять лампочку, мы замеряли напряжение на клеммах аккумулятора:

И как только подсоединяли лампочку, у нас напряжение на аккумуляторе становилось меньше.

Разница напряжения, то есть 0,3 Вольта (12,09-11,79) у нас падало на так называемом внутреннем сопротивлении r 😉 Оно же и есть ВЫХОДНОЕ СОПРОТИВЛЕНИЕ. Его также называют еще сопротивлением источника или эквивалентным сопротивлением.

У всех аккумуляторов есть это внутреннее сопротивление r, и “цепляется” оно последовательно с источником ЭДС (Е).

Но только ли аккумуляторы и различные батарейки обладают выходным сопротивлением? Не только. Выходным сопротивлением обладают все источники питания. Это может быть блок питания, генератор частоты, либо вообще какой-нибудь усилитель.

В теореме Тевенина (короче, умный мужик такой был) говорилось, что любую цепь, которая имеет две клеммы и содержит в себе туеву кучу различных источников ЭДС и резисторов разного номинала можно привести тупо к источнику ЭДС с каким-то значением напряжения (E_{эквивалентное}) и с каким-то внутренним сопротивлением (R_{эквивалентное}).

E_экв– эквивалентный источник ЭДС

R_экв– эквивалентное сопротивление

То есть получается, если какой-либо источник напряжения питает нагрузку, значит, в источнике напряжения есть ЭДС и эквивалентное сопротивление, оно же выходное сопротивление.

В режиме холостого хода (то есть, когда к выходным клеммам не подцеплена нагрузка) с помощью мультиметра мы можем замерить ЭДС (E). С замером ЭДС вроде бы понятно, но вот как замерить R_вых?

В принципе, можно устроить короткое замыкание. То есть замкнуть выходные клеммы толстым медным проводом, по которому у нас будет течь ток короткого замыкания I_кз.

В результате у нас получается замкнутая цепь с одним резистором. Из закона Ома получаем, что

Но есть небольшая загвоздка. Теоретически – формула верна. Но на практике я бы не рекомендовал использовать этот способ. В этом случае сила тока достигает бешеного значения, да вообще, вся схема ведет себя неадекватно.

Измерение выходного сопротивления на практике

Есть другой, более безопасный способ. Не буду повторяться, просто скопирую со статьи закон Ома для полной цепи, где мы находили внутреннее сопротивление аккумулятора. В той статье, мы к акуму цепляли галогенную лампочку, которая была нагрузкой R. В результате по цепи шел электрический ток. На лампочке и на внутреннем сопротивлении у нас падало напряжение, сумма которых равнялась ЭДС.

Итак, для начала замеряем напряжение на аккумуляторе без лампочки.

Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе U_r тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае E=12,09 Вольт.

Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем резисторе и на нагрузке, в данном случае на лампочке:

Сейчас на нагрузке (на галогенке) у нас упало напряжение U_R=11,79 Вольт, следовательно, на внутреннем резисторе падение напряжения составило U_r=E-U_R=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r:

Заключение

Входное и выходное сопротивление каскадов (блоков) в электронике играют очень важную роль. В этом мы убедимся, когда начнем рассматривать статью по согласованию узлов радиоэлектронных схем. Все качественные вольтметры и осциллографы также стараются делать с очень высоким входным сопротивлением, чтобы оно меньше сказывалось на замеряемый сигнал и не гасило его амплитуду.

С выходным сопротивлением все намного интереснее. Когда мы подключаем низкоомную нагрузку, то чем больше внутреннее сопротивление, тем больше напряжение падает на внутреннем сопротивлении. То есть в нагрузку будет отдаваться меньшее напряжение, так как разница осядет на внутреннем резисторе. Поэтому, качественные источники питания, типа блока питания либо генератора частоты, пытаются делать как можно с меньшим выходным сопротивлением, чтобы напряжение на выходе “не проседало” при подключении низкоомной нагрузки. Даже если сильно просядет, то мы можем вручную подкорректировать с помощью регулировки выходного напряжения, которые есть в каждом нормальном источнике питания. В некоторых источниках это делается автоматически.

Один из немаловажных характеристик усилителя, которые влияют на добротность всей системы, является его выходное сопротивление. От его величины зависит количество интермодуляционных искажений и коэффициент демпфирования.

Выходное сопротивление должно быть в пределах от 0,001 до 0,1% от импеданса нагрузки (сопротивления АС). Выходное сопротивление нынешних усилителей составляет примерно 0,01-0,1 Ом.

Для измерения выходного сопротивления на понадобятся: генератор звуковых частот, проверяемый усилитель, резистор (сопротивлением 4 — 8 Ом соответствующей мощности), вольтметр переменного тока (мультиметр).

На выходе усилителя, параллельно подключить вольтметр, а с генератора звуковых частот подать сигнал с частотой 1000 Гц, регулятором громкости выставить показания вольтметра в пределах 1-5 вольт.

Сперва снимаем показания выходного напряжения без нагрузки, получаем показания Uxxx. (Пример. Uxxx=5 вольт)

Затем повторяем замер, но уже с нагрузкой (Uрез=8Ом) и получаем значение Uнагр= 4,9 Ом.

Имея необходимые показания можем рассчитать сопротивление усилителя по формуле Rвых=((Uxxx-Uнагр)/Uнагр))хRрез=((5-4,9)/4,9))x8=0,163 Ом

Вот таким методом можно измерить выходное сопротивление усилителя.

Топовые усилители имеют ровное сопротивление на всех частотах и оно очень близко к нулевому значению.

Расчет входного сопротивления транзистора. Расчет комплексного входного сопротивления цепи

В прошлой статье мы с вами говорили о самой простой схеме смещения транзистора. Эта схема (рисунок ниже) зависит от коэффициента бета , а он в свою очередь зависит от температуры, что не есть гуд. В результате на выходе схемы могут появиться искажения усиливаемого сигнала.

В случае транзистора можно рассчитать вакуумное напряжение и ток короткого замыкания, исключая расчет сопротивления эмиттера, оставив входной генератор активным и вычислив две величины, как показано на рисунке. Вычисление напряжения вакуума происходит немедленно. Поскольку излучатель не связан ни с чем, ток коллектора должен быть противоположен основанию, то есть.

Поскольку существует единственное решение. Так как базовый ток равен нулю, то длительное падение напряжения отсутствует, и поэтому напряжение эмиттера, а затем вакуум действительно. Если бы сопротивление эмиттера присутствовало, счет был бы длиннее. Для оценки тока короткого замыкания следует отметить, что и последовательно, и их голова есть напряжение, поэтому базовый ток стоит. Ток короткого замыкания определяется суммой и так.

Чтобы такого не произошло, в эту схему добавляют еще парочку резисторов и в результате получается схема с 4-мя резисторами:

Резистор между базой и эмиттером назовем R бэ , а резистор, соединенный с эмиттером, назовем R э . Теперь, конечно же, главный вопрос: «Зачем они нужны в схеме?»

И, наконец, разделив его на. Который по-прежнему является выражением. Обычно независимый генератор, оставшийся в схеме, упрощается, и результат не зависит от амплитуды сигнала. В этом случае сигнал, который активирует сеть, является нормальным входом схемы, и он также должен быть упрощен, так как в результате получается передаточная функция.

Прежде чем отказаться от раздела электротехнических методов, представлен формальный и абстрактный метод расчета метода импеданса, матрицы и детерминанта. Метод узлов или потенциала в узлах является очень общим и используется для анализа с калькулятор, позволяющий рассчитать размер сети.

Начнем, пожалуй, с R э .

Как вы помните, в предыдущей схеме его не было. Итак, давайте предположим, что по цепи +Uпит—->R к ——> коллектор—> эмиттер—>R э —-> земля бежит электрический ток, с силой в несколько миллиАмпер (если не учитывать крохотный ток базы, так как I э = I к + I б ) Грубо говоря, у нас получается вот такая цепь:

Основная идея метода узла заключается в том, чтобы написать операционные уравнения схемы, используя потенциалы различных узлов как неизвестные, а также известные термины используются токи входного тока. Генераторы с действующим напряжением должны иметь пилот-сигнал, задаваемый потенциалом на узле, или разность потенциалов между двумя узлами. Схема на рисунке 9 представляет собой обычную схему, подготовленную для анализа метода узлов. Входной сигнал был преобразован в генератор тока, а пилот-генератор теперь управляется напряжением, и его усиление является допустимым.

Следовательно, на каждом резисторе у нас будет падать какое-то напряжение. Его величина будет зависеть от силы тока в цепи, а также от номинала самого резистора.

Чуток упростим схемку:

Матричная система, описывающая схему, где — матрица допуска, может быть написана в поле зрения, если вы знаете метод направленной проводимости, иначе вам нужно сделать некоторую алгебру. Знаки токов принимаются положительно из каждого узла, также для генератора пилот-сигнала, размер пилот-сигнала которого должен быть записан последовательно с этим соглашением.

Также в матрице указаны термины, связанные с ведомым генератором. Поскольку выполняется поиск только импеданса на узле эмиттера, он работает только на матрице допусков, и искомый импеданс действителен. Где он является определителем матрицы допуска, и является алгебраическим дополнением к матрице допусков, удалив второй и второй столбцы, поскольку импеданс на узле 2 должен быть найден относительно ссылки. получает.

R кэ — это сопротивление перехода коллектор-эмиттер. Как вы знаете, оно в основном зависит от базового тока.

В результате, у нас получается простой делитель напряжения , где

И сброса допусков с соответствующими импедансами, которые у вас есть. Тот же результат впервые достигнут с работой со скукой! С формулой Блэкмана мы выходим из электротехнических методов и вступаем в систему ретроактивных электронных схем. Эти схемы, как правило, трудно анализировать, поскольку они требуют решения систем уравнений, поскольку экспериментальный генератор имеет величину пилот-сигнала, которая зависит от самого генератора. Метод Блэкмена позволяет вам отбросить эту зависимость, а учетные записи стали намного проще.

Где импеданс между двумя мертвыми терминалами, то есть с выбранным управляемым генератором, отменяется, устанавливается с нулевым коэффициентом усиления. Величины — это коэффициенты возврата, рассчитанные относительно выбранного управляемого генератора и терминалы, на которых он находится хочет найти импеданс короткого замыкания или разомкнутую цепь.

Мы видим, что на эмиттере уже НЕ БУДЕТ напряжения в ноль Вольт, как это было в прошлой схеме. Напряжение на эмиттере уже будет равняться падению напряжения на резисторе R э .

А чему равняется падение напряжения на R э ? Вспоминаем закон Ома и высчитываем:

В случае импеданса эмиттера имеется только один ведомый генератор, на котором будут выполняться различные операции. Помните, что отмена ведомого генератора означает, что его коэффициент усиления равен нулю, поэтому генератор тока превращается в разомкнутую цепь. Операция отмены — это «электротехническая» операция, выполняемая только на ведомом генераторе. Транзистор не отключается, что также меняет только усиление генератора, сопротивление и, возможно, все другие параметры зависят от коэффициента усиления, который они остаются неизменными: он работает на управляемом генераторе, а не на транзисторной модели.

Как мы видим из формулы, напряжение на эмиттере будет равняться произведению силы тока в цепи на номинал сопротивления резистора R э . С этим вроде как разобрались. Для чего вся эта канитель, мы разберем чуть ниже.

Какую же функцию выполняют резисторы R б и R бэ ?

Расчет отчетов о возврате

Сопротивление мертвого состояния оценивается, потому что больше нет генераторов и, конечно. Расчет коэффициента возврата выполняется с помощью следующих простых шагов. Расчет должен повторяться два раза, один с клеммами разомкнутой цепи и один в коротком замыкании. Часто один из двух отчетов о возврате является нулевым.

Две схемы для расчета коэффициентов возврата показаны на рисунке. Модельный генератор тока транзистора был удален и подключен к короткому замыканию, в противном случае генератор тока разомкнутой цепи сильно недоволен! Пилотный генератор все еще управляется током, который должен оцениваться в соответствии с тестовым током. Обратите внимание, что тестовый г

Расчет входного сопротивления. Расчет комплексного входного сопротивления цепи

ОБЩИЕ ПОЛОЖЕНИЯ

Для расчета транзисторных усилителей используются два способа: графоаналитический и аналитический . При графоаналитическом методе необходима информация о входных и выходных характеристиках транзистора (по справочнику). Аналитический метод расчета вытекает из теории полупроводниковых приборов и является приближенным. Однако на практике данный метод дает вполне удовлетворительные результаты.

Согласно ЕСКД по выполнению электрических схем в процессе проектирования необходимо составлять перечень элементов принципиально электронных схем (по аналогии со спецификацией механических устройств).

Для составления перечня элементов проектируемого усилителя, элементы его принципиальной схемы необходимо пронумеровать с использованием буквенно-цифровой системы обозначений, принятой в ГОСТ.

С-конденсаторы;

D-микросхемы;

DA-аналоговые микросхемы;

DD-цифровые микросхемы.

L-индуктивности;

R-резисторы;

VD-полупроводниковые диоды;

VT-транзисторы.

Нумерация элементов принципиальной схемы осуществляется в направлении «сверху вниз » и «слева направо ».

Краткие теоретические сведения

Схемы транзисторных усилителей классифицируются по названию заземленного (общего) электрода транзистора-эмиттера, коллектора и базы. Существует три схемы включения биполярных транзисторов: схемы с общим эмиттером , с общим коллектором , с общей базой .

Усилительные свойства транзистора характеризуются следующими статическими параметрами:

Статический коэффициент передачи тока эмиттера транзистора;

статический коэффициент передачи тока базы транзистора.

Параметры a и b связаны соотношениями:

a=b/(1+b) ; b=a/(1-a).

Схема с ОЭ является усилителем мощности входного сигнала. В данной схемевходной и выходной сигналы находятся в противофазе (сдвиг по фазе на угол ). Усилитель с ОЭ обладает сравнительно низким входным сопротивлением и достаточно высоким выходным сопротивлением (импедансом). Вместе с этим схема с ОЭ обеспечивает усиление, как по току , так и по напряжению .

Для обеспечения заданного коэффициента усиления по переменному току в схеме с ОЭ резистор R э в эмиттерной цепи транзистора шунтируется конденсатором С э. Поэтому импеданс эмиттерной цепи соответствует параллельному соединению резистора R э и емкостного сопротивления конденсатора С э.

Комплексный коэффициент усиления в схеме с ОЭ определяется выражением:

,

где R k , R э – активное сопротивление в коллекторной и эмиттерной цепи транзистора соответственно; фазовый сдвиг в эмиттерной цепи транзистора; круговая частота входного сигнала.

Рисунок 1 – Электрическая схема усилителя с общим эмиттером

Методика расчета усилителя с общим эмиттером

Расчет усилителей осуществляется в направлении с выхода к входу устройства (от нагрузки к источнику входного сигнала).

1. Выбор транзистора (по индивидуальному заданию)

Выбор транзистора осуществляется по типу проводимости и по
параметру b.(bºh 21э -статический коэффициент передачи тока базы для
различных транзисторов b лежит в диапазоне 10…150).

2. Расчет емкости разделительного конденсатора на выходе

Разделительный конденсатор С3 не пропускает постоянный потенциал коллектора в нагрузку. Совместно с сопротивлением нагрузки R н =R5, конденсатор С3 образует RС-цепь, которая подавляет низкие частоты и пропускает высокие частоты.

Величина конденсатора С3 определяются по формуле:

С 3 расч. ³1/(2pf сигн R н).

Рассчитанное значение емкости С3 будет соответствовать ослаблению входного сигнала в раз относительно сигнала на более высоких частотах. Для уменьшения ослабления входного сигнала и расширения за счет этого полосы пропускания усилителя расчетное значение емкости С 3расч увеличиваются на 1-2 порядка (в 10-100 раз).

3. Расчет тока коллектора

При заданном значении тока эмиттера I э ток коллектора I к определяется по формуле

4. Расчет сопротивления в коллекторной цепи транзистора

Для обеспечения усиления сигнала с минимальными искажениями потенциал коллектора относительно земли в статическом режиме U к0 (при отсутствии входного сигнала), выбирается из условия:

U к0 =0,5Е пит.

Сопротивление R к в цепи коллектора определяется по закону Ома

R к =R3= Uк 0 / I к =0,5Е пит /I к.

Определяется мощность Р 3 , рассеиваемая на сопротивлении R3 в коллекторной цепи транзистора

Р 3 = (I k) 2 *R3.

5. Расчет эквивалентного сопротивления нагрузки переменному току

При достаточно большой емкости разделительного конденсатора С3 эквивалентное сопротивление нагрузки на переменном токе R н.экв.оэ определяется параллельным соединением коллекторного резистора R к =R3 и сопротивления нагрузки R н =R5

R н.экв.оэ =.

6. Расчет сопротивления в цепи эмиттера

Сопротивление R э =R4 обеспечивает температурную стабилизацию режима транзистора по постоянному току. Для уменьшения влияния температуры на параметры усилителя в целом потенциал эмиттера U э относительно земли выбирается в диапазоне 1…2 В. Обычно U э =1В.

Сопротивление R э определяется по закону Ома:

R э = U э / I э.

Ток эмиттера I э выбирается в диапазоне (0,5…1,0)мА, либо задается
индивидуально.

Определяется мощность Р 4 , рассеиваемая на сопротивлении R э =R4 в эмиттерной цепи транзистора

Р 4 = (I э) 2 *R4.

7. Расчет входного сопротивления транзистора со стороны базы

Входное сопротивление транзистора со стороны базы h 11 определяется по формуле

h 11 =R э *(b+1).

8. Расчет резистивного делителя в цепи базы транзистора на постоянном токе.

Для температурной стабилизации режима транзистора по постоянному току (при отсутствии входного сигнала) необходимо следить за разностью потенциалов между эмиттером и базой при изменении температуры . Для обеспечения следящей обратной связи по температуре в цепь эмиттера вводится резистор R э =R4, а в цепь базы — резистивный делитель R1, R2, с помощью которого стабилизируется потенциал базы транзистора относительно земли. Если в режиме максимального сигнала ток делителя I д превышает ток базы I б, то потенциал базы U б будет определяться только напряжением питания Е пит и соотношением резисторов R1, R2. Поэтому обеспечения температурной стабилизации режима обеспечивается условие:

I д = Е п /(R1+R2)= I э.

По второму закону Кирхгофа определяется потенциал базы U б:

U б = j d +U э,

где j d — статический потенциал рn-перехода (для германиевых транзисторов j d =0,3…0,4 В; для кремневых транзисторов j d =0,6…0,8В).

По закону Ома определяются резисторы R1, R2:

R2=U б /I д = (j d +U э) /I э;

R1= (E пит -U б)/I д =(E пит -U б)/I э.

Определяются мощности Р 1 , Р 2 рассеиваемые на сопротивлениях делителя R1, R2:

Р 1 = (I д) 2 *R1;

Р 2 = (I д) 2 *R2.

9. Расчет резистивного делителя в цепи базы транзистора на
переменном токе.

При усилении сигналов переменного тока шина питания Е пит заземлена через конденсатор фильтра С Ф (имеет нулевой потенциал). Поскольку при достаточно большой емкости С Ф емкостное сопротивление фильтра Х С.Ф достаточно мало (X С.Ф =1/wС Ф ®0), резисторы R1, R2 по переменному току соединены параллельно .

Эквивалентное сопротивление делителя R1, R2 переменному току R д.экв определяется выражением

R д.экв = R1* R2/(R1 + R2).

10. Расчет входного сопротивления усилителя с ОЭ

На низких частотах, несоизмеримых с быстродействием выбранного транзистора, входное сопротивление усилителя R вх является чисто активным и соответствует параллельному соединению сопротивлений h 11 и R д.экв,

R вх. = h 11 * R д.экв / (h 11+ R д.экв).

Примечание . На высоких частотах, соизмеримых с быстродействием выбранного транзистора, сказываются межэлектродные емкости между выводами эмиттер – база , база – коллектор и эмиттер – коллектор . Поэтому в области высоких частот входное сопротивление (импеданс) является комплексной величиной .

11. Расчет входного конденсатора в цепи базы транзистора

Разделительный конденсатор С1 предназначен для отделения постоянной составляющей входного сигнала. Совместно с эквивалентным входным сопротивлением ЭП R вх.экв конденсатор С1 образует RС-цепь, которая не пропускает постоянный потенциал базы U б в источник входного сигнала, подавляет низкие частоты и пропускает высокие частоты.

Величина емкости конденсатора С1 определяется по формуле

С 1 расч. ³1/(2pf сигн R

2.2. Входное сопротивление

Входное сопротивление ЭП определяется как отношение малого приращения входного напряжения к изменению входного тока. Предположим, что в схеме на рис.2.1 в качестве сопротивления нагрузки выступает сопротивление R₁. Для рассматриваемой схемы входное напряжение — это напряжение на базе транзистора, а входной ток — ток базы. Входное сопротивление ЭП может быть определено по формуле

r_{вх =} dU_вх/dI_вх= (dU_бэ+dU_вых)/dI_б=dU_бэ/dI_б+dU_вых/dI_б=r_бэ+R₁dIэ/dI_б=r_бэ+ (β+1)R₁, где- коэффициент усиления транзистора по току.

Итак входное сопротивление эмиттерного повторителя равно

r_вх=r_бэ+ (β+1)R₁.

Пример. Найдем входное сопротивление эмиттерного повторителя при следующих исходных данных: ток коллектораI_к= 1 мА,R₁= 3 кОм, β = 100.

r_вх=r_бэ+ (β+1)R₁= βu_т /I_к+(β+1)R₁=

=100 25,5мВ/ 1 мА + 101 3 кОм = 2,55 кОм + 303 кОм = 305,6 кОм.

Из расчета видно, что в общем входном сопротивлении доля первого слагаемого (r_бэ) незначительная, поэтому часто использую более приближенную формулу для определения выходного сопротивления эмиттерного повторителя

2.3. Выходное сопротивление

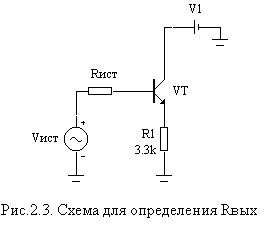
ЭП определяется, как отношение изменения выходного напряжения к изменению выходного тока r_вых= —dU_вых/dI_выхпри условии, что входное напряжение не изменяется, т.е.U_вх=const, аdU_вх= 0.

Для определения выходного сопротивления рассмотрим схему на рис.2.3. здесь R_ист– сопротивление источника входного сигнала.

rвых= —dUвых/dIвых= —dUвых/dIэ.

(2.3)

dU_вх =dU_Rист+dU_бэ+dU_вых.

Учитывая, что dU_вх= 0, и пренебрегаяdU_бэполучим

dU_вых= -dU_Rист= -dI_бR_ист= -dI_эR_ист /(β+1).

Подставим, найденное значение dU_выхв формулу (2.3) и найдем выходное сопротивление усилителя

r_вых= R_ист/(1+).

Из формулы видно, что выходное (внутреннее) сопротивление источника входного сигнала уменьшается в (+1) раз при подключении ЭП.

2.4. Смещение в эмиттерном повторителе

Схема на рис.2.1 пропускает на выход сигнал, который больше, чем 0.6В (U_бэоткрытого транзистора). Для того, чтобы схема могла усиливать разнополярные сигналы необходимо создатьсмещение, которое обеспечивает протекание коллекторного тока в течение полного периода сигнала. Смещение обеспечивается путем подачи положительного постоянного напряжения на базу транзистора. Переменный входной сигнал складывается с постоянным напряжением смещения. Величина напряжения смещения должна быть такой величины, чтобы при отрицательной амплитуде входного сигнала напряжение на базе было больше 0,6 В, т.е. транзистор был открыт.

С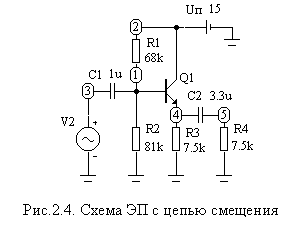мещение в усилителе можно задавать с помощью делителя напряжения R₁, R₂, как показано на рис.2.4. R₁и R₂выбраны так, чтобы на выходе формировался максимальный симметричный сигнал. Это можно обеспечить, если напряжение на эмиттере транзистора при отсутствии входного сигнала будет равно примерно половине напряжения питания U_п.При подаче на вход переменного напряжения на эмиттере сигнал будет изменяться относительно напряжения U_п / 2. Процесс выбора рабочих напряжений в схеме при отсутствии входного сигнала называетсяустановкой рабочей точки. Сопротивления R₁и R₂выбираются из условия, что ток протекающий через делитель (ток через сопротивление R₂) должен быть намного больше ( по крайней мере в 10 раз) тока базы транзистора, чтобы изменение тока базы при изменении входного сигнала оказывало малое влияние на изменение постоянной составляющей тока делителя.

Разделительная емкость С₁не пропускает постоянное напряжение смещения на вход источника сигнала, а емкость С₂пропускает в нагрузку только переменный полезный сигнал.

Разделительные емкости С₁и С₂образуют фильтры верхних частот, нижняя граничная частота которых должна быть выбрана так, чтобы полностью пропускались нижние частоты сигнала. Величины емкости могут быть определены по формуле

С 1/ 2fR_экв, где R_эквдля вычисления С1 равно параллельному соединению сопротивлений R1,R2 и r_вх. Для определения С2 предполагаем, что сопротивление нагрузки ЭП будет не меньше R3. Поэтому R_эквв этом случае выбирают равным R3.

Результаты моделирования схемы, показанной на рис.2.4 представлены на рис.2.5.

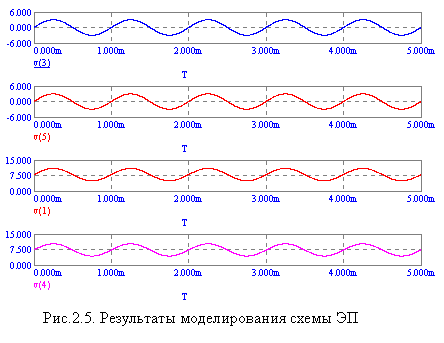
Из рисунка видно, что выходное напряжение v(5) практически полностью повторяет входное напряжение v(3). Переменное напряжение на базе v(1), по амплитуде равное входному напряжению, изменяется относительно постоянного напряжения смещения, примерно равное 7,5 В. Напряжение на эмиттере v(4) меньше напряжения на базе на U_бэ ≈ 0

Входное сопротивление Википедия

Двухполюсник и его эквивалентная схема

Вну́треннее сопротивле́ние двухполюсника — импеданс в эквивалентной схеме двухполюсника, состоящей из последовательно включённых генератора напряжения и импеданса (см. рисунок). Понятие применяется в теории цепей при замене реального источника идеальными элементами, то есть при переходе к эквивалентной схеме.

Введение[ | ]

Необходимость введения термина можно проиллюстрировать следующим примером. Сравним два химических источника постоянного тока с одинаковым напряжением:

Несмотря на одинаковое напряжение, эти источники значительно отличаются при работе на одинаковую нагрузку. Так, автомобильный аккумулятор способен отдать в нагрузку большой ток (от аккумулятора заводится двигатель автомобиля, при этом стартёр потребляет ток порядка 250 А), а от батареи элементов стартёр вообще не станет вращаться, так как напряжение батареи при подключении к зажимам стартёра упадёт до долей вольта. Дело не в относительно небольшой электрической ёмкости батареек: запасённой в ней энергии и заряде в один ампер-час хватило бы для того, чтобы вращать стартёр в течение 14 секунд (при токе 250 А).

В соответствии с законом Ома в источниках с одинаковым напряжением ток в одинаковой нагрузке также должен быть одинаковым. В приведённом примере это не выполняется потому, что утверждение верно только для идеальных источников ЭДС; реальные же источники в той или иной степени отличаются от идеальных. Для описания степени отличия реальных источников от идеальных применяется понятие внутреннее сопротивление.

Эквивалентная схема активного двухполюсника[ |

Входное сопротивление Википедия

Двухполюсник и его эквивалентная схема

Вну́треннее сопротивле́ние двухполюсника — импеданс в эквивалентной схеме двухполюсника, состоящей из последовательно включённых генератора напряжения и импеданса (см. рисунок). Понятие применяется в теории цепей при замене реального источника идеальными элементами, то есть при переходе к эквивалентной схеме.

Введение

Необходимость введения термина можно проиллюстрировать следующим примером. Сравним два химических источника постоянного тока с одинаковым напряжением:

Несмотря на одинаковое напряжение, эти источники значительно отличаются при работе на одинаковую нагрузку. Так, автомобильный аккумулятор способен отдать в нагрузку большой ток (от аккумулятора заводится двигатель автомобиля, при этом стартёр потребляет ток порядка 250 А), а от батареи элементов стартёр вообще не станет вращаться, так как напряжение батареи при подключении к зажимам стартёра упадёт до долей вольта. Дело не в относительно небольшой электрической ёмкости батареек: запасённой в ней энергии и заряде в один ампер-час хватило бы для того, чтобы вращать стартёр в течение 14 секунд (при токе 250 А).

В соответствии с законом Ома в источниках с одинаковым напряжением ток в одинаковой нагрузке также должен быть одинаковым. В приведённом примере это не выполняется потому, что утверждение верно только для идеальных источников ЭДС; реальные же источники в той или иной степени отличаются от идеальных. Для описания степени отличия реальных источников от идеальных применяется понятие внутреннее сопротивление.

Эквивалентная схема активного двухполюсника

Реальные активные двухполюсники хорошо описываются математически, если их рассматривать как эквивалентную схему, состоящую из (см. рисунок) последовательно включённых генератора напряжения и сопротивления (в общем случае — импеданса). Генератор напряжения представляет собственно источник энергии, находящийся в этом двухполюснике. Идеальный генератор мог бы отдать в нагрузку сколь угодно большие мощность и ток. Однако сопротивление, включённое последовательно с генератором, ограничивает мощность, которую данный двухполюсник может отдать в нагрузку. Это эквивалентное сопротивление и называется внутренним сопротивлением. Оно является лишь параметром абстрактной модели двухполюсника, то есть физического «резистора» как электронного компонента внутри двухполюсников обычно нет.

Формально, в реальных гальванических элементах это внутреннее сопротивление можно идентифицировать физически. Это суммарное сопротивление плюсового стержня (углерода, стали), самого корпуса (цинка и никеля), а также самого электролита (соли) и поглотителя водорода (в солевых элементах). Все эти материалы, как и поверхности раздела между ними, имеют конечное сопротивление, отличное от нуля.

В иных источниках это омическое сопротивление обусловлено сопротивлением обмоток и контактов, которое включено последовательно с собственно внутренним сопротивлением источника и снижают характеристики источников напряжения.

Контактные разности потенциалов имеют иную природу возникновения напряжения и являются неомическими, то есть здесь затраты энергии идут на работу выхода носителей заряда.

Сопротивление и внутреннее сопротивление

Основной характеристикой абстрактного двухполюсника является его внутреннее сопротивление (или, иначе, импеданс^[1]). Однако, описать двухполюсник одним только сопротивлением не всегда возможно. Дело в том, что термин сопротивление примени́м только для чисто пассивных элементов, то есть, не содержащих в себе источников энергии. Если двухполюсник содержит источник энергии, то понятие «сопротивление» к нему просто не применимо, поскольку закон Ома в формулировке U=I·r не выполняется^[2].

Таким образом, для двухполюсников, содержащих источники (то есть генераторы напряжения и генераторы тока) необходимо говорить именно о внутреннем сопротивлении (или импедансе). Если же двухполюсник не содержит источников^[3], то «внутреннее сопротивление» для такого двухполюсника означает то же самое, что и просто «сопротивление».

Родственные термины

Если в какой-либо системе можно выделить вход и/или выход (пара электрических контактов), то часто употребляют следующие термины:

• Входное сопротивление, часто входной импеданс, — внутреннее сопротивление, проявляемое этой парой контактов как двухполюсника, которым является вход системы ^[4]
• Выходное сопротивление, часто выходной импеданс, — внутреннее сопротивление, проявляемое этой парой контактов как двухполюсника, которым является выход системы.

Физические принципы

Несмотря на то, что на эквивалентной схеме внутреннее сопротивление представлено как один пассивный элемент (причём активное сопротивление, то есть резистор в нём присутствует обязательно), внутреннее сопротивление не обязательно сосредоточено в каком-либо одном элементе. Двухполюсник лишь внешне ведёт себя так, словно в нём имеется сосредоточенный внутренний импеданс и генератор напряжения. В действительности же, внутреннее сопротивление является внешним проявлением совокупности физических эффектов:

• Если в двухполюснике имеется только источник энергии без какой-либо электрической схемы (например, гальванический элемент), то внутреннее сопротивление носит чисто активный характер (в низкочастотных цепях), и оно обусловлено физическими эффектами, которые не позволяют мощности, отдаваемой этим источником в нагрузку, превысить определённый предел. Наиболее простой пример такого эффекта — ненулевое сопротивление проводников электрической цепи. Но, как правило, наибольший вклад в ограничение мощности вносят эффекты неэлектрической природы. Так, например, в химическом источнике мощность может быть ограничена площадью соприкосновения участвующих в реакции веществ, в генераторе гидроэлектростанции — ограниченным напором воды и т. д.
• В случае двухполюсника, содержащего внутри электрическую схему, внутреннее сопротивление «рассредоточено» в элементах схемы (в дополнение к перечисленным выше механизмам в источнике).

Отсюда также следуют некоторые особенности внутреннего сопротивления:

• Внутреннее сопротивление невозможно убрать из двухполюсника^[5]
• Внутреннее сопротивление не является стабильной величиной: оно может изменяться при изменении каких-либо внешних (нагрузка, ток) и внутренних (нагрев, истощение реагентов) условий.

Влияние внутреннего сопротивления на свойства двухполюсника

Эффект внутреннего сопротивления является неотъемлемым свойством любого активного двухполюсника. Основной результат наличия внутреннего сопротивления — это ограничение электрической мощности, которую можно получить в нагрузке, питаемой от этого двухполюсника.

Если к источнику с ЭДС^[6] генератора напряжения E и активным внутренним сопротивлением r подключена нагрузка с сопротивлением R, то ток, напряжение и мощность в нагрузке выражаются следующим образом:

I=Er+R,UR=Er+RR,PR=E2(r+R)2R.{\displaystyle I={\frac {E}{r+R}},\quad U_{R}={\frac {E}{r+R}}{R},\quad P_{R}={\frac {E^{2}}{(r+R)^{2}}}{R}.}

Нахождение внутреннего сопротивления

Расчёт

Понятие расчёт применимо к схеме (но не к реальному устройству). Расчёт приведён для случая чисто активного внутреннего сопротивления (отличия реактивного сопротивления будут рассмотрены далее).

Примечание: Строго говоря, любой реальный импеданс (в том числе и внутреннее сопротивление) обладает некоторой реактивной составляющей, поскольку любой проводник имеет паразитную индуктивность и ёмкость. Когда мы говорим о чисто активном сопротивлении, то имеем в виду не реальную систему, а её эквивалентную схему, содержащую только резисторы: реактивность была отброшена как несущественная при переходе от реального устройства к его эквивалентной схеме. Если же реактивность существенна при рассмотрении реального устройства (например, при рассмотрении системы на высоких частотах), то эквивалентная схема составляется с учётом этой реактивности. Более подробно смотри в статье «Эквивалентная схема».

Пусть, имеется двухполюсник, который может быть описан приведённой выше эквивалентной схемой. Двухполюсник обладает двумя неизвестными параметрами, которые необходимо найти:

• ЭДС генератора напряжения U
• Внутреннее сопротивление r

В общем случае, для определения двух неизвестных необходимо сделать два измерения: измерить напряжение на выходе двухполюсника (то есть разность потенциалов U_out = φ₂ − φ₁) при двух различных токах нагрузки. Тогда неизвестные параметры можно найти из системы уравнений:

Uout1=U−rI1Uout2=U−rI2{\displaystyle {\begin{matrix}U_{out1}=U-rI_{1}\\U_{out2}=U-rI_{2}\end{matrix}}}

(Напряжения)

где U_out1 — выходное напряжение при токе I₁, U_out2 — выходное напряжение при токе I₂. Решая систему уравнений, находим искомые неизвестные:

r=Uout1−Uout2I2−I1,U=Uout1+I1Uout1−Uout2I2−I1=Uout1+I1r{\displaystyle r={\frac {U_{out1}-U_{out2}}{I_{2}-I_{1}}},\quad U=U_{out1}+I_{1}{\frac {U_{out1}-U_{out2}}{I_{2}-I_{1}}}=U_{out1}+I_{1}r}

(ОбщийСлучай)

Обычно для вычисления внутреннего сопротивления используется более простая методика: находится напряжение в режиме холостого хода и ток в режиме короткого замыкания двухполюсника. В этом случае система (Напряжения) записывается следующим образом:

Uoc=U−00=U−rIsc{\displaystyle {\begin{matrix}U_{oc}=U-0\\0=U-rI_{sc}\end{matrix}}}

где U_oc — выходное напряжение в режиме холостого хода (англ. open circuit), то есть при нулевом токе нагрузки; I_sc — ток нагрузки в режиме короткого замыкания (англ. short circuit), то есть при нагрузке с нулевым сопротивлением. Здесь учтено, что выходной ток в режиме холостого хода и выходное напряжение в режиме короткого замыкания равны нулю. Из последних уравнений сразу же получаем:

r=UocIsc,U=Uoc{\displaystyle r={\frac {U_{oc}}{I_{sc}}},\quad U=U_{oc}}

(ВнутрСопр)

Таким образом, чтобы рассчитать внутреннее сопротивление и ЭДС эквивалентного генератора для двухполюсника, электрическая схема которого известна, необходимо:

• Рассчитать выходное напряжение двухполюсника в режиме холостого хода
• Рассчитать выходной ток двухполюсника в режиме короткого замыкания
• На основании полученных значений найти r и U по формуле (ВнутрСопр).

Измерение

Понятие измерение применимо к реальному устройству (но не к схеме). Непосредственное измерение омметром невозможно, поскольку нельзя подключить щупы прибора к выводам внутреннего сопротивления. Поэтому необходимо косвенное измерение, которое принципиально не отличается от расчёта — также необходимы напряжения на нагрузке при двух различных значениях тока. Однако воспользоваться упрощённой формулой (2) не всегда возможно, поскольку не каждый реальный двухполюсник допускает работу в режиме короткого замыкания.

Иногда применяется следующий простой способ измерения, не требующий вычислений:

• Измеряется напряжение холостого хода
• В качестве нагрузки подключается переменный резистор и его сопротивление подбирается таким образом, чтобы напряжение на нём составило половину от напряжения холостого хода.

После описанных процедур сопротивление резистора нагрузки необходимо измерить омметром — оно будет равно внутреннему сопротивлению двухполюсника.

Какой бы способ измерения ни использовался, следует опасаться перегрузки двухполюсника чрезмерным током, то есть ток не должен превышать максимально допустимого значениях для данного двухполюсника.

Реактивное внутреннее сопротивление

Если эквивалентная схема двухполюсника содержит реактивные элементы — конденсаторы и/или катушки индуктивности, то расчет реактивного внутреннего сопротивления выполняется также, как и активного, но вместо сопротивлений резисторов берутся комплексные импедансы элементов, входящих в схему, а вместо напряжений и токов — их комплексные амплитуды, то есть расчет производится методом комплексных амплитуд.

Измерение реактивного внутреннего сопротивления имеет некоторые особенности, поскольку оно является комплекснозначной функцией, а не скалярным значением:

• Можно искать различные параметры комплексного значения: модуль, аргумент, только вещественную или мнимую часть, а также комплексное число полностью. Соответственно, методика измерений будет зависеть от того, что хотим получить.
• Любой из перечисленных параметров зависит от частоты. Теоретически, чтобы получить путём измерения полную информацию о реактивном внутреннем сопротивлении, необходимо снять зависимость от частоты, то есть провести измерения на всех частотах, которые может генерировать источник данного двухполюсника.

Измерение сопротивления петли фаза-нуль

Результат измерения сопротивления петли фаза-нуль в розетке бытовой электросети

Частным случаем измерения внутреннего сопротивления является измерение сопротивления петли фаза-нуль в электроустановках. Двухполюсником в этом случае является пара проводников электроустановки: фазный и рабочий нулевой проводники или два фазных проводника. На фотографии показан результат такого измерения в розетке бытовой электросети напряжением 220 вольт:

• активная составляющая: 0,49 Ом
• реактивная составляющая: 0,09 Ом
• модуль полного сопротивления: 0,5 Ом
• ожидаемый ток короткого замыкания: 440 А

Прибор находит внутреннее сопротивление путём косвенного измерения методом падения напряжения на нагрузочном сопротивлении. Этот метод рекомендуется к использованию в приложении D ГОСТ Р 50571.16-99. Метод описывается приведённой выше формулой (ОбщийСлучай) при I₁=0.

Результат измерения считается удовлетворительным, если ожидаемый ток короткого замыкания достаточно велик для надежного срабатывания аппарата, защищающего эту цепь от сверхтока.

Применение

В большинстве случаев следует говорить не о применении внутреннего сопротивления, а об учете его негативного влияния, поскольку внутреннее сопротивление является скорее негативным эффектом. Тем не менее, в некоторых системах наличие внутреннего сопротивления с номинальным значением является просто необходимым.

Упрощение эквивалентных схем

Представление двухполюсника как совокупность генератора напряжения и внутреннего сопротивления является наиболее простой и часто используемой эквивалентной схемой двухполюсника.

Согласование источника и нагрузки

Согласование источника и нагрузки — это выбор соотношения сопротивления нагрузки и внутреннего сопротивления источника с целью достижения заданных свойств полученной системы (как правило, стараются достичь максимального значения какого-либо параметра для данного источника). Наиболее часто используются следующие типы согласования:

• Согласование по напряжению — получение в нагрузке максимального напряжения. Для этого сопротивление нагрузки должно быть как можно бо́льшим, по крайней мере, много больше, чем внутреннее сопротивление источника. Другими словами, двухполюсник должен быть в режиме холостого хода. При этом максимально достижимое в нагрузке напряжение равно ЭДС генератора напряжения E. Данный тип согласования применяется в электронных системах, когда носителем сигнала является напряжение, и его необходимо передать от источника к нагрузке с минимальными потерями.
• Согласование по току — получение в нагрузке максимального тока. Для этого сопротивление нагрузки должно быть как можно меньшим, по крайней мере, много меньше, чем внутреннее сопротивление источника. Другими словами, двухполюсник должен быть в режиме короткого замыкания. При этом максимально достижимый в нагрузке ток равен I_max=E/r. Применяется в электронных системах, когда носителем сигнала является ток. Например, при съеме сигнала с быстродействующего фотодиода целесообразно применять преобразователь ток-напряжение с минимальным входным сопротивлением. Малое входное сопротивление также решает проблему заужения полосы из-за паразитного RC-фильтра.
• Согласование по мощности — обеспечивает получение в нагрузке (что эквивалентно отбору от источника) максимально возможной мощности, равной P_max=E²/(4r)^[7]. В цепях постоянного тока: сопротивление нагрузки должно быть равно внутреннему сопротивлению r источника. В цепях переменного тока (в общем случае): импеданс нагрузки должен быть комплексно сопряженным внутреннему импедансу источника.
• Согласование по волновому сопротивлению — получение максимального коэффициента бегущей волны в линии передачи (в СВЧ технике и теории длинных линий). То же самое, что и согласование по мощности, но применительно к длинным линиям. Волновое сопротивление нагрузки должно быть равно внутреннему сопротивлению r. В СВЧ технике применяется практически всегда. Чаще всего термин согласованная нагрузка используется именно в этом смысле.

Согласование по току и мощности следует использовать с осторожностью, так как есть опасность перегрузить источник.

Понижение высоких напряжений

Иногда к источнику электропитания искусственно добавляют внешнее балластное сопротивление, соединённое последовательно с нагрузкой (оно суммируется с внутренним сопротивлением источника) для того, чтобы понизить получаемое от него напряжение, либо ограничить величину тока, отдаваемого в нагрузку. Однако добавление резистора в качестве дополнительного сопротивления (так называемый гасящий резистор) во многих случаях неприемлемо, так как ведёт к бесполезному выделению значительной мощности на нём^[8]. Чтобы не расходовать энергию впустую и не решать проблему охлаждения дополнительного сопротивления, в системах переменного тока используют реактивные гасящие импедансы. На основе гасящего конденсатора может быть построен конденсаторный блок питания. Аналогично, при помощи ёмкостного отвода от высоковольтной ЛЭП можно получить небольшие напряжения для питания каких-либо автономных устройств. Индуктивный балласт широко применяется для ограничения тока в цепи газоразрядных люминесцентных ламп.

Минимизация шума

При усилении слабых сигналов часто возникает задача минимизации шума, вносимого усилителем в сигнал. Для этого используются специальные малошумящие усилители, которые могут быть как низкоомные, например, на биполярных транзисторах, так и высокоомными на полевых транзисторах, однако спроектированы они таким образом, что наименьший коэффициент шума достигается лишь при полном согласовании выходного сопротивления источника сигнала и входного сопротивления самого усилителя. Например, если источник сигнала обладает меньшим выходным сопротивлением (например, микрофон с выходным сопротивлением 30 Ом), то следует применить между источником и усилителем повышающий трансформатор, который повысит выходное сопротивление (а также напряжение сигнала) до необходимого значения.

Ограничения

Понятие внутреннего сопротивления вводится через эквивалентную схему, поэтому имеют силу те же ограничения, что и для применимости эквивалентных схем.

Примеры

Значения внутреннего сопротивления относительны: то, что считается малым, например, для гальванического элемента, является очень большим для мощного аккумулятора. Ниже приведены примеры двухполюсников и значения их внутреннего сопротивления r. Тривиальные случаи двухполюсников без источников оговорены особо.

Малое внутреннее сопротивление

• Нулевым внутренним сопротивлением обладает только идеальный генератор напряжения. Если также рассматривать двухполюсники без источников, то сверхпроводящее короткое соединение тоже имеет нулевое внутреннее сопротивление (до величины токов, вызывающих потерю сверхпроводимости). Генератор со сверхпроводящей обмоткой при не слишком больших частотах и небольших токах также имеет активное внутреннее сопротивление, весьма близкое к нулю (индуктивный импеданс при определенных условиях может быть тоже довольно невелик).
• Автомобильная свинцово-кислотная стартёрная аккумуляторная батарея имеет r около 0,01 Ом. Благодаря столь низкому внутреннему сопротивлению ток, отдаваемый батареей при запуске двигателя, достигает 250 ампер и более (для легковых автомобилей).
• Бытовая сеть электроснабжения переменного тока в жилых помещениях имеет r от десятых долей Ом до 1 Ом и более (зависит от качества электропроводки). Высокое сопротивление соответствует плохой проводке: при подключении мощных нагрузок (например, утюга) напряжение падает, при этом заметно уменьшается яркость ламп освещения, подключенных к той же ветви сети. Повышается пожароопасность, поскольку на сопротивлении проводов выделяется значительная мощность. И наоборот, в хорошей сети с низким сопротивлением напряжение падает от допустимых нагрузок лишь незначительно. Ток при коротком замыкании в хорошей бытовой электросети достигает нескольких сотен ампер.
• Используя отрицательную обратную связь в электронных схемах, можно искусственно создавать источники, обладающие (при определённых условиях) очень низким внутренним сопротивлением. Такими свойствами обладают современные электронные стабилизаторы напряжения. Например, интегральный стабилизатор напряжения 7805 (выходное напряжение 5 В) имеет типичное выходное сопротивление менее 0,0009 Ома^[9]. Однако это вовсе не означает, что такой стабилизатор может отдать в нагрузку ток до 5500 А или мощность до 13 кВт при правильном согласовании. Характеристики стабилизатора нормированы только для рабочего диапазона токов, то есть в данном примере до 1,5 А. При превышении этого значения сработает защита, и стабилизатор отключится (при других конструкциях защиты ток ограничивается, а не отключается полностью).

Большое внутреннее сопротивление

Обычно двухполюсники с большим внутренним сопротивлением — это различного рода датчики, источники сигналов и т. п. Типичная задача при работе с такими устройствами — снятие с них сигнала без потерь из-за неправильного согласования. Для достижения хорошего согласования по напряжению сигнал с такого двухполюсника должен сниматься устройством, имеющим ещё большее входное сопротивление (как правило, сигнал с высокоомного источника снимается при помощи буферного усилителя).

• Бесконечным внутренним сопротивлением обладает только идеальный источник тока. Если также рассматривать двухполюсники без источников, то простой разрыв цепи (два вывода, ничем не соединённые) тоже имеет бесконечное внутреннее сопротивление.
• Конденсаторные микрофоны, пьезоэлектрические и пироэлектрические датчики, а также все остальные «конденсаторо-подобные» устройства имеют реактивное внутреннее сопротивление, модуль которого может достигать^[10] десятков и сотен мегаом. Поэтому такие источники требуют обязательного использования буферного усилителя для достижения согласования по напряжению. Конденсаторные микрофоны, как правило, уже содержат встроенный буферный усилитель, собранный на полевом транзисторе.
• Для измерения электрических потенциалов внутри живых клеток применяются электроды, представляющие собой стеклянный капилляр, заполненный проводящей жидкостью. Толщина такого проводника может быть порядка сотен ангстрем. Вследствие чрезвычайно малой толщины проводника такой «двухполюсник» (клетка с присоединёнными электродами) имеет внутреннее сопротивление порядка 100 мегаом. Высокое сопротивление и малое напряжение делают измерение напряжений внутри клетки непростой задачей.

Отрицательное внутреннее сопротивление

Существуют двухполюсники, внутреннее сопротивление которых имеет отрицательное значение. В обычном активном сопротивлении происходит диссипация энергии, в реактивном сопротивлении энергия запасается, а затем выделяется обратно в источник. Особенность отрицательного сопротивления в том, что оно само является источником энергии. Поэтому отрицательное сопротивление в чистом виде не встречается, оно может быть только имитировано электронной схемой, которая обязательно содержит источник энергии. Отрицательное внутреннее сопротивление может быть получено в схемах путём использования:

Системы с отрицательным сопротивлением потенциально неустойчивы и поэтому могут быть использованы для построения автогенераторов.

См. также

Входной импеданс антенны

Ссылки

Литература

• Зернов Н. В., Карпов В.Г. Теория радиотехнических цепей. — М. — Л.: Энергия, 1965. — 892 с.
• Джонс М. Х. Электроника — практический курс. — М.: Техносфера, 2006. — 512 с. ISBN 5-94836-086-5
• Tildon H. Glisson. Introduction to Circuit Analysis and Design. — Springer, 2011. — P. 768. — ISBN 9789048194421.

Примечания

1. ↑ Импеданс является обобщением понятия сопротивление для случая реактивных элементов. Более подробно смотри в статье Электрический импеданс
2. ↑ Применять закон Ома в такой формулировке к двухполюсникам с внутренними источниками некорректно, необходимо учитывать источники: U=Ir+ΣU_int, где ΣU_int — алгебраическая сумма ЭДС внутренних источников.
3. ↑ Отсутствие источников выражается в том, что напряжение на выводах двухполюсника при отсутствии нагрузки равно нулю. Сюда же относится случай, когда источники есть, но не влияют на выходное напряжение («никуда не подключены»).
4. ↑ Реза Ф., Сили С.Современный анализ электрических цепей Энергия, M.-Л., 1964 г., 480 с. с черт.
5. ↑ Исключение составляют случаи применения стабилизаторов компенсационного типа. Например, двухполюсник, содержащий батарею и ОУ, на некотором участке ВАХ может иметь как сколь угодно малое, так и отрицательное выходное сопротивление — до тех пор, пока избытка энергии в батарее хватает для компенсации.
6. ↑ То же самое, что и напряжение
7. ↑ 7.6. ЭНЕРГЕТИЧЕСКИЕ СООТНОШЕНИЯ В ЦЕПЯХ СИНУСОИДАЛЬНОГО ТОКА (неопр.). Дата обращения 6 апреля 2014.
8. ↑ Тем не менее, гасящие резисторы широко применяются для ограничения пускового тока тяговых электродвигателей постоянного тока на электротранспорте.
9. ↑ Изменение выходного напряжения не более 1,3 мВ в диапазоне выходных токов 0,005÷1,5 А. В более узком диапазоне токов 0,25÷0,75 А типичное выходное сопротивление ещё меньше — 0,0003 ома.
10. ↑ В рабочем диапазоне частот