Как найти сопротивление если известна сила тока и мощность: Как найти сопротивление, если известна мощность и сила тока

Содержание

Как найти сопротивление тока формула. Электрическое сопротивление. Определение, единицы измерения, удельное, полное, активное, реактивное

Одной из основных характеристик электрической цепи является сила тока. Она измеряется в амперах и определяет нагрузку на токопроводящие провода, шины или дорожки плат. Эта величина отражает количество электричества, которое протекло в проводнике за единицу времени. Определить её можно несколькими способами в зависимости от известных вам данных. Соответственно студенты и начинающие электрики из-за этого часто сталкиваются с проблемами при решении учебных заданий или практических ситуаций. В этой статье мы и расскажем, как найти силу тока через мощность и напряжение или сопротивление.

Если известна мощность и напряжение

Допустим вам нужно найти силу тока в цепи, при этом вам известны только напряжение и потребляемая мощность. Тогда чтобы её определить без сопротивления воспользуйтесь формулой:

После несложных мы получаем формулу для вычислений

Следует отметить, что такое выражение справедливо для цепей постоянного тока.

Но при расчётах, например, для электродвигателя учитывают его полную мощность или косинус Фи. Тогда для трёхфазного двигателя его можно рассчитать так:

Находим P с учетом КПД, обычно он лежит в пределах 0,75-0,88:

Р1 = Р2/η

Здесь P2 – активная полезная мощность на валу, η – КПД, оба этих параметра обычно указывают на шильдике.

Находим полную мощность с учетом cosФ (он также указывается на шильдике):

S = P1/cosφ

Определяем потребляемый ток по формуле:

Iном = S/(1,73·U)

Здесь 1,73 – корень из 3 (используется для расчетов трёхфазной цепи), U – напряжение, зависит от включения двигателя (треугольник или звезда) и количества вольт в сети (220, 380, 660 и т.д.). Хотя в нашей стране чаще всего встречается 380В.

Если известно напряжение или мощность и сопротивление

Но встречаются задачи, когда вам известно напряжение на участке цепи и величина нагрузки, тогда чтобы найти силу тока без мощности воспользуйтесь , с его помощью проводим расчёт силы тока через сопротивление и напряжение.

Но иногда случается так, что нужно определить силу тока без напряжения, то есть когда вам известна только мощность цепи и её сопротивление. В этом случае:

При этом согласно тому же закону Ома:

P=I 2 *R

Значит расчёт проводим по формуле:

I 2 =P/R

Или возьмем выражение в правой части выражения под корень:

I=(P/R) 1/2

Если известно ЭДС, внутреннее сопротивление и нагрузка

Ко студенческим задачам с подвохом можно отнести случаи, когда вам дают величину ЭДС и внутреннее сопротивление источника питания. В этом случае вы можете определить силу тока в схеме по закону Ома для полной цепи:

I=E/(R+r)

Здесь E – ЭДС, r – внутреннее сопротивление источника питания, R – нагрузки.

Закон Джоуля-Ленца

Еще одним заданием, которое может ввести в ступор даже более-менее опытного студента – это определить силу тока, если известно время, сопротивление и количество выделенного тепла проводником.

Для этого вспомним .

Его формула выглядит так:

Q=I 2 Rt

Тогда расчет проводите так:

I 2 =QRt

Или внесите правую часть уравнения под корень:

I=(Q/Rt) 1/2

Несколько примеров

В качестве заключения предлагаем закрепить полученную информацию на нескольких примерах задач, в которых нужно найти силу тока.

Из условия ясно, что нужно привести два варианта ответа для каждого из вариантов соединений. Тогда чтобы найти ток при последовательном соединении, сначала складывают сопротивления схемы, чтобы получить общее.

I=U/R=12/3=4 Ампера

При параллельном соединении двух элементов Rобщее можно рассчитать так:

Rобщ=(R1*R2)/(R1+R2)=1*2/3=2/3=0,67

Тогда дальнейшие вычисления можно проводить так:

В первую очередь нужно найти R общее параллельно соединенных R2 и R3, по той же формуле, что мы использовали выше.

Причиной написания данной статьи явилась не сложность этих формул, а то, что в ходе проектирования и разработки каких-либо схем часто приходится перебирать ряд значений чтобы выйти на требуемые параметры или сбалансировать схему. Данная статья и калькулятор в ней позволит упростить этот подбор и ускорить процесс реализации задуманного. Также в конце статьи приведу несколько методик для запоминания основной формулы закона Ома. Эта информация будет полезна начинающим. Формула хоть и простая, но иногда есть замешательство, где и какой параметр должен стоять, особенно это бывает поначалу.

В радиоэлектронике и электротехнике закон Ома и формула расчёта мощности используются чаше чем какие-либо из всех остальных формул. Они определяют жесткую взаимосвязь между четырьмя самыми ходовыми электрическими величинами: током, напряжением, сопротивлением и мощностью.

Закон Ома. Эту взаимосвязь выявил и доказал Георг Симон Ом в 1826 году. Для участка цепи она звучит так: сила тока прямо пропорциональна напряжению, и обратно пропорциональна сопротивлению

Так записывается основная формула:

Путем преобразования основной формулы можно найти и другие две величины:

Мощность. Её определение звучит так: мощностью называется произведение мгновенных значений напряжения и силы тока на каком-либо участке электрической цепи.

Формула мгновенной электрической мощности:

Ниже приведён онлайн калькулятор для расчёта закона Ома и Мощности. Данный калькулятор позволяет определить взаимосвязь между четырьмя электрическими величинами: током, напряжением, сопротивлением и мощностью. Для этого достаточно ввести любые две величины. Стрелками «вверх-вниз» можно с шагом в единицу менять введённое значение. Размерность величин тоже можно выбрать. Также для удобства подбора параметров, калькулятор позволяет фиксировать до десяти ранее выполненных расчётов с теми размерностями с которыми выполнялись сами расчёты.

Когда мы учились в радиотехническом техникуме, то приходилось запоминать очень много всякой всячины. И чтобы проще было запомнить, для закона Ома есть три шпаргалки. Вот какими методиками мы пользовались.

Первая — мнемоническое правило. Если из формулы закона Ома выразить сопротивление, то R = рюмка.

Вторая — метод треугольника. Его ещё называют магический треугольник закона Ома.

Если оторвать величину, которую требуется найти, то в оставшейся части мы получим формулу для её нахождения.

Третья. Она больше является шпаргалкой, в которой объединены все основные формулы для четырёх электрических величин.

Пользоваться ею также просто, как и треугольником. Выбираем тот параметр, который хотим рассчитать, он находиться в малом кругу в центре и получаем по три формулы для его расчёта. Далее выбираем нужную.

Этот круг также, как и треугольник можно назвать магическим.

Среди прочих показателей, характеризующих электрическую цепь, проводник, стоит выделить электрическое сопротивление. Оно определяет способность атомов материала препятствовать направленному прохождению электронов. Помощь в определении данной величины может оказать как специализированный прибор – омметр, так и математические расчеты на основании знаний о взаимосвязях между величинами и физическими свойствами материала. Измерение показателя производится в Омах (Ом), обозначением служит символ R.

Закон Ома – математический подход при определении сопротивления

Соотношение, установленное Георгом Омом, определяет взаимосвязь между напряжением, силой тока, сопротивлением, основанную на математическом взаимоотношении понятий. Справедливость линейной взаимосвязи – R = U/I (отношение напряжения к силе тока) – отмечается не во всех случаях.

Единица измерения [R] = B/A = Ом. 1 Ом – сопротивление материала, по которому идет ток в 1 ампер при напряжении в 1 вольт.

Эмпирическая формула расчета сопротивления

Объективные данные о проводимости материала следуют из его физических характеристик, определяющих как его собственно свойства, так и реакции на внешние влияния. Исходя из этого проводимость зависит от:

Размера.
Геометрии.
Температуры.

Атомы проводящего материала сталкиваются с направленными электронами, препятствуя их дальнейшему продвижению. При высокой концентрации последних атомы не способны им противостоять и проводимость оказывается высокой.

Большие значения сопротивления характерны для диэлектриков, которые отличаются практически нулевой проводимостью.

Одной из определяющих характеристик каждого проводника является его удельное сопротивление – ρ. Оно определяет зависимость сопротивления от материала проводника и воздействий извне. Это фиксированная (в пределах одного материала) величина, которая представляет данные проводника следующих размеров – длина 1 м (ℓ), площадь сечения 1 кв.м. Поэтому взаимосвязь между данными величинами выражается соотношением: R = ρ* ℓ/S:

Проводимость материала падает по мере увеличения его длины.

Увеличение площади сечения проводника влечет за собой снижение его сопротивления. Такая закономерность обусловлена уменьшением плотности электронов, а, следовательно, и контакт частиц материала с ними становится более редким.
Рост температуры материала стимулирует рост сопротивления, в то время как падение температуры влечет за собой его снижение.

Расчет площади сечения целесообразно производить согласно формуле S = πd 2 / 4. В определении длины поможет рулетка.

Взаимосвязь c мощностью (P)

Исходя из формулы закона Ома, U = I*R и P = I*U. Следовательно, P = I 2 *R и P = U 2 /R.
Зная величину силы тока и мощность, сопротивление можно определить как: R = P/I 2 .
Зная величину напряжения и мощности, сопротивление легко вычислить по формуле: R = U 2 /P.

Сопротивление материала и величины других сопутствующих характеристик могут быть получены с применением специальных измерительных приборов или на основании установленных математических закономерностей.

Одним из физических свойств вещества является способность проводить электрический ток. Электропроводимость (сопротивление проводника) зависит от некоторых факторов: длины электрической цепи, особенностей строения, наличия свободных электронов, температуры, тока, напряжения, материала и площади поперечного сечения.

Протекание электрического тока через проводник приводит к направленному движению свободных электронов. Наличие свободных электронов зависит от самого вещества и берется из таблицы Д. И. Менделеева, а именно из электронной конфигурации элемента. Электроны начинают ударяться о кристаллическую решетку элемента и передают энергию последней. В этом случае возникает тепловой эффект при действии тока на проводник.

При этом взаимодействии они замедляются, но затем под действием электрического поля, которое их ускоряет, начинают двигаться с той же скоростью. Электроны сталкиваются огромное количество раз. Этот процесс и называется сопротивлением проводника.

Следовательно, электрическим сопротивлением проводника считается физическая величина, характеризующая отношение напряжения к силе тока.

Что такое электрическое сопротивление: величина, указывающая на свойство физического тела преобразовывать энергию электрическую в тепловую, благодаря взаимодействию энергии электронов с кристаллической решеткой вещества. По характеру проводимости различаются:

Проводники (способны проводить электрический ток, так как присутствуют свободные электроны).
Полупроводники (могут проводить электрический ток, но при определенных условиях).
Диэлектрики или изоляторы (обладают огромным сопротивлением, отсутствуют свободные электроны, что делает их неспособными проводить ток).

Обозначается эта характеристика буквой R и измеряется в Омах (Ом) . Применение этих групп веществ является очень значимым для разработки электрических принципиальных схем приборов.

Для полного понимания зависимости R от чего-либо нужно обратить особое внимание на расчет этой величины.

Расчет электрической проводимости

Для расчета R проводника применяется закон Ома, который гласит: сила тока (I) прямо пропорциональна напряжению (U) и обратно пропорциональна сопротивлению.

Формула нахождения характеристики проводимости материала R (следствие из закона Ома для участка цепи): R = U / I.

Для полного участка цепи эта формула принимает следующий вид: R = (U / I) — Rвн, где Rвн — внутреннее R источника питания.

Способность проводника к пропусканию электрического тока зависит от многих факторов: напряжения, тока, длины, площади поперечного сечения и материала проводника, а также от температуры окружающей среды.

В электротехнике для произведения расчетов и изготовления резисторов учитывается и геометрическая составляющая проводника.

От чего зависит сопротивление: от длины проводника — l, удельного сопротивления — p и от площади сечения (с радиусом r) — S = Пи * r * r.

Формула R проводника: R = p * l / S.

Из формулы видно, от чего зависит удельное сопротивление проводника: R, l, S. Нет необходимости его таким способом рассчитывать, потому что есть способ намного лучше. Удельное сопротивление можно найти в соответствующих справочниках для каждого типа проводника (p — это физическая величина равная R материала длиною в 1 метр и площадью сечения равной 1 м².

Однако этой формулы мало для точного расчета резистора, поэтому используют зависимость от температуры.

Влияние температуры окружающей среды

Доказано, что каждое вещество обладает удельным сопротивлением, зависящим от температуры.

Для демонстрации это можно произвести следующий опыт. Возьмите спираль из нихрома или любого проводника (обозначена на схеме в виде резистора), источник питания и обычный амперметр (его можно заменить на лампу накаливания). Соберите цепь согласно схеме 1.

Схема 1 — Электрическая цепь для проведения опыта

Необходимо запитать потребитель и внимательно следить за показаниями амперметра. Далее следует нагревать R, не отключая, и показания амперметра начнут падать при росте температуры. Прослеживается зависимость по закону Ома для участка цепи: I = U / R. В данном случае внутренним сопротивлением источника питания можно пренебречь: это не отразится на демонстрации зависимости R от температуры. Отсюда следует, что зависимость R от температуры присутствует.

Физический смысл роста значения R обусловлен влиянием температуры на амплитуду колебаний (увеличение) ионов в кристаллической решетке. В результате этого электроны чаще сталкиваются и это вызывает рост R.

Согласно формуле: R = p * l / S, находим показатель, который зависит от температуры (S и l — не зависят от температуры). Остается p проводника. Исходя из это получается формула зависимости от температуры: (R — Ro) / R = a * t, где Ro при температуре 0 градусов по Цельсию, t — температура окружающей среды и a — коэффициент пропорциональности (температурный коэффициент).

Для металлов «a» всегда больше нуля, а для растворов электролитов температурный коэффициент меньше 0.

Формула нахождения p, применяемая при расчетах: p = (1 + a * t) * po, где ро — удельное значение сопротивления, взятое из справочника для конкретного проводника. В этом случае температурный коэффициент можно считать постоянным. Зависимость мощности (P) от R вытекает из формулы мощности: P = U * I = U * U / R = I * I * R. Удельное значение сопротивления еще зависит и от деформаций материала, при котором нарушается кристаллическая решетка.

При обработке металла в холодной среде при некотором давлении происходит пластическая деформация. При этом кристаллическая решетка искажается и растет R течения электронов. В этом случае удельное сопротивление также увеличивается. Этот процесс является обратимым и называется рекристаллическим отжигом, благодаря которому часть дефектов уменьшается.

При действии на металл сил растяжения и сжатия последний подвергается деформациям, которые называются упругими. Удельное сопротивление уменьшается при сжатии, так как происходит уменьшение амплитуды тепловых колебаний. Направленным заряженным частицам становится легче двигаться . При растяжении удельное сопротивление увеличивается из-за роста амплитуды тепловых колебаний.

Еще одним фактором, влияющим на проводимость, является вид тока, проходящего по проводнику.

Сопротивление в сетях с переменным током ведет себя несколько иначе, ведь закон Ома применим только для схем с постоянным напряжением. Следовательно, расчеты следует производить иначе.

Полное сопротивление обозначается буквой Z и состоит из алгебраической суммы активного, емкостного и индуктивного сопротивлений.

При подключении активного R в цепь переменного тока под воздействием разницы потенциалов начинает течь ток синусоидального вида. В этом случае формула выглядит: Iм = Uм / R, где Iм и Uм — амплитудные значения силы тока и напряжения. Формула сопротивления принимает следующий вид: Iм = Uм / ((1 + a * t) * po * l / 2 * Пи * r * r).

Емкостное сопротивление (Xc) обусловлено наличием в схемах конденсаторов. Необходимо отметить, что через конденсаторы проходит переменный ток и, следовательно, он выступает в роли проводника с емкостью.

Вычисляется Xc следующим образом: Xc = 1 / (w * C), где w — угловая частота и C — емкость конденсатора или группы конденсаторов. Угловая частота определяется следующим образом:

Измеряется частота переменного тока (как правило, 50 Гц).
Умножается на 6,283.

Индуктивное сопротивление (Xl) — подразумевает наличие индуктивности в схеме (дроссель, реле, контур, трансформатор и так далее). Рассчитывается следующим образом: Xl = wL, где L — индуктивность и w — угловая частота. Для расчета индуктивности необходимо воспользоваться специализированными онлайн-калькуляторами или справочником по физике. Итак, все величины рассчитаны по формулам и остается всего лишь записать Z: Z * Z = R * R + (Xc — Xl) * (Xc — Xl).

Для определения окончательного значения необходимо извлечь квадратный корень из выражения: R * R + (Xc — Xl) * (Xc — Xl). Из формул следует, что частота переменного тока играет большую роль, например, в схеме одного и того же исполнения при повышении частоты увеличивается и ее Z. Необходимо добавить, что в цепях с переменным напряжением Z зависит от таких показателей:

Длины проводника.
Площади сечения — S.
Температуры.
Типа материала.
Емкости.
Индуктивности.
Частоты.

Следовательно и закон Ома для участка цепи имеет совершенно другой вид: I = U / Z . Меняется и закон для полной цепи.

Расчеты сопротивлений требуют определенного количества времени, поэтому для измерений их величин применяются специальные электроизмерительные приборы, которые называются омметрами. Измерительный прибор состоит из стрелочного индикатора, к которому последовательно включен источник питания.

Измеряют R все комбинированные приборы , такие как тестеры и мультиметры. Обособленные приборы для измерения только этой характеристики применяются крайне редко (мегаомметр для проверки изоляции силового кабеля).

Прибор применяется для прозвонки электрических цепей на предмет повреждения и исправности радиодеталей, а также для прозвонки изоляции кабелей.

При измерении R необходимо полностью обесточить участок цепи во избежание выхода прибора из строя. Для это необходимо предпринять следующие меры предосторожности:

В дорогих мультиметрах есть функция прозвонки цепи, дублируемая звуковым сигналом, благодаря чему нет необходимости смотреть на табло прибора.

Таким образом, электрическое сопротивление играет важную роль в электротехнике. Оно зависит в постоянных цепях от температуры, силы тока, длины, типа материала и площади поперечного сечения проводника . В цепях переменного тока эта зависимость дополняется такими величинами, как частота, емкость и индуктивность. Благодаря этой зависимости существует возможность изменять характеристики электричества: напряжение и силу тока. Для измерений величины сопротивления применяются омметры, которые используются также и при выявлении неполадок проводки, прозвонки различных цепей и радиодеталей.

Доброго дня уважаемые радиолюбители!
Приветствую вас на сайте “ “

Формулы составляют скелет науки об электронике. Вместо того, чтобы сваливать на стол целую кучу радиоэлементов, а потом переподключать их между собой, пытаясь выяснить, что же появится на свет в результате, опытные специалисты сразу строят новые схемы на основе известных математических и физических законов. Именно формулы помогают определять конкретные значения номиналов электронных компонентов и рабочих параметров схем.

Точно так же эффективно использовать формулы для модернизации уже готовых схем. К примеру, для того, чтобы выбрать правильный резистор в схеме с лампочкой, можно применить базовый закон Ома для постоянного тока (о нем можно будет прочесть в разделе “Соотношения закона Ома” сразу после нашего лирического вступления). Лампочку можно заставить, таким образом, светить более ярко или, наоборот — притушить.

В этой главе будут приведены многие основные формулы физики, с которыми рано или поздно приходится сталкиваться в процессе работы в электронике. Некоторые из них известны уже столетия, но мы до сих пор продолжаем ими успешно пользоваться, как будут пользоваться и наши внуки.

Соотношения закона Ома

Закон Ома представляет собой взаимное соотношение между напряжением, током, сопротивлением и мощностью. Все выводимые формулы для расчета каждой из указанных величин представлены в таблице:

В этой таблице используются следующие общепринятые обозначения физических величин:

U — напряжение (В),

I — ток (А),

Р — мощность (Вт),

R — сопротивление (Ом),

Потренируемся на следующем примере: пусть нужно найти мощность схемы.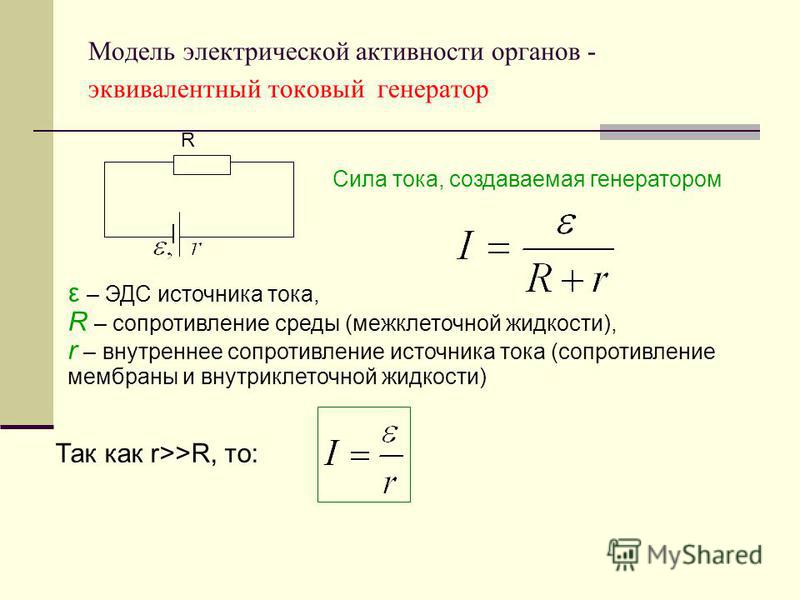 Известно, что напряжение на ее выводах составляет 100 В, а ток- 10 А. Тогда мощность согласно закону Ома будет равна 100 х 10 = 1000 Вт. Полученное значение можно использовать для расчета, скажем, номинала предохранителя, который нужно ввести в устройство, или, к примеру, для оценки счета за электричество, который вам лично принесет электрик из ЖЭК в конце месяца.

А вот другой пример: пусть нужно узнать номинал резистора в цепи с лампочкой, если известно, какой ток мы хотим пропускать через эту цепь. По закону Ома ток равен:

I = U / R

Схема, состоящая из лампочки, резистора и источника питания (батареи) показана на рисунке. Используя приведенную формулу, вычислить искомое сопротивление сможет даже школьник.

Что же в этой формуле есть что? Рассмотрим переменные подробнее.

> U пит (иногда также обозначается как V или Е): напряжение питания. Вследствие того, что при прохождении тока через лампочку на ней падает какое-то напряжение, величину этого падения (обычно рабочее напряжение лампочки, в нашем случае 3,5 В) нужно вычесть из напряжения источника питания. К примеру, если Uпит = 12 В, то U = 8,5 В при условии, что на лампочке падает 3,5 В.

> I : ток (измеряется в амперах), который планируется пропустить через лампочку. В нашем случае – 50 мА. Так как в формуле ток указывается в амперах, то 50 миллиампер составляет лишь малую его часть: 0,050 А.

> R : искомое сопротивление токоограничивающего резистора, в омах.

В продолжение, можно проставить в формулу расчета сопротивления реальные цифры вместо U, I и R:

R = U/I = 8,5 В / 0,050 А= 170 Ом

Расчёты сопротивления

Рассчитать сопротивление одного резистора в простой цепи достаточно просто. Однако с добавлением в нее других резисторов, параллельно или последовательно, общее сопротивление цепи также изменяется. Суммарное сопротивление нескольких соединенных последовательно резисторов равно сумме отдельных сопротивлений каждого из них. Для параллельного же соединения все немного сложнее.

Почему нужно обращать внимание на способ соединения компонентов между собой? На то есть сразу несколько причин.

> Сопротивления резисторов составляют только некоторый фиксированный ряд номиналов. В некоторых схемах значение сопротивления должно быть рассчитано точно, но, поскольку резистор именно такого номинала может и не существовать вообще, то приходится соединять несколько элементов последовательно или параллельно.

> Резисторы — не единственные компоненты, которые имеют сопротивление. К примеру, витки обмотки электромотора также обладают некоторым сопротивлением току. Во многих практических задачах приходится рассчитывать суммарное сопротивление всей цепи.

Расчет сопротивления последовательных резисторов

Формула для вычисления суммарного сопротивления резисторов, соединенных между собой последовательно, проста до неприличия. Нужно просто сложить все сопротивления:

Rобщ = Rl + R2 + R3 + … (столько раз, сколько есть элементов)

В данном случае величины Rl, R2, R3 и так далее — сопротивления отдельных резисторов или других компонентов цепи, а Rобщ — результирующая величина.

Так, к примеру, если имеется цепь из двух соединенных последовательно резисторов с номиналами 1,2 и 2,2 кОм, то суммарное сопротивление этого участка схемы будет равно 3,4 кОм.

Расчет сопротивления параллельных резисторов

Все немного усложняется, если требуется вычислить сопротивление цепи, состоящей из параллельных резисторов. Формула приобретает вид:

R общ = R1 * R2 / (R1 + R2)

где R1 и R2 — сопротивления отдельных резисторов или других элементов цепи, а Rобщ -результирующая величина. Так, если взять те же самые резисторы с номиналами 1,2 и 2,2 кОм, но соединенные параллельно, получим

776,47 = 2640000 / 3400

Для расчета результирующего сопротивления электрической цепи из трех и более резисторов используется следующая формула:

Расчёты ёмкости

Формулы, приведенные выше, справедливы и для расчета емкостей, только с точностью до наоборот. Так же, как и для резисторов, их можно расширить для любого количества компонентов в цепи.

Расчет емкости параллельных конденсаторов

Если нужно вычислить емкость цепи, состоящей из параллельных конденсаторов, необходимо просто сложить их номиналы:

Собщ = CI + С2 + СЗ + …

В этой формуле CI, С2 и СЗ — емкости отдельных конденсаторов, а Собщ суммирующая величина.

Расчет емкости последовательных конденсаторов

Для вычисления общей емкости пары связанных последовательно конденсаторов применяется следующая формула:

Собщ = С1 * С2 /(С1+С2)

где С1 и С2 — значения емкости каждого из конденсаторов, а Собщ — общая емкость цепи

Расчет емкости трех и более последовательно соединенных конденсаторов

В схеме имеются конденсаторы? Много? Ничего страшного: даже если все они связаны последовательно, всегда можно найти результирующую емкость этой цепи:

Так зачем же вязать последовательно сразу несколько конденсаторов, когда могло хватить одного? Одним из логических объяснений этому факту служит необходимость получения конкретного номинала емкости цепи, аналога которому в стандартном ряду номиналов не существует. Иногда приходится идти и по более тернистому пути, особенно в чувствительных схемах, как, например, радиоприемники.

Расчёт энергетических уравнений

Наиболее широко на практике применяют такую единицу измерения энергии, как киловатт-часы или, если это касается электроники, ватт-часы. Рассчитать затраченную схемой энергию можно, зная длительность времени, на протяжении которого устройство включено. Формула для расчета такова:

ватт-часы = Р х Т

В этой формуле литера Р обозначает мощность потребления, выраженную в ваттах, а Т — время работы в часах. В физике принято выражать количество затраченной энергии в ватт-секундах, или Джоулях. Для расчета энергии в этих единицах ватт-часы делят на 3600.

Расчёт постоянной ёмкости RC-цепочки

В электронных схемах часто используются RC-цепочки для обеспечения временных задержек или удлинения импульсных сигналов. Самые простые цепочки состоят всего лишь из резистора и конденсатора (отсюда и происхождение термина RC-цепочка).

Принцип работы RC-цепочки состоит в том, что заряженный конденсатор разряжается через резистор не мгновенно, а на протяжении некоторого интервала времени. Чем больше сопротивление резистора и/или конденсатора, тем дольше будет разряжаться емкость. Разработчики схем очень часто применяют RC-цепочки для создания простых таймеров и осцилляторов или изменения формы сигналов.

Каким же образом можно рассчитать постоянную времени RC-цепочки? Поскольку эта схема состоит из резистора и конденсатора, в уравнении используются значения сопротивления и емкости. Типичные конденсаторы имеют емкость порядка микрофарад и даже меньше, а системными единицами являются фарады, поэтому формула оперирует дробными числами.

T = RC

В этом уравнении литера Т служит для обозначения времени в секундах, R — сопротивления в омах, и С — емкости в фарадах.

Пусть, к примеру, имеется резистор 2000 Ом, подключенный к конденсатору 0,1 мкФ. Постоянная времени этой цепочки будет равна 0,002 с, или 2 мс.

Для того чтобы на первых порах облегчить вам перевод сверхмалых единиц емкостей в фарады, мы составили таблицу:

Расчёты частоты и длины волны

Частота сигнала является величиной, обратно пропорциональной его длине волны, как будет видно из формул чуть ниже. Эти формулы особенно полезны при работе с радиоэлектроникой, к примеру, для оценки длины куска провода, который планируется использовать в качестве антенны. Во всех следующих формулах длина волны выражается в метрах, а частота — в килогерцах.

Расчет частоты сигнала

Предположим, вы хотите изучать электронику для того, чтобы, собрав свой собственный приемопередатчик, поболтать с такими же энтузиастами из другой части света по аматорской радиосети. Частоты радиоволн и их длина стоят в формулах бок о бок. В радиолюбительских сетях часто можно услышать высказывания о том, что оператор работает на такой-то и такой длине волны. Вот как рассчитать частоту радиосигнала, зная длину волны:

Частота = 300000 / длина волны

Длина волны в данной формуле выражается в миллиметрах, а не в футах, аршинах или попугаях. Частота же дана в мегагерцах.

Расчет длины волны сигнала

Ту же самую формулу можно использовать и для вычисления длины волны радиосигнала, если известна его частота:

Длина волны = 300000 / Частота

Результат будет выражен в миллиметрах, а частота сигнала указывается в мегагерцах.

Приведем пример расчета. Пусть радиолюбитель общается со своим другом на частоте 50 МГц (50 миллионов периодов в секунду). Подставив эти цифры в приведенную выше формулу, получим:

6000 миллиметров = 300000 / 50 МГц

Однако чаще пользуются системными единицами длины — метрами, поэтому для завершения расчета нам остается перевести длину волны в более понятную величину. Так как в 1 метре 1000 миллиметров, то в результате получим 6 м. Оказывается, радиолюбитель настроил свою радиостанцию на длину волны 6 метров. Прикольно!

Закон Ома

Закон Ома — Один из самых применяемых законов в электротехнике. Данный закон раскрывает связь между тремя важнейшими величинами: силой тока, напряжением и сопротивлением. Выявил эту связь Георгом Омом в 1820-е годы именно поэтому этот закон и получил такое название.

Формулировка закона Ома следующая:
Величина силы тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку, и обратно пропорциональна его сопротивлению.

Эту зависимость можно выразить формулой:

I=U/R

Где I – сила тока, U — напряжение, приложенное к участку цепи, а R — электрическое сопротивление участка цепи.
Так, если известны две из этих величин можно легко вычислить третью.
Понять закон Ома можно на простом примере. Допустим, нам необходимо вычислить сопротивление нити накаливания лампочки фонарике и нам известны величины напряжения работы лампочки и сила тока, необходимая для ее работы (сама лампочка, чтобы вы знали имеет переменное сопротивление, но для примера примем его как постоянное). Для вычисления сопротивления необходимо величину напряжения разделить на величину силы тока. Как же запомнить формулу закона Ома, чтобы правильно провести вычисления? А сделать это очень просто! Вам нужно всего лишь сделать себе напоминалку как на указанном ниже рисунке.
Теперь закрыв рукой любую из величин вы сразу поймете, как ее найти. Если закрыть букву I, становится ясно, что чтобы найти силу тока нужно напряжение разделить на сопротивление.
Теперь давайте разберемся, что значат в формулировке закона слова « прямо пропорциональна и обратно пропорциональна. Выражение «величина силы тока на участке цепи прямо пропорциональна напряжению, приложенному к этому участку» означает, что если на участке цепи увеличится напряжение, то и сила тока на данном участке также увеличится. Простыми словами, чем больше напряжение, тем больше ток. И выражение «обратно пропорциональна его сопротивлению» значит, что чем больше сопротивление, тем меньше будет сила тока.
Рассмотрим пример с работой лампочки в фонарике. Допустим, что для работы фонарика нужны три батарейки, как показано на схеме ниже, где GB1 — GB3 — батарейки, S1 — выключатель, HL1 — лампочка.

Примем, что сопротивление лампочки условно постоянно, хотя нагреваясь её сопротивление увеличивается. Яркость лампочки будет зависеть от силы тока, чем она больше, тем ярче горит лампочка. А теперь, представьте, что вместо одной батарейки мы вставили перемычку, уменьшив тем самым напряжение.
Что случится с лампочкой?
Она будет светить более тускло (сила тока уменьшилась), что подтверждает закон Ома:
чем меньше напряжение, тем меньше сила тока.

Вот так просто работает этот физический закон, с которым мы сталкиваемся в повседневной жизни.
Бонус специально для вас шуточная картинка не менее красочно объясняющая закон Ома.

Это была обзорная статья. Более подробно об этом законе, мы говорим в следующей статье «Закон Ома для участка цепи», рассматривая всё на других более сложных примерах.

Если не получается с физикой, английский для детей (http://www.anylang.ru/order-category/?slug=live_language) как вариент альтернативного развития.

Если материал был полезен, вы можете отправить донат или поделиться данным материалом в социальных сетях:

РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ОНЛАЙН — ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЯ, ТОКА, МОЩНОСТИ И СЕЧЕНИЯ ПРОВОДНИКА

Наверное, каждый кто делал или делает ремонт электрики сталкивался с проблемой определения той или иной электрической величины. Для кого-то это становится настоящим камнем преткновения, а для кого-то все предельно ясно и каких-либо сложностей при определении той или иной величины нет. Данная статья посвящена именно первой категории – то есть для тех, кто не очень силен в теории электрических цепей и тех показателей, которые для них характерны.

Итак, для начала вернемся немного в прошлое и постараемся вспомнить школьный курс физики, касательно электрики. Как мы помним, основные электрические величины определяются на основании всего одного закона – закона Ома. Именно этот закон является базой проведения абсолютно для любых расчетов и имеет вид:

Отметим, что в данном случае речь идет о расчете самой простейшей электрической цепи, которая выглядит следующим образом:

Подчеркнем, что абсолютно любой расчет ведется именно посредством этой формулы. То есть путем не сложных математических вычислений можно определить ту или иную величину зная при этом два иных электрических параметра. Как бы там ни было, наш ресурс призван упростить жизнь тому кто делает ремонт, а поэтому мы упростим решение задачи определения электрических параметров, вывив основные формулы и предоставив возможность произвести расчет электрических цепей онлайн.

Как узнать ток зная мощность и напряжение?

В данном случае формула вычисления выглядит следующим образом:

Расчет силы тока онлайн:

(Не целые числа вводим через точку. Например: 0.5)

Как узнать напряжение зная силу тока?

Для того, чтобы узнать напряжение, зная при этом сопротивление потребителя тока можно воспользоваться формулой:

Расчет напряжения онлайн:

Если же сопротивление неизвестно, но зато известна мощность потребителя, то напряжение вычисляется по формуле:

Определение величины онлайн:

Как рассчитать мощность зная силу тока и напряжения?

Здесь необходимо знать величины действующего напряжения и действующей силы тока в электрической цепи. Согласно формуле предоставленной выше, мощность определяется путем умножения силы тока на действующее напряжение.

Расчет цепи онлайн:

Как определить потребляемую мощность цепи имея тестер, который меряет сопротивление?

Этот вопрос был задан в комментарие в одном из материалов нашего сайта. Поспешим дать ответ на этот вопрос. Итак, для начала измеряем тестером сопротивление электроприбора (для этого достаточно подсоединить щупы тестера к вилке шнура питания). Узнав сопротивление мы можем определить и мощность, для чего необходимо напряжение в квадрате разделить на сопротивление.

Онлайн расчет:

Формула расчета сечения провода и как определяется сечение провода

Довольно много вопросов связано с определением сечения провода при построении электропроводки. Если углубиться в электротехническую теорию, то формула расчета сечения имеет такой вид:

Конечно же, на практике, такой формулой пользуются довольно редко, прибегая к более простой схеме вычислений. Эта схема довольно проста: определяют силу тока, которая будет действовать в цепи, после чего согласно специальной таблице определяют сечение. Более детально по этому поводу можно почитать в материале – «Сечение провода для электропроводки»

Приведем пример. Есть бойлер мощностью 2000 Вт, какое сечение провода должно быть, чтобы подключить его к бытовой электропрводке? Для начала определим силу тока, которая будет действовать в цепи:

I=P/U=2000/220В = 9А

Как видим, сила тока получается довольно приличной. Округляем значение до 10 А и обращаемся к таблице:

Таким образом, для нашего бойлера потребуется провод сечением 1,7 мм. Для большей надежности используем провод сечением 2 или 2,5 мм.

Рекомендуем ознакомиться:

— БЛОК ПИТАНИЯ ДЛЯ СВЕТОДИОДНЫХ ЛЕНТ

— ЗАЩИТНОЕ ЗАНУЛЕНИЕ

— СВЕТОДИОДНЫЕ СВЕТИЛЬНИКИ — ЛУЧШЕ НЕ ПРИДУМАЕШЬ!

— АЛМАЗНАЯ РЕЗКА БЕТОНА И ЖБ КОНСТРУКЦИЙ

Автор — Антон Писарев

Как найти длину по формуле сопротивления. Если известно напряжение или мощность и сопротивление

Ом экспериментально установил закон, согласно которому сила тока, текущего по однородному (в смысле отсутствия сторонних сил) металлическому проводнику, пропорциональна падению напряжения V на проводнике:

Напомним, что в случае однородного проводника напряжение U совпадает с разностью потенциалов (см. (33.6)).

Обозначенная в формуле (34.1) буквой R величина называется электрическим сопротивлением проводника. Единицей сопротивления служит равный сопротивлению такого проводника, в котором при напряжении в 1 В течет ток силой 1 А.

Величина сопротивления зависит от формы и размеров проводника, а также от свойств материала, из которого он сделан. Для однородного цилиндрического проводника

где l — длина проводника, S — площадь его поперечного сечения, — зависящий от свойств материала коэффициент, называемый удельным электрическим сопротивлением вещества. Если то R численно равно . В СИ измеряется в ом-метрах (Ом-м).

Найдем связь между векторами j и Е в одной и той же точке проводника. В изотропном проводнике упорядоченное движение носителей тока происходит в направлении вектора Е.

Поэтому на правления векторов j и Е совпадают Выделим мысленно в окрестности некоторой точки элементарный цилиндрический объем с образующими, параллельными векторам j и Е (рис. 34.1). Через поперечное сечение цилиндра течет ток силой . Напряжение, приложенное к цилиндру, равно , где Е — напряженность поля в данном месте. Наконец, сопротивление цилиндра, согласно формуле (34.2), равно . Подставив эти значения в формулу (34.1), придем к соотношению

Воспользовавшись тем, что векторы j и Е имеют одинаковое направление, можно написать

Эта формула выражает закон Ома в дифференциальной форме.

Фигурирующая в (34.3) обратная величина называется удельной электрической проводимостью материала. Единица, обратная ому, называется сименсом (См). Соответственно единицей о является сименс на метр (См/м).

Допустим для простоты, что в проводнике имеются носители лишь одного знака. Согласно формуле (31.5) плотность тока в этом случае равна

Сравнение этого выражения с формулой (34.3) приводит к выводу, что скорость упорядоченного движения носителей тока пропорциональна напряженности поля Е, т. е. силе, сообщающей носителям упорядоченное движение. Пропорциональность скорости приложенной к телу силе наблюдается в тех случаях, когда кроме силы, вызвавшей движение, на тело действует сила сопротивления среды. Эта сила вызывается взаимодействием носителей тока с частицами, из которых построено вещество проводника. Наличие силы сопротивления упорядоченному движению носителей тока обусловливает электрическое сопротивление проводника.

Способность вещества проводить электрический ток характеризуется его удельным сопротивлением либо удельной проводимостью .

Их величина определяется химической природой вещества и условиями, в частности температурой, при которых оно находится.

Для большинства металлов при температурах, близких к комнатной, изменяется пропорционально абсолютной температуре Т:

При низких температурах наблюдаются отступления от этой закономерности (рис. 34.2). В большинстве случаев зависимость от Т следует кривой. Величина остаточного сопротивления рост в сильной степени зависит от чистоты материала и наличия остаточных механических напряжений в образце. Поэтому после отжига рост заметно уменьшается. У абсолютно чистого металла с идеально правильной кристаллической решеткой при абсолютном нуле

У большой группы металлов и сплавов при температуре порядка нескольких кельвинов сопротивление скачков обращается в нуль (кривая 2 на рис. 34.2). Впервые это явление, названное сверхпроводимостью, было обнаружено в 1911 г. Камерлинг-Оннесом для ртути. В дальнейшем сверхпроводимость была обнаружена у свинца, олова, цинка, алюминия и других металлов, а также у ряда сплавов. Для каждого сверхпроводника имеется своя критическая температура Т при которой он переходит в сверхпроводящее состояние. При действии на сверхпроводник магнитного поля сверхпроводящее состояние нарушается. Величина критического поля разрушающего сверхпроводимость, равна нулю при и растет с понижением температуры.

Полное теоретическое объяснение сверхпроводимости было дано академиком Н. Н. Боголюбовым и независимо от него Дж. Бардином, Л. Купером и Дж. Шриффером (см. § 56 тома 3).

Зависимость электрического сопротивления от температуры положена в основу термометров сопротивления. Такой термометр представляет собой металлическую (обычно платиновую) проволочку, намотанную на фарфоровый или слюдяной каркас. Проградуированный по постоянным температурным точкам термометр сопротивления позволяет измерять с погрешностью порядка несколько сотых градуса как низкие, так и высокие температуры. В последнее время все большее применение находят термометры сопротивления из полупроводников.

Содержание:

Появление электрического тока наступает при замыкании цепи, когда на зажимах возникает разность потенциалов. Перемещение свободных электронов в проводнике осуществляется под действием электрического поля. В процессе движения, электроны сталкиваются с атомами и частично передают им свою накопившуюся энергию. Это приводит к уменьшению скорости их движения. В дальнейшем, под влиянием электрического поля, скорость движения электронов снова увеличивается. Результатом такого сопротивления становится нагревание проводника, по которому течет ток. Существуют различные способы расчетов этой величины, в том числе и формула удельного сопротивления, применяющаяся для материалов с индивидуальными физическими свойствами.

Электрическое удельное сопротивление

Суть электрического сопротивления заключается в способности того или иного вещества превращать электрическую энергию в тепловую во время действия тока. Данная величина обозначается символом R, а в качестве единицы измерения используется Ом. Значение сопротивления в каждом случае связано со способностью того или иного .

В процессе исследований была установлена зависимость от сопротивления. Одним из основных качеств материала становится его удельное сопротивление, меняющееся в зависимости от длины проводника. То есть, с увеличением длины провода, возрастает и значение сопротивления. Данная зависимость определяется как прямо пропорциональная.

Другим свойством материала является площадь его поперечного сечения. Она представляет собой размеры поперечного среза проводника, независимо от его конфигурации. В этом случае получается обратно пропорциональная связь, когда с увеличением площади поперечного сечения уменьшается .

Еще одним фактором, влияющим на сопротивление, является сам материал. Во время проведения исследований была обнаружена различная сопротивляемость у разных материалов. Таким образом, были получены значения удельных электрических сопротивлений для каждого вещества.

Выяснилось, что самыми лучшими проводниками являются металлы. Среди них самой низкой сопротивляемостью и высокой проводимостью обладают и серебро. Они применяются в наиболее ответственных местах электронных схем, к тому же медь имеет сравнительно низкую стоимость.

Вещества, удельное сопротивление которых очень высокое, считаются плохими проводниками электрического тока. Поэтому они используются в качестве изоляционных материалов. Диэлектрические свойства более всего присущи фарфору и эбониту.

Таким образом, удельное сопротивление проводника имеет большое значение, поскольку с его помощью можно определить материал, из которого был изготовлен проводник. Для этого измеряется площадь сечения, определяется сила тока и напряжение. Это позволяет установить значение удельного электрического сопротивления, после чего, с помощью специальной таблицы можно легко определить вещество. Следовательно, удельное сопротивление относится к наиболее характерным признакам того или иного материала. Этот показатель позволяет определить наиболее оптимальную длину электрической цепи так, чтобы соблюдался баланс .

Формула

На основании полученных данных можно сделать вывод, что удельным сопротивлением будет считаться сопротивление какого-либо материала с единичной площадью и единичной длиной. То есть сопротивление, равное 1 Ом возникает при напряжении 1 вольт и силе тока 1 ампер. На этот показатель оказывает влияние степень чистоты материала. Например, если к меди добавить всего лишь 1% марганца, то ее сопротивляемость увеличится в 3 раза.

Удельное сопротивление и проводимость материалов

Проводимость и удельное сопротивление рассматриваются как правило при температуре 20 0 С. Эти свойства будут отличаться у различных металлов:

Медь . Чаще всего применяется для изготовления проводов и кабелей. Она обладает высокой прочностью, стойкостью к коррозии, легкой и простой обработкой. В хорошей меди доля примесей составляет не более 0,1%. В случае необходимости медь может использоваться в сплавах с другими металлами.
Алюминий . Его удельный вес меньше, чем у меди, однако у него более высокая теплоемкость и температура плавления. Чтобы расплавить алюминий, потребуется энергии значительно больше, чем для меди. Примеси в качественном алюминии не превышают 0,5%.
Железо . Наряду с доступностью и дешевизной, этот материал обладает высоким удельным сопротивлением. Кроме того, у него низкая устойчивость к коррозии. Поэтому практикуется покрытие стальных проводников медью или цинком.

Отдельно рассматривается формула удельного сопротивления в условиях низких температур. В этих случаях свойства одних и тех же материалов будут совершенно другими. У некоторых из них сопротивляемость может упасть до нулевой отметки. Такое явление получило название сверхпроводимости, при которой оптические и структурные характеристики материала остаются неизменными.

В своей работе электрик часто сталкивается с вычислением различных величин и преобразований. Так для корректного подбора кабеля приходится подбирать нужное сечение. Логика выбора сечения основана на зависимости сопротивления от длины линии и площади сечения проводника. В этой статье мы рассмотрим, как выполняется расчет сопротивления провода по его геометрическим размерам.

Формула для расчета

Любые вычисления начинаются с формулы. Основной формулой для расчета сопротивления проводника является:

R=(ρ*l)/S

Где R – сопротивление в Омах, ρ – удельное сопротивление, l – длина в м, S – площадь поперечного сечения провода в мм 2 .

Эта формула подходит для расчета сопротивления провода по сечению и длине. Из неё следует, что в зависимости от длины изменяется сопротивление, чем длиннее – тем больше. И от площади сечения – наоборот, чем толще провод (большое сечение), тем меньше сопротивление. Однако непонятной остаётся величина, обозначенная буквой ρ (Ро).

Удельное сопротивление

Удельное сопротивление – это табличная величина, для каждого металла она своя. Она нужна для расчета и зависит от кристаллической решетки металла и структуры атомов.

Из таблицы видно, что самое меньшее сопротивление у серебра, для медного кабеля оно равняется 0,017 Ом*мм 2 /м. Такая размерность говорит нам, сколько приходится Ом при сечении в 1 миллиметр квадратный и длине в 1 метр.

Кстати, серебряное покрытие используется в контактах коммутационных аппаратов, автоматических выключателей, реле и прочего. Это снижает , повышает срок службы и уменьшает . При этом в контактах измерительной и точной аппаратуры используют позолоченные контакты из-за того, что они слабо окисляются или вообще не окисляются.

У алюминия, который часто использовался в электропроводке раньше, сопротивление в 1,8 раза больше чем у меди, равняется 2,82*10 -8 Ом*мм 2 /м. Чем больше сопротивление проводника, тем сильнее он греется. Поэтому при одинаковом сечении алюминиевый кабель может передать меньший ток, чем медный, это и стало основной причиной почему все современные электрики используют . У нихрома, который используется в нагревательных приборах оно в 100 раз больше чем у меди 1,1*10 -6 Ом*мм 2 /м.

Расчет по диаметру

На практике часто бывает так, что площадь поперечного сечения жилы не известна. Без этого значения ничего рассчитать не получится. Чтобы узнать её, нужно измерить диаметр. Если жила тонка, можно взять гвоздь или любой другой стержень, намотать на него 10 витков провода, обычной линейкой измерить длину получившейся спирали и разделить на 10, так вы узнаете диаметр.

Ну, или просто замерить штангенциркулем. Расчет сечения выполняется по формуле:

Обязательны ли расчеты?

Как мы уже сказали, сечение провода выбирают исходя из предполагаемого тока и сопротивления металла, из которого изготовлены жилы. Логика выбора заключается в следующем: сечение подбирают таким способом, чтобы сопротивление при заданной длине не приводило к значительным просадкам напряжения. Чтобы не проводить ряд расчетов, для коротких линий (до 10-20 метров) есть достаточно точные таблицы:

В этой таблице указаны типовые значения сечения медных и алюминиевых жил и номинальные токи через них. Для удобства указана мощность нагрузки, которую выдержит эта линия. Обратите внимание на разницу в токах и мощности при напряжении 380В, естественно, что это предполагается трёхфазная электросеть.

Расчет сопротивления провода сводится к использованию пары формул, при этом вы можете скачать готовые калькуляторы из Плэй Маркета для своего смартфона, например, «Electrodroid» или «Мобильный электрик». Эти знания пригодятся для расчетов нагревательных приборов, кабельных линий, предохранителей и даже популярных на сегодняшний день спиралей для электронных сигарет.

Материалы

Инструкция

Найдите силу сопротивления движению, которая действует на равномерно прямолинейно движущееся тело. Для этого при помощи динамометра или другим способом измерьте силу, которую необходимо приложить к телу, чтобы оно двигалось равномерно и прямолинейно. По третьему закону Ньютона она будет численно равна силе сопротивления движения тела.

Определите силу сопротивления движению тела, которое перемещается по горизонтальной поверхности. В этом случае сила трения прямо пропорциональна силе реакции опоры, которая, в свою очередь равна силе тяжести, действующей на тело. Поэтому сила сопротивления движению в этом случае или сила трения Fтр равна произведению массы тела m, которая измеряется весами в килограммах, на ускорение свободного падения g≈9,8 м/с² и коэффициент пропорциональности μ, Fтр=μ∙m∙g. Число μ называется коэффициентом трения и зависит от поверхностей, входящих в контакт при движении. Например, для трения стали по дереву этот коэффициент равен 0,5.

Рассчитайте силу сопротивления движению тела, движущегося по . Кроме коэффициента трения μ, массы тела m и ускорения свободного падения g, она зависит от угла наклона плоскости к горизонту α. Чтобы найти силу сопротивления движению в этом случае, нужно найти произведения коэффициента трения, массы тела, ускорения свободного падения и косинуса угла, под которым плоскость к горизонту Fтр=μ∙m∙g∙сos(α).

При движении тела в воздухе на невысоких скоростях сила сопротивления движению Fс прямо пропорциональна скорости движения тела v, Fc=α∙v. Коэффициент α зависит от свойств тела и вязкости среды и рассчитывается отдельно. При движении на высоких скоростях, например, при падении тела со значительной высоты или движении автомобиля, сила сопротивления прямо пропорциональна квадрату скорости Fc=β∙v². Коэффициент β дополнительно рассчитывается для высоких скоростей.

Источники:

1 Общая формула для силы сопротивления воздуха На рисунке

Для определения силы сопротивления воздуха создайте условия, при которых тело начнет под действием силы тяжести двигаться равномерно и прямолинейно. Рассчитайте значение силы тяжести, оно будет равно силе сопротивления воздуха. Если тело движется в воздухе, набирая скорость, сила его сопротивления находится при помощи законов Ньютона, также силу сопротивления воздуха можно найти из закона сохранения механической энергии и специальных аэродинамических формул.

Вам понадобится

дальномер, весы, спидометр или радар, линейка, секундомер.

Инструкция

Перед измерением сопротивления б/у резистора обязательно выпаяйте его из старой платы или блока. Иначе он может быть шунтирован другими деталями схемы, и вы получите неправильные показания его сопротивления .

Видео по теме

Чтобы найти электрическое сопротивление проводника, воспользуйтесь соответствующими формулами. Сопротивление участка цепи находится по закону Ома. Если же известен материал и геометрические размеры проводника, его сопротивление можно рассчитать при помощи специальной формулы.

Вам понадобится

— тестер;
— штангенциркуль;
— линейка.

Инструкция

Вспомните, что подразумевает собой понятие резистора. В данном случае под резистором надо понимать любой проводник или элемент электрической цепи, имеющий активное резистивное сопротивление. Теперь важно задаться вопросом о том, как действует изменение значения сопротивления на значение силы тока и от чего оно зависит. Суть явления сопротивления заключается в том, что резистора формируют своего рода барьер для прохождения электрических зарядов. Чем выше сопротивление вещества, тем более плотно расположены атомы в решетке резистивного вещества. Данную закономерность и объясняет закон Ома для участка цепи. Как известно, закон Ома для участка цепи звучит следующим образом: сила тока на участке цепи прямо пропорциональна напряжению на участке и обратно пропорциональна сопротивлению самого участка цепи.

Изобразите на листе бумаги график зависимости силы тока от напряжения на резисторе, а также от его сопротивления, исходя из закона Ома. Вы получите график гиперболы в первом случае и график прямой во втором случае. Таким образом, сила тока будет тем больше, чем больше напряжение на резисторе и чем меньше сопротивление. Причем зависимость от сопротивления здесь более яркая, ибо она имеет вид гиперболы.

Обратите внимание, что сопротивление резистора также изменяется при изменении его температуры. Если нагревать резистивный элемент и наблюдать при этом за изменением силы тока, то можно заметить, как при увеличении температуры уменьшается сила тока. Данная закономерность объясняется тем, что при увеличении температуры увеличиваются колебания атомов в узлах кристаллической решетки резистора, уменьшая таким образом свободное пространство для прохождения заряженных частиц. Другой причиной, уменьшающей силу тока в данном случае, является тот факт, что при увеличении температуры вещества увеличивается хаотичное движение частиц, в том числе заряженных. Таким образом, движение свободных частиц в резисторе становится в большей степени хаотичным, чем направленным, что и сказывается на уменьшении силы тока.

Видео по теме

Собрав электрическую цепь, состоящую из источника тока, резистора, амперметра, вольтметра, ключа, можно показать, что сила тока (I ), протекающего через резистор, прямо пропорциональна напряжению (U ) на его концах: I — U . Отношение напряжения к силе тока U/I — есть величина постоянная .

Следовательно, существует физическая величина, характеризующая свойства проводника (резистора), по которому течёт электрический ток. Эту величину называют электрическим сопротивлением проводника, или просто сопротивлением. Обозначается сопротивление буквой R .

(R) – это физическая величина, равную отношению напряжения (U ) на концах проводника к силе тока (I ) в нём. R = U/I . Единица измерения сопротивления – Ом (1 Ом ).

Один Ом — сопротивление такого проводника, в котором сила тока равна 1А при напряжении на его концах 1В: 1 Ом = 1 В / 1 А.

Причина того, что проводник обладает сопротивлением, заключается в том, что направленному движению электрических зарядов в нём препятствуют ионы кристаллической решетки , совершающие беспорядочное движение. Соответственно, скорость направленного движения зарядов уменьшается.

Удельное электрическое сопротивление R ) прямо пропорционально длине проводника (l ), обратно пропорционально площади его поперечного сечения (S ) и зависит от материала проводника. Эта зависимость выражается формулой: R = p*l/S

р — это величина, характеризующая материал, из которого сделан проводник. Она называется удельным сопротивлением проводника , её значение равно сопротивлению проводника длиной 1 м и площадью поперечного сечения 1 м 2 .

Единицей удельного сопротивления проводника служит: [р] = 1 0м 1 м 2 / 1 м . Часто площадь поперечного сечения измеряют в мм 2 , поэтому в справочниках значения удельного сопротивления проводника приводятся как в Ом м так и в Ом мм 2 / м .

Изменяя длину проводника, а следовательно его сопротивление, можно регулировать силу тока в цепи. Прибор, с помощью которого это можно сделать, называется реостатом .

Как вычислить общее сопротивление цепи.

Доброго дня уважаемые радиолюбители!
Приветствую вас на сайте “ “

Соотношения закона Ома

В этой таблице используются следующие общепринятые обозначения физических величин:

U — напряжение (В),

I — ток (А),

Р — мощность (Вт),

R — сопротивление (Ом),

I = U / R

Что же в этой формуле есть что? Рассмотрим переменные подробнее.

> R : искомое сопротивление токоограничивающего резистора, в омах.

В продолжение, можно проставить в формулу расчета сопротивления реальные цифры вместо U, I и R:

R = U/I = 8,5 В / 0,050 А= 170 Ом

Расчёты сопротивления

Расчет сопротивления последовательных резисторов

Rобщ = Rl + R2 + R3 + … (столько раз, сколько есть элементов)

Расчет сопротивления параллельных резисторов

R общ = R1 * R2 / (R1 + R2)

776,47 = 2640000 / 3400

Расчёты ёмкости

Расчет емкости параллельных конденсаторов

Собщ = CI + С2 + СЗ + …

В этой формуле CI, С2 и СЗ — емкости отдельных конденсаторов, а Собщ суммирующая величина.

Расчет емкости последовательных конденсаторов

Для вычисления общей емкости пары связанных последовательно конденсаторов применяется следующая формула:

Собщ = С1 * С2 /(С1+С2)

где С1 и С2 — значения емкости каждого из конденсаторов, а Собщ — общая емкость цепи

Расчет емкости трех и более последовательно соединенных конденсаторов

Расчёт энергетических уравнений

ватт-часы = Р х Т

Расчёт постоянной ёмкости RC-цепочки

T = RC

Расчёты частоты и длины волны

Расчет частоты сигнала

Частота = 300000 / длина волны

Расчет длины волны сигнала

Ту же самую формулу можно использовать и для вычисления длины волны радиосигнала, если известна его частота:

Длина волны = 300000 / Частота

Результат будет выражен в миллиметрах, а частота сигнала указывается в мегагерцах.

6000 миллиметров = 300000 / 50 МГц

Если известна мощность и напряжение

После несложных мы получаем формулу для вычислений

Следует отметить, что такое выражение справедливо для цепей постоянного тока. Но при расчётах, например, для электродвигателя учитывают его полную мощность или косинус Фи. Тогда для трёхфазного двигателя его можно рассчитать так:

Находим P с учетом КПД, обычно он лежит в пределах 0,75-0,88:

Р1 = Р2/η

Здесь P2 – активная полезная мощность на валу, η – КПД, оба этих параметра обычно указывают на шильдике.

Находим полную мощность с учетом cosФ (он также указывается на шильдике):

S = P1/cosφ

Определяем потребляемый ток по формуле:

Iном = S/(1,73·U)

Если известно напряжение или мощность и сопротивление

При этом согласно тому же закону Ома:

P=I 2 *R

Значит расчёт проводим по формуле:

I 2 =P/R

Или возьмем выражение в правой части выражения под корень:

I=(P/R) 1/2

Если известно ЭДС, внутреннее сопротивление и нагрузка

I=E/(R+r)

Здесь E – ЭДС, r – внутреннее сопротивление источника питания, R – нагрузки.

Закон Джоуля-Ленца

Его формула выглядит так:

Q=I 2 Rt

Тогда расчет проводите так:

I 2 =QRt

Или внесите правую часть уравнения под корень:

I=(Q/Rt) 1/2

Несколько примеров

I=U/R=12/3=4 Ампера

При параллельном соединении двух элементов Rобщее можно рассчитать так:

Rобщ=(R1*R2)/(R1+R2)=1*2/3=2/3=0,67

Тогда дальнейшие вычисления можно проводить так:

Мы начинаем публикацию материалов новой рубрики “” и в сегодняшней статье речь пойдет о фундаментальных понятиях, без которых не проходит обсуждение ни одного электронного устройства или схемы. Как вы уже догадались, я имею ввиду ток, напряжение и сопротивление 😉 Кроме того, мы не обойдем стороной закон, который определяет взаимосвязь этих величин, но не буду забегать вперед, давайте двигаться постепенно.

Итак, давайте начнем с понятия напряжения .

Напряжение.

По определению напряжение – это энергия (или работа), которая затрачивается на перемещение единичного положительного заряда из точки с низким потенциалом в точку с высоким потенциалом (т. е. первая точка имеет более отрицательный потенциал по сравнению со второй). Из курса физики мы помним, что потенциал электростатического поля – это скалярная величина, равная отношению потенциальной энергии заряда в поле к этому заряду. Давайте рассмотрим небольшой пример:

В пространстве действует постоянное электрическое поле, напряженность которого равна E . Рассмотрим две точки, расположенные на расстоянии d друг от друга. Так вот напряжение между двумя точками представляет из себя ни что иное, как разность потенциалов в этих точках:

В то же время не забываем про связь напряженности электростатического поля и разности потенциалов между двумя точками:

И в итоге получаем формулу, связывающую напряжение и напряженность:

В электронике, при рассмотрении различных схем, напряжение все-таки принято считать как разность потенциалов между точками. Соответственно, становится понятно, что напряжение в цепи – это понятие, связанное с двумя точками цепи. То есть говорить, к примеру, “напряжение в резисторе” – не совсем корректно. А если говорят о напряжении в какой-то точке, то подразумевают разность потенциалов между этой точкой и “землей” . Вот так плавно мы вышли к еще одному важнейшему понятию при изучении электроники, а именно к понятию “земля” 🙂 Так вот “землей” в электрических цепях чаще всего принято считать точку нулевого потенциала (то есть потенциал этой точки равен 0).

Давайте еще пару слов скажем о единицах, которые помогают охарактеризовать величину напряжения . Единицей измерения является Вольт (В) . Глядя на определение понятия напряжения мы можем легко понять, что для перемещения заряда величиной 1 Кулон между точками, имеющими разность потенциалов 1 Вольт , необходимо совершить работу, равную 1 Джоулю . С этим вроде бы все понятно и можно двигаться дальше 😉

А на очереди у нас еще одно понятие, а именно ток .

Ток, сила тока в цепи.

Что же такое электрический ток ?

Давайте подумаем, что будет происходить если под действие электрического поля попадут заряженные частицы, например, электроны…Рассмотрим проводник, к которому приложено определенное напряжение :

Из направления напряженности электрического поля (E ) мы можем сделать вывод о том, что title=»Rendered by QuickLaTeX.com»> (вектор напряженности всегда направлен в сторону уменьшения потенциала). На каждый электрон начинает действовать сила:

Где e – это заряд электрона.

И поскольку электрон является отрицательно заряженной частицей, то вектор силы будет направлен в сторону противоположную направлению вектора напряженности поля. Таким образом, под действием силы частицы наряду с хаотическим движением приобретают и направленное (вектор скорости V на рисунке). В результате и возникает электрический ток 🙂

Ток – это упорядоченное движение заряженных частиц под воздействием электрического поля.

Важным нюансом является то, что принято считать, что ток протекает от точки с более положительным потенциалом к точке с более отрицательным потенциалом, несмотря на то, что электрон перемещается в противоположном направлении.

Носителями заряда могут выступать не только электроны. Например, в электролитах и ионизированных газах протекание тока в первую очередь связано с перемещением ионов, которые являются положительно заряженными частицами. Соответственно, направление вектора силы, действующей на них (а заодно и вектора скорости) будет совпадать с направлением вектора E . И в этом случае противоречия не возникнет, ведь ток будет протекать именно в том направлении, в котором движутся частицы 🙂

Для того, чтобы оценить ток в цепи придумали такую величину как сила тока. Итак, сила тока (I ) – это величина, которая характеризует скорость перемещения электрического заряда в точке. Единицей измерения силы тока является Ампер . Сила тока в проводнике равна 1 Амперу , если за 1 секунду через поперечное сечение проводника проходит заряд 1 Кулон .

Мы уже рассмотрели понятия силы тока и напряжения , теперь давайте разберемся каким образом эти величины связаны. И для этого нам предстоит изучить, что же из себя представляет сопротивление проводника .

Сопротивление проводника/цепи.

Термин “сопротивление ” уже говорит сам за себя 😉

Итак, сопротивление – физическая величина, характеризующая свойства проводника препятствовать (сопротивляться ) прохождению электрического тока.

Рассмотрим медный проводник длиной l с площадью поперечного сечения, равной S :

Сопротивление проводника зависит от нескольких факторов:

Удельное сопротивление – это табличная величина.

Формула, с помощью которой можно вычислить сопротивление проводника выглядит следующим образом:

Для нашего случая будет равно 0,0175 (Ом * кв. мм / м) – удельное сопротивление меди. Пусть длина проводника составляет 0.5 м , а площадь поперечного сечения равна 0.2 кв. мм . Тогда:

Как вы уже поняли из примера, единицей измерения сопротивления является Ом 😉

С сопротивлением проводника все ясно, настало время изучить взаимосвязь напряжения, силы тока и сопротивления цепи .

И тут на помощь нам приходит основополагающий закон всей электроники – закон Ома:

Сила тока в цепи прямо пропорциональна напряжению и обратно пропорциональна сопротивлению рассматриваемого участка цепи.

Рассмотрим простейшую электрическую цепь:

Как следует из закона Ома напряжение и сила тока в цепи связаны следующим образом:

Пусть напряжение составляет 10 В, а сопротивление цепи равно 200 Ом. Тогда сила тока в цепи вычисляется следующим образом:

Как видите, все несложно 🙂

Пожалуй на этом мы и закончим сегодняшнюю статью, спасибо за внимание и до скорых встреч! 🙂

Так записывается основная формула:

Путем преобразования основной формулы можно найти и другие две величины:

Формула мгновенной электрической мощности:

Первая — мнемоническое правило. Если из формулы закона Ома выразить сопротивление, то R = рюмка.

Вторая — метод треугольника. Его ещё называют магический треугольник закона Ома.

Если оторвать величину, которую требуется найти, то в оставшейся части мы получим формулу для её нахождения.

Этот круг также, как и треугольник можно назвать магическим.

Элементы электрической цепи можно соединить двумя способами. Последовательное соединение подразумевает подключение элементов друг к другу, а при параллельном соединении элементы являются частью параллельных ветвей. Способ соединения резисторов определяет метод вычисления общего сопротивления цепи.

Шаги

Последовательное соединение

Определите, является ли цепь последовательной. Последовательное соединение представляет собой единую цепь без каких-либо разветвлений. Резисторы или другие элементы расположены друг за другом.

Сложите сопротивления отдельных элементов. Сопротивление последовательной цепи равно сумме сопротивлений всех элементов, входящих в эту цепь. Сила тока в любых частях последовательной цепи одна и та же, поэтому сопротивления просто складываются.

Например, последовательная цепь состоит из трех резисторов с сопротивлениями 2 Ом, 5 Ом и 7 Ом. Общее сопротивление цепи: 2 + 5 + 7 = 14 Ом.

Если сопротивление каждого элемента цепи не известно, воспользуйтесь законом Ома: V = IR, где V – напряжение, I – сила тока, R – сопротивление. Сначала найдите силу тока и общее напряжение.

Подставьте известные значения в формулу, описывающую закон Ома. Перепишите формулу V = IR так, чтобы обособить сопротивление: R = V/I. Подставьте известные значения в эту формулу, чтобы вычислить общее сопротивление.

Например, напряжение источника тока равно 12 В, а сила тока равна 8 А. Общее сопротивление последовательной цепи: R O = 12 В / 8 А = 1,5 Ом.

Параллельное соединение

Определите, является ли цепь параллельной. Параллельная цепь на некотором участке разветвляется на несколько ветвей, которые затем снова соединяются. Ток течет по каждой ветви цепи.
Вычислите общее сопротивление на основе сопротивления каждой ветви. Каждый резистор уменьшает силу тока, проходящего через одну ветвь, поэтому она оказывает небольшое влияние на общее сопротивление цепи. Формула для вычисления общего сопротивления: , где R 1 – сопротивление первой ветви, R 2 – сопротивление второй ветви и так далее до последней ветви R n .
- Например, параллельная цепь состоит из трех ветвей, сопротивления которых равны 10 Ом, 2 Ом и 1 Ом.
  Воспользуйтесь формулой 1 R O = 1 10 + 1 2 + 1 1 {\displaystyle {\frac {1}{R_{O}}}={\frac {1}{10}}+{\frac {1}{2}}+{\frac {1}{1}}} , чтобы вычислить R O
  Приведите дроби к общему знаменателю : 1 R O = 1 10 + 5 10 + 10 10 {\displaystyle {\frac {1}{R_{O}}}={\frac {1}{10}}+{\frac {5}{10}}+{\frac {10}{10}}}
  1 R O = 1 + 5 + 10 10 = 16 10 = 1 , 6 {\displaystyle {\frac {1}{R_{O}}}={\frac {1+5+10}{10}}={\frac {16}{10}}=1,6}
  Умножьте обе части на R O: 1 = 1,6R O
  R O = 1 / 1,6 = 0,625 Ом.
Вычислите сопротивление по известной силе тока и напряжению. Сделайте это, если сопротивление каждого элемента цепи не известно.
Подставьте известные значения в формулу закона Ома. Если известны значения общей силы тока и напряжения в цепи, общее сопротивление вычисляется по закону Ома: R = V/I.
- Например, напряжение в параллельной цепи равно 9 В, а общая сила тока равна 3 А. Общее сопротивление: R O = 9 В / 3 А = 3 Ом.
Поищите ветви с нулевым сопротивлением. Если у ветви параллельной цепи вообще нет сопротивления, то весь ток будет течь через такую ветвь. В этом случае общее сопротивление цепи равно 0 Ом.

Комбинированное соединение

Разбейте комбинированную цепь на последовательную и параллельную. Комбинированная цепь включает элементы, которые соединены как последовательно, так и параллельно. Посмотрите на схему цепи и подумайте, как разбить ее на участки с последовательным и параллельным соединением элементов. Обведите каждый участок, чтобы упростить задачу по вычислению общего сопротивления.
- Например, цепь включает резистор, сопротивление которого равно 1 Ом, и резистор, сопротивление которого равно 1,5 Ом. За вторым резистором схема разветвляется на две параллельные ветви – одна ветвь включает резистор с сопротивлением 5 Ом, а вторая – с сопротивлением 3 Ом. Обведите две параллельные ветви, чтобы выделить их на схеме цепи.
Найдите сопротивление параллельной цепи. Для этого воспользуйтесь формулой для вычисления общего сопротивления параллельной цепи: 1 R O = 1 R 1 + 1 R 2 + 1 R 3 + . . . 1 R n {\displaystyle {\frac {1}{R_{O}}}={\frac {1}{R_{1}}}+{\frac {1}{R_{2}}}+{\frac {1}{R_{3}}}+…{\frac {1}{R_{n}}}} .
- В нашем примере параллельная цепь включает две ветви, сопротивления которых равны R 1 = 5 Ом и R 2 = 3 Ом.
  1 R p a r = 1 5 + 1 3 {\displaystyle {\frac {1}{R_{par}}}={\frac {1}{5}}+{\frac {1}{3}}}
  1 R p a r = 3 15 + 5 15 = 3 + 5 15 = 8 15 {\displaystyle {\frac {1}{R_{par}}}={\frac {3}{15}}+{\frac {5}{15}}={\frac {3+5}{15}}={\frac {8}{15}}}
  R p a r = 15 8 = 1 , 875 {\displaystyle R_{par}={\frac {15}{8}}=1,875} Ом.
Упростите цепь. После того как вы нашли общее сопротивление параллельной цепи, ее можно заменить одним элементом, сопротивление которого равно вычисленному значению.
- В нашем примере избавьтесь от двух параллельных ветвей и замените их одним резистором с сопротивлением 1,875 Ом.
Сложите сопротивления резисторов, соединенных последовательно. Заменив параллельную цепь одним элементом, вы получили последовательную цепь. Общее сопротивление последовательной цепи равно сумме сопротивлений всех элементов, которые включены в эту цепь.
- После упрощения цепи она состоит из трех резисторов со следующими сопротивлениями: 1 Ом, 1,5 Ом и 1,875 Ом. Все три резистора соединены последовательно: R O = 1 + 1 , 5 + 1 , 875 = 4 , 375 {\displaystyle R_{O}=1+1,5+1,875=4,375} Ом.

Мощность цепи — AP Physics 1

Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или другие ваши авторские права, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее в информацию, описанную ниже, назначенному ниже агенту. Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.

Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.

Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права. Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.

Чтобы отправить уведомление, выполните следующие действия:

Вы должны включить следующее:

Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно полагаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.

Отправьте жалобу нашему уполномоченному агенту по адресу:

Чарльз Кон Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105

Или заполните форму ниже:

ресурсов

Мощность

Мощность в электрической цепи относится к скорости, с которой электрическая энергия преобразуется в какую-либо другую форму, такую как тепло или магнетизм.Мощность, рассеиваемая в цепи, напрямую связана с приложенным напряжением и величиной тока, протекающего по цепи.

Диаграммы показывают, что увеличение мощности земного шара в цепи с тем же напряжением приводит к более высокому току, следовательно, рассеивается больше мощности, то есть больше тепла и света. Более высокий ток означает, что шар с высокой мощностью имеет меньшее сопротивление, чем шар с низкой мощностью.

Увеличение мощности

Единицей измерения мощности является Вт .

Кол-во	Символ	Установка	Аббревиатура	Значение
мощность	п.	ватт	Вт	Рассеиваемая мощность

Если есть увеличение напряжения, мощность увеличится в четыре раза.Если вы увеличиваете напряжение (или электрическое давление) в цепи, то ток (поток электронов) будет увеличиваться прямо пропорционально, например, если вы удвоите напряжение, ток удвоится.

Формула для расчета мощности:

P = VI

Следовательно, удвоение тока, умноженного на удвоенное напряжение, увеличит мощность в четыре раза.

Закон Ома для расчета рассеиваемой мощности

Простая схема

Проработанные примеры основаны на представленной принципиальной схеме.

Какая мощность будет рассеиваться резистором (R), если в цепи протекает ток (A) 2 А при приложенном напряжении (В) 24 В?
- P = VI
- P = 24 x 2
- P = 48 Вт
Какая мощность будет рассеиваться резистором (R), если в цепи протекает ток (А) 2 мкА при приложенном напряжении (В) 10 мВ?
- P = VI
- A и V являются частными кратными и должны быть преобразованы в базовые единицы
- А = 2 мкА = 2 х 0.000 001 = 0 000 002A
- В = 10 мВ = 10 x 0,001 = 0,01 В
- P = 0,01 x 0,000,002
- P = 0,000,000,02W или 20nW

Замена формулы

В соответствии с законом Ома рассеиваемая мощность напрямую зависит от приложенного напряжения и протекающего тока. Это напрямую связано с величиной сопротивления.Если известны любые два значения схемы, мы можем вычислить два других значения с помощью подстановки.

Пример

Простая схема.

В этом примере, если напряжение аккумулятора составляет 20 В, а сопротивление (R) имеет значение 100 Ом, то какой будет рассеиваемая мощность?
- Формула для расчета мощности:
- P = VI
- Мы не знаем текущий поток (I).
  Мы могли бы использовать закон Ома I = ^V/_R для расчета тока, а затем использовать вычисленное значение в приведенной выше формуле мощности.
- Ответ можно найти с помощью одной формулы:
- P = VI заменить I на ^V/_R
- Это даст вам формулу:
- P = ^{В x В}/_R вольт, умноженное на вольт, разделенное на сопротивление)
- Вольт, умноженное на вольт, выражается как V ² (вольт в квадрате).Итак, окончательная формула будет:
- P = V ² / R
- P = 20 ²/100, что совпадает с (20 x 20/100)
- P = 400/100
- P = 4 Вт
Если общее сопротивление цепи составляет 80 Ом, а ток равен 2 А, какова рассеиваемая мощность?
- P = VI мы не знаем напряжения, но по закону Ома V = IR.Следовательно, формула:
- P = I x R x I, что совпадает с I x I x R, которое совпадает с I ² R, поэтому формула:
- P = I ² R
- P = 2 ²/80
- P = 4/80
- P = 0,05 Вт или 7071 мВт
Если мощность, рассеиваемая в цепи, составляет 500 Вт, а текущий ток составляет 2 А, каково полное сопротивление?
- R = V / I — формула для расчета сопротивления, но напряжение неизвестно.
- Для определения напряжения можно использовать формулу мощности V = P / I, но ее можно подставить в первую формулу следующим образом:
- R = (P / I) / I (Сопротивление равно ваттам, разделенным на амперы, а затем снова разделенным на амперы.)
- Однако это уравнение можно упростить как P / (I x I) и, следовательно, можно выразить как:
- R = P / I ²
- R = 500/2 ²
- R = 125 Ом
Если мощность, рассеиваемая в цепи, составляет 10 Вт, а общее сопротивление составляет 5 Ом, каково приложенное напряжение?
- V = IR — формула для расчета напряжения, но текущее значение неизвестно.
- Формулу мощности V = P / I нельзя использовать для определения напряжения, потому что ток также неизвестен. Однако из-за прямой связи этих значений можно использовать замену формулы.
- Мы знаем, что напряжение будет равно V = P / I, а ток будет I = V / R, поэтому
- V = P / (V / R), что совпадает с V = PR / V, и после транспонирования это будет V ² = PR
- Мы хотим знать напряжение, а не квадрат напряжения, поэтому квадратный корень ( √ ) из PR даст ответ.
- Следовательно, формула:
- В = √PR
- В = √ (10 х 5)
- В = √50
- В = 7,071 В или 7071 мВ

19,4 Электроэнергия | Texas Gateway

Задачи обучения

К концу этого раздела вы сможете сделать следующее:

Определить электрическую мощность и описать уравнение электрической мощности
Расчет электрической мощности в цепях резисторов при последовательном, параллельном и сложном расположении

Основные термины раздела
электроэнергия

Энергия для многих ассоциируется с электричеством.Каждый день мы используем электроэнергию для работы наших современных приборов. Линии электропередачи — наглядные примеры электроэнергии, обеспечивающей мощность. Мы также используем электроэнергию для запуска автомобилей, работы компьютеров или освещения дома. Мощность — это скорость передачи энергии любого типа; электрическая мощность — это скорость, с которой электрическая энергия передается в цепи. В этом разделе мы узнаем не только, что это означает, но и какие факторы определяют электрическую мощность.

Для начала представим себе лампочки, которые часто характеризуются номинальной мощностью в ваттах.Давайте сравним лампочку мощностью 25 Вт с лампой мощностью 60 Вт (см. Рисунок 19.23). Хотя обе работают при одинаковом напряжении, лампа мощностью 60 Вт излучает больше света, чем лампа мощностью 25 Вт. Это говорит нам о том, что выходную мощность электрической цепи определяет нечто иное, чем напряжение.

Лампы накаливания, такие как две, показанные на рисунке 19.23, по сути являются резисторами, которые нагреваются, когда через них протекает ток, и становятся настолько горячими, что излучают видимый и невидимый свет. Таким образом, две лампочки на фото можно рассматривать как два разных резистора.В простой цепи, такой как электрическая лампочка с приложенным к ней напряжением, сопротивление определяет ток по закону Ома, поэтому мы можем видеть, что ток, а также напряжение должны определять мощность.

Рисунок 19.23 Слева лампочка мощностью 25 Вт, а справа лампочка мощностью 60 Вт. Почему их выходная мощность различается, несмотря на то, что они работают при одинаковом напряжении?

Формулу мощности можно найти путем анализа размеров. Рассмотрим единицы мощности. В системе СИ мощность указывается в ваттах (Вт), которые представляют собой энергию в единицу времени, или Дж / с.

Напомним, что напряжение — это потенциальная энергия на единицу заряда, что означает, что напряжение имеет единицы Дж / Кл.

Мы можем переписать это уравнение как J = V × CJ = V × C и подставить его в уравнение для ватт, чтобы получить

W = Js = V × Cs = V × Cs.W = Js = V × Cs = V × Cs.

Но кулон в секунду (Кл / с) — это электрический ток, который мы можем видеть из определения электрического тока, I = ΔQΔtI = ΔQΔt, где ΔΔ Q — заряд в кулонах, а ΔΔ t — время в секундах. Таким образом, приведенное выше уравнение говорит нам, что электрическая мощность равна напряжению, умноженному на ток, или

Это уравнение дает электрическую мощность, потребляемую цепью с падением напряжения В и током I .

Например, рассмотрим схему на рисунке 19.24. По закону Ома ток, протекающий по цепи, равен

19,49I = VR = 12 В 100 Ом = 0,12 AI = VR = 12 В 100 Ом = 0,12 А.

Таким образом, мощность, потребляемая цепью, составляет

19,50P = VI. = (12 В) (0,12 А) = 1,4 WP = VI = (12 В) (0,12 А) = 1,4 Вт.

Куда уходит эта мощность? В этой схеме мощность в основном идет на нагрев резистора в этой цепи.

Рисунок 19.24 Простая схема, потребляющая электроэнергию.

При вычислении мощности в цепи, показанной на рисунке 19.24, мы использовали сопротивление и закон Ома, чтобы найти ток.Закон Ома дает ток: I = V / RI = V / R, который мы можем вставить в уравнение для электроэнергии, чтобы получить

P = IV = (VR) V = V2R.P = IV = (VR) V = V2R.

Это дает мощность с точки зрения только напряжения и сопротивления.

Мы также можем использовать закон Ома, чтобы исключить напряжение из уравнения для электрической мощности и получить выражение для мощности, выраженное только через ток и сопротивление. Если мы запишем закон Ома как V = IRV = IR и используя это, чтобы исключить V в уравнении P = IVP = IV, мы получим

P = IV = I (IR) = I2R.P = IV = I (IR) = I2R.

Это дает мощность только по току и сопротивлению.

Таким образом, комбинируя закон Ома с уравнением P = IVP = IV для электроэнергии, мы получаем еще два выражения для мощности: одно через напряжение и сопротивление, а другое через ток и сопротивление. Обратите внимание, что в выражения для электрической мощности входят только сопротивление (не емкость или что-либо еще), ток и напряжение. Это означает, что физической характеристикой цепи, определяющей, сколько мощности она рассеивает, является ее сопротивление.Любые конденсаторы в цепи не рассеивают электроэнергию — напротив, конденсаторы либо накапливают электрическую энергию, либо отдают ее обратно в цепь.

Чтобы прояснить связь между напряжением, сопротивлением, током и мощностью, рассмотрим рисунок 19.25, на котором показано колесо формул . Количества в центральной четверти круга равны количествам в соответствующей внешней четверти круга. Например, чтобы выразить потенциал V через мощность и ток, мы видим из колеса формул, что V = P / IV = P / I.

Рисунок 19.25 Колесо формул показывает, как связаны между собой вольт, сопротивление, ток и мощность. Количества во внутренней четверти окружности равны количеству в соответствующей внешней четверти окружности.

Рабочий пример

Найдите сопротивление лампочки

Типичная старая лампа накаливания имела мощность 60 Вт. Если предположить, что к лампочке приложено 120 В, каков ток через лампочку?

СТРАТЕГИЯ

Нам даны напряжение и выходная мощность простой цепи, содержащей лампочку, поэтому мы можем использовать уравнение P = IVP = IV, чтобы найти ток I , протекающий через лампочку.

Решение

Решение P = IVP = IV для тока и вставка данных значений для напряжения и мощности дает

19,51 P = IVI = PV = 60 Вт 120 V = 0,50 А. P = IVI = PV = 60 Вт 120 В = 0,50 А.

Таким образом, при подаче напряжения 120 В через лампочку проходит половина ампера.

Обсуждение

Это значительное течение. Напомним, что в быту используется переменный, а не постоянный ток, поэтому 120 В, подаваемое от бытовых розеток, — это переменная, а не постоянная мощность. Фактически, 120 В — это усредненная по времени мощность, обеспечиваемая такими розетками.Таким образом, средний ток, протекающий через лампочку за период времени, превышающий несколько секунд, составляет 0,50 А.

Рабочий пример

Подогреватели ботинок

Чтобы согреть ботинки в холодные дни, вы решаете вшить цепь с некоторыми резисторами в стельку ботинок. Вам нужно 10 Вт тепла от резисторов в каждой стельке, и вы хотите, чтобы они работали от двух 9-вольтовых батарей (соединенных последовательно). Какое общее сопротивление вы должны приложить к каждой стельке?

СТРАТЕГИЯ

Нам известны требуемая мощность и напряжение (18 В, потому что у нас есть две батареи 9 В, соединенные последовательно), поэтому мы можем использовать уравнение P = V2 / RP = V2 / R, чтобы найти необходимое сопротивление.

Решение

Решая P = V2 / RP = V2 / R для сопротивления и вставляя заданные напряжение и мощность, получаем

19,52P = V2RR = V2P = (18 В) 210 Вт = 32 Ом. P = V2RR = V2P = (18 В) 210 Вт = 32 Ом.

Таким образом, общее сопротивление в каждой стельке должно быть 32 Ом.

Обсуждение

Давайте посмотрим, сколько тока пройдет через эту цепь. У нас есть 18 В, приложенное к сопротивлению 32 Ом, поэтому закон Ома дает

19,53 I = VR = 18 В 32 Ом = 0,56 А. I = VR = 18 В 32 Ом = 0,56 А.

На всех батареях есть этикетки, на которых указано, сколько заряда они могут обеспечить (в единицах силы тока, умноженного на время).Типичная щелочная батарея на 9 В может обеспечить заряд 565 мА · ч · мА · ч. (так что две батареи 9 В обеспечивают 1130 мА⋅ч мА⋅ч), поэтому эта система обогрева проработает в течение

19,54t = 1130 × 10−3 A⋅h0,56 A = 2,0 h.t = 1130 × 10−3 A⋅h0,56 A = 2,0 час.

Рабочий пример

Питание через ответвление цепи

Каждый резистор в приведенной ниже схеме имеет сопротивление 30 Ом. Какая мощность рассеивается средней ветвью схемы?

СТРАТЕГИЯ

Средняя ветвь схемы содержит последовательно включенные резисторы R3 и R5R3 и R5.Напряжение на этой ветви составляет 12 В. Сначала мы найдем эквивалентное сопротивление в этой ветви, а затем используем P = V2 / RP = V2 / R, чтобы найти мощность, рассеиваемую в ветви.

Решение

Эквивалентное сопротивление: R среднее = R3 + R5 = 30 Ом + 30 Ом = 60 Ом R среднее = R3 + R5 = 30 Ом + 30 Ом = 60 Ом. Мощность, рассеиваемая средней ветвью схемы, составляет

. 19,55P средний = V2R средний = (12 В) 260 Ом = 2,4 Вт. Средний = V2R средний = (12 В) 260 Ом = 2,4 Вт.

Обсуждение

Давайте посмотрим, сохраняется ли энергия в этой цепи, сравнив мощность, рассеиваемую в цепи, с мощностью, обеспечиваемой батареей.Во-первых, эквивалентное сопротивление левой ветви равно

. 19,56 Влево = 11 / R1 + 1 / R2 + R4 = 11/30 Ом + 1/30 Ом + 30 Ом = 45 Ом. Влево = 11 / R1 + 1 / R2 + R4 = 11/30 Ом + 1/30 Ом +30 Ом = 45 Ом.

Мощность через левую ветвь

19,57 Слева = V2R, слева = (12 В) 245 Ом = 3,2 Вт. Слева = V2R, слева = (12 В) 245 Ом = 3,2 Вт.

Правая ветвь содержит только R6R6, поэтому эквивалентное сопротивление Rright = R6 = 30 ΩRright = R6 = 30 Ω. Мощность через правую ветку

19,58 Правый = V2 Правый = (12 В) 230 Ом = 4,8 Вт. Правый = V2 Правый = (12 В) 230 Ом = 4,8 Вт.

Общая мощность, рассеиваемая схемой, представляет собой сумму мощностей, рассеиваемых в каждой ветви.

19,59P = складка + середина + прядь = 2,4 Вт + 3,2 Вт + 4,8 Вт = 10,4 WP = складка + середина + прядь = 2,4 Вт + 3,2 Вт + 4,8 Вт = 10,4 Вт

Мощность, обеспечиваемая аккумулятором, составляет

, где I — полный ток, протекающий через батарею. Поэтому мы должны сложить токи, проходящие через каждую ветвь, чтобы получить I . Ветви дают токи

19,61 слева = VR слева = 12 В 45 Ом = 0.2667 AIсредний = VR средний = 12 В 60 Ом = 0.20 AIright = VRright = 12 В 30 Ом = 0,40 A. Левый = VR Левый = 12 В 45 Ом = 0,2667 AI Средний = VR средний = 12 В 60 Ом = 0,20 AIright = VRright = 12 В 30 Ом = 0,40 А.

Суммарный ток

19,62 I = слева + Imiddle + I right = 0,2667 A + 0,20 A + 0,40 A = 0,87 A. I = I слева + Imiddle + I right = 0,2667 A + 0,20 A + 0,40 A = 0,87 A.

, а мощность, обеспечиваемая аккумулятором, составляет

19,63P = IV = (0,87 A) (12 В) = 10,4 Вт. P = IV = (0,87 A) (12 В) = 10,4 Вт.

Это та же мощность, которая рассеивается на резисторах схемы, что показывает, что в этой цепи сохраняется энергия.

Пример закона

Ома с решениями для средней школы

Экспериментально обнаружено, что когда напряжение или разность потенциалов $ \ Delta V $ прикладывается к концам определенных проводников, ток через них пропорционален приложенному напряжению, то есть $ I \ propto \ Delta V $.

Константа пропорциональности называется сопротивлением этого проводника .

Другими словами, сопротивление определяется как отношение напряжения на проводнике к току, протекающему по нему.\ [R \ Equiv \ frac {\ Delta V} {I} \] Эта простая взаимосвязь между разностью потенциалов и током известна как закон Ома .

Единицы измерения сопротивления в системе СИ — вольт на ампер , которые называются Ом ($ \ Omega $).

Проводник, который обеспечивает определенную величину сопротивления в электрической цепи, называется резистором .

Например, если резистор 10 Ом подключен к клеммам аккумулятора с напряжением 240 В, то через него проходит ток $ \ frac {240} {10} = 24 \, {\ rm A} $.

Напротив, в электронике также есть проводники или материалы, которые выше простой линейной зависимости между напряжением и током не соблюдаются, такие как диоды, транзисторы или люминесцентные лампы.

В таких материалах существует нелинейная зависимость напряжения от тока. Эти проводники называются неомическими материалами .

Готовитесь к экзамену AP Physics? Прочтите это:
Практических задач по схемам для экзамена AP Physics 2

Ниже приведены некоторые простые вопросы и ответы о законе Ома с подробными объяснениями.Все задачи подходят старшекласснику.

Примеры закона Ома

Пример (1): Электронное устройство имеет сопротивление 20 Ом и ток 15 А. Какое напряжение на устройстве?

Решение : сопротивление, ток и напряжение связаны законом Ома как $ V = IR $. Таким образом, напряжение устройства получается как \ begin {align *} V & = IR \\ & = 15 \ times 20 \\ & = 300 \ quad {\ rm V} \ end {align *}

Пример (2): разность потенциалов $ 3 — {\ rm V} $ приложена к резистору $ 6 \, {\ rm \ Omega} $.Какой ток протекает через резистор?

Решение : Закон Ома гласит, что разность потенциалов на резисторе равна сопротивлению, умноженному на ток, поэтому мы получаем \ begin {align *} I & = \ frac VR \\ & = \ frac {3} {6} \\ & = 0.5 \ четырехъядерный {\ rm A} \ end {align *}

Домашнее задание: В эксперименте по измерению тока через неизвестный резистор студент получил следующие данные.

Напряжение (В)	Ток (I)
3.0	0,151
6.0	0,310
9,0	0,448
12,0	0,511
15,0	0,750

(a) Нарисуйте график на бумаге и покажите взаимосвязь между током и напряжением.
(b) Используя этот график, определите сопротивление резистора.

Решение этой и 34 других домашних задач — здесь .

Пример (3): Ток величиной $ 0,2 \, {\ rm A} $ проходит через резистор $ 1,4 \, {\ rm k \ Omega} $. Какое напряжение на нем?

Решение : используя закон Ома, $ V = IR $, мы имеем \ begin {align *} V & = IR \\ & = (0.2 \, {\ rm A}) (1.4 \ times 1000 \, {\ rm \ Omega}) \\ & = 280 \ quad {\ rm V} \ end {align *}

Пример (4): В схеме, показанной ниже, какой ток показывает амперметр?

Решение : лампа представляет собой электронный компонент с высоким сопротивлением.На рисунке напряжение на нем такое же, как у батареи $ V = 20 \, {\ rm V} $. Ток, проходящий через него, связан с сопротивлением и падением напряжения по закону Ома \ begin {align *} I & = \ frac VR \\ & = \ frac {20} {8} \\ & = 1.25 \ quad {\ rm A} \ end {align *}

Пример (5): В цепи падение потенциала на резисторе 10 кОм составляет 100 В. Каков ток через резистор?

Решение : подставьте все известные числовые значения в уравнение Ома, $ V = IR $.\ begin {align *} I & = \ frac VR \\\\ & = \ frac {100 \, {\ rm V}} {10000 \, {\ rm \ Omega}} \\\\ & = 0.01 \ quad { \ rm A} \ end {align *}

Пример (6): в следующих схемах найдите неизвестные.

Решение : В каждой из схем используйте закон Ома $ V = IR $ и решите неизвестное. В левой цепи ток через резистор запрашивается в миллиамперах. Таким образом, \ begin {align *} I & = \ frac VR \\\\ & = \ frac {120} {100} \\\\ & = 1.2 \ quad {\ rm A} \ end {align *} Чтобы преобразовать его в миллиамперы, умножьте его на 1000, чтобы получить $ I = 1200 \, {\ rm mA} $.{-3}} \\\\ & = 40 \ quad {\ rm \ Omega} \ end {align *}

Пример (7): Кривая напряжение-ток для омического проводника строится, как показано на рисунке ниже. Какое сопротивление резисторов 1 и 2?

Решение: Закон Ома говорит нам, что сопротивление — это наклон кривой зависимости напряжения от тока $ R = \ frac {\ Delta V} {I} $. Напомним, что наклон $ m $ прямой между двумя точками $ A (x_1, y_1) $ и $ B (x_2, y_2) $ определяется как \ [m = \ frac {\ Delta y} {\ Delta x} = \ frac {y_2-y_1} {x_2-x_1} \] Таким образом, наклон кривой напряжение-ток, который представляет собой сопротивление, получается следующим образом:
Точки $ A (0,0) $ и $ B (2,20) $ находятся на линии (1): \ [R_1 = \ frac {20-0} {2-0} = 10 \ quad {\ rm \ Omega} \]
Точки $ A (0, 0) $ и $ B (4,10) $ находятся в строке (2): \ [R_2 = \ frac {10-0} {4-0} = 2.5 \ quad {\ rm \ Omega} \]

Пример (8): Поменяйте местами падение потенциала на проводнике и ток, проходящий через него в предыдущей задаче, чтобы получить вольт-амперную кривую. Теперь найдите сопротивление резисторов 1 и 2?

Решение: если мы изменим закон Ома как $ I = \ frac {1} {R} \ Delta V $, мы увидим, что наклон кривой вольт-амперной характеристики в этом случае дает обратное значение сопротивления . Следовательно, как и в предыдущей задаче, наклон линии (1)
равен \ [\ frac {1} {R_1} = \ frac {20-0} {2-0} = 10 \], что дает $ R_1 = 0.1 \, {\ rm \ Omega} $, а наклон линии (2) равен \ [\ frac {1} {R_2} = \ frac {10-0} {4-0} = 2,5 \], что дает $ R_2 = 0,4 \, {\ rm \ Omega} $.

Пример (9): Студент проводит эксперимент и измеряет ток и напряжение на двух неизвестных резисторах. Затем она строит свое открытие в координатах «ток-напряжение», как показано на рисунке. Что можно сказать о резисторах А и В?

Решение : омические материалы — это материалы, которые имеют постоянное сопротивление в широком диапазоне приложенных напряжений.Другими словами, в омическом проводнике отношение напряжения на нем к току через него, которое определяется как сопротивление, всегда является постоянным.

Таким образом, омические материалы имеют линейную зависимость тока от напряжения, и ее кривая проходит через начало координат. Напротив, материалы, имеющие сопротивление, которое изменяется при падении потенциала или токе, называются неомическими.

Кривая неомического материала не является линейной. Примерами неомических материалов, нарушающих закон Ома, являются диоды и транзисторы.

С этими пояснениями, поскольку кривая (A) линейна и проходит через начало координат, значит, это омический проводник, наклон которого дает обратное сопротивление. Как и в предыдущей задаче, его сопротивление рассчитывается как $ R_A = 5 \, {\ rm \ Omega} $.

Резистор (B) имеет нелинейную зависимость между напряжением на нем и током, поэтому это неомический проводник с переменным сопротивлением.

Закон Ома: практические проблемы с решением

Теперь мы хотим решить некоторые практические задачи, чтобы показать вам, как использовать закон Ома для решения проблем с электричеством.

Практическая задача (1): Будильник потребляет ток 0,5 А при подключении к цепи 120 В. Найдите его сопротивление.

Решение : заданы ток $ I = 0,5 \, {\ rm A} $ и падение напряжения $ V = 120 \, {\ rm V} $. Решите закон Ома для неизвестного $ R $ как \ begin {align *} R & = \ frac VI \\ \\ & = \ frac {120} {0.5} \\ \\ & = 240 \ quad {\ rm \ Omega} \ конец {align *}

Практическая проблема (2): сабвуферу требуется домашнее напряжение 110 В, чтобы протолкнуть ток 5.5 А через его катушку. Какое сопротивление сабвуфера?

Решение : Известны разность напряжений $ V = 110 \, {\ rm V} $ и ток $ I = 5.5 \, {\ rm A} $. Закон Ома связывает их следующим образом: \ begin {align *} R & = \ frac VI \\ \\ & = \ frac {110} {5.5} \\ \\ & = 20 \ quad {\ rm \ Omega} \ end {align *}

Проблема (3): Сколько тока потребляет цепь с резистором на 1000 Ом при питании от батареи с напряжением 1,5 В.

Решение : Сопротивление $ R = 1000 \, {\ rm \ Omega} $ и напряжение $ V = 1.5 \, {\ rm V} $ известны, поэтому у нас есть \ begin {align *} I & = \ frac VR \\\\ & = \ frac {1.5} {1000} \\\\ & = 1.5 \ quad { \ rm mA} \ end {align *}

Проблема (4): Электрический нагреватель имеет спиральный металлический провод, который потребляет ток 100 А. Сопротивление провода составляет 1,1 Ом. Рассчитайте напряжение, которое необходимо на нем установить.

Решение : Ток $ I = 100 \, {\ rm A} $ и сопротивление $ R = 1.1 \, {\ rm \ Omega} $ связаны как \ begin {align *} V & = IR \\ & = 100 \ раз 1.1 \\ & = 110 \ quad {\ rm V} \ end {align *}

Проблема (5): Максимальный ток, который проходит через лампочку с сопротивлением 5 Ом, составляет 10 А. Какое напряжение должно быть приложено к ее концам, прежде чем лампа сломается?

Решение : Максимальное напряжение можно найти с помощью закона Ома, как показано ниже \ begin {align *} V & = IR \\ & = 10 \ times 5 \\ & = 50 \ quad {\ rm V} \ end {align *} Если на схему подать напряжение выше этого значения, лампа перегорит.

Проблема (6): В цепи мы заменяем предыдущую 1,5-вольтовую батарею новой 3-вольтовой. Что происходит с этой схемой?

Решение : Закон Ома говорит нам, что, когда большее напряжение устанавливается в цепи, более высокий ток будет течь через резисторы в цепи, такой как электрические нагреватели, лампочки и т. Д.

Более высокий ток может вызвать повреждение или выход из строя бытовой техники. Например, лампочка с сопротивлением $ R = 1.5 \, {\ rm \ Omega} $ потребляет ток $ I = \ frac {1.5} {1.5} = 1 \, {\ rm A} $ с батареей $ 1.5 $ вольт и током $ I = \ frac { 3} {1.5} = 2 \, {\ rm A} $ с заменой новым. В этих случаях лампочка, скорее всего, перегорит.

Проблема (7): В цепи резистор $ 10 \, {\ rm \ Omega} $ удален и заменен резистором $ 20 \, {\ rm \ Omega} $. Что происходит с током в цепи.

Решение : Поскольку ничего не сказано о падении напряжения в цепи, мы предполагаем, что оно постоянное, скажем, $ V = 120 \, {\ rm V} $.Следовательно, используя формулу закона Ома, $ I = \ frac VR $, ток $ I = \ frac {120} {10} = 12 \, {\ rm A} $ течет через $ 10 \, {\ rm \ Omega} $ резистор и $ I = \ frac {120} {20} = 6 \, {\ rm A} $ через резистор $ 20 \, {\ rm \ Omega} $.

Мы видим, что для того же напряжения удвоение сопротивлений приводит к уменьшению, точнее, к уменьшению вдвое токов.

В этой статье мы узнали, , как решать задачи, связанные с законом Ома , на многих решенных примерах.

Автор: Dr.Али Немати
Страница создана: 06.12.2020
Последнее обновление: 19.01.2021

Закон Ома и Закон Уоттса

Калькулятор закона Ома и закона Ватта с примерами

Как пользоваться калькулятором:
Введите любые два известных значения и нажмите Вычислить , чтобы найти остальные.
Всегда нажимайте Reset перед каждым новым вычислением.

Закон Ома:
Устанавливает взаимосвязь между током (амперы), сопротивлением (Ом) и напряжением.
Вольт = Амперы x Ом
А = Вольт / Ом
Ом = Вольт / Ампер

Закон Ватта:
Устанавливает соотношение между мощностью (ватты), током (амперы) и напряжением.
Вт = Вольт x Ампер
Вольт = Ватт / Ампер
Ампер = Ватт / Вольт

Пример закона Ома: рассчитать сопротивление по напряжению и току
— Рейтинг роторов по сопротивлению

У вас есть коробка с роторами 27SI, и вам нужно определить, какие из них — 12 вольт, а какие — 24 вольт.

Вы хотите использовать омметр для проверки каждого ротора, но вы не знаете значение сопротивления (Ом) для каждого типа катушки ротора. Компания Delco-Remy опубликовала только значения тока возбуждения (амперы), но не сопротивления (Ом).

Процедура:
Используйте таблицу Delco-Remy 1G-188, чтобы узнать напряжение и потребление тока катушек ротора 27SI. Из диаграммы вы обнаружите, что:

Роторы на 12 В потребляют приблизительно 4,60 А при 12 В
на 24 В потребляют примерно 2 штуки.15 ампер при 24 вольт

Введите в калькулятор 12 вольт и 4,60 ампер, и он покажет сопротивление катушки как 2,61 Ом.

Введите 24 В и 2,15 А в калькулятор, и он покажет сопротивление катушки как 11,16 Ом.

Теперь, когда вы знаете значение сопротивления каждого типа катушки, вы можете быстро оценить каждый ротор. (Не забудьте отметить их!).

Полезные ссылки: Руководство по тестированию генератора
Delco-Remy 1G-188 Пример закона Ватта: вычисление ампер на основе ватт и напряжения
— Добавление аксессуара

Вы устанавливаете грузовик со снегоочистителем и хотите добавить фонари для плуга.
Вы выбрали лампы мощностью 65 Вт.

Вам необходимо определить две вещи:

Какое реле максимальной силы тока использовать.
Какого размера проводить провод от реле к фарам.

Это известные значения:

Максимальное рабочее напряжение фар: 14,5 В
Мощность каждой лампы: 65 Вт (поскольку есть две лампы, удвойте мощность)

Введите 14.

Как найти сопротивление тока формула. Электрическое сопротивление. Определение, единицы измерения, удельное, полное, активное, реактивное

Если известна мощность и напряжение

Если известно напряжение или мощность и сопротивление

Если известно ЭДС, внутреннее сопротивление и нагрузка

Закон Джоуля-Ленца

Несколько примеров

Закон Ома – математический подход при определении сопротивления

Эмпирическая формула расчета сопротивления

Взаимосвязь c мощностью (P)

Расчет электрической проводимости

Влияние температуры окружающей среды

Закон Ома

РАСЧЕТ ЭЛЕКТРИЧЕСКИХ ЦЕПЕЙ ОНЛАЙН — ОПРЕДЕЛЕНИЕ НАПРЯЖЕНИЯ, ТОКА, МОЩНОСТИ И СЕЧЕНИЯ ПРОВОДНИКА

Как узнать ток зная мощность и напряжение?

Как узнать напряжение зная силу тока?

Как рассчитать мощность зная силу тока и напряжения?

Как определить потребляемую мощность цепи имея тестер, который меряет сопротивление?

Формула расчета сечения провода и как определяется сечение провода

Как найти длину по формуле сопротивления. Если известно напряжение или мощность и сопротивление

Электрическое удельное сопротивление

Удельное сопротивление и проводимость материалов

Формула для расчета

Удельное сопротивление

Расчет по диаметру

Обязательны ли расчеты?

Как вычислить общее сопротивление цепи.

Если известна мощность и напряжение

Если известно напряжение или мощность и сопротивление

Если известно ЭДС, внутреннее сопротивление и нагрузка

Закон Джоуля-Ленца

Несколько примеров

Напряжение.

Ток, сила тока в цепи.

Сопротивление проводника/цепи.

Шаги

Последовательное соединение

Параллельное соединение

Комбинированное соединение

Мощность цепи — AP Physics 1

ресурсов

Мощность

19,4 Электроэнергия | Texas Gateway

Задачи обучения

Рабочий пример

Найдите сопротивление лампочки

СТРАТЕГИЯ

Рабочий пример

Подогреватели ботинок

СТРАТЕГИЯ

Рабочий пример

Питание через ответвление цепи

СТРАТЕГИЯ

Ома с решениями для средней школы

Примеры закона Ома

Закон Ома: практические проблемы с решением

Закон Ома и Закон Уоттса

Добавить комментарий Отменить ответ