Круговое движение — Википедия
- О разновидности перекрёстков: см. Круговой перекрёсток.
В физике кругово́е движе́ние — это вращательное движение материальной точки или тела, когда ось вращения в выбранной системе отсчёта неподвижна и не проходит через центр тела. В этом случае траектория точки или тела является кругом, круговой орбитой. Оно может быть равномерным (с постоянной угловой скоростью) или неравномерным (с переменной угловой скоростью). Вращение трёхмерного тела вокруг неподвижной оси включает в себя круговое движение каждой его части. Мы можем говорить о круговом движении объекта только если можем пренебречь его размерами, так что мы имеем движение массивной точки на плоскости. Например, центр масс тела может совершать круговое движение.
Примеры кругового движения: искусственный спутник на геосинхронной орбите, камень на верёвке, вращающийся по кругу (см. метание молота), болид, совершающий поворот, электрон, движущийся перпендикулярно постоянному магнитному полю, зубчатое колесо, вращающееся внутри механизма.
Круговое движение является ускоренным, даже если происходит с постоянной угловой скоростью, потому что вектор скорости объекта постоянно меняет направление. Такое изменение направления скорости вызывает ускорение движущегося объекта центростремительной силой, которая толкает движущийся объект по направлению к центру круговой орбиты. Без этого ускорения объект будет двигаться прямолинейно в соответствии с законами Ньютона.
Формулы для равномерного кругового движения[править | править код]
Рис. 1: Взаимосвязи векторов равномерного кругового движения; вектор Ω, представляющий вращение, перпендикулярен к плоскости орбиты.Для движения по кругу радиуса R длина окружности будет C = 2π R. Если период вращения есть
- ω=2πT .{\displaystyle \omega ={\frac {2\pi }{T}}\ .}
Скорость движения объекта равна
- v=2πRT=ωR{\displaystyle v\,={\frac {2\pi R}{T}}=\omega R}
Угол поворота θ за время t равен:
- θ=2πtT=ωt{\displaystyle \theta =2\pi {\frac {t}{T}}=\omega t}
Ускорение, вызванное изменением направления скорости, можно найти, если заметить, что скорость совершает полное изменение направления за то же самое время T, за которое объект делает один оборот. Тогда вектор скорости проходит путь длиной 2π v каждые T секунд, или:
- a=2πvT=ω2 R ,{\displaystyle a\,={\frac {2\pi v}{T}}=\omega ^{2}\ R\ ,}
и направлено радиально к центру.
Взаимосвязи векторов показаны на рис. 1. Ось вращения изображена вектором Ω, перпендикулярно плоскости орбиты и имеет величину ω = dθ / dt. Направление вектора Ω выбрано в соответствии с правилом правой руки. По этому соглашению скорость это векторное произведение вида:
- v=Ω×r ,{\displaystyle \mathbf {v} ={\boldsymbol {\Omega }}\times \mathbf {r} \ ,}
и есть вектор, перпендикулярный как Ω так и r ( t ), направленный по касательной к орбите и имеющий величину ω R. Аналогично, ускорение определяется как:
- a=Ω×v ,{\displaystyle \mathbf {a} ={\boldsymbol {\Omega }}\times \mathbf {v} \ ,}
Оно представляет собой вектор, перпендикулярный как Ω так и v ( t ), имеющий величину ω |v| = ω2R и направление строго противоположно к r ( t ).
В простейшем случае скорость, масса и радиус являются постоянными.
Рассмотрим тело массой один килограмм, движущееся по кругу радиуса один метр с угловой скоростью один радиан в секунду.
Теперь рассмотрим тело массы m{\displaystyle m}, движущееся по кругу радиуса r{\displaystyle r} с угловой скоростью w{\displaystyle w};{\displaystyle ;}
В круговом движении полную силу, приложенную к объекту, можно разложить на две составляющие: центростремительную, удерживающую тело на круговой орбите (т. е. меняющую направление вектора скорости), и тангенциальную, направленную по касательной к окружности и вызывающую изменение длины вектора скорости (т. е. меняющую скорость вращения тела по орбите). Величина центростремительной составляющей зависит от мгновенной скорости.
Для примера, когда камень привязан к концу верёвки, то он подвергается воздействию некоторой силы, которую мы можем разложить на радиальную и боковую составляющие. Радиальная направлена к центру (вовнутрь) окружности и вызвана тем, что веревка сопротивляется удлинению. А боковая составляющая определяет будет вращение камня ускоряться или замедляться.
Описание кругового движения в полярных координатах[править | править код]
Траектория кругового движения тела может быть описана в полярной системе координат значениями фиксированного расстояние R от центра орбиты, являющейся точкой отсчёта, и угла ориентации θ (t) от некоторого фиксированного направления (рис. 2). Вектор перемещения r→{\displaystyle {\stackrel {\vec {r}}{}}} является радиальным вектором от полюса до текущего положения:
- r→=Ru^R(t) ,{\displaystyle {\vec {r}}=R{\hat {u}}_{R}(t)\ ,}
где u^R(t){\displaystyle {\hat {u}}_{R}(t)} — единичный вектор, параллельный радиусу в момент t и направленный от полюса. Удобно также ввести единичный вектор, ортогональный к u^R{\displaystyle {\hat {u}}_{R}}, который назовём u^θ{\displaystyle {\hat {u}}_{\theta }}. Обычно его ориентация выбирается по направлению движения вдоль орбиты.
Скорость является производной перемещения по времени:
- v→=ddtr→(t)=dRdtu^R+Rdu^Rdt .{\displaystyle {\vec {v}}={\frac {d}{dt}}{\vec {r}}(t)={\frac {dR}{dt}}{\hat {u}}_{R}+R{\frac {d{\hat {u}}_{R}}{dt}}\ .}
Поскольку радиус окружности является константой, радиальная составляющая скорости равна нулю. Единичный вектор u^R{\displaystyle {\hat {u}}_{R}} имеет инвариантное по времени значение, так что при изменении времени его конец всегда лежит на окружности единичного радиуса, а угол θ такой же, как у r→(t){\displaystyle {\vec {r}}(t)}. Если произошло малое приращение угла dθ за время dt, тогда u^R{\displaystyle {\hat {u}}_{R}} описывает дугу единичной окружности со значением dθ (см. единичную окружность слева на рис. 2). Следовательно:
- du^Rdt=dθdtu^θ ,{\displaystyle {\frac {d{\hat {u}}_{R}}{dt}}={\frac {d\theta }{dt}}{\hat {u}}_{\theta }\ ,}
где направление изменения должно быть перпендикулярно к u^R{\displaystyle {\hat {u}}_{R}} (или, другими словами, вдоль u^θ{\displaystyle {\hat {u}}_{\theta }}), поскольку любое изменение du^R{\displaystyle {\hat {u}}_{R}} в направлении u^R{\displaystyle {\hat {u}}_{R}} будет изменять величину u^R{\displaystyle {\hat {u}}_{R}}. Знак положительный, потому что увеличение dθ влияет на объект и u^R{\displaystyle {\hat {u}}_{R}} передвигается в направлении u^θ{\displaystyle {\hat {u}}_{\theta }}. Следовательно, скорость становится:
- v→=ddtr→(t)=Rdu^Rdt=Rdθdtu^θ =Rωu^θ .{\displaystyle {\vec {v}}={\frac {d}{dt}}{\vec {r}}(t)=R{\frac {d{\hat {u}}_{R}}{dt}}=R{\frac {d\theta }{dt}}{\hat {u}}_{\theta }\ =R\omega {\hat {u}}_{\theta }\ .}
Ускорение тела также можно разложить на радиальную и тангенциальную составляющие. Ускорение есть производная скорости по времени:
- a→=ddtv→=ddt(R ω u^θ ) .{\displaystyle {\vec {a}}={\frac {d}{dt}}{\vec {v}}={\frac {d}{dt}}\left(R\ \omega \ {\hat {u}}_{\theta }\ \right)\ .}
- =R(dωdt u^θ+ω du^θdt) .{\displaystyle =R\left({\frac {d\omega }{dt}}\ {\hat {u}}_{\theta }+\omega \ {\frac {d{\hat {u}}_{\theta }}{dt}}\right)\ .}
Производная по времени от u^θ{\displaystyle {\hat {u}}_{\theta }} находится таким же путём, как и для u^R{\displaystyle {\hat {u}}_{R}}. Опять же, u^θ{\displaystyle {\hat {u}}_{\theta }} есть единичный вектор, и его конец расположен на единичной окружности, а угол равен π/2 + θ. Следовательно, приращение угла dθ вектора r→(t){\displaystyle {\vec {r}}(t)} перемещает u^θ{\displaystyle {\hat {u}}_{\theta }} по дуге на величину dθ, и поскольку u^θ{\displaystyle {\hat {u}}_{\theta }} перпендикулярен к u^R{\displaystyle {\hat {u}}_{R}}, мы имеем:
- du^θdt=−dθdtu^R=−ωu^R ,{\displaystyle {\frac {d{\hat {u}}_{\theta }}{dt}}=-{\frac {d\theta }{dt}}{\hat {u}}_{R}=-\omega {\hat {u}}_{R}\ ,}
где отрицательный знак необходим, чтобы сохранить u^θ{\displaystyle {\hat {u}}_{\theta }} перпендикулярным к u^R{\displaystyle {\hat {u}}_{R}}. (Иначе угол между u^θ{\displaystyle {\hat {u}}_{\theta }} и u^R{\displaystyle {\hat {u}}_{R}} будет уменьшаться с увеличением dθ, см. единичную окружность слева на рис. 2). Следовательно, ускорение равно:
- a→=R(dωdt u^θ+ω du^θdt){\displaystyle {\vec {a}}=R\left({\frac {d\omega }{dt}}\ {\hat {u}}_{\theta }+\omega \ {\frac {d{\hat {u}}_{\theta }}{dt}}\right)}
- =Rdωdt u^θ−ω2R u^R .{\displaystyle =R{\frac {d\omega }{dt}}\ {\hat {u}}_{\theta }-\omega ^{2}R\ {\hat {u}}_{R}\ .}
Центростремительное ускорение — это радиальная составляющая, направленная по радиусу вовнутрь:
- a→R=−ω2Ru^R ,{\displaystyle {\vec {a}}_{R}=-\omega ^{2}R{\hat {u}}_{R}\ ,}
тогда как тангенциальная составляющая изменяет значение скорости:
- a→θ=Rdωdt u^θ=dRωdt u^θ=d|v→|dt u^θ .{\displaystyle {\vec {a}}_{\theta }=R{\frac {d\omega }{dt}}\ {\hat {u}}_{\theta }={\frac {dR\omega }{dt}}\ {\hat {u}}_{\theta }={\frac {d|{\vec {v}}|}{dt}}\ {\hat {u}}_{\theta }\ .}
Описание кругового движения в комплексных числах[править | править код]
Круговое движение можно описать с использованием комплексных чисел. Пусть x{\displaystyle x} — ось вещественных чисел, а y{\displaystyle y} — ось мнимых чисел. Тогда положение тела может быть задано в виде комплексного «вектора» z{\displaystyle z}:
- z=x+iy=R(cosθ+isinθ)=Reiθ ,{\displaystyle z=x+iy=R(\cos \theta +i\sin \theta )=Re^{i\theta }\ ,}
где i{\displaystyle i} есть мнимая единица, и
- θ=θ(t) ,{\displaystyle \theta =\theta (t)\ ,}
есть угол комплексного вектора по отношению к вещественной оси как функция времени t. Поскольку радиус есть константа:
- R˙=R¨=0 ,{\displaystyle {\dot {R}}={\ddot {R}}=0\ ,}
где точка означает дифференциал по времени. В этих обозначениях скорость имеет вид :
- v=z˙=Rddt(iθ)eiθ=iRθ˙eiθ=iω⋅Reiθ=iωz{\displaystyle v={\dot {z}}=R{\frac {d}{dt}}\left(i\theta \right)e^{i\theta }=iR{\dot {\theta }}e^{i\theta }=i\omega \cdot Re^{i\theta }=i\omega z}
а ускорение:
- a=v˙=iω˙z+iωz˙=(iω˙−ω2)z{\displaystyle a={\dot {v}}=i{\dot {\omega }}z+i\omega {\dot {z}}=(i{\dot {\omega }}-\omega ^{2})z}
- =(iω˙−ω2)Reiθ{\displaystyle =\left(i{\dot {\omega }}-\omega ^{2}\right)Re^{i\theta }}
- =−ω2Reiθ+ω˙eiπ2Reiθ .{\displaystyle =-\omega ^{2}Re^{i\theta }+{\dot {\omega }}e^{i{\frac {\pi }{2}}}Re^{i\theta }\ .}
Первое слагаемое направлено против вектора перемещения, а второе — перпендикулярно ему, как и в предыдущих результатах.
Движение по окружности. |
|
|
Положение точки А, движущейся по окружности с постоянной по модулю скоростью v в любой момент времени t определяется углом φ между осью OX и радиус-ветором : |
|
Уравнение движения по окружности. Угловая скорость. Нормальное = центростремительное ускорение. Период, частота обращения (вращения). Связь линейной и угловой скорости: |
|
|
Угловая скорость [ω] = 1 рад/с = 1 с-1это: Отношение углового перемещения Δφ за промежуток времени Δt к этому промежутку: |
|
|
Кинематическое уравнение движения тела по окружности с постоянной по модулю скоростью :
|
|
|
Нормальное (центростремительное) ускорение: характеризует быстроту изменения вектора линейной скорости. Вектор всегда направлен к центру окружности, выражается так: |
|
ФИЗИКА: Задачи на Движение тела по окружности
Задачи на Движение тела по окружности с решениями
Формулы, используемые на уроках «Задачи на Движение тела по окружности».
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. Какова линейная скорость тела, движущегося по окружности радиусом 40 м с ускорением 2,5 м/с2 ?
Задача № 2. С какой наибольшей скоростью может двигаться автомобиль массой 1 т на повороте радиусом 100 м, чтобы его не «занесло», если максимальная сила трения 4 кН?
Задача № 3. Вентилятор вращается с постоянной скоростью и за две минуты совершает 2400 оборотов. Определите частоту вращения вентилятора, период обращения и линейную скорость точки, расположенной на краю лопасти вентилятора на расстоянии 10 см от оси вращения.
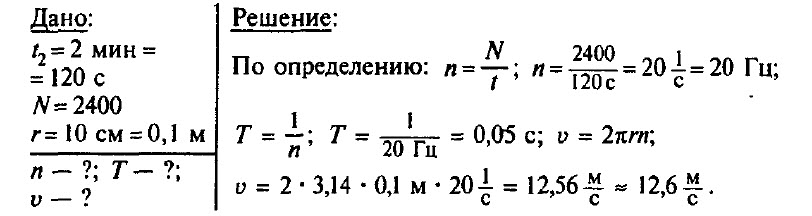
Задача № 4. Во сколько раз линейная скорость точки обода колеса радиусом 8 см больше линейной скорости точки, расположенной на 3 см ближе к оси вращения колеса?
Задача № 5. Велосипедист ехал со скоростью 25,2 км/ч. Сколько оборотов совершило колесо диаметром 70 см за 10 мин?
Задача № 6. Минутная стрелка часов в 1,5 раза длиннее часовой. Определите, во сколько раз линейная скорость конца часовой стрелки меньше, чем линейная скорость конца минутной стрелки.
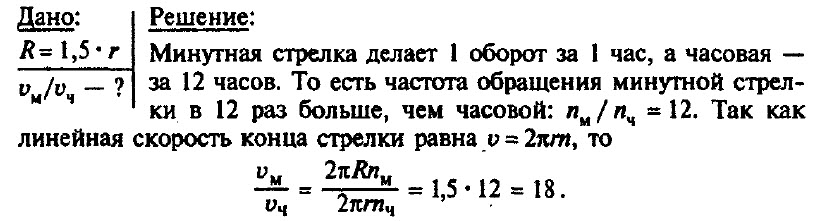
Задача № 7. Автомобиль движется по закруглению дороги, радиус которой равен 20 м. Определите скорость автомобиля, если центростремительное ускорение равно 5 м/с2.
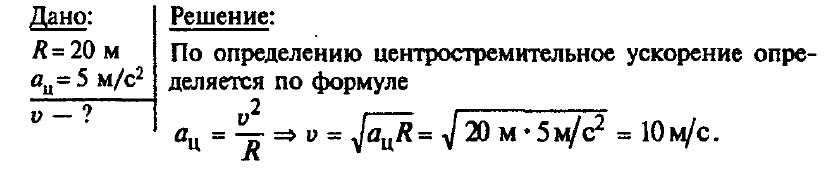
Задача № 8. Шкив радиусом 30 см имеет частоту вращения 120 об/мин. Определите частоту, период обращения, угловую скорость шкива и центростремительное ускорение точек шкива, наиболее удаленных от оси вращения.
Задача № 9. Для точек земной поверхности на широте Санкт-Петербурга (60°) определите линейную скорость и ускорение, испытываемое ими вследствие суточного вращения Земли. Радиус Земли считайте равным 6370 км.
Задача № 10. ОГЭ Точка движется равномерно по окружности. Как изменится её центростремительное ускорение, если скорость возрастёт вдвое, а радиус окружности вдвое уменьшится?
Задача № 11.
ЕГЭ
Линейная скорость точек обода вращающегося диска v1 = 3 м/с, а точек, находящихся на
Краткая теория для решения Задачи на Движение тела по окружности.
Это конспект по теме «ЗАДАЧИ на Движение тела по окружности». Выберите дальнейшие действия:
1.1.8 Движение тела по окружности. Угловая и линейная скорости точки. Центростремительное ускорение точки
Видеоурок: Движение по окружности
Лекция: Движение тела по окружности. Угловая и линейная скорости точки. Центростремительное ускорение точки
Движение по окружности
Траектория движения — окружность.
Так как скорость — векторная величина, то она зависит не только от модуля значения, но и от направления. Поэтому движение тела по окружности можно назвать равноускоренным. Даже если тело будет двигаться с постоянной по величине скоростью, её направление будет постоянно изменяться.
Любое криволинейное движение можно свести к нескольким движениям по окружности. Примером данного движения является бег по стадиону, ход стрелки часов, прогулка на корде лошади и другое.
Основные характеристики движения1. Линейная скорость
Мгновенная скорость (линейная) — на протяжении всего движения меняет свое направление вдоль касательной к траектории.Так как траектория движения точки — окружность, то в качестве пути в числителе находится формула длины перемещения.
Поэтому формула мгновенной скорости приобретает следующий вид, где Т — период:
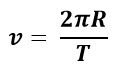
2. Центростремительное ускорение
Направлено перпендикулярно к линейной скорости на протяжении всего движения.Центростремительное ускорение определяется по формуле:
3. Период вращения
Период вращения — это величина, определяющая время, за которое тело делает одно полное вращение.
Период — это скалярная величина. Основной единицей периода является [Т]=1с.
Период определяется по формуле:
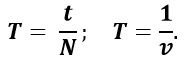
где N — количество оборотов, t — время, за которое они были совершены.
4. Частота вращения
Определяет, насколько часто совершаются обороты в единицу времени.
Частота — скалярная величина. Измеряется в [n] = 1с-1.
Частота определяется по формуле:
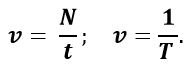
5. Угловое перемещение
Угловое перемещение — величина, которая определяется углом поворота радиуса, соединяющего центр описываемой окружности, с точкой, где находится тело, относительно начального его положения.
Данная величина может измеряться в градусной или радианной мере углов.
6. Угловая скорость
Это значение, которое определяет, насколько изменяется угловое перемещение со временем.
Измеряется в 1 рад/с.Определяется по формуле: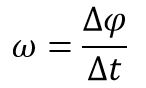
где
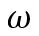— угловая скорость материальной точки, 1/с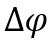
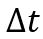— промежуток времени, сУгловое перемещение связано с линейной скоростью и центростремительным ускорением следующей формулой:
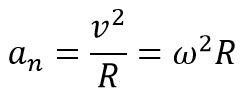
Вращательное движение (движение тела по окружности) | Формулы и расчеты онлайн
Законы, определяющие движение тела по окружности, аналогичны законам поступательного движения. Уравнения, описывающие вращательное движение, можно вывести из уравнений поступательного движения, произведя в последних следующие замены:
Если:
перемещение s — угловое перемещение (угол поворота) φ,
скорость u — угловая скорость ω,
ускорение a — угловое ускорение α
Вращательное движение, характеристики
| Вращательное движение | Угловая скорость | Угловое ускорение |
|---|---|---|
| Равномерное | Постоянная | Равно нулю |
| Равномерно ускоренное | Изменяется равномерно | Постоянно |
| Неравномерно ускоренное | Изменяется неравномерно | Переменное |
Угол поворота
Во всех уравнения вращательного движения углы задаются в радианах, сокращенно
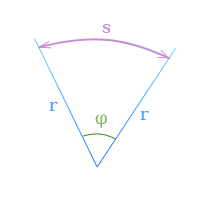Если
φ — угловое перемещение в радианах,
s — длина дуги, заключенной
между сторонами угла поворота,
r — радиус,
то по определению радиана
\[ φ = \frac{s}{r} \]
Соотношение между единицами угла
\[ \frac[-1.35]{φ_{рад}}{φ_{°}} = \frac[-1.2]{π}{180°} \]
$ 1 рад = 57.3° $ | $ 1° = 17.45 мрад $ | $ 1´ = 291 мкрад $ |
Обратите внимание: Наименование единицы радиан (рад) обычно указывается в формулах только в тех случаях, когда ее можно спутать с градусом. Поскольку радиан равен отношению длин двух отрезков
(1рад = 1м/ 1м = 1), он не имеет размерности.
Соотношение между угловой скоростью, угловым перемещением и временем для всех видов движения по окружности наглядно видны на графике угловой скорости (зависимость ω от t).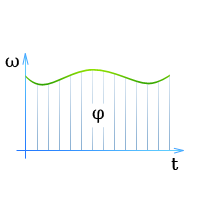 
Поэтому графику можно определить, какой угловой скоростью обладает тело в тот или иной момент времени и на какой угол с момента начала движения оно повернулось (он характеризуется площадью под кривой).
Кроме того, для представления соотношений между названными величинами используют график углового перемещения (зависимость φ от t) и график углового ускорения (зависимость α от t).
Число оборотов
Характеристикой всех видов вращения является число оборотов n или равноценная ей характеристика — частота f. Обе величины характеризуют число оборотов в единицу времени.
Единица СИ частоты (или числа оборотов)
\[ [n] = [f] = \frac{Обороты}{Секунда} = \frac{(об)}{с} = \frac{1}{c} = Герц \]
В технике число оборотов обычно измеряется в оборотах в минуту (об/мин) = 1/мин.
Таким образом, величина, обратная числу оборотов, есть продолжительность одного оборота.
Если
n — число оборотов,
f — частота,
T — продолжительность одного оборота, период,
φ — угловое перемещение,
N — полное число оборотов,
t — время, продолжительность вращения,
ω — угловая частота,
то
Период
\[ T = \frac{1}{f} = \frac{1}{n} \]
Угловое перемещение
Угловое перемещение равно произведению полного числа оборотов на 2π:
\[ φ = 2 π N \]
Угловая скорость
Из формулы для одного оборота следует:
\[ ω = 2 π f = \frac{2π}{T} \]
Обратите внимание:
• формулы (1)—(6) справедливы для всех видов вращательного движения — как для равномерного движения, так и для ускоренного. В них могут входить постоянные величины, средние значения, начальные и конечные значения, а также любые мгновенные значения.
• вопреки своему названию число оборотов n — это не число, а физическая величина.
• следует различать число оборотов n и полное число оборотов N.
В помощь студенту
Вращательное движение (движение тела по окружности) |
стр. 421 |
|---|
Формула угловой скорости в физике
Определение и формула угловой скорости
ОпределениеКруговым движением точки вокруг некоторой оси называют движение, при котором траекторией точки является окружность с центром, который лежит на оси вращения, при этом плоскость окружности перпендикулярна этой оси.
Вращением тела вокруг оси называют движение, при котором все точки тела совершают круговые движения около этой оси.
Перемещение при вращении характеризуют при помощи угла поворота . Часто используют вектор элементарного поворота , который равен по величине элементарному углу поворота тела замаленький отрезок времени dtи направлен по мгновенной оси вращения в сторону, откуда этот поворот виден реализующимся против часовой стрелки. Надо отметить, что только элементарные угловые перемещения являются векторами. Углы вращения на конечные величины векторами не являются.
ОпределениеУгловой скоростью называют скорость изменения угла поворота и обозначают ее обычно буквой . Математически определение угловой скорости записывают так:
Угловая скорость — векторная величина (это аксиальный вектор). Она имеет направление вдоль мгновенной оси вращения совпадающее с направлением поступательного правого винта, если его вращать в сторону вращения тела (рис.1).
Вектор угловой скорости может претерпевать изменения как за счет изменения скорости вращения тела вокруг оси (изменение модуля угловой скорости), так и за счет поворота оси вращения в пространстве ( при этом изменяет направление).
Равномерное вращение
Если тело за равные промежутки времени поворачивается на один и тот же угол, то такое вращение называют равномерным. При этом модуль угловой скорости находят как:
где – угол поворота, t – время, за которое этот поворот совершён.
Равномерное вращение часто характеризуют при помощи периода обращения (T), который является временем, за которое тело производит один оборот ). Угловая скорость связана с периодом обращения как:
С числом оборотов в единицу времени () угловая скорость связана формулой:
Равномерное движение по окружности | Физика для всех
Равномерное движение по окружности – это простейший пример криволинейного движения. Например, по окружности движется конец стрелки часов по циферблату. Скорость движения тела по окружности носит название линейная скорость.
При равномерном движении тела по окружности модуль скорости тела с течением времени не изменяется, то есть v = const, а изменяется только направление вектора скорости Тангенциальное ускорение в этом случае отсутствует (ar = 0), а изменение вектора скорости по направлению характеризуется величиной, которая называется центростремительное ускорение (нормальное ускорение) an или аЦС. В каждой точке траектории вектор центростремительного ускорения направлен к центру окружности по радиусу.
Модуль центростремительного ускорения равен
aЦС=v2 / R
Где v – линейная скорость, R – радиус окружности
Рис. 1.22. Движение тела по окружности.
Когда описывается движение тела по окружности, используется угол поворота радиуса – угол φ, на который за время t поворачивается радиус, проведённый из центра окружности до точки, в которой в этот момент находится движущееся тело. Угол поворота измеряется в радианах. Радиан равен углу между двумя радиусами окружности, длина дуги между которыми равна радиусу окружности (рис. 1.23). То есть если l = R, то
1 радиан= l / R
Так как длина окружности равна
l = 2πR
то
360о = 2πR / R = 2π рад.
Следовательно
1 рад. = 57,2958о = 57о18’
Угловая скорость равномерного движения тела по окружности – это величина ω, равная отношению угла поворота радиуса φ к промежутку времени, в течение которого совершён этот поворот:
ω = φ / t
Единица измерения угловой скорости – радиан в секунду [рад/с]. Модуль линейной скорости определяется отношением длины пройденного пути l к промежутку времени t:
v= l / t
Линейная скорость при равномерном движении по окружности направлена по касательной в данной точке окружности. При движении точки длина l дуги окружности, пройденной точкой, связана с углом поворота φ выражением
l = Rφ
где R – радиус окружности.
Тогда в случае равномерного движения точки линейная и угловая скорости связаны соотношением:
v = l / t = Rφ / t = Rω или v = Rω
Рис. 1.23. Радиан.
Период обращения – это промежуток времени Т, в течение которого тело (точка) совершает один оборот по окружности.Частота обращения – это величина, обратная периоду обращения – число оборотов в единицу времени (в секунду). Частота обращения обозначается буквой n.
n = 1 / T
За один период угол поворота φ точки равен 2π рад, поэтому 2π = ωT, откуда
T = 2π / ω
То есть угловая скорость равна
ω = 2π / T = 2πn
Центростремительное ускорение можно выразить через период Т и частоту обращения n:
aЦС = (4π2R) / T2 = 4π2Rn2