Равномерное движение по окружности. Скорость, ускорение
Автор — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: движение по окружности с постоянной по модулю скоростью, центростремительное ускорение.
Равномерное движение по окружности — это достаточно простой пример движения с вектором ускорения, зависящим от времени.
Пусть точка вращается по окружности радиуса . Скорость точки постоянна по модулю и равна . Скорость называется линейной скоростью точки.
Период обращения — это время одного полного оборота. Для периода имеем очевидную формулу:
. (1)
Частота обращения — это величина, обратная периоду:
.
Частота показывает, сколько полных оборотов точка совершает за секунду.
Пусть, например, . Это означает, что за время точка совершает один полный
оборот. Частота при этом получается равна: об/с; за секунду точка совершает 10 полных оборотов.
Угловая скорость.
Рассмотрим равномерное вращение точки в декартовой системе координат. Поместим начало координат в центре окружности (рис. 1).
| Рис. 1. Равномерное движение по окружности |
Пусть — начальное положение точки; иными словами, при точка имела координаты . Пусть за время точка повернулась на угол и заняла положение .
Отношение угла поворота ко времени называется угловой скоростью вращения точки:
. (2)
Угол , как правило, измеряется в радианах, поэтому угловая скорость измеряется в рад/с. За время, равное периоду вращения, точка поворачивается на угол . Поэтому
Поэтому
. (3)
Сопоставляя формулы (1) и (3), получаем связь линейной и угловой скоростей:
. (4)
Закон движения.
Найдём теперь зависимость координат вращающейся точки от времени. Видим из рис. 1, что
.
Но из формулы (2) имеем: . Следовательно,
. (5)
Формулы (5) являются решением основной задачи механики для равномерного движения точки по окружности.
Центростремительное ускорение.
Теперь нас интересует ускорение вращающейся точки. Его можно найти, дважды продифференцировав соотношения (5):
С учётом формул (5) имеем:
(6)
Полученные формулы (6) можно записать в виде одного векторного равенства:
(7)
где — радиус-вектор вращающейся точки.
Мы видим, что вектор ускорения направлен противоположно радиус-вектору, т. е. к центру окружности (см. рис. 1). Поэтому ускорение точки, равномерно движущейся по окружности, называется центростремительным.
Кроме того, из формулы (7) мы получаем выражение для модуля центростремительного ускорения:
(8)
Выразим угловую скорость из (4)
и подставим в (8). Получим ещё одну формулу для центростремительного ускорения:
.
Центрифугирование: как определить ускорение (число g) в зависимости от скорости вращения и диаметра ротора
Центрифугирование – способ разделения неоднородных, дисперсных жидких систем на фракции по плотности под действием центробежных сил. Центрифугирование осуществляют в центрифугах, принцип работы которых основан на создании центробежной силы, увеличивающей скорость разделения компонентов смеси по сравнению со скоростью их разделения только под влиянием силы тяжести. Разделение веществ с помощью центрифугирования основано на разном поведении частиц в центробежном поле. В центробежном поле частицы, имеющие разную плотность, форму или размеры, осаждаются с разной скоростью.
Скорость осаждения, или седиментации, зависит от центробежного ускорения (g), прямо пропорционального угловой скорости ротора (w, рад/с) и расстоянию между частицей и осью вращения (r, см): g = v2x
Центробежное ускорение тогда будет равно: g =p2x r x

Центробежное ускорение обычно выражается в единицах g (ускорение свободного падения, равное 980 м/с2) и называется относительным центробежным ускорением (ОЦУ), т.е. ОЦУ=g/980 или ОЦУ = 1,11 x 10-5 x r x n2 .
Относительное ускорение центрифуги (rcf) задается, как кратное от ускорения свободного падения (g). Оно является безразмерной величиной и служит для сравнения производительности разделения и осаждения. Относительное ускорение центрифуги
Существует номограмма, выражающая зависимость относительного ускорения центрифуги (rcf) от скорости вращения ротора (n) и радиуса (r) – среднего радиуса вращения столбика жидкости в центрифужной пробирке (т.е. расстояния от оси вращения до середины столбика жидкости). Радиус измеряется (см) от оси вращения ротора до середины столбика жидкости в пробирке, когда держатель находится в положении центрифугирования.
Номограмма для определения относительного ускорения центрифуги (
r – радиус ротора, см
n – скорость вращения ротора, оборотов в минуту
rcf (relative centrifuge force) – относительное ускорение центрифуги
Радиус центрифугирования rmax– это расстояние от оси вращения ротора до дна гнезда ротора.
Для определения ускорения с помощью линейки совмещаем значения радиуса и числа оборотов на и на шкале rcf определяем его величину.
Пример: на шкале А отмечаем значение rрадиуса для ротора – 7,2 см, на шкале С отмечаем значение скорости ротора –14,000 об/мин, соединяем эти две точки. Точка пересечения образованного отрезка со шкалой В показывает значение ускорения для данного ротора. В данном случае ускорение равно 15’000.
Вращательное движение
Вращательное движение является периодическим движением.
Период обозначается буквой T.
Чтобы найти период обращения, надо время вращения разделить на число оборотов:
|
Частота вращения обозначается буквой n.
Чтобы найти частоту вращения, надо число оборотов разделить на время, в течение которого эти обороты совершены:
Частота вращения и период обращения связаны друг с другом как взаимообратные величины:
Период измеряется в секундах: [T] = 1 с.
Единица частоты – секунда в минус первой степени: [n] = 1 с–1.
Эта единица имеет собственное название – 1 герц (1 Гц).
Проведем аналогию между вращательным и поступательным движениями.
Поступательно движущееся тело изменяет свое положение в пространстве относительно других тел.
Тела, совершающие вращательное движение поворачиваются на некоторый угол.
Если за любые равные промежутки времени поступательно движущееся тело совершает равные перемещения, движение называется равномерным.
Если за любые равные промежутки времени вращающееся тело поворачивается на один и тот же угол, то такое вращение называется равномерным. Характеристикой равномерного поступательного движения служит скорость Соответствующей характеристикой вращательного движения служит угловая скорость:
Угловая скорость – это физическая величина, равная отношению угла поворота тела ко времени, в течение которого этот поворот совершен.
Угловая скорость показывает, на какой угол поворачивается тело за единицу времени.
Чтобы получить единицу угловой скорости, нужно в ее определяющую формулу подставить единицу – 1 радиан, и времени – 1 с. Получаем: [ω] = 1
Аналогично можно ввести характеристику неравномерного вращения. Если видом неравномерного поступательного движения является равнопеременное движение, то для вращательного движения можно ввести понятие равнопеременного вращения.
Характеристикой равнопеременного поступательного движения является ускорение:
|
Продолжая аналогию дальше, запишем уравнение для перемещения при прямолинейном равноускоренном движении
Так как при вращении перемещению тела соответствует угол вращения, линейной скорости – угловая скорость, линейному ускорению – угловое ускорение, то аналогичное уравнение для вращательного движения будет иметь вид:
Другому уравнению для поступательного движения будет соответствовать уравнение для вращательного движения:
Метод, который использовался в данном случае, называется методом аналогий.
Точки тела, совершающего вращательное движение, поворачиваются относительно оси вращения на некоторые углы и движутся по дугам окружностей, проходя определенные пути.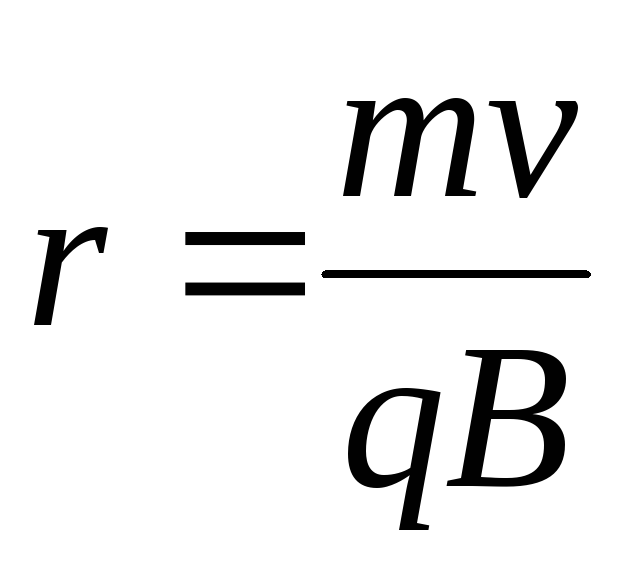 Таким образом, характеристиками вращательного движения являются и угловая, и линейная скорости.
Таким образом, характеристиками вращательного движения являются и угловая, и линейная скорости.
Линейная скорость точки направлена по касательной к окружности, по которой она движется.
Об этом свидетельствует слетающая с колес автомобиля грязь или искры, летящие от металлического предмета, прижатого к наждачному кругу.
Чем дальше от оси вращения находится точка, тем больше ее линейная скорость. Угловая же скорость точек, лежащих на одном радиусе, одинакова. Следовательно, линейная скорость точки прямо пропорциональна радиусу окружности, по которой она вращается.
За время, равное периоду, точка проходит путь, равный длине окружности. Её линейная скорость при этом равна Отношение же угла поворота ко времени поворота на этот угол равно угловой скорости
Таким образом, линейная скорость вращающейся точки связана с ее угловой скоростью соотношением:
При равномерном вращении скорость меняется по направлению, но не изменяется по величине.
|
Пусть вращающееся тело в начальный момент времени находится в точке A и скорость его направлена по касательной. В следующий момент времени тело находится в точке B. При этом скорость его изменилось только по направлению и направлена по касательной к окружности.
Найдем вектор разности скоростей, воспользовавшись правилом действия с векторами. Из чертежа видно, что вектор разности направлен в сторону близкую к центру окружности. Чем меньше угол поворота, тем ближе направлен вектор скорости
к направлению на центр вращения.
При малом времени движения изменение положения тела незначительно. Поэтому можно считать, что вектор скорости характеризующий изменение скорости по направлению, направлен на центр. Отсюда и происходит название центростремительного ускорения.
Угловое же ускорение, характеризующее изменение скорости по величине, называют еще касательным или тангенциальным ускорением (при неравномерном вращении).
Получим выражение для центростремительного ускорения. Будем считать, что угол поворота очень мал. Соединим точки A и B. Угол MAN = φ по построению.
Мы имеем два равнобедренных треугольника. Треугольник OAB, ребра которого R и AB, и треугольник MAN, ребра которого и
Так как треугольники подобны (по двум сторонам и углу между ними), то можно записать:
Дуга окружности и хорда практически равны из-за малости угла поворота. Поэтому дуга Следовательно, Получим
Разделив правую и левую части последнего уравнения на t, получим:
Отсюда Таким образом,
Полученная формула является формулой для расчета центростремительного ускорения.
Центростремительное ускорение, при движении тела по окружности, равно отношению квадрата скорости к радиусу окружности, по которой движется тело:
Урок 4. равномерное движение точки по окружности — Физика — 10 класс
Законы Кеплера
Орбиты небесных тел – траектории, по которым движутся в космическом пространстве Солнце, звёзды, планеты, кометы, а также искусственные космические аппараты (искусственные спутники Земли, Луны и других планет, межпланетные станции и т. п.). Формы орбит и скорости, с которыми движутся по ним небесные тела, определяются главным образом силой всемирного тяготения. При исследовании движения небесных тел в большинстве случаев допустимо считать их материальными точками.
Указанные упрощения приводят к так называемой задаче двух тел. Одно из решений этой задачи было дано И. Кеплером, полное решение задачи было получено И. Ньютоном.
Заслуга открытия законов движения планет принадлежит выдающемуся немецкому учёному Иоганну Кеплеру (1571–1630). В начале XVII в. Кеплер, изучая обращение Марса вокруг Солнца, установил три закона движения планет.
В начале XVII в. Кеплер, изучая обращение Марса вокруг Солнца, установил три закона движения планет.
Первый закон Кеплера. Каждая планета обращается по эллипсу, в одном из фокусов которого находится Солнце.
Второй закон Кеплера(закон площадей). Радиус-вектор планеты за одинаковые промежутки времени описывает равные площади.
Третий закон Кеплера. Квадраты звёздных периодов обращения планет относятся как кубы больших полуосей их орбит.
Ньютон доказал, что одна из притягивающихся материальных точек обращается вокруг другой по орбите, имеющей форму эллипса (или окружности, которая является частным случаем эллипса), параболы или гиперболы. В фокусе этой кривой находится вторая точка. Форма орбиты зависит: от масс рассматриваемых тел; от расстояния между ними; от скорости, с которой одно тело движется относительно другого.
Движение небесных тел
Чтобы начав движение вблизи поверхности Земли, тело преодолело земное притяжение и навсегда покинуло Землю по параболической орбите, необходимо сообщить ему начальную скорость не меньше 11,2 км/с. Эта скорость называется второй космической скоростью. Наименьшая начальная скорость, которую нужно сообщить телу, чтобы оно стало искусственным спутником Земли, называется первой космической скоростью. Она равна 7,91 км/с. Большинство тел Солнечной системы движется по эллиптическим орбитам. Только некоторые малые тела Солнечной системы – кометы, возможно, движутся по параболическим или гиперболическим орбитам. В задачах космического полёта наиболее часто встречаются эллиптические и гиперболические орбиты. Так, межпланетные станции отправляются в полет, имея гиперболическую орбиту относительно Земли; затем они движутся по эллиптическим орбитам относительно Солнца по направлению к планете назначения.
Эта скорость называется второй космической скоростью. Наименьшая начальная скорость, которую нужно сообщить телу, чтобы оно стало искусственным спутником Земли, называется первой космической скоростью. Она равна 7,91 км/с. Большинство тел Солнечной системы движется по эллиптическим орбитам. Только некоторые малые тела Солнечной системы – кометы, возможно, движутся по параболическим или гиперболическим орбитам. В задачах космического полёта наиболее часто встречаются эллиптические и гиперболические орбиты. Так, межпланетные станции отправляются в полет, имея гиперболическую орбиту относительно Земли; затем они движутся по эллиптическим орбитам относительно Солнца по направлению к планете назначения.
Ориентация орбиты в пространстве, её размеры и форма, а также положение небесного тела на орбите определяются шестью величинами, называемыми элементами орбиты. Орбиты небесных светил имеют некоторые характерные точки, которые получили собственные названия. Так, ближайшая к Солнцу точка орбиты небесного тела, движущегося вокруг Солнца, называется перигелием, а наиболее удалённая от него точка эллиптической орбиты – афелием. Если тело движется относительно Земли, то ближайшая к Земле точка орбиты называется перигеем, а самая далёкая – апогеем. В более общих задачах, когда под притягивающим центром можно подразумевать разные небесные тела, употребляют названия: перицентр (ближайшая к центру точка орбиты) и апоцентр (наиболее удалённая от центра точка орбиты).
Если тело движется относительно Земли, то ближайшая к Земле точка орбиты называется перигеем, а самая далёкая – апогеем. В более общих задачах, когда под притягивающим центром можно подразумевать разные небесные тела, употребляют названия: перицентр (ближайшая к центру точка орбиты) и апоцентр (наиболее удалённая от центра точка орбиты).
Методы, разработанные в небесной механике, позволяют очень точно на много лет вперёд определить положение любых тел Солнечной системы.
Сборник задач абитуриенту. КИНЕМАТИКА. Равномерное движение по окружности. Тема 4-1
КИНЕМАТИКА. Равномерное движение по окружности. Тема 4-1
1. Линейная скорость точек обода вращающегося колеса равна 50 см/с, а линейная скорость его точек, находящихся на 3 см ближе к оси вращения, равна 40 см/с. Определите радиус (в см) колеса.
Ответ2. Два шкива соединены ременной передачей. Ведущий шкив делает 600 об/мин. Ведомый шкив должен делать 3000 об/мин. Каким нужно сделать диаметр (в см) ведущего шкива, если диаметр ведомого колеса 10 см?
Каким нужно сделать диаметр (в см) ведущего шкива, если диаметр ведомого колеса 10 см?
3. Колесо катится без проскальзывания по горизонтальной дороге со скоростью 1 м/с. Определите скорость точки колеса лежащей на верхнем конце вертикального диаметра.
Ответ4. Минутная стрелка часов в три раза длиннее секундной. Каково отношение линейных скоростей концов этих стрелок?
Ответ5. Одно колесо равномерно вращается, совершая 50 оборотов в секунду. Второе колесо, равномерно вращаясь, делает 500 оборотов за 30 секунд. Во сколько раз угловая скорость первого колеса больше, чем второго?
Ответ6. За сколько секунд колесо, вращаясь равномерно с угловой скоростью 4$\pi$ рад/с, сделает 100 оборотов?
Ответ7. Угловая скорость лопастей вентилятора 20$\pi$ рад/с. Найдите число оборотов за 10 минут.
Ответ8. На плоскости диска проведена прямая от его центра к краю по радиусу. Диск начал равномерно вращаться, при этом прямая повернулась на угол (2/3)$\pi$ радиан за 7 c. Найдите период обращения диска.
Найдите период обращения диска.
9. С какой угловой скоростью вращается колесо, если линейная скорость точек его обода равна 0,5 м/с, а линейная скорость точек, находящихся на 4 см ближе к оси вращения, равны 0,3 м/с.
Ответ10. Минутная стрелка часов на 20 % длиннее секундной. Во сколько раз линейная скорость конца секундной стрелки больше, чем конца минутной стрелки?
Ответ11. При равномерном подъеме груза с помощью лебедки, диаметр барабана которой 18 см, скорость подъема груза равна 0,9 м/с. Найдите угловую скорость вращения барабана лебедки.
Ответ12. Пуля, выпущенная из винтовки, попадает во вращающийся с частотой 50 об/с тонкостенный цилиндр диаметром 20 см. Найдите скорость пули, если выстрел произведен в направлении диаметра цилиндра, а к моменту вылета пули из цилиндра входное отверстие сместилось на 1 см. $\pi$ = 3,14.
Ответ13. Во сколько раз линейная скорость точки поверхности Земли, лежащей на широте 600, меньше линейной скорости точки, лежащей на экваторе?
Ответ14. Определите величину центростремительного ускорения точки, движущейся по окружности с угловой скоростью 16 рад/с и линейной скоростью 2 м/с.
Определите величину центростремительного ускорения точки, движущейся по окружности с угловой скоростью 16 рад/с и линейной скоростью 2 м/с.
15. Во сколько раз увеличится центростремительное ускорение точек обода колеса, если период обращения колеса уменьшить в 5 раз?
Ответ16. Какова линейная скорость конца минутной стрелки часов на Спасской башне Московского Кремля, если длина стрелки 3,5 м? Сравните угловую скорость этой стрелки с угловой скоростью минутной стрелки наручных часов.
Ответ17. Колесо вращается вокруг неподвижной оси, проходящей через центр. Обладает ли любая точка на ободе колеса тангенциальным и нормальным ускорениями, если вращение происходит: а) с постоянной угловой скоростью; б) с постоянным угловым ускорением? Изменяются ли при этом модули этих ускорений?
Ответ18. Точка движется по окружности с постоянной по модулю скоростью 0,5 м/с. За 2 с вектор скорости изменяет свое направление на 300. Чему равно центростремительное ускорение?
Ответ19. При равномерном движении по окружности тело проходит 5 м за 2 c. Определите модуль центростремительного ускорения тела, если период обращения тела равен 5 c.
При равномерном движении по окружности тело проходит 5 м за 2 c. Определите модуль центростремительного ускорения тела, если период обращения тела равен 5 c.
20. Период обращения одного колеса вдвое меньше периода вращения другого колеса, а его радиус втрое больше радиуса вращения другого колеса. Во сколько раз отличаются их центростремительные ускорения?
Ответ21. Колесо радиусом 0,5 м равномерно вращается вокруг своей оси. Найти ускорение одной из точек его обода, если колесо за время 10 c совершит 120 оборотов.
Ответ22. На сколько километров орбита первого спутника Земли короче орбиты третьего спутника, если средние радиусы их орбит отличаются на $\Delta$R = 410 км?
Ответ23. Найти линейную скорость Луны, обусловленную ее обращением вокруг Земли. Период вращения Луны (синодический месяц) Т = 27,3 сут. Расстояние Земля – Луна R = 3,84$\cdot$105 км.
Ответ24. Корабль-спутник совершил N = 64 оборота вокруг Земли за t = 95 ч. Определить среднюю скорость полета v. Орбиту корабля можно считать круговой и отстоящей от поверхности Земли на h = 230 км.
Ответ25. Равномерно движущаяся по окружности точка делает полный оборот за T = 5 с. Чему равна угловая скорость точки $\omega$? Чему равен угол поворота точки за время $\Delta$t = 2 с?
Ответ26. Скорость точек рабочей поверхности шлифовального круга не должна превышать v = 100 м/с. Найти предельную частоту вращения круга n, диаметр которого d = 40 см. Определить нормальное ускорение an точек рабочей поверхности круга.
Ответ27. Большой шкив ременной передачи имеет радиус R1 = 32 см и вращается с частотой n1 = 120 об/мин. Малый шкив имеет радиус R2 = 24 см. Найти угловую скорость, число оборотов в секунду малого шкива и линейную скорость точек ремня, который движется без проскальзывания.
Ответ16,8; 160 об/мин; 4,02
28. Найти радиус R вращающегося колеса, если известно, что линейная скорость точек обода колеса в k = 2,5 раза больше линейной скорости точки, лежащей на расстоянии d = 5 см ближе к оси колеса.
Ответ29. Небольшое тело движется по окружности радиуса R = 1 м. Определить модуль перемещения за время, в течение которого тело делает: а) оборот; б) 1/2 оборота; в) 1/4 оборота; г) тело поворачивается на угол $\alpha$ = 600.
ОтветРавномерное движение тела по окружности – FIZI4KA
1. Движением тела по окружности называют движение, траекторией которого является окружность. По окружности движутся, например, конец стрелки часов, точки лопасти вращающейся турбины, вращающегося вала двигателя и др.
При движении по окружности направление скорости непрерывно изменяется. При этом модуль скорости тела может изменяться, а может оставаться неизменным. Движение, при котором изменяется только направление скорости, а её модуль сохраняется постоянным, называется равномерным движением тела по окружности. Под телом в данном случае имеют в виду материальную точку.
2. Движение тела по окружности характеризуется определёнными величинами. К ним относятся, прежде всего, период и частота обращения. Период обращения тела по окружности \( T \) — время, в течение которого тело совершает один полный оборот. Единица периода — \( [\,T\,] \) = 1 с.
Частота обращения \( (n) \) — число полных оборотов тела за одну секунду: \( n=N/t \). Единица частоты обращения — \( [\,n\,] \) = 1 с-1 = 1 Гц (герц). Один герц — это такая частота, при которой тело совершает один оборот за одну секунду.
Связь между частотой и периодом обращения выражается формулой: \( n=1/T \).
Пусть некоторое тело, движущееся по окружности, за время \( t \) переместилось из точки А в точку В. Радиус, соединяющий центр окружности с точкой А, называют радиусом-вектором. При перемещении тела из точки А в точку В радиус-вектор повернётся на угол \( \varphi \).
Быстроту обращения тела характеризуют угловая и линейная скорости.
Угловая скорость \( \omega \) — физическая величина, равная отношению угла поворота \( \varphi \) радиуса-вектора к промежутку времени, за которое этот поворот произошел: \( \omega=\varphi/t \). Единица угловой скорости — радиан в секунду, т.е. \( [\,\omega\,] \) = 1 рад/с. За время, равное периоду обращения, угол поворота радиуса-вектора равен \( 2\pi \). Поэтому \( \omega=2\pi/T \).
Линейная скорость тела \( v \) — скорость, с которой тело движется вдоль траектории. Линейная скорость при равномерном движении по окружности постоянна по модулю, меняется по направлению и направлена по касательной к траектории.
Линейная скорость равна отношению пути, пройденному телом вдоль траектории, ко времени, за которое этот путь пройден: \( \vec{v}=l/t \).2R \).
При движении тела по окружности его центростремительное ускорение постоянно по модулю и направлено к центру окружности.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. При равномерном движении тела по окружности
1) изменяется только модуль его скорости
2) изменяется только направление его скорости
3) изменяются и модуль, и направление его скорости
4) не изменяется ни модуль, ни направление его скорости
2. Линейная скорость точки 1, находящейся на расстоянии \( R_1 \) от центра вращающегося колеса, равна \( v_1 \). Чему равна скорость \( v_2 \) точки 2, находящейся от центра на расстоянии \( R_2=4R_1 \)?
1) \( v_2=v_1 \)
2) \( v_2=2v_1 \)
3) \( v_2=0,25v_1 \)
4) \( v_2=4v_1 \)
3. Период обращения точки по окружности можно вычислить по формуле:
1) \( T=2\pi\!Rv \)
2) \( T=2\pi\!R/v \)
3) \( T=2\pi v \)
4) \( T=2\pi/v \)
4.2 \)
3) \( \omega=vR \)
4) \( \omega=v/R \)
5. Угловая скорость вращения колеса велосипеда увеличилась в 2 раза. Как изменилась линейная скорость точек обода колеса?
1) увеличилась в 2 раза
2) уменьшилась в 2 раза
3) увеличилась в 4 раза
4) не изменилась
6. Линейная скорость точек лопасти винта вертолёта уменьшилась в 4 раза. Как изменилось их центростремительное ускорение?
1) не изменилось
2) уменьшилось в 16 раз
3) уменьшилось в 4 раза
4) уменьшилось в 2 раза
7. Радиус движения тела по окружности увеличили в 3 раза, не меняя его линейную скорость. Как изменилось центростремительное ускорение тела?
1) увеличилось в 9 раз
2) уменьшилось в 9 раз
3) уменьшилось в 3 раза
4) увеличилось в 3 раза
8. Чему равен период обращения коленчатого вала двигателя, если за 3 мин он совершил 600 000 оборотов?
1) 200 000 с
2) 3300 с
3) 3·10-4 с
4) 5·10-6 с
9.2/R \)
3) \( v/R \)
4) \( \omega R \)
5) \( 1/n \)
12. Период обращения колеса увеличился. Как изменились угловая и линейная скорости точки обода колеса и её центростремительное ускорение. Установите соответствие между физическими величинами в левом столбце и характером их изменения в правом столбце.
В таблице под номером физической величины левого столбца запишите соответствующий номер выбранного вами элемента правого столбца.
ФИЗИЧЕСКАЯ ВЕЛИЧИНА
A) угловая скорость
Б) линейная скорость
B) центростремительное ускорение
ХАРАКТЕР ИЗМЕНЕНИЯ ВЕЛИЧИНЫ
1) увеличилась
2) уменьшилась
3) не изменилась
Часть 2
13. Какой путь пройдёт точка обода колеса за 10 с, если частота обращения колеса составляет 8 Гц, а радиус колеса 5 м?
Ответы
Равномерное движение тела по окружности
2.9 (57.89%) 19 votesПланеты Солнечной системы: восемь и одна
Пять ближайших к Земле планет — Меркурий, Венера, Марс, Юпитер и Сатурн — были известны с древности.
Меркурий – ближайшая к Солнцу планета, среднее расстояние от Солнца 0,387 а.е (58 млн км), а расстояние до Земли колеблется от 82 до 217 млн км. Меркурий движется вокруг Солнца по сильно вытянутой эллиптической орбите, плоскость которой наклонена к плоскости эклиптики под углом 7°. Средний радиус планеты составляет 2440 км, масса 3,3 на 10 в 23 степени кг (0,055 массы Земли), а плотность почти такая же, как у Земли (5,43 г/см3). Средняя скорость движения Меркурия по орбите — 47,9 км/с. Период обращения вокруг Солнца (меркурианский год) составляет около 88 суток, период вращения вокруг своей оси равен 58,6 суткам (меркурианские звездные сутки), продолжительность солнечных суток на Меркурии равна 176 земным суткам – двум меркурианским годам.
Поверхность Меркурия, подобно лунной, покрыта кратерами. Атмосфера очень разреженная. Меркурий обладает крупным железным ядром, являющимся источником магнитного поля, по своей совокупности составляющим 0,1 от земного. Температура на поверхности Меркурия колеблется от 90 до 700 К (−180…430 °C). Планета названа в честь бога римского пантеона Меркурия, аналога греческого Гермеса и Вавилонского Набу. Естественных спутников у планеты нет.
Венера — вторая по удаленности от Солнца планета, среднее расстояние от Солнца 0,72 а.е. (108,2 млн км). Средний радиус планеты составляет 6051 км, масса — 4,9 на 10 в 24 степени кг (0,82 массы Земли), средняя плотность 5,24 г/см3. Орбита Венеры очень близка к круговой. Средняя скорость движения Венеры по орбите — 34,99 км/с. Наклон орбиты к плоскости эклиптики равен 3,4°. Венера вращается вокруг своей оси, наклоненной к плоскости орбиты на 2°, с востока на запад – в направлении, противоположном направлению вращения большинства планет. Период обращения вокруг Солнца — 224,7 суток, период вращения вокруг своей оси равен 243 суткам, продолжительность солнечных суток на планете — 116,8 земных суток.
Венера не имеет естественных спутников. Атмосфера ее состоит в основном из углекислого газа (96 %) и азота (почти 4 %). Давление у поверхности достигает 93 атмосфер, температура — 737 К. Причиной столь высокой температуры на Венере является парниковый эффект, создаваемый плотной углекислотной атмосферой. Поверхность Венеры в основном равнинная, сложена базальтами, обнаружены следы вулканической деятельности, ударные кратеры. Планета состоит преимущественно из камня и металла. Планета получила свое название в честь Венеры, богини любви из римского пантеона.
Земля — третья от Солнца планета Солнечной системы, среднее расстояние от Солнца 1 а.е. (149,6 млн км), средний радиус 6371,160 км (экваториальный 6378, 160 км, полярный 6356,777 км), масса – 6 на 10 в 24 степени кг. Орбита Земли близка к окружности с радиусом около 384400 км. Средняя скорость движения Земли по орбите равна 29,765 км/с. Период обращения вокруг Солнца 365,3 суток, период вращения вокруг своей оси – 23 часа 56 минут (звездные сутки), период вращения относительно Солнца (средние солнечные сутки) 24 часа. Имеет естественный спутник — Луну.
Марс – четвертая планета от Солнца, среднее расстояние от Солнца составляет 1,5 а.е. (227,9 млн км). Минимальное расстояние от Марса до Земли составляет 55,75 млн км, максимальное — около 401 млн. км. Экваториальный радиус Марса равен 3396,9 км, масса 6,4 на10 в 23 степени кг (0,108 массы Земли), плотность 3,95 г/см3. Отклонение орбиты по отношению к эклиптике — 1,9°. Средняя скорость обращения вокруг Солнца ‑ 24,13 км/с. Марс обращается вокруг Солнца за 687 земных суток, период вращения вокруг своей оси — 24 часа 37 минут.
Разреженная атмосфера состоит в основном из углекислого газа, среднее давление у поверхности 0,006 атм. Марс преимущественно состоит из камня и металла. Поверхность Марса — пыле-песчаная пустыня с каменистыми россыпями, потухшими вулканами, ударными кратерами, ветвящимися каньонами типа высохших русел рек. Известны два спутника Марса — Фобос и Деймос. Планету Марс в древности назвали в честь бога войны за кроваво-красный цвет.
Юпитер — пятая по счету от Солнца, а также крупнейшая планета Солнечной системы, среднее расстояние от Солнца 5,2 а.е.(778 млн км), экваториальный радиус равен 71,4 тыс. км, полярный – около 67 тысяч км, масса 1,9 на 10 в 27 степени кг (317,8 массы Земли), средняя скорость обращения вокруг Солнца — 13,06 км/с. Наклон плоскости орбиты к плоскости эклиптики 1,3°. Расстояние Юпитера от Земли меняется в пределах от 188 до 967 млн. км. Полный оборот вокруг Солнца Юпитер совершает за 11,9 года, период вращения вокруг своей оси – 9 часов 45 минут (для полярной зоны) и 9 часов 50,5 минут для экваториальной зоны. Экватор наклонен к плоскости орбиты под углом 3°5′; из-за малости этого угла сезонные изменения на Юпитере выражены весьма слабо.
Юпитер представляет собой газо-жидкое тело, твердой поверхности не имеет. Атмосфера состоит на 89 % из водорода и на 11 % гелия и напоминает по химическому составу Солнце. Планету Юпитер опоясывают кольца, состоящие из совокупности сравнительно мелких каменных частиц размером от нескольких мкм до нескольких метров. Юпитер назван в честь царя римских богов.
У Юпитера есть 63 известных естественных спутника. Четыре наиболее крупных спутника — Ио, Европа, Ганимед и Каллисто — были открыты в 1610 году Галилео Галилеем. Пятый спутник — Юпитер V, открытый в 1892 году, — самый близкий к планете, он удален от ее поверхности всего лишь на 2,54 экваториальных радиуса Юпитера. Все эти спутники движутся практически по круговым орбитам, плоскости которых совпадают с плоскостью экватора Юпитера.
К концу 1970‑х годов было известно о 13 спутниках Юпитера. В 1979 году американским космическим аппаратом «Вояджер‑1» были обнаружены еще три спутника. Начиная с 1999 года с помощью наземных телескопов нового поколения были открыты еще 47 спутников планеты, подавляющее большинство из которых имеют диаметр в 2-4 километра.
Сатурн — шестая планета от Солнца и вторая по размерам планета в Солнечной системе после Юпитера. Среднее расстояние Сатурна от Солнца 9,54 а.е. (1,427 млрд км), средний экваториальный радиус около 60,3 тысяч км, полярный — около 54 тысяч км, масса 5,68 на 10 в 26 степени кг (95,1 массы Земли). Средняя плотность Сатурна меньше плотности воды (около 0,7 г/см3). Период обращения вокруг Солнца 29,46 года, период вращения вокруг своей оси 10 часов 39 минут (экваториальные области вращаются на 5% быстрее полярных). Сатурн — наиболее сплющенная планета Солнечной системы.
Сатурн состоит на 93 % из водорода (по объему) и на 7 % — из гелия и не имеет твердой поверхности. Относится к типу газовых планет и имеет систему колец. Кольца Сатурна – концентрические образования различной яркости, как бы вложенные друг в друга, и образующие единую плоскую систему небольшой толщины, располагающуюся в экваториальной плоскости Сатурна. Километровой толщины кольца образованы из льда и пыли и состоят из бессчетного количества частиц разного размера: от 2,5 см до нескольких метров. Планета Сатурн была названа в честь греческого бога времени.
Известно уже 60 естественных спутников Сатурна, большая часть из которых обнаружены при помощи космических аппаратов. Большая часть спутников состоит из горных пород и льда. Крупнейший спутник — Титан, открытый в 1655 году Христианом Гюйгенсом, — по своей величине превосходит планету Меркурий. Диаметр Титана около 5200 км. Титан облетает вокруг Сатурна каждые 16 дней. Титан — единственный спутник, обладающий очень плотной атмосферой, в 1,5 раза больше Земной, и состоящей в основном из 90% азота, с умеренным содержанием метана.
Уран — седьмая от Солнца планета Солнечной системы. Планета была открыта в 1781 году английским астрономом Уильямом Гершелем и названа в честь греческого бога неба Урана. Среднее расстояние от Солнца 19,18 а.е. (2871 млн км), средний радиус 25560 км, масса 8,69 на 10 в 25 степени (14,54 массы Земли), средняя плотность — 1,27 г/см3. Орбитальная скорость — от 6,49 до 7,11 км/с. Наклон орбиты к плоскости эклиптики (градусы) 0,8°. Период обращения вокруг Солнца 84 года, период вращения вокруг своей оси — около 17 часов 14 минут.
Планета Уран имеет небольшое твердое железно-каменное ядро, над которым сразу начинается плотная атмосфера. Атмосфера на Уране имеет толщину не менее 8000 км и состоит примерно из 83 % водорода, 15 % гелия и 2 % метана.
Подобно другим газовым планетам, Уран имеет кольца. Кольцевая система была обнаружена в 1977 году. Ученым известно 13 отдельных колец планеты. Большинство колец Урана непрозрачны, их ширина не больше нескольких километров. Кольца состоят в основном из макрочастиц — объектов диаметром от 20 сантиметров до 20 метров — и пыли.
У планеты Уран открыты 27 естественных спутников, из них пять крупных. Крупнейшие — Титания, диаметр около 1600 км, и Оберон, диаметром около 1550 км. Титания и Оберон были обнаружены Уильямом Гершелем 11 января 1787 года, через шесть лет после открытия им Урана. Большие спутники Урана на 50% состоят из водяного льда, на 20% — из углеродных и азотных соединений, на 30% — из разных соединений кремния (силикатов).
Нептун — восьмая планета от Солнца и четвертая по размеру среди планет. Нептун открыт в Берлинской обсерватории 23 сентября 1846 года немецким астрономом Иоганном Галле на основании предсказаний, сделанных независимо математиком Джоном Адамсом в Англии и астрономом Урбеном Леверрье во Франции. Их вычисления опирались на несоответствия между наблюдаемой и предсказанной орбитами Урана, что астрономы объяснили гравитационным возмущениям неизвестной планеты.
Среднее расстояние планеты Нептун от Солнца 30,1 а.е. (4497 млн км), средний радиус около 25 тысяч км, масса 1,02 на 10 в 26 степени кг (17,2 массы Земли), плотность 1,64 г/см3. Наклонение орбиты к плоскости эклиптики равно 1°46′. Период обращения вокруг Солнца 164,8 года, период вращения вокруг своей оси 16 часов 6 минут. Расстояние от Земли — от 4,3 до 4,6 млрд км. У Нептуна, как и у других планет-гигантов, нет твердой поверхности. Атмосфера Нептуна на 98–99 % состоит из водорода и гелия. В ней содержится также 1–2 % метана.
У Нептуна есть кольцевая система. Кольца Нептуна очень темны и строение их неизвестно. У Нептуна известно 13 спутников, крупнейший из них — Тритон.
В 1930 году американский астроном Клод Томбо нашел на негативах медленно движущийся звездообразный объект, который назвали новой, девятой планетой Плутоном – в честь древнеримского бога подземного царства.
Международный астрономический союз официально признал Плутон планетой в мае 1930 года. В тот момент предполагали, что его масса сравнима с массой Земли, но позже было установлено, что масса Плутона почти в 500 раз меньше земной, даже меньше массы Луны. Масса Плутона 1,2 на 10 в22 степени кг (0,22 массы Земли). Среднее расстояние Плутона от Солнца 39,44 а.е. (5,9 на 10 в12 степени км), радиус около 1,65 тысяч км. Период обращения вокруг Солнца 248,6 года, период вращения вокруг своей оси 6,4 суток. Состав Плутона предположительно включает в себя камень и лед; планета имеет тонкую атмосферу, состоящую из азота, метана и углеродной одноокиси. У Плутона есть три спутника: Харон, Гидра и Никта.
В конце XX и начале XXI веков во внешней части Солнечной системы было открыто множество объектов. Стало очевидным, что Плутон — лишь один из наиболее крупных известных до настоящего времени объектов пояса Койпера. Более того, по крайней мере один из объектов пояса – Эрида — является более крупным телом, чем Плутон и на 27% тяжелее его. В связи с этим возникла идея не рассматривать более Плутон как планету. 24 августа 2006 года на XXVI Генеральной ассамблее Международного астрономического союза (МАС) было принято решение впредь называть Плутон не «планетой», а «карликовой планетой».
На конференции было выработано новое определение планеты, согласно которому планетами считаются тела, вращающиеся вокруг звезды (и сами не являющиеся звездой), имеющие гидростатически равновесную форму и «расчистившие» область в районе своей орбиты от других, более мелких, объектов. Карликовыми планетами будут считаться объекты, вращающиеся вокруг звезды, имеющие гидростатически равновесную форму, но не «расчистившие» близлежащее пространство и не являющиеся спутниками. Планеты и карликовые планеты — это два разных класса объектов Солнечной системы. Все прочие объекты, вращающиеся вокруг Солнца и не являющиеся спутниками, будут называться малыми телами Солнечной системы.
Таким образом, с 2006 года в Солнечной системе стало восемь планет: Меркурий, Венера, Земля, Марс, Юпитер, Сатурн, Уран, Нептун. Международным астрономическим союзом официально признаны пять карликовых планет: Церера, Плутон, Хаумеа, Макемаке, Эрида.
11 июня 2008 года МАС объявил о введении понятия «плутоид». Плутоидами решено называть небесные тела, обращающиеся вокруг Солнца по орбите, радиус которой больше радиуса орбиты Нептуна, масса которых достаточна, чтобы гравитационные силы придавали им почти сферическую форму, и которые не расчищают пространство вокруг своей орбиты (то есть, вокруг них обращается множество мелких объектов).
Поскольку для таких далеких объектов, как плутоиды, определить форму и тем самым отношение к классу карликовых планет пока затруднительно, ученые рекомендовали временно относить к плутоидам все объекты, абсолютная астероидная величина которых (блеск с расстояния в одну астрономическую единицу) ярче +1. Если позднее выяснится, что отнесенный к плутоидам объект карликовой планетой не является, его этого статуса лишат, хотя присвоенное имя оставят. К плутоидам были отнесены карликовые планеты Плутон и Эрида. В июле 2008 года в эту категорию был включен Макемаке. 17 сентября 2008 в список добавили Хаумеа.
Материал подготовлен на основе информации открытых источников
Математика движения спутников
Движение объектов подчиняется законам Ньютона. Те же простые законы, которые управляют движением объектов на Земле, также распространяются на небес , чтобы управлять движением планет, лун и других спутников. Математика, описывающая движение спутника, аналогична математике, представленной для кругового движения в Уроке 1. В этой части Урока 4 мы будем рассматривать множество математических уравнений, описывающих движение спутников.
Уравнение орбитальной скорости
Рассмотрим спутник с массой M sat , вращающийся вокруг центрального тела с массой M Central . Центральным телом может быть планета, солнце или другая большая масса, способная вызывать достаточное ускорение менее массивного соседнего объекта. Если спутник движется по кругу, то чистая центростремительная сила, действующая на этот орбитальный спутник, определяется соотношением
F net = (M sat • v 2 ) / RЭта чистая центростремительная сила является результатом гравитационной силы, которая притягивает спутник к центральному телу, и может быть представлена как
F грав = (G • M sat • M Central ) / R 2Поскольку F grav = F net , приведенные выше выражения для центростремительной силы и гравитационной силы могут быть установлены равными друг другу.Таким образом,
(M сб. • v 2 ) / R = (G • M сб. • M центральный ) / R 2Обратите внимание, что масса спутника присутствует в обеих частях уравнения; таким образом, его можно отменить, разделив на M sat . Затем обе части уравнения можно умножить на R , оставив следующее уравнение.
v 2 = (G • M Центральный ) / RВзяв квадратный корень из каждой стороны, получаем следующее уравнение для скорости спутника, движущегося вокруг центрального тела при круговом движении
, где G — 6.673 x 10 -11 Н • м 2 / кг 2 , M центральный — масса центрального тела, вокруг которого вращается спутник, а R — радиус орбиты спутника. .
Уравнение ускоренияАналогичные рассуждения можно использовать для определения уравнения ускорения нашего спутника, которое выражается через массы и радиус орбиты. Величина ускорения спутника равна ускорению свободного падения спутника в любом месте, по которому он вращается.В Уроке 3 уравнение ускорения свободного падения было дано как
. г = (G • M центральный ) / R 2Таким образом, ускорение спутника при круговом движении вокруг некоторого центрального тела определяется следующим уравнением
, где G составляет 6,673 x 10 -11 Н • м 2 / кг 2 , M центральный — это масса центрального тела, вокруг которого вращается спутник, а R — это масса центрального тела, вокруг которого вращается спутник. средний радиус орбиты спутника.
Уравнение периода обращенияПоследнее уравнение, которое полезно при описании движения спутников, — это форма Ньютона третьего закона Кеплера. Поскольку логика построения уравнения была представлена в другом месте, здесь будет представлено только уравнение. Период спутника ( T ) и среднее расстояние от центрального тела ( R ) связаны следующим уравнением:
, где T — период спутника, R — средний радиус орбиты спутника (расстояние от центра центральной планеты), а G — 6.673 x 10 -11 Н • м 2 / кг 2 .
Во всех трех уравнениях очевидна важная концепция — период, скорость и ускорение орбитального спутника не зависят от массы спутника.
Ни одно из этих трех уравнений не содержит в себе переменной M спутник . Период, скорость и ускорение спутника зависят только от радиуса орбиты и массы центрального тела, на орбите которого находится спутник.Так же, как и в случае движения снарядов по Земле, масса снаряда не влияет на ускорение по направлению к Земле и скорость в любой момент. Когда сопротивление воздуха незначительно и присутствует только сила тяжести, масса движущегося объекта не играет роли. Так обстоит дело с орбитальными спутниками.
Примеры проблемЧтобы проиллюстрировать полезность приведенных выше уравнений, рассмотрим следующие практические задачи.
| Практическая задача № 1 Спутник желает облететь Землю на высоте 100 км (приблизительно 60 миль) над поверхностью Земли. Определите скорость, ускорение и период обращения спутника. (Дано: M земля = 5,98 x 10 24 кг, R земля = 6,37 x 10 6 м) |
Как и большинство задач в физике, эта проблема начинается с определения известной и неизвестной информации и выбора соответствующего уравнения, способного разрешить неизвестное.Для этой проблемы известные и неизвестные перечислены ниже.
| Выдано / Известно: R = R земля + высота = 6,47 x 10 6 м M земля = 5.98×10 24 кг G = 6,673 x 10 -11 Н · м 2 / кг 2 | Неизвестный: v = ??? а = ??? Т = ??? |
Обратите внимание, что радиус орбиты спутника можно найти, зная радиус Земли и высоту спутника над Землей.Как показано на диаграмме справа, радиус орбиты спутника равен сумме радиуса Земли и высоты над землей. Эти две величины можно сложить, чтобы получить радиус орбиты. В этой задаче 100 км необходимо сначала преобразовать в 100 000 м перед добавлением к радиусу Земли. Уравнения, необходимые для определения неизвестного, перечислены выше. Начнем с определения орбитальной скорости спутника с помощью следующего уравнения:
v = SQRT [(G • M Центральный ) / R]Замена и решение следующие:
v = КОРЕНЬ [(6.673 x 10 -11 Н м 2 / кг 2 ) • (5,98 x 10 24 кг) / (6,47 x 10 6 м)]v = 7,85 x 10 3 м / с
Ускорение можно найти с помощью одного из следующих уравнений:
| (1) a = (G • M центральный ) / R 2 | (2) a = v 2 / R |
Уравнение (1) было получено выше.Уравнение (2) является общим уравнением кругового движения. Для расчета ускорения можно использовать любое уравнение. Здесь будет продемонстрировано использование уравнения (1).
a = (G • M центральный ) / R 2a = (6,673 x 10 -11 Н · м 2 / кг 2 ) • (5,98 x 10 24 кг) / (6,47 x 10 6 м) 2
a = 9,53 м / с 2
Обратите внимание, что это ускорение немного меньше, чем 9.8 м / с 2 ожидаемое значение на поверхности земли. Как обсуждалось в Уроке 3, увеличение расстояния от центра Земли снижает значение g.
Наконец, период можно рассчитать с помощью следующего уравнения:
Уравнение можно переписать к следующему виду
T = SQRT [(4 • pi 2 • R 3 ) / (G * M центральный )]Замена и решение следующие:
T = КОРЕНЬ [(4 • (3.1415) 2 • (6,47 x 10 6 м) 3 ) / (6,673 x 10 -11 Н м 2 / кг 2 ) • (5,98×10 24 кг)]T = 5176 с = 1,44 часа
| Практическая задача № 2 Период Луны составляет примерно 27,2 дня (2,35 x 10 6 с). Определите радиус орбиты Луны и орбитальную скорость Луны.(Дано: M земля = 5,98 x 10 24 кг, R земля = 6,37 x 10 6 м) |
Как и практическая задача № 2, эта проблема начинается с определения известных и неизвестных значений. Они показаны ниже.
| Выдано / Известно: T = 2,35 x 10 6 с M Земля = 5,98 x 10 24 кг G = 6.673 x 10 -11 Н м 2 / кг 2 | Неизвестный: R = ??? v = ??? |
Радиус орбиты можно рассчитать по следующей формуле:
Уравнение можно переписать к следующему виду
R 3 = [(T 2 • G • M центральный ) / (4 • pi 2 )]Замена и решение следующие:
R 3 = [((2.35×10 6 с) 2 • (6,673 x 10 -11 Н м 2 / кг 2 ) • (5,98×10 24 кг)) / (4 • (3,1415) 2 ) ]R 3 = 5,58 x 10 25 м 3
Взяв кубический корень из 5,58 x 10 25 м 3 , радиус можно определить следующим образом:
R = 3,82 x 10 8 мОрбитальная скорость спутника может быть вычислена по любому из следующих уравнений:
| (1) v = SQRT [(G • M Central ) / R] | (2) v = (2 • pi • R) / T |
Уравнение (1) было получено выше.Уравнение (2) является общим уравнением кругового движения. Любое уравнение можно использовать для расчета орбитальной скорости; здесь будет продемонстрировано использование уравнения (1). Подстановка значений в это уравнение и решение следующие:
v = SQRT [(6,673 x 10 -11 Н · м 2 / кг 2 ) * (5,98×10 24 кг) / (3,82 x 10 8 м)]v = 1,02 x 10 3 м / с
| Практическая задача № 3 Геостационарный спутник — это спутник, который вращается вокруг Земли с периодом обращения 24 часа, что соответствует периоду вращения Земли.Особый класс геостационарных спутников — геостационарный спутник. Геостационарный спутник вращается вокруг Земли за 24 часа по орбитальной траектории, параллельной воображаемой плоскости, проведенной через экватор Земли. Такой спутник оказывается постоянно закрепленным над тем же местом на Земле. Если геостационарный спутник желает облететь Землю за 24 часа (86400 с), то на какой высоте над земной поверхностью он должен быть расположен? (Дано: M земля = 5,98×10 24 кг, R земля = 6.37 x 10 6 м) |
Как и в предыдущей задаче, решение начинается с идентификации известных и неизвестных значений. Это показано ниже.
| Выдано / Известно: T = 86400 с M земля = 5.98×10 24 кг R земля = 6,37 x 10 6 м G = 6.673 x 10 -11 Н м 2 / кг 2 | Неизвестный: ч = ??? |
Неизвестным в этой задаче является высота ( h ) спутника над поверхностью земли. Но уравнения с переменной h нет. Затем решение включает сначала определение радиуса орбиты и использование этого значения R и R земли для определения высоты спутника над Землей.Как показано на диаграмме справа, радиус орбиты спутника равен сумме радиуса Земли и высоты над землей. Радиус орбиты можно найти с помощью следующего уравнения:
Уравнение можно переписать к следующему виду
R 3 = [(T 2 * G * M центральный ) / (4 * pi 2 )]Замена и решение следующие:
R 3 = [((86400 с) 2 • (6.673 x 10 -11 Н м 2 / кг 2 ) • (5,98×10 24 кг)) / (4 • (3,1415) 2 )]R 3 = 7,54 x 10 22 м 3
Взяв кубический корень из 7,54 x 10 22 м 3 , можно определить радиус
R = 4,23 x 10 7 мРадиус орбиты указывает расстояние, на котором спутник находится от центра Земли.Теперь, когда радиус орбиты найден, можно вычислить высоту над Землей. Поскольку поверхность Земли находится на расстоянии 6,37 x 10 6 м от ее центра (это радиус Земли), высота спутника должна составлять
м. 4,23 x 10 7 м — 6,37 x 10 6 м = 3,59 x 10 7 мнад поверхностью земли. Таким образом, высота спутника составляет 3,59 x 10 7 м .
На орбите Земли вращаются сотни искусственных спутников.Список геостационарных спутников можно найти на http://www.satsig.net/sslist.htm. Используйте виджет Спутниковая информация ниже, чтобы изучить различные свойства — скорость, высоту, орбитальную траекторию и т. Д. — любого существующего спутника. Просто введите имя (правильно) спутника и нажмите кнопку Получить информацию . Проверьте свое понимание1. Спутник вращается вокруг Земли.Какие из следующих переменных повлияют на скорость спутника?
а. масса спутникаг. высота над поверхностью земли
г. масса земли
2. Используйте информацию ниже и соотношение выше, чтобы вычислить отношение T 2 / R 3 для планет вокруг Солнца, Луны вокруг Земли и спутников Сатурна вокруг планеты Сатурн.Значение G составляет 6,673 x 10 -11 Н • м 2 / кг 2 .
| солнце | M = 2,0 x 10 30 кг |
| Земля | M = 6,0 x 10 24 кг |
| Сатурн | M = 5,7 x 10 26 кг |
а.T 2 / R 3 для планет около Солнцаг. T 2 / R 3 для Луны около Земли
г. T 2 / R 3 для спутников около Сатурна
3. Один из спутников Сатурна называется Мимас. Среднее орбитальное расстояние Mimas составляет 1,87 x 10 8 м. Средний орбитальный период Мимаса составляет примерно 23 часа (8.28×10 4 с). Используйте эту информацию, чтобы оценить массу планеты Сатурн.
4. Рассмотрим спутник, который находится на низкой орбите вокруг Земли на высоте 220 км над поверхностью Земли. Определите орбитальную скорость этого спутника. Используйте информацию, приведенную ниже.
| G = 6,673 x 10 -11 Нм 2 / кг 2 M Земля = 5.98 x 10 24 кг R земля = 6,37 x 10 6 м |
5. Предположим, что космический шаттл находится на орбите Земли на высоте 400 км над ее поверхностью. Используйте информацию, приведенную в предыдущем вопросе, для определения орбитальной скорости и периода обращения космического корабля «Шаттл».
Равномерное круговое движение
Введение
Равномерное круговое движение — это движение объекта, движущегося с постоянной (равномерной) скоростью по круговой траектории.Помимо скорости, есть несколько других переменных, которые используются для характеристики движения. Это радиус движения r , угловая скорость ω , период T и частота вращения f . Период — это время, необходимое для того, чтобы объект совершил один оборот движения. Угловая скорость — это угловое смещение в секунду, которое связано с частотой следующим образом: с ω в рад / с.Частота вращения — это количество оборотов в секунду, которое определяется по формуле: с f в Гц или сек -1 . Скорость объекта является касательной к окружности с величиной v = rω . Ускорение , a направлено к центру круга (центростремительное) с величиной, определяемой следующим образом: с a в м / с 2 . Чтобы объект массой м мог двигаться по окружности с постоянной скоростью, на объект должна действовать чистая центростремительная сила.Величина чистой силы F должна быть постоянной и связана с центростремительным ускорением вторым законом Ньютона: с F в N. Эта центростремительная сила может быть обеспечена за счет натяжения (как в этой лаборатории), трения (как для автомобиля, движущегося по кривой), нормальной силы (как в петлеобразных американских горках) или гравитации (как для движения спутника). В этом эксперименте вы будете измерять период объекта, совершающего равномерное круговое движение с фиксированным радиусом, но с различными значениями F .По периоду можно рассчитать угловую скорость. Используя эти известные значения и приведенные выше уравнения, вы можете найти эмпирическую массу вращающегося объекта и сравнить со значением массы, полученным путем непосредственного взвешивания его на весах.Аппарат UCM
Аппарат UCM состоит из платформы с регулируемой скоростью вращения . На расстоянии × от центра вращения находится узел боковой стойки , на котором висит объект массой м , называемый вращающейся массой (не путать со статической массой ).Вращающаяся масса прикреплена к пружине на центральной стойке с помощью струны и небольшого шкива. Когда платформа вращается, вращающаяся масса будет перемещаться по круговой траектории из-за силы, прилагаемой к ней струной (посредством натяжения пружины). Поскольку невозможно получить мгновенное считывание этой силы натяжения во время вращения платформы, косвенное измерение этой силы будет производиться с использованием веса статической массы, как показано и объяснено ниже.Рисунок 1
Когда платформа не вращается, вращающаяся масса не свисает вертикально с боковой стойки, а, скорее, втягивается внутрь за счет натяжения струны и пружины. При проведении эксперимента вы будете регулировать скорость вращения платформы до тех пор, пока вращающаяся масса не будет висеть вертикально на радиусе r . Оранжевый индикаторный диск поможет вам определить, когда вращающаяся масса достигла этого положения.Рисунок 2
Период вращения измеряется секундомером .Платформу можно вращать, поворачивая стержень с накаткой вручную.Процедура
Выравнивание предмета
Если платформа неровная, это отрицательно скажется на ваших результатах. Студенты первой лаборатории недели должны были уже выровнять прибор. Будем надеяться, что с тех пор аппарат не перемещали, и его не нужно будет снова выравнивать. Проверьте, выровнено ли ваше устройство, включив двигатель регулировки скорости и наблюдая за оранжевым индикаторным диском, чтобы увидеть, качается ли он вверх и вниз при вращении платформы.Если ваше устройство необходимо выровнять, выполните следующие действия.1
Чтобы примерно выровнять платформу, поместите пузырьковый уровень в середину платформы и отрегулируйте два регулировочных винта на основании устройства до тех пор, пока пузырь не будет отцентрирован.2
Поместите дополнительную массу (~ 500 г) на тот же конец вращающейся платформы, что и вращающаяся масса. Если платформа неровная, тяжелый конец будет качаться в низкую сторону.3
Отрегулируйте регулировочные винты на ножках основания до тех пор, пока конец платформы не будет качаться равномерно, когда ее осторожно поворачивают вручную.
Установка радиуса
1
Осторожно отсоедините вращающуюся массу от струн. Используйте весы, чтобы взвесить его, и запишите значение массы.2
Подвесьте вращающуюся гирю к боковой стойке и подсоедините шнур от пружины к гири.Убедитесь, что эта струна проходит под (а не за) маленьким шкивом на центральной стойке.3
Переместите кронштейн индикатора на центральной стойке в самое нижнее положение.4
Оттяните вращающуюся массу от центральной стойки, пока оранжевый индикатор не окажется в центре кронштейна. Если струна, поддерживающая вращающийся груз, не является вертикальной, когда индикатор выровнен с кронштейном, боковую стойку следует перемещать внутрь или наружу, пока струна не станет вертикальной.Используйте вертикальную линию на боковой стойке, чтобы облегчить это выравнивание. При затягивании боковой стойки, нажмите на платформу, чтобы убедиться, что она надежно удерживается в вертикальном положении, и избегайте чрезмерного затягивания и поломки пластикового винта с накатанной головкой!5
Измерьте и запишите радиус, а также оценку погрешности на основе центровки.6
Теперь ваш аппарат должен быть готов к работе в максимально широком диапазоне центростремительных сил.(Почему это важно?) Центростремительную силу можно изменять, перемещая опору пружины вверх и вниз, при этом другие части устройства остаются на месте. Этот диапазон движение по центральной стойке должно быть не менее 5 см, что соответствует диапазону натяжения пружины примерно 1,2 Н.
Установка величины центростремительной силы
В этой первой части процедуры вы будете использовать метод static (без вращения) для настройки устройства на известное значение центростремительной силы.1
Присоедините зажимной шкив к концу платформы, ближайшему к вращающейся массе. Прикрепите веревку к вращающейся массе и навесьте известную массу (начиная с 20 г) над зажимным шкивом. Отрегулируйте прижимной шкив вверх или вниз по мере необходимости так, чтобы веревка между шкивом и вращающаяся масса расположена горизонтально. (Почему это важно?)2
Запишите значение этой статической массы , которая будет определять центростремительную силу.3
Отрегулируйте опору пружины по вертикали, пока оранжевый индикаторный диск не окажется по центру кронштейна индикатора. Теперь устройство должно быть выровнено, чтобы точно знать радиус движения вращающейся массы, когда платформа вращается.
Контрольно-пропускной пункт 1:
Прежде чем продолжить, попросите ТА проверить ваше устройство.
Измерение периода
1
Удалите статическую массу и струну из вращающейся массы. (Почему?)2
Поверните устройство, равномерно поворачивая стержень с накаткой по часовой стрелке. Уделите минуту, чтобы прочувствовать поворот платформы с постоянной скоростью. Увеличивайте скорость до тех пор, пока оранжевый индикаторный диск не окажется по центру кронштейна индикатора на центральной стойке.Это указывает на то, что струна, поддерживающая вращающуюся массу, вертикальна и, следовательно, масса находится на желаемом радиусе.3
Когда один партнер по лаборатории вращает платформу, другой должен использовать секундомер для измерения времени, необходимого для совершения одного оборота. Сделайте десять таких измерений.4
Альтернативный метод измерения среднего периода — использовать секундомер для измерения времени для N (например, 10) оборотов и разделить на N, чтобы получить T .Сделайте это хотя бы для одного испытания и сравните со значением, полученным с помощью процедуры, приведенной на шаге 3. Какой метод, по вашему мнению, более точен?5
Прежде чем продолжить, проверьте свои результаты для этой единственной точки данных и убедитесь, что ваше эмпирическое значение для вращающейся массы является разумным. Если ваш результат не имеет смысла, проанализируйте свою процедуру и исправьте все ошибки, прежде чем брать дополнительные данные.
Контрольно-пропускной пункт 2:
Перед тем, как продолжить, ваш технический специалист должен проверить ваши данные и результаты расчетов.
Изменение центростремительной силы
Повторите описанную выше процедуру как минимум с пятью различными статическими массами (и, следовательно, пятью различными силами), которые охватывают максимально широкий диапазон значений (обычно от 40 до 150 г).Анализ
1
Вес статической массы, висящей на шкиве, равен центростремительной силе F , приложенной пружиной. Вычислите эту силу для каждого из пяти испытаний, умножив статическую массу на г , и запишите результаты.2
Для каждой центростремительной силы F вычислите средний период вращения T и его стандартную ошибку.3
Для каждого значения F рассчитайте ω 2 и его неопределенность из4
Постройте график ω 2 против F (с планками ошибок) и выполните аппроксимацию методом наименьших квадратов.5
Определите экспериментальное значение вращающейся массы, м , из наклона вашего графика и уравнения центростремительной силы.Определите пересечение и линейного соответствия вашим данным. Это то, чего вы ожидаете?
Обсуждение
Сравните значение м , полученное при подборе кривой, с измеренными значениями вращающейся массы м и радиуса движения r . Есть согласие в пределах неопределенностей? Если вы проведете этот эксперимент осторожно, вы сможете получить результаты с ошибкой менее 3%. Сравните значение интервала y с ожидаемым значением.Они согласны? Почему для этого (и большинства других) экспериментов важно получить данные в самом широком диапазоне значений? Каковы потенциальные последствия близкого расположения точек данных? Объясните, как вы собираете данные с помощью этого устройства, чтобы проверить следующую гипотезу: для данного значения центростремительной силы F радиус движения r обратно пропорционален квадрату угловой скорости ω .Авторские права © 2011 Advanced Instructional Systems, Inc. и Университет Северной Каролины | Кредиты
Скорость, ускорение и сила | Безграничная физика
Угол вращения и угловая скорость
Угол поворота — это мера того, как далеко вращается объект, а угловая скорость — это скорость его вращения.
Цели обучения
Выразите взаимосвязь между углом поворота и расстоянием
Основные выводы
Ключевые моменты
- Когда объект вращается вокруг оси, точки на краю объекта перемещаются по дугам.
- Угол, выходящий за пределы этих дуг, называется углом поворота и обычно обозначается символом theta .
- Мера того, насколько быстро объект вращается относительно времени, называется угловой скоростью. Обычно он представлен греческим символом омега . Как и его аналог линейной скорости, это вектор.
Ключевые термины
- радиан : угол, образуемый в центре окружности дугой той же длины, что и радиус окружности.
Угол вращения и угловая скорость
Когда объект вращается вокруг оси, как в случае с шиной автомобиля или записью на поворотной платформе, движение можно описать двумя способами. Точка на краю вращающегося объекта будет иметь некоторую скорость и будет перенесена по дуге на вращающемся объекте. Точка пройдет расстояние [latex] \ Delta \ text {S} [/ latex], но часто удобнее говорить о степени поворота объекта. Величина поворота объекта называется углом поворота и может измеряться в градусах или радианах.Поскольку угол поворота связан с расстоянием [latex] \ Delta \ text {S} [/ latex] и с радиусом [latex] \ text {r} [/ latex] уравнением [latex] \ Delta \ theta = \ frac {\ Delta \ text {S}} {\ text {R}} [/ latex], обычно удобнее использовать радианы.
Угол θ и длина дуги s : Радиус круга поворачивается на угол [латекс] \ дельта \ тета [/ латекс]. Длина дуги [латекс] \ Delta \ text {s} [/ latex] указывается на окружности.
Скорость вращения объекта определяется угловой скоростью, которая представляет собой скорость изменения угла поворота во времени.Хотя сам угол не является векторной величиной, угловая скорость — это вектор. Направление вектора угловой скорости перпендикулярно плоскости вращения в направлении, которое обычно задается правилом правой руки. Угловое ускорение дает скорость изменения угловой скорости. Угол, угловая скорость и угловое ускорение очень полезны при описании вращательного движения объекта.
Направление угловой скорости : Угловая скорость описывает скорость вращения и ориентацию мгновенной оси, вокруг которой происходит вращение.Направление угловой скорости будет вдоль оси вращения. В этом случае (вращение против часовой стрелки) вектор направлен вверх.
Когда ось вращения перпендикулярна вектору положения, угловую скорость можно вычислить, взяв линейную скорость [latex] \ text {v} [/ latex] точки на краю вращающегося объекта и разделив на радиус. Это даст угловую скорость, обычно обозначаемую [latex] \ omega [/ latex], в радианах в секунду.
Угловая скорость : Муха на краю вращающегося объекта фиксирует постоянную скорость [latex] \ text {v} [/ latex]. Объект вращается с угловой скоростью, равной [latex] \ frac {\ text {v}} {\ text {r}} [/ latex].
Центробежное ускорение
Центростремительное ускорение — это постоянное изменение скорости, необходимое объекту для поддержания круговой траектории.
Цели обучения
Выразите центростремительное ускорение через скорость вращения
Основные выводы
Ключевые моменты
- Чтобы объект сохранял круговое движение, он должен постоянно менять направление.
- Поскольку скорость является вектором, изменения направления представляют собой изменения скорости.
- Изменение скорости называется ускорением. Изменение скорости из-за кругового движения известно как центростремительное ускорение.
- Центростремительное ускорение можно рассчитать, разделив квадрат линейной скорости на радиус круга, по которому движется объект.
Ключевые термины
- ускорение : величина, на которую увеличивается скорость или скорость (и, следовательно, скалярная величина или векторная величина).
- круговое движение : движение по кругу.
- скорость : векторная величина, которая обозначает скорость изменения положения относительно времени или скорость с направленным компонентом.
Обзор
Как упоминалось в предыдущих разделах по кинематике, любое изменение скорости определяется ускорением. Часто изменения скорости являются изменениями по величине. Когда объект ускоряется или замедляется, это изменение скорости объекта.Изменения в величине скорости соответствуют нашему интуитивному и повседневному использованию термина «ускорение». Однако, поскольку скорость является вектором, у нее также есть направление. Следовательно, любое изменение направления движения объекта также должно сопровождаться ускорением.
Равномерное круговое движение означает, что объект движется по круговой траектории с постоянной скоростью. Поскольку скорость постоянна, обычно никто не думает, что объект ускоряется. Однако направление постоянно меняется, когда объект пересекает круг.Таким образом, говорят, что он ускоряется. Это ускорение можно почувствовать, катаясь на американских горках. Даже если скорость постоянна, быстрый поворот вызовет у гонщика чувство силы. Это ощущение ускорения.
Центростремительное ускорение : Краткий обзор центростремительного ускорения для школьников-физиков.
Расчет центростремительного ускорения
Для расчета центростремительного ускорения объекта, совершающего равномерное круговое движение, необходимо иметь скорость, с которой движется объект, и радиус круга, вокруг которого происходит движение.2 \ text {r} [/ latex]
, где омега — это скорость вращения, задаваемая [latex] \ frac {\ text {v}} {\ text {r}} [/ latex].
Центростремительное ускорение : Когда объект движется по окружности, направление вектора скорости постоянно меняется.
Центростремительная сила
Сила, которая вызывает движение по криволинейной траектории, называется центростремительной силой (равномерное круговое движение является примером центростремительной силы).
Цели обучения
Выразите уравнения для центростремительной силы и ускорения
Основные выводы
Ключевые моменты
- Когда объект находится в равномерном круговом движении, он постоянно меняет направление и, следовательно, ускоряется.Это угловое ускорение.
- Сила, действующая на объект при равномерном круговом движении (называемая центростремительной силой), действует на объект из центра круга.
Ключевые термины
- центростремительный : направлен или движется к центру.
- угловая скорость : векторная величина, описывающая объект в круговом движении; его величина равна скорости частицы, а направление перпендикулярно плоскости ее кругового движения.
Сила, вызывающая движение по криволинейной траектории, называется центростремительной силой. Равномерное круговое движение является примером действия центростремительной силы. Это можно увидеть на орбите спутников вокруг Земли, натяжении веревки в игре с тросом, петле-петле на американских горках или в ведре, вращающемся вокруг тела.
Обзор центростремительной силы : Краткий обзор центростремительной силы.
Ранее мы узнали, что любое изменение скорости — это ускорение.По мере того, как объект движется по круговой траектории, он постоянно меняет направление и, следовательно, ускоряется, вызывая постоянное воздействие на объект силы. Эта центростремительная сила действует по направлению к центру кривизны, по направлению к оси вращения. Поскольку объект движется перпендикулярно силе, путь, по которому он движется, является круговым. Именно эта сила удерживает мяч от выпадения из ведра, если вы непрерывно раскачиваете его по кругу.
Центростремительная сила : Когда объект движется по круговой траектории с постоянной скоростью, он испытывает центростремительную силу, ускоряющую его к центру.2 [/ латекс]
4.4 Равномерное круговое движение — Университетская физика, том 1
Цели обучения
К концу этого раздела вы сможете:
- Найдите центростремительное ускорение объекта, движущегося по круговой траектории.
- Используйте уравнения кругового движения, чтобы найти положение, скорость и ускорение частицы, совершающей круговое движение.
- Объясните разницу между центростремительным ускорением и тангенциальным ускорением, возникающим в результате неравномерного кругового движения.
- Оцените центростремительное и тангенциальное ускорение при неравномерном круговом движении и найдите вектор полного ускорения.
Равномерное круговое движение — это особый тип движения, при котором объект движется по кругу с постоянной скоростью. Например, любая точка пропеллера, вращающегося с постоянной скоростью, совершает равномерное круговое движение. Другими примерами являются секундная, минутная и часовая стрелки часов. Примечательно, что точки на этих вращающихся объектах действительно ускоряются, хотя скорость вращения постоянна.Чтобы увидеть это, мы должны проанализировать движение в терминах векторов.
Центростремительное ускорение
В одномерной кинематике объекты с постоянной скоростью имеют нулевое ускорение. Однако в двух- и трехмерной кинематике, даже если скорость постоянна, частица может иметь ускорение, если она движется по криволинейной траектории, такой как окружность. В этом случае вектор скорости меняется, или
Это показано на (Рисунок). Поскольку частица движется против часовой стрелки во времени
по круговой траектории, его вектор положения перемещается из
Спо
Вектор скорости имеет постоянную величину и касается пути, поскольку он изменяется от
. Спо
только меняет направление.Поскольку вектор скорости
перпендикулярно вектору положения
треугольников, образованных векторами положения и
и векторы скорости и
похожи. Кроме того, с
и
два равнобедренных треугольника. Из этих фактов мы можем сделать утверждение
или
Рисунок 4.18 (a) Частица движется по кругу с постоянной скоростью, временами имея векторы положения и скорости.и
(b) Векторы скорости, образующие треугольник. Два треугольника на рисунке похожи. Вектор
указывает на центр круга в пределах
Мы можем найти величину ускорения от
Направление ускорения также можно найти, отметив, что как
и, следовательно,
приближаются к нулю, вектор
приближается к направлению, перпендикулярному
В пределе
перпендикулярно
с
касается окружности, ускорение
указывает на центр круга.Таким образом, частица, движущаяся по кругу с постоянной скоростью, имеет ускорение с величиной
.Направление вектора ускорения — к центру круга ((Рисунок)). Это радиальное ускорение и называется центростремительным ускорением , поэтому мы даем ему индекс c. Слово центростремительный происходит от латинских слов centrum (что означает «центр») и petere (означает искать ») и, таким образом, принимает значение« поиск центра ».”
Рис. 4.19. Вектор центростремительного ускорения указывает на центр круговой траектории движения и представляет собой ускорение в радиальном направлении. Также показан вектор скорости, касающийся окружности.Давайте рассмотрим несколько примеров, которые иллюстрируют относительные величины скорости, радиуса и центростремительного ускорения.
Пример
Создание ускорения 1
gСамолет летит со скоростью 134,1 м / с по прямой и делает разворот по круговой траектории на уровне земли.Каким должен быть радиус окружности, чтобы пилот и самолет получил центростремительное ускорение 1 g к центру круговой траектории?
Стратегия
Учитывая скорость струи, мы можем найти радиус окружности в выражении для центростремительного ускорения.
Решение
Установите центростремительное ускорение равным ускорению свободного падения:
Решая для радиуса, находим
Значение
Чтобы создать у пилота большее ускорение, чем g , реактивный самолет должен либо уменьшить радиус своей круговой траектории, либо увеличить скорость на существующей траектории, либо и то, и другое.
Проверьте свое понимание
Радиус маховика 20,0 см. Какова скорость точки на краю маховика, если она испытывает центростремительное ускорение
?[показывать-ответ q = ”fs-id11651609 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id11651609 ″]
134,0 см / с
[/ hidden-answer]
Центростремительное ускорение может иметь широкий диапазон значений в зависимости от скорости и радиуса кривизны круговой траектории.Типичные центростремительные ускорения приведены в следующей таблице.
| Объект | Центростремительное ускорение (м / с 2 или коэффициент g ) |
|---|---|
| Земля вокруг Солнца | |
| Луна вокруг Земли | |
| Спутник на геостационарной орбите | 0.233 |
| Внешний край компакт-диска при воспроизведении | |
| Струя в бочке ролика | (2–3 г ) |
| Американские горки | (5 г ) |
| Электрон, вращающийся вокруг протона в простой модели атома Бора |
Уравнения движения для равномерного кругового движения
Частица, совершающая круговое движение, может быть описана своим вектором положения
(рисунок) показывает частицу, совершающую круговое движение против часовой стрелки.Когда частица движется по окружности, ее вектор положения выметает угол
с осью x- . Вектор
образующий угол
с осью x- показан с его компонентами вдоль осей x и y . Величина вектора положения
, а также радиус круга, так что с точки зрения его составляющих
Здесь,
— это постоянная, называемая угловой частотой частицы.Угловая частота измеряется в радианах (рад) в секунду и представляет собой просто количество радианов угловой меры, через которую проходит частица за секунду. Уголок
, которое вектор положения имеет в любой конкретный момент времени, равен
..
Если T — это период движения или время для завершения одного оборота (
рад), затем
Рис. 4.20. Вектор положения частицы, движущейся по кругу, с ее компонентами по осям x и y.Частица движется против часовой стрелки. Угол— угловая частота
в радианах в секунду, умноженное на t.
Скорость и ускорение можно получить из функции положения путем дифференцирования:
Из (Рисунок) можно показать, что вектор скорости тангенциальный к окружности в месте нахождения частицы с величиной
.Аналогично, вектор ускорения находится путем дифференцирования скорости:
Из этого уравнения мы видим, что вектор ускорения имеет величину
.и направлен против вектора положения, к началу координат, потому что
Пример
Круговое движение протона
Протон имеет скорость
и движется по окружности в плоскости xy радиуса r = 0.175 м. Каково его положение в плоскости xy в момент времени
?При t = 0 положение протона
и вращается против часовой стрелки. Набросайте траекторию.
Решение
По приведенным данным протон имеет период и угловую частоту:
Положение частицы в
с A = 0.175 м —
Из этого результата мы видим, что протон расположен немного ниже оси x . Это показано на (Рисунок).
Рис. 4.21 Вектор положения протона наПоказана траектория протона. Угол, под которым протон движется по окружности, составляет 5,712 рад, что немного меньше одного полного оборота.
Значение
Мы выбрали начальное положение частицы на оси x —.Это было совершенно произвольно. Если бы была дана другая начальная позиция, у нас было бы другое конечное положение при t = 200 нс.
Неравномерное круговое движение
Круговое движение не обязательно должно иметь постоянную скорость. Частица может двигаться по кругу и ускоряться или замедляться, показывая ускорение в направлении движения.
При равномерном круговом движении частица, совершающая круговое движение, имеет постоянную скорость, а круг имеет фиксированный радиус.Если скорость частицы тоже меняется, то мы вводим дополнительное ускорение в направлении, касательном к окружности. Такое ускорение происходит в точке на вершине, которая изменяет скорость вращения, или в любом ускоряющем роторе. В работе «Векторы смещения и скорости» мы показали, что центростремительное ускорение — это скорость изменения направления вектора скорости во времени. Если скорость частицы изменяется, то она имеет тангенциальное ускорение , то есть скорость изменения величины скорости во времени:
Направление тангенциального ускорения касается окружности, тогда как направление центростремительного ускорения радиально внутрь к центру окружности.Таким образом, частица, движущаяся по кругу с тангенциальным ускорением, имеет полное ускорение , которое является векторной суммой центростремительного и тангенциального ускорений:
Векторы ускорения показаны на (Рисунок). Обратите внимание, что два вектора ускорения
и
перпендикулярны друг другу, при этом
в радиальном направлении и
в тангенциальном направлении.Общее ускорение
точек под углом
и
Рис. 4.22. Центростремительное ускорение указывает на центр круга. Тангенциальное ускорение является касательным к окружности в месте расположения частицы. Общее ускорение — это векторная сумма тангенциального и центростремительного ускорений, которые перпендикулярны.Пример
Полное ускорение при круговом движении
Частица движется по окружности радиуса r = 2.0 мес. В течение интервала времени от t = 1,5 с до t = 4,0 с его скорость изменяется со временем в соответствии с
.Каково полное ускорение частицы при т = 2,0 с?
Стратегия
Нам даны скорость частицы и радиус круга, поэтому мы можем легко вычислить центростремительное ускорение. Направление центростремительного ускорения — к центру круга. Мы находим величину тангенциального ускорения, взяв производную по времени
, используя (рисунок) и оценив его как t = 2.0 с. Мы используем это и величину центростремительного ускорения, чтобы найти полное ускорение.
Решение
Центростремительное ускорение
направлен к центру круга. Касательное ускорение
Суммарное ускорение
и
от касательной к окружности. См. (Рисунок).
Рис. 4.23 Векторы тангенциального и центростремительного ускорения.Чистое ускорение— это векторная сумма двух ускорений.
Значение
Направления центростремительного и тангенциального ускорений можно описать более удобно в терминах полярной системы координат с единичными векторами в радиальном и тангенциальном направлениях. Эта система координат, которая используется для движения по криволинейным траекториям, подробно обсуждается позже в книге.
Сводка
- Равномерное круговое движение — это движение по окружности с постоянной скоростью.
- Центростремительное ускорение
— это ускорение, которое должна иметь частица, чтобы двигаться по круговой траектории. Центростремительное ускорение всегда направлено к центру вращения и имеет величину
. - Неравномерное круговое движение возникает, когда существует тангенциальное ускорение объекта, выполняющего круговое движение, так что скорость объекта изменяется. Это ускорение называется тангенциальным ускорением.
Величина тангенциального ускорения — это скорость изменения величины скорости во времени.Вектор тангенциального ускорения касается окружности, тогда как вектор центростремительного ускорения направлен радиально внутрь к центру окружности. Общее ускорение — это векторная сумма тангенциального и центростремительного ускорений.
- Объект, выполняющий равномерное круговое движение, можно описать уравнениями движения. Вектор положения объекта
, где A — величина
., который также является радиусом круга, и
— угловая частота.
Концептуальные вопросы
Может ли центростремительное ускорение изменить скорость частицы, совершающей круговое движение?
Может ли тангенциальное ускорение изменить скорость частицы, совершающей круговое движение?
[показывать-ответ q = ”fs-id116516
23 ″] Показать решение [/ показывать-ответ][скрытый-ответ a = ”fs-id116516
23 ″]да
[/ hidden-answer]
Проблемы
Маховик вращается со скоростью 30 об / с.Каков полный угол в радианах, на который точка маховика поворачивается за 40 с?
Частица движется по кругу радиусом 10 м с постоянной скоростью 20 м / с. Какая величина ускорения?
[show-answer q = ”fs-id11651685 ″] Показать решение [/ show-answer]
[скрытый-ответ a = ”fs-id11651685 ″]
[/ hidden-answer]
Кэм Ньютон из Carolina Panthers бросает идеальную футбольную спираль на отметке 8.0 об / с. Радиус профессионального футбола составляет 8,5 см по середине короткой стороны. Что такое центростремительное ускорение шнурков на футбольном мяче?
Выставочный аттракцион раскручивает своих пассажиров внутри контейнера в форме летающей тарелки. Если горизонтальный круговой путь, по которому следуют гонщики, имеет радиус 8,00 м, при скольких оборотах в минуту гонщики подвергаются центростремительному ускорению, равному ускорению силы тяжести?
[показывать-ответ q = ”fs-id11651661 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id11651661 ″]
, что равно
[/ hidden-answer]
Бегун, участвующий в забеге на 200 м, должен обойти конец трассы, имеющей дугу окружности с радиусом кривизны 30.0 мес. Бегун начинает забег с постоянной скоростью. Если она преодолевает 200-метровый рывок за 23,2 с и бежит с постоянной скоростью на протяжении всего забега, каково ее центростремительное ускорение при прохождении криволинейной части трассы?
Каково ускорение Венеры по направлению к Солнцу, если принять круговую орбиту?
[показывать-ответ q = ”fs-id11651611 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id11651611 ″]
Венера находится на расстоянии 108,2 миллиона км от Солнца и имеет период обращения 0.6152 г.
[/ hidden-answer]
Экспериментальная реактивная ракета движется вокруг Земли вдоль экватора прямо над ее поверхностью. С какой скоростью должна двигаться струя, если величина ее ускорения g ?
Вентилятор вращается с постоянной скоростью 360,0 об / мин. Какова величина ускорения точки на одной из лопастей на расстоянии 10,0 см от оси вращения?
[показывать-ответ q = ”fs-id1165168934870 ″] Показать решение [/ показывать-ответ]
[скрытый-ответ a = ”fs-id1165168934870 ″]
[/ hidden-answer]
Точка, расположенная на секундной стрелке больших часов, имеет радиальное ускорение
.Как далеко точка от оси вращения секундной стрелки?
Глоссарий
- угловая частота
скорость изменения угла, с которым объект движется по круговой траектории
- центростремительное ускорение
- Компонент ускорения объекта, движущегося по окружности, радиально направленной внутрь к центру окружности
- тангенциальное ускорение
- величина которого является временной скоростью изменения скорости.Его направление касается окружности.
- общее ускорение
- векторная сумма центростремительного и тангенциального ускорений
Калькулятор угловой скорости
Этот калькулятор угловой скорости представляет собой простой в использовании инструмент, который дает немедленный ответ на вопрос «Как найти угловую скорость?». В тексте вы найдете несколько формул угловой скорости, узнаете о различных единицах угловой скорости и, наконец, оцените угловую скорость Земли! Вы когда-нибудь задумывались, какова связь между угловой скоростью и угловой частотой или где применяется угловая скорость? Прочтите, чтобы узнать больше, и станьте экспертом в области кругового движения.
Что такое угловая скорость?
Угловая скорость описывает вращательное движение тел. Он измеряет, насколько быстро они перемещаются вокруг некоторого центра вращения. Мы можем думать о двух разных видах вращения. Первый описывает движение центра масс данного объекта вокруг определенной точки в пространстве , которую можно описать как начало координат. Некоторые примеры включают планеты, движущиеся вокруг Солнца, или автомобиль, съезжающий с шоссе.
Второй рассказывает о вращении тела вокруг собственного центра масс — спин (не путать с квантовым свойством частиц, также называемым спином).Вы наверняка видели, как баскетболист крутит мяч на пальце.
В целом можно сказать, что чем быстрее движение, тем выше угловая скорость. Чтобы определить некоторые конкретные значения, мы должны перейти к уравнениям угловой скорости, описанным в следующем разделе.
Формулы угловой скорости
В этом калькуляторе угловой скорости мы используем две разные формулы угловой скорости в зависимости от того, какие входные параметры у вас есть.
Первое уравнение угловой скорости аналогично уравнению для линейной скорости:
ω = (α₂ - α₁) / t = Δα / t ,
, где α₁ и α₂ — два значения углов на окружности, а Δα — их разница. t — время, за которое происходит изменение угла. Как видите, для нормальной скорости есть отношение изменения положения за период, а здесь мы используем угол вместо расстояния.
Вторая формула угловой скорости может быть получена из соотношения линейной скорости и радиуса с использованием векторного произведения, которое составляет:
v = ω × r .
Мы можем переписать это выражение, чтобы получить уравнение угловой скорости:
ω = r × v / | r | ² ,
, где все эти переменные — векторы , а | r | обозначает абсолютное значение радиуса.Фактически угловая скорость — это псевдовектор, направление которого перпендикулярно плоскости вращательного движения.
Единицы угловой скорости
Существует несколько единиц угловой скорости, и те, которые используются в нашем калькуляторе угловой скорости, указаны ниже:
рад / сили радиан в секунду — определение, которое происходит прямо из первой формулы угловой скорости. Он сообщает, насколько велико вращение (или угол), через которое тело движется за заданное время,об / минили оборотов в минуту — единица, наиболее часто встречающаяся на практике.С его помощью вы можете описать, с какой скоростью вращается колесо или двигатель. Вы легко можете себе представить разницу между10и100 об / мин.Гцили Гц — те же единицы измерения, которые используются для частоты, но редко используются в контексте угловой скорости. Это в некотором роде похоже наоб / мин, говорящее нам, сколько полных оборотов совершается за заданное время. Разница в том, что раньше базовой единицей времени была минута, а здесь — секунда.
Естественно, все эти единицы угловой скорости конвертируются между собой с использованием следующих соотношений:
1 RMP = 0,10472 рад / с = 0,01667 Гц ,
или наоборот:
1 Гц = 6,283 рад / с = 60 об / мин .
Зависимость угловой скорости от угловой частоты
Посмотрите определение угловой частоты:
ω = 2 * π * f ,
, где f — частота.Как видим, обозначается той же буквой. Кроме того, единица угловой частоты — рад / с , точно такая же, как и для угловой скорости. Так что может возникнуть вопрос: «В чем разница между угловой скоростью и угловой частотой?».
Ответ относительно прост. Соотношение между угловой частотой и угловой скоростью аналогично соотношению между , , скоростью , и скоростью . Первый — это величина второго, или, другими словами, угловая частота — это скаляр, а угловая скорость — это (псевдо) вектор.
Угловая частота обычно используется, когда говорят о гармоническом движении, примером которого является простой маятник. Как вы понимаете, движение не должно быть представлено стандартным вращением, а просто движением, которое периодически повторяет свое положение. Однако угловая скорость жестко связана с движением вокруг некоторой точки. Следовательно, мы можем сказать, что угловая частота является более общей величиной и может использоваться для описания широкого круга физических проблем, в то время как угловая скорость включает только вращательное движение.
Как найти угловую скорость Земли?
Как насчет того, чтобы использовать наш калькулятор угловой скорости? Оценим угловую скорость Земли! Во-первых, мы рассматриваем скорость вращения. Мы знаем, что Земля совершает полный оборот относительно далеких звезд примерно за 23 ч 56 мин 4 с , что составляет примерно 23,934 ч . Полное вращение составляет угол 2π рад , поэтому результирующая угловая скорость равна:
ω₁ = 2π рад / 23.934 ч = 0,2625 рад / ч = 0,00007292 рад / с ,
или 7,292 * 10⁻⁵ рад / с (в экспоненциальном представлении).
Теперь, когда мы знаем угловую скорость вращения Земли, мы можем оценить ее линейную скорость на экваторе. Для этого нам понадобится радиус Земли, который составляет примерно 6,371 км . Единственное, что нам нужно сделать, это вставить значения во вторую формулу угловой скорости:
v₁ = r₁ * ω₁ = 6,371 км * 7,292 * 10⁻⁵ рад / с = 0,4646 км / с = 464.6 м / с .
Чтобы вычислить линейную скорость относительно центра Земли, все, что вам нужно сделать, это умножить полученный результат на косинус широты вашего города. Кстати, вы когда-нибудь задумывались, почему ракеты обычно запускаются с космодромов, расположенных вблизи экватора, а не с полюсов? Ну, почти ускорение на 500 м / с в начале — это значительная часть его конечной скорости. Таким образом, перемещение начальной точки как можно ближе к экватору снижает количество топлива, необходимого для разгона ракеты.
После этого мы можем еще раз спросить, как найти угловую скорость Земли, но на этот раз орбитальную. Все расчеты аналогичны, но мы должны изменить время с 23,943 ч на один год, что составляет примерно 365,25 дня. Изменение угла такое же, полный оборот.
ω₂ = 2π рад / 23,934 h = 0,0000001991 рад / с = 1,991 * 10⁻⁷ рад / с ,
и линейная скорость Земли относительно Солнца (для среднего радиуса 1.496 * 10⁸ км ) составляет:
v₂ = 1,496 * 10⁸ км * 1,991 * 10⁻⁷ рад / с = 29,785 км / с .
Мы движемся довольно быстро, не так ли?
Физические величины, зависящие от угловой скорости
Существует множество физических величин, связанных с угловой скоростью, некоторые из которых перечислены ниже:
Угловое ускорение — описывает, как угловая скорость изменяется со временем. Чем больше разница угловых скоростей, тем больше значение углового ускорения.
Кинетическая энергия вращения — мера энергии при круговом движении. Как и в случае с кинетической энергией, зависимость (угловой) скорости квадратичная.
Центробежная сила — ее можно почувствовать в автомобиле, когда он поворачивает. Чем быстрее вы поворачиваете или чем он круче, тем выше становится центробежная сила, которую можно четко почувствовать.
Эффект Кориолиса — который заставляет объекты поворачиваться, если они помещены на вращающееся тело (например,грамм. на Земле) вместо того, чтобы двигаться по прямой.
Система шкивов — это не физическая величина, точнее говоря, это интересное устройство, все дело в угловой скорости. Самая простая система состоит из двух шкивов, обычно с разной окружностью или радиусом. Они связаны ремнем, поэтому их линейные скорости идентичны , но поскольку они имеют разные размеры, их угловые скорости изменяются пропорционально .Зная это и имея двигатель с четко определенной скоростью вращения, мы можем с хорошей точностью установить угловую скорость выходного элемента, просто отрегулировав его размер.
Сохранение момента импульса
Есть несколько фундаментальных правил, которые говорят нам о величинах, сохраняемых в изолированных системах. Самыми известными из них являются сохранение энергии и сохранение количества движения. Вместе с ними существует также сохранения углового момента .Если мы подумаем о двух моментах времени, правило можно записать как:
I₁ * ω₁ = I₂ * ω₂ ,
, где I₁ и I₂ — начальный и конечный массовые моменты инерции соответственно, величины, которые описывают распределение массы относительно центра тел.
Мы видим, что , если момент инерции увеличивается, угловая скорость уменьшается, и наоборот . Итак, каковы последствия этого явления? Представим, что вы фигурист.Когда вы вращаетесь, вы обладаете некоторой угловой скоростью. Если ваши руки широко раскрыты, момент инерции массы относительно велик. . Затем вы приближаете руки к остальному телу. Как следствие, ваш момент инерции уменьшается на , поэтому из-за того, что общий угловой момент должен быть сохранен, ваша угловая скорость увеличивается на — это означает, что вы будете вращаться быстрее! Это не магия, а просто физика!
Если кататься на коньках не любишь, можно попробовать проверить правило на обычном вращающемся кресле.Просто помните, безопасность превыше всего! Убедитесь, что для этого эксперимента достаточно места. После этого просто начните вращаться и посмотрите, как изменяется ваша угловая скорость, когда вы двигаете руками вперед и назад. Кроме того, вы можете усилить эффект, используя гантели. В результате вы можете объединить упражнения и развлечения в одно целое!
Использование уравнений кругового движения — Физика средней школы
Если вы считаете, что контент, доступный через Веб-сайт (как определено в наших Условиях обслуживания), нарушает или несколько ваших авторских прав, сообщите нам, отправив письменное уведомление («Уведомление о нарушении»), содержащее то информацию, описанную ниже, назначенному ниже агенту.Если репетиторы университета предпримут действия в ответ на ан Уведомление о нарушении, оно предпримет добросовестную попытку связаться со стороной, которая предоставила такой контент средствами самого последнего адреса электронной почты, если таковой имеется, предоставленного такой стороной Varsity Tutors.
Ваше Уведомление о нарушении прав может быть отправлено стороне, предоставившей доступ к контенту, или третьим лицам, таким как в качестве ChillingEffects.org.
Обратите внимание, что вы будете нести ответственность за ущерб (включая расходы и гонорары адвокатам), если вы существенно искажать информацию о том, что продукт или действие нарушает ваши авторские права.Таким образом, если вы не уверены, что контент находится на Веб-сайте или по ссылке с него нарушает ваши авторские права, вам следует сначала обратиться к юристу.
Чтобы отправить уведомление, выполните следующие действия:
Вы должны включить следующее:
Физическая или электронная подпись правообладателя или лица, уполномоченного действовать от их имени; Идентификация авторских прав, которые, как утверждается, были нарушены; Описание характера и точного местонахождения контента, который, по вашему мнению, нарушает ваши авторские права, в \ достаточно подробностей, чтобы позволить репетиторам университетских школ найти и точно идентифицировать этот контент; например нам требуется а ссылка на конкретный вопрос (а не только на название вопроса), который содержит содержание и описание к какой конкретной части вопроса — изображению, ссылке, тексту и т. д. — относится ваша жалоба; Ваше имя, адрес, номер телефона и адрес электронной почты; а также Ваше заявление: (а) вы добросовестно считаете, что использование контента, который, по вашему мнению, нарушает ваши авторские права не разрешены законом, владельцем авторских прав или его агентом; (б) что все информация, содержащаяся в вашем Уведомлении о нарушении, является точной, и (c) под страхом наказания за лжесвидетельство, что вы либо владелец авторских прав, либо лицо, уполномоченное действовать от их имени.
Отправьте жалобу нашему уполномоченному агенту по адресу:
Чарльз Кон
Varsity Tutors LLC
101 S. Hanley Rd, Suite 300
St. Louis, MO 63105
Или заполните форму ниже:
спутник НАСА ИЗОБРАЖЕНИЕ, Спросите у космического ученого Архив
НАСА ИЗОБРАЖЕНИЕ спутник, Спросите архив космического ученогоКак я могу рассчитать массу Земли, зная только расстояние до Луны а продолжительность лунного месяца?
Это один из самых захватывающих аспектов физики, с которым я столкнулся на ранний возраст, и с тех пор это меня очаровывает! Я до сих пор нахожу удивительным, что зная расстояние и время, вы можете вычислить массу и взвесить планета.Вот как это делается примерно. Для объекта массы м по круговой орбите или радиусу R, сила тяжести уравновешивается центробежной силой движения тел по кругу со скоростью V, поэтому из формул для этих двух сил вы получать:
Г М м
F (сила тяжести) = -------
2
р
а также
2
м V
F (Центробежный) = -------
р
Если вы уравновесите силы так, что F (сила тяжести) = F (центробежная сила), вы получите после
немного алгебры:
2 G M
V = ------
р
Удивительно, но масса спутника m уменьшилась с обеих сторон.
уравнения, и это означает, что не имеет значения, насколько большой спутник
вращение планеты по орбите вообще имеет значение, только ее расстояние R и скорость V имеют значение!
Теперь скорость на круговой орбите равна 2 x pi x R окружности,
разделить на орбитальное время спутника T, так что вы получите:
2 2
4 пи R G M
знак равно
2
T R
и с небольшой алгеброй вы можете решить для массы планеты, M, и получить
2 3
4 пи R
----------- = М
2
G T
Это работает, если масса спутника намного меньше массы спутника.
планету, которую вы взвешиваете.-8, и вы получите
ответ для массы Земли в граммах, что довольно близко к ее
реальная стоимость. Вы также можете взвесить Солнце, используя одну из планет или
Млечный Путь с использованием орбиты Солнца (8700 парсек и 224 миллиона лет).Вернитесь на главную страницу Спросите космического ученого.
Все ответы предоставлены доктором Стеном Оденвальдом (Raytheon STX).
для
НАСА ИЗОБРАЖЕНИЕ / ПОЭЗИЯ
Программа образования и информирования общественности.




