Формулы расчета резонансной частоты колебательного контура

Для генерации высокочастотных волн часто применяются схемы на основе колебательного контура. Подобрав параметры элементов цепи, можно производить частоты свыше 500 МГц. Схемы используются в ВЧ-генераторах, высокочастотном нагреве, телевизионных и радиоприемниках.

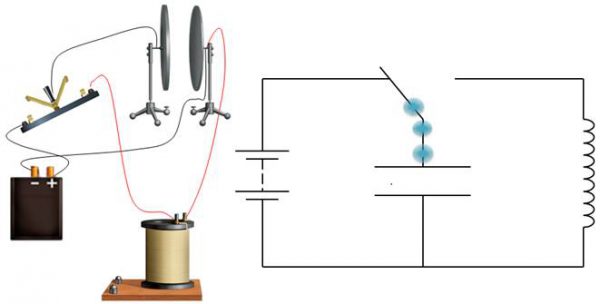
Колебательный контур

Колебательный контур

Колебательный контур – это последовательное или параллельное соединение индуктивных и конденсаторных элементов, генерирующих электромагнитные колебания любой заданной частоты. Оба компонента схемы способны хранить энергию.

Когда существует разность потенциалов на конденсаторных пластинах, он сохраняет энергию электрического поля. Аналогично энергия сохраняется в магнитном поле индуктивной катушки.

Работа колебательного контура

Когда первоначально конденсатор подключается к источнику постоянного тока, на нем возникает разность потенциалов. Одна пластина имеет избыток электронов и заряжена отрицательно, другая – недостаток электронов и заряжена положительно.

Что будет, если в цепь включить индуктивную катушку:

1. При замыкании контакта, соединяющего электроцепь, конденсатор начинает разряжаться через катушку индуктивности. Накопленная им энергия электрического поля снижается;
2. Ток, протекающий через катушку L, индуцирует ЭДС, противостоящую потоку электронов. Из-за этого скорость нарастания тока медленная. В катушке создается магнитное поле, которое начинает накапливать свою энергию. После полного разряда конденсатора поток электронов через катушку уменьшается до нуля. Электростатическая энергия, накопленная в конденсаторе, преобразуется в энергию магнитного поля катушки;
3. Когда конденсатор разряжен, магнитное поле начинает постепенно разрушаться, но, согласно закону Ленца, индукционный ток катушки способствует заряду конденсатора с противоположной полярностью. Энергия, связанная с магнитным полем, снова превращается в электростатическую;

Важно! В идеальном случае, когда нет потерь на L и С, конденсатор зарядился бы до первоначального значения с противоположным знаком.

4. После того, как уменьшающееся магнитное поле перезарядило конденсатор, он снова начинает разряжаться с потоком тока обратной направленности, а МП опять нарастает.

Последовательность зарядки и разрядки продолжается, то есть процесс преобразования электростатической энергии в магнитную и наоборот периодически повторяется, подобно маятнику, у которого потенциальная энергия циклически превращается в кинетическую и обратно.

Непрерывный процесс зарядки и разрядки приводит к меняющему направление движению электронов или к колебательному току.

Обмен энергией между L и С будет продолжаться бесконечно, если отсутствуют потери. Часть энергии теряется, рассеиваясь в виде тепла на проводах катушки, соединительных проводниках, из-за тока утечки конденсатора, электромагнитного излучения. Поэтому колебания будут затухающими.

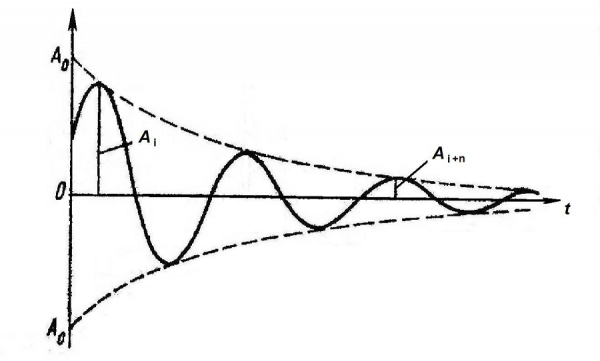
Затухающие колебания

Резонанс

Если схема с конденсатором, катушкой и резистором возбуждается напряжением, постоянно меняющимся во времени с определенной частотой, то также изменяются реактивные сопротивления: индуктивное и емкостное. Амплитуда и частота выходного сигнала будет изменяться по сравнению с входным.

Индуктивное сопротивление прямо пропорционально частоте:

X(L) = 2π x f x L,

а емкостное сопротивление обратно пропорционально этому показателю:

X(C) = 1/(2π x f x C).

Важно! На более низких частотах индуктивное сопротивление незначительное, а емкостное будет высоким и сможет создавать практически разомкнутый контур. На высоких частотах картина обратная.

При конкретной комбинации конденсатора и катушки схема становится резонансной, или настроенной, имеющей частоту колебаний, при которой индуктивное сопротивление идентично емкостному. И они компенсируют друг друга.

Следовательно, в цепи остается исключительно активное сопротивление, противостоящее протекающему току. Созданные условия получили наименование резонанса колебательного контура. Фазовый сдвиг между током и напряжением отсутствует.

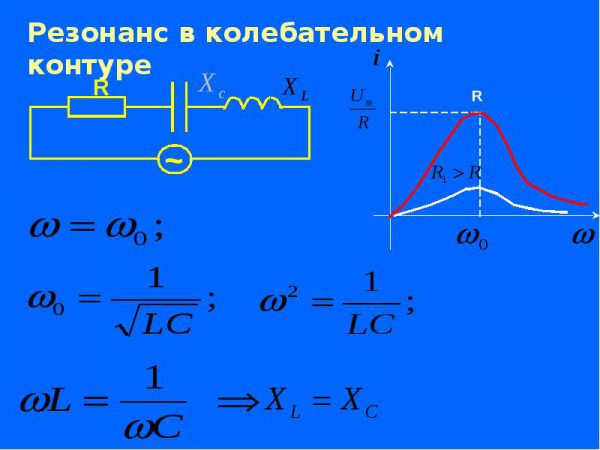
Резонанс LC-цепи

Для расчета резонансной частоты колебательного контура учитывается следующее условие:

X(L) = X(C).

Следовательно, 2π x f x L = 1/(2πx f x C).

Отсюда получается формула резонансной частоты:

f = 1/(2π x √(L x C)).

Расчет резонансной частоты, индуктивности и емкости можно сделать на онлайн калькуляторе, подставив конкретные значения.

Скорость, с которой рассеивается энергия от LC-схемы, должна быть такой же, как энергия, подаваемая на схему. Устойчивые, или незатухающие, колебания производятся электронными схемами генераторов.

LC-цепи используются либо для генерации сигналов на определенной частоте, либо для выделения частотного сигнала из более сложного. Они являются ключевыми компонентами многих электронных устройств, в частности радиооборудования, используемого в генераторах, фильтрах, тюнерах и частотных микшерах.

Видео

Оцените статью:

1. Формула резонансной частоты контура

2. Особенности распространения радиоволн различных диапазонов.

К коротким волнам относятся радиоволны длиной от 100 до 10 м (частоты 3-30 МГц). Преимуществом работы на коротких волнах по сравнению с работой на более длинных волнах является то, что в этом диапазоне можно создать направленные антенны. Короткие волны могут распространяться как земные и как ионосферные. С повышением частоты сильно возрастает поглощение волн в полупроводящей поверхности Земли. Поэтому при обычных мощностях передатчика земные волны коротковолнового диапазона распространяются на расстояния, не превышающие нескольких десятков километров.

К средним волнам относятся радиоволны длиной от 100 до 1000 м (частоты 3-0,3 МГц). Средние волны используются главным образом для вещания. Они могут распространяться как земные и как ионосферные волны. Средние волны испытывают значительное поглощение в полупроводящей поверхности Земли, дальность распространения земной волны ограничена расстоянием 500-700 км.

Радиоволны длиной от 1000 до 10000 м называют длинными (частота 300—30 кГц), а радиоволны длиной свыше 10000 м -сверхдлинными (частота менее 30 кГц). Длинные и особенно сверхдлинные волны мало поглощаются при прохождении в толще суши или моря. Так, волны длиной 20-30 км могут проникать в глубину моря на несколько десятков метров и, следовательно, могут использоваться для связи с погруженными подводными лодками, а также для подземной радиосвязи.

3. Особенности построения и работы оборудования исз (дальний космос)

ИСЗ — искусственный спутник Земли

Относится ко 2-ому классу. Спутниковая система Использование высоких элептических орбит, используются для построения спутниковых систем типа «Молния»

Для систем космической связи на элептических орбитах реально оказывает влияние доплировский сдвиг частоты.

,где с — скорость света, Фг — радиальная составляющая скорости спутника,

f1 — частота на участке ИСЗ, f2 — частота спутника Земли

+ приувеличении расстояния; — при уменьшении расстояния

Построение:

1)Ракетно-космический комплекс

2)Оснащённость ремонтным вспомогательным оборудованием

3)Оснащён системами: контроля показателей качества аппаратуры и каналов связи,

управления работы земных станций и ретрансляции, системой выполнения канальных распределений

Трасса Земля-ИСЗ (7,2-7,75 ГГц)

ЭКЗАМИНАЦИОННЫЙ БИЛЕТ №17-18

Основные параметры колебательного контура

Пусть конденсатор С, заряженный от внешнего источника, подключается к индуктивности

L (рис. 1а)

а)

б)

Разряд конденсатора не может произойти мгновенно, т.к. этому препятствует ЭДС самоиндукции, возникающая в элементе индуктивности.

В идеальном контуре, активное сопротивление которого равно нулю, и, следовательно, отсутствуют потери, запасенная в электрическом поле энергия полностью переходит в энергию магнитного поля индуктивности.

Затем происходит обратный переход энергии. Далее процессы повторяются. Таким образом, возникают незатухающие электрические колебания, имеющие форму косинусоиды. Графики

и представлены на рисунке 1, б.

Частота, с которой происходит колебания энергии между реактивными элементами при отключении источника, называется частотой свободных (собственных) незатухающих колебаний контура. Обозначение: или

_.

Т.к. в идеальном контуре величины напряжений на L и C одинаковы, то

, ,

или , .

В режиме свободных колебаний через элементы контура протекает ток. Сопротивление, которое оказывают элементы контура току на частоте собственных колебаний, называется

волновым (характеристическим).

Это сопротивление обозначается и определяется следующим образом:

, или . Т.к. , то

(Ом).

Из последнего выражения следует, что на частоте собственных колебаний волновое сопротивление равно одному из реактивных сопротивлений (рис. 2).

Рис. 2

На практике реальный КК всегда имеет потери активное сопротивление не равно 0, что приводит к затухающему характеру свободных колебаний (рис. 3).

Рис. 3

Для характеристики последнего свойства вводится понятие добротность контура (качество контура).

Добротность является энергетическим параметром и показывает во сколько раз реактивная мощность (за счет которой и происходят свободные колебания) больше активной:

Отметим, что данное определение относится не только к колебательным контурам, но и к отдельным деталям, например, к катушкам индуктивности, к конденсаторам.

Чем больше реактивная мощность, тем выше добротность и тем медленнее происходит затухание колебаний и наоборот.

Добротность КК, применяемых в технике связи, обычно составляет десятки-сотни, а в технике СВЧ и специальных устройствах добротность может достигать тысячи и больше.

8.1 Резонансная частота. Расстройка.

В цепи, содержащей реактивные элементы, произойдет резонанс, если цепь имеет резистивный характер:

Lώ=l/ώC, следовательно

, угловая резонансная частота.

Из формулы видно, что резонанс наступает, если частота питающего генератора равна собственным колебаниям контура.

При работе с колебательным контуром необходимо знать, совпадает ли частота генератора и частота собственных колебаний контура. Если частоты совпадают, то контур остается настроенным в резонанс, если не совпадает – то в контуре присутствует расстройка.

Настроить колебательный контур в резонанс можно тремя способами:

1 Изменять частоту генератора , при значениях емкости и индуктивности const, то есть изменяя частоту генератора мы подстраиваем эту частоту под частоту колебательного контура

2 Изменять индуктивность катушки, при частоте питания и емкости const;

3 Изменять емкость конденсатора , при частоте питания и индуктивности const.

Во втором и третьем способе изменяя частоту собственных колебаний контура, подстраиваем ее под частоту генератора.

При ненастроенном контуре частота генератора и контура не равны, то есть присутствует расстройка.

Расстройка – отклонение частоты от резонансной частоты.

Существует три вида расстройки:

1. Абсолютная – разность между данной частотой и резонансной

2. Обобщенная – отношение реактивного сопротивления к активному:

3. Относительная – отношение абсолютной расстройки к резонансной частоте:

При резонансе все расстройки равны нулю, если частота генератора меньше частоты контура, то расстройка считается отрицательной,

Если больше – положительной.

Таким образом добротность характеризует качество контура, а обобщенная расстройка- удаленность от резонансной частоты.

8.2 Построение зависимостейX, X_L, X_C от f.

При резонансе реактивные сопротивления равны, следовательно .

При — цепь носит емкостной характер,

— носит индуктивный характер.

Задачи:

1. Сопротивление контура 15 Ом, индуктивность 636 мкГн, Емкость 600 пФ, напряжение питающей сети 1,8 В. Найти собственную частоту контура, затухание контура, характеристическое сопротивление, ток, активную мощность, добротность, напряжение на зажимах контура.

Решение:

2. Напряжение на зажимах генератора 1 В, частота питающей сети 1 МГц, добротность 100, емкость 100 пФ. Найти: затухание, характеристическое сопротивление, активное сопротивление, индуктивность, частоту контура, ток, мощность, напряжения на емкости и индуктивности.

Решение:

Тестовые задания:

Отношение реактивного сопротивления к активному это :	А) Абсолютная расстройка; Б) Обобщенная расстройка; В) Относительная расстройка.

Тема занятия 9 : Входные и передаточные АЧХ и ФЧХ последовательного колебательного контура.

9.1 Входные АЧХ и ФЧХ.

В последовательном колебательном контуре:

, где

R – активное сопротивление;

X – реактивное сопротивление.

Учитывая, что

,то

ώ=0 ζ=-∞ Z=∞

ώ=ώ۪۪ζ=0 Z=R

ώ=∞ ζ=∞ Z=∞, следовательно график имеет вид:

Из графика видно, что контур обладает наименьшим сопротивлением на резонансной частоте, при увеличении расстройки сопротивление увеличивается.

ζ=0 φ=0 R

ζ=1 φ=45° RL

ζ=-1 φ=-45° RC

ζ=∞ φ=90° L

ζ=-∞ φ=-90° C.

Построим график:

На участке ζ=[-1;1]

ФЧХ имеет линейный

характер.

1. На участке ζ=[-∞;0] — цепь носит активно-емкостной характер;

2. На участке ζ=[0;∞]- цепь носит frnbdyj-индуктивный характер;

3. При ζ=0 — цепь носит активный характер;

2. Передаточные АЧХ и ФЧХ

передаточная характеристика АЧХ

ζ=-∞ k=0

ζ=0 k=Q

ζ=∞ k=0

Построим график зависимости:

Разделим k∕kо и получим передаточную

характеристику АЧХ в относительных

единицах, которая имеет вид:

Чтобы построить передаточную ФЧХ необходимо: построить входную ФЧХ, взять её зеркальное ее отображение и сместить на -90°.

На участке ζ=[-1;1] – передаточная ФЧХ носит линейный характер.

Coil32 — Собственный резонанс однослойной катушки

На заре развития радиотехники было обнаружено, что катушка не идеальная индуктивность. На определенной частоте она входит в режим резонанса даже при отсутствии внешней емкости, а выше этой частоты импеданс катушки носит уже емкостный характер. Для объяснения этого явления предположили, что кроме индуктивности реальная катушка обладает еще собственной емкостью (предположительно между соседними витками) и реальную катушку стали представлять в виде модели из сосредоточенных RLC элементов, в которой L —  индуктивность, C — собственная емкость, названная паразитной, а с помощью активного R учитываются различные потери в катушке. Такая модель катушки имеет одну резонансную частоту, которую назвали частотой собственного резонанса. Долгое время эта модель всех устраивала и стала классической моделью реальной катушки во всех учебниках.

 

Ведь катушки в подавляющем большинстве практических применений работают на частотах намного ниже частоты собственного резонанса и задачей конструктора является, по сути, обеспечение этого условия. При этом большинство инженеров с этой целью пытались уменьшить эту самую «межвитковую» паразитную емкость. В случае же, если катушка работает на частотах близких к собственному резонансу, как например в спиральных резонаторах или катушках Теслы, RLC-модель дает неверные результаты, но для таких случаев были разработаны альтернативные алгоритмы расчета и все остались довольны не особо задумываясь о причинах таких нестыковок. В нашу цифровую эпоху появились программы, которые дали возможность моделировать поведение любых высокочастотных устройств с высокой степени точности — так называемые электромагнитные симуляторы. Это мощные пакеты типа CST Studio, HFSS и многие другие. Давайте проведем исследование однослойной спиральной катушки в программе HFSS. В первой модели мы поместим катушку над идеальной проводящей поверхностью и запитаем от точечного источника с внутренним сопротивлением 50 МОм. Второй конец катушки заземлен. Расчет будем вести в режиме HFSS Design, использующий метод конечных элементов.Вторую катушку рассчитаем методом HFSS Design-IE, использующий метод моментов. В отличии от популярных у радиолюбителей симуляторов на основе ядра NEC, например MMANA, здесь сегментация идет не на отрезки провода, а по его поверхности на элементарные треугольные площадки. При такой сегментации для успешного расчета требуется не менее 8-16 Гб оперативной памяти компьютера. Запитаем катушку через короткие выводы от такого же источника. Поскольку катушка не заземлена, в этой модели первый резонанс — полуволновой.В результате исследования мы получили графики импеданса на зажимах источника относительно частоты. Из графиков видно, что у катушки не один, а множество резонансов. Из этого следует вывод, что наша катушка — это совсем не одиночный LC-контур с собственной индуктивностью и паразитной емкостью в виде сосредоточенных элементов, как принято считать, а длинная линия с распределенными параметрами. Такая линия состоит из одного провода, но это не должно никого смущать. То, что в даже одиночном проводе наблюдаются волновые резонансные явления, хорошо иллюстрирует пример полуволнового вибратора Герца. Ведь волновые явления как в длинных линиях, так и в вибраторе отображают тот факт, что электромагнитное взаимодействие распространяется с конечной скоростью. На то чтобы электромагнитное взаимодействие «добралось» от одного конца провода до другого затрачивается определенное время, и когда это время сравнимо с периодом колебаний рабочей частоты возникают явления резонанса. И катушка в этом плане недалеко ушла от вибратора, поскольку несмотря на малые ее габариты, длина провода, которым она намотана, может иметь величину сравнимую с длиной волны. Частоту собственного резонанса вибратора мы можем довольно легко определить зная его длину, учтя коэффициент укорочения. В катушке, кроме того, необходимо учесть связь между витками.

---

В учебниках по электродинамике [1] можно найти описание работы спиральных волноводов с поверхностными электромагнитными (ЭМ) волнами, распространяющимися вдоль провода спирали. Такие волноводы применяются как замедляющие структуры в спиральных антеннах и лампах бегущей волны. Длина одного витка и шаг намотки у них сравним с длиной волны. В частности, у спиральной антенны длина витка L равна длине волны, а шаг намотки p равен четверти длины волны.Фазовая скорость волны вдоль оси спирального волновода значительно ниже скорости света, на чем и основано его применение как замедляющей структуры.

[1]

где:

 

• v_ax — скорость волны вдоль оси спирали
• с — скорость света

Относительная фазовая скорость волны вдоль оси такого волновода зависит только от геометрии спирали и не зависит от частоты, поскольку влияние витков друг на друга минимально и ЭМ-волна распространяется вдоль провода такой спирали, так же как и у вибратора. Отметим, что фазовая скорость ЭМ волны относительно провода спирали в таком волноводе близка к скорости света.

---

В нашей же катушке, и длина отдельного витка, и даже длина всей намотки, и тем более шаг намотки намного меньше длины волны. В этом случае, кроме основной моды в таком спиральном волноводе существуют высшие моды колебаний, распространяющиеся непосредственно вдоль ее оси. Другими словами, ЭМ волна распространяется не только вдоль длины провода, но часть ее «перепрыгивает от витка к витку». Относительная фазовая скорость вдоль оси катушки определяется следующим приближенным выражением:

[2]

где:

 

• λ₀ — длина волны рабочей частоты в свободном пространстве

Как видно из формулы, скорость зависит от диаметра катушки, шага намотки и длины волны. По сути, катушка — тот же спиральный волновод с медленными волнами, но работающий в другом режиме колебаний. Во избежании различных спекуляций отметим то обстоятельство, что благодаря наличию высших мод, волна «добирается» до другого конца катушки быстрее чем непосредственно вдоль провода. Поэтому фазовая скорость волны относительно провода выше скорости света, причем в разы. Это не противоречит теории относительности. Достаточно упомянуть, что в полых волноводах фазовая скорость волны тоже выше скорости света. Для понимания этого кажущегося парадокса следует различать фазовую и групповую скорости электромагнитной волны. Для чего отсылаю к учебникам…

Катушка с одним заземленным концом резонирует на частотах nλ₀/4, где n – целое число, λ₀ — длина волны рабочей частоты и f_srf = v_ax/λ₀. Поэтому увеличение частоты собственного резонанса сводится к увеличению значения v_ax. Из-за наличия высших мод ЭМ-волны, частота первого резонанса катушки всегда выше частоты, рассчитанной исходя из длины провода. По этой же причине высшие по частоте резонансы не кратны первому и друг другу. При изменении шага намотки v_ax имеет максимум при шаге спирали примерно равном радиусу намотки (радиус a = D / 2). Однако катушки с большим шагом намотки (p ≈ a) не представляют практического интереса, поскольку имеют малую индуктивность. При увеличении шага намотки частота собственного резонанса катушки растет (при p < a), но рост этот идет за счет снижения величины индуктивности. При фиксированной индуктивности, если увеличивать шаг намотки, нам приходится добавлять витки и выигрыша мы практически не получаем.

У коротких катушек на каркасах большого диаметра последующие резонансы отстоят от первого далеко выше по частоте, что можно видеть по результатам HFSS моделирования:На частотах много ниже частоты первого резонанса пространственные задержки намного меньше периода колебаний, ЭМ-поле вокруг катушки представляет собой поле соленоида и скорость распространения волны вдоль ее оси можно не учитывать. В таком случае RLC-модель из сосредоточенных элементов будет вполне рабочей и достаточно точно отображает поведение катушки. Стоит только помнить, что паразитная собственная емкость — это вовсе не статическая емкость между витками. В таком режиме работают катушки из всех наших трех моделей в КВ диапазоне и ниже. Однако уже на частоте первого резонанса начинают проявляться волновые эффекты, связанные с ограниченной скоростью передачи электромагнитных взаимодействий и катушку следует рассматривать только как спиральный волновод. В этом случае RLC модель не только не годится для расчетов, но и приводит к неверному пониманию самого механизма возникновения резонансных явлений в катушке. В этой связи хочется отметить наличие в Сети ложной идеи о том, что в катушке одновременно происходят как волновой резонанс, так и LC-резонанс на сосредоточенных индуктивности и пресловутой «межвитковой емкости». Такое утверждение равносильно тому, что в катушке имеются два механизма распространения электромагнитных взаимодействий. Один происходит, как обычно, со скоростью света и определяет волновой резонанс. Второй осуществляется мгновенно с бесконечной скоростью в виртуальных сосредоточенных элементах катушки. Ведь фазовый сдвиг между током и напряжением в реактивных элементах — это совсем не то пространственное запаздывание, о котором идет речь. На самом деле катушка, как набор сосредоточенных RLC элементов, и катушка, как цепь с распределенными параметрами  — это две разные математические модели одной и той же реальной катушки. Первая модель не учитывает ограниченную скорость передачи взаимодействий, основана на предположении, что плотность тока во всех витках всегда одинакова, что не имеет место при собственном резонансе спирали. Поэтому эта модель ограничена и применима только на низких частотах. Вторая модель — более полная, учитывает то, что не учла первая и применима на любой частоте. В этом нет ничего необычного. Любая цепь, физические размеры которой сравнимы с длиной волны, не может рассматриваться как цепь из сосредоточенных элементов, в которой не учитывается ограниченная скорость передачи электромагнитных взаимодействий. Именно по этой причине О.Хевисайд и предложил в 1885 г. свою теорию длинных линий, а заодно кстати и само абстрактное математическое понятие «индуктивность». Как положительную реактивность.

Особо хотелось бы отметить следующий момент. На низких частотах, где, как мы выяснили, RLC модель справедлива, можно считать, что как индуктивность так и собственная емкость катушки не зависят от частоты, а определяются только геометрией намотки. Это общеизвестный факт, который зафиксирован например в формуле Нагаока. Однако реально параметры спиральной длинной линии зависят от частоты. Не только v_ax, но и погонная емкость и погонная индуктивность и, как следствие — величины собственной индуктивности и собственной емкости катушки в целом. Только на низких частотах эта зависимость пренебрежимо мала, а вот уже на частотах близких к первому резонансу значения индуктивности и собственной емкости катушки начинают заметно «плыть» по частоте. В итоге, мы сталкиваемся с ситуацией, что эти значения, измеренные или рассчитанные на низкой частоте, не пригодны для расчета частоты собственного резонанса катушки как LC резонанса по формуле Томсона. Расчет даст неверный результат! Неверный, Карл! Таким образом, мы приходим к выводу, что расчеты, основанные на понятии о LC-резонансе в катушке, полностью теряют смысл, что еще раз доказывает несостоятельность RLC-модели катушки не только для объяснения физических явлений при собственном резонансе, но и для расчетов в этой частотной области. Поэтому приходится прибегать к более сложному численному методу из работы [5], включающему в себя функции Бесселя и прочий суровый матан, что и делает Coil32.

Как видно из HFSS-моделей, у катушки как первый резонанс так и все последующие связаны исключительно с волновыми явлениями в катушке. Возможны практические случаи, когда катушка работает в диапазоне частот, в который попадает не только ее первый резонанс, но и более высокие. Очень хорошо такой случай описан в статье И.Гончаренко об анодном дросселе коротковолнового передатчика [2]. На этом примере хорошо видно, что для правильного понимания механизма резонансных явлений в катушке необходимо пользоваться теорией длинных линий.

 

Кроме фазовой скорости волны в катушке на частоту собственного резонанса оказывает влияние так называемый торцевой эффект, подобный хорошо известному аналогичному понятию из теории антенн, от которого зависит коэффициент укорочения вибратора. Этот эффект проявляется от того, что ЭМ-поле вокруг катушки занимает пространство большее, чем сама катушка. Наличие торцевого эффекта понижает резонансную частоту и этот эффект более выражен у коротких катушек с большим диаметром, что еще раз подтверждает родственную связь резонансных явлений в катушке и в вибраторе. Учитывая фазовую скорость вдоль оси катушки и явление торцевого эффекта мы можем рассчитать частоту собственного резонанса катушки по следующей весьма приближенной формуле от G3RBJ:

[3]

где:

 

• f_srf — частота собственного резонанса [МГц]
• ĺ_w — длина провода катушки с учетом торцевого эффекта [м]
• l_w — реальная длина провода катушки [м]
• D, p, l — диаметр, шаг и длина намотки, соответственно [м]
• 0,25 — коэффициент, определяющий четвертьволновый резонанс (для полуволнового — 0,5)

Если конструктору необходимо создать катушку, имеющую минимальные габариты и максимальную частоту собственного резонанса при заданной индуктивности, то наиболее оптимальна будет намотка с расстоянием между витками, равном диаметру провода,  при отношении l/D ≈ 1..1,5. Хотелось бы обратить внимание конструкторов, что здесь идет речь о вычислении собственной резонансной частоты «голой катушки в вакууме», т.е. одной проволочной спирали без учета влияния каркаса, сердечника, экрана, изоляции провода и т.п. Все эти, трудно поддаваемые учету факторы, приводят к уменьшению этой частоты. Причем влияние оказывает все — любой проводник, печатная плата, корпус конструкции. В наших HFSS-моделях влияющие факторы — это выводы спирали и, особенно, сплошная земля в 1-ой и 3-ей моделях. Даже если вы соберетесь измерить частоту собственного резонанса экспериментально, это будет непростой задачей, так как щупы измерительного оборудования также оказывают влияние, даже если катушка где то висит в воздухе!

---

Необходимо отметить, что строгого аналитического решения уравнений Максвелла для цилиндрической проволочной спирали не существует, поэтому в теории спиральный волновод представляют в виде эквивалентной модели из тонкостенного сплошного цилиндра с анизотропной проводимостью. Однако численные методы решения уравнений Максвелла (чем в принципе и занимается HFSS) приводят нас к вполне однозначным результатам. В итоге, следует иметь ввиду, что вышеприведенная простая аналитическая формула [3] является весьма приблизительной и не может быть применима к любой катушке с произвольной геометрией намотки. Поэтому в Coil32 расчет частоты собственного резонанса основан не на аналитическом, а на численном методе из работы [5], который проверен практическими измерениями. При этом не учитывается влияние экрана, каркаса и других факторов. Расчет имеет точность около 10% при 0,04 < l/D < 40. Для некоторых катушек, например для очень длинных соленоидов с большим числом витков, этот метод может давать неверный результат. На практике же следует придерживаться следующего простого условия: если длина провода, которым намотана катушка, меньше четверти длины волны на наивысшей рабочей частоте, то катушка будет работать ниже своего первого резонанса.

---

P.S: В заключении хотелось бы добавить несколько слов о концепции «Двух независимых резонансов в катушке — волновом и LC-резонансе». Эта концепция зиждется на трех ложных в своей основе предпосылках и поэтому в корне неверна:

1. Любую линейную замкнутую электрическую цепь можно представить как набор из сосредоточенных RLC-элементов. Основными законами этой цепи являются законы Ома и Кирхгофа. Любое изменение топологии цепи или добавление элементов в нее полностью меняет распределение токов и напряжений во всей цепи. Однако в концепции «двойного резонанса» длинная линия считается этаким себе «черным ящиком», равноценным какому-то особому четвертому сосредоточенному элементу, волновые процессы внутри которого существуют сами по себе. Но не стоит забывать, что другое название длинной линии — линия с распределенными параметрами, когда она представляется как цепь из бесконечного числа RLC-элементов. В ней также справедливы те же самые законы Ома и Кирхгофа, только представленные уже в дифференциальной форме. Мы просто перешли на более высокий уровень математической абстракции, при котором учитываются пространственно-временные задержки сигнала, но сути дела это не меняет. Поэтому, если мы подключим параллельно такой линии сосредоточенную емкость и будем считать, что характер распределения токов и напряжений внутри самой линии не изменится, мы просто отрицаем сами законы Ома и Кирхгофа. При этом не надо забывать, что характер распространения ЭМ-волны в линии и характер распределения токов и напряжений в ней — вещи жестко взаимосвязанные. Вывод — волновые процессы в линии не являются каким то особым ее свойством, которое существует само по себе, независимо от общих законов электрических цепей. Эти законы настолько фундаментальны, что в определенной мере отображены на еще более высоком уровне математической абстракции в уравнениях Максвелла, которые описывают свойства самой электромагнитной волны.
2. «При сворачивании линии в спираль мало что меняется». Это утверждение неверно. По крайней мере индуктивность значительно увеличивается, иначе зачем сворачивать? Кроме того, погонная емкость и погонная индуктивность такой линии уже становятся зависимыми от частоты. В результате, как отмечалось выше, формула Томсона для расчета частоты собственного резонанса в спиральной линии перестает работать.
3. В итоге, на основе этих неверных предпосылок, утверждается наличие двух независимых резонансов и нам выкатывают две формулы. Формулу Томсона, которая на самом деле в этом случае не работает, и формулу от Alane Payne (G3RBJ), которая, как мы отметили выше, является сильно приближенной. И по этим двум формулам уже идет развитие «теории двух независимых резонансов», которых в реальности не существует, что подтверждают и расчеты в HFSS и точные измерения. Повторюсь еще раз — все дело в разных математических моделях одной реальной катушки и разных уровнях математических абстракций в зависимости от конкретных условий расчета. Смешивать все это в одну кучу и подгонять под выдуманную теорию нельзя.

Ссылки по теме:

1. Техническая электродинамика, Семенов Н.А., Изд. «Связь» Москва, 1973, стр.318-323.
2. Моделирование анодного дросселя как распределенной структуры — И.Гончаренко 2007-2012
3. Паразитные резонансы в катушке П-контура — И.Гончаренко
4. Высокочастотные катушки, спиральные резонаторы и увеличение напряжения из-за когерентных пространственных мод 2001г. (Оригинал статьи здесь)
5. THE SELF-RESONANCE AND SELF-CAPACITANCE OF SOLENOID COILS — applicable theory, models and calculation methods. By David W Knight (G3YNH)
6. The self-resonance and self-capacitance of solenoid coils by David W Knight — основная статья с массой полезных ссылок по теме, в том числе на экспериментальные исследования с наглядными фото (G3YNH)
7. SELF-RESONANCE IN COILS and the self-capacitance myth. By Alane Payne (G3RBJ)
8. О собственной емкости катушки.

Нахождение резонансной емкости

В общем случае резонанс напряжений в цепи, содержащей реактивные элементы, наступает при равной нулю мнимой составляющей комплексного сопротивления Z_Im=0. Рассмотрим это на примере простой цепи, содержащей последовательно соединённые резистор, катушку и конденсатор.

R	C	L

Найдём комплексное сопротивление ветви:

Таким образом, в рассматриваемой цепи мнимая составляющая комплексного сопротивления равна нулю при равенстве сопротивлений конденсатора и катушки:

Или, если выразить реактивные сопротивления через параметры LиC:

Нетрудно увидеть, что при резонансе в рассматриваемой цепи сопротивление минимально. В соответствии с законом Ома: , ток при резонансе максимален.

Для экспериментального определения величины ёмкости, при которой в цепи наступит резонанс, пользуются зависимостью тока от ёмкости.

В заданной цепи изменяют ёмкость в определённых пределах, и снимают значение величины тока в ветви с конденсатором. Точка, в которой ток максимален показывает резонансную ёмкость.

§2.9. Примеры и задачи

2.9.1. Синусоидальные величины и их символическое изображение

Мгновенные значения синусоидальной величины определяются выражением:

,

где – амплитуда;

– действующее значение;

– угловая частота, [с^-1];

– линейная частота, [Гц];

– период колебаний [c];

 – начальная фаза, [рад].

Расчет цепей переменного тока облегчается, если изображать гармонические токи, напряжения и ЭДС векторами на комплексной плоскости.

Совокупность векторов, изображающих синусоидальные функции в заданный момент времени, называется векторной диаграммой.

Комплексное число может быть представлено в алгебраической и показательной форме:

.

Переход из показательной формы в алгебраическую форму осуществляется по формуле Эйлера:

.

При обратном переходе: , если вещественная часть алгебраической формы положительная, тоа если вещественная часть отрицательная, то

.

Комплексная синусоидальная функция представляется в виде вращающегося вектора на комплексной плоскости:

;

,

,

(при t = 0).

Мгновенное значение синусоидальной функции есть проекция вращающегося вектора на мнимую ось:

.

Обозначения:

i, u, e – мгновенные значения тока, напряжения, ЭДС.

I_m,U_m,E_m– комплексные амплитудные значения тока, напряжения, ЭДС.

I,U,E– комплексные действующие значения тока, напряжения, ЭДС.

Примеры

1.1. Дано синусоидальное напряжение .

Записать выражения для комплексного амплитудного и действующего значения.

Решение:

;

.

1.2. Комплексное действующее значение тока .

Записать выражение для мгновенных значений тока.

Решение:

;

.

2.10.2. Расчет линейных цепей с гармоническими источниками электрической энергии

2.10.2.1. Закон Ома в комплексной форме

Таблица 2.1.

Элемент	Связь между мгновенными значениями напряжения и тока	Связь между комплексными действующими значениями напряжения и тока	Векторная диаграмма	Применение
				Напряжение совпадает по фазе с током.
				Напряжение опережает ток на .
				Напряжение отстает от тока на .

2.10.2.2. Комплексное сопротивление двухполюсника

– активное сопротивление резистораR, [Ом];

– реактивное сопротивление катушки, [Ом];

– индуктивность катушки, [Гн];

– угловая частота, [с ^-1];

– реактивное сопротивление конденсатора, [Ом];

– емкость конденсатора, [Ф];

– комплексное сопротивление резистора;

– комплексное сопротивление катушки;

– комплексное сопротивление конденсатора.

Для цепи (рис. 1) комплексное сопротивление:

где – модуль комплексного сопротивления или полное сопротивление;

– угол сдвига фаз между напряжением и током.

6. Добротность и полоса пропускания резонансной цепи | 6. Резонанс | Часть2

6. Добротность и полоса пропускания резонансной цепи

Добротность и полоса пропускания резонансной цепи

Добротность (Q) резонансной цепи характеризует ее качество. Более высокое значение этого показателя соответствует более узкой полосе пропускания (что весьма желательно для многих схем). Если говорить проще, то добротность представляет собой отношение энергии, накопленной в реактивном сопротивлении цепи, к энергии, рассеиваемой активным сопротивлением этой цепи:

 

 

Данная формула применима к последовательным резонансным цепям, а также к параллельным резонансным цепям, если сопротивление в них включено последовательно с катушкой индуктивности. Действительно, в практических схемах нас часто беспокоит сопротивление катушки индуктивности, которое ограничивает добротность. Заметьте: Некоторые учебники в формуле «Q» для параллельных резонансных схем меняют местами X и R. Это верно для большого значения R, включенного параллельно с C и L. Наша формула верна для небольшого значения R, включенного последовательно с L.

Практическое применение добротности (Q) заключается в том, что напряжение на L или С в последовательной резонансной цепи в Q раз больше общего приложенного напряжения. В параллельной резонансной цепи ток через L или С в Q раз больше общего приложенного тока.

 

Последовательные резонансные цепи.

 

Резонанс последовательной LC цепи выражается в том, что полный импеданс этой цепи становится наименьшим и равным активному сопротивлению  (которое имеет сравнительно небольшую величину), а ток становится максимальным. Условием резонанса является равенство индуктивного и емкостного сопротивлений X_L = X_C. Когда частота генератора больше частоты контура, индуктивное сопротивление преобладает над емкостным и контур представляет для генератора сопротивление индуктивного характера. Если частота генератора меньше частоты контура, то емкостное сопротивление больше индуктивного и контур для генератора является сопротивлением емкостного характера.

 

 

Ток при резонансе имеет максимальное значение, а импеданс — минимальное. Величина тока определяется величиной сопротивления. На частоте, выше или ниже резонансной, импеданс увеличивается.

 

 

Пиковое значение тока при резонансе можно изменить путем подбора величины последовательного резистора, которая, в свою очередь, изменяет добротность. Все эти значения оказывают влияние на ширину полосы пропускания. Контур с низким сопротивлением и высокой добротностью имеет более узкую полосу пропускания, чем контур с высоким сопротивлением и низкой добротностью. Зависимость полосы пропускания контура от его резонансной частоты и добротности определяется следующей простой формулой:

 

 

 

Ширина полосы пропускания обычно определяется на уровне 0,707 от максимальной амплитуды тока. Уровню 0,707 соответствуют точки половинной мощности, равные P = I²R, (0,707)² = (0,5)

 

 

           Ппр = Δf = fв-fн = fc/Q 
           Где: fв = верхняя граница полосы пропускания,  
fн = нижняя граница полосы пропускания 
 
           fн = fc - Δf/2 
           fв = fc + Δf/2
           Где:  fc = резонансная частота

 

На представленном выше графике 100% тока — это 50мА. Уровню 70,7% соответствует величина тока 0,707(50мА) = 35,4 мА. Верхняя и нижняя границы полосы пропускания составляют 355 и 291 Гц соответственно. Ширина полосы пропускания равна 64 Гц, а точки половинной мощности составляют ± 32 Гц от центра резонансной частоты:

 

           Ппр = Δf = fв-fн = 355-291 = 64 
           fн = fc - Δf/2 = 323-32 = 291 
           fв = fc + Δf/2 = 323+32 = 355 

 

Поскольку П_пр = f_c/Q:

 

           Q = fc/Ппр = (323 Гц)/(64 Гц) = 5

 

Параллельные резонансные цепи

 

Резонанс параллельной LC цепи выражается в том, что полный импеданс этой цепи (между точками разветвления) становится максимальным, а ток принимает минимальное значение. Условием резонанса, как и в последовательной LC цепи,  является равенство индуктивного и емкостного сопротивлений X_L = X_C. Когда частота генератора больше частоты контура, емкостное сопротивление преобладает над индуктивным и контур представляет для генератора сопротивление емкостного характера. Если частота генератора меньше частоты контура, то индуктивное сопротивление больше емкостного и контур для генератора является сопротивлением индуктивного характера.

 

 

Импеданс при резонансе имеет максимальное значение, но на частотах, выше или ниже резонансной, он уменьшается. Поскольку напряжение пропорционально импедансу (U = IZ), при резонансе оно также имеет максимальное значение.

 

 

Низкая добротность (Q), обусловленная высоким сопротивлением (последовательно с катушкой индуктивности), производит низкий пик с широкой полосой пропускания. И наоборот, высокая добротность, обусловленная низким сопротивлением, производит высокий пик с узкой полосой пропускания. Высокая добротность достигается применением катушек индуктивности имеющих большой диаметр и малое сопротивление провода.

 

 

Ширина полосы пропускания кривой параллельного резонанса измеряется между точками половинной мощности. Поскольку мощность пропорциональна U², этим точкам соответствует уровень 70,7% от максимальной амплитуды напряжения ^{((0,707)2 = 0,5). Так как напряжение пропорционально импедансу, мы можем воспользоваться графиком импеданса.}

 

 

На представленном выше графике 100% сопротивления — это 500 Ом. Уровню 70,7% соответствует величина сопротивления 0,707(500) = 354 Ом. Верхняя и нижняя границы полосы пропускания составляют 343 и 281 Гц соответственно. Ширина полосы пропускания равна 62 Гц, а точки половинной мощности составляют ± 31 Гц от центра резонансной частоты:

 

           Ппр = Δf = fв-fн  = 343-281 = 62 
           fн = fc - Δf/2 = 312-31 = 281 
           fв = fc + Δf/2 = 312+31 = 343 

           Q = fc/Ппр = (312 Гц)/(62 Гц) = 5

Измерение ТС параметров динамиков

 

 

Более подробнее о физическом смысле параметров Тиля-Смола читайте в статье Параметры Тиля � Смолла: три карты акустики

 

 

Измерение параметров Тиля-Смолла

 

Внимание! Приведенная ниже методики действенна только для измерения параметров динамиков с резонансными частотами ниже 100Гц, на более высоких частотах погрешность возрастает.

Для получения максимально достоверных результатов все измерения рекомендуется производить несколько раз (3-5раз), затем за результат принимается средне-арифметическое значение.

 

Перед измерением параметров динамик необходимо �размять�. Дело в том, что у неработающего определенное время динамика или у нового динамика параметры будут отличаться, от тех которые мы измерим после того как динамик отыграет определенное время и будет регулярно работать. Поэтому смысл размятия динамика и заключается в получении достоверных параметров измерений. Бытует множество мнений как и сколько надо разминать: просто музыкой, синусоидальным сигналом (синусом) на частоте резонанса динамика Fs, синусом на 1000Гц, гонять синусом на разных частотах, белым и розовым шумом,� использовать тестовые диски.

Как разминать решать Вам, — это дело Ваших возможностей и времени, но разминать обязательно нужно.

От себя посоветую разминать в течении суток в различных комбинациях вышепречисленных способов, начать стоит с синуса частоты собственного резонанса Fs (взятую из паспорта динамика) на максимальное количество времени, потом уже использовать остальные способы. Можно использовать тестовые диски, лучше те которые содержат как музыкальные так и технические треки, т.е. сгенерированные сигналы различной формы, частоты и мощности, причем начать лучше с технических треков. Желательно разминать динамик на 50-100% от номинальной мощности, всё зависит от ваших условий, ушей и нервов.

 

 

Самыми основными параметрами, по которым можно рассчитать и изготовить акустическое оформление (корпус, ящик) являются:

• Резонансная частота динамика Fs (Герц)
• Эквивалентный объем Vas (литров или кубических футов)
• Полная добротность Qts
• Сопротивление постоянному току Re (Ом)

 

Для более серьезного подхода понадобится еще знать:

• Механическую добротность Qms
• Электрическую добротность Qes
• Площадь диффузора Sd (м²) или его диаметр D (см)
• Чувствительность SPL (dB)
• Индуктивность Le (Генри)
• Импеданс Z (Ом)
• Пиковую мощность Pe (Ватт)
• Массу подвижной системы Mms (г)
• Относительную жесткость Cms (метров/ньютон)
• Механическое сопротивление Rms (кг/сек)
• Двигательную мощность BL

 

 

Измерение резонансной частоты Fs, добротности динамика Qts

и ее составляющих электрической и механической добротности Qes, Qms

 

Метод 1

 

Для проведения измерений этих параметров вам понадобится следующее оборудование:

1. Вольтметр
2. Генератор сигналов звуковой частоты (это можно сделать при помощи компьютера и этой программы)
3. Частотомер
4. Мощный (не менее 2 ватт) резистор сопротивлением 1000 ом
5. Точный (+- 1%) резистор сопротивлением 10 ом
6. Провода, зажимы и прочая дребедень для соединения всего этого в единую схему.

 

Конечно, в этом списке возможны изменения. Например, большинство генераторов имеют собственную шкалу частоты и частотомер не является в таком случае необходимостью. Вместо генератора можно также использовать звуковую плату компьютера и соответствующее программное обеспечение (например, это), способное генерировать синусоидальные сигналы от 0 до 200Гц требуемой мощности. Либо мне еще приходилось делать так, когда не было рядом компьютера: я нарезал на диск треки с частотами от 20-120Гц, потом крутил его на DVD подключенный усилителю и затем уже подключал подвешенный динамик через сопротивление.

Схема для измерений

 

Калибровка:

Для начала необходимо откалибровать вольтметр. Для этого вместо динамика подсоединяется сопротивление 10 Ом и подбором напряжения, выдаваемого генератором, надо добиться напряжения 0,01 вольта. Если резистор другого номинала, то напряжение должно соответствовать 1/1000 номинала сопротивления в Омах. Например для калибровочного сопротивления 4 Ома напряжение должно быть 0,004 вольта.

 

Запомните! После калибровки регулировать выходное напряжение генератора (усилителя) НЕЛЬЗЯ до окончания всех измерений.

 

Определение Fs и Rmax

Динамик при этом и всех последующих измерениях должен находиться в свободном пространстве, обычно его подвешивают (обычно на люстре) подальше от стен и различныз предметов. Резонансная частота динамика находится по пику его импеданса (Z-характеристике). Для ее нахождения плавно увеличивайте частоту генератора, начиная примерно с 20Гц, и смотрите на показания вольтметра. Та частота, на которой напряжение на вольтметре будет максимальным (дальнейшее изменение частоты будет приводить к падению напряжения) и будет являться частотой основного резонанса для этого динамика. Для динамиков диаметром больше 16см эта частота должна лежать ниже 100Гц. Не забудьте записать не только частоту, но и показания вольтметра. Умноженные на 1000, они дадут сопротивление динамика на резонансной частоте Rmax, необходимое для расчета других параметров.

 

Определение Qms, Qes и Qts

Эти параметры определяются по следующим формулам:

Как видно, это последовательное нахождение дополнительных параметров Ro, Rx и измерение неизвестных нам ранее частот F₁ и F₂. Это частоты, при которых сопротивление динамика равно Rx. Поскольку Rx всегда меньше Rmax, то и частот будет две — одна несколько меньше Fs, а другая несколько больше. Вы можете проверить правильность своих измерений следующей формулой:

Если расчетный результат отличается от найденного ранее больше, чем на 1 герц, то нужно повторить все сначала и более аккуратно.

 

Определение сопротивление обмотки головки постоянному току Re

Теперь, подсоединив вместо калибровочного сопротивления динамик и выставив на генераторе частоту, близкую к 0 герц, мы можем определить его сопротивление постоянному току Re. Им будет являться показание вольтметра, умноженное на 1000. Впрочем, Re можно замерить и непосредственно омметром.

 

 

 

 

Метод 2

 

Схема измерений такая же как и в первом методе, элементы то же такие же: резистор на 1кОм и — генератор � либо генератор звуковой частоты способный выдавать напряжение 10-20В, либо сочетание генератор-усилитель, удовлетворяющее тому же требованию.

Размещаем динамик вдали от стен, потолка и пола (часто рекомендуют подвешивать). Подключаем вольтметр к точкам А и С (т.е. к выходу усилителя) , и устанавливаем напряжение равным 10-20 В на частоте 500-1000 Гц.

Подключаем вольтметр к точкам В и С (т.е. непосредственно к контактам динамика) �и изменяя частоту генератора находим частоту, на которой показания вольтметра максимальны, (как показано на рисунке ниже). Это и есть частота собственного резонанса динамика Fs. Записываем Fs и Us-показания вольтметра.

Изменяя частоту вверх относительно Fs, находим частоты, на которых показания вольтметра постоянны и значительно меньше Us (при дальнейшем повышении частоты напряжение опять начнет увеличиваться, пропорционально увеличению импеданса динамика). Запишем это значение, Um.

График импеданса динамика в свободном пространстве и в закрытом ящике выглядит приблизительно так.

 

Вычисляем напряжение U₁₂ по формуле:

 

Изменяя частоту, добиваемся показаний на вольтметре соответствующие напряжению U₁₂ , находим частоты F1 и F2.

 

Вычисляем Акустическую или механическую добротность по формуле:

Электрическую добротность:

 

И, на конец, полную добротность:

 

 

 

 

Метод 3 — Измерения параметров тиля-смолла при помощи фазоинвертора

 

Схема измерений такая же как и в первом методе, элементы то же такие же: калибровочного резистора R_k номиналом 10 Ом и активное сопротивление R, задающее ток в цепи, номиналом 1кОм. Можно взять сопротивления R_k и R других номиналов, выполняя условия:

— R_k — может быть любым, но близким к R_e

_— R/R_e > 200

где R_e — сопротивления постоянному току звуковой катушки

 

Измерения начинаются с наиболее точного определения сопротивления постоянному току звуковой катушки R_e и калибровочного резистора R_k при помощи цифрового вольтметра или мультиметра.

Затем вместо динамика включаем калибровочный резистор R_k и измеряем напряжение U_k на нем. Напряжение, соответствующее сопротивлению звуковой катушки постоянному току, находим по формуле:

 

Далее подключаем подвешенную, как можно дальше от других предметов, головку вместо калибровочного резистора. Плавно меняя частоту генератора, находим значение собственной резонансной частоты головки f_s, при которой показания вольтметра максимальны. Для повышения точности расчетов это и все последующие измерения проводим пять раз и в качестве результата принимаем среднее арифметическое значение измеренных величин.

Далее вычисляем U_1,2 по следующей формуле U_1,2=0.7U_s

Предположительно это напряжение соответствуют максимальной крутизне кривой [Z]. Далее определяем частоты f₁, f₂ ниже и выше резонансной, при которых напряжение на головке равно вычисленному U_1,2. Поскольку кривая модуля полного электрического сопротивления [Z] симметрична в логарифмическом масштабе, то можно сделать первую проверку выполненных измерений.

 

Расхождение с ранее измеренной частотой резонанса должно быть не более 1-1,5 Гц.

Теперь можно найти Q^�_ms , Q^�_es.

 

 

Далее помещаем головку в ФИ ящик. Настройка тоннеля значения не имеет или его вообще может не быть — только отверстие диаметром примерно 5 см. При выборе объема измерительного ящика можно воспользоваться рекомендациями, которые дает JBL SS.

Убеждаемся, что характеристика [Z] имеет вид как на рисунке приведенном ниже. Возникающие в некоторых случаях дополнительные максимумы и минимумы свидетельствуют о наличии щелей или воздушных пазух.

Находим частоты f_l, f_b, f_h, соответствующие максимуму и минимуму показаний вольтметра. Отмечаем также напряжение U_b в минимуме на частоте f_b. Резонансная частота головки с учетом присоединенной массы воздуха при работе в ФИ:

 

За счет увеличения соколеблющейся массы резонансная частота fs должна понизиться. Здесь можно провести еще одну проверку. Частоты f_s и f^�_s должны различаться не более чем на 5-10%. Эквивалентный объем подвижной системы головки и уточненные значения добротности находим по следующим формулам.

Формула для расчета полной добротности Q_ts справедлива только при работе от усилителя с нулевым выходным сопротивлением.

 

 

 

Измерения эквивалентного объема Vas

 

Есть несколько способов измерения эквивалентного объема, но в домашних условиях проще использовать два: метод «добавочной массы» и метод «добавочного объема». Первый из них требует из материалов несколько грузиков известного веса. Можно использовать набор грузиков от аптечных весов или воспользоваться старыми медными монетками 1,2,3 и 5 копеек, поскольку вес такой монетки в граммах соответствует номиналу. Второй метод требует наличия герметичного ящика заранее известного объема с соответствующим отверстием под динамик.

 

 

Определение эквивалентного объема методом добавочной массы

 

Для начала нужно равномерно нагрузить диффузор грузиками и вновь измерить его резонансную частоту, записав ее как F’s. Она должна быть ниже, чем Fs. Лучше если новая резонансная частота будет меньше на 30%-50%. Масса грузиков берется приблизительно 10 граммов на каждый дюйм диаметра диффузора. Т.е. для 12″ головки нужен груз массой около 120 граммов (1 дюйм равен 2,54 см). Я советую всё же использовать не монеты, ибо к примеру на 100грамм понадобится аж 20штук� 5-копеечных монет! А это согласитесь не очень удобно. Я использую обычный пластилин необходимый вес которого я подгоняю при помощи аптечных весов.

Итак эквивалентный объем вычисляется по формуле:

 

 

где: Sd — эффективная излучающая поверхность диффузора, м²;

������ Cms — относительная жесткость

 

Излучающая поверхность диффузора для самых низких частот (в зоне поршневого действия) она совпадает с конструктивной и равна:

 

Радиусом R в данном случае будет являться половина расстояния от середины ширины резинового подвеса одной стороны до середины резинового подвеса противоположной. Это связано с тем, что половина ширины резинового подвеса также является излучающей поверхностью. Обратите внимание что единица измерения этой площади — квадратные метры. Соответственно и радиус нужно в нее подставлять в метрах.

 

Рассчитываем относительную жесткость Cms на основе полученных результатов по формуле:

 

, м/Н (метров/Ньютон)

 

 

где М — масса добавленных грузиков в килограммах.

 

Определение эквивалентного объема методом добавочного объема

 

Для определения эквивалентного объема динамика методом добавочного объема герметичный измерительный ящик с круглой дыркой совпадающей по размеру с диаметром диффузора динамика. Объем ящика лучше выбрать ближе к тому, в котором мы потом собираемся этот динамик слушать. Нужно герметично закрепить динамик в измерительном ящике. Лучше всего это сделать магнитом наружу, поскольку динамику все равно, с какой стороны у него объем, а вам будет проще подключать провода. Да и лишних отверстий при этом меньше. герметизируем все щели.

Затем нужно произвести измерения Fс (резонансной частоты динамика в закрытом ящике) и, соответственно, вычислить механическую и электрическую добротность Qmc и Qec и добротность динамика в измерительном ящике Qts’ (Qtс). После чего уже вычисляем эквивалентный объем по формуле:

 

 

Практически с теми же результатами можно использовать и более простую формулу:

 

где: Vb — объем измерительного ящика, м³.

 

Выполняем проверку: вычисляем

 

и если измеренная в ящике Qts�=Qtc, ну или почти равна, значит — все сделано правильно, и можно переходить к проектированию акустической системы.

 

 

 

 

Выводы

 

Итак, мы нашли и рассчитали несколько основных параметров и можем на их основании делать некоторые выводы:

 

1.����� Если резонансная частота динамика выше 50Гц, то он имеет право претендовать на работу в лучшем случае как мидбас. О сабвуфере на таком динамике можно сразу забыть.

2.����� Если резонансная частота динамика выше 100Гц, то это вообще не низкочастотник. Можете использовать его для воспроизведения средних частот в трехполосных системах.

3.����� Если соотношение Fs/Qts у динамика составляет менее 50-ти, то этот динамик предназначен для работы исключительно в закрытых ящиках. Если больше 100 — исключительно для работы с фазоинвертором или в бандпассах. Если же значение находится в промежутке между 50 и 100, то тут нужно внимательно смотреть и на другие параметры — к какому типу акустического оформления динамик тяготеет.

 

Лучше всего для этого использовать специальные компьютерные программы, способные смоделировать в графическом виде акустическую отдачу такого динамика в разном акустическом оформлении. Правда при этом не обойтись без других, не менее важных параметров — Sd, Cms и Lе.

 

Полученных в результате всех этих измерений данных достаточно для дальнейшего расчета акустического оформления низкочастотного звена достаточно высокого класса.

 

 

 

Нахождение дополнительных параметров Сms, Re, Sd, Lе

 

Определение относительной жесткости Cms

 

Определение относительной жесткости описано в методике определения эквивалентного объема Vas методом добавочного массы (см. выше), и вычисляется по формуле:

 

, м/Н (метров/Ньютон)

 

где:

М � масса грузика, г;

Fs � резонансная частота головки, Гц;

F�s � резонансная частота головки в нагруженном состоянии под грузом М, Гц;

 

 

Нахождение сопротивления обмотки головки постоянному току Re

 

Сопротивление головки постоянному току Re определяется на частоте близкой к 0 Гц или измеряется и непосредственно омметром.

 

 

Нахождение площади диффузора Sd

Это так называемая эффективная излучающая поверхность диффузора. Для самых низких частот (в зоне поршневого действия) она совпадает с конструктивной и равна:

 

Радиусом R в данном случае будет являться половина расстояния от середины ширины резинового подвеса одной стороны до середины резинового подвеса противоположной. Это связано с тем, что половина ширины резинового подвеса также является излучающей поверхностью. Обратите внимание что единица измерения этой площади — квадратные метры. Соответственно и радиус нужно в нее подставлять в метрах.

 

 

Нахождение индуктивности катушки динамика Lе

 

Для этого нужны результаты одного из отсчетов из самого первого теста. Понадобится импеданс (полное сопротивление) звуковой катушки на частоте около 1000Гц. Поскольку реактивная составляющая (X_L) отстоит от активной Re на угол 90⁰, то можно воспользоваться теоремой Пифагора:

 

Поскольку Z (импеданс катушки на определенной частоте) и Re (сопротивление катушки по постоянному току) известны, то формула преобразуется к:

 

Найдя реактивное сопротивление X_L на частоте F можно рассчитать и саму индуктивность по формуле:

 

 

 

 

Более подробнее о физическом смысле параметров Тиля-Смола читайте в статье Параметры Тиля � Смолла: три карты акустики

 

Измерить параметры головок также можно при помощи программы JBL SpeakerShop, все вычисления при этом программа выполнит сама, об этом здесь здесь