Радиус окружности — что такое, формула, как найти ⚪

Основные понятия

Прежде чем погружаться в последовательность расчетов, важно понять разницу между понятиями.

Окружность — замкнутая плоская кривая, все точки которой равноудалены от центра, которая лежит в той же плоскости. Если говорить проще, то это замкнутая линия, как, например, обруч и кольцо.

Круг — множество точек на плоскости, которые удалены от центра на расстоянии равном радиусу. Иначе говоря, плоская фигура, ограниченная окружностью, как мяч и блюдце.

Радиус — это отрезок, который соединяет центр окружности и любую точку на ней. Общепринятое обозначение радиуса — латинская буква R.

Возможно тебе интересно узнать — как найти длину окружности?

Формула радиуса окружности

Определить способ вычисления проще, отталкиваясь от исходных данных. Далее рассмотрим девять формул разной степени сложности.

Если известна площадь круга

R = √ S : π, где S — площадь круга, π — это константа, которая выражает отношение длины окружности к диаметру, она всегда равна

3,14.

Если известна длина

R = P : 2 * π, где P — длина (периметр круга).

Если известен диаметр окружности

R = D : 2, где D — диаметр.

Диаметр — отрезок, который соединяет две точки окружности и проходит через центр. Радиус всегда равен половине диаметра.

 

Если известна диагональ вписанного прямоугольника

R = d : 2, где d — диагональ.

Диагональ вписанного прямоугольник делит фигуру на два прямоугольных треугольника и является их гипотенузой — стороной, лежащей напротив прямого угла. Если диагональ неизвестна, теорема Пифагора поможет её вычислить:

d = √ a² + b², где a, b — стороны вписанного прямоугольника.

Если известна сторона описанного квадрата

R = a : 2, где a — сторона.

Сторона описанного квадрата равна диаметру окружности.

Если известны стороны и площадь вписанного треугольника

R = (a * b * c) : (4 * S), где a, b, с — стороны, S — площадь треугольника.

Если известна площадь и полупериметр описанного треугольника

R = S : p, где S — площадь треугольника, p — полупериметр треугольника.

Полупериметр треугольника — это сумма длин всех его сторон, деленная на два.

Если известна площадь сектора и его центральный угол

R = √ (360° * S) : (π * α), где S — площадь сектора круга, α — центральный угол.

Площадь сектора круга — это часть S всей фигуры, ограниченной окружностью с радиусом.

Если известна сторона вписанного правильного многоугольника

R = a : (2 * sin (180 : N)), где a — сторона правильного многоугольника, N — количество сторон.

В правильном многоугольнике все стороны равны.

Скачать онлайн таблицу

У каждой геометрической фигуры много формул — запомнить все сразу бывает действительно сложно. В этом деле поможет регулярное решение задач и частый просмотр формул. Можно распечатать эту таблицу и использовать, как закладку в тетрадке или учебнике, и обращаться к ней по необходимости.

 

Урок 4. равномерное движение точки по окружности — Физика — 10 класс

Физика, 10 класс

Урок 04.Равномерное движение точки по окружности

Перечень вопросов, рассматриваемых на уроке:

1. Равномерное движение точки по окружности и его характеристики.
2. Центростремительное ускорение.

Глоссарий по теме

Криволинейное движение – это движение по дугам окружностей разных радиусов.

Ускорение – это векторная величина, равная отношению изменения скорости к промежутку времени, в течение которого это изменение произошло, при ∆t → 0

Равномерное движение точки по окружности — движение точки с постоянной по модулю скоростью (ν = const) по траектории, представляющей собой окружность.

Ключевые слова

Криволинейное движение; движение по окружности; скорость; радиус кривизны; изменение скорости; центростремительное ускорение.

Основная и дополнительная литература по теме урока:

Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика.10 класс. Учебник для общеобразовательных организаций М.: Просвещение, 2016. С.55-56

Марон Е.А., Марон А.Е. Сборник качественных задач по физике. М., Просвещение, 2006

Рымкевич А.П. Сборник задач по физике. 10-11 класс.-М.:Дрофа,2009.-С.20-22

Открытые электронные ресурсы:

http://kvant.mccme.ru/1986/11/kinematika_vrashchatelnogo_dvi.htm

Теоретический материал для самостоятельного изучения

1. Мы уже знакомы с равноускоренным движением. Как же меняются скорость и ускорение при криволинейном движении? Сегодня рассмотрим равномерное движение по окружности, узнаем, что такое центростремительное ускорение.

Если траектория движения тела прямая линия, то движение прямолинейное; если траектория кривая линия – криволинейное движение. Напомним, что траектория – это линия, вдоль которой двигалось тело.

При изучении равноускоренного движения мы заметили, что в некоторых случаях тело движется по прямой, например свободное падение тел, а в некоторых по кривой – тело, брошенное под углом к горизонту.

Рассмотрим движение тела, брошенного под углом к горизонту. Траекторией является парабола.

Возьмем разные точки на линии и нарисуем векторы скорости . Вектор скорости направлен по касательной, а ускорение свободного падения направлен вниз.

Векторы и не лежат на одной прямой, угол между ними не равен нулю.

Это естественно, так как, если ускорение образует угол со скоростью, то изменение скорости направлено не так, как скорость. Это приводит к изменению направления скорости. Изменение скорости направлено как ускорение. Скорость через некоторый промежуток времени образует некоторый угол с Итак, сформулируем первый вывод: если угол между векторами скорости и ускорения не равен нулю, то движение будет криволинейным.

2.Может ли быть движение одновременно равномерным и криволинейным? Да, например, движение по окружности.

Равномерное движение точки по окружности — это движение точки с постоянной по модулю скоростью (v = const) по траектории, представляющей собой окружность. Но, скорость – это векторная величина, а для векторной величины одинаково важны и модуль, и направление. Т.к. при движении по окружности скорость всегда направлена по касательной к траектории движения, то по направлению она изменяется. Если есть изменение скорости (точнее её направления), значит, есть ускорение

Сформулируем второй важный вывод: любое криволинейное движение является движением с ускорением, потому что меняется направление вектора скорости.

Решим задачу: найдем ускорение тела, равномерно движущегося по окружности.

Рассмотрим равномерное движение тела по окружности с центром в точке О. В какой-то момент времени, скорость тела в точке А была_.

Модули скоростей равны:

но вектора скоростей не равны.

Поэтому построим вектор для тела, движущегося по окружности. Перенесем вектор в начало вектораи найдем разность векторов.

направлен в сторону.

Вспомним, что векторнаправлен по касательной_, а касательная перпендикулярна радиусу окружности. Проведем радиусы к обеим точкам и обозначим угол между ними через ?.

Что можно сказать об угле между векторами ? Он равен малому углу, как углы с взаимно перпендикулярными сторонами.

Рассмотрим равнобедренный треугольник со сторонами , . Углы у основания равны.

Если угол φ стремится к нулю, то углы у основания совпадут и станут равными 90

0

Вектор будет перпендикулярен вектору в пределе_, а значит вектор ускорения тоже перпендикулярен т.е направлен по радиусу к центру окружности. Поэтому часто его называют центростремительным ускорением

Теперь следующая задача: как найти модуль вектора ускорения. Давайте рассмотрим два треугольника: треугольник, образованный векторами и треугольник, образованный радиусами и хордой. У этих треугольников углы при вершинах равны, они равнобедренные. Треугольники подобны и, следовательно, выполняются соотношения подобия.

Промежуток времени мал, поэтому очень мал и угол при вершине, в пределе он стремится к нулю.

Тогда можно сказать, что длина хорды s равна длине дуги АВ при

Длина дуги АВ это путь, пройденный точкой от А до В,

тогда запишем:

Умножим наи получим:

В левой части мы получили отношение изменения скорости за некоторый промежуток времени к этому промежутку времени т.е. ускорение:

Равномерное движение точки по окружности является движением с переменным ускорением и переменной скоростью. Модули скорости и ускорения остаются постоянными

1. Криволинейное движение — это движение по дугам окружностей разных радиусов.

А если меняется радиус, то меняется и центростремительное ускорение. Чем меньше радиус, тем больше ускорение при одинаковой скорости.

Всегда при равномерном криволинейном движении вектор ускорения перпендикулярен вектору скорости, поэтому центростремительное ускорение иногда называют нормальным ускорением, от слова нормаль, т.е. перпендикуляр.

Основные выводы:

— движение криволинейное, так как траекторией является окружность;

— движение равномерное, так как модуль скорости не меняется;

— вектор скорости направлен по касательной к окружности;

-вектор ускорения направлен к центру окружности;

— модуль центростремительного ускорения равен:

Примеры и разбор решения заданий

1.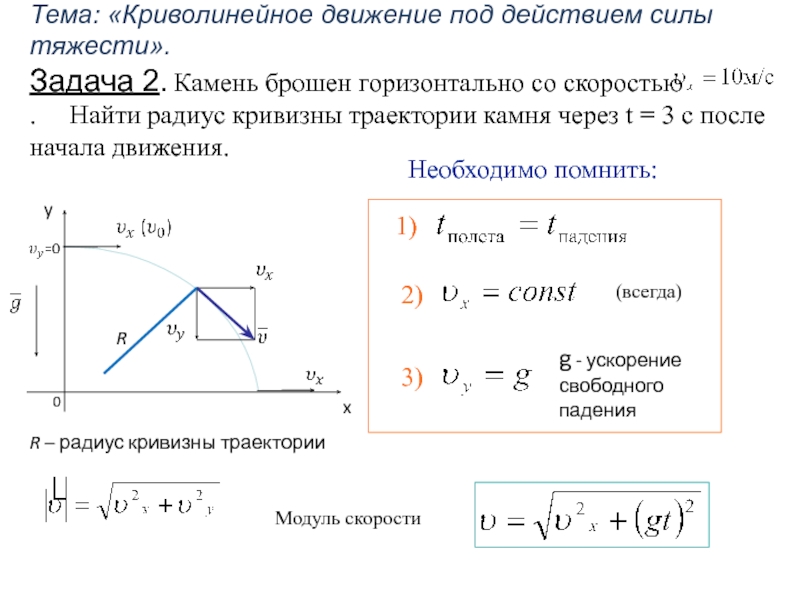 Велосипедист движется по закруглению дороги радиусом 50 м со скоростью 36 км/ч. С каким ускорением он проходит закругление?

При движении по окружности линейная скорость и центростремительное ускорение связаны соотношением

где R = 50 м; υ= км/ч = 10 м/с.

Тогда a_c = (10 м/с)² / 50 м = 2 м/с².

Ответ: 2 м/с²

2. Две материальные точки движутся по окружностям радиусами R₁ = 10 см и R₂ = 30 см с одинаковыми скоростями 0,20 м/с. Во сколько раз отличаются их центростремительные ускорения?

Дано:

R₁ =10см = 0,10 м

R₂ = 30см = 0,30 м

Найти —

Задано два объекта:

1) материальная точка, которая движется по окружности R₁;

2) материальная точка, которая движется по окружности R₂.

При движении по окружности центростремительное ускорение и линейная скорость связаны соотношением

Для тела 1 уравнение (1) примет вид:

для тела 2:

Тогда

Центростремительное ускорение тела (2) меньше ускорения тела (1) в 3 раза.

Как рассчитать угловую скорость и радиус поворота?

После всех этих ответов с имперскими единицами позвольте мне объяснить это с единицами Си, начиная с первых принципов. R-радиус, v-скорость полета, m-масса,g — гравитационная постоянная, Φ — угол крена и L-подъем.

Подъем должен быть равен весу (m·g) и центробежной силе (m·ω2·R = m·v2R

v2R

), так

L = (m ⋅ g ) 2 + (m ω ω 2 ⋅ R ) − − − − − − − − − − − − − − − √ = ρ 2 ⋅ v 2 ⋅ c L ⋅ S L=(m⋅g)2+(m⋅ω2⋅R)=ρ2⋅v2⋅cL⋅S

с ρ плотность воздуха, cL

cL

коэффициент подъемной силы и S площадь поверхности крыла. Теперь конвертируйте, чтобы вы получили v:

v = (m ⋅ g ) 2 (ρ 2 ⋅ c L ⋅ S ) 2 — (m R ) 2 − − − − − − − − − − − − − − − √ 4 v=(m⋅g)2(ρ2⋅cL⋅S)2−(mR)24

Теперь вы можете видеть, что номинатор не может стать нулевым или меньше, что дает вам минимальный радиус для заданной скорости и максимального коэффициента подъема c L m A x

cLmax

:

R ≥ 2 ⋅ m ρ 2 ⋅ c L m A x ⋅ S, R≥2⋅mρ2⋅cLmax⋅S,

и вообще:

R = 2 ⋅ m ρ 2 ⋅ c L ⋅ S = v ω = v 2 g ⋅ n 2 z− 1 − − − − − √ R=2⋅mρ2⋅cL⋅S=vω=v2g⋅nz2−1

Это похоже на «радиусный барьер»: повороты не могут лететь плотнее, чем это. Это происходит из-за увеличения центробежной силы, которая прибывает из более крутых поворотов полета. Чем круче поворот, тем быстрее вы должны лететь, чтобы создать достаточный подъем для компенсации веса и центробежной силы.

Что все еще увеличивается, так это ваша угловая скорость ω:

ω = v R = g ⋅ t A n Φ v = g ⋅ n 2 z− 1 − − − − − √ v ω=vR=g⋅tanΦv=g⋅nz2−1v

Внизу я построил планер. Вы можете ясно видеть радиус барьера на 40 м. Поверьте мне, это выглядит точно так же для авиалайнера, только цифры больше.

Если вам нужна быстрая формула для оценки радиуса, вам нужно использовать квадрат воздушной скорости, так что это не простая линейная зависимость. Для поворота с креном 30° (nz

nz

= 1.15), знаменатель уравнения радиуса составляет около 4, поэтому, чтобы вычислить радиус поворота в метрах, разделите квадрат воздушной скорости на 4 или возьмите квадрат половины вашей воздушной скорости в метрах в секунду.

Для скорости поворота в градусах в секунду разделите 220 на скорость полета в метрах в секунду. Полет медленнее позволяет более высокую скорость поворота.

Теперь о другой крайности: гиперзвуковым самолетам нужно много места для маневрирования. У меня есть здесь некоторые ценности, просто для удовольствия:

Высокая скорость делает это почти терпимым, в конце концов, половина оборота на Mach 6 и 2 g занимает всего 336 секунд, то есть менее 6 минут. Авиалайнеры крен только 30° или меньше, поэтому первая колонка действительна, если вы летите ваш гиперзвуковой автомобиль, как авиалайнер.

7.2: Классическая механика

Область классической механики включает изучение тел в движении, особенно физические законы, касающиеся тел, находящихся под воздействием сил. Большинство механических аспектов проектирования роботов тесно связано с концепциями из этой области. В данном блоке описываются несколько ключевых применяемых концепций классической механики.

СКОРОСТЬ — это мера того, насколько быстро перемещается объект. Обозначает изменение положения во времени (проще говоря, какое расстояние способен преодолеть объект за заданный период времени). Данная мера представлена в единицах расстояния, взятых в единицу времени, например, в количестве миль в час или футов в секунду.

ЧАСТОТА ВРАЩЕНИЯ – Скорость может также выражаться во вращении, то есть насколько быстро объект движется по кругу. Измеряется в единицах углового перемещения во времени (то есть в градусах в секунду), или в циклах вращения в единицу времени (например, в оборотах в минуту). Когда измерения представлены в оборотах в минуту (RPM), речь идет о частоте вращения. Есть речь идет об об/мин автомобильного двигателя, это означает, что измеряется скорость вращения двигателя.

УСКОРЕНИЕ – Изменение скорости во времени представляет собой ускорение. Чем больше ускорение, тем быстрее изменяется скорость. Если автомобиль развивает скорость от 0 до 60 миль в час за две секунды, в этом случае ускорение больше, чем когда он развивает скорость от 0 до 40 миль в час за тот же период времени. Ускорение — это мера изменения скорости. Отсутствие изменения означает отсутствие ускорения.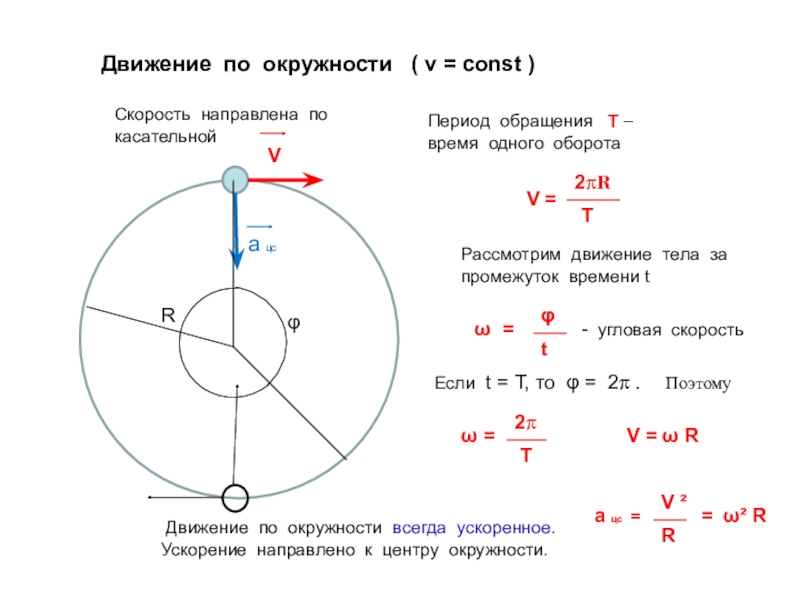 Если объект движется с постоянной скоростью — ускорение отсутствует.

СИЛА — Ускорение является следствием воздействия сил, которые провоцируют изменение в движении, направлении или форме. Если вы нажимаете на объект, это означает, что вы прикладываете к нему силу. Робот ускоряется под воздействием силы, которую его колеса прикладывают к полу. Сила измеряется в фунтах или ньютонах.

Например, масса объекта воздействует на объект как сила вследствие гравитации (ускорение объекта в направлении центра Земли).

КРУТЯЩИЙ МОМЕНТ – Сила, направленная по кругу (вращение объекта), называется крутящим моментом. Крутящий момент — это вращающая сила. Если к объекту приложен крутящий момент, на границе первого возникает линейная сила. В примере с колесом, катящемся по земле, крутящий момент, приложенный к оси колеса, создает линейную силу на границе покрышки в точке ее контакта с поверхностью земли. Так и определяется крутящий момент — как линейная сила на границе круга. Крутящий момент определяется величиной силы, умноженной на расстояние от центра вращения (Сила х Расстояние = Крутящий момент). Крутящий момент измеряется в единицах силы, умноженной на расстояние, например, фунто-дюймах или ньютон-метрах.

В примере с колесом, катящемся по земле, если известен крутящий момент, приложенный к оси с закрепленным на ней колесом, мы можем рассчитать количество силы, прикладываемой колесом к поверхности. В этом случае, радиус колеса является расстоянием силы от центра вращения.

Сила = Крутящий момент/Радиус колеса

В примере с рукой робота, удерживающей объект, мы можем рассчитать крутящий момент, требуемый для поднятия объекта. Если объект обладает массой, равной 1 ньютону, а рука имеет длину 0,25 метра (объект располагается на расстоянии 0,25 метра от центра вращения), тогда

Крутящий момент = Сила х Расстояние = 1 ньютон х 0,25 метра = 0,25 ньютон-метров.

Это означает, что для удержания объекта в неподвижном положении, необходимо применить крутящий момент, равный 0,25 ньютон-метров. Чтобы переместить объект вверх, роботу необходимо приложить к нему крутящий момент, значение которого будет превышать 0,25 ньютон-метров, так как необходимо преодолеть силу гравитации. Чем больше крутящий момент робота, тем больше силы он прикладывает к объекту, тем больше ускорение объекта, и тем быстрее рука поднимет объект.

Пример 7.2

Пример 7.3

Для данных примеров, мы можем рассчитать крутящий момент, необходимый для подъем этих объектов.

Пример 7.2 — Крутящий момент = Сила х Расстояние = 1 ньютон х 0,125 метра = 0,125 ньютон-метров.

Для данного примера, длина рука равна половине длины руки из Примера 1, поэтому значение требуемого крутящего момента также в два раза меньше. Значение длины руки пропорционально значению требуемого крутящего момента. При равных исходных характеристиках объекта, чем короче рука, тем меньший крутящий момент необходим для подъема.

Пример 7.3 — Крутящий момент = Сила * Расстояние = 1 ньютон х 0,5 метра = 0,5 ньютон-метров.

Для данного примера, длина рука равна удвоенной длине руки из Примера 1, поэтому значение требуемого крутящего момента также в два раза больше.

Еще одна точка зрения относительно ограниченного крутящего момента в соединении руки робота заключается в следующем: более короткая рука сможет поднять объект большей массы, чем более длинная рука; однако, для первой доступная высота подъема объекта будет меньше, чем для второй.

Пример 7.4

Пример 7.5

Эти примеры иллюстрируют руку робота, поднимающую объекты разной массы. Какова взаимосвязь с требуемым количеством крутящего момента?

Пример 4 — Крутящий момент = Сила х Расстояние = ½ ньютона х 0,25 метра = 0,125 ньютон-метров.

Пример 5 — Крутящий момент = Сила х Расстояние = 2 ньютона х 0,25 метра = 0,5 ньютон-метров.

Эти примеры иллюстрируют уменьшение значения требуемого крутящего момента по мере снижения массы объекта. Масса пропорциональна крутящему моменту, необходимому для ее подъема. Чем тяжелее объект, тем больше крутящий момент, требуемый для его подъема.

Проектировщики роботов должны обратить внимание на ключевые взаимосвязи между значениями крутящего момента, длины руки и массы объекта.

РАБОТА – Мера силы, приложенной на расстоянии, называется работой. Например, для удерживания объекта необходимо 10 фунтов силы. Далее, чтобы поднять этот объект на высоту 10 дюймов, требуется определенное количество работы. Количество работы, требуемое для подъема объекта на высоту 20 дюймов, удваивается. Работа также понимается как изменение энергии.

МОЩНОСТЬ — Большинство людей полагает, что мощность является термином из области электрики, но мощность также относится и к механике.

Мощность — это количество работы в единицу времени. Насколько быстро кто-то может выполнить работу?

В робототехнике принято понимать мощность как ограничение, так как соревновательные робототехнические системы имеют ограничения в части выходной мощности. Если роботу требуется поднять массу в 2 ньютона (прилагая 2 ньютона силы), скорость подъема будет ограничиваться количеством выходной мощности робота. Если робот способен произвести достаточное количество мощности, он сможет быстро поднять объект. Если он способен произвести лишь малое количество энергии, подъем объекта будет производиться медленно (либо не будет производиться вообще!).

Мощность определяется как Сила, умноженная на Скорость (насколько быстро выполняется толчок при постоянной скорости), и обычно выражается в Ваттах.

Мощность [Ватты] = Сила [Ньютоны] х Скорость [Метры в секунду]

1 Ватт = 1 (Ньютон х Метр) / Секунда

Как это применяется в соревновательной робототехнике? К проектам роботов применяются определенные ограничения. Проектировщики соревновательных роботов, использующие систему проектирования VEX Robotics Design, также должны учитывать физические ограничения, связанные с применением электромоторов. Электромотор обладает ограниченной мощностью, поэтому он может производить только определенное количество работы с заданной скоростью.

Примечание: все перспективные концепции имеют базовое описание. Более глубоко обсуждать эти физические свойства учащиеся будут в процессе обучения в ВУЗах, если выберут область STEM в качестве направления обучения.

 

Радиус кривизны траектории

В этой статье приведены две задачи, которые помогут вам научиться определять радиус кривизны траектории при движении тела под углом к горизонту. Каждая из  задач представляет собой целый набор, поэтому неясностей не должно остаться.

Задача 1. Тело брошено со скоростью 10 м/с под углом к горизонту. Найти радиусы кривизны траектории тела в начальный момент его движения, спустя время 0,5 с и в точке наивысшего подъема тела над поверхностью земли.
Как известно, радиус кривизны траектории связан с нормальным ускорением и скоростью формулой:

   

Откуда :

   

То есть, чтобы найти радиус кривизны траектории в любой точке, необходимо лишь знать скорость и нормальное ускорение, то есть ускорение, перпендикулярное вектору скорости. Рассмотрим все заданные точки и определим в них скорости и нужные составляющие ускорения.

К задаче 1

Самое простое – это определение этих величин в точке наивысшего подъема. Действительно, вертикальная составляющая скорости здесь равна нулю, поэтому скорость тела в данной точке равна горизонтальной составляющей, а ускорение, нормальное к вектору этой скорости – это ускорение свободного падения, поэтому

   

Вторая по простоте расчета – точка начала движения. Скорость в ней нам уже известна, осталось с ускорением разобраться. Ускорение свободного падения разложим на две составляющие: и . Первая – перпендикулярна скорости, она-то нам и нужна. Определяем радиус:

   

Наконец, точка, в которой тело окажется через пол-секунды.
Наше тело будет лететь по горизонтали с постоянной скоростью, равной . По вертикали тело будет двигаться равнозамедленно до середины траектории (наивысшей точки), а затем равноускоренно. Определим, успеет ли тело добраться до апогея:

   

   

   

Простой прикидочный расчет показывает, что нужная нам точка находится на первой половине траектории, где тело еще двигается вверх. Тогда его скорость по оси :

   

Определим полную скорость тела в момент времени :

   

Угол наклона вектора скорости к горизонту в этот момент равен:

   

А можно было сразу и косинус найти:

   

Тогда искомый радиус кривизны траектории равен:

   

Ответ: м, м, м.

 

Задача 2. Под каким углом к горизонту нужно бросить шарик, чтобы а) радиус кривизны траектории в начальный момент времени был в 8 раз больше, чем в вершине; б) центр кривизны вершины траектории находился бы на поверхности земли?
Запишем условие задачи так: а) , б).
а)Как и в предыдущей задаче, определяем радиус кривизны траектории в точке броска. Скорость нам известна, а нормальным ускорением будет проекция ускорения свободного падения:

   

Определим теперь радиус кривизны в вершине:

   

По условию :

   

   

   

   

   

б) Мы уже определили , осталась максимальная высота подъема.

   

Время определяем из условия равенства нулю вертикальной составляющей скорости так же, как мы это делали в предыдущей задаче:

   

   

   

Приравниваем и :

   

Откуда .

   

   

   

Ответ: а) , б) .

Скорость и скорость

Любой движущийся объект можно описать с помощью кинематических концепций, обсуждаемых в Блоке 1 Физического Класса. Движение движущегося объекта может быть объяснено либо с помощью законов Ньютона (блок 2 в классе физики) и векторных принципов (блок 3 в классе физики), либо с помощью теоремы работы-энергии (блок 5 в классе физики). Те же концепции и принципы, которые используются для описания и объяснения движения объекта, могут быть использованы для описания и объяснения параболического движения снаряда.В этом разделе мы увидим, что те же самые концепции и принципы могут также использоваться для описания и объяснения движения объектов, которые либо движутся по кругу, либо могут быть приближены к движущимся по кругу. Кинематические концепции и принципы движения будут применены к движению объектов по кругу, а затем будут расширены для анализа движения таких объектов, как американские горки, футболист, совершающий круговой поворот , и планета, вращающаяся вокруг Солнца. Мы увидим, что красота и сила физики заключаются в том, что несколько простых концепций и принципов могут быть использованы для объяснения механики всей вселенной.Урок 1 этого исследования начнется с разработки кинематических и динамических идей, которые можно использовать для описания и объяснения движения объектов по кругу.

Предположим, что вы ведете машину с повернутым рулевым колесом таким образом, что ваша машина движется по траектории идеального круга с постоянным радиусом. Предположим, что во время движения ваш спидометр постоянно показывает 10 миль в час. В такой ситуации движение вашего автомобиля можно описать как равномерное круговое движение. Равномерное круговое движение — это движение объекта по кругу с постоянной или постоянной скоростью.

Расчет средней скорости

Равномерное круговое движение — круговое движение с постоянной скоростью — это одна из многих форм кругового движения. Объект, движущийся равномерно по кругу, преодолеет такое же линейное расстояние за каждую секунду. При движении по кругу объект проходит расстояние по периметру круга.Таким образом, если ваша машина будет двигаться по кругу с постоянной скоростью 5 м / с, то она будет проходить 5 метров по периметру круга за каждую секунду. Расстояние одного полного цикла по периметру круга известно как окружности . С постоянной скоростью 5 м / с автомобиль мог совершить полный цикл по кругу с окружностью 5 метров. При этой равномерной скорости 5 м / с каждый цикл по окружности 5 м потребует 1 секунду. На скорости 5 м / с круг с окружностью 20 метров можно было сделать за 4 секунды; и при этой равномерной скорости каждый цикл по 20-метровой окружности круга будет занимать один и тот же период времени в 4 секунды. Эта связь между длиной окружности круга, временем завершения одного цикла по кругу и скоростью объекта является просто расширением уравнения средней скорости, изложенного в Блоке 1 Физического Класса.

Окружность любого круга может быть вычислена с использованием радиуса в соответствии с уравнением

Окружность = 2 * Пи * Радиус

Объединение этих двух приведенных выше уравнений приведет к новому уравнению, связывающему скорость объекта, движущегося в равномерном круговом движении, с радиусом круга и временем, чтобы сделать один цикл вокруг круга ( период ).

, где R представляет радиус окружности, а T представляет период. Это уравнение, как и все уравнения, можно использовать как алгебраический рецепт для решения проблемы. Его также можно использовать, чтобы направлять наши размышления о том, как переменные в уравнении связаны друг с другом. Например, уравнение предполагает, что для объектов, движущихся по кругам разного радиуса за один и тот же период, объект, пересекающий круг большего радиуса, должен двигаться с наибольшей скоростью. Фактически, средняя скорость и радиус круга прямо пропорциональны. Двукратное увеличение радиуса соответствует двукратному увеличению скорости; трехкратное увеличение радиуса соответствует трехкратному увеличению скорости; и так далее. Чтобы проиллюстрировать это, рассмотрим цепочку из четырех светодиодных ламп, расположенных в разных местах вдоль жилы. Прядь держится за один конец и быстро закручивается по кругу. Каждый светодиодный светильник проходит по кругу разного радиуса. Тем не менее, поскольку они подключены к одному проводу, период их вращения одинаков.Впоследствии светодиоды, которые находятся дальше от центра круга, перемещаются быстрее, чтобы охватить окружность большего круга за то же время. Если освещение в комнате выключено, светодиоды создают дугу, которая может казаться более длинной для тех светодиодов, которые перемещаются быстрее — светодиодов с наибольшим радиусом. Это показано на диаграмме справа.

Направление вектора скорости

Объекты, движущиеся равномерно по кругу, будут иметь постоянную скорость. Но означает ли это, что они будут иметь постоянную скорость? Вспомните из блока 1 Физического класса, что скорость и скорость относятся к двум совершенно различным величинам. Скорость — это скалярная величина, а скорость — это векторная величина. Скорость, будучи вектором, имеет как величину, так и направление. Величина вектора скорости — это мгновенная скорость объекта. Направление вектора скорости направлено в том же направлении, что и объект. Поскольку объект движется по кругу, его направление постоянно меняется.В какой-то момент объект движется на север так, что вектор скорости направлен на север. Четверть цикла спустя объект будет двигаться на восток, так что вектор скорости будет направлен на восток. Поскольку объект огибает круг, направление вектора скорости отличается от того, что было в предыдущий момент. Таким образом, хотя величина вектора скорости может быть постоянной, направление вектора скорости меняется. Лучшее слово, которое можно использовать для описания направления вектора скорости, — это слово тангенциальный . Направление вектора скорости в любой момент находится в направлении касательной линии, проведенной к окружности в месте расположения объекта. (Касательная линия — это линия, которая касается окружности в одной точке, но не пересекает ее.) На диаграмме справа показано направление вектора скорости в четырех разных точках для объекта, движущегося по часовой стрелке по окружности. Хотя фактическое направление объекта (и, следовательно, вектора скорости) изменяется, его направление всегда касается окружности.

Подводя итог, объект, движущийся равномерно по кругу, движется по периметру круга с постоянной скоростью. Пока скорость объекта постоянна, его скорость меняется. Скорость, будучи вектором, имеет постоянную величину, но меняющееся направление. Направление всегда направлено касательно окружности, и когда объект поворачивает круг, касательная линия всегда указывает в новом направлении.

Хотим предложить.. . Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного средства однородного кругового движения. Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивный модуль «Равномерное круговое движение» позволяет учащемуся интерактивно исследовать векторы скорости, ускорения и силы для объекта, движущегося по кругу.

Проверьте свое понимание

1. На стол кладут трубку, придающую ей форму круга в три четверти. Мяч для гольфа с большой скоростью проталкивается в трубку одним концом. Мяч катится по трубке и выходит на противоположном конце. Опишите путь мяча для гольфа, когда он выходит из трубы.

1.

4: Скорость и угловая скорость

Длина дуги на окружности

В разделе 1.3 мы узнали, что радианная мера угла равна длине дуги на единичной окружности, связанной с этим углом. Таким образом, дуга длины 1 на единичной окружности образует угол в 1 радиан. Бывают случаи, когда также будет полезно знать длину дуг на других окружностях, которые образуют тот же угол.

Рисунок \ (\ PageIndex {1} \): Дуги, заключенные под углом в 1 радиан.

На рисунке \ (\ PageIndex {1} \) внутренний круг имеет радиус 1, внешний круг имеет радиус \ (r \), а показанный угол имеет меру \ (\ theta \) радиан. . Таким образом, длина дуги на единичной окружности, образуемой углом, равна \ (\ theta \), и мы использовали s для обозначения длины дуги на окружности радиуса \ (r \), образуемой этим углом.

Напомним, что длина окружности радиуса \ (r \) равна \ (2 \ pi r \), а длина окружности радиуса 1 равна \ (2 \ pi \).Следовательно, отношение длины дуги \ (s \) на окружности радиуса \ (r \), которая образует угол в \ (\ theta \) радиан к соответствующей дуге единичной окружности, равно \ (\ dfrac {2 \ pi r} {2 \ pi} = r \). Отсюда следует, что

\ [\ dfrac {s} {\ theta} = \ dfrac {2 \ pi r} {\ pi} \]

\ [s = r \ theta \]

Определение

На окружности радиуса \ (r \) длина s дуги, пересекаемая центральным углом с радианами, равна

.

\ [s = r \ theta \]

Примечание

Важно помнить, что для расчета длины дуги необходимо измерить центральный угол в радианах.

(Непонятно, почему буква \ (s \) обычно используется для обозначения длины дуги. Одно из объяснений состоит в том, что дуга «расширяет» угол.)

Упражнение \ (\ PageIndex {1} \)

Использование кружков в начале действия для этого раздела:

1. Используйте формулу для длины дуги, чтобы определить длину дуги на окружности радиусом 10 футов, которая образует центральный угол в \ (\ dfrac {\ pi} {2} \) радиан. Результат равен одной четверти длины окружности?
2. Используйте формулу для длины дуги, чтобы определить длину дуги на окружности радиусом 20 футов, которая образует центральный угол в \ (\ dfrac {\ pi} {2} \) радиан. \ circ}) = \ dfrac {11 \ pi} {90} \) и \ [s = r \ theta = (3ft) \ dfrac {11 \ pi} {90} \] \ [s = \ dfrac {11 \ pi} {30} \] Длина дуги составляет \ (\ dfrac {11 \ pi} {30} \) футов или около \ (1.1519 \) футов.

Почему радианы?

Градус знаком и удобен, так почему же мы вводим единицу радиан? Это хороший вопрос, но на него есть тонкий ответ. Как мы только что видели, длина \ (s \) дуги на окружности радиуса \ (r \), образуемой углом в \ (\ theta \) радиан, равна \ (s = r \ theta \), поэтому \ (\ theta = \ dfrac {s} {r} \).В результате радиан представляет собой отношение двух длин (отношение длины дуги к радиусу окружности), что делает радиан безразмерной величиной. Таким образом, измерение в радианах можно рассматривать как действительное число. Это удобно для работы с длиной дуги (и угловой скоростью, как мы скоро увидим), и это также будет полезно при изучении периодических явлений в главе 2. По этой причине радианная мера повсеместно используется в математике, физике и технике как в отличие от степеней, потому что, когда мы используем градусную меру, мы всегда должны учитывать градусное измерение в вычислениях.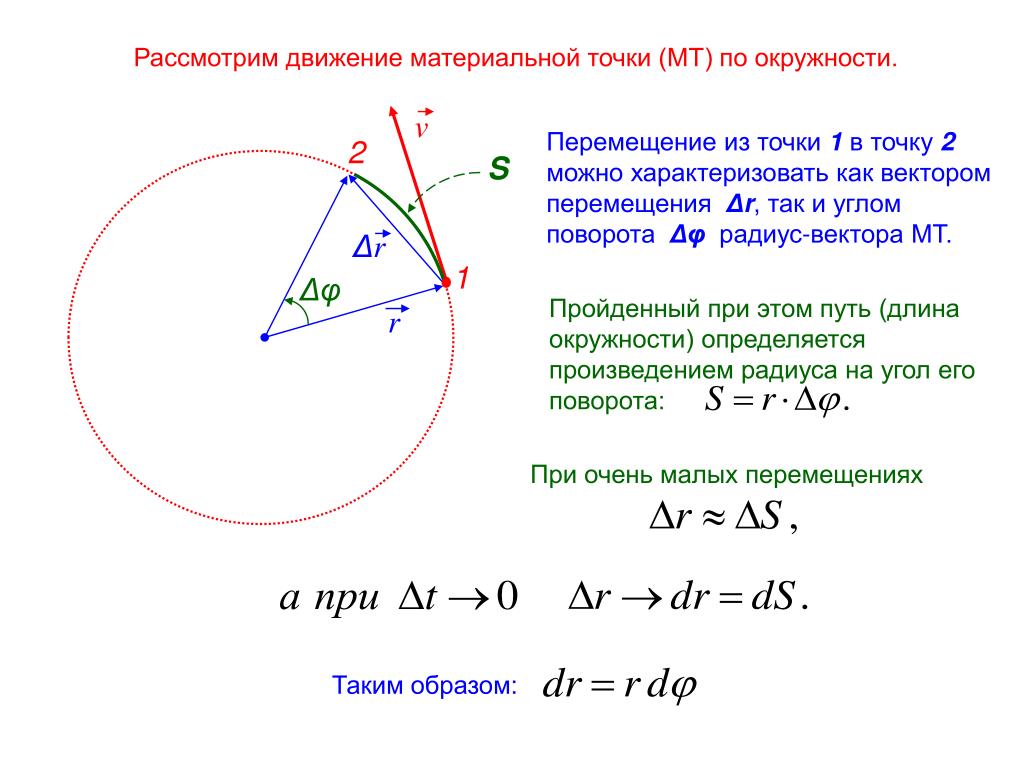 Это означает, что радианы на самом деле более естественны с математической точки зрения, чем градусы.

Линейная и угловая скорость

Связь между дугой на окружности и углом, который она образует, измеряемым в радианах, позволяет нам определять величины, относящиеся к движению по окружности. Объекты, движущиеся по круговым траекториям, обладают двумя типами скорости: линейной и угловой скоростью. Представьте себе вращение на карусели. Если вы уроните камешек с края движущейся карусели, камешек не упадет прямо вниз.Вместо этого он продолжит двигаться вперед со скоростью, которую имела карусель в тот момент, когда камешек был выпущен. Это линейная скорость гальки. Линейная скорость измеряет, как длина дуги изменяется во времени.

Рассмотрим точку \ (P \), движущуюся с постоянной скоростью по окружности радиуса \ (r \). Это называется равномерным круговым движением . Предположим, что P перемещается на расстояние s единиц за время \ (t \). Линейная скорость v точки \ (P \) — это расстояние, пройденное ею, деленное на прошедшее время.То есть \ (v = \ dfrac {s} {t} \). Расстояние s — это длина дуги, и мы знаем, что \ (s = r \ theta \).

Определение: линейная скорость

Рассмотрим точку \ (P \), движущуюся с постоянной скоростью по окружности радиуса \ (r \). Линейная скорость \ (v \) точки \ (P \) равна

\ [v = \ dfrac {s} {t} = \ dfrac {r \ theta} {t} \]

где \ (\ theta \) в радианах — это центральный угол, образованный дугой длиной \ (s \).

Другой способ измерить, насколько быстро объект движется с постоянной скоростью по круговой траектории, называется угловой скоростью. В то время как линейная скорость измеряет, как длина дуги изменяется с течением времени, угловая скорость является мерой того, насколько быстро изменяется центральный угол с течением времени.

Определение: угловая скорость

Рассмотрим точку P, движущуюся с постоянной скоростью по окружности радиуса r по дуге, соответствующей центральному углу измерения \ (\ theta \) (в радианах). Угловая скорость \ (\ omega \) точки — это величина в радианах угла \ (\ theta \), деленная на время t, необходимое для того, чтобы охватить этот угол. То есть

\ [\ omega = \ dfrac {\ theta} {t}. \]

Примечание

Символ \ (\ omega \) — это строчная греческая буква «омега». Также обратите внимание, что угловая скорость не зависит от радиуса r.

Это несколько специализированное определение угловой скорости, которое немного отличается от общепринятого термина, используемого для описания скорости вращения точки по окружности.Этот срок составляет оборотов в минуту или оборотов в минуту . Иногда используется единица измерения оборотов в секунду . Лучший способ представить количество оборотов в минуту — использовать «дробь единицы» \ (\ dfrac {rev} {min} \). Поскольку 1 оборот равен \ (2 \ pi \) радианам, мы видим, что если объект min движется со скоростью x оборотов в минуту, то

\ [\ omega = x \ dfrac {rev} {min} \ cdot \ dfrac {2 \ pi rad} {rev} = x (2 \ pi) \ dfrac {rad} {min}. \]

Упражнение \ (\ PageIndex {2} \)

Предположим, круглый диск вращается со скоростью 40 оборотов в минуту.Мы хотим определить линейную скорость v (в футах в секунду) точки, находящейся на расстоянии 3 футов от центра диска.

1. Определите угловую скорость \ (\ omega \) точки в радианах в минуту. Подсказка : Используйте формулу \ [\ omega = x \ dfrac {rev} {min} \ cdot \ dfrac {2 \ pi rad} {rev}. \]
2. Теперь мы знаем \ (\ omega = \ dfrac {\ theta} {t} \). Поэтому используйте формулу \ (v = \ dfrac {r \ theta} {t} \), чтобы определить \ (v \) в футах в минуту.
3. Наконец, преобразуйте линейную скорость v из футов в минуту в футы в секунду.

Ответ

1. Мы видим, что

\ [\ omega = 40 \ dfrac {rev} {min} \ times \ dfrac {2 \ pi \ space rad} {rev} \]
\ [\ omega = 80 \ pi \ dfrac {rad} {min} \ ]

2. Результат части (а) дает

\ [v = r (\ dfrac {\ theta} {r}) = r \ omega \]
\ [v = (3ft) \ times 80 \ pi \ dfrac {rad} {min} \]
\ [v = 240 \ pi \ dfrac {ft} {min} \]

3. Теперь мы переводим футы в минуту в футы в секунду.

\ [v = 240 \ pi \ dfrac {ft} {min} \ times \ dfrac {1 \ space min} {60 \ space sec} \]
\ [v = 4 \ pi \ dfrac {ft} {sec} \ около 12.566 \ dfrac {ft} {sec} \]

Обратите внимание, что в упражнении 1.18, как только мы определили угловую скорость, мы смогли определить линейную скорость. То, что мы сделали в этом конкретном случае, мы можем сделать в целом. Существует простая формула, которая напрямую связывает линейную скорость с угловой скоростью. Наша формула для линейной скорости: \ (v = \ dfrac {s} {t} \ dfrac {r \ theta} {t} \). Обратите внимание, что мы можем записать это как \ (v = r \ dfrac {\ theta} {t} \). То есть \ (v = r \ omega \)

Примечание

Рассмотрим точку \ (P \), движущуюся с постоянной (линейной) скоростью \ (v \) по окружности радиуса \ (r \).Если угловая скорость равна \ (\ omega \), то

\ [v = r \ omega \]

Итак, в упражнении 1. 18, когда мы определили, что \ (\ omega = 80 \ pi \ dfrac {rad} {min} \), мы могли бы определить v следующим образом:

\ [v = r \ omega = (3 \ space ft) (80 \ pi \ dfrac {rad} {min} = 240 \ pi \ dfrac {ft} {min}). \]

Обратите внимание, что, поскольку радианы «без единиц измерения», мы можем отбросить их при работе с уравнениями, такими как предыдущее.

Пример \ (\ PageIndex {1} \): линейная и угловая скорость

LP (долгоиграющая) или виниловая пластинка со скоростью 331 об / мин — это аналоговый носитель для хранения звука, который долгое время использовался для прослушивания музыки.LP обычно имеет диаметр 12 или 10 дюймов. Чтобы работать с нашими формулами для линейной и угловой скорости, нам нужно знать угловую скорость в радианах в единицу времени. Для этого мы преобразуем \ (33 \ dfrac {1} {3} \) оборотов в минуту в радианы в минуту. Мы будем использовать тот факт, что \ (33 \ dfrac {1} {3} = \ dfrac {100} {3} \)

\ [\ omega = \ dfrac {100} {3} \ dfrac {rev} {min} \ times \ dfrac {2 \ pi \ space rad} {1 \ space rev} = \ dfrac {200 \ pi} {3 } \ dfrac {rad} {min} \]

Теперь мы можем использовать формулу v D r! для определения линейной скорости точки на краю 12-дюймовой пластинки. Радиус 6 дюймов и так

\ [v = r \ omega = (6 \ пробел дюймов) (\ dfrac {200 \ pi} {3} \ dfrac {rad} {min}) = 400 \ pi \ dfrac {дюймы} {min} \]

Было бы удобнее выразить это как десятичное значение в дюймах в секунду. Получаем

\ [v = 400 \ pi \ dfrac {дюймы} {мин} \ times \ dfrac {1 \ space min} {60 \ space sec} \ приблизительно 20. 944 \ dfrac {дюймы} {sec} \]

Линейная скорость составляет приблизительно 20,944 дюйма в секунду.

Упражнение \ (\ PageIndex {3} \)

Для этих задач мы предположим, что Земля представляет собой сферу с радиусом 3959 миль.Когда Земля вращается вокруг своей оси, человек, стоящий на Земле, будет путешествовать по кругу, перпендикулярному оси.

1. Земля вращается вокруг своей оси каждые \ (24 \) часа. Определите угловую скорость Земли в радианах в час. (Оставьте свой ответ в виде числа �� \ (\ pi \).)
2. Когда Земля вращается, человек, стоящий на экваторе, будет путешествовать по кругу с радиусом 3959 миль. Определите линейную скорость этого человека в милях в час.\ circ \) север будет двигаться по кругу радиусом 2800 миль. Определите линейную скорость этого человека в милях в час и футах в секунду.

Ответ

1. Один оборот соответствует \ (2 \ pi \) радианам. Итак, \ [\ omega = \ dfrac {2 \ pi \ space rad} {24 \ space hr} = \ dfrac {\ pi \ space rad} {12 \ space hr}. \]
2. Для определения линейной скорости мы используем формулу \ (v = r \ omega \) \ [v = r \ omega = (3959mi) (\ dfrac {\ pi} {12} \ dfrac {rad} {hr}) = \ dfrac {3959 \ pi} {12} \ dfrac {mi} {hr} \] Линейная скорость приблизительно равна 1036.5 миль в час.
3. Чтобы определить линейную скорость, мы используем формулу \ (v = r \ omega \) \ [v = r \ omega = (2800mi) (\ dfrac {\ pi} {12} \ dfrac {rad} {hr}) = \ dfrac {2800 \ pi} {12} \ dfrac {mi} {hr} \] Линейная скорость составляет примерно 733,04 мили в час. Чтобы преобразовать это в футы в секунду, мы используем тот факт, что в одной миле 5280 футов, в часе 60 минут и в минуте 60 секунд. Итак

\ [v = (\ dfrac {2800 \ pi} {12} \ dfrac {mi} {hr}) (\ dfrac {5280 \ space ft} {1 \ space mi}) (\ dfrac {1 \ space hr } {60 \ space min}) (\ dfrac {1 \ space min} {60 \ space sec}) = \ dfrac {(2800 \ pi) (5280)} {12 \ cdot 60 \ cdot 60} \ dfrac {ft } {сек} \]

Таким образом, линейная скорость приблизительно равна \ (1075.1 \) футов в секунду.

Сводка

В этом разделе мы изучили следующие важные концепции и идеи:

• На окружности радиуса \ (r \) длина дуги \ (s \), пересеченная центральным углом с радианной мерой, равна \ [s = r \ theta \]
• Равномерное круговое движение — это когда точка движется с постоянной скоростью по окружности круга. Линейная скорость — это длина дуги, пройденная точкой, деленная на прошедшее время.В то время как линейная скорость измеряет, как длина дуги изменяется с течением времени, угловая скорость является мерой того, насколько быстро изменяется центральный угол с течением времени. Угловая скорость точки — это радианная мера угла, деленная на время, необходимое для того, чтобы подметать этот угол.
• Для точки \ (P \), движущейся с постоянной (линейной) скоростью v по окружности радиуса \ (r \), имеем \ [v = r \ omega \], где \ (\ omega \) — угловая скорость точки.

Движение по кругу — Математика A-Level, редакция

Эта страница описывает движение по кругу.

Угловая скорость

Представьте, что объект движется по круговой траектории.

Угловая скорость — это скорость изменения угла (который я пометил «a»). Таким образом, он измеряет, насколько быстро объект движется по кругу.

Угловая скорость обычно измеряется в радианах в секунду (рад с ^-1 ), то есть на сколько радиан проходит частица за секунду.Кроме того, его можно измерить в оборотах в секунду, т.е. сколько полных кругов объект проходит за секунду.

Существует формула, соединяющая «нормальную» скорость (обычно называемую «линейной скоростью») и угловую скорость:

где v — линейная скорость, r — радиус окружности, а w — угловая скорость.

Пример

Частица движется по окружности радиусом 10 см. Угловая скорость 2 рад с ^-1 .Найдите (линейную) скорость.

Нам нужен радиус в метрах, то есть 0,1 м. Используя формулу выше, получаем:

v = 0,1 × 2 = 0,2

Значит, скорость 0,2 мс ^-1 .

Обратите внимание, что если вам дана угловая скорость в оборотах в секунду, вам нужно сначала преобразовать в радианы в секунду. Для этого помните, что 1 оборот в секунду равен 2p радианам в секунду, потому что в круге 2p радиан.

Радиальное ускорение

Если тело движется по окружности, даже если оно движется с постоянной скоростью, оно ускоряется.Это потому, что он меняет направление (не движется по прямой).

Направление этого ускорения — к центру круга, а его величина определяется выражением:

где v — скорость, а r — радиус окружности.

Используя нашу формулу выше, это также можно записать как:

Какой из них вы будете использовать, будет зависеть от того, имеете ли вы дело со скоростью или угловой скоростью.

Ускорение происходит из-за действующей силы:

Представьте, что вы едете в машине, которая быстро свернет за поворот налево.Вы почувствуете, как сила тянет вас в сторону (левую сторону). Это сила, вызывающая ускорение. Сила действует по направлению к центру круга.

Конический маятник

Конический маятник выглядит примерно так:

P — частица. AP — это строка. P движется по синему кругу с угловой скоростью w.

Пример

Предположим, у нас есть конический маятник, как указано выше, где частица имеет массу 2 кг, а радиус круга, по которому движется частица, равен 0.5 м, а угол А составляет 45 градусов. Найти угловую скорость P.

Вес 2 г (W = мг), где g — ускорение свободного падения.

Вертикальное разрешение: Tcos45 = 2g
Следовательно (√2T) / 2 = 2g, поэтому T = 2√2 g (1)

Теперь используйте 2-й закон Ньютона, чтобы найти уравнение движения в радиальном направлении:
(«F = m r w ² «)
Tsin45 = 2 × 5 × w ²

Используйте (1), чтобы исключить T:
2√2 g × (√2) / 2 = 10w ²
g / 5 = w ²
Итак, w = √ (g / 5)

Принимая g = 9.8, мы находим, что угловая скорость составляет 1,4 рад с ^-1

Движение на береговой поверхности

Теперь рассмотрим движение частицы по «наклонной поверхности». Под этим я имею в виду, например, кольцевую гоночную трассу, которая наклонена вверх от центра, чтобы помочь автомобилям / мотоциклам оставаться на трассе на высоких скоростях.

Так вот, если машина едет очень быстро, она будет скользить по склону, двигаясь по кругу. Если он будет двигаться медленно, он поскользнется.

Если автомобиль не имеет тенденции к скольжению, силы и ускорение, действующие на кузов, будут такими, как на этой диаграмме (сила трения отсутствует):

Однако, если бы машина двигалась быстрее, она бы соскользнула по склону при движении по трассе. Таким образом, сила трения будет действовать, пытаясь предотвратить это:

6.1 Угол поворота и угловая скорость

Угловая скорость

Насколько быстро вращается объект? Мы можем ответить на этот вопрос, используя понятие угловой скорости.Рассмотрим сначала угловую скорость (ω) (ω) — это скорость, с которой изменяется угол поворота. В форме уравнения угловая скорость равна

6.2 ω = ΔθΔt, ω = ΔθΔt,

, что означает, что угловое вращение (Δθ) (Δθ) происходит за время ΔtΔt. Если объект поворачивается на больший угол поворота в данный момент времени, он имеет большую угловую скорость. Единицы измерения угловой скорости — радианы в секунду (рад / с).

Теперь давайте рассмотрим направление угловой скорости, а это значит, что теперь мы должны называть ее угловой скоростью.Направление угловой скорости — вдоль оси вращения. Для объекта, вращающегося по часовой стрелке, угловая скорость указывает от вас вдоль оси вращения. Для объекта, вращающегося против часовой стрелки, угловая скорость указывает на вас вдоль оси вращения.

Угловая скорость (ω) — это угловая версия линейной скорости v . Тангенциальная скорость — это мгновенная линейная скорость объекта во вращательном движении . Чтобы получить точное соотношение между угловой скоростью и тангенциальной скоростью, снова рассмотрим углубление на вращающемся компакт-диске.Эта яма перемещается по длине дуги (Δs) (Δs) за короткий промежуток времени (Δt) (Δt) , поэтому его тангенциальная скорость составляет

Из определения угла поворота, Δθ = ΔsrΔθ = Δsr, мы видим, что Δs = rΔθΔs ​​= rΔθ. Подставляя это в выражение для v , получаем

v = rΔθΔt = rω. v = rΔθΔt = rω.

Уравнение v = rωv = rω говорит, что тангенциальная скорость v пропорциональна расстоянию r от центра вращения. Следовательно, тангенциальная скорость больше для точки на внешнем крае CD (с большим r ), чем для точки ближе к центру CD (с меньшим r ).Это имеет смысл, потому что точка, находящаяся дальше от центра, должна покрывать большую длину дуги за то же время, что и точка ближе к центру. Обратите внимание, что обе точки по-прежнему будут иметь одинаковую угловую скорость, независимо от их расстояния от центра вращения. См. Рисунок 6.4.

Рисунок 6.4 Точки 1 и 2 вращаются на один и тот же угол (ΔθΔθ), но точка 2 перемещается на большую длину дуги (Δs2Δs2), поскольку она дальше от центра вращения.

Теперь рассмотрим другой пример: шина движущегося автомобиля (см. Рисунок 6.5). Чем быстрее вращается шина, тем быстрее движется машина — большое ωω означает большое v , потому что v = rωv = rω. Точно так же шина большего радиуса, вращающаяся с той же угловой скоростью ωω, будет создавать большую линейную (тангенциальную) скорость, v, для автомобиля. Это связано с тем, что больший радиус означает, что большая длина дуги должна касаться дороги, поэтому автомобиль должен двигаться дальше за то же время.

Рисунок 6.5 Автомобиль, движущийся со скоростью v, вправо, имеет шину, вращающуюся с угловой скоростью ωω.Скорость протектора шины относительно оси составляет v , такая же, как если бы автомобиль был поднят домкратом и колеса вращались, не касаясь дороги. Непосредственно под осью, где шина касается дороги, протектор шины движется назад по отношению к оси с тангенциальной скоростью v = rωv = rω, где r — радиус шины. Поскольку дорога неподвижна относительно этой точки шины, автомобиль должен двигаться вперед с линейной скоростью v . Большая угловая скорость шины означает большую линейную скорость автомобиля.

Однако есть случаи, когда линейная скорость и тангенциальная скорость не эквивалентны, например, когда автомобиль вращает свои колеса по льду. В этом случае линейная скорость будет меньше тангенциальной скорости. Из-за отсутствия трения под шинами автомобиля на льду длина дуги, по которой движутся протекторы шины, больше, чем линейное расстояние, по которому движется автомобиль. Это похоже на бег на беговой дорожке или на велотренажере; вы буквально никуда не денетесь.

Советы для успеха

Угловая скорость ω и тангенциальная скорость v являются векторами, поэтому мы должны включить величину и направление.Направление угловой скорости — вдоль оси вращения и указывает от вас для объекта, вращающегося по часовой стрелке, и к вам для объекта, вращающегося против часовой стрелки. В математике это описывается правилом правой руки. Тангенциальная скорость обычно описывается как вверх, вниз, влево, вправо, север, юг, восток или запад, как показано на рисунке 6.6.

Рис. 6.6. Поскольку муха на краю старинной виниловой пластинки движется по кругу, ее мгновенная скорость всегда направлена ​​по касательной к кругу.Направление угловой скорости в данном случае указано на странице.

Watch Physics

Взаимосвязь между угловой скоростью и скоростью

В этом видео рассматриваются определение и единицы угловой скорости и их связь с линейной скоростью. Здесь также показано, как преобразовать число оборотов в радианы.

Проверка захвата

Для объекта, движущегося по круговой траектории с постоянной скоростью, изменится ли линейная скорость объекта при увеличении радиуса пути?

1. Да, потому что тангенциальная скорость не зависит от радиуса.
2. Да, потому что тангенциальная скорость зависит от радиуса.
3. Нет, поскольку тангенциальная скорость не зависит от радиуса.
4. Нет, потому что тангенциальная скорость зависит от радиуса.

В поисках радиуса: формула и концепция — видео и стенограмма урока

А что насчет диаметра?

Есть еще один термин, связанный с радиусом, который вам нужно знать, и это , диаметр .Диаметр вдвое больше радиуса и представляет собой расстояние от края до края круга, проходящего через центр. Если радиус составляет 2 дюйма, то диаметр будет 4 дюйма. Всегда вдвойне. Давайте теперь посмотрим, как различные формулы для окружностей помогут нам найти радиус.

Определение радиуса по окружности

Нам только что дали длину окружности определенного круга, и теперь нам нужно найти радиус круга. Как мы продолжим?

Во-первых, нам нужна формула для окружности: C = 2 * pi * r .Когда у нас есть формула, мы можем подставить наши числа для длины окружности и константу Пи, чтобы найти r . Мы воспользуемся нашими навыками алгебры, чтобы переписать уравнение так, чтобы r было само по себе. Следуйте нашим инструкциям.

Начнем с нашей формулы окружности: C = 2 * pi * r . Наш следующий шаг — ввести все известные нам числа. Мы знаем, что длина окружности равна 8, и мы знаем, что постоянная пи всегда равна 3,14. После этого мы упростим, умножив 2 на пи.После этого делим на 6,28, чтобы r было само по себе. Когда r само по себе, мы вычислили радиус и теперь знаем, насколько велик радиус. В данном случае наш радиус составляет 1,27 метра.

Нахождение радиуса по площади

Если задана площадь круга, мы можем найти радиус, используя процедуру, аналогичную процедуре определения окружности. Мы подставляем значения в формулу для площади, а затем решаем для r .

Допустим, нам дана площадь 9.2. Мы используем навыки алгебры для решения нашей переменной r . Мы знаем, что постоянная пи всегда равна 3,14. Другое слово, связанное с радиусом, — это , диаметр , что всегда вдвое больше радиуса.

Резюме уравнения для величины центростремительной силы

Фелиция Черри
Менеджер по продуктам в области физических наук, физики и наук о Земле

Практически каждый урок физики изучает круговое движение.Студенты тратят много времени на изучение основной формулы и решение задач. В этой статье описывается вывод уравнения для центростремительной силы на основе алгебры.

Вывод уравнения

Это первое уравнение должно быть вам знакомо. Это, вероятно, наиболее часто используемое уравнение в любом первом курсе физики и способ, которым большинство студентов-физиков учатся выражать Второй закон Ньютона:

Уравнение 1.

Чистая сила, действующая на объект, равна массе объекта, умноженной на ускорение объекта. Уравнение 2 применяет этот принцип к объектам, движущимся с равномерным круговым движением, когда объект движется с постоянной скоростью, но продолжает менять направление, так что он движется по круговой траектории. На объект, движущийся в равномерном круговом движении, действует сила, направленная в центр круговой траектории, называемая центростремительной силой . Уравнение 2 переформулирует Уравнение 1 для объектов, движущихся с равномерным круговым движением. F _c обозначает центростремительную силу, а _c обозначает центростремительное ускорение.

Уравнение 2.

Уравнение для величины центростремительной силы имеет следующий вид:

Уравнение 3.

При описании линейного движения ускорение обычно описывается как изменение скорости, деленное на изменение во времени. Математически ускорение можно выразить так:

Уравнение 4.

Из Уравнение 2 и Уравнение 3 , центростремительное ускорение или _c , может быть выражено как:

Уравнение 5.

В следующем разделе будет объяснено, почему центростремительное ускорение равно квадрату скорости, деленному на радиус, как записано в Уравнение 5 .

В следующем списке определены символы, используемые в этом разделе:
F = величина силы (в ньютонах, Н)
F _c = центростремительная сила, направленная в центр круговой траектории (Н )
м = масса объекта, движущегося по круговой траектории (в килограммах, кг)
v = тангенциальная скорость объекта (метры в секунду, м / с)
v ₁ = начальная скорость (метры в секунду, м / с) (в некоторых текстах это vi или v ₀ )
v ₂ = конечная скорость (метры в секунду, м / с) (в некоторых текстах это v _f )
r = радиус круговой траектории (в метрах, м)
a = величина ускорения (в метрах в секунду в квадрате, м / с ² )
a _c = центростремительное ускорение, направленное в центр круговой траектории (м / с ² ) 9021 3 Δ обозначает изменение, например Δv = ( v ₂ — v ₁ )

Примечание: Этот вывод анализирует векторы, описывающие движение объекта, движущегося в равномерном круговом движении, и использует аналогичные треугольники, чтобы связать скорость объекта с радиусом круговой траектории.

Почему центростремительное ускорение равно квадрату скорости, деленному на радиус

Рассмотрим объект, движущийся с постоянной скоростью по круговой траектории. Скорость объекта постоянна, но скорость меняется, потому что направление объекта постоянно меняется. Рассмотрим скорость в два момента на круговой траектории. На рис. 1 v ₁ представляет начальную скорость. На рис. 2 v ₂ представляет скорость через короткий промежуток времени.

Уравнение 1.

Рисунок 1. Диаграммы 1 (слева) и 2 (справа) иллюстрируют изменение направления вектора скорости от времени 1 ко времени 2. На диаграмме 2 показано, что угол между векторами скорости равен углу между радиусами в момент времени 1 и момент времени 2.

Рис. 2. Диаграммы 3, 4 и 5.

Пока длина и направление векторов остаются неизменными, их можно рисовать любым удобным способом.На диаграмме 3 показано сложение и вычитание векторов v ₁ и v ₂ .

Векторы -v ₁ , v ₂ и Δv образуют треугольник, который похож на треугольник, образованный радиусами, нарисованными в момент времени 1 и момент времени 2, и хордой Δr .

Величина векторов v ₁ и v ₂ равна и имеет величину v.

│ v ₁ │ = │ v ₂ │ = v

Поскольку треугольники похожи, верно следующее:

Уравнение 6.

Δr = длина хорды между местоположением объекта в момент времени 1 и момент времени 2.
r = радиус окружности.

Круговой сегмент s представляет собой расстояние, пройденное объектом с момента 1 до момента 2.

Уравнение 7.

Если угол θ очень мал, можно сделать следующее приближение.

Уравнение 8.

Это позволяет сделать следующую замену:

Уравнение 9.

Подставляя v Δt вместо Δr в Уравнение 6 :

Уравнение 10.

Перестановка для Δ v / Δt дает Уравнение 11.

Уравнение 11.

Δv / Δt — это ускорение, как показано в уравнении 4 :

Умножение ускорения на массу объекта дает центростремительную силу, как показано в Уравнении 3 .

Уравнение 3 и Уравнение 4 можно использовать для решения многих физических задач.

Ресурсы

К этим изделиям могут применяться уравнения центростремительной силы и центростремительного ускорения.

Формула линейной скорости с физикой | Решенные и практические вопросы

Что такое линейная скорость?

Линейная скорость — это тема, в которой формулам уделяется большое внимание. Вам нужно запомнить несколько формул в этом конкретном подразделении. Если вы не можете запомнить формулы, не волнуйтесь, мы здесь, чтобы помочь! Линейная скорость — это расстояние, которое проходит движущийся объект. Скорость, с которой объект движется по линейной траектории, называется линейной скоростью. Проще говоря, мы можем понять, что линейная скорость — это расстояние, которое тело преодолевает за заданный промежуток времени.Давайте лучше поймем, что такое линейная скорость, а также решим несколько проблем!

Определение линейной скорости

Изменение расстояния во времени называется линейной скоростью. Это изменение может быть мгновенным или происходить в течение определенного периода времени. Когда линейная скорость измеряется в течение очень короткого интервала, она называется мгновенной линейной скоростью, а когда она измеряется в течение заданного периода времени, она называется средней линейной скоростью. Однако, когда линейная скорость измеряется за короткий промежуток времени, она оказывается более точной.

Формула для линейной скорости

V (линейная скорость) = ∆S / ∆T

Выше приведена формула средней линейной скорости. Это мера изменения линейной скорости во времени в течение заданного периода времени.

∆S представляет собой изменение расстояния

А ∆T представляет собой время, затрачиваемое телом на прохождение данного расстояния.

В (линейная скорость) = dS / dT

Выше приведена формула мгновенного измерения линейной скорости. Это измеряет изменение расстояния в пределах доли секунды движения.

Здесь dS представляет собой мгновенное изменение расстояния, а dT представляет собой долю секунды, необходимую для того, чтобы это изменение произошло. Мгновенная скорость является более точной, поскольку период, рассматриваемый при нахождении мгновенной линейной скорости, намного меньше.

Формула линейной скорости в круговом движении

Когда тело совершает круговое движение, оно имеет два разных вида скорости

1. Угловая скорость

2. Линейная скорость

Линейная скорость и угловая скорость вместе составляют скорость тела при круговом движении.Линейная скорость при круговом движении толкает тело вперед, тогда как угловая скорость вызывается центростремительной силой, которая заставляет тело продолжать движение по круговой траектории. Центростремительная сила создает притяжение внутрь и, следовательно, ограничивает движение круговой траекторией. Линейная скорость отвечает за движение тела. Без наличия линейной скорости круговое движение прекратится. Без наличия угловой скорости круговое движение будет нарушено, и движение продолжится в тангенциальном направлении.Следовательно, оба компонента одинаково важны для ограничения тела круговой траекторией.

Угловая линейная скорость

Как мы видели ранее, вращательное движение имеет два вида скоростей. Угловая скорость тела во вращательном движении возникает из-за ускорения, которое движет тело вперед и заставляет его двигаться по круговой траектории. Формула для линейной угловой скорости приведена ниже

V = rw

Где v — линейная скорость тела, r — радиус круговой траектории, а w — омега, угловая скорость тела, которая движется по круговой траектории.

Решенные ответы

Вопрос 1: Тело начинается с покоя и движется с ускорением 10 рад / с² по кругу радиусом 5 м. Найдите линейную скорость тела через 6 с.

Ответ:

Ускорение a = 10 рад с⁻²

Радиус r = 5 м

Время t = 6 с

Угловая скорость определяется как

ω = ω0 + при

= 0 + 10 ( 6)

= 60 рад⁻¹

Линейная скорость определяется как

v = r ω

= 5 м × 60 рад с⁻¹

v = 300 м / с.

Следовательно, линейная скорость данного тела составляет 300 м / с. Это означает, что если центростремительная сила, действующая на тело, будет снята, оно продолжит двигаться в тангенциальном направлении.

Вопрос 2: Найти линейную скорость тела, движущегося со скоростью 30 об / мин по круговой траектории с радиусом 5 м?

Ответ:

Учитывая

Угловая скорость = 30 об / мин

= 30 π / 30

= 1 рад / с

Радиус r = 2 м

Линейная скорость определяется как

v = r ω

v = 2 м × 1 рад / с

v = 2 м / с

Вопрос 3.