§ 4. Угловая скорость и угловое ускорение

Рассмотрим твердое тело, которое враща­ется вокруг неподвижной оси. Тогда от­дельные точки этого тела будут описывать окружности разных радиусов, центры ко­торых лежат на оси вращения. Пусть не­которая точка движется по окружности радиуса R (рис.6). Ее положение через промежуток времени t зададим углом . Элементарные (бесконечно малые) углы поворота рассматривают как векторы. Мо­дуль вектора d равен углу поворота, а его направление совпадает с направле­нием поступательного движения острия винта, головка которого вращается в на­правлении движения точки по окружности, т. е. подчиняется правилу правого, винта (рис.6). Векторы, направления которых связываются с направлением вращения, называются псевдовекторами или акси­альными векторами. Эти векторы не имеют определенных точек приложения: они мо­гут откладываться из любой точки оси вращения.

Угловой скоростью называется вектор­ная величина, равная первой производной угла поворота тела по времени:

Вектор «в направлен вдоль оси вращения по правилу правого винта, т. е. так же, как и вектор d (рис. 7). Размерность угловой скорости dim=T^-1, a . ее единица — радиан в секунду (рад/с).

Линейная скорость точки (см. рис. 6)

В векторном виде формулу для линейной скорости можно написать как вектор­ное произведение:

При этом модуль векторного произведе­ния, по определению, равен

, а направление совпадает с направлением поступательного движения правого винта при его вращении от  к R.

Если =const, то вращение равномер­ное и его можно характеризовать перио­дом вращения Т — временем, за которое точка совершает один полный оборот, т. е. поворачивается на угол 2. Так как промежутку времени t=T соответствует =2, то = 2/Т, откуда

Число полных оборотов, совершаемых телом при равномерном его движении по окружности, в единицу времени называет­ся частотой вращения:

Угловым ускорением называется век­торная величина, равная первой производ­ной угловой скорости по времени:

При вращении тела вокруг неподвижной оси вектор углового ускорения направлен вдоль оси вращения в сторону вектора элементарного приращения угловой ско­рости. При ускоренном движении вектор

13

 сонаправлен вектору  (рис.8), при замедленном.— противонаправлен ему (рис. 9).

Тангенциальная составляющая ускорения

Нормальная составляющая ускорения

Таким образом, связь между линейны­ми (длина пути s, пройденного точкой по дуге окружности радиуса

R, линейная ско­рость v, тангенциальное ускорение а_, нор­мальное ускорение а_n) и угловыми величи­нами (угол поворота , угловая скорость (о, угловое ускорение ) выражается сле­дующими формулами:

В случае равнопеременного движения точки по окружности (=const)

где ₀ — начальная угловая скорость.

Контрольные вопросы

• Что называется материальной точкой? Почему в механике вводят такую модель?

• Что такое система отсчета?

• Что такое вектор перемещения? Всегда ли модуль вектора перемещения равен отрезку пути,

пройденному точкой?

• Какое движение называется поступательным? вращательным?

• Дать определения векторов средней скорости и среднего ускорения, мгновенной скорости

и мгновенного ускорения. Каковы их направления?

• Что характеризует тангенциальная составляющая ускорения? нормальная составляющая

ускорения? Каковы их модули?

• Возможны ли движения, при которых отсутствует нормальное ускорение? тангенциальное

ускорение? Приведите примеры.

• Что называется угловой скоростью? угловым ускорением? Как определяются их направления?

• Какова связь между линейными и угловыми величинами?

Задачи

1.1. Зависимость пройденного телом пути от времени задается уравнением s = A+Вt+Сt²+Dt³ (С = 0,1 м/с², D = 0,03 м/с³). Определить: 1) через какое время после начала движения ускорение а тела будет равно 2 м/с²; 2) среднее ускорение <а> тела за этот промежуток времени. [ 1) 10 с; 2) 1,1 м/с²]

1.2. Пренебрегая сопротивлением воздуха, определить угол, под которым тело брошено к гори­зонту, если максимальная высота подъема тела равна 1/4 дальности его полета. [45°]

1.3. Колесо радиуса R = 0,1 м вращается так, что зависимость угловой скорости от времени задается уравнением  = 2At+5Вt⁴ (A=2 рад/с² и B=1 рад/с⁵). Определить полное ускорение точек обода колеса через t=1 с после начала вращения и число оборотов, сделан­ных колесом за это время. [а = 8,5 м/с²; N = 0,48]

14

1.4. Нормальное ускорение точки, движущейся по окружности радиуса r

=4 м, задается уравнением а_n=А+-Bt+Ct² (A=1 м/с², В=6 м/с³, С=3 м/с⁴). Определить: 1) тангенциальное ускорение точки; 2) путь, пройденный точкой за время t₁=5 с после начала движения; 3) полное ускорение для момента времени t₂=1 с. [ 1) 6 м/с²; 2) 85 м; 3) 6,32 м/с²]

1.5. Частота вращения колеса при равнозамедленном движении за t=1 мин уменьшилась от 300 до 180 мин^-1. Определить: 1) угловое ускорение колеса; 2) число полных оборотов, сделанных колесом за это время. [1) 0,21 рад/с

2; 2) 360]

1.6. Диск радиусом R=10 см вращается вокруг неподвижной оси так, что зависимость угла поворота радиуса диска от времени задается уравнением =A+Bt+Ct²+Dt³ (B = l рад/с, С=1 рад/с², D=l рад/с³). Определить для точек на ободе колеса к концу второй секунды после начала движения: 1) тангенциальное ускорение а_; 2) нормальное ускорение а_n; 3) полное ускорение а. [ 1) 0,14 м/с²; 2) 28,9 м/с²; 3) 28,9 м/с²]

Угловая скорость и ускорение. Определения и формулы для расчета.

Угловая скорость

Угловой скоростью называют скорость вращения тела, определяющаяся приращением угла поворота тела за промежуток времени.

Обозначение: ω (омега).

Формулы угловой скорости

Формула для расчета угловой скорости в зависимости от заданных параметров вращения может иметь вид:

• если известно количество оборотов n за единицу времени t:
  
• если задан угол поворота φ за единицу времени:
  

Размерности:

• Количество оборотов за единицу времени [об/мин], [c^-1].
• Угол поворота за единицу времени [рад/с].

Быстрота изменения угла φ (перемещения из положения П₁

в положение П₂) – это и есть угловая скорость:

ω=dφ/dt=φ’, рад/с; с^-1    (2.3)

Например, тело совершающее 1,5 оборота за одну секунду имеет угловую скорость

ω=1,5 с^-1=9,42 рад/с.

Приняв k как единичный орт положительного направления оси, получим:

Вектор угловой скорости – скользящий вектор: он может быть приложен к любой точке оси вращения и всегда направлен вдоль оси, при положительном значении угловой скорости направления ω и k совпадают, при отрицательном – противоположны.

Угловое ускорение

Изменение угловой скорости характеризуется угловым ускорением:

Единицы измерения углового ускорения: [рад/с²], [с^-2]

Вектор углового ускорения так же направлен по оси вращения. При ускоренном вращении их направления совпадают, при замедленном — противоположны.

Другими словами, при положительном ускорении угловая скорость нарастает, а при отрицательном вращение замедляется.

Для некоторых частных случаев вращательного движения твердого тела могут быть использованы формулы:

В технике угловая скорость часто задается в оборотах в минуту n [об/мин]. Один оборот – это 2π радиан:

ω=n2π/60=nπ/30 рад/с; с^-1.

Вращательное движение и угловая скорость твердого тела :: SYL.ru

В этой статье речь пойдет о физических величинах, которые характеризуют вращательное движение тела: угловая скорость, угловое перемещение, угловое ускорение, момент сил.

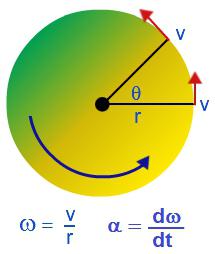
Твердым телом называют совокупность жестко связанных материальных точек. Когда твердое тело производит вращение относительно какой-либо оси, отдельные материальные точки, из которых оно складывается, двигаются по окружностям разных радиусов.

За определенный промежуток времени, например, за которое тело совершит один оборот, отдельные материальные точки, из которых состоит твердое тело, пройдут разные пути, следовательно, отдельные точки будут иметь разные линейные скорости. Описывать вращение твердого тела с помощью линейных скоростей отдельных материальных точек — сложно.

Угловое перемещение

Однако, анализируя движение отдельных материальных точек, можно установить, что за одинаковый промежуток времени все они поворачиваются вокруг оси на одинаковый угол. То есть для описания вращения твердого тела удобно пользоваться такой физической величиной, как угловое перемещение:

φ = φ(t).

Угловая скорость и угловое ускорение

Вращательное движение можно охарактеризовать угловой скоростью: ω = ∆φ/∆t.

Угловая скорость характеризует скорость вращения тела и равняется отношению изменения угла поворота ко времени, за которое оно произошло. Измеряется в радианах за секунду: [ω] = рад/с.

Угловая скорость вращения связана с линейной скоростью следующим соотношением: v = Rω, где R – радиус окружности, по которой двигается тело.

Вращательное движение тела характеризуется еще одной физической величиной — угловым ускорением, которое равно отношению изменения угловой скорости ко времени, за которое оно произошло: ε = ∆ω/∆t. Единица измерения углового ускорения: [ε] = рад/с².

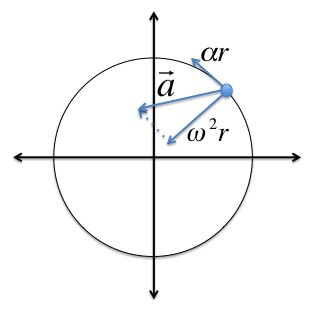
Угловая скорость и угловое ускорение являются псевдовекторами, направление которых зависит от направления вращения. Его можно определить по правилу правого винта.

Равномерное вращательное движение

Равномерное вращательное движение осуществляется с постоянной угловой скоростью и описывается такими уравнениями: ε = 0, ω = const, φ = φ₀ + ωt, где φ₀ – начальное значение угла поворота.

Равноускоренное вращательное движение

Равноускоренное вращательное движение происходит с постоянным угловым ускорением и описывается такими уравнениями: ε = const, ω = ω₀+ εt, φ = φ₀ + ω₀t + εt²/2.

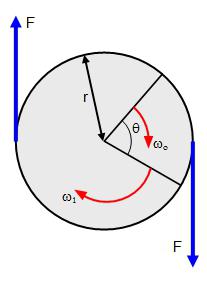
Во время вращения твердого тела центростремительное ускорение каждой точки этого тела можно найти так: ɑ_ц= v²/R = (ωR)²/R = ω²R.

Когда вращение твердого тела ускоренное, можно найти тангенциальное ускорение его точек по формуле: ɑ_t= ∆v/∆t= ∆(ωR)/∆t= R(∆ω/∆t) = Rε.

Момент сил

Если, рассматривая физическую проблему, мы имеем дело не с материальной точкой, а с твердым телом, то действие нескольких сил на него, приложенных к различным точкам этого тела, нельзя свести к действию одной силы. В этом случае рассматривают момент сил.

Моментом силы называют произведение силы на плечо. Это векторная величина, и ее находят по формуле: M = RFsinα, где α — угол между векторами R и F. Если на тело действует несколько моментов сил, то их действие можно заменить их равнодействующей, векторной суммой этих моментов: M = M₁ + M₂ + …+ M_n.

Эксперименты и опыт показывают, что под действием момента силы угловая скорость тела меняется, то есть тело имеет угловое ускорение. Выясним, как зависит угловое ускорение материальной точки (совокупности материальных точек) от приложенного момента сил: F = mɑ, RF = Rma = R²mβ, β= M/mR² = M/I, где I = mR² — момент инерции материальной точки. Заметим, что момент инерции тела имеет зависимость как от массы тела, так и от расположения этой массы относительно оси вращения.

Примеры решения задач

Задача 1. Ротор центрифуги делает 2•10⁴ об/мин. После того как выключили двигатель, его вращение прекращается через 8 мин. Найдите угловое ускорение, а также число оборотов, которое совершает ротор с момента выключения двигателя до его полной остановки, считая, что движение ротора равноускоренное.

Решение

Найдем угловое ускорение, учитывая, что угловая скорость при равноускоренном движении описывается уравнением: ω(t) = ω₀— εt.

Отсюда, учитывая, что в конце движения скорость равна нулю, найдем: ε = ω₀/t = 2πn/t.

Переведя данные задачи в систему единиц СИ (n = 333 об/с; t = 480 с), получим: ε = 2π333/480 = 4,36(рад/с²).

Угол поворота ротора центрифуги за время t будет: φ(t)= φ₀ + ω₀t + εt²/2. Учитывая выражение для углового ускорения и то, что φ₀ = 0, находим: φ(t)= ω₀t/2 = πnt.

Количество оборотов ротора за это время будет: N = φ(t)/2π = πnt/2π = nt = 8•10⁴ (об.).

Ответ: угловое ускорение равно 4,36 рад/с²; количество оборотов, сделанное ротором с момента выключения двигателя до его полной остановки, равно 8•10⁴ об.

Задача 2. Диск, имеющий массу 1 кг и радиус 20 см, вращается с частотой 120 об. в минуту. Под действием тормозного устройства на край диска начала действовать сила трения 10 Н. Найдите время остановки диска, после того как на него стала действовать сила трения.

Решение

Найдем тормозной момент сил, действующий на диск: M = RF.

Найдем угловое ускорение диска: ε = M/I = FR/mR² = F/mR.

Найдем время, за которое диск остановится: t = ω₀/ε, где ω₀ — начальная угловая скорость диска, которая равна 2πv.

Сделаем вычисления: t = 2πv/ ε = 2πvmR/F = 6,28•2•1•0,2/10 = 2,5 (с).

Ответ: время остановки равно 2,5 с.

Движение по окружности | LAMPA

Найдем угловую скорость. Известно, что ω=φt\omega=\frac{\varphi}{t}ω=tφ​. В качестве угла φ\varphiφ можно взять полный оборот, то есть угол 2π2\pi2π радиан, а в качестве времени — время одного полного оборота, то есть период TTT. Поэтому

ω=2πT,\omega=\frac{2\pi}{T}{,}ω=T2π​,ω=2πT=2π⋅1T=2πν.\omega=\frac{2\pi}{T}=2\pi\cdot\frac{1}{T}=2\pi\nu{.}ω=T2π​=2π⋅T1​=2πν.

Эти формулы мы тоже рекомендуем запомнить. Это будет полезно.

Единица измерения угловой скорости [ω]=радс[\omega]=\frac{\text{рад}}{\text{с}}[ω]=срад​.

Оказывается, что линейная скорость VVV и угловая скорость ω\omegaω связаны друг с другом. Рассмотрим пример из жизни. На детских площадках наверняка все видели карусель. Представьте, что карусель вращается. Вы сами сидите на сиденьи этой карусели, а ваш друг не стал сидеть на сиденьи, а «пролез» поближе к центру карусели.

Поскольку каждый из вас поворачивается вокруг карусели на один и тот же угол за то же время, то угловые скорости у вас равны: ωвы=ωдруг\omega_{вы}=\omega_{друг}ωвы​=ωдруг​. Но вот линейные скорости у вас не равны: Vвы≠VдругV_{вы}\neq V_{друг}Vвы​≠Vдруг​. Это нам подсказывает наш жизненный опыт. Тот, кто сидит поближе, двигается медленнее.

Чем ближе к центру находится тело — тем меньше его линейная скорость VVV. И наоборот: чем дальше от центра (чем больше расстояние от центра), тем больше скорость VVV.

Линейная скорость VVV также будет больше и в том случае, если будет больше быстрота поворота вокруг оси, то есть угловая скорость ω\omegaω.

По-простому: чем дальше сидишь от оси (чем больше RRR) и чем быстрее вращается тело (чем больше ω\omegaω), тем больше линейная скорость VVV.

Линейную скорость VVV можно пойти по формуле:

V=ω⋅R.V=\omega\cdot R{.}V=ω⋅R.

Эту формулу можно вывести строго. Возьмем уже известные нам формулы:

V=2πR⋅νV=2\pi R\cdot \nuV=2πR⋅ν и ω=2π⋅ν\omega=2\pi\cdot \nuω=2π⋅ν.

Из них видно, что в первой формуле вместо 2πν2\pi\nu2πν можно подставить ω\omegaω:

V=2πR⋅ν=2πνR=(2πν)⋅R=ω⋅RV=2\pi R\cdot \nu=2\pi\nu R=(2\pi\nu)\cdot R=\omega\cdot RV=2πR⋅ν=2πνR=(2πν)⋅R=ω⋅R.

Мы получили формулу V=ω⋅RV=\omega\cdot RV=ω⋅R.

Радиальное (нормальное) ускорение | Формулы и расчеты онлайн

При движении тела по криволинейной траектории возникает радиальное ускорение. Оно всегда перпендикулярно направлению мгновенной скорости.

Радиальное (нормальное) ускорение равно квадрату угловой скорости помноженному на радиус траектории (5).

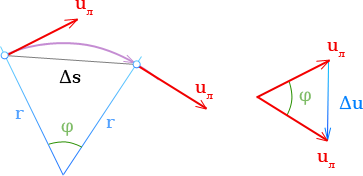
Для достаточно малого промежутка времени Δt справедливы следующие соотношения:

\[ \frac[-1.2]{Δs}{r} = \frac[-1.4]{Δu}{u_{л}} \]

Так как

\[ Δs = u_{л} Δt \]

имеем

\[ \frac[-1.4]{Δu}{u_{л}} = \frac[-1.2]{u_{л} Δt}{r} \]

или

\[ \frac{Δu}{Δt} = \frac{u_{л}^2}{r} \]

Отсюда получается радиальное ускорение

\[ a_{р} = \frac{u_{л}^2}{r} = ω^2 r \]

Тот же результат можно получить рассмотрев координаты лежащей на окружности точки Р, в которой в данный момент находится тело:

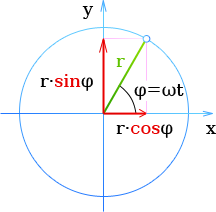
\[ \lvbig x = r \cos(φ)
y = r \sin(φ) \r.\]

Из выражения Равномерное движение тела по окружности [1] следует

\[ φ = ωt \]

Согласно формуле Мгновенное ускорение [2] ускорение представляет собой вторую производную перемещения по времени. Продифференцировав дважды координаты точки Р, найдем ускорения в направлении осей координат:

\[ \lvbig \diff{x} = -ωr \sin(ωt)
\diff{y} = ωr \cos(ωt) \r.\]

\[ \lvbig \diiff{x} = -ω^2 r \cos(ωt)
\diiff{y} = -ω^2 r \sin(ωt) \r.\]

Отсюда для результирующего ускорения имеем

\[ а_p^2 = (− ω^2 r \cos(ωt))^2 + (− ω^2 r \sin(ωt))^2 \] \[ а_p^2 = ω^4 r^2 (\cos^2(ωt) + \sin^2(ωt)) \] \[ а_p = \sqrt{ω^4 r^2} = ω^2 r \]

таким образом (11) и (5) совпадают.

Вычислить, найти радиальное (нормальное) ускорение по формуле (5) через линейную скорость

Вычислить, найти радиальное (нормальное) ускорение по формуле (5) через угловую скорость

В помощь студенту

Радиальное (нормальное) ускорение	стр. 435

Радиус кривизны траектории

В этой статье приведены две задачи, которые помогут вам научиться определять радиус кривизны траектории при движении тела под углом к горизонту. Каждая из  задач представляет собой целый набор, поэтому неясностей не должно остаться.

Задача 1. Тело брошено со скоростью 10 м/с под углом к горизонту. Найти радиусы кривизны траектории тела в начальный момент его движения, спустя время 0,5 с и в точке наивысшего подъема тела над поверхностью земли.
Как известно, радиус кривизны траектории связан с нормальным ускорением и скоростью формулой:

   

Откуда :

   

То есть, чтобы найти радиус кривизны траектории в любой точке, необходимо лишь знать скорость и нормальное ускорение, то есть ускорение, перпендикулярное вектору скорости. Рассмотрим все заданные точки и определим в них скорости и нужные составляющие ускорения.

К задаче 1

Самое простое – это определение этих величин в точке наивысшего подъема. Действительно, вертикальная составляющая скорости здесь равна нулю, поэтому скорость тела в данной точке равна горизонтальной составляющей, а ускорение, нормальное к вектору этой скорости – это ускорение свободного падения, поэтому

   

Вторая по простоте расчета – точка начала движения. Скорость в ней нам уже известна, осталось с ускорением разобраться. Ускорение свободного падения разложим на две составляющие: и . Первая – перпендикулярна скорости, она-то нам и нужна. Определяем радиус:

   

Наконец, точка, в которой тело окажется через пол-секунды.
Наше тело будет лететь по горизонтали с постоянной скоростью, равной . По вертикали тело будет двигаться равнозамедленно до середины траектории (наивысшей точки), а затем равноускоренно. Определим, успеет ли тело добраться до апогея:

   

   

   

Простой прикидочный расчет показывает, что нужная нам точка находится на первой половине траектории, где тело еще двигается вверх. Тогда его скорость по оси :

   

Определим полную скорость тела в момент времени :

   

Угол наклона вектора скорости к горизонту в этот момент равен:

   

А можно было сразу и косинус найти:

   

Тогда искомый радиус кривизны траектории равен:

   

Ответ: м, м, м.

 

Задача 2. Под каким углом к горизонту нужно бросить шарик, чтобы а) радиус кривизны траектории в начальный момент времени был в 8 раз больше, чем в вершине; б) центр кривизны вершины траектории находился бы на поверхности земли?
Запишем условие задачи так: а) , б).
а)Как и в предыдущей задаче, определяем радиус кривизны траектории в точке броска. Скорость нам известна, а нормальным ускорением будет проекция ускорения свободного падения:

   

Определим теперь радиус кривизны в вершине:

   

По условию :

   

   

   

   

   

б) Мы уже определили , осталась максимальная высота подъема.

   

Время определяем из условия равенства нулю вертикальной составляющей скорости так же, как мы это делали в предыдущей задаче:

   

   

   

Приравниваем и :

   

Откуда .

   

   

   

Ответ: а) , б) .

Формулы кинематики с пояснениями по физике / Блог :: Бингоскул

Кинематика — раздел физики, занимающийся исследованием законов движения идеальных тел.

Основные формулы с пояснениями, которые помогут в решении заданий ЕГЭ по физике: движение, скорость, ускорение.

 

Путь, время, скорость

S=v *t

• S — путь
• v — скорость
• t — время

Равномерное движение

x=x_0 + v*t

• x — координата
• x₀ — начальная координата
• v — скорость
• t — время

Равномерно ускоренное движение: ускорение

a=\frac { v — v_0 } { t }

• a — ускорение
• v — скорость
• v₀ — начальная скорость
• t — время

Равномерно ускоренное движение: скорость

v=v_0 + at

• v — скорость
• v₀ — начальная скорость
• a — ускорение
• t — время

Равномерно ускоренное движение: путь

S=vt + \frac { at^2 } { 2 }

• s — путь
• v — скорость
• t — время
• a — ускорение

Равномерно ускоренное движение: координата

x=x_0 + vt + \frac { at^2 } { 2 }

• x — координата
• x₀ — начальная координата
• v — скорость
• t — время
• a — ускорение

Высота тела, брошенного вертикально вверх (вниз)

h=h_0 + v_ { 0 } t — \frac { gt^2 } { 2 }

• h — высота
• h₀ — начальная высота
• v₀ — начальная скорость
• t — время
• g — ускорение свободного падения

Скорость тела, брошенного вертикально вверх (вниз)

v=v_0 — gt

• v — скорость
• v₀ — начальная скорость
• g — ускорение свободного падения
• t — время

Скорость, ускорение, время

v=at

• v — скорость
• a — ускорение
• t — время

Скорость свободно падающего тела

v=gt

• v — скорость
• g — ускорение свободного падения
• t — время

Центростремительное ускорение

a=\frac { v^2 } { R }

• a — центростремительное ускорение
• v — скорость
• R — радиус

Угловая скорость

\omega=\frac { \phi } { t }

• ω — угловая скорость
• φ — угол
• t — время

Равномерное круговое движение

l=R\phi

• l — длина дуги окружности
• R — радиус
• φ — угол

Равномерное круговое движение: линейная скорость

v=R \omega

• v — линейная скорость
• R — радиус
• ω — угловая скорость

 

Период вращения

T=\frac { t } { N }

• T — период
• t — время
• N — число вращений

T=\frac { 2 \pi R } { v }

• T — период
• R — радиус
• v — линейная скорость

T=\frac { 2 \pi } { \omega }

• T — период
• ω — угловая скорость

Центростремительное ускорение

a=\frac { 4 \pi^ { 2 } R } { T^2 }

• a — центростремительное ускорение
• R — радиус
• T — период вращения

a=4 \pi^ { 2 } Rn^2

• a — центростремительное ускорение
• R — радиус
• n — частота вращения

Частота вращения

n=\frac { 1 } { T }

• n — частота вращения
• T — период вращения

Центростремительное ускорение

a=\omega ^ { 2 } R

• a — центростремительное ускорение
• ω — угловая скорость
• R — радиус

Дальность броска тела, брошенного под углом к горизонту

x=v_0t \cos(\alpha)

• x — координата (дальность)
• v₀ — начальная скорость
• t — время
• α — угол

Высота подъема тела, брошенного под углом к горизонту

y=v_0t \sin (\alpha) — \frac { gt^2 } { 2 }

• y — координата (высота подъема )
• v₀ — начальная скорость
• t — время
• g — ускорение свободного падения
• α — угол

Вертикальная скорость тела, брошенного под углом к горизонту

v_y=v_0* \sin (\alpha) — gt

• v_y — вертикальная скорость
• v₀ — начальная скорость
• α — угол
• g — ускорение свободного падения
• t — время

Максимальная высота подъема тела, брошенного под углом к горизонту

h_max =\frac { v_0^2* \sin (\alpha)^ { 2 } } { 2g }

• h_макс — максимальная высота
• v₀ — начальная скорость
• α — угол
• g — ускорение свободного падения

Общее время движения тела, брошенного под углом к горизонту

t=\frac { 2v_0 * \sin (\alpha) } { g }

• t — время
• v₀ — начальная скорость
• α — угол
• g — ускорение свободного падения

Дальность броска тела, брошенного горизонтально

x=x_0 + vt

• x — координата (дальность)
• x₀ — начальная координата
• v — скорость
• t — время

Высота подъема тела, брошенного горизонтально

y=y_0 — \frac { gt^2 } { 2 }

• y — координата (высота подъема)
• y₀ — начальная координата (высота)
• g — ускорение свободного падения
• t — время

Общее время движения тела, брошенного горизонтально

t_max=\sqrt { \frac { 2h } { g } }

• t_макс — максимальное время
• h — высота
• g — ускорение свободного падения

---

Смотри также: