Формула работы

   

– работа (может обозначаться как ), – сила, – перемещение.

Единица измерения работы — Дж (джоуль).

Указанная формула применима к телу, движущемуся прямолинейно и постоянном значении воздействующей на него силы. Если между вектором силы и прямой, описывающей траекторию тела есть угол, то формула принимает вид:

   

Кроме того, понятие работы можно определить как изменение энергии тела:

   

Именно такое применение этого понятия чаще всего встречается в задачах.

Примеры решения задач по теме «Механическая работа»

Понравился сайт? Расскажи друзьям!

Работа | Формулы и расчеты онлайн

Если сила перемещает тело на некоторое расстояние, то она совершает над телом работу.

Работа W есть произведение силы F на перемещение s.

\[ W = F·s \]

Работа — величина скалярная.

Единица СИ работы

\[ [W] = [F][s] = Ньютон·метр \] \[ [W] = Джоуль (дж) = Вт · с = кг · \frac[-1.2]{метр^2}{сек^2} \]

Работа постоянной силы, формула

Если сила F постоянна во времени и ее направление совпадает с направлением перемещения тела, то работа W находится по формуле. \[ W = F·s \] Здесь: 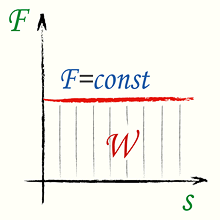W — совершенная работа (Джоуль), F — постоянная сила, совпадающая по направлению с перемещенем (Ньютон), s — перемещение тела (метр)

Вычислить, найти работу постоянной силы по формуле (4)

Работа постоянной силы, направленной под углом к перемещению, формула

Если сила и перемещение составляют между собой угол α 90º, то перемещение следует умножать на составляющую силы в направлении перемещения (или силу умножать на составляющую перемещения в направлении действия силы). В векторной форме \[ W = \vect{F}·\vect{s} \] \[ W = F·s·\cos(α) \] Здесь: 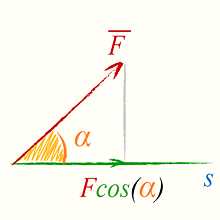α — угол между вектором силы и вектором перемещения, º

Вычислить, найти работу постоянной силы направленной под углом к перемещению по формуле (4)

Работа переменной силы, направленной под углом к перемещению, формула

Если сила не постоянна по величине и является функцией перемещения F = F(s), и направлена под углом α к перемещению, то работа есть интеграл от силы по перемещению. \[ W = \int\from{s_1}\to{s_2} \vect{F} d\vect{s} \]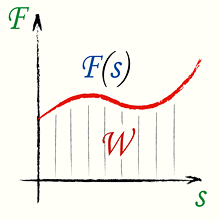

Площадь под кривой на графике зависимости F от s равна работе, произведенной данной силой

В помощь студенту

Формула работы — интернет энциклопедия для студентов

ОПРЕДЕЛЕНИЕ

Механическая работа — это произведение силы, приложенной к объекту, смещения, создаваемого этой силой.

A — произведение (может обозначаться как W), F — сила, S — движение.

Единицей измерения работы является Дж (джоуль).

Эта формула применима к телу, движущемуся по прямой и постоянному значению действующей на него силы. Если между вектором силы и прямой, описывающей траекторию тела, существует угол, то формула примет вид:

Кроме того, понятие работы можно определить как изменение энергии тела:

Именно это применение этой концепции чаще всего встречается в проблемах.

Примеры решения проблем на тему «Механические работы»

ПРИМЕР 1

Задача

Перемещение по кругу с радиусом 1 м, тело перемещается в противоположную точку круга под действием силы 9H. Найдите работу, проделанную этой силой.

Решение.

Согласно формуле, работу нужно искать на основе не пройденного расстояния, а перемещения, т. Е. Нет необходимости подсчитывать длину дуги окружности. Достаточно просто учесть, что при движении в противоположную точку круга тело совершает движение, равное диаметру круга, т. Е. 2 м. В соответствии с формулой:

Ответ.

Совершенная работа равна A = 18 Дж.

ПРИМЕР 2

Задача

Под действием определенной силы тело движется вверх по наклонной плоскости под углом к горизонту. Найдите силу, действующую на тело, если, когда тело движется на 5 м в вертикальной плоскости, ее энергия увеличивается на 19 Дж.

Решение

По определению изменение энергии тела — это проделанная на нем работа.

Однако мы не можем найти силу, подставляя исходные данные в формулу, так как мы не знаем движения тела. Мы знаем только его движение вдоль оси OY (обозначим ее через h). Найдите движение тела, используя определение функции sin:

Теперь вы можете заменить все в формуле:

Ответ

Сила равна

Формула работы | Все формулы

Сообщение от администратора:

Ребята! Кто давно хотел выучить английский?
Переходите по моей ссылке и получите два бесплатных урока

в школе английского языка SkyEng! 
Занимаюсь там сам — очень круто. Прогресс налицо.

В приложении можно учить слова, тренировать аудирование и произношение.

Попробуйте. Два урока бесплатно по моей ссылке!
Жмите СЮДА

  

 – работа (может обозначаться как ),  – сила,  – перемещение.

Единица измерения работы — Дж (джоуль).

Указанная формула применима к телу, движущемуся прямолинейно и постоянном значении воздействующей на него силы. Если между вектором силы и прямой, описывающей траекторию тела есть угол, то формула принимает вид:

  

Кроме того, понятие работы можно определить как изменение энергии тела:

  

Именно такое применение этого понятия чаще всего встречается в задачах.

Примеры решения задач по теме «Механическая работа»

ФИЗИКА: Задачи на механическую работу

Задачи на механическую работу с решениями

Формулы, используемые на уроках «Задачи на механическую работу».

Название величины	Обозначение	Единица измерения	Формула
Сила	F	H	F = mg
Путь	s	м	s = A / F
Масса	m	кг	m = АТ / (gh)
Высота	h	м	h = АТ / (mg)
Работа	A	Дж	A = Fs
Работа сил тяжести	Ат	Дж	АТ = mgh

 

---

---

---

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Задача № 1.  Шар катится по инерции по горизонтальной поверхности. а) Совершается ли при этом работа силой тяжести? б) Совершается ли в этом случае работа какой-либо другой силой?

Решение:
а) Работа силой тяжести не совершается, потому что перемещения в вертикальном направлении (то есть в направлении силы тяжести) не происходит.
б) Работа совершается силой трения

, так как шар остановится под действием этой силы.

---

Задача № 2. Какую работу надо совершить, чтобы положить гантель весом 100 Н на стол высотой 80 см?

Задача № 3.   Какая совершается работа при равномерном перемещении ящика на 25 м, если сила трения 450 Н?

---

Задача № 4.  Какую работу совершает сила тяжести при падении камня массой 0,5 кг с высоты 12 м?

---

Задача № 5.  Определите путь, пройденный автомобилем, если при силе тяги 25 кН совершенная работа равна 50 МДж.

---

Задача № 6.  Определите работу, совершенную краном при равномерном подъеме тела массой 3 т на высоту 7 м.

---

Задача № 7.  При равномерном подъеме из шахты нагруженной углем бадьи массой 10,5 т произведена работа 6200 кДж. Какова глубина шахты?

---

Задача № 8.  Давление воды в цилиндре нагнетательного насоса 1200 кПа. Чему равна работа при перемещении поршня площадью 400 см² на расстояние 50 см.

 

---

Теория для решения задач.

---

Конспект урока «Задачи на механическую работу с решениями».

Следующая тема: «Задачи на механическую мощность с решениями».

 

Формула работы в физике

Определение и формула работы

Определение

В том случае, если под воздействием силы происходит изменение модуля скорости движения тела, то говорят о том, что сила совершает работу. Считают, что если скорость увеличивается, то работа является положительной, если скорость уменьшается, то работа, которую совершает сила – отрицательна. Изменение кинетической энергии материальной точки в ходе ее движения между двумя положениями равно работе, которую совершает сила:

Действие силы на материальную точку можно охарактеризовать не только с помощью изменения скорости движения тела, но при помощи величины перемещения, которое совершает рассматриваемое тело под действием силы ().

Элементарная работа

Элементарная работа некоторой силы определяется как скалярное произведение:

радиус – вектор точки, к которой приложена сила, — элементарное перемещение точки по траектории, – угол между векторами и . Если является тупым углом работа меньше нуля, если угол острый, то работа положительная, при

В декартовых координатах формула (2) имеет вид:

где F_x,F_y,F_z – проекции вектора на декартовы оси.

При рассмотрении работы силы, приложенной к материальной точке можно использовать формулу:

где – скорость материальной точки, – импульс материальной точки.

Если на тело (механическую систему) действуют несколько сил одновременно, то элементарная работа, которую совершают эти силы над системой, равна:

где проводится суммирование элементарных работ всех сил, dt – малый промежуток времени, за который совершается элементарная работа над системой.

Результирующая работа внутренних сил, даже если твердое тело движется, равна нулю.

Пусть твердое тело вращается около неподвижной точки — начала координат (или неподвижной оси, которая проходит через эту точку). В таком случае, элементарная работа всех внешних сил (допустим, что их число равно n), которые действуют на тело, рав

Решение задач по теме «Механическая работа и мощность». Видеоурок. Физика 7 Класс

В ходе данного урока вы познакомитесь с методами решения задач на вычисление работы и мощности.

К бруску прикрепили динамометр и переместили брусок на расстояние 30 см. Показания динамометра равны 0,8 Н. Найти работу силы тяги по перемещению бруска (рис. 1).

Рис 1. К задаче №1

Прежде всего запишем краткое условие задачи и позаботимся, чтобы все данные были выражены в системе СИ (рис. 2).

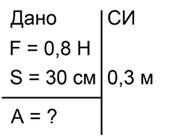
Рис 2. Краткое условие задачи №1

Для вычисления работы воспользуемся формулой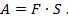

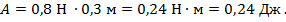
Полное решение задачи выглядит так (рис. 3).

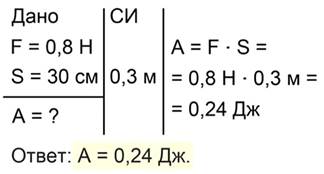
Рис 3. Полное решение задачи №1

Трактор перемещает платформу со скоростью 7,2 км/ч, развивая тяговое усилие в 25 кН. Какую работу совершит трактор за 10 мин (рис. 4)?

Рис 4. К задаче №2

Запишем краткое условие задачи и переведем все единицы измерения в систему СИ (рис. 5).

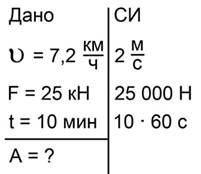
Рис 5. Краткое условие задачи №2

Для вычисления работы необходимо знать расстояние, пройденное телом. В условии задачи дана скорость движения трактора и время движения, поэтому воспользуемся формулой

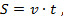
которую подставим в выражение для работы 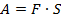 и получим рабочую формулу

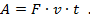
Подстановка данных из условия задачи дает

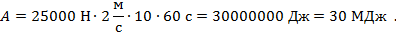
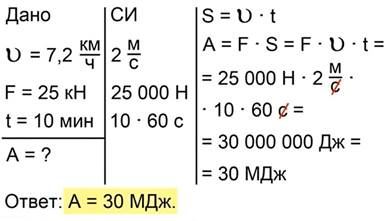
Рис 6. Полное решение задачи №2

Найдем работу силы тяжести при падении грузика.

Для решения задачи нам потребуется линейка и сам грузик. Измерим высоту, с которой будет падать грузик. Получаем 1 м. Масса грузика написана на нем самом и равна 100 г. Поднимем грузик на указанную высоту и отпустим его.

Краткое условие задачи будет выглядеть так (рис. 7):

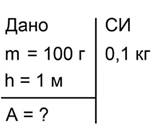
Рис 7. Краткое условие задачи №3

Для нахождения работы выразим силу тяжести через массу тела 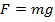, и учтем, что расстояние, пройденное телом, равно высоте, с которой оно упало: .

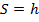Тогда

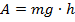
Подстановка чисел дает

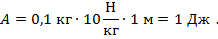
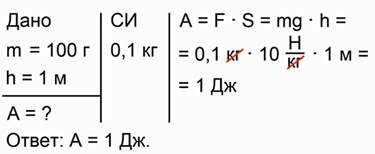
Рис 8. Полное решение задачи №3

Теперь у нас есть представление о том, насколько велика работа в 1 джоуль. Такая работа совершается при падении грузика массой 100 г со стола высотой 1 м.

Переходим к решению более сложных задач.

Со дна реки глубиной 4 м поднимают камень объемом 0,6 м³ на поверхность. Плотность камня 2500 кг/м³, плотность воды 1000 кг/м³. Найти работу по подъему камня.

Для решения задачи необходимо не только записать краткое условие задачи, но и сделать схематический рисунок и показать силы, действующие на камень. Это сила тяги F_т (работу именно этой силы мы будем находить), сила тяжести mg и сила Архимеда F_a. Кроме того, покажем высоту, на которую сила тяги перемещает камень (рис. 9).

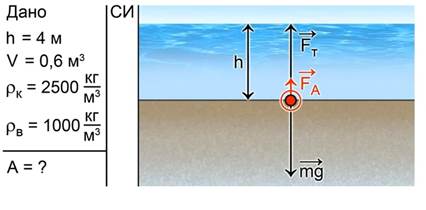
Рис 9. К решению задачи №4

Как видно из рисунка, искомая работа равна .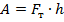

Для нахождения силы тяги воспользуемся условием равновесия тела: если оно неподвижно или движется с постоянной скоростью, то равнодействующая всех сил, приложенных к нему, равна нулю.

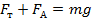, откуда .

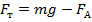Массу камня выразим через плотность камня и его объем, а силу Архимеда – через плотность воды и объем погруженной части камня (в этом задаче он равен объему всего камня). Объем камня и ускорение выносим за скобки.

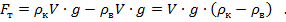
Остается подставить силу тяги в формулу для вычисления работы

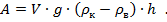
Поскольку рабочая формула получилась более сложной, единицы измерения результата определим отдельно от расчета его численного значения.

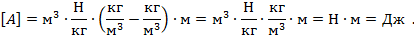
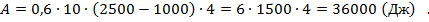
Рис 10. Полное решение задачи №4

Поршень двигателя перемещается на 20 см под давлением 800 кПа. Определите работу, совершаемую двигателем за один ход поршня, если площадь поршня 150 см² (рис. 11).

Рис 11. К задаче №5

Запишем краткое условие и выразим все единицы в системе СИ (рис. 12).

Рис. 12. Краткое условие задачи №5

В данной задаче работу выполняет сила давления газа в цилиндре двигателя. Для нахождения этой силы необходимо давление в цилиндре умножить на площадь поршня. Расстояние, пройденное поршнем, мы обозначили буквой l.

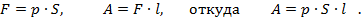
Единицы измерения результата:

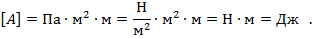
Численное значение результата:

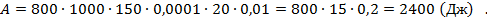
Рис 13. Полное решение задачи №5

Найти КПД (коэффициент полезного действия) наклонной плоскости (экспериментальная) (рис. 14).

Рис. 14. Груз поднимают вверх по наклонной плоскости

Поднимая груз по наклонной плоскости с помощью динамометра, измерим силу, которая для этого требуется. Она оказывается равной 2,2 Н. Расстояние, пройденное грузом вдоль плоскости, измеряем рулеткой. Оно составило 0,5 м. При этом груз поднялся над столом на высоту 20 см. Кроме того, известны масса бруска, равная 50 г, и общая масса трех поднимаемых грузов – 300 г.

Полученные опытные данные занесем в краткое условие задачи, выразим все величины в единицах системы СИ и сделаем схематический рисунок измерительной установки (рис. 15).

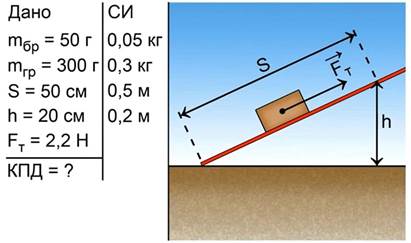
Рис 15. Краткое условие задачи №6

Коэффициентом полезного действия механизма называется физическая величина, равная отношению полезной работы, совершенной механизмом, к работе, затраченной для приведения его в действие.

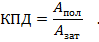
КПД также обозначают греческой буквой η (эта) и часто выражают в процентах.

В нашем случае механизмом является наклонная плоскость.

Полезная работа – эта работа, которую нужно совершить, чтобы поднять тело на высоту h.

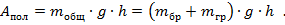
Затраченная работа совершается силой тяги, то есть силой упругости пружины динамометра.

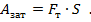
Тогда КПД равен

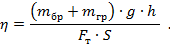
Определяем единицы измерения КПД

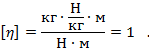
Такой результат означает, что КПД является безразмерной величиной (просто число без единиц измерения).

Его числовое значение

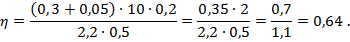
Обратите внимание, что коэффициент полезного действия не может быть больше единицы, поскольку полезная работа всегда меньше затраченной. Если у вас получилось наоборот, значит, либо при измерениях, либо в ходе вычислений допущена ошибка.

Рис 16. Полное решение задачи №6

Трактор равномерно тянет плуг, прилагая силу в 10 кН. За 10 мин он проходит путь 1,2 км. Определить мощность, развиваемую трактором (рис. 17).

Рис 17. К условию задачи №7

Запись краткого условия и перевод величин в систему СИ будет выглядеть так (рис. 18):

Рис 18. Краткое условие задачи №7

Для нахождения мощности нужно работу, выполненную трактором, разделить на время ее выполнения. Работа вычисляется как произведение силы тяги трактора на пройденное трактором расстояние. Таким образом, получаем:

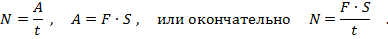
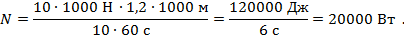
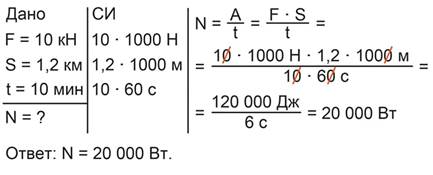
Рис 19. Полное решение задачи №7

Поезд массой 600 тонн равномерно движется со скоростью 36 км/ч. Определить развиваемую тепловозом мощность, если сила трения составляет 0,002 веса поезда.

 

Рис. 20. К условию задачи №8

Запишем краткое условие задачи, выразим величины в единицах системы СИ, сделаем рисунок, на котором покажем силу тяги тепловоза и силу трения (рис. 21).

 

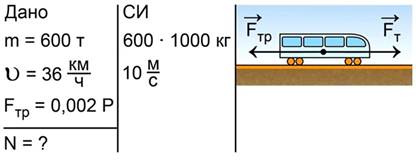
Рис. 21. Краткое условие задачи №8

Поскольку по условию задачи скорость поезда не изменяется и равна 36 км/ч, сила тяги равна силе трения 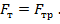 Вес в случае движения с постоянной скоростью равен силе тяжести  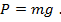Тогда сила тяги равна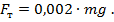

Для вычисления мощности воспользуемся формулой 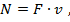 откуда

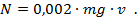
Подстановка данных из условия дает

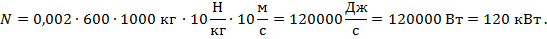
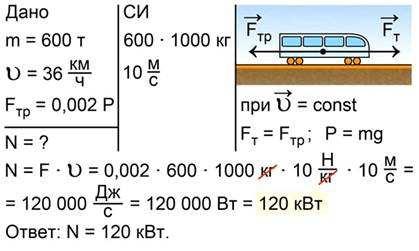
Рис. 22. Полное решение задачи №8

 

Список литературы

1. Перышкин А.В. Физика. 7 кл. – 14-е изд., стереотип. – М.: Дрофа, 2010.
2. Перышкин А.В. Сборник задач по физике, 7–9 кл.: 5-е изд., стереотип. – М: Издательство «Экзамен», 2010.
3. Лукашик В.И., Иванова Е.В. Сборник задач по физике для 7–9 классов общеобразовательных учреждений. – 17-е изд. – М.: Просвещение, 2004.

 

Домашнее задание

1. Лукашик В.И., Иванова Е.В. Сборник задач по физике для 7–9 классов №675–683, 706–712.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Единая коллекция Цифровых Образовательных Ресурсов (Источник).
2. Единая коллекция Цифровых Образовательных Ресурсов (Источник).