Период и частота обращения | Физика

Равномерное движение по окружности характеризуют периодом и частотой обращения.

Период обращения — это время, за которое совершается один оборот.

Если, например, за время t=4 с тело, двигаясь по окружности, совершило n = 2 оборота, то легко сообразить, что один оборот длился 2 с. Это и есть период обращения. Обозначается он буквой T и определяется по формуле

Итак, чтобы найти период обращения, надо время, за которое совершено n оборотов, разделить на число оборотов.

Другой характеристикой равномерного движения по окружности является частота обращения.

Частота обращения — это число оборотов, совершаемых за 1 с. Если, например, за время t = 2 с тело совершило n = 10 оборотов, то легко сообразить, что за 1 с оно успевало совершить 5 оборотов. Это число и выражает частоту обращения. Обозначается она греческой буквой ν (читается: ню) и определяется по формуле

Итак, чтобы найти частоту обращения, надо число оборотов разделить на время, в течение которого они произошли.

За единицу частоты обращения в СИ принимают частоту обращения, при которой за каждую секунду тело совершает один оборот. Эта единица обозначается так: 1/с или с^-1 (читается: секунда в минус первой степени). Раньше эту единицу называли «оборот в секунду», но теперь это название считается устаревшим.

Сравнивая формулы (6.1) и (6.2), можно заметить, что период и частота — величины взаимно обратные. Поэтому

Формулы (6.1) и (6.3) позволяют найти период обращения T, если известны число n и время оборотов t или частота обращения ν. Однако его можно найти и в том случае, когда ни одна из этих величин неизвестна. Вместо них достаточно знать скорость тела v и радиус окружности r, по которой оно движется. Для вывода новой формулы вспомним, что период обращения — это время, за которое тело совершает один оборот, т. е. проходит путь, равный длине окружности (l

окр = 2πr, где π≈3,14— число «пи», известное из курса математики). Но мы знаем, что при равномерном движении время находится делением пройденного пути на скорость движения. Таким образом,

Итак, чтобы найти период обращения тела, надо длину окружности, по которой оно движется, разделить на скорость его движения.

Видео, не по теме но интересно

1. Что такое период обращения? 2. Как можно найти период обращения, зная время и число оборотов? 3. Что такое частота обращения? 4. Как обозначается единица частоты? 5. Как можно найти частоту обращения, зная время и число оборотов? 6. Как связаны между собой период и частота обращения? 7. Как можно найти период обращения, зная радиус окружности и скорость движения тела?

Движение по окружности, период обращения и частота.

1. Равномерное движение по окружности

Внимание следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения.

Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу.

Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня.

Таким образом,

 Во время движения по кругу скорость в любой точке траектории направлена ​​по касательной к окружности в этой точке.

Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время меняется.

2. Период вращения и вращающаяся частота

Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения.

Период обращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот.

Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток.

При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле:

   

Если известен период обращения Т, то можно найти скорость тела v. За время t, равное периоду Т, тело проходит путь, равный длине окружности: . Итак,

   

Движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой:

частота вращения равна количеству полных оборотов за одну секунду.

Частота вращения и период обращения связаны следующим соотношением:

   

Частоту в СИ измеряют в

   

3. Вращательное движение

В природе довольно распространенный вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. Д.

Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусов.

Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу крупнейшего радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.

ПРОВЕРЬТЕ СЕБЯ

1. Приведите два-три примера криволинейного движения.
2. Приведите два-три примера равномерного движения по кругу.
3. Что такое вращательное движение? Приведите примеры такого движения.
4. Как направлена ​​мгновенная скорость при движении по кругу Приведите два-три примера.

1.Равномерное движение по кругу. Внимание учащихся следует обратить на то, что криволинейные движения более распространены, чем прямолинейные. Любой криволинейное движение можно рассматривать как движение по дугам окружностей с разными радиусами. Изучение движения по кругу дает также ключ к рассмотрению произвольного криволинейного движения. Мы будем изучать движение тел по окружности с постоянной по модулю скоростью. Такое движение называют равномерным движением по кругу. Наблюдения показывают, что маленькие частицы, которые отделяются от тела, вращающегося летят с той скоростью, которой владели в момент отрыва: грязь из-под колес автомобиля летит по касательной к поверхности колес; раскаленные частицы металла отрываются при заточке резца о точильный камень, вращающийся также летят по касательной к поверхности камня.

Таким образом, • Во время движения по кругу скорость в любой точке траектории направлена ​​по касательной к окружности в этой точке. Необходимо обратить внимание учащихся, что при равномерном движении по окружности модуль скорости тела остается постоянным, но направление скорости все время изменяется.

2. Период вращения и частота вращения. Движение тела по окружности часто характеризуют не скоростью движения, а промежутком времени, за которое тело совершает один полный оборот. Эта величина называется периодом вращения. • Период вращения — это физическая величина, равная промежутку времени, за который тело равномерно вращается, делает один оборот. Период вращения обозначается символом T. Например, Земля делает полный оборот вокруг Солнца за 365,25 суток. При расчетах период обычно выражают в секундах. Если период обращения равен 1с, это означает, что тело за одну секунду делает один полный оборот. Если за время t тело сделало N полных оборотов, то период можно определить по формуле: если известен период обращения Т, то можно найти скорость тела v.

За время t, равное периоду Т, тело проходит путь, равный длине окружности:. Итак, движение тела по окружности можно характеризовать еще одной величиной — числом оборотов по кругу за единицу времени. Ее называют вращающейся частотой: • вращающаяся частота равна количеству полных оборотов в одну секунду. Частота вращения и период обращения связаны следующим соотношением:  Частоту в СИ измеряют в обратных секундах.

3. Вращательного движения. В природе довольно распространенно вращательное движение: вращение колес, маховиков, Земли вокруг своей оси и т. д.Важной особенностью вращательного движения является то, что все точки тела движутся с тем же периодом, но скорости различных точек могут существенно отличаться, поскольку разные точки движутся по кругам различных радиусив. Например, при суточном вращении Земли быстрее других движутся точки, находящиеся на экваторе, так как они движутся по кругу самого большого радиуса — радиуса Земли. Точки же земной поверхности, находящиеся на других параллелях, движутся с меньшей скоростью, так как длина каждой из этих параллелей меньше длины экватора.

Движение по окружности, угловая скорость, частота, период, центростремительное ускорение. Формулы, определения, пояснения

Тестирование онлайн

Так как линейная скорость равномерно меняет направление, то движение по окружности нельзя назвать равномерным, оно является равноускоренным.

Угловая скорость

Выберем на окружности точку 1. Построим радиус. За единицу времени точка переместится в пункт 2. При этом радиус описывает угол. Угловая скорость численно равна углу поворота радиуса за единицу времени.

Период и частота

Период вращения T — это время, за которое тело совершает один оборот.

Частота вращение — это количество оборотов за одну секунду.

Частота и период взаимосвязаны соотношением

Связь с угловой скоростью

Линейная скорость

Каждая точка на окружности движется с некоторой скоростью. Эту скорость называют линейной. Направление вектора линейной скорости всегда совпадает с касательной к окружности. Например, искры из-под точильного станка двигаются, повторяя направление мгновенной скорости.

Рассмотрим точку на окружности, которая совершает один оборот, время, которое затрачено — это есть период T. Путь, который преодолевает точка — это есть длина окружности.

Центростремительное ускорение

При движении по окружности вектор ускорения всегда перпендикулярен вектору скорости, направлен в центр окружности.

Используя предыдущие формулы, можно вывести следующие соотношения

Точки, лежащие на одной прямой исходящей из центра окружности (например, это могут быть точки, которые лежат на спице колеса), будут иметь одинаковые угловые скорости, период и частоту. То есть они будут вращаться одинаково, но с разными линейными скоростями. Чем дальше точка от центра, тем быстрей она будет двигаться.

Закон сложения скоростей справедлив и для вращательного движения. Если движение тела или системы отсчета не является равномерным, то закон применяется для мгновенных скоростей. Например, скорость человека, идущего по краю вращающейся карусели, равна векторной сумме линейной скорости вращения края карусели и скорости движения человека.

Земля участвует в двух основных вращательных движениях: суточном (вокруг своей оси) и орбитальном (вокруг Солнца). Период вращения Земли вокруг Солнца составляет 1 год или 365 суток. Вокруг своей оси Земля вращается с запада на восток, период этого вращения составляет 1 сутки или 24 часа. Широтой называется угол между плоскостью экватора и направлением из центра Земли на точку ее поверхности.

Согласно второму закону Ньютона причиной любого ускорения является сила. Если движущееся тело испытывает центростремительное ускорение, то природа сил, действием которых вызвано это ускорение, может быть различной. Например, если тело движется по окружности на привязанной к нему веревке, то действующей силой является сила упругости.

Если тело, лежащее на диске, вращается вместе с диском вокруг его оси, то такой силой является сила трения. Если сила прекратит свое действие, то далее тело будет двигаться по прямой

Рассмотрим перемещение точки на окружности из А в В. Линейная скорость равна v_A и v_B соответственно. Ускорение — изменение скорости за единицу времени. Найдем разницу векторов.

Разница векторов есть . Так как , получим

В системе отсчета, связанной с колесом, точка равномерно вращается по окружности радиуса R со скоростью , которая изменяется только по направлению. Центростремительное ускорение точки направлено по радиусу к центру окружности.

Теперь перейдем в неподвижную систему, связанную с землей. Полное ускорение точки А останется прежним и по модулю, и по направлению, так как при переходе от одной инерциальной системы отсчета к другой ускорение не меняется. С точки зрения неподвижного наблюдателя траектория точки А — уже не окружность, а более сложная кривая (циклоида), вдоль которой точка движется неравномерно.

Мгновенная скорость определяется по формуле

Глава 7.

Вращательное движение. Кинематика и динамика

Как правило, в любом варианте задания ЕГЭ по физике представлены несколько задач на вращательное движение. Приведем основные определения и законы, необходимые для решения такого рода задач. Угловой скоростью тела, совершающего вращательное движение, называется отношение угла поворота к тому времени , за которое этот поворот произошел

(7.1)

В этом определении угол должен измеряться в радианах, поэтому размерность угловой скорости рад/с (или 1/с поскольку радиан — безразмерная величина). В принципе, определение (7.1) позволяет найти как среднюю (для больших интервалов времени ), так и мгновенную (при ) угловую скорость. Однако в школьном курсе физики рассматривается только движение с постоянной угловой скоростью, для которого определение (7.1) дает один и тот же результат для любых интервалов времени . Применяя определение (7. 1) к полному обороту тела (угол поворота — радиан), получим связь угловой скорости и периода вращения

(7.2)

Угловую скорость можно ввести не только для точечного тела, но и для протяженного тела. Действительно, при вращении неточечного тела вокруг любой оси все его точки поворачиваются за одинаковое время на одинаковый угол. Поэтому можно говорить об угловой скорости всего тела.

Из формулы (7.2) легко получить связь угловой и обычной скорости вращающегося точечного тела (в этом контексте последнюю всегда называют линейной скоростью). Умножая правую и левую часть формулы (7.2) на радиус окружности и учитывая, что – это длина пути, пройденного за период, получим

(7.3)

Конечно, для неточечного вращающегося тела нельзя ввести понятие линейной скорости, поскольку у разных точек этого тела линейные скорости будут разными.

Очевидно, при вращательном движении тело всегда имеет ускорение. Действительно, согласно определению (2.1) ускорение тела равно нулю, если не меняется вектор скорости этого тела (т.е. как величина скорости, так и ее направление). При вращательном движении направление скорости обязательно меняется. Можно доказать, что при вращательном движении точечного тела с постоянной по величине линейной скоростью вектор его ускорения в любой момент направлен от тела к центру траектории тела, а его величина равна

(7.4)

Ускорение (7.3) принято называть центростремительным. Если использовать связь линейной и угловой скорости тела при вращательном движении (7.3), то формулу для центростремительного ускорения можно записать и в таких формах

(7.5)

Согласно второму закону Ньютона ускорения сообщаются телам силами. Поэтому если тело совершает движение по окружности радиуса с постоянной по величине скоростью (и соответственно угловой скоростью ), на него должна действовать сила, направленная к центру окружности и равная по величине

(7.6)

Силу (7.6) принято называть центростремительной. Отметим, что термин «центростремительная» связан не с природой этой силы, а с тем, как она действует: в разных ситуациях центростремительной силой может быть и сила тяжести, и сила трения, и сила реакции, и другие силы или их комбинации.

Перечисленных законов и определений достаточно для решения любых задач ЕГЭ на вращательное движение. Рассмотрим их применение к решению задач, приведенных в первой части.

Если период вращения тела задан, то его угловая скорость может быть однозначно определена независимо от размеров тела или радиуса орбиты для точечного тела. В частности, секундная стрелка любых часов поворачивается на угол за одну минуту (конечно, при условии, что они идут «правильно»). Поэтому угловая скорость секундных стрелок любых часов равна рад/мин (задача 7.1.1 – ответ 2).

Для нахождения линейной скорости конца секундной стрелки часов (задача 7.1.2) используем связь угловой и линейной скоростей (7.5). Имеем

(правильный ответ – 2).

Применяя определение угловой скорости к колесу (задача 7.1.3), получаем

(правильный ответ 1).

Из формулы (7.2) имеем

(задача 7.1.4 – правильный ответ 4).

Используя известное расстояние от первой точки до оси вращения и ее центростремительное ускорение (задача 7.1.5), из формулы (7.5) находим квадрат угловой скорости диска

А теперь по формуле (7. 5) для второй точки получаем

(ответ 2).

Поскольку скорость автомобиля в задаче 7.1.6 не меняется в процессе движения для сравнения центростремительных ускорений автомобиля в разных точках траектории следует использовать формулу (7.4), из которой находим, что ускорение тем больше, чем меньше радиус траектории (правильный ответ – 3).

Ускорение мальчика из задачи 7.1.7 будет равно нулю, если его скорость относительно земли будет равна нулю. Поэтому при движении мальчика против движения карусели, его скорость относительно карусели равна скорости карусели относительно земли . Если мальчик пойдет в другую сторону с той же скоростью относительно карусели, его скорость относительно земли будет равна . Поэтому центростремительное ускорение мальчика будет равно

(ответ 4).

Тело, находящееся на поверхности вращающегося диска и вращающееся вместе с ним (задача 7.1.8), участвует в следующих взаимодействиях. Во-первых, тело притягивается к земле (сила тяжести), и на него действует поверхность диска (сила нормальной реакции и трения), причем сила трения в каждый момент времени направлена к оси вращения (см. рисунок). Действительно, в отсутствии силы трения тело либо будет оставаться на месте, а диск под ним будет вращаться, либо (если тело имеет скорость) слетит с поверхности диска. Именно сила трения «заставляет» тело вращаться вместе с диском. Поэтому сила трения служит в данной задаче цен-тростремительной силой. Остальные перечисления, данные в условии: «на тело действуют силы тяжести, трения, реакции опоры, центростремительная (или центробежная)» являются неправильными, поскольку в них смешиваются характеристики сил разных типов – первые три касаются природы взаимодействий, вторые – результат действия. Поэтому правильный ответ на вопрос задачи – 1. Кроме того, отметим, что центробежная сила возникает только в неинерциальных системах отсчета и в школьном курсе физики не рассматривается (поэтому лучше этим понятием вообще не пользоваться).

Поскольку тело в задаче 7.1.9 вращается с постоянной по величине скоростью по окружности, то его ускорение направлено к центру окружности, и, следовательно, согласно второму закону Ньютона, туда же направлена и результирующая сила, действующая на тело (ответ 2).

Применяя к данному в задаче 7.1.10 телу второй закон Ньютона и учитывая, что его ускорение равно м/с², получим для равнодействующей =2 Н (ответ 2).

Используя формулу для центростремительного ускорения , находим отношение ускорений материальных точек из задачи 7.2.1

(ответ 1).

Для сравнения центростремительных ускорений материальных точек в задаче 7. 2.2 удобно использовать формулу , поскольку в этой задаче одинаковы угловые скорости точек. Получаем

(ответ 3).

Для сравнения центростремительных ускорений тел в задаче 7.2.3 выразим ускорение через радиус окружности и период. Используя формулу (7.2) для периода и (7.5) для центростремительного ускорения, получим

(7.5)

Поэтому

(ответ 1).

Используя связь угловой и линейной скорости, находим скорости концов часовой и минутной стрелки (задача 7.2.4)

где и – угловые скорости часовой и минутной стрелки соответственно (в рад/час), и – длины часовой и минутной стрелок. Учитывая, что , получаем

(ответ 2).

Телу, вращающемуся вместе с диском на его горизонтальной поверхности (задача 7.2.5), центростремительное ускорение сообщается силой трения

Поэтому при увеличении угловой скорости вращения диска возрастает и сила трения между телом и диском. При некоторой угловой скорости сила трения достигнет максимально возможного для нее значения . Если еще увеличить угловую скорость диска, сила трения уже не сможет удержать тело на диске: тело начнет скользить по поверхности и слетит с поверхности диска. Поэтому значения угловой скорости, при которой тело может вращаться вместе с диском, находится из неравенства

(ответ 4).

В задаче 7. 2.6 центростремительной силой является сила натяжения нити. Поэтому из второго закона Ньютона с учетом формулы (7.5) для центростремительного ускорения имеем

(ответ 3).

В задаче 7.2.7 нужно использовать второй закон Ньютона для каждого тела. Силы, действующие на тела, показаны на рисунке. Проекция второго закона Ньютона для дальнего тела на координатную ось, направленную к центру диска, дает

(1)

На ближнее тело действуют силы натяжения и двух нитей (см. рисунок). Поэтому для него из второго закона Ньютона имеем

Подставляя в эту формулу силу из формулы (1), находим (ответ 2).

В задаче 7. 2.8 необходимо использовать то обстоятельство, что угловая скорость всех точек стержня одинакова. Обозначая расстояния от оси вращения до концов стержня как и , имеем

где = 1 м/с и = 2 м/с – линейные скорости концов стержня, м – его длина. Решая эту систему уравнений, найдем расстояния и , а затем и угловую скорость стержня . В результате получим

(ответ 3).

Среднее ускорение тела за некоторый интервал времени (не обязательно малый) определяется по формуле (2.1):

где и – скорости тела в конце и начале интервала времени . За половину периода вектор скорости поворачивается на 180°, поэтому величина разности равна . Поэтому среднее ускорение тела за половину периода равно

(задача 7. 2.9 – ответ 1).

Очевидно, при зубчатой передаче совпадают линейные скорости точек на ободе шестерней. Действительно, если бы эти скорости были разными, между поверхностями шестерней было бы проскальзывание, которому препятствуют зубцы шестерней (задача 7.2.10 – ответ 2).

Физика. Период и частота | Частная школа. 9 класс

Конспект по физике для 9 класса «Период и частота». Что такое период обращения. Что такое частота обращения. Как вычислить скорость и ускорение тела, движущегося по окружности, если известны его период и частота обращения.

Конспекты по физике    Учебник физики    Тесты по физике

---

Период и частота

Измерить скорость тела, движущегося по окружности, не всегда просто. Однако её можно вычислить, используя такие понятия, как период и частота обращения.

ПЕРИОД

Когда тело движется по окружности с постоянной по модулю скоростью, через определённые промежутки времени движение повторяется снова и снова. Примером этому может служить движение на обычной детской карусели.

Время, в течение которого тело совершает один полный оборот, называют периодом обращения. Период обращения принято обозначать буквой Т. Единица этой физической величины в СИ — секунда.

С понятием периода обращения вы уже знакомились при изучении географии. Например, период обращения Земли вокруг своей оси составляет 23 ч 56 мин 4 с, а период обращения Земли вокруг Солнца — 1,00004 земных года. Самый короткий период обращения вокруг Солнца в нашей Солнечной системе имеет планета Меркурий. Её период обращения составляет 0,24085 земных лет. Интересно, что самая большая планета Солнечной системы — Юпитер — имеет самый короткий период обращения вокруг своей оси — всего 9 ч 50 мин. В 226 000 000 лет оценивается период обращения Солнечной системы вокруг ядра Галактики.

ЧАСТОТА

Число оборотов в единицу времени, которое совершает тело при движении по окружности, называют частотой обращения. Частоту обращения обозначают греческой буквой ν.

Если, катаясь на карусели в парке, мы совершаем один оборот за 20 с, то период обращения в этом случае Т = 20 с. Как определить частоту обращения при этом движении? Сколько оборотов совершает карусель за 1 с?

Очевидно, ν = 1/Т = 1/20 ¹/с, т. е. за 1 с карусель совершает одну двадцатую часть своего полного оборота.

Таким образом, частота обращения является величиной, обратной периоду обращения:

Именно поэтому единица этой физической величины обратна секунде, т. е. ¹/с, или с^-1.

СВЯЗЬ МОДУЛЯ СКОРОСТИ С ПЕРИОДОМ И ЧАСТОТОЙ ОБРАЩЕНИЯ

Чтобы определить модуль скорости тела, движущегося по окружности, достаточно знать радиус окружности R и период или частоту обращения. Действительно, один полный оборот тело совершает за время, равное периоду обращения Т. Путь, пройденный телом, в этом случае равен длине окружности: l = 2πR. Тогда можно записать:

или с учётом формулы (1):

С учётом формул (2) и (3) можно найти центростремительное ускорение тела, выразив скорость через период или частоту обращения:

Часто мгновенную скорость движения по окружности называют линейной скоростью.

Модуль скорости движения тела по окружности рассчитывается по формуле:

Умение описывать движение тела по окружности чрезвычайно важно, так как движение по криволинейной траектории можно приближённо представить как движение по дугам окружностей различных радиусов.

РЕШЕНИЕ ЗАДАЧ

Задача 1. Найдём модуль скорости вращения ребёнка на карусели, если радиус окружности, по которой происходит движение, равен 2,3 м, а время, за которое карусель совершает один полный оборот, равно 20 с.

Ответ: υ = 0,722 м/с.

 

Задача 2.  Земля делает один оборот вокруг Солнца за 365 дней. Расстояние от Солнца до Земли составляет 149,6 • 10⁶ км. Определим линейную скорость движения Земли вокруг Солнца, считая орбиту окружностью.

Ответ: υ ≈ 30 км/с.

 

---

Вы смотрели Конспект по физике для 9 класса «Период и частота».

Вернуться к Списку конспектов по физике (Оглавление).

Кинематика — Физика — Теория, тесты, формулы и задачи

Оглавление:

 

Основные теоретические сведения

Система СИ

К оглавлению…

Основные единицы измерения величин в системе СИ таковы:

1. единица измерения длины — метр (1 м),
2. времени — секунда (1 с),
3. массы — килограмм (1 кг),
4. количества вещества — моль (1 моль),
5. температуры — кельвин (1 К),
6. силы электрического тока — ампер (1 А),
7. Справочно: силы света — кандела (1 кд, фактически не используется при решении школьных задач).

При выполнении расчетов в системе СИ углы измеряются в радианах.

Если в задаче по физике не указано, в каких единицах нужно дать ответ, его нужно дать в единицах системы СИ или в производных от них величинах, соответствующих той физической величине, о которой спрашивается в задаче. Например, если в задаче требуется найти скорость, и не сказано в чем ее нужно выразить, то ответ нужно дать в м/с.

Для удобства в задачах по физике часто приходится использовать дольные (уменьшающие) и кратные (увеличивающие) приставки. их можно применять к любой физической величине. Например, мм – миллиметр, кт – килотонна, нс – наносекунда, Мг – мегаграмм, ммоль – миллимоль, мкА – микроампер. Запомните, что в физике не существует двойных приставок. Например, мкг – это микрограмм, а не милликилограмм. Учтите, что при сложении и вычитании величин Вы можете оперировать только величинами одинаковой размерности. Например, килограммы можно складывать только с килограммами, из миллиметров можно вычитать только миллиметры, и так далее. При переводе величин пользуйтесь следующей таблицей.

Таблица дольных и кратных приставок в физике:

 

Путь и перемещение

К оглавлению…

Кинематикой называют раздел механики, в котором движение тел рассматривается без выяснения причин этого движения.

Механическим движением тела называют изменение его положения в пространстве относительно других тел с течением времени.

Всякое тело имеет определенные размеры. Однако, во многих задачах механики нет необходимости указывать положения отдельных частей тела. Если размеры тела малы по сравнению с расстояниями до других тел, то данное тело можно считать материальной точкой. Так при движении автомобиля на большие расстояния можно пренебречь его длиной, так как длина автомобиля мала по сравнению с расстояниями, которое он проходит.

Интуитивно понятно, что характеристики движения (скорость, траектория и т.д.) зависят от того, откуда мы на него смотрим. Поэтому для описания движения вводится понятие системы отсчета. Система отсчета (СО) – совокупность тела отсчета (оно считается абсолютно твердым), привязанной к нему системой координат, линейки (прибора, измеряющего расстояния), часов и синхронизатора времени.

Перемещаясь с течением времени из одной точки в другую, тело (материальная точка) описывает в данной СО некоторую линию, которую называют траекторией движения тела.

Перемещением тела называют направленный отрезок прямой, соединяющий начальное положение тела с его конечным положением. Перемещение есть векторная величина. Перемещение может в процессе движения увеличиваться, уменьшаться и становиться равным нулю.

Пройденный путь равен длине траектории, пройденной телом за некоторое время. Путь – скалярная величина. Путь не может уменьшаться. Путь только возрастает либо остается постоянным (если тело не движется). При движении тела по криволинейной траектории модуль (длина) вектора перемещения всегда меньше пройденного пути.

При равномерном (с постоянной скоростью) движении путь L может быть найден по формуле:

где: v – скорость тела, t – время в течении которого оно двигалось. При решении задач по кинематике перемещение обычно находится из геометрических соображений. Часто геометрические соображения для нахождения перемещения требуют знания теоремы Пифагора.

 

Средняя скорость

К оглавлению…

Скорость – векторная величина, характеризующая быстроту перемещения тела в пространстве. Скорость бывает средней и мгновенной. Мгновенная скорость описывает движение в данный конкретный момент времени в данной конкретной точке пространства, а средняя скорость характеризует все движение в целом, в общем, не описывая подробности движения на каждом конкретном участке.

Средняя скорость пути – это отношение всего пути ко всему времени движения:

где: L_полн – весь путь, который прошло тело, t_полн – все время движения.

Средняя скорость перемещения – это отношение всего перемещения ко всему времени движения:

Эта величина направлена так же, как и полное перемещение тела (то есть из начальной точки движения в конечную точку). При этом не забывайте, что полное перемещение не всегда равно алгебраической сумме перемещений на определённых этапах движения. Вектор полного перемещения равен векторной сумме перемещений на отдельных этапах движения.

• При решении задач по кинематике не совершайте очень распространенную ошибку. Средняя скорость, как правило, не равна среднему арифметическому скоростей тела на каждом этапе движения. Среднее арифметическое получается только в некоторых частных случаях.
• И уж тем более средняя скорость не равна одной из скоростей, с которыми двигалось тело в процессе движения, даже если эта скорость имела примерно промежуточное значение относительно других скоростей, с которыми двигалось тело.

 

Равноускоренное прямолинейное движение

К оглавлению. ..

Ускорение – векторная физическая величина, определяющая быстроту изменения скорости тела. Ускорением тела называют отношение изменения скорости к промежутку времени, в течение которого происходило изменение скорости:

где: v₀ – начальная скорость тела, v – конечная скорость тела (то есть спустя промежуток времени t).

Далее, если иное не указано в условии задачи, мы считаем, что если тело движется с ускорением, то это ускорение остается постоянным. Такое движение тела называется равноускоренным (или равнопеременным). При равноускоренном движении скорость тела изменяется на одинаковую величину за любые равные промежутки времени.

Равноускоренное движение бывает собственно ускоренным, когда тело увеличивает скорость движения, и замедленным, когда скорость уменьшается. Для простоты решения задач удобно для замедленного движения брать ускорение со знаком «–».

Из предыдущей формулы, следует другая более распространённая формула, описывающая изменение скорости со временем при равноускоренном движении:

Перемещение (но не путь) при равноускоренном движении рассчитывается по формулам:

В последней формуле использована одна особенность равноускоренного движения. При равноускоренном движении среднюю скорость можно рассчитывать, как среднее арифметическое начальной и конечной скоростей (этим свойством очень удобно пользоваться при решении некоторых задач):

С расчетом пути все сложнее. Если тело не меняло направления движения, то при равноускоренном прямолинейном движении путь численно равен перемещению. А если меняло – надо отдельно считать путь до остановки (момента разворота) и путь после остановки (момента разворота). А просто подстановка времени в формулы для перемещения в этом случае приведет к типичной ошибке.

Координата при равноускоренном движении изменяется по закону:

Проекция скорости при равноускоренном движении изменяется по такому закону:

Аналогичные формулы получаются для остальных координатных осей. Формула для тормозного пути тела:

 

Свободное падение по вертикали

К оглавлению…

На все тела, находящиеся в поле тяготения Земли, действует сила тяжести. В отсутствие опоры или подвеса эта сила заставляет тела падать к поверхности Земли. Если пренебречь сопротивлением воздуха, то движение тел только под действием силы тяжести называется свободным падением. Сила тяжести сообщает любым телам, независимо от их формы, массы и размеров, одинаковое ускорение, называемое ускорением свободного падения. Вблизи поверхности Земли ускорение свободного падения составляет:

Это значит, что свободное падение всех тел вблизи поверхности Земли является равноускоренным (но не обязательно прямолинейным) движением. Вначале рассмотрим простейший случай свободного падения, когда тело движется строго по вертикали. Такое движение является равноускоренным прямолинейным движением, поэтому все изученные ранее закономерности и фокусы такого движения подходят и для свободного падения. Только ускорение всегда равно ускорению свободного падения.

Традиционно при свободном падении используют направленную вертикально ось OY. Ничего страшного здесь нет. Просто надо во всех формулах вместо индекса «х» писать «у». Смысл этого индекса и правило определения знаков сохраняется. Куда направлять ось OY – Ваш выбор, зависящий от удобства решения задачи. Вариантов 2: вверх или вниз.

Приведем несколько формул, которые являются решением некоторых конкретных задач по кинематике на свободное падение по вертикали. Например, скорость, с которой упадет тело падающее с высоты h без начальной скорости:

Время падения тела с высоты h без начальной скорости:

Максимальная высота на которую поднимется тело, брошенное вертикально вверх с начальной скоростью v₀, время подъема этого тела на максимальную высоту, и полное время полета (до возвращения в исходную точку):

 

Горизонтальный бросок

К оглавлению…

При горизонтальном броске с начальной скоростью v₀ движение тела удобно рассматривать как два движения: равномерное вдоль оси ОХ (вдоль оси ОХ нет никаких сил препятствующих или помогающих движению) и равноускоренного движения вдоль оси OY.

Скорость в любой момент времени направлена по касательной к траектории. Ее можно разложить на две составляющие: горизонтальную и вертикальную. Горизонтальная составляющая всегда остается неизменной и равна v_x = v₀. А вертикальная возрастает по законам ускоренного движения v_y = gt. При этом полная скорость тела может быть найдена по формулам:

При этом важно понять, что время падения тела на землю никоим образом не зависит от того, с какой горизонтальной скоростью его бросили, а определяется только высотой, с которой было брошено тело. Время падения тела на землю находится по формуле:

Пока тело падает, оно одновременно движется вдоль горизонтальной оси. Следовательно, дальность полета тела или расстояние, которое тело сможет пролететь вдоль оси ОХ, будет равно:

Угол между горизонтом и скоростью тела легко найти из соотношения:

Также иногда в задачах могут спросить о моменте времени, при котором полная скорость тела будет наклонена под определенным углом к вертикали. Тогда этот угол будет находиться из соотношения:

Важно понять, какой именно угол фигурирует в задаче (с вертикалью или с горизонталью). Это и поможет вам выбрать правильную формулу. Если же решать эту задачу координатным методом, то общая формула для закона изменения координаты при равноускоренном движении:

Преобразуется в следующий закон движения по оси OY для тела брошенного горизонтально:

При ее помощи мы можем найти высоту на которой будет находится тело в любой момент времени. При этом в момент падения тела на землю координата тела по оси OY будет равна нулю. Очевидно, что вдоль оси OХ тело движется равномерно, поэтому в рамках координатного метода горизонтальная координата изменятся по закону:

 

Бросок под углом к горизонту (с земли на землю)

К оглавлению…

Максимальная высота подъема при броске под углом к горизонту (относительно начального уровня):

Время подъема до максимальной высоты при броске под углом к горизонту:

Дальность полета и полное время полета тела брошенного под углом к горизонту (при условии, что полет заканчивается на той же высоте с которой начался, т. е. тело бросали, например, с земли на землю):

Минимальная скорость тела брошенного под углом к горизонту – в наивысшей точке подъёма, и равна:

Максимальная скорость тела брошенного под углом к горизонту – в моменты броска и падения на землю, и равна начальной. Это утверждение верно только для броска с земли на землю. Если тело продолжает лететь ниже того уровня, с которого его бросали, то оно будет там приобретать все большую и большую скорость.

 

Сложение скоростей

К оглавлению…

Движение тел можно описывать в различных системах отсчета. С точки зрения кинематики все системы отсчета равноправны. Однако кинематические характеристики движения, такие как траектория, перемещение, скорость, в разных системах оказываются различными. Величины, зависящие от выбора системы отсчета, в которой производится их измерение, называют относительными. Таким образом, покой и движение тела относительны. Классический закон сложения скоростей:

Таким образом, абсолютная скорость тела равна векторной сумме его скорости относительно подвижной системы координат и скорости самой подвижной системы отсчета.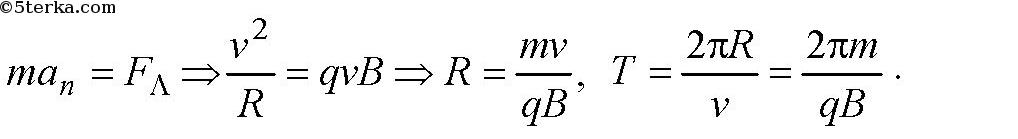 Или, другими словами, скорость тела в неподвижной системе отсчета равна векторной сумме скорости тела в подвижной системе отсчета и скорости подвижной системы отсчета относительно неподвижной.

 

Равномерное движение по окружности

К оглавлению…

Движение тела по окружности является частным случаем криволинейного движения. Такой вид движения также рассматривается в кинематике. При криволинейном движении вектор скорости тела всегда направлен по касательной к траектории. То же самое происходит и при движении по окружности (см. рисунок). Равномерное движение тела по окружности характеризуется рядом величин.

Период – время, за которое тело, двигаясь по окружности, совершает один полный оборот. Единица измерения – 1 с. Период рассчитывается по формуле:

Частота – количество оборотов, которое совершило тело, двигаясь по окружности, в единицу времени. Единица измерения – 1 об/с или 1 Гц. Частота рассчитывается по формуле:

В обеих формулах: N – количество оборотов за время t. Как видно из вышеприведенных формул, период и частота величины взаимообратные:

При равномерном вращении скорость тела будет определяется следующим образом:

где: l – длина окружности или путь, пройденный телом за время равное периоду T. При движении тела по окружности удобно рассматривать угловое перемещение φ (или угол поворота), измеряемое в радианах. Угловой скоростью ω тела в данной точке называют отношение малого углового перемещения Δφ к малому промежутку времени Δt. Очевидно, что за время равное периоду T тело пройдет угол равный 2π, следовательно при равномерном движении по окружности выполняются формулы:

Угловая скорость измеряется в рад/с. Не забывайте переводить углы из градусов в радианы. Длина дуги l связана с углом поворота соотношением:

Связь между модулем линейной скорости v и угловой скоростью ω:

При движении тела по окружности с постоянной по модулю скоростью изменяется только направление вектора скорости, поэтому движение тела по окружности с постоянной по модулю скоростью является движением с ускорением (но не равноускоренным), так как меняется направление скорости. В этом случае ускорение направлено по радиусу к центру окружности. Его называют нормальным, или центростремительным ускорением, так как вектор ускорения в любой точке окружности направлен к ее центру (см. рисунок).

Модуль центростремительного ускорения связан с линейной v и угловой ω скоростями соотношениями:

Обратите внимание, что если тела (точки) находятся на вращающемся диске, шаре, стержне и так далее, одним словом на одном и том же вращающемся объекте, то у всех тел одинаковые период вращения, угловая скорость и частота.

3)Формула для периода обращения заряда в однородном магнитном поле. Почему период обращения не зависит от скорости заряда.

4)

5)

6)

7) Почему при некоторм значение силытока солениоида электроны не достигаю анода

8)

9)

1. Магни́тный моме́нт, магни́тный дипо́льный моме́нт — основная величина, характеризующая магнитные свойства вещества. Источником магнетизма, согласно классической теории электромагнитных явлений, являются электрические макро- и микротоки. Элементарным источником магнетизма считают замкнутый ток. Магнитным моментом обладают элементарные частицы, атомные ядра, электронные оболочки атомов и молекул. Магнитный момент элементарных частиц (электронов, протонов, нейтронов и других), как показала квантовая механика, обусловлен существованием у них собственного механического момента — спина.

Магнитный момент измеряется в А⋅м² или Дж/Тл (СИ), либо эрг/Гс (СГС), 1 эрг/Гс = 10^-3 Дж/Тл. Специфической единицей элементарного магнитного момента является магнетон Бора.

Магни́тная инду́кция  — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой магнитное поле действует на заряд , движущийся со скоростью .

Более конкретно,  — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля^[1] на заряд , движущийся со скоростью , равна

где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора перпендикулярно им обоим и направлено по правилу буравчика).

Напряжённость магни́тного по́ля — (стандартное обозначение Н) это векторная физическая величина, равная разности вектора магнитной индукции B ивектора намагниченности M.

В СИ: , где — магнитная постоянная

В СГС: 

• В простейшем случае изотропной (по магнитным свойствам) среды и в приближении достаточно низких частот изменения поля B и H просто пропорциональны друг другу, отличаясь просто числовым множителем (зависящим от среды) B = μ H в системе СГС или B = μ₀μ H в системе СИ (см.Магнитная проницаемость, также см. Магнитная восприимчивость).

В системе СГС напряжённость магнитного поля измеряется в Эрстедах (Э), в системе СИ — в амперах на метр (А/м). В технике Эрстед постепенно вытесняется единицей СИ — ампером на метр, 1 Э = 1000/(4π) А/м = 79,5775 А/м.

Магни́тный пото́к — поток как интеграл вектора магнитной индукции через конечную поверхность . Определяется через интеграл по поверхности

при этом векторный элемент площади поверхности определяется как

где — единичный вектор, нормальный к поверхности.

Также магнитный поток можно рассчитать как скалярное произведение вектора магнитной индукции на вектор площади:

где α — угол между вектором магнитной индукции и нормалью к плоскости площади.

Магнитный поток через контур также можно выразить через циркуляцию векторного потенциала магнитного поля по этому контуру:

2. Закон электромагнитной идукции Фарадея

Интуитивно привлекательный, но ошибочный подход к использованию правила потока выражает поток через цепь по формуле Φ_B = B w ℓ, где w — ширина движущейся петли. Это выражение не зависит от времени, поэтому из этого неправильно следует, что никакой ЭДС не генерируется. Ошибка этого утверждения состоит в том, что в нём не учитывается весь путь тока через замкнутую петлю.

Для правильного использования правила потока мы должны рассмотреть весь путь тока, который включает в себя путь через ободы на верхнем и нижнем дисках. Мы можем выбрать произвольный замкнутый путь через ободы и вращающуюся петлю, и по закону потока найти ЭДС по этому пути. Любой путь, который включает сегмент, прилегающий к вращающейся петле, учитывает относительное движение частей цепи.

В качестве примера рассмотрим путь, проходящий в верхней части цепи в направлении вращения верхнего диска, а в нижней части цепи — в противоположном направлении по отношению к нижнему диску (показано стрелками на рис. 4). В этом случае если вращающаяся петля отклонилась на угол θ от коллекторной петли, то её можно рассматривать как часть цилиндра площадью A = r ℓ θ. Эта площадь перпендикулярна полю B, и вносимый ею вклад в поток равен:

где знак является отрицательным, потому что по правилу правой руки поле B, генерируемое петлёй с током, противоположно по направлению приложенному полю B’. Поскольку это только зависящая от времени часть потока, по закону потока ЭДС равна:

в согласии с формулой закона Лоренца.

3. Закон Био-Савара-Лапласа

Закон Био́—Савара—Лапла́са — физический закон для определения вектора индукции магнитного поля, порождаемого постояннымэлектрическим током. Был установлен экспериментально в 1820 году Био и Саваром и сформулирован в общем виде Лапласом. Лаплас показал также, что с помощью этого закона можно вычислить магнитное поле движущегося точечного заряда (считая движение одной заряженной частицы током).

Закон Био—Савара—Лапласа играет в магнитостатике ту же роль, что и закон Кулона в электростатике. Закон Био—Савара—Лапласа можно считать главным законом магнитостатики, получая из него остальные ее результаты.

В современной формулировке закон Био—Савара—Лапласа чаще рассматривают как следствие двух уравнений Максвелла для магнитного поля при условии постоянства электрического поля, т. е. в современной формулировке уравнения Максвелла выступают как более фундаментальные (прежде всего хотя бы потому, что формулу Био—Савара—Лапласа нельзя просто обобщить на общий случай полей, зависящих от времени).

4. Формула индукция магнитного поля в центре кругового тока

5)

6)

Как рассчитать менструальный цикл

Может быть, вы планируете день на пляже. Может быть, у вас есть ночевка с друзьями. Или, может быть, вы просто хотите знать, когда спрятать в сумке немного лишнего Always Ultra, чтобы вас не застали врасплох ежемесячный поток.

Знать, как рассчитать менструальный цикл, легко, и это может дать вам душевное спокойствие.

Итак, вот как это сделать.

Чтобы рассчитать менструальный цикл, вам нужно научиться отслеживать свой цикл.

Не волнуйтесь. Все очень просто. Все, что вам нужно сделать, это отметить начало менструации в календаре на несколько месяцев, чтобы понять, как считать дни цикла менструации и рассчитать среднюю продолжительность менструального цикла.

Вот как это работает. Отметьте в календаре первый день менструации. Первый день менструации — это день 1 менструального цикла. Начиная с первого дня менструации, начните считать.

День перед следующей менструацией — это последний день менструального цикла.Вот тогда ты перестанешь считать. Вот сколько дней у вас было в менструальном цикле в этом месяце. Например, если у вас начались месячные 5 июня, а следующая менструация наступила 2 июля, продолжительность вашего цикла в этом месяце составляла 27 дней.

Если вы будете делать это в течение нескольких месяцев, вы научитесь считать дни цикла менструации и сможете вычислить среднюю продолжительность цикла.

Сделайте это, сложив количество дней в каждом цикле. Затем разделите это число на количество циклов (то есть количество раз, когда у вас были месячные) с момента подсчета.Это даст вам среднее количество дней между периодами или среднюю продолжительность цикла.

Теперь выяснить, когда наступят ваши следующие месячные, проще простого. Начиная с первого дня вашей последней менструации, просто отсчитайте среднее количество дней между вашими менструациями (она же средняя длина цикла , которую вы рассчитали), и это даст вам прогнозируемую дату начала вашего следующего периода .

Вуаля! Теперь вы знаете, как рассчитать свой цикл. Подсчет менструации — это не точная наука, но знание того, как рассчитать менструальный цикл , даст вам хорошее приблизительное представление о том, когда у вас начнутся месячные.

Ваши месячные могут не наступать регулярно. Фактически, когда вы впервые начинаете менструацию, это совершенно нормально, — нерегулярные месячные. Вашему телу может потребоваться год или два, чтобы привыкнуть к регулярному режиму, поэтому продолжайте отслеживать.

Все это вас косило? Не волнуйся. Вы можете узнать больше об этом на always.com , поэтому проверьте онлайн и используйте календарь периодов на нашем веб-сайте. Знание того, как рассчитать свой __ менструальный цикл __, очень помогает подготовиться и быть уверенным в своем периоде.

Уравнение обмена — Обзор, формула и количественная теория денег

Что такое уравнение обмена?

Уравнение обмена — это математическое уравнение количественной теории денег в экономике, которое определяет взаимосвязь между факторами:

• Денежная масса
• Скорость денег
• Уровень цен
• Уровень расходов

Объяснение уравнения обмена

Уравнение обмена было выведено экономистом Джоном Стюартом Миллем.Уравнение утверждает, что общая сумма денег, которая переходит из рук в руки в экономике, всегда будет равна общей денежной стоимости товаров и услуг. услуга — это нематериальный объект, который возникает в результате перехода из рук в руки в экономике.

Другими словами, сумма номинальных расходов всегда будет равна сумме номинального дохода.

Уравнение обмена также используется для доказательства того, что темпы инфляции будут пропорциональны изменению денежной массы и что спрос на деньги можно разбить на:

1. Общий спрос на деньги для использования в транзакциях; и
2. Общий спрос на деньги для удержания в ликвидности Ликвидность На финансовых рынках ликвидность означает, насколько быстро инвестиция может быть продана без отрицательного влияния на ее цену.Чем более ликвидна инвестиция, тем быстрее ее можно продать (и наоборот) и тем легче ее продать по справедливой стоимости. При прочих равных, более ликвидные активы торгуются с премией, а неликвиды — с дисконтом.

Уравнение выглядит следующим образом:

Где:

• M _s = Денежная масса или средняя денежная единица в обращении за период времени
• V = Скорость обращения денег, или среднее количество раз, когда денежная единица переходила из рук в руки в течение периода времени
• P = Средний уровень цен на товары и услуги в течение периода времени
• T = Индекс реальной стоимости всех совокупных транзакций в течение времени период

«M _s x V» интерпретируется как общая сумма денег, потраченная в экономике за период времени

«P x T» интерпретируется как общая сумма потраченных денег внутри экономики в течение определенного периода времени.

Следовательно, как упоминалось ранее, уравнение утверждает, что общая сумма денег, потраченная в экономике за определенный период, всегда равна общей сумме денег, потраченной на товары и услуги в течение того же периода.

Уравнение можно переформулировать в следующем виде:

Где:

• M _s = Денежная масса или средняя денежная единица в обращении за период времени
• V = Скорость обращения деньги, или среднее количество раз, когда денежная единица переходила из рук в руки в течение периода времени
• P = Средний уровень цен на товары и услуги в течение периода времени
• Q = Индекс всех реальных расходов за период времени

«P x Q» интерпретируется как номинальный ВВП. Номинальный валовой внутренний продукт. Номинальный валовой внутренний продукт (номинальный ВВП) — это общая рыночная стоимость всех товаров и услуг, произведенных в экономике страны за определенный период в течение определенного периода времени.

В пересмотренном уравнении говорится, что общая сумма денег, потраченных в рамках экономики за определенный период, всегда равна общей сумме денег, заработанных за тот же период; или номинальные расходы всегда равны номинальному доходу.

Он представляет собой общее выражение количественной теории денег, которое используется для объяснения изменений денежной массы и ее отношения к общему уровню цен на товары и услуги.

Количественная теория денег

Количественная теория денег объясняет взаимосвязь между уровнями цен и денежной массой.Исходная «нео-количественная теория» утверждает, что существует фиксированная пропорциональная зависимость между изменением денежной массы в экономике и уровнями цен в экономике. Эта форма теории была основана на уравнении, выведенном экономистом Ирвингом Фишером.

Теория предполагает, что увеличение количества денег в обращении вызовет инфляцию и что любое увеличение инфляции приведет к увеличению количества денег в обращении. Это объясняется следующим примером:

Федеральная резервная система Федеральная резервная система (ФРС) Федеральная резервная система является центральным банком Соединенных Штатов и финансовым органом, стоящим за крупнейшей в мире свободной рыночной экономикой.решает удвоить количество денег в предложении, напечатав лишние деньги. Впоследствии это привело бы к резкому росту цен, поскольку больше долларов США преследуют такое же количество товаров. Спрос на товары и объем расходов должны увеличиться и оказать повышательное давление на цены.

Количественная теория денег на практике

В 2020 году произошла серьезная вспышка пандемии, известной как «Covid-19». Чтобы замедлить распространение вируса, мировая экономика остановилась, а целые группы населения остались на карантине дома.

Для поддержания экономики — когда доходы многих людей упали до нуля, — центральные банки и правительства ввели беспрецедентное количество стимулов в экономику, что значительно увеличило общую денежную массу.

Однако это не привело к пропорциональному увеличению цен, поскольку количественная теория денег предполагает, что увеличение денежной массы приведет непосредственно к увеличению расходов.

В таком сценарии вложенные в экономику деньги не сразу использовались для расходов, а скорее для сбережений или оплаты регулярных счетов вместо дохода.Это была ситуация, в которой количественная теория денег не действовала.

Дополнительные ресурсы

CFI является официальным поставщиком глобальной страницы программы коммерческого банковского и кредитного аналитика (CBCA) ™ — CBCAGet Сертификация CFI CBCA ™ и получение статуса коммерческого банковского и кредитного аналитика. Зарегистрируйтесь и продвигайтесь по карьерной лестнице с помощью наших программ и курсов сертификации. программа сертификации, призванная помочь любому стать финансовым аналитиком мирового уровня. Чтобы продолжить продвижение по карьерной лестнице, вам будут полезны следующие дополнительные ресурсы CFI:

• Спрос и предложение Спрос и предложение Законы спроса и предложения — это микроэкономические концепции, которые утверждают, что на эффективных рынках количество поставляемого товара и количество
• Равновесное количество Равновесие Количество Равновесное количество относится к количеству товара, поставляемому на рынок, когда количество, поставляемое продавцами, точно совпадает с
• Количественная теория денег Количественная теория денег связана с идеей о том, что количество доступных денег (денежная масса) растет. с той же скоростью, что и уровни цен
• Скорость обращения Скорость обращения Скорость обращения означает среднее количество раз, когда одна денежная единица переходила из рук в руки в экономике в течение определенного периода времени

Веб-сайт класса физики

Круговое движение и гравитация: обзор набора задач

Этот набор из 27 задач нацелен на вашу способность комбинировать законы Ньютона и уравнения кругового движения и гравитации для анализа движения объектов, движущихся по кругу, включая орбитальные спутники.Проблемы варьируются по сложности от очень простых и простых до очень сложных и сложных. Более сложные задачи обозначены цветом , синие задачи .

Характеристики движения объектов, движущихся по кругам.

Объекты, движущиеся по кругу, имеют скорость, равную пройденному за время пути расстоянию. Расстояние вокруг круга эквивалентно длине окружности и рассчитывается как 2 • pi • R, где R — радиус.Время одного оборота по окружности называется периодом и обозначается символом T. Таким образом, средняя скорость объекта, движущегося по кругу, определяется выражением 2 • pi • R / T. Часто в постановке задачи указывается частота вращения в оборотах в минуту или в оборотах в секунду. Каждый оборот по окружности эквивалентен длине окружности. Таким образом, умножение частоты вращения на длину окружности позволяет определить среднюю скорость объекта.

Ускорение объектов, движущихся по кругу, основано в первую очередь на изменении направления. Фактическая скорость ускорения зависит от скорости изменения направления и напрямую связана со скоростью и обратно пропорциональна радиусу поворота. В итоге ускорение определяется выражением v ² / R, где v — скорость, а R — радиус окружности.

Уравнения для средней скорости (v) и среднего ускорения (a) приведены ниже.

v = d / t = 2 • pi • R / T = частота • 2 • pi • R
а = v ² / R

Направленные величины для объектов, движущихся по кругам

Успешный математический анализ объектов, движущихся по кругу, во многом зависит от концептуального понимания направления вектора ускорения и результирующей силы. Движение по круговой траектории требует чистой силы, направленной к центру круга.В каждой точке пути результирующая сила должна быть направлена ​​внутрь. Хотя может существовать отдельная сила, направленная наружу, должна быть внутренняя сила, которая подавляет ее по величине и удовлетворяет требованию для внутренней чистой силы. Поскольку чистая сила и ускорение всегда в одном и том же направлении, ускорение объектов, движущихся по кругу, также должно быть направлено внутрь.

Диаграммы свободного тела и второй закон Ньютона

Часто силовой анализ должен проводиться для объекта, движущегося по кругу.Целью анализа является определение величины отдельной силы, действующей на объект, или использование значений отдельных сил для определения ускорения. Как и любая задача анализа сил, эти задачи должны начинаться с построения диаграммы свободного тела, показывающей тип и направление всех сил, действующих на объект. Из диаграммы F _net = m • можно написать уравнение. При написании уравнения помните, что F _net представляет собой векторную сумму всех индивидуальных сил.Лучше всего это записать, сложив все силы, действующие в направлении ускорения (внутрь), и вычтя те, которые ему противостоят. Два примера показаны на рисунке ниже.

Закон всемирного тяготения Ньютона

Спутники, движущиеся по орбите, — это просто снаряды — объекты, на которые действует только сила тяжести. Сила, управляющая их движением, — это сила гравитационного притяжения к объекту, который находится в центре их орбиты.Планеты вращаются вокруг Солнца в результате гравитационной силы притяжения к Солнцу. Естественные луны вращаются вокруг планет в результате гравитационной силы притяжения к планете. Гравитация — это сила, которая действует на больших расстояниях таким образом, что любые два объекта с массой будут притягиваться. Ньютон был первым, кто предложил теорию, чтобы описать это универсальное массовое притяжение и выразить его математически. Закон, известный как закон всемирного тяготения, гласит, что сила гравитационного притяжения прямо пропорциональна произведению масс и обратно пропорциональна квадрату расстояния между их центрами.В форме уравнения,

F _grav = G • m ₁ • m ₂ / d ²

где m ₁ и m ₂ — массы притягивающих объектов (в кг), d — расстояние разделения, измеренное от центра объекта к центру объекта (в метрах), а G — константа пропорциональности (иногда называемая всемирная гравитационная постоянная). Значение G составляет 6,673 x 10 ^-11 Н • м ² / кг ² .

Ускорение свободного падения

Поскольку на орбитальные спутники действует исключительно сила тяжести, их ускорение является ускорением силы тяжести (g). На земной поверхности это значение составило 9,8 м / с ² . Для местоположений, отличных от поверхности Земли, необходимо уравнение, которое выражает g через соответствующие переменные. Ускорение свободного падения зависит от массы объекта, который находится в центре орбиты (M _{, центральный} ), и расстояния разделения от этого объекта (d).Уравнение, связывающее эти две переменные с ускорением свободного падения, получено из закона всемирного тяготения Ньютона. Уравнение

g = G • M _{центральный} / d ²

где G составляет 6,673 x 10 ^-11 Н • м ² / кг ² .

Орбитальная скорость

Скорость, необходимая для того, чтобы спутник оставался на орбите вокруг центрального тела (планеты, солнца, другой звезды и т. Д.).) зависит от радиуса орбиты и массы центрального тела. Уравнение, выражающее взаимосвязь между этими переменными, получается путем объединения определений ускорения кругового движения с законом всемирного тяготения Ньютона. Уравнение

v = SQRT (G • M _{центральный} / R)

где M _central — масса центрального тела, вокруг которого вращается спутник, R — радиус орбиты, а G — 6,673 x 10 ^-11 Н • м ² / кг ² .

Орбитальный период

Для общего движения объекта по кругу период связан с радиусом круга и скоростью объекта уравнением v = 2 • pi • R / T. В случае орбитального спутника это уравнение для скорости можно приравнять к уравнению для орбитальной скорости, полученной из всемирного тяготения, чтобы получить новое уравнение для орбитального периода. Результат вывода:

T ² / R ³ = 4 • pi ² / (G • M _{центральный} )

где M _central — масса центрального тела, вокруг которого вращается спутник, R — радиус орбиты, а G — 6.673 x 10 ^-11 Н • м ² / кг ² . Выраженное таким образом уравнение показывает, что отношение квадрата периода к радиусу в кубе для любого спутника, вращающегося вокруг центрального тела, одинаково независимо от природы спутника или радиуса его орбиты. Это соотношение зависит только от массы объекта, который втягивает орбитальный спутник внутрь. Этот принцип согласуется с третьим законом движения планет Кеплера.

Резюме математических формул

Одна из трудностей, с которыми может столкнуться учащийся в этом наборе задач, — это путаница в выборе формулы.В таблице ниже представлено полезное резюме формул, относящихся к круговому движению и движению спутника. В таблице многие формулы получены из других уравнений. Таким образом, часто будет несколько способов определения неизвестной величины. Подходя к этим проблемам, рекомендуется практиковать обычные привычки эффективного решателя проблем; определить известные и неизвестные величины в виде символов физических формул, разработать стратегию использования известных для решения неизвестного, а затем, наконец, выполнить необходимые алгебраические шаги и замены, необходимые для решения.

Для расчета …	… используйте уравнение (а):
Скорость (v)	v = 2 • pi • R / T v = SQRT (G • M центральный / R) только для спутников
Разгон (а)	a = v 2 / R или a = F нетто / м a = g = G • M центральный / d 2 только для спутников
Чистая сила (F net )	F net = m • a или F net = m • v 2 / R F net = F grav = G • m sat • M центральный / d 2 только для спутников
Период (Т)	T = 2 • pi • R / v T 2 = 4 • pi 2 / (G • M центральный ) • R 3 только для спутников

Привычки эффективно решать проблемы

Эффективный решатель проблем по привычке подходит к физическим проблемам таким образом, чтобы отражать набор дисциплинированных привычек.Хотя не все эффективные специалисты по решению проблем используют один и тот же подход, все они имеют общие привычки. Эти привычки кратко описаны здесь. Эффективное решение проблем …

• … внимательно читает задачу и создает мысленную картину физической ситуации. При необходимости они набрасывают простую схему физической ситуации, чтобы помочь визуализировать ее.
• … определяет известные и неизвестные величины в организованном порядке, часто записывая их на диаграмме.Они приравнивают заданные значения к символам, используемым для представления соответствующей величины (например, m = 61,7 кг, v = 18,5 м / с, R = 30,9 м, F _norm = ???).
• … строит стратегию решения неизвестной величины; стратегия, как правило, сосредоточена вокруг использования физических уравнений и во многом зависит от понимания физических принципов.
• … определяет подходящую (ые) формулу (ы) для использования, часто записывая их. При необходимости они выполняют необходимое преобразование количеств в правильные единицы.
• … выполняет подстановки и алгебраические манипуляции, чтобы найти неизвестную величину.

Подробнее …

Дополнительная литература / Учебные пособия:

Следующие страницы из учебного пособия по физике могут быть полезны для понимания концепций и математики, связанных с этими проблемами.

Набор задач кругового движения и гравитации

Просмотреть набор задач

Решения с аудиогидом для кругового движения и гравитации

Просмотрите аудиогид решения проблемы:
1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 | 17 | 18 | 19 | 20 | 21 | 22 | 23 | 24 | 25 | 26 | 27

Скорость циркуляции — обзор

Основы циркуляции катализатора

Блок FCC — это операция «уравновешивания давления», которая в основном ведет себя аналогично водяному манометру.Перепад давления между регенератором и сосудами реактора является движущей силой, которая позволяет псевдоожиженному катализатору циркулировать между регенератором и сосудами реактора (типичный баланс давления см. На Рисунке 12.1). Задвижка или дроссельная заслонка, расположенная в линии дымовых газов регенератора, используется для регулирования перепада давления между регенератором и сосудами реактора. Давление в реакторе контролируется WGC.

Рисунок 12.1. Типичный баланс давления установки FCC.

Свежий катализатор добавляется для компенсации потерь катализатора из резервуаров реактора / регенератора, а также для компенсации потери активности катализатора. Запасы катализатора в установке регулируются периодическим отбором избыточного катализатора из регенерационной емкости.

Уровень катализатора в емкости для отпарки катализатора регулируется золотниковым или пробковым клапаном, расположенным в стояке для отработанного катализатора. В большинстве установок FCC температура крекинга регулируется путем регулирования потока катализатора из регенератора через золотниковые или пробковые клапаны, которые расположены в стояке регенерированного катализатора.В установках Model IV и Flexicracker FCC перепад давления между реактором и регенератором является основной контрольной точкой для регулирования циркуляции катализатора из регенератора в реактор.

В регенераторах FCC, которые работают в режиме частичного сгорания с регенерацией катализатора , расход воздуха для горения регулируется для достижения заданной концентрации монооксида углерода (CO) в дымовых газах регенератора и / или заданного уровня CRC.

В регенераторах FCC, которые работают в режиме полного сжигания регенерации катализатора, в дымовых газах регенератора поддерживается избыточная концентрация кислорода для обеспечения полного сгорания монооксида углерода (CO) до диоксида углерода (CO ₂ ).

Уровень «сырого» катализатора в регенераторе определяется путем измерения разности давлений между давлением над распределителем воздуха и давлением разбавления / верха регенератора. Часто имеется другой кран давления, примерно на 5 футов (152 см) выше воздухораспределителя, который используется для измерения плотности потока катализатора.

В реакторе / отпарной колонне уровень «сырого» катализатора определяется путем измерения перепада давления на дне отпарной колонны катализатора по сравнению с верхним давлением реактора.Фактический уровень катализатора можно рассчитать, используя показания плотности катализатора в отпарной колонне катализатора.

Скорость циркуляции катализатора зависит от следующих параметров:

•

Скорость подачи свежего сырья

•

Использование нафты, LCO, HCO или рециркуляции суспензии в стояк

Температура реактора

•

Температура подачи в стояк

•

Давления в реакторе и регенераторе

•

Температура плотного слоя регенератора.

Температура плотного слоя регенератора зависит от следующего:

•

Качество сырья

•

Скорость добавления свежего катализатора и / или его активность

•

состояние и температура нагнетания нагнетателя воздуха

•

Работа охладителя катализатора и / или другие схемы удаления

•

Эффективность работы форсунок подачи и удаления катализатора

•

Уровень дожигания

•

Концентрация CO в дымовых газах регенератора.

На «легкость» циркуляции катализатора в значительной степени влияет физическая структура устройства и свойства псевдоожижения катализатора. Некоторые крекеры для кошек легко циркулируют независимо от физических свойств катализатора. Однако в других конструкциях установка может испытывать трудности с циркуляцией из-за незначительных изменений свойств катализатора.

Что следует помнить при более высокой скорости циркуляции катализатора:

•

Давление на выходе золотникового клапана регенерированного катализатора повышается, в основном из-за более высокого напора и больших потерь на трение на J-образном изгибе / тройнике -сечение детали, а также поперек стояка.Это приведет к снижению Δ P на золотниковом клапане регенерированного катализатора (см. Также Пример 12.1).

•

Более высокая скорость циркуляции катализатора направленно увеличивает скорость потерь катализатора из циклонов реактора / регенератора. Это в значительной степени связано с более высокой загрузкой катализатора в циклоны и более высокой скоростью истирания катализатора.

•

Эффективность работы отпарной колонны катализатора снижается из-за «более высокой скорости потока» катализатора через отпарную колонну.Это особенно верно, поскольку большинство операторов не регулируют скорость отпарного пара с более высокой скоростью циркуляции катализатора.

•

Более высокая скорость циркуляции катализатора увлекает больше дымовых газов в стояк, что может привести к нагрузке на секцию улавливания паров FCC.

•

В долгосрочной перспективе более высокая скорость циркуляции катализатора отрицательно влияет на механическую надежность оборудования FCC.

Несмотря на недостатки, отмеченные выше, более высокая скорость циркуляции катализатора и последующее более высокое соотношение кат / масло часто доставляют больше жидких объемных продуктов из данного сырья для FCC, и это часто увеличивает рентабельность операций FCCU.

Стабильная и плавная циркуляция катализатора увеличивает уверенность, а также увеличивает «зону комфорта» оператора консоли для оптимизации производительности установки для кошачьего крекинга. Например, он или она сможет:

•

Увеличить подачу в установку

•

Увеличить отпарной пар, чтобы уменьшить вынос мягкого кокса и снизить температуру регенератора

•

Уменьшите температуру предварительного нагрева сырья для увеличения соотношения кат / масло

•

Увеличьте температуру крекинга, чтобы произвести больше олефинового сырья и / или увеличить октановое число бензина

•

Произвести больше пара из охладитель катализатора

•

Работает при более высоком содержании CO в дымовых газах при работе с частичным сжиганием.

Следовательно, возможность максимизировать скорость циркуляции катализатора чрезвычайно важна для долгосрочной надежности и прибыльности данной установки FCC.

Факторы, препятствующие циркуляции катализатора

Ключевые факторы, влияющие на способность катализатора FCC плавно течь в стояках, следующие (см. Также Пример 12.2):

•

Состояние катализатора до того, как он попадет в устье напорной трубы.Если катализатор не псевдоожижен «должным образом», трудно поддерживать его должным образом псевдоожиженным в стояке.

•

В зависимости от длины / высоты стояка может потребоваться дополнительное псевдоожижение для компенсации сжатия пузырьков газа, когда они движутся вниз вместе с катализатором. Чрезвычайно важны сухость и количество дополнительного дымового газа, а также расстояние между вентилями для аэрации. Кроме того, надежность измерения расхода аэрации для каждого крана или набора кранов играет ключевую роль в успехе псевдоожижения стояка.Слишком сильная аэрация может вызвать «перекрытие» потока катализатора, а недостаточная аэрация может вызвать поведение катализатора «прилипание / проскальзывание».

•

Catalyst PSD оказывает огромное влияние на легкость циркуляции катализатора, особенно в длинных стояках и / или U-образных коленах.

Средняя напорная труба должна обеспечивать давление напора 1 фунт / кв. Дюйм на каждые 4 фута высоты напорной трубы (0,07 бар / 1,2 м). Это увеличение давления должно быть равномерным по всей высоте стояка.Это увеличение давления соответствует примерно 35 фунт / фут ³ плотности потока катализатора (561 кг / м ³ ). Существуют стояки, в которых плотность потока катализатора находится в диапазоне 45 фунтов / фут ³ (721 кг / м ³ ).

Пример 12.1 Опережающий индикатор

Причины

Увеличение открытия золотникового клапана регенерированного катализатора
Индикатор: Открытие золотникового клапана регенерированного катализатора постепенно увеличилось с 40% до 60%
Доказательства
Полевая проверка: • Золотниковый клапан Δ P • Реактор – регенератор Δ P 3 9457 9457 • 9457 Температура плотного слоя регенератора • Скорость подачи.	1. Давление над золотниковым клапаном ниже стандартного: • Катализатор не создает достаточного давления в стояке • Катализатор входит в стояк не флюидизирован должным образом • Недостаточная аэрация вдоль стояка • Посторонний предмет, ограничивающий поток катализатора на входе в стояк • Посторонний предмет попал в ползун клапан. 2. Давление под золотниковым клапаном выше нормального: • Катализатор не полностью псевдоожижен в секции тройника или J-образного изгиба • Кокс Накопление кокса вокруг подающих форсунок • Кокс в циклонах реактора • Накопление кокса в паропроводе реактора • Загрязнение основной колонны и / или верхнего погона.

Пример 12.2 Опережающий индикатор

Неустойчивая циркуляция катализатора
Индикатор: Неустойчивая циркуляция катализатора 9018 9018 9018 9018		• Низкий Δ P Аварийный сигнал на входе и выходе из стояка свежего корма • Подъемник свежего корма не поддерживает заданное значение • Температура слоя регенератора колеблется.	• Баланс давления между реактором и регенератором отключен • Неправильная вентиляция в стояке • Неправильно отрегулирована скорость подачи воздуха 3 в колодец для отвода катализатора • Углерод на катушке низкий или неправильный размер частиц • Скорость подачи или сила тяжести нестабильны.

Определение оборачиваемости запасов: формула и расчет

Что такое оборачиваемость запасов?

Оборачиваемость запасов — это финансовый коэффициент, показывающий, сколько раз компания продавала и заменяла запасы в течение определенного периода.Затем компания может разделить дни в периоде по формуле оборачиваемости запасов, чтобы рассчитать дни, необходимые для продажи имеющихся запасов.

Расчет оборачиваемости запасов может помочь предприятиям принимать более обоснованные решения по ценообразованию, производству, маркетингу и закупке новых запасов.

Ключевые выводы

• Оборачиваемость запасов измеряет, сколько раз за определенный период компания может заменить проданные запасы.
• Низкая текучесть кадров означает слабые продажи и, возможно, избыточные запасы, в то время как более быстрое соотношение означает либо высокие продажи, либо недостаточные запасы.
• Отрасли с большими объемами и низкой маржой, такие как розничные торговцы и супермаркеты, обычно имеют самый высокий оборот товарных запасов.

Чтение оборота инвентаря

Формула и расчет товарооборота

Оборачиваемость запасов знак равно КОГС Средняя стоимость запасов куда: КОГС знак равно Стоимость проданных товаров \ begin {align} & \ text {Оборачиваемость запасов} = \ frac {\ text {COGS}} {\ text {Средняя стоимость запасов}} \\ & \ textbf {где:} \\ & \ text {COGS} = \ text {Себестоимость проданных товаров} \\ \ end {выровнены} Оборачиваемость запасов = Средняя стоимость запасов COGS, где: COGS = Себестоимость проданных товаров.

и:

Средний запас = (Начальный запас + Конечный запас) / 2

Компании также могут рассчитать оборачиваемость запасов по:

1. Расчет среднего запаса, который выполняется путем деления суммы начального и конечного запасов на два.
2. Разделение продаж на средний запас.

Как вы можете видеть выше, существует два основных метода расчета оборачиваемости запасов: один с использованием себестоимости проданных товаров (COGS), а другой с использованием продаж. Аналитики делят COGS на средний запас, а не на объем продаж, для большей точности при расчете оборачиваемости запасов, поскольку продажи включают наценку сверх затрат. Разделение продаж на средний запас увеличивает оборачиваемость запасов. В обеих ситуациях средний запас используется для устранения сезонных эффектов.

О чем говорит оборачиваемость товарно-материальных запасов

Оборачиваемость запасов измеряет, насколько быстро компания продает товарные запасы. Низкий оборот подразумевает слабые продажи и, возможно, избыток запасов, также известный как затоваривание. Это может указывать на проблему с товарами, выставленными на продажу, или быть результатом недостаточного маркетинга.

С другой стороны, высокий коэффициент означает либо высокие продажи, либо недостаточные запасы. Первое желательно, в то время как второе может привести к потере бизнеса.

Иногда низкая оборачиваемость запасов — это хорошо, например, когда ожидается рост цен (запасы предварительно позиционируются для удовлетворения быстро растущего спроса) или когда ожидается дефицит.

Скорость, с которой компания может продавать запасы, является критически важным показателем эффективности бизнеса. Розничные торговцы, которые перемещают запасы быстрее, как правило, выигрывают. Чем дольше товар хранится, тем выше будет стоимость его хранения и тем меньше причин, по которым покупателям придется возвращаться в магазин за новыми товарами.

Хороший пример можно увидеть в бизнесе fast fashion. Такие компании, как H&M и Zara, обычно ограничивают пробеги и быстро заменяют истощенные запасы новыми товарами. Медленно продаваемые товары означают более высокие затраты на хранение по сравнению с более быстро продаваемыми запасами. Существует также альтернативная стоимость низкой оборачиваемости запасов; предмет, на продажу которого уходит много времени, препятствует размещению новых предметов, которые могут быть проданы с большей готовностью.

Нуша Ашджаи {Авторские права}, Investopedia, 2019.

Оборачиваемость запасов и мертвый запас

Оборачиваемость запасов — это особенно важная часть данных для максимальной эффективности продажи скоропортящихся товаров и других товаров с ограниченным сроком действия. Некоторыми примерами могут быть молоко, яйца, продукты, быстрая мода, автомобили и периодические издания.

Избыток кашемировых свитеров может привести к непроданным товарным запасам и упущенной прибыли, особенно при смене сезонов, когда розничные торговцы пополняют запасы новыми сезонными товарами. Такие непроданные запасы известны как устаревшие запасы или мертвые запасы.

Оборачиваемость запасов и системы, открытые для покупки

Некоторые розничные торговцы могут использовать открытую для покупки систему, поскольку они стремятся более эффективно управлять своими запасами и пополнять свои запасы. Системы с открытыми покупками, по своей сути, представляют собой программные системы бюджетирования для закупок товаров. Такая система может использоваться для мониторинга товаров и может быть интегрирована в процессы финансирования и управления запасами розничного продавца.

Это может помочь мелким розничным торговцам лучше управлять решениями о том, сколько запасов нужно покупать, как оценивать, как работают запасы, и помогать с закупкой запасов в будущем.Такое программное обеспечение может быть адаптировано до некоторой степени, но не может быть полезным для всех типов товаров. Например, он может лучше всего работать с сезонными товарами и модой, но может не подходить для быстро продающихся потребительских товаров или основных предметов и продуктов первой необходимости.

Пример использования оборачиваемости запасов

Предположим, что объем продаж компании ABC составляет 1 миллион долларов, а COGS — 250 000 долларов. Средний запас составляет 25000 долларов. Используя эту информацию, мы можем увидеть, что товарооборот компании составляет 40, или 1 миллион долларов, разделенный на 25 000 долларов.Другими словами, в течение года компания ABC имеет тенденцию оборачивать свои запасы 40 раз.

Если пойти дальше, разделив 365 дней на оборачиваемость запасов, можно увидеть, сколько дней в среднем требуется компании, чтобы продать свои запасы. В случае компании ABC это 9.1.

В качестве альтернативы, используя другой метод — COGS / средний запас — оборот запасов составляет 10 или 250 000 долларов в COGS, разделенных на 25 000 долларов в запасах. При таком подходе запасы доступны в течение 36,5 дней, или 365/10.

Оборачиваемость запасов по сравнению с продажами запасов в днях

Оборачиваемость запасов показывает, насколько быстро компания может продать (обернуть) свои запасы. Между тем, дни инвентаризации (DSI) — это среднее время, в течение которого компания может превратить свои запасы в продажи.

DSI — это, по сути, обратная величина оборачиваемости запасов за определенный период, рассчитываемая как (инвентарь / COGS) * 365. По сути, DSI — это количество дней, которое требуется для превращения запасов в продажи, в то время как оборот запасов определяет, сколько раз в году запасы продается или используется.

Особые соображения

При сравнении или прогнозировании оборачиваемости запасов необходимо сравнивать аналогичные продукты и предприятия. Например, оборот автомобилей у автомобильного дилера может меняться намного медленнее, чем оборот товаров повседневного спроса (FMCG), продаваемых в супермаркете (закуски, сладости, безалкогольные напитки и т. Д.).

Еще одно соображение — это попытка манипулировать оборачиваемостью запасов с помощью скидок или распродаж, поскольку это может значительно снизить окупаемость инвестиций (ROI) и прибыльность.

Часто задаваемые вопросы

Как вы рассчитываете оборачиваемость запасов?

Оборачиваемость запасов — это показатель того, насколько быстро компания продает свои запасы в течение года, и часто используется в качестве показателя общей операционной эффективности.

Есть два популярных способа расчета оборачиваемости запасов. Первый метод состоит в делении годовых продаж компании на средний остаток запасов, тогда как второй метод делит годовую стоимость проданных товаров (COGS) на средние запасы.В любом случае средний остаток запасов часто оценивается путем деления суммы начальных и конечных запасов за год на 2.

Что такое хорошая оборачиваемость запасов?

То, что считается «хорошей» оборачиваемостью запасов, будет зависеть от рассматриваемой отрасли. Как правило, отрасли, в которых хранятся относительно недорогие товары, имеют тенденцию к более высокому оборачиваемости товарных запасов, тогда как более дорогие товары, когда покупатели обычно тратят больше времени на принятие решения о покупке, имеют тенденцию к более низкому оборачиваемости товарных запасов.

Например, компания, продающая дешевые продукты, может продавать в 30 раз больше своих запасов в год, тогда как компания, продающая крупное промышленное оборудование, может перебирать свои запасы только 3 раза. Следовательно, коэффициенты оборачиваемости запасов необходимо оценивать относительно отрасли компании и конкурентов, чтобы определить, являются ли они хорошими или плохими.

Высокая оборачиваемость запасов — это хорошо или плохо?

Компании почти всегда стремятся к высокой оборачиваемости товарных запасов.В конце концов, высокая оборачиваемость запасов снижает объем капитала, который они вложили в свои запасы, тем самым улучшая их ликвидность и финансовую устойчивость. Более того, поддержание высокой оборачиваемости запасов снижает риск того, что их запасы станут недоступными для продажи из-за порчи, повреждения, кражи или технологического устаревания.

5.1 Поток потока | Мониторинг и оценка

Что такое сток и почему он важен?

Поток или расход воды — это объем воды, который движется над определенной точкой за фиксированный период времени.Часто выражается в кубических футах в секунду (фут ³ / сек).

Расход ручья напрямую зависит от количества воды, уходящей с водораздела в русло ручья. На нее влияет погода, она увеличивается во время ливней и уменьшается в засушливые периоды. Он также меняется в разные сезоны года, снижаясь в летние месяцы, когда интенсивность испарения высока, а прибрежная растительность активно растет и удаляет воду с земли. Август и сентябрь — обычно месяцы самого низкого стока для большинства ручьев и рек на большей части страны.

Забор воды для целей орошения может серьезно истощить сток воды, как и промышленный забор воды. Плотины, используемые для выработки электроэнергии, особенно сооружения, предназначенные для выработки электроэнергии в периоды пиковой потребности, часто блокируют течение ручья, а затем выпускают его в виде скачка.

Расход зависит от объема и скорости воды. Это важно из-за своего воздействия на качество воды, а также на живые организмы и среду обитания в ручье. Крупные реки с быстрым течением могут получать сбросы загрязняющих веществ и подвергаться незначительному воздействию, в то время как небольшие реки обладают меньшей способностью разбавлять и разлагать отходы.

Скорость потока, которая увеличивается по мере увеличения объема воды в ручье, определяет виды организмов, которые могут жить в ручье (некоторым нужны участки с быстрым течением, другим нужны тихие бассейны). Это также влияет на количество ила и наносов, переносимых ручьем. Осадок, внесенный в тихие, медленно текущие потоки, быстро оседает на дно ручья. Быстро движущиеся потоки дольше удерживают осадок во взвешенном состоянии в толще воды. Наконец, быстро движущиеся потоки обычно имеют более высокий уровень растворенного кислорода, чем медленные потоки, потому что они лучше аэрируются.

В этом разделе описан один метод оценки потока в определенной области или на участке реки. Он адаптирован на основе методов, используемых несколькими программами мониторинга добровольцами, и использует поплавок (такой объект, как апельсин, мяч для пинг-понга, сосновая шишка и т. Д.) Для измерения скорости потока. Расчет расхода включает решение уравнения, которое исследует взаимосвязь между несколькими переменными, включая площадь поперечного сечения потока, длину потока и скорость воды. Один из способов измерения расхода — решить следующее уравнение:

Расход = ALC / T
Где:
А	=	Средняя площадь поперечного сечения ручья (ширина ручья, умноженная на среднюю глубину воды).
л	=	Измеренная длина участка ручья (обычно 20 футов)
С	=	Коэффициент или поправочный коэффициент (0,8 для ручьев с каменистым дном или 0,9 для потоков с илистым дном). Это позволяет вам скорректировать тот факт, что вода на поверхности движется быстрее, чем у дна ручья, из-за сопротивления гравия, булыжника и т. Д. Умножение скорости на поверхности на поправочный коэффициент уменьшает значение и дает более точное измерение общей протяженности потока. скорость.
т	=	Время в секундах, за которое поплавок проходит длину L

Как измерить и рассчитать поток воды

Задача 1 Подготовиться перед выездом на место отбора проб

См. Раздел 2.3 — Меры безопасности для получения подробной информации о подтверждении даты и времени отбора проб, соображениях безопасности, проверке расходных материалов, а также проверке погоды и направления. В дополнение к стандартному оборудованию для отбора проб и одежде, при измерении и расчете расхода, необходимо включать следующее оборудование:

• Шар из прочной струны, четыре колья и молоток для забивания кольев в землю.Трос будет натянут по ширине ручья перпендикулярно берегу в двух местах. Ставки заключаются в том, чтобы закрепить веревку на каждом берегу, чтобы сформировать линию разреза.
• Рулетка (минимум 20 футов)
• Водонепроницаемая линейка или другой прибор для измерения глубины воды
• Хомуты (для обозначения интервалов на нити линии трансекты)
• Апельсин и рыболовная сеть (чтобы вычерпать апельсин из ручья)
• Секундомер (или часы с секундной стрелкой)
• Калькулятор (опционально)

Задача 2 Выберите участок потока

Рисунок 5.4 Схема трансекты длиной 20 футов

Участок ручья, выбранный для измерения расхода, должен быть прямым (без изгибов), глубиной не менее 6 дюймов и не должен содержать области с медленной водой, например бассейн. Идеально подходят беспрепятственные перекаты или беговые дорожки. Выбранная длина будет равна L при решении уравнения потока. Двадцать футов — стандартная длина, используемая во многих программах. Измерьте свою длину и отметьте верхний и нижний конец, проведя линию разреза поперек ручья перпендикулярно берегу, используя веревку и колья (рис.5.4). Трос должен быть натянут и находиться у поверхности воды. Трансект выше по течению — это разрез №1, а нижний по течению — разрез №2.

Задача 3 Рассчитать среднюю площадь поперечного сечения

Площадь поперечного сечения (A в формуле) — произведение ширины ручья на среднюю глубину воды. Чтобы рассчитать среднюю площадь поперечного сечения для охвата исследуемого ручья, добровольцы должны определить площадь поперечного сечения для каждой трансекты, сложить результаты вместе, а затем разделить на 2, чтобы определить среднюю площадь поперечного сечения для участка протока.

Для измерения площади поперечного сечения:

1. Рисунок 5.5 Поперечный разрез для измерения ширины и глубины потока

2. Определите среднюю глубину вдоль разреза, отметив равные интервалы вдоль струны с помощью скрученных стяжек. Интервалы могут составлять одну четвертую, половину или три четверти расстояния через ручей.Измерьте глубину воды в каждой точке интервала (рис. 5.5). Чтобы рассчитать среднюю глубину для каждого разреза, разделите сумму трех измерений глубины на 4. (Вы делите на 4 вместо 3, потому что вам нужно учитывать нулевые глубины, которые встречаются на берегу). В примере, показанном на Рисунке 5.6. , средняя глубина трансекты № 1 составляет 0,575 футов, а средняя глубина трансекты № 2 составляет 0,625 футов.
3. Определите ширину каждого разреза, измерив расстояние от береговой линии до береговой линии.Просто сложите все интервалы ширины для каждого разреза, чтобы определить его ширину. В примере на Рисунке 5.6 ширина трансекты № 1 составляет 8 футов, а ширина трансекты № 2 — 10 футов.
4. Рассчитайте площадь поперечного сечения каждого разреза, умножив ширину на среднюю глубину. Пример, приведенный на Рисунке 5.6, показывает, что средняя площадь поперечного сечения трансекты № 1 составляет 4,60 квадратных футов, а средняя площадь поперечного сечения трансекты № 2 составляет 6,25 квадратных футов.
5. Чтобы определить среднюю площадь поперечного сечения всего участка ручья (A в формуле), сложите среднюю площадь поперечного сечения каждой трансекты и затем разделите на 2.Средняя площадь поперечного сечения ручья на Рисунке 5.6 составляет 5,42 квадратных футов.

Задача 4 Измерение времени в пути

Добровольцы должны отсчитывать с помощью секундомера, сколько времени требуется апельсину (или другому объекту), чтобы проплыть от верхнего к нижележащему разрезу. Апельсин — хороший объект для использования, потому что он обладает достаточной плавучестью, чтобы плавать чуть ниже поверхности воды. Именно в этом положении обычно возникает максимальная скорость.

Доброволец, позволяющий апельсину пройти на разрезе выше по течению, должен расположить его так, чтобы он тек в самое быстрое течение.Часы останавливаются, когда оранжевый полностью проходит под линией разреза вниз по течению. Оказавшись под линией трансекты, апельсин можно вычерпать из воды с помощью рыболовной сети. Это измерение «времени в пути» должно быть проведено не менее трех раз, а результаты усреднены — чем больше испытаний вы проведете, тем точнее будут ваши результаты. Усредненные результаты равны T в формуле. Рекомендуется размещать апельсин на разных расстояниях от берега, чтобы получить различные оценки скорости.Вы должны отказаться от любых попыток поплавка, если объект зависает в потоке (булыжниками, корнями, обломками и т. Д.).

Задача 5 Рассчитать расход

Напомним, что расход можно рассчитать по формуле:

Продолжая пример на рис. 5.6. скажем, среднее время прохождения апельсина между трансектом №1 и №2 составляет 15 секунд, а дно ручья было каменистым. Расчет расхода:

Где:
А	=	5.42 фут2
л	=	20 футов
С	=	0,8 (коэффициент для каменистого русла)
т	=	15 секунд

Расход = 15 секунд (5,42 футов 2 ) (20 футов) (0,8) / 15 секунд.

Расход = 86,72 фута 3 /15 сек.

Расход = 5,78 фут3 / сек.

Задача 6 Записать поток в форму данных

На следующей странице волонтеры могут использовать форму для расчета расхода ручья.

Список литературы

Фонд Adopt-A-Stream. Полевой справочник: инвентаризация водосборов и методы мониторинга водотоков, Том Мердок и Марта Чео. 1996. Эверетт, Вашингтон.

Mitchell, M.K., and W. Stapp. Полевое руководство по мониторингу качества воды. 5 ^{-е издание} . Принтеры Thompson Shore.

Команды потока Миссури. Добровольный мониторинг качества воды. Департамент природных ресурсов штата Миссури, P.O. Box 176, Джефферсон-Сити, Миссури 65102.

Форма данных для расчета расхода (PDF, 82,8 КБ)

Вам понадобится Adobe Acrobat Reader для просмотра файлов Adobe PDF на этой странице. См. Страницу EPA в формате PDF для получения дополнительной информации о получении и использовании бесплатного Acrobat Reader.

Плотность циркуляции и теорема Стокса

После завершения этого раздела вы должны …

В качестве последнего применения поверхностных интегралов мы теперь обобщаем циркуляционную версию теоремы Грина на поверхности.Используя ранее определенный ротор, мы готовы объяснить теорему Стокса.

Начнем с того, что покажем, как теорема Грина распространяется на 3D. Векторное поле на плоскости \ (\ vec F = \ left (M, N \ right) \) может быть расширено до 3D, написав \ (\ vec F = \ left (M, N, 0 \ right) \ text { .} \) Ротор — это \ (\ text {curl} \ vec F = \ left \ lt 0,0, N_x-M_y \ right> \ text {.} \) Вектор нормали к поверхности \ (S \) в плоскости \ (xy \) это \ (\ vec n = \ left \ lt 0,0,1 \ right> \ text {.} \) Мы можем записать теорему Грина как

\ begin {уравнение *} \ oint_C \ vec F \ cdot d \ vec r = \ oint_C Mdx + Ndy = \ iint_S \ text {curl} \ cdot \ vec n d \ sigma = \ iint_R \ left (N_x-M_y \ right) dA, \ end {уравнение *}

, где \ (C \) — простая замкнутая кривая на плоскости, а \ (S = R \) — плоская область внутри \ (C \ text {.} \)

Теорема 12.3.1 Теорема Стокса.

Предположим, \ (\ vec F (x, y, z) = (M, N, P) \ text {.} \) Предположим, что \ (S \) — поверхность на плоскости, граница которой — простая замкнутая кривая \ (C \ text {.} \) Предположим, что \ (\ vec n \) — непрерывный единичный вектор нормали к \ (S \) вдоль всей поверхности, где ориентация \ (\ vec n \) соответствует ориентации из \ (C \) в соответствии с правилом правой руки (это означает, что если вы согнете правую руку вокруг \ (\ vec n \), указав большим пальцем вдоль \ (\ vec n \ text {,} \), ваши пальцы будут следовать ориентации \ (\ vec C \)).2 = 9 \) в плоскости \ (y = 2 \ text {.} \) Кривая \ (C \) ориентирована против часовой стрелки, если смотреть на нее из начала координат.

(а)

Вычислите локон \ (\ vec F \ text {,} \) и задайте единичный вектор нормали \ (\ vec n \) к \ (S \), который ориентирован совместим с \ (C \ text {.} \ )

(б)

Задайте параметризацию \ (\ vec r (t) \) кривой \ (C \ text {.} \)

(c)

Проверьте теорему Стокса, вычислив обе части уравнения:

\ begin {уравнение *} \ int_C \ vec F \ cdot d \ vec r = \ iint_S \ text {curl} \ cdot \ vec n d \ sigma.3 \) и попадает в вершины \ ((2,0,0) \ text {,} \) \ ((0,3,0) \ text {,} \) и \ ((0,0,6) \ text {,} \) в этом порядке. Этот треугольник лежит в плоскости \ (S \), заданной формулой \ (\ ds \ frac x2 + \ frac y3 + \ frac z6 = 1 \ text {,} \) или, что эквивалентно, \ (z = 6-3x-2y \ text { .} \)

(а)

Дайте границы для \ (x \) и \ (y \) так, чтобы \ (\ vec r (x, y) = (x, y, 6-3x-2y) \) было параметризацией \ (S \ text {.} \)

(б)

Докажите, что циркуляция \ (\ vec F \) вдоль \ (C \) равна \ (- 18 \ text {,} \), используя теорему Стокса.2 \ right> \ text {.} \) Поверхность \ (S \ text {,} \), параметризованная \ (\ vec r (u, v) = \ left \ lt u \ cos v, u \ sin v, u \ right> \) для \ (0 \ leq u \ leq 1 \) и \ (0 \ leq v \ leq 2 \ pi \) является конусом. Граница \ (S \) — это кривая \ (C \) — окружность радиуса 1 на высоте \ (z = 1 \ text {.} \). Если мы выберем вектор нормали к \ (S \), наружу нормаль (от оси \ (z \) -), то, чтобы использовать теорему Стокса, мы должны ориентировать \ (C \) против часовой стрелки, если смотреть из-под поверхности.

(а)

Найдите \ (\ vec n d \ sigma \) (произведение должно позволять вам игнорировать величины).2 \ leq 1 \) на высоте \ (z = 1 \ text {,} \) имеет ту же границу \ (C \), что и поверхность \ (S \ text {.} \). Векторы нормали к \ (S_2 \) являются \ ((0,0, \ pm 1) \ text {.} \) Используйте теорему Стокса для вычисления обоих интегралов, указанных выше.

Творческий подход к выбору поверхности иногда может сделать проблему тривиальной.

Упражнение 12.3.4

Пусть \ (\ vec F (x, y, z) = (M, N, P) \) — непрерывно дифференцируемое векторное поле. Предположим, что \ (\ vec F \) имеет потенциал (так что \ (D \ vec F \) симметричен).

(а)

Вычислить производную от \ (F \) как квадратную матрицу.

(б)

Объясните, какие частные производные должны быть равны.

(в)

Используйте эту информацию, чтобы найти локон \ (\ vec F \), если \ (\ vec F \) имеет потенциал.

(г)

Согласно теореме Стокса, какова циркуляция \ (\ vec F \) по любому замкнутому пути, если \ (\ vec F \) имеет потенциал?

Заключение

После того, как вы выполнили задачи в этой \ chaptername и освоились с идеями, составьте короткий одностраничный план урока, содержащий примеры ключевых идей.У вас будет возможность преподавать из этого плана урока до сдачи экзамена. Затем войдите в Brainhoney и загрузите тест. После того, как вы пройдете тест, вы можете загрузить свою работу обратно в brainhoney, а затем загрузить ключ, чтобы увидеть, как вы справились. Если вам все еще нужно работать над усвоением некоторых идей, сделайте это, а затем продемонстрируйте свое мастерство с помощью исправлений викторины.

Заключение

На этом \ chaptername завершается. Посмотрите на цели в начале раздела.Сможете ли вы сделать все, что вам обещали? Review Guide Creation Ваше задание: организовать то, что вы узнали, в небольшую коллекцию примеров, иллюстрирующих ключевые концепции. Я назову это руководством по обзору вашего устройства. Я предоставлю вам шаблон, который включает ключевые концепции модуля из целей, поставленных в начале. После того, как вы закончите свое руководство по обзору, отсканируйте его в PDF-документ (используйте любой сканер в университетском городке или программное обеспечение для обработки фотографий) и загрузите его в Gradescope.