Последовательное соединение резисторов. Схема соединения и примеры расчета
Во многих электрических схемах мы можем обнаружить последовательное и параллельное соединение резисторов. Разработчик схем может, например, объединить несколько резисторов со стандартными значениями (E-серии), чтобы получить необходимое сопротивление.
Последовательное соединении резисторов — это такое соединение, при котором ток, протекающий через каждый резистор одинаков, поскольку имеется только одно направление для протекания тока. В тоже время падение напряжения будет пропорционально сопротивлению каждого резистора в последовательной цепи.
Последовательное соединение резисторов
На рисунке ниже, резисторы R1, R2 и R3 связаны друг с другом последовательно между точками А и В с общим током I, который протекает через них.
Эквивалентное сопротивление нескольких последовательно соединенных резисторов можно определить по следующей формуле:
R = R1 + R2 + R3
То есть, в нашем случае общее сопротивление цепи будет равно:
R = R1 + R2 + R3 = 1 кОм + 2 кОм + 6 кОм = 9 кОм
Таким образом, мы можем заменить эти три резистора всего лишь одним «эквивалентным» резистором, который будет иметь значение 9 кОм.
Там, где четыре, пять или более резисторов связаны вместе в последовательную цепь, общее или эквивалентное сопротивление всей цепи так же будет равно сумме сопротивлений отдельных резисторов.
Следует отметить, что общее сопротивление любых двух или более резисторов, соединенных последовательно всегда будет больше, чем самое большое сопротивление резистора входящего в эту цепь. В приведенном выше примере R = 9 кОм, тогда как наибольшее значение резистора только 6 кОм (R3).
Напряжение на каждом из резисторов, соединенных последовательно, подчинено другому правилу, нежели протекающий ток. Как известно, из приведенной выше схемы, что общее напряжение питания на резисторах равно сумме разности потенциала на каждом из них:
Используя закон Ома , напряжение на отдельных резисторов может быть вычислена следующим образом:
В итоге сумма разностей потенциалов на резисторах равна общей разности потенциалов всей цепи, нашем примере это 9В.
В частности, ряд резисторов, соединенных последовательно, можно рассматривать как делитель напряжения:
Пример № 1
Используя закон Ома, необходимо вычислить эквивалентное сопротивление серии последовательно соединенных резисторов (R1. R2, R3), а так же падение напряжения и мощность для каждого резистора:
Все данные могут быть получены с помощью закона Ома и для лучшего понимания представлены в виде следующей таблицы:
Пример № 2
Необходимо рассчитать падение напряжения на выводах «А» и «В»:
а) без подключенного резистора R3
б) с подключенным резистором R3
Как вы можете видеть, выходное напряжение U без нагрузочного резистора R3, составляет 6 вольт, но то же выходное напряжение при подключении R3 становится всего лишь 4 В. Таким образом, нагрузка, подключенная к делителю напряжения, провоцирует дополнительное падение напряжение. Данный эффект снижения напряжения может быть компенсирован с помощью потенциометра установленного вместо постоянного резистора, с помощью которого можно скорректировать напряжение на нагрузке.
Онлайн калькулятор расчета сопротивления последовательно соединенных резисторов
Чтобы быстро вычислить общее сопротивление двух и более резисторов, соединенных последовательно, вы можете воспользоваться следующим онлайн калькулятором:
Подведем итог
Когда два или несколько резисторов соединены вместе (вывод одного соединяется с выводом другого резистора) — то это последовательное соединение резисторов. Ток, протекающий через резисторы имеет одно и тоже значение, но падение напряжения на них не одно и то же. Оно определяется сопротивлением каждого резистора, которое рассчитывается по закону Ома (U = I * R).
Общее сопротивление цепи при последовательном соединении равно. Как найти сопротивление последовательной и параллельной цепей
Параллельное соединение электрических элементов (проводников, сопротивлений, емкостей, индуктивностей) — это такое соединение, при котором подключенные элементы цепи имеют два общих узла подключения.
Другое определение: сопротивления подключены параллельно, если они подключены одно и той же паре узлов.
Графическое обозначение схемы параллельного соеднинения
На приведенном рисунке показана схема параллельное подключения сопротивлений R1, R2, R3, R4. Из схемы видно, что все эти четыре сопротивления имеют две общие точки (узла подключения).
В электротехнике принято, но не строго требуется, рисовать провода горизонтально и вертикально. Поэтому эту же схему можно изобразить, как на рисунке ниже. Это тоже параллельное соединение тех же самых сопротивлений.
Формула для расчета параллельного соединения сопротивлений
При параллельном соединении обратная величина от эквивалентного сопротивления равна сумме обратных величин всех параллельно подключенных сопротивлений. Эквивалентная проводимость равна сумме всех параллельно подключенных проводимостей электрической схемы.
Для приведенной выше схемы эквивалентное сопротивление можно рассчитать по формуле:
В частном случае при подключении параллельно двух сопротивлений:
Эквивалентное сопротивление цепи определяется по формуле:
В случае подключения «n» одинаковых сопротивлений, эквивалентное сопротивление можно рассчитать по частной формуле:
Формулы для частного рассчета вытекают из основной формулы.
Формула для расчета параллельного соединения емкостей (конденсаторов)
При параллельном подключении емкостей (конденсаторов) эквивалентная емкость равна сумме параллельно подключенных емкостей:
Формула для расчета параллельного соединения индуктивностей
Необходимо обратить внимание, что в формуле не учтены взаимные индуктивности.
Пример свертывания параллельного сопротивления
Для участка электрической цепи необходимо найти параллельное соединение сопротивлений выполнить их преобразование до одного.
Из схемы видно, что параллельно подключены только R2 и R4. R3 не параллельно, т.к. одним концом оно подключено к E1. R1 — одним концом подключено к R5, а не к узлу. R5 — одним концом подключено к R1, а не к узлу. Можно так же говорить, что последовательное соединение сопротивлений R1 и R5 подключено параллельно с R2 и R4.
Ток при параллельном соединении
При параллельном соединении сопротивлений ток через каждое сопротивление в общем случае разный. Величина тока обратно пропорциональна величине сопротивления.
Напряжение при параллельном соединении
При параллельном соединении разность потенциалов между узлами, объединяющими элементы цепи, одинакова для всех элементов.
Применение параллельного соединения
1. В промышленности изготавливаются сопротивления определенных величин. Иногда необходимо получить значение сопротивления вне данных рядов. Для этого можно подключить несколько сопротивлений параллельно. Эквивалентное сопротивление всегда будет меньше самого большого номинала сопротивления.
2. Делитель токов.
Содержание:Во всех электрических схемах используются резисторы, представляющие собой элементы, с точно установленным значением сопротивления. Благодаря специфическим качествам этих устройств, становится возможной регулировка напряжения и силы тока на любых участках схемы.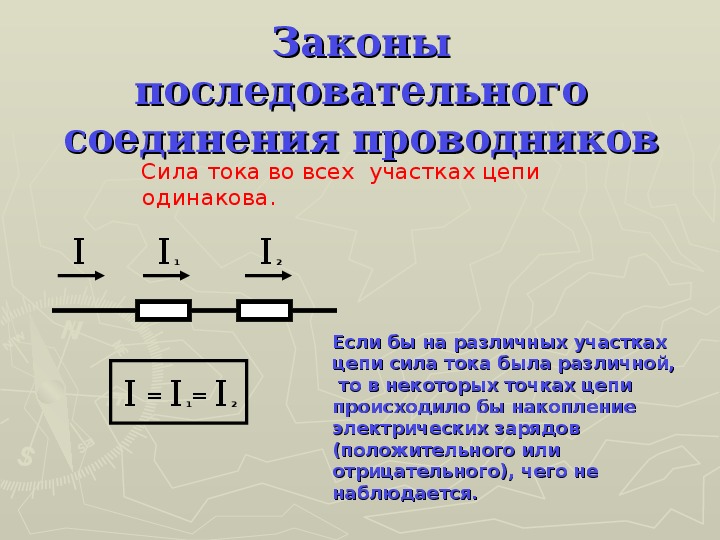 Данные свойства лежат в основе работы практически всех электронных приборов и оборудования. Так, напряжение при параллельном и последовательном соединении резисторов будет отличаться. Поэтому каждый вид соединения может применяться только в определенных условиях, чтобы та или иная электрическая схема могла в полном объеме выполнять свои функции.
Данные свойства лежат в основе работы практически всех электронных приборов и оборудования. Так, напряжение при параллельном и последовательном соединении резисторов будет отличаться. Поэтому каждый вид соединения может применяться только в определенных условиях, чтобы та или иная электрическая схема могла в полном объеме выполнять свои функции.
Напряжение при последовательном соединении
При последовательном соединении два резистора и более соединяются в общую цепь таким образом, что каждый из них имеет контакт с другим устройством только в одной точке. Иначе говоря, конец первого резистора соединяется с началом второго, а конец второго — с началом третьего и т.д.
Особенностью данной схемы является прохождение через все подключенные резисторы одного и того же значения электрического тока. С возрастанием количества элементов на рассматриваемом участке цепи, течение электрического тока становится все более затрудненным. Это происходит из-за увеличения общего сопротивления резисторов при их последовательном соединении.
Распределение напряжения, в соответствии с законом Ома, осуществляется на каждый резистор по формуле: V Rn = I Rn x R n . Таким образом, при увеличении сопротивления резистора, возрастает и падающее на него напряжение.
Напряжение при параллельном соединении
При параллельном соединении, включение резисторов в электрическую цепь выполняется таким образом, что все элементы сопротивлений подключаются друг к другу сразу обоими контактами. Одна точка, представляющая собой электрический узел, может соединять одновременно несколько резисторов.
Такое соединение предполагает течение отдельного тока в каждом резисторе. Сила этого тока находится в обратно пропорциональной . В результате, происходит увеличение общей проводимости данного участка цепи, при общем уменьшении сопротивления. В случае параллельного соединения резисторов с различным сопротивлением, значение общего сопротивления на этом участке всегда будет ниже самого маленького сопротивления отдельно взятого резистора.
На представленной схеме, напряжение между точками А и В представляет собой не только общее напряжение для всего участка, но и напряжение, поступающее к каждому отдельно взятому резистору. Таким образом, в случае параллельного соединения, напряжение, подаваемое ко всем резисторам, будет одинаковым.
В результате, напряжение при параллельном и последовательном соединении будет отличаться в каждом случае. Благодаря этому свойству, имеется реальная возможность отрегулировать данную величину на любом участке цепи.
Обычно все затрудняются ответить. А вот загадка эта в применении к электричеству решается вполне определенно.
Электричество начинается с закона Ома.
А уж если рассматривать дилемму в контексте параллельного или последовательного соединений — считая одно соединение курицей, а другое — яйцом, то сомнений вообще нет никаких.
Потому что закон Ома — это и есть самая первоначальная электрическая цепь. И она может быть только последовательной.
Да, придумали гальванический элемент и не знали, что с ним делать, поэтому сразу придумали еще лампочку. И вот что из этого получилось. Здесь напряжение в 1,5 В немедленно потекло в качестве тока, чтобы неукоснительно выполнять закон Ома, через лампочку к задней стенке того же элемента питания. А уж внутри самой батарейки под действием волшебницы-химии заряды снова оказались в первоначальной точке своего похода. И поэтому там, где напряжение было 1,5 вольта, оно таким и остается. То есть, напряжение постоянно одно, а заряды непрерывно движутся и последовательно проходят лампочку и гальванический элемент.
И это обычно рисуют на схеме вот так:
По закону Ома I=U/R
Тогда сопротивление лампочки (с тем током и напряжением, которые я написал) получится
R = 1/U , где R = 1 Ом
А мощность будет выделяться P = I * U , то есть P=2,25 Вm
В последовательной цепи, особенно на таком простом и несомненном примере, видно, что ток, который бежит по ней от начала до конца, — все время один и тот же.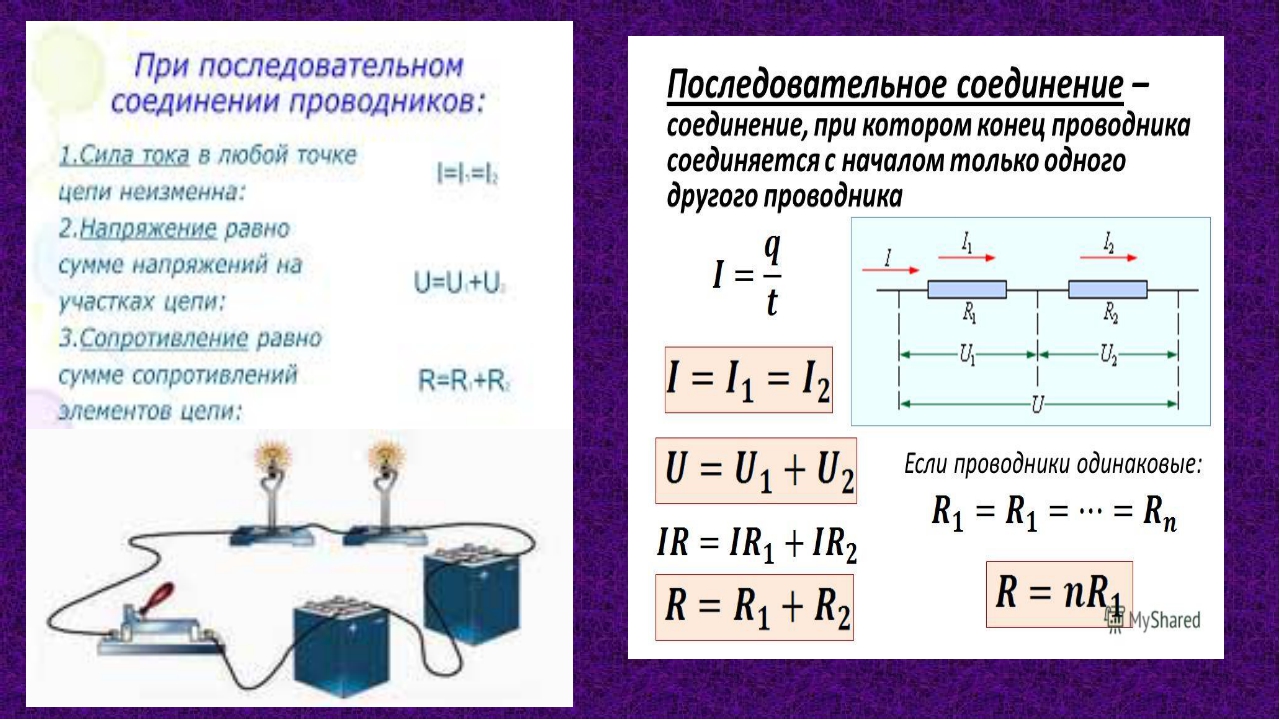 А если мы теперь возьмем две лампочки и сделаем так, чтобы ток пробегал сначала по одной, а потом по другой, то будет опять то же самое — ток будет и в той лампочке, и в другой снова одинаковым. Хотя другим по величине. Ток теперь испытывает сопротивление двух лампочек, но у каждой из них сопротивление как было, так и осталось, ведь оно определяется исключительно физическими свойствами самой лампочки. Новый ток вычисляем опять по закону Ома.
А если мы теперь возьмем две лампочки и сделаем так, чтобы ток пробегал сначала по одной, а потом по другой, то будет опять то же самое — ток будет и в той лампочке, и в другой снова одинаковым. Хотя другим по величине. Ток теперь испытывает сопротивление двух лампочек, но у каждой из них сопротивление как было, так и осталось, ведь оно определяется исключительно физическими свойствами самой лампочки. Новый ток вычисляем опять по закону Ома.
Он получится равным I=U/R+R,то есть 0,75А, ровно половина того тока, который был сначала.
В этом случае току приходится преодолевать уже два сопротивления, он становится меньше. Что и видно по свечению лампочек — они теперь горят вполнакала. А общее сопротивление цепочки из двух лампочек будет равно сумме их сопротивлений. Зная арифметику, можно в отдельном случае воспользоваться и действием умножения: если последовательно соединены N одинаковых лампочек, то общее их сопротивление будет равно N, умноженное на R, где R — сопротивление одной лампочки. Логика безупречная.
Логика безупречная.
А мы продолжим наши опыты. Теперь сделаем нечто подобное, что мы провернули с лампочками, но только на левой стороне цепи: добавим еще один гальванический элемент, точно такой, как первый. Как видим, теперь у нас в два раза увеличилось общее напряжение, а ток стал снова 1,5 А, о чем и сигнализируют лампочки, загоревшись снова в полную силу.
Делаем вывод:
- При последовательном соединении электрической цепи сопротивления и напряжения ее элементов суммируются, а ток на всех элементах остается неизменным.
Легко проверить, что это утверждение справедливо как для активных компонентов (гальванических элементов), так и для пассивных (лампочек, резисторов).
То есть это значит, что напряжение, измеренное на одном резисторе (оно называется падением напряжения), можно смело суммировать с напряжением, измеренным на другом резисторе, и в сумме получатся те же 3 В. А на каждом из сопротивлений оно окажется равным половине — то есть 1,5 В. И это справедливо. Два гальванических элемента вырабатывают свои напряжения, а две лампочки их потребляют. Потому что в источнике напряжения энергия химических процессов превращается в электроэнергию, принявшую вид напряжения, а в лампочках та же самая энергия из электрической превращается в тепловую и световую.
И это справедливо. Два гальванических элемента вырабатывают свои напряжения, а две лампочки их потребляют. Потому что в источнике напряжения энергия химических процессов превращается в электроэнергию, принявшую вид напряжения, а в лампочках та же самая энергия из электрической превращается в тепловую и световую.
Вернемся к первой схеме, подключим в ней еще одну лампочку, но иначе.
Теперь напряжение в точках, соединяющих две ветки, то же, что и на гальваническом элементе — 1,5 В. Но так как сопротивление у обеих лампочек тоже такое, как и было, то и ток через каждую из них пойдет 1,5 А — ток «полного накала».
Гальванический элемент теперь питает их током одновременно, следовательно, из него вытекают сразу оба эти тока. То есть общий ток из источника напряжения будет равен 1,5 А + 1,5 А = 3,0 А.
В чем же отличие этой схемы от схемы, когда те же самые лампочки были включены последовательно? Только в накале лампочек, то есть только в токе.
Тогда ток был 0,75 А, а теперь он стал сразу 3 А.
Получается, если сравнить с первоначальной схемой, то при последовательном соединении лампочек (схема 2) току сопротивления оказывалось больше (отчего он уменьшался, и лампочки теряли светимость), а параллельное подключение оказывает МЕНЬШЕ сопротивления, хотя сопротивление лампочек осталось неизменным. В чем тут дело?
А дело в том, что мы забываем одну интересную истину, что всякая палка о двух концах.
Когда мы говорим, что резистор сопротивляется току, то как бы забываем, что он ток все-таки проводит. И теперь, когда подключили лампочки параллельно, увеличилось суммарное для них свойство проводить ток, а не сопротивляться ему. Ну и, соответственно, некую величину G , по аналогии с сопротивлением R и следовало бы назвать проводимостью. И должна она в параллельном соединении проводников суммироваться.
Ну и вот она
Закон Ома тогда будет выглядеть
I = U * G &
И в случае параллельного соединения ток I будет равен U*(G+G) = 2*U*G, что мы как раз и наблюдаем.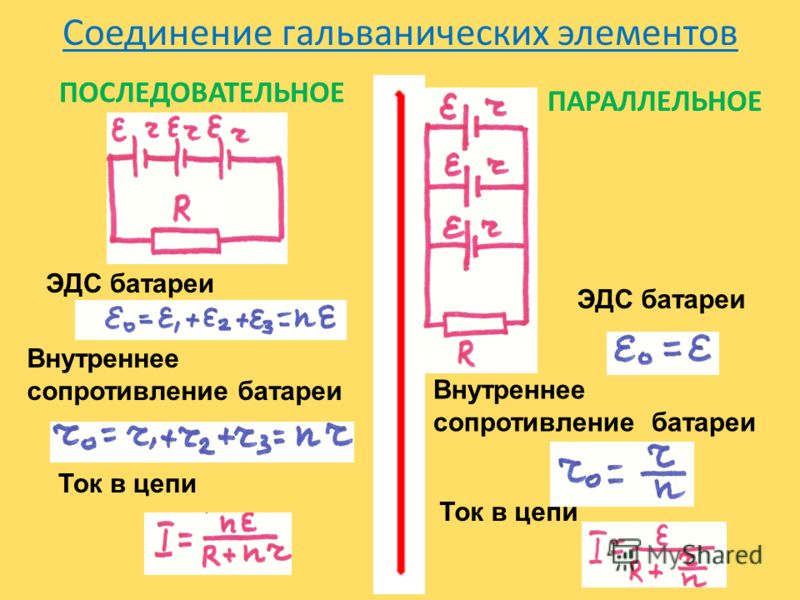
Замена элементов цепи общим эквивалентным элементом
Инженерам часто приходится узнавать токи и напряжения во всех частях схем. А реальные электрические схемы бывают достаточно сложными и разветвленными и могут содержать множество элементов, активно потребляющих электроэнергию и соединенных друг с другом в совершенно разных сочетаниях. Это называется расчет электрических схем. Он делается при проектировании энергоснабжения домов, квартир, организаций. При этом очень важно, какие токи и напряжения будут действовать в электрической цепи, хотя бы для того, чтобы выбрать подходящие им сечения проводов, нагрузки на всю сеть или ее части, и так далее. А уж насколько сложны бывают электронные схемы, содержащие тысячи, а то и миллионы элементов, думаю, понятно всякому.
Самое первое что, напрашивается — это воспользоваться знанием того, как ведут себя токи напряжения в таких простейших соединениях сети, как последовательное и параллельное. Делают так: вместо найденного в сети последовательного соединения двух или более активных устройств-потребителей (как наши лампочки) нарисовать один, но чтобы его сопротивление было таким же, как у обоих.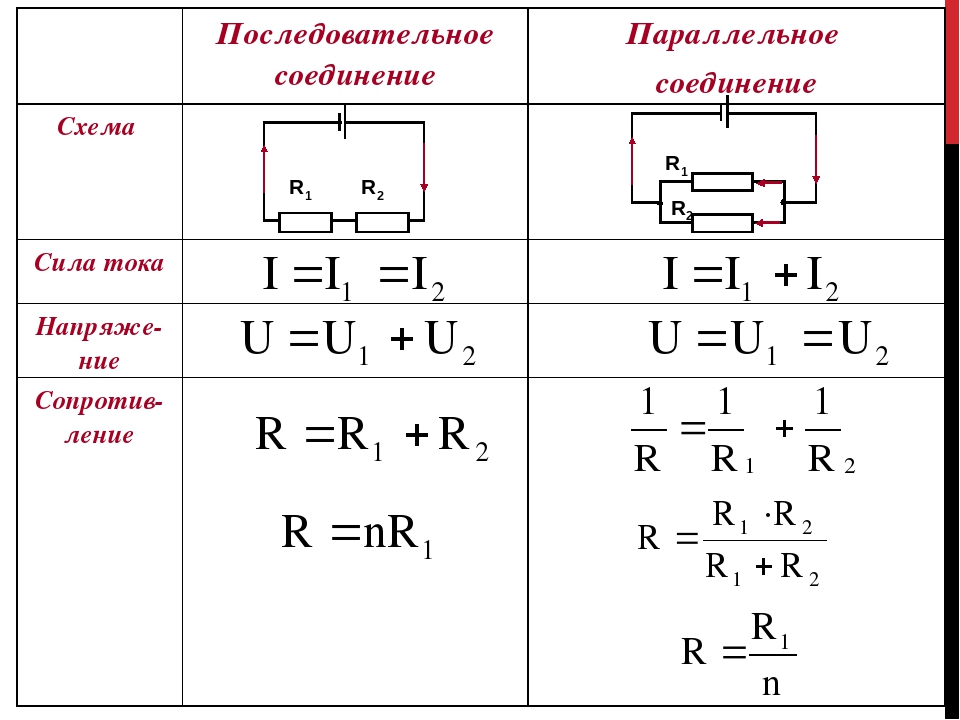 Тогда картина токов и напряжений в остальной части схемы не изменится. Аналогично и с параллельным соединением: вместо них нарисовать такой элемент, ПРОВОДИМОСТЬ которого была бы такой же, как у обоих.
Тогда картина токов и напряжений в остальной части схемы не изменится. Аналогично и с параллельным соединением: вместо них нарисовать такой элемент, ПРОВОДИМОСТЬ которого была бы такой же, как у обоих.
Теперь если схему перерисовать, заменив последовательные и параллельные соединения одним элементом, то получим схему, которая называется «схемой эквивалентного замещения».
Такую процедуру можно продолжать до тех пор, пока у нас не останется наипростейшая — которой мы в самом начале иллюстрировали закон Ома. Только вместо лампочки будет стоять одно сопротивление, которое и называют эквивалентным сопротивлением нагрузки.
Это первая задача. Она дает нам возможность по закону Ома рассчитать общий ток во всей сети, или общий ток нагрузки.
Вот это и есть полный расчет электрической сети.
Примеры
Пусть цепь содержит 9 активных сопротивлений. Это могут быть лампочки или что-то другое.
На ее входные клеммы подано напряжение в 60 В.
Значения сопротивлений для всех элементов следующие:
Найти все неизвестные токи и напряжения.
Надо пойти по пути поиска параллельных и последовательных участков сети, рассчитывать эквивалентные им сопротивления и постепенно упрощать схему. Видим, что R 3 , R 9 и R 6 соединены последовательно. Тогда им эквивалентное сопротивление R э 3, 6, 9 будет равно их сумме R э 3, 6, 9 = 1 + 4 + 1 Ом = 6 Ом.
Теперь заменяем параллельный кусочек из сопротивлений R 8 и R э 3, 6, 9, получая R э 8, 3, 6, 9 . Только при параллельном соединении проводников, складывать придется проводимости.
Проводимость измеряется в единицах, называемых сименсами, обратных омам.
Если перевернуть дробь, получим сопротивление R э 8, 3, 6, 9 = 2 Ом
Совершенно так же, как в первом случае, объединяем сопротивления R 2 , R э 8, 3, 6, 9 и R 5, включенные последовательно, получая R э 2, 8, 3, 6, 9, 5 = 1 + 2 + 1 = 4 Ом.
Осталось два шага: получить сопротивление, эквивалентное двум резисторам параллельного соединения проводников R 7 и R э 2, 8, 3, 6, 9, 5.
Оно равно R э 7, 2, 8, 3, 6, 9, 5 = 1/(1/4+1/4)=1/(2/4)=4/2 = 2 Ом
На последнем шаге просуммируем все последовательно включенные сопротивления R 1 , R э 7, 2, 8, 3, 6, 9, 5 и R 4 и получим сопротивление, эквивалентное сопротивлению всей цепи R э и равное сумме этих трех сопротивлений
R э = R 1 + R э 7, 2, 8, 3, 6, 9, 5 + R4 = 1 + 2 + 1 = 4 Ом
Ну и вспомним, в честь кого назвали единицу сопротивлений, написанную нами в последней из этих формул, и вычислим по его закону общий ток во всей цепи I
Теперь, двигаясь в обратном направлении, в сторону все большего усложнения сети, можно получать по закону Ома токи и напряжения во всех цепочках нашей достаточно простой схемы.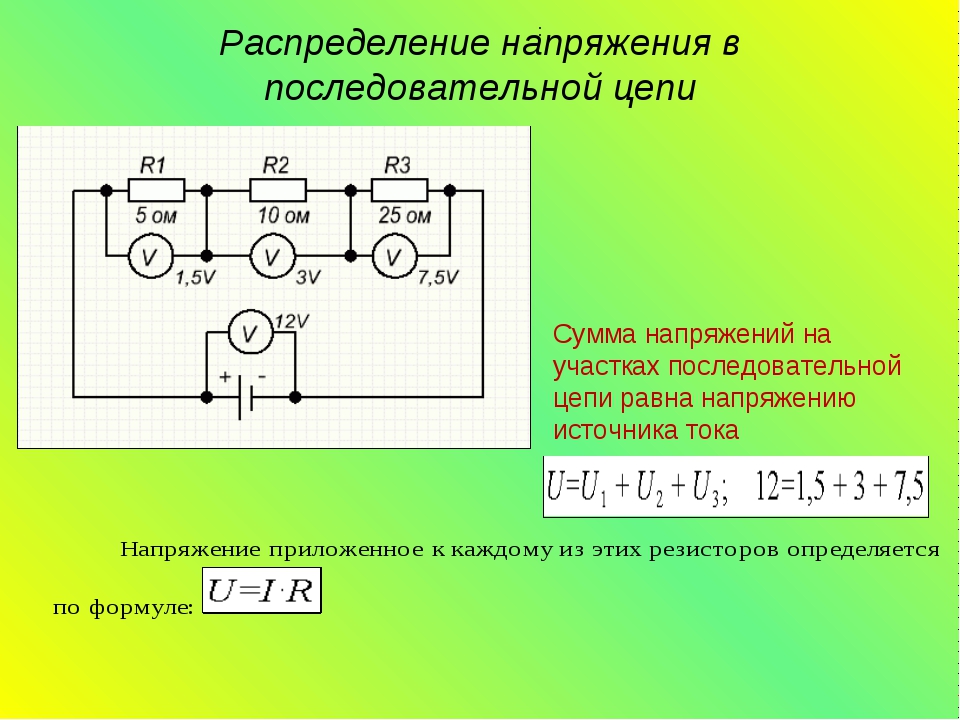
Так обычно и рассчитывают схемы электроснабжения квартир, которые состоят из параллельных и последовательных участков. Что, как правило, не годится в электронике, потому что там многое по-другому устроено, и все гораздо замысловатее. И вот такую, например, схему, когда не поймешь, параллельное это соединение проводников или последовательное, рассчитывают по законам Кирхгофа.
Последовательным называется такое соединение резисторов, когда конец одного проводника соединяется с началом другого и т.д. (рис. 1). При последовательном соединении сила тока на любом участке электрической цепи одинакова. Это объясняется тем, что заряды не могут накапливаться в узлах цепи. Их накопление привело бы к изменению напряженности электрического поля, а следовательно, и к изменению силы тока. Поэтому
Амперметр А измеряет силу тока в цепи и обладает малым внутренним сопротивлением (R A 0).
Включенные вольтметры V 1 и V 2 измеряют напряжение U 1 и U 2 на сопротивлениях R 1 и R 2 .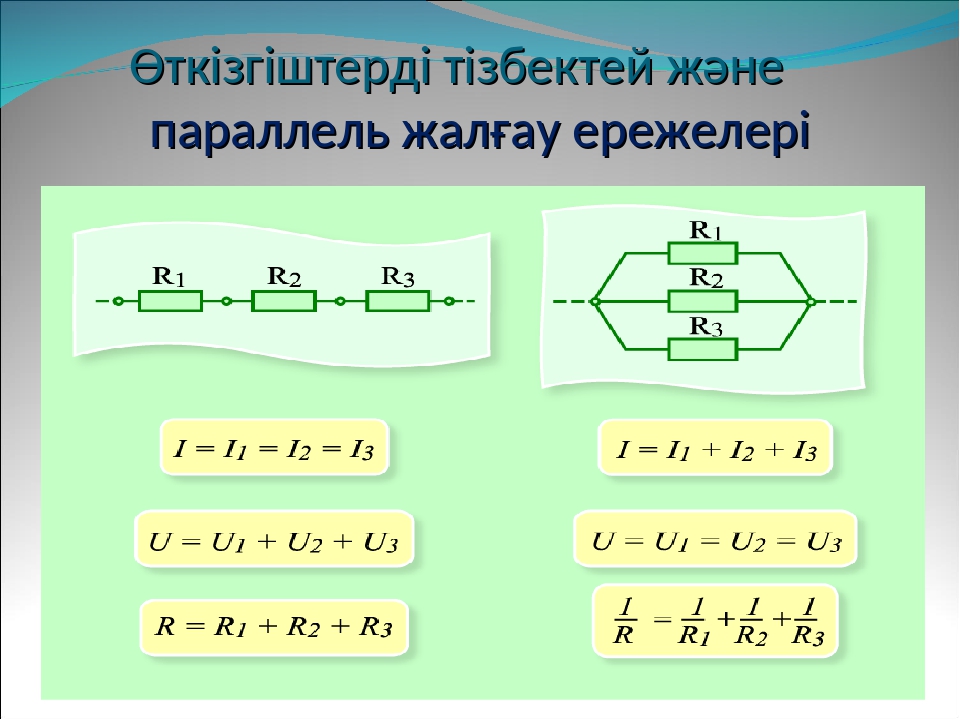 Вольтметр V измеряет подведенное к клеммам М и N напряжение U. Вольтметры показывают, что при последовательном соединении напряжение U равно сумме напряжений на отдельных участках цепи:
Вольтметр V измеряет подведенное к клеммам М и N напряжение U. Вольтметры показывают, что при последовательном соединении напряжение U равно сумме напряжений на отдельных участках цепи:
Применяя закон Ома для каждого участка цепи, получим:
где R — общее сопротивление последовательно соединенной цепи. Подставляя U, U 1 , U 2 в формулу (1), имеем
Сопротивление цепи, состоящей из n последовательно соединенных резисторов, равно сумме сопротивлений этих резисторов:
Если сопротивления отдельных резисторов равны между собой, т.е. R 1 = R 2 = … = R n , то общее сопротивление этих резисторов при последовательном соединении в n раз больше сопротивления одного резистора: R = nR 1 .
При последовательном соединении резисторов справедливо соотношение
т.е. напряжения на резисторах прямо пропорциональны сопротивлениям.
Параллельным называется такое соединение резисторов, когда одни концы всех резисторов соединены в один узел, другие концы — в другой узел (рис. 2). Узлом называется точка разветвленной цепи, в которой сходятся более двух проводников. При параллельном соединении резисторов к точкам М и N подключен вольтметр. Он показывает, что напряжения на отдельных участках цепи с сопротивлениями R 1 и R 2 равны. Это объясняется тем, что работа сил стационарного электрического поля не зависит от формы траектории:
2). Узлом называется точка разветвленной цепи, в которой сходятся более двух проводников. При параллельном соединении резисторов к точкам М и N подключен вольтметр. Он показывает, что напряжения на отдельных участках цепи с сопротивлениями R 1 и R 2 равны. Это объясняется тем, что работа сил стационарного электрического поля не зависит от формы траектории:
Амперметр показывает, что сила тока I в неразветвленной части цепи равна сумме сил токов I 1 и I 2 в параллельно соединенных проводниках R 1 и R 2:
Это вытекает и из закона сохранения электрического заряда. Применим закон Ома для отдельных участков цепи и всей цепи с общим сопротивлением R:
Подставляя I, I 1 и I 2 в формулу (2), получим.
Параллельные соединения резисторов, формула расчёта которых выводится из закона Ома и правил Кирхгофа, являются наиболее распространённым типом включения элементов в электрическую цепь. При параллельном соединении проводников два или несколько элементов объединяются своими контактами с обеих из сторон соответственно. Подключение их к общей схеме осуществляется именно этими узловыми точками.
Подключение их к общей схеме осуществляется именно этими узловыми точками.
Gif?x15027″ alt=»Общий вид»>
Общий вид
Особенности включения
Включённые таким образом проводники нередко входят в состав сложных цепочек, содержащих, помимо этого, последовательное соединение отдельных участков.
Для такого включения типичны следующие особенности:
- Общее напряжение в каждой из ветвей будет иметь одно и то же значение;
- Протекающий в любом из сопротивлений электрический ток всегда обратно пропорционален величине их номинала.
В частном случае, когда все включённые в параллель резисторы имеют одинаковые номинальные значения, протекающие по ним «индивидуальные» токи также будут равны между собой.
Расчёт
Сопротивления ряда соединённых в параллель проводящих элементов определяются по общеизвестной форме расчёта, предполагающей сложение их проводимостей (обратных сопротивлению величин).
Протекающий в каждом из отдельных проводников ток в соответствие с законом Ома, может быть найден по формуле:
I= U/R (одного из резисторов).
После ознакомления с общими принципами обсчёта элементов сложных цепочек можно перейти к конкретным примерам решения задач данного класса.
Типичные подключения
Пример №1
Нередко для решения стоящей перед конструктором задачи требуется путём объединения нескольких элементов получить в итоге конкретное сопротивление. При рассмотрении простейшего варианта такого решения допустим, что общее сопротивление цепочки из нескольких элементов должно составлять 8 Ом. Этот пример нуждается в отдельном рассмотрении по той простой причине, что в стандартном ряду сопротивлений номинал в 8 Ом отсутствует (есть только 7,5 и 8,2 Ом).
Решение этой простейшей задачи удаётся получить за счёт соединения двух одинаковых элементов с сопротивлениями по 16 Ом каждое (такие номиналы в резистивном ряду существуют). Согласно приводимой выше формуле общее сопротивление цепочки в этом случае вычисляется очень просто.
Из неё следует:
16х16/32=8 (Ом), то есть как раз столько, сколько требовалось получить.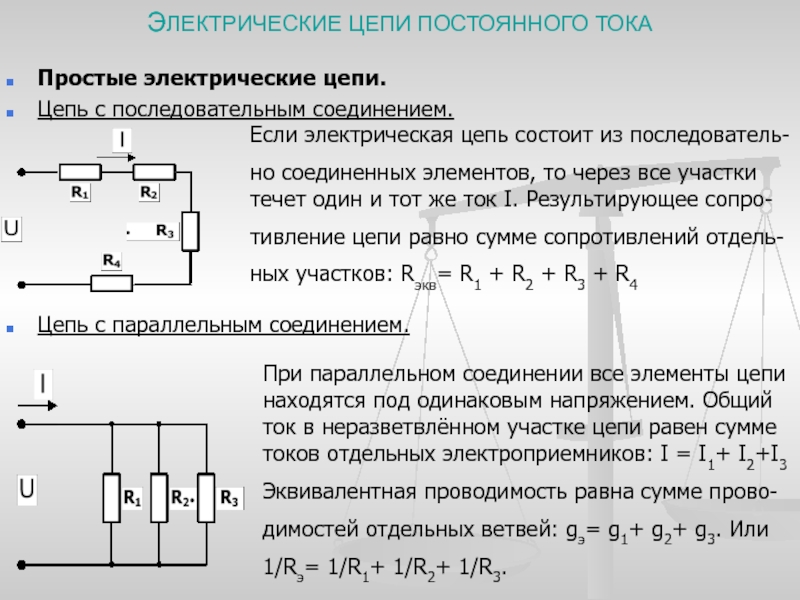
Таким сравнительно простым способом удаётся решить задачу формирования общего сопротивления, равного 8-ми Омам.
Пример №2
В качестве ещё одного характерного примера образования требуемого сопротивления можно рассмотреть построение схемы, состоящей из 3-х резисторов.
Общее значение R такого включения может быть рассчитано по формуле последовательного и параллельного соединения в проводниках.
Gif?x15027″ alt=»Пример»>
В соответствии с указанными на картинке значениями номиналов, общее сопротивление цепочки будет равно:
1/R = 1/200+1/220+1/470 = 0,0117;
R=1/0,0117 = 85,67Ом.
В итоге находим суммарное сопротивление всей цепочки, получаемой при параллельном соединении трёх элементов с номинальными значениями 200, 240 и 470 Ом.
Важно! Указанный метод применим и при расчёте произвольного числа соединенных в параллель проводников или потребителей.
Также необходимо отметить, что при таком способе включения различных по величине элементов общее сопротивление будет меньше, чем у самого малого номинала.
Расчёт комбинированных схем
Рассмотренный метод может применяться и при расчёте сопротивления более сложных или комбинированных схем, состоящих из целого набора компонентов. Их иногда называют смешанными, поскольку при формировании цепочек используются сразу оба способа. Смешанное соединение резисторов представлено на размещенном ниже рисунке.
Gif?x15027″ alt=»Смешанная схема»>
Смешанная схема
Для упрощения расчета сначала разбиваем все резисторы по типу включения на две самостоятельные группы. Одна из них представляет собой последовательное соединение, а вторая – имеет вид подключения параллельного типа.
Из приведённой схемы видно, что элементы R2 и R3 соединяются последовательно (они объединены в группу 2), которая, в свою очередь, включена в параллель с резистором R1, принадлежащим группе 1.
Соединение элементов питания и батарей
Источники напряжения обычно называют источниками питания. Для увеличения тока или напряжения, а может и того и другого источники питания (элементы, батареи) могут соединяться вместе. Существует три типа соединения элементов питания:
Для увеличения тока или напряжения, а может и того и другого источники питания (элементы, батареи) могут соединяться вместе. Существует три типа соединения элементов питания:
1. Последовательное соединение элементов.
2. Параллельное соединение элементов.
3. Последовательно-параллельное (смешанное) соединение элементов.
Последовательное соединение элементов.
При последовательном соединении элементов питания выделяются две схемы: последовательно-дополняющая и последовательно-препятствующая.
В последовательно-дополняющей схеме положительный вывод первого элемента питания соединяется с отрицательным выводом второго элемента питания; положительный вывод второго элемента питания соединяется с отрицательным выводом третьего элемента питания и т.д. (рисунок 3.11.)
Рисунок 3.11.Последовательное соединение элементов питания.
При таком соединении источников питания через все элементы будет течь одинаковый ток:
Iобщ=I1=I2=I3
Индексы в обозначениях токов указывают на номера отдельных источников питания (элементов или батарей питания)
А полное напряжение при последовательном соединении равно сумме напряжений (ЭДС) отдельных элементов:
Еобщ = Е1 + Е2 + Е3.
При последовательно-препятствующем включении источников питания, они соединяются друг с другом одноименными выводами. Но на практике такая схема не применяется или применяется, но очень редко.
Параллельное соединение элементов.
При параллельном соединении элементов питания, их одноименные выводы соединяются вместе, то есть плюс к плюсу, минус к минусу (рис 3.12).
Рисунок 3.11.Параллельное соединение элементов питания.
В этом случае общий ток будет равен сумме токов каждого элемента:
Iобщ=I1+I2+I3
Общее напряжение при параллельном включении источников питания будет равно напряжению каждого отдельного источника.
Еобщ = Е1 = Е2 = Е3.
Последовательно-параллельное соединение элементов напряжения.
Источники питания включают по последовательно-параллельной схеме для увеличения, как тока, так и напряжения. При этом основываются на том, что параллельное включение увеличивает силу тока, а последовательное увеличивает общее напряжение. На рисунке 3.13 показаны примеры последовательно-параллельных схем включения элементов питания.
На рисунке 3.13 показаны примеры последовательно-параллельных схем включения элементов питания.
Рисунок 3.11.Последовательно-параллельное соединение элементов питания.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Формула общего сопротивления при последовательном соединении. Электрическая цепь с последовательным соединением элементов
Отдельные проводники электрической цепи могут быть соединены между собой последовательно, параллельно и смешанно. При этом последовательное и параллельное соединение проводников являются основными видами соединений, а смешанное соединение это их совокупность.
Последовательным соединением проводников называется такое соединение, когда конец первого проводника соединен с началом второго, конец второго проводника соединен с началом третьего и так далее (рисунок 1).
Рисунок 1. Схема последовательного соединения проводников
Общее сопротивление цепи, состоящее из нескольких последовательно соединенных проводников, равно сумме сопротивлений отдельных проводников:
r = r 1 + r 2 + r 3 + … + r n .
Ток на отдельных участках последовательной цепи везде одинаков:
I 1 = I 2 = I 3 = I .
Видео 1. Последовательное соединение проводников
Пример 1. На рисунке 2 представлена электрическая цепь, состоящая из трех последовательно включенных сопротивлений r 1 = 2 Ом, r 2 = 3 Ом, r 3 = 5 Ом. Требуется определить показания вольтметров V 1 , V 2 , V 3 и V 4 , если ток в цепи равен 4 А.
Сопротивление всей цепи
r = r 1 + r 2 + r 3 = 2 + 3 + 5 =10 Ом.
Рисунок 2. Схема измерения напряжений на отдельных участках электрической цепи
В сопротивлении r 1 при протекании тока будет падение напряжения:
U 1 = I × r 1 = 4 × 2 = 8 В.
Вольтметр V 1 , включенный между точками а и б , покажет 8 В.
В сопротивлении r 2 также происходит падение напряжения:
U 2 = I × r 2 = 4 × 3 = 12 В.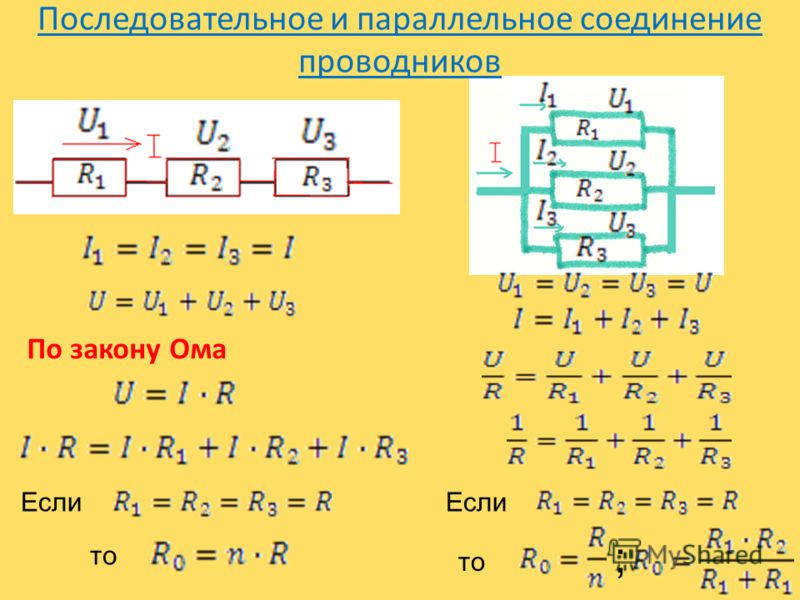
Вольтметр V 2 , включенный между точками в и г , покажет 12 В.
Падение напряжения в сопротивлении r 3:
U 3 = I × r 3 = 4 × 5 = 20 В.
Вольтметр V 3 , включенный между точками д и е , покажет 20 В.
Если вольтметр присоединить одним концом к точке а , другим концом к точке г , то он покажет разность потенциалов между этими точками, равную сумме падений напряжения в сопротивлениях r 1 и r 2 (8 + 12 = 20 В).
Таким образом, вольтметр V , измеряющий напряжение на зажимах цепи и включенный между точками а и е , покажет разность потенциалов между этими точками или сумму падений напряжения в сопротивлениях r 1 , r 2 и r 3 .
Отсюда видно, что сумма падений напряжения на отдельных участках электрической цепи равна напряжению на зажимах цепи.
Так как при последовательном соединении ток цепи на всех участках одинаков, то падение напряжения пропорционально сопротивлению данного участка.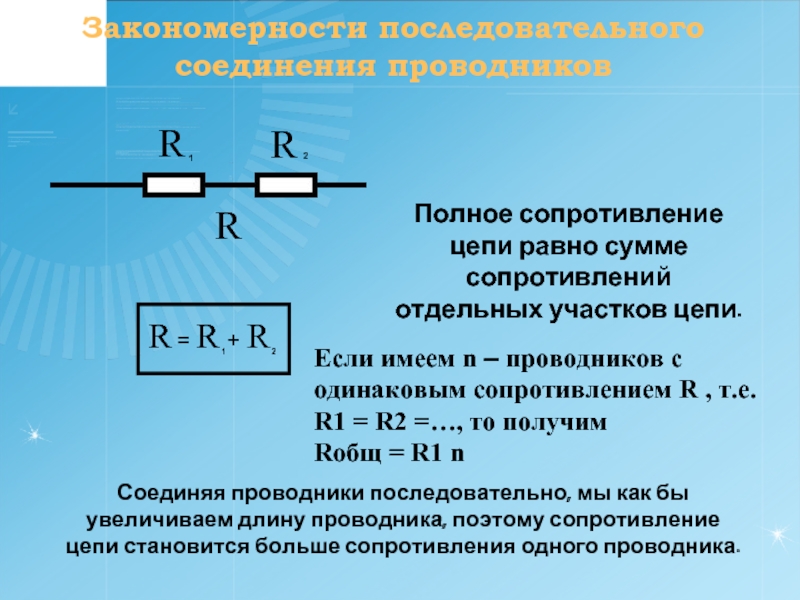
Пример 2. Три сопротивления 10, 15 и 20 Ом соединены последовательно, как показано на рисунке 3. Ток в цепи 5 А. Определить падение напряжения на каждом сопротивлении.
U 1 = I × r 1 = 5 ×10 = 50 В,
U 2 = I × r 2 = 5 ×15 = 75 В,
U 3 = I × r 3 = 5 ×20 = 100 В.
Рисунок 3. К примеру 2
Общее напряжение цепи равно сумме падений напряжений на отдельных участках цепи:
U = U 1 + U 2 + U 3 = 50 + 75 + 100 = 225 В.
Параллельное соединение проводников
Параллельным соединением проводников называется такое соединение, когда начала всех проводников соединены в одну точку, а концы проводников – в другую точку (рисунок 4). Начало цепи присоединяется к одному полюсу источника напряжения, а конец цепи – к другому полюсу.
Из рисунка видно, что при параллельном соединении проводников для прохождения тока имеется несколько путей. Ток, протекая к точке разветвления А , растекается далее по трем сопротивлениям и равен сумме токов, уходящих от этой точки:
I = I 1 + I 2 + I 3 .
Если токи, приходящие к точке разветвления, считать положительными, а уходящие – отрицательными, то для точки разветвления можно написать:
то есть алгебраическая сумма токов для любой узловой точки цепи всегда равна нулю. Это соотношение, связывающее токи в любой точке разветвления цепи, называется первым законом Кирхгофа . Определение первого закона Кирхгофа может звучать и в другой формулировке, а именно: сумма токов втекающих в узел электрической цепи равна сумме токов вытекающих из этого узла.
Видео 2. Первый закон Кирхгофа
Обычно при расчете электрических цепей направление токов в ветвях, присоединенных к какой либо точке разветвления, неизвестны. Поэтому для возможности самой записи уравнения первого закона Кирхгофа нужно перед началом расчета цепи произвольно выбрать так называемые положительные направления токов во всех ее ветвях и обозначить их стрелками на схеме.
Пользуясь законом Ома, можно вывести формулу для подсчета общего сопротивления при параллельном соединении потребителей.
Общий ток, приходящий к точке А , равен:
Токи в каждой из ветвей имеют значения:
По формуле первого закона Кирхгофа
I = I 1 + I 2 + I 3
Вынося U в правой части равенства за скобки, получим:
Сокращая обе части равенства на U , получим формулу подсчета общей проводимости:
g = g 1 + g 2 + g 3 .
Таким образом, при параллельном соединении увеличивается не сопротивление, а проводимость .
Пример 3. Определить общее сопротивление трех параллельно включенных сопротивлений, если r 1 = 2 Ом, r 2 = 3 Ом, r 3 = 4 Ом.
Пример 4. Пять сопротивлений 20, 30 ,15, 40 и 60 Ом включены параллельно в сеть. Определить общее сопротивление:
Следует заметить, что при подсчете общего сопротивления разветвления оно получается всегда меньше, чем самое меньшее сопротивление, входящее в разветвление.
Если сопротивления, включенные параллельно, равны между собой, то общее сопротивление r цепи равно сопротивлению одной ветви r 1 , деленному на число ветвей n :
Пример 5. Определить общее сопротивление четырех параллельно включенных сопротивлений по 20 Ом каждое:
Определить общее сопротивление четырех параллельно включенных сопротивлений по 20 Ом каждое:
Для проверки попробуем найти сопротивление разветвления по формуле:
Как видим, ответ получается тот же.
Пример 6. Пусть требуется определить токи в каждой ветви при параллельном их соединении, изображенном на рисунке 5, а .
Найдем общее сопротивление цепи:
Теперь все разветвления мы можем изобразить упрощенно как одно сопротивление (рисунок 5, б ).
Падение напряжения на участке между точками А и Б будет:
U = I × r = 22 × 1,09 = 24 В.
Возвращаясь снова к рисунку 5, а видим, что все три сопротивления окажутся под напряжением 24 В, так как они включены между точками А и Б .
Рассматривая первую ветвь разветвления с сопротивлением r 1 , мы видим, что напряжение на этом участке 24 В, сопротивление участка 2 Ом. По закону Ома для участка цепи ток на этом участке будет:
Ток второй ветви
Ток третьей ветви
Проверим по первому закону Кирхгофа
Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
Последовательное соединение резисторов . При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.
Последовательное соединение приемников поясняет рис. 25, а.
.Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:
E = IR 1 + IR 2 + IR 3 = I(R 1 + R 2 + R 3) = IR эк (19)
где R
эк
= R 1 + R 2 + R 3 .
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U 1 =IR 1 ; U 2 = IR 2 , U 3 = IR з и в данном случае E = U, то длярассматриваемой цепи
U = U 1 + U 2 +U 3 (20)
Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:
U 1: U 2: U 3 = R 1: R 2: R 3 (21)
т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.
В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:
При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Параллельное соединение резисторов . При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или
I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/R эк = 1/R 1 + 1/R 2 + 1/R 3 (24)
Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов :
G эк = G 1 + G 2 +G 3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
R эк =R 1 R 2 /(R 1 +R 2)
при трех параллельно включенных резисторах
R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
R эк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Смешанное соединение резисторов . Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле
R 123 =R 12 R 3 /(R 12 +R 3)=(R 1 +R 2)R 3 /(R 1 +R 2 +R 3).
При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:
R эк = R 123 + R 4 = (R 1 + R 2) R 3 / (R 1 + R 2 + R 3) + R 4
Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э.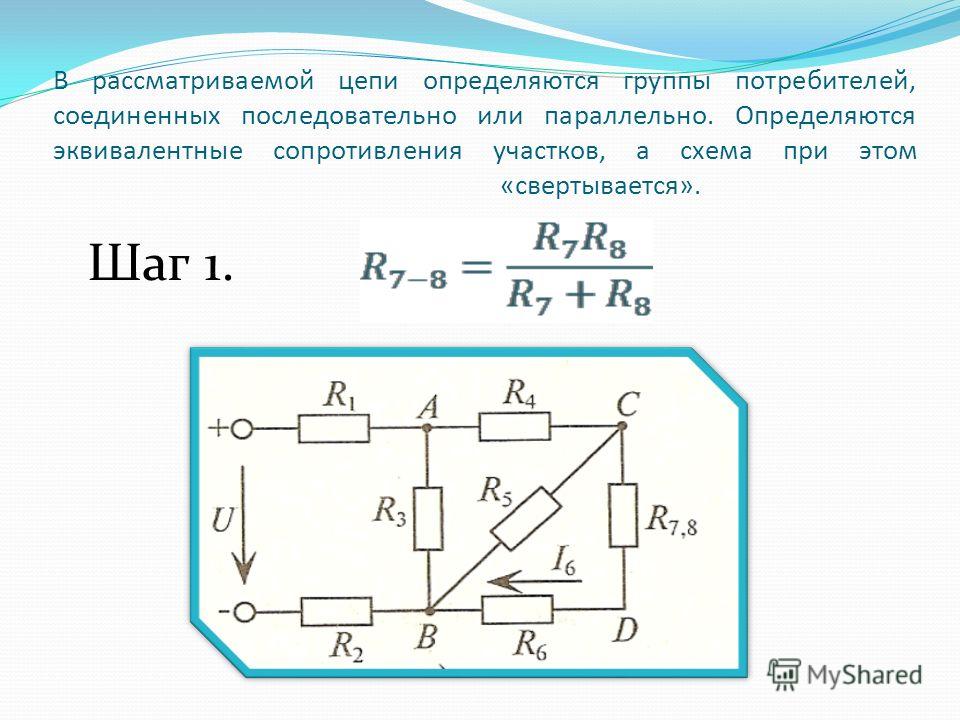 п. с. постоянного тока.
п. с. постоянного тока.
Параллельные соединения резисторов, формула расчёта которых выводится из закона Ома и правил Кирхгофа, являются наиболее распространённым типом включения элементов в электрическую цепь. При параллельном соединении проводников два или несколько элементов объединяются своими контактами с обеих из сторон соответственно. Подключение их к общей схеме осуществляется именно этими узловыми точками.
Gif?x15027″ alt=»Общий вид»>
Общий вид
Особенности включения
Включённые таким образом проводники нередко входят в состав сложных цепочек, содержащих, помимо этого, последовательное соединение отдельных участков.
Для такого включения типичны следующие особенности:
- Общее напряжение в каждой из ветвей будет иметь одно и то же значение;
- Протекающий в любом из сопротивлений электрический ток всегда обратно пропорционален величине их номинала.
В частном случае, когда все включённые в параллель резисторы имеют одинаковые номинальные значения, протекающие по ним «индивидуальные» токи также будут равны между собой.
Расчёт
Сопротивления ряда соединённых в параллель проводящих элементов определяются по общеизвестной форме расчёта, предполагающей сложение их проводимостей (обратных сопротивлению величин).
Протекающий в каждом из отдельных проводников ток в соответствие с законом Ома, может быть найден по формуле:
I= U/R (одного из резисторов).
После ознакомления с общими принципами обсчёта элементов сложных цепочек можно перейти к конкретным примерам решения задач данного класса.
Типичные подключения
Пример №1
Нередко для решения стоящей перед конструктором задачи требуется путём объединения нескольких элементов получить в итоге конкретное сопротивление. При рассмотрении простейшего варианта такого решения допустим, что общее сопротивление цепочки из нескольких элементов должно составлять 8 Ом. Этот пример нуждается в отдельном рассмотрении по той простой причине, что в стандартном ряду сопротивлений номинал в 8 Ом отсутствует (есть только 7,5 и 8,2 Ом).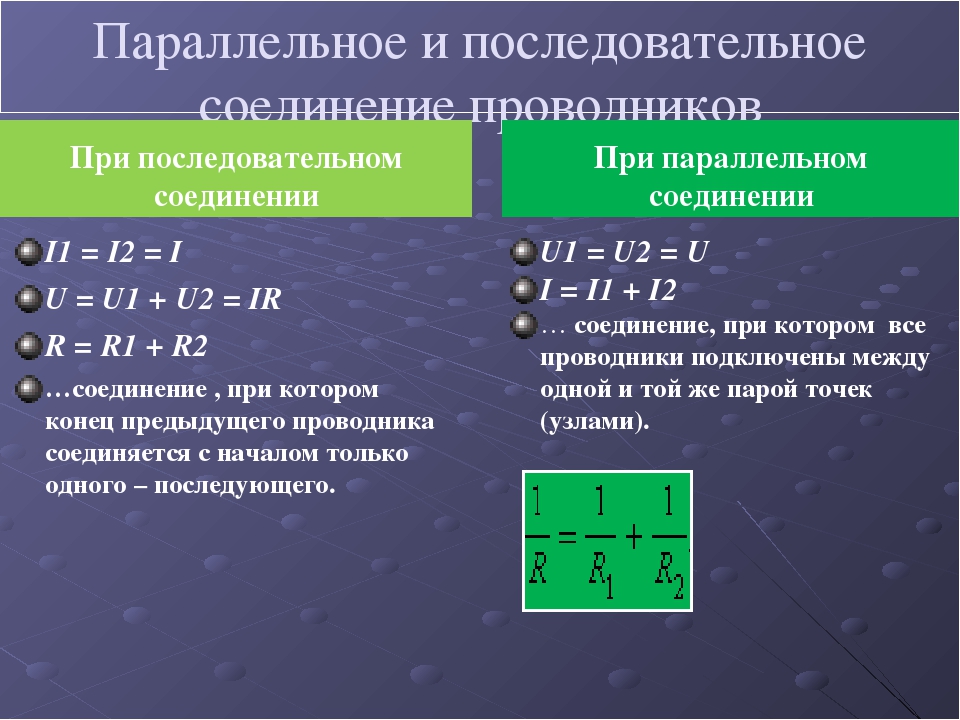
Решение этой простейшей задачи удаётся получить за счёт соединения двух одинаковых элементов с сопротивлениями по 16 Ом каждое (такие номиналы в резистивном ряду существуют). Согласно приводимой выше формуле общее сопротивление цепочки в этом случае вычисляется очень просто.
Из неё следует:
16х16/32=8 (Ом), то есть как раз столько, сколько требовалось получить.
Таким сравнительно простым способом удаётся решить задачу формирования общего сопротивления, равного 8-ми Омам.
Пример №2
В качестве ещё одного характерного примера образования требуемого сопротивления можно рассмотреть построение схемы, состоящей из 3-х резисторов.
Общее значение R такого включения может быть рассчитано по формуле последовательного и параллельного соединения в проводниках.
Gif?x15027″ alt=»Пример»>
В соответствии с указанными на картинке значениями номиналов, общее сопротивление цепочки будет равно:
1/R = 1/200+1/220+1/470 = 0,0117;
R=1/0,0117 = 85,67Ом.
В итоге находим суммарное сопротивление всей цепочки, получаемой при параллельном соединении трёх элементов с номинальными значениями 200, 240 и 470 Ом.
Важно! Указанный метод применим и при расчёте произвольного числа соединенных в параллель проводников или потребителей.
Также необходимо отметить, что при таком способе включения различных по величине элементов общее сопротивление будет меньше, чем у самого малого номинала.
Расчёт комбинированных схем
Рассмотренный метод может применяться и при расчёте сопротивления более сложных или комбинированных схем, состоящих из целого набора компонентов. Их иногда называют смешанными, поскольку при формировании цепочек используются сразу оба способа. Смешанное соединение резисторов представлено на размещенном ниже рисунке.
Gif?x15027″ alt=»Смешанная схема»>
Смешанная схема
Для упрощения расчета сначала разбиваем все резисторы по типу включения на две самостоятельные группы. Одна из них представляет собой последовательное соединение, а вторая – имеет вид подключения параллельного типа.
Из приведённой схемы видно, что элементы R2 и R3 соединяются последовательно (они объединены в группу 2), которая, в свою очередь, включена в параллель с резистором R1, принадлежащим группе 1.
Последовательным называется такое соединение резисторов, когда конец одного проводника соединяется с началом другого и т.д. (рис. 1). При последовательном соединении сила тока на любом участке электрической цепи одинакова. Это объясняется тем, что заряды не могут накапливаться в узлах цепи. Их накопление привело бы к изменению напряженности электрического поля, а следовательно, и к изменению силы тока. Поэтому
\(~I = I_1 = I_2 .\)
Амперметр А измеряет силу тока в цепи и обладает малым внутренним сопротивлением (R A → 0).
Включенные вольтметры V 1 и V 2 измеряют напряжение U 1 и U 2 на сопротивлениях R 1 и R 2 . Вольтметр V измеряет подведенное к клеммам Μ и N напряжение U . n R_i .\)
n R_i .\)
Если сопротивления отдельных резисторов равны между собой, т.е. R 1 = R 2 = … = R n , то общее сопротивление этих резисторов при последовательном соединении в n раз больше сопротивления одного резистора: R = nR 1 .
При последовательном соединении резисторов справедливо соотношение \(~\frac{U_1}{U_2} = \frac{R_1}{R_2}\), т.е. напряжения на резисторах прямо пропорциональны сопротивлениям.
Параллельным называется такое соединение резисторов, когда одни концы всех резисторов соединены в один узел, другие концы — в другой узел (рис. 2). Узлом называется точка разветвленной цепи, в которой сходятся более двух проводников. При параллельном соединении резисторов к точкам Μ и N подключен вольтметр. Он показывает, что напряжения на отдельных участках цепи с сопротивлениями R 1 и R 2 равны. Это объясняется тем, что работа сил стационарного электрического поля не зависит от формы траектории:
\(~U = U_1 = U_2 .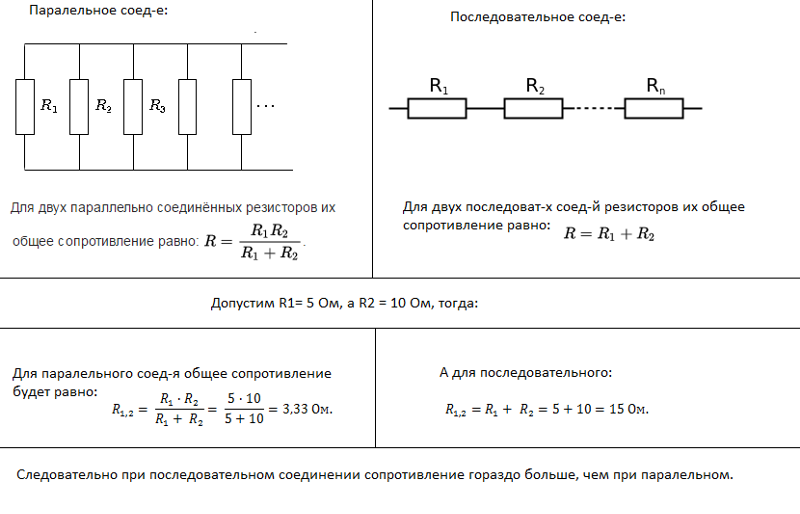 n \frac{1}{R_i} .\)
n \frac{1}{R_i} .\)
Если сопротивления всех n параллельно соединенных резисторов одинаковы и равны R 1 то \(~\frac 1R = \frac{n}{R_1}\) . Откуда \(~R = \frac{R_1}{n}\) .
Сопротивление цепи, состоящей из n одинаковых параллельно соединенных резисторов, в n раз меньше сопротивления каждого из них.
При параллельном соединении резисторов справедливо соотношение \(~\frac{I_1}{I_2} = \frac{R_2}{R_1}\), т.е. силы токов в ветвях параллельно соединенной цепи обратно пропорциональны сопротивлениям ветвей.
Литература
Аксенович Л. А. Физика в средней школе: Теория. Задания. Тесты: Учеб. пособие для учреждений, обеспечивающих получение общ. сред, образования / Л. А. Аксенович, Н.Н.Ракина, К. С. Фарино; Под ред. К. С. Фарино. — Мн.: Адукацыя i выхаванне, 2004. — C. 257-259.
Проверим справедливость показанных здесь формул на простом эксперименте.
Возьмём два резистора МЛТ-2 на 3 и 47 Ом и соединим их последовательно. Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Затем измерим общее сопротивление получившейся цепи цифровым мультиметром. Как видим оно равно сумме сопротивлений резисторов, входящих в эту цепочку.
Замер общего сопротивления при последовательном соединении
Теперь соединим наши резисторы параллельно и замерим их общее сопротивление.
Измерение сопротивления при параллельном соединении
Как видим, результирующее сопротивление (2,9 Ом) меньше самого меньшего (3 Ом), входящего в цепочку. Отсюда вытекает ещё одно известное правило, которое можно применять на практике:
При параллельном соединении резисторов общее сопротивление цепи будет меньше наименьшего сопротивления, входящего в эту цепь.
Что ещё нужно учитывать при соединении резисторов?
Во-первых, обязательно учитывается их номинальная мощность. Например, нам нужно подобрать замену резистору на 100 Ом и мощностью 1 Вт . Возьмём два резистора по 50 Ом каждый и соединим их последовательно. На какую мощность рассеяния должны быть рассчитаны эти два резистора?
Поскольку через последовательно соединённые резисторы течёт один и тот же постоянный ток (допустим 0,1 А ), а сопротивление каждого из них равно 50 Ом , тогда мощность рассеивания каждого из них должна быть не менее 0,5 Вт . В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .
В результате на каждом из них выделится по 0,5 Вт мощности. В сумме это и будет тот самый 1 Вт .
Данный пример достаточно грубоват. Поэтому, если есть сомнения, стоит брать резисторы с запасом по мощности.
Подробнее о мощности рассеивания резистора читайте .
Во-вторых, при соединении стоит использовать однотипные резисторы, например, серии МЛТ. Конечно, нет ничего плохого в том, чтобы брать разные. Это лишь рекомендация.
Соотношение токов и напряжений при параллельном соединении. Ток проводников в параллельном и последовательном соединении
Последовательное и параллельное соединение проводников это основные виды соединения проводников, встречающиеся на практике. Так как электрические цепи, как правило, не состоят из однородных проводников одинакового сечения. Как же найти сопротивление цепи, если известны сопротивления ее отдельных частей.
Рассмотрим два типичных случая. Первый из них это когда два или боле проводников обладающих сопротивлением включены последовательно. Последовательно значит, что конец первого проводника подключен к началу второго и так далее. При таком включении проводников сила тока в каждом из них будет одинакова. А вот напряжение на каждом из них будет различным.
Последовательно значит, что конец первого проводника подключен к началу второго и так далее. При таком включении проводников сила тока в каждом из них будет одинакова. А вот напряжение на каждом из них будет различным.
Рисунок 1 — последовательное соединение проводников
Падение напряжения на сопротивлениях можно определить исходя из закона Ома.
Формула 1 — Падение напряжения на сопротивлении
Сумма этих напряжений будет равна полному напряжению, приложенному к цепи. Напряжение на проводниках будет распределяться пропорционально их сопротивлению. То есть можно записать.
Формула 2 — соотношение между сопротивлением и напряжением
Суммарное же сопротивление цепи будет равно сумме всех сопротивлений включенных последовательно.
Формула 3 — вычисление суммарного сопротивления при параллельном включении
Второй случай, когда сопротивления в цепи включены параллельно друг другу. То есть в цепи есть два узла и все проводники обладающие сопротивлением подключаются к этим узлам. В такой цепи токи во всех ветвях в общем случае не равны друг другу. Но сумма всех токов в цепи после разветвления будет равна току до разветвления.
Рисунок 2 — Параллельное соединение проводников
Формула 4 — соотношение между токами в параллельных ветвях
Сила тока в каждой из разветвлённой цепи также подчиняется закону Ома. Напряжение на всех проводниках будет одинаково. Но сила тока будет разлучаться. В цепи, состоящей из параллельно соединенных проводников, токи распределяются пропорционально сопротивлениям.
Формула 5 — Распределение токов в параллельных ветвях
Чтобы найти полное сопротивление цепи в этом случае необходимо сложить величины обратные сопротивлениям то есть проводимости.
Формула 6 — Сопротивление параллельно включённых проводников
Также существует упрощённая формула для частного случая когда параллельно включены два одинаковых сопротивления.
Содержание:Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.
Последовательное соединение проводников
В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.
Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.
Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:
- Сила тока на всех участках цепи будет одинаковой.
- Общее напряжение цепи составляет сумму напряжений на каждом участке.
- Общее сопротивление включает в себя сопротивления каждого отдельного проводника.
Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.
Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R — общее сопротивление, R1 — сопротивление одного элемента, а n — количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.
Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.
Параллельное соединение проводников
В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.
Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.
После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 — силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.
С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.
В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.
Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях — увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.
Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.
Законы последовательного и параллельного соединения проводников
Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.
Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:
- Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
- параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
- Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
- При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
- Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.
Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.
Смешанное соединение проводников
В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.
В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.
Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.
При одновременном включении нескольких приемников электроэнергии в одну и ту же сеть, эти приемники можно легко рассматривать просто как элементы единой цепи, каждый из которых обладает собственным сопротивлением.
В ряде случаев такой подход оказывается вполне приемлемым: лампы накаливания, электрические обогреватели и т. п. — можно воспринимать как резисторы. То есть приборы можно заменить на их сопротивления, и легко произвести расчет параметров цепи.
Способ соединения приемников электроэнергии может быть одним из следующих: последовательный, параллельный или смешанный тип соединения.
Последовательное соединение
Когда несколько приемников (резисторов) соединяются в последовательную цепь, то есть второй вывод первого присоединяется к первому выводу второго, второй вывод второго соединяется с первым выводом третьего, второй вывод третьего с первым выводом четвертого и т. д., то при подключении такой цепи к источнику питания, через все элементы цепи потечет ток I одной и той же величины. Данную мысль поясняет приведенный рисунок.
Заменив приборы на их сопротивления, рисунок преобразуем в схему, тогда сопротивления с R1 по R4, соединенные последовательно, примут каждый на себя определенные напряжения, которые в сумме дадут значение ЭДС на зажимах источника питания. Для простоты здесь и далее изобразим источник в виде гальванического элемента.
Выразив падения напряжений через ток и через сопротивления, получим выражение для эквивалентного сопротивления последовательной цепи приемников: общее сопротивление последовательного соединения резисторов всегда равно алгебраической сумме всех сопротивлений, составляющих эту цепь. А поскольку напряжения на каждом из участков цепи можно найти из закона Ома (U = I*R, U1 = I*R1, U2 = I*R2 и т. д.) и E = U, то для нашей схемы получаем:
Напряжение на клеммах источника питания равно сумме падений напряжений на каждом из соединенных последовательно приемников, составляющих цепь.
Так как ток через всю цепь течет одного и того же значения, то справедливым будет утверждение, что напряжения на последовательно соединенных приемниках (резисторах) соотносятся между собой пропорционально сопротивлениям. И чем выше будет сопротивление, тем выше окажется и напряжение, приложенное к приемнику.
Для последовательного соединения резисторов в количестве n штук, обладающих одинаковыми сопротивлениями Rk, эквивалентное общее сопротивление цепи целиком будет в n раз больше каждого из этих сопротивлений: R = n*Rk. Соответственно и напряжения, приложенные к каждому из резисторов цепи будут между собой равны, и окажутся в n раз меньше напряжения, приложенного ко всей цепи: Uk = U/n.
Для последовательного соединения приемников электроэнергии характерны следующие свойства: если изменить сопротивление одного из приемников цепи, то напряжения на остальных приемниках цепи при этом изменятся; при обрыве одного из приемников ток прекратится во всей цепи, во всех остальных приемниках.
В силу этих особенностей последовательное соединение встречается редко, и используют его лишь там, где напряжение сети выше номинального напряжения приемников, в отсутствие альтернатив.
К примеру напряжением 220 вольт можно запитать две последовательно соединенные лампы равной мощности, каждая из которых рассчитана на напряжение 110 вольт. Ежели данные лампы при одинаковом номинальном напряжении питания будут обладать различной номинальной мощностью, то одна из них будет перегружена и скорее всего мгновенно перегорит.
Параллельное соединение
Параллельное соединение приемников предполагает включение каждого из них между парой точек электрической цепи с тем, чтобы они образовывали параллельные ветви, каждая из которых питается напряжением источника. Для наглядности опять заменим приемники их электрическими сопротивлениями, чтобы получить схему, по которой удобно вести расчет параметров.
Как уже было сказано, в случае параллельного соединения каждый из резисторов испытывает действие одного и того же напряжения. И в соответствии с законом Ома имеем: I1=U/R1, I2=U/R2, I3=U/R3.
Здесь I — ток источника. Первый закон Кирхгофа для данной цепи позволяет записать выражение для тока в неразветвленной ее части: I = I1+I2+I3.
Отсюда общее сопротивление для параллельного соединения между собой элементов цепи можно найти из формулы:
Величина обратная сопротивлению называется проводимостью G, и формулу для проводимости цепи, состоящей из нескольких параллельно соединенных элементов, также можно записать: G = G1 + G2 + G3. Проводимость цепи в случае параллельного соединения образующих ее резисторов равна алгебраической сумме проводимостей этих резисторов. Следовательно, при добавлении в цепь параллельных приемников (резисторов) суммарное сопротивление цепи уменьшится, а суммарная проводимость соответственно возрастет.
Токи в цепи состоящей из параллельно соединенных приемников, распределяются между ними прямо пропорционально их проводимостям, то есть обратно пропорционально их сопротивлениям. Здесь можно привести аналогию из гидравлики, где поток воды распределяется по трубам в соответствии с их сечениями, тогда большее сечение аналогично меньшему сопротивлению, то есть большей проводимости.
Если цепь состоит из нескольких (n) одинаковых резисторов, соединенных параллельно, то общее сопротивление цепи будет ниже в n раз, чем сопротивление одного из резисторов, а ток через каждый из резисторов будет меньше в n раз, чем общий ток: R = R1/n; I1 = I/n.
Цепь, состоящая из параллельно соединенных приемников, подключенная к источнику питания, отличается тем, что каждый из приемников находится под напряжением источника питания.
Для идеального источника электроэнергии справедливо утверждение: при подключении или отключении параллельно источнику резисторов, токи в остальных подключенных резисторах не изменятся, то есть при выходе из строя одного или нескольких приемников параллельной цепи, остальные будут продолжать работать в прежнем режиме.
В силу данных особенностей параллельное соединение обладает значительным преимуществом перед последовательным, и по этой причине именно соединение параллельное наиболее распространено в электрических сетях. Например, все электроприборы в наших домах предназначены для параллельного подключения к бытовой сети, и если отключить один, то остальным это ничуть не навредит.
Сравнение последовательных и параллельных цепей
Под смешанным соединением приемников понимают такое их соединение, когда часть или несколько из них соединены между собой последовательно, а другая часть или несколько — параллельно. При этом вся цепь может быть образована из разных соединений таких частей между собой. Для примера рассмотрим схему:
Три последовательно соединенных резистора подключены к источнику питания, параллельно одному из них подключены еще два, а третий — параллельно всей цепи. Для нахождения полного сопротивления цепи идут путем последовательных преобразований: сложную цепь последовательно приводят к простому виду, последовательно вычисляя сопротивление каждого звена, и так находят общее эквивалентное сопротивление.
Для нашего примера. Сначала находят общее сопротивление двух резисторов R4 и R5, соединенных последовательно, затем сопротивление параллельного соединения их с R2, потом прибавляют к полученному значению R1 и R3, и после — вычисляют значение сопротивления всей цепи, включая параллельную ветвь R6.
Различные способы соединения приемников электроэнергии применяют на практике для различных целей, чтобы решать конкретные поставленные задачи. Например, смешанное соединение можно встретить в схемах плавного заряда в мощных блоках питания, где нагрузка (конденсаторы после диодного моста) сначала получает питание последовательно через резистор, затем резистор шунтируется контактами реле, и нагрузка оказывается подключенной к диодному мосту параллельно.
Андрей Повный
Одним из китов, на котором держатся многие понятия в электронике, является понятие последовательного и параллельного подключения проводников. Знать основные отличия указанных типов подключения просто необходимо. Без этого нельзя понять и прочитать ни одной схемы.
Основные принципы
Электрический ток движется по проводнику от источника к потребителю (нагрузке). Чаще всего в качестве проводника выбирается медный кабель. Связано это с требованием, которое предъявляется к проводнику: он должен легко высвобождать электроны.
Независимо от способа подключения, электрический ток двигается от плюса к минусу. Именно в этом направлении убывает потенциал. При этом стоит помнить, что провод, по котору идет ток, также обладает сопротивлением. Но его значение очень мало. Именно поэтому им пренебрегают. Сопротивление проводника принимают равным нулю. В том случае, если проводник обладает сопротивлением, его принято называть резистором.
Параллельное подключение
В данном случае элементы, входящие в цепь, объединены между собой двумя узлами. С другими узлами у них связей нет. Участки цепи с таким подключением принято называть ветвями. Схема параллельного подключения представлена на рисунке ниже.
Если говорить более понятным языком, то в данном случае все проводники одним концом соединены в одном узле, а вторым — во втором. Это приводит к тому, что электрический ток разделяется на все элементы. Благодаря этому увеличивается проводимость всей цепи.
При подключении проводников в цепь данным способом напряжение каждого из них будет одинаково. А вот сила тока всей цепи будет определяться как сумма токов, протекающих по всем элементам. С учетом закона Ома путем нехитрых математических расчетов получается интересная закономерность: величина, обратная общему сопротивлению всей цепи, определяется как сумма величин, обратных сопротивлениям каждого отдельного элемента. При этом учитываются только элементы, подключенные параллельно.
Последовательное подключение
В данном случае все элементы цепи соединены таким образом, что они не образуют ни одного узла. При данном способе подключения имеется один существенный недостаток. Он заключается в том, что при выходе из строя одного из проводников все последующие элементы работать не смогут. Ярким примером такой ситуации является обычная гирлянда. Если в ней перегорает одна из лампочек, то вся гирлянда перестает работать.
Последовательное подключение элементов отличается тем, что сила тока во всех проводниках равна. Что касается напряжения цепи, то оно равно сумме напряжения отдельных элементов.
В данной схеме проводники включаются в цепь поочередно. А это значит, что сопротивление всей цепи будет складываться из отдельных сопротивлений, характерных для каждого элемента. То есть общее сопротивление цепи равно сумме сопротивлений всех проводников. Эту же зависимость можно вывести и математическим способом, используя закон Ома.
Смешанные схемы
Бывают ситуации, когда на одной схеме можно увидеть одновременно последовательное и параллельное подключение элементов. В таком случае говорят о смешанном соединении. Расчет подобных схем проводится отдельно для каждой из группы проводников.
Так, чтобы определить общее сопротивление, необходимо сложить сопротивление элементов, подключенных параллельно, и сопротивление элементов с последовательным подключением. При этом последовательное подключение является доминантным. То есть его рассчитывают в первую очередь. И только после этого определяют сопротивление элементов с параллельным подключением.
Подключение светодиодов
Зная основы двух типов подключения элементов в цепи, можно понять принцип создания схем различных электроприборов. Рассмотрим пример. во многом зависит от напряжения источника тока.
При небольшом напряжении сети (до 5 В) светодиоды подключают последовательно. Снизить уровень электромагнитных помех в данном случае поможет конденсатор проходного типа и линейные резисторы. Проводимость светодиодов увеличивают за счет использования системных модуляторов.
При напряжении сети 12 В может использоваться и последовательное, и параллельное подключение сети. В случае последовательного подключения используют импульсные блоки питания. Если собирается цепь из трех светодиодов, то можно обойтись без усилителя. Но если цепь будет включать большее количество элементов, то усилитель необходим.
Во втором случае, то есть при параллельном подключении, необходимо использование двух открытых резисторов и усилителя (с пропускной способностью выше 3 А). Причем первый резистор устанавливается перед усилителем, а второй — после.
При высоком напряжении сети (220 В) прибегают к последовательному подключению. При этом дополнительно используют операционные усилители и понижающие блоки питания.
Содержание:
Как известно, соединение любого элемента схемы, независимо от его назначения, может быть двух видов — параллельное подключение и последовательное. Также возможно и смешанное, то есть последовательно параллельное соединение. Все зависит от назначения компонента и выполняемой им функции. А значит, и резисторы не избежали этих правил. Последовательное и параллельное сопротивление резисторов это по сути то же самое, что и параллельное и последовательное подключение источников света. В параллельной цепи схема подключения подразумевает вход на все резисторы из одной точки, а выход из другой. Попробуем разобраться, каким образом выполняется последовательное соединение, а каким — параллельное. И главное, в чем состоит разница между подобными соединениями и в каких случаях необходимо последовательное, а в каких параллельное соединение. Также интересен и расчет таких параметров, как общее напряжение и общее сопротивление цепи в случаях последовательного либо параллельного соединения. Начать следует с определений и правил.
Способы подключения и их особенности
Виды соединения потребителей или элементов играют очень важную роль, ведь именно от этого зависят характеристики всей схемы, параметры отдельных цепей и тому подобное. Для начала попробуем разобраться с последовательным подключением элементов к схеме.
Последовательное соединение
Последовательное подключение — это такое соединение, где резисторы (равно, как и другие потребители или элементы схем) подключаются друг за другом, при этом выход предыдущего подключается на вход следующего. Подобный вид коммутации элементов дает показатель, равный сумме сопротивлений этих элементов схемы. То есть если r1 = 4 Ом, а r2 = 6 Ом, то при подключении их в последовательную цепь, общее сопротивление составит 10 Ом. Если мы добавим последовательно еще один резистор на 5 Ом, сложение этих цифр даст 15 Ом — это и будет общее сопротивление последовательной цепи. То есть общие значения равны сумме всех сопротивлений. При его расчете для элементов, которые подключены последовательно, никаких вопросов не возникает — все просто и ясно. Именно поэтому не стоит даже останавливаться более серьезно на этой.
Совершенно по другим формулам и правилам производится расчет общего сопротивления резисторов при параллельном подключении, вот на нем имеет смысл остановиться поподробнее.
Параллельное соединение
Параллельным называется соединение, при котором все входы резисторов объединены в одной точке, а все выходы — во второй. Здесь главное понять, что общее сопротивление при подобном подключении будет всегда ниже, чем тот же параметр резистора, имеющего наименьшее.
Имеет смысл разобрать подобную особенность на примере, тогда понять это будет намного проще. Существует два резистора по 16 Ом, но при этом для правильного монтажа схемы требуется лишь 8 Ом. В данном случае при задействовании их обеих, при их параллельном включении в схему, как раз и получатся необходимые 8 Ом. Попробуем понять, по какой формуле возможны вычисления. Рассчитать этот параметр можно так: 1/Rобщ = 1/R1+1/R2, причем при добавлении элементов сумма может продолжаться до бесконечности.
Попробуем еще один пример. Параллельно соединены 2 резистора, с сопротивлением 4 и 10 Ом. Тогда общее будет равно 1/4 + 1/10, что будет равным 1:(0.25 + 0.1) = 1:0.35 = 2.85 Ом. Как видим, хотя резисторы и имели значительное сопротивление, при подключении их параллельнообщий показатель стал намного ниже.
Так же можно рассчитать общее сопротивление четырех параллельно подключенных резисторов, с номиналом 4, 5, 2 и 10 Ом. Вычисления, согласно формуле, будут такими: 1/Rобщ = 1/4+1/5+1/2+1/10, что будет равным 1:(0.25+0.2+0.5+0.1)=1/1.5 = 0.7 Ом.
Что же касается тока, протекающего через параллельно соединенные резисторы, то здесь необходимо обратиться к закону Кирхгофа, который гласит «сила тока при параллельном соединении, выходящего из цепи, равна току, входящему в цепь». А потому здесь законы физики решают все за нас. При этом общие показатели тока разделяются на значения, которые являются обратно пропорциональными сопротивлению ветки. Если сказать проще, то чем больше показатель сопротивления, тем меньшие токи будут проходить через этот резистор, но в общем, все же ток входа будет и на выходе. При параллельном соединении напряжение также остается на выходе таким же, как и на входе. Схема параллельного соединения указана ниже.
Последовательно-параллельное соединение
Последовательно-параллельное соединение — это когда схема последовательного соединения содержит в себе параллельные сопротивления. В таком случае общее последовательное сопротивление будет равно сумме отдельно взятых общих параллельных. Метод вычислений одинаковый в соответствующих случаях.
Подведем итог
Подводя итог всему вышеизложенному можно сделать следующие выводы:
- При последовательном соединении резисторов не требуется особых формул для расчета общего сопротивления. Необходимо лишь сложить все показатели резисторов — сумма и будет общим сопротивлением.
- При параллельном соединении резисторов, общее сопротивление высчитывается по формуле 1/Rобщ = 1/R1+1/R2…+Rn.
- Эквивалентное сопротивление при параллельном соединении всегда меньше минимального подобного показателя одного из резисторов, входящих в схему.
- Ток, равно как и напряжение в параллельном соединении остается неизменным, то есть напряжение при последовательном соединении равно как на входе, так и на выходе.
- Последовательно-параллельное соединение при подсчетах подчиняется тем же законам.
В любом случае, каким бы ни было подключение, необходимо четко рассчитывать все показатели элементов, ведь параметры имеют очень важную роль при монтаже схем. И если ошибиться в них, то либо схема не будет работать, либо ее элементы просто сгорят от перегрузки. По сути, это правило применимо к любым схемам, даже в электромонтаже. Ведь провод по сечению подбирают также исходя из мощности и напряжения. А если поставить лампочку номиналом в 110 вольт в цепь с напряжением 220, несложно понять, что она моментально сгорит. Так же и с элементами радиоэлектроники. А потому — внимательность и скрупулезность в расчетах — залог правильной работы схемы.
Последовательность соединение и закономерности. Параллельное и последовательное соединение сопротивлений
Обычно все затрудняются ответить. А вот загадка эта в применении к электричеству решается вполне определенно.
Электричество начинается с закона Ома.
А уж если рассматривать дилемму в контексте параллельного или последовательного соединений — считая одно соединение курицей, а другое — яйцом, то сомнений вообще нет никаких.
Потому что закон Ома — это и есть самая первоначальная электрическая цепь. И она может быть только последовательной.
Да, придумали гальванический элемент и не знали, что с ним делать, поэтому сразу придумали еще лампочку. И вот что из этого получилось. Здесь напряжение в 1,5 В немедленно потекло в качестве тока, чтобы неукоснительно выполнять закон Ома, через лампочку к задней стенке того же элемента питания. А уж внутри самой батарейки под действием волшебницы-химии заряды снова оказались в первоначальной точке своего похода. И поэтому там, где напряжение было 1,5 вольта, оно таким и остается. То есть, напряжение постоянно одно, а заряды непрерывно движутся и последовательно проходят лампочку и гальванический элемент.
И это обычно рисуют на схеме вот так:
По закону Ома I=U/R
Тогда сопротивление лампочки (с тем током и напряжением, которые я написал) получится
R = 1/U , где R = 1 Ом
А мощность будет выделяться P = I * U , то есть P=2,25 Вm
В последовательной цепи, особенно на таком простом и несомненном примере, видно, что ток, который бежит по ней от начала до конца, — все время один и тот же. А если мы теперь возьмем две лампочки и сделаем так, чтобы ток пробегал сначала по одной, а потом по другой, то будет опять то же самое — ток будет и в той лампочке, и в другой снова одинаковым. Хотя другим по величине. Ток теперь испытывает сопротивление двух лампочек, но у каждой из них сопротивление как было, так и осталось, ведь оно определяется исключительно физическими свойствами самой лампочки. Новый ток вычисляем опять по закону Ома.
Он получится равным I=U/R+R,то есть 0,75А, ровно половина того тока, который был сначала.
В этом случае току приходится преодолевать уже два сопротивления, он становится меньше. Что и видно по свечению лампочек — они теперь горят вполнакала. А общее сопротивление цепочки из двух лампочек будет равно сумме их сопротивлений. Зная арифметику, можно в отдельном случае воспользоваться и действием умножения: если последовательно соединены N одинаковых лампочек, то общее их сопротивление будет равно N, умноженное на R, где R — сопротивление одной лампочки. Логика безупречная.
А мы продолжим наши опыты. Теперь сделаем нечто подобное, что мы провернули с лампочками, но только на левой стороне цепи: добавим еще один гальванический элемент, точно такой, как первый. Как видим, теперь у нас в два раза увеличилось общее напряжение, а ток стал снова 1,5 А, о чем и сигнализируют лампочки, загоревшись снова в полную силу.
Делаем вывод:
- При последовательном соединении электрической цепи сопротивления и напряжения ее элементов суммируются, а ток на всех элементах остается неизменным.
Легко проверить, что это утверждение справедливо как для активных компонентов (гальванических элементов), так и для пассивных (лампочек, резисторов).
То есть это значит, что напряжение, измеренное на одном резисторе (оно называется падением напряжения), можно смело суммировать с напряжением, измеренным на другом резисторе, и в сумме получатся те же 3 В. А на каждом из сопротивлений оно окажется равным половине — то есть 1,5 В. И это справедливо. Два гальванических элемента вырабатывают свои напряжения, а две лампочки их потребляют. Потому что в источнике напряжения энергия химических процессов превращается в электроэнергию, принявшую вид напряжения, а в лампочках та же самая энергия из электрической превращается в тепловую и световую.
Вернемся к первой схеме, подключим в ней еще одну лампочку, но иначе.
Теперь напряжение в точках, соединяющих две ветки, то же, что и на гальваническом элементе — 1,5 В. Но так как сопротивление у обеих лампочек тоже такое, как и было, то и ток через каждую из них пойдет 1,5 А — ток «полного накала».
Гальванический элемент теперь питает их током одновременно, следовательно, из него вытекают сразу оба эти тока. То есть общий ток из источника напряжения будет равен 1,5 А + 1,5 А = 3,0 А.
В чем же отличие этой схемы от схемы, когда те же самые лампочки были включены последовательно? Только в накале лампочек, то есть только в токе.
Тогда ток был 0,75 А, а теперь он стал сразу 3 А.
Получается, если сравнить с первоначальной схемой, то при последовательном соединении лампочек (схема 2) току сопротивления оказывалось больше (отчего он уменьшался, и лампочки теряли светимость), а параллельное подключение оказывает МЕНЬШЕ сопротивления, хотя сопротивление лампочек осталось неизменным. В чем тут дело?
А дело в том, что мы забываем одну интересную истину, что всякая палка о двух концах.
Когда мы говорим, что резистор сопротивляется току, то как бы забываем, что он ток все-таки проводит. И теперь, когда подключили лампочки параллельно, увеличилось суммарное для них свойство проводить ток, а не сопротивляться ему. Ну и, соответственно, некую величину G , по аналогии с сопротивлением R и следовало бы назвать проводимостью. И должна она в параллельном соединении проводников суммироваться.
Ну и вот она
Закон Ома тогда будет выглядеть
I = U * G &
И в случае параллельного соединения ток I будет равен U*(G+G) = 2*U*G, что мы как раз и наблюдаем.
Замена элементов цепи общим эквивалентным элементом
Инженерам часто приходится узнавать токи и напряжения во всех частях схем. А реальные электрические схемы бывают достаточно сложными и разветвленными и могут содержать множество элементов, активно потребляющих электроэнергию и соединенных друг с другом в совершенно разных сочетаниях. Это называется расчет электрических схем. Он делается при проектировании энергоснабжения домов, квартир, организаций. При этом очень важно, какие токи и напряжения будут действовать в электрической цепи, хотя бы для того, чтобы выбрать подходящие им сечения проводов, нагрузки на всю сеть или ее части, и так далее. А уж насколько сложны бывают электронные схемы, содержащие тысячи, а то и миллионы элементов, думаю, понятно всякому.
Самое первое что, напрашивается — это воспользоваться знанием того, как ведут себя токи напряжения в таких простейших соединениях сети, как последовательное и параллельное. Делают так: вместо найденного в сети последовательного соединения двух или более активных устройств-потребителей (как наши лампочки) нарисовать один, но чтобы его сопротивление было таким же, как у обоих. Тогда картина токов и напряжений в остальной части схемы не изменится. Аналогично и с параллельным соединением: вместо них нарисовать такой элемент, ПРОВОДИМОСТЬ которого была бы такой же, как у обоих.
Теперь если схему перерисовать, заменив последовательные и параллельные соединения одним элементом, то получим схему, которая называется «схемой эквивалентного замещения».
Такую процедуру можно продолжать до тех пор, пока у нас не останется наипростейшая — которой мы в самом начале иллюстрировали закон Ома. Только вместо лампочки будет стоять одно сопротивление, которое и называют эквивалентным сопротивлением нагрузки.
Это первая задача. Она дает нам возможность по закону Ома рассчитать общий ток во всей сети, или общий ток нагрузки.
Вот это и есть полный расчет электрической сети.
Примеры
Пусть цепь содержит 9 активных сопротивлений. Это могут быть лампочки или что-то другое.
На ее входные клеммы подано напряжение в 60 В.
Значения сопротивлений для всех элементов следующие:
Найти все неизвестные токи и напряжения.
Надо пойти по пути поиска параллельных и последовательных участков сети, рассчитывать эквивалентные им сопротивления и постепенно упрощать схему. Видим, что R 3 , R 9 и R 6 соединены последовательно. Тогда им эквивалентное сопротивление R э 3, 6, 9 будет равно их сумме R э 3, 6, 9 = 1 + 4 + 1 Ом = 6 Ом.
Теперь заменяем параллельный кусочек из сопротивлений R 8 и R э 3, 6, 9, получая R э 8, 3, 6, 9 . Только при параллельном соединении проводников, складывать придется проводимости.
Проводимость измеряется в единицах, называемых сименсами, обратных омам.
Если перевернуть дробь, получим сопротивление R э 8, 3, 6, 9 = 2 Ом
Совершенно так же, как в первом случае, объединяем сопротивления R 2 , R э 8, 3, 6, 9 и R 5, включенные последовательно, получая R э 2, 8, 3, 6, 9, 5 = 1 + 2 + 1 = 4 Ом.
Осталось два шага: получить сопротивление, эквивалентное двум резисторам параллельного соединения проводников R 7 и R э 2, 8, 3, 6, 9, 5.
Оно равно R э 7, 2, 8, 3, 6, 9, 5 = 1/(1/4+1/4)=1/(2/4)=4/2 = 2 Ом
На последнем шаге просуммируем все последовательно включенные сопротивления R 1 , R э 7, 2, 8, 3, 6, 9, 5 и R 4 и получим сопротивление, эквивалентное сопротивлению всей цепи R э и равное сумме этих трех сопротивлений
R э = R 1 + R э 7, 2, 8, 3, 6, 9, 5 + R4 = 1 + 2 + 1 = 4 Ом
Ну и вспомним, в честь кого назвали единицу сопротивлений, написанную нами в последней из этих формул, и вычислим по его закону общий ток во всей цепи I
Теперь, двигаясь в обратном направлении, в сторону все большего усложнения сети, можно получать по закону Ома токи и напряжения во всех цепочках нашей достаточно простой схемы.
Так обычно и рассчитывают схемы электроснабжения квартир, которые состоят из параллельных и последовательных участков. Что, как правило, не годится в электронике, потому что там многое по-другому устроено, и все гораздо замысловатее. И вот такую, например, схему, когда не поймешь, параллельное это соединение проводников или последовательное, рассчитывают по законам Кирхгофа.
Последовательным называют такое соединение элементов цепи, при котором во всех включенных в цепь элементах возникает один и тот же ток I (рис. 1.4).
На основании второго закона Кирхгофа (1.5) общее напряжение U всей цепи равно сумме напряжений на отдельных участках:
U = U 1 + U 2 + U 3 или IR экв = IR 1 + IR 2 + IR 3 ,
откуда следует
R экв = R 1 + R 2 + R 3 .
Таким образом, при последовательном соединении элементов цепи общее эквивалентное сопротивление цепи равно арифметической сумме сопротивлений отдельных участков. Следовательно, цепь с любым числом последовательно включенных сопротивлений можно заменить простой цепью с одним эквивалентным сопротивлением R экв (рис. 1.5). После этого расчет цепи сводится к определению тока I всей цепи по закону Ома
и по вышеприведенным формулам рассчитывают падение напряжений U 1 , U 2 , U 3 на соответствующих участках электрической цепи (рис. 1.4).
Недостаток последовательного включения элементов заключается в том, что при выходе из строя хотя бы одного элемента, прекращается работа всех остальных элементов цепи.
Электрическая цепь с параллельным соединением элементов
Параллельным называют такое соединение, при котором все включенные в цепь потребители электрической энергии, находятся под одним и тем же напряжением (рис. 1.6).
В этом случае они присоединены к двум узлам цепи а и b, и на основании первого закона Кирхгофа можно записать, что общий ток I всей цепи равен алгебраической сумме токов отдельных ветвей:
I = I 1 + I 2 + I 3 , т.е.
откуда следует, что
.
В том случае, когда параллельно включены два сопротивления R 1 и R 2 , они заменяются одним эквивалентным сопротивлением
.
Из соотношения (1.6), следует, что эквивалентная проводимость цепи равна арифметической сумме проводимостей отдельных ветвей:
g экв = g 1 + g 2 + g 3 .
По мере роста числа параллельно включенных потребителей проводимость цепи g экв возрастает, и наоборот, общее сопротивление R экв уменьшается.
Напряжения в электрической цепи с параллельно соединенными сопротивлениями (рис. 1.6)
U = IR экв = I 1 R 1 = I 2 R 2 = I 3 R 3 .
Отсюда следует, что
т.е. ток в цепи распределяется между параллельными ветвями обратно пропорционально их сопротивлениям.
По параллельно включенной схеме работают в номинальном режиме потребители любой мощности, рассчитанные на одно и то же напряжение. Причем включение или отключение одного или нескольких потребителей не отражается на работе остальных. Поэтому эта схема является основной схемой подключения потребителей к источнику электрической энергии.
Электрическая цепь со смешанным соединением элементов
Смешанным называется такое соединение, при котором в цепи имеются группы параллельно и последовательно включенных сопротивлений.
Для цепи, представленной на рис. 1.7, расчет эквивалентного сопротивления начинается с конца схемы. Для упрощения расчетов примем, что все сопротивления в этой схеме являются одинаковыми: R 1 =R 2 =R 3 =R 4 =R 5 =R. Сопротивления R 4 и R 5 включены параллельно, тогда сопротивление участка цепи cd равно:
.
В этом случае исходную схему (рис. 1.7) можно представить в следующем виде (рис. 1.8):
На схеме (рис. 1.8) сопротивление R 3 и R cd соединены последовательно, и тогда сопротивление участка цепи ad равно:
.
Тогда схему (рис. 1.8) можно представить в сокращенном варианте (рис. 1.9):
На схеме (рис. 1.9) сопротивление R 2 и R ad соединены параллельно, тогда сопротивление участка цепи аb равно
.
Схему (рис. 1.9) можно представить в упрощенном варианте (рис. 1.10), где сопротивления R 1 и R ab включены последовательно.
Тогда эквивалентное сопротивление исходной схемы (рис. 1.7) будет равно:
Рис. 1.10 | Рис. 1.11 |
В результате преобразований исходная схема (рис. 1.7) представлена в виде схемы (рис. 1.11) с одним сопротивлением R экв. Расчет токов и напряжений для всех элементов схемы можно произвести по законам Ома и Кирхгофа.
ЛИНЕЙНЫЕ ЦЕПИ ОДНОФАЗНОГО СИНУСОИДАЛЬНОГО ТОКА.
Получение синусоидальной ЭДС. . Основные характеристики синусоидального тока
Основным преимуществом синусоидальных токов является то, что они позволяют наиболее экономично осуществлять производство, передачу, распределение и использование электрической энергии. Целесообразность их использования обусловлена тем, что коэффициент полезного действия генераторов, электрических двигателей, трансформаторов и линий электропередач в этом случае оказывается наивысшим.
Для получения в линейных цепях синусоидально изменяющихся токов необходимо, чтобы э. д. с. также изменялись по синусоидальному закону. Рассмотрим процесс возникновения синусоидальной ЭДС. Простейшим генератором синусоидальной ЭДС может служить прямоугольная катушка (рамка), равномерно вращающаяся в однородном магнитном поле с угловой скоростью ω (рис. 2.1, б ).
Пронизывающий катушку магнитный поток во время вращения катушки abcd наводит (индуцирует) в ней на основании закона электромагнитной индукции ЭДС е . Нагрузку подключают к генератору с помощью щеток 1 , прижимающихся к двум контактным кольцам 2 , которые, в свою очередь, соединены с катушкой. Значение наведенной в катушке abcd э. д. с. в каждый момент времени пропорционально магнитной индукции В , размеру активной части катушки l = ab + dc и нормальной составляющей скорости перемещения ее относительно поля v н :
e = Blv н (2.1)
где В и l — постоянные величины, a v н — переменная, зависящая от угла α. Выразив скорость v н через линейную скорость катушки v , получим
e = Blv·sinα (2.2)
В выражении (2.2) произведение Blv = const. Следовательно, э. д. с., индуцируемая в катушке, вращающейся в магнитном поле, является синусоидальной функцией угла α .
Если угол α = π/2 , то произведение Blv в формуле (2.2) есть максимальное (амплитудное) значение наведенной э. д. с. E m = Blv . Поэтому выражение (2.2) можно записать в виде
e = E m sinα (2.3)
Так как α есть угол поворота за время t , то, выразив его через угловую скорость ω , можно записать α = ωt , a формулу (2.3) переписать в виде
e = E m sinωt (2.4)
где е — мгновенное значение э. д. с. в катушке; α = ωt — фаза, характеризующая значение э. д. с. в данный момент времени.
Необходимо отметить, что мгновенную э. д. с. в течение бесконечно малого промежутка времени можно считать величиной постоянной, поэтому для мгновенных значений э. д. с. е , напряжений и и токов i справедливы законы постоянного тока.
Синусоидальные величины можно графически изображать синусоидами и вращающимися векторами. При изображении их синусоидами на ординате в определенном масштабе откладывают мгновенные значения величин, на абсциссе — время. Если синусоидальную величину изображают вращающимися векторами, то длина вектора в масштабе отражает амплитуду синусоиды, угол, образованный с положительным направлением оси абсцисс, в начальный момент времени равен начальной фазе, а скорость вращения вектора равна угловой частоте. Мгновенные значения синусоидальных величин есть проекции вращающегося вектора на ось ординат. Необходимо отметить, что за положительное направление вращения радиус-вектора принято считать направление вращения против часовой стрелки. На рис. 2.2 построены графики мгновенных значений э. д. с. е и е» .
Если число пар полюсов магнитов p ≠ 1 , то за один оборот катушки (см. рис. 2.1) происходит p полных циклов изменения э. д. с. Если угловая частота катушки (ротора) n оборотов в минуту, то период уменьшится в pn раз. Тогда частота э. д. с., т. е. число периодов в секунду,
f = Pn / 60
Из рис. 2.2 видно, что ωТ = 2π , откуда
ω = 2π / T = 2πf (2.5)
Величину ω , пропорциональную частоте f и равную угловой скорости вращения радиус-вектора, называют угловой частотой. Угловую частоту выражают в радианах в секунду (рад/с) или в 1 / с.
Графически изображенные на рис. 2.2 э. д. с. е и е» можно описать выражениями
e = E m sinωt; e» = E» m sin(ωt + ψ e» ) .
Здесь ωt и ωt + ψ e» — фазы, характеризующие значения э. д. с. e и e» в заданный момент времени; ψ e» — начальная фаза, определяющая значение э. д. с. е» при t = 0. Для э. д. с. е начальная фаза равна нулю (ψ e = 0 ). Угол ψ всегда отсчитывают от нулевого значения синусоидальной величины при переходе ее от отрицательных значений к положительным до начала координат (t = 0). При этом положительную начальную фазу ψ (рис. 2.2) откладывают влево от начала координат (в сторону отрицательных значений ωt ), а отрицательную фазу — вправо.
Если у двух или нескольких синусоидальных величин, изменяющихся с одинаковой частотой, начала синусоид не совпадают по времени, то они сдвинуты друг относительно друга по фазе, т. е. не совпадают по фазе.
Разность углов φ , равная разности начальных фаз, называют углом сдвига фаз. Сдвиг фаз между одноименными синусоидальными величинами, например между двумя э. д. с. или двумя токами, обозначают α . Угол сдвига фаз между синусоидами тока и напряжения или их максимальными векторами обозначают буквой φ (рис. 2.3).
Когда для синусоидальных величин разность фаз равна ±π , то они противоположны по фазе, если же разность фаз равна ±π/2 , то говорят, что они находятся в квадратуре. Если для синусоидальных величин одной частоты начальные фазы одинаковы, то это означает, что они совпадают по фазе.
Синусоидальные напряжение и ток, графики которых представлены на рис. 2.3, описываются следующим образом:
u = U m sin(ω t + ψ u ) ; i = I m sin(ω t + ψ i ) , (2.6)
причем угол сдвига фаз между током и напряжением (см. рис. 2.3) в этом случае φ = ψ u — ψ i .
Уравнения (2.6) можно записать иначе:
u = U m sin(ωt + ψ i + φ) ; i = I m sin(ωt + ψ u — φ) ,
поскольку ψ u = ψ i + φ и ψ i = ψ u — φ .
Из этих выражений следует, что напряжение опережает по фазе ток на угол φ (или ток отстает по фазе от напряжения на угол φ ).
Формы представления синусоидальных электрических величин.
Любая, синусоидально изменяющаяся, электрическая величина (ток, напряжение, ЭДС) может быть представлена в аналитическом, графическом и комплексном видах.
1). Аналитическая форма представления
I = I m ·sin(ω·t + ψ i ), u = U m ·sin(ω·t + ψ u ), e = E m ·sin(ω·t + ψ e ),
где I , u , e – мгновенное значение синусоидального тока, напряжения, ЭДС, т. е. Значения в рассматриваемый момент времени;
I m , U m , E m – амплитуды синусоидального тока, напряжения, ЭДС;
(ω·t + ψ ) – фазовый угол, фаза; ω = 2·π/Т – угловая частота, характеризующая скорость изменения фазы;
ψ i , ψ u , ψ e – начальные фазы тока, напряжения, ЭДС отсчитываются от точки перехода синусоидальной функции через нуль к положительному значению до начала отсчета времени (t = 0). Начальная фаза может иметь как положительное так и отрицательное значение.
Графики мгновенных значений тока и напряжения показаны на рис. 2.3
Начальная фаза напряжения сдвинута влево от начала отсчёта и является положительной ψ u > 0, начальная фаза тока сдвинута вправо от начала отсчёта и является отрицательной ψ i φ . Сдвиг фаз между напряжением и током
φ = ψ u – ψ i = ψ u – (- ψ i) = ψ u + ψ i .
Применение аналитической формы для расчёта цепей является громоздкой и неудобной.
На практике приходится иметь дело не с мгновенными значениями синусоидальных величин, а с действующими. Все расчёты проводят для действующих значений, в паспортных данных различных электротехнических устройств указаны действующие значения (тока, напряжения), большинство электроизмерительных приборов показывают действующие значения. Действующий ток является эквивалентом постоянного тока, который за одно и то же время выделяет в резисторе такое же количество тепла, как и переменный ток. Действующее значение связано с амплитудным простым соотношением
2). Векторная форма представления синусоидальной электрической величины – это вращающийся в декартовой системе координат вектор с началом в точке 0, длина которого равна амплитуде синусоидальной величины, угол относительно оси х – её начальной фазе, а частота вращения – ω = 2πf . Проекция данного вектора на ось у в любой момент времени определяет мгновенное значение рассматриваемой величины.
Рис. 2.4
Совокупность векторов, изображающих синусоидальные функции, называют векторной диаграммой, рис. 2.4
3). Комплексное представление синусоидальных электрических величин сочетает наглядность векторных диаграмм с проведением точных аналитических расчётов цепей.
Рис. 2.5
Ток и напряжение изобразим в виде векторов на комплексной плоскости, рис.2.5 Ось абсцисс называют осью действительных чисел и обозначают +1 , ось ординат называют осью мнимых чисел и обозначают +j . (В некоторых учебниках ось действительных чисел обозначают Re , а ось мнимых – Im ). Рассмотрим векторы U и I в момент времени t = 0. Каждому из этих векторов соответствует комплексное число, которое может быть представлено в трех формах:
а). Алгебраической
U = U ’+ jU «
I = I ’ – jI «,
где U «, U «, I «, I » – проекции векторов на оси действительных и мнимых чисел.
б). Показательной
где U , I – модули (длины) векторов; е – основание натурального логарифма; поворотные множители, т. к. умножение на них соответствует повороту векторов относительно положительного направления действительной оси на угол, равный начальной фазе.
в). Тригонометрической
U = U ·(cosψ u + j sinψ u)
I = I ·(cosψ i – j sinψ i).
При решении задач в основном применяют алгебраическую форму (для операций сложения и вычитания) и показательную форму (для операций умножения и деления). Связь между ними устанавливается формулой Эйлера
е j ·ψ = cosψ + j sinψ .
Неразветвлённые электрические цепи
Причем это могут быть не только проводники, но и конденсаторы. Здесь важно не запутаться в том, как выглядит каждое из них на схеме. А уже потом применять конкретные формулы. Их, кстати, нужно помнить наизусть.
Как различить эти два соединения?
Внимательно посмотрите на схему. Если провода представить как дорогу, то машины на ней будут играть роль резисторов. На прямой дороге без каких-либо разветвлений машины едут одна за другой, в цепочку. Так же выглядит и последовательное соединение проводников. Дорога в этом случае может иметь неограниченное количество поворотов, но ни одного перекрестка. Как бы ни виляла дорога (провода), машины (резисторы) всегда будут расположены друг за другом, по одной цепочке.
Совсем другое дело, если рассматривается параллельное соединение. Тогда резисторы можно сравнить со спортсменами на старте. Они стоят каждый на своей дорожке, но направление движения у них одинаковое, и финиш в одном месте. Так же и резисторы — у каждого из них свой провод, но все они соединены в некоторой точке.
Формулы для силы тока
О ней всегда идет речь в теме «Электричество». Параллельное и последовательное соединение по-разному влияют на величину в резисторах. Для них выведены формулы, которые можно запомнить. Но достаточно просто запомнить смысл, который в них вкладывается.
Так, ток при последовательном соединении проводников всегда одинаков. То есть в каждом из них значение силы тока не отличается. Провести аналогию можно, если сравнить провод с трубой. В ней вода течет всегда одинаково. И все препятствия на ее пути будут сметаться с одной и той же силой. Так же с силой тока. Поэтому формула общей силы тока в цепи с последовательным соединением резисторов выглядит так:
I общ = I 1 = I 2
Здесь буквой I обозначена сила тока. Это общепринятое обозначение, поэтому его нужно запомнить.
Ток при параллельном соединении уже не будет постоянной величиной. При той же аналогии с трубой получается, что вода разделится на два потока, если у основной трубы будет ответвление. То же явление наблюдается с током, когда на его пути появляется разветвление проводов. Формула общей силы тока при :
I общ = I 1 + I 2
Если разветвление составлено из проводов, которых больше двух, то в приведенной формуле на такое же количество станет больше слагаемых.
Формулы для напряжения
Когда рассматривается схема, в которой выполнено соединение проводников последовательно, то напряжение на всем участке определяется суммой этих величин на каждом конкретном резисторе. Сравнить эту ситуацию можно с тарелками. Удержать одну из них легко получится одному человеку, вторую рядом он тоже сможет взять, но уже с трудом. Держать в руках три тарелки рядом друг с другом одному человеку уже не удастся, потребуется помощь второго. И так далее. Усилия людей складываются.
Формула для общего напряжения участка цепи с последовательным соединением проводников выглядит так:
U общ = U 1 + U 2 , где U — обозначение, принятое для
Другая ситуация складывается, если рассматривается Когда тарелки ставятся друг на друга, их по-прежнему может удержать один человек. Поэтому складывать ничего не приходится. Такая же аналогия наблюдается при параллельном соединении проводников. Напряжение на каждом из них одинаковое и равно тому, которое на всех них сразу. Формула общего напряжения такая:
U общ = U 1 = U 2
Формулы для электрического сопротивления
Их уже можно не запоминать, а знать формулу закона Ома и из нее выводить нужную. Из указанного закона следует, что напряжение равно произведению силы тока и сопротивления. То есть U = I * R, где R — сопротивление.
Тогда формула, с которой нужно будет работать, зависит от того, как выполнено соединение проводников:
- последовательно, значит, нужно равенство для напряжения — I общ * R общ = I 1 * R 1 + I 2 * R 2;
- параллельно необходимо пользоваться формулой для силы тока — U общ / R общ = U 1 / R 1 + U 2 / R 2 .
Далее следуют простые преобразования, которые основываются на том, что в первом равенстве все силы тока имеют одинаковое значение, а во втором — напряжения равны. Значит, их можно сократить. То есть получаются такие выражения:
- R общ = R 1 + R 2 (для последовательного соединения проводников).
- 1 / R общ = 1 / R 1 + 1 / R 2 (при параллельном соединении).
При увеличении числа резисторов, которые включены в сеть, изменяется количество слагаемых в этих выражениях.
Стоит отметить, что параллельное и последовательное соединение проводников по-разному влияют на общее сопротивление. Первое из них уменьшает сопротивление участка цепи. Причем оно оказывается меньше самого маленького из использованных резисторов. При последовательном соединении все логично: значения складываются, поэтому общее число всегда будет самым большим.
Работа тока
Предыдущие три величины составляют законы параллельного соединения и последовательного расположения проводников в цепи. Поэтому их знать нужно обязательно. Про работу и мощность необходимо просто запомнить базовую формулу. Она записывается так: А = I * U * t , где А — работа тока, t — время его прохождения по проводнику.
Для того чтобы определить общую работу при последовательном соединении нужно заменить в исходном выражении напряжение. Получится равенство: А = I * (U 1 + U 2) * t, раскрыв скобки в котором получится, что работа на всем участке равна их сумме на каждом конкретном потребителе тока.
Аналогично идет рассуждение, если рассматривается схема параллельного соединения. Только заменять полагается силу тока. Но результат будет тот же: А = А 1 + А 2 .
Мощность тока
При выведении формулы для мощности (обозначение «Р») участка цепи опять нужно пользоваться одной формулой: Р = U * I. После подобных рассуждений получается, что параллельное и последовательное соединение описываются такой формулой для мощности: Р = Р 1 + Р 2 .
То есть, как бы ни были составлены схемы, общая мощность будет складываться из тех, которые задействованы в работе. Именно этим объясняется тот факт, что нельзя включать в сеть квартиры одновременно много мощных приборов. Она просто не выдержит такой нагрузки.
Как влияет соединение проводников на ремонт новогодней гирлянды?
Сразу же после того, как перегорит одна из лампочек, станет ясно, как они были соединены. При последовательном соединении не будет светиться ни одна из них. Это объясняется тем, что пришедшая в негодность лампа создает разрыв в цепи. Поэтому нужно проверить все, чтобы определить, какая перегорела, заменить ее — и гирлянда станет работать.
Если в ней используется параллельное соединение, то она не перестает работать при неисправности одной из лампочек. Ведь цепь не будет полностью разорвана, а только одна параллельная часть. Чтобы отремонтировать такую гирлянду, не нужно проверять все элементы цепи, а только те, которые не светятся.
Что происходит с цепью, если в нее включены не резисторы, а конденсаторы?
При их последовательном соединении наблюдается такая ситуация: заряды от плюсов источника питания поступают только на внешние обкладки крайних конденсаторов. Те, что находятся между ними, просто передают этот заряд по цепочке. Этим объясняется то, что на всех обкладках появляются одинаковые заряды, но имеющие разные знаки. Поэтому электрический заряд каждого конденсатора, соединенного последовательно, можно записать такой формулой:
q общ = q 1 = q 2 .
Для того чтобы определить напряжение на каждом конденсаторе, потребуется знание формулы: U = q / С. В ней С — емкость конденсатора.
Общее напряжение подчиняется тому же закону, который справедлив для резисторов. Поэтому, заменив в формуле емкости напряжение на сумму, мы получим, что общую емкость приборов нужно вычислять по формуле:
С = q / (U 1 + U 2).
Упростить эту формулу можно, перевернув дроби и заменив отношение напряжения к заряду емкостью. Получается такое равенство: 1 / С = 1 / С 1 + 1 / С 2 .
Несколько по-другому выглядит ситуация, когда соединение конденсаторов — параллельное. Тогда общий заряд определяется суммой всех зарядов, которые накапливаются на обкладках всех приборов. А значение напряжения по-прежнему определяется по общим законам. Поэтому формула для общей емкости параллельно соединенных конденсаторов выглядит так:
С = (q 1 + q 2) / U.
То есть эта величина считается, как сумма каждого из использованных в соединении приборов:
С = С 1 + С 2.
Как определить общее сопротивление произвольного соединения проводников?
То есть такого, в котором последовательные участки сменяют параллельные, и наоборот. Для них по-прежнему справедливы все описанные законы. Только применять их нужно поэтапно.
Сперва полагается мысленно развернуть схему. Если представить ее сложно, то нужно нарисовать то, что получается. Объяснение станет понятнее, если рассмотреть его на конкретном примере (см. рисунок).
Ее удобно начать рисовать с точек Б и В. Их необходимо поставить на некотором удалении друг от друга и от краев листа. Слева к точке Б подходит один провод, а вправо направлены уже два. Точка В, напротив, слева имеет два ответвления, а после нее расположен один провод.
Теперь необходимо заполнить пространство между этими точками. По верхнему проводу нужно расположить три резистора с коэффициентами 2, 3 и 4, а снизу пойдет тот, у которого индекс равен 5. Первые три соединены последовательно. С пятым резистором они параллельны.
Оставшиеся два резистора (первый и шестой) включены последовательно с рассмотренным участком БВ. Поэтому рисунок можно просто дополнить двумя прямоугольниками по обе стороны от выбранных точек. Осталось применить формулы для расчета сопротивления:
- сначала ту, которая приведена для последовательного соединения;
- потом для параллельного;
- и снова для последовательного.
Подобным образом можно развернуть любую, даже очень сложную схему.
Задача на последовательное соединение проводников
Условие. В цепи друг за другом подсоединены две лампы и резистор. Общее напряжение равно 110 В, а сила тока 12 А. Чему равно сопротивление резистора, если каждая лампа рассчитана на напряжение в 40 В?
Решение. Поскольку рассматривается последовательное соединение, формулы его законов известны. Нужно только правильно их применить. Начать с того, чтобы выяснить значение напряжения, которое приходится на резистор. Для этого из общего нужно вычесть два раза напряжение одной лампы. Получается 30 В.
Теперь, когда известны две величины, U и I (вторая из них дана в условии, так как общий ток равен току в каждом последовательном потребителе), можно сосчитать сопротивление резистора по закону Ома. Оно оказывается равным 2,5 Ом.
Ответ. Сопротивление резистора равно 2,5 Ом.
Задача на параллельное и последовательное
Условие. Имеются три конденсатора с емкостями 20, 25 и 30 мкФ. Определите их общую емкость при последовательном и параллельном соединении.
Решение. Проще начать с В этой ситуации все три значения нужно просто сложить. Таким образом, общая емкость оказывается равной 75 мкФ.
Несколько сложнее расчеты будут при последовательном соединении этих конденсаторов. Ведь сначала нужно найти отношения единицы к каждой из этих емкостей, а потом сложить их друг с другом. Получается, что единица, деленная на общую емкость, равна 37/300. Тогда искомая величина получается приблизительно 8 мкФ.
Ответ. Общая емкость при последовательном соединении 8 мкФ, при параллельном — 75 мкФ.
Содержание:Течение тока в электрической цепи осуществляется по проводникам, в направлении от источника к потребителям. В большинстве подобных схем используются медные провода и электрические приемники в заданном количестве, обладающие различным сопротивлением. В зависимости выполняемых задач, в электрических цепях используется последовательное и параллельное соединение проводников. В некоторых случаях могут быть применены оба типа соединений, тогда этот вариант будет называться смешанным. Каждая схема имеет свои особенности и отличия, поэтому их нужно обязательно заранее учитывать при проектировании цепей, ремонте и обслуживании электрооборудования.
Последовательное соединение проводников
В электротехнике большое значение имеет последовательное и параллельное соединение проводников в электрической цепи. Среди них часто используется схема последовательного соединения проводников предполагающая такое же соединение потребителей. В этом случае включение в цепь выполняется друг за другом в порядке очередности. То есть, начало одного потребителя соединяется с концом другого при помощи проводов, без каких-либо ответвлений.
Свойства такой электрической цепи можно рассмотреть на примере участков цепи с двумя нагрузками. Силу тока, напряжение и сопротивление на каждом из них следует обозначить соответственно, как I1, U1, R1 и I2, U2, R2. В результате, получились соотношения, выражающие зависимость между величинами следующим образом: I = I1 = I2, U = U1 + U2, R = R1 + R2. Полученные данные подтверждаются практическим путем с помощью проведения измерений амперметром и вольтметром соответствующих участков.
Таким образом, последовательное соединение проводников отличается следующими индивидуальными особенностями:
- Сила тока на всех участках цепи будет одинаковой.
- Общее напряжение цепи составляет сумму напряжений на каждом участке.
- Общее сопротивление включает в себя сопротивления каждого отдельного проводника.
Данные соотношения подходят для любого количества проводников, соединенных последовательно. Значение общего сопротивления всегда выше, чем сопротивление любого отдельно взятого проводника. Это связано с увеличением их общей длины при последовательном соединении, что приводит и к росту сопротивления.
Если соединить последовательно одинаковые элементы в количестве n, то получится R = n х R1, где R — общее сопротивление, R1 — сопротивление одного элемента, а n — количество элементов. Напряжение U, наоборот, делится на равные части, каждая из которых в n раз меньше общего значения. Например, если в сеть с напряжением 220 вольт последовательно включаются 10 ламп одинаковой мощности, то напряжение в любой из них составит: U1 = U/10 = 22 вольта.
Проводники, соединенные последовательно, имеют характерную отличительную особенность. Если во время работы отказал хотя-бы один из них, то течение тока прекращается во всей цепи. Наиболее ярким примером является , когда одна перегоревшая лампочка в последовательной цепи, приводит к выходу из строя всей системы. Для установления перегоревшей лампочки понадобится проверка всей гирлянды.
Параллельное соединение проводников
В электрических сетях проводники могут соединяться различными способами: последовательно, параллельно и комбинированно. Среди них параллельное соединение это такой вариант, когда проводники в начальных и конечных точках соединяются между собой. Таким образом, начала и концы нагрузок соединяются вместе, а сами нагрузки располагаются параллельно относительно друг друга. В электрической цепи могут содержаться два, три и более проводников, соединенных параллельно.
Если рассматривать последовательное и параллельное соединение, сила тока в последнем варианте может быть исследована с помощью следующей схемы. Берутся две лампы накаливания, обладающие одинаковым сопротивлением и соединенные параллельно. Для контроля к каждой лампочке подключается собственный . Кроме того, используется еще один амперметр, контролирующий общую силу тока в цепи. Проверочная схема дополняется источником питания и ключом.
После замыкания ключа нужно контролировать показания измерительных приборов. Амперметр на лампе № 1 покажет силу тока I1, а на лампе № 2 — силу тока I2. Общий амперметр показывает значение силы тока, равное сумме токов отдельно взятых, параллельно соединенных цепей: I = I1 + I2. В отличие от последовательного соединения, при перегорании одной из лампочек, другая будет нормально функционировать. Поэтому в домашних электрических сетях используется параллельное подключение приборов.
С помощью такой же схемы можно установить значение эквивалентного сопротивления. С этой целью в электрическую цепь добавляется вольтметр. Это позволяет измерить напряжение при параллельном соединении, сила тока при этом остается такой же. Здесь также имеются точки пересечения проводников, соединяющих обе лампы.
В результате измерений общее напряжение при параллельном соединении составит: U = U1 = U2. После этого можно рассчитать эквивалентное сопротивление, условно заменяющее все элементы, находящиеся в данной цепи. При параллельном соединении, в соответствии с законом Ома I = U/R, получается следующая формула: U/R = U1/R1 + U2/R2, в которой R является эквивалентным сопротивлением, R1 и R2 — сопротивления обеих лампочек, U = U1 = U2 — значение напряжения, показываемое вольтметром.
Следует учитывать и тот фактор, что токи в каждой цепи, в сумме составляют общую силу тока всей цепи. В окончательном виде формула, отражающая эквивалентное сопротивление будет выглядеть следующим образом: 1/R = 1/R1 + 1/R2. При увеличении количества элементов в таких цепях — увеличивается и число слагаемых в формуле. Различие в основных параметрах отличают друг от друга и источников тока, позволяя использовать их в различных электрических схемах.
Параллельное соединение проводников характеризуется достаточно малым значением эквивалентного сопротивления, поэтому сила тока будет сравнительно высокой. Данный фактор следует учитывать, когда в розетки включается большое количество электроприборов. В этом случае сила тока значительно возрастает, приводя к перегреву кабельных линий и последующим возгораниям.
Законы последовательного и параллельного соединения проводников
Данные законы, касающиеся обоих видов соединений проводников, частично уже были рассмотрены ранее.
Для более четкого их понимания и восприятия в практической плоскости, последовательное и параллельное соединение проводников, формулы следует рассматривать в определенной последовательности:
- Последовательное соединение предполагает одинаковую силу тока в каждом проводнике: I = I1 = I2.
- параллельное и последовательное соединение проводников объясняет в каждом случае по-своему. Например, при последовательном соединении, напряжения на всех проводниках будут равны между собой: U1 = IR1, U2 = IR2. Кроме того, при последовательном соединении напряжение составляет сумму напряжений каждого проводника: U = U1 + U2 = I(R1 + R2) = IR.
- Полное сопротивление цепи при последовательном соединении состоит из суммы сопротивлений всех отдельно взятых проводников, независимо от их количества.
- При параллельном соединении напряжение всей цепи равно напряжению на каждом из проводников: U1 = U2 = U.
- Общая сила тока, измеренная во всей цепи, равна сумме токов, протекающих по всем проводникам, соединенных параллельно между собой: I = I1 + I2.
Для того чтобы более эффективно проектировать электрические сети, нужно хорошо знать последовательное и параллельное соединение проводников и его законы, находя им наиболее рациональное практическое применение.
Смешанное соединение проводников
В электрических сетях как правило используется последовательное параллельное и смешанное соединение проводников, предназначенное для конкретных условий эксплуатации. Однако чаще всего предпочтение отдается третьему варианту, представляющему собой совокупность комбинаций, состоящих из различных типов соединений.
В таких смешанных схемах активно применяется последовательное и параллельное соединение проводников, плюсы и минусы которых обязательно учитываются при проектировании электрических сетей. Эти соединения состоят не только из отдельно взятых резисторов, но и довольно сложных участков, включающих в себя множество элементов.
Смешанное соединение рассчитывается в соответствии с известными свойствами последовательного и параллельного соединения. Метод расчета заключается в разбивке схемы на более простые составные части, которые считаются отдельно, а потом суммируются друг с другом.
1. Находят эквивалентное сопротивление участков цепи с параллельным соединением резисторов. Рисунок 2. Последовательное соединение резисторов. Для расчета сопротивления таких соединений, всю цепь разбивают на простейшие участки, из параллельно или последовательно соединенных резисторов.
Этот результат следует из того, что в точках разветвления токов (узлы A и B) в цепи постоянного тока не могут накапливаться заряды. Этот результат справедлив для любого числа параллельно включенных проводников.
На рис. 1.9.3 приведен пример такой сложной цепи и указана последовательность вычислений. Следует отметить, что далеко не все сложные цепи, состоящие из проводников с различными сопротивлениями, могут быть рассчитаны с помощью формул для последовательного и параллельного соединения.
При последовательном соединении проводников сила тока во всех проводниках одинакова. При параллельном соединении падение напряжения между двумя узлами, объединяющими элементы цепи, одинаково для всех элементов.
Т.е чем большее сопротивление резистора, тем большее напряжение на него падает. В результате к одной точке (электрическому узлу) может быть присоединено несколько резисторов. При таком соединении, через каждый резистор потечет отдельный ток. Сила данного тока будет обратно пропорциональна сопротивлению резистора.
Таким образом, при параллельном подсоединении резисторов с разным сопротивлением, общее сопротивление будет всегда меньше значения самого маленького отдельного резистора. Напряжение между точками A и B является как общим напряжением для всего участка цепи, так и напряжением, падающим на каждый резистор в отдельности. Смешанным соединением называют участок цепи, где часть резисторов соединяются между собой последовательно, а часть параллельно.
Цепь разбивают на участки с только пареллельным или только последовательным соединением. Вычисляют общее сопротивление для каждого отдельного участка. Вычисляют общее сопротивление для всей цепи смешанного соединения. Также существует более быстрый способ расчета общего сопротивления для смешанного соединения. Если резисторы соединяются последоватеьно — складывать.
То есть при последовательном соединении резисторы подключатся друг за другом. На рисунке 4 показан простейший пример смешанного соединения резисторов. После расчета эквивалентных сопротивлений резисторов перерисовывают схему. Обычно получается цепь из последовательно соединенных эквивалентных сопротивлений.4. Рисунок 5. Расчет сопротивления участка цепи при смешанном соединении резисторов.
В результате вы научитесь с нуля не тольно разрабатывать собственные устройства, но и сопрягать с ними различную переферию! Узел — точка разветвления цепи, в которой соединяются не менее трёх проводников. Последовательное соединение резисторов применяется для увеличения сопротивления.
Напряжение при параллельном соединении
Как видно, вычислить сопротивление двух параллельных резисторов значительно удобнее. Параллельное соединение резисторов часто используют в случаях, когда необходимо сопротивление с большей мощностью. Для этого, как правило, используют резисторы с одинаковой мощностью и одинаковым сопротивлением.
Общее сопротивление Rобщ
Такое соединение сопротивлений называется последовательным. Мы получили таким образом, что U = 60 В, т. е. несуществующее равенство ЭДС источника тока и его напряжения. Будем теперь включать амперметр поочередно в каждую ветвь цепи, запоминая показания прибора. Следовательно, при параллельном соединении сопротивлений напряжение на зажимах источника тока равно падению напряжения на каждом сопротивлении.
Такое разветвление тока в параллельных ветвях сходно с течением жидкости по трубам. Рассмотрим теперь, чему будет равно общее сопротивление внешней цепи, состоящей из двух параллельно соединенных сопротивлений.
Вернемся к цепи, показанной на рис. 3, и посмотрим, чему будет равно эквивалентное сопротивление двух параллельно соединенных сопротивлений. Точно так же для каждой ветви I1 = U1 / R1, I2 = U2 / R2, где I1 и I2 — токи в ветвях; U1 и U2 — напряжение на ветвях; R1 и R2 — сопротивления ветвей.
Это значит, что общее сопротивление цепи всегда будет ниже любого параллельно включенного резистора. 2. Если эти участки включают последовательно соединенные резисторы, то сначала вычисляют их сопротивление. Применяя закон Ома для участка цепи, можно доказать, что полное сопротивление при последовательном соединении равно сумме сопротивлений отдельных проводников.
Как различать последовательное и параллельное соединение. Как найти сопротивление последовательной и параллельной цепей
В предыдущем конспекте был установлено, что сила тока в проводнике зависит от напряжения на его концах. Если в опыте менять проводники, оставляя напряжение на них неизменным, то можно показать, что при постоянном напряжении на концах проводника сила тока обратно пропорциональна его сопротивлению. Объединив зависимость силы тока от напряжения и его зависимость от сопротивления проводника, можно записать: I = U/R . Этот закон, установленный экспериментально, называется закон Ома (для участка цепи).
Закон Ома для участка цепи : сила тока в проводнике прямо пропорциональна приложенному к его концам напряжению и обратно пропорциональна сопротивлению проводника. Прежде всего закон всегда верен для твёрдых и жидких металлических проводников. А также для некоторых других веществ (как правило, твёрдых или жидких).
Потребители электрической энергии (лампочки, резисторы и пр.) могут по-разному соединяться друг с другом в электрической цепи. Д ва основных типа соединения проводников : последовательное и параллельное. А также есть еще два соединения, которые являются редкими: смешанное и мостовое.
Последовательное соединение проводниковПри последовательном соединении проводников конец одного проводника соединится с началом другого проводника, а его конец — с началом третьего и т.д. Например, соединение электрических лампочек в ёлочной гирлянде. При последовательном соединении проводников ток проходит через все лампочки. При этом через поперечное сечение каждого проводника в единицу времени проходит одинаковый заряд. То есть заряд не скапливается ни в какой части проводника.
Поэтому при последовательном соединении проводников сила тока в любом участке цепи одинакова: I 1 = I 2 = I .
Общее сопротивление последовательно соединённых проводников равно сумме их сопротивлений : R 1 + R 2 = R . Потому что при последовательном соединении проводников их общая длина увеличивается. Она больше, чем длина каждого отдельного проводника, соответственно увеличивается и сопротивление проводников.
По закону Ома напряжение на каждом проводнике равно: U 1 = I* R 1 , U 2 = I*R 2 . В таком случае общее напряжение равно U = I ( R 1 + R 2) . Поскольку сила тока во всех проводниках одинакова, а общее сопротивление равно сумме сопротивлений проводников, то полное напряжение на последовательно соединённых проводниках равно сумме напряжений на каждом проводнике : U = U 1 + U 2 .
Из приведённых равенств следует, что последовательное соединение проводников используется в том случае, если напряжение, на которое рассчитаны потребители электрической энергии, меньше общего напряжения в цепи.
Для последовательного соединения проводников справедливы законы :1) сила тока во всех проводниках одинакова; 2) напряжение на всём соединении равно сумме напряжений на отдельных проводниках; 3) сопротивление всего соединения равно сумме сопротивлений отдельных проводников.
Параллельное соединение проводниковПримером параллельного соединения проводников служит соединение потребителей электрической энергии в квартире. Так, электрические лампочки, чайник, утюг и пр. включаются параллельно.
При параллельном соединении проводников все проводники одним своим концом присоединяются к одной точке цепи. А вторым концом к другой точке цепи. Вольтметр, подключенный к этим точкам, покажет напряжение и на проводнике 1, и на проводнике 2. В таком случае напряжение на концах всех параллельно соединённых проводников одно и то же: U 1 = U 2 = U .
При параллельном соединении проводников электрическая цепь разветвляется. Поэтому часть общего заряда проходит через один проводник, а часть — через другой. Следовательно при параллельном соединении проводников сила тока в неразветвлённой части цепи равна сумме силы тока в отдельных проводниках: I = I 1 + I 2 .
В соответствии с законом Ома I = U/R, I 1 = U 1 /R 1 , I 2 = U 2 /R 2 . Отсюда следует: U/R = U 1 /R 1 + U 2 /R 2 , U = U 1 = U 2 , 1/R = 1/R 1 + 1/R 2 Величина, обратная общему сопротивлению параллельно соединенных проводников, равна сумме величин, обратных сопротивлению каждого проводника.
При параллельном соединении проводников их общее сопротивление меньше, чем сопротивление каждого проводника. Действительно, если параллельно соединены два проводника, имеющие одинаковое сопротивление г , то их общее сопротивление равно: R = г/2 . Это объясняется тем, что при параллельном соединении проводников как бы увеличивается площадь их поперечного сечения. В результате уменьшается сопротивление.
Из приведённых формул понятно, почему потребители электрической энергии включаются параллельно. Они все рассчитаны на определённое одинаковое напряжение, которое в квартирах равно 220 В. Зная сопротивление каждого потребителя, можно рассчитать силу тока в каждом из них. А также соответствие суммарной силы тока предельно допустимой силе тока.
Для параллельного соединения проводников справедливы законы:1) напряжение на всех проводниках одинаково; 2) сила тока в месте соединения проводников равна сумме токов в отдельных проводниках; 3) величина, обратная сопротивлению всего соединения, равна сумме величин, обратных сопротивлениям отдельных проводников.
Последовательное, параллельное и смешанное соединения резисторов. Значительное число приемников, включенных в электрическую цепь (электрические лампы, электронагревательные приборы и др.), можно рассматривать как некоторые элементы, имеющие определенное сопротивление. Это обстоятельство дает нам возможность при составлении и изучении электрических схем заменять конкретные приемники резисторами с определенными сопротивлениями. Различают следующие способы соединения резисторов (приемников электрической энергии): последовательное, параллельное и смешанное.
Последовательное соединение резисторов . При последовательном соединении нескольких резисторов конец первого резистора соединяют с началом второго, конец второго — с началом третьего и т. д. При таком соединении по всем элементам последовательной цепи проходит
один и тот же ток I.
Последовательное соединение приемников поясняет рис. 25, а.
.Заменяя лампы резисторами с сопротивлениями R1, R2 и R3, получим схему, показанную на рис. 25, б.
Если принять, что в источнике Ro = 0, то для трех последовательно соединенных резисторов согласно второму закону Кирхгофа можно написать:
E = IR 1 + IR 2 + IR 3 = I(R 1 + R 2 + R 3) = IR эк (19)
где R
эк
= R 1 + R 2 + R 3 .
Следовательно, эквивалентное сопротивление последовательной цепи равно сумме сопротивлений всех последовательно соединенных резисторов.Так как напряжения на отдельных участках цепи согласно закону Ома: U 1 =IR 1 ; U 2 = IR 2 , U 3 = IR з и в данном случае E = U, то длярассматриваемой цепи
U = U 1 + U 2 +U 3 (20)
Следовательно, напряжение U на зажимах источника равно сумме напряжений на каждом из последовательно включенных резисторов.
Из указанных формул следует также, что напряжения распределяются между последовательно соединенными резисторами пропорционально их сопротивлениям:
U 1: U 2: U 3 = R 1: R 2: R 3 (21)
т. е. чем больше сопротивление какого-либо приемника в последовательной цепи, тем больше приложенное к нему напряжение.
В случае если последовательно соединяются несколько, например п, резисторов с одинаковым сопротивлением R1, эквивалентное сопротивление цепи Rэк будет в п раз больше сопротивления R1, т. е. Rэк = nR1. Напряжение U1 на каждом резисторе в этом случае в п раз меньше общего напряжения U:
При последовательном соединении приемников изменение сопротивления одного из них тотчас же влечет за собой изменение напряжения на других связанных с ним приемниках. При выключении или обрыве электрической цепи в одном из приемников и в остальных приемниках прекращается ток. Поэтому последовательное соединение приемников применяют редко — только в том случае, когда напряжение источника электрической энергии больше номинального напряжения, на которое рассчитан потребитель. Например, напряжение в электрической сети, от которой питаются вагоны метрополитена, составляет 825 В, номинальное же напряжение электрических ламп, применяемых в этих вагонах, 55 В. Поэтому в вагонах метрополитена электрические лампы включают последовательно по 15 ламп в каждой цепи.
Параллельное соединение резисторов . При параллельном соединении нескольких приемников они включаются между двумя точками электрической цепи, образуя параллельные ветви (рис. 26, а). Заменяя
лампы резисторами с сопротивлениями R1, R2, R3, получим схему, показанную на рис. 26, б.
При параллельном соединении ко всем резисторам приложено одинаковое напряжение U. Поэтому согласно закону Ома:
I 1 =U/R 1 ; I 2 =U/R 2 ; I 3 =U/R 3 .
Ток в неразветвленной части цепи согласно первому закону Кирхгофа I = I 1 +I 2 +I 3 , или
I = U / R 1 + U / R 2 + U / R 3 = U (1/R 1 + 1/R 2 + 1/R 3) = U / R эк (23)
Следовательно, эквивалентное сопротивление рассматриваемой цепи при параллельном соединении трех резисторов определяется формулой
1/R эк = 1/R 1 + 1/R 2 + 1/R 3 (24)
Вводя в формулу (24) вместо значений 1/R эк, 1/R 1 , 1/R 2 и 1/R 3 соответствующие проводимости G эк, G 1 , G 2 и G 3 , получим: эквивалентная проводимость параллельной цепи равна сумме проводимостей параллельно соединенных резисторов :
G эк = G 1 + G 2 +G 3 (25)
Таким образом, при увеличении числа параллельно включаемых резисторов результирующая проводимость электрической цепи увеличивается, а результирующее сопротивление уменьшается.
Из приведенных формул следует, что токи распределяются между параллельными ветвями обратно пропорционально их электрическим сопротивлениям или прямо пропорционально их проводимостям. Например, при трех ветвях
I 1: I 2: I 3 = 1/R 1: 1/R 2: 1/R 3 = G 1 + G 2 + G 3 (26)
В этом отношении имеет место полная аналогия между распределением токов по отдельным ветвям и распределением потоков воды по трубам.
Приведенные формулы дают возможность определить эквивалентное сопротивление цепи для различных конкретных случаев. Например, при двух параллельно включенных резисторах результирующее сопротивление цепи
R эк =R 1 R 2 /(R 1 +R 2)
при трех параллельно включенных резисторах
R эк =R 1 R 2 R 3 /(R 1 R 2 +R 2 R 3 +R 1 R 3)
При параллельном соединении нескольких, например n, резисторов с одинаковым сопротивлением R1 результирующее сопротивление цепи Rэк будет в n раз меньше сопротивления R1, т.е.
R эк = R1 / n (27)
Проходящий по каждой ветви ток I1, в этом случае будет в п раз меньше общего тока:
I1 = I / n (28)
При параллельном соединении приемников, все они находятся под одним и тем же напряжением, и режим работы каждого из них не зависит от остальных. Это означает, что ток, проходящий по какому-либо из приемников, не будет оказывать существенного влияния на другие приемники. При всяком выключении или выходе из строя любого приемника остальные приемники остаются вклю-
ченными. Поэтому параллельное соединение имеет существенные преимущества перед последовательным, вследствие чего оно получило наиболее широкое распространение. В частности, электрические лампы и двигатели, предназначенные для работы при определенном (номинальном) напряжении, всегда включают параллельно.
На электровозах постоянного тока и некоторых тепловозах тяговые двигатели в процессе регулирования скорости движения нужно включать под различные напряжения, поэтому они в процессе разгона переключаются с последовательного соединения на параллельное.
Смешанное соединение резисторов . Смешанным соединением называется такое соединение, при котором часть резисторов включается последовательно, а часть — параллельно. Например, в схеме рис. 27, а имеются два последовательно включенных резистора сопротивлениями R1 и R2, параллельно им включен резистор сопротивлением Rз, а резистор сопротивлением R4 включен последовательно с группой резисторов сопротивлениями R1, R2 и R3.
Эквивалентное сопротивление цепи при смешанном соединении обычно определяют методом преобразования, при котором сложную цепь последовательными этапами преобразовывают в простейшую. Например, для схемы рис. 27, а вначале определяют эквивалентное сопротивление R12 последовательно включенных резисторов с сопротивлениями R1 и R2: R12 = R1 + R2. При этом схема рис. 27, а заменяется эквивалентной схемой рис. 27, б. Затем определяют эквивалентное сопротивление R123 параллельно включенных сопротивлений и R3 по формуле
R 123 =R 12 R 3 /(R 12 +R 3)=(R 1 +R 2)R 3 /(R 1 +R 2 +R 3).
При этом схема рис. 27, б заменяется эквивалентной схемой рис. 27, в. После этого находят эквивалентное сопротивление всей цепи суммированием сопротивления R123 и последовательно включенного с ним сопротивления R4:
R эк = R 123 + R 4 = (R 1 + R 2) R 3 / (R 1 + R 2 + R 3) + R 4
Последовательное, параллельное и смешанное соединения широко применяют для изменения сопротивления пусковых реостатов при пуске э. п. с. постоянного тока.
Одним из китов, на котором держатся многие понятия в электронике, является понятие последовательного и параллельного подключения проводников. Знать основные отличия указанных типов подключения просто необходимо. Без этого нельзя понять и прочитать ни одной схемы.
Основные принципы
Электрический ток движется по проводнику от источника к потребителю (нагрузке). Чаще всего в качестве проводника выбирается медный кабель. Связано это с требованием, которое предъявляется к проводнику: он должен легко высвобождать электроны.
Независимо от способа подключения, электрический ток двигается от плюса к минусу. Именно в этом направлении убывает потенциал. При этом стоит помнить, что провод, по котору идет ток, также обладает сопротивлением. Но его значение очень мало. Именно поэтому им пренебрегают. Сопротивление проводника принимают равным нулю. В том случае, если проводник обладает сопротивлением, его принято называть резистором.
Параллельное подключение
В данном случае элементы, входящие в цепь, объединены между собой двумя узлами. С другими узлами у них связей нет. Участки цепи с таким подключением принято называть ветвями. Схема параллельного подключения представлена на рисунке ниже.
Если говорить более понятным языком, то в данном случае все проводники одним концом соединены в одном узле, а вторым — во втором. Это приводит к тому, что электрический ток разделяется на все элементы. Благодаря этому увеличивается проводимость всей цепи.
При подключении проводников в цепь данным способом напряжение каждого из них будет одинаково. А вот сила тока всей цепи будет определяться как сумма токов, протекающих по всем элементам. С учетом закона Ома путем нехитрых математических расчетов получается интересная закономерность: величина, обратная общему сопротивлению всей цепи, определяется как сумма величин, обратных сопротивлениям каждого отдельного элемента. При этом учитываются только элементы, подключенные параллельно.
Последовательное подключение
В данном случае все элементы цепи соединены таким образом, что они не образуют ни одного узла. При данном способе подключения имеется один существенный недостаток. Он заключается в том, что при выходе из строя одного из проводников все последующие элементы работать не смогут. Ярким примером такой ситуации является обычная гирлянда. Если в ней перегорает одна из лампочек, то вся гирлянда перестает работать.
Последовательное подключение элементов отличается тем, что сила тока во всех проводниках равна. Что касается напряжения цепи, то оно равно сумме напряжения отдельных элементов.
В данной схеме проводники включаются в цепь поочередно. А это значит, что сопротивление всей цепи будет складываться из отдельных сопротивлений, характерных для каждого элемента. То есть общее сопротивление цепи равно сумме сопротивлений всех проводников. Эту же зависимость можно вывести и математическим способом, используя закон Ома.
Смешанные схемы
Бывают ситуации, когда на одной схеме можно увидеть одновременно последовательное и параллельное подключение элементов. В таком случае говорят о смешанном соединении. Расчет подобных схем проводится отдельно для каждой из группы проводников.
Так, чтобы определить общее сопротивление, необходимо сложить сопротивление элементов, подключенных параллельно, и сопротивление элементов с последовательным подключением. При этом последовательное подключение является доминантным. То есть его рассчитывают в первую очередь. И только после этого определяют сопротивление элементов с параллельным подключением.
Подключение светодиодов
Зная основы двух типов подключения элементов в цепи, можно понять принцип создания схем различных электроприборов. Рассмотрим пример. во многом зависит от напряжения источника тока.
При небольшом напряжении сети (до 5 В) светодиоды подключают последовательно. Снизить уровень электромагнитных помех в данном случае поможет конденсатор проходного типа и линейные резисторы. Проводимость светодиодов увеличивают за счет использования системных модуляторов.
При напряжении сети 12 В может использоваться и последовательное, и параллельное подключение сети. В случае последовательного подключения используют импульсные блоки питания. Если собирается цепь из трех светодиодов, то можно обойтись без усилителя. Но если цепь будет включать большее количество элементов, то усилитель необходим.
Во втором случае, то есть при параллельном подключении, необходимо использование двух открытых резисторов и усилителя (с пропускной способностью выше 3 А). Причем первый резистор устанавливается перед усилителем, а второй — после.
При высоком напряжении сети (220 В) прибегают к последовательному подключению. При этом дополнительно используют операционные усилители и понижающие блоки питания.
Всем доброго времени суток. В прошлой статье я рассмотрел , применительно к электрическим цепям, содержащие источники энергии. Но в основе анализа и проектирования электронных схем вместе с законом Ома лежат также законы баланса , называемым первым законом Кирхгофа, и баланса напряжения на участках цепи, называемым вторым законом Кирхгофа, которые рассмотрим в данной статье. Но для начала выясним, как соединяются между собой приёмники энергии и какие при этом взаимоотношения между токами, напряжениями и .
Приемники электрической энергии можно соединить между собой тремя различными способами: последовательно, параллельно или смешано (последовательно — параллельно). Вначале рассмотрим последовательный способ соединения, при котором конец одного приемника соединяют с началом второго приемника, а конец второго приемника – с началом третьего и так далее. На рисунке ниже показано последовательное соединение приемников энергии с их подключением к источнику энергии
Пример последовательного подключения приемников энергии.
В данном случае цепь состоит из трёх последовательных приемников энергии с сопротивлением R1, R2, R3 подсоединенных к источнику энергии с U. Через цепь протекает электрический ток силой I, то есть, напряжение на каждом сопротивлении будет равняться произведению силы тока и сопротивления
Таким образом, падение напряжения на последовательно соединённых сопротивлениях пропорциональны величинам этих сопротивлений.
Из вышесказанного вытекает правило эквивалентного последовательного сопротивления, которое гласит, что последовательно соединённые сопротивления можно представить эквивалентным последовательным сопротивлением величина, которого равна сумме последовательно соединённых сопротивлений. Это зависимость представлена следующими соотношениями
где R – эквивалентное последовательное сопротивление.
Применение последовательного соединения
Основным назначением последовательного соединения приемников энергии является обеспечение требуемого напряжения меньше, чем напряжение источника энергии. Одними из таких применений является делитель напряжения и потенциометр
Делитель напряжения (слева) и потенциометр (справа).
В качестве делителей напряжения используют последовательно соединённые резисторы, в данном случае R1 и R2, которые делят напряжение источника энергии на две части U1 и U2. Напряжения U1 и U2 можно использовать для работы разных приемников энергии.
Довольно часто используют регулируемый делитель напряжения, в качестве которого применяют переменный резистор R. Суммарное сопротивление, которого делится на две части с помощью подвижного контакта, и таким образом можно плавно изменять напряжение U2 на приемнике энергии.
Ещё одним способом соединения приемников электрической энергии является параллельное соединение, которое характеризуется тем, что к одним и тем же узлам электрической цепи присоединены несколько преемников энергии. Пример такого соединения показан на рисунке ниже
Пример параллельного соединения приемников энергии.
Электрическая цепь на рисунке состоит из трёх параллельных ветвей с сопротивлениями нагрузки R1, R2 и R3. Цепь подключена к источнику энергии с напряжением U, через цепь протекает электрический ток с силой I. Таким образом, через каждую ветвь протекает ток равный отношению напряжения к сопротивлению каждой ветви
Так как все ветви цепи находятся под одним напряжением U, то токи приемников энергии обратно пропорциональны сопротивлениям этих приемников, а следовательно параллельно соединённые приемники энергии можно заметь одним приемником энергии с соответствующим эквивалентным сопротивлением, согласно следующих выражений
Таким образом, при параллельном соединении эквивалентное сопротивление всегда меньше самого малого из параллельно включенных сопротивлений.
Смешанное соединение приемников энергии
Наиболее широко распространено смешанное соединение приемников электрической энергии. Данной соединение представляет собой сочетание последовательно и параллельно соединенных элементов. Общей формулы для расчёта данного вида соединений не существует, поэтому в каждом отдельном случае необходимо выделять участки цепи, где присутствует только лишь один вид соединения приемников – последовательное или параллельное. Затем по формулам эквивалентных сопротивлений постепенно упрощать данные участи и в конечном итоге приводить их к простейшему виду с одним сопротивлением, при этом токи и напряжения вычислять по закону Ома. На рисунке ниже представлен пример смешанного соединения приемников энергии
Пример смешанного соединения приемников энергии.
В качестве примера рассчитаем токи и напряжения на всех участках цепи. Для начала определим эквивалентное сопротивление цепи. Выделим два участка с параллельным соединением приемников энергии. Это R1||R2 и R3||R4||R5. Тогда их эквивалентное сопротивление будет иметь вид
В результате получили цепь из двух последовательных приемников энергии R 12 R 345 эквивалентное сопротивление и ток, протекающий через них, составит
Тогда падение напряжения по участкам составит
Тогда токи, протекающие через каждый приемник энергии, составят
Как я уже упоминал, законы Кирхгофа вместе с законом Ома являются основными при анализе и расчётах электрических цепей. Закон Ома был подробно рассмотрен в двух предыдущих статьях, теперь настала очередь для законов Кирхгофа. Их всего два, первый описывает соотношения токов в электрических цепях, а второй – соотношение ЭДС и напряжениями в контуре. Начнём с первого.
Первый закон Кирхгофа гласит, что алгебраическая сумма токов в узле равна нулю. Описывается это следующим выражением
где ∑ — обозначает алгебраическую сумму.
Слово «алгебраическая» означает, что токи необходимо брать с учётом знака, то есть направления втекания. Таким образом, всем токам, которые втекают в узел, присваивается положительный знак, а которые вытекают из узла – соответственно отрицательный. Рисунок ниже иллюстрирует первый закон Кирхгофа
Изображение первого закона Кирхгофа.
На рисунке изображен узел, в который со стороны сопротивления R1 втекает ток, а со стороны сопротивлений R2, R3, R4 соответственно вытекает ток, тогда уравнение токов для данного участка цепи будет иметь вид
Первый закон Кирхгофа применяется не только к узлам, но и к любому контуру или части электрической цепи. Например, когда я говорил о параллельном соединении приемников энергии, где сумма токов через R1, R2 и R3 равна втекающему току I.
Как говорилось выше, второй закон Кирхгофа определяет соотношение между ЭДС и напряжениями в замкнутом контуре и звучит следующим образом: алгебраическая сумма ЭДС в любом контуре цепи равна алгебраической сумме падений напряжений на элементах этого контура. Второй закон Кирхгофа определяется следующим выражением
В качестве примера рассмотрим ниже следующую схему, содержащую некоторый контур
Схема, иллюстрирующая второй закон Кирхгофа.
Для начала необходимо определится с направлением обхода контура. В принципе можно выбрать как по ходу часовой стрелки, так и против хода часовой стрелки. Я выберу первый вариант, то есть элементы будут считаться в следующем порядке E1R1R2R3E2, таким образом, уравнение по второму закону Кирхгофа будет иметь следующий вид
Второй закон Кирхгофа применяется не только к цепям постоянного тока, но и к цепям переменного тока и к нелинейным цепям.
В следующей статье я рассмотрю основные способы расчёта сложных цепей с использованием закона Ома и законов Кирхгофа.
Теория это хорошо, но без практического применения это просто слова.
Содержание:
Как известно, соединение любого элемента схемы, независимо от его назначения, может быть двух видов — параллельное подключение и последовательное. Также возможно и смешанное, то есть последовательно параллельное соединение. Все зависит от назначения компонента и выполняемой им функции. А значит, и резисторы не избежали этих правил. Последовательное и параллельное сопротивление резисторов это по сути то же самое, что и параллельное и последовательное подключение источников света. В параллельной цепи схема подключения подразумевает вход на все резисторы из одной точки, а выход из другой. Попробуем разобраться, каким образом выполняется последовательное соединение, а каким — параллельное. И главное, в чем состоит разница между подобными соединениями и в каких случаях необходимо последовательное, а в каких параллельное соединение. Также интересен и расчет таких параметров, как общее напряжение и общее сопротивление цепи в случаях последовательного либо параллельного соединения. Начать следует с определений и правил.
Способы подключения и их особенности
Виды соединения потребителей или элементов играют очень важную роль, ведь именно от этого зависят характеристики всей схемы, параметры отдельных цепей и тому подобное. Для начала попробуем разобраться с последовательным подключением элементов к схеме.
Последовательное соединение
Последовательное подключение — это такое соединение, где резисторы (равно, как и другие потребители или элементы схем) подключаются друг за другом, при этом выход предыдущего подключается на вход следующего. Подобный вид коммутации элементов дает показатель, равный сумме сопротивлений этих элементов схемы. То есть если r1 = 4 Ом, а r2 = 6 Ом, то при подключении их в последовательную цепь, общее сопротивление составит 10 Ом. Если мы добавим последовательно еще один резистор на 5 Ом, сложение этих цифр даст 15 Ом — это и будет общее сопротивление последовательной цепи. То есть общие значения равны сумме всех сопротивлений. При его расчете для элементов, которые подключены последовательно, никаких вопросов не возникает — все просто и ясно. Именно поэтому не стоит даже останавливаться более серьезно на этой.
Совершенно по другим формулам и правилам производится расчет общего сопротивления резисторов при параллельном подключении, вот на нем имеет смысл остановиться поподробнее.
Параллельное соединение
Параллельным называется соединение, при котором все входы резисторов объединены в одной точке, а все выходы — во второй. Здесь главное понять, что общее сопротивление при подобном подключении будет всегда ниже, чем тот же параметр резистора, имеющего наименьшее.
Имеет смысл разобрать подобную особенность на примере, тогда понять это будет намного проще. Существует два резистора по 16 Ом, но при этом для правильного монтажа схемы требуется лишь 8 Ом. В данном случае при задействовании их обеих, при их параллельном включении в схему, как раз и получатся необходимые 8 Ом. Попробуем понять, по какой формуле возможны вычисления. Рассчитать этот параметр можно так: 1/Rобщ = 1/R1+1/R2, причем при добавлении элементов сумма может продолжаться до бесконечности.
Попробуем еще один пример. Параллельно соединены 2 резистора, с сопротивлением 4 и 10 Ом. Тогда общее будет равно 1/4 + 1/10, что будет равным 1:(0.25 + 0.1) = 1:0.35 = 2.85 Ом. Как видим, хотя резисторы и имели значительное сопротивление, при подключении их параллельнообщий показатель стал намного ниже.
Так же можно рассчитать общее сопротивление четырех параллельно подключенных резисторов, с номиналом 4, 5, 2 и 10 Ом. Вычисления, согласно формуле, будут такими: 1/Rобщ = 1/4+1/5+1/2+1/10, что будет равным 1:(0.25+0.2+0.5+0.1)=1/1.5 = 0.7 Ом.
Что же касается тока, протекающего через параллельно соединенные резисторы, то здесь необходимо обратиться к закону Кирхгофа, который гласит «сила тока при параллельном соединении, выходящего из цепи, равна току, входящему в цепь». А потому здесь законы физики решают все за нас. При этом общие показатели тока разделяются на значения, которые являются обратно пропорциональными сопротивлению ветки. Если сказать проще, то чем больше показатель сопротивления, тем меньшие токи будут проходить через этот резистор, но в общем, все же ток входа будет и на выходе. При параллельном соединении напряжение также остается на выходе таким же, как и на входе. Схема параллельного соединения указана ниже.
Последовательно-параллельное соединение
Последовательно-параллельное соединение — это когда схема последовательного соединения содержит в себе параллельные сопротивления. В таком случае общее последовательное сопротивление будет равно сумме отдельно взятых общих параллельных. Метод вычислений одинаковый в соответствующих случаях.
Подведем итог
Подводя итог всему вышеизложенному можно сделать следующие выводы:
- При последовательном соединении резисторов не требуется особых формул для расчета общего сопротивления. Необходимо лишь сложить все показатели резисторов — сумма и будет общим сопротивлением.
- При параллельном соединении резисторов, общее сопротивление высчитывается по формуле 1/Rобщ = 1/R1+1/R2…+Rn.
- Эквивалентное сопротивление при параллельном соединении всегда меньше минимального подобного показателя одного из резисторов, входящих в схему.
- Ток, равно как и напряжение в параллельном соединении остается неизменным, то есть напряжение при последовательном соединении равно как на входе, так и на выходе.
- Последовательно-параллельное соединение при подсчетах подчиняется тем же законам.
В любом случае, каким бы ни было подключение, необходимо четко рассчитывать все показатели элементов, ведь параметры имеют очень важную роль при монтаже схем. И если ошибиться в них, то либо схема не будет работать, либо ее элементы просто сгорят от перегрузки. По сути, это правило применимо к любым схемам, даже в электромонтаже. Ведь провод по сечению подбирают также исходя из мощности и напряжения. А если поставить лампочку номиналом в 110 вольт в цепь с напряжением 220, несложно понять, что она моментально сгорит. Так же и с элементами радиоэлектроники. А потому — внимательность и скрупулезность в расчетах — залог правильной работы схемы.
Напряжение на компонентах в последовательной цепи — Практические электрические и электронные схемы — National 5 Physics Revision
Мы измеряем напряжения в цепи с помощью вольтметра.
Вольтметр подключается параллельно компоненту.
Напряжение питания распределяется между компонентами в последовательной цепи, поэтому сумма напряжений на всех компонентах в последовательной цепи равна напряжению питания \ ({V_s} \).
Цепь с ячейкой, замкнутым переключателем и тремя последовательно соединенными лампамиМы можем записать это соотношение напряжений как:
\ [{V_s} = {V_1} + {V_2} + {V_3} +…. \]
Напряжение на каждом из компонентов, включенных последовательно, находится в той же пропорции, что и их сопротивление:
- , если два идентичных компонента соединены последовательно, напряжение питания делится между ними поровну
- , если один компонент имеет в два раза больше сопротивления, чем у другого, напряжение на компоненте с более высоким сопротивлением в два раза больше напряжения на компоненте с более низким сопротивлением. закрыто?
Положение 1: 0 В, 3 В или 6 В
Положение 2: 0 В, 3 В или 6 В
Положение 3: 0 В, 3 В или 6 В
Последовательная цепь- Показать ответ
Положение 1 = 6 В
Положение 2 = 3 В
Положение 3 = 3 В
Пример 1: Найдите полное эквивалентное сопротивление в следующей цепи
Пример 2: Для следующей цепи:
- Найдите полное сопротивление
- Найдите текущий i
- Найдите напряжение на резисторе 10 Ом
Решение
- Общее сопротивление
Ток можно рассчитать как
Напряжение на резисторе 10 Ом
Пример 3: Для следующей цепи:
- Найдите общее значение сопротивления R T
- Найдите текущий i
- Найдите напряжение на отдельных резисторах
- Проверить закон напряжения Кирхгофа
Пример 4: Для следующей цепи:
- Найти V 1
- Найти V 2
- Проверить закон напряжения Кирхгофа вокруг замкнутого контура
Отдел напряжения :В следующей схеме ток через все последовательно включенные резисторы равен
. Эквивалентный резистор R eq является суммой номинала резистора.Чтобы найти падение напряжения v i на резисторе R i , мы используем ток и значение резистора
.Правая часть уравнения дает нам уравнение деления напряжения.
Примеры:Пример 5: Для следующей схемы
- Найдите общее значение сопротивления R T
- Найдите текущий i
- Найдите напряжение на резисторах
- Проверить закон напряжения Кирхгофа
Пример 6: Найдите ток для следующей цепи
Практические задачи :(Щелкните изображение, чтобы просмотреть решение)
Задача 1: Найдите следующую схему.
Просмотреть решение
Решение:
Применить закон Кирхгофа о напряжении
Задача 2: Рассчитайте напряжения для следующей цепи.
Просмотреть решение
Решение:
текущий,
Применение закона Кирхгофа:
Проблема 3: Найдите приложенное напряжение к следующей цепи, используя предоставленную информацию
Просмотреть решение
Проблема 4: Найдите значение резистора R , используя предоставленную информацию
Просмотреть решение
Проблема 5 : Найти V x
Просмотреть решение
Упражнения:Основные операции, уход и техническое обслуживание, а также расширенное устранение неисправностей для квалифицированных специалистов
Устранить проблему можно с помощью теста напряжения или сопротивления.Наиболее практично выбрать испытание напряжением. С помощью теста сопротивления вы должны сначала отключить проверяемый компонент от цепи, и, пока вы удаляете проводку, вы можете столкнуть предметы и, возможно, изменить схему, что может временно устранить проблему. Другими словами, вы можете и не найти проблему.
При использовании вольтметра для устранения неполадок вы обнаружите либо разомкнутый переключатель, либо отказавшую нагрузку. Вы можете сделать это, не перемещая никаких проводов и никоим образом не меняя схему.Затем вы можете снять устройство и дважды проверить его омметром.
Падения напряжения в последовательных цепях
В последовательных цепях полное напряжение является суммой отдельных падений напряжения в цепи, и уравнение E = IR используется для расчета падения напряжения на каждом резисторе. Поскольку ток через каждый резистор одинаков, падение напряжения на каждом резисторе прямо пропорционально значению сопротивления. Другими словами, чем больше номинал резистора в последовательной цепи, тем больше падение напряжения.Рассмотрим простую последовательную схему на рисунке 1.
Рисунок 1 — Последовательная цепь
Из значений, приведенных выше, вы можете легко рассчитать падение напряжения на каждом резисторе по следующей формуле:
E 1 = I 1 × R 1 = 2 A × 40 Ом = 80 В
E 2 = I 2 × R 2 = 2 A × 20 Ом = 40 ВПадение напряжения 80 В на резисторе 40 Ом в два раза превышает падение напряжения на резисторе 20 Ом.
См. Рисунок 2.Если между резисторами R 1 и R 2 возникает разрыв (например, путем отсоединения провода), ток через цепь, конечно, прерывается. Если нет тока, падение напряжения на каждом из резистивных элементов равно нулю (поскольку E = I × R).
Однако разность потенциалов источника все еще существует на открытом воздухе. Если вольтметр подключен через разрыв, показания такие же, как если бы он был подключен непосредственно к клеммам источника питания.
Рисунок 2 — Напряжение в цепи и разрыв цепи
В последовательной цепи освещения вы можете легко определить, какая лампа перегорела, просто измерив напряжение на клеммах держателя лампы, последовательно, пока не будет измерено полное напряжение источника.
Осторожно! Поскольку напряжение источника все еще присутствует в отверстии в последовательной цепи, это представляет опасность поражения электрическим током. Будьте осторожны, не прикасайтесь к токоведущим частям цепи! Точно так же, если переключатель разомкнут, на контактах переключателя появится полное напряжение источника.Даже если напряжение на нагрузочных устройствах может быть нулевым, если какая-либо из этих нагрузок находится перед переключателем, они будут запитаны с полным напряжением относительно земли.
Калькулятор серийи параллельных цепей
Калькулятор эквивалентной последовательной и параллельной цепейЗдесь мы изучаем расчет эквивалентной или полной последовательной цепи и параллельной цепи.
Во-первых, вы должны знать об основных понятиях, таких как последовательное и параллельное соединение цепей с соединенными различными элементами.
В предыдущем учебном пособии я объяснил последовательную цепь и параллельную цепь на примере.
1. Калькулятор последовательной цепи —
При последовательном соединении ряд электрических элементов или компонентов соединены последовательно или последовательно.
Например, данная схема называется последовательной схемой, когда компоненты электроники (такие как сопротивление R1, R2 и R3) соединены одним путем с подключенным источником напряжения (Vs).
Когда в цепь подается напряжение, течет такой же ток (I). Но другое (или падение) напряжения (V1, V2 и V3) произошло на всем последовательно подключенном сопротивлении.
Сумма падений напряжения на отдельных последовательно соединенных сопротивлениях равна приложенному напряжению (т.е. V = V1 + V2 + V3).
Давайте проверим, вот несколько важных формул для различных компонентов, соединенных последовательно.
Для расчета тока в серии:
Общий ток, (Ieq) = (I1 = I2 = I3 = I4 = 15 =...... = In) (Единица - Ампер)
Примечание: Один и тот же ток течет или возникает на разных подключенных компонентах в последовательной цепи.
Для расчета напряжения в серии:
Общий ток, (Veq) = (V1 + V2 + V3 + V4 = V5 = ...... = Vn) (Единица - Вольт)
Для расчета сопротивления в серии:
Общее сопротивление, (Треб.) = (R1 + R2 + R3 + R4 + R5 + ...... + Rn) (Единицы - Ом)
Для расчета проводимости серий:
Общая проводимость, (Geq) = [1 / ((1 / G1) + (1 / G2) + (1 / G3) + (1 / G4) + (1 / G5) +...... + (1 / Gn))] (Блок - Сименс)
Для расчета емкости в серии:
Общая емкость, (Ceq) = [1 / ((1 / C1) + (1 / C2) + (1 / C3) + (1 / C4) + (1 / C5) + ...... + ( 1 / Cn))] (Единица - Фарад)
Для расчета индуктивности в серии:
Общая индуктивность, (Leq) = (L1 + L2 + L3 + L4 + L5 ...... + Ln) (Единица - Генри)
Это простое описание последовательной цепи с различными формулами.
2. Вычислитель параллельной цепи:
При параллельном соединении ряд электрических элементов или компонентов соединяются параллельно.
Например, когда электронные компоненты (такие как сопротивление R1, R2 и R3) подключены в параллельную ветвь с подключенным источником напряжения (Vs).
Когда в цепь подается напряжение, течет такой же ток (I). Но разное (или падение) напряжения (V1, V2 и V3) произошло на всем параллельно подключенном сопротивлении.
Сумма падений напряжения на отдельных параллельно соединенных сопротивлениях равна приложенному напряжению (т.е. V = V1 + V2 + V3).
Давайте проверим, вот несколько важных формул для различных подключенных компонентов в параллельной цепи.
Для расчета параллельного тока:
Общий ток, (Ieq) = (I1 + I2 + I3 + I4 + 15 + ...... + In) (Единица - Ампер)
Для расчета параллельного напряжения:
Общее напряжение, (Veq) = (V1 = V2 = V3 = V4 = V5 =...... + Vn) (Единица- Вольт)
Примечание: одинаковое напряжение или разность потенциалов возникают на разных подключенных компонентах.
Для расчета сопротивления параллельно:
Общее сопротивление, (Треб.) = [1 / ((1 / R1) + (1 / R2) + (1 / R3) + (1 / R4) + (1 / R5) + ...... + ( 1 / Rn))] (Единица- Ом)
Для расчета проводимости серий:
Общая проводимость, (Geq) = (G1 + G2 + G3 + G4 + G5 +...... + Gn) (Единица- Сименс)
Для расчета емкости в серии:
Общая емкость, (Ceq) = (C1 + C2 + C3 + C4 + C5 + ...... + Cn) (единица- Фарады)
Для расчета индуктивности в серии:
Общая индуктивность, (Leq) = [1 / ((1 / L1) + (1 / L2) + (1 / L3) + (1 / L4) + (1 / L5) + ...... + ( 1 / Ln))] (Блок - Генри)
Это простое описание параллельной схемы с различными формулами.
Серияи параллельные электрические соединения
Серия и параллельнаяЕсть 2 способа подключить несколько устройств к источнику питания (например,грамм. динамики к усилителю), последовательно и параллельно. Ну … Хорошо, есть еще последовательный / параллельный. Но мы расскажем об этом на следующей странице.
Серийные динамикиВ последовательной цепи (как в двух вышеупомянутых) ток должен протекать через одно устройство, чтобы добраться до следующего устройства. Это означает, что скорость протекания тока через все устройства одинакова. Напряжение на каждом устройстве зависит от его полного сопротивления / сопротивления каждого устройства и тока, протекающего по цепи. При добавлении дополнительных компонентов в последовательную цепь ток уменьшается, если приложенное напряжение остается постоянным.
динамика параллельноВ параллельной схеме (как в двух приведенных выше примерах) каждое устройство напрямую подключается к источнику питания. Это означает, что каждое устройство получает одинаковое напряжение. Сила тока, протекающего через каждое устройство, зависит от импеданса / сопротивления этого конкретного устройства. Если устройства добавляются к источнику питания в параллельной конфигурации, ток потребления / потока от источника питания увеличивается.
На 2 диаграммах ниже вы можете увидеть взаимосвязь между током на выходе из усилителя и количеством динамиков.Вы можете видеть, что четыре динамика потребляют от усилителя в два раза больше тока, чем конфигурация с двумя динамиками.
При подключении к любому источнику питания вы должны знать пределы источника, чтобы предотвратить повреждение источника. Это означает, что если вы подключите слишком много динамиков с параллельной проводкой к усилителю (в данном случае источнику питания), он может выйти из строя и не подлежит ремонту. Я видел, как это происходило, особенно когда усилитель был неправильно вставлен.
Для тех, кто хочет заниматься математикой …На диаграммах / тексте выше у нас были либо последовательные ИЛИ параллельные цепи. В этом разделе показано, что происходит с напряжением, током и рассеиваемой мощностью в последовательной / параллельной цепи. Как было сказано ранее, в последовательной цепи «ток» в каждом устройстве одинаков. В параллельной цепи «напряжение» одинаково на каждом устройстве. В следующей схеме вы можете видеть, что два резистора на 1000 Ом последовательно соединены с одним резистором на 400 Ом.Мы знаем, что напряжение на двух резисторах 1000 Ом будет одинаковым (потому что они подключены параллельно). Мы также знаем, что общий ток, протекающий через два параллельно соединенных резистора, будет равен току, протекающему через резистор 400 Ом.
Чтобы рассчитать полный ток, сначала следует упростить схему. Это означает, что нам нужно найти полное сопротивление параллельной сети. Для простой схемы с двумя резисторами равного номинала мы можем просто разделить сопротивление отдельного компонента на общее количество компонентов.Для этой параллельной сети у нас есть два резистора по 1000 Ом.
Общее сопротивление параллельных резисторов = сопротивление отдельного компонента / количество резисторов
Общее сопротивление параллельных резисторов = 1000/2
Общее сопротивление параллельных резисторов = 500 ОмЕсли бы у нас было 3 параллельных резистора, мы бы разделили 1000 на 3, чтобы найти общее сопротивление параллельных резисторов.
Общее сопротивление параллельных резисторов = 1000/3
Общее сопротивление параллельных резисторов = 333.33 …. ОмТеперь, когда мы знаем, что параллельные резисторы равны одному резистору на 500 Ом. Теперь, когда у нас есть, по сути, один резистор на 500 Ом, соединенный последовательно с резистором на 400 Ом, мы можем рассчитать полный ток в цепи. Мы знаем, что у нас есть источник питания на 12 вольт. Мы также знаем, что резистор на 500 Ом, включенный последовательно с резистором на 400 Ом, равен резистору на 900 Ом.
Ток через цепь = напряжение в цепи / общее сопротивление цепи
Прохождение тока через цепь = 12/900
Прохождение тока через цепь = 0.0133 амперТеперь мы можем найти напряжение на отдельных компонентах. Чтобы избежать путаницы, сначала рассчитайте напряжение на единственном резисторе.
Напряжение на резисторе = сопротивление резистора * ток, протекающий через резистор
Напряжение на резисторе = 400 * 0,0133
Напряжение на резисторе = 5,333 ВВ последовательной цепи все напряжения на всех отдельных компонентах серии будут равны напряжению источника питания.Если у нас есть источник 12 В, а напряжение на резисторе 400 Ом составляет 5,333 В, мы знаем, что напряжение на параллельной паре резисторов будет 6,67 В (12-5,333 = 6,67). Чтобы вычислить ток через параллельные компоненты …
Ток через один резистор 1000 Ом = напряжение на резисторе / сопротивление
Ток через один резистор 1000 Ом = 6,67 / 1000
Ток через один резистор 1000 Ом = 0,0067 ампераТеперь, когда мы знаем напряжение на каждом из компонентов и ток от до на каждом из компонентов, мы можем вычислить рассеиваемую мощность для каждого компонента.На самом деле мы могли бы это сделать, как только узнали бы напряжение на компонентах, но я решил пойти по «живописному» маршруту.
Рассеиваемая мощность на резисторе 400 Ом = напряжение на компоненте * ток через компонент
Рассеиваемая мощность на резисторе 400 Ом = 5,33 * 0,013
Рассеиваемая мощность на резисторе 400 Ом = 0,071 ВтРассеиваемая мощность на каждом резисторе 1000 Ом = напряжение на компоненте * ток на компоненте
Рассеиваемая мощность на каждом резисторе 1000 Ом = 6.67 * .0067
Рассеиваемая мощность на каждом резисторе 1000 Ом = 0,045 ВтВ этом примере использовались резисторы, но те же вычисления будут работать для любого резистивного устройства. Хотя громкоговорители не являются чисто резистивными при работе с переменным напряжением, приведенные здесь расчеты можно использовать для грубых расчетов напряжения, тока и рассеиваемой мощности в громкоговорителях.
Сопротивление серии— Инструменты для установки
Общее сопротивление в последовательной цепи равно сумме всех частей этой цепи, как показано в уравнении ниже.
R
T = R1 + R2 + R3… и т. Д., где
R T = общее сопротивление
R1, R2 и R3 = последовательное сопротивлениеПример:
Последовательная цепь включает последовательно включенные резисторы 60 Ом, 100 Ом и 150 Ом (Рисунок 18). Какое полное сопротивление цепи?
Рисунок 18 Сопротивление в последовательной цепи
Решение:
РТ = R1 + R2 + R3
РТ = 60 + 100 + 150
RT = 310 Ом
Общее напряжение в последовательной цепи равно сумме напряжений на каждом резисторе в цепи (Рисунок 19), как показано в уравнении ниже.
VT = V1 + V2 + V 3… и т. Д.
где
VT = общее напряжение
V1 = напряжение на R1
V2 = напряжение на R2
V3 = напряжение на R3
Рисунок 19 Падения напряжения в последовательной цепи
ЗаконОма теперь может применяться ко всей последовательной цепи или к отдельным составным частям цепи. При использовании на отдельных компонентах напряжение на этой части равно току, умноженному на сопротивление этой части.Для схемы, показанной на рисунке 20, напряжение можно определить, как показано ниже.
V1 = IR1
V2 = IR2
V3 = IR3VT = V1 + V2 + V3
VT = 10 вольт + 24 вольт + 36 вольт
VT = 70 вольтРисунок 20 Суммарное напряжение в последовательной цепи
Чтобы найти полное напряжение в последовательной цепи, умножьте ток на общее сопротивление, как показано в уравнении ниже.
В
Т = I. R Тгде
VT = общее напряжение
I = ток
R T = общее сопротивлениеПример 1:
Последовательная цепь включает последовательно включенные резисторы 50 Ом, 75 Ом и 100 Ом (Рисунок 21).Найдите напряжение, необходимое для получения тока 0,5 ампер.
Рисунок 21 Пример 1 последовательной цепи
Решение:
Шаг 1: Найдите ток в цепи. Как мы уже знаем, ток в последовательной цепи один и тот же, он уже составляет 0,5 ампер.
Шаг 2: Найдите R T
РТ = R1 + R2 + R3
RT = 50 Ом + 75 Ом + 100 Ом
RT = 225 Ом
Шаг 3: Найдите VT.
Используйте закон Ома. V T = I. R Т
VT = 0,5 x 225
VT = 112,5 вольт
Пример 2:
Аккумулятор на 120 В соединен последовательно с тремя резисторами: 40 Ом, 60 Ом и 100 Ом (Рисунок 22). Найдите напряжение на каждом резисторе.
Рисунок 22 Пример 2 последовательной цепи
Решение:
Шаг 1: Найдите полное сопротивление.
РТ = R1 + R2 + R3
RT = 40 Ом + 60 Ом + 100 Ом
RT = 200 Ом
Шаг 2: Найдите ток в цепи (I).
Используйте закон Ома. V T = I. R Т
Решение для I
I = V T / R T
I = 120/200 = 0,6 ампер
Шаг 3: Найдите напряжение на каждом компоненте.
V1 = IR1
V1 = (0,6 А) (40 Ом)
V1 = 24 ВV2 = IR2
V2 = (0,6 А) (60 Ом)
V2 = 36 ВV3 = IR3
V3 = (0,6 А) (100 Ом)
V3 = 60 ВНапряжения V1, V2 и V3 в Примере 2 известны как «падения напряжения» или «падения IR».Их эффект заключается в уменьшении доступного напряжения, подаваемого на другие компоненты схемы. Сумма падений напряжения в любой последовательной цепи всегда равна приложенному напряжению. Мы можем проверить наш ответ в примере 2, используя уравнение
ниже.VT = V1 + V2 + V3
120 В = 24 В + 36 В + 60 В
120 вольт = 120 вольт
Базовая электрическая теория в двух словах
теория к electrician2.com
Правила цепей постоянного тока серииПравило № 1:
Одинаковый ток течет через каждую часть серии схема. Правило № 2:
Общее сопротивление последовательной цепи равно сумма отдельных сопротивлений. Правило № 3:
Общее напряжение в последовательной цепи равно сумме индивидуальных падений напряжения. Правило № 4:
Падение напряжения на резисторе в последовательной цепи пропорционально размеру резистора. Правило № 5:
Общая мощность, рассеиваемая в последовательной цепи, составляет равняется сумме индивидуальных потерь мощности. РЕЗЮМЕ ФОРМУЛ ЗАКОНА OHMS АМПЕР =
ВОЛЬТ
СОПРОТИВЛЕНИЕСОПРОТИВЛЕНИЕ =
ВОЛЬТ
АМПЕРВОЛЬТ =
АМПЕР x СОПРОТИВЛЕНИЕ
- Параллельная цепь постоянного тока
Правила
Правило № 1:
Такое же напряжение присутствует на каждой ветви параллельная цепь и равна напряжению источника. Правило № 2:
Ток через ответвление параллельной сети обратно пропорциональна величине сопротивления ветви. Правило № 3:
Суммарный ток параллельной цепи равен сумма токов отдельных ветвей цепи. Правило № 4:
Суммарное сопротивление параллельной цепи равно к сумме обратных величин отдельных сопротивлений схемы. Правило № 5:
Общая мощность, рассеиваемая в параллельной цепи, составляет равняется сумме индивидуальных потерь мощности.
СВОДКА ПРАВИЛ ПАРАЛЛЕЛЬНЫХ ЦЕПЕЙ ОБЩЕЕ НАПРЯЖЕНИЕ =
E (1) = E (2) = E (3) … и т. Д. ИТОГО СОПРОТИВЛЕНИЕ =
ВОЛЬТ
АМПЕРВОЛЬТ =
ОБЩЕЕ НАПРЯЖЕНИЕ
ОБЩИЙ АМПЕР
К ОПРЕДЕЛИТЕ ПОЛНОЕ СОПРОТИВЛЕНИЕ В ПАРАЛЛЕЛЬНОЙ ЦЕПИ ПРИ ПОЛНОМ ТОКЕ И ОБЩЕЕ НАПРЯЖЕНИЕ ПРИ НЕИЗВЕСТНОМ ИСПОЛЬЗОВАНИИ СЛЕДУЮЩЕЙ ФОРМУЛЫ:RT =
1
___________________
1 + 1 + 1 +…… и т. д.
R1 R2 R3ДЛЯ ДВУХ РЕЗИСТОРОВ ПАРАЛЛЕЛЬНО ИСПОЛЬЗУЙТЕ ЭТО FORMULA НАЗЫВАЕТСЯ «ПРОДУКТ ПРЕВЫШАЕТ СУММУ» РТ =
R (1) * Р (2)
к. (1) + к. (2)МОЩНОСТЬ В ОДНОЙ ФАЗЕ РЕЗИСТИВНЫЕ ЦЕПИ
ГДЕ КОЭФФИЦИЕНТ МОЩНОСТИ 100 ПРОЦЕНТОВ
(ЭТИ ФОРМУЛЫ ОБЫЧНО ИСПОЛЬЗУЮТСЯ ДЛЯ РЕШЕНИЯ БОЛЬШИНСТВА ПРОБЛЕМ С ПИТАНИЕМ ЦЕПЕЙ ПРИ ИСПЫТАНИЯХ)К ОПРЕДЕЛЕНИЕ МОЩНОСТИ, ПОТРЕБЛЯЕМОЙ ОТДЕЛЬНЫМ РЕЗИСТОРОМ В СЕРИЙНОЙ ЦЕПИ ИСПОЛЬЗУЙТЕ ДАННУЮ ФОРМУЛУ:
К ОПРЕДЕЛЕНИЕ МОЩНОСТИ, ПОТРЕБЛЯЕМОЙ ОТДЕЛЬНЫМ РЕЗИСТОРОМ В ПАРАЛЛЕЛЬНОЙ ЦЕПИ ИСПОЛЬЗУЙТЕ ДАННУЮ ФОРМУЛУ:
К ОПРЕДЕЛИТЕ ОБЩУЮ МОЩНОСТЬ, ПОТРЕБЛЯЕМУЮ ОТДЕЛЬНОЙ ЦЕПЕЙ, ИСПОЛЬЗУЙТЕ ДАННУЮ ФОРМУЛУ:
МОЩНОСТЬ = E (ОБЩЕЕ НАПРЯЖЕНИЕ) x I (ОБЩИЙ ТОК)
ПРАВИЛА БОЛЬШОГО ПАЛЬЦА:- THE ОБЩЕЕ СОПРОТИВЛЕНИЕ РЕЗИСТОРОВ ПО ПАРАЛЛЕЛЬНОМУ ВСЕГДА МЕНЬШЕ, ЧЕМ ЗНАЧЕНИЕ ЛЮБОГО ОДНОГО РЕЗИСТОРА.
- THE ОБЩЕЕ СОПРОТИВЛЕНИЕ ПАРАЛЛЕЛЬНЫХ РЕЗИСТОРОВ, ИМЕЮЩИЕ ВСЕ ОДИНАКОВЫЕ ЗНАЧЕНИЯ, ТАКОЕ ЗНАЧЕНИЕ, ОТДЕЛЕННОЕ НА КОЛИЧЕСТВО РЕЗИСТОРОВ.
- ВСЕГДА ИСПОЛЬЗУЙТЕ ПРЕВЫШАЮЩИЕ ПРАВИЛО ПРОДУКТА, ЧТОБЫ РАЗБИРАТЬ ДВА ПАРАЛЛЕЛЬНЫХ РЕЗИСТОРА НА ОДИН РЕЗИСТОР. ЭТО НАМНОГО проще, чем пытаться решить большую алгебраику. ВЫРАЖЕНИЯ.
- 746 ВАТЫ РАВНЫ ОДНОЙ ЛОШАДИ
- ЭФФЕКТИВНОСТЬ РАВНО ВЫХОДУ, РАЗДЕЛЕННОМ НА ВХОД
- В ИНДУКТИВНЫЕ ЦЕПИ, ТОК, ЗАПИСЫВАЕТ НАПРЯЖЕНИЕ.
- В ЕМКОСТНЫЕ ЦЕПИ ТОКОВЫЕ ПРОВОДЫ НАПРЯЖЕНИЕ.
- СИЛА КОЭФФИЦИЕНТ ЯВЛЯЕТСЯ МЕРОПРИЯТИЕМ ДЛЯ ДАЛЬНЕЙШИХ ТОКОВЫХ ПРОВОДОВ ИЛИ ЗАПИСИ НАПРЯЖЕНИЯ.
ПИТАНИЕ В ПЕРЕМЕННОЙ ТЕКУЩИЕ ЦЕПИ, КОГДА КОЭФФИЦИЕНТ МОЩНОСТИ НЕ 100 ПРОЦЕНТОВ(Истинная СИЛА) = E x I x КОЭФФИЦИЕНТ МОЩНОСТИ (ДЛЯ ОДНА ФАЗА)
(Истинная СИЛА) = E x I x 1.732 Х КОЭФФИЦИЕНТ МОЩНОСТИ (ДЛЯ ТРЕХФАЗА)
ЭТО ВЛАСТЬ ТАКЖЕ НАЗЫВАЕТСЯ ИСТИННОЙ ВЛАСТЬЮ, ИЛИ РЕАЛЬНОЙ ВЛАСТЬЮ, ПРОТИВ ВИДНОЙ ВЛАСТИ. НАЙДЕНА ПО РАСЧЕТУ АМПЕР НАПРЯЖЕНИЯ.
Ваттметры показывают значение True Power.
Полная мощность = ВОЛЬТ-АМПЕР = E x I (FOR ОДНА ФАЗА)
Полная мощность = ВОЛЬТ-АМПЕР = E x I x 1,732 (ДЛЯ ТРЕХФАЗА)
IT МОЖЕТ БЫТЬ ОПРЕДЕЛЕНА АЛГЕБРЫ, ЧТО
КОЭФФИЦИЕНТ МОЩНОСТИ =
ИСТИННАЯ СИЛА
ВНЕШНЯЯ МОЩНОСТЬДВИГАТЕЛЬ ФОРМУЛЫ ПРИМЕНЕНИЯ
ПОДВЕСКА =
(для трехфазных двигателей)1.732 x ВОЛЬТ x АМПЕР x КПД x коэффициент мощности
746ТРЕХФАЗНЫЙ АМПЕР =
(для трехфазных двигателей)746 x ПОДСТАВКА
1,732 x НАПРЯЖЕНИЕ x КПД x КОЭФФИЦИЕНТ МОЩНОСТИСИНХРОННЫЙ Обороты =
ГЕРЦ х 120
КОЛИЧЕСТВО ПОЛЮСОВДВИГАТЕЛЬ МАРКИРОВКА И ПОДКЛЮЧЕНИЯ
СОЕДИНЕНИЯ ДЛЯ ДЕВЯТИ СВИНЦА
ТРИ ФАЗНЫЕ ДВИГАТЕЛИТРИ ФАЗА ЗВЕЗДА ИЛИ Y
СОЕДИНЕНИЕ ЗВЕЗДА Напряжение Строка 1 Строка 2 Строка 3 Вместе Низкий 1 и 7 2 и 8 3 и 9 4 и 5 и 6 Высокий 1 2 3 4 и 7, 5 и 8, 6 и 9 ТРИ ФАЗА ДЕЛЬТА
СОЕДИНЕНИЕ ТРЕУГОЛЬНИКОМ Напряжение Строка 1 Строка 2 Строка 3 Вместе Низкий 1 и 6 и 7 2 и 4 и 8 3 и 5 и 9 НИКТО Высокий 1 2 3 4 и 7, 5 и 8, 6 и 9 ДЕЛЬТА ТРУБКА ДЛЯ ТРАНСФОРМАТОРА
ДВИГАТЕЛЬ КОНТРОЛЛЕР С ТРЕМЯ
ПУСК ОСТАНОВКИ
(ХОЛДИНГ КОНТАКТЫ НЕ ПОКАЗАНЫ)ТРАНСФОРМАТОР ОБОРОТОВ
Ep = Tp
Es TsГде
Ep — первичное напряжение
Es — вторичное напряжение
Tp — количество витков первичной обмотки
Ts — количество витков во вторичной обмотке.Подсоединение переключателя
4-ходовой
D — S, E — R, F — T, G — W
3-ходовой
от A до Z, от B до Y, от C до X
Пример заполнения кабельного лотка
Раствор Для многожильных кабелей на 2000 В и где кабели 4/0 и более устанавливаются с кабелями менее 4/0 по размеру см. Раздел 392.22 (А) (1) (с).
Сумма сечений всех кабелей меньшего размера чем 4/0 не должна превышать максимально допустимую площадь заполнения в результате расчет в столбце 2 таблицы 392.22 (A) для соответствующего кабельного лотка ширина.
В этой таблице sd = сумма диаметров кабелей 4/0 и больше.
Тогда
Сумма поперечных сечений для кабелей меньше 4/0 (СУММ) <= X - 1,2 x стандартное отклонение
X определяет ширину кабельного лотка из Таблицы 392.22 (А).
X> = СУММ + (1,2 x стандартное отклонение)
СУММ = 6 x 3,14 x 0,5 x 0,5 кв. Дюйма
СУММ = 4,71 кв. Дюйма
sd = 3 x 2 дюйма
sd = 6 дюймов
X> = 4,71 + (1,2 x 6)
X> = 11,91
Из таблицы 392.22 (A) следующий больший X равен 14, и это преобразует к кабельному лотку шириной 12,0 дюймов в колонне 1.
Следует отметить, что кабели 4/0 и больше должны быть установлен в один слой.
Максимальная мощность
для NEMA-Rated
Пускатели двигателяОднофазный Трехфазный NEMA
Размер115
Вольт230
Вольт208/230
Вольт460/575
Вольт00 1/3 1 1.5 2 0 1 2 3 5 1 2 3 7,5 10 2 3 7,5 15/10 25 3 25/30 50 4 40/50 100 5 75/100 200 РЕЙТИНГ NEMA ДЛЯ КОРПУСОВ
NEMA и другие организации создали стандарты конструкции корпуса для управляющего оборудования.В основном, оборудование будет закрыто по одной или нескольким из следующих причин:
- Избегайте случайного контакта с токоведущими частями.
- Защитите контроль от вредного воздействия окружающей среды условия.
- Предотвратить взрыв или возгорание, которые могут возникает из-за электрической дуги, вызванной регулятором.
NEMA I — ОБЩЕГО НАЗНАЧЕНИЯ
Корпус общего назначения предназначен в первую очередь для предотвращения случайного контакта с закрытым аппаратом.Это подходит для общего применения внутри помещений, где он не подвергается воздействию необычным условиям эксплуатации. Корпус NEMA I служит защитой от пыли и легких непрямых брызг, но не пыленепроницаемый.
NEMA 3 — DUSTTIGHT, RAINTIGHT
Этот корпус предназначен для подходящая защита от указанных погодных опасностей. Корпус NEMA 3 подходит для применения на открытом воздухе, на корабельных доках, каналах и строительстве работа, и для применения в метро и туннелях.Он также устойчив к мокрому снегу.
NEMA 3R — ДОЖДЕВОЙ, УСТОЙЧИВЫЙ НА СЛОИ
Этот корпус защищает от помех в работе встроенного оборудования из-за дождя и сопротивляется повреждениям от воздействия мокрого снега. Он разработан со ступицами для кабелепровода и внешним креплением, а также дренажные положения.
NEMA 4 — ВОДОСНАБЖЕНИЕ
Разработан водонепроницаемый корпус. чтобы выдержать испытание шланга, описанное в следующем примечании: «Корпуса должны быть испытанным погружением в струю воды.Шланг с однодюймовым соплом должны использоваться и должны обеспечивать скорость не менее 65 галлонов в минуту. Вода должно быть направлено на ограждение с расстояния не менее 10 стопы и в течение пяти минут. В этот период может быть направлено в любом одном или нескольких направлениях по желанию. Не должно быть утечки вода в корпус в этих условиях ».
Корпус NEMA 4 подходит для применение на открытом воздухе в доках судов, на молочных заводах, пивоварнях и т. д.
NEMA 4X — ВОДОНЕПРОНИЦАЕМЫЙ, КОРРОЗИОННЫЙ
Эти корпуса обычно изготавливаются в соответствии с корпусами NEMA 4, за исключением того, что они сделаны из материала что очень устойчиво к коррозии.По этой причине они идеальны в таких приложениях, как бумажные фабрики, упаковка мяса, удобрения и химикаты заводы, на которых загрязняющие вещества обычно разрушают стальную ограду над Период времени.
NEMA 7 — ОПАСНЫЕ ЗОНА — КЛАСС Я
Эти корпуса предназначены для требования к применению Национального электрического кодекса для класса Я опасные места. В этом типе оборудования прерывание цепи происходит в воздухе.
«Объектами класса I являются те, в которых легковоспламеняющиеся газы или пары присутствуют или могут присутствовать в воздухе в количествах достаточно для образования взрывоопасных или горючих смесей.»
NEMA 9 ОПАСНЫЕ ЗОНА — КЛАСС II
Эти корпуса предназначены для требования к применению Национального электрического кодекса для класса II опасные места.
«Объектами класса II являются те, которые опасны из-за наличия горючей пыли ».
Буква или буквы, следующие за номер типа указывает на конкретную группу или группы опасных мест (как определено в Национальном электротехническом кодексе), для которого разработан.



