Как найти кпд рычага формула в физике: Рычаг в физике. Формула для определения КПД рычага. Пример задачи – Ответы Mail.ru: Надо определить КПД… — groupnk.ru — Группа НК — комплексные поставки электрооборудования в Москве и регионах

Содержание

Рычаг в физике. Формула для определения КПД рычага. Пример задачи

Любая машина или механизм, которые созданы человеком, призваны выполнять некоторую полезную работу. Для ее совершения следует затратить энергию. Вопрос соотношения затраченной и полезной работы рассмотрим на примере определения КПД рычага.

О рычаге

Рычагом называют любой простой механизм, который служит для преобразования силы по величине и направлению. Он состоит из балки и опоры, в общем случае имеет два плеча. На каждое из плеч оказывает действие сила. Обе силы стремятся повернуть плечи в противоположных направлениях. Поэтому одна из них всегда совершает работу против другой.

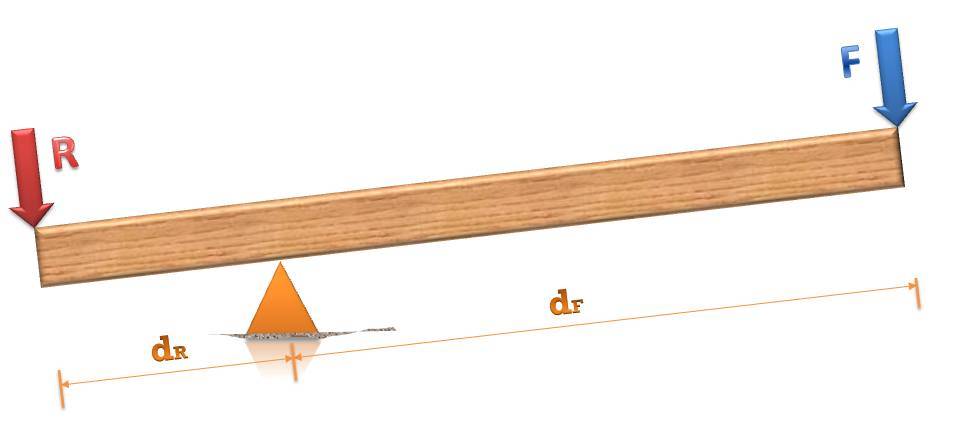
Рычаг позволяет выиграть в пути или в силе, при этом будет наблюдаться проигрыш в силе или в пути соответственно. Главная формула рычага, которая описывает равновесие его плеч, указана ниже:

F/R = d_R/d_F.

Здесь сила F совершает работу против веса груза R, действуя на плечо длиной d_F. Груз находится на плече длиной d_R. Формула отражает обратную пропорциональность между отношениями сил и плеч.

Следующий момент. Когда плечи начинают перемещаться, то одно из них поднимается на высоту h₁, другое же опускается на высоту h₂. Поскольку угол поворота плеч будет одинаковый, то, в отсутствие других сил, формулу выше можно переписать так:

F/R = h₁/h₂.

Дальше эта формула будет использоваться для определения КПД рычага.

КПД простого механизма

Напомним, что работой в физике называется величина, равная произведению силы на путь, в течение которого она действовала:

A = F * l.

КПД любого механизма характеризует эффективность его работы. Вычислить его можно по такой формуле:

КПД = А_п/А_з* 100%.

Где А_п — полезная работа, выполненная механизмом, А_з — работа, которую пришлось затратить.

Человечество на протяжении всей истории пытается создать механизмы, в которых бы А_з = А_п, но достичь этого равенства еще никому не удавалось. Затраченная работа всегда больше значения А_п.

Используя формулу для рычага, полученную в предыдущем пункте, можно записать формулу определения КПД рычага:

А_п = R * h₁; А_з = F * h₂;
КПД = А_п/А_з* 100% = R * h₁/(F * h₂) * 100%.

Если учесть соответствующее выражение для рычага, то может показаться, что КПД для него будет равен 100 %. Тем не менее это не так, поскольку постоянно существует трение в оси вращения и трение о воздух. В результате этих процессов затраченная работа частично расходуется на нагрев окружающей среды и деталей рычага, поэтому КПД механизма оказывается всегда меньше 100 %.

Задача на определение КПД

Предположим, что прилагаемая к рычагу сила F = 18 Н привела к подъему груза массой 3 кг на высоту 0,3 метра. Учитывая, что плечо приложения силы F опустилось при этом на 0,6 метра, вычислите КПД рычага.

Вычисляем полезную и затраченную работы:

А_п = R * h₁ = m * g * h₁ = 3 * 9,81 * 0,3 = 8,829 Дж;
А_з = F * h₂ = 18 * 0,6 = 10,8 Дж.

Как видно, А_з> А_п. КПД рычага равен:

КПД = А_п/А_з* 100% = 8,829/10,8 * 100% = 81,75 %.

Увеличить это значение КПД можно, если применить смазку в оси вращения рычага.

Рычаг в физике. Формула для определения КПД рычага. Пример задачи

О рычаге

F/R = d_R/d_F.

F/R = h₁/h₂.

Дальше эта формула будет использоваться для определения КПД рычага.

КПД простого механизма

A = F * l.

КПД любого механизма характеризует эффективность его работы. Вычислить его можно по такой формуле:

КПД = А_п/А_з* 100%.

Где А_п — полезная работа, выполненная механизмом, А_з — работа, которую пришлось затратить.

А_п = R * h₁; А_з = F * h₂;
КПД = А_п/А_з* 100% = R * h₁/(F * h₂) * 100%.

Задача на определение КПД

Вычисляем полезную и затраченную работы:

А_п = R * h₁ = m * g * h₁ = 3 * 9,81 * 0,3 = 8,829 Дж;
А_з = F * h₂ = 18 * 0,6 = 10,8 Дж.

Как видно, А_з> А_п. КПД рычага равен:

КПД = А_п/А_з* 100% = 8,829/10,8 * 100% = 81,75 %.

Увеличить это значение КПД можно, если применить смазку в оси вращения рычага.

Рычаг — Википедия

Использование рычага для получения бо́льшего усилия на коротком плече, за счёт приложения меньшей силы на длинном.

Рыча́г — твёрдое тело, которое может вращаться вокруг неподвижной опоры.

Рычаг относится к простейшим механизмам. Представляет собой любой предмет, имеющий возможность вращаться вокруг неподвижной точки опоры (подвеса). Части предмета от точки опоры до точки приложения сил называют плечами рычага. Относительно точки опоры места приложения сил могут быть по разные стороны (рычаг I рода) или с одной стороны (рычаг II рода)^[1].

Рычаг используется для создания большего усилия на коротком плече с помощью меньшего усилия на длинном плече (или для получения большего перемещения на длинном плече с помощью меньшего перемещения на коротком плече). Сделав плечо рычага достаточно длинным, теоретически, можно развить любое усилие.

Частными случаями рычага являются также два других простейших механизма: дифференциальный ворот и блок.

Человек стал использовать рычаг ещё в доисторические времена, интуитивно понимая его принцип. Такие инструменты, как мотыга или весло, применялись, чтобы уменьшить силу, которую необходимо было прикладывать человеку. В пятом тысячелетии до нашей эры в Месопотамии применялись весы, использовавшие принцип рычага для достижения равновесия.^[2]^[3] Позже, в Греции, был изобретён безмен, позволивший изменять плечо приложения силы, что сделало использование весов более удобным. Около 1500 года до н. э. в Египте и Индии появляется шадуф (колодец с «журавлём»), прародитель современных кранов, устройство для поднимания сосудов с водой.

[4]

Гравюра из «Журнала механики», изданного в Лондоне в 1842 году, изображающая Архимеда, переворачивающего Землю с помощью рычага.

Неизвестно, пытались ли мыслители тех времён объяснить принцип работы рычага. Первое письменное объяснение дал в III веке до н. э. Архимед, связав понятия силы, груза и плеча. Закон равновесия, сформулированный им, используется до сих пор и звучит как: «Усилие, умноженное на плечо приложения силы, равно нагрузке, умноженной на плечо приложения нагрузки, где плечо приложения силы — это расстояние от точки приложения силы до опоры, а плечо приложения нагрузки — это расстояние от точки приложения нагрузки до опоры». По легенде, осознав значение своего открытия, Архимед воскликнул: «Дайте мне точку опоры, и я переверну Землю!»

[4].

В современном мире принцип действия рычага используется повсеместно. Практически любой механизм, преобразующий механическое движение, в том или ином виде использует рычаги. Подъёмные краны, двигатели, плоскогубцы, ножницы, а также тысячи других механизмов и инструментов используют рычаги в своей конструкции.

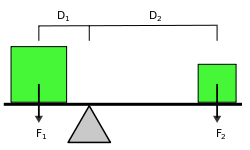Схема рычага. В равновесии F1D1=F2D2{\displaystyle F_{1}D_{1}=F_{2}D_{2}}

Принцип работы рычага является прямым следствием закона сохранения энергии. Чтобы переместить рычаг на расстояние Δh2{\displaystyle \Delta h_{1}} сила, действующая со стороны груза, должна совершить работу равную:

A1=F1Δh2{\displaystyle \ A_{1}=F_{1}\Delta h_{1}}.

Если посмотреть с другой стороны, сила, приложенная с другой стороны, должна совершать работу

A2=F2Δh3{\displaystyle \ A_{2}=F_{2}\Delta h_{2}},

где Δh3{\displaystyle \Delta h_{2}} — это перемещение конца рычага, к которому приложена сила F2{\displaystyle F_{2}}. Чтобы выполнялся закон сохранения энергии для замкнутой системы, работа действующей и противодействующей сил должны быть равны, то есть:

A1=A2{\displaystyle \ A_{1}=A_{2}},

F1Δh2=F2Δh3{\displaystyle \ F_{1}\Delta h_{1}=F_{2}\Delta h_{2}}.

По определению подобия треугольников, отношение перемещений двух концов рычага будет равно отношению его плеч:

Δh2Δh3=D1D2{\displaystyle {\frac {\Delta h_{1}}{\Delta h_{2}}}={\frac {D_{1}}{D_{2}}}}, следовательно

F1D1=F2D2{\displaystyle \ F_{1}D_{1}=F_{2}D_{2}}.

Учитывая, что произведение силы и расстояния от точки опоры до линии действия силы является модулем момента силы, можно сформулировать принцип равновесия для рычага. Рычаг находится в равновесии, если сумма моментов сил (с учётом знака), приложенных к нему, равна нулю. (Точнее, если векторная сумма моментов сил, приложенных к нему, равна нулю.)

Для рычагов, как и для других механизмов, вводят характеристику, показывающую механический эффект, который можно получить за счёт рычага. Такой характеристикой является передаточное отношение, оно показывает, как соотносятся нагрузка и приложенная сила:

i=F1F2=D2D1{\displaystyle i={\frac {F_{1}}{F_{2}}}={\frac {D_{2}}{D_{1}}}}.

Нужно отметить, что как и у любого механизма, у рычага полезная работа меньше полной. Например, у большинства рычагов коэффициент полезного действия (КПД) равен ~ 80 %. Остальные 20 процентов работы расходуются на преодоление силы трения и т. п.

В специальной теории относительности теория рычага существенно отличается от принятой в классической механике (парадокс рычага).

Составной рычаг представляет собой систему из двух и более простых рычагов, соединённых таким образом, что выходное усилие одного рычага является входным для следующего. Например, для системы из двух последовательно связанных рычагов, если на входное плечо первого рычага приложена сила F1{\displaystyle F_{1}}, на другом конце этого рычага выходное усилие окажется F2{\displaystyle F_{2}}, и связаны они будут с помощью передаточного отношения:

i1=F1F2{\displaystyle i_{1}={\frac {F_{1}}{F_{2}}}}.

При этом на входное плечо второго рычага будет воздействовать такое же усилие F2{\displaystyle F_{2}}, а выходным усилием второго рычага и всей системы будет F3{\displaystyle F_{3}}, передаточное отношение второй ступени будет равно:

i2=F2F3{\displaystyle i_{2}={\frac {F_{2}}{F_{3}}}}.

При этом механический эффект всей системы, то есть всего составного рычага, будет вычисляться как отношение входного и выходного усилия для всей системы, то есть:

i=F1F3=F1F3F2F2=F1F2F2F3=i1i2{\displaystyle i={\frac {F_{1}}{F_{3}}}={\frac {F_{1}}{F_{3}}}{\frac {F_{2}}{F_{2}}}={\frac {F_{1}}{F_{2}}}{\frac {F_{2}}{F_{3}}}=i_{1}i_{2}}.

Таким образом, передаточное отношение составного рычага, состоящего из двух простых будет равно произведению передаточных отношений входящих в него простых рычагов.

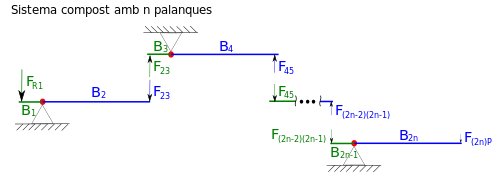$i={\frac {F_{1}}{F_{3}}}={\frac {F_{1}}{F_{3}}}{\frac {F_{2}}{F_{2}}}={\frac {F_{1}}{F_{2}}}{\frac {F_{2}}{F_{3}}}=i_{1}i_{2}$

Составной рычаг в общем случае, состоящий из n простых рычагов

Такой же подход решения можно применять и для более сложной системы, состоящей, в общем случае из n рычагов. В этом случае в системе будет присутствовать 2n плеч. Передаточное отношение для такой системы будет вычисляться по формуле:

iC=FR1F(2n−1)−P=FR1F23⋅F23F45⋅…⋅F(2n−2)−(2n−1)F(2n−1)−P=B2B1⋅B4B3⋅…⋅B(2n)B(2n−1){\displaystyle i_{C}={\frac {F_{R1}}{F_{(2n-1)-P}}}={\frac {F_{R1}}{F_{23}}}\cdot {\frac {F_{23}}{F_{45}}}\cdot …\cdot {\frac {F_{(2n-2)-(2n-1)}}{F_{(2n-1)-P}}}={\frac {B_{2}}{B_{1}}}\cdot {\frac {B_{4}}{B_{3}}}\cdot …\cdot {\frac {B_{(2n)}}{B_{(2n-1)}}}},

где:

Bi{\displaystyle \ B_{i}} — это i-ое плечо системы;
F(i−1)i{\displaystyle \ F_{(i-1)i}} — сила, передаваемая с плеча (i-1) на плечо i;
iC{\displaystyle \ i_{C}} — передаточное отношение всей системы.

Как видно из формулы для этого случая также верно, что передаточное отношение составного рычага равно произведению передаточных отношений входящих в него элементов.

Различают рычаги 1 рода, в которых точка опоры располагается между точками приложения сил, и

рычаги 2 рода, в которых точки приложения сил располагаются по одну сторону от опоры. Среди рычагов 2 рода выделяют рычаги 3 рода^[5], с точкой приложения внешней силы ближе к точке опоры, чем нагрузки, что даёт выигрыш в скорости и пути.

Примеры: рычаги первого рода — детские качели (перекладина), ножницы; рычаги второго рода — тачка (точка опоры — колесо), приподнимание предмета ломом движением вверх; рычаги третьего рода — метла дворника, грабли; задняя дверь багажника или капот легковых автомобилей на гидравлических телескопических упорах, подъём кузова самосвала (с гидроцилиндром в центре), движение мышцами рук и ног человека и животных.

Простые механизмы. КПД простых механизмов

В процессе труда человек больше опирается не на свою силу, а на свой ум. С древности люди при передвижении тяжелых грузов пользовались простейшими механизмами.

Простые механизмы – это устройства для преобразования силы, точнее, для увеличения и перенаправления силы. Например: рычаг, блок, лебедка, клин и даже наклонная плоскость.

Блок

Блок – устройство, состоящее из колесика и веревки. Веревка, двигаясь по окружности колеса, обеспечивает движения груза. Он не даёт выигрыша в силе, но позволяет менять его направление.

Рычаг
Это устройство, где длинное тело, вращаясь вокруг неподвижной опоры, обеспечивает преобразование малой силы, в большую силу.

Длина стержня от точки опоры до места приложения силы называется плечом силы.
Сила прикладываемая и сила, получаемая на выходе, связанны следующим равенством:
L1 – плечо силы F1
L2 – плечо силы F2
А выигрыш в силе можно рассчитать, разделив большее плечо силы на меньшее.
Наклонная плоскость
Для подъёма тела необходима маленькая сила, но при этом тело проходит большее расстояние.
Сила необходимая для движения по плоскости и сила необходимая для подъема, связанны следующим равенством:
Необходимо, отметить, что выше такие механизмы (рычаг, наклонная плоскость, лебедка и т.д) дают выигрыш только в силе, при выигрыш в работе отсутствует.
КПД механизмов
Коэффициент полезного действия показывает, насколько эффективна система. Она определяется как отношение полезной работы, то есть затраченной на выполнение самого действия, к полной работе.
КПД удобней вычислять в процентах, это можно сделать, умножив отношение полезной работы к полной работе на 100\%.
Чтобы повысить КПД, уменьшают вес механизмов, трение и т.д., совершенствуют конструкцию.
Пример задачи
Рассмотрим задачу, тело массой 200 кг, подняли на высоту 0.1 м. К длинному плечу рычага приложили силу 500H, вследствие чего оно опустилось на 0.5 м. Вычислить КПД рычага.
Для начала определим вес груза, то есть, какую силу нужно приложить, что бы поднять груз:
P = mg = 200 кг * 10 м/c2= 2000H
Полезная работа будет равна:
Aпол= Fh2= 2000H 0.1м= 200 Дж
Общая работа, необходимая для подъема груза будет равна:
Aобщ= Fh3= 500H 0.5 м = 250 Дж
КПД находим как отношение полезной работы к общей, в процентах:
Ƞ= Aпол/ Aобщ= (200 Дж / 250 Дж)100\% = 80\%
Простые механизмы. КПД простых механизмов – FIZI4KA
1. Простые механизмы — приспособления, которые сконструировал и использовал человек, чтобы облегчить работу по перемещению тяжёлых предметов. К ним относят: рычаг, блок, наклонную плоскость. Разновидностями этих механизмов являются: клин, ворот и винт.
Все простые механизмы позволяют преобразовать силу, действующую на тело: либо уменьшить её, либо изменить её направление.
2. Рычаг — это стержень, вращающийся вокруг неподвижной опоры или оси (рис. 51). На рисунке показан рычаг, который может вращаться вокруг точки О, расположенный между концами рычага. К одному концу рычага подвешен груз, действующий на рычаг с силой $ F_1 $, равной весу груза. Действуя на длинный конец рычага с силой $ F_2 $, человек поднимает груз. При этом сила $ F_1 $ стремится повернуть рычаг по часовой стрелке, а груз $ F_2 $ — против часовой стрелки.
Плечом силы называют кратчайшее расстояние (перпендикуляр) от точки опоры до линии действия силы. Так, плечом силы $ F_1 $ является расстояние ОА $ (l_1) $, плечом силы $ F_2 $ — расстояние ОВ $ (l_2) $.
Из эксперимента следует, что рычаг находится в равновесии, если произведение силы, вращающей рычаг по часовой стрелке, и её плеча равно произведению силы, вращающей рычаг против часовой стрелки, и её плеча, т.е. $ F_1l_1=F_2l_2 $. Произведение силы, действующей на рычаг, и её плеча называют моментом силы: $ Fl=M $. Соответственно, если рычаг находится в равновесии, то $ M_1=M_2 $.
Условие равновесия рычага можно записать по-другому:$ \frac{F_1}{F_2}=\frac{l_2}{l_1} $. Это равенство означает, что рычаг находится в равновесии, если силы, действующие на него, обратно пропорциональны их плечам. Оно называется условием равновесия рычага.
Рычаг другого типа вращается вокруг точки, находящейся на конце рычага. Примером такого рычага может служить тачка. Когда используется такой рычаг, то вес груза направлен вниз, а человек действует на свободный конец рычага с силой, направленной вверх. Для такого рычага также справедливо условие равновесия, приведенное выше.
3. При подъеме груза работа силы, действующей на груз, равна $ A_1=F_1h_1 $, работа силы, приложенной к другому концу рычага, равна $ A_2=F_2h_2 $. Рассмотрение треугольников AOC и BOD позволяет сделать вывод о том, что они подобны и $ \frac{AO}{BO}=\frac{AC}{BD} $ или $ \frac{l_1}{l_2}=\frac{h_1}{h_2} $. Поскольку $ F_1l_1=F_2l_2 $, то $ F_1h_1=F_2h_2 $, т.е. $ A_1=2 $. Таким образом, рычаг, позволяя выиграть в силе, не даёт выигрыша в работе.
4. Ещё одним простым механизмом является блок. Блок — это колесо с желобом, по которому пропускается трос и которое может вращаться относительно оси О (см. рис. ниже).
Если ось блока закреплена, то блок не перемещается, и он называется неподвижным.
Неподвижный блок можно рассматривать как рычаг, вращающийся вокруг точки, лежащей посередине рычага. Плечи такого рычага равны друг другу: OA = OB. В соответствии с условием равновесия рычага приложенные к блоку силы тоже равны: $ P=F $. Следовательно, неподвижный блок не даёт выигрыша в силе, но он позволяет поднимать груз, прикладывая силу, направленную не вверх, а вниз, что облегчает перемещение груза.
Чтобы получить выигрыш в силе используют подвижный блок (рис. 53). К нему непосредственно прикрепляется груз, один конец троса закрепляется, а к другому прикладывают силу и, таким образом, перебирая трос, поднимают блок с грузом.
В этом случае точкой вращения блока является точка А (см. рис. 52).
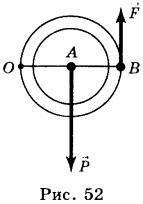
Плечи действующих сил равны соответственно: AO и AB, при этом AB = 2AO. В соответствии с условием равновесия рычага: $ P=2F $. Таким образом, подвижный блок даёт выигрыш в силе в 2 раза: $ F=P/2 $.
Измерив расстояние $ h_1 $, которое проходит груз, и расстояние $ h_2 $, на которое перемещается конец троса, можно обнаружить, что расстояние $ h_2=2h_1 $. Таким образом, подвижный блок даёт выигрыш в силе в 2 раза и в 2 раза проигрыш в пути. Соответственно, работа $ Ph_1=Fh_2 $, т.е. $ A_1=2 $. Подвижный блок, так же как и рычаг, не даёт выигрыша в работе.
5. Наклонная плоскость используется в том случае, если нужно поднять объемный тяжёлый груз на какую-либо высоту (рис. 54).
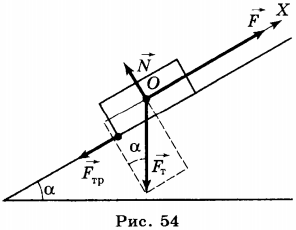
Например, нужно погрузить ящик с металлическими деталями в кузов грузовика. В этом случае кладут массивную доску так, что она образует наклонную плоскость, один конец которой находится на земле, а другой на грузовике, и по этой плоскости втаскивают ящик. Чтобы поднять ящик вертикально вверх нужно приложить к нему силу, равную его весу $ P $. Перемещая равномерно ящик по наклонной плоскости, в отсутствие трения прикладывают силу, равную $ F=P\sin\alpha $, т.е. меньшую веса ящика, но при этом, выигрывая в силе, проигрывают в расстоянии. Работа по подъёму ящика по вертикали равна работе, совершаемой при его перемещении вдоль наклонной плоскости. Это справедливо, если сила сопротивления движению пренебрежимо мала. При наличии трения перемещение ящика вдоль наклонной плоскости требует совершения большей работы, чем при его движении вертикально вверх. В этом случае говорят о коэффициенте полезного действия (КПД) наклонной плоскости. Он равен отношению полезной работы ко всей совершённой работе: $ \mathbf{КПД}=A_п/A_с\cdot 100 \% $, где $ A_п $ — полезная работа, $ A_п=mgh $; $ A_с $ — совершённая работа при перемещении ящика вдоль наклонной плоскости, $ A_c=Fl $, где $ F $ — приложенная сила, $ l $ — длина наклонной плоскости.
ПРИМЕРЫ ЗАДАНИЙ
Часть 1
1. Исследуя условия равновесия рычага, ученик выполнил соответствующую лабораторную работу. В таблице представлены значения сил и их плеч для рычага, находящегося в равновесии. Определите, чему равно плечо $ l_1 $?
1) 12,8 м
2) 2,5 м
3) 0,8 м
4) 0,25 м
2. Ученик выполнял лабораторную работу по исследованию условий равновесия рычага. Результаты для сил и их плеч, которые он получил, представлены в таблице.
Чему равна сила $ F_1 $, если рычаг находится в равновесии?
1) 100 Н
2) 50 Н
3) 25 Н
4) 9 Н
3. Рычаг находится в равновесии под действием двух сил. Сила $ F_1 $ = 6 Н. Чему равна сила $ F_2 $, если длина рычага 50 см, а плечо силы $ F_1 $ равно 30 см?
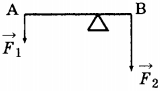
1) 0,1 Н
2) 3,6 Н
3) 9 Н
4) 12 Н
4. Выигрыш в силе, приложенной к грузу, нельзя получить с помощью
1) подвижного блока
2) неподвижного блока
3) рычага
4) наклонной плоскости
5. С помощью неподвижного блока в отсутствие трения силе
1) выигрывают в 2 раза
2) не выигрывают, но и не проигрывают
3) проигрывают в 2 раза
4) возможен и выигрыш, и проигрыш
6. С помощью подвижного блока в отсутствие трения
1) выигрывают в работе в 2 раза
2) проигрывают в силе в 2 раза
3) не выигрывают в силе
4) выигрывают в силе в 2 раза
7. На рисунке изображён неподвижный блок, с помощью которого, прикладывая к свободному концу нити силу 20 Н, равномерно поднимают груз. Если трением пренебречь, то масса поднимаемого груза равна
1) 4 кг
2) 2 кг
3) 0,5 кг
4) 1 кг
8. Наклонная плоскость даёт выигрыш в силе в 2 раза. В работе при отсутствии силы трения эта плоскость
1) даёт выигрыш в 2 раза
2) даёт выигрыш в 4 раза
3) не даёт ни выигрыша, ни проигрыша
4) даёт проигрыш в 2 раза
9. Вдоль наклонной плоскости длиной 5 м поднимают груз массой 40 кг, прикладывая силу 160 Н. Чему равна высота наклонной плоскости, если трение при движении груза пренебрежимо мало?
1) 1,25 м
2) 2 м
3) 12,5 м
4) 20 м
10. Груз массой 10 кг поднимают по наклонной плоскости длиной 2 м и высотой 0,5 м, прикладывая силу 40 Н. Чему равен КПД наклонной плоскости?
1) 160%
2) 62,5%
3) 16%
4) 6,25%
11. Груз поднимают с помощью подвижного блока радиусом $ R $ (см. рисунок). Установите соответствие между физическими величинами (левый столбец) и формулами, по которым они определяются (правый столбец).
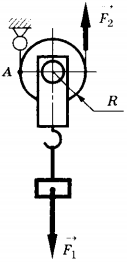
Запишите в таблицу выбранные цифры под соответствующими буквами. Цифры в ответе могут повторяться.
ФИЗИЧЕСКИЕ ВЕЛИЧИНЫ
A) плечо силы $ \vec{F}_1 $ относительно точки A
Б) плечо силы $ \vec{F}_2 $ относительно точки A
B) момент силы $ \vec{F}_1 $ относительно точки A
ФОРМУЛЫ
1) $ F_1R $
2) $ 2F_1R $
3) $ \frac{F_1}{R} $
4) $ R $
5) $ 2R $
12. Из перечня приведённых ниже высказываний выберите два правильных и запишите их номера в таблицу.
1) Любой простой механизм даёт выигрыш в силе.
2) Ни один простой механизм не даёт выигрыша в работе.
3) Наклонная плоскость выигрыша в силе не даёт.
4) Коэффициент полезного действия показывает, какая часть совершенной работы является полезной.
5) Неподвижный блок даёт выигрыш в силе в 2 раза.
Часть 2
13. Чему равна сила, с которой действуют на брусок массой 0,2 кг, перемещая его по наклонной плоскости длиной 1,6 м и высотой 0,4 м, если КПД наклонной плоскости 80%.
Ответы
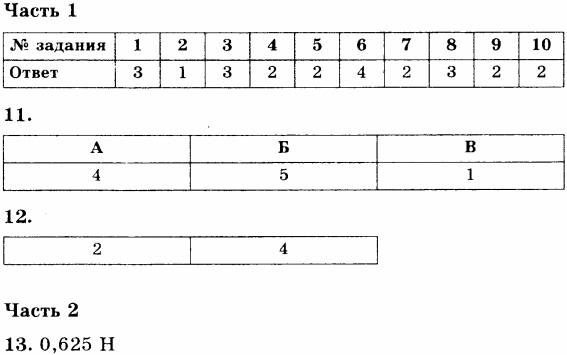
Простые механизмы. КПД простых механизмов
Оценка
Конспект «Рычаг. Равновесие рычага. Момент силы»
«Рычаг. Равновесие рычага.
Момент силы. Правило моментов»
Рычагом называют твердое тело, которое может вращаться вокруг неподвижной точки. Неподвижную точку называют точкой опоры. Расстояние от точки опоры до линии действия силы называют плечом этой силы.
Условие равновесия рычага: рычаг находится в равновесии, если приложенные к рычагу силы F₁ и F₂ стремятся вращать его в противоположных направлениях, причем модули сил обратно пропорциональны плечам этих сил: F₁/F₂ = l₂/l₁Это правило было установлено Архимедом. По легенде он воскликнул: Дайте мне точку опоры и я подниму Землю.
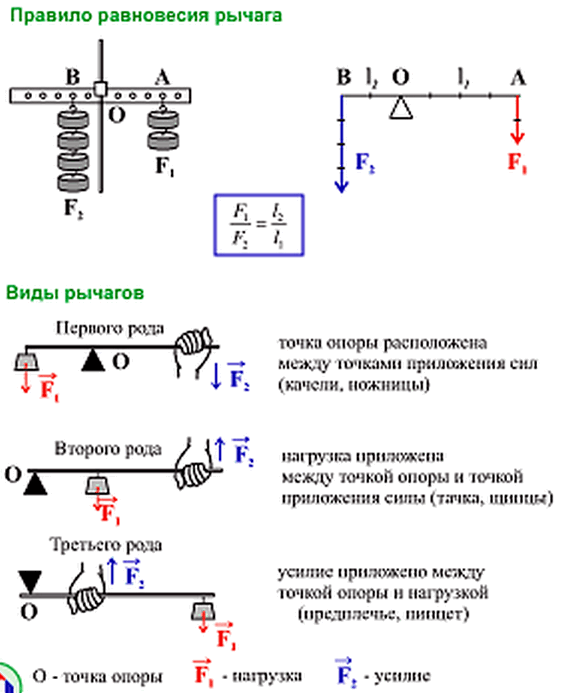
Для рычага выполняется «золотое правило» механики (если можно пренебречь трением и массой рычага).
Прикладывая к длинному рычагу некоторую силу, можно другим концом рычага поднимать груз, вес которого намного превышает эту силу. Это означает, что, используя рычаг, можно получить выигрыш в силе. При использовании рычага выигрыш в силе обязательно сопровождается таким же проигрышем в пути.
Момент силы. Правило моментов
Произведение модуля силы на ее плечо называют моментом силы. M = Fl, где М — момент силы, F — сила, l — плечо силы.
Правило моментов: рычаг находится в равновесии, если сумма моментов сил, стремящихся вращать рычаг в одном направлении, равна сумме моментов сил, стремящихся вращать его в противоположном направлении. Это правило справедливо для любого твердого тела, способного вращаться вокруг закрепленной оси.
Момент силы характеризует вращающее действие силы. Это действие зависит как от силы, так и от ее плеча. Именно поэтому, например, желая открыть дверь, стараются приложить силу как можно дальше от оси вращения. С помощью небольшой силы при этом создают значительный момент, и дверь открывается. Открыть ее, оказывая давление около петель, значительно труднее. По той же причине гайку легче отворачивать более длинным гаечным ключом, шуруп легче вывернуть с помощью отвертки с более широкой ручкой и т. д.
Единицей момента силы в СИ является ньютон-метр* (1 Нм). Это момент силы 1 Н, имеющей плечо 1 м.

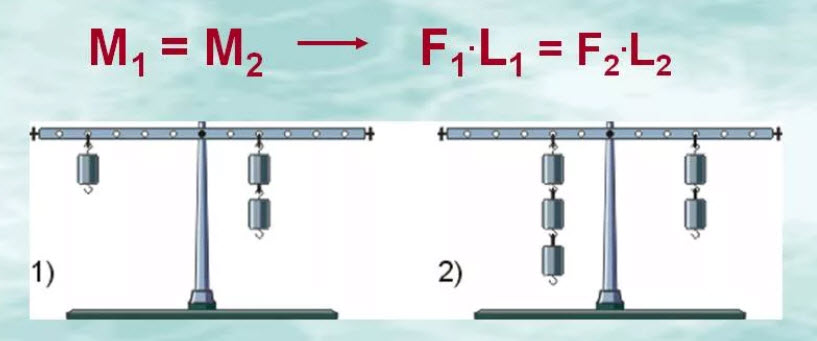
Конспект урока «Рычаги. Равновесие рычага. Момент силы».*
Следующая тема: «Механическая энергия. Закон сохранения энергии».

ФИЗИКА: Задачи на простые механизмы — Ответы и решения
Задачи на простые механизмы с решениями
Формулы, используемые на уроках «Задачи на простые механизмы,
условия равновесия рычага, блоки, золотое правило механики».
Название величины
Обозначение
Единица измерения
Формула
Сила
F
Н
F₁l₁ = F₂l₂
Плечо силы
l
м
Момент силы
M
Нм
M = Fl
ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ
Задача № 1. С помощью рычага рабочий поднимает плиту массой 120 кг. Какую силу он прикладывает к большему плечу рычага, равному 2,4 м, если меньшее плечо 0,8 м?
Задача № 2. На концах рычага действуют силы 20 Н и 120 Н. Расстояние от точки опоры до большей силы равно 2 см. Определите длину рычага, если рычаг находится в равновесии.
Задача № 3. На рисунке изображен рычаг, имеющий ось вращения в точке О. Груз какой массы надо подвесить в точке В для того, чтобы рычаг был в равновесии?
Задача № 4. На меньшее плечо рычага действует сила 300 Н, на большее — 20 Н. Длина меньшего плеча 5 см. Определите длину большего плеча.
Задача № 5. Рычаг длиной 60 см находится в равновесии. Какая сила приложена в точке В?
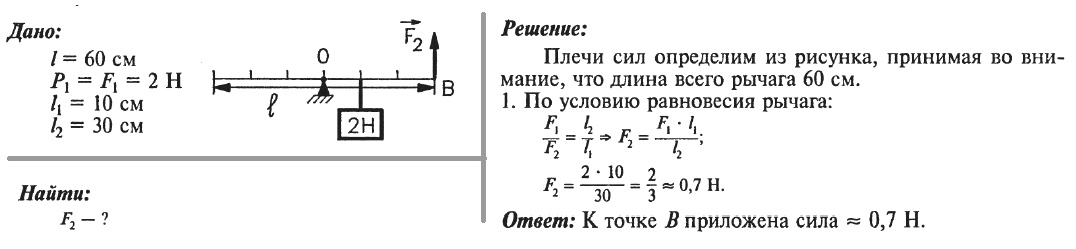
Задача № 6. **Момент силы действующей на рычаг, равен 20 Н*м. Найти плечо силы 5 Н, если рычаг находится в равновесии.
Задача № 7. Какое усилие необходимо приложить, чтобы поднять груз 1000 Н с помощью подвижного блока? Какая совершится работа при подъеме груза на 1 м? (Вес блока и трение не учитывать).
Задача № 8. Система блоков находится в равновесии. Определите вес правого груза. (Вес блоков и силу трения не учитывать).
Задача № 9. При помощи подвижного блока поднимают груз, прилагая силу 105 Н. Определите силу трения, если вес блока равен 20 Н, а вес груза 180 Н.
Задача № 10. ОГЭ Стержень цилиндрической формы длиной l = 40 см состоит на половину своей длины из свинца и наполовину — из железа. Найти его центр тяжести. Плотность свинца p₁ = 11,4 г/см³, плотность железа p₂ = 7,8 г/см³.
Решение. Центр тяжести тела (центр масс) — точка приложения силы притяжения его к земле — веса тела P.
У тел, имеющих какую-либо симметрию, он совпадает с центром симметрии. Например, у однородного цилиндра центр тяжести расположен на его оси в центре цилиндра.
Тело, закреплённое на оси, проходящей через его центр тяжести, находится в состоянии безразличного равновесия. Мысленно закрепим стержень AB на оси, перпендикулярной стержню и проходящей через его центр тяжести C, отстоящий от его геометрического центра O на расстояние x в сторону более тяжёлой половины стержня.
Задача № 11. ЕГЭ Масса якоря корабля m = 50 кг. Радиус барабана, на который наматывают якорную цепь, R = 0,2 м, длина каждой из двух ручек ворота l = 1 м. Какую силу нужно приложить к каждой из них, чтобы поднять якорь?
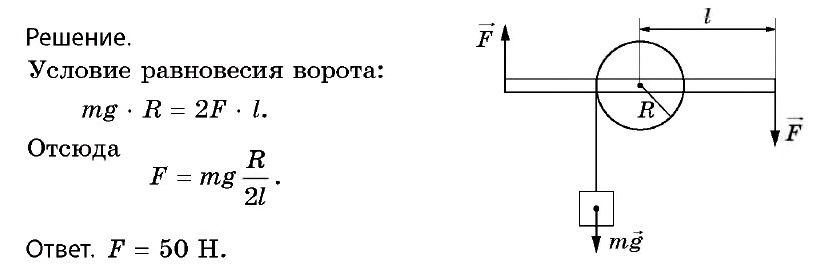
Краткая теория для решения задачи на простые механизмы.**

Конспект урока «Задачи на простые механизмы с решениями».
Следующая тема: «Задачи на КПД простых механизмов».

Название величины	Обозначение	Единица измерения	Формула
*Сила*	F	Н	*F₁l₁ = F₂l₂*
*Плечо силы*	l	м
*Момент силы*	M	Нм	M = Fl

Как найти кпд рычага формула в физике: Рычаг в физике. Формула для определения КПД рычага. Пример задачи – Ответы Mail.ru: Надо определить КПД…

Рычаг в физике. Формула для определения КПД рычага. Пример задачи

О рычаге

КПД простого механизма

Задача на определение КПД

Рычаг в физике. Формула для определения КПД рычага. Пример задачи

О рычаге

КПД простого механизма

Задача на определение КПД

Рычаг — Википедия

Простые механизмы. КПД простых механизмов

Блок

Рычаг

Наклонная плоскость

КПД механизмов

Пример задачи

Простые механизмы. КПД простых механизмов – FIZI4KA

ПРИМЕРЫ ЗАДАНИЙ

Часть 1

Часть 2

Ответы

Конспект «Рычаг. Равновесие рычага. Момент силы»

«Рычаг. Равновесие рычага.Момент силы. Правило моментов»

Момент силы. Правило моментов

ФИЗИКА: Задачи на простые механизмы — Ответы и решения

Задачи на простые механизмы с решениями

Название величины

Обозначение

Единица измерения

Формула

Сила

F

Н

F1l1 = F2l2

Плечо силы

l

м

Момент силы

M

Нм

M = Fl

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ

Краткая теория для решения задачи на простые механизмы.

Добавить комментарий Отменить ответ

«Рычаг. Равновесие рычага.
Момент силы. Правило моментов»

F₁l₁ = F₂l₂