Формула электрического заряда, q

Определение и формула электрического заряда

Фундаментальным свойством электрического заряда является существование двух видов зарядов: положительных и отрицательных. Заряды, имеющие один знак, отталкиваются. Взаимодействие зарядов разного знака определяют как притяжение. Телу можно сообщить заряд любого знака. В макроскопическом теле заряды разных знаков могут взаимно компенсировать друг друга.

Электрический заряд является релятивистски инвариантной величиной. Это значит, что величина заряда не зависит от системы отсчета, не важно, движется заряд (заряженное тело) или покоится.

Электрический заряд тела находят как суммарный заряд его частей.

Разделения электрических зарядов разных знаков можно добиться путем электризации посредством непосредственного контакта тел (например, трением) или без контакта, например посредством электрической индукции. При зарядке тела, мы создаем на нем избыток электронов или недостаток в сравнении с их нормальным количеством, при котором тело не имеет заряда. При этом электроны берутся у другого тела или удаляются из заряжаемого тела, но не уничтожаются или создаются. Важно запомнить, что процесс зарядки и разрядки тел является процедурой перераспределения электронов, при этом общее их число не изменяется.

При соединении заряженного проводника с незаряженным, заряд перераспределяется между обоими телами. Допустим, что одно тело несет отрицательный заряд, его соединяют с незаряженным телом. Электроны заряженного тела под воздействием сил взаимного отталкивания переходят на незаряженное тело. При этом заряд первого тела уменьшается, заряд второго увеличивается, до тех пор, пока не наступит равновесие.

Элементарный заряд

Немецкий физик и физиолог Г. Гельмгольц обратил внимание на то, что заряды, которые переносят ионы при явлении электролиза, являются целыми, кратными некоторой величине, равной Кл. Каждый одновалентный ион переносит такой заряд. Любой двухвалентный ион несет заряд, равный Кл, и так далее. Гельмгольц сделал вывод о том, что заряд Кл является минимальным количеством электричества, которое существует в природе. Данный заряд получил название элементарного заряда.

Закон сохранения заряда

Закон сохранения заряда является фундаментальным законом природы. Он был установлен на основании обобщения экспериментальных данных. Подтвержден в 1843 г. английским физиком М. Фарадеем.

Формулировка закона: В любой замкнутой системе алгебраическая сумма зарядов – это неизменная величина, и не важно, какие процессы происходят в этой системе:

   

где N – количество зарядов.

Закон Кулона

На вопрос: С какими силами взаимодействуют неподвижные точечные заряды? Отвечает закон Кулона, который можно записать в виде формулы как:

   

где – сила, с которой заряд действует на заряд ; – радиус вектор, который проведен от второго заряда к первому; – электрическая постоянная; – диэлектрическая проницаемость вещества в котором находятся заряды. В соответствии с третьим законом Ньютона первый заряд действует на второй с силой равной по модулю и противоположной по направлению силе Обратите внимание, что заряды в формуле (2) точечные.

Примеры решения задач по теме «Электрический заряд»

Закон Кулона простым языком: формулировка, формула, применение

Взаимодействия электрических зарядов исследовали ещё до Шарля Кулона. В частности, английский физик Кавендиш в своих исследованиях пришёл к выводу, что неподвижные заряды при взаимодействии подчиняются определённому закону. Однако он не обнародовал своих выводов. Повторно закон Кулона был открыт французским физиком, именем которого был назван этот фундаментальный закон.

Рисунок 1. Закон Кулона

История открытия

Эксперименты с заряженными частицами проводили много физиков:

• Г. В. Рихман;
• профессор физики Ф. Эпинус;
• Д. Бернулли;
• Пристли;
• Джон Робисон и многие другие.

Все эти учёные очень близко подошли к открытию закона, но никому из них не удалось математически обосновать свои догадки. Несомненно, они наблюдали взаимодействие заряженных шариков, но установить закономерность в этом процессе было непросто.

Кулон проводил тщательные измерения сил взаимодействия. Для этого он даже сконструировал уникальный прибор – крутильные весы (см. Рис. 2).

Рис. 2. Крутильные весы

У придуманных Кулоном весов была чрезвычайно высокая чувствительность. Прибор реагировал на силы порядка 10

-9 Н. Коромысло весов, под действием этой крошечной силы, поворачивалось на 1^º. Экспериментатор мог измерять угол поворота, а значит и приложенную силу, пользуясь точной шкалой.

Благодаря гениальной догадке учёного, идея которой состояла в том, что при соприкосновении заряженного и незаряженного шариков, электрический заряд делился между ними поровну. На это сразу реагировали крутильные весы, коромысло которых поворачивалось на определённый угол. Заземляя неподвижный шарик, Кулон мог нейтрализовать на нём полученный заряд.

Таким образом, учёный смог уменьшать первоначальный заряд подвижного шарика кратное число раз. Измеряя угол отклонения после каждого деления заряда, Кулон увидел закономерность в действии отталкивающей силы, что помогло ему сформулировать свой знаменитый закон.

Формулировка

Кулон исследовал взаимодействие между шариками, ничтожно малых размеров, по сравнению с расстояниями между ними. В физике такие заряженные тела называются точечными. Другими словами, под определение точечных зарядов подпадают такие заряженные тела, если их размерами, в условиях конкретного эксперимента, можно пренебречь.

Для точечных зарядов справедливо утверждение: Силы взаимодействия между ними направлены вдоль линии, проходящей через центры заряженных тел. Абсолютная величина каждой силы прямо пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними (см. рис. 3). Данную зависимость можно выразить формулой:

|F₁|=|F₂|=(k_e*q₁*q₂) / r²

Рис. 3. Взаимодействие точечных зарядов

Остаётся добавить, что векторы сил направлены друг к другу для разноименных зарядов, и противоположно, в случае с одноимёнными зарядами. То есть между разноимёнными зарядами действует электрическое притяжение, а между одноимёнными – отталкивание.

Таким образом, закон Кулона описывает взаимодействие между двумя электрическими зарядами, которое лежит в основе всех электромагнитных взаимодействий.

Для того чтобы действовал сформулированный выше закон, необходимо выполнение следующий условий:

• соблюдение точечности зарядов;
• неподвижность заряженных тел;
• закон выражает зависимости между зарядами в вакууме.

Границы применения

Описанная выше закономерность при определённых условиях применима для описания процессов квантовой механики. Правда, закон Кулона формулируется без понятия силы. Вместо силы используется понятие потенциальной энергии кулоновского взаимодействия. Закономерность получена путём обобщения экспериментальных данных.

Следует отметить, что на сверхмалых расстояниях (при взаимодействиях элементарных частиц) порядка 10 — 18 м проявляются электрослабые эффекты. В этих случаях закон Кулона, строго говоря, уже не соблюдается. Формулу можно применять с учётом поправок.

Нарушение закона Кулона наблюдается и в сильных электромагнитных полях (порядка 10¹⁸ В/м), например поблизости магнитаров (тип электронных звёзд). В такой среде кулоновский потенциал уменьшается не обратно пропорционально, а экспоненциально.

Кулоновские силы подпадают под действие третьего закона Ньютона: F₁ = – F₂. Они используются для описания законов всемирного тяготения. В этом случае формула приобретает вид:

F = ( m₁* m₂ ) / r² , где m₁ и m₂ – массы взаимодействующих тел, а r – расстояние между ними.

Закон Кулона стал первым открытым количественным фундаментальным законом, обоснованным математически. Его значение в исследованиях электромагнитных явлений трудно переоценить. С момента открытия и обнародования закона Кулона началась эра изучения электромагнетизма, имеющего огромное значение в современной жизни.

Коэффициент k

Формула содержит коэффициент пропорциональности k, который для согласования соразмерностей в международной системе СИ. В этой системе единицей измерения заряда принято называть кулоном (Кл) – заряд, проходящий за 1 секунду сквозь проводник, где силы тока составляет 1 А.

Коэффициент k в СИ выражается следующим образом: k = 1/4πε₀, где ε₀ – электрическая постоянная:   ε₀ = 8,85 ∙10^-12 Кл²/Н∙м². Выполнив несложные вычисления, мы находим: k = 9×10⁹ H*м² / Кл². В метрической системе СГС k =1.

На основании экспериментов было установлено, что кулоновские силы, как и принцип суперпозиции электрических полей, в законах электростатики описывают уравнения Максвелла.

Если между собой взаимодействуют несколько заряженных тел, то в замкнутой системе результирующая сила этого взаимодействия равняется векторной сумме всех заряженных тел. В такой системе электрические заряды не исчезают – они передаются от тела к телу.

Закон Кулона в диэлектриках

Выше было упомянуто, что формула, определяющая зависимость силы от величины точечных зарядов и расстояния между ними, справедлива для вакуума. В среде сила взаимодействия уменьшается благодаря явлению поляризации. В однородной изотопной среде уменьшение силы пропорционально определённой величине, характерной для данной среды. Эту величину называют диэлектрической постоянной. Другое название –  диэлектрическая проницаемость. Обозначают её символом ε. В этом случае k = 1/4πεε₀.

Диэлектрическая постоянная воздуха очень близка к 1. Поэтому закон Кулона в воздушном пространстве проявляется так же как в вакууме.

Интересен тот факт, что диэлектрики могут накапливать электрические заряды, которые образуют электрическое поле. Проводники лишены такого свойства, так как заряды, попадающие на проводник, практически сразу нейтрализуются. Для поддержания электрического поля в проводнике необходимо непрерывно подавать на него заряженные частицы, образуя замкнутую цепь.

Применение на практике

Вся современная электротехника построена на принципах взаимодействия кулоновских сил.  Благодаря открытию Клоном этого фундаментального закона развилась целая наука, изучающая электромагнитные взаимодействия. Понятие термина электрического поля также базируется на знаниях кулоновских сил. Доказано, что электрическое поле неразрывно связано с зарядами элементарных частиц.

Грозовые облака не что иное как скопление электрических зарядов. Они притягивают к себе индуцированные заряды земли, в результате чего появляется молния. Это открытие позволило создавать эффективные молниеотводы для защиты зданий и электротехнических сооружений.

На базе электростатики появилось много изобретений:

• конденсатор;
• различные диэлектрики;
• антистатические материалы для защиты чувствительных электронных деталей;
• защитная одежда для работников электронной промышленности и многое другое.

На законе Кулона базируется работа ускорителей заряженных частиц, в частности, функционирование Большого адронного коллайдера (см. Рис. 4).

Рис. 4. Большой адронный коллайдер

Ускорение заряженных частиц до околосветовых скоростей происходит под действием электромагнитного поля, создаваемого катушками, расположенными вдоль трассы. От столкновения распадаются элементарные частицы, следы которых фиксируются электронными приборами. На основании этих фотографий, применяя закон Кулона, учёные делают выводы о строении элементарных кирпичиков материи.

Использованная литература:

1. Сивухин Д. В. Общий курс физики. — М.: Физматлит; Изд-во МФТИ, 2004.
2. Ландау Л. Д., Лифшиц Е. М. Теоретическая физика: Учеб. пособ.: Для вузов.
3. Ландсберг Г. С. Элементарный учебник физики. Том II. Электричество и магнетизм.

Видео по теме

Электрический заряд — Википедия

Электри́ческий заря́д (коли́чество электри́чества) — это физическая скалярная величина, определяющая способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии. Впервые электрический заряд был введён в законе Кулона в 1785 году. Электрический заряд не существует без носителя заряда.

Единица измерения электрического заряда в Международной системе единиц (СИ) — кулон — совокупный электрический заряд носителей элементарных электрических зарядов, проходящих через поперечное сечение проводника с током 1 А за время 1 с. Электрический заряд в один кулон очень велик. Если бы два тела, каждое из которых обладает электрическим зарядом (q₁ = q₂ = 1 Кл) расположили в вакууме на расстоянии 1 м, то они взаимодействовали бы с силой 9⋅10⁹H, то есть с силой равной по величине силе, с которой гравитация Земли притягивает предмет массой порядка 1 миллиона тонн.

Бенджамин Франклин проводит свой знаменитый опыт с летающим змеем, в котором доказывает, что молния — это электричество.

Ещё в глубокой древности было известно, что янтарь (др.-греч. ἤλεκτρον — электрон), потёртый о шерсть, притягивает лёгкие предметы. А уже в конце XVI века английский врач Уильям Гильберт назвал тела, способные после натирания притягивать лёгкие предметы, наэлектризованными.

В 1729 году Шарль Дюфе установил, что существует два рода зарядов. Один образуется при трении стекла о шёлк, а другой — смолы о шерсть. Поэтому Дюфе назвал заряды «стеклянным» и «смоляным» соответственно. Понятие о положительном и отрицательном заряде ввёл Бенджамин Франклин.

В начале XX века американский физик Роберт Милликен опытным путём показал, что электрический заряд дискретен, то есть заряд любого тела составляет целое кратное от элементарного электрического заряда.

Электростатикой называют раздел учения об электричестве, в котором изучаются взаимодействия и свойства систем электрических зарядов, неподвижных относительно выбранной инерциальной системы отсчета.

Величина электрического заряда (иначе, просто электрический заряд) может принимать и положительные, и отрицательные значения; она является численной характеристикой носителей заряда и заряженных тел. Эта величина определяется таким образом, что силовое взаимодействие, переносимое полем между зарядами, прямо пропорционально величине зарядов, взаимодействующих между собой частиц или тел, а направления сил, действующих на них со стороны электромагнитного поля, зависят от знака зарядов.

Электрический заряд любой системы тел состоит из целого числа элементарных зарядов, равных примерно 1,6⋅10⁻¹⁹Кл^[1] в системе СИ или 4,8⋅10⁻¹⁰ед. СГСЭ^[2]. Носителями электрического заряда являются электрически заряженные элементарные частицы. Наименьшей по массе устойчивой в свободном состоянии частицей, имеющей один отрицательный элементарный электрический заряд, является электрон (его масса равна 9,11⋅10⁻³¹ кг). Наименьшая по массе устойчивая в свободном состоянии античастица с положительным элементарным зарядом — позитрон, имеющая такую же массу, как и электрон^[3]. Также существует устойчивая частица с одним положительным элементарным зарядом — протон (масса равна 1,67⋅10⁻²⁷ кг) и другие, менее распространённые частицы. Выдвинута гипотеза (1964 г.), что существуют также частицы с меньшим зарядом (±⅓ и ±⅔ элементарного заряда) — кварки; однако они не выделены в свободном состоянии (и, по-видимому, могут существовать лишь в составе других частиц — адронов), в результате любая свободная частица несёт лишь целое число элементарных зарядов.

Электрический заряд любой элементарной частицы — величина релятивистски инвариантная. Он не зависит от системы отсчёта, а значит, не зависит от того, движется этот заряд или покоится, он присущ этой частице в течение всего времени её жизни, поэтому элементарные заряженные частицы зачастую отождествляют с их электрическими зарядами. В целом, в природе отрицательных зарядов столько же, сколько положительных. Электрические заряды атомов и молекул равны нулю, а заряды положительных и отрицательных ионов в каждой ячейке кристаллических решеток твёрдых тел скомпенсированы.

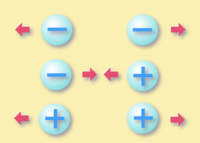Взаимодействие электрически заряженных тел: одноимённо заряженные тела отталкиваются, разноимённо — притягиваются друг к другу

Самое простое и повседневное явление, в котором обнаруживается факт существования в природе носителей электрических зарядов, — электризация тел при соприкосновении^[4]. Способность носителей электрических зарядов как к взаимному притяжению, так и к взаимному отталкиванию объясняется существованием двух различных видов электрических зарядов^[5]. Один вид электрического заряда называют положительным, а другой — отрицательным. Разноимённо заряженные тела притягиваются, а одноимённо заряженные — отталкиваются друг от друга.

При соприкосновении двух электрически нейтральных тел в результате трения заряды переходят от одного тела к другому. В каждом из них нарушается равенство суммы положительных и отрицательных зарядов, и тела заряжаются разноимённо.

При электризации тела через влияние в нём нарушается равномерное распределение носителей зарядов. Они перераспределяются так, что в одной части тела возникает избыток носителей положительных зарядов, а в другой — отрицательных. Если две эти части разъединить, то они будут заряжены разноимённо.

Закон сохранения электрического заряда[править | править код]

Совокупный электрический заряд замкнутой системы^[6] сохраняется во времени и квантуется — изменяется порциями, кратными элементарному электрическому заряду, то есть, другими словами, алгебраическая сумма электрических зарядов тел или частиц, образующих электрически изолированную систему, не изменяется при любых процессах, происходящих в этой системе.

В рассматриваемой системе могут образовываться новые электрически заряженные частицы, например, электроны — вследствие явления ионизации атомов или молекул, ионы — за счёт явления электролитической диссоциации и др. Однако, если система электрически изолирована, то алгебраическая сумма зарядов всех частиц, в том числе и вновь появившихся в такой системе, всегда сохраняется.

Закон сохранения электрического заряда — один из основополагающих законов физики. Он был впервые экспериментально подтверждён в 1843 году английским учёным Майклом Фарадеем и считается на настоящее время одним из фундаментальных законов сохранения в физике (подобно законам сохранения импульса и энергии). Всё более чувствительные экспериментальные проверки закона сохранения заряда, продолжающиеся и поныне, пока не выявили отклонений от этого закона.

В зависимости от концентрации свободных носителей электрических зарядов тела делятся на проводники, диэлектрики и полупроводники.

• Проводники — тела, в которых носители электрического заряда могут перемещаться по всему его объёму. Проводники делятся на две группы: 1) проводники первого рода (металлы), в которых перемещение носителей элементарных электрических зарядов (свободных электронов) не сопровождается химическими превращениями; 2) проводники второго рода (например, расплавленные соли, растворы кислот), в которых перенос носителей зарядов (положительных и отрицательных ионов) ведёт к химическим изменениям.
• Диэлектрики (например стекло, пластмасса) — тела, в которых практически отсутствуют свободные носители электрического заряда.
• Полупроводники (например, германий, кремний) занимают промежуточное положение между проводниками и диэлектриками.

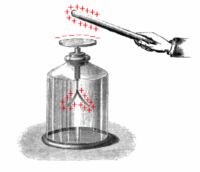Простейший электроскоп

Для обнаружения и измерения совокупного электрического заряда тела применяется электроскоп, который состоит из металлического стержня — электрода и подвешенных к нему двух листочков фольги. При прикосновении к электроду заряженным телом носители электрического заряда стекают через электрод на листочки фольги, листочки оказываются одноимённо заряженными и поэтому отклоняются друг от друга.

Также может применяться электрометр, в простейшем случае состоящий из металлического стержня и стрелки, которая способна вращаться вокруг горизонтальной оси. При соприкосновении электрически заряженного тела со стержнем электрометра носители электрического заряда распределяются по стержню и стрелке, и силы отталкивания, действующие между носителями одноимённых электрических зарядов на стержне и стрелке, вызывают её поворот. Для измерения малых электрических зарядов используются более чувствительные электронные электрометры.

1. ↑ Или, более точно, 1,602176487(40)⋅10⁻¹⁹ Кл.
2. ↑ Или, более точно, 4,803250(21)⋅10⁻¹⁰ ед СГСЭ.
3. ↑ Обычная для позитрона неустойчивость, связанная с аннигиляцией электрон-позитронной пары, при этом не рассматривается
4. ↑ Но это далеко не единственный способ электризации тел. Электрические заряды могут возникнуть, например, под действием света
5. ↑ Сивухин Д. В. Общий курс физики. — М.: Физматлит; Изд-во МФТИ, 2004. — Т. III. Электричество. — С. 16. — 656 с. — ISBN 5-9221-0227-3.
6. ↑ Электрически замкнутая система — это система, у которой через ограничивающую её поверхность не могут проникать электрически заряженные частицы (система, не обменивающаяся зарядами с внешними телами).

Электрический заряд. Закон сохранения заряда. Видеоурок. Физика 10 Класс

С электричеством вы сталкиваетесь постоянно. Вы видели молнию, вы освещаете комнату с помощью электрической лампочки, электрообогреватель выделяет тепло – все эти явления связаны с движением электрического заряда. С неподвижным электрическим зарядом вы тоже сталкивались, когда после расчесывания получали наэлектризованные волосы. Они разлетаются в разные стороны. Электрические заряды находятся без преувеличения везде, из них состоит любое вещество! На этом уроке мы выясним то, что нам известно про заряды.

Как известно, в природе встречаются заряды двух типов – положительные и отрицательные. Разноименные заряды притягиваются, одноименные – отталкиваются. Это взаимодействие происходит на любом расстоянии. Как же они тогда взаимодействуют? Для этого существует электрическое поле. Вокруг каждого заряда существует такое поле и если в него попадает еще один заряд, то он начинает «чувствовать» это поле: на него начинают действовать силы притяжения или отталкивания соответственно.

В природе есть много ненаблюдаемого. Например, мы не видим ветер, но видим, как он раскачивает ветви деревьев. Мы не видим температуру, но мы видим, как нагретые тела расширяются. По расширению, например, ртути в термометре, мы можем температуру измерять (см. рис. 1).

Рис. 1. Расширение ртути

Т. е. мы наблюдаем проявление чего-то и на основе этих наблюдений судим о том, чего непосредственно не наблюдаем. Заряд мы тоже изучаем по его проявлению. Мы не видим заряды, но наблюдаем их взаимодействие. Один заряд действует на другой на расстоянии через электрическое поле. Поле заряда – это пространство, где на другие заряды будет действовать сила.

Взаимодействие тел через поле нам уже знакомо. Тело, обладающее массой, создает вокруг себя поле – гравитационное, которое проявляется в действии на другое тело, обладающее массой. Их взаимодействие подчиняется закону всемирного тяготения (см. рис. 2).

Рис. 2. Взаимодействие массивных тел

---

Закон всемирного тяготения

Вокруг тела, обладающего массой, возникает гравитационное поле. Посредством этого поля массы взаимодействуют, притягиваются. Сила их притяжения пропорциональна величине каждой из масс и обратно пропорциональна квадрату расстояния между ними (см. рис. 3):

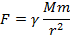
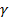 – константа, гравитационная постоянная, равна .

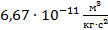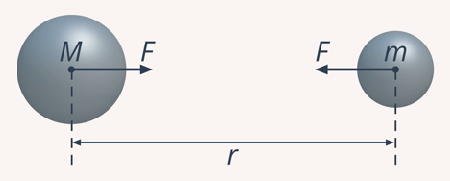
Рис. 3. Закон всемирного тяготения

Квадрат расстояния встречается во многих физических формулах, так что это позволяет говорить о законе, связывающем величину эффекта с квадратом расстояния от источника воздействия:

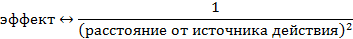
Эта пропорциональность справедлива для гравитационного, электрического, магнитного действия, силы звука, света, радиации, распространяющихся от источника. Связано это, конечно, с тем, что площадь поверхности сферы распространения эффекта увеличивается пропорционально квадрату расстояния (см. рис. 4). Это будет выглядеть естественным, если вспомнить, что площадь сферы пропорциональна квадрату радиуса:

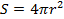
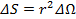
и тогда понятно, что сила действия от источника вдали от него должна распределяться по сфере всё большего радиуса.

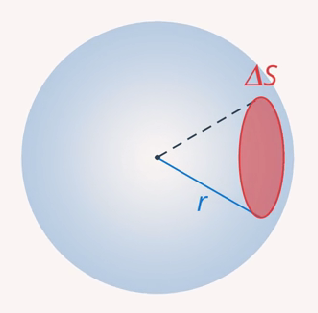
Рис. 4. Площадь сферы распространения эффекта увеличивается с увеличением радиуса сферы

---

 Итак, электрические заряды взаимодействуют через электрическое поле, которое они вокруг себя создают.

Электрический заряд – физическая величина, которая показывает способность тел участвовать в электромагнитных взаимодействиях.

Разные заряды будут взаимодействовать с разными силами. Измерить силы обычным способом – это легко разрешимая задача. По величине силы мы можем судить о величине заряда. Понятно, что чем больше заряды, тем сильнее они взаимодействуют. Но понятия больший или меньший заряд – нечеткие, а величину заряда нужно измерить точно.

Измерить заряд, используя уже известные единицы измерения, не получится. Мы не измерим заряд ни в метрах, ни, например, в килограммах. Это сущность, для которой нужна новая единица измерения. Единица измерения заряда – кулон.

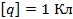
Обозначается заряд чаще всего буквой .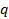

---

Единицы измерения заряда

Заряд проявляется в воздействии на другой заряд. Измерять его можно по этому воздействию, то есть измерять силу, с которой этот заряд действует на другой заряд на некотором расстоянии. Тогда единицы измерения заряда можно выразить через килограмм, метр и секунду. Так раньше и поступали в системе СГС. В системе СИ заряд удобно измерять в Кл (кулонах).

Процесс сообщения телу электрического заряда называется электризацией. Часто он происходит при трении тел друг о друга. Например, если потереть эбонитовую палочку о шерсть (см. рис. 5), то и она, и шерсть приобретут электрические заряды (эбонитовая палочка зарядится отрицательно, а шерсть – положительно).

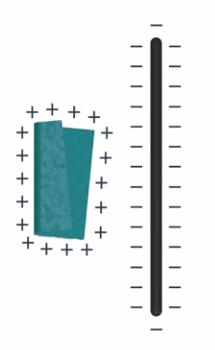
Рис. 5. Заряжание эбонитовой палочки

Проверить это просто: если поднести два наэлектризованных кусочка шерсти друг к другу, то они будут отталкиваться, так как заряжены зарядом одинакового знака (см. рис. 6).

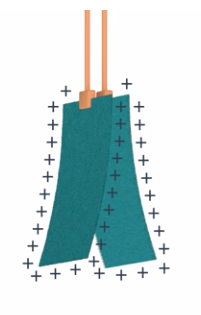
Рис. 6. Оба кусочка шерсти заряжены положительно

Из этого следует вывод, что заряды одного типа отталкиваются. Если расчесывать волосы, то расческа заряжается отрицательно, а волосы – положительно (см. рис. 7).

Рис. 7. Заряжание волос

Собственно, поэтому, после расчесывания, волосы разлетаются в разные стороны (каждый волос заряжен положительно и отталкивается от остальных (см. рис. 8)).

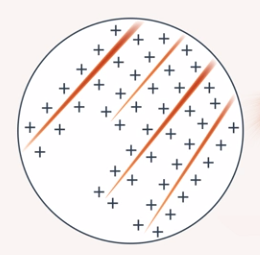
Рис. 8. Каждый волос заряжен положительно

Путем простых опытов мы обнаружили, что существует два типа зарядов, которые взаимодействуют следующим образом: однотипные заряды отталкиваются, разнотипные – притягиваются.

---

Как определить, какой именно заряд приобретает тело при трении

Мы проводим много опытов с расческами, тканями и палочками, чтобы они приобретали электрический заряд. Одна и та же шерсть заряжается отрицательно при трении о стекло и положительно при трении о полиэтилен. Как можно заранее знать, какой тип заряда приобретает материал? Есть ли какое-то правило? Можно заниматься практическим определением (такие опыты были проведены много раз), и были получены трибоэлектрические ряды некоторых материалов (см. рис. 9), в которых любой взятый материал при трении с материалом, расположенным ниже него в ряду, заряжается положительно, и наоборот. Разные экспериментаторы получали свои ряды, и на рисунке их можно увидеть.

Рис. 9. Трибоэлектрические ряды

---

Сейчас известно, что носителями двух типов заряда являются элементарные частицы: электрон и протон. Элементарные частицы неделимы, поэтому заряд одной частицы, равный 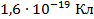, – это минимальный заряд, обозначается часто  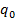или 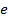. Эти частицы имеют массу:  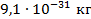и 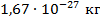 для электрона и протона соответственно.

Что же происходит с телами при электризации? Представьте себе два одинаковых металлических шара, но только один из них заряжен отрицательно, а другой не заряжен (см. рис. 10).

Рис. 10. Заряженный и незаряженный шары

Известно, что все тела состоят из атомов, а те, в свою очередь, состоят из протонов, нейтронов, электронов (см. рис. 11).

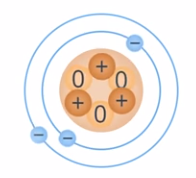
Рис. 11. Атом

Протоны заряжены положительно, электроны – отрицательно. Будем называть их элементарными зарядами, то есть неделимыми. Так вот, в большинстве случаев в атоме количество протонов равняется количеству электронов и получается, что они полностью компенсируют друг друга и в целом атом нейтрален. Важно понимать, что в атоме заряды никуда не исчезают, там по-прежнему есть положительные и отрицательные частицы, просто их действие на далекие предметы полностью компенсируется (см. рис. 12).

Рис. 12. Действие частиц компенсировано

А вот в шаре, заряженном отрицательно, электронов больше, чем протонов, поэтому в целом в теле количество отрицательных элементарных зарядов больше, чем количество положительных элементарных зарядов, и тело заряжено отрицательно (см. рис. 13).

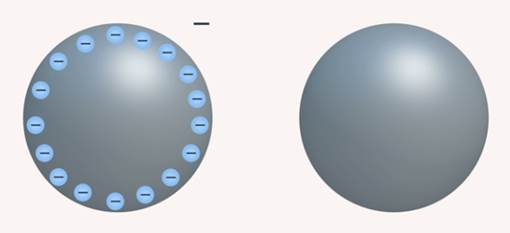
Рис. 13. Количество электронов в заряженном шаре

Заряд макроскопического тела (состоящего из большого количества атомов) – это величина, показывающая разность между положительными и отрицательными зарядами в теле. Если это количество одинаково, то заряд нулевой. Величина элементарного заряда известна и равна 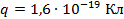. Соответственно, заряд протона договорились считать положительным 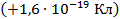, а заряд электрона – отрицательным .

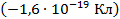Что же происходит при трении тел друг о друга, например пластика о шерсть? Электроны с внешних оболочек атомов, входящих в состав шерсти, «перепрыгивают» на пластмассу (см. рис. 14).

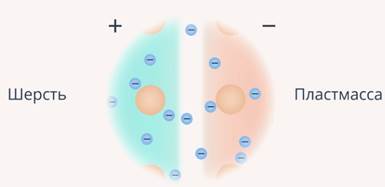
Рис. 14. Движение электронов при трении

Получается, что в шерсти становится меньше отрицательных электронов и она заряжается положительно, а пластмасса – отрицательно, так как в ней появляется избыточное количество электронов. Можно даже сказать: если при контакте заряд одного тела увеличивается, то у другого уменьшается.

Что касается искр между людьми, то это происходит, если хотя бы один человек «заряжен» (допустим, человек ходил по шерстяному ковру, при трении подошвами по нему), и если другой человек не заряжен также, то заряд будет перетекать с одного человека на другого, иногда это перетекание может быть даже по воздуху, в таком случае и появляется искра. Стоит отметить, что искра появляется только благодаря движению электронов, протоны находятся в ядрах атомов, они менее подвижны и не могут покидать атомов отличие от электронов.

Зарядить тело можно и без контакта – через влияние электрическим полем. Представьте себе незаряженный шар, к которому подносят положительно заряженную палочку – разноименные заряды притягиваются, поэтому электроны, которые были в шаре, притянутся к положительно заряженной палочке и скопятся в той части шара, которая ближе к ней (см. рис. 15).

Рис. 15. Влияние положительно заряженной палочки на электроны

---

Почему незаряженные частицы фольги притягиваются к заряженной расческе?

Оказывается, незаряженный кусочек фольги будет притягиваться к заряженной расческе. Как же так? В целом кусочек фольги электрически нейтрален. Давайте посмотрим, что произойдет, если мы поднесем отрицательно заряженную расческу к кусочку фольги – отрицательно заряженная расческа притягивает к себе положительный заряд и отталкивает отрицательный. Поэтому электроны отодвинутся дальше от границы, а сторона, которая находится ближе к расческе, будет заряжена положительно (см. рис. 16) и притяжение будет сильнее, чем отталкивание, потому что положительная часть фольги находится ближе к расческе.

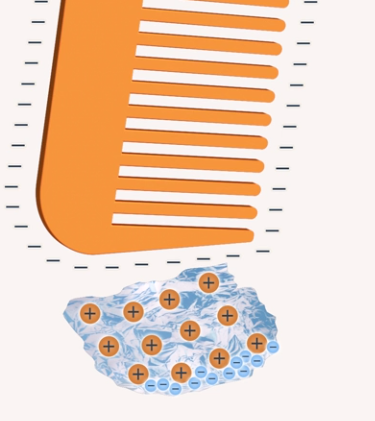
Рис. 16. Расположение электронов в фольге при поднесении расчески

Так как основным принципом физики является принцип, по которому «ничто не исчезает бесследно», то выполняется закон сохранения электрического заряда: в электрически замкнутой системе алгебраическая сумма зарядов неизменна. Электрически замкнутая система – это модель. Это такая система, которую не покидают и не пополняют электрические заряды.

Пылинка, имеющая положительный заряд 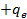, потеряла электрон. Каким стал заряд пылинки?

В задаче описано тело, теряющее заряд. По закону сохранения заряд не исчезает бесследно, в электрически замкнутой системе суммарный заряд не изменяется. Выберем, какую систему считать электрически замкнутой. Пылинку покидает электрон, поэтому саму пылинку считать электрически замкнутой нельзя. Замкнутой можно считать систему, в которую входит пылинка и электрон (см. рис. 17).

Рис. 17. Замкнутая система

По закону сохранения заряда заряд системы до потери пылинкой электрона равен заряду после потери. Запишем это: заряд пылинки был 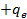. После взаимодействия заряд системы состоит из нового заряда пылинки и заряда электрона и равен заряду системы до потери:

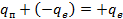
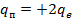
где 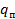 – новый заряд пылинки. Заряд пылинки стал равен .

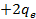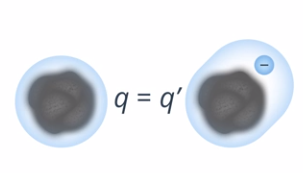
Рис. 18. Заряд системы до и после потери электрона

Ответ: заряд пылинки стал равен .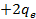

На этом наш урок окончен. Спасибо за внимание!

 

Список литературы

1. Мякишев Г.Я., Буховцев Б.Б., Сотский Н.Н. Физика: учеб. для общеобразоват. учреждений. Базовый и профильный уровни. 19-е издание. – М.: Просвещение, 2010.

2. Касьянов В.А. Физика. 10 кл.: Профильный уровень. 13-е издание. – М.: 2013 – 432 с.

 

Дополнительные рекомендованные ссылки на ресурсы сети Интернет

1. Интернет-сайт «Медицинская энциклопедия» (Источник)

2. Интернет-сайт nscience.ru (Источник)  

3. Интернет-сайт «Класс!ная физика» (Источник)

4. Интернет-сайт «Электрик PRO» (Источник)

 

Домашнее задание

1. Сформулируйте закон сохранения электрического заряда.

2. Чему равен заряд электрона?

3. Верно ли утверждение: «Одноименные заряды отталкиваются»?

Основные законы и формулы

58

ЭЛЕКТРОСТАТИКА. ПОСТОЯННЫЙ ТОК

Закон Кулона:

,

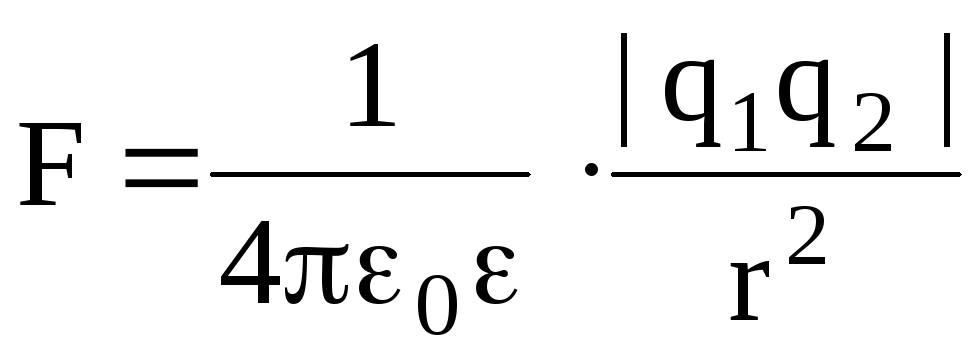где F – сила взаимодействия двух точечных зарядов q₁ и q₂; r – расстояние между зарядами;  — диэлектрическая проницаемость среды; ₀ — электрическая постоянная

.

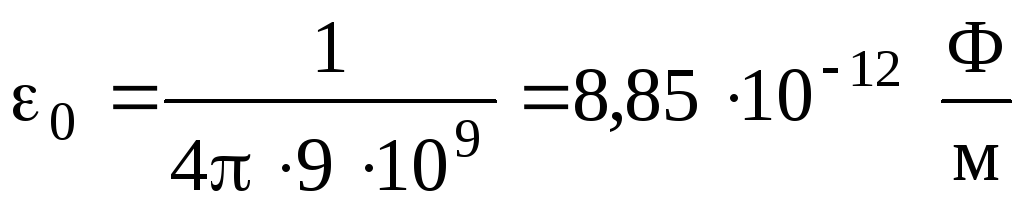Закон сохранения заряда:

,

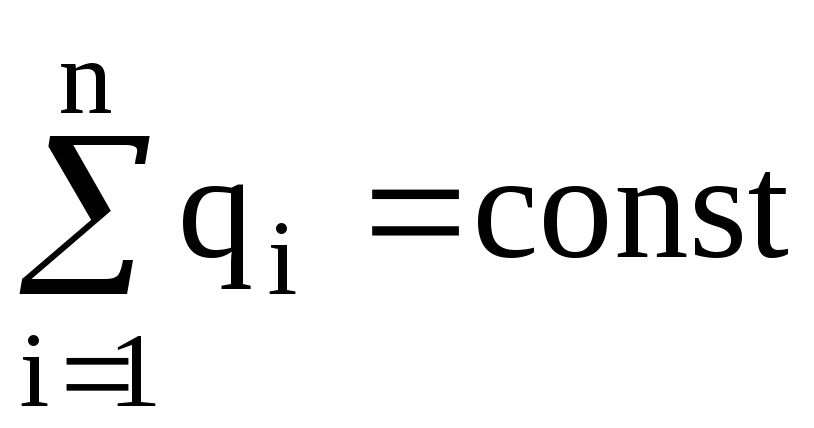где 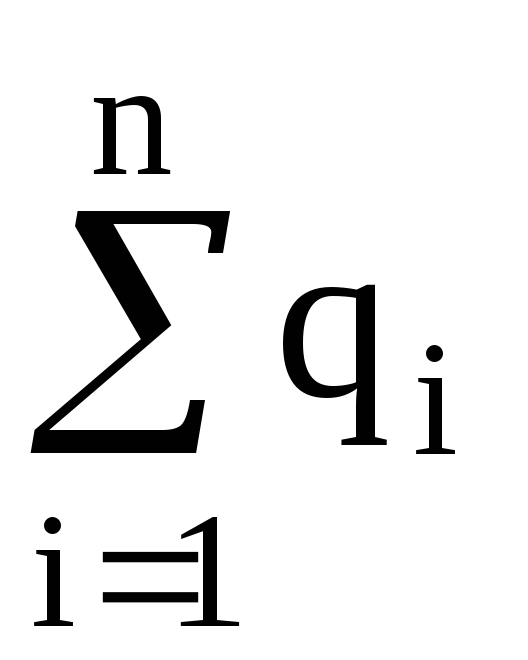– алгебраическая сумма зарядов, входящих в изолированную систему;n – число зарядов.

Напряженность и потенциал электростатического поля:

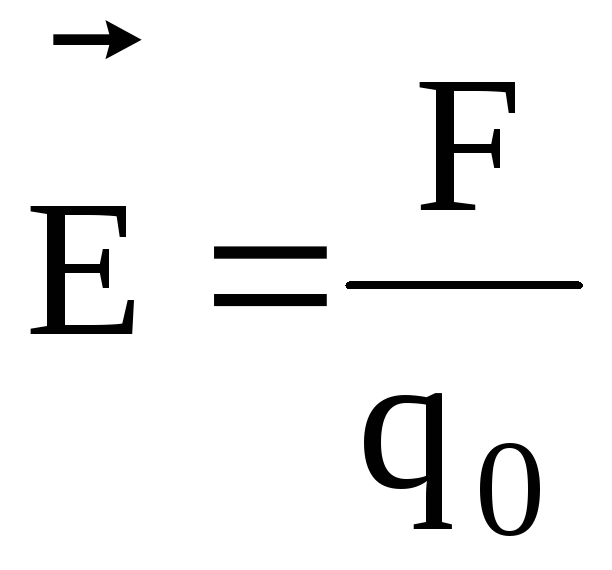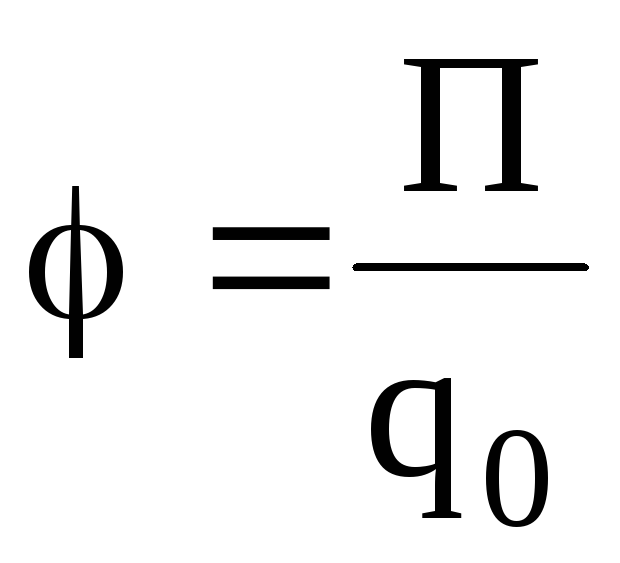; , или,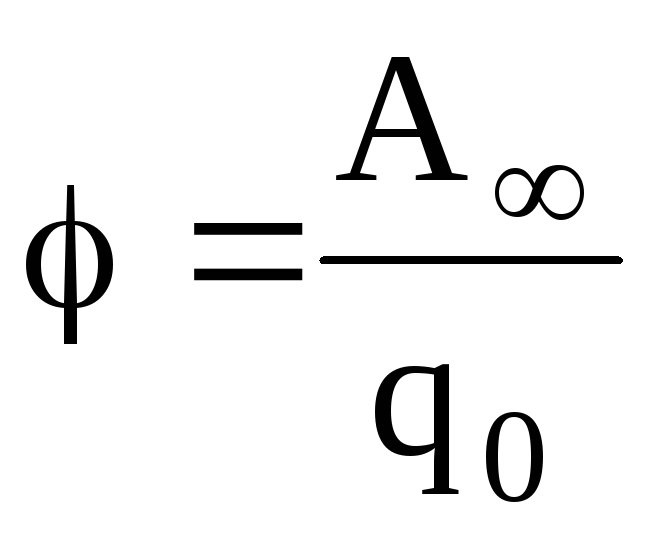

где – сила, действующая на точечный положительный зарядq₀, помещенный в данную точку поля; П – потенциальная энергия заряда; А_∞ — работа, затраченная на перемещение заряда q₀ из данной точки поля в бесконечность.

Поток вектора напряженности электрического поля:

а) через произвольную поверхность S, помещенную в неоднородное поле:

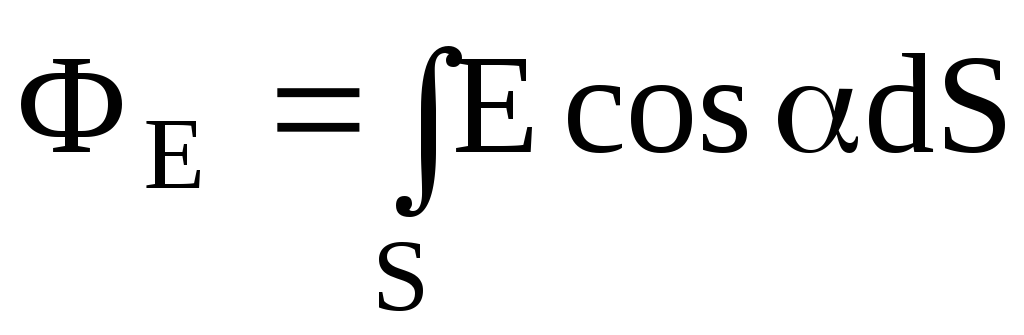, или ,

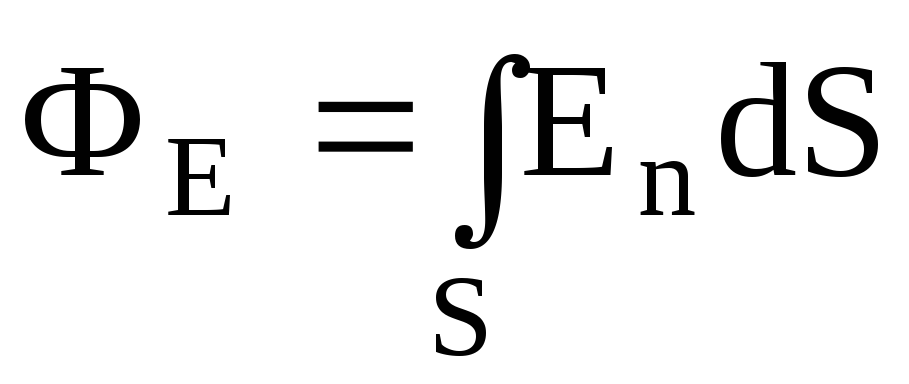где  – угол между вектором напряженности и нормальюк элементу поверхности;dS – площадь элемента поверхности; E_n – проекция вектора напряженности на нормаль;

б) через плоскую поверхность, помещенную в однородное электрическое поле:

.

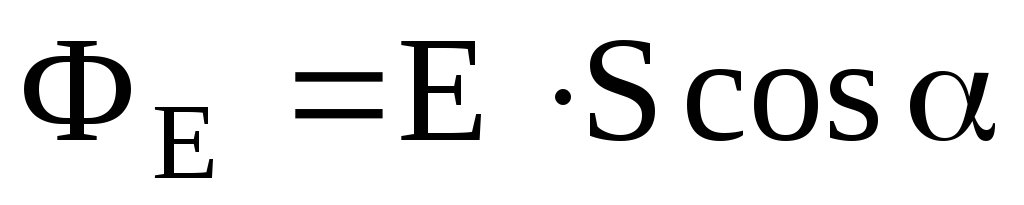Поток вектора напряженности через замкнутую поверхность –

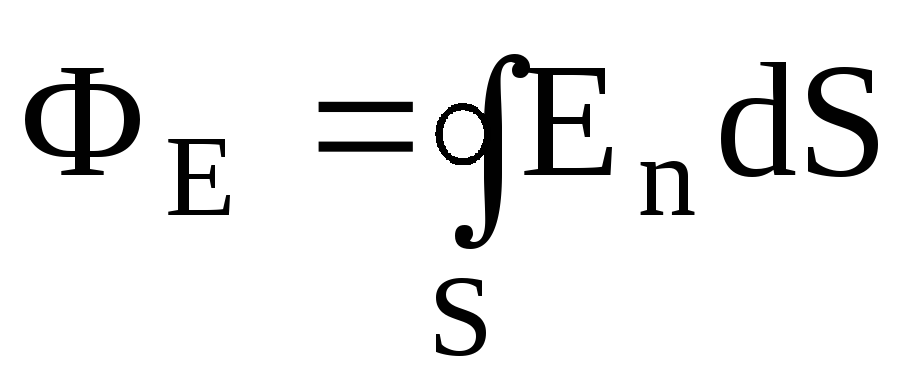
(интегрирование ведется по всей поверхности).

Теорема Остроградского-Гаусса. Поток вектора напряженностичерез любую замкнутую поверхность, охватывающую зарядыq1,q2, …,qn, –

,

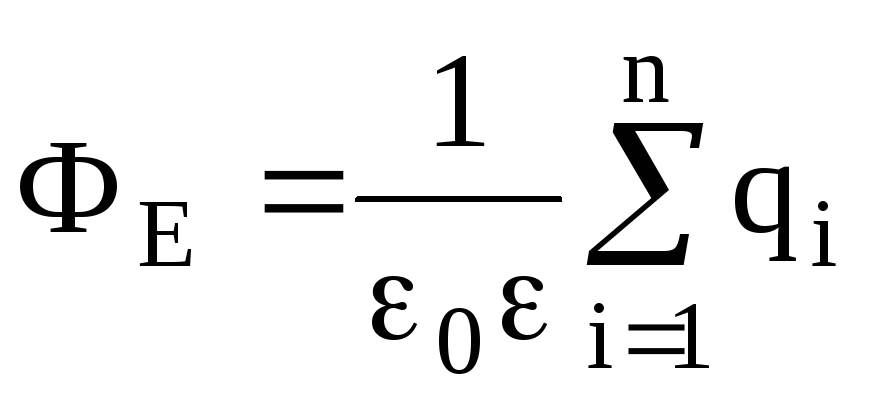где 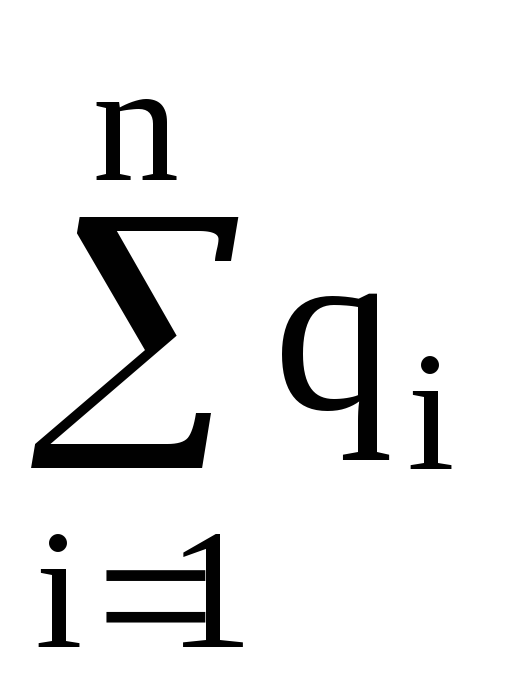– алгебраическая сумма зарядов, заключенных внутри замкнутой поверхности; n – число зарядов.

Напряженность электростатического поля, создаваемого точечным зарядом q на расстоянии r от заряда, –

.

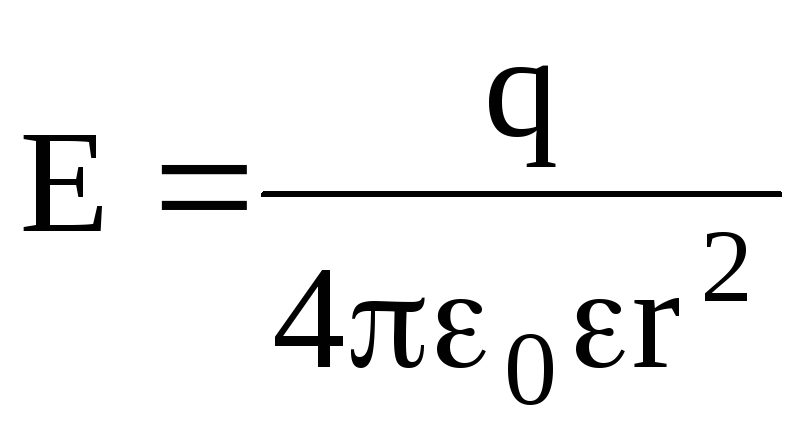Напряженность электрического поля, создаваемого сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы такова:

внутри сферы (r R) Е=0;

на поверхности сферы (r=R) ;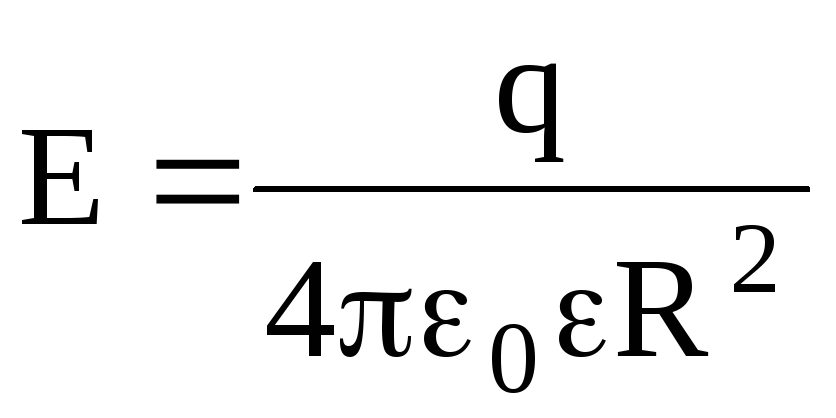

вне сферы (r  R) .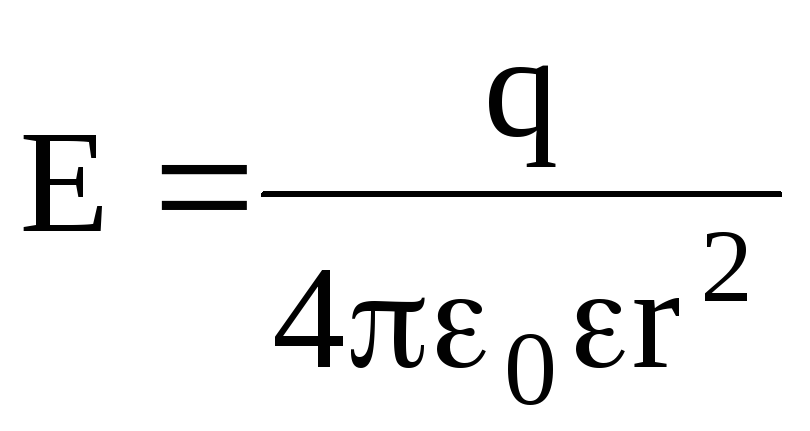

Принцип суперпозиции (наложения) электростатических полей, согласно которому напряженность результирующего поля, созданного двумя (и более) точечными зарядами, равна векторной (геометрической) сумме напряженностей складываемых полей, выражается формулой

.

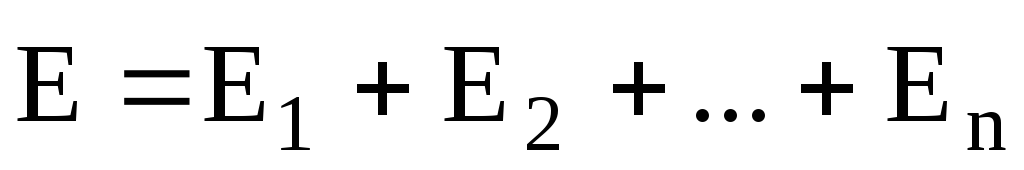В случае двух электрических полей с напряженностями иабсолютное значение вектора напряженности составляет

,

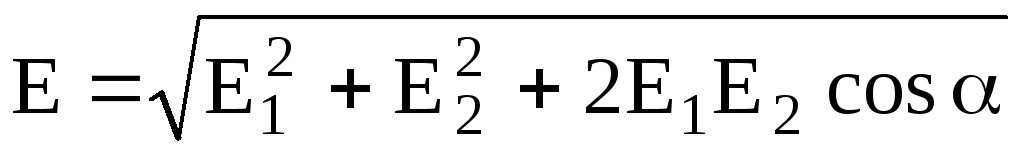где  — угол между векторами 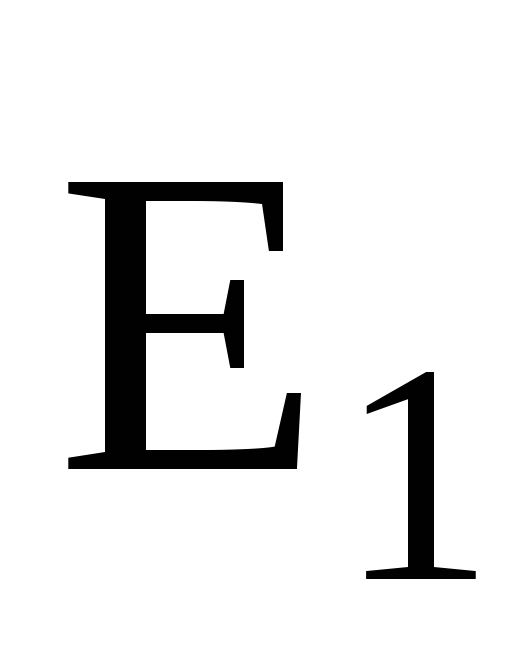и.

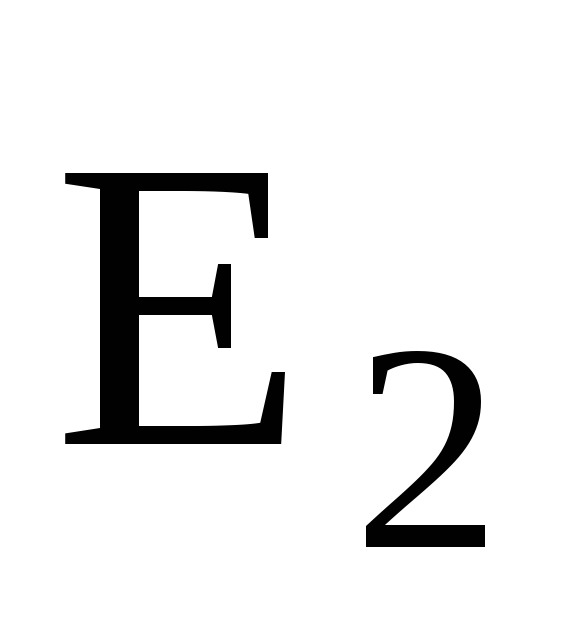Напряженность поля, создаваемого бесконечно длинной и равномерно заряженной нитью (или цилиндром) на расстоянии r от ее оси, –

,

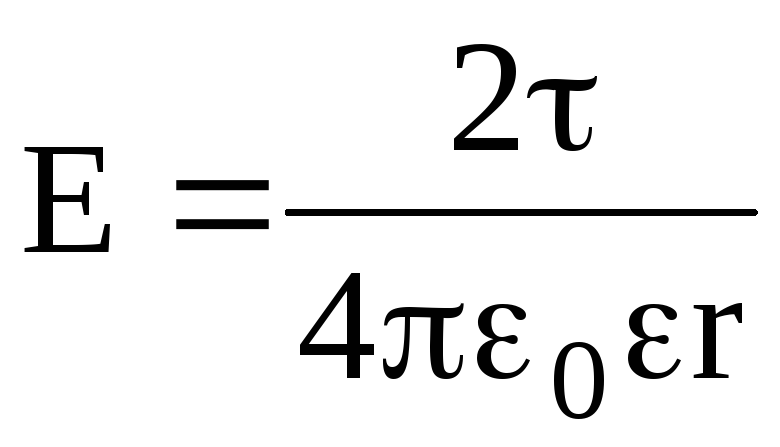где  — линейная плотность заряда.

Линейная плотность заряда есть величина, равная его отношению к длине нити (цилиндра):

.

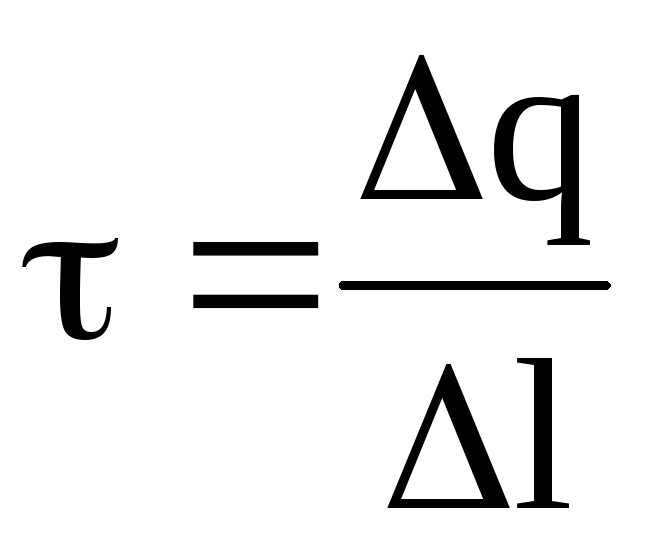Напряженность поля, создаваемого бесконечной равномерно заряженной плоскостью, –

,

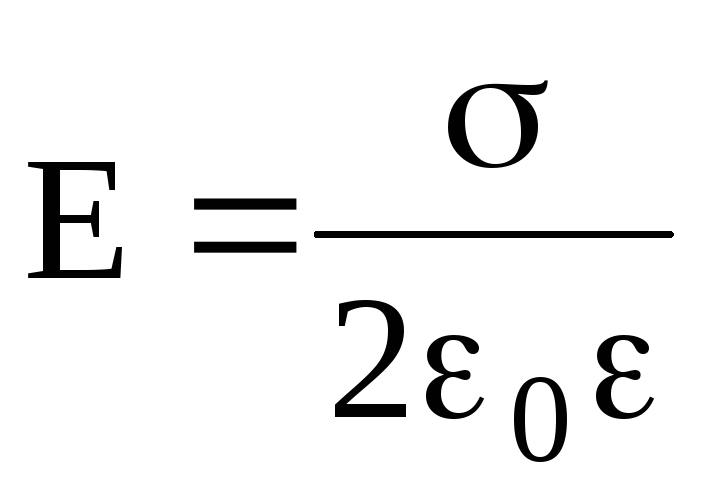где  — поверхностная плотность заряда.

Поверхностная плотность заряда есть величина, равная отношению заряда, распределенного по поверхности, к ее площади:

.

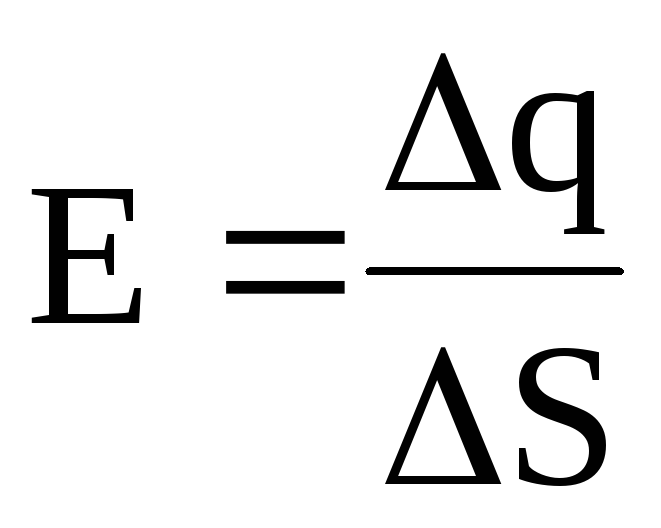Напряженность поля, создаваемого двумя бесконечными и параллельными плоскостями, заряженными равномерно и разноименно, с одинаковой по абсолютному значению поверхностной плотностью заряда (поле плоского конденсатора) –

.

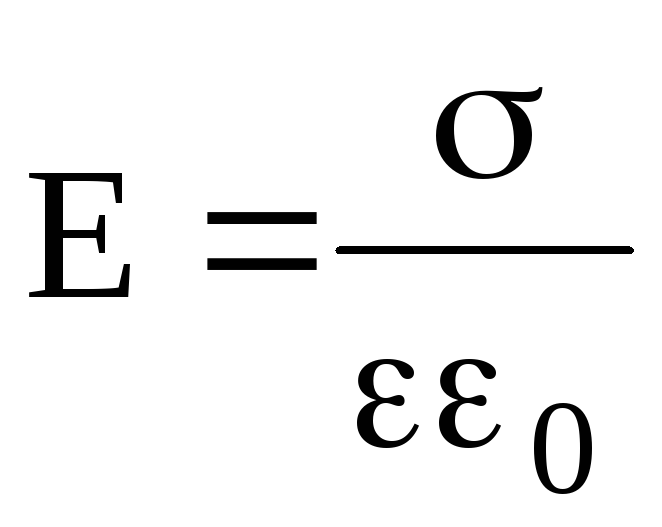Приведенная формула справедлива при вычислении напряженности поля между пластинами плоского конденсатора (в его средней части) только в том случае, если расстояние между пластинами намного меньше линейных размеров пластин конденсатора.

Электрическое смещение связано с напряженностьюэлектрического поля соотношением

,

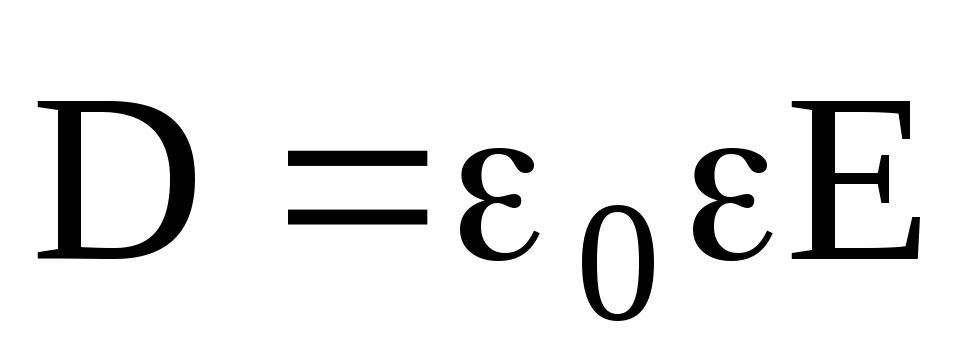которое справедливо только для изотропных диэлектриков.

Потенциал электрического поля есть величина, равная отношению потенциальной энергии и точечного положительного заряда, помещенного в данную точку поля:

.

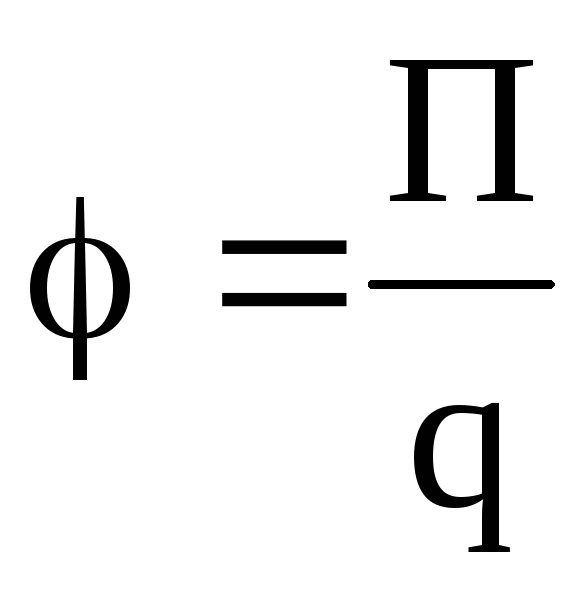Иначе говоря, потенциал электрического поля есть величина, равная отношению работы сил поля по перемещению точечного положительного заряда из данной точки поля в бесконечность к величине этого заряда:

.

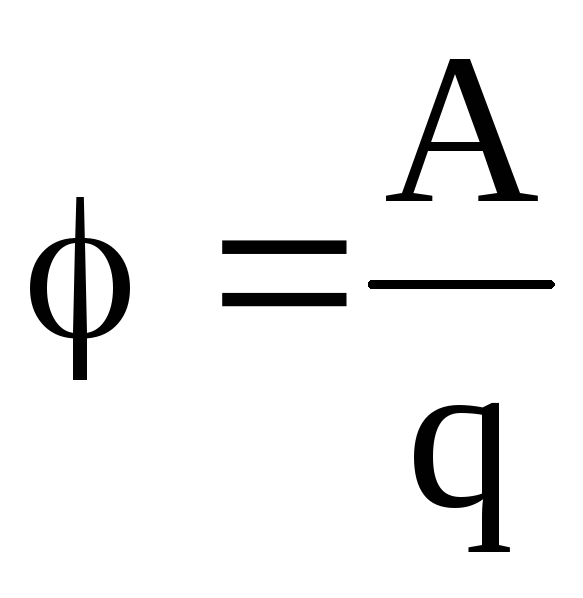Потенциал электрического поля в бесконечности условно принят равным нулю.

Потенциал электрического поля, создаваемый точечным зарядом q на

расстоянии r от заряда, –

.

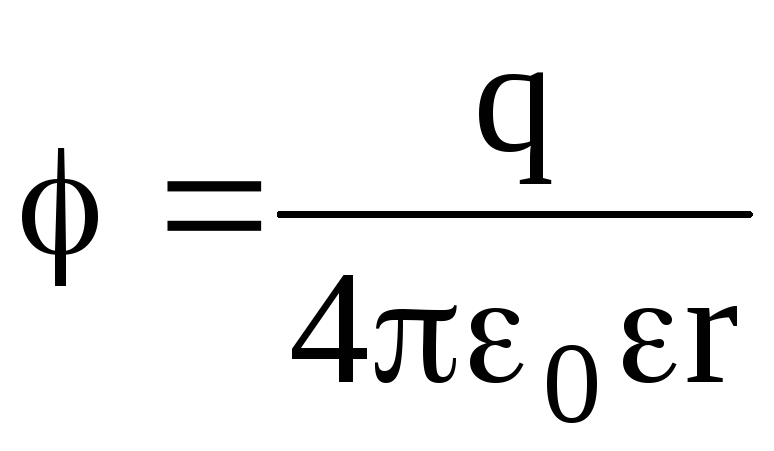Потенциал электрического поля, создаваемый металлической сферой, имеющей радиус R и несущей заряд q, на расстоянии r от центра сферы таков:

внутри сферы (r  R) ;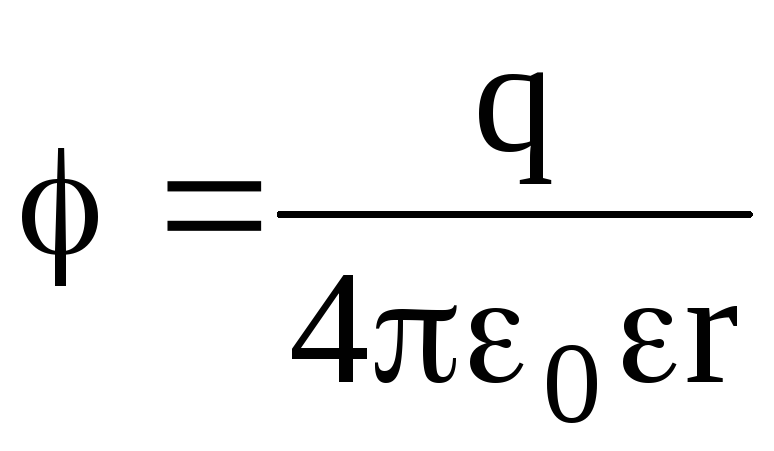

на поверхности сферы (r = R) ;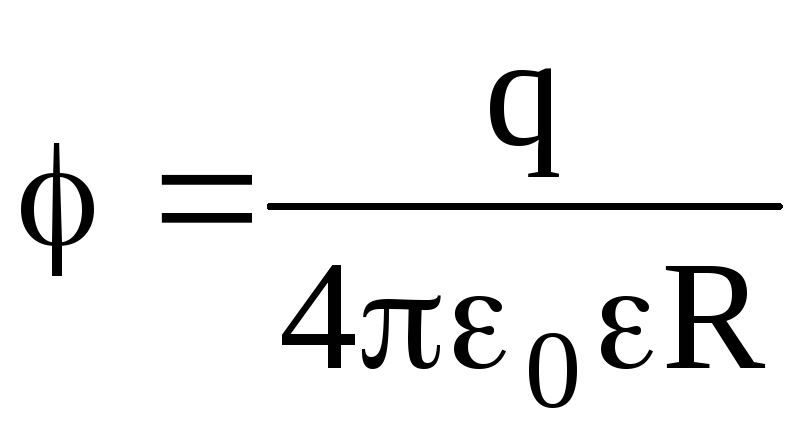

вне сферы (r  R) .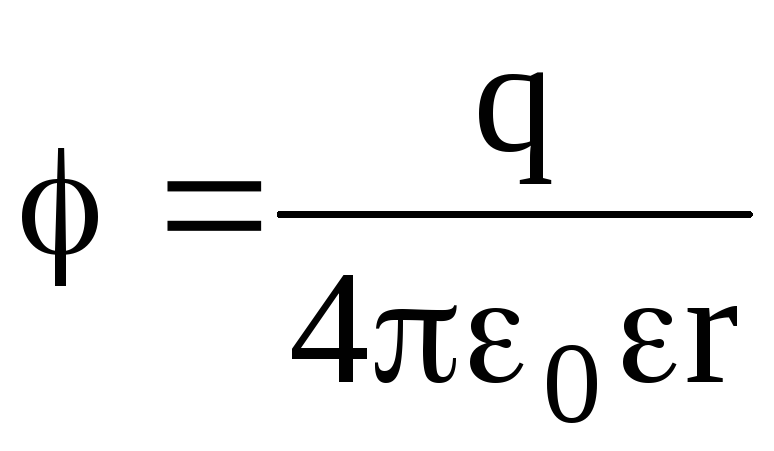

Во всех формулах, приведенных для потенциала заряженной сферы,  есть диэлектрическая проницаемость однородного безграничного диэлектрика, окружающего сферу.

Потенциал электрического поля, образуемого системой n точечных зарядов в данной точке в соответствии с принципом суперпозиции электрических полей, равен алгебраической сумме потенциалов 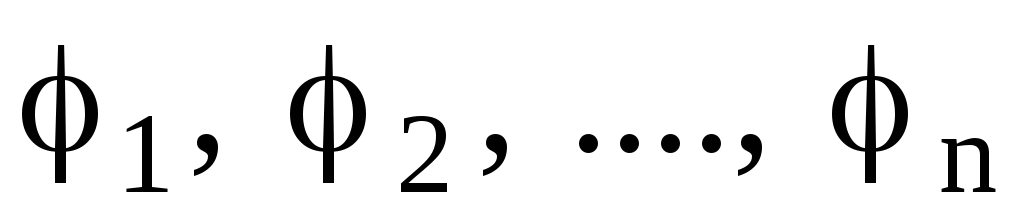, создаваемых отдельными точечными зарядами:

.

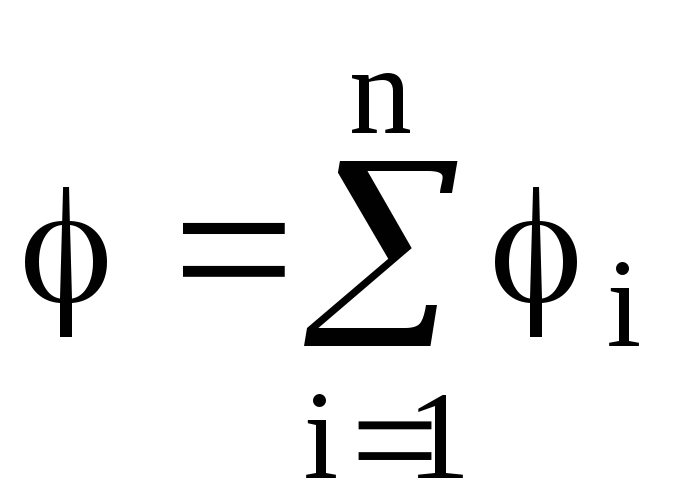Энергия W взаимодействия системы точечных зарядов 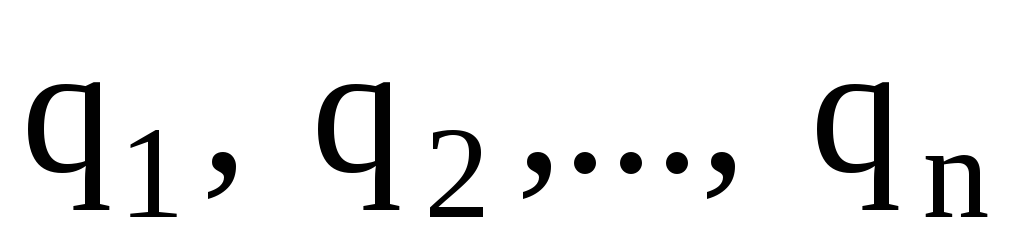определяется работой, которую эта система может совершить при удалении их относительно друг друга в бесконечность, и выражается формулой

,

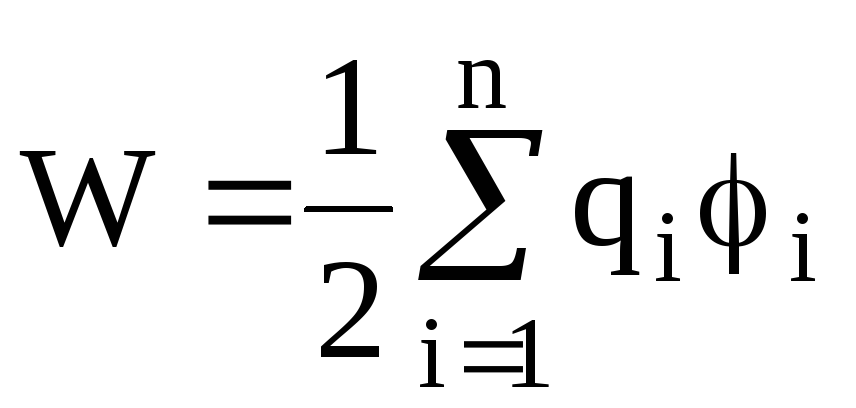где — потенциал поля, создаваемый всеми (n-1) зарядами (за исключением i-го) в точке, где находится заряд .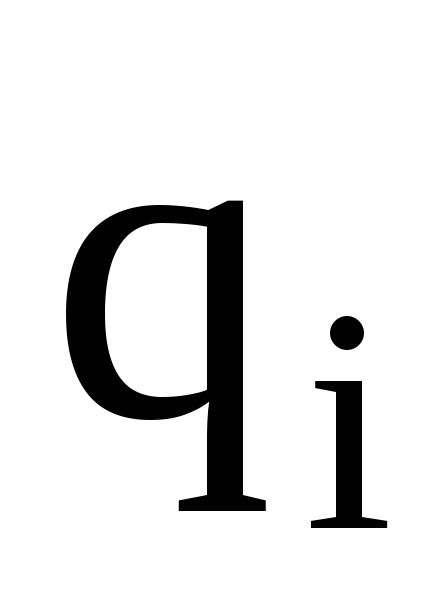

Потенциал связан с напряженностью электрического поля соотношением

.

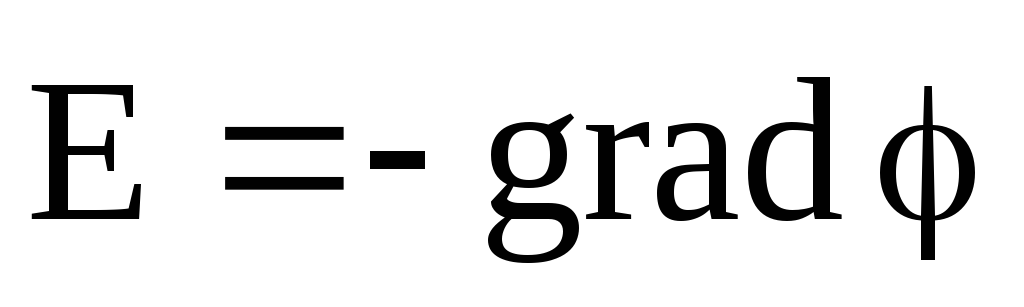В случае электрического поля, обладающего сферической симметрией, эта связь выражается формулой

,

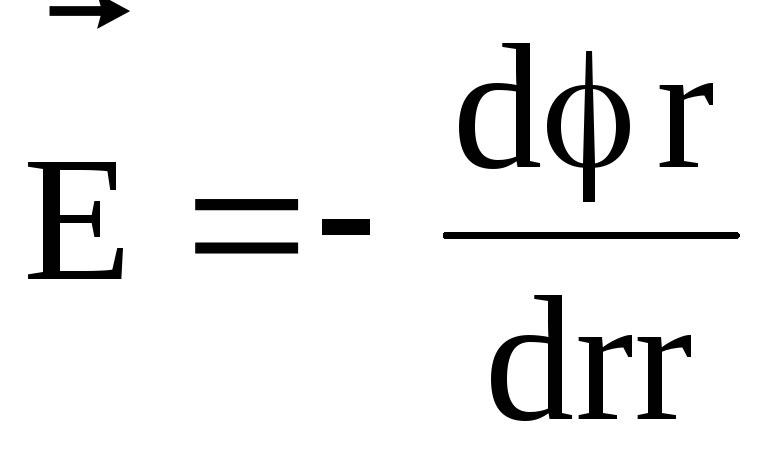или в скалярной форме

.

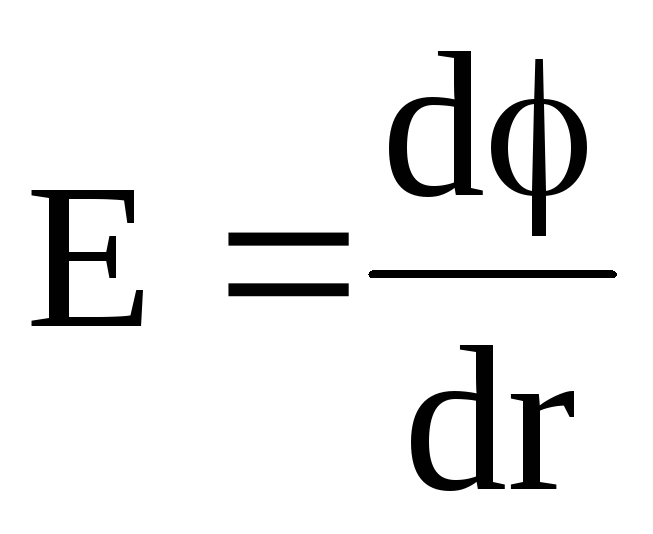В случае однородного поля, т.е. поля, напряженность которого в каждой его точке одинакова как по абсолютному значению, так и по направлению, –

,

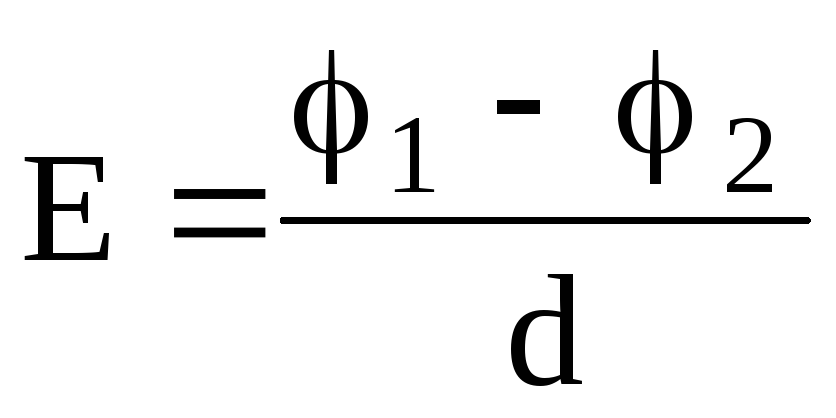где ₁ и ₂ – потенциалы точек двух эквипотенциальных поверхностей; d — расстояние между этими поверхностями вдоль электрической силовой линии.

Работа, совершаемая электрическим полем при перемещении точечного заряда q из одной точки поля, имеющей потенциал ₁, в другую, имеющую потенциал ₂, равна

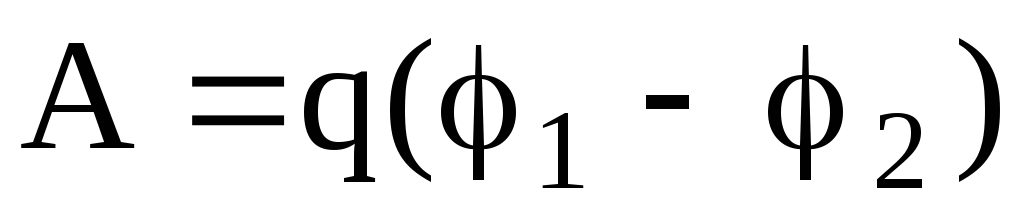, или ,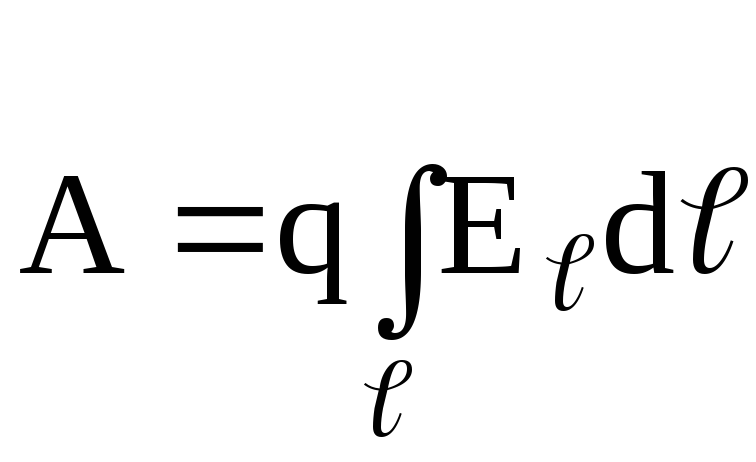

где E – проекция вектора на направление перемещения;— перемещение.

В случае однородного поля последняя формула принимает вид

,

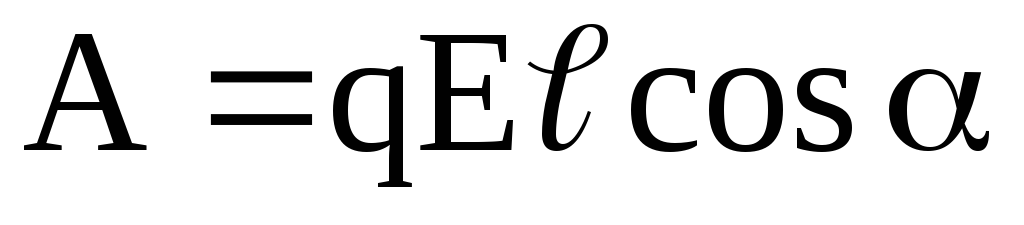где 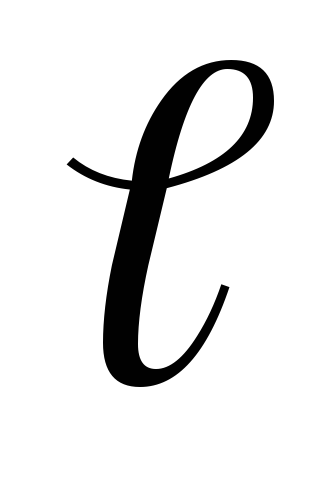– перемещение; — угол между направлениями вектора и перемеще-ния.

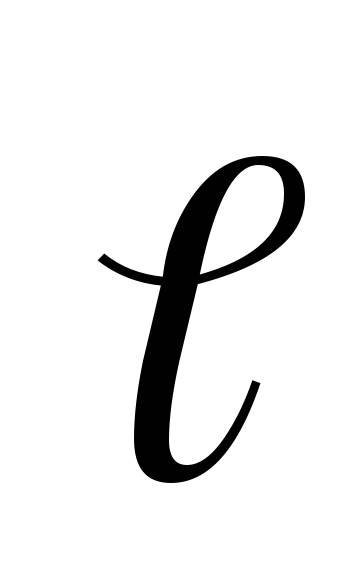Диполь есть система двух точечных (равных по абсолютному значению и противоположных по знаку) зарядов, находящихся на некотором расстоянии друг от друга.

Электрический момент диполя есть вектор, направленный от отрицательного заряда к положительному, равный произведению заряда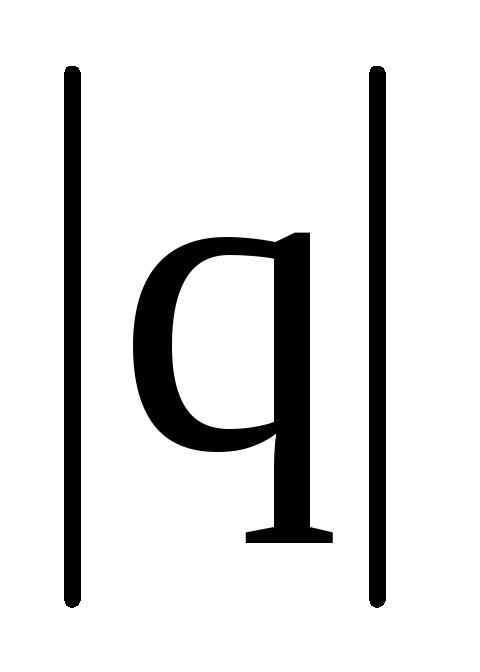на вектор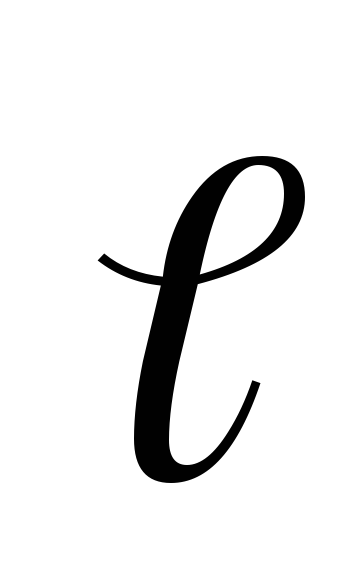, проведенный от отрицательного заряда к положительному, и называемый плечом диполя, т.е.

.

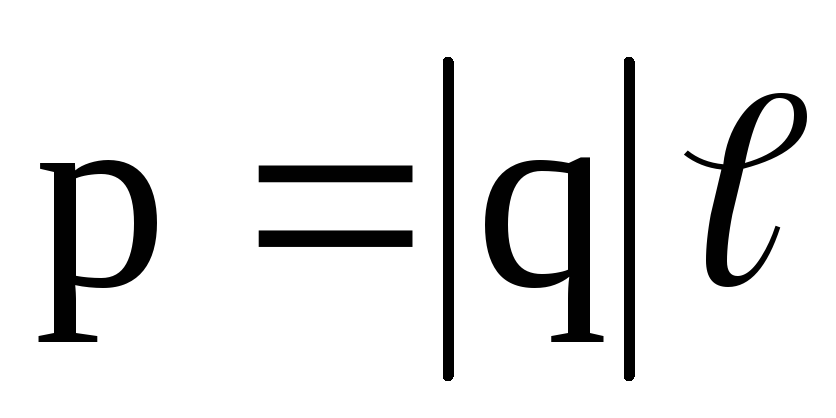Диполь называется точечным, если его плечо 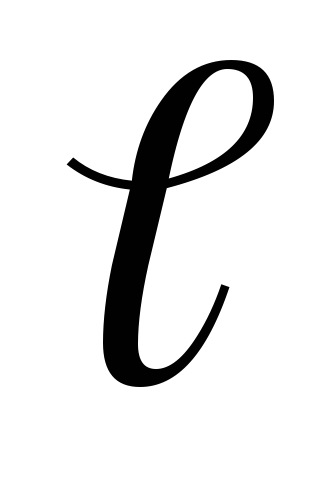намного меньше расстоянияr от центра диполя до точки, в которой нас интересует действие диполя ( r), см. рис. 1.

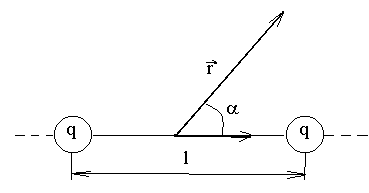
Рис. 1

Напряженность поля точечного диполя:

,

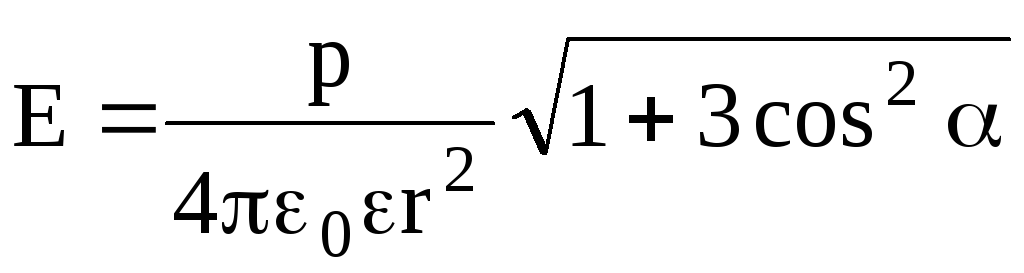где р – электрический момент диполя; r – абсолютное значение радиус-вектора, проведенного от центра диполя к точке, напряженность поля в которой нас интересует;  — угол между радиус-вектором 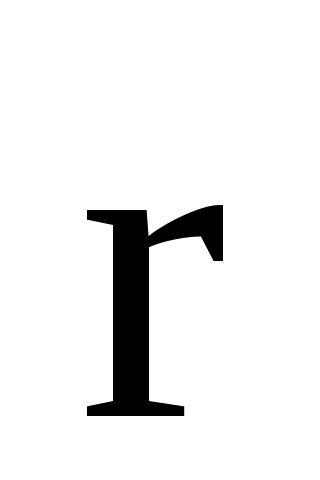и плечом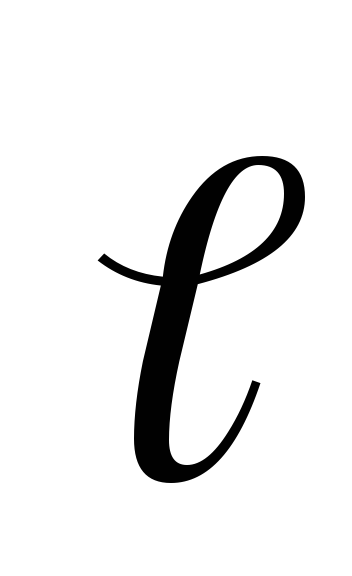диполя.

Напряженность поля точечного диполя в точке, лежащей на оси диполя

(=0), находится по формуле

;

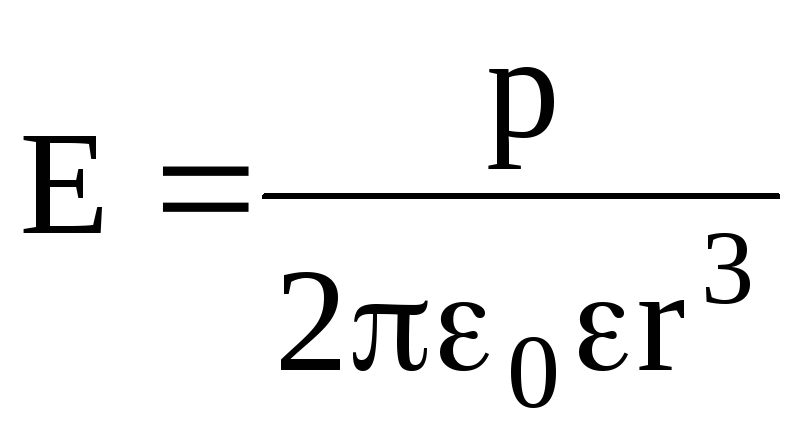в точке, лежащей на перпендикуляре к плечу диполя, восстановленном из его середины , – по формуле

.

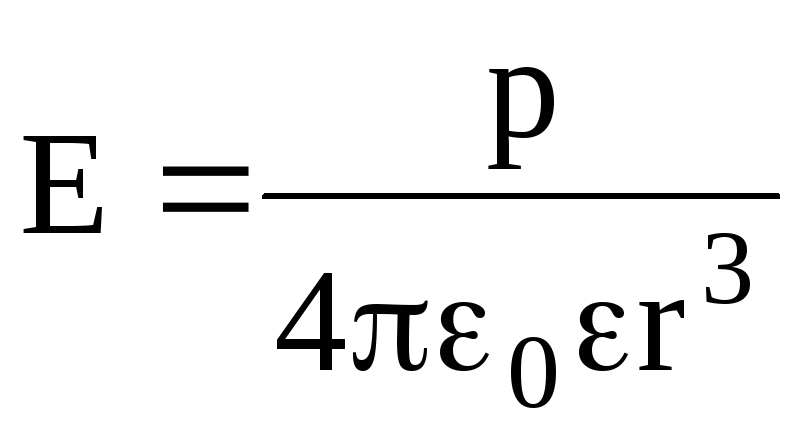Потенциал поля точечного диполя в точке, лежащей на оси диполя (=0), составляет

,

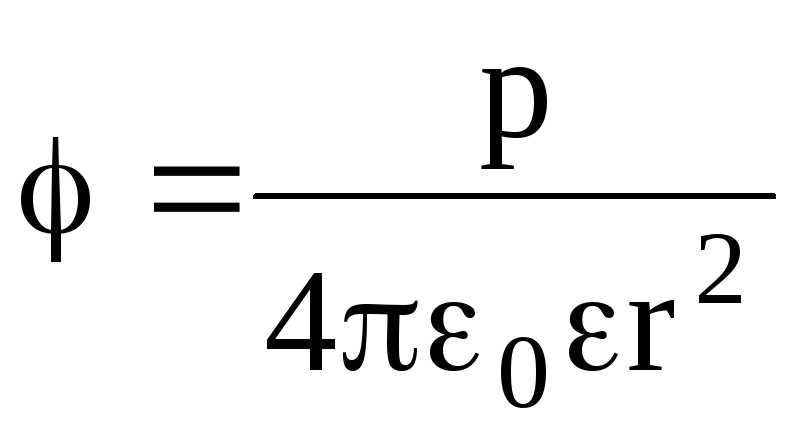а в точке, лежащей на перпендикуляре к плечу диполя, восстановленном из его середины , –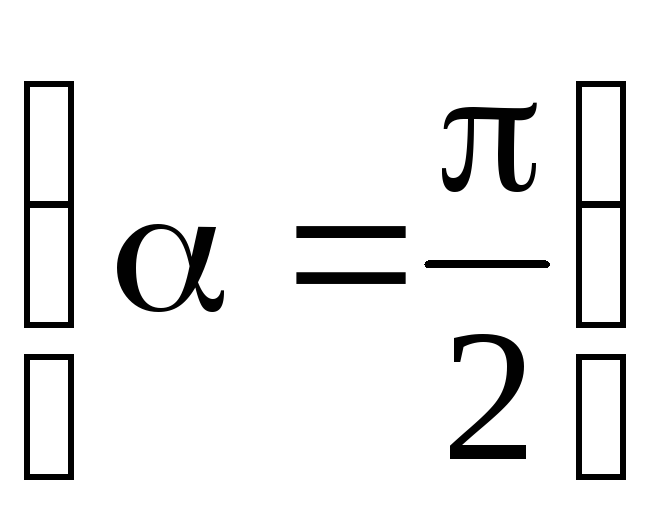

=0.

Напряженность и потенциал неточечного диполя определяются так же как и для системы зарядов.

Механический момент, действующий на диполь с электрическим моментом р, помещенный в однородное электрическое поле с напряженностью Е, –

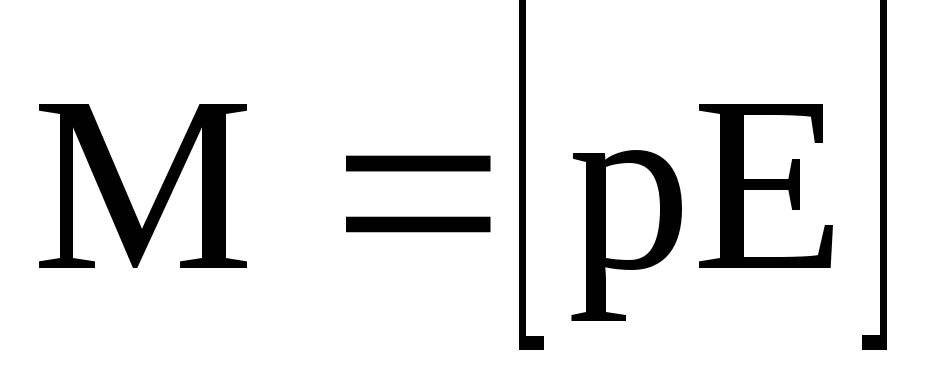, или ,

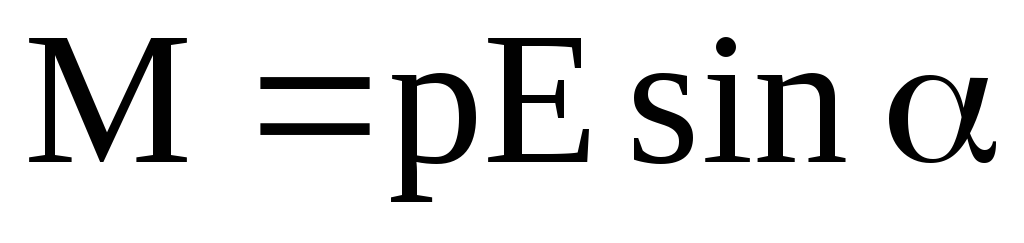где  — угол между направлениями векторов 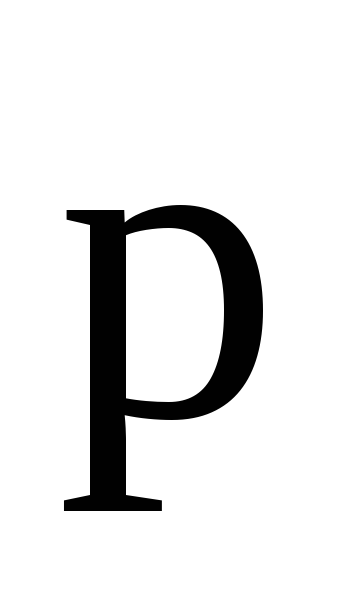и.

Электроемкость уединенного проводника или конденсатора –

,

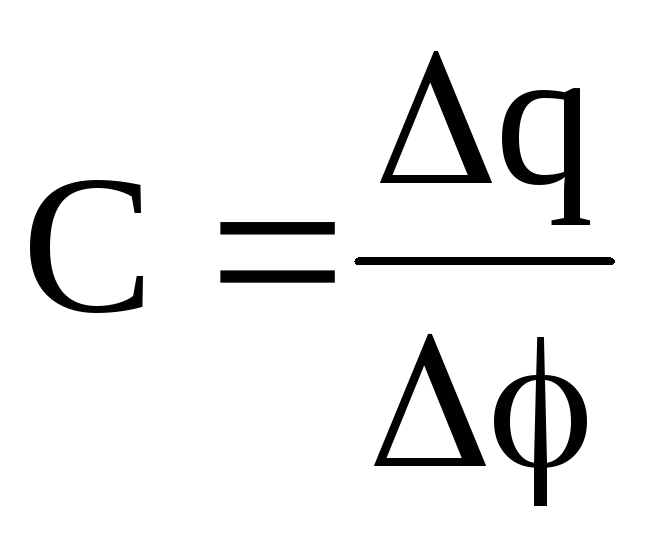где q – заряд, сообщенный проводнику; — изменение потенциала, вызванное этим зарядом.

Электроемкость уединенной проводящей сферы радиусом R, находящейся в бесконечной среде с диэлектрической проницаемостью , –

.

Если сфера полая и заполнена диэлектриком, то ее электроемкость при этом не изменяется.

Электроемкость плоского конденсатора:

,

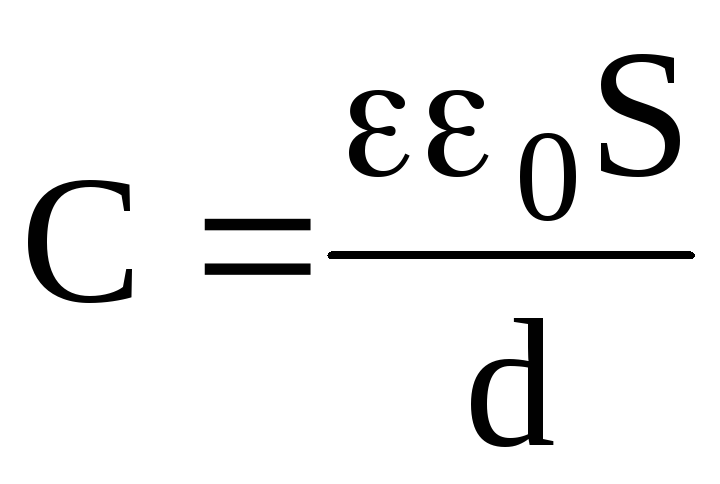где S – площадь каждой пластины конденсатора; d – расстояние между пластинами;  — диэлектрическая проницаемость диэлектрика, заполняющего пространство между пластинами.

Электроемкость плоского конденсатора, заполненного n слоями диэлектрика толщиной d_i и диэлектрической проницаемостью _i каждый (слоистый конденсатор), составляет

.

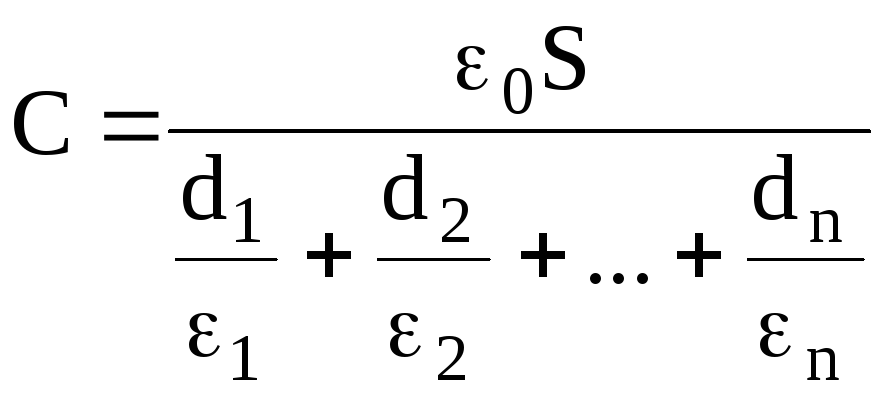Электроемкость сферического конденсатора (две концентрические сферы радиусом R₁ и R₂ , пространство между которыми заполнено диэлектриком с диэлектрической проницаемостью ) находится так:

.

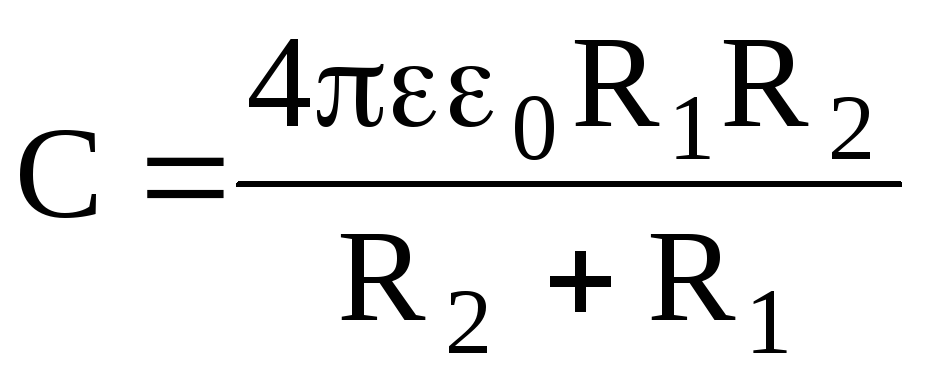Электроемкость последовательно соединенных конденсаторов составляет:

в общем случае –

,

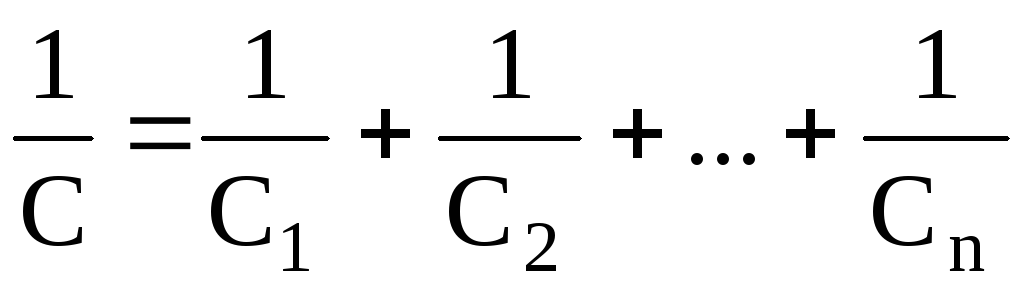где n – число конденсаторов;

в случае двух конденсаторов –

;

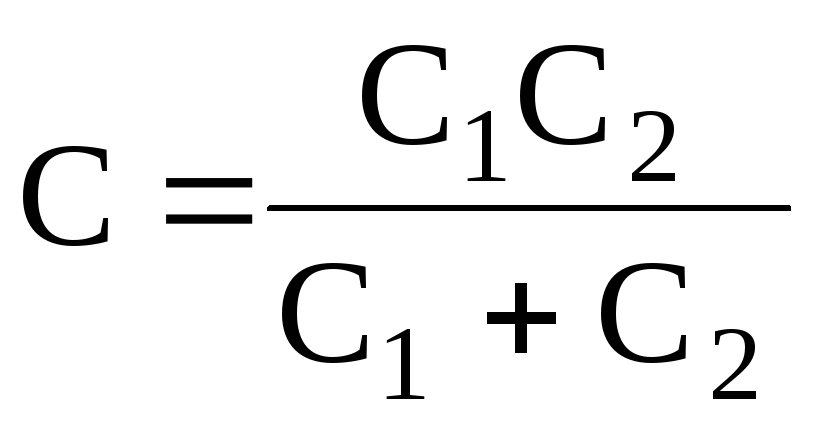в случае n одинаковых конденсаторов с электроемкостью С₁ каждый –

.

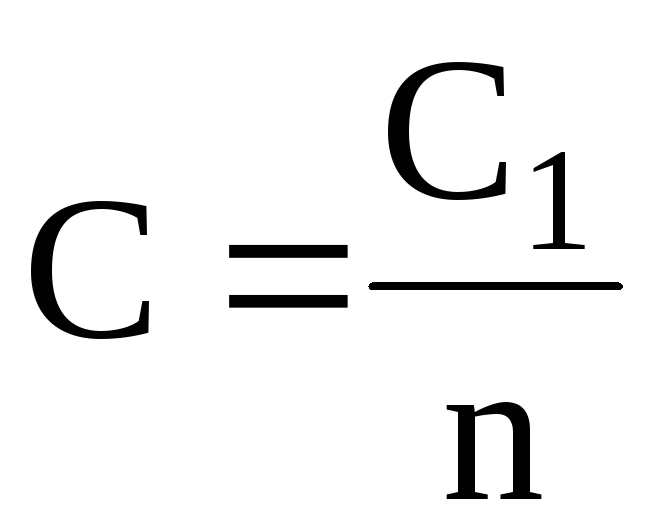Электроемкость параллельно соединенных конденсаторов определяется следующим образом:

в общем случае –

С=С₁+С₂+…+С_n;

в случае двух конденсаторов –

С= С₁+С₂;

в случае n одинаковых конденсаторов с электроемкостью С₁ каждый –

С=nС₁.

Энергия заряженного проводника выражается через заряд q, потенциал  и электроемкость С проводника следующим образом:

.

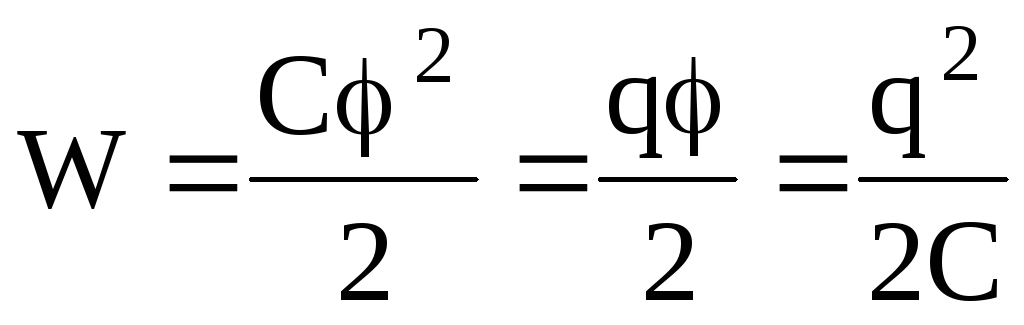Энергия заряженного конденсатора –

,

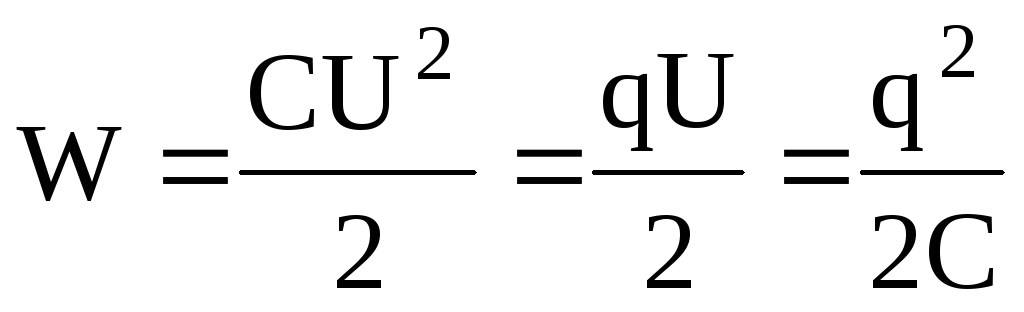где q – заряд конденсатора; С – электроемкость конденсатора; U – разность потенциалов на его пластинах.

Электрическое поле – FIZI4KA

Электродинамика – раздел физики, изучающий свойства и взаимодействия электрических зарядов, осуществляемые посредством электромагнитного поля.

Электростатикой называется раздел электродинамики, в котором рассматриваются свойства и взаимодействия неподвижных электрически заряженных тел или частиц.

Электромагнитное взаимодействие – это взаимодействие между электрически заряженными частицами или макротелами.

Точечный заряд – заряженное тело, размер которого мал по сравнению с расстоянием, на котором оценивается его действие.

Электризация тел

Электризация – процесс сообщения телу электрического заряда, т. е. нарушение его электрической нейтральности. Процесс электризации представляет собой перенесение с одного тела на другое электронов или ионов. В результате электризации тело получает возможность участвовать в электромагнитном взаимодействии.

Способы электризации:

• трением, – например, электризация эбонитовой палочки при трении о мех. При тесном соприкосновении двух тел часть электронов переходит с одного тела на другое; в результате этого на поверхности у одного из тел создается недостаток электронов и тело получает положительный заряд, а у другого – избыток, и тело заряжается отрицательно. Величины зарядов тел одинаковы;
• через влияние (электростатическая индукция) – тело остается электрически нейтральным, электрические заряды внутри него перераспределяются так, что разные части тела приобретают разные по знаку заряды;
• при соприкосновении заряженного и незаряженного тела – заряд при этом распределяется между этими телами пропорционально их размерам. Если размеры тел одинаковы, то заряд распределяется между ними поровну;
• при ударе;
• под действием излучения – под действием света с поверхности проводника могут вырываться электроны, при этом проводник приобретает положительный заряд.

Взаимодействие зарядов. Два вида зарядов

Электрический заряд – скалярная физическая величина, характеризующая способность тела участвовать в электромагнитных взаимодействиях.

Обозначение – ​\( q \)​, единица измерения в СИ – кулон (Кл).

Существуют два вида электрических зарядов: положительный и отрицательный. Наименьший отрицательный заряд имеет электрон (–1,6·10^-19 Кл), наименьший положительный заряд (1,6·10^-19 Кл) – протон. Минимальный заряд, который может быть сообщен телу, равен заряду электрона (элементарный заряд). Если тело имеет избыточные (лишние) электроны, то тело заряжено отрицательно, если у тела недостаток электронов, то тело заряжено положительно.

Величина заряда тела будет равна

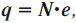
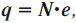
где ​\( N \)​ — число избыточных или недостающих электронов;
​\( e \)​ — элементарный заряд, равный 1,6·10^-19 Кл.

Важно!
Частица может не иметь заряда, но заряд без частицы не существует.

Электрические заряды взаимодействуют:

• заряды одного знака отталкиваются:

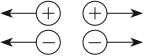
• заряды противоположных знаков притягиваются:

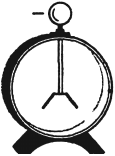
Прибор для обнаружения электрического заряда называется электроскоп. Основная часть прибора – металлический стержень, на котором закреплены два листочка металлической фольги, помещенные в стеклянный сосуд. При соприкосновении заряженного тела со стержнем электроскопа заряды распределяются между листочками фольги. Так как заряд листочков одинаков по знаку, они отталкиваются.

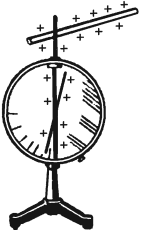
Для измерения зарядов можно использовать и электрометр. Основные части его – металлический стержень и стрелка, которая может вращаться вокруг горизонтальной оси. Стержень со стрелкой закреплен в пластмассовой втулке и помещен в металлический корпус, закрытый стеклянными крышками. При соприкосновении заряженного тела со стержнем стержень и стрелка получают электрические заряды одного знака. Стрелка поворачивается на некоторый угол.

Закон сохранения электрического заряда

Систему называют замкнутой (электрически изолированной), если в ней не происходит обмена зарядами с окружающей средой.

В любой замкнутой (электрически изолированной) системе сумма электрических зарядов остается постоянной при любых взаимодействиях внутри нее.

Полный электрический заряд ​\( (q) \)​ системы равен алгебраической сумме ее положительных и отрицательных зарядов ​\( (q_1, q_2 … q_N) \)​:

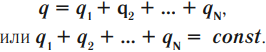
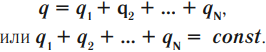
Важно!
В природе не возникают и не исчезают заряды одного знака: положительный и отрицательный заряды могут взаимно нейтрализовать друг друга, если они равны по модулю.

Закон Кулона

Закон Кулона был открыт экспериментально: в опытах с использованием крутильных весов измерялись силы взаимодействия заряженных шаров.

Закон Кулона формулируется так:
сила взаимодействия ​\( F \)​ двух точечных неподвижных электрических зарядов в вакууме прямо пропорциональна их модулям ​\( q_1 \)​ и \( q_2 \) и обратно пропорциональна квадрату расстояния между ними ​\( r \)​:

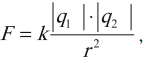
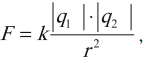
где ​\( k=\frac{1}{4\pi\varepsilon_0}=9\cdot10^9 \)​ (Н·м²)/Кл² – коэффициент пропорциональности,
​\( \varepsilon_0=8.85\cdot10^{-12} \)​ Кл²/(Н·м²) – электрическая постоянная.

Коэффициент ​\( k \)​ численно равен силе, с которой два точечных заряда величиной 1 Кл каждый взаимодействуют в вакууме на расстоянии 1 м.

Сила Кулона направлена вдоль прямой, соединяющей взаимодействующие заряды. Заряды взаимодействуют друг с другом с силами, равными по величине и противоположными по направлению.

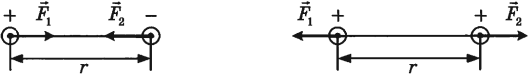
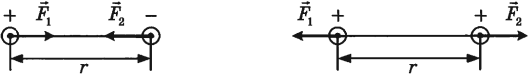
Значение силы Кулона зависит от среды, в которой они находятся. В этом случае формула закона:

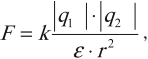
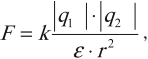
где ​\( \varepsilon \)​ – диэлектрическая проницаемость среды.

Закон Кулона применим к взаимодействию

• неподвижных точечных зарядов;
• равномерно заряженных тел сферической формы.

В этом случае ​\( r \)​ – расстояние между центрами сферических поверхностей.

Важно!
Если заряженное тело протяженное, то его необходимо разбить на точечные заряды, рассчитать силы их попарного взаимодействия и найти равнодействующую этих сил (принцип суперпозиции).

Действие электрического поля на электрические заряды

Электрическое поле – это особая форма материи, существующая вокруг электрически заряженных тел.

Впервые понятие электрического поля было введено Фарадеем. Он объяснял взаимодействие зарядов следующим образом: каждый заряд создает вокруг себя электрическое поле, которое с некоторой силой действует на другой заряд.

Свойства электрического поля заключаются в том, что оно:

• материально;
• создается зарядом;
• обнаруживается по действию на заряд;
• непрерывно распределено в пространстве;
• ослабевает с увеличением расстояния от заряда.

Действие заряженного тела на окружающие тела проявляется в виде сил притяжения и отталкивания, стремящихся поворачивать и перемещать эти тела по отношению к заряженному телу.

Силу, с которой электрическое поле действует на заряд, можно рассчитать по формуле:

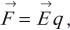
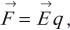
где ​\( \vec{E} \)​ – напряженность электрического поля, ​\( q \)​ – заряд.

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов механики с учетом закона Кулона и вытекающих из него следствий.

Алгоритм решения задач о точечных зарядах и системах, сводящихся к ним:

• сделать рисунок; указать силы, действующие на точечный заряд, помещенный в электрическое поле;
• записать для заряда условие равновесия или основное уравнение динамики материальной точки;
• выразить силы электрического взаимодействия через заряды и поля и подставить эти выражения в исходное уравнение;
• если при взаимодействии заряженных тел между ними происходит перераспределение зарядов, к составленному уравнению добавить уравнение закона сохранения зарядов;
• записать математически все вспомогательные условия;
• решить полученную систему уравнений относительно неизвестной величины;
• проверить решение

Напряженность электрического поля

Напряженность электрического поля ​\( \vec{E} \)​ – векторная физическая величина, равная отношению силы ​\( F \)​, действующей на пробный точечный заряд, к величине этого заряда ​\( q \)​:

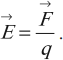
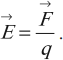
Обозначение – \( \vec{E} \), единица измерения в СИ – Н/Кл или В/м.

Напряженность поля точечного заряда в вакууме вычисляется по формуле:

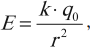
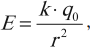
где \( k=\frac{1}{4\pi\varepsilon_0}=9\cdot10^9 \) (Н·м²)/Кл²,
​\( q_0 \)​ – заряд, создающий поле,
​\( r \)​ – расстояние от заряда, создающего поле, до данной точки.

Напряженность поля точечного заряда в среде вычисляется по формуле:

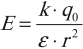
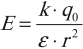
где ​\( \varepsilon \)​ – диэлектрическая проницаемость среды.

Важно!
Напряженность электрического поля не зависит от величины пробного заряда, она определяется величиной заряда, создающего поле.

Направление вектора напряженности в данной точке совпадает с направлением силы, с которой поле действует на положительный пробный заряд, помещенный в эту точку.

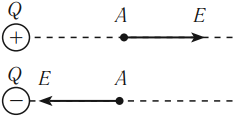
Линией напряженности электрического поля называется линия, касательная к которой в каждой точке направлена вдоль вектора напряженности ​\( \vec{E} \)​.

Линии напряженности электростатического поля начинаются на положительных электрических зарядах и заканчиваются на отрицательных электрических зарядах или уходят в бесконечность от положительного заряда и приходят из бесконечности к отрицательному заряду.

Распределение линий напряженности вокруг положительного и отрицательного точечных зарядов показано на рисунке.

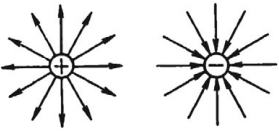
Определяя направление вектора ​\( \vec{E} \)​ в различных точках пространства, можно представить картину распределения линий напряженности электрического поля.

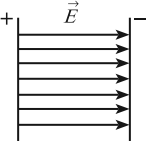
Поле, в котором напряженность одинакова по модулю и направлению в любой точке, называется однородным электрическим полем. Однородным можно считать электрическое поле между двумя разноименно заряженными металлическими пластинами. Линии напряженности в однородном электрическом поле параллельны друг другу.

Принцип суперпозиции электрических полей

Каждый электрический заряд создает в пространстве электрическое поле независимо от наличия других электрических зарядов.

Принцип суперпозиции электрических полей: напряженность электрического поля системы ​\( N \)​ зарядов равна векторной сумме напряженностей полей, создаваемых каждым из них в отдельности:

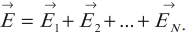
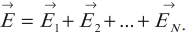
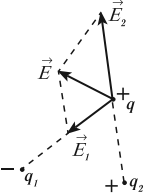
Электрические поля от разных источников существуют в одной точке пространства и действуют на заряд независимо друг от друга.

Потенциальность электростатического поля

Электрическое поле с напряженностью ​\( \vec{E} \)​ при перемещении заряда ​\( q \)​ совершает работу. Работа ​\( A \)​ электростатического поля вычисляется по формуле:

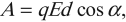
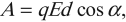
где ​\( d \)​ – расстояние, на которое перемещается заряд,
​\( \alpha \)​ – угол между векторами напряженности электрического поля и перемещения заряда.

Важно!
Эта формула применима для нахождения работы только в однородном электростатическом поле.

Работа сил электростатического поля при перемещении заряда из одной точки поля в другую не зависит от формы траектории, а определяется только начальным и конечным положением заряда.

Потенциальным называется поле, работа сил которого по перемещению заряда по замкнутой траектории равна нулю.

Важно!
Работа сил электростатического поля при перемещении заряда по любой замкнутой траектории равна нулю. Электростатическое поле является потенциальным.

Работа электростатического поля по перемещению заряда равна изменению потенциальной энергии, взятому с противоположным знаком. В электродинамике энергию принято обозначать буквой ​\( W \)​, так как буквой ​\( E \)​ обозначают напряженность поля:

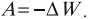
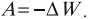
Потенциальная энергия заряда ​\( q \)​, помещенного в электростатическое поле, пропорциональна величине этого заряда. Потенциальная энергия взаимодействия зарядов вычисляется относительно нулевого уровня (аналогично потенциальной энергии поля силы тяжести). Выбор нулевого уровня потенциальной энергии определяется исходя из соображений удобства при решении задачи.

Потенциал электрического поля. Разность потенциалов

Потенциал – скалярная физическая величина, равная отношению потенциальной энергии электрического заряда в электростатическом поле к величине этого заряда.

Обозначение – ​\( \varphi \)​, единица измерения в СИ – вольт (В).

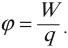
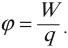
Потенциал \( \varphi \) является энергетической характеристикой электростатического поля.

Разность потенциалов численно равна работе, которую совершает электрическая сила при перемещении единичного положительного заряда между двумя точками поля:

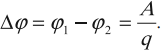
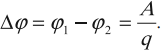
Обозначение – ​\( \Delta\varphi \)​, единица измерения в СИ – вольт (В).

Иногда разность потенциалов обозначают буквой ​\( U \)​ и называют напряжением.

Важно!
Разность потенциалов \( \Delta\varphi=\varphi_1-\varphi_2 \), а не изменение потенциала \( \Delta\varphi=\varphi_2-\varphi_1 \). Тогда работа электростатического поля равна:

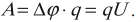
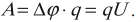
Важно!
Эта формула позволяет вычислить работу электростатических сил в любом поле.

В электростатике часто вычисляют потенциал относительно бесконечно удаленной точки. В этом случае потенциал поля в данной точке равен работе, которую совершают электрические силы при удалении единичного положительного заряда из данной точки в бесконечность.

Потенциал поля точечного заряда ​\( q \)​ в точке, удаленной от него на расстояние ​\( r \)​, вычисляется по формуле:

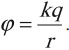
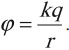
Для наглядного представления электрического поля используют эквипотенциальные поверхности.

Важно!
Внутри проводящего шара потенциал всех точек внутри шара равен потенциалу поверхности шара и вычисляется по формуле потенциала точечного заряда (​\( r =R \)​, где ​\( R \)​ – радиус шара). Напряженность поля внутри шара равна нулю.

Эквипотенциальной поверхностью, или поверхностью равного потенциала, называется поверхность, во всех точках которой потенциал имеет одинаковое значение.

Свойства эквипотенциальных поверхностей

• Вектор напряженности перпендикулярен эквипотенциальным поверхностям и направлен в сторону убывания потенциала.
• Работа по перемещению заряда по эквипотенциальной поверхности равна нулю.

В случае однородного поля эквипотенциальные поверхности представляют собой систему параллельных плоскостей. Для точечного заряда эквипотенциальные поверхности представляют собой концентрические окружности.

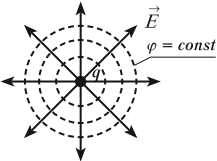
Разность потенциалов и напряженность связаны формулой:

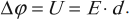
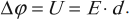
Из принципа суперпозиции полей следует принцип суперпозиции потенциалов:

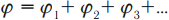
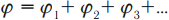
Потенциал результирующего поля равен сумме потенциалов полей отдельных зарядов.

Важно!
Потенциалы складываются алгебраически, а напряженности – по правилу сложения векторов.

Решение задач о точечных зарядах и системах, сводящихся к ним, основано на применении законов сохранения, теоремы об изменении кинетической энергии заряда с учетом работы электростатических сил.

Алгоритм решения таких задач:

• установить характер и особенности электростатических взаимодействий объектов системы;
• ввести характеристики (силовые и энергетические) этих взаимодействий, сделать рисунок;
• записать законы сохранения и движения для объектов;
• выразить энергию электростатического взаимодействия через заряды, потенциалы, напряженности;
• составить систему уравнений и решить ее относительно искомой величины;
• проверить решение.

Проводники в электрическом поле

Проводниками называют вещества, в которых может происходить упорядоченное перемещение электрических зарядов, т. е. протекать электрический ток.

Проводниками являются металлы, водные растворы солей, кислот, ионизованные газы. В проводниках есть свободные электрические заряды. В металлах валентные электроны взаимодействующих друг с другом атомов становятся свободными.

Если металлический проводник поместить в электрическое поле, то под его действием свободные электроны проводника начнут перемещаться в направлении, противоположном направлению напряженности поля. В результате на одной поверхности проводника появится избыточный отрицательный заряд, а на противоположной – избыточный положительный заряд.

Эти заряды создают внутри проводника внутреннее электрическое поле, вектор напряженности которого направлен противоположно вектору напряженности внешнего поля. Под действием внешнего электростатического поля электроны проводимости в металлическом проводнике перераспределяются так, что напряженность результирующего поля в любой точке внутри проводника равна нулю. Электрические заряды расположены на поверхности проводника.

Важно!
Если внутри проводника есть полость, то напряженность в ней будет равна нулю независимо от того, какое поле имеется вне проводника и как заряжен проводник. Внутренняя полость в проводнике экранирована (защищена) от внешних электростатических полей. На этом основана электростатическая защита.

Явление перераспределения зарядов во внешнем электростатическом поле называется электростатической индукцией.

Заряды, разделенные электростатическим полем, взаимно компенсируют друг друга, если проводник удалить из поля. Если такой проводник разрезать, не вынося из поля, то его части будут иметь заряды разных знаков.

Важно!
Во всех точках поверхности проводника вектор напряженности направлен перпендикулярно к его поверхности. Поверхность проводника является эквипотенциальной (потенциалы всех точек поверхности проводника равны).

Диэлектрики в электрическом поле

Диэлектриками называют вещества, не проводящие электрический ток. Диэлектриками являются стекло, фарфор, резина, дистиллированная вода, газы.

В диэлектриках нет свободных зарядов, все заряды связаны. В молекуле диэлектрика суммарный отрицательный заряд электронов равен положительному заряду ядра. Различают полярные и неполярные диэлектрики.

В молекулах полярных диэлектриков ядра и электроны расположены так, что центры масс положительных и отрицательных зарядов не совпадают и находятся на некотором расстоянии друг от друга. То есть молекулы представляют собой диполи независимо от наличия внешнего электрического поля. В отсутствие внешнего электрического поля из-за теплового движения молекул диполи расположены хаотично, поэтому суммарная напряженность поля всех диполей диэлектрика равна нулю.

Если в отсутствие внешнего электрического поля центры масс положительных и отрицательных зарядов в молекуле диэлектрика совпадают, то он называется неполярным. Пример такого диэлектрика – молекула водорода. Если такой диэлектрик поместить во внешнее электрическое поле, то направления векторов сил, действующих на положительные и отрицательные заряды, будут противоположными. В результате молекула деформируется и превращается в диполь. При внесении диэлектрика в электрическое поле происходит его поляризация.

Поляризация диэлектрика – процесс смещения в противоположные стороны разноименных связанных зарядов, входящих в состав атомов и молекул вещества в электрическом поле.

Если диэлектрик неполярный, то в его молекулах происходит смещение положительных и отрицательных зарядов. На поверхности диэлектрика появятся поверхностные связанные заряды. Связанными эти заряды называют потому, что они не могут свободно перемещаться отдельно друг от друга.

Внутри диэлектрика суммарный заряд равен нулю, а на поверхностях заряды не скомпенсированы и создают внутри диэлектрика поле, вектор напряженности которого направлен противоположно вектору напряженности внешнего поля. Это значит, что внутри диэлектрика поле имеет меньшую напряженность, чем в вакууме.

Физическая величина, равная отношению модуля напряженности электрического поля в вакууме к модулю напряженности электрического поля в однородном диэлектрике, называется диэлектрической проницаемостью вещества:

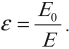
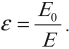
В полярном диэлектрике во внешнем электрическом поле происходит поворот диполей, и они выстраиваются вдоль линий напряженности.

Если внесенный в электрическое поле диэлектрик разрезать, то его части будут электрически нейтральны.

Электрическая емкость. Конденсатор

Электрическая емкость (электроемкость) – скалярная физическая величина, характеризующая способность уединенного проводника удерживать электрический заряд.

Обозначение – ​\( C \)​, единица измерения в СИ – фарад (Ф).

Уединенный проводник – это проводник, удаленный от других проводников и заряженных тел.

Фарад – электроемкость такого уединенного проводника, потенциал которого изменяется на 1 В при сообщении ему заряда 1 Кл:

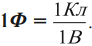
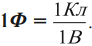
Формула для вычисления электроемкости:

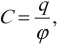
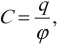
где ​\( q \)​ – заряд проводника, ​\( \varphi \)​ – его потенциал.

Электроемкость зависит от его линейных размеров и геометрической формы. Электроемкость не зависит от материала проводника и его агрегатного состояния. Электроемкость проводника прямо пропорциональна диэлектрической проницаемости среды, в которой он находится.

Конденсатор – это система из двух проводников, разделенных слоем диэлектрика, толщина которого мала по сравнению с размерами проводников.

Проводники называют обкладками конденсатора. Заряды обкладок конденсатора равны по величине и противоположны по знаку заряда. Электрическое поле сосредоточено между обкладками конденсатора. Конденсаторы используют для накопления электрических зарядов.

Электроемкость конденсатора рассчитывается по формуле:

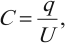
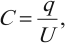
где ​\( q \)​ – модуль заряда одной из обкладок,
​\( U \)​ – разность потенциалов между обкладками.

Электроемкость конденсатора зависит от линейных размеров и геометрической формы и расстояния между проводниками. Электроемкость конденсатора прямо пропорциональна диэлектрической проницаемости вещества между проводниками.

Плоский конденсатор представляет две параллельные пластины площадью ​\( S \)​, находящиеся на расстоянии ​\( d \)​ друг от друга.

Электроемкость плоского конденсатора:

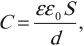
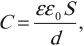
где ​\( \varepsilon \)​ – диэлектрическая проницаемость вещества между обкладками,
\( \varepsilon_0 \) – электрическая постоянная.

На электрической схеме конденсатор обозначается:

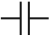
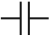
Виды конденсаторов:

• по типу диэлектрика – воздушный, бумажный и т. д.;
• по форме – плоский, цилиндрический, сферический;
• по электроемкости – постоянной и переменной емкости.

Конденсаторы можно соединять между собой.

Параллельное соединение конденсаторов

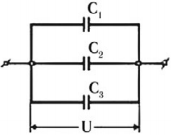
При параллельном соединении конденсаторы соединяются одноименно заряженными обкладками. Напряжения конденсаторов равны:

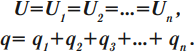
Общая емкость:

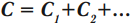
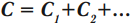
Последовательное соединение конденсаторов

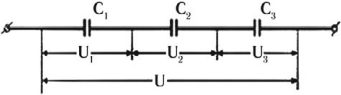
При последовательном соединении конденсаторов соединяют их разноименно заряженные обкладки.

Заряды конденсаторов при таком соединении равны:

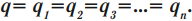
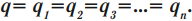
Общее напряжение:

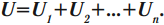
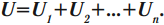
Величина, обратная общей емкости:

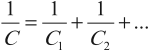
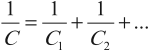
При таком соединении общая емкость всегда меньше емкостей отдельных конденсаторов.

Важно!
Если конденсатор подключен к источнику тока, то разность потенциалов между его обкладками не изменяется при изменении электроемкости и равна напряжению источника. Если конденсатор заряжен до некоторой разности потенциалов и отключен от источника тока, то его заряд не изменяется при изменении электроемкости.

Применение конденсаторов
Конденсаторы используются в радиоэлектронных приборах как накопители заряда, для сглаживания пульсаций в выпрямителях переменного тока.

Энергия электрического поля конденсатора

Энергия заряженного конденсатора равна работе внешних сил, которую необходимо затратить, чтобы зарядить конденсатор.

Электрическая энергия конденсатора сосредоточена в пространстве между обкладками конденсатора, то есть в электрическом поле, поэтому ее называют энергией электрического поля. Формулы для вычисления энергии электрического поля:

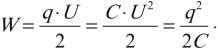
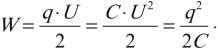
Так как напряженность электрического поля прямо пропорциональна напряжению, то энергия электрического поля конденсатора пропорциональна квадрату напряженности.

Плотность энергии электрического поля:

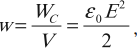
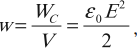
где ​\( V \)​ – объем пространства между обкладками конденсатора.

Плотность энергии не зависит от параметров конденсатора, а определяется только напряженностью электрического поля.

Основные формулы раздела «Электрическое поле»

Электрическое поле

5 (100%) 1 vote

Электричество — Основные формулы

1. Электростатика

1.1 Закон Кулона

q₁, q₂ — величины точечных зарядов,
r — расстояние между зарядами.

1.2 Напряженность поля уединенного точечного заряда

q — величина уединенного точечного заряда,
r — расстояние от заряда.

1.3 Потенциал точки в поле точечного заряда

q — величина уединенного точечного заряда,
r — расстояние от заряда.

1.4 Потенциальная энергия заряда в электростатическом поле

φ — потенциал,
q₁ — величина заряда.

1.5 Потенциальная энергия заряда q₁ в поле точечного заряда

q — величина уединенного точечного заряда, который создает поле,
r — расстояние между зарядами.

1.6 Теорема Гаусса

N — поток вектора напряженности электрического поля через замкнутую поверхность,
q — полный заряд, находящийся внутри замкнутой поверхности.

1.7 Напряженность электрического поля вблизи от поверхности проводника

σ — поверхностная плотность заряда.

1.8 Емкость плоского кондесатора

q — заряд конденсатора,
U — модуль разности потенциалов между обкладками.

1.9 Энергия плоского кондесатора

q — заряд конденсатора,
U — модуль разности потенциалов между обкладками.

2. Постоянный электрический ток

2.1 Закон Ома для участка однородной цепи

U — напряжение на концах участка,
R — сопротивление участка цепи.

2.2 Закон Ома для замкнутой цепи с источником тока

 — ЭДС (электродвижущая сила),
r — внутреннее сопротивление источника ЭДС.

2.3 Работа постоянного тока

U — напряжение на концах участка цепи,
t — время, за которое совершается работа.

2.4 Закон Джоуля-Ленца

Q — теплота,
R — сопротивление проводника,
t — время, за которое выделяется теплота.

2.5 Полная мощность, развиваемая источником тока

 — ЭДС источника тока,
R — сопротивление цепи,
r — внутреннее сопротивление источника тока.

2.6 Полезная мощность

 — ЭДС источника тока,
R — сопротивление цепи,
r — внутреннее сопротивление источника тока.

2.7 Коэффициент полезного действия источника тока

R — сопротивление цепи,
r — внутреннее сопротивление источника тока.

2.8 Первое правило Кирхгофа

n — число проводников, сходящихся в узле;
I_k — сила тока в k-м проводнике.

2.9 Второе правило Кирхгофа

n — число неразветвленных участков в контуре;
m — число ЭДС в контуре.