Глава 17. Взаимодействие электрических зарядов. Закон Кулона, принцип суперпозиции
Взаимодействие электрических зарядов описывается законом Кулона, который утверждает, что сила взаимодействия двух покоящихся точечных зарядов в вакууме равна
(17.1) |
где и — модули зарядов, — расстояние между ними. Коэффициент пропорциональности в формуле (17.1) зависит от системы единиц. В международной системе единиц СИ этот коэффициент принято записывать в виде
(17.2) |
где величина называется электрической постоянной, размерность величины сводится к отношению размерности длины к размерности электрической емкости (Фарада). Электрические заряды бывают двух типов, которые условно принято называть положительным и отрицательным. Как показывает опыт, заряды притягиваются, если они разноименные и отталкиваются, если одноименные.
В любом макроскопическом теле содержится огромное количество электрических зарядов, поскольку они входят в состав всех атомов: электроны заряжены отрицательно, протоны, входящие в состав атомных ядер — положительно. Однако большинство тел, с которыми мы имеем дело, не заряжены, поскольку количество электронов и протонов, входящих в состав атомов, одинаково, а их заряды по абсолютной величине в точности совпадают. Тем не менее, тела можно зарядить, если создать в них избыток или недостаток электронов по сравнению с протонами. Для этого нужно передать электроны, входящие в состав какого-нибудь тела, другому телу. Тогда у первого возникнет недостаток электронов и соответственно положительный заряд, у второго — отрицательный. Такого рода процессы происходят, в частности, при трении тел друг о друга.
Если заряды находятся в некоторой среде, которая занимает все пространство, то сила их взаимодействия ослабляется по сравнению с силой их взаимодействия в вакууме, причем это ослабление не зависит от величин зарядов и расстояния между ними, а зависит только от свойств среды. Характеристика среды, которая показывает, во сколько раз ослабляется сила взаимодействия зарядов в этой среде по сравнению с силой их взаимодействия в вакууме, называется диэлектрической проницаемостью этой среды и, как правило, обозначается буквой . Формула Кулона в среде с диэлектрической проницаемостью принимает вид
Характеристика среды, которая показывает, во сколько раз ослабляется сила взаимодействия зарядов в этой среде по сравнению с силой их взаимодействия в вакууме, называется диэлектрической проницаемостью этой среды и, как правило, обозначается буквой . Формула Кулона в среде с диэлектрической проницаемостью принимает вид
(17.3) |
Если имеется не два, а большее количество точечных зарядов для нахождения сил, действующих в этой системе, используется закон, который называется принципомсуперпозиции1. Принцип суперпозиции утверждает, что для нахождения силы, действующей на один из зарядов (например, на заряд ) в системе из трех точечных зарядов , и надо сделать следующее. Сначала надо мысленно убрать заряд и по закону Кулона найти силу, действующую на заряд со стороны оставшегося заряда . Затем следует убрать заряд и найти силу, действующую на заряд со стороны заряда . Векторная сумма полученных сил и даст искомую силу.
Принцип суперпозиции дает рецепт поиска силы взаимодействия неточечных заряженных тел. Следует мысленно разбить каждое тело на части, которые можно считать точечными, по закону Кулона найти силу их взаимодействия с точечными частями, на которое разбивается второе тело, просуммировать полученные вектора. Ясно, что такая процедура математически очень сложна, хотя бы потому, что необходимо сложить бесконечное количество векторов. В математическом анализе разработаны методы такого суммирования, однако в школьный курс физики они не входят. Поэтому, если такая задача и встретится, то суммирование в ней должно легко выполняться на основе тех или иных соображений симметрии. Например, из описанной процедуры суммирования следует, что сила, действующая на точечный заряд, помещенный в центр равномерно заряженной сферы, равна нулю.
Кроме того, школьник должен знать (без вывода) формулы для силы, действующей на точечный заряд со стороны равномерно заряженной сферы и бесконечной плоскости. Если имеется сфера радиуса , равномерно заряженная зарядом , и точечный заряд , расположенный на расстоянии от центра сферы, то величина силы взаимодействия равна
Если имеется сфера радиуса , равномерно заряженная зарядом , и точечный заряд , расположенный на расстоянии от центра сферы, то величина силы взаимодействия равна
(17.4) |
если точечный заряд находится снаружи сферы, и
(17.5) |
если заряд находится внутри (причем не обязательно в центре). Из формул (17.4), (17.5) следует, что сфера снаружи создает такое же электрическое поле как весь ее заряд, помещенный в центре, а внутри — нулевое.
Если имеется очень большая плоскость с площадью , равномерно заряженная зарядом , и точечный заряд , то сила их взаимодействия равна
(17.6) |
где величина имеет смысл поверхностной плотности заряда плоскости. Как следует из формулы (17. 6) сила взаимодействия точечного заряда и плоскости не зависит от расстояния между ними. Обратим внимание читателя на то, что формула (17.6) является приближенной и «работает» тем точнее, чем дальше точечный заряд находится от ее краев. Поэтому при использовании формулы (17.6) часто говорят, что она справедлива в рамках пренебрежения «краевыми эффектами», т.е. когда плоскость считается бесконечной.
6) сила взаимодействия точечного заряда и плоскости не зависит от расстояния между ними. Обратим внимание читателя на то, что формула (17.6) является приближенной и «работает» тем точнее, чем дальше точечный заряд находится от ее краев. Поэтому при использовании формулы (17.6) часто говорят, что она справедлива в рамках пренебрежения «краевыми эффектами», т.е. когда плоскость считается бесконечной.
Согласно закону Кулона (17.1) величина силы взаимодействия двух зарядов из задачи 17.1.1 выражается формулой
Заряды отталкиваются (ответ 2).
Поскольку капелька воды из задачи 17.1.2 имеет заряд ( – заряд протона), то она имеет в избытке электронов по сравнению с протонами. Значит при потере трех электронов их избыток уменьшится, и заряд капельки станет равен (ответ 2).
Если заряды двух точечных тел увеличить в раз при неизменном расстоянии между ними, то сила их взаимодействия, как это следует из закона Кулона (17.1), увеличится в раз (задача 17.1.4 — ответ 3).
При увеличении одного заряда в 2 раза, а второго в 4, числитель закона Кулона (17.1) увеличивается в 8 раз, а при увеличении расстояния между зарядами в 8 раз — знаменатель увеличивается в 64 раза. Поэтому сила взаимодействия зарядов из задачи 17.1.5 уменьшится в 8 раз (ответ
При заполнении пространства диэлектрической средой с диэлектрической проницаемостью = 10, сила взаимодействия зарядов согласно закону Кулона в среде (17.3) уменьшится в 10 раз (задача 17.1.6 — ответ 2).
Сила кулоновского взаимодействия (17. 1) действует как на первый, так и на второй заряд, а поскольку их массы одинаковы, то ускорения зарядов, как это следует из второго закона Ньютона, в любой момент времени одинаковы (задача 17.1.7 — ответ 3).
1) действует как на первый, так и на второй заряд, а поскольку их массы одинаковы, то ускорения зарядов, как это следует из второго закона Ньютона, в любой момент времени одинаковы (задача 17.1.7 — ответ 3).
Похожая задача, но массы шариков разные. Поэтому при одинаковой силе ускорение шарика с меньшей массой в 2 раза больше ускорения шарика с меньшей массой , причем этот результат не зависит от величин зарядов шариков (
Поскольку электрон заряжен отрицательно, он будет отталкиваться от шара (задача 17.1.9). Но поскольку начальная скорость электрона направлена к шару, он будет двигаться в этом направлении, но его скорость будет уменьшаться. В какой-то момент он на мгновение остановится, а потом будет двигаться от шара с увеличивающейся скоростью (ответ 4).
В системе двух заряженных шариков, связанных нитью (задача 17.1.10), действуют только внутренние силы. Поэтому система будет покоиться и для нахождения силы натяжения нити можно использовать условия равновесия шариков.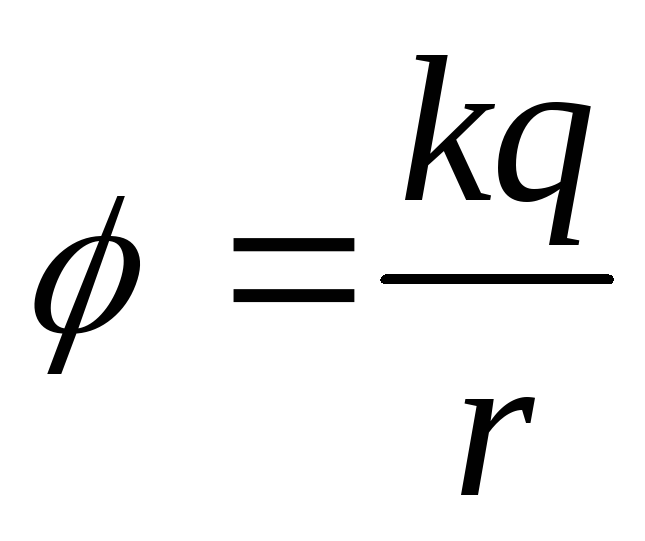
Отсюда
где (ответ 1).
Система трех шариков в задаче 17.2.1 покоится, поэтому силы натяжения должны компенсировать силы кулоновского отталкивания крайних зарядов. Последние найдем по закону Кулона и принципу суперпозиции. Каждый крайний заряд отталкивается от центрального заряда и другого крайнего. Для суммы этих сил получаем
Этой величине и будет равна сила натяжения нитей (ответ 4). Отметим, что рассмотрение условия равновесия центрального заряда не помогло бы найти силу натяжения, а привело бы к заключению, что силы натяжения нитей одинаковы (впрочем, это заключение и так очевидно благодаря симметрии задачи).
Для нахождения силы, действующей на заряд — в задаче 17.2.2, используем принцип суперпозиции. На заряд — действуют силы притяжения к левому и правому зарядам (см. рисунок). Поскольку расстояния от заряда — до зарядов одинаковы, модули этих сил равны друг другу и они направлены под одинаковыми углами к прямой, соединяющей заряд — с серединой отрезка — . Поэтому сила, действующая на заряд — направлена вертикально вниз (вектор результирующей силы выделен жирным на рисунке; ответ 4).
Задача 17.2.3 похожа на предыдущую, но изменен знак одного из зарядов. Поэтому сила, действующая на заряд — со стороны правого заряда, не изменившись по величине, изменится по направлению (см. рисунок). Поэтому вектор результирующей силы будет направлен влево (вектор результирующей силы выделен жирным на рисунке; ответ 1). |
|
На каждый заряд в задаче 17. |
Из-за равенства значений сил-слагаемых параллелограмм сложения сил представляет собой ромб, и, следовательно, вектор результирующей силы направлен вдоль биссектрисы треугольника из зарядов (выделен жирным на рисунке). Поэтому угол, отмеченный на рисунке дугой равен 30°, а значение результирующей силы равно
(ответ 3).
Из формулы (17.6) заключаем, что правильный ответ в задаче 17.2.5 — 4. В задаче 17.2.6 нужно использовать формулу для силы взаимодействия точечного заряда и сферы (формулы (17.4), (17.5)). Имеем = 0 (ответ 3).
В задаче 17. 2.7 необходимо применить принцип суперпозиции к двум сферам. Принцип суперпозиции утверждает, что взаимодействие каждой пары зарядов не зависит от наличия других зарядов. Поэтому каждая сфера действует на точечный заряд независимо от другой сферы, и для нахождения результирующей силы нужно сложить силы со стороны первой и второй сфер. Поскольку точечный заряд расположен внутри внешней сферы, она не действует на него (см. формулу (17.5)), внутренняя действует с силой
2.7 необходимо применить принцип суперпозиции к двум сферам. Принцип суперпозиции утверждает, что взаимодействие каждой пары зарядов не зависит от наличия других зарядов. Поэтому каждая сфера действует на точечный заряд независимо от другой сферы, и для нахождения результирующей силы нужно сложить силы со стороны первой и второй сфер. Поскольку точечный заряд расположен внутри внешней сферы, она не действует на него (см. формулу (17.5)), внутренняя действует с силой
где . Поэтому и результирующая сила равна этому выражению (ответ 2)
В задаче 17.2.8 также следует использовать принцип суперпозиции. Если заряд поместить в точку , то силы, действующие на него со стороны зарядов и , направлены влево. Поэтому по принципу суперпозиции имеем для равнодействующей силы
где — расстояния от зарядов до исследуемых точек. Если поместить положительный заряд в точку , то силы будут направлены противоположно, и на основании принципа суперпозиции находим результирующую силу
Если поместить положительный заряд в точку , то силы будут направлены противоположно, и на основании принципа суперпозиции находим результирующую силу
В точке на заряд будут действовать силы, направленные направо, и потому
Из этих формул следует, что наибольшей сила будет в точке — ответ 1.
Пусть, для определенности, заряды шариков и в задаче 17.2.9 положительны. Так как шарики одинаковы, заряды после их соединения распределяться между ними равномерно и для сравнения сил, нужно сравнить друг с другом величины
(1) |
которые представляют собой произведения зарядов шариков до и после их соединения. После извлечения квадратного корня сравнение (1) сводится к сравнению среднего геометрического и среднего арифметического двух чисел. А поскольку среднее арифметическое любых двух чисел больше их среднего геометрического, то сила взаимодействия шариков возрастет независимо от величин их зарядов (ответ 1).
А поскольку среднее арифметическое любых двух чисел больше их среднего геометрического, то сила взаимодействия шариков возрастет независимо от величин их зарядов (ответ 1).
Задача 17.2.10 очень похожа на предыдущую, а ответ — другой. Непосредственной поверкой легко убедиться, что сила может как увеличиться, так и уменьшиться в зависимости от величин зарядов. Например, если заряды равны по величине, то после соединения шариков их заряды станут равны нулю, поэтому нулевой будет и сила их взаимодействия, которая, следовательно, уменьшится. Если один из первоначальных зарядов равен нулю, то после соприкосновения шариков заряд одного из них распределится между шариками поровну, и сила их взаимодействия увеличится. Таким образом, правильный ответ в этой задаче — 3.
Формула силы тока в физике
Содержание:
Определение и формула силы тока
Определение
Электрическим током называют упорядоченное движение носителей зарядов. В металлах таковыми являются электроны, отрицательно
заряженные частицы с зарядом, равным элементарному заряду. Направлением тока считают направление движения положительно заряженных частиц.
В металлах таковыми являются электроны, отрицательно
заряженные частицы с зарядом, равным элементарному заряду. Направлением тока считают направление движения положительно заряженных частиц.
Силой тока (током) через некоторую поверхность S называют скалярную физическую величину, которую обозначают I, равную:
$$I=\frac{d q}{d t}$ (1)$где q – заряд, проходящий сквозь поверхность S, t – время прохождения заряда. Выражение (1) определяет величину силы тока в момент времени t (мгновенное значение величины силы тока).
Некоторые виды силы тока
Ток носит название постоянного, если его сила и направление с течением времени не изменяются, тогда:
$$I=\frac{q}{t}(2)$$Формула (2) показывает, что сила постоянного тока равна заряду, который проходит сквозь поверхность S в единицу времени.
Если ток является переменным, то выделяют мгновенную силу тока (1), амплитудную силу тока и эффективную силу тока. Эффективной величиной силы переменного тока (Ieff) называют такую силу постоянного тока, которая выполнит работу равную работе переменного тока в течение одного периода (T):
$$I_{e f f}=\sqrt{\frac{1}{T} \int_{0}^{T} I^{2} d t}(3)$$Если переменный ток можно представить как синусоидальный:
$$I=I_{m} \sin \omega t$$то Im – амплитуда силы тока ($\omega$ – частота силы переменного тока).
Плотность тока
Распределение электрического тока по сечению проводника характеризуют при помощи вектора плотности тока ($\bar{j}$). При этом:
$$j_{n}=j \cos \alpha=\frac{d I}{d S}(5)$$где $\alpha$ – угол между векторами $\bar{j}$ и $\bar{n}$ ( $\bar{n}$ – нормаль к элементу поверхности dS), jn – проекция вектора плотности тока на направление нормали ($\bar{n}$).
Сила тока в проводнике определяется при помощи формулы:
$$I=\int_{S} j d S(6)$$где интегрирование в выражении (6) проводится по всему поперечному сечению проводника S ($\alpha \equiv 0$)
Для постоянного тока имеем:
$I = jS (7)$Если рассматривать два проводника с сечениями S1 и S2 и постоянными токами, то выполняется соотношение:
$$\frac{j_{1}}{j_{2}}=\frac{S_{2}}{S_{1}}(8)$$Сила тока в соединениях проводников
При последовательном соединении проводников сила тока в каждом из них одинакова:
$$I=I_{1}=I_{2}=\cdots=I_{i}(9)$$При параллельном соединении проводников сила тока (I) вычисляется как сумма токов в каждом проводнике (Ii):
$$I=\sum_{i=1}^{n} I_{i}(10)$$Закон Ома
Сила тока входит в один из основных законов постоянного тока – закон Ома (для участка цепи):
$$I=\frac{\varphi_{1}-\varphi_{2}+\varepsilon}{R}(11)$$где $\varphi_{1}$ —
$\varphi_{2}$ – разность потенциалов на концах, рассматриваемого участка,
$\varepsilon$ — ЭДС источника, который входит в участок цепи, R – сопротивление участка цепи. {6}=(30-6)=24$ (Кл)
{6}=(30-6)=24$ (Кл)
Ответ. q=24 Кл
Слишком сложно?
Формула силы тока не по зубам? Тебе ответит эксперт через 10 минут!
Пример
Задание. Плоский конденсатор составлен из двух квадратных пластин со стороной A, находящихся на расстоянии dдруг от друга. Этот конденсатор подключен к источнику постоянного напряжения U. Конденсатор погружают в сосуд с керосином (пластины конденсатора вертикальны) со скоростью v=const. Какова сила тока, которая будет течь по подводящим проводам в описанном выше процессе. Считать, что диэлектрическая проницаемость керосина равна $\varepsilon$.
Решение. Основой для решения задачи станет формул для вычисления силы тока вида:
$$I=\frac{d q}{d t}(2.1)$$При погружении в керосин на глубину xописанной выше системы мы получаем два конденсатора, соединенных параллельно (над керосином и в керосине) рис. 2. Для такой системы конденсаторов напряжение на каждом из них одинаково, поэтому уравнение для изменения заряда при движении удобно искать в виде:
$dq = UdC (2. {2}-A v t\right) \rightarrow C_{2}=\frac{\varepsilon \varepsilon_{0}(A v t)}{d}(2.4)$$
{2}-A v t\right) \rightarrow C_{2}=\frac{\varepsilon \varepsilon_{0}(A v t)}{d}(2.4)$$где $\varepsilon_{0}$ – электрическая постоянная, переменной величиной при погружении системы в керосин является площадь обкладок S:
$$S_{2}=A \cdot v \cdot t ; S_{1}=A \cdot(A-v t)$$Из выражений (2.4), (2.5) и условий задачи имеем:
$$d C=d C_{1}+d C_{2}=\frac{\varepsilon \varepsilon_{0} A v d t}{d}-\frac{\varepsilon_{0}}{d} A v d t(2.6)$$Тогда подставив dC в формулу для силы тока (2.1) получаем:
$$I=U\left(\frac{\varepsilon \varepsilon_{0} A v}{d}-\frac{\varepsilon_{0}}{d} A v\right)=\frac{\varepsilon_{0} U A v}{d}(\varepsilon-1)$$Ответ. $I=\frac{\varepsilon_{0} U A v}{d}(\varepsilon-1)$
Читать дальше: Формула силы.
Работа и мощность тока — урок. Физика, 8 класс.
Напряжение показывает, какую работу совершает электрическое поле при перемещении единичного положительного заряда из одной точки в другую.
U=Aq, где \(U\) – напряжение, \(А\) – работа тока, \(q\) – электрический заряд.
Таким образом, говоря другими словами,
напряжение на концах участка цепи численно равно работе, которая совершается при прохождении по этому участку электрического заряда в 1 Кл.
При прохождении по этому же участку электрического заряда, равного не \(1\) Кл, а, например, \(10\) Кл, совершённая работа будет в \(10\) раз больше.Это означает, чтобы определить работу электрического тока на каком-либо участке цепи, надо напряжение на концах этого участка цепи умножить на электрический заряд, прошедший по нему: A=U⋅q,
Для выражения любой из величин можно использовать приведенные ниже рисунки.
Электрический заряд, прошедший по участку цепи, можно определить, измерив силу тока и время его прохождения: q=I⋅t. Используя это соотношение и подставляя его в формулу A=U⋅q, получим формулу для нахождения работы электрического тока: A=U⋅I⋅t.
Работа электрического тока на участке цепи равна произведению напряжения на концах этого участка на силу тока и на время, в течение которого совершалась работа.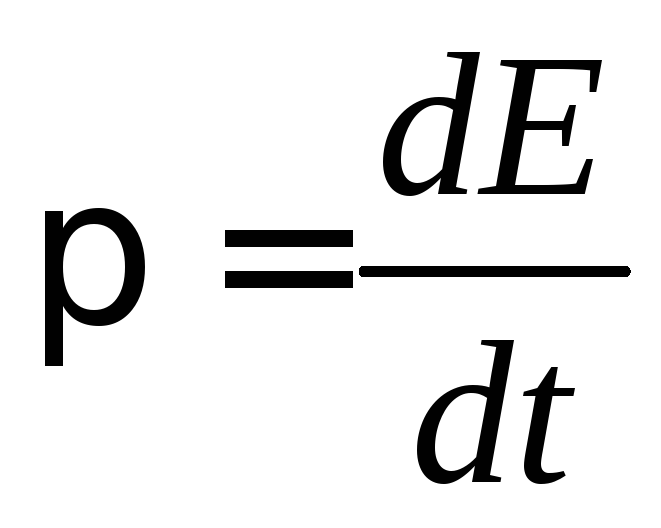
Чтобы выразить любую из величин из данной формулы, можно воспользоваться рисунком
Как известно, работу измеряют в джоулях, напряжение — в вольтах, силу тока — в амперах и время в секундах.
Тогда 1 джоуль = 1 вольт · 1 ампер · 1 секунду, или 1 Дж = 1 В · А ·С.
Из выше сказанного следует, что для измерения работы электрического тока нужны вольтметр, амперметр и часы. Например, для определения работы, которую совершает электрический ток, проходя по спирали лампы накаливания, необходимо собрать цепь, изображенную на рисунке. Вольтметром измеряется напряжение на лампе, амперметром – сила тока в ней. А при помощи часов (секундомера) засекается время горения лампы.
Например,
I = 1,2 АU = 5 Вt = 1,5 мин = 90 сА = U⋅I⋅t = 5⋅1,2⋅90 = 540 (Дж)
Обрати внимание!
Работа чаще всего выражается в килоджоулях или мегаджоулях.\(1\) кДж = 1000 Дж или \(1\) Дж = \(0,001\) кДж;
\(1\) М Дж = 1000000 Дж или \(1\) Дж = \(0,000001\) МДж.
На практике работу электрического тока
измеряют специальными приборами — счётчиками. Счётчики электроэнергии можно видеть в каждом доме.
Из курса физики известно, что мощность численно равна работе, совершённой в единицу времени N = Аt. Следовательно, чтобы найти мощность электрического тока, надо его работу A=U⋅I⋅t разделить на время.
В отличие от механической мощности мощность тока обозначают буквой \(Р\).
P=At=U⋅I⋅tt=U⋅I. Отсюда следует, чтомощность электрического тока равна произведению напряжения на силу тока: P=U⋅I.
Из этой формулы можно определить и другие физические величины.
Для удобства можно использовать приведенные ниже рисунки.
За единицу мощности принят ватт; \(1\) Вт = \(1\) Дж/с.
Из формулы P=U⋅I следует, что
\(1\) ватт =\(1\) вольт х \(1\) ампер, или \(1\) Вт = \(1\) В ∙ А.
Обрати внимание!
Используют также единицы мощности, кратные ватту: гектоватт (гВт), киловатт (кВт), мегаватт (МВт).
\(1\) гВт = \(100\) Вт или \(1\) Вт = \(0,01\) гВт;
\(1\) кВт = \(1000\) Вт или \(1\) Вт = \(0,001\) кВт;
\(1\) МВт = \(1 000 000\) Вт или \(1\) Вт = \(0,000001\) МВт.
Измерить мощность электрического тока можно с помощью вольтметра и амперметра.
Чтобы вычислить искомую мощность, необходимо напряжение умножить на силу тока. Значение силы тока и напряжение определяют по показаниям приборов.
I = 1,2 АU = 5 ВP = U⋅I = 5⋅1,2 = 6 (Вт)
Существуют специальные приборы — ваттметры, которые непосредственно измеряют мощность электрического тока в цепи. Они бывают аналоговые и цифровые. В зависимости от сферы применения у них различаются пределы измерения.
аналоговый ваттметр | аналоговый ваттметр | аналоговый ваттметр | цифровой ваттметр |
Подключим к цепи по очереди две лампочки накаливания, сначала одну, а затем другую и измерим силу тока в каждой из них.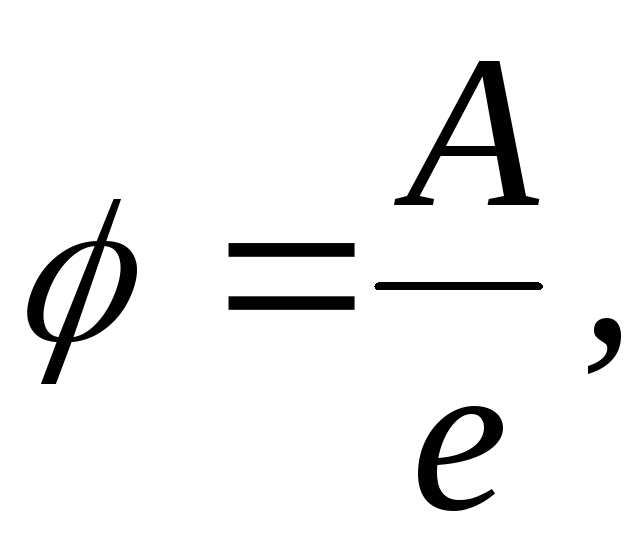 Она будет разной.
Она будет разной.
Сила тока в лампочке мощностью \(25\) ватт будет составлять \(0.1\) А. Лампочка мощностью \(100\) ватт потребляет ток в четыре раза больше — \(0.4\) А. Напряжение в этом эксперименте неизменно и равно \(220\) В. Легко можно заметить, что лампочка в 100 ватт светится гораздо ярче, чем \(25\)-ваттовая лампочка. Это происходит от того, что ее мощность больше. Лампочка, мощность которой в \(4\) раза больше, потребляет в \(4\) раза больше тока. Это показывает, что
Обрати внимание!
мощность прямо пропорциональна силе тока.
Что произойдет, если одну и ту же лампочку подсоединить к источникам различного напряжения? В данном случае используется напряжение \(110\) и \(220\) В.
Можно заметить, что при большем напряжении лампочка светится ярче, значит, в этом случае ее мощность будет больше. Это означает, что
Обрати внимание!
мощность зависит от напряжения.
Рассчитаем мощность лампочки в каждом случае:
| I=0,2АU=110ВP =U⋅I=110⋅0,2=22(Вт) | I=0,4АU=220ВP =U⋅I=220⋅0,4=88(Вт) |
Можно сделать вывод, что при увеличении напряжения в \(2\) раза мощность увеличивается в \(4\) раза.
Не следует путать эту мощность с номинальной мощностью лампы (мощность, на которую рассчитана лампа). Номинальная мощность лампы (а соответственно — ток через нить накала и её расчётное сопротивление) указываются только для номинального напряжения лампы (указано на баллоне, цоколе или упаковке).
В таблице дана мощность потребляемая различными приборами и устройствами:
Название | Рисунок | Мощность |
| калькулятор | \(0,001\) Вт | |
| лампы дневного света | \(15 — 80\) Вт | |
| лампы накаливания | \(25 — 5000\) Вт | |
| компьютер | \(200 — 450\) Вт | |
| электрический чайник | \(650 – 3100\) Вт | |
| пылесос | \(1500 — 3000\) Вт | |
| стиральная машина | \(2000 — 4000\) Вт | |
| трамвай | \(150 000 – 240000\) Вт |
Источники:
Перышкин А. В Физика. 8 класс // ДРОФА, 2013
В Физика. 8 класс // ДРОФА, 2013
http://уроки.мирфизики.рф/%d1%80%d0%b0%d0%b1%d0%be%d1%82%d0%b0-%d0%b8-%d0%bc%d0%be%d1%89%d0%bd%d0%be%d1%81%d1%82%d1%8c-%d1%8d%d0%bb%d0%b5%d0%ba%d1%82%d1%80%d0%b8%d1%87%d0%b5%d1%81%d0%ba%d0%be%d0%b3%d0%be-%d1%82%d0%be%d0%ba/
http://phscs.ru/physicsus/electric-power
http://class-fizika.narod.ru/8_34.htm
Как найти время зная силу тока и заряд? Формулу пожалуйста
Объём жидкости в аквариуме равен 8 мл. Выразите этот объём в метрах кубических (м³) и дециметрах кубических (дм³).
Срочно надо за 25 минут даю 30 балов
11 задание срочно нужно за 25 минут
Нужно ответит за 25 минут срочно
Світловий промінь переходить із повітря у воду. Кут падіння 75°, а кут заломлення47°. Визначити швидкість світла у воді?надо срочно
Составьте рассказ об устройстве власти в Риме, заменив выделенные определения слов их наименованием (в случае затруднения
обращайтесь к тексту учебник
… а и словам для справки). Государственная власть в Риме принадлежала 1) общенародному собранию, которое созывалось для принятия решений, важных для всей общины. Оно избирало 2) должностных лиц для повседневного управления государством. Во время выбора народ отдавал свои голоса самым видным гражданам – 3)представителям римской аристократии, в переводе с латинского «потомки отцов», но затем и 4)представители низшего сословия римского народа добились права избирать 5)особых должностных лиц для защиты своих интересов.
Перед выборами по территориальным округам 6)те, кого называли претендентами на избрание на какую-либо должность в государственном управлении, появились на 7)главной площади города в белоснежной, как цвет их намерений, одежде и просили о поддержке. Изгнанных царей заменили в 8)Римской системе управления, при которой государством руководят всенародно избранные должностные лица, в переводе с латыни «общее дело», 9)два высших должностных лица, созывавших сенат и народное собрание. По истечении срока они становились членами 10)совета старейшин, созданного Ромулом и включавшего 100, а потом 300 и более знатных граждан».
Государственная власть в Риме принадлежала 1) общенародному собранию, которое созывалось для принятия решений, важных для всей общины. Оно избирало 2) должностных лиц для повседневного управления государством. Во время выбора народ отдавал свои голоса самым видным гражданам – 3)представителям римской аристократии, в переводе с латинского «потомки отцов», но затем и 4)представители низшего сословия римского народа добились права избирать 5)особых должностных лиц для защиты своих интересов.
Перед выборами по территориальным округам 6)те, кого называли претендентами на избрание на какую-либо должность в государственном управлении, появились на 7)главной площади города в белоснежной, как цвет их намерений, одежде и просили о поддержке. Изгнанных царей заменили в 8)Римской системе управления, при которой государством руководят всенародно избранные должностные лица, в переводе с латыни «общее дело», 9)два высших должностных лица, созывавших сенат и народное собрание. По истечении срока они становились членами 10)совета старейшин, созданного Ромулом и включавшего 100, а потом 300 и более знатных граждан». Слова для справки: сенат, патриции, комиции, плебеи, кандидат, трибуны, республика, форум, магистраты, народное собрание, консул,патроны, цивитас
Слова для справки: сенат, патриции, комиции, плебеи, кандидат, трибуны, республика, форум, магистраты, народное собрание, консул,патроны, цивитас
29. Амперметр сопротивлением 0,1 Ом неопытный школь- ник зашунтировал сопротивлением 5 Ом. Во сколько раз возрос- ла цена деления прибора?
Оболонка кулі-зонда об’ємом 4 м³, наповнена гелієм, важить 30 Н.Якої маси прилади зможе підняти куля? СРОЧНООООО
Период полураспада – это время, за которое распадается половина радиоактивного вещества (масса исходного вещества уменьшается в 2 раза). Сколько грамм … урана надо взять, чтобы через время, равное 3 периодам полураспада, осталось 8 грамм урана?
При починке стиральной машины мастер сдвинул ее на 0,5 м Учитывая что стиральную машину он двигал приклвдывая силу 500 н Вычислите какую работу соверш … ил мастерПлиз решение
Электрический заряд. Суммарный и отрицательный заряды
Автор статьи — профессиональный репетитор, автор учебных пособий для подготовки к ЕГЭ Игорь Вячеславович Яковлев
Темы кодификатора ЕГЭ: электризация тел, взаимодействие зарядов, два вида заряда, закон сохранения электрического заряда.
Электромагнитные взаимодействия принадлежат к числу наиболее фундаментальных взаимодействий в природе. Силы упругости и трения, давление газа и многое другое можно свести к электромагнитным силам между частицами вещества. Сами электромагнитные взаимодействия уже не сводятся к другим, более глубоким видам взаимодействий.
Столь же фундаментальным типом взаимодействия является тяготение — гравитационное притяжение любых двух тел. Однако между электромагнитными и гравитационными взаимодействиями имеется несколько важных отличий.
1. Участвовать в электромагнитных взаимодействиях могут не любые, а только заряженные тела (имеющие электрический заряд).
2. Гравитационное взаимодействие — это всегда притяжение одного тела к другому. Электромагнитные взаимодействия могут быть как притяжением, так и отталкиванием.
3. Электромагнитное взаимодействие гораздо интенсивнее гравитационного. Например, сила электрического отталкивания двух электронов в раз превышает силу их гравитационного притяжения друг к другу.
Каждое заряженное тело обладает некоторой величиной электрического заряда . Электрический заряд — это физическая величина, определяющая силу электромагнитного взаимодействия между объектами природы. Единицей измерения заряда является кулон (Кл).
Два вида заряда
Поскольку гравитационное взаимодействие всегда является притяжением, массы всех тел неотрицательны. Но для зарядов это не так. Два вида электромагнитного взаимодействия — притяжение и отталкивание — удобно описывать, вводя два вида электрических зарядов: положительные и отрицательные.
Заряды разных знаков притягиваются друг к другу, а заряды разных знаков друг от друга отталкиваются. Это проиллюстрировано на рис. 1; подвешенным на нитях шарикам сообщены заряды того или иного знака.
Рис. 1. Взаимодействие двух видов зарядов
Повсеместное проявление электромагнитных сил объясняется тем, что в атомах любого вещества присутствуют заряженные частицы: в состав ядра атома входят положительно заряженные протоны, а по орбитам вокруг ядра движутся отрицательно заряженные электроны.
Заряды протона и электрона равны по модулю, а число протонов в ядре равно числу электронов на орбитах, и поэтому оказывается, что атом в целом электрически нейтрален. Вот почему в обычных условиях мы не замечаем электромагнитного воздействия со стороны окружающих тел: суммарный заряд каждого из них равен нулю, а заряженные частицы равномерно распределены по объёму тела. Но при нарушении электронейтральности (например, в результате электризации) тело немедленно начинает действовать на окружающие заряженные частицы.
Почему существует именно два вида электрических зарядов, а не какое-то другое их число, в данный момент не известно. Мы можем лишь утверждать, что принятие этого факта в качестве первичного даёт адекватное описание электромагнитных взаимодействий.
Заряд протона равен Кл. Заряд электрона противоположен ему по знаку и равен Кл. Величина
Кл
называется элементарным зарядом. Это минимальный возможный заряд: свободные частицы с меньшей величиной заряда в экспериментах не обнаружены. Физика не может пока объяснить, почему в природе имеется наименьший заряд и почему его величина именно такова.
Физика не может пока объяснить, почему в природе имеется наименьший заряд и почему его величина именно такова.
Заряд любого тела всегда складывается из целого количества элементарных зарядов:
Если , то тело имеет избыточное количество электронов (по сравнению с количеством протонов). Если же , то наоборот, у тела электронов недостаёт: протонов на больше.
Электризация тел
Чтобы макроскопическое тело оказывало электрическое влияние на другие тела, его нужно электризовать. Электризация — это нарушение электрической нейтральности тела или его частей. В результате электризации тело становится способным к электромагнитным взаимодействиям.
Один из способов электризовать тело — сообщить ему электрический заряд, то есть добиться избытка в данном теле зарядов одного знака. Это несложно сделать с помощью трения.
Так, при натирании шёлком стеклянной палочки часть её отрицательных зарядов уходит на шёлк.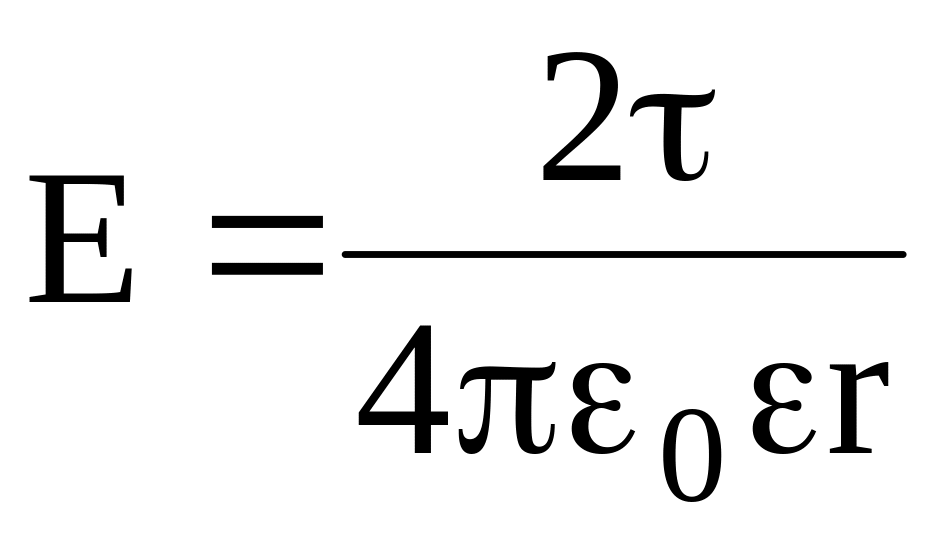 В результате палочка заряжается положительно, а шёлк — отрицательно. А вот при натирании шерстью эбонитовой палочки часть отрицательных зарядов переходит с шерсти на палочку: палочка заряжается отрицательно, а шерсть — положительно.
В результате палочка заряжается положительно, а шёлк — отрицательно. А вот при натирании шерстью эбонитовой палочки часть отрицательных зарядов переходит с шерсти на палочку: палочка заряжается отрицательно, а шерсть — положительно.
Данный способ электризации тел называется электризацией трением. С электризацией трением вы сталкиваетесь всякий раз, когда снимаете свитер через голову 😉
Другой тип электризации называется электростатической индукцией, или электризацией через влияние. В этом случае суммарный заряд тела остаётся равным нулю, но перераспределяется так, что в одних участках тела скапливаются положительные заряды, в других — отрицательные.
Рис. 2. Электростатическая индукция
Давайте посмотрим на рис. 2. На некотором расстоянии от металлического тела находится положительный заряд . Он притягивает к себе отрицательные заряды металла (свободные электроны), которые скапливаются на ближайших к заряду участках поверхности тела. На дальних участках остаются нескомпенсированные положительные заряды.
На дальних участках остаются нескомпенсированные положительные заряды.
Несмотря на то, что суммарный заряд металлического тела остался равным нулю, в теле произошло пространственное разделение зарядов. Если сейчас разделить тело вдоль пунктирной линии, то правая половина окажется заряженной отрицательно, а левая — положительно.
Наблюдать электризацию тела можно с помощью электроскопа. Простой электроскоп показан на рис. 3 (изображение с сайта en.wikipedia.org).
Рис. 3. Электроскоп
Что происходит в данном случае? Положительно заряженная палочка (например, предварительно натёртая) подносится к диску электроскопа и собирает на нём отрицательный заряд. Внизу, на подвижных листочках электроскопа, остаются нескомпенсированные положительные заряды; отталкиваясь друг от друга, листочки расходятся в разные стороны. Если убрать палочку, то заряды вернутся на место и листочки опадут обратно.
Явление электростатической индукции в грандиозных масштабах наблюдается во время грозы. На рис. 4 мы видим идущую над землёй грозовую тучу.
На рис. 4 мы видим идущую над землёй грозовую тучу.
Рис. 4. Электризация земли грозовой тучей
Внутри тучи имеются льдинки разных размеров, которые перемешиваются восходящими потоками воздуха, сталкиваются друг с другом и электризуются. При этом оказывается, что в нижней части тучи скапливается отрицательный заряд, а в верхней — положительный.
Отрицательно заряженная нижняя часть тучи наводит под собой на поверхности земли заряды положительного знака. Возникает гигантский конденсатор с колоссальным напряжением между тучей и землёй. Если этого напряжения будет достаточно для пробоя воздушного промежутка, то произойдёт разряд — хорошо известная вам молния.
Закон сохранения заряда
Вернёмся к примеру электризации трением — натирании палочки тканью. В этом случае палочка и кусок ткани приобретают равные по модулю и противоположные по знаку заряды. Их суммарный заряд как был равен нулю до взаимодействия, так и остаётся равным нулю после взаимодействия.
Мы видим здесь закон сохранения заряда, который гласит: в замкнутой системе тел алгебраическая сумма зарядов остаётся неизменной при любых процессах, происходящих с этими телами:
Замкнутость системы тел означает, что эти тела могут обмениваться зарядами только между собой, но не с какими-либо другими объектами, внешними по отношению к данной системе.
При электризации палочки ничего удивительного в сохранении заряда нет: сколько заряженных частиц ушло с палочки — столько же пришло на кусок ткани (или наоборот). Удивительно то, что в более сложных процессах, сопровождающихся взаимными превращениями элементарных частиц и изменением числа заряженных частиц в системе, суммарный заряд всё равно сохраняется!
Например, на рис. 5 показан процесс , при котором порция электромагнитного излучения (так называемый фотон) превращается в две заряженные частицы — электрон и позитрон . Такой процесс оказывается возможным при некоторых условиях — например, в электрическом поле атомного ядра.
Рис. 5. Рождение пары электрон–позитрон
Заряд позитрона равен по модулю заряду электрона и противоположен ему по знаку. Закон сохранения заряда выполнен! Действительно, в начале процесса у нас был фотон, заряд которого равен нулю, а в конце мы получили две частицы с нулевым суммарным зарядом.
Закон сохранения заряда (наряду с существованием наименьшего элементарного заряда) является на сегодняшний день первичным научным фактом. Объяснить, почему природа ведёт себя именно так, а не иначе, физикам пока не удаётся. Мы можем лишь констатировать, что эти факты подтверждаются многочисленными физическими экспериментами.
формулы расчета мощности в проводнике
Прохождение электрического тока через любую проводящую среду объясняется наличием в ней некоторого количества носителей заряда: электронов – для металлов, ионов – в жидкостях и газах. Как найти её величину, определяет физика силы тока.
Электрический ток в проводнике
В спокойном состоянии носители движутся хаотично, но при воздействии на них электрического поля движение становится упорядоченным, определяемым ориентацией этого поля – возникает сила тока в проводнике. Количество носителей, участвующих в переносе заряда, определяется физической величиной – силой тока.
Количество носителей, участвующих в переносе заряда, определяется физической величиной – силой тока.
От концентрации и заряда частиц-носителей, или количества электричества, напрямую зависит сила тока, проходящего через проводник. Если принять во внимание время, в течение которого это происходит, тогда узнать, что такое сила тока, и как она зависит от заряда, можно, используя соотношение:
Зависимость силы тока от электрического заряда
Входящие в формулу величины:
- I – сила электрического тока, единицей измерения является ампер, входит в семь основных единиц системы Си. Понятие «электрический ток» ввёл Андре Ампер, единица названа в честь этого французского физика. В настоящее время определяется как ток, вызывающий силу взаимодействия 2×10-7 ньютона между двумя параллельными проводниками, при расстоянии 1 метр между ними;
- Величина электрического заряда, применённая здесь для характеристики силы тока, является производной единицей, измеряется в кулонах.
 Один кулон – это заряд, проходящий через проводник за 1 секунду при токе 1 ампер;
Один кулон – это заряд, проходящий через проводник за 1 секунду при токе 1 ампер; - Время в секундах.
Сила тока через заряд может вычисляться с применением данных о скорости и концентрации частиц, угла их движения, площади проводника:
I = (qnv)cosαS.
Также используется интегрирование по площади поверхности и сечению проводника.
Определение силы тока с использованием величины заряда применяется в специальных областях физических исследований, в обычной практике не используется.
Связь между электрическими величинами устанавливается законом Ома, который указывает на соответствие силы тока напряжению и сопротивлению:
Сила тока участка цепи и цепи с источником тока
Сила электрического тока здесь как отношение напряжения в электрической цепи к её сопротивлению, эти формулы используются во всех областях электротехники и электроники. Они верны для постоянного тока с резистивной нагрузкой.
В случае косвенного расчета для переменного тока следует учитывать, что измеряется и указывается среднеквадратичное (действующее) значение переменного напряжения, которое меньше амплитудного в 1,41 раза, следовательно, максимальная сила тока в цепи будет больше во столько же раз.
При индуктивном или емкостном характере нагрузки вычисляется комплексное сопротивление для определённых частот – найти силу тока для такого рода нагрузок, используя значение активного сопротивления постоянному току, невозможно.
Так, сопротивление конденсатора постоянному току практически бесконечно, а для переменного:
RC = 1/ FC.
Здесь RC – сопротивление того же конденсатора ёмкостью С, на частоте F, которое во многом зависит от его свойств, сопротивления разных типов ёмкостей для одной частоты значительно различаются. В таких цепях сила тока по формуле, как правило, не определяется – используются различные измерительные приборы.
Для нахождения значения силы тока при известных значениях мощности и напряжения, применяются элементарные преобразования закона Ома:
Тут сила тока – в амперах, сопротивление – в омах, мощность – в вольт-амперах.
Электрический ток имеет свойство разделяться по разным участкам цепи. Если их сопротивления различны, то и сила тока будет разной на любом из них, так находим общий ток цепи.
I = I1 + I2 + I3
Общий ток цепи равен сумме токов на её участках – при полном проходе через электрическую замкнутую цепь ток разветвляется, затем принимает исходное значение.
Видео
Оцените статью:Эл заряд определение. Формула заряда
Простые опыты по электризации различных тел иллюстрируют следующие положения.
1. Существуют заряды двух видов: положительные (+) и отрицательные (-). Положительный заряд возникает при трении стекла о кожу или шелк, а отрицательный — при трении янтаря (или эбонита) о шерсть.
2. Заряды (или заряженные тела ) взаимодействуют друг с другом. Одноименные заряды оттал-киваются, а разноименные заряды притягиваются.
3. Состояние электризации можно передать от одного тела к другому, что связано с переносом электрического заряда . При этом телу можно передать больший или меньший заряд, т. е. заряд имеет величину. При электризации трением заряд приобретают оба тела, причем одно — поло-жительный, а другое — отрицательный. Следует подчеркнуть, что абсолютные величины зарядов наэлектризованных трением тел равны, что подтверждается многочисленными измерениями заря-дов с помощью электрометров.
Объяснить, почему тела электризуются (т. е. заряжаются) при трении, стало возможным после открытия электрона и изучения строения атома. Как известно, все вещества состоят из атомов; атомы , в свою очередь, состоят из элементарных частиц — отрицательно заряженных электронов , положительно заряженных протонов и нейтральных частиц — нейтронов . Электроны и протоны являются носителями элементарных (минимальных) электрических зарядов.
Элементарный электрический заряд (е ) — это наименьший электрический заряд, положи-тельный или отрицательный, равный величине заряда электрона:
е = 1,6021892(46) · 10 -19 Кл .
Заряженных элементарных частиц существует много, и почти все они обладают зарядом +e или -e , однако эти частицы весьма недолговечны. Они живут меньше миллионной доли се-кунды. Только электроны и протоны существуют в свободном состоянии неограниченно долго.
Протоны и нейтроны (нуклоны) составляют положительно заряженное ядро атома , вокруг которого вращаются отрицательно заряженные электроны, число которых равно числу протонов, так что атом в целом электроцентралей.
В обычных условиях тела, состоящие из атомов (или молекул), электрически нейтральны. Однако в процессе трения часть электронов, покинувших свои атомы, может перейти с одного тела на другое. Перемещения электронов при этом не превышают размеров межатомных расстояний. Но если тела после трения разъединить, то они окажутся заряженными; тело, которое отдало часть своих электронов, будет заряжено положительно, а тело, которое их приобрело, — отрицательно.
Итак, тела электризуются, т. е. получают электрический заряд, когда они теряют или приоб-ретают электроны. В некоторых случаях электризация обусловлена перемещением ионов. Новые электрические заряды при этом не возникают. Происходит лишь разделение имеющихся заря-дов между электризующимися телами: часть отрицательных зарядов переходит с одного тела на другое.
Определение заряда.
Следует особо подчеркнуть, что заряд является неотъемлемым свойством частицы. Частицу без заряда представить себе можно, но заряд без частицы — нельзя.
Проявляют себя заряженные частицы в притяжении (разноименные заряды) либо в отталкивании (одноименные заряды) с силами, на много порядков превышающими гравитационные. Так, сила электрического притяжения электрона к ядру в атоме водорода в 10 39 раз больше силы гра-витационного притяжения этих частиц. Взаимодействие между заряженными частицами называется электромагнитным взаимодействием , а электрический заряд определяет интенсивность электромагнитных взаимодействий.
В современной физике так определяют заряд:
Электрический заряд — это физическая величина , являющаяся источником электрического поля, посредством которого осуществляется взаимодействие частиц, обладающих зарядом.
Электрический заряд – физическая величина, которая определяет способность тела принимать участие в электромагнитных взаимодействиях. Тело, обладающее ненулевым зарядом, образует вокруг себя электрическое поле, которое взаимодействует с любым другим телом, имеющим заряд.
В чем измеряется заряд
Для того чтобы ответить на вопрос, как найти заряд, нужно знать в чем он измеряется и какие формулы применять. Заряд измеряется в кулонах (Кл). Названа единица измерения в честь Шарля Кулона – физика и инженера, сделавшего значительный вклад в развитие познаний об электричестве.
Задачи о том, как найти заряд q (этой буквой обозначается эта физическая величина), изучаются в школе в рамках электростатики – части курса физики. Главным законом электростатики является закон Кулона, который записывается математически следующим образом:
F = k (q1 * q2) / r2, (1)
где F – сила, с которой действуют друг на друга заряженные тела, q – заряды тел, r – расстояние между ними, k — коэффициент.
Если известна сила, заряд одного из тел и расстояние между ними, то задача о том, как найти электрический заряд второго тела, решается из уравнения (1) очень просто.
Какие частицы заряжены
Зарядом обладают элементарные частицы – электроны и протоны. Причём модули зарядов этих частиц одинаковы. Отличаются лишь их знаки. Каждый атом, состоит из одинакового числа этих частиц. Соответственно, суммарный заряд атома равен нулю.
Протоны (вместе с нейтронами, имеющими нулевой заряд) составляют ядро атома. Вокруг ядра на большом (по меркам размера самого ядра) расстоянии вращаются электроны. Сила, описанная формулой (1), удерживает электроны на своих орбитах. Однако атомы некоторых веществ удерживают электроны, находящие на высших энергетических уровнях (наиболее удалённые от ядра), довольно слабо, и эти электроны легко отрываются и «путешествуют» между атомами.
Если часть этих электронов отнять у одного тела и передать другому, то оба тела станут электрически заряженными. Первое получит положительный заряд (за счёт дефицита электронов), второе – отрицательный (за счёт их переизбытка). Атомы, потерявшие или получившие лишние электроны, называются ионами. Соответственно процесс отдачи или получения дополнительных электронов называется ионизацией.
В школьном курсе химии и физики также встречаются задачи о том, как находить заряд ядра атома. Сделать это очень просто: нужно умножить количество протонов, присутствующих в ядре, на заряд одного протона. Заряд протона – одна из элементарных физических констант.
Чтобы узнать количество протонов в ядре атома, следует заглянуть в таблицу Менделеева: этим числом является порядковый номер нужного вещества. Например, заряд атома цинка (который имеет в периодической таблице элементов номер 30) равен:
gzn=30*1.602*10(-19) Кл=48,06*10(-19)Кл
где, gzn- заряд атома цинка; Кл — измерение заряда в кулонах.
Изучение электродинамики начнем с простейшего случая — с электростатики, в которой рассматривается взаимодействие неподвижных относительно друг друга электрических зарядов и создаваемое ими неизменное во времени электростатическое поле.
§ 1. Электрический заряд. Закон Кулона
Электрический заряд и электрическое поле — первичные понятия, подобно понятиям массы и гравитационного поля в механике. Это значит, что их нельзя определить через другие, более простые понятия. Все, что мы можем сделать — это описать их свойства.
Электрический заряд. Электрический заряд характеризует способность тела к определенному взаимодействию, описываемому на языке сил. В отличие от гравитационного взаимодействия, проявляющегося всегда как притяжение между телами, электрическое взаимодействие может быть как притяжением, так и отталкиванием. Известным из опыта фундаментальным свойством электрического заряда является то, что он существует в двух видах, условно называемых положительными и отрицательными зарядами. Заряды одного знака отталкиваются. Взаимодействие зарядов противоположных знаков заключается в их взаимном притяжении.
Макроскопическому телу можно сообщить заряд любого знака. Когда эти заряды присутствуют в одинаковых количествах, тело называют электрически нейтральным или незаряженным. Другими словами, в макроскопическом теле положительные и отрицательные заряды могут компенсировать друг друга. Незаряженное тело при равномерном распределении входящих в него положительных и отрицательных зарядов электрически не взаимодействует с другими заряженными телами.
Электрический заряд макроскопического тела определяется суммарным зарядом образующих его элементарных частиц. Окружающий нас мир представляет собой хорошо скомпенсированную смесь положительных и отрицательных зарядов. Такая компенсация неудивительна, поскольку одноименные заряды отталкиваются.
Причина, по которой электрический заряд существует именно в двух видах, в современной физике до конца не выяснена. Возможно, что в этом находит свое отражение определенная симметрия.
Положительный и отрицательный заряды можно рассматривать как противоположные проявления одного качества, аналогично тому как понятия «правое» и «левое» выступают противоположными проявлениями свойства пространственной симметрии. Оказывается, что вопрос симметрии «правого» и «левого» тесно связан с этой двойственностью электрического заряда и с другой фундаментальной симметрией, а именно с симметрией по отношению к обращению времени. Некоторый свет на эти вопросы проливает физика элементарных частиц.
Электризация тел. Простейшие эксперименты, в которых на качественном уровне могут быть обнаружены описанные закономерности взаимодействия электрических зарядов, известны еще со времен Б. Франклина (вторая половина XVIII века).
Рис. 1. Электростатическая машина
Рис. 2. Простейший электроскоп
Существуют разные способы электризации тел, т. е. превращения электрически нейтральных тел в заряженные. В частности, это возможно путем трения тел друг о друга (электризация трением).
Разделение электрических зарядов противоположных знаков возможно и путем электризации через влияние, без непосредственного контакта между телами (электрическая индукция). Наиболее распространенный прибор для разделения зарядов — электростатическая машина (рис. 1). Обнаружить у тела наличие электрического заряда можно с помощью электроскопа (рис. 2) или более современного прибора — электрометра (рис. 3), Имеющего, в отличие от электроскопа, экранирующий металлический корпус, благодаря которому его показания не подвержены влиянию посторонних окружающих тел.
Проводники и диэлектрики. По поведению зарядов в наэлектризованном теле все вещества делятся на проводники и изоляторы (диэлектрики). У диэлектриков сообщенный им заряд остается в том месте, куда он был помещен при электризации. В проводниках сообщенный заряд может свободно перемещаться по всему телу. Именно благодаря этому свойству проводящие тела можно заряжать электризацией через влияние. В равновесии из-за взаимного отталкивания свободные заряды располагаются на внешней поверхности проводника.
Рис. 3. Электрометр и устройство его механизма
Среди большого числа разнообразных электростатических экспериментов немало таких, которые для своего объяснения даже на качественном уровне требуют привлечения весьма сложных и тонких понятий. Примером может служить широко известный опыт по притягиванию незаряженных клочков бумаги наэлектризованной расческой.
Закон Кулона. Первые экспериментальные количественные результаты, относящиеся к взаимодействию неподвижных электрических зарядов, были получены Ш. Кулоном в конце XVIII столетия. Для измерения сил, действующих между зарядами, Кулон использовал созданный им прибор, называемый крутильными весами (рис. 4а). На тонкой упругой нити подвешено легкое коромысло К из изолятора, на одном конце которого укреплен проводящий шарик А, а на другом — противовес П. Рядом с шариком А можно поместить другой такой же неподвижный шарик В. Стеклянный цилиндр защищает чувствительные части прибора от движения воздуха.
Чтобы установить зависимость силы взаимодействия от расстояния между зарядами, шарикам А и В сообщают произвольные заряды, прикасаясь к
Рис. 4. Крутильные весы Кулона
ним третьим заряженным шариком С, укрепленным на ручке из диэлектрика. По углу закручивания упругой нити (рис. 46) можно измерить силу отталкивания одноименно заряженных шариков, а по шкале прибора — расстояние между ними. В результате этих опытов Кулон установил, что сила взаимодействия направлена вдоль линии, соединяющей оба заряда, и обратно пропорциональна квадрату расстояния между ними:
Зависимость силы взаимодействия от заряда можно установить следующим образом. Когда заряженный проводящий шарик приводится в соприкосновение с таким же незаряженным шариком, то естественно предположить, что в силу симметрии заряд между ними распределится поровну. При этом оказывается, что сила взаимодействия между шариками, на одном из которых описанным способом заряд уменьшен вдвое, также уменьшается в два раза при том же расстоянии между шариками. Повторяя эту процедуру несколько раз, можно убедиться, что при уменьшении заряда любого из шариков в два, четыре и т. д. раз сила взаимодействия оказывается пропорциональной заряду каждого шарика.
Обобщая результаты таких опытов, можно сформулировать закон, описывающий силу взаимодействия неподвижных электрических зарядов, — закон Кулона. Сила взаимодействия двух точечных зарядов в вакууме пропорциональна произведению зарядов и обратно пропорциональна квадрату расстояния между ними:
Чтобы формула давала не только значения модуля силы, но и ее направление, удобно записать закон Кулона в векторном виде:
Здесь — сила, действующая на заряд со стороны заряда — разность радиусов-векторов точечных зарядов т. е. вектор, проведенный от заряда к заряду (рис. 5). Легко видеть, что формула (2) дает правильное направление силы при любых знаках зарядов т. е. и при отталкивании ( рис. 5а), и при притяжении ( рис. 5б) этих зарядов.
Выражение для силы действующей на заряд со стороны получается из (2) перестановкой индексов 1 и 2 и находится в полном соответствии с третьим законом Ньютона:
которому удовлетворяет взаимодействие неподвижных относительно друг друга электрических зарядов.
Точность, которая может быть достигнута в опытах с крутильными весами, сравнительно невелика. Наша убежденность в том, что закон Кулона точно описывает электростатическое взаимодействие, основана на большом количестве подтверждающих его других экспериментальных данных. Оказывается, что закон Кулона выполняется точно как для очень больших, так и для очень малых расстояний. В частности, исследования атомных явлений позволяют заключить, что он справедлив по крайней мере вплоть до расстояний порядка размеров атомного ядра
Рис. 5. Взаимодействие точечных зарядов (закон Кулона)
Отметим, что электростатическое взаимодействие тел со сферически-симметричным распределением заряда описывается такими же выражениями (1) и (2), как и взаимодействие точечных зарядов, помещенных в центры этих тел.
Единицы заряда. Коэффициент к, фигурирующий в формулах (1) и (2), зависит от выбора единиц. В физике получили широкое распространение две системы единиц, в которых введение единиц электромагнитных величин основано на разных физических законах. В так называемой системе СГСЭ (абсолютная электростатическая система), построенной на трех основных единицах — длины, времени и массы, — единица электрического заряда является производной. Она выбирается на основе закона Кулона так, чтобы коэффициент к в нем был равен единице. Такая единица заряда называется абсолютной электростатической единицей. Это такой заряд, который действует в вакууме на равный ему заряд, удаленный на расстояние один сантиметр, с силой, равной одной дине. Размерность заряда в системе СГСЭ устанавливается из формулы (1) при
Формула, выражающая закон Кулона, в системе ГСЭ имеет вид
В Международной системе единиц в числе семи основных единиц фигурирует единица силы электрического тока — ампер Эта единица устанавливается на основе магнитного взаимодействия токов, о чем будет подробно рассказано при изучении магнитного поля тока. Единица заряда — кулон (Кл) — является производной и выражается через две основные единицы — силы тока и времени. По определению один кулон — это заряд, проходящий за одну секунду через поперечное сечение проводника, в котором поддерживается постоянный электрический ток силой один ампер:
В электродинамике показывается, что между кулоном и абсолютной электростатической единицей заряда имеется следующее соотношение:
Поскольку в СИ единица заряда установлена независимо от закона Кулона, коэффициент к в (1) уже не равен единице. Его принято записывать в виде где — некоторая размерная постоянная, называемая электрической постоянной. Выражение для закона Кулона в СИ имеет вид
Значение электрической постоянной можно найти с помощью соотношения (6) между кулоном и единицей заряда СГСЭ. Пусть имеется два точечных заряда Кл, удаленных на расстояние Тогда согласно формуле (4) сила взаимодействия равна
С другой стороны, согласно (7), эта же сила равна
Элементарный электрический заряд. В природе электрические заряды существуют только в виде заряженных частиц, которые условно считаются простейшими или элементарными. Наличие электрического заряда — неотъемлемое свойство некоторых элементарных частиц. Носителями отрицательных зарядов являются
электроны, положительных зарядов — протоны. Заряд всех протонов одинаков и равен минимальному встречающемуся в природе заряду — так называемому элементарному электрическому заряду
Заряд всех электронов также одинаков и по абсолютной величине равен элементарному электрическому заряду. Атом любого элемента содержит столько же электронов в электронной оболочке, сколько протонов находится в его ядре, и потому атом электрически нейтрален.
Нейтральными будут молекулы и макроскопические тела, построенные из атомов. Всякий процесс электризации тел связан с разделением электрических зарядов, когда на одном из тел (или части тела) появляется избыток положительных зарядов, а на другом (или другой части тела) — избыток отрицательных зарядов. Общее число положительных и отрицательных зарядов при этом сохраняется, заряды только перераспределяются между телами. Как правило, электризация связана с переносом электронов, масса которых чрезвычайно мала ( кг). Поэтому можно перенести на макроскопическое тело или убрать с него огромное число электронов без заметного изменения его массы, сообщив телу при этом значительный электрический заряд.
Закон сохранения электрического заряда. Сохранение электрического заряда представляет собой важнейшее известное из опыта его свойство: в изолированной системе алгебраическая сумма зарядов всех тел остается неизменной. Справедливость этого закона подтверждается не только в процессах электризации, но и в наблюдениях над огромным числом рождений, уничтожений и взаимных превращений элементарных частиц.
Закон сохранения электрического заряда — один из самых фундаментальных законов природы. Не известно ни одного случая его нарушения. Даже в тех случаях, когда происходит рождение новой заряженной частицы, одновременно обязательно рождается другая частица с равным и противоположным по знаку зарядом. «Зарядить» элементарную частицу, т. е. изменить ее заряд, нельзя — мы просто получим при этом другую частицу.
Электрический заряд элементарной частицы не зависит ни от выбора системы отсчета, ни от состояния движения частицы, ни от ее взаимодействия с другими частицами. Поэтому заряд макроскопического тела не зависит ни от движения составляющих его частиц, ни от движения тела как целого.
Задачи
1. Электрон в атоме водорода. В планетарной модели атома предполагается, что электрон движется вокруг ядра под действием кулоновской силы притяжения к ядру. Считая, что движение электрона подчиняется законам
классической механики, определите скорость электрона на круговой орбите радиуса в атоме водорода.
Решение. Когда электрические заряды движутся медленно, т. е. их скорость много меньше скорости света, взаимодействие между ними в первом приближении будет таким же, как и между неподвижными зарядами.
2. Заряженные шарики. Два одинаковых металлических шарика, находящихся на расстоянии, большом по сравнению с их размерами, притягиваются друг к другу, причем известно, что один из них обладает втрое большим зарядом. Как изменится сила-их взаимодействия, если шарики привести в соприкосновение, а затем развести на прежнее расстояние?
Решение. Так как сначала шарики притягивались, то они обладали зарядами противоположных знаков. При соприкосновении одинаковых шариков вследствие симметрии полный заряд распределится между ними поровну. Абсолютная величина заряда одного из шариков по условию втрое больше другого. Поэтому после частичной нейтрализации заряда при соприкосновении шариков каждый из них будет иметь заряд одного и того же знака, причем модуль этого заряда равен меньшему из модулей первоначальных зарядов. Отсюда ясно, что шарики будут отталкиваться с силой, втрое меньшей первоначальной силы притяжения.
Почему в условии задачи говорится о том, что размеры шариков малы по сравнению с расстоянием между ними? При решении мы молчаливо опирались на закон Кулона, справедливый для взаимодействия точечных зарядов. Поэтому линейные размеры шариков должны быть малы, чтобы можно было не думать ни о том, что заряды распределены на шариках неравномерно, ни о том, как изменяется это распределение при их перезарядке.
Какие опыты свидетельствуют о том, что существует два вида электрического заряда?
Почему в окружающем нас мире макроскопические тела, как правило, электрически нейтральны?
Объясните принцип действия электроскопа (рис. 2).
Как зарядить электрометр или электроскоп, используя электризацию трением и электризацию через влияние? Объясните происходящие при этом процессы.
Опишите, каким образом устанавливается зависимость силы взаимодействия от значения заряда в опытах Кулона, учитывая, что при этом нет независимого способа измерения заряда.
Поясните, как от выражающей закон Кулона формулы (I) перейти к векторному выражению (2) для силы взаимодействия зарядов.
Выведите размерность заряда системе СГСЭ.
Получите выражение для размерности электрической постоянной .
В чем заключается закон сохранения электрического заряда? Может ли измениться заряд отдельных частиц и суммарный электрический заряд при ядерных реакциях и взаимных превращениях элементарных частиц?
Почему при решении задачи 1 можно не учитывать силу гравитационного притяжения электрона к ядру? Во сколько раз она меньше силы электростатического притяжения?
Одна из базовых физических величин, которая имеет непосредственное отношение к электричеству и в частности к электротехнике — это электрический заряд . Мы привыкли к тому, что в электротехнике заряд измеряется в кулонах , но мало кто знает, что есть и другие единицы измерения электрического заряда. При расчётах электрических схем, при использовании электроизмерительных приборов применяют международную систему единиц СИ. Но знаете ли вы, что есть и другие системы измерения?
Эта единица измерения заряда известна многим ещё со школы. Относится она, как вы уже поняли, к системе единиц СИ. Это производная величина, которая не является в системе СИ базовой. Она выводится из других величин и определяется другими величинами.
Единица измерения носит название учёного — Шарля де Огюстена Кулона, открывшего закон взаимодействия зарядов, и соответственно, электрический заряд. Обозначают сокращённо величину заряда буквами Кл , а когда речь идёт о количестве заряда — пишут его с прописными буквами — кулон .
Определение электрического заряда в системе СИ следующее:
Электрический заряд в один кулон — это такой заряд, который проходит через сечение проводника при силе тока в один ампер за время равное одной секунде.
Между зарядом и единицей в ампер-час существует связь. Один кулон электричества равен 1/3600 ампер-часа.
Ещё одна единица и измерения заряда, которая названа в честь американского изобретателя и физика — Бенджамина Франклина. Его портрет можно увидеть на стодолларовой купюре США. Эта единица относится к системе величин СГСЭ, в которой базовыми являются такие единицы как сантиметр, грамм и секунда. По другому эту систему единиц называют абсолютной системой физических единиц и она широко использовалась до принятия системы СИ (принята в 1960 году).
Сокращённо единица измерения записывается как Фр (русское) или Fr (английское).
Определение электрического заряда в системе СГСЭ следующее:
Количество электрического заряда в один Франклин — это такое количество заряда, что два разноимённых заряда по одному франклину, находящихся в вакууме на расстоянии одного сантиметра, будут притягиваться друг к другу с силой в один дин.
Как видно из определения, оно отличается от того, что приведено для системы СИ. Разница прежде всего в том, что в системе СИ заряд выражается через силу тока и исходя из этого определяется, а в системе СГСЭ заряд выражен через .
Система СГСЭ удобна для вычислений и исследований в физике, а система СИ более удобна для практических нужд электротехники.
Закон Кулона, имеющий непосредственное отношение к зарядам, в системе СИ и СГС (СГСЭ), записываются по разному. Единицу заряда в 1 Кл можно перевести в 1 Фр и наоборот.
Существует также планковская система естественных единиц измерения и в ней также имеется электрический заряд. Эта система была впервые предложена немецким физиком Максом Планком 1899 году на основе скорости света и гравитационной постоянной и ещё двух введённых им констант.
Электрический заряд – физическая величина, характеризующая способность тел вступать в электромагнитные взаимодействия. Измеряется в Кулонах.
Элементарный электрический заряд – минимальный заряд, который имеют элементарные частицы (заряд протона и электрона).
e = Кл
Тело имеет заряд , значит имеет лишние или недостающий электроны. Такой заряд обозначается q = ne . (он равен числу элементарных зарядов).
Наэлектризовать тело – создать избыток и недостаток электронов. Способы: электризация трением и электризация соприкосновением .
Точечный заря д – заряд тела, которое можно принять за материальную точку.
Пробный заряд () – точечный, малый по величине заряд, обязательно положительный – используется для исследования электрического поля.
Закон сохранения заряда : в изолированной системе алгебраическая сумма зарядов всех тел сохраняется постоянной при любых взаимодействиях этих тел между собой .
Закон Кулона : силы взаимодействия двух точечных зарядов пропорциональны произведению этих зарядов, обратно пропорциональны квадрату расстояния между ними, зависят от свойств среды и направлены вдоль прямой, соединяющей их центры .
,
где
Ф/м,
Кл 2 /нм 2 – диэлектр. пост.
вакуума
— относит. диэлектрическая проницаемость (>1)
— абсолютная диэлектрическая прониц. среды
Электрическое поле – материальная среда, через которую происходит взаимодействие электрических зарядов.
Свойства электрического поля:
Характеристики электрического поля:
Напряжённость (E ) – векторная величина, равная силе, действующей на единичный пробный заряд, помещённый в данную точку.
Измеряется в Н/Кл.
Направление – такое же, как и у действующей силы.
Напряжённость не зависит ни от силы, ни от величины пробного заряда.
Суперпозиция электрических полей : напряжённость поля, созданного несколькими зарядами, равна векторной сумме напряжённостей полей каждого заряда:
Графически электронное поле изображают с помощью линий напряжённости.
Линия напряжённости – линия, касательная к которой в каждой точке совпадает с направлением вектора напряжённости.
Свойства линий напряжённости : они не пересекаются, через каждую точку можно провести лишь одну линию; они не замкнуты, выходят из положительного заряда и входят в отрицательный, либо рассеиваются в бесконечность.
Виды полей:
Однородное электрическое поле – поле, вектор напряжённости которого в каждой точке одинаков по модулю и направлению.
Неоднородное электрическое поле – поле, вектор напряжённости которого в каждой точке неодинаков по модулю и направлению.
Постоянное электрическое поле – вектор напряжённости не изменяется.
Непостоянное электрическое поле – вектор напряжённости изменяется.
Работа электрического поля по перемещению заряда .
, где F – сила, S – перемещение, — угол между F и S.
Для однородного поля: сила постоянна.
Работа не зависит от формы траектории; работа по перемещению по замкнутой траектории равна нулю.
Для неоднородного поля:
Потенциал электрического поля – отношение работы, которое совершает поле, перемещая пробный электрический заряд в бесконечность, к величине этого заряда.
— потенциал – энергетическая характеристика поля. Измеряется в Вольтах
Разность потенциалов :
Если
,
то
,
значит
— градиент потенциала.
Для однородного поля: разность потенциалов
– напряжение :
. Измеряется в Вольтах, приборы – вольтметры.
Электроёмкость – способность тел накапливать электрический заряд; отношение заряда к потенциалу, которое для данного проводника всегда постоянно.
.
Не зависит от заряда и не зависит от потенциала. Но зависит от размеров и формы проводника; от диэлектрических свойств среды.
, где r – размер,
— проницаемость среды вокруг тела.
Электроёмкость увеличивается, если рядом находятся любые тела – проводники или диэлектрики.
Конденсатор – устройство для
накопления заряда. Электроёмкость:
Плоский конденсатор – две металлические пластины, между которыми находится диэлектрик. Электроёмкость плоского конденсатора:
, где S – площадь пластин, d – расстояние между пластинами.
Энергия заряженного конденсатора равна работе, которую совершает электрическое поле при переносе заряда с одной пластины на другую.
Перенос малого заряда
,
напряжение измениться на
,
совершится работа
.
Так как
,
а С = const,
.
Тогда
.
Интегрируем:
Энергия электрического поля :
,
где V=Sl –
объём, занимаемый электрическим полем
Для неоднородного поля :
.
Объёмная плотность электрического
поля :
.
Измеряется в Дж/м 3 .
Электрический диполь – система, состоящая из двух равных, но противоположных по знаку точечных электрических зарядов, расположенных на некотором расстоянии друг от друга (плечо диполя — l).
Основная характеристика диполя – дипольный момент – вектор, равный
произведению заряда на плечо диполя,
направленный от отрицательного заряда
к положительному. Обозначается
.
Измеряется в Кулон-метрах.
Диполь в однородном электрическом поле.
На каждый из зарядов диполя действуют
силы:
и
.
Эти силы противоположно направлены и
создают момент пары сил – вращающий
момент:
,
где
М – вращающий момент F – силы, действующие на диполь
d – плечо сил l – плечо диполя
p – дипольный момент E – напряжённость
— угол между p и Е q – заряд
Под действием вращающего момента, диполь повернётся и установится по направлению линий напряжённости. Векторы p и Е будут параллельны и однонаправлены.
Диполь в неоднородном электрическом поле.
Вращающий момент есть, значит диполь повернётся. Но силы будут неравны, и диполь будет двигаться туда, где сила больше.
— градиент напряжённости . Чем выше градиент напряжённости, тем выше боковая сила, которая стаскивает диполь. Диполь ориентируется вдоль силовых линий.
Собственное поле диполя .
Но . Тогда:
.
Пусть диполь находится в точке О, а его плечо мало. Тогда:
.
Формула получена с учётом:
Таким образом разность потенциалов зависит от синуса половинного угла, под которым видны точки диполя, и проекции дипольного момента на прямую, соединяющие эти точки.
Диэлектрики в электрическом поле.
Диэлектрик – вещество, не имеющее свободных зарядов, а значит и не проводящее электрический ток. Однако на самом же деле проводимость существует, но она ничтожно мала.
Классы диэлектриков:
с полярными молекулами (вода, нитробензол): молекулы не симметричны, центры масс положительных и отрицательных зарядов не совпадают, а значит, они обладают дипольным моментом даже в случае, когда электрического поля нет.
с неполярными молекулами (водород, кислород): молекулы симметричны, центры масс положительных и отрицательных зарядов совпадают, а значит, они не имеют дипольного момента при отсутствии электрического поля.
кристаллические (хлорид натрия): совокупность двух подрешёток, одна из которых заряжен положительно, а другая – отрицательно; в отсутствии электрического поля суммарный дипольный момент равен нулю.
Поляризация – процесс пространственного разделения зарядов, появления связанных зарядов на поверхности диэлектрика, что приводит к ослаблению поля внутри диэлектрика.
Способы поляризации:
1 способ – электрохимическая поляризация :
На электродах – движение к ним катионов и анионов, нейтрализация веществ; образуются области положительных и отрицательных зарядов. Ток постепенно уменьшается. Скорость установления механизма нейтрализации характеризуется временем релаксации – это время, в течение которого ЭДС поляризации увеличится от 0 до максимума от момента наложения поля. = 10 -3 -10 -2 с.
2 способ – ориентационная поляризация:
На поверхности диэлектрика образуются некомпенсированные полярные, т.е. происходит явление поляризации. Напряжённость внутри диэлектрика меньше внешней напряжённости. Время релаксации: = 10 -13 -10 -7 с. Частота 10 МГц.
3 способ – электронная поляризация:
Характерна для неполярных молекул, которые становятся диполями. Время релаксации: = 10 -16 -10 -14 с. Частота 10 8 МГц.
4 способ – ионная поляризация:
Две решётки (Na и Cl) смещаются относительно друг друга.
Время релаксации:
5 способ – микроструктурная поляризация:
Характерен для биологических структур, когда чередуются заряженные и незаряженные слои. Происходит перераспределение ионов на полупроницаемых или непроницаемых для ионов перегородках.
Время релаксации: =10 -8 -10 -3 с. Частота 1 КГц
Числовые характеристики степени поляризации:
Электрический ток – это упорядоченное движение свободных зарядов в веществе или в вакууме.
Условия существования электрического тока :
наличие свободных зарядов
наличие электрического поля, т.е. сил, действующих на эти заряды
Сила тока – величина, равная заряду, который проходит через любое поперечное сечение проводника за единицу времени (1 секунду)
Измеряется в Амперах.
n – концентрация зарядов
q – величина заряда
S – площадь поперечного сечения проводника
— скорость направленного движения частиц.
Скорость движения заряженных частиц в электрическом поле небольшая – 7*10 -5 м/с, скорость распространения электрического поля 3*10 8 м/с.
Плотность тока – величина заряда, проходящего за 1 секунду через сечение в 1 м 2 .
. Измеряется в А/м 2 .
— сила, действующая на ион со стороны эл поля равна силе трения
— подвижность ионов
— скорость направленного движения ионов =подвижность, напряжённость поля
Удельная проводимость электролита тем больше, чем больше концентрация ионов, их заряд и подвижность. При повышении температуры возрастает подвижность ионов и увеличивается электропроводность.
Как рассчитать электрический заряд
Обновлено 17 сентября 2019 г.
Автор S. Hussain Ather
Будь то статическое электричество, исходящее от пушистой шерсти, или электричество, от которого питаются телевизоры, вы можете узнать больше об электрическом заряде, изучив лежащая в основе физика. Методы расчета заряда зависят от природы самого электричества, например, принципов распределения заряда по объектам. Эти принципы одинаковы, независимо от того, где вы находитесь во Вселенной, поэтому электрический заряд является фундаментальным свойством самой науки.
Формула электрического заряда
Существует множество способов вычисления электрического заряда для различных контекстов в физике и электротехнике.
Закон Кулона обычно используется при вычислении силы, создаваемой частицами, несущими электрический заряд, и является одним из наиболее распространенных уравнений электрического заряда, которые вы будете использовать. Электроны несут отдельные заряды -1,602 × 10 -19 кулонов (Кл), а протоны несут такое же количество, но в положительном направлении, 1.2}
, в котором k — постоянная k = 9,0 × 10 9 Нм 2 / C 2 . Физики и инженеры иногда используют переменную e для обозначения заряда электрона.
Обратите внимание, что для зарядов противоположных знаков (плюс и минус) сила отрицательная и, следовательно, притягивающая между двумя зарядами. Для двух зарядов одного знака (плюс и плюс или минус и минус) сила отталкивающая. Чем больше заряды, тем сильнее сила притяжения или отталкивания между ними.
Электрический заряд и гравитация: сходства
Закон Кулона поразительно похож на закон Ньютона для силы тяжести F G = G м 1 м 2 / r 2 для гравитационной силы F G , масс м 1 и м 2 и гравитационной постоянной G = 6,674 × 10 −11 м 3 / кг с 2 .Оба они измеряют разные силы, изменяются с большей массой или зарядом и зависят от радиуса между обоими объектами во второй степени. Несмотря на сходство, важно помнить, что гравитационные силы всегда притягивают, в то время как электрические силы могут быть притягивающими или отталкивающими.
Следует также отметить, что электрическая сила обычно намного сильнее гравитации, исходя из различий в экспоненциальной мощности констант законов. Сходство между этими двумя законами является еще большим показателем симметрии и закономерностей среди общих законов Вселенной.
Сохранение электрического заряда
Если система остается изолированной (т. Е. Без контакта с чем-либо еще вне ее), она будет сохранять заряд. Сохранение заряда означает, что общее количество электрического заряда (положительный заряд минус отрицательный заряд) остается неизменным для системы. Сохранение заряда позволяет физикам и инженерам вычислять, сколько заряда перемещается между системами и их окружением.
Этот принцип позволяет ученым и инженерам создавать клетки Фарадея, в которых используются металлические экраны или покрытия для предотвращения утечки заряда.Клетки Фарадея или щиты Фарадея используют тенденцию электрического поля к перераспределению зарядов внутри материала, чтобы нейтрализовать действие поля и предотвратить повреждение или проникновение зарядов внутрь. Они используются в медицинском оборудовании, таком как аппараты магнитно-резонансной томографии, для предотвращения искажения данных, а также в защитном снаряжении для электриков и электромонтажников, работающих в опасных средах.
Вы можете рассчитать чистый поток начислений для объема пространства, вычислив общую сумму вводимых затрат и вычитая общую сумму оставленных сборов.Благодаря электронам и протонам, несущим заряд, заряженные частицы могут создаваться или разрушаться, чтобы уравновесить себя согласно закону сохранения заряда.
Число электронов в заряде
Зная, что заряд электрона равен -1,602 · 10 −19 Кл, заряд −8 · 10 −18 Кл будет состоять из 50 электронов. Вы можете найти это, разделив количество электрического заряда на величину заряда отдельного электрона.
Расчет электрического заряда в цепях
Если вам известен электрический ток , поток электрического заряда через объект, проходящий по цепи и продолжительность действия тока, вы можете рассчитать электрический заряд, используя уравнение для тока Q = Это , где Q — общий заряд, измеренный в кулонах, I — ток в амперах, а t — время, в течение которого приложен ток, в секундах.Вы также можете использовать закон Ома ( В = IR ) для расчета тока по напряжению и сопротивлению.
Для цепи с напряжением 3 В и сопротивлением 5 Ом, приложенной в течение 10 секунд, соответствующий ток будет равен I = В / R = 3 В / 5 Ом = 0,6 А, а общий заряд будет Q = It = 0,6 A × 10 с = 6 C.
Если вам известна разность потенциалов ( В, ) в вольтах, приложенная к цепи, и работа ( Вт, ) в джоулях, выполненная за период, за который он применяется, заряд в кулонах, Q = Вт / В .
Формула электрического поля
••• Syed Hussain Ather
Электрическое поле , электрическая сила на единицу заряда, распространяется радиально наружу от положительных зарядов к отрицательным зарядам и может быть рассчитана с помощью E = F E / q , в котором F E — электрическая сила, а q — заряд, создающий электрическое поле. Учитывая, насколько фундаментальными являются поле и сила для вычислений в электричестве и магнетизме, электрический заряд можно определить как свойство вещества, которое заставляет частицу иметь силу в присутствии электрического поля.
Даже если общий или общий заряд объекта равен нулю, электрические поля позволяют различным образом распределять заряды внутри объектов. Если внутри них есть распределения зарядов, которые приводят к ненулевому чистому заряду, эти объекты имеют поляризацию , а заряд, вызываемый этими поляризациями, известен как связанный заряд .
Чистый заряд Вселенной
Хотя ученые не все согласны с тем, каков общий заряд Вселенной, они сделали обоснованные предположения и проверили гипотезы с помощью различных методов.Вы можете заметить, что гравитация является доминирующей силой во Вселенной в космологическом масштабе, и, поскольку электромагнитная сила намного сильнее гравитационной силы, если бы у Вселенной был чистый заряд (положительный или отрицательный), вы бы были возможность видеть доказательства этого на таких огромных расстояниях. Отсутствие этих доказательств привело исследователей к мысли, что Вселенная заряжена нейтрально.
Всегда ли Вселенная была нейтральной по заряду или как заряд Вселенной изменился после Большого взрыва, также являются вопросами, которые вызывают споры.Если бы у Вселенной был чистый заряд, то ученые могли бы измерить их тенденции и влияние на все силовые линии электрического поля таким образом, чтобы вместо того, чтобы соединять положительные заряды с отрицательными, они никогда не закончились бы. Отсутствие этого наблюдения также указывает на аргумент, что у Вселенной нет чистого заряда.
Расчет электрического потока с зарядом
••• Сайед Хуссейн Атер
Электрический поток через планарную (т. Е.плоская) площадь A электрического поля E — поле, умноженное на составляющую площади, перпендикулярной полю. Чтобы получить этот перпендикулярный компонент, вы используете косинус угла между полем и интересующей плоскостью в формуле для потока, представленный как Φ = EA cos ( θ ) , где θ — угол между линией, перпендикулярной площади, и направлением электрического поля.
Это уравнение, известное как закон Гаусса , также говорит вам, что для поверхностей, подобных этим, которые вы называете гауссовскими поверхностями , любой чистый заряд будет находиться на ее поверхности плоскости, потому что было бы необходимо создать электрическое поле.
Поскольку это зависит от геометрии площади поверхности, используемой при расчете потока, она меняется в зависимости от формы. Для круглой области площадь потока A будет π_r_ 2 с r в качестве радиуса круга, или для криволинейной поверхности цилиндра площадь потока будет Ch , в которой C — это длина окружности круглой поверхности цилиндра, а h — высота цилиндра.
Заряд и статическое электричество
Статическое электричество возникает, когда два объекта не находятся в электрическом равновесии (или электростатическом равновесии ), или когда существует чистый поток зарядов от одного объекта к другому.Когда материалы трутся друг о друга, они переносят заряды друг на друга. Эти виды электричества могут генерироваться при натирании носков о ковер или резинкой надутого воздушного шара о волосы. Шок переносит эти избыточные заряды обратно, чтобы восстановить состояние равновесия.
Электрические проводники
Для проводника (материала, передающего электричество), находящегося в электростатическом равновесии, электрическое поле внутри равно нулю, а общий заряд на его поверхности должен оставаться в электростатическом равновесии.Это связано с тем, что, если бы было поле, электроны в проводнике перераспределялись бы или перестраивались в ответ на поле. Таким образом, они отменили бы любое поле в момент его создания.
Алюминий и медная проволока являются общими проводящими материалами, используемыми для передачи токов, также часто используются ионные проводники, которые представляют собой решения, в которых используются свободно плавающие ионы, позволяющие легко проходить заряду. Полупроводники , такие как микросхемы, которые позволяют компьютерам функционировать, также используют свободно циркулирующие электроны, но не так много, как проводники.Полупроводники, такие как кремний и германий, также требуют больше энергии для циркуляции зарядов и обычно имеют низкую проводимость. Напротив, изоляторы , такие как дерево, не позволяют заряду легко проходить через них.
При отсутствии поля внутри для гауссовой поверхности, лежащей непосредственно внутри поверхности проводника, поле должно быть везде нулевым, чтобы поток был равен нулю. Это означает, что внутри проводника нет чистого электрического заряда. Из этого вы можете сделать вывод, что для симметричных геометрических структур, таких как сферы, заряд равномерно распределяется по поверхности гауссовой поверхности.
Закон Гаусса в других ситуациях
Поскольку чистый заряд на поверхности должен оставаться в электростатическом равновесии, любое электрическое поле должно быть перпендикулярно поверхности проводника, чтобы материал мог передавать заряды. Закон Гаусса позволяет вычислить величину этого электрического поля и магнитного потока для проводника. Электрическое поле внутри проводника должно быть нулевым, а снаружи оно должно быть перпендикулярно поверхности.
Это означает, что для цилиндрического проводника с полем, излучаемым от стенок под перпендикулярным углом, полный поток равен просто 2_E__πr_ 2 для электрического поля E и радиус r круглой поверхности цилиндрического проводника.Вы также можете описать чистый заряд на поверхности, используя σ , плотность заряда на единицу площади, умноженную на площадь.
Калькулятор закона Кулона
Этот калькулятор электрической силы позволит вам определить силу отталкивания или притяжения между двумя статическими заряженными частицами. Продолжайте читать, чтобы лучше понять закон Кулона, условия его действия и физическую интерпретацию полученного результата.
Как использовать закон Кулона
Закон Кулона, также известный как закон обратных квадратов Кулона, описывает электростатическую силу, действующую между двумя зарядами.Сила действует по кратчайшей линии, соединяющей заряды. Отталкивает, если оба заряда имеют одинаковый знак, и притягивает, если они имеют противоположные знаки.
Закон Кулона формулируется следующим образом:
F = k e q₁q₂ / r² где:
-
F— электростатическая сила между зарядами (в Ньютонах), -
q₁— величина первого заряда (в кулонах), -
q₂— величина второго заряда (в кулонах), -
r— кратчайшее расстояние между зарядами (в м), -
k e— постоянная Кулона.Оно равно8,98755 × 10⁹ Н · м² / К2. Это значение уже заложено в калькулятор — запоминать его необязательно 🙂
Просто введите любые три значения в наш калькулятор электрической силы, чтобы в результате получить четвертое.
Электрозарядные
Единицей электрического заряда является кулон (обозначение: C). Он определяется как заряд, переносимый постоянным током в 1 ампер в течение 1 секунды. Следовательно, 1 C = 1 A * 1 с , выраженное в единицах СИ.
Если вы не помните, что такое ампер, обратитесь к нашему калькулятору закона Ома.
Условия действия
Три основных условия должны быть выполнены для того, чтобы вычислитель электростатической силы возвращал действительные значения:
- Заряды должны быть неподвижными — они не могут двигаться относительно друг друга. Предполагается
- баллов. Это предположение также верно для любых сферических и симметричных зарядов. Например, заряженный металлический шар удовлетворяет этому условию, а заряженный металлический ящик — нет.
- Заряды не могут перекрываться — они должны быть различимы и иметь хотя бы минимальное расстояние между ними.
Интерпретация результатов
Сила, полученная с помощью нашего калькулятора закона Кулона, может быть как положительной, так и отрицательной. Положительная сила подразумевает отталкивающее взаимодействие между зарядами. Отрицательная сила означает, что взаимодействие является привлекательным.
Вы заметили, что единицей заряда по умолчанию в нашем калькуляторе закона Кулона является наноКулон (нКл)? Это потому, что типичный порядок величины электрического заряда составляет 10 -6 C или даже 10 -9 C .
Заинтересованы в электричестве? Также ознакомьтесь с нашим калькулятором стоимости электроэнергии!
электричество | Определение, факты и типы
Электростатика — это изучение электромагнитных явлений, которые происходят при отсутствии движущихся зарядов, то есть после установления статического равновесия. Заряды быстро достигают положения равновесия, потому что электрическая сила чрезвычайно велика. Математические методы электростатики позволяют рассчитывать распределения электрического поля и электрического потенциала по известной конфигурации зарядов, проводников и изоляторов.И наоборот, имея набор проводников с известными потенциалами, можно рассчитать электрические поля в областях между проводниками и определить распределение заряда на поверхности проводников. Электрическую энергию набора зарядов в состоянии покоя можно рассматривать с точки зрения работы, необходимой для сборки зарядов; в качестве альтернативы, можно также считать, что энергия находится в электрическом поле, создаваемом этой сборкой зарядов. Наконец, энергия может храниться в конденсаторе; энергия, необходимая для зарядки такого устройства, хранится в нем как электростатическая энергия электрического поля.
Изучите, что происходит с электронами двух нейтральных объектов, тренных друг о друга в сухой среде.
Объяснение статического электричества и его проявлений в повседневной жизни.
Encyclopædia Britannica, Inc. Посмотреть все видео к этой статьеСтатическое электричество — это знакомое электрическое явление, при котором заряженные частицы передаются от одного тела к другому. Например, если два предмета трутся друг о друга, особенно если они являются изоляторами, а окружающий воздух сухой, предметы приобретают равные и противоположные заряды, и между ними возникает сила притяжения.Объект, теряющий электроны, становится заряженным положительно, а другой — отрицательно. Сила — это просто притяжение между зарядами противоположного знака. Свойства этой силы описаны выше; они включены в математическое соотношение, известное как закон Кулона. Электрическая сила на заряде Q 1 в этих условиях, вызванная зарядом Q 2 на расстоянии r , задается законом Кулона,
Жирным шрифтом в уравнении обозначается вектор характер силы, а единичный вектор r̂ — это вектор, который имеет размер один и указывает от заряда Q 2 до заряда Q 1 .Константа пропорциональности k равна 10 −7 c 2 , где c — скорость света в вакууме; k имеет числовое значение 8,99 × 10 9 ньютонов на квадратный метр на квадратный кулон (Нм 2 / C 2 ). На рисунке 1 показано усилие на Q 1 , создаваемое Q 2 . Числовой пример поможет проиллюстрировать эту силу. И Q 1 и Q 2 выбраны произвольно в качестве положительных зарядов, каждый с величиной 10 −6 кулонов.Заряд Q 1 расположен в координатах x , y , z со значениями 0,03, 0, 0 соответственно, а Q 2 имеет координаты 0, 0,04, 0. Все координаты даны в метрах. Таким образом, расстояние между Q 1 и Q 2 составляет 0,05 метра.
Получите подписку Britannica Premium и получите доступ к эксклюзивному контенту. Подпишитесь сейчасВеличина силы F на заряде Q 1 , рассчитанная с использованием уравнения (1), равна 3.6 ньютонов; его направление показано на рисунке 1. Сила, действующая на Q 2 из-за Q 1 , составляет — F , что также имеет величину 3,6 ньютона; его направление, однако, противоположно направлению F . Сила F может быть выражена через ее составляющие по осям x и y , поскольку вектор силы лежит в плоскости x y . Это делается с помощью элементарной тригонометрии из геометрии рисунка 1, а результаты показаны на рисунке 2.Таким образом, в ньютонах. Закон Кулона математически описывает свойства электрической силы между зарядами в состоянии покоя. Если заряды имеют противоположные знаки, сила будет притягивающей; притяжение будет указано в уравнении (1) отрицательным коэффициентом единичного вектора r̂. Таким образом, электрическая сила на Q 1 будет иметь направление, противоположное единичному вектору r̂ , и будет указывать от Q 1 к Q 2 .В декартовых координатах это привело бы к изменению знаков компонентов силы x и y в уравнении (2).
компоненты кулоновской силыРисунок 2: Составляющие x и y силы F на рисунке 4 (см. Текст).
Предоставлено Департаментом физики и астрономии Университета штата МичиганКак можно понять эту электрическую силу на Q 1 ? По сути, сила возникает из-за наличия электрического поля в позиции Q 1 .Поле создается вторым зарядом Q 2 и имеет величину, пропорциональную размеру Q 2 . При взаимодействии с этим полем первый заряд на некотором расстоянии либо притягивается, либо отталкивается от второго заряда, в зависимости от знака первого заряда.
электрический заряд — Calculator.org
Что такое электрический заряд?
В физике электрический заряд — это фундаментальное свойство некоторых субатомных частиц, которое сохраняется и определяет, как эти частицы взаимодействуют электромагнитно.Вся электрически заряженная материя создает электромагнитные поля и находится под их влиянием. Если электрический заряд движется и взаимодействует с электромагнитным полем, возникает электромагнитная сила. Эта результирующая сила считается одной из четырех фундаментальных сил, действующих в нашей Вселенной. Единицей измерения электрического заряда в системе СИ является кулон, названный в честь французского физика Шарля-Огюстена де Кулона.
Электрический заряд на теле может быть как положительным, так и отрицательным. На два тела с одинаковым электрическим зарядом будет действовать сила взаимного отталкивания, в то время как на два тела с противоположными зарядами будет действовать сила взаимного притяжения.Классическая электродинамика объясняет, как взаимодействуют заряженные тела, предполагая, что человек работает с телами, достаточно большими, чтобы квантовые эффекты были незначительными.
На протяжении двадцатого века многие эксперименты продемонстрировали, что электрический заряд квантуется. То есть электрический заряд не распределяется по континууму возможных зарядов, которые можно увеличить на любую величину. Фактически, минимальная сумма, которая может быть добавлена к уже существующему электрическому заряду, — это величина элементарного заряда e, и она равна 1.602 x 10 -19 кулонов. В атоме протон имеет положительный заряд e, а электрон имеет заряд -e. Область квантовой электродинамики — это изучение того, как эти заряженные частицы взаимодействуют и опосредуются фотонами.
В повседневной жизни статическое электричество становится реальностью, когда вы идете по ковру холодным январским утром и испытываете раздражающий шок, когда дотрагиваетесь до дверной ручки. Удар, который вы только что получили, представляет собой электростатический разряд, который возникает из-за того, что вы фактически создаете разницу в заряде между вами и дверной ручкой.Разряд происходит как способ вернуть общий электрический заряд в системе к равновесию. Хотя можно подумать, что во время этого процесса через нас проходит электрический ток, продолжительность разряда слишком мала, чтобы это было правдой.
Электрический ток — это поток заряда через какое-либо электропроводящее тело. Это также считается производной заряда по времени, записываемой как:
I = dQ / dt
Если взять интеграл по времени от обеих частей вышеприведенного уравнения относительно определенного периода времени, можно также вычислить общий заряд Q, накопленный за это время, с помощью интеграла:
Q = ∫ I dt
, где интеграл — это определенный интеграл от t начального до t конечного .Такое уравнение можно использовать для определения общего заряда, накопленного на поверхности конденсатора для данного тока и временного интервала.
Добавьте эту страницу в закладки в своем браузере, используя Ctrl и d или используя одну из следующих служб: (открывается в новом окне)Электрическое поле | Электростатика | Сиявула
Рассчитайте напряженность электрического поля \ (\ text {20} \) \ (\ text {m} \) от заряда \ (\ text {7} \) \ (\ text {nC} \).
Нам нужно вычислить электрическое поле на расстоянии от данного заряда.{-1} $} \ end {align *}
Два заряда \ ({Q} _ {1} = — \ text {6} \ text {pC} \) и \ ({Q} _ {2} = — \ text {8} \ text {pC} \ ) разделены расстоянием \ (\ text {3} \) \ (\ text {km} \). Какова напряженность электрического поля в точке, которая находится \ (\ text {2} \) \ (\ text {km} \) от \ ({Q} _ {1} \) и \ (\ text {1} \ ) \ (\ text {km} \) из \ ({Q} _ {2} \)? Точка находится между \ ({Q} _ {1} \) и \ ({Q} _ {2} \).
Нам нужно вычислить электрическое поле на расстоянии от двух заданных зарядов.{-1} $} \) в направлении заряда \ (- \ text {8} \) \ (\ text {pC} \).
Учебное пособие по физике: Закон Кулона
Взаимодействие между заряженными объектами — это неконтактная сила, действующая на некотором расстоянии друг от друга. Заряд, заряд и расстояние. Каждое электрическое взаимодействие включает в себя силу, которая подчеркивает важность этих трех переменных. Будь то пластиковая трубка для гольфа, притягивающая кусочки бумаги, два отталкивающих одинаково заряженных шара или заряженная пластина из пенополистирола, взаимодействующая с электронами в куске алюминия, всегда есть два заряда и расстояние между ними как три критических переменных, которые влияют на прочность. взаимодействия.В этом разделе Урока 3 мы исследуем важность этих трех переменных.
Электрическая сила, как и все силы, обычно выражается в единицах Ньютон. Сила электрического взаимодействия является векторной величиной, которая имеет как величину, так и направление. Направление электрической силы зависит от того, заряжены ли заряженные объекты одинаковым или противоположным зарядом, а также от их пространственной ориентации.Зная тип заряда на двух объектах, можно определить направление силы, действующей на любой из них, с небольшими рассуждениями. На диаграмме ниже объекты A и B имеют одинаковый заряд, заставляющий их отталкиваться друг от друга. Таким образом, сила на объект A направлена влево (от B), а сила на объект B направлена вправо (от A). С другой стороны, объекты C и D имеют противоположный заряд, заставляя их притягиваться друг к другу. Таким образом, сила, действующая на объект C, направлена вправо (к объекту D), а сила, действующая на объект D, направлена влево (к объекту C).Когда дело доходит до вектора электрической силы, возможно, лучший способ определить его направление — это применить фундаментальные правила взаимодействия зарядов (противоположности притягиваются, а любит отталкиваться), используя небольшие рассуждения.
Электрическая сила также имеет величину или силу. Как и большинство типов сил, на величину электрической силы влияет множество факторов. Два одинаково заряженных шара будут отталкивать друг друга, и сила их силы отталкивания может быть изменена путем изменения трех переменных.Во-первых, количество заряда на одном из воздушных шаров влияет на силу отталкивающей силы. Чем больше заряжен воздушный шар, тем больше сила отталкивания. Во-вторых, количество заряда на втором воздушном шаре будет влиять на силу отталкивающей силы. Аккуратно натрите два шарика шерстью животных, и они немного оттолкнутся. Сильно потрите два шара, чтобы передать им больший заряд, и они сильно оттолкнутся. Наконец, расстояние между двумя воздушными шарами будет иметь значительное и заметное влияние на силу отталкивания.Электрическая сила наиболее сильна, когда воздушные шары находятся максимально близко друг к другу. Уменьшение разделительного расстояния увеличивает силу. Величина силы и расстояние между двумя воздушными шарами составляет , обратно пропорционально .
Уравнение закона КулонаКоличественное выражение влияния этих трех переменных на электрическую силу известно как закон Кулона. Закон Кулона гласит, что электрическая сила между двумя заряженными объектами прямо пропорциональна произведению количества заряда на объектах и обратно пропорциональна квадрату разделительного расстояния между двумя объектами.В форме уравнения закон Кулона можно представить как
, где Q 1 представляет количество заряда на объекте 1 (в кулонах), Q 2 представляет количество заряда на объекте 2 (в кулонах), а d представляет собой расстояние между два объекта (в метрах). Символ k — это константа пропорциональности, известная как постоянная закона Кулона. Значение этой постоянной зависит от среды, в которую погружены заряженные объекты.В случае воздуха это значение составляет приблизительно 9,0 x 10 9 Н • м 2 / C 2 . Если заряженные объекты присутствуют в воде, значение k может быть уменьшено в 80 раз. Стоит отметить, что единицы на k таковы, что при подстановке в уравнение единицы на зарядке (кулоны) и единицы расстояния (метры) будут отменены, оставив Ньютон в качестве единицы силы.
Уравнение закона Кулона обеспечивает точное описание силы между двумя объектами, когда объекты действуют как точечных зарядов .Заряженная проводящая сфера взаимодействует с другими заряженными объектами так, как будто весь ее заряд находится в ее центре. Хотя заряд равномерно распределен по поверхности сферы, центр заряда можно рассматривать как центр сферы. Сфера действует как точечный заряд, избыточный заряд которого находится в центре. Поскольку закон Кулона применяется к точечным зарядам, расстояние d в уравнении — это расстояние между центрами заряда для обоих объектов (а не расстояние между их ближайшими поверхностями).
Символы Q 1 и Q 2 в уравнении закона Кулона представляют собой количества заряда на двух взаимодействующих объектах. Поскольку объект может быть заряжен положительно или отрицательно, эти величины часто выражаются в виде значений «+» или «-». Знак заряда просто показывает, есть ли в объекте избыток электронов (отрицательно заряженный объект) или недостаток электронов (положительно заряженный объект).Может возникнуть соблазн использовать знаки «+» и «-» при вычислении силы. Хотя такая практика не рекомендуется, в этом нет никакого вреда. При использовании знаков «+» и «-» в расчете силы результат будет таков, что значение «-» для силы является признаком силы притяжения, а значение «+» для силы означает силу отталкивания. Математически значение силы будет положительным, если Q 1 и Q 2 имеют одинаковый заряд — либо оба «+», либо оба «-».И значение силы будет отрицательным, если Q 1 и Q 2 имеют противоположный заряд — один — «+», а другой — «-». Это согласуется с концепцией, что противоположно заряженные объекты обладают притягивающим взаимодействием, а одноименные заряженные объекты — отталкивающим. В конце концов, если вы мыслите концептуально (а не просто математически), вы сможете определить природу силы — притягивающую или отталкивающую — без использования знаков «+» и «-» в уравнении.
Расчеты по закону Кулона В курсах физики закон Кулона часто используется как разновидность алгебраического рецепта для решения словесных задач физики. Здесь показаны три таких примера.
| Пример A Предположим, что два точечных заряда, каждый с зарядом +1,00 Кулона, разделены расстоянием 1.00 метр. Определите величину электрической силы отталкивания между ними. |
Это не самая сложная математическая задача, которую можно было выбрать. Он определенно был выбран не из-за его математической строгости. Используемая здесь стратегия решения проблем может показаться ненужной, учитывая простоту данных значений. Тем не менее, эта стратегия будет использоваться, чтобы проиллюстрировать ее полезность для решения любой проблемы закона Кулона.
Первым шагом стратегии является идентификация и перечисление известной информации в переменной форме.Здесь мы знаем заряды двух объектов (Q 1 и Q 2 ) и расстояние между ними (d). Следующий шаг стратегии включает перечисление неизвестной (или желаемой) информации в переменной форме. В этом случае проблема запрашивает информацию о силе. Так что F elect — это неизвестное количество. Результаты первых двух шагов показаны в таблице ниже.
Дано: Q 1 = 1.00 С | Найдите: F избранный = ??? |
Следующий и последний шаг стратегии включает подстановку известных значений в уравнение закона Кулона и использование соответствующих алгебраических шагов для поиска неизвестной информации. Этот шаг показан ниже.
F elect = k • Q 1 • Q 2 / d 2F elect = (9,0 x 10 9 Н • м 2 / C 2 ) • (1,00 C) • (1,00 C) / (1,00 м) 2
F избранный = 9,0 x 10 9 N
Сила отталкивания двух +1.00 кулоновских зарядов, находящихся на расстоянии 1 метра друг от друга, составляет 9 миллиардов ньютонов. Это невероятно большая сила, по величине сопоставимая с массой более 2000 лайнеров.
Эта задача была выбрана в первую очередь из-за ее концептуального послания. Объекты просто не получают зарядов порядка 1,00 кулонов. Фактически, более вероятные значения Q составляют порядка 10 -9 или, возможно, 10 -6 кулонов. По этой причине греческий префикс часто используется перед кулоном в качестве единицы заряда. Заряд часто выражается в единицах микрокулонов (мкКл) и нанокулонов (нКл). Если проблема указывает заряд в этих единицах, рекомендуется сначала преобразовать в кулоны перед подстановкой в уравнение закона Кулона.Следующие эквиваленты единиц измерения помогут в таком преобразовании.
1 кулон = 10 6 микрокулон1 кулон = 10 9 нано-кулон
Стратегия решения проблем, использованная в примере A, включала три этапа:
- Определите и перечислите известную информацию в переменной форме.
- Перечислите неизвестную (или желаемую) информацию в переменной форме.
- Подставьте известные значения в уравнение закона Кулона и, используя соответствующие алгебраические шаги, найдите неизвестную информацию.(В некоторых случаях и для некоторых студентов может быть проще сначала выполнить алгебру, используя переменные, а затем выполнить замену в качестве последнего шага.)
Эта же стратегия решения проблем продемонстрирована в примере B ниже.
| Пример B Два шара заряжаются одинаковым количеством и типом заряда: -6,25 нКл. Их разделяют на расстоянии 61.7 см. Определите величину электрической силы отталкивания между ними. |
В задаче указано значение Q 1 и Q 2 . Поскольку эти значения выражены в единицах нанокулонов (нКл), необходимо выполнить преобразование в кулоны. В задаче также указано расстояние разделения (d). Поскольку расстояние указывается в сантиметрах (см), необходимо также выполнить преобразование в метры. Эти преобразования необходимы, поскольку единицами заряда и расстояния в постоянной Кулона являются кулоны и метры.Неизвестная величина — электрическая сила (F). Результаты первых двух шагов показаны в таблице ниже.
Дано: Q 1 = -6,25 нКл = -6,25 x 10 -9 С | Найдите: F избранный = ??? |
Последний шаг стратегии включает подстановку известных значений в уравнение закона Кулона и использование соответствующих алгебраических шагов для решения неизвестной информации.Эта подстановка и алгебра показаны ниже.
F elect = k • Q 1 • Q 2 / d 2F elect = (9,0 x 10 9 Н • м 2 / C 2 ) • (6,25 x 10 -9 C) • (6,25 x 10 -9 C) / (0,617 м) 2
F электр. = 9,23 x 10 -7 N
Обратите внимание, что знак «-» был удален из значений Q 1 и Q 2 до подстановки в уравнение закона Кулона.Как упоминалось выше, использование знаков «+» и «-» в уравнении приведет к положительному значению силы, если Q 1 и Q 2 одинаково заряжены, и отрицательному значению силы, если Q 1 и Q 2 заряжены противоположным образом. Полученные в результате знаки «+» и «-» на F обозначают, является ли сила притягивающей (значение «-» F) или отталкивающей (значение «+» F).
| Пример C Два шара с зарядом +3.37 µC и -8,21 µC притягивают друг друга с силой 0,0626 Ньютона. Определите расстояние между двумя воздушными шарами. |
В задаче указано значение Q 1 и Q 2 . Поскольку эти значения выражены в микрокулонах (мкКл), будет выполнено преобразование в кулоны. В задаче также указывается электрическая сила (F). Неизвестная величина — это расстояние разделения (d). Результаты первых двух шагов показаны в таблице ниже.
Дано: Q 1 = +3,37 мкКл = +3,37 x 10 -6 ° С | Найдите: d = ??? |
Как упоминалось выше, использование знаков «+» и «-» необязательно.Однако, если они используются, то они должны использоваться последовательно для значений Q и F. Их использование в уравнении проиллюстрировано в этой задаче.
Последний шаг стратегии включает подстановку известных значений в уравнение закона Кулона и использование соответствующих алгебраических шагов для решения неизвестной информации. В этом случае сначала выполняется алгебра, а в последнюю — подстановка. Эта алгебра и подстановка показаны ниже.
F elect = k • Q 1 • Q 2 / d 2d 2 • F elect = k • Q 1 • Q 2
d 2 = k • Q 1 • Q 2 / F elect
d = SQRT (k • Q 1 • Q 2 ) / F elect
d = КОРЕНЬ [(9.0 x 10 9 Н • м 2 / C 2 ) • (-8,21 x 10 -6 C) • (+3,37 x 10 -6 C) / (-0,0626 Н)]
d = Sqrt [+3,98 м 2 ]
d = +1,99 м
Сравнение электрических и гравитационных силЭлектрическая сила и гравитационная сила — это две бесконтактные силы, обсуждаемые в учебном пособии по физике.Уравнение закона Кулона для электрической силы очень похоже на уравнение Ньютона для всемирного тяготения.
Эти два уравнения имеют очень похожую форму. Оба уравнения показывают обратную квадратичную зависимость между силой и разделительным расстоянием. И оба уравнения показывают, что сила пропорциональна произведению количества, вызывающего силу, — заряда в случае электрической силы и массы в случае силы тяжести. Однако между этими двумя силами есть поразительные различия.Во-первых, сравнение констант пропорциональности — k и G — показывает, что постоянная закона Кулона (k) значительно больше, чем универсальная гравитационная постоянная Ньютона (G). Впоследствии единица заряда будет притягивать единицу заряда со значительно большей силой, чем единица массы притягивает единицу массы. Во-вторых, гравитационные силы только притягивают; электрические силы могут быть как притягивающими, так и отталкивающими.
Обратное квадратичное соотношение между силой и расстоянием, вплетенное в уравнение, является общим для обеих бесконтактных сил.Эта взаимосвязь подчеркивает важность разделительного расстояния, когда речь идет об электрической силе между заряженными объектами. Этому и посвящен следующий раздел Урока 3.
Мы хотели бы предложить … Иногда просто прочитать об этом недостаточно. Вы должны с ним взаимодействовать! И это именно то, что вы делаете, когда используете один из интерактивных материалов The Physics Classroom. Мы хотели бы предложить вам совместить чтение этой страницы с использованием нашего интерактивного приложения по закону Кулона.Вы можете найти его в разделе Physics Interactives на нашем сайте. Интерактивный закон Кулона позволяет учащемуся исследовать влияние заряда и разделительного расстояния на величину электрической силы между двумя заряженными объектами.
Используйте свое понимание, чтобы ответить на следующие вопросы. По завершении нажмите кнопку, чтобы просмотреть ответы.
1. Q в уравнении закона Кулона обозначает _____.
а. масса заряженного объекта
г. # избыточных электронов на объекте
г. ток заряженного объекта
г. расстояние между заряженными объектами
e.заряд заряженного объекта
2. Символ d в уравнении закона Кулона обозначает расстояние от ___.
а. От A до B
г. От A до D
г.От B до C
г. От B до D
e. C по D
ф. От A до G
г. От B до F
ч. C по E
3.Определите электрическую силу притяжения между двумя воздушными шарами с отдельными зарядами +3,5 x 10 -8 C и -2,9 x 10 -8 C при разделении на расстояние 0,65 м.
4. Определите электрическую силу притяжения между двумя воздушными шарами, заряженными противоположным типом заряда, но одинаковым количеством заряда. Заряд на воздушных шарах составляет 6,0 x 10 -7 C, и они разделены расстоянием 0.50 м.
5. Джоанна натерла шарик шерстью, чтобы получить заряд -1,0 x 10 -6 C. Затем она достает пластиковую трубку для гольфа с зарядом +4,0 x 10 -6 C, локализованным в заданном месте. должность. Она удерживает место заряда на пластиковой трубке для гольфа на расстоянии 50,0 см над воздушным шаром. Определите электрическую силу притяжения между трубкой для гольфа и воздушным шаром.
6. Баллон с зарядом 4,0 мкКл удерживают на расстоянии 0,70 м от второго баллона с таким же зарядом. Рассчитайте величину силы отталкивания.
7. На каком расстоянии разделения должны быть расположены два заряда размером 1,00 микрокулонов, чтобы сила отталкивания между ними была эквивалентна весу (на Земле) 1.00-кг масса?
1.5 Расчет электрических полей распределения зарядов — Введение в электричество, магнетизм и схемы
ЦЕЛИ ОБУЧЕНИЯ
К концу этого раздела вы сможете:
- Объясните, что такое непрерывное распределение заряда источника и как оно связано с концепцией квантования заряда
- Опишите линейные, поверхностные и объемные заряды
- Вычислить поле непрерывного распределения заряда источника любого знака
Распределение заряда, которое мы видели до сих пор, было дискретным: оно состояло из отдельных точечных частиц.Это контрастирует с непрерывным распределением заряда , которое имеет по крайней мере одно ненулевое измерение. Если распределение заряда является непрерывным, а не дискретным, мы можем обобщить определение электрического поля. Мы просто делим заряд на бесконечно малые части и рассматриваем каждую часть как точечный заряд.
Обратите внимание, что поскольку заряд квантуется, не существует такой вещи, как «действительно» непрерывное распределение заряда. Однако в большинстве практических случаев полный заряд, создающий поле, включает такое огромное количество дискретных зарядов, что мы можем спокойно игнорировать дискретную природу заряда и считать его непрерывным.Именно такое приближение мы делаем, когда имеем дело с ведром с водой как сплошной жидкостью, а не с набором молекул h3Oh3O.
Нашим первым шагом является определение плотности заряда для распределения заряда вдоль линии, по поверхности или в объеме, как показано на рисунке 1.5.1.
(рисунок 1.5.1)
Рисунок 1.5.1. Конфигурация элементов разности зарядов для (а) линейного заряда, (б) слоя заряда и (в) объема заряда.Также обратите внимание, что (d) некоторые компоненты полного электрического поля уравновешиваются, а оставшаяся часть приводит к чистому электрическому полю.Определения плотности заряда:
Затем для линейного заряда, поверхностного заряда и объемного заряда сумма в уравнении 1.4.2 становится интегралом, и
заменяется на, или соответственно:
(1.5.1)
(1.5.2)
(1.5.3)
(1.5.4)
Интегралы являются обобщением выражения для поля точечного заряда.Они неявно включают и предполагают принцип суперпозиции. «Уловка» их использования почти всегда заключается в том, чтобы придумать правильные выражения для
, или, в зависимости от обстоятельств, выразить через, а также соответствующим образом выразить функцию плотности заряда. Может быть постоянным; это может зависеть от местоположения.
Внимательно обратите внимание на значение
в этих уравнениях: это расстояние от элемента заряда до интересующего места (точка в пространстве, где вы хотите определить поле).Однако не путайте это со значением; мы используем его и векторные обозначения для записи трех интегралов одновременно. То есть уравнение 1.5.2 на самом деле равно
.ПРИМЕР 1.5.1
Электрическое поле линейного участка
Найдите электрическое поле на расстоянии
выше середины отрезка прямой линии длины, несущего однородную линейную плотность заряда.
Стратегия
Так как это непрерывное распределение заряда, мы концептуально разбиваем сегмент провода на разные отрезки длиной
, каждый из которых несет разную величину заряда.Затем мы вычисляем дифференциальное поле, создаваемое двумя симметрично расположенными кусками провода, используя симметрию установки, чтобы упростить расчет (рисунок 1.5.2). Наконец, мы интегрируем это выражение дифференциального поля по длине провода (фактически, по половине, как мы объясним ниже), чтобы получить полное выражение электрического поля.
(рисунок 1.5.2)
Рисунок 1.5.2 Равномерно заряженный отрезок провода. Электрическое поле в точке можно найти, применив принцип суперпозиции к симметрично расположенным элементам заряда и интегрировав.Решение
Прежде чем мы перейдем к этому, как мы ожидаем, что поле «будет выглядеть» издалека? Поскольку это конечный отрезок линии, издалека он должен выглядеть как точечный заряд. Мы проверим полученное выражение, чтобы убедиться, что оно соответствует этому ожиданию.
Электрическое поле для линейного заряда дается общим выражением
Симметрия ситуации (наш выбор двух идентичных дифференциальных зарядов) подразумевает, что горизонтальные (
) -компоненты поля сокращаются, так что чистое поле указывает в -направлении.Проверим формально.
Итоговое поле
— это векторная сумма полей каждого из двух элементов начисления (назовите их и сейчас):
Потому что два элемента заряда идентичны и находятся на одинаковом расстоянии от точки
, где мы хотим вычислить поле, поэтому эти компоненты отменяются. Остается
Эти компоненты также равны, поэтому имеем
, где в этом примере находится наш дифференциальный линейный элемент
, поскольку мы интегрируем вдоль линии заряда, лежащей на оси -оси.(Пределы интегрирования заключаются в том, что мы построили чистое поле из двух разностных частей заряда. Если мы проинтегрируем по всей длине, мы получим ошибочный множитель.)
В принципе на этом полно. Однако, чтобы фактически вычислить этот интеграл, нам нужно исключить все переменные, которые не указаны. В этом случае и
, иизменяются по мере того, как мы интегрируем наружу до конца линейного заряда, поэтому от этих переменных следует избавиться.Мы можем сделать это так же, как и с двумя точечными зарядами: заметив, что
и
Подставляя, получаем
, что упрощается до
(1.5.5)
Значение
Еще раз обратите внимание на использование симметрии для упрощения задачи. Это очень распространенная стратегия расчета электрических полей. Поля несимметричного распределения заряда должны обрабатываться с помощью множественных интегралов, и может потребоваться численный расчет на компьютере.
ПРОВЕРЬТЕ ПОНИМАНИЕ 1.4
Как изменится использованная выше стратегия для расчета электрического поля в точке на расстоянии
над одним концом конечного отрезка линии?
ПРИМЕР 1.5.2
Электрическое поле бесконечной линии заряда
Найдите электрическое поле на расстоянии
выше середины бесконечной линии заряда, которая несет однородную линейную плотность заряда.
Стратегия
Это точно так же, как в предыдущем примере, за исключением того, что пределы интеграции будут
до.
Решение
Опять же, горизонтальные компоненты уравновешиваются, поэтому мы получаем
., где в этом примере находится наш дифференциальный линейный элемент
, поскольку мы интегрируем вдоль линии заряда, лежащей на оси -оси. Опять же,
Подставляя, получаем
, что упрощается до
Значение
Наша стратегия работы с непрерывным распределением зарядов также дает полезные результаты для зарядов с бесконечной размерностью.
В случае конечной линии заряда обратите внимание, что для
преобладает в знаменателе, так что уравнение 1.5.5 упрощается до
Если вы помните, что
, общий заряд на проводе, мы получили выражение для поля точечного заряда, как и ожидалось.
В пределе
, с другой стороны, мы получаем поле бесконечного прямого провода , который представляет собой прямой провод, длина которого намного, намного больше любого из его других размеров, а также намного, намного больше, чем расстояние, на котором рассчитывается поле:
(1.5.6)
Интересным артефактом этого бесконечного предела является то, что мы потеряли обычную зависимость
, к которой мы привыкли. Это станет еще более интригующим в случае с бесконечной плоскостью.
ПРИМЕР 1.5.3
Электрическое поле от зарядного кольца
Кольцо имеет однородную плотность заряда
с единицами кулонов на единицу дуги. Найдите электрический потенциал в точке на оси, проходящей через центр кольца.
Стратегия
Используем ту же процедуру, что и для заряженного провода. Разница здесь в том, что заряд распределяется по кругу. Мы разделим круг на бесконечно малые элементы в виде дуг на окружности и воспользуемся полярными координатами, показанными на рисунке 1.5.3.
(рисунок 1.5.3)
Рисунок 1.5.3 Система и переменная для расчета электрического поля, создаваемого кольцом заряда.Решение
Электрическое поле для линейного заряда дается общим выражением
Общий элемент дуги между
и имеет длину и, следовательно, содержит заряд, равный.Элемент находится на расстоянии от, угол равен, следовательно, электрическое поле равно
.Значение
Как обычно, симметрия упростила эту проблему, в данном случае приводя к тривиальному интегралу. Кроме того, когда мы берем предел
, мы обнаруживаем, что
, как мы и ожидали.
ПРИМЕР 1.5.4
Поле диска
Найдите электрическое поле круглого тонкого диска радиусом
и однородной плотностью заряда на расстоянии выше центра диска (рисунок 1.5.4).
(рисунок 1.5.4)
Рисунок 1.5.4 Равномерно заряженный диск. Как и в примере линейного заряда, поле над центром этого диска можно рассчитать, воспользовавшись симметрией распределения заряда.Стратегия
Электрическое поле для поверхностного заряда равно
.Для решения задач поверхностного заряда мы разбиваем поверхность на симметричные дифференциальные «полосы», соответствующие форме поверхности; здесь мы будем использовать кольца, как показано на рисунке.Опять же, из-за симметрии горизонтальные компоненты сокращаются, и поле полностью находится в вертикальном направлении
. Вертикальная составляющая электрического поля извлекается умножением на, так что
Как и раньше, нам нужно переписать неизвестные множители в подынтегральном выражении в терминах заданных величин. В данном случае
(Обратите внимание на два разных «
с» здесь; это расстояние от дифференциального кольца заряда до точки, где мы хотим определить поле, тогда как это расстояние от центра диска до дифференциального кольца. заряда.) Также мы уже выполнили интеграл по полярному углу в записи.
Решение
Подставив все это, получаем
или, проще говоря,
(1.5.7)
Значение
Опять же, можно показать (с помощью расширения Тейлора), что когда
, это сокращается до
, что является выражением точечного заряда
.
ПРОВЕРЬТЕ ПОНИМАНИЕ 1.5
Как изменится указанный выше предел при использовании равномерно заряженного прямоугольника вместо диска?
Как
, Уравнение 1.5.7 сводится к полю бесконечной плоскости , которая представляет собой плоский лист, площадь которого намного, намного превышает его толщину, а также намного, намного превышает расстояние, на котором должно быть вычислено поле:
(1.5.8)
Обратите внимание, что это поле является постоянным. Этот удивительный результат, опять же, является артефактом нашего предела, хотя мы будем неоднократно использовать его в будущем. Чтобы понять, почему это происходит, представьте, что вас помещают над бесконечной плоскостью постоянного заряда.Изменится ли самолет, если вы измените высоту? Нет, вы все еще видите, как самолет уходит в бесконечность, независимо от того, как далеко вы от него. Важно отметить, что уравнение 1.5.8 вызвано тем, что мы находимся над плоскостью. Если бы мы были ниже, поле указывало бы в направлении
.
ПРИМЕР 1.5.5
Поле двух бесконечных плоскостей
Найдите повсюду электрическое поле, возникающее из двух бесконечных плоскостей с равными, но противоположными плотностями заряда (Рисунок 1.5.5).
(рисунок 1.5.5)
Рисунок 1.5.5 Две заряженные бесконечные плоскости. Обратите внимание на направление электрического поля.Стратегия
Мы уже знаем электрическое поле, возникающее из одной бесконечной плоскости, поэтому мы можем использовать принцип суперпозиции, чтобы найти поле из двух.
Решение
Электрическое поле направлено от положительно заряженной плоскости к отрицательно заряженной. Поскольку
иравны и противоположны, это означает, что в области за пределами двух плоскостей электрические поля компенсируют друг друга до нуля.
Однако в области между плоскостями электрические поля складываются, и мы получаем
для электрического поля.
— это потому, что на рисунке поле указывает в направлении.
Значение
Системы, которые можно представить как две бесконечные плоскости такого типа, предоставляют полезные средства для создания однородных электрических полей.




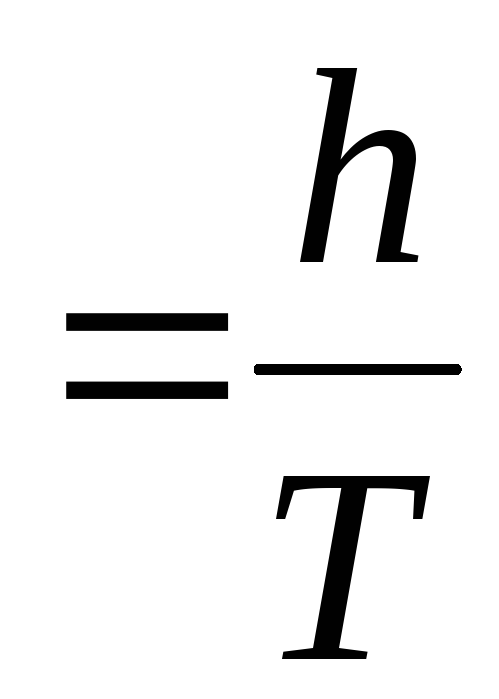 2.4 действуют силы отталкивания со стороны двух других зарядов (см. рисунок), причем значения этих сил одинаковы (из-за равенства величин всех зарядов и расстояний между ними) и равны
2.4 действуют силы отталкивания со стороны двух других зарядов (см. рисунок), причем значения этих сил одинаковы (из-за равенства величин всех зарядов и расстояний между ними) и равны Один кулон – это заряд, проходящий через проводник за 1 секунду при токе 1 ампер;
Один кулон – это заряд, проходящий через проводник за 1 секунду при токе 1 ампер;