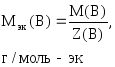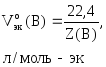Эквивалентная ёмкость конденсаторов
| Эквивалентная ёмкость конденсаторов при последовательном соединении |
| Альтернативное отображение |
| Эквивалентная ёмкость конденсаторов при паралельном соединении |
| Альтернативное отображение |
Последовательное соединение
Написав бот, расчета размерностей Система единиц измерения онлайн теперь начнем осваивать такую многогранную и сложную область как электротехника.
И первое, что нам пригодится, это расчет эквивалентных характеристик основных электрических элементов( ёмкость, индуктивность, сопротивление).
Хотелось бы напомнить, что ёмкости некоторых типовых конструкций мы уже умеем рассчитывать Ёмкость конденсатора онлайн
Сами по себе формулы очень просты, но нюанс состоит в том, как нам точно посчитать ёмкость двух последовательно соединенных конденсаторов если один из конденсаторов имеет ёмкость 10 пФ, а второй 250нФ. Размерность показывает что они различаются в 1000 раз. Можно конечно все перевести в абсолютные значения, но это при большом количестве конденсаторов способствует возникновению ошибок.
Итак, последовательное соединение конденсаторов имеет следующий вид
И формула расчета эквивалентной ёмкости выглядит так
Паралельное СОЕДИНЕНИЕ
Последовательное соединение нескольних конденсаторов выглядит так, как показано на рисунке
А формула становится до безобразия простой и наглядной
Синтаксис
Он очень прост
calc_e список емкостей с размерностями через запятую.
В ответе мы получим эквививалентное значение ёмкости при последовательном и паралельных соединениях.
Важное замечание: размерности нужно писать на русском языке. Для пользователей сайта, не знающих русский язык, можем по запросу добавить обработку англоязычных наименований приставок и размерностей. Это не сложно.
Примеры
Рассчитать ёмкость трех конденсаторов следующих номиналов: 10 пФ, 0.2нФ и 344мФ
В запросе так и пишем calc_e 10пФ,0.2нФ,344мФ
Ответ не заставит себя долго ждать и выглядит вот так
| Эквивалентная ёмкость конденсаторов при паралельном соединении |
|
9.5238095235459пикофарад |
| Альтернативное отображение |
| Эквивалентная ёмкость конденсаторов при последовательном соединении |
|
344.00000021милифарад |
| Альтернативное отображение |
Удачи в расчетах!
- Эквивалентное сопротивление онлайн >>
Задачи на определение эквивалентных емкостей
Задачи, связанные с определением эквивалентной емкости системы конденсаторов, или системы пластин, да если еще между ними вводят диэлектрик – для некоторых являются сложными. Также в таких задачах нужно уметь определять потенциалы, или заряды емкостей при различных соединениях пластин, а также и напряжения на них.
Задача 1. Два плоских конденсатора с емкостями 
 , обладающих зарядами
, обладающих зарядами  и
и  , включают в цепь так, что положительно заряженная пластина одного соединяется с отрицательно заряженной пластиной другого. Определить заряд каждого конденсатора в этом случае.
, включают в цепь так, что положительно заряженная пластина одного соединяется с отрицательно заряженной пластиной другого. Определить заряд каждого конденсатора в этом случае.Соединение разноименных пластин повлечет за собой нейтрализацию части заряда. Так как заряды будут перераспределяться, то вместе с изменением заряда конденсаторов будет меняться и напряжение: до соединения напряжения на обоих конденсаторах разные, а после – станут одинаковыми.

К задаче 1
Тогда можно записать, что по закону сохранения заряда
![Rendered by QuickLaTeX.com \[q_1-q_2=q_{11}+q_{22}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a4f6bf4097a0afa68120f44e65e3c33a_l3.png)
Где 
 – новые заряды конденсаторов.
– новые заряды конденсаторов.После соединения напряжения уравняются:
![Rendered by QuickLaTeX.com \[U_1=U_2\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d648a8e6c75dfbf13424ee23383a2b85_l3.png)
![Rendered by QuickLaTeX.com \[\frac{q_{11}}{C_1}=\frac{ q_{22}}{C_2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d23fcb309ceda5adfaca3544d3bcef91_l3.png)
Выразим один из зарядов:
![Rendered by QuickLaTeX.com \[q_{11}=\frac{C_1}{C_2} q_{22}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a063b4def73b3237223b13e7903bca23_l3.png)
Тогда:
![Rendered by QuickLaTeX.com \[q_1-q_2=\frac{C_1}{C_2} q_{22}+q_{22}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-d4f8019bb569793e54add157b48979bd_l3.png)
![Rendered by QuickLaTeX.com \[q_1-q_2= q_{22}\left(\frac{C_1}{C_2} +1 \right)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-e5bd7344f7329afe2f113135ec85a8d1_l3.png)
![Rendered by QuickLaTeX.com \[q_{22}=\frac{ q_1-q_2}{\left(\frac{C_1}{C_2} +1 \right)}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-632e1b0b33ac602adae72e044c86c278_l3.png)
![Rendered by QuickLaTeX.com \[q_{22}=\frac{ C_2(q_1-q_2)}{C_1+C_2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2b5e858fe3e4d34318c41bd07be7e9b8_l3.png)
Тогда определим и заряд на первом конденсаторе:
![Rendered by QuickLaTeX.com \[q_{11}=\frac{ C_1(q_1-q_2)}{C_1+C_2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-3184d1622be26a885a478fec6e5c9fd8_l3.png)
Ответ:  ,
,  .
.
Задача 2. Рассчитать электроемкость системы, состоящей из трех металлических пластин толщиной 
 каждая и одной диэлектрической пластины толщиной
каждая и одной диэлектрической пластины толщиной  и площадью
и площадью  и диэлектрической проницаемостью
и диэлектрической проницаемостью 

Задача 2
Такое соединение пластин эквивалентно следующей схеме соединения конденсаторов:

К задаче 2 – эквивалентная схема замещения
Тогда емкость 
![Rendered by QuickLaTeX.com \[C_2=\frac{S}{2} \frac{\varepsilon_0}{d}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-6c667308e551c9d6c2762f88decf9f75_l3.png)
Емкость конденсатора с диэлектриком:
![Rendered by QuickLaTeX.com \[C_3=\frac{S}{2} \frac{\varepsilon_0 \varepsilon}{d}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-1a35c5a5e0bf5f171f1d47b655f16de6_l3.png)
Эти два конденсатора соединены параллельно, их общая емкость равна сумме емкостей:
![Rendered by QuickLaTeX.com \[C_{23}=C_2+C_3=\frac{\varepsilon_0 S}{2d}\left(1+\varepsilon\right)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-7602198f1c8c29f928df6ad5a986e433_l3.png)
Емкость  равна:
равна:
![Rendered by QuickLaTeX.com \[C_1=\frac{S\varepsilon_0}{d}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-2ba5dfdef9499f041eb666512c87b747_l3.png)
Она соединена последовательно с объединением  :
:
![Rendered by QuickLaTeX.com \[C_{ekv}=\frac{C_1 C_{23}}{C_1+ C_{23}}=\frac{\frac{\varepsilon_0 S}{2d}\left(1+\varepsilon\right)\cdot\frac{S\varepsilon_0}{d}}{\frac{\varepsilon_0 S}{2d}\left(1+\varepsilon\right)+\frac{S\varepsilon_0}{d}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-bdb99b16fa30cffa2625348c3ac8a957_l3.png)
![Rendered by QuickLaTeX.com \[C_{ekv}=\frac{\varepsilon_0 S\left(1+\varepsilon\right)}{2d\left(2+\varepsilon\right)}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-c3f0ccc3c20e5c022f8d6f5ab7444ccf_l3.png)
Ответ: 
Задача 3. Рассчитать электроемкость системы, состоящей из трех металлических пластин толщиной  и площадью
и площадью  каждая и двух диэлектрических пластин толщиной
каждая и двух диэлектрических пластин толщиной  и площадью
и площадью  . Диэлектрическая проницаемость первой пластины
. Диэлектрическая проницаемость первой пластины  , второй –
, второй –  . Расположение пластин показано на рисунке.
. Расположение пластин показано на рисунке.

К задаче 3
Как в предыдущей задаче, такая система пластин может быть представлена следующим соединением конденсаторов:

К задаче 3 – схема замещения
Тогда последовательное соединение  и
и 
![Rendered by QuickLaTeX.com \[C_{12}=\frac{C^2}{2C}=\frac{C}{2}=\frac{\varepsilon_0 S }{2d}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-0bc08451d113314f1dd4d4b993b086b1_l3.png)
Емкости конденсаторов с диэлектриком:
![Rendered by QuickLaTeX.com \[C_3=\frac {\varepsilon_0\varepsilon_1 S }{2d}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-feb222bbff8a9741c65cd883c177e19e_l3.png)
![Rendered by QuickLaTeX.com \[C_4=\frac {\varepsilon_0\varepsilon_2 S }{2d}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a6ed788726d441b2417f2587c0bea61a_l3.png)
Так как они соединены параллельно, то их эквивалентная емкость – сумма их емкостей.
![Rendered by QuickLaTeX.com \[C_{34}=C_3+C_4=\frac {\varepsilon_0 S }{2d}(\varepsilon_1 +\varepsilon_2)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8d827b789d6a4fb4c37a19f15ded147d_l3.png)
Наконец, считаем последовательное соединение  и
и  :
:
![Rendered by QuickLaTeX.com \[C_{ekv}=\frac{C_{12}C_{34}}{ C_{12}+C_{34}}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8310b8ed328a0cdd84085e5dcd85867d_l3.png)
![Rendered by QuickLaTeX.com \[C_{ekv}=\frac{\frac{\varepsilon_0 S }{2d}\frac {\varepsilon_0 S }{2d}(\varepsilon_1 +\varepsilon_2)}{\frac{\varepsilon_0 S }{2d}+\frac {\varepsilon_0 S }{2d}(\varepsilon_1 +\varepsilon_2)}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-026adbdfaeec6fe86b44cc73a444e402_l3.png)
![Rendered by QuickLaTeX.com \[C_{ekv}=\frac{\varepsilon_0 S }{2d}\frac{\varepsilon_1 +\varepsilon_2}{ 1+\varepsilon_1 +\varepsilon_2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a6ae49f2b83fbb316a7dd623440472d0_l3.png)
Ответ: 
Задача 4. Плоский конденсатор находится во внешнем электрическом поле напряженностью  В/м, перпендикулярном пластинам. Площадь пластины конденсатора
В/м, перпендикулярном пластинам. Площадь пластины конденсатора  м
м . Какие заряды окажутся на каждой из пластин, если конденсатор замкнуть проводником накоротко? Пластины конденсатора до замыкания не заряжены. Влиянием силы тяжести пренебречь.
. Какие заряды окажутся на каждой из пластин, если конденсатор замкнуть проводником накоротко? Пластины конденсатора до замыкания не заряжены. Влиянием силы тяжести пренебречь.
Заряд конденсатора 
Напряжение между двумя точками в однородном электрическом поле равно: 
Тогда заряд
![Rendered by QuickLaTeX.com \[q=\frac{\varepsilon_0 S Ed}{d}=\varepsilon_0 S E=8,85\cdot10^{-12}\cdot10^{-2}\cdot10^3=0,9\cdot10^{-10}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b6300c2ccf96fd40905481836413c29b_l3.png)
Ответ: 
Задача 5. В схеме емкость батареи конденсаторов не изменится при замыкании ключа К. Определите емкость конденсатора  .
.

К задаче 5
До замыкания ключа имеем две ветви в параллель. В одной ветви (сверху) – последовательное соединение  и
и  , во второй (снизу) – последовательное соединение
, во второй (снизу) – последовательное соединение  и
и  .
.
Тогда для верхней ветви запишем:
![Rendered by QuickLaTeX.com \[C_{verh}=\frac{2C\cdotC}{2C+C}=\frac{2C}{3}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-879f1003318ff5e76099becb16549b95_l3.png)
Для нижней ветви:
![Rendered by QuickLaTeX.com \[C_{niz}=\frac{C_x\cdotC}{C_x+C}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-4ad41f668135ec739ced75df17ccd3db_l3.png)
Так как ветви соединены параллельно, емкости сложатся:
![Rendered by QuickLaTeX.com \[C_{ekv1}=C_{verh}+ C_{niz}=\frac{2C}{3}+\frac{C_x\cdotC}{C_x+C}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-623b71bd157eea8dce74392d1de2f072_l3.png)
![Rendered by QuickLaTeX.com \[C_{ekv1}=C _{verh}+ C_{niz}=\frac{2C(C_x+C)+3C_xC}{3(C_x+C)}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ce871b41bf9d52ff423e7af44ce25ae8_l3.png)
Теперь ключ замыкают, и оказывается, что емкости  и
и  соединены параллельно, и также параллельно соединены и емкости
соединены параллельно, и также параллельно соединены и емкости  и
и  . Емкость левой части схемы:
. Емкость левой части схемы:
![Rendered by QuickLaTeX.com \[C_{lev}=C+C_x\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-fe9ff41efd777555639daa01a59298bd_l3.png)
Емкость правой части схемы:
![Rendered by QuickLaTeX.com \[C_{prav}=2C+C=3C\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-acc98e12f37ee5d4431240c3d5d3fbba_l3.png)
Эквивалентная емкость после замыкания:
![Rendered by QuickLaTeX.com \[C_{ekv2}=\frac{3C(C_x+C)}{4C+C_x}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-56765545ebc69410370b30b1138f8598_l3.png)
В задаче сказано, что как до, так и после замыкания емкость всей системы одна и та же, тогда приравняем обе эквивалентные емкости:
![Rendered by QuickLaTeX.com \[C_{ekv1}= C_{ekv2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f8537d689100ffd7b0c0b60784696ec0_l3.png)
![Rendered by QuickLaTeX.com \[\frac{2C(C_x+C)+3C_xC}{3(C_x+C)}= \frac{3C(C_x+C)}{4C+C_x}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-99883c604e4929ad350af6899317e2b7_l3.png)
Упрощаем:
![Rendered by QuickLaTeX.com \[\frac{5C_x+2C)}{3(C_x+C)}= \frac{3(C_x+C)}{4C+C_x}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-cc5936f045bfe80c44225d4ee1e5f79d_l3.png)
![Rendered by QuickLaTeX.com \[9(C_x+C)^2=20CC_x+5c_x^2+8C^2+2CC_x\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-65a6238034c8298885e78b3e60323b29_l3.png)
![Rendered by QuickLaTeX.com \[9C_x^2+18CC_x+9C^2-8C^2-5C_x^2-22CC_x=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-0a360c28eb0cba49dcd79fe52f4df3af_l3.png)
Или получаем квадратное уравнение:
![Rendered by QuickLaTeX.com \[4C_x^2-4CC_x+C^2=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-695e29642c570e9109f6d06a25f70e87_l3.png)
![Rendered by QuickLaTeX.com \[D=16C^2-4\cdot4C^2=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-a7b6635ef03cdcf8a85ef84a5ddd9bc8_l3.png)
![Rendered by QuickLaTeX.com \[C_x=\frac{C}{2}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-454ee135dfb186915702b5f8ce3883cc_l3.png)
Ответ: 
Задача 6. Три незаряженных конденсатора, емкости которых  ,
,  и
и  , соединены, как показано на рисунке, и подключены к точкам
, соединены, как показано на рисунке, и подключены к точкам  ,
,  и
и  , потенциалы которых
, потенциалы которых  ,
,  и
и  . Определите потенциал точки
. Определите потенциал точки  .
.

К задаче 6
Заряд первой емкости равен:
![Rendered by QuickLaTeX.com \[q_1=C_1(\varphi_A-\varphi_O)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-627585c585603034141b05e5112a3d57_l3.png)
Аналогично для двух других емкостей:
![Rendered by QuickLaTeX.com \[q_2=C_2(\varphi_B-\varphi_O)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-b7a7de2bb48d9cebea783fe7521a2530_l3.png)
![Rendered by QuickLaTeX.com \[q_1=C_3(\varphi_K-\varphi_O)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-8ecd7f88b53bbd844de398f017c9d769_l3.png)
Заряд в точке  равен сумме зарядов всех конденсаторов и равен 0:
равен сумме зарядов всех конденсаторов и равен 0:
![Rendered by QuickLaTeX.com \[q_O=q_1+q_2+q_3=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-aca21f719b4f7739e2e2b68f113ac9e0_l3.png)
![Rendered by QuickLaTeX.com \[C_1(\varphi_A-\varphi_O)+ C_2(\varphi_B-\varphi_O)+ C_3(\varphi_K-\varphi_O)=0\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-f636410d1c0ecca6e644ce3c2a9a01b3_l3.png)
![Rendered by QuickLaTeX.com \[\varphi_AC_1+\varphi_B C_2+\varphi_K C_3=\varphi_O(C_1+C_2+C_3)\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-ee61f5fb24caf1e62247bd9defbcb098_l3.png)
Откуда потенциал точки  равен
равен
![Rendered by QuickLaTeX.com \[\varphi_O=\frac{\varphi_AC_1+\varphi_B C_2+\varphi_K C_3}{ C_1+C_2+C_3}\]](/800/600/https/easy-physic.ru/wp-content/ql-cache/quicklatex.com-aef284d58f9ffc4769e80d81d18a884d_l3.png)
Ответ: 
Пр. 1. конденсаторы
ПРАКТИЧАСКАЯ РАБОТА №1
«Расчет эквивалентной емкости при смешанном соединении конденсаторов, а также распределения зарядов и напряжений»
На рисунке 1 дана схема соединения конденсаторов. Значение емкостей конденсаторов и значение одного из напряжений или зарядов для своего варианта взять из таблицы 1.
Вычислить эквивалентную емкость батареи конденсаторов; напряжение сети, напряжение на каждом конденсаторе; общий заряд и заряд на каждом конденсаторе; энергию, накопленную батареей, а также потенциал заданной точки.
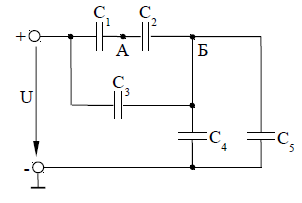
Рисунок 1
Таблица 1
№ вар. | Емкость конденсатора, мкФ | Напряжение, заряд | Точка, потенциал которой следует вычислить | ||||||
С1 | С2 | С3 | С4 | С5 | |||||
1 | 120 | 280 | 16 | 80 | 70 | U=20 В | Б | ||
2 | 600 | 200 | 150 | 400 | 200 | Q3=72∙10-4 Кл | Б | ||
3 | 24 | 12 | 2 | 16 | 14 | U5=25 В | А | ||
4 | 30 | 20 | 12 | 20 | 16 | Q4=4∙10-4 Кл | Б | ||
5 | 10 | 15 | 24 | 6 | 9 | U1=15 В | А | ||
6 | 12 | 6 | 5 | 9 | 9 | Q2=282∙10-6 Кл | А | ||
7 | 30 | 15 | 10 | 65 | 15 | Q5=6∙10-4 Кл | А | ||
8 | 18 | 9 | 12 | 15 | 21 | U2=84 В | Б | ||
9 | 140 | 60 | 6 | 30 | 18 | U3=50 В | А | ||
10 | 150 | 50 | 37,5 | 30 | 20 | Q1=3∙10-4 Кл | Б | ||
11 | 200 | 300 | 40 | 160 | 100 | U=40 В | Б | ||
12 | 540 | 150 | 90 | 380 | 120 | Q3=54∙10-4 Кл | А | ||
13 | 46 | 26 | 8 | 34 | 28 | U5=45 В | Б | ||
14 | 60 | 45 | 25 | 40 | 30 | Q4=8∙10-4 Кл | А | ||
15 | 30 | 25 | 46 | 20 | 18 | U1=30 В | Б | ||
16 | 25 | 15 | 10 | 20 | 15 | Q2=564∙10-6 Кл | Б | ||
17 | 60 | 30 | 45 | 120 | 25 | Q5=15∙10-4 Кл | Б | ||
18 | 36 | 18 | 24 | 30 | 44 | U2=160 В | А | ||
19 | 300 | 140 | 12 | 50 | 38 | U3=100 В | Б | ||
20 | 280 | 100 | 70 | 65 | 45 | Q1=6∙10-4 Кл | А | ||
21 | 60 | 150 | 9 | 40 | 25 | U=10 В | Б | ||
22 | 300 | 100 | 70 | 200 | 90 | Q3=36∙10-4 Кл | А | ||
23 | 14 | 6 | 4 | 8 | 10 | U5=15 В | А | ||
24 | 90 | 60 | 25 | 40 | 26 | Q4=12∙10-4 Кл | Б | ||
25 | 6 | 8 | 12 | 4 | 12 | U1=7 В | А | ||
26 | 46 | 18 | 15 | 27 | 18 | Q2=846∙10-6 Кл | Б | ||
27 | 90 | 45 | 30 | 190 | 65 | Q5=18∙10-4 Кл | А | ||
28 | 560 | 35 | 25 | 45 | 20 | U2=320 В | А | ||
29 | 400 | 240 | 15 | 35 | 100 | U3=150 В | А | ||
30 | 390 | 150 | 200 | 90 | 180 | Q1=9∙10-4 Кл | Б | ||
ПРИМЕР
На рисунке 2 приведена схема соединения конденсаторов. Определить эквивалентную
емкость Сэкв батареи конденсаторов, общий заряд Q, напряжение сети U, напряжение и заряд на каждом конденсаторе, если дано: C1=24 мкФ; С2=С3=8 мкФ; С4=12 мкФ; С5=6 мкФ; напряжение на пятом конденсаторе U5=30 В.
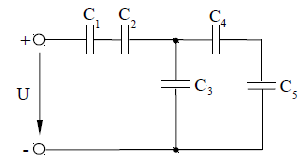
Рисунок 2
Дано:
C1=24 мкФ;
С2=С3=8 мкФ;
С4=12 мкФ;
С5=6 мкФ;
U5=30 В
Определить: U, Q, Сэкв, U1, U2, U3, U4, Q1.
Решение:
1. Общая емкость последовательно соединенных конденсаторов С4 и С5:
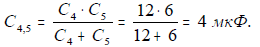
2. Общая емкость параллельно соединенных конденсаторов С3 иС4,5:

3. Общая емкость последовательно соединенных конденсаторов С1, С2 и С3,4,5, которая и является
эквивалентной емкостью батареи конденсаторов:
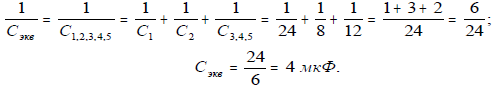
4. По заданному напряжению U5 и емкости конденсатора С5 определяем заряд, накапливаемый
этим конденсатором:

5. Заряд конденсатора С4 Q4=Q5=Q4,5=180・10-6 Кл, т. к. конденсаторы С4 и С5 соединены
последовательно.
6. Напряжение на четвертом конденсаторе:

7. Напряжение на третьем конденсаторе:

8. Заряд конденсатора С3:
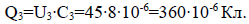
9. Общий заряд батареи и заряды конденсаторов С1 и С2:
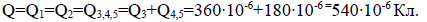
10. Напряжение на первом и втором конденсаторах:
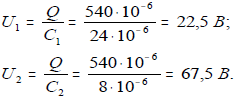
11. Напряжение сети (напряжение последовательно соединенных конденсаторов С1, С2, С3,4,5):
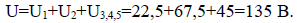
12. Энергия электрического поля батареи:

Расчет эквивалентной емкости электрической цепи — Мегаобучалка
Выполнить расчеты эквивалентной емкости конденсаторов. Схему и данные для расчетов взять из таблицы 1, 2.
Таблица 1.
| №вар | С1 | С2 | С3 | С4 | С5 | С6 | №вар | С1 | С2 | С3 | С4 | С5 | С6 |
| 1. | 13. | ||||||||||||
| 2. | 14. | ||||||||||||
| 3. | 15. | ||||||||||||
| 4. | 16. | ||||||||||||
| 5. | 17. | ||||||||||||
| 6. | 18. | ||||||||||||
| 7. | 19. | ||||||||||||
| 8. | 20. | ||||||||||||
| 9. | 21. | ||||||||||||
| 10. | 22. | ||||||||||||
| 11. | 23. | ||||||||||||
| 12. | 24. |
Таблица 2
| №вар | Схемы | №вар | Схемы |
| 1 |
| 2 |
| 3 |
| 4 |
| 5 |
| 6 |
| 7 |
| 8 |
| 9 |
| 10 |
| 11 |
| 12 |
| 13 |
| 14 |
| 15 |
| 16 |
| 17 |
| 18 |
| 19 |
| 20 |
| 21 |
| 22 |
| 23 |
| 24 |
Требования при выполнении задания.
1. Начертить схему. Обозначить элементы схемы.
2. Переписать условие задания.
3. Указать неизвестные параметры.
4. Решение выполнять поэтапно, вычерчивать схемы замещения и делать пояснения.
Методические рекомендации по выполнению задания 1.
Для выполнения данной работы необходимо знать расчетные формулы последовательного и параллельного соединения конденсаторов.
Схемы соединения емкостных элементов.
Рисунок 1-Схема последовательного соединения конденсаторов
Последовательное соединение: + +
Для схемы из двух конденсаторов: Cэкв =
Рисунок 2-Схема параллельного соединения конденсаторов
Параллельное соединение: Cэкв=C1+C2+C3
Задание 2.
Расчет эквивалентного сопротивления
Электрической цепи.
Выполнить расчеты эквивалентной сопротивления цепи. Схему и данные для расчетов взять из таблицы 1.
Требования при выполнении задания.
1. Начертить схему. Обозначить элементы схемы.
2. Переписать условие задания.
3. Указать неизвестные параметры.
4. Решение выполнять поэтапно, вычерчивать схемы замещения и делать пояснения.
Таблица 1.
Продолжение таблицы 1.
Методические рекомендации по выполнению задания 2.
Для выполнения данной работы необходимо знать расчетные формулы последовательного и параллельного соединения резисторов.
Последовательное соединение:Rэкв = R1+R2+R3
Параллельное соединение: + +
Для схемы из двух резисторов: Rэкв=
Задание 3.
Расчет сложных электрических цепей с помощью
законов Кирхгофа.
Выполнить расчеты по определению токов в ветвях электрической цепи. Данные для расчетов по вариантам взять в таблице.
Выполняя данное задание, проработать порядок расчетов по методическим указаниям.
Таблица 1.
Продолжение таблицы 1
Рассчитать эквивалентную емкость, напряжение и заряд батареи конфденсаторов при смешанном соединении конденсаторов .
<a href=»/» rel=»nofollow» title=»15907216:##:1OQmRak»>[ссылка заблокирована по решению администрации проекта]</a>
Для заданной схемы (рисунок 1.5) определить эквивалентную емкость батареи конденсаторов, заряды и напряжение каждого конденсатора, а также напряжение, приложенное к зажимам электрической цепи. Схема замещения цепи показана на рисунке 1.5. Исходные данные указаны в таблице вариантов. Рисунок 1.5 – Схема замещения расчетной цепи Таблица 1.1 – Исходные данные к контрольной работе № вар. С1 , мкФ С2 , мкФ С3 , мкФ С4 , мкФ С5 , мкФ С6 , мкФ Известный параметр 1 6 10 9 5 3 7 q 3 =4·10ˉ³Кл 2 8 10 15 12 8 5 U4=100В 3 10 12 16 10 8 10 q 2 =5·10ˉ³Кл 4 7 4 5 8 7 10 q 6 =4·10ˉ³Кл 5 5 8 7 6 8 12 U1=50В 6 4 6 8 10 10 15 U5=80В 7 12 10 10 14 8 8 q 4 =5·10ˉ³Кл 8 11 10 12 16 20 10 q 5 =4·10ˉ4Кл 9 3 5 3 4 6 8 U4=180В 10 9 10 7 5 4 10 q 1 =5·10ˉ4Кл 2 Расчет смешанного соединения резисторов
Эквивалентная объем — Справочник химика 21
Алюминий массой 0,752 г при взаимодействии с кислотой вытеснил водород объемом 0,936 л (н. у.). Определите эквивалентный объем водорода. Эквивалентная масса алюминия 8,99 г/моль. [c.9]Р е ш е н II е. Зная, что эквивалентный объем водорода равен [c.9]
Эквивалентный объем стандартного раствора можно найти и расчетным способом по формулам (5.7), вытекающим из а 5. [c.241]
Эквивалентным объемом называется объем, занимаемый при данных условиях 1 эквивалентом вещества. Значение эквивалентного объема вещества, находящегося в газообразном состоянии, можно найти, зная, что в мольном объеме любого газа, состоящего из одноатомных молекул, содержится 1 моль атомов, состоящего из двухатомных молекул — 2 моля атомов и т. д. Так, в 22,4 л Н2 содержатся при нормальных условиях 2 моля атомов водорода. Поскольку эквивалент водорода равен 1 моль, то в 22,4 л Hj содержатся 2 эквивалента водорода значит, эквивалентный объем водорода равен 22,4/2= 11,2 л/моль. [c.8]
Поскольку при нормальных условиях эквивалентный объем водорода равен 11,2 л/моль, а кислорода — 5,6 л/моль, то получаем [c.193]
Основные формулы для вычислений. Число грамм-эквивалентов вещества, находящихся в 1 л раствора, называют нормальностью (или ъор-мальной концентрацией) раствора. Нормальность раствора обозначают в формулах буквой N. Для вычисления главное значение имеет следующая очень важная характеристика этого числа если умножить объем данного раствора (I/) на нормальность (М) этого раствора, то аолучитхя эквивалентный объем точно однонормального раствора. [c.285]
Точка эквивалентности. Объем титрующего раствора К.ЛОз, л [c.155]
В обоих случаях эквивалентный объем титранта можно также найти расчетным методом. [c.249]
Здесь V —объем выделившегося газа, л I s — его эквивалентный объем, л/моль. [c.193]
Как правило, задача потенциометрического титрования сводится к определению объема титранта (стандартного раствора), который содержит такое количество стандартного вещества, которое эквивалентно количеству определяемого вещества в титруемом (анализируемом) растворе, т. е. к определению эквивалентного объема или, иначе говоря, точки эквивалентности (т. экв). Зная эквивалентный объем стандартного раствора, рассчитывают концентрацию или количество определяемого вещества. [c.239]
Эквивалентный объем фильтрата выражается равенством [c.31]
Что такое эквивалентный объем водорода [c.7]
Введя в это уравнение эквивалентный объем фильтрата У экв в соответствии с равенством (11,29), после небольших преобразований получим [c.153]
Само собой разумеется, что любой сепаратор будет работать так, как он запроектирован, если поток, поступающий в пего, состоит из двух фаз. Несмотря на наличие этих фаз, производительность сепаратора выражается в стандартных кубических метрах. Для этого к объему газовой фазы прибавляется объем газа, получаемый после перевода с помощью табл. 6 объема жидкости в эквивалентный объем газа. [c.68]
При титровании удельная электропроводность раствора уменьшается (на рис. 25, й от точки N до точки эквивалентности А), так как у ионов Ыа+, заменяющих в процессе титрования иоиы Н+, абсолютная скорость, а следовательно, эквивалентная электропро-иодпость при бесконечнодг разведении раствора значительно меньше, чем у иона Н+ (точнее Н3О+) Яц+, о = 349, а Яка+, о = 50,1 Ом Х Хсм -г-.экв» . Ионы Н+ (и ОН ) в отличие от других ионов переносят заряды через раствор путем специ([)ического обмена с молекулой воды. Когда в титруемую соляную кислоту введен эквивалентный объем раствора гидроокиси натрия и реакция нейтрализации завершена, электропроводность исследуемой системы становится минимальной, равной электропроводности раствора хлорида нат- [c.115]
Широко используется также понятие эквивалентный объем. Это объем, который занимает при нормальных условиях эквивалент взятого вещества. Например, эквивалентный объем кислорода 5,6 л, водорода 11,2 л. Поэтому пользуются и другой формулировкой закона эквивалентов [c.25]
Решение. Эквивалентный объем водорода 1/, (Нг) = = 11,2 л/моль (н. у.). [c.8]
При нормальных условиях (и. у.), т. е. давлении р, равном 101 325 Па, и температуре 7 = 273,15 К (О °С), I моль различных газов занимает объем 22,4 л (точнее, 22,41383 л). Такой объем называется молярным объемом газа и имеет размерность литр на моль (л/моль). По аналогии эквивалентный объем — объем, который занимает при данных условиях 1 моль эквивалента газооб разного вещества. Например, эквивалентный объем молекулярного водорода при нормальных условиях раве 22,4/2= 11,2 л/моль молекулярного кислорода — 22,4/4 = = 5,6 л/моль. [c.12]
Решение. В момент эквивалентности объем увеличится в два раза и концентрация соли составит 0,05 н. [c.98]
Зная объем водорода при нормальных условиях, можно вычислить эквивалент металла, пользуясь тем, что эквивалентный объем водорода равен 11,2 л/моль [c.46]
Напомним (см. [12]), что в распределении Гиббса может фигурировать любая свободная энергия — и Гельмгольца Р и Гиббса О (термодинамический потенциал). Выбор энергий Гельмгольца или Гиббса обусловлен лишь заданием естественных внешних параметров. Если последние суть Т и V, то используют Р О используют при г и р. в нашем случае длина эквивалентна объему, а растягивающее напряжение давлению. — Прим. ред. [c.141]
Например, если скачок потенциала возникает при п добавлениях 0,1 мл титранта, то в точке эквивалентности объем титранта /г-0,1. В предыдущих точках, начиная от т.э., объем можно выразить как п—1) 0,1 (п—2) 0,1 и т. д., а в последующих точках (п+1) 0,1 п + 2) 0,1 и т. д. Объем титранта в к.т.т. (Ук.т.т.) находят в пределах л-0,1-ь(п—1)0,1 мл. Он отличается от л-0,1 на вторые разности. Узнают, какая часть объема приходится на изменение ЭДС в 1 мВ. Умножив полученное число на а, находят долю объема, соответствующую из- [c.94]
Эквивалентная масса магния равна массе магния, вытесняющей 11,2 л водорода (эквивалентный объем водорода прн давлении 1,013-10 . Па и температуре О°С). [c.33]
Если грамм-эквивалентный объем водорода равен 11,2 л — —= H 2, это значит, [c.90]
Для газообразного вещества В его эквивалентный объем определяется так [c.42]
Так, если в некоторой реакции zq =2, то эквивалентный объем (н. у.) газообразного дихлора равен [c.42]
Если в реакции принимает участие газообразное вещество, то не обязательно пересчитывать объемные единицы в весо
5. Количество вещества эквивалентов.
Обозначение nэк(В), единицы измерения моль-эк. Если известна масса вещества и молярная масса эквивалентов, то количество вещества эквивалентов рассчитывают по формуле:
 (21)
(21)
где m(В) – масса вещества, г;
Мэк(В) – молярная масса эквивалентов вещества, г/моль-эк.
Для газообразных веществ можно рассчитать nэк(В), зная объем газа, который он имеет при н.у.:
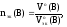 (22)
(22)
где Vo(В) – объем газа при н.у., л;
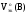 –молярный
объем эквивалентов газа при н.у., л/моль-эк
–молярный
объем эквивалентов газа при н.у., л/моль-эк
Между количеством вещества эквивалентов nэк(В) и количеством вещества n(В) существует простая зависимость :
nэк(В) = n(В) · Z(В) (23)
Пример. Рассчитать Z(В),
Мэк(В) всех веществ, принимающих участие
в реакциях а) и б), а так же 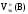 газообразных веществ в реакции а).
газообразных веществ в реакции а).
а) Fe2O3 (т) + 3CO(г) = 2Fe(т) + 3CO2(г)
б) Al2(SO4)3 + 6NaOH = 2Al(OH)3 + 3Na2SO4
Решение. Прежде всего необходимо определить к какому типу реакций (обменная или окислительно — восстановительная) относится данная реакция, для чего рассчитывают степени окисления атомов или групп атомов в формульных единицах всех веществ.
Реакция а)

является окислительно-восстановительной.
Находим атомы, которые изменяют степени окисления, и выписываем их, с учетом числа в составе одной формульной единицы и числа отданных и принятых электронов:
а) для реагентов
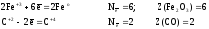
б) для продуктов
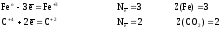
Расчеты всех величин приведены в таблице 5.
Таблица 5
ФЕ | | Z(B) | M(B), г/моль | | |
Fe2O3 | 6 | 6 | 160,0 | 26,7 | — |
CO | 2 | 2 | 28,0 | 14,0 | 11,2 |
Fe | 3 | 3 | 56,0 | 18,7 | — |
CO2 | 2 | 2 | 44,0 | 22,0 | 11,2 |
Реакция б)

является обменной, т.к. степени окисления атомов и групп атомов в ходе реакции не изменяются. Далее необходимо выбрать те части формульных единиц (положительно или отрицательно заряженных) по которым будет производится расчет суммарного заряда замещающихся ионов, а далее – Z(B) и Мэк(В). Расчеты приведены в таблице 6.
Таблица 6.
ФЕ | Замещаю- щиеся ионы | qi | Ni | Z(В)= Ni·│qi│ | М(В), г/моль | |
Al2(SO4)3 | SO4–2 | –2 | 3 | 3·2=6 | 342,0 | 57,0 |
NaOH | Na+ | +1 | 1 | 1·1=1 | 40,0 | 40,0 |
Al(OH)3 | OH– | –1 | 3 | 3·1=3 | 78,0 | 26,0 |
Na2SO4 | Na+ | +1 | 2 | 2·1=2 | 142,0 | 71,0 |
6. Закон эквивалентов.
Согласно закону эквивалентов все вещества реагируют и образуются в эквивалентных количествах.
Например, для реакции
2CO + O2 = 2CO2 (24)
nэк(CO) = nэк(O2)=nэк(CO2) (25)
Для реакции в общем виде:
nAA + nBB = nCC + nDD , (26)
где A,B – реагенты;
C,D – продукты реакции;
nA,nB,nC,nD – стехиометрические коэффициенты,
закон эквивалентов имеет вид:
nэк(A) = nэк(B) = nэк(C) = nэк(D) (27)
Т.е. количество вещества эквивалентов всех участвующих в реакции (26) веществ (реагентов А и В и образовавшихся продуктов C и D) одинаковы. Поэтому, если количество вещества эквивалентов одного из веществ (реагента или продукта) известно по условию задачи, то определены и nэк всех остальных веществ, участвующих в реакции, и необходимость их расчета отпадает. В этом состоит преимущество проведения расчетов по закону эквивалентов.
Для любой химической реакции (см. уравнение реакции в общем виде (26)) соблюдается условие (27), которое также может быть представлено следующим образом:
n(А) · Z(A)= n(В) · Z(B)= n(С) · Z(C)= n(D) · Z(D) (28)
Условие (28) упрощает определение эквивалентного числа в сложных реакциях.
Пример. Определить Z(Cr2(SO4)3) в обменной реакции, выраженной уравнением
Cr2(SO4)3 + 12KOH = 2K3[Cr(OH)6] + 3K2SO4
Решение. Для приведенной реакции запишем условие (28):
n( Cr2(SO4)3) · Z(Cr2(SO4)3)= n( KOH) · Z(KOH)
Из уравнения реакции:
n( Cr2(SO4)3) = 1 n(KOH) = 12
Поскольку Z(KOH) = 1 (не может быть другим, см. табл. 2), то


Если известны массы веществ, участвующих в реакции, то используя уравнения (21) и (27) можно записать:
 (29)
(29)
или
 (30)
(30)
Уравнение (30) является математическим выражением закона эквивалентов.
Если одно из веществ уравнения (26), например B, находится в газообразном состоянии и известен его объем при н.у., то количество вещества эквивалентов этого газа можно рассчитать по уравнению (22), а математическая запись закона эквивалентов для веществ A и B будет иметь вид:
 (31)
(31)
Пример. Рассчитать массу алюминия, вступившего в реакцию с разбавленной серной кислотой, если в результате реакции образуется 10,2 л водорода (н.у.).
Решение. Запишем уравнение реакции и укажем степени окисления атомов и заряды ионов:
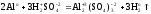
Реакция окислительно-восстановительная. Находим атомы, которые изменяют степени окисления, и выписываем их, с учетом числа в составе одной формульной единицы и числа отданных и принятых электронов:
Alo – 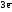 =
Al+3
=
Al+3 Z(Al) = 3
Z(Al) = 3
H2o –  =
2H+1Z(H2)
= 2
=
2H+1Z(H2)
= 2
Согласно закону эквивалентов:
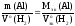 .
.
Отсюда выражаем массу алюмиия:
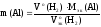
Рассчитаем
Мэк(Al)
и 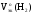 :
:

Подставив
полученные значения Мэк(Al)
и 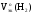 ,
а так жеVo(H2),
рассчитаем массу алюминия:
,
а так жеVo(H2),
рассчитаем массу алюминия: