Формула ЭДС
Здесь – ЭДС, – работа сторонних сил, – величина заряда.
Единица измерения напряжения – В (вольт).
ЭДС – скалярная величина. В замкнутом контуре ЭДС равна работе сил по перемещению аналогичного заряда по всему контуру. При этом ток в контуре и внутри источника тока будут течь в противоположных направлениях. Внешняя работа, которая создаёт ЭДС, должна быть не электрического происхождения (сила Лоренца, электромагнитная индукция, центробежная сила, сила, возникающая в ходе химических реакций). Эта работа нужна для преодоления сил отталкивания носителей тока внутри источника.
Если в цепи идёт ток, то ЭДС равна сумме падений напряжений во всей цепи.
Примеры решения задач по теме «Электродвижущая сила»
| Понравился сайт? Расскажи друзьям! | |||
схема, расчет, рисунок, как вычислить?
В разгар учебного года многим ученым деятелям требуется эдс формула для разных расчетов. Эксперименты, связанные с гальваническим элементом, так же нуждаются в информации об электродвижущей силе. Но для начинающих не так-то просто понять, что же это такое.
Формула нахождения эдс
Первым делом разберемся с определением. Что означает эта аббревиатура?
ЭДС или электродвижущая сила – это параметр характеризующий работу любых сил не электрической природы, работающих в цепях где сила тока как постоянного, так и переменного одинакова по всей длине. В сцепленном токопроводящем контуре ЭДС приравнивается работе данных сил по перемещению единого плюсового (положительного) заряда вдоль всего контура.
Ниже на рисунке представлена эдс формула.

Аст – означает работу сторонних сил в джоулях.
q – это переносимый заряд в кулонах.
Сторонние силы – это силы которые выполняют разделение зарядов в источнике и в итоге образуют на его полюсах разность потенциалов.
Для этой силы единицей измерения является вольт. Обозначается в формулах она буквой
Только в момент отсутствия тока в батареи, электродвижущая си-а будет равна напряжению на полюсах.
ЭДС индукции:

ЭДС индукции в контуре, имеющем N витков:

При движении:

Электродвижущая сила индукции в контуре, крутящемся в магнитном поле со скоростью

Таблица значений

Простое объяснение электродвижущей силы
Предположим, что в нашей деревне имеется водонапорная башня. Она полностью наполнена водой. Будем думать, что это обычная батарейка. Башня — это батарейка!
Вся вода будет оказывать сильное давление на дно нашей башенки. Но сильным оно будет только тогда, когда это строение полностью наполнено H2O.
В итоге чем меньше воды, тем слабее будет давление и напор струи будет меньше. Открыв кран, заметим, что каждую минуту дальность струи будет сокращаться.
В результате этого:
- Напряжение – это сила с которой вода давит на дно. То есть давление.
- Нулевое напряжение — это дно башни.
С батареей все аналогично.
Первым делом подключаем источник с энергией в цепь. И соответственно замыкаем ее. Например, вставляем батарею в фонарик и включаем его. Изначально заметим, что устройство горит ярко. Через некоторое время его яркость заметно понизится. То есть электродвижущая сила уменьшилась (вытекла если сравнивать с водой в башне).
Если брать в пример водонапорную башню, то ЭДС это насос качающие воду в башню постоянно. И она там никогда не заканчивается.
Эдс гальванического элемента – формула
Электродвижущую силу батарейки можно вычислить двумя способами:
- Выполнить расчет с применением уравнения Нернста. Нужно будет рассчитать электродные потенциалы каждого электрода, входящего в ГЭ. Затем вычислить ЭДС по формуле .
- Посчитать ЭДС формуле Нернста для суммарной ток образующей реакции, протекающей при работе ГЭ.

Таким образом вооружившись данными формулами рассчитать электродвижущую силу батарейки будет проще.
Где используются разные виды ЭДС?
- Пьезоэлектрическая применяется при растяжении или сжатии материала. С помощью нее изготавливают кварцевые генераторы энергии и разные датчики.
- Химическая используется в гальванических элементах и аккумуляторах.
- Индукционная появляется в момент пересечения проводником магнитного поля. Ее свойства применяют в трансформаторах, электрических двигателях, генераторах.
- Термоэлектрическая образуется в момент нагрева контактов разнотипных металлов. Свое применение она нашла в холодильных установках и термопарах.
- Фото электрическая используется для продуцирования фотоэлементов.
Batareykaa.ru
Формула связи между ЭДС (электродвижущей силой) и напряжением.
В задачах на электрический ток в качестве дано или найти присутствуют напряжение и ЭДС (электродвижущая сила). Есть достаточно простая связь между этими параметрами. Введём любую цепь (рис. 1).
Рис. 1. Связь между ЭДС и напряжением
Пусть дан источник с ЭДС
, напряжение во внешней цепи . Внутреннее сопротивление источника — , а сопротивление внешней цепи — . В данной системе течёт электрический ток . Тогда: (1) (2)Логично предположить, что количество электронов, сгенерированных источником, равно количеству электронов, ушедших в цепь, тогда приравниваем (1) и (2):
Откуда:
(3)Соотношение (3) — связь между ЭДС и напряжением в полной цепи постоянного тока.
В условиях идеальной цепи (внутреннее сопротивление источника равно нулю
), ЭДС численно равно напряжению.Вывод: приведенные соотношения помогают в ряде задач, в которых даны параметры источника тока/напряжения, а необходимо найти силу тока или напряжения на каком-либо элементе цепи (резистор, катушка, лампа и т.д.), и наоборот.
Поделиться ссылкой:
Понравилось это:
Нравится Загрузка…
| Электродвижущая сила. | |
Роль источника тока: разделить заряды за счет совершения работы сторонними силами. Любые силы, действующие на заряд, за исключением потенциальных сил электростатического происхождения (т. е. кулоновских) называютсторонними силами. (Сторонние силы объясняются электромагнитным взаимодействием между электронами и ядрами) |
|
ЭДС — энергетическая характеристика источника. Это физическая величина, равная отношению работы, совершенной сторонними силами при перемещении электрического заряда по замкнутой цепи, к этому заряду: Измеряется в вольтах (В). |
|
Еще одна характеристика источника — внутреннее сопротивление источника тока: r. |
|
Закон Ома для полной цепи. | |
Энергетические преобразования в цепи:
(А — работа сторонних сил; Авнеш.— работа тока на внешнем участке цепи сопротивлением R; Авнутр.— работа тока на внутреннем сопротивлении источникаr.) |
|
|
|
Закон Ома |
|
Следствия: |
|
1. Если R>>r, то ε=U. Измеряют e высокоомным вольтметром при разомкнутой внешней цепи. |
|
2.Если R<<r  — максимальный ток для данной цепи (ток короткого замыкания). Опасно, т.к. — максимальный ток для данной цепи (ток короткого замыкания). Опасно, т.к. 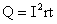 — возрастает — возрастает | e= U1+U2 |
3. На внутреннем участке цепи: Aвнутр=U1q , на внешнем участке цепи: Aвнеш=U2q. A=Aвнутр+ Aвнеш. Тогда: εq=U1q+U2q. Следовательно: ЭДС источника тока равна сумме падений напряжений на внешнем и внутреннем участках цепи. |
|
4. Если R растет, то I уменьшается. |
|
5. Мощность: а) Полная.. б) Полезная. в) Теряемая. г) КПД |
|
Соединение источников тока. | |
1. Последовательное соединение источников: полная ЭДС цепи равнаалгебраической сумме ЭДС отдельных источников, полное внутреннее сопротивление равно сумме внутренних сопротивлений всех источников тока. Если все источники одинаковы и включены в одном направлении, то Тогда з-н Ома запишется в виде: |
|
2. Параллельное соединение источников: один из источников (с наибольшейЭДС) работает как источник, остальные — как потребители (на этом принципе основана зарядка аккумулятора). Расчет по правилам Кирхгофа (см.). Если все источники одинаковы , то закон Ома запишется в виде:. |
|
Закон Ома для неоднородного участка цепи . | |
|
|
Правила Кирхгофа. | |
1. Алгебраическая сумма сил токов в каждом узле (точке разветвления) равна 0. |
|
2. В любом замкнутом контуре цепи алгебраическая сумма произведений сил токов в отдельных участках на их сопротивления равна алгебраической сумме ЭДС источников в этих контурах. |
|
Направление токов выбирают произвольно. Если после вычислений значение силы тока отрицательно, то направление противоположно. Замкнутый контур обходят в одном направлении. Если направление обхода совпадает с направлением тока, то IR>0. Если при обходе приходят к «+» источника, то его ЭДС отрицательна. В полученную систему уравнений должны входить все ЭДС и все сопротивления. Т.о. система должна состоять из одного уравнения для токов и k-1 — го уравнения для ЭДС (k — количество замкнутых контуров). |
|
Закон Ома для полной цепи
Если закон Ома для участка цепи знают почти все, то закон Ома для полной цепи вызывает затруднения у школьников и студентов. Оказывается, все до боли просто!
Идеальный источник ЭДС
Имеем источник ЭДС

Давайте вспомним, что такое ЭДС. ЭДС – это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогенных ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.
Или проще:
Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.
Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем аккумуляторе был идеальный источник ЭДС, тогда бы напряжение на клеммах аккумулятора никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока потребляет нагрузка. Что-то здесь не так. Но почему так происходит?
Внутреннее сопротивление источника ЭДС
Дело все в том, что в аккумуляторе “спрятано” сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой “r “.
Выглядит все это в аккумуляторе примерно вот так:
Цепляем лампочку
Итак, что у нас получается в чистом виде?
Лампочка – это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:
Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.
На резисторе R падает напряжение UR , а на внутреннем резисторе r падает напряжение Ur .
Теперь вспоминаем статью делитель тока. Сила тока, протекающая через последовательно соединенные сопротивления везде одинакова.
Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что

Далее



Закон Ома для полной цепи
Итак, последнее выражение носит название “закон Ома для полной цепи”

где
Е – ЭДС источника питания, В
R – сопротивление всех внешних элементов в цепи, Ом
I – сила ток в цепи, А
r – внутреннее сопротивление источника питания, Ом
Просадка напряжения
Итак, знакомьтесь, автомобильный аккумулятор!
Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус
Наш подопечный готов к бою.
Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на “ближний” свет.
Первым делом давайте замеряем напряжение на клеммах аккумулятора
12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.
Подключаем галогенную лампу к аккумулятору и снова замеряем напряжение:
Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!
А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:
Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр – силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.
Смотрим на показания приборов:
Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.
Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла
Смотрим показания:
Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.
Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.
Как найти внутреннее сопротивление источника ЭДС
Давайте снова вернемся к этой фотографии
Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе Ur тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.
Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем сопротивлении и на нагрузке, в данном случае на лампочке:
Сейчас на нагрузке (на галогенке) у нас упало напряжение UR=11,79 Вольт, следовательно, на внутреннем сопротивлении падение напряжения составило Ur=E-UR=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r


Резюме
Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.
Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень сильно просядет напряжение. Это можно увидеть, если замкнуть клеммы аккумулятора толстым медным проводом и замерять в это время напряжение на клеммах. Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R ), тем меньшее влияние оказывает эта нагрузка на источник электрической энергии.
Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осциллограф имеют ну очень большое сопротивление между своими щупами.
Работа 217 Определение ЭДС неизвестного источника
ОПРЕДЕЛЕНИЕ ЭДС НЕИЗВЕСТНОГО ИСТОЧНИКА МЕТОДОМ КОМПЕНСАЦИИ
Цель работы: Ознакомление с методом компенсации и его применение для определения электродвижущей силы (ЭДС) неизвестного источника.
Введение
Гальванические элементы, аккумуляторы, электрические генераторы и другие устройства, которые преобразуют различные виды энергий (химическую, механическую, световую и др.) в электрическую энергию, являются источниками ЭДС. Устройство способное поддерживать определённую разность потенциалов и обеспечить поток электрических зарядов во внешней цепи, называются источниками ЭДС.
Разность потенциалов на клеммах гальванического элемента при разомкнутой внешней цепи называется электродвижущей силой (ЭДС) и обозначается E. Когда сила тока во внешней цепи отсутствует, напряжение на клеммах равно ЭДС. Когда к клеммам гальванического элемента подключается внешняя нагрузка (например, сопротивление вольтметра), т.е. во внешней цепи протекает электрический ток, согласно закону Ома для неоднородной электрической цепи этот ток равен:
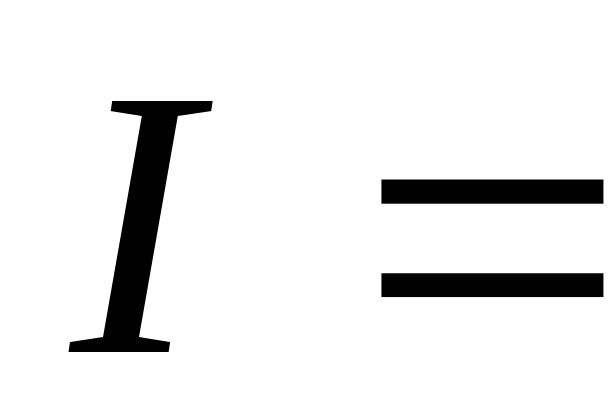
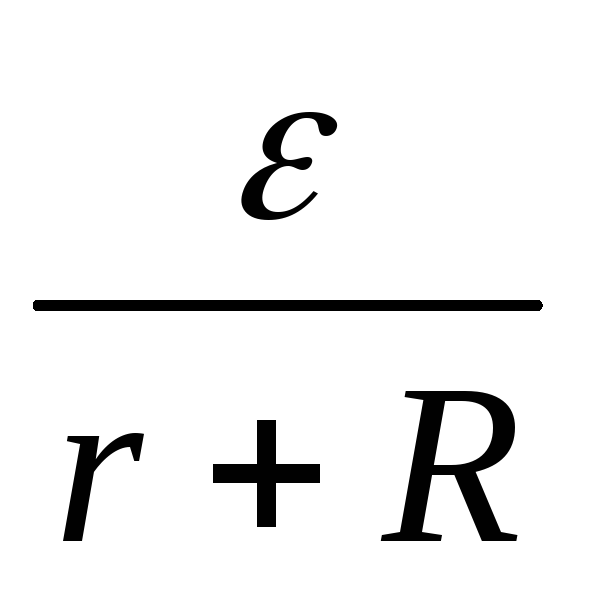 , тогда E
= Ir + IR, (1)
, тогда E
= Ir + IR, (1)
следовательно, напряжение на клеммах гальванического элемента оказывается ниже величины ЭДС из-за падения напряжения на внутреннем сопротивлении источника ЭДС и равно:
IR = E – Ir, (2)
где E — ЭДС источника тока, R – внешнее сопротивление, r – внутреннее сопротивление источника тока, I – сила тока.
Электродвижущая сила численно равна работе, совершаемой сторонними силами по перемещению единичного положительного заряда:
E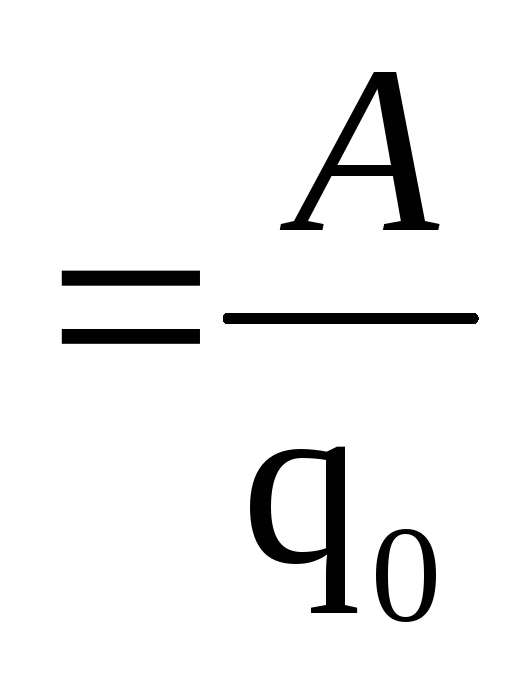 .
(3)
.
(3)
Эта работа производится за счёт энергии, затрачиваемой в источнике тока.

Рис. 1.
Напряжение U на участке 1-2 электрической цепи (см. рис. 1) называется физическая величина, определяемая работой, совершаемой суммарным полем кулоновских и сторонних сил при перемещении единичного положительного заряда на этом участке:
U12 = 1 –2 + E12. (4)
Если на участке цепи не действует ЭДС, напряжение на концах участка цепи равна разности потенциалов на этом участке.
Разность потенциалов численно равна работе, совершаемой силами электростатического поля по перемещению единичного положительного заряда:
1 – 2 = (5)
(5)
Для определения величины электродвижущей силы используется метод компенсации («нулевой метод»). В этом методе ток текущий через источник с неизвестной ЭДС – Eх, компенсируется током от какого-либо внешнего источника ЭДС – E. При этом разность потенциалов на зажимах неизвестного источника будет равна его ЭДС.
Принципиальная схема установки, служащей для измерений ЭДС неизвестного источника изображена на рис. 2.

Рис. 2.
В цепи, благодаря разности потенциалов между точками А и В через резистор R со скользящим контактом D создаётся постоянный ток. Резистор R может представлять собой однородный провод (реохорд) по которому скользит контакт D, что позволяет изменять величину сопротивления между А и D. Исследуемый источник ЭДС Eх присоединяется через гальванометр G ( с нулём на середине шкалы) к движку D и концу реохорда АВ таким образом, чтобы внешний источник ЭДС и исследуемый источник были включены навстречу друг другу. Только в этом случае возможна компенсация.
Контакт реохорда перемещают до тех пор, пока стрелка гальванометра не установится на нуле шкалы. В этом положении контакта D ток от источника неизвестной ЭДС равен нулю, а напряжение между точками АD равно Eх:
UАD = Eх
Это равенство справедливо только при условии, что сила тока через гальванометр равна нулю, т.к. в противном случае наблюдалось бы падение напряжения на внутреннем сопротивлении источника неизвестной ЭДС и сопротивлении гальванометра. Сила тока I через резистор R не равна нулю, и если обозначать через Rх сопротивление между точками А и D реохорда R то:
Eх = IRх. (6)
Затем необходимо произвести ещё одно измерение, подключив в установке вместо Eх «стандартный элемент» — источник EN ЭДС которого известна с высокой точностью. Контакт D переводят в новое положение D`, в котором гальванометр вновь не регистрирует тока. В этом положении справедливо равенство:
EN = IRN, (7)
где RN – сопротивление между точками А и D`. Т.к. через R протекает ток той же величины I, то:
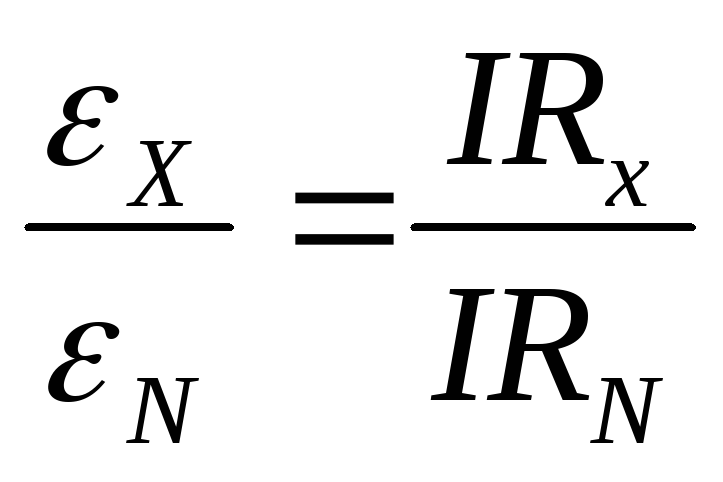 ,
,
или
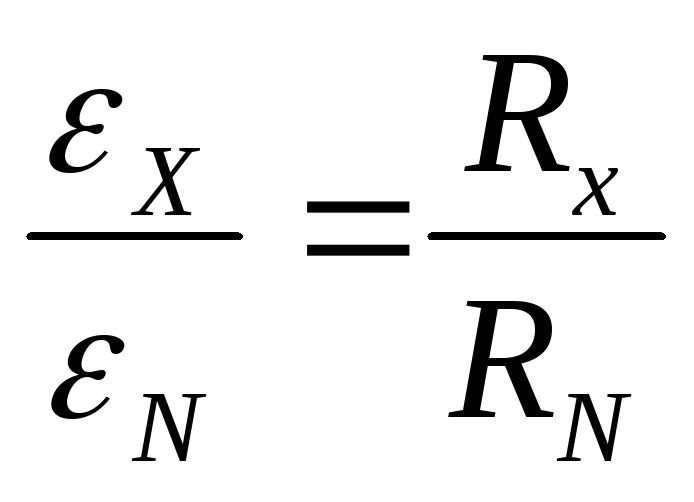 ,
,
отсюда:
 .
(8)
.
(8)
Т.к. резистор R представляет собой однородную проволоку, то сопротивления Rх и RN пропорциональны соответствующим длинам плеч реохорда lx и lN, поэтому окончательно получаем:
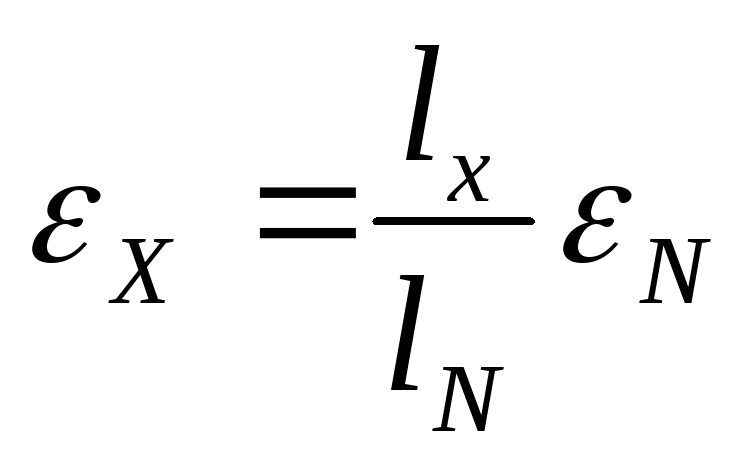 .
(9)
.
(9)
Следовательно, экспериментально определив длины плеч реохорда в двух случаях — в случае включения в компенсационную схему источника с неизвестной ЭДС Eх и в случае включения источника с известной ЭДС EN можно по формуле (9) рассчитать ЭДС неизвестного источника Eх. В компенсационном методе роль измерительного прибора, гальванометра сводится не к измерению тока, а к установлению его отсутствия на участке цени с источником неизвестной ЭДС. Поэтому в компенсационных схемах применяются не точные, но очень чувствительные гальванометры (так называемые ноль-гальванометры).
Приборы и принадлежности: источник питания, нормальный элемент Вестона (или другой эталонный источник), исследуемый источник ЭДС (гальванический элемент или другие источники ЭДС), потенциометр (или реохорд), вольтметр V с нулём посередине шкалы, ключ включения источника питания, переключатель Eх — EN с нейтральным положением.
Порядок выполнения работы
1. Ознакомиться с принципом работы компенсационной схемы и её применением в данной лабораторной работе, т. е. с монтажной компенсационной схемой, представленной на рис. 3. Здесь К1 — ключ включения источника E питания, К2 — переключатель для ввода в цепь попеременно исследуемого и эталонного источников ЭДС. В лабораторной установке реохорд АВ заменен потенциометром АВ с движком D. При этом выводы расчётной формулы (9) остаются справедливыми. Остальные обозначения соответствуют обозначениям схемы, представленной на рис. 2.
2. Ознакомиться с эксплуатационными особенностями схемы (см. последующие пункты).
3. Замкнуть переключатель К2 (двойной ключ) на исследуемый элемент Eх.
4. Замкнуть ключ К1.
Замыкание ключей необходимо производить только в указанном порядке.
Цепь должна замыкаться только на короткое время во избежание неэкономного расходования источника напряжения.
5. Добившись полного отсутствия тока в цепи вольтметра V передвижением подвижного контакта потенциометра, произвести измерение lх с помощью линейки, установленной на потенциометре. Аналогичным образом измерить lN, замкнув элемент EN ключом К2. Измерения проделать 4 (четыре) раза. Найти средние значения lх и lN. Полученные данные занести в таблицу1.
6. По окончании работы переключатель К2 обязательно поставить в среднее (нейтральное) положение!
7. Рассчитать значение Eх по формуле (9), используя средние значения lх ср и lN ср и занести результат в таблицу 1.

Рис. 3.
Таблица 1
Источники ЭДС | Длина плеча потенциометра l, мм | ЭДС источника, В | ||||
1 | 2 | 3 | 4 | Среднее значение, lср | ||
Исследуемый | ||||||
Эталонный | 1,018 | |||||
8. Определить предельную относительную погрешность измерений по формуле:
δE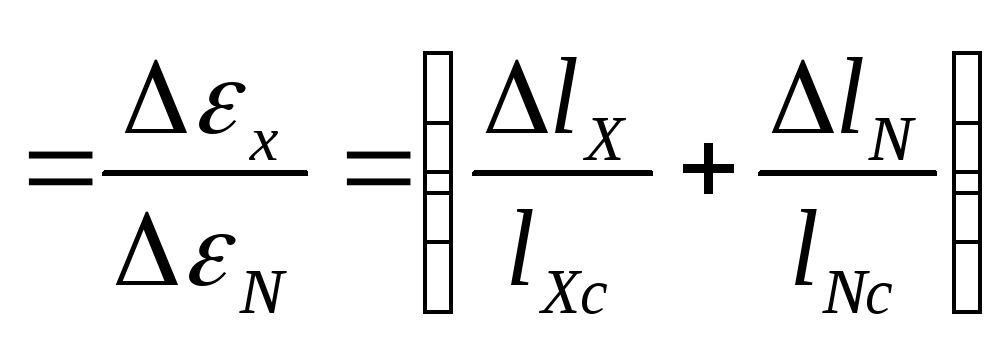 ,
(10)
,
(10)
считая, что в данной работе преобладают приборные ошибки.
Контрольные вопросы
1. В чем суть метода компенсации? Зарисовать схему цепи.
2. Написать уравнения Кирхгофа для контуров цепи компенсационной схемы.
3. Какие преимущества имеет метод компенсации по сравнению с другими методами измерения ЭДС?
4. Сформулировать закон Ома для замкнутой цепи, участка цепи, содержащего ЭДС и участка цепи, не содержащего ЭДС.
5. Как устроен гальванический элемент?
6. Что называется ЭДС?
7. Что называется напряжением?
8. В каких единицах измеряются ЭДС и напряжение в международной системе единиц?
9. Может ли резистор обладать ЭДС?
10. Может ли напряжение на клеммах батареи превышать её ЭДС?
Список литературы
1.Савельев И. В. Курс общей физики. – М., Наука, 2001.-Т.2 .
2. Яворский Б.М., Детлаф А.А. Курс физики. – М. «Высшая школа», 2003.
3. Колотилова В.Г. Определение ЭДС неизвестного источника методом компенсации. – М. МИИТ, 1987.
Учебно-методическое издание
Кули-Заде Тофик Салман-Оглы
Васильев Евгений Васильевич
ОПРЕДЕЛЕНИЕ ЭДС НЕИЗВЕСТНОГО
ИСТОЧНИКА МЕТОДОМ КОМПЕНСАЦИИ
Методические указания к лабораторной работе №217
под редакцией доцента Харитонова Ю.Н.
Подписано к печати Заказ № Формат 60х84х21/16
Усл.-печ. л. Изд. № 192-10 Тираж 300 экз.
127994, Москва, ул. Образцова д. 9, стр. 9.
Типография МИИТа
10
Электродвижущая сила (эдс) гальванического элемента
Причиной возникновения электрического тока в гальваническом элементе является разность электродных потенциалов двух окислительно-восстановительных систем. Эту разность обозначают символом ∆Е и называют электродвижущей силой (ЭДС) гальванического элемента. Поскольку ЭДС — величина положительная, её находят кАк разность между большим (катод) и меньшим (анод) значениями электродных потенциалов:
∆Е = Е(катода) – Е(анода).
Таблица стандартных окислительно-восстановительных потенциалов
Чаще всего в таких таблицах полуреакции восстановления приводятся не в порядке увеличения значений Ео, а группируются по признаку содержания в них определённых элементов, например, соединения азота, марганца, хрома и т.д. Обратите внимание на следующее. В таблице, в соответствии с рекомендациями ИЮПАК, все полуреакции записаны в виде процессов восстановления, хотя в ходе любой ОВР полуреакция восстановления всегда сочетается с полуреакцией окисления. Запомните, что из двух полуреакций восстановления слева направо всегда протекает полуреакция с бóльшим значением Ео. Другая полуреакция с меньшим значением Ео всегда протекает в обратном направлении и является фактически полуреакцией окисления. Поэтому при составлении уравнений ОВР полуреакцию с меньшим значением Ео нужно «превратить» в полуреакцию окисления. Для этого в соответствующем уравнении необходимо поменять местами окисленную и восстановленную формы, оставив электроны в левой части, но перед их числом изменить знак с «плюса» на «минус». Учтите, что при этом знак электродного потенциала не меняется!
Используя значения электродных или окислительно-восстановительных потенциалов полуреакций, можно выполнить следующие операции:
1. Оценить окислительно-восстановительные свойства веществ.
Из нескольких веществ более сильными восстановительными свойствами обладает то вещество, которому соответствует полуреакция с более низким значением потенциала. И наоборот: более сильными окислительными свойствами обладает то вещество, которому соответствует полуреакция с более высоким значением потенциала.
2. Предсказать принципиальную возможность осуществления реакции в
указанном направлении.
Протекание окислительно-восстановительной реакции в данном направлении возможно лишь тогда, когда потенциал полуреакции с участием используемого окислителя будет больше потенциала полуреакции с участием используемого восстановителя.
3. Определить направление протекания реакции.
Любая ОВР всегда протекает в том направлении, в котором осуществляется полуреакциия с более высоким значением потенциала. Этому направлению соответствует положительное значение ЭДС реакции. Однако необходимо помнить, что в данном направлении реакция протекает практически необратимо при ЭДС, большей либо равной 0,4 В. Если же разность потенциалов оказывается меньше 0,4 В, то ОВР протекает обратимо и направление реакции определяется условиями ее проведения.
4. Выбрать наиболее вероятную реакцию из нескольких возможных.
Из всех возможных ОВР наиболее вероятной будет та реакция, которой соответствует максимальное значение (ЭДС).
3. Окислительно-восстановительные процессы с участием электрического тока. Электролиз расплавов и водных растворов электролитов. Электролиз с инертными и активными электродами. Схемы процессов на электродах. Получение неорганических веществ и их очистка при помощи электрического тока. Химические источники тока.
1. с. 155-159; 2. с. 285-295; 3. с. 350-358; 4. с. 236; 6. с. 285-287.
Э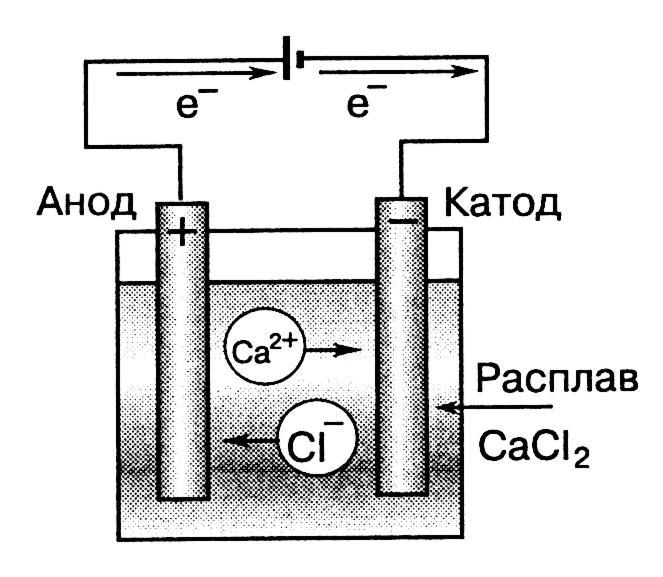 лектролиз – электрохимический
окислительно-восстановительный процесс,
протекающий на электродах при прохождении
постоянного электрического тока через
расплавы или растворы электролитов.
лектролиз – электрохимический
окислительно-восстановительный процесс,
протекающий на электродах при прохождении
постоянного электрического тока через
расплавы или растворы электролитов.
При электролизе энергия электрического тока превращается в химическую энергию и при этом осуществляется процесс, обратный происходящему в гальваническом элементе.
О
Рис.5.
Схема процесса электролиза расплава хлорида кальция
братите внимание, что заряды электродов при электролизе противоположны зарядам электродов в гальваническом элементе. Поэтому:Катод – отрицательно заряженный электрод, соединённый с отрицательным полюсом источника тока. Катод при электролизе является восстановителем. На его поверхности протекают процессы катодного восстановления. Катод всегда изготавливается из инертных материалов (графит, платина, золото, иридий и др.)
Анод – положительно заряженный электрод, который при электролизе является окислителем. На его поверхности всегда протекают процессы анодного окисления. Анод может быть изготовлен как из инертных материалов («инертный» или «нерастворимый» анод), так и из металлов, способных в ходе электролиза переходить в раствор («растворимый анод»).
При пропускании электрического тока через расплав или раствор электролита содержащиеся в нём ионы принимают направленное движение: положительно заряженные катионы направляются к отрицательно заряженному катоду, а отрицательно заряженные анионы – к положительно заряженному катоду (Рис. 6).
Процессы на катоде.
В расплавах электролитов на катоде всегда происходит восстановление катионов металлов по схеме: Меn+ + ne— = Me0 .
В водных растворах электролитов характер процессов на катоде определяется природой катионов:
а) катионы H+ : 2Н+ + 2е— = Н2.
б) катионы [Li+ – Al3+ ] и катионы NH4+: 2Н2О + 2е— = Н2 + 2ОН—.
в) катионы [Bi3+ – Au3+]: Меn+ + ne— = Me0 .
г) катионы [Mn2+ – Pb2+]: одновременно восстанавливаются катионы металлов и молекулы воды.
Процессы на инертном аноде.
В расплавах электролитов.
а) анионы ОН—: 4ОН— — 4е— = О2 + 2Н2О;
б) галогенид-анионы: 2Гал— -2е— = Гал20;
в) сульфид- и селенид-анионы: Э2- — 2е— = Э0;
В водных растворах электролитов.
а) анионы ОН—: 4ОН— — 4е— = О2 + 2Н2О;
б) анионы Гал— кроме F—: 2Гал— -2е— = Гал20;
в) сульфид- и селенид-анионы: Э2- — 2е— = Э0;
г) анионы кислородсодержащих неорганических кислот и анионы F—:
2H2O – 4e— = O2 + 4H+
д) анионы карбоновых кислот: 2RCOO— -2e— = R2 + 2CO2.
При электролизе с растворимым анодом происходит его окисление по схеме:
Ме0 – ne— = Men+.
Образующиеся при этом катионы переходят в раствор и восстанавливаются на катоде. Таким образом, электролиз с растворимым анодом заключается в переносе металла с анода на катод.
Пример.
С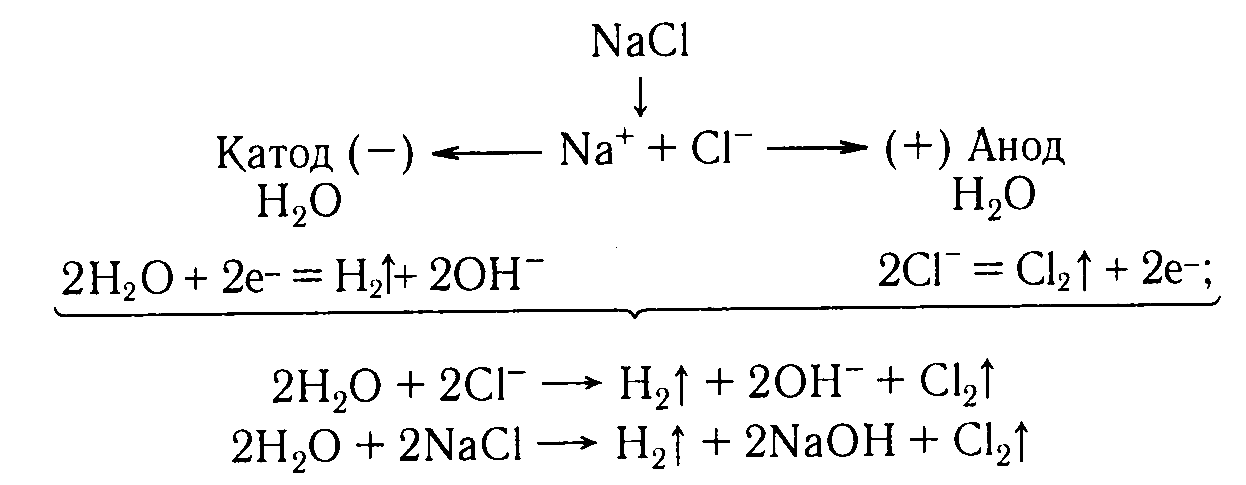 оставим
схемы процессов, протекающих на электродах
при электролизе раствора хлорида натрия
и общее уравнение процесса.
оставим
схемы процессов, протекающих на электродах
при электролизе раствора хлорида натрия
и общее уравнение процесса.
П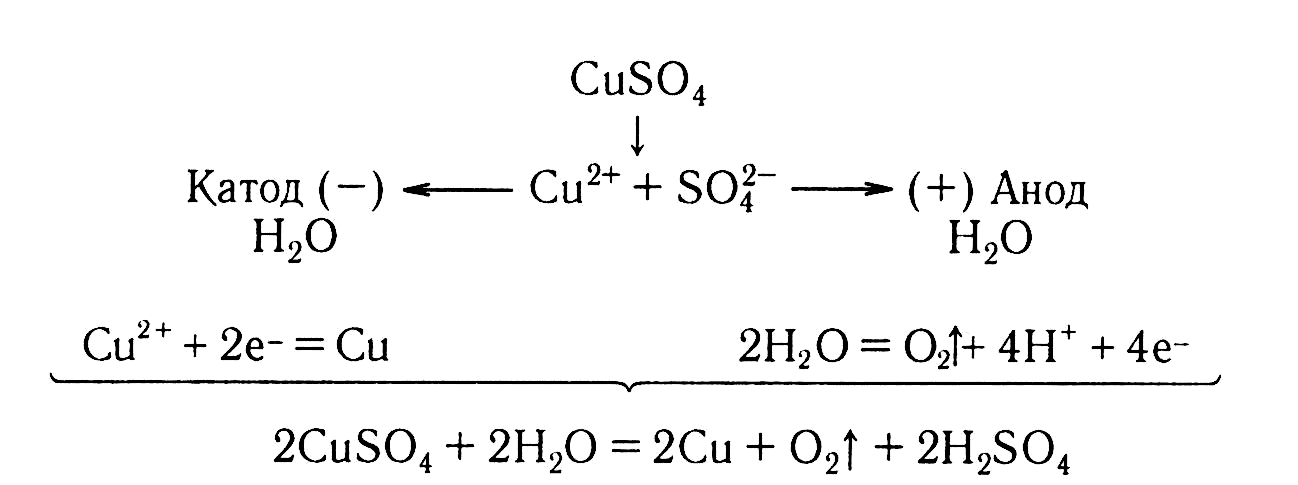 ример.
Составим схемы процессов, протекающих
на электродах при электролизе раствора
сульфата меди(II) и общее уравнение
процесса.
ример.
Составим схемы процессов, протекающих
на электродах при электролизе раствора
сульфата меди(II) и общее уравнение
процесса.
Пример. Составим схемы процессов, протекающих на электродах при электролизе раствора сульфата калия и общее уравнение процесса.




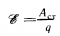
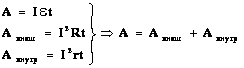 — закон сохранения энергии
— закон сохранения энергии

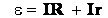
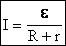
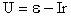 — при уменьшении силы тока в цепи напряжение увеличивается!
— при уменьшении силы тока в цепи напряжение увеличивается!
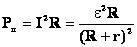 .
.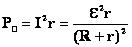 .
.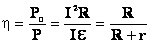 .
.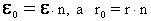 .
. 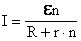
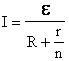
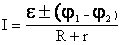 — знаки «+» или «-« выбираются в зависимости от того, в одну или в противоположные стороны направлены токи создаваемые источником ЭДС и электрическим полем.
— знаки «+» или «-« выбираются в зависимости от того, в одну или в противоположные стороны направлены токи создаваемые источником ЭДС и электрическим полем.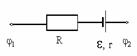
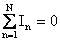 — следствие закона сохранения электрического заряда.
— следствие закона сохранения электрического заряда.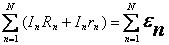 — следствие закона Ома для неоднородного участка цепи.
— следствие закона Ома для неоднородного участка цепи.