3. Примечание. Время установления скорости движения шара много меньше общего времени движения.

ДАЮ 74 Б, НУЖНО ОБЪЯСНЕНИЕ СРОЧНО! 7 класс.Решаю вот физику…., наткнулась на задачку с решением, не понимаю, откуда в формале вместе с А 100 стоит? … Причём она тут? В целом, объясните мне задачку, пожалуйста, кому несложно.Задача:Вычислите КПД неподвижного блока, если груз массой 50 кг поднят на высоту 20 м, при этом была приложена сила 800 НРешение:https://tex.z-dn.net/?f=%5Ceta%3D%20%5Cfrac%7B100A_%5Cpi%7D%7BA_3%7D%3D%20%5Cfrac%7B100F_1h%7D%7BF_2h%7D%3D%20%5Cfrac%7B100mg%7D%7BF_2%7D%20%5C%5C%20%5Ceta%3D%20%5Cfrac%7B100*50*10%7D%7B800%7D%3D62%2C5Заранее спасибо!!

Малое массивное тело массой m1 начинает соскальзывать с вершины гладкой полусферы массой m2 и радиусом R, лежащей на гладкой горизонтальной плоскости, … причём m1 = m2. На какой высоте тело оторвется от полусферы?

В стакан, содержащий 200 г воды, опускают нагреватель мощностью P= 50 Вт. Максимальная температура воды после длительного нагревания составляет в этом … случае t1= 55°С.

За какое время вода остынет на t = 1°C после выключения нагревателя? Оцените максимальную температуру воды в стакане при увеличении напряжения в на 20%. Температура воздуха to = 20°С.

в стакан, содержащий 200 г воды, опускают нагреватель мощностью P= 50 Вт. Максимальная температура воды после длительного нагревания составляет в этом … случае t1= 55°С. За какое время вода остынет на t = 1°C после выключения нагревателя? Оцените максимальную температуру воды в стакане при увеличении напряжения в на 20%. Температура воздуха to = 20°С.

титановая и медная пластинки содержат одинаковое количетсво вещества.определите массу медной пластинки,если масса титановой равно 120 гр

Сталева пилка масою 3 кг під час роботи протягом 5 хв нагрілася на 100 °С. Вважаючи, що на нагрівання пилки пішло 60 % усієї енергії, визначте виконан … у роботу та корисну потужність, що розвивається при цьому.

Свинцовую дробь, нагретую до 100 °С, в количестве 100 г смешивают с 50 г льда при 0 °С. Какой будет температура смеси после установления теплового рав … новесия?

Электродвижущая сила. | Объединение учителей Санкт-Петербурга

Электродвижущая сила.
Роль источника тока: разделить заряды за счет совершения работы сторонними силами. Любые силы, действующие на заряд, за исключением потенциальных сил электростатического происхождения (т. е. кулоновских) называютсторонними силами. (Сторонние силы объясняются электромагнитным взаимодействием между электронами и ядрами)
ЭДС — энергетическая  характеристика источника. Это физическая величина, равная отношению работы, совершенной сторонни­ми силами при перемещении электрического заряда по замкнутой цепи, к этому заряду: Измеряется в вольтах (В).
Еще одна характеристика источника — внутреннее сопротивление источника тока: r.
Закон Ома для полной цепи.
Энергетические преобразования в цепи: — закон сохранения энергии (А — работа сторонних сил; Авнеш.— работа тока на внешнем участке цепи сопротивлением  R; Авнутр.— работа тока на внутреннем сопротивлении источникаr.)
Закон Ома: Сила тока в цепи постоянного тока прямо пропорциональна ЭДС источника тока и обратно пропорциональна полному сопротивлению электрической цепи.
Следствия:
1. Если R>>r, то ε=U. Измеряют e высокоомным вольтметром при разомкнутой внешней цепи.
2.Если R<<r, то ток   — максимальный ток для данной цепи (ток короткого замыкания).  Опасно, т.к.  — возрастает	e= U1+U2
3. На внутреннем участке цепи:   Aвнутр=U1q , на внешнем участке цепи: Aвнеш=U2q. A=A внутр+ Aвнеш. Тогда: εq=U1q+U2q. Следовательно: ε= U1+U2 ЭДС источника тока равна сумме падений напряжений на внешнем и внутреннем   участках цепи.
4.   Если R растет, то I уменьшается.  — при уменьшении силы тока в цепи напряжение увеличивается!
5. Мощность: а) Полная.. б) Полезная.  . в) Теряемая. . г) КПД   .
Соединение источников тока.
1. Последовательное соединение источников:  полная ЭДС цепи равнаалгебраической сумме ЭДС отдельных источников, полное внутреннее сопротивление равно сумме внутренних сопротивлений всех источников тока. Если все источники одинаковы и включены в одном направлении, то .  Тогда з-н Ома запишется в виде:
2.  Параллельное соединение источников: один из источников (с наибольшейЭДС) работает как источник, остальные — как потребители (на этом принципе основана зарядка аккумулятора). Расчет по правилам Кирхгофа (см.). Если все источники одинаковы , то закон Ома запишется в виде:.
Закон Ома для  неоднородного участка цепи .
—  знаки «+» или «-« выбираются в зависимости от того, в одну или в противоположные стороны направлены токи создаваемые источником ЭДС и электрическим полем.
Правила Кирхгофа.
1. Алгебраическая сумма сил токов в каждом узле (точке разветвления) равна 0.    — следствие закона сохранения электрического заряда.
2. В любом замкнутом контуре цепи алгебраическая сумма произведений сил токов в отдельных участках на их сопротивления равна алгебраической сумме ЭДС источников в этих контурах.    — следствие закона Ома для неоднородного участка цепи.
Направление токов выбирают произвольно. Если после вычислений значение силы тока отрицательно, то направление противоположно. Замкнутый контур обходят в одном направлении. Если направление обхода совпадает с направлением тока, то IR>0. Если при обходе приходят к «+» источника, то его ЭДС отрицательна. В полученную систему уравнений должны входить все ЭДС и все сопротивления. Т.о. система должна состоять из одного уравнения для токов и  k-1 — го уравнения для ЭДС (k — количество замкнутых контуров).

Определить ЭДС аккумулятора, если при нагрузке в 5 А он отдает во внешнюю цепь 10 Вт

Условие задачи:

Определить ЭДС аккумулятора, если при нагрузке в 5 А он отдает во внешнюю цепь 10 Вт, а при сопротивлении внешней цепи 0,25 Ом – 16 Вт. 2} + 1,2r = 0\]

\[r\left( {3,9r + 1,2} \right) = 0\]

\[\left[ \begin{gathered}
r = 0 \hfill \\
r = – \frac{{12}}{{39}} \hfill \\
\end{gathered} \right.\]

Понятно, что внутреннее сопротивление отрицательным быть не может, значит оно все-таки равно нулю. Тогда ЭДС \(\rm E\) можно найти по одной из этих формул (мы же воспользуемся первой):

\[\left[ \begin{gathered}
{\rm E} = {I_1}{R_1} \hfill \\
{\rm E} = \sqrt {{P_2}{R_2}} \hfill \\
\end{gathered} \right.\]

\[{\rm E} = 5 \cdot 0,4 = 2\;В\]

Ответ: 2 В.

Если Вы не поняли решение и у Вас есть какой-то вопрос или Вы нашли ошибку, то смело оставляйте ниже комментарий.

Нахождение внутреннего сопротивления и ЭДС источника.

В статье расчёт в маткаде переходных процессов в ёмкостном фильтре исследовался переходный процесс в фильтре поставленном на выходе однофазного однополупериодного выпрямителя, при этом в схеме замещения выпрямитель с источником переменного напряжения заменены последовательным соединением источника ЭДС и резистора, такая замена делает возможным расчёт схем но при этом для расчётов требуется найти ЭДС источника и его внутреннее сопротивление.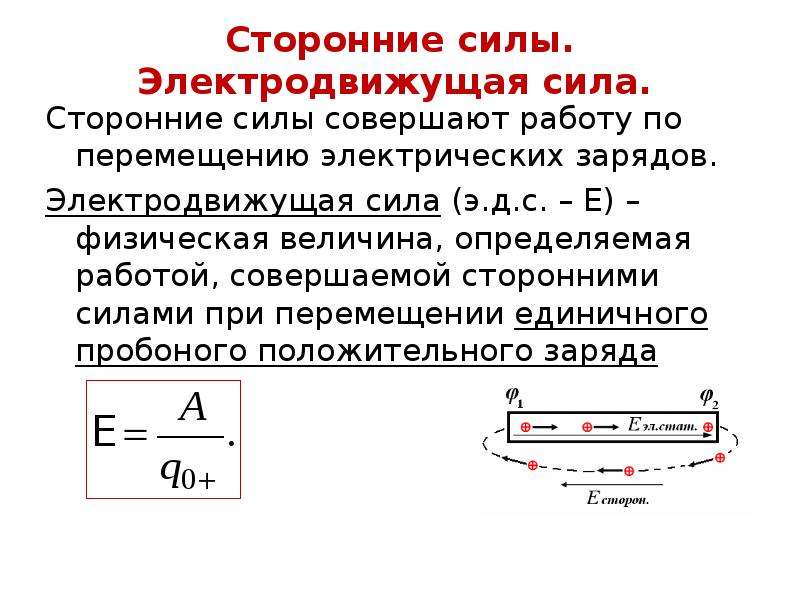 Найти ЭДС источника и его внутреннее сопротивление эксперементально можно проделав опыт холостого хода и опыт короткого замыкания но это не всегда возможно, например когда необходимо найти ЭДС и внутреннее сопротивление источника представляющего собой вторичную обмотку трансформатора, поэтому бывает необходимо определить параметры схемы замещения источника не внося больших изменений сопротивления нагрузки в схему. Рассмотрим схему на рисунке 1:

Рисунок 1 — Схема для определения параметров схемы замещения источника.

В этой схеме значения ЭДС источника и его внутреннего сопротивления неизвестны, известны только показания амперметра и вольтметра. Учтём что тока в цепи вольтметра нет, так как у него большое сопротивление и его проводимостью можно пренебреч а сопротивление амперметра настолько мало что им тоже можно пренебреч и заменить амперметр перемычкой. Ток в этой цепи обозначим как I1 (его показывает амперметр) а напряжение на R1 и G обозначим как U1 (его показывает вольтметр) при этом будем считать что ток направлен как показано на рисунке 1, а напряжения на R1 и r направлены в туже сторону что и ток.  Рассмотрим схему на рисунке 2 в которой изменено (в нашем случае увеличено) сопротивление реостата:

Рисунок 2 — Схема для определения параметров схемы замещения источника с изменённым сопротивлением реостата.

В этой схеме показание амперметра обозначим как I2 а показание вольтметра как U2.

Из схемы на рисунке 1, составим уравнение по второму закону Кирхгофа для контура который остаётся если заменить вольтметр разрывом:

Здесь E — ЭДС источника, U1 — напряжение на реостате (показывает вольтметр), I1 — ток в цепи (показывает амперметр), r — внутреннее сопротивление источника. Выразим из уравнения (1) напряжение U1:

Аналогично найдём U2, используя схему на рисунке 2:

Подставим (1) в (3):

Выразим из уравнения (4) внутреннее сопротивление источника r:

 Подставим (6) в (1) и найдём ЭДС источника:

По формулам (6) и (7) находятся параметры схемы замещения источника электрической энергии (по формуле (7) его ЭДС, по формуле (6) его внутреннее сопротивление).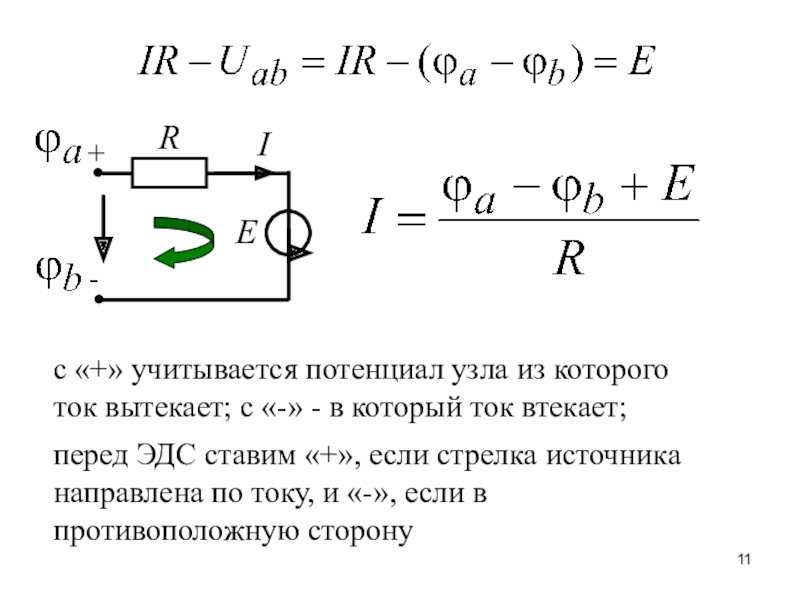 Последовательно с реостатом можно поставить измерительный резистор и использовать его для измерения тока вольтметром тогда измерения можно проводить одним вольтметром сначала подключая его паралельно источнику G, а потом паралельно измерительному резистору.
Для расчёта внутреннего сопротивления и ЭДС источника можно воспользоваться программой:
Первое измерение должно быть с меньшим сопротивлением реостата, а второе с большим.

Как найти эдс внутреннего сопротивления

Величина, характеризующая количество энергетических потерь, возникающих при протекании тока через его источник, определяется как внутреннее сопротивление источника тока. Как и обычное сопротивление, имеет единицу измерения, равную 1 Ом. Ток, двигаясь через источник, теряет часть своей энергии, которая переходит в тепло, точно так же, как на любом нагрузочном сопротивлении. Это значит, что величина напряжения на выводах источника зависит от величины тока, а не от ЭДС.

Если рассмотреть замкнутую электрическую цепь, в которую включён источник тока (батарейка, аккумулятор или генератор), и нагрузку R, то ток течёт и внутри источника. Внутреннее сопротивление источника, обозначаемое буквой r, ему препятствует.

У генератора r – это внутреннее сопротивление обмоток статора, у аккумулятора – сопротивление электролита.

Измерение сопротивления петли фаза-нуль

Петля «фаза – нуль» – это электрическая цепь переменного тока, которая может возникнуть в результате короткого замыкания между проводами: «фаза» и «ноль» или «фаза» и «фаза». Разрушение изоляции, механические повреждения или случайное соединение оголённых участков кабеля между собой могут стать этому причиной. В установках с глухо заземлённой нейтралью нулевой проводник физически связан с нейтралью трансформатора, она подключена к контуру заземления. При замыкании на корпус или соединении фаз между собой образуется цепь (петля).

Главная задача проводимых измерений – узнавать, каким будет величина тока через петлю при КЗ. Это обязательно для расчёта и подбора защитного оборудования. Хорошим результатом будет маленькое сопротивление петли, тогда ток Iк. з. будет наибольшим. От его величины зависит, как быстро сработает защитный автоматический выключатель.

Чем меньше времени будет затрачено на отключение повреждённой или закороченной цепи, тем больше шансов предотвратить пожар от возгорания кабельной сети. При попадании человека под удар электрического тока в результате прикосновения или короткого замыкания автоматическое снятие напряжения спасёт ему жизнь.

На предприятиях ежегодно проводится комплекс измерений защитного заземления и сопротивления петли фаза – ноль. При неудовлетворительных результатах проводится ряд мероприятий:

• заменяются участки провода, не отвечающие требованиям по диаметру сечения;
• перекручиваются болтовые соединения с обязательной установкой врезных шайб;
• вскрываются контуры защитных заземлений и осматриваются на предмет целостности сварных соединений и состояния элементов заземления;
• при необходимости в контур защитного заземления добавляются дополнительные элементы;
• исключается последовательное подключение корпусов устройств к общей шине заземления.

После выполнения комплекса мероприятий измерения проводятся повторно.

Нахождение внутреннего сопротивления

Его можно находить двумя путями: рассчитать или измерить. Первым путём идут при работе с электрическими схемами, второй – выбирают, занимаясь с реальными устройствами.

Простой расчёт производится с использованием формулы Закона Ома для участка полной цепи:

Чтобы узнать силу тока, нужно напряжение ЭДС делить на сумму сопротивлений.

Выразив отсюда r, получают формулу для его вычисления:

где:

• r – внутреннее сопротивление источника;
• ε – ЭДС источника;
• I – сила тока в полной цепи;
• R – сопротивление в полной цепи.

Комплекс измерений этого параметра у настоящего устройства не подразумевает непосредственных замеров. Тестируются напряжения на нагрузочном сопротивлении в двух режимах тока: холостом и КЗ.

Так как не любой источник может выдержать даже кратковременный режим замыкания, берётся метод измерения без вычислений.

В схему включается внешнее сопротивление нагрузки в виде подстроечного резистора Rн. Выставляется такое значение, при котором падение напряжения на резисторе равнялось бы 1/2 U холостого хода. Тогда измеренное омметром Rн будет соответствовать внутреннему сопротивлению источника.

Малое внутреннее сопротивление

Малой величины внутреннего сопротивления добиваются применением обратной связи в схемах, куда включён двухполюсник. В стабилизаторах напряжения r достигает значений менее 9*10-4 Ом. Автомобильная АКБ 6СТ-60 обладает сопротивлением около 0,01 Ом. Если произвести измерения петли фаза-ноль бытовой сети, то норма значения лежит в пределах 0,05-1 Ом.

Реактивное внутреннее сопротивление

Кроме гальванических и электролитических двухполюсников, существуют источники питания, схемы которых включают в себя реактивные элементы. При определении их внутреннего сопротивления используют метод комплексных амплитуд. Он подразумевает использовать при расчётах комплексные сопротивления элементов, включённых в схему. Величины токов и напряжений заменяются значениями их комплексных амплитуд. Сам алгоритм вычисления такой же, как при расчёте активного сопротивления.

Процесс измерений r-реактивного немного отличается от измерения активной составляющей сопротивления. Методы зависят от того, какие параметры этой комплексной функции нужно узнать: отдельные составляющие или комплексное число.

На эти параметры влияет частота, поэтому, чтобы при тестировании добиться информации о внутреннем реактивном значении r, нужно убрать частотную зависимость. Это достигается комплексом замеров на всём диапазоне частот, генерируемых таким двухполюсником.

Большое внутреннее сопротивление

Пьезоэлектрические датчики, конденсаторные микрофоны и другие источники импульсов обладают повышенным внутренним импедансом. Чтобы эффективно использовать такие устройства, нужно правильно согласовать схему считывания сигнала. При неудачном согласовании неизбежны потери.

Важно! Удачное согласование по напряжению получается при использовании для снятия сигнала устройства, с большим входным сопротивлением, чем у источника сигнала. В случае высокоомного источника для считывания сигнала применяется буферный усилитель.

Внутреннее сопротивление и импеданс

Импеданс – полное (комплексное) внутреннее сопротивление эквивалентного двухполюсника переменному току. Обозначается буквой Z и так же измеряется в Омах.

Двухполюсник и его эквивалентная схема

Двухполюсник представляет собой электрическую цепь, содержащую две точки присоединения к другим цепям. Бывает два вида электрических цепей:

• цепи, содержащие источник тока или напряжения;
• двухполюсники, не являющиеся источниками.

Первые характеризуются электрическими параметрами: силой тока, напряжением и импедансом. Для расчёта параметров таких двухполюсников предварительно производят замену реальных элементов цепи на идеальные элементы. Комбинация, которая получается в результате подобной замены, называется эквивалентной схемой.

Внимание! При работе со сложными электрическими схемами с учётом того, что устройство работает на одной частоте, допустимо преобразовывать последовательные и параллельные ветви до получения простой схемы, доступной для расчёта параметров.

Второй вид двухполюсников можно охарактеризовать только величиной внутреннего сопротивления.

Влияние внутреннего сопротивления на свойства двухполюсника

Чем оно выше, тем меньшую мощность выдаёт источник при подключении нагрузки. Определить мощность в нагрузке можно по формуле:

где:

• E – напряжение ЭДС;
• R – сопротивление нагрузки;
• r – активное внутреннее сопротивление двухполюсника.

Формула применима к двухполюсникам, не отдающим энергию.

К сведению. Когда величина внутреннего сопротивления двухполюсника приближается по своему значению к сопротивлению нагрузки, передача мощности достигает максимума.

Разрядная емкость источника

Величина, зависящая от силы тока разряда, называется разрядной ёмкостью источника. Это электрический заряд, который отдаёт источник в процессе эксплуатации в зависимости от тока нагрузки. Эту величину можно считать постоянной условно. Так, стартерный аккумулятор, имеющий разрядную ёмкость С = 55 А*ч, при токе разряда 5,5 А проработает 10 часов. При запусках холодного или имеющего неисправность автомобиля аккумулятор можно разрядить за несколько минут.

Для того чтобы найти остаточную разрядную ёмкость, производят циклы «заряд – разряд». Они выполняются при помощи нагрузочных сопротивлений. Разряд на нагрузочное сопротивление производят до минимально допустимых значений плотности электролита. При этом замеряется время работы под нагрузкой. Это актуально при сезонном обслуживании аккумуляторов для выявления процессов саморазряда.

Внутреннее сопротивление источников тока – важная величина. Методы, применяемые для её снижения, являются прямыми путями увеличения отдаваемой мощности источника, значит, повышения производительности двухполюсников. Правильное измерение и вычисление импеданса эквивалентных схем позволяют приблизить двухполюсник к идеальному источнику.

Видео

Величина, характеризующая количество энергетических потерь, возникающих при протекании тока через его источник, определяется как внутреннее сопротивление источника тока. Как и обычное сопротивление, имеет единицу измерения, равную 1 Ом. Ток, двигаясь через источник, теряет часть своей энергии, которая переходит в тепло, точно так же, как на любом нагрузочном сопротивлении. Это значит, что величина напряжения на выводах источника зависит от величины тока, а не от ЭДС.

Если рассмотреть замкнутую электрическую цепь, в которую включён источник тока (батарейка, аккумулятор или генератор), и нагрузку R, то ток течёт и внутри источника. Внутреннее сопротивление источника, обозначаемое буквой r, ему препятствует.

У генератора r – это внутреннее сопротивление обмоток статора, у аккумулятора – сопротивление электролита.

Измерение сопротивления петли фаза-нуль

Петля «фаза – нуль» – это электрическая цепь переменного тока, которая может возникнуть в результате короткого замыкания между проводами: «фаза» и «ноль» или «фаза» и «фаза». Разрушение изоляции, механические повреждения или случайное соединение оголённых участков кабеля между собой могут стать этому причиной. В установках с глухо заземлённой нейтралью нулевой проводник физически связан с нейтралью трансформатора, она подключена к контуру заземления. При замыкании на корпус или соединении фаз между собой образуется цепь (петля).

Главная задача проводимых измерений – узнавать, каким будет величина тока через петлю при КЗ. Это обязательно для расчёта и подбора защитного оборудования. Хорошим результатом будет маленькое сопротивление петли, тогда ток Iк.з. будет наибольшим. От его величины зависит, как быстро сработает защитный автоматический выключатель.

Чем меньше времени будет затрачено на отключение повреждённой или закороченной цепи, тем больше шансов предотвратить пожар от возгорания кабельной сети. При попадании человека под удар электрического тока в результате прикосновения или короткого замыкания автоматическое снятие напряжения спасёт ему жизнь.

На предприятиях ежегодно проводится комплекс измерений защитного заземления и сопротивления петли фаза – ноль. При неудовлетворительных результатах проводится ряд мероприятий:

• заменяются участки провода, не отвечающие требованиям по диаметру сечения;
• перекручиваются болтовые соединения с обязательной установкой врезных шайб;
• вскрываются контуры защитных заземлений и осматриваются на предмет целостности сварных соединений и состояния элементов заземления;
• при необходимости в контур защитного заземления добавляются дополнительные элементы;
• исключается последовательное подключение корпусов устройств к общей шине заземления.

После выполнения комплекса мероприятий измерения проводятся повторно.

Нахождение внутреннего сопротивления

Его можно находить двумя путями: рассчитать или измерить. Первым путём идут при работе с электрическими схемами, второй – выбирают, занимаясь с реальными устройствами.

Простой расчёт производится с использованием формулы Закона Ома для участка полной цепи:

Чтобы узнать силу тока, нужно напряжение ЭДС делить на сумму сопротивлений.

Выразив отсюда r, получают формулу для его вычисления:

где:

• r – внутреннее сопротивление источника;
• ε – ЭДС источника;
• I – сила тока в полной цепи;
• R – сопротивление в полной цепи.

Комплекс измерений этого параметра у настоящего устройства не подразумевает непосредственных замеров. Тестируются напряжения на нагрузочном сопротивлении в двух режимах тока: холостом и КЗ.

Так как не любой источник может выдержать даже кратковременный режим замыкания, берётся метод измерения без вычислений.

В схему включается внешнее сопротивление нагрузки в виде подстроечного резистора Rн. Выставляется такое значение, при котором падение напряжения на резисторе равнялось бы 1/2 U холостого хода. Тогда измеренное омметром Rн будет соответствовать внутреннему сопротивлению источника.

Малое внутреннее сопротивление

Малой величины внутреннего сопротивления добиваются применением обратной связи в схемах, куда включён двухполюсник. В стабилизаторах напряжения r достигает значений менее 9*10-4 Ом. Автомобильная АКБ 6СТ-60 обладает сопротивлением около 0,01 Ом. Если произвести измерения петли фаза-ноль бытовой сети, то норма значения лежит в пределах 0,05-1 Ом.

Реактивное внутреннее сопротивление

Кроме гальванических и электролитических двухполюсников, существуют источники питания, схемы которых включают в себя реактивные элементы. При определении их внутреннего сопротивления используют метод комплексных амплитуд. Он подразумевает использовать при расчётах комплексные сопротивления элементов, включённых в схему. Величины токов и напряжений заменяются значениями их комплексных амплитуд. Сам алгоритм вычисления такой же, как при расчёте активного сопротивления.

Процесс измерений r-реактивного немного отличается от измерения активной составляющей сопротивления. Методы зависят от того, какие параметры этой комплексной функции нужно узнать: отдельные составляющие или комплексное число.

На эти параметры влияет частота, поэтому, чтобы при тестировании добиться информации о внутреннем реактивном значении r, нужно убрать частотную зависимость. Это достигается комплексом замеров на всём диапазоне частот, генерируемых таким двухполюсником.

Большое внутреннее сопротивление

Пьезоэлектрические датчики, конденсаторные микрофоны и другие источники импульсов обладают повышенным внутренним импедансом. Чтобы эффективно использовать такие устройства, нужно правильно согласовать схему считывания сигнала. При неудачном согласовании неизбежны потери.

Важно! Удачное согласование по напряжению получается при использовании для снятия сигнала устройства, с большим входным сопротивлением, чем у источника сигнала. В случае высокоомного источника для считывания сигнала применяется буферный усилитель.

Внутреннее сопротивление и импеданс

Импеданс – полное (комплексное) внутреннее сопротивление эквивалентного двухполюсника переменному току. Обозначается буквой Z и так же измеряется в Омах.

Двухполюсник и его эквивалентная схема

Двухполюсник представляет собой электрическую цепь, содержащую две точки присоединения к другим цепям. Бывает два вида электрических цепей:

• цепи, содержащие источник тока или напряжения;
• двухполюсники, не являющиеся источниками.

Первые характеризуются электрическими параметрами: силой тока, напряжением и импедансом. Для расчёта параметров таких двухполюсников предварительно производят замену реальных элементов цепи на идеальные элементы. Комбинация, которая получается в результате подобной замены, называется эквивалентной схемой.

Внимание! При работе со сложными электрическими схемами с учётом того, что устройство работает на одной частоте, допустимо преобразовывать последовательные и параллельные ветви до получения простой схемы, доступной для расчёта параметров.

Второй вид двухполюсников можно охарактеризовать только величиной внутреннего сопротивления.

Влияние внутреннего сопротивления на свойства двухполюсника

Чем оно выше, тем меньшую мощность выдаёт источник при подключении нагрузки. Определить мощность в нагрузке можно по формуле:

где:

• E – напряжение ЭДС;
• R – сопротивление нагрузки;
• r – активное внутреннее сопротивление двухполюсника.

Формула применима к двухполюсникам, не отдающим энергию.

К сведению. Когда величина внутреннего сопротивления двухполюсника приближается по своему значению к сопротивлению нагрузки, передача мощности достигает максимума.

Разрядная емкость источника

Величина, зависящая от силы тока разряда, называется разрядной ёмкостью источника. Это электрический заряд, который отдаёт источник в процессе эксплуатации в зависимости от тока нагрузки. Эту величину можно считать постоянной условно. Так, стартерный аккумулятор, имеющий разрядную ёмкость С = 55 А*ч, при токе разряда 5,5 А проработает 10 часов. При запусках холодного или имеющего неисправность автомобиля аккумулятор можно разрядить за несколько минут.

Для того чтобы найти остаточную разрядную ёмкость, производят циклы «заряд – разряд». Они выполняются при помощи нагрузочных сопротивлений. Разряд на нагрузочное сопротивление производят до минимально допустимых значений плотности электролита. При этом замеряется время работы под нагрузкой. Это актуально при сезонном обслуживании аккумуляторов для выявления процессов саморазряда.

Внутреннее сопротивление источников тока – важная величина. Методы, применяемые для её снижения, являются прямыми путями увеличения отдаваемой мощности источника, значит, повышения производительности двухполюсников. Правильное измерение и вычисление импеданса эквивалентных схем позволяют приблизить двухполюсник к идеальному источнику.

Видео

Приборы и принадлежности, используемые в работе:

1. Источник электрической энергии.
2. Амперметр.
3. Вольтметр.
4. Реостат.
5. Ключ.
6. Соединительные провода.

Цель работы:

1. Научится собирать, заданную электрическую схему.

2. Используя закон ОМА для всей цепи, определить опытным путём величину внутреннего сопротивления и ЭДС источника электрической цепи.

Формула закона Ома для всей цепи имеет вид:

, (1)

Е — ЭДС источника электрической энергии

R — сопротивление внешней части цепи

r — внутреннее сопротивление источника

I — сила тока в цепи.

Перепишем формулу (I) в виде:

(2)

Величина является напряжением на внешней части цепи. Тогда формула (2) примет вид:

(3)

Если в полной цепи менять внешнее сопротивление, то будут меняться величины I и U (ток в цепи и напряжение на внешней её части). Пусть при силе тока в цепи , напряжение на внешней цепи равно , а при силе тока равно . Тогда дважды запишем формулу (3).

(4)

Левые части у уравнений одинаковые, поэтому приравняем правые части:

и получим формулу для нахождения г внутреннего сопротивления источника:

(5)

Подставив (5) в одно из уравнений системы (4), получим формулу для нахождения Е ЭДС источника:

;

(6)

1. Определить цену деления амперметра и вольтметра.

2. Собрать следующую схему:

При сборке схемы соблюдать следующие требования:

— Собирать схему только при разомкнутом ключе К.

— Приступать к включению схемы и измерениям только после того, как преподаватель или лаборант проверят, правильно ли собрана Ваша схема.

— При замыкании ключа особое внимание обратить на показания амперметра — он не должен зашкаливать.

3. Изменяя величину внешнего сопротивления реостатом, получить 7 различных значений силы тока и напряжения во внешней цепи.

4. По формуле (5) вычислить 7 различных значений внутреннего сопротивления источника.

5. По формуле (6) вычислить 7 различных значений ЭДС источника электрической энергии.

6. Результаты измерений I и U, а также вычислений r и Е занести в таблицу.

В таблице n— число делений, на которое отклонилась стрелка амперметра или вольтметра при очередном измерении.

В следующую колонку после n записывается сила тока или напряжение в цепи, которые вычисляются по формуле:

(цена деления);

Таблица результатов измерений и вычислений

Цена одного деления амперметра = .

Цена одного деления вольтметра =.

7. Вычислить погрешности с которыми определены внутреннее сопротивление и ЭДС источника электрической энергии, по формулам:[13]

; s_r = D r_ср/ r_ср × 100%

;

8. Значение погрешностей занести в таблицу и по результатам, полученным в лабораторной работе сделать вывод[14].

КОНТРОЛЬНЫЕ ВОПРОСЫ ПЕРВОГО УРОВНЯ.

1. Закон Ома для всей цепи (формула и формулировка).

2.Закон Ома при параллельном, последовательном и смешанном соединении одинаковых источников электрической энергии (формулы, схемы).

3. Определение цены деления многопредельного прибора.

КОНТРОЛЬНЫЕ ВОПРОСЫ ВТОРОГО И ТРЕТЬЕГО УРОВНЯ.

4.Закон Ома для участка цепи с ЭДС (3 случая и общий закон) и для всей цепи при нескольких ЭДС.

5.Что называется ЭДС источника электрической энергии? Единицы ЭДС.

6. Понятие внутреннего сопротивления источника.

7.Измерительные приборы вольтметр и амперметр[15].
Лабораторная работа № 8.

Не нашли то, что искали? Воспользуйтесь поиском:

Лучшие изречения: Да какие ж вы математики, если запаролиться нормально не можете. 8459 — | 7349 — или читать все.

91.146.8.87 © studopedia.ru Не является автором материалов, которые размещены. Но предоставляет возможность бесплатного использования. Есть нарушение авторского права? Напишите нам | Обратная связь.

Отключите adBlock!
и обновите страницу (F5)
очень нужно

Закон Ома для полной цепи

Если закон Ома для участка цепи знают почти все, то  закон Ома для полной цепи вызывает затруднения у школьников и студентов. Оказывается, все до боли просто!

Идеальный источник ЭДС

Имеем источник ЭДС

Давайте вспомним, что такое ЭДС. ЭДС – это что-то такое, что создает электрический ток. Если к такому источнику напряжения подцепить любую нагрузку (хоть миллиард галогенных ламп, включенных параллельно), то он все равно будет выдавать такое же напряжение, какое-бы он выдавал, если бы мы вообще не цепляли никакую нагрузку.

Или проще:

Короче говоря, какая бы сила тока не проходила через цепь резистора, напряжение на концах источника ЭДС будет всегда одно и тоже. Такой источник ЭДС называют идеальным источником ЭДС.

Но как вы знаете, в нашем мире нет ничего идеального. То есть если бы в нашем аккумуляторе был идеальный источник ЭДС, тогда бы напряжение на клеммах аккумулятора никогда бы не проседало. Но оно проседает и тем больше, чем больше силы тока потребляет нагрузка. Что-то здесь не так. Но почему так происходит?

Внутреннее сопротивление источника ЭДС

Дело все в том, что в аккумуляторе “спрятано” сопротивление, которое условно говоря, цепляется последовательно с источником ЭДС аккумулятора. Называется оно внутренним сопротивлением или выходным сопротивлением. Обозначается маленькой буковкой “r “.

Выглядит все это в аккумуляторе примерно вот так:

Цепляем лампочку

Итак, что у нас получается в чистом виде?

Лампочка – это нагрузка, которая обладает сопротивлением. Значит, еще больше упрощаем схему и получаем:

Имеем идеальный источник ЭДС, внутреннее сопротивление r и сопротивление нагрузки R. Вспоминаем статью  делитель напряжения. Там говорится, что напряжение источника ЭДС равняется сумме падений напряжения на каждом сопротивлении.

На резисторе R падает напряжение U_R , а на внутреннем резисторе r падает напряжение U_r .

Теперь вспоминаем статью делитель тока. Сила тока, протекающая  через последовательно соединенные сопротивления везде одинакова.

Вспоминаем алгебру за 5-ый класс и записываем все то, о чем мы с вами сейчас говорили. Из закона Ома для участка цепи получаем, что

Далее

Закон Ома для полной цепи

Итак, последнее выражение носит название “закон Ома для полной цепи”

где

Е – ЭДС источника питания, В

R – сопротивление всех внешних элементов в цепи, Ом

I – сила ток в цепи, А

r – внутреннее сопротивление источника питания, Ом

Просадка напряжения

Итак, знакомьтесь, автомобильный аккумулятор!

Для дальнейшего его использования, припаяем к нему два провода: красный на плюс, черный на минус

Наш подопечный готов к бою.

Теперь берем автомобильную лампочку-галогенку и тоже припаяем к ней два проводка с крокодилами. Я припаялся к клеммам на “ближний” свет.

Первым делом давайте замеряем напряжение на клеммах аккумулятора

12,09 вольт. Вполне нормально, так как наш аккумулятор выдает именно 12 вольт. Забегу чуток вперед и скажу, что сейчас мы замерили именно ЭДС.

Подключаем  галогенную лампу к аккумулятору и снова замеряем напряжение:

Видели да? Напряжение на клеммах аккумулятора просело до 11,79 Вольт!

А давайте замеряем, сколько потребляет тока наша лампа в Амперах. Для этого составляем вот такую схемку:

Желтый мультиметр у нас будет замерять напряжение, а красный мультиметр – силу тока. Как замерять с помощью мультиметра силу тока и напряжение, можно прочитать в этой статье.

[quads id=1]

Смотрим на показания приборов:

Как мы видим, наша лампа потребляет 4,35 Ампер. Напряжение просело до 11,79 Вольт.

Давайте вместо галогенной лампы поставим простую лампочку накаливания на 12 Вольт от мотоцикла

Смотрим показания:

Лампочка потребляет силу тока в 0,69 Ампер. Напряжение просело до 12 Вольт ровно.

Какие выводы можно сделать? Чем больше нагрузка потребляет силу тока, тем больше просаживается напряжение на аккумуляторе.

Как найти внутреннее сопротивление источника ЭДС

Давайте снова вернемся к этой фотографии

Так как у нас в этом случае цепь разомкнута (нет внешней нагрузки), следовательно сила тока в цепи I равняется нулю. Значит, и падение напряжение на внутреннем резисторе U_r тоже будет равняться нулю. В итоге, у нас остается только источник ЭДС, у которого мы и замеряем напряжение. В нашем случае ЭДС=12,09 Вольт.

Как только мы подсоединили нагрузку, то у нас сразу же упало напряжение на внутреннем сопротивлении и на нагрузке, в данном случае на лампочке:

Сейчас на нагрузке (на галогенке) у нас упало напряжение U_R=11,79 Вольт, следовательно, на внутреннем сопротивлении падение напряжения составило U_r=E-U_R=12,09-11,79=0,3 Вольта. Сила тока в цепи равняется I=4,35 Ампер. Как я уже сказал, ЭДС у нас равняется E=12,09 Вольт. Следовательно, из закона Ома для полной цепи высчитываем, чему у нас будет равняться внутреннее сопротивление r

Вывод

Внутреннее сопротивление бывает не только у различных химических источников напряжения. Внутренним сопротивлением также обладают и различные измерительные приборы. Это в основном вольтметры и осциллографы.

Дело все в том, что если подключить нагрузку R, сопротивление у которой будет меньше или даже равно r, то у нас очень сильно просядет напряжение. Это можно увидеть, если замкнуть клеммы аккумулятора толстым медным проводом и замерять в это время напряжение на клеммах. Но я не рекомендую этого делать ни в коем случае! Поэтому, чем высокоомнее нагрузка (ну то есть чем выше сопротивление нагрузки R ), тем меньшее влияние оказывает эта нагрузка на источник электрической энергии.

Вольтметр и осциллограф при замере напряжения тоже чуть-чуть просаживают напряжение замеряемого источника напряжения, потому как являются нагрузкой с большим сопротивлением. Именно поэтому самый точный вольтметр и осциллограф имеют ну очень большое сопротивление между своими щупами.

определение и формула, в чём измеряется, работа источника электродвижущей силы

Электрический ток не протекает в медном проводе по той же причине, по которой остаётся неподвижной вода в горизонтальной трубе. Если один конец трубы соединить с резервуаром таким образом, чтобы образовалась разность давлений, жидкость будет вытекать из одного конца. Аналогичным образом, для поддержания постоянного тока необходимо внешнее воздействие, перемещающее заряды. Это воздействие называется электродвижущая сила или ЭДС.

От электростатики к электрокинетике

Между концом XVIII и началом XIX века работы таких учёных, как Кулон, Лагранж и Пуассон, заложили математические основы определения электростатических величин. Прогресс в понимании электричества на этом историческом этапе очевиден. Франклин уже ввёл понятие «количество электрической субстанции», но пока ещё и он, ни его преемники не смогли его измерить.

Следуя за экспериментами Гальвани, Вольта пытался найти подтверждения того, что «гальванические жидкости» животного были одной природы со статическим электричеством. В поисках истины он обнаружил, что когда два электрода из разных металлов контактируют через электролит, оба заряжаются и остаются заряженными несмотря на замыкание контура нагрузкой. Это явление не соответствовало существующим представлениям об электричестве потому, что электростатические заряды в подобном случае должны были рекомбинировать.

Вольта ввёл новое определение силы, действующей в направлении разделения зарядов и поддержании их в таком состоянии. Он назвал её электродвижущей. Подобное объяснение описания работы батареи не вписывалось в теоретические основы физики того времени. В Кулоновской парадигме первой трети XIX века э. д. с. Вольта определялась способностью одних тел вырабатывать электричество в других.

Важнейший вклад в объяснение работы электрических цепей внёс Ом. Результаты ряда экспериментов привели его к построению теории электропроводности. Он ввёл величину «напряжение» и определил её как разность потенциалов на контактах. Подобно Фурье, который в своей теории различал количество тепла и температуру в теплопередаче, Ом создал модель по аналогии, связывающую количество перемещаемого заряда, напряжение и электропроводность. Закон Ома не противоречил накопленным знаниям об электростатическом электричестве.

Затем, благодаря Максвеллу и Фарадею, пояснительные модели тока получили новую теорию поля. Это позволило разработать связанную с полем концепцию энергии как для статических потенциалов, так и для электродвижущей силы. Основные даты эволюции понятия ЭДС:

• 1800 г. — создание Вольтой гальванической батареи;
• 1826 г. — Ом формулирует свой закон для полной цепи;
• 1831 г. — обнаружение электромагнитной индукции Фарадеем.

Определение и физический смысл

Приложение некоторой разности потенциалов между двумя концами проводника создаст перетекание электронов от одного конца к другому. Но этого недостаточно для поддержания потока зарядов в проводнике. Дрейф электронов приводит к уменьшению потенциала до момента его уравновешивания (прекращение тока). Таким образом, для создания постоянного тока необходимы механизмы, непрерывно возвращающие описанную систему в первоначальную конфигурацию, то есть, препятствующие агрегации зарядов в результате их движения. Для этой цели используются специальные устройства, называемые источники питания.

В качестве иллюстрации их работы удобно рассматривать замкнутый контур из сопротивления и гальванического источника питания (батареи). Если предположить, что внутри батареи тока нет, то описанная проблема объединения зарядов остаётся неразрешённой. Но в цепи с реальным источником питания электроны перемещаются постоянно. Это происходит благодаря тому, что поток ионов протекает и внутри батареи от отрицательного электрода к положительному. Источник энергии, перемещающий эти заряды в батарее — химические реакции. Такая энергия называется электродвижущей силой.

ЭДС является характеристикой любого источника энергии, способного управлять движением электрических зарядов в цепи. В аналогии с замкнутым гидравлическим контуром работа источника э. д. с. соответствует работе насоса для создания давления воды. Поэтому значок, обозначающий эти устройства, неотличим на гидравлических и электрических схемах.

Несмотря на название, электродвижущая сила на самом деле не является силой и измеряется в вольтах. Её численное значение равно работе по перемещению заряда по замкнутой цепи. ЭДС источника выражается формулой E=A/q, в которой:

• E — электродвижущая сила в вольтах;
• A — работа сторонних сил по перемещению заряда в джоулях;
• q — перемещённый заряд в кулонах.

Из этой формулы ЭДС следует, что электродвижущая сила не является свойством цепи или нагрузки, а есть способность генератора электроэнергии к разделению зарядов.

Сравнение с разностью потенциалов

Электродвижущая сила и разность потенциалов в цепи очень похожие физические величины, так как оба измеряются в вольтах и определяются работой по перемещению заряда. Одно из основных смысловых различий заключается в том, что э. д. с. (E) вызывается путём преобразования какой-либо энергии в электрическую, тогда как разность потенциалов (U) реализует электрическую энергию в другие виды. Другие различия выглядят так:

• E передаёт энергию всей цепи. U является мерой энергии между двумя точками на схеме.
• Е является причиной U, но не наоборот.
• Е индуцируется в электрическом, магнитном и гравитационном поле.
• Концепция э. д. с. применима только к электрическому полю, в то время как разность потенциалов применима к магнитным, гравитационным и электрическим полям.

Напряжение на клеммах источника питания, как правило, отличается от ЭДС источника. Это происходит из-за наличия внутреннего сопротивления источника (электролита и электродов, обмоток генератора). Связывающая разность потенциалов и ЭДС источника тока формула выглядит как U=E-Ir. В этом выражении:

• U — напряжение на клеммах источника;
• r — внутреннее сопротивление источника;
• I — ток в цепи.

Из этой формулы электродвижущей силы следует, что э. д. с. равна напряжению когда ток в цепи не течёт. Идеальный источник ЭДС создаёт разность потенциалов независимо от нагрузки (протекающего тока) и не обладает внутренним сопротивлением.

В природе не может существовать источника с бесконечной мощностью при замыкании на клеммах, как и материала с бесконечной проводимостью. Идеальный источник используется как абстрактная математическая модель.

Источники электродвижущей силы

Суть источника ЭДС заключается в преобразовании других видов энергии в электрическую с помощью сторонних сил. С точки зрения физики обеспечения э. д. с различают следующие два основных вида источников:

• гальванические;
• электромагнитные.

Первые представляют собой электрохимические источники, основанные на вовлечение в химическую реакцию процесса переноса электронов. В обычных условиях химические взаимодействия сопровождаются выделением или поглощением тепла, но существует немало реакций, в результате которых генерируется электрическая энергия.

Электрохимические процессы в большинстве случаев обратимы, поскольку энергия электрического тока может быть использована, чтобы заставить реагировать вещества между собой. Эта возможность позволяет создавать возобновляемые гальванические источники — аккумуляторы.

В генераторах тока э. д. с. создаётся другим способом. Разделение зарядов происходит с помощью явления электромагнитной индукции, которое заключается в том, что изменение величины или направления магнитного поля создаёт ЭДС. Согласно закону Фарадея, нахождение э. д. с. индукции возможно из выражения E=—dФ/dt. В этой формуле:

• Ф — магнитный поток;
• t — время.

ЭДС индукции измеряется также в вольтах. В зависимости от того, каким способом вызываются изменения магнитного потока, различают:

• Динамически индуцированную. Когда в стационарном магнитном поле перемещается проводник. Характерен для генераторов.
• Статически индуцированную. Когда изменения потока возникают из-за изменений магнитного поля вокруг неподвижного проводника. Так работают трансформаторы.

Существуют также источники э. д. с, не основанные на электрохимии или магнитной индукции. К таким устройствам можно отнести полупроводниковые фотоэлементы, контактные потенциалы и пьезокристаллы. Понятие ЭДС имеет практическое применение прежде всего как параметр выбора источников питания для тех или иных целей. Чтобы получить максимальный эффект от работы устройств в цепи, нужно согласовывать их возможности и характеристики. Прежде всего внутреннее сопротивление источника ЭДС силы с характеристиками подключаемой нагрузки.

Как измерить выходную мощность от батареи

Батареи выдают мощность, когда они подключены к цепи. Батарея, которая не подключена к цепи, не дает тока и, следовательно, не выводит энергию. Однако после того, как вы подключили батарею к цепи, вы можете определить выходную мощность, измерив падение напряжения на нагрузке цепи. Если вы знакомы с уравнениями, связывающими мощность с напряжением, током и сопротивлением, вы сможете легко перемещаться между этими понятиями.

Расчет мощности

Мощность — это произведение тока и напряжения. Следовательно, чтобы рассчитать выходную мощность батареи, вы должны измерить эти два аспекта цепи. Ток — это поток заряда в единицу времени, а напряжение — это электрическая потенциальная энергия. Единицами измерения тока и напряжения являются амперы и вольт соответственно. Кроме того, напряжение — это произведение тока и сопротивления. Сопротивление — это величина сопротивления току.Предметы, подверженные электрическому потенциалу или напряжению, обладают характеристическим сопротивлением. Сопротивление измеряется в Ом. Из-за взаимосвязанного характера мощности, напряжения, тока и сопротивления вы можете определить мощность, даже если вам известны только две другие величины. Например, мощность равна квадрату тока, умноженному на сопротивление, или квадрату напряжения, деленному на сопротивление.

Проведение измерений

Чтобы измерить выходную мощность батареи, вы должны измерить ее, когда она подключена к внешнему сопротивлению, также называемому сопротивлением нагрузки.В противном случае аккумулятор не будет работать и, следовательно, не будет обеспечивать выходную мощность. Сопротивление нагрузки создает измеримое падение напряжения. Если вы знаете сопротивление нагрузки, вы можете определить ток. Используйте мультиметр, чтобы проверить падение напряжения на нагрузке. Поверните шкалу мультиметра, чтобы контролировать напряжение постоянного тока. Затем поместите два провода измерителя по обе стороны от нагрузки. Полярность значения не имеет. Разделите это напряжение на сопротивление нагрузки, чтобы получить ток. Как только у вас есть ток и напряжение, умножьте их, чтобы получить выходную мощность.Вы заметите, что выходная мощность батареи варьируется в зависимости от цепи, в которой она запитана. Это связано с тем, что ток изменяется в зависимости от сопротивления нагрузки.

Напряжение замкнутой и разомкнутой цепи

Напряжение батареи изменяется в зависимости от того, приложено ли оно к цепи. Подробное описание батареи часто включает цифры напряжения как в замкнутой, так и в разомкнутой схемах. Напряжение замкнутой цепи аккумулятора также называется напряжением на его клеммах.Кроме того, эти напряжения могут варьироваться в зависимости от состояния заряда аккумулятора и тока зарядки, где это применимо. Это еще одна причина, по которой вы должны измерять напряжение батареи, когда она подключена к цепи.

Внутреннее сопротивление

Батарея показывает внутреннее сопротивление в дополнение к любому сопротивлению в цепи. По мере увеличения этого внутреннего сопротивления выходная мощность батареи уменьшается, поскольку некоторая мощность рассеивается внутри. Когда это происходит, напряжение на клеммах аккумулятора уменьшается.Если внутреннее сопротивление батареи становится слишком высоким, батарея больше не будет обеспечивать достаточный потенциал для пропускания тока через нагрузку.

Номинальные характеристики аккумуляторов

Аккумуляторы имеют несколько напечатанных номинальных значений их емкости и мощности. Общий электростатический потенциал батареи указывается в вольтах. Это одна из самых выдающихся характеристик батареи, и она имеет большое значение для выходной мощности батареи: как правило, чем выше номинальное напряжение, тем больше выходная мощность.Также емкость аккумулятора указана в ампер-часах. Это выражение количества ампер, которое батарея будет выдавать в течение заданного количества часов. Например, батарея на 140 ампер-час может выдавать ток 7 ампер в течение 20 часов, прежде чем потребуется зарядка.

Электродвижущая сила и внутреннее сопротивление

Электродвижущая сила (э) или э.д.с. это энергия, обеспечиваемая элементом или батареей на один кулон заряда, проходящего через них, это , измеренное в вольтах (В). Равен разности потенциалов на выводах ячейки при отсутствии тока.

• e = электродвижущая сила в вольтах, В
• E = энергия в джоулях, Дж
• Q = заряд в кулонах, Кл

Батареи и элементы имеют внутреннее сопротивление (r) , что составляет единиц измерения в омах (Вт). Когда электричество течет по цепи, внутреннее сопротивление самого элемента сопротивляется протеканию тока, и поэтому тепловая энергия теряется в самом элементе.

• e = электродвижущая сила в вольтах, В
• I = ток в амперах, А
• R = сопротивление нагрузки в цепи в Ом, Вт
• r = внутреннее сопротивление ячейки в Ом, Вт

Мы можем изменить приведенное выше уравнение;

, а затем на

В этом уравнении ( В, ) появляется разность потенциалов , измеренная в вольтах (В). Это разность потенциалов на выводах ячейки, когда в цепи протекает ток, она всегда меньше, чем e.м.ф. ячейки.

Пример;

Q1) p.d. на выводах элемента составляет 3,0 В, когда он не подключен к цепи и не течет ток. Когда ячейка подключена к цепи и течет ток 0,37 А, клемма p.d. падает до 2,8 В. Какое внутреннее сопротивление ячейки?

График терминальных п.о. против нынешних

Если мы построим график зависимости разности потенциалов на клеммах (V) от тока в цепи (I), мы получим прямую линию с отрицательным градиентом.

Мы можем им переставить э.д.с. уравнение сверху, чтобы соответствовать общему выражению для прямой линии, y = mx + c.

Из красных прямоугольников выше видно;

• точка пересечения по оси Y равна ЭДС. ячейки
• градиент графика равен -r, где r — внутреннее сопротивление ячейки.

Электрогенераторы | Физика

Цели обучения

К концу этого раздела вы сможете:

• Рассчитайте ЭДС, наведенную в генераторе.
• Рассчитайте пиковую ЭДС, которая может быть наведена в конкретной генераторной системе.

Электрические генераторы индуцируют ЭДС, вращая катушку в магнитном поле, как кратко обсуждается в разделе «Индуцированная ЭДС и магнитный поток». Теперь мы рассмотрим генераторы более подробно. Рассмотрим следующий пример.

Пример 1. Расчет ЭДС, наведенной в катушке генератора

Катушка генератора, показанная на Рисунке 1, поворачивается на одну четверть оборота (от θ, = 0º до θ, = 90º) на 15.0 мс. Круглая катушка с 200 витками имеет радиус 5,00 см и находится в однородном магнитном поле 1,25 Тл. Какая средняя наведенная ЭДС?

Рис. 1. Когда катушка генератора вращается на одну четверть оборота, магнитный поток Φ изменяется от максимального до нуля, вызывая ЭДС.

Стратегия

Мы используем закон индукции Фарадея, чтобы найти среднюю ЭДС, индуцированную за время Δ t :

[латекс] \ text {emf} = — N \ frac {\ Delta \ Phi} {\ Delta t} \\ [/ latex].

Мы знаем, что N = 200 и Δ t = 15,0 мс, и поэтому мы должны определить изменение потока Δ Φ , чтобы найти ЭДС.

Раствор

Поскольку площадь петли и напряженность магнитного поля постоянны, мы видим, что

[латекс] \ Delta \ Phi = \ Delta \ left (BA \ cos \ theta \ right) = AB \ Delta \ left (\ cos \ theta \ right) \\ [/ latex].

Теперь Δ (cos θ ) = -1,0, поскольку было дано, что θ изменяется от 0 ° до 90 °.{-3} \ text {s}} = 131 \ text {V} \\ [/ latex].

Обсуждение

Это практическое среднее значение, аналогичное 120 В, используемому в бытовой электросети.

ЭДС, рассчитанная в Примере 1 выше, является средним значением за одну четверть оборота. Какова ЭДС в любой момент времени? Он меняется в зависимости от угла между магнитным полем и перпендикуляром к катушке. Мы можем получить выражение для ЭДС как функции времени, рассматривая ЭДС движения на вращающейся прямоугольной катушке шириной × и высотой × в однородном магнитном поле, как показано на рисунке 2.

Рис. 2. Генератор с одной прямоугольной катушкой, вращающейся с постоянной угловой скоростью в однородном магнитном поле, создает ЭДС, синусоидально изменяющуюся во времени. Обратите внимание, что генератор похож на двигатель, за исключением того, что вал вращается для выработки тока, а не наоборот.

На заряды в проводах петли действует магнитная сила, потому что они движутся в магнитном поле. Заряды в вертикальных проводах испытывают силы, параллельные проводу, вызывая токи.Но те, кто находится в верхнем и нижнем сегментах, ощущают силу, перпендикулярную проводу, которая не вызывает тока. Таким образом, мы можем найти наведенную ЭДС, рассматривая только боковые провода. Движущаяся ЭДС дается равной ЭДС = Bℓv , где скорость v перпендикулярна магнитному полю B . Здесь скорость находится под углом θ с B , так что ее составляющая, перпендикулярная B , составляет v sin θ (см. Рисунок 2).Таким образом, в этом случае ЭДС, индуцированная с каждой стороны, составляет ЭДС = Bℓv sin θ , и они имеют одинаковое направление. Суммарная ЭДС вокруг контура тогда составляет

.

[латекс] \ text {emf} = 2 {B \ ell v} \ sin \ theta \\ [/ latex].

Это выражение допустимо, но оно не дает ЭДС как функцию времени. Чтобы найти зависимость ЭДС от времени, предположим, что катушка вращается с постоянной угловой скоростью ω . Угол θ связан с угловой скоростью соотношением θ = ωt , так что

[латекс] \ text {emf} = 2 {B \ ell v} \ sin \ omega t \\ [/ latex].

Итак, линейная скорость v связана с угловой скоростью ω соотношением v = rω . Здесь r = w /2, так что v = ( w /2) ω и

[латекс] \ text {emf} = 2 B \ ell \ frac {w} {2} \ omega \ sin \ omega t = \ left (\ ell w \ right) B \ omega \ sin \ omega t \\ [ /латекс].

Отметив, что площадь петли составляет A = ℓ w , и учитывая N петель, мы находим, что

[латекс] \ text {emf} = NAB \ omega \ sin \ omega t \\ [/ latex]

— это ЭДС , индуцированная в обмотке генератора из N, витков и площади A, , вращающейся с постоянной угловой скоростью ω в однородном магнитном поле B .Это также может быть выражено как

[латекс] \ text {emf} = {\ text {emf}} _ {0} \ sin \ omega t \\ [/ latex],

где

[латекс] {\ text {emf}} _ {0} = NAB \ omega \\ [/ latex]

— это максимальная (пиковая) ЭДС . Обратите внимание, что частота колебаний составляет f = ω / 2π , а период составляет T = 1/ f = 2π / ω . На рисунке 3 показан график зависимости ЭДС от времени, и теперь кажется разумным, что напряжение переменного тока является синусоидальным.

Рис. 3. ЭДС генератора направляется на лампочку с показанной системой колец и щеток. График показывает зависимость ЭДС генератора от времени. emf0 — пиковая ЭДС. Период равен T = 1/ f = 2π / ω, где f — частота. Обратите внимание, что сценарий E означает emf.

Тот факт, что пиковая ЭДС ₀ = NABω , имеет смысл. Чем больше катушек, тем больше их площадь и чем сильнее поле, тем больше выходное напряжение.Интересно, что чем быстрее раскручивается генератор (больше ω ), тем больше ЭДС. Это заметно на велосипедных генераторах — по крайней мере, на более дешевых моделях. Один из авторов, будучи подростком, находил забавным ездить на велосипеде достаточно быстро, чтобы погасить его свет, пока ему не пришлось ехать домой без света одной темной ночью. На рис. 4 показана схема, по которой генератор может вырабатывать импульсный постоянный ток. Более сложные конструкции из нескольких катушек и разрезных колец могут обеспечить более плавный постоянный ток, хотя для создания постоянного тока без пульсаций обычно используются электронные, а не механические средства.

Рис. 4. Разделенные кольца, называемые коммутаторами, в этой конфигурации создают импульсный выходной сигнал ЭДС постоянного тока.

Пример 2. Расчет максимальной ЭДС генератора

Рассчитайте максимальную ЭДС, ЭДС ₀ генератора, который был предметом примера 1.

Стратегия

После определения ω , угловой скорости, ЭДС ₀ = NABω может использоваться для нахождения ЭДС ₀ . Все остальные количества известны.

Раствор

Угловая скорость определяется как изменение угла в единицу времени:

[латекс] \ omega = \ frac {\ Delta \ theta} {\ Delta t} \\ [/ latex].

Одна четвертая оборота равна π / 2 радиан, а время 0,0150 с; таким образом,

[латекс] \ begin {array} {lll} \ omega & = & \ frac {\ pi / 2 \ text {rad}} {0.0150 \ text {s}} \\ & = & 104.7 \ text {rad / s } \ end {array} \\ [/ latex].

104,7 рад / с — это ровно 1000 об / мин. Мы подставляем это значение вместо ω и информацию из предыдущего примера в ЭДС ₀ = NABω , что дает

[латекс] \ begin {array} {lll} {\ text {emf}} _ {0} & = & NAB \ omega \\ & = & 200 \ left (7.{2} \ right) \ left (1.25 \ text {T} \ right) \ left (104.7 \ text {rad / s} \ right) \\ & = & 206 \ text {V} \ end {array} \\ [/латекс].

Обсуждение

Максимальная ЭДС больше, чем средняя ЭДС 131 В, найденная в предыдущем примере, как и должно быть.

В реальной жизни электрические генераторы сильно отличаются от рисунков в этом разделе, но принципы те же. Источником механической энергии, вращающей катушку, может быть падающая вода (гидроэнергия), пар, образующийся при сжигании ископаемого топлива, или кинетическая энергия ветра.На фиг.5 — паровая турбина в разрезе; пар движется по лопастям, соединенным с валом, который вращает катушку внутри генератора.

Рисунок 5. Паровая турбина / генератор. Пар, образующийся при сжигании угля, ударяет по лопаткам турбины, вращая вал, соединенный с генератором. (Источник: Nabonaco, Wikimedia Commons)

Генераторы, показанные в этом разделе, очень похожи на двигатели, показанные ранее. Это не случайно. Фактически, двигатель становится генератором, когда его вал вращается.В некоторых ранних автомобилях стартер использовался в качестве генератора. В Back Emf мы более подробно рассмотрим действие двигателя как генератора.

Сводка раздела

• Электрический генератор вращает катушку в магнитном поле, вызывая ЭДС, задаваемую как функцию времени

  [латекс] \ text {emf} = 2 {B \ ell v} \ sin \ omega t \\ [/ latex],

  , где A — площадь витка N , вращающегося с постоянной угловой скоростью ω в однородном магнитном поле B .

• Пиковая ЭДС ЭДС ₀ генератора равна

  ЭДС ₀ = NABω

Концептуальные вопросы

1. Используя RHR-1, покажите, что ЭДС на сторонах контура генератора на Рисунке 4 имеют одинаковое значение и, таким образом, складываются.
2. Источником выработки электрической энергии генератора является работа по вращению его катушек. Как работа, необходимая для включения генератора, связана с законом Ленца?

Задачи и упражнения

1.Вычислите пиковое напряжение генератора, который вращает свою 200-витковую катушку диаметром 0,100 м со скоростью 3600 об / мин в поле 0,800 Тл.

2. При какой угловой скорости в об / мин пиковое напряжение генератора будет 480 В, если его 500-витковая катушка диаметром 8,00 см вращается в поле 0,250 Тл?

3. Какова пиковая ЭДС, генерируемая при вращении катушки с 1000 витками диаметром 20,0 см в магнитном поле Земли 5,00 × 10 ⁻⁵ Тл, учитывая, что плоскость катушки изначально перпендикулярна полю Земли и вращается быть параллельно полю в 10.0 мс?

4. Какова пиковая ЭДС, генерируемая радиусом 0,250 м, катушка с 500 витками вращается на одну четверть оборота за 4,17 мс, первоначально ее плоскость перпендикулярна однородному магнитному полю. (Это 60 об / с.)

5. (a) Велогенератор вращается со скоростью 1875 рад / с, создавая пиковую ЭДС 18,0 В. Он имеет прямоугольную катушку размером 1,00 на 3,00 см в поле 0,640 Тл. Сколько витков в катушке? (b) Практично ли такое количество витков провода для катушки 1,00 на 3,00 см?

6. Integrated Concepts Эта проблема относится к велосипедному генератору, рассмотренному в предыдущей задаче. Он приводится в движение колесом диаметром 1,60 см, которое катится по внешнему ободу велосипедной шины. а) Какова скорость велосипеда, если угловая скорость генератора составляет 1875 рад / с? (b) Какова максимальная ЭДС генератора, когда велосипед движется со скоростью 10,0 м / с, учитывая, что в исходных условиях она составляла 18,0 В? (c) Если сложный генератор может изменять собственное магнитное поле, какая напряженность поля ему потребуется при 5.00 м / с для создания максимальной ЭДС 9,00 В?

7. (a) Автомобильный генератор вращается со скоростью 400 об / мин при работе двигателя на холостом ходу. Его прямоугольная катушка с 300 витками, 5,00 на 8,00 см вращается в регулируемом магнитном поле, так что она может производить достаточное напряжение даже при низких оборотах в минуту. Какая напряженность поля необходима для создания пиковой ЭДС 24,0 В? (b) Обсудите, как эта требуемая напряженность поля сравнивается с имеющейся у постоянных магнитов и электромагнитов.

8. Покажите, что если катушка вращается с угловой скоростью ω , период ее выхода переменного тока равен 2π / ω .

9. Катушка с 75 витками диаметром 10,0 см вращается с угловой скоростью 8,00 рад / с в поле 1,25 Тл, начиная с плоскости катушки, параллельной полю. а) Что такое пиковая ЭДС? (б) В какое время впервые достигается пиковая ЭДС? (c) В какое время ЭДС становится наиболее отрицательной? (d) Каков период выходного напряжения переменного тока?

10. (a) Если ЭДС катушки, вращающейся в магнитном поле, равна нулю при t = 0 и увеличивается до своего первого пика при t = 0.100 мс, какова угловая скорость катушки? б) В какое время наступит его следующий максимум? (c) Каков период вывода? (d) Когда выход составляет первую четверть от максимума? (e) Когда это следующая четверть от максимума?

11. Необоснованные результаты Катушка на 500 витков с площадью 0,250 м ² вращается в поле Земли 5,00 × 10 ⁻⁵ Тл, создавая максимальную ЭДС 12,0 кВ. (а) С какой угловой скоростью нужно вращать катушку? б) Что неразумного в этом результате? (c) Какое предположение или предпосылка ответственны?

Глоссарий

электрогенератор:

устройство для преобразования механической работы в электрическую энергию; он индуцирует ЭДС, вращая катушку в магнитном поле

ЭДС, индуцированная в катушке генератора:

ЭДС = NAB ω sin ωt , где A — площадь витка N , вращающегося с постоянной угловой скоростью ω в однородном магнитном поле B , за период времени т

пиковая ЭДС:

ЭДС ₀ = NABω

Избранные решения проблем и упражнения

1.474 В

3. 0,247 В

5. (a) 50 (b) да

7. (a) 0,477 Тл (b) Эта напряженность поля достаточно мала, чтобы ее можно было получить с помощью постоянного магнита или электромагнита.

9. (а) 5,89 В (б) При t = 0 (в) 0,393 с (г) 0,785 с

11. (a) 1,92 × 10 ⁶ рад / с (b) Эта угловая скорость неоправданно высока, выше, чем может быть получена для любой механической системы. (c) Предположение, что может быть получено напряжение до 12,0 кВ, является необоснованным.

Mr Toogood Physics — ЭДС и внутреннее сопротивление

Внутреннее сопротивление

Элементы и батареи преобразуют химическую энергию в электрический потенциал, который затем используется в цепи. Однако ни одна ячейка не эффективна на 100% при таком переносе. Никакая передача энергии не эффективна на 100%, и электрические элементы и источники питания не исключение. Электрический элемент состоит из трех частей: анода, катода и электролита. Анод и катод изготовлены из двух разных металлов или из одного металла и углеродной пленки, а электролит представляет собой ионную жидкость, такую ​​как гидроксид калия.Когда ячейка включается в цепь, химическая реакция начинается на аноде и катоде. На аноде реакция окисления удаляет электроны из металла, и они начинают течь в цепь. Это оставляет анод положительно заряженным, что притягивает больше электронов из электролита. Анод в отрицательной клемме ячейки. Возвращающиеся электроны собираются на катоде, и он восстанавливается. Катод — это положительный вывод. Через некоторое время анод потеряет почти все свои электроны, и электролит не сможет подавать больше, поэтому реакция замедляется, и ЭДС ячейки падает.

Рисунок 1: Упрощенный пример того, как работает ячейка.

Когда происходят химические реакции, а также вырабатывается электричество, элемент выделяет небольшое количество тепла, которое излучается от системы и теряется. Поскольку энергия, теряемая элементом, представляет собой тепло, его можно смоделировать, как если бы это был резистор, выделяющий тепло, и он называется внутренним сопротивлением ( r ) элемента. Скорость потери энергии ячейкой, конечно, измеряется в $ \ units {ваттах} $, и для ее описания можно использовать уравнения мощности для резистора.

Рисунок 2: Когда элемент генерирует ток, он также выделяет тепло.

Иногда на принципиальных схемах резистор соединен последовательно с ячейкой для обозначения внутреннего сопротивления; конечно, на самом деле внутри ячейки нет резистора, это просто полезный способ описания энергии, потерянной в цепи. Внутреннее сопротивление — это аналог эффективности ячейки. Чем больше внутреннее сопротивление, тем больше тепла он выделяет, производя электричество, и тем менее эффективен.Внутреннее сопротивление также будет иметь разность потенциалов на нем, что означает, что напряжение, измеренное на клеммах при протекании тока, ниже фактического истинного значения ЭДС ячейки. Истинная ЭДС ячейки — это «потерянных вольт» плюс напряжение на клеммах .

ЭДС = клемма p.d. + потеряно вольт

Рисунок 3: ЭДС равна конечной п.о. плюс «потерянные вольт».

Мы можем сформулировать это математически как:

$$ ε = IR + Ir $$

Где:

• ε — ЭДС в $ \ units {V} $
• I — ток в $ \ units {A} $
• R — полное сопротивление цепи в $ \ units {Ω} $
• r — внутреннее сопротивление ячейки в $ \ units {Ω} $

Термин $ IR $ представляет собой терминал p.d. а член $ Ir $ — это потерянные вольты. Приведенное выше уравнение можно упростить до:

$$ \ large ε = I \ left (R + r \ right) $$

Часто в примерах схем внутренним сопротивлением пренебрегают и предполагается идеальный элемент без внутреннего сопротивления. Однако на уровне A вы должны будете выполнять вычисления в цепях, которые имеют значительное внутреннее сопротивление. Типичное внутреннее сопротивление для современных ячеек находится в диапазоне от $ \ amount {100} {mΩ} $ до $ \ quantity {900} {mΩ} $.

К началу

---

Рабочий пример

Батарея соединена последовательно с резистором $ \ amount {10} {Ω} $ и переключателем.К аккумулятору подключен вольтметр. Когда переключатель разомкнут (выключен), вольтметр показывает $ \ amount {1.45} {V} $. Когда переключатель замкнут, отображается значение $ \ amount {1.26} {V} $.

Какое внутреннее сопротивление аккумулятора?

1. $ \ amount {0,66} {Ω} $
2. $ \ amount {0.76} {Ω} $
3. $ \ amount {1.3} {Ω} $
4. $ \ amount {1.5} {Ω} $

Этот вопрос с несколькими вариантами ответов включает относительно простые вычисления, но в этих вопросах с несколькими вариантами ответов важно работать эффективно, чтобы вы не теряли время зря.

Мы знаем, что ЭДС ячейки равна $ \ amount {1.45} {V} $, а конечная p.d. падает до $ \ amount {1.26} {V} $, когда ток течет через резистор $ \ amount {10} {Ω} $, поэтому ток через резистор можно рассчитать как:

\ begin {align} I & = \ frac {V} {R} \\ I & = \ frac {\ amount {1.26} {V}} {\ amount {10} {Ω}} \\ \\ I & = \ количество {0.126} {A} \ end {align}

Разность потенциалов на внутреннем сопротивлении равна $ \ amount {1.45} {V} — \ amount {1.45} {V} = \ amount {0.19} {V}

долл. США

Теперь мы можем использовать это значение тока и значение потерянных вольт, чтобы найти значение внутреннего сопротивления:

$$ R = \ frac {V} {I} = {\ amount {0.19} {V}} {\ amount {0.126} {A}} = \ amount {1.5} {Ω} $$

К началу

---

Внутреннее сопротивление и протекание тока

Чем больше тока течет из элемента, тем выше скорость реакции в элементе и выделяется больше тепла, и, соответственно, чем выше потери вольт .Между током и энергией, теряемой внутренним сопротивлением, существует прямо пропорциональная зависимость.

Когда ток не течет, внутреннее сопротивление и вывод p.d. не теряют энергию. будет равняться ЭДС. На практике ЭДС ячейки можно определить с помощью мультиметра, который обычно имеет очень высокое сопротивление, и измерения на клемме p.d., которая будет эдс, поскольку через измеритель не будет протекать ток.

Чем больше ток, протекающий через ячейку, тем больше разница между ЭДС и выводом p.д .. Если график терминального п.д. и ток нанесен на график, ЭДС может быть найдена из точки пересечения оси y, а градиент будет представлять внутреннее сопротивление.

Рисунок 4: График терминального п.о. против тока для клетки. Внутреннее сопротивление можно найти по градиенту.

Вы выполните это упражнение для своего CAP, но вам нужно будет разработать схему и предложить подходящий диапазон сопротивлений для проверки.

К началу

---

Рабочий пример

Студент исследует, как мощность, рассеиваемая на переменном резисторе Y, изменяется при изменении сопротивления.

На схеме ниже показана схема, которую использует ученик. Y подключен к батарее с ЭДС ε и внутренним сопротивлением r .

Рисунок 5: Простая схема с ячейкой и переменным резистором.

На графике показаны результаты, полученные учеником при изменении сопротивления Y от $ \ amount {0.5} {Ω} $ до $ \ amount {6.5} {Ω} $.

Рисунок 6: График, показывающий, как мощность, рассеиваемая переменным резистором, изменяется в зависимости от его сопротивления. {2}} {R} $.Когда внешнее сопротивление меньше внутреннего сопротивления, он будет иметь меньший p.d. поперек него, поэтому он будет иметь меньшую мощность, чем внутреннее сопротивление. Когда внешнее сопротивление равно внутреннему, они оба будут иметь одинаковую разность потенциалов и, следовательно, будут иметь одинаковую мощность. По мере увеличения переменного резистора, превышающего внутреннее сопротивление, мощность снова уменьшается, поскольку мощность обратно пропорциональна сопротивлению.

Это известно как теорема максимальной мощности, т.е.е. максимальная мощность от источника питания (в данном случае ячейки) получается при нагрузке, либо внешнее сопротивление равно внутреннему сопротивлению источника питания.

ЭДС батареи составляет $ \ amount {6.0} {V} $, а сопротивление Y установлено равным $ \ amount {0.80} {Ω} $.

1. Используйте данные из графика , чтобы вычислить ток через батарею.

При чтении данных с графика рекомендуется тщательно аннотировать диаграмму карандашом и линейкой, чтобы гарантировать точность считываемых значений.{2} R $ на поиск текущих:

\ begin {align} I & = \ sqrt {\ frac {P} {R}} \\ I & = \ sqrt {\ frac {\ quantity {1.95} {W}} {\ amount {0.80} {Ω}}} \\ \\ I & = \ amount {1.56} {A} \ end {align}

В подобном вопросе легко забыть найти квадратный корень из $ \ frac {P} {R} $, поэтому будьте особенно осторожны при использовании калькулятора.

2. Рассчитайте напряжение на Y.

Теперь, когда мы знаем ток и сопротивление, мы можем использовать закон Ома, $ V = IR $, чтобы найти напряжение или p.d. по Ю.

$$ V = \ amount {1.56} {A} \ times \ amount {0.80} {Ω} = \ amount {1.2} {V} $$
3. Рассчитайте внутреннее сопротивление аккумулятора.

Это можно либо вычислить по уравнению $ ε = V + Ir $, либо считать по графику, используя теорему о максимальной мощности, как описано выше. Мы уже вычислили значения $ V $ и $ I $, поэтому, используя уравнение, сделав $ r $ объектом:

\ begin {align} r & = \ frac {\ left (ε-V \ right)} {I} \\ r & = \ frac {\ left (\ amount {6.0} {V} — \ amount {1.2} {V} \ right)} {\ amount {1.56} {A}} \\ \\ г & = \ количество {3.1} {Ω} \ end {align}

Даже если вам не удалось вычислить предыдущие значения для тока и разности потенциалов, вы можете прочитать значение сопротивления на пике графика, если вы укажете, что максимальная мощность будет рассеиваться, когда $ Y = r $ и четко аннотируйте график.

Студент повторяет эксперимент с батареей с такой же ЭДС, но с незначительным внутренним сопротивлением.Сформулируйте и объясните, как вы теперь ожидаете, что мощность, рассеиваемая в Y, будет изменяться при увеличении сопротивления Y с $ \ amount {0.5} {Ω} $ до $ \ amount {6.5} {Ω} $.

При незначительном внутреннем сопротивлении p.d. по оси Y будет равна ЭДС ячейки. Как p.d. теперь является постоянным, а соотношение между мощностью и сопротивлением, поскольку постоянное напряжение является обратным, мощность будет уменьшаться с увеличением значения Y.

Это вопрос, на который студенты, как правило, очень плохо отвечают, и легко предположить, что форма графика будет аналогичной, но будет иметь более низкое или более высокое значение пиковой мощности.{2}} {R} $, чтобы по мере увеличения ресурса мощность уменьшалась, и график выглядел бы так:

Рисунок 8: График, показывающий, как мощность, рассеиваемая переменным резистором, изменяется в зависимости от его сопротивления, когда внутреннее сопротивление ячейки незначительно.

К началу

---

---

Пример проблемы ЭДС электрохимической ячейки

Электродвижущая сила ячейки или ЭДС ячейки — это суммарное напряжение между полуреакциями окисления и восстановления, имеющими место между двумя полуреакциями окислительно-восстановительного потенциала.ЭДС ячейки используется, чтобы определить, является ли ячейка гальванической. В этом примере задачи показано, как рассчитать ЭДС ячейки с использованием стандартных восстановительных потенциалов.
Для этого примера необходима таблица стандартных восстановительных потенциалов. В домашней задаче вам должны быть предоставлены эти значения или доступ к таблице.

Пример расчета ЭДС

Рассмотрим окислительно-восстановительную реакцию:

• Mg (тв) + 2 H ⁺ (водн.) → Mg ²⁺ (водн.) + H ₂ (г)
  • a) Рассчитайте ЭДС ячейки для реакции.
  • б) Определите, является ли реакция гальванической.
• Решение:
  • Шаг 1: Разбейте окислительно-восстановительную реакцию на полуреакции восстановления и окисления.
    Ионы водорода, H ⁺ , приобретают электроны при образовании газообразного водорода, H ₂ . Атомы водорода восстанавливаются за счет полуреакции:
    2 H ⁺ + 2 e ^— → H ₂
    Магний теряет два электрона и окисляется в ходе полуреакции:
    Mg → Mg ²⁺ + 2 e ^—
  • Шаг 2: Найдите стандартные восстановительные потенциалы для полуреакций.
    Восстановление: E ⁰ = 0,0000 В
    В таблице показаны полуреакции восстановления и стандартные потенциалы восстановления. Чтобы найти E ⁰ для реакции окисления, переверните реакцию.
  • Обратная реакция:
    Mg ²⁺ + 2 e ^— → Mg
    Эта реакция имеет E ₀ = -2,372 В.
    E ⁰ _{Окисление} = — E ⁰ _{Восстановление}
    E _{0 Окисление} = — (-2,372 В) = + 2,372 В
  • Шаг 3: Сложите два E ⁰ вместе, чтобы найти общую ЭДС ячейки, E ⁰ _ячейку
    E ⁰ _ячейку = E ⁰ _{сокращение} + E ⁰ _{окисление}
    E ⁰ _ячейка = 0.0000 В + 2,372 В = +2,372 В
  • Шаг 4: Определите, является ли реакция гальванической. Окислительно-восстановительные реакции с положительным значением E ⁰ _ячейки являются гальваническими.
    Эта реакция E ⁰ _ячейка является положительной и, следовательно, гальванической.
• Ответ:
  ЭДС ячейки реакции составляет +2,372 Вольт и является гальванической.

Внутреннее сопротивление, ЭДС и разность потенциалов

В любой цепи есть компоненты, которые передают энергию из в схему, и компоненты, которые отбирают энергию из .С этого момента мы будем говорить, что любое устройство, передающее энергию в цепь, обеспечивает электродвижущую силу (ЭДС) , и любое устройство, вынимающее ее, имеет разность потенциалов (pd) на нем.

И ЭДС, и pd измеряются в вольт, В, , поскольку они описывают, сколько энергии вводится или снимается на один кулон заряда, проходящего через этот участок цепи.

Лучше всего думать о них:

ЭДС — это количество энергии любой формы, которое превращается в электрическую энергию на кулон заряда.

pd — количество электрической энергии, которая преобразуется в другие формы энергии на один кулон заряда.

Источники ЭДС:

Элемент, аккумулятор (комбинация элементов), солнечный элемент, генератор, динамо-машина, термопара.

Элементы и батареи не идеальны (что, конечно, не считая момента окончания вашего последнего экзамена?). Используйте их некоторое время, и вы заметите, что они нагреваются.

Откуда поступает тепловая энергия?

Это от тока, проходящего через внутреннюю часть ячейки.Сопротивление внутри ячейки превращает часть производимой ею электроэнергии в тепловую при движении электронов через нее.

Это легко объяснить, если вы вообразите, что каждая ячейка идеальна, за исключением того, что по какой-то странной причине (вероятно, часть заговора по захвату мира, задуманного доктором Злом) производители включили резистор последовательно с ячейкой внутри кожух.

Таким образом, внутри ячейки энергия передается в цепь ячейкой (ЭДС), но часть этой энергии отбирается из цепи внутренним резистором (pd).

Таким образом, pd, доступный для остальной части схемы (внешней цепи, поскольку некоторые вопросы могут относиться к ней), это ЭДС минус pd, потерянный внутри ячейки:

V = E — Ir

Где :

В = pd по внешней цепи (В)

E = ЭДС ячейки (В)

I = ток через элемент (А)

r = значение внутреннего сопротивления (& Omega;)

( Ir = p.d. на внутреннем резисторе)

Примечание: V иногда называют клеммой pd , поскольку это pd на клеммах ячейки

Пример 1:

Что такое клемма p.d. для ячейки ЭДС 2В и внутреннего сопротивления 1 Ом при подключении к резистору 9 Ом?

Ответ:

Просто представьте, что внутреннее сопротивление — это один из нормальных резисторов в цепи.Нарисуйте его на принципиальной схеме рядом с ячейкой, чтобы весь ток, проходящий через ячейку, также проходил через резистор.

Чтобы найти V, клемму pd (или напряжение, доступное для внешней цепи), вычислите ток I для всей цепи:

Примечание: V _T и R _T — это напряжение и сопротивление для всей цепи, включая внешнее и внутреннее сопротивление.

Таким образом, 9 & Omega; резистор получает V = IR = 0.2 x 9 = 1,8 В

Таким образом, эта ячейка ЭДС на 2 В фактически подает 1,8 В во внешнюю цепь.

Пример 2:

Теперь поменяйте местами 9 & Omega; резистор в последнем примере для 1 & Omega; резистор.

Ответ:

Найдите V, терминал pd, снова используя тот же метод:

Теперь ячейка ЭДС 2V подает только 1V во внешнюю цепь !!! Другой 1 В теряется, из-за чего ячейка нагревается. Не очень эффективно.

Примечание: При принятии решения о том, подходит ли ячейка для использования в конкретной цепи, необходимо учитывать внутреннее сопротивление. Для максимальной эффективности внешнее сопротивление должно быть намного больше внутреннего сопротивления ячейки. Однако для максимальной мощности, передаваемой во внешнюю цепь, внутреннее сопротивление должно быть равно сопротивлению внешней цепи, хотя эффективность ячейки будет только 50%.

Источники питания с низким напряжением и более высокими токами, например автомобильный аккумулятор, должны иметь низкое внутреннее сопротивление, как показано выше.Источники питания высокого напряжения, вырабатывающие тысячи вольт, должны иметь чрезвычайно высокое внутреннее сопротивление, чтобы ограничить ток, который может протекать в случае случайного короткого замыкания.

Поскольку V = E — Ir, если вы построите график зависимости pd, V от тока, I, градиент графика будет равен внутреннему сопротивлению ячейки. (отрицательный, потому что график наклоняется вниз)

Записывая значения тока и клеммы pd по мере изменения внешнего сопротивления, вы можете построить график и найти внутреннее сопротивление и ЭДС ячейки.

Если последовательно подключено более одной ячейки, необходимо сложить внутренние сопротивления ячеек.

Формула ЭДС — уравнения, решенные примеры и часто задаваемые вопросы

Электродвижущая сила — одно из важных понятий, которые помогают нам понять процесс электромагнетизма. Электродвижущая сила сокращенно называется ЭДС и тесно связана с более распространенным понятием напряжения. Электродвижущая сила — это полная энергия, обеспечиваемая батареей или элементом на кулон q заряда, проходящего через нее.

Величина ЭДС равна разности потенциалов на клеммах ячейки, когда нет тока, протекающего через данную электрическую цепь, и используемая формула известна как формула ЭДС. В этой статье мы подробно изучим формулу электродвижущей силы, идею физики ЭДС и, наконец, с помощью уравнения ЭДС с несколькими решенными примерами.

EMF Physics

Электродвижущая сила может быть определена как полное напряжение или разность потенциалов на клеммах батареи в разомкнутой цепи или, другими словами, когда через нее не течет ток.Это может не выглядеть так, поскольку это будет отличаться, но каждая батарея будет построена с определенным внутренним сопротивлением. Это связано с регулярным сопротивлением, которое уменьшает ток в электрической цепи, но оно заключено только внутри самой батареи.

Мы знаем, что когда цепь разомкнута, ток не будет течь через элемент, это означает, что внутреннее сопротивление батареи ничего не изменит, потому что нет тока для его уменьшения или замедления.Таким образом, электродвижущую силу можно рассматривать как максимальную разность потенциалов или напряжение на двух выводах в идеализированном состоянии. Это объясняет физику ЭДС, и из этого мы можем понять, что электродвижущая сила — это частный случай разности напряжений.

Теперь возник вопрос, хотя электродвижущая сила вообще не является формой силы, тогда почему ее называют электродвижущей силой, в чем разница между ЭДС и регулярной разностью потенциалов и что будет источник ЭДС? Чтобы ответить на эти сомнения, рассмотрим простую электрическую схему лампы, подключенной к батарее.

Мы знаем, что любое гальваническое устройство можно представить как двухполюсное устройство, которое поддерживает один вывод с более высоким потенциалом, а другой вывод — с более низким потенциалом. Более высокий электрический потенциал обычно известен как положительный полюс и обычно обозначается знаком плюс. Клемма с более низким потенциалом называется отрицательной клеммой и обозначается знаком минус. Это называется источником ЭДС.

Когда источник электродвижущей силы отключен от лампы i.е., когда цепь разомкнута, то нет никакого чистого движения зарядов в данном источнике ЭДС. После того, как цепь будет замкнута или повторно подключена к лампе, заряды будут перемещаться от одной клеммы батареи через лампу, что в дальнейшем приведет к тому, что лампа начнет светиться и вернется к другой клемме батареи.

Если мы рассмотрим обычный поток электрического тока, то есть положительный ток, положительные заряды имеют тенденцию покидать положительный вывод, проходить через лампу и попадать на отрицательный конец источника ЭДС.Так устроен источник ЭМП. В то же время электродвижущая сила батареи — это разность потенциалов, развиваемая на обоих концах данной батареи.

Таким образом, физика ЭДС объясняет, что электродвижущая сила — это полная энергия, поставляемая батареей или элементом на кулон заряда, проходящего через нее. Общая величина ЭДС равна напряжению или разности потенциалов на клеммах батареи, когда в данной электрической цепи нет тока.

Уравнение ЭДС

Мы знаем, что заряды циркулируют в электрической цепи, для движения зарядов в данной электрической цепи нам необходимо приложить к ней внешнюю силу. Мы говорим, что внешний источник электричества, такой как батарея, использует такую ​​силу, которая придает ускорение зарядам, и это называется электродвижущей силой. Несмотря на свое название, это не форма силы, а разность потенциалов, на самом деле, это частный случай разности потенциалов, который обычно обозначается символом.

Теперь давайте посмотрим на уравнение ЭДС:

Согласно определению физики ЭДС и ЭДС формула ЭДС имеет вид:

\ [\ Rightarrow EMF = \ varepsilon = \ frac {E} { Q} \]… .. (1)

Где,

E — Полная энергия батареи

Q — Полный заряд, протекающий через данную цепь

Уравнение (1) можно использовать, если мы знаем общую энергия батареи, используемой в цепи. Электродвижущая сила — это также разность потенциалов, возникающая в цепи, поэтому формулу ЭДС можно также найти с помощью закона Ома.Следовательно, мы пишем:

ε = IR… .. (2)

Где,

I — полный ток, протекающий в цепи

R — полное сопротивление, используемое в цепи

Поскольку мы знаем, что ЭДС зависит от при внутреннем сопротивлении батареи мы должны заменить сопротивление суммой сопротивления и внутреннего сопротивления. Таким образом, уравнение (2) принимает следующий вид:

ε = I (r + R)

ε = Ir + IR

ε = V + Ir ……. (3)

Где,

V — Общая разность потенциалов в цепи

I — Полный ток, протекающий в цепи

r — Внутреннее сопротивление батареи

Следовательно, уравнение (1) и уравнение (3) известны как формула ЭДС или уравнение ЭДС.Давайте разберемся с формулой ЭДС и как найти ЭДС или как рассчитать ЭДС на нескольких решенных примерах.

Примеры:

1. Рассмотрим электрическую цепь с разностью потенциалов 5 В с током 1 А. Если внутреннее сопротивление используемой батареи составляет 0,8 Ом. Затем определите ЭДС цепи, используя формулу ЭДС.

Sol:

Дано,

Разность потенциалов электрической цепи = V = 5 вольт

Суммарный ток, протекающий по цепи = I = 1 A

Внутреннее сопротивление батареи = r = 0.8 Ом

Нас просят определить ЭДС цепи, используя уравнение ЭДС. Мы знаем, что ЭДС цепи можно рассчитать по формуле, приведенной ниже:

ε = V + Ir ……. (1)

Где,

V — Полная разность потенциалов, развиваемая в цепи

I — Суммарный ток, протекающий в цепи

r — Внутреннее сопротивление батареи

Подставляя значение разности потенциалов, тока и внутреннего сопротивления в уравнение (1), получаем:

ε = V + Ir

ε = 5 + (10.8)

ε = 5,8 В

Следовательно, ЭДС схемы по формуле ЭДС составляет 5,8 Вольт.

2. Рассчитайте разность потенциалов на клеммах батареи, когда она подключена к нагрузке 10 Ом с ЭДС батареи, ε = 3 вольта и внутреннее сопротивление батареи 2 Ом.

Sol:

Дано,

Суммарная ЭДС батареи = ε = 3 вольта

Внешняя нагрузка, приложенная к батарее = R _L = 10 Ом

Внутреннее сопротивление батареи = r = 2 Ом

Теперь нас просят определить разность потенциалов на клеммах аккумулятора.Перед этим рассчитаем ток, протекающий по данной цепи. согласно закону Ома мы знаем, что:

\ [\ Rightarrow I = \ frac {V} {R} = \ frac {\ varepsilon} {r + R_ {L}} \]…. (1)

I = 3/12 = 0,25 А

Теперь давайте определим разность потенциалов на клеммах аккумулятора. Формула ЭДС определяется следующим образом:

ε = V + Ir …….