Измерение потенциала проводника
Что такое потенциал проводника
Как уже неоднократно отмечалось, напряженность поля внутри проводника равна нулю. Из этого следует, что проводник эквипотенциален по всему объему, то есть во всех точках проводника потенциалы одинаковы, значит, разность потенциалов двух любых точек проводника равна:
Значение потенциала, равное во всех точках проводника называют потенциалом проводника.
Допустим, что мы имеем изолированный, заряженный проводник. Заряд этого проводника создаёт электрическое поле в веществе вокруг проводника. Примем нормировку потенциала на ноль в бесконечности. В таком случае потенциал проводника выразим как:
где путь интегрирования начинается в любой точке проводника и заканчивается в бесконечности.
Как измерить потенциал проводника
Прибором для измерения разности потенциалов между двумя проводниками может служить электроскоп, листочки или стрелка которого окружены металлической оболочкой, при этом его называют электрометром. При этом один проводник соединяют с шариком электрометра, другой с оболочкой (рис. 1). Стрелка электрометра примет потенциал тела (1), а оболочка — потенциал тела (2). Возникнет электрическое поле, силовые линии которого идут от оболочки к стрелке или в обратном направлении. При этом угол отклонения стрелки определен напряженностью и конфигурацией возникшего поля. При этом поле внутри замкнутой оболочки из металла ни как не зависит от внешнего поля. Оно определяется разностью потенциалов между оболочкой и стрелкой.
Значит, угол отклонения стрелки есть мера разности потенциалов тел (1) и (2).
Подобный прибор можно градуировать в вольтах. Очень часто в качестве второго тела используют Землю, то есть оболочку электрометра заземляют. В таком случае электрометр покажет потенциал тела (1) относительно Земли.

Рис. 1
Не имеет принципиального значения, какое из тел заземлять, оболочку или шарик. От этого зависит только направление силовых линий. Угол отклонения стрелки в обоих случаях будет одним. Понятно, что электрометр может служить измерительным прибором для потенциала тела, только если его стрелка защищена не полностью от внешних полей. Но при этом связь стрелки с внешними телами должна быть слабой. Для этого отверстие в оболочке металлического экрана (шарика) и наружная часть стержня, которая соединяет шарик со стрелкой, должны быть небольшими. В противном случае, на этих частях электрометра могут возникать существенные заряды, которые индуцируются посторонними внешними телами. Они вносили бы искажения при переходе на стрелку, и разность потенциалов измерялась бы неверно. Провода, которые соединяют тела (1) и (2) по такой же причине должны быть тонкими. Используя электрометр легко убедиться, что поверхность проводника всегда является эквипотенциальной. Если соединять электрометр с разными точками заряженного проводника, то отклонение стрелки его изменяться не будет.
Метод электрического зонда
Для измерения разности потенциалов в жидком или газообразном диэлектрике используют метод электрического зонда. Зонд состоит из небольшого металлического тельца (например, шарик или диск), которое соединено проволочкой с шариком электрометра. Оболочка электрометра заземлена. Зонд помещают в точку диэлектрика, потенциал которой измеряют. При этом электрометр покажет разность потенциалов между стрелкой и оболочкой (тоже самое: между зондом и Землей). При этом необходимо заметить, что зонд существенно изменяет потенциал точки, в которую он помещается. Причиной этому являются индукционные заряды, которые появляются на зонде и шарике электрометра. Поэтому для того, чтобы была возможность истинного измерения потенциала надо, чтобы при внесении зонда в исследуемую точку зонд и соединенный с ним шарик электроскопа приняли потенциал, который был в нашей точке до внесения зонда. Это достигается если убрать индукционные заряды с зонда. Так, например, в капельном зонде телом служит маленькое ведерко, которое наполняется проводящей жидкостью. В дне ведерка есть очень маленькое отверстие. Капли жидкости, стекающие из этого отверстия, уносят индукционный заряд, который возникает на зонде. Заряды противоположного знака переходят на стрелку электрометра. Угол отклонения стрелки изменяется. В стационарном состоянии, когда зонд не заряжен, потенциал зонда равен потенциалу окружающего пространства. Так как зонд соединен проводником с шариком электрометра, то потенциал шарика измерительного прибора будет таким же. В результате электрометр покажет потенциал, который необходимо измерить. Индукционные заряды удаляют и другими методами, например, используют «пламенный зонд». В этом случае зондом является кончик металлической проволоки, который выступает из диэлектрической трубки, которая играет роль газовой горелки. Из-за высокой температуры пламени воздух вокруг нее слегка ионизируется и становится проводящим. Ионы уносят индукционные заряды с зонда с потоком газа. Похожая идея реализуется и в радиоактивном зонде.
Пример 1
Задание: Опыты показали, что земной шар заряжен отрицательно. В среднем напряженность поля около самой поверхности Земли составляет 130$\frac{В}{м}$. Разность потенциалов уровней у ног человека и у головы составляет примерно 200 В. Почему при таких условиях человек не поражается электрическим током?
Решение:
Человеческое тело является хорошим проводником. Как и любой другой проводник, тело человека сильно искажает электрическое поле. При помещении тела человека происходит перераспределение зарядов на поверхности его тела, но это перемещение идет короткий промежуток времени и оно очень слабо. Силовые линии поля подходят к поверхности тела перпендикулярно, а эквипотенциальные поверхности огибают его, так же как металлический предмет. Весь объем тела человека эквипотенциален, то есть все точки тела имеют равные потенциалы. Напряженность поля зависит от разности потенциалов поля, если разность потенциалов равна нулю, значит и напряженность поля нуль. Поэтому человек не чувствует разности потенциалов электрического поля Земли.
Пример 2
Задание: Если коснуться электроскопа пальцем, то он разрядится. Будет ли разряжаться электроскоп, если недалеко от него поместить изолированное от Земли заряженное тело?
Решение:
Если к электроскопу поднести заряженное тело, то на стержне прибора возникнут индуцированные заряды. Причем на внешнем конце заряды будут иметь противоположный знак по отношению к зарядам тела, на внутреннем конце такой же знак, что и заряд тела. Следовательно, электроскоп не разрядится на электрометре останется индуцированный заряд.
Пример 3
Задание: Измерения электрическим зондом показывают, что изменение потенциала электрического поля Земли изменяется в среднем на 100 В на каждый метр подъема от поверхности. Вычислите заряд Земли, если считать, что поле создается этим зарядом. Радиус Земли принять равным R=6400 км.
Решение:
Изменение модуля напряженности поля можно связать c изменением потенциала Земли в нашей задаче с помощью формулы:
\[\left|E\right|=\frac{\triangle \varphi }{\triangle x}(3.1)\]судя по размерности в нашей задаче указан именно $\left|E\right|$.
По теореме Остроградского — Гаусса запишем, что:
\[ES=\frac{q}{\varepsilon {\varepsilon }_0}\left(3.2\right),\]где $S=4\pi R^2$, где поверхность, через которую рассмотрен поток вектора напряженности, совпала со сферой радиуса Земли. Выразим искомый заряд:
Будем считать, что $\varepsilon =1$, подставим в (3.3) выражение (1.1), учтем, что$\ S=4\pi R^2$ получим:
\[q=\frac{\triangle \varphi }{\triangle x}4\pi R^2\varepsilon {\varepsilon }_0.\]Переведем радиус Земли в СИ, получим: $R=6,4\cdot {10}^6м.$ Проведем вычисления заряда Земли:
\[q=\frac{100\cdot 4\cdot 3,14\cdot 8,85\cdot {10}^{-12}\cdot {\left(6,4\cdot {10}^6\right)}^2}{1}\approx 4,55\cdot {10}^5\ \left(Кл\right).\]Ответ: Заряд Земли равен $4,55\cdot {10}^5Кл\ $.
Измерение потенциала проводника
Как мы уже отмечали ранее, поле внутри проводника имеет нулевую напряженность. Следовательно, он является эквипотенциальным по всему объему. Иными словами, значения потенциалов будут одинаковы во всех его точках.
Разность потенциалов двух любых точек проводника будет равна:
Определение 1Потенциал проводника – это значение его потенциала, одинаковое для всех точек.
Рассмотрим ситуацию с изолированным заряженным проводником. Вокруг него имеется электрическое поле, создаваемое зарядом и распространяемое в веществе вокруг него. Нормировка потенциала будет равна нулю в бесконечности. Тогда его потенциал может быть выражен так:
Интегрирование может начинаться в любой точке проводника и заканчиваться в бесконечности.
Измерение с помощью электрометра
Определение 2Электроскоп — прибор для измерения разности потенциалов между двумя проводниками.
Если его стрелка или листочки заключены в металлическую оболочку, то его называют электрометром. Для измерения нам надо соединить один проводник с его оболочкой, а второй – с шариком, после чего стрелка прибора примет потенциал измеряемого тела. При этом образуется электрическое поле с силовыми линиями, направленными от стрелки к оболочке или наоборот. От напряженности и конфигурации этого поля будет зависеть величина отклонения стрелки. Важно отметить, что поле внутри металлической оболочки не будет зависеть от внешнего поля, а будет определяться только разностью потенциалов между стрелкой и оболочкой.
Определение 3Мерой разности потенциалов двух измеряемых тел является угол отклонения стрелки электрометра.
Градуировка на таком приборе может быть и в вольтах. Зачастую при измерении вторым телом выступает земля, то есть выполняется заземление оболочки электрометра. В таком случае его показания будут означать потенциал тела относительно Земли.

Рисунок 1
Можно заземлять как оболочку, так и шарик, это не имеет значения. Это определит только направление, в котором будут идти силовые линии, а угол отклонения стрелки окажется одинаковым.
Очевидно, что стрелка должна иметь слабую связь с внешними полями, чтобы точность измерения электрометром была высокой. Однако слишком сильная связь искажает показания. Чтобы создать нужный уровень защиты, в оболочке экрана или шарика, а также в наружной части стержня, соединяющего стрелку с шариком, оставляют небольшое отверстие. Если контакт с внешними полями будет слишком интенсивным, то на этих частях прибора возникнут посторонние заряды, индуцированные внешними полями, которые будут вносить искажения при переходе на с
Потенциал электрического поля — Основы электроники
В зависимости от количества зарядов и их величины изменяется энергия электрического поля, создаваемого этими зарядами. Очевидно, что величина энергии электрического поля, образованного одним ‘зарядом, будет отличаться от величины энергии поля, образованного двумя или тремя такими же зарядами.
В практике очень часто приходится сравнивать различные по величине поля. Это сравнение производится по действиям полей на единичный положительный заряд (так называемый пробный заряд). Поясним это.
Определение: Единичным называется заряд, величина которого равна одной единице заряда.
Пусть, например, поле образовано некоторым положительным зарядом. Чтобы внести в какую-то точку этого поля единичный положительный заряд, необходимо затратить определенную работу на преодоление силы отталкивания между основным и единичным зарядами. Величина потенциальной энергии поля при этом возрастает.
Попробуем теперь внести единичный заряд в другое поле, образованное в два раза большим электрическим зарядом. Очевидно, что при этом придется затратить большую работу, чем в первом случае. Следовательно, и потенциальная энергия поля возрастет больше, чем в первом случае.
В электротехнике для характеристики поля вводится специальное понятие — электрический потенциал.
Определение; Электрический потенциал некоторой точки поля численно равен работе, затрачиваемой при внесении единичного положительного заряда из-за пределов поля в данную точку.
Измеряется потенциал электрического поля в вольтах. Такое название единицы для измерения потенциала дано по имени итальянского физика Алессандро Вольта (1745—1827), открывшего закон взаимодействия электрических токов и предложившего первую гипотезу для объяснения магнитных свойств вещества.
Характеристика поля с помощью электрического потенциала очень удобна. Она позволяет сравнивать не только различные электрические поля, но и отдельные точки одного и того же поля. Вместо того, например, чтобы говорить «шар А наэлектризован более сильно, чем шар Б», можно сказать: «потенциал шара А выше потенциала шара Б». Потенциал точки поля обычно обозначается буквой φ.
Электрическое поле может создаваться не только положительным или отрицательным зарядом, но и их совокупностью. В таком поле отдельные точки могут иметь как отрицательные, так и положительные потенциалы. Чтобы в этом случае сравнивать потенциалы различных точек, ввели условное понятие о точке с нулевым потенциалом, т. е. стали считать, что одна из точек (или несколько точек) имеет потенциал, равный нулю. Потенциалы остальных точек поля определяются относительно точки нулевого потенциала. Этот метод аналогичен методу измерения температур. Там также определенная температура (температура тающего льда) принимается за нулевую точку и по отношению к ней определяется температура других тел.
В электротехнике условно считают, что нулевой потенциал имеет поверхность земли.
Если потенциал в данной точке выше потенциала земли, то мы говорим, что точка обладает положительным потенциалом. Если же, наоборот, потенциал точки ниже потенциала земли, то точка обладает отрицательным потенциалом.
Измеряя потенциалы различных точек электрического поля относительно земли, можно убедиться в том, что они неодинаковы. Значит, между отдельными точками может быть некоторая разность потенциалов.
Определение: Разность потенциалов между двумя точками электрического поля называется напряжением. Напряжение, так же как и потенциал, измеряется в вольтах.
Сказанное поясним примером.
На рис. 1 мы условно показали четыре точки: А—с потенциалом + 20 в, Б — с потенциалом +40 в, В — с нулевым потенциалом (земля) и Г — с потенциалом—15 в.
Рисунок 1. Разность потенциалов между различными точками электрического поля
Разность потенциалов между точками Б и А =40—20=20 в;
Разность потенциалов между точками А и В =20— 0=20 в;
Разность потенциалов между точками Б и В =40— 0=40 в;
Разность потенциалов между точками А и Г=20—(—15) =35 в.
Потенциал точки Б выше потенциалов точек А, В и Г. Потенциал точки А выше потенциалов точек В и Г, но ниже потенциала точки Б. Потенциал точки В ниже потенциалов точек А и Б, но выше потенциала точки Г.
Следует обратить внимание на то, что точки отрицательного потенциала имеют более низкий потенциал, чем тонки нулевого потенциала.
Можно и иначе определить напряжение между двумя точками. Для этого рассмотрим две точки А и Б электрического поля.
Допустим, что потенциал точки А равен φА потенциал точки Б равен φБ. Потенциал точки А (или Б) определяется той работой, которую необходимо затратить на перенос единичного положительного заряда из-за пределов поля в точку А (или Б). Если для переноса единичного положительного заряда из-за предела поля в точку А и в точку Б требуется затратить различную по величине работу, то φА не равно φБ и между точками А и Б существует некоторая разность потенциалов, или напряжение. Это напряжение определяется разностью φА — φБ т. е. работой, совершаемой силами поля при переносе единичного положительного заряда из точки А в точку Б.
ПОНРАВИЛАСЬ СТАТЬЯ? ПОДЕЛИСЬ С ДРУЗЬЯМИ В СОЦИАЛЬНЫХ СЕТЯХ!
Похожие материалы:
Добавить комментарий
Измерение потенциалов точек электрической цепи и построение потенциальной диаграммы
любой ветви схемы можно найти по закону Ома для участка цепи, содержащего ЭДС. Для того чтобы можно было применить закон Ома, необходимо знать потенциалы узлов схемы. Метод расчета электрических цепей, в котором за неизвестные принимают потенциалы узлов схемы, называют методом узловых потенциалов.
Допустим, что в схеме n узлов. Так как любая (одна) точка схемы может быть заземлена без изменения токораспределения в схеме, то один из узлов схемы можно мысленно заземлить, т. е. принять потенциал его равным нулю. При этом число неизвестных уменьшается с n до n-1.
Число неизвестных в методе узловых потенциалов равно числу уравнений, которые необходимо составить для схемы по первому закону Кирхгофа. Метод узловых потенциалов, как и метод контурных токов, — один из основных расчетных приемов. В том случае, когда число узлов без единицы меньше числа независимых контуров в схеме, данный метод является более экономичным, чем метод контурных токов.
Вывод основных расчетных уравнений проведем применительно
к схеме рис. 2, в которой три узла. Если узел 3 мысленно заземлить, т. е.
принять  =0, то необходимо определить потенциалы
только двух узлов:
=0, то необходимо определить потенциалы
только двух узлов: ,
,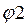
Запишем уравнения по первому закону Кирхгофа для независимых узлов, причем токи, направленные к узлу берем со знаком минус, а от узла – со знаком плюс.
Для первого узла  ,
,
Для второго узла  .
.

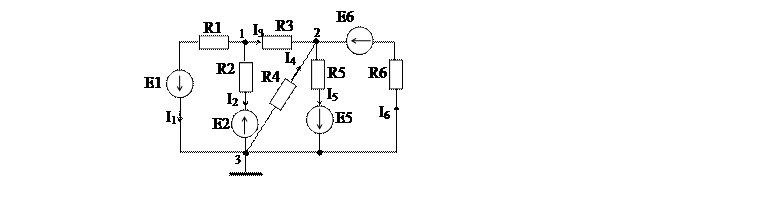
Рис. 2. Схема для расчета по методу узловых потенциалов
Запишем токи по закону Ома:
 ,
,  ,
,  ,
,  ,
, 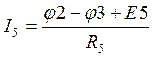 ,
, 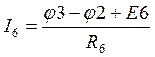 .
.
Подставим токи в уравнения по первому закону Кирхгофа:
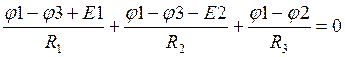
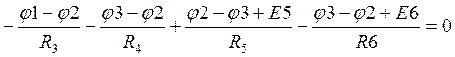 .
.
Перепишем уравнения:
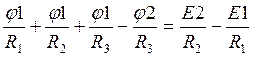 ,
,
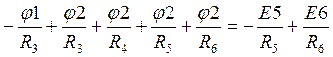 ;
;
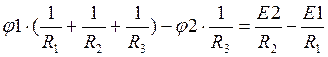 ,
,
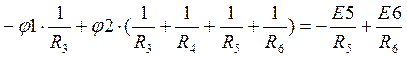 ;
;

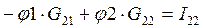 , где
, где 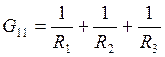 ,
, 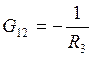 ,
, 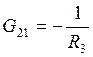 ,
, 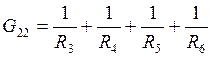 ,
,
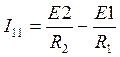 ,
, 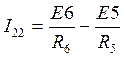 ,
,
G11— сумма проводимостей ветвей, сходящихся в первом узле,
G12— сумма проводимостей ветвей, соединяющих первый и второй узлы, взятая со знаком минус,
G21— сумма проводимостей ветвей, соединяющих первый и второй узлы, взятая со знаком минус,
G11— сумма проводимостей ветвей, сходящихся во втором узле,
I11— узловой ток первого узла,
I22 — узловой ток второго узла.
Запишем уравнения в матричной форме:
 ,
,
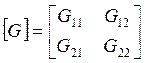 ,
, 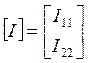 ,
,  .
.
Решим эти уравнения относительно искомых потенциалов и выразим токи ветвей, используя закон Ома.
После нахождения токов ветвей любым методом всегда делается проверка по первому закону Кирхгофа.
Потенциальная диаграмма.
Под потенциальной диаграммой понимают график
распределения потенциала вдоль какого-либо участка цепи или замкнутого контура.
По оси абсцисс на нем откладывают сопротивления вдоль контура, начиная с какой-либо
произвольной точки, по оси ординат – потенциалы. Каждой точке участка цепи или
замкнутого контура соответствует своя точка на потенциальной диаграмме.
Построим потенциальную диаграмму для контура на рис.3. Пусть R1=10 Ом, R2=5 Ом, R3=15
Ом, E1=20 В, E2=10 В, I=1A. 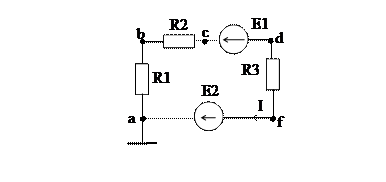
Рис.3. Контур для построения потенциальной диаграммы
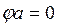 ,
,
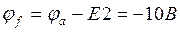 ,
,
 ,
,
 ,
,
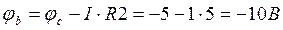 ,
,
 .
.
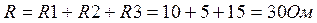
Построим график.

Рис. 4. Потенциальная диаграмма для контура на рис.3.
Таблица 1. Исходные данные
Схема | R1 | R2 | R3 | R4 | R5 | R6 | E1 | E2 | |
Рис. | Ом | Ом | Ом | Ом | Ом | Ом | В | В | |
Вариант 1 | 5 | 15 | 10 | 25 | 20 | 10 | 30 | 100 | 60 |
Вариант 2 | 6 | 4 | 6 | 3 | 2 | 5 | 6 | 35 | 25 |
Вариант 3 | 7 | 5 | 1 | 6 | 4 | 2 | 6 | 10 | 30 |
Вариант 4 | 8 | 3 | 6 | 9 | 10 | 6 | 8 | 55 | 40 |
Вариант 5 | 5 | 6 | 6 | 8 | 8 | 10 | 12 | 70 | 45 |
Вариант 6 | 6 | 4 | 2 | 4 | 5 | 6 | 3 | 15 | 35 |
Вариант 7 | 7 | 1 | 2 | 5 | 1 | 3 | 3 | 10 | 15 |
Вариант 8 | 8 | 25 | 50 | 15 | 25 | 20 | 30 | 150 | 75 |

Порядок выполнения работы:
1. Нарисовать схему. Записать данные.
2. Найти токи ветвей методом контурных токов.
3. Сделать проверку по первому закону Кирхгофа.
4. Найти токи ветвей методом узловых потенциалов.
5. Рассчитанные токи занести в таблицу 2.
Таблица 2
I1,A | I2,A | I3,A | I4,A | I5,A | I6,A | |
расчет | ||||||
эксперимент |
6. Составить баланс мощностей.
7. Потенциалы точек отмеченных на схеме занести в таблицу 3.
Таблица 3
|
|
|
|
| |
расчет | |||||
эксперимент |
8. Собрать схему в программе Electronics Workbench.
9. Измерить токи во всех ветвях. Для чего в каждую ветвь включить амперметр. Результаты измерений занести в таблицу 2.
10. Заземлить узел, который заземляли при расчете по методу узловых потенциалов.
11. Измерить потенциалы точек, отмеченных на схеме. Результаты занести в таблицу 3.
12. Построить потенциальную диаграмму заданного контура.
13. Сравнить измеренные данные с расчетными.
14. Сделать вывод.
Содержание отчета:
1. Тема, цель, приборы и оборудование.
2. Схема заданной цепи. Исходные данные.
3. Расчет по методу контурных токов и методу узловых потенциалов.
4. Заполненная таблица 2.
5. Проверка по первому закону Кирхгофа.
6. Баланс мощностей.
7. Заполненная таблица 3.
8. Токи ветвей и потенциалы узлов цепи, измеренные в программе Electronics Workbench .
9. Потенциальная диаграмма.
10. Вывод.
Вопросы на защиту:
1. Суть метода контурных токов.
2. Суть метода узловых потенциалов.
3. Какой используется закон Кирхгофа для составления уравнений по методу контурных токов? Сформулировать его.
4. Какой используется закон Кирхгофа для составления уравнений по методу узловых потенциалов? Сформулировать его.
5. Как называется сопротивление R11? Как оно находится?
6. Как называется сопротивление R12? Как оно находится?
7. Что такое Е11 в матричной записи уравнений по методу контурных токов?
8. Как находится собственная проводимость узла по методу узловых потенциалов?
9. Матричная форма записи уравнений по методу узловых потенциалов.
10. Как строится потенциальная диаграмма контура сложной цепи
РАСЧЕТ ПОТЕНЦИАЛОВ ТОЧЕК ЦЕПИ — Мегаобучалка
Чтобы найти ток в цепи с несколькими источниками надо:
1) Сложить все Е, направленные в одну сторону;
2) Вычесть все Е, направленные в другую сторону
3) Разделить на сумму всех сопротивлений цепи
Ток течет в сторону большей суммы Е.
Пусть Е1 > Е2, тогда
Если ток и ЭДС совпадают по направлению, то источник работает в режиме генератора, если нет, то в режиме потребителя.
Е1 — генератор; Е2— потребитель
Потенциалом точки цепи называется напряжение между данной точкой и заземлённой.
φ0 = 0
При переходе через источник в режиме генератора потенциал повышается на величину ЭДС минус падение напряжения внутри источника.
φА = φ0 + Е1 — I∙Ri1
При переходе через резистор потенциал понижается на величину падения напряжений в нём:
φВ = φА — I∙R
При переходе через источник в режиме потребителя потенциал понижается на величину ЭДС и на величину падения напряжения внутри источника.
φ0 = φB — E2 — I∙Ri2
Потенциальная диаграмма — это график зависимости потенциалов точек цепи от величины сопротивления цепи.
Рассмотрим построение потенциальной диаграммы на конкретном примере. Одну точку цепи заземляем. Расставляем точки вдоль направления тока. При расчете снова должен получиться равным нулю
Пример решения задачи:
Дано:
Е1 = 25 B
Е2 = 35 В
Е3 = 18 В
Ri1 = 2 Ом
Ri2 = 1 Ом
Ri3 =2 Ом
R1 = 12 Ом
R2 = 5 Ом
R3 = 14 Ом
R4 = 6 Ом
1) Рассчитаем ток в цепи и определяем его направление:
A
2) Рассчитаем потенциалы точек:
φ0 = 0
φ1 = φ0 — I∙R1 = 0 — 12 = -12 B
φ2 = φ1 + Е1 — I∙Ri1 = -12 + 25 — 2 = 11 B
φ3 = φ2 — I∙R2 = 11 — 5 = 6 B
φ4 = φ3 + E2 — I∙Ri2 = 6 + 35 — 1 = 40 B
φ5 = φ4 — E3 — I∙Ri3 = 40 — 18 — 2 = 20 B
φ6 = φ5 — I∙R3 = 20 — 14 = 6 B
φ0 = φ6 — I∙R4 = 6 — 6 = 0
Вывод: При переходе через резистор потенциал понижается плавно, через источник в режиме генератора резко увеличивается, а в режиме потребителя резко уменьшается.
Тестовые задания:
| Задание | Варианты ответов |
| 1.Являются ли напряжение между данной точкой цепи и заземленной потенциалом точки этой цепи? | Да; Нет. |
| 2. Источник работает в режиме генератора если… | а) ЭДС и ток направлены в разные стороны; б) ЭДС и ток направлены в одну сторону. |
РАБОТА ИСТОЧНИКА НА НАГРУЗКУ С ПЕРЕМЕННЫМ СОПРОТИВЛЕНИЕМ.
Построение зависимостей I, U, η = F(R).
Пусть сопротивление нагрузки изменяется от Rкз=0 до Rxx= . Рассмотрим величину тока в трех режимах короткое замыкание, холостой ход и согласованный режим.
1) Iкз = =
2) Iхх =
3)
Вывод 1: с ростом величины сопротивления ток в цепи уменьшается;
Вывод 2: ток максимальный в режиме короткого замыкания;
Рассмотрим величину напряжения в трех режимах
1) Uкз=
2)
3)
Вывод 1: с ростом величины сопротивления напряжение на зажимах источника растет;
Вывод 2: напряжение максимально в режиме Х.Х.
Рассмотрим величину К.П.Д. в трех режимах
Вывод: η стремиться к 1 в режиме Х.Х., но использовать на практике этот режим невозможно, так как цепь разомкнута.
Построение зависимостей Pu, Pн = F(R)
Рассмотрим величину мощности источника в трех режимах
Pu = E∙I = E∙
Вывод: мощность источника максимальна в режиме короткого замыкания.
Рассмотрим величину мощности нагрузки в трех режимах
Исследуя функцию Pн = f(R) на экстремум доказано, что максимальная мощность выделяется в нагрузке при согласованном режиме. Поэтому линии связи и другие устройства работают в этом режиме. И хотя η = 50%, но в слаботочных цепях это не имеет значения.
Тестовые задания:
| Задание | Режим работы | Варианты ответов |
| 4.Укажите при каких режимах работы перечисленные в ответах величины максимальны. | 1) режим холостого хода; 2) режим короткого замыкания; 3) согласованный режим. | а) мощность источника; б) ток цепи; в) мощность нагрузки напряжение на зажимах источника. |
разность потенциалов в электротехнике и физике
Понятие “потенциал” широко используется в физике для характеристики различных полей и сил. Наиболее известны такие применения:
- Электромагнитный – характеристика электромагнитного поля;
- Гравитационный – характеристика полей гравитации;
- Механический – определение сил;
- Термодинамический – мера внутренней энергии тел термодинамической системы;
- Химический;
- Электродный.
Разность потенциалов
В свою очередь, электромагнитный делится на два понятия:
- Электростатический (скалярный), как характеристика электрического поля;
- Векторный, характеризующий магнитное поле.
Напряженность изменяющегося электрического поля находится через электрический потенциал, в то время как статичное поле характеризуется электростатическим.
Разность потенциалов
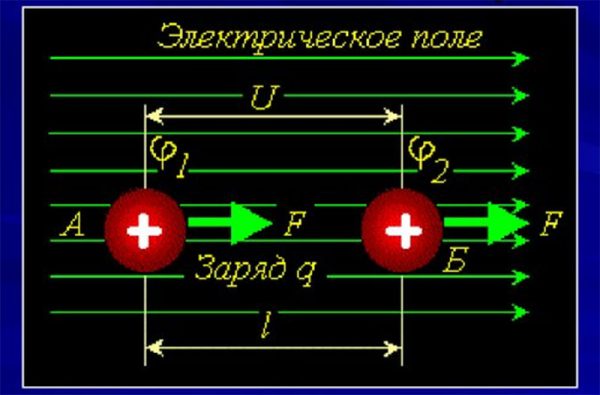
Разность потенциалов, или напряжение, – одно из основных понятий электротехники. Ее можно определить как работу электрического поля, затраченную на перенос заряда между двумя точками. Тогда на вопрос, что такое потенциал, можно ответить, что это работа по переносу единичного заряда из данной точки в бесконечность.
Как и в случае гравитационных сил, заряд, подобно телу с потенциальной энергией, имеет определенный электрический потенциал при внесении его в электрическое поле. Чем выше напряженность электрического поля, и больше величина заряда, тем выше его электрический потенциал.
Для определения напряжения существует формула:
U=A/q,
которая связывает работу А по перемещению заряда q из одной точки в другую.
Проведя преобразование, получим:
А=Uq.
То есть чем выше напряжение, тем большую работу электрическим полем (электричеством) надо затратить по переносу зарядов.
Данное определение позволяет понять суть мощности источника питания. Чем выше его напряжение, разность потенциалов между клеммами, тем большее количество работы он может обеспечить.
Разность потенциалов измеряется в вольтах. Для измерения напряжения созданы измерительные приборы, которые именуются вольтметрами. Они основаны на принципах электродинамики. Ток, проходя по проволочной рамке вольтметра, под действием измеряемого напряжения создает электромагнитное поле. Рамка находится между полюсами магнитов.
Взаимодействие полей рамки и магнита заставляет последнюю отклониться на некоторый угол. Большая разность потенциалов создает больший ток, в результате угол отклонения увеличивается. Шкала прибора пропорциональна углу отклонения рамки, то есть разности потенциалов и проградуирована в вольтах.

Вольтметр
В руках современного электрика имеются не только стрелочные, но и цифровые измерительные приборы, которые не только измеряют электрический потенциал в определенной точке схемы, но и другие величины, характеризующие электрическую цепь. Напряжения в точках измеряются по отношению к другим, которым условно присваивают значение нуля. Тогда измеренное значение между нулевым и потенциальным выводами даст искомое напряжение.
Сказанное выше относится к напряжению как разности потенциалов между двумя зарядами. В электротехнике эта разность измеряется на участке цепи при протекании по нему тока. В случае переменного тока, то есть изменяющего во времени амплитуду и полярность, напряжение в цепи изменяется по такому же закону. Это справедливо только при наличии в схеме активных сопротивлений. Реактивные элементы в цепи переменного тока вызывают сдвиг фазы относительно протекающего тока.
Потенциометры
Напряжение источников питания, в особенности автономных, таких как аккумуляторы, химические источники, солнечные и тепловые батареи, является постоянным и не поддается регулировке. Для получения меньших значений используются, в простейшем случае, потенциометрические делители напряжения с использованием трехвыводного переменного резистора (потенциометра). Как работает потенциометр? Переменный резистор представляет собой резистивный элемент с двумя выводами, по которому может перемещаться контактный ползунок с третьим выводом.

Потенциометр-реостат
Переменный резистор может включаться двумя способами:
- Реостатным;
- Потенциометром.
В первом случае у переменного резистора используются два вывода: один – основной, другой – с ползунка. Перемещая ползунок по телу резистора, изменяют сопротивление. Включив реостат в цепь электрического тока последовательно с источником напряжения, можно регулировать ток в цепи.
Реостатное включение
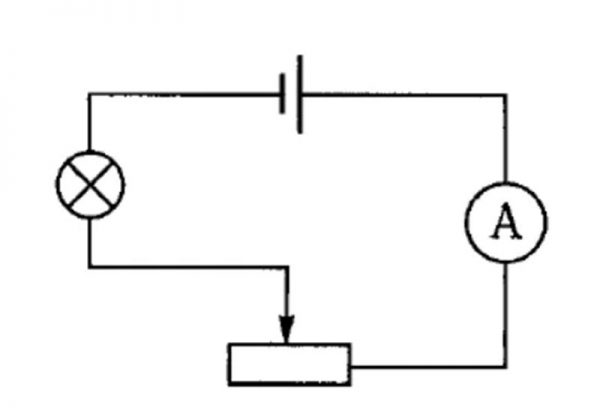
Включение потенциометром требует использования всех трех выводов. Основные выводы подключаются параллельно источнику питания, а пониженное напряжение снимается с ползунка и одного из выводов.
Принцип действия потенциометра заключается в следующем. Через резистор, подключенный к источнику питания, проходит ток, который создает падение напряжения между ползунком и крайними выводами. Чем меньше сопротивление между ползунком и выводом, тем меньше напряжение. Данная схема имеет недостаток, она сильно нагружает источник питания, поскольку для корректной и точной регулировки требуется, чтобы сопротивление переменного резистора было в несколько раз меньше сопротивления нагрузки.

Потенциометрическое включение
Обратите внимание! Название «потенциометр» в данном случае не совсем корректно, поскольку из названия следует, что это устройство для измерения, но так как по принципу действия оно схоже с современным переменным резистором, то это название за ним прочно закрепилось, особенно в любительской среде.
Многие понятия в физике схожи и могут служить примером друг другу. Это справедливо и для такого понятия, как потенциал, который может быть как механической величиной, так и электрической. Сам по себе потенциал измерить невозможно, поэтому речь идет о разности, когда один из двух зарядов принимается за точку отсчета – нуль или заземление, как принято в электротехнике.
Видео
Оцените статью:Как определить потенциалы точек
Понятие потенциала нашло очень широкое распространение не только в науке и технике, но и в быту. Так напряжение в электрической сети – это разность потенциалов. Наиболее четко это понятие исследовано в теории поля, где оно возникает при изучении специальных полей, часть которых являются потенциальными.
Векторное поле образует векторная величина, заданная в виде функции поля М(x,y,z). Обозначается как F=F(M)=F(x,y,z) или F=i∙P(x,y,z)+j∙Q(x,y,z)+k∙R(x,y,z), где P, Q, R — координатные функции. Наибольшее применение векторные поля получили в теории электромагнитного поля.
Векторное поле называется потенциальным в некоторой области, если его можно представить в видеF(M)=grad(f(M)). При этом f(M)=f(x,y,z) называется скалярным потенциалом векторного поля. Если F(M)={P, Q, R}, то P=&partf/&partх, Q=&partf/&party, R=&partf/&partz. Известно, что для любой скалярной функции f ротор ее градиента rot(gradf)=0. Это равенство является необходимым и достаточным условием потенциальности F(M). Его можно перефразировать в виде:∂Q/∂х=∂P/∂y, ∂P/∂z=∂R/∂х, ∂R/∂y=∂Q/∂z.
Как определить bпотенциалы/b точек» rel=»gallery-step-images»>Вычисление потенциала f потенциального поля F=i∙P(x,y,z)+j∙Q(x,y,z)+k∙R(x,y,z) производится на основе того, что в силу определения df= F∙dr (имеется в виду скалярное произведение).Тогда f=∫(Мо М) F∙dr=∫(Мо М)P∙dx+Q∙dy+R∙dz представляет собой криволинейный интеграл второго рода вдоль произвольной линии от Мо к переменной точке М. Проще всего использовать ломанную, отрезки которой параллельны координатным осям (условие потенциальности совпадает с условием независимости криволинейного интеграла от пути интегрирования) (см. рис. 1).
Приступите к решению. Обозначьте x*, y*, z* координаты переменной точки на пути интегрирования. На отрезке МоА y*=yo, z*=zo, dy*=0, dz*=0 и ∫(Мо А) Fdr=∫(xо x)P(x*,yo,zo)∙dx*.На АВ x*=x, z*=zo, dx*=0, dz*=0 и ∫(А В) F∙dr=∫(yо y)Q(x,y*,zo)∙dy*.На ВМ x*=x, y*=y, dx*=0, dy*=0 и ∫(В М) F∙dr=∫(zо z)R(x,y,z*)∙dz*. Окончательно, f=∫(xо x)P(x*,yo,zo)∙dx*+∫(yо y)Q(x,y*,zo)∙dy*+∫(zо z)R(x,y,z*)∙dz*.
Пример. Дано векторное поле F(x,y,z)=(2x∙y+z)i + (x^2-2y)∙j+x∙k. Найти его потенциал в точке М(1,2,1). Решение. Проверьте, является ли заданное поле потенциальным. Для этого можно вычислить его ротор, но проще использовать равенства ∂Q/∂х=∂P/∂y, ∂P/∂z=∂R/∂х, ∂R/∂y=∂Q/∂z. Здесь P=2x∙y+z, Q=x^2-2y, R=x. ∂Q/∂х=2x, ∂P/∂y=2x – первое равенство выполнено. ∂P/∂z=1, ∂R/∂х=1 второе равенство выполнено. ∂R/∂y=0, ∂Q/∂z=0 – выполнено и третье равенство.Теперь вычислите потенциал, приняв за начальную точку (0,0,0) – это проще всего. f=∫(0 x)0∙dx*+∫(0 y)∙(x^2-y*)∙dy*+∫(0 z)∙x∙dz*=(x^2)∙y-y^2+x∙z.f(1,2,1)=-1.




 A, B
A, B