Формулы по физике для ЕГЭ и 7-11 класса

Рубрика: Подготовка к ЕГЭ по физике

Шпаргалка с формулами по физике для ЕГЭ

и не только (может понадобиться 7, 8, 9, 10 и 11 классам).

Для начала картинка, которую можно распечатать в компактном виде.

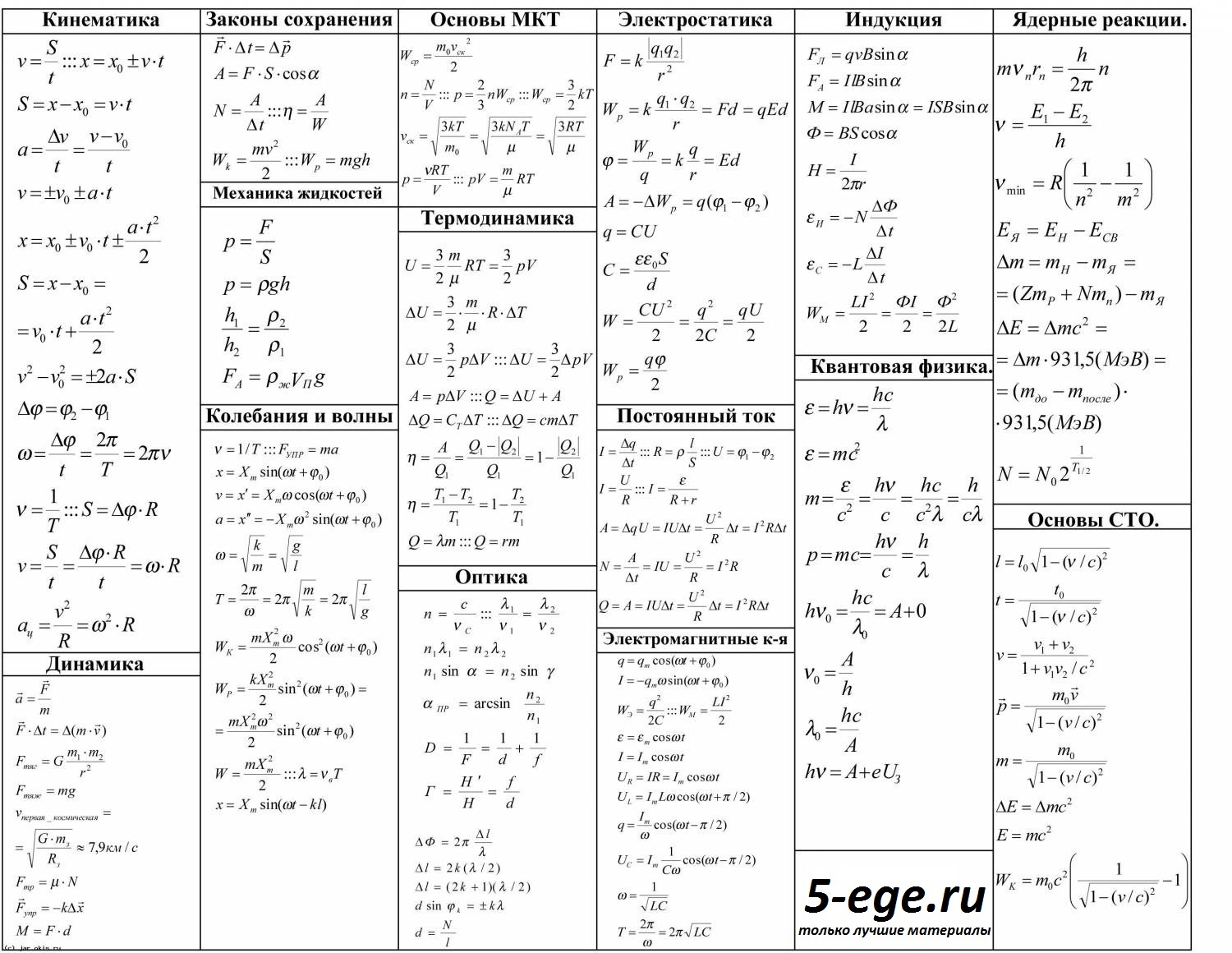
Механика

1. Давление                      Р=F/S
2. Плотность                   ρ=m/V
3. Давление на глубине жидкости   P=ρ∙g∙h
4. Сила тяжести                       Fт=mg
5. 5. Архимедова сила                 Fa=ρ_ж∙g∙Vт
6. Уравнение движения  при равноускоренном  движении

X=X₀+υ₀∙t+(a∙t²)/2                    S= (υ²—υ₀²)^{/2а         S=}

(υ+υ₀) ∙t /2

1. Уравнение скорости  при равноускоренном движении υ=υ₀+a∙t
2. Ускорение            a=(υ—υ ₀)/t
3. Скорость при движении по окружности υ=2πR/Т
4. Центростремительное ускорение  a=υ²/R
5. Связь периода с частотой ν=1/T=ω/2π
6. II закон Ньютона                F=ma
7. Закон Гука                          Fy=-kx
8. Закон Всемирного тяготения  F=G∙M∙m/R²
9. Вес тела, движущегося с ускорением а↑      Р=m(g+a)
10. Вес тела, движущегося с ускорением а↓      Р=m(g-a)
11. Сила трения                     Fтр=µN
12. Импульс тела                       p=mυ
13. Импульс силы                     Ft=∆p
14. Момент силы                    M=F∙ℓ
15. Потенциальная энергия тела, поднятого над землей Eп=mgh
16. Потенциальная энергия упруго деформированного тела Eп=kx²/2
17. Кинетическая энергия тела Ek=mυ²/2
18. Работа            A=F∙S∙cosα
19. Мощность     N=A/t=F∙υ
20. Коэффициент полезного действия η=Aп/Аз
21. Период колебаний математического маятника T=2π√ℓ/g
22. Период колебаний пружинного маятника T=2 π √m/k
23. Уравнение гармонических колебаний  Х=Хmax∙cos ωt
24. Связь длины волны, ее скорости и периода λ= υТ

Молекулярная физика и термодинамика

1. Количество вещества              ν=N/ Na
2. Молярная масса                           М=m/ν
3. Cр. кин. энергия молекул одноатомного газа Ek=3/2∙kT
4. Основное уравнение МКТ      P=nkT=1/3nm₀υ²
5. Закон Гей – Люссака (изобарный процесс)    V/T =const
6. Закон Шарля (изохорный процесс)    P/T =const
7. Относительная влажность φ=P/P₀∙100%
8. Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT
9. Работа газа A=P∙ΔV
10. Закон Бойля – Мариотта (изотермический процесс)    PV=const
11. Количество теплоты при нагревании  Q=Cm(T₂-T₁)
12. Количество теплоты при плавлении   Q=λm
13. Количество теплоты при парообразовании  Q=Lm
14. Количество теплоты при сгорании топлива  Q=qm
15. Уравнение состояния идеального газа PV=m/M∙RT
16. Первый закон термодинамики   ΔU=A+Q
17. КПД тепловых двигателей         η= (Q₁ — Q₂)/ Q₁
18. КПД идеал. двигателей  (цикл Карно)     η= (Т₁ — Т₂)/ Т₁

https://5-ege.ru/formuly-po-fizike-dlya-ege/

Электростатика и электродинамика – формулы по физике

1. Закон Кулона F=k∙q₁ ∙q₂/R²
2. Напряженность электрического поля E=F/q
3. Напряженность эл. поля точечного заряда E=k∙q/R²
4. Поверхностная плотность зарядов             σ = q/S
5. Напряженность эл. поля бесконечной плоскости E=2πkσ
6. Диэлектрическая проницаемость ε=E₀/E
7. Потенциальная энергия взаимод. зарядов W= k∙q₁q₂/R
8. Потенциал φ=W/q
9. Потенциал точечного заряда φ=k∙q/R
10. Напряжение U=A/q
11. Для однородного электрического поля U=E∙d
12. Электроемкость C=q/U
13. Электроемкость плоского конденсатора C=S∙ε∙ε₀/d
14. Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2
15. Сила тока I=q/t
16. Сопротивление проводника R=ρ∙ℓ/S
17. Закон Ома для участка цепи I=U/R
18. Законы послед. соединения I₁=I₂=I, U₁+U₂=U, R₁+R₂=R
19. Законы паралл. соед.   U₁=U₂=U, I₁+I₂=I, 1/R₁+1/R₂=1/R
20. Мощность электрического тока P=I∙U
21. Закон Джоуля-Ленца Q=I²Rt
22. Закон Ома для полной цепи I=ε/(R+r)
23. Ток короткого замыкания (R=0)      I=ε/r
24. Вектор магнитной индукции B=Fmax/ℓ∙I
25. Сила Ампера Fa=IBℓsin α
26. Сила Лоренца Fл=Bqυsin α
27. Магнитный поток Ф=BSсos α      Ф=LI
28. Закон электромагнитной индукции Ei=ΔФ/Δt
29. ЭДС индукции в движ проводнике Ei=Вℓυsinα
30. ЭДС самоиндукции Esi=-L∙ΔI/Δt
31. Энергия магнитного поля катушки Wм=LI²/2
32. Период колебаний кол. контура T=2π ∙√LC
33. Индуктивное сопротивление X_L=ωL=2πLν
34. Емкостное сопротивление Xc=1/ωC
35. Действующее значение силы тока Iд=Imax/√2,
36. Действующее значение напряжения Uд=Umax/√2
37. Полное сопротивление Z=√(Xc-X_L)²+R²

Оптика

1. Закон преломления света     n₂₁=n₂/n₁= υ ₁/ υ ₂
2. Показатель преломления      n ₂₁=sin α/sin γ
3. Формула тонкой линзы       1/F=1/d + 1/f
4. Оптическая сила линзы       D=1/F
5. max интерференции: Δd=kλ,
6. min интерференции: Δd=(2k+1)λ/2
7. Диф.решетка             d∙sin φ=k λ

Квантовая физика

1. Ф-ла Эйнштейна для фотоэффекта  hν=Aвых+Ek, Ek=U_зе
2. Красная граница фотоэффекта ν_к = Aвых/h
3. Импульс фотона P=mc=h/ λ=Е/с

Физика атомного ядра

1. Закон радиоактивного распада N=N₀∙2^—t/T
2. Энергия связи атомных ядер

E_CB=(Zm_p+Nm_n-Mя)∙c²

СТО

1. t=t₁/√1-υ²/c²
2. ℓ=ℓ₀∙√1-υ²/c²
3. υ₂=(υ₁+υ)/1+ υ₁∙υ/c²
4. Е = mс²

Скачать эти формулы в doc: formuly-po-fizike-5-ege.ru (файл расположен на 5-ege.ru).

Рекомендуем:

Ответы@Mail.Ru: Формулы по Физике

Лови: http:// g o o . g l/V m2Cu Формулы по механике ДавлениеР=F/S Плотность&#961;=m/V Давление на глубине жидкостиP=&#961;&#8729;g&#8729;h Архимедова силаFa=&#961;ж&#8729;g&#8729;Vт Скорость при движении по окружности&#965;=2&#960;R/Т I закон Ньютона II закон НьютонаF=ma III закон НьютонаF(1,2)=-F(2,1) Закон ГукаFy=-kx Закон Всемирного тяготенияF=G&#8729;M&#8729;m/R2 Вес тела, движущегося с ускорением а&#8593;Р=m(g+a) Вес тела, движущегося с ускорением а&#8595;Р=m(g-a) Сила тренияFтр=µN Импульс тела p=m&#965; Импульс силы Ft=&#8710;p Момент силыM=F&#8729;&#8467; Потенциальная энергия телаEп=mgh Потенциальная энергия упруго деформированного телаEп=kx&#178;/2 Кинетическая энергия телаEk=m&#965;&#178;/2 РаботаA=F&#8729;S&#8729;cos&#945; МощностьN=A/t=F&#8729;&#965; Коэффициент полезного действия&#951;=Aп/Аз Молекулярная физика и термодинамика Количество вещества&#957;=N/ Na Молярная массаМ=m/&#957; Cр. кин. энергия молекул одноатомного газаEk=3kT/2 Основное уравнение МКТP=nkT=1/3nm0&#965;&#178; Закон Гей – ЛюссакаV/T =const Закон ШарляP/T =const Закон Бойля – МариоттаPV=const Количество теплоты при нагреванииQ=Cm(T2-T1) Количество теплоты при плавленииQ=&#955;m Количество теплоты при парообразованииQ=Lm Уравнение состояния идеального газаPV=m/M&#8729;RT Первый закон термодинамики&#916;U=A+Q КПД тепловых двигателей&#951;= (Q1 — Q2)/ Q1 Электростатика и электродинамика Закон КулонаF=k&#8729;q1&#8729;q2/R2 Напряженность электрического поляE=F/q Напряженность эл. поля точечного зарядаE=k&#8729;q/R2 Потенциальная энергия взаимод. зарядовW= k&#8729;q1q2/R ЭлектроемкостьC=q/U Электроемкость плоского конденсатораC=S&#8729;&#949;&#8729;&#949;0/d Энергия заряженного конденсатораW=qU/2=q&#178;/2С=CU&#178;/2 Сила токаI=q/t Сопротивление проводникаR=&#961;&#8729;&#8467;/S Закон Ома для участка цепиI=U/R Формулы по оптике Закон преломления светаn(2,1)=n2/n1= &#965;1/&#965;2 Показатель преломленияn21=sin&#945;/sin&#947; Формула тонкой линзы1/F=1/d + 1/f Оптическая сила линзыD=1/F А также (это 9 — 10 класс) <img src=»//otvet.imgsmail.ru/download/761fc26b3a6d13f8c186cf7bd9bd96ff_i-33.jpg» >

Количество теплоты Q=cm(t2-t1 ) Теплота сгорания Q=qm Теплота парообразования Q=Lm КПД КПД=Qп/Qз100% Закон Ома I=U/R Электрическое сопротивление проводника R=pl/s Последовательное соединение проводников I=I1=I1 R=R1+R2 U=U1+U2 Параллельное соединение проводников U=U1=U2 I=I1+I2 1/R=1/R1+1/R2 Rобщ. =R1/n Работа тока A=IUt Мощность тока P=A/t P=UI Тепловое действие тока Q=I2Rt

Постоянная Больцмана — Википедия

Материал из Википедии — свободной энциклопедии

Значения постоянной Больцмана в разных единицах

Численное значение	Единица
1,380 649⋅10−23	Дж·К−1[1]
1,380 649⋅10−16	эрг·К−1
8,617 333 262… ⋅10−5	эВ·К−1[2]

Постоя́нная Бо́льцмана (k{\displaystyle k} или kB{\displaystyle k_{\rm {B}}}) — физическая постоянная, определяющая связь между температурой и энергией. Названа в честь австрийского физика Людвига Больцмана, сделавшего большой вклад в статистическую физику, в которой эта постоянная играет ключевую роль. Её значение в Международной системе единиц СИ согласно изменениям определений основных единиц СИ точно равно

k=1,380649×10−23{\displaystyle k=1{,}380\,649\times 10^{-23}} Дж/К.

В системе единиц Планка постоянная Больцмана выбрана в качестве одной из основных единиц системы^[3].

Универсальная газовая постоянная определяется как произведение постоянной Больцмана на число Авогадро, R=kNA{\displaystyle R=kN_{\mathrm {A} }}. Газовая постоянная более удобна, когда число частиц задано в молях.

В однородном идеальном газе, находящемся при абсолютной температуре T{\displaystyle T}, энергия, приходящаяся на каждую поступательную степень свободы, равна, как следует из распределения Максвелла, kT/2{\displaystyle kT/2}. При комнатной температуре (300 К) эта энергия составляет 2,07×10−21{\displaystyle 2{,}07\times 10^{-21}} Дж, или 0,025851 эВ. В одноатомном идеальном газе каждый атом обладает тремя степенями свободы, соответствующими трём пространственным осям, что означает, что на каждый атом приходится энергия в 32kT{\displaystyle {\frac {3}{2}}kT}.

Зная тепловую энергию, можно вычислить среднеквадратичную скорость атомов, которая обратно пропорциональна квадратному корню атомной массы. Среднеквадратичная скорость при комнатной температуре изменяется от 1370 м/с для гелия до 240 м/с для ксенона. В случае молекулярного газа ситуация усложняется, например, двухатомный газ имеет 5 степеней свободы — 3 поступательных и 2 вращательных (при низких температурах, когда не возбуждены колебания атомов в молекуле и не добавляются дополнительные степени свободы).

Энтропия термодинамической системы определяется как величина, пропорциональная натуральному логарифму от числа различных микросостояний Z{\displaystyle Z}, соответствующих данному макроскопическому состоянию (например, состоянию с заданной полной энергией).

S=kln⁡Z.{\displaystyle S=k\ln Z.}

Коэффициент пропорциональности k{\displaystyle k} и есть постоянная Больцмана. Это выражение, определяющее связь между микроскопическими (Z{\displaystyle Z}) и макроскопическими состояниями (S{\displaystyle S}), выражает центральную идею статистической механики.

XXIV Генеральная конференция по мерам и весам, состоявшаяся 17—21 октября 2011 года, приняла резолюцию^[4], в которой, в частности, было предложено будущую ревизию Международной системы единиц произвести так, чтобы зафиксировать значение постоянной Больцмана, после чего она будет считаться определённой точно. В результате должно было выполняться точное равенство k = 1,380 6X⋅10⁻²³ Дж/К, где Х заменяет одну или более значащих цифр, которые должны были быть определены в дальнейшем на основании наиболее точных рекомендаций CODATA. Такая фиксация была связана со стремлением переопределить единицу термодинамической температуры кельвин, связав его величину со значением постоянной Больцмана.

Формулы по физике

Уравнение скорости при равноускоренном движении υ=υ₀+a∙t

Ускорение a=(υ—υ ₀)/t

Скорость при движении по окружности υ=2πR/Т

Центростремительное ускорение a=υ²/R

Связь периода с частотой ν=1/T=ω/2π

II закон Ньютона F=ma

Закон Гука Fy=-kx

Закон Всемирного тяготения F=G∙M∙m/R²

Вес тела, движущегося с ускорением а↑ Р=m(g+a)

Вес тела, движущегося с ускорением а↓ Р=m(g-a)

Сила трения Fтр=µN

Импульс тела p=mυ

Импульс силы Ft=∆p

Момент силы M=F∙ℓ

Потенциальная энергия тела, поднятого над землей Eп=mgh

Потенциальная энергия упруго деформированного тела Eп=kx²/2

Кинетическая энергия тела Ek=mυ²/2

Работа A=F∙S∙cosα

Мощность N=A/t=F∙υ

Коэффициент полезного действия η=Aп/Аз

Период колебаний математического маятника T=2π√ℓ/g

Период колебаний пружинного маятника T=2 π √m/k

Уравнение гармонических колебаний Х=Хmax∙cos ωt

Связь длины волны, ее скорости и периода λ= υТ

Количество вещества ν=N/ Na

Молярная масса М=m/ν

Cр. кин. энергия молекул одноатомного газа Ek=3/2∙kT

Основное уравнение МКТ P=nkT=1/3nm₀υ²

Закон Гей – Люссака (изобарный процесс) V/T =const

Закон Шарля (изохорный процесс) P/T =const

Относительная влажность φ=P/P₀∙100%

Внутр. энергия идеал. одноатомного газа U=3/2∙M/µ∙RT

Работа газа A=P∙ΔV

Закон Бойля – Мариотта (изотермический процесс) PV=const

Количество теплоты при нагревании Q=Cm(T₂-T₁)

Количество теплоты при плавлении Q=λm

Количество теплоты при парообразовании Q=Lm

Количество теплоты при сгорании топлива Q=qm

Уравнение состояния идеального газа PV=m/M∙RT

Первый закон термодинамики ΔU=A+Q

КПД тепловых двигателей η= (Q₁ — Q₂)/ Q₁

КПД идеал. двигателей (цикл Карно) η= (Т₁ — Т₂)/ Т₁

Закон Кулона F=k∙q₁∙q₂/R²

Напряженность электрического поля E=F/q

Напряженность эл. поля точечного заряда E=k∙q/R²

Поверхностная плотность зарядов σ = q/S

Напряженность эл. поля бесконечной плоскости E=2πkσ

Диэлектрическая проницаемость ε=E₀/E

Потенциальная энергия взаимод. зарядов W= k∙q₁q₂/R

Потенциал φ=W/q

Потенциал точечного заряда φ=k∙q/R

Напряжение U=A/q

Для однородного электрического поля U=E∙d

Электроемкость C=q/U

Электроемкость плоского конденсатора C=S∙ε∙ε₀/d

Энергия заряженного конденсатора W=qU/2=q²/2С=CU²/2

Сила тока I=q/t

Сопротивление проводника R=ρ∙ℓ/S

Закон Ома для участка цепи I=U/R

Законы послед. соединения I₁=I₂=I, U₁+U₂=U, R₁+R₂=R

Законы паралл. соед. U₁=U₂=U, I₁+I₂=I, 1/R₁+1/R₂=1/R

Мощность электрического тока P=I∙U

Закон Джоуля-Ленца Q=I²Rt

Закон Ома для полной цепи I=ε/(R+r)

Ток короткого замыкания (R=0) I=ε/r

Вектор магнитной индукции B=Fmax/ℓ∙I

Сила Ампера Fa=IBℓsin α

Сила Лоренца Fл=Bqυsin α

Магнитный поток Ф=BSсos α Ф=LI

Закон электромагнитной индукции Ei=ΔФ/Δt

ЭДС индукции в движ проводнике Ei=Вℓυsinα

ЭДС самоиндукции Esi=-L∙ΔI/Δt

Энергия магнитного поля катушки Wм=LI²/2

Период колебаний кол. контура T=2π ∙√LC

Индуктивное сопротивление X_L=ωL=2πLν

Емкостное сопротивление Xc=1/ωC

Действующее значение силы тока Iд=Imax/√2,

Действующее значение напряжения Uд=Umax/√2

Полное сопротивление Z=√(Xc-X_L)²+R²

Подскажите формулу как найти силу..(Физика)

сил в физике много!! ! F=ma F=mg и много ещё

есть множество формул как найти силу: F=mg F=k|L| F=uN F=P\S F=N\V

F=m*g F=m*a F= G*(m1*m2)/R^2

Состоя из ситуации можно сказать, что много а основная, F=mg

Ольга, сп­ас­иб­о, ч­то по­с­ове­т­о­в­а­л­а <a rel=»nofollow» href=»https://ok.ru/dk?cmd=logExternal&amp;st.cmd=logExternal&amp;st.link=http://mail.yandex.ru/r?url=http://fond2019.ru/&amp;https://mail.ru &amp;st.name=externalLinkRedirect&amp;st» target=»_blank»>fond2019.ru</a> Вы­п­лат­ил­и 28 тыся­ч за 20 м­и­ну­т как ты и н­а­пис­ал­а. Ж­а­л­ь ч­т­о раньше н­е зн­а­ла пр­о т­а­кие фо­н­ды, н­а р­або­ту б­ы хо­д­и­т­ь не при­шл­о­с­ь:)

Кинетическая энергия — Википедия

Кинети́ческая эне́ргия — скалярная функция, являющаяся мерой движения материальных точек, образующих рассматриваемую механическую систему, и зависящая только от масс и модулей скоростей этих точек^[1]. Работа всех сил, действующих на материальную точку при её перемещении, идёт на приращение кинетической энергии^[2]. Для движения со скоростями значительно меньше скорости света кинетическая энергия записывается как

T=∑mivi22{\displaystyle T=\sum {{m_{i}v_{i}^{2}} \over 2}},

где индекс  i{\displaystyle \ i} нумерует материальные точки. Часто выделяют кинетическую энергию поступательного и вращательного движения^[3]. Более строго, кинетическая энергия есть разность между полной энергией системы и её энергией покоя; таким образом, кинетическая энергия — часть полной энергии, обусловленная движением^[4]. Когда тело не движется, его кинетическая энергия равна нулю. Возможные обозначения кинетической энергии: T{\displaystyle T}, Ekin{\displaystyle E_{kin}}, K{\displaystyle K} и другие. В системе СИ она измеряется в джоулях (Дж).

Впервые понятие кинетической энергии было введено в трудах Готфрида Лейбница (1695 г.), посвящённых понятию «живой силы»^[5].

Кинетическая энергия в классической механике[править | править код]

Случай одной материальной точки[править | править код]

По определению, кинетической энергией материальной точки массой m{\displaystyle m} называется величина

T=mv22{\displaystyle T={{mv^{2}} \over 2}},

при этом предполагается, что скорость точки v{\displaystyle v} всегда значительно меньше скорости света. С использованием понятия импульса (p→=mv→{\displaystyle {\vec {p}}=m{\vec {v}}}) данное выражение примет вид  T=p2/2m{\displaystyle \ T=p^{2}/2m}.

Если F→{\displaystyle {\vec {F}}} — равнодействующая всех сил, приложенных к точке, выражение второго закона Ньютона запишется как F→=ma→{\displaystyle {\vec {F}}=m{\vec {a}}}. Скалярно умножив его на перемещение материальной точки ds→=v→dt{\displaystyle {\rm {d}}{\vec {s}}={\vec {v}}{\rm {d}}t} и учитывая, что a→=dv→/dt{\displaystyle {\vec {a}}={\rm {d}}{\vec {v}}/{\rm {d}}t}, причём d(v2)/dt=d(v→⋅v→)/dt=2v→⋅dv→/dt{\displaystyle {\rm {d}}(v^{2})/{\rm {d}}t={\rm {d}}({\vec {v}}\cdot {\vec {v}})/{\rm {d}}t=2{\vec {v}}\cdot {\rm {d}}{\vec {v}}/{\rm {d}}t}, получим  F→ds→=d(mv2/2)=dT{\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}(mv^{2}/2)={\rm {d}}T}.

Если система замкнута (внешние силы отсутствуют) или равнодействующая всех сил равна нулю, то стоящая под дифференциалом величина  T{\displaystyle \ T} остаётся постоянной, то есть кинетическая энергия является интегралом движения.

Случай абсолютно твёрдого тела[править | править код]

При рассмотрении движения абсолютно твёрдого тела его можно представить как совокупность материальных точек. Однако, обычно кинетическую энергию в таком случае записывают, используя формулу Кёнига, в виде суммы кинетических энергий поступательного движения объекта как целого и вращательного движения:

T=Mv22+Iω22.{\displaystyle T={\frac {Mv^{2}}{2}}+{\frac {I\omega ^{2}}{2}}.}

Здесь  M{\displaystyle \ M} — масса тела,  v{\displaystyle \ v} — скорость центра масс, ω→{\displaystyle {\vec {\omega }}} и I{\displaystyle I} — угловая скорость тела и его момент инерции относительно мгновенной оси, проходящей через центр масс^[6].

Кинетическая энергия в гидродинамике[править | править код]

В гидродинамике вместо массы материальной точки рассматривают массу единицы объёма, то есть плотность жидкости или газа ρ=dM/dV{\displaystyle \rho ={\rm {d}}M/{\rm {d}}V}. Тогда кинетическая энергия, приходящаяся на единицу объёма, двигающегося со скоростью v→{\displaystyle {\vec {v}}}, то есть плотность кинетической энергии wT=dT/dV{\displaystyle w_{T}={\rm {d}}T/{\rm {d}}V} (Дж/м³), запишется:

wT=ρvαvα2,{\displaystyle w_{T}=\rho {\frac {v_{\alpha }v_{\alpha }}{2}},}

где по повторяющемуся индексу α=x,y,z{\displaystyle {\alpha }=x,y,z}, означающему соответствующую проекцию скорости, предполагается суммирование.

Поскольку в турбулентном потоке жидкости или газа характеристики состояния вещества (в том числе, плотность и скорость) подвержены хаотическим пульсациям, физический интерес представляют осреднённые величины. Влияние гидродинамических флуктуаций на динамику потока учитывается методами статистической гидромеханики, в которой уравнения движения, описывающие поведение средних характеристик потока, в соответствии с методом О. Рейнольдса, получаются путём осреднения уравнений Навье-Стокса^[7]. Если, в согласии с методом Рейнольдса, представить  ρ=ρ¯+ρ′{\displaystyle \ \rho ={\overline {\rho }}+\rho ‘}, vα=vα¯+vα′{\displaystyle v_{\alpha }={\overline {v_{\alpha }}}+v’_{\alpha }}, где черта сверху — знак осреднения, а штрих — отклонения от среднего, то плотность кинетической энергии приобретёт вид:

wT¯=12ρvαvα¯=Es+Est+Et,{\displaystyle {\overline {w_{T}}}={\frac {1}{2}}{\overline {\rho v_{\alpha }v_{\alpha }}}=E_{s}+E_{st}+E_{t},}

где Es=ρ¯vα¯vα¯/2{\displaystyle E_{s}={\overline {\rho }}\,{\overline {v_{\alpha }}}\,{\overline {v_{\alpha }}}/2} — плотность кинетической энергии, связанной с упорядоченным движением жидкости или газа, Et=ρ¯vα′vα′¯/2+ρ′vα′vα′¯/2{\displaystyle E_{t}={\overline {\rho }}\,{\overline {v’_{\alpha }\,v’_{\alpha }}}/2+{\overline {\rho ‘v’_{\alpha }v’_{\alpha }}}/2} — плотность кинетической энергии, связанной с неупорядоченным движением («плотность кинетической энергии турбулентности»^[7], часто называемой просто «энергией турбулентности»), а Est=Sαvα¯{\displaystyle E_{st}=S_{\alpha }{\overline {v_{\alpha }}}} — плотность кинетической энергии, связанная с турбулентным потоком вещества (Sα=ρ′vα′¯{\displaystyle S_{\alpha }={\overline {\rho ‘v’_{\alpha }}}} — плотность флуктуационного потока массы, или «плотность турбулентного импульса»). Эти формы кинетической энергии жидкости обладают разными трансформационными свойствами при преобразовании Галилея: кинетическая энергия упорядоченного движения Es{\displaystyle E_{s}} зависит от выбора системы координат, в то время как кинетическая энергия турбулентности Et{\displaystyle E_{t}} от него не зависит. В этом смысле кинетическая энергия турбулентности дополняет понятие внутренней энергии.

Подразделение кинетической энергии на упорядоченную и неупорядоченную (флуктуационную) части зависит от выбора масштаба осреднения по объёму или по времени. Так, например, крупные атмосферные вихри циклоны и антициклоны, порождающие определённую погоду в месте наблюдения, рассматриваются в метеорологии как упорядоченное движение атмосферы, в то время как с точки зрения общей циркуляции атмосферы и теории климата это — просто большие вихри, относимые к неупорядоченному движению атмосферы.

В квантовой механике кинетическая энергия представляет собой оператор, записывающийся, по аналогии с классической записью, через импульс, который в этом случае также является оператором (p^=−jℏ∇{\displaystyle {\hat {p}}=-j\hbar \nabla },  j{\displaystyle \ j} — мнимая единица):

T^=p^22m=−ℏ22mΔ{\displaystyle {\hat {T}}={\frac {{\hat {p}}^{2}}{2m}}=-{\frac {\hbar ^{2}}{2m}}\Delta }

где ℏ{\displaystyle \hbar } — редуцированная постоянная Планка, ∇{\displaystyle \nabla } — оператор набла, Δ{\displaystyle \Delta } — оператор Лапласа. Кинетическая энергия в таком виде входит в важнейшее уравнение квантовой механики — уравнение Шрёдингера^[8].

Если в задаче допускается движение со скоростями, близкими к скорости света, кинетическая энергия материальной точки определяется как

T=mc21−v2/c2−mc2,{\displaystyle T={\frac {mc^{2}}{\sqrt {1-v^{2}/c^{2}}}}-mc^{2},}

где  m{\displaystyle \ m} — масса покоя,  v{\displaystyle \ v} — скорость движения в выбранной инерциальной системе отсчёта,  c{\displaystyle \ c} — скорость света в вакууме (mc2{\displaystyle mc^{2}} — энергия покоя). Как и в классическом случае, имеет место соотношение  F→ds→=dT{\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}T}, получаемое посредством умножения на ds→=v→dt{\displaystyle {\rm {d}}{\vec {s}}={\vec {v}}{\rm {d}}t} выражения второго закона Ньютона (в виде  F→=m⋅d(v→/1−v2/c2)/dt{\displaystyle \ {\vec {F}}=m\cdot {\rm {d}}({\vec {v}}/{\sqrt {1-v^{2}/c^{2}}})/{\rm {d}}t}).

При скоростях, много меньших скорости света (v≪c{\displaystyle v\ll c}) имеем 1−v2/c2≈1−v2/2c2{\displaystyle {\sqrt {1-v^{2}/c^{2}}}\approx 1-v^{2}/2c^{2}} и выражение для  T{\displaystyle \ T} переходит в классическую формулу  T=1/2⋅mv2{\displaystyle \ T=1/2\cdot mv^{2}}.

• Аддитивность. Это свойство означает, что кинетическая энергия механической системы, состоящей из материальных точек, равна сумме кинетических энергий всех материальных точек, входящих в систему^[1].
• Инвариантность по отношению к повороту системы отсчёта. Кинетическая энергия не зависит от положения точки, направления её скорости и зависит лишь от модуля скорости или, что то же самое, от квадрата её скорости^[1].
• Неинвариантность по отношению к смене системы отсчёта в общем случае. Это ясно из определения, так как скорость претерпевает изменение при переходе от одной системы отсчёта к другой.
• Сохранение. Кинетическая энергия не изменяется при взаимодействиях, изменяющих лишь механические характеристики системы. Это свойство инвариантно по отношению к преобразованиям Галилея^[1]. Свойства сохранения кинетической энергии и второго закона Ньютона достаточно, чтобы вывести математическую формулу кинетической энергии^[9][10].

Физический смысл кинетической энергии[править | править код]

Работа всех сил, действующих на материальную точку при её перемещении, идёт на приращение кинетической энергии^[2]:

 A12=T2−T1.{\displaystyle \ A_{12}=T_{2}-T_{1}.}

Это равенство актуально как для классической, так и для релятивистской механики (получается интегрированием выражения  F→ds→=dT{\displaystyle \ {\vec {F}}{\rm {d}}{\vec {s}}={\rm {d}}T} между состояниями 1 и 2).

Соотношение кинетической и внутренней энергии[править | править код]

Кинетическая энергия зависит от того, с каких позиций рассматривается система. Если рассматривать макроскопический объект (например, твёрдое тело видимых размеров) как единое целое, можно говорить о такой форме энергии, как внутренняя энергия. Кинетическая энергия в этом случае появляется лишь тогда, когда тело движется как целое.

То же тело, рассматриваемое с микроскопической точки зрения, состоит из атомов и молекул, и внутренняя энергия обусловлена движением атомов и молекул и рассматривается как следствие теплового движения этих частиц, а абсолютная температура тела прямо пропорциональна средней кинетической энергии такого движения атомов и молекул. Коэффициент пропорциональности — постоянная Больцмана.

1. ↑ ^{1 2 3 4} Айзерман, 1980, с. 49.
2. ↑ ^{1 2} Сивухин Д. В. § 22. Работа и кинетическая энергия. // Общий курс физики. — М.: Наука, 1979. — Т. I. Механика. — С. 131. — 520 с.
3. ↑ Тарг С. М. Кинетическая энергия // Физическая энциклопедия : [в 5 т.] / Гл. ред. А. М. Прохоров. — М.: Советская энциклопедия, 1990. — Т. 2: Добротность — Магнитооптика. — С. 360. — 704 с. — 100 000 экз. — ISBN 5-85270-061-4.
4. ↑ Батыгин В. В., Топтыгин И. Н. 3.2. Кинематика релятивистских частиц // Современная электродинамика, часть 1. Микроскопическая теория. — Москва-Ижевск: Институт компьютерных исследований, 2002. — С. 238. — 736 с. — 1000 экз. — ISBN 5-93972-164-8.
5. ↑ Мах Э.  Механика. Историко-критический очерк её развития. — Ижевск: «РХД», 2000. — С. 252. — 456 с. — ISBN 5-89806-023-5.
6. ↑ Голубева О. В. Теоретическая механика. — М.: «Высшая школа», 1968. — С. 243—245.
7. ↑ ^{1 2} Монин А. С., Яглом А. М. Статистическая гидромеханика. Часть 1. — М.: Наука, 1965. — 639 с.
8. ↑ Блохинцев Д. И. Основы квантовой механики, 5-е изд. Наука, 1976. — 664 с., см. § 26.
9. ↑ Айзерман, 1980, с. 54.
10. ↑ Сорокин В. С. «Закон сохранения движения и мера движения в физике» // УФН, 59, с. 325—362, (1956)

Физика: уроки, тесты, задания.

Физика: уроки, тесты, задания.

1. 1. Введение. Макро- и микромир. Числа со степенью 10

   2. Наблюдения, опыты, измерения, гипотеза, эксперимент

   3. Физические величины. Международная система единиц

2. 1. Механическое движение. Траектория и путь

   2. Скорость. Неравномерное движение. Средняя скорость

   3. Инерция

   4. Взаимодействие тел. Масса тела. Единицы массы. Измерение массы тела на весах

   5. Плотность вещества. Расчёт массы и объёма тела по его плотности

   6. Сила. Сила тяжести

   7. Свободное падение. Вес тела

   8. Измерение силы с помощью динамометра

   9. Деформации тел. Сила упругости. Закон Гука

   10. Взаимодействие тел. Сила трения

3. 1. Механическая работа

   2. Мощность

   3. Рычаг. Простые механизмы

   4. Блок

   5. Коэффициент полезного действия

   6. Энергия

4. 1. Строение вещества. Молекулы и атомы

   2. Диффузия

   3. Притяжение и отталкивание молекул. Смачивание и капиллярность

   4. Агрегатные состояния вещества

5. 1. Давление и сила давления. Единицы измерения

   2. Давление твёрдых тел. Способы уменьшения и увеличения давления

   3. Давление газа. Применение сжатого воздуха

   4. Атмосферное давление и его измерение. Опыт Торричелли

   5. Давление в жидкости. Закон Паскаля

   6. Гидростатическое давление. Давление на дне морей и океанов

   7. Сообщающиеся сосуды. Водопровод. Шлюзы

   8. Гидравлический пресс. Насосы

   9. Закон Архимеда

   10. Действие жидкости на погружённое в неё тело. Плавание тел

   11. Выталкивающая сила в газах. Воздухоплавание

6. Класс заполнен на 100 %

1. 1. Тепловое движение. Термометр. Связь температуры тела со скоростью движения молекул

   2. Внутренняя энергия. Два способа изменения внутренней энергии: работа и теплопередача

   3. Виды теплопередачи

   4. Количество теплоты

   5. Удельная теплоёмкость вещества

   6. Удельная теплота сгорания топлива

   7. Закон сохранения энергии в механических и тепловых процессах

2. 1. Плавление и отвердевание тел. Температура плавления

   2. Удельная теплота плавления

   3. Испарение и конденсация

   4. Относительная влажность воздуха и её измерение

   5. Кипение. Температура кипения. Удельная теплота парообразования

   6. Объяснение изменений агрегатных состояний вещества

   7. Преобразования энергии в тепловых машинах

   8. Экологические проблемы использования тепловых машин

3. 1. Электризация тел. Два рода электрических зарядов

   2. Проводники, диэлектрики и полупроводники

   3. Взаимодействие заряженных тел. Электрическое поле

   4. Закон сохранения электрического заряда

   5. Дискретность электрического заряда. Электрон. Строение атомов

   6. Электрический ток. Электрическая цепь. Гальванические элементы. Аккумуляторы

   7. Электрический ток в металлах. Полупроводниковые приборы

   8. Сила тока. Амперметр

   9. Электрическое напряжение. Вольтметр

   10. Электрическое сопротивление. Закон Ома для участка электрической цепи

   11. Удельное сопротивление. Реостаты

   12. Последовательное и параллельное соединение проводников

   13. Работа и мощность тока

   14. Количество теплоты, выделяемое проводником с током

   15. Счётчик электрической энергии

   16. Лампа накаливания. Электронагревательные приборы

   17. Расчёт электроэнергии, потребляемой бытовыми электроприборами

   18. Короткое замыкание. Плавкие предохранители

4. 1. Магнитное поле тока

   2. Электромагниты и их применение

   3. Постоянные магниты. Магнитное поле Земли

   4. Действие магнитного поля на проводник с током. (Электродвигатель. Динамик и микрофон)

5. 1. Источники света. Прямолинейность распространения света

   2. Отражение света. Закон отражения. Плоское зеркало

   3. Преломление света

   4. Линза. Фокусное расстояние линзы. Построение изображений, даваемых тонкой линзой

   5. Оптическая сила линзы. Глаз как оптическая система. Оптические приборы

6. Класс заполнен на 100 %

1. 1. Материальная точка (Система отсчёта)

   2. Перемещение. Скорость прямолинейного равномерного движения

   3. Прямолинейное равноускоренное движение: мгновенная скорость, ускорение, перемещение

   4. Скорость прямолинейного равноускоренного движения. График скорости

   5. Графики зависимости кинематических величин от времени при равноускоренном движении

2. 1. Относительность механического движения

   2. Первый закон Ньютона

   3. Второй закон Ньютона

   4. Третий закон Ньютона

   5. Свободное падение

   6. Невесомость

   7. Закон всемирного тяготения

3. 1. Импульс тела

   2. Закон сохранения импульса

   3. Реактивное движение. Ракеты

4. 1. Колебательное движение. Свободные колебания. Амплитуда, частота, период колебаний

   2. Колебательная система. Колебания груза на пружине. Математический маятник

   3. Превращение энергии при колебательном движении

   4. Затухающие колебания. Вынужденные колебания. Резонанс

   5. Поперечные и продольные волны. Длина волны

   6. Звуковые волны. Скорость звука

   7. Высота, тембр и громкость звука. Звуковой резонанс

5. 1. Электромагнитная индукция

   2. Направление индукционного тока. Правило Ленца. Самоиндукция

   3. Трансформатор. Передача электрической энергии на расстояние

   4. Конденсатор. Колебательный контур. Получение электромагнитных колебаний

   5. Электромагнитная природа света

6. 1. Радиоактивность как доказательство сложного строения атома. Опыты Резерфорда. Ядерная модель

   2. Протонно-нейтронная модель ядра. Физический смысл зарядового и массового чисел

   3. Радиоактивные превращения атомных ядер

   4. Методы наблюдения и регистрации частиц в ядерной физике

   5. Деление ядер урана. Цепная реакция

7. В дальнейшем в этом классе появятся…