ТОП-100 Важнейших формул по физике — Физика — Теория, тесты, формулы и задачи
Знание формул по физике является основой для успешной подготовки и сдачи различных экзаменов, в том числе и ЦТ или ЕГЭ по физике. Формулы по физике, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении физических задач. На этой странице сайта представлены 100 важнейших формул по физике.
Изучать ТОП-100 Важнейших формул по физике онлайн:
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день.
Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач. - Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Основные формулы по физике — Физика — Теория, тесты, формулы и задачи
Формулы по физике, которые надежно хранятся в памяти ученика — это основной инструмент, которым он должен оперировать при решении физических задач. На этой странице сайта представлены основные формулы по школьной физике в двух частях. В первой части Вы найдете самые важные физические формулы, а во второй — дополнительный набор полезных формул по физике.
Оглавление:
Основные формулы по школьной физике (Часть I)
К оглавлению…
Основные формулы по школьной физике (Часть II)
К оглавлению…
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
- Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию.
Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка. Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Еще больше физических формул и свойств — Физика — Теория, тесты, формулы и задачи
На этой странице представлен исчерпывающий список формул по физике и важнейших физических свойств для успешной подготовки к ЦТ или ЕГЭ.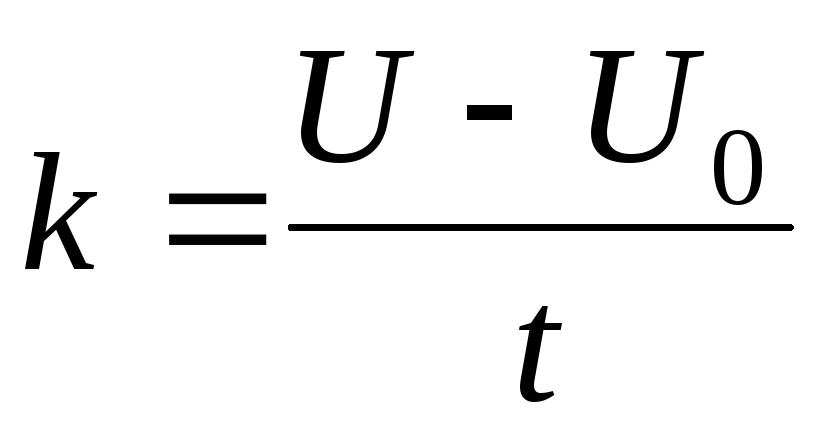
Изучать еще больше формул по физике и физических свойств онлайн:
Как успешно подготовиться к ЦТ по физике и математике?
Для того чтобы успешно подготовиться к ЦТ по физике и математике, среди прочего, необходимо выполнить три важнейших условия:
- Изучить все темы и выполнить все тесты и задания приведенные в учебных материалах на этом сайте. Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
- Выучить все формулы и законы в физике, и формулы и методы в математике. На самом деле, выполнить это тоже очень просто, необходимых формул по физике всего около 200 штук, а по математике даже чуть меньше. В каждом из этих предметов есть около десятка стандартных методов решения задач базового уровня сложности, которые тоже вполне можно выучить, и таким образом, совершенно на автомате и без затруднений решить в нужный момент большую часть ЦТ. После этого Вам останется подумать только над самыми сложными задачами.
- Посетить все три этапа репетиционного тестирования по физике и математике. Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.
Для этого нужно всего ничего, а именно: посвящать подготовке к ЦТ по физике и математике, изучению теории и решению задач по три-четыре часа каждый день. Дело в том, что ЦТ это экзамен, где мало просто знать физику или математику, нужно еще уметь быстро и без сбоев решать большое количество задач по разным темам и различной сложности. Последнему научиться можно только решив тысячи задач.
Каждый РТ можно посещать по два раза, чтобы прорешать оба варианта. Опять же на ЦТ, кроме умения быстро и качественно решать задачи, и знания формул и методов необходимо также уметь правильно спланировать время, распределить силы, а главное правильно заполнить бланк ответов, не перепутав ни номера ответов и задач, ни собственную фамилию. Также в ходе РТ важно привыкнуть к стилю постановки вопросов в задачах, который на ЦТ может показаться неподготовленному человеку очень непривычным.Успешное, старательное и ответственное выполнение этих трех пунктов, а также ответственная проработка итоговых тренировочных тестов, позволит Вам показать на ЦТ отличный результат, максимальный из того, на что Вы способны.
Нашли ошибку?
Если Вы, как Вам кажется, нашли ошибку в учебных материалах, то напишите, пожалуйста, о ней на электронную почту (адрес электронной почты здесь). В письме укажите предмет (физика или математика), название либо номер темы или теста, номер задачи, или место в тексте (страницу) где по Вашему мнению есть ошибка.
Также опишите в чем заключается предположительная ошибка. Ваше письмо не останется незамеченным, ошибка либо будет исправлена, либо Вам разъяснят почему это не ошибка.
Квадратное уравнение с чётным вторым коэффициентом
Если в квадратном уравнении ax2 + bx + c = 0 второй коэффициент b является чётным, то решение этого уравнения можно немного упростить. Дискриминант для такого уравнения можно вычислить по формуле D1 = k2 − ac, а корни по формулам и .
Примеры
Решим квадратное уравнение x2 + 6x − 16 = 0. В нём второй коэффициент является чётным. Чтобы воспользоваться формулами для чётного коэффициента, нужно сначала узнать чему равна переменная k.
Любое четное число n можно представить в виде произведения числа 2 и числа k, то есть 2k.
n = 2k
Например, число 10 можно представить как 2 × 5.
10 = 2 × 5
В этом произведении k = 5.
Число 12 можно представить как 2 × 6.
12 = 2 × 6
В этом произведении k = 6.
Число −14 можно представить как 2 × (−7)
В этом произведении k = −7.
Как видим, сомножитель 2 не меняется. Меняется только сомножитель k.
В уравнении x2 + 6x − 16 = 0 вторым коэффициентом является число 6. Это число можно представить как 2 × 3. В этом произведении k = 3. Теперь можно воспользоваться формулами для чётного коэффициента.
Найдем дискриминант по формуле D1 = k2 − ac
D1 = k2 − ac = 32 − 1 × (−16) = 9 + 16 = 25
Теперь вычислим корни по формулам: и .
Значит корнями уравнения x2 + 6x − 16 = 0 являются числа 2 и −8.
В отличие от стандартной формулы для вычисления дискриминанта (D=b2 − 4ac), в формуле D1 = k2 − ac не нужно выполнять умножение числа 4 на ac.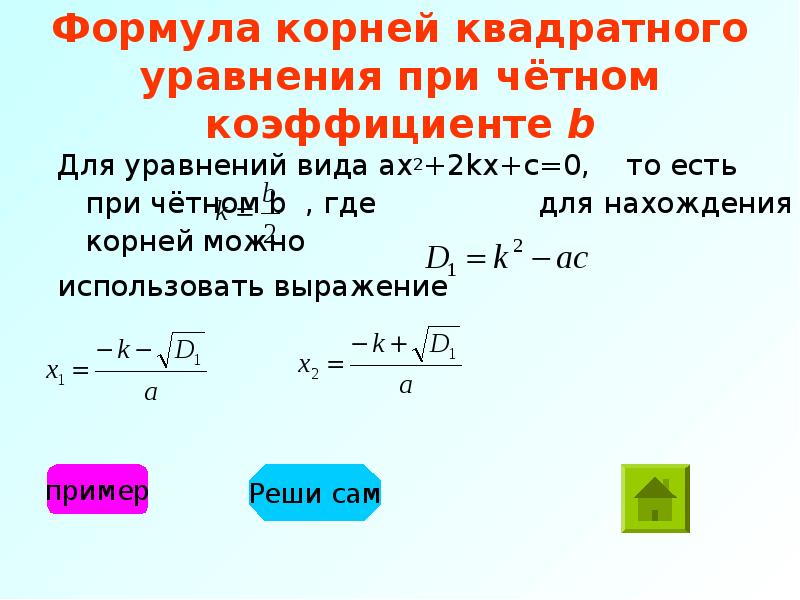
И в отличие от формул и формулы и не содержат в знаменателе множитель 2 что опять же освобождает нас от дополнительных вычислений.
Пример 2. Решить квадратное уравнение 5x2 − 6x + 1=0
Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−3). То есть k = −3. Найдём дискриминант по формуле D1 = k2 − ac
D1 = k2 − ac = (−3)2 − 5 × 1 = 9 − 5 = 4
Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и
Пример 3. Решить квадратное уравнение x2 − 10x − 24 = 0
Второй коэффициент является чётным числом. Его можно представить в виде 2 × (−5). То есть k = −5. Найдём дискриминант по формуле D1 = k2 − ac
D1 = k2 − ac = (−5)2 − 1 × (−24) = 25 + 24 = 49
Дискриминант больше нуля.
Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и
Обычно для определения числа k поступают так: делят второй коэффициент на 2.
Действительно, если второй коэффициент b является чётным числом, то его можно представить как b = 2k. Чтобы из этого равенства выразить сомножитель k, нужно произведение b разделить на сомножитель 2
Например, в предыдущем примере для определения числа k можно было просто разделить второй коэффициент −10 на 2
Пример 5. Решить квадратное уравнение
Коэффициент b равен . Это выражение состоит из множителя 2 и выражения . То есть оно уже представлено в виде 2k. Получается, что
Найдём дискриминант по формуле D1 = k2 − ac
Дискриминант больше нуля. Значит уравнение имеет два корня. Для их вычисления воспользуемся формулами и
При вычислении корня уравнения получилась дробь, в которой содержится квадратный корень из числа 2.
Квадратный корень из числа 2 извлекается только приближённо. Если выполнить это приближённое извлечение, а затем сложить результат с 2, и затем разделить числитель на знаменатель, то получится не очень красивый ответ.
В таких случаях ответ записывают, не выполняя приближённых вычислений. В нашем случае первый корень уравнения будет равен .
Вычислим второй корень уравнения:
Вывод формул
Давайте наглядно увидим, как появились формулы для вычисления корней квадратного уравнения с чётным вторым коэффициентом.
Рассмотрим квадратное уравнение ax2 + bx + c = 0. Допустим, что коэффициент b является чётным числом. Тогда его можно обозначить как 2k
b = 2k
Заменим в уравнении ax2 + bx + c = 0 коэффициент b на выражение 2k
ax2 + 2kx + c = 0
Теперь вычислим дискриминант по ранее известной формуле:
D = b2 − 4ac = (2k)2 − 4ac = 4k2 − 4ac
Вынесем в получившемся выражении за скобки общий множитель 4
D = b2 − 4ac = (2k)2 − 4ac = 4k2 − 4ac = 4(k2 − ac)
Что можно сказать о получившемся дискриминанте? При чётном втором коэффициенте он состоит из множителя 4 и выражения k2 − ac.
В выражении 4(k2 − ac) множитель 4 постоянен. Значит знак дискриминанта зависит от выражения k2 − ac. Если это выражение меньше нуля, то и D будет меньше нуля. Если это выражение больше нуля, то и D будет больше нуля. Если это выражение равно нулю, то и D будет равно нулю.
То есть выражение k2 − ac это различитель — дискриминант. Такой дискриминант принято обозначать буквой D1
D1 = k2 − ac
Теперь посмотрим как выводятся формулы и .
В нашем уравнении ax2 + bx + c = 0 коэффициент b заменён на выражение 2k. Воспользуемся стандартными формулами для вычисления корней. То есть формулами и . Только вместо b будем подставлять 2k. Также на забываем, что D у нас равно выражению 4(k2 − ac)
Но ранее было сказано, что выражение k2 − ac обозначается через D1.
Тогда в наших преобразованиях следует сделать и эту замену:
Теперь вычислим квадратный корень, расположенный в числителе. Это квадратный корень из произведения — он равен произведению корней. Остальное перепишем без изменений:
Теперь в получившемся выражении вынесем за скобки общий множитель 2
Сократим получившуюся дробь на 2
Аналогично вывóдится формула для вычисления второго корня:
Задания для самостоятельного решения
Задание 1. Решить уравнение:
Решение:
Ответ: 1; 0,6
Задание 2. Решить уравнение:
Решение:
Ответ:Задание 3. Решить уравнение:
Решение:
Ответ: 1; −1,4
Задание 4. Решить уравнение:
Решение:
Ответ:Задание 5. Решить уравнение:
Решение:
Ответ:Задание 6. Решить уравнение:
Решение:
Ответ:Задание 7.
Решить уравнение:
Решение:
Ответ:Понравился урок?
Вступай в нашу новую группу Вконтакте и начни получать уведомления о новых уроках
Возникло желание поддержать проект?
Используй кнопку ниже
Навигация по записям
Калейдоскоп формул для пи
Калейдоскоп формул для пи«…я считал, что есть две математики — алгебраическая и геометрическая, и что геометрическая математика принципиально “трансцендентна” для алгебраической. Возьмите, например, формулу длины окружности — там есть “геометрическое” число $\pi$. Или, скажем, синус — он определяется чисто геометрически.
Когда я обнаружил, что синус можно записать алгебраически в виде ряда, барьер обрушился, математика стала единой.»
— из интервью И. М. Гельфанда
«Калейдоскоп» ниже состоит из нескольких «алгебраических» формул для $\pi$ с краткими комментариями.
2$ (последнее равенство — это, по сути, основная теорема арифметики).
Более серьезное обсуждение вопроса можно найти, например, в книге «Введение в теорию чисел» Харди и Райта.
4. Формула Валлиса
Если подставить $x=\pi/2$ в разложение Эйлера синуса в бесконечное произведение, то получается равенство $$ \frac\pi2= \frac{2\cdot2\cdot4\cdot4\cdot6\cdot6\cdot\ldots}{1\cdot3\cdot3\cdot5\cdot5\cdot7\cdot\ldots} $$ Впрочем, Джон Валлис нашел эту формулу уже в середине XVII века, почти за 100 лет до формулы Эйлера, вычисляя некоторые интегралы.
В упоминавшейся выше статье Ягломов при помощи элементарной тригонометрии доказывается и формула Валлиса. А J. Wästlund нашел и доказательство (в духе «геометрического суммирования»), непосредственно связывающее произведение Валлиса с площадью круга — см. его статью (AMM, 2007) или лекцию Д. Кнута.
При помощи формулы Валлиса можно доказать, что если подкинуть монету $2n$ раз, то вероятность того, что орлов и решек выпадет в точности поровну, приблизительно равна $1/\sqrt{\pi n}$.
наверх
Закон гука сила упругости — определение, формулы
Сила: что это за величина
В повседневной жизни мы часто встречаем, как любое тело деформируется (меняет форму или размер), ускоряется или тормозит, падает. В общем, чего только с разными телами в реальной жизни не происходит. Причиной любого действия или взаимодействия является сила.
Сила — это физическая векторная величина, которую воздействует на данное тело со стороны других тел.
Она измеряется в Ньютонах — это единица измерения названа в честь Исаака Ньютона.
Сила — величина векторная. Это значит, что, помимо модуля, у нее есть направление. От того, куда направлена сила, зависит результат.
Вот стоите вы на лонгборде: можете оттолкнуться вправо, а можете влево — в зависимости от того, в какую сторону оттолкнетесь, результат будет разный. В данном случае результат выражается в направлении движения.
Деформация
Деформация — это изменение формы и размеров тела (или части тела) под действием внешних сил
Происходит деформация из-за различных факторов: при изменении температуры, влажности, фазовых превращениях и других воздействиях, вызывающих изменение положения частиц тела.
Деформация является деформацией, пока сила, вызывающая эту деформацию, не приведет к разрушению.
На появление того или иного вида деформации большое влияние оказывает характер приложенных к телу напряжений. Одни процессы деформации связаны с преимущественно перпендикулярно (нормально) приложенной силой, а другие — преимущественно с силой, приложенной по касательной.
По характеру приложенной к телу нагрузки виды деформации подразделяют следующим образом:
- Деформация растяжения
- Деформация сжатия
- Деформация сдвига
- Деформация при кручении
- Деформация при изгибе
Сила упругости: Закон Гука
Давайте займемся баскетболом.
Начнем набивать мяч о пол, он будет чудесно отскакивать. Этот удар можно назвать упругим. Если при ударе деформации не будет совсем, то он будет называться абсолютно упругим.
Если вы перепутали мяч и взяли пластилиновый, он деформируется при ударе и не оттолкнется от пола. Такой удар будет называться абсолютно неупругим.
Деформацию тоже можно назвать упругой (при которой тело стремится вернуть свою форму и размер в изначальное состояние) и неупругой (когда тело не стремится вернуться в исходное состояние).
При деформации возникает сила упругости— это та сила, которая стремится вернуть тело в исходное состояние, в котором оно было до деформации.
Сила упругости, возникающая при упругой деформации растяжения или сжатия тела, пропорциональна абсолютному значению изменения длины тела. Выражение, описывающее эту закономерность, называется законом Гука.
Закон Гука Fупр = kx Fупр — сила упругости [Н] |
Важно раз
Изменение длины может обозначаться по-разному в различных источниках. Варианты обозначений: x, ∆x, ∆l.
Это равноценные обозначения — можно использовать любое удобное.
Важно два
Поскольку сила упругости направлена против направления силы, с которой это тело деформируется (она же стремится все «распрямить»), в Законе Гука должен быть знак минус. Часто его и можно встретить в разных учебниках. Но поскольку мы учитываем направление этой силы при решении задач, знак минус можно не ставить.
Задачка
На сколько удлинится рыболовная леска жесткостью 0,3 кН/м при поднятии вверх рыбы весом 300 г?
Решение:
Сначала определим силу, которая возникает, когда мы что-то поднимаем.
Это, конечно, сила тяжести.
Не забываем массу представить в единицах СИ – килограммах.
СИ — международная система единиц.
«Перевести в СИ» означает перевод всех величин в метры, килограммы, секунды и другие единицы измерения без приставок. Исключение составляет килограмм с приставкой «кило».
m = 300 г = 0,3 кг
Если принять ускорение свободного падения равным 10 м/с*с, то модуль силы тяжести равен :
F = mg = 0,3*10 = 3 Н.
Тогда из Закона Гука выразим модуль удлинения лески:
F = kx
Выражаем модуль удлинения:
x = F/k
Подставим числа, жесткость лески при этом выражаем в Ньютонах:
x=3/(0,3 * 1000)=0,01 м = 1 см
Ответ: удлинение лески равно 1 см.
Параллельное и последовательное соединение пружин
В Законе Гука есть такая величина, как коэффициент жесткости— это характеристика тела, которая показывает его способность сопротивляться деформации. Чем больше коэффициент жесткости, тем больше эта способность, а как следствие из Закона Гука — и сила упругости.
Чаще всего эта характеристика используется для описания жесткости пружины. Но если мы соединим несколько пружин, то их суммарная жесткость нужно будет рассчитать. Разберемся, каким же образом.
Последовательное соединение системы пружин
Последовательное соединение характерно наличием одной точки соединения пружин.
При последовательном соединении общая жесткость системы уменьшается. Формула для расчета коэффициента упругости будет иметь следующий вид:
Коэффициент жесткости при последовательном соединении пружин 1/k = 1/k₁ + 1/k₂ + … + 1/k_i k — общая жесткость системы [Н/м] k1, k2, …, — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-] |
Параллельное соединение системы пружин
Последовательное соединение характерно наличием двух точек соединения пружин.
В случае когда пружины соединены параллельно величина общего коэффициента упругости системы будет увеличиваться. Формула для расчета будет выглядеть так:
Коэффициент жесткости при параллельном соединении пружин k = k₁ + k₂ + … + k_i k — общая жесткость системы [Н/м] k1, k2, …, ki — отдельные жесткости каждого элемента [Н/м] i — общее количество всех пружин, задействованных в системе [-] |
Задачка
Какова жесткость системы из двух пружин, жесткости которых k₁ = 100 Н/м, k₂ = 200 Н/м, соединенных: а) параллельно; б) последовательно?
Решение:
а) Рассмотрим параллельное соединение пружин.
При параллельном соединении пружин общая жесткость
k = k₁ + k₂ = 100 + 200 = 300 Н/м
б) Рассмотрим последовательное соединение пружин.
При последовательном соединении общая жесткость двух пружин
1/k = 1/k₁ + 1/k₂ + … + 1/k
1/k = 1/100 + 1/200 = 0,01 + 0,005 = 0,015
k = 1000/15 = 200/3 ≃ 66,7 Н/м
Очень-очень важно!
Не забудь при расчете жесткости при последовательном соединении в конце перевернуть дробь.
График зависимости силы упругости от жесткости
Закон Гука можно представить в виде графика. Это график зависимости силы упругости от изменения длины и по нему очень удобно можно рассчитать коэффициент жесткости. Давай рассмотрим на примере задач.
Задачка 1
Определите по графику коэффициент жесткости тела.
Решение:
Из Закона Гука выразим коэффициент жесткости тела:
F = kx
k = F/x
Снимем значения с графика. Важно выбрать одну точку на графике и записать для нее значения обеих величин.
Например, возьмем вот эту точку.
В ней удлинение равно 2 см, а сила упругости 2 Н.
Переведем сантиметры в метры: 2 см = 0,02 м И подставим в формулу: k = F/x = 2/0,02 = 100 Н/м
Ответ:жесткость пружины равна 100 Н/м
Задачка 2
На рисунке представлены графики зависимости удлинения от модуля приложенной силы для стальной (1) и медной (2) проволок равной длины и диаметра. Сравнить жесткости проволок.
Решение:
Возьмем точки на графиках, у которых будет одинаковая сила, но разное удлинение.
Мы видим, что при одинаковой силе удлинение 2 проволоки (медной) больше, чем 1 (стальной). Если выразить из Закона Гука жесткость, то можно увидеть, что она обратно пропорциональна удлинению.
k = F/x
Значит жесткость стальной проволоки больше.
Ответ: жесткость стальной проволоки больше медной.
Размещения, перестановки, сочетания с повторениями. Формула включения — исключения
Размещения с повторениями
Определение. Отображение множества первых натуральных чисел в данное множество , называется размещением с повторениями, составленным из данных элементов по .
Размещения с повторениями называются также конечными последовательностями.
Два размещения с повторениями одинаковы тогда и только тогда, когда на одинаковых местах находятся одни и те же элементы.
Если в размещении с повторениями некоторый элемент ставится в соответствие различным натуральным числам, т.е., иначе говоря, данный элемент занимает различных мест, то говорят, что этот элемент повторяется в размещении раз.
Пример. Всевозможные размещения с повторениями из трех элементов по 2:
Теорема. Число всевозможных размещений с повторениями из элементов по равно
Доказательство. По индукции. При теорема верна, так как сами элементы составляют всевозможные размещения элементов по одному, то число этих размещений равно .
Предположим, что число размещений с повторениями из элементов по равно . Составим из данных элементов всевозможные размещения с повторениями по элементу. Во всяком размещении с повторениями по элементу
первые элементов
образуют некоторое размещение с повторениями из по элементов. В качестве последнего -го элемента может быть взят любой из элементов. При различных выборах получаются различные размещения. Кроме того, два различные размещения -го порядка дают два различные размещения -го порядка.
Таким образом, число всех размещений -го порядка равно
Задача. Имеется различных книг, каждая в экземплярах. Сколькими способами может быть сделан выбор книг из числа данных?
Перестановки с повторениями
Всякое размещение с повторениями, в котором элемент повторяется раз, элемент повторяется раз и т.д. элемент повторяется раз, где , , , — данные числа, называется перестановкой с повторениями порядка
в которой данные элементы повторяются соответственно , , раз.
Теорема. Число различных перестановок с повторениями из элементов , в которых элементы повторяются соответственно раз, равно
Доказательство. Если мы будем считать все элементов перестановки с повторениями различными, то всего различных вариантов перестановок элементов — . Однако среди этих перестановок не все различны. В самом деле, все элементы мы можем переставлять местами друг с другом, и от этого перестановка не изменится. Точно так же, можем переставлять элементы , , , . Таким образом, всякая перестановка может быть записана способами. Следовательно, число различных перестановок с повторениями равно
Задача. Дано различных предметов. Сколькими способами можно разбить эти предметы на 3 группы так, чтобы первая группа содержала предметов, вторая предметов, а третья предметов?
Показать решение
Ответ.
Сочетания с повторениями
Определение. Если каждому элементу некоторого конечного множества поставлено в соответствие целое неотрицательное число — кратность данного элемента, то говорят, что задано сочетание с повторениями. Сумма кратностей всех элементов называется порядком сочетания.
Всякое сочетание с повторениями -го порядка, составленное из множества, содержащего элементов, называется также сочетанием с повторением из элементов по .
Если — кратности элементов , то по определению есть порядок сочетания
Теорема. Число сочетаний с повторениями из элементов по выражается формулой
Пример. В кондитерском магазине продавались 4 сорта пирожных: наполеоны, эклеры, песочные и картошка. Сколькими способами можно купить 7 пирожных?
Решение. Положим пирожные в коробку, а чтобы они не перепутались, разделим их картонными разделителями. Нужно 3 разделителя. Обозначения: 0 (картонки-разделители) и 1 — пирожные. Примерная покупка: 1110101101 — три наполеона, 1 эклер, 2 песочных и 1 картошка.
Итак два класса объектов 1 (7 штук) и 0 (3 штуки) — покупка — 10 объектов.
Два способа рассуждения:
(1) задача сводится к выбору мест для 7 пирожных (или для 3 разделителей) среди 10 объектов.
(2) другой способ рассуждения (эквивалентный). Надо разбить 10 мест на две группы: для 7 пирожных и 3 разделителей.
В чем особенность: объекты повторяются, причем один эклер на вкус неотличим от другого. Отсюда название: сочетания с повторениями. Можно представлять себе, что пирожные непрерывно пекут, так что они не переводятся, сколько ни ешь. Это совсем другая ситуация, чем в обычных сочетаниях!!!
Пусть заданы два числа: — число выбираемых элементов, и — число типов элементов, из которых производится выбор. Число сочетаний с повторениями порядка из элементов типов равно числу способов выбора мест для собственно выбираемых элементов различных классов, или, что то же: для разделителей между ними.
Итак, основная формула:
Задача. Имеется одинаковых предметов. Сколькими способами можно распределить эти предметы между лицами?
Сочетания с повторениями с дополнительными условиями
Сколько существует сочетания с повторениями таких, что в них обязательно входят элементы фиксированных типов?
Сразу возьмем по одному элементу указанного типа, и тогда уже сразу окажутся заняты мест. Остальные мест можно заполнять элементами прежних типов.
В частности, пусть число типов — числа выбранных элементов. Сколько существует сочетаний с повторениями, так что представлены хотя бы по одному все типы элементов?
Пример. шаров размещаются по ящикам. Сколько существует способов разместить их так, что пустых ящиков нет?
Решение. Пусть нолики — шарики, а единички — стенки ящиков (потребуется единичек). Две единички сразу кладем по краям.
Теперь положим между ними шарики-нолики, а далее нужно заполнить некоторые промежутки между ними так, чтобы между любыми двумя ноликами находилась не более одной единички. Значит, из промежутков между шариками нужно выбрать места для единичек. Всего таких способов .
Метод координат. Подсчет числа путей
Рассмотрим координатную сетку: двигаясь по ней, помечаем каждый перекресток — производим суммирование числа возможных путей, ведущих на каждый перекресток. Получаем известный треугольник Паскаля.
Поскольку на перекресток на уровне (считая сверху и принимая верхний уровень за нулевой) ведет путей (число способов выбрать движений направо вниз из общего числа движений вниз), то свойство суммирования путей на перекрестке можно записать как
По прежнему остается справедливым свойство симметрии .
Формула включения — исключения
Определение. Число элементов множества называется мощностью множества и обозначается .
Теорема. Пусть даны множества . Тогда количество элементов в объединении этих множеств можно найти по формуле:
Доказательство проводится по индукции. Пусть . Нужно доказать формулу
Действительно, множество состоит из всех элементов множества и тех элементов множества , которые не содержатся в множестве . Тогда, сложив количества элементов во множествах и , мы два раза посчитаем количество элементов, общих для множеств и .
Предположим, что формула включения — исключения справедлива для множеств.
Докажем ее для множеств. Множество можно представить в виде
Тогда получаем (первое равенство по формуле включения — исключения для двух множеств):
Используя формулу
и формулу включения — исключения для множеств, получаем
В эту формулу подставляем выражение, полученное ранее, и теорема доказана.
Задачи.
1. Есть три билета в различные театры. Сколькими способами они могут быть распределены между 25 школьниками, если каждый школьник может получить только один билет?
2. Есть три билета на КВН 1 апреля. Сколькими способами они могут быть распределены между 25 школьниками (более одного билета в руки не давать!!!)?
3. Телефонный номер состоит из 7 цифр. Насколько легче угадать правильный номер, если знать, что все его цифры различны?
4. В буфете продаются 5 сортов пирожков: с яблоками, с капустой, картошкой, мясом и грибами (цена всех пирожков одинакова). Скольким числом способов можно сделать покупку из 10 пирожков?
5. (Продолжение). Скольким числом способов можно сделать покупку так, чтобы попробовать пирожков всех видов?
6. (Продолжение). Скольким числом способов можно сделать покупку так, чтобы в нее вошло не менее двух пирожков с мясом и хотя бы один пирожок с яблоками?
7. Скольким числом способов можно вывести на арену цирка 5 львов и 4 тигра так, чтобы никакие два тигра не шли друг за другом (оказавшись рядом, они начинают драться)?
8. За круглым столом короля Артура сидят 12 рыцарей. Из них каждый враждует со своими соседями. Для участия в спецоперации по освобождению заколдованной принцессы нужно выбрать 5 рыцарей, но при этом нельзя посылать вместе рыцарей, враждующих друг с другом. Скольким числом способов это можно сделать?
9. Докажите формулу
10. Докажите, что число различных решений уравнения
в неотрицательных целых числах равно .
11. Докажите, что число различных решений уравнения
в натуральных числах равно .
12. Сколькими способами можно разложить 15 одинаковых шаров по 5 различным ящикам так, чтобы оказалось не более двух пустых ящиков?
13. Сколькими способами можно разложить 20 одинаковых шаров по 5 различным ящикам так, чтобы в каждом ящике оказалось не менее двух шаров?
14. Сколькими способами можно разложить 20 одинаковых шаров по 6 различным ящикам так, чтобы в каждом ящике оказалось не более 5 шаров?
15. Докажите, что число таких перестановок чисел , которые удовлетворяют условию при всех , равно
n Выберите формулу k — Выучите формулу комбинаций
«Выбрать» означает «выбрать». «n выбрать k формула» используется для определения количества способов выбора k вещей из n вещей. Иногда мы предпочитаем выбирать, но не забываем их заказывать. Например, вы собираете чемоданы в поездку и хотите взять с собой 5 платьев из 10 имеющихся у вас новых платьев. Это можно сделать разными способами, неважно, в каком порядке вы их выбрали, но все имеет значение, какие платья вы выбрали.Давайте изучим формулу n выбираем k вместе с несколькими решенными примерами.
Что такое n Choose k Formula?
«n выберите k» обозначается C (n, k) (или) \ (n_ {C_ {k}} \) (или) \ (_ {n} C_ {k} \) (или) \ (\ left (\ begin {array} {l} n \\ k \ end {array} \ right) \). Он также известен как биномиальный коэффициент. Он используется, чтобы найти количество способов выбрать k разных вещей из n разных вещей. Формула n выберите k также известна как формула комбинаций (так мы называем способ выбора вещей, которые должны быть комбинацией).Эта формула включает факториалы.
Формула n Choose k:
C (N, К) = п! / [(п-к)! к! ]
Решенных примеров с использованием формулы n Choose k
Пример 1Найдите количество способов сформировать команду из 5 человек из 10.
Решение
Найти: Количество способов формирования команды из 5 человек из 10.
Здесь общее количество участников n = 10.
Количество членов, которые должны быть выбраны для формирования команды, равно k = 5.
Это можно сделать C (n, k) способами, и мы найдем это, используя формулу n choose k.
C (N, К) = п! / [(п-к)! к! ]
С (10, 5) = 10! / [(10 — 5)! 5! ]
C (10, 5) = (10 × 9 × 8 × 7 × 6 × 5!) / (5! 5!)
C (10, 5) = (10 × 9 × 8 × 7 × 6) / (5 × 4 × 3 × 2 × 1)
С (10, 5) = 252.
Ответ : Количество способов формирования команды из 5 человек = 252.
Пример 2На вечеринке 50 человек. Среди них каждый ровно один раз пожимает друг другу руку. Тогда сколько рукопожатий там должно произойти?
Решение
Чтобы найти: Общее количество рукопожатий на вечеринке.
Всего на вечеринке n = 50 человек.
Чтобы рукопожатие произошло, должны быть два человека.
Таким образом, количество рукопожатий равно количеству способов выбора 2 человек из 50 человек.Итак, k = 2.
Используя формулу n выберите k,
C (N, К) = п! / [(п-к)! к! ]
С (50, 2) = 50! / [(50 — 2)! 2! ]
С (50, 2) = (50 × 49 × 48!) / (48! 2!)
С (50, 2) = (50 × 49) / (2 × 1)
С (50, 2) = 1225,
Ответ: Количество рукопожатий = 1225.
Завершение
Площадь: С вы всегда выполняете одну и ту же процедуру каждый раз, когда находите вершину форма, процедура может быть выполнена символически (используя y = ax 2 + bx + c вместо ввода чисел), поэтому вы получите формулу, которую вы можно использовать вместо того, чтобы каждый раз выполнять процесс завершения квадрата.Вот как это выглядит:
Тогда вершина ( h , k ) для любого заданная квадратичная y = ax 2 + bx + c подчиняется формуле: Практически говоря, вы можете просто запомнить, что h = — b / (2 a ), а затем подставьте свое значение для « h » вернитесь к « y =», чтобы вычислить « k ».Если вам разрешено использовать эту формулу, вы сможете быстрее найти вершина, потому что простое вычисление h = — b / (2 a ), а затем нахождение k намного быстрее, чем завершение квадрата. С другой стороны, даже если вы не «должны» использовать эту формулу, вы все равно можете использовать это для проверки вашей работы. Если вы не уверены, завершили ли вы квадрат правильно на тесте, вы всегда можете использовать шаблонный ответ, чтобы проверить (или исправьте) все, что вы придумали. Однако если вы запомнили квадратичный Формула, ты можешь вероятно, легко запомнить формулу здесь для k . Дискриминант в квадратичной формуле: b 2 — 4 ac . Возьми отрицательное значение, чтобы получить обратное вычитание: формула для h имеет знаменатель 2 a ; удвойте это значение, чтобы получить знаменатель 4 a .Сложите их вместе, и вы получите формулу для k . << Предыдущий Наверх | 1 | 2 | Возвращение в индекс
| Этот урок можно распечатать для личного пользования. |
Формула постоянной пружины | Формулы постоянной пружины с использованием закона Гука
Формула постоянной пружины является неотъемлемой частью простого гармонического движения.Чтобы понять формулу жесткости пружины, сначала мы рассмотрим, что такое SHM или то, что мы называем простым гармоническим движением. После того, как мы подробно ознакомимся с концепцией SHM, мы рассмотрим, как пружины связаны с простым гармоническим движением, а затем, наконец, формулу жесткости пружины. Подробное объяснение, представленное здесь, также пытается разработать формулу жесткости пружины с использованием закона Гука.
Простое гармоническое движение
Простое гармоническое движение — это в основном повторяющееся движение вперед и назад через центральное положение, так что максимальное смещение на одной стороне этого положения равно максимальному смещению на другой стороне.Временной интервал каждой полной вибрации одинаков. Сила, отвечающая за движение, всегда направлена в сторону равновесия и прямо пропорциональна расстоянию от него.
Пружины обычно имеют ШМ. У пружин есть свои естественные «пружинные константы», которые определяют их жесткость. Закон Хука — известный закон, который объясняет SHM и дает формулу для приложенной силы с использованием постоянной пружины.
Закон Гука
Закон Гука определяет соотношение между приложенной силой и расстоянием, растянутым в пружине.Сила, необходимая для сжатия или растяжения пружины, прямо пропорциональна расстоянию, на которое она растягивается.
Согласно третьему закону движения Ньютона, он оттягивается с возвращающей силой при натяжении пружины. Эта восстанавливающая сила подчиняется закону Гука, который связывает силу пружины с постоянной пружиной.
(изображение будет загружено в ближайшее время)
Сила пружины = — (Постоянная пружины) x (Смещение)
\ [F = — \ frac {K} {X} \]
Знак минус указывает на обратное направление силы реакции.
Где,
F: Восстанавливающая сила пружины, направленная к равновесию.
K: Постоянная пружины в Нм-1.
X: смещение пружины из положения равновесия.
Константа пружины (K)
Теперь жесткость пружины определяется как сила, требуемая на единицу растяжения пружины. Зная жесткость пружины, мы можем легко определить, какое усилие необходимо для деформации пружины.
\ [K = — \ frac {F} {x} \]
Его единица измерения — Н / м (Ньютон на метр).
Как постоянная пружины зависит от длины?
Предположим, у нас есть пружина 6 см с жесткостью пружины k. Что произойдет, если мы разделим пружину на две части равного размера? Для одной из этих более коротких пружин будет новая жесткость пружины, которая будет составлять 2k. В более общем смысле, жесткость пружины обратно пропорциональна длине пружины, предполагая, что мы говорим о пружине из определенного материала и ее толщине.
Итак, предположим, что в приведенном выше примере мы разрезали пружину точно на две, сделав две более короткие пружины длиной по 3 см каждая.Жесткость пружины, которая в два раза больше исходной, будет применима для меньших пружин. Это потому, что она обратно пропорциональна жесткости пружины и ее длине. Это означает, что на более короткой пружине при первоначальной массе 30 г можно было бы растянуть только на 1 мм. Чем больше постоянная пружины, тем меньше растяжение, создаваемое данной силой.
График закона Гука
График закона Гука представлен ниже. Здесь материал демонстрирует упругие свойства до предела текучести, после чего материал теряет эластичность и проявляет пластичность.
(изображение будет загружено в ближайшее время)
Прямая линия означает, что материал следует закону Гука от источника до пропорционального предела, приближающегося к мощности текучести. Материал теряет свое упругое существование за пределом упругости между пределом пропорциональности и пределом текучести и начинает проявлять пластичность. Площадь от начала координат до предела пропорциональности под кривой находится ниже диапазона упругости. В диапазоне пластичности площадь под кривой находится от пропорционального предела до точки разрыва / разрушения.
Уголок Джея 4
Уголок Джея 4Формула для C (n, k)
Мы хотели бы получить формулу для вычисления C (n, k) без записи треугольника Паскаля (хотя, честно говоря, обычно быстрее записать треугольник Паскаля, чем использовать эту формулу, особенно если вам нужно число этих биномиальных коэффициентов). Для этого мы подсчитаем количество подмножеств размера k в наборе размера n.Прежде чем начать подсчет, нам нужно посмотреть на разницу между упорядоченными наборами (схемами) и неупорядоченными наборами (выборками).В упорядоченном наборе есть первый элемент, второй элемент, третий элемент и так далее. Изменение того, какой элемент считается первым, а какой — вторым, и так далее, изменяет упорядоченный набор, даже если используемые элементы не меняются. Предположим, у нас есть три элемента A, B и C. Количество упорядоченных наборов, которые мы могли бы сделать из них, равно 6, то есть ABC, ACB, BAC, BCA, CAB и CB A. Простой способ увидеть, как эти упорядоченные множества Приходится рисовать «дерево решений» (мы обычно рисуем дерево так, чтобы оно росло вниз, а не вверх), например:
С самого начала мы рисуем ветвь к каждому элементу, который может быть первым элементом упорядоченного набора.От каждого из этих элементов мы рисуем ветвь к элементу, который может быть вторым элементом упорядоченного набора, а затем из них мы рисуем ветви к элементам, которые могут быть третьими элементами. В любой момент рисования дерева мы должны помнить, что мы использовали некоторые элементы, чтобы добраться до этой точки, поэтому они недоступны для продолжения. Мы вынуждены прекратить расширение дерева, когда больше нет элементов, которые можно использовать. Теперь каждый путь вдоль ветвей, начиная сверху и всегда спускаясь к нижнему уровню, соответствует упорядоченному набору, упорядоченному набору меток, через который вы проходите, путешествуя по этому пути.
Здесь я указал два таких пути, красный и зеленый, давая упорядоченные множества A C B и C A B. Легко подсчитать количество путей. Вначале есть 3 ветви, и для каждой из них есть 2 ветви, которые могут продолжить путь (всего 6 = 3 (2) двухветвевых пути), и, наконец, каждый из этих 6 может быть продолжен в только один путь, поэтому мы получаем 6 = 3 (2) (1) путей. Если бы мы начали с 4 элементов вместо 3 (вы должны нарисовать дерево для этого самостоятельно), мы получили бы 24 = 4 (3) (2) (1) пути.Поскольку числа этой формы часто встречаются в математике, мы приняли для них специальные обозначения, определив n! = п (п-1) (п-2) … (3) (2) (1) . Итак, 3! = 3 (2) (1) = 6, 4! = 4 (3) (2) (1) = 24 и 5! = 5 (4) (3) (2) (1) = 120. Это обозначение читается как «n факториал». Подводя итог, количество упорядоченных наборов с n элементами тогда дается n !.
Вопрос : Что такое 6 !, 7! и 8 !.
Далее следует рассмотреть несколько иную проблему. Сколько упорядоченных наборов, содержащих только два элемента, можно составить из набора из четырех элементов? Легко видеть, что мы можем ответить на этот вопрос, начав рисовать дерево решений для всех упорядоченных наборов из четырех элементов, но затем остановившись на втором уровне.
Мы видим, что ответ 12 = 4 (3). Если бы мы хотели, чтобы количество упорядоченных наборов размера 3 было изготовлено из набора размера 8, было бы 336 = 8 (7) (6). В общем, количество упорядоченных наборов размера k, которые могут быть изготовлены из набора размера n, обозначается P (n, k) и равно числу n (n-1) (n-2). . (п-к + 1). Обратите внимание, что здесь умножается ровно k чисел.
Вопрос : Найдите значения для P (5,2), P (7,4), P (6,1), P (3,3) и P (4,3).
Обратите внимание, что предыдущая проблема определения количества всех упорядоченных множеств с n элементами на самом деле является частным случаем этой второй проблемы.Другими словами, P (n, n) = n !.
Теперь мы можем найти формулу для C (n, k). Мы сделаем это, найдя другой способ подсчитать количество упорядоченных наборов размера k, которые можно сделать из набора размера n. Пересмотрите проблему нахождения количества упорядоченных наборов размера 2 в наборе размера 4. Мы можем получить эти наборы, сначала выбрав подмножество размера 2 из набора размера 4 (их C (4,2)). ), а затем упорядочить элементы этого подмножества (что можно сделать P (2,2) = 2! способами).Для каждого из подмножеств C (4,2) мы получим P (2,2) упорядоченных наборов размера 2, поэтому общее количество упорядоченных наборов размера 2 равно произведению C (4,2) P (2,2 ). Но мы уже знаем, что ответ P (4,2), поэтому мы должны иметь P (4,2) = C (4,2) P (2,2). Записывая это в числах, мы имеем 12 = 4 (3) = C (4,2) 2! = 2 С (4,2). Итак, решая для C (4,2), мы получаем 12/2 = 6. В целом то же самое дает нам P (n, k) = C (n, k) P (k, k). Итак, мы можем решить для C (n, k) и получить:
Иногда эту формулу пишут немного иначе, умножая верхнюю и нижнюю часть дроби на (n-k)! и используя тот факт, что n (n-1)… (п-к + 1) (п-к)! = n !, можно написать:
Вопрос : Найдите C (5,3), C (10,2), C (12,3) и C (6,4), используя эту формулу.
Ответы :
6! = 6 (5) (4) (3) (2) (1) = 720
7! = 7 (6) (5) (4) (3) (2) (1) = 5040
8! = 8 (7) (6) (5) (4) (3) (2) (1) = 40320
Обратите внимание, как быстро эти числа становятся большими. Какое наибольшее факториальное число может обработать ваш калькулятор?
P (5,2) = 5 (4) = 20
P (7,4) = 7 (6) (5) (4) = 840
P (6,1) = 6
P (3,3) = 3 (2) (1) = 6
P (4,3) = 4 (3) (2) = 24
C (5,3) = 5 (4) (3) / 3 (2) (1) = 10
C (10,2) = 10 (9) / 2 (1) = 45
C (12,3) = 12 (11) (10) / 3 (2) (1) = 220
C (6, 4) = 6 (5) (4) (3) / 4 (3) (2) (1) = 15
Вы должны сверить их с результатами Треугольника Паскаля.
Цветок сливы Stone-K Formula
Plum Flower® Modern Masters ™ Stone-K Formula (結石 靈 Jié Shí Líng, «Эффективный камень») первоначально в Китае назывался Niào Shí Tōng (尿 石 通 «Чистый камень мочи»). Исследование этой формулы финансировалось Национальным фондом естественных наук Китайской Народной Республики. Эмпирический рецепт Ниао Ши Тун был разработан доктором Лю Цзи Моком на протяжении двадцати лет на основе сочетания теории традиционной китайской медицины и его клинического опыта, накопленного за десятилетия медицинской практики в качестве главного врача Исследовательского института мочевого камня. Город Донг Гуань в провинции Гуандун.Эта уникальная формула основана на концепциях традиционной китайской медицины, но сформулирована и оценена с точки зрения западной науки и медицины. Исследования на животных и контролируемые рандомизированные клинические испытания проводились в четырех научно-исследовательских институтах и пяти больницах Китайской Народной Республики. В пятибольничном исследовании более 50% участников испытали полное исчезновение своих симптомов. Результаты продемонстрировали значительное улучшение по сравнению с прежним стандартом лечения в КНР, который заключался в применении Shi Lin Tong Pian, таблетированного экстракта одной китайской травы Guǎng jīn qián cǎo / Herba Desmodii.
В рамках диагностических стандартов традиционной китайской медицины формула Stone-K предназначена для лечения ши лин 石淋 или «каменной преграды» с застоем ци, сохранением сырости в нижних отделах цзяо и лежащим в основе дефицитом ци почек, поскольку для этого необходимо достаточное количество ци почек. способствовать нормальной функции мочеиспускания. Мочевые камни образуются, когда тепло или влажное тепло накапливаются в нижнем цзяо. Присутствие тепла или влажного тепла в этой области вызывает высыхание и застывание жидкостей, что в конечном итоге приводит к образованию непроходимости мочевыводящих путей или лин чжэн 淋, характеризующемуся присутствием в моче кристаллов, похожих на песок.Хотя генетика и ожирение являются предрасполагающими факторами, 80% этих кристаллов представляют собой оксалат кальция, что вызвано потреблением продуктов с высоким содержанием оксалатов и низким потреблением жидкости. Добавки кальция, витамина D и витамина C, а также высокое потребление фруктовых соков и животного белка также могут быть причиной.
Клинические признаки включают язык, который может быть от красного до темно-красного с жирным желтым налетом, а пульс может быть напряженным, напряженным и, возможно, частым. У человека могут возникать позывы к мочеиспусканию, подтекание после мочеиспускания и почечная колика.Другие симптомы, включая потливость, тошноту, рвоту, гематурию и сильную боль, могут потребовать дополнительного медицинского вмешательства.
Этот лечебный принцип этой формулы состоит в том, чтобы очистить тепло (qing re 清熱), выпустить влагу (qu shi 祛濕), переместить ци, изгнать застой (xing qi zhu yu 行 氣 逐瘀), продвинуть мочу и изгнать камень (тонг Лин Пай Ши 通淋 排 石). Запатентованная смесь ингредиентов формулы:
Функции ингредиентов
Guǎng jīn qián cǎo (廣 金錢草) / Desmodium styracifolium herb — главная трава формулы.Он сладкий, мягкий и холодный и используется для снятия жара, стимулирования мочеиспускания, прекращения неуверенности в мочеиспускании и изгнания камней.
Fú líng (茯苓) / гриб Poria cocos сладкий, мягкий и нейтральный. Выступая в качестве главного заместителя, он используется для стимулирования мочеиспускания, отвода сырости и укрепления селезенки.
Chē qián zĭ (車前子) / Трава подорожника азиатского сладкая, мягкая, холодная и скользкая. Это еще один помощник, который сильно очищает и отводит влажное тепло в нижнем цзяо и способствует мочеиспусканию.
Sī guā luò (絲瓜絡) / Губка Luffa cylindrica сладкая и мягкая, она действует как помощник, устраняя токсичность, уменьшая отек и трансформируя мокроту.
Qĭng má zĭ (茼 麻子) / Семя Abutilon theophrastii горькое и нейтральное и служит дополнительным помощником, так как снимает жар, устраняет сырость и останавливает подтекание после мочеиспускания.
Huái niú xī (淮 牛膝) / Корень Achyranthes bidentata горький, кислый и нейтральный.Хотя Нюси тонизирует печень и почки, он используется в этой формуле, чтобы помочь избавиться от влажного тепла из нижнего цзяо и для его эмпирической функции, чтобы остановить подтекание и боль после мочеиспускания.
Hǎi jīn shā (海金沙) / Lygodium japonicum spore сладкий, мягкий, холодный и направленный вниз. Он служит еще одним помощником, способствуя мочеиспусканию, разблокируя подтекание после мочеиспускания и удаляя камни.
Zhĭ zhí (枳實) / Citrus aurantium fruit-незрелый — горький, едкий, слегка холодный, тонущий и направленный вниз.Чжу чжи выступает в качестве ориентира в формуле, направляя действие вниз, разрушая застойную ци, трансформируя мокроту и уменьшая накопление.
Chuān mù tōng (川 木 通) / Стебель Clematis armandii мягкий, горький и холодный. Чуан Му Тонг — еще один помощник, который способствует мочеиспусканию, устраняет влажное тепло и разблокирует подтекание и боль после мочеиспускания.
Plum Flower® Modern Masters ™ Stone-K Formula — это клинически проверенная ценная травяная формула, доступная только для профессионального использования.Этот травяной подход предлагает практикующим врачам проверенный нефармацевтический вариант поддержки здоровой функции мочеиспускания.
| Биография: Skye Sturgeon, DAOM, L.Ac. Скай — менеджер по обеспечению качества и специальный консультант Mayway, США. Скай был бывшим заведующим кафедрой иглоукалывания и восточноазиатской медицины и основным преподавателем в Университете Бастира, основным преподавателем и председателем совета факультетов Американского колледжа традиционной китайской медицины, а также президентом и старшим профессором Колледжа акупунктуры и интегративной медицины в Беркли.Прежде чем сделать выбор в пользу китайской медицины, Скай в течение 12 лет занимал различные должности в индустрии натуральных продуктов, а до этого был клиническим биохимиком и токсикологом. |
символов формулы — K
Математические символы
Математические термины
Обозначения формул
A — B — C — D — E — F — G — H — I — J — K — L — M — N — O — P — Q — R — S — T — U — V — W — X — Y — Z
К
| Символ | Греческий символ | Определение | US | Метрическая система | Значение |
|---|---|---|---|---|---|
| \ (K \) | – | Константа К-фактора | постоянная | постоянная | – |
| \ (Ка \) | – | Карловиц номер | безразмерный | безразмерный | – |
| \ (К_С \) | – | Кеулеган – Карпентер номер | безразмерный | безразмерный | – |
| \ (KE \), \ (\; E_k \) | – | кинетическая энергия | \ (фут-фунт-сила \) | \ (Дж \) | – |
| \ (ф_к \) | – | кинетическое трение | \ (фунт-сила \) | \ (н \) | – |
| \ (\ mu_k \) | му | коэффициент кинетического трения | безразмерный | безразмерный | – |
| \ (\ nu \) | ню | кинетическая вязкость | \ (дюйм ^ 2 \; / \; сек \) | \ (мм ^ 2 \; / \; с \) | – |
| \ (\ nu \) | ню | кинематическая вязкость | \ (дюйм ^ 2 \; / \; сек \) | \ (мм ^ 2 \; / \; с \) | – |
| \ (Kn \) | – | Число Кнудсена | безразмерный | безразмерный | – |
| \ (К \) | – | Кутателадзе № | безразмерный | безразмерный | – |
A — B — C — D — E — F — G — H — I — J — K — L — M — N — O — P — Q — R — S — T — U — V — W — X — Y — Z
MULTITHERA® 1 КАПСУЛА FORMULA PLUS K
Комплексные продукты для получения необходимых питательных микроэлементов, без железа
Эта комплексная мультивитаминная / минеральная добавка похожа на нашу формулу MultiThera ® на 1 таблетку, но количество кальция, магния и некоторых других питательных веществ было уменьшено, чтобы формула вписывалась в 6 капсул в день для сохранения соответствия.MultiThera ® 1 Capsule Formula сохраняет важный баланс жиро- и водорастворимых антиоксидантов, витаминов B-комплекса и других питательных веществ, составляющих прочную основу питания. Как и в случае таблеток MultiThera ® , активированные формы фолиевой кислоты (Метафолин ® ‡ L-5-метилтетрагидрофолат) и витамина B 12 (метилкобаламин) используются для улучшения абсорбции и биоактивности. MultiThera ® 1 Capsule Formula содержит полный спектр биодоступных микроэлементов, за исключением железа.Витамин К является необязательным ингредиентом в этой формуле, что делает его подходящим для тех, кто принимает антикоагулянтные препараты и не желает принимать это питательное вещество. Вегетарианские капсулы из растительной целлюлозы используются для приготовления одной капсулы MultiThera ® и всех других инкапсулированных продуктов ProThera ® . MultiThera ® 1 Capsule Formula хорошо подходит для тех, кто предпочитает капсулы или испытывает затруднения при глотании, так как капсулы при желании можно разделить, а содержимое смешать с пищей.
| Размер порции 6 капсул | ||
| Количество на 6 капсул | % дневная стоимость | |
|---|---|---|
| Витамин A (64% (1500 мкг RAE) в виде натуральных каротинов (бета-каротин, альфа-каротин и бета-криптоксантин) из D. salina и 36% (750 мкг RAE) в виде пальмитата витамина A) | 2250 мкг RAE | 250% |
| Витамин C (как L-аскорбиновая кислота) | 750 мг | 833% |
| Витамин D 3 (в виде холекальциферола) | 25 мкг | 125% |
| Витамин E (87% в виде сукцината RRR-альфа-токофериловой кислоты, 13% в виде RRR-альфа-токоферола) | 268 мг | 1,787% |
| Витамин K (67% в виде витамина K 1 (фитонадион) и 33% в виде витамина K 2 (менахинон-7)) | 60 мкг | 50% |
| Тиамин (как тиамин гидрохлорид) | 50 мг | 4 167% |
| Рибофлавин | 25 мг | 1,923% |
| Ниацин (75% в виде ниацинамида, 25% в виде ниацина) | 100 мг NE | 625% |
| Витамин B 6 (в виде гидрохлорида пиридоксина) | 25 мг | 1,471% |
| Фолат (как Метафолин ® ‡ L-5-метилтетрагидрофолат кальция) | 1360 мкг DFE (800 мкг) | 340% |
| Витамин B 12 (как метилкобаламин) | 200 мкг | 8 333% 90 204 |
| Биотин (D-биотин) | 300 мкг | 1000% |
| Пантотеновая кислота (в виде D-пантотената кальция) | 150 мг | 3 000% |
| Холин (в виде битартрата холина) | 100 мг | 18 и |
| Кальций (91% в виде комплекса цитрат-малат кальция и 9% в виде D-пантотената кальция) | 188 мг | 14% |
| Йод (в виде йодида калия) | 150 мкг | 100% |
| Магний (75% в виде малата димагния и 25% в виде хелата бисглицината магния TRAACS ® ‡‡ ) | 250 мг | 60% |
| Цинк (в виде хелата аргината цинка TRAACS ® ‡‡ ) | 15 мг | 136% |
| Селен (как L-селенометионин) | 200 мкг | 364% |
| Медь (как хелат бисглицината меди TRAACS ® ‡‡ ) | 2 мг | 222% |
| Марганец (как хелат бисглицината марганца TRAACS ® ‡‡ ) | 2 мг | 87% |
| Хром (в виде хелата глицината никотината хрома TRAACS ® ‡‡ ) | 200 мкг | 571% |
| Молибден (в виде хелата глицината молибдена TRAACS ® ‡‡ ) | 150 мкг | 333% |
| Бор (в виде аспартат-цитратного комплекса бора) | 2 мг | * |
| Ванадий (бисглицинато оксованадий) (BGOV) | 100 мкг | * |
| Инозитол | 25 мг | * |
| пара -Аминобензойная кислота | 50 мг | * |
| Цитрусовый биофлавоноидный комплекс (85 мг в виде экстракта биофлавоноидов цитрусовых ( Citrus aurantium ) (плод / кожура) (стандартизован до 50% биофлавоноидов гесперидина) и 15 мг в виде гесперидинметилхалкона (полученный из экстракта Citrus aurantium ) (плоды) )) | 100 мг | * |
| Природные смешанные токоферолы (RRR-бета, RRR-дельта, RRR-гамма) | 8 мг | * |
| Натуральные смешанные каротиноиды (лютеин и зеаксантин из D.салина ) | 30 мкг | * |
| * Суточная доза не определена | ||
Другие ингредиенты:
Вегетарианские капсулы (гидроксипропилметилцеллюлоза, вода), диоксид кремния, аскорбилпальмитат и натуральный цитрусовый ароматизатор.
‡ Metafolin ® является зарегистрированным товарным знаком компании Merck KGaA, Дармштадт, Германия.
‡‡ Albion ® и TRAACS ® являются зарегистрированными товарными знаками Albion ® Laboratories, Inc.
Рекомендуемое использование
Взрослые: 6 капсул во время еды или по назначению врача. Дети от 4 до 14 лет: принимать до 3 капсул в день или по назначению врача. Дети до 4 лет: по назначению врача.
Заявление об аллергии
Не содержит следующих распространенных аллергенов: молоко / казеин, яйца, рыба, моллюски, древесные орехи, арахис и пшеница.Не содержит искусственных красителей, ароматизаторов или консервантов.
Осторожно
Если вы беременны, кормите грудью, страдаете заболеванием или принимаете рецептурные лекарства, проконсультируйтесь с врачом перед использованием этого продукта. ХРАНИТЕ В НЕДОСТУПНОМ ДЛЯ ДЕТЕЙ МЕСТЕ.
MultiThera® 1 Capsule Formula Plus Vitamin K — это высокоэффективная мультивитаминная / минеральная добавка для поддержания оптимального здоровья взрослых мужчин и женщин. † Он содержит полный спектр биодоступных витаминов, минералов, микроэлементов, антиоксидантов и натуральных каротиноидов. MultiThera® 1 Capsule Formula Plus Vitamin K является частью линейки полинутриентов MultiThera®. Он не содержит железа, содержит витамин К и выпускается в форме капсул.
MultiThera® 1 Capsule Formula Plus Vitamin K содержит все витамины, содержащиеся в обычных поливитаминных продуктах, и включает дополнительное количество витаминов C, E и витаминов группы B, а также кальций, магний и другие важные минералы и микроэлементы.Кроме того, этот продукт содержит RRR-альфа-токоферол (витамин Е в натуральной форме) и бета-каротин (витамин А) для поддержки оптимального усвоения и использования организмом. †
Уровни питательных веществRDA определяются на основе их способности предотвращать дефицит. Исследования показывают, что прием некоторых необходимых питательных веществ выше этих уровней может не только предотвратить дефицит, но и поддержать здоровье другими способами. MultiThera® 1 Capsule Formula Plus Vitamin K содержит многие из своих ингредиентов в биодоступных формах и в количествах, превышающих рекомендованную суточную норму, для поддержания оптимального здоровья. †
MultiThera® 1 Capsule Formula Plus Vitamin K содержит полный спектр витаминов, минералов, микроэлементов, антиоксидантов и натуральных каротиноидов. По сравнению со многими другими поливитаминными и минеральными продуктами, эти ингредиенты представлены в биодоступных формах и в количествах, равных или превышающих рекомендованную суточную норму потребления для поддержания оптимального здоровья. †
MultiThera® 1 Capsule Formula Plus Vitamin K содержит полный спектр витаминов, минералов, микроэлементов, антиоксидантов и натуральных каротиноидов.Многие из этих ингредиентов предоставляются по рекомендованной суточной или превышающей ее суточной норме для поддержания оптимального здоровья. † Кроме того, биодоступные формы некоторых витаминов и минералов обычно имеют более крупные молекулярные структуры, что требует более высоких общих количеств в миллиграммах для обеспечения эквивалентного элементарного питания. В результате физически невозможно доставить количество биодоступных питательных веществ в MultiThera® 1 Capsule Formula Plus Vitamin K всего за 1 или 2 капсулы в день.
MultiThera® 1 Capsule Formula Plus Vitamin K содержит биодоступные ингредиенты для поддержки оптимального усвоения и действия в организме. † Например, витамины E и бета-каротин (витамин A) поставляются в их «естественных» формах (т.е. распознаются организмом) по сравнению с синтетическими формами, содержащимися в некоторых других продуктах. Витамин B 12 , кальций и другие минералы, такие как магний, представлены в формах, которые легко усваиваются по сравнению с формами, которые обычно встречаются в других полинутриентных продуктах. † Фолат представлен в запатентованной активной форме под названием Metafolin® ‡ , которая может абсорбироваться и использоваться непосредственно организмом. † Кроме того, каждая партия MultiThera® 1 Capsule Formula Plus Vitamin K тестируется в соответствии с официальными протоколами Фармакопеи США, чтобы гарантировать, что капсулы разрушаются в течение 45 минут или меньше после приема внутрь.
Фолиевая кислота и витамин B 12 помогают поддерживать нормальное метилирование и метаболизм таких веществ, как гомоцистеин. † Биологически активные формы фолиевой кислоты (Metafolin® ‡ L-5-метилтетрагидрофолат) и витамина B 12 (метилкобаламин) используются в MultiThera® 1 Capsule Formula Plus Vitamin K.
MultiThera® 1 Capsule Formula Plus Vitamin K — это мощный продукт, предлагаемый медицинскими работниками в качестве основы питания для терапевтических программ. † MultiThera® 1 Capsule Formula Plus Vitamin K и другие продукты Klaire Labs ™ производятся в соответствии со строгими производственными стандартами и включают доступ к профессиональному обучению и поддержке. Чтобы поддерживать стандарты качества и результаты, Klaire Labs ™ сотрудничает с профессионалами в области здравоохранения, чтобы рекомендовать свои продукты.
Да, количество каждого питательного вещества в MultiThera® 1 Capsule Formula Plus Vitamin K ниже верхнего предела, рекомендованного государственными учреждениями и экспертами по питанию.
Две формы витамина К включены в MultiThera® 1 Capsule Formula Plus Vitamin K для поддержки оптимального питания витамином K. † Витамин К 1 (фитонадион) необходим для свертывания крови и поддержания здоровья костей. † Витамин K 2 (менахинон-7 или MK-7) поддерживает здоровье костей, а также функцию сосудов. †
MultiThera® 1 Capsule Formula Plus Vitamin K содержит полный спектр биодоступных витаминов, минералов, микроэлементов, антиоксидантов и натуральных каротиноидов для поддержания оптимального здоровья взрослых мужчин и женщин, которым не требуется дополнительное железо и которые ищут дополнительные добавки витамина К. . †
Принимайте 1 капсулу MultiThera® Formula Plus с витамином К в разделенных дозах во время еды. Три капсулы утром и 3 капсулы вечером — это обычно удобный способ приема этого продукта.
MultiThera® 1 Capsule Formula Plus Vitamin K содержит необходимые питательные вещества, которые поддерживают оптимальное здоровье, включая сердечно-сосудистую, иммунную и нервную системы, метаболизм глюкозы, энергию, антиоксидантную защиту, здоровье костей и здоровье глаз. †
Техническая информация доступна исключительно зарегистрированным специалистам в области здравоохранения и их уполномоченным пациентам.