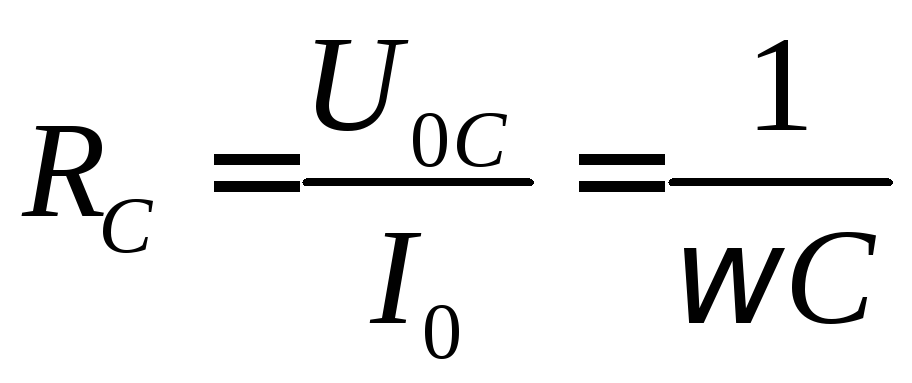Индуктивность в цепи переменного тока

Рассмотрим идеальную цепь состоящая только из индуктивности и источника питания, ток в которой изменяется по закону:
i = Imsinωt
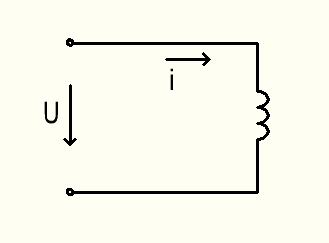
При изменении тока, протекающего по катушки, в ней наводится ЭДС самоиндукции.
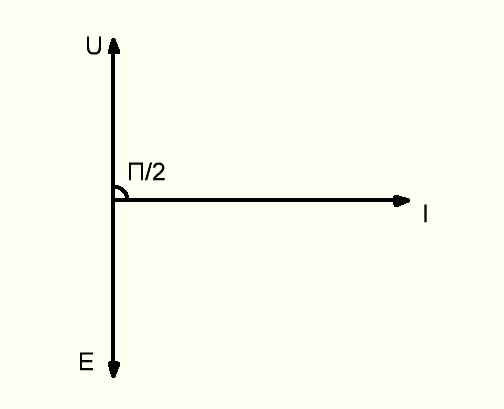
В данной цепи ток отстаёт от напряжения по фазе на угол π/2.
i = Imsinωt
u = Umsin(ωt+π/2)
ω = 2fπ
где: f — частота питающей сети по стандарту 50 Гц, но в условии задачи могут указать другую.
Индуктивное сопротивление XL
XL = ωL
где: L — индуктивность
Мгновенная мощность цепи с индуктивностью
При нарастании тока, независимо от его направления, происходит накопление магнитной энергии от 0 до максимального значения которое поступает от генератора таким образом цепь работает в режиме потребителя, что соответствует положительному значению мощности.
При уменьшении тока энергия магнитного поля уменьшается от максимального значения до 0, и это энергия возвращается цепью генератору. То есть цепь работает в режиме генератора, что соответствует определённому значению мощности.
В целом за период P=0. Максимальное значение Р цепи с индуктивности называется
Q = XL*I2 [Вар]
Если в замкнутом контуре течет непостоянный ток, то магнитное поле, создаваемое этим током, также непостоянно. В проводе (катушке) под влиянием изменения ее собственного магнитного потока индуктируется ЭДС, называемая ЭДС самоиндукции. Согласно закону Ленца, ЭДС самоиндукции всегда противоположна вызвавшей ее причине. Если ток в цепи возрастает, то ЭДС самоиндукции стремится замедлить нарастание тока. Если ток в цепи уменьшается, ЭДС самоиндукции препятствует спаданию тока.
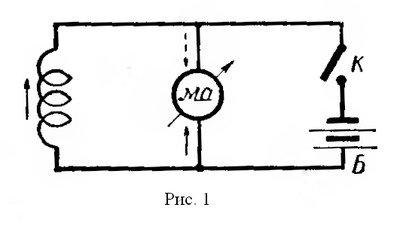
Характерным примером явления самоиндукции служат так называемые экстратоки замыкания и размыкания. При питании цепей постоянным током ЭДС самоиндукции возникает и оказывает влияние на изменение тока только в моменты замыкания и размыкания цепи (рис.1).
 В проводниках различной формы величина ЭДС самоиндукции различна. Прямолинейный проводник имеет слабое магнитное поле и поэтому ЭДС самоиндукции невелика. Она заметно сказывается только в очень длинных проводниках или при очень быстрых изменениях тока. Значительная ЭДС возникает в проводниках, образующих катушку.
В проводниках различной формы величина ЭДС самоиндукции различна. Прямолинейный проводник имеет слабое магнитное поле и поэтому ЭДС самоиндукции невелика. Она заметно сказывается только в очень длинных проводниках или при очень быстрых изменениях тока. Значительная ЭДС возникает в проводниках, образующих катушку.При включении в цепь переменного тока катушки индуктивности (рис.2) образуется переменное магнитное поле и в витках катушки наводится ЭДС самоиндукции. Для создания и поддержания переменного тока в цепи катушки необходимо преодолеть действие ЭДС самоиндукции.
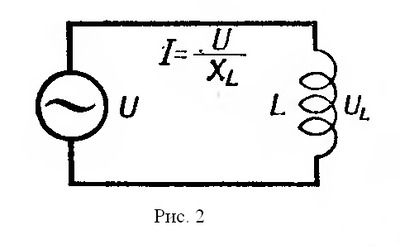 Сопротивление, которое вносит в цепь переменного тока катушка индуктивности, называется индуктивным сопротивлением. Индуктивное сопротивление возникает вместе с появлением ЭДС самоиндукции, а величина последней зависит от величины индуктивности L и скорости изменения магнитного потока в катушке, то есть скорости изменения величины тока в ней. Таким образом индуктивное сопротивление зависит от частоты переменного тока. Чем больше частота переменного тока, тем больше индуктивное сопротивление катушки.
Сопротивление, которое вносит в цепь переменного тока катушка индуктивности, называется индуктивным сопротивлением. Индуктивное сопротивление возникает вместе с появлением ЭДС самоиндукции, а величина последней зависит от величины индуктивности L и скорости изменения магнитного потока в катушке, то есть скорости изменения величины тока в ней. Таким образом индуктивное сопротивление зависит от частоты переменного тока. Чем больше частота переменного тока, тем больше индуктивное сопротивление катушки.В тех случаях, когда необходимо иметь катушку с очень малой индуктивностью, применяют бифилярную намотку (рис.3). При такой намотке в каждых двух соседних витках ток имеет противоположное направление и суммарный магнитный поток равен нулю.
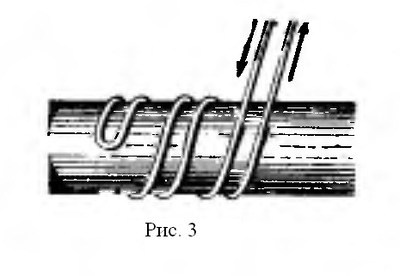 Всякий проводник или катушка обладают также и активным сопротивлением, но иногда для упрощения считают, что катушка обладает только индуктивным сопротивлением. Такую индуктивность считают идеальной.
Всякий проводник или катушка обладают также и активным сопротивлением, но иногда для упрощения считают, что катушка обладает только индуктивным сопротивлением. Такую индуктивность считают идеальной.Предположим, что идеальная индуктивность L подключена к источнику переменного тока в тот момент, когда его напряжение равно амплитудному значению. Ток в катушке не сразу достигнет амплитудного значения (рис. 4), так как возникающая в ней ЭДС самоиндукции u
Величина индуктивного сопротивления выражается следующей формулой:
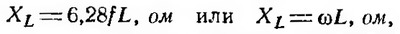 где f — частота тока, гц; L — индуктивность катушки, гн; ω — угловая частота.
где f — частота тока, гц; L — индуктивность катушки, гн; ω — угловая частота. 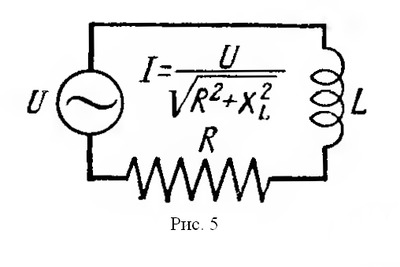 Если включить в цепь переменного тока последовательно индуктивное и активное сопротивление (рис. 5), полное сопротивление такой цепи будет равно геометрической сумме сопротивлений; его можно определить по формуле:
Если включить в цепь переменного тока последовательно индуктивное и активное сопротивление (рис. 5), полное сопротивление такой цепи будет равно геометрической сумме сопротивлений; его можно определить по формуле: 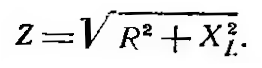
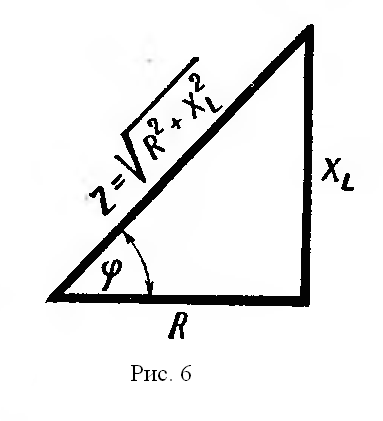 В цепи, содержащей индуктивное и активное сопротивления, сдвиг фаз между током и напряжением меньше 90° и зависит от отношения величины активного сопротивления к величине полного сопротивления R/Z. Из треугольника сопротивлений видно, что R/Z=cos φ. Если X
В цепи, содержащей индуктивное и активное сопротивления, сдвиг фаз между током и напряжением меньше 90° и зависит от отношения величины активного сопротивления к величине полного сопротивления R/Z. Из треугольника сопротивлений видно, что R/Z=cos φ. Если XЕсли подсчитать мгновенные значения мощности как произведения мгновенных значений тока и напряжения по формуле p = ui и построить в некотором масштабе график мощности, то мы получим синусоиду, частота которой в два раза больше частоты проходящего по катушке тока. Энергия, поступающая в катушку индуктивности в течение первой и третьей четверти периода, идет на образование магнитного поля. Однако в течение второй и четвертой четверти периода магнитное поле отдает эту запасенную энергию обратно в цепь источника тока (рис. 7).
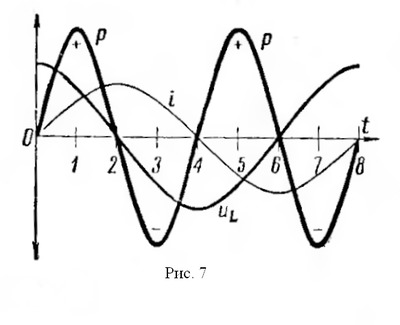 Как известно, мощность, потребляемая чисто активным сопротивлением, равняется произведению действующих значений тока и напряжения. Мощность. потребляемая чисто индуктивным сопротивлением, за период равна нулю. Для цепи, содержащей R и XL потребляемая мощность зависит от соотношения этих величин. Чем меньше сдвиг фаз между током и напряжением, тем большую мощность потребляет цепь.
Как известно, мощность, потребляемая чисто активным сопротивлением, равняется произведению действующих значений тока и напряжения. Мощность. потребляемая чисто индуктивным сопротивлением, за период равна нулю. Для цепи, содержащей R и XL потребляемая мощность зависит от соотношения этих величин. Чем меньше сдвиг фаз между током и напряжением, тем большую мощность потребляет цепь.Величина мощности определяется по формуле:
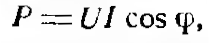 где U и I действующие значения тока и напряжения.
где U и I действующие значения тока и напряжения.Мощность переменного тока, поглощаемую нагрузкой, называют активной и измеряют в ваттах (Вт) или киловаттах (кВт).
Мощность, отдаваемая источником в течение одной части периода и возвращаемая в течение другой части периода, называется реактивной мощностью. Величина этой мощности определяется по формуле:
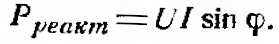
Цепь переменного тока с индуктивностью
Дата публикации: .
Категория: Электротехника.
В статье «ЭДС самоиндукции и индуктивность цепи» говорится, что при включении и при всяком изменении тока в электрической цепи вследствие пересечения проводника своим же собственным магнитным полем в нем возникает индуктированная электродвижущая сила (ЭДС). Эту ЭДС мы назвали ЭДС самоиндукции. ЭДС самоиндукции имеет реактивный характер. Так, например, при увеличении тока в цепи ЭДС самоиндукции будет направлена против ЭДС источника напряжения, и поэтому ток в электрической цепи не может установиться сразу. И, наоборот, при уменьшении тока в цепи индуктируется ЭДС самоиндукции такого направления, что, мешая току исчезать, она поддерживает этот убывающий ток.

Рисунок 1. Цепь переменного тока, содержащая индуктивность
Как нам уже известно, ЭДС самоиндукции зависит от скорости изменения тока в цепи и от индуктивности этой цепи (числа витков, наличия стальных сердечников).

В цепи переменного тока ЭДС самоиндукции возникает непрерывно, так как ток в цепи непрерывно изменяется.
На рисунке 1 представлена схема цепи переменного тока, содержащей катушку с индуктивностью L без стального сердечника. Для простоты будем считать сначала, что активное сопротивление катушки очень мало и им можно пренебречь.
Рассмотрим внимательнее изменение переменного тока за время одного периода. На рисунке 2 показана кривая изменения переменного тока. Первая половина периода разбита на мелкие одинаковые части.

Рисунок 2. Определение скорости изменения переменного тока
За промежуток времени 0 – 1 величина тока изменилась от нуля до 1 – 1’. Прирост величины тока за это время равен а.
За время, обозначенное отрезком 1 – 2, мгновенная величина выросла до 2 – 2’, причем прирост величины тока равен б.
В течение времени, обозначенного отрезком 2 – 3, ток увеличивается до 3 – 3’, прирост тока показывает отрезок в и так далее.
Так, с течением времени переменный ток возрастет до максимума (при 90°). Но, как видно из чертежа, прирост тока делается все меньше и меньше, пока, наконец, при максимальном значении тока этот прирост не станет равным нулю.
При дальнейшем изменении тока от максимума до нуля убыль величины тока становится все больше и больше, пока, наконец, около нулевого значения ток, изменяясь с наибольшей скоростью, не исчезнет, но тут же появляется вновь, протекая в обратном направлении.
Рассматривая изменение тока в течение периода, мы видим, что с наибольшей скоростью изменяется ток около своих нулевых значений. Около максимальных значений скорость изменения тока падает, а при максимальном значении тока прирост его равен нулю. Таким образом, переменный ток меняется не только по величине и направлению, но также и по скорости своего изменения. Переменный ток, проходя по виткам катушки, создает переменное магнитное поле. Магнитные линии этого поля, пересекая витки своей же катушки, индуктируют в них ЭДС самоиндукции.
На рисунке 3 кривая i показывает изменение переменного тока в катушке. Как было уже указано, величина ЭДС самоиндукции зависит от скорости изменения тока и от индуктивности катушки. Но так как индуктивность катушки в нашем случае остается без изменения, ЭДС самоиндукции будет зависеть только от скорости изменения тока. Выше было показано, что наибольшая скорость изменения тока имеет место около нулевых значений тока. Следовательно, наибольшее изменение ЭДС самоиндукции имеет те же моменты.


Рисунок 3. ЭДС самоиндукции в катушке, включенной в цепь переменного тока
В момент а ток резко и быстро увеличивается от нуля, а поэтому, как следует из вышеприведенной формулы, ЭДС самоиндукции (кривая eL) имеет отрицательное максимальное значение. Так как ток увеличивается, то ЭДС самоиндукции по правилу Ленца должна препятствовать изменению (здесь увеличению) тока. Поэтому ЭДС самоиндукции при возрастании тока будет иметь направление, обратное току (положение б), что следует также из указанной формулы. Скорость изменения тока по мере приближения его к максимуму уменьшается. Поэтому ЭДС самоиндукции также уменьшается, пока, наконец, при максимуме тока, когда изменения его будут равны нулю, она не станет равной нулю (положение в).
Переменный ток, достигнув максимума, начинает убывать. По правилу Ленца ЭДС самоиндукции будет мешать току убывать и, направленная уже в сторону протекания тока, будет его поддерживать (положение г).
При дальнейшем изменении переменный ток быстро убывает до нуля. Резкое уменьшение тока в катушке повлечет за собой также быстрое уменьшение магнитного поля и в результате пересечения магнитными линиями витков катушки в них будет индуктироваться наибольшая ЭДС самоиндукции (положение д).


Рисунок 4. Ток в катушке опережает ЭДС самоиндукции по фазе на 90°
Во вторую половину периода изменения тока картина повторяется и снова при возрастании тока ЭДС самоиндукции будет мешать ему, имея направление, обратное току (положение е).
При убывании тока ЭДС самоиндукции, имея направление в сторону тока, будет поддерживать его, не давая ему исчезнуть сразу (положение з).
На рисунке видно, что ЭДС самоиндукции отстает по фазе от тока на 90° или на ¼ периода. Так как магнитный поток совпадает по фазе с током, то можно сказать, что ЭДС, наводимая магнитным потоком, отстает от него по фазе на 90° или на ¼ периода.
Нам уже известно, что две синусоиды, сдвинутые одна относительно другой на 90°, можно изобразить векторами, расположенными под углом 90° (рисунок 4).
Так как ЭДС самоиндукции в цепях переменного тока непрерывно противодействует изменениям тока, то, чтобы дать возможность току протекать по виткам катушки, напряжение сети должно уравновешивать ЭДС самоиндукции. Иными словами, напряжение сети в каждый момент времени должно быть равно и противоположно ЭДС самоиндукции.


Рисунок 5. Приложенное к катушке напряжение сети опережает ток на 90° и противоположно ЭДС самоиндукции
Вектор напряжения сети, равный и противоположный ЭДС самоиндукции eL, мы обозначим через U (рисунок 5). Только при условии, что к зажимам катушки будет приложено напряжение сети, равное и противоположное ЭДС самоиндукции, и, стало быть, это напряжение сети U уравновесит ЭДС самоиндукции eL, по катушке сможет проходить переменный ток I.
Но в этом случае напряжение сети U будет опережать по фазе ток I на 90°.
Таким образом, в цепях переменного тока ЭДС самоиндукции, возникая непрерывно, вызывает сдвиг фаз между током и напряжением. Возвращаясь к рисунку 3, мы видим, что ток i по катушке будет проходить и тогда, когда напряжение сети (кривая uL) равно нулю (положение в), и даже тогда, когда напряжение сети направлено в сторону, обратную току (положение г и з).
Итак отметим, что в цепи переменного тока, когда ЭДС самоиндукции отсутствует, напряжение сети и ток совпадают по фазе. Индуктивная же нагрузка в цепях переменного тока (обмотки электродвигателей и генераторов, обмотки трансформаторов, индуктивные катушки) всегда вызывает сдвиг фаз между током и напряжением.
Можно показать, что скорость изменения тока пропорциональна угловой частоте ω. Следовательно, действующее значение ЭДС самоиндукции eL может быть найдено по формуле:
eL = ω × L × I = 2 × π × f × L × I .
Как было отмечено выше, напряжение, приложенное к зажимам цепи, содержащей индуктивность, в каждый момент времени должно быть по величине равно ЭДС самоиндукции:
uL = eL.
Поэтому
uL = 2 × π × f × L × I .
Обозначая 2 × π × f × L = xL , получим
uL = xL × I .
Формула закона Ома для цепи переменного тока, содержащего индуктивность, будет такова:


Величина xL называется индуктивным сопротивлением цепи, или реактивным сопротивлением индуктивности, и измеряется в омах. Таким образом, реактивное индуктивное сопротивление представляет собой своеобразное препятствие, которое оказывает цепь изменениям тока в ней. Оно равно произведению индуктивности на угловую частоту. Формула индуктивного сопротивления имеет вид:
xL = ω × L .
Индуктивное сопротивление проводника зависит от частоты переменного тока и индуктивности проводника. Поэтому индуктивное сопротивление катушки, включаемой в цепь токов различной частоты, будет различным. Например, если имеется катушка индуктивностью 0,05 Гн, то путем расчета индуктивного сопротивления выяснится, что в цепи частотой 50 Гц ее индуктивное сопротивление будет:
xL1 = 2 × π × f1 × L = 2 × 3,14 × 50 × 0,05 = 15,7 Ом ,
а в цепи тока частотой 400 Гц
xL2 = 2 × π × f2 × L = 2 × 3,14 × 400 × 0,05 = 125,6 Ом .
Та часть напряжения сети, которая идет на преодоление (уравновешивание) ЭДС самоиндукции, называется индуктивным падением напряжения или реактивной слагающей напряжения.
uL = xL × I .
Рассмотрим теперь, какая мощность потребляется от источника переменного напряжения, если к его зажимам подключена индуктивность.


Рисунок 6. Кривые мгновенных значений напряжения, тока и мощности для цепи, содержащей индуктивность
На рисунке 6 даны кривые мгновенных значений напряжения, тока и мощности для этого случая. Мгновенное значение мощности равно произведению мгновенных значений напряжения и тока:
p = u × i .
Из чертежа видно, что если u и i имеют одинаковые знаки, то кривая p положительная и располагается выше оси ωt. Если же u и i имеют разные знаки, то кривая p отрицательна и располагается ниже оси ωt.
В первую четверть периода ток, а в месте с ним и магнитный поток катушки увеличиваются. Катушка забирает из сети мощность. Площадь, заключенная между кривой p и осью ωt, есть работа (энергия) электрического тока. За первую четверть периода энергия, забираемая из сети, идет на создание магнитного поля вокруг витков катушки (мощность положительная). Количество энергии, запасаемое в магнитном поле за время роста тока, можно определить по формуле:


За вторую четверть периода ток убывает. ЭДС самоиндукции, которая в первую четверть периода стремилась помешать возрастанию тока, теперь, когда ток начинает уменьшаться, будет мешать ему уменьшаться. Сама катушка становится как бы генератором электрической энергии. Она возвращает в сеть энергию, запасенную в ее магнитном поле. Мощность отрицательна, и на рисунке 6 кривая p располагается ниже оси ωt.
За вторую половину периода явление повторяется. Таким образом, между источником переменного напряжения и катушкой, содержащей индуктивность, происходит обмен мощностью. В течение первой и третьей четвертей периода мощность поглощается катушкой, в течение второй и четвертой мощность возвращается источнику.
В этом случае, в среднем, расхода мощности не будет, несмотря на то, что на зажимах цепи есть напряжение U и в цепи протекает ток I.
Тот же результат мы получим, если вычислим среднюю или активную мощность по формуле, приведенной выше:
P = U × I × cos φ .
В нашем случае между напряжением и током существует сдвиг фаз, равный 90°, и cos φ = 90° = 0.
Поэтому активная мощность также равна нулю, то есть расхода мощности нет.
Источник: Кузнецов М. И., «Основы электротехники» — 9-е издание, исправленное — Москва: Высшая школа, 1964 — 560 с.
Индуктивность в цени переменного тока. В любом проводнике, по которому протекает переменный ток, возникает ЭДС самоиндукции. Поэтому ни одна электрическая цепь не обладает только активным сопротивлением.
,
то колебания напряжения на катушке описываются уравнением
или
, (70.1)
т.е. колебания напряжения опережают по фазе колебания силы тока на .Произведение является амплитудой колебаний напряжения:
. (70.2)
Индуктивное сопротивление. Произведение циклической частоты на индуктивность называют индуктивным сопротивлением. Обозначив индуктивное сопротивление , запишем
. (70.3)
Связь между амплитудой колебаний напряжения на концах проводника индуктивностью с амплитудой колебаний силы тока в нем совпадает по форме с выражением закона Ома для участка цепи постоянного тока:
(70.4)
Зависимость индуктивного сопротивления от частоты. Хотя выражения (43.3). и (70.4) совпадают по форме, между ними имеются принципиальные отличия по существу. Электрическое сопротивление проводника при данной температуре является постоянной величиной, характеризующей проводник. Индуктивное сопротивление не является постоянной величиной, его значение прямо пропорционально частоте переменного тока. Поэтому амплитуда колебаний силы тока в проводнике индуктивностью при постоянном значении амплитуды колебаний напряжения убывает обратно пропорционально частоте:
(70.5)
Емкость в цепи переменного тока. Рассмотрим процессы, протекающие в электрической цепи переменного тока с конденсатором. При включении конденсатора последовательно с источником постоянного тока в цепи возникает кратковременный импульс тока, заряжающий конденсатор до напряжения источника, а затем ток прекращается.
Если заряженный конденсатор отключить от источника постоянного тока и соединить его обкладки с выводами лампы накаливания, то конденсатор будет разряжаться, при этом наблюдается кратковременная вспышка лампы.
При включении конденсатора в цепь переменного тока, как и в случае цепи постоянного тока, через диэлектрик, разделяющий обкладки конденсатора, электрические заряды проходить не будут. Но в результате периодически повторяющихся процессов зарядки и разрядки конденсатора в проводах, соединенных с его выводами, появится переменный ток. Лампа накаливания, включенная последовательно с конденсатором в цепь переменного тока, кажется горящей непрерывно, так как человеческий глаз при высокой частоте колебаний силы тока не замечает периодического ослабления свечения нити лампы.
При изменениях напряжения на обкладках конденсатора по гармоническому закону:
(70.6)
заряд на его обкладках изменяется также по гармоническому закону:
. (70.7)
Электрический ток в цепи возникает в результате изменения заряда конденсатора, поэтому колебания силы тока в цепи будут происходить по закону:
или , т.е.
(70.8)
Сравнение выражений (70.6) и (70.8) показывает, что гармонические колебания напряжения на обкладках конденсатора в цепи переменного тока отстают по фазе от колебаний силы тока на .
Произведение является амплитудой колебаний силы тока:
. (70.9)
Емкостное сопротивление. Величину, обратную произведению циклической частоты на электроемкость конденсатора, называют емкостным сопротивлением конденсатора. Обозначив емкостное сопротивление , запишем
(70.10)
Связь между амплитудным значением силы тока и амплитудным значением напряжения по форме совпадает с выражением закона Ома для участка цепи постоянного тока, в котором вместо электрического сопротивления используется емкостное сопротивление конденсатора :
(70.11)
Для действующих значений напряжения и силы тока выполняется такое же соотношение.
Как и индуктивное сопротивление катушки, емкостное сопротивление конденсатора не является постоянной величиной. Его значение обратно пропорционально частоте переменного тока. Поэтому амплитуда колебаний силы тока в цепи конденсатора при постоянной амплитуде колебаний напряжения на конденсаторе возрастает прямо пропорционально частоте .
ТРАНСФОРМАТОР
Передача электрической энергии. Передача электрической энергии от электростанции на значительное расстояние до большого города или промышленного центра является сложной научно-технической проблемой.
Потери энергии на нагревание проводов прямо пропорциональны квадрату силы тока в линии электропередачи. Поэтому для уменьшения потерь необходимо уменьшить силу тока в линии. Мощность тока равна произведению силы тока на напряжение. Чтобы при уменьшении силы тока в линии не уменьшалась передаваемая мощность, следует увеличить напряжение во столько же раз, во сколько раз была уменьшена сила тока.
При высоком напряжении переменный ток передается на большие расстояния с малыми потерями, но для использования на промышленных предприятиях, транспорте, в быту необходимо понижение напряжения. Повышение и понижение напряжения переменного тока осуществляются трансформаторами.
Трансформатор. Трансформатор был изобретен в 1878 г. русским ученым Павлом Николаевичем Яблочковым (1847-1894). Самый простой трансформатор переменного тока состоит из двух катушек.
Одна из катушек, концы которой подключаются к источнику переменного напряжения, называется первичной катушкой (обмоткой), другая — вторичной катушкой (обмоткой). При подключении выводов первичной катушки к источнику переменного напряжения в катушке возникает переменный ток. Если напряжение изменяется со временем по гармоническому закону с частотой , то по гармоническому закону с той же частотой происходят изменения силы тока в катушке и магнитного потока , создаваемого этим током:
.
При изменениях магнитного потока в каждом витке провода первичной катушки возникает изменяющаяся по гармоническому закону ЭДС самоиндукции:
.
Произведение является амплитудой колебаний ЭДС в одном витке:
.
Если число витков в первичной катушке , а ЭДС самоиндукции в одном витке равна , то мгновенное значение ЭДС самоиндукции в первичной катушке равно
. (72.1)
Вторичную катушку пронизывает тот же самый магнитный поток, который проходит через первичную катушку. При изменениях магнитного потока в каждом ее витке возникает ЭДС индукции, изменяющаяся по гармоническому закону, амплитуда изменений ЭДС индукции в одном витке имеет такое же значение, что и ЭДС самоиндукции в одном витке первичной катушки. Если число витков провода вторичной катушки , то мгновенное значение ЭДС в ней равно
. (72.2)
Отношение ЭДС самоиндукции в первичной катушке к ЭДС индукции во вторичной катушке равно отношению числа витков в первичной катушке к числу витков во вторичной катушке:
(72.3)
Если активное сопротивление провода первичной катушки мало по сравнению с его индуктивным сопротивлением, то приложенное напряжение в любой момент времени примерно равно ЭДС самоиндукции, взятой с противоположным знаком.
При разомкнутой цепи вторичной катушки — режим холостого хода трансформатора — напряжение на ее концах в любой момент времени равно ЭДС индукции , взятой с противоположным знаком. Поэтому из выражения (72.3) следует, что
(72.4)
Это отношение называется коэффициентом трансформации :
При трансформатор понижающий, при — повышающий.
При подключении нагрузки к концам вторичной катушки во вторичной цепи возникает переменный ток. Мощность тока в первичной и вторичной цепях, если пренебречь потерями, одинакова. Поэтому увеличение напряжения на выходе повышающего трансформатора в раз сопровождается уменьшением силы тока во вторичной катушке в раз. Трансформаторы для преобразования переменных токов больших мощностей обладают высокими КПД, достигающими 98-99,5%. Снижение КПД трансформатора обусловлено потерями энергии на нагревание проводов его обмоток и стального сердечника. Сердечник нагревается в результате перемагничивания и возникновения в нем вихревых индукционных токов. Для уменьшения вихревых токов сердечники трансформаторов обычно изготавливают из тонких стальных листов, изолированных друг от друга. Это приводит к значительному увеличению электрического сопротивления сердечника и уменьшению потерь на его нагревание вихревыми токами.
2.2.Индуктивность в цепи переменного тока
 Если
катушка индуктивности
Если
катушка индуктивности 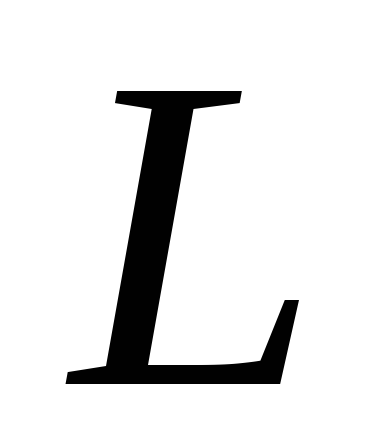 находится в контуре с переменным током,
то в ней все время будет возникать ЭДС
самоиндукции, которая противодействует
внешний переменной ЭДС. Вследствие
этого катушка будет создавать сопротивление
(дополнительное к активному) переменному
току, который называют индуктивным
сопротивлением. Найдем это сопротивление.
находится в контуре с переменным током,
то в ней все время будет возникать ЭДС
самоиндукции, которая противодействует
внешний переменной ЭДС. Вследствие
этого катушка будет создавать сопротивление
(дополнительное к активному) переменному
току, который называют индуктивным
сопротивлением. Найдем это сопротивление.
Пусть
активное сопротивление катушки очень
мало ( ).
Тогда на индуктивности создается падение
напряжения
).
Тогда на индуктивности создается падение
напряжения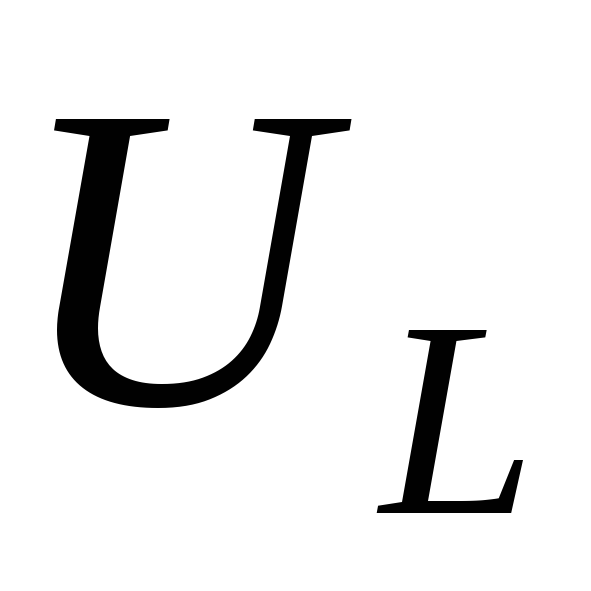 ,
которое равняется минус ЭДС самоиндукции
(ЭДС самоиндукции противодействует
внешнему напряжению),
,
которое равняется минус ЭДС самоиндукции
(ЭДС самоиндукции противодействует
внешнему напряжению),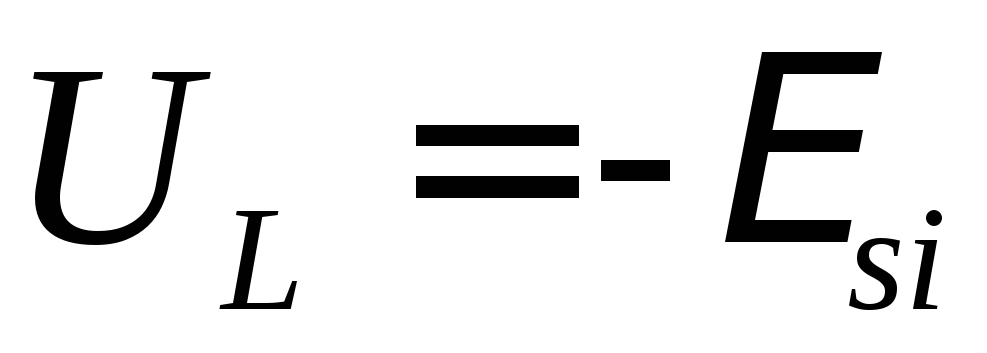 .
Подставив выражение для силы тока (1) в
выражение для ЭДС самоиндукции (11*),
получим значение напряжения на
индуктивности
.
Подставив выражение для силы тока (1) в
выражение для ЭДС самоиндукции (11*),
получим значение напряжения на
индуктивности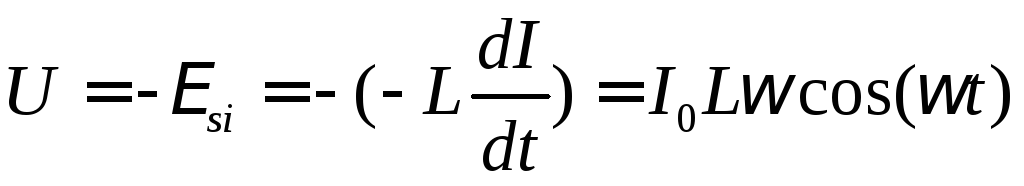 ,
или учитывая, что
,
или учитывая, что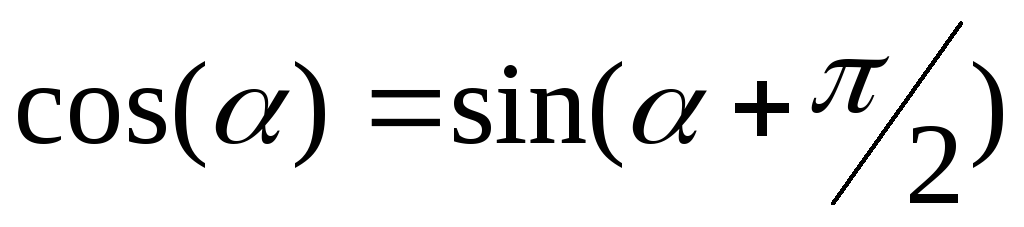
| (3) |
Величина 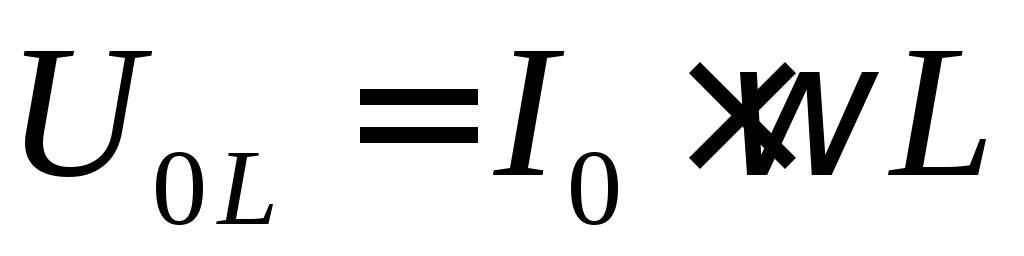 является амплитудным значением напряжения
на индуктивности, а отношение
является амплитудным значением напряжения
на индуктивности, а отношение
| (4) |
называют индуктивным
сопротивлением. Анализируя это выражение, можно сделать
вывод, что катушка индуктивности хорошо
пропускает постоянный ток (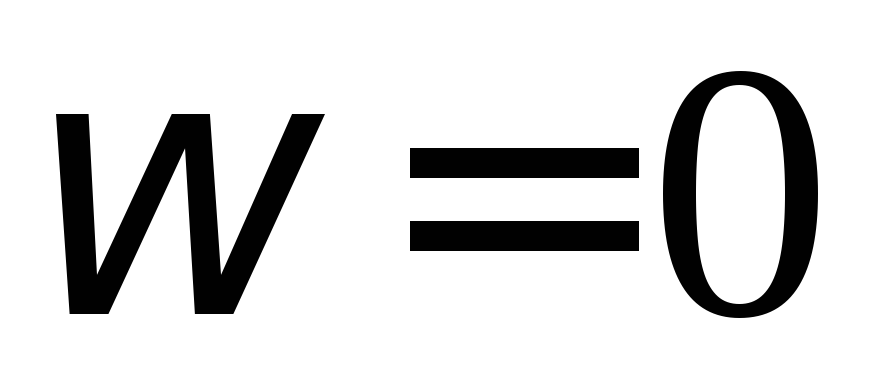 )
и хуже пропускает переменный ток (
)
и хуже пропускает переменный ток (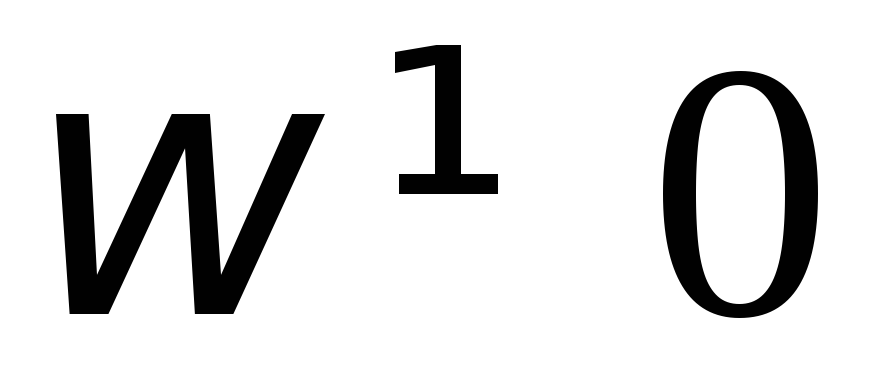 ).
В отличие от активного сопротивления,
индуктивное сопротивление не вызывает
выделение джоулева тепла.
).
В отличие от активного сопротивления,
индуктивное сопротивление не вызывает
выделение джоулева тепла.
И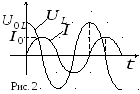 з
сравнения выражений для силы тока (1) и
напряжения (3) на индуктивности вытекает,
что колебания напряжения на катушке
опережают колебания тока на
з
сравнения выражений для силы тока (1) и
напряжения (3) на индуктивности вытекает,
что колебания напряжения на катушке
опережают колебания тока на 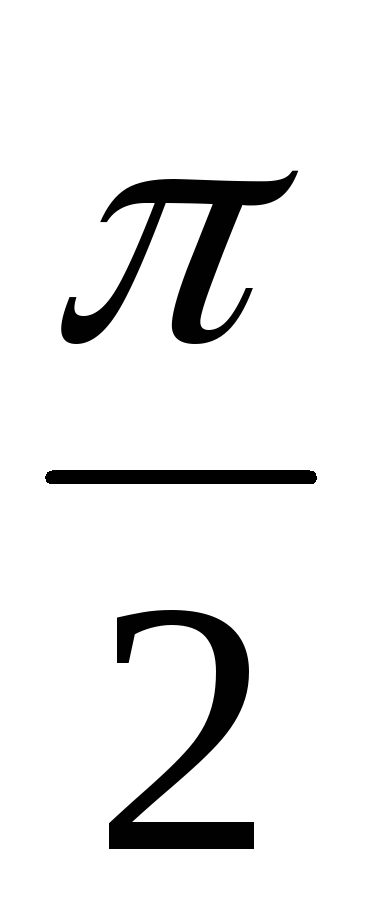 (рис. 2). Это означает, что на катушке
сначала возникает напряжение – ЭДС
самоиндукции, а уже потом начинает
возрастать ток (мгновенному росту тока
мешает ЭДС самоиндукции, которая
противодействует первичной переменной
ЭДС). Когда ток достигает максимального
значения – напряжение на катушке
минимально (производная в максимуме
равна нулю), И наоборот, когда напряжение
максимально – ток равняется нулю.
(рис. 2). Это означает, что на катушке
сначала возникает напряжение – ЭДС
самоиндукции, а уже потом начинает
возрастать ток (мгновенному росту тока
мешает ЭДС самоиндукции, которая
противодействует первичной переменной
ЭДС). Когда ток достигает максимального
значения – напряжение на катушке
минимально (производная в максимуме
равна нулю), И наоборот, когда напряжение
максимально – ток равняется нулю.
2.3. Емкость в цепи переменного тока
Р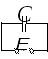 ассмотрим
электрическую цепь, которая состоит
только из источника переменного тока
и конденсатора
ассмотрим
электрическую цепь, которая состоит
только из источника переменного тока
и конденсатора  .
Как известно, конденсатор (две металлические
пластины, между которыми – диэлектрик)
вообще не пропускает постоянный ток
(ток будет протекать только до тех пор,
пока конденсатор заряжается, а потом
исчезает). Но если на конденсатор подавать
переменное напряжение, он все время
будет перезаряжаться, то есть через
конденсатор может идти переменный ток
.
Как известно, конденсатор (две металлические
пластины, между которыми – диэлектрик)
вообще не пропускает постоянный ток
(ток будет протекать только до тех пор,
пока конденсатор заряжается, а потом
исчезает). Но если на конденсатор подавать
переменное напряжение, он все время
будет перезаряжаться, то есть через
конденсатор может идти переменный ток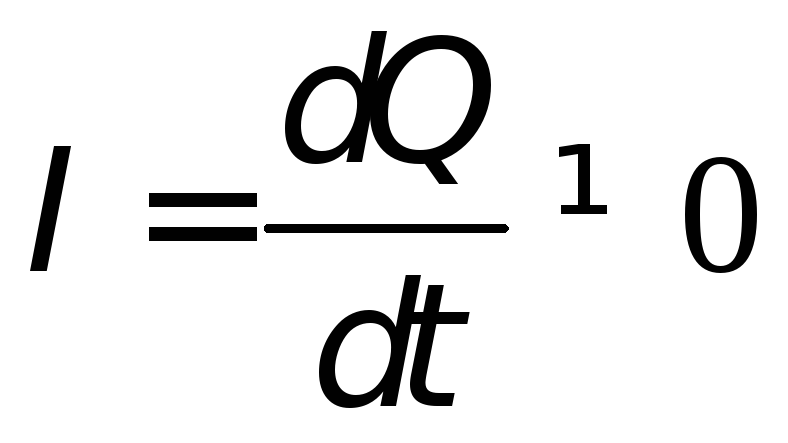 .
Чем больше частота переменного тока и
емкость конденсатора, тем лучше он
пропускает ток, тем меньшим будет егоемкостное
сопротивление.
Найдем это сопротивление, то есть
сопротивление, которое создает конденсатор
переменному току.
.
Чем больше частота переменного тока и
емкость конденсатора, тем лучше он
пропускает ток, тем меньшим будет егоемкостное
сопротивление.
Найдем это сопротивление, то есть
сопротивление, которое создает конденсатор
переменному току.
Пусть
через конденсатор течет ток, который
меняется по закону (1) 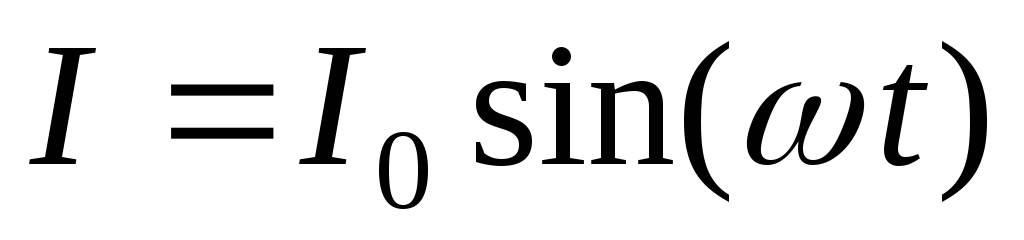 .
Из определения силы тока (1*)
.
Из определения силы тока (1*)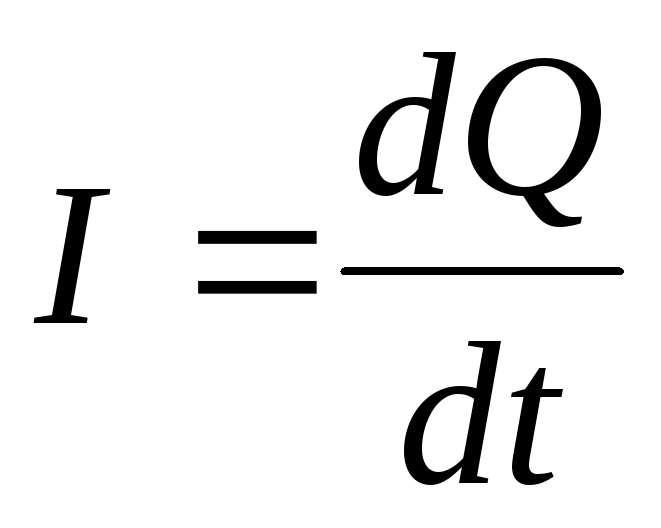 ,
можно найти заряд
,
можно найти заряд на обкладках конденсатора:
на обкладках конденсатора: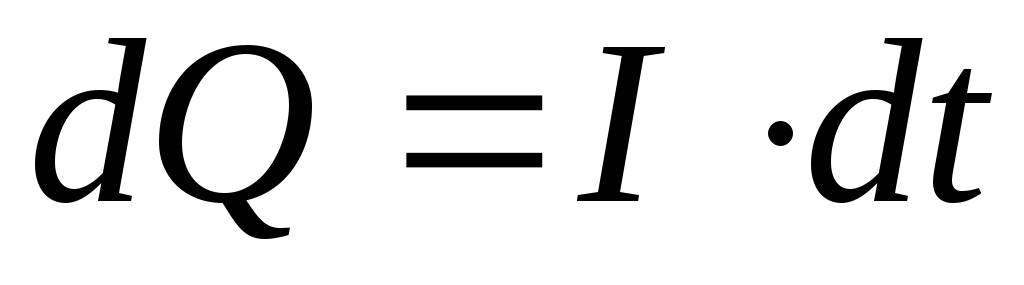 ,
,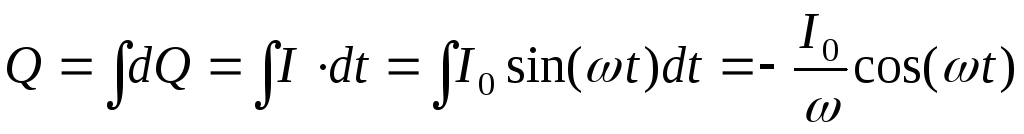 .
Учитывая, что
.
Учитывая, что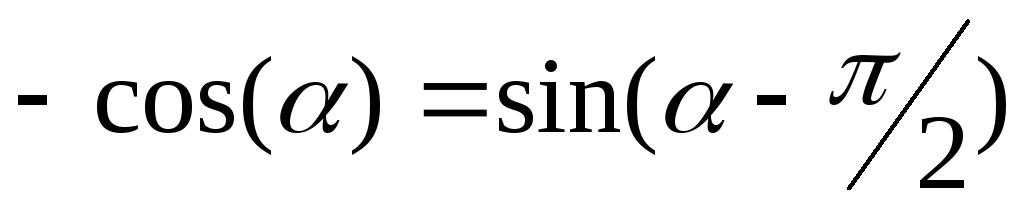 ,
получаем
,
получаем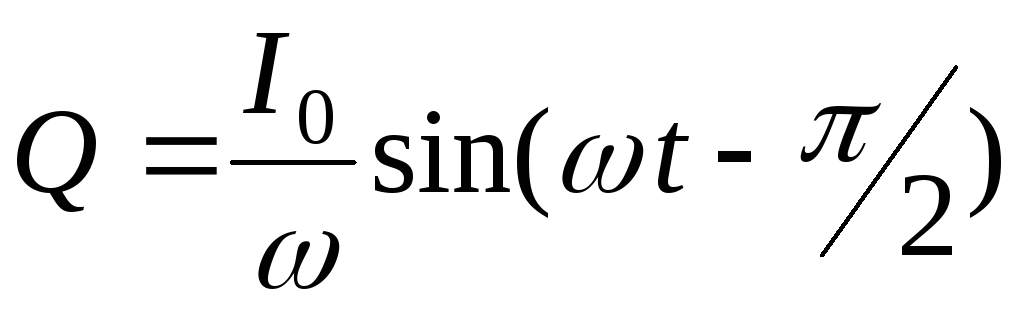 .
Из определения электроемкости конденсатора
(7)
.
Из определения электроемкости конденсатора
(7)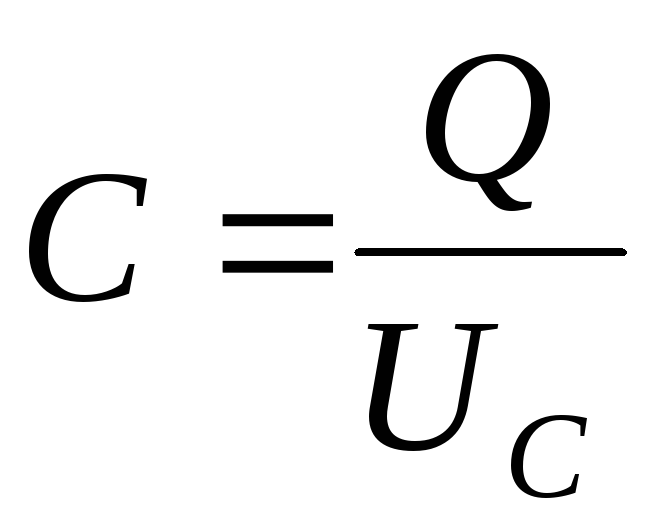 ,
вытекает, что напряжение на его обкладках
будет
,
вытекает, что напряжение на его обкладках
будет
| (5) |
Величина 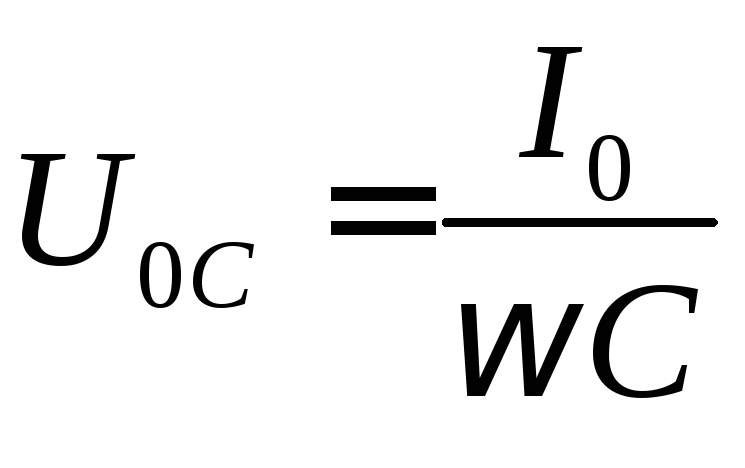 является амплитудным значением напряжения
на емкости, а отношение
является амплитудным значением напряжения
на емкости, а отношение
| (6) |
называют емкостным сопротивлением. На емкостном сопротивлении, как и на индуктивном, джоулево тепло не выделяется. Анализируя это выражение, можно сделать вывод, что конденсатор хорошо пропускает переменный ток высокой частоты и хуже пропускает ток малой частоты.
И з
сравнения выражений для силы тока (1) и
напряжения (5) на конденсаторе вытекает,
что колебания напряжения на конденсаторе
отстают от колебаний тока на
з
сравнения выражений для силы тока (1) и
напряжения (5) на конденсаторе вытекает,
что колебания напряжения на конденсаторе
отстают от колебаний тока на 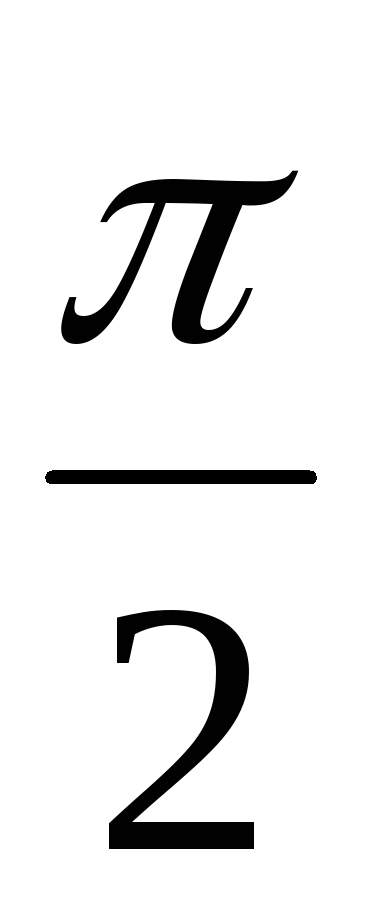 (рис. 3). То есть сначала через конденсатор
протекает ток (конденсатор заряжается),
а уже потом на нем возникает напряжение.
Когда ток достигает максимального
значения – напряжение на конденсаторе
равняется нулю, и наоборот, когда
напряжение максимальное – ток равняется
нулю.
(рис. 3). То есть сначала через конденсатор
протекает ток (конденсатор заряжается),
а уже потом на нем возникает напряжение.
Когда ток достигает максимального
значения – напряжение на конденсаторе
равняется нулю, и наоборот, когда
напряжение максимальное – ток равняется
нулю.
Список всех статей на технические темы
Простая электротехника все статьи
Сначала читаем статью «Переменный ток — краткие сведения»
Все электротехнические устройства состоят из сопротивлений индуктивностей и емкостей
Соотношение индуктивности емкости в цепи переменного тока принципиально определяют свойства цепи переменного тока.
Активное сопротивление R — это такой элемент электрической цепи, который оказывает сопротивление току с выделением тепла. Ведет себя одинаково в цепях постоянного и переменного тока, хотя величина сопротивления несколько отличается, это придется учитывать в точных расчетах.
Индуктивность L –это такой элемент электрической цепи, который состоит из витков провода и при протекании тока создает магнитное поле, это магнитное поле противодействует изменениям тока.
При протекании постоянного тока индуктивность ведет себя как проволока и не считается сопротивлением. Сопротивлением она является только для переменного тока, чем больше частота переменного тока, тем больше сопротивление индуктивности.
Емкость C – это такой элемент электрической цепи, который накапливает заряд, и проводит ток, только пока заряжается, или разряжается, поэтому в цепях постоянного тока, тока не проводит, а в цепях переменного тока все время заряжается – разряжается и, значит, проводит ток. Сопротивление емкости переменному току тем меньше, чем выше частота переменного тока.
Емкость и индуктивность взаимно противоположные по свойствам элементы, значит, они могут снижать взаимное влияние в цепях переменного тока или совсем отключать друг друга. Емкость и индуктивность оказывают сопротивление переменному току, но не могут выделить тепла, поэтому на них не происходит прямых потерь мощности.
Активное сопротивление R в цепи переменного тока
Что нам интересно знать про простейшую электрическую цепь содержащую R ?
Какой ток протекает в ней, какое напряжение на ней действует? и какая мощность может быть получена.
Здесь изображены две синусоиды, которые нельзя сравнивать и говорить какая больше, какая меньше. Они разные для удобства рассмотрения. Красная синусоида изображает переменное напряжение, а синяя синусоида изображает переменный ток
Если через активное R сопротивление протекает переменный синусоидальный ток, то на нем действует переменное синусоидальное напряжение. Ток и напряжение имеют одинаковую частоту и совпадают по фазе.
Мощность на активном сопротивлении определяется как произведение тока и напряжения. Действующая мощность будет равна произведению действующего значения тока на действующее значение напряжения.
Черные полуволны показывают, что мощность выделяемая в цепи на активном сопротивление изменяется также по синусоидальному закону,
Только знак остается все время положительным, это значит, что поток мощности однонаправлен. Мощность получается как произведение каждой точки синусоиды тока на каждую точку синусоиды напряжения в один и тот же момент. Плюс напряжения на плюс тока даст нам плюс мощности. Минус напряжения на минус тока даст нам плюс мощности.
Это значит, что при протекании тока через активное сопротивление R, электрическая мощность приводит к выделению тепла.
P=UI U = Uа√2 ; I = Iа√2 P = UаIа/2
Средняя мощность за период равна постоянной составляющей мощности
Uа Iа/2
Физический смысл этого явления состоит в том, что активное сопротивление потребляет энергию от источника, выделяет энергию в виде тепла. Электрическая мощность, которая превращается в тепло, называется активной мощностью и обозначается, как и в цепях постоянного тока, буквой P
Активными сопротивлениями в цепях переменного тока являются нагревательные и осветительные приборы, а также резисторы в сигнальных схемах, кроме того, как активные сопротивления проявляют себя все устройства, на которых выделяется полезная мощность в любом виде. Например, электрический мотор, звуковые динамики и т. п.
Индуктивное сопротивление в цепи переменного тока
XL = ωL
Чтобы сделать сосредоточенную индуктивность, кусок проволоки сматывают в катушку
Если к цепи с индуктивностью подключить переменное синусоидальное напряжение, то в ней должен протекать переменный синусоидальный ток.
Что же происходит в цепи с индуктивностью при протекании переменного тока.
Оказывается, ток и напряжение действуют не одновременно,
то есть, сдвинуты по фазе
На активном сопротивлении R, появление напряжения сразу – в тот же момент, вызывает появление тока, и они действуют в одной фазе.
На индуктивности так не получается.
Если напряжение от источника начинает нарастать, то ток за ним не успевает.
Почему? В индуктивности изменение тока, приводит к появлению ЭДС самоиндукции, а эта ЭДС направлена на встречу изменения тока. Напряжение растет, и ток хочет расти, но ЭДС самоиндукции препятствует нарастанию тока. Это примерно также, как сила инерции мешает разогнать тележку, когда мы сдвигаем ее с места.
Ток преодолевает сопротивление направленной навстречу ему ЭДС самоиндукции, и начинает нарастать, но это происходит, когда напряжение уже достигло максимального значения. Ток, наконец, достигает максимального значения, но напряжение в этот момент уже снизилось до нуля. Так и повторяется – ток все время отстает от напряжения на 900 то есть на π/2. Значит, фаза тока отрицательна и составляет — π/2
Откуда берется эта ЭДС самоиндукции, и почему она не мешает в цепи с сопротивлением R. Это связано с тем, что катушка индуктивности, в отличие от сопротивления R, создает сильное магнитное поле, благодаря большому количеству витков. Магнитное поле не может мгновенно изменяться, оно и рождает внутри провода ЭДС, которая препятствует изменению тока.
Более подробно об ЭДС самоиндукции смотри в статье Начальные представления об электромагнетизме
Красная синусоида напряжения пресекает ноль каждый раз раньше зеленой синусоиды тока на π/2
Вывод: В цепи с индуктивностью напряжение впереди тока на 90°.
Любое сопротивление ограничивает ток, но бывает активное сопротивление, бывает реактивное..
R — активное сопротивление — на нем выделяется тепло
X — реактивное сопротивление на нем не выделятся тепло
XL – сопротивление индуктивности
XL – сопротивление индуктивности L является реактивным, оно равно XL = ωL, то есть, оно прямо пропорционально частоте ω и индуктивности L, чем больше индуктивность, тем больше реактивное сопротивление и чем выше частота тем больше реактивное сопротивление.
Индуктивность тем сильнее ограничивает ток, чем выше частота тока.
Индуктивность пропускает переменный ток тем лучше, чем меньше индуктивность и чем меньше частота. Постоянный ток – частный случай переменного тока при частоте равной нулю, поэтому постоянный ток индуктивность пропускает без всякого сопротивления
Мощность на индуктивности
Мощность определяется как произведение тока на напряжение. Для каждого момента времени точка синусоиды тока умножается на точку синусоиды напряжения и получается точка синусоида мощности. Синусоида мощности получается двунаправленной, положительные полупериоды сменяются отрицательными, значит, мощность пол периода выделяется и пол периода поглощается. Это значит, что индуктивность L полпериода накапливает энергию в магнитном поле, а затем полпериода возвращает ее в источник.
Частота синусоиды мощности вдвое больше частоты тока и напряжения.
На индуктивности не получается выделение тепла, и никакой полезной мощности получить нельзя. Поэтому мощность, которая получается на индуктивности, называется реактивной и обозначается не Р, а другой буквой – QL
Емкость в цепи переменного тока
XC = 1/ ωc
При включении емкости под переменное напряжение во время t=0, конденсатор полностью разряжен, напряжение на конденсаторе равно 0, и он начинает заряжаться. Поэтому мгновенно появляется ток зарядки. По мере зарядки конденсатора на нем начинает расти напряжение, которое тормозит процесс зарядки, а значит, ток зарядки начинает уменьшаться.
Когда U на конденсаторе достигает максимума, это значит, что оно достигло максимума напряжения источника, зарядка продолжаться не может, поэтому ток становится равным 0.
Синусоида тока (синяя) каждый раз пресекает ноль на π/2 раньше, чем (красная) синусоида напряжения.
То есть, максимальному напряжению на емкости соответствует ток, равный 0, а это значит, что ток на емкости С впереди напряжения на 90° или π/2
XC — сопротивление емкости
XC — сопротивление емкости является реактивным, оно равно XC = 1/ ωc, то есть оно обратно пропорционально частоте и емкости, чем больше емкость, тем меньше реактивное сопротивление и чем выше частота тем меньше меньше реактивное сопротивление.
Емкость пропускает переменный ток тем лучше, чем больше емкость и чем выше частота. Постоянный ток – частный случай переменного тока при частоте равной нулю, поэтому постоянный ток емкость вообще не пропускает.
Конденсатор часто ставят в участки цепей, в которых не должен проходить постоянный ток
Мощность в цепи с емкостью
Произведение тока и напряжения для емкости дает синусоиду, которая состоит из положительных и отрицательных полуволн, значит, средняя за период мощность равна 0.
Физический смысл состоит в том, что емкость за пол периода получает энергию, а затем пол периода возвращает ее в источник. Энергия накапливается в электрическом поле емкости, а затем возвращается в источник. Частота синусоиды мощности вдвое больше частоты тока и напряжения.
Таким образом, на емкости не получается выделение тепла и никакой полезной мощности получить нельзя. Поэтому мощность, которая получается на емкости, называется реактивной и обозначается буквой – Qc.
Реактивные сопротивления
Индуктивность и емкость проявляют себя в электрических цепях как сопротивления.
XC – реактивное сопротивление емкости
XL — реактивное сопротивление индуктивности
Формулы сопротивлений позволяют их использовать для расчета задач по закону Ома для участка цепи.
Формула XC = 1/ ωc показывает, что сопротивление емкости зависит от частоты ω. Это означает, что емкость по-разному пропускает ток низкой и высокой частоты.
Емкость пропускает переменный ток тем лучше, чем выше частота.
Емкость вообще не пропускает постоянный ток, и это ее важнейшее свойство. Одно из главных применений емкости (конденсатора) состоит в том, что его ставят в те ветви схем, где запрещено протекание постоянного тока.
Формула XL = ωL показывает, что сопротивление индуктивности зависит от частоты. Это означает, что индуктивность по-разному пропускает ток низкой и ток высокой частоты.
Индуктивность хуже пропускает переменный ток высокой частоты
Чем больше частота. Тем труднее проходит переменный ток. Катушка индуктивности используется для ограничения переменного тока.
Конденсатор и катушка являются противоположностями.
Конденсатор пропускает переменный ток и не пропускает постоянный
Катушка пропускает постоянный ток и не пропускает переменный
Такие цепи содержат сопротивление R, индуктивность L, и ёмкость C.
Реальное сопротивление цепи, содержащей одновременно R, L и C, зависит от величины каждого элемента цепи, и от частоты переменного тока, который протекает в этой цепи.
Расчет цепей переменного тока по аналогии с расчетом цепей постоянного тока невозможен, потому, что необходимо учитывать фазовый сдвиг между током и напряжением.
Можно упростить цепи, если какой-то элемент: R, L или C пренебрежительно мал.
Задачи на переменный ток решаются методом векторных диаграмм.
Ток и напряжение являются векторными величинами.Их изображают как вращающиеся радиус -векторы, в этом смысле они отличаются от векторов сил и скоростей в механике, но правила сложения и вычитания векторов аналогичны.
Метод векторных диаграмм
Мы уже пользуемся векторными диаграммами, по которым наблюдаем соотношения токов и напряжения в цепях переменного тока. Векторная диаграмма это стоячее изображение вращающихся векторов.
В предыдущих рассуждениях, было сказано, что линейно развернутая диаграмма переменного процесса, (в простом случае синусоидального), точно показывает изменение мгновенного значения переменной величины, то есть происходит все именно так как показывает синусоида и каждая ее точка и есть переменная величина в данный момент. Но оказывается нам интересно не это, нам нужно знать какое значение тока и напряжения и мощности действует в цепи в течение времени, то есть действует длительное время, пока цепь работает.
Анализ синусоид нескольких величин, одновременно действующих в разных фазах, позволяет рассчитать все свойства и режимы работы цепи переменного тока, но гораздо проще это сделать, если отвлечься от синусоид и просто построить соотношение векторов, которые, собственно, и образуют эти синусоиды. Вся информация синусоид заложена в их радиус – векторах. Мы останавливаем эти векторы на рисунке, понимая, что они вращающиеся, но факт их вращения учитываем угловой частотой в расчетных формулах векторной диаграммы.
Итак, векторная диаграмма заменяет линейно развернутую синусоидальную диаграмму, потому, что любая информация, заложенная в синусоиду, есть и в соответствующем ей радиус-векторе.
Если нам приходится рассматривать несколько действующих одновременно синусоидальных процессов, то они изображаются векторной диаграммой, где длина каждого вектора, соответствует действующему значению синусоидальной величины, направление вектора соответствует начальной фазе, синусоидальной величины.
Результирующие значения одновременно действующих напряжений рассчитывается как векторная сумма, где угол между векторами определяется сдвигом фаз между ними.
Расчет цепей переменного тока сводится к расчету треугольников, которые состоят из соответствующих векторов.
Например, можно определить суммарное напряжение, частичные напряжения, и сдвиг фаз между ними.
На основании векторных диаграмм можно построить подобные векторным диаграммам треугольники сопротивлений и треугольники мощностей, решением которых можно определить соотношения сопротивлений, и мощности которые действуют в цепях переменного тока.
Векторная диаграмма напряжений представляет собой векторный треугольник напряжений
Последовательное соединение L R.
Любая катушка наматывается проволокой, а проволока обладает сопротивлением, которое приходится учитывать.
Получается, что реальная цепь, содержащая только L, просто невозможна. В некоторых случаях значением R пренебрегают, и получается, что вроде бы цепь с только L, на самом деле она конечно L R.
Реально, кроме проволоки, в цепи всегда есть и какие – то другие элементы R, поэтому интерес представляют именно цепи L R,
Ток, при последовательном соединении, один и тот же через все сопротивления, а напряжения разные, но общее напряжение не равно просто сумме напряжений на каждом сопротивлении, оно равно векторной сумме, то есть вектор общего напряжения равен сумме векторов напряжений на каждом участке. Для расчетов напряжений надо построить векторную диаграмму.
Векторная диаграмма строится так.
Выберем фазу общего тока равной 0, вектор тока откладывается как горизонтальный вектор слева на право. Далее строим векторную диаграмму напряжений. Сначала откладывается вектор напряжения на сопротивлении R. Этот вектор, пойдет горизонтально, так как его фаза совпадает с фазой тока. Затем строят вектор напряжения на индуктивности L. Его надо откладывать под углом 900 вверх, это потому, что напряжение на индуктивности впереди на 900.
Второй вектор переносится из центра вращения. Прикладываем его к концу вектора напряжения на активном сопротивлении. Таковы правила сложения векторов.
Теперь остается построить вектор полного напряжения на обоих элементах. Это вектор суммы, он, как известно, строится из начала первого вектора к концу второго.
Получился прямоугольный треугольник. Любую сторону этого треугольника можно найти по теореме Пифагора.
Острый угол этого треугольника и есть реальный сдвиг фаз в этой цепи между током и общим напряжением. Он обязательно меньше 90 градусов, потому что только на идеально индуктивности он составляет 90 градусов. Активное сопротивление обязательно уменьшает сдвиг фаз.
Соотношение сопротивлений в такой цепи соответствует треугольнику сопротивлений. Общее сопротивление, обозначается Z, определяется как гипотенуза прямоугольного треугольника, где катеты Rа и XL
Z2, = Rа2 + X2L
В цепи L R, в отличие от цепи только с L, появляется активная мощность, следовательно она потребляет энергию источника и выделяет тепло.
Соотношение мощностей такой цепи соответствует треугольнику мощностей. Где S – полная мощность, определяется как гипотенуза треугольника, где катеты Р и QL
S2 = Р2 + Q2L
Векторная диаграмма и все треугольники сопротивления и мощностей подобные, значит, угол φ (сдвиг фаз) является общим для всех треугольников.
Последовательное соединение RC
Конденсаторы очень часто включают последовательно с сопротивлениями, но если даже специального сопротивления нет, любой конденсатор обладает определённой величиной активного сопротивления, которую необходимо учитывать в точных расчетах. Есть понятие «добротность» конденсатора, которая проявляет активную составляющую его сопротивления
При последовательном соединении, через все элементы цепи протекает один ток, который называем – общий.
Сначала откладываем вектор тока, фазу которого принимаем равной нулю. Вектор напряжения на активном сопротивлении, откладываем в том же направлении, так как на активном сопротивлении ток и напряжение совпадают по фазе.
К концу вектора напряжения на активном сопротивлении прикладываем начало вектора напряжения на емкости. Фаза напряжения на емкости отстает от фазы напряжения на активном сопротивлении на 90 градусов, а вектор отстающего напряжения откладывается вниз.
Векторная диаграмма напряжений представляет собой прямоугольный треугольник, который позволяет определить все составляющие по теореме Пифагора.
Активное сопротивление R включенное в цепь с катушкой или конденсатором уменьшает угол сдвига фаз.
Соотношение сопротивлений в такой цепи соответствует треугольнику сопротивлений. Общее сопротивление обозначается буквой Z, определяется как гипотенуза прямоугольного треугольника, где катеты Rа и XС
Z 2 = Rа2 + X2С
В цепи L C, в отличие от цепи только с C, появляется активная мощность, следовательно она потребляет энергию источника и выделяет тепло.
Соотношение мощностей такой цепи соответствует треугольнику мощностей. Где S – полная мощность, определяется как гипотенуза треугольника, где катеты Р и QС
S2 = Р2 + Q2С
Векторная диаграмма и все треугольники сопротивления и мощностей подобные, значит, угол φ (сдвиг фаз) является общим для всех треугольников
Параллельное соединение RL
При параллельном соединении RL одинаковое напряжение на всех элементах цепи, а токи разные и сдвинутые по фазе. Ток через сопротивление совпадает по фазе с напряжением, а ток через катушку отстает по фазе от напряжения. на 900. Общий ток отстает от напряжения меньше чем на 900.
Для цепей с параллельным соединением элементов, гораздо удобнее использовать не сопротивления (активные и реактивные) а их обратные величины, которые называются проводимости. Вместо r используется g, вместо XL используется bL, вместо Xc используется bc
Параллельное соединение RC
При параллельном соединении RС одинаковое напряжение на всех элементах цепи, а токи разные и сдвинутые по фазе. Ток через сопротивление совпадает по фазе с напряжением, а ток через конденсатор опережает по фазе от напряжения. на 900. Общий ток опережает напряжение меньше чем на 900
Значение Cos φ
Cos φ в практической электротехнике имеет очень важное значение. Реальные нагрузки, типа электромоторов и трансформаторов, имеют большую индуктивную составляющую сопротивления, то есть, фактически, представляют собой цепи RL. Для таких цепей неизбежно существует сдвиг фаз, который приводит к тому, что полная мощность S значительно превышает активную мощность (P).
Из формулы видно, что чем меньше Cos φ (Чем больше угол сдвига фаз), тем меньшую часть активная мощность составляет от полной мощности .
Только активная мощность является полезной, если источник затрачивает полную мощность, а от нагрузки мы можем получить только активную мощность, значит, Cos φ имеет смысл электротехнического КПД или коэффициента мощности.
В идеале источник должен отдавать такую мощность, которую будет потреблять нагрузка. Реальные устройства неизбежно содержат индуктивности (катушки, обмотки, и т.п.), значит, источник вынужден отдавать полную мощность, которая значительно больше, активной.
Проектирование устройств и электрических цепей должно иметь целью получить значение Cos φ как можно ближе к единице, то есть влияние индуктивности надо свести к минимуму. Плохие значения Cos φ приводят к большим неоправданным затратам электроэнергии.
Цепи RLC
Цепи, которые содержат R, L и C, могут иметь разные варианты соединений. Цепи могут быть последовательными, разветвленными, и имеющие последовательные соединения в ветвях. Рассмотрим простые варианты. RLC последовательно.
В некоторых случаях цепи RL (моторы, трансформаторы и т. п.) имеют слишком маленький Cos φ. То есть в них слишком сильно влияние индуктивной составляющей. В такие цепи специально включают компенсационные конденсаторы, которые уменьшают фазовый сдвиг, Это разгружает источники электроэнергии от избыточной реактивной нагрузки, и обеспечивает значительную экономию электроэнергии.
RLC последовательно
Как будет выглядеть векторная диаграмма в общем случае?
При последовательном соединении сопротивлений на каждом сопротивлении действует своя часть напряжения. На большем сопротивлении будет большая часть напряжения.
На первой векторной диаграмме видно, что напряжение на конденсаторе Uc больше, чем на катушке UL тогда суммарный вектор общего напряжения направлен вниз, и видно, xnj угол сдвига фаз отрицательный. На второй диаграмме видно, что напряжение на конденсаторе Uc, значительно меньше, чем UL , и вектор общего напряжения оказался направленным вверх, угол сдвига фаз стал положительным.
В первом случае цепь имеет емкостный характер, во втором индуктивный.
На определенной частоте наступает равенство Uc = Ul, такое явление называется резонанс напряжений
Условие резонанса XL = XC
При резонансе напряжений Общее сопротивление цепи становится минимально, а ток становится максимальным, что может быть опасно для источника и требует надежной защиты.
RLC параллельно
Векторные диаграммы токов при параллельном соединении
При параллельно соединении элементов RLC напряжение на всех элементах действует одно и то же, а токи разные, чем меньше сопротивление ветви, тем больше ток. В первом случае ток катушки значительно больше тока конденсатора. Вектор общего тока направлен вниз. Во втором случае ток катушки значительно меньше тока конденсатора и вектор тока направлен вверх.
В первом случае цепь имеет индуктивный характер, во втором емкостный
На определенной частоте наступает равенство токов Ic = IL такое явление называется резонанс токов.
При резонансе токов сопротивление цепи становится максимальным и ток уменьшается до величины, которая определяется сопротивлением R, которое остается в цепи.
Условия резонанса
Резонанс широко применяется в радиотехнических и различных электронных схемах.
XL = XC
Устройства для переменного тока и устройства для постоянного тока
Устройства. Которые включаются электрические цепи
Лампочки
Нагреватели
Электромоторы
Электроинструмент
Бытовые приборы
Электроника
И т. п.
Лампочки и нагреватели работают одинаково в цепях переменного и постоянного тока. В некоторых случаях разница может быть заметной, так как активное сопротивление в цепи постоянного тока (омическое) может отличаться от сопротивления в цепи переменного тока.
Электромоторы и электроинструмент рассчитанный на переменный ток, при подключении в цепь постоянного тока скорее всего сгорят, так как, у них пропадает индуктивное сопротивление и ток сильно возрастает.
Если моторы, и инструмент рассчитанные на постоянный ток, включены на переменный ток, они сильно потеряют мощность, так как появившееся индуктивное сопротивление и сильно ограничит потребляемый ток.
Цепь с индуктивностью — Знаешь как
Содержание статьи
Напряжение и ток
 Цепь, изображенная на рис. 5-14, обладает индуктивностью и ничтожно малым активным сопротивлением
Цепь, изображенная на рис. 5-14, обладает индуктивностью и ничтожно малым активным сопротивлением
(r = 0)
При прохождении по цепи тока
i = Iм sin ωt в ней индуктируется э. д. с. самоиндукции;
еL = —L(di : dt)
Для замкнутой цепи согласно второму правилу Кирхгофа u + eL = ir = 0 следовательно, напряжение на зажимах индуктивности
u = — eL = L(di : dt)
Рис. 5-14. Цепь с индуктивностью.
Написанное уравнение, с одной стороны, показывает, что под действием приложенного
напряжения в цепи устанавливается такой ток, который в каждый момент времени индуктирует э. д. с. самоиндукции, равную по величине и противоположную по направлению приложенному напряжению, т. е. э. д. с, уравновешивающую напряжение.
С другой стороны, уравнение показывает, что напряжение на индуктивности пропорционально скорости изменения тока по времени.
При синусоидальном токе (рис. 5-15) скорость изменения его
di : dt = Iм(d sin ωt : dt) = ωIмcosωt

т. е. скорость изменения пропорциональна косинусу. Следовательно, при прохождении тока через максимум скорость его изменения равна нулю, а при прохождении тока через нулевое значение скорость его изменения наибольшая (рис. 5-15).
Рис. 5-15. Графики тока, магнитного потока, напряжения и мощности цепи с индуктивностью.
Напряжение на индуктивности
и = L(di : dt ) = LωIмcosωt = LωIмsin (ωt + π:2)
Таким образом, при синусоидальном токе напряжение на индуктивности также синусоидально, но по фазе опережает ток на угол π/2 (рис. 5-16).
Индуктированная в цепи э. д. с. самоиндукции
eL = — и = — LωIM sin (ωt + π:2) = LωIM sin (ωt — π:2)
сдвинута по фазе от напряжения на половину периода.
Векторная диаграмма цепи с индуктивностью дана на рис. 5-16.

Рис. 5-16. Векторная диаграмма цепи с индуктивностью.
Индуктивное сопротивление
Из выражений следует, что максимальное значение, напряжения и равное ему максимальное значение э. д. с.
Uм = ELм= LωIM
Разделив написанные выражения на √2, получим действующие значения напряжения и э. д. с.
U = EL = LωI
откуда действующее значение тока I = U : ωL = U : xL
Величина, определяемая отношением напряжения к току цепи:
U : I = ωL = 2πfL = xL
называется реактивным сопротивлением индуктивности или просто индуктивным сопротивлением.
Индуктивное сопротивление пропорционально индуктивности и частоте переменного тока. При изменении частоты от f = 0 (постоянный ток) до f = ∞ оно изменяется от xL = 0 до xL = ∞.
Мощность
Мгновенное значение мощности
р = ui = Uм сos 2ωt = UI sin 2ωt
Приняв во внимание, что sin ωt cos ωt = 1/2 sin 2 ωt, получим: p = 1/2UмIм sin 2ωt = UI sin 2ωt
На рис. 5-15 показан график мгновенной мощности. Мгновенная мощность в цепи с индуктивностью изменяется с двойной частотой,; достигая то положительного максимума UI = I2 ωL, то такого же по величине отрицательного максимума.
При нарастании тока, а следовательно, и магнитного потока (первая и третья четверти периода, рис. 5-15), независимо от его направления, происходит: накопление энергии магнитного поля от пуля до максимального значений: Wм = 1/2LI2м = LI2
которая получается от генератора; таким образом, цепь работает в режиме потребителя, что соответствует положительному значению мощности цепи.
При спадании тока, а следовательно, и магнитного потока (вторая и четвертая четверти периода, рис. 5-15) происходит уменьшение энергии магнитного поля от максимального значения до нуля, которая возвращается цепью генератору. Таким образом, в эти части периода цепь работает в режиме генератора, что соответствует отрицательному значению мощности цепи с индуктивностью.
Средняя мощность Р в цепи с индуктивностью равна нулю.
Максимальное значение мощности Q в цепи с индуктивностью принято называть реактивной мощностью.
Из (5-27) следует, что Q = 1/2UмIм = UI = I2ωL = ωWм
Единица измерения реактивной мощности носит название вольт-ампер реактивный (вар).
Пример 5-5. Катушка с индуктивностью 0,01 гн включена в сеть
с напряжением 127 в и частотой 50 гц.
1. Определить реактивное сопротивление, ток цепи и реактивную мощность:
xL = 2πfL = 2π • 50 • 0,01 = 3,14 ом;
I= U/ xL= 127 : 3,14 = 40,5 а
Q = UI = 127 • 40,5 = 5143,5 вар.
2. Определить реактивное сопротивление и ток при частоте 500 гц:
xL =2πfL = 2π • 500 • 0,01=31,4 ом;
I = U / xL = 127 : 31,4 = 4,05 a
Зависимость между э. д. с. и магнитным потоком
При расчете цепей переменного тока со сталью часто индуктированную з. д. с. выражают через магнитный поток. Амплитудное значение потокосцепления самоиндукции
Ψм = LIм
Если все витки контура пронизываются одним магнитным потоком, то Ψм = ɯФм
В этом случае э. д. с. самоиндукции или равное ей напряжение можно выразить:
U=EL=ωL(Iм/√2) = 2πf(ɯФм /√2) = 4,44ɯФм
Статья на тему Цепь с индуктивностью
Что такое чисто индуктивная цепь? — Phasor Diagram & Waveform
Цепь, которая содержит только индуктивность (L), а не любые другие величины, такие как сопротивление и емкость в цепи, называется Pure индуктивной цепью. В схеме этого типа ток отстает от напряжения на угол 90 градусов.
Содержание:
Катушка индуктивности — это тип катушки, которая запасает электрическую энергию в магнитном поле, когда через нее протекает ток.Индуктор состоит из провода, который намотан в виде катушки. Когда ток, протекающий через индуктор, изменяется, изменяющееся во времени магнитное поле вызывает ЭДС, которая препятствует протеканию тока. Индуктивность измеряется в Генри . Противостояние потока тока известно как индуктивное сопротивление .
Объяснение и вывод индуктивной схемы
Схема, содержащая чистую индуктивность, показана ниже:
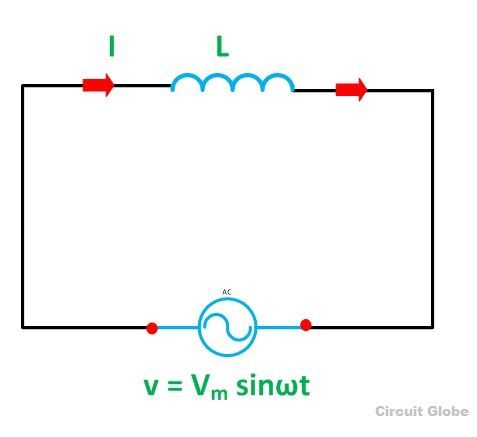 Схема
Схемачистой индуктивной схемы
Пусть переменное напряжение, подаваемое на цепь, определяется уравнением:
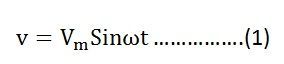
В результате переменный ток i протекает через индуктивность, которая индуцирует в нем ЭДС.Уравнение показано ниже:
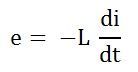
ЭДС, которая индуцируется в цепи, равна и противоположна приложенному напряжению. Следовательно, уравнение становится,

Положив значение е в уравнении (2), получим уравнение как
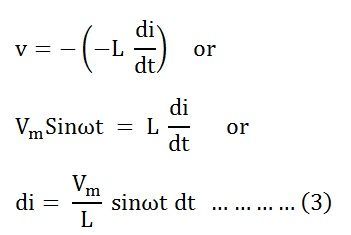
Интегрируя обе части уравнения (3), мы получим
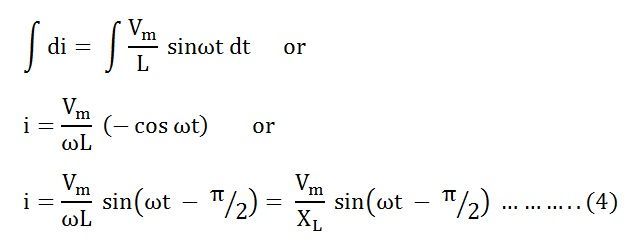 , где X L = ω L — сопротивление, предлагаемое потоку переменного тока чистой индуктивностью и называемое индуктивным реактивным сопротивлением.
, где X L = ω L — сопротивление, предлагаемое потоку переменного тока чистой индуктивностью и называемое индуктивным реактивным сопротивлением.
Значение тока будет максимальным, когда sin (ωt — π / 2) = 1
Следовательно,
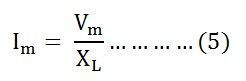
Подставляя это значение в I м из уравнения (5) и подставляя его в уравнение (4), мы получим 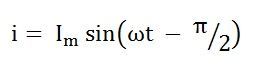
Диаграмма вектора и кривая мощности индуктивной цепи
Ток в чистой индуктивной цепи переменного тока отстает от напряжения на 90 градусов. Форма волны, кривая мощности и фазовая диаграмма чисто индуктивного контура показаны ниже
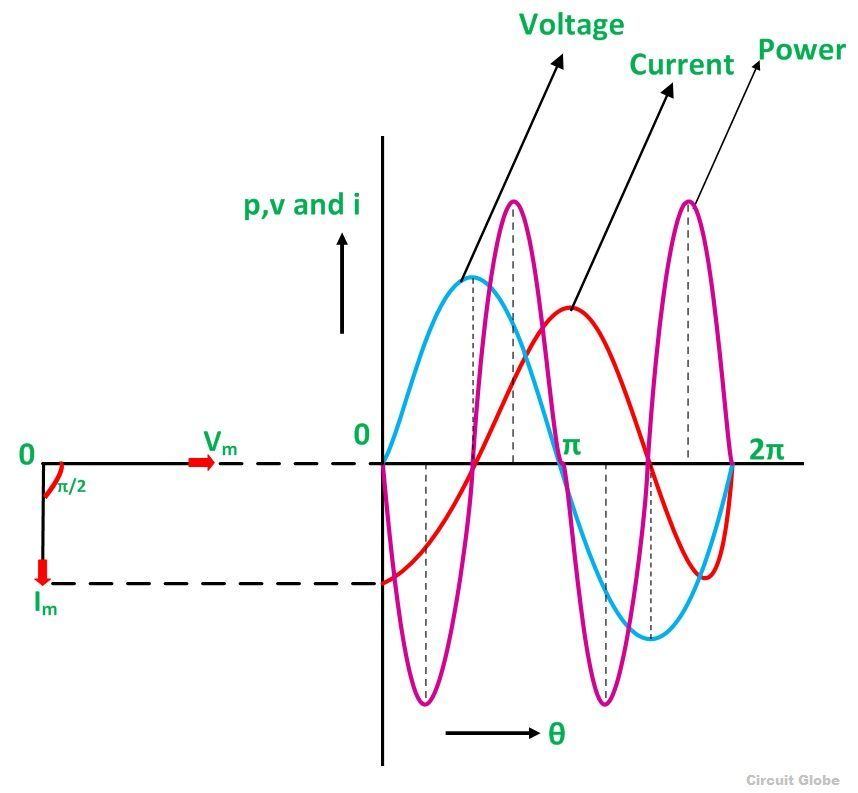
Диаграмма вектора и форма волны чистой индуктивной цепи
Форма волны напряжения, тока и мощности показана синим, красным и розовым цветами соответственно.Когда значения напряжения и тока находятся на своем пике в качестве положительного значения, мощность также является положительной, и аналогично, когда напряжение и ток дают отрицательный сигнал, мощность также станет отрицательной. Это из-за разности фаз между напряжением и током.
Когда напряжение падает, значение тока изменяется. Когда значение тока достигает своего максимального или максимального значения, напряжение в этот момент времени будет равно нулю, и, следовательно, напряжение и ток не совпадают по фазе друг с другом на угол 90 градусов.
Диаграмма вектора также показана на левой стороне формы сигнала, где текущее (I м ) запаздывающее напряжение (V м ) под углом π / 2.
Власть в чистой индуктивной цепи
Мгновенная мощность в индуктивной цепи задается
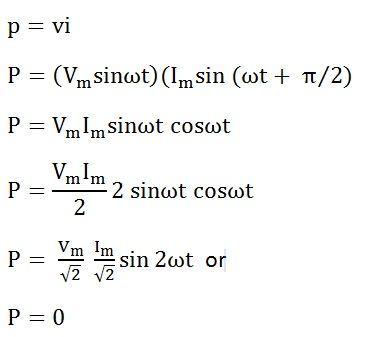
Следовательно, средняя мощность, потребляемая в чисто индуктивной цепи, равна нулю.
Средняя мощность в одном изменении, то есть в полупериоде, равна нулю, так как отрицательная и положительная петли находятся под кривой мощности, то же самое.
В чисто индуктивной цепи в течение первой четверти цикла мощность, подаваемая источником, сохраняется в магнитном поле, установленном вокруг катушки. В следующем цикле четверти магнитное поле уменьшается, и энергия, которая была сохранена в цикле первой четверти, возвращается источнику.
Этот процесс продолжается в каждом цикле, и, таким образом, в цепи не расходуется энергия.
, однофазных цепей переменного тока MCQ (пояснительные ответы) X L ). - Непосредственно
- Обратно
- Нет эффекта
Показать пояснительный ответ
Ответ: 1… Прямо пропорционально
Объяснение:
X L = 2πfL…., т.е. …. X L ∞ f ……, а также… ..L ∞ f
2. В случае индуктивной цепи частота ___________ пропорциональна току.
- Непосредственно
- Обратно
- Нет эффекта
Показать пояснительный ответ
Ответ: 2… Обратно пропорционально
Объяснение: 



3. В случае индуктивной цепи индуктивность (L) равна ___________ Пропорциональной к индуктивному сопротивлению ( X L ).
- Непосредственно
- Обратно
- Нет эффекта
Показать пояснительный ответ
Ответ: 1… Непосредственно
Объяснение:
X L = 2πfL… .. т.е. X L ∞L.
4. В индуктивной цепи при увеличении индуктивности (L) или индуктивного сопротивления (X L ) ток цепи уменьшается, но коэффициент мощности цепи ________?
- Увеличивается
- Также уменьшается
- Остается прежним
- Ничего из вышеперечисленного
Показать пояснительный ответ
Ответ: 2… Также уменьшается
Объяснение:
Предположим, когда индус (L) = 0.02H
V = 220, R = 10 Ом, L = 0,02 H, f = 50 Гц.
X L = 2πfL = 2 x 3,1415 x 50 x 0,02 = 6,28 Ом
Z = √ (R 2 + X L 2 ) = √ (10 2 + 6,28 2 ) = 11,8 Ом
I = V / Z = 220 / 11,8 = 18,64 A
Cos θ = R / Z = 10 / 11,05 = 0,85
Теперь мы увеличиваем индуктивность (L) с 0,02 H до 0,04 H,
V = 220, R = 10 Ом, L = 0,04 H, f = 50 Гц.
X L = 2πfL = 2 x 3.1415 x 50 x 0,04 = 12,56 Ω
Z = √ (R 2 + X L 2 ) = √ (10 2 + 12,56 2 ) = 16,05 Ω
I = V / Z = 220 / 16,05 = 13,70 A
Cos θ = R / Z = 10 / 16,05 = 0,75
Вывод:
Мы можем видеть, что когда индуктивность (L) была 0,02, то ток в цепи составлял 18,64 A, а мощность в цепи коэффициент был (Cos θ) = 0,85.
Но когда индуктивность цепи увеличилась с 0,02 до 0,04 Гц, то ток уменьшился с 13.70 A до 18,64 A, также коэффициент мощности (Cos θ) снизился с 0,85 до 0,75.
Следовательно, доказано,
В индуктивной цепи, когда индуктивное сопротивление X L увеличивается, ток цепи уменьшается, но коэффициент мощности цепи также уменьшается.
5. В индуктивной цепи, когда увеличивается индуктивность (L) или индуктивное сопротивление (X L ), ток цепи ________?
- Также увеличивается
- Уменьшается
- Остается прежним
- Ничего из вышеперечисленного
Показать пояснительный ответ
Ответ:… 2… Уменьшается
Мы знаем, что I = V / R,
, но индуктивно схема, I = V / X L
Т.о. ток обратно пропорционален току (в индуктивной цепи.
Давайте проверим на примере.
Предположим, когда индуктивность (L) = 0,02H
V = 220, R = 10 Ом, L = 0,02 H, f = 50 Гц.
X L = 2πfL = 2 x 3,1415 x 50 x 0,02 = 6,28 Ом
Z = √ (R 2 + X L 2 ) = √ (10 2 + 6,28 2 ) = 11,8 Ω
I = V / Z = 220 / 11,8 = 18,64 A
Теперь мы увеличиваем индуктивность (L) с 0,02 H до 0,04 H,
V = 220, R = 10 Ω, L = 0.04 H, f = 50 Гц.
X L = 2πfL = 2 x 3,1415 x 50 x 0,04 = 12,56 Ом
Z = √ (R 2 + X L 2 ) = √ (10 2 + 12,56 2 ) = 16,05 Ω
I = V / Z = 220 / 16,05 = 13,70 A
Вывод:
Мы можем видеть, что, когда индуктивность (L) была 0,02, то ток цепи был 18,64 A,
, но, когда индуктивность цепи увеличилась с 0,02 H до 0,04 H, ток уменьшился с 13,70 A до 18.64А.
Следовательно доказано,
В индуктивной цепи, когда индуктивное сопротивление X L увеличивается, ток в цепи уменьшается, и наоборот.
6. В случае емкостной цепи частота составляет ___________ Пропорционально емкости (C) или емкостному сопротивлению ( X C ).
- Непосредственно
- Обратно
- Без последствий
Показать пояснительный ответ
Ответ: 2.Обратно
Объяснение:
В емкостном контуре
X C = 1 / 2πfC и
f = 1 / 2πX C C
Итак, мы видим, что
f = 1 / C… а также… f = 1 / X C.
Таким образом, в емкостном контуре частота обратно пропорциональна Емкости (C) и Емкостному сопротивлению (Xc)
7. В случае емкостной цепи частота ___________ пропорциональна току.
- Непосредственно
- Обратно
- Без последствий
Показать пояснительный ответ
Ответ: 1 Непосредственно
Объяснение:
Мы знаем, что
I = V / R
, но в емкостная цепь
I = V / Xc …… (1)
Но мы также знаем, что
Xc = 1 / 2πfC…. (2)… .. то есть… .. Xc ∞ 1 / f
Puttint (2) в (1)
I = V / (1 / 2πfC)… то есть ..I = V x 2πfC
Следовательно доказано, I ∞ f
8. В случае емкостной цепи Ёмкость (C) ___________ пропорциональна емкостному сопротивлению ( X C ).
- Непосредственно
- Обратно
- Без эффекта
Показать пояснительный ответ
Ответ: 2. Обратно
Объяснение:
В емкостной цепи,
X C = 1 / 2πfC, … Т. Е.
Xc ∞ 1 / C
Итак, в емкостном контуре емкость (C) обратно пропорциональна емкостному сопротивлению (Xc)
9. В емкостной цепи, когда емкость (C) увеличивается (ток цепи также увеличивается), тогда коэффициент мощности схемы ________?
- Увеличивается
- Уменьшается
- Остается прежним
- Ничего из вышеперечисленного
Показать пояснительный ответ
Ответ: 1. Увеличивается.
Объяснение:
Предположим, когда емкость (C) = 500 мкФ = или 5 × 10 -04 F
V = 220, R = 10 Ом, C = 500 мкФ = (5 × 10 -04 F), f = 50 Гц.
X C = 1 / 2πfC = 1 / (2 x 3,1415 x 50 x 5 × 10 -04 F) = 6,37 Ом
Z = √ (R 2 + X C 2 ) = √ (10 2 + 6,37 2 ) = 11,85 Ом
I = V / Z = 220 / 11,8 = 18,56 A
Cos θ = R / Z = 10 / 11,85 = 0,84
Теперь мы увеличили Емкость (C) = 1000 мкФ = или 1 × 10 -3 F,
В = 220, R = 10 Ом, C = 1000 мкФ = 1 × 10 -3 F
X C = 1 / 2πfC = 1 / (2 х 3.1415 x 50 x 1 × 10 -3 F) = 3,18 Ом
Z = √ (R 2 + X C 2 ) = √ (10 2 + 3,18 2 ) = 10,49 Ω
I = V / Z = 220 / 11,8 = 20,97A = 21A
Cos θ = R / Z = 10 / 11,85 = 0,95
Вывод:
Мы можем видеть, что когда емкость (C) была 500 мкФ, то ток в цепи был 18,56 А, а коэффициент мощности в цепи был (Cos θ) = 0,84.
Но когда мы увеличили емкость цепи с 500 мкФ до 1000 мкФ, ток также увеличился с 18.56 А до 21 А, также Коэффициент мощности (Cos θ) увеличился с 0,84 до 0,95.
Следовательно, доказано,
В индуктивной цепи, когда емкость C увеличивается, ток цепи также увеличивается, более того, также увеличивается коэффициент мощности схемы.
10. В емкостном контуре при увеличении емкостного сопротивления коэффициент мощности контура ________?
- Увеличивается
- Уменьшается
- Остается прежним
- Ничего из вышеперечисленного
Показать пояснительный ответ
Ответ: 2.Уменьшается
Объяснение:
Предположим, когда емкостное сопротивление (Xc) = 6 Ом
В = 220, R = 10 Ом, Xc = 6 Ом
Z = √ (R 2 + X C 2 ) = √ (10 2 + 6 2 ) = 11,66 Ом
Cos θ = R / Z = 10 / 11,66 = 0,85
Теперь мы увеличили емкостное сопротивление = 10 Ом
В = 220 , R = 10 Ом, Xc = 10 Ом
Z = √ (R 2 + X C 2 ) = √ (10 2 + 10 2 ) = 14.14 Ом
Cos θ = R / Z = 10 / 14,14 = 0,70
Вывод:
Мы можем видеть, что, когда емкостное реактивное сопротивление (Xc) = 6 Ом, тогда коэффициент мощности схемы был (Cos θ) = 0,85 ,
Но когда мы увеличили емкостное сопротивление с 6 Ом до 10 Ом, коэффициент мощности (Cos θ) снизился с 0,85 до 0,70.
Следовательно, доказано,
В емкостном контуре, когда емкостное реактивное сопротивление (Xc) увеличивается, коэффициент мощности контура также увеличивается.
11. Если ток и напряжение не соответствуют фазе на 90 градусов, то мощность (P) будет __________.
- Бесконечный
- Максимальный
- Нормальный
- Минимум
- Ноль
Показать пояснительный ответ
Ответ: 5. Ноль
Объяснение: Если ток и напряжение не превышают фазу на 90 градусов Тогда мощность (P) будет равна нулю. Причина в том, что
Мы знаем, что мощность в цепи переменного тока
P = V I Cos φ
, если угол между током и напряжением составляет 90 (φ = 90) градусов.затем
Мощность P = V I Cos (90) = 0
[Обратите внимание, что Cos (90) = 0]
Поэтому, если вы установите Cos 90 = 0 → Тогда мощность будет равна нулю
12. В чистой индуктивной цепи мощность равна __________?
- Бесконечный
- Максимальный
- Нормальный
- Минимум
- Ноль
Показать пояснительный ответ
Ответ 5. Ноль
Объяснение: Мы знаем, что в чисто индуктивной цепи ток запаздывает на 90 градусов от напряжения (другими словами, напряжение опережает 90 градусов от тока) i.Разница между током и напряжением составляет 90 градусов.
Итак, если ток и напряжение не соответствуют фазе на 90 градусов, то мощность (P) будет равна нулю. Причина в том, что
Мы знаем, что мощность в цепи переменного тока
P = V I Cos φ
, если угол между током и напряжением составляет 90 (φ = 90) градусов. затем
Мощность P = V I Cos (90) = 0
[Обратите внимание, что Cos (90) = 0]
Поэтому, если вы установите Cos 90 = 0 → Тогда мощность будет нулевой (в чистой индуктивной цепи)
13. В чистой емкостной цепи мощность равна __________?
- Бесконечный
- Максимум
- Нормальный
- Минимум
- Ноль
Показать пояснительный ответ
Ответ: 5.Ноль
Объяснение:
Мы знаем, что в чистой емкостной цепи ток идет на 90 градусов от напряжения (другими словами, напряжение отстает на 90 градусов от тока), то есть разность фаз между током и напряжением составляет 90 градусов.
Итак, если ток и напряжение не соответствуют фазе на 90 градусов, то мощность (P) будет равна нулю. Причина в том, что
Мы знаем, что мощность в цепи переменного тока
P = V I Cos φ
, если угол между током и напряжением составляет 90 (φ = 90) градусов.затем
Мощность P = V I Cos (90) = 0
[Обратите внимание, что Cos (90) = 0]
Поэтому, если вы установите Cos 90 = 0 → Тогда мощность будет нулевой (в чистой емкостной цепи)
14. Если коэффициент мощности = Cos θ = 1, это означает, что _____________.
- Вход = Выход
- P IN = P OUT
- Цепь только резистивная
- Угол (θ) между напряжением и током равен нулю.
Показать пояснительный ответ
Ответ: 4. Треугольник θ между напряжением и током равен нулю
Объяснение: Мы знаем, что коэффициент мощности = Cos θ
Данное значение коэффициента мощности равно = 1.
Но это возможно только при θ = 0 (в случае коэффициента мощности = Cos θ).
Т.е., Cosθ = Cos (0) = 1.
15. Используя формулу P = VI Cos φ, мы можем найти _______.
- Мощность однофазной цепи.
- Напряжение однофазной цепи
- Ток однофазной цепи.
- Коэффициент мощности однофазной цепи
- Все вышеперечисленное
- Ни один из вышеперечисленных
Показать пояснительный ответ
Ответ: 5. Все вышеперечисленное
Объяснение: Как мы знаем, что это зависит от заданных значений или данных. но, как правило, мы можем найти все эти количества по этой формуле.
для мощности: P = VI Cos φ
для напряжения = V = P / (I Cos φ)
для тока = I = P / (V Cos φ)
для коэффициента мощности = Cos φ = P / VI
16. Взаимное значение коэффициента мощности = _________?
- Q-фактор
- Коэффициент спроса
- Коэффициент разнесения
- Коэффициент использования
Показать пояснительный ответ
Ответ: 1. Q-фактор
Объяснение:
Противоположный коэффициент называется добротностью или добротностью катушки или ее достоинства.
коэффициент Q = 1 / коэффициент мощности = 1 / Cosθ = Z / R… (где коэффициент мощности Cosθ = R / Z)
, если R слишком мал по отношению к реактивности
, то коэффициент Q = Z / R = ωL / R = 2πfL / R… (ωL / R = 2πf)
Также Q = 2π (максимальная энергия, хранимая / энергия, рассеиваемая за цикл) в катушке.
для более подробной информации: добротность в электротехники и электроники
17 . Коэффициент мощности (Cos θ) = _________?
- кВт / кВА
- R / Z
- Косинус угла между током и напряжением
- Все вышеперечисленное
Показать пояснительный ответ
Ответ.4. Все вышеперечисленное.
Объяснение: Как известно, мощность в однофазных цепях переменного тока = P = VI Cos θ. Следовательно, Cos θ = P / V I ===> Cos θ = P (в ваттах) / V I (в вольт-амперах) ===> Cos θ = W / VI.
И Cos θ = R / Z = отношение между сопротивлением и импедансом = Сопротивление / Импеданс = R / Z
Также Cos θ = Косинус угла между Током и напряжением = P = V I Cos θ.
18 . Отношение между импедансом (Z) и допуском (Y) составляет ___________?
- Z = 1 / Y
- Z = 1 + Y
- Z = 1-Y
- Z = Y 2
Показать пояснительный ответ
Ответ: 1.Z = 1 / Y
Объяснение:
Импеданс: Общее сопротивление в цепи переменного тока называется импедансом . Он представлен Z, и единица полного сопротивления такая же, как и сопротивление, т. Е. = Ом (Ом), где
Импеданс = Z = √ (R 2 + X L 2 )…. В случае индуктивной цепи (* X L = индуктивное сопротивление)
Импеданс = Z = √ (R 2 + X C 2 )… в случае, если емкостная цепь (* X c = емкостная Реактивность)
допуск : допуск определяется как обратное сопротивление, так же как электропроводность является обратной величиной сопротивления i.е. оно обозначено как Y.
Вход,
Y = 1 / Z
= 1 / (V / I)
= I / V ———> I = VY
Единицей допуска является Siemens и его единичный символ — S.
. Вы также можете прочитать о зачислении здесь.
Что такое зачисление и как его рассчитать?
19. Среднее значение синусоидального переменного сигнала составляет ————- для полного цикла.
- Максимум
- Ноль
- Конечное значение
- Бесконечно
Показать пояснительный ответ
Ответ: (2)
Для синусоидального переменного сигнала среднее значение равно значению устойчивого состояния тот электрический параметр, который передает то же самое изменение через цепь как его чередующийся аналог.Он определяется путем усреднения всех мгновенных значений электрического параметра. Поскольку синусоидальная волна является симметричной, среднее значение в положительном цикле будет равно средним значениям в отрицательном цикле. Следовательно, это ноль для полного цикла.
20. Среднее значение синусоидального переменного сигнала равно ————–
- равно максимальному значению
- Половина максимального значения
- в 637 раз превышает максимальное значение
- Ничего из вышеперечисленного
Показать пояснительный ответ
Отв.(3)
Рассмотрим синусоидальный сигнал переменного тока, приведенный ниже.


Это синусоидальная форма волны тока, где значение тока в любой точке имеет вид:
i = I м sinθ
Для небольшого сегмента толщины dθ площадь будет: idθ
Интегрируя для полупериода, площадь будет: 

Среднее значение будет иметь вид: 

21.Форм-фактор для синусоидального сигнала:
- 1,21
- 0,5
- 1,11
- 0
Показать пояснительный ответ
Ответ: (3)
Форм-фактор для синусоидального сигнала — это отношение его среднеквадратичное значение и его среднее значение. Среднеквадратичное значение — это значение этого электрического параметра, который выделяет такое же количество тепла в цепи, что и его аналог постоянного тока
Математически, форм-фактор, 

22.Пиковый коэффициент для синусоидальной формы волны:
- 1,3
- 1,02
- 1,14
- 0,5
Показать пояснительный ответ
Ответ: (1,14)
Пиковый коэффициент представляет собой отношение максимального значения к среднеквадратическому значению. Это указывает на максимальное значение.
Математически, 

23. Синусоидальные волны одной и той же частоты можно представить с помощью одного и того же вектора
- Верно
- False
Показать пояснительный ответ
Ответ: (1)
Phasor Diagram — это представление синусоидальной волны с использованием одной линии, вращающейся в направлении против часовой стрелки с постоянной скоростью.В то время как длина линии представляет величину, то есть максимальное значение переменного параметра, ее ориентация с осью X представляет частоту. Две синусоидальные волны одинаковой частоты были бы представлены вращающимися векторами, которые поддерживают фиксированное положение относительно друг друга.
24. Для приведенной ниже схемы приблизительное значение реактивного сопротивления, импеданса, тока и коэффициента мощности составляет ———– соответственно.


- 35 Ом, 90 Ом, 1 Ампер, 1
- 4 Ом, 104.8 Ом, 1,9 А, 0,95
- 40 Ом, 100 Ом, 5 Ампер, 0,5
- 50 Ом, 200 Ом, 2 Ампер, 0,7
Показать пояснительный ответ
Отв. (2)
Для вышеупомянутой цепи индуктивное сопротивление определяется следующим образом:
Сопротивление, R = 100 Ом
Подставляя значения, f = 50 Гц, L = 0,1H, получаем = 31,4 Ом прибл.
Сопротивление дается как:


Подставляя соответствующие значения, получаем Z = 104.8 Ом ок.
Значение тока, I = V / Z = 1,9 Ампер
Разность фаз дается как: 

Вычисление получается, ∅ = 17,43 градуса
Следовательно, коэффициент мощности, cos∅ = 0,95
25. Для схемы, приведенной в предыдущем вопросе, потребляемая мощность составляет —
- 200 Вт
- 361 Вт
- 300 Вт
- 500 Вт
Показать пояснительный ответ
Ответ: (2)
Средняя потребляемая мощность — это мощность, потребляемая резистором, поскольку идеальный индуктор не потребляет энергию.Таким образом, потребляемая мощность определяется как:
P = VIOS∅
В = Напряжение питания = 200 Вольт
Теперь сверху I = 1,9 Ампер
Коэффициент мощности, cos∅ = 0,95
Следовательно, P = 361 Ватт
26. Коэффициент мощности для приведенной ниже цепи: ——–


- 1
- 0,8
- 0,9
- 0,5
Показать пояснительный ответ
Ответы: ( 2)
Имеются следующие параметры с учетом
Неиндуктивное сопротивление, R = 100 Ом
Индуктивность катушки, L = 0.1 H
Сопротивление катушки, R L = 10 Ом
Частота, f = 50 Гц
Напряжение питания, В = 200 Вольт
Индуктивное сопротивление, X L = 2 πfl = 31,4 Ом
Следовательно, полное сопротивление катушки, = 

Общее сопротивление, Z = Z L + R = 132,95 Ом
Общий ток, проходящий через цепь, I = V / Z = 1,5 Ампер
Теперь, мощность коэффициент только для катушки, cosθ = R L / Z L = 0.3
Напряжение на катушке, В L = IZ L = 49,425 Вольт
Мощность, потребляемая катушкой, P L = V L Icosθ = 22,24 Вт
Мощность, потребляемая неиндуктивным сопротивлением , P R = I 2 R = 225 Вт
Общая потребляемая мощность или реальная мощность, P rl = P L + P R = 247,4 Вт
Общая входная мощность, P A = VI = 300 Вт
Следовательно, общий коэффициент мощности, p f = P rl / P A = 0.8
27. Для схемы, приведенной в вопросе 6, предположим, что катушка индуктивности заменена на конденсатор емкостью 75 мкФ. Потребляемая мощность, максимальный заряд и максимальная энергия в цепи — соответственно
- 300 Вт, 0,1 С, 4 Дж 900 000
- 339 Вт, 0,2 С, 3 Дж
- 100 Вт, 0,01 С, 12 Дж
- 150 Вт, 0,4 C, 2 Дж
Показать пояснительный ответ
Ответ: (2)
Аналогично индуктору, мощность, потребляемая конденсатором, также равна нулю или почти ничтожна.Следовательно, для схемы потребляемая мощность — это мощность, потребляемая только сопротивлением.
Следовательно, потребляемая мощность = I 2 R
Теперь I = В / З
В = Напряжение питания = 200 Вольт
Z = Полное сопротивление, данное как: 

Теперь ток I = 1,84 Ампер
Следовательно, потребляемая мощность = 338,56 Ватт = 339 Ватт прибл.
Максимальный заряд в конденсаторе, Q макс. = CV м = CV√2 = 0,02 Колумба
Максимальная энергия, E макс. = 0.5CV м 2 = 3 Дж на внешней поверхности
Ноль в ядре Показать пояснительный ответ
Ответ:
Для прямого провода переменный ток создает магнитный поток, который больше в центре по сравнению с поверхностью.Это приводит к тому, что индуктивность оказывается больше в центре, чем на поверхности. Таким образом, ток больше на внешней поверхности, где индуктивность меньше. Следовательно, полезное поперечное сечение проводника меньше, чем фактическое, а эффективное сопротивление выше.
29. Для последовательных цепей RLC в резонансе падение напряжения на емкостных и индуктивных компонентах составляет — — — —
- Большое
- Малое
- Ноль
- Бесконечное
Показать пояснительный ответ
Ответ: (1)
Когда ток в последовательной цепи RLC находится в фазе с напряжением питания, говорят, что он находится в резонансе.Рассмотрим схему RLC ниже серии.


Емкостная реактивность = X C = 1 / 2πfC
Индуктивная реактивность = X L = 2πfL
Поскольку ток находится в фазе с напряжением питания, общая разность фаз будет равна нулю и, следовательно, X С = Х , Л .
Следовательно, полное сопротивление, Z = R и ток, I = V / Z = V / R
Поскольку сопротивление току обусловлено только резистором, максимальный ток протекает по цепи и, следовательно, падение напряжения на емкостном и индуктивные компоненты максимальны.Таким образом, в энергосистемах исключается последовательный резонанс.
30. Параллельные системы переменного тока используются чаще, чем системы переменного тока серии
- Правда
- Ложь
Показать пояснительный ответ
Ответ: (1)
Параллельные системы переменного тока используются чаще, чем серии Системы переменного тока, потому что все электрические приборы или устройства работают с одинаковым напряжением питания, а также каждый из них должен работать независимо с помощью соответствующего переключателя.
Почему ток уменьшается при увеличении индуктивности и реактивности? В индуктивной цепи, почему уменьшается ток в цепи (I), когда увеличивается индуктивность (L) или индуктивное сопротивление (X L )?
Еще один вопрос из серии вопросов и ответов на вопросы в области электротехники и электроники.
Объясните утверждение: « В индуктивной цепи, когда индуктивность (L) или индуктивное сопротивление (X L ) увеличивается, ток в цепи (I) уменьшается на ».


Смежный вопрос: почему ток увеличивается при увеличении емкости или уменьшении емкостного сопротивления?
Объяснение:
Мы знаем, что в цепях постоянного тока:
I = V / R,
Но в случае цепей переменного тока:
I = V / Z
Где «общее сопротивление цепей переменного тока = Полное сопротивление = Z = √ (R 2 + (X L — X C 2 ) ”
В случае индуктивной цепи:
- Z = √ (R 2 + X L 2 )
- I = V / X L или I = V / Z
Показывает, что в индуктивной цепи ток обратно пропорционален индуктивному сопротивлению, а также индуктивности «L» в качестве индуктивности и индуктивности реактивные сопротивления «X L » прямо пропорциональны друг другу.
Давайте проверим на примере, чтобы увидеть, как ток уменьшается индуктивным сопротивлением.
Когда индуктивность = 0,02 H
Предположим, что индуктивная цепь где:
- Индуктивность = L = 0,02 Генри
- Напряжение = V = 220 В
- Сопротивление = R = 10 Ом
- Частота = f = 50 Гц
Найти индуктивное сопротивление;
X L = 2π f L
X L = 2 x 3.1415 x 50 x 0,02
X L = 6,28 Ом
Теперь полное сопротивление цепи:
Z = √ (R 2 + X L 2 )
Z = √ (10 2 + 6,28 2 )
Z = 11,8 Ом
Наконец, ток в индуктивной цепи:
I = В / З
I = 220 В / 11,8 Ом
I = 18,64 A
Вопросы, связанные с данной:
Когда индуктивность = 0,04 H
Теперь мы увеличили индуктивность (L) индуктивности формы 0.02 H до 0,04 H,
V = 220 В, R = 10 Ом, L = 0,04 H, f = 50 Гц.
X L = 2π f L = 2 x 3,1415 x 50 x 0,04 = 12,56 Ом
Z = √ (R 2 + X L 2 ) = √ (10 2 + 12,56 2 ) = 16,05 Ω
I = V / Z = 220 В / 16,05 Ω
I = 13,70 A
Вопросы, относящиеся:
Вывод:
Мы видим, что при индуктивности (L) было 0.02 Генри , тогда ток цепи был 18,64 A ,
Но когда индуктивность цепи увеличилась с 0,02 H до 0,04 H , то ток уменьшился с 18,64 A до 13,70 A .
Следовательно, доказано,
В индуктивной цепи, когда индуктивное сопротивление X L увеличивается, ток цепи уменьшается и наоборот.
В устной или устной форме
- Индуктивное сопротивление — это своего рода сопротивление.Когда сопротивление увеличивается, ток в цепи уменьшается и наоборот.
- Индуктивность прямо пропорциональна индуктивному реактивному сопротивлению
L ∝ X L
- Ток обратно пропорционален индуктивности и индуктивному сопротивлению.
I ∝ 1 / L и I ∝ 1 / X L
Похожие вопросы / ответы:
. Почему коэффициент мощности уменьшается при увеличении индуктивности и реактивности? В индуктивной цепи, почему коэффициент мощности ( Cos θ ) уменьшается, когда увеличивается индуктивность (L) или индуктивное сопротивление (X L )?
Следующий вопрос из серии вопросов и ответов на вопросы в области электротехники и электроники.
Объясните утверждение, что « В индуктивной цепи, когда индуктивность (L) или индуктивное реактивное сопротивление (X L ) увеличивается, коэффициент мощности цепи (Cos θ) уменьшается на ».


Объяснение:
Мы знаем, что в цепях постоянного тока:
I = V / R,
Но в случае цепей переменного тока:
I = V / Z
где «общее сопротивление Цепи переменного тока = полное сопротивление = Z = √ (R 2 + (X L — X C 2 ) »
В случае индуктивной цепи:
- Z = √ (R 2 + X L 2 )
- I = V / X L или I = V / Z
Вопросы, связанные с данной:
Показывает, что в индуктивной цепи ток обратно пропорционален индуктивному реактивному сопротивлению, а также индуктивность «L» как индуктивность и индуктивное сопротивление «X L » прямо пропорциональны друг другу.Это означает, что если индуктивность увеличивается, ток в цепи уменьшается, что приводит к снижению коэффициента мощности. Аналогичным образом, когда ток в цепи увеличивается из-за уменьшения индуктивности или индуктивного сопротивления, общий коэффициент мощности будет улучшен, поскольку коэффициент мощности прямо пропорционален индуктивности и индуктивным сопротивлениям.
Давайте проверим на решенном примере, чтобы увидеть, как снижается коэффициент мощности при увеличении индуктивности и индуктивного сопротивления.
При индуктивности = 0.01 H
Предположим, что индуктивная цепь где:
- Индуктивность = L = 0,01 Генри
- Напряжение = V = 230 В
- Сопротивление = R = 12 Ом
- Частота = f = 60 Гц
Найти индуктивное сопротивление;
X L = 2π f L
X L = 2 x 3,1415 x 60 x 0,01
X L = 3,77 Ом
Теперь сопротивление цепи:
Z = √ (R 2 + X L 2 )
Z = √ (12 2 + 3.77 2 )
Z = 12,58 Ом
Наконец, коэффициент мощности в индуктивной цепи:
Cos θ = R / Z
Cos θ = 12 Ом / 12,58 Ом
Cos θ = 0,95
Когда индуктивность = 0,03 H
Теперь мы увеличили индуктивность (L) индуктивности с 0,01 H до 0,03 H .
В = 230 В, R = 12 Ом, L = 0,03 Н, Ф, = 60 Гц.
X L = 2π f L = 2 x 3.1415 x 60 x 0,03 = 11,30 Ω
Z = √ (R 2 + X L 2 ) = √ (12 2 + 11,30 2 ) = 16,48 Ω
Коэффициент мощности = Cos θ = R / Z = 12 Ом / 16,48 Ом
Cos θ = 0,73
Вопросы, относящиеся:
Вывод:
Мы можем видеть, что, когда индуктивность (L) была 0,01 Генри , то схема коэффициент мощности составлял , 0,95, ,
,, но когда индуктивность цепи увеличилась с 0.01 H до 0,03 H , затем коэффициент мощности уменьшился с с 0,95 до 0,73 .
Следовательно, доказано,
В индуктивной цепи, когда индуктивность или индуктивное сопротивление X L увеличивается, коэффициент мощности цепи уменьшается, и наоборот.
В устной или устной форме,
- Индуктивное сопротивление является разновидностью сопротивления. Когда индуктивное сопротивление увеличивается, коэффициент мощности цепи уменьшается, и наоборот.
- Индуктивность прямо пропорциональна индуктивному реактивному сопротивлению
L ∝ X L
- Индуктивность прямо пропорциональна индуктивному реактивному сопротивлению и току.
L ∝ I и L ∝ X L
- Коэффициент мощности обратно пропорционален индуктивности и индуктивному сопротивлению.
Cos θ ∝ 1 / L и Cos θ ∝ 1 / X L
Похожие вопросы / ответы:
.
Объяснение:
X L = 2πfL…., т.е. …. X L ∞ f ……, а также… ..L ∞ f
Объяснение:
X L = 2πfL… .. т.е. X L ∞L.
Объяснение:
Предположим, когда индус (L) = 0.02H
Мы знаем, что I = V / R,
, но индуктивно схема, I = V / X L
Т.о. ток обратно пропорционален току (в индуктивной цепи.
Давайте проверим на примере.
Объяснение:
Мы знаем, что
Puttint (2) в (1)
I = V / (1 / 2πfC)… то есть ..I = V x 2πfC
Объяснение:
В емкостной цепи,
Объяснение:
Предположим, когда емкостное сопротивление (Xc) = 6 Ом
Объяснение: Если ток и напряжение не превышают фазу на 90 градусов Тогда мощность (P) будет равна нулю. Причина в том, что
Мы знаем, что мощность в цепи переменного тока
P = V I Cos φ
, если угол между током и напряжением составляет 90 (φ = 90) градусов.затем
Мощность P = V I Cos (90) = 0
[Обратите внимание, что Cos (90) = 0] Поэтому, если вы установите Cos 90 = 0 → Тогда мощность будет равна нулю
Объяснение: Мы знаем, что в чисто индуктивной цепи ток запаздывает на 90 градусов от напряжения (другими словами, напряжение опережает 90 градусов от тока) i.Разница между током и напряжением составляет 90 градусов.
Итак, если ток и напряжение не соответствуют фазе на 90 градусов, то мощность (P) будет равна нулю. Причина в том, что
Мы знаем, что мощность в цепи переменного тока
P = V I Cos φ
, если угол между током и напряжением составляет 90 (φ = 90) градусов. затем
Мощность P = V I Cos (90) = 0
[Обратите внимание, что Cos (90) = 0] Поэтому, если вы установите Cos 90 = 0 → Тогда мощность будет нулевой (в чистой индуктивной цепи)
Объяснение:
Мы знаем, что в чистой емкостной цепи ток идет на 90 градусов от напряжения (другими словами, напряжение отстает на 90 градусов от тока), то есть разность фаз между током и напряжением составляет 90 градусов.
Итак, если ток и напряжение не соответствуют фазе на 90 градусов, то мощность (P) будет равна нулю. Причина в том, что
Мы знаем, что мощность в цепи переменного тока
P = V I Cos φ
, если угол между током и напряжением составляет 90 (φ = 90) градусов.затем
Мощность P = V I Cos (90) = 0
[Обратите внимание, что Cos (90) = 0] Поэтому, если вы установите Cos 90 = 0 → Тогда мощность будет нулевой (в чистой емкостной цепи)
Объяснение: Мы знаем, что коэффициент мощности = Cos θ
Данное значение коэффициента мощности равно = 1.
Но это возможно только при θ = 0 (в случае коэффициента мощности = Cos θ).
Т.е., Cosθ = Cos (0) = 1.
Объяснение: Как мы знаем, что это зависит от заданных значений или данных. но, как правило, мы можем найти все эти количества по этой формуле.
И Cos θ = R / Z = отношение между сопротивлением и импедансом = Сопротивление / Импеданс = R / Z
Также Cos θ = Косинус угла между Током и напряжением = P = V I Cos θ.
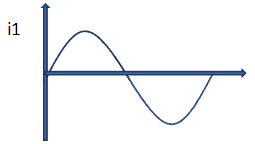

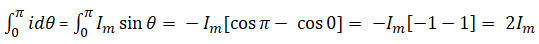
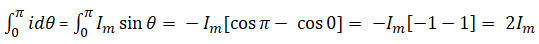
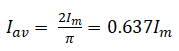
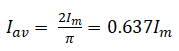
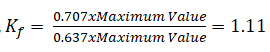
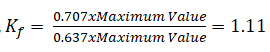
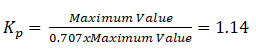
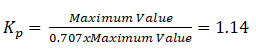
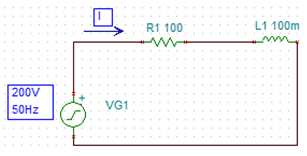

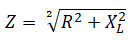
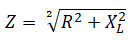
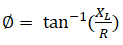
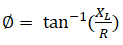
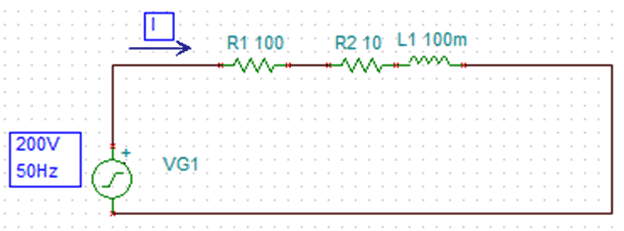

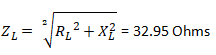
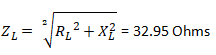
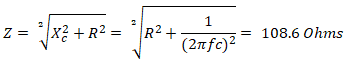
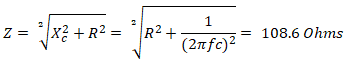
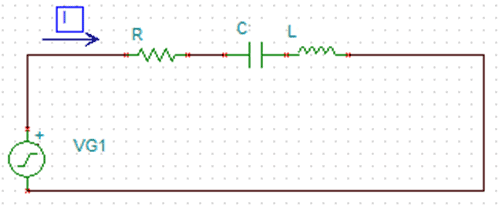

В индуктивной цепи, почему уменьшается ток в цепи (I), когда увеличивается индуктивность (L) или индуктивное сопротивление (X L )?
Еще один вопрос из серии вопросов и ответов на вопросы в области электротехники и электроники.
Объясните утверждение: « В индуктивной цепи, когда индуктивность (L) или индуктивное сопротивление (X L ) увеличивается, ток в цепи (I) уменьшается на ».


Смежный вопрос: почему ток увеличивается при увеличении емкости или уменьшении емкостного сопротивления?
Объяснение:
Мы знаем, что в цепях постоянного тока:
I = V / R,
Но в случае цепей переменного тока:
I = V / Z
Где «общее сопротивление цепей переменного тока = Полное сопротивление = Z = √ (R 2 + (X L — X C 2 ) ”
В случае индуктивной цепи:
- Z = √ (R 2 + X L 2 )
- I = V / X L или I = V / Z
Показывает, что в индуктивной цепи ток обратно пропорционален индуктивному сопротивлению, а также индуктивности «L» в качестве индуктивности и индуктивности реактивные сопротивления «X L » прямо пропорциональны друг другу.
Давайте проверим на примере, чтобы увидеть, как ток уменьшается индуктивным сопротивлением.
Когда индуктивность = 0,02 H
Предположим, что индуктивная цепь где:
- Индуктивность = L = 0,02 Генри
- Напряжение = V = 220 В
- Сопротивление = R = 10 Ом
- Частота = f = 50 Гц
Найти индуктивное сопротивление;
X L = 2π f L
X L = 2 x 3.1415 x 50 x 0,02
X L = 6,28 Ом
Теперь полное сопротивление цепи:
Z = √ (R 2 + X L 2 )
Z = √ (10 2 + 6,28 2 )
Z = 11,8 Ом
Наконец, ток в индуктивной цепи:
I = В / З
I = 220 В / 11,8 Ом
I = 18,64 A
Вопросы, связанные с данной:
Когда индуктивность = 0,04 H
Теперь мы увеличили индуктивность (L) индуктивности формы 0.02 H до 0,04 H,
V = 220 В, R = 10 Ом, L = 0,04 H, f = 50 Гц.
X L = 2π f L = 2 x 3,1415 x 50 x 0,04 = 12,56 Ом
Z = √ (R 2 + X L 2 ) = √ (10 2 + 12,56 2 ) = 16,05 Ω
I = V / Z = 220 В / 16,05 Ω
I = 13,70 A
Вопросы, относящиеся:
Вывод:
Мы видим, что при индуктивности (L) было 0.02 Генри , тогда ток цепи был 18,64 A ,
Но когда индуктивность цепи увеличилась с 0,02 H до 0,04 H , то ток уменьшился с 18,64 A до 13,70 A .
Следовательно, доказано,
В индуктивной цепи, когда индуктивное сопротивление X L увеличивается, ток цепи уменьшается и наоборот.
В устной или устной форме
- Индуктивное сопротивление — это своего рода сопротивление.Когда сопротивление увеличивается, ток в цепи уменьшается и наоборот.
- Индуктивность прямо пропорциональна индуктивному реактивному сопротивлению
L ∝ X L
- Ток обратно пропорционален индуктивности и индуктивному сопротивлению.
I ∝ 1 / L и I ∝ 1 / X L
Похожие вопросы / ответы:
.В индуктивной цепи, почему коэффициент мощности ( Cos θ ) уменьшается, когда увеличивается индуктивность (L) или индуктивное сопротивление (X L )?
Следующий вопрос из серии вопросов и ответов на вопросы в области электротехники и электроники.
Объясните утверждение, что « В индуктивной цепи, когда индуктивность (L) или индуктивное реактивное сопротивление (X L ) увеличивается, коэффициент мощности цепи (Cos θ) уменьшается на ».


Объяснение:
Мы знаем, что в цепях постоянного тока:
I = V / R,
Но в случае цепей переменного тока:
I = V / Z
где «общее сопротивление Цепи переменного тока = полное сопротивление = Z = √ (R 2 + (X L — X C 2 ) »
В случае индуктивной цепи:
- Z = √ (R 2 + X L 2 )
- I = V / X L или I = V / Z
Вопросы, связанные с данной:
Показывает, что в индуктивной цепи ток обратно пропорционален индуктивному реактивному сопротивлению, а также индуктивность «L» как индуктивность и индуктивное сопротивление «X L » прямо пропорциональны друг другу.Это означает, что если индуктивность увеличивается, ток в цепи уменьшается, что приводит к снижению коэффициента мощности. Аналогичным образом, когда ток в цепи увеличивается из-за уменьшения индуктивности или индуктивного сопротивления, общий коэффициент мощности будет улучшен, поскольку коэффициент мощности прямо пропорционален индуктивности и индуктивным сопротивлениям.
Давайте проверим на решенном примере, чтобы увидеть, как снижается коэффициент мощности при увеличении индуктивности и индуктивного сопротивления.
При индуктивности = 0.01 H
Предположим, что индуктивная цепь где:
- Индуктивность = L = 0,01 Генри
- Напряжение = V = 230 В
- Сопротивление = R = 12 Ом
- Частота = f = 60 Гц
Найти индуктивное сопротивление;
X L = 2π f L
X L = 2 x 3,1415 x 60 x 0,01
X L = 3,77 Ом
Теперь сопротивление цепи:
Z = √ (R 2 + X L 2 )
Z = √ (12 2 + 3.77 2 )
Z = 12,58 Ом
Наконец, коэффициент мощности в индуктивной цепи:
Cos θ = R / Z
Cos θ = 12 Ом / 12,58 Ом
Cos θ = 0,95
Когда индуктивность = 0,03 H
Теперь мы увеличили индуктивность (L) индуктивности с 0,01 H до 0,03 H .
В = 230 В, R = 12 Ом, L = 0,03 Н, Ф, = 60 Гц.
X L = 2π f L = 2 x 3.1415 x 60 x 0,03 = 11,30 Ω
Z = √ (R 2 + X L 2 ) = √ (12 2 + 11,30 2 ) = 16,48 Ω
Коэффициент мощности = Cos θ = R / Z = 12 Ом / 16,48 Ом
Cos θ = 0,73
Вопросы, относящиеся:
Вывод:
Мы можем видеть, что, когда индуктивность (L) была 0,01 Генри , то схема коэффициент мощности составлял , 0,95, ,
,, но когда индуктивность цепи увеличилась с 0.01 H до 0,03 H , затем коэффициент мощности уменьшился с с 0,95 до 0,73 .
Следовательно, доказано,
В индуктивной цепи, когда индуктивность или индуктивное сопротивление X L увеличивается, коэффициент мощности цепи уменьшается, и наоборот.
В устной или устной форме,
- Индуктивное сопротивление является разновидностью сопротивления. Когда индуктивное сопротивление увеличивается, коэффициент мощности цепи уменьшается, и наоборот.
- Индуктивность прямо пропорциональна индуктивному реактивному сопротивлению
L ∝ X L
- Индуктивность прямо пропорциональна индуктивному реактивному сопротивлению и току.
L ∝ I и L ∝ X L
- Коэффициент мощности обратно пропорционален индуктивности и индуктивному сопротивлению.
Cos θ ∝ 1 / L и Cos θ ∝ 1 / X L
Похожие вопросы / ответы:
.



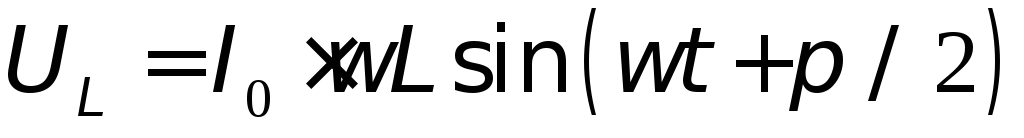 .
.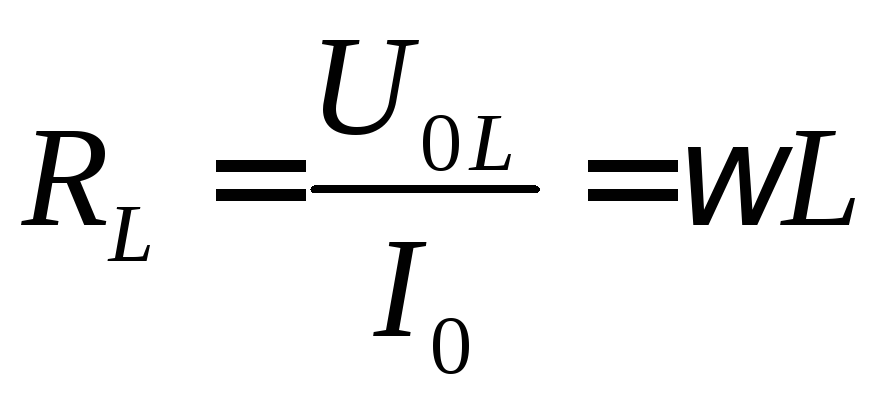
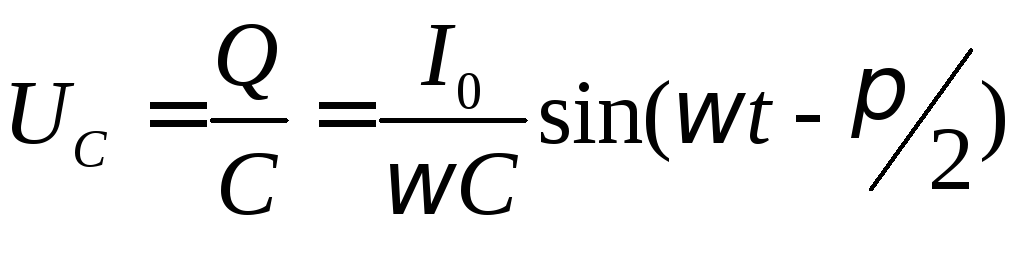 .
.