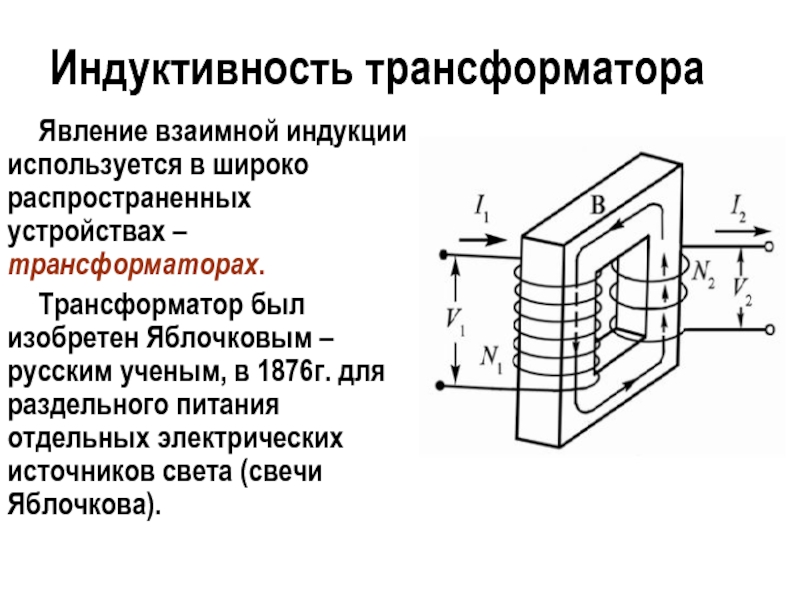
чему равна индуктивность катушки, если за время 0,5с ток в цепи изменился от 20 до 5А? при
СРОЧНО!!! Квадрокоптер, несущий небольшой тяжёлый груз, летел горизонтально с постоянной скоростью. Внезапно он выронил груз. Еще τ=2 с он летел с той … же скоростью, а затем начал погоню за грузом. За какое минимальное время квадрокоптер может настигнуть груз? Ответ выразите в секундах, округлив до целого числа. Считайте, что усилие, создаваемое движителями, примерно постоянно и не зависит от направления движения. При этом оно позволяет квадрокоптеру подниматься вертикально с ускорением до 2,5 м/с2 и опускаться вертикально вниз с ускорением до 22,5 м/с2 (сила сопротивления воздуха пренебрежимо мала). Ускорение свободного падения считать равным 10 м/с2.
Кинематика помогите пожалуйста
На ровном склоне горы, наклон которого к горизонту α=30∘, на высоте h=20 м друг над другом находятся два школьника. Они
… одновременно бросают камни с одинаковыми скоростями: нижний — перпендикулярно склону, верхний — в горизонтальном направлении.
Срочно! Самолёт летит горизонтально по прямой со скоростью 300 м/с на высоте 6 км. В тот момент, когда он пролетает точно над зенитным орудием, устано … вленном на поверхности Земли, с него сбрасывают тяжёлое ядро, а орудие производит выстрел. Скорость вылета снаряда из орудия равна 500 м/с, и снаряд попадает точно в ядро. Пренебрегая сопротивлением воздуха, найдите время полёта снаряда. Ответ выразите в с, округлив до десятых.
Если КПД двигателя 20%, а полезная развиваемая мощность по паспорту 100 кВт, то какова затрачиваемая тепловая мощность?
Если яблоко поместить под воду на глубину 40 см, то какая сила, действующая на него, будет больше: сила тяжести или сила Архимеда?
СРОЧНО!!! На лёгкой нерастяжимой верёвке с помощью трёх блоков подвешены три груза. Блоки лёгкие, вращаются без трения, верёвка по ним не скользит. Гр
… узы с массами m1=1 кг, m2=4 кг и m3=2 кг сначала удерживают неподвижно, затем отпускают без начальной скорости. Определите проекцию ускорения груза 2 на ось x, направленную вертикально вверх. Ответ дайте в м/с2, округлив до целого числа. Ускорение свободного падения g=10 м/с2.
Блоки лёгкие, вращаются без трения, верёвка по ним не скользит. Гр
… узы с массами m1=1 кг, m2=4 кг и m3=2 кг сначала удерживают неподвижно, затем отпускают без начальной скорости. Определите проекцию ускорения груза 2 на ось x, направленную вертикально вверх. Ответ дайте в м/с2, округлив до целого числа. Ускорение свободного падения g=10 м/с2.
Помогите пожалуйста
Помогите пожалуйста
Как найти Объем шара , если известно только диаметр и вес??? 50 БАЛЛОВ ДАМ
Плотность бумаги формата А4 80г/м кв. Сколько весит упаковка из 5 пачек, если в каждой пачке 500 листов размером 297см х 209 см ?
индуктивность колебательного контура
индуктивность колебательного контура
Задача 60501
На рисунке приведен график зависимости силы тока от времени в ходе свободных электромагнитных колебаний в идеальном колебательном контуре, индуктивность катушки которого равняется 0,45 мГн.
а) Вычислите емкость конденсатора и полную энергию колебательного контура.
б) Определите, какими будут через 1,0 мкс после начала отсчета времени: фаза колебаний, сила тока в контуре, энергия магнитного поля катушки, энергия электрического поля конденсатора, заряд на пластинах конденсатора.
в) Через какой наименьший интервал времени энергия магнитного поля катушки будет в два раза больше энергии электрического поля конденсатора?
Задача 12199
Индуктивность L колебательного контура равна 0,5 мГн. Какова должна быть электроемкость С контура, чтобы он резонировал на длину волны λ = 300 м?
Задача 15179
Индуктивность колебательного контура L = 1,5 мГн. Какова должна быть емкость контура С, чтобы он резонировал на длину волны λ = 300 м?
Задача 15188
Индуктивность колебательного контура L = 0,5 мГн. Какова должна быть емкость контура С, чтобы он резонировал на длину волны λ = 400 м?
Задача 15203
Индуктивность колебательного контура L = 0,2 мГн. Какова должна быть емкость контура С, чтобы он резонировал на длину волны λ = 600 м?
Какова должна быть емкость контура С, чтобы он резонировал на длину волны λ = 600 м?
Задача 15210
Индуктивность колебательного контура L = 2,5 мГн. Какова должна быть емкость контура С, чтобы он резонировал на длину волны λ = 500 м?
Задача 15218
Индуктивность колебательного контура L = 0,18 мГн. Какова должна быть емкость контура С, чтобы он резонировал на длину волны λ = 360 м?
Задача 15237
Индуктивность колебательного контура L = 23 мГн. Какова должна быть емкость контура С, чтобы он резонировал на длину волны λ = 230 м?
Задача 16200
В колебательном контуре с индуктивностью L = 10–3 Гн происходят свободные гармонические колебания. При этом максимальные значения силы тока и заряда на обкладках конденсатора соответственно равны I
Задача 17974
В колебательном контуре с индуктивностью катушки 150 мГн совершаются электромагнитные колебания с частотой 410 Гц. Колебания напряжения на обкладках включенного в контур конденсатора описываются уравнением U = Um0·e–β·t·сos(ω·t), где Um0 = 15 В и β = 0,021 с–1. Постройте график убывания амплитуды напряжения на конденсаторе. Найдите минимальное (критическое) сопротивление резистора, который нужно включить в контур, чтобы колебания в контуре не возникали.
Колебания напряжения на обкладках включенного в контур конденсатора описываются уравнением U = Um0·e–β·t·сos(ω·t), где Um0 = 15 В и β = 0,021 с–1. Постройте график убывания амплитуды напряжения на конденсаторе. Найдите минимальное (критическое) сопротивление резистора, который нужно включить в контур, чтобы колебания в контуре не возникали.
Задача 19286
Определить энергию WL магнитного поля катушки индуктивности колебательного контура, после того, как с момента начала колебаний пройдет время, составляющее 1/8 периода. Максимальное напряжение на конденсаторе U0 = 500 В, емкость конденсатора С = 1 мкФ. Активным сопротивлением пренебречь.
Задача 19315
Индуктивность колебательного контура равна 2 мГн. При какой емкости контур резонирует на длину волны 600 м? Как изменится длина волны, если индуктивность контура увеличить в два раза?
Задача 19475
В колебательном контуре с индуктивностью 350 мГн возникли гармонические колебания с периодом 6 мс. Найдите уравнение колебаний для заряда на конденсаторе, которые возникнут в контуре, если в контур включить последовательно дополнительный конденсатор емкостью 3 мкФ, зарядить оба конденсатора до общего напряжения 45 В и затем подключить конденсаторы к катушке индуктивности. Постройте график зависимости заряда от времени. Вычислите максимальную электрическую энергию этого колебательного контура.
Найдите уравнение колебаний для заряда на конденсаторе, которые возникнут в контуре, если в контур включить последовательно дополнительный конденсатор емкостью 3 мкФ, зарядить оба конденсатора до общего напряжения 45 В и затем подключить конденсаторы к катушке индуктивности. Постройте график зависимости заряда от времени. Вычислите максимальную электрическую энергию этого колебательного контура.
Задача 19647
Магнитный поток Фs самоиндукции, пронизывающий катушку индуктивности колебательного контура, в котором происходят ЭМК, изменяется со временем так, как показано на рисунке. Какой точке, из выделенных на графике, соответствует максимальный ток самоиндукции?
Задача 22226
В колебательном контуре с индуктивностью 350 мГн возникли гармонические колебания с периодом 6 мс. Запишите уравнение колебаний для заряда на обкладках конденсатора, которые возникнут в контуре, если в контур включить последовательно с имеющимся конденсатором дополнительный конденсатор емкостью 3 мкФ, зарядить оба конденсатора до общего напряжения 45 В и затем подключить конденсаторы к катушке индуктивности.
Калькулятор взаимной индукции — последовательное соединение индуктивностей • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения
Этот калькулятор определяет взаимоиндукцию и эквивалентную индуктивность двух связанных и соединенных последовательно катушек индуктивности.
Пример. Рассчитать эквивалентную индуктивность двух катушек индуктивности 10 мкГн и 5 мкГн, соединенных последовательно и согласно с коэффициентом связи 0,5.
Входные данные
Индуктивность первой катушки, L1
генри (Гн)миллигенри (мГн)микрогенри (мкГн)наногенри (нГн)пикогенри (пГн)
Индуктивность второй катушки, L2
миллигенри (мГн)
Коэффициент связи, k
0 ≤ k ≤ 1
Тип включения катушек
Встречно
Согласно
Выходные данные
Взаимоиндукция
M миллигенри (мГн)
Полная индуктивность
Lt миллигенри (мГн)
Введите тип связи, величины индуктивностей и коэффициента связи, выберите единицы индуктивности в генри (Гн), миллигенри (мГн), микрогенри (мкГн) или пикогенри (пГн) и нажмите кнопку Рассчитать.
В Калькуляторе сопротивлений мы показали, что полное сопротивление соединенных последовательно резисторов равно сумме их сопротивлений. То же относится и к индуктивностям. Общая индуктивность определяется по аналогичному закону и если несколько соединенных последовательно катушек индуктивности не связаны между собой, их общая индуктивность равна сумме индуктивностей отдельных катушек. Если посмотреть на приведенную ниже иллюстрацию последовательно соединенных индуктивностей, мы увидим, что витки катушек составляют одну общую катушку и, следовательно, их индуктивности также складываются:
Это равенство работает только в том случае, если между отдельными катушками индуктивности нет связи. Отметим, что это бывает только в идеальном случае. В реальной жизни магнитные поля катушек пронизывают витки соседних катушек даже в том случае, если расстояние между ними достаточно велико. Если две индуктивности соединены последовательно и влияют одна на другую, то возможны две ситуации. Если магнитные потоки, образованные вокруг катушек в результате протекания в них тока, направлены в одну сторону, говорят, что такие катушки включены согласно. Если же магнитные потоки, образованные вокруг катушек в результате протекания в них тока, направлены в разные стороны, говорят, что такие катушки включены встречно.
Если магнитные потоки, образованные вокруг катушек в результате протекания в них тока, направлены в одну сторону, говорят, что такие катушки включены согласно. Если же магнитные потоки, образованные вокруг катушек в результате протекания в них тока, направлены в разные стороны, говорят, что такие катушки включены встречно.
Последовательно соединенные катушки с согласным включением
Последовательно соединенные катушки с согласным включением
Рассмотрим две взаимно связанные катушки индуктивности L₁ и L₂, соединенные последовательно. Катушка L₁ индуктивно связана с катушкой L₂ и их взаимоиндукция равна M₁₂. Катушка L₂, в свою очередь, также индуктивно связана с катушкой L₁ и их взаимоиндукция равна M₂₁. Поскольку их магнитные поля направлены в одну сторону, они складываются. В результате складываются и индуктивности:
Согласно принципу обратимости, M₂₁ = M₁₂, следовательно, имеем
Здесь М — взаимоиндукция двух катушек, а L₁ и L₂ — самоиндукции двух катушек. В Калькуляторе взаимной индукции было показано, что взаимная индукция определяется как
В Калькуляторе взаимной индукции было показано, что взаимная индукция определяется как
Подставляя это в вышеприведенную формулу, получаем используемую в этом калькуляторе формулу для расчета общей индуктивности двух включенных согласно катушек индуктивности с коэффициентом связи k:
Последовательно соединенные катушки со встречным включением
Последовательно соединенные катушки со встречным включением
Если две катушки индуктивности L₁ и L₂ соединены, как показано на этом рисунке, то один и тот же ток, текущий в каждой катушке, направлен в противоположную сторону в каждой из них. ЭДС, появляющаяся в катушке L₁ под влиянием взаимной индуктивности катушки L₂, направлена противоположно ЭДС, вызванной самоиндукцией катушки L₁. То же можно сказать относительно ЭДС в катушке L₂, вызванной магнитным полем катушки L₁. Мы видим, что в этом случае взаимная индукция уменьшает, иными словами «гасит» самоиндукцию. Поэтому вместо знака плюс в формуле общей индуктивности появляется знак минус:
Эта формула и используется в данном калькуляторе для расчета общей индуктивности двух катушек со встречным включением L₁ и L₂ с коэффициентом связи k.
Катушки индуктивности на плате блока питания: трансформаторы отмечены красными стрелками, дроссели — синими стрелками
Автор статьи: Анатолий Золотков
Калькулятор параллельных индуктивностей • Электротехнические и радиотехнические калькуляторы • Онлайн-конвертеры единиц измерения
Калькулятор определяет индуктивность нескольких параллельно соединенных катушек индуктивности.
Пример. Рассчитать эквивалентную индуктивность двух соединенных параллельно катушек индуктивности 10 мкГн и 5 мкГн.
Входные данные
Добавить катушку индуктивности
Выходные данные
Общая индуктивность
L миллигенри (мГн)
Введите величины индуктивностей в поля L1, L2 и т.д., добавляя при необходимости нужное количество полей для ввода, выберите единицы индуктивности в генри (Гн), миллигенри (мГн), микрогенри (мкГн) или пикогенри (пГн) и нажмите кнопку
1 мГн = 0,001 Г. 1 мкГн = 0,000001 = 10⁻⁶ Гн. 1 нГн = 0,000000001 = 10⁻⁹ Гн. 1 пГн = 0,000000000001 = 10⁻¹² Г. Подробнее о единицах измерения индуктивности.
1 нГн = 0,000000001 = 10⁻⁹ Гн. 1 пГн = 0,000000000001 = 10⁻¹² Г. Подробнее о единицах измерения индуктивности.
Индуктивность характеризует способность электрического проводника преобразовывать электрический ток в изменение электрического потенциала в данном проводнике (самоиндукция) и в расположенных рядом проводниках (взаимоиндукция). Индуктивность обычно обозначается символом L в честь русского физика немецкого происхождения Эмилия Христиановича Ленца (Heinrich Lenz).
По определению самоиндукции напряжение v(t)
На всех соединенных параллельно катушках индуктивности имеется одно и то же напряжение V. В соответствии с правилом Кирхгофа для тока общий ток I равен сумме токов, протекающих через отдельные катушки:
Общая индуктивность Leq соединенных параллельно трех катушек индуктивности, расположенных далеко друг от друга и не имеющих общего магнитного поля равна величине, обратной сумме величин, обратных их индуктивностям:
Или для n несвязанных катушек индуктивности:
Эта формула для Leq используется для расчетов в этом калькуляторе. Например, общая индуктивность трех катушек индуктивности 10, 15 and 20 мкГн, соединенных параллельно, будет равна
Например, общая индуктивность трех катушек индуктивности 10, 15 and 20 мкГн, соединенных параллельно, будет равна
мкГн.
Отметим, что если одна или несколько величин индуктивности равны нулю, то Leq стремится к нулю. Представьте себе очень короткий прямой проводник, шунтирующий катушку индуктивности — он и будет иметь почти нулевую индуктивность. Отметим также, что невозможно создать схему с нулевой индуктивностью.
Если параллельно соединены только две катушки индуктивности, имеем:
или
Эквивалентная индуктивность n одинаковых соединенных параллельно катушек индуктивности L равна
Отметим, что формула для расчета общей индуктивности нескольких катушек индуктивности, соединенных параллельно, используется и для расчета сопротивления группы резисторов, соединенных параллельно.
Отметим также, что для группы из любого количества соединенных параллельно катушек индуктивности эквивалентная индуктивность всегда будет меньше самой малой индуктивности в группе катушек индуктивности, а добавление еще одной катушки всегда будет уменьшать эквивалентную индуктивность группы.
Тороидальные катушки индуктивности в модуле питания принтера
Если индукторы расположены в магнитном поле друг друга, эти формулы работать не будут из-за явления взаимоиндукции (взаимной индукции), которое рассматривается в нашем калькуляторе взаимной индукции. Эффект взаимоиндукции может уменьшить или увеличить общую индуктивность катушек в зависимости от того как работает магнитная связь между катушками. Величина взаимной индукции зависит от расстояния между катушками и их ориентации. При этом взаимоиндукция может увеличивать или уменьшать общую индуктивность.
Если несколько катушек индуктивности соединены последовательно, их эквивалентная индуктивность определяется простым сложением индуктивностей отдельных катушек.
Для n соединенных последовательно катушек индуктивности имеем
Возможно, вы уже заметили, что катушки индуктивности ведут себя точно так же, как резисторы: если катушки соединены последовательно, их эквивалентные индуктивности всегда будет выше, чем индуктивности отдельных катушек, соединенных последовательно, а при параллельном соединении эквивалентная индуктивность всегда будет меньше индуктивностей отдельных катушек.
Многослойная пакетная спиральная катушка индуктивности в микросхеме и ее упрощенная эквивалентная схема
Зачем соединять катушки последовательно, если можно просто намотать большую катушку индуктивности? Вот один из примеров.
В микроэлектронике для реализации довольно больших индуктивностей на единицу площади интегральной микросхемы используется комбинирование спиральных катушек в нескольких слоях металлизации. Для этой цели используется многослойная пакетная конфигурация катушек индуктивности. Несколько слоев металлизации со спиральными катушками располагают точно один над другим. Катушки соединяют последовательно, чтобы индуктивности складывались для получения одной большой катушки индуктивности. Без такого пакетного расположения при использовании планарной технологии было бы невозможно создать большие индуктивности. Благодаря такому пакетному расположению коэффициент связи катушек k ≈ 1.
В этом калькуляторе мы рассматриваем только идеальные катушки индуктивности. Однако мы живем в реальном мире, где реальные катушки обладают как активным сопротивлением, так и емкостью. В другом калькуляторе мы рассмотрим характеристики неидеальных катушек индуктивности, обладающих сопротивлением, которые описываются эквивалентной схемой из последовательно соединенных индуктивности и сопротивления, в частности их временные характеристики.
Однако мы живем в реальном мире, где реальные катушки обладают как активным сопротивлением, так и емкостью. В другом калькуляторе мы рассмотрим характеристики неидеальных катушек индуктивности, обладающих сопротивлением, которые описываются эквивалентной схемой из последовательно соединенных индуктивности и сопротивления, в частности их временные характеристики.
Бескаркасные катушки индуктивности без сердечников в радиочастотном модуле
Автор статьи: Анатолий Золотков
Индуктивность / Хабр
Выше мы рассматривали два основных понятия в электротехнике — идеальный генератор напряжения и идеальный генератор тока.
Идеальный генератор напряжения выдает заданное напряжения U (давление в водопроводной аналогии) на любой нагрузке (сопротивлении внешней цепи).
При этом в соответствии с законом Ома I=U/R, даже если R стремится к нулю, а ток возрастает до бесконечности.
Внутренне сопротивление идеального генератора напряжения равно 0.
Идеальный генератор тока выдает заданный ток I (поток в водопроводной аналогии), даже если сопротивление внешней цепи стремится к бесконечности. Напряжение на нагрузке при этом также стремится к бесконечности U=I*R.
Напряжение на нагрузке при этом также стремится к бесконечности U=I*R.
Внутреннее сопротивление идеального генератора тока равно ∞.
Тут можно увидеть определенную симметрию, дуализм.
Мы рассматривали конденсатор С который может накапливать заряд (потому и называется — емкость) С=Q/U. Чем больше емкость, тем медленнее растет напряжение (давление) при закачке в конденсатор заряда U=Q/C.
Если емкость заряда очень большая (стремится к бесконечности), то такой конденсатор бесконечной емкости будет являться идеальным генератором напряжения. Он никогда не разрядится и при этом может выдать ток любой величины, и напряжение на нем будет оставаться постоянным.
Симметричным (дуальным) к конденсатору элементом будет являться индуктивность. Индуктивность обозначается буквой L (см схему ниже).
Обычно сам электронный компонент называется катушка индуктивности, а его параметр — индуктивность L.
Если конденсатор является генератором напряжения, то индуктивность является генератором тока. Индуктивность стремиться поддерживать ток в цепи постоянным, то есть препятствует изменению тока в цепи.
Индуктивность бесконечной величины является идеальным генератором тока, то есть будет бесконечно гнать заданный ток I независимо от сопротивления нагрузки.
Как хорошо сказано в wiki — “При сопоставлении силы электрического тока со скоростью в механике и электрической индуктивности с массой в механике ЭДС самоиндукции сходна с силой инерции.”
Это похоже как если вы подойдете к стоящей на рельсах вагонетке и станете ее толкать (приложите к ней силу). Вагонетка начнет медленно разгоняться и «ток все быстрее и быстрее побежит по проводам». А потом попробуйте вагонетку тормозить и она будет медленно останавливаться.
Так и в индуктивности, после подачи напряжения ток будет постепенно расти (вагонетка разгоняется), а при подаче напряжения другой полярности — постепенно уменьшаться (вагонетка тормозится).
Отсюда следует вывод «Поезд мгновенно остановить нельзя!»
«Ток в индуктивности мгновенно остановить нельзя!»
То есть даже если щелкнуть выключателем S4 на схеме и разомкнуть цепь, ток в первый момент после этого будет продолжать идти! На практике это приводит к тому, что в момент размыкания контактов в выключателе между ними будет проскакивать искра.
Сопротивление при размыкании контактов увеличивается до бесконечности (в реальности до очень больших величин) и протекающий ток создаст на этом сопротивлении напряжение очень большой величины, так что воздушный промежуток между контактами будет пробит.
В водопроводной аналогии этому явлению можно сопоставить гидравлический удар, когда масса воды в водопроводе набирает скорость, и при резком закрытии крана вода, продолжая двигаться по инерции, создает высокое давление, что может привести к разрыву трубы.
Причины по которой индуктивность имеет такие свойства (поддержание тока в цепи) хорошо описаны в wiki — https://ru. wikipedia.org/wiki/Самоиндукция
wikipedia.org/wiki/Самоиндукция
“При изменении тока в контуре пропорционально меняется и магнитный поток через поверхность, ограниченную этим контуром. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС. Это явление называется самоиндукцией. Направление ЭДС самоиндукции всегда оказывается таким, что при возрастании тока в цепи ЭДС самоиндукции препятствует этому возрастанию (направлена против тока), а при убывании тока — убыванию (сонаправлена с током). Явление самоиндукции проявляется в замедлении процессов исчезновения и установления тока.”
По отношению к конденсатору , основным отличием индуктивности, если говорить простыми словами, является то, что конденсатор пропускает переменный ток и не пропускает постоянный, а индуктивность наоборот — пропускает постоянный ток и не пропускает переменный.
Тут есть некий момент — постоянный ток это ток, который не меняется со временем, то, что называется «постоянная составляющая» частотой равной 0 Гц. Ее конденсатор не пропускает. Совсем.
Ее конденсатор не пропускает. Совсем.
А вот индуктивность совсем не пропускает переменный ток бесконечной частоты. А просто переменный ток любой конечной частоты немножко пропускает.
Но к понятию напряжения переменного тока мы вернемся позже.
Рассмотрим цепь на рис. 13 — подключение катушки индуктивности к генератору напряжения.
Ниже представлен график тока в индуктивности при подаче на нее постоянного напряжения от генератора напряжения.
При подаче на индуктивность постоянного напряжения ток в ней линейно возрастает со временем.
Мы помним аналогичную картину для конденсатора.
Напряжение на конденсаторе линейно возрастает при его заряде постоянным током.
А что будет, если запитать индуктивность от генератора тока?
рис 15. Подключение индуктивности к генератору тока. Ну тут из серии «кто кого заборет — слон или кит».
Попробуйте проанализировать работу схемы (hint — вообще схема изображена с ошибкой. В чем она заключается? Как нарисовать схему правильно?)
Цепи, содержащие конденсатор и индуктивность
Как было отмечено выше, индуктивность в электротехнике играет ту же роль, что масса в механике. А что является аналогом конденсатора в механике? Конденсатор является генератором напряжения, то есть создает силу, которая двигает поток заряда по проводам. Выше мы приводили аналог конденсатора в виде водонапорной башни, которая заполняется водой (зарядом) и давление (напряжение) в ней увеличивается.
Но можно также представить конденсатор в виде пружины — при заряде пружина сжимается и сила сжатия (напряжение) увеличивается. Емкость в этом случае величина обратная жесткости пружины. Чем пружина жестче, тем быстрее возрастает сила при сжатии. То есть соединение конденсатора и индуктивности эквивалентно вагонетке закрепленной на пружине. )
Что же будет происходить, если конденсатор соединить с индуктивностью, например как в схеме на рис. 16
16
Пусть конденсатор С заряжен до напряжения U. Ключ S2 замыкается и в цепи начинает течь ток. Это эквивалентно тому, как если бы мы сжали пружину и затем в какой-то момент отпустили (замкнули ключ S2).
В первый момент после замыкания ключа ток в цепи будет равен 0, так как индуктивность препятствует изменению тока. К вагонетке приложили силу, но в первый момент времени ее скорость равна 0. Затем ток начинает возрастать (вагонетка разгоняется). Пружина разжимается все больше и больше, скорость вагонетки (ток) растет и в какой-то момент времени пружина оказывается не сжата. Конденсатор разрядился до 0. Но. Мы помним что «ток в индуктивности мгновенно остановить нельзя!» Вагонетка разогналась и даже если мы не будем ее толкать, она будет двигаться по инерции. То есть индуктивность будет поддерживать ток и при этом заряжать конденсатор, но уже в другой полярности — заряды теперь будут скапливаться на другой обкладке конденсатора. Растущее напряжение противоположного знака на конденсаторе будет препятствовать движению зарядов, и в конце концов ток в цепи станет равным нулю. Но при этом конденсатор уже зарядился напряжением U другой полярности!
Растущее напряжение противоположного знака на конденсаторе будет препятствовать движению зарядов, и в конце концов ток в цепи станет равным нулю. Но при этом конденсатор уже зарядился напряжением U другой полярности!
То есть цепь пришла в состояние когда конденсатор заряжен, ток в ней равен нулю.
Хм.. но это то же состояние, с которого мы начали, только полярность напряжения противоположная. Следовательно процесс повторится, только ток потечет уже в другую сторону и система вернется в исходное состояние. Вагонетка поедет обратно, проедет положение равновесия и по инерции снова сожмет пружину.
Возникнет колебательный процесс. То есть вагонетка на пружине так и будет кататься туда-сюда и в отсутствие потерь энергии (трения) этот процесс будет длиться бесконечно.
Таким образом соединение конденсатора с индуктивностью образует колебательное звено. Такие звенья широко используются в электротехнике для создания генераторов и фильтров напряжения переменного тока.
Понятие переменного тока рассмотрим в следующей статье.
UPD.
Поскольку возник диспут экспоненциально ли растет ток при подключении катушки индуктивности к генератору напряжения или линейно, скажу еще пару слов по этому вопросу.
Откуда же берется экспонента роста тока в схеме на рис.13?
Ответ- ниоткуда. Ее там нет. Ток растет линейно и зависимость тока от напряжения описывается формулой
ЭДС самоиндукции в цепи прямо пропорциональна скорости изменения силы тока в этой цепи.
Чтобы обеспечить U=const (а U – это производная от тока в катушке), ток должен линейно расти.
А откуда тогда вообще зашел разговор об экспоненте? А зашел он потому, что ток линейно растет только в идеальном случае — в схеме с идеальным генератором напряжения (бесконечной мощности и с нулевым внутренним сопротивлением) и идеальной индуктивностью (с нулевым внутренним сопротивлением).
В реальном случае с учетом внутреннего сопротивления схема будет выглядеть так.

На схеме рис.17 R символизирует собой внутреннее сопротивление генератора и катушки индуктивности. (они все равно включены последовательно, поэтому можно обойтись одним R, как суммой этих сопротивлений)
В этом случае процесс разворачивается следующим образом. При замыкании ключа S4 цепь замкнется и должен был бы пойти ток. Однако, катушка индуктивности препятствует изменению тока, и в первый момент времени после замыкания ключа ток останется равным 0! По сути дела катушка в этот момент представляет собой разрыв цепи с бесконечным сопротивлением. Поэтому напряжение U будет приложено к катушке целиком. Можно и по другому подойти — Ur=I*R. Падение напряжения на резисторе равно I*R, I у нас равен 0, поэтому напряжение на резисторе тоже равно 0, и к катушке будет приложено полное напряжение U. Дальше ток в катушке будет расти. В области 0 линейно кстати (см рис 19 «Переход Суворова через Альпы» «Экспонента проходит через 0 под углом 45 градусов»). Ток будет расти и падение напряжения на резисторе тоже будет расти. А на катушке соответственно падать, потому что часть напряжения будет забирать на себя резистор. Поэтому со временем линейность роста тока в цепи будет нарушаться. Когда падение напряжения на резисторе I*R сравняется с напряжением генератора U рост тока прекратится совсем, потому что напряжение на катушке будет равно 0 (все напряжение будет падать на резисторе).
А на катушке соответственно падать, потому что часть напряжения будет забирать на себя резистор. Поэтому со временем линейность роста тока в цепи будет нарушаться. Когда падение напряжения на резисторе I*R сравняется с напряжением генератора U рост тока прекратится совсем, потому что напряжение на катушке будет равно 0 (все напряжение будет падать на резисторе).
Вот в этом случае и получится такой экспоненциальный график роста тока в индуктивности.
Рис. 18 Экспоненциальный график роста тока в индуктивности.ис 19 «Экспонента проходит через 0 под углом 45 градусов»зы. В интернете столько разнообразной ереси на тему катушек индуктивности. Просто диву даешься.
«Катушка индуктивности обладает также очень интересным свойством. При подаче на катушку постоянного напряжения, в катушке возникает на короткий промежуток времени противоположное напряжение. Это противоположное напряжение называется ЭДС самоиндукции. Эта ЭДС зависит от значения индуктивности катушки. Поэтому, в момент подачи напряжения на катушку сила тока в течение долей секунд плавно меняет свое значение от 0 до некоторого значения, потому что напряжение, в момент подачи электрического тока, также меняет свое значение от ноля и до установившегося значения. »
»
Ну.. поскольку про резистор в цепи ничего не сказано, то не на короткий промежуток, а пока входное напряжение не будет снято. Вторая часть звучит бредово, но направление верное — ток с цепи растет от нуля до.. без резистора до бесконечности, с резистором до I=Uвх/R.
Предположим, что обычная катушка индуктивности подключена к источнику напряжения через ключ. При замыкании ключа на индуктивность подается напряжение, вызывающее быстрое изменение протекающего через нее тока. Когда приложенное напряжение увеличивается от нуля до пикового значения (за короткое время), индуктивность противодействует изменяющемуся через нее току, индуцируя напряжение, противоположное по полярности приложенному напряжению. Индуцированное напряжение при подаче питания на катушку индуктивности называется обратной ЭДС и определяется по формуле 1:
VL = – L*(di/dt), (1)
где:
VL – напряжение (обратная ЭДС), индуцированная на катушке;
L – индуктивность катушки;
di/dt – скорость изменения тока во времени.
Видимо здесь попытались описать начальный момент возникновения ЭДС самоиндукции, но получилась ерунда. Говорить, что «индуцированное напряжение противоположно по полярности приложенному напряжению» это то же самое, что «падение напряжения на резисторе противоположно по полярности приложенному напряжению.» Ага, точно, приложенное напряжение сложили с падением напряжения и после резистора получили 0. Так и есть, лол.
«ЭДС самоиндукции» в катушке это аналог «падения напряжения» на резисторе. Только в резисторе электрическая энергия рассеивается, переходит в тепло, а в индуктивности — накапливается, переходит в энергию магнитного поля. В водопроводной аналогии индуктивность это такая турбинка, вставленная в водопроводную трубу, и которая имеет момент инерции. Турбинка пропускает воду только когда вращается. И вот крантель открыли, давление к турбинке приложили, она начала вращаться и пошел ток дальше по трубе. И чем быстрее турбинка вращается, тем больше ее пропускная способность. Турбинка раскручивается, ток возрастает и так до бесконечности. Это если нет потерь энергии — резистора. А если есть резистор (трение), то часть давления расходуется на преодоление трения. И когда вся входная энергия будет расходоваться на трение, турбинка перестанет ускоряться и ток достигнет максимальной величины.
И чем быстрее турбинка вращается, тем больше ее пропускная способность. Турбинка раскручивается, ток возрастает и так до бесконечности. Это если нет потерь энергии — резистора. А если есть резистор (трение), то часть давления расходуется на преодоление трения. И когда вся входная энергия будет расходоваться на трение, турбинка перестанет ускоряться и ток достигнет максимальной величины.
Картинка неправильная. В правильном варианте при отключении источника, подключался резистор и цепь оставалась замкнутой.
Рассмотрим следующую цепь
Рис.21 Цепь с индуктивностью и переключателемВопрос на засыпку: Чему будет равно напряжение на индуктивности в первый момент после переключения ключа S из верхнего положения в нижнее?
Hint: Не надо выносить себе мозг, пытаясь сообразить с каким там знаком возникнет ЭДС самоиндукции и что с ней будет дальше. Надо применять простое правило:
Ток в индуктивности в первый момент времени после переключения сохраняется неизменным.
Дальше применять закон Ома.
Помогите решить / разобраться (Ф)
EUgeneUS в [url=/post1354947.html#p1354947]сообщении #1354947[/url] писал(а):
Подскажите, как получают квадратичную зависимость?
Примерно, как Вы и написали.
Важно понимать вот что: квадратичная зависимость получается при некоторой идеализации — 100% магнитосцеплении. То есть 100% магнитного потока от одного любого витка проходят через каждый другой виток.
Да конечно, коэффициент связи идеальных контуров, у меня равен 1. Просто я пытался понять логику получения квадратичной зависимости от числа витков .
— 18.11.2018, 15:13 —
realeugene в [url=/post1354964.html#p1354964]сообщении #1354964[/url] писал(а):
Это взаимоиндукция идеальных витков?
Нет, если вы рассматриваете индуктивность одной катушки целиком. У вас один общий контур, а не два контура. В котором ни один виток сам по себе не является замкнутым контуром. Поэтому, на мой взгляд, про взаимоиндукцию витков тут лучше не рассуждать.
Можно ли аналог катушки, составить из идеальных несвязных (общим током) контуров расположенных на близком расстоянии друг от друга?
Если да, то получаем взаимоиндукцию и эффект квадратичной зависимости общей индуктивности от числа контуров (витков).
— 18.11.2018, 15:33 —
EUgeneUS в [url=/post1354957.html#p1354957]сообщении #1354957[/url] писал(а):
Kiev
Если Вы проследите ход Ваших рассуждений\вычислений, то увидите, что используется (явно или не явно) условие: магнитный поток от одного витка полностью проходит через каждый другой виток. В реальном мире
а) это может выполняться приближенно, и с хорошей точностью — тогда зависимость индуктивности от количества витков можно считать квадратичной.
б) для некоторых геометрий катушек это может выполняться приближенно, но характер зависимости остается квадратичным, например, для «толстой катушки».
в) для некоторых геометрий катушек может приводить к неточной формуле для индуктивности. Например, если мы смотаем провод в соленоид, то его индуктивность будет пропорциональная количеству витков в квадрате, а значит квадрату длины провода. Далее начинаем вытягивать соленоид в прямой провод, а у прямого провода зависимость индуктивности от длины уже не квадратичная.
Далее начинаем вытягивать соленоид в прямой провод, а у прямого провода зависимость индуктивности от длины уже не квадратичная.
Да я взял 100%-й коэффициент связи витков по полю, то есть бесконечно близко их сблизил (наложил), при этом сказал что токи не суммируются (ток последовательный, как и в катушке).
Мне главное было понять, логику происхождения ~ в идеальном случае.
— 18.11.2018, 15:55 —
Простое объяснение зависимости ~
У изолированных витков с током есть только — самоиндукция.
У связных (в катушку) витков появляется и взаимоиндукция.
И сумма Самоиндукций и Взаимоиндукций даёт .
В отличии от суммы Самоиндукций которые дают только .
Чему равна индуктивность цепи
Рассмотрим цепь, содержащую в себе катушку индуктивности , и предположим, что активное сопротивление цепи, включая провод катушки, настолько мало, что им можно пренебречь. В этом случае подключение катушки к источнику постоянного тока вызвало бы его короткое замыкание, при котором, как известно, сила тока в цепи оказалась бы очень большой.
Иначе обстоит дело, когда катушка присоединена к источнику переменного тока. Короткого замыкания в этом случае не происходит. Это говорит о том. что катушка индуктивности оказывает сопротивление проходящему по ней переменному току .
Каков характер этого сопротивления и чем оно обусловливается?
Чтобы ответить ил этот вопрос, вспомним явление самоиндукции. Всякое изменение тока в катушке вызывает появление в ней ЭДС самоиндукции, препятствующей изменению тока. Величина ЭДС самоиндукции прямо пропорциональна величине индуктивности катушки и скорости изменения тока в ней. Но так как переменный ток непрерывно изменяется, то непрерывно возникающая в катушке ЭДС самоиндукции создает сопротивление переменному току.
Для уяснения процессов, происходящих в цепи переменного тока с катушкой индуктивности, обратимся к графику. На рисунке 1 построены кривые линии, характеризующие соответственно тик в цепи, напряжение на катушке и возникающую в ней ЭДС самоиндукции. Убедимся в правильности произведенных па рисунке построений.
Цепь переменного тока с катушкой индуктивности
С момента t = 0, т. е. с начального момента наблюдения за током, он начал быстро возрастать, но по мере приближения к своему максимальному значению скорость нарастания тока уменьшалась. В момент, когда ток достиг максимальной величины, скорость его изменения на мгновение стала равной нулю, т. е. прекратилось изменение тока. Затем ток начал сначала медленно, а потом быстро убывать и по истечении второй четверти периода уменьшился до нуля. Скорость же изменения тока за эту четверть периода, возрастая от пуля, достигла наибольшей величины тогда, когда ток станет равным нулю.
Рисунок 2. Характер изменений тока во времени в зависимости от величины тока
Из построений на рисунке 2 видно, что при переходе кривой тока через ось времени увеличение тока за небольшой отрезок времени t больше, чем за этот же отрезок времени, когда кривая тока достигает своей вершины.
Следовательно, скорость изменения тока уменьшается по мере увеличения тока и увеличивается по мере его уменьшения, независимо от направления тока в цепи.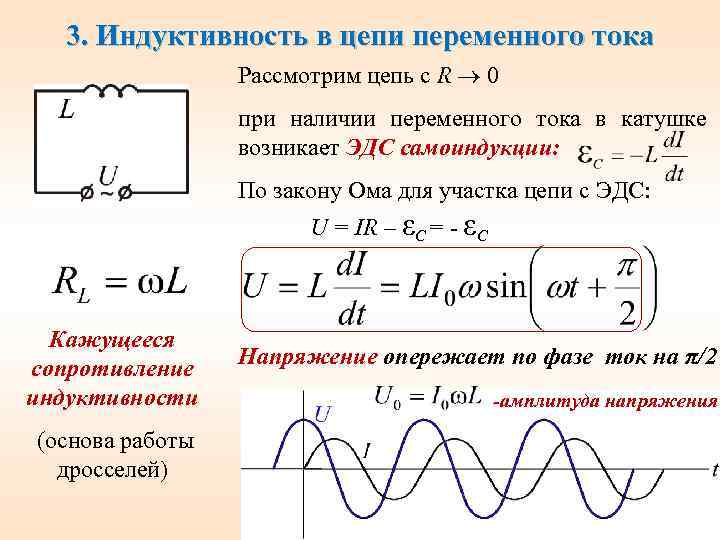
Очевидно, и ЭДС самоиндукции в катушке должна быть наибольшей тогда, когда скорость изменения тока наибольшая, и уменьшаться до нуля, когда прекращается его изменение. Действительно, на графике кривая ЭДС самоиндукции e L за первую четверть периода, начиная от максимального значения, упала до нуля (см. рис. 1).
На протяжении следующей четверти периода ток от максимального значения уменьшался до нуля, однако скорость его изменения постепенно возрастала и была наибольшей в момент, когда ток стал равным нулю. Соответственно и ЭДС самоиндукции за время этой четверти периода, появившись вновь в катушке, постепенно возрастала и оказалась максимальной к моменту, когда ток стал равным нулю.
Однако направление свое ЭДС самоиндукции изменила на обратное, так как возрастание тока в первой четверти периода сменилось во второй четверти его убыванием.
Цепь с индуктивностью
Продолжив дальше построение кривой ЭДС самоиндукции, мы убеждаемся в том, что за период изменения тока в катушке и ЭДС самоиндукции совершит в ней полный период своего изменения. Направление ее определяется законом Ленца: при возрастании тока ЭДС самоиндукции будет направлена против тока (первая и третья четверти периода), а при убывании тока, наоборот, совпадать с ним по направлению (вторая и четвертая четверти периода).
Направление ее определяется законом Ленца: при возрастании тока ЭДС самоиндукции будет направлена против тока (первая и третья четверти периода), а при убывании тока, наоборот, совпадать с ним по направлению (вторая и четвертая четверти периода).
Таким образом, ЭДС самоиндукции, вызываемая самим переменным током, препятствует его возрастанию и , наоборот, поддерживает его при убывании .
Обратимся теперь к графику напряжения на катушке (см. рис. 1). На этом графике синусоида напряжения на зажимах катушки изображена равной и противоположной синусоиде ЭДС самоиндукции. Следовательно, напряжение на зажимах катушки в любой момент времени равно и противоположно ЭДС самоиндукции, возникающей в ней. Напряжение это создается генератором переменного тока и идет на то, чтобы погасить действие в цепи ЭДС самоиндукции.
Таким образом, в катушке индуктивности, включенной в цепь переменного тока, создается сопротивление прохождению тока. Но так как такое сопротивление вызывается в конечном счете индуктивностью катушки , то и называется оно индуктивным сопротивлением.
Индуктивное сопротивление обозначается через X L и измеряется, как и активное сопротивление, в омах.
Индуктивное сопротивление цепи тем больше, чем больше частота источника тока, питающего цепь, и чем больше индуктивность цепи. Следовательно, индуктивное сопротивление цепи прямо пропорционально частоте тока и индуктивности цепи; определяется оно по формуле X L = ω L , где ω — круговая частота, определяемая произведением 2π f . — индуктивность цепи в гн.
Закон Ома для цепи переменного тока, содержащей индуктивное сопротивление, звучит так: величина тока прямо пропорциональна напряжению и обратно пропорциональна индуктивному сопротивлению це п и , т. е. I = U / X L , где I и U — действующие значения тока и напряжения, а X L — индуктивное сопротивление цепи.
Рассматривая графики изменения тока в катушке. ЭДС самоиндукции и напряжения на ее зажимах, мы обратили внимание на то, что изменение этих в еличин не совпадает по времени. Иначе говоря, синусоиды тока, напряжения и ЭДС самоиндукции оказались для рассматриваемой нами цепи сдвинутыми по времени одна относительно другой. В технике переменных токов такое явление принято называть сдвигом фаз .
В технике переменных токов такое явление принято называть сдвигом фаз .
Если же две переменные величины изменяются по одному и тому же закону (в нашем случае по синусоидальному) с одинаковыми периодами, одновременно достигают своего максимального значения как в прямом, так и в обратном направлении, а также одновременно уменьшаются до нуля, то такие переменные величины имеют одинаковые фазы или, как говорят, совпадают по фазе.
В качестве примера на рисунке 3 приведены совпадающие по фазе кривые изменения тока и напряжения. Такое совпадение фаз мы всегда наблюдаем в цепи переменного тока, состоящей только из активного сопротивления.
В том случае, когда цепь содержит индуктивное сопротивление, фазы тока и напряжения, как это видно из рис. 1 не совпадают, т. е. имеется сдвиг фаз между этими переменными величинами. Кривая тока в этом случае как бы отстает от кривой напряжения на четверть периода.
Следовательно, при включении катушки индуктивности в цепь переменного тока в цепи появляется сдвиг фаз между током и напряжением, причем ток отстает по фазе от напряжения на четверть периода . Это значит, что максимум тока наступает через четверть периода после того, как наступил максимум напряжения.
Это значит, что максимум тока наступает через четверть периода после того, как наступил максимум напряжения.
ЭДС же самоиндукции находится в противофазе с напряжением на катушке, отставая, в свою очередь, от тока на четверть периода. При этом период изменения тока, напряжения, а также и ЭДС самоиндукции не меняется и остается равным периоду изменения напряжения генератора, питающего цепь. Сохраняется также и синусоидальный характер изменения этих величин.
Рисунок 3. Совпадение по фазе тока и напряжения в цепи с активным сопротивлением
Выясним теперь, каково отличие нагрузки генератора переменного тока активным сопротивлением от нагрузки его индуктивным сопротивлением.
Когда цепь переменного тока содержит в себе лишь одно активное сопротивление, то энергия источника тока поглощается в активном сопротивлении, нагревая проводник.
Когда же цепь не содержит активного сопротивления (мы условно считаем его равным нулю), а состоит лишь из индуктивного сопротивления катушки, энергия источника тока расходуется не на нагрев проводов, а только на создание ЭДС самоиндукции, т. е. она превращается в энергию магнитного поля. Однако переменный ток непрерывно изменяется как по величине, так и по направлению, а следовательно, и магнитное поле катушки непрерывно изменяется в такт с изменением тока. В первую четверть периода, когда ток возрастает, цепь получает энергию от источника тока и запасает ее в магнитном поле катушки. Но как только ток, достигнув своего максимума, начинает убывать, он поддерживается за счет энергии, запасенной в магнитном поле катушки посредством ЭДС самоиндукции.
е. она превращается в энергию магнитного поля. Однако переменный ток непрерывно изменяется как по величине, так и по направлению, а следовательно, и магнитное поле катушки непрерывно изменяется в такт с изменением тока. В первую четверть периода, когда ток возрастает, цепь получает энергию от источника тока и запасает ее в магнитном поле катушки. Но как только ток, достигнув своего максимума, начинает убывать, он поддерживается за счет энергии, запасенной в магнитном поле катушки посредством ЭДС самоиндукции.
Таким образом, источник тока, отдав в течение первой четверти периода часть своей энергии в цепь, в течение второй четверти получает ее обратно от катушки, выполняющей при этом роль своеобразного источника тока. Иначе говоря, цепь переменного тока, содержащая только индуктивное сопротивление, не потребляет энергии : в данном случае происходит колебание энергии между источником и цепью. Активное же сопротивление, наоборот, поглощает в себе всю энергию, сообщенную ему источником тока.
Говорят, что катушка индуктивности, в противоположность омическому сопротивлению, не активна по отношению к источнику переменного тока, т. е. реактивна . Поэтому индуктивное сопротивление катушки называют также реактивным сопротивлением .
Кто в школе не изучал физику? Для кого-то она была интересна и понятна, а кто-то корпел над учебниками, пытаясь выучить наизусть сложные понятия. Но каждый из нас запомнил, что мир основан на физических знаниях. Сегодня мы поговорим о таких понятиях, как индуктивность тока, индуктивность контура, и узнаем, какие бывают конденсаторы и что такое соленоид.
Электрическая цепь и индуктивность
Самоиндукция и измерение индуктивности
Индуктивностью называется величина, которая равна отношению магнитного потока, проходящего по всем виткам контура к силе тока:
Индуктивность контура находится в зависимости от формы, размеров контура и от магнитных свойств среды, в которой он находится. Если в замкнутом контуре протекает электрический ток, то возникает изменяющееся магнитное поле. Это впоследствии приведет к возникновению ЭДС. Рождение индукционного тока в замкнутом контуре носит название «самоиндукция». По правилу Ленца величина не дает изменяться току в контуре. Если обнаруживается самоиндукция, то можно применять электрическую цепь, в которой параллельно включены резистор и катушка с железным сердечником. Последовательно с ними подсоединены и электрические лампы. В этом случае сопротивление резистора равно сопротивлению на постоянном токе катушки. Результатом будет яркое горение ламп. Явление самоиндукции занимает одно из главных мест в радиотехнике и электротехнике.
Это впоследствии приведет к возникновению ЭДС. Рождение индукционного тока в замкнутом контуре носит название «самоиндукция». По правилу Ленца величина не дает изменяться току в контуре. Если обнаруживается самоиндукция, то можно применять электрическую цепь, в которой параллельно включены резистор и катушка с железным сердечником. Последовательно с ними подсоединены и электрические лампы. В этом случае сопротивление резистора равно сопротивлению на постоянном токе катушки. Результатом будет яркое горение ламп. Явление самоиндукции занимает одно из главных мест в радиотехнике и электротехнике.
Как найти индуктивность
Формула, которая является простейшей для нахождения величины, следующая:
где F – магнитный поток, I – ток в контуре.
Через индуктивность можно выразить ЭДС самоиндукции:
Из формулы напрашивается вывод о численном равенстве индукции с ЭДС, которое возникает в контуре при изменении силы тока на один амперметр за одну секунду.
Переменная индуктивность дает возможность найти и энергию магнитного поля:
«Катушка ниток»
Катушка индуктивности представляет собой намотанную изолированную медную проволоку на твердое основание. Что касается изоляции, то выбор материала широк – это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.
Что касается изоляции, то выбор материала широк – это и лак, и проводная изоляция, и ткань. Величина магнитного потока зависит от площади цилиндра. Если увеличить ток в катушке, то магнитное поле будет становиться все больше и наоборот.
Если подать электрический ток на катушку, то в ней возникнет напряжение, противоположное напряжению тока, но оно внезапно исчезает. Такого рода напряжение называется электродвижущей силой самоиндукции. В момент включения напряжения на катушку сила тока меняет свое значение от 0 до некоего числа. Напряжение в этот момент тоже меняет значение, согласно закону Ома:
где I характеризует силу тока, U – показывает напряжение, R – сопротивление катушки.
Еще одной особенной чертой катушки является следующий факт: если разомкнуть цепь «катушка – источник тока», то ЭДС добавится к напряжению. Ток тоже вначале вырастет, а потом пойдет на спад. Отсюда вытекает первый закон коммутации, в котором говорится, что сила тока в катушке индуктивности мгновенно не меняется.
Катушку можно разделить на два вида:
- С магнитным наконечником. В роли материала сердца выступают ферриты и железо. Сердечники служат для повышения индуктивности.
- С немагнитным. Используются в случаях, когда индуктивность не больше пяти миллиГенри.
Устройства различаются и по внешнему виду, и внутреннему строению. В зависимости от таких параметров находится индуктивность катушки. Формула в каждом случае разная. Например, для однослойной катушки индуктивность будет равна:
- L = 10µ0ΠN 2 R 2 : 9R + 10l.
А вот уже для многослойной другая формула:
- L= µ0N 2 R 2 : 2Π(6R + 9l + 10w).
Основные выводы, связанные с работой катушек:
- На цилиндрическом феррите самая большая индуктивность возникает в середине.
- Для получения максимальной индуктивности необходимо близко наматывать витки на катушку.
- Индуктивность тем меньше, чем меньше количество витков.
- В тороидальном сердечнике расстояние между витками не играет роли катушки.

- Значение индуктивности зависит от «витков в квадрате».
- Если последовательно соединить индуктивности, то их общее значение равно сумме индуктивностей.
- При параллельном соединении нужно следить, чтобы индуктивности были разнесены на плате. В противном случае их показания будут неправильными за счет взаимного влияния магнитных полей.
Соленоид
Под этим понятием понимается цилиндрическая обмотка из провода, который может быть намотан в один или несколько слоев. Длина цилиндра значительно больше диаметра. За счет такой особенности при подаче электрического тока в полости соленоида рождается магнитное поле. Скорость изменения магнитного потока пропорциональна изменению тока. Индуктивность соленоида в этом случае рассчитывается следующим образом:
Еще эту разновидность катушек называют электромеханическим исполнительным механизмом с втягиваемым сердечником. В данном случае соленоид снабжается внешним ферромагнитным магнитопроводом – ярмом.
- Первая способна контролировать линейное давление.
- Вторая модель отличается от других принудительным управлением блокировки муфты в гидротрансформаторах.
- Третья модель содержит в своем составе регуляторы давления, отвечающие за работу переключения скоростей.
- Четвертая управляется гидравлическим способом или клапанами.
Необходимые формулы для расчетов
Чтобы найти индуктивность соленоида, формула применяется следующая:
где µ0 показывает магнитную проницаемость вакуума, n – это число витков, V – объем соленоида.
Также провести расчет индуктивности соленоида можно и с помощью еще одной формулы:
где S – это площадь поперечного сечения, а l – длина соленоида.
Чтобы найти индуктивность соленоида, формула применяется любая, которая подходит по решению к данной задаче.
Работа на постоянном и переменном токе
Магнитное поле, которое создается внутри катушки, направлено вдоль оси, и равно:
где µ0 – это магнитная проницаемость вакуума, n – это число витков, а I – значение тока.
Когда ток движется по соленоиду, то катушка запасает энергию, которая равна работе, необходимая для установления тока. Чтобы вычислить в этом случае индуктивность, формула используется следующая:
где L показывает значение индуктивности, а E – запасающую энергию.
ЭДС самоиндукции возникает при изменении тока в соленоиде.
В случае работы на переменном токе появляется переменное магнитное поле. Направление силы притяжения может изменяться, а может оставаться неизменным. Первый случай возникает при использовании соленоида как электромагнита. А второй, когда якорь сделан из магнитомягкого материала. Соленоид на переменном токе имеет комплексное сопротивление, в которое включаются сопротивление обмотки и ее индуктивность.
Самое распространенное применение соленоидов первого типа (постоянного тока) – это в роли поступательного силового электропривода. Сила зависит от строения сердечника и корпуса. Примерами использования являются работа ножниц при отрезании чеков в кассовых аппаратах, клапаны в двигателях и гидравлических системах, язычки замков. Соленоиды второго типа применяются как индукторы для индукционного нагрева в тигельных печах.
Соленоиды второго типа применяются как индукторы для индукционного нагрева в тигельных печах.
Колебательные контуры
Простейшей резонансной цепью является последовательный колебательный контур, состоящий из включенных катушек индуктивности и конденсатора, через которые протекает переменный ток. Чтобы определить индуктивность катушки, формула используется следующая:
где XL показывает реактивное сопротивление катушки, а W – круговая частота.
Если используется реактивное сопротивление конденсатора, то формула будет выглядеть следующим образом:
При параллельном колебательном контуре включены два реактивных элемента с разной силой реактивности. Использование такого вида контура подразумевает знание, что при параллельном включении элементов нужно складывать только их проводимости, но не сопротивления. На резонансной частоте суммарная проводимость контура равна нулю, что говорит о бесконечно большом сопротивлении переменному току. Для контура, в котором параллельно включены емкость (C), сопротивление (R) и индуктивность, формула, объединяющая их и добротность (Q), следующая:
При работе параллельного контура за один период колебаний дважды происходит энергетический обмен между конденсатором и катушкой. В этом случае появляется контурный ток, который значительно больше значения тока во внешней цепи.
В этом случае появляется контурный ток, который значительно больше значения тока во внешней цепи.
Работа конденсатора
Устройство представляет собой двухполюсник малой проводимости и с переменным или постоянным значением емкости. Когда конденсатор не заряжен, сопротивление его близко к нулю, в противном случае оно равно бесконечности. Если источник тока отсоединить от данного элемента, то он становится этим источником до своей разрядки. Использование конденсатора в электронике заключается в роли фильтров, которые удаляют помехи. Данное устройство в блоках питания на силовых цепях применяются для подпитки системы при больших нагрузках. Это основано на способности элемента пропускать переменную составляющую, но непостоянный ток. Чем выше частота составляющей, тем меньше у конденсатора сопротивление. В результате через конденсатор глушатся все помехи, которые идут поверх постоянного напряжения.
Сопротивление элемента зависит от емкости. Исходя из этого, правильнее будет ставить конденсаторы с различным объемом, чтобы улавливать разного рода помехи.![]() Благодаря способности устройства пропускать постоянный ток только в период заряда его используют как времязадающий элемент в генераторах или как формирующее звено импульса.
Благодаря способности устройства пропускать постоянный ток только в период заряда его используют как времязадающий элемент в генераторах или как формирующее звено импульса.
Конденсаторы бывают многих типов. В основном используется классификация по типу диэлектрика, так как этот параметр определяет стабильность емкости, сопротивление изоляции и так далее. Систематизация по данной величине следующая:
- Конденсаторы с газообразным диэлектриком.
- Вакуумные.
- С жидким диэлектриком.
- С твердым неорганическим диэлектриком.
- С твердым органическим диэлектриком.
- Твердотельные.
- Электролитические.
Существует классификация конденсаторов по назначению (общий или специальный), по характеру защиты от внешних факторов (защищенные и незащищенные, изолированные и неизолированные, уплотненные и герметизированные), по технике монтажа (для навесного, печатного, поверхностного, с выводами под винт, с защелкивающимися выводами). Также устройства можно различить по способности к изменению емкости:
- Постоянные конденсаторы, то есть у которых емкость остается всегда постоянной.

- Подстроечные. У них емкость не меняется при работе аппаратуры, но можно ее регулировать разово или периодически.
- Переменные. Это конденсаторы, которые допускают в процессе функционирования аппаратуры изменение ее емкости.
Индуктивность и конденсатор
Токоведущие элементы устройства способны создавать его собственную индуктивность. Это такие конструктивные части, как кладки, соединительные шины, токоотводы, выводы и предохранители. Можно создать дополнительную индуктивность конденсатора путем присоединения шин. Режим работы электрической цепи зависит от индуктивности, емкости и активного сопротивления. Формула расчета индуктивности, которая возникает при приближении к резонансной частоте, следующая:
- Ce = C : (1 – 4Π 2 f 2 LC),
где Ce определяет эффективную емкость конденсатора, C показывает действительную емкость, f – это частота, L – индуктивность.
Значение индуктивности всегда должно учитываться при работе с силовыми конденсаторами. Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.
Для импульсных конденсаторов наиболее важна величина собственной индуктивности. Их разряд приходится на индуктивный контур и имеет два вида – апериодический и колебательный.
Индуктивность в конденсаторе находится в зависимости от схемы соединения элементов в нем. Например, при параллельном соединении секций и шин эта величина равна сумме индуктивностей пакета главных шин и выводов. Чтобы найти такого рода индуктивность, формула следующая:
где Lk показывает индуктивность устройства, Lp –пакета, Lm – главных шин, а Lb – индуктивность выводов.
Если при параллельном соединении ток шины меняется по ее длине, то тогда эквивалентная индуктивность определяется так:
- Lk = Lc : n + µ0 l х d : (3b) + Lb,
где l – длина шин, b – ее ширина, а d – расстояние между шинами.
Если в катушке, изображенной на рис. 20.1, магнитное поле создается собственным током i, то магнитный поток называется потоком самоиндукции и обозначается ФL, а индуцируемая в катушке ЭДС еL – ЭДС самоиндукции. В соответствии с формулой (20.1) она равна:
В соответствии с формулой (20.1) она равна:
где ψ – потокосцепление самоиндукции, величина, пропорциональная протекающему по катушке току: ψ = Li.
Коэффициент пропорциональности L между потокосцеплением и током называется собственной индуктивностью или просто индуктивностью катушки (контура). Она зависит от формы и размеров катушки, а также от магнитной проницаемости сердечника. Ее размерность В x с/А=Ом x с. Эта единица измерения называется генри (Гн).
Подставляя последнее выражение в (2.15) и полагая L = const, получаем следующую формулу, определяющую ЭДС самоиндукции:
На рис. 2.18 показано изображение индуктивности на электрической схеме; uL – напряжение на зажимах катушки, обусловленное электродвижущей силой самоиндукции, или другими словами, напряжение, наведенное в катушке собственным переменным магнитным полем.
Рис. 2.18 – Обозначение индуктивности
Все три стрелки на схеме (i, eL, uL) принято направлять в одну сторону. Раньше мы видели, что при одинаковых направлениях стрелок напряжения и ЭДС они имеют разные знаки. Поэтому:
Раньше мы видели, что при одинаковых направлениях стрелок напряжения и ЭДС они имеют разные знаки. Поэтому:
Знак минус в правой части формулы (2.16) обусловлен принципом Ленца, определяющим направление индуцированной ЭДС. В рассматриваемом случае он может быть сформулирован следующим образом:
ЭДС самоиндукции направлена так, что своим действием препятствует причине, вызвавшей ее появление.
Причина появления ЭДС самоиндукции – изменение тока. Поэтому при возрастании тока она направлена ему навстречу, при уменьшении тока – в одну с ним сторону.
Препятствуя изменению тока, ЭДС самоиндукции оказывает ему сопротивление, которое называется индуктивным и обозначается хL. В соответствии с формулой (2.16) его величина определяется индуктивностью и скоростью изменения тока, т.е. частотой. Формула, определяющая индуктивное сопротивление, имеет вид:
В цепях постоянного тока такого понятия мы не встречали, так как при постоянных магнитных полях ЭДС самоиндукции не возникает. Пусть ток, протекающий по индуктивности, определяется выражением (2.13). Тогда напряжение на ее зажимах, в соответствии с формулой (2.17), равно:
Пусть ток, протекающий по индуктивности, определяется выражением (2.13). Тогда напряжение на ее зажимах, в соответствии с формулой (2.17), равно:
Это – мгновенное значение напряжения. Его амплитуда равна:
Аналогичное выражение получается (после деления на √2) и для действующих значений:
где Bl – индуктивная проводимость.
Запишем соответствующие формулы в символической форме:
Аналогично для действующих значений
Уравнения, связывающие напряжение и ток в индуктивности, как в вещественных, так и в комплексных числах, представляют собой закон Ома для индуктивности.
Начальная фаза напряжения больше начальной фазы тока на 90° . В индуктивности ток отстает от напряжения на четверть периода. Выражение закона Ома, записанное в символическое форме, указывает на этот сдвиг фаз. Вспомним, что умножение вектора на j приводит к его повороту на угол 90° против часовой стрелки.
Рис. 2.19 – Векторная диаграмма напряжения и тока в индуктивности
Согласно уравнениям (2.18) UL получается путем умножения произведения IxL на j, в результате чего вектор UL оказывается повернутым относительно вектора I.
Пример 2.5. Мгновенное значение напряжения на индуктивности определяется выражением uL = 200 sin(ωt+60°)В. Записать выражение мгновенного значения тока, если L = 63,67 мГн, а частота питающего напряжения f = 50 Гц. Построить векторные диаграммы напряжения и тока.
Решение. При частоте f = 50 Гц циклическая частота ω = 314 с-1, и индуктивное сопротивление xL = ωL = 20 Ом. Амплитуда тока равна:
Так как в индуктивности ток отстает от напряжения на четверть периода, его начальная фаза меньше начальной фазы напряжения на 90° : ψi = ψu – 90° = 60–90–30°.
Итак, i = 10sin (ωt–30°). Векторная диаграмма показана на рис. 2.20.
Индуктивность — Энциклопедия Нового Света
| Электромагнетизм | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Электричество · Магнетизм | |||||||||
Магнитостатика
| |||||||||
Электродинамика
| |||||||||
Тензоры в теории относительности
| |||||||||
Индуктивность — это свойство электрической цепи, при котором изменение тока, протекающего по цепи, индуцирует электродвижущую силу (ЭДС), которая препятствует изменению тока.В электрических цепях любой электрический ток (i {\ displaystyle i}) создает магнитное поле вокруг проводника с током, создавая общий магнитный поток (Φ {\ displaystyle \ Phi}), действующий на цепь. Этот магнитный поток имеет тенденцию действовать, чтобы противодействовать изменениям потока, генерируя напряжение (противо-ЭДС), которое противодействует или имеет тенденцию уменьшать скорость изменения тока. Отношение магнитного потока к току называется самоиндуктивностью , которую обычно называют просто индуктивностью цепи.
Свойство индуктивности особенно заметно и полезно в виде электрических устройств, известных как индукторы . Катушка индуктивности часто представляет собой катушку с проволокой, обернутую вокруг материала, называемого сердечником . Когда электрический ток проходит через катушку, вокруг нее образуется магнитное поле, и это поле заставляет катушку индуктивности сопротивляться изменениям в величине тока, проходящего через нее.
Катушки индуктивностиимеют различное практическое применение. Например, в сочетании с конденсаторами они используются в качестве дросселей в источниках питания и для создания настроенных схем для радиоприема и радиовещания.Кроме того, индукторы используются в трансформаторах для электрических сетей и в качестве накопителей энергии в некоторых импульсных источниках питания.
Свойство индуктивности отводится при использовании электрических устройств, известных как индукторы , некоторые из которых показаны здесь.Условные обозначения и единицы
Термин «индуктивность» был введен Оливером Хевисайдом в феврале 1886 года. [1]
Принято использовать символ L {\ displaystyle L} для обозначения индуктивности, возможно, в честь физика Генриха Ленца. [2] [3]
В честь Джозефа Генри единице индуктивности присвоено имя генри (H):
- 1 H = 1 Вебер на ампер (Вт / А).
Индуктивность — это мера величины ЭДС, генерируемой при единичном изменении тока. Например, катушка индуктивности с индуктивностью 1 генри создает ЭДС 1 вольт, когда ток через катушку индуктивности изменяется со скоростью 1 ампер в секунду.
Определения
Количественное определение (само) индуктивности проволочной петли в единицах СИ (веберов на ампер):
- L = NΦi {\ displaystyle \ displaystyle L = {\ frac {N \ Phi} {i}}}
где Φ {\ displaystyle \ Phi} обозначает магнитный поток через область, охватываемую петлей, а N количество витков провода.Таким образом, потокосцепление λ = NΦ {\ displaystyle \ lambda = N \ Phi}
- NΦ = Li {\ displaystyle \ displaystyle N {\ Phi} = Li}.
Однако могут быть вклады от других цепей. Рассмотрим, например, две цепи C1 {\ displaystyle C_ {1}}, C2 {\ displaystyle C_ {2}}, по которым проходят токи i1 {\ displaystyle i_ {1}}, i2 {\ displaystyle i_ {2}}. Потоковые связи C1 {\ displaystyle C_ {1}} и C2 {\ displaystyle C_ {2}} задаются формулой
- N1Φ1 = L11i1 + L12i2, {\ displaystyle \ displaystyle N_ {1} \ Phi _ {1} = L_ {11} i_ {1} + L_ {12} i_ {2},}
- N2Φ2 = L21i1 + L22i2.{\ displaystyle \ displaystyle N_ {2} \ Phi _ {2} = L_ {21} i_ {1} + L_ {22} i_ {2}.}
Согласно приведенному выше определению, L11 {\ displaystyle L_ { 11}} и L22 {\ displaystyle L_ {22}} — это самоиндуктивности C1 {\ displaystyle C_ {1}} и C2 {\ displaystyle C_ {2}} соответственно. Можно показать (см. Ниже), что два других коэффициента равны: L12 = L21 = M {\ displaystyle L_ {12} = L_ {21} = M}, где M {\ displaystyle M} называется взаимной индуктивностью пары контуров.
Число витков N1 {\ displaystyle N_ {1}} и N2 {\ displaystyle N_ {2}} в приведенном выше определении встречается несколько асимметрично.{K} L_ {m, n} i_ {m} i_ {n}}
для энергии магнитного поля, создаваемого электрическими цепями K {\ displaystyle K}, где в {\ displaystyle i_ {n}} — ток в n-й цепи. Это уравнение является альтернативным определением индуктивности, которое также применяется, когда токи не ограничиваются тонкими проводами, поэтому не сразу понятно, какая область охватывает цепь, и как следует определять магнитный поток, проходящий через цепь.
Определение L = NΦ / i {\ displaystyle L = N \ Phi / i}, напротив, более прямое и интуитивно понятное.Можно показать, что эти два определения эквивалентны, если приравнять производную W по времени к электрической мощности, передаваемой в систему.
Свойства индуктивности
Взяв производную по времени от обеих сторон уравнения NΦ = Li {\ displaystyle N \ Phi = Li}, получим:
- NdΦdt = Ldidt + dLdti {\ displaystyle N {\ frac {d \ Phi} {dt}} = L {\ frac {di} {dt}} + {\ frac {dL} {dt}} i \,}
В большинстве физических случаев индуктивность постоянна во времени, поэтому
- NdΦdt = Ldidt {\ displaystyle N {\ frac {d \ Phi} {dt}} = L {\ frac {di} {dt}}}
По закону индукции Фарадея мы имеем:
- NdΦdt = −E = v {\ displaystyle N {\ frac {d \ Phi} {dt}} = — {\ mathcal {E}} = v}
где E {\ displaystyle {\ mathcal {E} }} — электродвижущая сила (ЭДС), а v {\ displaystyle v} — индуцированное напряжение.{t} v (\ tau) d \ tau + i (0)}
Эти уравнения вместе утверждают, что для постоянного приложенного напряжения v, ток изменяется линейно со скоростью , пропорциональной приложенное напряжение, но обратно пропорциональное индуктивности. И наоборот, если ток через катушку индуктивности изменяется с постоянной скоростью, индуцированное напряжение остается постоянным.
Влияние индуктивности можно понять на примере одиночного витка провода. Если напряжение внезапно приложено между концами проволочной петли, ток должен измениться с нуля на ненулевой.Однако ненулевой ток индуцирует магнитное поле по закону Ампера. Это изменение магнитного поля индуцирует ЭДС, противоположную изменению тока. Сила этой ЭДС пропорциональна изменению тока и индуктивности. Когда эти противодействующие силы уравновешены, результатом является ток, который линейно увеличивается со временем, причем скорость этого изменения определяется приложенным напряжением и индуктивностью.
Умножение приведенного выше уравнения для di / dt {\ displaystyle di / dt} на Li {\ displaystyle Li} приводит к
- Lididt = ddtL2i2 = iv {\ displaystyle Li {\ frac {di} {dt}} = {\ frac {d} {dt}} {\ frac {L} {2}} i ^ {2} = iv}
Поскольку iv — энергия, передаваемая системе за время, отсюда следует, что (L / 2) i2 {\ displaystyle \ left (L / 2 \ right) i ^ {2}} — это энергия магнитного поля, создаваемого током.
Анализ схем и полное сопротивление
При использовании векторов эквивалентное сопротивление индуктивности определяется по формуле:
- ZL = V / I = jLω {\ displaystyle Z_ {L} = V / I = jL \ omega \,}
где
- j — мнимая единица,
- L — индуктивность,
- ω = 2πf {\ displaystyle \ omega = 2 \ pi f \,} — угловая частота,
- f — частота, а
- Lω = XL {\ displaystyle L \ omega \ = X_ {L}} — индуктивное реактивное сопротивление.
Индуцированная ЭДС
Поток Φi {\ displaystyle \ Phi _ {i} \ \!} Через i -ю цепь в наборе определяется выражением:
- Φi = ∑jMijIj = LiIi + ∑j ≠ iMijIj {\ displaystyle \ Phi _ {i} = \ sum _ {j} M_ {ij} I_ {j} = L_ {i} I_ {i} + \ sum _ { j \ neq i} M_ {ij} I_ {j} \,}
так, чтобы наведенная ЭДС, E {\ displaystyle {\ mathcal {E}}} определенной цепи, i , в любом заданном набор может быть задан напрямую:
- E = −dΦidt = −ddt (LiIi + ∑j ≠ iMijIj) = — (dLidtIi + dIidtLi) −∑j ≠ i (dMijdtIj + dIjdtMij).{\ displaystyle {\ mathcal {E}} = — {\ frac {d \ Phi _ {i}} {dt}} = — {\ frac {d} {dt}} \ left (L_ {i} I_ {i } + \ sum _ {j \ neq i} M_ {ij} I_ {j} \ right) = — \ left ({\ frac {dL_ {i}} {dt}} I_ {i} + {\ frac {dI_ {i}} {dt}} L_ {i} \ right) — \ sum _ {j \ neq i} \ left ({\ frac {dM_ {ij}} {dt}} I_ {j} + {\ frac { dI_ {j}} {dt}} M_ {ij} \ right).}
Связанные индукторы
Принципиальная схема взаимно индуктирующих катушек индуктивности. Две вертикальные линии между индукторами указывают на твердый сердечник , вокруг которого намотаны провода индуктора.«n: m» показывает отношение количества обмоток левого индуктора к количеству обмоток правого индуктора. На этом рисунке также показано условное обозначение точек.Взаимная индуктивность возникает, когда изменение тока в одной катушке индуктивности индуцирует напряжение в другой соседней катушке индуктивности. Это важно как механизм работы трансформаторов, но он также может вызвать нежелательное соединение между проводниками в цепи.
Взаимная индуктивность, M , также является мерой связи между двумя индукторами.Взаимная индуктивность цепи i в цепи j определяется двойным интегралом формулы Неймана, см. # Методы расчета
Между взаимной индуктивностью также существует соотношение:
- M21 = N1N2P21 {\ displaystyle M_ {21} = N_ {1} N_ {2} P_ {21} \!}
где
- M21 {\ displaystyle M_ {21}} — взаимная индуктивность, а нижний индекс определяет отношение напряжения, индуцированного в катушке 2, к току в катушке 1.
- N1 {\ displaystyle N_ {1}} — количество витков в катушке 1,
- N2 {\ displaystyle N_ {2}} — количество витков в катушке 2,
- P21 {\ displaystyle P_ {21}} — проницаемость пространства, занимаемого потоком.
Взаимная индуктивность также связана с коэффициентом связи . Коэффициент связи всегда находится в диапазоне от 1 до 0, и это удобный способ указать взаимосвязь между определенной ориентацией индуктора с произвольной индуктивностью:
- M = kL1L2 {\ displaystyle M = k {\ sqrt {L_ {1} L_ {2}}} \!}
где
- k — коэффициент связи и 0 ≤ k ≤ 1,
- L1 {\ displaystyle L_ {1}} — индуктивность первой катушки, а
- L2 {\ displaystyle L_ {2}} — индуктивность второй катушки.
Как только этот коэффициент взаимной индуктивности M определен, его можно использовать для прогнозирования поведения цепи:
- V1 = L1dI1dt + MdI2dt {\ displaystyle V_ {1} = L_ {1} {\ frac {dI_ {1}} {dt}} + M {\ frac {dI_ {2}} {dt}}}
где
- В — напряжение на интересующей катушке индуктивности,
- L1 {\ displaystyle L_ {1}} — индуктивность интересующей катушки индуктивности,
- dI1 / dt {\ displaystyle dI_ {1} / dt} — производная по времени тока через интересующий индуктор,
- M {\ displaystyle M} — взаимная индуктивность, а
- dI2 / dt {\ displaystyle dI_ {2} / dt} — производная по времени тока через катушку индуктивности, соединенную с первой катушкой индуктивности.
Когда одна катушка индуктивности тесно связана с другой катушкой индуктивности через взаимную индуктивность, например, в трансформаторе, напряжения, токи и количество витков могут быть связаны следующим образом:
- Vs = VpNsNp {\ displaystyle V_ {s} = V_ {p} {\ frac {N_ {s}} {N_ {p}}}}
где
- Vs {\ displaystyle V_ {s}} — это напряжение на вторичной катушке индуктивности,
- Vp {\ displaystyle V_ {p}} — это напряжение на первичной катушке индуктивности (той, которая подключена к источнику питания),
- Ns {\ displaystyle N_ {s}} — количество витков во вторичной катушке индуктивности, а
- Np {\ displaystyle N_ {p}} — количество витков в первичной катушке индуктивности.
Обратный ток:
- Is = IpNpNs {\ displaystyle I_ {s} = I_ {p} {\ frac {N_ {p}} {N_ {s}}}}
где
- Is {\ displaystyle I_ {s}} — ток через вторичную катушку индуктивности,
- Ip {\ displaystyle I_ {p}} — ток через первичный индуктор (тот, который подключен к источнику питания),
- Ns {\ displaystyle N_ {s}} — количество витков во вторичной катушке индуктивности, а
- Np {\ displaystyle N_ {p}} — количество витков в первичной катушке индуктивности.
Обратите внимание, что мощность через один индуктор равна мощности через другой. Также обратите внимание, что эти уравнения не работают, если оба трансформатора работают принудительно (с источниками питания).
Когда обе стороны трансформатора представляют собой настроенную цепь, величина взаимной индуктивности между двумя обмотками определяет форму кривой частотной характеристики. Хотя границы не определены, это часто называют слабой, критической и избыточной связью. Когда две настроенные схемы слабо связаны через взаимную индуктивность, полоса пропускания будет узкой.По мере увеличения взаимной индуктивности полоса пропускания продолжает расти. Когда взаимная индуктивность превышает критическую точку, пик на кривой отклика начинает падать, и центральная частота будет ослабляться сильнее, чем ее прямые боковые полосы. Это называется избыточной связью.
Методика расчетов
Взаимная индуктивность
Взаимная индуктивность цепи i в цепи j определяется двойным интегралом формулы Неймана
- Mij = Б.CE ; 04π∮Ci∮Cjdsi⋅dsj | Rij | {\ displaystyle M_ {ij} = {\ frac {\ mu _ {0}} {4 \ pi}} \ oint _ {C_ {i}} \ oint _ {C_ {j}} {\ frac {\ mathbf {ds} _ {i} \ cdot \ mathbf {ds} _ {j}} {| \ mathbf {R} _ {ij} |}}}
константа г. до н.э. ; 0 {\ displaystyle \ mu _ {0}} — проницаемость свободного пространства (4π {\ displaystyle \ pi} × 10 -7 H / m), Ci {\ displaystyle C_ {i}} и Cj { \ displaystyle C_ {j}} — это кривые, натянутые на провода, Rij {\ displaystyle R_ {ij}} — расстояние между двумя точками. См. Вывод этого уравнения.
Собственная индуктивность
Формально самоиндукция проволочной петли может быть задана приведенным выше уравнением с i = j . Однако 1 / R {\ displaystyle 1 / R} теперь становится сингулярным, а конечный радиус a {\ displaystyle a} и Необходимо учитывать распределение тока в проводе. Остается вклад от интеграла по всем точкам, где | R | ≥a / 2 {\ displaystyle | R | \ geq a / 2} и поправочный член,
- Ljj = L = ( г. до н. Э.E. ; 04π∮C∮C′ds⋅ds ′ | R |) | R | ≥a / 2 + г. до н. Э. ; 02πlY {\ displaystyle L_ {jj} = L = \ left ({\ frac {\ mu _ {0}} {4 \ pi}} \ oint _ {C} \ oint _ {C ‘} {\ frac { \ mathbf {ds} \ cdot \ mathbf {ds} ‘} {| \ mathbf {R} |}} \ right) _ {| \ mathbf {R} | \ geq a / 2} + {\ frac {\ mu _ {0}} {2 \ pi}} lY}
Здесь {\ displaystyle a} и l {\ displaystyle l} обозначают радиус и длину провода, а Y {\ displaystyle Y} — константа, которая зависит от в распределение тока в проводе: Y = 0 {\ displaystyle Y = 0}, когда ток течет по поверхности провода. (скин-эффект), Y = 1/4 {\ displaystyle Y = 1/4}, когда ток в проводе однородный.Вот вывод этого уравнения.
Метод изображений
В некоторых случаях разные распределения тока создают одинаковое магнитное поле в некоторой части пространства. Этот факт может быть использован для связи самоиндуктивностей (метод изображений). В качестве примера рассмотрим:
- A) Провод на расстоянии d / 2 {\ displaystyle d / 2} перед идеально проводящей стеной (которая является обратной стороной)
- B) Два параллельных провода на расстоянии d {\ displaystyle d} с противоположным током
Магнитные поля двух систем совпадают (в полупространстве).Таким образом, энергия магнитного поля и индуктивность системы B вдвое больше, чем у системы A.
Самоиндукция простых электрических цепей в воздухе
Собственная индуктивность многих типов электрических цепей может быть дана в замкнутой форме. Примеры приведены в таблице.
| Тип | Индуктивность / г. {2}} {3l }} \ left \ {- 8w + 4 {\ frac {\ sqrt {1 + m}} {m}} \ left (K \ left ({\ frac {m} {1 + m}} \ right) — \ left (1-m \ right) E \ left ({\ frac {m} {1 + m}} \ right) \ right) \ right \}} = r2N2πl (1−8w3π + w22 − w44 + 5w616−35w864 +.{2}} | |
|---|---|---|
| Коаксиальный кабель, высокочастотный | l2πlna1a {\ displaystyle {\ frac {l} {2 \ pi}} \ ln {\ frac {a_ {1}} {a}}} | a 1 : Внешний радиус a: Внутренний радиус l {\ displaystyle l}: Длина |
| Круговая петля | р⋅ (ln8ra − 2 + Y) {\ displaystyle r \ cdot \ left (\ ln {\ frac {8r} {a}} — 2 + Y \ right)} | r: радиус петли a: радиус проволоки |
| Прямоугольник | 1π (bln2ba + dln2da− (b + d) (2 − Y) + 2b2 + d2 − b⋅arsinhbd − d⋅arsinhdb) {\ displaystyle {\ frac {1} {\ pi }} \ left (b \ ln {\ frac {2b} {a}} + d \ ln {\ frac {2d} {a}} — \ left (b + d \ right) \ left (2-Y \ right ) +2 {\ sqrt {b ^ {2} + d ^ {2}}} — b \ cdot \ operatorname {arsinh} {\ frac {b} {d}} — d \ cdot \ operatorname {arsinh} {\ гидроразрыв {d} {b}} \ right)} | b, d: длина границы d >> a, b >> a a: радиус проволоки |
| Пара параллельных проводов | lπ (lnda + Y) {\ displaystyle {\ frac {l} {\ pi}} \ left (\ ln {\ frac {d} {a}} + Y \ right)} | a: радиус провода d: расстояние, d ≥ 2a l {\ displaystyle l}: длина пары |
| Пара параллельных проводов , высокая частота | l2πarcosh (d22a2−1) {\ displaystyle {\ frac {l} {2 \ pi}} \ operatorname {arcosh} \ left ({\ frac {d ^ {2}} {2a ^ {2}}} — 1 \ справа)} | a: радиус провода d: расстояние, d ≥ 2a l {\ displaystyle l}: длина пары |
| Провод параллельно идеально проводящей стене | l2π (ln2da + Y) {\ displaystyle {\ frac {l} {2 \ pi}} \ left (\ ln {\ frac {2d} {a}} + Y \ right)} | a: радиус провода d: расстояние, d ≥ a l {\ displaystyle l}: длина |
| Провод параллельно проводящей стене , высокая частота | l4πarcosh (2d2a2−1) {\ displaystyle {\ frac {l} {4 \ pi}} \ operatorname {arcosh} \ left ({\ frac {2d ^ {2}} {a ^ {2}}} — 1 \ справа)} | a: радиус провода d: расстояние, d ≥ a l {\ displaystyle l}: длина |
Константа B.C.E. ; 0 {\ displaystyle \ mu _ {0}} — проницаемость свободного пространства (4π {\ displaystyle \ pi} × 10 -7 H / m). Для высоких частот электрический ток течет по поверхности проводника. (скин-эффект), а в зависимости от геометрии иногда необходимо различать индуктивности низкой и высокой частоты. Это назначение константы Y: Y = 0, когда ток равномерно распределен по поверхности провода (скин-эффект), Y = 1/4, когда ток равномерно распределен по поперечному сечению провода.В случае высокой частоты, если проводники приближаются друг к другу, по их поверхности протекает дополнительный экранирующий ток, и выражения, содержащие Y, становятся недействительными.
Индуктивность соленоида
Соленоид — это длинная тонкая катушка, т.е. катушка, длина которой намного больше диаметра. В этих условиях и без использования какого-либо магнитного материала плотность магнитного потока B {\ displaystyle B} внутри катушки практически постоянна и определяется выражением
- B = B. н. Э .; 0Ni / l {\ displaystyle \ displaystyle B = \ mu _ {0} Ni / l}
, где г. до н. Э. ; 0 {\ displaystyle \ mu _ {0}} — проницаемость свободного пространства, N {\ displaystyle N} — количество витков, i {\ displaystyle i} — текущий, l {\ displaystyle l} — длина катушка. Игнорируя концевые эффекты, общий магнитный поток, проходящий через катушку, получается путем умножения плотности потока B {\ displaystyle B} на площадь поперечного сечения A {\ displaystyle A} и количество витков N {\ displaystyle N}:
- Φ = В.{2} A / l.}
Это, а также индуктивность более сложных форм, можно получить из уравнений Максвелла. Для жестких катушек с воздушным сердечником индуктивность зависит от геометрии катушки и количества витков и не зависит от тока.
Аналогичный анализ применим к соленоиду с магнитопроводом, но только если длина катушки намного больше, чем произведение относительной магнитной проницаемости магнитопровода на диаметр. Это ограничивает простой анализ сердечниками с низкой проницаемостью или очень длинными тонкими соленоидами.{2} A / l.}
Обратите внимание, что, поскольку проницаемость ферромагнитных материалов изменяется в зависимости от приложенного магнитного потока, индуктивность катушки с ферромагнитным сердечником обычно изменяется в зависимости от тока.
Индуктивность коаксиальной линии
Пусть внутренний проводник имеет радиус ri {\ displaystyle r_ {i}} и проницаемость до н.э. ; i {\ displaystyle \ mu _ {i}}, пусть диэлектрик между внутренним и внешним проводником имеет проницаемость до н.э. ; d {\ displaystyle \ mu _ {d}}, и пусть внешний проводник имеет внутренний радиус ro1 {\ displaystyle r_ {o1}}, внешний радиус ro2 {\ displaystyle r_ {o2}} и проницаемость B.{2}}} \ right) — {\ frac {\ mu _ {o}} {8 \ pi}}}
Однако для типичного приложения коаксиальной линии нас интересует передача (не постоянного тока) сигналов на частоты, для которых нельзя пренебрегать резистивным скин-эффектом. В большинстве случаев членами внутреннего и внешнего проводников можно пренебречь, и в этом случае можно приблизиться к
- dLdl≈ до н. Э. ; d2πlnro1ri {\ displaystyle {\ frac {dL} {dl}} \ приблизительно {\ frac {\ mu _ {d}} {2 \ pi}} \ ln {\ frac {r_ {o1}} {r_ {i}}}}
См. также
Банкноты
Список литературы
- Гриффитс, Дэвид Дж.1999. Введение в электродинамику, 3-е изд. Река Аппер Сэдл, штат Нью-Джерси: Prentice Hall. ISBN 013805326X.
- Гровер, Фредерик Уоррен. 1962. Расчеты индуктивности, рабочие формулы и таблицы . Нью-Йорк: Дувр. OCLC 299921393.
- Хевисайд, Оливер. 1894. Электротехнические статьи. Нью-Йорк: Макмиллан.
- Хьюз, Эдвард и др. 2002. Электрические и электронные технологии, 8-е изд. Харлоу: Прентис Холл. ISBN 058240519X.
- Вангснесс, Роальд К. 1986. Электромагнитные поля, 2-е изд. Нью-Йорк: Вили. ISBN 0471811866.
Внешние ссылки
Все ссылки получены 2 марта 2018 г.
Кредиты
New World Encyclopedia Писатели и редакторы переписали и завершили статью Wikipedia в соответствии со стандартами New World Encyclopedia . Эта статья соответствует условиям лицензии Creative Commons CC-by-sa 3.0 (CC-by-sa), которая может использоваться и распространяться с указанием авторства.Кредит предоставляется в соответствии с условиями этой лицензии, которая может ссылаться как на участников Энциклопедии Нового Света, участников, так и на самоотверженных добровольцев Фонда Викимедиа. Чтобы процитировать эту статью, щелкните здесь, чтобы просмотреть список допустимых форматов цитирования. История более ранних публикаций википедистов доступна исследователям здесь:
История этой статьи с момента ее импорта в Энциклопедию Нового Света :
Примечание. Некоторые ограничения могут применяться к использованию отдельных изображений, на которые распространяется отдельная лицензия.
Что такое индуктор? — ES Components
Катушка индуктивности , также называемая катушкой , дросселем или реактором , представляет собой пассивный двухконтактный электрический компонент, который накапливает энергию в магнитном поле, когда через него протекает электрический ток. Индуктор обычно состоит из изолированного провода, намотанного в катушку вокруг сердечника.
Когда ток, протекающий через катушку индуктивности, изменяется, изменяющееся во времени магнитное поле индуцирует электродвижущую силу ( e.м.ф. ) (напряжение) в проводнике, описываемое законом индукции Фарадея. Согласно закону Ленца, индуцированное напряжение имеет полярность (направление), которая противодействует изменению тока, который его создал. В результате катушки индуктивности препятствуют любым изменениям тока через них.
Катушка индуктивности характеризуется своей индуктивностью, которая представляет собой отношение напряжения к скорости изменения тока. В Международной системе единиц (СИ) единицей индуктивности является генри (Н), названный в честь американского ученого 19 века Джозефа Генри.При измерении магнитных цепей он эквивалентен Веберу / Амперу. Индукторы имеют значения, которые обычно находятся в диапазоне от 1 мкГн (10-6 Гн) до 20 Гн. Многие индукторы имеют магнитный сердечник из железа или феррита внутри катушки, который служит для увеличения магнитного поля и, следовательно, индуктивности. Наряду с конденсаторами и резисторами, индукторы являются одним из трех пассивных элементов линейной цепи, составляющих электронные схемы. Индукторы широко используются в электронном оборудовании переменного тока (AC), особенно в радиооборудовании.Они используются для блокировки переменного тока, позволяя проходить постоянному току; индукторы, предназначенные для этой цели, называются дросселями. Они также используются в электронных фильтрах для разделения сигналов разных частот и в сочетании с конденсаторами для создания настроенных схем, используемых для настройки радио- и ТВ-приемников.
Катушки индуктивности широко используются в аналоговых схемах и обработке сигналов. Применения варьируются от использования больших катушек индуктивности в источниках питания, которые в сочетании с фильтрующими конденсаторами устраняют пульсации, кратные частоте сети (или частоте переключения для импульсных источников питания) на выходе постоянного тока, до небольшой индуктивности. ферритовой бусины или торца, установленных вокруг кабеля, чтобы предотвратить передачу радиочастотных помех по проводу.Индукторы используются в качестве накопителя энергии во многих импульсных источниках питания для выработки постоянного тока. Катушка индуктивности подает энергию в схему для поддержания протекания тока в периоды выключения и позволяет создавать топографии, в которых выходное напряжение выше входного.
Источник: Википедия
Промышленное производство | Базовая электроника: что такое индуктивность?
Венделл С. Райс 10 мая 2004 г.
Катушка индуктивности — это устройство, которое при воздействии увеличивающегося электрического тока генерирует обратное напряжение, противодействующее этому току.Индуктивность определяет количество энергии, которое может хранить катушка индуктивности.
Катушка индуктивности состоит как минимум из одной обмотки провода, но обычно ее больше. В зависимости от области применения индуктор может иметь или не иметь сердечник, который обычно изготавливается из какого-либо магнитного материала. Но некоторые индукторы или катушки с воздушным сердечником намотаны на картон, пластик или другой материал, чтобы катушка сохраняла свою форму.
Индуктивность и магнетизм
Взаимосвязь тока, магнетизма и движения важна для индуктивности.У электронов есть заряд; когда они находятся в движении, течет ток. Этот поток вызывает магнитное поле. Когда заряд и, следовательно, магнитное поле приводится в движение, он создает силу, которая может вызывать движение или оказывать давление.
Магнитный домен — это область магнитного материала, которая сохраняет одно направление намагничивания. Магнитные линии потока также называют силовыми линиями и силовыми линиями . Перемещение электрического проводника, такого как провод, через магнитное поле индуцирует в проводнике напряжение.Пропускание тока через проводник создает магнитное поле вокруг проводника (см. «Факты и примеры индуктивности и магнетизма»). Сила поля пропорциональна величине тока. Увеличение тока расширяет поле; уменьшение тока вызывает схлопывание поля.
Когда ток постоянный, магнитное поле статично. Поле присутствует, но не расширяется и не сжимается. Однако, если ток перестанет течь, поле схлопнется.Поскольку коллапсирующее магнитное поле движется в направлении, противоположном тому, в котором оно было создано, напряжение, которое оно индуцирует в проводе, имеет полярность, противоположную напряжению, создавшему его. Это явление известно как закон наведенного тока Ленца (см. «Законы индуктивности»).
При зацикливании проводника напряженность магнитного поля увеличивается пропорционально количеству витков. Чем быстрее движется магнитное поле, тем выше индуцированное напряжение. Намотайте проводник в катушку, и напряжение будет индуцировано в каждой петле (рис.1). Согласно закону Фарадея, два контура удваивают напряжение, три контура удваивают напряжение, семь контуров индуцируют в семь раз большее напряжение и так далее (см. «Законы индуктивности»).
Предположим, что в теоретической катушке с четырьмя петлями протекает ток через одну петлю, которая создает вокруг нее магнитное поле. Это поле прорезает остальные три петли, вызывая напряжение в каждой из них, но с полярностью, противоположной напряжению, которое изначально создавало поле (закон Ленца). Ток через контур 1 вызывает противодействующее напряжение в контурах 2, 3 и 4; ток в контуре 2 индуцирует напряжение в контурах 1, 3 и 4; и ток в контуре 3 индуцирует напряжение в контурах 1, 2 и 4.Трансформаторы основаны на этом принципе.
Частота и индуктивность
Обратная электродвижущая сила (ЭДС) присутствует только тогда, когда магнитное поле расширяется или сжимается. Если приложенное напряжение является постоянным, магнитное поле нарастает при первом приложении, а затем становится постоянным. Обратная ЭДС возникает только при увеличении напряженности поля. Это противодействующее напряжение пытается остановить прохождение тока.
Когда напряжение постоянного тока достигает своего пика, поле перестает расширяться и индуцированное напряжение падает до нуля.С катушкой установившееся состояние магнитного поля похоже на состояние прямого куска проволоки. Вокруг него есть поле — а количество витков провода умножает напряженность поля — но силовые линии не меняются. Наведенное напряжение отсутствует, если магнитное поле не меняется. Когда постоянное напряжение снимается, коллапсирующее поле индуцирует противоположное напряжение, которое пытается поддерживать ток, возвращая накопленную энергию (рис. 2).
При переменном напряжении скорость нарастания напряжения и расширения результирующего магнитного поля замедляется с уменьшением частоты.Следовательно, индуцированное напряжение, которое противодействует приложенному напряжению, ниже. Более высокие частоты увеличивают напряжение с большей скоростью, что увеличивает результирующее магнитное поле с большей скоростью. Это вызывает большее противодействующее напряжение. В результате катушка индуктивности создает большее сопротивление более высокочастотным напряжениям, чем низкочастотным напряжениям. Когда частота переменного напряжения уменьшается до нуля, напряжение становится постоянным (без изменения направления). Противодействие протеканию тока уменьшается, и сопротивление провода остается единственным ограничением для протекания тока.
Как измеряется индуктивность
Индуктивность измеряется в генри и обычно обозначается в формулах заглавными буквами L . Стоимость индуктора определяет количество энергии, которое он может хранить. Один генри (Гн) — это мера индуктивности замкнутой цепи, которая дает 1 В при изменении тока 1 А / сек.
Обычными единицами индуктивности являются генри (Гн), миллигенри (мГн или 1/1000 генри) и микрогенри (
1 H = 1000 мH = 1000000
Индуктивность увеличивается с увеличением количества витков провода или количества витков.Увеличение размера петли также увеличивает значение индуктивности, как и улучшение индуктивной связи от петли к петле. Расположение петель таким образом, чтобы они были ближе друг к другу, и увеличение магнитных свойств сердечника — это факторы, улучшающие индуктивную связь. Железный сердечник позволяет соединять силовые линии магнитного поля лучше, чем воздух; Форма сердечника пончика обеспечивает большее сцепление, чем форма сердечника стержня.
Дроссели и конденсаторы
Катушки индуктивности и конденсаторы накапливают энергию.В цепи постоянного тока при первоначальном приложении напряжения энергия начинает накапливаться, как и магнитное поле. Ток в цепи задерживается относительно момента подачи напряжения. Вы не можете производить энергию. Но вы можете хранить его и использовать — но не одновременно.
Как только поле создается, энергия заставляет ток течь в цепи. Когда напряжение снимается, накопленная энергия возвращается в цепь и немного дольше сохраняет ток. Пиковое значение протекающего тока отстает от пикового значения напряжения.
То же самое происходит в цепи переменного тока, за исключением того, что периодически реагирует на в зависимости от частоты переменного тока. Во время первого поток падает, а затем поле схлопывается, вызывая протекание тока. Прохождение тока задерживается на цикла после напряжения (рис. 3).
В конденсаторе, с другой стороны, ток в цепи протекает немедленно, начиная заряжать конденсатор. По мере увеличения заряда напряжение на конденсаторе увеличивается. Во второй
С индукторами, ток отстает от напряжения; напряжение приводит к току.С конденсаторами ток ведет к напряжению ; напряжение отстает от тока. Независимо от того, какое объяснение вы используете, если вы примените его к чистой индуктивности, это будет полная противоположность чистой емкости.
В той же цепи конденсатор накапливает заряд, в то время как магнитное поле вокруг катушки индуктивности разрушается. Конденсатор разряжается, в то время как магнитное поле индуктора расширяется. Это основа для настроенных схем и частотно-зависимых фильтров.
Катушки индуктивностимогут использоваться в электрических и электронных схемах в виде катушек, дросселей, трансформаторов, соленоидов, реле и фильтров.В сочетании с конденсаторами катушки индуктивности используются для настраиваемых схем, фильтров, шумоподавления и других приложений.
Факты и примеры индуктивности и магнетизма
| Факт | Пример |
| Когда сила перемещает проводник через магнитное поле, она индуцирует ток в проводе. | Звук — это сила, которая перемещает диафрагму, прикрепленную к катушке, движущуюся через магнитное поле.В результате получился микрофон. |
| Поток воды или пара — это сила, которая вращает турбину, вал которой соединен с катушками, движущимися в магнитном поле. В результате получился генератор энергии. | |
| Прохождение тока через проводник во внешнем магнитном поле создает силу на проводнике. | Ток через звуковую катушку передает возникающую силу на диафрагму или диффузор. В результате получился громкоговоритель. |
| Ток через катушки, установленные на валу, вызывает вращение.В результате получился мотор. | |
| Ток, протекающий через проводник, создает магнитное поле и создает силу. | Ток через катушку, намотанную на фиксированный железный стержень, создает внешнюю силу. В результате получился электромагнит. |
| Ток через катушку, намотанную на подвижный железный стержень, создает внутреннюю силу, которая перемещает стержень. В результате получился соленоид. |
| Информация об авторе |
| Венделл Райс (Wendell Rice), инженер по приборам и системам управления, Parsons Infrastructure & Technology, Пасадена, Калифорния, работал инженером по системам управления более 25 лет.С ним можно связаться по телефону 765-245-5357 или [email protected]. В настоящее время г-н Райс работает над проектом в Ньюпорте, штат Индиана, который обеспечивает поддержку программы армии США по нейтрализации химического оружия. |
Законы об индуктивности
Lenz — Напряжение, индуцированное в проводнике, будет противодействовать вызвавшей его силе.
Фарадей — Величина наведенного напряжения пропорциональна тому, насколько быстро силовые линии проходят через проводник, и количеству витков провода.
Hitachi FAQ | Что такое индуктивность?
A: Индуктор — это электронный компонент, состоящий просто из катушки с проволокой . Если по проводу проходит постоянный электрический ток, это создает магнитное поле. Если ток меняется, меняется и магнитное поле. Единицей измерения индуктивности является генри (H), названный в честь Джозефа Генри, американского физика, который открыл ее независимо примерно в то же время, что и английский физик Майкл Фарадей.
Один генри — это величина индуктивности, которая требуется для создания одного вольт электродвижущей силы, когда ток изменяется со скоростью один ампер в секунду. С индуктивностью связаны три закона. Эти:
- Закон Эрстеда: , который гласит, что постоянный электрический ток создает магнитное поле вокруг проводника.
- Закон Фарадея: , который гласит, что изменяющееся магнитное поле индуцирует ток в проводнике.
- Закон Ленца: , который гласит, что этот индуцированный ток имеет направление, противоположное изменению тока, создавшего магнитное поле. Это явление называется самоиндукцией.
Одним из важных применений индукторов является то, что они имеют тенденцию блокировать высокочастотные сигналы, пропуская низкочастотные колебания. Это противоположная функция конденсаторов, которые позволяют переменному току свободно течь, блокируя постоянный ток после того, как конденсатор заряжен. Вот почему конденсаторы постоянного тока часто используются в качестве фильтров нижних или верхних частот.Если схема представляет собой цепь переменного тока и чувствительна к шуму постоянного тока (как в случае микрофонных входов или соединений между аудиокомпонентами), то конденсатор постоянного тока, включенный последовательно перед остальной частью схемы, будет пропускать только сигналы переменного тока. Это называется блокировкой цепи. Однако, если между сигналом и землей установлен конденсатор, это предотвратит прохождение сигналов переменного тока. Это известно как схема развязки постоянного тока, и они часто используются для удаления пульсаций напряжения с источников питания постоянного тока, чтобы они обеспечивали более чистое напряжение.
Таким образом, комбинируя два компонента (то есть конденсаторы и катушки индуктивности) в любой цепи, можно выборочно фильтровать или генерировать колебания практически любой желаемой частоты. Однако современные схемы редко используют индукторы, потому что они могут достичь практически всех тех же результатов с микросхемами и конденсаторами.
Определение индуктивности по Merriam-Webster
в · дукт · танс | \ in-ˈdək-tən (t) s \ 1а : свойство электрической цепи, посредством которого в ней индуцируется электродвижущая сила за счет изменения тока либо в самой цепи, либо в соседней цепи. б : мера этого свойства, равная отношению наведенной электродвижущей силы к скорости изменения индуцирующего тока.2 : цепь или устройство, обладающие индуктивностью.
14.2: Взаимная индуктивность — Physics LibreTexts
ЦЕЛИ ОБУЧЕНИЯ
К концу этого раздела вы сможете:
- Сопоставьте две соседние цепи, которые переносят изменяющиеся во времени токи, с ЭДС, индуцированной в каждой цепи
- Опишите примеры, в которых взаимная индуктивность может быть желательной или нежелательной
Индуктивность — это свойство устройства, которое говорит нам, насколько эффективно оно индуцирует ЭДС в другом устройстве. Другими словами, это физическая величина, которая выражает эффективность данного устройства.
Когда две цепи, несущие изменяющиеся во времени токи, близки друг к другу, магнитный поток через каждую цепь изменяется из-за изменяющегося тока I в другой цепи. Следовательно, ЭДС индуцируется в каждой цепи изменяющимся током в другой. Поэтому этот тип ЭДС называется взаимно индуцированной ЭДС , а возникающее явление известно как взаимная индуктивность ( M ) . В качестве примера рассмотрим две туго намотанные катушки (рисунок \ (\ PageIndex {1} \)).Катушки 1 и 2 имеют \ (N_1 \) и \ (N_2 \) витки и переносят токи \ (I_1 \) и \ (I_2 \) соответственно. Поток через один виток катушки 2, создаваемый магнитным полем тока в катушке 1, равен \ (\ Phi_ {12} \), тогда как поток через один виток катушки 1 из-за магнитного поля \ (I_2 \) равно \ (\ Phi_ {12} \).
Рисунок \ (\ PageIndex {1} \): Некоторые силовые линии магнитного поля, создаваемые током в катушке 1, проходят через катушку 2.Взаимная индуктивность \ (M_ {21} \) катушки 2 относительно катушки 1 равна отношение потока через \ (N_2 \) витков катушки 2, создаваемого магнитным полем тока в катушке 1, деленное на этот ток, то есть
\ [M_ {21} = \ dfrac {N_2 \ Phi_ {21}} {I_1}.\ label {12.24} \]
Точно так же взаимная индуктивность катушки 1 относительно катушки 2 составляет
\ [M_ {12} = \ dfrac {N_1 \ Phi_ {12}} {I_2}. \ label {12.25} \]
Как и емкость, взаимная индуктивность является геометрической величиной. Это зависит от формы и относительного положения двух катушек и не зависит от токов в катушках. Единица СИ для взаимной индуктивности M называется генри (H) в честь Джозефа Генри (1799–1878), американского ученого, который открыл наведенную ЭДС независимо от Фарадея.Таким образом, имеем \ (1 \, H = 1 \, V \ cdot s / A \). Из уравнений \ ref {12.24} и \ ref {12.25} мы можем показать, что \ (M_ {21} = M_ {12} \), поэтому мы обычно опускаем индексы, связанные с взаимной индуктивностью, и пишем
\ [M = \ dfrac {N_2 \ Phi_ {21}} {I_1} = \ dfrac {N_1 \ Phi_ {12}} {I_2}. \ Label {14.3} \]
ЭДС, возникающая в любой катушке, находится путем объединения закона Фарадея и определения взаимной индуктивности. Поскольку \ (N_2 \ Phi_ {21} \) — это полный поток через катушку 2 из-за \ (I_1 \), получаем
\ [\ begin {align} \ epsilon_2 & = — \ dfrac {d} {dt} (N_2 \ Phi_ {21}) \\ [4pt] & = — \ dfrac {d} {dt} (MI_1) \\ [4pt] & = — M \ dfrac {dI_1} {dt} \ label {14.4} \ end {align} \]
, где мы использовали тот факт, что \ (M \) не зависит от времени, потому что геометрия не зависит от времени. Аналогично имеем
\ [\ epsilon_1 = — M \ dfrac {dI_2} {dt}. \ label {14.5} \]
В уравнении \ ref {14.5} мы можем увидеть значение предыдущего описания взаимной индуктивности (\ (M \)) как геометрической величины. Значение \ (M \) аккуратно инкапсулирует физические свойства элементов схемы и позволяет нам отделить физическую схему схемы от динамических величин, таких как ЭДС и ток.Уравнение \ ref {14.5} определяет взаимную индуктивность в терминах свойств в цепи, тогда как предыдущее определение взаимной индуктивности в уравнении \ ref {12.24} определяется в терминах испытываемого магнитного потока, независимо от элементов цепи. Вы должны быть осторожны при использовании формул \ ref {14.4} и \ ref {14.4}, потому что \ (\ epsilon_1 \) и \ (\ epsilon_2 \) не обязательно представляют общие ЭДС в соответствующих катушках. Каждая катушка может также иметь наведенную в ней ЭДС из-за ее самоиндукции (самоиндукция будет обсуждаться более подробно в следующем разделе).
Большая взаимная индуктивность M может быть или нежелательна. Мы хотим, чтобы трансформатор имел большую взаимную индуктивность. Но такой прибор, как электрическая сушилка для одежды, может вызвать опасную ЭДС на металлическом корпусе, если взаимная индуктивность между его катушками и корпусом велика. Один из способов уменьшить взаимную индуктивность — это использовать катушки противотока, чтобы нейтрализовать создаваемое магнитное поле (Рисунок \ (\ PageIndex {2} \)).
Рисунок \ (\ PageIndex {2} \): Нагревательные катушки электрической сушилки для белья могут быть намотаны в противоположную сторону, так что их магнитные поля нейтрализуют друг друга, что значительно снижает взаимную индуктивность по сравнению с корпусом сушилки.Цифровая обработка сигналов — еще один пример, в котором взаимная индуктивность снижается за счет обмотки встречных катушек. Быстрая ЭДС включения / выключения, представляющая единицы и нули в цифровой схеме, создает сложное зависящее от времени магнитное поле. ЭДС может возникать в соседних проводниках. Если этот проводник также передает цифровой сигнал, наведенная ЭДС может быть достаточно большой, чтобы переключить единицы и нули, с последствиями от неудобных до катастрофических.
Пример \ (\ PageIndex {1} \): взаимная индуктивность
На рисунке \ (\ PageIndex {3} \) показана катушка из \ (N_2 \) витков и радиуса \ (R_2 \), окружающая длинный соленоид длиной \ (l_1 \), радиусом \ (R_1 \) и \ ( N_1 \) оборотов.
- Какова взаимная индуктивность двух катушек?
- Если \ (N_1 = 500 \, витков, \, N_2 = 10 \, витков, \, R_1 = 3.10 \, см, \, l_1 = 75.0 \, см \), и ток в соленоиде изменяется с при скорости 200 А / с, какая ЭДС индуцируется в окружающей катушке?
Стратегия
Вне соленоида магнитное поле отсутствует, а поле внутри имеет величину \ (B_1 = \ mu_0 (N_1 / l_1) I_1 \) и направлено параллельно оси соленоида.{-3} В. \ end {align *} \]
Значение
Обратите внимание, что M в части (a) не зависит от радиуса \ (R_2 \) окружающей катушки, потому что магнитное поле соленоида ограничено его внутренней частью. В принципе, мы также можем вычислить M , найдя магнитный поток через соленоид, создаваемый током в окружающей катушке. Этот подход намного сложнее, потому что \ (\ Phi_ {12} \) очень сложен. Однако, поскольку \ (M_ {12} = M_ {21} \), нам известен результат этого вычисления.{-2} \, V \)
Авторы и авторство
Сэмюэл Дж. Линг (Государственный университет Трумэна), Джефф Санни (Университет Лойола Мэримаунт) и Билл Мобс со многими авторами. Эта работа лицензирована OpenStax University Physics в соответствии с лицензией Creative Commons Attribution License (4.0).
Что такое индуктивность? Последовательная и параллельная цепь
Индуктивность — это свойство материала, благодаря которому он препятствует любому изменению величины и направления электрического тока, проходящего через проводник.Другими словами, это свойство катушки, в которой ЭДС индуцируется из-за изменения магнитного потока.
Индуктивность добавляется в цепь через катушку индуктивности. Индуктор — это в основном катушка из проводов, которая концентрирует магнитное поле в цепи.
Индуктивность обозначается (L), а ее единица — Генри. Считается, что индуктивность равна одному Генри, когда ток в один ампер проходит через катушку или проводник изменяется со скоростью в секунду, а напряжение на катушке индуцируется со скоростью один вольт.
Состав:
Описание и типы индукторов
Индуктор образуется при скручивании провода конечной длины в катушку. Когда ток течет через катушку, образуется электромагнитное поле. Электромагнитное поле изменяется при изменении направления тока.
Это изменение электромагнитного поля индуцирует напряжение (v) на катушке и определяется уравнением, показанным ниже:
Где I — ток, протекающий через катушку индуктивности, в амперах.
Напряжение на катушке индуктивности будет равно нулю, если ток, протекающий через нее, останется постоянным. Это означает, что когда через индуктор протекает постоянный устойчивый ток, он ведет себя как короткозамкнутая катушка в установившемся состоянии. Если есть небольшое изменение направления или силы тока, появится индуктивность.
Если мы поместим значение dt как ноль (dt = 0) в уравнение (1), то увидим, что при мгновенном изменении тока в течение нулевого времени возникает бесконечное напряжение на катушке индуктивности, что не является допустимым условием, и, таким образом, в катушке индуктивности нельзя резко изменить ток .
Таким образом, после переключения постоянного напряжения катушки индуктивности действуют как разомкнутые катушки.
Мощность, потребляемая индуктором, определяется по приведенному ниже уравнению:
Подставив значение v из уравнения (1) в уравнение (2), мы получим мощность как:
Энергия, поглощаемая индуктором, определяется как:
Катушка индуктивности накапливает конечное количество энергии, даже если напряжение на ней может быть незначительным.
Катушки индуктивности классифицируются в зависимости от различных факторов, таких как размер, используемый материал сердечника, тип обмоток и т. Д.Сердечник играет важную роль при выборе индуктора.
В зависимости от материала сердечника используются следующие типы индукторов:
- Индуктор с ферромагнитным или железным сердечником
- Индуктор с воздушным сердечником
- Индуктор с тороидальным сердечником
- Индуктор с ламинированным сердечником
- Индуктор с активным сердечником
Последовательное и параллельное соединение индуктора
Цепь индуктивности серииВ последовательной цепи индуктивности несколько катушек индуктивности подключены последовательно в цепи, и одинаковое количество тока будет протекать в каждой из подключенных катушек индуктивности.Например, если L 1 , L 2 , L 3 …… индукторы подключены последовательно и ток I течет по цепи, как показано на рисунке ниже:
Ток на катушке индуктивности L 1 , L 2 , L 3 будет равен I 1 , I 2 , I 3 соответственно. Значение тока на каждой катушке индуктивности будет одинаковым.
IL 1 = IL 2 = IL 3 = I MN
Полная или эквивалентная индуктивность определяется уравнением
Цепь параллельного индуктора
Если несколько индукторов подключены параллельно друг другу, то цепь называется параллельной цепью индуктивности.В этом типе схемы схема разделена на каждую ветвь схемы, как показано на рисунке ниже:
Ток I 1 протекает в катушке индуктивности L 1 , и аналогично, ток I 2 в L 2 и I 3 в L 3 катушке индуктивности и I T составляет общее количество ток, протекающий в цепи. Эквивалентная индуктивность определяется уравнением, показанным ниже:
Применение индуктора
Некоторые из применений индуктора следующие:
- Используется в электронном оборудовании, таком как радиоприемники
- В аппарате связи
- Электронные испытательные приборы
- В качестве накопителя энергии
- В датчиках, трансформаторах, двигателях и различных фильтрах.